| Issue |
A&A
Volume 678, October 2023
Solar Orbiter First Results (Nominal Mission Phase)
|
|
|---|---|---|
| Article Number | A52 | |
| Number of page(s) | 19 | |
| Section | The Sun and the Heliosphere | |
| DOI | https://doi.org/10.1051/0004-6361/202245582 | |
| Published online | 02 October 2023 | |
SPICE point spread function correction: General framework and capability demonstration
1
Southwest Research Institute, 1050 Walnut St., Suite 300, Boulder, CO 80302, USA
e-mail: jplowman@boulder.swri.edu
2
Université Paris-Saclay, CNRS, Institut d’Astrophysique Spatiale, Bâtiment 121, 91405 Orsay, France
3
Max-Planck-Institut für Sonnensystemforschung, Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
4
RAL Space, UKRI STFC Rutherford Appleton Laboratory, Didcot, Oxfordshire OX11 0QX, UK
Received:
29
November
2022
Accepted:
30
April
2023
We present a new method of removing point spread function (PSF) artifacts and improving the resolution of multidimensional data sources, including imagers and spectrographs. Rather than deconvolution, which is translationally invariant, the method we present is based on sparse matrix solvers. This allows it to be applied to spatially varying PSFs as well as to combined observations from instruments with radically different spatial, spectral, or thermal response functions (e.g., SDO/AIA and RHESSI). The method was developed to correct PSF artifacts in Solar Orbiter Spectral Imaging of the Coronal Environment, so the motivation, presentation of the method, and the results revolve around this type of application. However, it can be used as a more robust (e.g., with respect to spatially varying PSFs) alternative to deconvolution of 2D image data, as well as similar problems, and is also relevant to more general linear inversion problems.
Key words: line: profiles / techniques: imaging spectroscopy / instrumentation: spectrographs / techniques: high angular resolution / Sun: abundances / Sun: corona
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The Spectral Imaging of the Coronal Environment (SPICE; Spice Consortium 2020; Fludra et al. 2021) is an extreme ultraviolet (EUV) slit scanning spectrograph on board the Solar Orbiter spacecraft (García Marirrodriga et al. 2021). It was made to discriminate between current models of the slow solar wind source region by using compositional signatures of the wind to identify in situ wind streams with particular outflowing regions on the solar disk. SPICE has a unique capability to produce (comparatively) high resolution time resolved maps of outflow velocity and ionic composition that, compared with a relatively large field of view (nearly 1024 pixels along the slit with 1 arcsecond plate scale, or the equivalent of roughly 0.3 arcsec from Earth when Solar Orbiter is at 0.3 AU perihelion; see below for more detailed instrument specifics), uniquely enable tracing of individual wind streams from the surface of the Sun to in situ measurements from the Solar Orbiter spacecraft by using the wind’s variability and compositional signature to identify each stream.
Despite decades of study, the origin of the slow solar wind is still not known. Several widely disparate models of the slow wind’s origin exist, including the boundary between coronal holes and streamers, small transient open regions in the quiet Sun, diffusion through streamer tops, or plasmoid ejection into the streamer belt (e.g., Suess et al. 1998; Fisk & Zurbuchen 2006; Woo & Martin 1997; Wang et al. 1999). Existing static ultraviolet Dopplergrams of the quiet transition region and low corona show many regions that are blue-shifted by roughly 10 km s−1 and nearly as many red-shifted regions (e.g., Popescu & Doyle 2005; Hassler et al. 1999). Thus, in order to identify the features that are relevant to the solar wind, more detailed time-resolved studies and association with in situ measurements are required.
Slow wind streams vary strongly in speed and density, with correlated variations in ionization temperature, concentration of elements with a low first ionization potential (FIP) of each element, and mass-to-charge ratio (M/q) fractionation. With the point spread function (PSF) correction we introduce in this paper, SPICE is able to produce images of outflow in the lower solar atmosphere with a sensitivity of 5 km s−1 (Spice Consortium 2020) and simultaneous compositional signatures in the in situ-relevant ion sequences. This allows temporal sequences and compositional and kinetic signatures on the Sun (in the chromosphere and low corona) to be compared with with plasma properties observed in situ, which in turn enables unambiguous mapping of solar wind packets (observed in situ) and their corresponding solar origins (remotely sensed on the Sun).
A primary design objective of SPICE is to trace how plasma outflows in the photosphere and the low corona connect to the heliosphere at large – primarily by connecting abundances observed in situ by various spacecraft with those sensed remotely by SPICE. This relies on accurate identification of particular emission lines at a variety of temperatures, lines which have varying susceptibility to ionization (i.e., the FIP effect; see Spice Consortium 2020; Fludra et al. 2021, for more detail). An additional important feature of SPICE for diagnosing connectedness is the use of the Doppler effect to discriminate upflows from downflows and to identify potential solar wind outflow regions deep in the corona and transition region.
Although SPICE is not a high-resolution instrument by design, these and other observables, along with their driving science objectives, require resolution within the limits of its design (given the mission’s nominal requirements; see Spice Consortium 2020). Degraded resolution beyond the design limits will impact the ability of SPICE to achieve its science goals. This paper reports on some issues that degrade SPICE’s resolution and discusses a novel data processing methodology that will remove the degradation.
We use a set of coordinated SPICE and high spectral and spatial resolution Interface Region Imaging Spectrograph (IRIS; De Pontieu et al. 2014) data for the examples and demonstrations in this paper, with IRIS data used as “ground truth” to assess the quality of the PSF correction and constrain the effective SPICE PSF. IRIS observes spectral lines that sample the same regions of the corona as SPICE, with very similar temperature response, and its high resolution makes a good starting point for degrading resolution to that of SPICE. The observation data were taken on March 7, 2022, when SPICE’s orbit placed it on the Earth-Sun line, with the same perspective as IRIS. We compare the SPICE C III 977 Å observations with IRIS Si IV 1394 Å observations. These two lines have very close formation temperatures, log T [K] of 4.78 and 4.81, when in ionization equilibrium (e.g., Table 1 of Peter et al. 2006). An image showing the larger context of this region is shown in Fig. 1.
 |
Fig. 1. Context images of the primary IRIS and SPICE observations used for demonstration and testing in this paper. Left panel a: Context image of the SPICE-IRIS coordinated observation data. The image was made from one of the full-size SPICE rasters. It is a spectral sum over the C III 977 Å window. The detailed comparisons in this paper focus on the smaller region outlined in this image. Upper-right panel b: Spectral line fit amplitude image of the smaller region from IRIS. Lower-right panel c: Spectral line fit amplitude image of the smaller region from SPICE. |
2. Overview of SPICE point spread function problem and possible solution
2.1. Point spread function issues and need for correction
SPICE has an approximately 1.1 arcsec per pixel spatial plate scale along the slit and several slit widths ranging from 2 to 3 arcsec, while the spectral plate scale is about 0.009 nm per pixel. The focal plane has two detector arrays of 1024 × 1024 pixels each covering two spectral bands – one from 70.4 to 79.0 nm and the other from 97.3 to 104.9 nm. The slit scanning mechanism can cover up to 16 arcmin, while the slit covers 14 arcmin on the detector plane. The overall raster image dimensions are up to 960 × 840 arcsec. SPICE’s observing distance varies between about 0.3 and 1.0 AU, which must be considered when comparing these numbers with Earth-based instruments.
Since SPICE is a scanning slit spectrograph, its observables are in three dimensions: spectral (λ), slit-aligned (y), and slit-perpendicular (x, the scanning direction). (There is actually a fourth time dimension, but we do not consider it here because we assume the source and PSF do not change with time.) The SPICE PSF is similarly three-dimensional, extending in all three of these directions. The issue this paper addresses is caused by a PSF that is both elongated and rotated with respect to these axes, rather than being aligned with them. We have observed that the SPICE PSF is rotated both within the slit plane (i.e., y − λ) and, in some cases, in the scanning plane as well. This is shown for an example slit plane in Fig. 2. This slit plane passes through the middle of the green circled region in Fig. 1. A rotation on the detector (i.e., y − λ) plane of ∼15° is evident. This angle will appear different if the pixels are not square and can vary with the different slit width. We note that this paper focuses on the 2 arcsec slit. We believe the PSF issue is caused by a combination of astigmatism on the primary mirror and defocus. The suggested PSF shown in Fig. 2 was chosen through trial and error to best match the appearance of the SPICE data. We discuss it in more detail in subsequent sections.
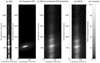 |
Fig. 2. Spectra from a particular slit position in the SPICE and IRIS data. This slit position was chosen for good agreement between SPICE and IRIS, and it passes through the middle of the green circled region in Fig. 1. Panel a: IRIS spectra. Panel b: Proposed SPICE PSF with SPICE pixelization. Panel c: IRIS data (“synthetic SPICE”) with this PSF and pixelization. Panel d: Actual observed SPICE data. The elongation and apparent rotation of the PSF are evident, as is the agreement between (synthetic) IRIS and SPICE. |
The elongation and rotation of the SPICE spectro-spatial PSF impacts its ability to diagnose connectedness and other important instrument capabilities in a variety of ways. For instance, it can reduce the definition with which SPICE can resolve boundaries of regions with differing connectedness. The degradation also hampers its ability to resolve fainter spectral lines when there are neighboring bright spectral lines. This is especially critical because the selection of lines that adequately sample both abundance and temperature is very limited (the aforementioned spectral blends are a case in point).
Even more challenging is that the tilt of the PSF between the spatial and spectral directions causes a bright feature at one location, creating the illusion of a neighboring dim feature, which is Doppler shifted relative to the true feature (i.e., bright features appear to have Doppler shift lobes next to them). Together with Doppler fitting, the elongated and rotated “effective” PSF in the y − λ plane acts as an edge detection filter, causing bright features to be “aliased” from intensity into Doppler. (As previously mentioned, we believe this issue is ultimately caused by a combination of astigmatism on the primary mirror and defocus.) This PSF artifact confounds attempts to understand connectedness and dynamics by looking at Doppler shifts, and we have seen this kind of feature in the SPICE data.
To illustrate the issue, we show (in the lower panels of Fig. 3) the Doppler fits to the IRIS data, the IRIS data degraded with the SPICE PSF, and the actual SPICE data for the region of interest already highlighted by Fig. 1. We note that before fitting, the IRIS data on the left were first binned down 2 × 2 to better match the SPICE pixel size. Strong Doppler features are evident in the IRIS data degraded with SPICE PSF and the SPICE data, which are not present in the original IRIS data. In the figure, we have circled three of the most prominent Doppler features in the map. Each of these coincide with bright features (e.g., ridges) in intensity, as can be seen in the lower panels of Fig. 3. Because the features are absent from the original (plus down-binning) IRIS data, their appearance in the IRIS with the SPICE PSF clearly implicates the PSF in creating these artifacts. A similar effect and artifacts have been previously noted for the Hinode EUV Imaging Spectrometer (EIS; Culhane et al. 2007). This is primarily discussed in an online EIS software note (Ugarte-Urra 2016) but is also alluded to in other papers, such as Young et al. (2012).
 |
Fig. 3. Amplitude (upper row) and Doppler (lower row) fits to the IRIS (panel a), IRIS with SPICE PSF and pixelization (“IRIS synthetic SPICE”; panel b), and SPICE (panel c). Before fitting, the IRIS data on the left were first binned down 2 × 2 to better match the SPICE pixel size. Both the “synthetic SPICE” and real SPICE Doppler (panels b and c) show clear ridge artifacts that are absent from the IRIS Doppler (panel a). Some specific artifacts are highlighted. Comparison with the amplitudes in the upper row shows that these artifacts are associated with bright features in intensity. The elongated, rotated effective y − λ PSF causes bright intensity features to alias into Doppler, as further discussed in the text. |
The Doppler shift artifacts have fortunately been reduced thanks to the efforts of the SPICE team. This was done by adjusting the SPICE focus position and checking the results during instrument calibration campaigns. Consequently, the team has determined a focus position where the aberrations are significantly reduced. The results shown here use data that takes advantage of this improved focus position.
2.2. Solution method: General linear (sparse) solvers and why we are using them
These examples sufficiently illustrate that this PSF effect seriously degrades the quality of Doppler data observed by SPICE. A means of removing it is highly desirable, and the objective of this work is to develop a method that could ultimately be applied to all data at some level of its data pipeline. The conventional way of removing PSFs is via convolution (e.g., Poduval et al. 2013). Convolution in this context is the translationally invariant special case of the general linear transform, and it usually also assumes that the input and output of the transform have the same dimensions (e.g., nx by ny pixels). Rather than treating the problem under this special case, however, we instead treat it as an example of the full general linear transform. There are a number of reasons for this choice, including:
-
Pragmatically, we expect these PSF artifacts to vary over the image plane, which a convolution cannot represent.
-
The general transform provides a somewhat more straightforward framework for applying other constraints, such as positivity and regularization. We have already had success with this framework in other contexts (Plowman & Caspi 2020; Plowman 2021).
-
The general full linear problem is far more broadly applicable than the (de)convolution problem. Once properly developed, the same tools used for this problem with SPICE can be applied to almost every other coronal remote sensing problem, to similarly good effect. See Plowman (2021) for an early example. We return to this point at the end of the paper.
-
The tools for tackling the inverse part of this problem have already been extensively developed by the computer science communities in the form of high performance sparse matrix solvers. All we need to do, therefore, is implement the forward transform in the appropriate fashion (i.e., as a sparse matrix).
The reason we use a sparse matrix approach, as opposed to some more complex method (e.g., a deep learning approach), on the other hand, is because the forward problem is inherently a linear matrix operator. Sparse matrix inversions are specifically designed to solve linear inverse problems, and the most direct and straightforward approach that captures the problem well is often the best. A wide variety of problems in remote sensing fall under the linear category, and the utility of direct sparse solvers to this domain is underappreciated. The large size of the corresponding full matrices may give the impression that the problem is intractable by this approach, but this is not the case, as the subsequent examples will show. In this paper, we add the nonlinear mapping from Plowman & Caspi (2020), which enables the use of a positivity constraint and some additional flexibility in terms of regularization.
We turn next to our implementation of this method. The derivation shown next presupposes a 3D PSF as a function of x, y, and λ (the most general case for SPICE). In practice, our understanding of the problem is that it can be represented by two PSFs. The first blurs in x and y but does not affect λ. Therefore, this PSF does not contribute to the Doppler artifacts we are trying to correct. The other “effective” y − λ PSF is assumed to affect y and λ but not x. This is the PSF that is elongated in λ and rotated approximately 15°, and which causes the Doppler artifacts. We have done a variety of tests with 2D and 3D PSFs and found that correcting this effective PSF sufficiently removes the Doppler artifacts, working as well as the 3D correction while also being much faster. We wrote the derivation in 3D since it seemed that a 3D method may be necessary. In the event it appears a 2D correction will suffice, we retain the 3D derivation since it is more general. The code for the correction is written to be agnostic to the dimensionality of the problem, as the 1D and 2D examples demonstrate.
3. Introducing our solution method (formalism)
3.1. SPICE point spread function as instance of general linear forward problem
3.1.1. The SPICE forward problem
To begin, we suppose that SPICE observes some static (meaning it does not change over the time of observation) cube in the sky with spectral radiance L(xs, ys, λs) as a function of sky longitude and latitude (which we write as xs, ys) and wavelength λs. These are projected onto the detector plane by the PSF, P(xd, yd, λd, xs, ys, λs), which is a function of both sky coordinates (xs, ys, λs) and detector plane coordinates (xd, yd, λd). In reality, xd and λd are time multiplexed onto the same surface (although not necessarily the same axis) by the grating, slit, and scanning mechanism, but we treat them as independent for clarity of our demonstration. The flux density E(xd, yd, λd) on the detector plane observed for this cube is the integral of the cube against the PSF overall sky angles:
where we have made the small angle approximation and placed the Sun at the equator of the coordinate system, which allows us to set the cos ys weight in the integral to one. The sensors divide the detector plane into pixels, which we index by i, j, and k, each of which have weight functions (typically nonoverlapping “bins”) θijk(xd, yd, λd). The fluxes Φijk into each of these pixels are the integrals of the detector plane flux densities against each of these weight functions:
At this point, we point out what we call the overall response function of the {ijk}th pixel of the instrument,
The name of the game is to find the spectral radiance, L, which is an unknown continuous function and therefore has an infinite number of degrees of freedom. To limit the number of degrees of freedom without loss of generality (in practice, if not in principle), we can define L in terms of a linear combination of a set of appropriately chosen basis functions, Blmn(xs, ys, λs):
where clmn are the coefficients of the linear combination. The set of basis functions ought to be linearly independent (i.e., no basis function can be expressed as a linear combination of the others). It is useful for our present purpose if each basis function is spatially compact and does not overlap much (or at all) with the other basis functions. The basis functions should also cover the sky plane at least as well as the pixels cover the detector plane. A set of pixel-like “bins” in {xs, ys, λs} with equivalent (or denser) spacing to the pixels is sufficient and is what we used in this paper. The indices {l, m, n} are intended to reflect the identification of the bins with the coordinate axes. In terms of this, the pixel fluxes are:
If we recognize an array of what might be called “response coupling terms” (i.e., the coefficients that define how each source element is coupled to each detector element and how the detector elements respond to the source elements),
(the constituents of this are all known and computable, being composed of the basis functions and the principlally known instrument response functions) we are left with the following linear equation relating the unknowns (clmn) to the knowns (ϕijk):
We used three indices each of the coefficients and the observables, but this is simply a notational convenience that allows us to identify each of the coordinate axes with its own index. Mathematically, we can “flatten” all the indices down to a pair of indices (one for the coefficients and one for the observables) by relabeling according to the following one-to-one correspondence:
Our linear equation then becomes
which we recognize as a familiar matrix equation, with the array of coupling terms becoming a “forward response matrix”. Any N-dimensional linear discrete or integral transform can be similarly treated, and nonlinear ones may be amenable to a linearization and iteration approach, so this can be a very powerful and general method for dealing with these problems.
3.1.2. One- and two-dimensional examples
In this section, we present a pair of lower dimensional examples using “dummy” data to illustrate our approach. The first example is the spectrum for a single pixel, that is, a function only of (for example) wavelength. This spectrum is equivalent to the differential emission measure (DEM) problem presented by Plowman & Caspi (2020), with the only difference being that instead of the instrument temperature response functions found there, we have a combination of the wavelength PSF and pixel bin functions:
The forward matrix is
This is illustrated graphically in Figs. 4 and 5. The only difference between them is that the individual steps are depicted in Fig. 4, whereas all of these steps are combined into the forward matrix in Fig. 5. Combining the steps is possible because all of the individual steps are linear operations.
 |
Fig. 4. One-dimensional example of the linear process relating a source model to observations. The input to the model (panel a) is a set of coefficients. These are multiplied by a set of basis functions at various wavelengths (one is shown in panel b), and the result is added to produce a spectrum (panel c). The spectrum in turn is multiplied by the PSF at each wavelength (panel d), and the result is added to produce a detector plane spectrum (panel e). Lastly, each of the sensor response functions (panel f) are integrated against the detector plane spectrum to produce count rates in each detector element (panel g). |
 |
Fig. 5. One-dimensional example of the linear process applied using a matrix in a single step. Input (source coefficients; panel a) and outputs (detector count rates; panel c) in this figure are identical to Fig. 4 but with all of the intermediate operations carried out by a single matrix (panel b). This figure is specifically constructed so that the vertical axis of the matrix is aligned with the source element index, while the horizontal axis is aligned with the detector element index in order to make the matrix nature of the operation visually apparent. |
Figures 6 and 7 are of the same format and show how the same treatment can be scaled up to two dimensions (spatial, in this example, although it makes no difference in the mathematical treatment). Essentially, the additional dimension in the source and the detector are simply multiplexed down to the one “input” (conventionally, the columns) and one “output” dimension of the forward matrix. Mathematically, the only difference is the addition of a multiplexing (e.g., by “flattening” in numpy or reforming to a 1D vector in the Interactive Data Language – IDL) step at the beginning and, if desired, a demultiplexing step at the end (e.g., by using reform in IDL or reshape in numpy), but these are trivial 1-to-1 operations. The additional multiplexing step is shown in the top-left and bottom-center panels of Fig. 7, which is otherwise identical in format to the one-dimensional example in Fig. 5. The output resolution of these examples differs from the input because, in general, the resolutions of the solar sources are different from those of our detectors, which enables us to demonstrate that this framework can accommodate such resolution differences.
 |
Fig. 6. Two-dimensional example of the linear process relating a source model to observations. Identical to Fig. 4 except that in this case, the source and observations are two-dimensional. The output resolution of these examples differs from the input because, in general, the resolution of solar sources differs from that of our detectors, demonstrating that this framework can accommodate such resolution differences. |
 |
Fig. 7. Two-dimensional example of the linear process applied using a matrix in a single step. The input source coefficient image (panel a) and outputs (detector count rates image; panel e) in this figure are identical to Fig. 6, but all the intermediate operations were carried out by a single matrix (shown as an image at top right; panel c). The vertical axis of this matrix is aligned with the source element index, while the horizontal axis is aligned with the detector element index. This two-dimensional case is equivalent to the 1D example except that there is a multiplexing step that “flattens” the 2D input to 1D (panel b) prior to multiplication by the forward matrix (top right). The result of this multiplication (panel d) can then be demultiplexed to produce the output image (panel e). |
The SPICE forward problem for the effective (y − λ) PSF is equivalent to this 2D correction, while the full forward problem follows the same trend from 1D to 2D to 3D – the same multiplexing and demultiplexing operations suffice for converting the problem into matrix form. The practical implementation of the construction of this forward matrix can be conceptually thorny due to the arbitrary number of dimensions, the need to avoid aliasing if the source and detector resolution do not match, and the need to avoid evaluating the PSFs where their contributions are negligible (in higher dimensions the computational penalty can be extreme). Nevertheless, we have developed a general N-Dimensional, coordinate-aware framework in Python for computing these matrices. This is described in more detail in Sect. 3.4, and the framework is also available for download (see Sect. 3.4).
3.1.3. Sparse matrix algorithms
As is clear from the examples provided above, the forward matrix is very large, even for images of modest size. However, only detector elements within the PSF range of the source elements have non-zero entries, and the PSF is much smaller than the overall image. Therefore, this matrix is sparse. There are a wide variety of specialized sparse matrix algorithms that exist to work with such matrices, and they drastically reduce the real-world memory and processing requirements of working with these matrices. Standard examples can be found in Press et al. (2002), for instance. Additionally, solving linear problems based on sparse matrices is a well-developed field in computer science, and by casting the problem in this form, we can avail ourselves of the tools that have been developed. Our framework for computing the forward matrices is built on these algorithms. Specifically, we make use of the scipy.sparse sparse matrix package.
3.2. Solving the SPICE forward problem
The fundamentals of this solution method have also been recently discussed in Plowman & Caspi (2020), Plowman (2021), but we also cover them in order to show how they apply to this case. We begin by considering the forward problem in the linear least squares framework (Press et al. 2002).
We seek the “best fit” coefficient vector (cj in Eq. (10)) that minimizes the sum of squares (hence, the “least squares”) of the deviation of our model prediction for the data – Φi from Eq. (10) – with the data, di. These squared deviations are weighted by the inverse of the square of the errors in the data, σi. This weighted sum is also known as a χ2 statistic:
The above equation assumes that the errors in the data are normally distributed, which can be seen by noting that the log likelihood is −χ2. Because this merit function is convex, it has only one minimum that occurs where the gradient of χ2 with respect to the coefficient vector is zero. Better yet, because χ2 is quadratic, its derivative is linear. The best fit coefficient vector is therefore found by solving the following matrix equation (cf. the chapter in Press et al. 2002, on Linear Least Squares):
where
This is the standard form for matrix problems in linear algebra, and in principle the linear least squares best fit solution is
Reality is never quite so simple, of course. Thus, we need to apply some additional constraints to ensure a well-posed solution, which we discuss next.
3.3. Positivity constraint and regularization
The ATA matrix is likely to be poorly conditioned even if it is not outright singular. The blurring caused by the PSF means that details we want to resolve are degraded by the forward transform – it loses information – even if the number of data points is equal to the number of coefficients. In this case, ATA would be poorly conditioned, and detector noise would lead to instabilities in the reconstruction. If the number of data points is less than the number of coefficients, then ATA would be singular, and simply inverting Eq. (14) would not be possible. To resolve this issue, we apply a positivity constraint and regularization.
3.3.1. Regularization
Regularization typically takes the form of adding a term to χ2 and minimizing their sum instead of χ2 alone. In this derivation, we took this added term to be of the form
In other words, instead of minimizing χ2 by itself, we seek to minimize the merit function
where X is a matrix specifying the regularization. This matrix can be as simple as the identity matrix, in which case the regularization makes the solver prefer solutions with a smaller l2 norm (i.e., c ⋅ c). Exactly how much smaller depends on the size of the ϵ parameter, which tunes the strength of the regularization. In Plowman & Caspi (2020), the operator was composed of the derivatives (i.e., WRT temperature) of the basis functions integrated against each of the other basis functions. This results in a regularization operator that makes the solver prefer solutions with smaller derivatives, specifically the log of the derivative in that case.
The addition of the regularization term changes the matrix equation we wish to solve from Eq. (14) to
In other words, the matrix that needs to be inverted simply has the regularization matrix times the tunable parameter (ϵX) added to it.
For this class of problem, ϵ is often chosen to make each of the residuals of the fit to be some number χ0 (typically equal to the number of data points, or “reduced” χ2 of order unity). Noting that the residuals are b − A ⋅ c and with a slight rearrangement of Eq. (19), this requirement is equivalent to
We want to solve this for ϵ. But this is just one parameter, and it cannot satisfy each component of this vector equation. Instead, we minimize the RMS of the LHS of this equation over ϵ. The result is
But we do not know c either. Therefore, we use an initial guess for c to determine our ϵ. We will need a guess later on when we introduce the positivity constraint.
It turns out that a simple initial guess can be formed using FT ⋅ d. An analogy can be made to upscaling an image by an integer factor. More generally, the results of this procedure are roughly a model that has been subjected to the source response function twice. Such a model will be much smoother, but features will be in the right place. This is desirable for regularization since it is more conservative than regularization using a sharper guess and therefore avoids overfitting. It does result in an over-smoothed solution as well; however, the amount of which depends on how much sharper the source is than the results of the instrument resolution degradation. To mitigate this, we apply a final correction factor to scale ϵ. The SPICE sources are significantly sharper than the SPICE PSF, so this final scaling factor for ϵ is about 0.1 (i.e., ϵ is reduced by a factor of ten compared with Eq. (21)). Multiplying another factor in this way is of course not ideal, but a priori estimation of regularization parameters has something of a circular dependence since one does not mathematically know the sharpness of the source prior to reconstructing it. This final factor is a way of instructing the code regarding how sharp the source is likely to be, while initial ϵ estimate allows the code to automatically adjust for varying intensity and error levels in the data.
The amplitude needs to be rescaled (since F is not normalized). We choose this scaling factor to be the one that minimizes the χ2 in the initial guess compared with the data, resulting in the following initial guess for c:
The framework, as currently constructed, uses regularization based on the l2 norm. The derivative-based regularization used in Plowman & Caspi (2020) could also be employed here, but it would require constructing gradient operator matrices with respect to image position and wavelength, which is doable but too involved to include in the present publication. However, it will be implemented in future work, which will open up a variety of possibilities for including more physical constraints on inversions using this framework, as well as some other intrinsic benefits.
3.3.2. Positivity constraint: Nonlinear mapping
One condition that the sources of these data must satisfy is positivity, as spectral radiances cannot be negative. This is a nonlinear constraint that cannot be directly captured by linear formalism. Instead, we use the same nonlinear mapping on the coefficients as in Plowman & Caspi (2020). We express cj in terms of a second set of parameters, sj, such that
We then choose the mapping function, g, to be one whose range is limited to the non-negative numbers. Two such examples are 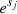 and
and 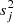 . We use the former (exponential) mapping here, as it seems to produce better convergence properties. We then linearize and iterate beginning from an initial guess. The results of this are described in more detail in Plowman & Caspi (2020), and we do not repeat all the steps of the derivation here, although we have changed the notation somewhat in an attempt at better clarity. The one difference is that in Plowman & Caspi (2020), only the case where the regularization acts on the sj, rather than the cj, was considered. If the regularization acts on the cj instead, there are additional terms (shown below). The result is the following matrix equation
. We use the former (exponential) mapping here, as it seems to produce better convergence properties. We then linearize and iterate beginning from an initial guess. The results of this are described in more detail in Plowman & Caspi (2020), and we do not repeat all the steps of the derivation here, although we have changed the notation somewhat in an attempt at better clarity. The one difference is that in Plowman & Caspi (2020), only the case where the regularization acts on the sj, rather than the cj, was considered. If the regularization acts on the cj instead, there are additional terms (shown below). The result is the following matrix equation
where
and
where h(si) is the mapping function for the regularization. It is also equal to g(si) if the regularization is with respect to c and to h(si) = si if it is with respect to s. The primes on g or h represent their derivatives with respect to their arguments. The coefficient parameters from the previous step of the iteration are represented by 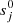 . There is no reason the regularization could not use some other mapping function of s, but we do not consider that possibility further here. We use the same mapping for both χ2 and the regularization (h(x) = g(x)). The regularization strength, ϵ, likewise changes to
. There is no reason the regularization could not use some other mapping function of s, but we do not consider that possibility further here. We use the same mapping for both χ2 and the regularization (h(x) = g(x)). The regularization strength, ϵ, likewise changes to
These equations suffice to ensure positivity, which in addition to being required by the physics, makes the solutions more well-posed in many situations. It does require an iteration, but the convergence is generally good, provided the mapping functions are monotonic (this makes the overall optimization problem convex, so the figure of merit has a single global minimum).
3.3.3. Summary of derivation
In summary, given input data of variable dimensions (which may be a cube Dijk or spectral-spatial image Dij), instrument PSF P (which depends on sky coordinates, wavelength, and detector plane coordinates), pixel binning functions θ (which depend only on detector plane coordinates), and basis functions B (which depend only on sky coordinates and wavelength), the PSF correction is defined by the following equations. The source luminosity to be estimated (compare to Eq. (4)) is a linear combination of the basis functions:
In the second part of the equation, we express the nonlinear exponential mapping (ci ≡ e(si)) that enforces positivity. We take the basis functions to be top hat functions in the variables (e.g., x, y, and/or λ. In the standard application we perform in this paper, the variables are y and λ). As a result of this choice of basis functions, these coefficients behave analogously to pixels. They can be interpreted as the corrected data, though technically the basis functions must also be remembered to be fully correct.
The overall response of a given pixel in the instrument to a given source is the integral of the product of basis function, PSF, and pixel binning function over sky angle and detector plane. In full generality, this can be written (see Eqs. (3) and (5)) in terms of the following array of response coupling terms:
where
This is the three-variable form of the equation, but in practice we omit the x direction (and i and l indices), performing the inversion only in y and λ. We also “flatten” the multiple source and detector indices into a single pair of indices, turning the overall pixel response into a standard matrix equation:
The one index terms here are identical to their multi-index versions above, following the index relabeling described in Sect. 3.1.1.
Given these definitions, an initial guess 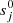 and the mapped coefficients sj (and therefore the coefficients themselves, which are what we seek) are solved by inverting
and the mapped coefficients sj (and therefore the coefficients themselves, which are what we seek) are solved by inverting
where
and
The mapping functions are represented by h(s) for the regularization and g(s) for the forward problem. The derivatives of these functions are h′(s) and g′(s), respectively. In our case, they are both es, and so h′ and g′ are also both es. The regularization matrix Xij is the identity matrix, and the regularization parameter ϵ is
Lastly, the initial guess for the coefficients c is
where the A matrix is just the forward matrix modulated by the measurement errors σj:
3.3.4. Solvers: GMRes and Bicstab
Since these forward matrices are very large and sparse (though they would not be solvable if they were not sparse), they require sparse solvers. These generally rely on some sort of iterative process in order to avoid dealing with the fully populated matrix. The code for applying these corrections was developed in Python, so we have been using the solver algorithms included in the sparse package of SciPy (Virtanen et al. 2020b). Specifically, the stabilized biconjugate gradient (bicgstab; van der Vorst 1992) and the “loose” generalized minimal residual (lgmres; Baker et al. 2005) algorithms. Both of these algorithms have a long heritage. They are variants of algorithms mentioned in the 1992 edition of Press et al. (2002), namely, the biconjugate gradient and generalized minimal residual methods. We tested both algorithms and found their convergence and performance to be comparable and more than acceptable for the problem at hand.
3.4. Implementation details and practical considerations
To accompany this formalism, we have developed a flexible coordinate-aware Python framework that can compute basis functions, PSF, and response matrices for arbitrary sources and detector dimensions. It contains the following components:
-
Basis functions: Rectilinear N-Dimensional “bin” and “triangle” functions are provided as examples, and others can easily be added.
-
Point spread functions: These are functions specifying how an N-Dimensional detector plane is illuminated by a point source at a particular location. A Gaussian-based “boilerplate” PSF is included as an example (see Sect. 3.5 below).
-
Coordinate grids: These represent the standard notion of an N-Dimensional array of coordinate points indexed to a grid. They are defined in terms of a coordinate system and a transform from grid indices to a set of coordinate points. The transform may be defined in terms of an origin (the location of the center of the element with all indices equaling zero), a set of sizes (Δx, Δy, etc.), and the dimensions of the array, but more complex transforms are also possible. This transform must be one-to-one.
-
Source and detector element grids: These represent the standard notion of a gridded array of elements and can be either a set of source basis elements or detector elements (pixels). Source and detector element grids are defined in terms of the coordinate grids and registered to them, but they add code for returning the coordinates and amplitude of a particular basis element and for returning the response of all detector elements to a particular point source. Sources and detectors are independent and each have their own coordinate system.
-
Coordinate transform: These are a transformation operator from the coordinate system of the source model to the coordinate system of the detector. This is built to interface with the coordinate grids and is also setup with the astropy (Astropy Collaboration 2013, 2018) and sunpy (SunPy et al. 2020) coordinate systems in mind, but for these examples, we used a trivial identity transform, leaving the source defined in terms of detector units, and registered to the same grid. This transform does not need to be one-to-one (i.e., it can map from a set of 3D spatial points on the sky to a 2D detector plane).
This framework should be able to accommodate detectors whose elements are not gridded in the usual way. The Reuven Ramaty High Energy Solar Spectroscopic Imager (Lin et al. 2002) could be an example of this, but we do not explore the possibility further in this paper. Likewise, we leave providing a detailed description of the framework to its code base and example usage software, which will be made available along with the published paper.
3.5. Boilerplate point spread function model
For the work shown next, we used a “boilerplate” model of the PSF that consists of a two-component, 2D Gaussian where each component can be raised by an additional exponent to weight it more toward its wings or its core. We found that setting this exponent to approximately 1.5 made for a closer match between the IRIS line profiles (with our PSF added) and the SPICE line profiles, although the effect on the corrected Doppler shifts was very small. The mathematical expression for these Gaussians is:
where Δr is the difference between the coordinate vector of the source and the coordinate vector on the image plane (for the x − y − λ PSF case, this would be {xd − xs, yd − ys, λd − λs} in Eq. (1)). The covariance matrix of the Gaussian is represented by Σ, and γ is the exponent (an exponent of one is a standard Gaussian). We specify the covariance matrix in terms of a set of initial axis lengths (the uncertainties of the principal axes without rotation) and rotation angles, in which case one begins with a diagonal covariance matrix that has the principal axis uncertainties on the diagonals and then rotates the matrix to its final position with a succession of rotation matrices(s) – one in the 2D case and three in the 3D case. Our implementation includes an example implementation of this PSF that works in both 2D and 3D.
4. Testing and application
To begin, we show the method applied to the one- and two-dimensional examples shown earlier. Figure 8 shows a reconstruction of the example shown in Fig. 4, while Fig. 9 shows a reconstruction of the example in Fig. 6. In both cases, the reconstruction recovers most of the features of the source that are not evident in the data, despite the presence of PSF, noise, and (in the 2D example) a lower pixel resolution. Apparent noise is amplified by this process, but this is an inevitable consequence of the flow of information in this problem, as below some threshold, noise and features cannot be distinguished.
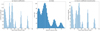 |
Fig. 8. Reconstruction of the one-dimensional example case previously shown in Fig. 4 using our method. Panel a: Original “source” model. Panel b: Data corresponding to source model (including PSF, pixelization, and noise). Panel c: Reconstruction of the source model. |
 |
Fig. 9. Reconstruction of the two-dimensional example case previously shown in Fig. 6 using our method. Panel a: Original “source” model. Panel b: Data corresponding to source model (including PSF, pixelization, and noise). Panel c: Reconstruction of the source model. |
To illustrate the capability to recover an arbitrarily spatially varying PSF, we also show a reconstruction of the same field of view presented in Fig. 9 but with a PSF that is increasingly larger when it is farther from the center of the field of view and that rotates about it. This is shown in Fig. 10. In this figure, our method is called the Sparse NLMap (for “nonlinear map”) reconstruction. The figure also shows a standard Richardson-Lucy (R–L) deconvolution that does not capture spatial variation of the PSF for comparison. We used the average of the PSFs in the field for the R–L deconvolution. The specific R–L algorithm used is the Python skimage package’s restoration.richardson_lucy code.
 |
Fig. 10. Two-dimensional example reconstructions with spatially varying PSF. Upper row: Test pattern of dots to show how the PSF appear. Panel a: Original pattern of dots. Panel b: Pattern with the PSF applied. Panel c: Pattern with the PSF and our correction algorithm. Here our algorithm is called “Sparse NLMap”, with “NL” standing for “nonlinear”. Panel d: Attempt to correct the data with a standard Richardson-Lucy (R–L) deconvolution. This approach does not incorporate a spatially varying PSF. With no noise and well-isolated features, resolution comparable to the original can be restored with our Sparse NLMap algorithm, but R–L fails to recover the original test pattern. Lower row: Application to AIA image also shown in Fig. 9 except at full rather than half AIA resolution. Panel e: Original image. Panel f: Image with varying PSF (same as upper panels) and noise applied. Panel g: Sparse NLMAP correction applied. Panel h: Attempt to correct with R-L. The reconstruction of AIA is much sharper and closer to the original source than the “data” is, although it is inevitably impacted somewhat by noise. The R–L deconvolution, on the other hand, shows many obvious artifacts of the variation and elongation of the PSF. |
Since the exact shape of the PSF can be difficult to discern from a complex Solar Dynamics Observatory Atmospheric Imaging Assembly (AIA; Lemen et al. 2012) image, Fig. 10 also shows an application to a much simpler image that is a grid of “dots”. Unlike in Fig. 9, the source image in Fig. 10 is at the full AIA resolution, rather than being binned down 2 × 2. We also made the detector gridding the same as the source gridding, since the R-L algorithm does not incorporate differing source and detector sampling grids. Simulated instrument noise was added for the AIA example as before but not for the test pattern of dots. For the test pattern of dots, the reconstruction demonstrates that sharpness close to the original is achievable. The reconstruction of AIA is much sharper and closer to the original source than the “data” is, although it is inevitably impacted somewhat by noise.
4.1. Application to SPICE data and comparison with coordinated IRIS data
We show next an application to the example SPICE data shown earlier. As previously mentioned, we are treating the overall SPICE spatio-spectral response function as an x − y response function representing (primarily) the main (spatial focusing) mirror followed by a y − λ “effective” response function representing the elements that contribute to the spectral PSF, including the grating and final pixelization. To reduce the size of the inverse problem, this example incorporates the downsampling in y, including a 2-pixel binning in that direction, into the x − y response function. This is not strictly required, although it does also help to increase the S/N. The wavelength resolution change, of course, all happens as part of the response function.
The correction uses the full IRIS resolution in wavelength. Even though this is considerably higher than the SPICE resolution, it is necessary to properly resolve the spectral line. The combination of positivity constraint, regularization, and the fact that the modulation transfer function of the PSF does not completely go to zero means that the correction can somewhat exceed the standard Airy/Nyquist criteria, especially since the spectral direction is mostly composed of a near-zero amplitude signal. This super resolution can result in some ringing and overfitting features due to noise, however, so we applied a new forward matrix that applies a “nominal”-sized SPICE PSF and returns the pixel scale to that of the original data. The size of this “nominal” PSF is based on the resolutions described in the SPICE instrument paper (Spice Consortium 2020). The parameters of the PSF used are shown in Table 1, along with the slightly different parameters (just the PSF angle in this case) used for the correction of the region discussed in Sect. 4.2. These parameters were developed by trial and error, looking for the set which best fits the visual appearance of the SPICE data while best improving the resolution of SPICE and providing the largest reduction in the Doppler artifacts. The same PSF is shown as the “suggested SPICE PSF” in Fig. 2.
Parameters of the PSF used for the correction of the two regions.
Figure 11 shows the same slit position as Fig. 2, with the higher spectral resolution, while Fig. 12 shows our final correction with this nominal (or “ideal”) SPICE PSF and pixelization. Each figure shows correction of both the SPICE data and the IRIS-based “synthetic” SPICE data (IRIS with proposed SPICE PSF and pixelization). All show good removal of the rotation artifacts of the PSF, and the degraded then corrected IRIS data show a good match to the originals (though not exact, which is to be expected considering the much lower resolution). The high-resolution correction for SPICE (Fig. 11) shows the ringing and noise features mentioned, but these are absent when the resolution is reduced back the nominal SPICE values (Fig. 12).
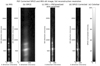 |
Fig. 11. High-resolution “raw” corrected spectra from the same slit position as shown in Fig. 2. Panel a: IRIS data. Panel b: SPICE data. Panel c: Correction applied to the degraded IRIS data. Panel d: Correction applied to SPICE data. The last two panels are at a higher spectral resolution than the input SPICE data. The higher resolution was necessary to resolve the spectral line. This over-resolution results in some noise-induced ringing and other ripples in the SPICE data, which we resolved by returning the image to SPICE pixel scale plus a “nominal” PSF, shown in Fig. 12. Otherwise, the original IRIS line width was recovered, while the elongation and tilt of the SPICE PSF was removed. |
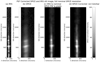 |
Fig. 12. Corrected spectra from the same slit position as shown in Fig. 2. Panel a: IRIS data. Panel b: SPICE data. Panel c: Correction applied to the degraded IRIS data. Panel d: Correction applied to SPICE. The last two panels have the same pixel scale as the input SPICE data with a “nominal” PSF applied as well. The “raw” corrected data (Fig. 11) is at a higher resolution, which is necessary to resolve the spectral line. This over-resolution results in some noise-induced ringing and other ripples in the SPICE data. These effects were resolved in the figure by returning the image to SPICE pixel scale plus a “nominal” PSF. The original IRIS line width was recovered, while the elongation and tilt of the SPICE PSF was removed. |
More importantly, the PSF correction does remove the Doppler artifacts, both in the degraded then corrected IRIS data and in the SPICE data. This is shown in Fig. 13. This figure shows the degraded then corrected IRIS Doppler data, the degraded IRIS Doppler data, and the corrected SPICE data (for the original IRIS and SPICE data, see Fig. 3). The degraded then corrected IRIS data is essentially identical to the original (plus binned down) IRIS data, and the SPICE data is quite similar to the IRIS data. The artifacts previously seen at the circled locations are no longer present. There is some extra coarseness in the SPICE data due to noise. There are also some artifacts in low signal regions that are likely due to a combination of noise and the interpolation applied to the SPICE L2 data, which we used. The interpolation can be mitigated by the use of an intermediate data product (with dark correction and flat fielding but no interpolation), but the same cannot be done for the low noise limit, since the noise results in a loss of information that cannot be recovered.
 |
Fig. 13. Corrected Doppler shifts for both the degraded IRIS data and the SPICE data. Panel a: Binned down IRIS data. Panel b: Original SPICE data (for comparison). Panel c: Degraded, then corrected IRIS Doppler data. The data shown is essentially identical to the original (with down binning) IRIS data, which demonstrates that the correction is formally sound. Panel d: Degraded, noise added, and then corrected IRIS data. The read noise data were set to 0.75 SPICE L2 data units, while the shot noise data were both set to 0.75 SPICE L2 data units times the square root of the data level at each pixel. Panel e: Corrected SPICE data. The data looks very similar to the degraded, noise added IRIS data (for the degraded IRIS data, see Fig. 3). This demonstrates that the correction also works on the real SPICE data. |
To further investigate the quality of the correction, we show the difference between the corrected “synthetic” IRIS Doppler data and the IRIS Doppler data without the degradation and correction in Fig. 14. In the figure, we still applied the “nominal” PSF previously mentioned so that the two images should be equivalent in resolution and pixel dimension. Except in areas with a very low signal (also shown in the figure for reference), the degraded then corrected IRIS Doppler data match the artifact PSF-free IRIS Doppler data to within 3 km s−1, well under the 5 km s−1 mentioned in the SPICE instrument paper (Spice Consortium 2020). Detector noise, of course, adds scatter to the Doppler shifts.
 |
Fig. 14. Doppler residuals for the “synthetic” SPICE data made from IRIS observations. Residuals are compared with data with the “nominal” symmetric SPICE PSF and detector scale applied – free of the PSF artifacts. Panel a: Original IRIS amplitude (for context). Panel b: Magnitude of the difference between the corrected Doppler and the Doppler with only the “nominal” symmetric SPICE PSF and detector scale applied. This image is free of PSF artifacts and looks essentially identical to panel a of Fig. 13 except for the smaller pixel size, so it is not shown. Panel c: Difference between the uncorrected Doppler and the same nominal Doppler in panel b. Except for areas with a very low signal (see panel a), the corrected Doppler is within 3 km s−1 of the nominal, whereas the uncorrected Doppler is essentially above 3 km s−1 everywhere. |
4.2. Correction applied to second region
Last, we show correction to a second part of the coordinated IRIS and SPICE observing campaign. This region is more characteristic of the quiet Sun, as it does not show bright extended EUV features and only has a couple of isolated bright features, which are nevertheless significantly dimmer than in the other region. The maximum intensities in the blue, orange, and green circled regions shown in Fig. 15 are 19.8, 6.4, and 7.3 W m−2 sr−1nm−1s, respectively, compared with 15.9, 23.2, and 44.7 for the brightest features in the other region, shown in Fig. 1.
 |
Fig. 15. Panel a: Context image of the SPICE-IRIS coordinated observation data for the second considered region. This image is made from one of the full-size SPICE rasters. It is a spectral sum over the C III 977 Å window. Panel b: Detailed image of the line fit amplitudes in the region from IRIS. Panel c: Detailed image of the line fit amplitudes in the region from SPICE. Doppler fits are shown in Fig. 16. |
Removal of artifacts from these features is another good test of the PSF correction. A context image for these observations is shown in Fig. 15, while Doppler images for the region are shown in Fig. 16. The correction removed almost all the artifacts and results in a Doppler image similar to the IRIS data, although somewhat less so than before. An exception to this is the small, relatively bright region (circled in blue) in the upper left of Fig. 16. The feature appears to still have some strong Doppler signals that are not present in the IRIS data. The mean Doppler shift in this region is largely unchanged, going from 17.8 to 18.1 km s−1. However, this region has a highly complex spectral structure and varies rapidly both spatially and temporally in IRIS, so a close match between SPICE and IRIS is not expected here. The corrected “synthetic” SPICE data (IRIS degraded with noise added) do not show this artifact, so it would not seem to be an issue with the correction method itself. Nevertheless, it appears as if the “corrected” SPICE data may not be fully corrected in that location. Other differences can be attributed to the lower signal in the region and possibly also to more dissimilarities between the region, as seen through comparison of the IRIS data with the SPICE data. For instance, the intensities appear more different than in the previous region, and the mean absolute difference between the SPICE and the “synthetic” SPICE intensities, after scaling the synthetic ones so that the overall means match, is 0.46 times the mean intensity in this case, compared to 0.29 for the previous one. We also had to increase the rotation angle of the PSF from 15° to 20° to best remove the artifacts. The rotation angle does appear to change across the field. We tried a variety of PSF rotation angles for both regions, and the ones that best reduced the Doppler artifacts are shown. The correction can account for per-pixel and/or field-wide variation in the PSF; however, it is just a (perhaps not so simple) matter of quantifying that variation.
 |
Fig. 16. Doppler shifts for a second region (see Fig. 15 for context) of the coordinated SPICE and IRIS observations. Panel a: IRIS data. Panel b: SPICE data. Panel c: Corrected SPICE data. This second region has a lower signal compared to the first region and a small, highly complex region (blue circle at top left of each image) that shows a strong (likely artifact) feature in SPICE but not in IRIS. Generally, the correction removes the artifacts, although the agreement with IRIS is less strong than in the first region (Fig. 13). See text for further discussion. |
5. Conclusions
We have shown the presence of Doppler artifacts in the SPICE data and demonstrated that their likely cause is an elongated and rotated effective (i.e., y − λ) PSF. We have further demonstrated a novel method for correcting these artifacts by representing the forward transformation as a sparse matrix and then performing a regularized inversion of this matrix with a method based on minimizing χ2 and the L2 norm with a positivity constraint.
The correction methods described in this paper appear to work well. They accurately reproduce the IRIS Doppler shifts when applied to “synthetic” data (IRIS data with SPICE-like PSF and pixelization applied) and quantitatively reproduce the IRIS Doppler shifts in most places when applied to real SPICE data. There are some regions where the S/N is too low to correct the PSF, and the reconstruction fails for that reason. There are fundamental information limitations regarding the ability to recover a high-resolution source from a blurred signal, but they do not appear to preclude correction of the Doppler artifacts and restoration of SPICE’s nominal effective PSF. Other issues that presently affect the reconstruction include interpolation of the L2 data and uncertainty in the SPICE PSF, which we hope to rectify using modified data products and further coordinated observations with IRIS and Hinode EIS.
The correction method is also interesting in its applicability to a variety of other problems. The positivity constraint and regularization affords a degree of super-resolution capability, especially when the data being inverted have a high contrast, and so the method may also be useful for improving the sharpness of high-resolution imagery. Unlike many sharpening methods, this method returns a true, improved resolution version of its source, maintaining photometry, because its inversion remains consistent with the forward problem and original data. It should also be capable of inverting data from multiple instruments simultaneously, even from those with differing resolutions. We may investigate reapplying the method to the DEM problem, for example, for computing DEMs using data from AIA and the Hinode X-Ray Telescope (Golub et al. 2007) simultaneously. Plowman (2021) applies a similar method to 3D reconstruction of the corona, demonstrating the method’s flexibility.
In subsequent papers on this topic for SPICE, we intend to work on determining the best characterization of the PSF. Particular attention will be paid to determining how the PSF varies over the detector planes and with scan position. Further coordinated observation campaigns with IRIS along those lines are already in progress. We hope to produce, as a result, a map of the SPICE PSF at each point on the detector plane. Future work will also include a survey of the results of PSF correction for each spectral window, including effectiveness of the correction for the spectral windows and for various signal-to-noise ratios.
The corrections shown in this work were all done on a laptop computer with a 2.6 GHz 6 core Intel Core i7. Although the results shown have been reduced in size, we also carried out correction of full resolution data on the same laptop. These took approximately 2 h, considerably less than the average acquisition rate of the SPICE data set as a whole (the cropped and binned down regions we showed took approximately 6 min). Therefore, the CPU load is easily within the capacity of a central server to reprocess the data as well as of individual users who would reprocess the data on their own. Currently, the code base has been provided to other members of the SPICE team for beta testing. Once this is finished, the code will be made publicly available. In the meantime, the code will be provided upon request, pending approval of the SPICE team. The code was written in Python, making use of Numpy (Harris et al. 2020), Astropy (Astropy Collaboration 2013, 2018), SciPy (Virtanen et al. 2020b), and (optionally) SunPy (SunPy et al. 2020).
References
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Baker, A. H., Jessup, E. R., & Manteuffel, T. 2005, SIAM J. Matrix Anal. App., 26, 962 [CrossRef] [Google Scholar]
- Culhane, J. L., Harra, L. K., James, A. M., et al. 2007, Sol. Phys., 243, 19 [Google Scholar]
- De Pontieu, B., Title, A. M., Lemen, J. R., et al. 2014, Sol. Phys., 289, 2733 [Google Scholar]
- Fisk, L. A., & Zurbuchen, T. H. 2006, J. Geophys. Res. Space Phys., 111, A09115 [NASA ADS] [CrossRef] [Google Scholar]
- Fludra, A., Caldwell, M., Giunta, A., et al. 2021, A&A, 656, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García Marirrodriga, C., Pacros, A., Strandmoe, S., et al. 2021, A&A, 646, A121 [CrossRef] [EDP Sciences] [Google Scholar]
- Golub, L., Deluca, E., Austin, G., et al. 2007, Sol. Phys., 243, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hassler, D. M., Dammasch, I. E., Lemaire, P., et al. 1999, Science, 283, 810 [Google Scholar]
- Lemen, J. R., Title, A. M., Akin, D. J., et al. 2012, Sol. Phys., 275, 17 [Google Scholar]
- Lin, R. P., Dennis, B. R., Hurford, G. J., et al. 2002, Sol. Phys., 210, 3 [Google Scholar]
- Peter, H., Gudiksen, B. V., & Nordlund, Å. 2006, ApJ, 638, 1086 [Google Scholar]
- Plowman, J. 2021, ApJ, 922, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Plowman, J., & Caspi, A. 2020, ApJ, 905, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Poduval, B., DeForest, C. E., Schmelz, J. T., & Pathak, S. 2013, ApJ, 765, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Popescu, M. D., & Doyle, J. G. 2005, Astrophys. Space Sci. Lib., 320, 235 [Google Scholar]
- Press, W., Teukolsky, S., Vetterling, W., & Flannery, B. 2002, Numerical recipes in C: the art of scientific computing (Cambridge University Press) [Google Scholar]
- Spice Consortium (Anderson, M., et al.) 2020, A&A, 642, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suess, S. T., Poletto, G., Wang, A. H., Wu, S. T., & Cuseri, I. 1998, Sol. Phys., 180, 231 [NASA ADS] [CrossRef] [Google Scholar]
- SunPy, C., Barnes, W. T., Bobra, M. G., et al. 2020, ApJ, 890, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Ugarte-Urra, I. 2016, EIS Point Spread Function [Google Scholar]
- van der Vorst, H. A. 1992, SIAM J. Sci. Stat. Comput., 13, 631 [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020b, Nat. Methods, 17, 261 [Google Scholar]
- Wang, Y. M., Sheeley, N. R. Jr., Howard, R. A., Rich, N. B., & Lamy, P. L. 1999, Geophys. Res. Lett., 26, 1349 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, R., & Martin, J. M. 1997, Geophys. Res. Lett., 24, 2535 [NASA ADS] [CrossRef] [Google Scholar]
- Young, P. R., O’Dwyer, B., & Mason, H. E. 2012, ApJ, 744, 14 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Context images of the primary IRIS and SPICE observations used for demonstration and testing in this paper. Left panel a: Context image of the SPICE-IRIS coordinated observation data. The image was made from one of the full-size SPICE rasters. It is a spectral sum over the C III 977 Å window. The detailed comparisons in this paper focus on the smaller region outlined in this image. Upper-right panel b: Spectral line fit amplitude image of the smaller region from IRIS. Lower-right panel c: Spectral line fit amplitude image of the smaller region from SPICE. |
| In the text | |
 |
Fig. 2. Spectra from a particular slit position in the SPICE and IRIS data. This slit position was chosen for good agreement between SPICE and IRIS, and it passes through the middle of the green circled region in Fig. 1. Panel a: IRIS spectra. Panel b: Proposed SPICE PSF with SPICE pixelization. Panel c: IRIS data (“synthetic SPICE”) with this PSF and pixelization. Panel d: Actual observed SPICE data. The elongation and apparent rotation of the PSF are evident, as is the agreement between (synthetic) IRIS and SPICE. |
| In the text | |
 |
Fig. 3. Amplitude (upper row) and Doppler (lower row) fits to the IRIS (panel a), IRIS with SPICE PSF and pixelization (“IRIS synthetic SPICE”; panel b), and SPICE (panel c). Before fitting, the IRIS data on the left were first binned down 2 × 2 to better match the SPICE pixel size. Both the “synthetic SPICE” and real SPICE Doppler (panels b and c) show clear ridge artifacts that are absent from the IRIS Doppler (panel a). Some specific artifacts are highlighted. Comparison with the amplitudes in the upper row shows that these artifacts are associated with bright features in intensity. The elongated, rotated effective y − λ PSF causes bright intensity features to alias into Doppler, as further discussed in the text. |
| In the text | |
 |
Fig. 4. One-dimensional example of the linear process relating a source model to observations. The input to the model (panel a) is a set of coefficients. These are multiplied by a set of basis functions at various wavelengths (one is shown in panel b), and the result is added to produce a spectrum (panel c). The spectrum in turn is multiplied by the PSF at each wavelength (panel d), and the result is added to produce a detector plane spectrum (panel e). Lastly, each of the sensor response functions (panel f) are integrated against the detector plane spectrum to produce count rates in each detector element (panel g). |
| In the text | |
 |
Fig. 5. One-dimensional example of the linear process applied using a matrix in a single step. Input (source coefficients; panel a) and outputs (detector count rates; panel c) in this figure are identical to Fig. 4 but with all of the intermediate operations carried out by a single matrix (panel b). This figure is specifically constructed so that the vertical axis of the matrix is aligned with the source element index, while the horizontal axis is aligned with the detector element index in order to make the matrix nature of the operation visually apparent. |
| In the text | |
 |
Fig. 6. Two-dimensional example of the linear process relating a source model to observations. Identical to Fig. 4 except that in this case, the source and observations are two-dimensional. The output resolution of these examples differs from the input because, in general, the resolution of solar sources differs from that of our detectors, demonstrating that this framework can accommodate such resolution differences. |
| In the text | |
 |
Fig. 7. Two-dimensional example of the linear process applied using a matrix in a single step. The input source coefficient image (panel a) and outputs (detector count rates image; panel e) in this figure are identical to Fig. 6, but all the intermediate operations were carried out by a single matrix (shown as an image at top right; panel c). The vertical axis of this matrix is aligned with the source element index, while the horizontal axis is aligned with the detector element index. This two-dimensional case is equivalent to the 1D example except that there is a multiplexing step that “flattens” the 2D input to 1D (panel b) prior to multiplication by the forward matrix (top right). The result of this multiplication (panel d) can then be demultiplexed to produce the output image (panel e). |
| In the text | |
 |
Fig. 8. Reconstruction of the one-dimensional example case previously shown in Fig. 4 using our method. Panel a: Original “source” model. Panel b: Data corresponding to source model (including PSF, pixelization, and noise). Panel c: Reconstruction of the source model. |
| In the text | |
 |
Fig. 9. Reconstruction of the two-dimensional example case previously shown in Fig. 6 using our method. Panel a: Original “source” model. Panel b: Data corresponding to source model (including PSF, pixelization, and noise). Panel c: Reconstruction of the source model. |
| In the text | |
 |
Fig. 10. Two-dimensional example reconstructions with spatially varying PSF. Upper row: Test pattern of dots to show how the PSF appear. Panel a: Original pattern of dots. Panel b: Pattern with the PSF applied. Panel c: Pattern with the PSF and our correction algorithm. Here our algorithm is called “Sparse NLMap”, with “NL” standing for “nonlinear”. Panel d: Attempt to correct the data with a standard Richardson-Lucy (R–L) deconvolution. This approach does not incorporate a spatially varying PSF. With no noise and well-isolated features, resolution comparable to the original can be restored with our Sparse NLMap algorithm, but R–L fails to recover the original test pattern. Lower row: Application to AIA image also shown in Fig. 9 except at full rather than half AIA resolution. Panel e: Original image. Panel f: Image with varying PSF (same as upper panels) and noise applied. Panel g: Sparse NLMAP correction applied. Panel h: Attempt to correct with R-L. The reconstruction of AIA is much sharper and closer to the original source than the “data” is, although it is inevitably impacted somewhat by noise. The R–L deconvolution, on the other hand, shows many obvious artifacts of the variation and elongation of the PSF. |
| In the text | |
 |
Fig. 11. High-resolution “raw” corrected spectra from the same slit position as shown in Fig. 2. Panel a: IRIS data. Panel b: SPICE data. Panel c: Correction applied to the degraded IRIS data. Panel d: Correction applied to SPICE data. The last two panels are at a higher spectral resolution than the input SPICE data. The higher resolution was necessary to resolve the spectral line. This over-resolution results in some noise-induced ringing and other ripples in the SPICE data, which we resolved by returning the image to SPICE pixel scale plus a “nominal” PSF, shown in Fig. 12. Otherwise, the original IRIS line width was recovered, while the elongation and tilt of the SPICE PSF was removed. |
| In the text | |
 |
Fig. 12. Corrected spectra from the same slit position as shown in Fig. 2. Panel a: IRIS data. Panel b: SPICE data. Panel c: Correction applied to the degraded IRIS data. Panel d: Correction applied to SPICE. The last two panels have the same pixel scale as the input SPICE data with a “nominal” PSF applied as well. The “raw” corrected data (Fig. 11) is at a higher resolution, which is necessary to resolve the spectral line. This over-resolution results in some noise-induced ringing and other ripples in the SPICE data. These effects were resolved in the figure by returning the image to SPICE pixel scale plus a “nominal” PSF. The original IRIS line width was recovered, while the elongation and tilt of the SPICE PSF was removed. |
| In the text | |
 |
Fig. 13. Corrected Doppler shifts for both the degraded IRIS data and the SPICE data. Panel a: Binned down IRIS data. Panel b: Original SPICE data (for comparison). Panel c: Degraded, then corrected IRIS Doppler data. The data shown is essentially identical to the original (with down binning) IRIS data, which demonstrates that the correction is formally sound. Panel d: Degraded, noise added, and then corrected IRIS data. The read noise data were set to 0.75 SPICE L2 data units, while the shot noise data were both set to 0.75 SPICE L2 data units times the square root of the data level at each pixel. Panel e: Corrected SPICE data. The data looks very similar to the degraded, noise added IRIS data (for the degraded IRIS data, see Fig. 3). This demonstrates that the correction also works on the real SPICE data. |
| In the text | |
 |
Fig. 14. Doppler residuals for the “synthetic” SPICE data made from IRIS observations. Residuals are compared with data with the “nominal” symmetric SPICE PSF and detector scale applied – free of the PSF artifacts. Panel a: Original IRIS amplitude (for context). Panel b: Magnitude of the difference between the corrected Doppler and the Doppler with only the “nominal” symmetric SPICE PSF and detector scale applied. This image is free of PSF artifacts and looks essentially identical to panel a of Fig. 13 except for the smaller pixel size, so it is not shown. Panel c: Difference between the uncorrected Doppler and the same nominal Doppler in panel b. Except for areas with a very low signal (see panel a), the corrected Doppler is within 3 km s−1 of the nominal, whereas the uncorrected Doppler is essentially above 3 km s−1 everywhere. |
| In the text | |
 |
Fig. 15. Panel a: Context image of the SPICE-IRIS coordinated observation data for the second considered region. This image is made from one of the full-size SPICE rasters. It is a spectral sum over the C III 977 Å window. Panel b: Detailed image of the line fit amplitudes in the region from IRIS. Panel c: Detailed image of the line fit amplitudes in the region from SPICE. Doppler fits are shown in Fig. 16. |
| In the text | |
 |
Fig. 16. Doppler shifts for a second region (see Fig. 15 for context) of the coordinated SPICE and IRIS observations. Panel a: IRIS data. Panel b: SPICE data. Panel c: Corrected SPICE data. This second region has a lower signal compared to the first region and a small, highly complex region (blue circle at top left of each image) that shows a strong (likely artifact) feature in SPICE but not in IRIS. Generally, the correction removes the artifacts, although the agreement with IRIS is less strong than in the first region (Fig. 13). See text for further discussion. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



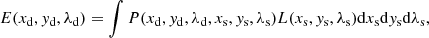
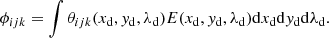
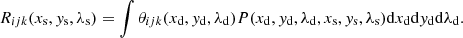
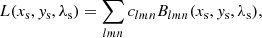
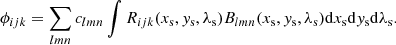
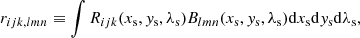
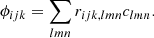
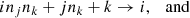
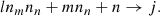
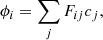
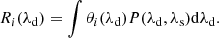
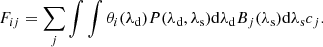
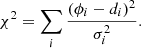
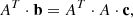
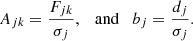
![$$ \begin{aligned} \mathbf{c} = {[A^T A]}^{-1}\cdot {A^T \cdot \mathbf{b}}. \end{aligned} $$](/articles/aa/full_html/2023/10/aa45582-22/aa45582-22-eq16.gif)
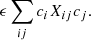
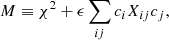
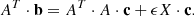
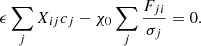
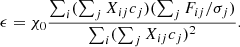
![$$ \begin{aligned} \mathbf{c}^0 \equiv F_T\cdot \mathbf{d} \Big [\frac{\mathbf{d} \cdot A \cdot A^T \cdot \mathbf{d}}{\vert A \cdot F^T \cdot \mathbf{d}\vert ^2}\Big ]. \end{aligned} $$](/articles/aa/full_html/2023/10/aa45582-22/aa45582-22-eq22.gif)
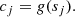
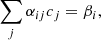
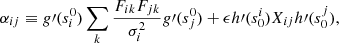
![$$ \begin{aligned} \nonumber \beta _i&\equiv \sum _j g\prime (s_i^0)\frac{F_{ji}}{\sigma _j^2}\big [d_j - \sum _k F_{jk} (g(s_k^0)-s_k^0g\prime (s_k^0))\big ] \\&\quad - \epsilon h\prime (s_i^0)X_{ij}\big [h(s_j^0)-s_j^0h\prime (s_j^0)\big ], \end{aligned} $$](/articles/aa/full_html/2023/10/aa45582-22/aa45582-22-eq28.gif)
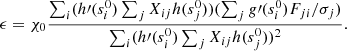
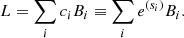
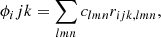
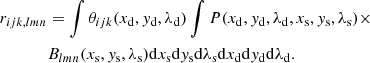
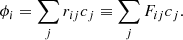
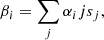
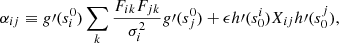
![$$ \begin{aligned} \nonumber \beta _i&\equiv&\sum _j g\prime (s_i^0)\frac{F_{ji}}{\sigma _j^2}\big [d_j - \sum _k F_{jk} (g(s_k^0)-s_k^0g\prime (s_k^0))\big ] \\&- \epsilon h\prime (s_i^0)X_{ij}\big [h(s_j^0)-s_j^0h\prime (s_j^0)\big ]. \end{aligned} $$](/articles/aa/full_html/2023/10/aa45582-22/aa45582-22-eq38.gif)
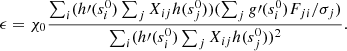
![$$ \begin{aligned} \mathbf{c}^0 \equiv F_T\cdot \mathbf{d} \Big [\frac{\mathbf{d} \cdot A \cdot A^T \cdot \mathbf{d}}{\vert A \cdot F^T \cdot \mathbf{d}\vert ^2}\Big ], \end{aligned} $$](/articles/aa/full_html/2023/10/aa45582-22/aa45582-22-eq40.gif)
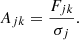
![$$ \begin{aligned} P(\Delta \boldsymbol{r}) = \exp \Big [-\frac{1}{2}\big (\Delta \boldsymbol{r}^T \Sigma ^{-1} \Delta \boldsymbol{r}\big )^\gamma \Big ], \end{aligned} $$](/articles/aa/full_html/2023/10/aa45582-22/aa45582-22-eq42.gif)