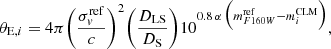EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 676 (August 2023) A&A, 676 (2023) A40 Full HTML
Open Access
Issue
A&A
Volume 676, August 2023
Article Number A40
Number of page(s) 17
Section Cosmology (including clusters of galaxies)
DOI https://doi.org/10.1051/0004-6361/202346283
Published online 04 August 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Strong gravitational lensing is a powerful tool for studying the mass distribution of galaxies and galaxy clusters and for testing cosmological models. Over recent decades, strong lensing has been exploited, for example, to analyse galaxy structures and study their evolution (e.g. Treu & Koopmans 2002; Auger et al. 2010; Sonnenfeld et al. 2013); to measure the value of the Hubble constant using time-delay measurements (e.g. Suyu et al. 2017, 2020; Grillo et al. 2018; Millon et al. 2020; Moresco et al. 2022); to constrain the dark energy equation of state (e.g. Jullo et al. 2010; Cao et al. 2012; Collett & Auger 2014; Caminha et al. 2022); and to estimate the dark matter fraction in massive early-type galaxies (e.g. Grillo 2010; Tortora et al. 2010; Sonnenfeld et al. 2015). On cluster-scales, strong-lensing models allow the study of the inner total mass distribution of clusters by exploiting an increasing number of multiple images of background sources (e.g. Caminha et al. 2017, 2019; Acebron et al. 2018; Bergamini et al. 2019, 2021a; Lagattuta et al. 2019, 2022). In addition, the strong lensing magnification enables clusters to be used as cosmic telescopes, allowing us to explore the intrinsic properties of otherwise undetectable faint (lensed) high-redshift sources (e.g. Swinbank et al. 2009; Richard et al. 2011; Vanzella et al. 2020, 2021).

Recently, by utilising cluster mass maps from high-precision strong-lensing models, Meneghetti et al. (2020, 2022) reported an excess of galaxy–galaxy strong lensing (GGSL) events in galaxy clusters compared with expectations based on the ΛCDM structure formation model. This has sparked debate over whether such an excess could be due to limitations in cosmological simulations (e.g. in the mass resolution or in the treatment of baryonic physics) or to more fundamental aspects related to the properties of dark matter (Meneghetti et al. 2022 and references therein).

This study is focused on a search for GGSL systems embedded in galaxy cluster halos. In this environment, the probability of GGSLs is generally higher than in the field for a given lens mass owing to the contribution of the cluster-scale lensing effect. Traditionally, GGSLs are identified through the visual inspection of candidates selected with spectroscopic or photometric criteria (e.g. Le Fèvre & Hammer 1988; Jackson 2008; Sygnet et al. 2010; Pawase et al. 2014). However, this will not be a viable method with upcoming data-intensive surveys based on next-generation facilities, such as the European Space Agency (ESA) Euclid satellite (Laureijs et al. 2011) and the Vera Rubin Observatory (Ivezić et al. 2019), which are expected to find tens of thousands of galaxy clusters and approximately 105 GGSLs (LSST Dark Energy Science Collaboration 2012; Euclid Collaboration 2019).

Several techniques have recently been developed to handle this unprecedented amount of survey imaging data. These range from semi-automatic algorithms searching for arc and ring-shaped features (e.g. More et al. 2012; Gavazzi et al. 2014; Sonnenfeld et al. 2018), to crowd sourcing science (e.g. Marshall et al. 2016; Sonnenfeld et al. 2020). In this context, machine learning and deep-learning methods appear to be a reliable and efficient means to identify GGSLs (see e.g. the discussion in Metcalf et al. 2019), although they need to be trained on appropriate simulated datasets. Moreover, the restricted number of confirmed strong-lensing examples in galaxy clusters prevents us from training machine learning methods with real data. Moreover, the large redshift range over which GGSLs are searched for, and their different morphologies, colours, and magnitudes, require realistic simulations to make deep-learning-based methods effective in detecting real strong lenses.

To this aim, significant efforts have been made over recent years to simulate GGSL populations such as those observed by current and upcoming surveys. Mock images of strong lensing events are obtained by co-adding simulated lensed sources to foreground galaxies with different methods. For example, dark matter halos and galaxies can be extracted from semi-analytical catalogues (e.g. with the Millennium Observatory project, as done by Metcalf et al. 2019, or by Leuzzi et al., in prep.) using mass density profiles (e.g. Collett 2015; He et al. 2020; Lanusse et al. 2018) or deep learning algorithms (Lanusse et al. 2021). Other studies opted for a hybrid approach, which consists in modelling the mass density profile of photometrically selected galaxies (e.g. Petrillo et al. 2017, 2019; Li et al. 2020, 2021; Gentile et al. 2022; Cañameras et al. 2021; Akhazhanov et al. 2022). Similarly, lensed sources can be simulated by modelling their surface brightness distributions (e.g. Petrillo et al. 2017, 2019; Li et al. 2020, 2021; Gentile et al. 2022) or sampled from observations (e.g. Meneghetti et al. 2008, 2010; Metcalf et al. 2019) and then co-added to real or synthetic images through ray-tracing techniques (e.g. GLAMERMetcalf & Petkova 2014; Petkova et al. 2014, GRAVLENSKeeton 2001).

In this work, we present a novel approach, which exploits accurate cluster-deflection fields to generate thousands of strong galaxy–galaxy lenses in galaxy clusters. The deflection angle maps are provided by high-precision cluster lens models constructed by Bergamini et al. (2019, 2021a) and Caminha et al. (2019) with the LensTool software (Kneib et al. 1996; Jullo et al. 2007; Jullo & Kneib 2009), which uses large numbers of spectroscopic multiple images. These models accurately describe both the cluster-scale mass component and the subhalo mass distribution associated to the cluster member galaxies (CLMs) –which together affect the morphology, brightness, and frequency of galaxy-scale lensing events– for a given distribution of background sources. Thus, GGSLs can be simulated with a realistic description of the CLMs acting as lenses in combination with the cluster-scale deflection field.

We test this methodology by injecting background source galaxies in multi-band images obtained with the Hubble Space Telescope (HST) Advanced Camera for Survey (ACS) as part of dedicated campaigns over the last decade, such as the Cluster Lensing And Supernova survey with Hubble (CLASH, Postman et al. 2012), Hubble Frontier Fields (HFF, Lotz et al. 2017), and the Reionization Lensing Cluster Survey (RELICS, Coe et al. 2019). This high-quality imaging dataset is completed with intensive spectroscopic programs, such as the CLASH-VLT (Rosati et al. 2014) with VIMOS (Visible MultiObject Spectrograph, Le Fèvre et al. 2003) and MUSE observations (Multi Unit Spectroscopic Explorer, Bacon et al. 2012, 2014, 2015) from the Very Large Telescope (VLT), and GLASS (Grism Lens-Amplified Survey from Space, Treu et al. 2015; Schmidt et al. 2014), which offer a three-dimensional view of approximately 50 clusters, providing spectra for several thousand galaxies. We exploit the combination of imaging and spectroscopic datasets to construct our convolutional neural network (CNN) knowledge base (KB).

This paper is structured as follows. In Sect. 2, we describe the two implemented convolutional neural networks. In Sect. 3, we illustrate the simulation methodology and dataset configuration. We detail the network performances in Sect. 4, including a complete analysis of the network misclassifications as a function of the physical parameters. In Sect. 5, we test the generalisation capabilities acquired by the networks by processing a set of known GGSLs. Finally, we draw our conclusions in Sect. 6.

Throughout the paper, we adopt a flat ΛCDM cosmological model with ΩM = 0.3, ΩΛ = 0.7, and H0 = 70 km s−1 Mpc−1. All astronomical images are oriented north to the top and east to the left. Unless otherwise specified, magnitudes are in the AB system.

2. Convolutional neural network

Among the deep learning methods, CNNs (LeCun et al. 1989, 1998) have become a popular tool with which to search for GGSLs in imaging surveys, owing to their ability to automatically extract information from raw data (e.g. Petrillo et al. 2017, 2019; Spiniello et al. 2018; Jacobs et al. 2019a,b; Cañameras et al. 2020; Huang et al. 2020; Li et al. 2020, 2021; Gentile et al. 2022). Here, we present the results achieved by two CNN architectures1, both of which are inspired by the Visual Group Geometry network (Simonyan & Zisserman 2014). The first network (similarly to the one described in Angora et al. 2020), hereafter named VGG, consists of a chain of convolution and pooling layers, whose ensemble of extracted feature maps is connected to the output through two dense layers. The second network consists of parallel VGGs, each of which processes a single HST band; we therefore name this architecture single-channel VGG (SC-VGG). As we use the F435W, F606W, and F814W bands in this work, the SC-VGG is composed of three parallel VGGs. Therefore, while the VGG performs a (linear) combination of filters in the first convolutional layer, the SC-VGG separates the informative contribution carried by the three bands. To obtain a single probability value, we average the probabilities for a GGSL event derived from each parallel VGG, and use this to measure the loss function and to update the training parameters. For both networks, we set the binary cross-entropy as the loss function (Goodfellow et al. 2016), the Leaky version of the Rectified Linear Unit (LeReLU, Maas et al. 2013) as the activation function for each layer, and Adadelta (Zeiler 2012) as the optimiser.

Furthermore, we include (i) an early stopping regularisation criterion (Prechelt 1997; Raskutti et al. 2011), which prevents overfitting; and (ii) a gradual reduction of the learning rate on the plateau of the loss function (as a function of iterations; Bengio 2012). These techniques evaluate the network performance during the training phase using a validation set previously extracted from the whole KB. At the same time, we opt for a stratified k-fold approach (Kohavi 1995; Hastie et al. 2009) to handle the training–testing split, where a fraction of the training image cutouts are augmented through flipping and rotations, as described in Angora et al. (2020).

Finally, to avoid memory loss, the networks were trained with input data batches, which include 32 and 16 patterns, respectively, for the VGG and the SC-VGG models. All networks were implemented through keras (Chollet et al. 2015), with tensorflow (Abadi et al. 2016) as back-end system.

3. Methodology

3.1. The simulation process

To simulate the GGSL events, we exploit the deflection angle maps of eight galaxy clusters obtained from cluster lens models2 provided by Bergamini et al. (2019, 2021a) and Caminha et al. (2019). The cluster sample is described in Table 1, while three of the clusters are shown in Fig. 1. The cluster total mass distribution of each cluster is modelled with a parametric description of the overall lensing potential, which includes a cluster-scale term composed of a dark matter halo and the smooth intracluster hot-gas mass from Chandra X-ray data when available (Bonamigo et al. 2017, 2018), and a clumpy component associated to the CLMs. For the latter, the mass density profile of each subhalo –these contain both dark matter and baryons– is modeled with a circular, singular dual-pseudo isothermal profile (Limousin et al. 2005; Elíasdóttir et al. 2007) and further calibrated with the measured stellar velocity dispersions of a large sample of CLMs (Bergamini et al. 2021b). Such lens models are able to reproduce the observed positions of many multiple images (ranging from ∼20 to ∼200; see Table 1) with a typical accuracy of ≲0.5″.

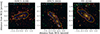thumbnail Fig. 1.

HST colour-composite images (combining the F435W, F606W, F814W filters) of three of the clusters in the sample (see Table 1). The tangential critical lines corresponding to four different redshifts, z = [1.5, 3.0, 4.5, 6.0], are shown in cyan, green, orange, and red, respectively.

Table 1.

Description of the cluster sample included in the GGSL simulation.

LensTool reconstructs the cluster potential by minimising the difference between the observed and model-predicted positions of the multiple images given a set of model parameter values. The deflection angle maps, α, describe the relation between the source real position (β) and its observed position (θ) via the lens equation: β = θ − α. The simulation process is carried out with PyLensLib (Meneghetti 2021) and can be summarised as follows:

– From the deflection angle maps, we derive the convergence and the shear maps, that is, the elements of the Jacobian matrix describing the image deformation, whose inverse matrix is the so-called magnification tensor. Then, the critical curves are found where the magnification goes to infinity. Examples of tangential critical curves –corresponding to sources at four different redshifts– are shown in Fig. 1, overlaid onto the HST field of view (FoV).

– To avoid the primary critical lines associated to the cluster potential and very small-scale galaxies, we select the secondary critical lines whose equivalent (circularised) Einstein radius is 0.2″ < θE < 3.5″, which is consistent with the expected distribution of the equivalent Einstein radii associated to secondary critical lines in galaxy clusters (see e.g. Fig. 7 in Meneghetti et al. 2022). Moreover, we assign a selection probability proportional to θE (i.e. larger critical lines are more likely to be extracted). In this way, a mass-limited sample of lens galaxies is selected from the secondary critical lines, circumventing any photometric selection (see the left panel in Fig. 2).

thumbnail Fig. 2.

Example of a GGSL simulation. Left panel: HST image of the cluster M1206 at z = 0.439 (∼2′ across), with the critical lines (in white) at z = 2.5 from the lens model (Bergamini et al. 2019). A specific secondary critical line is marked in red, with a zoomed-in image shown in the upper left ∼10″ inset. The green spot indicates the position of the corresponding caustic on the source plane. Central panel: source plane at z = 2.5 showing the caustic (in red) corresponding to the selected critical line, including the buffer (black dotted line) delimiting the injecting region; the injected source has a Sérsic profile (index n = 1.5, Reff = 0.14″), magF814W = 26.3, and the SED of a star-forming galaxy. Right panel: colour-composite image of the resulting simulated GGSL system, together with the critical line (red dotted line, with a circularised θE = 1.7″); the cutout is ∼10″ across.

– The selected secondary critical line is mapped into the corresponding caustic on the source plane (see the central panel in Fig. 2) using the lens equation.

– The source is simulated by injecting a Sérsic surface brightness profile (Sérsic 1963, 1968), I(β), within the caustic, including a buffer whose width is set equal to half of the source effective radius. Therefore, as the lens mapping conserves the surface brightness, that is, I(θ) = I(β), the observed surface brightness is computed as I(θ = β + α). The resulting GGSL is finally generated by convolving the simulated multiple-image system with the HST point spread function (PSF) for each band and is then co-added to the HST ACS image in a given filter (right panel in Fig. 2). The used PSFs are estimated with morphofit (Tortorelli & Mercurio 2023, see also Tortorelli et al. 2018, 2023).

In this work, we adopt a source spectral energy distribution (SED) of a star-forming galaxy template from Kinney et al. (1996). The list of Sérsic parameters and their adopted value ranges are shown in Table 2. The Sérsic index is extracted from a uniform distribution between n = 1.0 and 2.0 typical of late-type galaxy star-burst profiles. The axis ratio and the position angle values are randomly extracted from uniform distributions in (0.2, 1.0) and (0, π), respectively. To closely reproduce the HST observations, we do not use a uniform sampling for the other parameters. Specifically, for the source magnitudes and redshifts, we estimate the number counts in the i-band (i.e. the number of galaxies per square degree per magnitude bin) from the COSMOS 2015 catalogue (Scoville et al. 2007; Laigle et al. 2016), complemented with HST Deep Field North and South observations (Williams et al. 1996; Metcalfe et al. 2001) in F814W (taken from Capak et al. 2007), which extends the galaxy counts to the faint end, down to F814W = 29 mag (see the left panel of Fig. 3). In each of the six magnitude bins (with i limits = {22, 24, 25, 26, 27, 28, 29} mag), we use the COSMOS photometric redshift catalogue to estimate a redshift probability density function (PDF), that is, p(z |Δi), by fitting it with a simple function of the form p(z |Δi) = Az2e−z/z0 for i ∈ [22, 24) and p(z |Δi) = Az2e−(z/z0)1/2 for the other magnitude bins (see e.g. Lombardi & Bertin 1999; Lombardi et al. 2005). The redshift limit of the COSMOS catalogue is z ∼ 7, which is appropriate for our studies in which the reddest band is F814W. The six modelled PDFs are shown in the right panels of Fig. 3. For a given total number of galaxies injected into the cluster field, which is chosen in such a way as to be appropriate for the depth of the HST observations, we then use these PDFs to assign a source magnitude and redshift to each background galaxy. We also impose a minimum value for the source redshift of zsrc = zcls + 0.4, as suggested by Meneghetti et al. (2022), who measured the lensing cross-section for the galaxy clusters considered in this work, finding that it becomes significantly larger than zero for zsrc ≳ zcls + 0.4.

thumbnail Fig. 3.

Background source population. Left panel: galaxy number counts estimated from the COSMOS i-band catalogue (grey bars), compared with the results of Capak et al. (2007 black line), together with the 5σ HFF and CLASH F814W depth limit (cyan and green vertical lines). Galaxy counts added in the faint end to match the HST deep counts are coloured in magenta. Right panels: redshift distributions for six magnitude bins, p(z|Δm), coloured according to the magnitude bin from which they are extracted (left plot).

Table 2.

Sérsic parameters and their adopted value ranges for the injected sources.

Finally, to assign an effective radius value to the background galaxies, we exploit an empirical relation proposed by Shibuya et al. (2015) that describes the redshift evolution of the physical sizes of galaxies, which these authors approximated with a function of the form: Re = B(1 + z)β (fitted by combining galaxy radii estimated in the UV and optical bands). However, as a comparison of these values with the effective radii measured by Tortorelli et al. (2018) for low-z galaxies reveals a significant overestimate, we limit the application of this relation to z > 1, adopting a constant value at z ≤ 1 (see the fourth row in Table 2 and the left panel in Fig. 4). As suggested by the Shibuya et al. (2015) analysis, we assume a scatter of σ = 0.25 kpc over the entire redshift range, and randomly extract a value of Re at a given redshift z within the [ − 1.5σ, +1σ] range (see the left panel in Fig. 4). The chosen asymmetrical range allows us to sample Re values down to Re ≲ 0.5 kpc at z ≳ 4 (as shown in the left panel of Fig. 4).

thumbnail Fig. 4.

Simulation details. Left panel: adopted relation for the redshift evolution of Re, constant for z ≤ 1, and taken from Shibuya et al. (2015) for z > 1, together with the upper and lower limits within which Re is extracted (light red area). The black dashed line shows the 0.070″ threshold – under which the source size is indistinguishable from the PSF – after the convolution. Right panel: resulting scaling relation, i.e. θE vs. F160W, compared to those from Bergamini et al. (2019, 2021a) and Caminha et al. (2019), in red.

In an effort to verify that our simulated galaxy-scale lenses statistically reproduce the observations, we compare the θE − mF160W relation obtained for our mock GGSL sample with the CLM velocity dispersion scaling relation measured by Bergamini et al. (2019, 2021a) and used to build the lens models, that is, 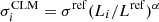σ i CLM = σ ref ( L i / L ref ) α $ \sigma^{\rm CLM}_i = \sigma^{\rm ref} (L_i/L^{\rm ref})^\alpha $ (see also Brainerd et al. 1996; Jullo et al. 2007). To this aim, we compute the expected Einstein radius as a function of the magnitude of the lens galaxy F160W by assuming a singular isothermal sphere for the lens galaxy mass density profile (Schneider 2006):

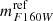θ E , i = 4 π ( σ v ref c ) 2 ( D LS D S ) 10 0.8 α ( m F 160 W ref − m i CLM ) , $$ \begin{aligned} \theta _{\mathrm{E},i} = 4\pi \Bigg (\frac{\sigma _v^\mathrm{ref}}{c}\Bigg )^2 \Bigg (\frac{D_{\rm LS}}{D_{\rm S}}\Bigg ) 10^{0.8\,\alpha \,\Big (m^\mathrm{ref}_{F160W} - m^\mathrm{CLM}_i\Big )}, \end{aligned} $$

where m F 160 W ref $ m^{\mathrm{ref}}_{F160W} $ is the F160W reference magnitude, which corresponds to the brightest cluster galaxy (BCG); 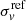σ v ref $ \sigma_v^{\rm ref} $ is a free parameter of the lens model (the normalization of the σ − m scaling relation); DS is the angular diameter distance to the source, and DLS is that between the lens and the source. The value of the slope of the scaling relation, α, is the one used in the lens models (directly inferred from the stellar velocity dispersion measurements Bergamini et al. 2019, 2021a). In Fig. 4, we show the latter relation as a red line and remark that it closely follows the distribution of effective Einstein radius values inferred from the secondary critical lines.

3.2. Building the knowledge base

The described methodology can simulate an arbitrary number of realistic GGSLs embedded in the complex environment of galaxy clusters as observed with the HST. To build a KB containing a large variety of GGSLs, we generate twice as many mock GGSLs as non-GGSLs (NGGSLs, i.e. the negative class for the classification problem). To this aim, we exploit the spectroscopic information obtained by combining the CLASH-VLT VIMOS programme with the MUSE archival observations and extract 10″ cutouts centred on the CLM positions belonging to 16 clusters, with a rest-frame velocity separation of |v|≤5000 km s−1, (see Table 3). As some of these cutouts may contain strong-lensing features, a visual inspection process was carried out by lensing experts in our group in order to build a fiducial sample of non-GGSLs. To help this classification process, each RGB image cutout was inspected together with the F435W, F606W, F814W bands, with knowledge of any nearby spectroscopic source with zs ≥ zcluster + 0.1. A score of +1, +0.5, or −1 was assigned to each CLM in case of a reliable GGSL, a less likely GGSL, or a non-GGSL, respectively. The cutouts containing bright stars, nearby bright galaxies, and/or those with an incomplete multi-band coverage near the edge of the FoV were also excluded. In this way, using the average scores, a visual inspection of 16 galaxy clusters led to the classification of a pure sample 1453 non-GGSLs. At the same time, 320 were classified as candidate GGSLs, and 282 cutouts were excluded.

Table 3.

Description of the cluster sample used in the non-GGSL selection.

Therefore, the resulting KB comprises 1453 observed non-GGSLs and 3000 simulated GGSLs. This initial mismatch, motivated by the need for a sufficient diversity of mock GGSLs, is later compensated during the extraction of the validation subset and the augmentation process, which leads to a training set of approximately 3800 images for each class. The KB dataset is then built by extracting 128 × 128 pixel cutouts (3.84″ by side)3. By studying the distribution of the distances of the multiple images with respect to lens centres, we find that all the cutouts contain at least one lensed image.

A sample of simulated GGSLs and cutouts classified as non-GGSLs is shown in Fig. 5, where the input images are indicated as red squares. GGSLs are sorted in order of increasing θE (across columns) and source intrinsic F814W magnitude (across rows). Besides the typical arc-like and ring-like features, several GGSL mock images do not reveal any apparent strong-lensing feature. This may occur (i) when the injected source is too faint, meaning that the lens galaxy outshines the GGSL signal (30% of sources have F814W > 28 mag); (ii) for small-scale lenses (small θE), where the lens galaxy halo hides multiple images (32% of lenses have θE < 0.5″); (iii) or when both of these latter two cases apply (10% of GGSLs have both F814W > 28 mag and θE < 0.5″). Although these cutouts represent the most challenging cases for the classifier, they act as adversarial examples (Szegedy et al. 2013), preventing network overfitting and allowing the network to gain a high degree of generalisation (Goodfellow et al. 2014; Zhao et al. 2020; Kong et al. 2020). We also performed some experiments to verify this by removing faint sources and small-scale lenses from the training phase. Even though the network achieves nearly perfect results, it appears unable to identify real strong lensing events, lacking enough generalisation capabilities. Finally, we note that the same CLM cutout can be used in the training set as a mock GGSL or a non-GGLS (i.e. no background source is injected); however, we expect this to have a negligible impact on the CNN performance.

thumbnail Fig. 5.

Examples of RGB cutouts of GGSLs and non-GGSL obtained by combining the F435W, F606W, and F814W bands. GGSL cutouts are sorted in order of increasing θE (along columns) and F814W magnitude (along rows) values. The images have been stretched to emphasise faint features by clipping values within ±3σ and normalising them. Cutouts are ∼9″ across; red squares indicate the 4 × 4″ areas processed by the networks. The labels at the bottom of each image indicate the values of zs, θE, and F814W magnitude.

4. Network performances

4.1. Statistical metrics

In order to assess the network classification performance, we use a set of metrics that are computed from the binary confusion matrix (Stehman 1997; see middle panel of Fig. 6), namely the average efficiency (AE), purity (pur), completeness (compl), and the F1-score, which is the harmonic mean between purity and completeness. The accuracy represents a global average score, which includes both classes, while the other three estimators are measured for each class. In this work, we refer to the GGSLs as the ‘positive’ class. Therefore, the four elements of a binary confusion matrix assume the following meaning: true positives (TPs) are GGSLs correctly classified, false positives (FPs) are non-GGSLs incorrectly flagged as GGSLs, false negatives (FNs) are GGSLs incorrectly predicted to be non-GGSLs, and true negatives (TNs) are correctly classified non-GGSLs. These estimators, as well as the confusion matrix, are computed by assuming a given threshold on the probability assigned by the CNN to each object. Unless otherwise specified, such a probability threshold is set to 0.50. The performance assessment is completed by including the so-called receiver operating characteristic curve (ROC; Hanley & McNeil 1982), which represents the trade-off between the TP rate (TPR; i.e. the completeness rate) and the FP rate (FPR; i.e. the contamination rate) as a function of the probability threshold (see the middle panel in Fig. 6). The area under this curve (AUC) can be used as an additional estimator of the network classification capabilities. Finally, as the training-test split has been implemented with a k-fold approach, we can also analyse the metric fluctuations over the ten folds (see Angora et al. 2020) and represent them graphically, as in the bottom panel of Fig. 6. For each metric, the box delimits the 25th and 75th percentiles, that is, the first and third quartiles (Q1 and Q3); their difference, the so-called interquartile range, IQR = Q3 − Q1; the error bars (ranging from Q1 − 1.5 ⋅ IQR to Q3 + 1.5 ⋅ IQR) correspond to 90.3% of the data (i.e. within ±2.698σ values); and the horizontal line indicates the median value.

thumbnail Fig. 6.

Comparison between the performance of the two networks under study (in all panels, the VGG and SC-VGG results are shown in green and in cyan, respectively). Top panel: statistical performance estimators for the GGSL and non-GGSL classes. Middle panel: ROC curves for the GGSL classification, i.e. TPR vs FPR (the lines and the coloured areas represent the mean and the 1σ level, respectively); here, the AUC values are quoted in the legend and the normalised confusion matrices are also shown. Bottom panel: box plots for the GGSL metrics and AE for both classes (see Sect. 4.1 for details).

4.2. Performances

A summary of the performances is shown in Table A.1 and in the top panel of Fig. 6 in terms of the statistical estimators (purity, completeness, F1-score, and average efficiency) for both classes. Globally, CNNs correctly classified at least 87% of the sources. Concerning the GGSL identification, both CNNs appear more pure than complete, with pur–compl differences ranging from 1.4% to 4.8%. As for the non-GGSLs, the networks reveal an opposite behaviour and a wider trade-off (pur–compl of between −8.7% and −2.7%). Such a dichotomy results from an unclear distinction between the two classes for a fraction of sources, which in our example is the case for faint sources and small-scale lenses (i.e. the adversarial examples). As mentioned above, these images prevent model overfitting when included in the training set; however, we measure the statistical estimators with and without these adversarial images in the test sets to quantify their effect on estimating the model performances. These re-estimated metrics (i.e. without the adversarial cutouts) are marked with an asterisk in Table A.1. Clearly, the non-GGSL completeness is not affected by this modification, while the non-GGSL purity increases by 15.6% and 11.9%, reaching 92.3% and 93.3%, respectively, for the VGG and SC-VGG models. Correspondingly, the F1-score increases to ∼88%, with an improvement of 7.6% for the VGG and 5.7% for the SC-VGG. Regarding the GGSL set, we find a more balanced trade-off between purity and completeness: the drop in purity (∼6%) is balanced by a gain in completeness (∼3%); while the F1-score drop remains at ≲2%.

A further analysis of the CNN performances is illustrated in Fig. 6. In the middle panel, the ROC curves and the corresponding AUC values are similar (within 1%), whereas the bottom panel shows the network classification capabilities in greater detail, quantifying the performance fluctuations (values listed in Table A.2). Both networks have similar GGSL purity (median, ∼93%, first and third quartile, Q1 ∼ 92% and Q3 ∼ 94%, and inter-quartile range IQR = 2.1%). More significant variations occur for the other GGSL metrics: the SC-VGG performances show an overall significant improvement in terms of completeness (median: 2.8%, Q1 and Q3: 4.5%, 2.1%), which in turn is reflected in an F1-score gain (from 0.8% to 3.8%). Concerning the non-GGSL metrics (only listed in Table A.2), SC-VGG achieves larger purity values (4.7%), while VGG shows better completeness (1.0%). SC-VGG achieves the best non-GGSL F1 score, with an average improvement of 1.6%. Based on this analysis, SC-VGG shows the best purity-completeness trade-off for both GGSL and non-GGSL (92.4%–82.8% vs. 91.0%–81.1%); it appears more robust when dealing with adversarial examples and is less subject to metric fluctuations (⟨IQR⟩SC-VGG = 2.1% vs ⟨IQR⟩VGG = 3.4%), particularly for the GGSL completeness.

Furthermore, we also perform an experiment using single-band cutouts (the F435W, F606W and F814W independently), that is, removing the multi-band information. The results are outlined in Table A.3, to be compared with the performances of the VGG and SC-VGG models. Although single-band performances reproduce the VGG and SC-VGG purity-completeness trends, the use of single-band data implies a loss of performance based on all metrics: an average reduction of 1.8%, 1.3%, and 3.5% for the AE, GGSL, and non-GGSL F1-scores, respectively. However, this moderate performance loss suggests that GGSLs can also be classified using single bands when multi-band imagining is not available (see also Petrillo et al. 2017, 2019; Li et al. 2021, who use the Kilo-Degree Survey data by de Jong et al. 2015). When using single band information, our tests show a better performance with the blue filter, owing to the larger contrast between the lens galaxy (red) and the strong-lensing features (generally blue).

We also tested the network performance using a KB built with cutouts of twice the size (256 pixels ≃7.7″ side). These experiments show a 10% drop in the performance metrics. Considering the significant extra burden of computing resources, we did not pursue this strategy further.

Finally, we compare the predictions made by our neural networks with the outcome of the visual inspection by gravitational lensing experts. As pointed out, as we aim to produce a highly pure non-GGSL sample, the resulting set of GGSL candidates is strongly contaminated, as it includes objects with uncertain visual classification (conservatively excluded from the non-GGSL set). Therefore, a human–machine comparison is more appropriate for identifying non-GGSLs than it is for identifying GGSLs. Indeed, considering the approximately 1800 visually inspected sources, we measure a high fraction of non-GGSLs also predicted by our neural network (∼95%), whereas this percentage for GGSLs is just ∼35%. However, by increasing the CNN probability threshold from 0.50 to 0.75, we find that all the 105 candidates are classified as GGSLs by both neural networks and astronomers, underscoring the high effectiveness of the CNN developed in this work.

4.3. False positives and false negatives

In this section, we specifically analyse the properties of the FPs and FNs produced by the CNN, which are characterised based on the galaxy magnitude and colour of FPs, and the GGSL system properties of FNs (source redshift and intrinsic magnitude, together with the lens Einstein radius).

Concerning the non-GGSLs mistakenly classified as strong lenses, a selection of FPs common to both VGG and SC-VGG models is displayed in Fig. 7. In Fig. 8, we show the TN, FP, and the FPR (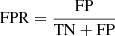 FPR = FP TN + FP $ \mathrm{FPR} = \frac{\mathrm{FP}}{\mathrm{TN+FP}} $) as a function of the CLM photometry: F814W magnitude (left panel) and the normalised colour (right panel), whose values are summarised in Table A.4. We use the galaxy red-sequence dependence on the redshift to compensate for the K-correction of CLMs, thus obtaining a normalised colour. We use the Girardi et al. (2015) relation, (F814W − F606W)norm = (F814W − F606W)obs − CM(F814W), which is the difference between the observed galaxy colour and the one determined from the colour–magnitude (CM) relation at a given F814W magnitude. We fit the CM sequence for the spectroscopically confirmed CLMs using a robust linear regression (Cappellari et al. 2013) that considers a possible intrinsic data scatter and clips out outliers, adopting the least trimmed squares technique (Rousseeuw & Driessen 2006). With this correction, red galaxies are centred around zero, while blue galaxies have colours of ≲ − 0.2 mag regardless of their redshift.

thumbnail Fig. 7.

Selection of FPs common to both the VGG and SC-VGG models. The probability of belonging to the GGSL class is shown in each thumbnail (referred to the SC-VGG model). Cutouts are ∼4″ across.

The number of FPs correlates both with the non-GGSL magnitudes and colours for F814W > 19 and (F606W − F814W)norm > −0.5 (see the approximately constant FPR in the bottom panels of Fig. 8). There are two FP excesses in the brighter and bluer part of the parameter space. The FPs increase in number for progressively bluer objects (7% for objects bluer than −0.5 mag, up to 90% and 50%, respectively for VGG and SC-VGG, in the bin around −0.7 mag). These are disc galaxies with a red bulge surrounded by blue spiral-like structures (see the first row in Fig. 7) or generally blue galaxies, which are under-represented in the KB because our sample is extracted from cluster cores mainly populated by red CLMs.

thumbnail Fig. 8.

FP dependences. TN and FP analysis related to the VGG and SC-VGG performances as a function of the galaxy lens photometry: F814W magnitude (left panel), (F606W − F814W)norm normalised colour (right panel). In both panels, the TNs are plotted with purple and magenta lines, while the FPs are shown with red and orange lines (respectively for the SC-VGG and VGG): in both cases, solid for SC-VGG, dashed for VGG. The FPR is plotted at the bottom of each panel (as a purple line for VGG, red for SC-VGG). In both panels, only sources with available and reliable magnitudes are plotted.

The two models also have similar trends as a function of the F814W magnitude, with a constant FPR of ∼0.16 for F814W > 19.5 and an FP excess in the brightest bins. This could be due to embedded lensed features in the training cutouts, which are outshone by the galaxy halo, meaning that when bright lens galaxies are present, the networks are trained to predict the existence of a GGSL with hidden lensed features (see the second row in Fig. 7). Indeed, these non-GGSL images are similar in appearance to mock GGSLs with hidden lensed features included in the training set. A bidimensional representation of the distribution of FPRs in the CM space is also shown in the top panels of Fig. A.1 for the VGG and SC-VGG models, which illustrates the trends discussed above.

Regarding the strong lenses misclassified as non-GGSLs (i.e. the FNs), Fig. 9 shows the distributions of FN, TP, and the FN ratio (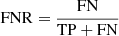 FNR = FN TP + FN $ \mathrm{FNR}=\frac{\mathrm{FN}}{\mathrm{TP+FN}} $) as a function of the source redshift (top left panel), galaxy-lens θE (top right panel), and the source intrinsic F814W magnitude (middle right panel). The main dependencies are also summarised in Table A.5. The number of FN decreases with θE, with an FNR of ≲0.06 for θE ≳ 2″. On the other hand, FNs are mainly associated with small-scale galaxy lenses (FNR ≳ 0.10 for θE < 0.5″). Likewise, misclassifications increase with the source magnitude, with an FN fraction of ∼0.10 for F814W ≥ 27. The VGG and SC-VGG FN ratios are similar (∼0.05) down to F814W = 27, whereas the VGG FNR continues to increase up to 0.20 at fainter magnitudes. A 2D distribution of the FNR as a function of θE and F814W is shown in the middle panels of Fig. A.1 for both CNNs. These plots clearly show that the SC-VGG model outperforms the VGG network for faint sources and small-scale lenses (FNRVGG ≃ 2 × FNRSC-VGG).

thumbnail Fig. 9.

FN dependences. TPs (green lines) and FNs (blue lines) distributions as a function of source redshift (zsrc, top panel), Einstein radius (θE, middle panel), and source intrinsic F814W magnitude (bottom panel) for the VGG (dashed lines) and SC-VGG (solid lines) models. The corresponding FN ratio is plotted at the bottom of each panel. In all panels, only sources with available and reliable magnitudes are plotted.

Similarly, the dependence of the FNR on the source redshift is comparable for the VGG and SC-VGG models (∼0.10) up to z ∼ 3, which represents 70% of the whole FN set. However, the VGG FNR significantly deteriorates (up to ∼0.21) at larger redshifts, whereas SC-VGG FNR remains approximately constant. The better performance of the SC-VGG model over the VGG at z ≳ 3 is likely connected to the drop-out effect for lensed galaxies due to the Lyman-break shift out of the bluest filter. In the VGG model, images in the three filters are combined in the first convolution layer, which mixes the multi-band information. Instead, with the single-channel approach, only filters that carry information (useful to disentangle GGSLs from non-GGSLs) contribute to the classification. In contrast, the drop-out images (no signal) are down-weighted by the network model.

We also verify that there is no significant dependence of the FNR on the source effective radius (re), as illustrated in the bottom panel of Fig. A.1, where FNR values ≳0.3 are mainly confined to the high-redshift bin for the VGG model only, as discussed above.

A selection of FNs is shown in Fig. 10. The first row includes the adversarial examples containing faint sources (F814W > 27.5) and small-scale lenses (0.10″ < θE < 0.25″). These cases should be compared with the FPs discussed above (see the second row in Fig. 7). The second row includes bonafide GGSLs, with visible arc-like features. All the adversarial FNs have probabilities (to be a GGSL) equal to zero, whereas bonafide GGSLs have probabilities not far below the adopted threshold of 0.50. This suggests that these FNs could be recovered by lowering the GGSL probability threshold. For example, one could adopt a threshold corresponding to the value where the purity and the completeness functions intersect. Figure 11 shows that this value is Pr = 0.25 for the SC-VGG model. By adopting this threshold, all FNs in the second row of Fig. 10 are recovered; while analysing the entire sample, we find that the completeness increases by 3.5% at the expense of a 1.8% drop in purity. The optimal strategy on the Pr value will depend on the number of GGSL candidates in a given imaging dataset and specific science objectives.

thumbnail Fig. 10.

Selection of FNs common to both the VGG and SC-VGG models. The probability of being a GGSL is shown in each thumbnail (estimated by the SC-VGG model). Cutouts are ∼4″ across.

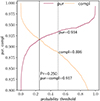thumbnail Fig. 11.

Purity (red) and completeness (orange) as a function of the GGSL probability threshold. Vertical lines correspond to the purity-completeness intersection at Pr = 0.25 (as a solid line) and to the classical threshold at Pr = 0.50 (as a dotted line). Purity and completeness values at Pr = 0.25 and Pr = 0.5 are indicated.

The analysis carried out in this section can be compared with other studies in blank field (i.e. not in clusters) based on different imaging datasets, adopting a similar methodology. For example, Petrillo et al. (2019) and Gentile et al. (2022) use the KiDS (de Jong et al. 2015) and VOICE (Vaccari et al. 2016) imaging surveys to search for GGSLs with similar CNNs. They trained their networks with simulated lensed galaxies, adopting simple Singular Isothermal Sphere models for early-type lens galaxies. A comparison of our FN distributions as a function of θE (middle panel in Fig. 9) with those from these studies shows similar FNR ranges, especially in the case of Petrillo et al. (2019), who found FNR values in the 4%–15% range (see their Fig. 3), while Gentile et al. (2022) obtained larger FNR values (10%–35%, see their Fig. 6).

5. Searching for strong lenses in galaxy clusters

The experiments described in the previous sections are mostly focused on the classification efficiency of the image-based CNN with simulated lenses by evaluating its dependence on several observational parameters, such as magnitude, colour, and Einstein radius. In this section, we are mainly interested in evaluating the degree of generalisation achieved by the trained CNNs in classifying real sources as GGSLs. This process step is commonly referred to as a ‘run’ in a machine learning context. To maximise the parameter space sampling, we do not use the k-fold approach utilised for performance testing but rather exploit the whole KB by excluding the validation set used for the regularisation processes.

To test the network generalisation capability, we perform a run on 24 candidate GGSLs previously known in the HST sample of galaxy clusters. These systems are listed in Table A.6 and shown in Fig. 12. We assume as ‘secure’ those objects whose GGSL nature is based on the presence of clear strong-lensing features, in some cases with spectroscopic confirmation; those with uncertain classification are flagged as ‘uncertain’, that is, those to be confirmed with further observations. We note that some of these secure GGSLs (panels E2, E4, E5, E6, G2) are part of multiple image systems produced by the cluster-deflection field in addition to the lens galaxy. We consider 20 of these candidates as secure. We organise the CNN predictions according to three probability intervals: Pr > 0.5, 0.2 ≤ Pr < 0.5, and Pr ≤ 0.2, defined as TP, quasi-true positive (qTP), and FN, respectively. Out of the 24 processed GGSLs, both CNN models yield the same classification for 15 objects (17 by including qTPs), 13 of which are correctly classified (15 by including qTPs). By adopting a probability threshold Pr > 0.2, out of 20 secure GGSLs, the TPs are 18 and 16 for the VGG and SC-VGG, respectively (16 and 14 by excluding the qTPs).

thumbnail Fig. 12.

Known GGSLs processed by both VGG and SC-VGG networks (see Table A.6). The GGSL probability is reported in each thumbnail (referred to the VGG and SC-VGG, respectively). Cutouts are 7.7″ across. The inner red squares enclose the area processed by the networks (∼4″). According to the classification probability, cutouts are surrounded by a box coloured in green (at least one probability is > 0.5), orange (at least one probability is ∈(0.2, 0.5]), or grey (otherwise).

All typical lenses, with arc-like or ring-like features, have been correctly classified (see e.g. the Einstein rings shown in panels A2, C1, I1, and L2, or the arc-like structures in panels D2, E3, E4, F1, K1, and L1). The system in panel B1 in Fig. 12, visually identified as a GGSL by Desprez et al. (2018) in Abell 383, is predicted to be a non-GGSL by both CNNs. However, further inspection, including also the HST/WFC3 bands, shows that the faint sources, in a seemingly Einsten cross configuration, have different colours, suggesting a correct CNN classification (for this reason, we set this classification as TN in Table A.6).

Concerning the FNs, the system in panel E1 is a spectroscopic multiply imaged system in M0416 (named ID.14) studied by Caminha et al. (2016) and Vanzella et al. (2017). This somewhat surprising misclassification may be due to a peculiar lens configuration with two CLMs, which is a situation not well represented in the training set (less than 0.01% of the input lenses). Other FNs (E2, G2) seem to be associated with cluster-scale lensing features, a category which somewhat bridges GGSLs and giant arcs. Interestingly, the remaining systems (G4, H1 and J2) with uncertain classification (see Table A.6) are characterised by almost complementary probabilities by the two CNN models. This behaviour underscores the hard challenge of the (human or machine-based) GGSL classification process when faced with peculiar or complex morphologies.

6. Conclusions

In this work, we build a methodology to search for galaxy-scale strong lensing systems in the HST multi-band imaging of galaxy clusters using deep learning techniques. We present a novel approach to simulating GGSLs in galaxy clusters, which takes advantage of extensive spectroscopic information on CLMs in eight clusters whose inner total mass distribution is determined with high accuracy through strong lensing modelling. Accurate knowledge of the deflection field in each cluster allows us to inject background sources near the secondary caustics associated with the CLMs and to simulate highly realistic GGSL systems in the HST cluster field. To this aim, we sampled the magnitude and photometric redshift distributions of background galaxies using Sérsic light profiles with a physical size estimated from an empirical redshift evolution of the effective radius of distant galaxies and a given star-forming SED.

In this way, we generate thousands of mock GGSLs, which reproduce the observations with high fidelity, preserving the full complexity of the real data. We use the image cutouts of these simulated GGSL systems in three ACS filters as a knowledge base with which to train two main CNNs. Their efficiency in identifying and classifying GGSLs in HST images down to F814W = 29 is quantified using several standard metrics. The main results of our study can be summarised as follows.

  • We investigated two CNN architectures: one combines the F435W, F606W, and F814W ACS bands (VGG model), while the other processes the three channels independently (SC-VGG model). We find that both models achieve a very good trade-off between purity and completeness (85%–95%). This reflects the comprehensive sampling of the parameter space describing the source and lens properties and a highly pure classification of non-GGSL events based on the visual inspection of lensing experts. We also find that performance fluctuations –estimated by iteratively varying the portion of the dataset used as an independent test set (the so-called k-fold approach)– are within 2%–4%, underlying the robustness of the network efficiency.

  • The analysis of FP and FN rates shows that FPs are typically spiral or disc galaxies whose structure is sometimes mistaken for lensing features. Interesting categories of FPs and FNs are bright galaxies and small cross-section lenses (small Einstein radii), respectively, for which the lens galaxy outshines possible multiple images. Although this category encompasses a significant fraction of misclassification, its inclusion in the KB is important in order to avoid network overfitting.

  • Overall, the SC-VGG model performs slightly better than the VGG model based on all the adopted metrics. This is particularly evident for faint and relatively red lensed sources, for which the single-channel approach seems to better take into account the K-correction effects.

  • When testing our CNN models on GGSLs previously known from the literature in 12 CLASH and HFF clusters, both networks are able to identify almost all systems deemed secure GGSLs, which demonstrates the high degree of generalisation of these networks. These TP cases include a wide range of galaxy-scale strong-lensing configurations, while the FNs seem to be generally associated with GGSLs whose configuration suggests a significant contribution from cluster-scale lensing.

In a forthcoming paper, we plan to perform a systematic search for GGSLs around CLMs in approximately 50 galaxy clusters included as targets in several HST programs (CLASH, HFF, and RELICS). In future works, we also intend to extend this methodology to the forthcoming ground- and space-based datasets, such as the Euclid (Laureijs et al. 2011) and Vera Rubin Observatory (Ivezić et al. 2019) wide-area surveys, and the James Webb Space Telescope (Gardner et al. 2006) NIRCAM imaging data, whose extraordinary potential in the study of strongly lensed sources has been shown in the first observations of galaxy cluster cores (e.g. Treu et al. 2022; Adams et al. 2023). Moreover, we will explore other deep learning networks, such as deep auto-encoders (Goodfellow 2010) and generative adversarial networks (Mirza & Osindero 2014), in an effort to automate the search and classification of strong-lensing events in these next-generation datasets. In this context, other deep architectures (e.g. region-based CNN, Ren et al. 2015, or masked-region CNN, He et al. 2017) can be tested by exploiting the trained convolutional layers developed in this paper.

1

We tested different network architectures, e.g. Residual Net X (He et al. 2015; Xie et al. 2016) and Inception Net (Szegedy et al. 2014). Due to their lower performances and higher computational cost, we limit the description of our results to deep models that achieved the best performances.

2

The cluster lens models are publicly available at https://www.fe.infn.it/astro/lensing/

3

We also studied the network behaviour using 256 × 256 pixel cutouts (7.68″ by side) and find that the performances are poorer (8%−15% in terms of accuracy) whilst entraining a four times higher training computing time. These tests suggest that the ∼4″ cutouts offer the best strategy.

Acknowledgments

We thank the anonymous referee for the helpful feedback and suggestions. We acknowledge financial support through grants PRIN-MIUR 2015W7KAWC, 2017WSCC32, and 2020SKSTHZ. MB acknowledges financial contributions from the agreement ASI/INAF 2018-23-HH.0, Euclid ESA mission – Phase D. A.A. has received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Skłodowska-Curie grant agreement No. 101024195 – ROSEAU. M.M. thanks INAF for support through Minigrant “The Big-Data era of cluster lensing”. We gratefully acknowledge the support of NVIDIA Corporation, with the donation of the Titan Xp GPUs used for this research. In this work several public softwares were used: Topcat (Taylor 2005), Astropy (Astropy Collaboration 2013, 2018), TensorFlow (Abadi et al. 2016), Keras (Chollet et al. 2015) and Scikit-Learn (Pedregosa et al. 2011).

References

  1. Abadi, M., Agarwal, A., Barham, P., et al. 2016, ArXiv e-prints arXiv e-prints[arXiv:1603.04467] [Google Scholar]
  2. Acebron, A., Cibirka, N., Zitrin, A., et al. 2018, ApJ, 858, 42 [NASA ADS] [CrossRef] [Google Scholar]
  3. Adams, N. J., Conselice, C. J., Ferreira, L., et al. 2023, MNRAS, 518, 4755 [Google Scholar]
  4. Akhazhanov, A., More, A., Amini, A., et al. 2022, MNRAS, 513, 2407 [NASA ADS] [CrossRef] [Google Scholar]
  5. Angora, G., Rosati, P., Brescia, M., et al. 2020, A&A, 643, A177 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
  8. Auger, M. W., Treu, T., Gavazzi, R., et al. 2010, ApJ, 721, L163 [Google Scholar]
  9. Bacon, R., Accardo, M., Adjali, L., et al. 2012, The Messenger, 147, 4 [NASA ADS] [Google Scholar]
  10. Bacon, R., Vernet, J., Borisova, E., et al. 2014, The Messenger, 157, 13 [NASA ADS] [Google Scholar]
  11. Bacon, R., Brinchmann, J., Richard, J., et al. 2015, A&A, 575, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Bengio, Y. 2012, ArXiv e-prints [arXiv:1206.5533] [Google Scholar]
  13. Bergamini, P., Rosati, P., Mercurio, A., et al. 2019, A&A, 631, A130 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Bergamini, P., Rosati, P., Vanzella, E., et al. 2021a, A&A, 645, A140 [EDP Sciences] [Google Scholar]
  15. Bergamini, P., Agnello, A., & Caminha, G. B. 2021b, A&A, 648, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  16. Bonamigo, M., Grillo, C., Ettori, S., et al. 2017, ApJ, 842, 132 [NASA ADS] [CrossRef] [Google Scholar]
  17. Bonamigo, M., Grillo, C., Ettori, S., et al. 2018, ApJ, 864, 98 [Google Scholar]
  18. Brainerd, T. G., Blandford, R. D., & Smail, I. 1996, ApJ, 466, 623 [NASA ADS] [CrossRef] [Google Scholar]
  19. Cañameras, R., Schuldt, S., Suyu, S. H., et al. 2020, A&A, 644, A163 [Google Scholar]
  20. Cañameras, R., Schuldt, S., Shu, Y., et al. 2021, A&A, 653, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  21. Caminha, G. B., Grillo, C., Rosati, P., et al. 2016, A&A, 587, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Caminha, G. B., Grillo, C., Rosati, P., et al. 2017, A&A, 607, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  23. Caminha, G. B., Rosati, P., Grillo, C., et al. 2019, A&A, 632, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  24. Caminha, G. B., Suyu, S. H., Grillo, C., & Rosati, P. 2022, A&A, 657, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Cao, S., Covone, G., & Zhu, Z.-H. 2012, ApJ, 755, 31 [NASA ADS] [CrossRef] [Google Scholar]
  26. Capak, P., Aussel, H., Ajiki, M., et al. 2007, ApJS, 172, 99 [Google Scholar]
  27. Cappellari, M., Scott, N., Alatalo, K., et al. 2013, MNRAS, 432, 1709 [Google Scholar]
  28. Chollet, F., et al. 2015, Keras, https://keras.io [Google Scholar]
  29. Coe, D., Salmon, B., Bradač, M., et al. 2019, ApJ, 884, 85 [Google Scholar]
  30. Collett, T. E. 2015, ApJ, 811, 20 [NASA ADS] [CrossRef] [Google Scholar]
  31. Collett, T. E., & Auger, M. W. 2014, MNRAS, 443, 969 [NASA ADS] [CrossRef] [Google Scholar]
  32. de Jong, J. T. A., Verdoes Kleijn, G. A., Boxhoorn, D. R., et al. 2015, A&A, 582, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  33. Desprez, G., Richard, J., Jauzac, M., et al. 2018, MNRAS, 479, 2630 [Google Scholar]
  34. Diego, J. M., Broadhurst, T., Benitez, N., Lim, J., & Lam, D. 2015, MNRAS, 449, 588 [Google Scholar]
  35. Elíasdóttir, Á., Limousin, M., Richard, J., et al. 2007, ArXiv e-prints [arXiv:0710.5636] [Google Scholar]
  36. Euclid Collaboration (Adam, R., et al.) 2019, A&A, 627, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  37. Gardner, J. P., Mather, J. C., Clampin, M., et al. 2006, Space Sci. Rev., 123, 485 [Google Scholar]
  38. Gavazzi, R., Marshall, P. J., Treu, T., & Sonnenfeld, A. 2014, ApJ, 785, 144 [Google Scholar]
  39. Gentile, F., Tortora, C., Covone, G., et al. 2022, MNRAS, 510, 500 [Google Scholar]
  40. Girardi, M., Mercurio, A., Balestra, I., et al. 2015, A&A, 579, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. Goodfellow, I. J. 2010, Technical Report: Multidimensional, Downsampled Convolution for Autoencoders, Tech. Rep. [Google Scholar]
  42. Goodfellow, I. J., Shlens, J., & Szegedy, C. 2014, ArXiv e-prints [arXiv:1412.6572] [Google Scholar]
  43. Goodfellow, I., Bengio, Y., & Courville, A. 2016, Deep Learning (MIT Press), http://www.deeplearningbook.org [Google Scholar]
  44. Grillo, C. 2010, ApJ, 722, 779 [NASA ADS] [CrossRef] [Google Scholar]
  45. Grillo, C., Rosati, P., Suyu, S. H., et al. 2018, ApJ, 860, 94 [Google Scholar]
  46. Hanley, J. A., & McNeil, B. J. 1982, Radiology, 143, 29 [Google Scholar]
  47. Hastie, T., Tibshirani, R., & Friedman, J. 2009, The Elements of Statistical Learning: Data Mining, Inference, and Prediction, Second Edition, Springer Series in Statistics (New York: Springer) [Google Scholar]
  48. He, K., Zhang, X., Ren, S., & Sun, J. 2015, ArXiv e-prints [arXiv:1512.03385] [Google Scholar]
  49. He, K., Gkioxari, G., Dollár, P., & Girshick, R. 2017, ArXiv e-prints [arXiv:1703.06870] [Google Scholar]
  50. He, Z., Er, X., Long, Q., et al. 2020, MNRAS, 497, 556 [NASA ADS] [CrossRef] [Google Scholar]
  51. Huang, X., Storfer, C., Ravi, V., et al. 2020, ApJ, 894, 78 [NASA ADS] [CrossRef] [Google Scholar]
  52. Ivezić, Ž., Kahn, S. M., Tyson, J. A., et al. 2019, ApJ, 873, 111 [Google Scholar]
  53. Jackson, N. 2008, MNRAS, 389, 1311 [NASA ADS] [CrossRef] [Google Scholar]
  54. Jacobs, C., Collett, T., Glazebrook, K., et al. 2019a, ApJS, 243, 17 [Google Scholar]
  55. Jacobs, C., Collett, T., Glazebrook, K., et al. 2019b, MNRAS, 484, 5330 [NASA ADS] [CrossRef] [Google Scholar]
  56. Jullo, E., & Kneib, J. P. 2009, MNRAS, 395, 1319 [NASA ADS] [CrossRef] [Google Scholar]
  57. Jullo, E., Kneib, J. P., Limousin, M., et al. 2007, New J. Phys., 9, 447 [Google Scholar]
  58. Jullo, E., Natarajan, P., Kneib, J. P., et al. 2010, Science, 329, 924 [Google Scholar]
  59. Keeton, C. R. 2001, ArXiv e-prints [arXiv:astro-ph/0102340] [Google Scholar]
  60. Kinney, A. L., Calzetti, D., Bohlin, R. C., et al. 1996, ApJ, 467, 38 [NASA ADS] [CrossRef] [Google Scholar]
  61. Kneib, J. P., Ellis, R. S., Smail, I., Couch, W. J., & Sharples, R. M. 1996, ApJ, 471, 643 [Google Scholar]
  62. Kohavi, R. 1995, Proceedings of the 14th International Joint Conference on Artificial Intelligence – Volume 2, IJCAI’95 (San Francisco: Morgan Kaufmann Publishers Inc.), 1137 [Google Scholar]
  63. Kong, K., Li, G., Ding, M., et al. 2020, ArXiv e-prints [arXiv:2010.09891] [Google Scholar]
  64. Lagattuta, D. J., Richard, J., Bauer, F. E., et al. 2019, MNRAS, 485, 3738 [NASA ADS] [Google Scholar]
  65. Lagattuta, D. J., Richard, J., Bauer, F. E., et al. 2022, MNRAS, 514, 497 [NASA ADS] [CrossRef] [Google Scholar]
  66. Laigle, C., McCracken, H. J., Ilbert, O., et al. 2016, ApJS, 224, 24 [Google Scholar]
  67. Lanusse, F., Ma, Q., Li, N., et al. 2018, MNRAS, 473, 3895 [Google Scholar]
  68. Lanusse, F., Mandelbaum, R., Ravanbakhsh, S., et al. 2021, MNRAS, 504, 5543 [CrossRef] [Google Scholar]
  69. Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
  70. LeCun, Y., Boser, B., Denker, J. S., et al. 1989, Neural Comput., 1, 541 [NASA ADS] [CrossRef] [Google Scholar]
  71. LeCun, Y., Bottou, L., Bengio, Y., & Haffner, P. 1998, Proc. Inst. Radio Eng., 86, 2278 [Google Scholar]
  72. Le Fèvre, O., & Hammer, F. 1988, ApJ, 333, L37 [CrossRef] [Google Scholar]
  73. Le Fèvre, O., Saisse, M., Mancini, D., et al. 2003, SPIE Conf. Ser., 4841, 1670 [Google Scholar]
  74. Li, R., Napolitano, N. R., Tortora, C., et al. 2020, ApJ, 899, 30 [Google Scholar]
  75. Li, R., Napolitano, N. R., Spiniello, C., et al. 2021, ApJ, 923, 16 [NASA ADS] [CrossRef] [Google Scholar]
  76. Limousin, M., Kneib, J.-P., & Natarajan, P. 2005, MNRAS, 356, 309 [Google Scholar]
  77. Lombardi, M., & Bertin, G. 1999, A&A, 342, 337 [NASA ADS] [Google Scholar]
  78. Lombardi, M., Rosati, P., Blakeslee, J. P., et al. 2005, ApJ, 623, 42 [NASA ADS] [CrossRef] [Google Scholar]
  79. Lotz, J. M., Koekemoer, A., Coe, D., et al. 2017, ApJ, 837, 97 [Google Scholar]
  80. LSST Dark Energy Science Collaboration 2012, ArXiv e-prints [arXiv:1211.0310] [Google Scholar]
  81. Maas, A. L., Hannun, A. Y., & Ng, A. Y. 2013, ICML Workshop on Deep Learning for Audio, Speech and Language Processing, 30 [Google Scholar]
  82. Marshall, P. J., Verma, A., More, A., et al. 2016, MNRAS, 455, 1171 [NASA ADS] [CrossRef] [Google Scholar]
  83. Meneghetti, M. 2021, Introduction to Gravitational Lensing, 1st edn. (Springer International Publishing) [CrossRef] [Google Scholar]
  84. Meneghetti, M., Melchior, P., Grazian, A., et al. 2008, A&A, 482, 403 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Meneghetti, M., Rasia, E., Merten, J., et al. 2010, A&A, 514, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  86. Meneghetti, M., Davoli, G., Bergamini, P., et al. 2020, Science, 369, 1347 [Google Scholar]
  87. Meneghetti, M., Ragagnin, A., Borgani, S., et al. 2022, A&A, 668, A188 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Metcalf, R. B., & Petkova, M. 2014, MNRAS, 445, 1942 [NASA ADS] [CrossRef] [Google Scholar]
  89. Metcalf, R. B., Meneghetti, M., Avestruz, C., et al. 2019, A&A, 625, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  90. Metcalfe, N., Shanks, T., Campos, A., McCracken, H. J., & Fong, R. 2001, MNRAS, 323, 795 [Google Scholar]
  91. Millon, M., Galan, A., Courbin, F., et al. 2020, A&A, 639, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Mirza, M., & Osindero, S. 2014, ArXiv e-prints [arXiv:1411.1784] [Google Scholar]
  93. More, A., Cabanac, R., More, S., et al. 2012, ApJ, 749, 38 [NASA ADS] [CrossRef] [Google Scholar]
  94. Moresco, M., Amati, L., Amendola, L., et al. 2022, Liv. Rev. Relat., 25, 6 [NASA ADS] [Google Scholar]
  95. Pawase, R. S., Courbin, F., Faure, C., Kokotanekova, R., & Meylan, G. 2014, MNRAS, 439, 3392 [NASA ADS] [CrossRef] [Google Scholar]
  96. Pedregosa, F., Varoquaux, G., Gramfort, A., et al. 2011, J. Mach. Learn. Res., 12, 2825 [Google Scholar]
  97. Petkova, M., Metcalf, R. B., & Giocoli, C. 2014, MNRAS, 445, 1954 [NASA ADS] [CrossRef] [Google Scholar]
  98. Petrillo, C. E., Tortora, C., Chatterjee, S., et al. 2017, MNRAS, 472, 1129 [Google Scholar]
  99. Petrillo, C. E., Tortora, C., Vernardos, G., et al. 2019, MNRAS, 484, 3879 [Google Scholar]
  100. Postman, M., Coe, D., Benítez, N., et al. 2012, ApJS, 199, 25 [Google Scholar]
  101. Prechelt, L. 1997, Neural Networks: Tricks of the Trade, Volume 1524 of LNCS, Chapter 2 (Springer-Verlag), 55 [Google Scholar]
  102. Raskutti, G., Wainwright, M. J., & Yu, B. 2011, 2011 49th Annual Allerton Conference on Communication, Control, and Computing (Allerton), 1318 [CrossRef] [Google Scholar]
  103. Ren, S., He, K., Girshick, R., & Sun, J. 2015, ArXiv e-prints [arXiv:1506.01497] [Google Scholar]
  104. Richard, J., Kneib, J.-P., Ebeling, H., et al. 2011, MNRAS, 414, L31 [Google Scholar]
  105. Rosati, P., Balestra, I., Grillo, C., et al. 2014, The Messenger, 158, 48 [NASA ADS] [Google Scholar]
  106. Rousseeuw, P. J., & Driessen, K. 2006, Data Min. Knowl. Discov., 12, 29 [CrossRef] [Google Scholar]
  107. Schmidt, K. B., Treu, T., Brammer, G. B., et al. 2014, ApJ, 782, L36 [Google Scholar]
  108. Schneider, P. 2006, Extragalactic Astronomy and Cosmology (Berlin, Heidelberg: Springer-Verlag) [Google Scholar]
  109. Scoville, N., Aussel, H., Brusa, M., et al. 2007, ApJS, 172, 1 [Google Scholar]
  110. Sérsic, J. L. 1963, Boletin de la Asociacion Argentina de Astronomia La Plata Argentina, 6, 41 [Google Scholar]
  111. Sérsic, J. L. 1968, Atlas de Galaxias Australes (Cordoba, Argentina: Observatorio Astronomico) [Google Scholar]
  112. Shibuya, T., Ouchi, M., & Harikane, Y. 2015, ApJS, 219, 15 [Google Scholar]
  113. Simonyan, K., & Zisserman, A. 2014, ArXiv e-prints [arXiv:1409.1556] [Google Scholar]
  114. Smith, G. P., Kneib, J.-P., Smail, I., et al. 2005, MNRAS, 359, 417 [NASA ADS] [CrossRef] [Google Scholar]
  115. Sonnenfeld, A., Treu, T., Gavazzi, R., et al. 2013, ApJ, 777, 98 [Google Scholar]
  116. Sonnenfeld, A., Treu, T., Marshall, P. J., et al. 2015, ApJ, 800, 94 [Google Scholar]
  117. Sonnenfeld, A., Chan, J. H. H., Shu, Y., et al. 2018, PASJ, 70, S29 [Google Scholar]
  118. Sonnenfeld, A., Verma, A., More, A., et al. 2020, A&A, 642, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  119. Spiniello, C., Agnello, A., Napolitano, N. R., et al. 2018, MNRAS, 480, 1163 [NASA ADS] [CrossRef] [Google Scholar]
  120. Stehman, S. V. 1997, Remote Sens. Environ., 62, 77 [NASA ADS] [CrossRef] [Google Scholar]
  121. Suyu, S. H., Bonvin, V., Courbin, F., et al. 2017, MNRAS, 468, 2590 [Google Scholar]
  122. Suyu, S. H., Huber, S., Cañameras, R., et al. 2020, A&A, 644, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  123. Swinbank, A. M., Webb, T. M., Richard, J., et al. 2009, MNRAS, 400, 1121 [NASA ADS] [CrossRef] [Google Scholar]
  124. Sygnet, J. F., Tu, H., Fort, B., & Gavazzi, R. 2010, A&A, 517, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  125. Szegedy, C., Zaremba, W., Sutskever, I., et al. 2013, ArXiv e-prints [arXiv:1312.6199] [Google Scholar]
  126. Szegedy, C., Liu, W., Jia, Y., et al. 2014, ArXiv e-prints [arXiv:1409.4842] [Google Scholar]
  127. Taylor, M. B. 2005, ASP Conf. Ser., 347, 29 [Google Scholar]
  128. Tortora, C., Napolitano, N. R., Romanowsky, A. J., & Jetzer, P. 2010, ApJ, 721, L1 [NASA ADS] [CrossRef] [Google Scholar]
  129. Tortorelli, L., & Mercurio, A. 2023, Front. Astron. Space Sci., 10, 51 [NASA ADS] [CrossRef] [Google Scholar]
  130. Tortorelli, L., Mercurio, A., Paolillo, M., et al. 2018, MNRAS, 477, 648 [NASA ADS] [CrossRef] [Google Scholar]
  131. Tortorelli, L., Mercurio, A., Granata, G., et al. 2023, A&A, 671, L9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  132. Treu, T., & Koopmans, L. V. E. 2002, ApJ, 575, 87 [NASA ADS] [CrossRef] [Google Scholar]
  133. Treu, T., Schmidt, K. B., Brammer, G. B., et al. 2015, ApJ, 812, 114 [Google Scholar]
  134. Treu, T., Roberts-Borsani, G., Bradac, M., et al. 2022, ApJ, 935, 110 [NASA ADS] [CrossRef] [Google Scholar]
  135. Umetsu, K., Sereno, M., Tam, S.-I., et al. 2018, ApJ, 860, 104 [Google Scholar]
  136. Vaccari, M., Covone, G., Radovich, M., et al. 2016, The 4th Annual Conference on High Energy Astrophysics in Southern Africa (HEASA 2016), 26 [Google Scholar]
  137. Vanzella, E., Castellano, M., Meneghetti, M., et al. 2017, ApJ, 842, 47 [Google Scholar]
  138. Vanzella, E., Meneghetti, M., Caminha, G. B., et al. 2020, MNRAS, 494, L81 [Google Scholar]
  139. Vanzella, E., Caminha, G. B., Rosati, P., et al. 2021, A&A, 646, A57 [EDP Sciences] [Google Scholar]
  140. Williams, R. E., Blacker, B., Dickinson, M., et al. 1996, AJ, 112, 1335 [NASA ADS] [CrossRef] [Google Scholar]
  141. Xie, S., Girshick, R., Dollár, P., Tu, Z., & He, K. 2016, ArXiv e-prints [arXiv:1611.05431] [Google Scholar]
  142. Zeiler, M. D. 2012, ArXiv e-prints [arXiv:1212.5701] [Google Scholar]
  143. Zhao, L., Liu, T., Peng, X., & Metaxas, D. 2020, ArXiv e-prints [arXiv:2010.08001] [Google Scholar]

Appendix A: Complementary tables and figures

In this Appendix, we include additional tables and figures related to the CNN performance evaluation. Table A.1 shows a comparison between the VGG and the SC-VGG in terms of statistical estimators by also excluding the adversarial examples from the metric computation (quoted with an asterisk). The analysis of performance fluctuations (for both VGG and SC-VGG) evaluated over the ten folds is summarised in Table A.2. Table A.3 shows a comparison of the results achieved by the networks trained with the three ACS bands (the adopted method) with performances obtained using a single band. A summary of the FP and FN distributions is outlined in Table A.4 and Table A.5, respectively. Figure A.1 shows the FPRs and FNRs as 2D histograms. Table A.6 illustrates the run performed by both VGG and SC-VGG by processing a set of known GGSLs in a sample of galaxy clusters observed with HST.

thumbnail Fig. A.1.

FPR and FNR represented by 2D histograms. Top panels: FPRs on a galaxy colour–magnitude diagram (i.e. (F606W − F814W)norm vs F814W). Middle panels: FNRs on a lens θE vs source F814W magnitude diagram. Bottom panels: FNRs on a source re vs source redshift diagram. The VGG and the SC-VGG results are shown in the left and right panels, respectively. The regions of the parameter space with zero TN or zero TP values are left white.

Table A.1.

Performance comparison between the two CNN architectures.

Table A.2.

Fluctuations of the performances for the VGG and SC-VGG models.

Table A.3.

Network performances trained with three HST/ACS bands (VGG, SC-VGG) compared with single-band training.

Table A.4.

Summary of FP distributions for the VGG and SC-VGG networks.

Table A.5.

Summary of the FN distributions, split between VGG and SC-VGG network.

Table A.6.

Catalogue of known GGSLs processed by both the VGG and SC-VGG networks.

All Tables

Table 1.

Description of the cluster sample included in the GGSL simulation.

In the text
Table 2.

Sérsic parameters and their adopted value ranges for the injected sources.

In the text
Table 3.

Description of the cluster sample used in the non-GGSL selection.

In the text
Table A.1.

Performance comparison between the two CNN architectures.

In the text
Table A.2.

Fluctuations of the performances for the VGG and SC-VGG models.

In the text
Table A.3.

Network performances trained with three HST/ACS bands (VGG, SC-VGG) compared with single-band training.

In the text
Table A.4.

Summary of FP distributions for the VGG and SC-VGG networks.

In the text
Table A.5.

Summary of the FN distributions, split between VGG and SC-VGG network.

In the text
Table A.6.

Catalogue of known GGSLs processed by both the VGG and SC-VGG networks.

In the text

All Figures

thumbnail Fig. 1.

HST colour-composite images (combining the F435W, F606W, F814W filters) of three of the clusters in the sample (see Table 1). The tangential critical lines corresponding to four different redshifts, z = [1.5, 3.0, 4.5, 6.0], are shown in cyan, green, orange, and red, respectively.
In the text
thumbnail Fig. 2.

Example of a GGSL simulation. Left panel: HST image of the cluster M1206 at z = 0.439 (∼2′ across), with the critical lines (in white) at z = 2.5 from the lens model (Bergamini et al. 2019). A specific secondary critical line is marked in red, with a zoomed-in image shown in the upper left ∼10″ inset. The green spot indicates the position of the corresponding caustic on the source plane. Central panel: source plane at z = 2.5 showing the caustic (in red) corresponding to the selected critical line, including the buffer (black dotted line) delimiting the injecting region; the injected source has a Sérsic profile (index n = 1.5, Reff = 0.14″), magF814W = 26.3, and the SED of a star-forming galaxy. Right panel: colour-composite image of the resulting simulated GGSL system, together with the critical line (red dotted line, with a circularised θE = 1.7″); the cutout is ∼10″ across.
In the text
thumbnail Fig. 3.

Background source population. Left panel: galaxy number counts estimated from the COSMOS i-band catalogue (grey bars), compared with the results of Capak et al. (2007 black line), together with the 5σ HFF and CLASH F814W depth limit (cyan and green vertical lines). Galaxy counts added in the faint end to match the HST deep counts are coloured in magenta. Right panels: redshift distributions for six magnitude bins, p(z|Δm), coloured according to the magnitude bin from which they are extracted (left plot).
In the text
thumbnail Fig. 4.

Simulation details. Left panel: adopted relation for the redshift evolution of Re, constant for z ≤ 1, and taken from Shibuya et al. (2015) for z > 1, together with the upper and lower limits within which Re is extracted (light red area). The black dashed line shows the 0.070″ threshold – under which the source size is indistinguishable from the PSF – after the convolution. Right panel: resulting scaling relation, i.e. θE vs. F160W, compared to those from Bergamini et al. (2019, 2021a) and Caminha et al. (2019), in red.
In the text
thumbnail Fig. 5.

Examples of RGB cutouts of GGSLs and non-GGSL obtained by combining the F435W, F606W, and F814W bands. GGSL cutouts are sorted in order of increasing θE (along columns) and F814W magnitude (along rows) values. The images have been stretched to emphasise faint features by clipping values within ±3σ and normalising them. Cutouts are ∼9″ across; red squares indicate the 4 × 4″ areas processed by the networks. The labels at the bottom of each image indicate the values of zs, θE, and F814W magnitude.
In the text
thumbnail Fig. 6.

Comparison between the performance of the two networks under study (in all panels, the VGG and SC-VGG results are shown in green and in cyan, respectively). Top panel: statistical performance estimators for the GGSL and non-GGSL classes. Middle panel: ROC curves for the GGSL classification, i.e. TPR vs FPR (the lines and the coloured areas represent the mean and the 1σ level, respectively); here, the AUC values are quoted in the legend and the normalised confusion matrices are also shown. Bottom panel: box plots for the GGSL metrics and AE for both classes (see Sect. 4.1 for details).
In the text
thumbnail Fig. 7.

Selection of FPs common to both the VGG and SC-VGG models. The probability of belonging to the GGSL class is shown in each thumbnail (referred to the SC-VGG model). Cutouts are ∼4″ across.
In the text
thumbnail Fig. 8.

FP dependences. TN and FP analysis related to the VGG and SC-VGG performances as a function of the galaxy lens photometry: F814W magnitude (left panel), (F606W − F814W)norm normalised colour (right panel). In both panels, the TNs are plotted with purple and magenta lines, while the FPs are shown with red and orange lines (respectively for the SC-VGG and VGG): in both cases, solid for SC-VGG, dashed for VGG. The FPR is plotted at the bottom of each panel (as a purple line for VGG, red for SC-VGG). In both panels, only sources with available and reliable magnitudes are plotted.
In the text
thumbnail Fig. 9.

FN dependences. TPs (green lines) and FNs (blue lines) distributions as a function of source redshift (zsrc, top panel), Einstein radius (θE, middle panel), and source intrinsic F814W magnitude (bottom panel) for the VGG (dashed lines) and SC-VGG (solid lines) models. The corresponding FN ratio is plotted at the bottom of each panel. In all panels, only sources with available and reliable magnitudes are plotted.
In the text
thumbnail Fig. 10.

Selection of FNs common to both the VGG and SC-VGG models. The probability of being a GGSL is shown in each thumbnail (estimated by the SC-VGG model). Cutouts are ∼4″ across.
In the text
thumbnail Fig. 11.

Purity (red) and completeness (orange) as a function of the GGSL probability threshold. Vertical lines correspond to the purity-completeness intersection at Pr = 0.25 (as a solid line) and to the classical threshold at Pr = 0.50 (as a dotted line). Purity and completeness values at Pr = 0.25 and Pr = 0.5 are indicated.
In the text
thumbnail Fig. 12.

Known GGSLs processed by both VGG and SC-VGG networks (see Table A.6). The GGSL probability is reported in each thumbnail (referred to the VGG and SC-VGG, respectively). Cutouts are 7.7″ across. The inner red squares enclose the area processed by the networks (∼4″). According to the classification probability, cutouts are surrounded by a box coloured in green (at least one probability is > 0.5), orange (at least one probability is ∈(0.2, 0.5]), or grey (otherwise).
In the text
thumbnail Fig. A.1.

FPR and FNR represented by 2D histograms. Top panels: FPRs on a galaxy colour–magnitude diagram (i.e. (F606W − F814W)norm vs F814W). Middle panels: FNRs on a lens θE vs source F814W magnitude diagram. Bottom panels: FNRs on a source re vs source redshift diagram. The VGG and the SC-VGG results are shown in the left and right panels, respectively. The regions of the parameter space with zero TN or zero TP values are left white.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.