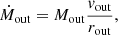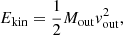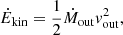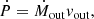| Issue |
A&A
Volume 675, July 2023
|
|
|---|---|---|
| Article Number | A58 | |
| Number of page(s) | 25 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202245408 | |
| Published online | 30 June 2023 | |
A radio-jet-driven outflow in the Seyfert 2 galaxy NGC 2110?
1
Centro de Astrobiología (CAB), CSIC-INTA, Camino Bajo del Castillo s/n, 28692 Villanueva de la Cañada, Madrid, Spain
e-mail: lperalta@cab.inta-csic.es; aalonso@cab.inta-csic.es
2
Observatorio de Madrid, OAN-IGN, Alfonso XII, 3, 28014 Madrid, Spain
3
Department of Physics, University of Oxford, Keble Road, Oxford, OX1 3RH
UK
4
Centro de Astrobiología (CAB), CSIC-INTA, Carretera de Ajalvir km 4, 28850 Torrejón de Ardoz, Madrid, Spain
5
Instituto de Astrofísica de Canarias (IAC), Calle Vía Láctea, s/n, 38205 La Laguna, Tenerife, Spain
6
Departamento de Astrofísica, Universidad de La Laguna, 38206 La Laguna, Tenerife, Spain
7
Max-Planck-Institut für Extraterrestrische Physik, Postfach 1312, 85741 Garching, Germany
8
School of Mathematics, Statistics and Physics, Newcastle University, Newcastle upon Tyne, NE1 7RU
UK
9
School of Physics & Astronomy, University of Southampton, Southampton, SO17 1BJ Hampshire, UK
10
Space Telescope Science Institute, 3700 San Martin Dr, Baltimore, MD, 21218
USA
11
The University of Texas at San Antonio, 1 UTSA Circle, San Antonio, TX, 78249
USA
12
National Astronomical Observatory of Japan, National Institutes of Natural Sciences (NINS), 2-21-1 Osawa, Mitaka, Tokyo, 181-8588
Japan
13
Instituto de Física Fundamental, CSIC, Calle Serrano 123, 28006 Madrid, Spain
14
Departamento de Física de la Tierra y Astrofísica, Fac. de CC Físicas, Universidad Complutense de Madrid, 28040 Madrid, Spain
15
Instituto de Física de Partículas y del Cosmos IPARCOS, Fac. CC Físicas, Universidad Complutense de Madrid, 28040 Madrid, Spain
16
Department of Physics & Astronomy, University of Alaska Anchorage, Anchorage, AK, 99508-4664
USA
17
Telespazio UK for the European Space Agency, ESAC, Camino Bajo del Castillo s/n, 28692 Villanueva de la Cañada, Spain
18
Núcleo de Astronomía de la Facultad de Ingeniería, Universidad Diego Portales, Av. Ejército Libertador 441, Santiago, Chile
19
Kavli Institute for Astronomy and Astrophysics, Peking University, Beijing, 100871
PR China
20
School of Sciences, European University Cyprus, Diogenes Street, Engomi, 1516 Nicosia, Cyprus
Received:
8
November
2022
Accepted:
8
May
2023
We present a spatially resolved study of the ionized gas in the central 2 kpc of the Seyfert 2 galaxy NGC 2110 and investigate the role of its moderate-luminosity radio jet (kinetic radio power of Pjet = 2.3 × 1043 erg s−1). We used new optical integral-field observations taken with the MEGARA spectrograph at the Gran Telescopio Canarias, which cover the 4300 − 5200 Å and 6100 − 7300 Å ranges with a spectral resolution of R ≃ 5000 − 5900. We fitted the emission lines with a maximum of two Gaussian components, except at the position of the active galactic nucleus (AGN), where we used three. Aided by existing stellar kinematics, we used the observed velocity and velocity dispersion (σ) of the emission lines to classify the different kinematic components. The disk component is characterized by lines with σ ≃ 60 − 200 km s−1. The outflow component has typical values of σ ≃ 700 km s−1 and is confined to the central 2.5″ ≃ 400 pc, which is coincident with the linear part of the radio jet detected in NGC 2110. At the AGN position, the [O III]λ5007 line shows high velocity components that reach at least 1000 km s−1. This and the high velocity dispersions indicate the presence of outflowing gas outside the galaxy plane. Spatially resolved diagnostic diagrams reveal mostly low ionization (nuclear) emitting region-like excitation in the outflow and some regions in the disk, which could be due to the presence of shocks. However, there is also Seyfert-like excitation beyond the bending of the radio jet, which probably traces the edge of the ionization cone that intercepts with the disk of the galaxy. NGC 2110 follows the observational trends between the outflow properties and the jet radio power found for a few nearby Seyfert galaxies. All these pieces of information suggest that part of the observed ionized outflow in NGC 2110 might be driven by the radio jet. However, the radio jet was bent at radial distances of ∼200 pc (in projection) from the AGN, and beyond there, most of the gas in the galaxy disk is rotating.
Key words: galaxies: active / galaxies: Seyfert / galaxies: ISM / ISM: jets and outflows / techniques: imaging spectroscopy
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Active galactic nuclei (AGNs) are crucial for understanding galaxy evolution. Active galactic nucleus feedback has been proposed as one mechanism to reproduce the observed number of the most massive galaxies, because in its absence star formation would have been too efficient (e.g., Silk & Mamon 2012). In particular, in moderate-luminosity AGN, the relationship between radiation-driven outflows and radio jets remains an open problem. From the theoretical point of view, it is expected that galaxies that host radio jets could drive outflowing material (e.g., Weinberger et al. 2017; Mukherjee et al. 2018; Talbot et al. 2022; Meenakshi et al. 2022). From the observational side, the capacity of high power radio jets to produce energetic outflows is well demonstrated (e.g., Nesvadba et al. 2008; Vayner et al. 2017).
The impact of low- to moderate-luminosity radio jets on the interstellar medium (ISM) of their host galaxies has mostly been studied in local Seyfert galaxies, low-luminosity AGN, and quasars. It has been shown that in the presence of a good geometrical coupling, these jets can successfully transfer mechanical energy to the ISM of their host galaxies (e.g., Combes et al. 2013; García-Burillo et al. 2014; Morganti et al. 2015; García-Bernete et al. 2021; Maccagni et al. 2021; Pereira-Santaella et al. 2022; Cazzoli et al. 2022; Speranza et al. 2022; Audibert et al. 2023). Using a small sample of Seyfert galaxies, Venturi et al. (2021) detected enhanced widths of optical lines in regions perpendicular to the radio jet, while Seyfert-like excited conical shapes were aligned with the radio jet. They interpreted this as the result of the interaction between the radio jet and outflowing material. In this context, they proposed scaling relationships between both the ionized gas mass and kinetic energy in the regions with an enhanced line width and radio jet power.
NGC 2110 is an early-type spiral galaxy (SAB0) that hosts a Seyfert 2 nucleus (McClintock et al. 1979), observed at an intermediate inclination i = 42 − 65° (see, e.g., Wilson & Baldwin 1985; González Delgado et al. 2002; Kawamuro et al. 2020, and Fig. 1). It contains a radio jet, whose “S” shape was proposed to be the result of its bending via the ram pressure of the host galaxy’s rotating gas (Ulvestad & Wilson 1983). The jet appears brighter on the north side, which allowed Pringle et al. (1999) to postulate that it is at an intermediate orientation with respect to the plane of the galaxy. The luminosity of this jet lies at the high end of the 20 cm radio luminosity distribution of the early-type Seyfert galaxies studied by Nagar et al. (1999).
 |
Fig. 1. HST/WFPC2 optical image of NGC 2110 obtained with the F791W filter, shown on a linear scale (gray colors and blue contours). The orange contours (also on a linear scale) are the VLA radio 6 cm emission from Ulvestad & Wilson (1983). We also mark with a red rectangle the approximate size of the GTC/MEGARA FoV of 12.5″ × 11.3″. The dashed and dotted lines are the PA of the galaxy major axis (PA ≃ 163° measured from the north to the east; see Ferruit et al. 2004) and the minor axis, respectively. The dashed-dotted line is the PA of the slit used by González Delgado et al. (2002) and discussed in Sect. 3.3. |
Several works have studied NGC 2110 in detail using optical integral field unit (IFU) spectroscopy (González Delgado et al. 2002; Ferruit et al. 2004; Schnorr-Müller et al. 2014) with spectral resolutions R = λ/Δλ ≃ 1000 − 2000. They all detected the presence of complex noncircular motions in the ionized gas, which were interpreted as being due to the presence of an outflow, inflow, and/or a minor merger. Moreover, Rosario et al. (2010) demonstrated that the radio jet has sufficient ram pressure to drive the emission-line outflow. Finally, using Atacama Large Millimeter Array (ALMA) CO(2−1) observations, Rosario et al. (2019) discovered a nuclear region with faint cold molecular gas emission (termed the “lacuna”), which is oriented in the approximate direction of the radio jet and filled with warm molecular hydrogen emission. These authors suggested that the radio jet and/or an AGN wind could be responsible for this phenomenon.
As part of the Galactic Activity, Torus, and Outflow Survey (GATOS), we obtained new optical IFU observations of several Seyfert galaxies, including NGC 2110, using the Multi-Espectrógrafo en GTC de Alta Resolución para Astronomía (MEGARA; Gil de Paz et al. 2016; Carrasco et al. 2018) at the 10.4-m Gran Telescopio Canarias (GTC) with R = 5000 − 5900. Our observations cover the ∼4300–5200 Å and ∼6100–7300 Å spectral ranges, which allowed us to spatially resolve both the gas kinematics and the excitation mechanisms in NGC 2110. By revisiting this well-studied target, we plan to use it as a benchmark for other forthcoming analyses of MEGARA observations within the GATOS survey.
This paper is structured as follows. Section 2 describes the data employed in this work. Section 3 explains the analysis, the classification of gas components, and the construction of the two-dimensional maps. We discuss the properties of the disk and outflow regions of NGC 2110 in Sects. 4 and 5, respectively. Finally, the summary and conclusions are presented in Sect. 6. We assume a systemic velocity of 2335 ± 20 km s−1, based on measurements of stellar absorptions from the magnesium b triplet at ∼5175 Å by Nelson & Whittle (1995). We adopt a Λ cold dark matter cosmology with H0 = 70 km s−1 Mpc−1, Ωm = 0.3, and ΩΛ = 0.7, which translates to a luminosity distance of DL = 33.6 Mpc and a physical scale of 160.2 pc/″.
2. Observations
2.1. Optical IFU data from MEGARA
We observed the central region of NGC 2110 (Program GTC27-19B, PI: Alonso Herrero) using the large compact bundle (LCB) of fibers of MEGARA (i.e., the IFU mode of this instrument). This IFU provides a field of view (FoV) of 12.5″ × 11.3″ (see Fig. 1), using 567 fibers of 0.62″ in diameter. The physical region covered for NGC 2110 by our MEGARA observations is 2.0 × 1.8 kpc2. We used two volume-phased holographic gratings. The low resolution B (LR-B) grating covers the spectral range ∼4300–5200 Å with R ∼ 5000. Hβ and the [O III]λλ4959, 5007 doublet are within this range for NGC 2110. The low resolution R (LR-R) grating covers the ∼6100–7300 Å range with R ∼ 5900, thus including [O I]λ6300, Hα, [N II]λλ6548, 6583, and [S II]λλ6716, 6731. The on-source integration times were ∼1 h (7 exposures of 520 s each) for LR-B and half hour (5 exposures of 360 s each) for LR-R.
The observations were taken in two consecutive observation blocks on the night of 9 February 2021. The observing conditions were a dark photometric sky and a seeing of 0.9″. The position angle (PA) of the observations was −0.598°, which is practically equivalent to the regular orientation north up, east to the left.
The data reduction was performed using the official MEGARA pipeline (Pascual et al. 2021). The data reduction process of this software includes bias subtraction, bad-pixels masking, tracing fibers, wavelength calibration (including versions corrected and uncorrected of barycentric velocity), flat-field correction, flux calibration, sky subtraction and cube construction. The flat-field images were taken with a continuum halogen lamp and close in time to the target exposures. This allows us to use them for tracing fibers without dealing with their known shifts that depend on the ambient temperature. Also, just before the target exposures, we obtained images illuminated with a thorium-argon hollow cathode lamp, which were used for the wavelength calibration. The spectrophotometric standard star HR 1544/HR 4554 was used for the flux calibration of the observations with the LR-B/LR-R grating. The final data cubes were produced with 0.3″ spaxels, which is the recommended size by the pipeline developers.
We note that NGC 2110 was also observed as part of the Siding Spring Southern Seyfert Spectroscopic Snapshot Survey (S7; Thomas et al. 2017), using the WiFeS instrument on the Australian National University (ANU) 2.3 m telescope. Although their FoV is larger (25″ × 38″) than that provided by MEGARA, our data have higher spatial resolution due to both the smaller MEGARA fiber diameter (0.62″) versus the S7 spaxel (1″ × 1″) and better seeing conditions (MEGARA 0.9″ versus S7 1.4″). In addition, our MEGARA observations have higher spectral resolution in the blue range (5000 versus 3000 for the S7 survey).
As the absolute flux calibration has a direct impact on the outflow properties (Sect. 5.4), we compare our calibration with those provided by other authors. Davies et al. (2020) presented Very Large Telescope (VLT) X-shooter observations of NGC 2110 and measured observed fluxes (not corrected for extinction) of 7.85 ± 0.10 × 10−15 erg s−1 cm−2 and 41.1 ± 0.5 × 10−15 erg s−1 cm−2 for the Hβ and Hα lines for an aperture of 1.8″ × 1.8″ under seeing conditions ranging between 0.50″ and 0.58″. We reproduced their aperture on our GTC/MEGARA data and we obtained 25.6 × 10−15 erg s−1 cm−2 and 101.8 × 10−15 erg s−1 cm−2, respectively. Thomas et al. (2017), as part of the S7 survey, reported a dereddened flux of 384.8 × 10−15 erg s−1 cm−2 for the Hβ line for a circular 4″ diameter aperture and a seeing of 1.4″. Undoing the dereddening in the same way as these authors (i.e., a Fitzpatrick 1999 reddening law with RV = 3.1 and AV = 2.39 mag) leads to a non-dereddened flux of 29.5 × 10−15 erg s−1 cm−2. We extracted a spectrum with the same aperture from our IFU data and we obtained a flux of 45.1 × 10−15 erg s−1 cm−2.
It is worth mentioning that both works subtracted the stellar continuum from their spectra before measuring the line fluxes. Consequently, we also subtracted the stellar continuum around Hβ line for the above estimates (see Sect. 3), while that correction was assumed negligible for Hα. However, we noticed that the selection of stellar continuum template contributes significantly to these differences. For instance, the above value for the comparison with Thomas et al. (2017) was obtained using the stellar fit by Burtscher et al. (2021), while using the one from Davies et al. (2020) leads to a non-dereddened Hβ flux of 38.1 × 10−15 erg s−1 cm−2, and when the stellar continuum is not subtracted, we found 37.7 × 10−15 erg s−1 cm−2 (see Sect. 3 for more details about stellar continuum templates). In summary, our absolute flux calibration is 2.5 and 3.3 times higher than the estimates by Davies et al. (2020) for the Hβ and Hα lines, respectively. However, it is only 20–50 per cent higher for Hβ than that of the larger apertures used by Thomas et al. (2017). Part of the differences with Davies et al. (2020) might be attributed to centering differences.
Additionally, we checked that our relative flux calibration within each of the GTC/MEGARA gratings provides similar line ratios to those in Davies et al. (2020). We measured [O III]λ5007/Hβ = 4.96 and [N II]λ6583/Hα = 1.62 using the same aperture as these authors, while they reported a value of 4.76 and 1.37 for these same ratios. In what follows, we use our own flux calibration throughout this work and take into account the uncertainty in the absolute calibration when needed.
2.2. Ancillary radio observations
In order to interpret our MEGARA observations and their potential relationship with the radio jet of NGC 2110, we downloaded from NASA/IPAC Extragalactic Database (NED)1 a radio map observed at 6 cm (4885 MHz) by Ulvestad & Wilson (1983, 1984, 1989). These observations were taken on 15 March 1982, using the A configuration of the Very Large Array (VLA) at the National Radio Astronomy Observatory. The observations consisted of two exposures of 12 min each. Calibration and self-calibration of the data followed the standard procedures (e.g., Wilson & Ulvestad 1982). The radio map has a half-power beam width of 0.44″ × 0.35″ at a PA = −1°.
Ulvestad & Wilson (1983) found that the optical nucleus (observed by Clements 1983) and the central radio component were coincident. We retrieved an optical image of NGC 2110 from ESASky (Baines et al. 2017; Giordano et al. 2018). The observations were taken with the Hubble Space Telescope (HST) WFPC2 instrument using the F791W filter. We adjusted the HST astrometry using the Gaia information from stars in the field and found that the positions of the nuclear radio and optical peaks agreed with each other, as can be seen from Fig. 1. This fact allowed us to assume that both the MEGARA continuum peak and the VLA peak mark the position of the AGN.
3. Analysis of the MEGARA observations
3.1. Emission line fitting
For the analysis of the emission lines of the MEGARA IFU data of NGC 2110, we developed a new Python tool named ALUCINE2. This Spanish acronym stands for Ajuste de Líneas para Unidades de Campo Integral de Nebulosas en Emisión, or IFU line fitting for emission-line nebulae. This is a general purpose tool designed to fit emission lines in integral-field data, using a user-specified number of components. At each spaxel, the fit of the line (or lines) is performed automatically and independently. We already used this tool with IFU observations obtained with the Mid-InfraRed Instrument (MIRI) instrument on the James Webb Space Telescope (see García-Bernete et al. 2022).
Before we fitted the emission lines of the MEGARA observations, we subtracted the stellar continuum around the Hβ region (i.e., within the wavelength range stated for that line in Table 1) from the LR-B cube on a spaxel-by-spaxel basis. This is especially important for the Hβ emission line fluxes since they are affected by stellar absorption, while it was assumed negligible for the other emission lines. We tried three different approaches, namely, subtracting the stellar templates provided by Burtscher et al. (2021) and Davies et al. (2020), and not subtracting any template. In particular, when subtracting a stellar template we scaled it to match the continuum level measured in the Hβ continuum region (defined in Table 1) for each spaxel. For the figures included in this work and all the subsequent analysis, we made the correction with the template provided by Burtscher et al. (2021). However, it is worth mentioning that we checked that results of this work are not affected if we used the template from Davies et al. (2020) or even if we did not subtract the stellar continuum. For the LR-R data cube, we did not subtract a stellar template. However, the impact of this correction on the Hα fluxes and [N II]/Hα line ratios is reduced when compared with Hβ and line ratios involving this line because Hα is brighter. Moreover, Bellocchi et al. (2019) demonstrated that the effects of the stellar template on the gas Hα kinematics were not critical.
Parameters employed for the construction of cubelets and their line fits.
In what follows, we describe the steps followed to perform the line fitting of our MEGARA observations. We first spatially smoothed the cubes. Specifically, we assigned to each spaxel the mean value in a square box of 3 spaxels (0.9″ × 0.9″) around it. We chose this size for the box because it corresponds to the seeing value of the observations. Second, we built cubelets from the MEGARA cubes, that is to say, we created smaller cubes by cutting spectral slices of the cubes covering the emission lines to be analyzed. The resulting five cubes and their wavelength ranges are listed in Table 1. We then estimated the noise in each spaxel of each cubelet using regions where the continuum level is flat. These continuum regions are detailed in Table 1. Finally, given the good quality of the GTC/MEGARA observations, we fitted independently the emission line(s) at each spaxel of each cubelet. Thus, the method does not assume that all the emission lines share the same kinematics. We allowed for a maximum of two Gaussian components.
In ALUCINE, the number of components to fit the emission lines at each spaxel is decided as follows. We started with zero components by default. If we detected a line above a specified threshold on amplitude over noise (AoN; see below), we tried to fit it and we trusted the resulting fit if it had a specified value of the minimum amplitude (Amin). In the case of having added one component, we iterated the criteria starting from the residual derived from the previous fit. The values of AoN and Amin were tuned for each cubelet, seeking a compromise between maximizing the signal and minimizing the noise in the resulting maps. The final values of these two parameters for each cubelet are listed in Table 1. We should highlight that, if AoN values in this table were set to a value of 3.0, only a few spaxels would be affected by this change. This is because the cuts introduced by the Amin values do in practice also mean that spaxels with low AoN are not fitted. The fitting model (e.g., the number of Gaussians or other line profiles) depends on the cubelet and the nature of each emission line.
In particular for the MEGARA data sets, we used a baseline for adjusting the continuum level plus the following models. For Hβ, each component for this singlet is one Gaussian with three free parameters, namely, amplitude, central wavelength, and line width. Each component of the [O III]λλ4959, 5007, doublet is a set of two Gaussians sharing the same kinematics and with a fixed ratio between amplitudes of A[O III] λ4959 = 0.350 A[O III] λ5007. Although [O I]λ6300 is a doublet with the line at 6364 Å, they are well separated in our GTC/MEGARA spectra. Moreover, the latter line is not close to any other line of interest in this work. We therefore decided to fit only the [O I]λ6300 line. For Hα + [N II]λλ6548, 6583 we use a set of three Gaussians. Two share the same kinematics and have an amplitude ratio of A[N II] λ6548 = 0.340 A[N II] λ6583 in order to fit the [N II]λλ6548, 6583 doublet. The third Gaussian fits the Hα line with its own three free parameters. The amplitude of the Hα line is that employed to evaluate if it passes the threshold value Amin explained above. Each component of the [S II]λλ6716, 6731 doublet is a set of two Gaussians sharing the same kinematics and the ratio between amplitudes of them is a free parameter.
When fitting the lines with a particular model, we imposed a constraint that the fitted lines had widths equal to or higher than the instrumental resolution of our data, that is, 0.78 Å at full width at half maximum (FWHM) for the LR-B grating and 1.0–1.1 Å for the LR-R grating. As ALUCINE also allows the user to apply limits to the velocities and line widths, we used this feature to a fix spurious fits of the lines in a few spaxels. This did not affect the results when compared to those provided with the fits without this fine tuning.
We decided to use a maximum of two Gaussian components because they provided good quality fits to the emission lines in most of the spaxels of our MEGARA observations. In the nuclear region of NGC 2110, we nevertheless find that a three-Gaussian-component fit gives a significantly better performance. In Fig. 2, we show this fit for a spectrum extracted with a 0.9″ × 0.9″ aperture and the [O III]λλ4959, 5007 doublet. The fits for the rest of the emission lines can be seen in Appendix A. Table 2 lists the fluxes, velocities, and velocity dispersions for each of the three components for all the emission lines.
 |
Fig. 2. GTC/MEGARA nuclear spectrum of NGC 2110 in the spectral region around the [O III]λλ4959, 5007 doublet. The orange line is the observed spectrum after the subtraction of the continuum and extracted with a 0.9″ × 0.9″ aperture. The fit (dashed black line) is the sum of three Gaussian components. The dotted blue lines show each component of the fit, with lines of increasing thickness for the components with increasing velocity dispersions. The green lines are the line wavelengths. |
Measurements from the nuclear spectrum using a model with three Gaussian components.
3.2. Distributions of the fitted velocity dispersions
As explained in Sect. 3.1, we fitted the optical emission lines with one or two components on a spaxel-by-spaxel basis. We termed them narrow and broad (see below) when two Gaussian components were fitted, and narrow if one Gaussian component provided a good fit. Figures 3 and B.1 show the distribution of the velocity dispersions, corrected for instrumental resolution, for Hβ and [O III]λλ4959, 5007, and [O I]λ6300, Hα, [N II]λλ6548, 6583, and [S II]λλ6716, 6731, respectively.
 |
Fig. 3. Observed distribution of the velocity dispersions (corrected for the instrumental resolution) fitted on a spaxel-by-spaxel basis and using a maximum of two Gaussian components from lines observed with the GTC/MEGARA LR-B grating, i.e., Hβ and [O III]λλ4959, 5007 lines. Blue and orange lines correspond to the narrow and broad components, respectively (see text). |
The velocity dispersion distributions for the narrow component are narrow and clearly unimodal, peaking at 50–100 km s−1. These values are similar to the values derived from VLT/MUSE observations for other Seyfert 2 galaxies, like NGC 5643 (García-Bernete et al. 2021) and NGC 7130 (Comerón et al. 2021). Regarding the broad component, most of the distributions tend to be bimodal, with one peak with velocity dispersions at 100 − 150 km s−1, thus broader than the narrow component. The second peak of the broad component is at σ∼200–350 km s−1, followed by a tail toward high velocity dispersions. The latter reaches values of up to ∼500–700 km s−1, mostly in [O III]λλ4959, 5007 and [N II]λλ6548, 6583. The distributions of the fitted velocity dispersions in the MEGARA LR-R data cube are similar to those of Schnorr-Müller et al. (2014).
3.3. Comparison with the stellar kinematics
To classify the different ionized gas components according to their kinematics, in this section we compare the gas velocities with those measured from stellar absorption features. Figure 4 shows the velocities of the two components fitted for the [O III]λ5007 line versus the stellar kinematics along three different slit PAs. The top and middle panels are the stellar kinematics along the galaxy major (PA = 163°) and minor (PA = 73°) axes from Ferruit et al. (2004), while the bottom panel is along PA = 6° from González Delgado et al. (2002). For reference, we show the orientation of these slits in Fig. 1.
 |
Fig. 4. Comparison between the velocities of the ionized gas derived from fits using a maximum of two Gaussian components for the [O III]λλ4959, 5007 doublet and the stellar velocities. From top to bottom, the stellar velocities are along the major and minor axes of the galaxy from Ferruit et al. (2004) and along PA = 6° from González Delgado et al. (2002). Circles represent the narrow component or that when only one Gaussian is required to fit the line, while triangles correspond to the broad component. Stars show stellar velocities. The color and size of the circles and triangles depend on the velocity dispersion of each component. Black and red edges have been added to the circles and triangles, respectively, for velocity dispersions below and above 60/200 km s−1 in order to illustrate the component classification explained in Sect. 3.1. The horizontal dashed line shows the systemic velocity and the horizontal gray region its error. |
Figure 4 already reveals the difficulty in classifying the different ionized gas kinematic components in NGC 2110. Along the NGC 2110 major axis, our MEGARA observations detected two components out to a radial distance of approximately 4″ to the southeast and 6″ to the northwest. Along the minor axis, the two components are seen in the inner ∼4″. In this central region and along the minor axis, the [O III] narrow component follows relatively well the stellar kinematics (middle panel of Fig. 4). When comparing with the stellar kinematics of González Delgado et al. (2002) along PA = 6°, the ionized gas component with the intermediate velocity dispersions agrees well with the stars (bottom panel of Fig. 4).
Along the major axis of the galaxy to the northwest and in the central ∼2″, the velocities of the gas narrow component are comparable to those of the stars, while beyond 2″ they are redshifted. To the southeast the gas velocities are redshifted with respect to those of the stars (top panel of Fig. 4). This is similar to the findings of Ferruit et al. (2004). The broad component with σ ≃ 250 − 670 km s−1 in the inner 4″ is likely tracing an outflow, which we analyze in more detail in Sect. 5. In the outer regions to the northwest and along the galaxy major axis, the component with intermediate values of velocity dispersion traces well the stellar kinematics. The narrowest gas component (circles in the figure) to the southeast at radial distances > 2″ deviates the most from the stellar velocities, with gas velocities faster than the stellar ones.
A plausible scenario accounting for a slower rotation of the stars relative to the gas in some parts of the galaxy would invoke a rotation lag in thick stellar disks or a comparatively larger contribution of the velocity dispersion in the stellar component. However, the behavior is the opposite in the northwest side. Here, the reported asymmetry of the gas kinematics in NGC 2110 could be explained by an uneven impact left by the radio jet on the gas motions, which probably slowed down the gas with the lowest observed velocity dispersions on the northern side of the disk. The secondary peak of the ALMA millimeter emission (see panel c of Fig. 1 of Rosario et al. 2019) identifies the region where the jet was probably diverted. We discuss the impact of the radio jet in more detail in Sect. 5.5.
Based on this comparison, where we identify the rotating gas with the intermediate velocity dispersion component, we define the following components for the ionized gas.
Disk component. At a particular spaxel, if only one component was required to fit the emission line, this is identified with the disk. If there are two components, we apply the following criteria for assigning the component whose kinematics is closer to the stellar one: (i) If both are below σ = 200 km s−1 (for the [O III] doublet), the broader component is assigned to the disk, (ii) If one of them is above 200 km s−1 (for the [O III] doublet), the narrow component is assigned to the disk. It is worth mentioning that we detected no spaxels in which both components were broader than 200 km s−1, nor in any of the one-component spaxels did the velocity dispersion exceed 200 km s−1. The typical values for the velocity dispersion of the disk component are 60 − 200 km s−1.
Outflow component. This component includes those spaxels where one of the components of the [O III] doublet was fitted with a velocity dispersion above ≃200 km s−1. Most of these spaxels lie in the central 4″.
Noncircular component. If at a particular spaxel the line requires two components, the component that is not assigned to the disk is termed noncircular. We found that these components lie outside the outflow region and generally include spaxels whose lines were fitted with low values of the velocity dispersion (< 60 km s−1).
This component classification differs from that proposed by Schnorr-Müller et al. (2014) for NGC 2110. Although for each spaxel they also fitted the emission lines in the red part of the spectrum with two components, they classified them into four categories only according to increasing velocity dispersion values, namely, outflow, warm gas disk, cold gas disk, and a north cloud. With this approach, they sought to interpret the asymmetry in the velocity field and proposed two incomplete rotating disk components (see their Figs. 5 and 6). Our kinematic classification has only one disk component, which includes a large fraction of the spaxels in their cold and warm disk components. On the other hand, we agreed with their velocity dispersion classification for the outflow component. We nevertheless find that, for the goals pursued by this work, it is sufficient to perform a classification that allows us to separate the outflow component from that of the disk and other noncircular components.
3.4. Two-dimensional maps
With the kinematics classification adopted in the previous section, we created maps of the line intensity, velocity, and velocity dispersion for the disk component and the outflow+noncircular component. For the latter, the outflow component is confined to the central 4″ and thus is easily distinguished from the other noncircular motions by inspecting the velocity dispersion map. In Figs. 5–7, we show the MEGARA LR-B grating maps for the intensity, velocity, and velocity dispersion, respectively, for Hβ and [O III]. These maps capture the most remarkable aspects of both gratings. The LR-R grating maps can be found in Appendix B.
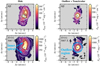 |
Fig. 5. Flux maps of the disk (left) and the outflow+noncircular (right) components for the lines observed with the GTC/MEGARA LR-B grating, i.e., the Hβ and [O III]λ5007 lines. All the color bars use a square root scale and are saturated at the half maximum value of each map. Contour levels correspond to 30, 60, 70, 80, and 90 per cent of the maximum value of each map. Crosses indicate the location of the nucleus (as defined by the peak of the continuum). The northeast compass, the hatched circle indicating the seeing size, and physical size bar on the bottom-right map apply to all the maps. |
 |
Fig. 6. Velocity maps of the disk (left) and the outflow+noncircular (right) components for the lines observed with the GTC/MEGARA LR-B grating, i.e., the Hβ and [O III]λλ4959, 5007 lines. Values are referred to the systemic velocity. The lines indicate the orientation of the slit PA in Fig. 4 (see text for details). Other symbols are the same as in Fig. 5. |
 |
Fig. 7. Velocity dispersion maps of the disk (left) and the outflow+noncircular (right) components for the lines observed with the GTC/MEGARA LR-B grating, i.e., the Hβ and [O III]λλ4959, 5007 lines. Contours show the VLA radio jet (Sect. 2.2). Symbols are the same as in Fig. 5. |
Diagnostic diagrams based on optical line ratios, also known as Baldwin, Phillips, Terlevich (BPT) diagnostic diagrams, are tools for identifying the dominant gas excitation mechanism in galaxies. Initially proposed by Baldwin et al. (1981) and Veilleux & Osterbrock (1987), they use a comparison of the [O III]/Hβ ratio versus the [S II]/Hα, [O I]/Hα and [N II]/Hα ratios. These diagrams can be used to distinguish between mechanisms such as photoionization by young stars in star-forming regions, photoionization from an AGN, or low ionization (nuclear) emission regions (LI(N)ERs). The last type is associated with the presence of shocks, as well as ionization by hot, low-mass evolved stars (see also Sect. 4). BPT diagrams derived from IFU spectroscopy are routinely applied to local AGN (e.g., Bremer et al. 2013; Davies et al. 2016; Husemann et al. 2019; Mingozzi et al. 2019; D’Agostino et al. 2019; Smirnova-Pinchukova et al. 2019, 2022; Shimizu et al. 2019; Perna et al. 2020; Venturi et al. 2021; Comerón et al. 2021; Juneau et al. 2022; Cazzoli et al. 2022). Figures 8 and 9 display the [O III]/Hβ versus [N II]/Hα, [S II]/Hα, and [O I]/Hα diagnostic diagrams, and their associated spatially resolved maps, for the disk and outflow+noncircular components, respectively.
 |
Fig. 8. Spatially resolved BPT diagnostic diagrams (left panels) and maps (right panels) for the disk component. The top, middle, and bottom diagrams of the left panels correspond to [O III]λ5007/Hβ versus [N II]λ6583/Hα, ([S II]λ6716 + λ6731)/Hα, and [O I]λ6300/Hα, respectively. The points in the red color scale are spaxels in the AGN or Seyfert region, those in the blue color scale are spaxels in the star-forming region, and those in the green color scale in the composite-like or LI(N)ER region. Solid curves are theoretical upper limits of starburst models from Kewley et al. (2001). The dashed curve in the [N II] diagram is the demarcation between starburst galaxies and AGN proposed by Kauffmann et al. (2003). Dashed lines in the [S II] and [O I] diagrams are classification lines proposed by Kewley et al. (2006) to split Seyfert and LI(N)ER emission. Dotted lines in the diagnostic diagrams mark bisector lines between the loci of points for the shock-excited NGC 1482 and the AGN-excited NGC 1365 (Sharp & Bland-Hawthorn 2010). For reference, the error bars represent the measurement uncertainties in a spaxel outside the outflow region, at ≃2.4″ north of the AGN. The right panels are diagnostic maps color coded in the same way as their corresponding diagrams to the left. Contours in the maps show the radio jet using the VLA data described in Sect. 2.2. |
 |
Fig. 9. Spatially resolved BPT diagnostic diagrams (left) and maps (right) for the outflow+noncircular component. All symbols, colors, and lines are the same as in Fig. 8. |
Finally, we computed electron density maps using the fluxes from the [S II] λλ6716, 6731 doublet. In particular, we used the method Atom.getTemDen of PYNEB (Luridiana et al. 2015), and assumed a typical electron temperature of 104 K. This method computes densities in the range 20–5.7 × 104 cm−3 for [S II]λ6731/[S II]λ6716 ratios between 0.7 and 2.2. We assigned the minimum and maximum densities to those ratios that are below and above the mentioned interval, respectively. However, the upper value is only reached at one spaxel within the central region and at a spurious location of the noncircular component. The resulting electron density maps are in Fig. 10. For comparison, we also estimated the electron densities using the ionization parameter (U) method proposed by Baron & Netzer (2019). This method only applies to gas excited by a central source (like an AGN). Given the likely mix of shock and AGN ionization in some regions of NGC 2110 (see below), the interpretation of the electron density maps using the U method are not straightforward. The maps are shown Fig. C.1.
 |
Fig. 10. Maps of electron densities for the disk (left) and the outflow+noncircular (right) components using the [S II] doublet ratio method. Values in top-left corners indicate the median density in each map. |
4. The disk component
The maps of the emission line fluxes for the disk component are the left panels of Figs. 5 and B.2 for Hβ and [O III]λ5007, and [O I]λ6300, Hα, [N II]λ6583, [S II]λ6716, and [S II]λ6731, respectively. We detected the disk component filling approximately the full MEGARA FoV along the major axis of the galaxy and approximately 8″ along the minor axis of the galaxy. The ionized gas morphology of the disk component is dominated by the nucleus, with the extended emission tracing the disk orientation and some of the spiral morphology (marked in the bottom-left panel of Fig. 5), seen in the HST image in Fig. 1 and especially in the optical color maps (see, for instance, Fig. 1 of Schnorr-Müller et al. 2014).
Figures 6 and B.3 (left panels) are the velocity maps of the disk component. They all show a similar structure, namely a rotation pattern in which the north half approaches the observer and the south half recedes from the observer. The absolute values of velocities in the north half are lower than those in the south half. Our results for this component are in line with the observations by Wilson & Baldwin (1985), González Delgado et al. (2002), Ferruit et al. (2004), and Rosario et al. (2010). A few spaxels close to the nucleus have high negative velocities in the maps from the [N II]λλ6548, 6583, and [S II]λλ6716, 6731 doublets, and correspond to spurious fits of our automatic algorithm. We also observe some discontinuities in the velocity and velocity dispersion maps, especially in transition regions between lines fitted with two components and only one component. It is possible that in some spaxels, in particular in the central and transition regions, the lines present other additional velocity components that cannot be resolved with the current spectral resolution.
Figures 8 and 9 present, for the first time, the spatially resolved BPT diagrams of the central part of the disk and outflow region of NGC 2110. All the spaxels of the disk component fall in the AGN zone in the [N II] diagnostic diagram (Fig. 8, top-left panel). There appears to be a gradient of increasing excitation to the north of the AGN location, which might also be caused by an uneven impact of the radio jet, as discussed in Sect. 3.3. LI(N)ER emission predominates in the diagnostic diagrams from [S II] and [O I] (Fig. 8, middle and bottom-left panels, respectively). However, in these two last maps, there are some regions with Seyfert-like excitation, that is, gas photoionized by the AGN. These are near the AGN position as well as beyond the bending of the radio jet, both to the north and south of the AGN, at projected distances reaching at least 5″ ≃ 800 pc. These regions appear to be coincident with the inner spiral arms marked in Fig. 5 (bottom-right panel). They are likely tracing gas in the disk that is being illuminated by the AGN, as has been found in other Seyfert galaxies in the MAGNUM sample (Mingozzi et al. 2019). In fact, this morphology could be understood in the context of the geometry proposed by Rosario et al. (2010) in their Fig. 7. The Seyfert-like excitation regions could plausibly arise by the intersection of a wider-angle ionization cone with the galaxy disk. This could also explain the relatively low ionization of the entire observable ionization cone, as we are only seeing the part that is on the edge of the cone due to the geometry of illumination. This region is likely to correspond to the continuation of the AGN-photoionized plume identified by Rosario et al. (2010).
Since NGC 2110 is an early-type spiral galaxy, LI(N)ER-like line ratios may not necessarily be interpreted as evidence for shocks. To rule out a dominant contribution from ionization by evolved stars, we constructed diagrams comparing the equivalent width of Hα (WHα) with the [N II]/Hα line ratio, also known as WHAN diagrams (Cid Fernandes et al. 2010, 2011) for both the disk and outflow components. As can be seen from Fig. 11, the majority of spaxels of the disk and outflow component lie outside the region occupied by retired and passive galaxies. According to these authors, the gas excitation galaxies with very weak line emission is believed to be due to evolved stars. We can rule out that in the central disk and outflow regions of NGC 2110, the LI(N)ER-like emission is dominated by excitation from evolved stars. Therefore, considering the results from the WHAN diagrams and the seeing conditions, we can conclude that there is LI(N)ER-like excitation in galaxy regions well beyond what could be expected from beam smearing.
 |
Fig. 11. WHAN diagrams (left panels) for the disk component (top) and for the outflow and noncircular motion components (bottom) and the corresponding spatial distribution of the WHAN regions (right panels). See Cid Fernandes et al. (2011) for details regarding the different region definitions: star-forming galaxies (SF), strong AGN (sAGN), weak AGN (wAGN), and retired galaxies (RG). |
5. The outflow component
5.1. Morphology and excitation conditions
The intensity of the outflow component of the ionized gas peaks at the AGN position (central region in the right panels of Figs. 5 and B.2), and can be easily distinguished from the other noncircular motions by the velocity and velocity dispersion maps (right panels of Figs. 6, B.3, 7, and B.4). Nevertheless, we marked the outflow region in the bottom-right panel of Fig. 5. The outflow emission is oriented along the northwest-southeast direction at a PA that is similar to that of −35° observed in the X-ray Fe-Kα line by Kawamuro et al. (2020). The outflow region is clearly resolved along the north-south direction, with a projected size (FWHM) of 1.34″ ≃ 214 pc at the [O III] wavelength compared with the measured FWHM of 0.93″ from the calibration star at the same wavelength and direction. We obtained these measurements from the data cubes before we spatially smoothed them (see Sect. 3.1). Assuming a simple broadening in quadrature, the intrinsic size would be approximately 1″ ≃ 160 pc (FWHM). It is just resolved in the east-west direction with a FWHM = 1.2″, compared with the standard star size of FWHM = 0.96″ along this direction.
The VLA radio emission (Ulvestad & Wilson 1983) of NGC 2110 shows a collimated linear structure in an almost north-south direction in the inner 2″. This is in agreement with the size of the outflow region. Beyond this, the radio jet bends to the northeast and southwest direction in an inverted S-shaped morphology, which coincides with the noticeable drop observed in the MEGARA velocity dispersion maps. Within the central ∼2″, the broad component flux maps (see also Ferruit et al. 2004) resolve the “outer plume” (see the middle right panel of Fig. B.2) detected by Rosario et al. (2010) in the HST narrow-band Hβ+[O III] and Hα+[N II] images, as well as some fainter spiral morphology seen on larger scales. The “inner plume” identified by Rosario et al. (2010), extends only approximately 0.4″ from the nucleus, and is not resolved in our MEGARA observations.
The outflow component shows AGN excitation in the [N II] diagnostic diagram (top-right panel of Fig. 9) and a LI(N)ER excitation in the other two diagrams (middle and bottom-right panels of Fig. 9), as found in other AGN (see, e.g., Perna et al. 2017). The outflow component of NGC 2110 is relatively compact and does not reveal a clear conical shape illuminated by the central AGN. This contrasts with the results for the Seyfert galaxies in the MAGNUM survey (Cresci et al. 2015; Mingozzi et al. 2019) and other works (see, e.g., Juneau et al. 2022), in which ionization cones with AGN photoionized emission, with their edges showing lower ionization, are frequently revealed in their diagnostic diagrams.
As shown above, a large fraction of the spaxels in the disk and outflow component of NGC 2110 have line ratios in the LI(N)ER region in two BPT diagrams, where the gas excitation can be explained by shocks (see Perna et al. 2017; Mingozzi et al. 2019; Cazzoli et al. 2022, and references therein) but also by X-ray radiation from the AGN and evolved stars. However, Fig. 11 (right panels) shows that most spaxels are outside the region occupied by retired and passive galaxies where the LI(N)ER excitation is produced by evolved stars. Comparing with Fig. 8 of Mingozzi et al. (2019), it would be possible to reproduce the observed line ratios for the outflow component and some regions in the disk with shock models. Such shocks might be driven by the radio jet impacting the ISM in the galaxy disk. Indeed, recent simulations show that low-power radio jets, such as those observed in Seyfert galaxies, can drive ∼ kpc-scale outflows, which can affect the inner galaxy disk (Mukherjee et al. 2018; Talbot et al. 2022; Meenakshi et al. 2022). The effects are especially noticeable when jets are launched at low inclinations with respect to the disk of the galaxy. Finally, we have only been able to measure all the line ratios of the noncircular component in a small number of spaxels. The north part appears to be located in the AGN area of the [N II] diagram and the LI(N)ER region in the [S II] and [O I] diagrams. The south part, at an approximate radial distance from the AGN of ∼4″, appears in the composite regime and the star-forming area in the BPT diagrams.
5.2. Kinematics
The velocity fields of the outflow component (central region in the right panels of Figs. 6 and B.3) present moderate values of the peak velocity relative to the systemic value, typically in the ∼50 − 100 km s−1 range. The typical values of the velocity dispersion in the outflow region are 700 km s−1. The [O III]λλ4959, 5007, Hα and [N II]λλ6548, 6583 maps show a linear structure almost 4″ in size, with high blueshifts from the northeast to the southwest through the nucleus, reaching velocities of ∼300 km s−1. This region is coincident with a high-σ strip seen in some of the outflow component velocity dispersion maps (Figs. 7 and B.4) and is also seen in the disk component. It has already been reported by González Delgado et al. (2002) and Schnorr-Müller et al. (2014). This high-σ strip is close to the minor axis of the galaxy, so it is possible that smearing of the rotation curve and other noncircular velocities could partly explain it.
The MEGARA [O III]λ5007 position-velocity (p-v) diagrams along the major and minor axis of the galaxy (Fig. 12) are useful to identify the velocities of the outflow. We constructed these diagrams from the LR-B data cube after continuum subtraction and using an aperture of 0.9″. The diagram for the major axis can be compared with that presented by Rosario et al. (2010) for their HST slit-A spectroscopy (cf. their Fig. 3). We note that the PA of their slit is not exactly along the major axis of the galaxy, but it is close enough for this comparison. As can be seen from left panel of Fig. 12, the MEGARA p-v diagram reproduces the HST observations well considering our ∼0.9″ seeing conditions. This p-v diagram also reveals the asymmetric rotation curve discussed in Sect. 3.3. To the southeast of the AGN, at distances of ≃2.5″, it clearly shows the two velocity components fitted in Fig. 4. The outflow can be seen as much higher velocities in the central ≃2″, both blueshifted to velocities in excess of −1000 km s−1 and redshifted to velocities of several hundreds of km s−1. The largest values of the blueshifted velocities are mostly concentrated in the nuclear region while some more moderate redshifted and blueshifted velocities are observed along the major axis to the northwest of the AGN.
 |
Fig. 12. GTC/MEGARA p-v diagrams extracted for the [O III]λ5007 line after continuum subtraction, along the major (PA = 163°, left panel) and minor (PA = 73°, right panel) axes of NGC 2110. The first contour is plotted at three times the noise at approximately 1350 km s−1. The second contour is at five times the noise, reaching velocities of −650/500 km s−1, and the rest of the contours are on a linear scale. |
Along the galaxy minor axis, the MEGARA p-v diagram shows a broad range of velocities, both redshifted and blueshifted velocities, at the nuclear position, with the blueshifted velocities reaching maximum outflow velocities in excess of ≃ − 1000 km s−1 at the AGN position. We note that in the blue part of the spectrum in the p-v diagrams the two [O III] lines start mixing as they are about 2870 km s−1 apart. Nevertheless, the observed high velocities are beyond the range of velocities attributable to any possible effect of smearing of rotation curve at the AGN position ( ≃ 400 km s−1). The large blueshifts observed along both axes can be associated with the broadest of the three components fitted for the nuclear spectrum (see Table 2 and Fig. 2), with σ = 662 km s−1. Finally, there is [O III] emission in the two quadrants forbidden by disk rotation along the major axis p-v diagram. They show velocities of a few hundred km s−1, seen as redshifted motions to the northwest and blueshifted motions to the southeast. If we assumed these motions are in the plane of the galaxy, they would imply counter-rotation. However, given the velocities and velocity dispersions fitted in the outflow region, it is more reasonable to assume that they trace outflowing gas outside the plane of the galaxy in NGC 2110.
5.3. Electron densities
Figure 10 shows the electron density maps for each of the two kinematic components using the [S II] method. The outflow region presents a median value of ne ∼ 600 cm−3, which is considerably higher than the values of the noncircular motions and the disk. The latter has a median value of ∼175 cm−3. Analogous to our work, Kakkad et al. (2018) studied the spatial distribution of electron density for the outflow component of NGC 2110 (their Fig. 9). Although the comparison is not straightforward, mainly due to their poorer seeing conditions, they found the same tendency of higher values within the outflow region and smaller values for higher distances of this component.
Davies et al. (2020) estimated the electron density for an aperture of 1.8″ × 1.8″ around the nucleus with three different methods without splitting the flux in different kinematic components. In particular, they found a value of 350 cm−3 from the [S II] doublet. This is in the middle of our estimations for the two components, indicating a good agreement with those authors. We note, however, that with the ionization parameter method they derived values of the electron density of up to 43 000 cm−3, in agreement with our estimates using the same method (see the electron density maps in Fig. C.1).
5.4. Outflow properties
In this section we compute the outflow properties using the [O III] line, as in Davies et al. (2020), to allow for a comparison with their work. In the next section we also estimate some outflow properties using Hα. Before we estimated the outflowing gas mass from the [O III] luminosity (see below), we computed the extinction in the outflow region, using the integrated Hα and Hβ fluxes. We made use of the extinction law from Cardelli et al. (1989) with a parameter RV = 3.1, assuming an intrinsic ratio between the Balmer lines of Hα and Hβ of 3.1. We then used the derived extinction to correct the observed [O III] flux. Our median extinction value (AV = 0.82 mag) over the outflow region is lower than the values reported by Davies et al. (2020) and Thomas et al. (2017), which are 1.7 and 2.4 mag, respectively. Apart from the different physical sizes used for the spectra extraction, we also checked whether the differences are mainly due to the fact that these works did not split the flux in kinematic components for their estimations. Interestingly, we derived an extinction of AV = 2.0 mag for the disk component for an aperture as that of Davies et al. (2020). Thus, this may explain thus the differences. Nevertheless, we corrected the [O III] fluxes within the outflow region with the corresponding median value of the extinction.
Considering Eq. (B.3) of Fiore et al. (2017), the mass of ionized gas based on the [O III] luminosity can be expressed as (see also Carniani et al. 2015)
where C is the condensation factor and [O/H] the oxygen abundance ratio (i.e., the ratio of AGN oxygen abundance compared to that of the Sun on a logarithmic scale), we derived an [O III] mass map. For simplicity, we assumed that the gas clouds have the same electron density, leading to a value of C = 1. A(X) is the elemental abundance expressed as the logarithm of the number of atoms of an element X per 1012 atoms of hydrogen. The oxygen abundance ratio is related to a AGN oxygen abundance and that of the Sun as follows: [O/H] = A(O)−A(O)⊙, where the required oxygen abundances for NGC 2110 and the Sun are known from the literature: A(O) = 8.87 (Dors et al. 2015) and A(O)⊙ = 8.86 (Centeno & Socas-Navarro 2008).
Finally, for estimating the total outflowing mass of ionized gas M in each spaxel (using the corresponding value of the electron density), we used the approximation adopted by Fiore et al. (2017) in terms of the [O III] outflowing mass:
We obtained an ionized mass in the outflow of 9.8 × 104 M⊙. We note that in the following section we provide another estimate of the outflowing mass of ionized gas using Hα measurements.
For the NGC 2110 outflow it seems reasonable to adopt a constant outflow history through a cone/sphere to the outflow properties (see Lutz et al. 2020). This assumption leads to the following equations for the mass outflow rate, Ṁout, the kinetic energy, Ekin, the kinetic power, Ėkin, and the momentum rate, Ṗ:
where Mout is the ionized gas mass integrated within the outflow region, vout the outflow velocity, and rout the outflow radius.
In order to estimate the outflow velocity vout, we used a similar approach to that of Davies et al. (2020). We computed the percentiles 2 and 98 of the velocity distribution inferred from the outflow profile of the [O III] doublet, measured their differences with respect to the systemic velocity, and chose whichever is larger. We obtained a maximum outflowing velocity of v98 = 1167 km s−1, whereas they reported a value of 1665 km s−1. We note that apart from the different extraction sizes, they assumed that the whole profile is dominated by the outflow, while we built the outflow profile stacking the line profiles of the noncircular component in each spaxel within the outflow region. As a note, our kinematic decomposition allowed us to estimate that approximately half of the flux of the whole profile in the ∼4″ region comes from the disk component.
For the outflow radius we took rout = 400 pc (projected value; see Fig. 5), which is 2.7 times larger than the value adopted by Davies et al. (2020). The outflow region size is approximately consistent with two times the measured FWHM at the wavelength of [O III] (see Sect. 5.1). We also checked that our estimation is equivalent to that employed by Kang & Woo (2018), who defined the outflow radius as the distance in which the velocity dispersion from the [O III] doublet changes with respect to the stellar values. Indeed, the observed velocity dispersions in the outflow region of NGC 2110 (see, e.g., Fig. 7) are higher than the stellar velocity dispersion (220 − 260 km s−1; see Nelson & Whittle 1995; González Delgado et al. 2002; Burtscher et al. 2021). However, the measured radius for NGC 2110 falls approximately 4σ below the expected value from the correlation between the outflow size and [O III] luminosity reported by Kang & Woo (2018) for more luminous AGN. Table 3 summarizes the properties of the outflow.
Outflow properties from the [O III] line.
Davies et al. (2020) also computed the outflow properties of NGC 2110 and derived a mass outflow rate that is approximately an order magnitude lower. Their L[O III] is 0.12 dex lower than ours. Their lower flux calibration (by 0.40 dex; see Sect. 2.1) is compensated with their extinction correction, which is 0.39 dex higher. Therefore, the difference in luminosity is due to their light loss caused by their smaller aperture (0.20 dex), even though they assumed that all the light can be attributed to the outflow. Regarding Mout, they obtained a value 1.59 dex lower, which is mainly due to their much higher value of the electron density. For the ionized gas mass rate Ṁout, the difference decreases to 0.99 dex because we considered an outflowing velocity 0.15 dex lower and a radius 0.43 higher (which in both cases help alleviate the difference). The same happens for the kinetic power Ėkin. All this highlights the importance of understanding the assumptions for estimating the outflow properties while comparing with results from other works.
5.5. Are the outflow properties linked with the radio jet?
NGC 2110 follows well the scaling relation of the ionized mass outflow rate and the AGN bolometric luminosity derived by Fiore et al. (2017) for luminous AGN using log LAGN = 44.5 erg s−1 from Davies et al. (2020). However, it falls below the scaling relation with the kinetic power. In this respect, NGC 2110 behaves like other AGN of similar luminosities (see, e.g., Fig. 10 of García-Bernete et al. 2021), which show a large range of kinetic powers. Moreover, NGC 2110 lies in the upper envelop of this observed large scatter at a given AGN luminosity. It is possible that, at least in cases such as NGC 2110, some of the kinetic power, in addition to that provided by the AGN radiation pressure, might be due to the effect of a moderate power radio jet. In this section we explore this scenario in NGC 2110.
Venturi et al. (2021) observed in a small sample of Seyfert galaxies that regions with high velocity dispersion were generally perpendicular to the orientation of the radio jet. In NGC 2110, the increased velocity dispersions, compared to those of the disk, are observed both perpendicular and parallel to the radio jet. Equally conspicuous is the fact that the bending of the radio jet, to the northeast and southwest within the outflow region of NGC 2110, coincides with the sharp transition in velocity dispersions seen in the region with the noncircular motions (right panels of Figs. 7 and B.4). The length of the linear part of the radio jet nearly matches that of the outflow region. In this this region, there is also weak CO(2−1) emission, termed the lacuna, along the northwest-southeast direction (PA ≃ −25°) passing through the AGN location (Rosario et al. 2019). In this section we investigate whether the outflow properties of NGC 2110 follow the relations between the jet radio power and the outflowing ionized mass and kinetic energy found by Venturi et al. (2021).
We estimated the kinetic power of the radio jet for NGC 2110 from the 20 cm radio flux reported by Nagar et al. (1999). We converted the total radio flux into kinetic power using Eq. (16) of Bîrzan et al. (2008), as done by Venturi et al. (2021). We note, however, that other calibrations might provide kinetic powers differing by up to an order of magnitude. We obtained Pjet = 2.3 × 1043 erg s−1 for NGC 2110, which is slightly higher than that of NGC 1068 and approximately a factor of two less powerful than the jet in IC 5063 (Venturi et al. 2021).
To make a proper comparison with Venturi et al. (2021), we estimated the outflowing mass with our extinction corrected Hα luminosity and their Eq. (1), instead of our Eqs. (1) and (2). Unlike their work, for NGC 2110 we only included the mass from the outflow component. With this approach, the outflowing ionized mass within the outflow region is 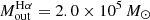 , which is a factor of two higher than our value estimated from the [O III] line (Table 3). Finally, we would like to emphasize that our mass estimates and theirs are based on electron densities from the [S II] method. Following Venturi et al. (2021), the kinetic energy of the jet is
, which is a factor of two higher than our value estimated from the [O III] line (Table 3). Finally, we would like to emphasize that our mass estimates and theirs are based on electron densities from the [S II] method. Following Venturi et al. (2021), the kinetic energy of the jet is 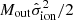 . We measured the velocity dispersion of the [O III] profile including both components, as in their work, that is to say, from its second-order moment. We obtained
. We measured the velocity dispersion of the [O III] profile including both components, as in their work, that is to say, from its second-order moment. We obtained 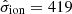 km s−1.
km s−1.
In Fig. 13 we compare NGC 2110 with the trends observed by Venturi et al. (2021) between the outflow properties and the jet radio power. NGC 2110 appears to follow well the trends suggested by their galaxies, except for the more extreme properties of NGC 1068. The derived kinetic energy in NGC 2110 is between NGC 5643 and IC 5063, which are well known for hosting a radio jet that is close to the disk of the galaxy and driving a multiphase energetic outflow (see Morganti et al. 2015; Venturi et al. 2021, and references therein). On the other hand, in these diagrams NGC 1068 is well above the trends. As in NGC 2110, the radio jet of NGC 1068 suffers a reorientation due probably to the impact with a gas cloud in the disk of the galaxy, and further away (a few hundred parsecs from the AGN) the radio morphology resembles a bow-shock (García-Burillo et al. 2014, 2017). However, unlike in NGC 2110, shocks in NGC 1068 only dominate the gas excitation at the radio jet location, while AGN and star formation excitation dominate in other regions (D’Agostino et al. 2019).
 |
Fig. 13. Outflow mass (left panel) and a proxy for the kinetic energy (right panel) versus the jet radio power. Circles are galaxies from Venturi et al. (2021), while the star corresponds to NGC 2110 (see Sect. 5.5). For this galaxy, the outflowing ionized gas mass corresponds only to that observed in the outflow region. The horizontal error bars for NGC 2110 take the errors in Eq. (16) of Bîrzan et al. (2008) into account, while vertical error bars include the uncertainties related to the extinction correction and the relative flux calibration between the two MEGARA gratings, as well as the uncertainty from the absolute flux calibration. |
Considering the above observational evidence, we speculate that the radio jet propagated through the nuclear region of NGC 2110 and shocked the gas producing highly turbulent motions, both parallel and perpendicular to the radio jet. Indeed, Ulvestad & Wilson (1983) proposed that that the radio jet morphology of NGC 2110 is due to ram pressure bending by a dense rotating disk. Simulations predict that the gas would expand like a bubble (e.g., Wagner & Bicknell 2011; Mukherjee et al. 2018). Since in NGC 2110 the jet is not perpendicular to the galaxy disk (Pringle et al. 1999), the jet-inflated bubble probably ended up impacting the ISM of the galaxy disk. As a result the jet was deflected and probably decelerated. This may have caused a decrease in the turbulence of the gas, and thus lower observed velocity dispersions in the noncircular component outside the outflow region. In the disk of the galaxy we observe shock-like emission in the central region where the jet is still operating but at distances beyond the radio bend the dominance of shocks diminishes and it is then possible to identify gas excited by the AGN (see Fig. 8).
In summary, the discussion above provides additional support for the scenario where part of the observed ionized gas outflow in NGC 2110 could be driven by the radio jet when it expands laterally and radially in the disk of the galaxy.
6. Summary and conclusions
In this paper we present new GTC/MEGARA IFU observations of the central ∼13″ × 11″ (∼2 kpc × 1.8 kpc in projection) region of NGC 2110 with R ≃ 5000 − 5900. We used two gratings to observe the most prominent nebular emission lines in the 4300 − 5200 Å and 6100 − 7300 Å spectral ranges. The goal was to study the spatially resolved properties of the ionized gas in the central 2 kpc of NGC 2110, including its outflow, and evaluate the role of its radio jet. We fitted the emission lines with a maximum of two Gaussian components, which was sufficient in the majority of spaxels, except at the AGN position. We performed a kinematic separation using the observed velocities and velocity dispersions and a comparison with the stellar kinematics from González Delgado et al. (2002) and Ferruit et al. (2004).
We identified the ionized gas rotation in the disk of the galaxy with an intermediate velocity dispersion component (σ ≃ 60 − 200 km s−1). It is detected in all the bright emission lines ([O III], Hα, [N II], and [S II]) over an area of ∼8″ × 12″ (1.3 × 1.9 kpc2 in projection), which corresponds to most of the MEGARA FoV along the major axis of the galaxy.
The noncircular component covers an area of ∼4″ × 8″ and presents different properties in two distinct regions. The first is a spatially resolved region, mostly in the north-south direction, with a total size of ∼2.5″ ∼ 400 pc around the nucleus. It presents the highest velocity dispersions, typically 700 km s−1, and is identified with the ionized outflow in this galaxy. The extent of the outflow region, as traced by the [O III] line, is approximately equal to the linear part of the radio jet. Outside the outflow region, beyond the edges of the radio source and where it is deflected, the kinematics of the gas with noncircular motions changes drastically. The velocity dispersion drops to < 60 km s−1. These are likely noncircular motions taking place in the disk of the galaxy, possibly unrelated to the inner outflow and the radio jet.
We fitted the AGN nuclear spectrum of NGC 2110 with three Gaussian components, with the broadest [O III] component reaching a velocity dispersion of 662 km s−1. The [O III] p-v diagrams along the major and minor axes of the galaxy reveal observed velocities in excess of 1000 km s−1 at the AGN position, both blueshifted and redshifted. There are other redshifted and blueshifted components of several hundreds of km s−1 in the p-v diagram along the major axis of the galaxy. Their location in the two quadrants forbidden by rotation indicates that part of the outflowing gas is outside the disk of the galaxy.
The spatially resolved BPT diagnostic diagrams of the outflow region reveal mostly LI(N)ER-like excitation. The observed line ratios are consistent with predictions from shock models. In the disk of the galaxy, there is a large number of spaxels with LI(N)ER-like excitation, but also “Seyfert-like” excitation due to AGN photoionization. The latter excitation appears in regions beyond, although close to, the region where the radio jet is bent, at projected distances greater than approximately 1 − 2″, reaching at least 5″ ≃ 800 pc. This is likely gas in the host galaxy disk being illuminated by AGN photons at the intersection of an ionization cone with the galaxy disk (see also Rosario et al. 2010).
Using the outflow component of the [O III]λ5007 line, we derive an outflowing ionized gas mass, ionized mass outflow rate, and outflow kinetic power of Mout = 9.8 × 104 M⊙, Ṁout = 0.29 M⊙ yr−1, and Ėkin = 1.3 × 1041 erg s−1, respectively. As found in other Seyfert galaxies, NGC 2110 lies below the correlation between the AGN bolometric luminosity and the kinetic power of the ionized outflow derived for luminous AGN. However, NGC 2110 shows an increased kinetic power when compared to other Seyferts of similar AGN luminosity. We explored the possibility that part of the kinetic power might be due to the effect of the moderate power radio jet detected in this galaxy. To do so, we compared NGC 2110 outflowing gas mass and kinetic power properties with its jet radio power. NGC 2110 follows the observational trends between these quantities found by Venturi et al. (2021) for a few Seyfert galaxies. We propose that the ionized gas outflow in the inner ≃400 pc region of NGC 2110 is driven in part by the radio jet. This is supported by the presence of shock-like emission, presumably induced by the passage of the moderate-luminosity radio jet through the disk. However, beyond the outflow region there is also gas photoionized by the AGN in the central 2 kpc of NGC 2110. This gas is rotating and located in regions bordering and past the radio jet bending, where it is being illuminated by AGN photons.
Available on Gitlab at https://gitlab.com/lperalta_ast/alucine
Acknowledgments
We would like to thank the referee for insightful comments and O. González-Martín for providing constructive feedback. L.P.d.A., A.A.H., S.G.B., and M.V.M. acknowledge financial support from grant PGC2018-094671-B-I00 funded by MCIN/AEI/10.13039/501100011033 and by ERDF A way of making Europe. A.A.H. and M.V.M. also acknowledge financial support from grant PID2021-124665NB-I00 funded by the Spanish Ministry of Science and Innovation and the State Agency of Research MCIN/AEI/ 10.13039/501100011033 and ERDF A way of making Europe. S.G.B. acknowledges support from the research project PID2019-106027GA-C44 of the Spanish Ministerio de Ciencia e Innovación. I.G.B. and D.R. acknowledge support from STFC through grant ST/S000488/1. B.G.L. acknowledges support from grants PID2019-107010GB-100 and the Severo Ochoa CEX2019-000920-S. C.R.A. acknowledges the project “Feeding and feedback in active galaxies”, with reference PID2019-106027GB-C42, funded by MICINN-AEI/10.13039/501100011033, and the European Union’s Horizon 2020 research and innovation programme under Marie Skłodowska-Curie grant agreement No 860744 (BID4BEST). C.R.A. and A.A. acknowledge the project “Quantifying the impact of quasar feedback on galaxy evolution”, with reference EUR2020-112266, funded by MICINN-AEI/10.13039/501100011033 and the European Union NextGenerationEU/PRTR; the Consejería de Economía, Conocimiento y Empleo del Gobierno de Canarias and the European Regional Development Fund (ERDF) under grant “Quasar feedback and molecular gas reservoirs”, with reference ProID2020010105, ACCISI/FEDER, UE. E.B. acknowledges the María Zambrano program of the Spanish Ministerio de Universidades funded by the Next Generation European Union and is also partly supported by grant RTI2018-096188-B-I00 funded by MCIN/AEI/10.13039/501100011033. C.R. acknowledges support from the Fondecyt Iniciacion grant 11190831 and ANID BASAL project FB210003. D.R. acknowledges support from University of Oxford John Fell Fund. Based on observations made with the Gran Telescopio Canarias (GTC), installed in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias, in the island of La Palma. This work is based on data obtained with MEGARA instrument, funded by European Regional Development Funds (ERDF), through Programa Operativo Canarias FEDER 2014-2020. This research made use of NumPy (Harris et al. 2020), SciPy (Virtanen et al. 2020), Matplotlib (Hunter 2007) and Astropy (Astropy Collaboration 2013, 2018). This research has made use of the NASA/IPAC Extragalactic Database (NED), which is funded by the National Aeronautics and Space Administration and operated by the California Institute of Technology. This research has made use of ESASky, developed by the ESAC Science Data Centre (ESDC) team and maintained alongside other ESA science mission’s archives at ESA’s European Space Astronomy Centre (ESAC, Madrid, Spain).
References
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Audibert, A., Ramos Almeida, C., García-Burillo, S., et al. 2023, A&A, 671, L12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baines, D., Giordano, F., Racero, E., et al. 2017, PASP, 129, 028001 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [Google Scholar]
- Baron, D., & Netzer, H. 2019, MNRAS, 486, 4290 [Google Scholar]
- Bellocchi, E., Ascasibar, Y., Galbany, L., et al. 2019, A&A, 625, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bîrzan, L., McNamara, B. R., Nulsen, P. E. J., Carilli, C. L., & Wise, M. W. 2008, ApJ, 686, 859 [Google Scholar]
- Bremer, M., Scharwächter, J., Eckart, A., et al. 2013, A&A, 558, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Burtscher, L., Davies, R. I., Shimizu, T. T., et al. 2021, A&A, 654, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Carniani, S., Marconi, A., Maiolino, R., et al. 2015, A&A, 580, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carrasco, E., Gil de Paz, A., Gallego, J., et al. 2018, SPIE Conf. Ser., 10702, 1070216 [NASA ADS] [Google Scholar]
- Cazzoli, S., Hermosa Muñoz, L., Márquez, I., et al. 2022, A&A, 664, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Centeno, R., & Socas-Navarro, H. 2008, ApJ, 682, L61 [NASA ADS] [CrossRef] [Google Scholar]
- Cid Fernandes, R., Stasińska, G., Schlickmann, M. S., et al. 2010, MNRAS, 403, 1036 [Google Scholar]
- Cid Fernandes, R., Stasińska, G., Mateus, A., & Vale Asari, N. 2011, MNRAS, 413, 1687 [Google Scholar]
- Clements, E. D. 1983, MNRAS, 204, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Combes, F., García-Burillo, S., Casasola, V., et al. 2013, A&A, 558, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Comerón, S., Knapen, J. H., Ramos Almeida, C., & Watkins, A. E. 2021, A&A, 645, A130 [EDP Sciences] [Google Scholar]
- Cresci, G., Marconi, A., Zibetti, S., et al. 2015, A&A, 582, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Agostino, J. J., Kewley, L. J., Groves, B. A., et al. 2019, MNRAS, 487, 4153 [Google Scholar]
- Davies, R. L., Dopita, M. A., Kewley, L., et al. 2016, ApJ, 824, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R., Baron, D., Shimizu, T., et al. 2020, MNRAS, 498, 4150 [Google Scholar]
- Dors, O. L., Cardaci, M. V., Hägele, G. F., et al. 2015, MNRAS, 453, 4102 [Google Scholar]
- Ferruit, P., Mundell, C. G., Nagar, N. M., et al. 2004, MNRAS, 352, 1180 [CrossRef] [Google Scholar]
- Fiore, F., Feruglio, C., Shankar, F., et al. 2017, A&A, 601, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [Google Scholar]
- García-Bernete, I., Alonso-Herrero, A., García-Burillo, S., et al. 2021, A&A, 645, A21 [EDP Sciences] [Google Scholar]
- García-Bernete, I., Rigopoulou, D., Alonso-Herrero, A., et al. 2022, A&A, 666, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Combes, F., Usero, A., et al. 2014, A&A, 567, A125 [Google Scholar]
- García-Burillo, S., Viti, S., Combes, F., et al. 2017, A&A, 608, A56 [Google Scholar]
- Gil de Paz, A., Carrasco, E., Gallego, J., et al. 2016, SPIE Conf. Ser., 9908, 99081K [Google Scholar]
- Giordano, F., Racero, E., Norman, H., et al. 2018, Astron. Comput., 24, 97 [NASA ADS] [CrossRef] [Google Scholar]
- González Delgado, R. M., Arribas, S., Pérez, E., & Heckman, T. 2002, ApJ, 579, 188 [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Husemann, B., Scharwächter, J., Davis, T. A., et al. 2019, A&A, 627, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Juneau, S., Goulding, A. D., Banfield, J., et al. 2022, ApJ, 925, 203 [NASA ADS] [CrossRef] [Google Scholar]
- Kakkad, D., Groves, B., Dopita, M., et al. 2018, A&A, 618, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kang, D., & Woo, J.-H. 2018, ApJ, 864, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003, MNRAS, 346, 1055 [Google Scholar]
- Kawamuro, T., Izumi, T., Onishi, K., et al. 2020, ApJ, 895, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Dopita, M. A., Sutherland, R. S., Heisler, C. A., & Trevena, J. 2001, ApJ, 556, 121 [Google Scholar]
- Kewley, L. J., Groves, B., Kauffmann, G., & Heckman, T. 2006, MNRAS, 372, 961 [Google Scholar]
- Luridiana, V., Morisset, C., & Shaw, R. A. 2015, A&A, 573, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lutz, D., Sturm, E., Janssen, A., et al. 2020, A&A, 633, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maccagni, F. M., Serra, P., Gaspari, M., et al. 2021, A&A, 656, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McClintock, J. E., van Paradijs, J., Remillard, R. A., et al. 1979, ApJ, 233, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Meenakshi, M., Mukherjee, D., Wagner, A. Y., et al. 2022, MNRAS, 516, 766 [NASA ADS] [CrossRef] [Google Scholar]
- Mingozzi, M., Cresci, G., Venturi, G., et al. 2019, A&A, 622, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morganti, R., Oosterloo, T., Oonk, J. B. R., Frieswijk, W., & Tadhunter, C. 2015, A&A, 580, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mukherjee, D., Bicknell, G. V., Wagner, A. Y., Sutherland, R. S., & Silk, J. 2018, MNRAS, 479, 5544 [NASA ADS] [CrossRef] [Google Scholar]
- Nagar, N. M., Wilson, A. S., Mulchaey, J. S., & Gallimore, J. F. 1999, ApJS, 120, 209 [Google Scholar]
- Nelson, C. H., & Whittle, M. 1995, ApJS, 99, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvadba, N. P. H., Lehnert, M. D., De Breuck, C., Gilbert, A. M., & van Breugel, W. 2008, A&A, 491, 407 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pascual, S., Cardiel, N., Picazo-Sanchez, P., Castillo-Morales, A., & Gil De Paz, A. 2021, https://doi.org/10.5281/zenodo.2206856 [Google Scholar]
- Pereira-Santaella, M., Álvarez-Márquez, J., García-Bernete, I., et al. 2022, A&A, 665, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perna, M., Lanzuisi, G., Brusa, M., Cresci, G., & Mignoli, M. 2017, A&A, 606, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Perna, M., Arribas, S., Catalán-Torrecilla, C., et al. 2020, A&A, 643, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pringle, J. E., Antonucci, R. R. J., Clarke, C. J., et al. 1999, ApJ, 526, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Rosario, D. J., Whittle, M., Nelson, C. H., & Wilson, A. S. 2010, MNRAS, 408, 565 [Google Scholar]
- Rosario, D. J., Togi, A., Burtscher, L., et al. 2019, ApJ, 875, L8 [NASA ADS] [CrossRef] [Google Scholar]
- Schnorr-Müller, A., Storchi-Bergmann, T., Nagar, N. M., et al. 2014, MNRAS, 437, 1708 [Google Scholar]
- Sharp, R. G., & Bland-Hawthorn, J. 2010, ApJ, 711, 818 [Google Scholar]
- Shimizu, T. T., Davies, R. I., Lutz, D., et al. 2019, MNRAS, 490, 5860 [Google Scholar]
- Silk, J., & Mamon, G. A. 2012, Res. Astron. Astrophys., 12, 917 [Google Scholar]
- Smirnova-Pinchukova, I., Husemann, B., Busch, G., et al. 2019, A&A, 626, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smirnova-Pinchukova, I., Husemann, B., Davis, T. A., et al. 2022, A&A, 659, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Speranza, G., Ramos Almeida, C., Acosta-Pulido, J. A., et al. 2022, A&A, 665, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Talbot, R. Y., Sijacki, D., & Bourne, M. A. 2022, MNRAS, 514, 4535 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, A. D., Dopita, M. A., Shastri, P., et al. 2017, ApJS, 232, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Ulvestad, J. S., & Wilson, A. S. 1983, ApJ, 264, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Ulvestad, J. S., & Wilson, A. S. 1984, ApJ, 285, 439 [Google Scholar]
- Ulvestad, J. S., & Wilson, A. S. 1989, ApJ, 343, 659 [NASA ADS] [CrossRef] [Google Scholar]
- Vayner, A., Wright, S. A., Murray, N., et al. 2017, ApJ, 851, 126 [Google Scholar]
- Veilleux, S., & Osterbrock, D. E. 1987, ApJS, 63, 295 [Google Scholar]
- Venturi, G., Cresci, G., Marconi, A., et al. 2021, A&A, 648, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Wagner, A. Y., & Bicknell, G. V. 2011, ApJ, 728, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Weinberger, R., Ehlert, K., Pfrommer, C., Pakmor, R., & Springel, V. 2017, MNRAS, 470, 4530 [CrossRef] [Google Scholar]
- Wilson, A. S., & Baldwin, J. A. 1985, ApJ, 289, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, A. S., & Ulvestad, J. S. 1982, ApJ, 263, 576 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: MEGARA fits with three components for the nuclear region
Figures A.1, A.2, A.3, and A.4 display the spectra from 3-spaxel square extractions in the nuclear region and their fits with three components, like Fig. 2, which shows the spectral region around the [O III]λλ4959, 5007 doublet in the main text. The physical parameters of these fits are provided in Table 2.
 |
Fig. A.1. Spectrum of the Hβ line extracted in the nuclear region fitted with three components. All lines are as in Fig. 2. |
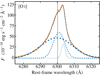 |
Fig. A.2. Spectrum of the [O I]λ6300 line extracted in the nuclear region fitted with three components. All lines are the same as in Fig. 2. |
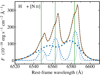 |
Fig. A.3. Spectrum of the Hα line and the [N II]λλ6548, 6583 doublet extracted in the nuclear region fitted with three components. All lines are the same as in Fig. 2. |
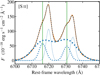 |
Fig. A.4. Spectrum of the [S II] λλ6716, 6731 doublet extracted in the nuclear region fitted with three components. All lines are the same as in Fig. 2. |
Appendix B: Figures for the emission lines observed with the MEGARA LR-R grating
In this Appendix, Figs. B.1, B.2, B.3, and B.4 show the same information as Figs. 3, 5, 6, and 7 but for the emission-lines in the MEGARA LR-R grating.
 |
Fig. B.1. Distributions of the velocity dispersion (corrected for instrumental resolution) measured on a spaxel-by-spaxel basis of the fits using a maximum of two Gaussian components from lines observed with the MEGARA LR-R grating, i.e., the [O I]λ6300, Hα, [N II]λλ6548, 6583, and [S II]λλ6716, 6731 lines. Colors have the same meanings as in Fig. 3. |
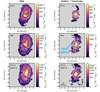 |
Fig. B.2. Flux maps of the disk and outflow+noncircular components for lines observed with the MEGARA LR-R grating, i.e., the [O I]λ6300, Hα, [N II]λ6583, [S II]λ6716, and [S II] λ6731 lines. Contour and symbol definitions are the same as in Fig. 5. |
 |
Fig. B.2. Continued. |
 |
Fig. B.3. Velocity maps of the disk and outflow+noncircular components for lines observed with the MEGARA LR-R grating, i.e., the [O I]λ6300, Hα, [N II]λλ6548, 6583, and [S II]λλ6716, 6731 lines. Colors and lines have the same meanings as in Fig. 6. |
 |
Fig. B.4. Velocity-dispersion maps of the disk and outflow+noncircular components for lines observed with the MEGARA LR-R grating, i.e., the [O I]λ6300, Hα, [N II]λλ6548, 6583, and [S II]λλ6716, 6731 lines. Colors and contours have the same meanings as in Fig. 7. |
Appendix C: Electron densities from the ionization parameter method
In this appendix, Fig. C.1 shows the estimation of the electron densities using the ionization parameter method proposed by Baron & Netzer (2019). See the main text for details and caveats related to this method.
 |
Fig. C.1. Maps of electron densities for the disk (left) and outflow+noncircular (right) components using the ionization parameter method (see text for details). |
All Tables
Measurements from the nuclear spectrum using a model with three Gaussian components.
All Figures
 |
Fig. 1. HST/WFPC2 optical image of NGC 2110 obtained with the F791W filter, shown on a linear scale (gray colors and blue contours). The orange contours (also on a linear scale) are the VLA radio 6 cm emission from Ulvestad & Wilson (1983). We also mark with a red rectangle the approximate size of the GTC/MEGARA FoV of 12.5″ × 11.3″. The dashed and dotted lines are the PA of the galaxy major axis (PA ≃ 163° measured from the north to the east; see Ferruit et al. 2004) and the minor axis, respectively. The dashed-dotted line is the PA of the slit used by González Delgado et al. (2002) and discussed in Sect. 3.3. |
| In the text | |
 |
Fig. 2. GTC/MEGARA nuclear spectrum of NGC 2110 in the spectral region around the [O III]λλ4959, 5007 doublet. The orange line is the observed spectrum after the subtraction of the continuum and extracted with a 0.9″ × 0.9″ aperture. The fit (dashed black line) is the sum of three Gaussian components. The dotted blue lines show each component of the fit, with lines of increasing thickness for the components with increasing velocity dispersions. The green lines are the line wavelengths. |
| In the text | |
 |
Fig. 3. Observed distribution of the velocity dispersions (corrected for the instrumental resolution) fitted on a spaxel-by-spaxel basis and using a maximum of two Gaussian components from lines observed with the GTC/MEGARA LR-B grating, i.e., Hβ and [O III]λλ4959, 5007 lines. Blue and orange lines correspond to the narrow and broad components, respectively (see text). |
| In the text | |
 |
Fig. 4. Comparison between the velocities of the ionized gas derived from fits using a maximum of two Gaussian components for the [O III]λλ4959, 5007 doublet and the stellar velocities. From top to bottom, the stellar velocities are along the major and minor axes of the galaxy from Ferruit et al. (2004) and along PA = 6° from González Delgado et al. (2002). Circles represent the narrow component or that when only one Gaussian is required to fit the line, while triangles correspond to the broad component. Stars show stellar velocities. The color and size of the circles and triangles depend on the velocity dispersion of each component. Black and red edges have been added to the circles and triangles, respectively, for velocity dispersions below and above 60/200 km s−1 in order to illustrate the component classification explained in Sect. 3.1. The horizontal dashed line shows the systemic velocity and the horizontal gray region its error. |
| In the text | |
 |
Fig. 5. Flux maps of the disk (left) and the outflow+noncircular (right) components for the lines observed with the GTC/MEGARA LR-B grating, i.e., the Hβ and [O III]λ5007 lines. All the color bars use a square root scale and are saturated at the half maximum value of each map. Contour levels correspond to 30, 60, 70, 80, and 90 per cent of the maximum value of each map. Crosses indicate the location of the nucleus (as defined by the peak of the continuum). The northeast compass, the hatched circle indicating the seeing size, and physical size bar on the bottom-right map apply to all the maps. |
| In the text | |
 |
Fig. 6. Velocity maps of the disk (left) and the outflow+noncircular (right) components for the lines observed with the GTC/MEGARA LR-B grating, i.e., the Hβ and [O III]λλ4959, 5007 lines. Values are referred to the systemic velocity. The lines indicate the orientation of the slit PA in Fig. 4 (see text for details). Other symbols are the same as in Fig. 5. |
| In the text | |
 |
Fig. 7. Velocity dispersion maps of the disk (left) and the outflow+noncircular (right) components for the lines observed with the GTC/MEGARA LR-B grating, i.e., the Hβ and [O III]λλ4959, 5007 lines. Contours show the VLA radio jet (Sect. 2.2). Symbols are the same as in Fig. 5. |
| In the text | |
 |
Fig. 8. Spatially resolved BPT diagnostic diagrams (left panels) and maps (right panels) for the disk component. The top, middle, and bottom diagrams of the left panels correspond to [O III]λ5007/Hβ versus [N II]λ6583/Hα, ([S II]λ6716 + λ6731)/Hα, and [O I]λ6300/Hα, respectively. The points in the red color scale are spaxels in the AGN or Seyfert region, those in the blue color scale are spaxels in the star-forming region, and those in the green color scale in the composite-like or LI(N)ER region. Solid curves are theoretical upper limits of starburst models from Kewley et al. (2001). The dashed curve in the [N II] diagram is the demarcation between starburst galaxies and AGN proposed by Kauffmann et al. (2003). Dashed lines in the [S II] and [O I] diagrams are classification lines proposed by Kewley et al. (2006) to split Seyfert and LI(N)ER emission. Dotted lines in the diagnostic diagrams mark bisector lines between the loci of points for the shock-excited NGC 1482 and the AGN-excited NGC 1365 (Sharp & Bland-Hawthorn 2010). For reference, the error bars represent the measurement uncertainties in a spaxel outside the outflow region, at ≃2.4″ north of the AGN. The right panels are diagnostic maps color coded in the same way as their corresponding diagrams to the left. Contours in the maps show the radio jet using the VLA data described in Sect. 2.2. |
| In the text | |
 |
Fig. 9. Spatially resolved BPT diagnostic diagrams (left) and maps (right) for the outflow+noncircular component. All symbols, colors, and lines are the same as in Fig. 8. |
| In the text | |
 |
Fig. 10. Maps of electron densities for the disk (left) and the outflow+noncircular (right) components using the [S II] doublet ratio method. Values in top-left corners indicate the median density in each map. |
| In the text | |
 |
Fig. 11. WHAN diagrams (left panels) for the disk component (top) and for the outflow and noncircular motion components (bottom) and the corresponding spatial distribution of the WHAN regions (right panels). See Cid Fernandes et al. (2011) for details regarding the different region definitions: star-forming galaxies (SF), strong AGN (sAGN), weak AGN (wAGN), and retired galaxies (RG). |
| In the text | |
 |
Fig. 12. GTC/MEGARA p-v diagrams extracted for the [O III]λ5007 line after continuum subtraction, along the major (PA = 163°, left panel) and minor (PA = 73°, right panel) axes of NGC 2110. The first contour is plotted at three times the noise at approximately 1350 km s−1. The second contour is at five times the noise, reaching velocities of −650/500 km s−1, and the rest of the contours are on a linear scale. |
| In the text | |
 |
Fig. 13. Outflow mass (left panel) and a proxy for the kinetic energy (right panel) versus the jet radio power. Circles are galaxies from Venturi et al. (2021), while the star corresponds to NGC 2110 (see Sect. 5.5). For this galaxy, the outflowing ionized gas mass corresponds only to that observed in the outflow region. The horizontal error bars for NGC 2110 take the errors in Eq. (16) of Bîrzan et al. (2008) into account, while vertical error bars include the uncertainties related to the extinction correction and the relative flux calibration between the two MEGARA gratings, as well as the uncertainty from the absolute flux calibration. |
| In the text | |
 |
Fig. A.1. Spectrum of the Hβ line extracted in the nuclear region fitted with three components. All lines are as in Fig. 2. |
| In the text | |
 |
Fig. A.2. Spectrum of the [O I]λ6300 line extracted in the nuclear region fitted with three components. All lines are the same as in Fig. 2. |
| In the text | |
 |
Fig. A.3. Spectrum of the Hα line and the [N II]λλ6548, 6583 doublet extracted in the nuclear region fitted with three components. All lines are the same as in Fig. 2. |
| In the text | |
 |
Fig. A.4. Spectrum of the [S II] λλ6716, 6731 doublet extracted in the nuclear region fitted with three components. All lines are the same as in Fig. 2. |
| In the text | |
 |
Fig. B.1. Distributions of the velocity dispersion (corrected for instrumental resolution) measured on a spaxel-by-spaxel basis of the fits using a maximum of two Gaussian components from lines observed with the MEGARA LR-R grating, i.e., the [O I]λ6300, Hα, [N II]λλ6548, 6583, and [S II]λλ6716, 6731 lines. Colors have the same meanings as in Fig. 3. |
| In the text | |
 |
Fig. B.2. Flux maps of the disk and outflow+noncircular components for lines observed with the MEGARA LR-R grating, i.e., the [O I]λ6300, Hα, [N II]λ6583, [S II]λ6716, and [S II] λ6731 lines. Contour and symbol definitions are the same as in Fig. 5. |
| In the text | |
 |
Fig. B.2. Continued. |
| In the text | |
 |
Fig. B.3. Velocity maps of the disk and outflow+noncircular components for lines observed with the MEGARA LR-R grating, i.e., the [O I]λ6300, Hα, [N II]λλ6548, 6583, and [S II]λλ6716, 6731 lines. Colors and lines have the same meanings as in Fig. 6. |
| In the text | |
 |
Fig. B.4. Velocity-dispersion maps of the disk and outflow+noncircular components for lines observed with the MEGARA LR-R grating, i.e., the [O I]λ6300, Hα, [N II]λλ6548, 6583, and [S II]λλ6716, 6731 lines. Colors and contours have the same meanings as in Fig. 7. |
| In the text | |
 |
Fig. C.1. Maps of electron densities for the disk (left) and outflow+noncircular (right) components using the ionization parameter method (see text for details). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} M^{[{\text{ O}}{\small {\uppercase {\text{ III}}}}]} = 4.0 \times 10^7 \,{M_\odot } \frac{C}{10^\mathrm{[O/H]} } \frac{L^{[{\text{ O}}{\small {\uppercase {\text{ III}}}}]}}{10^{44} \, \mathrm {erg \, s}^{-1} } \frac{1000 \, \mathrm {cm}^{-3} }{n_\mathrm{e} }, \end{aligned} $$](/articles/aa/full_html/2023/07/aa45408-22/aa45408-22-eq1.gif)
![$$ \begin{aligned} M_{\rm out} = 3 \times M^{[{\text{ O}}{\small {\uppercase {\text{ III}}}}]}. \end{aligned} $$](/articles/aa/full_html/2023/07/aa45408-22/aa45408-22-eq2.gif)