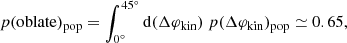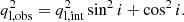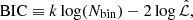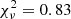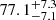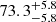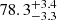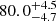| Issue |
A&A
Volume 673, May 2023
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 21 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202345878 | |
| Published online | 24 April 2023 | |
TDCOSMO
XII. Improved Hubble constant measurement from lensing time delays using spatially resolved stellar kinematics of the lens galaxy⋆
1
Department of Astronomy & Astrophysics, University of Chicago, Chicago, IL 60637, USA
e-mail: ajshajib@uchicago.edu
2
Kavli Institute for Cosmological Physics, University of Chicago, Chicago, IL 60637, USA
3
Department of Physics and Astronomy, University of California, Davis, CA 95616, USA
4
Department of Physics and Astronomy, University of California, Los Angeles, CA 90095, USA
5
Sub-Department of Astrophysics, Department of Physics, University of Oxford, Denys Wilkinson Building, Keble Road, Oxford OX1 3RH, UK
6
Technical University of Munich, TUM School of Natural Sciences, Department of Physics, James-Franck-Str. 1, Garching 85748, Germany
7
Max Planck Institute for Astrophysics, Karl-Schwarzschild-Str. 1, Garching 85748, Germany
8
Institute of Astronomy and Astrophysics, Academia Sinica, 11F of ASMAB, No. 1, Section 4, Roosevelt Road, Taipei 10617, Taiwan
9
Physics Department, California Polytechnic State University, San Luis Obispo, CA 93407, USA
10
Fermi National Accelerator Laboratory, PO Box 500 Batavia, IL 60510, USA
11
STAR Institute, Quartier Agora, Allée du Six Août, 19c, 4000 Liège, Belgium
12
Kavli Institute for Particle Astrophysics and Cosmology and Department of Physics, Stanford University, Stanford, CA 94305, USA
13
SLAC National Accelerator Laboratory, Menlo Park, CA 94025, USA
14
Department of Physics and Astronomy, Stony Brook University, Stony Brook, NY 11794, USA
15
Institute of Physics, Laboratory of Astrophysics, École Polytechnique Fédérale de Lausanne (EPFL), Observatoire de Sauverny, 1290 Versoix, Switzerland
Received:
10
January
2023
Accepted:
1
February
2023
Strong-lensing time delays enable the measurement of the Hubble constant (H0) independently of other traditional methods. The main limitation to the precision of time-delay cosmography is mass-sheet degeneracy (MSD). Some of the previous TDCOSMO analyses broke the MSD by making standard assumptions about the mass density profile of the lens galaxy, reaching 2% precision from seven lenses. However, this approach could potentially bias the H0 measurement or underestimate the errors. For this work, we broke the MSD for the first time using spatially resolved kinematics of the lens galaxy in RXJ1131−1231 obtained from the Keck Cosmic Web Imager spectroscopy, in combination with previously published time delay and lens models derived from Hubble Space Telescope imaging. This approach allowed us to robustly estimate H0, effectively implementing a maximally flexible mass model. Following a blind analysis, we estimated the angular diameter distance to the lens galaxy Dd = 865−81+85 Mpc and the time-delay distance DΔt = 2180−271+472 Mpc, giving H0 = 77.1−7.1+7.3 km s−1 Mpc−1 – for a flat Λ cold dark matter cosmology. The error budget accounts for all uncertainties, including the MSD inherent to the lens mass profile and line-of-sight effects, and those related to the mass–anisotropy degeneracy and projection effects. Our new measurement is in excellent agreement with those obtained in the past using standard simply parametrized mass profiles for this single system (H0 = 78.3−3.3+3.4 km s−1 Mpc−1) and for seven lenses (H0 = 74.2−1.6+1.6 km s−1 Mpc−1), or for seven lenses using single-aperture kinematics and the same maximally flexible models used by us (H0 = 73.3−5.8+5.8 km s−1 Mpc−1). This agreement corroborates the methodology of time-delay cosmography.
Key words: distance scale / gravitational lensing: strong / Galaxy: kinematics and dynamics / galaxies: elliptical and lenticular, cD / galaxies: individual: RXJ1131−1231
Reduced Keck Cosmic Web Imager data analyzed in this paper are also available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/673/A9
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
The Hubble constant, H0, the current value of the Universe’s expansion rate, is a crucial cosmological parameter that also sets the extragalactic distance scale. Recently, tension has emerged between early- and late-Universe estimates of H0 (e.g., Freedman 2021; Abdalla et al. 2022). The temperature and polarization fluctuations in the cosmic microwave background (CMB) provide an estimate of the Hubble parameter at the last scattering surface H(z ≈ 1100), which can be extrapolated to the current epoch using Λ cold dark matter (ΛCDM) cosmology. The CMB measurements from Planck give H0 = 67.4 ± 0.5 km s−1 Mpc−1 (Planck Collaboration VI 2020) and H0 = 67.6 ± 1.1 km s−1 Mpc−1 (Aiola et al. 2020). In the local Universe, H0 can be estimated using the cosmic distance ladder, which uses luminosity distances of type Ia supernovae (SNe Ia) with their absolute brightness calibrated using different classes of stars. The Supernova H0 for the Equation of State of the dark energy (SH0ES) team used Cepheids and parallax distances for this calibration, and they find H0 = 73.04 ± 1.04 km s−1 Mpc−1 (Riess et al. 2022). This value is in 5σ tension with the Planck CMB-based measurements. If this difference is not due to systematic errors in either of these measurements (e.g., Efstathiou 2021), then this tension could point to new physics beyond the ΛCDM cosmological model (e.g., Knox & Millea 2020).
To determine whether this “Hubble tension” is due to systematics or new physics, multiple independent methods to measure H0 are needed (e.g., Verde et al. 2019; Di Valentino et al. 2021; Freedman 2021). The Carnegie–Chicago Hubble Project used the tip of the red giant branch (TRGB) to calibrate the SNe Ia absolute brightness and measured H0 = 69.6 ± 1.9 km s−1 Mpc−1 (Freedman et al. 2019, 2020). This TRGB-calibrated measurement is statistically consistent with both the SH0ES measurement and the CMB-based measurements. However, several independent local probes have strengthened the Hubble tension by measuring values consistent with the SH0ES value. For example, the Megamaser Cosmology Project (MCP) estimated H0 = 73.9 ± 3.0 km s−1 Mpc−1 (Pesce et al. 2020), the surface brightness fluctuation (SBF) method measured H0 = 73.7 ± 0.7 ± 2.4 km s−1 Mpc−1 (Blakeslee et al. 2021), and the Tully–Fisher-relation-based method calibrated with Cepheids measured H0 = 75.1 ± 0.2 ± 0.3 km s−1 Mpc−1 Kourkchi et al. 2020.
Strong-lensing time delays provide an independent measurement of H0 (Refsdal 1964; for an up-to-date review: Treu et al. 2022; Birrer et al. 2022a, and for a historical perspective: Treu & Marshall 2016). In strong lensing, a background source appears as multiple images due to the gravitational deflection of photons by a massive foreground galaxy or galaxy cluster. The photons that were emitted at the same time from the background source arrive in different images with a relative time delay. This time delay carries cosmological information through a combination of angular diameter distances involved in the lensing system. This combination is called the “time-delay distance”, which is inversely proportional to H0 (Refsdal 1964; Schneider et al. 1992; Suyu et al. 2010). The Time-Delay COSMOgraphy (TDCOSMO) collaboration has analyzed seven time-delay lenses to measure H0 with a 2% error, with H0 = 74.2 ± 1.6 km s−1 Mpc−1, assuming a power-law or composite – that is stars and a Navarro–Frenk–White (NFW) halo (Navarro et al. 1996, 1997) – mass profile for the lensing galaxies (Millon et al. 2020b). The TDCOSMO collaboration encompasses the COSmological MOnitoring of GRAvItational Lenses (COSMOGRAIL; Courbin et al. 2005; Millon et al. 2020a), the H0 Lenses in COSMOGRAIL’s Wellspring (H0LiCOW; Suyu et al. 2010, 2013; Bonvin et al. 2017; Birrer et al. 2019; Rusu et al. 2020; Wong et al. 2020), the Strong-lensing High Angular Resolution Programme (SHARP; Chen et al. 2019), and the STRong-lensing Insights into the Dark Energy Survey (STRIDES; Treu et al. 2018; Shajib et al. 2020) collaborations.
The simple parametric lens models, for example, the power law, adopted in the TDCOSMO analyses are “industry standard” consistent with nonlensing measurements. The TDCOSMO collaboration has performed various systematic checks on the adopted lens modeling procedure. These checks find potential systematic biases to be lower than the acceptable limit (∼1%) from the choice of mass model parametrization (i.e., power law or composite, Millon et al. 2020b), from ignoring dark substructures in the lens galaxy’s halo (Gilman et al. 2020), from ignoring disky or boxy-ness in the baryonic distribution (Van de Vyvere et al. 2022a), from using different lens modeling software (Shajib et al. 2022a), and from ignoring potential isodensity twists and ellipticity gradients in the lens galaxy (Van de Vyvere et al. 2022b). However, a significant source of potential systematics could arise due to the relatively simple parametrization of the lens mass profile (Kochanek 2020). The well-known mass-sheet degeneracy (MSD) does not allow one to constrain the mass profile shape of the deflector galaxy from imaging observables alone (Falco et al. 1985; Schneider & Sluse 2013, 2014). Nonlensing observables, such as the deflector galaxy’s velocity dispersion or the source’s unlensed intrinsic brightness, are required to break the mass-sheet degeneracy and simultaneously constrain H0 and the mass profile shape (Treu & Koopmans 2002; Shajib et al. 2018; Yıldırım et al. 2020, 2021; Birrer et al. 2020, 2022b).
The TDCOSMO collaboration has redesigned the experiment to mitigate this systematic by relaxing the simple parametric assumptions in the mass profile and constraining the profile shape solely from the stellar velocity dispersion measurements of the lensing galaxies (Birrer et al. 2020). Relaxing the assumption on the mass profile leads to an increase in the H0 uncertainty from 2 to 8% – which is dominated by the uncertainty of the measured velocity dispersion – giving 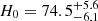 km s−1 Mpc−1. One approach to improving the precision is to incorporate prior information on the mass profile shape from the measured velocity dispersions of a larger sample of external lenses without measured time delays. Assuming that the Sloan Lens ACS (SLACS) survey’s lens galaxies are drawn from the same population as the TDCOSMO lens galaxies and using their velocity dispersions to constrain the mass profile shape, the uncertainty on H0 improves to 5%, giving
km s−1 Mpc−1. One approach to improving the precision is to incorporate prior information on the mass profile shape from the measured velocity dispersions of a larger sample of external lenses without measured time delays. Assuming that the Sloan Lens ACS (SLACS) survey’s lens galaxies are drawn from the same population as the TDCOSMO lens galaxies and using their velocity dispersions to constrain the mass profile shape, the uncertainty on H0 improves to 5%, giving 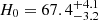 km s−1 Mpc−1 (Birrer et al. 2020). We note that this estimate is statistically consistent within 1σ with the larger 8% H0 measurement above. However, the shift could also arise from systematic differences, for example, a difference between the parent populations of time-delay and non-time-delay lenses (Gomer et al. 2022). Such differences could arise, for example, from evolutionary effects, as the SLACS sample is at lower redshift than the TDCOSMO lenses (e.g., Sonnenfeld et al. 2015, for a discussion of the evolution of mass density profiles of massive elliptical galaxies).
km s−1 Mpc−1 (Birrer et al. 2020). We note that this estimate is statistically consistent within 1σ with the larger 8% H0 measurement above. However, the shift could also arise from systematic differences, for example, a difference between the parent populations of time-delay and non-time-delay lenses (Gomer et al. 2022). Such differences could arise, for example, from evolutionary effects, as the SLACS sample is at lower redshift than the TDCOSMO lenses (e.g., Sonnenfeld et al. 2015, for a discussion of the evolution of mass density profiles of massive elliptical galaxies).
Spatially resolved velocity dispersion measurements of lens galaxies for systems with measured time delays are critical to drastically improving the H0 precision, given the limited sample size of time-delay lenses (Shajib et al. 2018; Yıldırım et al. 2021). The spatially resolved nature of the measured velocity dispersion is especially powerful in simultaneously breaking the MSD and the mass-anisotropy degeneracy (Cappellari 2008; Barnabè et al. 2009, 2012; Collett et al. 2018; Shajib et al. 2018). Spatially resolved velocity dispersion measurements for ∼40 time-delay lens galaxies will yield an independent ≲2% H0 measurement without any mass profile assumption (Birrer & Treu 2021). Additional constraints from velocity dispersion measurements of non-time-delay lens galaxies or magnification information for standardizable lensed type Ia supernovae can further improve the uncertainty to ≲1% (Birrer & Treu 2021; Birrer et al. 2022b).
In this paper, we measured the spatially resolved velocity dispersion for the lens galaxy in the strongly lensed quasar system RXJ1131−1231 using the Keck Cosmic Web Imager (KCWI) integral field spectrograph on the W. M. Keck Observatory (Morrissey et al. 2012, 2018). We constrained H0 without any mass profile assumption from this single time-delay lens system. This is the first application of spatially resolved velocity dispersion from a time-delay lens to measure H0. This lens system was previously used to measure H0 by combining the observed imaging data, single-aperture velocity dispersion, time delays, and analysis of the line-of-sight environment (Suyu et al. 2013, 2014). However, these previous studies assumed simple parametrizations for the mass profile, such as a power law or a combination of the NFW profile and the stellar profile with constant mass-to-light ratio, which is the industry standard in modeling of galaxy-scale lenses (Shajib et al. 2022b). Birrer et al. (2016) marginalized over the MSD effect for the system RXJ1131−1231 to constrain H0 using a single-aperture velocity dispersion measurement. Here in this paper, we allowed the maximal freedom in the MSD by introducing one free parameter on top of the simply parametrized mass profile constrained by lens modeling, which is completely degenerate with H0.
This paper is organized as follows. In Sect. 2, we describe the observational strategy and data reduction. In Sect. 3, we describe the procedures to extract the spatially resolved kinematics map from the KCWI data. In Sect. 4, we briefly review the lensing and dynamical formalisms and how we combine the two to mitigate the MSD in our analysis. Then in Sect. 5, we describe our dynamical models and present results. We infer the cosmological parameters from our analysis in the Sect. 6. We discuss our results in Sect. 7 and conclude the paper in Sect. 8.
We performed the cosmological inference blindly in this paper. The measurement of velocity dispersion was not blinded. However, we blinded the cosmological and other model parameters directly related to cosmological parameters in the dynamical modeling. Before unblinding, this analysis went through an internal collaboration-wide review and code review. After all the coauthors had agreed that the necessary systematic checks were satisfactorily performed, we froze the analysis and unblinded on 5 January 2023. All the sections in this paper except for the final discussion in Sect. 7 and summary in Sect. 8 were written before unblinding. After unblinding, we only made minor edits for clarity and grammatical corrections in the previous sections and added the unblinded numbers where relevant in the abstract, main text, and plots.
2. Observations and data reduction
In this section, we provide a brief description of the lens system RXJ1131−1231 (Sect. 2.1), the spectroscopic observation with KCWI (Sect. 2.2), and the data reduction procedure (Sect. 2.3).
2.1. Description of lens system
The quadruply imaged quasar lens system RXJ1131−1231 was discovered by Sluse et al. (2003). The deflector in this system is an elliptical galaxy with redshift zd = 0.295, and the source redshift is zs = 0.657 (Sluse et al. 2003). Due to its low redshifts, the system is relatively bright and large in angular size. The Einstein ring in this system contains intricate features, providing a wealth of information to constrain the lens mass model (Fig. 1). Due to its early discovery and information-rich features, this system is one of the most studied lensed quasar systems. The time delays for this system were measured by Tewes et al. (2013). Suyu et al. (2013, 2014) performed cosmographic analyses of this system. These authors combined simply parametrized lens models based on the high-resolution imaging from the HST’s Advanced Camera for Surveys (ACS) instrument (HST-GO 9744; PI: Kochanek), the measured time delays, single-aperture velocity dispersion, and external convergence estimate to infer 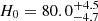 km s−1 Mpc−1. However, such simply parametrized lens models implicitly break the MSD. Birrer et al. (2016) performed an independent mass modeling of this system while marginalizing the MSD with a prior on the source size. These authors found the prior choice on the anisotropy in the dynamical modeling to be the dominant systematic in inferring H0.
km s−1 Mpc−1. However, such simply parametrized lens models implicitly break the MSD. Birrer et al. (2016) performed an independent mass modeling of this system while marginalizing the MSD with a prior on the source size. These authors found the prior choice on the anisotropy in the dynamical modeling to be the dominant systematic in inferring H0.
 |
Fig. 1. HST/ACS image of RXJ1131−1231 in the F814W band. The four quasar images are labeled with A, B, C, and D. The central deflector is marked with G, of which we are measuring the spatially resolved velocity dispersion. An arrow points to the nearby satellite S, which we mask out in the velocity dispersion measurement. The north and east directions and 1″ scale are also illustrated. |
2.2. KCWI spectroscopy
We obtained integral field unit (IFU) spectroscopy of RXJ1131−1231 on 16 May and 7 June 2021 with the KCWI instrument on the Keck Observatory (Morrissey et al. 2012, 2018). We chose KCWI with the small IFU slicer and the low-resolution blue grating (BL) with a field-of-view (FoV) of 8″.4 × 20″.4. The spectral resolution is R ≈ 3600, corresponding to an instrumental dispersion σinst ∼ 35 km s−1. The reciprocal dispersion is 0.5 Å per pixel. The observed wavelength range 3600−5600 Å covers the Ca H&K lines with wavelengths λλ3933, 3968 Å at the redshift of the lens galaxy (zd = 0.295). We primarily used these lines to determine the stellar velocity dispersion. The redshifted 4304 Å G-band is beyond the observed range, so it is not accessible with the KCWI for the RXJ1131−1231 system.
We aligned the FoV’s longer side with the north direction (i.e., PA = 0°) and dithered the individual exposures by 9″ along the north-south direction. As the extent of the RXJ1131−1231 system is smaller than the FoV, each exposure contained the entire lens system within the FoV. In different exposures, the lens system occupied the upper or lower portion of the FoV. Thus, the sky in an exposure with the system occupying the upper portion can be subtracted using another exposure with the system occupying the lower portion, and vice versa. We obtained six exposures with a total integration time of 10 560 s on 16 May and three with a total integration time of 5400 s on 7 June. Therefore, the total exposure time is texp = 15 960 s. The airmass ranged from 1.2 to 1.48 over the integrating period.
2.3. Data reduction
We used the official PYTHON-based data reduction pipeline1 (DRP) to reduce our data. The DRP converts the 2D raw data captured on the detector into a 3D datacube. It performs geometry correction, differential atmospheric refraction correction, and wavelength calibration and produces a final standard-star-calibrated 3D datacube for each exposure. The calibration with the standard star corrects for instrumental response and scales the data to flux units (Morrissey et al. 2018). We used the final output file with the suffix “_icubes” for further analysis.
We stacked the dithered datacubes through drizzling (Fruchter & Hook 2002). Since the exposures are obtained on different dates, the world coordinate system information is not accurate enough to determine the relative positions of the dithered exposures. We followed Chen et al. (2021b) to determine the relative positions by simultaneously fitting the point spread function (PSF) to the four quasar image positions. To perform the drizzling on the datacubes, we repurposed the drizzling routine of the DRP for OSIRIS, another IFU spectrograph on the Keck Observatory2. For the drizzling process, we set pixfrac = 0.7 as recommended to reduce correlated uncertainties between the drizzled pixels (Avila et al. 2015). We calculated the drizzled weight image and ensured that the ratio of rms/median < 0.2 in the region of interest so that the trade-off is balanced between improving the image resolution and increasing the background noise (Gonzaga et al. 2012). The rectangular pixel size 0″.1457 × 0″.3395 of the KCWI was kept the same in the drizzled output. We transformed the datacube to have square pixels of size 0″.1457 × 0″.1457 through resampling while conserving the total flux. We converted the pixels into square sizes for the convenience of Voronoi binning the spectra using the software VORBIN as described in Sect. 3.2.
We directly estimated the PSF from the observed data. We produced a 2D image from the datacube by summing along the wavelength axis (Fig. 2). We created a model for this KCWI image using a high-resolution template from the HST imaging (Fig. 1) that has a pixel size 0″.05 and PSF full width at half maximum (FWHM) 0″.10. In the model, the template was convolved with a Gaussian PSF with a free FWHM parameter, and the positioning of the template on the KCWI image grid was fitted with two additional free parameters. By optimizing the model, we estimated that the PSF FWHM is 0″.96.
 |
Fig. 2. Illustration of the KCWI data for RXJ1131−1231. Left: 2D representation (summed across wavelength) of the 3D KCWI datacube. The yellow contour traces the region with 1″.5 radial extent from the center selected for stellar kinematic measurement. A circular region with 0″.5 radius around image D and the spaxel containing the satellite S are excluded from this selected region. All the individual spaxels within this region have continuum S/N > 1.4 Å−1 for the lens galaxy’s light within 3985−4085 Å (the purple shaded range in the right panel). Right: the spectra (gray) from an example pixel (gray box in the left panel) and the estimate of the signal from the lens galaxy’s spectra (orange) after removing the contribution from the quasar light (blue). The full model of the spectra is presented with the red line, and the model’s residual is plotted in emerald color. The vertical purple shaded region marks where we compute the continuum S/N. |
3. Kinematics maps
This section describes our procedure to obtain the final kinematics map. We use the PPXF package3 to fit the spectra with a library of stellar templates and extract the velocity dispersion (Cappellari 2017, 2022). In Sect. 3.1, we describe the stellar templates used for the analysis. In Sect. 3.2, we present the measurement of the spatially resolved kinematics map of the lens galaxy. In Sect. 3.3, we test the systematics of the velocity dispersion measurement.
3.1. Library of stellar templates
The popularly used template libraries Medium-resolution Isaac Newton Telescope library of empirical spectra (MILES; Sánchez-Blázquez et al. 2006) and INDO-US templates (Valdes et al. 2004) are both too low resolution to fit our datasets. The KCWI’s instrumental resolution of R ≈ 3600 leads to σinst ∼ 35 km s−1 for a Gaussian line spread function (LSF)4. MILES has a resolution of σtemplate ∼ 64 km s−1 (i.e., R ∼ 2000), and the INDO-US templates have an approximately constant-wavelength resolution of 1.2 Å, which corresponds to σtemplate = 39 km s−1 over the Ca H&K wavelength range. Therefore, we chose the X-shooter Spectral Library (XSL), which contains 628 stars covering three segments, including UVB, Vis, and NIR bands (Gonneau et al. 2020). As our data cover the rest-frame blue/UV range, we only used the UVB segment to fit the data, where its resolution is R ∼ 9700 and σtemplate ∼ 13 km s−1.
3.2. Measuring the velocity dispersion
We chose a cutout centered on the lens system with 6″.235 × 6″.235 (43 pixels × 43 pixels) to initiate the analysis (Fig. 2). We estimated the lens galaxy light’s signal-to-noise ratio (S/N) in each spatial pixel (hereafter, spaxel) within this initial cutout. We then selected a region with sufficient S/N from the lens galaxy and relatively low quasar contamination for measuring the velocity dispersion (the yellow contour in Fig. 2’s left panel). We performed Voronoi binning within this selected region to preserve the maximal spatial resolution and reduce the bias in the lower-S/N region (Cappellari & Copin 2003). We elaborate on these steps below.
To estimate the lens galaxy’s S/N in each spaxel, we first simultaneously fitted the quasar and the lens galaxy in each spaxel to calculate the signal from each. We performed this fitting within the wavelength range 3400−4300 Å. As the four quasar images surround the lens galaxy, each spaxel receives a different contribution from the quasar light. We took spectra at the central spaxel of image A as the quasar template, ignoring the lens galaxy’s small contribution. Later in Sect. 3.3, we would also choose the quasar template from images B and C to account for the associated systematic uncertainty, that is, the potential impact of chromatic microlensing that may change the contrast between the line and the continuum (e.g., Sluse et al. 2007).
We determined a single optimal template spectrum for the lens galaxy template. For this purpose, we binned the spectra from spaxels within a circular region of radius 0″.5 centered on the lens galaxy and fitted it with PPXF using the 628 stellar templates from the XSL and the quasar template. We also included a Legendre polynomial of degree 3 as a component in the fitting to account for any residual gradient in the continuum. PPXF chose 39 out of the 628 stellar templates and built the optimal template by taking a weighted linear combination of them. Figure 3 illustrates the weighted distribution of spectral types of the full template library and that of the 39 stars selected by PPXF. Among those stars in the XSL with stellar classes specified by the SIMBAD database (Wenger et al. 2000), G-type stars were selected with the highest total weight, consistent with the fact that massive elliptical galaxy spectra are dominated by G- and K-type stars. In the PPXF fitting procedure, the stellar templates were broadened, corresponding to a freely varying velocity dispersion, but the velocity dispersion did not broaden the quasar template.
 |
Fig. 3. Distribution of the stellar spectral types in the XSL according to the SIMBAD database. Unspecified stars are grouped in the “∼” class. The dark gray color represents the full library of 628 stars. Set 1 (orange) refers to the 39 stars selected by PPXF out of the full library to construct an optimal template 1. Set 2 (blue) refers to 32 stars selected from a random half of the full library and set 3 (emerald) refers to 33 stars selected from the other half. Sets 2 and 3 have 15 and 17 stars, respectively, in common with Set 1. The alternating light gray and white vertical regions divide the spectral classes for easier visualization. |
Once the optimal galaxy template was constructed, we used this template and the quasar template to fit the spectrum of each spaxel individually. We used this optimal template to fit the galaxy spectra in individual spaxels instead of the full template library to avoid large spurious fluctuations in the measured velocity dispersion from spaxel to spaxel. We show the decomposition of the spectra from one example spaxel into different components after fitting with PPXF in Fig. 2. We calculated the signal of the lens galaxy’s spectrum in each spaxel by subtracting the modeled quasar component from the observed spectra. The noise was estimated by adding in quadrature the Poisson noise of the total signal and the background noise estimated from an empty patch of the sky. The noise values were multiplied by 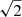 to account for the fact that the square pixels are created from the rectangular pixels about double the size through resampling. We estimated the S/N using the restframe wavelength range 3985−4085 Å, slightly above the Ca H&K absorption lines in wavelength (illustrated by the purple shaded region in Fig. 2).
to account for the fact that the square pixels are created from the rectangular pixels about double the size through resampling. We estimated the S/N using the restframe wavelength range 3985−4085 Å, slightly above the Ca H&K absorption lines in wavelength (illustrated by the purple shaded region in Fig. 2).
To perform Voronoi binning before the velocity dispersion measurement, we selected the spaxels within a radius of 1″.55 from the lens galaxy center that avoid the brightest spaxels containing images A, B, and C and the lensed arcs. We also excluded a circular region around image D with radius 0″.5. To avoid any potential bias due to contamination from the satellite galaxy S, we excluded the spaxel at its position (ΔRA = 0″.09, ΔDec = 0″.54 from the galaxy center, Suyu et al. 2013). We also excluded pixels with S/N < 1 Å−1. In the end, the spaxels within the selected region have S/N > 1.4 Å−1 (Fig. 2 illustrates the selected region). We performed Voronoi binning using VORBIN6 given the estimated S/N values for each spaxel. In Fig. 4, we show the 41 Voronoi bins obtained by setting the target S/N ≈ 23 Å−1 for each bin. This target S/N was chosen so that the resultant S/N ≳ 20 Å−1 for each bin, which is standard practice (Fig. 4, only bin 16 has S/N ≈ 18 Å−1).
 |
Fig. 4. Left: Voronoi binning of the selected spaxels within 1″.5 from the galaxy center that avoid lensed arcs, quasar images, and the satellite galaxy S. The different colors illustrate the regions for each Voronoi bin in a cartographic manner for easier visualization, with the bin number specified within each bin. We perform the binning with a target S/N ≈ 23 Å−1 for each bin, which results in 41 bins in total. Right: resultant S/N for each Voronoi bin (red points). |
For each Voronoi bin, we measured the velocity dispersion by fitting the binned spectra using PPXF using the optimal galaxy template described above, the quasar template, and the additive Legendre polynomial to model any slight gradient in the population. A few examples of PPXF fit of the binned spectra are shown in Fig. 5.
 |
Fig. 5. PPXF fitting to the spectra from four examples of Voronoi bins. The bin number and the measured velocity dispersion for the corresponding bin are specified in each panel. The gray line presents the full spectra, the red line traces the best-fit model, and the blue line shows the quasar component in the best-fit model. |
3.3. Estimation of systematic uncertainty
To estimate the systematic uncertainties in the velocity dispersion measurement, we considered a range of plausible choices in the extraction procedure: the degrees of the additive Legendre polynomial used to correct the template continuum shape between 2 and 4; the quasar template obtained from images A, B, and C; the fitted wavelength range chosen from 3300−4200 Å, 3350−4250 Å, and 3400−4300 Å; and three sets of template spectra used in the fitting. The first set of template spectra contains the complete XSL of 628 stars. The second set contains half of the entire sample that is randomly selected, and the third set contains the other half. The numbers of stars selected by PPXF in the three sets are 39, 32, and 33, respectively. Sets 2 and 3 have 15 and 17 stars, respectively, in common with Set 1. Figure 3 shows the distribution of spectral types in all three sets and the entire library. We did not take the quasar template from image D as it is much fainter than the other images, and thus the galaxy contribution in the brightest spaxel on image D is nonnegligible. Taking a combination of all of these choices yields 81 different setups. We illustrate the shift in the extracted velocity dispersion maps for one change of setting at a time in Figs. 6 and 7.
 |
Fig. 6. Absolute difference in km s−1 between the extracted velocity dispersion from two setups that differ by one setting. The baseline setup has the range: 3400−4300 Å, polynomial degree: 3, stellar template set 1, and quasar template from image A. The different setting for each case is specified at the top of each panel. |
 |
Fig. 7. Same as Fig. 6, but the difference is normalized by the statistical uncertainty of the baseline setup. |
We estimated the variance-covariance matrix of the binned velocity dispersions from these 81 setups. To do this, we generated 1000 random realizations of the measured velocity dispersion map for each of the 81 setups using the corresponding statistical uncertainty. We created the variance-covariance matrix from the 81 000 realizations combined from all the setups. In this way, the diagonal terms of the variance-covariance matrix encode the total variance from systematic and statistical uncertainties, and the off-diagonal terms encode the systematic covariances. For example, if all 81 setups hypothetically provided the same velocity dispersion map and uncertainty, then the off-diagonal terms would be zero, and the diagonal terms would reflect only the statistical uncertainties. We show the systematic variance-covariance relative to the statistical variance in Fig. 8. The systematic variance is subdominant relative to the statistical variance (with a median of 0.47 of the ratio between systematic and statistical covariances along the diagonal) except for bins 29 and 31. These two bins are closest to quasar images A and C, and thus largely susceptible to the choice of quasar template (Figs. 6 and 7.)
 |
Fig. 8. Illustration of the systematic covariance relative to the statistical covariance. Σ is the variance-covariance matrix of the Voronoi-binned velocity dispersions (with target S/N ≈ 23 Å−1 for each bin), σstat, x is the statistical uncertainty in bin number x from our fiducial setup, and diag(σstat) is a diagonal matrix. We assume no covariance in the statistical uncertainty from each setup for kinematic measurement. Thus the off-diagonal terms in the variance-covariance matrix purely represent the systematic covariance. Most diagonal terms are < 1 (with a median of 0.47), showing that the systematic variances are subdominant to the statistical variances except for bins 29 and 31. These bins are close to images A and C. Thus, they are largely susceptible to the choice of the quasar template, as seen in Figs. 6 and 7. |
We show the velocity dispersion and mean velocity maps averaged over the 81 setups in Fig. 9. We estimated a systematic velocity of 182 km s−1 using the PAFIT7 software program (Krajnović et al. 2006) and subtracted it from the mean velocity map. The systematic velocity is the result of a slight deviation in the true redshift from the fiducial value. The mean velocity map does not show any significant evidence of ordered rotation above the systematic and statistical noise levels. Thus it is consistent with the lens galaxy being a slow rotator. We used this systematic-averaged velocity dispersion map and the variance-covariance matrix estimated above when computing the likelihood function for dynamical modeling in Sect. 5.
 |
Fig. 9. Maps of extracted velocity dispersion (top row) and mean velocity (bottom row) in Voronoi bins along with the corresponding uncertainties (right column). The Voronoi binning was tuned to achieve S/N ≈ 23 Å−1 for each bin. The illustrated maps (left column) correspond to the average values after combining 81 model setups, and the uncertainty maps correspond to the square root of the diagonal of the variance-covariance matrices. A systematic velocity of 182 km s−1 was subtracted from the mean velocity map. |
To test the impact of our choice for the Voronoi binning scheme, we adopted an alternative target S/N ≈ 28 Å−1 for each bin, which results in 27 bins. We similarly produced another set of 81 model setups in this binning scheme and produced the variance-covariance matrix for these binned velocity dispersions. We would test the systematic impact of this different binning scheme on the cosmological measurement later in Sect. 5.2. We show the difference in the extracted kinematics between the two binning schemes in Fig. 10.
 |
Fig. 10. Absolute (left) and uncertainty-normalized (right) difference in the extracted velocity dispersion between two Voronoi binning schemes. The two binning schemes are obtained by setting the target S/N to 23 Å−1 and 28 Å−1 for each bin. We take the case with target S/N ≈ 23 Å−1 for each bin as the baseline in our analysis. |
4. Overview of lens and dynamical modeling
This section reviews the theoretical formalism for lens modeling (Sect. 4.1), dynamical modeling (Sect. 4.2), cosmological inference from combining the lensing and dynamical constraints (Sect. 4.3), and the Bayesian framework (Sect. 4.4).
4.1. Lensing observables and modeling
We briefly review the strong lensing formalism in the context of time-delay cosmography in Sect. 4.1.1, describe the mass-sheet transform (MST) in Sect. 4.1.2, and explain the internal and external components of the MST in Sect. 4.1.3.
4.1.1. Strong lensing formalism
In the thin lens approximation applicable in this case, lensing observables are described using the surface mass density Σ(R) projected from the 3D mass density distribution ρ(r) in the lens galaxy. Formally, the lensing observables depend on the dimensionless convergence defined as
which is the surface mass density normalized by the critical density
Here, c is the speed of light, G is the gravitational constant, Ds is the angular diameter distance between the observer and the source, Dd is the angular diameter distance between the observer and the lens galaxy, and Dds is the angular diameter distance between the lens galaxy and the source. The on-sky deflection angle α(θ) relates to the convergence as
The time delay between two quasar images labeled A and B is given by
where θA is the angular position of image A, ς is the source’s angular position, ψ(θ) is the lensing potential, and the time-delay distance DΔt is defined as
4.1.2. Description of the MST
The MST is a mathematical transform of the convergence profile that leaves invariant all the imaging observables, such as the image positions and the flux ratios (Falco et al. 1985; Schneider & Sluse 2014). This transform scales the convergence and the unknown source position as
where λMST is the transformation parameter. The predicted time delay Δt scales under the transform as
Then, the inferred time-delay distance DΔt and the Hubble constant H0 based on the observed time delays will change as
However, the MST changes the predicted velocity dispersion, thus measuring it breaks the MSD. Notably, the MST also rescales the lensing magnifications. Thus, standardizable candles can also be used to break the MSD (Bertin & Lombardi 2006; Birrer et al. 2022b) provided that microlensing and millilensing can be mitigated (e.g., Yahalomi et al. 2017; More et al. 2017; Foxley-Marrable et al. 2018).
4.1.3. Internal and external MST
We can express the “true” (i.e., physically present) lensing mass distribution as
where κgal is the mass distribution of the central lens galaxy (or galaxies) that is (are) considered in the lens modeling, and κext is called the external convergence, which approximates the projected mass distribution of line-of-sight structures as a mass sheet. Since limθ → ∞κgal = 0 has to be satisfied, we find that limθ → ∞κtrue = κext, hence the interpretation of κext as the lensing mass far from (or, “external” to) the central deflector(s).
All the lensing observables including imaging observables result from κtrue. However, since only the central galaxies are usually considered in lens modeling with imaging observables, the lens model provides 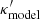 with
with 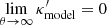 . This
. This 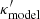 is an MST of κtrue for λMST = 1/(1 − κext) as
is an MST of κtrue for λMST = 1/(1 − κext) as
Lens mass models are usually described with simply parametrized models, such as the power law or a combination of the NFW profile and the observed stellar distribution. In that case, the assumption of a simple parametric form implicitly breaks the MSD. Therefore, the simply parametrized model κmodel can be expressed as another approximate MST of the 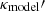 as
as
where λint is called the internal MST parameter, and κs is a “variable” mass sheet with limθ → ∞κs(θ) = 0 to ensure that both 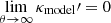 and limθ → ∞κmodel = 0 are satisfied. However, for Eq. (11) to be an approximate MST, the variable mass-sheet needs to satisfy κs(θ)≃1 within the central region that lensing observables are sensitive to θ ≲ 2θE (Schneider & Sluse 2013). This can be achieved with the formulation (Blum et al. 2020)
and limθ → ∞κmodel = 0 are satisfied. However, for Eq. (11) to be an approximate MST, the variable mass-sheet needs to satisfy κs(θ)≃1 within the central region that lensing observables are sensitive to θ ≲ 2θE (Schneider & Sluse 2013). This can be achieved with the formulation (Blum et al. 2020)
where θs ≫ θE is a scale radius where the variable mass-sheet smoothly transitions from 1 − λint to 0. This approximate MST converges to the pure MST in the limit θs → ∞. Thus, the actual mass distribution of the central deflector(s) relates to the modeled mass distribution as
The external convergence κext can be estimated by using relative number counts of line-of-sight galaxies near the central deflector(s) (e.g., Suyu et al. 2010; Greene et al. 2013; Rusu et al. 2017; Buckley-Geer et al. 2020), or by using weak lensing of distant galaxies by the line-of-sight mass distribution (e.g., Tihhonova et al. 2018). The measured velocity dispersion then constrains the internal MST parameter λint (Birrer et al. 2020; Yıldırım et al. 2021).
4.2. Dynamical modeling
In this section, we describe the Jeans anisotropic multi-Gaussian-expansion (JAM) framework to model our dynamical observable, which is the spatially resolved stellar velocity dispersion measured in Sect. 3. The orbital motions of the stars, that is, the distribution function f(x, v) of position x and velocity v, in the galactic potential Φ is described by the steady-state collisionless Boltzmann equation (Binney & Tremaine 1987, Eqs. (4)–(13)b)
We assume an axisymmetric case (i.e., ∂Φ/∂ϕ = ∂f/∂ϕ = 0 with ϕ being the polar angle in the spherical coordinate system), a spherically aligned velocity ellipsoid, and the anisotropy for each Gaussian component in the multi-Gaussian expansion (MGE; Emsellem et al. 1994; Cappellari 2002) to be spatially constant. Slow rotators such as the deflector galaxy in RXJ1131−1231 are in general expected to be weakly triaxial or oblate but never flat and instead quite close to spherical in their central parts (e.g., Cappellari 2016). For this reason, we expect the spherical alignment of the velocity ellipsoid of JAMsph (Cappellari 2020) to provide a better approximation to the galaxy dynamics than the cylindrical alignment JAMcyl solution (Cappellari 2008). Then, the above equation gives two Jeans equations in spherical coordinates (Jeans 1922; Bacon et al. 1983; de Zeeuw et al. 1996; Cappellari 2020)
where the following notations are used
Here, β is the anisotropy parameter, and the velocity dispersion ellipsoid is assumed to be spherically aligned, giving ⟨vrvθ⟩ = 0.
The line-of-sight second moment 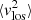 is the integral given by
is the integral given by
where S(x, y) is the surface density of the dynamical tracer. Given that there is no evidence of significant ordered rotation and the only significantly nonzero velocities are likely due to systematic errors (Fig. 9), we assume ⟨vlos⟩ = 0 and define 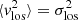 . The observed line-of-sight velocity dispersion is given a luminosity-weighted integral as
. The observed line-of-sight velocity dispersion is given a luminosity-weighted integral as
where the symbol “⊗ PSF” denotes a convolution with the PSF. In the equation above, we have chosen the surface brightness profile I(x, y) as a substitute for the surface density S(x, y) of the dynamical tracer since the constant factor between surface brightness and surface number density cancels out in this expression.
We use the dynamical modeling software JAMPY8 to compute the observed velocity dispersion by solving the Jeans equation from Eq. (15) for a given 3D potential Φ(r) and anisotropy profile β(r). Specifically, we use the jam_axi_proj() routine with the keyword align=‘sph’. We refer to Cappellari (2008, 2020) for a detailed formalism in computing Eq. (18) by JAMPY.
4.3. Cosmological inference from combining dynamical and lensing observables
We parametrize the 3D potential Φ(r) using the lens model parameters ξmass and the internal MST parameter λint to conveniently use the lens model posterior from Suyu et al. (2013) as a mass model prior in the dynamical modeling. Thus from Eq. (13), the surface mass density for our dynamical model is given by
We include DΔt and Dd as free parameters in our model, which give the critical density Σcr as
where 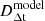 is the time-delay distance predicted by the lens mass model κmodel(θ) for the time delays observed by Tewes et al. (2013).
is the time-delay distance predicted by the lens mass model κmodel(θ) for the time delays observed by Tewes et al. (2013).
We approximate the surface mass density Σ(θ) with an MGE (Emsellem et al. 1994; Cappellari 2002; Shajib 2019) using the software program MGEFIT9. JAMPY deprojects the MGE components into an oblate or prolate spheroid with an inclination angle i (Cappellari 2002). The deprojected 3D mass density provides the 3D potential Φ for the kinematic computation. We also take the MGE of the surface brightness I(x, y) for deprojection to 3D with the inclination angle i for the kinematic computation by JAMPY.
The combination of lens imaging observables and the stellar kinematics is sensitive to λint(1 − κext)Ds/Dds (Birrer et al. 2016; Chen et al. 2021a). We apply a prior on κext using the estimated κext distribution from Suyu et al. (2014) to help break the degeneracy in distributing the total MSD into external and internal components.
4.4. Bayesian framework
According to Bayes’ theorem, the posterior of the model parameters 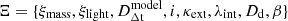 as
as
where p(𝒟 ∣ Ξ) is the likelihood given data 𝒟 and p(Ξ) is the prior. In this study, the data 𝒟 is the measured velocity dispersions in Voronoi bins (Fig. 9). The observational information from the published time delays, lens models using HST imaging, and the line-of-sight effects (Tewes et al. 2013; Suyu et al. 2013, 2014) is incorporated by adopting those previous posteriors as the prior on our model parameters. The likelihood of the observed velocity dispersion vector σlos ≡ [σ1, …, σNbin], with Nbin being the number of Voronoi bins, is given by
where Σ is the variance-covariance matrix. Specific priors used in this Bayesian framework are given in Sect. 5. We obtain the posterior probability distribution function (PDF) of the model parameters using the Markov chain Monte Carlo (MCMC) method using the affine-invariant ensemble sampler EMCEE (Goodman & Weare 2010; Foreman-Mackey et al. 2013). We ensure the MCMC chains’ convergence by running the chains for ≳20 times the autocorrelation length after the chains have stabilized (Foreman-Mackey et al. 2013).
5. Dynamical models
We first describe our baseline dynamical model in Sect. 5.1 and then perform various checks on systematics in Sect. 5.2.
5.1. Baseline dynamical model
This subsection describes the baseline settings in our dynamical model, namely the specific parametrization of the mass model (Sect. 5.1.1), the dynamical tracer profile (Sect. 5.1.2), the probability of oblate or prolate axisymmetry (Sect. 5.1.3), the inclination angle (Sect. 5.1.4), and the choice of anisotropy profile (Sect. 5.1.5).
5.1.1. Parametrization of the mass model
We adopted the power-law mass model as our baseline model. In this model, the mass profile is defined with Einstein radius θE, logarithmic slope γ, projected axis ratio qm, and position angle φmass. The convergence profile κmodel in Eq. (19) for the power-law model is given by
Here, the coordinates (θ1, θ2) are rotated by φmass from the (RA, Dec) coordinate system. We adopted the lens model posterior from Suyu et al. (2013) as a prior in our dynamical model. For simplicity, we set the position angle φmass the same as the observed position angle of light φlight. We used the estimated κext distribution for the power-law model as the prior (Fig. 3 of Suyu et al. 2014).
We set θs = 12″ (≃7.5θE) in the approximate mass-sheet κs (Eq. (12)) so that the imaging constraints alone cannot differentiate the power-law mass profile and its approximate MST from Eq. (11). We obtained this lower limit by running the JUPYTER notebook that produces Fig. 3 of Birrer et al. (2020)10. However, we adjusted the fiducial lens model parameters in the notebook to match with those for RXJ1131−1231. We took a uniform prior for the internal MST parameter λint ∼ 𝒰(0.5, 1.13). The upper limit of 1.13 was set by the requirement that the transformed mass profile under the approximate MST must be monotonic so that the MGE can approximate the transformed profile sufficiently well (Shajib et al. 2019). Previous studies also found similar or more restrictive upper limits for λint to satisfy the physical requirement of nonnegative density (Birrer et al. 2020; Yıldırım et al. 2021).
The appropriate number of MGE components for the mass or light profile was automatically chosen by JAMPY with a maximum of 20 components. We checked that the MGE approximates the input mass or light profile very well (with a maximum 1% deviation at < 10″ and maximum 10% deviation between 10″ − 50″). These deviations from the density profile have an oscillatory pattern due to the MGE approximation’s nature, except near the end of the fitted ranges. Thus, the deviation in the integrated mass profile often averages out in the line-of-sight integration up to a very large radius. We performed the MGE fitting up to 100″. Thus, the large mismatch between the MGE approximation and the original profile occurs largely outside the integration limit ∼70″. The chosen number of maximum Gaussian components is not a dominant source of numerical error. Setting this maximum number to a very high value, such as 100, shifts the computed velocity dispersion by only < 0.5% within the observed region, which is insignificant compared to the 1% numerical stability targeted by JAMPY.
5.1.2. Dynamical tracer profile
We updated the light profile fitting for the lens galaxy from Suyu et al. (2013) using a larger HST image cutout than that therein, which did not contain the full extent of the lens galaxy’s light profile (Fig. 11). The lensed arcs and quasar images were first subtracted from the cutout using the prediction of the best-fit lens model from Suyu et al. (2013). We used the software package LENSTRONOMY11 to fit the residual light distribution attributed to the lens galaxy (Birrer & Amara 2018; Birrer et al. 2021). Following Suyu et al. (2013), we used the double Sérsic model to fit the light profile, which is a superposition of two concentric Sérsic profiles. The Sérsic profile is defined as
 |
Fig. 11. Fit of the lens galaxy’s surface brightness profile. Left: the HST/ACS imaging in the F814W filter of the lens system RXJ1131−1231 with the quasar images and the lensed arcs subtracted using the prediction from the best-fit lens model from Suyu et al. (2013), thus leaving only the lens galaxy’s light to be fitted. The orange circle shows the large circular region considered for fitting in our analysis, and the yellow square shows the smaller cutout used for lens modeling by Suyu et al. (2013). The cyan annulus contains the region where pixels were fitted to reconstruct the source by Suyu et al. (2013). Thus the lensed arcs from the quasar host galaxy were subtracted only within this annulus. The red contours mark quasar image positions with significant residuals due to saturated pixels, which we mask. Middle: the fitted light profile with a double Sérsic model. The black pixels correspond to masked pixels. The additional masked pixels within the orange circle not described above are randomly selected through an iterative process that performs outlier rejection while preserving the Gaussian tail (Sect. 5.1.2 for details). Right: normalized residual of the best-fit model. |
where Ieff the amplitude, ql is the axis ratio, θeff is the effective radius, ns is the Sérsic index, and bn = 1.999n − 0.327 is a normalizing factor so that θeff becomes the half-light radius (Sérsic 1968). The coordinates (θ1, θ2) are rotated by φlight from the (RA, Dec) coordinate system.
We first masked circular regions at the quasar image positions due to slightly saturated pixels producing significant residuals in the subtracted cutout (Fig. 11). We then iteratively masked the other pixels with significant residuals above statistical expectations to effectively perform an outlier rejection while preserving the shape of a Gaussian tail. For each iteration of this process, we took a discrepancy threshold, which we decreased from 5σ to 2σ with step size 0.5σ across these iterations. We then randomly masked a subset of the pixels with residuals more than the discrepancy level at the given iteration such that the number of remaining pixels with such high residuals is statistically expected. The final masked area after the iterations is illustrated in Fig. 11. We tabulate the best-fit light model parameters in Table 1 and compare them with those from Suyu et al. (2013). The circularized half-light radius for our best-fit model is θeff = 1″.91, which is slightly larger than the value θeff = 1″.85 from Suyu et al. (2013) based on the same imaging data but from a smaller cutout (illustrated in Fig. 11). We then took the MGE of the fitted double Sérsic profile as the light distribution I(x, y) in our dynamical modeling. We propagated the uncertainties and covariances from the light profile fitting into the dynamical modeling. To do that, we sampled from the multivariate normal distribution corresponding to all the light model parameters for each call of the likelihood function within the MCMC process and then took the MGE of the light profile given the sampled parameters.
Values of the light model parameters for the double Sérsic model in our fitting of a large cutout and those from Suyu et al. (2013).
5.1.3. Oblate or prolate shape of the axisymmetry
The oblateness, prolateness, or triaxiality of a slow rotator galaxy can, in principle, be constrained from the kinematic misalignment angle Δφkin ≡ |φkin−φlight|. However, we do not detect any significant rotational pattern in the vmean map (Fig. 9). Thus, the uncertainty for the constrained kinematic major axes is too large to be meaningful, and we cannot directly constrain this galaxy’s oblateness from the data. Instead, we obtained the probability of oblateness from a population prior based on 189 slow rotator elliptical galaxies that are in the Sloan Digital Sky Survey’s (SDSS’s) Mapping Nearby Galaxies at APO (MaNGA) sample (Abolfathi et al. 2018; Graham et al. 2018). We took the distribution of Δφkin for this sample of slow rotators (Li et al. 2018), where Δφkin = 0° corresponds to a purely oblate shape, and Δφkin = 90° corresponds to a purely prolate shape. Li et al. (2018) find two distinct peaks in the distribution at Δφkin = 0° and Δφkin = 90° (Fig. 12). We, therefore, fitted the data points with a double Gaussian profile with the means set at Δφkin = 0° and Δφkin = 90° (Fig. 12 illustrates the fit). Although the slow rotators with 0° < Δφkin < 90° have triaxial shapes, we chose only oblate or prolate axisymmetric shapes in our dynamical modeling for computational simplicity. Therefore, we took Δφkin < 45° as the oblate case and Δφkin > 45° as the prolate case. We obtained the prior probability p(oblate)pop of the galaxy being oblate as
 |
Fig. 12. Population prior on kinematic misalignment angle Δφkin ≡ |φkin−φlight| for a sample of slow rotator elliptical galaxies from the SDSS’s MaNGA dataset (Li et al. 2018). Here, Δφkin = 0° corresponds to a purely oblate shape, and Δφkin = 90° corresponds to a purely prolate shape. The vertical dashed gray lines mark Δφkin = 0°, 45°, and 90°. The red points with error bars show the measurements from Li et al. (2018). We fit this distribution with a double Gaussian model (blue line) with the means fixed to Δφkin = 0° and Δφkin = 90°. We take Δφkin < 45° as the oblate case and Δφkin > 45° as the prolate case. Integrating the double Gaussian model from 0° to 45° gives the prior probability of oblateness p(oblate)pop ≃ 0.65. |
and thus p(prolate)pop = 1 − p(oblate)pop ≃ 0.35.
The JAMPY software package, by default, adopts the oblate case for deprojection. We implemented the prolate case in JAMPY by setting qprolate = 1/q > 1 and switching the x and y axes in the input coordinate system. Due to the switching of x and y axes, σ parameters of the MGEs for mass and light models were scaled as σprolate = qσ.
5.1.4. Inclination
The observed axis ratio of light ql, obs = 0.850 ± 0.002 relates to ql, int through the inclination angle i as
We imposed a prior on the intrinsic axis ratio ql, int from a sample of massive elliptical galaxies in the SDSS with stellar mass 10.8 < log10(M⋆/M⊙) < 11.5 at 0.04 < z < 0.08 (Chang et al. 2013). The distribution of ql, int by Chang et al. (2013) is different for oblate and prolate assumptions. Therefore, we adopted the specific prior corresponding to the oblate or the prolate case (Fig. 13).
 |
Fig. 13. Prior on the intrinsic axis ratio ql, int of light for oblate (solid line) and prolate (dashed line) cases from Chang et al. (2013). The priors correspond to massive elliptical galaxies from the SDSS survey at 0.04 < z < 0.08 with 10.8 < log10(M⋆/M⊙) < 11.5. |
5.1.5. Anisotropy profile
We investigated two choices to parametrize the anisotropy profile. The first choice is a single spatially constant 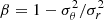 value for all the light MGE components. Numerically, we sampled σθ/σr with a uniform prior (σθ/σr)∼𝒰(0.78, 1.14). This range of σθ/σr allows −0.31 < β < 0.38. We adopted this range using the β values of eight slow rotator galaxies measured by Cappellari et al. (2007, Fig. 2). These measurements of β by Cappellari et al. (2007) are from Schwarzschild modeling of data with one of the highest S/N values in the literature, allowing to constrain the Gauss–Hermite moments up to order six. Applying the student’s t-distribution on the sample mean of this small sample, we find the 95% confidence interval of the population mean for β to be [−0.10, 0.17] and the standard deviation to be 0.16. These values infer that 95% of the population is contained within β ∈ [ − 0.31, 0.38], which we took as the boundaries of our prior range. The second choice of the anisotropy profile has two free parameters: the inner light MGE components with σ < rbreak = θeff = 1″.91 were assigned one value for (σθ/σr)inner and the outer light MGE components with σ ≥ rbreak were assigned another independent value of (σθ/σr)outer. Thus, this parametrization with two free parameters allows radial variability in the anisotropy profile. Both the inner and outer ratios had uncorrelated uniform priors (σθ/σr)∼𝒰(0.78, 1.14). For these two choices of parametrization, we computed the Bayesian information criterion (BIC) given by
value for all the light MGE components. Numerically, we sampled σθ/σr with a uniform prior (σθ/σr)∼𝒰(0.78, 1.14). This range of σθ/σr allows −0.31 < β < 0.38. We adopted this range using the β values of eight slow rotator galaxies measured by Cappellari et al. (2007, Fig. 2). These measurements of β by Cappellari et al. (2007) are from Schwarzschild modeling of data with one of the highest S/N values in the literature, allowing to constrain the Gauss–Hermite moments up to order six. Applying the student’s t-distribution on the sample mean of this small sample, we find the 95% confidence interval of the population mean for β to be [−0.10, 0.17] and the standard deviation to be 0.16. These values infer that 95% of the population is contained within β ∈ [ − 0.31, 0.38], which we took as the boundaries of our prior range. The second choice of the anisotropy profile has two free parameters: the inner light MGE components with σ < rbreak = θeff = 1″.91 were assigned one value for (σθ/σr)inner and the outer light MGE components with σ ≥ rbreak were assigned another independent value of (σθ/σr)outer. Thus, this parametrization with two free parameters allows radial variability in the anisotropy profile. Both the inner and outer ratios had uncorrelated uniform priors (σθ/σr)∼𝒰(0.78, 1.14). For these two choices of parametrization, we computed the Bayesian information criterion (BIC) given by
where k is the number of free model parameters, Nbin is the number of data points, and 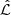 is the maximum likelihood. We approximated
is the maximum likelihood. We approximated 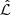 from the highest likelihood value sampled in the MCMC chain. The single-parameter β model provides the lowest BIC value excluding the two-parameter β model with ΔBIC ≈ 3.7 (i.e., positively excluded; Raftery 1995). We checked that the difference between the highest and the second highest likelihood values among the MCMC samples is negligibly smaller than ΔBIC, thus this ΔBIC value is robust against our approximation of
from the highest likelihood value sampled in the MCMC chain. The single-parameter β model provides the lowest BIC value excluding the two-parameter β model with ΔBIC ≈ 3.7 (i.e., positively excluded; Raftery 1995). We checked that the difference between the highest and the second highest likelihood values among the MCMC samples is negligibly smaller than ΔBIC, thus this ΔBIC value is robust against our approximation of 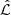 from the highest likelihood value in the sampled chain. The nondetection of varying anisotropy in our data is consistent with that observed in nearby elliptical galaxies, as even high-S/N SAURON data for a large sample of galaxies are accurately described by JAM models with constant anisotropy, as used here, within the noise of the kinematics (e.g., Cappellari et al. 2013). We compared the posterior distributions of the model parameters for the two anisotropy models in Fig. 14. An example of a best-fit kinematic model and the corresponding residual with the single-parameter β model and oblate axisymmetry is illustrated in Fig. 15. The reduced
from the highest likelihood value in the sampled chain. The nondetection of varying anisotropy in our data is consistent with that observed in nearby elliptical galaxies, as even high-S/N SAURON data for a large sample of galaxies are accurately described by JAM models with constant anisotropy, as used here, within the noise of the kinematics (e.g., Cappellari et al. 2013). We compared the posterior distributions of the model parameters for the two anisotropy models in Fig. 14. An example of a best-fit kinematic model and the corresponding residual with the single-parameter β model and oblate axisymmetry is illustrated in Fig. 15. The reduced 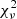 value is 0.83 with ν = 41 degrees of freedom. The distribution of residuals is similar to a normal distribution expected from a perfect model for data with Gaussian noise, illustrating that our model is appropriate for the data. We show the range of velocity dispersion radial profiles sampled by our model in Fig. 16 and compare it with the radially averaged measurements of the velocity dispersion. This illustration shows that our model reproduces the uncertainty range of the measurement.
value is 0.83 with ν = 41 degrees of freedom. The distribution of residuals is similar to a normal distribution expected from a perfect model for data with Gaussian noise, illustrating that our model is appropriate for the data. We show the range of velocity dispersion radial profiles sampled by our model in Fig. 16 and compare it with the radially averaged measurements of the velocity dispersion. This illustration shows that our model reproduces the uncertainty range of the measurement.
 |
Fig. 14. Constraints from axisymmetric JAM modeling on the power-law mass model parameters (θE, γ, and qm), internal MST parameter λint, external convergence κext, anisotropy profile parameter(s), and the cosmological distances DΔt and Dd. assuming two anisotropy parametrizations: (i) one single constant β ≡ 1 − (σθ/σr)2 for all light MGE components (orange contours), and (ii) one free (σθ/σr)inner ≡ (σθ/σr) for light MGE components with σ < rbreak = θeff = 1″.91 and another free (σθ/σr)outer for light MGE components with σ > rbreak (blue contours). The blinded parameters are blinded as pblinded ≡ p/⟨p⟩−1 so that the distributions only reveal fractional uncertainties. The darker and lighter shaded regions in the 2D plots trace 68% and 95% credible regions, respectively. The mass model parameters Einstein radius θE, power-law slope γ, axis ratio q, and position angle PA are additionally constrained through a prior from the imaging data from Suyu et al. (2013). The two anisotropy parametrizations provide equally good fits to the kinematics data. However, the BIC selects the constant-β anisotropy model over the other one with one additional free parameter (ΔBIC value is 3.5). |
 |
Fig. 15. Observed velocity dispersion map in Voronoi bins (first panel), the best-fit dynamical model with a power-law mass model, constant β anisotropy profile, and oblate shape (second panel), the normalized residual for the best-fit dynamical model (third panel), and the distribution of the normalized residual (orange, fourth panel). The reduced χ2 quantity is |
 |
Fig. 16. Radial profile of the line-of-sight velocity dispersion. The red points are radially binned values from the 2D maps, with the horizontal error bars illustrating the widths of the annuli. The lines show the radial profiles for random samples from the dynamical model posterior. The radial profile of the model is averaged over the major, minor, and intermediate axes. The solid purple lines correspond to 65 random samples for the oblate case, and the dashed green lines correspond to 35 random samples for the prolate case. We note that the model was fit to the 2D kinematics data. However, we illustrate the 1D radial profile only for visualization. |
5.2. Checking potential systematics due to modeling choices
This section describes several checks performed on potential systematics for different choices in the dynamical model setup.
5.2.1. Comparison between power-law and composite mass models
In addition to the power-law mass model, Suyu et al. (2014) also adopted a composite mass model individually describing the lens galaxy’s dark matter and baryonic components. The dark matter distribution was modeled with an elliptical NFW profile in the potential. The parameters in this profile are the normalization of the NFW component κs, the NFW scale radius rscale, and the mass axis ratio qm. The baryonic component was modeled with a mass-follow-light profile with a free mass-to-light ratio (M/L) parameter. Thus, this mass model parametrization has one more free parameter than the power-law model. We refer to Suyu et al. (2014) for parametric definitions of these profiles. We implemented this composite mass profile as 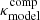 in Eq. (19) and adopted the model posterior from Suyu et al. (2014) as a prior in our model. We appropriately converted the ellipticity defined in the potential by Suyu et al. (2014) to an ellipticity defined in the convergence in our model. We took the MGE of this composite surface density model as done for the power-law surface density model. However, since the dark matter and baryonic components have different ellipticities, we took the MGE of each component separately to preserve the ellipticity information in deprojection. Specifically, We took the MGE of the approximate MST with λint of the dark matter profile and the MGE of an accordingly rescaled baryonic profile, which effectively results in the total mass profile being transformed as the approximate MST with λint.
in Eq. (19) and adopted the model posterior from Suyu et al. (2014) as a prior in our model. We appropriately converted the ellipticity defined in the potential by Suyu et al. (2014) to an ellipticity defined in the convergence in our model. We took the MGE of this composite surface density model as done for the power-law surface density model. However, since the dark matter and baryonic components have different ellipticities, we took the MGE of each component separately to preserve the ellipticity information in deprojection. Specifically, We took the MGE of the approximate MST with λint of the dark matter profile and the MGE of an accordingly rescaled baryonic profile, which effectively results in the total mass profile being transformed as the approximate MST with λint.
This mass model with one more free parameter than the power-law model has a higher BIC score with ΔBIC = 3.8. Thus, the BIC excludes the composite model with positive evidence (Raftery 1995). The median values of Dd from the power-law and composite mass models differ by 0.9% (0.07σ, Fig. 17), and the median DΔt values differ by 1.26% (0.06σ). Therefore, we conclude that our power-law mass model with an additional degree of freedom to scale with the MST robustly describes the observed data.
 |
Fig. 17. Comparison of the constrained Dd from power-law (blue contours) and composite (orange contours) mass models. The blinded parameters are blinded as pblinded ≡ p/⟨p⟩−1 so that the distributions only reveal fractional uncertainties. The darker and lighter shaded regions in the 2D plots trace 68% and 95% credible regions, respectively. |
5.2.2. Comparison between prolate and oblate axisymmetry
We compare the inferred Dd between the purely oblate and purely prolate cases in the deprojected 3D spheroidal shape of the mass and light models in Fig. 18. The median Dd values from these two cases differ by 3.6% (0.3σ), and the median DΔt values differ by 0.94% (0.04σ). Our final distance posterior is the combination of oblate and prolate cases, with weights p(oblate)pop = 0.65 and 1 − p(oblate)pop = 0.35, respectively. Thus, this difference between the oblate and prolate cases is marginalized in our final cosmological distance posterior.
 |
Fig. 18. Comparison of the constrained Dd between oblate (blue) and prolate (blue) cases of the deprojected spheroidal shape in the dynamical model. The blinded parameters are blinded as pblinded ≡ p/⟨p⟩−1 so that the distributions only reveal fractional uncertainties. The darker and lighter shaded regions in the 2D plots trace 68% and 95% credible regions, respectively. |
We also compare the predictions from axisymmetric and spherical mass models in Fig. 18. The median Dd from the spherical model matches very well with the axisymmetric prolate model, but the median DΔt differs by 2.0% (0.08σ). The galaxy is only mildly elliptical in projection (ql ∼ 0.85), and the resulting axisymmetric models are not very flat. For this reason, the relatively small difference between the axisymmetric and spherical models is not surprising.
5.2.3. Comparison between Voronoi binning schemes
Here, we compare the Voronoi binning schemes with two choices for the target S/N in each bin: ≈23 Å−1 and ≈28 Å−1. The two cases match very well with only a 0.21% difference (0.02σ) in the median values of Dd (Fig. 19) and 0.28% difference (0.01σ) in the median DΔt values. As a result, we conclude that our choice of the Voronoi binning scheme is not a significant source of systematic error in our analysis.
 |
Fig. 19. Comparison of the constrained Dd between two choices of the target S/N for each bin in the Voronoi binning scheme. The blinded parameters are blinded as pblinded ≡ p/⟨p⟩−1 so that the distributions only reveal fractional uncertainties. The darker and lighter shaded regions in the 2D plots trace 68% and 95% credible regions, respectively. |
Based on the systematics tests performed above, we adopted a robust final distance posterior from the model with the power-law parametrization for the mass profile that the approximate internal MST is applied to. We marginalize the oblate and prolate axisymmetrical cases by combining the posteriors from these two choices with weights of 0.65 and 0.35, respectively. In the next section, we present the unblinded values from the distance posterior and infer the value of H0 from it.
6. Cosmological inference
We inferred cosmological parameters from the joint distribution of Dd and DΔt, accounting for their covariance. The unblinded point estimates of these distances are 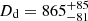 Mpc (a 9.6% measurement) at zd = 0.295, and
Mpc (a 9.6% measurement) at zd = 0.295, and 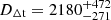 Mpc (a 17% measurement) for zs = 0.657.
Mpc (a 17% measurement) for zs = 0.657.
We inferred H0 and Ωm from our distance posterior for a flat ΛCDM cosmology (Fig. 20, left panel). We left the exploration of more exotic cosmologies based on our distance posterior for future studies. We approximated the likelihood function ℒ(H0, Ωm ∣ Dd, DΔt) of the cosmological parameters using a 2D Gaussian kernel density estimate (KDE) from the 2D distance posterior. We adopted two choices of prior for Ωm: one is a uniform prior Ωm ∼ 𝒰(0.05, 0.5), and the other is a Gaussian prior Ωm ∼ 𝒩(0.334, 0.018) from the Pantheon+ analysis of type Ia supernovae relative distances (Brout et al. 2022). We inferred the posterior joint PDF of H0 and Ωm by performing MCMC sampling using EMCEE, given the likelihood function and prior choice.
 |
Fig. 20. Unblinded cosmological constraints from our analysis. Left: final 2D posterior of the time-delay distance DΔt and the angular diameter distance Dd (emerald contour). The darker and lighter shaded regions in the 2D plots trace 68% and 95% credible regions, respectively. We infer H0 and Ωm from this distance posterior accounting for the covariance in a flat ΛCDM cosmology. We take a wide uniform prior on H0 ∼ 𝒰(0, 150) km s−1 Mpc−1. The blue-shaded region corresponds to a uniform prior Ωm ∼ 𝒰(0.05, 0.5) and the orange-shaded region corresponds to a Gaussian prior Ωm ∼ 𝒩(0.334, 0.018) from the Pantheon+ analysis of type Ia supernovae relative distances (Brout et al. 2022). Right: posterior PDF of H0 and Ωm in flat ΛCDM cosmology. We constrain H0 to 9.4% and 9.1% precision for the uniform and Pantheon+ Ωm-priors, respectively. We show the cosmological parameter posterior from only the 1D Dd posterior with dashed contours with colors matching the associated Ωm prior. In this case, the H0 precision is 10.3% and 9.6% for the uniform and Gaussian priors, respectively. The Dd-only constraint on the H0 is lower by ∼1.4% (0.15σ) than the constraint from the full 2D posterior, for the uniform Ωm-prior. |
We find 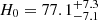 km s−1 Mpc−1 (a 9.4% measurement) with the uniform Ωm-prior, and
km s−1 Mpc−1 (a 9.4% measurement) with the uniform Ωm-prior, and 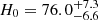 km s−1 Mpc−1 (a 9.1% measurement) with the Pantheon+ Ωm-prior (solid contours in the right panel of Fig. 20). We show the DΔt − Dd region allowed by our priors in the left panel of Fig. 20, which also shows the region allowed by our distance posterior that provides information for the cosmological inference. Other cosmological models beyond flat ΛCDM (e.g., Bonvin et al. 2017; Wong et al. 2020) or combining other cosmological probes in a cosmology-independent manner (e.g., Taubenberger et al. 2019) can utilize the additional cosmological information contained by our full 2D posterior outside the regions probed by our cosmological priors.
km s−1 Mpc−1 (a 9.1% measurement) with the Pantheon+ Ωm-prior (solid contours in the right panel of Fig. 20). We show the DΔt − Dd region allowed by our priors in the left panel of Fig. 20, which also shows the region allowed by our distance posterior that provides information for the cosmological inference. Other cosmological models beyond flat ΛCDM (e.g., Bonvin et al. 2017; Wong et al. 2020) or combining other cosmological probes in a cosmology-independent manner (e.g., Taubenberger et al. 2019) can utilize the additional cosmological information contained by our full 2D posterior outside the regions probed by our cosmological priors.
For comparison, we also performed cosmological inference using only the 1D posterior of Dd (dashed contours in right panel of Fig. 20). This gives 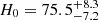 km s−1 Mpc−1 (a 10.3% measurement) for the uniform Ωm-prior, and
km s−1 Mpc−1 (a 10.3% measurement) for the uniform Ωm-prior, and 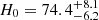 km s−1 Mpc−1 (a 9.6% measurement) for the Pantheon+ Ωm-prior. The Dd-only constraints are lower by ∼1.4% (0.15σ) than that from the full 2D distance posterior (for the uniform Ωm-prior). This slight difference arises from the projection difference of the 2D posterior along the Dd direction and along the narrow track allowed by our choice of cosmological priors.
km s−1 Mpc−1 (a 9.6% measurement) for the Pantheon+ Ωm-prior. The Dd-only constraints are lower by ∼1.4% (0.15σ) than that from the full 2D distance posterior (for the uniform Ωm-prior). This slight difference arises from the projection difference of the 2D posterior along the Dd direction and along the narrow track allowed by our choice of cosmological priors.
7. Discussion
We now compare our results with previous works (Sect. 7.1), discuss the improvement of the constraint in this paper over single-aperture stellar kinematics (Sect. 7.2), and describe the limitations of this work (Sect. 7.3).
7.1. Comparison with previous time-delay H0 measurements
Our measured value 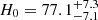 km s−1 Mpc−1 is consistent with previous measurements from lensing time delays with different treatments of the MSD (as illustrated in Fig. 21). These previous studies can be divided into two approaches: the first breaks the MSD by assuming simple parametric mass profiles such as the power law or composite (i.e., NFW halo and stars with constant mass-to-light ratio), and the second breaks the MSD based solely on stellar kinematics. Our study belongs to the second approach by allowing the freedom in the model to be maximally degenerate with H0 and constraining it solely from the spatially resolved stellar kinematics. However, it is illustrative to compare our result with the first approach to discuss the validity of their mass model assumptions.
km s−1 Mpc−1 is consistent with previous measurements from lensing time delays with different treatments of the MSD (as illustrated in Fig. 21). These previous studies can be divided into two approaches: the first breaks the MSD by assuming simple parametric mass profiles such as the power law or composite (i.e., NFW halo and stars with constant mass-to-light ratio), and the second breaks the MSD based solely on stellar kinematics. Our study belongs to the second approach by allowing the freedom in the model to be maximally degenerate with H0 and constraining it solely from the spatially resolved stellar kinematics. However, it is illustrative to compare our result with the first approach to discuss the validity of their mass model assumptions.
 |
Fig. 21. Comparison of our 9.4% H0 measurement (red, |
Following the first approach, Suyu et al. (2013, 2014) measured 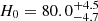 km s−1 Mpc−1 from this same system RXJ1131−1231 with simple parametric mass profiles using HST imaging. Chen et al. (2019) combined the HST imaging and adaptive-optics-assisted imaging from the Keck Telescope to measure
km s−1 Mpc−1 from this same system RXJ1131−1231 with simple parametric mass profiles using HST imaging. Chen et al. (2019) combined the HST imaging and adaptive-optics-assisted imaging from the Keck Telescope to measure 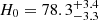 km s−1 Mpc−1. Although these studies used single-aperture stellar kinematics, the MSD was already broken by the assumption of parametric mass profiles, and the single-aperture velocity dispersion helped tighten the constraint and made the inferred H0 values from the power-law and composite models more consistent (Suyu et al. 2014). Our measured value – albeit with a larger uncertainty due to the maximal freedom allowed in the mass model – has a median value very close to these previous measurements. Such a good agreement in the medians suggests that these previous studies’ simple parametric mass models are close to the ground truth, and no bias is detected within the precision afforded by the data. Future spatially resolved velocity dispersion measurements for more time-delay lens systems or better quality data for this system – for example, from the James Webb Space Telescope (JWST) – will allow us to make a more definitive statement on the validity of the parametric mass model assumptions.
km s−1 Mpc−1. Although these studies used single-aperture stellar kinematics, the MSD was already broken by the assumption of parametric mass profiles, and the single-aperture velocity dispersion helped tighten the constraint and made the inferred H0 values from the power-law and composite models more consistent (Suyu et al. 2014). Our measured value – albeit with a larger uncertainty due to the maximal freedom allowed in the mass model – has a median value very close to these previous measurements. Such a good agreement in the medians suggests that these previous studies’ simple parametric mass models are close to the ground truth, and no bias is detected within the precision afforded by the data. Future spatially resolved velocity dispersion measurements for more time-delay lens systems or better quality data for this system – for example, from the James Webb Space Telescope (JWST) – will allow us to make a more definitive statement on the validity of the parametric mass model assumptions.
Following the second approach, Birrer et al. (2016) analyzed this same system RXJ1131−1231 using HST imaging and single-aperture velocity dispersion. These authors marginalized the effect of MSD by incorporating a prior on the source but found that the H0 posterior strongly depends on the shape of the anisotropy prior. These authors used two different choices for this prior to find 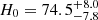 km s−1 Mpc−1 and
km s−1 Mpc−1 and 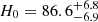 km s−1 Mpc−1. This large difference illustrates that single aperture velocity dispersion imposes only a weak constraint on the anisotropy profile and, thus, on the MSD. This result highlights the need for spatially resolved velocity dispersion, such as the one presented in this study. Our measured H0 has a precision of 9% while allowing the data to constrain the MSD effect that is maximally degenerate with H0, illustrating the power of spatially resolved kinematics in constraining the anisotropy profile and the MSD, despite the seeing-limited nature of our data. In the future, exquisite data from the JWST will provide an even more dramatic improvement (4% H0 precision forecasted, Yıldırım et al. 2021).
km s−1 Mpc−1. This large difference illustrates that single aperture velocity dispersion imposes only a weak constraint on the anisotropy profile and, thus, on the MSD. This result highlights the need for spatially resolved velocity dispersion, such as the one presented in this study. Our measured H0 has a precision of 9% while allowing the data to constrain the MSD effect that is maximally degenerate with H0, illustrating the power of spatially resolved kinematics in constraining the anisotropy profile and the MSD, despite the seeing-limited nature of our data. In the future, exquisite data from the JWST will provide an even more dramatic improvement (4% H0 precision forecasted, Yıldırım et al. 2021).
We also compare our result with the measured values of H0 from the current TDCOSMO sample of seven time-delay lenses. With the power-law mass model assumptions, the combination of seven time-delay lenses gives a 2% measurement with 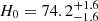 km s−1 Mpc−1 (Wong et al. 2020; Millon et al. 2020b). However, relaxing this mass profile assumption and constraining the MSD solely from the single-aperture stellar kinematics of the TDCOSMO sample leads to a 9% uncertainty on the resultant
km s−1 Mpc−1 (Wong et al. 2020; Millon et al. 2020b). However, relaxing this mass profile assumption and constraining the MSD solely from the single-aperture stellar kinematics of the TDCOSMO sample leads to a 9% uncertainty on the resultant 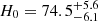 km s−1 Mpc−1. In this study, we achieve the same 9% precision from a single system, highlighting the superb constraining power of spatially resolved kinematics over single-aperture ones.
km s−1 Mpc−1. In this study, we achieve the same 9% precision from a single system, highlighting the superb constraining power of spatially resolved kinematics over single-aperture ones.
It is also worth comparing with the result obtained by Birrer et al. (2020) when combining the seven TDCOSMO lenses with information obtained from the external SLACS sample of non-time-delay lenses, 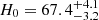 km s−1 Mpc−1. Given the uncertainties, our new measurement is not statistically inconsistent with that result, although the difference is clearly important from a cosmological standpoint. With the data in hand, we cannot conclude whether (a) the difference is real and the SLACS sample cannot, therefore, be combined with the TDCOSMO sample, or whether (b) it is due to a statistical fluctuation. This study demonstrates that, as we gather more and better data for spatially resolved kinematics and external samples of nonlenses, we will soon be able to conclude whether the difference is real or not.
km s−1 Mpc−1. Given the uncertainties, our new measurement is not statistically inconsistent with that result, although the difference is clearly important from a cosmological standpoint. With the data in hand, we cannot conclude whether (a) the difference is real and the SLACS sample cannot, therefore, be combined with the TDCOSMO sample, or whether (b) it is due to a statistical fluctuation. This study demonstrates that, as we gather more and better data for spatially resolved kinematics and external samples of nonlenses, we will soon be able to conclude whether the difference is real or not.
In the context of the Hubble tension, our new measurement strengthens the tension by reaffirming the previously obtained time-delay H0 measurements that agreed with other local measurement values, for example, from SH0ES (Riess et al. 2022). Although the 9% uncertainty in H0 from our measurement alone is not sufficient to resolve the tension, it demonstrates that time-delay cosmography can provide a powerful independent perspective with the help of future data from telescopes such as Keck, JWST, and the extremely large telescopes (e.g., Shajib et al. 2018; Yıldırım et al. 2021; Birrer & Treu 2021). We cannot help noticing that the median of our measurement is somewhat higher than the mean of the local values (∼73 km s−1 Mpc−1). However, the difference is not significant, given the uncertainties. Therefore our likely explanation is that the difference originates from the inevitable statistical fluctuation pertaining to this system, as the initial H0 measurements using simple parametric assumption all provided such higher values (Suyu et al. 2013, 2014; Birrer et al. 2016; Chen et al. 2019). We conclude by stressing that some dispersion around the mean is, of course, expected, and indeed Millon et al. (2020b) shows that the seven TDCOSMO lenses scatter around the mean by an amount consistent with the estimated errors.
7.2. Improvement from the spatial resolution of the stellar kinematics
We investigate the improvement in constraints provided by the spatially resolved nature of the stellar kinematics presented in this paper over the unresolved or single-aperture case. Suyu et al. (2013) presented a single-aperture measurement of the line-of-sight velocity dispersion σlos = 323 ± 20 km s−1 obtained within a 0″.81 × 0″.7 aperture with a 0″.7 seeing. This measurement was from the Low-Resolution Imaging Spectrometer (LRIS; Oke et al. 1995) on the Keck Observatory. The probed wavelength range was ∼3900−4700 Å, which probed mostly the redward range of the Ca H&K lines with a little overlap with the range probed by our data (i.e., 3300−4200 Å). If we take a luminosity-weighted-sum of the spatially resolved velocity dispersion map within the same 0″.81 × 0″.7 aperture, we get 288 ± 5 km s−1, which is 1.7σ (11%) lower than the previous single-aperture measurement. Although the 1.7σ difference is not statistically significant, some parts of it can be due to potential systematics in the kinematic extraction procedure or due to different wavelength ranges probed. Considering systematics, the minimum error on velocity dispersion measurements is generally assumed to be 5%, even for very high-S/N data.
However, to illustrate the improvement in precision from the spatially resolved nature of the velocity dispersion presented in this study, we took a fiducial single-aperture measurement value of 288 ± 18 km s−1. This mean value is from the luminosity-weighted sum within the single aperture mentioned above, and the 18 km s−1 uncertainty comes from applying the 6% uncertainty of the 323 ± 20 km s−1 measurement on the fiducial mean. We took the galaxy’s major axis to align with the rectangular aperture’s longer side. Rotating the aperture by 90° only changes the predicted velocity dispersion integrated within the aperture by ≲0.1%, which is unsurprising given the mild ellipticity (ql ∼ 0.85) of the galaxy and the 0″.96 seeing. We compare the key dynamical model parameters between the spatially resolved and single-aperture cases in Fig. 22. As expected, the internal MST parameter λint and the anisotropy profile parameter σθ/σr are almost completely unconstrained in the case of the single-aperture stellar kinematics due to the mass-anisotropy degeneracy (Treu & Koopmans 2002; Courteau et al. 2014). However, the angular diameter distance Dd can be constrained to 15.7% precision, largely by the anisotropy prior (cf. the 9.6% constraint on Dd from the spatially resolved data). This single-aperture precision level on Dd agrees very well with the 17.9% precision on Dd (=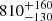 Mpc) obtained by Jee et al. (2019) from the same system RXJ1131−1231 based on the previously available single-aperture stellar kinematics mentioned above. The Hubble constant H0 can be inferred to 12.5% precision with the uniform Ωm prior from the full 2D posterior of the fiducial single-aperture case. The improvement in H0 precision (by ∼3%) from the spatially resolved kinematics, however, does not appear to be dramatic, this is because the projection of DΔt − Dd posterior along the narrow track allowed by our chosen prior happens to give a small difference between the two cases. The improvement could have appeared more drastic if the full 2D posterior had a different orientation from the prior region. In reality, the full cosmological information (illustrated by the area enclosed within the 95% contour) contained by the single-aperture data is much less than that from the spatially resolved data presented in this study (Fig. 22).
Mpc) obtained by Jee et al. (2019) from the same system RXJ1131−1231 based on the previously available single-aperture stellar kinematics mentioned above. The Hubble constant H0 can be inferred to 12.5% precision with the uniform Ωm prior from the full 2D posterior of the fiducial single-aperture case. The improvement in H0 precision (by ∼3%) from the spatially resolved kinematics, however, does not appear to be dramatic, this is because the projection of DΔt − Dd posterior along the narrow track allowed by our chosen prior happens to give a small difference between the two cases. The improvement could have appeared more drastic if the full 2D posterior had a different orientation from the prior region. In reality, the full cosmological information (illustrated by the area enclosed within the 95% contour) contained by the single-aperture data is much less than that from the spatially resolved data presented in this study (Fig. 22).
 |
Fig. 22. Comparison of the distance constraints between spatially resolved velocity dispersion and single-aperture velocity dispersion. Here, the integrated velocity dispersion is taken as the fiducial value of 287 ± 18 km s−1 to match the mean of our spatially resolved measurement, but the uncertainty of a single-aperture velocity dispersion measurement (Suyu et al. 2013). The darker and lighter shaded regions in the 2D plots trace 68% and 95% credible regions, respectively. The single-aperture velocity dispersion cannot constrain the anisotropy profile parameter σθ/σr and the internal MST parameter λint, with both limited by the prior. As a result, the DΔt − Dd posterior is constrained much more weakly. |
7.3. Limitations of this study
One limitation of our study is the data quality. Although our data are the first of their kind from a cutting-edge ground-based facility such as the Keck Observatory, there are opportunities to obtain better-quality data. The KCWI instrument is seeing-limited. Thus the S/N on the lensing galaxy is degraded by contamination from the nearby quasars, and the spatial resolution of the velocity dispersion map is limited by the seeing. Adaptive-optics-assisted IFU spectroscopy from the ground or observations from space, for example, with the JWST, can deliver exquisite spatially resolved data for improved H0 precision in the future (Yıldırım et al. 2020, 2021).
Future data with higher spatial resolution will be particularly powerful in constraining the anisotropy profile better. Our measurement has only weak constraints on the anisotropy profile, which is largely bounded by the adopted uniform prior (Fig. 14). This prior was obtained from a sample of eight local massive ellipticals with one of the highest quality spatially resolved kinematics. However, this is a small sample size. A tighter anisotropy prior from larger samples of massive ellipticals, even better if they are from a redshift range that matches with the one for our system, will be helpful to mitigate further the degeneracy induced by the anisotropy profile, that is, the mass-anisotropy degeneracy (Treu & Koopmans 2002; Courteau et al. 2014).
8. Conclusion
We measured the spatially resolved stellar velocity dispersion of the lens galaxy in RXJ1131−1231 using the KCWI IFU spectrograph on the Keck Observatory. We combined the new spatially resolved stellar kinematics with previously obtained lens models derived from HST imaging data, observed time delays, and estimated line-of-sight lensing effects (i.e., the external convergence) to infer H0. Combining the spatially resolved velocity dispersion with lens imaging and time delays simultaneously alleviates the MSD in the measured DΔt and additionally measures the angular diameter distance Dd.
We blindly performed the dynamical modeling and cosmographic inference to prevent conscious or unconscious experimenter bias. We unblinded the H0 value after all the co-authors had agreed on the modeling choices after various checks on systematics and the analysis had been frozen. The main conclusions from our study are as follows:
-
The 2D distance posterior of Dd and DΔt gives
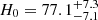 km s−1 Mpc−1 for a uniform prior on Ωm ∼ 𝒰(0.05, 0.5), and
km s−1 Mpc−1 for a uniform prior on Ωm ∼ 𝒰(0.05, 0.5), and 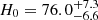 km s−1 Mpc−1 for a Gaussian prior on Ωm from the Pantheon+ analysis (Brout et al. 2022).
km s−1 Mpc−1 for a Gaussian prior on Ωm from the Pantheon+ analysis (Brout et al. 2022). -
Our 9.4% measurement from a single system with spatially resolved kinematics provides a similar precision as, and is in excellent agreement with, the current TDCOSMO sample of seven time-delay lenses based only on single-aperture stellar kinematics (H0 =
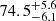 km s−1 Mpc−1, Birrer et al. 2020). We note that the system RXJ1131−1231 analyzed here is part of that sample of seven.
km s−1 Mpc−1, Birrer et al. 2020). We note that the system RXJ1131−1231 analyzed here is part of that sample of seven. -
The median value of H0 from our analysis is very close to the previously inferred values assuming simple parametric mass models (e.g., H0 =
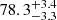 km s−1 Mpc−1, Chen et al. 2019). Thus we do not detect any potential bias in those mass profile assumptions within the precision afforded by our data.
km s−1 Mpc−1, Chen et al. 2019). Thus we do not detect any potential bias in those mass profile assumptions within the precision afforded by our data. -
Our measurement is in excellent agreement with that obtained by Millon et al. (2020a), based on the standard assumption of simply parameterized forms for the mass density profile of the lens to break the MSD (
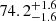 km s−1 Mpc−1).
km s−1 Mpc−1).
In conclusion, our study provides an important validation of previous work by our collaboration on the determination of H0 from time-delay cosmography (summarized in Fig. 21). This analysis also showcases the power of spatially resolved kinematics in breaking the degeneracies that limit the H0 precision when mass profile assumptions on the galaxy density profile are relaxed. As the first application of such methodology performed on real data, this study is an important proof of concept to pioneer future studies on many more time-delay lens systems.
In the broader context of the Hubble tension, the measurement presented here is on the high end of the distribution. However, the precision is insufficient to rule out the values below 70 km s−1 Mpc−1, which is generally favored by early-Universe probes (Abdalla et al. 2022). Larger samples of time-delay lenses with spatially resolved kinematics are needed to reach a conclusive answer without making assumptions about the mass density profile of the deflectors. With JWST data already scheduled to be obtained and additional ground-based data similar to those presented here for 7 systems, ∼3% precision should be attainable in a relatively short time scale (Birrer & Treu 2021). Beyond that, a sample of ∼40 lensed quasars or supernovae with spatially resolved kinematics can provide the ∼1.2% precision on H0 that is necessary to resolve or confirm the Hubble tension at 5σ confidence level, with maximally flexible models, thanks to spatially resolved stellar kinematics (Birrer & Treu 2021).
Developed by Luca Rizzi, Don Neill, Max Brodheim; https://kcwi-drp.readthedocs.io/
We quantitatively verified that the shape of the instrumental LSF is Gaussian (cf. Fig. 28 of Morrissey et al. 2018). Thus, the treatment of the instrumental LSF in PPXF is self-consistent and avoids any systematic bias due to inconsistent definitions of the LSF’s FWHM (Robertson 2013).
Acknowledgments
We thank Elizabeth Buckley-Geer, Thomas E. Collett, Philip J. Marshall, and Chiara Spiniello for useful discussions and comments that improved this study and the manuscript. Support for this work was provided by NASA through the NASA Hubble Fellowship grant HST-HF2-51492 awarded to AJS by the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Inc., for NASA, under contract NAS5-26555. T.T. and G.C.F.C. acknowledge support by National Science Foundation (NSF) through grants AST-1906976 and AST-1836016, and from the Moore Foundation through grant 8548. P.M. and C.D.F. acknowledge support for this work from the NSF under grant AST-1907396. S.H.S. thanks the Max Planck Society for support through the Max Planck Research Group and the Max Planck Fellowship. S.H.S. is supported in part by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311. This project has received funding from SNSF and from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (COSMICLENS: grant agreement No. 787886). V.N.B. gratefully acknowledges assistance from NSF Research at Undergraduate Institutions (RUI) grant AST-1909297. We note that findings and conclusions do not necessarily represent views of the NSF. This work used computational and storage services associated with the Hoffman2 Shared Cluster provided by UCLA Institute for Digital Research and Education’s Research Technology Group. The data presented herein were obtained at the W. M. Keck Observatory, which is operated as a scientific partnership among the California Institute of Technology, the University of California and the National Aeronautics and Space Administration. The Observatory was made possible by the generous financial support of the W. M. Keck Foundation. The authors wish to recognize and acknowledge the very significant cultural role and reverence that the summit of Maunakea has always had within the indigenous Hawaiian community. We are most fortunate to have the opportunity to conduct observations from this mountain. This research made use of JAMPY (Cappellari 2008, 2020), PPXF (Cappellari 2017, 2022), PAFIT (Krajnović et al. 2006), VORBIN (Cappellari & Copin 2003), MGEFIT (Cappellari 2002), LENSTRONOMY (Birrer & Amara 2018; Birrer et al. 2021), NUMPY (Oliphant 2015), SCIPY (Jones et al. 2001), ASTROPY (Astropy Collaboration 2013, 2018), JUPYTER (Kluyver et al. 2016), MATPLOTLIB (Hunter 2007), SEABORN (Waskom et al. 2014), EMCEE (Foreman-Mackey et al. 2013), and GETDIST (https://github.com/cmbant/getdist).
References
- Abdalla, E., Abellán, G. F., Aboubrahim, A., et al. 2022, J. High Energy Astrophys., 34, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Abolfathi, B., Aguado, D. S., Aguilar, G., et al. 2018, ApJS, 235, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Aiola, S., Calabrese, E., Maurin, L., et al. 2020, JCAP, 2020, 047 [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A. M., et al.) 2018, AJ, 156, 123 [Google Scholar]
- Avila, R., Koekemoer, A., Mack, J., & Fruchter, A. 2015, Instrument Science Report WFC3 2015-04, 17 [Google Scholar]
- Bacon, R., Simien, F., & Monnet, G. 1983, A&A, 128, 405 [NASA ADS] [Google Scholar]
- Barnabè, M., Czoske, O., Koopmans, L. V. E., et al. 2009, MNRAS, 399, 21 [CrossRef] [Google Scholar]
- Barnabè, M., Dutton, A. A., Marshall, P. J., et al. 2012, MNRAS, 423, 1073 [Google Scholar]
- Bertin, G., & Lombardi, M. 2006, ApJ, 648, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic Dynamics (Princeton: Princeton University Press) [Google Scholar]
- Birrer, S., & Amara, A. 2018, Phys. Dark Univ., 22, 189 [Google Scholar]
- Birrer, S., & Treu, T. 2021, A&A, 649, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birrer, S., Amara, A., & Refregier, A. 2016, JCAP, 8, 020 [CrossRef] [Google Scholar]
- Birrer, S., Treu, T., Rusu, C. E., et al. 2019, MNRAS, 484, 4726 [Google Scholar]
- Birrer, S., Shajib, A. J., Galan, A., et al. 2020, A&A, 643, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birrer, S., Shajib, A. J., Gilman, D., et al. 2021, J. Open Source Softw., 6, 3283 [NASA ADS] [CrossRef] [Google Scholar]
- Birrer, S., Millon, M., Sluse, D., et al. 2022a, Space Sci. Rev., submitted [arXiv:2210.10833] [Google Scholar]
- Birrer, S., Dhawan, S., & Shajib, A. J. 2022b, ApJ, 924, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Blakeslee, J. P., Jensen, J. B., Ma, C.-P., Milne, P. A., & Greene, J. E. 2021, ApJ, 911, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Blum, K., Castorina, E., & Simonović, M. 2020, ApJ, 892, L27 [Google Scholar]
- Bonvin, V., Courbin, F., Suyu, S. H., et al. 2017, MNRAS, 465, 4914 [NASA ADS] [CrossRef] [Google Scholar]
- Brout, D., Scolnic, D., Popovic, B., et al. 2022, ApJ, 938, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Buckley-Geer, E. J., Lin, H., Rusu, C. E., et al. 2020, MNRAS, 498, 3241 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2002, MNRAS, 333, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2008, MNRAS, 390, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2016, ARA&A, 54, 597 [Google Scholar]
- Cappellari, M. 2017, MNRAS, 466, 798 [Google Scholar]
- Cappellari, M. 2020, MNRAS, 494, 4819 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2022, MNRAS, submitted [arXiv:2208.14974] [Google Scholar]
- Cappellari, M., & Copin, Y. 2003, MNRAS, 342, 345 [Google Scholar]
- Cappellari, M., Emsellem, E., Bacon, R., et al. 2007, MNRAS, 379, 418 [Google Scholar]
- Cappellari, M., Scott, N., Alatalo, K., et al. 2013, MNRAS, 432, 1709 [Google Scholar]
- Chang, Y.-Y., van der Wel, A., Rix, H.-W., et al. 2013, ApJ, 773, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, G. C. F., Fassnacht, C. D., Suyu, S. H., et al. 2019, MNRAS, 490, 1743 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, G. C.-F., Fassnacht, C. D., Suyu, S. H., et al. 2021a, A&A, 652, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, G. C. F., Treu, T., Fassnacht, C. D., et al. 2021b, MNRAS, 508, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Collett, T. E., Oldham, L. J., Smith, R. J., et al. 2018, Science, 360, 1342 [CrossRef] [Google Scholar]
- Courbin, F., Eigenbrod, A., Vuissoz, C., Meylan, G., & Magain, P. 2005, IAU Symp., 225, 297 [NASA ADS] [Google Scholar]
- Courteau, S., Cappellari, M., de Jong, R. S., et al. 2014, Rev. Mod. Phys., 86, 47 [Google Scholar]
- de Zeeuw, P. T., Evans, N. W., & Schwarzschild, M. 1996, MNRAS, 280, 903 [NASA ADS] [Google Scholar]
- Di Valentino, E., Mena, O., Pan, S., et al. 2021, Class. Quant. Grav., 38, 153001 [NASA ADS] [CrossRef] [Google Scholar]
- Efstathiou, G. 2021, MNRAS, 505, 3866 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Monnet, G., Bacon, R., & Nieto, J.-L. 1994, A&A, 285, 739 [NASA ADS] [Google Scholar]
- Falco, E. E., Gorenstein, M. V., & Shapiro, I. I. 1985, ApJ, 289, L1 [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Foxley-Marrable, M., Collett, T. E., Vernardos, G., Goldstein, D. A., & Bacon, D. 2018, MNRAS, 478, 5081 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L. 2021, ApJ, 919, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Madore, B. F., Hatt, D., et al. 2019, ApJ, 882, 34 [Google Scholar]
- Freedman, W. L., Madore, B. F., Hoyt, T., et al. 2020, ApJ, 891, 57 [Google Scholar]
- Fruchter, A. S., & Hook, R. N. 2002, PASP, 114, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Gilman, D., Birrer, S., & Treu, T. 2020, A&A, 642, A194 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gomer, M. R., Sluse, D., Van de Vyvere, L., Birrer, S., & Courbin, F. 2022, A&A, 667, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonneau, A., Lyubenova, M., Lançon, A., et al. 2020, A&A, 634, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gonzaga, S., Hack, W., Fruchter, A., & Mack, J. 2012, The DrizzlePac Handbook, HST Data Handbook [Google Scholar]
- Goodman, J., & Weare, J. 2010, Commun. Appl. Math. Comput. Sci., 5, 65 [Google Scholar]
- Graham, M. T., Cappellari, M., Li, H., et al. 2018, MNRAS, 477, 4711 [Google Scholar]
- Greene, Z. S., Suyu, S. H., Treu, T., et al. 2013, ApJ, 768, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jeans, J. H. 1922, MNRAS, 82, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Jee, I., Suyu, S. H., Komatsu, E., et al. 2019, Science, 365, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001, SciPy: Open Source Scientific Tools for Python, http://www.scipy.org [Google Scholar]
- Kluyver, T., Ragan-Kelley, B., Pérez, F., et al. 2016, in Positioning and Power in Academic Publishing: Players, Agents and Agendas, eds. F. Loizides, & B. Schmidt (Amsterdam, Netherlands: IOS Press BV), 87 [Google Scholar]
- Knox, L., & Millea, M. 2020, Phys. Rev. D, 101, 043533 [Google Scholar]
- Kochanek, C. S. 2020, MNRAS, 493, 1725 [NASA ADS] [CrossRef] [Google Scholar]
- Kourkchi, E., Tully, R. B., Eftekharzadeh, S., et al. 2020, ApJ, 902, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Krajnović, D., Cappellari, M., de Zeeuw, P. T., & Copin, Y. 2006, MNRAS, 366, 787 [Google Scholar]
- Li, H., Mao, S., Cappellari, M., et al. 2018, ApJ, 863, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Millon, M., Courbin, F., Bonvin, V., et al. 2020a, A&A, 640, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millon, M., Galan, A., Courbin, F., et al. 2020b, A&A, 639, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- More, A., Suyu, S. H., Oguri, M., More, S., & Lee, C.-H. 2017, ApJ, 835, L25 [Google Scholar]
- Morrissey, P., Matuszewski, M., Martin, C., et al. 2012, Proc. SPIE, 8446, 844613 [NASA ADS] [CrossRef] [Google Scholar]
- Morrissey, P., Matuszewski, M., Martin, D. C., et al. 2018, ApJ, 864, 93 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [Google Scholar]
- Oke, J. B., Cohen, J. G., Carr, M., et al. 1995, PASP, 107, 375 [Google Scholar]
- Oliphant, T. E. 2015, Guide to NumPy, 2nd edn. (USA: CreateSpace Independent Publishing Platform) [Google Scholar]
- Pesce, D. W., Braatz, J. A., Reid, M. J., et al. 2020, ApJ, 891, L1 [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Raftery, A. E. 1995, Sociol. Methodol., 25, 111 [CrossRef] [Google Scholar]
- Refsdal, S. 1964, MNRAS, 128, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Yuan, W., Macri, L. M., et al. 2022, ApJ, 934, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, J. G. 2013, PASA, 30, e048 [NASA ADS] [CrossRef] [Google Scholar]
- Rusu, C. E., Fassnacht, C. D., Sluse, D., et al. 2017, MNRAS, 467, 4220 [NASA ADS] [CrossRef] [Google Scholar]
- Rusu, C. E., Wong, K. C., Bonvin, V., et al. 2020, MNRAS, 498, 1440 [Google Scholar]
- Sánchez-Blázquez, P., Peletier, R. F., Jiménez-Vicente, J., et al. 2006, MNRAS, 371, 703 [Google Scholar]
- Schneider, P., & Sluse, D. 2013, A&A, 559, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, P., & Sluse, D. 2014, A&A, 564, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, P., Ehlers, J., & Falco, E. E. 1992, Gravitational Lenses (New York: Springer-Verlag) [Google Scholar]
- Sérsic, J. L. 1968, Atlas de Galaxias Australes (Cordoba, Argentina: Observatorio Astronomico) [Google Scholar]
- Shajib, A. J. 2019, MNRAS, 488, 1387 [NASA ADS] [CrossRef] [Google Scholar]
- Shajib, A. J., Treu, T., & Agnello, A. 2018, MNRAS, 473, 210 [Google Scholar]
- Shajib, A. J., Birrer, S., Treu, T., et al. 2019, MNRAS, 483, 5649 [Google Scholar]
- Shajib, A. J., Birrer, S., Treu, T., et al. 2020, MNRAS, 494, 6072 [Google Scholar]
- Shajib, A. J., Glazebrook, K., Barone, T., et al. 2022a, ApJ, 938, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Shajib, A. J., Vernardos, G., Collett, T. E., et al. 2022b, Space Sci. Rev., submitted [arXiv:2210.10790] [Google Scholar]
- Sluse, D., Surdej, J., Claeskens, J.-F., et al. 2003, A&A, 406, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sluse, D., Claeskens, J.-F., Hutsemékers, D., & Surdej, J. 2007, A&A, 468, 885 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sonnenfeld, A., Treu, T., Marshall, P. J., et al. 2015, ApJ, 800, 94 [Google Scholar]
- Suyu, S. H., Marshall, P. J., Auger, M. W., et al. 2010, ApJ, 711, 201 [Google Scholar]
- Suyu, S. H., Auger, M. W., Hilbert, S., et al. 2013, ApJ, 766, 70 [Google Scholar]
- Suyu, S. H., Treu, T., Hilbert, S., et al. 2014, ApJ, 788, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Taubenberger, S., Suyu, S. H., Komatsu, E., et al. 2019, A&A, 628, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tewes, M., Courbin, F., Meylan, G., et al. 2013, A&A, 556, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tihhonova, O., Courbin, F., Harvey, D., et al. 2018, MNRAS, 477, 5657 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., & Koopmans, L. V. E. 2002, MNRAS, 337, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., & Marshall, P. J. 2016, A&ARv, 24, 11 [Google Scholar]
- Treu, T., Agnello, A., Baumer, M. A., et al. 2018, MNRAS, 481, 1041 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., Suyu, S. H., & Marshall, P. J. 2022, A&ARv, 30, A8 [NASA ADS] [CrossRef] [Google Scholar]
- Valdes, F., Gupta, R., Rose, J. A., Singh, H. P., & Bell, D. J. 2004, ApJS, 152, 251 [Google Scholar]
- Van de Vyvere, L., Gomer, M. R., Sluse, D., et al. 2022a, A&A, 659, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Van de Vyvere, L., Sluse, D., Gomer, M. R., & Mukherjee, S. 2022b, A&A, 663, A179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verde, L., Treu, T., & Riess, A. G. 2019, Nat. Astron., 3, 891 [Google Scholar]
- Waskom, M., Botvinnik, O., Hobson, P., et al. 2014, https://zenodo.org/record/12710 [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wong, K. C., Suyu, S. H., Chen, G. C. F., et al. 2020, MNRAS, 498, 1420 [Google Scholar]
- Yahalomi, D. A., Schechter, P. L., & Wambsganss, J. 2017, ArXiv e-prints [arXiv:1711.07919] [Google Scholar]
- Yıldırım, A., Suyu, S. H., & Halkola, A. 2020, MNRAS, 493, 4783 [Google Scholar]
- Yıldırım, A., Suyu, S. H., Chen, G. C. F., & Komatsu, E. 2021, A&A, submitted [arXiv:2109.14615] [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Values of the light model parameters for the double Sérsic model in our fitting of a large cutout and those from Suyu et al. (2013).
All Figures
 |
Fig. 1. HST/ACS image of RXJ1131−1231 in the F814W band. The four quasar images are labeled with A, B, C, and D. The central deflector is marked with G, of which we are measuring the spatially resolved velocity dispersion. An arrow points to the nearby satellite S, which we mask out in the velocity dispersion measurement. The north and east directions and 1″ scale are also illustrated. |
| In the text | |
 |
Fig. 2. Illustration of the KCWI data for RXJ1131−1231. Left: 2D representation (summed across wavelength) of the 3D KCWI datacube. The yellow contour traces the region with 1″.5 radial extent from the center selected for stellar kinematic measurement. A circular region with 0″.5 radius around image D and the spaxel containing the satellite S are excluded from this selected region. All the individual spaxels within this region have continuum S/N > 1.4 Å−1 for the lens galaxy’s light within 3985−4085 Å (the purple shaded range in the right panel). Right: the spectra (gray) from an example pixel (gray box in the left panel) and the estimate of the signal from the lens galaxy’s spectra (orange) after removing the contribution from the quasar light (blue). The full model of the spectra is presented with the red line, and the model’s residual is plotted in emerald color. The vertical purple shaded region marks where we compute the continuum S/N. |
| In the text | |
 |
Fig. 3. Distribution of the stellar spectral types in the XSL according to the SIMBAD database. Unspecified stars are grouped in the “∼” class. The dark gray color represents the full library of 628 stars. Set 1 (orange) refers to the 39 stars selected by PPXF out of the full library to construct an optimal template 1. Set 2 (blue) refers to 32 stars selected from a random half of the full library and set 3 (emerald) refers to 33 stars selected from the other half. Sets 2 and 3 have 15 and 17 stars, respectively, in common with Set 1. The alternating light gray and white vertical regions divide the spectral classes for easier visualization. |
| In the text | |
 |
Fig. 4. Left: Voronoi binning of the selected spaxels within 1″.5 from the galaxy center that avoid lensed arcs, quasar images, and the satellite galaxy S. The different colors illustrate the regions for each Voronoi bin in a cartographic manner for easier visualization, with the bin number specified within each bin. We perform the binning with a target S/N ≈ 23 Å−1 for each bin, which results in 41 bins in total. Right: resultant S/N for each Voronoi bin (red points). |
| In the text | |
 |
Fig. 5. PPXF fitting to the spectra from four examples of Voronoi bins. The bin number and the measured velocity dispersion for the corresponding bin are specified in each panel. The gray line presents the full spectra, the red line traces the best-fit model, and the blue line shows the quasar component in the best-fit model. |
| In the text | |
 |
Fig. 6. Absolute difference in km s−1 between the extracted velocity dispersion from two setups that differ by one setting. The baseline setup has the range: 3400−4300 Å, polynomial degree: 3, stellar template set 1, and quasar template from image A. The different setting for each case is specified at the top of each panel. |
| In the text | |
 |
Fig. 7. Same as Fig. 6, but the difference is normalized by the statistical uncertainty of the baseline setup. |
| In the text | |
 |
Fig. 8. Illustration of the systematic covariance relative to the statistical covariance. Σ is the variance-covariance matrix of the Voronoi-binned velocity dispersions (with target S/N ≈ 23 Å−1 for each bin), σstat, x is the statistical uncertainty in bin number x from our fiducial setup, and diag(σstat) is a diagonal matrix. We assume no covariance in the statistical uncertainty from each setup for kinematic measurement. Thus the off-diagonal terms in the variance-covariance matrix purely represent the systematic covariance. Most diagonal terms are < 1 (with a median of 0.47), showing that the systematic variances are subdominant to the statistical variances except for bins 29 and 31. These bins are close to images A and C. Thus, they are largely susceptible to the choice of the quasar template, as seen in Figs. 6 and 7. |
| In the text | |
 |
Fig. 9. Maps of extracted velocity dispersion (top row) and mean velocity (bottom row) in Voronoi bins along with the corresponding uncertainties (right column). The Voronoi binning was tuned to achieve S/N ≈ 23 Å−1 for each bin. The illustrated maps (left column) correspond to the average values after combining 81 model setups, and the uncertainty maps correspond to the square root of the diagonal of the variance-covariance matrices. A systematic velocity of 182 km s−1 was subtracted from the mean velocity map. |
| In the text | |
 |
Fig. 10. Absolute (left) and uncertainty-normalized (right) difference in the extracted velocity dispersion between two Voronoi binning schemes. The two binning schemes are obtained by setting the target S/N to 23 Å−1 and 28 Å−1 for each bin. We take the case with target S/N ≈ 23 Å−1 for each bin as the baseline in our analysis. |
| In the text | |
 |
Fig. 11. Fit of the lens galaxy’s surface brightness profile. Left: the HST/ACS imaging in the F814W filter of the lens system RXJ1131−1231 with the quasar images and the lensed arcs subtracted using the prediction from the best-fit lens model from Suyu et al. (2013), thus leaving only the lens galaxy’s light to be fitted. The orange circle shows the large circular region considered for fitting in our analysis, and the yellow square shows the smaller cutout used for lens modeling by Suyu et al. (2013). The cyan annulus contains the region where pixels were fitted to reconstruct the source by Suyu et al. (2013). Thus the lensed arcs from the quasar host galaxy were subtracted only within this annulus. The red contours mark quasar image positions with significant residuals due to saturated pixels, which we mask. Middle: the fitted light profile with a double Sérsic model. The black pixels correspond to masked pixels. The additional masked pixels within the orange circle not described above are randomly selected through an iterative process that performs outlier rejection while preserving the Gaussian tail (Sect. 5.1.2 for details). Right: normalized residual of the best-fit model. |
| In the text | |
 |
Fig. 12. Population prior on kinematic misalignment angle Δφkin ≡ |φkin−φlight| for a sample of slow rotator elliptical galaxies from the SDSS’s MaNGA dataset (Li et al. 2018). Here, Δφkin = 0° corresponds to a purely oblate shape, and Δφkin = 90° corresponds to a purely prolate shape. The vertical dashed gray lines mark Δφkin = 0°, 45°, and 90°. The red points with error bars show the measurements from Li et al. (2018). We fit this distribution with a double Gaussian model (blue line) with the means fixed to Δφkin = 0° and Δφkin = 90°. We take Δφkin < 45° as the oblate case and Δφkin > 45° as the prolate case. Integrating the double Gaussian model from 0° to 45° gives the prior probability of oblateness p(oblate)pop ≃ 0.65. |
| In the text | |
 |
Fig. 13. Prior on the intrinsic axis ratio ql, int of light for oblate (solid line) and prolate (dashed line) cases from Chang et al. (2013). The priors correspond to massive elliptical galaxies from the SDSS survey at 0.04 < z < 0.08 with 10.8 < log10(M⋆/M⊙) < 11.5. |
| In the text | |
 |
Fig. 14. Constraints from axisymmetric JAM modeling on the power-law mass model parameters (θE, γ, and qm), internal MST parameter λint, external convergence κext, anisotropy profile parameter(s), and the cosmological distances DΔt and Dd. assuming two anisotropy parametrizations: (i) one single constant β ≡ 1 − (σθ/σr)2 for all light MGE components (orange contours), and (ii) one free (σθ/σr)inner ≡ (σθ/σr) for light MGE components with σ < rbreak = θeff = 1″.91 and another free (σθ/σr)outer for light MGE components with σ > rbreak (blue contours). The blinded parameters are blinded as pblinded ≡ p/⟨p⟩−1 so that the distributions only reveal fractional uncertainties. The darker and lighter shaded regions in the 2D plots trace 68% and 95% credible regions, respectively. The mass model parameters Einstein radius θE, power-law slope γ, axis ratio q, and position angle PA are additionally constrained through a prior from the imaging data from Suyu et al. (2013). The two anisotropy parametrizations provide equally good fits to the kinematics data. However, the BIC selects the constant-β anisotropy model over the other one with one additional free parameter (ΔBIC value is 3.5). |
| In the text | |
 |
Fig. 15. Observed velocity dispersion map in Voronoi bins (first panel), the best-fit dynamical model with a power-law mass model, constant β anisotropy profile, and oblate shape (second panel), the normalized residual for the best-fit dynamical model (third panel), and the distribution of the normalized residual (orange, fourth panel). The reduced χ2 quantity is |
| In the text | |
 |
Fig. 16. Radial profile of the line-of-sight velocity dispersion. The red points are radially binned values from the 2D maps, with the horizontal error bars illustrating the widths of the annuli. The lines show the radial profiles for random samples from the dynamical model posterior. The radial profile of the model is averaged over the major, minor, and intermediate axes. The solid purple lines correspond to 65 random samples for the oblate case, and the dashed green lines correspond to 35 random samples for the prolate case. We note that the model was fit to the 2D kinematics data. However, we illustrate the 1D radial profile only for visualization. |
| In the text | |
 |
Fig. 17. Comparison of the constrained Dd from power-law (blue contours) and composite (orange contours) mass models. The blinded parameters are blinded as pblinded ≡ p/⟨p⟩−1 so that the distributions only reveal fractional uncertainties. The darker and lighter shaded regions in the 2D plots trace 68% and 95% credible regions, respectively. |
| In the text | |
 |
Fig. 18. Comparison of the constrained Dd between oblate (blue) and prolate (blue) cases of the deprojected spheroidal shape in the dynamical model. The blinded parameters are blinded as pblinded ≡ p/⟨p⟩−1 so that the distributions only reveal fractional uncertainties. The darker and lighter shaded regions in the 2D plots trace 68% and 95% credible regions, respectively. |
| In the text | |
 |
Fig. 19. Comparison of the constrained Dd between two choices of the target S/N for each bin in the Voronoi binning scheme. The blinded parameters are blinded as pblinded ≡ p/⟨p⟩−1 so that the distributions only reveal fractional uncertainties. The darker and lighter shaded regions in the 2D plots trace 68% and 95% credible regions, respectively. |
| In the text | |
 |
Fig. 20. Unblinded cosmological constraints from our analysis. Left: final 2D posterior of the time-delay distance DΔt and the angular diameter distance Dd (emerald contour). The darker and lighter shaded regions in the 2D plots trace 68% and 95% credible regions, respectively. We infer H0 and Ωm from this distance posterior accounting for the covariance in a flat ΛCDM cosmology. We take a wide uniform prior on H0 ∼ 𝒰(0, 150) km s−1 Mpc−1. The blue-shaded region corresponds to a uniform prior Ωm ∼ 𝒰(0.05, 0.5) and the orange-shaded region corresponds to a Gaussian prior Ωm ∼ 𝒩(0.334, 0.018) from the Pantheon+ analysis of type Ia supernovae relative distances (Brout et al. 2022). Right: posterior PDF of H0 and Ωm in flat ΛCDM cosmology. We constrain H0 to 9.4% and 9.1% precision for the uniform and Pantheon+ Ωm-priors, respectively. We show the cosmological parameter posterior from only the 1D Dd posterior with dashed contours with colors matching the associated Ωm prior. In this case, the H0 precision is 10.3% and 9.6% for the uniform and Gaussian priors, respectively. The Dd-only constraint on the H0 is lower by ∼1.4% (0.15σ) than the constraint from the full 2D posterior, for the uniform Ωm-prior. |
| In the text | |
 |
Fig. 21. Comparison of our 9.4% H0 measurement (red, |
| In the text | |
 |
Fig. 22. Comparison of the distance constraints between spatially resolved velocity dispersion and single-aperture velocity dispersion. Here, the integrated velocity dispersion is taken as the fiducial value of 287 ± 18 km s−1 to match the mean of our spatially resolved measurement, but the uncertainty of a single-aperture velocity dispersion measurement (Suyu et al. 2013). The darker and lighter shaded regions in the 2D plots trace 68% and 95% credible regions, respectively. The single-aperture velocity dispersion cannot constrain the anisotropy profile parameter σθ/σr and the internal MST parameter λint, with both limited by the prior. As a result, the DΔt − Dd posterior is constrained much more weakly. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



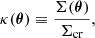
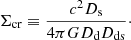
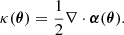
![$$ \begin{aligned} \begin{aligned} \Delta t_{\rm AB} = \frac{D_{\rm \Delta t}}{c} \left[ \frac{(\boldsymbol{\theta }_{\rm A} - \boldsymbol{\varsigma })^2}{2} - \frac{(\boldsymbol{\theta }_{\rm B} - \boldsymbol{\varsigma })^2}{2} - \psi (\boldsymbol{\theta }_{\rm A}) + \psi (\boldsymbol{\theta }_{\rm B})\right], \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/05/aa45878-23/aa45878-23-eq14.gif)
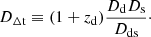
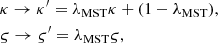
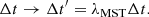
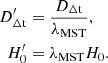
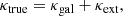
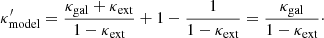
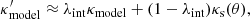
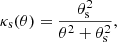
![$$ \begin{aligned} \kappa _{\rm gal} \approx (1 - \kappa _{\rm ext}) \left[\lambda _{\rm int} \kappa _{\rm model} + (1 - \lambda _{\rm int}) \kappa _{\rm s} (\theta )\right]. \end{aligned} $$](/articles/aa/full_html/2023/05/aa45878-23/aa45878-23-eq28.gif)
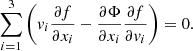
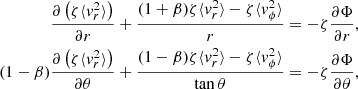
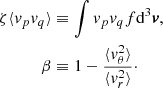
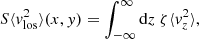
![$$ \begin{aligned} \left[\sigma ^2_{\rm los}\right]_{\rm obs} = \left[\langle {v_{\rm los}^2}\rangle \right]_{\rm obs} = \frac{\int _{\rm ap} \mathrm{d} x\mathrm{d} { y}\ I \langle {v_{\rm los}^2}\rangle \otimes \mathrm{PSF}}{\int _{\rm ap} \mathrm{d} x\mathrm{d} { y} \ I \otimes \mathrm{PSF}}, \end{aligned} $$](/articles/aa/full_html/2023/05/aa45878-23/aa45878-23-eq35.gif)
![$$ \begin{aligned} \Sigma (\boldsymbol{\theta }) = \Sigma _{\rm cr} (1 - \kappa _{\rm ext}) \left[ \lambda _{\rm int}\ \kappa _{\rm model}(\boldsymbol{\theta }) + (1 - \lambda _{\rm int}) \kappa _{\rm s}(\theta ) \right]. \end{aligned} $$](/articles/aa/full_html/2023/05/aa45878-23/aa45878-23-eq36.gif)
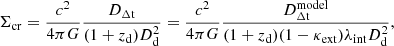
![$$ \begin{aligned} \mathcal{L} ({\boldsymbol{\sigma }}_{\rm los} \mid \Xi ) \propto \exp \left[-\frac{1}{2} {\boldsymbol{\sigma }}_{\rm los}^\mathrm{T} \Sigma ^{-1} {\boldsymbol{\sigma }}_{\rm los} \right], \end{aligned} $$](/articles/aa/full_html/2023/05/aa45878-23/aa45878-23-eq41.gif)
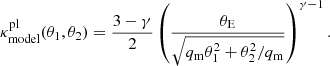
![$$ \begin{aligned} I(\theta _1, \theta _2) = I_{\rm eff} \exp \left[-b_{\rm n} \left(\frac{\sqrt{q_{\rm l} \theta _1^2 + \theta _2^2/q_{\rm l}}}{\theta _{\rm eff}}\right)^{1/n_{\rm s}} + b_{\rm n} \right], \end{aligned} $$](/articles/aa/full_html/2023/05/aa45878-23/aa45878-23-eq43.gif)