| Issue |
A&A
Volume 675, July 2023
|
|
|---|---|---|
| Article Number | A21 | |
| Number of page(s) | 20 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202142318 | |
| Published online | 28 June 2023 | |
TDCOSMO
XIII. Cosmological distance measurements in light of the mass-sheet degeneracy: Forecasts from strong lensing and integral field unit stellar kinematics
1
Max Planck Institute for Astrophysics, Karl-Schwarzschild-Str. 1, 85748 Garching, Germany
e-mail: yildirim@mpa-garching.mpg.de
2
Technical University of Munich, TUM School of Natural Sciences, Department of Physics, James-Franck-Str. 1, 85748 Garching, Germany
3
Institute of Astronomy and Astrophysics, Academia Sinica, 11F of ASMAB, No.1, Section 4, Roosevelt Road, Taipei, 10617
Taiwan
4
Department of Physics and Astronomy, University of California, Los Angeles, CA, 90095
USA
5
Kavli Institute for the Physics and Mathematics of the Universe (Kavli IPMU, WPI), UTIAS, The University of Tokyo, Chiba, 277-8583
Japan
Received:
28
September
2021
Accepted:
3
May
2023
Time-delay distance measurements of strongly lensed quasars have provided a powerful and independent probe of the current expansion rate of the Universe (H0). However, in light of the discrepancies between early- and late-time cosmological studies, current efforts revolve around the characterisation of systematic uncertainties in the methods. In this work we focus on the mass-sheet degeneracy (MSD), which is commonly considered a significant source of systematics in time-delay strong lensing studies, and aim to assess the constraining power provided by integral field unit (IFU) stellar kinematics. To this end, we approximated the MSD with a cored, two-parameter extension to the adopted lensing mass profiles (with core radius rc and mass-sheet parameter λint), which introduces a full degeneracy between λint and H0 from lensing data alone. In addition, we utilised spatially resolved mock IFU stellar kinematics of time-delay strong lenses, given the prospects of obtaining such high-quality data with the James Webb Space Telescope (JWST) in the near future. We constructed joint strong lensing and generalised two-integral axisymmetric Jeans models, where the time delays, mock imaging, and IFU observations are used as input to constrain the mass profile of lens galaxies at the individual galaxy level and consequently yield joint constraints on the time-delay distance (DΔt) and the angular diameter distance (Dd) to the lens. We find that mock JWST-like stellar kinematics constrain the amount of internal mass sheet that is physically associated with the lens galaxy and limit its contribution to the uncertainties of DΔt and Dd, each at the ≤4% level, without assumptions on the background cosmological model. Incorporating additional uncertainties due to external mass sheets associated with mass structures along the lens line of sight, these distance constraints would translate to a ≲4% precision measurement on H0 in flat Λ cold dark matter cosmology for a single lens. Our study shows that future IFU stellar kinematics of time-delay lenses will be key in lifting the MSD on a per lens basis, assuming reasonable and physically motivated core sizes. However, even in the limit of infinite rc, where DΔt is fully degenerate with λint and is thus not constrained, stellar kinematics of the deflector, time delays, and imaging data will provide powerful constraints on Dd, which becomes the dominant source of information in the cosmological inference.
Key words: gravitational lensing: strong / Galaxy: kinematics and dynamics / distance scale
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model.
Open access funding provided by Max Planck Society.
1. Introduction
The current expansion rate of the Universe (H0) is a fiercely debated issue. By means of many independent probes, and efforts spanning multiple decades, a picture has now emerged in which there appears to be a clear discrepancy between early- and late-time cosmological studies (Planck Collaboration VI 2020; Riess et al. 2022; Wong et al. 2020; Abbott et al. 2018; Pesce et al. 2020; Verde et al. 2019). At the heart of this debate is nothing less than our understanding of our standard cosmological model, and, at face value, this discrepancy can only be resolved by as yet unknown and unaccounted for physics (e.g. Poulin et al. 2019; Agrawal et al. 2019; Knox & Millea 2020) or by our lack of accounting for systematic uncertainties in the methods (e.g. Freedman et al. 2019; Shanks et al. 2019). We refer readers to recent reviews on the Hubble tension (e.g. Di Valentino et al. 2021; Riess 2020) for a broad overview and for more details.
Given the possibly drastic implications, the assessment of the systematics has been of particular interest lately. In the context of time-delay strong lensing (TDSL; Refsdal 1964; Treu & Marshall 2016; Suyu et al. 2018), the prominent mass-sheet degeneracy (MSD; Falco et al. 1985) is commonly quoted as a fundamental source of uncertainty (Schneider & Sluse 2013; Kochanek 2020). In brief, the MSD manifests itself through a degeneracy between the lens potential and the observationally inaccessible source position and size. That is, a transformation of the former can be compensated for by a translation and scaling of the latter (see Eqs. (6)–(12) in Yıldırım et al. 2020, hereafter Y20, and references therein). This mass-sheet transformation (MST) leaves many observables invariant and thus recovers, for example, the image positions and time delays equally well. With the time-delay distance, and hence H0, being sensitive to the (functional form of the) lens potential (Wucknitz 2002; Sonnenfeld 2018; Kochanek 2020, 2021), accounting for the MSD is crucial for obtaining an unbiased measurement of H0 with realistic uncertainties.
To reduce the complexity of the MSD, we followed the classification introduced in Suyu et al. (2010) and differentiated between two kinds of mass sheets: (i) an internal mass sheet that is physically associated with the strong-lens galaxy and hence affects its stellar kinematics, and (ii) an external mass sheet that is attributed to mass structures along the strong-lens line of sight (LOS) that are not physically associated with the strong-lens galaxy and thus do not affect its stellar kinematics. We provide a brief overview on ways to constrain the external mass sheet and focus on the internal mass sheet in the rest of this work. The H0LiCOW (H0 Lenses in COSMOGRAIL’s1 Wellspring; Suyu et al. 2017) and TDCOSMO2 collaborations account for external mass sheets by explicitly modelling, for example, the nearest and brightest galaxies (in projection) along the LOS and comparing observed galaxy counts in the vicinity of the strong-lens system to counts from ray tracing through simulations (e.g. Sluse et al. 2017; Rusu et al. 2017, 2020). Tihhonova et al. (2018, 2020) have further employed weak lensing to obtain independent estimates of external convergence that are in agreement with the results based on galaxy counts. New approaches for quantifying the external convergence have been developed (e.g. McCully et al. 2014, 2017; Fleury et al. 2021), and McCully et al. (2017) show that the external convergence estimate is more precise when including more detailed information on individual LOS objects.
The H0LiCOW programme, together with COSMOGRAIL (Courbin et al. 2018) and the Strong lensing at High Angular Resolution Program (SHARP; Chen et al. 2019), showed that a final precision of 2.4% on H0 is achieved from an ensemble of six time-delay strong lenses when well-motivated mass models for the lens galaxies are adopted (Wong et al. 2020). However, if these mass model assumptions are relaxed and a model with an internal mass sheet – that is maximally degenerate with H0 – is used, then the constraint on H0 degrades to 5% or 8%, depending on whether or not external priors (obtained from non-time-delay lenses) for the orbital anisotropy are adopted (Birrer et al. 2020, TDCOSMO IV).
In order to gain back the precision lost by this more general and inclusive approach, several avenues can be explored. These range from acquiring even more stellar kinematic data of non-time-delay lenses (to further constrain the orbital anisotropy and mass profile of lens galaxies at the galaxy population level) to high-quality, partially resolved stellar kinematics (i.e. kinematics within azimuthally averaged rings from the ground) of individual time-delay lenses (Birrer & Treu 2021, TDCOSMO V).
Given our previous work (Y20) on forecasting cosmological distance measurements with high-spatially resolved stellar kinematics from the next-generation telescopes, such as the James Webb Space Telescope (JWST) or the planned European Extremely Large Telescope (E-ELT), this study aims to reassess the constraining power of joint strong lensing and stellar dynamical models for cosmological purposes, while incorporating a more general family of mass models that closely mimics the contribution of an internal mass-sheet component. The mass-sheet component used in this work resembles the parameterisation presented in Blum et al. (2020, hereafter B20) of a cored mass-density distribution, which has been tailored to be insensitive to the lensing data and is therefore maximally degenerate with H0. Adopting this cored density distribution hence allows us to fully explore the uncertainties associated with the MSD and the prospects of limiting its impact effectively by means of integral field unit (IFU) data, which is otherwise not possible unless, for example, aided by additional distance indicators, the assumption of a cosmological world model (Chen et al. 2021), or the aforementioned use of prior information (Birrer et al. 2020). Even though this particular choice of parameterising the contribution of a mass sheet is a deliberate one, it provides the necessary freedom in the models while simultaneously providing a physical argument for its presence (Blum & Teodori 2021). Other parameterisations of a mass sheet can be mathematically more convenient but usually lack any argument for a physical counterpart. In general, our approach outlined in Sect. 3 can be adjusted in the future by accommodating different parameterisations for the lens mass distribution.
The main novelty of our current work is the use of a more flexible, self-consistent lensing and dynamical mass model. Instead of spherical Jeans modelling for the kinematics that were used in previous TDCOSMO studies, we employ an axisymmetric mass distribution (in 3D) for both the lensing and kinematic analysis. This allows us to exploit the spatially resolved kinematic maps to their full extent in order to constrain the internal mass sheet. A detailed comparison to and discussion of earlier TDCOSMO studies are provided in Sect. 4.4. Throughout this paper we adopt a standard cosmological model with H0 = 82.5 km s−1 Mpc−1, a matter density of Ωm = 0.27, and a dark energy density of ΩΛ = 0.73, where our particular choice for H0 is driven by the time-delay distance measurement of RXJ1131−1231 in Suyu et al. (2014)3.
2. Data
As a test-bed for our study, we made use of RXJ1131−1231, which was discovered by Sluse et al. (2003). Being part of the H0LiCOW base sample (Suyu et al. 2017), RXJ1131−1231 represents one of the most prominent TDCOSMO systems with exquisite data, consisting of Hubble Space Telescope (HST) imaging (Fig. 1) and highly precise time-delay measurements (Tewes et al. 2013a; Millon et al. 2020a). In addition, an aperture-averaged stellar velocity dispersion measurement for the lensing galaxy of σ = 323 ± 20 km s−1 is available (Suyu et al. 2013).
 |
Fig. 1. HST ACS F814W imaging cutout of RXJ1131−1231, illustrating the prominent lens configuration with a quadruply imaged background quasar (A, B, C, and D) and a nearby satellite (S). Spectroscopic measurements locate the lens and quasar at redshifts zd = 0.295 and zs = 0.654, respectively. We generated mock imaging data that closely resemble the archival HST data shown here, based on a best-fitting lensing model and excluding the satellite. Overlaid is the JWST NIRSpec nominal FOV of 3″×3″, within which we create mock stellar kinematics of the foreground lens at 0.1″ pixel−1 resolution. The FOV is oriented such that the x-axis is aligned with the galaxy major axis. |
Following the procedure outlined in Y20, we make use of a hybrid data strategy, where the archival HST data (GO: 9744; PI: Kochanek) and literature time-delays (Tewes et al. 2013b) are aided by mock IFU stellar kinematics. In detail, the HST observations have been used to re-mock the imaging data. This is achieved by means of the best-fitting COMPOSITE (i.e. stars and NFW halo) lensing model achieved on the HST lens image (Fig. 1), as obtained in Suyu et al. (2014). In this model, the extended source has been reconstructed on a source grid with a resolution of 64 × 64 pixels. Unlike the COMPOSITE lens model in Suyu et al. (2014), we excluded the nearby satellite (S in Fig. 1) in our mock HST image, to ensure consistency with the mock IFU stellar kinematics, where the satellite has also been omitted (see Sect. 3 for further explanation). The stellar kinematics of RXJ1131−1231 have been generated based on this COMPOSITE lens mass model and using arbitrary dynamical model parameters (see Sect. 3). Utilising the axisymmetric Jeans formalism for mocking up the stellar kinematics (Binney & Tremaine 1987; Cappellari 2008; Barnabè et al. 2012), we obtain IFU data at JWST resolution (i.e. 0.1″ pixel−1), covering a 3″ × 3″ field-of-view (FOV). The mock IFU data closely resemble the Near-Infrared Spectrograph (NIRSpec) properties and characteristics, assuming that the kinematics have been measured with a single pointing centred on RXJ1131−1231 (Fig. 1)4.
The mock kinematics are further convolved with a single Gaussian point spread function (PSF) of 0.08″ FWHM, which is already two times larger than the diffraction limit of JWST. Difficulties in properly measuring the kinematic PSF size have been shown to be of minimal concern (Y20), which is why this PSF is employed for both the mock and modelling stage5.
Since the signal-to-noise ratio (S/N) in each spatial resolution element is usually insufficient to reliably measure the stellar kinematics across the entire FOV, we performed a spatial binning of the mock data (Cappellari & Copin 2003). To this end, the surface brightness (SB) distribution at the JWST resolution was obtained from parameterised fits to the HST imaging data. This SB distribution of RXJ1131−1231 was then used to achieve a desired S/N level, by means of JWST’s exposure time calculator (ETC V1.3) Within the 3″×3″ FOV, this S/N map was, in turn, used to spatially bin the individual pixels to a target S/N of ∼40 per bin. Our procedure results in ∼80 spatially resolved measurements of the line-of-sight velocity distribution (LOSVD) across the entire FOV, achievable with reasonable observation times (including overheads) of 8–10h.
To imitate realistic observations, various sources of statistic and systematic uncertainties are added to the mock input kinematics  . Here, we focus on two individual datasets. Following the notation in Y20, the IDEAL data incorporate random Gaussian errors only (δvstat). More specifically, the random error in each bin l (i.e. δvstat, l) is drawn from a Gaussian distribution with a mean of zero and a standard deviation (σstat, l) that is inversely proportional to its S/N. Given that all bins reach the target S/N of 40, this approach yields
. Here, we focus on two individual datasets. Following the notation in Y20, the IDEAL data incorporate random Gaussian errors only (δvstat). More specifically, the random error in each bin l (i.e. δvstat, l) is drawn from a Gaussian distribution with a mean of zero and a standard deviation (σstat, l) that is inversely proportional to its S/N. Given that all bins reach the target S/N of 40, this approach yields 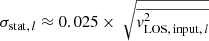 . The IDEAL data hence reflect a best-case scenario for breaking the MSD, where the results will be unaffected by, for example, systematic effects in the measurement of the stellar kinematics. In the second dataset, which we label as FIDUCIAL, we incorporate systematic errors in addition to the random Gaussian noise in the IDEAL dataset. That is, the FIDUCIAL dataset contains a 2% systematic shift downwards of all mock
. The IDEAL data hence reflect a best-case scenario for breaking the MSD, where the results will be unaffected by, for example, systematic effects in the measurement of the stellar kinematics. In the second dataset, which we label as FIDUCIAL, we incorporate systematic errors in addition to the random Gaussian noise in the IDEAL dataset. That is, the FIDUCIAL dataset contains a 2% systematic shift downwards of all mock 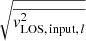 values
values 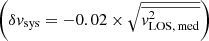 , where
, where  is the median of
is the median of 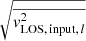 from all bins. This systematic shift to the downside is introduced to account for possible systematics in the measurement of the stellar kinematics (e.g. due to stellar template mismatches; Emsellem et al. 2004; Falcón-Barroso et al. 2017; Collett et al. 2018). The mock kinematics can be quickly summarised as follows:
from all bins. This systematic shift to the downside is introduced to account for possible systematics in the measurement of the stellar kinematics (e.g. due to stellar template mismatches; Emsellem et al. 2004; Falcón-Barroso et al. 2017; Collett et al. 2018). The mock kinematics can be quickly summarised as follows:
It is worth mentioning here that the inverse correlation between the S/N of the observations and the corresponding kinematic errors have been extensively tested via, for example, simulations of ground-based IFU data (Emsellem et al. 2004), and found to be quite accurate in realistic observing conditions (Yıldırım et al. 2017). The adoption of the systematic errors quoted here, however, will require more extensive checks based on the actual data. For the sake of completeness, we adopted various levels of statistical and systematic uncertainties, which we deemed achievable and present the corresponding modelling results in the Appendix. To check for consistency with real observations, we collapsed the mock IFU data within an 0.8″ wide aperture for the IDEAL case, which yields a mock single second-order velocity moment along the LOS of 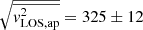 km s−1. This mock value is in excellent agreement with the literature stellar velocity dispersion measurement, assuming that rotation is minimal, and confirms the validity of our approach.
km s−1. This mock value is in excellent agreement with the literature stellar velocity dispersion measurement, assuming that rotation is minimal, and confirms the validity of our approach.
The mock HST observations, time-delay measurements and mock kinematics are then employed as constraints for our joint modelling machinery and the modelling results for both mock datasets (i.e. IDEAL and FIDUCIAL) are presented and discussed in Sects. 3 and 4.
3. Theoretical framework
3.1. Strong lensing under the internal MST
We adopted the COMPOSITE mass model of RXJ1131−1231 as our baseline model (Y20). This model consists of a baryonic and non-baryonic component. The former is parameterised by multiple pseudo-isothermal elliptical profiles (PIEMDs; Kassiola & Kovner 1993), to resemble a two-component Sérsic distribution, multiplied with a spatially constant stellar mass-to-light ratio (Υ), and the latter by a Navarro-Frenk-White (NFW) profile (Navarro et al. 1996, 1997). Moreover, we add a cored density distribution to the COMPOSITE model, here also parameterised as a PIEMD, with a core radius of θc = 20″, which is well beyond the Einstein radius (θE ≈ 1.6″)6. As introduced in B20, such a cored density distribution is built to mimic an internal mass sheet with constant convergence κint. It is therefore a convenient way to parameterise and incorporate the internal MSD into the lens mass model, especially since the lensing properties (e.g. deflection angles) of PIEMD can be readily computed. In addition to the baseline COMPOSITE mass model, we also consider a softened power-law elliptical mass distribution (SPEMD; Barkana 1998) for comparison, and similarly add a PIEMD as an approximate internal mass sheet.
In concordance with earlier notations, we define
with
By scaling the total convergence profile according to
where κcomposite(θ) is the original COMPOSITE profile with θ = (θ1, θ2) as the angular coordinates, this MST leaves all observables invariant, provided the time-delay distance (DΔt),
scales as
Here zd is the redshift to the lens, Dd, Ds and Dds are angular diameter distances to the lens, to the source and between the lens and the source, respectively. Incorporating further the effect of an external mass sheet (κext) yields
whereas Dd is fully invariant under the external MST7 (Jee et al. 2015):
In concordance with B20, our adopted cored density distribution has the special attribute of leaving the mean convergence within θE (∼1.6″) virtually identical and making it thus inaccessible for strong lensing studies alone. However, the above transformation introduces changes in the radial 3D mass distribution, depending on the extent of the core radius, to which spatially resolved stellar kinematics can be sensitive. Here, the choice of a core radius is particularly important. Our core radius of 20″ might seem deliberate at first, but was adopted after intensive testing. Larger core radii will mimic a scenario in which the original density profile of the galaxy (κcomposite) is effectively unchanged (see Appendix C), that is, both the lensing and kinematic data will be insensitive, whereas core radii that are too small will have a more noticeable imprint on the stellar kinematics, but might not be a valid MST in the sense that the lensing data will start to become sensitive to such a transformation of the mass profile (see also Fig. 3 in Birrer et al. 2020). The core radius of 20″ was chosen to probe a worst-case scenario of sorts, where the MST is still intact from a lensing point of view while the imprint on the kinematic data is big enough to allow for meaningful constraints on λint. Our distinction between an internal and external mass-sheet is therefore a practical one; we assume that the internal MST does not conspire in a way that it becomes undetectable for both lensing and stellar kinematics within θE. We also note that the adopted core radius of 20″ corresponds to a physical radius of ≈80 kpc at our lens distance. It is therefore sufficiently large to test physically motivated mechanisms that could produce extended cored density distributions, such as those put forward by ultra-light dark matter (see e.g. Blum & Teodori 2021).
3.2. Stellar dynamics under the internal MST
Here we briefly revisit the theoretical framework for mocking up and modelling the stellar kinematics. We provide a list of variables with descriptions in Table 1 as a convenient reference. As outlined in Y20, our models are based on the solution of the axisymmetric Jeans equations (Jeans 1922; Binney & Tremaine 1987), assuming alignment of the velocity ellipsoid with the cylindrical coordinate (R, ϕ, z) system as well as a flattening in the meridional plane (Cappellari et al. 2007; Cappellari 2008). This yields the two equations,
and
which link the tracer density (ρ*) and gravitational potential (ψD) to three intrinsic second-order velocity moments (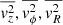 ). Once the tracer density ρ* is measured (by means of the SB distribution) and a gravitational potential is adopted, we can readily solve Eq. (10) for
). Once the tracer density ρ* is measured (by means of the SB distribution) and a gravitational potential is adopted, we can readily solve Eq. (10) for 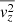 and Eq. (9) for
and Eq. (9) for 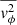 and obtain
and obtain 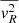 via
via 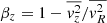 . The intrinsic second-order moments can then be projected along the LOS to predict a second-order velocity moment:
. The intrinsic second-order moments can then be projected along the LOS to predict a second-order velocity moment:
where x′ and y′ are the Cartesian coordinates on the plane of the sky, z′ is the coordinate along the LOS, ζ is the inclination angle (with 90° being edge-on), μ is the observed SB and v and σ the observed mean LOS velocity and velocity dispersion, respectively.
In our self-consistent modelling approach, both the intrinsic tracer and mass density for the dynamics are constructed by deprojecting the SB and surface mass density (SMD) distribution from the lens models, which are constrained by the quasar image positions, time delays and the spatially extended Einstein ring. As mentioned in Sect. 3.1, the projected SMD consists of a COMPOSITE and PIEMD profile and is subject to the internal MST. More specifically,
where Σsmd denotes the (projected) physical SMD and
is the critical SMD8. With Eq. (4), we rewrite the projected SMD as
The SMD is expanded by multiple Gaussians (MGE; Emsellem et al. 1994) and deprojected into a 3D mass density. Assuming an oblate axisymmetric system, the intrinsic total density of each Gaussian in the fit (MGEfit; Cappellari 2002) is obtained via
and related to ψD through Poisson’s equation. We use index i to denote the MGE components of the mass density. It is of importance to note that, based on our finite core size, our treatment and implementation of the MST is an approximate one, with κint ≈ const. within θc. This, however, is a good enough approximation of the perfect MST (i.e. θc → ∞), where the deviation in, for example, the deflection angles are small enough (i.e. α(θ; θc → ∞)≈ α(θ; θc = 20″), with α as the deflection angle), such that the models fully capture the degeneracies associated with it (see Sect. 4).
In Eq. (15), 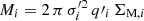 denotes the total mass of the individual Gaussians,
denotes the total mass of the individual Gaussians, 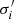 the projected dispersion,
the projected dispersion, 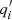 the projected flattening and ΣM, i the peak SMD. In our case of a MGE of the SMD, the gravitational potential assigned to each Gaussian is
the projected flattening and ΣM, i the peak SMD. In our case of a MGE of the SMD, the gravitational potential assigned to each Gaussian is
with
and 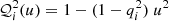 . Here, σi is the intrinsic dispersion of the Gaussians, qi their intrinsic long versus short axis ratio, and (R, z) the intrinsic cylindrical coordinate system. Similarly, the SB distribution can also be expanded by multiple Gaussians. Denoting the MGE components of the luminosity distribution by index j (in contrast to i for the mass density), the intrinsic luminosity density of each Gaussian is
. Here, σi is the intrinsic dispersion of the Gaussians, qi their intrinsic long versus short axis ratio, and (R, z) the intrinsic cylindrical coordinate system. Similarly, the SB distribution can also be expanded by multiple Gaussians. Denoting the MGE components of the luminosity distribution by index j (in contrast to i for the mass density), the intrinsic luminosity density of each Gaussian is
with Lj now expressing the total luminosity of the individual Gaussians. In general, the set of Gaussians describing the SB and SMD are not identical (i.e. i ≠ j and hence σi ≠ σj and qi ≠ qj) unless mass-follows-light. For instance, the Gaussians describing the mass and tracer density distribution in the SPEMD model differ, whereas the Gaussians describing the light profile in the Composite mass model are transformed into a corresponding stellar mass density distribution by assigning each Gaussian the same Υ. In principle, this framework also allows for a radially varying Υ, by assigning the luminous Gaussians in the Composite mass model individual Υ values. Given the spatial coverage of ∼1 Re (effective radius) however, spatial variations in the Υ are expected to be small, which is why we refrain from probing a radially varying Υ in our Composite mass model.
The second-order moments of a single Gaussian tracer distribution j – embedded in the gravitational potential ψD = ∑iψD, i – is then obtained via
where we simply solved Eq. (10) for ![$ [\overline{{\mathit{v}_{z}^{2}}}]_{j} $](/articles/aa/full_html/2023/07/aa42318-21/aa42318-21-eq45.gif) , assuming a single luminous Gaussian component j tracing the total mass density distribution generated by all Gaussians i and using
, assuming a single luminous Gaussian component j tracing the total mass density distribution generated by all Gaussians i and using 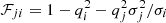 (see Cappellari 2008; van de Ven et al. 2010, for analytical expressions of all velocity moments involved in Eq. (9) and (10)). It is worth noting that absolute lengths in the plane of the sky scale linearly with the distance (r ∝ Dd, int). Hence, when moving from angular to physical units, this dependence translates to
(see Cappellari 2008; van de Ven et al. 2010, for analytical expressions of all velocity moments involved in Eq. (9) and (10)). It is worth noting that absolute lengths in the plane of the sky scale linearly with the distance (r ∝ Dd, int). Hence, when moving from angular to physical units, this dependence translates to
It is immediately evident from Eq. (14) that the deprojected (i.e. intrinsic) 3D mass distribution is subject to the MST. The impact on the radial 3D mass distribution is highlighted in Fig. 2, where we scale λint (and hence DΔt, int and κmst, int) with respect to the mock input values. Stellar kinematic measurements of the galaxies primarily constrain the mass enclosed within spherical radii (Menc, 3D) covering the region of kinematic measurements. With a single aperture average velocity dispersion measurement with 5% uncertainty, we would get a single Menc, 3D constraint of ∼10% uncertainty (since Menc, 3D ∼ v2). On the other hand, spatially resolved kinematics with velocity measurements in multiple spatial bins can be viewed as providing multiple Menc, 3D constraints at different radii. Fig. 2 illustrates the dependence of Menc, 3D on our model parameters. In particular, differences in the total enclosed mass within JWST’s FOV amount to roughly 5% for λint = 0.9, a value that was deemed necessary to align RXJ1131−1231’s H0 measurement with that obtained by the cold microwave background (B20). Moreover, the MST translates not only to differences in the total enclosed mass, but also changes the slope of the mass profile to which spatially resolved kinematics are sensitive (Cappellari 2020).
 |
Fig. 2. Total enclosed mass profile in 3D and its sensitivity to λint and Dd, int. Top: Total enclosed mass profile in 3D as a function of intrinsic radius ( |
3.3. Models
We construct joint strong lensing and stellar dynamical models as introduced in Y20. In brief, these models rely on a pixelated source fitting algorithm (Suyu et al. 2006, 2010, 2013) and the solution of the Jeans equations in axisymmetry (Cappellari 2008, JAMPY). The model parameter space thus includes those listed in Table 2 for the COMPOSITE and SPEMD mass models, including the time-delay distance DΔt, int, the lens distance Dd, int, the orbital anisotropy parameter βz, inclination ζ and absolute strength/amplitude of the internal mass-sheet parameter λint. In line with Y20, we do not include the satellite in our fits to both the lensing and kinematic data. Given that the contribution of the satellite to the SMD is ≤1% at the lens centre, any uncertainties due to the missing satellite are subdominant with respect to the other sources of uncertainties in the models. Moreover, we do not constrain the parameter range by physical arguments other than the fact that the MST is not supposed to yield negative convergences within a FOV that is more than twice as large as the core radius, which penalises models with λint ⪆ 1.059 (see Sect. 4). Besides that, the priors are identical to those adopted in Y20 (with e.g. a Gaussian prior for the NFW scale radius; Gavazzi et al. 2007), with λint being flat within the aforementioned prior range of [0.5, 1.5]. We note that our kinematic data have been mocked up without any contribution from a mass sheet (i.e. λint = 1.0, as described in Sect. 2). Moreover, we do not assume a ratio of Dd/Dds. That is, our inferred values for DΔt, int and Dd, int are based solely on the data and are not constrained by assuming a cosmological world model.
Model parameters and priors for our joint strong lensing and dynamical models.
We explore the posterior probability density function (PDF) by means of EMCEE (Foreman-Mackey et al. 2013). We investigate different modelling runs by adopting different source grid resolutions, which (for a given mass model parameterisation and in the absence of a MSD) constitutes the biggest source of uncertainty on H0 (Suyu et al. 2013, Y20). The grid resolutions span a range of 56 × 56 to 68 × 68 pixels in the source plane, with source pixel sizes roughly of the order of 0.05 ± 0.01″ pixel−1. The grid size is sufficiently large to allow for a proper reconstruction of the extended source, without artificially constraining the parameter space in λint, as will be shown for the lensing-only models in Sect. 4.1. In a last step, we then combine the constraints from different source resolutions by assigning equal weights to the chains.
In the case of the FIDUCIAL dataset, we sample over an additional velocity fractional shift parameter fv in the model to account for the systematic uncertainties. For a given value of fv, the mock kinematic data  in Eq. (1) is scaled by
in Eq. (1) is scaled by 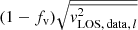 . We consider a uniform distribution of fv ∈ [ − 0.02, 0.02]; that is to say, we assume the mock kinematic data in all kinematic bins have equal likelihood in being systematically shifted by an amount within 2%. Such a systematic fractional offset in the measured kinematic data could arise from, for example, stellar template mismatches. In practice, such a systematic shift in the kinematic data leads to a shift in Dd, int, leaving other model parameters unchanged. To obtain the cosmological distance measurements in the FIDUCIAL dataset, we then marginalise over the parameter fv from [ − 0.02, 0.02].
. We consider a uniform distribution of fv ∈ [ − 0.02, 0.02]; that is to say, we assume the mock kinematic data in all kinematic bins have equal likelihood in being systematically shifted by an amount within 2%. Such a systematic fractional offset in the measured kinematic data could arise from, for example, stellar template mismatches. In practice, such a systematic shift in the kinematic data leads to a shift in Dd, int, leaving other model parameters unchanged. To obtain the cosmological distance measurements in the FIDUCIAL dataset, we then marginalise over the parameter fv from [ − 0.02, 0.02].
4. Results and discussions
4.1. Distance measurements without cosmological model assumptions
The probability distributions for the various datasets are displayed in Fig. 3. As expected, the introduction of a constant internal mass sheet is degenerate with the mass model. By scaling the mass model parameters accordingly, the lensing data (consisting of the multiple image positions, the SB distribution of the quasar host galaxy and the time delays) can easily be recovered, while allowing for a large variation in the contribution of λint. Consequently, we observe a posterior probability distribution function (PDF) for λint and DΔt, int (grey) that is essentially flat within the prior bounds. The PDF for the lens distance Dd, int and the anisotropy parameter βz is also flat, since these are anchored by the kinematic data only. It is worth noting here that the effect depicted in Fig. 3 for the lensing-only data is neither new nor unexpected, but simply a manifestation of the MSD. The degeneracy is well captured by our models and this exercise also serves the purpose of illustrating the differences in the constraining power of a mass sheet with and without high-spatially resolved stellar kinematic data.
 |
Fig. 3. Measurements from our joint strong lensing and stellar dynamical models, without any kinematic data (grey) and with mock IFU stellar kinematics (orange and blue). The corner plot shows the most relevant parameters in the fit, consisting of the lens distance, Dd, int, time-delay distance, DΔt, int, internal mass-sheet parameter, λint, and orbital anisotropy, βz. The contours highlight the 1σ, 2σ, and 3σ confidence regions. The black points (lines) depict the mock input values. Without any kinematics, DΔt, int and λint are highly degenerate, while Dd, int and βz are unconstrained. The posterior PDFs for Dd, int and βz are virtually flat in this case, which is why we only show the 2D contours in the DΔt, int–λint space. IFU data will considerably tighten the constraints. In the IDEAL case, the mock input values are recovered within 2σ. In the FIDUCIAL case, the mock input values are also recovered within the 2σ bands, but with larger relative uncertainties for the lens distance (δDd, int/Dd, int ≈ 4%). These measurements are independent of cosmological model assumptions. |
The corresponding probability distributions for our joint lensing and dynamical models are also shown in Fig. 3, where the IDEAL (orange) and FIDUCIAL (blue) mock IFU observations were employed10. In contrast to the highly degenerate lensing-only run, an internal mass-sheet component is constrained when IFU stellar kinematics are available. We observe tight constraints for any contribution from an internal mass sheet with a core radius of 20″ of 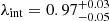 . The sensitivity of the 2D kinematics to changes in the radial mass distribution translates to tight measurements on the distances, too. We measure Dd, int and DΔt, int with a precision of ∼ 1.6% and ∼3.7%, respectively (see Table 3) in the IDEAL case. Yet, the constraint for the lens distance degrades significantly when the FIDUCIAL data are employed instead, where Dd, int is only measured with a ∼4% precision. In both cases, however, the mock input values are generally recovered within the 1–2σ uncertainty bands. The results can be explained as follows; the statistical uncertainty in the mock kinematic data (δvstat) sets the overall precision for measuring λint and DΔt, int, whereas the systematic offset (δvsys) dictates the best precision to be achieved for Dd, int. Hence, with the same statistical uncertainties of 2.5% in both the IDEAL and FIDUCIAL data, the final modelling uncertainties for λint and DΔt, int are identical (see Fig. 3), while the uncertainties on Dd, int in the FIDUCIAL case can readily be obtained from the IDEAL PDF, by utilising the analytic relationship in Eq. (20)11. This yields the final PDF in Fig. 3.
. The sensitivity of the 2D kinematics to changes in the radial mass distribution translates to tight measurements on the distances, too. We measure Dd, int and DΔt, int with a precision of ∼ 1.6% and ∼3.7%, respectively (see Table 3) in the IDEAL case. Yet, the constraint for the lens distance degrades significantly when the FIDUCIAL data are employed instead, where Dd, int is only measured with a ∼4% precision. In both cases, however, the mock input values are generally recovered within the 1–2σ uncertainty bands. The results can be explained as follows; the statistical uncertainty in the mock kinematic data (δvstat) sets the overall precision for measuring λint and DΔt, int, whereas the systematic offset (δvsys) dictates the best precision to be achieved for Dd, int. Hence, with the same statistical uncertainties of 2.5% in both the IDEAL and FIDUCIAL data, the final modelling uncertainties for λint and DΔt, int are identical (see Fig. 3), while the uncertainties on Dd, int in the FIDUCIAL case can readily be obtained from the IDEAL PDF, by utilising the analytic relationship in Eq. (20)11. This yields the final PDF in Fig. 3.
Parameter constraints from our lensing-only and joint strong lensing and stellar dynamical models.
While we recover the key parameters of our mass models within the 1–2σ regions as shown in Fig. 3, we note here some of the effects that affect the shape of the posterior PDF of the model parameters. First of all, the amount of noise in the mock datasets the size of the posterior PDF – the higher the amount of noise, the broader the PDF (as further illustrated in Appendix A). Secondly, the posterior distribution of λint is highly asymmetric due to the imposed physical condition of positive mass density. Finally, models with different source pixelisations lead to slightly different optimisations, resulting in shifts of the PDF from individual source pixelisations relative to each other (Suyu et al. 2013, Y20). The final PDF is obtained by combining the individual PDFs for each source resolution, giving equal weighting to all due to indistinguishable kinematic goodness of fit values (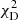 ), in order to account for the model uncertainties due to source pixelisation. This is in contrast to Y20, where the Bayesian information criterion (BIC; Schwarz 1978) was utilised effectively to down-weight individual source resolutions that are too far away from the mock input values, but no longer applicable in the presence of a MST to further constrain this source of uncertainty in the models.
), in order to account for the model uncertainties due to source pixelisation. This is in contrast to Y20, where the Bayesian information criterion (BIC; Schwarz 1978) was utilised effectively to down-weight individual source resolutions that are too far away from the mock input values, but no longer applicable in the presence of a MST to further constrain this source of uncertainty in the models.
For the orbital anisotropy, we picked a mock input value of βz = 0.15. Our choice of mild radial anisotropy was motivated by the findings from extensive modelling of massive elliptical galaxies in the local universe (Cappellari et al. 2007, 2013). Regardless of this particular choice, Fig. 3 is a powerful illustration of how time delays and high-spatially resolved kinematic data will enable us to lift the MSD and mass-anisotropy degeneracy (van der Marel & Franx 1993; Gerhard 1993) simultaneously, providing tight constraints also on the orbital anisotropy parameter, which is otherwise difficult unless higher order moments of the LOSVD are available.
The anisotropy in our mock data and models was, so far, assumed to be constant as a function radius. We also explored the scenario of allowing for spatially varying anisotropy profiles to assess its impact on the inference of the cosmological distances in the fit. We present the results in Fig. 4, where we compare the constraints for the two different parameterisations of the orbital anisotropy profile. Models that adopt a constant value for the anisotropy fit the data exceptionally well and recover the mock input values within the 1σ confidence levels (indigo). This is identical to Fig. 3, but shown here for a single source resolution of 64 × 64 pixels. Models with a radially varying anisotropy profile have been implemented, where the anisotropy profile is parameterised according to
 |
Fig. 4. Measurements from our joint strong lensing and stellar dynamical models with mock IFU stellar kinematics (IDEAL), but for two different parameterisations of the orbital anisotropy profile, βz. The corner plot shows the relevant parameters in the fit, consisting of the lens distance, Dd, int, time-delay distance, DΔt, int, and internal mass-sheet parameter, λint. The mock data are mildly anisotropic (i.e. βz(r) = 0.15 is non-zero and independent of radius) and fitted with both a radially constant (indigo) and radially varying anisotropy profile (teal). The contours highlight the 1σ, 2σ, and 3σ confidence regions, with the black points (lines) depicting the mock input values. The radially constant mock input anisotropy can be recovered from models with a radially varying anisotropy profile. |
with α ∈ [ − 0.3, 0.3] and | β |∈[0, 0.5]. This parameterisation provides enough freedom to allow for a wide range of anisotropy profiles, while ensuring a smooth transition from the central to the outermost bins. It is also tailored to account for the coarser sampling in the remote regions. Models with a radially varying anisotropy profile are capable of recovering the mock input value within 1σ (teal), with α = 0.13 ± 0.02 and β = 0.0 ± 0.1. Despite the increased freedom in the anisotropy profile, we do not observe inflated errors for the cosmological distances in the fit, showing that the orbit distribution has limited power for compensating for the effects of the distances and mass-sheet, as illustrated in Fig. 2.
We further highlight the difference in the model-predicted 2D kinematics of the IDEAL mock data between the best-fitting model without a mass sheet (λint ≈ 1.0) and the best-fitting model with a (fixed) mass sheet of λint ≈ 0.85 in Fig. 5. The mock data are exceptionally well fitted without a mass sheet and generally recovered within the 1–2σ errors.
 |
Fig. 5. Mock kinematic data and model comparisons. First: IDEAL mock IFU |
The difference between the overall best-fitting model without a mass sheet (i.e. λint = 1.0) and the best-fitting model with a significant mass-sheet contribution of λint ≈ 0.85 is Δχ2 = 6. With the IDEAL and FIDUCIAL mock kinematics, the value of λint ≈ 0.85 can be ruled out at the ≈3σ level whereas the input value of λint = 1 is recovered within 1σ (see Table 3). Given the same priors for the two models above (with or without the internal mass sheet), the ratio of the posterior probabilities is determined by the Bayes factor, which we approximate by means of the BIC difference (Y20), and which yields a posterior odd of 0.05 for the model with a mass sheet against the model without a mass sheet. We therefore anticipate that spatially resolved kinematics from future JWST observations will be valuable in placing constraints on the internal mass sheet in the lens galaxy.
We also constructed models with a SPEMD and, again, added a PIEMD profile to mimic the contribution of an internal mass sheet. In agreement with our earlier studies (Y20), the SPEMD provides a considerably worse fit to the mock kinematics. The best-fitting SPEMD
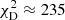 , as opposed to
, as opposed to 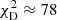 for the COMPOSITE mass model. The corresponding reduced
for the COMPOSITE mass model. The corresponding reduced 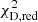 are ∼3 and ∼1 for the SPEMD and COMPOSITE models, respectively, given the ∼80 kinematic measurements, and the ∼4 ‘free’ parameters unconstrained by lensing (λint, Dd, int, ζ, βz). Whereas the BIC differences are insufficient to discriminate between the various source resolutions of a given mass model, the BIC differences are sufficient to rule out mass density parameterisations that deviate strongly from the input model, even in light of the increased freedom provided by the MSD. Therefore, including the SPEMD models in our final chains leaves the constraints for the various parameters in the fit unchanged, given that these are assigned zero weighting.
are ∼3 and ∼1 for the SPEMD and COMPOSITE models, respectively, given the ∼80 kinematic measurements, and the ∼4 ‘free’ parameters unconstrained by lensing (λint, Dd, int, ζ, βz). Whereas the BIC differences are insufficient to discriminate between the various source resolutions of a given mass model, the BIC differences are sufficient to rule out mass density parameterisations that deviate strongly from the input model, even in light of the increased freedom provided by the MSD. Therefore, including the SPEMD models in our final chains leaves the constraints for the various parameters in the fit unchanged, given that these are assigned zero weighting.
In Fig. 5, the high levels of residuals in the kinematic data associated with SPEMD are mostly in the central region, which is unsurprising given that it is in the central region of θ ≲ 0.5″ that the SPEMD and COMPOSITE models deviate from one another due to the lack of lensing constraints in the central region (see Fig. 2 of Suyu et al. 2014). Spatially resolved kinematic data are therefore crucial for constraining the inner mass density profile. As advocated in Y20, we recommend exploring a large set of physically motivated lens potentials using spatially resolved kinematics in future time-delay cosmographic studies in order to minimise systematic errors associated with lens mass parameterisations.
The final parameter constraints for Dd, int, DΔt, int, and λint are summarised in Table 3. In concordance with Y20, we observe tight measurements for Dd, int and DΔt, int when IFU data are available. The uncertainties on Dd, int are dominated by those of the kinematic data, yet significantly better than expected from, for example, a single-aperture-averaged velocity dispersion (Chen et al. 2021; Jee et al. 2019), given the roughly 80 (almost) independent measurements of the LOSVD across the entire FOV. The precision of DΔt, int also greatly benefits from high-spatially resolved kinematics (Y20), with |δDΔt, int/DΔt, int|∼|δλint/λint|, but is highly sensitive to the statistical errors in the measurement of the LOSVD. For illustration purposes, we also present an even more conservative scenario in Appendix A, in which we increase δvstat to 3.5% instead, which further highlights the impact of δvstat in constraining λint and DΔt, int.
4.2. Cosmographic forecast in flat ΛCDM
Unlike earlier findings without an internal MST, where much of the constraining power in measuring H0 came from DΔt, int only (with the small δDΔt, int propagating almost linearly into the error budget on H0), Dd, int is now expected to add substantial constraining power to DΔt, int in measuring H0 (Jee et al. 2016; Chen et al. 2021).
To this end, we utilise the joint distance measurements of Dd, int and DΔt, int to obtain cosmological forecasts in flat Lambda cold dark matter (ΛCDM). We first fit the marginalised DΔt, int–Dd, int distribution (from all chains across various source resolutions) with a kernel density estimator and account for mass structures along the lens LOS with an external convergence (κext) distribution, following the number counts approach from numerical simulations in Suyu et al. (2013, 2014). We draw random samples of {H0, Ωm, κext} with uniform priors on H0 of [50,120] km s−1 and on Ωm of [0.05, 0.5] and with the P(κext) distribution, compute the corresponding DΔt, int and Dd, int following Eqs. (7) and (8), and importance sample given the P(Dd, int, DΔt, int) posterior. This yields a final value of H0
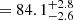 km s−1 Mpc−1 (H0
km s−1 Mpc−1 (H0
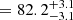 km s−1 Mpc−1), which is a 3.2% precision measurement (3.7%) for the IDEAL (FIDUCIAL) case, recovering the input value of 82.5 km s−1 Mpc−1.
km s−1 Mpc−1), which is a 3.2% precision measurement (3.7%) for the IDEAL (FIDUCIAL) case, recovering the input value of 82.5 km s−1 Mpc−1.
Figure 6 shows how the inclusion of 2D stellar kinematics of the lens not only helps in tightly constraining the lens distance, but also leads to improved constraints on cosmological parameters beyond H0, even for a single lens. This conclusion has already been drawn in Y20 and is now corroborated even in the presence of a MST, assuming that the stellar kinematics can be measured with high accuracy and precision. Otherwise, more systems will be needed to provide more meaningful constraints beyond H0.
 |
Fig. 6. H0 and Ωm constraints from our models in flat ΛCDM cosmology, for the IDEAL (left) and FIDUCIAL (right) datasets with statistical uncertainties of δvstat = 2.5%. We adopted uniform priors on H0 of [50, 120] km s−1 Mpc−1 and Ωm of [0.05, 0.5]. The green shaded regions show the 1σ, 2σ, and 3σ confidence regions based on the constraint on DΔt only, i.e. P(DΔt) after marginalising over other mass model parameters, including Dd. The red shaded regions show the corresponding constraints based on P(Dd), after marginalising over DΔt. The grey histogram shows the constraints based on P(Dd, DΔt); we have omitted the 2D contours for ease of viewing. Different tilts in the H0–Ωm space, when marginalised over Dd and DΔt, respectively, can break some of the degeneracies, also leading to improved constraints on Ωm. |
4.3. View of Dd and core size
It is of great importance to recapitulate our findings within a more comprehensive and broader context: despite employing a model that is maximally degenerate with DΔt, int, and hence with H0 through the MST, we have shown that high-quality, high-spatially resolved stellar kinematics can break the internal MSD and constrain DΔt, int. Furthermore, time delays and (spatially resolved) kinematics also provide leverage for constraining Dd (Paraficz & Hjorth 2009) regardless of the MST (Jee et al. 2015, 2019; Chen et al. 2021). Previous analyses in TDCOSMO using two families of mass models with single-aperture velocity dispersion measurements and without MST yield joint constraints on DΔt and Dd, but with substantially tighter constraints on DΔt compared to Dd. When allowing for a MST, the precision on DΔt degrades. On the other hand, Dd is nearly insensitive to the internal MST (and completely insensitive to the external MST). With high-quality spatially resolved kinematics, the precision on Dd can become better than that of DΔt (Sects. 4.1 and 4.2 and Y20). Therefore, the DΔt-centric view in TDSL can be complemented by the new Dd-centric view; namely, the combination of the two distances provide robust H0 even in the presence of the MST.
The results presented here rest upon the assumption of an extended, yet finite core size of θc = 20″, but it may be useful to emphasise again the role played by Dd in the two limiting cases of θc ≪ θE and θc ≫ θE. First, when θc ≪ θE, the approximation of a pure MST is no longer valid (Birrer et al. 2020) and lensing data are sensitive to transformations of the lens mass profile, particularly the λint values. In this scenario, the precision of DΔt is mainly limited by the precision of the lensing and time-delay observations, whereas the precision of Dd mainly depends on the time delays and kinematics. Both DΔt and Dd can be measured almost equally well in this case (see also Y20), thus leading to tight constraints on the inferred cosmological parameters. Second, when θc ≫ θE, the kinematic data no longer constrains the internal mass sheet, as the corresponding density profile effectively vanishes (Appendix C). Under these circumstances, no improvement in the measurement of DΔt and H0 can be expected, leaving it prone to the full degeneracy introduced by the MST. However, the kinematics still improve the constraint on Dd significantly on a single lens basis, which then becomes the dominant source of information in the final cosmological inference. While this was expected from previous studies on the subject (Jee et al. 2015, 2016, 2019; Chen et al. 2021), our results demonstrate this explicitly and quantitatively using mock JWST observations.
4.4. Comparison to previous TDCOSMO studies
We compare our approach to previous analyses of TDCOSMO, particularly TDCOSMO I (Millon et al. 2020b), IV (Birrer et al. 2020), V (Birrer & Treu 2021) and VI (Chen et al. 2021) that involve lens mass modelling. We start by summarising previous studies, and explain the similarities and differences.
In TDCOSMO I, Millon et al. (2020b) investigated potential sources of systematic uncertainties connected to lens mass modelling by employing two families of physically motivated mass models, the power-law and composite mass models, without internal MST. They find the two families of models yield the same H0 within 1% uncertainty from the sample of lens systems that were previously modelled by the H0LiCOW, SHARP, and STRIDES collaborations (Suyu et al. 2013, 2014; Wong et al. 2017; Birrer et al. 2019; Chen et al. 2019; Rusu et al. 2020; Shajib et al. 2020). The comparison of these two families of model demonstrates that there is no evidence for significant residual systematic uncertainties associated with the lens mass modelling.
To further explore the MST as a source of uncertainty for measuring H0, Birrer et al. (2020) in TDCOSMO IV relaxed the assumptions on the lens mass profiles and allowed for an internal MST of the power-law model. The MST parameter λint is then constrained through spherical Jeans modelling (with a radially varying anisotropy profile) and the stellar kinematic data of the lens galaxy, which are mostly single-aperture-averaged stellar velocity dispersions. A subset of the SLACS lens galaxies is further combined with the seven TDCOSMO lenses through a hierarchical analysis to constrain λint and infer H0 in flat ΛCDM. The uncertainties on H0 are 8% from TDCOSMO lenses only, or 5% from TDCOSMO and SLACS lenses. Birrer & Treu (2021) in TDCOSMO V then estimated the precisions of H0 measurements from current and future samples of time-delay lenses, with various levels of velocity dispersion measurements, ranging from single-aperture-averaged velocity dispersions to IFU kinematic maps with 30 radially averaged velocity bins. With seven TDCOSMO lenses and future velocity dispersion measurements in 10 radial bins for each lens, Birrer & Treu (2021) anticipate a precision on H0 in flat ΛCDM of 3.5%–4.7%, depending on the quality of the kinematic data. An expansion of the sample to 40 time-delay lenses and 200 non-time-delay lenses would improve the precision to 1.5% and 1.2%, respectively.
The analyses of TDCOSMO IV and V assumed the flat ΛCDM model, which reduces the range of plausible λint in the MST given the tight correlation between Dd and DΔt. Chen et al. (2021) in TDCOSMO VI relaxed the assumption of flat ΛCDM by considering the measurements of DΔt and Dd in generic cosmological models, while allowing for the MST. By combining the lenses together with relative distance indicators such as Type Ia supernovae and baryon acoustic oscillations, Chen et al. (2021) showed that λint and DΔt can be constrained in generic cosmological models. In this work, spherical Jeans modelling and aperture-averaged kinematic measurements are used.
Our current paper is similar to TDCOSMO IV, V, and VI in that we also considered a parameterised profile with an internal MST characterised by λint. While TDCOSMO IV, V, and VI used only the power-law profile with mass sheets, we considered both families of mass models (composite and power-law profiles that were used in TDCOSMO I) with additional mass sheets. We find that spatially resolved kinematics not only allow us to constrain the MST parameter λint, but also to distinguish between the families of mass models. Our setup is similar to TDCOSMO VI in that we aim to measure the distances DΔt and Dd without assuming a background cosmological model, in contrast to TDCOSMO IV and V that assumed flat ΛCDM.
The key difference and novelty of our current work are the use of a self-consistent lensing and dynamical mass model that is axisymmetric in 3D, in contrast to the spherical Jeans modelling employed in previous TDCOSMO studies for the kinematics. Furthermore, we considered 2D spatially resolved kinematic data with angular structure, which help constrain both λint and DΔt, even when allowing for radially varying anisotropy profiles. With our forecast of JWST-like spatially resolved kinematics of ∼80 bins for RXJ1131−1231, we find that we can constrain H0 with this single lens with better than 4% precision. This is based on the assumption of a uniformly distributed systematic uncertainty of 2% with fv varying between [−0.02,0.02], although we show in Appendix B that a Gaussian distributed systematic uncertainty of 2% increases the H0 uncertainty only slightly from 3.8% to 4.1% for our mock kinematic data with δvstat = 2.5%. In comparison to TDCOSMO V that adopted a 3% systematic uncertainty (in each of the 10 radial velocity bins for their spherical Jeans modelling) that is larger than our 2%, our forecast of ≤4% uncertainty on H0 constrained from a single lens is more precise, as expected. Once we account for the difference in the assumed kinematic data quality, the two studies (this and TDCOSMO V) should provide consistent results, under similar modelling assumptions. A direct comparison of the two dynamical modelling approaches (axisymmetric Jeans in this paper and spherical Jeans in TDCOSMO V) would require modelling the same kinematic, lensing and time delay dataset, which is not the focus of our current paper. We summarise the various TDCOSMO modelling papers in Table 4.
Summary of TDCOSMO studies.
For completeness, however, we assessed the changes in the parameter constraints, when running our axisymmetric models in the spherically symmetric limit. That is, we fixed the flattening q to be ∼1 for our COMPOSITE mass model components12. Based on this limited testing scenario, we find two main trends. First, the uncertainties on DΔt, int and Dd, int degrade significantly to 7.4% and 2.1%, respectively, in the spherical model (i.e. a loss by a factor of 2 in the constraining power of DΔt, int when compared to our axisymmetric models). Second, the spherical assumption introduces a systematic shift of the mean towards higher values, of the order of 3–4% for both DΔt, int and Dd, int. We attribute the larger uncertainties in these models to the degeneracy between the (now) spherically symmetric mass model and the spherically symmetric sheet (the sheet is assumed to be circular in projection, with b/a = 1, and hence spherical in deprojection), while the shift in the mean values is most likely induced by the limited freedom in the geometric shape of the mass components. A more thorough investigation is warranted to properly assess the effects of the geometry. Nonetheless, we strongly urge the community to refrain from overly simplistic models, when IFU kinematic data are available.
One other key difference to TDCOSMO IV, V, and VI is that with the anticipated high-quality JWST kinematic data, we can constrain the parameters for the mass sheet (λint) and for the anisotropy of the stellar orbits from the JWST kinematic data, without having to rely on external samples of non-time-delay lenses (in TDCOSMO IV and V) and/or other relative distance indicators (in TDCOSMO VI). We therefore see the individual analyses of lenses with high-quality data to be complementary to the hierarchical analyses with external samples – the combination of both approaches in future studies would give us the maximal amount of cosmological information especially in measuring H0.
5. Summary
In order to assess the constraining power on a mass-sheet component in TDSL studies, we have performed a suite of simulations. For this purpose, we used the prominent lens system RXJ1131−1231 as a test-bed for our studies.
We mocked up high-quality, high-spatially resolved IFU stellar kinematics (as is expected from the next generation of ground- and space-based telescopes) together with mock HST imaging, and used long-baseline time-delay measurements. Following the prescription of a cored density distribution (B20), a variable internal mass-sheet component was included in our models. Our findings can be summarised as follows:
-
Without any kinematic data (i.e. for pure strong-lens models), we observe the well-known degeneracy between the mass model parameters and any internal mass-sheet component, λint. The lensing data allow for a wide range of λint values, which can adversely affect the time-delay distance measurement, DΔt, int, according to Eq. (6).
-
Future IFU stellar kinematics with the next generation of telescopes (such as JWST and E-ELT) will be able to effectively break the internal MSD, by placing tight constraints on the contribution of any internal mass-sheet component with a core radius ⪅20″. This finding is specific to RXJ1131−1231; however, with θE/Re ≈ 0.9 (where Re is the effective radius), RXJ1131−1231 is not a particular outlier in the H0LiCOW sample (Millon et al. 2020b).
-
Using realistic mock IFU observations, provided by assuming total observation times with JWST of 8–10 h (including overheads), we show that future measurements of λint (and hence DΔt, int) could be as precise as 4% per lens. These uncertainties propagate almost linearly into the error budget on H0, whereas the precise Dd, int measurements (δDd, int/Dd, int ≤ 4%) allow further reductions in the H0 uncertainties. This yields a high-precision measurement on H0 of ≤4% from this single lens system, assuming flat ΛCDM cosmology and a mock H0 value of 82.5 km s−1 Mpc−1.
-
High-spatially resolved stellar kinematics of the lens can constrain cosmological parameters beyond H0. However, more systems are needed to provide more meaningful information on, for example, Ωm.
-
The modelling approach presented here is fully self-consistent and more flexible than literature studies where spherical symmetry is commonly employed for modelling the stellar kinematic data. The 2D angular structure in the kinematic data together with the lensing information allow us to place tight constraints on the anisotropy parameters of the stellar orbits. In particular, we implemented models where the stellar anisotropy is parameterised according to Eq. (21). Despite the increased flexibility (which provides additional freedom to account for radial variations in the stellar anisotropy), the models are capable of recovering the radially constant anisotropy of the mock data without yielding inflated errors for the cosmological distances in the fit.
-
We did not use (and thus did not rely on) informative priors at the galaxy population level. This approach presents an alternative and complementary method to that presented in Birrer et al. (2020), to gain back much of the precision lost by accounting for the MSD. In addition, spatially resolved kinematics can be used, in turn, to verify if external datasets can be combined with the TDCOSMO lenses from the galaxy population point of view.
-
Our final inference of the angular diameter distances Dd, int and DΔt, int are independent of cosmological model assumptions.
Our analysis shows that the mass-sheet parameter, λint, can be constrained at the few percent level by means of JWST-like stellar kinematics, unless the core radius associated with the mass sheet is rc ⪆ 100 kpc. Even though there is currently no observational evidence for the presence of a mass sheet at the 8% level based on existing kinematic data on lensed quasars (Birrer et al. 2020), spatially resolved kinematics will allow us to put tighter limits on the internal mass sheet. This will be helpful in further constraining physical models that are put forward for producing cored density distributions. Until the internal mass sheet is detected with significance from observations, we will refrain from speculating further on its physical plausibility and origin13.
Given this forecast, much of the precision lost by incorporating a maximally degenerate model can be regained, such that only a few systems with similar precision will be sufficient to address the H0 tension between late- and early-time cosmological probes. JWST is scheduled to observe the first lensed quasar systems with the NIRSpec IFU14, and our work provides the modelling framework for measuring distances while allowing for the internal MSD. Moreover, our approach of simulating mock JWST-like data can be used to identify further strong lensing systems that will provide the biggest gain in precision and hence the fastest route to tackling the aforementioned tension. As new IFU facilities come online in the next few years, we advocate for utilising this unique combination of lensing and dynamics, particularly with spatially resolved kinematics, as a powerful probe of cosmology.
COSmological MOnitoring of GRAvItational Lenses; https://cosmograil.epfl.ch
Time-Delay COSMOgraphy: https://ui.adsabs.harvard.edu/abs/2020A%26A...639A.101M/abstract
This value is based on the best-fitting composite mass model of the quadruple lens system RXJ1131−1231 in Suyu et al. (2014) in order to simulate realistic kinematic data that are compatible with the measured time delays. Despite more recent investigations pointing towards a lower H0 value for this particular system, the adopted value is sufficient for our purposes, since we are interested in the relative uncertainties.
The actual observing strategy for JWST cycle 1 observations of RXJ1131−1231 (PI: Suyu) will employ a four-point mosaic pattern, which retains the high S/N for the central parts, while also reaching into the fainter arcs. This setup will help ancillary science cases, such as those of studying the kinematic state of the source galaxy. However, as illustrated in Fig. 1, a single (three-dither) pointing strategy can be adopted instead, which will provide sufficient depth to make substantial gains in the constraining power, even in light of the MSD (Sect. 4).
In contrast, the PSF for the imaging data is crucial for the lens parameter inference (e.g. Shajib et al. 2022), and methods have been developed to reconstruct the PSF based on the multiple quasar images of lens systems (e.g. Chen et al. 2016).
We refer to θc as the angular core radius. The physical core radius rc in units of kpc is obtained via rc = θc Dd. See also Appendix C.
The angular diameter distance to the lens, Dd, is also approximately invariant under the internal MST with a single-aperture-averaged velocity dispersion and for λint ∈[0.8, 1.2] (Chen et al. 2021).
Our FOV within which we carry out the MGE has to be large enough to avoid a premature exponential fall off of the Gaussians, which can adversely impact the predicted 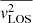 . We find that a FOV ≥2 × θc is sufficiently large to adequately describe the profile of the cored density distribution. Within this FOV, however, the convergence profile is not allowed to be negative, since this would yield negative SMDs. This translates into an upper bound for our constraints on λint of ≈1.05.
. We find that a FOV ≥2 × θc is sufficiently large to adequately describe the profile of the cored density distribution. Within this FOV, however, the convergence profile is not allowed to be negative, since this would yield negative SMDs. This translates into an upper bound for our constraints on λint of ≈1.05.
In detail, the final uncertainties for Dd, int in the FIDUCIAL case are obtained by marginalising over models with various realisations of the systematic offset fv. In practice, we create 9 realisations corresponding to the values of fv = { − 0.02, −0.015, −0.01, −0.005, 0.,0.005, 0.01, 0.015, 0.02}, and combine the resulting chains from these realisations with equal weights.
We adopt spherically symmetric mass components for the dynamical part, but axisymmetric mass components for the lens modelling. While this is consistent with the literature approach of carrying out joint strong lensing and dynamical models, it breaks the self-consistency of our models and thus diminishes its modelling capacity.
We used κcomposite for consistency with Sect. 3.1, but the results presented here are valid irrespective of the parameterisation of the lens mass profile.
Acknowledgments
The authors thank S. Birrer, F. Courbin, D. Sluse and T. Treu for helpful discussions on the manuscript, and the anonymous referees for comments that improved the presentation of this work. AY and SHS thank the Max Planck Society for support through the Max Planck Research Group for SHS. G C.-F. C acknowledges support from the National Science Foundation through grants NSF-AST-1906976 and NSF-AST-1836016. G. C.-F. C. acknowledges support from the Moore Foundation through grant 8548. SHS and EK are supported in part by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under Germany’s Excellence Strategy – EXC-2094 – 390783311. The Kavli IPMU is supported by World Premier International Research Center Initiative (WPI), MEXT, Japan.
References
- Abbott, T. M. C., Abdalla, F. B., Annis, J., et al. 2018, MNRAS, 480, 3879 [Google Scholar]
- Agrawal, P., Cyr-Racine, F.-Y., Pinner, D., & Randall, L. 2019, ArXiv eprints [arXiv:1904.01016] [Google Scholar]
- Barkana, R. 1998, ApJ, 502, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Barnabè, M., Dutton, A. A., Marshall, P. J., et al. 2012, MNRAS, 423, 1073 [Google Scholar]
- Binney, J., & Tremaine, S. 1987, Galactic Dynamics (Princeton, NJ, USA: Princeton University Press) [Google Scholar]
- Birrer, S., & Treu, T. 2021, A&A, 649, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Birrer, S., Treu, T., Rusu, C. E., et al. 2019, MNRAS, 484, 4726 [Google Scholar]
- Birrer, S., Shajib, A. J., Galan, A., et al. 2020, A&A, 643, A165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blum, K., & Teodori, L. 2021, Phys. Rev. D, 104, 123011 [CrossRef] [Google Scholar]
- Blum, K., Castorina, E., & Simonović, M. 2020, ApJ, 892, L27 [Google Scholar]
- Cappellari, M. 2002, MNRAS, 333, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2008, MNRAS, 390, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2020, MNRAS, 494, 4819 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Copin, Y. 2003, MNRAS, 342, 345 [Google Scholar]
- Cappellari, M., Emsellem, E., Bacon, R., et al. 2007, MNRAS, 379, 418 [Google Scholar]
- Cappellari, M., Scott, N., Alatalo, K., et al. 2013, MNRAS, 432, 1709 [Google Scholar]
- Chen, G. C. F., Suyu, S. H., Wong, K. C., et al. 2016, MNRAS, 462, 3457 [CrossRef] [Google Scholar]
- Chen, G. C. F., Fassnacht, C. D., Suyu, S. H., et al. 2019, MNRAS, 490, 1743 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, G. C. F., Fassnacht, C. D., Suyu, S. H., et al. 2021, A&A, 652, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Collett, T. E., Oldham, L. J., Smith, R. J., et al. 2018, Science, 360, 1342 [CrossRef] [Google Scholar]
- Courbin, F., Bonvin, V., Buckley-Geer, E., et al. 2018, A&A, 609, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Valentino, E., Mena, O., Pan, S., et al. 2021, CQG, 38, 153001 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Monnet, G., & Bacon, R. 1994, A&A, 285, 723 [NASA ADS] [Google Scholar]
- Emsellem, E., Cappellari, M., Peletier, R. F., et al. 2004, MNRAS, 352, 721 [Google Scholar]
- Falco, E. E., Gorenstein, M. V., & Shapiro, I. I. 1985, ApJ, 289, L1 [Google Scholar]
- Falcón-Barroso, J., Lyubenova, M., van de Ven, G., et al. 2017, A&A, 597, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fleury, P., Larena, J., & Uzan, J.-P. 2021, CQG, 38, 085002 [NASA ADS] [CrossRef] [Google Scholar]
- Foreman-Mackey, D., Hogg, D. W., Lang, D., & Goodman, J. 2013, PASP, 125, 306 [Google Scholar]
- Freedman, W. L., Madore, B. F., Hatt, D., et al. 2019, ApJ, 882, 34 [Google Scholar]
- Gavazzi, R., Treu, T., Rhodes, J. D., et al. 2007, ApJ, 667, 176 [Google Scholar]
- Gerhard, O. E. 1993, MNRAS, 265, 213 [Google Scholar]
- Jeans, J. H. 1922, MNRAS, 82, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Jee, I., Komatsu, E., & Suyu, S. H. 2015, J. Cosmol. Astropart. Phys., 11, 033 [CrossRef] [Google Scholar]
- Jee, I., Komatsu, E., Suyu, S. H., & Huterer, D. 2016, J. Cosmol. Astropart. Phys., 4, 031 [CrossRef] [Google Scholar]
- Jee, I., Suyu, S. H., Komatsu, E., et al. 2019, Science, 365, 1134 [NASA ADS] [CrossRef] [Google Scholar]
- Kassiola, A., & Kovner, I. 1993, ApJ, 417, 450 [Google Scholar]
- Knox, L., & Millea, M. 2020, Phys. Rev. D, 101, 043533 [Google Scholar]
- Kochanek, C. S. 2020, MNRAS, 493, 1725 [NASA ADS] [CrossRef] [Google Scholar]
- Kochanek, C. S. 2021, MNRAS, 501, 5021 [Google Scholar]
- McCully, C., Keeton, C. R., Wong, K. C., & Zabludoff, A. I. 2014, MNRAS, 443, 3631 [NASA ADS] [CrossRef] [Google Scholar]
- McCully, C., Keeton, C. R., Wong, K. C., & Zabludoff, A. I. 2017, ApJ, 836, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Millon, M., Courbin, F., Bonvin, V., et al. 2020a, A&A, 640, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Millon, M., Galan, A., Courbin, F., et al. 2020b, A&A, 639, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1996, ApJ, 462, 563 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [Google Scholar]
- Paraficz, D., & Hjorth, J. 2009, A&A, 507, L49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pesce, D. W., Braatz, J. A., Reid, M. J., et al. 2020, ApJ, 891, L1 [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poulin, V., Smith, T. L., Karwal, T., & Kamionkowski, M. 2019, Phys. Rev. Lett., 122 [CrossRef] [Google Scholar]
- Refsdal, S. 1964, MNRAS, 128, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G. 2020, Nat. Rev. Phys., 2, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Riess, A. G., Yuan, W., Macri, L. M., et al. 2022, ApJ, 934, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Rusu, C. E., Fassnacht, C. D., Sluse, D., et al. 2017, MNRAS, 467, 4220 [NASA ADS] [CrossRef] [Google Scholar]
- Rusu, C. E., Wong, K. C., Bonvin, V., et al. 2020, MNRAS, 498, 1440 [Google Scholar]
- Schneider, P., & Sluse, D. 2013, A&A, 559, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarz, G. 1978, Ann. Statist., 6, 461 [Google Scholar]
- Shajib, A. J., Birrer, S., Treu, T., et al. 2020, MNRAS, 494, 6072 [Google Scholar]
- Shajib, A. J., Wong, K. C., Birrer, S., et al. 2022, A&A, 667, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shanks, T., Hogarth, L. M., & Metcalfe, N. 2019, MNRAS, 484, L64 [Google Scholar]
- Sluse, D., Surdej, J., Claeskens, J.-F., et al. 2003, A&A, 406, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sluse, D., Sonnenfeld, A., Rumbaugh, N., et al. 2017, MNRAS, 470, 4838 [NASA ADS] [CrossRef] [Google Scholar]
- Sonnenfeld, A. 2018, MNRAS, 474, 4648 [Google Scholar]
- Suyu, S. H., Marshall, P. J., Hobson, M. P., & Blandford, R. D. 2006, MNRAS, 371, 983 [Google Scholar]
- Suyu, S. H., Marshall, P. J., Auger, M. W., et al. 2010, ApJ, 711, 201 [Google Scholar]
- Suyu, S. H., Auger, M. W., Hilbert, S., et al. 2013, ApJ, 766, 70 [Google Scholar]
- Suyu, S. H., Treu, T., Hilbert, S., et al. 2014, ApJ, 788, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Suyu, S. H., Bonvin, V., Courbin, F., et al. 2017, MNRAS, 468, 2590 [Google Scholar]
- Suyu, S. H., Chang, T.-C., Courbin, F., & Okumura, T. 2018, Space Sci. Rev., 214, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Tewes, M., Courbin, F., & Meylan, G. 2013a, A&A, 553, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tewes, M., Courbin, F., Meylan, G., et al. 2013b, A&A, 556, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tihhonova, O., Courbin, F., Harvey, D., et al. 2018, MNRAS, 477, 5657 [NASA ADS] [CrossRef] [Google Scholar]
- Tihhonova, O., Courbin, F., Harvey, D., et al. 2020, MNRAS, 498, 1406 [NASA ADS] [CrossRef] [Google Scholar]
- Treu, T., & Marshall, P. J. 2016, A&ARv., 24, 11 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, R. P., & Franx, M. 1993, ApJ, 407, 525 [Google Scholar]
- van de Ven, G., Falcón-Barroso, J., McDermid, R. M., et al. 2010, ApJ, 719, 1481 [Google Scholar]
- Verde, L., Treu, T., & Riess, A. G. 2019, Nat. Astron., 3, 891 [Google Scholar]
- Wong, K. C., Suyu, S. H., Auger, M. W., et al. 2017, MNRAS, 465, 4895 [NASA ADS] [CrossRef] [Google Scholar]
- Wong, K. C., Suyu, S. H., Chen, G. C. F., et al. 2020, MNRAS, 498, 1420 [Google Scholar]
- Wucknitz, O. 2002, MNRAS, 332, 951 [Google Scholar]
- Yıldırım, A., van den Bosch, R. C. E., van de Ven, G., et al. 2017, MNRAS, 468, 4216 [Google Scholar]
- Yıldırım, A., Suyu, S. H., & Halkola, A. 2020, MNRAS, 493, 4783 [Google Scholar]
Appendix A: Statistical error sensitivity
We present the distance constraints and cosmological forecast from our joint strong lensing and stellar dynamical models, based on the IDEAL and FIDUCIAL data. Unlike the results shown in Fig. 3 and Fig. 6, the statistical error (δvstat) in the mock kinematics (Eq. 1) has been increased from 2.5% to 3.5%, while δvsys remains −2% for the FIDUCIAL data. This roughly corresponds to a target S/N of 30 per bin. As before, we assume a uniform distribution of fv ∈ [ − 0.02, 0.02]. Fig. A.1 effectively illustrates how the increased statistical uncertainty in the kinematics translates into larger modelling uncertainties on DΔt, int and λint, whereas the uncertainty on Dd, int depends mainly on the fractional offset fv distribution that accounts for the systematic uncertainties in the kinematic measurements. Given the degraded mock kinematics, the uncertainties on DΔt, int (further amplified by the degeneracy between DΔt, int and λint) become significant, such that most of the constraining power in the cosmological inference hinges on the accuracy and precision of Dd, int (Fig. A.2). This is most obvious when drawing a direct comparison between the IDEAL and FIDUCIAL cosmological forecast here. We obtain a final H0 measurement of 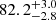 km s−1 Mpc−1 in the IDEAL case, whereas the FIDUCIAL data yields
km s−1 Mpc−1 in the IDEAL case, whereas the FIDUCIAL data yields 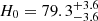 km s−1 Mpc−1. The shift in the mean value for the FIDUCIAL data is mainly caused by the significant drop in the constraining power of DΔt, int. With the systematic offset in the velocity moments for the FIDUCIAL case, the mean H0 is also biased. This is in contrast to our findings without a mass sheet in Y20 (see Table 3) where, despite increased statistical errors in the kinematic data, both DΔt, int and Dd, int contribute almost equally to an accurate and precise H0 measurement. We summarise the results in Table A.1.
km s−1 Mpc−1. The shift in the mean value for the FIDUCIAL data is mainly caused by the significant drop in the constraining power of DΔt, int. With the systematic offset in the velocity moments for the FIDUCIAL case, the mean H0 is also biased. This is in contrast to our findings without a mass sheet in Y20 (see Table 3) where, despite increased statistical errors in the kinematic data, both DΔt, int and Dd, int contribute almost equally to an accurate and precise H0 measurement. We summarise the results in Table A.1.
 |
Fig. A.1. Measurements from our joint strong lensing and stellar dynamical models, without any kinematic data (grey) and with mock IFU stellar kinematics (orange and blue) and an increased statistical error of δvstat = 3.5% for the kinematics. In concordance with Fig. 3, the plot shows the constraints for the most relevant parameters in the fit: the lens distance, Dd, int, time-delay distance DΔt, int, internal mass-sheet parameter, λint, and orbital anisotropy, βz. The contours highlight the 1σ, 2σ, and 3σ confidence regions. The black points (lines) depict the mock input values. The increased error of 3.5% for each velocity bin translates to larger uncertainties on DΔt, int and λint. The uncertainties on Dd, int are dictated by the systematic offset (δvsys) and are unchanged with respect to the models in Sect. 4.1, given the same bias of −2% in |
 |
Fig. A.2. H0 and Ωm constraints from our models in flat ΛCDM cosmology, for the IDEAL (left) and FIDUCIAL (right) datasets, with increased statistical errors of δvstat = 3.5%. We adopted uniform priors on H0 of [50, 120] km s−1 Mpc−1 and on Ωm of [0.05, 0.5]. The green shaded regions show the 1σ, 2σ, and 3σ confidence regions based on the constraint on DΔt only, i.e. P(DΔt) after marginalising over other mass model parameters, including Dd. The red shaded regions show the corresponding constraints based on P(Dd), after marginalising over DΔt. The grey histogram shows the constraints based on P(Dd, DΔt); we have omitted the 2D contours for ease of viewing. In principle, the different tilts in the H0-Ωm space, when marginalised over Dd or DΔt, can break some of the degeneracies. However, this requires highly accurate and precise measurements of the LOSVD. Errors of δvstat = 3.5% are already insufficient to provide powerful constraints on, for example, Ωm on a single lens basis when accounting for the MST. |
Parameter constraints and cosmological forecast from our lensing-only and joint strong lensing and stellar dynamical models.
Appendix B: Systematic error sampling sensitivity
To facilitate a direct comparison with the cosmological forecast in Birrer & Treu (2021), we perform the joint modelling of the strong lensing and stellar kinematic data with δvstat = 2.5% and δvsys = −2% (orange) and δvstat = 3.5% and δvsys = −2% (blue), and show the corresponding parameter constraints in Fig. B.1. In contrast to Sect. 4.1 where fv was uniformly distributed between [ − 0.02, 0.02], fv is now assumed to be a Gaussian distribution with a standard deviation of 0.02, for which we create 25 realisations of fv, covering a range of [−0.06, 0.06] in steps of 0.005, and apply a weighting of each chain given by w = exp(−0.5(fv/σv)2), with σv = 0.02. The corresponding cosmological forecast for flat ΛCDM is presented in Fig. B.2, with the results summarised in Table B.1.
 |
Fig. B.1. Measurements from our joint strong lensing and stellar dynamical models, without any kinematic data (grey) and with mock IFU stellar kinematics (orange and blue). In both cases, we adopt δvsys = −2% and a statistical error of δvstat = 2.5% (orange) and δvstat = 3.5% (blue). We adopt and marginalise over a Gaussian distribution for fv within the range [−0.06, 0.06] for both. In concordance with Fig. 3, the plot shows the constraints for the most relevant parameters in the fit: the lens distance, Dd, int, time-delay distance, DΔt, int, internal mass-sheet parameter, λint, and orbital anisotropy, βz. The contours highlight the 1σ, 2σ, and 3σ confidence regions. The black points (lines) depict the mock input values. The increased error of 3.5% for each velocity bin translates to larger uncertainties on DΔt, int and λint. The uncertainties on Dd, int are dictated by the systematic offset (δvsys) and are almost identical for both mock kinematic datasets, given the same bias of −2% in |
 |
Fig. B.2. H0 and Ωm constraints from our models in flat ΛCDM cosmology, for the FIDUCIAL datasets with δvstat= 3.5% (left) and δvstat= 2.5% (right). The systematic uncertainty is δvsys = −2.0%, but assuming a Gaussian distribution for fv within the range [−0.06, 0.06] for both. We adopted uniform priors on H0 of [50, 120] km s−1 Mpc−1 and on Ωm of [0.05, 0.5]. The green shaded regions show the 1σ, 2σ, and 3σ confidence regions based on the constraint on DΔt only, i.e. P(DΔt) after marginalising over other mass model parameters, including Dd. The red shaded regions show the corresponding constraints based on P(Dd), after marginalising over DΔt. The grey histogram shows the constraints based on P(Dd, DΔt); we have omitted the 2D contours for ease of viewing. In principle, the different tilts in the H0-Ωm space, when marginalised over Dd or DΔt, can break some of the degeneracies. However, this requires highly accurate and precise measurements of the LOSVD. Errors of δvstat = 3.5% (left) are already insufficient to provide powerful constraints on, for example, Ωm on a single lens basis when accounting for the MST. The different statistical uncertainties on the velocity measurements, δvstat (between the left and right panels), primarily affect the constraints on DΔt and hence H0, as shown by the green contours and histograms. |
Parameter constraints and cosmological forecast from our lensing-only and joint strong lensing and stellar dynamical models.
Appendix C: Kinematic insensitivity to large core radii
In this appendix we show in more detail that a MST with a large core radius for the cored SMD profile (that approximates a mass sheet) effectively yields a vanishing 3D mass density profile and does not influence the stellar kinematics of the lens galaxy.
We start from Eq. (14) for the projected SMD,
The term (1 − λint) represents the mass sheet, and following B20, we approximate it as a cored dimensionless SMD distribution15,
where a0 is a normalisation parameter that is directly proportional to the SMD of the mass sheet. For θc ≫ θ, the cored mass-density profile approximates well a mass sheet of constant convergence. Assuming spherical symmetry, the 3D mass density corresponding to the (projected) dimensionless SMD above is
where Σcrit is given by Eq. (13). In other words, ρcore is the deprojection of κcore.
Substituting Eq. (C.2) into Eq. (C.1), we obtain
In order to predict the 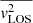 through the Jeans equation, we would first deproject the SMD to obtain the mass density
through the Jeans equation, we would first deproject the SMD to obtain the mass density
where the deprojection for Deproj[κcomposite(θ)] can be done through the MGEs described in Sect. 3.2. For large rc (≳400 kpc for our case), ρcore(r)→ 0 and we obtain
Substituting Eq. (6) into the above equation for DΔt, int, the λint in the numerator and denominator cancels and we find that
Therefore, when rc is large, this mass density is independent of λint and thus the associated internal MST does not affect the stellar kinematics16.
All Tables
Parameter constraints from our lensing-only and joint strong lensing and stellar dynamical models.
Parameter constraints and cosmological forecast from our lensing-only and joint strong lensing and stellar dynamical models.
Parameter constraints and cosmological forecast from our lensing-only and joint strong lensing and stellar dynamical models.
All Figures
 |
Fig. 1. HST ACS F814W imaging cutout of RXJ1131−1231, illustrating the prominent lens configuration with a quadruply imaged background quasar (A, B, C, and D) and a nearby satellite (S). Spectroscopic measurements locate the lens and quasar at redshifts zd = 0.295 and zs = 0.654, respectively. We generated mock imaging data that closely resemble the archival HST data shown here, based on a best-fitting lensing model and excluding the satellite. Overlaid is the JWST NIRSpec nominal FOV of 3″×3″, within which we create mock stellar kinematics of the foreground lens at 0.1″ pixel−1 resolution. The FOV is oriented such that the x-axis is aligned with the galaxy major axis. |
| In the text | |
 |
Fig. 2. Total enclosed mass profile in 3D and its sensitivity to λint and Dd, int. Top: Total enclosed mass profile in 3D as a function of intrinsic radius ( |
| In the text | |
 |
Fig. 3. Measurements from our joint strong lensing and stellar dynamical models, without any kinematic data (grey) and with mock IFU stellar kinematics (orange and blue). The corner plot shows the most relevant parameters in the fit, consisting of the lens distance, Dd, int, time-delay distance, DΔt, int, internal mass-sheet parameter, λint, and orbital anisotropy, βz. The contours highlight the 1σ, 2σ, and 3σ confidence regions. The black points (lines) depict the mock input values. Without any kinematics, DΔt, int and λint are highly degenerate, while Dd, int and βz are unconstrained. The posterior PDFs for Dd, int and βz are virtually flat in this case, which is why we only show the 2D contours in the DΔt, int–λint space. IFU data will considerably tighten the constraints. In the IDEAL case, the mock input values are recovered within 2σ. In the FIDUCIAL case, the mock input values are also recovered within the 2σ bands, but with larger relative uncertainties for the lens distance (δDd, int/Dd, int ≈ 4%). These measurements are independent of cosmological model assumptions. |
| In the text | |
 |
Fig. 4. Measurements from our joint strong lensing and stellar dynamical models with mock IFU stellar kinematics (IDEAL), but for two different parameterisations of the orbital anisotropy profile, βz. The corner plot shows the relevant parameters in the fit, consisting of the lens distance, Dd, int, time-delay distance, DΔt, int, and internal mass-sheet parameter, λint. The mock data are mildly anisotropic (i.e. βz(r) = 0.15 is non-zero and independent of radius) and fitted with both a radially constant (indigo) and radially varying anisotropy profile (teal). The contours highlight the 1σ, 2σ, and 3σ confidence regions, with the black points (lines) depicting the mock input values. The radially constant mock input anisotropy can be recovered from models with a radially varying anisotropy profile. |
| In the text | |
 |
Fig. 5. Mock kinematic data and model comparisons. First: IDEAL mock IFU |
| In the text | |
 |
Fig. 6. H0 and Ωm constraints from our models in flat ΛCDM cosmology, for the IDEAL (left) and FIDUCIAL (right) datasets with statistical uncertainties of δvstat = 2.5%. We adopted uniform priors on H0 of [50, 120] km s−1 Mpc−1 and Ωm of [0.05, 0.5]. The green shaded regions show the 1σ, 2σ, and 3σ confidence regions based on the constraint on DΔt only, i.e. P(DΔt) after marginalising over other mass model parameters, including Dd. The red shaded regions show the corresponding constraints based on P(Dd), after marginalising over DΔt. The grey histogram shows the constraints based on P(Dd, DΔt); we have omitted the 2D contours for ease of viewing. Different tilts in the H0–Ωm space, when marginalised over Dd and DΔt, respectively, can break some of the degeneracies, also leading to improved constraints on Ωm. |
| In the text | |
 |
Fig. A.1. Measurements from our joint strong lensing and stellar dynamical models, without any kinematic data (grey) and with mock IFU stellar kinematics (orange and blue) and an increased statistical error of δvstat = 3.5% for the kinematics. In concordance with Fig. 3, the plot shows the constraints for the most relevant parameters in the fit: the lens distance, Dd, int, time-delay distance DΔt, int, internal mass-sheet parameter, λint, and orbital anisotropy, βz. The contours highlight the 1σ, 2σ, and 3σ confidence regions. The black points (lines) depict the mock input values. The increased error of 3.5% for each velocity bin translates to larger uncertainties on DΔt, int and λint. The uncertainties on Dd, int are dictated by the systematic offset (δvsys) and are unchanged with respect to the models in Sect. 4.1, given the same bias of −2% in |
| In the text | |
 |
Fig. A.2. H0 and Ωm constraints from our models in flat ΛCDM cosmology, for the IDEAL (left) and FIDUCIAL (right) datasets, with increased statistical errors of δvstat = 3.5%. We adopted uniform priors on H0 of [50, 120] km s−1 Mpc−1 and on Ωm of [0.05, 0.5]. The green shaded regions show the 1σ, 2σ, and 3σ confidence regions based on the constraint on DΔt only, i.e. P(DΔt) after marginalising over other mass model parameters, including Dd. The red shaded regions show the corresponding constraints based on P(Dd), after marginalising over DΔt. The grey histogram shows the constraints based on P(Dd, DΔt); we have omitted the 2D contours for ease of viewing. In principle, the different tilts in the H0-Ωm space, when marginalised over Dd or DΔt, can break some of the degeneracies. However, this requires highly accurate and precise measurements of the LOSVD. Errors of δvstat = 3.5% are already insufficient to provide powerful constraints on, for example, Ωm on a single lens basis when accounting for the MST. |
| In the text | |
 |
Fig. B.1. Measurements from our joint strong lensing and stellar dynamical models, without any kinematic data (grey) and with mock IFU stellar kinematics (orange and blue). In both cases, we adopt δvsys = −2% and a statistical error of δvstat = 2.5% (orange) and δvstat = 3.5% (blue). We adopt and marginalise over a Gaussian distribution for fv within the range [−0.06, 0.06] for both. In concordance with Fig. 3, the plot shows the constraints for the most relevant parameters in the fit: the lens distance, Dd, int, time-delay distance, DΔt, int, internal mass-sheet parameter, λint, and orbital anisotropy, βz. The contours highlight the 1σ, 2σ, and 3σ confidence regions. The black points (lines) depict the mock input values. The increased error of 3.5% for each velocity bin translates to larger uncertainties on DΔt, int and λint. The uncertainties on Dd, int are dictated by the systematic offset (δvsys) and are almost identical for both mock kinematic datasets, given the same bias of −2% in |
| In the text | |
 |
Fig. B.2. H0 and Ωm constraints from our models in flat ΛCDM cosmology, for the FIDUCIAL datasets with δvstat= 3.5% (left) and δvstat= 2.5% (right). The systematic uncertainty is δvsys = −2.0%, but assuming a Gaussian distribution for fv within the range [−0.06, 0.06] for both. We adopted uniform priors on H0 of [50, 120] km s−1 Mpc−1 and on Ωm of [0.05, 0.5]. The green shaded regions show the 1σ, 2σ, and 3σ confidence regions based on the constraint on DΔt only, i.e. P(DΔt) after marginalising over other mass model parameters, including Dd. The red shaded regions show the corresponding constraints based on P(Dd), after marginalising over DΔt. The grey histogram shows the constraints based on P(Dd, DΔt); we have omitted the 2D contours for ease of viewing. In principle, the different tilts in the H0-Ωm space, when marginalised over Dd or DΔt, can break some of the degeneracies. However, this requires highly accurate and precise measurements of the LOSVD. Errors of δvstat = 3.5% (left) are already insufficient to provide powerful constraints on, for example, Ωm on a single lens basis when accounting for the MST. The different statistical uncertainties on the velocity measurements, δvstat (between the left and right panels), primarily affect the constraints on DΔt and hence H0, as shown by the green contours and histograms. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




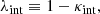
![$$ \begin{aligned} {\lambda _{\rm int}} \in [0.5, 1.5]. \end{aligned} $$](/articles/aa/full_html/2023/07/aa42318-21/aa42318-21-eq10.gif)
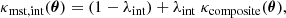
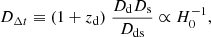
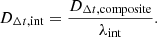
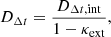
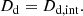
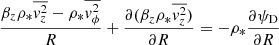
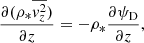
![$$ \begin{aligned} \begin{aligned} \overline{{ v}_{\mathrm{LOS} }^{2}} =&\frac{1}{\mu (x\prime ,{ y}\prime )}\;\int _{-\infty }^{\infty }\;\rho _*\Big [(\overline{{ v}_{R}^{2}}\sin ^{2}\phi +\overline{{ v}_{\phi }^{2}}\cos ^{2}\phi )\sin ^{2}\zeta \\&+\overline{{ v}_{z}^{2}}\cos ^{2}\zeta -\overline{{ v}_{R}{ v}_{z}}\sin \phi \sin (2\zeta )\Big ]\mathrm{d}z\prime \;\equiv \;{ v}^{2}+\sigma ^{2}, \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/07/aa42318-21/aa42318-21-eq32.gif)
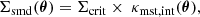
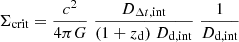
![$$ \begin{aligned} \begin{aligned} \Sigma _{\rm smd}(\boldsymbol{\theta })&= \bigg [ \frac{c^{2}}{4\pi G}\;\frac{{{D_{{\Delta t},\mathrm{int}}}}}{(1+{z_{\rm d}})\;{D_{\mathrm{d} ,\mathrm{int}}}}\;\frac{1}{{D_{\mathrm{d} ,\mathrm{int}}}}\bigg ]\\&\times \bigg [(1-{\lambda _{\rm int}})+{\lambda _{\rm int}}\;\kappa _{\rm composite}(\boldsymbol{\theta }) \bigg ].\\ \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/07/aa42318-21/aa42318-21-eq35.gif)
![$$ \begin{aligned} \rho _{i}(R, z) = \frac{M_{i}}{(\sigma _{i} \sqrt{2 \pi })^3\;q_{i}}\;\exp \bigg [-\frac{1}{2\sigma _{i}^{2}}\;\Bigg (R^{2} + \frac{z^2}{q_{i}^2} \Bigg )\bigg ], \end{aligned} $$](/articles/aa/full_html/2023/07/aa42318-21/aa42318-21-eq36.gif)
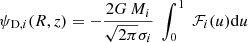
![$$ \begin{aligned} \mathcal{F} _{i}(u) = \exp \bigg [-\frac{u^{2}}{2\sigma ^{2}_{i}}\Bigg (R^{2}+\frac{z^2}{\mathcal{Q} ^{2}_{i}(u)}\Bigg )\bigg ]\frac{1}{\mathcal{Q} _{i}(u)} \end{aligned} $$](/articles/aa/full_html/2023/07/aa42318-21/aa42318-21-eq41.gif)
![$$ \begin{aligned} \rho _{*,j}(R, z) = \frac{L_{j}}{(\sigma _{j} \sqrt{2 \pi })^3\;q_{j}}\;\exp \bigg [-\frac{1}{2\sigma _{j}^{2}}\;\Bigg (R^{2} + \frac{z^2}{q_{j}^2} \Bigg )\bigg ], \end{aligned} $$](/articles/aa/full_html/2023/07/aa42318-21/aa42318-21-eq43.gif)
![$$ \begin{aligned}[\overline{{ v}_{z}^{2}}]_{j} = 4\pi \,G \sum _{i} \frac{\Sigma _{\mathrm{M} , i}\,q\prime _{i}}{\sqrt{2\pi }\sigma _{i}}\int _{0}^{1}q_{j}^{2}\sigma _{j}^{2}\frac{\mathcal{F} _{i}(u)u^{2}}{1-\mathcal{F} _{ji}u^{2}}\mathrm{d}u, \end{aligned} $$](/articles/aa/full_html/2023/07/aa42318-21/aa42318-21-eq44.gif)
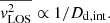
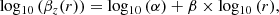
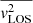


![$$ \begin{aligned} \begin{aligned} \Sigma _{\rm smd}(\boldsymbol{\theta })&= \bigg [ \frac{c^{2}}{4\pi G}\;\frac{{{D_{{\Delta t},\mathrm{int}}}}}{(1+{z_{\rm d}})\;{D_{\mathrm{d} ,\mathrm{int}}}^2}\bigg ]\\&\times \bigg [(1-{\lambda _{\rm int}})+{\lambda _{\rm int}}\;\kappa _{\rm composite}(\boldsymbol{\theta }) \bigg ].\\ \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/07/aa42318-21/aa42318-21-eq98.gif)
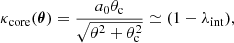
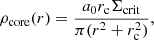
![$$ \begin{aligned} \begin{aligned} \Sigma _{\rm smd}(\boldsymbol{\theta })&= \bigg [ \frac{c^{2}}{4\pi G}\;\frac{{{D_{{\Delta t},\mathrm{int}}}}}{(1+{z_{\rm d}})\;{D_{\mathrm{d} ,\mathrm{int}}}^2}\bigg ] \bigg [\kappa _{\rm core} + {\lambda _{\rm int}}\;\kappa _{\rm composite}(\boldsymbol{\theta }) \bigg ].\\ \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/07/aa42318-21/aa42318-21-eq101.gif)
![$$ \begin{aligned} \begin{aligned} \rho (r)&= \bigg [ \frac{c^{2}}{4\pi G}\;\frac{{{D_{{\Delta t},\mathrm{int}}}}}{(1+{z_{\rm d}})\;{D_{\mathrm{d} ,\mathrm{int}}}^2}\bigg ]\\&\times \bigg [\rho _{\rm core}(r) + {\lambda _{\rm int}}\;\mathrm{Deproj}\left[\kappa _{\rm composite}(\boldsymbol{\theta })\right] \bigg ],\\ \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/07/aa42318-21/aa42318-21-eq103.gif)
![$$ \begin{aligned} \begin{aligned} \rho (r)&= \frac{c^{2}}{4\pi G}\;\frac{{{D_{{\Delta t},\mathrm{int}}}}\; {\lambda _{\rm int}}}{(1+{z_{\rm d}})\;{D_{\mathrm{d} ,\mathrm{int}}}^2} \;\mathrm{Deproj}\left[\kappa _{\rm composite}(\boldsymbol{\theta })\right].\\ \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/07/aa42318-21/aa42318-21-eq104.gif)
![$$ \begin{aligned} \begin{aligned} \rho (r)&= \frac{c^{2}}{4\pi G}\;\frac{{D_{\Delta t, \mathrm{composite}}}}{(1+{z_{\rm d}})\;{D_{\mathrm{d} ,\mathrm{int}}}^2} \;\mathrm{Deproj}\left[\kappa _{\rm composite}(\boldsymbol{\theta })\right].\\ \end{aligned} \end{aligned} $$](/articles/aa/full_html/2023/07/aa42318-21/aa42318-21-eq105.gif)