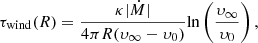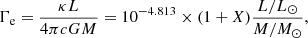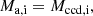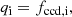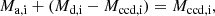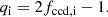EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 672 (April 2023) A&A, 672 (2023) A198 Full HTML
Open Access
Issue
A&A
Volume 672, April 2023
Article Number A198
Number of page(s) 19
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202245378
Published online 21 April 2023

© The Authors 2023

Licence Creative CommonsOpen Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.

1. Introduction

Massive stars are known to affect multiple aspects of the evolution of our Universe (Haiman & Loeb 1997; Mac Low & Klessen 2004; Langer 2012). They regulate star formation in galaxies (Mac Low et al. 2005; Crowther 2019) and drive chemical evolution (Burbidge et al. 1957; Pignatari et al. 2010; Thielemann et al. 2011; Kasen et al. 2017; Kajino et al. 2019) where the dominant contribution may come from the most massive stars, particularly at sub-solar metallicity (Kozyreva et al. 2014; Crowther et al. 2016). They further produce supernova explosions (Burrows et al. 1995; Burrows & Vartanyan 2021; Aguilera-Dena et al. 2023), neutron stars (Baym et al. 2018; Vidaña 2018), stellar-mass black holes (BHs, Orosz et al. 2011; Miller-Jones et al. 2021), and gravitational wave events (Abbott et al. 2016, 2019, 2021).

Recent observations have provided empirical evidence of massive stars being preferentially born in binaries and higher order multiples with at least one nearby companion (Sana et al. 2012, 2013, 2014; Moe & Di Stefano 2017; Banyard et al. 2022). The proximity of such a companion has a strong impact on the evolution of both stars (Podsiadlowski 1992; de Mink et al. 2013; De Marco & Izzard 2017; Kruckow et al. 2018; Wang et al. 2020; Klencki et al. 2020). In this situation, comparing binary evolution model predictions to observed populations of massive binaries (Vanbeveren et al. 1998a; Han et al. 2003; de Mink et al. 2007; Eldridge et al. 2017; Menon et al. 2021; Abdul-Masih et al. 2021; Sen et al. 2022; El-Badry et al. 2022; Patrick et al. 2022) is of paramount importance to place constraints on the uncertainties associated with massive star evolution (Langer 2012; Crowther 2019).

The growing stellar radius during core hydrogen burning leads to mass transfer via Roche-lobe overflow in short-period massive binaries (Pols 1994; Vanbeveren et al. 1998b; Nelson & Eggleton 2001; de Mink et al. 2007; Sen et al. 2022). This so-called Case A mass transfer is unique in the sense that it contains a nuclear timescale mass transfer phase (slow Case A) and has the Algol binaries (Surkova & Svechnikov 2004; Malkov 2020; Li et al. 2022) as long-lived observational counterparts. Slow Case A mass transfer occurs because after the mass ratio inversion during the foregoing fast (thermal timescale) Case A mass transfer phase, any further mass transfer widens the orbit (Soberman et al. 1997; Wellstein et al. 2001). Consequently, after the mass donor becomes thermally relaxed, mass transfer is only driven by its expansion on the nuclear timescale. During this phase, the binary systems fulfil the so-called Algol paradox (named after β Per = Algol, Eggen 1957), with a less massive mass donor being more evolved than its more massive companion (Paczyński 1971; Batten 1989; Pustylnik 1998).

Algols binaries present a distinct opportunity to test stellar and binary evolution physics, and in particular to constrain the mass-transfer efficiency of the important fast mass transfer phase, during which the majority of the donor’s envelope mass is removed (de Mink et al. 2007; Sen et al. 2022). These systems are also expected to be the progenitors of short-period Wolf-Rayet (WR)+OB star binaries (van der Hucht 2001; Petrovic et al. 2005), high-mass X-ray binaries (Valsecchi et al. 2010; Qin et al. 2019; Quast et al. 2019; Sen et al. 2021), and, possibly, double compact binaries and merging black holes (Bond & Carr 1984; Voss & Tauris 2003; Belczynski et al. 2008, 2020; Dominik et al. 2012; Stevenson et al. 2017; Mandel & Farmer 2022; Chruslinska et al. 2018; Kruckow et al. 2018; Spera et al. 2019; Vigna-Gómez et al. 2019; Antonini & Gieles 2020; Mapelli 2020; Kremer et al. 2020; Gallegos-Garcia et al. 2021; Marchant et al. 2021; Bavera et al. 2021; Broekgaarden et al. 2022; van Son et al. 2022; Briel et al. 2023). Only the detailed reproduction of the observed properties of massive binaries in the early stages of binary evolution (Sen et al. 2022; Wang et al. 2020, 2022) can ensure that errors in the models for these stages do not propagate into our predictions of later binary evolution stages (e.g. Olejak et al. 2021; Belczynski et al. 2022).

For initial primary star masses below ∼40 M⊙, detailed analyses of binary models following Case A evolution have been performed (see references above). They essentially confirmed the classical picture of Algol binary evolution derived from intermediate-mass models (e.g. van Rensbergen & de Greve 2021)1. While these models still cannot explain all of the individual massive Algol binaries (de Mink et al. 2007; Sen et al. 2022), they are able to reproduce the overall properties of the majority of them, such as the distribution of orbital periods and mass ratios, implying that the evolutionary state of the observed Algol binaries is well understood.

In contrast, detailed models of very massive binaries (with initial donor masses ≥40 M⊙) are sparse in the literature (Wellstein & Langer 1999; Petrovic et al. 2005; Eldridge et al. 2017; Shenar et al. 2020a; Fragos et al. 2023; Pauli et al. 2022), while rapid binary evolution models are generally unable to make accurate predictions for the Algol phase. Here, we try to remedy this by analysing models from a recent large grid of detailed models for very massive binary stars at LMC metallicity (Pauli et al. 2022), with a focus on the evolution phase after the fast Case A mass transfer during which both components are still burning hydrogen in their cores.

Our paper is organised as follows. Section 2 describes the physics assumptions used in the binary evolution models. In Sect. 3, we discuss the salient features of Case A evolution in very massive binaries, and their relation to the Eddington limit. We estimate the initial binary parameter space for reverse Algol evolution in Sect. 4 and show an animated view of reverse Algol evolution on the Hertzsprung-Russell (HR) diagram in Sect. 5. We compare the models with observations of very massive semi-detached binaries and hydrogen-rich luminous WR stars in Sect. 6. Finally, we discuss relevant uncertainties in massive binary modelling and their effects on our results in Sect. 7, before summarising our work in Sect. 8.

2. Method

In this section, we briefly summarise the most relevant physics assumptions in the analysed detailed binary evolution models of Pauli et al. (2022), and we refer the reader to their work for more details. Furthermore, we describe our method for assigning an optical depth parameter to a given stellar model, which will allow us to argue which of the models may correspond to WR-type stars rather than to O stars.

2.1. Stellar physics

The models discussed in our paper have been calculated with version 10 398 of the one-dimensional stellar evolution code MESA (Paxton et al. 2011, 2013, 2015, 2018, 2019). The metallicity and initial chemical composition of the binary components correspond to that of the stars observed in young star-forming regions of the Large Magellanic Cloud (LMC). They are set as in Brott et al. (2011), with hydrogen, helium, and metal mass fractions of 0.7391, 0.2562, and 0.0047, respectively, and account for the non-solar metal-abundance ratios in the LMC. Custom-made OPAL opacity tables (Iglesias & Rogers 1996) for these initial abundances have been used. The models take into account differential rotation (Heger et al. 2000; Spruit 2002), magnetic angular momentum transport (Spruit 2002; Heger et al. 2005), and rotational mixing via the Eddington-Sweet circulation, the Goldreich-Schubert-Fricke instability, and the secular and dynamic shear instability (Heger et al. 2000).

The adopted wind mass-loss rates depend on the surface-hydrogen mass fraction XH and effective temperature Teff of the stellar model. For hot stars (Teff > 25 kK) with XH > 0.7, the prescription of Vink et al. (2001) is used. For cooler stars (Teff < 25 kK) with XH > 0.7, the maximum of the mass-loss rate of Vink et al. (2001) and Nieuwenhuijzen & de Jager (1990) is adopted. For stars with XH < 0.4, the Nugis & Lamers (2000) mass-loss rate is implemented with a wind clumping factor of D = 3 instead of 10 (Pauli et al. 2022, see also Yoon 2017). Finally, for stars with XH between 0.4 and 0.7, the mass-loss rate is linearly interpolated between the Vink et al. (2001) rate and the reduced Nugis & Lamers (2000) rate. Mass-loss rates for more evolved types of stars, such as hydrogen-free WR stars, are not relevant here.

Regions of convective instability inside the star are determined using the Ledoux criterion. Convection is modelled using the standard mixing length theory (MLT) of Böhm-Vitense (1960), with a mixing length parameter of αMLT = 1.5. In superadiabatic regions with a stabilising molecular gradient, semi-convection is assumed to occur (Langer et al. 1983; Langer 1991) with an efficiency parameter of αsc = 1 (Schootemeijer et al. 2019). Thermohaline mixing is modelled following the work of Cantiello & Langer (2010). Overshooting above the convective core is implemented as a step function extending the core by 0.335 times the local pressure scale height at the core boundary (Brott et al. 2011). To account for the composition gradients in the rejuvenation process of mass-gaining stars (Braun & Langer 1995), we only allow overshooting in regions with nearly constant composition (Marchant 2017).

2.2. Binary physics

The binary models are calculated from the start of their hydrogen burning, assuming that both stars start burning hydrogen at the same time. The orbits are assumed to be circular, and the initial rotation period of the stars is set as equal to the initial orbital period of the binary, with the spin axes perpendicular to the plane of the orbit. Time-dependent tides are modelled as in Detmers et al. (2008). The tidal synchronisation timescale is taken from the dynamical tide model of Zahn (1977), since our work focuses on main-sequence stars with radiative envelopes.

In the case of the Roche-lobe overflow of one star, the mass-transfer rate is calculated such that the donor star marginally fills its Roche lobe. When both stars fill their Roche lobes, we apply the contact binary scheme from Marchant et al. (2016), also described in detail in Menon et al. (2021). The evolution of models during the contact phase is stopped if the binary undergoes L2 overflow. Angular momentum accretion of the mass-gaining star is based on the results of Lubow & Shu (1975) and Ulrich & Burger (1976), implemented as in de Mink et al. (2013), where a distinction is made between ballistic and disc modes of accretion.

We assume that mass transfer in our binary models is conservative unless the mass accreting star spins up to critical rotation. When the accretor is critically rotating, we remove the excess transferred mass from the binary via an enhanced stellar wind, with a specific angular momentum equal to the specific orbital angular momentum of the accretor. Since in close binaries, tides impair the accretor’s spin-up, the mass transfer efficiency in the models depends on the orbital period, with higher mass transfer efficiencies obtained for shorter period binaries. Finally, when the energy required to remove the excess mass exceeds the combined luminosity of both stars, the model calculation is stopped. For a comprehensive discussion of these physics assumptions, see Marchant (2017) and Sen et al. (2022).

2.3. Optical-depth parameter

In order to derive the frequency-dependant emergent photon spectrum of a stellar model, detailed model atmosphere calculations are required (e.g. Groh et al. 2013; Jung et al. 2022). While this is beyond the scope of our paper, we aim to assess which of the analysed stellar models would produce an emission-line-dominated spectrum and thus correspond to the class of WR stars. To this end, we followed Aguilera-Dena et al. (2022) and Pauli et al. (2022) to compute the optical depth parameter of the adopted stellar winds.

We followed De Loore et al. (1982) and Langer (1989) in assuming a β = 1 wind-velocity law (Vink et al. 2001) to estimate the optical depth of a stellar wind with a mass-loss rate of Ṁ for a star with radius, R, as

(1)

using the electron scattering opacity as κ = 0.2(1 + XH) cm2 g−1. Here, υ∞ is the terminal wind speed, υ0 is the expansion velocity near the stellar surface taken as 20 km s−1, and XH is the mass fraction of hydrogen at the stellar surface. For stars with 4.4 < log Teff < 4.7, we assume υ∞ = 2.6υesc, and for cooler stars υ∞ = 1.3υesc (as in Pauli et al. 2022). For the escape velocity υesc, we account for the electron scattering Eddington factor, which is given by

(2)

where L and M are the luminosity and mass of the star, respectively. We ignore the dependence of the terminal wind speed on metallicity Z (υ∞ ∝ Z0.1 − 0.2, Vink & Sander 2021; Marcolino et al. 2022), as it is not expected to affect our results significantly.

Due to the rough approximations required for our approach (e.g. on the opacity), we do not expect the optical depth parameters computed for the models to accurately represent the true optical depth in the corresponding stellar winds. However, they include the main dependencies on mass-loss rate, wind velocity, and stellar radius, and as such they may be valid order-of-magnitude estimates. Moreover, these parameters can be meaningfully compared relatively to each other, that is, for different stellar models, and, importantly, to the optical-depth parameters computed in the same way for observed stars. From this ansatz, Aguilera-Dena et al. (2022) and Pauli et al. (2022) find a threshold optical-depth parameter for hydrogen-free WR stars of τwind ≃ 1.5, and Pauli et al. (2022) suggest a significantly smaller value for hydrogen-rich WR stars. In Sect. 6.2, we show that for the models investigated here, a threshold value as low as τwind ≃ 0.1 may be appropriate.

3. Distinct effects in the evolution of very massive Case A binaries

In this section, we highlight four fundamental effects that occur only in the evolution of very massive binaries. The mass limits above which they exhibit these effects are gauged here based on the LMC binary model grid, but they may depend on metallicity. All four effects are related to the proximity of very massive stars to their Eddington limit and therefore occur naturally in all detailed binary evolution models. The reverse Algol configuration in particular can be found in models of Sybesma (1986) and of Stanway & Eldridge (2018), but the unique implications of this evolutionary path we raise here have not been identified before. We describe specific binary models in detail in the appendix to illustrate our findings and only discuss their underlying physics here. In Sect. 4, we identify the initial binary parameter space in which the reverse Algol scenario (Sect. 3.2) is expected to play a role. We discuss uncertainties in our inherent assumptions in Sect. 7.

3.1. Most very massive binaries undergo Case A mass transfer

Massive main-sequence stars (∼20 M⊙) typically expand by a factor of three during their main-sequence evolution. Case A mass transfer is therefore usually associated with orbital periods of the order of a few days (Fig. 5 of Sen et al. 2022). However, due to the proximity to the Eddington limit and corresponding envelope inflation in very massive core-hydrogen-burning stars (Brott et al. 2011; Gräfener et al. 2012; Sanyal et al. 2015, 2017), the limiting orbital period for Case A evolution increases sharply at higher mass. For example, Pauli et al. (2022) find this limiting initial orbital period in LMC binary models to be at 16 d, 120 d, and 2000 d for initial donor masses of 32 M⊙, 50 M⊙, and 56 M⊙, respectively. This can be understood by considering single-star evolution models. In the LMC models of Brott et al. (2011), the initial mass at which envelope inflation shifts the terminal-age-main-sequence (TAMS) effective temperature to about halfway between the zero-age main sequence (ZAMS) and the Hayashi line, is about 40 M⊙. Consequently, at higher mass, the majority of all interacting binaries will undergo Case A mass transfer.

Due to the large luminosity-to-mass ratio of very massive stars, it is also more likely that very massive binaries can undergo highly non-conservative mass transfer without merging. In the models studied here, it is assumed that a merger occurs when the available photon energy is insufficient to push the transferred mass that cannot be accreted by the donor to infinity (Marchant 2017). As this condition is more easily avoided for more massive stars, we find that most of our very massive Case A binaries with initial periods even up to ∼1000 d can avoid merging. In the appendix, we show a detailed example of a very massive binary with an initial orbital period of 100 d (Fig. A.1).

3.2. Donors may remain the more massive binary component

In the classical picture of Case A binary evolution in intermediate and massive stars, once mass transfer commences it occurs on the rapid, thermal timescale. The reason is that any transfer of mass from the donor to the accretor leads to a shrinking orbit until the mass ratio is inverted. Since for the mass donor to remain within its Roche volume, it needs to be more compact than it can be in thermal equilibrium, the fast mass transfer can only end after the mass ratio has inverted and the orbit widens again.

In very massive binaries, Case A mass transfer starts on the thermal timescale. However, the fast mass-transfer phase can end before mass-ratio inversion for two reasons. Firstly, fast Case A mass transfer ends when the donor is stripped so far that helium-enriched matter appears at its surface, since, from that moment on, any mass loss from the donor leads to a decreasing thermal equilibrium stellar radius. And secondly, as discussed in the next subsection, the donor’s stellar wind mass loss can become so strong that the orbit widens already before the mass ratio is inverted. We discuss consequences for the slow (nuclear timescale) Case A mass transfer in Sect. 3.4.

Surface helium enrichment before mass-ratio inversion in very massive binaries occurs due to the large convective core fractions of very massive stars – an effect of their large Eddington factors. The fraction of the total mass which forms the unprocessed envelope of a massive star decreases with mass. The convective core mass fractions (excluding the overshooting region) at the beginning of core hydrogen burning are roughly 0.3, 0.5, and 0.8 for stars of 10 M⊙, 30 M⊙, and 80 M⊙, respectively. Therefore, in binaries with 10 M⊙ donors, the mass ratio of the binary will invert long before helium-enriched matter appears at its surface. In contrast, for stars above ∼30 M⊙, mass transfer via Roche-lobe overflow may remove the envelope of the donor without producing a mass-ratio inversion of the binary. The consequence is a nuclear timescale Case A mass transfer phase, during which the more massive star is transferring mass to the less massive companion, that is, a reverse Algol configuration (see Fig. A.1).

Reverse Algol evolution becomes more likely the higher the initial mass of the donor star is. While this is due to the larger convective core mass fraction (see above), another effect corroborates this. We find that mass transfer may be less conservative in more massive binaries since more energy is available to remove mass from the binary system. This allows binaries with more extreme initial mass ratios to avoid merging. Results from the recent detailed binary model grid of Pauli et al. (2022) show that binaries with initial companion masses of 50%, 30%, and 20% of the initial donor mass can still survive Case A mass transfer for initial donor masses of 32 M⊙, 50 M⊙, and 80 M⊙, respectively. We explore the Reverse Algol parameter space more comprehensively in Sect. 4.

While ordinary Algol evolution also occurs in some of the analysed models; that is, they undergo a mass-ratio inversion during fast Case A mass transfer. But in some of them, the donor still remains the more luminous star (Appendix B). We find models of such binaries in both the semi-detached and the detached configurations (Figs. A.1 and B.1). The less massive yet more luminous star may also show WR characteristics (Sect. 3.3), as we expect its optical-depth parameter may be similar to that of observed hydrogen-rich WN stars (see the wind mass-loss rates in Figs. A.1 and B.1).

3.3. Donors may obtain WR-type winds

As the wind mass-loss rate for O-type stars increases steeply with luminosity (see, e.g. Eq. (12) of Vink et al. 2001), and the optical depth parameter is proportional to the wind mass-loss rate (Eq. (1)), one may expect that moving up in mass, eventually even unenriched main-sequence stars have winds with WR characteristics. Indeed, luminous and very hydrogen-rich WR stars – with surface hydrogen mass fractions of up to XH = 0.7 – are observed and often interpreted as core-hydrogen-burning single stars (Hainich et al. 2014). We designate the stellar mass above which unenriched main-sequence single stars have WR-type winds (here at LMC metallicity) as MWNH.

In very massive binaries, as we discussed above, the fast mass transfer reduces the stellar mass to the initial convective core mass of the mass donor, such that when the fast mass transfer ends, the donor’s hydrogen surface abundance is still close to its initial value (Fig. A.1). At this stage, the donor’s luminosity is close to its luminosity before the fast mass transfer (Fig. A.3). This is linked to the mass-luminosity relation for core-hydrogen-burning stars, where a smaller mass implies a smaller luminosity, but an increased average mean molecular weight implies a larger luminosity, such that both dependencies counteract each other (Fig. 17 in Köhler et al. 2015). Consequently, our donor stars have an elevated luminosity-to-mass ratio, that is, they are closer to their Eddington limit compared to single stars of the same mass. This implies that our yet unenriched donors may develop WR-type winds at masses well below the corresponding single star mass limit MWNH.

The very massive Case A donors evolve after the fast mass transfer with a surface-hydrogen mass fraction close to their initial surface-hydrogen mass fraction. Further on during core hydrogen burning, the slow mass transfer and/or the enhanced stellar wind lead to a decrease of their surface-hydrogen mass fraction and to a corresponding increase in their surface-helium mass fraction. We may therefore expect very massive Case A donors with a surface-hydrogen mass fraction, XH, in the range of 0.7 − 0.2 (Fig. A.1), with WR-type winds.

In Sect. 3.2, we showed that the donors may remain the more massive components in the binaries. On top of that, they also have a larger average mean molecular weight. So, they may be far more luminous than their companion, which therefore may be difficult to spot in the combined spectrum. Since some of our binary models with such parameters have long orbital periods, it could be difficult to detect the binary status in corresponding observed systems.

3.4. Donors may underfill their Roche lobes

The classical Case A mass-transfer evolution leads to donor stars which, after the fast Case A mass transfer, keep transferring mass on the nuclear timescale throughout the remainder of their core-hydrogen-burning evolution (Pols 1994; Wellstein et al. 2001; Sen et al. 2022). In the very massive Case A binaries, this may be different, due to the high stellar wind mass-loss of the donors (Petrovic et al. 2005). We find that in many of the investigated models, the wind mass-loss rate exceeds the nuclear timescale mass transfer rate (Fig. A.1).

In this situation, the stellar mass loss may indeed slow down the nuclear timescale radius growth of the donor, or – as the donor becomes ever more helium-enriched at the surface – even reverse it (right panel of Fig. A.1). On top of that, despite mass being transferred to the less massive star in the reverse Algol situation, the stellar wind mass loss may lead to a widening of the orbit and an increase of the orbital period (see Appendix A.3). We indeed find that only ∼20% of the donors in the very massive models fill their Roche lobes, and in some cases the Roche-lobe filling factors drop considerably during the core-hydrogen-burning evolution.

4. The parameter space for reverse Algol evolution

The effects discussed in Sect. 3 occur only in stellar models that are close to their Eddington limit. This naturally translates to a limiting donor mass, below which we expect these effects do not occur. However, this mass limit can be different for the four different mentioned effects, and some will also depend on the initial stellar metallicity and other physics assumptions. Consequently, we cannot comprehensively derive the initial binary parameter space where the effects are operating. However, we can quantify the parameter space for reverse Algol evolution through our Fig. 1.

thumbnail Fig. 1.

Initial convective core mass of mass donor (Mccd, i thick black line) and initial accretor mass Ma, i (thin coloured lines) for five initial mass ratios qi = Ma, i/Md, i (0.2, 0.4, 0.6, 0.8, 1.0) as a function of the initial donor mass Md, i in massive binary systems. For highly non-conservative mass transfer, reverse Algol evolution cannot occur above the thick black line (yellow region), only below it (blue region), whereas for conservative evolution it cannot occur above the yellow line. The symbols mark the positions of VFTS 094 and VFTS 176 in this diagram, assuming inefficient (blue) or conservative (yellow) mass transfer, with the ordinate value giving their initial accretor masses. The black dashed line shows the limiting initial companion mass above which the models of Pauli et al. (2022) that avoid a contact phase, also avoid merging during Case A mass transfer. The dash-dotted line shows the limiting initial companion mass below which all models merge. Between these two lines, whether the models merge or not is a function of their initial orbital period, and the fraction of models that merge increases for lower initial accretor masses. Lighter shading is used to indicate that not all models avoid merging. It is also assumed that all binaries with qi < 0.2 (grey line) merge before entering the Algol stage.

Figure 1 shows the donors’ initial convective core mass, Mccd, i, as a function of their initial mass, Md, i, which is the key quantity to estimate whether a reverse Algol phase follows the fast mass transfer in a given binary system. In the case of highly inefficient mass transfer (none of the transferred matter remains on the accretor), models in which the initial convective core mass of the donor exceeds the initial mass of the companion may become reverse Algols, since the donor is stripped to its initial convective core mass during fast Case A mass transfer. The borderline for reverse Algol evolution is thus defined as

(3)

where Ma, i is the initial mass of the accretor, or

(4)

with qi = Ma, i/Md, i and fccd, i = Mccd, i/Md, i. It is expressed by the thick black line in Fig. 1. Only binaries above it can invert their mass ratio and develop an ordinary Algol phase, whereas models below that line may become reverse Algol systems.

In the case of conservative mass transfer, the borderline between ordinary and reverse Algol evolution is defined by the accretor’s mass after a fast Case A mass transfer equaling the donor’s initial convective core mass, that is,

(5)

which implies

(6)

This condition corresponds to the yellow line in Fig. 1.

These two borderlines for reverse Algol evolution are model-independent. They are not affected by stellar wind mass loss of the mass donor as long as the wind does not uncover helium-enriched layers, but wind mass loss of the mass gainer before the onset of mass transfer might shift both lines slightly upwards. While the reverse Algol parameter space shrinks for more efficient mass transfer, we still expect reverse Algol systems for sufficiently high donor masses, even for conservative evolution. The reason is that the initial envelope-mass fraction of the donor becomes even smaller for higher initial masses. Below, we discuss the reverse Algol parameter space possible for inefficient mass transfer in more detail, which closely corresponds to the investigated grid of binary evolution models.

The thin coloured lines in Fig. 1 indicate selected initial binary mass ratios as a function of the initial donor mass. For a given initial mass ratio, reverse Algols can only form to the right of the intersection of these lines, with the line giving the initial convective core mass of the donor. We can find a line of constant initial mass ratio that intersects with the line for the donor’s initial convective core mass for any chosen donor mass. The corresponding initial mass ratio is the maximum value for which reverse Algol evolution can occur at this donor mass. For example, we can see that binaries with an initial donor mass above ∼35 M⊙ are not expected to invert their mass ratio during fast Case A mass transfer if their initial mass ratios are below ∼0.6.

For non-conservative mass transfer, the yellow and blue areas in Fig. 1 indicate where ordinary or reverse Algol evolution is possible. However, when an Algol or reverse Algol evolution is indicated for a given (Md, i, Ma, i) in Fig. 1, some or even all such models may merge before the (reverse) Algol phase is reached, depending on their initial orbital period. The dashed and dashed-dotted lines in Fig. 1 indicate this for the detailed binary model grid of Pauli et al. (2022). They imply that – when ignoring the shortest period binaries which develop contact and merge (see Figs. 1 and F.1 of Sen et al. 2022; see also Menon et al. 2021) – all models above the dashed line avoid merging, and all models below the black dash-dotted line merge. In between these two lines (indicated by lighter shading), the fraction of surviving models drops from one to zero, with shorter period Case A models surviving near the dashed line but merging near the dash-dotted line (Fig. 2). The binary models with small initial mass ratios (qi < 0.2) and those with the shortest initial orbital periods (Pi < 2 − 3 d) are assumed to merge during the fast Case A.

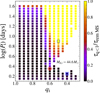thumbnail Fig. 2.

Initial orbital period and initial mass ratio of models of considered binary evolution grid with an initial donor mass of 44.6 M⊙ (small squares). We only show models that do not merge during the fast Case A mass transfer (see Figs. 1 and F.1 of Sen et al. 2022). The colour indicates the fraction of the lifetime of the donor after the fast Case A mass-transfer phase during which the donor is more massive than the accretor (see colour bar to the right). The model discussed in the right panel of Fig. A.1 is highlighted with a black frame. The large red diamond and large blue square show the estimated positions of VFTS 094 and VFTS 176 assuming a highly non-conservative mass transfer, respectively (see text).

Figure 2 shows the fraction of the time span from the end of fast Case A mass transfer to core hydrogen exhaustion of the donor star during which its mass exceeds that of the accretor, for models with an initial donor mass of 44.6 M⊙. The region dominated by black colour corresponds to models with a long-lived ordinary Algol phase, while other colours indicate a long-lived reverse Algol evolution. For initial periods above ∼4 d, the border between both regions corresponds roughly to qi = 0.65. When we compare this to Fig. 1, we obtain a very similar answer. The initial convective core masses of 44.6 M⊙ stars are about 28.5 M⊙, which corresponds to a critical initial donor mass for reverse Algol evolution of the same value, that is, to a critical initial mass ratio of 0.64.

Figure 2 also shows the limitation of our simple approach. It reveals a slight dependence of the critical mass ratio on the initial orbital period for initial periods above 4 d, and a shift of the critical mass ratio towards smaller values for shorter initial periods. The main reason is that in the shorter period binaries, tides may delay or prevent the spin-up of the accretor, which increases the mass-transfer efficiency (see Fig. F.2 of Sen et al. 2022), such that the critical mass ratio shifts from Eqs. (4)–(6).

For the models with an initial donor mass of ∼44.6 M⊙, about 40% of the surviving Case A binary models undergo reverse Algol evolution. Therefore, we expect observable counterparts of such models, in which overluminous and near Roche-lobe filling primaries orbit less massive and less luminous secondary stars.

5. An animated view of massive Algol models

Here, we discuss the evolution of massive Algol binaries in the Hertzsprung-Russell diagram through the animation of a coeval population of massive binary stars. We used the detailed binary evolution models introduced in Wang et al. (2020), which were calculated at a metallicity suitable for the Small Magellanic Cloud (SMC). In Sect. 7.5, we briefly discuss the effect of metallicity on our results.

The grid consists of 2078 binary evolution models with initial primary masses greater than 5 M⊙, covering an initial mass ratio range of 0.3−0.95 and initial orbital periods of 1 day to 8.6 years. A Monte Carlo method was used to sample initial binary model parameters assuming a Salpeter initial mass function (Salpeter 1955), a flat distribution of mass ratios, and a flat distribution of the logarithm of initial orbital periods. The stellar physics assumptions are the same as in Brott et al. (2011) and the binary physics assumptions are the same as in Sen et al. (2022). For more details, we refer the reader to Wang et al. (2020).

Our animation shows the positions of both binary components for the coeval population of binary stars in the HR diagram and covers the first 40 Myr of their evolution. An interpolation of stellar parameters between the binary evolution models is not needed. Only an interpolation in time for each binary model was performed. Due to the high time resolution of the MESA models, this did not lead to noticeable errors in the animation (Wang et al. 2020). Figure 3 shows four snapshots of the animation to describe its features.

thumbnail Fig. 3.

Four snapshots of the animation showing positions of both components of detailed massive binary models in the HR diagram, considering a coeval population following a Salpeter initial mass function and flat initial distributions of mass ratios and logarithms of the initial orbital periods. The snapshots correspond to an age of 2.5 Myr (top left panel), 4 Myr (top right panel), 7.5 Myr (bottom left panel), and 10 Myr (bottom right panel). Translucent grey circles indicate components of pre-interaction binaries, grey squares indicate Case A merger products, and triangles and diamonds indicate mass donors and accretors after the onset of mass transfer, respectively. Components of Case A binaries after the onset of mass transfer are shown in colour, denoting the fraction of critical rotation rotation (v/vcrit). The two components of semi-detached binaries are connected by solid black lines with an arrow indicating the direction of mass transfer. The two components of binaries that have interacted in the past are connected with grey dotted lines. A black frame around a mass donor symbol (triangle) indicates a surface hydrogen mass fraction below 0.1, and a black frame around the symbol for a mass accretor (diamond) indicates a surface helium mass fraction above 0.3. The current age of the population is displayed in the centre bottom with a time bar that fills up as the animation moves forward in time. The table above the legend indicates (from the top) the current number of (i) Algol binaries, i.e. models in the slow Case A mass transfer phase; (ii) core hydrogen burning main-sequence merger products and (iii) cool red supergiants (log Teff < 3.7); (iv) and (v) Case A or Case-B main-sequence mass gainers, respectively, with a neutron star (white dot on symbol) or black hole (black dot on symbol) companion; (vi) core-collapse events that occurred up to the current age; and (vii) pre-interaction binaries brighter than the indicated luminosity threshold, which is 1.5 dex below the luminosity of the brightest hydrogen-burning single star at the current age.

Since thermal timescale mass transfer is too fast to be resolved in the animation, the highlighted mass-transferring binaries are binaries undergoing slow Case A mass transfer. The first such case appears with a donor mass near 40 M⊙ at t ∼ 1.55 Myr in the classical Algol configuration. Around t ∼ 2.5 Myr (Fig. 3, top left panel), we begin to see binary models in the semi-detached configuration where the more luminous star is transferring mass to a less luminous companion.

With time, more semi-detached binaries appear where the more luminous donor is found to transfer mass to a less luminous companion. For example, at 4 Myr (Fig. 3, top right panel), we find 19 binaries in the semi-detached configuration, 11 of which are in the classical Algol configuration and eight are in the reverse Algol configuration. We see that there are more semi-detached binaries in the reverse Algol configuration at higher luminosities than at lower luminosities. There are no reverse Algol binaries below log (L/L⊙) = 5.3, because less luminous stars are generally less massive, and the parameter space for reverse Algol evolution decreases for lower masses (Fig. 1).

Our animation further shows that in ordinary as well as in reverse Algols, the donor star is generally cooler than the accretor. This implies that in ordinary Algols, the bolometric correction of the donor will be less than that of the more luminous accretor, which helps to identify the donor in the combined spectrum. In reverse Algols, the effect goes the other way. The less luminous accretor is also hotter and may therefore be hard to identify spectroscopically. For example, a donor star of a reverse Algol model in the right panel of Fig. 3 is found at Teff ≃ 11 kK, while the accretor has Teff ≃ 37 kK. Together with a luminosity ratio of 6.3, it implies that the mass donor is about 5.2 mag brighter in the visual spectral range, and it will therefore completely outshine the mass gainer.

As time progresses in our animation, the initial masses of the stars that evolve into semi-detached systems decrease, and the corresponding initial mass ranges move below the initial mass threshold for reverse Algol formation. We find that the last reverse Algol model disappears after an age of ∼7.5 Myr (Fig. 3, bottom left panel), whereafter all semi-detached binaries appear in the ordinary Algol configuration (Fig. 3, bottom right panel). This time corresponds to the hydrogen-burning lifetime of a 25 M⊙ star, and it is thereby in good agreement with the simple prediction derived from Fig. 1.

6. Comparison with observations

Here, we discuss several observed binary systems in which the reverse Algol channel has likely occurred. We compare detailed binary evolution models to observed binaries and look for indications that may support the reverse Algol scenario as such.

6.1. Reverse Algols in the Tarantula Nebula

The recent Tarantula Massive Binary Monitoring (TMBM) programme (Almeida et al. 2017; Mahy et al. 2020a,b) investigated the radial velocity variable O stars that were recognised as such as part of the VLT Flames Tarantula Survey (VFTS, Evans et al. 2011; Sana et al. 2013). As the Tarantula region in the LMC has been found to be particularly rich in very massive stars (Schneider et al. 2018), it appears well suited to search for reverse Algol systems. In this sample, Mahy et al. (2020a) identified five semi-detached binaries, roughly as expected from recent binary evolution models (Sen et al. 2022).

From these five systems, Mahy et al. (2020a) found two -VFTS 094 and VFTS 176- in which the Roche lobe filling component is the more massive star in the binary (see Sect. 3.2 and panel ‘a’ of Fig. A.1). While in principle, those could be systems caught during the fast Case A mass transfer, and as such be progenitors of ordinary Algol systems, this is only expected for about one in one hundred semi-detached binaries. Finding two out of five semi-detached binaries with more massive donors points strongly towards all five systems evolving on the nuclear timescale, and thus for VFTS 094 and VFTS 176 being two genuine reverse Algol binaries.

The two mass donors in VFTS 094 and VFTS 176 have dynamical masses of 30.5 M⊙ and 28.3 M⊙, respectively. When we assume that these masses correspond to their initial convective core masses, their initial stellar masses are expected to be about 46 M⊙ and 43 M⊙, respectively (Fig. 1). For non-conservative mass transfer, the initial masses of the accretors would be similar to their current masses, that is, about 28 M⊙ and 17 M⊙, leading to initial mass ratios of ∼0.6 and ∼0.4, respectively. Figure 1 shows that under these assumptions, both systems are located inside the blue shaded area (large symbols), and their status as reverse Algol is therefore consistent with our simple estimate.

Assuming conservative mass transfer leads to initial masses for the accretors of VFTS 094 and VFTS 176 to be 13.0 M⊙ and 2.0 M⊙ respectively, and thus to initial mass ratios of VFTS 094 and VFTS 176 to be 0.28 and 0.05, respectively. Conservative binary models in this parameter range are not available, but they are unlikely to avoid a merging of the two stars during fast Case A mass transfer since the thermal-timescale ratio in massive main-sequence binaries is roughly equal to 1/q2, that is, of the order of ten for VFTS 094 and about 160 for VFTS 176. The mass gainers might therefore quickly swell up and lead to a contact configuration (Wellstein et al. 2001). We conclude that certainly VFTS 176 and probably VFTS 094 have evolved through a non-conservative, fast, Case A mass-transfer phase.

This expectation is confirmed when we compare with corresponding detailed binary evolution models of Pauli et al. (2022), as we can see from Fig. 2. For VFTS 094, binary models with an initial mass ratio of 0.6 can undergo an ordinary or reverse Algol phase depending on the orbital period. At the shortest orbital periods, tides prevent the spin-up of the accretor that leads to a mass transfer efficiency of up to 70%. Therefore, the corresponding models in Fig. 2 develop only a short or no reverse Algol phase. Consequently, the observed masses of VFTS 094 imply that the mass transfer efficiency in these models is overestimated. We conclude that while the models of Pauli et al. (2022) do not fit the main parameters of VFTS 094, similar models with a reduced mass transfer efficiency have a good chance of reproducing this reverse Algol binary.

For VFTS 176, the initial mass ratio is more extreme. At the shortest orbital periods (see Fig. F.2 of Sen et al. 2022), the models shown in Fig. 2 undergo near-conservative mass transfer and do not show an extended reverse Algol phase. As for VFTS 094, the implication is that the mass transfer efficiency in the corresponding models of Pauli et al. (2022) is far too high. A mass transfer efficiency of 70% implies an initial mass ratio of qi = 0.17 for VFTS 176, while the short-period models in Fig. 2 avoid merging only for qi ≳ 0.3. Therefore, models that might reproduce VFTS 176 require a mass transfer efficiency that is much lower than 70%. Again, such models have a good chance of reproducing this reverse Algol system, because, for the lowest mass transfer efficiency, merging is always avoided.

The discussion above shows that VFTS 094 and VFTS 176 may be understood as reverse Algol systems. While current detailed models do not reproduce these two binaries, models that adopt less efficient mass transfer likely can. This raises the question of how nature might achieve this. For the short orbital periods found in these two binaries, tides are expected to be efficient and to avoid a spin-up of the accretor to critical rotation, which is confirmed by their observed rotation rates (Mahy et al. 2020b). Stellar rotation may therefore be of limited use for driving the excess mass out of the system during fast mass transfer, and the mass transfer scheme adopted in Pauli et al. (2022) needs to be revised for very massive short-period binaries. Hence, these reverse Algol binaries provide a new pathway to constrain input physics assumptions in massive binary evolution.

6.2. Wolf-Rayet stars from the reverse Algol channel

As detailed in Sect. 3.3, we expect the donor stars of Case A binaries after the fast Case A mass transfer to be overluminous. As such, their stellar wind mass-loss rate will be elevated compared to single stars of the same luminosity. Since the donor’s surface may still be un-enriched in helium at this stage, we expect O stars (evolving as single stars) and WR stars (Algol donors), both hydrogen-rich, at the same position in the HR diagram (Fig. A.3).

The stripping of the donor star due to Roche-lobe overflow will occur in essentially the same way in ordinary and reverse Algol binaries. In reverse Algols, however, the donor, or the WR component, may outshine the companion more easily, because it is more massive and has a higher average mean molecular weight, which both contribute to making it the more luminous of the two stars. When the mass ratio is more extreme, the companion star may not be detected at all, and the WR component could be misinterpreted as a hydrogen-rich single WR star.

The majority of the observed WR stars are expected to undergo core helium burning (Pauli et al. 2022). However, the analysis of luminous hydrogen-rich WN stars in the LMC and the Galaxy showed some of them are likely to be core hydrogen burning stars (de Koter et al. 1997; Martins et al. 2013). To compare our donor models with observed WR stars, one needs a quantitative criterion allowing us to assess whether a given model corresponds to a WR star or not. For this purpose, we considered the optical depth parameter introduced in Sect. 2.3.

Figure 4 (top panels) shows the evolution of the optical depth parameter τwind (Eq. (1)) for the donor stars of our two example binary models (Appendix A). For the more massive model (left panel), we find τwind ≃ 0.2 before any mass is transferred. This corresponds to a high wind mass-loss rate of more than ∼10−5 M⊙ yr−1 shortly before the onset of mass transfer (Fig. A.1). After the fast Case A mass-transfer phase, the wind mass-loss rate increases slightly because about 10 M⊙ are removed from the donor. This in turn only leads to an increase of the donor’s optical depth parameter to ∼0.3. Since the radius of the donor star is slowly increasing (Fig. A.1), this binary model remains in the semi-detached configuration, while the orbital period is also slowly increasing. Likewise, the wind mass-loss rate is also increasing during this slow Case A mass transfer phase. These two effects compensate each other such that the optical depth parameter of the donor star remains nearly constant (see Eq. (1)) until the end of core hydrogen burning. After core hydrogen depletion and the thermal timescale Case AB mass transfer, the wind mass-loss rate increases again and the donor radius shrinks drastically, leading to a sharp rise of the optical depth parameter.

thumbnail Fig. 4.

Time evolution of optical depth parameter τwind (top panels) and electron scattering Eddington factor Γe (bottom panels, Eq. (2)) of the donor (black lines) for our two example models (Appendix A). The x-axis limits are the same as in Fig. A.1. The green vertical lines indicate the age at which the central hydrogen mass fraction of the donor is equal to 0.01, that is, the donor completes core hydrogen burning. The red and blue horizontal lines denote the calculated optical depth parameter of the observed LMC WN stars and Of or Of/WN stars, respectively, which have a surface hydrogen mass fraction of XH ≥ 0.4 (Table 1).

For the less massive model (right panel), the optical depth parameter of the donor is very low (∼0.03) before the onset of mass transfer as its wind mass-loss rate is more than one order of magnitude smaller than that of the model discussed above. During fast Case A mass transfer, both the wind mass-loss rate and the optical depth parameter of the donor rise by almost one order of magnitude (Fig. A.1). The optical depth parameter grows to a value near unity during the remainder of the core hydrogen burning evolution of the donor, and to even higher values afterwards.

In order to deduce from the optical depth parameters of the models whether they may correspond to WR stars, we calculated the optical depth parameters of observed hydrogen-rich WN and Of stars in the LMC. For this, we used the observed stellar radius, terminal wind velocity, and wind mass-loss rate in Eq. (1). Table 1 shows that the optical depth parameters of the Of and Of/WN stars fall in the τwind = 0.10 − 0.20 range, while those of the remaining WN stars cover τwind = 0.17 − 1.53. Therefore, it seems reasonable to adopt a threshold of τwind ≳ 0.2 for assuming that a given donor model represents a hydrogen-rich WR star.

Table 1.

Stellar and optical depth parameter τwind of binary and single WN stars in the LMC with a surface-hydrogen mass fraction of XH ≥ 0.40.

In doing so, we see from the more massive binary model in Fig. 4 that the donor may already develop WR characteristics before the mass transfer starts. Therefore, this would equally apply to a single star with the same initial mass. This consideration shows that above a certain initial mass limit, single stars may become WR stars during core hydrogen burning, as has been anticipated before in the literature (e.g. Shenar et al. 2020a). According to our example, this initial mass limit could be just above 60 M⊙ in the LMC. However, for smaller mass-loss rates (Björklund et al. 2021; Hawcroft et al. 2021; Brands et al. 2022) the limiting mass may be significantly larger.

Our second example binary shows that, for an initial mass of ∼45 M⊙, the donor star will not show WR characteristics before the mass transfer. However, Fig. 4 suggests that, in this case, the elevated L/M-ratio after fast Case A mass transfer pushes the donor into the WR regime, and during its reverse Algol-like phase the WR characteristics become stronger with time. Here, the donor has a mass that would clearly not lead it to become a hydrogen-burning WR star if it were a single star, but in a binary system it evolves into an ∼28 M⊙ hydrogen-rich, core hydrogen-burning WN star.

In previous works, the occurrence of WR-type winds has been attributed to the proximity of the WR stars to their Eddington limit (Gräfener & Hamann 2008; Gräfener et al. 2011; Sander & Vink 2020). For very massive main-sequence stars in the LMC, Bestenlehner et al. (2014) identified a transition between optically thin O star winds and enhanced WR-type winds at electron scattering Eddington factors of Γe ≈ 0.4. The post-Case A donors in our example models show similarly high values of Γe of about 0.4 and 0.5 (bottom panels of Fig. 4), supporting the interpretation that they represent WR stars.

After this phase, for a short period after the thermal-timescale Case AB mass transfer (see panel b of Fig. A.1), the Eddington factor increases even further to values of 0.6 and 0.7, respectively. Finally, when the core helium-burning WR phase is reached, it settles back down to values in the range of 0.4−0.5. Again, the Eddington factors of the models during the reverse Algol phase are similar to those of the same models during core helium burning – where they clearly correspond to hydrogen-poor WR stars (Pauli et al. 2022) – supports the WR interpretation during their reverse Algol phase.

6.3. Observed counterpart Wolf-Rayet stars

With their moderate hydrogen deficiencies and low effective temperatures, the models described above are reminiscent of hydrogen-rich WNL stars as those observed in the LMC sample of Hainich et al. (2014), at luminosities of log(L/L⊙)≈5.5 − 5.9 (see their Fig. 8). These objects have luminosities comparable to classical WR stars, but show much lower mass-loss rates (Fig. 6 in Hainich et al. 2014), indicating a physical nature distinct from classical WR stars.

Table 1 lists all hydrogen-rich WR stars in the LMC (XH ≥ 0.4). The orbital periods of the detected binaries are either shorter than 5 d or longer than 150 d. Since it appears unlikely that no WN binary with an orbital period in the range of 5−150 d exists in the LMC (e.g. Langer et al. 2020), some of the apparently single WN stars from this list may also have main-sequence companions. That they are not detected implies that they are significantly less luminous than the WR stars, which means they could be counterparts of our post-mass-transfer Case A models in which the primary star remains more luminous or even more massive (Sect. 3.2).

The three very luminous WN stars in long-period binaries listed in Table 1 could just be wind stripped, that is, their initial masses might be larger than MWNH, which is defined in Sect. 3.3. This is particularly true for BAT99 #116 (see also Tehrani et al. 2019) and BAT99 #119 (see also Shenar et al. 2017), which contain very luminous WR stars. However, due to the effect of envelope inflation, binaries with initial orbital periods of up to ∼2000 d can undergo Case A mass transfer (Sect. 3.1), such that an Algol evolution cannot be excluded for BAT99#107.

Of the short-period binaries listed in Table 1, BAT99#113 is the only one in which the WR component is known to be significantly more massive than the companion. The WR component appears to be close to Roche lobe filling, and its high hydrogen abundance excludes a previous Case-B mass transfer. Using the luminosity and dynamical mass estimate for the WR component of Shenar et al. (2019) yields a luminosity-to-mass ratio of logℒ/ℒ⊙ = 4.41 with ℒ = (4πσG)−1L/M. Notably, this value is only about 0.2 dex from the electron-scattering Eddington limit (logℒ/ℒ⊙ = 4.6, Langer & Kudritzki 2014), whereas corresponding single-star models as hot as the WR star in BAT99#113 (Teff ≃ 45 kK) remain below logℒ/ℒ⊙ = 4.2 (see Fig. 18 of Köhler et al. 2015).

In the detailed binary evolution grid, the model with the initial parameters (M1,i,M2,i,Pi) = (79.4 M⊙,19.8 M⊙, 15.8 d) obtains, after fast Case A mass transfer, (M1, M2, P) = 53 M⊙, 20 M⊙, 4.5 d), which fits well with the values derived by Shenar et al. (2019) of 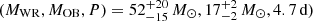. At an effective temperature of 43 kK, the donor’s luminosity-to-mass ratio is logℒ/ℒ⊙ = 4.37. A merging of both stars is avoided. We conclude that BAT99#113 constitutes a strong case for reverse Algol evolution. This argues for stable mass transfer in very massive binaries even for rather extreme initial mass ratios (here qi = 0.25) due to highly non-conservative mass transfer.

Figure 5 shows the evolution of luminosity and effective temperature of both components of the binary model mentioned above. When the more luminous donor fills its Roche volume at the coolest point of the track, fast Case A mass transfer is initiated, and the reverse Algol phase starts immediately thereafter. The donor remains more massive and more luminous than the accretor, in contrast with the ordinary Algol evolution in less massive binaries (Pols 1994; Nelson & Eggleton 2001; Sen et al. 2022). Since the mass transfer efficiency in this model is low, the accretor evolves similarly to a single star of the corresponding mass. The HRD positions of both model components after the fast Case A mass transfer match the observed positions of the WR star and its companion in BAT99#113. We note that Shenar et al. (2019) attempted to derive the initial parameters and evolutionary state of the WR binaries listed in Table 1 by comparing with the binary evolution grid of Eldridge et al. (2008) and Eldridge & Stanway (2016). However, for BAT99#113, no satisfactory fit could be obtained.

thumbnail Fig. 5.

HR diagram showing evolution of luminosity and surface temperature of donor and accretor star from a binary evolution model with initial donor (Md, i) and accretor masses (Ma, i) of 79.4 M⊙ and 19.8 M⊙, respectively, and an initial orbital period of 15.8 d. Dots are placed along the tracks every 50 000 yr. Coloured lines and symbols (red for the donor and blue for the accretor) are used as long as the donor undergoes core hydrogen burning. The remaining evolution of both stars is shown in grey. The zero-age main sequence is shown as a dashed grey line. The red triangle and blue diamond indicate the position of the WR star and its companion in BAT99#113, respectively, with their error bars.

7. Discussion and uncertainties

7.1. Envelope inflation

Sanyal et al. (2015, 2017) studied the detailed single-star models of Brott et al. (2011) and Köhler et al. (2015) and found that models exceeding ∼40 M⊙ at LMC metallicity reach their Eddington limit inside the stellar envelope towards the end of core hydrogen burning. The stellar envelope expands, and the donors grow to red supergiant proportions towards core hydrogen exhaustion. Due to this inflation, Pauli et al. (2022) found that binary models with an initial donor mass of ∼50 M⊙ and ∼56.2 M⊙ can undergo Case A mass transfer for initial orbital periods of up to 120 d and 2000 d, respectively. This leads to a very large parameter space for reverse Algol evolution in very massive binaries.

However, the extent of the envelope inflation in 1D models depends on the mixing length parameter (Sanyal et al. 2015), or, more generally, on the employed model for convective energy transport. For more efficient convection, inflation is reduced, and so would be the orbital period range for Case A binaries above ∼40 M⊙. In this case, the mass range for reverse Algol evolution would remain the same, but the number of systems experiencing it would be reduced. Notably, in the Case-B binaries that would instead be produced, the donor star would be significantly less massive and more helium-rich than a comparable Case A binary.

7.2. Mass transfer efficiency and stability of mass transfer

Recently, Sen et al. (2022) showed that an accretor spin-dependent mass transfer efficiency can explain many observed massive Algol binaries reasonably well. Observations of individual binary systems also indicate that the mass transfer efficiency can vary from binary to binary. While some binaries favour low mass transfer efficiency (Langer et al. 2003), others indicate a need for higher mass transfer efficiency (Wellstein & Langer 1999). Petrovic et al. (2005) and de Mink et al. (2007) also found evidence of a mass ratio and orbital-period-dependent mass transfer efficiency, respectively.

The accretor spin-dependent mass transfer efficiency results in an orbital period and mass ratio dependence of the mass transfer efficiency (Langer et al. 2020; Sen et al. 2022). As already discussed, inefficient mass transfer leads to more massive binaries being able to undergo the reverse Algol evolution. When the mass transfer efficiency decreases with increasing orbital period, we found that the reverse Algol evolution also shows an orbital period dependence (see Fig. 2). For a fixed initial mass ratio, lower orbital period models are more likely to invert their mass ratio during fast Case A mass transfer and vice versa.

Pauli et al. (2022) determine the stability of their binary models during inefficient mass transfer by assuming that the combined photon energy from both the binary components is larger than the gravitational energy needed to remove the excess mass transferred when the accretor reaches critical rotation. As discussed in Sect. 6.1, the two reverse Algol binaries in the Tarantula region require less efficient mass transfer than provided by this mechanism.

The mass transfer efficiency also affects the state of double black hole systems. If the accretion efficiency is small, then the initially more massive star is expected to produce the more massive black hole (e.g. Fig. 7 of Langer et al. 2020). For conservative evolution, however, this is so only in the binaries with the lowest initial mass ratios, while in many systems the initially more massive star becomes the less massive one after mass transfer (e.g. in the classical Algol evolution), and it may form the lower mass black hole. As the spin parameters of the first and second formed black holes are potentially different, the measured spins in black hole mergers may have an inference on the mass transfer efficiency in massive binaries (Mould et al. 2022) and thus on the fraction of very massive binaries undergoing the reverse Algol evolution.

7.3. Wind mass-loss rates

It has been shown that the WR mass-loss rates given by Nugis & Lamers (2000) are not adequate to explain the luminosity distribution of WC- and WO-type stars and the observed properties of SN Ic progenitors (Yoon 2017). It was also recommended Yoon (2017) to use a clumping factor of D = 4 instead of the usual D = 10, which is compatible with the Nugis & Lamers (2000) prescription, to reproduce the distribution of Galactic WN and WC stars (see also Pauli et al. 2022). Quantitatively, using a lower clumping factor in the Nugis & Lamers (2000) prescription increases the wind mass-loss rates of mildly helium-enriched stars.

The models used here include this updated wind-mass loss prescription of Yoon (2017) with a clumping factor of D = 3 (see Pauli et al. 2022). Hence, the wind mass-loss rates of our stripped donors on the main sequence have a greater wind mass-loss rate than previous models in the literature. This makes our donors more likely to develop an optically thick wind after fast Case A mass transfer (see Eq. (1)).

Recent theoretical and observational studies indicate that the work of Vink et al. (2001) may overestimate the wind mass-loss rate of O-type stars by a factor of 2−3 (Björklund et al. 2021; Hawcroft et al. 2021; Brands et al. 2022). A lower mass-loss rate for O stars means that it will be harder for single stars to be wind-stripped and show a WR-like spectrum. A lower wind mass-loss rate would also reduce the optical depth parameter just after the end of the fast Case A mass transfer phase. The jump in the wind mass-loss rate of the donor stars after fast Case A mass transfer due to an increased Eddington factor will still remain. Moreover, since the surface hydrogen mass fraction decreases below 0.7 shortly after the fast Case A phase, when the mass-loss rate is calculated by interpolating between the Vink et al. (2001) and Nugis & Lamers (2000) rates, we expect that the effect of a lower wind mass-loss rate of O stars will not affect our results significantly during the majority of the reverse Algol phase.

7.4. Mass of the convective core

The overshooting parameter in the models was calibrated to αov = 0.335 (Brott et al. 2011) against observations of the rotational velocities of massive stars in the FLAMES Survey of Massive Stars (Hunter et al. 2008), at masses around 16 M⊙. This value was confirmed by Castro et al. (2014), who compared their sample of Galactic massive stars to single star models. However, they found that while this value of the overshooting parameter works for stars of mass ∼16 M⊙, a smaller or larger value is preferred for stars that are less or more massive than ∼16 M⊙, respectively. A more recent study by Castro et al. (2018) on SMC OB field stars (Lamb et al. 2016) found that an overshooting parameter of 0.335 was able to reproduce the derived tentative TAMS line of these massive stars (see also Gilkis et al. 2021).

Recent observations of massive stars, via gravity mode asteroseismology of B stars (Pedersen et al. 2021) and eclipsing binary systems (Claret & Torres 2019), have indicated that their convective cores are larger than what is adopted in many stellar evolution models (Maeder & Meynet 1988; Alongi et al. 1993). Following this empirical evidence (see also Tkachenko et al. 2020), theoretical studies have shown that convective penetration in early-type stars can increase the size of the convective core by ∼10%−30% of the pressure scale height at the core boundary (Anders et al. 2022; Jermyn et al. 2022). A larger increase of the convective core size will lead to smaller envelope masses, therefore increasing the likelihood of reverse Algol evolution in even lower mass binaries. A quantification of this effect is however outside the scope of this work.

7.5. Metallicity

Wind mass-loss from hot massive stars (for a review, see Puls et al. 2008) is known to depend on their metallicity (e.g. Mokiem et al. 2007; Vink et al. 2001; Vink & Sander 2021; Björklund et al. 2021). In the LMC, the initial mass threshold for single stars to show WR-like winds is around 60 M⊙. We showed that binary stripping can increase the luminosity-to-mass ratio of the donor such that stripped stars with masses above 40 M⊙ can develop a WR-like wind spectrum. For lower (higher) metallicity environments, the wind mass-loss rates are lower (higher) as well, decreasing (increasing) the mass threshold for ordinary single stars to exhibit the WR phenomenon (Shenar et al. 2020a).

For binary-stripped donors, the wind mass-loss rate increase due to the enhanced luminosity-to-mass ratio occurs independent of the metallicity (Vink et al. 2001), with the mass-loss rate of a binary stripped donor being higher than that of a single star of the same mass. The mass threshold for binary stripped donors to show a WR-type spectrum also decreases (increases) for higher (lower) metallicity, with the absolute value at each metallicity being lower for the case of binary stripping than for the single-star scenario. As also discussed in the literature (Shenar et al. 2020a), we expect a range of masses (and in turn luminosities) where only binary stripping can produce these hydrogen-rich WR stars at each metallicity.

8. Conclusions

Semi-detached binary systems serve as an excellent test bed for binary evolution and the involved physical processes (de Mink et al. 2007; Mennekens & Vanbeveren 2017; Sen et al. 2022). The existence of a nuclear-timescale mass-transfer phase not only enables us to observe mass-transferring binaries to which we can compare the models, but it also gives us a window to understand the elusive but dominant thermal-timescale mass transfer.

In this work, we studied detailed binary evolution models with initial donor masses above 40 M⊙. We focused on the configuration of semi-detached binaries in which the Roche-lobe filling donor star performs nuclear-timescale mass transfer as the more massive component of the binary (Fig. A.1). This reverse Algol evolutionary channel in very massive binaries occurs due to the higher ratio of core to envelope mass in more massive stars. Provided the initial mass ratio of the binary is small enough (Fig. 1), the envelope stripping of the donor does not remove enough mass to invert the mass ratio of the binary. We find that these stripped donors may remain hydrogen-rich and are highly overluminous for their masses.

We identify two massive semi-detached binaries, VFTS 094 and VFTS 176 (Mahy et al. 2020a,b), as likely observational counterparts of reverse Algol systems. However, their properties are shown to be incompatible with conservative fast Case A mass transfer, and they require an even lower mass transfer efficiency than what is provided by the detailed binary evolution models of Pauli et al. (2022).

In sufficiently massive binaries, the overluminosity of the donor may induce an elevated stellar wind mass loss, leading to optical depth parameters comparable to those of the observed hydrogen-rich WN stars (Fig. 4). We show that the WR binary BAT99#113 (Shenar et al. 2019) is well explained by the reverse Algol scenario. We also identify several other LMC WR binaries as potential reverse Algol counterparts and argue that some of the apparently single hydrogen-rich WR stars in the LMC (Table 1) might also currently be in this phase.

Some very massive Case A binaries may be progenitors of high-mass black hole binaries and double black hole systems. A comprehensive study of corresponding model grids is required to develop a deeper understanding of their evolution. Population synthesis based on rapid binary evolution models will have difficulty achieving this due to the complexity of Case A mass transfer. Besides more detailed evolutionary calculations for very massive binaries, refined models for fast mass transfer need to be developed (Dessart et al. 2003; Lu et al. 2023) and tested against the observed Algol binary population.

Movie

Movie 1 associated with Fig. 3 (CaseA) Access here

1

We note that at low mass, when stars have convective envelopes, the character of Case A evolution is very different (Giuricin et al. 1983; Lanza & Rodonò 1999; Richards & Albright 1993; Zavala et al. 2002).

Acknowledgments

We thank the anonymous referee for the helpful comments that improved the manuscript. This research was funded in part by the National Science Center (NCN), Poland under grant number OPUS 2021/41/B/ST9/00757. T.S. acknowledges support from the European Union’s Horizon 2020 under the Marie Skłodowska-Curie grant agreement No. 101024605. The research leading to these results has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement number 772225: MULTIPLES).

References

  1. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2016, Phys. Rev. X, 6, 041015 [Google Scholar]
  2. Abbott, B. P., Abbott, R., Abbott, T. D., et al. 2019, Phys. Rev. X, 9, 031040 [Google Scholar]
  3. Abbott, R., Abbott, T. D., Abraham, S., et al. 2021, Phys. Rev. X, 11, 021053 [Google Scholar]
  4. Abdul-Masih, M., Sana, H., Hawcroft, C., et al. 2021, A&A, 651, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Aguilera-Dena, D. R., Langer, N., Antoniadis, J., et al. 2022, A&A, 661, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Aguilera-Dena, D. R., Müller, B., Antoniadis, J., et al. 2023, A&A, 671, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Almeida, L. A., Sana, H., Taylor, W., et al. 2017, A&A, 598, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  8. Alongi, M., Bertelli, G., Bressan, A., et al. 1993, A&AS, 97, 851 [NASA ADS] [Google Scholar]
  9. Anders, E. H., Jermyn, A. S., Lecoanet, D., & Brown, B. P. 2022, ApJ, 926, 169 [NASA ADS] [CrossRef] [Google Scholar]
  10. Antonini, F., & Gieles, M. 2020, Phys. Rev. D, 102, 123016 [NASA ADS] [CrossRef] [Google Scholar]
  11. Banyard, G., Sana, H., Mahy, L., et al. 2022, A&A, 658, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Batten, A. H. 1989, Space Sci. Rev., 50, 1 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bavera, S. S., Fragos, T., Zevin, M., et al. 2021, A&A, 647, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  14. Baym, G., Hatsuda, T., Kojo, T., et al. 2018, Rep. Progr. Phys., 81, 056902 [CrossRef] [PubMed] [Google Scholar]
  15. Belczynski, K., Kalogera, V., Rasio, F. A., et al. 2008, ApJS, 174, 223 [Google Scholar]
  16. Belczynski, K., Klencki, J., Fields, C. E., et al. 2020, A&A, 636, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  17. Belczynski, K., Romagnolo, A., Olejak, A., et al. 2022, ApJ, 925, 69 [NASA ADS] [CrossRef] [Google Scholar]
  18. Bestenlehner, J. M., Gräfener, G., Vink, J. S., et al. 2014, A&A, 570, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  19. Björklund, R., Sundqvist, J. O., Puls, J., & Najarro, F. 2021, A&A, 648, A36 [EDP Sciences] [Google Scholar]
  20. Böhm-Vitense, E. 1960, IAU Symp., 12, 338 [Google Scholar]
  21. Bond, J. R., & Carr, B. J. 1984, MNRAS, 207, 585 [NASA ADS] [CrossRef] [Google Scholar]
  22. Brands, S. A., de Koter, A., Bestenlehner, J. M., et al. 2022, A&A, 663, A36 [Google Scholar]
  23. Braun, H., & Langer, N. 1995, A&A, 297, 483 [NASA ADS] [Google Scholar]
  24. Briel, M. M., Stevance, H. F., & Eldridge, J. J. 2023, MNRAS, 520, 5724 [Google Scholar]
  25. Broekgaarden, F. S., Berger, E., Stevenson, S., et al. 2022, MNRAS, 516, 5737 [NASA ADS] [CrossRef] [Google Scholar]
  26. Brott, I., de Mink, S. E., Cantiello, M., et al. 2011, A&A, 530, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Burbidge, E. M., Burbidge, G. R., Fowler, W. A., & Hoyle, F. 1957, Rev. Mod. Phys., 29, 547 [NASA ADS] [CrossRef] [Google Scholar]
  28. Burrows, A., & Vartanyan, D. 2021, Nature, 589, 29 [CrossRef] [PubMed] [Google Scholar]
  29. Burrows, A., Hayes, J., & Fryxell, B. A. 1995, ApJ, 450, 830 [NASA ADS] [CrossRef] [Google Scholar]
  30. Cantiello, M., & Langer, N. 2010, A&A, 521, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  31. Castro, N., Fossati, L., Langer, N., et al. 2014, A&A, 570, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Castro, N., Oey, M. S., Fossati, L., & Langer, N. 2018, ApJ, 868, 57 [NASA ADS] [CrossRef] [Google Scholar]
  33. Chruslinska, M., Belczynski, K., Klencki, J., & Benacquista, M. 2018, MNRAS, 474, 2937 [CrossRef] [Google Scholar]
  34. Claret, A., & Torres, G. 2019, ApJ, 876, 134 [Google Scholar]
  35. Crowther, P. A. 2019, Galaxies, 7, 88 [Google Scholar]
  36. Crowther, P. A., Caballero-Nieves, S. M., Bostroem, K. A., et al. 2016, MNRAS, 458, 624 [Google Scholar]
  37. de Koter, A., Heap, S. R., & Hubeny, I. 1997, ApJ, 477, 792 [Google Scholar]
  38. De Loore, C., Hellings, P., & Lamers, H. J. G. 1982, in Wolf-Rayet Stars: Observations, Physics, Evolution, eds. C. W. H. De Loore, & A. J. Willis, 99, 53 [NASA ADS] [CrossRef] [Google Scholar]
  39. De Marco, O., & Izzard, R. G. 2017, PASA, 34, e001 [Google Scholar]
  40. de Mink, S. E., Pols, O. R., & Hilditch, R. W. 2007, A&A, 467, 1181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  41. de Mink, S. E., Langer, N., Izzard, R. G., Sana, H., & de Koter, A. 2013, ApJ, 764, 166 [Google Scholar]
  42. Dessart, L., Langer, N., & Petrovic, J. 2003, A&A, 404, 991 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Detmers, R. G., Langer, N., Podsiadlowski, P., & Izzard, R. G. 2008, A&A, 484, 831 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  44. Dominik, M., Belczynski, K., Fryer, C., et al. 2012, ApJ, 759, 52 [Google Scholar]
  45. Eggen, O. J. 1957, The Observatory, 77, 191 [NASA ADS] [Google Scholar]
  46. El-Badry, K., Conroy, C., Quataert, E., et al. 2022, MNRAS, 516, 3602 [NASA ADS] [CrossRef] [Google Scholar]
  47. Eldridge, J. J., & Stanway, E. R. 2016, MNRAS, 462, 3302 [Google Scholar]
  48. Eldridge, J. J., Izzard, R. G., & Tout, C. A. 2008, MNRAS, 384, 1109 [Google Scholar]
  49. Eldridge, J. J., Stanway, E. R., Xiao, L., et al. 2017, PASA, 34, e058 [Google Scholar]
  50. Evans, C. J., Taylor, W. D., Hénault-Brunet, V., et al. 2011, A&A, 530, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Fragos, T., Andrews, J. J., Bavera, S. S., et al. 2023, ApJS, 264, 45 [NASA ADS] [CrossRef] [Google Scholar]
  52. Gallegos-Garcia, M., Berry, C. P. L., Marchant, P., & Kalogera, V. 2021, ApJ, 922, 110 [NASA ADS] [CrossRef] [Google Scholar]
  53. Gilkis, A., Shenar, T., Ramachandran, V., et al. 2021, MNRAS, 503, 1884 [NASA ADS] [CrossRef] [Google Scholar]
  54. Giuricin, G., Mardirossian, F., & Mezzetti, M. 1983, ApJS, 52, 35 [NASA ADS] [CrossRef] [Google Scholar]
  55. Gräfener, G., & Hamann, W.-R. 2008, A&A, 482, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Gräfener, G., Vink, J. S., de Koter, A., & Langer, N. 2011, A&A, 535, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Gräfener, G., Owocki, S. P., & Vink, J. S. 2012, A&A, 538, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  58. Groh, J. H., Meynet, G., Georgy, C., & Ekström, S. 2013, A&A, 558, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Haiman, Z., & Loeb, A. 1997, ApJ, 483, 21 [NASA ADS] [CrossRef] [Google Scholar]
  60. Hainich, R., Rühling, U., Todt, H., et al. 2014, A&A, 565, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Han, Z., Podsiadlowski, P., Maxted, P. F. L., & Marsh, T. R. 2003, MNRAS, 341, 669 [NASA ADS] [CrossRef] [Google Scholar]
  62. Hawcroft, C., Sana, H., Mahy, L., et al. 2021, A&A, 655, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  63. Heger, A., Langer, N., & Woosley, S. E. 2000, ApJ, 528, 368 [NASA ADS] [CrossRef] [Google Scholar]
  64. Heger, A., Woosley, S. E., & Spruit, H. C. 2005, ApJ, 626, 350 [Google Scholar]
  65. Hunter, I., Lennon, D. J., Dufton, P. L., et al. 2008, A&A, 479, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  66. Iglesias, C. A., & Rogers, F. J. 1996, ApJ, 464, 943 [NASA ADS] [CrossRef] [Google Scholar]
  67. Jermyn, A. S., Anders, E. H., Lecoanet, D., & Cantiello, M. 2022, ApJ, 929, 182 [NASA ADS] [CrossRef] [Google Scholar]
  68. Jung, M.-K., Yoon, S.-C., & Kim, H.-J. 2022, ApJ, 925, 216 [NASA ADS] [CrossRef] [Google Scholar]
  69. Kajino, T., Aoki, W., Balantekin, A. B., et al. 2019, Progr. Part. Nucl. Phys., 107, 109 [NASA ADS] [CrossRef] [Google Scholar]
  70. Kasen, D., Metzger, B., Barnes, J., Quataert, E., & Ramirez-Ruiz, E. 2017, Nature, 551, 80 [Google Scholar]
  71. Klencki, J., Nelemans, G., Istrate, A. G., & Pols, O. 2020, A&A, 638, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  72. Köhler, K., Langer, N., de Koter, A., et al. 2015, A&A, 573, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Kozyreva, A., Yoon, S. C., & Langer, N. 2014, A&A, 566, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Kremer, K., Spera, M., Becker, D., et al. 2020, ApJ, 903, 45 [NASA ADS] [CrossRef] [Google Scholar]
  75. Kruckow, M. U., Tauris, T. M., Langer, N., Kramer, M., & Izzard, R. G. 2018, MNRAS, 481, 1908 [CrossRef] [Google Scholar]
  76. Lamb, J. B., Oey, M. S., Segura-Cox, D. M., et al. 2016, ApJ, 817, 113 [NASA ADS] [CrossRef] [Google Scholar]
  77. Langer, N. 1989, A&A, 210, 93 [NASA ADS] [Google Scholar]
  78. Langer, N. 1991, A&A, 252, 669 [NASA ADS] [Google Scholar]
  79. Langer, N. 2012, ARA&A, 50, 107 [CrossRef] [Google Scholar]
  80. Langer, N., & Kudritzki, R. P. 2014, A&A, 564, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  81. Langer, N., Fricke, K. J., & Sugimoto, D. 1983, A&A, 126, 207 [NASA ADS] [Google Scholar]
  82. Langer, N., Wellstein, S., & Petrovic, J. 2003, IAU Symp., 212, 275 [Google Scholar]
  83. Langer, N., Schürmann, C., Stoll, K., et al. 2020, A&A, 638, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  84. Lanza, A. F., & Rodonò, M. 1999, A&A, 349, 887 [Google Scholar]
  85. Li, F.-X., Qian, S.-B., & Liao, W.-P. 2022, AJ, 163, 203 [NASA ADS] [CrossRef] [Google Scholar]
  86. Lu, W., Fuller, J., Quataert, E., & Bonnerot, C. 2023, MNRAS, 519, 1409 [Google Scholar]
  87. Lubow, S. H., & Shu, F. H. 1975, ApJ, 198, 383 [NASA ADS] [CrossRef] [Google Scholar]
  88. Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [Google Scholar]
  89. Mac Low, M.-M., Balsara, D. S., Kim, J., & de Avillez, M. A. 2005, ApJ, 626, 864 [NASA ADS] [CrossRef] [Google Scholar]
  90. Maeder, A., & Meynet, G. 1988, A&AS, 76, 411 [NASA ADS] [Google Scholar]
  91. Mahy, L., Sana, H., Abdul-Masih, M., et al. 2020a, A&A, 634, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  92. Mahy, L., Almeida, L. A., Sana, H., et al. 2020b, A&A, 634, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Malkov, O. Y. 2020, MNRAS, 491, 5489 [NASA ADS] [CrossRef] [Google Scholar]
  94. Mandel, I., & Farmer, A. 2022, Phys. Rep., 955, 1 [NASA ADS] [CrossRef] [Google Scholar]
  95. Mapelli, M. 2020, Front. Astron. Space Sci., 7, 38 [NASA ADS] [CrossRef] [Google Scholar]
  96. Marchant, P. 2017, PhD Thesis, University of Bonn, Germany [Google Scholar]
  97. Marchant, P., Langer, N., Podsiadlowski, P., Tauris, T. M., & Moriya, T. J. 2016, A&A, 588, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  98. Marchant, P., Pappas, K. M. W., Gallegos-Garcia, M., et al. 2021, A&A, 650, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  99. Marcolino, W. L. F., Bouret, J. C., Rocha-Pinto, H. J., Bernini-Peron, M., & Vink, J. S. 2022, MNRAS, 511, 5104 [NASA ADS] [CrossRef] [Google Scholar]
  100. Martins, F., Depagne, E., Russeil, D., & Mahy, L. 2013, A&A, 554, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  101. Mennekens, N., & Vanbeveren, D. 2017, A&A, 599, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  102. Menon, A., Langer, N., de Mink, S. E., et al. 2021, MNRAS, 507, 5013 [NASA ADS] [CrossRef] [Google Scholar]
  103. Miller-Jones, J. C. A., Bahramian, A., Orosz, J. A., et al. 2021, Science, 371, 1046 [Google Scholar]
  104. Moe, M., & Di Stefano, R. 2017, ApJS, 230, 15 [Google Scholar]
  105. Mokiem, M. R., de Koter, A., Vink, J. S., et al. 2007, A&A, 473, 603 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  106. Mould, M., Gerosa, D., Broekgaarden, F. S., & Steinle, N. 2022, MNRAS, 517, 2738 [CrossRef] [Google Scholar]
  107. Nelson, C. A., & Eggleton, P. P. 2001, ApJ, 552, 664 [NASA ADS] [CrossRef] [Google Scholar]
  108. Nieuwenhuijzen, H., & de Jager, C. 1990, A&A, 231, 134 [NASA ADS] [Google Scholar]
  109. Nugis, T., & Lamers, H. J. G. L. M. 2000, A&A, 360, 227 [NASA ADS] [Google Scholar]
  110. Olejak, A., Belczynski, K., & Ivanova, N. 2021, A&A, 651, A100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  111. Orosz, J. A., McClintock, J. E., Aufdenberg, J. P., et al. 2011, ApJ, 742, 84 [NASA ADS] [CrossRef] [Google Scholar]
  112. Packet, W. 1981, A&A, 102, 17 [NASA ADS] [Google Scholar]
  113. Paczyński, B. 1971, ARA&A, 9, 183 [Google Scholar]
  114. Patrick, L. R., Thilker, D., Lennon, D. J., et al. 2022, MNRAS, 513, 5847 [Google Scholar]
  115. Pauli, D., Langer, N., Aguilera-Dena, D. R., Wang, C., & Marchant, P. 2022, A&A, 667, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  116. Paxton, B., Bildsten, L., Dotter, A., et al. 2011, ApJS, 192, 3 [Google Scholar]
  117. Paxton, B., Cantiello, M., Arras, P., et al. 2013, ApJS, 208, 4 [Google Scholar]
  118. Paxton, B., Marchant, P., Schwab, J., et al. 2015, ApJS, 220, 15 [Google Scholar]
  119. Paxton, B., Schwab, J., Bauer, E. B., et al. 2018, ApJS, 234, 34 [NASA ADS] [CrossRef] [Google Scholar]
  120. Paxton, B., Smolec, R., Schwab, J., et al. 2019, ApJS, 243, 10 [Google Scholar]
  121. Pedersen, M. G., Aerts, C., Pápics, P. I., et al. 2021, Nat. Astron., 5, 715 [NASA ADS] [CrossRef] [Google Scholar]
  122. Petrovic, J., Langer, N., & van der Hucht, K. A. 2005, A&A, 435, 1013 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  123. Pignatari, M., Gallino, R., Heil, M., et al. 2010, ApJ, 710, 1557 [Google Scholar]
  124. Podsiadlowski, P. 1992, PASP, 104, 717 [CrossRef] [Google Scholar]
  125. Pols, O. R. 1994, A&A, 290, 119 [Google Scholar]
  126. Puls, J., Vink, J. S., & Najarro, F. 2008, A&ARv, 16, 209 [NASA ADS] [CrossRef] [Google Scholar]
  127. Pustylnik, I. 1998, Astron. Astrophys. Trans., 15, 357 [NASA ADS] [CrossRef] [Google Scholar]
  128. Qin, Y., Marchant, P., Fragos, T., Meynet, G., & Kalogera, V. 2019, ApJ, 870, L18 [Google Scholar]
  129. Quast, M., Langer, N., & Tauris, T. M. 2019, A&A, 628, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  130. Richards, M. T., & Albright, G. E. 1993, ApJS, 88, 199 [NASA ADS] [CrossRef] [Google Scholar]
  131. Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
  132. Sana, H., de Mink, S. E., de Koter, A., et al. 2012, Science, 337, 444 [Google Scholar]
  133. Sana, H., de Koter, A., de Mink, S. E., et al. 2013, A&A, 550, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  134. Sana, H., Le Bouquin, J. B., Lacour, S., et al. 2014, ApJS, 215, 15 [Google Scholar]
  135. Sander, A. A. C., & Vink, J. S. 2020, MNRAS, 499, 873 [Google Scholar]
  136. Sanyal, D., Grassitelli, L., Langer, N., & Bestenlehner, J. M. 2015, A&A, 580, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  137. Sanyal, D., Langer, N., Szécsi, D., Yoon, S.-C., & Grassitelli, L. 2017, A&A, 597, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  138. Schneider, F. R. N., Sana, H., Evans, C. J., et al. 2018, Science, 359, 69 [NASA ADS] [CrossRef] [Google Scholar]
  139. Schootemeijer, A., Langer, N., Grin, N. J., & Wang, C. 2019, A&A, 625, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  140. Sen, K., Xu, X. T., Langer, N., et al. 2021, A&A, 652, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  141. Sen, K., Langer, N., Marchant, P., et al. 2022, A&A, 659, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  142. Shenar, T., Richardson, N. D., Sablowski, D. P., et al. 2017, A&A, 598, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  143. Shenar, T., Sablowski, D. P., Hainich, R., et al. 2019, A&A, 627, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  144. Shenar, T., Gilkis, A., Vink, J. S., Sana, H., & Sander, A. A. C. 2020a, A&A, 634, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  145. Shenar, T., Sablowski, D. P., Hainich, R., et al. 2020b, A&A, 641, C2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  146. Soberman, G. E., Phinney, E. S., & van den Heuvel, E. P. J. 1997, A&A, 327, 620 [NASA ADS] [Google Scholar]
  147. Spera, M., Mapelli, M., Giacobbo, N., et al. 2019, MNRAS, 485, 889 [Google Scholar]
  148. Spruit, H. C. 2002, A&A, 381, 923 [CrossRef] [EDP Sciences] [Google Scholar]
  149. Stanway, E. R., & Eldridge, J. J. 2018, MNRAS, 479, 75 [NASA ADS] [CrossRef] [Google Scholar]
  150. Stevenson, S., Vigna-Gómez, A., Mandel, I., et al. 2017, Nat. Commun., 8, 14906 [Google Scholar]
  151. Surkova, L. P., & Svechnikov, M. A. 2004, VizieR Online Data Catalog: II/256 [Google Scholar]
  152. Sybesma, C. H. B. 1986, A&A, 168, 147 [NASA ADS] [Google Scholar]
  153. Tehrani, K. A., Crowther, P. A., Bestenlehner, J. M., et al. 2019, MNRAS, 484, 2692 [NASA ADS] [CrossRef] [Google Scholar]
  154. Thielemann, F. K., Arcones, A., Käppeli, R., et al. 2011, Progr. Part. Nucl. Phys., 66, 346 [NASA ADS] [CrossRef] [Google Scholar]
  155. Tkachenko, A., Pavlovski, K., Johnston, C., et al. 2020, A&A, 637, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  156. Ulrich, R. K., & Burger, H. L. 1976, ApJ, 206, 509 [NASA ADS] [CrossRef] [Google Scholar]
  157. Valsecchi, F., Glebbeek, E., Farr, W. M., et al. 2010, Nature, 468, 77 [NASA ADS] [CrossRef] [Google Scholar]
  158. Vanbeveren, D., De Donder, E., Van Bever, J., Van Rensbergen, W., & De Loore, C. 1998a, New Astron., 3, 443 [CrossRef] [Google Scholar]
  159. Vanbeveren, D., De Loore, C., & Van Rensbergen, W. 1998b, A&ARv, 9, 63 [Google Scholar]
  160. van der Hucht, K. A. 2001, New Astron. Rev., 45, 135 [CrossRef] [Google Scholar]
  161. van Rensbergen, W., & de Greve, J.-P. 2021, Galaxies, 9, 19 [NASA ADS] [CrossRef] [Google Scholar]
  162. van Son, L. A. C., de Mink, S. E., Callister, T., et al. 2022, ApJ, 931, 17 [NASA ADS] [CrossRef] [Google Scholar]
  163. Vidaña, I. 2018, Eur. Phys. J. Plus, 133, 445 [CrossRef] [Google Scholar]
  164. Vigna-Gómez, A., Justham, S., Mandel, I., de Mink, S. E., & Podsiadlowski, P. 2019, ApJ, 876, L29 [CrossRef] [Google Scholar]
  165. Vink, J. S., & Sander, A. A. C. 2021, MNRAS, 504, 2051 [NASA ADS] [CrossRef] [Google Scholar]
  166. Vink, J. S., de Koter, A., & Lamers, H. J. G. L. M. 2001, A&A, 369, 574 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  167. Voss, R., & Tauris, T. M. 2003, MNRAS, 342, 1169 [Google Scholar]
  168. Wang, C., Langer, N., Schootemeijer, A., et al. 2020, ApJ, 888, L12 [NASA ADS] [CrossRef] [Google Scholar]
  169. Wang, C., Langer, N., Schootemeijer, A., et al. 2022, Nat. Astron., 6, 480 [NASA ADS] [CrossRef] [Google Scholar]
  170. Wellstein, S., & Langer, N. 1999, A&A, 350, 148 [NASA ADS] [Google Scholar]
  171. Wellstein, S., Langer, N., & Braun, H. 2001, A&A, 369, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  172. Yoon, S.-C. 2017, MNRAS, 470, 3970 [NASA ADS] [CrossRef] [Google Scholar]
  173. Zahn, J. P. 1977, A&A, 500, 121 [NASA ADS] [Google Scholar]
  174. Zavala, R. T., McNamara, B. J., Harrison, T. E., et al. 2002, AJ, 123, 450 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Examples of reverse Algol evolution models

In this section, we show two examples of Case A mass transfer for very massive binary models and discuss their differences compared to the typical nuclear-timescale, Case A mass-transfer phase studied in the literature (Nelson & Eggleton 2001; de Mink et al. 2007; Sen et al. 2022).

A.1. Mass and mass transfer efficiency

Figure A.1 (left panel) shows the evolution of a massive binary model with a donor of an initial mass of 63 M⊙ in a 100 d orbit around an accretor with an initial mass of 31.5 M⊙. While both the binary components are burning hydrogen at their cores (Panel ‘f’), the donor star (red line) fills its Roche lobe (Panel ‘c’) at around 3.71 Myr, thereby commencing the Case A mass-transfer phase. The mass-transfer rate (thick red line) rises to about 10−3 M⊙ yr−1 (Panel ‘b’) during the so-called fast Case A mass-transfer phase, that is, of the order of Md/τKH, where Md is the mass of the donor and τKH is the thermal timescale of the donor at the onset of mass transfer.

thumbnail Fig. A.1.

Examples of reverse Algol evolution. Left panel: Model that undergoes nuclear-timescale, slow, Case A mass transfer in the reverse Algol configuration. The initial donor mass, mass ratio, and orbital period of the model are 63.0 M⊙, 0.5, and 100 d, respectively. Right panel: Model that detaches after fast Case A mass transfer. The initial donor mass, mass ratio, and orbital period of the model are 44.6 M⊙, 0.5, and 7.9 d, respectively. We show selected stellar parameters as a function of time, where t = 0 denotes the ZAMS of both stars. (a): Donor (red) and accretor (blue) mass. (b): Mass transfer rate Ṁt (thick red line) and wind mass-loss rate of the donor (− Ṁw,d, red dotted line). (c): Ratio of the donor and accretor radius to their respective Roche lobe radii. (d): Orbital period. (e): Orbital velocity of donor and accretor. (f): Central helium mass fraction of donor and accretor. (g): Surface helium mass fraction. (h): Surface nitrogen mass fraction enhancement factor.

The fast Case A mass transfer continues at the thermal timescale because the mass transfer occurs while the binary is going towards a mass ratio of unity and is hence decreasing its orbital separation. When the envelope stripping reaches the mass coordinate of the initial convective core, however, the mass-radius exponent in the hydrogen-helium gradient region is different such that the radius of the donor now only increases on the nuclear timescale. Then, the system enters a nuclear-timescale mass-transfer phase at around 3.73 Myr. The donor loses most of its mass during the thermal-timescale mass-transfer phase (Panel ‘d’), while very little mass is lost via Roche-lobe overflow during the slow Case A mass-transfer phase.

Contrary to the usual Algol evolution (Sen et al. 2022), we see that the mass ratio of the binary is not inverted during the entire Case A mass-transfer phase (Panel ‘a’). In this configuration, the currently more massive donor is transferring mass to its less massive companion on the nuclear timescale. This constitutes the reverse Algol evolution in very massive binaries. We note that the donor eventually detaches towards the end of its main-sequence evolution. At core hydrogen exhaustion, the donor expands again and initiates the thermal timescale Case AB mass-transfer phase.

The right panel of Fig. A.1 shows the evolution of a massive binary model with a 44.6 M⊙ donor in a 7.9 d orbit around an accretor with an initial mass of 22.3 M⊙. The donor star (red line) fills its Roche lobe (Panel ‘c’) at around 4.3 Myr, initiating a thermal-timescale, fast, Case A mass-transfer phase where the mass-transfer rate rises above 10−3 M⊙ yr−1 (Panel ‘b’). During this short time, the donor loses ∼30% of its total mass (Panel ‘a’). Similarly to the semi-detached model, the mass ratio does not invert during the fast Case A phase, that is, the donor remains the more massive star of the binary.

Unlike the semi-detached model, however, this model detaches after the fast Case A mass-transfer phase (see the decline in R/RRL in Panel ‘c’) and has no nuclear-timescale, slow, Case A mass-transfer phase. The sharp decline in the donor mass increases the luminosity-to-mass ratio of the donor. This increases the wind mass-loss rate of the donor (Vink et al. 2001, Panel ‘b’). Due to this increased wind mass-loss rate, the radius of the donor shrinks upon mass loss (Petrovic et al. 2005) instead of the usual increase in stellar radius during the main sequence. The increased wind mass-loss rate may also enable the donor to develop an optically thick wind and be observable as a hydrogen-rich WR star.

For both the example models, the initial masses of the accretors are half of those of the donors. Hence, the wind mass-loss rates of the accretors are much lower compared to the donors, such that the accretors hardly decrease in mass after the fast Case A mass-transfer phase. Due to the very high mass of the binary components, the orbital velocities are of the order of 100 km s−1 (Panel ‘e’), even though the orbital period of the semi-detached model is around 100 d (Panel ‘d’). This may facilitate the detection of these reverse Algol systems, despite some of them having a high orbital period.

Figure A.2 shows the evolution of the internal structure of the donor and accretor of the binary model that detaches after the fast Case A mass transfer. We see the retreating convective core of the donor (left panel) during the main sequence. The fast Case A mass transfer removes the outer envelope of the star up to the initial extent of the convective core. The convective core of the donor hardly reacts to the mass loss, decreasing its mass only slightly. After the fast Case A mass transfer, the star loses mass faster via wind mass-loss than before since the wind mass-loss rate has increased (see Fig. A.1). The convective core of the donor continues to recede as well.

thumbnail Fig. A.2.

Kippenhahn diagram showing internal structure of the donor and accretor of the model with initial donor mass, mass ratio, and orbital period of 44.6 M⊙, 0.5, and 7.9 d, respectively, as a function of the stellar age. The green hatched line shows the regions of the star that are unstable to convection. The purple cross-hatched line shows the extent of convective overshooting above the convective core. The yellow hatching denotes the regions of thermohaline mixing. Red shows the regions of semi-convective mixing. The black line gives the total mass of the star as a function of stellar age.

The convective core of the accretor (right panel) remains almost constant in mass. Since the accretor is only half as massive as the donor, the main-sequence lifetime of the accretor is much greater than that of the donor, and for this reason the recession of its convective core is much slower compared to that of the donor. The accretor in this model reaches critical rotation soon after accreting very little mass from the donor (Packet 1981, see also Sen et al. 2022, Fig. 9), because the tidal forces are not strong enough to halt its spin-up. Accordingly, our mass-transfer prescription leads to a low mass-transfer efficiency. Since the mass-transfer efficiency is low, the accretor only gains ∼2 M⊙ during the fast Case A mass transfer.

A.2. Surface abundances

The nitrogen mass fraction inside the convective core of a massive star becomes equal to the CNO equilibrium value soon after the onset of hydrogen burning. Panels ‘g’ and ‘h’ of Fig. A.1 show that the surface-nitrogen mass fraction enhancement of the donors becomes equal to the CNO equilibrium value for the LMC, while the surface-helium mass fraction is only slightly increased during fast Case A mass transfer. This implies that the fast Case A mass-transfer phase removes the envelope of the donors up to the depth where the convective core had developed at the beginning of its main sequence.

During the slow Case A mass-transfer phase, the wind mass-loss removes material from the hydrogen-helium gradient region that forms due to the recession of the convective core during the main sequence. Layers that are increasingly enriched in helium appear successively at the surface of the donor. It is only during the Case AB mass-transfer phase that the envelope stripping reaches the very deep layers of the donor where the helium mass fraction is ∼0.75. Since the mass-transfer efficiency in both models is low, the surface-helium and -nitrogen mass fractions of the accretor hardly increase from their initial values. Moreover, efficient thermohaline mixing quickly combines the helium- and nitrogen-enriched material from the donor throughout the envelope of the accretor.

A.3. Orbital period evolution

We note that the wind mass-loss rate of the donor (dotted red line in Panel ‘b’ of Fig. A.1) exceeds the nuclear-timescale mass-transfer rate. This is also captured by the evolution of the orbital period of the model (Panel ‘d’). Before the onset of fast Case A mass transfer, the orbital period of the models gradually increased from 100 d to 120 d (left panel) and from 7.9 d to 8.6 d (right panel), primarily due to the wind mass loss from the donor. Then, during the fast Case A mass-transfer phase, the orbital period decreases rapidly because the binary evolves towards equal masses of both components (Wellstein et al. 2001). However, after the fast Case A mass transfer phase, the orbital period starts increasing again, despite the binary evolving towards a mass ratio of unity. This is because the primary source of mass loss from the binary is through the stellar wind of the mass donor and it dominates over the effect of nuclear-timescale mass transfer.

In contrast, conventional Algols have a positive orbital period derivative after the fast Case A phase (Sen et al. 2022) because the mass ratio of the binary has already inverted (Wellstein et al. 2001), mass transfer is occurring at the nuclear timescale, and the wind mass-loss rate is lower than the nuclear-timescale mass-transfer rate (see Fig. 2 of Sen et al. 2022). Hence, we expect the ratio of the orbital period to its derivative for Algol binaries to capture the nuclear timescale of the donor (Sen et al. 2022). For the case of the reverse Algols, however, we expect this ratio to capture the wind mass-loss timescale of the donor, which is smaller than its nuclear timescale.

A.4. Evolution in the Hertzsprung-Russell diagram

Figure A.3 shows the luminosity and surface temperature of the stellar components in the two binary models. In both models, the donors are 3-6 times more luminous than the accretors at the beginning of core hydrogen burning. During the main-sequence evolution before the interaction, the more massive donor (left panel) reaches lower effective temperatures than the less massive donor (right panel), because the envelope of the more massive donor has a larger Eddington factor. The luminosity of the donors does not decrease significantly during the fast Case A mass-transfer phase (see Fig. 1 of Wellstein et al. 2001), with the dip in luminosity being smaller for the more massive donor. This is because of the decreasing amount of envelope mass that is removed by the Case A mass-transfer phase with an increase in the mass of the donor.

thumbnail Fig. A.3.

Same as Fig. 5, but for two of the exemplary models discussed in Appendix A. Left panel: Binary model with an initial orbital period of 100 d, which experiences a semi-detached reverse Algol phase. Right panel: Model with an initial orbital period of 7.9 d, which experiences a detached reverse Algol phase. See also, Fig. A.1.

Notably, the donors remain more luminous than the accretors after the fast Case A mass transfer phase for the remainder of their main-sequence evolution. This is in contrast to the inversion of the luminosity ratio seen in lower mass Algol binaries, where the accretors are both more massive and more luminous than the donors during the slow Case A mass-transfer phase (Wellstein et al. 2001). Also, the more massive donor stays cooler than its accretor as well as the less massive donor after the fast Case A mass-transfer phase. In fact, the more massive donor remains within the main-sequence band, while the less massive donor becomes hot enough to migrate to the left of the main sequence towards the end of its core hydrogen-burning phase. Since the mass-transfer efficiency in both models is low, the mass accretors evolve similarly to a single star of their corresponding mass once they regain thermal equilibrium after the fast Case A mass transfer.

The mass donors, after undergoing the thermal timescale fast Case AB mass transfer, are stripped of most of their remaining hydrogen envelope (Sen et al. 2022). They become much hotter than the main-sequence stars and spend their remaining lifetime on the left of the ZAMS line (denoted in grey). The mass accretors, on the other hand, evolve similarly to single stars and spend their post-main sequence lifetime as red supergiants.

Appendix B: Two more Case A mass-transfer scenarios

Figure B.1 shows two more examples of binary models where the mass ratio is inverted after the fast Case A mass-transfer phase (Panel ‘a’), but the donors are so overluminous for their mass that their absolute luminosity remains higher than the accretor (Panel ‘c’). We see that the model with an initial donor mass of 44.6 M⊙ goes through a classical Algol phase, but the luminosity of the donor does not dip significantly after the fast Case A mass transfer phase (see Fig. 1 of Wellstein et al. 2001). This leads to another unique configuration in an Algol binary where the less massive donor is more luminous than the accretor. We also see that the model with an initial donor mass of 63 M⊙ detaches after the fast Case A mass transfer. This leads to a peculiar configuration in a detached binary where the less massive star is more luminous than the more massive star while on the main sequence band in the HR diagram.

thumbnail Fig. B.1.

Similar to Fig. A.1, but with Panel ‘c’ showing the luminosity of the donor and the accretor. Left panel: Initial donor mass, mass ratio, and orbital period of the model are 44.6 M⊙, 0.8, and ∼7.9 d, respectively. Right panel: Initial donor mass, mass ratio, and orbital period of the model are 63.0 M⊙, 0.8, and ∼31.6 d, respectively.

All Tables

Table 1.

Stellar and optical depth parameter τwind of binary and single WN stars in the LMC with a surface-hydrogen mass fraction of XH ≥ 0.40.

In the text

All Figures

thumbnail Fig. 1.

Initial convective core mass of mass donor (Mccd, i thick black line) and initial accretor mass Ma, i (thin coloured lines) for five initial mass ratios qi = Ma, i/Md, i (0.2, 0.4, 0.6, 0.8, 1.0) as a function of the initial donor mass Md, i in massive binary systems. For highly non-conservative mass transfer, reverse Algol evolution cannot occur above the thick black line (yellow region), only below it (blue region), whereas for conservative evolution it cannot occur above the yellow line. The symbols mark the positions of VFTS 094 and VFTS 176 in this diagram, assuming inefficient (blue) or conservative (yellow) mass transfer, with the ordinate value giving their initial accretor masses. The black dashed line shows the limiting initial companion mass above which the models of Pauli et al. (2022) that avoid a contact phase, also avoid merging during Case A mass transfer. The dash-dotted line shows the limiting initial companion mass below which all models merge. Between these two lines, whether the models merge or not is a function of their initial orbital period, and the fraction of models that merge increases for lower initial accretor masses. Lighter shading is used to indicate that not all models avoid merging. It is also assumed that all binaries with qi < 0.2 (grey line) merge before entering the Algol stage.
In the text
thumbnail Fig. 2.

Initial orbital period and initial mass ratio of models of considered binary evolution grid with an initial donor mass of 44.6 M⊙ (small squares). We only show models that do not merge during the fast Case A mass transfer (see Figs. 1 and F.1 of Sen et al. 2022). The colour indicates the fraction of the lifetime of the donor after the fast Case A mass-transfer phase during which the donor is more massive than the accretor (see colour bar to the right). The model discussed in the right panel of Fig. A.1 is highlighted with a black frame. The large red diamond and large blue square show the estimated positions of VFTS 094 and VFTS 176 assuming a highly non-conservative mass transfer, respectively (see text).
In the text
thumbnail Fig. 3.

Four snapshots of the animation showing positions of both components of detailed massive binary models in the HR diagram, considering a coeval population following a Salpeter initial mass function and flat initial distributions of mass ratios and logarithms of the initial orbital periods. The snapshots correspond to an age of 2.5 Myr (top left panel), 4 Myr (top right panel), 7.5 Myr (bottom left panel), and 10 Myr (bottom right panel). Translucent grey circles indicate components of pre-interaction binaries, grey squares indicate Case A merger products, and triangles and diamonds indicate mass donors and accretors after the onset of mass transfer, respectively. Components of Case A binaries after the onset of mass transfer are shown in colour, denoting the fraction of critical rotation rotation (v/vcrit). The two components of semi-detached binaries are connected by solid black lines with an arrow indicating the direction of mass transfer. The two components of binaries that have interacted in the past are connected with grey dotted lines. A black frame around a mass donor symbol (triangle) indicates a surface hydrogen mass fraction below 0.1, and a black frame around the symbol for a mass accretor (diamond) indicates a surface helium mass fraction above 0.3. The current age of the population is displayed in the centre bottom with a time bar that fills up as the animation moves forward in time. The table above the legend indicates (from the top) the current number of (i) Algol binaries, i.e. models in the slow Case A mass transfer phase; (ii) core hydrogen burning main-sequence merger products and (iii) cool red supergiants (log Teff < 3.7); (iv) and (v) Case A or Case-B main-sequence mass gainers, respectively, with a neutron star (white dot on symbol) or black hole (black dot on symbol) companion; (vi) core-collapse events that occurred up to the current age; and (vii) pre-interaction binaries brighter than the indicated luminosity threshold, which is 1.5 dex below the luminosity of the brightest hydrogen-burning single star at the current age.
In the text
thumbnail Fig. 4.

Time evolution of optical depth parameter τwind (top panels) and electron scattering Eddington factor Γe (bottom panels, Eq. (2)) of the donor (black lines) for our two example models (Appendix A). The x-axis limits are the same as in Fig. A.1. The green vertical lines indicate the age at which the central hydrogen mass fraction of the donor is equal to 0.01, that is, the donor completes core hydrogen burning. The red and blue horizontal lines denote the calculated optical depth parameter of the observed LMC WN stars and Of or Of/WN stars, respectively, which have a surface hydrogen mass fraction of XH ≥ 0.4 (Table 1).
In the text
thumbnail Fig. 5.

HR diagram showing evolution of luminosity and surface temperature of donor and accretor star from a binary evolution model with initial donor (Md, i) and accretor masses (Ma, i) of 79.4 M⊙ and 19.8 M⊙, respectively, and an initial orbital period of 15.8 d. Dots are placed along the tracks every 50 000 yr. Coloured lines and symbols (red for the donor and blue for the accretor) are used as long as the donor undergoes core hydrogen burning. The remaining evolution of both stars is shown in grey. The zero-age main sequence is shown as a dashed grey line. The red triangle and blue diamond indicate the position of the WR star and its companion in BAT99#113, respectively, with their error bars.
In the text
thumbnail Fig. A.1.

Examples of reverse Algol evolution. Left panel: Model that undergoes nuclear-timescale, slow, Case A mass transfer in the reverse Algol configuration. The initial donor mass, mass ratio, and orbital period of the model are 63.0 M⊙, 0.5, and 100 d, respectively. Right panel: Model that detaches after fast Case A mass transfer. The initial donor mass, mass ratio, and orbital period of the model are 44.6 M⊙, 0.5, and 7.9 d, respectively. We show selected stellar parameters as a function of time, where t = 0 denotes the ZAMS of both stars. (a): Donor (red) and accretor (blue) mass. (b): Mass transfer rate Ṁt (thick red line) and wind mass-loss rate of the donor (− Ṁw,d, red dotted line). (c): Ratio of the donor and accretor radius to their respective Roche lobe radii. (d): Orbital period. (e): Orbital velocity of donor and accretor. (f): Central helium mass fraction of donor and accretor. (g): Surface helium mass fraction. (h): Surface nitrogen mass fraction enhancement factor.
In the text
thumbnail Fig. A.2.

Kippenhahn diagram showing internal structure of the donor and accretor of the model with initial donor mass, mass ratio, and orbital period of 44.6 M⊙, 0.5, and 7.9 d, respectively, as a function of the stellar age. The green hatched line shows the regions of the star that are unstable to convection. The purple cross-hatched line shows the extent of convective overshooting above the convective core. The yellow hatching denotes the regions of thermohaline mixing. Red shows the regions of semi-convective mixing. The black line gives the total mass of the star as a function of stellar age.
In the text
thumbnail Fig. A.3.

Same as Fig. 5, but for two of the exemplary models discussed in Appendix A. Left panel: Binary model with an initial orbital period of 100 d, which experiences a semi-detached reverse Algol phase. Right panel: Model with an initial orbital period of 7.9 d, which experiences a detached reverse Algol phase. See also, Fig. A.1.
In the text
thumbnail Fig. B.1.

Similar to Fig. A.1, but with Panel ‘c’ showing the luminosity of the donor and the accretor. Left panel: Initial donor mass, mass ratio, and orbital period of the model are 44.6 M⊙, 0.8, and ∼7.9 d, respectively. Right panel: Initial donor mass, mass ratio, and orbital period of the model are 63.0 M⊙, 0.8, and ∼31.6 d, respectively.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.