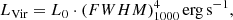| Issue |
A&A
Volume 669, January 2023
|
|
|---|---|---|
| Article Number | A135 | |
| Number of page(s) | 22 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202244177 | |
| Published online | 24 January 2023 | |
Statistical analysis of Al III and C III] emission lines as virial black hole mass estimators in quasars⋆
1
Instituto de Astronomía, UNAM, Circuito de la Investigación Científica S/N, Ciudad Universitaria, Coyoacán 04510, Mexico
e-mail: tbuendia@astro.unam.mx
2
CONACyT Research Fellow – Instituto de Astronomía, UNAM, Circuito de la Investigación Científica S/N, Ciudad Universitaria, Coyoacán 04510, Mexico
3
INAF, Osservatorio astronomico di Padova, vicolo dell’ Osservatorio 5, 35122 Padova, Italy
Received:
2
June
2022
Accepted:
7
September
2022
Aims. We test the usefulness of the intermediate ionisation lines Al IIIλ1860 and C III]λ1909 as reliable virial mass estimators for quasars.
Methods. We identified a sample of 309 quasars from the Sloan Digital Sky Survey Data Release 16 (SDSS DR16) in the redshift range 1.2 ≤ z ≤ 1.4 that have [O II]λ3728 recorded on the same spectrum as Al IIIλ1860, Si III]λ1892, and C III]λ1909. We set the systemic quasar redshift using careful measurements of [O II]λ3728. We then classified the sources as Population A (Pop. A), extreme Population A (Pop. xA), and Population B (Pop. B), and analysed the 1900 Å blend using multi-component models to look for systematic line shifts of Al IIIλ1860 and C III]λ1909 along the quasar main sequence.
Results. We do not find significant shifts of the Al IIIλ1860 line peak in Pop. B or in the vast majority of Pop. A. For Pop. xA, a small median blueshift of −250 km s−1 was observed, motivating a decomposition of the Al III line profile into a virialised component centred at rest frame and a blueshifted component for an outflow emission. For Pop. B objects, we proved the empirical necessity to fit a redshifted very broad component, clearly seen in C III], and analysed the physical implications on a Pop. B composite spectrum using CLOUDY simulations. We find consistent black hole mass estimations using Al III and C III] as virial estimators for the bulk of Pop. A.
Conclusions. Al III (and even C III]) is a reliable virial black hole mass estimator for Pop. A and Pop. B objects. The Pop. xA sources deserve special attention due to the significant blueshifted excess observed in the line profile of Al III, although it is not as large as the excess observed in C IVλ1549.
Key words: quasars: emission lines / galaxies: active / quasars: general / quasars: supermassive black holes / galaxies: nuclei / galaxies: high-redshift
Table described in Appendix B is only available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/A135/669
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
In 1992, Boroson & Green (1992) carried out a principal component analysis (PCA) on a sample of ∼80 Palomar-Green quasars. Their analysis identified a first eigenvector dominated by an anti-correlation between the [O III]λ5007 peak intensity and the strength of optical Fe II emission. In this first eigenvector (from now on ‘Eigenvector 1’; E1), two dimensions, (1) the full width at half maximum of Hβ (FWHM(Hβ)), and (2) the Fe II emission parameterised by the ratio of the equivalent widths (EWs) of the Fe II emission at 4750 Å and Hβ, RFeII = EW(FeIIλ4750)/EW(Hβ), define what is known as the optical plane of the main sequence (MS, Marziani et al. 2018) of quasars. In this way the MS is an empirical sequence based on optical parameters that are easy to measure in single-epoch spectra. The spectroscopic trends led Sulentic et al. (2000a) to distinguish two populations: quasars with FWHM(Hβ) < 4000 km s−1 belong to Population A (Pop. A), while objects with FWHM(Hβ) > 4000 km s−1 are Population B (Pop. B).
The E1 gained two more dimensions over the years, becoming the 4DE1 (Sulentic et al. 2000a,c, 2007). The 4DE1 involves optical, UV, and X-ray data, and its additional dimensions are: (3) the photon index in the soft X-ray domain (below 2 keV), Γsoft (Wang et al. 1996), and (4) the systematic blueshift of the high-ionisation line (HIL) C IVλ1549 (Sulentic et al. 2000c, 2007), which is especially prominent among Pop. A objects. The soft X-ray excess (Singh et al. 1985) is a dominant component of the X-ray spectra of many active galactic nuclei (AGN). It was adopted as a critical parameter of the 4DE1 that correlates opposite extremes of populations A and B (Bensch et al. 2015). Sources with higher values of soft X-ray excess (corresponding to a value of the soft-X photon index Γsoft ≈ 3 − 4) concentrate among the highly accreting Pop. A quasars (Grupe et al. 2004; Sulentic et al. 2008), while Pop. B quasars typically have Γsoft ≈ 2. The most widely accepted interpretation of the excess detected in soft X-rays is a measure of comptonised emission in a corona connected with the innermost accretion disc (Walter & Fink 1993; Petrucci et al. 2020 and references therein). The systematic high amplitude of the C IVλ1549 blueshift of quasars with a high Eddington ratio may indicate the presence of strong outflows most likely originating in a disc wind (Netzer 2015; Coatman et al. 2016, 2017). Sulentic et al. (2007) introduced the line centroid velocity shift at half maximum (see Zamfir et al. 2010, for a more detailed description) of C IV as the UV E1 measurement in the 4DE1 parameter space. The observational definition of the accretion and outflow processes is the motivation behind the two additional dimensions. In this paper, we shall consider the C IV only, as it is available for most quasars at z ≳ 1.4 surveyed by the Sloan Digital Sky Survey (SDSS). The division between the two populations is not enough to reflect the spectral diversity (e.g., Marziani et al. 2010). Sulentic et al. (2002) made subdivisions of ΔFWHM(Hβ) = 4000 km s−1 and ΔRFeII = 0.5 to emphasise the trends in spectral properties seen especially in Pop. A sources as a function of RFeII (e.g., Du et al. 2016; Shen & Ho 2014; Sun & Shen 2015). This division defines the A1, A2, A3, and A4 bins as RFeII increases, and B1, B1+, and B1++ (as well as B2 and B2+ in the range of RFeII 0.5–1) as FWHM(Hβ) increases. Spectra belonging to the same bin should have similar characteristics concerning the line profiles and optical and UV line ratios (Sulentic et al. 2007; Zamfir et al. 2010).
A quasar spectrum can be characterised using two physical parameters: the Eddington ratio (defined as the ratio of the bolometric and Eddington luminosities, REdd = Lbol /LEdd) and the black hole mass (MBH), which can be only coarsely estimated employing the MS of quasars (Panda et al. 2019b). This is why it is necessary to accurately obtain MBH either with the reverberation mapping technique (Netzer & Peterson 1997; Panda et al. 2019a; Dalla Bontà al. 2020) or with methods based on single-epoch spectra (Shen 2013). The MBH relates the evolutionary stage of the quasar with the accretion process (Small & Blandford 1992; Di Matteo et al. 2003; Fraix-Burnet et al. 2017). The knowledge of the MBH allows us to assess the strength of the gravitational forces and gain inferences on the dynamics of the region surrounding the black hole (e.g., Ferland et al. 2009; Marconi et al. 2009; Netzer & Marziani 2010). The definition of the virial mass as used in this paper is:
where r is the distance of the line emitting gas from the central black hole, δvr is the line broadening due to virial motions, and G is the gravitational constant. f is the virial factor dependent on the geometry, orientation, and kinematics of the emitting region (e.g., Peterson et al. 1993; Liu et al. 2017; Mejía-Restrepo et al. 2018). The parameter f is intended to take into account phenomena that affect the measure of the line broadening (usually FWHM or velocity dispersion), which may include radiation-pressure effects (Netzer & Marziani 2010; Liu et al. 2017), as well non-virial kinematical components due to outflow or inflow. All methods using optical and UV broad lines are based on estimating the distance of the broad line region (BLR) from the central continuum source, rBLR. At low redshifts (z ≤ 0.8), one can estimate MBH using FWHM(Hβ) as the δvr, but the higher the redshift, the less practical this measure becomes. Thus only two options are left: (1) following the Hβ line into the infrared, a feat requiring large telescopes and IR spectrometers; or (2) adopting other broad lines (e.g., Mg IIλ2800, Al IIIλ1860, or C IVλ1549) as surrogate virial estimators if z > 1.
The use of the C IVλ1549 emission line in the UV as a virial mass estimator is problematic due to its strong blueshift with respect to the rest frame frequently observed (Richards et al. 2011, and references therein), associating the HIL (≥40 eV) with outflowing winds (Gaskell 1982; Marziani et al. 1996). This outflow indicates that the emitting gas is not in virial equilibrium, and therefore is not a reliable mass indicator due to the systematic biases. Other HILs such as [O III]λλ4959,5007 could also present blueshifts arising from an outflowing gas (Zamanov et al. 2002), possibly associated with a disc wind. Hence, the narrow-line region (NLR) in sources showing spectroscopic blueshifts is not likely to be dynamically related to the gravitational potential of the host galaxy. To avoid systematic shifts in the velocity dispersion estimates (as well as in the proper rest frame), the width of [S II]λλ6716,6731 or the doublet [O II]λλ3727,3729 (hereafter [O II]λ3728) was proposed as an alternative to [O III]λλ4959,5007 (Komossa & Xu 2007; Salviander et al. 2007). Narrow low-ionisation lines (LILs) serve as better rest-frame references, as they provide a value closest to the one of the host galaxy (Marziani & Sulentic 2012; Bon et al. 2020).
To avoid the HILs in the UV spectral range, we propose working with the LILs or the intermediate ionisation lines (IILs, ∼20–40 eV). A possible strategy is to use high signal-to-noise ratio (S/N) of Hβ as a template to model the IILs Al IIIλ1860 and Si III]λ1892 (among others). Velocity-resolved reverberation mapping (Bentz et al. 2009; Denney et al. 2010; Feng et al. 2021) detect inflow and outflow motions, although the effects seem to be relatively minor as far as the width of the LILs is concerned. We emphasise the importance of finding a reliable virial mass estimator in the UV range that is paired to LIL Hβ and we propose the surrogate lines Al III and C III] present in the 1900 Å blend. The blend includes the IILs Al IIIλ1860, Si III]λ1892, and C III]λ1909. Al IIIλ1860 is a resonant doublet (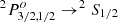 ) in the sodium isoelectronic configuration, while Si III]λ1892 and C III]λ1909 are due to the inter-combination transitions (
) in the sodium isoelectronic configuration, while Si III]λ1892 and C III]λ1909 are due to the inter-combination transitions (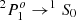 ) with widely different critical densities (≈2 × 1012 cm−3 and 3.2 × 109 cm−3, respectively; Negrete et al. 2012; Marziani et al. 2020). The parent ionic species imply intermediate ionisation potentials between LILs and HILs.
) with widely different critical densities (≈2 × 1012 cm−3 and 3.2 × 109 cm−3, respectively; Negrete et al. 2012; Marziani et al. 2020). The parent ionic species imply intermediate ionisation potentials between LILs and HILs.
The usefulness of Si III] and Al III as virial estimators is suggested by their profiles, which show consistent width and shape with the profile of HβBC (Marziani et al. 2010, 2022). They are symmetric and are usually not affected by strong outflows often observed in the C IVλ1549 profile (Marziani et al. 2017; Martínez-Aldama et al. 2018). The rest frame of the 1900 Å blend based on the quasar redshift derived from the [O II]λ3728 line (Bon et al. 2020) would prove the effectiveness of Al III and C III] as virial broadening estimators in the absence of systematic blueshifts.
The main objectives of the present work are: (1) to test the consistency of the Al III and C III] emission lines with the systemic redshift derived from the [O II] line, and in the cases where a systematic shift is found, to propose a correction; and (2) to probe the usefulness of the IILs Al III and C III] as reliable virial mass estimators. The outline of the paper is as follows. Section 2 is a description of the sample and the employed selection criteria. Section 3 describes the analysis of the redshift estimation, as well as the multi-component fitting of the 1900 Å blend and the [O II]λ3728 region. In Sect. 4 we present our results for the entire sample and by population, analysing the trends and correlations obtained, along with the physical parameters. Section 5 discusses the virial MBH obtained from Al III and C III], virial luminosity estimates for the extreme Population A (Pop. xA) sub-sample, and the inter-comparison between C IV and Al III, along with a schematic interpretation of the λ1900 blend in Pop. B. Section 6 provides the summary and conclusions.
2. Sample description
The spectroscopic quasar sample used in this work was selected from the SDSS data release 16 (DR16, Lyke et al. 2020), limited with the following filters: (1) 1.2 < z < 1.4 to cover the 1900 Å blend and the [O II]λ3728 doublet line simultaneously; and (2) a high S/N > 20 (measured in the continuum range around 1700 Å) to be able to decompose the blend at 1900 Å. These criteria gave us a sample of 1379 objects.
Not all spectra have a visible [O II] emission. To determine the visibility of [O II] in the selected objects, we used a third criterion applied to all spectra normalised by a continuum region around the line: (3) the ratio f[OII], defined as the intensity ratio of [O II] in the range 3722–3734 Å (F([OII]), and the observed continuum over the range 3670–3700 Å (F(cont), composed of the AGN continuum and strong Fe II emission contaminating the region), f[OII] = [F([OII]) + F(cont)]/F(cont), with the constriction of f[OII] > 1.3. Only 309 spectra satisfied this last condition.
[O II]λ3728 is a relatively weak line that is also affected by the emission of the Fe II multiplet (e.g., Vanden Berk et al. 2001). The fact that [O II]λ3728 was detected in only 22% of the objects in the initial sample (with a S/N > 20) may be due to two reasons. The first one is that it may be severely contaminated by sky subtraction residuals, whose emission is strong at the red end of the spectra. The second reason is attributed to the intrinsic [O II]λ3728 emission. We already know the trends of the MS in regard to oxygen; in Sulentic et al. (2000a, right panel of their Fig. 2), it is very clear that for Pop. A quasars, the oxygen is fainter than in Pop. B, and it decreases along the sequence, indicating that the higher the accretion (bins A3-A4), the less prominent oxygen lines we observe (Sulentic et al. 2000a; Shen & Ho 2014). So, discarding spectra with no detectable [O II]λ3728 creates a bias against highly accreting sources.
The next step was to separate Pops. A and B (Sect. 3.3). For this purpose, it was necessary to apply the luminosity-dependent criterion of Sulentic et al. (2017), which brings the limit at FWHM ≈ 4000 km s−1 to significantly higher values for sources of bolometric luminosity log Lbol ≳ 46 ergs s−1: FWHMAB ≈ 3500 + 500(Lbol/3.69 × 1044)0.15 km s−1 (applied to the C III] line) to separate Pops. A and B. In our sample, Pop. A FWHM(Al IIIλ1860) goes from ∼2500 km s−1 to almost 4500 km s−1, and only one source had a value less than 2000 km s−1 (Sect. 4.2). Afterwards, we looked for extreme Pop. A sources (xA or highly accreting quasars) using the UV line ratios from Marziani & Sulentic (2014, hereafter MS14): Al IIIλ1860/Si III]λ1892 ≥ 0.5 and C III]λ1909/Si III]λ1892 ≤ 1 (see Sect. 3.3 for a more detailed description), finding 11 xA quasar candidates.
The median value of the S/N distribution of our final sample is ≈31. The redshift distribution is reported in Fig. 1 (left). The z range is small, due to the values of the line wavelength range needed to have both Al III and [O II] recorded on the same spectrum: Al III is at the blue edge and [O II] at the red edge of each spectrum (see Fig. 2, upper panel, for an example). This z range is the most relevant condition to ensure that the systemic redshift of the quasar is measured precisely (see also Sect. 3.1). In Fig. 1 (right), the Lbol distribution of our sample shows that our sample is made of luminous AGN. The luminosity median values are log Lbol = 46.8 ergs s−1 for Pop. A objects (including xA quasars) and log Lbol = 46.6 ergs s−1 for Pop B. Previous works usually found 50% Pop. A and 50 % Pop. B in flux-limited samples (Zamfir et al. 2010; Marziani et al. 2013). The larger sample size of Pop. A might be due to the flux limit of the Sloan survey along with the relatively high redshift z ∼ 1 (Sulentic et al. 2014) that might have caused a Malmquist-type bias yielding an excess of Pop. A sources (i.e. radiating at a relatively high Eddington ratio) with respect to Pop. B (radiating at a lower Eddington ratio).
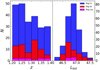 |
Fig. 1. Distribution of redshift (left) and of bolometric luminosity (right) for the total sample (309 objects). Colour code: Pops. A, xA, and B in blue, magenta and red, respectively. |
3. Data analysis
Optical spectral data used in this work were wavelength- and flux-calibrated by the SDSS DR16 pipeline. For the Galactic dust extinction, we used the reddening estimates from Schlafly & Finkbeiner (2011), assuming the value of the RV coefficient as 3.1. The Galactic absorption median value was 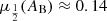 , ranging from 0.03 up to ∼0.6. We chose to apply this correction only in correspondence of the redshifted 1900 Å blend, where the median AB implies a flux increase of 14%. The chosen value only affected the luminosity computation, not the spectral slope between the blue and red edge of the 1900 Å blend. Redshift and flux corrections of the spectra were first done using the z values provided by the SDSS DR16. An additional z correction was applied using the rest frame estimated with the [O II]λ3728 line, as described below.
, ranging from 0.03 up to ∼0.6. We chose to apply this correction only in correspondence of the redshifted 1900 Å blend, where the median AB implies a flux increase of 14%. The chosen value only affected the luminosity computation, not the spectral slope between the blue and red edge of the 1900 Å blend. Redshift and flux corrections of the spectra were first done using the z values provided by the SDSS DR16. An additional z correction was applied using the rest frame estimated with the [O II]λ3728 line, as described below.
3.1. [OII]λ3728 redshift estimation
The SDSS redshift estimates can be biased (Hewett & Wild 2010). We observed discrepancies between the peak and rest frame wavelength of [O II] (as seen in Fig. 2) after the SDSS-based z correction. We applied an additional redshift correction using the peak intensity wavelength of [O II]λ3728 as described in Sect. 3.2.2 with a more careful fitting using the specfit task (Kriss 1994) from the Image Reduction and Analysis Facility (lmttIRAF, Tody 1986).
 |
Fig. 2. Redshift estimation and comparison with the SDSS meassurements. Upper panel: example of a spectrum from our sample. Vertical lines are the prominent emission lines of our work: Al IIIλ1860, C III]λ1909, and [O II]λ3728. The abscissa scale is rest frame wavelength in Å. The ordinate scale is the normalised flux at 1700 Å. Lower left panel: zSDSS vs. Δz for the sample. The red point corresponds to the values of Δz and z of the upper panel spectrum. Lower right panel: distribution of Δz. The lime line shows the shift Δz median value: 4.918 × 10−4 equivalent to ∼65 km s−1. |
We compare the differences between the SDSS DR16 redshift and the z values obtained from the narrow line [O II] in Fig. 2. The median value of Δz = z[OII] − zSDSS = 4.918 × 10−4 (roughly ∼70 km s−1 in the rest frame, dotted green line in Fig. 2) indicates that the SDSS z values were underestimated. A fraction of the objects, ∼25% of the sample, showed a difference in the rest frame z higher than 150 km s−1 (up to ∼450 km s−1). The distribution is not symmetric around the median value. The main reason for these systematic differences is probably a bias of the SDSS due to the usage of HILs.
3.2. Multi-component fitting
The UV range covered in the sample is populated by blended, intermediate-ionisation lines. To analyse the emission lines of the spectra, multi-component fits were done using the task specfit. This routine allowed us to simultaneously fit all the components present in the spectrum: continuum, Fe II features, and emission lines, computing the χ2 parameter that measures the difference between the original spectra and the fitted one. The task specfit minimises the χ2 to find the best fit. Intensity measures of [O II]λ3728 were carried out with the splot task within lmttIRAF.
The primary continuum source in the UV region is well known to be originated from the accretion disc (e.g., Malkan & Sargent 1982; Wandel & Petrosian 1988; Capellupo et al. 2016). In the absence of extinction, the most widely used model for the continuum is a single power law over a limited spectral range (see e.g., Śniegowska et al. 2020). We fitted a local continuum for two spectral ranges centred on the 1900 Å blend and [O II]λ3728, the most important emission lines relevant to this work (see Fig. 3).
 |
Fig. 3. Analysis of the 1900 Å blend and the [O II]λ3728 region (small box within the figure) as described in Sect. 3.2. The abscissa scale is rest frame wavelength in Å. The ordinate scale is the specific flux in units of 10−17 ergs s−1 cm−2 Å−1. Top: example of a Pop. A source fitted with a Lorentzian profile. Bottom: example of a Pop. B source fitted with a Gaussian profile. The black lines identify the BC of Al IIIλ1860, Si III]λ1892, and C III]λ1909 (red and grey lines are the VBC and NC of C III]λ1909, respectively, if present). The dashed blue line is the multi-component model obtained by specfit. Green lines trace the adopted Fe II (pale) and Fe III templates (dark). |
Along the E1 main sequence, it is possible to model the Hβ line profile with three components with blueshifted, unshifted, and redshifted centroids (blue [BLUE], broad [BC], and very broad components [VBC], respectively; Marziani et al. 2010). Then, we can use this model for all strong broad lines by varying the relative intensity of the components. The model considering the BC and VBC separation applies to Pop. B sources and is consistent with stratification of the BLR (Sulentic et al. 2000b; Snedden & Gaskell 2007; Wolf et al. 2020). The BC (hydrogen density nH ∼ 1012 cm−3, ionisation parameter log U ∼ −2, and column density Nc ≳ 1023 cm−2) is present in almost all type-1 quasars and corresponds most likely to the virialised part of the BLR, while the VBC can be interpreted as the emitted gas in the innermost BLR (e.g., Sulentic et al. 2000b; Marziani et al. 2003a, 2010; Wang & Li 2011; Wolf et al. 2020). The BLUE component is apparent as a blueshifted excess superimposed to the blue wing of the BC (Leighly & Moore 2004).
The 1900 Å blend contains the same emission lines for both Pops. A and B: Al III, Si III], and C III]λ1909, which are the strongest features (see also Table 1 from Negrete et al. 2012). Figure 3 shows example fits of a Pop. A and B sources, where we used a Lorentzian function for Pop. A and a Gaussian function for Pop B. For Pop. B spectra, we included an additional Gaussian component for the VBC. A detailed description of the phenomenology of the line profiles can be found in Sulentic et al. (2000a, 2002) and Marziani et al. (2022, and references therein). In greater detail, we considered the components described in Sects. 3.2.1 and 3.2.2 for a complete model of each spectrum.
3.2.1. Region 1: 1750–2050 Å.
Continuum. We adopted a single power law to fit the region 1700–2050 Å, using a continuum window at 1700 Å, as seen in Francis et al. (1991).
FeIIIand FeII. Emission of the Fe III multiplets can be strong in the vicinity of C III]λ1909, as seen in the average quasar spectrum from Vanden Berk et al. (2001). They appear to be strong when Al III is also strong (Hartig & Baldwin 1986). Strong Fe III and Al III emissions further strengthen the conclusion that the BLR densities, at least in Pop. A sources, are very high (on the basis of photoionisation models, ∼1011 − 1012 cm−3, Korista et al. 1997; Kuraszkiewicz et al. 2000). For the Fe III template, we adopted the multiplet obtained by Vestergaard & Wilkes (2001). The specfit task scaled and broadened the template to reproduce the observed emission (Boroson & Green 1992). In most cases, we fitted the multiplet Fe II UV191 (seen blueward of the 1900 Å blend, Moore 1945) as an isolated Gaussian in the rest frame. We adopted a Gaussian profile because the feature is a blend of several individual Fe II lines belonging to the same multiplet. If the Fe II multiplet was prominent, an extra component was added: Fe IIIλ1914 to fit an excess seen near the red wing of C III]λ1909 associated with unresolved Fe III template emission in Pop. A quasars (Negrete et al. 2012). This Fe IIIλ1914 emission is a single line, so we fitted it using a Lorentzian profile to be consistent with the profile of the BCs. The spectrum of I Zw 1 shows this effect: both C III] and Fe IIIλ1914 were needed to account for the double-peaked feature at 1910 Å that was too broad to be explained by a single line (Negrete et al. 2012, 2013). This criterion rested on the assumption that Fe IIIλ1914 and the Fe II UV multiplet #191 are enhanced by Lyα fluorescence (Sigut & Pradhan 1998; Johansson et al. 2000).
CIII]λ1909. Strengths and FWHM were left free to vary in the specfit model with one restriction: FWHM(C III]λ1909) ≤ FWHM(Al IIIλ1860) or FWHM(Si III]λ1892), to avoid a divergence of the FWHM(C III]λ1909) due to the Fe III emission on the red side of the blend. In the case where the model did not successfully follow this condition, the FWHM of both lines were forced to be the same to avoid a larger FWHM(C III]). We also added a narrow component (NC), if needed, with a fixed upper limit of FWHM ∼ 1000 km s−1 at the rest frame wavelength as an initial condition. The distribution of the peak emission around 1909 Å shows a fraction of quasars with a shorter wavelength than the one expected for the laboratory wavelength of C III]λ1909 (Fig. 4). This phenomenon could be due to two main reasons. First, we are looking at the prohibited line [C III]λ1906 (dotted line, Fig. 4) also observed in the NLR. Second, we are looking at a blueshifted emission of C III] NC due to an outflow in the NLR.
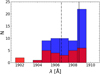 |
Fig. 4. Distribution of the peak blend wavelength around 1909 Å, for Pop. A (blue) and Pop. B (red). The vertical lines identify the rest frame wavelength of [C III]λ1906 (dotted) and C III]λ1909 (solid). |
For Pop. B objects, we included a redshifted VBC whose strengths and FWHM were left free to vary with an FWHM lower limit ≈7000 km s−1. In Fig. 5 we illustrate the necessity of using an additional component in the C III] profile. Looking at the residuals and the χ2 values, the best fit (according to the F distribution for the ratio of the χ2, Bevington & Robinson 2003) is the one with the VBC as seen for the SDSS spectrum J012726.39+154153.8 with a χ2VBC ≈ 0.1676 in contrast to χ2 ≈ 0.4451 obtained without VBC (see Sect. 5.4 for its interpretation).
 |
Fig. 5. Analysis of the 1900 Å blend (continuum extracted for simplicity in both spectra) of SDSS J012726.39+154153.8 as described for Fig. 3. The C III] profile fitted with only a BC and with a BC+VBC are shown in the top and bottom panels, respectively. The abscissa scale is rest-frame wavelength in Å. The ordinate scale is the normalised specific flux obtained from specfit. |
SiIII]λ1892. Strengths and shifts were free to vary, with one restriction: FWHM(Si III]λ1892) ≥ FWHM(C III]λ1909). We had some difficulties due to the nature of the blend itself. The line tended to be blueshifted in order to ‘fill’ its blue side, and therefore Al IIIλ1860 also presented a blueshift as seen in Martínez-Aldama et al. (2018). In the cases where the shift was completely unreal under a visual inspection, we fixed the central wavelength of Si III] to the rest frame.
AlIIIλ1860. The doublet was resolved and the blue component shifts, FWHM, and intensity were allowed to vary, with the red one tied to the blue one by an identical FWHM and a fixed wavelength ratio. The ratio between the intensity of the red and blue components of the doublet was kept fixed 0.8 (Laor et al. 1997). Rarely, a different ratio up to 0.98 was assumed according to the observed doublet profile. However, doublet total strengths and shifts were left free to vary. Regarding C III]λ1909, the condition FWHM(Al IIIλ1860) ≥ FWHM(C III]λ1909) was imposed. The FWHM(C III]) limit comes from the low value of the C III]λ1909 critical density. Conversely, the Al III line emitted via a permitted transition has no well-defined critical density (Baldwin et al. 1995; Korista et al. 1997).
Other lines. Two lines, not as prominent as those described before, were detected on the blue side of the 1900 Å blend: N III]λ1750 and Si IIλ1816. We assumed them to be at the rest frame as an initial condition, although their shifts, strength, and FWHM were left free to vary.
3.2.2. Region 2: 3550–3950 Å.
The [O II]λ3728 doublet emission line is one of the main emission features of this spectral range. Hence, the components are the same for all spectra:
Continuum. A strong pseudo-continuum associated with Fe II emission is expected to be present in the spectral range around [O II]λ3728 between 3500 Å and 3850 Å (Vanden Berk et al. 2001). However, the limited range 3700–3770 Å is smooth enough to permit the use of a power law to model the sum of the AGN continuum and the FeII emission.
[OII]λ3728. Our spectra have unresolved or almost unresolved [O II]λλ3727,3729 lines because the spectral resolution at the observed wavelength around 8200 Å is λ/δλ ≈ 2250, so the spectral purity is 3.64 Å, which is larger than the doublet separation. Therefore, we used a single Gaussian fit (Bon et al. 2020).
3.3. Spectral types along the E1
In order to classify the objects, we attempted to use, as a first approximation, the Sulentic et al. (2000c) spectral types. However, this classification is based on the FWHM Hβ that increases systematically for higher L objects, and we expect the same effect for the IILs. We identified 242 and 67 Pop. A and B objects, respectively. In a few cases, we had fits with both profiles, almost ∼5% of the sample, but with a different FWHM(C III]). For these sources, with a value of FWHM near the 4000 km s−1 limit, it was necessary to choose the best fit according to the χ2 values using the F distribution (Bevington & Robinson 2003). To separate highly accreting candidates of spectral type A3 and A4 (xA) from the A1-A2 sources defined in Sect. 1, we used the UV diagnostics ratios of MS14. The Pop. A quasars located at the extreme of the MS are considered to be sources radiating close to the Eddington if they satisfy the following criterion (e.g., Du et al. 2016):
An equivalent condition has been proposed at intermediate to high redshifts (z ≳ 1) where the Hβ line is no longer visible in the optical range, using the 1900 Å emission line blend of Al IIIλ1860, Si III]λ1892, and C III]λ1909 (MS14). The blend involving these lines constrains the physical conditions in the broad-line emitting gas the same way as extreme optical Fe II emission. Measures of high-S/N spectra of MS14 yielded the selection criterion based on two related ratios: (1) Al IIIλ1860 / Si III]λ1892 ≥ 0.5; and (2) C III]λ1909/Si III]λ1892 ≤ 1.0.
The emitting region of the IILs corresponds to the densest emitting region likely associated with the production of LILs, such as the CaII IR triplet (Matsuoka et al. 2008) and FeII (Baldwin et al. 2004). We made a bin separation for the bins A1-A2, which we called Pop.  1, and the A3-A4 bins are our Pop. xA candidates. In Fig. 6 we show the A1-A2 bins in blue, and in magenta we identify 11 xA quasars.
1, and the A3-A4 bins are our Pop. xA candidates. In Fig. 6 we show the A1-A2 bins in blue, and in magenta we identify 11 xA quasars.
 |
Fig. 6. Distribution of Pop. A sources in the plane defined by the ratios C III]λ1909/Si III]λ1892 vs. Al IIIλ1860/Si III]λ1892. The blue dots are quasars within populations A1-A2 (Pop. |
4. Results
Table B.1 lists the results of the line fitting procedures of Sect. 3.2, and the luminosity and MBH computations of Sect. 5. The table also reports the redshifts from the SDSS and our z estimations using [O II], the continuum flux and the normalisation at 1700 Å, and the line profile classification (Lorentzian or Gaussian). From the specfit analysis, we report the intensity, FWHM, shift from the rest frame, and EW for each emission line of the 1900 Å blend. For the [O II] region, we report the intensity and FWHM. The last part of Table B.1 contains the UV diagnostic ratios, the black hole mass, the Eddington ratio, and the virial luminosity (computed only for xA sources, see Sect. 5.2). Table 1 presents a summary of the physical parameter values where we report the median and average values by Population. The reported uncertainties are the semi-interquartile ranges (sIQR) of the parameter distributions. For luminosity estimates we adopted an uncertainty of 10%.
Average and median values of the sample physical parameters by population.
We organise the presentation of our results on line widths and shifts of the 1900 Å blend along the MS, separating Pops.  (A1-A2), xA, and B. The MS is expected to trace changes in the dynamical and physical conditions inside the quasars (Marziani et al. 2003a; La Mura et al. 2009; Popović & Kovačević-Dojčinović 2019). Line widths (e.g., FWHMs) of LILs and IILs measure the kinematics of the BLR. We assume that Doppler motions in a virialised region produce unshifted and symmetric line broadening. Wavelength shifts of Al IIIλ1860 and C III]λ1909 were measured with respect to the [OII]λ3728 rest frame. They may be due to Doppler effect because of radial gas motions plus obscuration along our line of sight. The differences in line widths observed in the same spectrum might be due to emissions from regions of non-virialised motions (e.g., outflows), as usually seen in Pop. A and also in high-luminosity Pop. B objects (Sulentic et al. 2017). Line width differences in type-1 quasars are also associated with the stratification of the emitting region, where broader lines trace the kinematics of the regions closer to the supermassive black hole (e.g., Sulentic et al. 2000b; Peterson & Wandel 2000; Snedden & Gaskell 2007; Wolf et al. 2020; Li et al. 2021). Last, FWHM differences may be due to different orientations of the accretion disc (expected to provide the reference plane of symmetry of the BLR) with respect to our line of sight.
(A1-A2), xA, and B. The MS is expected to trace changes in the dynamical and physical conditions inside the quasars (Marziani et al. 2003a; La Mura et al. 2009; Popović & Kovačević-Dojčinović 2019). Line widths (e.g., FWHMs) of LILs and IILs measure the kinematics of the BLR. We assume that Doppler motions in a virialised region produce unshifted and symmetric line broadening. Wavelength shifts of Al IIIλ1860 and C III]λ1909 were measured with respect to the [OII]λ3728 rest frame. They may be due to Doppler effect because of radial gas motions plus obscuration along our line of sight. The differences in line widths observed in the same spectrum might be due to emissions from regions of non-virialised motions (e.g., outflows), as usually seen in Pop. A and also in high-luminosity Pop. B objects (Sulentic et al. 2017). Line width differences in type-1 quasars are also associated with the stratification of the emitting region, where broader lines trace the kinematics of the regions closer to the supermassive black hole (e.g., Sulentic et al. 2000b; Peterson & Wandel 2000; Snedden & Gaskell 2007; Wolf et al. 2020; Li et al. 2021). Last, FWHM differences may be due to different orientations of the accretion disc (expected to provide the reference plane of symmetry of the BLR) with respect to our line of sight.
4.1. Systematic shifts
In the virialised region, one can expect a modest shift (≲|±200| km s−1) associated with the measurement of the uncertainties. We consider ±200 km s−1 as an uncertainty limit, given the instrumental resolution of the SDSS spectra on their blue side, which is where the 1900 Å blend falls in the observed rest frame. Considering our complete sample, the median values of the Al III and C III] shifts in the histograms of panels a and c in Fig. 7 are 10±120 km s−1 and 40±190 km s−1, respectively (see also Table 1). In almost 90% of Pop.  and B Al III profiles, we find that the shifts are lower than the uncertainty limit. However, panel a of Fig. 7 shows an asymmetric distribution of Al IIIλ1860 shifts with an extended tail of blueshifts reaching several hundred km s−1. Blueshifts larger than 200 km s−1 imply that we are most likely looking at a mixture of two non-resolved components in the line profiles: a virialised plus an outflow component. Even though a blueshifted component in Al III may not be as intense as the blue component of C IVλ1549, it is essential to be aware of its presence: significant shifts would introduce a bias in the estimation of the rest frame, as the Al III blue component would broaden and shift the full profile. The C III]λ1909 line shows a more uniform distribution in the shift of Pop.
and B Al III profiles, we find that the shifts are lower than the uncertainty limit. However, panel a of Fig. 7 shows an asymmetric distribution of Al IIIλ1860 shifts with an extended tail of blueshifts reaching several hundred km s−1. Blueshifts larger than 200 km s−1 imply that we are most likely looking at a mixture of two non-resolved components in the line profiles: a virialised plus an outflow component. Even though a blueshifted component in Al III may not be as intense as the blue component of C IVλ1549, it is essential to be aware of its presence: significant shifts would introduce a bias in the estimation of the rest frame, as the Al III blue component would broaden and shift the full profile. The C III]λ1909 line shows a more uniform distribution in the shift of Pop.  (Fig. 7, panel c), with a slight net shift to the red ∼100 km s−1, smaller than the typical uncertainty in the individual shift measurements.
(Fig. 7, panel c), with a slight net shift to the red ∼100 km s−1, smaller than the typical uncertainty in the individual shift measurements.
 |
Fig. 7. Distribution of shift with respect to the rest frame and FWHM of Al IIIλ1860 and C III]λ1909, top and bottom panels, respectively. Shift and FWHM are in units of km s−1. The colour-code is the same as for Fig. 1. |
4.1.1. Population 
Panel a in Fig. 7 shows that only 39 out of our 231 Pop.  objects have Al III blueshifts larger than the uncertainty limit (33 objects have shifts < −300 km s−1). This trend can also be seen in panel a of Fig. 8, where we plot the Al III shift as a function of its FWHM in bins2 of ΔFWHM(Al III) = 1000 km s−1. The plot shows that, on average, Pop.
objects have Al III blueshifts larger than the uncertainty limit (33 objects have shifts < −300 km s−1). This trend can also be seen in panel a of Fig. 8, where we plot the Al III shift as a function of its FWHM in bins2 of ΔFWHM(Al III) = 1000 km s−1. The plot shows that, on average, Pop.  sources (blue circles) do not present systematic shifts in Al III that significantly affect the FWHM measurements. This behaviour confirms the reliability of the rest frame of the Al IIIλ1860 for sources within the A1-A2 populations. In the relations of the Al III shift with the bolometric luminosity or Eddington ratio (Fig. 8, panels c and e) we also do not find displacements larger than the uncertainty limit. Data were divided into sub-samples of Δ log Lbol = 0.2 dex and ΔREdd = 0.5.
sources (blue circles) do not present systematic shifts in Al III that significantly affect the FWHM measurements. This behaviour confirms the reliability of the rest frame of the Al IIIλ1860 for sources within the A1-A2 populations. In the relations of the Al III shift with the bolometric luminosity or Eddington ratio (Fig. 8, panels c and e) we also do not find displacements larger than the uncertainty limit. Data were divided into sub-samples of Δ log Lbol = 0.2 dex and ΔREdd = 0.5.
 |
Fig. 8. Behaviour of Al IIIλ1860 (left) and C III]λ1909 (right) by population. a),b): shift with respect to rest frame vs. FWHM. c),d): shift vs. log Lbol. e),f): ratio of shift over FWHM vs. REdd. g),h): FWHM vs. log Lbol. Lines are the luminosity-dependent limit between Pop. A and Pop. B. of Sulentic et al. (2017, gold) and the empirical separation of Sulentic et al. (2000c, dashed). Colour-coding: Pop. |
Regarding the behaviour of C III] in Pop.  sources, in panel b of Fig. 7, we find 11 objects (∼4%) that show blueshifts larger than −300 km s−1. As observed for Al III relations, in C III] we do not see clear tendencies of Lbol and REdd(C III]) with the shift (Fig. 8, panels d and f), although ∼17% Pop. A sources show a displacement as large as ∼ + 300 km s−1 (52 objects, Fig. 7, panel c). This displacement towards the red is most likely due to the effect of the strong Fe III emission heavily blended with C III].
sources, in panel b of Fig. 7, we find 11 objects (∼4%) that show blueshifts larger than −300 km s−1. As observed for Al III relations, in C III] we do not see clear tendencies of Lbol and REdd(C III]) with the shift (Fig. 8, panels d and f), although ∼17% Pop. A sources show a displacement as large as ∼ + 300 km s−1 (52 objects, Fig. 7, panel c). This displacement towards the red is most likely due to the effect of the strong Fe III emission heavily blended with C III].
4.1.2. Extreme Population A
The spectral fitting of our 11 xA objects are shown in Fig. A.1. Panels a and c of Fig. 8 present our xA sub-sample using magenta points, which show Al IIIλ1860 blueshifts reaching several hundred km s−1. However, those shifts are much lower than those found in C IVλ1549 (e.g., Sulentic et al. 2007; Sect. 5.3). Nine out of 11 xA sources of panel c of Fig. 8 show a blueshift in Al III, with a median shift of ∼−340 km s−1 and a maximum of ∼ − 1000 km s−1. The figure reveals that there is no dependence on luminosity for the Al III shift. Panel e of Fig. 8 shows that not only a blueshift is detected for xA sources, but that the blueshift is also significant, ∼10% of the FWHM. On the other hand, we note that 50 Pop. A objects (∼17% of the sample) have a REdd higher than that of xA sources. As described in Sect. 3.3 and discussed in Sect. 5.1, we expect a higher REdd for xA objects).
C III]λ1909 shifts in Pop. xA sources seem to be slightly redshifted (the median shift is 50±120 km s−1), so we do not take them into account for the analysis. A redshift of ∼300 km s−1 was found in three xA spectra where C III] is weak and is also affected by the Fe III emission at ≈1915–1920 Å.
4.1.3. Population B
Our Pop. B sample is represented by red squares in Fig. 8. In general, the Pop. B Al III profile show small displacements from the rest-frame wavelength within the uncertainty limit. Panel a of Fig. 8 shows that the shift distribution is symmetric around 0. Panels c and e of Fig. 8 are consistent with this trend: symmetric displacements around 0 shift, and no dependency on the bolometric luminosity and Eddington ratio obtained with Al III.
In panel b of Fig. 8, we observe a peak in the C III] shift with a median value of 160±90 km s−1. As seen in Fig. 5, this small redshift could indicate that sources above the 4000 km s−1 limit tends to ‘cover’ the VBC spectral range. This behaviour has also been observed for the LIL Hβ line (Zamfir et al. 2010). From panels d and f of Fig. 8, we observe a consistent behaviour for both C III] and Al III: there is no significant dependency on Lbol and REdd.
4.2. Line widths
4.2.1. Population 
From our spectral fitting, 111 Pop. A objects (excluding the 11 xA sources) have an FWHM of C III] and Al III that are not forced to be equal. We call them Pop.  *. In Fig. 9 we show Pop.
*. In Fig. 9 we show Pop.  * quasars in blue and xA quasars as magenta points. The grey line indicates the 1:1 relation, the black line is the best fit for the Pop.
* quasars in blue and xA quasars as magenta points. The grey line indicates the 1:1 relation, the black line is the best fit for the Pop.  * sources. Using the least-square method, it yields the equation FWHM(C III]) ≈ (663±348) + (0.709±0.061) FWHM(Al III). The Al III FWHM median value is 3550±230 km s−1. The orange line is set at FWHM(C III]) = 0.9 FWHM(Al III), according to the findings of Marziani et al. (2022, hereafter M22). The value that relates the FWHM of C III] and Al III should be in the range 0.8 − 1.1 for Pop A1-A2 sources. Indeed, as seen in Fig. 9, we have three objects with an FWHM(C III] BC) ∼ 1.1 FWHM(Al IIIλ1860). This behaviour indicates that A1-A2 lines are narrower than Hβ by ≈10%.
* sources. Using the least-square method, it yields the equation FWHM(C III]) ≈ (663±348) + (0.709±0.061) FWHM(Al III). The Al III FWHM median value is 3550±230 km s−1. The orange line is set at FWHM(C III]) = 0.9 FWHM(Al III), according to the findings of Marziani et al. (2022, hereafter M22). The value that relates the FWHM of C III] and Al III should be in the range 0.8 − 1.1 for Pop A1-A2 sources. Indeed, as seen in Fig. 9, we have three objects with an FWHM(C III] BC) ∼ 1.1 FWHM(Al IIIλ1860). This behaviour indicates that A1-A2 lines are narrower than Hβ by ≈10%.
 |
Fig. 9. FWHM(Al IIIλ1860) vs. FWHM(C III]λ1909) for Pop. |
4.2.2. Extreme Population A
The physical reason for using the ratio of the shift from the central wavelength over the FWHM in panels e and f of Fig. 8 resides in the effect of outflow motions on the BC. An outflow component leads to an increase in the profile width (as seen for C IVλ1549 and Mg IIλ2800, e.g., Marziani et al. 2016, 2013; Denney 2012; McLure & Jarvis 2002). The decomposition of the xA Al IIIλ1860 profiles shown in Appendix A validates this assumption. In our xA sub-sample, SDSS J003546.29-034118.2 is the source with the highest blueshift, −1010±80 km s−1, which is also the quasar with the largest FWHM(Al III) = 4200±340 km s−1. Another example is SDSS J152314.49+375928.9, with a shift of −850±30 km s−1 and an FWHM(Al III) = 4000±400 km s−1. The other nine xA Al III profiles show shifts between −500 and 270 km s−1 with an FWHM(Al III) between 2500 and 4000 km s−1. In the Al III case (Fig. 8, panel e), the largest ratio of shift/FWHM is ≲−0.15, which implies that the broadening effect might significantly affect the Al III line width.
4.2.3. Population B
The highest value of Al III FWHM observed in Pop. B objects is 6500 km s−1. Only one object shows an FWHM of 4000 km s−1, indicating that the Al III line is broader than in Pop. A spectra but not as wide as the C III] VBC. The median values are FWHM (C III] BC) = 5300±250 km s−1 and FWHM(C III] VBC) = 8124±410 km s−1. The inclusion of a VBC of C III] on the red side of the Pop. B spectra is evident, as seen in Fig. 5. In Pop. B objects, we do not expect strong contribution of Fe III, so the residual seen in the fit with no VCB (Fig. 5, upper panel) should be also part of C III].
The case of a VBC in Al III and Si III] is not so evident. It could be that for Al III and Si III] it is also necessary to add a VBC due to the large FWHM observed (up to ∼6500 km s−1 for Al III and 5800 km s−1 for Si III]). In the case of Al III, the blending is not extremely severe, so we are able to efficiently de-blend the BC (as seen in Fig. 3). The blend profile suggests that if Al III VBC is present, it might be very weak, probably unresolved, and not dominant in the emission line profile. A VBC might not be detected and might be lost in the spectral noise. In Sect. 5.4 we derive constraints on the Al III and Si III] VBC.
5. Discussion
The MBH computations are closely related to the FWHM of prominent broad components and the underlying continuum. Therefore, the decomposition of the line profile becomes important to isolate the virialised component from other components, either coming from an outflow (blueshifted) or possibly coming from an inflow region (redshifted, Wang et al. 2017). We explore different MBH estimators (Sects. 5.1 and 5.2) not as affected by shifts as C IVλ1549 (Sect. 5.3). For Pop. B objects, we analyse the possibility of a VBC in Al III and Si III] (Sect. 5.4).
5.1. Virial mass and Eddington ratio estimates with AlIIIλ1860
Using the FWHM of two prominent lines of the 1900 Å blend, Al III and C III], we computed the virial MBH with two methods: (1) M22 (Eqs. (3) and (4)) derived from the comparison of the FWHM of Hβ with Al III and C III]; (2) Vestergaard & Peterson (2006, hereafter VP06, Eqs. (5) and (7)) that are based on the Hβ and C IVλ1549 line widths.
The M22 scaling laws take the form:
Here ξ is a correction needed in the FWHM (Sect. 4.2.1), for ξAIII ≈ 1 and ξCIII] ≈ 1.25.
VP06 use the optical continuum luminosity Lλ(5100 Å) along with FWHM(HβBC), and the UV continuum Lλ(1350 Å) along with FWHM(C IVλ1549BC). Considering the different continuum windows of these equations, we found it necessary to extrapolate the continuum obtained from specfit to a wavelength as close as possible to 5100 Å or 1350 Å. We applied the ‘surrogate’ lines Al IIIλ1860 and C III]λ1909 in both equations of VP06. This means that we can directly compare the MBH(Al III) and MBH(C III]) from the scaling relations of M22 to the ones of VP06 using FWHM Al IIIλ1860 or C III]λ1909 in place of FWHM C IVλ1549 or Hβ.
The comparison of MBH from Eqs. (3) and (4) is presented in Fig. 10, along with the residuals of each set with δlog MBH = log MBH(Al III) − log MBH(C III]). In the figure, the grey line indicates the 1:1 relation, and the black line is the best fit for the Pop.  * sources using the least-square method. For the M22 results (Fig. 10, panela) the equation is log MBH(C III]) ≈ ( − 1.017 ± 0.095)+(1.131 ± 0.085)log MBH(Al III); the rms of the linear fit is 0.043 and the deviation from the 1:1 relation is 0.14. In the other two panels of Fig. 10, we used Eq. (7) of VP06 by replacing the FWHM of C IV with the FWHM of Al III and C III]. Panel b of Fig. 10 shows the relation for MBH(Al III) using Eq. (3) versus VP06 Eq. (7). There is very good agreement between the estimations: log MBH(Al III)M22 ≈ ( − 0.249 ± 0.045)+(1.037 ± 0.065)log MBH(Al III)VP06 with a Pearson correlation of 0.98; the standard error (STD err) of the linear fit is 0.015 and the deviation from the 1:1 relation is 0.08. Panel c of Fig. 10 displays the relation of MBH(C III]) using Eq. (4) versus VP06 Eq. (7). In this case, we also observe a good agreement between each estimation. The resultant equation is log MBH(C III])M22 ≈ (0.609 ± 0.085)+(0.935 ± 0.065) log MBH(C III])VP06 with a Pearson correlation of 0.99; the STD err of the lineal fit is 0.012 and the deviation from the 1:1 relation is 0.04. The scatter of panels b and c of Fig. 10 is smaller than in panel a, due to fact that the equations of M22 are based on VP06.
* sources using the least-square method. For the M22 results (Fig. 10, panela) the equation is log MBH(C III]) ≈ ( − 1.017 ± 0.095)+(1.131 ± 0.085)log MBH(Al III); the rms of the linear fit is 0.043 and the deviation from the 1:1 relation is 0.14. In the other two panels of Fig. 10, we used Eq. (7) of VP06 by replacing the FWHM of C IV with the FWHM of Al III and C III]. Panel b of Fig. 10 shows the relation for MBH(Al III) using Eq. (3) versus VP06 Eq. (7). There is very good agreement between the estimations: log MBH(Al III)M22 ≈ ( − 0.249 ± 0.045)+(1.037 ± 0.065)log MBH(Al III)VP06 with a Pearson correlation of 0.98; the standard error (STD err) of the linear fit is 0.015 and the deviation from the 1:1 relation is 0.08. Panel c of Fig. 10 displays the relation of MBH(C III]) using Eq. (4) versus VP06 Eq. (7). In this case, we also observe a good agreement between each estimation. The resultant equation is log MBH(C III])M22 ≈ (0.609 ± 0.085)+(0.935 ± 0.065) log MBH(C III])VP06 with a Pearson correlation of 0.99; the STD err of the lineal fit is 0.012 and the deviation from the 1:1 relation is 0.04. The scatter of panels b and c of Fig. 10 is smaller than in panel a, due to fact that the equations of M22 are based on VP06.
 |
Fig. 10. Comparison of MBH of Al III and C III], along with their residuals. Upper panels: log space of MBH(Al IIIλ1860) vs. MBH(C III]λ1909) computed with the scale relations of M22 and VP06 for the Pop. |
As for the case of Eq. (5) of VP06, by replacing the FWHM of Hβ for the FWHM of Al III and C III], we observed a discrepancy between estimations, a much larger scatter, and systematic changes probably associated with the extrapolation of the continuum from ≈4000 Å to 5100 Å. We see a similar situation for Al III and C III] for both comparisons, both of them with a Pearson correlation of ∼0.8 and a resultant equation of log MBH(Al III,C III])M22 ≈ 0.6 log MBH(Al III,C III])VP06. These findings prove that Al III and C III] are equivalent as virial broadening estimators for quasars (with a Pearson correlation coefficient of 0.93 for M22) at intermediate z from observations obtained from large surveys such as the SDSS.
In HILs such as C IVλ1549, the contamination of an outflow introduces a bias in the black hole mass estimations (see Sect. 5.3), because of over-broadening of the lines. The dynamic associated with a virialised system is different from the outflow that emerges from a system dominated by radiation pressure. A similar effect can be seen in the IIL Al III for xA objects, but the contribution of the outflow is much lower than in the case of C IVλ1549. This accounts for the good agreement found between between the scaling laws for C IVλ1549 by VP06 and by M22. The C IVλ1549 scaling law of VP06 was built around the assumption that the C IVλ1549 FWHM was as good as Hβ FWHM for virial mass estimation. Using the C III]λ1909 (or Al IIIλ1860), we use a line that is truly equivalent to Hβ M22 and is not strongly affected by any non-virial component.
Several authors have proposed that the Eddington ratio is driving the E1 MS (Marziani et al. 2001, 2003b; Shen & Ho 2014; Sun & Shen 2015). Trends in REdd are also reflected in the X-ray properties (Boller et al. 1996; Wang et al. 1996; Laor et al. 1997), C IVλ1549 line profiles (Wills et al. 1999; Sulentic et al. 2000c, 2007), and in virial MBH estimates using the width of the broad emission lines (Laor 2000; Boroson 2002; Dong et al. 2011). The distribution of MBH(Al III) versus REdd is shown in Fig. 11. Eddington luminosities were calculated based on masses obtained from the FWHM(Al IIIλ1860) following the relation: LEdd ≈ 1.5 × 1038(MBH/M⊙) [erg s−1] (e.g., Netzer & Marziani 2010; Netzer 2015). The bolometric correction for Lλ (1700 Å), 6.3, was taken from MS14, and the bolometric corrections for 1350 Å (5.75) and for 5100 Å (10.3) were taken from Richards et al. (2006).
 |
Fig. 11. Distribution of log MBH(Al IIIλ1860) vs. REdd. The colour-code is as follows: the scale relations of M22 are in blue, red, and magenta, and the scale relations of VP06 (Eq. (5)) are in light blue, orange, and light magenta, for Pops. |
Figure 11 shows that Pops. B and  appear to be segregated mainly on the basis of REdd: few Pop. B sources are in excess of REdd ≈ 0.5. The wide majority of Pop.
appear to be segregated mainly on the basis of REdd: few Pop. B sources are in excess of REdd ≈ 0.5. The wide majority of Pop.  is constrained in the range 0.4 ≲ REdd ≲ 1.2. A minority of data points scatter in the range 1.2 ≲ REdd ≲ 3. If orientation plays a role, and if pole-on orientation leads to narrower lines (McLure & Jarvis 2002; Collin et al. 2006; Decarli et al. 2011; Mejía-Restrepo et al. 2017, 2018), the MBH might be severely underestimated and the REdd overestimated. A similar effect has been already seen in the MBH versus luminosity diagram (e.g., Marziani et al. 2006).
is constrained in the range 0.4 ≲ REdd ≲ 1.2. A minority of data points scatter in the range 1.2 ≲ REdd ≲ 3. If orientation plays a role, and if pole-on orientation leads to narrower lines (McLure & Jarvis 2002; Collin et al. 2006; Decarli et al. 2011; Mejía-Restrepo et al. 2017, 2018), the MBH might be severely underestimated and the REdd overestimated. A similar effect has been already seen in the MBH versus luminosity diagram (e.g., Marziani et al. 2006).
We analysed the parameter space of the UV diagnostic ratios versus REdd plane for the Pop.  sources, but we found no strong correlation (Fig. 12). Table 1 reports the median values of the line ratios. The condition C III]λ1909/Si III]λ1892 ≲1 seems to be sufficient for identifying xA quasars. Yet, xA quasars are not associated with the highest REdd (see also Fig. 11). This might be a consequence of an over-broadening due to an outflow component, increasing MBH for xA sources, and therefore lowering the REdd. The median excess in the virial luminosity (rose bars in Fig. 13) suggests a median MBH overestimate δ log MBH ≈ 0.2. Pop.
sources, but we found no strong correlation (Fig. 12). Table 1 reports the median values of the line ratios. The condition C III]λ1909/Si III]λ1892 ≲1 seems to be sufficient for identifying xA quasars. Yet, xA quasars are not associated with the highest REdd (see also Fig. 11). This might be a consequence of an over-broadening due to an outflow component, increasing MBH for xA sources, and therefore lowering the REdd. The median excess in the virial luminosity (rose bars in Fig. 13) suggests a median MBH overestimate δ log MBH ≈ 0.2. Pop.  sources with REdd ≳ 2 might be orientated preferentially pole-on, leading to a strong underestimate of the MBH and hence to an overestimate of the Eddington ratio (as observed in Fig. 11, the REdd is up to ∼2.5).
sources with REdd ≳ 2 might be orientated preferentially pole-on, leading to a strong underestimate of the MBH and hence to an overestimate of the Eddington ratio (as observed in Fig. 11, the REdd is up to ∼2.5).
 |
Fig. 12. Distribution of the UV diagnostic ratios of MS14: Al IIIλ1860/Si III]λ1892 (left) and C III]λ1909/Si III]λ1892 (right) with respect to REdd (Al III) for Pop. |
5.2. Virial luminosities and outflow broadening
The physical parameters of xA quasars are correspondingly extreme, with a maximum radiative output per unit of mass close to their Eddington limit. This condition is predicted by accretion disc theory at high accretion rates: low radiative efficiency and the Eddington ratio saturating towards a limiting value (Mineshige et al. 2000; Sadowski 2011; Sądowski et al. 2014, and references therein). We also expect that the intensity ratios of the intermediate- and low-ionisation lines in xA quasars remain almost the same: only the line width increases with luminosity (Negrete et al. 2012, 2013). The spectral invariance with luminosity implies that the radius of the emitting regions should rigorously scale as L1/2; if not, the ionisation parameter U should change with luminosity (Marziani et al. 2021). Putting together these considerations: (1) L/LEdd = const.; (2) r ∝ L1/2; together with (3) the definition of Eq. (1) MBH ∝ rFWHM2, we obtain a relation linking luminosity and line width, known as the ‘virial luminosity equation’ (MS14):
where L0 = 7.88×1044 and the FWHM is of the virialised BC in units of 1000 km s−1 (see Eq. (6) in MS14 for the complete derivation). The FWHM of Al III is the adopted virial broadening estimator for our work. We calculated LVir for the 11 xA sources, and the average and median values are reported in Table 1. However, there are two effects that can significantly affect the luminosity estimations: an outflow that broadens the virial component, and an orientation effect that narrows it.
For xA sources, the Al III shift/FWHM ratio can be up to ∼ − 0.1 (Fig. 8, panel e). The dominant effect on our sources may be due to an outflow since the virial luminosities are larger than the cosmological ones. We have 11 extreme sources, of which six objects have δlog L = log Lbol −log LVir ≈ −0.2 (magenta bars in Fig. 13). SDSS J003546.29, J152314.49, and J023055.54 showed a difference between the cosmological and virial luminosities under -0.2 and are sources with an Al III blueshift. SDSS J003546.29 has a δlog L = −0.75 and shift Al III ≈ − 1000 km s−1.
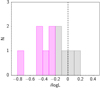 |
Fig. 13. Distribution of the luminosity difference between concordance cosmology determinations and virial ones, δlog L. Colour-code: Grey bars are the five objects that lie under our uncertainties of δlog L and the six objects in magenta are the ones that show an outflow effect (δlog L ≲ −0.2). |
5.3. CIVλ1549 and AlIIIλ1860 inter-comparison
The blueshift of C IVλ1549 is usually evidence of strong outflows (e.g., Richards et al. 2011) that, most likely, result from the presence of a radiation line-driven accretion-disc wind (Gallagher et al. 2015 and references therein). Therefore, a prominent blue component over the line profile is expected, especially at high and intermediate redshifts (Martínez-Aldama et al. 2018). However, when compared to samples with lower redshifts, Pop. A sources at intermediate redshifts tend to show broader and more blueshifted components of C IV. They are indicative of wind activities surrounding the central region (Deconto-Machado et al. 2022). Therefore, black hole masses based on the FWHM(C IV) emission line can be overestimated by a factor of four to five at large blueshifts and are biased due to this non-virial component (Coatman et al. 2016; Denney 2012).
A sub-sample from Shen et al. (2011) was extracted to compare the C IVλ1549 profile with our Al III sample. The criterion used was a luminosity distribution consistent with the one of the Al IIIλ1860 sample. The results are shown in Fig. 14, for the FWHM and peak shift of the line. The blue lines show the distribution of bootstrap replications of the bolometric luminosity distribution, for 300 objects pooled out of ∼50 000 sources from the Shen et al. (2011) catalogue. The luminosity distributions of the bootstrapped samples overlay the luminosity distribution of the present samples, since the source from Shen et al. (2011) were pooled preserving the relative prevalence of the Al IIIλ1860 luminosity (shaded histogram in Fig. 14). For both C IVλ1549 FWHM and shift, the distributions imply an extremely high probability that they are not consistent. In particular, the FWHM C IVλ1549 appears to be systematically broader than the one of Al III by ≈1500 km s−1. While the Al III blueshifts are modest (within |δvr|≲500 km s−1, and the distribution appears centred at rest frame and only slightly skewed to the blue, the C IVλ1549 line presents a systematic blueshift by ≈ − 600 km s−1.
 |
Fig. 14. Bootstrapped distributions for C IV luminosity, FWHM, and line peak shift. Left: inter-comparison between the Al IIIλ1860 of the present sample (hatched histograms) and the C IVλ1549 FWHM distribution of the sample of Shen et al. (2011), for matching luminosity distributions (top panel). In the bottom panel, the thin blue lines show the binned distributions of bootstrap replications of the Shen et al. (2011) data; the thick blue line is their average. Right: same as for the left panels, but for peak shift. |
The C IVλ1549 shift has been analysed with respect to Hβ (e.g., Leighly & Moore 2004; Marziani et al. 2010; Sulentic et al. 2017; Vietri et al. 2018), and interpreted as a strong wind contribution affecting the C IVλ1549 profile in the form of an excess blueshifted emission. The same difference has been revealed in a detailed same-source, inter-line comparison between Al III and C IVλ1549 in ≈20 xA sources (Martínez-Aldama et al. 2018). Figure 14 provides a statistical confirmation that the C IVλ1549 blueshifted emission considerably broadens and shifts the C IVλ1549 profile with respect to the profile of Al IIIλ1860.
5.4. A model for the Population B CIII]λ1909 profile
We ask ourselves whether our model of the 1900 Å blend is adequate. This work has convincingly shown the need to include a VBC to account for the C III]λ1909 profile. Even if the Si III]λ1892 is heavily blended, the fits detect an emission peak between Al III and C III]λ1909, implying that the Si III]λ1892 core component is always prominent. There is no doubt about the existence of a core component (i.e. the BC) for Al III. However, Al III is the weakest line in the blend, and some VBC emission could be lost in noise.
We can analyse the expectation of VBC emission considering that: (1) the velocity field of the emitting regions is predominantly virial in Pop. B sources, as established by early reverberation mapping studies (Peterson & Wandel 1999, 2000); and (2) the VBC is a heuristic representation of the innermost part of the BLR. This VBC could be physically associated with inflowing gas (Wang et al. 2017; Giustini & Proga 2019) or due to an effect of the gravitational redshift (Netzer 1977; Zheng & Sulentic 1990; Corbin 1995; Liu et al. 2017; Mediavilla et al. 2018). This component has been observed in sources with masses in the range 108–1010 M⊙ (Bon et al. 2015), comparable to the Pop. B mass values of the present sample, with mean log MBH = 9.1 [M⊙].
In this way, three empirical approaches are in order: (1) a fit with only the BCs (M1); (2) a fit in which one VBC is assumed for C III]λ1909 only (as done for all Pop. B sources, M2); (3) a fit in which three BCs and three VBCs are introduced, with restrictions on consistent shifts and widths for the BCs and VBCs (M3) as seen in panel a of Fig. 15. This last option implies eight free parameters (peak shifts and wavelengths are locked). It is probably the most appropriate in physical terms, but is very difficult to implement for individual sources. The three fits were carried out on an average composite for all Pop. B sources, and the resulting ratios are reported for the three models in Table 2. The basic inference is that the BC ratios Al IIIλ1860/Si III]λ1892 and Si III]λ1892/C III]λ1909 remain consistent if different models are assumed. A second result is that the VBC/BC ratio is < 1 and ≪1 for Si III]λ1892 and Al IIIλ1860, respectively.
 |
Fig. 15. Empirical fitting models for the Pop. B 1900 Å blend. Upper left: specfit model (M3) of the composite spectra of Pop. B sources with VBC (in red) added to the profiles of Al III, Si III], and C III]. Abscissa scales are rest frame wavelength in Å. The ordinate scale is the specific flux in units of 10−17ergs s−1 cm−2 Å−1. Upper right: synthetic model (M4) with BC+VBC in all three lines with the median value (dashed line) and the uncertainty regions of each profile in light and dark tones: red, green, and blue for Al III, Si III], and C III] BC – VBC, respectively. Grey lines are the M3 flux values as the initial condition. Lower panels: Gaussian distributions of the BC - VBC fluxes obtained with a million random iterations of M3, with values that satisfy the condition of χ2(M4)/χ2min(M4) < F(2σ). |
UV diagnostic ratios of MS14 values obtained on an average composite for all Pop. B sources with different considerations for the Al III, C III], and Si III] profile lines.
The physical implications for the line emitting regions were analysed using CLOUDY 17.02 (Ferland et al. 2017) arrays of photoionisation simulations computed for an unrelated work (Śniegowska et al. 2021). Briefly, they assumed a standard AGN continuum implemented in CLOUDY, solar metallicity, a canonical value of the Hydrogen column density (1023 cm−2), and no micro-turbulence. They were computed for an array of ionisation parameters and density covering the ranges (in log) −4.5 − 1, and 7 − 14 [cm−3], respectively.
Figure 16 shows the behaviour of the ratios Al IIIλ1860 //Si III]λ1892, Si III]λ1892/C III]λ1909, and Al IIIλ1860/C III]λ1909 as a function of ionisation parameter and hydrogen density. The typical ratios measured on the Pop. B sample and on the composite spectrum indicate that the BC is emitted in a region of moderate density and high ionisation (U ∼ 10−1, nH ∼ 1011 cm−3). Similar values are found for the VBC.
 |
Fig. 16. From top to bottom, maps of intensity ratios as a function of ionisation parameter and Hydrogen number density: log Al IIIλ1860/ Si III]λ1892, log Si III]λ1892/C III]λ1909 and log Al IIIλ1860/C III]λ1909. |
To push the analysis one step further, we consider the ratios estimated for Model 4 (a synthetic model with VBC and BC for the three lines, Table 2) as seen in panel b of Fig. 15. This model was made using M3 flux values as an initial condition, then we let the model adapt to the better statistical values (along very well defined physical ranges) varying the fit with a million random iterations. The significance of χ2 variations is described by F statistics appropriate for ratios of χ2 values (Bevington & Robinson 2003), F = 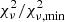 , with degrees of freedom ν ≈ 165. F ≈ 1.30 provides 2σ confidence ranges on the parameters. The final fluxes obtained for the M4 BC and VBC fluxes are the ones that satisfy F within a 2σ confidence level (F(2σ), Fig. 15, panel b). In panel b of Fig. 15, we can see the distributions in light and dark red, green, and blue for Al III, Si III], and C III] BC and VBC, respectively. The dotted line of each distribution show the median values used in the UV ratios in Table 2. Our synthetic models that satisfied the condition of the F(2σ) showed Gaussian distributions for the BC and VBC fluxes centred in one very well defined value, except for Si III] VBC (Fig. 15, panels c and d). The median values are marked for each distribution and correspond to the dotted black lines of Fig. 15, panel b.
, with degrees of freedom ν ≈ 165. F ≈ 1.30 provides 2σ confidence ranges on the parameters. The final fluxes obtained for the M4 BC and VBC fluxes are the ones that satisfy F within a 2σ confidence level (F(2σ), Fig. 15, panel b). In panel b of Fig. 15, we can see the distributions in light and dark red, green, and blue for Al III, Si III], and C III] BC and VBC, respectively. The dotted line of each distribution show the median values used in the UV ratios in Table 2. Our synthetic models that satisfied the condition of the F(2σ) showed Gaussian distributions for the BC and VBC fluxes centred in one very well defined value, except for Si III] VBC (Fig. 15, panels c and d). The median values are marked for each distribution and correspond to the dotted black lines of Fig. 15, panel b.
Figure 17 shows the regions in the parameter plane that are consistent with the ratios built from the three lines in the blend. For the BC there is a very well defined (U, nH) region where the three ratios cross; it means that in this region, the values of (U, nH) are able to reproduce the observed ratios: 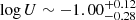 ,
, 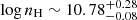 cm−3. Similar values are derived if the BC and VBC are added together:
cm−3. Similar values are derived if the BC and VBC are added together: 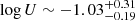 ,
, 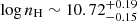 cm−3, where the uncertainty range has been set from the ±1σ uncertainties for the individual line ratios. These values indicate a moderate density and a fairly high ionisation, as expected for Pop. B sources (Negrete et al. 2013, 2014). We warn that our single-zone model is certainly not adequate to represent the complexity of the emitting region. In the case of Pop. B, there is most likely a range of densities, column densities, and ionisation parameters that make the locally optimised cloud model (Baldwin et al. 1995; Korista et al. 1997) the most appropriate.
cm−3, where the uncertainty range has been set from the ±1σ uncertainties for the individual line ratios. These values indicate a moderate density and a fairly high ionisation, as expected for Pop. B sources (Negrete et al. 2013, 2014). We warn that our single-zone model is certainly not adequate to represent the complexity of the emitting region. In the case of Pop. B, there is most likely a range of densities, column densities, and ionisation parameters that make the locally optimised cloud model (Baldwin et al. 1995; Korista et al. 1997) the most appropriate.
 |
Fig. 17. Isophotes tracing the loci of the parameter plane (log U, log nH) consistent with the observed intensity ratios Al IIIλ1860/Si III]λ1892, Si III]λ1892/C III]λ1909, and Al IIIλ1860/C III]λ1909 (shown in log scale). The crossing region defines the (U, nH) parameter range consistent with the values of the three ratios. Top: BC only. Middle: VBC. Bottom: BC+VBC. |
The case of the VBC deserves special attention. We are dealing with emission that is well-constrained only in the case of C III]λ1909, and that is presumably much weaker than the corresponding BC emission for Al IIIλ1860 and Si III]λ1892. Using the ratios of the best fit to the synthetic spectrum, we obtain 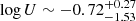 ,
, 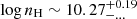 [cm−3]. Due to the very low Si III]λ1892/C III]λ1909 and Al IIIλ1860/Si III]λ1892 intensity ratios derived from the fit (actually consistent with 0 within the uncertainties), the lower limit of both U and nH are practically unconstrained.
[cm−3]. Due to the very low Si III]λ1892/C III]λ1909 and Al IIIλ1860/Si III]λ1892 intensity ratios derived from the fit (actually consistent with 0 within the uncertainties), the lower limit of both U and nH are practically unconstrained.
Further clues can be obtained considering that the line width should be inversely proportional to the square root of the radius of the emitting region: FWHM 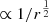 , as per Eq. (1). The BC over VBC FWHM ratio is ≈0.8, implying that the ratio of the radii should be ≈0.64. For constant nH, this would imply an increase in δ log U of ∼ + 0.38. The diagnostics from the blend for the VBC are very poor (a more refined analysis should involve measurements of at least C IVλ1549 and He IIλ1640, which are not covered in the spectra of our sample). However, there is a slight increase in U moving from the BLR to the VBLR, which does not suggest any gross inconsistency with the virial approach.
, as per Eq. (1). The BC over VBC FWHM ratio is ≈0.8, implying that the ratio of the radii should be ≈0.64. For constant nH, this would imply an increase in δ log U of ∼ + 0.38. The diagnostics from the blend for the VBC are very poor (a more refined analysis should involve measurements of at least C IVλ1549 and He IIλ1640, which are not covered in the spectra of our sample). However, there is a slight increase in U moving from the BLR to the VBLR, which does not suggest any gross inconsistency with the virial approach.
Figure 16 indicates that for a likely value of nH ∼ 1011 cm−3, moving from log U ∼ −1 towards higher U values, we may expect a lowering of the Si III]λ1892/C III]λ1909 ratio to a level that may make the VBC of Si III]λ1892 difficult to detect. At the same time, the Al IIIλ1860/Si III]λ1892 ratio might increase sharply for log U ≳ −0.5, reaching ≈1 for log U ≳ −0.0. At that value of the ionisation parameter, the Al IIIλ1860 VBC should be stronger than that of C III]λ1909. The composite profile (Fig. 15) disfavours the possibility that the Al IIIλ1860 VBC, and in turn the U, could be that high: in Pop. B, the intensity of Al IIIλ1860 is lower than that of Si III]λ1892 (Bachev et al. 2004; Kuraszkiewicz et al. 2004; Lira et al. 2017, 2018). The ionisation parameter log U ∼ −0.25 might be a possibility, entailing Al IIIλ1860/C III]λ1909≈0.3, Al IIIλ1860/Si III]λ1892 ≈ 2, and Si III]λ1892/C III]λ1909 ≈ 0.15 (assuming nH = 1011 cm−3).
In summary, these considerations justify the neglect of a Si III]λ1892 VBC. The possibility of an Al IIIλ1860 VBC dominating the Al IIIλ1860 cannot be excluded if the ionisation parameter is high. Against this prospect goes the empirical fact that the FWHM of Al IIIλ1860 and Si III]λ1892 BC are consistent.
6. Summary and conclusions
The present investigation has shown that the intermediate-ionisation lines are little affected by outflows, and that the Al III and C III] lines are equivalent (with some caveats) as virial broadening estimators for quasars, providing a suitable tool for MBH estimates at intermediate z from observations obtained from a big survey such as the SDSS. In greater detail, the results of the present investigation can be summarised as follows:
-
We carried out a redshift correction of the sample spectra using the narrow LIL [O II] rest frame wavelength. The rest frame of the 1900 Å blend corrected in redshift for the [O II] line proved the effectiveness of Al III and C III] as rest frame estimators.
-
We subdivided the sample into Pop. A and Pop. B. We took into account the luminosity-dependent relation of Sulentic et al. (2017). Within Pop. A, Pop. xA was considered separately.
-
Pop. A quasars constituted 78% of the sample with 11 sources classified as extreme accretors, and 22% were Pop. B quasars, out of a sample of 309 objects. We observed a bias against high-Eddington-ratio sources due to the absence of [O II] in the spectra, and a Malmquist-type bias at low Eddington ratios.
-
Applying the specfit routine of lmttIRAF, we were able to fit the most prominent emission lines of the 1900 Å blend simultaneously, proving that we can measure widths of Al III and C III] (and Si III]) even if they are blended.
-
In terms of tendencies observed for each population: Pop.
 showed no shifts in the median sub-samples from the Al III profile, Pop. B showed symmetric shifts around 0; only Pop. xA showed a median blueshift of -300 km s−1, indicating a mixture of two unresolved components: a virialised plus an outflow component. The xA sub-sample showed an Al III shift/FWHM ratio ∼10–15%, indicating that the displacement significantly affects the line width.
showed no shifts in the median sub-samples from the Al III profile, Pop. B showed symmetric shifts around 0; only Pop. xA showed a median blueshift of -300 km s−1, indicating a mixture of two unresolved components: a virialised plus an outflow component. The xA sub-sample showed an Al III shift/FWHM ratio ∼10–15%, indicating that the displacement significantly affects the line width. -
The virial black hole mass estimations of our sample using the FWHM (Al III) are consistent with the ones obtained with FWHM(C III]), using the VP06 and M22 scale relations.
-
Our xA sample (11 quasars) showed a broad consistency between the cosmological and virial luminosity computed with the equation derived by MS14; however, an excess in the virial luminosity with respect to the concordance one indicates that, in this case, the Al III width is affected by a non-virial broadening.
-
The comparison of the Al III and a large number of C IV bootstrapped samples extracted from Shen et al. (2011) matching the luminosity distribution showed that the Al III and C IV FWHM and shift distributions differ fundamentally, in the sense that the C IVλ1549 FWHM and shift distributions are much broader than those of Al III. Shift amplitudes of C IVλ1549 are a factor of roughly ten larger than the Al III ones.
-
Our single-zone model proved that there is a very well defined region in the log plane nH, U for the BC and BC+VBC models for the composite Pop. B spectra. As for the case of only VBC, log nH, U is not fully constrained. Nonetheless, the appearance of the blend and the intensity ratios of the components are consistent with the predominance of a virial velocity field, with a stratification of emission properties.
In conclusion, we can use the IILs Al III and C III] as reliable surrogate mass estimators for Pop.  and Pop. B objects. Highly accreting quasars show smaller blueshifts (on average ≪1000 km s−1) compared to those observed in C IV, and the method discussed in this paper may provide slight MBH overestimates by a factor of ≲2, as described in Sects. 5.1 and 5.2.
and Pop. B objects. Highly accreting quasars show smaller blueshifts (on average ≪1000 km s−1) compared to those observed in C IV, and the method discussed in this paper may provide slight MBH overestimates by a factor of ≲2, as described in Sects. 5.1 and 5.2.
Throughout Fig. 8, we report the median values for each bin.
Acknowledgments
D. Dultzin and C. A. Negrete acknowledge support form Grant IN111422 PAPIIT UNAM. C. A. Negrete acknowledges support form CONACyT project Paradigmas y Controversias de la Ciencia 2022-320020. The work of T. M. Buendia-Rios has been sponsored by CONACYT-Mexico through the Ph.D. scholarship No. 760641. Funding for the SDSS and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the U.S. Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, the Max Planck Society, and the Higher Education Funding Council for England. The SDSS website is http://www.sdss.org. The SDSS is managed by the Astrophysical Research Consortium for the Participating Institutions listed at the http://www.sdss.org.
References
- Bachev, R., Marziani, P., Sulentic, J. W., et al. 2004, ApJ, 617, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J., Ferland, G., Korista, K., & Verner, D. 1995, ApJL, 455, L119 [NASA ADS] [CrossRef] [Google Scholar]
- Baldwin, J. A., Ferland, G. J., Korista, K. T., Hamann, F., & LaCluyzé, A. 2004, ApJ, 615, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Bensch, K., del Olmo, A., Sulentic, J., Perea, J., & Marziani, P. 2015, J. Astrophys. Astron., 36, 467 [NASA ADS] [CrossRef] [Google Scholar]
- Bentz, M. C., Walsh, J. L., Barth, A. J., et al. 2009, ApJ, 705, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Bevington, P. R., & Robinson, D. K. 2003, Data reduction and error analysis for the physical sciences (Boston, MA: McGraw-Hill) [Google Scholar]
- Boller, T., Brandt, W. N., & Fink, H. 1996, A&A, 305, 53 [NASA ADS] [Google Scholar]
- Bon, N., Bon, E., Marziani, P., & Jovanović, P. 2015, Ap&SS, 360, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Bon, N., Marziani, P., Bon, E., et al. 2020, A&A, 635, A151 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boroson, T. A. 2002, ApJ, 565, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Boroson, T. A., & Green, R. F. 1992, ApJS, 80, 109 [Google Scholar]
- Capellupo, D. M., Netzer, H., Lira, P., Trakhtenbrot, B., & Mejía-Restrepo, J. 2016, MNRAS, 460, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Coatman, L., Hewett, P. C., Banerji, M., & Richards, G. T. 2016, MNRAS, 461, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Coatman, L., Hewett, P. C., Banerji, M., et al. 2017, MNRAS, 465, 2120 [Google Scholar]
- Collin, S., Kawaguchi, T., Peterson, B. M., & Vestergaard, M. 2006, A&A, 456, 75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Corbin, M. R. 1995, ApJ, 447, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Dalla Bontà, E., Peterson, B. M., Bentz, M. C., et al. 2020, ApJ, 903, 112 [CrossRef] [Google Scholar]
- Decarli, R., Dotti, M., & Treves, A. 2011, MNRAS, 413, 39 [CrossRef] [Google Scholar]
- Deconto-Machado, A., del Olmo, A., Marziani, P., Perea, J., & Stirpe, G. 2022, Astron. Nachr., 343, e210084 [NASA ADS] [CrossRef] [Google Scholar]
- Denney, K. D. 2012, ApJ, 759, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Denney, K. D., Peterson, B. M., Pogge, R. W., et al. 2010, ApJ, 721, 715 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, T., Croft, R. A. C., Springel, V., & Hernquist, L. 2003, ApJ, 593, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, X.-B., Wang, J.-G., Ho, L. C., et al. 2011, ApJ, 736, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Du, P., Wang, J.-M., Hu, C., et al. 2016, ApJ, 818, L14 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, H.-C., Hu, C., Li, S.-S., et al. 2021, ApJ, 909, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mexicana. Astron. Astrofis., 53, 385 [Google Scholar]
- Ferland, G. J., Hu, C., Wang, J., et al. 2009, ApJ, 707, L82 [NASA ADS] [CrossRef] [Google Scholar]
- Fraix-Burnet, D., Marziani, P., D’Onofrio, M., & Dultzin, D. 2017, Front. Astron. Space Sci., 4, 1 [NASA ADS] [Google Scholar]
- Francis, P. J., Hewett, P. C., Foltz, C. B., et al. 1991, ApJ, 373, 465 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, S. C., Everett, J. E., Abado, M. M., & Keating, S. K. 2015, MNRAS, 451, 2991 [NASA ADS] [CrossRef] [Google Scholar]
- Gaskell, C. M. 1982, ApJ, 263, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Giustini, M., & Proga, D. 2019, A&A, 630, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grupe, D., Wills, B. J., Leighly, K. M., & Meusinger, H. 2004, AJ, 127, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Hartig, G. F., & Baldwin, J. A. 1986, ApJ, 302, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Hewett, P. C., & Wild, V. 2010, MNRAS, 405, 2302 [NASA ADS] [Google Scholar]
- Johansson, S., Zethson, T., Hartman, H., et al. 2000, A&A, 361, 977 [NASA ADS] [Google Scholar]
- Komossa, S., & Xu, D. 2007, ApJ, 667, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Korista, K., Baldwin, J., Ferland, G., & Verner, D. 1997, ApJS, 108, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Kriss, G. 1994, in Astronomical Data Analysis Software and Systems III, eds. D. R. Crabtree, R. J. Hanisch, & J. Barnes, ASP Conf. Ser., 61, 437 [NASA ADS] [Google Scholar]
- Kuraszkiewicz, J., Wilkes, B. J., Czerny, B., & Mathur, S. 2000, ApJ, 542, 692 [NASA ADS] [CrossRef] [Google Scholar]
- Kuraszkiewicz, J. K., Green, P. J., Crenshaw, D. M., et al. 2004, ApJS, 150, 165 [NASA ADS] [CrossRef] [Google Scholar]
- La Mura, G., Di Mille, F., Ciroi, S., Popović, L. Č., & Rafanelli, P. 2009, ApJ, 693, 1437 [NASA ADS] [CrossRef] [Google Scholar]
- Laor, A. 2000, ApJ, 543, L111 [NASA ADS] [CrossRef] [Google Scholar]
- Laor, A., Fiore, F., Elvis, M., Wilkes, B. J., & McDowell, J. C. 1997, ApJ, 477, 93 [Google Scholar]
- Leighly, K. M., & Moore, J. R. 2004, ApJ, 611, 107 [Google Scholar]
- Li, S.-S., Yang, S., Yang, Z.-X., et al. 2021, ApJ, 920, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Lira, P., Botti, I., Kaspi, S., & Netzer, H. 2017, Front. Astron. Space Sci., 4, 71 [Google Scholar]
- Lira, P., Kaspi, S., Netzer, H., et al. 2018, ApJ, 865, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, H. T., Feng, H. C., & Bai, J. M. 2017, MNRAS, 466, 3323 [NASA ADS] [CrossRef] [Google Scholar]
- Lyke, B. W., Higley, A. N., McLane, J. N., et al. 2020, ApJS, 250, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Malkan, M. A., & Sargent, W. L. W. 1982, ApJ, 254, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Marconi, A., Axon, D. J., Maiolino, R., et al. 2009, ApJ, 698, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Aldama, M. L., del Olmo, A., Marziani, P., et al. 2018, A&A, 618, A179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez-Aldama, M. L., Del Olmo, A., Marziani, P., et al. 2018, Front. Astron. Space Sci., 4, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., del Olmo, A., Negrete, C. A., et al. 2022, ApJS, 261, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., del Olmo, A., Perea, J., D’Onofrio, M., & Panda, S. 2020, Atoms, 8, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Dultzin, D., del Olmo, A., et al. 2021, in Nuclear Activity in Galaxies Across Cosmic Time, eds. M. Pović, P. Marziani, J. Masegosa, et al., 356, 66 [NASA ADS] [Google Scholar]
- Marziani, P., Dultzin, D., Sulentic, J. W., et al. 2018, Front. Astron. Space Sci., 5, 6 [CrossRef] [Google Scholar]
- Marziani, P., Dultzin-Hacyan, D., & Sulentic, J. W. 2006, in New Developments in Black Hole Research, ed. P. V. Kreitler (New York: Nova Press), 123 [Google Scholar]
- Marziani, P., Martínez Carballo, M. A., Sulentic, J. W., et al. 2016, Ap&SS, 361, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Olmo, A., Martínez-Aldama, M., et al. 2017, Atoms, 5, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., & Sulentic, J. W. 2012, Astron. Rev., 7, 33 [NASA ADS] [Google Scholar]
- Marziani, P., & Sulentic, J. W. 2014, MNRAS, 442, 1211 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Sulentic, J. W., Dultzin-Hacyan, D., Calvani, M., & Moles, M. 1996, ApJS, 104, 37 [Google Scholar]
- Marziani, P., Sulentic, J. W., Zwitter, T., Dultzin-Hacyan, D., & Calvani, M. 2001, ApJ, 558, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Sulentic, J. W., Zamanov, R., & Calvani, M. 2003a, Mem. Soc. Astron. Ital., 74, 490 [Google Scholar]
- Marziani, P., Zamanov, R. K., Sulentic, J. W., & Calvani, M. 2003b, MNRAS, 345, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Sulentic, J. W., Negrete, C. A., et al. 2010, MNRAS, 409, 1033 [Google Scholar]
- Marziani, P., Sulentic, J. W., Plauchu-Frayn, I., & del Olmo, A. 2013, ApJ, 764, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Matsuoka, Y., Kawara, K., & Oyabu, S. 2008, ApJ, 673, 62 [NASA ADS] [CrossRef] [Google Scholar]
- McLure, R. J., & Jarvis, M. J. 2002, MNRAS, 337, 109 [Google Scholar]
- Mediavilla, E., Jiménez-Vicente, J., Fian, C., et al. 2018, ApJ, 862, 104 [Google Scholar]
- Mejía-Restrepo, J. E., Lira, P., Netzer, H., Trakhtenbrot, B., & Capellupo, D. 2017, Front. Astron. Space Sci., 4, 70 [Google Scholar]
- Mejía-Restrepo, J. E., Lira, P., Netzer, H., Trakhtenbrot, B., & Capellupo, D. M. 2018, Nat. Astron., 2, 63 [CrossRef] [Google Scholar]
- Mineshige, S., Kawaguchi, T., Takeuchi, M., & Hayashida, K. 2000, PASJ, 52, 499 [NASA ADS] [CrossRef] [Google Scholar]
- Moore, C. E. 1945, Contributions from the Princeton University Observatory, 20, 1 [Google Scholar]
- Negrete, C. A., Dultzin, D., Marziani, P., & Sulentic, J. W. 2012, ApJ, 757, 62 [NASA ADS] [CrossRef] [Google Scholar]
- Negrete, C. A., Dultzin, D., Marziani, P., & Sulentic, J. W. 2013, ApJ, 771, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Negrete, C. A., Dultzin, D., Marziani, P., & Sulentic, J. W. 2014, ApJ, 794, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H. 1977, MNRAS, 181, 89 [Google Scholar]
- Netzer, H. 2015, ARA&A, 53, 365 [Google Scholar]
- Netzer, H., & Marziani, P. 2010, ApJ, 724, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H., & Peterson, B. M. 1997, Astron. Time Ser., eds. D. Maoz, A. Sternberg, & E. M. Leibowitz (Dordrecht: Kluwer) 85 [Google Scholar]
- Panda, S., Marziani, P., & Czerny, B. 2019a, ApJ, 882, 79 [NASA ADS] [CrossRef] [Google Scholar]
- Panda, S., Martínez-Aldama, M. L., & Zajaček, M. 2019b, Front. Astron. Space Sci., 6, 75 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., & Wandel, A. 1999, ApJ, 521, L95 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., & Wandel, A. 2000, ApJ, 540, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Peterson, B. M., Ali, B., Horne, K., et al. 1993, ApJ, 402, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Petrucci, P. O., Gronkiewicz, D., Rozanska, A., et al. 2020, A&A, 634, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popović, L. Č., Kovačević-Dojčinović, J., & Marčeta-Mand ić, S., 2019, MNRAS, 484, 3180 [CrossRef] [Google Scholar]
- Richards, G. T., Kruczek, N. E., Gallagher, S. C., et al. 2011, AJ, 141, 167 [Google Scholar]
- Richards, G. T., Strauss, M. A., Fan, X., et al. 2006, AJ, 131, 2766 [Google Scholar]
- Sadowski, A. 2011, PhD thesis, Polish Academy of Sciences, Poland [Google Scholar]
- Salviander, S., Shields, G. A., Gebhardt, K., & Bonning, E. W. 2007, ApJ, 662, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Shen, Y. 2013, Bull. Astron. Soc. India, 41, 61 [NASA ADS] [Google Scholar]
- Shen, Y., & Ho, L. C. 2014, Nature, 513, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [Google Scholar]
- Sigut, T. A. A., & Pradhan, A. K. 1998, ApJ, 499, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Singh, K. P., Garmire, G. P., & Nousek, J. 1985, ApJ, 297, 633 [NASA ADS] [CrossRef] [Google Scholar]
- Sądowski, A., Narayan, R., McKinney, J. C., & Tchekhovskoy, A. 2014, MNRAS, 439, 503 [CrossRef] [Google Scholar]
- Small, T. A., & Blandford, R. D. 1992, MNRAS, 259, 725 [NASA ADS] [Google Scholar]
- Snedden, S. A., & Gaskell, C. M. 2007, ApJ, 669, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Śniegowska, M., Kozłowski, S., Czerny, B., Panda, S., & Hryniewicz, K. 2020, ApJ, 900, 64 [CrossRef] [Google Scholar]
- Śniegowska, M., Marziani, P., Czerny, B., et al. 2021, ApJ, 910, 115 [CrossRef] [Google Scholar]
- Sulentic, J. W., Marziani, P., & Dultzin-Hacyan, D. 2000a, ARA&A, 38, 521 [Google Scholar]
- Sulentic, J. W., Marziani, P., Zwitter, T., Dultzin-Hacyan, D., & Calvani, M. 2000b, ApJ, 545, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Sulentic, J. W., Zwitter, T., Marziani, P., & Dultzin-Hacyan, D. 2000c, ApJ, 536, L5 [Google Scholar]
- Sulentic, J. W., Marziani, P., Zamanov, R., et al. 2002, ApJ, 566, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Sulentic, J. W., Bachev, R., Marziani, P., Negrete, C. A., & Dultzin, D. 2007, ApJ, 666, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Sulentic, J. W., Zamfir, S., Marziani, P., & Dultzin, D. 2008, Rev. Mex. Astron. Astrofis. Conf. Ser., 32, 51 [NASA ADS] [Google Scholar]
- Sulentic, J. W., Marziani, P., del Olmo, A., et al. 2014, A&A, 570, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sulentic, J. W., del Olmo, A., Marziani, P., et al. 2017, A&A, 608, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sun, J., & Shen, Y. 2015, ApJ, 804, L15 [Google Scholar]
- Tody, D. 1986, in Instrumentation in astronomy VI, ed. D. L. Crawford, SPIE Conf. Ser., 627, 733 [Google Scholar]
- Vanden Berk, D. E., Richards, G. T., Bauer, A., et al. 2001, AJ, 122, 549 [Google Scholar]
- Vestergaard, M., & Peterson, B. M. 2006, ApJ, 641, 689 [Google Scholar]
- Vestergaard, M., & Wilkes, B. J. 2001, ApJS, 134, 1 [Google Scholar]
- Vietri, G., Piconcelli, E., Bischetti, M., et al. 2018, A&A, 617, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walter, R., & Fink, H. H. 1993, A&A, 274, 105 [NASA ADS] [Google Scholar]
- Wandel, A., & Petrosian, V. 1988, ApJ, 329, L11 [CrossRef] [Google Scholar]
- Wang, J., & Li, Y. 2011, ApJ, 742, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, T., Brinkmann, W., & Bergeron, J. 1996, A&A, 309, 81 [NASA ADS] [Google Scholar]
- Wang, J.-M., Du, P., Brotherton, M. S., et al. 2017, Nat. Astron., 1, 775 [NASA ADS] [CrossRef] [Google Scholar]
- Wills, B. J., Laor, A., Brotherton, M. S., et al. 1999, ApJ, 515, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, J., Salvato, M., Coffey, D., et al. 2020, MNRAS, 492, 3580 [NASA ADS] [CrossRef] [Google Scholar]
- Zamanov, R., Marziani, P., Sulentic, J. W., et al. 2002, ApJ, 576, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Zamfir, S., Sulentic, J. W., Marziani, P., & Dultzin, D. 2010, MNRAS, 403, 1759 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, W., & Sulentic, J. W. 1990, ApJ, 350, 512 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Extreme accretor source multi-component fits
The results of line profile fitting for the 1900Å blend are shown in Fig. A.1. Notes for some of the objects within the xA sub-sample are:
-
J152314.49+375928.9: one of the highest-blueshift sources: shift(Al III) = -850 ± 30 km s−1, with an FWHM(Al III) = 4000 ± 400 km s−1. This source is also the one with an additional component in Fe IIIλ1914 due to the high amount of iron emission observed on the red side of C III].
-
J100827.67+210931.1: the brightest quasar with a log Lbol = 47.06, with an FWHM(Al III) = 3610 ± 360 km s−1, it also give us one of the most massive xA quasars with a log MBH(Al III) = 8.92 (M/M⊙).
-
J235157.59+003610.6: this object was affected by the host galaxy emission. It was fitted with a positive continuum, and a few absorption lines on the red side of Si III]λ1892 and CIII]λ1909 are observed.
-
J095531.45+174340.3: one of the brightest sources with a log Lbol = 47.04, with a relatively high shift(Al III) = -430 ± 40 km s−1. This object has the highest Eddington ratio in the sub-sample, REdd = 1.34.
-
J092612.68+202326.6: this object presented an Al III redshift of 260 ± 30 km s−1 with an FWHM(Al III) = 3770 ± 370 km s−1.
-
J003546.29-034118.2: the highest-blueshifted source, shift(Al III) = -1010 ± 80 km s−1, FWHM(Al III) = 4190 ± 340 km s−1, with a δlog LVir = -0.75.
 |
Fig. A.1. Analysis of the 1900Å blend as described in Sect. 3.2 for the 11 xA sources in our work. Abscissa scales are rest frame wavelength in Å. The ordinate scale is the specific flux. Black lines identify the BC of Al IIIλ1860, Si III]λ1892, and CIII]λ1909. The dashed blue line is the multi-component model obtained by specfit. Green lines trace the adopted Fe II (pale) and Fe III templates (dark). |
 |
Fig. A.1. continued. |
Appendix B: Line fitting procedures and derived computations header table
Data obtained for this work can be described as follows by number of columns in Table B.1:
Header description of the sample with individual measurements.
(1) file SDSS name,
(2-5) z of this work obtained with [OII]λ3728 (Δz = z[OII] − zSDSS) and the SDSS extracted values with errors,
(6) signal-to-noise ratio around 1700Å,
(7-10) continuum flux at 1700Å and its normalisation flux with errors,
(11) assigned profile of the CIII]λ1909 line: Gaussian or Lorentzian, for xA sources it was added to the name the notation ‘xA’
(12-13) power-law index - α with error for REGION 1,
(14-41) flux, equivalent width, FWHM, shift of Al IIIλ1860, Si III]λ1892 and CIII]λ1909 BC,
(42-45) UV diagnostics ratios with errors,
(46-69) flux and FWHM of NIII]λ1750, Si IIλ1816, Fe II(UV191), Fe III(UV34), C III]VBC and NC with errors obtained by specfit,
(70) power-law index - α for REGION 2,
(71-74) flux and FWHM of [OII]λ3728 with errors,
(75-80) continuum flux at 1350Å and pseudo-continuum flux at 3700Å with errors,
(81-83) logarithmic line luminosity at 1860Å, 1892Å, and 1909Å,
(84-85) logarithmic bolometric luminosity,
(86) FWHM using the luminosity-dependant criterion,
(87-88) logarithmic black hole mass using CIII]λ1909 and Al IIIλ1860,
(89-92) Eddington ratio using CIII]λ1909 and Al IIIλ1860 with errors,
(93-94) logarithmic virial luminosity for Pop. xA sources with errors
All Tables
UV diagnostic ratios of MS14 values obtained on an average composite for all Pop. B sources with different considerations for the Al III, C III], and Si III] profile lines.
All Figures
 |
Fig. 1. Distribution of redshift (left) and of bolometric luminosity (right) for the total sample (309 objects). Colour code: Pops. A, xA, and B in blue, magenta and red, respectively. |
| In the text | |
 |
Fig. 2. Redshift estimation and comparison with the SDSS meassurements. Upper panel: example of a spectrum from our sample. Vertical lines are the prominent emission lines of our work: Al IIIλ1860, C III]λ1909, and [O II]λ3728. The abscissa scale is rest frame wavelength in Å. The ordinate scale is the normalised flux at 1700 Å. Lower left panel: zSDSS vs. Δz for the sample. The red point corresponds to the values of Δz and z of the upper panel spectrum. Lower right panel: distribution of Δz. The lime line shows the shift Δz median value: 4.918 × 10−4 equivalent to ∼65 km s−1. |
| In the text | |
 |
Fig. 3. Analysis of the 1900 Å blend and the [O II]λ3728 region (small box within the figure) as described in Sect. 3.2. The abscissa scale is rest frame wavelength in Å. The ordinate scale is the specific flux in units of 10−17 ergs s−1 cm−2 Å−1. Top: example of a Pop. A source fitted with a Lorentzian profile. Bottom: example of a Pop. B source fitted with a Gaussian profile. The black lines identify the BC of Al IIIλ1860, Si III]λ1892, and C III]λ1909 (red and grey lines are the VBC and NC of C III]λ1909, respectively, if present). The dashed blue line is the multi-component model obtained by specfit. Green lines trace the adopted Fe II (pale) and Fe III templates (dark). |
| In the text | |
 |
Fig. 4. Distribution of the peak blend wavelength around 1909 Å, for Pop. A (blue) and Pop. B (red). The vertical lines identify the rest frame wavelength of [C III]λ1906 (dotted) and C III]λ1909 (solid). |
| In the text | |
 |
Fig. 5. Analysis of the 1900 Å blend (continuum extracted for simplicity in both spectra) of SDSS J012726.39+154153.8 as described for Fig. 3. The C III] profile fitted with only a BC and with a BC+VBC are shown in the top and bottom panels, respectively. The abscissa scale is rest-frame wavelength in Å. The ordinate scale is the normalised specific flux obtained from specfit. |
| In the text | |
 |
Fig. 6. Distribution of Pop. A sources in the plane defined by the ratios C III]λ1909/Si III]λ1892 vs. Al IIIλ1860/Si III]λ1892. The blue dots are quasars within populations A1-A2 (Pop. |
| In the text | |
 |
Fig. 7. Distribution of shift with respect to the rest frame and FWHM of Al IIIλ1860 and C III]λ1909, top and bottom panels, respectively. Shift and FWHM are in units of km s−1. The colour-code is the same as for Fig. 1. |
| In the text | |
 |
Fig. 8. Behaviour of Al IIIλ1860 (left) and C III]λ1909 (right) by population. a),b): shift with respect to rest frame vs. FWHM. c),d): shift vs. log Lbol. e),f): ratio of shift over FWHM vs. REdd. g),h): FWHM vs. log Lbol. Lines are the luminosity-dependent limit between Pop. A and Pop. B. of Sulentic et al. (2017, gold) and the empirical separation of Sulentic et al. (2000c, dashed). Colour-coding: Pop. |
| In the text | |
 |
Fig. 9. FWHM(Al IIIλ1860) vs. FWHM(C III]λ1909) for Pop. |
| In the text | |
 |
Fig. 10. Comparison of MBH of Al III and C III], along with their residuals. Upper panels: log space of MBH(Al IIIλ1860) vs. MBH(C III]λ1909) computed with the scale relations of M22 and VP06 for the Pop. |
| In the text | |
 |
Fig. 11. Distribution of log MBH(Al IIIλ1860) vs. REdd. The colour-code is as follows: the scale relations of M22 are in blue, red, and magenta, and the scale relations of VP06 (Eq. (5)) are in light blue, orange, and light magenta, for Pops. |
| In the text | |
 |
Fig. 12. Distribution of the UV diagnostic ratios of MS14: Al IIIλ1860/Si III]λ1892 (left) and C III]λ1909/Si III]λ1892 (right) with respect to REdd (Al III) for Pop. |
| In the text | |
 |
Fig. 13. Distribution of the luminosity difference between concordance cosmology determinations and virial ones, δlog L. Colour-code: Grey bars are the five objects that lie under our uncertainties of δlog L and the six objects in magenta are the ones that show an outflow effect (δlog L ≲ −0.2). |
| In the text | |
 |
Fig. 14. Bootstrapped distributions for C IV luminosity, FWHM, and line peak shift. Left: inter-comparison between the Al IIIλ1860 of the present sample (hatched histograms) and the C IVλ1549 FWHM distribution of the sample of Shen et al. (2011), for matching luminosity distributions (top panel). In the bottom panel, the thin blue lines show the binned distributions of bootstrap replications of the Shen et al. (2011) data; the thick blue line is their average. Right: same as for the left panels, but for peak shift. |
| In the text | |
 |
Fig. 15. Empirical fitting models for the Pop. B 1900 Å blend. Upper left: specfit model (M3) of the composite spectra of Pop. B sources with VBC (in red) added to the profiles of Al III, Si III], and C III]. Abscissa scales are rest frame wavelength in Å. The ordinate scale is the specific flux in units of 10−17ergs s−1 cm−2 Å−1. Upper right: synthetic model (M4) with BC+VBC in all three lines with the median value (dashed line) and the uncertainty regions of each profile in light and dark tones: red, green, and blue for Al III, Si III], and C III] BC – VBC, respectively. Grey lines are the M3 flux values as the initial condition. Lower panels: Gaussian distributions of the BC - VBC fluxes obtained with a million random iterations of M3, with values that satisfy the condition of χ2(M4)/χ2min(M4) < F(2σ). |
| In the text | |
 |
Fig. 16. From top to bottom, maps of intensity ratios as a function of ionisation parameter and Hydrogen number density: log Al IIIλ1860/ Si III]λ1892, log Si III]λ1892/C III]λ1909 and log Al IIIλ1860/C III]λ1909. |
| In the text | |
 |
Fig. 17. Isophotes tracing the loci of the parameter plane (log U, log nH) consistent with the observed intensity ratios Al IIIλ1860/Si III]λ1892, Si III]λ1892/C III]λ1909, and Al IIIλ1860/C III]λ1909 (shown in log scale). The crossing region defines the (U, nH) parameter range consistent with the values of the three ratios. Top: BC only. Middle: VBC. Bottom: BC+VBC. |
| In the text | |
 |
Fig. A.1. Analysis of the 1900Å blend as described in Sect. 3.2 for the 11 xA sources in our work. Abscissa scales are rest frame wavelength in Å. The ordinate scale is the specific flux. Black lines identify the BC of Al IIIλ1860, Si III]λ1892, and CIII]λ1909. The dashed blue line is the multi-component model obtained by specfit. Green lines trace the adopted Fe II (pale) and Fe III templates (dark). |
| In the text | |
 |
Fig. A.1. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



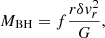
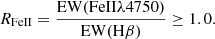
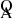
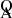
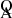
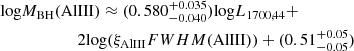
![$$ \begin{aligned}&\mathrm{log} M_{\rm BH} (\mathrm{CIII]} ) \approx (0.645^{+0.045}_{-0.045})\mathrm{log} L_{1700,44} + \nonumber \\&\qquad \qquad \qquad 2 {\log (\xi _{\rm CIII]} FWHM(\mathrm {CIII}]))} + (0.355^{+0.075}_{-0.045}). \end{aligned} $$](/articles/aa/full_html/2023/01/aa44177-22/aa44177-22-eq23.gif)