| Issue |
A&A
Volume 691, November 2024
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 24 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202449976 | |
| Published online | 25 October 2024 | |
Exploring the links between quasar winds and radio emission along the main sequence at high redshift⋆
1
Instituto de Astrofísica de Andalucía, IAA-CSIC, E-18008 Granada, Spain
2
INAF, Osservatorio Astronomico di Padova, IT 35122 Padova, Italy
⋆⋆ Corresponding authors; adeconto@iaa.es; chony@iaa.es; paola.marziani@inaf.it
Received:
14
March
2024
Accepted:
9
August
2024
Context. Despite the increasing prevalence of radio-loud (RL) sources at cosmic noon, our understanding of the underlying physics that governs the accretion disc outflows in these particular sources and its dissimilarity with radio-quiet (RQ) quasars remains somewhat limited.
Aims. Disentangling the real impact of the radio-loudness and accretion on the outflow parameters remains a challenge to this day. We present ten new spectra of high-redshift and high-luminosity quasars and combine these with previous data at both high and low redshift with the aim being to evaluate the role of the feedback from RL and RQ AGN. The final high-redshift (1.5 ≲ z ≲ 3.9), high-luminosity (47.1 ≤ log(L) ≤ 48.5) sample consists of a combination of 60 quasars from our ISAAC and the Hamburg-ESO surveys. The low-redshift (z ≤ 0.8) sample has 84 quasars that have been analyzed in the optical and with the Faint Object Spectrograph (FOS) data in the UV.
Methods. We perform a multicomponent analysis of optical and UV emission line profiles along the quasar main sequence, and provide a relation that can be used to estimate the main outflow parameters (mass rate, thrust, and kinetic power) in both the BLR and NLR through the analysis of the [O III]λ5007 and C IVλ1549 emission lines.
Results. Spectrophotometric properties and line profile measurements are presented for Hβ+[O III]λλ4959,5007, Si IVλ1397+O IV]λ1402, C IVλ1549+He IIλ1640, and the 1900 Å blend. High-ionization lines, such as C IVλ1549 and [O III]λ5007, usually present a significant asymmetry toward the blue, especially in radio-quiet sources. This is strong evidence of outflow motions. In the ISAAC sample, 72% of the quasars where [O III] is clearly detected present significant outflows, with centroid velocity at half intensity blueshifted to values of greater than ∼250 km s−1. Radio-loud quasars tend to present slightly more modest blueshifted components in both the UV and optical ranges. The behavior of [O III]λ5007 mirrors that of C IVλ1549, with blueshift amplitudes between the two lines showing a high degree of correlation, which appears unaffected by the presence of radio emission.
Conclusions. In contrast to the situation at low redshift, both RL and RQ AGN outflow parameters at high luminosity appear in the range needed to provide feedback effects on their host galaxies. Both high- and low-z RL quasars exhibit smaller outflows compared to RQ quasars, suggesting a potential role of radio-loudness in mitigating outflow effects. Nevertheless, the radio-loudness effect on AGN feedback is much less significant than the effect of accretion, with this latter emerging as the main driver of nuclear outflows.
Key words: quasars: emission lines / quasars: general / quasars: supermassive black holes
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
It is now established that quasar spectra do not scatter randomly around an average, and that a systematic scheme is needed to organize their spectral diversity. One of the most successful tools to analyze such objects makes use of independent observational properties obtained from the optical and UV emission lines, as well as from soft X-rays (the 4D Eigenvector 1 (4DE1) correlation space; Boroson & Green 1992; Sulentic et al. 2000b). As part of the 4DE1, it is possible to identify a sequence of quasars in the plane defined by two optical parameters: the full width at half maximum of the Hβ emission line (FWHM(Hβ)) and the ratio between the intensities of the blend of Fe II emission lines at 4570 Å and Hβ (RFe II). This relation has come to be known as the main sequence of quasars (MS; Sulentic et al. 2000a,b; Marziani et al. 2001; Shen & Ho 2014; Marziani et al. 2018). Several multifrequency correlations associated with the MS are well established at low redshift and low luminosity (e.g., see the summary tables in Sulentic et al. 2011; Fraix-Burnet et al. 2017).
At low redshift, it appears that the jetted1 (radio-loud, RL) sources show a preference for the Population B (Pop. B) domain in the MS, while the radio-quiet (RQ) sources are distributed equally between Population A (Pop. A) and Pop. B (Zamfir et al. 2008). This suggests potential differences in spectral and physical properties between RL and RQ sources. The phenomenology involves broader lines for RL than for RQ sources (as most RL sources are in Pop. B), and an optical spectrum showing lower Fe II and a higher ionization degree with respect to full samples of RQ quasars in both the broad-line region (BLR) and the narrow-line region (NLR) (Marziani et al. 2003b; Zamfir et al. 2010; Kovačević-Dojčinović & Popović 2015; Coziol et al. 2017; Ganci et al. 2019). Consequently, the low-z RQ sources seem to follow different distributions of Eddington ratio and black hole mass than the RL ones (Woo & Urry 2002; Marziani et al. 2003a; Sikora et al. 2007; Fraix-Burnet et al. 2017). In general, at low-z, RQ sources are the ones that usually present smaller masses and larger Eddington ratios.
Outflows appear to be ubiquitous in both the BLR and NLR (e.g., Coatman et al. 2019; Vietri et al. 2020; Marziani et al. 2022b, and references therein). However, at low z, mild-ionization gas outflows observed in jetted sources appear to be weaker than in the RQ ones (Marziani et al. 1996; Bachev et al. 2004; Punsly 2010; Richards et al. 2011). This may not be at odds with the higher ionization degree revealed in RLs (e.g., Buttiglione et al. 2010; Mengistue et al. 2023), although a full physical explanation is still missing, mainly because of the still-limited scope of detailed studies of accretion disk outflows in RL quasars. This difference between RQ and RL outflows is observed at both high and low redshift. A key distinction is however that at high redshift, the outflows appear significantly stronger compared to those at low redshift (Richards et al. 2011; Sulentic et al. 2017; Deconto-Machado et al. 2023). At low-redshift ranges, many authors have found ionized gas outflows on kiloparsec (kpc) scales; however their impact is only in the central region of the galaxies (e.g., Kim et al. 2023, and references therein).
An increasing number of RL sources are being discovered at cosmic noon (e.g., Patil et al. 2022; Breiding et al. 2023, and references therein). Their rest-frame optical properties remain poorly studied, as they require high-signal-to-noise-ratio (S/N) moderate-dispersion IR spectroscopy. For this reason, we obtained new IR spectroscopic observations for a further ten high-redshift (z ∼ 1.5 − 2.5) and high-luminosity (MB ≲ −27) quasars. The targets are intended to cover the rest-frame Hβ range, and include both RQ and jetted (or RL) objects, completing the sample reported in Deconto-Machado et al. (2023 hereafter Paper I). Our main aim is to clarify the origin of several phenomenological differences between RL and RQ and in particular the relation between accretion status, accretion disk outflows, and the presence of powerful relativistic ejections, exploiting the MS and its correlation with the C IVλ1549 and [O III]λλ4959,5007 emission.
In addition to the rest-frame optical data, we collected archival rest-frame UV data for the targets in the present paper and in Paper I, and we defined comparison samples for which both rest-frame UV and optical data are available (Section 2). The data analysis includes a discussion about UV and optical regions for the two different quasar populations and the spectral types that have been defined along the quasar MS (Section 3). The measurements carried out in both the optical (Fe II, Hβ, +[O III]λλ4959,5007) and UV (Si IVλ1397, C IVλ1549, and the 1900 Å blend) regions are reported in Section 4, and their interpretation in terms of the outflow dynamical parameters is presented in Section 5. We show that the RQ and RL populations are both associated with high Eddington ratios at high luminosity, and that BLR and NLR scale outflows are consistently powerful, albeit they are somewhat weaker in RL sources. This difference between RQ and RL outflows might be due to an apparently minor effect related to the propagation of the relativistic jet. In Section 6, we summarize our key findings and discuss some implications of our results.
2. Samples
2.1. The new ISAAC2 sample
New near-infrared (NIR) spectroscopic observations for ten quasars (hereafter ISAAC2 sample) were obtained to cover the high-redshift (1.55 ≤ z ≤ 2.45) and high-luminosity (47.18 ≤ log Lbol ≤ 48.14 [erg s−1]) ranges. The redshift range of this sample allows the detection and observation of the Hβ+[O III]λλ4959,5007 region through the transparent window in the NIR with the ISAAC spectrograph at the VLT. These spectra, together with those from Paper I complete what we refer to from now on as the ISAAC sample (32 sources in total), which is described in more detail in Sect. 2.2.
Table 1 lists the main properties of the ISAAC2 sample. The redshift was estimated using a similar approach to that used in Paper I. For five sources (PKS0226-038, PKS0858-279, CTSJ01.03, CTSJ03.14, and PKS1448-232), the redshift estimation relied on the observed wavelength of the narrow component (NC) of Hβ, which is also consistent with the central wavelength of the [O III] NC. For PKS0237-23, BZQJ0544-2241, [HB89]1559+088, and FBQS J2149-0811, the redshift was determined using the broad component (BC) of Hβ, whose peak wavelength agrees with the peak of a very faint Hβ NC in all cases except PKS0237-23 and [HB89]1559+088, where the NC is only barely detected. In the case of WB J0948+0855, the presence of strong telluric bands, combined with the fact that the Hβ region is at the edge of the spectrum, significantly affect the estimation of the Hβ peak centroid, leading to large uncertainties. Therefore, we used the Mg IIλλ2796,2803 doublet from the SDSS UV spectrum to determine the redshift for this source (see spectral fitting in Fig. 6 of the additional Zenodo file). The luminosity distance was estimated from the redshift using the approximation reported in Sulentic et al. (2006), which is valid for ΩM = 0.3, ΩΛ = 0.7, and H0 = 70 km s−1 Mpc−1.
Source identification of the ISAAC2 sample.
2.2. The complete ISAAC sample
Our complete ISAAC sample comprises 32 quasars, consisting of 22 sources from Paper I, along with the ten new objects presented in this work. These quasars are characterized by high redshift values, ranging from z = 1.55 to z = 3.80, and high luminosity (47.18 ≲ log Lbol ≲ 48.36 [erg s−1]), including both RL (10) and RQ (22) sources. The ISAAC sample was selected from the catalog of Véron-Cetty & Véron (2010, VCV), among the type 1 quasars observable from the Paranal Observatory, with declination δ ≤ 25°, and with a redshift of between 1 and 4 according to VCV (from where the first estimation of the redshift was obtained), which would allow good coverage of the Hβ and [O III] region through the NIR windows with the ISAAC spectrograph at the VLT. Figure 1 shows the distribution in z and Mi of the complete ISAAC sample, along with the other samples considered in this work (described in Sect. 2.3). The ISAAC2 sample exhibits a very similar Mi range to ISAAC1, although ISAAC1 has a more extended distribution in the z context, with some cases reaching redshifts of as high as ∼3.8.
 |
Fig. 1. Distributions of z and Mi for FOS, HEMS, ISAACI from Paper I, and the new ISAAC2 data. Each distribution was normalised separately. |
2.3. Other samples
This work includes two additional, previously published samples, at high and low redshift (including RL and RQ sources). Ultraviolet and optical spectra are available for both, and these were analyzed using the same approach for the decomposition of the emission line profiles. These two additional samples are as follows:
High-redshift Hamburg-ESO sample (hereafter, HEMS). The HEMS sample consists of the 28 high-luminosity and high-redshift objects with measurements reported by Sulentic et al. (2017), where a detailed analysis (based on the same methodology as that used for our ISAAC sample) of the Hβ and C IVλ1549 broad emission lines is presented. This sample was selected for having additional UV spectra from the original 52 sources with ISAAC Hβ observations of the Hamburg-ESO (HE) sample discussed in Sulentic et al. (2004, 2006) and Marziani et al. (2009). These sources are extremely luminous (47.5 ≲ log Lbol ≲ 48 [erg s−1]) and are located in a redshift range of 1.4 ≲ z ≲ 3.1. The radio properties of the HEMS sample are listed in Table 2 (available at the CDS), together with the UV and optical full profile measured parameters for this sample and used in this paper. From the 28 quasars, 24 are classified as RQ, while four are RL sources. We combine these data with our ISAAC1+ISAAC2 sources to build a high-luminosity sample to be analyzed in the present work. As can be seen in Fig. 1, the HEMS sample shares similar i-band absolute magnitudes with the ISAAC sample.
Low-redshift FOS data. The low-luminosity sample was selected from Sulentic et al. (2007), who analyzed the C IVλ1549 emission line parameters of 130 low-redshift sources observed with the Faint Object Spectrograph (FOS) on board HST. Of these 130 quasars, 84 have optical spectra available in the recent literature, and we reanalyzed them following the same approach as that used for the ISAAC data. We use this sample as a comparison sample at low L for both optical and UV spectral ranges. Table 2 also lists the radio properties and the UV and optical full profile parameters (velocity centroids at half (c(1/2)) and one-quarter (c(1/4)) of the intensity of C IV and [O III]) of the FOS sample. This sample includes both RQ and RL (50 and 34 sources, respectively) and has a typical bolometric luminosity of ∼45.6 [ergs−1] and a redshift of z ≤ 0.8, as shown in Fig. 1.
In the analysis carried out in Sects. 4 and 5, our high-z high-luminosity sample (including RQ and RL sources) consists of the combination of the full ISAAC (ISAAC1+ISAAC2) and HEMS samples, as they share similar redshift and luminosity ranges. This high-z sample consists of 60 sources in total (32 from ISAAC and 28 from HEMS), of which 58 objects have an [O III] detection. For the other 2, in the case of SDSSJ005700.18+143737.7, [O III] is located very close to the edge of the spectrum, and for WB J0948+0855, the region is completely affected by absorption lines. From these 58 sources, 34 are identified as blue outliers in [O III] (i.e., velocity shifts at half intensity c(1/2) higher than −250 km s−1; see Sect. 4.1), with 20 sources from ISAAC (representing ∼62% of the sample) and 14 from HEMS (∼50% of the sample). Regarding C IV at high z, data are available for 48 (20 from ISAAC and 28 from HEMS), wherein blueshifts are identified in all sources but HE2355–4621.
The low-z low-luminosity sample consists of the 84 reanalyzed FOS sources, for which measurement data are available for both [O III] and C IV. Among them, 11 sources in [O III] and 21 in C IV present a significant blueshifted component. For both emission lines, a source is classified as a blue outlier and consequently considered to have an outflow if its full profile exhibits a velocity centroid at half peak intensity c(1/2) < − 250 km s−1. Also for the FOS low-z sample, when the [O III] full profile shows slightly smaller c(1/2) blueshift, the object is identified with an outflow if its blueshifted component (after the spectral fitting; see Section 3.3) has a significant intensity (≳40%) relative to the full profile. The list of sources identified as outliers is reported in Table A.1.
Throughout Sections 4 and 5, the sample size depends on the analysis done. We consider the complete samples (i.e., the 60 sources at high z and 84 ones at low z) when discussing the general behavior of the profiles or, for example, of the effect of radio-loudness on the line profiles both in C IV and [O III]. However, when addressing outflows and their dynamical parameters, only the objects identified as exhibiting blueshifted components are taken into account.
3. Observations and data analysis
3.1. NIR observations and data reduction
The new spectra were taken in service mode in 2010 and 2011 under the ESO programme 086.B-0774(A), with the IR spectrometer ISAAC mounted at the Nasmyth A focus of VLT-U3 (Melipal) at the ESO Paranal Observatory. A summary of the observations is listed in Table 3.
Log of optical observations with VLT/ISAAC.
Reductions were performed following a standard methodology in NIR observations, that is, using standard IRAF routines, and following the procedures described in Paper I. Pairs of spectra were taken by nodding the telescope between two positions, A and B, displaced on the CCD frame and following an ABBA cycle, as this allows a better subtraction of the sky.
The wavelength calibration was achieved from xenon and argon arc spectra with rms residuals of 0.4 Å in J and 0.6 Å in sH. This wavelength calibration was corrected for small zero-order offsets by measuring the centroids of several OH sky lines against the arc calibration. The 2D wavelength-calibrated spectra (A and B) of each pair AB or BA were rebinned to a common linear wavelength scale. The sky background was then subtracted using the double-subtraction technique. For each rebinned wavelength 2D spectra, we computed a frame (A–B or B–A), so that the reduced image (AB or BA) consists of two spectra of the source, one positive and one negative, positioned as separated by the nod throw and in which the sky has been removed. We then extracted the 1D wavelength-calibrated spectra using the task apsum, creating one spectrum for each nodding position. The 1D –B (or –A) spectrum was subtracted again to obtain a final 1D A–(-B) = A+B spectrum for each observing AB and BA sequence of the ABBA cycle. Finally, all double-subtracted spectra were stacked together.
The absolute flux calibration was performed through observations of standard telluric stars, with the same setup as that used to obtain quasar spectra. The standard star spectral energy distributions (SEDs) were retrieved from the Library of Stellar Spectra for spectrophotometric calibration available at ESO2. The absolute flux scale for the standard star was provided by the Two Micron All Sky Survey (2MASS, Skrutskie et al. 2006) magnitudes. Each standard star SED spectrum was then divided by its corresponding spectrum in order to correct for the atmospheric absorption features (IRAF routine telluric). Spectra were also corrected for galactic extinction.
As a final step, we evaluated the absolute flux calibration uncertainty on the quasar spectra by performing a comparison between the J/H-band magnitudes estimated by convolving the J/H 2MASS filter with the observed spectrum and the J/H magnitudes in the NASA/IPAC Extragalactic Database (NED). The average difference between 2MASS and our flux estimations is 0.026 mag, with the largest value of 0.091 ± 0.018 mag found for CTSJ01.03.
3.2. Optical data
Eight out of the ten new sources from the ISAAC2 sample have rest-frame UV spectra that cover at least one of the three regions of our interest (i.e., Si IVλ1397+O IV]λ1402, C IVλ1549+He IIλ1402, and the 1900 Å blend regions). Table 4 reports the database or reference from which each UV spectrum was obtained. For four quasars (PKS0237-23, BZQJ0544-2241, PKS0858-279, and CTSJ01.03) it was necessary to digitize the spectra from the respective references reported in Table 4. This process was performed using the WebPlotDigitizer facility 3. The only sources for which we could not find useful UV spectra are PKS1448-232 and FBQS J2149-0811. For these two quasars, the available UV spectra have an insufficient S/N to perform the fittings.
UV spectra information.
3.3. Data analysis
We carried out our spectral analysis in two complementary ways, following the methodology described in Paper I. After setting the spectra at rest-frame, we performed a multicomponent fit using the specfit (Kriss 1994) routine from the IRAF package. This routine allows a simultaneous minimum-χ2 fit of the continuum approximated by a power law, a scalable Fe II (or Fe III) pseudo-continuum, and the spectral line components, yielding the full width at half maximum (FWHM), the peak wavelength, and the intensity of all line components (see Fig. 2 of Paper I for an illustration of the decomposition analysis of the broad lines). We also include absorption lines in the event that some emission profiles (usually those of C IV) are affected by them. In addition, we performed a study of the full broad emission line profiles after subtracting the continuum power law, Fe II, and the narrow components.
3.3.1. Hβ spectral region
In the Hβ region fittings, apart from the power law and the scalable Fe II template, for the Hβ BLR broad emission line, we include: (1) a broad component (BC), which is symmetric and typically set at the rest-frame wavelength (Lorentzian-like shape for Pop. A and Gaussian for Pop. B); a very broad component (VBC), representing the innermost part of the BLR, characterized by a Gaussian shape and only present in Pop. B; and (3) a blueshifted component (BLUE), if needed, represented by a Gaussian profile (with the option of being skewed). In addition, we include a narrow component superimposed on the broad Hβ that may include up to two components: the proper narrow component (NC), usually with FWHM ≤1200 km s−1 and fitted as an unshifted Gaussian; and a semi-broad component (SBC), represented by a blueshifted (symmetric or skewed) Gaussian profile with FWHM and shift similar to the [O III] semi-broad component, if present (see below for [O III] components). A final fitting for each spectrum –based on the best-fit model with the minimum χ2– was obtained after performing a set of models both as Pop. A and Pop. B.
Figure 2 shows the multicomponent decomposition of the Hβ+[O III] spectral region for one of our sources. The fittings of the complete ISAAC2 sample are shown on Zenodo, along with their respective VLT-ISAAC optical spectra. Measurements on the Hβ full broad profiles of the ISAAC2 sample are listed in Table 5, where properties derived from the Hβ region are also included. We calculated Lbol from the continuum flux at 5100 Å and by applying the bolometric correction factor expected for the respective luminosity range as established by Netzer (2019). The black hole mass MBH for each quasar was estimated using the Hβ scaling law of Vestergaard & Peterson (2006, Eq. (5)). We computed the Eddington ratio (L/LEdd) using the bolometric luminosity and with LEdd = 1.5 ⋅ 1038MBH. The corresponding individual components obtained from the specfit decomposition of the broad Hβ profile are reported in Table 6.
 |
Fig. 2. Example of an ISAAC spectrum and of the decomposition analysis of the emission lines. (a) Rest-frame optical spectrum of CTSJ01.03. The white area shows the spectral region used in the fitting. The gray dashed line indicates the continuum level obtained with the specfit multicomponent fitting. Fe II contributions are represented by the green line. (b) Example of the Hβ+[O III] emission line decomposition (upper panel) and its respective residuals (bottom panel). Black, orange, and blue lines indicate the broad, the narrow, and the blueshifted components of the profile, respectively. The final fit is shown by the pink dashed line. |
Measurements on the Hβ full broad line profile and derived properties of the Hβ region.
Results from specfit analysis on the broad and narrow profiles of Hβ.
The [O III]λλ4959,5007 emission line profiles were modeled assuming that each line consists of a narrower, centered Gaussian component (NC) and one (or more) skewed blueshifted Gaussian semi-broad component (SBC) representing bipolar outflow emissions, where the recessing side of the outflow remains obscured (see e.g., Zamanov et al. 2002; Kim et al. 2023, and references therein). Similarly to Hβ, the results obtained for the full profile and the components of [O III]λ5007 are reported in Table 7.
Measurements on the [O III]λ5007 line profile.
3.3.2. UV spectral region
The UV spectral analysis is performed for three different regions: one centred in the Si IVλ1397+O IV]λ1402 lines, one in which the C IVλ1549 dominates the emission together with a less strong He IIλ1640 line, and another region considering the emission lines from the 1900 Å blend (consisting mainly of the Al IIIλ1860 doublet, Si III]λ1892, and C III]λ1909). In the three spectral regions, the continuum was modeled locally by a power law, and the Fe III multiplets (e.g., the strong lines observed on the red side of the 1900 Å blend) were modeled using the Vestergaard & Wilkes (2001) empirical template. For some Pop. A sources, an additional Fe IIIλ1914 emission line is needed to fully represent the red side of C III]λ1909 (see e.g., Martínez-Aldama et al. 2018). The broad UV lines (Si IVλ1397, C IVλ1549, He IIλ1640, and C III]λ1909) are fitted by the same three model components employed for Hβ, varying their relative contribution to each line flux, as detailed in Paper I.
Table 8 provides measurements for the C IVλ1549 full broad profile, and information on the C IVλ1549 and He IIλ1640 individual components is given in Table 9. The FWHM and peak shift of the C IVλ1549 and He IIλ1640 components were suitable for representing the profiles in all cases apart from CTSJ03.14, for which the He IIλ1640 BLUE is much narrower than the C IVλ1549 component.
Measurements on the C IVλ1549 full broad profile.
Table 10 shows the measurements on the full profile of Si IVλ1397 and O IV]λ1402. Similar to the approach taken in Paper I, we also set the Si IVλ1397 BC at rest-frame and select a FWHM similar to that determined for C IVλ1549 BC as an initial guess.
Results from our specfit analysis of C IVλ1549 and He IIλ1640.
Measurements on the Si IVλ1397+O IV]λ1402 broad lines.
The measurements resulting from the specfit analysis of the 1900 Å blend are presented in Table 11. As Si III]λ1892 has the same peak rest-frame velocity and FWHM as Al IIIλ1860, we do not report these values for the Si III] line in the table.
Results from our specfit analysis of the 1900 Å blend.
3.4. Radio data
The radio properties for the complete ISAAC sample are reported in Table 12. The radio fluxes used to estimate these parameters were obtained from the 1.4-GHz NRAO VLA Sky Survey (NVSS, Condon et al. 1998) and from the VLA Faint Images of the Radio Sky at Twenty-Centimeters survey (FIRST, Gregg et al. 1996; Becker et al. 1995) catalogs. In the case of CTQ 0408, which is not covered by these two surveys, we estimated the upper limit for the flux from the SUMSS catalog (Mauch et al. 2003). The RK parameter is determined as the ratio between the rest-frame specific fluxes at 1.4 GHz and at the g-band effective wavelength (following Ganci et al. 2019). We then considered three different ranges of radio-loudness: radio-quiet (RQ; RK < 10), radio-intermediate (RI; 10 ≤ RK ≤ 70), and radio-loud (RL; RK ≥ 70).
Radio properties of the full ISAAC sample.
If the object is not detected (for the 50% of the sample: 16 sources, 15 from ISAAC1, and one from ISAAC2), an upper limit on the radio flux is set equal to a detection threshold (of ∼2 times the rms in both FIRST and NVSS catalogs) at the position of the source. Our preference is to rely on the FIRST detection limit as its maps have a higher sensitivity than NVSS and allow for a better restrictive upper limit. However, in cases where the position of the object does not fall within the current coverage of the FIRST catalog, we then use the NVSS detection limit. When considering the complete ISAAC sample, we have 10 RL, 2 RI, and 20 RQ sources.
For objects from both the HEMS and the FOS sample, we re-estimated the values of RK using the same methodology as that employed for the ISAAC data. Of the 28 sources of the HEMS sample, 4 are RL and 24 RQ. As mentioned in Section 2.3, in the low-luminosity FOS sample there are 34 RL and 50 RQ sources.
By default, we define that the sources initially classified as RI are considered together with the RQ objects, unless we have evidence that the source is jetted. The enhancement of the radio emission in RIs is possibly related to star formation (Condon et al. 2013; Bonzini et al. 2015; Caccianiga et al. 2015; Ganci et al. 2019), a powerful broad line region and extended ionized outflows (Panessa et al. 2019, and references therein), or intrinsic reddening in the optical fluxes.
4. Results
4.1. ISAAC1 and ISAAC2 basic results: Synopsis
The optical and UV main spectral properties of ISAAC1 and ISAAC2 are fully consistent.
Hβ. The dichotomy between Pop. A and Pop. B is preserved in the complete ISAAC sample, with Pop. A quasars usually presenting lower values of HβW and FWHM. However, it is noteworthy that the lowest FWHM(Hβ) values in ISAAC2 are observed in two Pop. B quasars (CTSJ03.14 and PKS1448-232), both of which are blazar candidates, and therefore the FWHM may be strongly influenced by the source orientation. Among the ISAAC2 Hβ Pop. A profiles, all are symmetric except for BZQJ0544-2241, which requires an additional (usually weak) BLUE component to fully represent the Hβ line. In contrast, the Hβ profiles in Pop. B sources are all redward asymmetric, with the exception of [HB89]1559+088, which is nearly symmetric and also requires a BLUE component. This additional component is added when the blueshift observed in the Hβ profile does not correspond to the blueshifted SBC observed in [O III]λ5007. The full ISAAC sample has eight quasars (five Pop. A and three Pop. B) with a BLUE component, whose contribution to the profile has an average value of ≈8%. The mean asymmetry index for the whole ISAAC sample Pop. B is 0.26 (same for only ISAAC2) and they have the full broad profile with an average velocity centroid c(1/4) of 1740 km s−1. This is attributed to the fact that, in Pop. B, the most prominent broad component is the VBC, which accounts for 54% of the Hβ profile in the ISAAC2 sample (57% for the whole ISAAC), with median FWHM and shift values of ≈10420 and 3149 km s−1, respectively. Consistent values are found for the full ISAAC sample, with a median FWHM and a shift of the VBC of 11760 and 3000 km s−1, respectively, in good agreement with the values obtained in HEMS sources (e.g., Vietri et al. 2018, 2020; Wolf et al. 2020, see also Marziani et al. 2009; Sulentic et al. 2017 for extremely broad Hβ profiles).
[O III]λλ4959,5007. In the full ISAAC sample, both populations (A and B) exhibit significant blueshifts, with the most pronounced ones observed in Pop. A sources. In most of the full ISAAC sample, both the [O III] SBC and NC are often not in the rest-frame. Additionally, for 18 out of the 32 sources from the whole ISAAC sample (16 from ISAAC1 and two from ISAAC2), the SBC is the strongest component, accounting for ∼64% of the flux in the case of Pop. A and ∼52% of the flux for Pop. B. Consequently, the two populations A and B also differ in terms of FWHM, with the Pop. A on average showing slightly broader profiles due to the presence of a stronger SBC. Moreover, in contrast to the low-z scenario, where the majority of the [O III]λ5007 profiles exhibit blueshift velocity centroids at half intensity, c(1/2), of lower than 250 km s−1 (Zamanov et al. 2002; Marziani et al. 2016a), in our complete high-z ISAAC sample, 62% of the sources have blueshifts in [O III] of greater than 250 km s−1 and are considered outliers. However, in ISAAC2, we do not observe the few very large [O III] profiles (FWHM ∼4000 km s−1) measured in ISAAC1. This may be a consequence of the fact that ISAAC1 is primarily composed of RQ sources (which typically exhibit broader [O III]λλ4959,5007 profiles than RL ones; see Sect. 4.5.2), while a significant fraction of ISAAC2 sources are classified as RL. Significant [O III] outflows appear to be a common feature at high redshift and have also been observed in other samples (see e.g., Kakkad et al. 2020). As discussed in Paper I, the [O III] profile almost always appears peculiar when compared to those of optically selected samples at low redshift (Zamanov et al. 2002; Marziani et al. 2003b; Bian et al. 2005; Zhang et al. 2011; Cracco et al. 2016), with higher shift amplitude and broader widths.
C IVλ1549. Consistent results with ISAAC1 are also observed for ISAAC2 C IVλ1549 profiles. In general, the Pop. B sources from ISAAC2 tend to exhibit slightly larger values of W than Pop. A. This is also observed in the full ISAAC sample (median W ∼ 27 Å for Pop. B vs. ∼21 Å for Pop. A). Conversely, Pop. A sources tend to show greater FWHM, asymmetry, and centroid velocity, which is in agreement with the HEMS sample (Sulentic et al. 2017). The BLUE is the strongest component in the full ISAAC sample, and contributes to ∼72% and ∼51% of the full C IVλ1549 flux for Pop. A and Pop. B, respectively. Consistently, the largest blueshifts are found for the BLUE components of Pop. A sources, which achieve a median value of c(1/2) of the full C IVλ1549 profile of ∼–2590 ± 1890 km s−1 for the entire ISAAC sample. In the case of Pop. B, this value is ∼–1530 ± 760 km s−1. Centroid shifts are comparable to those derived in recent works that followed a similar analysis strategy (Coatman et al. 2016; Vietri et al. 2018; Temple et al. 2023, and especially Sulentic et al. (2017), who analyze the HEMS sample). Both [O III]λλ4959,5007 and C IVλ1549 suggest the presence of extremely powerful winds in the NLR and BLR (Marziani et al. 2016b,a; Fiore et al. 2017; Bischetti et al. 2017). At variance with low-z, low-luminosity sources, the blueshifted emission associated with the winds is prominent in both Pop. A and B, as further discussed in Sects. 5.1 and 5.2.
1900 Å blend. In the ISAAC2 sample, we have 1900 Å blend data for six of the ten objects (two Pop. A and four Pop. B). The 1900 Å blend properties observed in the ISAAC2 sample also appear consistent with the full ISAAC sample, as well as with the expectations from recent works involving intermediate-redshift sources (Temple et al. 2020; Marziani et al. 2022a; Buendia-Rios et al. 2023). Considering the whole ISAAC sample (11 Pop. A and 9 Pop. B quasars), we find that the BLUE component in Al IIIλ1860 is detected in only 5 Pop. A sources, with an average blueshift of ∼ − 1720 km s−1 and accounts for ∼40% of the full profile. For Pop. B, all nine sources show Al IIIλ1860 profiles well-represented by a single rest-frame BC with averaged FWHM ∼4240 km s−1. For Si III]λ1892, only three Pop. A exhibit a BLUE component, with an average shift of ∼ − 1880 km s−1. Regarding the C III]λ1909 profiles, Pop. A sources are suitably represented by a rest-frame BC with FWHM ∼3370 km s−1. Of the 11 Pop. A sources, 9 required an additional Fe III component at ∼1914Å. The Pop. B C III]λ1909 profiles are fitted by the combination BC+VBC, where the VBC is weaker than that of Hβ, as it represents only 37% of the full profile, with an FWHM of ∼7240 km s−1.
4.2. The optical plane of the 4DE1 parameter space
The classification as population A or B on the quasar MS is based on two parameters that can only be measured from NIR spectra: the FWHM of the Hβ full broad profile and the strength of the Fe II blend at 4570 Å, defined as the ratio between the intensities of the blue blend of Fe II at 4750Å and Hβ, RFe II. We set the Pop. A/Pop. B limit according to the luminosity-dependent FWHM value, as explained in Paper I. We measured the RFe II parameter to assign a number from 1 to 4 to the spectral type (ST) covering the range 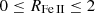 with a step of
with a step of 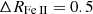 (Sulentic et al. 2002).
(Sulentic et al. 2002).
The location of the whole ISAAC sample on the MS optical plane is shown in Fig. 3, where the 28 sources belonging to the HEMS sample are also represented. As discussed in Paper I, the sources of high luminosity, such as the ten new quasars presented here, show a displacement in the direction of increasing FWHM(Hβ) by 1000–1500 km s−1 with respect to the low-luminosity, low-z samples (see also Sulentic et al. 2017). Of the ten new sources, six are classified as Pop. B and four as Pop. A. CTSJ03.14 and PKS1448-232 (see the models in Figs. 7 and 8 on Zenodo, respectively), two RLs classified as B1, are located below the Pop A/B boundary for their luminosity. Both sources are blazar candidates (see Massaro et al. (2014) for CTSJ03.14 and Massaro et al. (2015) for PKS1448-232), implying that the FWHM of Hβ may be significantly lowered by a pole-on orientation of the line-emitting region. In the complete sample considered in this work (ISAAC1+ISAAC2+HEMS), there are 30 sources classified as Pop. A (including 5 RL) and 30 classified as Pop. B (including 8 RL).
 |
Fig. 3. Location on the MS of the ten new sources for this work together with those from Paper I (circles) and the HEMS sample (squares). Pop. A quasars are represented by blue symbols and Pop. B by red symbols. The RL sources are surrounded by an open circle or square in the plot. The gray region indicates the distribution of the MS of quasars at low z. The purple-shaded area shows the luminosity-dependent boundary between Pops. A and B for high-luminosity sources, as described in detail in Paper I. |
4.3. The role of physical parameters
In Paper I, we show that while the bolometric luminosity, Lbol, and the black hole mass (MBH) exhibit trends with the C IV blueshifts, the primary correlation is observed with the Eddington ratio, with the higher C IV blueshift in the higher accretion rate (see e.g., Sect. 6.3 of Paper I, and references therein). These results are reconfirmed in the present work. By including the new data from ISAAC2 in the sample composed of both high- and low-z data, we find a relation between C IVc(1/4) blueshift (< –250 km s−1) and Lbol with a slope of 0.21 ± 0.07 (with a Pearson correlation coefficient c.c. of 0.61, ρ ∼ 10−9). The slope 0.14 ± 0.06, and Pearson c.c. ∼0.48 (ρ ∼ 10−6) suggest an even weaker relation between C IVc(1/4) and the black hole mass MBH. Regarding the Eddington ratio, we find the following relation (with a Pearson c.c. ∼ 0.66 and a ρ-value for the null hypothesis ∼10−11):
Similar results, albeit less significant, are observed for [O III]. When analyzing the 45 sources (34 high-z and 11 low-z) that exhibit significant [O III] outflows, we find a slope of 0.12 ± 0.07 between [O III] c(1/4) and Lbol (Pearson c.c. ∼0.31, ρ ∼ 10−2). Concerning L/LEdd, we obtain (Pearson c.c. ∼0.48, ρ ∼ 10−4):
In close agreement with these relations, Fig. 4 shows the dependence of c(1/4) on L/LEdd for the [O III]λ5007 and C IVλ1549 emission lines, where we include all the measurements of c(1/4) velocity centroids of both lines (blueshifted or not) and for both low- and high-z samples. For the two emission lines, strong outflows (i.e., ≳500 km −1 for [O III]λ5007 and ≳2000 km s−1 for C IVλ1549) are found at Eddington ratios of log L/LEdd ≳ −0.8 (L/LEdd ∼ 0.2), consistent with previous results (see e.g., Marziani et al. 2003b; Bian et al. 2005; Komossa et al. 2008; Marziani et al. 2016b; Cracco et al. 2016; Coatman et al. 2016; Wang et al. 2018; Ayubinia et al. 2023).
 |
Fig. 4. Velocity centroid c(1/4) versus L/LEdd for [O III]λ5007 (left) and C IVλ1549 (right). Dark green and blue symbols correspond, respectively, to RQ and RL sources at low-z, while orange (RQ) and red (RL) symbols represent high-z quasars. Within each color, filled squares represent Pop. B sources and the bullets Pop. A quasars. |
The effect of high Eddington ratio is strengthened at high luminosity. The high z to low z comparison is consistent with the weaker luminosity effect (outflow velocity 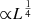 ) on both the RL and RQ samples, which is expected for radiation-driven winds and becomes appreciable when considering samples spread over a wide range of luminosities (Laor & Brandt 2002, cf. Sulentic et al. 2017).
) on both the RL and RQ samples, which is expected for radiation-driven winds and becomes appreciable when considering samples spread over a wide range of luminosities (Laor & Brandt 2002, cf. Sulentic et al. 2017).
The radio-loudness appears to play a role in reducing the outflow velocities in both [O III]λ5007 and C IVλ1549. The sources that present the most significant blueshifts in both [O III] and C IV in Fig. 4 are all RQ. Conversely, the RL sources (blue and red symbols) exhibit lower outflow velocities. This result is in good agreement with previous findings (e.g., Marziani et al. 2003b; Laor 2018) and is discussed in more detail in Sects. 4.4 and 4.5.
4.4. Inter-comparison between RL and RQ sources at low and high z: [O III]λ5007 versus C IVλ1549
Figure 5 presents a comparison between [O III] and C IV in terms of the relative intensity of the outflowing component (SBC for [O III]λ5007 and BLUE for C IVλ1549) with respect to the full profiles, IBLUE/Itot. In this case, we exclusively consider sources that are identified as blue outliers in [O III] and which also present blueshifts in C IV. Therefore, the sample shown in Fig. 5 has 28 high-z sources (14 from ISAAC and 14 from HEMS) and 9 low-z sources from the FOS sample. In addition, in the FOS sample, there are seven objects in which only a blueshifted SBC [O III] component (with no clear NC) is detected, which nevertheless present shifts in the c(1/2) of lower than −250. Clearly identifying any outflow in these cases would require higher resolution and an improved S/N compared to the data available in the present work.
 |
Fig. 5. Comparison between the relative intensities of the blueshifted component for both [O III]λ5007 and C IVλ1549. Low-z and high-z sources are represented in the left and right panels, respectively. |
At low redshift, the behavior of the BLUE component appears to be different in [O III] and C IV in terms of relative intensity: while the [O III] outflowing component can achieve a ISBC/Itot of up to nearly ∼ 100% of the total intensity of the full profile, the C IV outflowing component never surpasses ∼40% of the entire profile, with the lower values found for the RL sources
The right panel of Fig. 5 shows the same analysis but for the high-redshift range. At variance with the low-z sample, the [O III]λ5007 and C IVλ1549 emission lines exhibit very similar behavior with respect to their outflowing component, and their ratio IBLUE/Itot can vary from ∼20% to 100% of the full profile, with the largest contributions found in RQ sources. The RL–RQ difference at high redshift is consistent with that found at low redshift, with the RL sources presenting clearly fainter [O III]λ5007 SBC and C IVλ1549 BLUE.
We analyzed the RL and RQ blueshift distributions in an attempt to characterize other parameters affected by radio-loudness. Figure 6 shows the cumulative distribution functions of centroid velocities at one-quarter flux intensity (c(1/4)) of both [O III]λ5007 and C IVλ1549 emission lines for the samples by separating them according to the radio classification and the redshift range. All sources with [O III] or C IV spectral information have been taken into account regardless of the shift. Panel (a) shows a comparison between RL and RQ at low redshift for the [O III]λ5007 c(1/4). In this case, the Kolmogorov-Smirnov (KS) test reveals that the RL and RQ subsamples are statistically indistinguishable, although the RQ sources, in general, present larger values of c(1/4) towards the blue, which indicates stronger outflows than for RL sources. A similar result is found when comparing RL and RQ c(1/4) at high z (panel (b) of Fig. 6).
 |
Fig. 6. Centroid velocities at one-quarter intensity (c(1/4)) cumulative distributions of the samples separated by radio-loudness and redshift range for [O III]λ5007 (top panels) and C IVλ1549 (bottom panels). Kolmogórov-Smirnov tests were performed comparing different subsamples identified at the top of the panels. KS statistics for each comparison are shown in the top left corner of each plot together with the respective ρ-value. Vertical lines indicate the mean value for each subsample. |
Panel (c) of Fig. 6 compares the RL sources at high- and low-z ranges. The KS test indicates that the distributions are significantly different (∼0.88, ρ ∼ 10−8), with the RL sources at high redshift presenting higher outflow velocities (mean value ∼ −420 km s−1) than the ones at lower redshifts (∼ −40 km s−1). The same is found when comparing RQ sources at high and low redshift (panel (d)). The difference in this case is still significant due to a more prominent outflow at high z, with c(1/4) mean values ≈ − 740 and ≈ − 200 km s−1 for high and low z, respectively.
The bottom panels of Fig. 6 show the results for the C IVλ1549 emission line. In general, the c(1/4) of this line follows the same behavior as [O III], albeit with stronger outflows. In both RQs and RLs, there is a statistically very significant difference between the distributions of C IV c(1/4) at high and low redshift. The more extreme difference is found between RL sources at high and low z, where the distributions are completely different (KS coefficient of 0.97, and a probability of coming from the same distribution ρ ∼ 10−7). The significance is extremely high, even if the RL subsample in the case of C IVλ1549 at high z contains only seven sources.
The cumulative distributions of both [O III] and C IV centroid shifts demonstrate that the main difference between samples is when they widely differ in luminosity, not radio-loudness. In the two redshift domains considered (corresponding on average to a difference in luminosity of a factor ≈60), Figs. 4 and 6 show that there is second-order effect related to radio-loudness in both C IVλ1549 and [O III]λλ4959,5007. The effect is more significant at low-z (with a ρ ∼ 10−5), although a similar difference in shift amplitude is detected also at high redshift. In the latter case, the small number of sources means that our results regarding this effect are not statistically significant. In summary, the effect of radio-loudness is consistent in the low-z and high-z samples, with lower blueshifted velocities and outflows in the RLs, albeit weaker than the effects of luminosity and accretion rate (see section 4.3).
4.5. Trends with radio-loudness
4.5.1. Fe II
The relation between the RFe II with the radio-loudness parameter RK is shown in Fig. 7. In both low- and high-z ranges, the RQ sources are the ones that can present RFe II values from ∼0 up to more than 1, with the most extreme cases found for the low-redshift RQ Pop. A quasars. With the exception of these extreme sources, the RQ sources at high and low z present a very similar distribution, with a mean RFe II value for low-z RQ sources of ∼0.52, while for high-z RQ sources this value is ∼0.55.
 |
Fig. 7. Relation between radio-loudness RK and RFe II for low-z (left) and high-z (right) ranges. RK upper limits are indicated by arrows alongside the symbol. The color scheme is the same as that in Fig. 4. |
The RL quasars tend to present lower values of RFe II, which rarely exceeds the threshold of 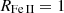 . The fact that the RL sources are weaker Fe II emitters than the RQ ones has already been observed in previous studies (e.g., Yuan & Wills 2003; Netzer et al. 2004; Sulentic et al. 2004). In general, the sources that present strong Fe II emission are found to also present very high Eddington ratios, which are more frequently typically found in RQ sources of Pop. A. Hence, this difference in RFe II between RL and RQ sources may also be linked to the accretion rate, which somehow can contribute to enhancing the Fe II emission in strong accretors.
. The fact that the RL sources are weaker Fe II emitters than the RQ ones has already been observed in previous studies (e.g., Yuan & Wills 2003; Netzer et al. 2004; Sulentic et al. 2004). In general, the sources that present strong Fe II emission are found to also present very high Eddington ratios, which are more frequently typically found in RQ sources of Pop. A. Hence, this difference in RFe II between RL and RQ sources may also be linked to the accretion rate, which somehow can contribute to enhancing the Fe II emission in strong accretors.
The mean RFe II values of low- and high-redshift RL sources are ∼0.25 and ∼0.40, respectively. This result is intriguing, although it could simply be related to differences in the Eddington ratios of the samples at high and low z, with missing high-z sources at the lowest Eddington ratios because they are too faint to be detected in major surveys such as the SDSS (Sulentic et al. 2014).
4.5.2. [O III]λ5007
Figure 8 shows the relation between RK and c(1/4) of [O III]λ5007 for low- and high-z ranges separately. In both ranges, RQ sources exhibit larger outflow velocities compared to RL sources, with the RQ sources achieving values of ∼ − 2000 at low z and ∼ − 2700 km s−1 at high z. This difference in outflow velocity between RQ and RL quasars has previously been reported (e.g., Marziani et al. 2003b, 2016a; Ganci et al. 2019, and references therein) and may be a consequence of the presence of relativistic jets in RL sources, which can potentially reduce the impact of the outflows on the optical emission. In contrast, RQ sources lack such strong radio jets, allowing the outflows to have a more significant influence on the optical emission (e.g., Padovani 2016).
 |
Fig. 8. Relation between radio-loudness and velocity centroid at one-quarter intensity of the [O III]λ5007 emission line for low-z (left) and high-z (right) ranges. Gray shaded areas in both plots indicate the c(1/4) range between 250 and −250 km s−1. RK upper limits are indicated by arrows alongside the symbol. The color scheme is the same as that in Fig. 4. |
At low redshifts, the majority of the sources (including both RQ and RL) do not exhibit [O III]λ5007 c(1/4) values that exceed 250 km s−1, and therefore do not present significant [O III]λ5007 outflows. Only eight objects (seven RQ and one RL) within this redshift range in our FOS sample present relevant [O III] c(1/4) blueshifts of ∼ − 500 km s−1.
The right panel of Fig. 8 shows the same analysis, but this time focuses on high-z sources. In this redshift range, ∼75% of the RQ sources present blueshifts of greater than 250 km s−1, and in some cases can achieve very strong velocities, as is the case of SDSS J212329.46-005052.9 (∼2700 km s−1). All the high-redshift RL sources from our sample present significant blueshifts, with a [O III]λ5007 c(1/4) range of between ∼230 and 1000 km s−1.
4.5.3. C IVλ1549
It has long since been known that [O III]λ5007 and C IVλ1549 show similarities in their phenomenology (e.g., Zamanov et al. 2002; Coatman et al. 2019; Deconto-Machado et al. 2023). In Fig. 9 we repeat the [O III]λλ4959,5007 analysis described in Sect. 4.5.2 for C IVλ1549. As for [O III]λ5007, the majority of RQ sources at low z present negative values of C IVλ1549 c(1/4), while the vast majority of RL sources show positive values or values very close to 0-500 km s−1 to the blue. Regarding the high-z range, it is already known that the largest shifts are also found in RQ sources (see e.g., Richards et al. 2011, 2021, and references therein). This is no different in our high-z sample, where almost all sources (including both RQ and RL) present very significant outflow velocities. The average C IVc(1/4) blueshift for RL sources is ∼1900 km s−1. The relation between the [O III]λ5007 and C IVλ1549 emission lines does not seem to be affected by the radio emission; however, the comparison between RQ and RL at high z for the C IVλ1549 emission line is limited by the fact that we have a very small sample of RL sources in this redshift range (only seven objects, two Pop. A and five Pop. B) and more data are definitely required.
 |
Fig. 9. Relation between radio-loudness and the velocity centroid at one-quarter intensity of the C IVλ1549 emission line for low-z (left) and high-z (right) ranges. RK upper limits are indicated by arrows alongside the symbol. The color scheme is the same as in Fig. 4. |
5. Discussion
5.1. Dominance of outflows
C IVλ1549 somehow seems to be a magnified version of [O III]λ5007, presenting very similar trends but with higher outflow velocities. The left plot of Fig. 10 shows the relation between the centroid velocity at half intensity (c(1/2)) for the full profiles of [O III]λ5007 and C IVλ1549 at high redshift, including the sources from HEMS, Paper I, and from the present paper. The result reported in Paper I is strengthened: ISAAC2 objects that present strong shifts in the [O III]λλ4959,5007 emission line profiles do present them also in C IVλ1549. The bisector linear relation after including all ISAAC data is
 |
Fig. 10. Centroid velocity at half flux intensity (c(1/2)) of C IVλ1549 vs. c(1/2) of [O III]λ5007 for the full (left) and outflow (right) profiles of the high-z sample. The magenta lines indicate the linear regression between c(1/2) of C IV and [O III] for both cases obtained through the bisector method. Dotted black lines represent the 1:1 relation. The color scheme is the same as in Fig. 4. |
with a correlation coefficient ≈0.51. This trend is consistent with the results reported by Coatman et al. (2019) and Vietri et al. (2020) at high redshift.
In both [O III] and C IV, the largest blueshifts are found in Pop. A sources (represented by orange bullets in the figures), which usually present the largest accretion rates. Figure 10 also shows that the largest outflow velocities in [O III] and in C IV are found in RQ sources, indicating that the accretion may be the main driver of these outflows (Nesvadba et al. 2007; Kukreti et al. 2023). A similar relation is found when considering the c(1/2) of only the outflowing (BLUE) components of both [O III]λ5007 and C IVλ1549 emission lines, as shown in the right plot of Fig. 10. In this case, the orthogonal linear relation (with a c.c. of 0.40) is given by
At high z, the outflows appear to be more prominent than at low z (see also Fig. 4), consolidating the idea that the accretion rate is the main driver of the outflows. The accretion rate in most of the sources at high z is higher (−0.6 ≲ log L/LEdd ≲ 0.4) than in the case of sources at low z (−2 ≲ log L/LEdd ≲ 0; see also e.g., Cavaliere & Vittorini 2000; Hopkins et al. 2006), even if the difference could be in part due to a selection effect, as mentioned in Section 4.5.
5.2. Dynamical parameters of the outflows
We estimated the mass-outflow rate (Ṁ), the kinetic power (Ėkin), and the thrust (Ṁvo) adopting a simple biconical outflow, and using an analogous methodology to that of Marziani et al. (2016a); Marziani et al. (2017); our methodology is summarized in Appendix B. In this framework, the relations are formally identical for [O III] and C IVλ1549, and namely:
where L is the outflow-emitted line luminosity, nH the electron density and Z the metallicity. The mass outflow rate (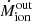 ) and the thrust (
) and the thrust (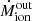 vout) at a radius r and with an outflow velocity vout, might be written as:
vout) at a radius r and with an outflow velocity vout, might be written as:
The kinetic power, Ėkin, is then given by 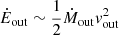 , which leads to
, which leads to
The parameters entering the previous equations are estimated using different relations for [O III] and C IV, and are briefly discussed in following sections and in Appendix B. The adopted parameters and relevant scaling relations are summarized in Table 13.
Summary of assumed scaling relations and parameter values for wind dynamics.
When estimating wind parameters in quasars, such as mass-outflow rate, thrust, and kinetic power, several sources of error can affect the accuracy of these measurements. These errors arise from various observational and methodological issues, including the complexity of the line profiles, spatial resolution limitations, and the assumptions made in the models used for interpretation, where the last two are expected to be the dominating sources of uncertainty in the estimation of the wind parameters. For C IVλ1549 in particular, the uncertainty in the conversion between line luminosity and ionized gas could be ∼3 at a 3σ confidence level. We have considered a range of densities of 0.5 dex around log nH radius of the emitting region; Z estimates in quasars suggest very high metallicity, and a range around 5 Z⊙, where between 2 and 20 times solar seems possible both at high and low redshifts (Hamann & Ferland 1993; Garnica et al. 2022; Floris et al. 2024). The geometry of the outflow would contribute a factor 3 via the comparison between the spherically symmetric case and a flat layer. The 1σ uncertainty in the emitting radius is ±30% if ascribed only to the uncertainty of the scaling law parameter, while uncertainty on the outflow velocity is typically ∼30%. Propagating these uncertainties quadratically would result in a typical factor of ≈5 at 1σ confidence level.
Similar considerations were applied to [O III]: a factor of ≈3 at 1σ in density, a factor of ≈2 in Z and in the luminosity-to-ionized mass gas conversion, and a factor of ≈2 in the zero point of the radius–luminosity (L([O III])) relation. These factors contribute to a comparable uncertainty estimate, a factor of ≈5 at 1σ confidence level, and should be taken into account in the interpretation of the analysis that follows.
5.2.1. [O III]λ5007
We consider a situation where the outflow radius r is allowed to vary depending on the [O III]λ5007 luminosity of each source. In the case of sources spanning four orders of magnitude in luminosity, it is nonphysical to assume that the size of the emitting region is constant, as there is evidence of compact emission at low-z (Zamanov et al. 2002), and of kiloparsec(kpc)-sized outflows at high luminosity (e.g., Harrison et al. 2014). Conventional scaling laws of narrow-line regions with luminosity are not expected to exclusively trace the outflowing [O III] component (Bennert et al. 2002, 2006).
Figure 11 shows the outflow radius as a function of the [O III]λ5007 luminosity for the integral field spectroscopy (IFU) data analyzed by Villar-Martín et al. (2016), Fischer et al. (2018), Tadhunter et al. (2018), Kakkad et al. (2020), and Singha et al. (2022), where we also show a least squares linear relation between these two quantities, imposing a slope of 0.5:
 |
Fig. 11. Relation between the outflow radio in kiloparsecs and the luminosity of the [O III]λ5007 emission line for the five plotted samples. The red dashed line represents the adopted least squares linear regression. Magenta vertical lines symbolise the minimum and maximum estimated radii in the Villar-Martin sample. Arrows correspond to upper limits. |
The slope 0.5, which gives a reasonable representation of the radius–L[OIII] relation in Fig. 11, is imposed to ensure consistent ionization conditions as a function of luminosity. This scaling relation was then applied to our sources, considering the luminosity of the entire [O III] emission line profile. Our low-z sample exhibits [O III] luminosities (full profile) ranging from approximately 1040.6 up to 1043.1 erg s−1, while the high-z sources have luminosities of between 1043.4 and 1044.9 erg s−1. Consequently, we find [O III] outflow radii r ranging from ∼ 0.04 to 0.71 kpc at low-z, in agreement with recent values obtained for IFU resolved [O III] in low-z AGN (see e.g. Deconto-Machado et al. 2022), and from 0.97 to 5.81 kpc at high-z.
The parameters used to estimate the outflow properties associated with the [O III]λ5007 emission line are listed in Table A.1.
The estimated values of the mass rate Ṁout derived from Equation (B.2) in the Appendix span from ∼0.08 to 3.43 M⊙ yr−1 for low luminosities (≲1046 erg s−1) and from ∼6.2 to 114.0 M⊙ yr−1 for higher luminosities.
The relations between the [O III] outflow kinetic power Ėkin and thrust 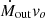 with the bolometric luminosity Lbol are shown in Fig. 12. We assume a density of nH = 103 cm−3 for both high- and low-z contexts. For metallicity, we adopt Z = 5 Z⊙ for low-z, considering the compactness of the outflow, and Z = 2 Z⊙ for high-z, aligning with the typical values used in the computations for the NLR metallicity at high z (see e.g., Xu et al. 2018). Additionally, as detailed in Appendix B.1, we assume the outflow velocity to be c(1/2) of the BLUE component. If instead we were to follow the assumption of c(1/2)+2σ as done by Fiore et al. (2017), this would result in an ∼2.5 larger outflow velocity in our estimates of the outflow parameters. Typical errors are represented in the error bars of Fig. 12. The results of the linear correlation analysis between these outflow parameters for [O III]λ5007 and C IVλ1549 are reported in Table 14. We find correlation coefficients of 0.66 and 0.74 (with ρ-value of ∼10−7 and ∼10−9, respectively) between the kinetic power and the thrust with the bolometric luminosity. Similar correlations have already been extensively discussed by other authors (e.g., Carniani et al. 2015; Feruglio et al. 2015; Fiore et al. 2017, and references therein).
with the bolometric luminosity Lbol are shown in Fig. 12. We assume a density of nH = 103 cm−3 for both high- and low-z contexts. For metallicity, we adopt Z = 5 Z⊙ for low-z, considering the compactness of the outflow, and Z = 2 Z⊙ for high-z, aligning with the typical values used in the computations for the NLR metallicity at high z (see e.g., Xu et al. 2018). Additionally, as detailed in Appendix B.1, we assume the outflow velocity to be c(1/2) of the BLUE component. If instead we were to follow the assumption of c(1/2)+2σ as done by Fiore et al. (2017), this would result in an ∼2.5 larger outflow velocity in our estimates of the outflow parameters. Typical errors are represented in the error bars of Fig. 12. The results of the linear correlation analysis between these outflow parameters for [O III]λ5007 and C IVλ1549 are reported in Table 14. We find correlation coefficients of 0.66 and 0.74 (with ρ-value of ∼10−7 and ∼10−9, respectively) between the kinetic power and the thrust with the bolometric luminosity. Similar correlations have already been extensively discussed by other authors (e.g., Carniani et al. 2015; Feruglio et al. 2015; Fiore et al. 2017, and references therein).
 |
Fig. 12. Kinetic power Ėkin (left) and thrust (right) vs. bolometric luminosity for the [O III]λ5007 outflow. The two outflow parameters were estimated by varying the outflow radius according to Eq. (9) and assuming vout = c(1/2). Magenta dashed lines indicate the least-squares linear regression. Black dotted, continuous, and dashed lines on the left plot show |
Least-squares linear relations (y = a + b * x) between different outflow properties and the bolometric luminosity.
In our analysis of [O III] Ėkin with luminosity-dependent r, none of the sources display a ratio reaching at least 5% of the bolometric luminosity (filled line in Fig. 12), a threshold needed for a significant impact on the host galaxy dynamics, and to account for the black hole mass–velocity dispersion correlation and host-spheroid co-evolution (e.g., Di Matteo et al. 2005). Star formation quenching might be easier, if an AGN outflow induces a wind in the diffuse interstellar medium that in turn induces a flattening and shredding of molecular clouds (Hopkins & Elvis 2010). A threshold for this effect occurs when the kinetic efficiency is much lower than the 5% limit, 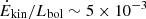 (short dashed line in Fig. 12). Based on the criteria of both Hopkins & Elvis (2010) and Di Matteo et al. (2005), the [O III]λ5007 outflow parameters do not provide an efficient feedback mechanism, at either low or high z (although see the discussion of Section 5.2.3). Similar results have recently been found at low redshift (Kim et al. 2023, and references therein). These latter authors derived
(short dashed line in Fig. 12). Based on the criteria of both Hopkins & Elvis (2010) and Di Matteo et al. (2005), the [O III]λ5007 outflow parameters do not provide an efficient feedback mechanism, at either low or high z (although see the discussion of Section 5.2.3). Similar results have recently been found at low redshift (Kim et al. 2023, and references therein). These latter authors derived 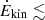 0.1% Lbol for a sample of low-z type-1 AGN. It is likely that part of the [O III] emitting gas has already dissipated part of its energy and momentum, as the emitting regions can extend over several kpc. Along the same line of reasoning, the AGN outflows traced by the [O III] emission are likely to impact the central kiloparsecs scales, but their effects on galactic scales are more debatable.
0.1% Lbol for a sample of low-z type-1 AGN. It is likely that part of the [O III] emitting gas has already dissipated part of its energy and momentum, as the emitting regions can extend over several kpc. Along the same line of reasoning, the AGN outflows traced by the [O III] emission are likely to impact the central kiloparsecs scales, but their effects on galactic scales are more debatable.
The thrust ranges from ∼2.2 × 1032 to 3.1 × 1034 g cm s−2 in the case of the low-luminosity sample; at high luminosity, the thrust increases significantly to the larger outflow masses and higher velocities and the values are found between ∼3.3 × 1034 and 3.5 × 1036 g cm s−2. In all cases, however, the [O III] thrust is ≪L/c, in agreement with Vietri et al. (2020).
5.2.2. C IVλ1549
The ionized gas mass producing the C IVλ1549 line was estimated following the results obtained from CLOUDY photoionization computations by using two different SEDs representing the two main samples of sources considered in this work: a SED from Mathews & Ferland (1987) for the low-z FOS sample, and the more appropriate SED from Krawczyk et al. (2013) for high-luminosity high-z ISAAC and HEMS samples, and taking also into account the constraints imposed by the measurements of the observed quantities in the spectra, such as the W(C IV) or the C IVλ1549/Hβ ratio. All the calculations and assumptions for the C IV outflow parameters are reported in Appendix B.2. For C IVλ1549, we consider that (at variance with [O III]) the C IV outflow is accelerated to a final outflow velocity of c(1/2)+2σ of the blueshifted component.
As in [O III], we estimated the radius r independently for each source, and based on the luminosity at 1350Å. In the case of C IV, we use the consolidated scaling relation of Kaspi et al. (2021):
where rBLR is the radius of the BLR.
For our sources, the specific luminosities at 1350Å range from approximately 1044.5 up to 1046.5 erg s−1 at low z and from 1045.9 to 1047.6 erg s−1 at high z. With these luminosity values, we find C IVλ1549 outflow radii varying from 0.06 to 0.37 pc at high z and 0.01 to 0.11 pc at low z.
Table A.1 lists the properties of the C IVλ1549 used in estimating the outflow parameters. The relations between the C IV outflow parameters and the bolometric luminosity are shown in Fig. 13 and the respective linear correlations are reported in Table 14. The outflow parameters considered in this work (kinetic power Ėkin and thrust 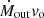 ) show very good correlations with the bolometric luminosity (as expected), reaching correlation coefficients of ∼ 0.9 and P ≪ 10−20 in both cases.
) show very good correlations with the bolometric luminosity (as expected), reaching correlation coefficients of ∼ 0.9 and P ≪ 10−20 in both cases.
 |
Fig. 13. Kinetic power Ėkin (left plot) and thrust (right) vs. bolometric luminosity for the C IVλ1549 emission line. The two outflow parameters were estimated by varying the outflow radius depending on λLλ as defined in Kaspi et al. (2021). Magenta dashed lines indicate the least squares linear regression. Black dotted, continuous, and dashed lines show |
The left plot of Fig. 13 shows the kinetic power of C IV outflows. We find that 15 of the 42 high-z sources present a Ėkin/Lbol ratio of ≳5 × 10−3, 8 of them show an Ėkin/Lbol of around 0.01, and 3 sources exhibit a ratio of close to 0.05 (between 1 to 3%). The situation is different when we consider the low-z sample. In this case, only two sources, [HB89]1259+593 and [HB89]1543+489, have a Ėkin/Lbol ratio of ≳5 × 10−3. This is hardly surprising considering that the luminosity of the BLUE component is highly correlated with 1350Å luminosity with a slope ≈1.8 ≫ 1, and that outflow velocities are systematically higher at high L. At high L, the kinetic power reaches values for which a substantial feedback effect might be possible: a considerable fraction of sources present 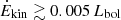 and some of them are close to the limit 0.05 Lbol, which is the minimum energetic requirement for feedback to lead to the black hole mass–host velocity dispersion relation according to Di Matteo et al. (2005).
and some of them are close to the limit 0.05 Lbol, which is the minimum energetic requirement for feedback to lead to the black hole mass–host velocity dispersion relation according to Di Matteo et al. (2005).
Average values and standard deviations of the [O III]λ5007 and C IVλ1549 outflow parameters for the different samples.
The right panel of Fig. 13 shows the behavior of the thrust in different luminosity ranges. Thrust values from ∼1035 to 1036 g cm s−2 at high luminosity and from ∼1032 to 1035 g cm −2 at low L. At high luminosity, the thrust values are slightly closer to their AGN L/c momentum rate than at low luminosity. It seems reasonable that the C IV-emitting gas in the inner BLR may not have yet suffered losses in energy and momentum (unlike [O III]), which would imply that, at least at high L, the outflow is somehow able to exploit the full luminosity of the continuum for its acceleration. Radiative acceleration is apparently less efficient at low z. The reason for the difference –at low luminosity, most sources remain substantially below the threshold lines at 0.005 Lbol and Lbol/c –is not entirely clear. A simple explanation is that the acceleration might involve a smaller fraction of the gas mass at low L. Lowering the gas density by an order of magnitude would reconcile the low-z values with the critical limits. A lower density (or a higher degree of ionization, see Appendix B.2) would increase the gas mass needed to explain the observed line luminosity and thus increase the outflowing gas mass proportionally. Lower-density gas might be associated with lower-column-density gas, which can be more efficiently accelerated (Netzer & Marziani 2010).
We conclude that there is the possibility of a significant feedback effect due to the mildly ionized BLR outflow from the high-ionization broad-line gas observed in luminous quasars at the cosmic noon, and that this possibility appears more remote for lower-luminosity, low-z quasars. This conclusion appears to be valid for both RQ and RL sources: the slightly lower velocities measured on the C IVλ1549 profile of the RLs are not enough to significantly affect the outflow dynamical parameters with respect to the RQ population (Fig. 13).
 |
Fig. 14. Comparison between the kinetic power Ėkin (left) and thrust (right) of [O III]λ5007 and C IVλ1549 outflows, for high-z (orange and red symbols) and low-z (blue and green symbols) sources. Both parameters have been estimated by evaluating the outflow radius in each source according Eqs. (9) and (10) for [O III] and C IV, respectively. Black dashed lines indicate the 1:1 relation. The color scheme is the same as in Fig. 4. |
5.2.3. Comparison between the outflow parameters of [O III]λ5007 and C IVλ1549
The average values and standard deviations of [O III]λ5007 and C IVλ1549 outflow parameters for the three analyzed samples (ISAAC and HEMS at high-z, and FOS at low-z) are listed in Table 15. Figure 14 presents a comparison between the estimated kinetic power and thrust for the [O III]λ5007 (left panel) and C IVλ1549 (right panel) emission lines. From the results obtained independently for [O III] and C IV and at high- and low-z, in the previous sections, as well as from the comparison of the outflow parameters in the BLR and NLR through the analysis of both lines, we make the following inferences:
-
The ISAAC and HEMS (high-redshift) samples share similar values for the outflow parameters, mass-outflow rate, thrust, and kinetic power. This is true for both [O III] and C IV, with the C IV emission line presenting consistently stronger wind parameters than those estimated from [O III]. The FOS (low-redshift) sample exhibits substantially lower values for all outflow parameters (≈ one and two orders of magnitude in [O III] and C IV, respectively).
-
At high redshift, the C IV outflow parameters indicate a significant influence: 16 out of 42 have
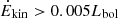 , and in some cases this value approaches ∼ 3% of Lbol. Regarding [O III], our results suggest that although the outflowing gas at high redshift seems to be induced by the AGN, its impact is possibly restricted to the central kiloparsecs due to its low efficiency.
, and in some cases this value approaches ∼ 3% of Lbol. Regarding [O III], our results suggest that although the outflowing gas at high redshift seems to be induced by the AGN, its impact is possibly restricted to the central kiloparsecs due to its low efficiency. -
In contrast to the outflows at low redshift, some of the C IV outflows at high redshift exhibit thrust values on the order of Lbol/c, suggesting that the outflowing gas in this scenario may be momentum-conserving. This characteristic is not observed in [O III] for either high- or low-redshift ranges.
-
It is intriguing that, at low-z, C IV and [O III] have consistent thrust values, which is at variance with high-luminosity sources (Fig. 14), even if both of them fall short of the L/c line. If this is accurate, it might be a consequence of the compactness of the emitting regions in low-z quasars:
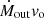 is inversely proportional to the radius and in the case of the low-luminosity NLSy1s, the [O III]-emitting regions might be very compact (≲10 pc), therefore preserving a signature of the AGN radiative acceleration.
is inversely proportional to the radius and in the case of the low-luminosity NLSy1s, the [O III]-emitting regions might be very compact (≲10 pc), therefore preserving a signature of the AGN radiative acceleration.
5.3. A tentative physical explanation for the RL/RQ difference in wind profiles
Observations of the C IVλ1549 line in the ISAAC sample suggest systematically lower blueshifts for RL than for RQ quasars, in agreement with previous studies both at high and low-z (see e.g., Wills et al. 1995; Sulentic et al. 1995; Corbin & Boroson 1996; Marziani et al. 1996; Richards et al. 2011). According to Sulentic et al. (2015, and references therein), two phenomena might be relevant here.
First, the pressure exerted by the jet in its propagation surpasses the thermal pressure of the BLR gas and the hydrostatic pressure of the expected emitting gas for the blueshifted component attributed to the accretion disc wind. This suggests the existence of an “avoidance zone” near the radio axis that may be wider in the case of powerful relativistic jets, potentially suppressing emission along radial lines close to the jet axis. The second important phenomenon to be considered is the impact on the inner BLR due to the cocoon associated with the relativistic ejection. The wind might start farther from the central BH due to cocoon pressure, reaching a lower terminal velocity.
6. Conclusions
We present an additional sample of ten high-redshift, high-luminosity quasars observed with the VLT/ISAAC spectrograph, completing our ISAAC sample, discussed in Paper I. These data cover the Hβ spectral range, shifted to the near-infrared due to its redshift, and are combined with rest-frame UV spectra observed in the optical and available in the literature. The analysis at high redshift involves 32 sources from our ISAAC sample and 28 sources from the HEMS survey, including both RL and RQ sources and with bolometric luminosities in the range from ≈1047 to 1048.5[erg s−1]. A comparison sample is made with 84 low-redshift, low-luminosity sources selected from the FOS data. We performed a spectroscopic exploration of UV and optical emission line diagnostics along the quasar main sequence, including a dedicated analysis of the differences between RL and RQ sources at both high and low redshifts. Additionally, we investigated the main feedback properties from both the BLR and NLR using high-ionization lines (C IV and [O III], respectively). Our main conclusions are as follows.
-
The shift in the main sequence toward broader Hβ profiles and higher R
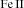 observed at high redshift in Paper I is reconfirmed with the inclusion of the ten new sources. RL quasars from our high-z sample consistently exhibit a tendency toward lower R
observed at high redshift in Paper I is reconfirmed with the inclusion of the ten new sources. RL quasars from our high-z sample consistently exhibit a tendency toward lower R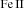 compared to the RQ ones.
compared to the RQ ones. -
High-z RL/RQ sources have stronger outflows than low-z RL/RQ sources as inferred from both [O III]λ5007 and C IVλ1549, which indicates that the accretion rate may be the primary driver of these outflows.
-
RL sources have smaller outflows compared to RQ sources in both high- and low-z ranges. This suggests that the radio-loudness has a second-order effect on the outflow. However, more data on high-z RL sources are needed.
-
Both RQ and RL outflows may induce a significant feedback effect at the high luminosities encountered in the high-z sample.
-
In the end, the outflow “power” is proportional to the AGN luminosity, via the line luminosity that enters linearly, and the increase in outflow velocity with luminosity that is expected to be weaker (
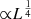 for a radiation driven wind). However, this increase becomes more significant if a luminosity range as large as ∼103 − 104 is considered, as in the case of the samples presented in this paper. Within limited luminosity ranges, the dominant effect is associated with the radiative output per unit mass (i.e., the Eddington ratio).
for a radiation driven wind). However, this increase becomes more significant if a luminosity range as large as ∼103 − 104 is considered, as in the case of the samples presented in this paper. Within limited luminosity ranges, the dominant effect is associated with the radiative output per unit mass (i.e., the Eddington ratio). -
The C IVλ1549 line follows the same trends as [O III]λ5007, albeit with larger outflow velocities and stronger outflow parameters. The relations between these two emission lines does not seem to be affected by the radio emission.
Our findings suggest that, regardless of the influence of accretion and radio emission, the outflow is likely to significantly affect the host galaxy at high luminosity. Less clear is the role of outflows from the BLR and NLR at low-z due to the much lower luminosity and smaller outflow velocity.
Data availability
Table 2 and spectra are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/691/A15.
The spectra and fittings of the ten new sources presented in this paper are available at https://zenodo.org/records/13332221
Here we define “jetted” sources the ones that present a radio-loudness parameter RK ≳ 1.8 (also called here as “radio-loud”, Ganci et al. 2019, see also Section 3.4).
Acknowledgments
The authors thank the anonymous referee for his/her valuable suggestions that helped us to improve the present paper. A.D.M. and A.d.O. acknowledge financial support from the Spanish MCIU through projects PID2019–106027GB–C41, PID2022-140871NB-C21 by “ERDF A way of making Europe”, and the Severo Ochoa grant CEX2021- 515001131-S funded by MCIN/AEI/10.13039/501100011033. A.D.M. acknowledges the support of the INPhINIT fellowship from “la Caixa” Foundation (ID 100010434). The fellowship code is LCF/BQ/DI19/11730018. A.D.M. is very thankful for the kind hospitality at the Padova Astronomical Observatory. This research has made use of the NASA/IPAC Extragalactic Database (NED) which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. In this work, we made use of astronomical tool IRAF, which is distributed by the National Optical Astronomy Observatories, and archival data from FIRST, NVSS, and 2MASS. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the U.S. Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org/.
References
- Ayubinia, A., Woo, J.-H., Rakshit, S., & Son, D. 2023, ApJ, 954, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Bachev, R., Marziani, P., Sulentic, J. W., et al. 2004, ApJ, 617, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [Google Scholar]
- Bennert, N., Falcke, H., Schulz, H., Wilson, A. S., & Wills, B. J. 2002, ApJ, 574, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Bennert, N., Jungwiert, B., Komossa, S., Haas, M., & Chini, R. 2006, A&A, 459, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bian, W., Yuan, Q., & Zhao, Y. 2005, MNRAS, 364, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Bischetti, M., Piconcelli, E., Vietri, G., et al. 2017, A&A, 598, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonzini, M., Mainieri, V., Padovani, P., et al. 2015, MNRAS, 453, 1079 [Google Scholar]
- Boroson, T. A., & Green, R. F. 1992, ApJS, 80, 109 [Google Scholar]
- Breiding, P., Chiaberge, M., Lambrides, E., et al. 2023, ApJ, 963, 91 [Google Scholar]
- Buendia-Rios, T. M., Negrete, C. A., Marziani, P., & Dultzin, D. 2023, A&A, 669, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Buttiglione, S., Capetti, A., Celotti, A., et al. 2010, A&A, 509, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caccianiga, A., Antón, S., Ballo, L., et al. 2015, MNRAS, 451, 1795 [NASA ADS] [CrossRef] [Google Scholar]
- Cano-Díaz, M., Maiolino, R., Marconi, A., et al. 2012, A&A, 537, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carniani, S., Marconi, A., Maiolino, R., et al. 2015, A&A, 580, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cavaliere, A., & Vittorini, V. 2000, ApJ, 543, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Coatman, L., Hewett, P. C., Banerji, M., & Richards, G. T. 2016, MNRAS, 461, 647 [NASA ADS] [CrossRef] [Google Scholar]
- Coatman, L., Hewett, P. C., Banerji, M., et al. 2019, MNRAS, 486, 5335 [Google Scholar]
- Condon, J. J., Cotton, W. D., Greisen, E. W., et al. 1998, AJ, 115, 1693 [Google Scholar]
- Condon, J. J., Kellermann, K. I., Kimball, A. E., Ivezić, Ž., & Perley, R. A. 2013, ApJ, 768, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Corbin, M. R., & Boroson, T. A. 1996, ApJS, 107, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Coziol, R., Andernach, H., Torres-Papaqui, J. P., Ortega-Minakata, R. A., & Moreno del Rio, F. 2017, MNRAS, 466, 921 [CrossRef] [Google Scholar]
- Cracco, V., Ciroi, S., Berton, M., et al. 2016, MNRAS, 462, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Deconto-Machado, A., Riffel, R. A., Ilha, G. S., et al. 2022, A&A, 659, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deconto-Machado, A., del Olmo Orozco, A., Marziani, P., Perea, J., & Stirpe, G. M. 2023, A&A, 669, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diamond-Stanic, A. M., Fan, X., Brandt, W. N., et al. 2009, ApJ, 699, 782 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Duras, F., Bongiorno, A., Piconcelli, E., et al. 2017, A&A, 604, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duras, F., Bongiorno, A., Ricci, F., et al. 2020, A&A, 636, A73 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mex. Astron. Astrofis., 53, 385 [NASA ADS] [Google Scholar]
- Feruglio, C., Fiore, F., Carniani, S., et al. 2015, A&A, 583, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fiore, F., Feruglio, C., Shankar, F., et al. 2017, A&A, 601, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, T. C., Kraemer, S. B., Schmitt, H. R., et al. 2018, ApJ, 856, 102 [Google Scholar]
- Floris, A., Marziani, P., Panda, S., et al. 2024, A&A, 689, A321 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fraix-Burnet, D., Marziani, P., D’Onofrio, M., & Dultzin, D. 2017, Front. Astron. Space Sci., 4, 1 [NASA ADS] [Google Scholar]
- Ganci, V., Marziani, P., D’Onofrio, M., et al. 2019, A&A, 630, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garnica, K., Negrete, C. A., Marziani, P., et al. 2022, A&A, 667, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gregg, M. D., Becker, R. H., White, R. L., et al. 1996, AJ, 112, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Hamann, F., & Ferland, G. 1993, ApJ, 418, 11 [Google Scholar]
- Harrison, C. M., Alexander, D. M., Mullaney, J. R., & Swinbank, A. M. 2014, MNRAS, 441, 3306 [Google Scholar]
- Hopkins, P. F., & Elvis, M. 2010, MNRAS, 401, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2006, ApJS, 163, 1 [Google Scholar]
- Jin, C., Done, C., Ward, M., et al. 2023, MNRAS, 518, 6065 [Google Scholar]
- Kakkad, D., Mainieri, V., Vietri, G., et al. 2020, A&A, 642, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kaspi, S., Brandt, W. N., Maoz, D., et al. 2021, ApJ, 915, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, C., Woo, J.-H., Luo, R., et al. 2023, ApJ, 958, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Kinney, A. L., Rivolo, A. R., & Koratkar, A. P. 1990, ApJ, 357, 338 [CrossRef] [Google Scholar]
- Komossa, S., Xu, D., Zhou, H., Storchi-Bergmann, T., & Binette, L. 2008, ApJ, 680, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Kovačević-Dojčinović, J., & Popović, L. Č. 2015, ApJS, 221, 35 [Google Scholar]
- Krawczyk, C. M., Richards, G. T., Mehta, S. S., et al. 2013, ApJS, 206, 4 [Google Scholar]
- Kriss, G. 1994, ASP Conf. Ser., 61, 437 [NASA ADS] [Google Scholar]
- Kukreti, P., Morganti, R., Tadhunter, C., & Santoro, F. 2023, A&A, 674, A198 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laor, A. 2018, MNRAS, 482, 5513 [Google Scholar]
- Laor, A., & Brandt, W. N. 2002, ApJ, 569, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Aldama, M. L., del Olmo, A., Marziani, P., et al. 2018, A&A, 618, A179 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marziani, P., Sulentic, J. W., Dultzin-Hacyan, D., Calvani, M., & Moles, M. 1996, ApJS, 104, 37 [Google Scholar]
- Marziani, P., Sulentic, J. W., Zwitter, T., Dultzin-Hacyan, D., & Calvani, M. 2001, ApJ, 558, 553 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Sulentic, J. W., Zamanov, R., et al. 2003a, ApJS, 145, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Zamanov, R. K., Sulentic, J. W., & Calvani, M. 2003b, MNRAS, 345, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Sulentic, J. W., Stirpe, G. M., Zamfir, S., & Calvani, M. 2009, A&A, 495, 83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Marziani, P., Martínez Carballo, M. A., Sulentic, J. W., et al. 2016a, Ap&SS, 361, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Sulentic, J. W., Stirpe, G. M., et al. 2016b, Ap&SS, 361, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Negrete, C. A., Dultzin, D., et al. 2017, Front. Astron. Space Sci., 4, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Dultzin, D., Sulentic, J. W., et al. 2018, Front. Astron. Space Sci., 5, 6 [CrossRef] [Google Scholar]
- Marziani, P., Deconto-Machado, A., & Del Olmo, A. 2022a, Galaxies, 10, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Marziani, P., Olmo, A. d., Negrete, C. A., et al. 2022b, ApJS, 261, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Massaro, F., Giroletti, M., D’Abrusco, R., et al. 2014, ApJS, 213, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Massaro, E., Maselli, A., Leto, C., et al. 2015, Ap&SS, 357, 75 [Google Scholar]
- Mathews, W. G., & Ferland, G. J. 1987, ApJ, 323, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Mauch, T., Murphy, T., Buttery, H. J., et al. 2003, MNRAS, 342, 1117 [Google Scholar]
- Mengistue, S. T., Del Olmo, A., Marziani, P., et al. 2023, MNRAS, 525, 4474 [CrossRef] [Google Scholar]
- Nesvadba, N. P. H., Lehnert, M. D., De Breuck, C., Gilbert, A., & van Breugel, W. 2007, A&A, 475, 145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Netzer, H. 2019, MNRAS, 488, 5185 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H., & Marziani, P. 2010, ApJ, 724, 318 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H., Shemmer, O., Maiolino, R., et al. 2004, ApJ, 614, 558 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei (Sausalito, CA, USA: University Science Books) [Google Scholar]
- Padovani, P. 2016, A&ARv, 24, 13 [Google Scholar]
- Panessa, F., Baldi, R. D., Laor, A., et al. 2019, Nat. Astron., 3, 387 [Google Scholar]
- Patil, P., Whittle, M., Nyland, K., et al. 2022, ApJ, 934, 26 [Google Scholar]
- Perlman, E. S., Padovani, P., Giommi, P., et al. 1998, AJ, 115, 1253 [Google Scholar]
- Punsly, B. 2010, ApJ, 713, 232 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Kruczek, N. E., Gallagher, S. C., et al. 2011, AJ, 141, 167 [Google Scholar]
- Richards, G. T., McCaffrey, T. V., Kimball, A., et al. 2021, AJ, 162, 270 [NASA ADS] [CrossRef] [Google Scholar]
- Shemmer, O., Trakhtenbrot, B., Anderson, S. F., et al. 2010, ApJ, 722, L152 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., & Ho, L. C. 2014, Nature, 513, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Sikora, M., Stawarz, Ł., & Lasota, J.-P. 2007, ApJ, 658, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Singha, M., Husemann, B., Urrutia, T., et al. 2022, A&A, 659, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Śniegowska, M., Marziani, P., Czerny, B., et al. 2021, ApJ, 910, 115 [CrossRef] [Google Scholar]
- Stickel, M., Kuehr, H., & Fried, J. W. 1993, A&AS, 97, 483 [NASA ADS] [Google Scholar]
- Sulentic, J. W., Marziani, P., Dultzin-Hacyan, D., Calvani, M., & Moles, M. 1995, ApJ, 445, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Sulentic, J. W., Marziani, P., & Dultzin-Hacyan, D. 2000a, ARA&A, 38, 521 [Google Scholar]
- Sulentic, J. W., Zwitter, T., Marziani, P., & Dultzin-Hacyan, D. 2000b, ApJ, 536, L5 [Google Scholar]
- Sulentic, J. W., Marziani, P., Zamanov, R., et al. 2002, ApJ, 566, L71 [NASA ADS] [CrossRef] [Google Scholar]
- Sulentic, J. W., Stirpe, G. M., Marziani, P., et al. 2004, A&A, 423, 121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sulentic, J. W., Repetto, P., Stirpe, G. M., et al. 2006, A&A, 456, 929 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sulentic, J. W., Bachev, R., Marziani, P., Negrete, C. A., & Dultzin, D. 2007, ApJ, 666, 757 [NASA ADS] [CrossRef] [Google Scholar]
- Sulentic, J., Marziani, P., & Zamfir, S. 2011, Balt. Astron., 20, 427 [NASA ADS] [Google Scholar]
- Sulentic, J. W., Marziani, P., del Olmo, A., et al. 2014, A&A, 570, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sulentic, J. W., Martínez-Carballo, M. A., Marziani, P., et al. 2015, MNRAS, 450, 1916 [NASA ADS] [CrossRef] [Google Scholar]
- Sulentic, J. W., del Olmo, A., Marziani, P., et al. 2017, A&A, 608, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tadhunter, C., Rodríguez Zaurín, J., Rose, M., et al. 2018, MNRAS, 478, 1558 [NASA ADS] [CrossRef] [Google Scholar]
- Temple, M. J., Ferland, G. J., Rankine, A. L., et al. 2020, MNRAS, 496, 2565 [NASA ADS] [CrossRef] [Google Scholar]
- Temple, M. J., Matthews, J. H., Hewett, P. C., et al. 2023, MNRAS, 523, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Tytler, D., O’Meara, J. M., Suzuki, N., et al. 2004, AJ, 128, 1058 [NASA ADS] [CrossRef] [Google Scholar]
- Véron-Cetty, M. P., & Véron, P. 2010, A&A, 518, A10 [Google Scholar]
- Vestergaard, M., & Peterson, B. M. 2006, ApJ, 641, 689 [Google Scholar]
- Vestergaard, M., & Wilkes, B. J. 2001, ApJS, 134, 1 [Google Scholar]
- Vietri, G., Piconcelli, E., Bischetti, M., et al. 2018, A&A, 617, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vietri, G., Mainieri, V., Kakkad, D., et al. 2020, A&A, 644, A175 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Villar-Martín, M., Arribas, S., Emonts, B., et al. 2016, MNRAS, 460, 130 [Google Scholar]
- Wang, J., Xu, D. W., & Wei, J. Y. 2018, ApJ, 852, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkes, B. J., Wright, A. E., Jauncey, D. L., & Peterson, B. A. 1983, PASA, 5, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Wills, B. J., Thompson, K. L., Han, M., et al. 1995, ApJ, 447, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, J., Salvato, M., Coffey, D., et al. 2020, MNRAS, 492, 3580 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J.-H., & Urry, C. M. 2002, ApJ, 581, L5 [Google Scholar]
- Wu, J., Brandt, W. N., Anderson, S. F., et al. 2012, ApJ, 747, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, F., Bian, F., Shen, Y., et al. 2018, MNRAS, 480, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Yuan, M. J., & Wills, B. J. 2003, ApJ, 593, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Zamanov, R., Marziani, P., Sulentic, J. W., et al. 2002, ApJ, 576, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Zamfir, S., Sulentic, J. W., & Marziani, P. 2008, MNRAS, 387, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Zamfir, S., Sulentic, J. W., Marziani, P., & Dultzin, D. 2010, MNRAS, 403, 1759 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, K., Dong, X.-B., Wang, T.-G., & Gaskell, C. M. 2011, ApJ, 737, 71 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Additional table
Properties of the [O III]λ5007 and C IVλ1549 outflows for the objects of each sample considered in this work that present clear outflows.
Appendix B: Details on the estimations of the outflow parameters
B.1. [O III]λλ4959,5007
The expressions for the [O III]λ5007 outflow parameters were derived by Marziani et al. (2017) assuming a bipolar outflow structure (c.f. Kim et al. 2023, and references therein). All the [O III]λ5007 outflow equations reported here are in accordance with the work of Cano-Díaz et al. (2012) and Fiore et al. (2017).
The [O III]λ5007 luminosity can be related to the outflow mass by
where L[OIII],44out is the outflow-emitted luminosity of [O III]λ5007 emission line in units of 1044 erg s−1, the density (nH) and the metallicity (Z) have been scaled to 103 cm−3 and 5 times solar, respectively.
If we assume that the outflow is confined to a solid angle Ω, then the mass outflow rate 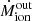 at a distance r can be written as:
at a distance r can be written as:
Even if part of a nuclear outflow, the [O III]λλ4959,5007 emitting gas is probably not being anymore accelerated by radiation pressure, and so we consider as maximum outflow velocity vo the centroid at 1/2 intensity of the BLUE component. If we assume the [O III]λ5007 outflow to be nuclear, we can then suppose a super-solar chemical composition Z = 5 Z⊙ at low redshift, that is also consistent with the metallicity derived for the most metal rich bulge stars. At high redshift, there is no estimation we are aware of the chemical composition of the outflowing gas. A proxy is provided by the metallicity of the stellar component of the host galaxy (Xu et al. 2018), expected to be twice the solar value.
The thrust might be written as:
Similarly, the kinetic power Ėout is then given by 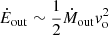 , which leads to
, which leads to
B.2. C IVλ1549
Both C IVλ1549 and [O III]λλ4959,5007 are predominantly produced by collisional excitation, for which the collisional excitation rate of Eq. 3.20 from Osterbrock & Ferland (2006) applies:
where hν is the energy of the photon emitted in the transition (1.28×10−11 erg in the case of C IVλ1549), and k is the Boltzmann’s constant in erg K−1. Υ is the collision strength and is almost independent from temperature Osterbrock & Ferland (2006) yield Υ ≈ 8.91). The g1 = (2J + 1) = 2, as the lower level of the transition is the ground state ( ). The exponential argument is
). The exponential argument is 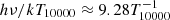 , and dominates over the factor
, and dominates over the factor 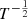 .
.
The mass of ionized gas is given by
Here LCIV is the C IVλ1549 luminosity, (hν)CIV the C IVλ1549 photon energy, [C/H] the relative abundance of Carbon with respect to Hydrogen, in number: 8.43 ≈ 12 + log[C/H] for solar abundance, implying [C/H] ≈2.69 ⋅ 10−4. The factor XC+3 = [C+3]/∑i[C+i] ≤ 1 is the ionic fraction of triply ionized Carbon, and μmP is the molecular mass of the gas, with μ ≈ 1.4 (neglecting the mass of the metals), and mP the proton mass.
The mass of the emitting gas strongly depends on temperature. A single value of the dynamical temperature could be assumed, in keeping with the simplest assumptions. However, the T value should be chosen carefully.
B.2.1. Observational constraints
To estimate a typical value of the dynamical temperature, we can apply two main observational constraints on the blueshifted emission due to the outflow:
-
C IVλ1549 equivalent width: in super-Eddington candidates, the equivalent width is typically very low W ∼ 10 Å and in Population A W ≲ 30 Å (Kinney et al. 1990; Sulentic et al. 2000b; Marziani et al. 2016a; Martínez-Aldama et al. 2018). The sources that are radiating at high Eddington ratio are the ones showing the lowest W along the E1 main sequence, with a large fraction of them being weak lined quasars (WLQs) (Shemmer et al. 2010; Wu et al. 2012; Marziani et al. 2016a; Martínez-Aldama et al. 2018; Jin et al. 2023). Even for the Pop. B sources of the HEMS and ISAAC samples W C IVλ1549 is usually below ≈ 50 Å.
-
C IVλ1549/Hβ ratio: its value, due to the absence of a strong Hβ blueshifted component, can be assumed to be C IVλ1549/Hβ ≳5 ∼ 10 for blueshifted components.
The decomposition of the C IVλ1549 profile in two components reveals very different properties and physical conditions for the outflow and virial component. In the outflow case, the C IVλ1549 equivalent width is in the range from the detectability limit of a few Å to a few tens Å. This observational constraint suggests that the outflow component of the C IVλ1549 profile is not produced by gas in physical conditions optimized for its emission.
B.2.2. Photoionization modeling
The diagrams of Fig. B.1 show the W of C IVλ1549 (left panels) and the C IV/Hβ ratio (right panels) as a function of the ionization parameter U, according to CLOUDY 17.02 (Ferland et al. 2017) computations, assuming two cases: (1) MBH = 109 M⊙, five times solar metallicity, and a standard AGN SED representative for low-redshift sources that have Eddington ratios ≳0.1 − 0.2 (Mathews & Ferland 1987) (upper panels); and (2) in bottom panels for MBH = 109.5 M⊙, five times solar metallicity and the SED defined by Krawczyk et al. (2013), more appropriate for representing our high-z high luminosity sources (see more details below). Very low W is possible in conditions of Carbon under-ionization and over-ionization with respect to C+3. For the blueshifted component, a high-ionization solution has been found with typical values log U ∼ −0.5 − 0 (Śniegowska et al. 2021; Garnica et al. 2022).
The upper left panel of Fig. B.1 shows that the expected W(C IVλ1549) at U ∼ 1 is several tens of Å, consistent with the observations if the covering factor is moderate (∼0.2 − 0.5), with a marginal dependence on density. The C IVλ1549/Hβ ratio is constrained to be ≳5, with C IVλ1549/Hβ ∼10 for the density range 109.5 − 1010 cm−3.
The electron temperature associated with these conditions is high (T ∼ 20 000 K), implying a very high efficiency for the collisional excitation. The point here is that, even if the collisional efficiency is high, the ionic fraction of C+3 is very low (∼0.01), yielding a 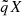 factor ≈(3 − 4)⋅10−11 cm3 s−1.
factor ≈(3 − 4)⋅10−11 cm3 s−1.
At high luminosity, however, the softening of the accretion disk emission due to large masses makes the SED significantly different from that of Mathews & Ferland (1987). The peak of the disk emission can be displaced toward lower frequency by a factor ∼10 (Duras et al. 2017, 2020), reducing significantly the amount of ionizing photons. We therefore considered a different SED, defined for intermediate redshift quasars with W(C IV) ≲30 Å (Krawczyk et al. 2013). The simulations predict lower W(C IV) by a factor ≈5 (bottom panels on Fig. B.1) with respect to the Mathews & Ferland (1987) SED. The W(C IV) and the C IV/Hβ ratio provide some constraints over the ionization parameter and density. The C IV/Hβ ratio falls within a range of ∼ 8 - 33 for the ISAAC sources where the BLUE of Hβ has been detected, and the W ∼ 10Å. For log nH ≈ 9.5, these conditions imply a log U between -0.7 and 0.3. In this case, for log U ≈ −0.2, and computing a weighted average over r2, we obtain a much higher efficiency, 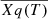 to ≈1.22 ⋅ 10−10 cm3 s−1. Much lower efficiencies are possible if log U → 0 and log nH → 9. In this case the predicted W(C IV) might be below 10 Å, as found for weak lined quasars (Diamond-Stanic et al. 2009; Shemmer et al. 2010; Marziani et al. 2016a).
to ≈1.22 ⋅ 10−10 cm3 s−1. Much lower efficiencies are possible if log U → 0 and log nH → 9. In this case the predicted W(C IV) might be below 10 Å, as found for weak lined quasars (Diamond-Stanic et al. 2009; Shemmer et al. 2010; Marziani et al. 2016a).
 |
Fig. B.1. Relation between W C IVλ1549 (left panels) and intensity ratio C IVλ1549/Hβ (right panels) with the ionization parameter U for three density values log nH = 9, 9.5, 10 [cm−3] (black, blue, and magenta symbols, respectively), column density Nc = 1022 cm−2, 5 times solar metallicity. Top: For log MBH = 109 [M⊙], and a Mathews & Ferland (1987) SED. Bottom: log MBH = 109.5 [M⊙], and a Krawczyk et al. (2013) SED. |
 |
Fig. B.2. Behavior of ionization parameter, electron temperature, C IVλ1549 luminosity, and ionic fraction as a function of radius for density value log nH = 9.5 [cm−3], and for the two adopted SEDs for the low (top panels) and high-z (bottom panels) samples. Top, upper panel: behavior of the ionization parameter (left axis scale, blue dots) and electron temperature (right axis scale, green dots) as a function of radius for a MBH = 109 M⊙ radiating at Eddington limit and illuminating a slab of gas. We assume column density Nc = 1022 cm−2, Mathews & Ferland (1987) SED, and the metallicity five times solar in all cases. Top, lower panel: logarithm of C IVλ1549 luminosity (black dots) and ionic fraction as a function of radius. The blue and red line represent the ionic stages higher and lower than 3, respectively, and the black circles ionic stage 3. Bottom, upper and lower panels: same as top panels, for log MBH= 9.5 [M⊙], and SED from Krawczyk et al. (2013). In both the top and bottom panels, the horizontal gray bands indicate the range of ionization parameters consistent with the observed C IV equivalent width and the C IV/Hβ ratio. The vertical bands represent the corresponding range of permitted radii. |
Fig. B.2 shows the trends expected for the ionization parameter and electron temperature as a function of radius, for the value of the density log nH = 9.5 [cm−3]. The intercepts between the expected range of ionization parameter and radius does not fall in correspondence of the peak ionization fraction in the case of the Mathews & Ferland (1987) SED, while it does in the high-luminosity case due to the “softer” Krawczyk et al. (2013) SED (bottom panels of Fig. B.2). The lower limit assumed for log U ≈ −0.5 implies a condition of over-ionization for the line emitting gas. Electron temperature is around Te ≈ 20 000 K.
The photoionization computations predict an equivalent width more than an order of magnitude higher than the observed value if C IVλ1549 emission is due to gas at log U ∼ −1.3 in the case of the Mathews & Ferland (1987) SED appropriate for low-z sources (upper right panel of Fig. B.1). In addition, the distance expected for log U = −1.3 and log nH ≈ 9.0 is log r ≈ 18.8 [cm], more than one order of magnitude higher than the scaling radius of Kaspi et al. (2021), log r ≈ 17.43 [cm] (see the ionic fraction distribution in the lower half of the upper panel of Fig. B.2).
Taking into account previous considerations, we use for the ionized mass the following expression:
which incorporates the average over density in the range 109.5 − 1010.5 cm−3 of Xq(T) for log U = 0, 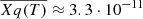 cm3 s−1. Averaging over log U = − 0.5, 0, + 0.5, would imply an increase of
cm3 s−1. Averaging over log U = − 0.5, 0, + 0.5, would imply an increase of  to ≈5.65 ⋅ 10−11 cm3 s−1, by a factor ≈1.7. Such increase in the efficiency in C IV production would only reinforce the conclusion on the weakness of the outflows at low-z.
to ≈5.65 ⋅ 10−11 cm3 s−1, by a factor ≈1.7. Such increase in the efficiency in C IV production would only reinforce the conclusion on the weakness of the outflows at low-z.
B.2.3. Wind dynamical parameters
To estimate the wind dynamical parameters we assume the same simple model utilized for [O III]λλ4959,5007. The mass outflow rate is therefore given by:
where 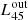 is the luminosity of the blueshifted component in units of 1045 erg s−1, the outflow velocity v5000 is scaled to 5000 km s−1, the gas density is in units of 10 9.5, and the radius is now in parsec units. For this paper, we assume that the C IV outflow is accelerated to a final, terminal velocity v ≈ c(1/2) + 2σ ≈ c(1/2) + FWHMBLUE/1.18, where c(1/2) corresponds to the centroid velocity at half intensity of the C IV BLUE component.
is the luminosity of the blueshifted component in units of 1045 erg s−1, the outflow velocity v5000 is scaled to 5000 km s−1, the gas density is in units of 10 9.5, and the radius is now in parsec units. For this paper, we assume that the C IV outflow is accelerated to a final, terminal velocity v ≈ c(1/2) + 2σ ≈ c(1/2) + FWHMBLUE/1.18, where c(1/2) corresponds to the centroid velocity at half intensity of the C IV BLUE component.
The thrust  and kinetic power can then be computed as:
and kinetic power can then be computed as:
These expressions, used to calculate the dynamical parameters of the outflows for our low-z FOS sample, are quantitatively similar to the ones reported in earlier works (Marziani et al. 2016a, 2017). Those authors assumed an ad hoc temperature to account for the low C IVλ1549 radiative efficiency of the emitting gas suggested by the observed low equivalent width of C IVλ1549.
At high luminosity, for the ISAAC and HEMS samples, and by considering the results from the CLOUDY computations by using the more appropriate SED from Krawczyk et al. (2013) and for an estimated log U ≈ −0.2, and an efficiency, 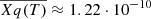 cm3 s−1 (see section B.2.2), Eqs. B.7, B.8, B.9, and B.10 should be divided by a factor ≈3.63. Eqs. B.7, once the constants are divided by the factor reported above yields estimates that are in basic agreement with those of Vietri et al. (2020): they differ by a factor ∼ 2-3 in Mion, and the difference comes from the assumed efficiency of the C IVλ1549 emission. Additional factors accounting for differences in the estimated values concern the geometry: a factor 3 from the assumption of a thin flat layer in place of a spherical surface element, and an additional factor of 2 for the unseen contribution of the receding cone enters in Eqs. B.7, B.8, B.9 and B.10.
cm3 s−1 (see section B.2.2), Eqs. B.7, B.8, B.9, and B.10 should be divided by a factor ≈3.63. Eqs. B.7, once the constants are divided by the factor reported above yields estimates that are in basic agreement with those of Vietri et al. (2020): they differ by a factor ∼ 2-3 in Mion, and the difference comes from the assumed efficiency of the C IVλ1549 emission. Additional factors accounting for differences in the estimated values concern the geometry: a factor 3 from the assumption of a thin flat layer in place of a spherical surface element, and an additional factor of 2 for the unseen contribution of the receding cone enters in Eqs. B.7, B.8, B.9 and B.10.
All Tables
Measurements on the Hβ full broad line profile and derived properties of the Hβ region.
Least-squares linear relations (y = a + b * x) between different outflow properties and the bolometric luminosity.
Average values and standard deviations of the [O III]λ5007 and C IVλ1549 outflow parameters for the different samples.
Properties of the [O III]λ5007 and C IVλ1549 outflows for the objects of each sample considered in this work that present clear outflows.
All Figures
 |
Fig. 1. Distributions of z and Mi for FOS, HEMS, ISAACI from Paper I, and the new ISAAC2 data. Each distribution was normalised separately. |
| In the text | |
 |
Fig. 2. Example of an ISAAC spectrum and of the decomposition analysis of the emission lines. (a) Rest-frame optical spectrum of CTSJ01.03. The white area shows the spectral region used in the fitting. The gray dashed line indicates the continuum level obtained with the specfit multicomponent fitting. Fe II contributions are represented by the green line. (b) Example of the Hβ+[O III] emission line decomposition (upper panel) and its respective residuals (bottom panel). Black, orange, and blue lines indicate the broad, the narrow, and the blueshifted components of the profile, respectively. The final fit is shown by the pink dashed line. |
| In the text | |
 |
Fig. 3. Location on the MS of the ten new sources for this work together with those from Paper I (circles) and the HEMS sample (squares). Pop. A quasars are represented by blue symbols and Pop. B by red symbols. The RL sources are surrounded by an open circle or square in the plot. The gray region indicates the distribution of the MS of quasars at low z. The purple-shaded area shows the luminosity-dependent boundary between Pops. A and B for high-luminosity sources, as described in detail in Paper I. |
| In the text | |
 |
Fig. 4. Velocity centroid c(1/4) versus L/LEdd for [O III]λ5007 (left) and C IVλ1549 (right). Dark green and blue symbols correspond, respectively, to RQ and RL sources at low-z, while orange (RQ) and red (RL) symbols represent high-z quasars. Within each color, filled squares represent Pop. B sources and the bullets Pop. A quasars. |
| In the text | |
 |
Fig. 5. Comparison between the relative intensities of the blueshifted component for both [O III]λ5007 and C IVλ1549. Low-z and high-z sources are represented in the left and right panels, respectively. |
| In the text | |
 |
Fig. 6. Centroid velocities at one-quarter intensity (c(1/4)) cumulative distributions of the samples separated by radio-loudness and redshift range for [O III]λ5007 (top panels) and C IVλ1549 (bottom panels). Kolmogórov-Smirnov tests were performed comparing different subsamples identified at the top of the panels. KS statistics for each comparison are shown in the top left corner of each plot together with the respective ρ-value. Vertical lines indicate the mean value for each subsample. |
| In the text | |
 |
Fig. 7. Relation between radio-loudness RK and RFe II for low-z (left) and high-z (right) ranges. RK upper limits are indicated by arrows alongside the symbol. The color scheme is the same as that in Fig. 4. |
| In the text | |
 |
Fig. 8. Relation between radio-loudness and velocity centroid at one-quarter intensity of the [O III]λ5007 emission line for low-z (left) and high-z (right) ranges. Gray shaded areas in both plots indicate the c(1/4) range between 250 and −250 km s−1. RK upper limits are indicated by arrows alongside the symbol. The color scheme is the same as that in Fig. 4. |
| In the text | |
 |
Fig. 9. Relation between radio-loudness and the velocity centroid at one-quarter intensity of the C IVλ1549 emission line for low-z (left) and high-z (right) ranges. RK upper limits are indicated by arrows alongside the symbol. The color scheme is the same as in Fig. 4. |
| In the text | |
 |
Fig. 10. Centroid velocity at half flux intensity (c(1/2)) of C IVλ1549 vs. c(1/2) of [O III]λ5007 for the full (left) and outflow (right) profiles of the high-z sample. The magenta lines indicate the linear regression between c(1/2) of C IV and [O III] for both cases obtained through the bisector method. Dotted black lines represent the 1:1 relation. The color scheme is the same as in Fig. 4. |
| In the text | |
 |
Fig. 11. Relation between the outflow radio in kiloparsecs and the luminosity of the [O III]λ5007 emission line for the five plotted samples. The red dashed line represents the adopted least squares linear regression. Magenta vertical lines symbolise the minimum and maximum estimated radii in the Villar-Martin sample. Arrows correspond to upper limits. |
| In the text | |
 |
Fig. 12. Kinetic power Ėkin (left) and thrust (right) vs. bolometric luminosity for the [O III]λ5007 outflow. The two outflow parameters were estimated by varying the outflow radius according to Eq. (9) and assuming vout = c(1/2). Magenta dashed lines indicate the least-squares linear regression. Black dotted, continuous, and dashed lines on the left plot show |
| In the text | |
 |
Fig. 13. Kinetic power Ėkin (left plot) and thrust (right) vs. bolometric luminosity for the C IVλ1549 emission line. The two outflow parameters were estimated by varying the outflow radius depending on λLλ as defined in Kaspi et al. (2021). Magenta dashed lines indicate the least squares linear regression. Black dotted, continuous, and dashed lines show |
| In the text | |
 |
Fig. 14. Comparison between the kinetic power Ėkin (left) and thrust (right) of [O III]λ5007 and C IVλ1549 outflows, for high-z (orange and red symbols) and low-z (blue and green symbols) sources. Both parameters have been estimated by evaluating the outflow radius in each source according Eqs. (9) and (10) for [O III] and C IV, respectively. Black dashed lines indicate the 1:1 relation. The color scheme is the same as in Fig. 4. |
| In the text | |
 |
Fig. B.1. Relation between W C IVλ1549 (left panels) and intensity ratio C IVλ1549/Hβ (right panels) with the ionization parameter U for three density values log nH = 9, 9.5, 10 [cm−3] (black, blue, and magenta symbols, respectively), column density Nc = 1022 cm−2, 5 times solar metallicity. Top: For log MBH = 109 [M⊙], and a Mathews & Ferland (1987) SED. Bottom: log MBH = 109.5 [M⊙], and a Krawczyk et al. (2013) SED. |
| In the text | |
 |
Fig. B.2. Behavior of ionization parameter, electron temperature, C IVλ1549 luminosity, and ionic fraction as a function of radius for density value log nH = 9.5 [cm−3], and for the two adopted SEDs for the low (top panels) and high-z (bottom panels) samples. Top, upper panel: behavior of the ionization parameter (left axis scale, blue dots) and electron temperature (right axis scale, green dots) as a function of radius for a MBH = 109 M⊙ radiating at Eddington limit and illuminating a slab of gas. We assume column density Nc = 1022 cm−2, Mathews & Ferland (1987) SED, and the metallicity five times solar in all cases. Top, lower panel: logarithm of C IVλ1549 luminosity (black dots) and ionic fraction as a function of radius. The blue and red line represent the ionic stages higher and lower than 3, respectively, and the black circles ionic stage 3. Bottom, upper and lower panels: same as top panels, for log MBH= 9.5 [M⊙], and SED from Krawczyk et al. (2013). In both the top and bottom panels, the horizontal gray bands indicate the range of ionization parameters consistent with the observed C IV equivalent width and the C IV/Hβ ratio. The vertical bands represent the corresponding range of permitted radii. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



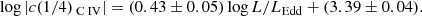
![$$ \begin{aligned} \log |c(1/4)_{\rm [{\text{ O}}{\small {\uppercase {\text{ III}}}}] }|= (0.33 \pm 0.09)\log L/L_{\mathrm{Edd} }+(2.91 \pm 0.04). \end{aligned} $$](/articles/aa/full_html/2024/11/aa49976-24/aa49976-24-eq12.gif)
![$$ \begin{aligned} c(1/2)_{{{\text{ C}}{\small {\uppercase {\text{ IV}}}}}}=(1.42 \pm 0.23)\times c(1/2)_{{[{\text{ O}}{\small {\uppercase {\text{ III}}}}]}}+(-1071\pm 148), \end{aligned} $$](/articles/aa/full_html/2024/11/aa49976-24/aa49976-24-eq15.gif)
![$$ \begin{aligned} c(1/2)_{{{\text{ C}}{\small {\uppercase {\text{ IV}}}},{\text{ BLUE}}}}=(1.27 \pm 0.99)\times c(1/2)_{{[{\text{ O}}{\small {\uppercase {\text{ III}}}}],{\text{ BLUE}}}}+(-1432\pm 1323). \end{aligned} $$](/articles/aa/full_html/2024/11/aa49976-24/aa49976-24-eq16.gif)
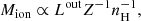
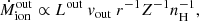
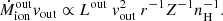
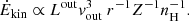
![$$ \begin{aligned} \log \left(r\right) = (0.5)\times \log \left(L_{\mathrm{[O III],full}}\right) + (-21.7\pm 0.1). \end{aligned} $$](/articles/aa/full_html/2024/11/aa49976-24/aa49976-24-eq32.gif)
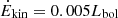
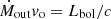
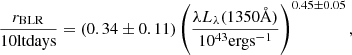
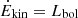
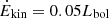
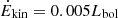
![$$ \begin{aligned} M_{\mathrm{ion}}=1\times 10^7\ L^\mathrm{out} _{\mathrm{[OIII],44}}\left(\frac{Z}{5Z_{\odot }}\right)^{-1}n_{\rm H,3}^{-1} \ \ [ \mathrm M_\odot ] , \end{aligned} $$](/articles/aa/full_html/2024/11/aa49976-24/aa49976-24-eq59.gif)
![$$ \begin{aligned} \dot{M}_{\mathrm{ion}}=30\,L_{\mathrm{[OIII],44}}^{\mathrm{out}}\ \ v_{\mathrm{o,1000}}\ \ r_{\mathrm{1kpc}}^{-1}\left(\frac{Z}{5Z_{\odot }}\right)^{-1} n_{\rm H,3}^{-1}\ [\mathrm{M}_{\odot } \mathrm{yr}^{-1}]. \end{aligned} $$](/articles/aa/full_html/2024/11/aa49976-24/aa49976-24-eq61.gif)
![$$ \begin{aligned} \dot{M}_{\mathrm{ion} }v_{\mathrm{o} }=1.9\times 10^{35}L_{\mathrm{[OIII],44} }^{\mathrm{out} }\ v^2_{\mathrm{o,1000} }\ r^{-1}_{\mathrm{1kpc} }\left(\frac{Z}{5Z_{\odot }}\right)^{-1}n_{\rm H,3}^{-1}\ [\mathrm{g cm s}^{-2}]. \end{aligned} $$](/articles/aa/full_html/2024/11/aa49976-24/aa49976-24-eq62.gif)
![$$ \begin{aligned} \dot{\epsilon }_{\mathrm{kin} }=9.6\times 10^{42}L_{\mathrm{[OIII],44} }^{\mathrm{out} }\ v_{\mathrm{o,1000} }^3\ r_{\mathrm{1kpc} }^{-1}\left(\frac{Z}{5Z_{\odot }}\right)^{-1}n_{\rm H,3}^{-1}\ [\mathrm{erg s}^{-2}]. \end{aligned} $$](/articles/aa/full_html/2024/11/aa49976-24/aa49976-24-eq64.gif)
![$$ \begin{aligned} q_{12} = \frac{8.629\cdot 10^{-6}}{T^\frac{1}{2}} \frac{\Upsilon }{g_1} \exp {(-h\nu /{kT})}\, \, [\mathrm {cm}^{+3} s^{-1}] \end{aligned} $$](/articles/aa/full_html/2024/11/aa49976-24/aa49976-24-eq65.gif)
![$$ \begin{aligned} M_{\rm c^{+3}} \sim \frac{L_{\rm CIV}}{(h\nu )_{\rm CIV} q_{12} n_{\rm H} \mathrm{[C/H]} X_{C^{+3}} } \cdot \mu \ m_{\rm P}. \end{aligned} $$](/articles/aa/full_html/2024/11/aa49976-24/aa49976-24-eq69.gif)
![$$ \begin{aligned} M_{\mathrm{ion}} \approx 6.5 \cdot 10^2 L_{{\mathrm{CIV}},45}^{\mathrm{out}} \left[\frac{Z}{5Z_\odot }\right]^{-1} n_{\mathrm{H,9.5}}^{-1} [{\mathrm{M}}_{\odot }] \end{aligned} $$](/articles/aa/full_html/2024/11/aa49976-24/aa49976-24-eq72.gif)
![$$ \begin{aligned} \dot{M}_{\mathrm{ion}} \approx 10\, L^{\mathrm{out}}_{{\mathrm{CIV}},45}\ v_{5000}\ r_{1{\mathrm{pc}}}^{-1} \left(\frac{Z}{5Z_\odot }\right)^{-1} n_{{\mathrm{H}},9.5}^{-1}\ [{\mathrm{M}}_\odot \ {\mathrm{yr}}^{-1}] \end{aligned} $$](/articles/aa/full_html/2024/11/aa49976-24/aa49976-24-eq75.gif)
![$$ \begin{aligned} \dot{M}_{\mathrm{ion}}v\approx 3.15 \cdot 10^{35} L^{\mathrm{out}}_{{\mathrm{CIV}}45},\,v_{5000}^2\,r_{1{\mathrm{pc}}}^{-1}\left(\frac{Z}{5Z_\odot }\right)^{-1}n_{{\mathrm{H}},9.5}^{-1}\ [{\mathrm{g\,cm\,s}}^{-2}] \end{aligned} $$](/articles/aa/full_html/2024/11/aa49976-24/aa49976-24-eq78.gif)
![$$ \begin{aligned} {\dot{E}}_{kin}=\frac{1}{2}{\dot{M}}_{\mathrm{ion}} v^{2} \approx 7.9\cdot 10^{43} L^{\mathrm{out}}_{{\mathrm{CIV}},45}v_{5000}^3 r_{1{\mathrm{pc}}}^{-1}\left(\frac{Z}{5Z_\odot }\right)^{-1}n_{{\mathrm{H}},9.5}^{-1} [{\mathrm{erg s}}^{-2}] \end{aligned} $$](/articles/aa/full_html/2024/11/aa49976-24/aa49976-24-eq79.gif)