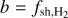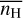| Issue |
A&A
Volume 669, January 2023
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 22 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202243902 | |
| Published online | 13 January 2023 | |
3D chemical structure of the diffuse turbulent interstellar medium
II. The origin of CH+: A new solution to an 80-year mystery
1
Observatoire de Paris, Université PSL, Sorbonne Université, LERMA,
75014
Paris, France
e-mail: benjamin.godard@obspm.fr
2
Laboratoire de Physique de l’École Normale Supérieure, ENS, Université PSL, CNRS, Sorbonne Université, Université de Paris,
75005
Paris, France
3
Université Paris-Saclay, CNRS, Institut d’Astrophysique Spatiale,
91405
Orsay, France
4
Laboratoire AIM, CEA/IRFU, CNRS/INSU, Université Paris-Diderot, CEA-Saclay,
91191
Gif-Sur-Yvette, France
5
Harvard-Smithsonian Center for Astrophysics,
60 Garden Street,
Cambridge, MA, USA
6
Department of Physics, Graduate School of Science, Nagoya University,
Furo-cho, Chikusa-ku,
Nagoya
464-8602, Japan
Received:
29
April
2022
Accepted:
16
September
2022
Aims. The high abundances of CH+ in the diffuse interstellar medium (ISM) are a long-standing issue of our understanding of the thermodynamical and chemical states of the gas. We investigate here the formation of CH+ in turbulent and multiphase environments, where the heating of the gas is almost solely driven by the photoelectric effect.
Methods. The diffuse ISM is simulated using the magnetohydrodynamic (MHD) code RAMSES which self-consistently computes the dynamical and thermal evolution of the gas along with the time-dependent evolutions of the abundances of H+, H, and H2. The rest of the chemistry, including the abundance of CH+, is computed in post-processing, at equilibrium, under the constraint of out-of-equilibrium H+, H, and H2. The comparison with the observations is performed taking into account an often neglected yet paramount piece of information, namely the length of the intercepted diffuse matter along the observed lines of sight.
Results. Almost all of the mass of CH+ originates from unstable gas, in environments where the kinetic temperature is higher than 600 K, the density ranges between 0.6 and 10 cm−3, the electronic fraction ranges between 3 × 10−4 and 6 × 10−3, and the molecular fraction is smaller than 0.4. Its formation is driven by warm and out-of-equilibrium H2 initially formed in the cold neutral medium (CNM) and injected in more diffuse environments, and even the warm neutral medium (WNM) through a combination of advection and thermal instability. The simulation that displays the closest agreement with the HI-to-H2 transition and the thermal pressure distribution observed in the solar neighborhood is found to naturally reproduce the observed abundances of CH+, the dispersion of observations, the probability of occurrence of most of the lines of sight, the fraction of nondetections of CH+, and the distribution of its line profiles. The amount of CH+ and the statistical properties of the simulated lines of sight are set by the fraction of unstable gas rich in H2, which is controlled on Galactic scales by the mean density of the diffuse ISM (or, equivalently, its total mass), the amplitude of the mean UV radiation field, and the strength of the turbulent forcing.
Conclusions. This work offers a new and natural solution to an 80-yr-old chemical riddle. The almost ubiquitous presence of CH+ in the diffuse ISM likely results from the exchange of matter between the CNM and the WNM induced by the combination of turbulent advection and thermal instability, without the need to invoke ambipolar diffusion or regions of intermittent turbulent dissipation. Through two-phase turbulent mixing, CH+ might thus be a tracer of the H2 mass loss rate of CNM clouds.
Key words: ISM: structure / ISM: molecules / ISM: kinematics and dynamics / ISM: clouds / methods: numerical / methods: statistical
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1 Introduction
The methylidyne cation CH+ is among the molecules the most frequently seen in the diffuse interstellar medium. Since its first detection in 1941 by Douglas & Herzberg (1941), CH+ has been observed in absorption along a great variety of diffuse Galactic lines of sight, first with optical facilities (see Appendix A) and later on with the Herschel Space Telescope (e.g., Falgarone et al. 2010; Godard et al. 2012). Surprisingly, very few lines of sight are dark in CH+. The presence of CH+ in the diffuse ISM is so ubiquitous that this molecular ion is now frequently detected in external galaxies, including nearby objects (e.g., Rangwala et al. 2011; Spinoglio et al. 2012; Ritchey et al. 2015) and Starburst galaxies at high redshift (e.g., Falgarone et al. 2017).
The high abundances and the remarkable coverage of CH+ raise a chemical conundrum. Easily destroyed by collisions with H, H2, and e−, or by photodissociation, CH+ requires an efficient formation pathway. The only reaction capable of balancing its fast destruction is C+ + H2 → CH+ + H, a highly endothermic chemical process (ΔE/k ~ 4640 K, where k is the Boltzmann constant). On the one hand, the formation of CH+ can only proceed at high effective temperature (see Eq. (2.1) of Pineau des Forêts et al. 1986). On the other hand, it requires molecular hydrogen, which is mainly formed in cold environments.
One possible solution to this issue is the release of suprathermal energy induced by the intermittent dissipation of interstellar turbulence. This scenario, initially proposed by Elitzur & Watson (1978, 1980), was studied using 1D idealized structures of turbulent dissipation such as magnetohydrodynamic (MHD) shocks (e.g., Draine 1986; Pineau des Forêts et al. 1986; Flower & Pineau des Forêts 1998) or magnetized vortices (Godard et al. 2009, 2014). In particular, Godard et al. (2014) found that the observed abundances of CH+ and many other molecular species can be explained if all the mechanical energy of the cold neutral medium (CNM) is dissipated in the CNM itself, in structures where the dissipation occurs through ambipolar diffusion with a typical ion-neutral velocity drift of ~3 km s−1, three stringent necessary conditions.
These studies were recently followed by 2D numerical simulations of hydrodynamic turbulence (Lesaffre et al. 2020) and 3D numerical simulations of ideal MHD turbulence (Myers et al. 2015; Moseley et al. 2021) applied to the CNM. Myers et al. (2015) and Moseley et al. (2021) argued that the distribution of the ion-neutral velocity drift expected in the CNM is sufficient to explain the observed abundances of CH+. However, their estimation of the velocity drift, obtained in the framework of ideal MHD with no feedback on the magnetic field strength, constant ionization and molecular fractions, and a single momentum transfer rate coefficient, leads to artificially large velocity drifts in the low density gas (nH ~ 1 cm−3) where most of the CH+ is produced. As pointed out by Moseley et al. (2021), the effect is so large that an arbitrary cutoff at 5 km s−1 needs to be applied to prevent the ambipolar heating rate from exceeding the driving power of their simulations. Moreover, by focusing on the CNM, these simulations neglect the transfer of kinetic energy between the CNM and the WNM that naturally occurs in multiphase environments.
The above discussion shows that while the scenario of turbulent dissipation offers a plausible solution, it suffers from two major caveats. First, it surmises that the mechanical energy dissipated in the CNM is on the order of the mechanical energy of CNM clouds, which is debatable. Second, it requires reliable descriptions of the distribution of the ion-neutral velocity drift in regions of turbulent dissipation, which are currently uncertain and overestimated in the framework of ideal MHD.
Another possible yet poorly explored solution to the formation of CH+ in the diffuse ISM is the exchange of matter between the WNM and the CNM induced by turbulent mixing (Lesaffre et al. 2007) or a combination of turbulent advection and thermal instability (Valdivia et al. 2017). In this scenario, cold molecular hydrogen initially formed in the CNM is naturally transported into the warm unstable phase where it survives long enough to activate the formation of CH+. Valdivia et al. (2017) showed that this process greatly increases the production of CH+ although to a level 3–10 times lower than the observations. This result was derived, however, from the outputs of a single simulation with no exploration of the parameter domain. In particular, the distribution of the column densities of H2 predicted by the simulation was in poor statistical agreement with the observations of the HI-to-H2 transition in the local ISM (see Fig. 13 of Valdivia et al. 2016). In addition, the comparisons with the observations were performed without taking into account the distribution of lengths of the observed diffuse lines of sight.
All these limitations were recently obviated by Bellomi et al. (2020, hereafter Paper I) who performed a large parametric study, including 305 numerical simulations, of the turbulent and multiphase diffuse ISM. The results of their standard simulation were shown to simultaneously explain the position, the width, the dispersion, and most of the statistical properties of the HI-to-H2 transition observed in the local ISM with a precision never achieved by any previous theoretical model. The parametric study led to the conclusion that the observed HI-to-H2 transition is statistical in nature and traces the distributions and sizes of warm and cold phases mostly set by the mean density of the local diffuse ISM and the density of OB stars, with little dependence on the strength or the nature of the turbulent forcing.
In the present paper we reinvestigate the scenario of formation of CH+ induced by the turbulent and multiphase nature of the interstellar medium applying the methodology of Paper I. The observational sample is presented in Sect. 2. The setup, the updates, and the main properties of the numerical simulations are described in Sect. 3. The comparison with the observations and the exploration of the parameters are performed in Sects. 4 and 5. Discussion of our results and the main conclusions are presented in Sects. 6 and 7.
 |
Fig. 1 Properties of the observed lines of sight. Top: Aitoff projection, in Galactic longitude and latitude coordinates, of the background sources of the CH+ observational sample (see Table A.1). The color-coding indicates the distance of background sources, and the symbol shapes correspond to the lines of sight where CH+ is detected (circles) or not detected (triangles). Bottom: distribution of the lengths of the intercepted diffuse material computed with Eq. (1) along all the lines of sight of the observational sample. The orange sample corresponds to lines of sight where CH+ is detected and the green sample to those for which an upper limit on N(CH+) has been derived (see the bottom part of Table A.1). The two samples are summed in order to display the total number of sources observed in each bin. |
2 Observational sample
The observational sample is described in detail in Appendix A and Table A.1. It contains 229 lines of sight where the 4232 Å line of CH+ was searched in absorption against the optical continuum of background stars. This sample, which to date forms the most complete set of observations of CH+ in the local diffuse ISM, includes 175 detections and 54 upper limits. The position of the sources in Galactic coordinates and their distances derived from recent measurements of their parallaxes are shown in the top panel of Fig. 1. The lines of sight are rather homogeneously distributed in Galactic longitude. In contrast, and similarly to the sample studied in Paper I, about two-thirds of the sources are located at a Galactic latitude below 15°, following the distribution of stars in the solar neighborhood.
Because the amount of gas exponentially decreases as a function of the distance from the midplane of the Galaxy, the length of material intercepted by any line of sight is not always equal to the distance of the background source. Following the simple prescription adopted in Paper I, we assume a height above the midplane of 100 pc and compute this length as
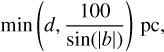 (1)
(1)
where d is the distance of the background source and b is its Galactic latitude (see Table A.1). The distribution of lengths of the intercepted diffuse gas is shown in the bottom panel of Fig. 1 and extends over more than two orders of magnitude, from ~10 pc to a few kpc. We find that the length of the intercepted diffuse material follows a flat distribution in log scale from 0.1 to 2 kpc, as was found for the observations of the HI-to-H2 transitions in the solar neighborhood (Paper I). Interestingly, CH+ is never detected along lines of sight shorter than ~100 pc. Conversely, the number of nondetections of CH+ rapidly decreases with the length of the line of sight and reaches zero at ~1 kpc. As explained in Paper I, this distribution of length of the intercepted material is of paramount importance to accurately compare the results of numerical simulations with the distribution of chemical composition observed in the diffuse ISM.
3 Theoretical models of the multiphase ISM
3.1 Numerical setup
The theoretical models used in this work are updates of the large grid of MHD simulations of the multiphase diffuse ISM presented in length in Paper I. In a nutshell, the diffuse, turbulent, and multiphase neutral medium is modeled using the RAMSES code (Teyssier 2002; Fromang et al. 2006). The simulations follow a magnetized and partially ionized gas with a mean proton density 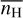 over a box of size L with periodic boundary conditions and illuminated from all sides by the standard isotropic UV radiation field (Mathis et al. 1983) scaled by a factor G0. The z-axis is chosen as the direction perpendicular to the Galactic midplane. A z-dependent gravitational potential is included to mimic the presence of stars and dark matter, while a homogeneous initial magnetic field Bx is set along the x-axis. Throughout the simulations, mechanical energy is regularly injected in the gas at large scale (~L/2) via random fluctuations of the acceleration field in Fourier space (e.g., Schmidt et al. 2009; Federrath et al. 2010). The amplitude of this forcing and the relative power injected in compressive modes are controlled by two parameters, F and ζ, respectively (e.g., Saury et al. 2014). All the models are run without adaptative mesh refinement: the number of grid cells is therefore equal to the numerical resolution R.
over a box of size L with periodic boundary conditions and illuminated from all sides by the standard isotropic UV radiation field (Mathis et al. 1983) scaled by a factor G0. The z-axis is chosen as the direction perpendicular to the Galactic midplane. A z-dependent gravitational potential is included to mimic the presence of stars and dark matter, while a homogeneous initial magnetic field Bx is set along the x-axis. Throughout the simulations, mechanical energy is regularly injected in the gas at large scale (~L/2) via random fluctuations of the acceleration field in Fourier space (e.g., Schmidt et al. 2009; Federrath et al. 2010). The amplitude of this forcing and the relative power injected in compressive modes are controlled by two parameters, F and ζ, respectively (e.g., Saury et al. 2014). All the models are run without adaptative mesh refinement: the number of grid cells is therefore equal to the numerical resolution R.
In this configuration, RAMSES follows the thermodynamical evolution of the gas, taking into account heating and cooling processes, and the out-of-equilibrium evolution of H+, H, and H2, as described below. Each simulation is run over a few turnover timescales until it reaches a steady state where the physical properties of the multiphase ISM (the fraction of gas in the different phases, the mean pressure, the mean velocity dispersion, and the mean molecular fraction) are roughly stationary. The standard set of parameters is given in Table 1. It slightly differs from that adopted in Paper I, with a mean density 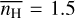 cm−3 (instead of 2 cm−3), a turbulent forcing strength F = 1.5 × 10−3 kpc Myr−2 (instead of 9 × 10−4 kpc Myr−2), and a resolution of 5123 (instead of 2563).
cm−3 (instead of 2 cm−3), a turbulent forcing strength F = 1.5 × 10−3 kpc Myr−2 (instead of 9 × 10−4 kpc Myr−2), and a resolution of 5123 (instead of 2563).
Several physical and chemical processes have been modified compared to those treated in the simulations used in Paper I. These modifications, described in the next two sections, include updates of the heating and cooling processes, the calculation of the time dependent evolution of the abundance of H+, and updates of the treatment of the photodissociation of H2.
Standard values of the simulation parameters.
3.2 Updates of the heating and cooling processes
In Paper I, the thermodynamical evolution of the gas was computed taking into account the heating induced by the photoelectric effect and the cosmic ray particles, the radiative cooling induced by the Lyman α line and the fine structure lines of OI and CII, and the cooling due to the recombination of electrons onto grains.
To account for the impact of H2 on the thermodynamical evolution of the gas, we include here three additional mechanisms: the heating induced by the formation of H2, the heating that follows its photodestruction, and the radiative cooling induced by the collisional excitation of its rovibrational levels. The first two heating rates are modeled using Eqs. (13) and (14) of Valdivia et al. (2016) who assumed that one-third of the binding energy of H2 (4.5 eV) is released in the gas during its formation and that 0.4 eV is released in the gas per photodestruction (Black & Dalgarno 1977). The cooling induced by the collisional excitation of H2 is calculated using the analytical functions prescribed by Moseley et al. (2021, Eqs. (17)-(21) of their paper) who performed fits of the cooling rate of H2, calculated with updated collisional rate coefficients, valid for kinetic temperatures below 5000 K.
Regarding the photoelectric effect, we adopt here the photoelectric heating rate given by Weingartner & Draine (2001) who provide a specific prescription for the diffuse interstellar medium (see Eq. (44) of their paper and the last line of their Table 2). Following Wolfire et al. (2003), and to ensure self-consistency between the computations of the photoelectric heating and the fractional abundance of H+ (see Sect. 3.3), we adopt a grain charging parameter
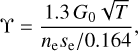 (2)
(2)
which depends on the sticking coefficient of electrons onto polycyclic aromatic hydrocarbons (PAHs), se. In the above formula, T is the kinetic temperature of the gas and ne is the density of electrons. The resulting photoelectric heating rate therefore writes
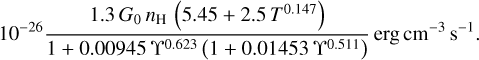 (3)
(3)
The factor 1.3 in Eqs. (2) and (3) accounts for the ratio between the energy density of the Mathis field (Mathis et al. 1983), used as reference in this work, and that of the Habing field (Habing 1968), used as reference by Weingartner & Draine (2001). Throughout this work, the sticking coefficient of electrons onto PAHs is set to 1 for the computations of both the photoelectric heating rate and the out-of-equilibrium abundance of H+.
Reaction rates of the formation and destruction processes of H+, PAH, PAH0, and PAH+ included in the simulations.
3.3 Treatment of the chemistry
The timescale required for the electron abundance to reach chemical equilibrium spans several orders of magnitude depending on the physical conditions of the ISM. Expected to be short for CNM conditions (~104 yr), this equilibrium timescale considerably increases in WNM environments (a few 106 yr) where it becomes larger than the dynamical timescale. To account for potential out-of-equilibrium effects in the unstable and the WNM phases, we model the fractional abundance of electrons as x(e−) = x(C+) + x(H+), where the fractional abundance of C+, x(C+), is set to a constant value of 1.4 × 10−4, while that of H+, x(H+), is computed in the simulation. Following Wolfire et al. (2003), we assume that the fractional abundance of H+ in the diffuse neutral ISM is driven by the ionization of H induced by extreme ultraviolet (EUV) photons, soft X-rays, and cosmic rays, and by the recombination of H+ on negatively charged and neutral PAHs1. The abundances of PAHs in their different ionization states are supposed to be driven by photodetachment and photoionization processes, on the one hand, and by recombination with free electrons, on the other. The rates adopted for all these processes are given in Table 2. The size of the PAHs is set to 5 Å and their fractional abundance to 10−6, which corresponds to a total abundance of carbon of 6 × 10−5 in very small grains (Weingartner & Draine 2001). In diffuse interstellar conditions, the timescale required for the PAHs, in any ionized state, to reach their equilibrium abundance is less than 10 yr, which is far shorter than the dynamical timescale of the gas and the equilibrium timescale of H+. The abundances of negatively charged, neutral, and positively charged PAHs can therefore be computed at equilibrium. This consideration leads to a simplified differential equation for the abundance of H+ which is solved in each cell and at each timestep in the simulation using the splitting operator method.
As in Paper I, the out-of-equilibrium evolution of the abundances of H and H2 are computed in the simulation, taking into account the formation of H2 onto grains and its photodestruction by UV photons. In particular, the photodestruction rate of H2 is modeled as
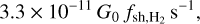 (4)
(4)
where the shielding factor, 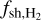 , is computed by averaging at any point the shielding factor due to dust extinction and the self-shielding factor of H2 over 12 solid angles evenly spread over the polar coordinates (Valdivia et al. 2016). In Paper I the self-shielding of H2 was derived using the prescription of Draine & Bertoldi (1996). This prescription is reliable for diffuse gas at low temperature, but becomes less reliable for high temperature environments (T > 500 K) where the collisional excitation of H2 in its rovibrational levels reduces the efficiency of the self-shielding (Wolcott-Green et al. 2011). To account for this effect, we use here the self-shielding function given by Wolcott-Green et al. (2011, Eq. (12) in their paper with α = 1.1) using a Doppler broadening parameter of 2 km s−1 in favor of the small-scale self-shielding (see Sects. 5.5 and 5.6 of Paper I).
, is computed by averaging at any point the shielding factor due to dust extinction and the self-shielding factor of H2 over 12 solid angles evenly spread over the polar coordinates (Valdivia et al. 2016). In Paper I the self-shielding of H2 was derived using the prescription of Draine & Bertoldi (1996). This prescription is reliable for diffuse gas at low temperature, but becomes less reliable for high temperature environments (T > 500 K) where the collisional excitation of H2 in its rovibrational levels reduces the efficiency of the self-shielding (Wolcott-Green et al. 2011). To account for this effect, we use here the self-shielding function given by Wolcott-Green et al. (2011, Eq. (12) in their paper with α = 1.1) using a Doppler broadening parameter of 2 km s−1 in favor of the small-scale self-shielding (see Sects. 5.5 and 5.6 of Paper I).
Only the abundances of H+, H, and H2 are computed during the numerical simulation. The rest of the chemical composition of the diffuse and multiphase ISM is computed in post-treatment using a chemical solver presented in Appendix A of Valdivia et al. (2017). This solver computes the abundances of atomic and molecular species, assuming chemical equilibrium for all species except for H+, H, and H2, which, depending on the choice of the user, can be given as input parameters or computed at equilibrium. The chemical network used by the solver is taken from the Meudon PDR code2 (Le Petit et al. 2006) and includes 151 species interacting through a network of 2715 reactions. In this network, the chemistry of CH+ is mainly driven by five different reactions, its formation through the hydrogenation of C+, and its destruction by photodissociation and reactive collisions with H, H2, and e−. The rates adopted for these processes are given in Table 3.
Reaction rates of the main formation and destruction processes of CH+ and associated references.
3.4 Physical properties of the standard simulation
The updates described in the previous sections have an important impact on the thermochemical properties of the multiphase ISM simulated with RAMSES compared with the simulations presented in Paper I. In particular, the cooling induced by the excitation of the rovibrational levels of H2 suppresses the thermal instability process in fully molecular media. This cooling mechanism therefore efficiently prevents CNM clouds from evaporating back into the WNM as long as H2 is not destroyed, at least partly. The updates performed on the photoelectric effect and the computation of the out-of-equilibrium abundance of H+ are found to boost the efficiency of the photoelectric heating and produce a multiphase gas at higher thermal pressure than those reported in Fig. 4 of Paper I.
Given the differences between our two studies, we discuss here the choice of the standard setup and compare its main physical properties to those derived in the local diffuse ISM. The standard setup corresponds to a neutral diffuse ISM extending over 200 pc, illuminated by the interstellar radiation field of Mathis et al. (1983) and with a mean density 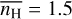 cm−3 (see Table 1). As discussed in Paper I (Sect. 3.5), the scale of illumination of the gas is comparable to the typical distances between OB star associations in the solar neighborhood (e.g., Zari et al. 2018). Given the uncertainties on the volume filling factor of the fully ionized gas (see Sect. 5.3 of Paper I), the mean density is in agreement with the standard Galactic midplane density of HI at a galactocentric distance of 8.5 kpc (Kalberla & Kerp 2009) derived from the measurement of the mass surface density of HI in the solar neighborhood (e.g., Nakanishi & Sofue 2016).
cm−3 (see Table 1). As discussed in Paper I (Sect. 3.5), the scale of illumination of the gas is comparable to the typical distances between OB star associations in the solar neighborhood (e.g., Zari et al. 2018). Given the uncertainties on the volume filling factor of the fully ionized gas (see Sect. 5.3 of Paper I), the mean density is in agreement with the standard Galactic midplane density of HI at a galactocentric distance of 8.5 kpc (Kalberla & Kerp 2009) derived from the measurement of the mass surface density of HI in the solar neighborhood (e.g., Nakanishi & Sofue 2016).
The standard simulation reaches a steady state in ~30 Myr. The WNM (defined here by T > 3000 K), the CNM (defined here by T < 300 K), and the unstable gas at intermediate temperature, the lukewarm neutral medium (LNM), encompass respectively 35%, 54%, and 11% of the total mass of the gas. We display in Fig. 2 the 2D probability histogram of the column densities of H and H2 obtained with the standard simulation3 and the probability distribution function of the pressure (normalized to its maximum) predicted in the CNM. As found in Paper I, the multiphase ISM simulated with the RAMSES code reproduces, to an outstanding level, the statistical properties of the HI-to-H2 transition observed in the local interstellar medium, which include the position of the transition, its width, the dispersion of observations, and the occurrence of most of the lines of sight. In addition, as shown in the bottom panel of Fig. 2, the distribution of thermal pressure obtained in the cold neutral medium is in agreement with the pressure distribution derived by Jenkins & Tripp (2011, Eq. (3) in their paper) from the observations of the excitation of the fine structure levels of atomic carbon. This last result significantly differs from Paper I where the standard simulation was underpredicting the mean thermal pressure of the ISM by a factor of ~3.5 (see Fig. 4 in Paper I). The width of the pressure probability distribution function is controlled by the strength of the turbulent forcing, which is set here to F = 1.5 × 10−3 kpc Myr−2. We find that such a turbulent forcing not only ensures that the CNM covers the same thermal pressure range than that inferred from the observations, but also leads to a 1D turbulent velocity dispersion of the WNM (calculated using Eqs. (17), (19), and (20) in Paper I) of ~5.4 km s−1, in agreement with the velocity dispersion deduced from HI emission spectra at high Galactic latitude (Kalberla et al. 2005; Haud & Kalberla 2007).
The turbulent forcing and the homogeneous magnetic field applied in the simulation lead to an equipartition between the kinetic and magnetic energy densities at a level of ~1.6 × 10−12 erg cm−3. In comparison, the impinging UV radiation field4 (Mathis et al. 1983) has an energy density of 6.1 × 10−14 erg cm−3 between 6 and 13.6 eV (Weingartner & Draine 2001). However, these reservoirs of energy have very different cycling timescales. The dissipation of the mechanical energy is almost entirely mediated by numerical viscosity. The cycling of the mechanical energy typically occurs on a turnover timescale, implying an artificial turbulent heating rate of ~1.5 × 10−27 erg cm−3 s−1. Because of the fast cycling of the UV radiative energy, this turbulent heating rate is far lower than the heating induced by the photoelectric effect ~ 10−25 erg cm−3 s−1, which effectively dominates the heating of the gas and sets its thermal energy density at a level of 9.9 × 10−13 erg cm−3. The main physical properties of the standard simulation are summarized in Table 4.
 |
Fig. 2 Comparison of the main thermochemical properties of the standard simulation with observations of the local diffuse ISM. Top: comparison of the observational dataset of the HI-to-H2 transition of Paper I (black points) to the 2D probability histogram obtained with the standard simulation after application of the reconstruction algorithm (see Sect. 3.8 of Paper I). Observations include detections of H2 (circles) and upper limits on its column density (arrows). The color-coding indicates the fraction of lines of sight (in logarithmic scale) contained in each bin. Bottom: probability distribution function of the thermal pressure of the cold neutral medium in the standard simulation (blue histograms) compared with the probability distribution function of the thermal pressure deduced from the observation of the fine structure levels of carbon (Jenkins & Tripp 2011; black curve). Both distributions are normalized to their maximum value to facilitate comparison. |
Main physical properties of the standard simulation.
3.5 Origin of CH+
The chemical composition of the gas at any point of the simulation, such as the fractional abundance of CH+, x(CH+), depends on several local quantities which include the density, nH; the kinetic temperature, T; the electronic fraction, x(e−); and the molecular fraction5, f(H2). In addition, the molecular fraction also depends on the shielding factor of H2 from the UV dissociative radiation field, 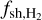 (see Eq. (4)). The regions responsible for the production of CH+ in the standard simulation are shown in Fig. 3, which displays the 2D probability distribution functions of the fraction of mass of CH+ as a function of nH and nHT (top panel), x(CH+) and x(e−) (middle panel), and f(H2) and
(see Eq. (4)). The regions responsible for the production of CH+ in the standard simulation are shown in Fig. 3, which displays the 2D probability distribution functions of the fraction of mass of CH+ as a function of nH and nHT (top panel), x(CH+) and x(e−) (middle panel), and f(H2) and 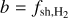 (bottom panel). Figure 3 shows that 90% of the mass of CH+ originates from the warm and unstable gas with 0.6 < nH < 10 cm−3, 600 < T < 8000 K, 3 × 10−4 < x(e−) < 6 × 10−3, 2 × 10−3 < f(H2) < 0.4, and
(bottom panel). Figure 3 shows that 90% of the mass of CH+ originates from the warm and unstable gas with 0.6 < nH < 10 cm−3, 600 < T < 8000 K, 3 × 10−4 < x(e−) < 6 × 10−3, 2 × 10−3 < f(H2) < 0.4, and 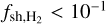 . The corresponding gas encompasses only ~3.5% of the mass of the diffuse ISM and occupies only ~1.5% of its total volume. Its physical conditions imply that CH+ is primarily destroyed by collision with H6, yet its production through the hydrogenation of C+ is so efficient that CH+ reaches typical fractional abundances between 3 × 10−9 and 4 × 10−6. In these regions, CH+ can therefore carry as much as ~3% of the elemental abundance of carbon7. Interestingly, we find that the total mass of CH+ predicted by the simulation strongly depends on whether the abundance of H2 is computed at equilibrium by the chemical solver (M(CH+) ~ 3.1 × 10−4 M⊙) or out-of-equilibrium during the simulation itself (M(CH+) ~ 1.1 × 10−2 M⊙). All these behaviors result from the following physical processes.
. The corresponding gas encompasses only ~3.5% of the mass of the diffuse ISM and occupies only ~1.5% of its total volume. Its physical conditions imply that CH+ is primarily destroyed by collision with H6, yet its production through the hydrogenation of C+ is so efficient that CH+ reaches typical fractional abundances between 3 × 10−9 and 4 × 10−6. In these regions, CH+ can therefore carry as much as ~3% of the elemental abundance of carbon7. Interestingly, we find that the total mass of CH+ predicted by the simulation strongly depends on whether the abundance of H2 is computed at equilibrium by the chemical solver (M(CH+) ~ 3.1 × 10−4 M⊙) or out-of-equilibrium during the simulation itself (M(CH+) ~ 1.1 × 10−2 M⊙). All these behaviors result from the following physical processes.
The steady state obtained in numerical simulations of turbulent and multiphase ISM is statistical in nature (e.g., Seifried et al. 2011; Saury et al. 2014; Paper I). The forcing applied at large scale at regular time intervals and the resulting turbulent cascade lead to strong pressure variations and the formation of CNM structures at all scales that are not at thermodynamical equilibrium. Because the volume and the mass of the gas are fixed, the combined actions of the turbulent forcing and the thermal instability induce mass exchanges between the two stable phases, the WNM (T ~ 8000 K) and the CNM (T < 300 K), thus the existence of a substantial amount of gas in the lukewarm neutral medium (LNM) at intermediate temperatures. Whether this unstable phase triggers the formation of CH+ or not depends on the history of the gas. Because the WNM is poor in H2 (f(H2) ~ 10−7, see Paper I), LNM gas transiting from the WNM to the CNM weakly contributes to the production of CH+. The formation of CH+ in the LNM is thus necessarily dominated by the evaporation of CNM clouds, initially rich in H2. This scenario requires that the H2 injected in the warm phase survives long enough to allow the production of CH+ and that the formation of CH+ occurs quickly. Because of the efficient shielding of the surrounding environment, the H2 injected in the LNM has a destruction timescale up to 2 × 106 yr (see bottom panel of Fig. 3 and Eq. (4)), a period longer than the dynamical timescale (< 105 yr). In comparison, the rates given in Table 3 and the conditions of production of CH+ shown in Fig. 3 imply that CH+ reaches its local equilibrium abundance on timescales of less than ~100 yr. This short timescale not only ensures a maximum production of CH+, but also justifies, a posteriori, the use of the chemical solver to post-process the simulation.
 |
Fig. 3 Two-dimensional probability distribution functions of the fraction of mass of CH+ in the fiducial simulation d[M(CH+)/Mtot(CH+)]/[dlog(a) dlog(b)] displayed in a a = nH and b = nHT diagram (top panel), a a = x(CH+) and b = x(e−) diagram (middle panel), and a a = f(H2) and |
 |
Fig. 4 Maps of the column densities of H2 (left panel) and CH+ (right panel) predicted with the standard simulation (see Table 1) and obtained by integrating the densities along the x-axis over the entire box of size L = 200 pc. |
4 Comparison with observations
The maps of the column densities of H2 and CH+ integrated along the x-axis across the standard simulation are shown in Fig. 4. The production of CH+ induced by the injection of H2 in the warm and diffuse ISM leads to a substantial amount of lines of sight rich in CH+ with column densities higher than 1012 cm−2 and up to ~1014 cm−2. The surface filling factor of these lines of sight over a box of 200 pc of diffuse neutral gas is 56%. Because the size L of neutral medium is fixed, these distributions of column densities cannot be directly compared with the observations. A quantitative and statistical comparison with the observational data requires to take into account the length of diffuse neutral material intercepted by the observed lines of sight.
4.1 Distribution of simulated lines of sight
The comparison with the observations is performed statistically, using the methodology proposed in Paper I (Sect. 3.8 and Fig. 5). We assume that a simulation of size L is a building-block of the neutral diffuse ISM. We construct a random sample of 105 lines of sight with a length distribution given by the distribution of the observed sample (bottom panel of Fig. 1). Each line of sight is supposed to intercept diffuse neutral matter, but also hot and fully ionized gas. The fraction of the line of sight occupied by this hot ionized medium is set to a constant value of 0.5 (see Sect. 5.3 of Paper I). The total proton column density, NH, and the column density of CH+, N(CH+), along each line of sight are built by integrating the abundances along the x-axis8 over a fraction of the simulation if the length occupied by the neutral material is smaller than L, or by stacking together several random lines of sight of size L if the length occupied by the neutral material is longer than L.
The resulting 2D probability histograms of NH and N(CH+) are shown and compared with the observations in Fig. 5. The color-coding indicates the fraction of simulated lines of sight with a given chemical composition (NH,N(CH+)). The results shown here correspond to the fiducial simulation (Table 1), which is found to display an outstanding statistical agreement with the observations of the HI-to-H2 transitions (see Fig. 2). If the abundance of H2 is computed at equilibrium, the simulation underestimates the column densities of CH+ by about two orders of magnitude (top panel of Fig. 5). However, if H2 is computed out-of-equilibrium, the very same setup appears to naturally reproduce the distribution of observations of NH and N(CH+) (bottom panel of Fig. 5). For NH > 1021 cm−2, the simulation predicts that most of the lines of sight should have high column densities of CH+, with log[N(CH+)/NH] ~ −8.57 ± 0.28 in remarkable agreement with the mean and dispersion values of the observational sample in this domain (−8.37 ± 0.32). For NH < 1021 cm−2, the simulated and observed samples must be compared by taking into account the number of nondetections. The observations show a limit of detection of CH+ of ~1012 cm−2. For NH < 1020 cm−2, 98% of the simulated lines of sight have a column density of CH+ below 1012 cm−2 in agreement with the number of nondetections in this domain (100%). For 1020 < NH < 1021 cm−2, the predicted and observed fractions of nondetections similarly drop to 60% and 65%, respectively. In this domain the simulated lines of sight with N(CH+) > 1012 cm−2 verify log[N(CH+)/NH] ~ −8.27 ± 0.32, in agreement with, although slightly lower than, the observed values (−7.85 ± 0.54).
It is important to note that the mass flow rate between the CNM and the WNM induced by large-scale turbulence not only produces an amount of CH+ comparable to the observations, but also naturally generates all the statistical properties seen in the observations. As shown in Fig. 5, this process simultaneously explains the probabilities of occurrence of most of the lines of sight, the probabilities of nondetections of CH+, the mean fractional abundances of CH+, and their dispersions, all as functions of the total proton column density NH. Such a precise description of the observational data has never been achieved, nor even been searched for, by any previous theoretical model.
In the following section, we deepen the analysis by comparing the results of the simulation to another important, yet poorly studied, observational signature: the kinematic information carried in the line profiles of CH+.
 |
Fig. 5 Comparison of the observational dataset (black points) with the 2D probability histogram of NH and N(CH+) predicted by the fiducial simulation (colored histogram) after application of the chemical solver and the lines of sight reconstruction algorithm. The observational dataset include detections (open circles) and nondetections (filled triangles) of CH+. The color-coding indicates the fraction of lines of sight (in logarithmic scale) contained in each bin. Two cases are shown: the chemical solver computes the abundance of H2 at equilibrium (top panel) or uses the out-of-equilibrium abundance of H2 calculated during the simulation (bottom panel). |
4.2 Distribution of line profiles
The observations performed in the optical and submillimeter domains have long revealed the kinematic signatures of CH+ (e.g., Crane et al. 1995). Multi-Gaussian fits of the observations systematically show that the CH+ absorption lines have typical linewidths of a few km s−1 and are broader than the absorption lines of most of the molecules and molecular ions observed in the diffuse ISM (e.g., Crane et al. 1995; Godard et al. 2012). Principal component analyses of absorption spectra show that the kinematic profile of CH+ is similar to that of HI (Neufeld et al. 2015). Such broad absorption profiles are a firm signature of the regions that produce CH+. Because they follow the 3D dynamical, thermal, and chemical states of the gas, the simulations used in this work open the possibility to perform a comparative study between observational and theoretical line profiles. This analysis is done by applying the following methodology.
Synthetic spectra of the X1Σ+ − A1∏ 4232 Å line of CH+ are computed across the standard simulation along 200 random lines of sight with N(CH+) > 1012 cm−2, a value chosen from the observational detection limit of CH+ (see Fig. 5). Because the density and the kinetic temperature are too low to significantly excite the A1∏ state of CH+, the emissivity of this line is negligible along the line of sight. The velocity dependent specific intensity I(v) relative to that of the continuum background Ic is thus simply calculated as
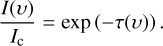 (5)
(5)
The line opacity τ(υ) is integrated along the x-axis
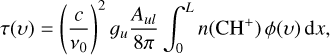 (6)
(6)
where v0, Au1, and gu are respectively the line rest frequency, its spontaneous emission rate, and the degeneracy of the upper level; c is the speed of light; and n(CH+) is the local density of CH+. The local line profile ϕ(υ) is assumed to be Gaussian and is computed as
![$\phi \left( \upsilon \right) = {1 \over {\sqrt {2\pi } \sigma }}\exp \left( { - {1 \over 2}{{\left[ {{{\upsilon - {\upsilon _0}} \over \sigma }} \right]}^2}} \right),$](/articles/aa/full_html/2023/01/aa43902-22/aa43902-22-eq16.png) (7)
(7)
where υ0 is the local velocity of the gas projected along the x-axis and σ is the local 1D velocity dispersion
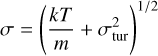 (8)
(8)
set by the local kinetic temperature, T; the mass of CH+, m; and the micro-turbulent velocity dispersion, σtur, at the resolution scale of the simulation. Because σtur is, by construction, inaccessible from the simulation, its value is set from the velocity dispersion–size relation of molecular clouds (e.g., Larson 1981; Hennebelle & Falgarone 2012) as
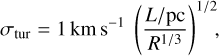 (9)
(9)
where L is the size of the simulated box expressed in pc and R is the numerical resolution. This choice implies that the microturbulent velocity dispersion of the standard simulation, σtur = 0.625 km s−1, is always smaller than the thermal velocity dispersion of the gas producing CH+ (T > 600 K, see Fig. 3), and therefore has a weak impact on the resulting line profiles.
Once computed, the 200 synthetic spectra are analyzed with the same method as that applied to real observations. The opacity profile of each spectrum is decomposed into velocity components by performing a multi-Gaussian fit using the curve fit optimization algorithm provided by the SciPy python library. The number of components is chosen as the minimum number of Gaussian features required to reproduce the spectrum with residual opacities about ten times below the peak opacity of the spectrum. Examples of the synthetic spectra obtained across the standard simulations and their multi-Gaussian decompositions are displayed in Fig. 6. The detection limit N(CH+) > 1012 cm−2 implies typical peak opacities of the 4232 Å line of CH+ greater than ~0.01. The distribution of phases along the lines of sight, the large-scale velocity dispersion of the diffuse ISM set by the turbulent forcing, and the velocity dispersion of the gas producing CH+ frequently lead to blended features that require more than one Gaussian component. A total of 24%, 37%, 29%, 8%, and 2% of the spectra across 200 pc of diffuse neutral medium are fitted with one, two, three, four, and five Gaussian components respectively. In total, the 200 synthetic spectra are decomposed into 457 velocity components.
The resulting distribution of the full width at half maximum ∆V of the velocity components of CH+ is shown in Fig. 7 (bottom panel) and compared to the distribution extracted from optical observations of CH+ in the local ISM (top panel). Surprisingly, the thermodynamical properties of the turbulent multiphase ISM obtained in the standard simulation are found to naturally explain the observed distribution of the CH+ absorption profiles. Most of the velocity components of CH+ are predicted to have linewidths between 1.5 and 5 km s−1, with a tail up to ~10 km s−1, as seen in the observational sample. The distribution obtained with the numerical simulation leads to an expected linewidth ∆V ~ 3.44 ± 0.87 km s−1 in agreement with the mean and dispersion values of the observational dataset (3.59 ± 1.18 km s−1).
The results displayed in Fig. 7 are promising and open new prospects for statistical comparisons between simulations and observations. It would be tempting, for instance, to perform a more advanced analysis of these distributions including the number of velocity components per line of sight and the probability of occurrence of each linewidth; however, such a detailed comparison requires to slightly adapt the methodology. First of all, the fact that the simulated spectra are built without noise necessarily leads to more and narrower velocity components than those extracted from real observational data. Moreover, a detailed comparison with the observations would require to compute synthetic spectra along lines of sight that follow the length distribution of the observed sample (bottom panel of Fig. 1) as was done above for the comparisons of the column densities. Finally, the micro-turbulent velocity dispersion (which has no impact on the current predictions) should be described more carefully. On the one hand, and because of numerical diffusion, the micro-turbulent velocity is probably underestimated and should be derived at slightly larger scales than the numerical resolution scale. On the other hand, this micro-turbulent velocity dispersion is deduced from the velocity dispersion–size relation of molecular clouds, which has no reason to apply to the evaporating medium responsible for the production of CH+. All these considerations are beyond the scope of the present paper.
5 Exploration of the parameters
In this section we discuss the dependence of the production of CH+ on several key parameters including the resolution of the simulation, R; the mean density, 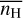 ; the UV illumination factor, G0; the strength of the turbulent forcing, F; and its compressive ratio, ζ. The exploration is performed over a set of 26 simulations. Each run is post-processed with the chemical solver using the out-of-equilibrium abundance of H2 computed during the simulation. A simulated sample of lines of sight is then drawn following the distribution of length of the observed sample. The influence of the parameters are estimated and discussed based on their impact on the probability histograms of NH and N(CH+) compared to that of the fiducial setup (Fig. 5).
; the UV illumination factor, G0; the strength of the turbulent forcing, F; and its compressive ratio, ζ. The exploration is performed over a set of 26 simulations. Each run is post-processed with the chemical solver using the out-of-equilibrium abundance of H2 computed during the simulation. A simulated sample of lines of sight is then drawn following the distribution of length of the observed sample. The influence of the parameters are estimated and discussed based on their impact on the probability histograms of NH and N(CH+) compared to that of the fiducial setup (Fig. 5).
5.1 Influence of the resolution
In Paper I, we found that the HI-to-H2 transition is independent of the resolution over about one order of magnitude (643 ⩽ R ⩽ 5123). This is understood by the fact that H2 is almost entirely produced in the CNM. The predicted distribution of the column densities of H2 therefore only depends on whether the simulation accurately resolves the CNM structures that carry most of the mass and volume of H2. While simulations at high resolution allow the formation of dense structures on small scales, they have a negligible impact on the mass of H2 and the volume it occupies. This result is expected to hold for any other chemical tracer as long as it is formed in the same regions as H2. This is not the case of CH+.
The impact of the resolution on the production of CH+ is shown in Fig. 8, which displays the total mass of CH+ contained in simulations at different resolutions, and in Fig. 9, which compares two isocontours of the 2D probability histograms of NH and N(CH+) for R = 643, 2563, and 5123. Unlike the HI-to-H2 transition, Figs. 8 and 9 show that the distribution of the column densities of CH+ strongly depends on the resolution for R < 2563, and is almost independent of the resolution for R ⩾ 2563. Quantitatively, the mass of CH+ produced in the simulation at R = 643 is ~5 times higher than that produced for R = 5123. In comparison, the simulation at R = 2563 produces only ~20% more CH+ than the simulation at R = 5123. This behavior, which significantly differs from that of the HI-to-H2 transition, is due to the origin of CH+. While H2 is built in the CNM, CH+ is entirely produced in the unstable diffuse ISM (LNM). As described in Sect. 3.5, the total mass of CH+ in these regions not only depends on their physical conditions (density, temperature, electronic fraction, and molecular fraction), which set the local abundance of CH+, but also on the rate at which H2 is injected from the CNM to the LNM. Interestingly, the analysis of the simulations at different resolutions show that the physical conditions of these regions are independent of the resolution. The observed dependence therefore solely results from changes in the rate of injection of H2 in the LNM. The results displayed in Figs. 8 and 9 suggest that this injection rate is dominated by numerical diffusion for R < 2563 and by a real physical process for R ⩾ 2563. The nature of this process is discussed in Sect. 5.3.
The weak dependence of the 2D probability histograms of NH and N(CH+) for a resolution R ⩾ 2563 indicates that the numerical convergence is reached at high resolution. Moreover, it justifies using simulations with a moderate numerical resolution to study the production of CH+ in the diffuse interstellar medium. The exploration of the parameter domain in the following sections are therefore performed for R = 2563.
 |
Fig. 6 Examples of absorption profiles of the 4232 Å line of CH+ computed along the x-axis across the standard simulation (see Table 1). The black histograms are the computed spectra. The colored curves are the results of a multi-Gaussian fit applied to the line opacity and display the individual Gaussian components (dashed red curves) and their sum (solid blue curves). The spectra are classified in increasing order of their maximum opacity (from top to bottom) and in increasing order of the number of Gaussian components used in the fit (from left to right). |
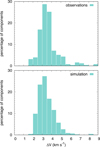 |
Fig. 7 Probability distributions of the full width at half maximum ΔV of the 4232 A line of CH+ derived from the observations (top panel) and from synthetic spectra (see Fig. 6) computed across the standard simulation (bottom panel). The observational sample includes 254 velocity components extracted along 120 lines of sight by Federman (1982; Table 2), Lambert & Danks (1986; Table 1), Crane et al. (1995; Table 2), Pan et al. (2004; Table 4), Ritchey et al. (2006; Table 4), and Sheffer et al. (2008; Table 3). This dataset includes all the lines of sight where CH+ has been observed (see Table A.1), except those observed or compiled by Gredel et al. (2002) and Rachford et al. (2002), who do not provide measurements of the CH+ linewidth. |
 |
Fig. 8 Total mass of CH+, Mtot(CH+), contained in simulations at different resolutions R (blue points). The data are fitted with the function a/Rb/3 + c, where a, b, and c are adjustable coefficients. The best fit (black curve) corresponds to the function 1.57 × 102/R2/3 + 1.05 × 10−2 and tends toward the constant value 1.05 × 10−2 (blue line) at high resolution. |
 |
Fig. 9 Isocontours of the 2D probability histograms of NH and N(CH+) predicted by simulations with a resolution R = 643 (green curve), 2563 (blue curve), and 5123 (pink curve), after application of the chemical solver and the lines of sight reconstruction algorithm. This representation shows, in a simplified manner, the effect of the resolution on the result displayed in Fig. 5. The isocontours chosen at 8 × 10−5 (top panel) and 8 × 10−4 (bottom panel) highlight the changes in the distribution of the most probable lines of sight. These values correspond to the turquoise blue and orange levels of the 2D probability histograms of NH and N(CH+) (see Fig. 5). |
5.2 Impact of G0 and 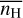
The impacts of the mean density and the strength of the UV radiation field are displayed in Fig. 10 (top frame), which shows comparisons of the 2D probability histograms of NH and N(CH+), predicted for various values of 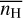 and G0, to the observational sample. The results obtained here are a direct consequence of those displayed in Fig. 9 in Paper I, which shows the dependence of the HI-to-H2 transition on these two parameters over a wider range of mean density
and G0, to the observational sample. The results obtained here are a direct consequence of those displayed in Fig. 9 in Paper I, which shows the dependence of the HI-to-H2 transition on these two parameters over a wider range of mean density 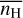 . Since the amount of CH+ is proportional to the rate of injection of H2 in the LNM, CH+ is tightly linked to the reservoir of H2 itself. An (under-) overestimation of the column densities of H2 in the local diffuse ISM directly translates into an (under-)overestimation of the column densities of CH+. Interestingly, we find that the statistical distribution of the observed column densities of CH+ can only be reproduced if the statistical distribution of the observed column densities of H2 are reproduced as well (see Fig. 2). These separated constraints emphasize the coherence of the chemical composition predicted with the standard setup.
. Since the amount of CH+ is proportional to the rate of injection of H2 in the LNM, CH+ is tightly linked to the reservoir of H2 itself. An (under-) overestimation of the column densities of H2 in the local diffuse ISM directly translates into an (under-)overestimation of the column densities of CH+. Interestingly, we find that the statistical distribution of the observed column densities of CH+ can only be reproduced if the statistical distribution of the observed column densities of H2 are reproduced as well (see Fig. 2). These separated constraints emphasize the coherence of the chemical composition predicted with the standard setup.
As explained in Paper I, the strong dependences of the results on 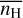 and G0 only weakly originate from changes in the local physical conditions. They are in fact a consequence of the statistical distributions of phases along random lines of sight. The thermal instability applied to diffuse gas with a constant volume and a constant mass implies that decreasing
and G0 only weakly originate from changes in the local physical conditions. They are in fact a consequence of the statistical distributions of phases along random lines of sight. The thermal instability applied to diffuse gas with a constant volume and a constant mass implies that decreasing 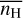 or increasing G0 considerably reduce the mass and the volume occupied by of the cold and dense CNM. This not only reduces the total mass of H2, but also the probability of obtaining lines of sight with large molecular fraction. Such lines of sight therefore occur at higher total column density, NH, and their molecular fractions exhibit a larger dispersion around the mean value. As expected from the interpretative framework given in Sect. 3.5, and as shown in the top frame of Fig. 10, the column densities and the total mass of CH+ reveal exactly the same dependences as the molecular fraction and the total mass of H2.
or increasing G0 considerably reduce the mass and the volume occupied by of the cold and dense CNM. This not only reduces the total mass of H2, but also the probability of obtaining lines of sight with large molecular fraction. Such lines of sight therefore occur at higher total column density, NH, and their molecular fractions exhibit a larger dispersion around the mean value. As expected from the interpretative framework given in Sect. 3.5, and as shown in the top frame of Fig. 10, the column densities and the total mass of CH+ reveal exactly the same dependences as the molecular fraction and the total mass of H2.
Figures 2 and 5 indicate that the fiducial setup slightly overestimates the mean pressure of the ISM, and slightly underestimates the total mass of H2 and CH+ (by a factor ~1.5). As shown in Fig. 10, these shallow discrepancies could be solved by slightly adjusting the mean density (above 1.5 cm−3) or the impinging radiation field (below 1). We consider such fine-tuning of the model parameters superfluous given the uncertainties on the key underlying microphysical processes discussed in Sect. 6 and on the turbulent forcing.
 |
Fig. 10 Comparison of the observational dataset (black points) with the 2D probability histograms of NH and N(CH+) predicted by numerical simulations (colored histograms) after application of the chemical solver and the lines of sight reconstruction algorithm. The observational dataset include detections (open circles) and nondetections (filled triangles) of CH+. Each panel in the top frame shows the prediction of a different simulation with G0 varying between 0.5 and 4 (from left to right) and |
5.3 Impact of F and ζ
The strength and the nature of the turbulent forcing are known to have a significant influence on the physics of the multiphase ISM (e.g., Seifried et al. 2011). The variations in pressure and the shear motions induced at all scales by the turbulent forcing perturb the gas out of its thermal equilibrium states, and also reduce the time spent in the WNM, LNM, and CNM (Seifried et al. 2011). On the one hand, the turbulent forcing thus modifies the mass and volume distributions of the phases. Increasing the strength of the turbulent forcing leads to a decrease in the mass of the CNM to the benefit of the LNM and the WNM; however, this effect is much larger for a solenoidal forcing than a compressive forcing because solenoidal motions efficiently prevent the gas from condensating back to the CNM (see Fig. 4 and Sect. 3.7 of Paper I). On the other hand, the turbulent forcing modifies the rate at which mass is exchanged between the different phases. Increasing the strength of the turbulent forcing leads to an increase in the mass transfer rate between the CNM, the WNM, and the LNM.
The impact on the HI-to-H2 transition is presented and discussed in Sect. 4.6 of Paper I. In a nutshell, the HI-to-H2 transition is found to weakly depend on the strength of the turbulent forcing if the forcing is dominated by compressive motions, and to be sensitive to the strength of the forcing if the forcing is dominated by solenoidal motions. Overall, the turbulent forcing has a moderate impact because the HI-to-H2 transition is only sensitive to the distributions of mass and volume occupied by the different phases. This is not the case of CH+, which also depends on the mass loss rate of the CNM.
The influence of the strength and the nature of the turbulent forcing on the production of CH+ are displayed in Fig. 10 (bottom frame) which shows comparisons of the 2D probability histograms of NH and N(CH+), predicted for various values of F and ζ, to the observational sample. The dependence of CH+ on the turbulent forcing is significantly different from that of the HI-to-H2 transition. For a kinetic energy density (which is roughly proportional to F) above the thermal energy density (F ⩾ 1.5 × 10−3 kpc Myr−2, see Table 4), the distribution of the column densities of CH+ is found to strongly depend on the strength of the turbulent forcing regardless of its compressive or solenoidal nature. Increasing the strength of the turbulent forcing from F = 1.5 × 10−3 kpc Myr−2 to F = 1.5 × 10−2 kpc Myr−2 leads to an increase in the total mass of CH+ by about an order of magnitude. The amplitude of this effect depends on the nature of the forcing and is slightly smaller if the forcing is dominated by solenoidal motions. All these behaviors confirm the interpretation given in Sect. 3.5. The amount of CH+ is proportional to the rate of injection of H2 in the LNM. This rate increases with the strength of the turbulent forcing (if the kinetic energy density is higher than the thermal energy density) and slightly decreases with the fraction of power injected in the solenoidal modes which efficiently reduce the mass of the CNM. Interestingly, the closest agreement with the observations of CH+ and the HI-to-H2 transition is obtained for a forcing that is not purely solenoidal (ζ ⩽ 0.5) with F ~ 1.5 × 10−3 kpc Myr−2. We recall that this forcing induces a 1D turbulent velocity dispersion of the WNM of ~5.4 km s−1 (see Sect. 3.4), in agreement with the velocity dispersion derived from HI emission spectra at high Galactic latitude (Kalberla et al. 2005; Haud & Kalberla 2007).
Interestingly, Fig. 10 indicates that the turbulent forcing has a weak impact on the production of CH+ if the kinetic energy density is below or close to the thermal energy density (F ⩽ 1.5 × 10−3 kpc Myr−2). This result should be considered with caution. A study of the numerical convergence was performed for F = 1.5 × 10−3 kpc Myr−2 (see Figs. 8 and 9). While convergence is expected to be reached for higher values of F, it is not necessarily the case for lower values where the evaporation process of CNM clouds could be mediated by artificial thermal conduction. Confirmation of this result would require performing a convergence study for lower values of the strength of the turbulent forcing or even without forcing where the turbulence is sustained by the thermal instability itself (Iwasaki & Inutsuka 2014).
6 Discussion
The simulations presented in this work show that it is possible to build a coherent physical model of the multiphase diffuse ISM that simultaneously explains a great variety of observations, including chemical correlations, statistical distributions, and line profiles, within the constraints set by the structure of the ISM observed at Galactic scales (e.g., ISM midplane mean density, UV interstellar radiation field, and illumination scales). We call this model the standard simulation. It is important to note, however, that such a model is not unique and depends on the prescriptions used for several microphysical processes. Any uncertainty on these processes will likely result in an update of the so-called standard simulation.
The mean pressure of the diffuse ISM depends on the efficiency of the photoelectric heating (e.g., Wolfire et al. 2003). This efficiency, in turn, depends on the abundance of very small grains, on their recombination rate with free electrons, on the photoelectric yield, and on their very nature including their composition and structure. Weingartner & Draine (2001) estimate that the uncertainties on the yield and the recombination rate alone implies an uncertainty on the photoelectric heating rate of about a factor of 3. In this paper we model very small grains as carbonaceous PAHs, with a fractional abundance of 10−6, and assume a sticking coefficient of free electrons of 1. These choices lead to a photoelectric efficiency about twice as high as the reference model of Weingartner & Draine (2001). Other prescriptions for the photoelectric effect could be adopted, but would require modifying the standard setup in order to account for the observed mean pressure of the CNM.
Although not displayed in this paper, the effect of the initial homogeneous magnetic field has been explored. As long as the magnetic energy density is below equipartition, this parameter is found to have a small influence on the distribution of pressure and the statistical distribution of the HI-to-H2 transition. A reduced strength of the magnetic field leads, however, to an increase in the total mass of CH+ because it facilitates the exchanges of mass between the CNM and the WNM. We find that reducing the magnetic field intensity by a factor of 5 leads to an amount of CH+ twice as large as in the standard setup.
The column densities predicted by the simulations obviously depend on the chemical rates adopted for the formation and the destruction of CH+. We note that the rates used in this work (see Table 3) are significantly different from those used in other theoretical studies (Myers et al. 2015; Moseley et al. 2021). The fact that the formation rate of CH+ by hydrogenation of C+ and the destruction rate of CH+ by reactive collision with H are both higher than those adopted by Myers et al. (2015) by a factor of 5 evidently has no impact on our results, but highlights the need for reliable chemical rates. A more robust treatment would be to take into account the impact of the local distribution of H2 in its excited levels in the computation of the formation rate of CH+ (Agúndez et al. 2010; Zanchet et al. 2013), which would lead to a lower formation rate than that prescribed by Hierl et al. (1997). In contrast, we note that the destruction rate of CH+ by collision with H prescribed by Plasil et al. (2011) and adopted in this work appears to overestimate the rate measured at high temperatures (T > 800 K) by Federer et al. (1984, 1985). We find that implementing the state-to-state chemical rates for the formation of CH+ and modifying the destruction of CH+ by collision with H to match the measurements performed at high temperatures reduces the amount of CH+ only by a factor of two, which is well within the uncertainty expected given the loose constraints on the strength of the turbulent forcing and the strength of the magnetic field in the local diffuse ISM.
7 Conclusions
The high abundances and spatial coverage of CH+ has long been recognized as a deep mystery of the chemical state and evolution of the diffuse interstellar matter. In this paper we explore the impact of the multiphase and turbulent nature of the ISM on the production of CH+ and on its kinematic signatures through detailed comparisons of the results of numerical simulations with observations of CH+ in the solar neighborhood. Because of the long chemical timescale of H2 and the short chemical timescale of CH+, the chemical composition of the ISM is modeled by solving the out-of-equilibrium abundance of H2 during the simulation itself and by computing the rest of the chemistry at equilibrium in post-processing.
The first and most important outcome of this work is the validation of the method proposed in Paper I and reapplied here to confront numerical simulations and observations. The validity of the results of a model is estimated from its capacity to account for the full statistical information contained in an observational sample, which include not only the correlations between the column densities of different species, but also the rate of nondetections of these species, and the probability of occurrence of any groups of lines of sight. On the one hand, this detailed and quantitative comparison requires taking into account the distribution of lengths of the intercepted diffuse matter for the construction of a simulated sample of lines of sight. On the other hand, the method requires the observed dataset to be unbiased. In particular, it relies on the fact that the observational sample corresponds to random lines of sight that are not selected depending on the opacity of the foreground medium. Moreover, it relies on the fact that the information is complete and that upper limits are systematically given if the species is not detected. As far as we know, both conditions are fulfilled in the observational sample of CH+ studied here.
The methylidyne cation CH+ is usually considered a tracer of the intermittent dissipation of turbulence in regions with large ion-neutral velocity drift. The present paper shows, for the first time, that the production of CH+ might be a natural consequence of the exchanges of mass between the CNM and the WNM induced by the combination of large-scale turbulence and thermal instability. The results of a single simulation of the turbulent multiphase ISM are able to reproduce most of the statistical properties of the observations of CH+ with a precision never achieved before by any theoretical model. In particular, the model explains the probabilities of occurrence of most of the lines of sight, the probabilities of nondetections of CH+, the range of observed column densities, and the mean fractional abundances of CH+ and their dispersions, all as functions of the total proton column density along the lines of sight (Fig. 5). In addition, the combined dynamical and thermochemical properties of the regions responsible for the production of CH+ lead to a distribution of line profiles almost identical to that derived from the observational data (Fig. 7). All these results are obtained without tuning any parameter, but by simply using the setup found to reproduce the statistical properties of the HI-to-H2 transition and the distribution of thermal pressure observed in the local diffuse ISM. These separated chemical and physical constraints highlight the remarkable coherence of the chemical composition obtained with simulations of the turbulent multiphase ISM.
The quasi-totality of the mass of CH+ originates from the warm and unstable gas produced by the evaporation of CNM clouds that injects out-of-equilibrium H2 in warmer and more diffuse environments. This process depends on the mass and volume distributions of the CNM, primarily set by the mean density of the diffuse ISM and the intensity of the UV radiation field, and the evaporation timescale of the CNM set by the strength of the turbulent forcing. The physical conditions (i.e., density, kinetic temperature, molecular fraction, and electronic fraction) of the regions responsible for the production of CH+ weakly depend on the model parameters. The amount of CH+ in the diffuse ISM therefore traces the injection rate of H2 in the unstable gas.
This injection rate can be roughly estimated using the following argument. Let us consider a volume of CNM in expansion. Since its dynamical timescale is shorter than the destruction timescale of H2, the mass of H2 contained in the volume is initially conserved. However, the expansion reduces the self-shielding of H2 and its destruction timescale. The mass of H2 is thus conserved as long as the dynamical timescale is shorter than the chemical timescale, and then exponentially decreases as a function of time. We estimate that this turning point happens for a self-shielding factor  . It follows that the total mass of warm H2 (T > 600 K) contained in the standard simulation (~ 600 M⊙) survives for a timescale of ~105 yr, leading to an injection rate of H2 from the CNM to the LNM of ~10−9 M⊙ yr−1 per pc3 of neutral diffuse ISM.
. It follows that the total mass of warm H2 (T > 600 K) contained in the standard simulation (~ 600 M⊙) survives for a timescale of ~105 yr, leading to an injection rate of H2 from the CNM to the LNM of ~10−9 M⊙ yr−1 per pc3 of neutral diffuse ISM.
The natural follow-up to this work is to extend the parametric study of the multiphase ISM and the methodology proposed for the comparison between simulations and observations to other chemical and kinematic tracers. Such investigations and their impact on the interpretation of future observations using the James Webb Space Telescope and the Square Kilometer Array are underway.
Acknowledgements
We are very grateful to the referee for their thorough reading and their clever comments which greatly improved the content of the paper. The research leading to these results has received fundings from the European Research Council, under the European Community’s Seventh framework Programme, through the Advanced Grant MIST (FP7/2017-2022, No. 742719). The grid of simulations used in this work has been run on the computing cluster Totoro of the ERC MIST, administered by MesoPSL. We would also like to acknowledge the support from the Programme National “Physique et Chimie du Milieu Interstellaire” (PCMI) of CNRS/INSU with INC/INP co-funded by CEA and CNES.
Appendix A Observations of CH+ in the diffuse local ISM
The diffuse Galactic CH+ has been the target of many observational studies during the past 40 yr. First limited to optical observations (e.g., Federman 1982; Sheffer et al. 2008), these studies were recently extended to the infrared domain thanks to the Herschel Space Telescope (e.g., Falgarone et al. 2010; Godard et al. 2012), which allowed the observations of the submillimeter spectra of many hydrides previously unaccessible from the ground due to large atmospheric absorption lines (Gerin et al. 2016). In the optical, CH+ is observed in absorption against the continuum of bright nearby stars. The resulting lines of sight therefore sample nearby diffuse material over distances up to ~2 kpc (see Fig. 1). In contrast, observations of CH+ in the submillimeter domain are performed in absorption against the infrared continuum of distant massive star forming regions located at small Galactic latitude. The resulting lines of sight therefore sample diffuse material across the entire Galactic disk over distances up to ~12 kpc. To avoid the complexity of modeling the Galactic structure and the necessary variations of physical conditions (e.g., the mean density of the diffuse gas, the density of OB stars, or the amount of mechanical energy injected at large scale) along extended lines of sight, we limited our present study to optical observations and refer to the sampled material as the solar neighborhood diffuse gas.
The observational sample studied in this paper is given in Table A.1, which provides the Galactic coordinates of the sources, their distances, the total proton column density NH, and the column densities of CH+. The column densities of CH+ are taken from Federman (1982), Lambert & Danks (1986), Crane et al. (1995), Rachford et al. (2002), Gredel et al. (2002), Pan et al. (2004), Ritchey et al. (2006), and Sheffer et al. (2008). When available, all the other quantities listed in Table A.1 are taken from the recent compilation of observations performed by Bellomi et al. (2020) (Table A.1). If not available in this compilation, the quantities are derived as follows. The distances are computed from the parallaxes published in the Gaia EDR3 catalog (Gaia Collaboration et al. 2016, 2021) or alternatively provided on the SIMBAD astronomical database (Wenger et al. 2000). The total proton column density NH is derived from measurements of the reddening E(B − V), as NH = 5.8 × 1021 E(B − V) cm−2 if these measurements are available. If not, NH is derived from the Galactic dust extinction maps AV, available on the NASA/IPAC infrared science archive (Schlafly & Finkbeiner 2011), as NH = 1.87 × 1021 AV cm−2. The relations between NH, E(B − V), and AV are chosen assuming a standard Galactic extinction curve and the average interstellar ratio RV = AV/E(B − V) = 3.1 (Fitzpatrick & Massa 1986; Fitzpatrick 1999).
Observational dataset used in this work.
References
- Agúndez, M., Goicoechea, J. R., Cernicharo, J., Faure, A., & Roueff, E. 2010, ApJ, 713, 662 [Google Scholar]
- Bellomi, E., Godard, B., Hennebelle, P., et al. 2020, A&A, 643, A36 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Black, J. H., & Dalgarno, A. 1977, ApJS, 34, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Bowen, D. V., Jenkins, E. B., Tripp, T. M., et al. 2008, ApJS, 176, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Cartledge, S. I. B., Lauroesch, J. T., Meyer, D. M., & Sofia, U. J. 2004, ApJ, 613, 1037 [NASA ADS] [CrossRef] [Google Scholar]
- Chaffee, F. H. J., & White, R. E. 1982, ApJS, 50, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Crane, P., Lambert, D. L., & Sheffer, Y. 1995, ApJS, 99, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Diplas, A., & Savage, B. D. 1994, ApJS, 93, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Douglas, A. E., & Herzberg, G. 1941, ApJ, 94, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1986, ApJ, 310, 408 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Draine, B. T., & Bertoldi, F. 1996, ApJ, 468, 269 [Google Scholar]
- Draine, B. T., & Sutin, B. 1987, ApJ, 320, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M., & Watson, W. D. 1978, ApJ, 222, L141 [NASA ADS] [CrossRef] [Google Scholar]
- Elitzur, M., & Watson, W. D. 1980, ApJ, 236, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Falgarone, E., Godard, B., Cernicharo, J., et al. 2010, A&A, 521, L15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Falgarone, E., Zwaan, M. A., Godard, B., et al. 2017, Nature, 548, 430 [NASA ADS] [CrossRef] [Google Scholar]
- Federer, W., Villinger, H., Howorka, F., et al. 1984, Phys. Rev. Lett., 52, 2084 [CrossRef] [Google Scholar]
- Federer, W., Villinger, H., Tosi, P., et al. 1985, in NATO Advanced Study Institute (ASI) Series C, NATO Advanced Study Institute (ASI) Series C, eds. G. H. F. Diercksen, W. F. Huebner, & P. W. Langhoff, 157, 649 [NASA ADS] [Google Scholar]
- Federman, S. R. 1982, ApJ, 257, 125 [Google Scholar]
- Federman, S. R., Strom, C. J., Lambert, D. L., et al. 1994, ApJ, 424, 772 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Roman-Duval, J., Klessen, R. S., Schmidt, W., & MacLow, M. M. 2010, A&A, 512, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 1986, ApJ, 307, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Flower, D. R., & Pineau des Forêts, G. 1998, MNRAS, 297, 1182 [NASA ADS] [CrossRef] [Google Scholar]
- Fromang, S., Hennebelle, P., & Teyssier, R. 2006, A&A, 457, 371 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fruscione, A., Hawkins, I., Jelinsky, P., & Wiercigroch, A. 1994, ApJS, 94, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gerin, M., Neufeld, D. A., & Goicoechea, J. R. 2016, ARA&A, 54, 181 [NASA ADS] [CrossRef] [Google Scholar]
- Godard, B., Falgarone, E., & Pineau des Forêts, G. 2009, A&A, 495, 847 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Godard, B., Falgarone, E., Gerin, M., et al. 2012, A&A, 540, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Godard, B., Falgarone, E., & Pineau des Forêts, G. 2014, A&A, 570, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gredel, R., Pineau des Forêts, G., & Federman, S. R. 2002, A&A, 389, 993 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habing, H. J. 1968, Bull. Astron. Inst. Netherlands, 19, 421 [Google Scholar]
- Haud, U., & Kalberla, P. M. W. 2007, A&A, 466, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heays, A. N., Bosman, A. D., & van Dishoeck, E. F. 2017, A&A, 602, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hennebelle, P., & Falgarone, E. 2012, A&Av, 20, 55 [NASA ADS] [Google Scholar]
- Hierl, P. M., Morris, R. A., & Viggiano, A. A. 1997, J. Chem. Phys., 106, 10145 [Google Scholar]
- Iwasaki, K., & Inutsuka, S.-I. 2014, ApJ, 784, 115 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, E. B., & Tripp, T. M. 2011, ApJ, 734, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., & Kerp, J. 2009, ARA&A, 47, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lambert, D. L., & Danks, A. C. 1986, ApJ, 303, 401 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Lesaffre, P., Gerin, M., & Hennebelle, P. 2007, A&A, 469, 949 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lesaffre, P., Todorov, P., Levrier, F., et al. 2020, MNRAS, 495, 816 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- McEwan, M. J., Scott, G. B. I., Adams, N. G., et al. 1999, ApJ, 513, 287 [Google Scholar]
- Moseley, E. R., Draine, B. T., Tomida, K., & Stone, J. M. 2021, MNRAS, 500, 3290 [Google Scholar]
- Myers, A. T., McKee, C. F., & Li, P. S. 2015, MNRAS, 453, 2747 [Google Scholar]
- Nakanishi, H., & Sofue, Y. 2016, PASJ, 68, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., Godard, B., Gerin, M., et al. 2015, A&A, 577, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pan, K., Federman, S. R., Cunha, K., Smith, V. V., & Welty, D. E. 2004, ApJS, 151, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Paul, D., Grieser, M., Grussie, F., et al. 2022, ApJ, 939, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Pineau des Forêts, G., Flower, D. R., Hartquist, T. W., & Dalgarno, A. 1986, MNRAS, 220, 801 [CrossRef] [Google Scholar]
- Plasil, R., Mehner, T., Dohnal, P., et al. 2011, ApJ, 737, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Rachford, B. L., Snow, T. P., Tumlinson, J., et al. 2002, ApJ, 577, 221 [Google Scholar]
- Rangwala, N., Maloney, P. R., Glenn, J., et al. 2011, ApJ, 743, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Ritchey, A. M., Martinez, M., Pan, K., Federman, S. R., & Lambert, D. L. 2006, ApJ, 649, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Ritchey, A. M., Welty, D. E., Dahlstrom, J. A., & York, D. G. 2015, ApJ, 799, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Saury, E., Miville-Deschênes, M. A., Hennebelle, P., Audit, E., & Schmidt, W. 2014, A&A, 567, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Savage, B. D., Meade, M. R., & Sembach, K. R. 2001, ApJS, 136, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
- Schmidt, W., Federrath, C., Hupp, M., Kern, S., & Niemeyer, J. C. 2009, A&A, 494, 127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seifried, D., Schmidt, W., & Niemeyer, J. C. 2011, A&A, 526, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sheffer, Y., Rogers, M., Federman, S. R., et al. 2008, ApJ, 687, 1075 [Google Scholar]
- Spinoglio, L., Pereira-Santaella, M., Busquet, G., et al. 2012, ApJ, 758, 108 [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [CrossRef] [EDP Sciences] [Google Scholar]
- Valdivia, V., Hennebelle, P., Gérin, M., & Lesaffre, P. 2016, A&A, 587, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valdivia, V., Godard, B., Hennebelle, P., et al. 2017, A&A, 600, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Dishoeck, E. F., & Black, J. H. 1989, ApJ, 340, 273 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJS, 134, 263 [CrossRef] [Google Scholar]
- Welsh, B. Y., Sasseen, T., Craig, N., Jelinsky, S., & Albert, C. E. 1997, ApJS, 112, 507 [NASA ADS] [CrossRef] [Google Scholar]
- Welty, D. E., & Crowther, P. A. 2010, MNRAS, 404, 1321 [NASA ADS] [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolcott-Green, J., Haiman, Z., & Bryan, G. L. 2011, MNRAS, 418, 838 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., McKee, C. F., Hollenbach, D., & Tielens, A. G. G. M. 2003, ApJ, 587, 278 [Google Scholar]
- Zanchet, A., Godard, B., Bulut, N., et al. 2013, ApJ, 766, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Zari, E., Hashemi, H., Brown, A. G. A., Jardine, K., & de Zeeuw, P. T. 2018, A&A, 620, A172 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Version 1.5.2 available at http://ism.obspm.fr
The total interstellar radiation field, excluding the cosmic microwave background, integrated over all wavelengths has an energy density of ~1.6 × 10−12 erg cm−3 (Draine 2011, Table 12.1), in equipartition with the kinetic and magnetic energy densities of the standard simulation.
All Tables
Reaction rates of the formation and destruction processes of H+, PAH, PAH0, and PAH+ included in the simulations.
Reaction rates of the main formation and destruction processes of CH+ and associated references.
All Figures
 |
Fig. 1 Properties of the observed lines of sight. Top: Aitoff projection, in Galactic longitude and latitude coordinates, of the background sources of the CH+ observational sample (see Table A.1). The color-coding indicates the distance of background sources, and the symbol shapes correspond to the lines of sight where CH+ is detected (circles) or not detected (triangles). Bottom: distribution of the lengths of the intercepted diffuse material computed with Eq. (1) along all the lines of sight of the observational sample. The orange sample corresponds to lines of sight where CH+ is detected and the green sample to those for which an upper limit on N(CH+) has been derived (see the bottom part of Table A.1). The two samples are summed in order to display the total number of sources observed in each bin. |
| In the text | |
 |
Fig. 2 Comparison of the main thermochemical properties of the standard simulation with observations of the local diffuse ISM. Top: comparison of the observational dataset of the HI-to-H2 transition of Paper I (black points) to the 2D probability histogram obtained with the standard simulation after application of the reconstruction algorithm (see Sect. 3.8 of Paper I). Observations include detections of H2 (circles) and upper limits on its column density (arrows). The color-coding indicates the fraction of lines of sight (in logarithmic scale) contained in each bin. Bottom: probability distribution function of the thermal pressure of the cold neutral medium in the standard simulation (blue histograms) compared with the probability distribution function of the thermal pressure deduced from the observation of the fine structure levels of carbon (Jenkins & Tripp 2011; black curve). Both distributions are normalized to their maximum value to facilitate comparison. |
| In the text | |
 |
Fig. 3 Two-dimensional probability distribution functions of the fraction of mass of CH+ in the fiducial simulation d[M(CH+)/Mtot(CH+)]/[dlog(a) dlog(b)] displayed in a a = nH and b = nHT diagram (top panel), a a = x(CH+) and b = x(e−) diagram (middle panel), and a a = f(H2) and |
| In the text | |
 |
Fig. 4 Maps of the column densities of H2 (left panel) and CH+ (right panel) predicted with the standard simulation (see Table 1) and obtained by integrating the densities along the x-axis over the entire box of size L = 200 pc. |
| In the text | |
 |
Fig. 5 Comparison of the observational dataset (black points) with the 2D probability histogram of NH and N(CH+) predicted by the fiducial simulation (colored histogram) after application of the chemical solver and the lines of sight reconstruction algorithm. The observational dataset include detections (open circles) and nondetections (filled triangles) of CH+. The color-coding indicates the fraction of lines of sight (in logarithmic scale) contained in each bin. Two cases are shown: the chemical solver computes the abundance of H2 at equilibrium (top panel) or uses the out-of-equilibrium abundance of H2 calculated during the simulation (bottom panel). |
| In the text | |
 |
Fig. 6 Examples of absorption profiles of the 4232 Å line of CH+ computed along the x-axis across the standard simulation (see Table 1). The black histograms are the computed spectra. The colored curves are the results of a multi-Gaussian fit applied to the line opacity and display the individual Gaussian components (dashed red curves) and their sum (solid blue curves). The spectra are classified in increasing order of their maximum opacity (from top to bottom) and in increasing order of the number of Gaussian components used in the fit (from left to right). |
| In the text | |
 |
Fig. 7 Probability distributions of the full width at half maximum ΔV of the 4232 A line of CH+ derived from the observations (top panel) and from synthetic spectra (see Fig. 6) computed across the standard simulation (bottom panel). The observational sample includes 254 velocity components extracted along 120 lines of sight by Federman (1982; Table 2), Lambert & Danks (1986; Table 1), Crane et al. (1995; Table 2), Pan et al. (2004; Table 4), Ritchey et al. (2006; Table 4), and Sheffer et al. (2008; Table 3). This dataset includes all the lines of sight where CH+ has been observed (see Table A.1), except those observed or compiled by Gredel et al. (2002) and Rachford et al. (2002), who do not provide measurements of the CH+ linewidth. |
| In the text | |
 |
Fig. 8 Total mass of CH+, Mtot(CH+), contained in simulations at different resolutions R (blue points). The data are fitted with the function a/Rb/3 + c, where a, b, and c are adjustable coefficients. The best fit (black curve) corresponds to the function 1.57 × 102/R2/3 + 1.05 × 10−2 and tends toward the constant value 1.05 × 10−2 (blue line) at high resolution. |
| In the text | |
 |
Fig. 9 Isocontours of the 2D probability histograms of NH and N(CH+) predicted by simulations with a resolution R = 643 (green curve), 2563 (blue curve), and 5123 (pink curve), after application of the chemical solver and the lines of sight reconstruction algorithm. This representation shows, in a simplified manner, the effect of the resolution on the result displayed in Fig. 5. The isocontours chosen at 8 × 10−5 (top panel) and 8 × 10−4 (bottom panel) highlight the changes in the distribution of the most probable lines of sight. These values correspond to the turquoise blue and orange levels of the 2D probability histograms of NH and N(CH+) (see Fig. 5). |
| In the text | |
 |
Fig. 10 Comparison of the observational dataset (black points) with the 2D probability histograms of NH and N(CH+) predicted by numerical simulations (colored histograms) after application of the chemical solver and the lines of sight reconstruction algorithm. The observational dataset include detections (open circles) and nondetections (filled triangles) of CH+. Each panel in the top frame shows the prediction of a different simulation with G0 varying between 0.5 and 4 (from left to right) and |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.