| Issue |
A&A
Volume 664, August 2022
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 21 | |
| Section | Astronomical instrumentation | |
| DOI | https://doi.org/10.1051/0004-6361/202141958 | |
| Published online | 09 August 2022 | |
Large Interferometer For Exoplanets (LIFE)
II. Signal simulation, signal extraction, and fundamental exoplanet parameters from single-epoch observations
1
ETH Zurich, Institute for Particle Physics & Astrophysics,
Wolfgang-Pauli-Str. 27,
8093
Zurich, Switzerland
e-mail: fdannert@phys.ethz.ch
2
National Center of Competence in Research PlanetS
3
Institute of Astronomy,
KU Leuven, Celestijnenlaan 200D,
3001
Leuven, Belgium
4
STAR Institute, University of Liège,
19C allée du Six Août,
4000
Liège, Belgium
5
Centre Spatial de Liège, Université de Liège,
Avenue Pré-Aily,
4031
Angleur, Belgium
6
Institut de Ciències de l’Espai (ICE, CSIC),
Campus UAB, C/Can Magrans s/n,
08193
Bellaterra, Spain
7
Space Telescope Science Institute,
3700 San Martin Drive,
Baltimore,
MD 21218
USA
8
University of Oxford, Atmospheric, Oceanic and Planetary Physics, Department of Physics,
Sherrington Road, Oxford OX1 3PU,
UK
9
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg, Germany
10
Faculty of Aerospace Engineering, Delft University of Technology,
Kluyverweg 1,
2629
Delft, The Netherlands
Received:
5
August
2021
Accepted:
1
March
2022
Context. The Large Interferometer For Exoplanets (LIFE) initiative is developing the science and a technology road map for an ambitious space mission featuring a space-based mid-infrared (MIR) nulling interferometer in order to detect the thermal emission of hundreds of exoplanets and characterize their atmospheres.
Aims. In order to quantify the science potential of such a mission, in particular in the context of technical trade-offs, an instrument simulator is required. In addition, signal extraction algorithms are needed to verify that exoplanet properties (e.g., angular separation and spectral flux) contained in simulated exoplanet data sets can be accurately retrieved.
Methods. We present LIFEsim, a software tool developed for simulating observations of exoplanetary systems with an MIR space-based nulling interferometer. It includes astrophysical noise sources (i.e., stellar leakage and thermal emission from local zodiacal and exozodiacal dust) and offers the flexibility to include instrumental noise terms in the future. Here, we provide some first quantitative limits on instrumental effects that would allow the measurements to remain in the fundamental noise limited regime. We demonstrate updated signal extraction approaches to validating signal-to-noise ratio (S/N) estimates from the simulator. Monte Carlo simulations are used to generate a mock survey of nearby terrestrial exoplanets and determine to which accuracy fundamental planet properties can be retrieved.
Results. LIFEsim provides an accessible way to predict the expected S/N of future observations as a function of various key instrument and target parameters. The S/Ns of the extracted spectra are photon noise dominated, as expected from our current simulations. Signals from multi-planet systems can be reliably extracted. From single-epoch observations in our mock survey of small (R < 1.5 REarth) planets orbiting within the habitable zones of their stars, we find that typical uncertainties in the estimated effective temperature of the exoplanets are ≲10%, for the exoplanet radius ≲20%, and for the separation from the host star ≲2%. Signal-to-noise-ratio values obtained in the signal extraction process deviate by less than 10% from purely photon-counting statistics-based S/Ns.
Conclusions. LIFEsim has been sufficiently well validated so that it can be shared with a broader community interested in quantifying various exoplanet science cases that a future space-based MIR nulling interferometer could address. Reliable signal extraction algorithms exist, and our results underline the power of the MIR wavelength range for deriving fundamental exoplanet properties from single-epoch observations.
Key words: methods: data analysis / techniques: interferometric / techniques: high angular resolution / planets and satellites: detection / planets and satellites: terrestrial planets / planets and satellites: fundamental parameters
© ESO 2022
1 Introduction
Ever since the first detection of an exoplanet orbiting a solar-like star (Mayor & Queloz 1995), thousands of exoplanets have been detected from the ground and with dedicated space missions. Ongoing and future space missions, such as the CHaracterizing ExOPlanet Satellite (CHEOPS; Benz et al. 2021), the James Webb Space Telescope (JWST), and the Atmospheric Remote-sensing Infrared Exoplanet Large-survey (ARIEL; Tinetti et al. 2018), will focus on characterizing a subset of the known exoplanets and their atmospheres in greater detail. All of these missions rely on investigating exoplanets that transit in front of their host stars, but the vast majority of exoplanets do not transit. Hence, the characterization space is limited and biased toward close-in and large planets. In order to investigate the atmospheric properties of hundreds of terrestrial exoplanets, including dozens that are potentially habitable, optimized large-scale space missions that rely on a direct detection technique will be required. This could be either a single aperture ultraviolet, optical or near-infrared telescope to characterize exoplanets in reflected light (e.g., the HabEx and LUVOIR concepts; Gaudi et al. 2020; The LUVOIR Team 2019) or a mid-infrared (MIR) nulling interferometer to probe the thermal emission of exoplanets. In Quanz et al. (2022), we introduce the Large Interferometer For Exoplanets (LIFE) initiative, which aims at developing the science objectives, requirements, and a concept (including a technology development road map) for such a space-based MIR nulling interferometer mission. Of significant importance in the current phase of the LIFE initiative is the availability of a simulator environment that, under well-defined assumptions, can assess the performance of a certain interferometer architecture and instrument concept in terms of scientific output. Similarly, a solid understanding of how well a measured signal can be extracted from the simulated data is crucial. The longer-term objective is to develop and maintain a flexible framework that incorporates the fundamental properties of various interferometer architectures and includes all relevant noise sources (astrophysical and instrumental). Such a framework can then be used for even more sophisticated scientific simulations and trade-offs (e.g., prioritization of targets), but also to understand and quantify the impact of technical trade-offs.
The structure of the paper is as follows: in Sect. 2 we give a brief introduction to the basic principles of nulling interferometry needed to describe the measuring process of LIFE. We describe the implementation of the measurement process into the publicly available LIFEsim mission simulator and further introduce the most dominant astrophysical noise terms, explain how the signal-to-noise ratio (S/N) of a measurement can be quantified, and provide simulations of an Earth-twin exoplanet seen at a distance of 10 pc as a specific example. In Sect. 3 we revisit the assumption of the photon-based S/N calculations and present a signal extraction method that enables locating exoplanets in the vicinity of their host stars and estimating their fluxes. In Sect. 4, we investigate how accurately the physical properties (such as position and flux and, from this, effective temperature and radius) of simulated exoplanets can be extracted based on single-epoch observations. We do this by reanalyzing parts of the Monte Carlo simulations presented in Quanz et al. (2022). We discuss the results and conclude in Sect. 5. Throughout this work, we assume that the measurement is primarily disturbed by astrophysical noise sources and not by noise emerging from instrumental effects. In Appendix A, we examine this assumption by presenting estimates for the required instrument stability using an explicit treatment of the instrumental noise.
2 Signal Simulation
2.1 Nulling Interferometry
Bracewell (1978) was the first to propose nulling interferometry as a method to detect and characterize exoplanets. The general goal of a nulling interferometer is to enable measurements of a faint source (i.e., an exoplanet) despite the presence of a much brighter source close by. The simplest realization, a single Bracewell interferometer, consists of two collector apertures that are separated by a baseline b. By combining the collected light coherently, the response of the instrument is a sinusoidal fringe pattern with spacing λ/b projected onto the plane of the sky, λ being the observing wavelength (e.g., Bracewell 1978; Lay 2004). By adding a π-phase shift to the beam of one of the collectors, the central minimum of the fringe pattern coincides with the position of the star so that its signal is effectively suppressed (i.e., “nulled”). Nulling the on-axis stellar light is hence a way to optically separate the star light from other nearby sources, such as exoplanets.
An interferometer has the advantage that it provides higher “spatial resolution” than a single-aperture telescope with aperture size D: the first positive transmission peak in the fringe pattern is located at λ/2b, while the spatial resolution of a telescope is ∝ λ/D. Furthermore, in the case of a free-flying space interferometer, as foreseen for LIFE, the baselines are reconfigurable and generally much larger (up to hundreds of meters) than the apertures of a single-dish telescope (i.e., b >> D).
In a static, monochromatic configuration, the single Bracewell interferometer provides only limited coverage of the uv-plane in the form of a single baseline. Increasing this coverage will allow for the retrieval of more complex signals from the measurements. One possible method for enhancing coverage without changing the configuration of the array itself can be achieved by rotation of the array (cf. rotation synthesis; Paresce & Crane 1997). By continuously rotating the interferometer around its line of sight, the projected fringe pattern will also rotate, and while the on-axis star remains nulled, any planet in its vicinity moves through the pattern of varying transmission and its signal is modulated. The uv-plane coverage can be additionally increased by adding collector apertures to the array and hence raising the number of baselines, or by performing multi-wavelength observations.
Nonetheless, the single Bracewell interferometer is insufficient for the detection of Earth-like exoplanets (e.g., Angel & Woolf 1997; Defrère et al. 2010)1. Furthermore, because the transmission pattern is symmetric, an ambiguity of 180° exists for the position angle of any detected exoplanet.
Driven by the ultimate goal to detect Earth-like exoplanets, extensive studies of interferometer configurations consisting of more than two apertures led to two major space mission concepts in the early 2000s: the Darwin concept led by the European Space Agency (Cockell et al. 2009) and NASA’s Terrestrial Planet Finder-Interferometer (TPF-I; Lawson et al. 2007). LIFE leverages the heritage of these concepts by rooting its design in analyses performed in the context of the Darwin and TPF-I missions.
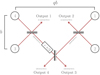 |
Fig. 1 Assumed beam combination scheme of the LIFE array. Four collector spacecraft are located on a 6:1 rectangle with the combiner spacecraft located in the geometric center. The shorter distance between the collectors, b, is called the nulling baseline, and the longer distance is the imaging baseline, qb. The dual chopped Bracewell beam combination scheme, consisting of an interconnection of two single Bracewell combiners, is shown. We note that the collector spacecraft and the interferometric outputs are numbered for the subsequent calculation and that the spacecraft diameters are not to scale. |
2.1.1 Beam Combination in an X-array Configuration
For LIFE we assume an X-array architecture. It consists of four free-flying collector spacecraft, arranged in a rectangular configuration (see Fig. 1) in a plane perpendicular to the line of sight. Because the spacecraft are free-flying, the baselines can be scaled depending on the desired spatial extent of the fringe pattern. At the moment, the ratio between the length of the long so-called imaging baseline and that of the short so-called nulling baseline is chosen to be 6:1 (cf. Defrère et al. 2010). Compared to smaller ratios, the 6:1 configuration is better suited for advanced post-processing techniques aimed at removing a part of the instrumental effects on the measurement called instability noise (Lay 2006). Further investigations and trade-offs are required to validate and confirm this choice for the LIFE mission. The fifth spacecraft, in which the beams are combined coherently and the signal is detected, is located in the geometric center of the array. However, this beam combiner spacecraft could either be located in the same plane as the collector spacecraft or, alternatively, it could fly several hundreds of meters above this plane. This trade-off mostly affects stray light and viewing zone considerations and while it is of no concern for the following analyses, it does significantly affect the field of regard of the mission (cf. Lay et al. 2007).
The beam combination for such complex array configurations need to be captured by a suitable formalism. The following presents such a formalism, as described by Guyon et al. (2013).
To calculate the coherent beam combination, a nulling interferometer can be fully described by N apertures, each defined by its respective position and radius (xk, yk, rk) in a two-dimensional plane, where k ϵ [1,…, N]. The complex field amplitude generated in the kth aperture by a point source with projected angular offset (α,β) from the central line of sight is given by
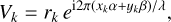 (1)
(1)
where λ is the wavelength. The interferometric combinations can then be represented by a matrix, U, which describes the linear mapping from input amplitude vector, V, to the output amplitude vector,
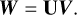 (2)
(2)
Based on the heritage of the Darwin and TPF-I concepts, for this work we assume that light picked up by the collector spacecraft is merged using a dual chopped Bracewell combiner (Lay 2004). The matrix
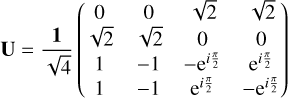 (3)
(3)
describes a realizable (matrix is unitary, cf. Guyon et al. 2013) and lossless (matrix is orthonormal, cf. Laugier et al. 2020) implementation of this combiner.
The rows of this matrix reflect the two-stage approach of the beam combination (Fig. 1). In a first stage, the collector apertures are grouped and combined into two single Bracewell combiners. The respective constructive outputs, denoted as Outputs 1 and 2, are captured by the first two rows of the matrix U, which do not induce any phase delays. The destructive outputs of the first stage are expressed by the eiπ phase difference between entries one and two or three and four in the last two rows of the combiner matrix. In a second stage, these destructive outputs are combined again, with one of the destructive outputs receiving an additional phase shift of 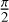 . This produces two complementary nulled outputs that can be used to apply phase chopping to the final output, which reduces the susceptibility of the measurement to instrumental noise effects (Lay 2004). The outputs of this second combination stage are denoted as the destructive Outputs 3 and 4 and are captured by the rows 3 and 4 in the matrix U. We note that the analyses presented in this paper are solely based on these destructive outputs.
. This produces two complementary nulled outputs that can be used to apply phase chopping to the final output, which reduces the susceptibility of the measurement to instrumental noise effects (Lay 2004). The outputs of this second combination stage are denoted as the destructive Outputs 3 and 4 and are captured by the rows 3 and 4 in the matrix U. We note that the analyses presented in this paper are solely based on these destructive outputs.
2.1.2 Transmission and Differential Maps
The two-dimensional projected intensity transmission, Tm, which describes the amount of signal originating from a point in the sky at position (α, β) that transmits to the output, m, can be expanded from Eq. (2) as a combination of the input beams, Vk, as
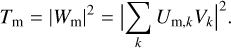 (4)
(4)
In the following, the transmission map of one of the interferometric outputs is calculated analytically to illustrate the basic principle. In a coordinate system that has its origin in the center of the interferometer array, the aperture positions xk and yk are given as ±L and ±qL, respectively, with L representing half the nulling baseline b, and q being the ratio between the imaging baseline and the nulling baseline. The transmission of Output 3 as a function of angular separation (α, β) is given by
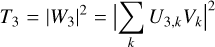 (5)
(5)
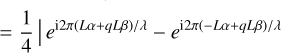 (6)
(6)
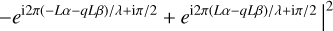 (7)
(7)
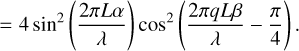 (8)
(8)
To apply phase chopping, Outputs 3 and 4 are subtracted from each other. This yields the differential map
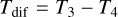 (9)
(9)
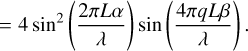 (10)
(10)
This map is antisymmetric with respect to its central point. Thus, any point symmetric emission source (e.g., a homogeneous exozodiacal dust clouds disks) will not transmit through the differential map and will only contribute to the statistical shot noise (e.g., Defrère et al. 2010). An example of the two destructive output transmission maps, T3 and T4, as well as the differential map is shown in Fig. 2.
 |
Fig. 2 Transmission maps for the chopped dual Bracewell nulling interferometer. Left and middle: Tm of Outputs 3 and 4 calculated for a wavelength λ = 10 µm, a nulling baseline b = 12m, and a 6:1 baseline ratio. These two outputs have destructive interference at their vertical center and are used to create the differential map. The axes show the distance from the center in milliarcseconds. The white star indicates the position of the star in the center of the map. Right: Differential map, Tdif, which is the difference between T3 and T4. The dashed red line shows the path of a hypothetical planet at 100 mas through the differential map as the interferometer array describes a full rotation. |
2.1.3 Signal Modulation
To study the signal transmission of a potential planet, the differential map is examined in polar coordinates as shown in the top panel of Fig. 3. Any (static) source at some angular separation θ from the central star will move through this map on a horizontal line as the telescope array is rotated by an angle ϕ. Thus, the normalized signal generated by such a source over one array rotation corresponds to the value of the differential map on a horizontal line through the map at the corresponding radial distance. The normalized signal transmission as a function of rotation angle (i.e., the modulated signal) of that point source is shown in the bottom panel of Fig. 3.
The modulation efficiency ξ indicates the part of the incoming signal that can be used for signal extraction and corresponds to the root-mean-square (rms) of the differential map upon a complete array rotation (Lay 2004). The modulation efficiency over a full array rotation as a function of θ is given by
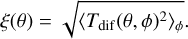 (11)
(11)
Because the spatial extent of the fringe pattern depends on the baseline configuration of the interferometer and the considered wavelength, this is also true for the modulation efficiency. Figure 4 shows ξ(θ) for three different MIR wavelengths for the baseline configuration used in Fig. 2. The curve for λ = 10 µm, which is based on the differential map shown in Figs. 2 and 3, has its first peak and global maximum at 100 mas. For shorter wavelengths the pattern shrinks and the peak transmission is located closer to the star; for longer wavelengths the pattern expands and the peak transmission moves away from the star. The position of the maximum of ξ(θ) can be calculated numerically as
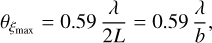 (12)
(12)
which is slightly more than the separation corresponding to the first maximum in the transmission maps at λ/2b.
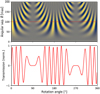 |
Fig. 3 Modulation of the planet signal. Top: Differential map in polar coordinates, normalized from −1 (blue) to 1 (yellow). The dashed red line at 100 mas angular separation corresponds to the path of the planet shown in the right panel of Fig. 2 for a full rotation of the array. Bottom: Normalized signal transmission intensity of the planet as a function of rotation angle. |
 |
Fig. 4 Modulation efficiency, ξ(θ), as a function of angular separation for the three wavelengths λ = 5 µm, 10 µm, and 20 µm. The vertical red line indicates an angular separation of 100 mas, which corresponds to the separation of the planet shown in the right panel of Fig. 2. |
2.2 Astrophysical Sources
In the following we describe how various relevant astrophysical sources and their photon flux are implemented in LIFEsim.
2.2.1 Host Star and Exopanets
To first order, thermal radiation emitted by an exoplanet and its host star can be approximated as blackbody radiation. Because we will base our S/N calculation on the principles of photon statistics, we are interested in the received spectral photon flux in units of [ph s−1 m−2 m−1],
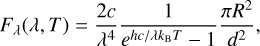 (13)
(13)
where h is Planck’s constant, c is the speed of light, kB is the Boltzmann constant, T and R are the effective temperature and radius of either the planet or the star, and d is the distance from the observer.
Throughout this paper the star is modeled as a blackbody with effective temperature Ts and radius Rs. Limb darkening is not taken into account, and thus the stellar brightness is distributed uniformly across the projected circular disk. Because of the principle of geometric stellar leakage, as described further below in Sect. 2.2.2, this is thought to be a conservative approximation.
As one of the objectives of LIFE is the atmospheric characterization of (terrestrial) exoplanets by measuring wavelength-dependent absorption features in their emission spectra, modeling their emission with blackbody radiation is a simplification. Therefore, LIFEsim has the option to either select a simple blackbody model for the planet or to upload a simulated or observed emission spectrum. In the following subsections we make use of both options. When using a blackbody, we denote the radius and the effective temperature of the exoplanets with Rp and Tp. We use a simulated Earth’s spectrum for illustrative purposes when calculating the expected S/N of an Earth-twin in Sect. 2.4.
2.2.2 Stellar Leakage
Even with a perfect nulling interferometer, photons from the observed star “leak” through the instrument. If the central null fringe is positioned on the center of the star, the stellar flux is not completely suppressed because of the star’s finite size. This phenomenon is described as geometric stellar leakage (e.g., Lay 2004). The photon noise contribution from geometric stellar leakage is determined by applying the transmission maps to the surface area of the star. As such, it depends on the surface brightness and angular size of the star as well as on the baseline configuration.
2.2.3 Local Zodiacal Dust
Our Solar System contains diffuse dust that is mostly located near the ecliptic plane. The dust adds a radiation background to any astronomical observation either coming from sunlight that is scattered off the dust particles or as thermal radiation emitted by the dust itself. As LIFE works in the MIR, we concentrate solely on the thermal emission. The local zodiacal surface brightness is described by a sky-position-dependent model developed for the DarwinSim science simulator (Den Hartog & Karlsson 2005). The parametrization, which is based on data from the COsmic Background Explorer (COBE) mission (Kelsall et al. 1998), gives the spectral surface brightness
![$ \matrix{ \hfill {{I_\lambda }\left( {\lambda ,{\lambda _{{\rm{rel}}}},\beta } \right) = \tau \left[ {{B_\lambda }\left( {\lambda ,{T_{{\rm{eff}}}}} \right) + A \cdot {B_\lambda }\left( {\lambda ,{T_ \odot }} \right){{\left( {{{{R_ \odot }} \over {1.5\,{\rm{AU}}}}} \right)}^2}} \right]} \cr \hfill { \cdot \left[ {{{\pi /\arccos \left( {\cos \left( {{\lambda _{{\rm{rel}}}}} \right)\cos \left( \beta \right)} \right)} \over {{{\sin }^2}\left( \beta \right) + 0.6 \cdot {{\left( {{\lambda \over {11\,{\rm{\mu m}}}}} \right)}^{ - 0.4}}{{\cos }^2}\left( \beta \right)}}} \right],} \cr } $](/articles/aa/full_html/2022/08/aa41958-21/aa41958-21-eq15.png) (14)
(14)
where λ is the wavelength, λrel = λecl − λecl,⊙ is the ecliptic longitude relative to the Sun, β is the ecliptic latitude, τ = 4 × 10−8 is the optical depth toward the ecliptic poles, Bλ(T) is the Plank function, Teff = 265 K is the effective temperature of the local zodiacal dust cloud at 1 AU, T⊙ = 5778 K is the effective temperature of the Sun, A = 0.22 is the near-IR dust albedo, and R⊙ is the radius of the Sun. Since the local-zodiacal light received by the interferometer is diffuse, it cannot be brought to interfere destructively. Therefore, it is not possible to remove the local-zodi emission by virtue of the rotating nulling interferometer. Subsequently, the most effective way of minimizing the noise at long wavelengths is to observe in directions where the local-zodi emission is weak (see Appendix C).
Compared to the original COBE data, the DarwinSim model overestimates the flux from the zodiacal dust in the 6–20 µm range and for a line of sight with a relative latitude of more than 90° from the Sun by 10–20%. For wavelengths below 6 µm the difference increases to a factor of two to three at 3 µm. However, at these wavelengths the photon noise contribution by the zodiacal dust is several orders of magnitude lower than the photon noise from the stellar leakage as we will show below in Sect. 2.3.
2.2.4 Exozodiacal Dust
Exozodiacal dust clouds (“exozodis” for short) are the equivalent to the local zodiacal dust in other stellar systems. Even if the dust density is as low as in the Solar System, integrated over the full field-of-view the MIR radiation emitted by the dust is two to three orders of magnitude higher than that of an Earth-like planet (e.g., Defrère et al. 2010) and can thus significantly affect the integration time required to detect (terrestrial) exoplanets.
The exozodiacal dust distribution and its surface brightness are simulated according to the model described by Kennedy et al. (2015). It assumes a dust distribution in exoplanetary systems similar to the one in the Solar System, except for a global scaling factor z, the number of “zodis2.” The model assumes that the dust emission is optically thin and the dimensionless, face-on surface density, Σ(r), is approximated by a power law distribution. The emission is modeled as blackbody radiation with the temperature-radius profile of the disk following the equilibrium temperature
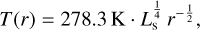 (15)
(15)
where r is given in AU and Ls in solar luminosities. The spectral surface brightness of the disk as seen face-on is then given by
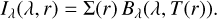 (16)
(16)
Due to the high temperature and surface density close to the star, much of the emitted radiation originates from the central regions.
It is important to note that the given definition of the zodi level z is coupled to the surface density and not to the spectral flux or the total luminosity of the disk. For constant z, the total emitted radiation at a given wavelength, as well as the luminosity of the disk, scale with the surface area of the disk and thus with the stellar luminosity 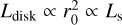 . For high-luminosity stars, which are expected to have larger exozodi disks in this model, the total emitted flux by the disk is thus also larger than for low-luminosity stars.
. For high-luminosity stars, which are expected to have larger exozodi disks in this model, the total emitted flux by the disk is thus also larger than for low-luminosity stars.
At the moment, the exozodi dust disks are assumed to be homogeneous and symmetric around the star and always viewed face-on. Therefore, they only contribute to the shot noise (see Sect. 2.3 below). The influence of asymmetric or clumpy exo-zodiacal disks viewed at an inclination i > 0° is investigated in Defrère et al. (2010) and Defrère et al. (2012) and we discuss these points and their potential impact on exoplanet detection yield in Quanz et al. (2022).
2.3 Signal-to-noise Ratio Calculations
2.3.1 Astrophysical Noise Sources
The astrophysical sources located within the field-of-view of the collector apertures create a scene that is described by the surface brightness Ι(θ, λ). It depends on the position θ within the field-of-view and on the wavelength, and is here assumed to be time-independent.
When the photons emitted by the different sources reach the interferometer, they are detected in one of the interferometric outputs. The signal (Sm) collected by output m, described by the transmission map (Tm) after some integration time is given by the integral of the total surface brightness (Ι(θ, λ)) superimposed with the transmission map over the complete field-of-view,
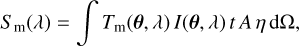 (17)
(17)
with t the integration time, A the total collecting area, and η a detection efficiency factor combining multiple effects. The efficiency factor, η, and the size of the field-of-view are generally also wavelength-dependent. In this work, η is the product of the quantum efficiency of the detector ηQE and the overall instrument throughput ηt. Until a more concrete instrument design is available, it is assumed that both parameters are wavelength-independent. As motivated in more detail in Quanz et al. (2022), we chose ηQE = 0.7 and ηt = 0.05 as default values. The effective field-of-view is assumed to be FoV = λ/D in diameter as we assume the light will be coupled into single-mode fibers.
The spectral signal generated by a single planet, approximated as a point source at location θp, is thus given by
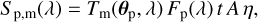 (18)
(18)
where Fp(λ) is the planet flux. Over a full array rotation, the quadratic mean of the modulated signal Sp = S3,p – S4,p detected from the planet is given by
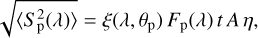 (19)
(19)
where ξ(λ, θ) is the wavelength-dependent modulation efficiency at angular separation θ from the star (see Eq. (11)).
If only rotationally symmetric sources, such as the central star, the local zodiacal background or a homogeneous, face-on exozodiacal dust cloud are considered, the detected signal does not depend on the rotation angle of the array. If the source is only point-symmetric, such as a smooth exozodiacal disk with some inclination i > 0°, the signal per output varies with rotation angle, but is always equal for the two destructive Outputs 3 and 4. Thus, point-symmetric sources do not contribute to the modulated signal.
However, as Mugnier et al. (2006) pointed out, the linear combination of detected signals is an incoherent combination, since it is performed numerically after detection (i.e., in post processing). Removing the contribution of symmetrically distributed sources by incoherent combination is therefore only effective for the signal part of the data, but the sources still contribute to the statistical noise. Hence, the S/N per spectral wavelength bin, denoted as S/Nλ and defined as the ratio between detected exoplanet photons and detected photons from the various noise terms, is calculated as
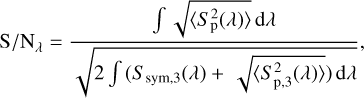 (20)
(20)
where Ssym,3 is the contribution from symmetric background sources to the signal in Output 3 and Sp,3 is the signal of the planet only3. The integral runs over the wavelength range covered by the wavelength bin.
Following Lay (2004), for a measurement across several wavelength bins and under the assumption that the noise is uncorrelated between the bins, the integrated S/N over the full wavelength range, or summed over all wavelength bins, is given by
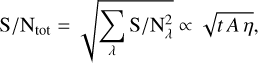 (21)
(21)
which scales, as expected, with the square root of integration time, area and detection efficiency.
In LIFEsim, each noise term from the different sources is calculated individually to avoid numerical discretization errors, as the angular extents of the sources have different scales. For the local and exozodiacal dust, the transmission map as well as the surface brightness distribution are calculated and integrated over a two-dimensional artificial image covering the full field-of-view defined by the instrumental parameters. For the stellar leakage, it is only integrated over the solid angle covered by the stellar disk, but with much higher resolution. The planet signal transmission efficiency is calculated analytically using Eq. (18). All terms are calculated for each predefined wavelength bin, with varying angular extent of the field-of-view and possibly varying bin width, and are then combined to an integrated S/N as given in Eq. (21).
The calculated S/N depends strongly on the baseline of the array. The mean modulated planet signal (Eq. (19)) scales with the modulation efficiency, which in turn depends on the baseline as demonstrated in Sect. 2.1.3. For the contribution from background sources, the amount of stellar leakage contribution depends on the broadness of the central null. This broadness of the null in the transmission map is also governed by the baseline configuration. Thus, maximizing the S/N by changing the length of the baselines poses a trade-off between the amount of planetary signal received over the amount of stellar leakage affecting the measurement. Ideally, to reduce the integration time required for detection, the baselines of the interferometer should thus be chosen such that the S/N across the full wavelength range is high for projected separations that are of major interest. For instance, maximizing the chances of detecting an Earth-like planet orbiting within the habitable zone (HZ) around nearby stars can be achieved by maximizing the S/N across the projected HZ. As discussed in Quanz et al. (2022), for LIFE it is currently assumed that the baselines can indeed be reconfigured depending on the target star where the minimum and maximum separation between two spacecraft is 10 m and 600 m, respectively.
2.3.2 Instrumental Noise Terms
Instrument perturbations such as intensity variations and optical path difference (OPD) errors can degrade the null and lead to additional stellar leakage as well as instability noise (Lay 2004; Defrere 2009). Similarly, detector noise (e.g., dark current) and thermal background noise from the instrument can also deteriorate the measurement. In the current version of LIFEsim, it is assumed that the instrument will be designed such that photon shot noise will dominate over these additional instrumental noise sources. Appendix A presents a preliminary analysis of the aforementioned instrumental effects and constrains the maximum level of allowed perturbations to operate in this fundamental noise limited regime.
2.4 A Simple Case Study: Earth-Twin at 10 pc
We applied the above described S/N calculation to the example of an Earth-like planet located around a Sun-like star at 10 pc, with the aim to illustrate the effects of the different noise sources on the S/N and their wavelength dependence. Instrument parameters and properties of the simulated sources are given in Table1.
Figure 5 (top panel) shows the total fluxes received from the different sources as well as the “leakage” terms (i.e., the part of the flux that is not nulled). These leakage terms contribute to the shot noise. It can be seen that at short wavelengths the stellar leakage dominates strongly, while for longer wavelengths the emission from the local zodiacal dust contributes most to the shot noise.
In the bottom panel of Fig. 5, we show the detected signal from the planet (averaged over each spectral bin) as well as the shot noise and the S/N for the parameters listed in Table 1. Integrating over the full wavelength range gives a S/N ≈ 9.7. The maximum S/N per bin of ≈3 is reached around 11 µm. For wavelengths shorter than 8 µm the S/N decreases rapidly, due to a decrease in planet signal and the increasing shot noise due to stellar leakage.
Instrumental parameters and properties of the simulated sources for the S/N calculation of an Earth-like planet at 10 pc.
3 Signal Extraction
The approach and the simulated spectrum presented in the previous section are based on photon counting statistics. It was implicitly assumed that the signal extraction can be performed with sufficient accuracy.
In practice, data processing and signal extraction algorithms will be of great importance, in particular if a mission like LIFE features an initial search phase4: in addition to separating the planetary signal from the various noise sources, it will be crucial to accurately derive physical characteristics of the exoplanet (e.g., radius, effective temperature and separation from the host star) from single-epoch data in order to identify and rank-order the most interesting objects for in-depth follow-up observations during the characterization phase. For both the Darwin and the TPF-I missions, multiple signal analysis algorithms were proposed. Draper et al. (2006) presented an algorithm that was based on an advanced correlation process. For Darwin, Mugnier et al. (2006) and Thiébaut & Mugnier (2005) presented a signal extraction scheme based on the maximum-likelihood method (MLM). While in the meantime significant progress has been made in many areas of data post-processing, especially thanks to machine-learning-based approaches, the before-mentioned methods still offer a straight-forward framework to deal with the unique characteristics of nulling interferometry with respect to the modulation of the planet signal.
In the following subsections, the MLM will be described, modified, and applied to simulated LIFE data. The goal is to find a metric to quantify the robustness of an exoplanet detection and compare the extracted S/N to that from the photon statistics used in the previous section. Additionally, the signal extraction for multi-planet systems will be investigated. Furthermore, we will revisit the Monte Carlo simulations presented in Quanz et al. (2022) and quantify how accurately we can expect exoplanet properties to be determined from single-epoch data during the search phase.
 |
Fig. 5 Simulated spectra for the observation of an Earth-twin. Top: comparison of the various input signals in our example of an Earthlike planet at 10 pc. The solid lines indicate the total flux received from the respective sources: planet (red), star (black), exozodiacal dust (gray), and local zodiacal dust (blue). The dotted lines with the same color code indicate the fraction of the flux that contributes to the shot noise. Bottom: detected planet signal (red line) and total shot noise (dashed blue line) averaged over each wavelength bin and for an integration time of 200 000 s (values refer to the y axis on the left). The resulting spectral S/N is shown as the black line and is calculated as described in Sect. 2.3 (values refer to the y axis on the right). Integrated over the full wavelength range, one obtains a S/N ≈ 9.7. |
3.1 Maximum-likelihood method
As described in Sect. 2.3, the signal measurement with a nulling interferometer can be described as a noisy time series. Following Mugnier et al. (2006) and Thiébaut & Mugnier (2005), it is modeled as
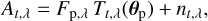 (22)
(22)
where At,λ is the recorded amplitude at time t and for effective wavelength λ, Tt,λ(θp) is the response of the instrument (i.e., the value of the differential map Tdif) at the location of the planet θp as a function of time and wavelength, Fp,λ is the discretized planet flux and nt,λ denotes the noise, which is assumed to be spectrally independent normal noise and whose variance σ2(t, λ) can be estimated from the data. In a first step and as a simplification, only the case with one (detectable) planet per system is considered to derive the signal analysis; afterward, the approach will be extended to multiple planets.
The MLM enables estimating the planet position θp and spectral flux Fp(λ) from the modulated signal by searching 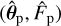 that maximize the likelihood L(θp, Fp). Maximizing the likelihood is equivalent to minimizing the negative log-likelihood or cost function
that maximize the likelihood L(θp, Fp). Maximizing the likelihood is equivalent to minimizing the negative log-likelihood or cost function
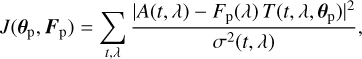 (23)
(23)
which measures the discrepancy between the data A and the model of the data for the estimated set of parameters (θp,Fp), based on the differential map T. Fp denotes the set of flux values at all measured wavelengths. It has been shown in the previously mentioned papers that for a given planet position θp the optimal spectral flux is obtained by maximizing J (as defined in Eq. (B.5)) with respect to all F(λ):
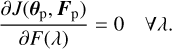 (24)
(24)
To ensure the result is physical, a positivity constraint has to be introduced on the estimated flux. The most likely planet position is then found by globally maximizing the cost function over a grid by inserting the optimized flux values back into the cost function. The estimation of the planet position and the wavelength-dependent flux can be further improved if an agreement of the estimated parameters with a priori information is enforced (Thiébaut & Mugnier 2005). This can be done by introducing a regularization term Jprior, which estimates the roughness of a sampled planet spectral flux:
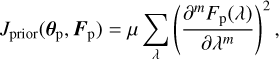 (25)
(25)
where µ is a parameter that allows the relative weight of regularization to be tuned. The mth order derivative is computed by finite differences (Thiébaut & Mugnier 2005). To smooth the estimated flux, only second order derivatives are taken into account (m = 2). The calculation of the optimal flux values and the cost function with and without regularization is further outlined in Appendix A. In accordance with the previous works, we denote by J′ the cost function that is optimized with respect to the fluxes, and by J″ the cost function that has an additional positivity constraint on the flux. The cost functions can be computed on a grid of possible initial planet positions spanning the full or only a part of the field-of-view. The most likely planet position 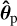 is then the location of the maximum of J″(θp) on the grid.
is then the location of the maximum of J″(θp) on the grid.
It is noted here that the cost function is closely related to the cross correlation of an ideal modulated signal generated by a noiseless point source with the template functions (the transmission maps). The cross correlation across a two-dimensional grid gives the demodulated signal function of the interferometer (Defrère et al. 2010). This is shown in Fig. 6 for a single wavelength and for the combination of multiple wavelength bins by addition of the maps.
 |
Fig. 6 Cross-correlation of the modulated signal of a noiseless point source located at [−100, 0] mas with the transmission map. Left: cross-correlation at a single wavelength. The resulting image can be understood as the demodulated signal function of such a point source at the considered wavelength. The image is antisymmetric with respect to the image center. Right: combined cross-correlation across the full wavelength range considered for the ideal point source. Considering a broader wavelength range reduces the side lobes and allows for a better location of the point source. |
3.2 Detection Criterion
To create a link between the outcome of the maximum likelihood signal extraction method and a quantitative detection criterion we further investigate the noise propagation and the probability of false alarm (PFA) in the following. As introduced in Sect. 2.3, and following the definition of Mugnier et al. (2009), the S/N of the estimated planet signal at a single wavelength is given by
![$ S/{N_\lambda }\left( {{{\bf{\theta }}_{\rm{p}}}} \right) = S/N\left[ {{{\hat F}_{\rm{p}}}\left( {{\bf{\theta }},\lambda } \right)} \right]\hat = {{{{\hat F}_{\rm{p}}}\left( {{\bf{\theta }},\lambda } \right)} \over {\sigma \left( {{{\hat F}_{\rm{p}}}\left( {{\bf{\theta }},\lambda } \right)} \right)}}, $](/articles/aa/full_html/2022/08/aa41958-21/aa41958-21-eq30.png) (26)
(26)
with 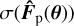 the standard deviation of the estimated flux. Given the high photon flux values of the astrophysical sources introduced in Sect. 2.2 (cf. Fig. 5), the noise in a measurement can be approximated by a normal distribution. To get an estimated value for the integrated S/N, the individual wavelength bins could be combined naively by
the standard deviation of the estimated flux. Given the high photon flux values of the astrophysical sources introduced in Sect. 2.2 (cf. Fig. 5), the noise in a measurement can be approximated by a normal distribution. To get an estimated value for the integrated S/N, the individual wavelength bins could be combined naively by
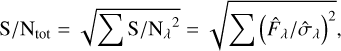 (27)
(27)
as is done to calculate the integrated S/N from the predicted photon noise in Sect. 2.3. However, this does not take into account the random nature of the measurement; in reality, even repeating the exact same observations will result in a slightly different estimated S/N.
Flasseur et al. (2020) presents a method that allows us to derive a detection criterion combining measurements at multiple wavelengths with uncorrelated noise on the basis of the cost function for direct imaging methods. With some modifications, this approach can also be applied to nulling interferometry. We note that the dominant and normally distributed background noise in the modulated signal propagates as a linear combination to the S/Nλ maps. This means that in the absence of point sources the distribution of S/Nλ values over a large enough field-of-view also follows a normal distribution. Thus, the random values of the combined cost function J′ map are expected to follow a χ2 distribution 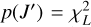 with L degrees of freedom, where L is the number of wavelength bins (Flasseur et al. 2020). For the simulated measurements presented above, a spectral resolution of R = 20 and a wavelength range from 4 µm to 18.5 µm is used (unless otherwise noted), which results in L = 31 wavelength bins (with varying bin widths).
with L degrees of freedom, where L is the number of wavelength bins (Flasseur et al. 2020). For the simulated measurements presented above, a spectral resolution of R = 20 and a wavelength range from 4 µm to 18.5 µm is used (unless otherwise noted), which results in L = 31 wavelength bins (with varying bin widths).
Figure 7 (top left) shows the cost function J′ calculated for a simulated measurement without any point sources. The non uniformity of the image is a result of the statistical fluctuations of the background noise. The bottom panel in Fig. 7 shows the corresponding distribution of the J′ values in a histogram. The simulated data follow the χ2 distribution with L = 31 degrees of freedom very closely. Following the derivation by Flasseur et al. (2020), the PFA in a data set containing no point sources but only background noise is given by 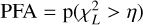 , where η is the detection threshold, which has to be determined. To obtain a PFA corresponding to a 5-σ confidence level, one needs to solve
, where η is the detection threshold, which has to be determined. To obtain a PFA corresponding to a 5-σ confidence level, one needs to solve
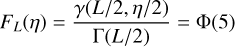 (28)
(28)
for η. Here, FL is the cumulative distribution function of the 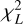 distribution, which can be expressed in terms of the lower incomplete gamma function γ and the gamma function Γ, and Φ is the cumulative distribution function of the standard normal distribution. Solving Eq. (28) for η gives a detection threshold for J′ of η ≈ 87. If the J′ value of the most likely planet position is greater than η it can be considered a detection.
distribution, which can be expressed in terms of the lower incomplete gamma function γ and the gamma function Γ, and Φ is the cumulative distribution function of the standard normal distribution. Solving Eq. (28) for η gives a detection threshold for J′ of η ≈ 87. If the J′ value of the most likely planet position is greater than η it can be considered a detection.
Using J′ as a detection criterion is, however, unsatisfactory as explained above, and J″– with positivity constraint on the flux – is better suited. At a single wavelength, and without any point sources being present, 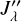 follows a χ2 distribution with one degree of freedom – the distribution of squares of normally distributed values – with a threshold at 0 due to the positivity constraint on the estimated flux values:
follows a χ2 distribution with one degree of freedom – the distribution of squares of normally distributed values – with a threshold at 0 due to the positivity constraint on the estimated flux values:
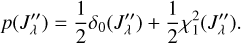 (29)
(29)
The probability distribution of the sum of L-independent values following the above distribution is given by
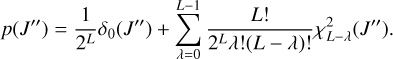 (30)
(30)
In Fig. 7, the bottom panel shows as a blue histogram the distribution of the J″ values found in the map on the top-right panel. It follows the expected distribution from Eq. (29).
Thus, similar to Eq. (28), a detection criterion J″ > η can be defined by finding η such that
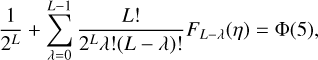 (31)
(31)
with the left-hand side being the cumulative distribution function of the probability distribution defined in Eq. (30).
Solving Eq. (31) with L = 31 for η gives a detection threshold of η ≈ 65 for the cost function with positivity constraint. A value of η = 65 in the cost map J″ thus corresponds to a 5σ detection.
The detection measure presented here does not include spectral regularization. While a regularization term improves the contrast of the detection maps (see Fig. B.1), it adds an interdependence between the wavelength bins. Thus, the estimated signal, as well as the noise terms in the individual wavelength bins, are no longer mutually independent. Because the derivation of the detection criterion was based on the assumption of uncorrelated noise, it cannot be applied directly in the case of regularization. However, it was already pointed out by Mugnier et al. (2006), and is also indicated by the example presented in Fig. B.1, that regularization is mostly needed for the detection of planets with a low underlying S/N ≲ 5.
 |
Fig. 7 Effect of the positivity constraint of the cost function. Top: different versions of the cost function, J, for a simulated observation without any point sources. L = 31 wavelength bins are used. Top left: J′ without positivity constraint on the flux. The image is point-symmetric with respect to the image center. Top right: J″ with a positivity constraint on the planet flux. Compared to the left image, the strict point symmetry is lifted and the mean value is lower. Bottom: probability distribution of the cost function maps shown above. The gray histogram shows the J′ values obtained from the panel on the top left. The solid red line shows the probability density function of a χ2 distribution with L = 31 degrees of freedom. The blue histogram shows the J″ values obtained from the panel on the top right. The solid orange line shows the theoretically expected distribution of the J″ values given in Eq. (30). The dashed vertical lines indicate the detection criteria of η = 87 and η = 65 as derived by Eq. (28) and Eq. (31), respectively. |
4 Signal Analysis
4.1 Single Planet: Earth-Twin at 10 pc
We applied the signal extraction method to the case study example of an Earth-twin planet orbiting a Sun-like star at 10 pc (see Table 1). We compared the S/N of the extracted signal to predictions based on photon statistics and determined the position of the signal. We simulated the planet at 100 mas projected angular separation from the star. We remind the reader that for an assumed integration time of 55 h one obtains a predicted integrated S/Npred = 9.7. The top panel of Fig. 8 shows the noisy time series resulting from the simulation. The maximum likelihood analysis was performed on a grid out to 200 mas angular separation from the central star, with a resolution of ~0.5 mas. The middle panel of Fig. 8 shows the cost function map J″ without regularization (µ = 0) for a single simulated measurement. The relatively high S/N allows for a clear detection of the planet in the upper right corner. The detection criterion as derived in Sect. 3.2 is fulfilled and the planet location is estimated correctly within the resolution provided by the grid. The estimated extracted spectral flux of the located planet is shown in the bottom panel in Fig. 8. The extracted spectrum agrees with the underlying true spectrum within the expected uncertainties.
Estimates for the location and the spectrum have been extracted from the simulated data, but we still need to quantify the S/N and compare it to the expected value. Applying Eq. (27) results in S/Nest = 10.45, compared to the predicted S/Npred = 9.7. The discrepancy is due to the statistical nature of the simulated data as mentioned previously. If the simulation is repeated, the outcome is slightly different as would be the case for a real measurement. To better estimate the performance of the signal extraction process in general, and the S/N estimation in particular, the simulated measurement was repeated 1000 times with the same setup. For each run the planet position and spectral flux were estimated from the simulated data.
The top panel in Fig. 9 shows the distribution of the estimated angular separation of the planets. The average of the estimated angular separation is 99.7 ± 1.5 mas. The azimuthal position was extracted correctly for all simulated planets within the resolution of the grid (±1°). While the extracted spectra are all noisy and are qualitatively similar to the example shown in the bottom panel of Fig. 8, the bottom panel of Fig. 9 shows the mean and the standard deviation of the extracted flux values per wavelength bin over the Ν = 1000 simulations in comparison with the input spectrum. Apart from the short wavelength range, where the low flux and high noise levels result in large uncertainties, the extracted mean spectrum agrees very well with the input data.
4.2 Multi-Planet Systems
As most exoplanetary systems are expected to contain multiple planets, it is important that extraction algorithms can deal with multiple objects. The modulation signal recorded with a nulling interferometer is a superposition of the signals from different sources within the field-of-view. The most straightforward approach to differentiate individual planets is to find their positions and the estimated fluxes one after another. To do so, the most likely planet position, in absolute terms, is accepted as a detection provided it fulfills the detection criterion described above, and the spectral flux is estimated for that planet. The estimated planet signal is subtracted from the data and the process is repeated until no other significant signal remains in the data.
We applied the signal extraction process outlined above to a simulated 3-planet system. All planets have a radius Rp = 1 R⊕ and are located around a Sun-like star at 10 pc. Their semimajor axes, ap, were set at 0.8, 1.0, and 1.2 AU, respectively. All planets were assumed to radiate as black bodies with an equilibrium temperature of 276 Κ scaled by the inverse square root of the semimajor axis, 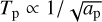 . The system is seen face-on, such that all planets appear at their respective maximum angular separation. The azimuthal position of the planets was chosen randomly. The system was assumed to harbor an exozodi disk with z = 3. For an integration time of 55 h the predicted S/Ns of the three planets are 15.8, 10.4, and 6.9, respectively.
. The system is seen face-on, such that all planets appear at their respective maximum angular separation. The azimuthal position of the planets was chosen randomly. The system was assumed to harbor an exozodi disk with z = 3. For an integration time of 55 h the predicted S/Ns of the three planets are 15.8, 10.4, and 6.9, respectively.
Figure 10 shows the three detection maps for the iterative signal extraction process applied to the simulated data. In the left panel, the highest values for the cost function indicate the correct position of the planet closest to the host star, which has the highest expected S/N. In addition to the side lobes of the first planet, the positions of the other planets, as well as their side lobes, are also visible. However, because the cost values of these features are similar, it is unclear which signal corresponds to a true source and which does not. The subtraction of the highest S/N signal removes also its side lobes and the second planet can be identified by the strongest remaining peak. Removing the second signal allows the third source to be detected. After the third source, no further point source is found above the detection criterion. Extracting the signal of the three planets leads to estimated S/N values of 16.0, 10.1, and 7.1, respectively. To test the robustness of the extraction process with respect to the planet position we again iterated the signal extraction for multiplanetary systems over distinct realizations of the noise. We find that the angular separation and the position angle of the planet is retrieved accurately within the given uncertainties. These uncertainties scale in accordance to the respective photon noise S/Ns, meaning that the innermost planet is extracted to the highest precision.
We fitted the extracted spectra of the three planets with a blackbody spectrum to estimate their radii and effective temperatures as this will also be done as one of the first steps for any planet candidates detected with LIFE. Figure 11 shows the estimated values along with 1σ confidence contours derived from the uncertainties in the extracted flux values. The true values are indicated by crosses. The uncertainty in the estimated temperatures and radii increases with decreasing S/N, from about σT ≈ 20 Κ and σR ≈ 0.15 R⊕, for the brightest planet to σT ≈ 35 K and σR ≈ 0.4 R⊕ for the faintest. As the spectral shape of an emitting blackbody depends more strongly on the temperature than on its size, the relative uncertainty in the derived temperature is much smaller than the relative uncertainty in the radius.
 |
Fig. 8 Extraction of spectrum from noisy observation. Top: noisy time series signal from simulated data for an Earth-like planet around a Sun-like star at 10 pc (in blue). The underlying noiseless planet signal is indicated by the red curve. Middle: detection map for simulated data of the Earth-like planet. The photon-noise-based S/N is 9.7 (cf. Sect. 2.4). The planet is correctly found in the upper right of the map. Bottom: spectral flux of the Earth-like planet as estimated from the simulated data (red data points with 1σ error bars). The blue line shows the true flux of the simulated planet, and the blue shaded region indicates ±1σ based on the photon statistics. |
 |
Fig. 9 Robustness of the single planet extraction. Top: distribution of the estimated angular separation from the host star of 1000 simulated Earth-twins. The underlying true value is θ = 100 mas, and the average estimated value is 99.7 ± 1.5 mas. The spacing of the bars corresponds to the angular resolution of the grid on which the analysis was performed. Bottom: mean (red dots) with standard deviation (red error bars) of the distribution of the estimated flux values over 1000 simulations of the same artificial planet. The blue line shows the true spectrum, with the blue shaded region enclosing ±1σ based on the photon statistics. |
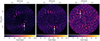 |
Fig. 10 Cost function detection map for the iterative detection of three simulated planets (indicated by the white arrows). The simulation parameters are given in Sect. 4.2. The left image shows the detection map calculated from the full simulated data. Subtracting the estimated signal contribution of the source detected in the first map and recalculating the detection map results in the second image, and after repeating this the third one. Removing a detected source from the data also removes the side lobes created by the source, thus allowing for a clear iterative detection. |
4.3 Rocky, Habitable Zone Exoplanets from LIFE Search Phase
In the previous sections, we investigate how well the signal of individual exoplanets can be extracted and their basic properties, such as effective temperature, radius and position, can be estimated. We now turn to a larger sample of objects covering a broader range of properties and different noise characteristics (e.g., spectral type of host star and exozodi level). The extraction algorithm is applied to a subset of simulated exoplanet population that was used for the detection yield estimation in Paper I (Quanz et al. 2022). Specifically, we focus on the rocky, HZ planets5 that are detectable in a 2.5 yr search phase with four D = 2 m apertures and investigate in detail how well their properties can be determined from single-epoch observations, assuming the planets radiate as black bodies at their respective equilibrium temperature. From the 500 Monte Carlo runs that we carried out in Quanz et al. (2022) in order to estimate the expected detection yield of the LIFE mission, we randomly selected 100 runs. These runs contained approximately 4400 rocky, HZ planets with predicted S/N ≥ 7, which is considered the detection threshold in Paper I. Figure 12 shows the distribution of the predicted S/N of these planets (based on photon noise statistics), their temperature, radius, and their projected angular separation from their host star. The median of the S/N distribution is ≈13.3, thus nearly twice the detection threshold. While, on average, the planet radii are >1.0 R⊕, the mean temperature of the detected planets is only Tp ≈ 235K, which is less than Earth’s effective temperature.
Our signal extraction method was applied to each planet individually and the detection maps were calculated without reg-ularization of the estimated spectra. The detection criterion as derived in Sect. 3.2 was applied. We find that ≈1.5% of the simulated planets do not fulfill the detection criterion. For a few additional planets the position was extracted incorrectly. Overall, about 98% of the planets were detected at a separation deviating ≤15% from the true value and with an error in position angle ≥10°.
For the detected planets, the temperature and radius were estimated by fitting a blackbody spectrum to the extracted flux. Additionally, the S/N was estimated from the extracted flux as described in Sect. 4.1. Because each of the estimated parameters has a broad distribution among the simulated planets, the relative deviation of the estimated values from the underlying true values is analyzed. The results of the parameter extraction are presented in Fig. 13. The corner plot shows the distribution of the predicted S/N and the ratios between the estimated and the true values of the planetary parameters (i.e., temperature, radius, and separation) as well as the ratio between the estimated and the purely photon-statistic-based S/Ns. From the first column it is evident that the estimation of all parameters improves with increasing S/N of the planet, as the statistical distribution of the estimates becomes narrower. Overall, the S/N is slightly underestimated, even for relatively high S/N values > 25. This can be explained by an overestimated noise variance from the simulated data, as it is calculated as the variance of the full data including possible planet signals.
The deviation of the estimates of the temperature and the radius from the true values are approximately symmetric in terms of over- or underestimation. Across the full sample, the temperature is estimated to 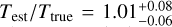 and the radius to Rest/Rtrue = 0.97 ± 0.18. As expected, the estimate of the temperature and the radius are highly correlated as both parameters are positively correlated with the total emitted radiation of the planet. The separation is estimated to θest/θtrue = 0.99 ± 0.01.
and the radius to Rest/Rtrue = 0.97 ± 0.18. As expected, the estimate of the temperature and the radius are highly correlated as both parameters are positively correlated with the total emitted radiation of the planet. The separation is estimated to θest/θtrue = 0.99 ± 0.01.
 |
Fig. 11 Temperature and radius estimates for the three simulated planets with Rp = 1 R⊕ and varying temperatures. The true values are indicated by crosses and the estimated values by dots with corresponding 1σ confidence ellipses. The values are estimated by fitting a blackbody curve to the estimated spectra of the point sources, whose locations are inferred from the detection maps shown in Fig. 10. |
 |
Fig. 12 Distribution of properties of detectable rocky, HZ planets from the detection yield estimates presented in Quanz et al. (2022) normalized over 100 Monte Carlo runs. From top to bottom: Predicted S/N (based on photon noise), effective temperature, radius, and projected angular separation. |
5 Discussion and conclusions
We have investigated the signal extraction process for simulated interferometric measurements to study the detectability of potential exoplanets and the ability to characterize them. We implemented a maximum-likelihood algorithm previously proposed for the Darwin mission and applied it to simulated data. This yields three important results: (a) this method can be successfully applied to multi-planet systems, (b) the signal extraction method is able to reproduce S/N estimates that are in agreement with expectations from photon noise statistics, and (c) planetary properties inferred by the signal extraction are of high accuracy. These results are especially interesting in the context of Quanz et al. (2022), since this publication predicts the exo-planet yield of the LIFE mission based on a synthetic planet population without considering the impact of signal extraction. Our results indicate that an inclusion of the signal extraction in these simulations would not fundamentally alter the results.
Yet, under certain conditions the signal extraction is especially demanding. In the low-S/N regime, we have qualitatively shown how spectral regularization can help to disentangle the planet signal from the background noise. However, as spectral regularization relies on a priori assumptions about the planet spectrum, it is not free of bias and adds a degree of freedom to the analysis. To apply regularization to a large set of simulated planets, a detection criterion that depends on the amount of enforced spectral regularization would have to be defined. Additionally, it has to be investigated how the regularization quantitatively affects the estimated planet spectrum.
To further assess potential limitations when dealing with multi-planet systems, studies with more diverse planet properties or very small projected angular separations could be envisaged. Potential improvements when dealing with several signals were already presented by Thiébaut & Mugnier (2005). These authors discussed an extrapolation of the MLM to estimate the planet positions and spectra for multiple planets at once, which avoids error propagation from the estimation of the first detected planet to the other ones. This generalized approach is computationally more expensive; a simplified option estimates the planet positions one after the other but recomputes the optimal flux of all detected planets at each iteration.
Furthermore, the ability to correctly extract multi-planet systems is also governed by the effective angular resolution of the array. Therefore, a study of diverse multi-planet extractions would be able to provide minimum requirements for the angular resolution. Since the angular resolution has been shown to be a dominant factor in the design of nulling interferometers (Lay 2005), such a study will become vital in the ongoing development of LIFE.
Going forward, one could easily imagine that new approaches involving modern machine-learning-based signal extraction algorithms should be tested and their performance compared. While already being explored in other fields (e.g., Cuoco et al. 2020; Gebhard et al. 2019, 2020), nulling interferometry has not yet been a focus point of these efforts. This will be particularly important as soon as systematic noise terms can be simulated in a realistic way.
An additional factor degrading the quality of the measurement can be the occurrence of instrumental noise. Within the LIFE project, the current working assumption is that the instrumental noise can be neglected based on its contribution being significantly smaller than the fundamental noise. We show that this assumption places strict requirements on the instrumental stability and prompts continued technical developments, for example in the fields of low dark current detectors or highly precise OPD control techniques.
Similarly, signal extraction has been shown to play an integral role in the prediction of instrumental noise (Lay 2004). Certain steps in the signal retrieval, for example the explicit fitting and removal of systematic noise, can significantly relax technical requirements (Lay 2006). As LIFEsim progresses to include the simulation of instrumental noise, the removal of such noise should be considered with the methods presented here.
In future work, we aim to shift from the fundamental noise limited regime into a regime in which some instrumental noise is retained in the signal. A prerequisite for this is that the instrumental noise is well understood, tracked, and considered in the interpretation of the measurements. Defrère et al. (2010) offers a list of techniques targeted at facilitating this treatment of instrumental noise. The goal of this future work will be to achieve the scientific output postulated by the LIFE mission with technology closer to contemporary and near-future instrumentation.
In summary, we present a publicly available6 tool for simulating the exoplanet search phase of the LIFE mission called LIFEsim7. Using the presented planetary signal extraction methods, we have shown that the synthetic exoplanet population used for the mission yield evaluation in Quanz et al. (2022) can be retrieved. We have demonstrated the precise extraction of planetary radius and temperature, which is of special interest since they are fundamentally important parameters for characterizing the (atmospheric) properties of exoplanets and for categorizing and prioritizing objects for potential in-depth follow-up investigations. We remind the reader that these two parameters are much more difficult to derive from reflected light measurements as there is a degeneracy between planet size and geometric albedo and no immediate information about the effective temperature can be obtained. These results illustrate the high quality of information one can expect from single-epoch observations with LIFE and how this information will complement the results from future reflected light missions.
 |
Fig. 13 Corner plot showing the predicted S/N based on photon statistics (cf. top panel in Fig. 12) and the estimated values for S/N, temperature, radius, and angular separation relative to the true values based on the signal analysis of ≈4400 rocky, HZ planets. We note that the discretization of the values for the estimated angular separation corresponds to the resolution of the spatial grid on which the analysis was performed. At the top of each column the mean and the standard deviation of the distributions are given. |
Acknowledgements
We thank the anonymous referee for a critical and constructive review of the original manuscript which helped improve the quality of the paper significantly. This work has been carried out within the framework of the National Centre of Competence in Research PlanetS supported by the Swiss National Science Foundation. S.P.Q. acknowledges the financial support of the SNSF. TL was supported by the Simons Foundation (SCOL award No. 611576). This research has made use of the following Python packages: astropy (Astropy Collaboration 2013, 2018), matplotlib (Hunter 2007), numpy (Van Der Walt et al. 2011), scipy (Virtanen et al. 2020). Author contributions: M.O. and F.D. contributed equally to this paper. M.O. wrote the original LIFEsim tool, carried out the main analyses and wrote part of the manuscript. F.D. contributed to the main analyses and the LIFEsim tool, programmed the publicly available github version, led the instrumental noise analyses and wrote part of the manuscript. S.P.Q. initiated and guided this project and wrote part of the manuscript. R.L., E.F. and A.Gh. contributed to the LIFEsim tool. All authors discussed the results and commented on the manuscript. D.D. and R.L. acknowledge the support from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement CoG-866070).
Appendix A Fundamental noise limit
Section 2.3.2 states that for the analysis presented in this paper a measurement dominated by photon noise originating from the astrophysical sources is assumed. In the following, this state will be referred to as the fundamental noise limited regime. Considering the technical complexity of nulling interferometers, it is important to substantiate this assumption and offer proof that it is well founded. The aim of this appendix is the implementation of an instrumental noise model and the subsequent prediction of the maximum levels of perturbations to the instrument that allow the system to stay in the fundamental noise dominated regime.
Appendix A.1 Assumptions
The term fundamental noise limited is readily used in literature as well as in the LIFE paper series. Under the goal of producing quantitative results, this must be translated into a more tangible constraint. The perfect instrument will only be subject to the photon noise by the astrophysical noise sources σfund8. Perturbing the instrument will give rise to two additional types of noise terms. First and foremost, a systematic perturbation (e.g., a variation in the amplitude response of one of the interferometric arms) of the instrument will introduce a systematic noise term σs,inst arising from an additional photon rate introduced by the perturbations. These additional photons can resemble a signal as would be produced by a target exoplanet. Second, additional photon noise sources such as a detector dark current or thermal emission within the instrument can be considered. Moreover, the systematic perturbations of the central destructive fringe will average to a mean reduction in the effective null-depth. This will increase the overall amount of photons received from the target star and subsequently also increase the photon noise. We collect all additional photon noise sources into the instrumental photon noise term σp,inst and define the instrumental noise term
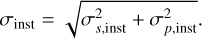
The fundamental noise limited case is then interpreted as the measurement being dominated by the photon noise arising in the perfect instrument over the instrumental noise. Therefore, we define the fundamental noise limited case as
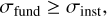 (A.1)
(A.1)
where the fundamental noise contribution is larger that the instrumental noise contribution. Semantically, it could also be argued that the fundamental noise being a multiple of the instrumental noise could be required. Therefore, we also present the case of a five-times larger fundamental noise in the following.
For the array and instrument configuration, we mirrored the setup described in Sect. 2.1 and Table 1. This includes the simulation of phase chopping, which is assumed to be facilitated by subtracting two simultaneous realizations of phase-inverted outputs. This simplifies the calculation of instrumental noise terms as, contrary to Lay (2004), we do not have to include errors at the chopping frequency. All astrophysical sources were simulated according to the models described in Sect. 2.2. If not stated otherwise, this appendix analyzes an observation of an Earth-twin around a Sun-like star located at a distance of 10 pc with a z = 3 exozodi level (cf. Table 1).
In the following simulations, we assume a non-perfect instrument affected by perturbations. Systematic perturbations are assumed to affect the amplitude response A, the phase response ϕ and the polarization rotation θ of each of the four interferometric arms as well as the position x and y of the collector spacecraft.
These dynamic perturbations follow a perturbation spectrum centered around values for the configuration of the ideal instrument9. In this work, we omit any constant static offsets from the ideal instrument configuration (e.g. a constant amplitude response offset in one of the arms). This omission is based on static offsets being more easily calibrated and removed compared to dynamic perturbations. Due to a lack of reliable empirical data, we stay agnostic to how these perturbations are generated and assume the general noise profiles listed in Table A.1. Apart from the aforementioned general systematic perturbations, we examine two more sources of perturbation in an effort to illustrate the allowed magnitude of the remaining perturbation terms. We consider the detector dark current ID and the thermal background seen by a detector in an environment of temperature T. We assume a detector with physical pixel dimensions of the JWST Mid-Infrared Instrument (MIRI) detectors (25 µm pixel pitch; see Rieke et al. 2015) and a spectral sampling of 2.2 pixels per wavelength channel.
Parameters of the instrument perturbations at a reference wavelength of 10 µm.
 |
Fig. A.1 Wavelength dependence of noise contributions for observations of an Earth-twin located at 10 pc with LIFE in the baseline scenario. Panel a): Division of the fundamental noise into its individual sources. Panel b): Instrumental noise sources split into systematic noise sources (green) and additional photon noise sources arising from instrumental effects. Panel c): Planet signal, fundamental noise, and instrumental noise contributions. A S/N using only fundamental noise (orange bars) represents the fundamental noise limited case used in the LIFE paper series. The green bars show the full S/N, which additionally considers the instrumental noise as well as the fundamental noise. |
Appendix A.2 Methods
The simulations are largely based on the approach presented in Lay (2004). This paper was published in the context of the TPF-I mission and offers a comprehensive framework for estimating the instrumental noise for nulling interferometers. The following paragraphs will sparsely trace the calculations performed in Lay (2004) to highlight fundamental properties.
First, the overall interferometric response is decomposed into a sum of responses of the individual baselines:
![$ N = \sum\limits_j {\sum\limits_k {{A_j}{A_k}\left[ {\cos \left( {{\phi _j} - {\phi _k}} \right){{\bar B}_{{\rm{sym}},jk}} - i\,\sin \left( {{\phi _j} - {\phi _k}} \right){{\bar B}_{{\rm{asym}},jk}}} \right]} .} $](/articles/aa/full_html/2022/08/aa41958-21/aa41958-21-eq45.png) (A.2)
(A.2)
Here, N is the detected photon rate, An and ϕn are the amplitude and phase responses of the n interferometric arms and  is the Fourier transform of the (anti)symmetric sky brightness distribution under the baseline from the nth to the mth collector spacecraft. Equation (A.2) reflects an intrinsic symmetry property of nulling interferometers: baselines with π-multiple phase difference respond to symmetric (with respect to the line of sight) source while baselines with π/2-multiple phase differences respond to antisymmetric sources. The sensitivity of the photon rate against perturbations of the instrument (here in phase δϕn and relative amplitude δan = δAn/An) is captured in a second order Taylor expansion,
is the Fourier transform of the (anti)symmetric sky brightness distribution under the baseline from the nth to the mth collector spacecraft. Equation (A.2) reflects an intrinsic symmetry property of nulling interferometers: baselines with π-multiple phase difference respond to symmetric (with respect to the line of sight) source while baselines with π/2-multiple phase differences respond to antisymmetric sources. The sensitivity of the photon rate against perturbations of the instrument (here in phase δϕn and relative amplitude δan = δAn/An) is captured in a second order Taylor expansion,
![$ \matrix{ {\delta N \approx } \hfill & {\sum\limits_j {\left| {{{\partial N} \over {\partial {A_j}}}{A_j}\delta {a_j} + {{\partial N} \over {\partial {\phi _j}}}\delta {\phi _j}} \right|} } \hfill \cr {} \hfill & { + \sum\limits_j {\sum\limits_k {\left[ {{1 \over 2}{{{\partial ^2}N} \over {\partial {A_j}\partial {A_k}}}{A_j}{A_k}\delta {a_j}\delta {a_k}} \right.} } } \hfill \cr {} \hfill & { + \left. {{{{\partial ^2}N} \over {\partial {A_j}\partial {\phi _k}}}{A_j}\delta {a_j}\delta {\phi _k} + {1 \over 2}{{{\partial ^2}N} \over {\partial {\phi _j}\partial {\phi _k}}}\partial {\phi _j}\partial {\phi _k}} \right].} \hfill \cr } $](/articles/aa/full_html/2022/08/aa41958-21/aa41958-21-eq47.png) (A.3)
(A.3)
The partial derivatives in this equation represent the sensitivity that the photon rate exhibits against a perturbation of respective kind and order. We note the appearance of second order terms as well as amplitude-phase cross terms.
At this point in the calculation, the symmetry of the sources is used to simplify the expressions and arrive at the sensitivity to the perturbations. This will be demonstrated using the sensitivity to stellar leakage. In first approximation, the brightness distribution of the stellar disk is centrally symmetric, leading to  . This reduces Eq. (A.2) to
. This reduces Eq. (A.2) to
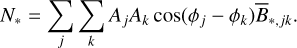
Now the sensitivity of the photon rate toward, for example, first order amplitude perturbations is given by
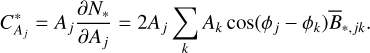
Here, 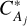 is called the first order stellar leakage sensitivity coefficient, and all remaining sensitivity coefficients in Eq. (A.3) can be determined in the same fashion.
is called the first order stellar leakage sensitivity coefficient, and all remaining sensitivity coefficients in Eq. (A.3) can be determined in the same fashion.
In a final step, the photon rates Ν and δΝ are cross-correlated with planetary template functions, which represents the signal extraction process. The photon noise of the instrument then corresponds to the square root of the mean photon rate and is therefore given by
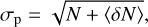
where 〈〉 denotes the ensemble average over all perturbed states of the system. In this description, we identify the following correspondences to the variables defined in the previous Sect. A.1: 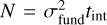 and
and 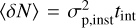 where tint is the integration time.
where tint is the integration time.
The systematic noise is accessed via
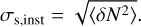
Up to second order, the method of phase chopping is able to remove all systematic noise contributions except for one first order phase (δϕn) and one amplitude-phase cross term (δanδϕm). We remind the reader that the order of the term is not connected to its impact but refers to the proportionality between the perturbation and the photon rate in Eq. (A.3). Identifying the perturbation with the noise spectra given in Table A.1 enables the calculation of the required noise sources. We refer the reader to Lay (2004) for the full details of the methods described in this section.
 |
Fig. A.2 Ratio of fundamental noise to instrumental noise on a grid of amplitude and phase perturbations for the shortest-wavelength bin at λb = 4.1 µm with width ∆λb = 0.2 µm. The perturbations are assumed to be pink noise with the specified reference rms at 10 µm, and the phase perturbation is converted to an OPD. The contours indicate where the fundamental noise dominates the systematic noise by a factor of one, five, or ten, respectively, for the λb = 4.1 µm case (in red) and for comparison the λb = 6.1 µm (in orange) and λb = 10.1 µm (in cyan) cases. The crosses indicate the reference levels specified by Table A.1. |
Appendix A.3 Results
The signal and noise contributions using the assumptions laid out above for every wavelength channel defined in the LIFE baseline scenario are shown in Fig. A.1. For the comparison of the fundamental noise sources in Panel a), we reconfirm the behavior described in Sect. 2.4: the short-wavelength end of the spectrum is dominated by the stellar leakage term, while the long-wavelength end of the spectrum is dominated by the local-zodiacal dust emission, which cannot be suppressed by nulling due to its incoherent nature. For the first and second order systematic noise terms shown in Panel b) we stress again that the use of phase chopping removes all systematic noise terms except for the first order phase deviations and the second order amplitudephase deviation cross terms. This removal helps to relax the technical requirements imposed by the systematic noise. We reproduce the finding of Lay (2004) that the second order term is generally larger than the first order term. Panel b) also shows that the instrumental noise is either white or increases toward shorter wavelengths. This is driven by the perturbation scaling with wavelength described in Table A.1 and by the increased amount of stellar light emitted in this regime.
Panel c) of Fig. A.1 presents the impact of the additional noise sources on the S/N. Here, we assume a detector environment temperature of T = 11 K and a dark current of ID = 10−4 e− px−1 s−1. As expected, the largest relative S/N reduction is induced toward the shorter wavelength end of the spectrum where the systematic noise is most dominant.
In the fundamental noise limit, the condition in Eq. (A.1) must be valid for all wavelength bins. The relative trends of instrumental and fundamental noise in Fig. A.1 indicate that this condition should be tested toward the shorter wavelength end of the spectrum. We therefore select three discrete wavelength bins below 10 µm for evaluation10. For completeness, we list the numerical values for the relative signal and noise contribution in this shortest-wavelength bin in Table A.2.
To infer the acceptable systematic noise levels, we ran the simulations over a grid of pink noise amplitude and phase perturbations with varying root-mean-squared (rms) values11. The rms is specified at a reference wavelength of 10 µm and scaled according to Table A.1. Phase errors were converted to OPD errors to allow for a better comparison with literature. The ratio of instrumental to fundamental noise on this grid is shown in Fig. A.2.
Firstly, the figure confirms that certain regions allow for a trade-off between the OPD error rms and the amplitude error rms, where increasing one allows for a reduction of the other. Outside of these regions, there exist hard upper limits for the maximally allowed rms error for both amplitude and OPD. It will be vital for the design of the instrument to stay clear of these limits, since they imply that, if reached in one perturbation rms, any improvement to the other perturbation rms does not improve instrument performance. Additionally, we can reconfirm that the requirements are much less strict in the longer-wavelength regime.
This grid can serve as a rough predictor for the maximally acceptable noise levels: acceptable and too high levels of noise are divided by the contour tracing a ratio of one between the fundamental and systematic noise. Within the presented framework, this produces sets of allowable noise levels shown in Table A.3. These values can only be seen as rough predictors, since we are not presenting a complete instrument model and additional noise sources not considered in the present analysis could further increase the noise requirements.
Approximate predictions for the maximum allowed perturbation rms to stay in the fundamental noise dominated case.
A similar analysis can be done for the instrumental photon noise sources. As representative terms for thermal background emission and white shot noise term we analyzed the thermal emission as seen by the detector and a dark current term for the detector.
 |
Fig. A.3 Ratio of fundamental noise to instrumental noise on a grid of the detector environment temperature and the detector dark current for the shortest-wavelength bin at λb = 4.1 µm with width ∆λb = 0.2 µm. The temperature induces blackbody thermal emission that is propagated directly into the detector. The dark current is assumed to be constant with temperature. The instrument is configured according to the reference state in Table A.1. The contours indicate where the fundamental noise dominates the systematic noise by a factor of one or five. The cross indicates the reference levels of Τ = 11 Κ and ID = 10−4 e− px−1 s−1 used in Fig. A.1. |
Figure A.3 shows an expected behavior. Since both noise sources are independent of each other, there exists an absolute upper limit for the acceptable level of both terms (see Table A.4).
We note that while meeting the requirement for the thermal background temperature of the detector does not appear too challenging, the requirements on the dark current seem to be at least one order of magnitude more stringent than what has been achieved so far for both Si: As IBC detector arrays and MIR MCT devices (e.g., Rieke et al. 2015; Cabrera et al. 2019; Roellig et al. 2020; Gáspár et al. 2020). The challenges related to MIR detector technology (and availability) has already been discussed in LIFE paper I (Quanz et al. 2022). An interesting alternative approach could be using kinetic inductance detectors or transition edge sensor detectors, which may also be applicable for the LIFE wavelength range (e.g., Perido et al. 2020; Nagler et al. 2021).
The acceptable perturbation levels will depend on the configuration of the observed system. First and foremost, the properties of the star and exozodiacal disk will influence both, the amount of fundamental noise received and how the amount of systematic noise scales with a given level of perturbation. Apart from this there are additional, subtler effects that change the noise levels. Prominent examples are the scaling of the array baseline with the host star luminosity (see Sect. 2.3.1), relative shifts in main emission wavelength between the astrophysical objects and scaling of absolute flux with the target distance.
A full study of all the aforementioned effects is vital, but out of the scope of this paper. Nevertheless, a simulation varying only the stellar type and the distance was performed to confirm low impact on the acceptable noise levels and find an order-of-magnitude estimate for the relative change.
To simulate the observation around a different stellar type, an Earth-twin was placed around HD 23297912, an MO.5V-type star at 10 pc distance. For this target as well as for an Earth-twin system at 5 pc distance, the ratio of fundamental to instrumental noise over amplitude and OPD perturbations is shown in Fig. A.4.
It is apparent that the change in system configuration undertaken here changes the acceptable perturbation levels by less than one order of magnitude. Away from the amplitude and phase limits (toward the center of Fig. A.4), the acceptable levels show almost no change. This can be taken as validation for the approach of this appendix to retrieve order-of-magnitude estimates using only a single representative Earth-twin target. However, it must also be a reminder that this will propagate systematic biases into the sample of detectable planets, making an analysis of the full sample a top priority for future work.
An additional interesting property found here is that decreasing the distance to the target increases the strictness of the OPD error requirement while decreasing the strictness of the amplitude error requirement. The same effect can be seen when moving to hotter host stars.
Appendix A.4 Discussion
Approximate predictions for the asymptotic upper limits in detector thermal background and detector dark current perturbation to stay in the fundamental noise dominated case.
 |
Fig. A.4 Impact of the target system configuration on the ratio of fundamental noise to instrumental noise on a grid of amplitude and phase perturbations for the shortest-wavelength bin at λb = 4.1 µm with width ∆λb = 0.2 µm. The system parameters assumed for the M-star target are given in the text. The contours indicate where the fundamental noise dominates the systematic noise by a factor of one, five, or ten, respectively. The cross indicates the 4 µm reference level specified by Table A.1. |
In Table A.3 and Table A.4, we present an estimate for the maximum allowed noise level to stay in the fundamental noise limited regime. We cross-validated the simulations that produce these results with those of Lay (2004). While the maximum allowed noise levels can confidently be used as an order-of-magnitude approximation, we briefly discuss the most prominent factors that will influence these values as work on LIFE continues to progress.
First, in Fig. A.4 we demonstrate three different configurations of the target systems that do not produce significantly different requirements toward instrument perturbations. However, the LIFE mission aims at observing a much more diverse sample than what is represented in Fig. A.4. Therefore, in order to gain an understanding about the requirements to remain in the fundamental noise limited regime for every target, we will apply the presented simulation to the full synthetic planetary sample described in Quanz et al. (2022) in future work.
Secondly, the presented analysis assumes a specific type of beam combination (double Bracewell). The LIFE initiative is still in the process of evaluating other combiner techniques (Hansen et al. 2022). An adoption of a significantly different technique would certainly also change the requirements on maximum allowed perturbations and the types of perturbations that dominate the noise.
Thirdly, the assumptions about the perturbations themselves are not directly based on real data or a detailed instrument model. On the one hand, an approach more strongly based onexperi-ments could inform a more detailed model for the shape of the perturbation spectra. As is shown in Defrère et al. (2010) the shape can significantly influence the requirements for maximal perturbations. On the other hand, it would enable the connection of requirements as presented in this report to a component level breakdown. This would enable an evaluation of the feasibility of reaching the required levels of perturbation.
Meeting these requirements for amplitude and especially OPD error described in Table A.3 will be a considerable challenge. For comparison, currently planned lab experiments in the context of the LIFE mission (Gheorghe et al. 2020) plan to achieve similar amplitude mismatch. The planned OPD error, however, is one order of magnitude larger compared to what is presented in this work. Based on these experiments, it will be difficult to predict whether the requirements in Table A.3 are achievable in the mid-term future. In turn, this raises the question if it is strictly required to operate the instrument in the fundamental noise limited regime over the whole wavelength range to accomplish the science goals proposed for the LIFE mission.
Allowing for more OPD and amplitude perturbation will increase the instrumental noise at short wavelengths. However, these wavelength bands are routinely dominated by stellar geometric leakage (fundamental noise) and offer very little signal at least for temperate exoplanets (see Fig. 5). Accordingly, for those targets, wavelengths below 6 µm do not contribute to the bulk detection nor the atmospheric retrieval (cf. Konrad et al. 2022). We therefore expect that allowing for appropriately larger perturbations will not significantly alter the results presented in this paper and in Quanz et al. (2022).
Appendix B Implementation of the maximum likelihood method
We describe the implementation of the MLM for the setting described in Sect. 2.3, with symmetrical noise sources that contribute by shot noise only. The time dependence of the transmission map originates only from the rotation of the array, such that T(t, λ, θp) = T(ϕ(t), λ, θp). The ideal modulation profiles for all possible planet positions θp are already contained in the transmission map shown earlier in Fig. 3 as horizontal lines. Additionally, the noise variance is time-independent: σ2(t, λ) = σ2(λ) and can be estimated from the recorded data A(t, λ).
For simplicity, here J labels the total cost function including the regularization term. To enforce smoothness on the spectrum, the second order derivative m = 2 is used. The discretized cost function is given by
![$ \matrix{ {J\left( {{\bf{\theta }},{\bf{F}}} \right) = } \hfill & {\sum\limits_\lambda {\left[ {\sum\limits_t { - 2{F_\lambda }} } \right.\sum\limits_t {{{{A_{t,\lambda }}{T_{t,\lambda }}} \over {\sigma _\lambda ^2}}} + F_\lambda ^2\sum\limits_t {{{T_{t,\lambda }^2} \over {\sigma _\lambda ^2}}} } } \hfill \cr {} \hfill & {\left. {\quad \quad + \mu {{\left( {{{{F_{\lambda + 1}} - 2{F_\lambda } + {F_{\lambda - 1}}} \over {{{\left( {{\rm{\Delta }}\lambda } \right)}^2}}}} \right)}^2}} \right]} \hfill \cr } , $](/articles/aa/full_html/2022/08/aa41958-21/aa41958-21-eq56.png) (B.1)
(B.1)
where the dependence of A and Τ on the considered position θp is omitted in the notation on the right-hand side. To switch to matrix notation, the following parameters are defined:
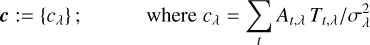 (B.2)
(B.2)
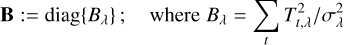 (B.3)
(B.3)
 (B.4)
(B.4)
where c corresponds to the un-regularized flux estimate vector, and D is the second order derivation matrix, which is symmetric. Equation (B.1) can then be rewritten in matrix notation as
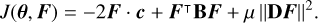 (B.5)
(B.5)
The condition for minimizing the cost function with respect to the flux, Eq. (24), then directly returns the optimized flux vector as
![$ J''\left( {\bf{\theta }} \right) = J\left[ {{\bf{\theta }},{{{\bf{\hat F}}}_{{\rm{pos}}}}\left( {\bf{\theta }} \right)} \right] = - {{\bf{\hat F}}_{{\rm{pos}}}} \cdot {\bf{c}}{\bf{.}} $](/articles/aa/full_html/2022/08/aa41958-21/aa41958-21-eq61.png) (B.6)
(B.6)
which now also includes the regularization enforced by D. If the optimized flux is inserted back into Eq. (B.5), we get the cost function 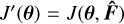 , which is optimized with respect to the flux:
, which is optimized with respect to the flux:
![$ J''\left( {\bf{\theta }} \right) = J\left[ {{\bf{\theta }},{{{\bf{\hat F}}}_{{\rm{pos}}}}\left( {\bf{\theta }} \right)} \right] = - {{\bf{\hat F}}_{{\rm{pos}}}} \cdot {\bf{c}}{\bf{.}} $](/articles/aa/full_html/2022/08/aa41958-21/aa41958-21-eq63.png) (B.7)
(B.7)
where only c depends on the recorded data. As with the unregularized cost function in Sect. 3.1, a positivity constraint can be applied on the regularized estimated flux:
![$ J''\left( {\bf{\theta }} \right) = J\left[ {{\bf{\theta }},{{{\bf{\hat F}}}_{{\rm{pos}}}}\left( {\bf{\theta }} \right)} \right] = - {{\bf{\hat F}}_{{\rm{pos}}}} \cdot {\bf{c}}{\bf{.}} $](/articles/aa/full_html/2022/08/aa41958-21/aa41958-21-eq64.png) (B.8)
(B.8)
The computation of the likelihood maps can be performed on any grid of possible planet positions and does not necessarily have to cover the whole field-of-view of the telescope.
 |
Fig. B.1 Different versions of the cost function, J, which is calculated on a grid up to 100 mas angular separation from the star. An artificial planet with a photon-based S/N~ 5 is located in the lower right at 67 mas from the center. Left: J′ without positivity constraint on the flux. The image is symmetric, and the contrast is low such that the planet position cannot be inferred. Middle: J″ with a simple positivity constraint on the planet flux. The spatial degeneracy is removed, and the most likely planet position in the lower right indicates the correct planet position. Two side lobes with similar cost values to the true planet position are visible. Right: Cost function Jreg with a positivity constraint on the flux and spectral regularization. The overall contrast is enhanced, and the side lobes are suppressed compared with the un-regularized cost function. |
In Fig. B.1 we show a concrete example for how the different cost functions behave.
Appendix C Local zodiacal emission
Figure 5 indicates that the local-zodiacal thermal emission is the dominant astrophysical noise source in LIFE’S long-wavelength regime. Figure C.1 depicts a visual representation this emission according to Formula (14). It shows that with respect to local-zodi leakage it is generally favorable to observe targets at high ecliptic latitudes and longitudes close to the anti-Sun direction.
 |
Fig. C.1 Surface brightness distribution of the local zodiacal dust cloud for wavelengths of 5 µm, 10 µm, and 20 µm (from top to bottom). The flux is given in MJy sr−1 to allow for a comparison with the DARWIN-SIM technical report (Den Hartog & Karlsson 2005) and other models for the local zodiacal dust, e.g., the one used for sensitivity predictions for the MIRI instrument on board the JWST (Glasse et al. 2015). We note the different color scale for each wavelength. |
References
- Angel, J. R. P., & Woolf, N. J. 1997, ApJ, 475, 373 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T.P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astropy Collaboration (Price-Whelan, A.M., et al.) 2018, AJ, 156, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Benz, W., Broeg, C., Fortier, A., et al. 2021, Exp. Astron., 51, 109 [Google Scholar]
- Bracewell, R. N. 1978, Nature, 274, 780 [NASA ADS] [CrossRef] [Google Scholar]
- Cabrera, M. S., McMurtry, C. W., Forrest, W. J., et al. 2019, J. Astron. Telescopes Instrum. Syst., 6, 1 [CrossRef] [Google Scholar]
- Cockell, C. S., Herbst, T., Léger, A., et al. 2009, Exp. Astron., 23, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Cuoco, E., Powell, J., Cavaglià, M., et al. 2020, Mach. Learn.: Sci. Technol., 2, 011002 [CrossRef] [Google Scholar]
- Dandumont, C., Defrère, D., Kammerer, J., et al. 2020, J. Astron. Telescopes Instrum. Syst., 6, 035004 [NASA ADS] [Google Scholar]
- Defrere, D. 2009, PhD thesis, University of Liege, Belgium [Google Scholar]
- Defrère, D., Absil, O., Den Hartog, R., Hanot, C., & Stark, C. 2010, A&A, 509, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Defrère, D., Stark, C., Cahoy, K., & Beerer, I. 2012, in Space Telescopes and Instrumentation 2012: Optical, Infrared, and Millimeter Wave, eds. M.C. Clampin, G.G. Fazio, H.A. MacEwen, & J. Oschmann, SPIE Conf. Ser., 8442, 84420M [Google Scholar]
- Den Hartog, R., & Karlsson, A. 2005, The DarwinSim science simulator, Tech. rep., ESA [Google Scholar]
- Draper, D. W., Elias, N.M.II, Noecker, M.C., et al. 2006, AJ, 131, 1822 [NASA ADS] [CrossRef] [Google Scholar]
- Ertel, S., Defrère, D., Hinz, P., et al. 2020, AJ, 159, 177 [Google Scholar]
- Flasseur, O., Denis, L., Thiébaut, E., & Langlois, M. 2020, A&A, 637, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A.G.A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gáspár, A., Rieke, G. H., Guillard, P., et al. 2020, PASP, 133, 014504 [Google Scholar]
- Gaudi, B. S., Seager, S., Mennesson, B., et al. 2020, ArXiv e-prints, [arXiv:2001.06683] [Google Scholar]
- Gebhard, T. D., Bonse, M. J., Quanz, S. P., & Schölkopf, B. 2020, ArXiv e-prints, [arXiv:2010.05591] [Google Scholar]
- Gebhard, T.D., Kilbertus, N., Harry, I., & Schölkopf, B. 2019, Phys. Rev. D, 100 [Google Scholar]
- Gheorghe, A., Glauser, A. M., Ergenzinger, K. J., et al. 2020, in Optical and Infrared Interferometry and Imaging VII, ed. A. Mérand, S. Sallum, & P.G. Tuthill, 11446 [Google Scholar]
- Glasse, A., Rieke, G. H., Bauwens, E., et al. 2015, PASP, 127, 686 [NASA ADS] [CrossRef] [Google Scholar]
- Guyon, O., Mennesson, B., Serabyn, E., & Martin, S. 2013, PASP, 125, 951 [NASA ADS] [CrossRef] [Google Scholar]
- Hansen, J. T., Ireland, M. J., & The LIFE Collaboration 2022, A&A, in press https://doi.org/10.1051/0004-6361/43107 [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Kelsall, T., Weiland, J., Franz, B., et al. 1998, ApJ, 508, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Kennedy, G. M., Wyatt, M. C., Bailey, V., et al. 2015, ApJS, 216 [Google Scholar]
- Konrad, B. S., Alei, E., Angerhausen, D., et al. 2022, A&A, 664, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laugier, R., Cvetojevic, N., & Martinache, F. 2020, A&A, 642, A202 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lawson, P. R., Lay, O. P., Martin, S. R., et al. 2007, in Techniques and Instrumentation for Detection of Exoplanets III, ed. D. R. Coulter, SPIE Conf. Ser., 6693, 669308 [NASA ADS] [CrossRef] [Google Scholar]
- Lay, O. P. 2004, Appl. Opt., 43, 6100 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lay, O. P. 2005, Appl. Opt., 44, 5859 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lay, O. P. 2006, in SPIE Astronomical Telescopes + Instrumentation, eds. J.D. Monnier, M. Schöller, & W.C. Danchi (SPIE), 62681A-14 [Google Scholar]
- Lay, O. P., Martin, S. R., & Hunyadi, S. L. 2007, Techniques and Instrumentation for Detection of Exoplanets III, 6693, 66930A [NASA ADS] [CrossRef] [Google Scholar]
- Mayor, M., & Queloz, D. 1995, Nature, 378, 355 [Google Scholar]
- Mugnier, L., Thiébaut, E., Belu, A., et al. 2006, EAS Pub. Ser., 22, 69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mugnier, L. M., Cornia, A., Sauvage, J.-F., et al. 2009, J. Opt. Soc. Am. A, 26, 1326 [NASA ADS] [CrossRef] [Google Scholar]
- Nagler, P.C., Sadleir, J.E., & Wollack, E.J. 2021, J. Astron. Telescopes Instrum. Syst., 7, 1 [Google Scholar]
- Paresce, F., & Crane, P., eds. 1997, Science with the VLT Interferometer: Proceedings of the ESO Workshop Held at Garching, Germany, 18-21 June 1996, ESO Astrophysics Symposia (Berlin, Heidelberg: Springer Berlin Heidelberg) [Google Scholar]
- Perido, J., Glenn, J., Day, P., et al. 2020, J. Low Temp. Phys., 199, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Quanz, S. P., Ottiger, M., Fontanet, E., et al. 2022, A&A, 664, A21 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rieke, G. H., Ressler, M. E., Morrison, J. E., et al. 2015, PASP, 127, 665 [NASA ADS] [CrossRef] [Google Scholar]
- Roellig, T. L., McMurtry, C., Greene, T., et al. 2020, J. Astron. Telescopes Instrum. Syst., 6 [Google Scholar]
- The LUVOIR Team 2019, ArXiv e-prints, [arXiv:1912.06219] [Google Scholar]
- Thiébaut, E., & Mugnier, L. 2005, Proc. Int. Astron. Union, 1, 547 [CrossRef] [Google Scholar]
- Tinetti, G., Drossart, P., Eccleston, P., et al. 2018, Exp. Astron., 46, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Van Der Walt, S., Colbert, S.C., & Varoquaux, G. 2011, Comput. Sci. Eng., 13, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Meth., 17, 261 [Google Scholar]
We refer the reader to Dandumont et al. (2020) for recent detection yield estimates for Bracewell interferometers with various aperture sizes.
A probability distribution for z was derived by the HOSTS survey carried out at the Large Binocular Telescope (LBTI; Ertel et al. 2020).
The baseline mission scenario features a 2.5 yr search phase for detecting previously unknown exoplanets, followed by a 2.5–3.5 yr characterization phase (Quanz et al. 2022).
Defined as planets with radii Rp in the range 0.5 R⊕ ≤ Rp ≤ 1.5 R⊕ orbiting within the spectral-type-dependent empirical HZ of their host star. For a Sun-like star, the empirical HZ corresponds to an insolation range of 0.32 S⊕ ≤ Sp ≤ 1.76 S⊕, where S⊕ corresponds to the present-day insolation level of the Earth.
Effective temperature Teff = 4047 K, effective radius Reff = 0.57 R⊙, luminosity L = 0.079 L⊙ (Gaia Collaboration et al. 2016, 2018), planet separation scaled to a = 0.31 according to a planetary equilibrium temperature of Teq = 265 K.
All Tables
Instrumental parameters and properties of the simulated sources for the S/N calculation of an Earth-like planet at 10 pc.
Approximate predictions for the maximum allowed perturbation rms to stay in the fundamental noise dominated case.
Approximate predictions for the asymptotic upper limits in detector thermal background and detector dark current perturbation to stay in the fundamental noise dominated case.
All Figures
 |
Fig. 1 Assumed beam combination scheme of the LIFE array. Four collector spacecraft are located on a 6:1 rectangle with the combiner spacecraft located in the geometric center. The shorter distance between the collectors, b, is called the nulling baseline, and the longer distance is the imaging baseline, qb. The dual chopped Bracewell beam combination scheme, consisting of an interconnection of two single Bracewell combiners, is shown. We note that the collector spacecraft and the interferometric outputs are numbered for the subsequent calculation and that the spacecraft diameters are not to scale. |
| In the text | |
 |
Fig. 2 Transmission maps for the chopped dual Bracewell nulling interferometer. Left and middle: Tm of Outputs 3 and 4 calculated for a wavelength λ = 10 µm, a nulling baseline b = 12m, and a 6:1 baseline ratio. These two outputs have destructive interference at their vertical center and are used to create the differential map. The axes show the distance from the center in milliarcseconds. The white star indicates the position of the star in the center of the map. Right: Differential map, Tdif, which is the difference between T3 and T4. The dashed red line shows the path of a hypothetical planet at 100 mas through the differential map as the interferometer array describes a full rotation. |
| In the text | |
 |
Fig. 3 Modulation of the planet signal. Top: Differential map in polar coordinates, normalized from −1 (blue) to 1 (yellow). The dashed red line at 100 mas angular separation corresponds to the path of the planet shown in the right panel of Fig. 2 for a full rotation of the array. Bottom: Normalized signal transmission intensity of the planet as a function of rotation angle. |
| In the text | |
 |
Fig. 4 Modulation efficiency, ξ(θ), as a function of angular separation for the three wavelengths λ = 5 µm, 10 µm, and 20 µm. The vertical red line indicates an angular separation of 100 mas, which corresponds to the separation of the planet shown in the right panel of Fig. 2. |
| In the text | |
 |
Fig. 5 Simulated spectra for the observation of an Earth-twin. Top: comparison of the various input signals in our example of an Earthlike planet at 10 pc. The solid lines indicate the total flux received from the respective sources: planet (red), star (black), exozodiacal dust (gray), and local zodiacal dust (blue). The dotted lines with the same color code indicate the fraction of the flux that contributes to the shot noise. Bottom: detected planet signal (red line) and total shot noise (dashed blue line) averaged over each wavelength bin and for an integration time of 200 000 s (values refer to the y axis on the left). The resulting spectral S/N is shown as the black line and is calculated as described in Sect. 2.3 (values refer to the y axis on the right). Integrated over the full wavelength range, one obtains a S/N ≈ 9.7. |
| In the text | |
 |
Fig. 6 Cross-correlation of the modulated signal of a noiseless point source located at [−100, 0] mas with the transmission map. Left: cross-correlation at a single wavelength. The resulting image can be understood as the demodulated signal function of such a point source at the considered wavelength. The image is antisymmetric with respect to the image center. Right: combined cross-correlation across the full wavelength range considered for the ideal point source. Considering a broader wavelength range reduces the side lobes and allows for a better location of the point source. |
| In the text | |
 |
Fig. 7 Effect of the positivity constraint of the cost function. Top: different versions of the cost function, J, for a simulated observation without any point sources. L = 31 wavelength bins are used. Top left: J′ without positivity constraint on the flux. The image is point-symmetric with respect to the image center. Top right: J″ with a positivity constraint on the planet flux. Compared to the left image, the strict point symmetry is lifted and the mean value is lower. Bottom: probability distribution of the cost function maps shown above. The gray histogram shows the J′ values obtained from the panel on the top left. The solid red line shows the probability density function of a χ2 distribution with L = 31 degrees of freedom. The blue histogram shows the J″ values obtained from the panel on the top right. The solid orange line shows the theoretically expected distribution of the J″ values given in Eq. (30). The dashed vertical lines indicate the detection criteria of η = 87 and η = 65 as derived by Eq. (28) and Eq. (31), respectively. |
| In the text | |
 |
Fig. 8 Extraction of spectrum from noisy observation. Top: noisy time series signal from simulated data for an Earth-like planet around a Sun-like star at 10 pc (in blue). The underlying noiseless planet signal is indicated by the red curve. Middle: detection map for simulated data of the Earth-like planet. The photon-noise-based S/N is 9.7 (cf. Sect. 2.4). The planet is correctly found in the upper right of the map. Bottom: spectral flux of the Earth-like planet as estimated from the simulated data (red data points with 1σ error bars). The blue line shows the true flux of the simulated planet, and the blue shaded region indicates ±1σ based on the photon statistics. |
| In the text | |
 |
Fig. 9 Robustness of the single planet extraction. Top: distribution of the estimated angular separation from the host star of 1000 simulated Earth-twins. The underlying true value is θ = 100 mas, and the average estimated value is 99.7 ± 1.5 mas. The spacing of the bars corresponds to the angular resolution of the grid on which the analysis was performed. Bottom: mean (red dots) with standard deviation (red error bars) of the distribution of the estimated flux values over 1000 simulations of the same artificial planet. The blue line shows the true spectrum, with the blue shaded region enclosing ±1σ based on the photon statistics. |
| In the text | |
 |
Fig. 10 Cost function detection map for the iterative detection of three simulated planets (indicated by the white arrows). The simulation parameters are given in Sect. 4.2. The left image shows the detection map calculated from the full simulated data. Subtracting the estimated signal contribution of the source detected in the first map and recalculating the detection map results in the second image, and after repeating this the third one. Removing a detected source from the data also removes the side lobes created by the source, thus allowing for a clear iterative detection. |
| In the text | |
 |
Fig. 11 Temperature and radius estimates for the three simulated planets with Rp = 1 R⊕ and varying temperatures. The true values are indicated by crosses and the estimated values by dots with corresponding 1σ confidence ellipses. The values are estimated by fitting a blackbody curve to the estimated spectra of the point sources, whose locations are inferred from the detection maps shown in Fig. 10. |
| In the text | |
 |
Fig. 12 Distribution of properties of detectable rocky, HZ planets from the detection yield estimates presented in Quanz et al. (2022) normalized over 100 Monte Carlo runs. From top to bottom: Predicted S/N (based on photon noise), effective temperature, radius, and projected angular separation. |
| In the text | |
 |
Fig. 13 Corner plot showing the predicted S/N based on photon statistics (cf. top panel in Fig. 12) and the estimated values for S/N, temperature, radius, and angular separation relative to the true values based on the signal analysis of ≈4400 rocky, HZ planets. We note that the discretization of the values for the estimated angular separation corresponds to the resolution of the spatial grid on which the analysis was performed. At the top of each column the mean and the standard deviation of the distributions are given. |
| In the text | |
 |
Fig. A.1 Wavelength dependence of noise contributions for observations of an Earth-twin located at 10 pc with LIFE in the baseline scenario. Panel a): Division of the fundamental noise into its individual sources. Panel b): Instrumental noise sources split into systematic noise sources (green) and additional photon noise sources arising from instrumental effects. Panel c): Planet signal, fundamental noise, and instrumental noise contributions. A S/N using only fundamental noise (orange bars) represents the fundamental noise limited case used in the LIFE paper series. The green bars show the full S/N, which additionally considers the instrumental noise as well as the fundamental noise. |
| In the text | |
 |
Fig. A.2 Ratio of fundamental noise to instrumental noise on a grid of amplitude and phase perturbations for the shortest-wavelength bin at λb = 4.1 µm with width ∆λb = 0.2 µm. The perturbations are assumed to be pink noise with the specified reference rms at 10 µm, and the phase perturbation is converted to an OPD. The contours indicate where the fundamental noise dominates the systematic noise by a factor of one, five, or ten, respectively, for the λb = 4.1 µm case (in red) and for comparison the λb = 6.1 µm (in orange) and λb = 10.1 µm (in cyan) cases. The crosses indicate the reference levels specified by Table A.1. |
| In the text | |
 |
Fig. A.3 Ratio of fundamental noise to instrumental noise on a grid of the detector environment temperature and the detector dark current for the shortest-wavelength bin at λb = 4.1 µm with width ∆λb = 0.2 µm. The temperature induces blackbody thermal emission that is propagated directly into the detector. The dark current is assumed to be constant with temperature. The instrument is configured according to the reference state in Table A.1. The contours indicate where the fundamental noise dominates the systematic noise by a factor of one or five. The cross indicates the reference levels of Τ = 11 Κ and ID = 10−4 e− px−1 s−1 used in Fig. A.1. |
| In the text | |
 |
Fig. A.4 Impact of the target system configuration on the ratio of fundamental noise to instrumental noise on a grid of amplitude and phase perturbations for the shortest-wavelength bin at λb = 4.1 µm with width ∆λb = 0.2 µm. The system parameters assumed for the M-star target are given in the text. The contours indicate where the fundamental noise dominates the systematic noise by a factor of one, five, or ten, respectively. The cross indicates the 4 µm reference level specified by Table A.1. |
| In the text | |
 |
Fig. B.1 Different versions of the cost function, J, which is calculated on a grid up to 100 mas angular separation from the star. An artificial planet with a photon-based S/N~ 5 is located in the lower right at 67 mas from the center. Left: J′ without positivity constraint on the flux. The image is symmetric, and the contrast is low such that the planet position cannot be inferred. Middle: J″ with a simple positivity constraint on the planet flux. The spatial degeneracy is removed, and the most likely planet position in the lower right indicates the correct planet position. Two side lobes with similar cost values to the true planet position are visible. Right: Cost function Jreg with a positivity constraint on the flux and spectral regularization. The overall contrast is enhanced, and the side lobes are suppressed compared with the un-regularized cost function. |
| In the text | |
 |
Fig. C.1 Surface brightness distribution of the local zodiacal dust cloud for wavelengths of 5 µm, 10 µm, and 20 µm (from top to bottom). The flux is given in MJy sr−1 to allow for a comparison with the DARWIN-SIM technical report (Den Hartog & Karlsson 2005) and other models for the local zodiacal dust, e.g., the one used for sensitivity predictions for the MIRI instrument on board the JWST (Glasse et al. 2015). We note the different color scale for each wavelength. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


