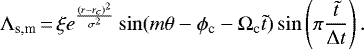| Issue |
A&A
Volume 656, December 2021
|
|
|---|---|---|
| Article Number | A115 | |
| Number of page(s) | 12 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/202142176 | |
| Published online | 09 December 2021 | |
Kepler-223 resonance holds information about turbulence during the gas-disk phase
1
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117
Heidelberg,
Germany
e-mail: huehn@mpia.de
2
Division of Geological and Planetary Sciences, California Institute of Technology,
1200 E. California Blvd.,
Pasadena,
CA
91125,
USA
Received:
8
September
2021
Accepted:
24
October
2021
Context. Planet formation remains an open field of research, and many fundamental physical processes regarding planetary formation in protoplanetary disks are still imperfectly understood. It remains to be investigated how different conditions in these protoplanetary disks affect the emergence of different types of observed systems. An elusive phenomenon is the turbulence in these disks. Observations are available of planetary systems and of some protoplanetary disks, which can serve as a starting point for these investigations. The detected systems reveal different architectures of planets. One particularly interesting case to consider is the Kepler-223 system, which contains a rare configuration of four planets in a resonance chain. This implies a certain migration history.
Aims. We aim to use the orbital configuration of the Kepler-223 planets to constrain the parameters of the protoplanetary disk that allow the formation of a chain of mean-motion resonances that resembles the resonances of Kepler-223. We primarily investigate the disk viscosity and surface density.
Methods. We used the swift_symba N-body integrator with additional dissipative forces to mimic planet-disk interactions.
Results. We constrained the surface densities and viscosities that allow the formation of a resonant chain like that of Kepler-223. We find that surface densities of up to a few minimum mass solar nebula surface densities and disk viscosity parameters α of a few × 10−3 up to × 10−2 are most successful at reproducing the architecture of this particular planetary system. We describe the connection of these two quantities with each other, considering the success of reproducing the chain. We find that higher disk surface densities in turn require lower viscosities to build the chain.
Conclusions. Our results show that well-characterized observed planetary systems hold information about their formation conditions in the protoplanetary disks and that it is possible to extract this information, namely the initial disk surface density and viscosity. This helps to constrain planet formation.
Key words: protoplanetary disks / planet-disk interactions / planets and satellites: dynamical evolution and stability / methods: numerical
© L.-A. Hühn et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access funding provided by Max Planck Society.
1 Introduction
The study of exoplanetary systems is a key element for understanding the formation and evolution of planets, as well as the assembly of planetary systems and their dynamical evolution. Currently, the exoplanet sample is largely dominated by data from the Kepler mission, which provided well-constrained planetary radii and orbital periods using the transit detection method. Out of all detected planets, small and close-in planets, the so-called super-Earths and mini-Neptunes, are thought to be orbiting up to 50% of Sun-like stars (Howard et al. 2012; Mayor et al. 2011; Mulders et al. 2018), and they often occur in multiplanetary configurations, in which the planets within each system mostly have similar masses and radii (e.g., Millholland et al. 2017; Weiss et al. 2018).
A notable example is the planetary system hosted by Kepler-223, which is a G5V star with a mass of 1.1 M⊙. Four sub-Neptunian planets in mean-motion resonance (MMR) are orbiting it (Mills et al. 2016). In addition to orbital periods and radii, Mills et al. (2016) used transit-timing variations (TTVs) to obtain masses, eccentricities, and inclinations of the planets. The masses are given by 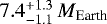 ,
, 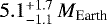 ,
, 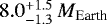 , and
, and 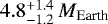 for planets b-e, respectively. The period ratios of the planets are 8:6:4:3 starting from the innermost planet Kepler-223 b. This suggests the existence of individual MMRs of the pairs of planets in the MMR chain, that is, a 4:3 resonance for the first pair, a 3:2 resonance for the second pair, and a 4:3 resonance for the third pair. Mills et al. (2016) confirmed the resonant nature of the system, showing librating Laplace angles. More detailed information about the planets orbiting Kepler-223 is presented in Table 1.
for planets b-e, respectively. The period ratios of the planets are 8:6:4:3 starting from the innermost planet Kepler-223 b. This suggests the existence of individual MMRs of the pairs of planets in the MMR chain, that is, a 4:3 resonance for the first pair, a 3:2 resonance for the second pair, and a 4:3 resonance for the third pair. Mills et al. (2016) confirmed the resonant nature of the system, showing librating Laplace angles. More detailed information about the planets orbiting Kepler-223 is presented in Table 1.
While capture into an MMR is a natural outcome of type I migration, this is found very infrequently in the exoplanetary sample. It was suggested that capture into a resonance chain does not often produce dynamically stable systems if the disk in inviscid (McNally et al. 2019). Another frequently studied reason for the rarity of MMRs is their instability during (e.g., Liu et al. 2017) or after the dispersal of the protoplanetary disk (e.g., Izidoro et al. 2017, 2021; Pichierri & Morbidelli 2020; Lambrechts et al. 2019). Thus, the existence of the particular configuration of the Kepler-223 system, as well as other resonant chains such as that of Trappist-1 (Gillon et al. 2016, 2017; Luger et al. 2017) or GJ-876 (Marcy et al. 2001; Rivera et al. 2005), poses a definite challenge to formation scenarios of planetary systems. For Kepler-223, the resonant state appears to be long-term stable (it is, e.g., protected from instabilities due to the emergence from secondary resonances; Pichierri & Morbidelli 2020), raising the question of which condition brought about this particular configuration. These exotic orbital configurations indeed offer a unique opportunity, as the current state can be used to constrain the parameters of models that describe the protoplanetary disk in which they formed.
Important disk parameters that could be constrained this way, for example, are the surface density or a description of turbulent viscosity in the disk. The surface density is a measure for the mass, which in turn is an important parameter for the migration speed (Kley & Nelson 2012; Baruteau et al. 2014) and is also relevant, for example, for gravitational instabilities.Turbulence in disks can arise from different hydrodynamical instabilities, for instance, the global baroclinic instability (Klahr & Bodenheimer 2003) or the vertical shear instability (Richard et al. 2016; Flock et al. 2017; Manger et al. 2020), or from the magnetorotational instability (MRI) (Balbus & Hawley 1991). Turbulent viscosity is a key element of many planet formation scenarios and disk evolution models. It is supported by Atacama Large Millimeter/submillimeter Array (ALMA) data of disks that might show still ongoing planetary formation (Teague et al. 2018; Pinte et al. 2018; Keppler et al. 2018), and is typically described in terms of the α parameter (Shakura & Sunyaev 1972). Despite its significance and recent improvements, the α parameter is not very well constrained observationally, with values typically ranging between ×10−4 and about 4 × 10−2, as studies of disks observable by ALMA have shown (Rafikov 2017; Dullemond et al. 2018; Flaherty et al. 2017, 2018). These values are also consistent with hydrodynamical and MRI simulations (e.g., Turner et al. 2014).
In this work, we use the fact that turbulence causes stochastic fluctuations of the disks density structure, leading to stochastic forces on the planets, to study its effects on the formation of the Kepler-223 resonance chain. The main idea is that turbulence can be a reason for destroying or preventing the formation of an MMR chain even before the disk has dissipated (e.g., Batygin & Adams 2017). The aim of this investigation is to constrain the α parameter in combination with other disk parameters from observational information contained in the current state of the planetary system alone.
The methods we used to investigate Kepler-223 are laid out in Sect. 2. Kepler-223 serves as a test case for the method we use to determine constraints on the disk turbulence and surface density. However, the methods we apply are general and can be applied to other systems with resonant chains. The results of our investigation are presented in Sect. 3. We discuss implications and shortcomings of our investigation in Sect. 4.
Parameters of the planets orbiting Kepler-223 (Mills et al. 2016).
2 Methods
We reproduced the Kepler-223 resonance chain using N-body simulations using the swift_simba code. Additional dissipative forces were implemented to mimic the interactions of the planets with the protoplanetary disk, including the effects of stochastic surface density changes caused by turbulence.
2.1 Type I migration
As a model for the effects on the semimajor axis and eccentricity resulting from planet-disk interactions, the prescription developed by Cresswell & Nelson (2008) was implemented. The effects of eccentricity damping and type I migration are viewed as two separate contributions. The former is described by
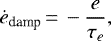 (1)
(1)
with the timescale τe given by
![\begin{equation*}\begin{split}\tau_e\,{=}\,\frac{\tau_{\textrm{wave}}}{{0.780}}\left[1-0.14\left(\frac{e}{H/r}\right){}^2+0.06\left(\frac{e}{H/r}\right){}^3\right.\\\left.+0.18\left(\frac{e}{H/r}\right)\left(\frac{i}{H/r}\right){}^2\right]{}\end{split}.\end{equation*}](/articles/aa/full_html/2021/12/aa42176-21/aa42176-21-eq6.png) (2)
(2)
Here, τwave is the typical type I migration timescale,
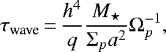 (3)
(3)
where 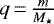 is the fraction of the planetary to stellar mass, h = H∕r is the disk aspect ratio, and the subscript p denotes that the quantity is evaluated at the location of the planets. Planetary type I migration is modeled given the negative torque,
is the fraction of the planetary to stellar mass, h = H∕r is the disk aspect ratio, and the subscript p denotes that the quantity is evaluated at the location of the planets. Planetary type I migration is modeled given the negative torque,
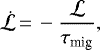 (4)
(4)
with a migration timescale of
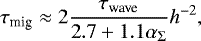 (5)
(5)
again in the limit of low eccentricities, with the power law of the surface density αΣ (see below). The resulting change in semimajor axis can then be calculated as
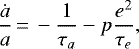 (6)
(6)
with τa = τmig∕2 and p ≈ 2 for small e. The migration speed scales linearly with q and the surface density Σ. The ratio of the migration to eccentricity damping timescale, the K-factor (Ramos et al. 2017), is given by
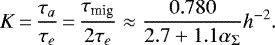 (7)
(7)
Equation (7) shows that for typical values for h and αΣ, eccentricity damping occurs on a much shorter timescale than migration. In this regime, the planets are therefore expected to have vanishing eccentricities before they are captured into resonance.
To stop migration at the inner edge of the protoplanetary disk, a planetary trap is implemented. To model the sign flip of the torque and its radial dependence, which ultimately stops planetary migration when the planet reaches the inner edge (Masset et al. 2006; Flock et al. 2019), a multiplier 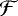 is applied to the acceleration of the planets (Pichierri et al. 2018). It is given by
is applied to the acceleration of the planets (Pichierri et al. 2018). It is given by
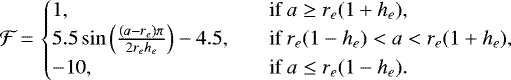 (8)
(8)
Here, re is the location of the edge (in AU) and he is the aspect ratio of the disk at re. This implementation does not affect eccentricity damping.
2.2 Disk-driven turbulence
Our prescription for disk turbulence follows an implementation of Ogihara et al. (2007) based on results from hydrodynamical simulations investigating MRI turbulence (Laughlin et al. 2004). Turbulent modes are generated with a turbulent strength parameter γ. We summarize this method in the following. The stochastic force exerted by the turbulent disk is described by
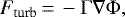 (9)
(9)
where the parameter Γ is given by
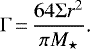 (10)
(10)
The potential is described by a superposition of individual modes,
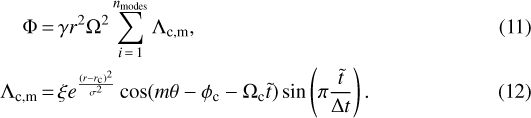
In Eq. (12), ξ describes a Gaussian distribution with σ = 1 and (r, θ) the radial and azimuthal position of the planet, while rc and ϕc describe the center of the density fluctuations caused by the turbulent modes. The azimuthal extent of the modes is given by 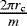 , while the radial extent is given by
, while the radial extent is given by 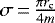 . The time dependence of the modes is given by Δt. A mode is created at time t0 and dies when
. The time dependence of the modes is given by Δt. A mode is created at time t0 and dies when 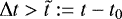 . For Δt, the sound-crossing time in angular direction (
. For Δt, the sound-crossing time in angular direction (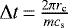 ) was chosen. To create a new mode, rc is randomly generated inside the considered edges of our system rin and rout and ϕc ∈ [0, 2π) is also chosen randomly. The wave number m is chosen from a logarithmic random distribution in the range of 2 ≤ m ≤ 64. The resulting torque Γt is then given by
) was chosen. To create a new mode, rc is randomly generated inside the considered edges of our system rin and rout and ϕc ∈ [0, 2π) is also chosen randomly. The wave number m is chosen from a logarithmic random distribution in the range of 2 ≤ m ≤ 64. The resulting torque Γt is then given by
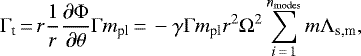 (13)
(13)
Here, mpl denotes the planetary mass in order to avoid confusion with the wave number m.
The stochastic force strength parameter γ can be related to the α parameter that is typically used to describe turbulence in current disk models. To this end, we used on the one hand a relation for the diffusion coefficient in the eccentricity De to the model strength parameter (Ida et al. 2008; Okuzumi & Ormel 2013), where the numerical prefactor we used was modified to fit the setup used here (see Appendix A),
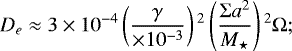 (15)
(15)
on the other hand, we used a similar relation involving the α parameter (Okuzumi & Ormel 2013),
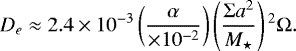 (16)
(16)
This yields a conversion between the two parameters that reads
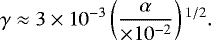 (17)
(17)
This relation should be considered valid as an order-of-magnitude correspondence between γ (the parameter used in the disk model for generating turbulent waves) and α (the commonly used turbulence parameter).
3 Results
The results are presented in two parts. First, we show our considerations of the Kepler-223 system without including effects of turbulence on the formation of the resonance chain in Sect. 3.1. A selection of stable systems in the correct resonance chain, described in that section, are used as the basis for the inclusion of turbulence into our simulations. The insights gained from that are presented in Sect. 3.2.
3.1 Results without turbulence
3.1.1 Treatment of individual planet pairs
As a starting point, we treated all three planet pairs of the Kepler-223 system separately. We first simulated each resonant pair separately for varying surface density values 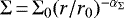 in order to obtain a first overview of the effects of the surface density distribution on each individual pair. For allsimulations conducted here and in later sections, the aspect ratio was fixed at h = 0.05. The power law of the surface density αΣ was kept constant at a value of αΣ = 1.5. The reference distance r0 was chosen to be r0 = 1 AU. For the purposes of this step, we set the trap at the inner disk edge at the position of the inner planet in each pair under investigation. This allowed the inner planet to be fixed, allowing a clear investigation of the convergent migration behavior, and it means in turn that Σ0 sufficiently describes the surface density. The planets are also captured in order, from the innermost to the outermost, when the case of all four planets is considered. This is therefore a good simplification to make to gain first insights into the migration behavior.
in order to obtain a first overview of the effects of the surface density distribution on each individual pair. For allsimulations conducted here and in later sections, the aspect ratio was fixed at h = 0.05. The power law of the surface density αΣ was kept constant at a value of αΣ = 1.5. The reference distance r0 was chosen to be r0 = 1 AU. For the purposes of this step, we set the trap at the inner disk edge at the position of the inner planet in each pair under investigation. This allowed the inner planet to be fixed, allowing a clear investigation of the convergent migration behavior, and it means in turn that Σ0 sufficiently describes the surface density. The planets are also captured in order, from the innermost to the outermost, when the case of all four planets is considered. This is therefore a good simplification to make to gain first insights into the migration behavior.
When turbulence is not considered and the planet parameters are fixed, the migration timescale is the quantity that mainly defines the migration behavior and speed, and thus the final resonance. It is a function of the surface density, which makes it an important quantity to investigate for migration. It is important to keep in mind that we do not know at which distance from the star the four Kepler-223 planets formed, nor do we know the time. For the purposes of this initial step, the planets of each pair were therefore initially placed wide of the 2:1 MMR, only in order to find a rough first estimate for the values for Σ0 that we expect to work for the formation of the specific resonance chain. For a higher surface density, resonances with lower k are skipped as a general rule. This subsequently leads to a capture into a resonance with a higher k (Batygin 2015). We therefore considered a range of values for Σ0 for the individual pairs and verified the index k of the resonance into which the pairs are captured. Considering the different locations and different masses of the pairs, we expect a value for Σ0 to lead to different final k for each individual pair. We then compared these final k to the resonance indices measured by Mills et al. (2016) to determine a range of surface densities that allow capture into the correct resonance.
The result of this consideration is shown in Fig. 1. Under the strong assumption that the planets formed outside of the 2:1 MMR, we cannot find a surface density power-law prescription that allows all pairs to individually be captured into the correct resonance. While in principle other slope values αΣ than the value of 3∕2 we used are possible, this statement is independent of this parameter. However, when individual pairs are placed in front of the desired resonances, there is no lower limit for the surface density that allows the planets to be captured into that resonance. In this case, surface density values that allow the formation of the observed resonance for all pairs individually can indeed be found. All in all, this investigation is insufficient for the problem at hand, and should rather be taken as an estimate for the relevant range of Σ0 for a more complete consideration. When a resonant chain of four planets is considered, four-planet dynamics need to be taken into account, which also changes the outcome with respect to the final configuration per surface density.
3.1.2 Treatment of all four planets together
The next natural step to investigate the capture into a resonant chain of the Kepler-223 system is thus to consider all four planets at once. We considered different surface densities because we expect the densities to affect the migration timescale and different initial planet locations. For the planet locations, we took a pragmatic approach. As we already mentioned, their initial formation location cannot be inferred from observations and could in principle have been in a configuration in which individual planet pairs lie far outside the currently observed resonances. For the purpose of this investigation, however, the planets were placed just outside the resonances in which they are observed today. The reason for this is that because the innermost planet is locked at the inner edge of the disk (Masset et al. 2006; Ataiee & Kley 2021), migration is typically convergent in any case (see below). If a planet pair is observed today in a certain MMR, it is therefore natural to assume, within the framework of our investigation, that they once lay just wider of that specific period ratio. This initial placement does not contradict the results of Sect. 3.1.1. In this section, the premise was to determine a range of potential surface density values that locally allow the formation of a resonance with index k that matches the observations by Mills et al. (2016). This was achieved by considering the analytically well-understood case of a two-planet system without turbulence. In the investigation in this section, the dynamics of the four-planet system including effects of turbulence are considered. In this scenario, planets are able to reach the position where we place them at the start of the simulation, even if they do form wider away from the resonances in which they are presently observed and have to migrate inward. The distance to an unperturbed semimajor axis ratio is parameterized by ε,
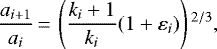 (18)
(18)
where i = 1, 2, 3 denotes the planet pair of the chain, and ki is the resonance index, with k1 = 4, k2 = 3, and k3 = 4. The initial semimajor axis of the first planet was set to a1 = 0.076 AU, which is close to the current location of Kepler-223 b given by Kepler’s third law, ab = 0.0772 AU (Mills et al. 2016).
We ran N-body simulations for values of Σ0 ranging between 0.1 and 10 ΣMMSN for all combinations of values for εi out of {0.02,0.035,0.05} representing small, medium, and large initial separations between the planets. Even for the largest initial separation, the planet pair was always placed in such a way that no first-order MMR had to be crossed in order to reach the intended MMR. After the integration, a system was considered to exhibit the correct chain of resonances if their period ratios were wide of the observed resonance, as well as the corresponding resonant angles showing libration. The system configuration of the periods was considered to be compatible with observations if the ratio of the periods of each individual planet pair exceeded the nominal value, but with a relative error below 0.1%. We are interested in the first-order question of reproducing the period ratios corresponding to the observed MMR chain. Thus, we do not considerthe question of reproducing the observed libration centers that take into account additional resonances between non-adjacent planets (Delisle 2017). The result of this investigation is shown in Fig. 2. It shows the surface density value at which the migration timescale is too short to be able to form the Kepler-223 resonance chain because the required resonances are skipped, as expected. Thi
s occurs beyond a surface density corresponding to ~6 ΣMMSN. This demonstrates at face value that at least without any treatment of turbulence, the minimum-mass extrasolar nebula (MMEN, Chiang & Laughlin 2013) cannot accurately describe protoplanetary disks of extrasolar systems such as Kepler-223. It predicts a surface density of ~ 7ΣMMSN at 0.1 AU, which would not allow the formation of the Kepler-223 system.
From the figure, it appears as if the capturing process of this four-planet system into resonance is chaotic and therefore depends very sensitively on both the initial separation and the surface density, where even a small change in the initial distance to the resonance may make the difference between a successful formation or failure to create the correct chain.
 |
Fig. 1 Range of surface density values Σ0 that allow the individual Kepler-223 planet pairs to be captured into the correct resonance as a function of the semimajor axis of the outer planet of each pair. The error that is related to the mass error of the planets is indicated in red (Mills et al. 2016). The dotted black lines clarify that within the errors, no value for Σ0 can be found that allows each separate pair to be captured into the correct resonance if the pairs are initially wide of the 2:1 MMR. The dotted blue vertical lines indicate that this does not hold if the planets are instead placed just wide of the correct MMR, which eliminates the lower limit for Σ0. |
 |
Fig. 2 Buildup of the resonance chain of the four Kepler-223 planets, without considering turbulence. The investigated parameter space is two dimensional: The surface density is varied, as is the initial separation of the planet pairs from the final resonance. The configurations in which the correct chain was built are indicated by green triangles, while those who failed to do so are shown as red crosses. The vales for ε are ordered such that ε1 is the topmost value. Simulations whose symbol is encircled share their initial parameters with those considered for a consideration including disk turbulence (Sect. 3.2). |
3.2 Results with turbulence
Some of the initial conditions that lead to the successful creation of the Kepler-223 chain were used to investigate the effects of turbulence on the formation of the chain. Three different initial separations were chosen, for which the surface densities ranged between 0.72 ΣMMSN and 3.93 ΣMMSN. These surface densities were chosen because they allow for most of the successful simulations. Higher surface densities give a migration speed that is too high, which is unfavorable for the formation of the resonance chain, while lower surface densities do not offer great constraints for the simulations that include turbulence. The initial conditions that were used are denoted with a blue circle in Fig. 2.
After finding initial conditions that are favorable for the formation of the resonance chain, we investigated the effects of turbulence on the formation of the chain to determine constraints for the turbulence strength in the protoplanetary disk during the formation of the chain. We based our analysis on 100 simulations per initial setup. The integration time was not based on physical properties of the system because the remaining disk lifetime at the point of formation of the chain is not known, and neither is the effect of a possible time variability of α. The integration time was instead chosen as a compromise between simulation run time and stability of the results; we found that integrating for ×105 years achieves this compromise. We also investigated the effects of a longer integration for a particular case and found that while some initially stable configuration became unstable, the difference was below 10%. This shows that it does not significantly change the results presented in Fig. 3.
Four different strengths of turbulence were considered, ranging between α = ×10−4 and α = 5 × 10−2. The resulting trend is depicted in Fig. 3. Several trends are worth pointing out. First, a larger turbulence strength generally leads to less success in forming the Kepler-223 resonance chain. The point at which the formation of the chain becomes significantly improbable lies at lower α for higher surface densities, which fulfills the expectation that the strength of the random kicks is dependent on the product 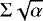 (cf. Eqs. (13), (17)). This can be further seen by considering individual columns in the figure, where a larger number of simulations leads to the formation of the resonance chain when the surface density is lower at constant α. However,this trend does not hold for the lower turbulence strengths. This can be seen as an indication that simple analytical trends derived for the two-planet case (Batygin & Adams 2017) are not applicable when the strength of the turbulent kicks is not sufficient to disrupt chains that have already established their resonant configuration (see below), while they can serve as an order-of-magnitude approximation when the turbulence is strong enough to disrupt formed chains. In the former case, disruption has to take place during the capturing process, where simple assumptions do not hold for four planets.
(cf. Eqs. (13), (17)). This can be further seen by considering individual columns in the figure, where a larger number of simulations leads to the formation of the resonance chain when the surface density is lower at constant α. However,this trend does not hold for the lower turbulence strengths. This can be seen as an indication that simple analytical trends derived for the two-planet case (Batygin & Adams 2017) are not applicable when the strength of the turbulent kicks is not sufficient to disrupt chains that have already established their resonant configuration (see below), while they can serve as an order-of-magnitude approximation when the turbulence is strong enough to disrupt formed chains. In the former case, disruption has to take place during the capturing process, where simple assumptions do not hold for four planets.
Systems can fail to recreate the Kepler-223 resonance chain for a variety of reasons. Frequent examples include the second planet pair skipping the desired 3:2 resonance and being captured into a 4:3 resonance instead, which can lead to other pairs failing to be captured into or stay in the correct resonance. The second planet pair is especially prone to temporary capture because its desired resonance has the lowest index k and its outer planetis more massive than its inner planet (Deck & Batygin 2015). Even in the event of successful capture of the second pair,planets can skip their desired resonance during the initial capturing process of the chain or break out of it later on. Another possible path to failure is created by the brief divergent migration of the third pair, which occurs because its inner planet is more massive than the outer planet. If the more massive planet is not captured fast enough into the 3:2 resonance of pair 2, pair 3 can cross the 3:2 resonance from the inside, which is known to cause a rapid excitation of eccentricity. The rapid excitation usually breaks the resonances of other pairs. The frequency at which the third pair crosses the 3:2 resonance is related to the initial separation of the planets. When a desired resonance is skipped, the planets may either be captured into a resonance with higher index k or collide. A pair is rarely captured into a second-order resonance.
Figure 3 also contains the results of a simulation corresponding to initial conditions that without considering turbulence, were not favorable for the creation of the Kepler-223 resonance chain. These initial conditions are indicated in red. When turbulence is considered, the probability of the successful formation of the correct chain does not differ significantly from all other initial conditions we considered, even though they allowed for a correct chain in the nonturbulent case. This suggests that turbulence in this case is necessary, while even weak turbulence strengths are sufficient to bring the probability in line with other similar initial conditions. The reason for this, however, remains to be investigated in future work.
The trend that fewer simulations lead to the formation of the Kepler-223 system if the turbulence strength is higher is not apparent for lower values for α, but it is clearly visible for higher α. It might be expected that for an increase in turbulence strength, the number of simulations that successfully recreate the Kepler-223 resonance chain drops. While this expectation is fulfilled for larger α, it is not as clear for lower α, where simulations with lower surface densities (i.e., lower turbulence strength) apparently do not reproduce Kepler-223 as often as those with ahigher surface density. When the strength of the turbulence lies beyond a critical value, the disruption of the resonance chain is significantly more efficient than below this value. We propose that this is because turbulence below a certain threshold can only disrupt chain formation while the planets are migrating to the correct semimajor axes, while turbulence beyond this threshold can also efficiently disrupt chains after the planets have already fully been captured in resonance. This can also serve as an explanation as to why expected trends for the formation of the resonance chain are not as clear for turbulence below that threshold. In the case of only two planets, Batygin & Adams (2017) developed an order-of-magnitude criterion for turbulent disruption of formed resonance chains. It is given by
![\begin{equation*}\frac{h}{20}\frac{M}{m_1+m_2}\sqrt{\frac{3\alpha}{f}}\,{\times}\,\left[\frac{\Sigma\langle a\rangle^2}{kM}\sqrt{\frac{\Sigma\langle a\rangle^2}{m_1+m_2}}\right]^{1/3}\gtrsim 1{.}\end{equation*}](/articles/aa/full_html/2021/12/aa42176-21/aa42176-21-eq30.png) (19)
(19)
Here, m1 and m2 are the masses of the planets, M is the stellar mass, ⟨a⟩ is the average semimajor axis, and f is a factor that accommodates different implementations of the rate of change in the semimajor axis. For our considerations, we applied Eq. (19) to the second planet pair because it is observed to be in a 3:2 resonance, which has the lowest resonance index of the chain and should therefore be the least stable. The resulting critical value αcrit, obtained by solving Eq. (19) toward α, is also indicated in Fig. 3. The analytical values match the results from the simulations in order of magnitude. In the four-planet case, values for α that lie slightly below the predicted αcrit from two-planet considerations lead to the disruption of the formed chain.
Furthermore, the validity of Eq. (19) was tested by considering an initial setup in which the four planets are already in resonance. Two initial conditions were considered, the first with a surface density of Σ = 1.39ΣMMSN and ϵ = (0.05, 0.02, 0.035), and the second with Σ = 3.93ΣMMSN and ϵ = (0.05, 0.035, 0.035). Equation (19) gives αcrit = 6.4 × 10−2 and αcrit = 2.3 × 10−2, respectively.Figure 4 shows simulations for which these conditions were implemented. It is apparent that the criterion is a good order-of-magnitude approximation in the four-planet case as well, and the behavior of the general case in which the planets start outside of the resonances is well explained by the destruction of chains that formed beyond αcrit, where the destruction of formed chains becomes possible at lower values for α than αcrit because the four-planet case is more sensitive than the two-planet case.
 |
Fig. 3 Number of successful creations of the Kepler-223 resonance chain for various initial conditions, with varying initial separations and surface densities. For each initial setup, four turbulence strengths α were considered. The green bar denotes successful formations. Generally, a larger turbulence strength leads to fewer successful runs. For each setup, there is a critical value αcrit (cf. Eq. (19)), for which stronger turbulence significantly hinders the creation of the resonance chain (Batygin &Adams 2017). This is depicted in the plot. This critical value decreases with increasing gas surface density, which is also the case for the number of successful runs for an increasing surface density at constant α (cf. Eq. (3)). The setup marked in red did not reproduce the Kepler-223 resonance chain without turbulence, but it does not differ significantly from those that did when the effects of the turbulent disk were considered, indicating that turbulence is a necessary ingredient for this particular setup. This remains to be investigated in future work. |
 |
Fig. 4 Two setups, also represented in Fig. 3, in which turbulence was activated in the simulations only after the formation of the resonance chain. For case (a), Eq. (19) gives αcrit = 6.4 × 10−2, and for case (b), it yields αcrit = 2.3 × 10−2. The resulting number of successful simulations as a function of α is shown, which was compared to the expected critical αcrit value (cf. Eq. (19)). The results match the theoretical expectations on the order of magnitude. |
3.2.1 Constraining the minimum turbulence level
While the results from Fig. 3 can give an upper limit for the strength of disk turbulence during the formation of the Kepler-223 resonance chain, they do not provide a lower limit. The libration amplitude of the Laplace angles can help determining a lower limit, as Mills et al. (2016) provided the observed amplitudes of these angles.
From an analytical perspective, we would expect the amplitude of the Laplace angles to grow like 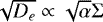 because thediffusion coefficient governs the average evolution of the eccentricity e, which in turn gives the evolution of the resonance and Laplace angles. The scaling is the same as for the turbulence strength (cf. Eq. (13)). For a fixed Σ0, this relation can therefore be used to set bounds on α. In Fig. 5, the libration amplitudes for every Laplace angle, grouped by turbulence strength, are shown for the simulations in which the correct chain was formed. The figure demonstrates that the libration amplitudes indeed scale like
because thediffusion coefficient governs the average evolution of the eccentricity e, which in turn gives the evolution of the resonance and Laplace angles. The scaling is the same as for the turbulence strength (cf. Eq. (13)). For a fixed Σ0, this relation can therefore be used to set bounds on α. In Fig. 5, the libration amplitudes for every Laplace angle, grouped by turbulence strength, are shown for the simulations in which the correct chain was formed. The figure demonstrates that the libration amplitudes indeed scale like 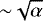 for a constant surface density, allowing the use of the Laplace angle amplitudes for determining a lower limit for α. For the lowest turbulence strength of α = × 10−4, the amplitudes of the Laplace angles for the formed chain are smaller than the observed angles. For × 10−3 ≤ α ≤×10−2, an agreement between the observed amplitudes and those resulting from the simulations can be found. For the highest strength of 5 × 10−2, the number of successful simulations is smaller than at other strengths, and they are mostly limited to low surface densities. With this in mind, the amplitudes for ϕ3 do not agree with the simulations, while the amplitudes for ϕ1 and ϕ2 can match the expected values.
for a constant surface density, allowing the use of the Laplace angle amplitudes for determining a lower limit for α. For the lowest turbulence strength of α = × 10−4, the amplitudes of the Laplace angles for the formed chain are smaller than the observed angles. For × 10−3 ≤ α ≤×10−2, an agreement between the observed amplitudes and those resulting from the simulations can be found. For the highest strength of 5 × 10−2, the number of successful simulations is smaller than at other strengths, and they are mostly limited to low surface densities. With this in mind, the amplitudes for ϕ3 do not agree with the simulations, while the amplitudes for ϕ1 and ϕ2 can match the expected values.
 |
Fig. 5 Libration amplitudes of the Laplace angles for successful simulations depicted in Fig. 3, grouped by turbulence strength. The positions of the peaks scale with
|
3.2.2 Eccentricities of the planets
Because Mills et al. (2016) also provided the eccentricities of the planets in the Kepler-223 system, they can be compared to the eccentricities that result from the simulations. The comparison between the averaged final eccentricity for cases in which the correct resonance chain was formed to the eccentricities measured by Mills et al. (2016) is depicted in Fig. 6. The different turbulence strength values that correspond to the successful simulations are indicated by different colors. In the two-planet case, we would not expect the final eccentricities to depend on the turbulence strength. The reason for this is that random kicks as produced by turbulence only lead to a change around the analytical equilibrium point, the value itself is independent of α and Σ0, however. The analytical value for the two-planet case can be found as (Goldreich & Schlichting 2014)
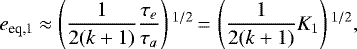 (20)
(20)
where the subscript 1 denotes an evaluation for the inner planet, and K is the K-factor as defined in Eq. (7). This result holds true in the limit of a massless inner planet moving outward toward a massive planet on a fixed circular orbit (circular restricted three-body problem). A more general description shows that a similar relation also holds for the equilibrium eccentricity of the outer planet, 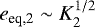 (Pichierri et al. 2018). Equations (20) and (7) show that the equilibrium eccentricity is proportional to h and is a function of k. The eccentricity distribution shown in Fig. 6 exhibits multiple peaks, which means that the four-planet case depends on the turbulence strength and initial separation, unlike in the case of only two planets. When comparing our result for the eccentricities with the measured values, we find that there is a mismatch for the two innermost planets. This could be due to restrictions in our setup, where the inner edge of the protoplanetary disk is modeled by applying high opposing accelerations to the planets close to it, which may not represent the physical situation to high accuracy. The planet trap could be caused by a sharp drop in surface density, which also affects the eccentricity damping timescale and therefore the equilibrium eccentricity of the planets that are pushed into the trap. By just applying a factor to the acceleration of the semimajor axis, this effect is not considered, resulting in final eccentricities that are lower than they should be. We also note that the eccentricities depend on the aspect ratio, which was fixed at a constant value of h = 0.05. Increasing the aspect ratio of the disk can therefore in principle lead to a better agreement in the eccentricities.
(Pichierri et al. 2018). Equations (20) and (7) show that the equilibrium eccentricity is proportional to h and is a function of k. The eccentricity distribution shown in Fig. 6 exhibits multiple peaks, which means that the four-planet case depends on the turbulence strength and initial separation, unlike in the case of only two planets. When comparing our result for the eccentricities with the measured values, we find that there is a mismatch for the two innermost planets. This could be due to restrictions in our setup, where the inner edge of the protoplanetary disk is modeled by applying high opposing accelerations to the planets close to it, which may not represent the physical situation to high accuracy. The planet trap could be caused by a sharp drop in surface density, which also affects the eccentricity damping timescale and therefore the equilibrium eccentricity of the planets that are pushed into the trap. By just applying a factor to the acceleration of the semimajor axis, this effect is not considered, resulting in final eccentricities that are lower than they should be. We also note that the eccentricities depend on the aspect ratio, which was fixed at a constant value of h = 0.05. Increasing the aspect ratio of the disk can therefore in principle lead to a better agreement in the eccentricities.
 |
Fig. 6 Final averaged planet eccentricities of successfully formed resonant chains, as shown in Fig. 3. The different turbulence strengths |
4 Discussion
In Sect. 3.2.1 we showed that a lower limit for α can be inferred by considering that a certain level of turbulence is needed to reach an excitation of the Laplace angle amplitudes that match those inferred by Mills et al. (2016). While the α values that allow a formation of the Kepler-223 system with the correct Laplace angle libration amplitudes also depend on the disk surface density, a lower limit is given by α ~×10−3. This value is consistent with turbulence values inferred for an MRI “dead-zone” (Flock et al. 2019). Even though α has a space dependence across the protoplanetary disk, the assumption of a constant α is not too strong for our approach, considering that the planetesimals that formed the initial embryos resulting in the Kepler-223 planets formed close to each other, as suggested by embryo growth simulations (e.g., Voelkel et al. 2020, 2021).
To apply the concept of inferring disk parameters from a planetary system after the disk itself has already dissipated, we adopted the prescription by Cresswell & Nelson (2008) for the additional dissipative forces added to the N-body integrator. This description of planetary migration is comparatively simple, therefore allowing us to obtain gross estimates of parameter ranges and giving agood overview over the idea of this method. For a more thorough investigation, more sophisticated prescriptions for planetary migration in protoplanetary disk may be implemented. While this can be achieved by integrating hydrodynamical models that are commonly used for investigations of this kind (see, e.g., Bitsch & Kley 2010; McNally et al. 2019; Ataiee & Kley 2020), the goal is to do so with the less computation-intensive method of N-body integration including dissipative forces. In this case, for example, adopting models from Paardekooper et al. (2011) and Jiménez & Masset (2017), a main aspect is the fact that the disk torques responsible for migration in fact exhibit a viscosity dependence, which was not considered here. In addition, these models can include more physically accurate models for the inner edge of the protoplanetary disk, where the positive torque acting as a planetary trap is caused by the slopeof the density profile, which changes rapidly close to the inner edge. Adopting these considerations in a self-consistent way including stochastic forces as they are caused by the disk turbulence would allow for a more detailed picture of resonant systems, while in principle applying the same arguments as with the simplified approach.
While an N-body approach is not as detailed as a full hydrodynamical consideration, it serves as a good way to reduce the large parameter space because the N-body approach saves a significant amount of computation time compared to a full hydrodynamical approach. We ran 6000 simulations for × 105 years of physical time to produce Fig. 3, which corresponds to about 5 × 106 orbits of the innermost planet Kepler-223 b. One simulation used 24 CPU hours on average, so that one orbit required ~ 4.8 × 10−6 CPU hours (~ 17 ms). Under the assumption that a typical hydrodynamical approach takes 4 min to integrate one orbit, the methods applied here would have required about 3.3 × 106 CPU hours (~38 yr) per simulation. The number of simulations and high integration time that we employed for our considerations would therefore be unfeasible for a hydrodynamical approach.
While planetary systems with long chains of MMRs are not common due to the reasons stated above, Kepler-223 is certainly not the only system with such a peculiar configuration. Another prominent example is the Trappist-1 system, which consists of seven resonant planets. Similarly to the approach taken for Kepler-223, we can infer parameters of the protoplanetary disk in the phase in which planetary migration was relevant, even though the disk has already dissipated, by imposing that the disk must allow such a system to form and remain stable during the timescales we observe. This can supplement studies concerning the properties of observable protoplanetary disks, for instance, with ALMA (Rafikov 2017; Dullemond et al. 2018; Flaherty et al. 2017, 2018). More broadly, any system with a rare orbital configuration that in turn offers constraints to a protoplanetary disk that would have formed such a rare system can be used in this way to infer parameter estimates that offer insights into the formation of protoplanetary systems in general.
5 Conclusions
The observed orbital configuration of the Kepler-223 system can be used to infer information about the protoplanetary disk out of which the system formed. By exploring different parameters of the disk at the time of the assembly of the chain, we were able to show how some configurations prevent the system from a dynamical evolution that would allow the presently observed configuration to exist.
- 1.
Treatment of the dynamical evolution of the system, in a manner that is adequate for our purpose, can be achieved without the need of computationally expensive codes that consider the full hydrodynamical picture.Instead, we simply employ an N-body integrator with additional dissipative forces mimicking the relevant planet-disk interactions. However, the approach demonstrated in this work should be seen as a proof-of-concept rather than providing detailed results about the disk parameters that governed the late evolution of the Kepler-223 system because this simple model has a number of limits: no evolution of the protoplanetary disk over time is considered, and neither is the space- (or time-) dependence of α. Considering this can affect the formation of the chain (Ataiee & Kley 2020) and also the long-term stability (e.g., Pichierri et al. 2018; Pichierri & Morbidelli 2020). Moreover, we acknowledge that this method only probes the evolutionary phase in which migration of planets and disk turbulence are the dominating effects. Nevertheless, our method clearly shows that the dynamical constraint from planetary systems in resonance can be used to constrain the disk parameters during planet formation.
- 2.
For a fixed surface density value Σ0, this approach can be used to determine constraints for the turbulence parameter α by requiring the formation of the resonance chain under these turbulent conditions. This is done under the simplifying assumption that the planets under investigation can be considered to be close to the resonances that they are observed in today. This can be seen as not too restrictive, considering that it is safe to assume that the planets reached an orbital state close to where they are observed at some point in time. Conversely, under the assumption of a fixed α, the required range of surface densities can be inferred, implying whether the planets of Kepler-223 have formed during the early time of high surface density or the late time of lower surface density.
- 3.
For lower values for α, it is not straightforward to conclude whether the formation of all aspects of the Kepler-223 orbital architecture can be ensured. This is because for weak turbulence, meaning such that captured resonance chains cannot be disrupted, simple analytical insights cannot be put into use and the impact of the turbulent environment is relevant mostly during the formation stage of the chain. The points at which we recover analytical considerations is reached when an established chain can also be disrupted. The limiting parameter αcrit can be estimated from two-planet results following Batygin & Adams (2017), as described in Eq. (19).
- 4.
The values of α that were considered in this work are in the range of α = ×10−4 to 4 × 10−2, which is the range found by studies of disks that can be observed with ALMA (Rafikov 2017; Dullemond et al. 2018; Flaherty et al. 2017, 2018). These observations are also consistent with hydrodynamical and MRI simulations (e.g., Turner et al. 2014). When the assembly of the correct chain of MMRs is considered alone, it is not possible to give a lower limit for α using the method we employed here. However, because the amplitudes of the Laplace angles are also known for the Kepler-223 system (Mills et al. 2016), an additional constraint can be provided. As shown in Fig. 5, a certain level of turbulence is needed to reproduce the correct amplitudes of the Laplace angles, which is about 15° for ϕ1 and 30° for ϕ2 and ϕ3, peak to peak. As a lower limit for α, the consideration of the Laplace angle amplitudes gives α ~×10−3, which is consistent with values typically considered for an MRI dead zone (Flock et al. 2019). Our measurement of viscosity comes with the uncertainty of an unknown value for the surface density because our simulations allow us to make statements about
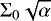 . For example, a higher turbulent viscosity can be consistent with our results if we adopt a lower surface density. It was also found that even if the correct MMR chain is formed, the system can still fail to reproduce the correct amplitudes for the Laplace angles and can therefore not be considered to have correctly reproduced the observations; this is mainly important at high α.
. For example, a higher turbulent viscosity can be consistent with our results if we adopt a lower surface density. It was also found that even if the correct MMR chain is formed, the system can still fail to reproduce the correct amplitudes for the Laplace angles and can therefore not be considered to have correctly reproduced the observations; this is mainly important at high α. - 5.
While the described methods can be used to determine rough constraints for disk parameters during the later stages of planet formation and the assembly of planetary systems, it has shortcomings that can be seen by the example of the final planet eccentricities as depicted in Fig. 6. The eccentricities of the inner two planets as measured by Mills et al. (2016) were not reproduced here. However, this does not invalidate our method because on the one hand, a global mismatch of the eccentricities can be fixed by modifying the aspect ratio prescription, where an increase could lead to a shift in eccentricities that provides a better match with the observed values (Goldreich & Schlichting 2014; Pichierri et al. 2018). On the other hand, we propose the model of the inner edge of the protoplanetary disk as a reason for the presented mismatch, which is strongly simplified and does not accurately represent all physical properties. While the focus of this investigation was on the method itself, this issue could be fixed by employing more physically accurate models (e.g., Izidoro et al. 2017; Izidoro et al. 2021).
Our method clearly shows that the currently observed system architectures hold imprints of their formation history. Especially systems with multiple planets in resonance can help to constrain disk parameters. This is especially important to also probe different environments, like in the Trappist-1 system, which orbits an M dwarf, where constraints from disk observations are even rarer.
Acknowledgements
L.-A.H, G.P. and B.B. thank the European Research Council (ERC Starting Grant 757448-PAMDORA) for their financial support.
Appendix A Diffusion coefficient fit for the eccentricity evolution
To derive the prefactor of Eq. (15), the diffusion coefficient was derived for different γ by computing the standard deviation between 100 simulations for a fixed time and fitting a square-root dependence. For these simulations, migration was disabled. Figure A.1 shows the resulting diffusion coefficient, where another fit lead to the prefactor of 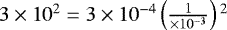 for the relation between the turbulence strength parameter γ and the diffusion coefficient of the eccentricity, De, as seen in Eq. (15).
for the relation between the turbulence strength parameter γ and the diffusion coefficient of the eccentricity, De, as seen in Eq. (15).
 |
Fig. A.1 Diffusion coefficients De that are realized by three different turbulence strength parameters γ in simulations with the setup used throughout this work. A quadratic fit was used to determine the prefactor that describes the order-of-magnitude relation as described in Eq. (15). |
Appendix B Simulation parameters
This appendix presents all constant parameters we employed for the prescription of migration (Cresswell & Nelson 2008) and stochastic forces mimicking turbulence (Ogihara et al. 2007). They are shown in Table B.1.
Model parameters employed for the simulations.
References
- Ataiee, S., & Kley, W. 2020, A&A, 635, A204 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ataiee, S., & Kley, W. 2021, A&A, 648, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1991, ApJ, 376, 214 [Google Scholar]
- Baruteau, C., Crida, A., Paardekooper, S. J., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 667 [Google Scholar]
- Batygin, K. 2015, MNRAS, 451, 2589 [NASA ADS] [CrossRef] [Google Scholar]
- Batygin, K., & Adams, F. C. 2017, AJ, 153, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Bitsch, B., & Kley, W. 2010, A&A, 523, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chiang, E., & Laughlin, G. 2013, MNRAS, 431, 3444 [Google Scholar]
- Cresswell, P., & Nelson, R. P. 2008, A&A, 482, 677 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deck, K. M., & Batygin, K. 2015, ApJ, 810, 119 [Google Scholar]
- Delisle, J. B. 2017, A&A, 605, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dullemond, C. P., Birnstiel, T., Huang, J., et al. 2018, ApJ, 869, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Flaherty, K. M., Hughes, A. M., Rose, S. C., et al. 2017, ApJ, 843, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Flaherty, K. M., Hughes, A. M., Teague, R., et al. 2018, ApJ, 856, 117 [CrossRef] [Google Scholar]
- Flock, M., Nelson, R. P., Turner, N. J., et al. 2017, ApJ, 850, 131 [Google Scholar]
- Flock, M., Turner, N. J., Mulders, G. D., et al. 2019, A&A, 630, A147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Jehin, E., Lederer, S. M., et al. 2016, Nature, 533, 221 [Google Scholar]
- Gillon, M., Triaud, A. H. M. J., Demory, B.-O., et al. 2017, Nature, 542, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Goldreich, P., & Schlichting, H. E. 2014, AJ, 147, 32 [Google Scholar]
- Howard, A. W., Marcy, G. W., Bryson, S. T., et al. 2012, ApJS, 201, 15 [Google Scholar]
- Ida, S., Guillot, T., & Morbidelli, A. 2008, ApJ, 686, 1292 [Google Scholar]
- Izidoro, A., Ogihara, M., Raymond, S. N., et al. 2017, MNRAS, 470, 1750 [Google Scholar]
- Izidoro, A., Bitsch, B., Raymond, S. N., et al. 2021, A&A, 650, A152 [EDP Sciences] [Google Scholar]
- Jiménez, M. A., & Masset, F. S. 2017, MNRAS, 471, 4917 [Google Scholar]
- Keppler, M., Benisty, M., Müller, A., et al. 2018, A&A, 617, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Klahr, H. H., & Bodenheimer, P. 2003, ApJ, 582, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Kley, W., & Nelson, R. P. 2012, ARA&A, 50, 211 [Google Scholar]
- Lambrechts, M., Morbidelli, A., Jacobson, S. A., et al. 2019, A&A, 627, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laughlin, G., Steinacker, A., & Adams, F. C. 2004, ApJ, 608, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, B., Ormel, C. W., & Lin, D. N. C. 2017, A&A, 601, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luger, R., Sestovic, M., Kruse, E., et al. 2017, Nat. Astron., 1, 0129 [Google Scholar]
- Manger, N., Klahr, H., Kley, W., & Flock, M. 2020, MNRAS, 499, 1841 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., Butler, R. P., Fischer, D., et al. 2001, ApJ, 556, 296 [Google Scholar]
- Masset, F. S., Morbidelli, A., Crida, A., & Ferreira, J. 2006, ApJ, 642, 478 [Google Scholar]
- Mayor, M., Marmier, M., Lovis, C., et al. 2011, ArXiv e-prints [1109.2497] [Google Scholar]
- McNally, C. P., Nelson, R. P., & Paardekooper, S.-J. 2019, MNRAS, 489, L17 [Google Scholar]
- Millholland, S., Wang, S., & Laughlin, G. 2017, ApJ, 849, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Mills, S. M., Fabrycky, D. C., Migaszewski, C., et al. 2016, Nature, 533, 509 [Google Scholar]
- Mulders, G. D., Pascucci, I., Apai, D., & Ciesla, F. J. 2018, AJ, 156, 24 [Google Scholar]
- Ogihara, M., Ida, S., & Morbidelli, A. 2007, Icarus, 188, 522–34 [CrossRef] [Google Scholar]
- Okuzumi, S., & Ormel, C. W. 2013, ApJ, 771, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Paardekooper, S.-J., Baruteau, C., & Kley, W. 2011, MNRAS, 410, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Pichierri, G., & Morbidelli, A. 2020, MNRAS, 494, 4950 [Google Scholar]
- Pichierri, G., Morbidelli, A., & Crida, A. 2018, Celest. Mech. Dyn. Astron., 130, 54 [Google Scholar]
- Pinte, C., Ménard, F., Duchêne, G., et al. 2018, A&A, 609, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rafikov, R. R. 2017, ApJ, 837, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos, X. S., Charalambous, C., Benítez-Llambay, P., & Beaugé, C. 2017, A&A, 602, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richard, S., Nelson, R. P., & Umurhan, O. M. 2016, MNRAS, 456, 3571 [NASA ADS] [CrossRef] [Google Scholar]
- Rivera, E. J., Lissauer, J. J., Butler, R. P., et al. 2005, ApJ, 634, 625 [Google Scholar]
- Shakura, N. I., & Sunyaev, R. A. 1972, A&A, 24, 337 [Google Scholar]
- Teague, R., Bae, J., Bergin, E. A., Birnstiel, T., & Foreman-Mackey, D. 2018, ApJ, 860, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Turner, N. J., Fromang, S., Gammie, C., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning (Tucson: University of Arizona Press), 411 [Google Scholar]
- Voelkel, O., Klahr, H., Mordasini, C., Emsenhuber, A., & Lenz, C. 2020, A&A, 642, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Voelkel, O., Deienno, R., Kretke, K., & Klahr, H. 2021, A&A, 645, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Weiss, L. M., Marcy, G. W., Petigura, E. A., et al. 2018, AJ, 155, 48 [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Range of surface density values Σ0 that allow the individual Kepler-223 planet pairs to be captured into the correct resonance as a function of the semimajor axis of the outer planet of each pair. The error that is related to the mass error of the planets is indicated in red (Mills et al. 2016). The dotted black lines clarify that within the errors, no value for Σ0 can be found that allows each separate pair to be captured into the correct resonance if the pairs are initially wide of the 2:1 MMR. The dotted blue vertical lines indicate that this does not hold if the planets are instead placed just wide of the correct MMR, which eliminates the lower limit for Σ0. |
| In the text | |
 |
Fig. 2 Buildup of the resonance chain of the four Kepler-223 planets, without considering turbulence. The investigated parameter space is two dimensional: The surface density is varied, as is the initial separation of the planet pairs from the final resonance. The configurations in which the correct chain was built are indicated by green triangles, while those who failed to do so are shown as red crosses. The vales for ε are ordered such that ε1 is the topmost value. Simulations whose symbol is encircled share their initial parameters with those considered for a consideration including disk turbulence (Sect. 3.2). |
| In the text | |
 |
Fig. 3 Number of successful creations of the Kepler-223 resonance chain for various initial conditions, with varying initial separations and surface densities. For each initial setup, four turbulence strengths α were considered. The green bar denotes successful formations. Generally, a larger turbulence strength leads to fewer successful runs. For each setup, there is a critical value αcrit (cf. Eq. (19)), for which stronger turbulence significantly hinders the creation of the resonance chain (Batygin &Adams 2017). This is depicted in the plot. This critical value decreases with increasing gas surface density, which is also the case for the number of successful runs for an increasing surface density at constant α (cf. Eq. (3)). The setup marked in red did not reproduce the Kepler-223 resonance chain without turbulence, but it does not differ significantly from those that did when the effects of the turbulent disk were considered, indicating that turbulence is a necessary ingredient for this particular setup. This remains to be investigated in future work. |
| In the text | |
 |
Fig. 4 Two setups, also represented in Fig. 3, in which turbulence was activated in the simulations only after the formation of the resonance chain. For case (a), Eq. (19) gives αcrit = 6.4 × 10−2, and for case (b), it yields αcrit = 2.3 × 10−2. The resulting number of successful simulations as a function of α is shown, which was compared to the expected critical αcrit value (cf. Eq. (19)). The results match the theoretical expectations on the order of magnitude. |
| In the text | |
 |
Fig. 5 Libration amplitudes of the Laplace angles for successful simulations depicted in Fig. 3, grouped by turbulence strength. The positions of the peaks scale with
|
| In the text | |
 |
Fig. 6 Final averaged planet eccentricities of successfully formed resonant chains, as shown in Fig. 3. The different turbulence strengths |
| In the text | |
 |
Fig. A.1 Diffusion coefficients De that are realized by three different turbulence strength parameters γ in simulations with the setup used throughout this work. A quadratic fit was used to determine the prefactor that describes the order-of-magnitude relation as described in Eq. (15). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.