| Issue |
A&A
Volume 655, November 2021
|
|
|---|---|---|
| Article Number | A80 | |
| Number of page(s) | 28 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202141757 | |
| Published online | 24 November 2021 | |
ATOMIUM: halide molecules around the S-type AGB star W Aquilae
1
Department of Physics and Astronomy, Institute of Astronomy,
KU Leuven, Celestijnenlaan 200D,
3001
Leuven, Belgium
e-mail: taissa.danilovich@kuleuven.be
2
University of Leeds, School of Chemistry,
Leeds
LS2 9JT, UK
3
Astrophysics Research Centre, School of Mathematics and Physics, Queen’s University Belfast, University Road,
Belfast
BT7 1NN, UK
4
LSAMA, Department of Physics, Faculty of Sciences, University Tunis El Manar, Campus Universitaire,
1060
Tunis, Tunisia
5
Harvard-Smithsonian Center for Astrophysics,
60 Garden Street,
Cambridge,
MA
02138, USA
6
JBCA, Department Physics and Astronomy, University of Manchester,
Manchester
M13 9PL, UK
7
Department of Space, Earth and Environment, Chalmers University of Technology, Onsala Space Observatory,
43992
Onsala, Sweden
8
Université de Bordeaux, Laboratoire d’Astrophysique de Bordeaux,
33615
Pessac, France
9
University of Amsterdam, Anton Pannekoek Institute for Astronomy,
1090 GE
Amsterdam, The Netherlands
10
National Astronomical Research Institute of Thailand,
Chiangmai
50180, Thailand
11
Institut d’Astronomie et d’Astrophysique, Université Libre de Bruxelles (ULB), CP 226, 1060
Brussels, Belgium
12
Max-Planck-Institut für Radioastronomie,
53121
Bonn, Germany
13
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université de Paris,
5 place Jules Janssen,
92195
Meudon, France
14
Université Côte d’Azur, Laboratoire Lagrange, Observatoire de la Côte d’Azur,
06304
Nice Cedex 4, France
15
Universität zu Köln, I. Physikalisches Institut,
50937
Köln, Germany
16
California Institute of Technology, Jet Propulsion Laboratory,
Pasadena,
CA
91109, USA
17
SRON Netherlands Institute for Space Research,
3584 CA
Utrecht, The Netherlands
18
Radboud University, Institute for Mathematics, Astrophysics and Particle Physics (IMAPP),
Nijmegen, The Netherlands
19
Institut de Radioastronomie Millimétrique,
300 rue de la Piscine,
38406
Saint Martin d’Hères, France
20
University College London, Department of Physics and Astronomy,
London
WC1E 6BT, UK
21
University of Hong Kong, Laboratory for Space Research,
Pokfulam, Hong Kong
22
School of Physical Sciences, The Open University,
Walton Hall,
Milton Keynes,
MK7 6AA, UK
Received:
9
July
2021
Accepted:
9
September
2021
Context. S-type asymptotic giant branch (AGB) stars are thought to be intermediates in the evolution of oxygen- to carbon-rich AGB stars. The chemical compositions of their circumstellar envelopes are also intermediate but have not been studied in as much detail as their carbon- and oxygen-rich counterparts. W Aql is a nearby S-type star, with well-known circumstellar parameters, making it an ideal object for in-depth study of less common molecules.
Aims. We aim to determine the abundances of AlCl and AlF from rotational lines, which have been observed for the first time towards an S-type AGB star. In combination with models based on PACS observations, we aim to update our chemical kinetics network based on these results.
Methods. We analyse ALMA observations towards W Aql of AlCl in the ground and first two vibrationally excited states and AlF in the ground vibrational state. Using radiative transfer models, we determine the abundances and spatial abundance distributions of Al35Cl, Al37Cl, and AlF. We also model HCl and HF emission and compare these models to PACS spectra to constrain the abundances of these species.
Results. AlCl is found in clumps very close to the star, with emission confined within 0′′.1 of the star. AlF emission is more extended, with faint emission extending 0′′.2 to 0′′.6 from the continuum peak. We find peak abundances, relative to H2, of 1.7 × 10−7 for Al35Cl, 7 × 10−8 for Al37Cl, and 1 × 10−7 for AlF. From the PACS spectra, we find abundances of 9.7 × 10−8 and ≤10−8, relative to H2, for HCl and HF, respectively.
Conclusions. The AlF abundance exceeds the solar F abundance, indicating that fluorine synthesised in the AGB star has already been dredged up to the surface of the star and ejected into the circumstellar envelope. From our analysis of chemical reactions in the wind, we conclude that AlF may participate in the dust formation process, but we cannot fully explain the rapid depletion of AlCl seen inthe wind.
Key words: stars: AGB and post-AGB / circumstellar matter / submillimeter: stars / stars: individual: W Aql / stars: individual: χ Cyg
© ESO 2021
1 Introduction
Stars on the asymptotic giant granch (AGB) of the Hertzsprung-Russell diagram are an evolved form of low- and intermediate-mass stars with initial masses in the range ~0.8–8 M⊙. The AGB evolutionary stage is characterised by intense mass loss, of the order of ~10−8–10−4 M⊙ yr−1 (Höfner & Olofsson 2018). The gas ejected by these stars forms molecules and dust in an expanding region surrounding the star, known as a circumstellar envelope (CSE). The CSEs of AGB stars are rich chemical laboratories, and a large number of different molecular species have been detected towards various AGB stars (Agúndez et al. 2020).
The chemical composition of the CSE is, to the first order, determined by the photospheric abundances of C and O of the star. We define AGB stars as oxygen-rich if C/O < 1 and carbon-rich if C/O > 1. Generally speaking, more oxygen-bearing molecules are found in the CSEs of oxygen-rich stars, while carbon-bearing molecules are more prevalent in the CSEs of carbon-rich stars. There is thought to be an evolutionary progression such that all stars are oxygen-rich when they transition to the AGB and then a subset of these gradually become carbon-rich as freshly nucleosynthesised carbon is dredged up from the core of the star to the surface, increasing the C/O ratio. S-type stars, with C/O ~ 1, are thought to be transition objects that arise during this evolutionary process (Herwig 2005). The circumstellar chemistry of S-type stars has been generally found to be intermediate between carbon- and oxygen-rich chemistry (see, for example, Danilovich et al. 2014).
Halogen-bearing molecules have not been extensively studied in the CSEs of many AGB stars. Chlorine has been found to be a tracer of metallicity (Maas et al. 2016), and fluorine is thought to be produced in AGB stars and dredged up to the surface of the star (Kobayashi et al. 2020). By understanding the total abundance of Cl or F around AGB stars, we can better understand their metallicities or AGB ages, respectively. To date, halide molecules have been studied in most detail towards the nearby, high mass-loss rate carbon star CW Leo (IRC+10216), towards which AlCl, NaCl, KCl, AlF, HCl, and HF have been detected (Cernicharo & Guelin 1987; Cernicharo et al. 2010; Agúndez et al. 2011, 2012). Aside from CW Leo, halogen-bearing molecules have only been detected towards a handful of AGB stars, such as Al35 Cl tentatively seen towards the oxygen-rich stars IK Tau and R Dor (Decin et al. 2017), and NaCl seen towards IK Tau (Milam et al. 2007; Decin et al. 2018) and tentatively R Dor (De Beck & Olofsson 2018). No spectrally resolved halogen-bearing species have been previously reported towards any S-type stars1, although spectrally unresolved infrared observations of HCl in the atmosphere of the S-type star R And have been reported by Yamamura et al. (2000).
Agúndez et al. (2020) undertook an extensive study of molecular abundances in the inner regions of AGB CSEs under the assumption of thermochemical equilibrium, making several predictions for molecular abundances in the inner 10 stellar radii (R⋆). They predict AlF and AlCl to be the dominant F- and Cl-bearing molecules from ~ 3R⋆ outwards for S-type stars, with HF and HCl dominating the innermost regions (≲ 3R⋆). Hence, we should expect to see both aluminium and hydrogen halides towards S-type stars.
In recent years, W Aql has become the most-studied S-type AGB star, thanks to a combination of its proximity (374 ± 22 pc, Gaia Collaboration 2016, 2021; Lindegren et al. 2021), moderately high mass-loss rate (3 × 10−6 M⊙ yr−1, Ramstedt et al. 2017), and equatorial position in the sky (declination ~−7°). It has been observed by two instruments aboard Herschel2 (Mayer et al. 2013; Danilovich et al. 2014) and the Atacama Large Millimetre/sub-millimetre Array (ALMA, Ramstedt et al. 2017; Brunner et al. 2018), as well as a variety of other telescopes (see for example De Beck & Olofsson 2020), which helped constrain the conditions in its CSE. In addition to (sub)millimetre observations, optical and infrared observations have provided information on the dust around this star (Hony et al. 2009; Mayer et al. 2013; Ramstedt et al. 2011) and its companion, which has been characterised as an F9 main sequence star (Danilovich et al. 2015a) located at a projected distance of 0′′.46 (Ramstedt et al. 2011), which corresponds to approximately 170 AU at the distance given by Gaia.
In this study we focus on the rotational lines of halogen-bearing molecules towards W Aql, especially AlCl and AlF, which were observed with ALMA. These data are presented in Sect. 2. Additionally, we examine observations of HCl and HF obtained by Herschel/PACS (Sect. 3). Radiative transfer modelling is performed for all four of these molecules (Sect. 4), with the results presented in Sect. 5. We discuss our results in the context of the literature and use them to update our chemical kinetics model in Sect. 6. Section 7 summarises our conclusions.
2 ALMA observations of AlCl and AlF
As part of the ATOMIUM3 programme (2018.1.00659.L, PI: L. Decin), W Aql was observed with three configurations of ALMA, which we refer to as the compact (angular resolution 1′′.11 × 0′′.88 at 262.2 GHz and maximum recoverable scale (MRS) = 8′′.9), mid (angular resolution 0′′.374 × 0′′.250 and MRS = 3′′.9), and extended (angular resolution 0′′.024 × 0′′.021 and MRS = 0′′.4) arrays (see Decin et al. 2020; Gottlieb et al. 2021, for details). These three datasets were combined to produce more sensitive data cubes to allow us to examine the observations in more detail. When data from the different ALMA configurations are combined, different resolutions can be chosen to emphasise different aspects of the data. We found the most useful combined data to have angular resolution of 32 × 30 mas for AlCl and 150 × 130 mas for AlF. Forthis study, we aim to use the best dataset in each context, as will be discussed in detail below.
We detected Al35Cl in the ground, first, and second excited vibrational states (v = 0, 1, 2), Al37 Cl in the ground and first excited vibrational states (v = 0, 1), and AlF in the ground vibrational state (v = 0). We also use tentative or undetected lines of Al35Cl in the third vibrationally excited state, Al37Cl in the second vibrationally excited state, and AlF in the first vibrationally excited state as upper limits when we perform our radiative transfer analysis of the data (see Sects. 4 and 5). These lines are listed with their frequencies, upper level energies and central velocities in Table 1. The central velocities were found by fitting Gaussian profiles to spectra extracted from the combined cubes. Based on these central velocities, we find an average LSR velocity of − 23.1 ± 0.9 km s−1, which is in good agreement with the values found by Danilovich et al. (2014) and De Beck & Olofsson (2020) from single dish observations of a variety of molecules.
Angular sizes are given in Table 1 for sufficiently bright lines. They have been measured by: examining zeroth moment maps (of the velocity-integrated emission) of each line over the velocity range indicated in Table 1; and creating contours enclosing the flux at the 2σ level. The 2σ level was chosen since this gives a more accurate estimate of total extent, including weaker emission, than the 3σ level. Isolated islands only detected at 2σ levels are not included since we require at least 3σ certainty to consider emission to be detected. This gave a table of x and y values of the coordinates enclosing the flux, centred on the star, which could be transformed to polar coordinates r, θ. To reduce random noise affecting the contour, we binned and averaged the values with at least 10 samples per bin, corresponding to angular ranges of ≥ 60°. We then measured the longest (Rmax) and shortest (Rmin) radial distances from the continuum peak to the binned contour. To give an indication of the regularity or irregularity of the shape of the emission, we also note the angle (θR) between the radii of the nearest and farthest angle of the contour. If these are orthogonal the radii can correspond to semi-major and semi-minor axes, suggesting a more regular distribution, but if the angle is very different from 90°, then the distribution is asymmetric. For AlF the measurement was done for data that had been combined with a taper of 0′′.2, giving a lower resolution image but avoiding the irregularities seen in Fig. 3. The uncertainty in the radii is ~ 3 mas for AlCl and ~18 mas for AlF.
We characterise the 1D spectra extracted from ALMA cubes by an aperture size, which is the size of a circular region over which the spectrum has been extracted, and is always centred on the continuum peak. Since the AlF (7 → 6) v = 0 line is relatively weak, we average channels to give a lower velocity resolution of ~ 2.5 km s−1 (compared with ~1.1 km s−1 for AlCl) and a higher signal-to-noise ratio. For our modelling, we also use what we refer to as azimuthally averaged radial profiles of the ALMA lines. These are extracted from the zeroth moment maps by obtaining the average flux in concentric annuli, plus the flux in the central circular region, centred on the continuum peak. These radial profiles allow us to more easily compare ALMA data with our spherically symmetric models (see Sect. 4 for details of modelling).
Properties of lines of AlCl and AlF covered by ATOMIUM towards W Aql.
 |
Fig. 1 Channel maps of Al35Cl (18 → 17) observed towards W Aql using ALMA in the extended array configuration. The dotted red contours enclose 50% of the total continuum flux. The white contours indicate levels of 3 and 5σ. The ellipses in the bottom left of each panel indicate the synthetic beams for the molecular emission (white) and continuum emission (red). |
2.1 AlCl
The AlCl lines seen towards W Aql are all fairly compact, including the v = 0 lines. The channel maps for Al35Cl (18 → 17) in the ground vibrational state, observed with the ALMA extended array, are shown in Fig. 1. There it can be seen that the emission is resolved and clumpy, but seen within 0′′.1 of the star. The Al35Cl v = 1 lines and the Al37Cl (16 → 15) line in the ground vibrational state are found in similar regions but are seen less clearly, due to their expected lower intensities. We show the zeroth moment maps of Al35Cl (18 → 17) and Al37 Cl (16 → 15) in the ground vibrational state, and (17 → 16) in the first vibrationally excited state in Fig. 2. The zeroth moment maps were all constructed so as to include all of the line flux with no contamination from adjacent lines and with minimal dilution due to line-free noise-dominated channels. The zeroth moment map of Al35Cl v = 0 (18 → 17) shows the emission is not centred on the star, with more emission seen to the south-east than the north-west. However, the emission from the other transitions shown in Fig. 2 is not consistently offset in the same direction. We conclude that the cause of this asymmetry is either noise or clumpy emission, rather than a specific directional bias for the formation of AlCl, though such bias is not decisively ruled out. The spectral lines of AlCl are presented in conjunction with our models in Sect. 5, where we show all the lines extracted for an aperture of radius 0′′.08 and include the Al35Cl v = 0 (18 → 17) line extracted for a radius of 0′′.2, to ensure all the flux is captured for the purposes of comparisons with our model.
 |
Fig. 2 Zeroth moment maps of AlCl observed towards W Aql using ALMA in the extended array configuration. Transitionsare labelled in the top right of each panel. The black contours indicate levels of 3, 5, and 10σ. The dotted red contour encloses 50% the total continuum flux. The ellipses in the bottom left of each panel indicate the synthetic beams for the molecular emission (white) and continuum emission (red). |
2.2 AlF
The ground state AlF emission is more extended than AlCl. It has a bright central region, within ~ 0′′.15 of the star, and a more extended region of faint, clumpy emission. The extended emission is seen most clearly in a zeroth moment map with a lower angular resolution of150 × 130 mas (Fig. 3), which allows us to see the faint emission above the noise, with dashed white contours outlining the emission down to the 3σ level. As can be seen in Fig. 3, the extended diffuse emission is mostly found to the north of thestellar position. Relative to the stellar continuum peak, the diffuse emission extends to ~ 0′′.5 north, ~ 0′′.6 east, ~ 0′′.4 west, and only ~ 0′′.2 south. We include contours of the Al35Cl (18 → 17) zeroth moment map (with an angular resolution of 32 × 30 mas) in Fig. 3. Although the offsets noted for AlF and Al35 Cl are not in the same direction, we find that the central peak of AlF emission corresponds reasonably well with the region of Al35 Cl emission.
3 Observations of other halide molecules
3.1 NaCl and KCl
Several transitions of NaCl and KCl were covered in the ATOMIUM observations but not detected towards W Aql. ATOMIUM detections of these two molecules were made towards the higher mass-loss rate oxygen-rich stars (and the red supergiant VX Sgr) and will be examined in more detail in a future work. We calculate the rms values as detection limits for NaCl and KCl towards W Aql in Appendix A.1.
In their recent study, De Beck & Olofsson (2020) analysed a spectral survey of W Aql conducted by the Atacama Pathfinder Experiment (APEX). They find emission from 13 species and their isotopologues, in addition to two unidentified lines (the latter falling outside of our observed frequency range). They do not detect AlCl or AlF but report tentative detections of NaCl, both of which fall within our observed frequency range at 247.2397 GHz for the (19 → 18) line and 260.2231 GHz for the (20 → 19) line.
The line at 247.2397 GHz falls on the edge of a band in our data; however a clear partial detection is visible, both in the spectrum and the channel maps. After correcting for the LSR velocity of − 23 km s−1 (Danilovich et al. 2014), we found that the 247.2397 GHz line did not coincide with the emission we detect. A more likely carrier of the emission seen near this band edge isthe 30SiO (6 → 5) line in the v = 4 state at 247.244 GHz, owing to a better agreement with the systemic velocity of W Aql for the spatially compact emission of this line. In the case of the possible NaCl line at 260.2231 GHz, emission is present at this frequency; however we identify it as the 260.2248 GHz line of H13CN, with J = 3 → 2 in the ν2 = 1 excited bending vibrational level, which is in better agreement with the systemic velocity of W Aql. The H13 CN line is also similar in brightness and appearance to the other component of the l-type doublet (with the same J and ν2 values) seen at 258.9361 GHz, thereby confirming the assignment. An additional line of NaCl, (17 → 16) at 221.2601 GHz, was covered in our observations and by De Beck & Olofsson (2020), but was not detected in either case.
 |
Fig. 3 Zeroth moment map of the AlF (7 → 6) line in the ground vibrational state (colours and white dashed contours) plotted with the zeroth moment map of the Al35 Cl (18 → 17) line in the ground vibrational state (black solid contours). The contours are plotted at levels of 3, 5, and 10σ for AlF and 5 and 10σ for Al35 Cl. The red star indicates the position of the continuum peak. The white and black ellipses in the bottom right indicate the synthetic beam sizes for the AlF and Al35 Cl emission, respectively. |
HCl and HF lines covered by Herschel/PACS towards W Aql.
3.2 HCl and HF
A search of the literature revealed that, aside from the metal halides discussed above, the only other published detections of halogen-bearing molecules towards AGB stars are the hydrides HCl and HF towards the carbon star CW Leo (Cernicharo et al. 2010; Agúndez et al. 2011). The frequencies of both HCl and HF are well outside of the observing window of the ATOMIUM project. However, some transitions of HCl and HF were covered by the Herschel/PACS spectrograph (Pilbratt et al. 2010; Poglitsch et al. 2010) and observed towards several AGB stars (Groenewegen et al. 2011; Nicolaes et al. 2018). Although spectrally resolved transitions of HCl and HF were observed by Agúndez et al. (2011) towards CW Leo with Herschel/HIFI (de Graauw et al. 2010), all of these lines are outside of the frequency range at which W Aql was observed with Herschel/HIFI (Danilovich et al. 2014).
We searched the PACS spectrum of W Aql (Nicolaes et al. 2018) and found evidence of H35 Cl and H37 Cl emission in the J = 3 → 2 and J = 4 → 3 lines. In both cases, there is a partial overlap of the H35Cl and H37 Cl lines, since the emission is not spectrally resolved by PACS. The H37Cl (4 → 3) line is also known to be blended with H13CN (29 → 28) at 120.12 μm and SiO (58 → 57) at 120.14 μm. Without spectrally resolved observations available, we cannot disentangle the contributions of these lines to the H37 Cl (4 → 3) line, but they are the most likely reason that the H37Cl appears brighter than the more abundant H35Cl. We do not find clear detections of the J = 6 → 5 and J = 7 → 6 lines for either HCl isotopologue. However, we still compare the PACS spectrum in the region of these two lines to our model results (see Sect. 5.3.1), so that they can serve as upper limits. The details of these lines are listed in Table 2. We also include the measured fluxes of the detected lines, which were calculated by fitting Gaussians to the spectra.
We also searched the PACS spectrum for HF, for which three transitions fall within the observed PACS range: J = 2 → 1, J = 3 → 2, and J = 4 → 3 (see Table 2). The lowest energy of these lines, at 121.70 μm, is unfortunately blended with a bright ortho-H2O line at 121.721 μm. Higher spectral resolution observations would be needed to distinguish these two lines if the HF line is indeed present. We did not conclusively detect the two higher energy lines, although there is a faint line (~ 2σ) that we tentatively attribute to HF (4 → 3). As for HCl, we include these lines in our model so that they might allow us to derive an upper limit for the abundance of HF.
Stellar and circumstellar parameters of W Aql used in radiative transfer modelling.
4 Modelling overview
4.1 Radiative transfer model
Radiative transfer modelling was performed to determine the abundances and abundance distributions of our observed halide molecules. For the radiative transfer modelling of AlCl and AlF, we used a spherically symmetric model and the accelerated lambda iteration method (ALI, Rybicki & Hummer 1991), previously used to model various molecules in the CSE of W Aql (Danilovich et al. 2014; Ramstedt et al. 2017; Brunner et al. 2018). For this study, we used the circumstellar parameters derived by Danilovich et al. (2014), including the assumption of silicate dust, and included the adjusted mass-loss rate found by Ramstedt et al. (2017). The velocity profile4 from Danilovich et al. (2014) was also used here:
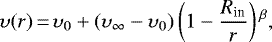 (1)
(1)
with the parameters listed in Table 3 with the other circumstellar and stellar parameters. The gas kinetic temperature was derived in Danilovich et al. (2014) and Ramstedt et al. (2017) from CO radiative transfer modelling (see Schöier & Olofsson 2001; Danilovich et al. 2014, for a discussion of the heating and cooling terms). As plotted in Fig. 4, we extended the kinetic temperature profile inwards such that the stellar effective temperature is not exceeded at the stellar surface.
For consistency with previous models, we used the distance for W Aql obtained by Danilovich et al. (2014) of 395 pc, which was found using a period-luminosity relation. This value is within the uncertainties of the parallax value from the Gaia Early Data Release 3 (Gaia Collaboration 2016, 2021), which gives a distance of 374 ± 22 pc after applying the corrections of Lindegren et al. (2021).
For AlCl and AlF, we used a combination of spectral lines and azimuthally averaged radial profiles (centred on the continuum peak) to determine the molecular abundances and extents of the molecular envelopes. From earlier models of spatially resolved ALMA observations (such as Danilovich et al. 2019), we found that this method was best for finding the abundance distribution of the inner wind – most clearly seen in the ALMA azimuthal profile – while still constraining the outer wind. In general, fainter outer emission is often below the noise in the azimuthal profiles, but its signatures are more clearlyseen in spectral lines, especially those with emitting regions farther out in the CSE, such as the v = 0 AlF line.
Since the emitting regions for AlCl and AlF are quite different (see Fig. 3), there are some differences in how we treat the two molecules, particularly with respect to how dust is implemented in the models. AlF is treated similarly to other molecules in Brunner et al. (2018), using the dust characteristics obtained by Danilovich et al. (2014), since a significant portion of the AlF emission is detected outside the dust condensation radius (Rin = 2 × 1014 cm, Danilovich et al. 2014).
From the ALMA observations, AlCl is predominantly found within 0′′.05 (≈ 3 × 1014 cm) of the star – that is, a significant portion of the AlCl is located within the dust condensation radius. One limitation of our ALI code is that it is not possible to simultaneously consider a dust-free inner region and a dusty outer region. To overcome this limitation, we run a dust-free model for AlCl but include an additional infrared radiation field, based on a blackbody with a temperature of 700 K, which is close to the dust temperature at 3 × 1014 cm in the Danilovich et al. (2014) model. This method is only used for AlCl since it is the most compact emission we see. For HCl and HF, we start our model at 2 × 1014 cm (i.e. the dust condensation radius), following the method in Danilovich et al. (2014), since we have no observational information on the behaviour of these molecules in the inner wind.
Although AlF is more extended than AlCl, it is still relatively compact, compared with, for example, the molecules studied towards W Aql by Brunner et al. (2018), notably CS, SiS, and (quasi-thermal) SiO, which extend out to ~ 2′′ from the continuum peak. The predicted distributions of HCl and HF (see Sect. 4.3) are more similar in spatial extent to the molecules modelled by Brunner et al. (2018), so we include the overdensity derived in that study, increasing the density of the wind by a factor of five between 8 × 1015 cm and 1.5 × 1016 cm. This overdensity, intended to represent the denser region of a spiral arm (see Ramstedt et al. 2017, for plots of the CO distribution), is outside of the region modelled for AlF or AlCl, but may contribute to the flux of the HCl and HF lines, which extend past the overdense region.
 |
Fig. 4 Radial gas kinetic temperature profile used in our modelling of W Aql. |
4.2 Molecular data
A radiative transfer analysis of molecular observations requires a comprehensive list of molecular energy levels and transitions, including Einstein A coefficients and collisional (de-)excitation rates. We prefer to use collisional (de-)excitation rates measured or calculated for collisions between the target molecule and H2, but these are not always available – or are not available for our domain of interest – so some substitutions must be made. For most of the molecules studied here, we obtained the level and radiative information from the ExoMol database5 (Tennyson et al. 2016) and the collisional rates from a variety of sources detailed for each molecule in Appendix B. In particular, we use newly updated collisional rates for AlF, which cover the high temperatures seen for AGB CSEs and are described in detail in Appendix B.2.
Generally, collisional rates have only been calculated for the ground vibrational states of various molecules. Hence, we ensured that the rates used cover, at minimum, all levels that participate in our observed transitions in the ground vibrational state. Often, the available collisional rates are calculated for lower temperatures than seen in our models, for example, rates calculated for maximum kinetic temperatures of 300 K are common. In these cases, collisional rates for higher kinetic temperatures are linearly extrapolated in log–log space from the given rates.
4.3 Radial distribution of HCl and HF from chemical modelling
In the absence of spatially resolved observations of HCl and HF, and having only a small number of spectrally unresolved lines, we turned to predictions from chemical models to determine the HCl and HF abundance distributions. We use the 1D chemical kinetics model of Van de Sande et al. (2018) and the publicly available gas-phase only RATE12 reaction network6 (McElroy et al. 2013). The chemical model assumes the same mass-loss rate and stellar radius as the radiative transfer model, and a constant expansion velocity of 16.5 km s−1. The retrieved gas temperature profile (Fig. 4) was reproduced in the chemical model using two power-laws (r < 2 × 1014 cm, 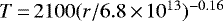 K; r ≥ 2 × 1014 cm,
K; r ≥ 2 × 1014 cm, 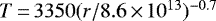 K).
K).
To estimate the shape of the abundance profiles of HF and HCl, we assumed an initial abundance of F and Cl corresponding to their solar abundance minus the inner abundances calculated for AlCl and AlF from early models (see Sects. 5.1 and 5.2). Both halogens are efficiently hydrogenised into HF and HCl at the start of the model. The other Cl- and F-bearing species included in the reaction network (which does not include AlCl or AlF) play a negligible role. Our chemical model is expanded to include Al chemistry in Sect. 6.5, where we discuss the reactions important in the syntheses of AlCl and AlF.
The shape of the predicted radial abundance distribution does not change with changes in initial Cl or F abundances.Hence, in our radiative transfer analysis, we find the best fitting model by scaling the radial abundance distribution until the model lines best reproduce the observed data. When finding upper limits on the abundance, we scale the radial abundance profile such that the model lines do not exceed the observed lines.
 |
Fig. 5 Spectra of Al35Cl observed towards W Aql with ALMA (black histograms), with calculated line profiles (red curves) superposed on the observed profiles. Nearby lines of other molecules are labelled in blue. |
5 Model results
5.1 AlCl
In attempting to fit the observed spectral lines of Al35Cl, we started with a constant radial abundance profile to first determine the outer extent of the molecular envelope. To also fit the inner part of the azimuthally averaged radial profile, we needed to include a step down in abundance in the inner region. Our final best-fitting model, which agreed well with the radial profile and the spectral lines, had an inner abundance f0 = 8.5 × 10−8, relative to H2, from the stellar surface out to Rstep = 1.4 × 1014 cm (≈ 3.6 R⋆). Then between 1.4 × 1014 cm and an outer radius Rmax = 5 × 1014 cm (≈ 13 R⋆ ≈ 0′′.08), we find a relative abundance of 1.7 × 10−7. The model lines are plotted with the observed spectra in Fig. 5. We also plot the observed and modelled azimuthally averaged radial profiles in Fig. 6, with a residual plot showing the difference between the modelled and observed radial profile points. As can be seen in those plots, our model reproduces the observed data well. The main deviation between our model and the observations is the small ‘tail’ in the radial profile seen around 0′′.1. We were not able to reproduce this with our model, possibly because it is caused by asymmetry in the detected emission (see Figs. 1 and 2). When we increased the outer radius of the model we reproduced the tail but failed to reproduce the shapes of the spectral line profiles. Using a larger outer radius in our model tended to increase the amount of emission coming from outside of 2 × 1014 cm, which is the region in which the gas accelerates. Emission from outside of 2 × 1014 cm is generally broader and a model that reproduced the tail caused the calculated line profile to have a broad base with wings approximately 30% of the peak line flux. This is contrary to what is seen in the observations, especially for the v = 0 (18 → 17) line, which has the highest signal-to-noise ratio. Our best model includes part of the acceleration region, resulting in small wings on the model lines that are consistent with the observations.
For Al37Cl we used a similar modelling strategy. The lower abundance of the 37Cl isotopologue leads to fainter lines and a noisier azimuthally averaged radial profile. Therefore, it is more difficult to fit a model to the radial profile. We find that a model with the same outer radius as for Al35 Cl fits the data well. However, we do not require a step function to fit the radial profile of Al37 Cl. In fact, a test using a step function with the same f0∕f1 as for Al35Cl did not reproduce the Al37Cl data as well. Instead we find the best model to have a constant abundance of 7 × 10−8 relative to H2. If we require the abundance profile to have the same f0∕f1 as for Al35Cl, then we can only obtain models with higher χ2 values and, although we can find a model with a radial profile within most of the uncertainties of the observed radial profile, we are unable to reproduce the central point in this way. This is most likely a result of noise in the observations or could be because Al37 Cl is present or excited in different clumps to Al35Cl, leading to a difference in the azimuthally averaged profile (see Figs. 1 and 2). Since it best reproduces our data, we use the constant abundance model as our best fit model. The difference in the Al35 Cl and Al37 Cl distributions can be seen in the left and centre panels of Fig. 2, where we plot the zeroth moment maps of the v = 0 lines for both isotopologues. The calculated line profiles from our best model are plotted with the observed spectra in Fig. 7 and the model and observed azimuthal profiles are plotted together in Fig. 6, along with a residual plot showing the difference between the modelled and observed radial profile points. Our results are tabulated in Table 4.
Since we do not find the same shape for the Al35Cl and Al37Cl abundance distributions, we are unable to determine a single 35Cl/37Cl ratio across the entire emitting region. In the inner region of our model (inside 1.7 × 1014 cm) we find Al35Cl/Al37Cl = 1.2 and in the outer region we find it is twice as high: Al35 Cl/Al37Cl = 2.4. However, given the uncertainties of our observations (see Fig. 6 and Sect. 5.4), it is possible that the difference in these ratios may actually be less than a factor of two. Since the outer regionrepresents a larger total volume of our circumstellar model, we adopt this value as the ratio for 35Cl/37Cl.
 |
Fig. 6 Azimuthally averaged radial profiles extracted from ALMA v = 0 lines of AlCl(black dotted lines and points with error bars) plotted with the corresponding modelled radial profiles (red lines and squares). Residuals are plotted in the lower panels, showing the difference between the observed and modelled lines, with error bars from the observations included. |
 |
Fig. 7 Spectra of Al37Cl observed towards W Aql with ALMA (black histograms), with calculated line profiles (red curves) superposed on the observed profiles. |
5.2 AlF
For AlF we also started with a constant abundance model and then introduced a step function to fit the observed data. The azimuthally averaged radial profile (Fig. 8) has a bright inner component out to ~ 0′′.2, then what looks like an extended plateau from ~0′′.2 to ~0′′.5. These features roughly correspond to the central inner region and the more diffuse emission seen in the zeroth moment map in Fig. 3. Since the emission seen in Fig. 3 is not centred on the star, our spherically symmetric model is unable to reproduce it perfectly. Also, as noted in Sect. 4.1, we include dust in the AlF model as described in Danilovich et al. (2014), since the majority of the AlF emission comes from beyond the dust condensation radius. Although we assume silicate dust opacities in our model (based on the results of Danilovich et al. 2014), W Aql does not have strong silicate features in its infrared spectrum (see Hony et al. 2009, and discussion in Sect 6.1.2). Hence, we also tested an AlF model with amorphous carbon dust (Suh 2000) in place of silicate dust. Using silicate dust, we find the best model with an abundance of f0 = 1 × 10−7 relative to H2 in the inner region, with a step down at Rstep = 6 × 1014 cm (≈ 0′′.1 ≈ 15.6 R⋆) to f1 = 4 × 10−8 relative to H2, and the outer radius of the model at Rmax = 3.5 × 1015 cm (≈ 0′′.6 ≈ 90 R⋆). Using a model with amorphous carbon dust instead, we find a slightly lower inner abundance of f0 = 7.2 × 10−8 but the same values for Rstep, f1, and Rmax. This difference, of less than 30%, is most likely owing to radiative pumping, since the term energies of the AlF vibrational levels (12.6 μm for v = 1 up to 2.2 μm for v = 6) overlap with the wavelengths for which dust (re)radiation contributes significantly to the radiation field. In the absence of a detailed characterisation of S-type AGB dust and for consistency with our other results, and previous studies of W Aql (Danilovich et al. 2014; Ramstedt et al. 2017; Brunner et al. 2018), we preferentially refer to the model results for silicate dust, unless otherwise specified.
The calculated line profiles for the silicate dust model are plotted with the observed lines in Fig. 9. The narrow central component and broader wings of the line profiles are the result of the velocity profile (Eq. (1)) and are a good fit to the observed spectral lines. As can also be seen in Fig. 9, the model predicts a very faint v = 1 line for AlF, with flux lower than the noise of the observed spectrum7. The model and observed radial profiles are plotted together in Fig. 8, with a residual plot showing the difference between the modelled and observed radial profile points. The plateau part of the model radial profile mainly fits within the error bars of the observed radial profile, the discrepancy arising from the lack of spherical symmetry in the data. The innermost few points are underpredicted by 7% or less and were not notably improved by adding a third step up in abundance in innermost regions.
We note that the relative abundance in the inner region of our AlF model exceeds the solar abundance of F (7.2 × 10−8 Asplund et al. 2009)by almost 40%. This is discussed in more detail in Sect. 6.3.
Detailed model results for W Aql.
 |
Fig. 8 Azimuthally averaged radial profile of AlF, extracted from the ALMA (7 → 6) v = 0 line (black dotted lines and points with error bars) plotted with the corresponding modelled radial profiles (red lines and squares). Residuals are plotted in the lower panels, showing the difference between the observed and modelled lines, with error bars from the observations included. |
 |
Fig. 9 Spectra of AlF observed towards W Aql with ALMA (black histograms), with calculated line profiles (red curves) superposed on the observed profiles. |
5.3 Models of PACS observations
The PACS spectrum of W Aql (Figs. 10 and 11) is noisiest in the 80 μm region (the B2B band, see Poglitsch et al. 2010, for band ranges); therefore, the HCl (6 → 5) and the HF (3 → 2) lines are not tightly constrained by the data. Although the HCl and HF lines in the 60 μm region (the B2A band) are not formally detected above the noise, there are suggestive tentative detections of both of the HCl (7 → 6) lines and the HF (4 → 3) line at the expected wavelengths. We use these features as upper limits for our models.
5.3.1 HCl
Taking the abundance distribution calculated from the chemical model described in Sect. 4.3, we scaled the abundance by a constant factor until we found a model that best fit our data without overpredicting any of our undetected lines (Table 2). We also fixed the H35 Cl/H37Cl abundance ratio to 2.4, based on the outer Al35 Cl/Al37Cl ratio (which is found in a region overlapping with the assumed inner part of the HCl distribution).
Our best fitting model had an inner H35Cl abundance of 6.8 × 10−8, relative to H2, and an inner H37Cl abundance of 2.9 × 10−8. Although the model was fit to the detected lines (see Table 2), the uncertainties inherent in the PACS data, particularly with regards to possible line blends, mean that these results should be considered upper limits. The model results, convolved with the PACS spectral resolution, are shown with the observed spectra in Fig. 10.
 |
Fig. 10 PACS spectra (black histograms) and model results (blue curves) for HCl towards W Aql. For each pair of lines, H35 Cl is shown on the left since it has the shorter wavelength and H37Cl is on the right, with the longer wavelength. Some known nearby and blended lines are indicated in orange (but not all nearby lines have been identified). |
5.3.2 HF
No lines of HF were clearly detected in the PACS spectrum of W Aql. Nevertheless, we use the same method as for HCl, scaling the abundance distribution derived from the chemical model described in Sect. 4.3. For consistency with our χ Cyg results (see Sect. 6.1.1 and Appendix C), we set the inner radius for HF as Rin = 2R⋆. We find an upper limit on the HF abundance of ≤1 × 10−8 relative to H2.
A plot of our HF model, convolved to the PACS spectral resolution, is shown in Fig. 11, with the observed spectra. For the HF (2 → 1) line, which is blended with the H2O line at 121.721 μm, we use the H2O model intensity from Danilovich et al. (2014) as a proxy for the H2O contributionto the observed PACS line (shown in grey in Fig. 11). The sum of our HF model line and the H2O line is in good agreement with the line seen in the PACS spectrum.
5.4 Model uncertainties
The formal uncertainties on our models for a 90% confidence interval are around 20% for AlCl and 5% for AlF, when χ2 statistics are calculated primarily from the radial profiles. However, our 1D model cannot account for the 3D effects that produce deviations from spherical symmetry, especially in the case of AlF (see Fig. 3). This means that our actual uncertainties are much larger than the formal uncertainties and cannot easily be quantified. This holds even though the error bars on the azimuthally averaged radial profiles (shown in Figs. 6 and 8) take into account deviations from azimuthal symmetry in the distribution of emission, as well as stochastic noise.
The uncertainties on the HCl and HF model abundances are also larger than can be easily quantified from the formal errors. Owing to the low spectral resolution of PACS, there is substantial uncertainty as to whether the lines of interest are blended with nearby lines (for example, the H35Cl and H37Cl (3 → 2) lines are separated by almost 3 GHz, despite overlapping in their wings at the PACS resolution). This uncertainty can only be alleviated with spectrally resolved observations.
An additional source of uncertainty in our models, particularly for the case of AlF (see Sect. 5.2), is the choice of dust type. We primarily use silicate dust for consistency with Danilovich et al. (2014), who also performed SED modelling to derive the dust optical depths. When we tested amorphous carbon dust with our AlF model, we used the same optical depth for the dust since running new SED models is beyond the scope of the present study. However, Hony et al. (2009) found that dust around S-type stars bears some similarities to M-type dust with some variation in features (see Sect. 6.1.2).
Another source of uncertainty comes from our extrapolation of the CSE model of Danilovich et al. (2014) inwards towards the star. Our model does not consider gas infall or stellar pulsations, which are likely to have an effect on material in the innermost regions of the CSE. The gas number density of our model in these inner regions is extrapolated inwards following the power law n = Ṁ∕(4πr2υ(r)), which assumes an expanding CSE with a constant mass-loss rate. However, recent models of the warm molecular layer close to AGB stars (including W Aql, Khouri et al. 2016) have yielded higher number densities (by around an order of magnitude) in this region. Since part of the AlCl and AlF emission is thought to come from this innermost warm molecular layer, this adds further uncertainty to the inner 2–3R⋆ (~ 15 mas) of our models.
6 Discussion
6.1 Halogens towards other AGB stars
We searchedthe literature and in Table 5 we have compiled the measured abundances of the aluminium and hydrogen halides for AGB stars. In the following subsections, we discuss the abundances of these molecules for individual sources, grouped into S-type AGB stars (Sect. 6.1.1), carbon stars (Sect. 6.1.2), and oxygen-rich AGB stars (Sect. 6.1.3). We also touch on mid-infrared observations of HCl and HF in Sect. 6.1.4.
 |
Fig. 11 PACS spectra (black histograms) and model results (blue curves) for HF towards W Aql. The HF (2 → 1) line is dominated by a blend with the o-H2O line at 121.721 μm, which is plotted in grey. See text for details. |
Abundances relative to H2 of halide molecules found towards AGB stars.
6.1.1 S-type AGB stars
No halide molecules (i.e. AlF, AlCl, NaCl, KCl) were detected towards π1 Gru, the only other S-type star in the ATOMIUM survey. This may be partly because the unusual torus + bipolar structure of the CSE of π1 Gru (Doan et al. 2017; Homan et al. 2020) could make it harder to detect less abundant molecules or might even interfere with molecule formation. We are not aware of any other detections of halide molecules towards S-type stars with ALMA.
PACS spectra were taken for only three S-type AGB stars: W Aql, π1 Gru and χ Cyg (Groenewegen et al. 2011; Nicolaes et al. 2018). We checked the PACS spectra of π1 Gru and χ Cyg for the signatures of HCl and HF. We found evidence of HCl and HF towards χ Cyg and, tentatively, HF towards π1 Gru. The aforementioned complex circumstellar structure of π1 Gru is such that it cannot be modelled under the assumption of spherical symmetry (see also the unusual CO line structure presented in Danilovich et al. 2015b). However, we are able to run radiative transfer models models for χ Cyg –q see details in Appendix C. We find inner relative abundances of 4.6 × 10−8 and 1.9 × 10−8 for H35 Cl and H37 Cl, respectively(assuming, in the absence of other data, the same 35Cl/37Cl ratio as for W Aql), and 1.2 × 10−8 for HF.
The HCl abundances are around 50% higher for W Aql than for χ Cyg, and the HF abundance is 20% higher for χ Cyg than the upper limit found for W Aql. For both molecules, these differences are within the observational uncertainties of the PACS data, especially for the very weak lines detected towards W Aql. The relative proximity of χ Cyg (150 pc, Schöier et al. 2011) results in lines with higher signal to noise ratios in the PACS spectrum (see Fig. C.1), despite the similar abundances between the two stars, and the lower mass-loss rate of χ Cyg (7 × 10−7 M⊙ yr−1, Schöier et al. 2011). From the available data, we are unable to conclude whether the abundances of HCl and HF have a mass-loss rate dependence, as has been seen for some other molecules (e.g. SiO González Delgado et al. 2003; Ramstedt et al. 2009). Following similar arguments, we are also unable to conclude whether the abundances of HCl and HF depend on the C/O ratio of the star, despite W Aql (S6/6e) and χ Cyg (S8/1) being categorised as one grade away from the SC and MS classifications, respectively (Turnshek et al. 1985; Gray et al. 2009; Danilovich et al. 2015a). A larger sample is required to draw firmer conclusions.
6.1.2 Carbon stars
CW Leo (IRC+10216) is the closest carbon star and all the halide molecules mentioned thus far have been detected in its CSE. It is also the only other AGB star for which abundances of HCl and HF have been calculated from radiative transfer modelling. Agúndez et al. (2011) found an inner abundance of 8 × 10−8 relative to H2 for H35 Cl (and an H35 Cl/H37Cl ratio of 3.3) and of 8 × 10−9 for HF. TheHCl abundance for CW Leo is comparable to that found for W Aql but 50% higher than that found for χ Cyg. Conversely, the HF abundance is comparable to the upper limit found for W Aql but 33% lower than that found for χ Cyg. The observed abundances towards CW Leo of these two molecules are a factor of ~ 5 lower for HCl and an order of magnitude higher for HF than the predictions made by the chemical kinetics model of Cherchneff (2012), which considers shocks for models of the inner 5R⋆ of the CSE.
Based on observations with the IRAM 30 m telescope (with beam sizes ranging from 7′′ to 30′′), abundances of the halide molecules AlCl, AlF, NaCl, and KCl, were modelled by Agúndez et al. (2012) for CW Leo. In the data presented by Agúndez et al. (2012), there are no detections of any vibrationally excited lines for any of these halide molecules (though NaCl in the v = 1 state was subsequently seen by Quintana-Lacaci et al. 2016, using ALMA). Despite AlCl and AlF having significantly lower dipole moments than NaCl and KCl, Agúndez et al. (2012) saw similar line strengths for all four halogen-bearing species. They conclude that this is due to the higher abundances of AlCl and AlF compared with NaCl and KCl, which is borne out by their model results (7 × 10−8 and 1 × 10−8 for AlCl and AlF compared with 1.8 × 10−9 and 5 × 10−10 for NaCl and KCl). The most striking difference between their model results for CW Leo and ours for W Aql is the much larger molecular envelope sizes of AlCl and AlF towards CW Leo. Although Agúndez et al. (2012) do not list specific parameters for the sizes of the envelopes, from their Fig. 13 it can be seen that AlCl is present at an appreciable abundance (~ 1 × 10−9 relative to H2) out to ~ 2 × 1016 cm and AlF out to ~ 4 × 1016 cm. This is much larger than our outer radii of 5 × 1014 cm and 3.5 × 1015 cm for AlCl and AlF. They also observe AlCl and AlF lines with expansion velocities around 14.5 km s−1, equal to the terminal gas expansion velocity used in their models. This is in contrast with what we see for W Aql, where AlCl is found in a region very close to the star (see Figs. 1 and 12) and the expansion velocity of AlCl, as derived from the vibrational ground state, is around 4 km s−1 – that is, much lower than the terminal expansion velocity of 16.5 km s−1 (Danilovich et al. 2014) or the maximum velocity found by Gottlieb et al. (2021) (see Figs. 5 and 7).
Quintana-Lacaci et al. (2016) observed Al35Cl, Al37Cl, and AlF with ALMA towards CW Leo. In all cases, they found there was resolved out flux in the ALMA observations, when compared with spectra obtained from the IRAM 30 m telescope. Al37Cl was less affected than the other two species and, from the plots presented (Figs. 12 and 13 of Quintana-Lacaci et al. 2016), it can be seen that the Al37Cl extends out to ~2′′ from the continuum peak. Assuming a distance of 130 pc (Agúndez et al. 2012), this corresponds to ~ 4 × 1015 cm, which is almost an order of magnitude larger than what we see for W Aql (see Fig. 12). Another difference we see from comparison to the Quintana-Lacaci et al. (2016) data is a lack of v > 0 AlCl detections towards CW Leo, despite v = 1, 2 lines being present in the covered frequency range, and even though the v = 0 AlCl lines in the CW Leo dataset have flux densities almost 18 times higher than our W Aql data, when measured in an equivalent aperture8. The absenceof vibrationally excited lines could indicate different formation pathways if AlCl is not present as close to the star in the CSE of CW Leo compared with W Aql.
The AlF emission observed by Quintana-Lacaci et al. (2016) for the (8 → 7) transition is significantly resolved out by ALMA. Based on their observing setup, the authors estimate that smooth emission larger than 13–14′′ was filtered out. From their plot of the recovered AlF emission, it seems that the emission around the central ~ 15 km s−1 was the most resolved out. Based on their estimate of the maximum resolvable scale, we can expect that AlF emission extends out to at least 6.5–7′′ from the star, assuming relatively symmetric emission. At a distance of 130 pc, this corresponds to ~ 1.3 × 1016 cm or about five times larger than our AlF model for W Aql.
Since the temperatures (agreement within 30 K) and luminosities (CW Leo 17% more luminous) of the two stars are similar, we can conclude that the differences between AlCl and AlF distributions should mainly be because of the different chemical compositions and wind densities of the two CSEs (the latter dependent mainly on the mass-loss rates: Ṁ = 2 × 10−5 M⊙ yr−1 for CW Leo compared with Ṁ = 3 × 10−6 M⊙ yr−1 for W Aql).This in itself is an interesting result since the equilibrium models of Agúndez et al. (2020) predict very similar abundances between carbon stars and S-type stars for both Cl- and Al-bearing molecules.
Another possibility is that dust composition and interactions between gas and dust species could also contribute to the differences seen between W Aql and CW Leo. As a carbon star, CW Leo is surrounded by carbon-rich dust. As an S-type star, the dust around W Aql is less well understood. Hony et al. (2009) analyse infrared spectra from ISO/SWS for several AGB stars, with a focuson S-type stars. They note that there are weak features in the spectrum of W Aql (and other S stars) that are similar to but broader and less structured than the silicate and aluminium oxide features present in M-type AGB stars. Smolders et al. (2012) studied a large sample of S-type stars (not including W Aql) observed with Spitzer, and found that around half of them did not exhibit any alumina features. Although rotational lines of AlO were not detected towards W Aql, despite two lines in the ground vibrational state being covered by the ATOMIUM programme, and despite a lack of clear aluminium features in the infrared spectrum, it is possible that AlCl is incorporated into dust, hence explaining why it is seen only in regions close to the star. AlF may also be partly incorporated into dust, hence explaining the step down in abundance at approximately the same distance from the star as the outer edge of our AlCl model. Both the step down in AlF abundance and the outer radius of AlCl are within a factor of ~ 3 of the dust condensation radius. The persistence of AlF further out in the envelope, after AlCl has been destroyed, is likely to be at least partially due to the higher binding energy of AlF compared with AlCl (681 kJ mol−1 for AlF and 507 kJ mol−1 for AlCl, Curtiss et al. 2007). A more detailed discussion of chemistry is given in Sect. 6.5.
 |
Fig. 12 Abundance profiles for the halide molecules modelled here. Abundances for 35Cl and 37Cl isotopologues have been combined. Vertical dashed lines indicate the outer radius of the corresponding model and short vertical lines indicate the inner radii of the HCl and HF models. The dotted curve and corresponding shading indicates an upper limit abundance for HF. See text for details. |
6.1.3 Oxygen-rich AGB stars
Aside from W Aql, in this study, and CW Leo, we have found no other published observations of AlF towards AGB stars. However, we note that AlF has been detected around several oxygen-rich ATOMIUM sources (Wallström et al., in prep.), which will be modelled in a future study. In the ATOMIUM sample, AlCl was also detected towards the oxygen-rich AGB star GY Aql, which will also be studied in a future publication.
Al35Cl has also been tentatively detected at relatively low abundances towards the oxygen-rich stars R Dor (low mass-loss rate, Ṁ = 1.6 × 10−7 M⊙ yr−1) and IK Tau (higher mass-loss rate, Ṁ = 5 × 10−6 M⊙ yr−1), as reported by Decin et al. (2017). For both stars, Al35Cl was found to be confined to the region close to the central star, similar to our results for W Aql (although our ALMA observations are at a higher spatial resolution and can put more stringent constraints on the AlCl emission region). Based on models that only considered rotational levels in the ground vibrational state of Al35Cl, Decin et al. (2017) derived abundances are 2.5 × 10−8 and 9 × 10−10 relative to H2 for R Dor and IK Tau, respectively. These abundances are around one to two orders of magnitude lower than the Al35Cl abundance we found for W Aql. Gaseous AlO and AlOH have also been detected around the same two oxygen-rich stars (Decin et al. 2017; Danilovich et al. 2020), but at low enough abundances that we would not expect their presence to inhibit the production of AlCl.
NaCl and KCl have been detected towards several oxygen-rich stars, including some in the ATOMIUM sample, to be presented ina future study. Spectral scans of IK Tau, carried out using single-dish telescopes, detected several NaCl lines but no KCl lines (Milam et al. 2007; Velilla Prieto et al. 2017). A spectral scan of R Dor and IK Tau using ALMA found clumpy NaCl emission towards IK Tau (Decin et al. 2018), no NaCl emission towards R Dor, and no KCl towards either star, although De Beck & Olofsson (2018) tentatively find NaCl towards R Dor in an APEX spectral scan. NaCl and KCl in the ground and several vibrationally excited states have been seen towards extreme OH/IR stars, oxygen-rich stars with high mass-loss rates (≳ 10−5 M⊙ yr−1), including OH 26+0.6 (Justtanont et al. 2019) and OH 30.1–0.7 (Danilovich et al., in prep.). Tentatively, it seems that there is a positive correlation between higher abundances of NaCl and KCl and higher mass-loss rates for oxygen-rich AGB stars, though this will be explored in more detail in a future study.
The chemical kinetics model of Gobrecht et al. (2016) considered shocks in the inner wind and included chloride species for a model based on IK Tau. They predict an average abundance for HCl of 3.8 × 10−7 relative to H2, around 4 times higher than our S-star results. They also predict a very low abundance of AlCl, with 3.8 × 10−12 close to the stellar surface and 2.2 × 10−10 at 6R⋆. This is lower than the Decin et al. (2018) observational result for IK Tau of 9 × 10−10, by a factor of around four at 6R⋆ and by two orders of magnitude close to the stellar surface. This corresponds to 3 to 5 orders of magnitude lower than our W Aql results. In the Gobrecht et al. (2016) model, NaCl was a more significant carrier of Cl than AlCl but only reached ~ 3% of the HCl abundance in the outer part of their model (at 9R⋆).
6.1.4 Rovibrational observations of halides
Thus far we have discussed observations of rotational transitions of halide molecules, but observations of rovibrational bands in the mid-infrared are also possible. Yamamura et al. (2000) report HCl lines in the spectrum of R And, an S-type star with a moderately low mass-loss rate (5.3 × 10−7 M⊙ yr−1, Danilovich et al. 2015b). A rough comparison between their reported column density and CO gives an approximate relative abundance of HCl of 1.5 × 10−8, which is within an order of magnitude of our values for W Aql and χ Cyg.
Jorissen et al. (1992) observed a sample of AGB stars of different chemical types (and some non-AGB stars) and used mid infrared lines of HF as a proxy for the fluorine abundance. They find photospheric F abundances consistently higher in AGB stars than the solar abundance of fluorine. Abia et al. (2015) find similarly enhanced F abundances for their sample mostly of carbon and SC-type AGB stars, albeit to a lesser extent. The ramifications of their results will be discussed in Sect. 6.3, but the purely observational implication is that HF should be detectable for many AGB stars, if only the rotational lines were not so difficult to access from the ground.
6.2 Chlorine abundance and isotopic ratio
Both stable isotopes of chlorine, 35Cl and 37Cl, are believed to be primarily formed during the hydrostatic and explosive oxygen burning stages of supernova explosions (Woosley & Weaver 1995), through different nuclear reactions (and predominantly through core-collapse supernovae Kobayashi et al. 2020). Esteban et al. (2015) and Henry et al. (2004) found a weak trend towards decreasing Cl abundance with galactic radius, based on data from HII regions and planetary nebulae (PNe). They also found very similar relations between Cl and O gradients with galactic radius, suggesting that the production of Cl and O are correlated (Maas et al. 2016; Maas & Pilachowski 2021) and hence that Cl can be used as a tracer of metallicity. From a study of PNe, Delgado-Inglada et al. (2015) found that Cl is a good indicator of metallicity in the progenitors of PNe (i.e. AGB stars). Hence, the comparison of an AGB Cl abundance with the solar abundance might indicate a higher or lower metallicity of the natal environment of the AGB star, without obfuscation from elements actively synthesised by AGB stars (which 35Cl is not, based on the investigation of Maas et al. 2016). However, the solar abundance of chlorine is very difficult to measure, for reasons discussed in detail by Maas et al. (2016). For the purposes of our study, we assume a solar abundance of Cl, relative to H2, of 6.3 × 10−7, based on the value given by Asplund et al. (2009), when referring to solar chlorine abundance.
The highest total chlorine abundance we find for W Aql, by summing the abundance of HCl and the higher abundance of AlCl, is just over half that of the solar abundance. While we can determine from non-detections in our ALMA observations that the abundances of NaCl and KCl are less significant than those of HCl and AlCl, we cannot be certain whether other molecules do not contribute to the total Cl abundance. For example, Agúndez et al. (2020) predict that more unusual and as yet undetected molecules (such as CaCl2, SiCl, ZrCl2) may contribute a few percent to the overall Cl abundance, although they predict AlCl, HCl and atomic Cl to be the dominant species for S-stars. Furthermore, their models only look at the inner regions of AGB CSEs (out to 10R⋆) under chemical equilibrium conditions and make no predictions for abundances outside of these regions. Hence, although wefind a lower total Cl abundance for W Aql than solar, we cannot with certainty say that W Aql must have alower metallicity than solar. The uncertainty of our HCl abundance is also significant and improved models based on spectrally resolved HCl lines would give rise to firmer conclusions. Although there are likely differences between carbon and S-type stars in terms of the formation and destruction of Cl-bearing molecules (see Sect. 6.1.2), we can make a first-order approximation of the difference in total Cl abundance by considering the sum of abundances of the observed Cl-bearing molecules for W Aql and CW Leo (see Table 5and Agúndez et al. 2012). Considering similar inner regions of the CSEs (where our AlCl and HCl models overlap for W Aql), we find a factor of two more Cl detected around W Aql than CW Leo. This could be because different chemical processes are in play for the different types of stars, or, if we assume the chemical processes are similar, this difference could indicate that W Aql formed from a natal cloud with higher metallicity than CW Leo.
The solar system 35Cl/37Cl ratio of 3.1 is well established (see for example Asplund et al. 2009). In close agreement with the solar value, Agúndez et al. (2011) found 35Cl/37Cl = 3.3 ± 0.3 towards CW Leo from the modelling of HIFI observations of HCl, which is also in agreement with studies of metal chlorides in the same star (e.g. 2.9 ± 0.3 from the Agúndez et al. 2012, study of NaCl, KCl and AlCl). Some variation has been found for this ratio in other astronomical sources, however. For example, Peng et al. (2010) observed the (1 → 0) transition of both isotopologues of HCl towards several different galactic sources, including star-forming regions, molecular clouds and carbon stars9. For sources towards which both isotopologues were detected, they found a spread of 35Cl/37Cl ratios, mostly in the 2.0–2.6 range, with values below 1 for two locations in the W3 star forming region and ~ 5 for DR21(OH), a region of massive star formation. Maas & Pilachowski (2018) found 35Cl/37Cl ratios ranging from 1.76 to 3.42 for a sample of six M giants. All of these results point to significant variation in 35Cl/37Cl across the galaxy. The stellar evolution models of Cristallo et al. (2015) and Karakas & Lugaro (2016) predict modest decreases in 35Cl/37Cl during the AGB phase, depending on metallicity and initial mass. For example, the most significant decrease in 35Cl/37Cl (to 2.17 at the end of the AGB phase) in the Karakas & Lugaro (2016) models is seen for a low metallicity star (Z = 0.007) with initial mass 2.75 M⊙.
The 35Cl/37Cl values we find for W Aql from AlCl are 1.2 in the innermost region and 2.4 in the outer region of the AlCl emission. Since the AlCl emission is relatively faint, especially in the case of Al37Cl, it is unclear to what extent the different isotopic ratios are real or a product of observational uncertainty and noise, especially since chemical fractionation is not expected to play a significant role. This uncertainty could be reduced if we had sensitive observations of additional Al35Cl and Al37Cl lines in the ground vibrational state, rather than just one line for each isotopologue. Alternatively, checking for a similar discrepancy in another molecule could confirm it more strongly if it were found. For example, spectrally and spatially resolved observations of H35Cl and H37Cl (1 → 0) are possible with ALMA and could give us more information about the spatial dependence of the 35Cl/37Cl ratio. Additionally, spectrally (but not spatially) resolved observations of H35Cl and H37Cl up to (4 → 3) are possible with SOFIA10, and would allow us to independently determine the H35Cl and H37Cl abundances and constrain our HCl models better than the PACS data alone.
6.3 Abundance of fluorine
The cosmic origin of fluorine has not yet been fully constrained, with nucleosynthesis models under-predicting observed fluorine abundances (Lugaro et al. 2004; Kobayashi et al. 2020). A significant portion of the local fluorine abundance is thought to have been produced by AGB stars, around 51%, according to the models of Kobayashi et al. (2020). However, there are at present still several uncertainties in the calculations of nucleosynthesis yields, particularly when it comes to the treatment of convection and mass loss (Kobayashi et al. 2020). In a detailed study of the uncertainties in the nuclear reaction rates for 19 F, Lugaro et al. (2004) concluded that these cause uncertainties in theoretical models of fluorine production of a factor of two to seven, depending on the initial stellar mass. A recent study by Ryde et al. (2020) argues for multiple sites of fluorine production, in particular at different metallicities. Nevertheless, it has been clear for some time that AGB stars play a significant role in the production of fluorine. Jorissen et al. (1992) first determined fluorine abundances for sources outside of the solar system. From their observations of atmospheric HF, they concluded that, not only is F more abundant in M, S and carbon stars than in the Sun, it is generally further enhanced in carbon and S-type stars compared with M-type stars. Further evidence of the synthesis of F in AGB stars is provided by Zhang & Liu (2005), who find abundances of F in PNe higher than the solar abundance, hence surmising that F is produced in the AGB progenitors of PNe.
The solar abundance of elemental fluorine is still somewhat uncertain, not least because fluorine is the least abundant element in the range of atomic numbers from 6 to 20 (carbon to calcium, Asplund et al. 2009), and is more difficult to measure. Nevertheless, the recent solar fluorine abundance found by Maiorca et al. (2014) is in agreement within the uncertainties with earlier determinations (Lodders 2003; Asplund et al. 2009). Converting their values to abundances relative to H2 for comparison with our results, we find solar abundances of F in the range 5.0–7.2 × 10−8, with uncertainties at, or close to, a factor of two. Whichever value we adopt for the solar abundance of F, our abundance of AlF for W Aql is higher than the solar F abundance, and increases if we include the upper limit we found for HF. This indicates that F synthesised in the AGB star has already been dredged up to the surface and injected into the wind.
As discussed in Sect. 6.1, fluorine-bearing molecules have not been extensively studied towards AGB stars, with the carbon star CW Leo being the only example of AlF and rotational lines of HF predating the present study. The total abundance of F found from AlF and HF for CW Leo (see Table 5) is almost an order of magnitude less than what we find for W Aql and lower than (any determination of) the solar abundance. This could be a result of different chemical processes in the winds of the two stars, or could be explained by CW Leo having formed from a lower-metallicity natal cloud than W Aql, which would affect the initial (and hence total) F abundance. Although the chemical equilibrium predictions of Agúndez et al. (2020) predict that AlF and HF will be the dominant carriers of F in the inner winds of carbon stars as well as S-type stars (with very similar molecular abundances of F-bearing species between the two AGB types), it is possible there are some additional non-equilibrium processes at play that more strongly affect carbon stars and were not taken into account for that study. For example, the presence of H2O in the inner regions of CW Leo is a clear indicator of non-equilibrium processes in those regions (Decin et al. 2010).
An interesting direction of future study would be a more extensive look at AlF and HF towards a larger sample of AGB stars, especially S-type stars. As previously mentioned, AlF was detected towards some of the oxygen-rich AGB stars in the ATOMIUM sample, and will be analysed in future work. Additional observations of AlF towards S-type stars do not currently exist but could be obtained with ALMA, potentially of multiple rotational lines. Observations of HF are more difficult to obtain, with rotational HF (found in the THz range) not presently accessible11. Nevertheless, photospheric abundance determinations from infrared observations of HF towards AGB stars with known mass-loss rates and well-studied CSEs (including abundances of other molecules) would help fill out our understanding of F towards these stars. In particular, comparing the abundances of AlF + HF with physical parameters, such as mass-loss rates, pulsation periods, luminosity, expansion velocity, etc, could tell us about the evolutionary history of the star, especially in light of the synthesis of F during the AGB phase.
6.4 Constraints on aluminium abundance
AlO and AlOH were not detected towards W Aql, despite being detected towards some of the oxygen-rich ATOMIUM sources (to be presented in a future study). This is notable since AlO and especially AlOH are expected to be the dominant carriers of Al under thermochemical equilibrium (Agúndez et al. 2020) and steady-state chemical models, even in the case of S-type stars. The absence or very low abundance (quantified below) of AlO and AlOH is indicative of other processes, such as dust formation or growth, limiting the gas-phase abundance of these molecules. In Appendix A.2, we calculate rms values as detection limits for AlO and AlOH. Additionally, we ran some radiative transfer models to obtain abundance upper limits for AlO and AlOH.
We tested two abundance distributions for both AlO and AlOH: 1) a model with a constant abundance of the molecule from the stellar surface out to 4 × 1014 cm, based partly on the results found for the oxygen-rich stars in Decin et al. (2017); and 2) a model with an abundance profile based on the predictions of the chemical model described in Sect. 4.3 and expanded on in Sect. 6.5. In both cases, the abundance was scaled until the lines predicted by the model were equal to and/or did not exceed the rms values given in Table A.1 (using the same extraction apertures). The molecular data used here is taken from Decin et al. (2017) and Danilovich et al. (2020) for the AlOH and AlO models, respectively. For the constant abundance models, we found upper limits of fAlO ≤ 6 × 10−9 and fAlOH ≤ 3 × 10−8, relative to H2. For the abundance distributions predicted by the chemical model, we found upper limits of fAlO, peak ≤ 6.6 × 10−9 and fAlOH, peak ≤ 6.5 × 10−8, relative to H2. Both sets of upper limits are plotted in Fig. A.1. The AlOH upper limit exceeds the abundances found for the M-type stars R Dor and IK Tau by around an order of magnitude, but the AlO upper limit is around an order of magnitude smaller than the abundances found for the same stars (Decin et al. 2017).
6.5 Chemistry of AlCl and AlF
After the initial chemical model results were used as input for the radiative transfer modelling of HCl and HF (i.e. see Sect. 4.3 and the derived abundance results in Fig. 12), we extended the RATE12 chemical model by including reactions describing the chemistry of aluminium, in an attempt to reproduce the observed abundance distributions of the halide species. The aluminium halides studied here can be produced by the exothermic reactions of Al, AlOH and AlO with the corresponding hydrogen halides:
 (R1)
(R1)
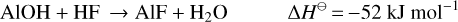 (R2)
(R2)
 (R3)
(R3)
 (R4)
(R4)
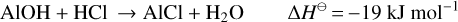 (R5)
(R5)
 (R6)
(R6)
The standard reaction enthalpies, ΔH⊖, (at 0 K) are calculated using the very accurate G4 method within the Gaussian suite of programs (Frisch et al. 2016). Theoretical calculations of the rate coefficients for reactions R1 to R6 (i.e. k1 to k6) and the reverse reactions R-1 to R-6 (k−1 to k−6) are described in Appendix D and the rate coefficients are listed in Table 6. We note that the theoretical estimate of k5 is in good agreement with a measurement between 475 and 1275 K (Rogowski et al. 1989). The aluminium halides can be removed by reaction with H (reactions R-1 and R-4), with H2O (R-2 and R-5) or with OH (R-3 and R-6). In addition, they can undergo photolysis:
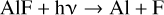

The chemical outflow model used here is based on McElroy et al. (2013) and adapted by Van de Sande et al. (2018), as described in Sect. 4.3. The complete list of reactions added to the network is given in Table D.5 and discussed in Appendix D.
The first-order rates (s−1) for the formation and destruction of AlF and AlCl (R1 to R6, R-1 to R-6, and J1 and J2) can now be calculated as a function of radius in the outflow, using the temperature and concentrations of H2O, OH, H, HF and HCl from the 1D model of W Aql (Van de Sande et al. 2018). These rates are plotted in Figs. 13a and b for AlF and AlCl, respectively, along with the molecular expansion rate (expressed as 2υ∞∕R, where υ∞ = 16.5 km s−1). This shows that the production and loss rates of both AlF and AlCl are slower than the expansion rate out to 2 × 1016 cm. In the case of AlF, Fig. 13a shows that AlF is mostly produced in the inner region of the model by the reaction of Al with HF (R1), although production by AlO + HF (R3) becomes more important beyond 2 × 1015 cm. Removal of AlF by reaction with H2O (R-2) is most important in the inner region between 2 × 1014 and 1.5 × 1015 cm, because R-1 has a substantial activation energy so that reactions with H are not a competitive loss term for AlF, and the abundance of OH is relatively low. At distances>2 × 1015 cm, photolysis by interstellar radiation becomes the dominant removal process.
The newly modelled concentration profiles of the halogen species are shown as a function of radius in Fig. 14, plotted with the results of the radiative transfer models (Sect. 5). The model successfully simulates the observed absolute relative abundance of AlF at radii < 3 × 1015 cm (cf. Fig. 12). However, the AlF photolysis rate does not start to approach the expansion rate until a radial distance of 5 × 1016 cm. Hence, AlF is nearly unchanged until >1016 cm (Fig. 14), in comparison with the observed disappearance of AlF around 3 × 1015 cm (Fig. 12). This discrepancy probably indicates that AlF is efficiently removed in the cooler part of the outflow (> 1015 cm, where the temperature is below 400 K) by clustering with other metallic molecules such as oxides (e.g. FeO and MgO) and hydroxides (FeOH and MgOH), as well as small dust particles (e.g. (Al2 O3)n, (FeMgSiO4)n, n > 1). The total concentration of the major metals (Mg, Fe, Al and Na) relative to H2 is 7.6 × 10−5 (Asplund et al. 2009). Clustering is likely to be fast because metal-containing molecules have large dipole moments. Assuming a clustering rate coefficient of 5 × 10−10 cm3 molecule−1 s−1 (i.e. a typical dipole-dipole capture frequency Saunders & Plane 2006), then the blue line in Fig. 13(a) shows that the first-order clustering rate in this cooler region is faster than the expansion rate out to 2 × 1016 cm. This means that the observed disappearance of AlF by 4 × 1015 cm (Fig. 12) could be explained by cluster formation or uptake on dust particles.
In the case of AlCl, the production and loss rates as a function of distance are illustrated in Fig. 13b. The reaction of Al with HCl (R4) is the most important AlCl production term over the entire outflow, and photolysis dominates AlCl removal beyond 2 × 1014 cm. The newly simulated HCl density (Fig. 14) is in good accord with observations, including its disappearance beyond 1016 cm. However, the location of the drop-off in HCl abundance is not tightly constrained by our current radiative transfer model, in the absence of higher quality data (see Sect. 5.3.1). Although the model simulates well the absolute AlCl density out to 5 × 1014 cm, it fails to reproduce the rapid decrease in AlCl further out. The reason(s) for this are unclear. Removal of AlCl on dust or molecular clustering might be an explanation, but this would require that AlCl was removed much more efficiently than AlF, which seems unlikely because AlF is much less volatile than AlCl. For example, the heat of vaporisation of AlF from AlF3 is 1227 kJ mol−1 at 1000 K, whereas that of AlCl from AlCl3 is only 620 kJ mol−1 (Chase et al. 1985). So this remains an interesting challenge for future study.
 |
Fig. 13 (a) Calculated first-order rates for conversion of HF to AlF by reaction with Al, AlOH and AlO; and loss of AlF by photolysis and reaction with H, H2O and OH. The clustering rate with metallic compounds (blue line, see text for further details) is shown in the region where the temperature is below 500 K. (b) Calculated first-order rates for conversion of HCl to AlCl by reaction with Al, AlOH and AlO; and loss of AlCl by photolysis and reaction with H, H2O and OH. The red lines show the molecular expansion rate of the outflow at a constant velocity of 16.5 km s−1. |
 |
Fig. 14 Fractional abundance relative to H2 of AlCl and HCl (left panel), and AlF and HF (right panel), obtained from chemical modelling (solid lines), plotted with the results of the radiative transfer models (dotted lines). The assumed physical conditions and parent species are given in the text and Appendix D. |
7 Conclusions
We presented observations of AlCl and AlF towards an S-type AGB star for the first time. We detected rotational lines of AlCl up to the second vibrationally excited state and one rotational line of AlF in the ground vibrational state. AlCl was found in regions very close to the star, within 0′′.1, while AlF was found in a larger region of the envelope, out to 0′′.2–0′′.6. The distribution of both molecules was slightly asymmetric, probably due to regions of higher and lower density around the star.
The observations of AlCl and AlF were azimuthally averaged and analysed using 1D non-LTE radiative transfer models. We found step-function abundance profiles best reproduce the ALMA observations, with Al35Cl increasing at ~3.6R⋆ from an abundance of 8.5 × 10−8 to 1.7 × 10−7, relative to H2, and no longer present from ~13R⋆. For Al37Cl we did not find a step-function in abundance (possibly due to the fainter data) and instead found a constant abundance of 7 × 10−8 relative to H2, also out to ~13R⋆. For AlF we found a higher abundance in the inner region close to the star, with abundance 1 × 10−7 relative to H2 out to ~ 16R⋆, after which it dropped down to 4 × 10−8 until ~90R⋆, beyond which it was not detected. The AlCl and AlF abundances found for W Aql are higher than those seen for the carbon star CW Leo, and distributed differently in the CSE. This points to different chemical processes taking part in the creation and destruction of these molecules in the S-type W Aql and the carbon-rich CW Leo.
In addition to the ALMA observations of AlCl and AlF, we used radiative transfer models and unresolved PACS spectra of HCl and HF towards W Aql to constrain the abundances of those molecules, using predictions from chemical models to determine the size of the corresponding molecular envelopes. We found an HCl abundance of 9.7 × 10−8, relative to H2, and were able to put an upper limit on HF of ≤1 × 10−8. We also modelled HCl and HF for another S-type AGB star: χ Cyg and found a slightly lower abundance of HCl (6.5 × 10−8 relative to H2) and a higher abundance of HF (1.2 × 10−8).
The total abundance of F calculated for W Aql (even if we exclude the upper limit found for HF) is higher than the solar abundance of F. This indicates that not only has F been synthesised in W Aql, as is expected for AGB stars, but it has also been dredged up to the surface and ejected into the CSE.
From an analysis of chemical reactions in the wind, we find that gas-phase reactions alone cannot explain the abundance distributions of AlCl and AlF found from the observations and radiative transfer modelling. We conclude that AlF is most likely removed from the gas phase due to clustering (i.e. as part of the dust formation process). However, the very rapid removal of AlCl may be due to an additional factor that cannot yet be fully explained.
Acknowledgements
We thank the anonymous referee for their thoughtful feedback on the manuscript. T.D., M.V.dS. and S.H.J.W. acknowledge support from the Research Foundation Flanders (FWO) through grants 12N9920N, 12X6419N, and 1285221N, respectively. T.J.M. is grateful to the STFC for support through grant ST/P000312/1. J.M.C.P. was supported by STFC grant number ST/T000287/1. L.D., J.M.C.P., W.H., S.H.J.W., D.G. acknowledge support from ERC consolidator grant 646758 AEROSOL. E.D.B. acknowledges support from the Swedish National Space Agency. E.C. acknowledges funding from the KU Leuven C1 grant MAESTRO C16/17/007. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2018.1.00659.L. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. We acknowledge excellent support from the UK ALMA Regional Centre (UK ARC), which is hosted by the Jodrell Bank Centre for Astrophysics (JBCA) at the University of Manchester. The UK ARC Node is supported by STFC Grant ST/P000827/1. PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM (France); MPIA (Germany); INAF-IFSI/OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI/INAF (Italy), and CICYT/MCYT (Spain). This work has made use of data from the European Space Agency (ESA) mission Gaia (https://www.cosmos.esa.int/gaia), processed by the Gaia Data Processing and Analysis Consortium (DPAC, https://www.cosmos.esa.int/web/gaia/dpac/consortium). Funding for the DPAC has been provided by national institutions, in particular the institutions participating in the Gaia Multilateral Agreement.
Appendix A Non-detections of other halogen- and aluminium-bearing molecules
A.1 NaCl and KCl
No NaCl or KCl lines were detected towards W Aql in the ATOMIUM survey. To give an indication of the detection limits of our data, we measured the rms values of the spectra near the vibrational ground state NaCl and KCl lines covered by ATOMIUM. For each line listed in Table A.1 we calculated the rms over a velocity range of 100 km s−1, centred on the line frequency. The calculation was done for the spectrum extracted from the extended array with a 0′′.1 radius aperture and for the spectrum from the mid array extracted with a 0′′.6 radius aperture. These were chosen because we do not know a priori the extent of the possible NaCl or KCl lines and by checking for compact and more extended emission we can be sure of the non-detection of the salt lines. Where a line fell close to the edge of a band or close to a detected line, we measured the rms only for the unaffected half of the spectrum (over a velocity range of 50 km s−1). The NaCl (20 → 19) line at 260.223 GHz was excluded from the measurement since it is dominated by an overlap with a ν2 = 1 H13 CN line. The rms values are given in Table A.1.
 |
Fig. A.1 Upper limits for AlO (blue) and AlOH (orange) abundance distributions. Dotted lines show the constant abundance models and dashed lines show abundance distributions predicted by chemical models. See text for details. |
A.2 AlO and AlOH
We performed similar measurements for AlO and AlOH, with the rms values also listed in Table A.1. For these two molecules we additionally ran some radiative transfer models to ascertain the upper limits on their abundances. The results for two sets of models are shown in Fig. A.1. This was done for the aluminium-bearing molecules because they are expected to play a key role in circumstellar chemistry (see Sect. 6.5).
Measured rms values for undetected lines of NaCl, KCl, AlO, and AlOH towards W Aql.
Appendix B Molecular data and collisional rates
B.1 AlCl
For both AlCl isotopologues, we included molecular data for levels with J ≤ 40 and v ≤ 10. The maximum vibrationally excited level of v = 10 was chosen because the term energy of this level is 2.2 μm, close to the wavelength of peak flux for W Aql, as seen from its SED (Danilovich et al. 2014). The radiative information used in our AlCl models comes from Yousefi & Bernath (2018), accessed via the ExoMol database. The only AlCl collisional rates we found were for AlCl-He collisions by Pamboundom et al. (2016). However, the rates calculated in that study only go up to the J =17, v = 0 rotational level of AlCl, whereas our ALMA observations cover the J = 18 → 17, v = 0 transition. Hence, using the rates of Pamboundom et al. (2016) would not give us the most accurate model results, even if they were scaled to account for the different mass of the AlCl-H2 system.
We searched for available rates for a molecule with similar characteristics to AlCl. Via the BASECOL12 database (Dubernet et al. 2013), we found rates calculated by Kłos & Lique (2008) for collisions between SiS-H2, considering both ortho- and para-H2 and going up to the J = 40 rotational level, in the ground vibrational state. SiS has a dipole moment of 1.74 D (Hoeft et al. 1969; Murty & Curl 1969), very close to the dipole moment of AlCl: 1.63 D (Yousefi & Bernath 2018). SiS and AlCl also have very similar molecular masses and comparable level energies. These similar properties suggest that the collisional rates of SiS with H2 are an adequate stand-in for the collisional rates of AlCl with H2. For our model, we weighted the rates assuming an H2 ortho-to-para ratio of 3, as is typical for warm environments.
B.2 AlF
For AlF we include molecular data for levels with J ≤ 30 and v ≤ 6. As for AlCl, the maximum vibrationally excited level was chosen for its term energy, which is also 2.2 μm, close to the peak flux of W Aql. We neglect the hyperfine structure of AlF because the separation of the hyperfine components is smaller than the spectral resolution of our observations (based on parameters calculated by Wyse et al. 1970). The radiative information used in our AlF models comes from Yousefi & Bernath (2018), accessed via the ExoMol database.
For the collisional rates, a new calculation was performed to obtain rates for sufficiently high temperatures as seen in our circumstellar model. This calculation is an extension of the earlier work by Gotoum et al. (2012), in which rates were given for temperatures up to 70 K. Using the potential energy surface (PES) for AlF-H2 given by Gotoum et al. (2012), we broadened the calculations of the integral cross-sections for kinetic energy up to 10000 cm−1. Indeed the earlier work was limited for total energy Ec ≤ 350 cm−1 where cross-sections were calculated in the quantum mechanical close coupling formalism (CC, Arthurs & Dalgarno 1960). We broadened the calculation up to 500 cm−1 using the CC method with Jmax = 20, then up to 10000 cm−1 using the coupled-state (CS) approach (McGuire & Kouri 1974) with Jmax = 50. The following energy steps were considered, where all values are in cm−1: 1 for 350 ≤ E ≤ 500, 5 for 500 ≤ E ≤ 1000, 20 for 1000 ≤ E ≤ 2000 and finally with uniform steps of 50 up to 10000. All these computations are done using the MOLSCAT package (Hutson & Green 2012).
In Fig. B.1, we present the rotational quenching cross-sections of AlF in collision with H2 for the J = 1 to 12 rotational levels. This figure shows that for low kinetic energies cross-sections present shape and Feshbach resonances and a large overlap between them. The quenching cross-sections for J = 1 and J = 2 are separated from the others from Ec = 20 cm−1, while the others explode at around 500 to 1000 cm−1.
 |
Fig. B.1 Rotational quenching cross-sections of AlF induced by collision with H2 as a functionof the kinetic energy, presented with colour diagram, with J = 1 in black to J= 12 in red. |
Generally, as the rotational level increases, the energy gap of the rotational transitions increases, and the efficiency of the rotational quenching decreases. That is why the quenching cross-sections vary only slightly as a function of rotational levels for J >2.
These cross-sections were averaged over the Boltzmann dis- tribution of velocities to determine the downward rate coefficients of AlF in collision with H2 for kinetic temperature up to 2000 K. We present in Fig. B.2 these rates as a function of tem- perature for ΔJ = −1, with J from 1 to 12. The rate curves ex- hibit the same trends and increase with increasing J, and the gap between the plots narrow considerably. In addition, the collision rate coefficients reflect the same behaviour as the general trends observed previously for its valence isomers: AlOH-H2 (Naouai et al. 2019)and HCP-H2 (Hammami et al. 2008). We should note here that the reason this latter behaviour is also observed for the quenching cross-sections for high energy values is probably because of the small rotational constant of AlF (~ 0.5). In this case the kinetic energy is very large compared to the rotational energies and hence the statistical approach can be valid.
 |
Fig. B.2 Log-log scale variation in downward rate coefficients for transitions with ΔJ = −1, as a function of the kinetic temperature. |
B.3 HCl
For HCl we include molecular data for levels with J ≤ 16 and v ≤ 2, neglecting hyperfine structure since our PACS observations are spectrally unresolved. The spectroscopic information used in ourmodels of HCl comes from Gordon et al. (2017). We used HCl-H2 collisional rates from Lanza et al. (2014) accessed from BASECOL (Dubernet et al. 2013). Lanza et al. (2014) calculate rates for both ortho- and para-H2 and we again weighted these assuming an H2 ortho-to-para ratio of 3.
B.4 HF
For HF we use a molecular data file obtained from the LAMDA database13 (Schöier et al. 2005; van der Tak et al. 2020), which includes levels up to J ≤8 for v = 0 and up to J ≤ 6 for v = 1. The data for theground vibrational state was taken from Nolt et al. (1987) via the JPL Molecular Spectroscopy Database14 (Pickett et al. 1998). Rovibrational transition frequencies came from Goddon et al. (1991) and Einstein A values were computed from Pine et al. (1985). We used the collisional rates for HF-H2 calculated by Guillon & Stoecklin (2012), again assuming an H2 ortho-to-para ratio of 3.
Appendix C χ Cyg HCl and HF
As noted in Sect. 6.1.1, we found evidence of HCl and HF emission in the PACS spectrum of χ Cyg. To be able to directly com- pare the abundances of HCl and HF between χ Cyg and W Aql, we also ran radiative transfer models for χ Cyg, using the same methods we used for W Aql in Sections 5.3.1 and 5.3.2. For the HCl and HF abundance distributions, we re-ran the chemical model described in Sect. 4.3, adjusted for the mass-loss rate and expansion velocity of χ Cyg (Ṁ = 7 × 10−7 M⊙ yr−1 and υ∞ = 8.5 km s−1, Schöier et al. 2011). The stellar and circumstellar parameters for χ Cyg were taken from Schöier et al. (2011). As for W Aql, we used the non-detected lines to constrain the upper limits of the models.
For the HCl model, we found that the results were more strongly dependent on the choice of inner radius for χ Cyg than they were for W Aql. The inner radius used by Schöier et al. (2011) Rin = 2 × 1014 cm resulted in models that significantly under-predited the higher-J HCl lines. When we treated the inner radius as a free parameter, we found the best fitting model to have Rin = 1.2 × 1014 cm and abundances of 4.6 × 10−8 for H35Cl and 1.9 × 10−8 for H37Cl. The 35Cl/37Cl ratio was fixed based on our W Aql AlCl results, since the PACS data are not of sufficiently high quality to independently determine the isotopic ratio. The PACS spectra of HCl are plotted with the model HCl lines in Fig. C.1 and the radial abundance profile is shown in Fig. C.2. The fact that changing the Rin from 2 × 1014 cm to 1.2 × 1014 cm had little effect on the intensity of the (3 → 2) model line but an increasingly significant effect on the higher-J lines suggests that these lines are probably emitted from the 1.2–2 × 1014 cm region. However, higher quality observations, preferably spectrally and spatially resolved, are needed to con- firm this.
For HF, we found that the (3 → 2) and (4 → 3) lines were more clearly seen towards χ Cyg than W Aql, possibly due to the closer proximity of that star (150 pc for χ Cyg compared with 395 pc for W Aql). As for W Aql, the (2 → 1) line towards χ Cyg is blended with H2O. However, although Schöier et al. (2011) modelled H2O towards χ Cyg (to find an abundance about 80% of the W Aql H2O abundance),their model was based only on HIFI observations and did not include any PACS data. Hence we are unable to estimate the contributionof H2O to the H2O+HF line blend, as was done for W Aql. Instead, we focus our HF modelling on the other two HF lines, which are not known to be blended. Similar to HCl, we found that the line ratios of these two HF lines were very sensitive to the choice of inner radius. Leaving Rin as a free parameter again, we found the best fitting model had Rin = 6 × 1013 cm ≈ 2R⋆ and an innerHF abundance of 1.2 × 10−8 relative to H2. These best fitting model lines are plotted with the PACS spectra of HF in Fig. C.3 and the radial abundance profile is shown in Fig. C.2.
 |
Fig. C.1 PACS spectra (black histograms) and model results (blue curves) for HCl towards χ Cyg. For each pair of lines, H35Cl is shown on the left since it has the shorter wavelength and H37Cl is on the right, with the longer wavelength. Some known nearby and blended lines are indicated in orange (but not all nearby lines have been identified). |
 |
Fig. C.2 Radial abundance profiles for HCl (green) and HF (red) as derived for χ Cyg. The short vertical lines indicate the inner radius of the corresponding model. |
 |
Fig. C.3 PACS spectra (black histograms) and model results (blue curves) for HF towards χ Cyg. The HF (2 → 1) line is blended with the o-H2O line at 121.721 μm, which is notshown here. See text for details. |
Appendix D Supplementary information concerning the chemistry of AlF and AlCl
The rate coefficients for the reactions of Al, AlO and AlOH with HF and HCl to produce AlF and AlCl, respectively, were estimated by combining electronic structure calculations with Rice- Ramsperger-Kassel-Markus (RRKM) statistical rate theory. Accurate energies, geometries and vibrational frequencies were determined at the G4 level of theory (Curtiss et al. 2007) within the Gaussian 16 suite of programs (Frisch et al. 2016). The Cartesian coordinates, rotational constants, vibrational frequencies and heats of formation of the relevant molecules are listed in Table D.2 for reactions producing AlF (R1 – R3), and Table D.3 for the AlCl-forming reactions (R4 – R6). The potential energy surfaces for the six reactions are illustrated in Figs. D.1 and D.2, which also show the geometries of the stationary points. We note that the relative energies include zero-point energy corrections.
Capture rate coefficients calculated using long range transition state theory (Georgievskii & Klippenstein 2005).
The Master Equation Solver for Multi-Energy well Reac- tions (MESMER) program (Glowacki et al. 2012) was then used to estimate rate coefficients. Apart from R4, these reactions proceed via the formation of an energised adduct. This adduct can dissociate back to the reactants, dissociate to bimolecular products sometimes involving a barrier (R1, R2, and R5, but not R3 or R6), or be stabilised by collision with a third body (which in the case of the outflow is H2). The internal energies of the sta- tionary points on the surface (i.e. reactants, intermediates, tran- sition states and products) were divided into a contiguous set of grains (width = 150 cm−1) containing abundle of rovibrational states. The density of states of each stationary point was calculated using the vibrational frequencies and rotational constants listed in Tables D.2 and D.3. The vibrations were treated as harmonic oscillators, and a classical densities of states treatment was used for the rotational modes.
Each adduct grain was then assigned a set of microcanon- ical rate coefficients for dissociation to the reactants and prod- ucts. These were determined using inverse Laplace transformation to link them directly to the relevant capture rates. These cap- ture rates were calculated using long-range transition state theory (Georgievskii & Klippenstein 2005), and are listed in Table D.1.
The probability of collisional transfer between grains was estimated using the exponential down model (Gilbert & Smith 1990): the average energy for downward transitions, 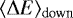 , was set to 200 cm−1 with no temperature dependence, and the probabilities for upward transitions are determined by detailed balance. The collision rate of H2 with the adduct as a function of temperature was calculated using Lennard-Jones parameters (σ = 3.0 Å and ε∕k = 200 K) to characterise the intermolecular potential. The ME, which describes the evolution with time of the adduct grain populations, was then expressed in matrix form and solved to yield the rate coefficients for recombination and bimolecular reaction at a specified pressure and temperature. In fact, at the low pressures in the outflow ([H2] < 108 cm−3 beyond a radius of 2 × 1014 cm), it is only the bimolecular channels that matter. The rate coefficients for the reverse reactions were calculated by detailed balance, using the molecular parameters in Tables D.2 and D.3 to calculate the relevant equilibrium constants. In the case of reaction R6 between AlO and HCl, the AlOH + Cl channel is 44 kJ mol−1 more exothermic than AlCl + OH, and so AlOH is the major product (91% at 900 K, 79% at 1900 K).
, was set to 200 cm−1 with no temperature dependence, and the probabilities for upward transitions are determined by detailed balance. The collision rate of H2 with the adduct as a function of temperature was calculated using Lennard-Jones parameters (σ = 3.0 Å and ε∕k = 200 K) to characterise the intermolecular potential. The ME, which describes the evolution with time of the adduct grain populations, was then expressed in matrix form and solved to yield the rate coefficients for recombination and bimolecular reaction at a specified pressure and temperature. In fact, at the low pressures in the outflow ([H2] < 108 cm−3 beyond a radius of 2 × 1014 cm), it is only the bimolecular channels that matter. The rate coefficients for the reverse reactions were calculated by detailed balance, using the molecular parameters in Tables D.2 and D.3 to calculate the relevant equilibrium constants. In the case of reaction R6 between AlO and HCl, the AlOH + Cl channel is 44 kJ mol−1 more exothermic than AlCl + OH, and so AlOH is the major product (91% at 900 K, 79% at 1900 K).
The absorption cross-sections for AlF and AlCl were calculated by first optimising their geometries at the B3LYP/6-311+g(2d,p) level of theory (Frisch et al. 2016), before deter- mining the vertical excitation energies and transition dipole moments for transitions from their ground electronic states to the first 50 electronically excited states, using the time-dependent density function theory (TD-DFT) method (Bauernschmitt & Ahlrichs 1996). The resulting cross-sections are illustrated in Fig. D.3. Because the AlF bond strength is so large (681 kJ mol−1 at the G4 level of theory, Curtiss et al. 2007) compared with that of AlCl (507 kJ mol−1), the wavelength threshold for photolysis of AlF is 175 nm compared with 235 nm for AlCl. Interstellar radiation is attenuated by dust within the outflow, where the extinction is assumed to be equal to that of the ISM, namely 1.87× 1021 atoms cm−2 mag−1 (Cardelli et al. 1989).
The outflow model was initialised with the parent species listed in Table D.4. Additional reactions, beyond those published in McElroy et al. (2013) as part of RATE12 are listed in Table D.5. The tabulated constants give the rate coefficient via a temperature-dependent Arrhenius-type formula:
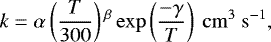 (D.1)
(D.1)
except for reactions with (interstellar) photons (hν), which are parameterised as
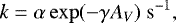 (D.2)
(D.2)
where AV is the dust extinction at visible wavelengths.
The rate coefficients for R1 to R6 were adjusted by varying the heights of the transition states within the expected uncertainty of the G4 level of theory (6 kJ mol−1) to optimise agreement with the observations in Fig. 12. These rate coefficients are listed in Table D.1.
Molecular properties and heats of formation (at 0 K) of the stationary points on the Al, AlOH and AlO + HF potential energy surfaces.
Molecular properties and heats of formation (at 0 K) of the stationary points on the Al, AlOH and AlO + HCl potential energy surfaces.
Parent species initial fractional abundances relative to H2.
Additional reactions for halide and aluminium-bearing molecules included in our chemical modelling.
 |
Fig. D.1 Potential energy surfaces calculated at the G4 level of theory for: (a) Al + HF (R1); (b) AlOH + HF (R2); (c) AlO + HF (R3). Note that the very endothermic channels are not shown. |
 |
Fig. D.2 Potential energy surfaces calculated at the G4 level of theory for: (a) Al + HCl (R1); (b) AlOH + HCl (R2); (c) AlO + HCl (R3). Note that the very endothermic channels are not shown. |
 |
Fig. D.3 Absorption cross-sections of AlF and AlCl calculated at the TD-B3LYP//6-311+g(2d,p) level of theory (Frisch et al. 2016). Photolysis is possible in the portions of the absorption curves shown with solid lines. |
References
- Abia, C., Cunha, K., Cristallo, S., & de Laverny, P. 2015, A&A, 581, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Agúndez, M., Cernicharo, J., Waters, L. B. F. M., et al. 2011, A&A, 533, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Agúndez, M., Fonfría, J. P., Cernicharo, J., et al. 2012, A&A, 543, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Agúndez, M., Martínez, J. I., de Andres, P. L., Cernicharo, J., & Martín-Gago, J. A. 2020, A&A, 637, A59 [Google Scholar]
- Apponi, A. J., Barclay, W. L., J., & Ziurys, L. M. 1993, ApJ, 414, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Arthurs, A. M., & Dalgarno, A. 1960, Proc. R. Soc. London Ser. A, 540 [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Atkinson, R., Baulch, D. L., Cox, R. A., et al. 2006, Atmos. Chem. Phys., 6, 3625 [NASA ADS] [CrossRef] [Google Scholar]
- Barton, E. J., Chiu, C., Golpayegani, S., et al. 2014, MNRAS, 442, 1821 [NASA ADS] [CrossRef] [Google Scholar]
- Bauernschmitt, R., & Ahlrichs, R. 1996, Chem. Phys. Lett., 256, 454 [CrossRef] [Google Scholar]
- Brunner, M., Danilovich, T., Ramstedt, S., et al. 2018, A&A, 617, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cabezas, C., Cernicharo, J., Quintana-Lacaci, G., et al. 2016, ApJ, 825, 150 [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
- Caris, M., Lewen, F., & Winnewisser, G. 2002, Z. Naturf. Teil A, 57, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Caris, M., Lewen, F., Müller, H. S. P., & Winnewisser, G. 2004, J. Mol. Struct., 695, 243 [CrossRef] [Google Scholar]
- Cernicharo, J., & Guelin, M. 1987, A&A, 183, L10 [Google Scholar]
- Cernicharo, J., Decin, L., Barlow, M. J., et al. 2010, A&A, 518, L136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chase, M. W., Davies, C. A., Downey, J. R., et al. 1985, NIST-JANAF Thermochemical Tables 1985 Version 1.0 (Gaithersburg, MD: National Institute of Standards and Technology Gaithersburg) [Google Scholar]
- Cherchneff, I. 2012, A&A, 545, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clouser, P. L., & Gordy, W. 1964, Phys. Rev., 134, A863 [NASA ADS] [CrossRef] [Google Scholar]
- Cristallo, S., Straniero, O., Piersanti, L., & Gobrecht, D. 2015, ApJS, 219, 40 [Google Scholar]
- Curtiss, L. A., Redfern, P. C., & Raghavachari, K. 2007, J. Chem. Phys., 126, 084108 [NASA ADS] [CrossRef] [Google Scholar]
- Danilovich, T., Bergman, P., Justtanont, K., et al. 2014, A&A, 569, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovich, T., Olofsson, G., Black, J. H., Justtanont, K., & Olofsson, H. 2015a, A&A, 574, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovich, T., Teyssier, D., Justtanont, K., et al. 2015b, A&A, 581, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovich, T., Richards, A. M. S., Karakas, A. I., et al. 2019, MNRAS, 484, 494 [CrossRef] [Google Scholar]
- Danilovich, T., Gottlieb, C. A., Decin, L., et al. 2020, ApJ, 904, 110 [NASA ADS] [CrossRef] [Google Scholar]
- De Beck, E., & Olofsson, H. 2018, A&A, 615, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Beck, E., & Olofsson, H. 2020, A&A, 642, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Graauw, T., Helmich, F. P., Phillips, T. G., et al. 2010, A&A, 518, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decin, L., Agúndez, M., Barlow, M. J., et al. 2010, Nature, 467, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Decin, L., Richards, A. M. S., Waters, L. B. F. M., et al. 2017, A&A, 608, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decin, L., Richards, A. M. S., Danilovich, T., Homan, W., & Nuth, J. A. 2018, A&A, 615, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decin, L., Montargès, M., Richards, A. M. S., et al. 2020, Science, 369, 1497 [Google Scholar]
- Delgado-Inglada, G., Rodríguez, M., Peimbert, M., Stasińska, G., & Morisset, C. 2015, MNRAS, 449, 1797 [NASA ADS] [CrossRef] [Google Scholar]
- Doan, L., Ramstedt, S., Vlemmings, W. H. T., et al. 2017, A&A, 605, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dubernet, M.-L., Alexander, M. H., Ba, Y. A., et al. 2013, A&A, 553, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Duran, C. A., Gusten, R., Risacher, C., et al. 2021, IEEE Trans. Terahertz Sci. Technol., 11, 194 [CrossRef] [Google Scholar]
- Esteban, C., García-Rojas, J., & Pérez-Mesa, V. 2015, MNRAS, 452, 1553 [NASA ADS] [CrossRef] [Google Scholar]
- Frisch, M. J., Trucks, G. W., Schlegel, H. B., et al. 2016, Gaussian 16 Revision B.01, (Wallingford, CT: Gaussian Inc.) [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2021, A&A, 649, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gao, Y., Alecu, I. M., Hsieh, P.-C., et al. 2006, J. Phys. Chem. A, 110, 6844 [NASA ADS] [CrossRef] [Google Scholar]
- Georgievskii, Y., & Klippenstein, S. J. 2005, J. Chem. Phys., 122, 194103 [Google Scholar]
- Gilbert, R. G., & Smith, S. C. 1990, Theory of Unimolecular and Recombination Reactions (Oxford, Boston, Brookline Village, Mass.: Blackwell Scientific Publications Publishers’ Business Services Distributor) [Google Scholar]
- Glowacki, D. R., Liang, C.-H., Morley, C., Pilling, M. J., & Robertson, S. H. 2012, J. Phys. Chem. A, 116, 9545 [NASA ADS] [CrossRef] [Google Scholar]
- Gobrecht, D., Cherchneff, I., Sarangi, A., Plane, J. M. C., & Bromley, S. T. 2016, A&A, 585, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goddon, D., Groh, A., Hanses, H. J., Schneider, M., & Urban, W. 1991, J. Mol. Spectr., 147, 392 [NASA ADS] [CrossRef] [Google Scholar]
- González Delgado, D., Olofsson, H., Kerschbaum, F., et al. 2003, A&A, 411, 123 [Google Scholar]
- Gordon, I., Rothman, L., Hill, C., et al. 2017, J. Quant. Spectr. Rad. Transfer (HITRAN2016 Special Issue), 203, 3 [Google Scholar]
- Gotoum, N., Hammami, K., Owono Owono, L. C., & Jaidane, N.-E. 2012, Ap&SS, 337, 553 [CrossRef] [Google Scholar]
- Gottlieb, C. A., Decin, L., Richards, A. M. S., et al. 2021, A&A, submitted [Google Scholar]
- Gray, R., Corbally, C., & Burgasser, A. 2009, Stellar Spectral Classification, Princeton Series in Astrophysics (Princeton University Press) [CrossRef] [Google Scholar]
- Groenewegen, M. A. T., Waelkens, C., Barlow, M. J., et al. 2011, A&A, 526, A162 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guillon, G., & Stoecklin, T. 2012, MNRAS, 420, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Hammami, K., Nkem, C., Owono Owono, L. C., Jaidane, N., & Ben Lakhdar Z. 2008, J. Chem. Phys., 129, 204305 [CrossRef] [Google Scholar]
- Heays, A. N., Bosman, A. D., & van Dishoeck, E. F. 2017, A&A, 602, A105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henry, R. B. C., Kwitter, K. B., & Balick, B. 2004, ApJ, 127, 2284 [Google Scholar]
- Hensel, K. D., Styger, C., Jäger, W., Merer, A. J., & Gerry, M. C. L. 1993, J. Chem. Phys., 99, 3320 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F. 2005, ARA&A, 43, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeft, J., Lovas, F. J., Tiemann, E., & Törring, T. 1969, Z. Naturforsch. A, 24, 1422 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeft, J., Lovas, F. J., Tiemann, E., & Törring, T. 1970, Z. Naturforsch. A, 25, 1029 [CrossRef] [Google Scholar]
- Höfner, S., & Olofsson, H. 2018, A&ARv, 26, 1 [Google Scholar]
- Homan, W., Montargès, M., Pimpanuwat, B., et al. 2020, A&A, 644, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hony, S., Heras, A. M., Molster, F. J., & Smolders, K. 2009, A&A, 501, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hutson, J. M., & Green, S. 2012, MOLSCAT: MOLecular SCATtering v. 14 [Google Scholar]
- Jorissen, A., Smith, V. V., & Lambert, D. L. 1992, A&A, 261, 164 [NASA ADS] [Google Scholar]
- Justtanont, K., Muller, S., Barlow, M. J., et al. 2019, in IAU Symposium, 343, eds. F. Kerschbaum, M. Groenewegen, & H. Olofsson, 436 [NASA ADS] [Google Scholar]
- Karakas, A. I., & Lugaro, M. 2016, ApJ, 825, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Khouri, T., Vlemmings, W. H. T., Ramstedt, S., et al. 2016, MNRAS, 463, L74 [NASA ADS] [CrossRef] [Google Scholar]
- Kłos, J., & Lique, F. 2008, MNRAS, 390, 239 [CrossRef] [Google Scholar]
- Kobayashi, C., Karakas, A. I., & Lugaro, M. 2020, ApJ, 900, 179 [Google Scholar]
- Kumaran, S. S., Lim, K. P., & Michael, J. V. 1994, J. Chem. Phys., 101, 9487 [NASA ADS] [CrossRef] [Google Scholar]
- Lanza, M., Kalugina, Y., Wiesenfeld, L., & Lique, F. 2014, J. Chem. Phys., 140, 064316 [NASA ADS] [CrossRef] [Google Scholar]
- Lindegren, L., Bastian, U., Biermann, M., et al. 2021, A&A, 649, A4 [EDP Sciences] [Google Scholar]
- Lodders, K. 2003, ApJ, 591, 1220 [Google Scholar]
- Lugaro, M., Ugalde, C., Karakas, A. I., et al. 2004, ApJ, 615, 934 [CrossRef] [Google Scholar]
- Maas, Z. G., & Pilachowski, C. A. 2018, AJ, 156, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Maas, Z. G., & Pilachowski, C. A. 2021, AJ, 161, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Maas, Z. G., Pilachowski, C. A., & Hinkle, K. 2016, AJ, 152, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Maiorca, E., Uitenbroek, H., Uttenthaler, S., et al. 2014, ApJ, 788, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Mangan, T. P., Douglas, K. M., Lade, R. E., et al. 2021, ACS Earth Space Chem., submitted [Google Scholar]
- Mayer, A., Jorissen, A., Kerschbaum, F., et al. 2013, A&A, 549, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McElroy, D., Walsh, C., Markwick, A. J., et al. 2013, A&A, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGuire, P., & Kouri, D. J. 1974, J. Chem. Phys., 60, 2488 [CrossRef] [Google Scholar]
- Milam, S. N., Apponi, A. J., Woolf, N. J., & Ziurys, L. M. 2007, ApJ, 668, L131 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [Google Scholar]
- Murty, A. N., & Curl, R. F. 1969, J. Mol. Spectr., 30, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Naouai, M., Najar, F., & Hammami, K. 2019, Phys. Chem. Chem. Phys., 21, 20137 [NASA ADS] [CrossRef] [Google Scholar]
- Nicolaes, D., Groenewegen, M. A. T., Royer, P., et al. 2018, A&A, 618, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Nolt, I., Radostitz, J., DiLonardo, G., et al. 1987, J. Mol. Spectr., 125, 274 [NASA ADS] [CrossRef] [Google Scholar]
- Pamboundom, M., Tchakoua, T., & Nsangou, M. 2016, Ap&SS, 361, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, R., Yoshida, H., Chamberlin, R. A., et al. 2010, ApJ, 723, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, J. Quant. Spectr. Rad. Transf., 60, 883 [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pine, A. S., Fried, A., & Elkins, J. W. 1985, J. Mol. Spectr., 109, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Plane, J. M. C., Daly, S. M., Feng, W., Gerding, M., & Gómez Martín, J. C. 2021, J. Geophys. Res.: Space Phys., 126, e28792 [NASA ADS] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Quintana-Lacaci, G., Cernicharo, J., Agúndez, M., et al. 2016, ApJ, 818, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Ramstedt, S., Schöier, F. L., & Olofsson, H. 2009, A&A, 499, 515 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramstedt, S., Maercker, M., Olofsson, G., Olofsson, H., & Schöier, F. L. 2011, A&A, 531, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramstedt, S., Mohamed, S., Vlemmings, W. H. T., et al. 2017, A&A, 605, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rogowski, D. F., Marshall, P., & Fontijn, A. 1989, J. Phys. Chem., 93, 1118 [CrossRef] [Google Scholar]
- Rybicki, G. B., & Hummer, D. G. 1991, A&A, 245, 171 [NASA ADS] [Google Scholar]
- Ryde, N., Jönsson, H., Mace, G., et al. 2020, ApJ, 893, 37 [CrossRef] [Google Scholar]
- Saunders, R., & Plane, J. 2006, J. Atm. Sol.-Terr. Phys., 68, 2182 [NASA ADS] [CrossRef] [Google Scholar]
- Schöier, F. L., & Olofsson, H. 2001, A&A, 368, 969 [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [Google Scholar]
- Schöier, F. L., Maercker, M., Justtanont, K., et al. 2011, A&A, 530, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smolders, K., Neyskens, P., Blommaert, J. A. D. L., et al. 2012, A&A, 540, A72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stevens, P. S., Brune, W. H., & Anderson, J. G. 1989, J. Phys. Chem., 93, 4068 [CrossRef] [Google Scholar]
- Suh, K.-W. 2000, MNRAS, 315, 740 [NASA ADS] [CrossRef] [Google Scholar]
- Tennyson, J., Yurchenko, S. N., Al-Refaie, A. F., et al. 2016, J. Mol. Spectr., 327, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Timp, B. A., Doran, J. L., Iyer, S., Grabow, J.-U., & Leopold, K. R. 2012, J. Mol. Spectr., 271, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Tizniti, M., Le Picard, S. D., Lique, F., et al. 2014, Nat. Chem., 6, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Törring, T., & Herrmann, R. 1989, Mol. Phys., 68, 1379 [CrossRef] [Google Scholar]
- Turnshek, D. E., Turnshek, D. A., & Craine, E. R. 1985, An atlas of digital spectra of cool stars [Google Scholar]
- Uehara, H., Horiai, K., Nakagawa, K., & Fujimoto, T. 1989, J. Mol. Spectr., 134, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Van de Sande,M., Sundqvist, J. O., Millar, T. J., et al. 2018, A&A, 616, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van der Tak, F. F. S., Lique, F., Faure, A., Black, J. H., & van Dishoeck, E. F. 2020, Atoms, 8, 15 [Google Scholar]
- Velilla Prieto, L., Sánchez Contreras, C., Cernicharo, J., et al. 2017, A&A, 597, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [Google Scholar]
- Wyse, F. C., & Gordy, W. 1972, J. Chem. Phys., 56, 2130 [NASA ADS] [CrossRef] [Google Scholar]
- Wyse, F. C., Gordy, W., & Pearson, E. F. 1970, J. Chem. Phys., 52, 3887 [NASA ADS] [CrossRef] [Google Scholar]
- Yamada, C., Cohen, E. A., Fujitake, M., & Hirota, E. 1990, J. Chem. Phys., 92, 2146 [NASA ADS] [CrossRef] [Google Scholar]
- Yamamura, I., Kawaguchi, K., & Ridgway, S. T. 2000, ApJ, 528, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Yousefi, M., & Bernath, P. F. 2018, ApJS, 237, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., & Liu, X. W. 2005, ApJ, 631, L61 [NASA ADS] [CrossRef] [Google Scholar]
Aside from a misidentification of NaCl towards W Aql by De Beck & Olofsson (2020), which will be discussed further in Sect. 3.1.
We note our use of the expansion velocity implemented in previous radiative transfer models of W Aql, υ∞ = 16.5 km s−1 (Danilovich et al. 2014; Ramstedt et al. 2017; Brunner et al. 2018), which is smaller than the maximum velocity derived by Gottlieb et al. (2021), of υ∞ = 27.1 km s−1, partly due to low-intensity, high-velocity wings. As discussed in Danilovich et al. (2014), larger expansion velocities can be found for W Aql due to an auxiliary feature seen in the blue part of many molecular line profiles. This is routinely excluded from 1D radiative transfer modelling, an especially valid approach here, since we do not detect this feature or any other high-velocity components in the AlCl or AlF emission.
The ALMA beam size and rms are ~0′′.7, 4 mJy and 0′′.023, 1 mJy for the CW Leo data and our data, respectively. The v = 2 line covered by both observations (considered since the v = 1 is close to a brighter SiO line), has a total flux density of 13 mJy over a few beam areas at the line peak for W Aql. The proportional flux density for the CW Leo data, when compared with the v = 0 line, would be 23 mJy/beam. This is just over 5σ but it is possible for weak emission to be missed in masking for cleaning, especially in the Cycle 0 data with fewer antennas and less refined calibration.
CW Leo was the only carbon star for which Peng et al. (2010) observed both isotopologues of HCl. Their ratio is lower than that found by Agúndez et al. (2011) but still agrees within uncertainties. We consider only the Agúndez et al. (2011) value here since they use more HCl transitions and more detailed radiative transfer models to obtain their result.
At 1232.476 GHz (Nolt et al. 1987; Pickett et al. 1998), the J = 1 → 0 line falls close to a water line and just outside of the feasible observing ranges SOFIA is currently equipped for (Duran et al. 2021).
All Tables
Stellar and circumstellar parameters of W Aql used in radiative transfer modelling.
Measured rms values for undetected lines of NaCl, KCl, AlO, and AlOH towards W Aql.
Capture rate coefficients calculated using long range transition state theory (Georgievskii & Klippenstein 2005).
Molecular properties and heats of formation (at 0 K) of the stationary points on the Al, AlOH and AlO + HF potential energy surfaces.
Molecular properties and heats of formation (at 0 K) of the stationary points on the Al, AlOH and AlO + HCl potential energy surfaces.
Additional reactions for halide and aluminium-bearing molecules included in our chemical modelling.
All Figures
 |
Fig. 1 Channel maps of Al35Cl (18 → 17) observed towards W Aql using ALMA in the extended array configuration. The dotted red contours enclose 50% of the total continuum flux. The white contours indicate levels of 3 and 5σ. The ellipses in the bottom left of each panel indicate the synthetic beams for the molecular emission (white) and continuum emission (red). |
| In the text | |
 |
Fig. 2 Zeroth moment maps of AlCl observed towards W Aql using ALMA in the extended array configuration. Transitionsare labelled in the top right of each panel. The black contours indicate levels of 3, 5, and 10σ. The dotted red contour encloses 50% the total continuum flux. The ellipses in the bottom left of each panel indicate the synthetic beams for the molecular emission (white) and continuum emission (red). |
| In the text | |
 |
Fig. 3 Zeroth moment map of the AlF (7 → 6) line in the ground vibrational state (colours and white dashed contours) plotted with the zeroth moment map of the Al35 Cl (18 → 17) line in the ground vibrational state (black solid contours). The contours are plotted at levels of 3, 5, and 10σ for AlF and 5 and 10σ for Al35 Cl. The red star indicates the position of the continuum peak. The white and black ellipses in the bottom right indicate the synthetic beam sizes for the AlF and Al35 Cl emission, respectively. |
| In the text | |
 |
Fig. 4 Radial gas kinetic temperature profile used in our modelling of W Aql. |
| In the text | |
 |
Fig. 5 Spectra of Al35Cl observed towards W Aql with ALMA (black histograms), with calculated line profiles (red curves) superposed on the observed profiles. Nearby lines of other molecules are labelled in blue. |
| In the text | |
 |
Fig. 6 Azimuthally averaged radial profiles extracted from ALMA v = 0 lines of AlCl(black dotted lines and points with error bars) plotted with the corresponding modelled radial profiles (red lines and squares). Residuals are plotted in the lower panels, showing the difference between the observed and modelled lines, with error bars from the observations included. |
| In the text | |
 |
Fig. 7 Spectra of Al37Cl observed towards W Aql with ALMA (black histograms), with calculated line profiles (red curves) superposed on the observed profiles. |
| In the text | |
 |
Fig. 8 Azimuthally averaged radial profile of AlF, extracted from the ALMA (7 → 6) v = 0 line (black dotted lines and points with error bars) plotted with the corresponding modelled radial profiles (red lines and squares). Residuals are plotted in the lower panels, showing the difference between the observed and modelled lines, with error bars from the observations included. |
| In the text | |
 |
Fig. 9 Spectra of AlF observed towards W Aql with ALMA (black histograms), with calculated line profiles (red curves) superposed on the observed profiles. |
| In the text | |
 |
Fig. 10 PACS spectra (black histograms) and model results (blue curves) for HCl towards W Aql. For each pair of lines, H35 Cl is shown on the left since it has the shorter wavelength and H37Cl is on the right, with the longer wavelength. Some known nearby and blended lines are indicated in orange (but not all nearby lines have been identified). |
| In the text | |
 |
Fig. 11 PACS spectra (black histograms) and model results (blue curves) for HF towards W Aql. The HF (2 → 1) line is dominated by a blend with the o-H2O line at 121.721 μm, which is plotted in grey. See text for details. |
| In the text | |
 |
Fig. 12 Abundance profiles for the halide molecules modelled here. Abundances for 35Cl and 37Cl isotopologues have been combined. Vertical dashed lines indicate the outer radius of the corresponding model and short vertical lines indicate the inner radii of the HCl and HF models. The dotted curve and corresponding shading indicates an upper limit abundance for HF. See text for details. |
| In the text | |
 |
Fig. 13 (a) Calculated first-order rates for conversion of HF to AlF by reaction with Al, AlOH and AlO; and loss of AlF by photolysis and reaction with H, H2O and OH. The clustering rate with metallic compounds (blue line, see text for further details) is shown in the region where the temperature is below 500 K. (b) Calculated first-order rates for conversion of HCl to AlCl by reaction with Al, AlOH and AlO; and loss of AlCl by photolysis and reaction with H, H2O and OH. The red lines show the molecular expansion rate of the outflow at a constant velocity of 16.5 km s−1. |
| In the text | |
 |
Fig. 14 Fractional abundance relative to H2 of AlCl and HCl (left panel), and AlF and HF (right panel), obtained from chemical modelling (solid lines), plotted with the results of the radiative transfer models (dotted lines). The assumed physical conditions and parent species are given in the text and Appendix D. |
| In the text | |
 |
Fig. A.1 Upper limits for AlO (blue) and AlOH (orange) abundance distributions. Dotted lines show the constant abundance models and dashed lines show abundance distributions predicted by chemical models. See text for details. |
| In the text | |
 |
Fig. B.1 Rotational quenching cross-sections of AlF induced by collision with H2 as a functionof the kinetic energy, presented with colour diagram, with J = 1 in black to J= 12 in red. |
| In the text | |
 |
Fig. B.2 Log-log scale variation in downward rate coefficients for transitions with ΔJ = −1, as a function of the kinetic temperature. |
| In the text | |
 |
Fig. C.1 PACS spectra (black histograms) and model results (blue curves) for HCl towards χ Cyg. For each pair of lines, H35Cl is shown on the left since it has the shorter wavelength and H37Cl is on the right, with the longer wavelength. Some known nearby and blended lines are indicated in orange (but not all nearby lines have been identified). |
| In the text | |
 |
Fig. C.2 Radial abundance profiles for HCl (green) and HF (red) as derived for χ Cyg. The short vertical lines indicate the inner radius of the corresponding model. |
| In the text | |
 |
Fig. C.3 PACS spectra (black histograms) and model results (blue curves) for HF towards χ Cyg. The HF (2 → 1) line is blended with the o-H2O line at 121.721 μm, which is notshown here. See text for details. |
| In the text | |
 |
Fig. D.1 Potential energy surfaces calculated at the G4 level of theory for: (a) Al + HF (R1); (b) AlOH + HF (R2); (c) AlO + HF (R3). Note that the very endothermic channels are not shown. |
| In the text | |
 |
Fig. D.2 Potential energy surfaces calculated at the G4 level of theory for: (a) Al + HCl (R1); (b) AlOH + HCl (R2); (c) AlO + HCl (R3). Note that the very endothermic channels are not shown. |
| In the text | |
 |
Fig. D.3 Absorption cross-sections of AlF and AlCl calculated at the TD-B3LYP//6-311+g(2d,p) level of theory (Frisch et al. 2016). Photolysis is possible in the portions of the absorption curves shown with solid lines. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


