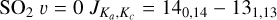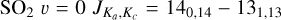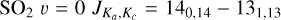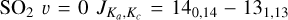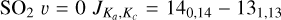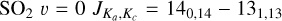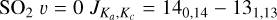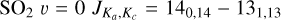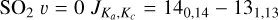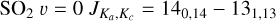| Issue |
A&A
Volume 681, January 2024
|
|
|---|---|---|
| Article Number | A50 | |
| Number of page(s) | 41 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/202347632 | |
| Published online | 09 January 2024 | |
ATOMIUM: Molecular inventory of 17 oxygen-rich evolved stars observed with ALMA★
1
Institute of Astronomy, KU Leuven,
Celestijnenlaan 200D,
3001
Leuven,
Belgium
e-mail: sofia.wallstrom@kuleuven.be
2
School of Physics & Astronomy, Monash University,
Wellington Road,
Clayton
3800,
Victoria,
Australia
3
ARC Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D),
Clayton
3800,
Australia
4
Universität zu Köln, I. Physikalisches Institut,
50937
Köln,
Germany
5
Harvard-Smithsonian Center for Astrophysics,
60 Garden Street,
Cambridge,
MA
02138,
USA
6
School of Physics and Astronomy, University of Leeds,
Leeds
LS2 9JT,
UK
7
School of Chemistry, University of Leeds,
Leeds
LS2 9JT,
UK
8
JBCA, Department Physics and Astronomy, University of Manchester,
Manchester
M13 9PL,
UK
9
Université de Bordeaux, Laboratoire d’Astrophysique de Bordeaux,
33615
Pessac,
France
10
Department of Mathematics, Kiel University,
Heinrich-Hecht-Platz 6,
24118
Kiel,
Germany
11
Anton Pannekoek Institute for Astronomy, University of Amsterdam,
Science Park 904,
1098 XH
Amsterdam,
The Netherlands
12
Departamento de Fisica, Universidad de Santiago de Chile,
Av. Victor Jara 3659,
Santiago,
Chile
13
Center for Interdisciplinary Research in Astrophysics and Space Exploration (CIRAS), USACH,
Chile
14
Department of Chemistry and Molecular Biology, University of Gothenburg,
Kemigården 4,
412 96
Gothenburg,
Sweden
15
School of Engineering and Applied Sciences and Department of Earth and Planetary Sciences, Harvard University,
Cambridge,
MA
02138,
USA
16
National Astronomical Research Institute of Thailand,
Chiangmai
50180,
Thailand
17
Max-Planck-Institut für Radioastronomie,
53121
Bonn,
Germany
18
National Solar Observatory,
Makawao,
HI
96790,
USA
19
LESIA, Observatoire de Paris, Université PSL, CNRS, Sorbonne Université, Université Paris Cité,
5 place Jules Janssen,
92195
Meudon,
France
20
Department of Space, Earth and Environment, Chalmers University of Technology,
Onsala Space Observatory,
43992
Onsala,
Sweden
21
Université Côte d’Azur, Laboratoire Lagrange, Observatoire de la Côte d’Azur,
06304
Nice Cedex 4,
France
22
School of Physical Sciences, The Open University,
Walton Hall,
Milton Keynes,
MK7 6AA,
UK
23
Astrophysics Research Centre, School of Mathematics and Physics, Queen’s University Belfast,
University Road,
Belfast
BT7 1NN,
UK
24
NASA Goddard Space Flight Center,
8801 Greenbelt Road,
Greenbelt,
MD
20071,
USA
25
Jet Propulsion Laboratory, MS 183-900, California Institute of Technology,
Pasadena,
CA
91109,
USA
26
Department of Astrophysics/IMAPP, Radboud University,
PO Box 9010,
6500 GL
Nijmegen,
The Netherlands
27
SRON Netherlands Institute for Space Research Sorbonnelaan 2,
3584 CA
Utrecht,
The Netherlands
28
Theoretical Astrophysics, Department of Physics and Astronomy, Uppsala University,
Box 516,
751 20
Uppsala,
Sweden
29
Institut de Radioastronomie Millimétrique,
300 rue de la Piscine,
38406
Saint-Martin-d’Hères,
France
30
University College London, Department of Physics and Astronomy,
London
WC1E 6BT,
UK
Received:
2
August
2023
Accepted:
27
October
2023
Context. The dusty winds of cool evolved stars are a major contributor of the newly synthesised material enriching the Galaxy and future generations of stars. However, the details of the physics and chemistry behind dust formation and wind launching have yet to be pinpointed. Recent spatially resolved observations show the importance of gaining a more comprehensive view of the circumstellar chemistry, but a comparative study of the intricate interplay between chemistry and physics is still difficult because observational details such as frequencies and angular resolutions are rarely comparable.
Aims. Aiming to overcome these deficiencies, ATOMIUM is an ALMA Large Programme to study the physics and chemistry of the circumstellar envelopes of a diverse set of oxygen-rich evolved stars under homogeneous observing conditions at three angular resolutions between ~0.02″−1.4″. Here we summarize the molecular inventory of these sources, and the correlations between stellar parameters and molecular content.
Methods. Seventeen oxygen-rich or S-type asymptotic giant branch (AGB) and red supergiant (RSG) stars have been observed in several tunings with ALMA Band 6, targeting a range of molecules to probe the circumstellar envelope and especially the chemistry of dust formation close to the star. We systematically assigned the molecular carriers of the spectral lines and measured their spectroscopic parameters and the angular extent of the emission of each line from integrated intensity maps.
Results. Across the ATOMIUM sample, we detect 291 transitions of 24 different molecules and their isotopologues. This includes several first detections in oxygen-rich AGB/RSG stars: PO v = 1, SO2 v1 = 1 and v2 = 2, and several high energy H2O transitions. We also find several first detections in S-type AGB stars: vibrationally excited HCN v2 = 2,3 and SiS v = 4,5,6, as well as first detections of the molecules SiC, AlCl, and AlF in W Aql. Overall, we find strong correlations between the following molecular pairs: CS and SiS, CS and AlF, NaCl and KCl, AlO and SO, SO2 and SO, and SO2 and H2O; meaning both molecules tend to have more detected emission lines in the same sources. The measured isotopic ratios of Si and S are found to be consistent with previous measurements, except for an anomalously high 29Si/30Si ratio of 4 ± 1 in the RSG VX Sgr.
Conclusions. This paper presents the overall molecular inventory and an initial analysis of the large ATOMIUM dataset, laying the groundwork for future work deriving molecular abundances and abundance profiles using radiative transfer modeling which will provide more rigorous tests for chemical models.
Key words: stars: AGB and post-AGB / supergiants / circumstellar matter / line: identification / instrumentation: interferometers / astrochemistry
Tables A.1–A.5 are available at the CDS via anonymous ftp to cdsarc.cds.unistra.fr (130.79.128.5) or via https://cdsarc.cds.unistra.fr/viz-bin/cat/J/A+A/681/A50
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
Cool evolved stars are a major contributor of the gas and dust returned to the interstellar medium (Tielens 2005) through their dusty winds which can reach mass-loss rates of up to 10−4 M⊙ yr−1 (Höfner & Olofsson 2018). Low- and intermediate-mass (~0.8−8 M⊙) asymptotic giant branch (AGB) stars are known to have dust-driven winds, while the mass-loss mechanism of the rarer, more massive red supergiant (RSG) stars remains uncertain. In both cases, however, the details of the physics and chemistry behind dust formation and wind launching have yet to be pinpointed, a vital step in understanding how newly synthesised material from AGB and RSG stars enriches the Galaxy and future generations of stars.
These AGB and RSG stars and their accompanying circum-stellar envelopes (CSEs) provide useful chemical laboratories for studying dust and molecule formation due to their relatively simple overall spherical structure and their (mostly) radial velocity fields. Other chemically interesting cool environments, such as star-forming regions or (proto)planetary disks, tend to have more complex spatial and velocity structures, making it more difficult to disentangle the effects of chemistry. The overall chemical composition of an AGB CSE depends on the C/O ratio of the central star (see, for example, Habing & Olofsson 2003), as most of the less abundant element is locked up in CO. An oxygen-rich or M-type star (C/O < 1) has more free oxygen to form for example silicate dust and oxygen-bearing molecules – such as SO, TiO, AlO – while a carbon-rich star (C/O > 1) has more free carbon to form for example amorphous carbon dust and molecules such as HC3N and SiC2. Stars with C/O ~ 1 are called S-type stars and have a mixed chemistry. The more massive RSGs are all oxygen-rich stars, due to extra nucleosynthesis processes such as hot-bottom burning (Herwig 2005), resulting in oxygen-rich CSEs.
To date more than 100 molecules and 15 dust species have been detected around AGB and RSG stars (Decin 2021). The difficult-to-observe H2 is by far the most abundant molecule, but it is followed in abundance by CO, whose lower energy rotational transitions are easily excited over much of the CSE and readily observable with ground-based telescopes. Observations of CO and other molecular lines provide dynamical and physical information about the CSE, and help constrain chemical models of dust and molecule formation. A very efficient means of determining the molecular contents of diverse Galactic sources are spectral line surveys, covering wide frequency bands in the millimeter and sub-millimeter domain. A range of surveys has been carried out for evolved stars with single-dish telescopes, which have discovered a wealth of new molecules. For example, Tenenbaum et al. (2010) report the first detections of PO, AlO and AlOH in space, in the RSG VY CMa, as well as the first detections of NaCl, PN, NS, and HCO+ in an oxygen-rich source; Velilla Prieto et al. (2017) report the first detections of NO and H2CO in an oxygen-rich source, namely IK Tau (a.k.a. NML Tau); De Beck & Olofsson (2020) report the first detections of silicon- and carbon-bearing species SiC2, SiN, C2H, and HC3N towards an S-type star, W Aql; and in the extensively studied, high mass-loss rate carbon-rich star CW Leo (a.k.a. IRC+10216) refractory metal-containing species such as AlCl, AlF, MgNC, MgCN, NaCN, NaCl, and KCl are reported by Cernicharo et al. (2000), He et al. (2008), Pardo et al. (2022), alongside cyanopolyynes of the family HC2n+1N, carbon chain radials up to C8H, and cyclic compounds such as c-C3H2.
However, these single-dish observations at low angular resolution (typically 10″−40″) struggle to probe the spatial distributions of molecules in the CSE, which provide further vital constraints on chemical models. Greatly increased angular resolution is achieved with interferometry, alongside increased sensitivity allowing fainter molecular lines to be detected. This results in more accurate information on the relative excitation and formation of different species, and is especially useful for detecting rarer or short-lived species which are typically only seen close to the star – especially those suspected to play a part in dust condensation, such as AlO or carbon chains (Agundez et al. 2020). To date, only a handful of interferometric molecular line surveys of AGB stars have been carried out due to the large observing time requirements. These include studies of some sources that also were covered by single-dish surveys: the carbon-rich CW Leo (Patel et al. 2011) and the two oxygen-rich stars R Dor and IK Tau (Decin et al. 2017, 2018). The RSG VY CMa has also been studied in this way (Kamiński et al. 2013).
Patel et al. (2011) observed the carbon-rich AGB star CW Leo with a 3″ beam using the Submillimeter Array (SMA). They detect ~200 new lines of the molecules known from previous single-dish surveys, including narrow vibrationally excited lines (many from HCN) close to the star (see also Patel et al. 2009). They note that many of their unassigned lines are also narrow, possibly produced by vibrationally excited transitions of polyatomic molecules for which laboratory measurements of rest frequencies were not yet available. With measurements of both emission sizes and velocities for a range of lines they are also able to characterise the wind acceleration, parameterised by a beta law velocity profile (Lamers & Cassinelli 1999) with a fast acceleration (β = 0.5).
Kamiński et al. (2013) observed the very high mass-loss rate (4 × 10−4 M⊙ yr−1) and asymmetric RSG VY CMa with a 0.9” beam, again using the SMA. They detect over 200 lines from 19 molecules, including AlCl, rotational emission from TiO for the first time in an oxygen-rich evolved star, and TiO2 for the first time in space. A large number of lines of oxygen-rich molecules like SO2 and SO are seen, as well as many lines of the relatively refractory NaCl including vibrationally excited transitions up to v = 3. Most of the observed lines show multiple velocity components, and the molecular emission shows similar spatial complexity.
Decin et al. (2017, 2018) observed two archetypal oxygen-rich AGB stars, the high mass-loss rate (5 × 10−6 M⊙ yr−1) IK Tau and the low mass-loss rate (1 × 10−7 M⊙ yr−1) R Dor, at ~0.15″ angular resolution with the Atacama Large Millimeter and sub-millimeter Array (ALMA). They detect ~200 lines from 15 different molecules, including dust precursors such as SiO, AlO, AlOH, TiO, and TiO2. Highly vibrationally excited SiO (up to v = 5) is detected in both sources close to the star, and AlO is detected far beyond the dust condensation radius showing that this molecule does not become entirely locked up in dust grains. The data is also used to characterise the wind acceleration of both sources, showing much slower accelerations than for the carbon-rich CW Leo (6 ~ 5−10).
These interferometric surveys demonstrate the importance of spatially resolved observations for obtaining a more comprehensive view of the circumstellar chemistry, as different molecules and transitions can show emission at different spatial scales and with different morphologies. However, it is difficult to draw more general conclusions about AGB or RSG stars from the study of single sources. Even in aggregate, various studies have different sensitivities, frequency coverage, and angular resolutions, and hence are difficult to compare. The next step to elucidate the circumstellar chemistry is to observe a sample of stars with a range of stellar parameters, with identical observing setups. By performing homogeneous high-angular-resolution observations, we can directly compare the chemical inventories of different sources, and compare them with stellar parameters.
ALMA Tracing the Origins of Molecules forming dUst in oxygen-rich M-type stars (ATOMIUM, Program ID: 2018.1.00659.L) is an ALMA Large Programme to observe 17 oxygen-rich AGB and RSG stars at high angular resolution in a range of molecular transitions (Decin et al. 2020; Gottlieb et al. 2022). The ATOMIUM targets were chosen to represent a range of AGB mass-loss rates, chemical types (M-type and S-type stars), and pulsation behaviors (semi-regular variables (SR), long-period variables (LPV), and regular Mira variables). The sample also includes three RSG stars, and is summarised in Table 1. ATOMIUM is the first ALMA Large Programme for stellar evolution, and consists of a set of homogeneous high-resolution observations that allow unambiguous comparison of the physicochemical properties of the winds of the 17 evolved stars, expanding the sample of evolved stars studied at such high angular resolution by a factor of four. It also provides a detailed picture of the chemical and dynamical processes throughout the stellar wind, including measurements of isotopic ratios which provide an important tracer of nucleosynthesis in the core of the star. Alongside the ATOMIUM overview paper (Gottlieb et al. 2022), several in-depth studies of individual sources (Homan et al. 2020, 2021; Danilovich et al. 2023), specific molecules (Danilovich et al. 2021; Baudry et al. 2023), and comparisons with optical polarized light (Montargès et al. 2023) have already resulted from this data.
This paper presents the molecular inventory of the 17 oxygen-rich AGB and RSG sources of the ATOMIUM sample. Section 2 briefly describes the observations undertaken with ALMA as part of the ATOMIUM Large Programme, and we summarize how the carriers of the spectral lines were assigned to specific molecules and how the spectroscopic parameters of the rotational lines (flux density, line width, and integrated area) were determined. In Sect. 3 we present our results, and Sect. 4 contains the conclusions. Additionally, the accompanying online tables include full lists of the molecular lines identified in the sample and in each source, including line parameters and molecular emission sizes, and all the spectra.
ATOMIUM sources and their stellar parameters.
2 Data
2.1 ALMA observations
The ATOMIUM ALMA Large Programme covers a frequency range of ~213–270 GHz in 16 spectral tunings, with a total bandwidth of 27 GHz. Observations were carried out at three different spatial resolutions – low-resolution with beam sizes of ~0.8″–1.4″, medium-resolution with beam sizes of ~0.2″–0.5″, and high-resolution with beam sizes of ~0.02″–0.05″. The maximum scales which can be imaged (maximum recoverable scale, MRS) for each resolution are approximately 8–10”, 1.5–4”, and 0.4–0.6”, respectively (see Gottlieb et al. 2022, Table E.3). The field of view (to half maximum sensitivity) is 22”–26”, depending on frequency. Only half the tunings, covering CO and some of the other lines with the most extended emission, were observed at the lowest spatial resolution. There is, however, missing flux for at least some molecules (notably CO) in some of our sources. This can occur both for lines with angular extent larger than the field of view, and for emission which is smooth on scales larger than the MRS. For example, in R Hya about 40% of the CO flux is resolved out (Homan et al. 2021), π1 Gru is missing ~30–70% of the CO flux (Homan et al. 2020), and W Aql is missing 66% of the CO flux (Danilovich et al. 2023). There is likely also missing flux for other molecules such as HCN and some transitions of SO2, in at least some sources. The full extent of missing flux has not been quantified as single-dish spectra of the same frequency ranges are not available for most of our sources.
Observations took place between 2018 and 2021. All the high resolution data were taken during June-July in 2019, and hence essentially samples, for each source, only one part of the stellar phase (see Gottlieb et al. 2022, for details). Calibration and imaging were performed in CASA (McMullin et al. 2007) following standard ALMA procedures. The line-free continuum (mostly stellar emission) was identified and used for self-calibration, which was applied to all data, ensuring that the data for each star had a consistent position and flux density scale (measured in Jy beam−1 for the image cubes, and Jy for the extracted spectra). See Table E.2 in Gottlieb et al. (2022) for details of the continuum image properties. Image cubes were made (after continuum subtraction) for each separate spatial resolution. The channel spacing of 0.9765625 MHz gives a velocity resolution of 1.1–1.4 kms−1 depending on frequency. The rms noise σrms per spectral channel is ~1–5 mJy, depending on target elevation and requested noise level; the high-resolution data usually have the lowest noise and are the most sensitive to compact or clumpy emission, while the low-resolution data has the greatest surface brightness sensitivity. The observations and data reduction are described fully in Gottlieb et al. (2022), and the characteristics such as the rms noise level, σrms, and angular resolution of each spectral cube are given in their Table E.3. Note that in some cases (such as very bright, compact emission or weak, extended emission) the standard reduction parameters may leave low-level artefacts in the images for individual lines; papers on specific lines or targets, using optimised imaging and combination of the different spatial resolutions, may give slightly different values from those reported here (and in Gottlieb et al. 2022). To allow for this and for the propagation of errors when combining data taken at different epochs, we adopt a conservative flux scale uncertainty of 15% (although in some cases it may be much better than this).
Extract of Table A.5 which lists all measured lines in each source.
2.2 Processing and analysis
We used spectra of each source at high, medium, and low angular resolution to identify the various molecular transitions. Spectra were extracted in circular apertures, centered on the continuum peak, with diameters of 0.04″, 0.08″, and 0.12″ for the high-resolution data; diameters of 0.4″, 1.2″, and 3.6″ for the medium-resolution data; and diameters of 1.2″, 3.6″, and 10.8″ for the low-resolution data. At each resolution, the smallest aperture was chosen to be the average beam size rounded up to one significant figure, for consistency.
In each spectrum the line identification was carried out in a systematic way. Starting from a list of expected lines based on the line survey of IK Tau and R Dor by Decin et al. (2018), at the position of each potential line a soft parabola function (as defined in De Beck et al. 2010) was fit with a least squares fitting algorithm. A visual inspection then ruled out spurious fits, added missing lines, and adjusted the fit of weak and blended lines. The rms (σ) was measured from the parts of the spectrum more than three times the wind expansion velocity (vexp) away from any line, and any potential lines below 2.5σ are considered non-detections. Any previously unknown lines were added to the line list, and identified if possible. Inspection of integrated intensity (moment 0) maps by eye further ensured any weak lines correspond to coherent emission across several channels rather than a noise fluctuation. We have also checked the intrinsic brightness (at 300 K) of the various transitions to ensure that the detected lines of each molecule are among the brightest lines in our frequency range. We do not exclude the possibility that further lines may be detected with a different data reduction method or by stacking data; however, we leave this to future papers.
Example medium and high angular resolution spectra of R Hya are shown in Appendix C, with molecular identifications, while Appendix A contains more detailed information about the identified lines. Additional information about the lines and molecular data can be found in Appendix A.1, Table A.1 gives a full list of identified molecules by source, Table A.2 gives the maximum radial extent of each molecule in each source, Table A.3 lists all identified molecular lines with references for the line parameters, and Table A.4 lists all the unidentified lines. Tables 2 and A.5 list all detected lines in each source, and gives measurements taken at each spatial resolution (high, medium, low) where the line was detected. Each line was measured separately in the spectra extracted with the three different apertures given above.
Line parameters were extracted from each spectrum, and for each detected line its peak flux, integrated intensity, velocity width (full width at zero power), and angular extent (from its integrated intensity map, see below) was measured. The peak flux was taken to be the flux in the brightest channel included within the line extent. The spectral extent of a line was measured between the channels where each line wing reaches 2.5σ% with a minimum width of four channels (≈5kms−1), thus defining the velocity width and integrated intensity. As this was done automatically, broad weak lines may have their velocity widths and hence integrated intensities underestimated. The uncertainty on the peak flux was taken to be the rms plus the 15% absolute flux uncertainty (see Sect. 2.1), and the uncertainty on the line width was taken to be the channel width.
Potentially blended lines and lines with absorption or double-peaked profiles were checked manually to ensure that the correct line region was chosen. For lines which are blended or truncated by the edge of an observing band, only a peak flux is reported, as measured at the line center, and for lines with absorption the “peak” flux value is actually the positive or negative extremum value. Note that some lines show (partial) absorption only at certain apertures, most commonly the smaller apertures. The measured line width was used to make integrated intensity (moment 0) maps by summing the intensities of all the spectral channels covered by a line. From these maps the maximum radial extent of the emission from each line was measured, defined as the maximum radial extent of the 3σ contour enclosing the star (centered on the peak of the continuum emission). The contours were azimuthally smoothed (in bins with at least ten samples, corresponding to angular ranges of ≥60°) to limit deviations due to noise, following the method in Danilovich et al. (2021). Note that for transitions with clumpy emission, this method may underestimate the extent of the emission. For transitions with no measured extent from this method an upper limit is given, equal to half the major axis of the restoring beam (bmaj/2). We also note that there may be diffuse extended emission of various molecules which is not properly imaged, or which is filtered out if its size is similar to (or greater than) the maximum recoverable scale. Such emission may be brought out with different data reduction techniques or spectral averaging.
A majority of detected lines are seen in the data at multiple angular resolutions, as expected; however some transitions are only seen in the high-resolution data. We note that this data is more sensitive so faint lines are more likely to be detected. Furthermore, very compact emission (less than a few hundred milliarcsec in diameter) is best detected in the highest angular resolution data, as it may otherwise be diluted in large extraction apertures or with larger beams, or have its apparent flux reduced by imaging artefacts.
2.3 Mass-loss rate uncertainties
Mass-loss rates (Ṁ) for the ATOMIUM sample were gathered from literature studies (see references in Table 1). However, these mass-loss rate determinations often assumed different distances to the stars than is used in this paper, and hence the mass-loss rate must be scaled to the new distance. This has been done using a simple formula to account for the dilution factor stemming from the distance to the star:
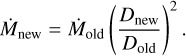 (1)
(1)
Table 3 lists the factor by which this has changed the literature mass-loss rate, alongside more details about how the mass-loss rates were derived.
Updating the distances to these sources has changed the derived mass-loss rate by at most a factor of 2.5. However, we expect the literature mass-loss rate values to have uncertainties larger than this (though they are seldom quantified), with determinations frequently based on only one or two independent observations which makes it difficult to disentangle the degeneracies between for example the mass-loss rate, temperature profile, and the outer radius of the wind. Sources with derived mass-loss rates based on more than two independent observational data points are highlighted in green, which is the case for only five sources: IRC+10011, π1 Gru, R Hya, VX Sgr, and W Aql. W Aql has undoubtedly the best constrained mass-loss rate as it is based on direct modeling of 21 individual CO lines, and even here the model has an estimated uncertainty of a factor ~3 (Danilovich et al. 2014; Ramstedt et al. 2017). Furthermore, many of the mass-loss rates are derived using empirical formulae, based on CO line fluxes and some stellar parameters, rather than direct radiative transfer modelling of CO observations. These formulae involve a large number of assumptions resulting in uncertainties of at least a factor ~3–5 (De Beck et al. 2010; Olofsson et al. 1993), when they are quantified at all. Two of the mass-loss rates are derived from empirical formulae using the observed 60 µm flux (labeled “a” in Table 3), which requires further assumptions about the wind velocity, dust properties, and gas-to-dust ratio.
The derived mass-loss rates also generally assume a constant and spherically symmetric mass loss, but the ATOMIUM observations have shown this is not true for any of our sources (Decin et al. 2020): they all show significant structure in their winds, and some – like π1 Gru and R Hya – are highly asymmetric. This is interpreted as the likely presence of a companion. If the companion shapes the wind into an equatorial density enhancement, this could change the derived mass-loss rate by a factor of up to three if the system is seen face-on, and potentially much more if the system is seen edge-on (El Mellah et al. 2020). Furthermore, simply the assumption of a constant mass-loss rate has been shown to change the derived mass-loss rate by a factor of a few (Kemper et al. 2003; Decin et al. 2007).
Taken together, these factors result in typical uncertainties on the mass-loss rates of up to an order of magnitude. However, the mass-loss rate still provides a useful way to order the sources to look for general trends, and in the absence of more precise estimates we will continue to use the values in Table 1 in our analysis. Improving the mass-loss rate estimates for the ATOM-IUM sources will be undertaken in a future publication, using radiative transfer modelling of homogeneous single-dish observations of at least four CO transitions per source, combined with the spatial information from the ALMA observations.
Mass-loss rates from literature.
3 Results and discussion
This section presents an overview of the molecular inventory in Sect. 3.1, molecular emission sizes in Sect. 3.2, correlations between various stellar parameters and their molecular content in Sect. 3.3, an analysis of the spatial distributions of SO and SO2 in Sect. 3.4, isotopic ratios for a subset of the molecules in Sect. 3.5, and a discussion of the unidentified lines in Sect. 3.6
3.1 Overview of molecular inventory
Across the variety of 17 AGB and RSG sources in the ATOM-IUM sample, we detect 287 molecular lines of which 29 remain unidentified. Emission from a total of 24 molecules has been identified, namely: AlCl, AlF, AlO, AlOH, CO, CN, CS, H2O, H2S, HC3N, HCN, KCl, NaCl, OH, PO, SO, SO2, SiC, SiC2, SiN, SiO, SiS, TiO, and TiO2; and 19 isotopologues thereof containing one or more of atoms of 13C, 170,29Si, 30Si, 33S, 34S, and37 C1.
This includes some first detections in oxygen-rich AGB and RSG stars:
PO in the vibrationally excited v = 1 transition, detected in the RSG AH Sco and the AGB stars IRC+10011, IRC-10529, R Hya, and S Pav.
SO2 in the high-energy vibrationally excited v2 = 2 and v1 = 1 transitions, detected in the RSGs AH Sco and VX Sgr, respectively.
Of the ten detected rotational transitions from various vibrational states of H2O, all but one are the first identifications in space, as is one high energy transition of OH (see Baudry et al. 2023, who also detect further OH transitions by stacking data).
and first detections in S-type AGB stars:
High vibrational level transitions of HCN v2 = 2, 3 in π1 Gru and W Aql. Vibrationally excited HCN has been studied for C-rich AGB stars by Jeste et al. (2022);
High vibrational level transitions of SiS v = 4,5,6 in π1 Gru and W Aql. Such high vibrational levels have previously been observed in CW Leo by Patel et al. (2011);
Two transitions of the SiS double isotopologue29 Si33 S in W Aql, previously observed in CW Leo by Patel et al. (2011);
Four transitions of HC3N in W Aql, confirming the tentative stacking detection by De Beck & Olofsson (2020);
One transition of SiC in W Aql, to be more thoroughly discussed in Danilovich et al. (2023). SiC has previously been detected in 12 C-rich sources by Massalkhi et al. (2018);
Several transitions of AlCl and one transition of AlF in W Aql, as discussed in Danilovich et al. (2021).
A visual overview of the molecules detected in each source can be seen in Fig. 1, where the sources are arranged in order of increasing mass-loss rate (note that molecules detected in only one source – TiO2 in VX Sgr; and AlCl, 13CN, SiN, SiC, SiC2, and HC3N in W Aql - are not included).
Looking at the overall molecular content, we can group together some similar sources:
The two S-type sources, π1 Gru and W Aql, are unsurprisingly different from the other, oxygen-rich sources. They are notably lacking in oxygen-bearing molecules, such as SO and SO2, and show a large number of SiS lines, however W Aql is significantly more molecule-rich than π1 Gru.
IRC + 10011 and IRC-10529 are very similar in molecular content, showing, for example, a range of Al - and Cl-bearing molecules, relatively few SO2 lines, and a relatively large number of SiS lines. GY Aql also has a similar molecular content to IRC+10011 and IRC-10529, though it shows comparatively more SO2 and fewer SiS lines.
Two sources are very line-poor: U Del and the RSG KW Sgr. Beyond the molecules seen in all sources (CO, SiO, HCN) these two sources only contain a single H2O line each and KW Sgr exhibits two SO lines. An explanation may lie in the lack of detection of high-v SiO lines (see below) in both sources, which may indicate weak shocks in the inner wind and hence post-shock temperatures too low to drive a rich chemistry and excite many of the high-v molecular lines. Furthermore, KW Sgr is a younger RSG than AH Sco or VX Sgr, with a spectral classification of M2, similar to Betelgeuse which is also known to be relatively poor in molecules (Huggins et al. 1994).
From Fig. 1 we can see that CO, HCN, and SiO are ubiquitous, as expected from previous studies, with similar numbers of lines detected in almost all sources (excepting the large number of vibrationally excited HCN lines in W Aql). All sources show vibrationally excited (up to v = 4) lines of SiO except the line-poor KW Sgr (up to v = 2) and U Del (up to v = 1), and also SV Aqr (up to v = 1). Three sources also show 30SiO lines up to v = 5: R Aql, R Hya, and S Pav. Note that the v = 5 transitions of the main SiO isotopologue were not covered by our observations. Many of the SiO lines have maser components, especially the high-v lines but also some v = 0 lines (Pimpanuwat et al., in prep.).
SO and SO2 are detected in a majority of sources, excepting the line-poor U Del and KW Sgr (in which SO but not SO2 is seen), and the S-type sources π1 Gru and W Aql. A large number of SO2 v = 0 and v2 = 1 lines are detected in many sources, and the two RSGs AH Sco and VX Sgr also show a few high-energy v1 = 1 or v2 = 2 transitions. SO2 is one of the most widespread species in our sample, partially due to its nature as an asymmetric top which exhibits many different energy levels throughout its energy ladder, which are fairly easily populated by radiation and collisions. The other sulfur-bearing molecules – H2S, SiS, and CS – are expected to have abundances that scale with mass-loss rate, and hence are more likely to be seen in high mass-loss-rate sources (Decin et al. 2018; Danilovich et al. 2017, 2018). Indeed, we only see H2S in the highest mass-loss-rate sources, but for SiS and CS there is no clear trend with mass-loss rate. Danilovich et al. (2016, 2020a) also found a difference in the spatial distributions of SO and SO2 in low-and high-mass-loss-rate sources, which is discussed further in Sect. 3.4.
SiS shows transitions from several isotopologues, and high-v lines (up to v = 5–6) are seen in both S-type sources, π1 Gru and W Aql, which are expected to have higher SiS abundances (Schöier et al. 2007; Danilovich et al. 2018). All other sources only show lines of SiS up to v = 1, except IRC+10011 and IRC-10529 where v = 3 is reached.
H2O is detected in all the sources in our sample except the two S-type stars, in several high-lying rotational transitions with lower state energy levels above ~3900 K, including high vibrational energy states. Four OH hyperfine split transitions with similar high energies (Elow ≳ 4800 K) are also detected. This includes many first detections of these transitions in space; they are discussed in detail in Baudry et al. (2023) and hence will not be extensively discussed here.
The halide-bearing molecules – AlF, NaCl, and KCl – are mostly found in high mass-loss-rate sources, although AlF (and AlOH) are also seen in the intermediate mass-loss-rate source U Her. Specifically the chlorine-bearing molecules KCl and NaCl are found only in IRC+10011, IRC-10529, and GY Aql. It is perhaps unexpected that the chlorides are missing in the RSGs AH Sco and VX Sgr, as NaCl is very strong in the RSG VY CMa (Tenenbaum et al. 2010; Quintana-Lacaci et al. 2023), however VY CMa is a more evolved RSG with a higher mass-loss rate than the RSGs in our sample. Furthermore, another chlorine-bearing molecule, AlCl, is only found in the S-type star W Aql, in which we do not detect NaCl or KCl, so AlCl seems to require different formation and/or excitation conditions.
W Aql is also the only source to show transitions of 13CN, SiN, SiC, SiC2, and HC3N (note 12CN was not covered by our observations). This is unsurprising as it is a bright, nearby S-type star with a fairly carbon-rich outflow (De Beck & Olofsson 2020). The other molecule only seen in a single source is TiO2 in VX Sgr, which may be because VX Sgr is the highest-mass-loss-rate source in our sample and so its denser wind may allow less abundant molecules to be detected.
 |
Fig. 1 Overview of how many lines of each molecule are detected in each source. The sources are listed in order of increasing mass-loss rate |
Maximum measured radial extent of each molecule across all sources.
3.2 Angular extents of molecules
While a full analysis of the spatial distributions of various molecules is beyond the scope of this paper, we found it useful as a first step to simply compare their observationally measured extents, as defined in Sect. 2.2. Table 4 shows the measured angular extent of each molecule across the 17 ATOMIUM sources. For each molecule, we have taken the maximum measured angular extent (rmax) in each source, and then give the range and median of these measurements in units of the stellar radius, R⋆ (see Table 1 for R⋆ values of each source). The maximum rmax for each molecule is also given in arcseconds. The maximum extents of CO are almost certainly underestimates because the emission of this molecule typically extends beyond the field of view of the observations.
Some of the smallest emission extents are found for the molecules TiO2, OH, AlOH, and AlF. It is not surprising that these molecules are mainly seen close to the star, in the densest part of the wind, as this is predicted by chemical models (Agúndez et al. 2020; Mangan et al. 2021), especially for the Al-bearing molecules which are expected to participate in dust formation. However, OH is a special case as the observed transitions all have very high lower state energies (Elow ≥ 4800 K) which will only be excited close to the star. In fact, 1.6 GHz OH maser emission has been measured up to ~ 100–1000 R⋆ in for example IRC+10011 and R Aql (Bowers et al. 1983), U Her (Chapman et al. 1994), and the RSG VX Sgr (Szymczak & Cohen 1997).
The largest angular extents, >1.5″, are mainly found for molecules which are seen in a majority of sources: CO, SiO, SO, SO2, CS, SiS, and HCN. However, for almost all molecules there are some sources where the maximum measured extent is very small. Which source it is varies by molecule, and its value is often an outlier among the sample. For example, in CO the smallest rmax of 29 R⋆ in the line-poor RSG KW Sgr is much smaller than the next smallest value of 530 R⋆ in AH Sco. V PsA has the smallest measured rmax in HCN, SO, and SO2; R Hya shows the smallest extents in SiS and CS; and the smallest measured rmax in SiO is in π1 Gru.
There are some interesting observations to be made from this summary from a chemical standpoint. First, AlO extends further out than AlOH, though this is only true for the RSGs VX Sgr and AH Sco, which have much larger AlO extents than the other sources: ≥100 R⋆. They also have the largest rmax in AlOH, at 45 and 8 R⋆, respectively – smaller than their AlO extents. This is unexpected as AlOH is formed from AlO (by reaction with H2O and H2), although AlOH is also easily photolysed back to AlO (Mangan et al. 2021). The other three AGB sources with detections of both AlOH and AlO show slightly larger extents in AlOH. So here we have a dichotomy between the RSG and AGB sources, where perhaps the photolysis of AlOH to AlO is more efficient in the RSGs explaining their large AlO extents.
Another surprising observation is that TiO extends further out than TiO2 in the only star where TiO2 is detected: the RSG VX Sgr. VX Sgr shows a maximum extent in TiO of 65 R⋆, larger than the 14 R⋆ extent in TiO2. This might indicate that TiO2 is depleted because it is taking part in the formation of dust particles in the inner wind.
3.3 Correlations
To get an overview of how the molecular content varies by source, we have calculated Kendall’s τb rank correlation coefficients (Kendall 1945) for various stellar parameters and the molecular content of each source. These are shown in Fig. 2. Kendall’s rank correlations are chosen as a non-parametric measure of correlation, that does not assume linear relationships between variables and is applicable to ordinal data. This allows us to use the differing number of detected lines of a given molecule as a (very rough) proxy for its relative abundance in different sources. The number of detected lines is a function of molecular parameters and excitation conditions as well as abundance, which we cannot properly take into account without radiative transfer modeling. However, by ranking the sources by the number of detected lines we can nevertheless determine which groups of molecules tend to coincide by having relatively large numbers of lines in the same sources. We also negate the need to normalize different molecules by the absolute number of potentially detectable lines in our frequency range. Many alternative techniques, such as Pearson’s correlations or principal component analysis, assume linear relationships between variables and hence are less applicable to our data at this initial analysis stage.
To calculate the Kendall’s τb correlation coefficients the sources were ranked (by measured value for stellar parameters and by number of detected lines for molecules) for each variable, and the ranks between every pair of variables were compared (adjusting for ties). This assesses how well the relationship between the two variables can be described by a monotonic function, that is, whether the first variable tends to increase as the second does and vice versa. The variables being correlated are the effective temperatures, mass-loss rates, terminal expansion velocities, and pulsation periods (as given in Table 1), and the number of lines detected for each molecule and its isotopologues. Molecules which are found in only one source (TiO2 in VX Sgr, and AlCl, HC3N, SKC2, SiN, and 13CN in W Aql) have not been included. Generally, we assume that a larger number of detected lines of a given molecule implies a higher molecular abundance; however there may be additional effects making the detection of, for example, highly vibrationally excited lines more likely. These will be discussed for each molecule in the following sections.
As we have more than ten sources to compare, the sampling distribution of Kendall’s τb is approximately a normal Gaussian distribution (Kendall 1938). We therefore use p-values1 corresponding to 1σ (p < 0.15865), 2σ (p < 0.02275), and 3σ (p < 0.00135) to determine which correlations are significant. We consider a correlation coefficient ≳0.5 to be a strong correlation, which is generally only seen for correlations with at least 2σ significance. Correlations with 3σ significance have coefficients ≥0.64 and hence will be termed very strong correlations. For simplicity, we use a single term to refer to both significance and strength of correlation, as they are strongly related, and will refer to correlations with 2σ significance as strong correlations, and those with 1σ significance as weak correlations. Figure 2 is colorized by the value of the correlation coefficient, with stronger positive correlations in a darker blue. For further visual differentiation, 3σ correlation coefficients are written in boldface, 2σ in regular font, and 1σ in small italics. Correlation coefficients with p-values above 0.15865 (that is lower than 1σ significance) are not included in our analysis or in the figure.
The molecular correlations with at least a 1σ significance were then used to calculate a dendrogram (see Fig. 3) of the hierarchical relationships between the different parameters, using the farthest point (a.k.a. complete linkage) algorithm for hierarchical clustering. This dendrogram shows which parameters are most similar to each other in terms of their correlations to all the other parameters, and groups them into seven clusters shown with different colors. Note that this grouping may split up pairs of parameters that are strongly correlated with each other but have dissimilar correlations with other parameters. These clusters are reflected in Fig. 2, and the calculated correlations will now be discussed cluster by cluster for simplicity.
Cluster 1: HCN and CO is shown with green lines in Fig. 3 and discussed in Sect. 3.3.1; Cluster 2: AlF, CS, H2S, and AlOH is shown with red lines and discussed in Sect. 3.3.2; Cluster 3: vexp and P is shown with cyan lines and discussed in Sect 3.3.3; Cluster 4: SiS, 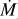 , NaCl, and KCl is shown with purple lines discussed in Sect 3.3.4; Cluster 5: AlO and SO is shown with yellow lines and discussed in Sect. 3.3.5; Cluster 6: PO, TiO, SO2, H2O, OH, and SiO is shown with black lines and discussed in Sect. 3.3.6; and Cluster 7: Teff is discussed in Sect. 3.3.7.
, NaCl, and KCl is shown with purple lines discussed in Sect 3.3.4; Cluster 5: AlO and SO is shown with yellow lines and discussed in Sect. 3.3.5; Cluster 6: PO, TiO, SO2, H2O, OH, and SiO is shown with black lines and discussed in Sect. 3.3.6; and Cluster 7: Teff is discussed in Sect. 3.3.7.
3.3.1 Cluster 1: HCN, CO
The first cluster contains the correlated molecules HCN and CO. For these molecules the v = 0 transitions of the main isotopologues are seen in all sources, so more detected lines means the detection of isotopologues (13CO, C17O, H13CN) or vibrationally excited transitions (CO v = 1; HCN v2 = 1, 2, 3; H13CN v2 = 1).
The isotopologues of HCN and CO tend to be detected in the same sources, as one might expect for both isotopologues with 13C. 13CO is detected in all sources except SV Aqr, and H13CN is detected in all sources except SV Aqr, U Del, and V PsA. C17O is only detected in two sources: IRC-10529 and W Aql. From this we can assume that SV Aqr, U Del, and V PsA either have relatively low 13C abundances or faint HCN emission, while IRC-10529 may have relatively high 17O abundances and W Aql is the source with by far the brightest emission in the main CO isotopologue. Similarly, the vibrationally excited transitions in HCN and CO tend to coincide. Vibrationally excited HCN is detected in six sources: IRC+10011, π1 Gru, R Hya, W Aql, and the RSGs AH Sco and VX Sgr, four of which also show vibrationally excited H13CN. These six sources are also among the 11 which show emission in the CO v = 1 line.
Detecting more lines of HCN and CO is correlated with more detected lines of AlF, CS, SiS, AlO, TiO, and SiO, as well as a higher mass-loss rate 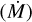 . Additionally, CO is correlated with detecting more lines of H2S, NaCl, KCl, and PO; while HCN is correlated with detecting more lines of AlOH, SO, and SO2, as well as a larger expansion velocity (vexp). The detection of more isotopologues and vibrationally excited lines of CO and HCN at higher mass-loss rates is due to a denser wind, and most of the correlated molecules are also preferentially seen in denser winds. Some of these molecules, such as SiS and H2S, are known tracers of higher mass-loss rate winds (Danilovich et al. 2017, 2018). Others, such as AlF, AlOH, AlO, and KCl, are expected to have fairly low abundances (Agúndez et al. 2020) and hence would only be detectable in a sufficiently dense wind. To further explain the observed correlations, a higher
. Additionally, CO is correlated with detecting more lines of H2S, NaCl, KCl, and PO; while HCN is correlated with detecting more lines of AlOH, SO, and SO2, as well as a larger expansion velocity (vexp). The detection of more isotopologues and vibrationally excited lines of CO and HCN at higher mass-loss rates is due to a denser wind, and most of the correlated molecules are also preferentially seen in denser winds. Some of these molecules, such as SiS and H2S, are known tracers of higher mass-loss rate winds (Danilovich et al. 2017, 2018). Others, such as AlF, AlOH, AlO, and KCl, are expected to have fairly low abundances (Agúndez et al. 2020) and hence would only be detectable in a sufficiently dense wind. To further explain the observed correlations, a higher 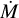 is also correlated with a higher expansion velocity, and some of the molecules like SiO, PO, and SO2 show vibrationally excited transitions in similar sources as vibrationally excited CO and HCN, which may imply these molecules are excited in similar regions of the wind.
is also correlated with a higher expansion velocity, and some of the molecules like SiO, PO, and SO2 show vibrationally excited transitions in similar sources as vibrationally excited CO and HCN, which may imply these molecules are excited in similar regions of the wind.
 |
Fig. 2 Kendall’s τb rank correlation coefficients between the expansion velocity (vexp), pulsation period (P), mass-loss rate |
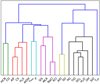 |
Fig. 3 Dendrogram of the correlations in Fig. 2, showing the hierarchical relationships between the different parameters. A closer connection point (lower down in the diagram) between two parameters signals a stronger relationship. The dark blue lines indicate the top-level division into seven clusters, and the other colors are simply to guide the eye in distinguishing between the different clusters. |
3.3.2 Cluster 2: AlF, CS, H2S, AlOH
The second cluster contains the molecules AlF, CS, H2S, and AlOH. AlF is detected in 7/17 sources – GY Aql, IRC+10011, IRC-10529, U Her, W Aql, and the RSGs AH Sco and VX Sgr – of which W Aql also shows the corresponding v = 1 transition. CS is detected in one transition in 10/17 sources, of which five sources also show a 13CS line: GY Aql, IRC+10011, IRC-10529, VX Sgr, and W Aql. H2S has one detected transition, in 5/17 sources: AH Sco, GY Aql, IRC+10011, IRC-10529, and VX Sgr. AlOH has two v = 0 transitions, and is detected in 5/17 sources: AH Sco, GY Aql, IRC+10011, U Her, and VX Sgr.
AlF and CS are very strongly correlated, with all five sources showing 13CS also detected in AlF. Further, all four molecules in this cluster are strongly correlated with each other and tend to be detected in the same sources. 4/5 sources showing H2S also show AlOH, and all sources with either molecule also show AlF. All four molecules are also correlated with a longer pulsation period (P), higher mass-loss rate 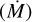 , and detecting more lines of SiS, NaCl, AlO, and SO. Three-out-of-four molecules are further correlated with detecting more lines of HCN, CO, KCl, and PO, as well as a larger expansion velocity (vexp).
, and detecting more lines of SiS, NaCl, AlO, and SO. Three-out-of-four molecules are further correlated with detecting more lines of HCN, CO, KCl, and PO, as well as a larger expansion velocity (vexp).
These correlations can largely be explained by the similarities between the four sources AH Sco, GY Aql, IRC+10011, and VX Sgr. These sources have the second to eighth longest periods, and highest to seventh highest mass-loss rates. They all show a fair number of SiS lines, and include two of the three sources with detections of NaCl (see Sect. 3.3.4). The RSGs AH Sco and VX Sgr are the two sources which show the most lines of both AlO and SO (see further discussion in Sect. 3.3.5). Regarding HCN and CO: all four sources show their 13C isotopologues and the CO v = 1 transition, three show vibrationally excited HCN and two also show vibrationally excited H13CN. IRC+10011 is one of two sources showing KCl emission. All four sources are among the 11 showing PO emission, and the group contains 2/5 sources showing vibrationally excited transitions of PO. Finally, these four sources have the third to ninth largest expansion velocities.
The strong correlation between AlOH and AlO is expected due to their close chemical coupling (Mangan et al. 2021; Gobrecht et al. 2022). The strong correlation between AlOH and AlF probably comes from AlF’s formation reaction AlOH + HF → AlF + H2O; and the correlation between AlO and AlF also follows from the lesser formation reaction AlO + HF → AlF + OH (Danilovich et al. 2021).
3.3.3 Cluster 3: vexp, P
The third cluster contains expansion velocity (vexp) and pulsation period (P), which are weakly correlated with each other. The clustering of these parameters is not unexpected, as for AGB stars both expansion velocity and pulsation period tend to increase as they evolve (Habing & Olofsson 2003), along with the mass-loss rate. In fact, for a constant and spherical mass loss we expect a perfect correlation between vexp and the mass-loss rate, so the correlation of 0.48 seen here is further evidence of wind asymmetries.
A larger expansion velocity and longer pulsation period is correlated with detecting more lines of AlF, H2S, AlOH, and SiS, as well as a larger mass-loss rate. The expansion velocity is also correlated with detecting more lines of HCN, while the pulsation period is correlated with detecting more lines of CS, AlO, and SO. As discussed in Sect. 3.3.1, most of these molecules are preferentially detected in a dense (higher 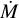 ) wind.
) wind.
3.3.4 Cluster 4: SiS, 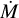 , NaCl, KCl
, NaCl, KCl
The fourth cluster contains the molecules SiS, NaCl, and KCl, along with the mass-loss rate 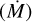 . NaCl is detected in three sources: GY Aql, IRC+10011, and IRC-10529, of which IRC+10011 and IRC-10529 also show vibrationally excited transitions and transitions of Na37Cl. KCl is detected only in these same two sources: IRC+10011 and IRC-10529. SiS is detected in 10/17 sources, while its various isotopologues of 29Si, 30Si, 33S, and 34S are detected in between five and seven sources, including GY Aql, IRC+10011, and IRC-10529. GY Aql also shows vibrationally excited transitions of SiS up to v = 1, while IRC+10011 and IRC-10529 show vibrationally excited transitions up to v = 3. The only sources showing higher vibrationally excited transitions of SiS (up to v = 6) are the two S-type sources π1 Gru and W Aql, which are expected to have higher SiS abundances (Danilovich et al. 2018), and also show transitions in all the isotopologues. Furthermore, IRC+10011, IRC-10529, GY Aql, π1 Gru, and W Aql have between the second and ninth highest mass-loss rates in our sample.
. NaCl is detected in three sources: GY Aql, IRC+10011, and IRC-10529, of which IRC+10011 and IRC-10529 also show vibrationally excited transitions and transitions of Na37Cl. KCl is detected only in these same two sources: IRC+10011 and IRC-10529. SiS is detected in 10/17 sources, while its various isotopologues of 29Si, 30Si, 33S, and 34S are detected in between five and seven sources, including GY Aql, IRC+10011, and IRC-10529. GY Aql also shows vibrationally excited transitions of SiS up to v = 1, while IRC+10011 and IRC-10529 show vibrationally excited transitions up to v = 3. The only sources showing higher vibrationally excited transitions of SiS (up to v = 6) are the two S-type sources π1 Gru and W Aql, which are expected to have higher SiS abundances (Danilovich et al. 2018), and also show transitions in all the isotopologues. Furthermore, IRC+10011, IRC-10529, GY Aql, π1 Gru, and W Aql have between the second and ninth highest mass-loss rates in our sample.
Detecting more lines of SiS and a higher mass-loss rate are correlated with detecting more lines of HCN, CO, AlF, CS, H2S, AlOH, and of course NaCl and KCl, along with larger expan sion velocities (vexp) and longer pulsation periods (P). These correlations can largely be explained by the molecular content of GY Aql, IRC+10011, IRC-10529, π1 Gru, and W Aql. As noted above, these sources show many lines of SiS and high mass-loss rates. Most of them are detected in vibrationally excited transi tions of HCN, and IRC-10529 and W Aql are the only sources to show a transition of the 17O isotopologue of CO. All but π1 Gru show transitions of AlF and CS, and they make up 3/5 and 2/5 of the sources showing transitions of H2S and AlOH, respec tively. When it comes to expansion velocities π1 Gru has by far the largest, and the other sources are up to the tenth largest. They also have the fourth to eighth longest periods, except π1 Gru which instead has one of the shortest periods in our sample. Fur thermore, as noted in Sect. 3.3.3, AGB stars tend to increase in mass-loss rate, expansion velocity, and pulsation period as they evolve, explaining their correlation.
Within this cluster, the chemically similar KCl and NaCl are very strongly correlated with each other. They are also correlated with detecting more lines of CO, AlF, CS, H2S, and PO. NaCl is additionally correlated with detecting more lines of AlOH. The strong correlation between KCl and NaCl is because they are both formed from reactions of the metal atom with HCl (Plane et al. 1989; Helmer & Plane 1993). The correlation with another halogen-bearing molecule, AlF, implies that these chem ically related molecules may coexist in similar environments in the stellar wind, though note that the only source where AlCl is detected, W Aql, does not show any transitions of KCl or NaCl. Through AlF the correlations with AlOH and the sulfur-bearing CS and H2S can be explained (see Sect. 3.3.2), and the correlation with PO may be due to the main sources containing NaCl and KCl – IRC+10011 and IRC-10529 – also showing all the detected PO transitions, although they are only 2/5 sources to do so.
3.3.5 Cluster 5: AlO, SO
The fifth cluster contains the molecules AlO and SO, which are strongly correlated with each other. AlO is detected in 9/17 sources of which four also show vibrationally excited transitions: R Aql, U Her, and the RSGs AH Sco and VX Sgr. SO is detected in 14/17 sources, ten of which also show 34SO. The less abun dant isotopologue33 SO is detected in five sources, and the single detected SO v = 1 transition is observed in seven sources. Of the sources showing transitions of AlO, the vast majority are detected in either both isotopologues or one isotopologue and the v = 1 transition of SO. Three of these sources – AH Sco, U Her, and VX Sgr – are seen in both SO isotopologues and its v = 1 transition.
The detection of more lines of AlO and SO is correlated with detecting more lines of HCN, AlF, CS, H2S, AlOH, PO, TiO, SO2, H2O, and OH, as well as longer pulsation periods (P). Additionally, detecting more lines of AlO is correlated with detecting more lines of CO and a higher mass-loss rate (Ṁ). Overall, AlO and SO are correlated with the other oxygen-bearing molecules, as expected, but also with the molecules in Cluster 1 (HCN, CO) and Cluster 2 (AlF, CS, H2S, AlOH). As explained in Sect 3.3.2, the strong correlation between AlO and AlOH stems from their close chemical coupling, but the chem ical links to SO and H2S are less clear. One might suspect a connection through the sulfur chemistry, as both AlO and SO are also correlated with CS, but neither is correlated with SiS. However, it may be that the conditions required to populate the higher energy levels of SiS (and hence have more detected lines of SiS) differ from the conditions that excite more transitions of (vibrationally excited) AlO and (vibrationally excited and/or isotopologues of) SO. Overall, both Cluster 1 and Cluster 2 molecules tend to have many detected lines in the three sources showing the most lines of AlO and SO – AH Sco, U Her, and VX Sgr – which may explain the correlations. The grouping of the low mass-loss rate AGB star U Her with the high mass-loss rate RSGs AH Sco and VX Sgr here is unexpected, and will be explored further in a future paper.
3.3.6 Cluster 6: PO, TiO, SO2, H2O, OH, SiO
The sixth cluster contains the remaining oxygen-bearing molecules: PO, TiO, SO2, H2O, OH, and SiO. A PO doublet is detected in 11/17 sources, of which five sources – IRC+10011, IRC-10529, R Hya, S Pav, and the RSG AH Sco – also show the corresponding v = 1 doublet. TiO is detected in 7/17 sources, with vibrationally excited transitions detected in three sources: R Hya, and the RSGs AH Sco and VX Sgr. SO2 is detected in 13/17 sources, with 34SO2 in nine sources and vibrationally excited transitions detected in seven sources. Six of these sources have detections of both 34SO2 and vibrationally excited SO2: AH Sco, R Aql, R Hya, RW Sco, U Her, and VX Sgr. H2O is detected in 15/17 sources, with intrinsically fainter and/or higher energy transitions in progressively fewer sources. OH is detected in 6/17 sources, of which five show both detected v = 0 doublets: R Aql, R Hya, S Pav, T Mic, and VX Sgr. SiO is detected in all sources: the main isotopologue in v = 0 and v = 1 and both 29SiO and 30SiO in a v = 0 transition. So more detected transi tions implies the detection of more highly vibrationally excited transitions: up to v = 4 in the main isotopologue, which is seen in 13/17 sources; up to 29SiO v = 3 which is seen in six sources – IRC+10011, IRC-10529, R Aql, R Hya, S Pav, and W Aql; and up to 30SiO v = 5 which is seen in four sources – IRC+10011, R Aql, R Hya, and S Pav.
The molecules in this cluster are all correlated with each other, as expected, and most also show correlations with the other oxygen-bearing molecules. PO, TiO, and SiO are corre lated with CO; PO, TiO, SO2, and H2O are correlated with AlOH; and all except SiO are correlated with AlO and SO.
PO is very strongly correlated with H2O, which supports experimental findings that the reaction of excited P atoms with H2O is a major formation route for PO (Douglas et al. 2022). The five sources with the most detected PO lines – that is the ones showing the v = 1 transition: AH Sco, IRC+10011, IRC-10529, R Hya, and S Pav – are also among the sources with the most detected H2O lines, including R Hya which is the only source to show all ten H2O transitions. Conversely, the six sources with no detected PO transitions – KW Sgr, π1 Gru, SV Aqr, U Del, V PsA, and W Aql – also show the fewest detected H2O lines. The two S-type sources, π1 Gru and W Aql, show neither PO nor H2O lines, and the others only have one to two H2O lines and are overall quite line-poor. However, from the dendrogram in Fig. 3 we can see that PO is less closely grouped with H2O than SO2, TiO, and OH are. This is likely due to PO showing correlations that H2O lacks with a range of molecules – CO, CS, H2S, NaCl, and KCl – in addition to their shared correlations with the other oxygen-bearing molecules. This may be mostly due to IRC+10011 and IRC-10529 which are, for example, two of the three sources with detected NaCl or KCl, and two of the five sources showing H2S. Conversely, in R Hya and S Pav, which show the most H2O lines, we do not detect any transitions of NaCl, KCl, or H2S.
Detecting more lines of TiO is correlated with detecting more lines of HCN, CO, and H2S, alongside its correlations with the other oxygen-bearing molecules. There are up to nine TiO lines, with vibrationally excited transitions in v = 1, with Elow values around 1500 K, and v = 2, with Elow values around 3000 K. Hence detecting more lines of TiO implies more vibrationally excited lines, as is also the case for HCN and CO. The three sources with the most TiO lines – AH Sco, R Hya, and VX Sgr – are also the only sources to show vibrationally excited TiO transitions. The 13C isotopologues of HCN and CO are detected in all three of these sources, as are the CO v = 1 and HCN v2 = 1 transitions. The vibrationally excited CO v = 1 has an Elow value around 3000 K, just as the v = 2 transitions of TiO do, and the HCN v2 = 1 transitions have Elow values around 1000 K, roughly similar to the v = 1 transitions of TiO. This implies that these vibrationally excited transitions may origi nate in similar regions of the circumstellar envelope, potentially explaining their correlation.
SO2 and H2O are very strongly correlated with each other, and SO2 is also very strongly correlated with SO. The four sources with the most transitions of SO2 – AH Sco, R Hya, U Her, and VX Sgr – are also the four with the most SO tran sitions: this includes transitions of its 33S and 34S isotopologues, as well as the one vibrationally excited SO transition. These four sources are also in the half of the sample with the most detected H2O transitions, as indeed are all seven of the sources with the most SO2 transitions.
SO2 and SO are chemically connected by the fast reaction SO + OH → SO2 + H (DeMore et al. 1997). As SO2 is created from SO, one would expect these molecules to be anti-correlated, but this is probably ameliorated by photolysis of SO2 back to SO. This reaction also helps explain the strong correlation between SO2 and OH, and its correlation with H2O as observationally the photodissociation of H2O into OH is linked with an abun dance peak in SO (Danilovich et al. 2016). We detect up to 66 lines of SO2 in our sources, with vibrational levels up to v2 = 2. A majority (~65%) of all the detected SO2 lines are in the v = 0 state, and most of the rest are in the v2 = 1 state. The energy of the lower transition level (Elow) values are up to 2300 K, with the v = 0 transitions spanning the whole range, while the v2 = 1 transitions have Elow values above 750 K, and the four v1 = 1 and three v2 = 2 transitions all have energies above 1500 K. The single vibrationally excited transition of SO has an Elow value around 1600 K. The 10 detected H2O lines have much higher Elow values (≥3900 K) and many are in vibrationally excited states. There is some indication that in sources with more detected transitions of SO2, SO, and H2O, these tran sitions are probing a hotter gas as they generally have high Elow values. However, the H2O transitions we can detect have much higher energies than any SO2 or SO transitions, implying they are probing a different region of the wind, and furthermore these sources also show more transitions of 33S and 34S isotopologues. Therefore, the strong correlations between SO2 and SO, and SO2 and H2O seem to also reflect increased abundances of all three molecules in certain sources.
OH only shows significant correlations with the other oxygen-bearing molecules: strong correlations with SO2, H2O, and TiO, and weak correlations with AlO, SO, PO, and SiO. The strong correlation between OH and SO2 can be explained by the fast SO2 formation reaction described above. OH and H2O are expected to be chemically related, we only detect transitions at high energies – ≥3900 K for H2O, and ≥4700 K for OH – which are likely to be excited in similar regions around the star. The strong correlation between OH and TiO is surpris ing from a chemical standpoint as they would be expected to be anti-correlated due to the fast reaction TiO + OH → TiO2 + H. However, the two molecules are not necessarily co-located even if they are found in the same sources, so this reaction may not be very prominent. The detection of TiO2 does not help resolve this issue as its transitions are inherently fairly weak, and hence not unexpectedly TiO2 is detected in only the highest mass-loss rate source, VX Sgr.
SiO shows strong correlations with CO, H2O, and PO; and weak correlations with larger pulsation amplitudes, and detect ing more lines of HCN, SO2, TiO, and OH. SiO is seen in every source due to its strong v = 0 and v = 1 lines, but some sources show more highly vibrationally excited transitions up to v = 5, and lines from the 29SiO and 30SiO isotopologues. The five sources with the most PO transitions – AH Sco, IRC+10011, IRC-10529, R Hya, and S Pav – are among the seven sources with the most SiO transitions. These sources also have among the most CO and H2O transitions. Most of the SiO transitions with v > 0 are dominated by maser emission and weak masers are seen even in v = 0 for some stars (Pimpanuwat et al., in prep.). The strong correlations with CO, H2O and PO may indi cate these high-v SiO masers, with Elow values up to ~8600 K, form in similar regions around the star as the high-energy lines of H2O and PO, and the v = 1 line of CO. Similarly, sources with more detected transitions of HCN, SO2, TiO, and Oh also tend to show vibrationally excited lines of these molecules, which may also form in similar regions.
3.3.7 Cluster 7: Teff
Finally, we have a cluster containing only the effective tempera ture of the star, Teff, which shows the only significant negative correlation: a weak negative correlation with detecting more lines of AlOH. There are two detected lines of AlOH, and both are low energy v = 0 transitions. Two lines of AlOH are detected in GY Aql, IRC+10011, and the RSG VX Sgr, while a single line is detected in U Her and the RSG AH Sco. GY Aql, IRC+10011, and U Her have effective temperatures at or below the median value for our sources, while the RSGs VX Sgr and AH Sco have the highest effective temperatures. So this negative correlation between effective temperature and detections of AlOH seems to mainly hold for AGB sources. The correlation might potentially be explained by a relative lack of alumina dust (and hence more free Al to form AlOH) in these sources. There is some evidence for alumina dust being the major dust component in warmer semi-regular variable AGB stars, as it can form and survive at higher temperatures than silicate dust (Gobrecht et al. 2016, and references therein), and GY Aql, IRC+10011, and U Her are all relatively cool Mira variables.
3.4 SO and SO2 spatial distributions
While a full analysis of the spatially resolved molecular data, including a radiative transfer analysis to obtain molecular abun dance distributions, is beyond the scope of this paper, we have performed an initial analysis of the spatial distributions of SO and SO2 and how they relate to the mass-loss rate of the source. As was first put forward by Danilovich et al. (2016), there are two classes of SO distributions around AGB stars. For the lower mass-loss rate stars, the SO abundance peak is centred on the star, whereas for the higher mass-loss rate AGB stars, the rela tive SO abundance has a shell-like distribution. Danilovich et al. (2016) found that the e-folding radius (the radius at which the abundance has dropped by a factor of 1/e) of SO for the low mass-loss rate stars and the radius of the abundance peak for the higher mass-loss rate stars closely corresponded to the photodissociation radius of H2O (that is, the radius at which the abundance of OH, the photodissociation product of H2O, peaks – see the empirical relation from Netzer & Knapp 1987; Maercker et al. 2016). This was interpreted to be the result of different SO formation pathways with varying wind density. A similar analysis could not be performed in that work for SO2 since there were not enough detected lines for the higher mass-loss rate stars.
Here, we carefully examine the data to ascertain whether our observations are consistent with the distributions first pro posed by Danilovich et al. (2016). Hence we must define the two classes of SO and SO2 distributions observationally. We con sider a centralized SO or SO2 distribution to be one where, for the majority of detected lines, the peak of the molecular emission in centred on the continuum peak and decreases monotonically with distance from the star. Conversely, for a shell-like distribu tion, the molecular emission for most lines does not decrease uniformly with angular distance from the star: the radial dis tribution is either flat or shows a second peak offset from the continuum peak and often associated with a (broken) ring-like structure. The shell-like distributions may be apparent in inte grated intensity maps, but are generally more clearly seen in channel maps (see Appendix B). They are also more clearly detectable in lower-energy lines.
SO and SO2 were detected for most of the stars in the ATOM-IUM sample. The only stars without SO and SO2 detections are the two S-type stars, W Aql and π1 Gru, and the line-poor U Del. The line-poor RSG KW Sgr was detected in SO but not in SO2. Henceforth, when referring to “all” stars in discussing SO and SO2 detections, these sources are not included.
In Appendix B we show channel maps of the bright SO2 v = 0 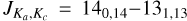 line at 244.254 GHz in all the sources. The channel maps of R Aql, GY Aql, IRC-10529, and IRC+10011 (Figs. B.7–B.10), as well as VX Sgr (Fig. B.12), clearly show an overall shell-like structure. A similar shell-like structure is also seen for SO in these sources (shown around R Aql in the v = 0 NJ = 55 −44 line at 215.221 GHz in Fig. B.13), but the SO emission is brighter closer to the continuum peak – that is, the star itself – with fainter extended structures dis tributed similarly to the SO2. These minor differences suggest that SO2 is predominantly found further from the star than SO is, which could be the result of SO2 being a daughter species (formed from SO) for this group of stars. A similar trend is not seen for the stars with centralized SO2 emission, where SO and SO2 are both distributed similarly close to the continuum peaks. If anything, there is a slight tendency among the centralized SO2 sources for the SO emission to be more extended than the SO2 emission, but this could be a result of different abundances, some SO lines being inherently brighter than many SO2 lines, or differing excitation conditions between the examined lines.
line at 244.254 GHz in all the sources. The channel maps of R Aql, GY Aql, IRC-10529, and IRC+10011 (Figs. B.7–B.10), as well as VX Sgr (Fig. B.12), clearly show an overall shell-like structure. A similar shell-like structure is also seen for SO in these sources (shown around R Aql in the v = 0 NJ = 55 −44 line at 215.221 GHz in Fig. B.13), but the SO emission is brighter closer to the continuum peak – that is, the star itself – with fainter extended structures dis tributed similarly to the SO2. These minor differences suggest that SO2 is predominantly found further from the star than SO is, which could be the result of SO2 being a daughter species (formed from SO) for this group of stars. A similar trend is not seen for the stars with centralized SO2 emission, where SO and SO2 are both distributed similarly close to the continuum peaks. If anything, there is a slight tendency among the centralized SO2 sources for the SO emission to be more extended than the SO2 emission, but this could be a result of different abundances, some SO lines being inherently brighter than many SO2 lines, or differing excitation conditions between the examined lines.
3.4.1 AGB stars
The two brightest SO lines covered by our frequency setup are NJ = 55 − 44 at 215.221 GHz and NJ = 65 − 54 at 251.826 GHz, the two lines with ΔN = ΔJ = −1 and v = 0. These two lines are detected for all 14 stars with any SO detections. Overall six SO lines in the v = 0 vibrational ground state are detected in our sample, with Elow ~ 10–90 K. The most energetic line detected in our sample is the NJ = 67 − 56 line at 259.857 GHz (Elow = 1635 K) in the first vibrationally excited state (v = 1), which was detected for ten stars. The only other line in v = 1 that was covered by our observations has a predicted intensity (fol lowing the intensity calculations of Pickett et al. 1998, at 300 K) almost three orders of magnitude lower than the detected line, so we do not expect to detect it. With such a small number of SO lines covered over a relatively narrow range of energies, aside from the single line in v = 1, it is difficult to draw any firm con clusions about trends across the sample. Without a more detailed analysis involving radiative transfer modelling, which is beyond the scope of the present work, we cannot easily determine which lines were not detected for a particular source because of exci tation conditions in the CSE or because of the sensitivity of our observations.
SO2 gives us more opportunity for such an analysis since many more lines, coming from a wide range of energy levels, fall in the covered frequency range and many of these were detected by our observations. One source, V PsA shows only two detected SO2 lines: 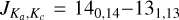 at 244.254 GHz and
at 244.254 GHz and 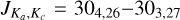 at 259.599 GHz. These are the lines with the highest predicted intensities (at 300 K) suggesting that sensitivity is the main limitation to detecting further SO2 lines. With so few lines, we cannot draw any further conclusions for V PsA and exclude it from further discussion of SO2. The other ten AGB stars for which we detect SO2 (GY Aql, IRC+10011,
at 259.599 GHz. These are the lines with the highest predicted intensities (at 300 K) suggesting that sensitivity is the main limitation to detecting further SO2 lines. With so few lines, we cannot draw any further conclusions for V PsA and exclude it from further discussion of SO2. The other ten AGB stars for which we detect SO2 (GY Aql, IRC+10011,
IRC–10529, R Aql, R Hya, RW Sco, S Pav, SV Aqr, T Mic, and U Her), all have detections of at least six lines in the ground vibrational state (with 30 K ≤ Elow≤ 280 K). Four stars (R Aql, R Hya, U Her and S Pav) also have detections of at least four lines in the v2 = 1 vibrational state.
The observational categories defined above, with shell-like or centralized SO2 distributions, approximately correspond to the categories put forward by Danilovich et al. (2016) for SO, and are applicable to SO2 as the emission of these two molecules for the same star tends to be broadly similar. Ordering the sources with SO2 detections by mass-loss rate, as in Table 5, shows a general tendency for the low mass-loss-rate sources to have centralized distributions and higher mass-loss-rate sources to have shell-like distributions. We note, however, that the mass-loss rates for many of the stars in the ATOMIUM sample are uncertain (see Sect. 2.3).
From an examination of the detected SO2 lines for each AGB source, we also found a tendency for the sources with shell like emission to be detected in lower-energy SO2 lines, while the sources with centralized emission tended to be detected in more higher-energy lines (in addition to the lower-energy lines). Three out of the six stars with centralized distributions (R Hya, U Her and S Pav) also show vibrationally excited emission. In contrast, only one star with shell-like emission (R Aql) has vibrationally excited SO2 detections. Furthermore, some of the highest energy SO2 lines in the ground vibrational state (such as 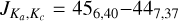 at 229.750 GHz with Elow = 1034 K) are only detected in the centralized AGB sources. To quantify this trend, Table 5 includes the average of the lower energy levels of each detected line for each star. Overall, there is a trend for the sources with a shell-like distribution to have lower median Elow values than the sources with a centralized distribution. This trend is confounded by RW Sco and SV Aqr, two centralized sources with median Elow values below 100 K. However, these sources both show faint SO2 emission, making the classification of their emission distribution more difficult. They also have the fewest SO2 detections among the centralized sources, tending to show only the brightest SO2 lines which generally have low Elow values.
at 229.750 GHz with Elow = 1034 K) are only detected in the centralized AGB sources. To quantify this trend, Table 5 includes the average of the lower energy levels of each detected line for each star. Overall, there is a trend for the sources with a shell-like distribution to have lower median Elow values than the sources with a centralized distribution. This trend is confounded by RW Sco and SV Aqr, two centralized sources with median Elow values below 100 K. However, these sources both show faint SO2 emission, making the classification of their emission distribution more difficult. They also have the fewest SO2 detections among the centralized sources, tending to show only the brightest SO2 lines which generally have low Elow values.
The observed trend between SO2 line energy and spatial dis tribution is not a consequence of naturally having greater spatial resolution for the nearest sources, since our two most distant sources (IRC–10529 and IRC+10011 see Table 1) have shell like distributions of SO2 lines, while two of the nearest sources (T Mic and R Hya) have centralized SO2 lines. It is also not caused by lines with different energies being excited at differ ent distances from the star, since this dichotomy holds if we use only the 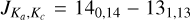 line at 244.254 GHz, which is one of the brightest and most frequently detected lines, to make the determination. We also note that there is a general tendency for centralized sources to have more SO2 lines detected than the shell-like sources: the maximum radial extent of SO2 is found to be negatively correlated (r ~ −0.3) with the median Elow val ues and the number of SO2 lines detected in each source. This is most likely a consequence of the excitation conditions. The SO2 in centralized sources is found closer to the star and hence in a warmer environment, while a significant portion of the shell-like emission originates further out in a cooler region of the wind. At higher temperatures where there are more potential SO2 transi tions to be excited, and hence unsurprising that more (and more energetic) SO2 lines are detected.
line at 244.254 GHz, which is one of the brightest and most frequently detected lines, to make the determination. We also note that there is a general tendency for centralized sources to have more SO2 lines detected than the shell-like sources: the maximum radial extent of SO2 is found to be negatively correlated (r ~ −0.3) with the median Elow val ues and the number of SO2 lines detected in each source. This is most likely a consequence of the excitation conditions. The SO2 in centralized sources is found closer to the star and hence in a warmer environment, while a significant portion of the shell-like emission originates further out in a cooler region of the wind. At higher temperatures where there are more potential SO2 transi tions to be excited, and hence unsurprising that more (and more energetic) SO2 lines are detected.
We can also compare the measured extents of SO2 in our AGB sources with what is expected from the chemical model of Van de Sande et al. (2018), for which calculations for each ATOMIUM source (using the stellar parameters in Table 1) is shown in Fig. 4. The sources are arranged as in Table 5, in order of increasing mass-loss rate, and for each the colored bar shows the modeled e-folding radius of the SO2 abundance, and the black line the maximum measured 3σ extent of SO2 lines from our observations. The chemical model assumes a power-law tem perature profile with exponent ɛ, as implemented in Van de Sande et al. (2018) and Maes et al. (2023):
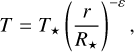 (2)
(2)
where T★ is the surface temperature of the AGB star and R★ the stellar radius. As the temperature profile in the outflows is gen erally not known, a range of models with different temperature profiles, varying ɛ from 0.3 to 1.0 (in steps of 0.05), were calcu lated. This range of models is included in Fig. 4 as an uncertainty on the model result.
An increase in the SO2 radius with increasing mass-loss rate is clearly seen from the model results, and the observationally measured extents broadly follow the same trend. In general, the measured SO2 extents are larger than the modeled e-folding radii, and some discrepancy is expected when comparing mod eled abundances with measured emission intensities, which does not take, for example, excitation effects into account. There are, however, two significant outliers: RW Sco which has a much larger measured SO2 extent than expected from the models, and R Hya whose measured extent is much smaller than expected. There are several reasons to suspect the mass-loss rate we use for RW Sco is underestimated, which would explain its larger mea sured extent. First, its SO2 distribution is shell-like rather than centralized, suggesting it should have a relatively high mass-loss rate to follow the SO2 distribution trend. Second, the mass-loss rate value is taken from Groenewegen et al. (1999), who use an empirical formula from Olofsson et al. (1993) linking the integrated CO intensity with the mass-loss rate. Olofsson et al. (1993) see evidence that their formula underestimates the mass-loss rates for low mass-loss rate objects, like RW Sco. This is in addition to the inherent uncertainties in the formula, which are a factor of ~5. The discrepancy between the measured extent of SO2 and the prediction from the chemical model is further evidence that the mass-loss rate of RW Sco may be underesti mated. As for the unexpectedly small observed extent of SO2 in R Hya, its geometry may provide an explanation: Homan et al. (2021) find evidence for an equatorial density enhance ment, and possible rotating disk, in the inner 0.4″ of the wind, which corresponds to ~35 R★. This is similar to the maxi mum measured extent of SO2 (51 R★), so it may be that SO2 is largely confined to this disk, or not abundant enough to be detected outside it. Furthermore, the equatorial density enhance ment increases the uncertainty of the calculated mass-loss rate by a factor of a few (El Mellah et al. 2020). Some discrep ancy may also be caused by the limitations of the chemical model: it assumes a smooth, spherically symmetric outflow, with a constant expansion velocity and mass-loss rate. R Hya, with its equatorial density enhancement, deviates significantly from these assumptions. Additionally, most of the ATOMIUM sources show additional structure or deviations from spherical symmetry (Decin et al. 2020; Gottlieb et al. 2022) which may affect the chemistry in the wind.
SO2 spatial distributions, radial extents, and median lower level energies in all sources.
 |
Fig. 4 Emission sizes of SO2 as expected from chemical models, and our maximum measured line extents, for each source. |
3.4.2 RSG stars
The two red supergiants, VX Sgr and AH Sco, are detected in seven and six SO transitions, respectively, out of the seven total detected in ATOMIUM. They are also extensively detected in SO2, with more than 45 lines seen for each star, and approx imately a third of this count lying in the v2 = 1 excited state. There are additionally three tentative detections of SO2 towards AH Sco in the v2 = 2 state and four tentative detections towards VX Sgr in the v1 = 1 state. Previous studies of the more mas sive and highly evolved red supergiants VY CMa and NML Cyg (Adande et al. 2013; Andrews et al. 2022) report asymmetric and localised emission for both stars, including multiple components of SO and SO2. In contrast, when considering only the lower-energy ground vibrational state SO and SO2 emission observed by ATOMIUM, we do not see directed outflows for VX Sgr or AH Sco. Based on observations of other molecular lines, it is likely that both of these stars have complex circumstellar struc tures. However, when considering only the SO and SO2 lines, we can place both RSGs into the categories we have defined here for AGB stars: VX Sgr has shell-like SO2 and SO emission, while AH Sco has more uniform emission resembling the centralized AGB stars. Since both stars have high mass-loss rates and many high-energy SO2 line detections, making them the two stars with the highest mean energy levels across the SO2 lines, they do not fit the trends observed for AGB stars. In light of this and the pre vious studies of SO and SO2 for RSGs, it is likely that different factors contribute to RSG SO and SO2 distributions, possibly including different formation mechanisms, compared with the AGB stars. However, a more detailed analysis of the ATOMIUM RSGs is beyond the scope of this paper.
3.5 Isotopic ratios
In order to calculate molecular abundances from our obser vational data, extensive radiative transfer modeling would be required. However, with a few assumptions we can calculate iso-topic ratios from observations of different isotopologues in the same transitions. These ratios provide constrains on the nucle osynthesis within AGB and RSG stars, their stellar mass and age, and the Galactic environment in which they were born. We have limited the calculation of isotopic ratios to pairs of transitions in v = 0 with at least one minor isotope in both molecules, to avoid the problem of potential missing flux or high optical depth in the main isotopologue lines. Hence we assume all the lines used to calculate isotopic ratios are optically thin and have no miss ing flux; assumptions which are supported by their narrow line shapes and limited angular extents. We have also checked that the chosen lines don’t appear to be masing, as none are exces sively bright or narrow. In practise, this limits us to calculations with isotopologues of SiS, as some lines of for example SiO isotopologues fall outside our observed frequency ranges.
We also need to account for the differences in line strength between different isotopologues, so to calculate the isotopic ratio between example isotopologues aX and bX we have used the following formula (Danilovich et al. 2020b):
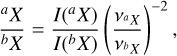 (3)
(3)
where I is the integrated intensity and v the transition frequency for each isotopologue. For each pair of transitions we measured the integrated intensity in the spectrum where the sum of the intensities of both transitions is maximized. By taking the inte grated intensities from spectra extracted at the same angular resolution and aperture size, the beam filling factors should be the same for both transitions. The calculated ratios are given in Table 6. In cases where an isotopic ratio can be calculated from multiple pairs of transitions for a single source, Table 6 contains the weighted average of these ratios.
The silicon 29Si/30Si isotopic ratios are found to be generally in the range 1–2 for our oxygen-rich and S-type AGB stars, with the RSG VX Sgr showing a larger ratio of ~4. Previously mea sured values in oxygen-rich sources are also in the range 1–2: 1.7 in IK Tau (Danilovich et al. 2019); 1.58 in R Dor (De Beck & Olofsson 2018); between 0.99 and 1.35 in a sample of ten M-type AGB stars, and around 1.5 in two RSG stars (Peng et al. 2013). The solar value of 1.52 (Asplund et al. 2021) is similarly in the same range as the AGB stars.
The high29 Si/30 Si ratio of 4 ± 1 measured in VX Sgr is out side the range of almost all measured Si ratios in evolved stars and in the local galaxy in general. 29Si/30Si ratios measured from presolar SiC grains are all close to the solar ratio of 1.52 (Zinner et al. 2006), as are measurements of various sources at different Galactic radii (Monson et al. 2017). The only literature ratio we were able to find that matches VX Sgr are ratios ~ 1–10 from infrared observations of the red giant EU Del (Pavlenko et al. 2020). EU Del is a very low-mass and metal-poor star, located below the tip of the red giant branch (McDonald et al. 2016), so it is not similar to the high mass-loss rate RSG VX Sgr. 29Si/30Si ratios above 2 have also been measured in the AGB stars x Cyg (2.4) and V1111 Oph (2.9) by Ukita & Kaifu (1988), as well as a measured value of 3 ± 1.5 in IK Tau by Decin et al. (2010), consistent with the value of 1.7 cited above. We note that VX Sgr has been shown to have some puzzling characteristics (Tabernero et al. 2021), so this anomalous 29Si/30Si ratio may be another signature of its odd nature.
For most oxygen-rich AGB stars we do not expect the 29Si/30Si ratio to change during the AGB phase (Zinner et al. 2006), so the measured ratios reflect those from the stars’ natal clouds. The primary isotope of silicon, 28Si, is an α-process element, while the two isotopes 29Si and 30Si form largely from 25Mg and 26Mg during Ne burning, which creates simi lar amounts of both isotopes (within a factor ~1.5, Woosley & Weaver 1995), as well as during core-collapse Type II super-novae. According to the models of Kobayashi et al. (2011),29 Si/30 Si ratios of ~2–4 can be formed in the core-collapse super-novae of 25–30 M⊙ progenitors, though the supernovae of both lower and higher mass progenitors produce much lower ratios. Some 29Si and 30Si also forms from 28Si in the He-burning shells of AGB stars, but in small and similar amounts (Monson et al. 2017).
The sulfur 33S/34S isotopic ratio is only measured in the S-type star W Aql, where it is found to be 0.4 ± 0.3. This ratio has been measured to be 0.19 ± 0.03 in IK Tau (Danilovich et al. 2019), and 0.17 ± 0.02 in R Dor (Danilovich et al. 2020b). The solar value is 0.17 (Asplund et al. 2021), consistent with the two oxygen-rich AGB stars and also with W Aql within the uncertainties.
The sulfur 34S/32S isotopic ratio is found to be 0.06 ± 0.02 in the S-type star W Aql, and 0.04 ± 0.02 and 0.11 ± 0.06 in IRC+10011 and IRC-10529, two high mass-loss rate oxygen-rich sources. A slightly lower ratio of 0.03 is found in IK Tau (Danilovich et al. 2019), while a value of 0.04 is found in the oxygen-rich RN Cnc (Winters et al. 2022), and both R Dor and the Sun have similar values of 0.05 (Danilovich et al. 2020b; Asplund et al. 2021). Hence all our measured 34S/32S ratios are consistent with the solar value, within uncertainties.
Both the main sulfur isotope 32S and the second most abundant isotope 34S are primarily produced through explosive nucleosynthesis during Type II supernovae, so these values measured in AGB stars reflect the abundances in the stars’ natal clouds. However, the abundance of the 33S isotope may increase during the AGB phase via the slow neutron capture process (Anders & Grevesse 1989). This is consistent with its detection in the S-type star W Aql, which is more evolved than the oxygen-rich stars in our sample.
Isotopic ratios calculated from single and double isotopologues of SiS.
3.6 Unidentified lines
Table A.4 lists the 28 unidentified lines in the ATOMIUM sample, and in which sources they are detected. Four of these lines -U221.507, U254.791, U255.023, and U259.329 - are coincident with calculated lines of SO2 in its v3=1 state. The lines were observed toward stars with SO2 lines in v = 0 and v2 = 1 such that the assignments appear to be reasonable. On the other hand, except for S Pav, toward which two such lines were detected, only one line was detected for the other stars and none of these stars displayed emissions in v2 = 2 or v1 = 1. We would therefore have to invoke very selective excitations, which appears to be too speculative at present even if this cannot be ruled out entirely. Therefore, we refrain from viewing these assignments even as tentative ones.
U253.973, seen in AH Sco, IRC-10529, and VX Sgr, is possibly due to NS, a blend of its ν = 0 J = 11/2 − 9/2, Ω = 1/2, F = 13/2 − 11/2f transition at 253.968 GHz, and J = 11/2 − 9/2, Ω = 1/2, F = 11/2 − 9/2f at 253.971 GHz. Facts in favor of this assignment are that these are the brightest NS lines covered by our observations, and the NS molecule has been detected in IK Tau (Velilla Prieto et al. 2017). Unfortunately, the corresponding F = 13/2 − 11/2e and F = 11/2 − 9/2e transitions around 253.570 GHz are not covered by our observations, and the U-line is blended with an SO2 line in AH Sco and VX Sgr, making the assignment to NS very tentative.
Comparing all the U-line frequencies with the rotational lines of the following species – MgO, CaO, NaO, FeO, ZrO, MgOH, CaOH, NaOH, ZrS, MgS, and CaS – we tentatively conclude that there is no evidence for new metal oxides, hydroxides, and sulfides in the ATOMIUM survey. Furthermore, we would not expect most of these species to exist at observable levels because of the high concentrations of H and H2 in the winds of these stars (Decin et al. 2018).
4 Conclusions
We have observed 17 oxygen-rich AGB and RSG sources at high angular resolution (0.02″ −0.05″), and complementary lower resolutions (up to 1.4″), with the ALMA interferometer as part of the ATOMIUM Large Programme, detecting 291 transitions of 24 different molecules and their isotopologues.
We find a range of conclusions, both major and minor:
We have first detections in oxygen-rich AGB and RSG stars of several vibrationally excited transitions: PO ν = 1, SO2 v1 = 1 and v2 = 2, and high energy H2O transitions (as examined in more detail in Baudry et al. 2023).
We also have several first detections in S-type AGB stars: vibrationally excited HCN v2 = 2, 3 and SiS v = 4, 5, 6; as well as first detections of the molecules SiC, AlCl, and AlF in W Aql (Danilovich et al. 2021, 2023, as examined in more detail in).
We have calculated correlations between the molecular content of different sources, finding strong correlations (with 3σ significance and correlation coefficients above 0.64) between sources with more detected lines of: CS and SiS, CS and AlF, NaCl and KCl, AlO and SO, SO2 and SO, an SO2 and H2O. Some of these correlations are expected from previous results (for example, CS and SiS both trace more dense winds) or chemical reactions (for example, NaCl and KCl both form from reactions of the metal atom with HCl), while the correlations of, for example, CS and AlF, or AlO and SO, have less clear origins:
Two of our sources are found to be extremely line-poor: the AGB star U Del and the RSG KW Sgr. We speculate this may be indicative of weak shocks in the inner wind;
The spatial distributions of SO and SO2 are found to be generally consistent with previous results, with a centralized distribution for low mass-loss rate sources and a shell-like distribution for high mass-loss rate sources;
The isotopic ratios of Si and S are generally in line with previously measured ratios (including solar ratios) except for an anomalously high 29Si/30Si ratio of 4 ± 1 in the RSG VX Sgr.
This paper has presented the overall molecular inventory and an initial analysis of the large ATOMIUM dataset, laying the groundwork for future work deriving molecular abundances and abundance profiles using radiative transfer modeling which will provide more rigorous tests for chemical models.
Acknowledgements
We thank the referee for their helpful comments improving the manuscript, and Kelvin Lee for his contributions to the line identification strategy. S.H.J.W. acknowledges support from the Research Foundation Flanders (FWO) through grant 1285221N, and the ERC consolidator grant 646758 AEROSOL. T.D. acknowledges support from the Research Foundation Flanders (FWO) through grant 12N9920N, and the Australian Research Council through a Discovery Early Career Researcher Award (DE230100183). H.S.P.M. acknowledges support by the Deutsche Forschungsgemeinschaft through the collaborative research grant SFB 956 (project ID 184018867). S.M. and L.D. acknowledge support from the ERC consolidator grant 646758 AEROSOL, from the KU Leuven C1 excellence grant C16/17/007 MAESTRO, and from the FWO research grant 6099720N. M.V.d.S. acknowledges support from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 882991. A.B. and F.H. acknowledge funding from the French National Research Agency (ANR) project PEPPER (ANR-20-CE31-0002). D.G. was funded by the project grant ‘The Origin and Fate of Dust in Our Universe’ from the Knut and Alice Wallenberg Foundation. M.M. acknowledges funding from the Programme Paris Region fellowship supported by the Région Ile-de-France. J.M.C.P. was supported by STFC grant number ST/T000287/1. R.S.’s contribution to the research described in this publication was carried out at the Jet Propulsion Laboratory, California Institute of Technology, under a contract with NASA. K.T.W. acknowledges support from the ERC under the European Union’s Horizon 2020 research and innovation programme (Grant agreement no. 883867, project EXWINGS). This paper makes use of the following ALMA data: ADS/JAO.ALMA#2018.1.00659.L. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada), NSC and ASIAA (Taiwan), an KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. We also acknowledge excellent support from the UK ALMA Regional Centre (UK ARC), which is hosted by the Jodrell Bank Centre for Astrophysics (JBCA) at the University of Manchester. The UK ARC Node is supported by STFC Grant ST/P000827/1. This project has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie Grant agreement No. 945298, and was supported in part by the Australian Research Council Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D) through project number CE170100013. This work has made use of Python packages Astropy (Robitaille et al. 2013; Price-Whelan et al. 2018, 2022), SciPy (Virtanen et al. 2020), pandas (McKinney 2010), NumPy (Harris et al. 2020), and Matplotlib (Hunter 2007).
Appendix A Molecular data, line identifications and measured parameters
Appendix A.1 Laboratory spectroscopic background on line identifications
Spectroscopic data were retrieved from the Cologne Database for Molecular Spectroscopy, CDMS,2 (Müller et al. 2001; Müller et al. 2005; Endres et al. 2016) unless stated otherwise. Several of the accessed entries were created, updated, or extended in vibrational quanta υ to support the ATOMIUM project. While all of the relevant laboratory or observational data were considered for these entries, other data are not always up-to-date. We mention only cases in which our observations may be affected. We usually list the most important references for species with more than one line in ATOMIUM, possibly supplemented by references for data that encompass the ATOMIUM frequency range or are close to it. We list in Table A.3 references of lines identified in ATOMIUM; we may refrain from listing additional background information for species with only one or two lines in ATOMIUM.
We point out that Hund’s case (b) quantum numbers are given in the CDMS catalog throughout because of the spfit and spcat programs (Pickett 1991) employed for most of the CDMS entries. Hund’s case (a) quantum numbers may be more appropriate for some of the radical species, and these are listed in most cases in Table A.3. The CDMS documentation file usually contains information on how to convert Hund’s case (b) quantum numbers to Hund’s case (a). The quantum numbers N, J, and F indicate the total rotational angular momentum, the total rotational angular momentum including the electronic spin, and the total rotational angular momentum including the electronic and nuclear spin, respectively. For non-radicals, J = N, and J is usually given instead of N. The quantum numbers Ka and Kc designate projection of the total rotational angular momentum onto the a- and c-axis, respectively, in the case of asymmetric top molecules such as SO2, H2O, TiO2, and SiC2. Rotational levels are usually designated as 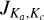 . Vibrational quanta are usually designated with υ; a subscript indicated the number of the vibrational mode. The triply excited bending mode of a triatomic molecule is indicated as υ2 = 3. Multiple excitations of triatomics, for example, υ2 = 3, υ3 = 1, are often given as triple (υ1υ2υ3), where υ; indicates the excitation in the vibrational mode i; in the above case (031). The Greek letter ν is used to designate vibrational bands; ν1 could also be witten as (100) − (000) and v1 − v3 as (100) − (001).
. Vibrational quanta are usually designated with υ; a subscript indicated the number of the vibrational mode. The triply excited bending mode of a triatomic molecule is indicated as υ2 = 3. Multiple excitations of triatomics, for example, υ2 = 3, υ3 = 1, are often given as triple (υ1υ2υ3), where υ; indicates the excitation in the vibrational mode i; in the above case (031). The Greek letter ν is used to designate vibrational bands; ν1 could also be witten as (100) − (000) and v1 − v3 as (100) − (001).
The references for CO, CS, H2S, and 13CN are given in Table A.3 only.
The HCN rest frequencies are from a combined fit to laboratory data for υ2 ≤ 3, υ3 = 1, and υ1 = 1. The rotational data for υ2 = 0 and 1 are largely from Ahrens et al. (2002) and Thorwirth et al. (2003), respectively; data for higher excited rotational data are largely from Zelinger et al. (2003). The H13CN rest frequencies are from an equvalent fit. The υ2 = 0 and 1 data are from Fuchs et al. (2004); additional extensive υ = 0 data were taken from Cazzoli & Puzzarini (2005). Important for both fits were IR data from Maki et al. (2000).
The SiO rest frequencies were derived from Müller et al. (2013) who performed Fourier transform microwave (FTMW) spectroscopy on several isotopic species up to very high vibrational states along with millimeter and submillimeter measurements of several isotopic species in their ground vibrational states. Additional FTMW data of SiO, 29SiO (and Si18O) were taken from Sanz et al. (2003). Excited vibrational data of the main isotopologue were published by Mollaaghababa et al. (1991). Noteworthy are furthermore IR data from Campbell et al. (1995).
The current rest frequencies of SO rely mostly on Bogey et al. (1997) and Klaus et al. (1996), those of the isotopic species mostly on the latter work. Additional older data were also used at lower frequencies; some references are given in Table A.3. We point out that Hund’s case (a) quantum numbers may be found in the older literature, usually designated as JN, whereas Hund’s case (b) quantum numbers are more common in the more recent literature, designated as NJ.
The SO2 υ2 = 0 and 1 data were derived from Müller & Brünken (2005) with important additional rest frequencies for υ = 0 from Belov et al. (1998) and for both vibrational states from Alekseev et al. (1996) and Helminger & De Lucia (1985). The υ2 = 2 and υ1 = 1 data are based on an unpublished fit by one of us (HSPM) and employ besides own new data published rotational transition frequencies from Steenbeckeliers (1968), unpublished data communicated by the late Walter Lafferty, presumably associated with Pine et al. (1996), and IR data from Sattler et al. (1981) and Flaud et al. (1993). The 34SO2 υ = 0 data are largely based on Belov et al. (1998) with important additional rest frequencies from Alekseev et al. (1996) and Helminger & De Lucia (1985).
The SiS rest frequencies were derived from Müller et al. (2013) who performed Fourier transform microwave (FTMW) spectroscopy on several isotopic species up to very high vibrationa states along with millimeter and submillimeter measurments of several isotopic species mostly in their ground vibrational states. Additional FTMW data of SiS, 29SiS and Si34S) were taken from Sanz et al. (2003). Important were also IR data, in particular from Frum et al. (1990).
The H2O data pertaining to the lowest five vibrational states were based on the JPL catalog (Pickett et al. 1998; Pearson et al. 2010) entry which, in turn, is based on Yu et al. (2012). Besides extensive new data, this work employs additional rotational and rovibrational data from a plethora of sources. Coudert et al. (2014) presented a similar study including the next three vibrational states, but, unfortunately, calculated transition frequencies for these start only at 300 GHz. Therefore, we inspected the HITRAN2020 (Gordon et al. 2022) and W2020 (Furtenbacher et al. 2020) compilations for highly vibrationally excited H2O transitions. As these were deemed to be quite uncertain, we resorted to the transition frequencies determined in our study on H2O and OH (Baudry et al. 2023).
The initial OH data were taken from the JPL catalog and bear on Drouin (2013). This analysis is based on a plethora of laboratory spectroscopic investigations. The Λ-doubling transition with high rotational quanta, however, are rather uncertain and display systematic deviations, see for example Khouri et al (2019) and Baudry et al. (2023). In our study on H2O and OH (Baudry et al. 2023), we combined the data gathered in Drouin (2013) with Λ-doubling transition frequencies from our own astronomical observations and those from Khouri et al. (2019) to improve the calculations of the OH Λ-doubling transition frequencies in the upper millimeter and submillimeter regions (Baudry et al. 2023).
Calculations of the PO rest frequencies rely mainly on Bailleux et al. (2002) with additional υ = 0 data from Kawaguchi et al. (1983).
The TiO rest frequencies are based on an unpublished iso-topic invariant fit by one of us (HSPM). The main source of experimental data are those from the minor Ti isotopologues from Lincowski et al. (2016). Additional important data relevant for our study are the ground state rotational data of 46,48,50TiO from Kania et al. (2008), those of 48TiO from Namiki et al. (1998), and the extensive IR data for all Ti isotopologues from Witsch et al. (2021).
Calculations on the rotational spectrum of TiO2 are based on Kania et al. (2011). Besides our own upper millimeter and lower submillimeter data of 46,48,50TiO2, the analysis also employs microwave data of the same isotopologues from Brünken et al. (2008). The rotational temperatures were of order of 30 K and 3 K, respectively, which limited the quantum number range accessed. Transition frequencies involving higher rotational excitation may be quite uncertain as a consequence. The Ka = 6−5 Q-branch transitions with J = 25, 27, and 29 display larger uncertainties, such that their true transition freaquencies may differ from the calculated ones by more than 1 MHz.
The ground state rotational data of AlO were taken from Yamada et al. (1990) and from Törring & Herrmann (1989); transition frequencies of v = 1 and 2 were published by Goto et al. (1994).
The AlOH data were taken from the JPL catalog; they are derived from Apponi et al. (1993).
The AlF rest frequencies are mainly based on the rotational data of Wyse et al. (1970). Additional rotational data are from Hoeft et al. (1970), and rovibrational data are mainly from Hedderich & Bernath (1992).
Calculations of the rotational spectrum of AlCl and Al37Cl depends mainly on rotational data of Wyse & Gordy (1972). Very accurate frequencies of the J = 1 − 0 transitions by Hensel et al. (1993) were also employed as were rovibrational transitions taken from Hedderich et al. (1993).
The NaCl and KCl rest frequencies rely mainly on measurements by Caris et al. (2002) and Caris et al. (2004), respectively.
The SiN rest frequencies are based on Bizzocchi et al. (2006), with the important lower frequency data taken from Saito et al. (1983).
The SiC transition frequencies are based on Bogey et al. (1990) and on Cernicharo et al. (1989).
The current calculation of SiC2 v = 0 transition frequencies were derived from Müller et al. (2012). Important additional data besides HIFI-Herschel data from that work come from laboratory measurements by Gottlieb et al. (1989) and from astronomical observations by Cernicharo et al. (2000).
The ground state rotational data of HC3N depend on Thor-wirth et al. (2000) with additional contributions mainly from Yamada et al. (1995).
Appendix B SO2 and SO channel maps
 |
Fig. B.1 Channel map of the |
 |
Fig. B.2 Channel map of the |
 |
Fig. B.3 Channel map of the |
 |
Fig. B.4 Channel map of the |
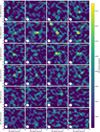 |
Fig. B.5 Channel map of the |
 |
Fig. B.6 Channel map of the |
 |
Fig. B.7 Channel map of the |
 |
Fig. B.8 Channel map of the |
 |
Fig. B.9 Channel map of the |
 |
Fig. B.10 Channel map of the |
 |
Fig. B.11 Channel map of the |
 |
Fig. B.12 Channel map of the |
 |
Fig. B.13 Channel map of the SO υ = 0 NJ = 55 − 44 line at 215.221 GHz observed towards R Aql at medium angular resolution. See caption of Figure B.1. |
Appendix C Spectra
 |
Fig. C.1 Spectrum of R Hya, in the 16 observed frequency bands. The top spectrum is extracted in a 1.2″-diameter circular aperture from the medium resolution spectrum, and the bottom shows the high resolution spectrum extracted in a 0.08″ -diameter aperture. All identified lines are marked, though note that some are more easily seen at other resolutions or extraction apertures. |
References
- Adande, G. R., Edwards, J. L., & Ziurys, L. M. 2013, ApJ, 778, 22 [NASA ADS] [CrossRef] [Google Scholar]
- Agúndez, M., Martinez, J. I., Andres, P. L. d., Cernicharo, J., & Martin-Gago, J. A. 2020, A&A, 637, A59 [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Ahrens, V., Lewen, F., Takano, S., et al. 2002, Z. Naturforsch. A, 57, 669 [NASA ADS] [CrossRef] [Google Scholar]
- Alekseev, E. A., Dyubko, S. F., Ilyushin, V. V., & Podnos, S. V. 1996, J. Mol. Spectr., 176, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Anders, E., & Grevesse, N. 1989, Geochim. Cosmochim. Acta, 53, 197 [Google Scholar]
- Andrews, H., De Beck, E., & Hirvonen, P. 2022, MNRAS, 510, 383 [Google Scholar]
- Andriantsaralaza, M., Ramstedt, S., Vlemmings, W. H. T., & De Beck, E. 2022, A&A, 667, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Apponi, A. J., Barclay, W. L., J., & Ziurys, L. M. 1993, ApJ, 414, L129 [NASA ADS] [CrossRef] [Google Scholar]
- Arroyo-Torres, B., Wittkowski, M., Marcaide, J. M., & Hauschildt, P. H. 2013, A&A, 554, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M., Amarsi, A. M., & Grevesse, N. 2021, A&A, 653, A141 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailer-Jones, C. A. L., Rybizki, J., Fouesneau, M., Demleitner, M., & Andrae, R. 2021, AJ, 161, 147 [Google Scholar]
- Bailleux, S., Bogey, M., Demuynck, C., Liu, Y., & Walters, A. 2002, J. Mol. Spectr., 216, 465 [CrossRef] [Google Scholar]
- Baudry, A., Wong, K. T., Etoka, S., et al. 2023, A&A, 674, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belov, S. P., Tretyakov, M. Y., Kozin, I. N., et al. 1998, J. Mol. Spectr., 191, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Bizzocchi, L., Degli Esposti, C., & Dore, L. 2006, A&A, 455, 1161 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bogey, M., Demuynck, C., & Destombes, J. L. 1990, A&A, 232, L19 [NASA ADS] [Google Scholar]
- Bogey, M., Civiš, S., Delcroix, B., et al. 1997, J. Mol. Spectr., 182, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Bowers, P. F., Johnston, K. J., & Spencer, J. H. 1983, ApJ, 274, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Brünken, S., Muller, H. S. P., Menten, K. M., McCarthy, M. C., & Thaddeus, P. 2008, ApJ, 676, 1367 [CrossRef] [Google Scholar]
- Campbell, J. M., Klapstein, D., Dulick, M., Bernath, P. F., & Wallace, L. 1995, ApJS, 101, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Caris, M., Lewen, F., & Winnewisser, G. 2002, Z. Naturforsch. A, 57, 663 [NASA ADS] [CrossRef] [Google Scholar]
- Caris, M., Lewen, F., Müller, H. S. P., & Winnewisser, G. 2004, J. Mol. Struct., 695, 243 [CrossRef] [Google Scholar]
- Cazzoli, G., & Puzzarini, C. 2005, J. Mol. Spectr., 233, 280 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Gottlieb, C. A., Guelin, M., Thaddeus, P., & Vrtilek, J. M. 1989, ApJ, 341, L25 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Guélin, M., & Kahane, C. 2000, A&AS, 142, 181 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chapman, J. M., Sivagnanam, P., Cohen, R. J., & Le Squeren, A. M. 1994, MNRAS, 268, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., & Shen, Z. Q. 2008, IAU Symp., 252, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, X., Shen, Z.-Q., & Xu, Y. 2007, Chinese J. Astron. Astrophys., 7, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Coudert, L. H., Martin-Drumel, M.-A., & Pirali, O. 2014, J. Mol. Spectr., 303, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Danilovich, T., Bergman, P., Justtanont, K., et al. 2014, A&A, 569, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovich, T., De Beck, E., Black, J. H., Olofsson, H., & Justtanont, K. 2016, A&A, 588, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovich, T., Van de Sande, M., De Beck, E., et al. 2017, A&A, 606, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovich, T., Ramstedt, S., Gobrecht, D., et al. 2018, A&A, 617, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovich, T., Richards, A. M. S., Karakas, A. I., et al. 2019, MNRAS, 484, 494 [CrossRef] [Google Scholar]
- Danilovich, T., Gottlieb, C. A., Decin, L., et al. 2020a, ApJ, 904, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Danilovich, T., Richards, A. M. S., Decin, L., Van de Sande, M., & Gottlieb, C. A. 2020b, MNRAS, 494, 1323 [NASA ADS] [CrossRef] [Google Scholar]
- Danilovich, T., Van de Sande, M., Plane, J. M. C., et al. 2021, A&A, 655, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovich, T., Malfait, J., Van de Sande, M., & Montargès, M. 2023, Nat. Astron., in press [Google Scholar]
- De Beck, E., & Olofsson, H. 2018, A&A, 615, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Beck, E., & Olofsson, H. 2020, A&A, 642, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Beck, E., Decin, L., de Koter, A., et al. 2010, A&A, 523, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decin, L. 2021, ARA&A, 59, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Decin, L., Hony, S., de Koter, A., et al. 2007, A&A, 475, 233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decin, L., De Beck, E., Brünken, S., et al. 2010, A&A, 516, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decin, L., Richards, A. M. S., Waters, L. B. F. M., et al. 2017, A&A, 608, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decin, L., Richards, A. M. S., Danilovich, T., Homan, W., & Nuth, J. A. 2018, A&A, 615, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Decin, L., Montarges, M., Richards, A. M. S., et al. 2020, Science, 369, 1497 [NASA ADS] [CrossRef] [Google Scholar]
- DeMore, W., Sander, S., Golden, D., et al. 1997, JPL Publ., 97-4, 1 [Google Scholar]
- Doan, L., Ramstedt, S., Vlemmings, W. H. T., et al. 2017, A&A, 605, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Douglas, K. M., Gobrecht, D., & Plane, J. M. C. 2022, MNRAS, 515, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Drouin, B. J. 2013, J. Phys. Chem. A, 117, 10076 [NASA ADS] [CrossRef] [Google Scholar]
- El Mellah, I., Bolte, J., Decin, L., Homan, W., & Keppens, R. 2020, A&A, 637, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Endres, C. P., Schlemmer, S., Schilke, P., Stutzki, J., & Müller, H. S. P. 2016, J. Mol. Spectr., 327, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Flaud, J. M., Perrin, A., Salah, L. M., Lafferty, W. J., & Guelachvili, G. 1993, J. Mol. Spectr., 160, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Frum, C. I., Engleman, R., J., & Bernath, P. F. 1990, J. Chem. Phys., 93, 5457 [NASA ADS] [CrossRef] [Google Scholar]
- Fuchs, U., Bruenken, S., Fuchs, G. W., et al. 2004, Z. Naturforsch. A, 59, 861 [NASA ADS] [CrossRef] [Google Scholar]
- Furtenbacher, T., Tóbiás, R., Tennyson, J., Polyansky, O. L., & Császár, A. G. 2020, J. Phys. Chem. Ref. Data, 49, 033101 [NASA ADS] [CrossRef] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gobrecht, D., Cherchneff, I., Sarangi, A., Plane, J. M. C., & Bromley, S. T. 2016, A&A, 585, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gobrecht, D., Plane, J. M. C., Bromley, S. T., et al. 2022, A&A, 658, A167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gordon, I. E., Rothman, L. S., Hargreaves, R. J., et al. 2022, J. Quant. Spec. Radiat. Transf., 277, 107949 [NASA ADS] [CrossRef] [Google Scholar]
- Goto, M., Takano, S., Yamamoto, S., Ito, H., & Saito, S. 1994, Chem. Phys. Lett., 227, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Gottlieb, C. A., Vrtilek, J. M., & Thaddeus, P. 1989, ApJ, 343, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Gottlieb, C. A., Decin, L., Richards, A. M. S., et al. 2022, A&A, 660, A94 [CrossRef] [EDP Sciences] [Google Scholar]
- Groenewegen, M. a. T., Baas, F., Blommaert, J. a. D. L., et al. 1999, A&AS, 140, 197 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Habing, H., & Olofsson, H., eds. 2003, Asymptotic Giant Branch Stars (A&A Library (Springer)) [Google Scholar]
- Harris, C. R., Millman, K. J., van der Walt, S. J., et al. 2020, Nature, 585, 357 [NASA ADS] [CrossRef] [Google Scholar]
- He, J. H., Kwok, S., Müller, H. S. P., et al. 2008, ApJS, 177, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Hedderich, H. G., & Bernath, P. F. 1992, J. Mol. Spectr., 153, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Hedderich, H. G., Dulick, M., & Bernath, P. F. 1993, J. Chem. Phys., 99, 8363 [NASA ADS] [CrossRef] [Google Scholar]
- Helmer, M., & Plane, J. M. C. 1993, J. Chem. Phys., 99, 7696 [NASA ADS] [CrossRef] [Google Scholar]
- Helminger, P. A., & De Lucia, F. C. 1985, J. Mol. Spectr., 111, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Hensel, K. D., Styger, C., Jäger, W., Merer, A. J., & Gerry, M. C. L. 1993, J. Chem. Phys., 99, 3320 [NASA ADS] [CrossRef] [Google Scholar]
- Herwig, F. 2005, ARA&A, 43, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Hoeft, J., Lovas, F. J., Tiemann, E., & Törring, T. 1970, Z. Naturforsch. A, 25, 1029 [CrossRef] [Google Scholar]
- Höfner, S. & Olofsson, H. 2018, A&ARv, 26, 1 [Google Scholar]
- Homan, W., Montargès, M., Pimpanuwat, B., et al. 2020, A&A, 644, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Homan, W., Pimpanuwat, B., Herpin, F., et al. 2021, A&A, 651, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Huggins, P. J., Bachiller, R., Cox, P., & Forveille, T. 1994, ApJ, 424, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Jeste, M., Gong, Y., Wong, K. T., et al. 2022, A&A, 666, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jura, M., & Kleinmann, S. G. 1990, ApJS, 73, 769 [NASA ADS] [CrossRef] [Google Scholar]
- Kamiński, T., Gottlieb, C. A., Young, K. H., Menten, K. M., & Patel, N. A. 2013, ApJS, 209, 38 [CrossRef] [Google Scholar]
- Kania, P., Giesen, T. F., Müller, H. S. P., Schlemmer, S., & Brünken, S. 2008, in 33rd International Conference on Infrared, Millimeter and Terahertz Waves, 1 [Google Scholar]
- Kania, P., Hermanns, M., Brünken, S., Müller, H. S. P., & Giesen, T. F. 2011, J. Mol. Spectr., 268, 173 [Google Scholar]
- Kawaguchi, K., Saito, S., & Hirota, E. 1983, J. Chem. Phys., 79, 629 [NASA ADS] [CrossRef] [Google Scholar]
- Kemper, F., Stark, R., Justtanont, K., et al. 2003, A&A, 407, 609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kendall, M. G. 1938, Biometrika, 30, 81 [Google Scholar]
- Kendall, M. G. 1945, Biometrika, 33, 239 [CrossRef] [Google Scholar]
- Khouri, T., Velilla-Prieto, L., De Beck, E., et al. 2019, A&A, 623, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kiss, L. L., Szabó, G. M., & Bedding, T. R. 2006, MNRAS, 372, 1721 [Google Scholar]
- Klaus, T., Saleck, A. H., Belov, S. P., et al. 1996, J. Mol. Spectr., 180, 197 [NASA ADS] [CrossRef] [Google Scholar]
- Knapp, G. R., & Morris, M. 1985, ApJ, 292, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Kobayashi, C., Karakas, A. I., & Umeda, H. 2011, MNRAS, 414, 3231 [Google Scholar]
- Lamers, H. J. G. L. M., & Cassinelli, J. P. 1999, Introduction to stellar winds (Cambridge, UK: Cambridge University Press) [CrossRef] [Google Scholar]
- Lincowski, A. P., Halfen, D. T., & Ziurys, L. M. 2016, ApJ, 833, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Loup, C., Forveille, T., Omont, A., & Paul, J. F. 1993, A&AS, 99, 291 [NASA ADS] [Google Scholar]
- Maercker, M., Danilovich, T., Olofsson, H., et al. 2016, A&A, 591, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maes, S., Van de Sande, M., Danilovich, T., De Ceuster, F., & Decin, L. 2023, MNRAS, 522, 4654 [NASA ADS] [CrossRef] [Google Scholar]
- Maki, A. G., Mellau, G. C., Klee, S., Winnewisser, M., & Quapp, W. 2000, J. Mol. Spectr., 202, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Mamon, G. A., Glassgold, A. E., & Huggins, P. J. 1988, ApJ, 328, 797 [Google Scholar]
- Mangan, T. P., Douglas, K. M., Lade, R. E., et al. 2021, ACS Earth Space Chem., 5, 3385 [NASA ADS] [CrossRef] [Google Scholar]
- Marigo, P., Girardi, L., Bressan, A., et al. 2008, A&A, 482, 883 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Massalkhi, S., Agúndez, M., Cernicharo, J., et al. 2018, A&A, 611, A29 [CrossRef] [EDP Sciences] [PubMed] [Google Scholar]
- Mauron, N., & Josselin, E. 2011, A&A, 526, A156 [CrossRef] [EDP Sciences] [Google Scholar]
- McDonald, I., Zijlstra, A. A., Sloan, G. C., et al. 2016, MNRAS, 456, 4542 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, W. 2010, Proceedings of the 9th Python in Science Conference, 56 [CrossRef] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, Astron. Soc. Pac. Conf. Ser., 376, 127 [Google Scholar]
- Mollaaghababa, R., Gottlieb, C. A., Vrtilek, J. M., & Thaddeus, P. 1991, ApJ, 368, L19 [NASA ADS] [CrossRef] [Google Scholar]
- Monson, N. N., Morris, M. R., & Young, E. D. 2017, ApJ, 839, 123 [Google Scholar]
- Montargès, M., Cannon, E., Koter, A. d., et al. 2023, A&A, 671, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morris, M. 1980, ApJ, 236, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Müller, H. S. P., & Brünken, S. 2005, J. Mol. Spectr., 232, 213 [CrossRef] [Google Scholar]
- Müller, H. S. P., Thorwirth, S., Roth, D. A., & Winnewisser, G. 2001, A&A, 370, L49 [Google Scholar]
- Müller, H. S. P., Schlöder, F., Stutzki, J., & Winnewisser, G. 2005, J. Mol. Struct., 742, 215 [Google Scholar]
- Müller, H. S. P., Cernicharo, J., Agúndez, M., et al. 2012, J. Mol. Spectr., 271, 50 [CrossRef] [Google Scholar]
- Müller, H. S. P., Spezzano, S., Bizzocchi, L., et al. 2013, J. Phys. Chem. A, 117, 13843 [Google Scholar]
- Namiki, K.-i., Saito, S., Robinson, J. S., & Steimle, T. C. 1998, J. Mol. Spectr., 191, 176 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, N., & Knapp, G. R. 1987, ApJ, 323, 734 [NASA ADS] [CrossRef] [Google Scholar]
- Olofsson, H., Eriksson, K., Gustafsson, B., & Carlstrom, U. 1993, ApJS, 87, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Olofsson, H., Delgado, D. G., Kerschbaum, F., & Schöier, F. L. 2002, A&A, 391, 1053 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pardo, J. R., Cernicharo, J., Tercero, B., et al. 2022, A&A, 658, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Patel, N. A., Young, K. H., Brünken, S., et al. 2009, ApJ, 692, 1205 [NASA ADS] [CrossRef] [Google Scholar]
- Patel, N. A., Young, K. H., Gottlieb, C. A., et al. 2011, ApJS, 193, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Pavlenko, Y. V., Yurchenko, S. N., & Tennyson, J. 2020, A&A, 633, A52 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pearson, J. C., Müller, H. S. P., Pickett, H. M., Cohen, E. A., & Drouin, B. J. 2010, JQSRT, 111, 1614 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, T.-C., Humphreys, E. M. L., Testi, L., et al. 2013, A&A, 559, A8 [Google Scholar]
- Perryman, M. a. C., Lindegren, L., Kovalevsky, J., et al. 1997, A&A, 323, L49 [NASA ADS] [Google Scholar]
- Pickett, H. M. 1991, J. Mol. Spectr., 148, 371 [Google Scholar]
- Pickett, H. M., Poynter, R. L., Cohen, E. A., et al. 1998, JQSRT, 60, 883 [NASA ADS] [CrossRef] [Google Scholar]
- Pine, A. S., Suenram, R. D., Brown, E. R., & Mcintosh, K. A. 1996, J. Mol. Spectr., 175, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Plane, J. M. C., Rajasekhar, B., & Bartolotti, L. 1989, J. Chem. Phys., 91, 6177 [NASA ADS] [CrossRef] [Google Scholar]
- Price-Whelan, A. M., Sipocz, B. M., Günther, H. M., et al. 2018, AJ, 156, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Price-Whelan, A. M., Lim, P. L., Earl, N., et al. 2022, ApJ, 935, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Quintana-Lacaci, G., Velilla-Prieto, L., Agúndez, M., et al. 2023, A&A, 669, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ramstedt, S., Mohamed, S., Vlemmings, W. H. T., et al. 2017, A&A, 605, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robitaille, T. P., Tollerud, E. J., Greenfield, P., et al. 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saito, S., Endo, Y., & Hirota, E. 1983, J. Chem. Phys., 78, 6447 [NASA ADS] [CrossRef] [Google Scholar]
- Samus’, N. N., Kazarovets, E. V., Durlevich, O. V., Kireeva, N. N., & Pastukhova, E. N. 2017, Astron. Rep., 61, 80 [Google Scholar]
- Santander-García, M., Bujarrabal, V., Koning, N., & Steffen, W. 2015, A&A, 573, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sanz, M. E., McCarthy, M. C., & Thaddeus, P. 2003, J. Chem. Phys., 119, 11715 [NASA ADS] [CrossRef] [Google Scholar]
- Sattler, J. P., Worchesky, T. L., & Lafferty, W. J. 1981, J. Mol. Spectr., 88, 364 [NASA ADS] [CrossRef] [Google Scholar]
- Schöier, F. L., & Olofsson, H. 2001, A&A, 368, 969 [Google Scholar]
- Schöier, F. L., Bast, J., Olofsson, H., & Lindqvist, M. 2007, A&A, 473, 871 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Steenbeckeliers, G. 1968, Ann. Soc. Sci. Bruxelles, Ser. III, 82, 331 [Google Scholar]
- Szymczak, M., & Cohen, R. J. 1997, MNRAS, 288, 945 [NASA ADS] [Google Scholar]
- Tabernero, H. M., Dorda, R., Negueruela, I., & Marfil, E. 2021, A&A, 646, A98 [EDP Sciences] [Google Scholar]
- Tenenbaum, E. D., Dodd, J. L., Milam, S. N., Woolf, N. J., & Ziurys, L. M. 2010, ApJS, 190, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Thorwirth, S., Müller, H. S. P., & Winnewisser, G. 2000, J. Mol. Spectr., 204, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Thorwirth, S., Müller, H. S. P., Lewen, F., et al. 2003, ApJ, 585, L163 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2005, The Physics and Chemistry of the Interstellar Medium (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Törring, T., & Herrmann, R. 1989, Mol. Phys., 68, 1379 [CrossRef] [Google Scholar]
- Ukita, N., & Kaifu, N. 1988, in Atmospheric Diagnostics of Stellar Evolution: Chemical Peculiarity, Mass Loss, and Explosion, ed. K. Nomoto, Lecture Notes in Physics (Berlin, Heidelberg: Springer), 51 [Google Scholar]
- Van de Sande, M., Sundqvist, J. O., Millar, T. J., et al. 2018, A&A, 616, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Velilla Prieto, L., Sánchez Contreras, C., Cernicharo, J., et al. 2017, A&A, 597, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Vlemmings, W. H. T., & Langevelde, H. J. v. 2007, A&A, 472, 547 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winters, J. M., Hoai, D. T., Wong, K. T., et al. 2022, A&A, 658, A135 [CrossRef] [EDP Sciences] [Google Scholar]
- Witsch, D., Breier, A. A., Doring, E., et al. 2021, J. Mol. Spectr., 377, 111439 [NASA ADS] [CrossRef] [Google Scholar]
- Wittkowski, M., Arroyo-Torres, B., Marcaide, J. M., et al. 2017, A&A, 597, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Woosley, S. E., & Weaver, T. A. 1995, ApJS, 101, 181 [Google Scholar]
- Wyse, F. C., & Gordy, W. 1972, J. Chem. Phys., 56, 2130 [NASA ADS] [CrossRef] [Google Scholar]
- Wyse, F. C., Gordy, W., & Pearson, E. F. 1970, J. Chem. Phys., 52, 3887 [NASA ADS] [CrossRef] [Google Scholar]
- Yamada, C., Fujitake, M., Hirota, E., & Cohen, E. A. 1990, J. Chem. Phys., 92, 2146 [NASA ADS] [CrossRef] [Google Scholar]
- Yamada, K. M. T., Moravec, A., & Winnewisser, G. 1995, Z. Naturforsch. A, 50, 1179 [NASA ADS] [CrossRef] [Google Scholar]
- Young, K. 1995, ApJ, 445, 872 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, S., Pearson, J. C., Drouin, B. J., et al. 2012, J. Mol. Spectr., 279, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Zelinger, Z., Amano, T., Ahrens, V., et al. 2003, J. Mol. Spectr., 220, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Zinner, E., Nittler, L. R., Gallino, R., et al. 2006, ApJ, 650, 350 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
SO2 spatial distributions, radial extents, and median lower level energies in all sources.
All Figures
 |
Fig. 1 Overview of how many lines of each molecule are detected in each source. The sources are listed in order of increasing mass-loss rate |
| In the text | |
 |
Fig. 2 Kendall’s τb rank correlation coefficients between the expansion velocity (vexp), pulsation period (P), mass-loss rate |
| In the text | |
 |
Fig. 3 Dendrogram of the correlations in Fig. 2, showing the hierarchical relationships between the different parameters. A closer connection point (lower down in the diagram) between two parameters signals a stronger relationship. The dark blue lines indicate the top-level division into seven clusters, and the other colors are simply to guide the eye in distinguishing between the different clusters. |
| In the text | |
 |
Fig. 4 Emission sizes of SO2 as expected from chemical models, and our maximum measured line extents, for each source. |
| In the text | |
 |
Fig. B.1 Channel map of the |
| In the text | |
 |
Fig. B.2 Channel map of the |
| In the text | |
 |
Fig. B.3 Channel map of the |
| In the text | |
 |
Fig. B.4 Channel map of the |
| In the text | |
 |
Fig. B.5 Channel map of the |
| In the text | |
 |
Fig. B.6 Channel map of the |
| In the text | |
 |
Fig. B.7 Channel map of the |
| In the text | |
 |
Fig. B.8 Channel map of the |
| In the text | |
 |
Fig. B.9 Channel map of the |
| In the text | |
 |
Fig. B.10 Channel map of the |
| In the text | |
 |
Fig. B.11 Channel map of the |
| In the text | |
 |
Fig. B.12 Channel map of the |
| In the text | |
 |
Fig. B.13 Channel map of the SO υ = 0 NJ = 55 − 44 line at 215.221 GHz observed towards R Aql at medium angular resolution. See caption of Figure B.1. |
| In the text | |
 |
Fig. C.1 Spectrum of R Hya, in the 16 observed frequency bands. The top spectrum is extracted in a 1.2″-diameter circular aperture from the medium resolution spectrum, and the bottom shows the high resolution spectrum extracted in a 0.08″ -diameter aperture. All identified lines are marked, though note that some are more easily seen at other resolutions or extraction apertures. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.