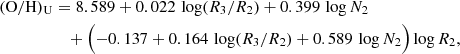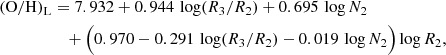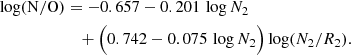EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 655 (November 2021) A&A, 655 (2021) A58 Full HTML
Free Access
Issue
A&A
Volume 655, November 2021
Article Number A58
Number of page(s) 10
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/202141522
Published online 19 November 2021

© ESO 2021

1. Introduction

The chemical composition of galaxies plays an important role in their formation and evolution during the lifetime of the Universe. Hence, the oxygen abundance correlates with other integrated characteristics of galaxies, as in the well-known case of the mass–metallicity relation (MZR), where the average oxygen abundance increases with stellar mass (or luminosity) of a galaxy (Searle 1971; Shields & Searle 1978; Vila-Costas & Edmunds 1992; Zaritsky et al. 1994; Thuan et al. 2010; Pérez-Montero et al. 2013; Sánchez et al. 2014, 2019; Zinchenko et al. 2019a; Yates et al. 2020). In the individual disc galaxies, the oxygen abundance depends diversely on the galactocentric distance, but at the present epoch and on average it decreases with radius, forming the so-called radial metallicity gradient (Sánchez et al. 2012, 2014; Pilyugin et al. 2014; Sánchez-Menguiano et al. 2016, 2018; Zinchenko et al. 2016, 2019a,b; Belfiore et al. 2017; Kreckel et al. 2019; Zurita et al. 2021).

Negative metallicity gradients can be explained by the inside-out growth of the galactic discs (Matteucci & Francois 1989; Boissier & Prantzos 1999; Chiappini et al. 2001). However, the chemical enrichment and, therefore, formation of the shape of the radial metallicity distribution in a galaxy is a complex process that depends on its star formation history (SFH), the gas inflows and outflows as a whole, and also the different evolution timescales of its local parts (Troncoso et al. 2014; Zahid et al. 2014; Bothwell et al. 2016). This has two important implications regarding the formation of metallicity gradients in disc galaxies. First, galaxies with different histories should show different slopes of the radial metallicity distribution. From the observational point of view, this is revealed in a large measured scatter of metallicity gradient slopes, which is reported in many works (e.g., Sánchez et al. 2014; Pérez-Montero et al. 2016; Zinchenko et al. 2016; Belfiore et al. 2017). Second, radial metallicity gradients depend on integrated properties of galaxies that reflect their evolution.

The most obvious parameter that defines the evolution of a galaxy is its mass. Some studies suggest that the oxygen abundance gradient may depend on the stellar mass of a galaxy (Ho et al. 2015; Belfiore et al. 2017; Carton et al. 2018; Zinchenko et al. 2019b), while other works do not report such a correlation (Sánchez et al. 2014; Pérez-Montero et al. 2016; Sánchez-Menguiano et al. 2016, 2018).

A correlation between the global (average) gas-phase oxygen abundance and the D(4000) index, which is an indicator of stellar age, has been found by Lian et al. (2015) and Sánchez-Menguiano et al. (2020). Moreover, Sánchez-Menguiano et al. (2020) reported a positive correlation for the local oxygen abundance as well.

Negative nitrogen-to-oxygen (N/O) gradients have been reported for a majority of galaxies (Pilyugin et al. 2004; Pérez-Montero et al. 2016; Belfiore et al. 2017). The mass–N/O relation was studied for the first time by Pérez-Montero & Contini (2009), who showed that the N/O ratio is larger at higher stellar masses, similarly to the case of the MZR for oxygen. Theoretical models suggest that other variables, such as the time delay in nitrogen enrichment, the infall timescale, or the star formation efficiency could affect the N/O ratio (Mollá et al. 2006). A possible correlation between the N/O gradient and the stellar mass was studied by Pérez-Montero et al. (2016) for 350 spiral galaxies from the CALIFA survey. They did not find a statistically significant correlation between the N/O gradient and the stellar mass. Later, for a larger sample of 550 galaxies from the MaNGA survey, Belfiore et al. (2017) reported a steepening of the N/O gradient with the stellar mass.

In this work, we studied the distributions of the oxygen abundance and the N/O abundance ratio for a large sample of 1431 nearby galaxies from the Mapping Nearby Galaxies at Apache Point Observatory (MaNGA; Bundy et al. 2015) survey data release 15 (DR15), which is a part of the Sloan Digital Sky Survey IV (SDSS IV; Blanton et al. 2017). Our main goal is to explore the connection between the gas-phase metallicity gradients and the stellar age of a galaxy. We consider oxygen abundance gradients as well as N/O gradients and their connection with the stellar mass. The robust estimation of the chemical abundance is crucial for studying such relations, therefore we take advantage of two precise strong line methods, which are based on different observational and theoretical sets of calibration data.

The paper is structured as follows. In Sect. 2, we describe the data, the sample selection criteria, and the spectral fitting procedure. In Sect. 3, we discuss the methods used to determine O/H, N/O, and the corresponding radial gradients in our sample, and we explore how the abundance gradients are connected to the stellar age. Finally, in Sect. 4 we summarise the main results of our work.

2. Data

For this study, we prepared a sample of galaxies from the MaNGA SDSS DR15 survey (Bundy et al. 2015). We analysed the MaNGA spectra following Zinchenko et al. (2016). In brief, the stellar background in all spaxels is fitted using the public version of the STARLIGHT code (Cid Fernandes et al. 2005; Mateus et al. 2006; Asari et al. 2007), adapted for execution in the NorduGrid ARC1 environment of the Ukrainian National Grid. To fit the stellar spectra, we used simple stellar population (SSP) spectra from the evolutionary synthesis models by Bruzual & Charlot (2003) with ages from 1 Myr up to 13 Gyr and metallicities Z of 0.004, 0.02, and 0.05. The resulting stellar spectrum is subtracted from the observed spectrum to obtain a pure gas spectrum. The line intensities in the gas spectrum were measured by fitting single Gaussian profiles on the pure emission spectra.

To fit the emission lines, we used our code ELF3D for emission line fitting in the optical spectra. The code is based on the iminuit library (Dembinski et al. 2020), which in turn is based on the SEAL Minuit2 code (James & Roos 1975). Since Minuit2 is sensitive to the choice of the initial parameters, we implemented an option of the Monte Carlo (MC) approach to choose the initial parameters of the fit. This approach significantly increases the robustness of line fluxes estimation. The computational time per one data cube in the robust MC mode has been reduced owing to the MPI parallelisation of the code. Our sample of galaxies was processed on two clusters, MareNostrum4 at the Barcelona Supercomputing Center (BSC) and Golowood at the Main Astronomical Observatory of the National Academy of Sciences of Ukraine.

For each spectrum, we measured fluxes of the [O II]λ λ3727,3729, Hβ, [O III]λ4959, [O III]λ5007, [N II]λ6548, Hα, [N II]λ6584, and [S II]λ6717,6731 lines. The line fluxes were corrected for interstellar reddening using the analytical approximation of the Whitford interstellar reddening law (Izotov et al. 1994), assuming the Balmer line ratio of Hα/Hβ = 2.86. When the measured value of Hα/Hβ is less than 2.86, the reddening is set to zero.

We applied the log([O III]λ5007/Hβ) – log([N II]λ6584/Hα) diagram (Baldwin et al. 1981) and the dividing line proposed by Kauffmann et al. (2003a) to classify objects in two groups based on their main ionisation source, which is either massive stars or gas shocks and/or active galactic nuclei (AGNs). We only selected spectra with the signal-to-noise ratio S/N > 5 in all the [O II]λ λ3727,3729, Hβ, [O III]λ5007, Hα, [N II]λ6584, and [S II]λ6717,6731 lines.

Since the measurement of the radial metallicity gradient in the distant and edge-on galaxies may be affected by significant systematical and statistical errors, we only selected galaxies at distances shorter than 300 Mpc, which corresponds to z ∼ 0.07, and with the minor-to-major axis ratio of b/a > 0.35 or an inclination less than i ∼ 70°.

Stellar masses, effective radii, and colours for the MaNGA sample were taken from the NASA-Sloan Atlas (NSA) catalogue2. Stellar masses were derived from the K-correction fit for elliptical Petrosian fluxes using the Chabrier (2003) initial mass function and simple stellar population models from Bruzual & Charlot (2003). Effective radii are defined as Sersic 50% light radii along the major axis in the r band.

The inclination and the position angle of the major axis of the galaxies have been obtained from the Sersic fit to the surface brightness profile in the r band available in the NSA catalogue.

3. Gradients of O/H and N/O abundance ratios

3.1. Abundance determination

The oxygen abundance 12 + log(O/H) and the nitrogen-to-oxygen ratio log(N/O) were derived using the empirical R calibration (Pilyugin & Grebel 2016) and the Bayesian model-based code HII-CHI-MISTRY (HCM)3 (hereinafter HCm) (Pérez-Montero 2014). We used HCM version 4.1, assuming photoionisation models from Cloudy v.17.00 (Ferland et al. 2017) with SEDs from POPSTAR (Mollá et al. 2009) and linear interpolations on the grid of O/H and N/O. The R calibration for the oxygen abundance determination is divided in two branches, depending on the metallicity range,

(1)

for H II regions with log N2 ≥ −0.6 (the upper branch), and,

(2)

for log N2 < −0.6 (the lower branch). Here, (O/H)U and (O/H)L correspond to 12 + log(O/H) for the upper and lower branches, respectively. To determine the N/O ratio, we also used the following calibration from Pilyugin & Grebel (2016):

(3)

For the sake of consistency, in both strong line methods for the oxygen abundance determination we used the following set of emission lines: [O II]λ λ3727,3729, [O III]λ5007, and [N II]λ6584. The [N II]λ6584 line allows us to solve the double-valued problem, which is typical for calibrations based on metallicity indicators with only oxygen lines. The downside of this approach is that oxygen abundance indicators based on the [N II]λ6584 line may introduce the N/O dependence into the calibration relationship (Schaefer et al. 2020). To overcome this problem, the HCM code uses a grid of models with different N/O ratios. The R calibration adopts a three-dimensional relation that incorporates a correction for the N/O ratio by introducing indexes sensitive to the N/O ratio.

We note that the HCM code allows us to use the [S II]λ λ6717,6731 lines in addition to those three lines and that the S calibration proposed by Pilyugin & Grebel (2016) replaces the [O II]λ λ3727,3729 lines with the [S II]λ λ6717,6731 lines. However, S+ has a lower ionisation potential compared to O+ and, therefore, could be more contaminated by the diffuse ionised gas (DIG). Since MaNGA spectra have the [O II]λ λ3727,3729 lines starting from the rest frame, we prefer not to use the additional [S II]λ λ6717,6731 lines for the abundance determination.

We calculated the radial gradients for both 12 + log(O/H) and log(N/O) only for galaxies with at least 10 spaxels with measured 12 + log(O/H) and log(N/O) values. To make fits more robust, we required data points to be well spread along the galactocentric distance; that is, the galactocentric distance of the outermost data point should be at least 1Re higher than the distance of the innermost data point. To obtain the radial gradient and its error, a least-square linear fit was performed on 5000 bootstrap samples with a replacement. In the end, we selected 1431 galaxies for further analysis. Figure 1 illustrates an example of the radial gradients of 12 + log(O/H) and log(N/O) for one of the selected galaxies.

thumbnail Fig. 1.

Example of the radial gradients of O/H (upper panel) and N/O (lower panel) in the MaNGA galaxy 1-48157 using data from data cube 10001-12701. Grey points are values in each spaxel, derived from the empirical R calibration of Pilyugin & Grebel (2016). Red crosses are median values in bins. A solid line is the linear fit to the data.

Since the radial distribution of the oxygen abundance may be more complex than the pure linear distribution (Vilchez et al. 1988; Bresolin et al. 2009; Goddard et al. 2011; Rosales-Ortega et al. 2011; Sánchez-Menguiano et al. 2016, 2018; Belfiore et al. 2017; Pilyugin et al. 2017), in Fig. 2 we compare the oxygen abundances in the galaxy centres derived either by extrapolating the fits or by averaging in individual spaxels at R < 0.1Re. We see that the oxygen abundances in the centres of high-metallicity galaxies are lower when averaged over the innermost spaxels than when extrapolated from the fits, which is true both for the empirical and theoretical methods used. The abundances show the same behaviour when derived by either of the methods. Thus, we re-affirm the conclusion of previous studies, which found a flattening of the metallicity gradient in the central parts of massive galaxies (Belfiore et al. 2017; Sánchez-Menguiano et al. 2018; Zinchenko et al. 2019a). We see the same behaviour for the N/O ratio: in the centres of high-metallicity galaxies, it is generally lower when averaged rather than when it is extrapolated.

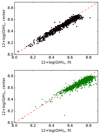thumbnail Fig. 2.

Comparison between O/H at galaxy centres derived by extrapolating the radial fits and by averaging in individual spaxels at R < 0.1Re. Upper panel: O/H derived from the empirical R calibration. Lower panel: O/H derived using the HCM code. Dashed lines represent the one-to-one correspondence.

The other widely reported feature of the radial metallicity distribution is its flattening in the outer parts of the disc (Bresolin et al. 2009; Goddard et al. 2011; Sánchez-Menguiano et al. 2016, 2018; Belfiore et al. 2017). We checked for the existence of this outer flattening and its possible effect on the calculated gradients. In Fig. 3, we compare the oxygen abundance and its gradient derived in a galactocentric radius either within 3Re or 5Re. However, it should be noted that the fraction of metallicity measurements in the outer part of galaxies is low: about 1% for R/Re > 3 and 0.2% for R/Re > 5. These two cases show no systematic difference either in the oxygen abundance extrapolated to the centre of a galaxy or in the slope of the fit. Neither of the N/O gradients show any dependence on the maximum galactocentric radius adopted for the calculation of the gradients. Therefore, for further analysis we use the gradients derived within 5Re.

thumbnail Fig. 3.

Comparison between fits to the derived O/H radial distributions at a galactocentric radius less than 3Re (horizontal axes) and less than 5Re (vertical axes). Upper panel: comparison of the extrapolated O/H abundances in the galaxy centres. Lower panel: comparison of the slopes of the fits. The oxygen abundances and their corresponding gradients were derived using the following two methods: the R calibration (black circles) or the HCM code (green triangles). Dashed lines represent the one-to-one correspondence.

3.2. Abundances and gradients as a function of mass

In Fig. 4, we show relations between the parameters of the derived linear radial fits for both O/H and N/O as a function of the stellar mass in the galaxies from our sample. We show the oxygen abundance at Re as a function of the stellar mass in the top left panel of Fig. 4. Both methods produce different abundances that differ by ∼0.1 dex for massive galaxies, and this difference grows to ∼0.3 dex in the low-mass regime. However, at the same time the oxygen abundance steeply increases up to stellar masses of some 1010 M⊙, and then it stalls for higher masses. This flattening at high masses is in agreement with many previous studies (e.g., Tremonti et al. 2004; Kewley & Ellison 2008; Thuan et al. 2010; Sánchez et al. 2019; Zinchenko et al. 2019a). The MZR relation in Fig. 4, obtained with the HCM-based O/H abundances, effectively reproduces the one obtained by Pérez-Montero et al. (2016) for the CALIFA sample using the same HCM code. In both cases, the median O/H abundance increases with the stellar mass from ∼8.5 dex to ∼8.7 dex having a flattening at high masses. This implies only ∼0.2 dex change in O/H across the MZR mass range, 8.7 < log(M/M⊙) < 10.7, which is significantly smaller compared to 0.4 dex in the case of the R calibration. Other studies based on R23 and O3N2 calibrations have also reported a bigger change in O/H of ∼0.4–0.5 dex across a mass range of 9 < log(M/M⊙) < 11 (Tremonti et al. 2004; Belfiore et al. 2017).

thumbnail Fig. 4.

Galaxy-centre oxygen abundance log(O/H), nitrogen-to-oxygen ratio log(N/O), and their gradients as a function of galaxy mass log(M/M⊙). Median values (solid lines) with 1-σ range scatter (shaded areas) are shown in each mass bin. The metallicity parameters were calculated using the following two methods: the R calibration (blue lines and areas) or the HCM method (red lines and areas). For the O/H and N/O gradients, dashed lines show linear fits as a function of the stellar mass.

The N/O ratio at Re also increases with the galaxy mass (see bottom left panel of Fig. 4). There is no bias between the R and HCM abundance ratios at low masses. Meanwhile, at high masses, the N/O ratio derived by the HCM method is on average up to 0.2 dex higher compared to the one derived using the R calibration. At the same time and compared to other studies, the R calibration yields the same range of the N/O ratio, from −1.3 dex at low masses through −0.8 dex at high masses, which is consistent with the results obtained by Belfiore et al. (2017) using calibrations of the R23 and O3N2 parameters and Pérez-Montero et al. (2016) using the HCM code version 2.0.

Both the R calibration and the HCM methods confirm negative oxygen abundance gradients for the majority of galaxies from our sample (see top right panel of Fig. 4). Median values of the oxygen abundance gradients are ( − 0.06 ± 0.06) dex/Re for the R abundances and ( − 0.03 ± 0.06) dex/Re for the HCM abundances. We note that the distribution of gradients is not symmetric: it has a steeper cut-off around zero and a longer tail at the lower end. On average, the oxygen abundance gradients calculated using the R calibration and the HCM methods are consistent for massive galaxies.

The slope of the oxygen abundance gradient with respect to the stellar mass is calculated by a linear fit to the data. The error of the linear fit is estimated by bootstrapping with 1000 random re-samplings of the data with replacement. For the R calibration, the slope is mildly positive while the HCM method yields a mild negative slope. Thus, the comparison between the linear fit, and the O/H gradient averaged in the mass bins shows that both relations are significantly non-linear and have a U-shape with the steepest average gradients around log(M/M⊙) = 10.0 and flatter average gradients in high- and low-mass bins. These U-shape profiles are consistent with the result obtained by Belfiore et al. (2017), who used the R23 parameter as calibrated by Maiolino et al. (2008), and that of Poetrodjojo et al. (2021), who compared a large set of strong line methods using 248 galaxies from the SAMI Galaxy Survey. Zinchenko et al. (2019a) and Pilyugin et al. (2019) reported a mild positive slope when applying the R calibration to a smaller sample containing relatively massive CALIFA and MaNGA galaxies. Thus, undersampling the low-mass galaxies produces only a positive correlation between the O/H gradient and the stellar mass for massive galaxies. The same positive correlation between the O/H gradient and the stellar mass was found by Tissera et al. (2019) for galaxies in the EAGLE simulation that have quiet merger histories.

We show the average N/O gradients as a function of mass in the bottom right panel of Fig. 4. Compared to the O/H gradients, the N/O gradients are steeper with median and standard deviation values of ( − 0.12  ±  0.09) dex/Re for the R abundances and ( − 0.18  ±  0.16) dex/Re for the HCM abundances. On average, the N/O gradients also correlate with the stellar mass. Both the R calibration and the HCM method produce steeper average N/O gradients for more massive galaxies, which is in line with the previous result of Belfiore et al. (2017). The R calibration provides a flatter slope of ( − 0.06  ±  0.005) dex/Re per dex in stellar mass compared to ( − 0.10  ±  0.01) dex/Re per dex in stellar mass obtained by the HCM method. However, considering this correlation in detail, we see a non-linear relation between the average N/O gradient and the stellar mass, which has the steepest slope in the intermediate mass range and some flattening in the high- and low-mass ranges.

3.3. Relation between O/H and N/O abundance gradients

In the previous sub-section, we show that the median N/O gradient correlates with the stellar mass of a galaxy. As has been suggested by Pérez-Montero & Contini (2009), this can be related not to the galaxy mass itself but to a correlation between the galaxy mass and its oxygen abundance (the mass–metallicity relation). In addition, at high metallicity, which is typical for the galaxies from our sample, nitrogen is mostly produced as a secondary element in the CNO cycle, which implies that a yield of N depends on the amount of C and O already present in the star. Therefore, the nitrogen production depends on metallicity, and at high metallicities the oxygen abundance and the N/O ratio are expected to have a non-linear relation (see Vila-Costas & Edmunds 1992; Pérez-Montero et al. 2013, 2016; Pilyugin & Grebel 2016; Vincenzo et al. 2016, among others). However, inflow and outflow of gas may change how the O/H abundance and the N/O ratio are related (Edmunds 1990; Köppen & Hensler 2005). These effects can be very significant at low metallicities (Amorín et al. 2010, 2012). The variation of the star formation efficiency (SFE) can also affect O/H and N/O ratios (Mollá et al. 2006, 2016). This mechanism is invoked as the probable cause of the observed N/O enhancement in the centres of barred galaxies (Florido et al. 2015; Zurita et al. 2021).

If the N/O ratio depends on the oxygen abundance, one can expect a correlation between the N/O gradient and the O/H gradient. Moreover, this correlation should have particular features. First, the N/O radial distribution should be flat if the O/H radial distribution is flat. Second, both gradients should be equal at low metallicity where nitrogen is mostly produced as a primary element and the N/O ratio is constant. At higher metallicity, when nitrogen is mostly produced as a secondary element, the N/O ratio gradient should be steeper compared to the O/H one.

All three features are seen in Fig. 5 for the R abundances (top panel). In the case of the abundances derived by the HCM method, the N/O gradients also increase with O/H gradients in the case of the galaxies with high metallicity (bottom panel in Fig. 5). Nevertheless, in the case of the HCM method, as can be seen in the top left panel of Fig. 4, almost all points lie above the low metallicity regime (i.e., 12 + log(O/H) > 8.4), so this can not be properly checked for this method.

thumbnail Fig. 5.

Comparison of oxygen abundance log(O/H) gradient and the log(N/O) ratio gradient for metallicities obtained from the R calibration (top panel) or the HCM method (bottom panel). Colour denotes the oxygen abundance at Re. Black dashed lines are zero gradients. Solid black line is a one-to-one correspondence for reference.

In the previous paragraph, we explained that, on average, the slope of the N/O gradient correlates with the slope of the O/H gradient as N/O correlates with O/H. However, this correlation does not exclude a simultaneous dependence of the slope of the N/O gradient on the stellar mass. To further investigate this, in Fig. 6 we represent the median N/O gradient as a function of the galaxy mass for a sample of galaxies with a flat oxygen abundance gradient (less than 0.02 dex/Re). The N/O gradients for a sample of galaxies with flat O/H gradients show the same behaviour with respect to the stellar mass as the ones in the full sample of galaxies. This confirms that the N/O gradient depends on the stellar mass independently of the O/H gradient.

thumbnail Fig. 6.

Median N/O ratio gradient as a function of the galaxy mass for a sample of galaxies with a flat oxygen abundance gradient. The abundances are either derived from the R calibration (blue solid) or using the HCM method (red dashed). Error bars show the standard deviation divided by the square root of the number of data points in each mass bin. For reference, a horizontal dashed line shows the zero level of the N/O ratio gradient.

3.4. The relation between abundance gradients and stellar age

As has been shown by Lian et al. (2015) and Sánchez-Menguiano et al. (2020), the FMR or the mass–metallicity relation may depend on the stellar age of the galaxy. These authors used the 4000 Å break strength D(4000) as a proxy to the stellar age (Kauffmann et al. 2003b; Gallazzi et al. 2005; Sánchez Almeida et al. 2012). In this section, we discuss the links between the O/H and N/O gradients and the average stellar age of the galaxy. Since it is not easy to directly measure the stellar age, we adopted D(4000) as a proxy to it. Another advantage of D(4000) is its sensitivity to the stellar age variations during the last few Gyr (Poggianti & Barbaro 1997; Noll et al. 2009), which is enough to see its relation with the evolution of chemical abundances.

We derived values and gradients of the D(4000) index by fitting linearly the radial distribution of the D(4000) index, calculated using the method of Balogh et al. (1999), at Voronoi bins, taken from the MaNGA Firefly value-added catalogue (Goddard et al. 2017; Parikh et al. 2018). To quantify the accuracy of the fit, we calculated the standard deviation of the residuals of the fit to the individual D(4000) values, which is 0.07 for our sample. A visual inspection of the fit confirms that it is a good estimation of the radial profile. Although for some galaxies, a higher order polynomial or segmented linear fit may better represent the local values of D(4000), the estimation of the general slope of D(4000) remains robust. Furthermore in this work, the D(4000) index of a galaxy is defined as a D(4000) value from the fit at radius R = 0.

First, we investigate how stellar age affects O/H and N/O gradients. Figure 7 shows the oxygen abundance gradient as a function of the stellar mass and the D(4000) index for abundances derived from either the R calibration or using the HCM method. Left panels present the O/H gradient against the mass as distributed in individual galaxies with colour-coded D(4000) index. Right panels show the median O/H gradient in mass bins for three sub-samples of galaxies with 1.0 < D(4000) < 1.4, 1.4 < D(4000) < 1.6, and 1.6 < D(4000) < 2.2, with a similar number of galaxies in each of them. Since the D(4000) value increases with the average stellar age, we refer to these three as young, intermediate, and old sub-samples. Error bars show 2σ confidence intervals for the median O/H gradients where σ is calculated in each bin as the standard deviation divided by the square root of the number of data points. Figure 8 presents the same diagram for the radial gradient of the N/O ratio.

thumbnail Fig. 7.

Oxygen abundance gradient as a function of the stellar mass and the D(4000) index for abundances derived either from the R calibration (top panels) or using the HCM method (bottom panels). Left panels: O/H gradient as a function of the stellar mass of a galaxy with colour-coded D(4000) for individual galaxies; crosses are median values in each mass bin. Right panels: median O/H gradient with 2σ CI in each mass bin for three sub-samples of galaxies with different ranges of the D(4000) index: 1.0–1.4 (black), 1.4–1.6 (blue), and 1.6–2.2 (red).

thumbnail Fig. 8.

Same as in Fig. 7, but for the N/O gradient as a function of the stellar mass and the D(4000) index. The layout of panels, the notations, and the three sub-samples of D(4000) are the same.

In the case of the oxygen abundance gradient, the same trend results from either the R calibration or by using the HCM method. For galaxies with log(M/M⊙) < 10.25 the oxygen abundance gradient differs depending on the D(4000) value, and it is steeper in the intermediate sub-sample compared to the young and old sub-samples. We see the same trend for the N/O gradient derived either from the R calibration or by using the HCM method.

Although galaxies with low D(4000) in our sample are not the progenitors of galaxies with higher D(4000), this index characterises how old the stellar population of a galaxy is. Therefore, if the galaxies in our sample were not simultaneously formed, then D(4000) provides us an indirect opportunity to trace their evolution. Bearing this in mind, the trends seen on these plots can be interpreted as an evolution of the gradients of oxygen and the N/O ratio with time. In the beginning, galaxies with young stellar populations develop shallow oxygen abundance gradients and likely shallow N/O ratio gradients as well. Then, with the ageing of the stellar population the gradients become steeper. This may be caused by faster chemical evolution of the inner and denser parts of the galaxies. However, the chemical enrichment is limited by the interstellar gas availability, so when a significant fraction of it has been consumed to form new stars in the central part of galaxies, the pace of the chemical enrichment in the outer parts becomes relatively faster. This leads to the flattening of the radial gradients of chemical elements in the galaxies with an old stellar population. In the current epoch, this trend can be seen as a flattening of the radial metallicity gradient in the most massive galaxies (Belfiore et al. 2017; Sánchez-Menguiano et al. 2018), which have at the same time old stellar populations and a very limited amount of interstellar gas. This can explain why our sample of galaxies does not show any correlation of the O/H and N/O gradients with the D(4000) index at high stellar masses. It is important to note that such trends are predicted by the inside-out growth scenario of the galactic discs (Matteucci & Francois 1989; Boissier & Prantzos 1999; Chiappini et al. 2001).

If the abundance gradient depends on the average stellar age, that is the D(4000) index of the galaxy, one could also expect that the abundance gradient correlates with the radial gradient of D(4000). In Fig. 9, we show the oxygen abundance gradient with respect to the stellar mass of a galaxy for galaxies with positive and negative radial gradient of D(4000). On average, galaxies with the positive gradient of D(4000) show significantly flatter oxygen abundance gradients compared to the ones with the negative gradient of D(4000) in almost any mass bin for abundances obtained by either of the strong line methods. As in the previous cases, the difference decreases for massive galaxies with log(M/M⊙) > 10.25.

thumbnail Fig. 9.

Oxygen abundance gradient as a function of the stellar mass and the gradient of the D(4000) index for abundances derived from either the R calibration (top panel) or using the HCM method (bottom panel). We show median O/H gradients with 2σ CI in each mass bin for two sub-samples of galaxies with negative (black) and positive (red) gradient of D(4000).

In Fig. 10, we present the same plot for N/O gradients. As in the case of the oxygen abundance gradients, it is evident that the N/O gradient flattens for galaxies with the positive gradient of D(4000) up to stellar masses of log(M/M⊙)≈10.25 for abundances derived using either of the both strong line methods.

thumbnail Fig. 10.

Same as in Fig. 9, but for the N/O gradient as a function of the stellar mass and the gradient of the D(4000) index. The notations and the two sub-samples of the D(4000) gradient are the same.

We first demonstrated that O/H and N/O gradients correlate with D(4000) and then with the gradient of D(4000) as well. In Fig. 11, we explore these two correlations in detail for the galaxies in a narrower stellar mass range of 9 < log(M/M⊙) < 10, where the correlation of abundance gradients with D(4000) is stronger and the range of D(4000) values is wide. In confirmation of the results described above in this section, both the O/H and N/O gradients depend, on average, on the D(4000) index and its gradient simultaneously. Another interesting behaviour, described above, is that the D(4000) gradient becomes steeper and negative when D(4000) increases. Since here we consider a relatively narrow range in stellar mass, we may see how stellar evolution along the discs correlates with the gradients of O/H and N/O.

thumbnail Fig. 11.

O/H gradient (top panel) and N/O gradient (bottom panel) as a function of the D(4000) index with colour-coded gradient of D(4000) for abundances derived from the R calibration (see the text for details). Crosses connected by solid lines present median abundance gradient values in each bin of D(4000).

3.5. Comparison with theoretical models

Next, we compare our results with the predictions from theoretical models. As we discussed above, the change of the radial metallicity gradient with D(4000) may be interpreted as its evolution with time. Indeed, a number of theoretical models predicts such changes although there is a significant disagreement in their conclusions regarding the evolution of the metallicity gradient. For example, models of a Milky Way-like galaxy by Mollá et al. (2019) predict a slight flattening of the gradient starting from z = 4 with a possible steepening from z = 1 to z = 0 in some models. An analytical model developed by Belfiore et al. (2019) also predicts a general flattening of the metallicity gradient with time, taking into account significant degeneracies between model parameters at the present-day epoch.

In contrast, Sharda et al. (2021) predicted that the metallicity gradient in massive galaxies has steepened over time until the advection-dominated regime changed to the accretion-dominated regime, when the metallicity gradient started to flatten. Assuming that D(4000) correlates with the time passed from the beginning of the active star formation in a galaxy, the relation presented in Fig. 11 can be explained by the Sharda et al. (2021) model. Moreover, their Fig. 12 shows that their model predicts a flattening of the present-day metallicity gradient with the stellar mass. The same trend has been observed in this work and in Belfiore et al. (2017) for massive galaxies in the MaNGA survey as well as for galaxies in the CALIFA survey (Zinchenko et al. 2019b).

4. Summary and conclusions

We derived the oxygen abundance, 12 + log(O/H), the nitrogen-to-oxygen abundance ratio, log(N/O), and their corresponding radial gradients normalised to the effective radius Re for a sample of 1431 galaxies from the MaNGA DR15 survey using both the empirical R calibration by Pilyugin & Grebel (2016) and the model-based Bayesian HII-CHI-MISTRY method (HCM) of Pérez-Montero (2014). Our main conclusions are the following:

  1. Both methods of abundance determination confirm negative oxygen abundance gradients for the majority of galaxies. Median values of the oxygen abundance gradients are −0.06 dex/Re according to the R calibration and −0.03 dex/Re for the HCM method.

  2. The median value of the N/O gradient is also negative, −0.12 dex/Re for the R calibration and −0.18 dex/Re for the HCM method, which is consistent with previous studies (Pilyugin et al. 2004; Pérez-Montero et al. 2016; Belfiore et al. 2017).

  3. Both methods of the abundance calculation show the correlation between the O/H gradient and the stellar mass of a galaxy. This relation is non-linear, with the steepest average gradients around log(M/M⊙)≈10.0 and flatter average gradients for galaxies with higher and lower masses, as has previously been shown by Belfiore et al. (2017) using calibrations of the R23 and R3N2 parameters.

  4. The relation between the N/O gradient and the stellar mass is non-linear with, on average, the steepest gradients in the intermediate mass range, flatter gradients for galaxies with high masses, and the flattest gradients for low-mass galaxies. However, the general trend of steepening N/O gradient for higher masses remains consistent with the result obtained by Belfiore et al. (2017).

  5. Massive galaxies with log(M/M⊙) > 10.25 show no significant correlation between the slopes of either the O/H or N/O gradients and the galaxy mean stellar age, as traced by the D(4000) index. For galaxies of lower masses, O/H gradients are steeper on average for intermediate values of D(4000) and flatter for low and high values of D(4000). We interpret this behaviour as an evolution of the oxygen abundance gradient with the age of the stellar population when young stellar systems have a flat oxygen abundance gradient, which becomes steeper with time up to the minimal value. After this point the oxygen abundance gradient again becomes flatter with time. This scenario can be naturally explained by the inside-out growth of galactic discs. The N/O ratio gradients demonstrate a similar behaviour for the N/O gradients derived by both the R calibration and the HCM method.

  6. The slopes of the O/H and N/O gradients are, on average, flatter in galaxies with a positive D(4000) gradient, as compared to those with a negative D(4000) gradient.

In conclusion, our results suggest that both the age of the stellar population and the stellar mass of the galaxy are linked to the formation of the metallicity gradient in disc galaxies.

Acknowledgments

We are grateful to the referee for his/her constructive comments. The work has been performed under the Project HPC-EUROPA3 (INFRAIA-2016-1-730897), with the support of the EC Research Innovation Action under the H2020 Programme; in particular, the authors gratefully acknowledge the support of the Instituto de Astrofísica de Andalucía, the computer resources and technical support provided by the Barcelona Supercomputing Center (BSC). I.A.Z., A.V.S. and M.S. acknowledge support by the National Academy of Sciences of Ukraine under the Research Laboratory Grant for young scientists No. 0120U100148. J.V.M., E.P.M. and S.D.P. acknowledge the support by projects “Estallidos7” PID2019-107408GB-C44 (Spanish Ministerio de Ciencia e Innovacion), the Junta de Andalucía for grant EXC/2011 FQM-7058 and the Spanish Science Ministry “Centro de Excelencia Severo Ochoa Program” under grant SEV-2017-0709. M.S. was partly supported by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) Project-ID 138713538, SFB 881 (“The Milky Way System”) and by the Volkswagen Foundation under the Trilateral Partnerships grant No. 97778. M.S. acknowledges support by the Fellowship of the National Academy of Science of Ukraine for young scientists 2020-2022. S.D.P. is grateful to the Fonds de Recherche du Québec – Nature et Technologies. Funding for the Sloan Digital Sky Survey IV has been provided by the Alfred P. Sloan Foundation, the U.S. Department of Energy Office of Science, and the Participating Institutions. SDSS-IV acknowledges support and resources from the Center for High-Performance Computing at the University of Utah. The SDSS web site is https://www.sdss.org/. SDSS-IV is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS Collaboration including the Brazilian Participation Group, the Carnegie Institution for Science, Carnegie Mellon University, the Chilean Participation Group, the French Participation Group, Harvard-Smithsonian Center for Astrophysics, Instituto de Astrofísica de Canarias, The Johns Hopkins University, Kavli Institute for the Physics and Mathematics of the Universe (IPMU)/University of Tokyo, Lawrence Berkeley National Laboratory, Leibniz Institut für Astrophysik Potsdam (AIP), Max-Planck-Institut für Astronomie (MPIA Heidelberg), Max-Planck-Institut für Astrophysik (MPA Garching), Max-Planck-Institut für Extraterrestrische Physik (MPE), National Astronomical Observatories of China, New Mexico State University, New York University, University of Notre Dame, Observatório Nacional/MCTI, The Ohio State University, Pennsylvania State University, Shanghai Astronomical Observatory, United Kingdom Participation Group, Universidad Nacional Autónoma de México, University of Arizona, University of Colorado Boulder, University of Oxford, University of Portsmouth, University of Utah, University of Virginia, University of Washington, University of Wisconsin, Vanderbilt University, and Yale University.

References

  1. Amorín, R. O., Pérez-Montero, E., & Vílchez, J. M. 2010, ApJ, 715, L128 [CrossRef] [Google Scholar]
  2. Amorín, R., Pérez-Montero, E., Vílchez, J. M., & Papaderos, P. 2012, ApJ, 749, 185 [CrossRef] [Google Scholar]
  3. Asari, N. V., Cid Fernandes, R., Stasińska, G., et al. 2007, MNRAS, 381, 263 [Google Scholar]
  4. Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [Google Scholar]
  5. Balogh, M. L., Morris, S. L., Yee, H. K. C., Carlberg, R. G., & Ellingson, E. 1999, ApJ, 527, 54 [Google Scholar]
  6. Belfiore, F., Maiolino, R., Tremonti, C., et al. 2017, MNRAS, 469, 151 [Google Scholar]
  7. Belfiore, F., Vincenzo, F., Maiolino, R., & Matteucci, F. 2019, MNRAS, 487, 456 [NASA ADS] [CrossRef] [Google Scholar]
  8. Blanton, M. R., Bershady, M. A., Abolfathi, B., et al. 2017, AJ, 154, 28 [Google Scholar]
  9. Boissier, S., & Prantzos, N. 1999, MNRAS, 307, 857 [NASA ADS] [CrossRef] [Google Scholar]
  10. Bothwell, M. S., Maiolino, R., Peng, Y., et al. 2016, MNRAS, 455, 1156 [NASA ADS] [CrossRef] [Google Scholar]
  11. Bresolin, F., Ryan-Weber, E., Kennicutt, R. C., & Goddard, Q. 2009, ApJ, 695, 580 [Google Scholar]
  12. Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
  13. Bundy, K., Bershady, M. A., Law, D. R., et al. 2015, ApJ, 798, 7 [Google Scholar]
  14. Carton, D., Brinchmann, J., Contini, T., et al. 2018, MNRAS, 478, 4293 [NASA ADS] [CrossRef] [Google Scholar]
  15. Chabrier, G. 2003, PASP, 115, 763 [Google Scholar]
  16. Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] [Google Scholar]
  17. Cid Fernandes, R., Mateus, A., Sodré, L., Stasińska, G., & Gomes, J. M. 2005, MNRAS, 358, 363 [Google Scholar]
  18. Dembinski, H., Ongmongkolkul, P., Deil, C., et al. 2020, https://doi.org/10.5281/zenodo.4310361 [Google Scholar]
  19. Edmunds, M. G. 1990, MNRAS, 246, 678 [NASA ADS] [Google Scholar]
  20. Ferland, G. J., Chatzikos, M., Guzmán, F., et al. 2017, Rev. Mex. Astron. Astrofis., 53, 385 [NASA ADS] [Google Scholar]
  21. Florido, E., Zurita, A., Pérez, I., et al. 2015, A&A, 584, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  22. Gallazzi, A., Charlot, S., Brinchmann, J., White, S. D. M., & Tremonti, C. A. 2005, MNRAS, 362, 41 [Google Scholar]
  23. Goddard, Q. E., Bresolin, F., Kennicutt, R. C., Ryan-Weber, E. V., & Rosales-Ortega, F. F. 2011, MNRAS, 412, 1246 [NASA ADS] [Google Scholar]
  24. Goddard, D., Thomas, D., Maraston, C., et al. 2017, MNRAS, 466, 4731 [NASA ADS] [Google Scholar]
  25. Ho, I. T., Kudritzki, R.-P., Kewley, L. J., et al. 2015, MNRAS, 448, 2030 [NASA ADS] [CrossRef] [Google Scholar]
  26. Izotov, Y. I., Thuan, T. X., & Lipovetsky, V. A. 1994, ApJ, 435, 647 [NASA ADS] [CrossRef] [Google Scholar]
  27. James, F., & Roos, M. 1975, Comput. Phys. Commun., 10, 343 [Google Scholar]
  28. Kauffmann, G., Heckman, T. M., Tremonti, C., et al. 2003a, MNRAS, 346, 1055 [Google Scholar]
  29. Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003b, MNRAS, 341, 33 [Google Scholar]
  30. Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [Google Scholar]
  31. Köppen, J., & Hensler, G. 2005, A&A, 434, 531 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  32. Kreckel, K., Ho, I. T., Blanc, G. A., et al. 2019, ApJ, 887, 80 [NASA ADS] [CrossRef] [Google Scholar]
  33. Lian, J. H., Li, J. R., Yan, W., & Kong, X. 2015, MNRAS, 446, 1449 [NASA ADS] [CrossRef] [Google Scholar]
  34. Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  35. Mateus, A., Sodré, L., Cid Fernandes, R., et al. 2006, MNRAS, 370, 721 [NASA ADS] [CrossRef] [Google Scholar]
  36. Matteucci, F., & Francois, P. 1989, MNRAS, 239, 885 [Google Scholar]
  37. Mollá, M., Vílchez, J. M., Gavilán, M., & Díaz, A. I. 2006, MNRAS, 372, 1069 [CrossRef] [Google Scholar]
  38. Mollá, M., García-Vargas, M. L., & Bressan, A. 2009, MNRAS, 398, 451 [CrossRef] [Google Scholar]
  39. Mollá, M., Díaz, A. I., Ascasibar, Y., et al. 2016, ArXiv e-prints [arXiv:1612.03348] [Google Scholar]
  40. Mollá, M., Díaz, Á. I., Cavichia, O., et al. 2019, MNRAS, 482, 3071 [NASA ADS] [Google Scholar]
  41. Noll, S., Burgarella, D., Giovannoli, E., et al. 2009, A&A, 507, 1793 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  42. Parikh, T., Thomas, D., Maraston, C., et al. 2018, MNRAS, 477, 3954 [Google Scholar]
  43. Pérez-Montero, E. 2014, MNRAS, 441, 2663 [CrossRef] [Google Scholar]
  44. Pérez-Montero, E., & Contini, T. 2009, MNRAS, 398, 949 [CrossRef] [Google Scholar]
  45. Pérez-Montero, E., Contini, T., Lamareille, F., et al. 2013, A&A, 549, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Pérez-Montero, E., García-Benito, R., Vílchez, J. M., et al. 2016, A&A, 595, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  47. Pilyugin, L. S., & Grebel, E. K. 2016, MNRAS, 457, 3678 [NASA ADS] [CrossRef] [Google Scholar]
  48. Pilyugin, L. S., Vílchez, J. M., & Contini, T. 2004, A&A, 425, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  49. Pilyugin, L. S., Grebel, E. K., & Kniazev, A. Y. 2014, AJ, 147, 131 [NASA ADS] [CrossRef] [Google Scholar]
  50. Pilyugin, L. S., Grebel, E. K., Zinchenko, I. A., Nefedyev, Y. A., & Vílchez, J. M. 2017, A&A, 608, A127 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  51. Pilyugin, L. S., Grebel, E. K., Zinchenko, I. A., Nefedyev, Y. A., & Vílchez, J. M. 2019, A&A, 623, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  52. Poetrodjojo, H., Groves, B., Kewley, L. J., et al. 2021, MNRAS, 502, 3357 [NASA ADS] [CrossRef] [Google Scholar]
  53. Poggianti, B. M., & Barbaro, G. 1997, A&A, 325, 1025 [NASA ADS] [Google Scholar]
  54. Rosales-Ortega, F. F., Díaz, A. I., Kennicutt, R. C., & Sánchez, S. F. 2011, MNRAS, 415, 2439 [NASA ADS] [CrossRef] [Google Scholar]
  55. Sánchez, S. F., Rosales-Ortega, F. F., Marino, R. A., et al. 2012, A&A, 546, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  56. Sánchez, S. F., Rosales-Ortega, F. F., Iglesias-Páramo, J., et al. 2014, A&A, 563, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  57. Sánchez, S. F., Barrera-Ballesteros, J. K., López-Cobá, C., et al. 2019, MNRAS, 484, 3042 [CrossRef] [Google Scholar]
  58. Sánchez Almeida, J., Terlevich, R., Terlevich, E., Cid Fernandes, R., & Morales-Luis, A. B. 2012, ApJ, 756, 163 [CrossRef] [Google Scholar]
  59. Sánchez-Menguiano, L., Sánchez, S. F., Pérez, I., et al. 2016, A&A, 587, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  60. Sánchez-Menguiano, L., Sánchez, S. F., Pérez, I., et al. 2018, A&A, 609, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Sánchez-Menguiano, L., Sánchez Almeida, J., Muñoz-Tuñón, C., & Sánchez, S. F. 2020, ApJ, 903, 52 [CrossRef] [Google Scholar]
  62. Schaefer, A. L., Tremonti, C., Belfiore, F., et al. 2020, ApJ, 890, L3 [NASA ADS] [CrossRef] [Google Scholar]
  63. Searle, L. 1971, ApJ, 168, 327 [Google Scholar]
  64. Sharda, P., Krumholz, M. R., Wisnioski, E., et al. 2021, MNRAS, 502, 5935 [NASA ADS] [CrossRef] [Google Scholar]
  65. Shields, G. A., & Searle, L. 1978, ApJ, 222, 821 [NASA ADS] [CrossRef] [Google Scholar]
  66. Thuan, T. X., Pilyugin, L. S., & Zinchenko, I. A. 2010, ApJ, 712, 1029 [NASA ADS] [CrossRef] [Google Scholar]
  67. Tissera, P. B., Rosas-Guevara, Y., Bower, R. G., et al. 2019, MNRAS, 482, 2208 [Google Scholar]
  68. Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [Google Scholar]
  69. Troncoso, P., Maiolino, R., Sommariva, V., et al. 2014, A&A, 563, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  70. Vila-Costas, M. B., & Edmunds, M. G. 1992, MNRAS, 259, 121 [NASA ADS] [CrossRef] [Google Scholar]
  71. Vilchez, J. M., Pagel, B. E. J., Diaz, A. I., Terlevich, E., & Edmunds, M. G. 1988, MNRAS, 235, 633 [CrossRef] [Google Scholar]
  72. Vincenzo, F., Belfiore, F., Maiolino, R., Matteucci, F., & Ventura, P. 2016, MNRAS, 458, 3466 [NASA ADS] [CrossRef] [Google Scholar]
  73. Yates, R. M., Schady, P., Chen, T. W., Schweyer, T., & Wiseman, P. 2020, A&A, 634, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Zahid, H. J., Dima, G. I., Kudritzki, R.-P., et al. 2014, ApJ, 791, 130 [NASA ADS] [CrossRef] [Google Scholar]
  75. Zaritsky, D., Kennicutt, R. C., Jr., & Huchra, J. P. 1994, ApJ, 420, 87 [NASA ADS] [CrossRef] [Google Scholar]
  76. Zinchenko, I. A., Pilyugin, L. S., Grebel, E. K., Sánchez, S. F., & Vílchez, J. M. 2016, MNRAS, 462, 2715 [Google Scholar]
  77. Zinchenko, I. A., Just, A., Pilyugin, L. S., & Lara-Lopez, M. A. 2019a, A&A, 623, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  78. Zinchenko, I. A., Dors, O. L., Hägele, G. F., Cardaci, M. V., & Krabbe, A. C. 2019b, MNRAS, 483, 1901 [CrossRef] [Google Scholar]
  79. Zurita, A., Florido, E., Bresolin, F., Pérez, I., & Pérez-Montero, E. 2021, MNRAS, 500, 2380 [Google Scholar]

All Figures

thumbnail Fig. 1.

Example of the radial gradients of O/H (upper panel) and N/O (lower panel) in the MaNGA galaxy 1-48157 using data from data cube 10001-12701. Grey points are values in each spaxel, derived from the empirical R calibration of Pilyugin & Grebel (2016). Red crosses are median values in bins. A solid line is the linear fit to the data.
In the text
thumbnail Fig. 2.

Comparison between O/H at galaxy centres derived by extrapolating the radial fits and by averaging in individual spaxels at R < 0.1Re. Upper panel: O/H derived from the empirical R calibration. Lower panel: O/H derived using the HCM code. Dashed lines represent the one-to-one correspondence.
In the text
thumbnail Fig. 3.

Comparison between fits to the derived O/H radial distributions at a galactocentric radius less than 3Re (horizontal axes) and less than 5Re (vertical axes). Upper panel: comparison of the extrapolated O/H abundances in the galaxy centres. Lower panel: comparison of the slopes of the fits. The oxygen abundances and their corresponding gradients were derived using the following two methods: the R calibration (black circles) or the HCM code (green triangles). Dashed lines represent the one-to-one correspondence.
In the text
thumbnail Fig. 4.

Galaxy-centre oxygen abundance log(O/H), nitrogen-to-oxygen ratio log(N/O), and their gradients as a function of galaxy mass log(M/M⊙). Median values (solid lines) with 1-σ range scatter (shaded areas) are shown in each mass bin. The metallicity parameters were calculated using the following two methods: the R calibration (blue lines and areas) or the HCM method (red lines and areas). For the O/H and N/O gradients, dashed lines show linear fits as a function of the stellar mass.
In the text
thumbnail Fig. 5.

Comparison of oxygen abundance log(O/H) gradient and the log(N/O) ratio gradient for metallicities obtained from the R calibration (top panel) or the HCM method (bottom panel). Colour denotes the oxygen abundance at Re. Black dashed lines are zero gradients. Solid black line is a one-to-one correspondence for reference.
In the text
thumbnail Fig. 6.

Median N/O ratio gradient as a function of the galaxy mass for a sample of galaxies with a flat oxygen abundance gradient. The abundances are either derived from the R calibration (blue solid) or using the HCM method (red dashed). Error bars show the standard deviation divided by the square root of the number of data points in each mass bin. For reference, a horizontal dashed line shows the zero level of the N/O ratio gradient.
In the text
thumbnail Fig. 7.

Oxygen abundance gradient as a function of the stellar mass and the D(4000) index for abundances derived either from the R calibration (top panels) or using the HCM method (bottom panels). Left panels: O/H gradient as a function of the stellar mass of a galaxy with colour-coded D(4000) for individual galaxies; crosses are median values in each mass bin. Right panels: median O/H gradient with 2σ CI in each mass bin for three sub-samples of galaxies with different ranges of the D(4000) index: 1.0–1.4 (black), 1.4–1.6 (blue), and 1.6–2.2 (red).
In the text
thumbnail Fig. 8.

Same as in Fig. 7, but for the N/O gradient as a function of the stellar mass and the D(4000) index. The layout of panels, the notations, and the three sub-samples of D(4000) are the same.
In the text
thumbnail Fig. 9.

Oxygen abundance gradient as a function of the stellar mass and the gradient of the D(4000) index for abundances derived from either the R calibration (top panel) or using the HCM method (bottom panel). We show median O/H gradients with 2σ CI in each mass bin for two sub-samples of galaxies with negative (black) and positive (red) gradient of D(4000).
In the text
thumbnail Fig. 10.

Same as in Fig. 9, but for the N/O gradient as a function of the stellar mass and the gradient of the D(4000) index. The notations and the two sub-samples of the D(4000) gradient are the same.
In the text
thumbnail Fig. 11.

O/H gradient (top panel) and N/O gradient (bottom panel) as a function of the D(4000) index with colour-coded gradient of D(4000) for abundances derived from the R calibration (see the text for details). Crosses connected by solid lines present median abundance gradient values in each bin of D(4000).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.