| Issue |
A&A
Volume 666, October 2022
|
|
|---|---|---|
| Article Number | A186 | |
| Number of page(s) | 18 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202141571 | |
| Published online | 26 October 2022 | |
Mass–metallicity and star formation rate in galaxies: A complex relation tuned to stellar age⋆
1
Département de Physique, de Génie Physique et d’Optique, Université Laval, et Centre de Recherche en Astrophysique du Québec (CRAQ), Québec, QC G1V 0A6, Canada
e-mail: salvador-manuel.duarte-puertas.1@ulaval.ca
2
Instituto de Astrofísica de Andalucía – CSIC, Glorieta de la Astronomía s.n., 18008 Granada, Spain
3
CIEMAT, Avda. Complutense 40, 28040 Madrid, Spain
4
Main Astronomical Observatory, National Academy of Sciences of Ukraine, 27 Akademika Zabolotnoho St., 03680 Kyiv, Ukraine
5
Institute of Theoretical Physics and Astronomy, Vilnius University, Sauletekio av. 3, 10257 Vilnius, Lithuania
6
Faculty of Physics, Ludwig-Maximilians-Universität, Scheinerstr. 1, 81679 Munich, Germany
Received:
16
June
2021
Accepted:
11
April
2022
Context. In this work we study the stellar mass–metallicity relation (MZR) of an extended sample of star-forming galaxies in the local Universe and its possible dependence on the star formation rate (SFR).
Aims. We selected a sample of approximately 195 000 Sloan Digital Sky Survey (SDSS) star-forming galaxies up to z = 0.22 with the aim of analysing the behaviour of the MZR with respect to SFR whilst taking into account the age of their stellar populations.
Methods. For the first time, with this sample, we obtained aperture corrected oxygen and nitrogen-to-oxygen abundances (O/H and N/O, respectively) and SFR using the empirical prescriptions from the Calar Alto Legacy Integral Field Area (CALIFA) survey. To perform this study we also make use of the stellar mass of the galaxies and the parameter Dn(4000) as a proxy for the age of the stellar population.
Results. We derive a robust MZR locus, which is found to be fully consistent with the ‘anchoring’ points of a selected set of well-studied nearby galaxies for which the chemical abundance has been derived using the direct method. We observe a complex relation between MZR and SFR across the whole range of galaxy mass and metallicity, where the slope changes seen in the O/H–SFR plane present a pattern that seems to be tuned to the stellar age of the galaxies, and therefore stellar age has to be taken into account in the stellar mass–metallicity–SFR relation.
Conclusions. In order to provide an answer to the question of whether or not the MZR depends on the SFR, it is essential to take into account the age of the stellar populations of galaxies. A strong dependence of the MZR on SFR is observed mainly for star-forming galaxies with strong SFR values and low Dn(4000). The youngest galaxies of our SDSS sample show the highest SFR measured for their stellar mass.
Key words: galaxies: general / galaxies: star formation / galaxies: abundances / galaxies: evolution
Full Table 1 with the values of oxygen and nitrogen-to-oxygen abundance ratios for ∼195 000 SDSS star-forming galaxies and related relevant data is only available in electronic form at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/666/A186
© S. Duarte Puertas et al. 2022
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe-to-Open model. Subscribe to A&A to support open access publication.
1. Introduction
Since the pioneering work of Lequeux et al. (1979), a plethora of studies have investigated the relation between metallicity and galaxy stellar mass, as well as their connections with other fundamental parameters of galaxies (e.g.Vila-Costas & Edmunds 1992; Garnett 2002; Pilyugin et al. 2004; Tremonti et al. 2004; Lee et al. 2006; Zahid et al. 2014; Sánchez et al. 2017; Maiolino & Mannucci 2019; Sánchez 2020). In all of these works, a clear correlation between total stellar mass (M⋆) and metallicity of galaxies was highlighted. The mass–metallicity relation (MZR) therefore remains a key ingredient in our understanding of the formation and evolution of galaxies. Theoretical models predict a tight relation (e.g. Mouhcine et al. 2008; Sakstein et al. 2011; Davé et al. 2011; Romeo Velonà et al. 2013; Okamoto et al. 2017; De Rossi et al. 2017; Torrey et al. 2018), illustrating how galaxy evolution is driven by galaxy mass and is modulated by gas accretion and outflows.
The MZR reaches a maximum near saturation at the high-mass end (log(M⋆/M⊙)≥10.5), maintaining a metallicity asymptotically close to the oxygen yield (e.g. Pilyugin et al. 2007). The study of this relation for galaxies of different masses can be used to better ascertain whether the MZR could be emerging from a local relationship within galaxies or rather represents a truly global scale relation, for example linked to galaxy mass. The overall shape of the MZR is believed to respond mainly to the action of galactic winds and enriched outflows in addition to metal astration driven by star formation and galaxy stellar mass, but other processes related to for example galaxy downsizing or massive gas accretion and star formation can also be involved (e.g. Finlator & Davé 2008).
Star formation rate (SFR) was originally introduced as a secondary parameter of the MZR, with the aim being to reduce the observed scatter, and in this way the so-called fundamental mass–metallicity–SFR relation was defined (MZSFR; e.g. Ellison et al. 2008; Mannucci et al. 2010; Lara-López et al. 2010b). In this fundamental relation, at a fixed galaxy stellar mass, SFR anti-correlates with metallicity, similarly to the predictions of some models used to study this possible secondary dependence of MZR on SFR (e.g.Dayal et al. 2013). An intense debate (e.g. Sánchez et al. 2013, 2017, 2019; Salim et al. 2014; Barrera-Ballesteros et al. 2017; Cresci et al. 2019) has developed since then over the existence (or not) of this second dependence on SFR. The observations of a large number of galaxies obtained with integral field spectroscopy (IFS) in CALIFA (Sánchez et al. 2012; García-Benito et al. 2015) and MANGA (Bundy et al. 2015) surveys, or with integrated spectra by Hughes et al. (2013), led to different conclusions preventing consensus in understanding the exact role played by the SFR, and the possible evolution of MZSFR with redshift.
One of the key differences among the above cited studies, and that investigated in the present work, is that the integrated galaxy analyses are usually performed using bright emission lines measured on single aperture spectroscopy of galaxies (e.g. spectra SDSS, VVDS, zCOSMOS, DEIMOS) to derive the oxygen abundance (O/H) of the ionised gas as a proxy of galaxy metallicity; and the SFR estimates for these galaxies were also derived from the same aperture spectral information, with present-day SFRs often computed from the luminosity of Hα emission. The aperture corrections are produced by incomplete or partial coverage of the observed galaxies (e.g. SDSS 3 arcsec fibre spectroscopy), and may produce critical effects, which must be corrected. IFS of a large sample of galaxies of CALIFA provided a method for correcting the emission lines by aperture and spatial sampling effects (Mast et al. 2014; Gomes et al. 2016; Iglesias-Páramo et al. 2016). It has been shown that aperture effects translate to clear flux deficits which, in the case of SFR for example, imply corrections of up to ∼0.6 dex (Iglesias-Páramo et al. 2013; Duarte Puertas et al. 2017); whereas model-based aperture corrections do not solve this problem. In the case of the emission-line fluxes, the situation is not trivial, as they and their corresponding extinction must be aperture corrected before deriving SFR or the different abundance ratios. In particular, differential extinction correction across the disks of galaxies cannot be overlooked. Iglesias-Páramo et al. (2016) provide empirical CALIFA-based aperture corrections for the relevant lines.
The SFR of galaxies can also be derived using multiparametric fitting of their spectral energy distribution (SED) using evolutionary population synthesis models and inverting population synthesis equations (with their own uncertainties). Recent spatially resolved studies using this latter technique found a clear correlation between O/H and SFR using the IFS CALIFA and MANGA data (e.g. Cresci et al. 2019). However, according to Sánchez (2020), whether or not a fundamental metallicity relation exists depends on the analysis of the data, that is, with the same CALIFA data set, Salim et al. (2014) found a dependence of sSFR on metallicity not found by Sánchez et al. (2013), who suggested that the MZSFR relation is an artifact of spectroscopy aperture bias. On the other hand, Cresci et al. (2019) concluded that the method used to calculate the stellar mass of galaxies, the other key ingredient in the MZR, also affects the obtained results. To these considerations, we need to add the fact that other authors have used IFS to study the relationship between O/H and other parameters (e.g.Barrera-Ballesteros et al. 2018, 2020; Sánchez-Menguiano et al. 2020), and propose that there might be some dependence, even indirectly, between gas-phase metallicity and stellar age at local and global scales. The two questions are related, and therefore the study of a possible evolution of the zero point and slope of the MZR with cosmic time and its dependence on SFR can shed light on how galaxies formed and how they were assembled and evolve, and could also provide insights into the infall and galactic wind phases of their chemical evolution. The MZR has been extensively studied as a general scaling relation of star-forming galaxies in the local Universe (e.g. Mannucci et al. 2010; Lara-López et al. 2010b; Kashino et al. 2016; Curti et al. 2020), as a function of galaxy environment (e.g. Ellison et al. 2009; Petropoulou et al. 2011, 2012; Peng & Maiolino 2014; Pilyugin et al. 2017), and in medium- and high-redshift surveys (e.g. Brown et al. 2016; Hunt et al. 2016; Kojima et al. 2017). Some evolution is expected for the shape and the zero point of the MZR (e.g. Lara-López et al. 2010a; Møller et al. 2013; Pilyugin et al. 2013); though, other works find no significant evolution for the MZSFR (e.g. Mannucci et al. 2010; Cresci et al. 2012).
In addition to the above uncertainties, we must also consider the well-known issue of metallicity derivation from spectroscopy in large samples, which has been discussed elsewhere (e.g. Curti et al. 2017 and references therein). As temperature-sensitive line fluxes are not available for the huge majority of these objects (e.g. in SDSS), abundance calibrations are applied to derive their metallicity. Not all abundance calibrations appear equally reliable when they are compared with oxygen abundances derived using the direct method. Recent empirical abundance calibrations provide an abundance which, statistically, is typically within 0.2 dex uncertainty of the direct value. In this respect, some support can be gained using complementary versions of the MZR relation; for example using stellar metallicity derived either from integrated young stellar populations (e.g. Gallazzi et al. 2005) or for individual massive stars (e.g. Bresolin et al. 2016); or deriving O/H directly from stacked spectra of mass-grouped star-forming galaxies (e.g. Andrews & Martini 2013). Also replacing O/H with nitrogen-to-oxygen abundance (N/O), an abundance ratio less dependent on electron temperature and recognise as a well-known ‘chemical clock’ (e.g. Edmunds & Pagel 1978; Pilyugin et al. 2003; Mollá et al. 2006), gives useful chemical evolution information. N/O also has a well-known relationship with stellar mass (Pérez-Montero & Contini 2009); for high metallicity, nitrogen has mainly a secondary origin, and as its derivation does not depend on the excitation of the gas, the study of the mass versus N/O relation (MNOR) can be very useful for better understanding the zero-point and the slope of the MZR. In addition, the combined study of mass, SFR, and N/O can also be used to better understand the dependence of metallicity on SFR. In the present work, we take into account the caveats mentioned above in our metallicity derivation and analysis, and we performed the corresponding sanity checks when appropriate.
In summary, in order to carry out an in-depth study of the relation between MZR and SFR, we must address the systematic effects involved, as discussed in Telford et al. (2016) and Cresci et al. (2019), such as those associated to signal-to-noise ratio (S/N), aperture effects, or the metallicity indicators used, among others, which can affect the derivation of the MZR and any possible dependence of MZR on SFR. This is the main objective of this work. To this end, we use the methodology and knowledge gained with the CALIFA survey to minimise systematic effects. We perform a detailed examination of the behaviour of the relation between MZR and SFR for a large and complete sample of SDSS star-forming galaxies (see Duarte Puertas et al. 2017 for details) using the total fluxes of their emission lines empirically corrected by extinction and aperture effects in a consistent manner. We analyse the MZR and SFR relationships, studying in particular the role of the age of stellar populations in galaxies using the parameter Dn(4000) as a proxy.
The structure of this paper is organised as follows: in Sect. 2 we describe the data, providing a description of the methodology used to select the sample (Sect. 2.1). The methodology followed to derive all the parameters used in this work is presented in Sect. 2.2. Our main results and a discussion are given in Sect. 3. Our conclusions are outlined in Sect. 4, and, finally, supplementary material is provided in Appendix A. Throughout the paper, we assume a Friedman-Robertson-Walker cosmology with ΩΛ0 = 0.7, Ωm0 = 0.3, and H0 = 70 km s−1 Mpc−1. We use the Kroupa (2001) universal initial mass function (IMF).
2. Data and sample
2.1. The sample of galaxies
Our study is based on the catalogue of 209276 star-forming galaxies extracted from SDSS-DR12 (Alam et al. 2015) and presented in Duarte Puertas et al. (2017). The galaxies span redshift (z) and stellar mass ranges of 0.005 ≤ z ≤ 0.22 and 8.5 ≤ log(M⋆/M⊙) ≤ 11.5, respectively. All the emission line fluxes (i.e. [OII]λλ 3727, 3729, [OIII]λ 5007, Hβ, [NII]λ 6584, and Hα), log(M⋆/M⊙), z, and Dn(4000)1 used in this work are taken from Max-Planck-Institut für Astrophysik and Johns Hopkins University (MPA-JHU) public catalogue2 (Kauffmann et al. 2003; Brinchmann et al. 2004; Tremonti et al. 2004; Salim et al. 2007). From this catalogue we have selected a subset of 194353 SDSS star-forming galaxies according to the following criteria:
(i) z ≥ 0.02. Due to the SDSS spectral range (3800–9200 Å), this is the minimum redshift required to include and measure [OII]λλ 3727, 3729; this emission lines are necessary to derive the metallicity (see Sect. 2.2) from our spectra (Pilyugin et al. 2012; Pérez-Montero et al. 2013).
(ii) A S/N ≥ 3 is imposed for all the line fluxes used to derive O/H and N/O.
For these objects, we determine the oxygen and nitrogen-to-oxygen abundances, following the prescriptions explained in Sect. 2.2. For the SFR, we use aperture corrected measurements from the database of Duarte Puertas et al. (2017).
2.2. Empirical aperture correction and chemical abundances
It is well known that the 3 arcsec diameter fibres of SDSS only cover a limited region of galaxies in the low-z Universe (z < 0.22). In order to obtain the total SFR for all the galaxies in our sample, we used the aperture-corrected SFR values from Duarte Puertas et al. (2017), where a detailed description of the aperture correction for the Hα flux measurements of SDSS is presented.
The aperture corrections for the Hα flux and the log([OIII]λ 5007/Hβ), log([NII]λ 6584/Hα), and Hα/Hβ flux ratios of our sample were performed using the prescriptions by Iglesias-Páramo et al. (2016). These corrections were derived for a sample of disk galaxies in the CALIFA survey that are representative of different types and masses (Iglesias-Páramo et al. 2016). The aperture correction recipe for [OII]λλ 3727, 3729 was also provided to us by Iglesias-Páramo et al. (private communication). Conversely, as shown in Belfiore et al. (2016), the Dn(4000) break strength index remains substantially constant across star-forming galaxies, given that their young stellar component appears well distributed throughout the entire galactic disk; hence no aperture correction was applied for it. In summary, for each galaxy in our sample, the line fluxes measured in the SDSS fibres (i.e. [OII]λλ 3727, 3729, [OIII]λ 5007, Hβ, [NII]λ 6584, and Hα) were corrected for extinction following Duarte Puertas et al. (2017), and were aperture-corrected by applying the equations in Table 20 of Iglesias-Páramo et al. (2016). These emission-line fluxes are necessary for the derivation of oxygen and nitrogen abundances, as explained.
In order to derive the metallicity of our sample galaxies, and given that the faint temperature-sensitive lines are not available, we must rely on bright-line abundance calibrations (including from [OII] to [NII]). It is well known that some calibrations produce different absolute values of O/H; special care was taken in this work in the selection of the abundance calibrations applied. We used three different methods: We first followed the study updated by Curti et al. (2017) for O/H derivation and selected their calibration of O3N2 which presents the wider O/H prediction range with the smallest dispersion. In addition, we adopted the empirical calibrations by Pilyugin & Grebel (2016) for nitrogen (their eq. 13) and oxygen (their eqs. 4, 5) abundances.
These calibrations are empirical, that is, they are calibrated against direct abundances calculated with electron temperature measurements. Finally, we used the abundances given by the code HII-CHI-MISTRY (Pérez-Montero 2014), which is based on photoionisation models, and reproduces chemical abundances consistent with their corresponding direct derivations3. For the sake of consistency, and in order to compare our findings with the literature and other works performed including spectroscopy of distant galaxies, oxygen and nitrogen-to-oxygen abundances for our sample galaxies were derived with the three methods mentioned above once they were free from aperture effects (given that the emission line fluxes used were all aperture corrected), corresponding to the entire galaxy. We also derived the value of oxygen and nitrogen-to-oxygen abundances within the SDSS fibre and we obtained that the values derived in the SDSS fibre for O/H and N/O are systematically higher than those that are aperture corrected. The mean oxygen abundance difference between the fibre and the value corrected for aperture, Δ(12+log(O/H)), is 0.04 dex (the standard deviation is 0.01 dex) for our sample of star-forming galaxies. In the case of the mean nitrogen-to-oxygen abundance difference, Δ(log(N/O)), we find a value of 0.06 dex (the standard deviation is 0.01 dex). All the abundances obtained for each object we found to be consistent within the errors, and overall, the three abundance outputs from the calibrations selected (and values in the fibre) are statistically consistent to within ∼0.15 dex; with the highest consistency and lowest errors being achieved for the nitrogen-to-oxygen abundance ratio. Taking this fact into account, in this work, we adopt the O/H and N/O abundances obtained from the methodology of Pilyugin & Grebel (2016) as representative for each galaxy. Table 1 shows a sample of the online table of 194353 star-forming galaxies, where their fluxes have been aperture corrected, showing the spectroscopic identifier from SDSS (specObjID), oxygen, as 12+log(O/H), the nitrogen-to-oxygen abundance ratio, as log(N/O), abundances, stellar mass as log(M⋆/M⊙), the SFR (in M⊙ yr−1 units), and the parameter Dn(4000); we use this latter as the stellar population age indicator. Table 1 also shows the uncertainties for each property considered4.
Compiled data for our sample of star-forming galaxies.
3. Discussion
In left panel of Fig. 1, we show the oxygen abundance, 12 + log(O/H), versus total stellar mass for the 194353 galaxies in our sample, which clearly reproduce the MZR relation. A further quality check of our MZR derivation is to compare it with the oxygen abundance and total stellar mass5 for the Milky Way6 and ten well-known nearby galaxies for which precise abundance values of their HII regions have been derived using the direct method from available electron temperature measurements. These nearby galaxies show well-defined spatially resolved radial abundance gradients, and therefore their representative abundance corresponding to the integrated galaxy flux can easily be derived using the IFS measurements in the CALIFA survey. To do so, we use the O/H measured in the characteristic radius (0.4 × R25; similar to the effective radius of the galaxy, e.g. Sánchez et al. 2013), which is the most suitable representative value of the whole galaxy abundance. According to Sánchez et al. (2013), for galaxies presenting 12 + log(O/H) abundance at the effective radius, 12 + log(O/H)Reff ≤ 8.6 dex, the mean difference between 12 + log(O/H) of the integrated galaxy flux and 12 + log(O/H)Reff is ∼ − 0.03 dex; whereas for galaxies with 12 + log(O/H)Reff above 8.6 dex, this difference amounts to ∼0.06 dex. We applied this conversion to calculate the representative 12 + log(O/H) abundances of our selected nearby galaxies; these objects are also shown in left panel of Fig. 1. In this panel, it can be seen that the selected sample of nearby galaxies and our sample of SDSS star-forming galaxies, free from aperture effects, show excellent agreement, delineating the local Universe MZR. As mentioned in Sect. 2.2, we derived (and compared) the O/H values using the empirical calibrations from Pilyugin & Grebel (2016), Pérez-Montero & Contini (2009); the direct method, using the electron temperature for objects with auroral line measurements; and the theoretical photoionisation models (HII-CHI-mistry) from Pérez-Montero (2014). All these methods lead to abundances that are consistent overall – within the errors – and the differences between them have already been discussed. In Fig. A.1 it can be seen that all galaxies where the electron temperature has been calculated show a high level of consistency between the O/H from the direct method and the corresponding values obtained in this work using empirical calibrators. Therefore, we consider that the oxygen abundances used are precisely estimated and better than others in the literature.
 |
Fig. 1. Relation between 12+log(O/H) and M⋆. Left panel: aperture corrected MZR for star-forming galaxies of our sample (grey dots), as well as the Milky Way (green mark) and other nearby galaxies (labelled; coloured points) with direct (from electron temperature) oxygen abundances are shown. Blue or red colour indicate galaxies with a flat or non-zero radial oxygen gradient, respectively. References as follows: galaxy name, O/H reference, stellar mass reference; SMC, LMC, and M81, Bresolin et al. (2016), Kudritzki et al. (2012); NGC 55, Magrini et al. (2017), Lee et al. (2006); MW, Fernández-Martín et al. (2017), Arellano-Córdova et al. (2021), Licquia & Newman (2015); M83, Bresolin et al. (2016), Hernandez et al. (2019), Kang et al. (2016); M33 and NGC 300, Bresolin et al. (2016), Kang et al. (2016); M 31, Zurita & Bresolin (2012), Fisher & Drory (2011); M 101, Croxall et al. (2016), Skibba et al. (2011); NGC 628, Berg et al. (2015), Cook et al. (2014; see also Vílchez et al. 2019). Right panel: aperture corrected MZR for star-forming galaxies, black points. Blue, green, red, cyan, magenta, lime, and yellow solid lines represent the fits to the running median of the SFR of the galaxies, calculated in bins of 1000 galaxy points, corresponding to seven SFR intervals as indicated. |
As we also want to see the role of the SFR in the MZR relation, we show, in right panel of Fig. 1, the diagram for the same MZR as in left panel, but overplotting the lines representing the fits to the running medians of seven different SFR intervals. The strong correlation between oxygen abundance and galaxy stellar mass shown in the MZR plot is also evident in all the shown SFR lines separately. We can also see how these iso-SFR loci tend to saturate at higher abundances and level off near solar metallicity7. We may also see that for a fixed log(M⋆/M⊙), galaxies with a higher metallicity present lower SFRs than their lower metallicity counterparts, in line with previous findings (e.g. Mannucci et al. 2010).
We now analyse the relationship between the abundances and the SFR. Panel (a) of Fig. 2 shows our aperture-corrected oxygen abundances, as 12 + log(O/H), versus the SFR for the galaxy sample (grey points) following the same statistical procedure as in the previous figure. We computed the running medians and plotted the corresponding fits for six intervals of log(M⋆/M⊙) with Δlog(M⋆/M⊙) = 0.5 dex each (see also Fig. A.2). The total covered range in galaxy stellar mass is 8.5 ≤ log(M⋆/M⊙) ≤ 11.5 in both panels. Both panels show the fits to the running median of the Dn(4000) index of the sample galaxies, calculated for six intervals from Dn(4000) < 1.1 to Dn(4000)∼1.5, with ΔDn(4000) = 0.1 dex each, as indicated in the plot; in parenthesis, the total number of points per interval is quoted. We can see a clear overall trend in 12 + log(O/H) versus SFR in our sample (grey points). Panel (b) shows the aperture-corrected log(N/O) versus SFR. There, we again show the log(N/O) versus SFR considering the same galaxy mass and Dn(4000) bins, and fits to the running median. A similar strong correlation is also present between these two properties. A wide range in log(N/O) is covered by our SDSS galaxy sample, going from over-solar8 values to the level typical of low-metallicity dwarf galaxies (log(N/O) ∼ −1.5). All the lines shown in Fig. 2 (i.e. black for stellar mass and coloured for Dn(4000)) represent the real statistical (median) loci of the galaxy points and are the result of the fit to the statistical distribution of the properties considered (i.e. Dn(4000), stellar mass, and O/H) for the SDSS star-forming galaxies sample used in this work.
 |
Fig. 2. Relation between 12+log(O/H) (panel a) and log(N/O) (panel b) and SFR for our sample of SDSS star-forming galaxies. Blue, green, red, cyan, magenta, and yellow solid lines represent the fits to the running median for bins of 1000 objects in six Dn(4000) bins. The number of star-forming galaxies in each Dn(4000) bin appears on the legend. Black dash-dotted lines show the 12+log(O/H) (panel a) and log(N/O) (panel b) vs. SFR fits to the running median for bins of 1000 objects in six log(M⋆/M⊙) bins (each box shows the considered log(M⋆/M⊙) range). |
It is important to bear in mind that Dn(4000) depends on stellar population age, and shows the lowest values for the youngest stellar populations, while the older ones show higher values (Balogh et al. 1999). In panels (a) and (b) of Fig. 2, we can see how, for a fixed log(M⋆/M⊙), galaxies with lower SFR present systematically higher values of Dn(4000), suggesting that they host older stellar populations. For Dn(4000) > 1.2, we can see that the lines corresponding to the most massive galaxies (log(M⋆/M⊙) > 10.5) tend to saturate, and seem to flatten above 12 + log(O/H) ≥ 8.55 and log(N/O) ≥ −0.9, irrespective of their SFR. For nearly the entire mass range of the sample (log(M⋆/M⊙) ≤ 11), oxygen abundance, 12 + log(O/H), shows a nearly flat or very mild decrease with respect to SFR along the black dotted lines. Although the usual assumption is that SFR depends on age, where an anticorrelation is seen between stellar age and SFR when the stellar mass is taken into account, this plot suggests that the two effects are disentangled. Figure 3 shows SFR as a function of Dn(4000) and is designed to highlight this SFR–age effect. In this figure, we see that at face value there is a correlation between high SFR and high Dn(4000) values. We also overplot the mass isolines and O/H isolines for six stellar mass bins and six O/H ranges, respectively, for our sample of SDSS star-forming galaxies. We can see how: (i) at fixed SFR the corresponding entire range of Dn(4000) is covered; (ii) at fixed stellar mass, the lower the SFR, the higher the Dn(4000); and (iii) at fixed O/H, we see that the relationship is more complex: from Dn(4000)∼1.2 towards the right, for O/H < 8.5 the SFR stops decreasing with Dn(4000). However, for the left region, the anticorrelation between SFR and Dn(4000) is very strong. We consider this relationship to be relevant and deserving of further exploration with our sample of star-forming galaxies.
 |
Fig. 3. Relation between SFR and Dn(4000) for our sample of star-forming galaxies. Blue, green, red, cyan, magenta, and yellow solid lines represent the running median for bins of 2000 objects in six O/H bins. Black dash-dotted lines show the fit to the running median for bins of 1000 objects in six log(M⋆/M⊙), bins, from low stellar mass (8.5, lower part of the figure) to high stellar mass (11.5, higher part of the figure). |
Depending on the stellar mass range, there is a value of SFR for which a change in O/H is observed. This SFR value varies depending on the stellar mass range considered. The iso-Dn(4000) line between 1.1 and 1.2 accompanies the change in the O/H–SFR relation depending on the stellar mass, which suggests that this line determines a statistical value for stellar mass, SFR, and age9. The data do not allow us to decipher the exact age at which the slope of these iso-mass lines changes in the O/H–SFR diagram, but our results do allow us to say that it must occur around that Dn(4000) value (shown by the green line). Therefore, in order to address this point, we proceeded as follows: (i) We derived 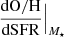 , that is, the derivative of O/H versus SFR at constant stellar mass, along all iso-mass lines below the range 10 ≤ log(M⋆/M⊙) < 10.5; (i.e. for four iso-mass lines); (ii) We obtained the value of log(SFR) for which the derivative presents the net measurable change, log(SFRderi), with a minimum value of −0.002, which is half of the value obtained for the iso-mass line of the range 8.5 ≤ log(M⋆/M⊙) < 9.0. This is the point where the slope starts to be steeper (and negative) than this value; (iii) The iso-mass line corresponding to this lowest mass range plotted shows a nearly constant derivative, approximately a straight line in the plot without any apparent change in its slope; therefore, any change in the derivative of this iso-mass line should have occurred for log(SFR) < −1.5 (alternatively, there exists no such change in the derivative of the subsample of SDSS galaxies in this stellar mass and SFR range, or it is small and we cannot statistically ‘see’ it); (iv) We determined log(SFRcut) as the SFR value at which each iso-Dn(4000) line cuts each iso-mass line in the O/H vs. SFR diagram in Fig. 2; and (v) We then computed the difference between log(SFRcut) and log(SFRderi), as Δlog(SFR) = log(SFRcut) − log(SFRderi), for each iso-mass line. As the iso-Dn(4000) line between 1.2 and 1.3 does not intersect the 8.5 ≤ log(M⋆/M⊙) < 9.0 iso-mass line in the O/H versus SFR diagram, we assume the position in this diagram at which it would intersect by slightly extrapolating the iso-Dn(4000) line for the sake of this test.
, that is, the derivative of O/H versus SFR at constant stellar mass, along all iso-mass lines below the range 10 ≤ log(M⋆/M⊙) < 10.5; (i.e. for four iso-mass lines); (ii) We obtained the value of log(SFR) for which the derivative presents the net measurable change, log(SFRderi), with a minimum value of −0.002, which is half of the value obtained for the iso-mass line of the range 8.5 ≤ log(M⋆/M⊙) < 9.0. This is the point where the slope starts to be steeper (and negative) than this value; (iii) The iso-mass line corresponding to this lowest mass range plotted shows a nearly constant derivative, approximately a straight line in the plot without any apparent change in its slope; therefore, any change in the derivative of this iso-mass line should have occurred for log(SFR) < −1.5 (alternatively, there exists no such change in the derivative of the subsample of SDSS galaxies in this stellar mass and SFR range, or it is small and we cannot statistically ‘see’ it); (iv) We determined log(SFRcut) as the SFR value at which each iso-Dn(4000) line cuts each iso-mass line in the O/H vs. SFR diagram in Fig. 2; and (v) We then computed the difference between log(SFRcut) and log(SFRderi), as Δlog(SFR) = log(SFRcut) − log(SFRderi), for each iso-mass line. As the iso-Dn(4000) line between 1.2 and 1.3 does not intersect the 8.5 ≤ log(M⋆/M⊙) < 9.0 iso-mass line in the O/H versus SFR diagram, we assume the position in this diagram at which it would intersect by slightly extrapolating the iso-Dn(4000) line for the sake of this test.
Figure 4 shows the resulting Δlog(SFR) for the different stellar mass ranges considered as a function of the iso-Dn(4000) ages. The symbols are coloured-coded according to the colour of the iso-Dn(4000) lines of Fig. 2. The green points show the closest values to Δlog(SFR) = 0. The mean value of Δlog(SFR) = 0.72,0.14−0.35,−0.75, and −1.02 for galaxies in the Dn(4000) ranges < 1.1, [1.1–1.2), [1.2–1.3), [1.3–1.4), and [1.4–1.5), respectively. The difference is proportionally larger as we move away from the iso-Dn(4000) with values between 1.1 and 1.2 (green line), that is, this iso-Dn(4000) line is the one with values of Δlog(SFR) closest to zero in all iso-masses considered in this figure. From this, we may consider that the iso-Dn(4000) line for 1.1 ≤ Dn(4000) < 1.2 (green line in Fig. 2) represents the best approximation to the locus where the change of the relation between oxygen abundance and SFR is observed for each stellar mass range and given SFR. Before this line, for Dn(4000) larger than 1.2, the slope of each O/H-SFR iso-mass line may be considered flat as its absolute value is smaller than 0.002.
 |
Fig. 4. Relation between Δlog(SFR) and the iso-Dn(4000) ranges. The symbols are colour-coded depending on the Dn(4000) range and according to Fig. 2, being Dn(4000) < 1.1 (blue), 1.1 ≤ Dn(4000) < 1.2 (green), 1.2 ≤ Dn(4000) < 1.3 (red), 1.3 ≤ Dn(4000) < 1.4 (cyan), and 1.4 ≤ Dn(4000) < 1.5 (magenta). The symbol type is related to the log(M⋆/M⊙) range considered, as labelled. For the stellar mass range 8.5–9.0 (circles), only a lower limit, if any, for Δlog(SFR) could be assumed from the present SDSS sample, leading to log(SFR) < −1.5. In the case of the iso-Dn(4000) line 1.2 ≤ Dn(4000) < 1.3, the value of the intersect position has been derived by slightly extrapolating this iso-Dn(4000). The mean value of Δlog(SFR) for each iso-Dn(4000), considering all the iso-masses, is shown by the coloured numbers (only lower limits of Δlog(SFR) for the 8.5 ≤ log(M⋆/M⊙) < 9.0 mass range are not considered). The black dotted line indicates Δlog(SFR) = 0. |
This way, for all galaxies with stellar mass log(M⋆/M⊙) ≤ 10.5, the green iso-Dn(4000) line defines, de facto, an effective isochrone, which marks the locus of the sudden change in the derivative of oxygen abundance against SFR in the sample galaxies. This plot may illustrate why the case for a universal negative relation between oxygen abundance and SFR is still controversial for some samples of galaxies. The exact region in which the negative slope of the metallicity–SFR relation may hold varies for each stellar mass range; a negative dependence of metallicity on SFR could be seen for a given galaxy mass range but only for those galaxies hosting the youngest stellar population (i.e. Dn(4000)≤1.1). A similar behaviour can be observed in panel (b) for log(N/O). Again for galaxies with log(M⋆/M⊙) ≲ 11, there is a mild dependence of log(N/O) on SFR, if any, except when the green iso-Dn(4000) line is reached. Beyond this point, moving towards larger SFR for a fixed stellar mass (i.e. along dash-dotted lines), a strong negative dependence of Δlog(N/O)/Δlog SFR is evident. The value of log(N/O) at which these changes in the slope can be seen range from the typical values in dwarf galaxies up to the solar log(N/O)⊙. The similar behaviour exhibited by the oxygen abundance versus SFR and the nitrogen-to-oxygen abundance ratio versus SFR, shown in the two panels of Fig. 2, provides information that can help us to understand the chemical evolution of our sample galaxies and the origin of the MZRSFR relationship.
We find loci in the planes 12 + log(O/H)–SFR and log(N/O)–SFR that delimit two broad regions domains in these diagrams for the sample galaxies. In one of them, the sample galaxies show a clear dependence of metallicity on SFR, whereas in the corresponding complementary region no dependence is seen, along each galaxy stellar mass sequence. These loci appear well represented on each plot by the line corresponding to galaxies with Dn(4000) < 1.2, for which a mean stellar age younger than 150 Myr is expected (Mateus et al. 2006). Along these two loci lines, it seems that the precise oxygen abundance (N/O ratio) and SFR, for each galaxy stellar mass (i.e. specific SFR) appear to be tuned10, defining, de facto, the effective isochrone corresponding to the average stellar population for each galaxy. This applies only to galaxies with log(M⋆/M⊙) ≲ 10.5; for more massive galaxies we do not observe this behaviour in our sample, because the lines of the Dn(4000) index converge at high metallicity (near solar to over-solar), and O/H and N/O do not show an observable decrease here, suggesting an evolution without metallicity loss and mainly driven by galaxy mass.
In Fig. 5, we show the MZSFR relation for the star-forming galaxies with Dn(4000) < 1.2 (left panel) and Dn(4000)≥1.2 (right panel). From this figure, it can be seen that galaxies with young and old stellar populations are located in different domains in the MZSFR three-dimensional diagram. As expected, galaxies with younger stellar populations (Dn(4000) < 1.2, represented as blue dots in the figure) are located in the zone where SFR is higher, at a fixed 12+log(O/H). In contrast, galaxies with older stellar populations (Dn(4000)≥1.2, represented as red dots in the figure) fall in the area where SFR is lower, at fixed 12+log(O/H). However, this plot shows a large dispersion, and we therefore analysed this possible dependence of the OH on SFR and on stellar age from another point of view, by using the classical method of representing residuals of a correlation as a function of other parameters. Figure 6 has three panels showing these plots. The first, on the left, shows the MZR relation with a polynomial fit overplotted and, at the bottom, the residuals of this relation. The middle panel shows these same residuals plotted as a function of SFR, with a least-square straight line overplotted and the corresponding residuals at the bottom. These residuals, within ±0.2 dex, are represented as a function of the Dn(4000) parameter in the right panel, where again a correlation appears. In this way, a third parameter, age, arises clearly as needing to be considered as well as stellar mass and SFR in our analysis of the MZR–SFR. In this last panel, a fit with two straight lines may also be acceptable because, as we claim above, for Dn(4000) > 1.2 the correlation is almost flat, while a strong slope appears in the younger objects with Dn(4000) < 1.2.
 |
Fig. 5. MZSFR for star-forming galaxies corrected for aperture. Colour-coded star-forming galaxies with Dn(4000) < 1.2 (blue in left panel, grey in right panel) and Dn(4000)≥1.2 (red in right panel, grey in left panel). Note the scale of the SFR axis decreases towards the right in the figures. |
 |
Fig. 6. Left panel: MZSFR for our sample of galaxies with a polynomial fit to these results overplotted (black dash-dotted line). In the bottom the residuals of the data fit, OH−OHfit,M, are represented as a function of stellar mass. Central panel: These residuals of OH−OHfit,M as a function of SFR with a minimum straight line fitting the points. The residual of this fit are represented at the bottom as a function of SFR: Right panel: residual of the latter fit, OH−OHfit,M−Resfit,SFR, as a function of the parameter Dn(4000). In the upper panels, the correlation coefficients for each fit are shown in the top right. |
Interestingly, a direct consequence of the above findings is the selection of a subsample of galaxies that populate the youngest part of the two diagrams of Fig. 2. This group of (8598) galaxies are ‘outliers’ of the sample, and cluster around the iso-line Dn(4000) < 1.1 on average in both panels of Fig. 2. It is for this group of very young galaxies that the largest changes in the slopes of the O/H–SFR relation are observed (similar for N/O–SFR). The galaxies in this group are mainly, but not only, dwarf galaxies; they sample a range in galaxy stellar mass, as shown, but always show the largest SFR measured for their stellar mass. This is clearly seen in Fig. 7, where the relation between SFR and M⋆ for our sample of SDSS star-forming galaxies is presented; galaxies are colour coded according to their Dn(4000) parameter. In this figure, for a fixed SFR nearly the entire range of Dn(4000) is covered, where the parameter Dn(4000) increases as the stellar mass increases; that is, more massive galaxies have higher Dn(4000) values than less massive ones. Similarly, for each fixed stellar mass, a range in SFR is observed where the largest SFR corresponds to the youngest objects.
 |
Fig. 7. Relation between SFR and M⋆ for star-forming galaxies colour-coded according to the Dn(4000) parameter (left panel) and its corresponding confidence limits from 1σ to 3σ (right panel). All the points and contours of the Dn(4000) parameter in the figures have the same colours as in Fig. 2. |
In order to explore the nature of these 8598 galaxies, we performed a sanity check to confirm their metallicity and SFR (see Figs. A.3, A.4, and A.5) and to gain more insight into the nature of this subsample of galaxies. We checked that the abundances and SFR derived for these galaxies were not affected by aperture corrections, performing a particular study of this subsample.
In Fig. 8 we summarise all the results concerning the O/H, SFR, and age of the stellar populations, making use of the ‘population box’ Dn(4000)–SFR–12+log(O/H) three-dimensional diagram, where values found for the star-forming galaxies are colour-coded according to the M⋆ of each galaxy. We find a clear correlation between Dn(4000), SFR, and 12+log(O/H). Galaxies with Dn(4000) values < 1.2 span the range of stellar masses log(M⋆/M⊙) = 8.5 to 11.5, where the majority of the sample galaxies have stellar masses of less than ∼10.5. The less massive galaxies (log(M⋆/M⊙) ≲ 9) mostly have values of Dn(4000) lower than 1.2, and, as expected, have the lowest 12+log(O/H). On the other hand, the most massive galaxies (log(M⋆/M⊙)≳ 11) are those with the highest 12+log(O/H) values (solar metallicity) and have Dn(4000) values greater than 1.1, although most galaxies have values above 1.2. According to the SFR–M⋆ relation, the higher the stellar mass, the higher the SFR.
 |
Fig. 8. Population box (Dn(4000)–SFR–12+log(O/H) diagram) for our sample of star-forming galaxies colour coded according to M⋆. |
The apparent metallicity–SFR anticorrelation appears to be controversial in the literature; this relation has been interpreted as the consequence of a possible selection effect, and/or possibly resulting from the existence of massive infall of mainly metal-poor gas onto these galaxies, which would produce a strong enhancement of the SFR and, as a consequence, should dilute the metallicity of the interstellar medium (Ellison et al. 2008; Mannucci et al. 2010; Yates et al. 2012) giving rise to an anticorrelation between 12 + log(O/H) and SFR. This picture seems to be supported by some theoretical work (e.g. Sakstein et al. 2011; Dayal et al. 2013), though recent observational studies have questioned this scenario (e.g. Sánchez et al. 2013, 2017, 2019). Here, we show that a deep and complex relationship exists between the MZR and SFR, which appears to be tuned to the mean age of the galaxy stellar population. The anticorrelation we find between oxygen abundance and SFR appears to be significant only for those galaxies hosting the youngest stellar populations. The massive infall scenario could be invoked to explain these high-SFR objects; however for these galaxies we can see that log(N/O) and SFR also show an anticorrelation, suggesting a more complex framework than the standard infall scenario, where N/O should not be significantly affected. Further deep spectroscopic observations of the extreme SFR subsample could provide valuable information for our understanding of the evolution of these very active star-forming galaxies.
4. Summary and conclusions
In this work, we derived O/H and N/O corrected for aperture effects. These empirical aperture corrections are based on the sample of 165 spiral galaxies from the CALIFA project Iglesias-Páramo et al. (2016). We studied the O/H–SFR and N/O–SFR relations, as well as their relation with the parameter Dn(4000), a proxy for the age of the stellar populations of the galaxies. We compared the location of the star-forming galaxies in the SFR–M⋆ and MZSFR diagrams according to the value of Dn(4000) for each galaxy.
Our main conclusions can be summarised as follows:
-
i)
We derive a robust stellar mass–metallicity relation (MZR) locus that is consistent with the ‘anchoring’ points of a selected set of well-studied nearby galaxies with a direct derivation of abundance. We observe a complex relation between MZR and SFR across the whole range of galaxy mass and metallicity, and find a pattern of slope changes of the MZR–SFR relation in the O/H versus SFR plane that appears tuned to the age of the stellar population of the galaxies.
-
ii)
From the study of the relation between the MZR and SFR, we find a new dependence of the O/H–SFR relation on the age of the stellar populations of the galaxies. The dependence of the MZR on SFR is strong mainly for star-forming galaxies with high SFR and low Dn(4000). Massive galaxies (log(M⋆/M⊙) ≳ 10.5) with older stellar populations (Dn(4000)≥1.2) tend to saturate, and seem to flatten in the O/H–SFR relation when 12+log(O/H) ≥ 8.55, irrespective of their SFR; which indicates that the metallicity remains constant only depending on the stellar mass of these massive galaxies. We also observe a dependence of the N/O–SFR relation on the age of the stellar populations of the galaxies, where those massive galaxies with oldest stellar populations seem to flatten when log(N/O) ≥ −0.9.
-
iii)
On the contrary, for galaxies with younger stellar populations (Dn(4000) < 1.2), we find a negative dependence of O/H on SFR (also of N/O on SFR) for less massive galaxies (log(M⋆/M⊙)≲10.5). This anticorrelation has been interpreted as the existence of massive infall of mainly metal-poor gas onto the galaxies, which would produce a strong enhancement of the SFR and, as a consequence, should dilute the metallicity of the interstellar medium.
-
iv)
This negative dependence found between O/H and SFR for galaxies with younger stellar populations holds in a metallicity range from typical dwarf values to solar values, covering a wide range of stellar masses, suggesting that galaxies with young stellar populations are not only composed of dwarf galaxies. These young galaxies of our SDSS sample always show the highest SFR measured for their stellar mass.
-
v)
Galaxies with young and old stellar populations are located in different domains in the three-dimensional MZSFR diagram: (i) galaxies with younger stellar populations (Dn(4000) < 1.2) are located in the zone where SFR is higher, at fixed 12+log(O/H); and (ii) galaxies with older stellar populations (Dn(4000)≥1.2) fall in the area where SFR is lower, at fixed 12+log(O/H).
We find a population of outlier galaxies in the O/H–SFR relation (and also in the N/O–SFR relation), with young stellar population ages. Further characterisation of the physical and chemical properties of these galaxies is necessary to understand how they evolve chemically and to unravel the O/H and N/O relation for these galaxies.
Dn(4000) corresponds to the narrow definition of the 4000 Å break strength from Balogh et al. (1999) that can be considered a proxy of stellar population age.
Available at http://www.mpa-garching.mpg.de/SDSS/
NGC 55, NGC 300, and M 33 stellar masses transformed from Chabrier (2003) to Kroupa (2001) IMF dividing by 0.943 (Mannucci et al. 2010).
An effective radius value of 5.9 kpc was assumed for the Milky Way (Sackett 1997; Yin et al. 2009).
Solar metallicity: 12 + log(O/H)⊙ = 8.69 (Asplund et al. 2009).
Solar log(N/O)⊙ = −0.86 (Asplund et al. 2009; Tsamis et al. 2011).
Acknowledgments
We thank the anonymous referee for very constructive suggestions that have helped us to improve this manuscript. SDP is grateful to the Fonds de Recherche du Québec - Nature et Technologies. SDP, JVM, JIP, CK, and EPM acknowledge financial support from the Spanish Ministerio de Economía y Competitividad under grants AYA2016-79724-C4-4-P and PID2019-107408GB-C44, from Junta de Andalucía Excellence Project P18-FR-2664, and also acknowledge support from the State Agency for Research of the Spanish MCIU through the ‘Center of Excellence Severo Ochoa’ award for the Instituto de Astrofísica de Andalucía (SEV-2017-0709). L.S.P acknowledges support within the framework of the program of the NAS of Ukraine Support for the development of priority fields of scientific research (CPCEL 6541230). I.A.Z acknowledges support by the National Academy of Sciences of Ukraine under the Research Laboratory Grant for young scientists No. 0120U100148. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the U.S. Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org. This study makes use of the results based on the Calar Alto Legacy Integral Field Area (CALIFA) survey (http://califa.caha.es/). This research made use of Python (http://www.python.org) and IPython (Pérez & Granger 2007); APLpy (Robitaille & Bressert 2012); Numpy (Van Der Walt et al. 2011); Pandas (McKinney et al. 2010); of Matplotlib (Hunter 2007), a suite of open-source Python modules that provides a framework for creating scientific plots. This research made use of Astropy, a community-developed core Python package for Astronomy (Astropy Collaboration 2013). The Astropy web site is http://www.astropy.org.
References
- Alam, S., Albareti, F. D., Allende Prieto, C., et al. 2015, ApJS, 219, 12 [Google Scholar]
- Andrews, B. H., & Martini, P. 2013, ApJ, 765, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Arellano-Córdova, K. Z., Esteban, C., García-Rojas, J., & Méndez-Delgado, J. E. 2021, MNRAS, 502, 225 [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balogh, M. L., Morris, S. L., Yee, H. K. C., Carlberg, R. G., & Ellingson, E. 1999, ApJ, 527, 54 [Google Scholar]
- Barrera-Ballesteros, J. K., Sánchez, S. F., Heckman, T., Blanc, G. A., & The MaNGA Team. 2017, ApJ, 844, 80 [CrossRef] [Google Scholar]
- Barrera-Ballesteros, J. K., Heckman, T., Sánchez, S. F., et al. 2018, ApJ, 852, 74 [Google Scholar]
- Barrera-Ballesteros, J. K., Utomo, D., Bolatto, A. D., et al. 2020, MNRAS, 492, 2651 [NASA ADS] [CrossRef] [Google Scholar]
- Belfiore, F., Maiolino, R., Maraston, C., et al. 2016, MNRAS, 461, 3111 [Google Scholar]
- Berg, D. A., Skillman, E. D., Croxall, K. V., et al. 2015, ApJ, 806, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Kudritzki, R.-P., Urbaneja, M. A., et al. 2016, ApJ, 830, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [Google Scholar]
- Brown, J. S., Martini, P., & Andrews, B. H. 2016, MNRAS, 458, 1529 [NASA ADS] [CrossRef] [Google Scholar]
- Bundy, K., Bershady, M. A., Law, D. R., et al. 2015, ApJ, 798, 7 [Google Scholar]
- Chabrier, G. 2003, ApJ, 586, L133 [NASA ADS] [CrossRef] [Google Scholar]
- Cook, D. O., Dale, D. A., Johnson, B. D., et al. 2014, MNRAS, 445, 899 [NASA ADS] [CrossRef] [Google Scholar]
- Cresci, G., Mannucci, F., Sommariva, V., et al. 2012, MNRAS, 421, 262 [NASA ADS] [Google Scholar]
- Cresci, G., Mannucci, F., & Curti, M. 2019, A&A, 627, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Croxall, K. V., Pogge, R. W., Berg, D. A., Skillman, E. D., & Moustakas, J. 2016, ApJ, 830, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Curti, M., Cresci, G., Mannucci, F., et al. 2017, MNRAS, 465, 1384 [Google Scholar]
- Curti, M., Mannucci, F., Cresci, G., & Maiolino, R. 2020, MNRAS, 491, 944 [Google Scholar]
- Davé, R., Finlator, K., & Oppenheimer, B. D. 2011, MNRAS, 416, 1354 [CrossRef] [Google Scholar]
- Dayal, P., Ferrara, A., & Dunlop, J. S. 2013, MNRAS, 430, 2891 [Google Scholar]
- De Rossi, M. E., Bower, R. G., Font, A. S., Schaye, J., & Theuns, T. 2017, MNRAS, 472, 3354 [Google Scholar]
- Duarte Puertas, S., Vilchez, J. M., Iglesias-Páramo, J., et al. 2017, A&A, 599, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edmunds, M. G., & Pagel, B. E. J. 1978, MNRAS, 185, 77P [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, S. L., Patton, D. R., Simard, L., & McConnachie, A. W. 2008, ApJ, 672, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Ellison, S. L., Simard, L., Cowan, N. B., et al. 2009, MNRAS, 396, 1257 [NASA ADS] [CrossRef] [Google Scholar]
- Fernández-Martín, A., Pérez-Montero, E., Vílchez, J. M., & Mampaso, A. 2017, A&A, 597, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Finlator, K., & Davé, R. 2008, MNRAS, 385, 2181 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, D. B., & Drory, N. 2011, ApJ, 733, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Gallazzi, A., Charlot, S., Brinchmann, J., White, S. D. M., & Tremonti, C. A. 2005, MNRAS, 362, 41 [Google Scholar]
- García-Benito, R., Zibetti, S., Sánchez, S. F., et al. 2015, A&A, 576, A135 [Google Scholar]
- Garnett, D. R. 2002, ApJ, 581, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes, J. M., Papaderos, P., Vílchez, J. M., et al. 2016, A&A, 586, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hernandez, S., Larsen, S., Aloisi, A., et al. 2019, ApJ, 872, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, T. M., Cortese, L., Boselli, A., Gavazzi, G., & Davies, J. I. 2013, A&A, 550, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L., Dayal, P., Magrini, L., & Ferrara, A. 2016, MNRAS, 463, 2002 [NASA ADS] [CrossRef] [Google Scholar]
- Hunter, J. D. 2007, Comput. Sci. Eng., 9, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Iglesias-Páramo, J., Vílchez, J. M., Galbany, L., et al. 2013, A&A, 553, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Iglesias-Páramo, J., Vílchez, J. M., Rosales-Ortega, F. F., et al. 2016, ApJ, 826, 71 [Google Scholar]
- Kang, X., Zhang, F., Chang, R., Wang, L., & Cheng, L. 2016, A&A, 585, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kashino, D., Renzini, A., Silverman, J. D., & Daddi, E. 2016, ApJ, 823, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003, MNRAS, 341, 33 [Google Scholar]
- Kojima, T., Ouchi, M., Nakajima, K., et al. 2017, PASJ, 69, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R.-P., Urbaneja, M. A., Gazak, Z., et al. 2012, ApJ, 747, 15 [CrossRef] [Google Scholar]
- Lara-López, M. A., Bongiovanni, A., Cepa, J., et al. 2010a, A&A, 519, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lara-López, M. A., Cepa, J., Bongiovanni, A., et al. 2010b, A&A, 521, L53 [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, H., Skillman, E. D., Cannon, J. M., et al. 2006, ApJ, 647, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Lequeux, J., Peimbert, M., Rayo, J. F., Serrano, A., & Torres-Peimbert, S. 1979, A&A, 80, 155 [Google Scholar]
- Licquia, T. C., & Newman, J. A. 2015, ApJ, 806, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Magrini, L., Gonçalves, D. R., & Vajgel, B. 2017, MNRAS, 464, 739 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., & Mannucci, F. 2019, A&ARv, 27, 3 [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Mast, D., Rosales-Ortega, F. F., Sánchez, S. F., et al. 2014, A&A, 561, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mateus, A., Sodré, L., Cid Fernandes, R., et al. 2006, MNRAS, 370, 721 [NASA ADS] [CrossRef] [Google Scholar]
- McKinney, W. 2010, in Proceedings of the 9th Python in Science Conference, eds. S. van der Walt, & J. Millman, 51 [Google Scholar]
- Mollá, M., Vílchez, J. M., Gavilán, M., & Díaz, A. I. 2006, MNRAS, 372, 1069 [CrossRef] [Google Scholar]
- Møller, P., Fynbo, J. P. U., Ledoux, C., & Nilsson, K. K. 2013, MNRAS, 430, 2680 [CrossRef] [Google Scholar]
- Mouhcine, M., Gibson, B. K., Renda, A., & Kawata, D. 2008, A&A, 486, 711 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Okamoto, T., Nagashima, M., Lacey, C. G., & Frenk, C. S. 2017, MNRAS, 464, 4866 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, Y.-J., & Maiolino, R. 2014, MNRAS, 438, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Pérez, F., & Granger, B. E. 2007, Comput. Sci. Eng., 9, 21 [Google Scholar]
- Pérez-Montero, E. 2014, MNRAS, 441, 2663 [CrossRef] [Google Scholar]
- Pérez-Montero, E., & Contini, T. 2009, MNRAS, 398, 949 [CrossRef] [Google Scholar]
- Pérez-Montero, E., Contini, T., Lamareille, F., et al. 2013, A&A, 549, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Petropoulou, V., Vílchez, J., Iglesias-Páramo, J., et al. 2011, ApJ, 734, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Petropoulou, V., Vílchez, J., & Iglesias-Páramo, J. 2012, ApJ, 749, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., & Grebel, E. K. 2016, MNRAS, 457, 3678 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Thuan, T. X., & Vílchez, J. M. 2003, A&A, 397, 487 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilyugin, L. S., Vílchez, J. M., & Contini, T. 2004, A&A, 425, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilyugin, L. S., Thuan, T. X., & Vílchez, J. M. 2007, MNRAS, 376, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Vílchez, J. M., Mattsson, L., & Thuan, T. X. 2012, MNRAS, 421, 1624 [CrossRef] [Google Scholar]
- Pilyugin, L. S., Lara-López, M. A., Grebel, E. K., et al. 2013, MNRAS, 432, 1217 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Grebel, E. K., Zinchenko, I. A., Nefedyev, Y. A., & Mattsson, L. 2017, MNRAS, 465, 1358 [CrossRef] [Google Scholar]
- Robitaille, T., & Bressert, E. 2012, APLpy: Astronomical Plotting Library in Python, Astrophysics Source Code Library [record ascl:1208.017] [Google Scholar]
- Romeo Velonà, A. D., Sommer-Larsen, J., Napolitano, N. R., et al. 2013, ApJ, 770, 155 [CrossRef] [Google Scholar]
- Sackett, P. D. 1997, ApJ, 483, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Sakstein, J., Pipino, A., Devriendt, J. E. G., & Maiolino, R. 2011, MNRAS, 410, 2203 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Rich, R. M., Charlot, S., et al. 2007, ApJS, 173, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Lee, J. C., Ly, C., et al. 2014, ApJ, 797, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F. 2020, ARA&A, 58, 99 [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012, A&A, 538, A8 [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Jungwiert, B., et al. 2013, A&A, 554, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., Barrera-Ballesteros, J. K., Sánchez-Menguiano, L., et al. 2017, MNRAS, 469, 2121 [CrossRef] [Google Scholar]
- Sánchez, S. F., Barrera-Ballesteros, J. K., López-Cobá, C., et al. 2019, MNRAS, 484, 3042 [CrossRef] [Google Scholar]
- Sánchez-Menguiano, L., Sánchez Almeida, J., Muñoz-Tuñón, C., & Sánchez, S. F. 2020, ApJ, 903, 52 [CrossRef] [Google Scholar]
- Skibba, R. A., Engelbracht, C. W., Dale, D., et al. 2011, ApJ, 738, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Telford, O. G., Dalcanton, J. J., Skillman, E. D., & Conroy, C. 2016, ApJ, 827, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Torrey, P., Vogelsberger, M., Hernquist, L., et al. 2018, MNRAS, 477, L16 [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [Google Scholar]
- Tsamis, Y. G., Walsh, J. R., Vílchez, J. M., & Péquignot, D. 2011, MNRAS, 412, 1367 [NASA ADS] [Google Scholar]
- Van Der Walt, S., Colbert, S. C., & Varoquaux, G. 2011, The NumPy array: a structure for efficient numerical computation, 13, 22 [Google Scholar]
- Vila-Costas, M. B., & Edmunds, M. G. 1992, MNRAS, 259, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Vílchez, J. M., Relaño, M., Kennicutt, R., et al. 2019, MNRAS, 483, 4968 [CrossRef] [Google Scholar]
- Yates, R. M., Kauffmann, G., & Guo, Q. 2012, MNRAS, 422, 215 [NASA ADS] [CrossRef] [Google Scholar]
- Yin, J., Hou, J. L., Prantzos, N., et al. 2009, A&A, 505, 497 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zahid, H. J., Dima, G. I., Kudritzki, R.-P., et al. 2014, ApJ, 791, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Zurita, A., & Bresolin, F. 2012, MNRAS, 427, 1463 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Supplementary material
 |
Fig. A.1. Distribution of oxygen abundance for SDSS star-forming galaxies with S/N([OIII]λ4363) > 5 using the Pilyugin & Grebel (2016) methodology (blue dashed histogram) and using the direct (electron-temperature-based) methodology (orange open histogram). |
In this Appendix, we show the O/H–SFR relation as a function of M⋆ and parameter Dn (4000) for the galaxies in Fig. 2 in detail. From the O/H–SFR relation, a subsample of 21 galaxies is randomly defined in selected zones below the isochrone Dn(4000) ≤ 1.2. Its location on the SFR–M⋆ diagram and its spectra and SDSS three-colour images are shown. An upcoming and more detailed characterisation of this subsample of galaxies will be presented in a forthcoming work (Duarte Puertas et al. in prep.).
We checked the SFR derived for these galaxies, confirming that these values were not produced by aperture corrections, because the correction applied to these outliers was in fact smaller than average. We searched and extracted the fluxes of the measured SDSS spectra and verified for all these galaxies with electron temperature (i.e. with S/N([OIII]λ4363) >5) that their direct (electron temperature based) abundances agree with our oxygen abundance values to within ∼-0.025 dex on average (see Fig. A.1), as expected.
Figure A.2 shows a density plot of our aperture-corrected O/H versus SFR in six ranges of Dn(4000). In each range of Dn(4000), the density plot of the O/H–SFR relation of the galaxies in that interval is shown and the contours 1σ, 2σ, and 3σ in each bin are represented, highlighting the fit to the running median.
Figure A.3 shows again the aperture corrected O/H–SFR relation (left panel) and the aperture-corrected SFR–M⋆ relation (right panel). As we find a population of galaxies in the zone where O/H dilution occurs, we defined a subsample of 21 randomly selected galaxies, distributed below the isochrone 1.1 < Dn(4000) ≤ 1.2 in the O/H–SFR diagram. We made the selection in such a way that some of them must be found in the isochrones of Dn(4000) < 1.1 and others in 1.1 < Dn(4000) ≤ 1.2, as well as in the iso-mass [9, 9.5). The positions of the 21 galaxies, as well as the positions of the subsample of galaxies that have values of Dn(4000) < 1.2 (blue colour) and of Dn(4000) ≥ 1.2 (red colour), are also shown in the SFR–M⋆ relation. Galaxies with values of Dn(4000) < 1.2 (found in the lower right of the O/H–SFR diagram) are located in the upper left of the SFR–M⋆ diagram. As expected from Fig. 2, galaxies with younger stellar populations have higher SFR values than older ones at a given stellar mass.
 |
Fig. A.2. Detailed analysis of the 12+log(O/H)–SFR density plot presenting confidence limits for each Dn(4000) bin. Density plots for the relation between the 12+log(O/H) and SFR for star-forming galaxies for six Dn(4000) ranges. All the lines have the same colours as in Fig. 2. The dashed lines represent the 1σ, 2σ, and 3σ contours in each Dn(4000) bin. |
As mentioned in the main text, in order to explore the nature of this subsample of 8598 galaxies, we performed a sanity check to confirm their metallicity and SFR, such as we show in Figures A.3, A.4, and A.5, in order to gain further insight into the nature of this subsample of galaxies. Figures A.4 and A.5 show the spectra and SDSS three-colour images of 21 selected galaxies. By focusing on the spectra of the galaxies found in the iso-mass [9, 9.5) (galaxies 6, 11, and 13), excitation can be seen to decrease as the age of the galaxy’s stellar populations and 12+log(O/H) increase. In the isochrone Dn(4000) < 1.1, the spectra of these three galaxies (galaxies 4, 11, and 15) look similar, while their morphologies are different.
 |
Fig. A.3. Selection of 21 galaxies from the 12+log(O/H) versus SFR diagram. Left panel: Relation between 12+log(O/H) and SFR for star-forming galaxies. All the lines have the same colours as in Fig. 2. A sample of 21 galaxies has been selected (as an example) in this diagram; their positions are shown with grey circles and have been labelled from 1 to 21 according to their SFR. Right panel: Relation between SFR and M⋆ for star-forming galaxies. The points are colour-coded according to their Dn(4000): blue if Dn(4000) < 1.2, and red if Dn(4000) ≥ 1.2. The dashed lines represent the 1σ, 2σ, and 3σ contours in each Dn(4000) subsample. Grey circles show the positions in the SFR–M⋆ diagram of the 21 galaxies. |
 |
Fig. A.4. Spectra of the 21 galaxies defined in Fig. A.3. Grey dotted lines show the locations of the emission lines studied in this paper. The galaxy label is indicated in each panel (right part). |
 |
Fig. A.4. continued. |
 |
Fig. A.5. SDSS three-colour images of 21 galaxies defined in Fig. A.3 in the SDSS-DR12 footprint. North is up and east is left. The galaxy label is indicated in each panel (upper right). |
 |
Fig. A.5. continued. |
All Tables
All Figures
 |
Fig. 1. Relation between 12+log(O/H) and M⋆. Left panel: aperture corrected MZR for star-forming galaxies of our sample (grey dots), as well as the Milky Way (green mark) and other nearby galaxies (labelled; coloured points) with direct (from electron temperature) oxygen abundances are shown. Blue or red colour indicate galaxies with a flat or non-zero radial oxygen gradient, respectively. References as follows: galaxy name, O/H reference, stellar mass reference; SMC, LMC, and M81, Bresolin et al. (2016), Kudritzki et al. (2012); NGC 55, Magrini et al. (2017), Lee et al. (2006); MW, Fernández-Martín et al. (2017), Arellano-Córdova et al. (2021), Licquia & Newman (2015); M83, Bresolin et al. (2016), Hernandez et al. (2019), Kang et al. (2016); M33 and NGC 300, Bresolin et al. (2016), Kang et al. (2016); M 31, Zurita & Bresolin (2012), Fisher & Drory (2011); M 101, Croxall et al. (2016), Skibba et al. (2011); NGC 628, Berg et al. (2015), Cook et al. (2014; see also Vílchez et al. 2019). Right panel: aperture corrected MZR for star-forming galaxies, black points. Blue, green, red, cyan, magenta, lime, and yellow solid lines represent the fits to the running median of the SFR of the galaxies, calculated in bins of 1000 galaxy points, corresponding to seven SFR intervals as indicated. |
| In the text | |
 |
Fig. 2. Relation between 12+log(O/H) (panel a) and log(N/O) (panel b) and SFR for our sample of SDSS star-forming galaxies. Blue, green, red, cyan, magenta, and yellow solid lines represent the fits to the running median for bins of 1000 objects in six Dn(4000) bins. The number of star-forming galaxies in each Dn(4000) bin appears on the legend. Black dash-dotted lines show the 12+log(O/H) (panel a) and log(N/O) (panel b) vs. SFR fits to the running median for bins of 1000 objects in six log(M⋆/M⊙) bins (each box shows the considered log(M⋆/M⊙) range). |
| In the text | |
 |
Fig. 3. Relation between SFR and Dn(4000) for our sample of star-forming galaxies. Blue, green, red, cyan, magenta, and yellow solid lines represent the running median for bins of 2000 objects in six O/H bins. Black dash-dotted lines show the fit to the running median for bins of 1000 objects in six log(M⋆/M⊙), bins, from low stellar mass (8.5, lower part of the figure) to high stellar mass (11.5, higher part of the figure). |
| In the text | |
 |
Fig. 4. Relation between Δlog(SFR) and the iso-Dn(4000) ranges. The symbols are colour-coded depending on the Dn(4000) range and according to Fig. 2, being Dn(4000) < 1.1 (blue), 1.1 ≤ Dn(4000) < 1.2 (green), 1.2 ≤ Dn(4000) < 1.3 (red), 1.3 ≤ Dn(4000) < 1.4 (cyan), and 1.4 ≤ Dn(4000) < 1.5 (magenta). The symbol type is related to the log(M⋆/M⊙) range considered, as labelled. For the stellar mass range 8.5–9.0 (circles), only a lower limit, if any, for Δlog(SFR) could be assumed from the present SDSS sample, leading to log(SFR) < −1.5. In the case of the iso-Dn(4000) line 1.2 ≤ Dn(4000) < 1.3, the value of the intersect position has been derived by slightly extrapolating this iso-Dn(4000). The mean value of Δlog(SFR) for each iso-Dn(4000), considering all the iso-masses, is shown by the coloured numbers (only lower limits of Δlog(SFR) for the 8.5 ≤ log(M⋆/M⊙) < 9.0 mass range are not considered). The black dotted line indicates Δlog(SFR) = 0. |
| In the text | |
 |
Fig. 5. MZSFR for star-forming galaxies corrected for aperture. Colour-coded star-forming galaxies with Dn(4000) < 1.2 (blue in left panel, grey in right panel) and Dn(4000)≥1.2 (red in right panel, grey in left panel). Note the scale of the SFR axis decreases towards the right in the figures. |
| In the text | |
 |
Fig. 6. Left panel: MZSFR for our sample of galaxies with a polynomial fit to these results overplotted (black dash-dotted line). In the bottom the residuals of the data fit, OH−OHfit,M, are represented as a function of stellar mass. Central panel: These residuals of OH−OHfit,M as a function of SFR with a minimum straight line fitting the points. The residual of this fit are represented at the bottom as a function of SFR: Right panel: residual of the latter fit, OH−OHfit,M−Resfit,SFR, as a function of the parameter Dn(4000). In the upper panels, the correlation coefficients for each fit are shown in the top right. |
| In the text | |
 |
Fig. 7. Relation between SFR and M⋆ for star-forming galaxies colour-coded according to the Dn(4000) parameter (left panel) and its corresponding confidence limits from 1σ to 3σ (right panel). All the points and contours of the Dn(4000) parameter in the figures have the same colours as in Fig. 2. |
| In the text | |
 |
Fig. 8. Population box (Dn(4000)–SFR–12+log(O/H) diagram) for our sample of star-forming galaxies colour coded according to M⋆. |
| In the text | |
 |
Fig. A.1. Distribution of oxygen abundance for SDSS star-forming galaxies with S/N([OIII]λ4363) > 5 using the Pilyugin & Grebel (2016) methodology (blue dashed histogram) and using the direct (electron-temperature-based) methodology (orange open histogram). |
| In the text | |
 |
Fig. A.2. Detailed analysis of the 12+log(O/H)–SFR density plot presenting confidence limits for each Dn(4000) bin. Density plots for the relation between the 12+log(O/H) and SFR for star-forming galaxies for six Dn(4000) ranges. All the lines have the same colours as in Fig. 2. The dashed lines represent the 1σ, 2σ, and 3σ contours in each Dn(4000) bin. |
| In the text | |
 |
Fig. A.3. Selection of 21 galaxies from the 12+log(O/H) versus SFR diagram. Left panel: Relation between 12+log(O/H) and SFR for star-forming galaxies. All the lines have the same colours as in Fig. 2. A sample of 21 galaxies has been selected (as an example) in this diagram; their positions are shown with grey circles and have been labelled from 1 to 21 according to their SFR. Right panel: Relation between SFR and M⋆ for star-forming galaxies. The points are colour-coded according to their Dn(4000): blue if Dn(4000) < 1.2, and red if Dn(4000) ≥ 1.2. The dashed lines represent the 1σ, 2σ, and 3σ contours in each Dn(4000) subsample. Grey circles show the positions in the SFR–M⋆ diagram of the 21 galaxies. |
| In the text | |
 |
Fig. A.4. Spectra of the 21 galaxies defined in Fig. A.3. Grey dotted lines show the locations of the emission lines studied in this paper. The galaxy label is indicated in each panel (right part). |
| In the text | |
 |
Fig. A.4. continued. |
| In the text | |
 |
Fig. A.5. SDSS three-colour images of 21 galaxies defined in Fig. A.3 in the SDSS-DR12 footprint. North is up and east is left. The galaxy label is indicated in each panel (upper right). |
| In the text | |
 |
Fig. A.5. continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


