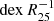| Issue |
A&A
Volume 679, November 2023
|
|
|---|---|---|
| Article Number | A83 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202347677 | |
| Published online | 15 November 2023 | |
The growth history of local M 33-mass bulgeless spiral galaxies
1
Yunnan Observatories, Chinese Academy of Sciences, 396 Yangfangwang, Guandu District, Kunming 650216, PR China
e-mail: kxyysl@ynao.ac.cn
2
Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, 396 Yangfangwang, Guandu District, Kunming 650216, PR China
3
International Centre of Supernovae, Yunnan Key Laboratory, Kunming 650216, PR China
4
LMU München, Universitätssternwarte, Scheinerstr. 1, 81679 München, Germany
5
Institute for Astronomy, University of Hawaii, 2680 Woodlawn Drive, Honolulu, HI 96822, USA
Received:
8
August
2023
Accepted:
13
September
2023
NGC 7793, NGC 300, M 33, and NGC 2403 are four nearby undisturbed and bulgeless low-mass spiral galaxies whose morphology and stellar mass are similar. They are ideal laboratories for studying disc formation scenarios and the histories of stellar mass growth. We constructed a simple chemical evolution model by assuming that discs grow gradually with continuous metal-free gas infall and metal-enriched gas outflow. By means of the classical χ2 method, applied to the model predictions, the best combination of free parameters capable of reproducing the corresponding present-day observations was determined, that is, the radial dependence of the infall timescale τ = 0.1r/Rd + 3.4 Gyr (Rd is the disc scale length) and the gas outflow efficiency bout = 0.2. The model results agree excellently with the general predictions of the inside-out growth scenario for the evolution of spiral galaxies. About 80% of the stellar mass of NGC 7793 was assembled within the last 8 Gyr, and 40% of the mass was assembled within the last 4 Gyr. By comparing the best-fitting model results of the three other galaxies, we obtain similar results: 72% (NGC 300), 66% (NGC 2403), and 79% (M 33) of the stellar mass were assembled within the last ∼8 Gyr (i.e. z = 1). These four disc galaxies simultaneously increased their sizes and stellar masses in time, and they grew in size at ∼0.30 times the rate at which they grew in mass. The scale lengths of these four discs now are 20%–25% larger than at z = 1. Our best-fitting model predicted the stellar mass-metallicity relation and the metallicity gradients, constrained by the observed metallicities from HII-region emission line analysis, agree well with the observations measured from individual massive red and blue supergiant stars and population synthesis of Sloan Digital Sky Survey galaxies.
Key words: galaxies: evolution / galaxies: individual: M 33 / galaxies: spiral / galaxies: individual: NGC 7793 / galaxies: individual: NGC 2403 / galaxies: individual: NGC 300
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Understanding the assembly of galaxies is crucial for understanding the overall picture of galaxy evolution. Spiral galaxies have a major role in the Universe today. Disc galaxies dominate the star formation at the present epoch (Brinchmann et al. 2004; Williams et al. 2011) and continue to form stars at a sustained rate throughout their evolution (Aumer & Binney 2009; Fraternali & Tomassetti 2012; Pezzulli et al. 2015). At the same time, the structure and star formation history (SFH) of disc galaxies are tightly linked with stellar mass (Casasola et al. 2017), and galaxies with stellar masses near or below the mass of the Milky Way (log(MMW, */M⊙)∼10.7) assemble their mass mainly from in situ star formation, not from mergers (Leitner & Kravtsov 2011; Qu et al. 2017; Behroozi et al. 2019; Pan et al. 2019). Furthermore, recent studies based on deep surveys detecting galaxy masses (log(M*/M⊙) < 10) have shown that very large populations of low-mass galaxies exist at all redshifts and that galaxy stellar mass functions exhibit a slightly steeper low-mass end (Baldry et al. 2008, 2012; Bauer et al. 2013; Kelvin et al. 2014). This highlights that we need to understand the growth of low-mass galaxies, which are the largest population of galaxies in the Universe.
Most spiral galaxies are difficult to study in detail because their bulges are complex (Byun & Freeman 1995) or because they are involved in mergers (Barnes & Hernquist 1992). While bulgeless discs appear to be excellent laboratories for studying the secular evolution of galactic discs, most of them are too distant to be studied in great detail. Fortunately, the nearby Universe (D < 4 Mpc) hosts four undisturbed and bulgeless (pure-disc) galaxies with a similar morphology and stellar mass (log(M*/M⊙) < 10): NGC 7793 (Sacchi et al. 2019), NGC 300 (Gogarten et al. 2010), M 33 (Williams et al. 2009), and NGC 2403 (Williams et al. 2013). The main properties of these four galaxies are summarized in Table 1. The wealth of available data, including both local and global data, such as gas mass, star formation rate (SFR), stellar mass (e.g. Leroy et al. 2008), gas-phase metallicity (e.g. Pilyugin et al. 2014), and specific SFR (sSFR; Muñoz-Mateos et al. 2007; Smith et al. 2021), for these four low-mass spiral galaxies can be used to constrain their theoretical models. Therefore, we can use the theoretical results to compare the detailed evolution of these discs. These comparative studies offer an ideal opportunity to search for clues to the processes that drive the galaxy disc growth histories, for instance, the inside-out formation scenario, which posits that the inner parts of the galaxy disc form faster than the outer parts (e.g. Larson 1976; Matteucci & Francois 1989; Chiappini et al. 2001; Grisoni et al. 2018; Frankel et al. 2019; Spitoni et al. 2021a).
Basic properties of NGC 7793, NGC 2403, NGC 300, and M 33.
On the other hand, observations in local star-forming galaxies have revealed a tight relation between stellar mass and gas metallicity: the stellar mass-metallicity relation (MZR). The more massive galaxies are more metal enriched (e.g. Tremonti et al. 2004; Kewley & Ellison 2008; Andrews & Martini 2013; Zahid et al. 2014). As for the stellar metallicity, the MZR is also found in star-forming galaxies (e.g. Gallazzi et al. 2005; Panter et al. 2008; Thomas et al. 2010; Zahid et al. 2017; Sextl et al. 2023). Bresolin et al. (2022) updated the MZR based on metallicity studies of stars in resolved star-forming galaxies. The MZR seems to be a Rosetta stone for understanding the formation and evolution of galaxies.
In addition to the global metallicities, the radial gradient in metallicity is also important for understanding the formation history of galaxies. Since the pioneering work by Aller (1942), the radial metallicity gradient has been studied for a long time. Based on long-slit spectroscopy and integral field unit (IFU) spectroscopy, most spiral galaxies in the local Universe exhibit negative metallicity gradients in gas and stars within their optical radius, that is, the centre of a galaxy has a higher metallicity than the outskirts (e.g. Zaritsky et al. 1994; Moustakas et al. 2010; Sánchez et al. 2014; Pilyugin et al. 2014, 2019; González Delgado et al. 2015; Ho et al. 2015; Zheng et al. 2017; Goddard et al. 2017; Bresolin 2019; Bresolin et al. 2022).
At the same time, spiral galaxies that show no clear evidence of an interaction present a common metallicity gradient if normalised to an appropriate scale length, such as the effective disc radius (Re; e.g. Sánchez et al. 2014), the disc scale length (Rd, e.g. Garnett et al. 1997), and the isophotal radius (R25, e.g. Zaritsky et al. 1994; Pilyugin et al. 2014, 2019; Ho et al. 2015; Bresolin 2019). The slope is independent of galaxy properties such as stellar mass, absolute magnitude, morphology, or the presence or absence of a bar.
The simple chemical evolution model has been widely used in studies of the chemical evolution and SFHs of nearby disc galaxies (e.g. Tinsley 1980; Chang et al. 1999, 2012; Boissier & Prantzos 2000; Chiappini et al. 2001; Mollá & Díaz 2005; Kubryk et al. 2015; Kang et al. 2017; Bresolin 2019), and our understanding of the formation and evolution of disc galaxies made great progress. Furthermore, the SFH is a vital aspect of the formation and evolution of any disc galaxy because it dominates its resulting stellar disc structure (Frankel et al. 2019). We therefore adopt a simple chemical evolution model to study the chemical evolution and SFHs of M 33-mass bulgeless spiral galaxies.
The main aim of this paper is to investigate the disc formation scenarios and stellar mass growth histories of M 33-mass bulgeless spiral galaxies, as well as to study whether the model-predicted results of these four galaxies can explain the MZR and the observed metallicity gradients. The chemical evolution and SFHs of M 33, NGC 300, and NGC 2403 have been studied in our previous works using a simple chemical evolution model (Kang et al. 2012, 2016, 2017). Before making comparative studies of these four galaxies, we therefore construct a simple chemical evolution model to explore the chemical evolution and SFH of NGC 7793 first.
The outline of this paper is as follows. Section 2 describes the main ingredients of the chemical evolution model. The observed data, including radial profiles and global properties of atomic hydrogen (HI) gas, SFR, sSFR, and gas-phase metallicity constraints of NGC 7793, are presented in Sect. 3. In Sect. 4 we investigate the chemical evolution and SFH of NGC 7793 using a simple chemical evolution model, and we provide the disc formation scenarios and stellar mass growth histories of M 33-mass spiral galaxies by comparing the evolution and SFH of NGC 7793 with those of M 33, NGC 300, and NGC 2403. Our conclusions are given in Sect. 5.
2. Model
Similar to our previous work (Chang et al. 1999; Kang et al. 2012, 2016, 2017), a star-forming galaxy disc was assumed to gradually build up due to continuous infall of metal-free gas (X = 0.7571, Yp = 0.2429, Z = 0) from its halo. It was composed of a set of independently evolved concentric rings, in the sense that no radial mass flows were allowed in the model. These flows can take place in real galaxies as a result of the presence of the bars (Sellwood & Wilkinson 1993), redistribution of angular momentum owing to viscosity (Ferguson & Clarke 2001), and radial stellar migration (Roškar et al. 2008). In particular, the age-metallicity relation in the solar neighbourhood of our Galaxy (e.g. Edvardsson et al. 1993; Haywood 2008; Schönrich & Binney 2009; Minchev & Famaey 2010; Feuillet et al. 2019; Xiang & Rix 2022) and the observed U-shaped colour profiles in galaxies (Azzollini et al. 2008; Bakos et al. 2008) place strong constraints on radial migration (e.g. Schönrich & Binney 2009; Minchev et al. 2012; Kubryk et al. 2013; Spitoni et al. 2015; Frankel et al. 2018; Buck 2020; Vincenzo & Kobayashi 2020; Chen et al. 2023). Moreover, metal-enriched gas outflows are considered in the model because both observations (Garnett 2002; Tremonti et al. 2004) and theoretical models (Erb 2008; Finlator & Davé 2008; Spitoni et al. 2020) showed that the gas-outflow process plays a key role during the chemical evolution of low-mass galaxies with stellar mass log(M*/M⊙) < 10.5. Finally, the model does not include the bulge, nor does it differentiate between the thin and thick disc (see e.g. Grisoni et al. 2017; Spitoni et al. 2019). Despite the simplifying assumption of independently evolving rings, the model has been successfully applied to investigate the formation and evolution of the Milky Way disc and other nearby disc galaxies (Chang et al. 1999; Boissier & Prantzos 2000; Muñoz-Mateos et al. 2011; Kang et al. 2012, 2016, 2017; Bouquin et al. 2018; Bresolin 2019).
Thus, main ingredients of the model include infalls of metal-free gas, star formation, metal production via stellar evolution, stellar mass return, and outflows of metal-enriched gas. The details of these ingredients are presented in the following. The instantaneous recycling approximation (IRA; Tinsley 1980) is adopted in the model by assuming that the gas return from stars to the interstellar medium (ISM) occurs on a timescale that is short compared with galactic evolution, and the gas is well mixed with stellar ejecta. Although IRA is a strong assumption in chemical evolution modelling, it still represents a good approximation for the abundance of chemical elements produced by massive stars with short lifetimes. The best example of such a chemical element is oxygen, which also represents the best proxy for the global metallicity of the galaxy ISM because it is the most abundant heavy element by mass. On the other hand, the ISM evolution of chemical elements produced by stars with long lifetimes cannot be followed by chemical evolution models working with the IRA assumption. Examples of such chemical elements are nitrogen, carbon, and iron. To consider the stellar lifetimes with a high level of detail, numerical chemical evolution models in which the IRA is relaxed should be adopted (see Matteucci 2012; Vincenzo et al. 2016).
The evolution in each ring can be described by the following differential equations from Tinsley (1980):
where Σtot(r, t) and Σgas(r, t) are the total (star + gas) and gas-mass surface density in the ring centred at galactocentric distance r at evolution time t, respectively, and Ψ(r, t) and Z(r, t) are the SFR and metallicity in the corresponding place and time, respectively. fin(r, t) and fout(r, t) are the gas-infall and -outflow rate in the corresponding place and time, respectively. R is the return fraction, and y is the nuclear synthesis yield. Both R and y are functions of the initial mass function (IMF) and depend weakly on metallicity and time (Vincenzo et al. 2016). Neither metallicity nor time dependence of R and y are further considered in our model because the oxygen yield is independent of metallicity and stellar lifetimes under our assumptions. Furthermore, galactic chemical enrichment significantly depends on the IMF (Vincenzo et al. 2016; Goswami et al. 2021). The Kroupa et al. (1993) IMF is favoured to describe the chemical evolution of spiral discs (Romano et al. 2010; Vincenzo et al. 2016), which we therefore adopted in this work. The values of R = 0.289 and y = 0.019 were obtained by averaging the values of R and yZ over metallicity in Table 2 of Vincenzo et al. (2016), which corresponds to the compilation of stellar yields of Romano et al. (2010). Zin is the metallicity of the infalling gas and is assumed to be metal free, that is, Zin = 0. Zout(r, t) is the metallicity of the outflowing gas. It is assumed to have the same metallicity as the ISM, that is, Zout(r, t) = Z(r, t) (Chang et al. 2010; Belfiore et al. 2016; Kang et al. 2012, 2016, 2017; Kang et al. 2021).
The metal-free gas-infall rate at each radius r and time t, fin(r, t) in units of M⊙ pc−2 Gyr−1 as a function of space and time was adopted as in Kang et al. (2012, 2016, 2017),
where τ is the gas-infall timescale, and it is a free parameter in our model. The range of the free parameter τ extends from 0.1 Gyr to 15.0 Gyr. As shown in Fig. 1 of Kang et al. (2016), the gas-infall rate we adopted in this work is low in the beginning and gradually increases with time. This gas-infall rate reaches the highest value when t = τ and then decreases. The case of τ = 0.1 Gyr corresponds to a time-declining gas infall rate, according to which most of the cold gas has been accreted to the disc in the early period of its history, while that of τ = 15.0 Gyr represents a time-increasing gas infall rate, according to which a large fraction of cold gas currently falls onto the disc of NGC 7793. We describe the derivation of the best-fitting value of τ in Sect. 4.1.
The function A(r) was determined iteratively so that the present-day model-predicted stellar mass surface density Σ*(r, tg) matched the observations (Kang et al. 2012, 2016, 2017). Σ*(r, tg) is well described by an exponential profile,
where Rd is the present-day disc scale length. Σ*(0, tg) is the present-day central stellar mass surface density, which can easily be obtained from 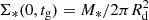 . We adopted the stellar mass and disc scale length of NGC 7793 as M* = 3.162 × 109 M⊙ and Rd = 1.3 kpc. These values were estimated from Infrared Array Camera (IRAC) images at 3.6 μm (Leroy et al. 2008). tg is the cosmic age, and we set tg = 13.5 Gyr according to the standard flat cosmology.
. We adopted the stellar mass and disc scale length of NGC 7793 as M* = 3.162 × 109 M⊙ and Rd = 1.3 kpc. These values were estimated from Infrared Array Camera (IRAC) images at 3.6 μm (Leroy et al. 2008). tg is the cosmic age, and we set tg = 13.5 Gyr according to the standard flat cosmology.
In our calculation, we adopted a value of the free parameter τ, started with a first estimate of A(r), and numerically solved Eqs. (1) and (2) adopting an SFR surface density Ψ(r, t) (see below). By comparing the model-predicted Σ*(r, tg) with its observed value, we adjusted the value of A(r) and repeated the calculation until the resulting Σ*(r, tg) fitted the observed radial distribution. Figure 1 plots the model-predicted radial profile of A(r). It shows that A(r) varies strongly with τ.
 |
Fig. 1. A(r) function. The dashed and solid lines correspond to two limiting cases of τ = 0.1 Gyr and τ = 15 Gyr, respectively. To facilitate comparison, the A(r) values of the model adopting τ = 15 Gyr have been multiplied by 4000. |
The SFR surface density Ψ(r, t) (in units of M⊙ pc−2 Gyr−1) describes how a disc galaxy of a given cold gas mass and scale radius forms its stars. Leroy et al. (2008) and Bigiel et al. (2008) reported that Ψ(r, t) appears to correlate strongly with the molecular hydrogen gas-mass surface density (ΣH2(r, t)) on sub-kiloparsec scales, rather than with the mass surface density of atomic hydrogen gas (ΣHI(r, t)) or the total gas (Σtot(r, t) = ΣH2(r, t)+ΣHI(r, t)). They also found that in their sample of spiral galaxies (including NGC 7793) the molecular hydrogen gas (H2) forms stars at a roughly constant efficiency at radii at which it can be detected (Leroy et al. 2008; Bigiel et al. 2008). Ψ(r, t) proportional to ΣH2(r, t) was used in disc models by Lagos et al. (2011), Kang et al. (2012, 2016, 2017), and Kubryk et al. (2015), and it is also adopted in this paper:
Here, tdep is the molecular gas depletion time, and its value was adopted as tdep = 1.9 Gyr (Leroy et al. 2008; Bigiel et al. 2008). In order to split Σgas(r, t) into ΣH2(r, t) and ΣHI(r, t) in our galaxy evolution model, we adopted the semi-empirical prescription by Blitz & Rosolowsky (2006) and Leroy et al. (2008) for the molecular-to-atomic ratio,
where Ph(r, t) is the mid-plane pressure of the ISM. P0 and αP are constants derived from the observations. We adopted P0/k = 1.7 × 104 cm−3 K and αP = 0.8 (Leroy et al. 2008).
The mid-plane pressure of the ISM in disc galaxies can be expressed as (Elmegreen 1989; Leroy et al. 2008)
where G is the gravitational constant, and cgas and c* are the (vertical) velocity dispersions of gas and stars, respectively. Observations reveal that cgas is a constant along the disc, and we adopted cgas = 11 km s−1 (Ostriker et al. 2010), while c* was estimated as 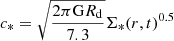 (see Appendix B.3 of Leroy et al. (2008) for more details).
(see Appendix B.3 of Leroy et al. (2008) for more details).
The feedback from supernovae gives rise to galactic outflows when the thermal energy of a galaxy exceeds the binding energy of gas. NGC 7793 is a low-mass disc galaxy with a shallower gravitational potential, which means that it is more susceptible to losing its ISM (Garnett 2002; Tremonti et al. 2004; Hirschmann et al. 2016; Lian et al. 2018a; Spitoni et al. 2021b). Thus, the gas-outflow process is important during the evolution and SFH of NGC 7793. We assumed that the outflowing gas does not return to the disc and that its metallicity is equal to that of the ISM at the time the outflow process is launched (Chang et al. 2010; Kang et al. 2012, 2016, 2017; Ho et al. 2015). The gas-outflow rate fout(r, t) is proportional to Ψ(r, t) (see Recchi et al. 2008; Spitoni et al. 2015, 2020),
where bout is the gas outflow efficiency. This is the other free parameter in our model. The assumption that fout(r, t) is proportional to Ψ(r, t) is reasonable if supernova and winds of massive stars are the main drivers of the galactic wind.
In summary, the gas-infall timescale τ and the gas-outflow efficiency bout are two free parameters in our model. The best-fitting model-predicted τ and bout obtained in Sect. 4.1 will be presented in Table 3. Moreover, a degeneracy between the yield y and the outflow parameter bout exists in that the model adopting a higher y needs a higher bout to reproduce the observed radial metallicity distribution. Because the reasonable range of y is short for a fixed IMF (Vincenzo et al. 2016) compared with the wide possible rang of bout, we can constrain bout by using the observed metallicity gradient. We emphasize that although the accurate value of the free parameters in our best-fitting model may change slightly, our results for the main trends of the SFHs of NGC 7793 are robust.
3. Observations
A successful chemical evolution model of NGC 7793, especially one involving free parameters, should reproduce as many observed constraints as possible, including both local (concerning the radial profiles) and global (concerning the whole disc) constraints. In this sense, the observed present-day cold gas, SFR, sSFR, and metallicity distributions provide crucial constraints on the model. Thus, we summarise the current available observations for the disc of NGC 7793 in this section.
3.1. Radial distributions of gas mass, SFR, sSFR, and metallicity
The stratification of HI of NGC 7793 was obtained from the Very Large Array (VLA) maps of the National Radio Astronomy Observatory (NRAO; Walter et al. 2008), and the radial distribution HI mass surface density (ΣHI) of NGC 7793 was taken from Leroy et al. (2008). The radial SFR surface density (ΣSFR) along the disc of NGC 7793 was estimated by combining the far-UV (FUV) with 24 μm maps (Leroy et al. 2008) and by the FUV emission corrected for the WISE 22 μm maps (Casasola et al. 2017).
The sSFR, defined as the SFR per unit of stellar mass, represents the ratio of young to old stars and shows the fraction of total star formation that occurred recently. Muñoz-Mateos et al. (2007) derived the radial sSFR profiles for NGC 7793 from GALEX and 2MASS (FUV−K) colour profiles after a proper SFR calibration of the UV luminosity and K-band mass-to-light ratio were adopted. Smith et al. (2021) calculated the radial sSFR profiles for NGC 7793 using broad-band indicators for the SFR (FUV + 24 μm flux) and stellar mass (3.6 μm flux).
The present-day distribution of the metallicity within an individual galaxy is the outcome of a complex pattern of evolution, advancing through infall of metal-free gas, star formation, energy feedback from stars, and metal-enriched outflows. Each of these processes reshuffles the metals present in and around the galaxy discs to various extents. Thus, the radial metallicity distribution of galaxies places important constraints on the galaxy chemical model (Boissier & Prantzos 2000; Ho et al. 2015; Kubryk et al. 2015; Kang et al. 2012, 2016, 2017; Kang et al. 2021; Bresolin 2019, and references therein). The radial metallicity gradient has been studied for a long time, starting with the pioneering work by Aller (1942). Most spiral galaxies in the local Universe exhibit negative metallicity gradients within their optical radius, that is, the centre of a galaxy has a higher metallicity than the outskirts (e.g. Zaritsky et al. 1994; Rupke et al. 2010; Moustakas et al. 2010; Sánchez et al. 2014; Pilyugin et al. 2014; Kudritzki et al. 2015; Ho et al. 2015; Bresolin 2019).
Because oxygen is the most abundant metal by mass in the Universe, it is a good tracer for the total metal content. Oxygen is also an element for which the IRA approximation is appropriate. We therefore use the oxygen abundance (i.e. 12 + log(O/H)) to represent the metallicity of NGC 7793 and adopt the solar value as 12 + log(O/H)⊙ = 8.69 (Asplund et al. 2009) throughout this work. The absolute gas-phase metallicity depends on the calibrations, and the classical Te method is generally considered to provide the most reliable oxygen abundances in HII regions (Izotov et al. 2006; Pilyugin et al. 2014). Thus, we used the oxygen abundances in HII regions determined with the Te method to constrain the model. The radial metallicity distribution from HII-region emission line analysis along the disc of NGC 7793 has been observed and quantified in many works (McCall et al. 1985; Zaritsky et al. 1994; Moustakas et al. 2010; Bibby & Crowther 2010; Pilyugin et al. 2014; Stanghellini et al. 2015), and the data from Bibby & Crowther (2010), Pilyugin et al. (2014), and Stanghellini et al. (2015) were used to constrain our model here. The linear radial metallicity gradient depends on the galaxy distance, and therefore, we scaled the metallicity gradient to the distance of 3.9 Mpc. The metallicity gradient of NGC 7793 is −0.07 ± 0.019 dex kpc−1 and 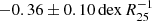 (Bibby & Crowther 2010), −0.0662 ± 0.0104 dex kpc−1 and
(Bibby & Crowther 2010), −0.0662 ± 0.0104 dex kpc−1 and 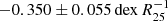 (Pilyugin et al. 2014), −0.054 ± 0.019 dex kpc−1, and
(Pilyugin et al. 2014), −0.054 ± 0.019 dex kpc−1, and 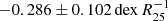 (Stanghellini et al. 2015).
(Stanghellini et al. 2015).
All the observed radial distributions of HI mass, SFR, sSFR, and metallicity are displayed in Fig. 2 to constrain the model with which we search for the best-fitting model of NGC 7793. The observed radial distribution of metallicity is also shown in Fig. 3.
 |
Fig. 2. Comparisons of model predictions with observations. The different line types correspond to different parameter groups (the dotted lines (τ, bout) show (0.1 Gyr, 0), the dashed lines (τ, bout) show (15 Gyr, 0), the dot-dashed lines (τ, bout) show (15 Gyr, 1.0), and the solid lines (τ, bout) show (0.1r/Rd + 3.4 Gyr, 0.2)). On the left side, the radial profiles of HI mass and SFR surface density are shown in the top and bottom panels, respectively. On the right side, the radial profiles of the sSFR and metallicity are displayed in the top and bottom panels, respectively. The different symbols correspond to observed data from different works. HI data from Leroy et al. (2008) are shown as filled red circles. SFR data obtained from Leroy et al. (2008) are denoted as filled red circles, and those from Casasola et al. (2017) are displayed as filled blue asterisks. The sSFR data from Muñoz-Mateos et al. (2007) and Smith et al. (2021) are denoted as open red triangles and open red diamonds, respectively. The 12 + log(O/H) data taken from Bibby & Crowther (2010), Pilyugin et al. (2014), and Stanghellini et al. (2015) are separately plotted as filled yellow asterisks, filled green circles, and filled red diamonds. |
3.2. Global properties of gas mass, SFR, sSFR, and metallicity
The HI gas mass of NGC 7793 is MHI = 1.26 × 109 M⊙ (Leroy et al. 2008) and MHI = 1.05 × 109 M⊙ (Muraoka et al. 2016). The molecular hydrogen (H2) gas mass of NGC 7793 is MH2 = 2.0 × 108 M⊙ (Muraoka et al. 2016). As a result, the gas fraction (fgas) of NGC 7793 can easily be calculated through 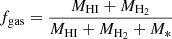 , and the value of fgas is ∼0.27 − 0.33.
, and the value of fgas is ∼0.27 − 0.33.
The current global SFR of NGC 7793 disc has been measured by using different tracers, 0.235 M⊙ yr−1 from a combination of FUV with 24 μm maps by Leroy et al. (2008), 0.45 M⊙ yr−1 from the observed Hα+[N II]λ6583 flux by Bibby & Crowther (2010), 0.26 M⊙ yr−1 from a combination of Hα with 24 μm maps by Kennicutt et al. (2011), 0.363 M⊙ yr−1 from a combination of FUV with total infrared (TIR) maps by Skibba et al. (2011), 0.52 M⊙ yr−1 calculated from the GALEX FUV corrected for dust attenuation (Calzetti et al. 2015), and 0.251 M⊙ yr−1 obtained from hybrids of FUV and 22 μm maps by Leroy et al. (2019).
The value of the sSFR for NGC 7793 is ∼(8.36 − 9.74)×10−11 yr−1, as derived using FUV−K colour (Muñoz-Mateos et al. 2007) and 8.06 × 10−11 yr−1, as estimated by Muraoka et al. (2016).
The metallicity value at the effective radius of the disc 12 + log(O/H)Re was used as a surrogate for the mean metallicity of a galaxy (Zaritsky et al. 1994; Sánchez et al. 2013). Re is equal to 1.685 times the radial scale length Rd of the disc (de Vaucouleurs & Pence 1978) and basically corresponds to 0.4R25 (Sánchez et al. 2013) in the local Universe, that is, Re = 1.685Rd = 0.4R25. The value of the mean metallicity for the disc of NGC 7793 is 8.466 ± 0.05 (Bibby & Crowther 2010), 8.31 ± 0.02 (calibration of Kobulnicky & Kewley 2004), 8.87 ± 0.01 (calibration of Pilyugin & Thuan 2005) (Moustakas et al. 2010), 8.378 ± 0.02 (Pilyugin et al. 2014), and 8.445 ± 0.063 (Stanghellini et al. 2015), respectively. These global observed properties for the disc of NGC 7793 are summarised in Table 2.
Global observational data for the disc of NGC 7793.
4. Results and discussion
In this section, we first investigate the influence of the free parameters on the model predictions and search for the best-fitting model for NGC 7793. We then study the properties of the stellar populations along the disc of NGC 7793. Finally, to search for clues to the processes that drive the disc formation scenarios and stellar mass growth histories, we compare the best-fitting model- predicted growth history of NGC 7793 with those of M 33, NGC 300, and NGC 2403, which were separately studied in our previous work (Kang et al. 2012, 2016, 2017).
4.1. Radial distributions
The aforementioned free parameters in the model are the gas-infall timescale τ and the gas-outflow efficiency bout. We explored the influence of these two free parameters on the model predictions by comparing the model predictions with observations. The comparison of the dotted, dashed and dot-dashed lines in Fig. 2 shows that the gas-outflow efficiency has a strong influence on the metallicity, but only a small effect on HI gas-mass surface density, SFR surface density, and sSFR, while the gas-infall timescale is important for the radial distribution of all four quantities. The reason for this mainly is that during the whole evolutionary history of a galaxy, the infalling gas supplies the reservoir for star formation, while the outflowing gas takes a fraction of metals away from the disc. Figure 2 also shows that the area between the dotted line (τ, bout) = (0.1 Gyr, 0) and the dot-dashed line (τ, bout) = (15 Gyr, 1.0) brackets almost the whole region of the observed data, which implies that it is possible to construct a model that can reproduce the main observed features of NGC 7793 disc.
The bottom right panel of Fig. 2 shows a negative metallicity gradient, that is, the central region has a higher metallicity than the outskirts. This is consistent with the scenario of an inside-out formation of the disc. Moreover, the SFH derived from the colour–magnitude diagrams (CMD) also certifies an inside-out growth for the disc of NGC 7793 (Sacchi et al. 2019). Thus, following the method adopted in our previous work (Kang et al. 2012, 2016, 2017), the form of the gas-infall timescale is assumed to be τ(r) = a × r/Rd + b. This means that gas takes longer to settle onto the disc in the outer regions, where a and b are the coefficients for τ(r). The inside-out growth mechanism was originally introduced in the theory of galaxy evolution on the basis of chemical evolution models (Larson 1976; Matteucci & Francois 1989) and a semi-analytic model of disc galaxies in the context of dark matter cosmologies (Kauffmann 1996; van den Bosch 1998). When we add the free parameter bout, there are now three free parameters (a, b, and bout) in our model that need to be determined.
In order to search for the best combination of free parameters (a, b, and bout) that can reproduce the main observed features of NGC 2403, we used the classical χ2 technique by comparing the model results with the corresponding observational data, such as the radial profiles of HI gas-mass surface density, SFR, sSFR, and 12 + log(O/H). The boundary conditions of a, b, and bout for NGC 7793 are separately assumed to be 0 < a ≤ 3.0, 1.0 ≤ b ≤ 5.0, and 0.1 ≤ bout ≤ 0.9. In practice, for each pair of a and b, we varied the value of bout to calculate the minimum value of χ2 that corresponds to the best combination of a, b, and bout. We obtained (a, b, bout) = (0.1, 3.4, 0.2), that is, (τ, bout) = (0.1r/Rd + 3.4 Gyr, 0.2) as the best-fitting model. The best combination of the free parameters is displayed in Table 3. The best-fitting model-predicted results are plotted by solid lines in Fig. 2. The agreement between the model results and the NGC 7793 observations is remarkable.
Main input properties and parameters of the best-fitting models for NGC 7793, NGC 2403, NGC 300, and M 33.
The lower right panel of Fig. 2 shows that the best-fitting model-predicted radial metallicity distribution does not show a constant gradient of 12 + log(O/H). Instead, the radial metallicity distribution is bent. This is mainly due to the fact that we used the observational data, such as the radial distributions of HI gas-mass surface density, SFR surface density, sSFR, and 12 + log(O/H), to constrain the model and to search for the best-fitting model that can simultaneously reproduce these observational data for NGC 7793. In order to further state that the best-fitting model describes the formation and evolution of NGC 7793 well, comparisons of the best-fitting model-predicted present-day 12 + log(O/H) distributions with the observed data are displayed in the upper panel of Fig. 3. The linear best fit and the 1σ uncertainty of the observed data are also shown in this panel. The deviations of the observed 12 + log(O/H) points from our best-fitting model-predicted 12 + log(O/H) and those from the corresponding linear best fit are shown in the lower panel of Fig. 3. The lower panel of Fig. 3 shows only little difference between the solid black and open blue circles. The mean deviation values of the filled black and open blue circles are 0.019 and 0.015, respectively. Figure 3 reinforces our results that the best-fitting model includes and describes the crucial ingredients of the main physical processes that regulate the formation and evolution history of NGC 7793 reasonably well.
 |
Fig. 3. Radial distribution of 12 + log(O/H). Upper panel: comparisons of the present-day radial distribution of 12 + log(O/H) predicted by our best-fitting model (solid black line) with the observational data. Different symbols denote the observed metallicity data from different works as filled yellow asterisks (Bibby & Crowther 2010), filled green circles (Pilyugin et al. 2014), and filled red diamonds (Stanghellini et al. 2015). The linear best fit to the observed data and 1σ uncertainty are plotted as the solid and dotted blue lines, respectively. Lower panel: filled black circles show the deviations of the observations from our best-fitting model predictions, derived by subtracting the solid black line from the observed data in the upper panel, and the open blue circles show those obtained from subtracting the linear best fit from the observational data in the upper panel. |
4.2. Stellar populations along the disc
To investigate the stellar populations along the disc of NGC 7793, Fig. 4 demonstrates the best-fitting model-predicted SFHs (upper panel) and stellar mass growth curves (lower panel) of three regions at different galactocentric distances for NGC 7793. The upper panel of Fig. 4 shows that the peak of the SFH moves to a later time from internal to more external regions of the disc, and regions at larger radii have more extended SFHs. The lower panel demonstrates that the stellar mass growth rate in the inner region is faster than that in the outer region. Figure 4 shows clear signatures of inside-out growth for the NGC 7793 disc.
 |
Fig. 4. Star formation histories (upper panel) and relative stellar mass growth (lower panel) of three regions at different galactocentric distances for the NGC 7793 disc. Different line types represent different regions along the disc, dotted red line for 1 − 2 kpc, dashed blue line for 4 − 5 kpc and solid black line for 7 − 8 kpc. Both the SFRs and stellar masses are normalised by their present-day values. The horizontal cyan dash-dotted line in the lower panel shows when each component achieves 50% of its final value. |
If the disc of NGC 7793 does form inside-out, we would expect to see a negative radial gradient in age. Figure 5 shows the mean stellar age along the disc of NGC 7793 predicted by the best-fitting model with the solid line. The stellar population in the inner region of the disc is older than that in the outer region, that is, the inner parts of the disc have a higher percentage of old stars than the outer parts. The mean stellar age, which decreases with radius, is indeed consistent with the inside-out growth scenario for the disc formation. In this picture, the inner regions of NGC 7793 are built up at earlier times than the outer parts, and as a result, they contain older stars than the outermost regions on average. The results presented in Figs. 4 and 5 are indicative of an inside-out formation scenario for the disc of NGC 7793. This is in line with the observed results derived by Muñoz-Mateos et al. (2007) and Sacchi et al. (2019).
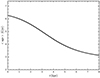 |
Fig. 5. Radial profile of the mean stellar age along the disc of NGC 7793 predicted by its own best-fitting model. |
Figure 6 displays the best-fitting model-predicted growth history of stellar mass for NGC 7793. It displays a relatively smooth build-up of its stellar mass. The best-fitting model results also show that about 80% of the stellar mass of NGC 7793 is assembled within the last 8 Gyr and 40% within the last 4 Gyr. This is consistent with what was found by the CMD-derived SFH for NGC 7793 in Radburn-Smith et al. (2012) and Sacchi et al. (2019). The content of this figure is further discussed in Sect. 4.3.1.
 |
Fig. 6. Stellar mass growth histories of NGC 7793 (solid line), NGC 300 (dashed line), M 33 (dotted line), and NGC 2403 (dash-dotted line) predicted by the respective best-fitting models. Stellar masses are normalised to their present-day values. The horizontal dashed lines mark when the stellar mass reaches 20% (green), 50% (cyan), and 60% (yellow) of its final value, and the vertical dotted red line denotes the galaxy evolutionary age at t = 5.75 Gyr (i.e. z = 1). |
4.3. Comparison with other three disc galaxies
NGC 7793, M 33, NGC 300, and NGC 2403 are four bulgeless disc galaxies with a similar morphology and stellar mass, and the chemical evolution and SFHs of NGC 300, M 33, and NGC 2403 have already been studied in our previous works (see Kang et al. 2012, 2016, 2017). In this section, we compare the best-fitting model-predicted SFH of NGC 7793 with those of M 33, NGC 300, and NGC 2403 to search for clues to the processes that drive the disc formation scenarios and stellar mass growth histories. Table 3 summarises the input properties (including the total stellar mass M* and the scale length Rd) and the best-fitting parameters for the main ingredients of the models, such as the star formation law and the gas-infall and -outflow rate. Physical details of the model description and of the search for the best-fitting models for M 33, NGC 300, and NGC 2403 are separately reported in Kang et al. (2012, 2016, 2017).
4.3.1. Evolution of stellar mass and SFR
Figure 6 plots the best-fitting model-predicted growth history of stellar mass for NGC 7793, NGC 300, M 33, and NGC 2403. Figure 6 shows that they also assembled their stellar mass steadily. Our results qualitatively agree with the results in Fig. 17 (bottom) of Sextl et al. (2023), who used the galaxy evolution model in Kudritzki et al. (2021) and found that the galaxy stellar masses at 10 Gyr ago are significantly lower than the final stellar masses. Figure 6 also shows that about 78% (NGC 7793), 66% (NGC 300), 72% (NGC 2403), and 79% (M 33) of the galaxy stars were formed between z = 1 and z = 0. That is, these four galaxies accumulated more than 50% of their total stellar mass within the past ∼8 Gyr (i.e. z = 1). This is supported by the previous results that late-type galaxies with stellar mass M* < 1011 M⊙ appear to assemble most of their stellar mass at z < 1 (Leitner & Kravtsov 2011; Sachdeva et al. 2015) because stellar mass contributes to the majority of the total baryonic budget at most epochs (z = 1).
The best-fitting model-predicted SFHs of these four galaxies are plotted in Fig. 7. It shows that the SFHs of NGC 7793, NGC 2403, and NGC 300 reach their peaks around 5.5 − 8 Gyr ago and then slowly drop to their present-day values, while the SFH of M 33 reaches a maximum about 4 Gyr ago and then stays constant until recently, before declining slightly. The more extended SFH of M 33 further indicates that the principal time of star formation in the discs of NGC 7793, NGC 2403, and NGC 300 is earlier than that in the disc of M 33. This may be due to an HI bridge between M 33 and M 31, in accordance with the statistical result of Guglielmo et al. (2015), who reported that galaxies of a given mass have different SFHs depending on their environment.
 |
Fig. 7. Evolution of the SFR for NGC 7793 (solid line), NGC 300 (dashed line), M 33 (dotted line), and NGC 2403 (dash-dotted line) predicted by the respective best-fitting models. SFRs are normalised to their present-day values. |
4.3.2. Evolution of the scale length Rd
Figure 8 plots the evolution of the scale length and total stellar mass (mass-size relation) from z = 1 to z = 0 for NGC 7793, NGC 300, M 33, and NGC 2403. As in Muñoz-Mateos et al. (2011), the disc scale length Rd at evolution time t was computed by fitting an exponential law to the total stellar mass surface density profile, Σ*(r, t) = Σ*(0, t)exp(−r/Rd(t)). The model predicts Rd = 1.25 kpc for NGC 7793, which agrees with its observed value Rd = 1.30 kpc (Leroy et al. 2008), considering the observed uncertainties. Figure 8 shows that stellar mass and scale length increase simultaneously with time, that is, these four spirals grow in size while they grow in mass, in perfect agreement with the previous mass–size trend (e.g. Muñoz-Mateos et al. 2011; Pezzulli et al. 2015; Sachdeva & Saha 2016). However, the details about the formation and growth of stellar discs in mass and size are not known from first principles. Significant observational effort is still required to shed light on the missing links from structure formation to galaxy formation.
 |
Fig. 8. Evolution of the scale length and total stellar mass predicted by our best-fitting models for NGC 7793 (solid line), NGC 300 (dashed line), M 33 (dotted line), and NGC 2403 (dash-dotted line). Each track follows the evolution of a galaxy from z = 1 (the z = 1 step is marked with an asterisk) to z = 0 (the z = 0 step is marked with a filled circle). |
Investigating the rate at which stellar discs grow sheds light on the interplay between the physical processes, such as metal-free gas infall, star formation, enriched gas outflows, and the global evolution of disc galaxies (Frankel et al. 2019). The specific stellar mass growth rate (νM) and specific radial scale-length growth rate (νR) represent the stellar mass and radial scale-length growth rates, defined as 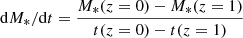 and
and 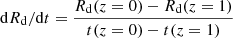 , normalised to the actual present-day value of stellar mass M*(z = 0) and scale length Rd(z = 0). Therefore, νR between z = 1 (i.e. t = 5.75 Gyr) and z = 0 (i.e. t = 13.5 Gyr) calculated by the respective best-fitting models are separately 0.0278 Gyr−1 for NGC 7793, 0.0281 Gyr−1 for NGC 300, 0.0252 Gyr−1 for NGC 2403, and 0.0327 Gyr−1 for M 33. We note that all these four disc galaxies have undergone a radial scale-length growth of ∼20%−25% since z = 1 until now, in perfect agreement with what was found by Muñoz-Mateos et al. (2011) and Pezzulli et al. (2015). At the same time, νM from z = 1 to z = 0 are 0.1007 Gyr−1 for NGC 7793, 0.0854 Gyr−1 for NGC 300, 0.0931 Gyr−1 for NGC 2403, and 0.1016 Gyr−1 for M 33. Comparing νR and νM, we conclude that these four disc galaxies grow in size at ∼0.30 times the rate at which they grow in mass. This is similar to the value ∼0.32 derived by Courteau et al. (2007) and ∼0.35 found by Pezzulli et al. (2015). Furthermore, the values of both νM and νR for M 33 are higher than that for other three galaxies, indicating that more star formation occurred along the M 33 disc recently than that in other three galaxies: The HI bridge between M 33 and M 31 may supply cold gas for star formation in the disc of M 33 (Wolfe et al. 2013).
, normalised to the actual present-day value of stellar mass M*(z = 0) and scale length Rd(z = 0). Therefore, νR between z = 1 (i.e. t = 5.75 Gyr) and z = 0 (i.e. t = 13.5 Gyr) calculated by the respective best-fitting models are separately 0.0278 Gyr−1 for NGC 7793, 0.0281 Gyr−1 for NGC 300, 0.0252 Gyr−1 for NGC 2403, and 0.0327 Gyr−1 for M 33. We note that all these four disc galaxies have undergone a radial scale-length growth of ∼20%−25% since z = 1 until now, in perfect agreement with what was found by Muñoz-Mateos et al. (2011) and Pezzulli et al. (2015). At the same time, νM from z = 1 to z = 0 are 0.1007 Gyr−1 for NGC 7793, 0.0854 Gyr−1 for NGC 300, 0.0931 Gyr−1 for NGC 2403, and 0.1016 Gyr−1 for M 33. Comparing νR and νM, we conclude that these four disc galaxies grow in size at ∼0.30 times the rate at which they grow in mass. This is similar to the value ∼0.32 derived by Courteau et al. (2007) and ∼0.35 found by Pezzulli et al. (2015). Furthermore, the values of both νM and νR for M 33 are higher than that for other three galaxies, indicating that more star formation occurred along the M 33 disc recently than that in other three galaxies: The HI bridge between M 33 and M 31 may supply cold gas for star formation in the disc of M 33 (Wolfe et al. 2013).
4.3.3. Stellar mass-metallicity relation
The shape of the MZR provides important constraints for understanding the chemical evolution of galaxies. Figure 9 shows a comparison of MZR predicted by our best-fitting models with results measured by other authors. In order to compare our best-fitting model-predicted MZR with that of young stellar population and individual supergiant stars, we first scaled the mean metallicities of these galaxies to solar ratios, that is, [Z] = 12 + log(O/H)gal − (12 + log(O/H)⊙) = 12 + log(O/H)gal − 8.69. Thus, the best-fitting model-predicted mean metallicities (defined as the metallicity at the effective radius Re) are −0.336 (NGC 7793), −0.161 (NGC 2403), −0.234 (NGC 300), and −0.208 (M 33), and their values are shown in Fig. 9. In Fig. 9 we plot the MZR based on abundance data obtained from the analysis of quantitative spectroscopy of individual objects in 17 nearby galaxies (see Fig. 9 and Table 4 in Bresolin et al. 2022). In this figure, we also display the MZR derived by Sextl et al. (2023) from the young stellar population of Sloan Digital Sky Survey (SDSS) local star-forming galaxies. For comparison, the mean metallicity of NGC 5194 (Kang et al. 2015) is also plotted in Fig. 9.
 |
Fig. 9. Comparison of the stellar mass-metallicity relation predicted by our best-fitting models (black star for NGC 7793, red triangle for NGC 2403, blue square for NGC 300, magenta diamond for M 33, and green pentagon for NGC 5194) with that published in the literature. The solid circles show the stellar metallicity of nearby galaxies measured from spectroscopy of individual blue supergiants (cyan), red supergiants (pink), and super star clusters (yellow; see Bresolin et al. 2022, reference therein). The thin orange diamonds are the MZR derived from the young stellar population of SDSS star-forming galaxies (Sextl et al. 2023). |
Figure 9 shows that our model-predicted MZR of these galaxies (including NGC 5194) agree with the MZR derived based on data of the young stellar population of SDSS star-forming galaxies and individual young massive supergiant stars (including super star clusters). Although our best-fitting models are constrained by the metallicities from HII-region emission line analysis, the model-predicted MZR is compatible with the empirical MZR measured from individual supergiant stars in nearby galaxies and the young stellar population in SDSS star-forming galaxies.
4.3.4. Metallicity gradient dependence on stellar mass
The dependence of the metallicity gradient on galaxy stellar mass is a matter of recent controversy. Isolated spiral galaxies share a characteristic metallicity gradient when normalised to an appropriate scale length, such as Rd, Re, or R25 (Zaritsky et al. 1994; Garnett et al. 1997; Sánchez et al. 2014; Bresolin & Kennicutt 2015; Ho et al. 2015; Lian et al. 2018b; Pilyugin et al. 2019; Bresolin 2019). On the other hand, Belfiore et al. (2017, based on MaNGA) and Poetrodjojo et al. (2018, based on SAMI) reported that the metallicity gradient in terms of 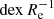 steepens with galaxy stellar mass until log(M⋆/M⊙)∼10.5 and remains roughly constant for higher masses. In addition, the metallicity gradients in interacting disc galaxies are shallower than the gradient in isolated disc galaxies because of effective mixing (e.g. Kewley et al. 2010; Rupke et al. 2010; Torrey et al. 2012).
steepens with galaxy stellar mass until log(M⋆/M⊙)∼10.5 and remains roughly constant for higher masses. In addition, the metallicity gradients in interacting disc galaxies are shallower than the gradient in isolated disc galaxies because of effective mixing (e.g. Kewley et al. 2010; Rupke et al. 2010; Torrey et al. 2012).
Pilyugin et al. (2014) measured the metallicity of 130 nearby late-type galaxies and derived a common metallicity gradient of 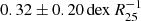 for 104 of their field galaxies (i.e. excluding mergers and close pairs). Sánchez et al. (2014) found that 146 galaxies from CALIFA that show no clear evidence of an interaction present a common metallicity gradient expressed in terms of
for 104 of their field galaxies (i.e. excluding mergers and close pairs). Sánchez et al. (2014) found that 146 galaxies from CALIFA that show no clear evidence of an interaction present a common metallicity gradient expressed in terms of 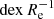 with a value
with a value 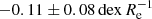 , independent of morphology, the existence of a bar, absolute magnitude, or mass. Ho et al. (2015) also studied 49 local field isolated spiral galaxies with absolute magnitudes −22 < MB < −16, and found evidence for a common metallicity gradient among their galaxies when the slope was expressed in units of the isophotal radius R25, that is,
, independent of morphology, the existence of a bar, absolute magnitude, or mass. Ho et al. (2015) also studied 49 local field isolated spiral galaxies with absolute magnitudes −22 < MB < −16, and found evidence for a common metallicity gradient among their galaxies when the slope was expressed in units of the isophotal radius R25, that is, 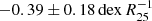 . Pilyugin et al. (2019) analysed 147 galaxies from MaNGA and found the metallicity gradient independent of galaxy stellar with the mean value
. Pilyugin et al. (2019) analysed 147 galaxies from MaNGA and found the metallicity gradient independent of galaxy stellar with the mean value  . Bresolin (2019) derived the common metallicity gradient with a value
. Bresolin (2019) derived the common metallicity gradient with a value 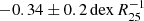 based on long-slit observations of nearby spiral galaxies. To compare the best-fitting model-predicted observed metallicity gradient with the observed common metallicity gradient, we must consider the different scale lengths. According to the relation between Re and R25, that is, Re = 0.4R25 (Zaritsky et al. 1994; Sánchez et al. 2013), we can convert the common metallicity gradient in Sánchez et al. (2014, 146 isolated spiral galaxies from CALIFA) into
based on long-slit observations of nearby spiral galaxies. To compare the best-fitting model-predicted observed metallicity gradient with the observed common metallicity gradient, we must consider the different scale lengths. According to the relation between Re and R25, that is, Re = 0.4R25 (Zaritsky et al. 1994; Sánchez et al. 2013), we can convert the common metallicity gradient in Sánchez et al. (2014, 146 isolated spiral galaxies from CALIFA) into 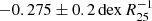 .
.
All this information indicates that it is worthwhile to investigate the metallicity gradients for the discs of NGC 7793, NGC 300, M 33, and NGC 2403. Both Fig. 3 of NGC 7793 in this work and Fig. 2 of NGC 2403 in Kang et al. (2017) show that the linear best fit to the observed data within the optical radius almost coincides with our best-fitting model-predicted metallicity distributions. Here, we also calculated the metallicity gradients of these four galaxies within their optical radii, and the corresponding values predicted by their own best-fitting models are −0.492 dex/R25 for NGC 7793, −0.384 dex/R25 for NGC 2403, −0.474 dex/R25 for NGC 300, and −0.127 dex/R25 for M 33. The metallicity gradient of NGC 7793 agrees well with its observations (Bibby & Crowther 2010; Pilyugin et al. 2014; Stanghellini et al. 2015). Interestingly, although the models for NGC 300 in Kang et al. (2016) and NGC 2403 in Kang et al. (2017) were constrained by observed metallicities from HII-region emission line analysis (Bresolin et al. 2009, NGC 300 and Berg et al. 2013, NGC 2403), their best-fitting model-predicted results agree excellently with the observed metallicity distributions and gradients from stellar spectral analysis of young massive supergiant stars (Kudritzki et al. 2008; Gazak et al. 2015, NGC 300 and Bresolin et al. 2022, NGC2403). For M 33, some new observational metallicity data obtained from HII-region emission line analysis (e.g. Alexeeva & Zhao 2022; Rogers et al. 2022) and stellar spectral analysis of young massive blue supergiant stars (Liu et al. 2022) were recently reported. It would be interesting to consider these metallicities to constrain the chemical evolution model of M 33. Fortunately, our best-fitting model results of M 33 (Kang et al. 2012) basically agree with these observations, taking into account the observed uncertainties and the calibration for determining metallicity. We emphasize that although the accurate values of free parameters in our best-fitting models are not unique, the main results do not impact our conclusion significantly.
Figure 10 displays the metallicity gradient versus stellar mass. The best-fitting model-predicted metallicity gradients exactly reproduce the observed data. The metallicity gradients of the isolated spiral galaxies NGC 7793, NGC 2403, and NGC 300 are similar and steeper than the gradient of M 33. This is the same behaviour as was found by Rupke et al. (2010), that is, the metallicity gradient in isolated galaxies is steeper than that in interacting galaxies because the interactions between M 33 and M 31 may change its metallicity gradient. The similar metallicity gradients in NGC 7793, NGC 2403, and NGC 300 indicate that they may follow a very similar chemical evolution when growing their discs (Prantzos & Boissier 2000; Ho et al. 2015).
 |
Fig. 10. Metallicity gradient vs. stellar mass predicted by the respective best-fitting models when the metallicity gradients are measured in |
5. Conclusions
NGC 7793 is an isolated loosely bound member of the Sculptor group, without a bar and with a very faint central bulge. In this work, we built a bridge for the disc of NGC 7793 between its observed properties and its evolutionary history by constructing a simple chemical evolution model. Our results show that the model predictions are very sensitive to the adopted infall timescale, but the outflow process mainly influences the metallicity distributions along the disc of NGC 7793 because it takes a fraction of metals away from the NGC 7793 due to its shallow gravitational potential. The best-fitting model results show that the disc of NGC 7793 forms inside-out, in excellent agreement with the general predictions of the inside-out growth scenario for the evolution of spiral galaxies. About 80% of the stellar mass of NGC 7793 was assembled within the last 8 Gyr, and 40% was assembled within the last 4 Gyr.
We also compared the best-fitting model results of NGC 7793 with those of M 33, NGC 300, and NGC 2403, which were studied in our previous work (Kang et al. 2012, 2016, 2017). We found that 78% (NGC 7793), 72% (NGC 300), 66% (NGC 2403), and 79% (M 33) of the galaxy stars were formed between z = 1 and z = 0. That is, these four galaxies accumulated more than 50% of their total stellar mass within the past ∼8 Gyr (i.e. z = 1). Our results also show that these four disc galaxies simultaneously increase their sizes and stellar masses with time, and they grow in size at ∼0.30 times the rate at which they grow in mass. This providing a perfect match to previous results (Courteau et al. 2007; Pezzulli et al. 2015). The best-fitting model-predicted MZR and gradients, constrained by the observed metallicities from HII-region emission line analysis, agree excellently with the metallicities measured from individual massive red and blue supergiant stars.
Acknowledgments
We thank the anonymous referee for constructive comments and suggestions, which improved the quality of our work greatly. Xiaoyu Kang and Fenghui Zhang are supported by the National Key R&D Program of China with (Nos. 2021YFA1600403 and 2021YFA1600400), the National Natural Science Foundation (NSF) of China (No. 11973081, 11573062, 11403092, 11773063), the Basic Science Centre project of the NSF of China (No. 12288102), the Science Research grants from the China Manned Space Project (No. CMS-CSST-2021-A08), International Centre of Supernovae, Yunnan Key Laboratory (No. 202302AN360001), the NSF of Yunnan Province (No. 2019FB006). Rolf Kudritzki acknowledges support by the Munich Excellence Cluster Origins Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under the German Excellence Strategy EXC-2094 390783311.
References
- Aller, L. H. 1942, ApJ, 95, 52 [CrossRef] [Google Scholar]
- Alexeeva, S., & Zhao, G. 2022, ApJ, 925, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, B. H., & Martini, P. 2013, ApJ, 765, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Aumer, M., & Binney, J. J. 2009, MNRAS, 397, 1286 [NASA ADS] [CrossRef] [Google Scholar]
- Azzollini, R., Trujillo, I., & Beckman, J. E. 2008, ApJ, 679, L69 [NASA ADS] [CrossRef] [Google Scholar]
- Bakos, J., Trujillo, I., & Pohlen, M. 2008, ApJ, 683, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Baldry, I. K., Glazebrook, K., & Driver, S. P. 2008, MNRAS, 388, 945 [NASA ADS] [Google Scholar]
- Baldry, I. K., Driver, S. P., Loveday, J., et al. 2012, MNRAS, 421, 621 [NASA ADS] [Google Scholar]
- Barnes, J. E., & Hernquist, L. 1992, ARA&A, 30, 705 [Google Scholar]
- Bauer, A. E., Hopkins, A. M., Gunawardhana, M., et al. 2013, MNRAS, 434, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Behroozi, P., Wechsler, R. H., Hearin, A. P., et al. 2019, MNRAS, 488, 3143 [NASA ADS] [CrossRef] [Google Scholar]
- Belfiore, F., Maiolino, R., & Bothwell, M. 2016, MNRAS, 455, 1218 [CrossRef] [Google Scholar]
- Belfiore, F., Maiolino, R., Tremonti, C., et al. 2017, MNRAS, 469, 151 [Google Scholar]
- Berg, D. A., Skillman, E. D., Garnett, D. R., et al. 2013, ApJ, 775, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Bibby, J. L., & Crowther, P. A. 2010, MNRAS, 405, 2737 [NASA ADS] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Blitz, L., & Rosolowsky, E. 2006, ApJ, 650, 933 [NASA ADS] [CrossRef] [Google Scholar]
- Boissier, S., & Prantzos, N. 2000, MNRAS, 312, 398 [Google Scholar]
- Bouquin, A. Y. K., Gil de Paz, A., Muñoz-Mateos, J. C., et al. 2018, ApJS, 234, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F. 2019, MNRAS, 488, 3826 [NASA ADS] [Google Scholar]
- Bresolin, F., & Kennicutt, R. C. 2015, MNRAS, 454, 3664 [CrossRef] [Google Scholar]
- Bresolin, F., Gieren, W., Kudritzki, R.-P., et al. 2009, ApJ, 700, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Bresolin, F., Kudritzki, R.-P., & Urbaneja, M. A. 2022, ApJ, 940, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [Google Scholar]
- Buck, T. 2020, MNRAS, 491, 5435 [NASA ADS] [CrossRef] [Google Scholar]
- Byun, Y. I., & Freeman, K. C. 1995, ApJ, 448, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Lee, J. C., Sabbi, E., et al. 2015, AJ, 149, 51 [Google Scholar]
- Casasola, V., Cassarà, L. P., Bianchi, S., et al. 2017, A&A, 605, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chang, R. X., Hou, J. L., Shu, C. G., & Fu, C. Q. 1999, A&A, 350, 38 [NASA ADS] [Google Scholar]
- Chang, R. X., Hou, J. L., Shen, S. Y., & Shu, C. G. 2010, ApJ, 722, 380 [NASA ADS] [CrossRef] [Google Scholar]
- Chang, R. X., Shen, S. Y., & Hou, J. L. 2012, ApJ, 753, L10 [CrossRef] [Google Scholar]
- Chen, B., Hayden, M. R., Sharma, S., et al. 2023, MNRAS, 523, 3791 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappini, C., Matteucci, F., & Romano, D. 2001, ApJ, 554, 1044 [NASA ADS] [CrossRef] [Google Scholar]
- Courteau, S., Dutton, A. A., van den Bosch, F. C., et al. 2007, ApJ, 671, 203 [Google Scholar]
- Dalcanton, J. J., Williams, B. F., Seth, A. C., et al. 2009, ApJS, 183, 67 [Google Scholar]
- de Vaucouleurs, G., & Pence, W. D. 1978, AJ, 83, 1163 [CrossRef] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G., et al. 1991, Sky Telesc., 82, 621 [NASA ADS] [Google Scholar]
- Edvardsson, B., Andersen, J., Gustafsson, B., et al. 1993, A&A, 500, 391 [NASA ADS] [Google Scholar]
- Elmegreen, B. G. 1989, ApJ, 338, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Erb, D. K. 2008, ApJ, 674, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Ferguson, A. M. N., & Clarke, C. J. 2001, MNRAS, 325, 781 [Google Scholar]
- Feuillet, D. K., Frankel, N., Lind, K., et al. 2019, MNRAS, 489, 1742 [Google Scholar]
- Finlator, K., & Davé, R. 2008, MNRAS, 385, 2181 [NASA ADS] [CrossRef] [Google Scholar]
- Frankel, N., Rix, H.-W., Ting, Y.-S., et al. 2018, ApJ, 865, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Frankel, N., Sanders, J., Rix, H.-W., et al. 2019, ApJ, 884, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Fraternali, F., & Tomassetti, M. 2012, MNRAS, 426, 2166 [NASA ADS] [CrossRef] [Google Scholar]
- Freedman, W. L., Madore, B. F., Gibson, B. K., et al. 2001, ApJ, 553, 47 [Google Scholar]
- Gallazzi, A., Charlot, S., Brinchmann, J., et al. 2005, MNRAS, 362, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Garnett, D. R. 2002, ApJ, 581, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Garnett, D. R., Shields, G. A., Skillman, E. D., et al. 1997, ApJ, 489, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Gazak, J. Z., Kudritzki, R., Evans, C., et al. 2015, ApJ, 805, 182 [NASA ADS] [CrossRef] [Google Scholar]
- Goddard, D., Thomas, D., Maraston, C., et al. 2017, MNRAS, 466, 4731 [NASA ADS] [Google Scholar]
- Gogarten, S. M., Dalcanton, J. J., Williams, B. F., et al. 2010, ApJ, 712, 858 [NASA ADS] [CrossRef] [Google Scholar]
- González Delgado, R. M., García-Benito, R., Pérez, E., et al. 2015, A&A, 581, A103 [Google Scholar]
- Goswami, S., Slemer, A., Marigo, P., et al. 2021, A&A, 650, A203 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grisoni, V., Spitoni, E., Matteucci, F., et al. 2017, MNRAS, 472, 3637 [Google Scholar]
- Grisoni, V., Spitoni, E., & Matteucci, F. 2018, MNRAS, 481, 2570 [NASA ADS] [Google Scholar]
- Guglielmo, V., Poggianti, B. M., Moretti, A., et al. 2015, MNRAS, 450, 2749 [NASA ADS] [CrossRef] [Google Scholar]
- Haywood, M. 2008, MNRAS, 388, 1175 [NASA ADS] [CrossRef] [Google Scholar]
- Hirschmann, M., De Lucia, G., & Fontanot, F. 2016, MNRAS, 461, 1760 [Google Scholar]
- Ho, I.-T., Kudritzki, R.-P., Kewley, L. J., et al. 2015, MNRAS, 448, 2030 [Google Scholar]
- Izotov, Y. I., Stasińska, G., Meynet, G., et al. 2006, A&A, 448, 955 [CrossRef] [EDP Sciences] [Google Scholar]
- Jarrett, T. H., Chester, T., Cutri, R., et al. 2003, AJ, 125, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, X., Chang, R., Yin, J., et al. 2012, MNRAS, 426, 1455 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, X., Chang, R., Zhang, F., et al. 2015, MNRAS, 449, 414 [NASA ADS] [CrossRef] [Google Scholar]
- Kang, X., Zhang, F., Chang, R., Wang, L., & Cheng, L. 2016, A&A, 585, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kang, X., Zhang, F., & Chang, R. 2017, MNRAS, 469, 1636 [CrossRef] [Google Scholar]
- Kang, X., Chang, R., Kudritzki, R.-P., et al. 2021, MNRAS, 502, 1967 [NASA ADS] [CrossRef] [Google Scholar]
- Karachentsev, I. D., Karachentseva, V. E., Huchtmeier, W. K., et al. 2004, AJ, 127, 2031 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G. 1996, MNRAS, 281, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Kelvin, L. S., Driver, S. P., Robotham, A. S. G., et al. 2014, MNRAS, 444, 1647 [Google Scholar]
- Kennicutt, R. C., Calzetti, D., Aniano, G., et al. 2011, PASP, 123, 1347 [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [Google Scholar]
- Kewley, L. J., Rupke, D., Zahid, H. J., et al. 2010, ApJ, 721, L48 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., & Kewley, L. J. 2004, ApJ, 617, 240 [CrossRef] [Google Scholar]
- Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Kubryk, M., Prantzos, N., & Athanassoula, E. 2013, MNRAS, 436, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Kubryk, M., Prantzos, N., & Athanassoula, E. 2015, A&A, 580, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kudritzki, R.-P., Urbaneja, M. A., Bresolin, F., et al. 2008, ApJ, 681, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Kudritzki, R.-P., Ho, I.-T., Schruba, A., et al. 2015, MNRAS, 450, 342 [Google Scholar]
- Kudritzki, R.-P., Teklu, A. F., Schulze, F., et al. 2021, ApJ, 910, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Lagos, C. D. P., Baugh, C. M., Lacey, C. G., et al. 2011, MNRAS, 418, 1649 [CrossRef] [Google Scholar]
- Larson, R. B. 1976, MNRAS, 176, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, J. C., Gil de Paz, A., Kennicutt, R. C., et al. 2011, ApJS, 192, 6 [CrossRef] [Google Scholar]
- Leitner, S. N., & Kravtsov, A. V. 2011, ApJ, 734, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Brinks, E., et al. 2008, AJ, 136, 2782 [Google Scholar]
- Leroy, A. K., Sandstrom, K. M., Lang, D., et al. 2019, ApJS, 244, 24 [Google Scholar]
- Lian, J., Thomas, D., & Maraston, C. 2018a, MNRAS, 481, 4000 [Google Scholar]
- Lian, J., Thomas, D., Maraston, C., et al. 2018b, MNRAS, 476, 3883 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, C., Kudritzki, R.-P., Zhao, G., et al. 2022, ApJ, 932, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Matteucci, F. 2012, Chemical Evolution of Galaxies: Astronomy and Astrophysics Library (Berlin, Heidelberg: Springer-Verlag) [CrossRef] [Google Scholar]
- Matteucci, F., & Francois, P. 1989, MNRAS, 239, 885 [Google Scholar]
- McCall, M. L., Rybski, P. M., & Shields, G. A. 1985, ApJS, 57, 1 [CrossRef] [Google Scholar]
- Minchev, I., & Famaey, B. 2010, ApJ, 722, 112 [Google Scholar]
- Minchev, I., Famaey, B., Quillen, A. C., et al. 2012, A&A, 548, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mollá, M., & Díaz, A. I. 2005, MNRAS, 358, 521 [CrossRef] [Google Scholar]
- Moustakas, J., Kennicutt, R. C., Tremonti, C. A., et al. 2010, ApJS, 190, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Mateos, J. C., Gil de Paz, A., Boissier, S., et al. 2007, ApJ, 658, 1006 [Google Scholar]
- Muñoz-Mateos, J. C., Boissier, S., Gil de Paz, A., et al. 2011, ApJ, 731, 10 [CrossRef] [Google Scholar]
- Muraoka, K., Takeda, M., Yanagitani, K., et al. 2016, PASJ, 68, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Ostriker, E. C., McKee, C. F., & Leroy, A. K. 2010, ApJ, 721, 975 [CrossRef] [Google Scholar]
- Pan, Z., Peng, Y., Zheng, X., et al. 2019, ApJ, 876, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Panter, B., Jimenez, R., Heavens, A. F., et al. 2008, MNRAS, 391, 1117 [NASA ADS] [CrossRef] [Google Scholar]
- Pezzulli, G., Fraternali, F., Boissier, S., et al. 2015, MNRAS, 451, 2324 [CrossRef] [Google Scholar]
- Pilyugin, L. S., & Thuan, T. X. 2005, ApJ, 631, 231 [CrossRef] [Google Scholar]
- Pilyugin, L. S., Grebel, E. K., & Kniazev, A. Y. 2014, AJ, 147, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Grebel, E. K., Zinchenko, I. A., et al. 2019, A&A, 623, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poetrodjojo, H., Groves, B., Kewley, L. J., et al. 2018, MNRAS, 479, 5235 [Google Scholar]
- Prantzos, N., & Boissier, S. 2000, MNRAS, 313, 338 [NASA ADS] [CrossRef] [Google Scholar]
- Prugniel, P., & Heraudeau, P. 1998, A&AS, 128, 299 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Qu, Y., Helly, J. C., Bower, R. G., et al. 2017, MNRAS, 464, 1659 [NASA ADS] [CrossRef] [Google Scholar]
- Radburn-Smith, D. J., Roškar, R., Debattista, V. P., et al. 2012, ApJ, 753, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Recchi, S., Spitoni, E., Matteucci, F., et al. 2008, A&A, 489, 555 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rogers, N. S. J., Skillman, E. D., Pogge, R. W., et al. 2022, ApJ, 939, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Romano, D., Karakas, A. I., Tosi, M., et al. 2010, A&A, 522, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roškar, R., Debattista, V. P., Stinson, G. S., et al. 2008, ApJ, 675, L65 [Google Scholar]
- Rupke, D. S. N., Kewley, L. J., & Chien, L.-H. 2010, ApJ, 723, 1255 [NASA ADS] [CrossRef] [Google Scholar]
- Sacchi, E., Cignoni, M., Aloisi, A., et al. 2019, ApJ, 878, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sachdeva, S., & Saha, K. 2016, ApJ, 820, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Sachdeva, S., Gadotti, D. A., Saha, K., et al. 2015, MNRAS, 451, 2 [CrossRef] [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Jungwiert, B., et al. 2013, A&A, 554, A58 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sánchez, S. F., Rosales-Ortega, F. F., Iglesias-Páramo, J., et al. 2014, A&A, 563, A49 [CrossRef] [EDP Sciences] [Google Scholar]
- Schönrich, R., & Binney, J. 2009, MNRAS, 396, 203 [Google Scholar]
- Sellwood, J. A., & Wilkinson, A. 1993, Rep. Progr. Phys., 56, 173 [CrossRef] [Google Scholar]
- Sextl, E., Kudritzki, R.-P., Zahid, H. J., et al. 2023, ApJ, 949, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Skibba, R. A., Engelbracht, C. W., Dale, D., et al. 2011, ApJ, 738, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. V., van Zee, L., Salim, S., et al. 2021, MNRAS, 505, 3998 [NASA ADS] [CrossRef] [Google Scholar]
- Spitoni, E., Romano, D., Matteucci, F., et al. 2015, ApJ, 802, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Spitoni, E., Cescutti, G., Minchev, I., et al. 2019, A&A, 628, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spitoni, E., Calura, F., Mignoli, M., et al. 2020, A&A, 642, A113 [EDP Sciences] [Google Scholar]
- Spitoni, E., Verma, K., Silva Aguirre, V., et al. 2021a, A&A, 647, A73 [EDP Sciences] [Google Scholar]
- Spitoni, E., Calura, F., Silva Aguirre, V., et al. 2021b, A&A, 648, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stanghellini, L., Magrini, L., & Casasola, V. 2015, ApJ, 812, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Thomas, D., Maraston, C., Schawinski, K., et al. 2010, MNRAS, 404, 1775 [NASA ADS] [Google Scholar]
- Tinsley, B. M. 1980, Fund. Cosmic Phys., 5, 287 [Google Scholar]
- Torrey, P., Cox, T. J., Kewley, L., et al. 2012, ApJ, 746, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [Google Scholar]
- van den Bosch, F. C. 1998, ApJ, 507, 601 [NASA ADS] [CrossRef] [Google Scholar]
- Vincenzo, F., & Kobayashi, C. 2020, MNRAS, 496, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Vincenzo, F., Matteucci, F., Belfiore, F., et al. 2016, MNRAS, 455, 4183 [CrossRef] [Google Scholar]
- Walter, F., Brinks, E., de Blok, W. J. G., et al. 2008, AJ, 136, 2563 [Google Scholar]
- Williams, B. F., Dalcanton, J. J., Dolphin, A. E., et al. 2009, ApJ, 695, L15 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, B. F., Dalcanton, J. J., Johnson, L. C., et al. 2011, ApJ, 734, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, B. F., Dalcanton, J. J., Stilp, A., et al. 2013, ApJ, 765, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfe, S. A., Pisano, D. J., Lockman, F. J., et al. 2013, Nature, 497, 224 [NASA ADS] [CrossRef] [Google Scholar]
- Xiang, M., & Rix, H.-W. 2022, Nature, 603, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Zahid, H. J., Dima, G. I., Kudritzki, R.-P., et al. 2014, ApJ, 791, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Zahid, H. J., Kudritzki, R.-P., Conroy, C., et al. 2017, ApJ, 847, 18 [Google Scholar]
- Zaritsky, D., Kennicutt, R. C., & Huchra, J. P. 1994, ApJ, 420, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Zheng, Z., Wang, H., Ge, J., et al. 2017, MNRAS, 465, 4572 [Google Scholar]
All Tables
Main input properties and parameters of the best-fitting models for NGC 7793, NGC 2403, NGC 300, and M 33.
All Figures
 |
Fig. 1. A(r) function. The dashed and solid lines correspond to two limiting cases of τ = 0.1 Gyr and τ = 15 Gyr, respectively. To facilitate comparison, the A(r) values of the model adopting τ = 15 Gyr have been multiplied by 4000. |
| In the text | |
 |
Fig. 2. Comparisons of model predictions with observations. The different line types correspond to different parameter groups (the dotted lines (τ, bout) show (0.1 Gyr, 0), the dashed lines (τ, bout) show (15 Gyr, 0), the dot-dashed lines (τ, bout) show (15 Gyr, 1.0), and the solid lines (τ, bout) show (0.1r/Rd + 3.4 Gyr, 0.2)). On the left side, the radial profiles of HI mass and SFR surface density are shown in the top and bottom panels, respectively. On the right side, the radial profiles of the sSFR and metallicity are displayed in the top and bottom panels, respectively. The different symbols correspond to observed data from different works. HI data from Leroy et al. (2008) are shown as filled red circles. SFR data obtained from Leroy et al. (2008) are denoted as filled red circles, and those from Casasola et al. (2017) are displayed as filled blue asterisks. The sSFR data from Muñoz-Mateos et al. (2007) and Smith et al. (2021) are denoted as open red triangles and open red diamonds, respectively. The 12 + log(O/H) data taken from Bibby & Crowther (2010), Pilyugin et al. (2014), and Stanghellini et al. (2015) are separately plotted as filled yellow asterisks, filled green circles, and filled red diamonds. |
| In the text | |
 |
Fig. 3. Radial distribution of 12 + log(O/H). Upper panel: comparisons of the present-day radial distribution of 12 + log(O/H) predicted by our best-fitting model (solid black line) with the observational data. Different symbols denote the observed metallicity data from different works as filled yellow asterisks (Bibby & Crowther 2010), filled green circles (Pilyugin et al. 2014), and filled red diamonds (Stanghellini et al. 2015). The linear best fit to the observed data and 1σ uncertainty are plotted as the solid and dotted blue lines, respectively. Lower panel: filled black circles show the deviations of the observations from our best-fitting model predictions, derived by subtracting the solid black line from the observed data in the upper panel, and the open blue circles show those obtained from subtracting the linear best fit from the observational data in the upper panel. |
| In the text | |
 |
Fig. 4. Star formation histories (upper panel) and relative stellar mass growth (lower panel) of three regions at different galactocentric distances for the NGC 7793 disc. Different line types represent different regions along the disc, dotted red line for 1 − 2 kpc, dashed blue line for 4 − 5 kpc and solid black line for 7 − 8 kpc. Both the SFRs and stellar masses are normalised by their present-day values. The horizontal cyan dash-dotted line in the lower panel shows when each component achieves 50% of its final value. |
| In the text | |
 |
Fig. 5. Radial profile of the mean stellar age along the disc of NGC 7793 predicted by its own best-fitting model. |
| In the text | |
 |
Fig. 6. Stellar mass growth histories of NGC 7793 (solid line), NGC 300 (dashed line), M 33 (dotted line), and NGC 2403 (dash-dotted line) predicted by the respective best-fitting models. Stellar masses are normalised to their present-day values. The horizontal dashed lines mark when the stellar mass reaches 20% (green), 50% (cyan), and 60% (yellow) of its final value, and the vertical dotted red line denotes the galaxy evolutionary age at t = 5.75 Gyr (i.e. z = 1). |
| In the text | |
 |
Fig. 7. Evolution of the SFR for NGC 7793 (solid line), NGC 300 (dashed line), M 33 (dotted line), and NGC 2403 (dash-dotted line) predicted by the respective best-fitting models. SFRs are normalised to their present-day values. |
| In the text | |
 |
Fig. 8. Evolution of the scale length and total stellar mass predicted by our best-fitting models for NGC 7793 (solid line), NGC 300 (dashed line), M 33 (dotted line), and NGC 2403 (dash-dotted line). Each track follows the evolution of a galaxy from z = 1 (the z = 1 step is marked with an asterisk) to z = 0 (the z = 0 step is marked with a filled circle). |
| In the text | |
 |
Fig. 9. Comparison of the stellar mass-metallicity relation predicted by our best-fitting models (black star for NGC 7793, red triangle for NGC 2403, blue square for NGC 300, magenta diamond for M 33, and green pentagon for NGC 5194) with that published in the literature. The solid circles show the stellar metallicity of nearby galaxies measured from spectroscopy of individual blue supergiants (cyan), red supergiants (pink), and super star clusters (yellow; see Bresolin et al. 2022, reference therein). The thin orange diamonds are the MZR derived from the young stellar population of SDSS star-forming galaxies (Sextl et al. 2023). |
| In the text | |
 |
Fig. 10. Metallicity gradient vs. stellar mass predicted by the respective best-fitting models when the metallicity gradients are measured in |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned}&\frac{\mathrm{d}[\Sigma _{\rm tot}(r,t)]}{\mathrm{d}t} = f_{\mathrm{in}}(r,t)-f_{\mathrm{out}}(r,t),\end{aligned} $$](/articles/aa/full_html/2023/11/aa47677-23/aa47677-23-eq1.gif)
![$$ \begin{aligned}&\frac{\mathrm{d}[\Sigma _{\rm gas}(r,t)]}{\mathrm{d}t} = -(1-R)\Psi (r,t)+f_{\mathrm{in}}(r,t)-f_{\mathrm{out}}(r,t),\end{aligned} $$](/articles/aa/full_html/2023/11/aa47677-23/aa47677-23-eq2.gif)
![$$ \begin{aligned}&\frac{\mathrm{d}[Z(r,t)\Sigma _{\rm gas}(r,t)]}{\mathrm{d}t} = { y}(1-R)\Psi (r,t)-Z(r,t)(1-R)\Psi (r,t)\nonumber \\&\qquad \qquad \qquad \qquad \quad +Z_{\mathrm{in}}f_{\mathrm{in}}(r,t)-Z_{\mathrm{out}}(r,t)f_{\mathrm{out}}(r,t), \end{aligned} $$](/articles/aa/full_html/2023/11/aa47677-23/aa47677-23-eq3.gif)
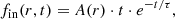
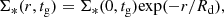
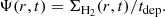
![$$ \begin{aligned} R_{\mathrm{mol}}(r,t) = {\Sigma _{{{\mathrm{H}}_2}}}(r,t)/{\Sigma _{{\mathrm{HI}}}(r,t)} = {\left[ {P_{\rm h}\left(r,t\right)/{P_0}} \right]^{\alpha _{\rm P}}}, \end{aligned} $$](/articles/aa/full_html/2023/11/aa47677-23/aa47677-23-eq8.gif)
![$$ \begin{aligned} P_{\rm h}\left( r,t \right) = \frac{\pi }{2}\mathrm{G}{\Sigma _{{\mathrm{gas}}}}\left( r,t \right)\left[ {{\Sigma _{{\mathrm{gas}}}}\left( r,t \right) + \frac{c_{\rm gas}}{c_{\rm *}}{\Sigma _*}\left( r,t \right)} \right], \end{aligned} $$](/articles/aa/full_html/2023/11/aa47677-23/aa47677-23-eq9.gif)