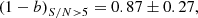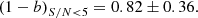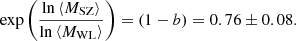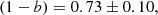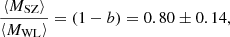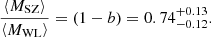| Issue |
A&A
Volume 655, November 2021
|
|
|---|---|---|
| Article Number | A115 | |
| Number of page(s) | 15 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202140382 | |
| Published online | 01 December 2021 | |
Velocity dispersion and dynamical mass for 270 galaxy clusters in the Planck PSZ1 catalogue⋆
1
Instituto de Astrofísica de Canarias (IAC), C/ Vía Láctea s/n, 38205 La Laguna, Tenerife, Spain
e-mail: ferragamoantonio@gmail.com
2
Universidad de La Laguna, Departamento de Astrofísica, C/ Astrofísico Francisco Sánchez s/n, 38206 La Laguna, Tenerife, Spain
3
Dipartimento di Fisica, Sapienza Università di Roma, Piazzale Aldo Moro, 00185 Roma, Italy
4
Gran Telescopio Canarias, La Palma, Spain
5
Purple Mountain Observatory, No. 8 Yuanhua Road, Qixia District, Nanjing 210034, PR China
6
Universidad Andrés Bello, Departemento de Ciencias Físicas, 7591538 Santiago de Chile, Chile
7
Max-Planck Institute for Astronomy, Königstuhl 17, 69117 Heidelberg, Germany
8
Tartu Observatory, University of Tartu, 61602 Tõravere, Tartumaa, Estonia
Received:
20
January
2021
Accepted:
23
August
2021
We present the velocity dispersion and dynamical mass estimates for 270 galaxy clusters included in the first Planck Sunyaev-Zeldovich (SZ) source catalogue, the PSZ1. Part of the results presented here were achieved during a two-year observational program, the ITP, developed at the Roque de los Muchachos Observatory (La Palma, Spain). In the ITP we carried out a systematic optical follow-up campaign of all the 212 unidentified PSZ1 sources in the northern sky that have a declination above −15° and are without known counterparts at the time of the publication of the catalogue. We present for the first time the velocity dispersion and dynamical mass of 58 of these ITP PSZ1 clusters, plus 35 newly discovered clusters that are not associated with the PSZ1 catalogue. Using Sloan Digital Sky Survey archival data, we extend this sample, including 212 already confirmed PSZ1 clusters in the northern sky. Using a subset of 207 of these galaxy clusters, we constrained the MSZ–Mdyn scaling relation, finding a mass bias of (1 − B) = 0.83 ± 0.07(stat) ± 0.02(sys). We show that this value is consistent with other results in the literature that were obtained with different methods (X-ray, dynamical masses, or weak-lensing mass proxies). This result cannot dissolve the tension between primordial cosmic microwave background anisotropies and cluster number counts in the ΩM–σ8 plane.
Key words: large-scale structure of Universe / galaxies: clusters: general / catalogs
Tables A.1–A.3 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/655/A115
© ESO 2021
1. Introduction
According to the bottom-up hierarchical scenario, Galaxy clusters (GCs) are the last bounded structures to form in our Universe (starting from about z ∼ 2). They reside in the deepest potential wells, which are generated by dark matter (DM) overdensities (e.g., Springel 2005). Galaxy clusters are multi-component structures. In addition to DM, haloes include baryonic matter in different forms and phases (see e.g., Allen et al. 2011, and references therein). In addition to galaxies, cold and hot gas and non-thermal plasma constitute the intra-cluster medium (ICM). This multi-component nature allows us to observe GCs at various wavelengths, taking advantage of the different physical processes involved in each case. For instance, we use X-rays and radio observations to probe the ICM or the visible/IR wavelengths to study the galactic component. Dark matter is usually studied through the deformation of images from the background galaxies. These multi-wavelength observations provide complementary information about the cluster physics.
Galaxy clusters are excellent tracers of the evolution of structures throughout the history of the Universe. Their abundance as a function of redshift and mass, the so-called cluster number counts, is very sensitive to cosmological parameters, and in particular, to the matter density parameter Ωm and to the amplitude of the density fluctuations σ8 (Vikhlinin et al. 2009; Mamon et al. 2010; Penna-Lima et al. 2017; Planck Collaboration XXIV 2016). The accuracy in the cluster mass determination is crucial for the determination of cosmological parameters. To this end, several mass proxies can be defined through scaling relations (see e.g., Pratt et al. 2019, and references therein). However, each mass proxy has its own biases that are linked to the methods of observation or the assumptions made to calculate it. To understand these biases, the analysis of cosmological simulations is a valuable tool, and the comparison of the masses obtained from different proxies becomes essential.
The Sunyaev-Zeldovich (SZ) effect (Sunyaev & Zeldovich 1972) is a spectral distortion of the cosmic microwave background (CMB), generated by the inverse Compton scattering of the CMB photons off the hot electrons in the ICM. As the brightness temperature of the resulting distortion is redshift independent, the SZ effect has recently become a powerful tool for detecting GCs.
The ESA Planck mission scanned the entire sky in microwaves with the aim of studying primary and secondary anisotropies of the CMB. The observations, which lasted four years, spanned nine bands between 30 GHz and 857 GHz. The results of these observations include two catalogues of objects detected by means of their SZ signature: PSZ1 (Planck Collaboration XXIX 2014; Planck Collaboration Int. XXXII 2015) and PSZ2 (Planck Collaboration XXVII 2016). These products were the first to provide the possibility of detecting GCs through the SZ effect in a full-sky survey. The catalogues contain 1227 and 1653 objects, respectively, with 937 objects in common. The total integrated SZ signal within a circle of radius (the so-called integrated Compton parameter, YSZ) is closely related to the cluster mass (e.g., Burgh et al. 2003). This Y500 observable has been used as the mass proxy by the Planck Collaboration, after calibrating it to X-ray measurements (Penna-Lima et al. 2017; Planck Collaboration XXIV 2016).
This paper is the third (and last) in the series of publications associated with the International Time Programme ITP13B-15A, a two-year (August 2013 to July 2014) long-term program in the Canary Islands Observatories dedicated to characterising PSZ1 sources in the northern sky without known optical counterparts at the time of publication of the PSZ1 catalogue. The publications were a continuation of the validation efforts carried out in Planck Collaboration Int. XXXVI (2016), within the context of the ITP 12-2 program. Paper I (Barrena et al. 2018) and Paper II (Barrena & Ferragamo 2020) described the ITP13B-15A program in detail, which included observations of 256 SZ sources with a declination above −15° (212 of them were previously unknown), finding optical counterparts for 152 SZ sources. This paper (number III in the series) presents all the spectroscopic observations of the program, including velocity dispersion and dynamical mass estimates.
In Sect. 2, we describe the PSZ1-North reference sample summarising the results of the ITP program. Sections 3 and 4 depict how we estimate GC velocity dispersion and dynamical masses, respectively. In Sect. 2 we describe the ITP and the Sloan Digital Sky Survey (SDSS) GC samples we used for the cosmological analyses of this work. In Sect. 6, we constrain the mass bias parameter, (1−B), explaining how much the Eddington bias affects our sample and detailing the importance of correcting for it. Finally, in Sect. 7, we compare our results with those from Planck Collaboration and those from the literature, using the velocity dispersion and the weak-lensing analysis as mass proxies. We also discuss the implications on the σ8 tension with CMB measurements.
Throughout this paper, we define R200 and R500 as the radius within which the mean cluster density is 200 and 500 times the critical density of the Universe at redshift z, respectively. The quantities with the subscripts 200 or 500 have to be considered as evaluated at or within R200 and R500, respectively. We assume a flat ΛCDM cosmology, with H0 = 100 h km s−1 Mpc−1, h = 0.678, and ΩM = 0.307 (Planck Collaboration XX 2014).
2. PSZ1-North sample
The PSZ1 catalogue (Planck Collaboration XXIX 2014; Planck Collaboration Int. XXXII 2015) contains 1227 sources detected by means of their SZ signature in the all-sky maps obtained during the first 15.5 months of Planck observations. These sources are detected by at least one of the three Planck cluster detection algorithms (MMF1, MMF3, and PwS) with a signal-to-noise ratio (S/N) of 4.5 or higher. Planck Collaboration XXIX (2014) describes these three algorithms, the selection, and the validation methods adopted in the construction of the catalogue in detail.
Following Papers I and II, we define the PSZ1-North sample as the 753 PSZ1 sources in the northern hemisphere with a declination Dec ≥ −15°. Of these, 541 were validated by the Planck Collaboration at the time of publication of the PSZ1 catalogue. The remaining 212 sources were studied within the ITP program.
2.1. ITP program
Planck Collaboration Int. XXXVI (2016), Barrena et al. (2018), and Barrena & Ferragamo (2020) have described our optical follow-up of the unknown PSZ1 sources in the northern sky that we carried out between the second semester of 2012 and first semester of 2015 by means of two International Time Projects (ITP 12-2 and ITP13-08, hereafter ITP). Table 3 in Barrena & Ferragamo (2020) presented the summary information of the full program, where we observed all the 212 PSZ1-North sources for which no counterparts were known, plus 44 of the already validated sources.
Papers I and II have presented the complete imaging results of the program and partial spectroscopic results, including the mean spectroscopic redshifts to the clusters, as well as the redshift of the BCG, when available. This Paper III presents for the first time the velocity dispersion and dynamical mass estimates for s with at least Ngal seven spectroscopic members. In total, 58 PSZ1-North clusters were characterised (see Table 1).
Summary of the data sets.
The majority of these results were obtained using multi-object spectroscopy (MOS), although for a few cases and when the MOS mode was not available, we used a combination of long-slit measurements. As described in previous papers, all the spectroscopic data for the ITP program have been acquired using three instruments at the Observatorio del Roque de Los Muchachos (ORM), located on the island of La Palma (Spain). OSIRIS at the 10.4 m Gran Telescopio Canarias (GTC) and DOLORES at the 3.5 m Telescopio Nazionale Galileo (TNG) were mainly used to obtain MOS, while ACAM at the 4.2 m William Herschel Telescope (WHT) provided some additional spectra that were retrieved through a long-slit setup. A detailed description of the instrument characteristics and the configuration adopted for these measurements has been presented in Papers I and II.
When the MOS technique was used with OSIRIS and DOLORES, we observed each field with a single mask containing between 45 and 60 slitlets on average. In this way, we were able to maximize the number of redshifts per observation, obtaining a median number of galaxy members of about 20 (see details in Paper II).
Table A1 contains the full list of the 58 ITP objects within PSZ1-North that we studied in this paper. The first, second, and third columns identify the index number, the Planck name of each cluster in the PSZ1 catalogue, and the signal-to-noise ratio of the SZ detection. Columns 4 and 5 indicate the equatorial coordinates (J2000) of the cluster optical centre. Column 6 indicates the distance from the optical centre to the nominal Planck coordinates. Columns 7 and 8 contain our spectroscopic redshift and the number of cluster members with spectroscopic measurements, respectively. Columns 9 to 11 contain the velocity dispersion, the dynamical mass, and the SZ mass estimates. The description of the process with which these numbers were derived is discussed in Sects. 3 and 4. Finally, cols. 12 and 13 indicate whether the cluster was used to constrain the scaling relation and if it was part of the Planck cosmological sample (hereafter, PlCS), as defined in Planck Collaboration XXIX (2014).
During this program, we also characterised 35 bona fide GCs that have not been associated with the SZ signal measured by Planck, either because they lie at a distance of more than 5′ from the nominal Planck pointing or because their velocity dispersion is too low. These objects were labelled Flag = 3 in our validation process (see details in Barrena et al. 2018; Barrena & Ferragamo 2020). These 35 clusters are listed in the column “Beyond PSZ1” in Table 1 and are presented in Table A3, using the same format as in Table A1.
The location of all these ITP clusters is shown in Fig. 1 in red. We obtained more than 2000 individual redshift measurements in this work. The mean number of galaxy members for these ITP clusters is Ngal = 15. All the spectra associated with these observations that we present here for the first time will be published online and are included in the VO database.
 |
Fig. 1. Sky distribution of all the PSZ1 clusters studied in this paper. The figure uses a Mollweide projection in Galactic coordinates. The Galactic plane is horizontal and centred at longitude zero. Red circles and blue triangles represent ITP (Sect. 2.1) and SDSS (Sect. 2.2) clusters, respectively, and the symbol size is proportional to the cluster mass. The shaded grey area represents the union mask used to produce the CMB map in the first Planck data release (downloaded from the Planck Legacy Archive). This mask excludes 27% of the sky, mostly in the region of the Galactic plane, the Magellanic Clouds, and point sources. |
2.2. SDSS archival data
With the aim of characterising the full PSZ1-North sample, we decided to enlarge our ITP sample by searching in the SDSS Data Release 14 (Aihara et al. 2011) for additional spectroscopic information. For each of the 401 PSZ1 sources within the SDSS footprint, we retrieved all spectroscopic redshifts within 15′ radius around the nominal Planck coordinates. We used the position of the brightest galaxy in the radial velocity catalogue as the cluster centre, within a range of ±2500 km s−1 around the Planck validation redshift. In most cases, this position corresponded to the BCG. If not, after a visual inspection of SDSS RGB images, we selected the centre as the position of a clear BCG (not observed spectroscopically). Alternatively, we used the cluster members mean coordinates as the optical centre.
For each individual PSZ1 field, we analysed the retrieved set of spectroscopic redshifts in the same way as we treated the clusters that were observed during the ITP program. However, due to the lack of (enough number of) spectra in some fields, it was only possible to characterise the spectroscopic properties for 212 regions. As in the previous case, we only considered the clusters for which we had at least Ngal seven spectroscopic members.
Table A2 contains the final list of PSZ1-North clusters with SDSS information that is discussed in this paper. The table format is identical to that of Table A1. The location of these 212 clusters is also shown in Fig. 1 in blue. We used ∼10 000 spectra in this analysis. The mean number of galaxy members for these clusters is Ngal = 35.
Finally, the joint ITP and SDSS sample consists of 270 GCs, 226 of which are also included in the PSZ2 catalogue. In our sample, the percentage of PSZ1 clusters that are also detected in the PSZ2 is therefore 85%. This number is slightly higher than the same fraction computed for the whole PSZ1 catalogue, 76% (see Table 10 in Planck Collaboration XXVII 2016).
3. Velocity dispersion estimates
For each, the final product of either our ITP observations or the SDSS archival data search is a catalogue of radial velocities of galaxies within a certain field. This means that the cluster is detected as an over-density in the radial velocity distribution of at least four galaxies in a range of ±5000 km s−1 around the velocity of the BCG. The membership selection is based on the galaxy position in the 2D projected phase space (r, cz), where r is the projected distance from the cluster centre, and cz is the galaxy line-of-sight (LoS) velocity. To minimize the presence of interlopers, we defined a region of membership by performing a cut at r = 2.5 Mpc (at the redshift of the cluster) and an iterative 2.5 − σ clipping in the cz coordinate, taking into account the radial profile of the expected velocity dispersion (Łokas & Mamon 2001). The first criterion restricts our galaxy sample to a distance between 1.5 and 2 R200 (depending on the cluster mass and redshift) and in this way limits the contamination of interlopers at large distances from the centre of the clusters.
Figure 2 shows two examples of the final velocity histogram of cluster members for two ITP clusters. Figure 3 shows the 2D projected phase-space and the velocity distribution of the stack of all cluster members selected using the procedure explained above for the ITP sub-sample (1432 clusters) and for the SDSS sub-sample (3879 clusters).
 |
Fig. 2. Two examples of the velocity distribution of cluster members: PSZ1 G103.94+25.81 (top) and PSZ1 G123.55–10.34 (bottom). Both clusters have been observed within the ITP program. The histograms contain 17 and 30 members, respectively. In both cases, the red line corresponds to a Gaussian distribution centred in the mean cluster velocity, and with σ equal to the estimated velocity dispersion σv. |
 |
Fig. 3. Projected phase-space and velocity histogram of the stack of all ITP clusters members (top) and all SDSS cluster members (bottom). In both cases, velocities are normalised to the cluster velocity dispersion. The dashed black lines indicate the 2.5 − σ clipping, and the dotted blue lines show the same clipping, but take the velocity dispersion radial profile as shown in Łokas & Mamon (2001) into account. The red line in the right panel represents a Gaussian fit of the stacked velocity histogram normalised to the total number of members. |
After this member selection was concluded, we estimated the velocity dispersion using the gapper estimator (Wainer & Thissen 1976). We followed the procedure outlined in Evrard et al. (2008), and we corrected this velocity dispersion estimate by taking the statistical bias introduced by the under-sampling and sigma clipping into account, as well as the physical bias due to the aperture radius. Our velocity dispersion results are listed in Col. 9 of Tables A1, A2, and A3.
4. Dynamical mass estimates
We computed the dynamical mass 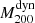 by using the bias-corrected mass estimator described in Evrard et al. (2008). This estimator is based on the AGN fit of the Miyatake et al. (2019) scaling relation, given by
by using the bias-corrected mass estimator described in Evrard et al. (2008). This estimator is based on the AGN fit of the Miyatake et al. (2019) scaling relation, given by
where A = 1177.0 and α = 0.364.
Following prescriptions described in Evrard et al. (2008), we corrected for the aperture radius bias. The physical bias correction due to the fraction of massive galaxies (which tends to reduce the mass of the clusters by 5 % at most) cannot be evaluated in this work because it requires a well-constrained luminosity function. This cannot be obtained because the clusters we analysed have only a few spectroscopic members.
It follows that the dynamical masses reported here are to be considered as a lower limit to the true mass. The derived mass bias is therefore to be considered as an upper limit. In order to compare our results with the SZ flux (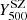 ) and SZ mass (
) and SZ mass (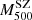 ) values derived by the Planck Collaboration, we need to rescale our values from M200 to M500.
) values derived by the Planck Collaboration, we need to rescale our values from M200 to M500.
To do this, we assumed an NFW density profile (Nagai 2006),
where ρs and rs are the characteristic density and the scale radius, respectively. These parameters are related to R200 and ρ200 ≡ 200 × ρc, where ρc is the critical density, through the concentration parameter c200, which is defined as
where g(x) = 1/[ln(1+x)−x/(1+x)]. The mass enclosed within a spherical over-density of radius rΔ can be written as
where Δ is the new density contrast at which we wish to obtain the mass (in our case, Δ = 500). Finally, we selected a mass-concentration relation to scale our masses (Krause et al. 2012). Following the procedure in Kelly (2007), we chose the da Silva et al. (2004) relation, which is constrained using N-body simulations and WMAP 5-year cosmological parameters,
5. Selection of a representative sub-sample
Here we describe the sub-sample of selected 207 PSZ1-North clusters that we used to characterise the scaling relation 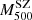 –
–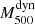 . This sub-sample contains all the 58 ITP objects and 149 SDSS clusters (see last column in Table 1) that were selected as explained below. This sub-sample represents 27.5 % of the full PSZ1-North catalogue.
. This sub-sample contains all the 58 ITP objects and 149 SDSS clusters (see last column in Table 1) that were selected as explained below. This sub-sample represents 27.5 % of the full PSZ1-North catalogue.
5.1. ITP sub-sample
Although our observational program has resulted in more confirmed clusters, we considered only the most reliable ones that had an unambiguous association with the Planck SZ signal to characterise the scaling relation. Because the measured SZ signal is the total integrated electron pressure along the line of sight, we cannot separate the fraction of the Y500 signal that corresponds to each cluster in the case of multiple cluster counterparts inside the same pointing. We therefore discarded these multiple counterparts for this analysis. In practice, this does not affect the ITP sample, and we kept all 58 ITP clusters within PSZ1-North, as listed in Table A1. The last column in the table indicates the objects that are included in the PlCS. By construction, this number is very small (only 2) because the ITP sample includes PSZ1-North objects with unknown counterparts at the time of publication of the catalogue.
Figure 4 shows the distribution of these 58 objects as a function of redshift (left panel) and the S/N of the SZ detection (right panel). The median redshift of this sub-sample is z = 0.31, and the median S/N is 4.9.
 |
Fig. 4. Number of ITP clusters as a function of redshift (left panel) and the S/N of the SZ detection (right panel) we used, normalised to 88, which is the total number of ITP-validated clusters (for details, see Barrena & Ferragamo 2020). |
5.2. SDSS sub-sample
From the full list of 212 SDSS objects discussed in Sect. 2.2, we only considered the 149 SZ clusters with a single optical counterpart at the same redshift as the validation counterpart reported in the PSZ1 catalogue. These clusters lie within 5′ from the nominal Planck pointing. Although these prescriptions (Ngal ≥ 7 and a single counterpart) leave us with only 37% of all the 401 PSZ1 clusters within the SDSS footprint, they guarantee a clean SDSS sample. A detailed and systematic study of the optical counterparts of previously validated clusters of the PSZ1 catalogue is beyond the scope of this work.
Figures 4 and 5 show the number of GCs in the ITP and our SDSS sample (green) as a function of the redshift (left panel) and of the S/N (right panel), respectively. The number of PlCS clusters contained in our SDSS sample is plotted in red. Most of the selected clusters are low-redshift systems with a low S/N. The median redshift and S/N are 0.17 and 5.74, respectively. It is also interesting to note that although the percentage of validated PSZ1 clusters comprised in SDSS is 25.8%, only 18.6% of the clusters are in the PlCS. However, 42 (28.2 %) of the 149 SDSS clusters that we selected are part of the PlCS, with a median redshift equal to 0.11 and a median S/N of 9.39. In our analysis below, we explore whether the measured mass bias differs for clusters within or outside the cosmological sample.
 |
Fig. 5. Number of SDSS clusters as a function of redshift (left panel) and SZ S/N (right panel) we used, normalised to the total number of PSZ1 sources within the SDSS footprint (green). Red histograms correspond to the subsample of SDSS clusters within the Planck cosmological sample. |
In Table A2 we list the velocity dispersion and the dynamical and the SZ mass for these 149 clusters selected from the SDSS sample. The selected objects are marked with a checkmark in the column “scaling”. We also indicate the clusters that are included in the cosmological sample.
6. Mdyn–MSZ relation
Here we describe the results of the 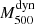 –
–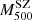 scaling relation using the PSZ1 GC samples selected in the previous section. Following the definition given in Penna-Lima et al. (2017), the bias of SZ-derived masses is given by
scaling relation using the PSZ1 GC samples selected in the previous section. Following the definition given in Penna-Lima et al. (2017), the bias of SZ-derived masses is given by
where 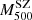 is the cluster SZ mass. This is estimated following the prescriptions in Planck Collaboration XXIX (2014) using the equation
is the cluster SZ mass. This is estimated following the prescriptions in Planck Collaboration XXIX (2014) using the equation
which is calibrated using X-ray observations of 71 clusters in the PSZ1 cosmological sample.
In general, because we cannot account for all the possible biases in the dynamical mass estimation, we defined a global bias of the dynamical mass as
Combining Eqs. (7) and (9), we obtain the Mdyn − MSZ relation as
where the mass bias (1 − B) is defined as the ratio of SZ and dynamical bias,
6.1. Linear regression method
We fit for the relation in Eq. (10) using a linear regression in logarithmic space because the high noise level of our dynamical mass estimates, with typical relative errors of ∼30%, could affect the estimation of the fitted parameters. In some cases, we also explored the possibility of a mass dependence by letting the exponent vary freely in the relation, fitting for the slope and intercept in
This problem requires carrying out a linear regression with errors in both axes, and accounting for intrinsic scatter. In order to select the most appropriate method for this problem, we tested five methods that are commonly used in literature, namely the orthogonal distance regression (ODR, implemented in the python scipy.odr package), the Nukers (Tremaine et al. 2002), the maximum likelihood estimator with uniform prior (MLEU), the bivariate correlated errors and intrinsic scatter (BCES, Akritas & Bershady 1996), and the complete maximum likelihood estimator (CMLE, Kay et al. 2012), on realistic mock realisations of PSZ1 sample. In a companion paper associated with the characterisation of the PSZ2 sample (Aguado-Barahona & Ferragamo 2020), we show that although all these five methods produced biased results in the recovered slope because of the high noise levels in our sample, the Nukers and the ODR present the lowest bias. For this reason, we adopted ODR as the reference regression method, and we tested it using simulations with realistic noise levels mimicking those present in our sample. See Appendix B in Aguado-Barahona & Ferragamo (2020) for a detailed description of the other estimators.
Figure 6 shows that after 500 realisations with realistic noise levels, the ODR method retrieves a mean mass bias parameter that is ∼6% larger than the input bias, (1 − B) = 0.8, for the case of a fixed slope (α = 1). We also obtain the same bias of ∼6% when the slope was left as a free parameter. This value was used later to correct for the final results.
 |
Fig. 6. Distribution of the mass bias parameter estimates using the ODR method to fit Eq. (12) with the slope fixed to 1. The vertical dotted lines represent the mean (recovered) value and the simulated (input) value (1 − B) = 0.8 in blue and red, respectively. |
6.2. Mass bias for the ITP and SDSS sub-samples
Figure 7 shows our fit for the ITP sample (left panel) and the SDSS sample (blue line in the right panel). Apparently, we find a different mass bias for the two sub-samples,
 |
Fig. 7.
|
Because the clusters in the two samples were analysed in the same way, this discrepancy cannot be explained by a heterogeneous mass calculation. We ascribe this discrepancy to the different S/N distribution of cluster samples. The median S/N for the ITP sample is 4.9, whereas the SDSS sample median S/N is 5.7. Moreover, if we divide the SDSS sample into two parts, the cosmo (the clusters in the PlCS) and the not cosmo, we find that they have a median S/N 9.4 and 5.2, respectively. The fit performed with these two new sub-samples, shown in the right panel of Fig. 7, yields (1−B) = 0.83 ± 0.11 (red line) and (1−B) = 1.02 ± 0.08 (green line) for the cosmo and not cosmo, respectively.
This evidence led us to investigate the effect of the S/N of clusters on the (1 − B) fits in more detail. We divided the whole catalogue (ITP+SDSS) into four S/N bins with the same number of clusters, performing the Mdyn − MSZ fit in each bin and for the whole sample. Figure 8 shows that the mass bias decreases from lower to higher value of S/N (see the second column of Table 2). This difference suggests that our clusters might be affected (totally or partially) by Eddington bias (hereafter EB, Dutton & Macciò 2014). The statistical noise scatters above the S/N threshold some objects with a mass that is lower than the observational limit, resulting in an over-estimation of these masses.
 |
Fig. 8. Fit of the scaling relation |
Value of the mass bias before and after the Eddington bias correction for the S/N bins.
We corrected for this EB effect by using the curves in van der Burg et al. (2016). These were obtained by constructing a 30.000 deg2 mock SZ catalogue that took the Tinker et al. (2008) halo mass function, the redshift-dependent comoving volume element, and the Planck noise maps properties into account. They reproduced the effect of the noise on the true S/N as a random Gaussian variable added to the true S/N. They showed that the effect of the bias is more severe the lower the threshold, and it becomes extremely strong for S/N ≤ 4.5. Moreover, they found that the effect of the EB also depends on the redshift. It affected the high-redshift clusters more because the halo mass function at a given S/N is steeper. Although these curves were created using the PSZ2 noise maps, they are a good approximation for the PSZ1 as well because they only depend on the mean S/N level and not on the particular noise level on the PSZ2 maps.
Figure 9 shows the 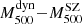 fit for the whole sample (blue line) and for the S/N bins (green, yellow, red, and magenta circles and lines), and after the EB correction, all the (1−B) values are clearly statistically compatible with each other within the 2 − σ level. The corrected values are listed in the last column of Table 2.
fit for the whole sample (blue line) and for the S/N bins (green, yellow, red, and magenta circles and lines), and after the EB correction, all the (1−B) values are clearly statistically compatible with each other within the 2 − σ level. The corrected values are listed in the last column of Table 2.
 |
Fig. 9. Scaling relation |
As shown in van der Burg et al. (2016), the magnitude of the EB depends on redshift. We quantified this by analysing the behaviour of the mass bias parameter as a function of redshift. Table 3 shows that the uncorrected SZ masses lead to different values of (1−B). In particular, the highest redshift bin differs at almost 3 − σ from the lowest bin. On the other hand, the 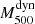 –
–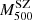 relations after the EB correction show more comparable values of the (1−B): all redshift bins are consistent within the 2 − σ level. Here we note that the bin containing the clusters at the redshift interval [0.11, 0.19] yields the highest (1 − B) value.
relations after the EB correction show more comparable values of the (1−B): all redshift bins are consistent within the 2 − σ level. Here we note that the bin containing the clusters at the redshift interval [0.11, 0.19] yields the highest (1 − B) value.
Value of the mass bias before and after correction for Eddigton bias for the redshift bins.
After the EB correction, the mass bias estimated for the two samples became
which is compatible within the 2 − σ level.
We also investigated the possible dependence of the estimated mass bias on the number of galaxies Ngal used to extract the dynamical masses after correction for EB. To do this, each sub-sample (ITP and SDSS) was sub-divided into two bins with the same number of s, according to the Ngal values. We labelled the bin containing lower (LN) and higher (HN) values Ngal than the median. We repeated our analysis for each of these bins. For the ITP sample, we obtained
whereas the fit for the SDSS sample gave
The bins for LN and HN are compatible within the 2 − σ level for both ITP and SDSS samples. However, when we consider the whole sample, the results for the LN and HN sub-samples differ slightly (at the 2.3 − σ level),
Although the residual effects due to Ngal should be accounted for in our method (Evrard et al. 2008), this result suggests that there might be some marginal residual dependence on Ngal in our velocity and mass estimators.
6.3. Final result for the mass bias
After the EB correction, by fitting the 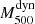 –
–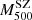 relation for the whole GCs sample and fixing the slope to unity, we obtain
relation for the whole GCs sample and fixing the slope to unity, we obtain
Each of the parameters and related errors shown so far was estimated as the mean and standard deviation of 10000 bootsrap resamples, respectively. However, taking the expected ∼6% bias introduced by the linear regression estimator into account, the corrected value of the mass bias should be
where the first error is the statistical error, and the second error is a systematic error associated with the bias of the ODR method.
The Planck analysis showed that the mass bias could be a function of the cluster mass (Penna-Lima et al. 2017). For this reason, we repeated our fit with the ODR method, but letting the slope free as well. In this case, after correcting for the bias due to the ODR method, we obtain
at the pivot mass 6 × 1014 M⊙. This result, which is compatible within 1 − σ with the result in Eq. (24), does not give indications about a mass dependence for the Mdyn–MSZ relation. Figure 10 shows the two fits of the 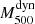 –
–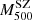 scaling relation, with the slope fixed to 1 (blue line) and with the slope free to vary (red line).
scaling relation, with the slope fixed to 1 (blue line) and with the slope free to vary (red line).
 |
Fig. 10. Scaling relation between |
7. Comparison with other works
The multi-component nature of GCs and multi-wavelength studies allows us to assess the relative bias of mass proxies based on different observables. Here we compare our results on (1 − B) with those obtained by other authors using different mass proxies and methods. The literature about this argument is very rich. We restrict our comparison to some of the recent works. Table 4 and Fig. 11 summarise all values obtained by all the surveys described below.
 |
Fig. 11. Value of the mass bias from previous studies. In blue we show the result from Penna-Lima et al. (2017), using a scaling relation from X-ray observations; in green we plot the mass bias from Mdyn–MSZ scaling relations, and in red we show those from weak-lensing studies. All these values are listed in Table 4. The grey shaded region represents the mass bias values that reconciles the tension between CMB and SZ number counts from Penna-Lima et al. (2017). The green star represents the mass bias value we found here. |
7.1. Mass bias from Planck Collaboration analysis
The Planck Collaboration calibrated the PSZ1 masses using X-ray observations of nearby relaxed clusters. For this reason, the mass bias they found is homologous to the hydrostatic equilibrium mass bias, 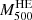 . To find the value of the mass bias
. To find the value of the mass bias 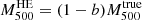 , they compared the Y500–M500 relation derived using data from seven simulations including different types of input physics (Munari et al. 2013; Yang et al. 2010; Sehgal et al. 2010; Komatsu et al. 2011; Battaglia et al. 2012; Hook et al. 2004; Sembolini et al. 2013), with the relation obtained by comparing Y500 and the hydrostatic mass (Penna-Lima et al. 2017). The main conclusion is that the dependence of bias on mass,
, they compared the Y500–M500 relation derived using data from seven simulations including different types of input physics (Munari et al. 2013; Yang et al. 2010; Sehgal et al. 2010; Komatsu et al. 2011; Battaglia et al. 2012; Hook et al. 2004; Sembolini et al. 2013), with the relation obtained by comparing Y500 and the hydrostatic mass (Penna-Lima et al. 2017). The main conclusion is that the dependence of bias on mass, 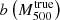 , is strong, which also translates into different slopes for the observed and true Y500–M500 relations. Because of this mass dependence, the Planck Collaboration selected a representative value for (1 − b) as the median value obtained for a mass pivot point M500 = 6 × 1014 M⊙ (Penna-Lima et al. 2017),
, is strong, which also translates into different slopes for the observed and true Y500–M500 relations. Because of this mass dependence, the Planck Collaboration selected a representative value for (1 − b) as the median value obtained for a mass pivot point M500 = 6 × 1014 M⊙ (Penna-Lima et al. 2017),
The reported confidence interval [0.7, 1] accounts for the scatter of the different simulations and measurements.
7.2. Bias from dynamical mass estimates
Several groups have studied the relation Mdyn–MSZ using SZ data from the Planck PSZ2 catalogue (Amodeo et al. 2017), the Atacama Cosmology Telescope (ACT) (Sifón et al. 2016), the South Pole Telescope (SPT) (Ruel et al. 2014), and spectroscopic data from the Gemini Multi-Object Spectrograph (GMOS), installed at the Gemini telescopes. Although these studies also compared the SZ and dynamical masses, each shows important differences in the method with respect to our analysis.
7.2.1. South Pole Telescope cluster sample
The first of these analyses was published by Ruel et al. (2014). Their analysis used 43 SZ-selected GCs within the SPT catalogues (Vanderlinde et al. 2010; Williamson et al. 2011; Reichardt et al. 2013). The sample consists of massive (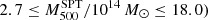 s at z ≥ 0.3 with more than 15 members. The most important differences with respect to our study are the scaling relation between observables and masses. From the SZ point of view,
s at z ≥ 0.3 with more than 15 members. The most important differences with respect to our study are the scaling relation between observables and masses. From the SZ point of view, 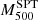 were calculated using the Y–M scaling in Reichardt et al. (2013). This relation presents a slightly fainter slope than the slope from Penna-Lima et al. (2017). This might result in some differences in the mass estimate, especially for the most massive clusters. From the dynamical mass point of view, the SPT group used the Saro et al. (2013) relation, which, as shown in Sifón et al. (2016), tends to overestimate the dynamical masses (especially for massive clusters) when compared to the Miyatake et al. (2019) relation we used here. Another difference is that following the prescription in Beers et al. (1990), they used the biweight as the velocity dispersion estimator applied on cluster members selected by an iterative 3 − σ clipping around the mean velocity. In contrast to what we did here, Ruel and collaborators decided to scale the SZ masses from
were calculated using the Y–M scaling in Reichardt et al. (2013). This relation presents a slightly fainter slope than the slope from Penna-Lima et al. (2017). This might result in some differences in the mass estimate, especially for the most massive clusters. From the dynamical mass point of view, the SPT group used the Saro et al. (2013) relation, which, as shown in Sifón et al. (2016), tends to overestimate the dynamical masses (especially for massive clusters) when compared to the Miyatake et al. (2019) relation we used here. Another difference is that following the prescription in Beers et al. (1990), they used the biweight as the velocity dispersion estimator applied on cluster members selected by an iterative 3 − σ clipping around the mean velocity. In contrast to what we did here, Ruel and collaborators decided to scale the SZ masses from 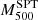 to
to 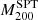 . However, in order to perform this transformation, they also assumed the same NFW density profile and the da Silva et al. (2004) mass-concentration relation as in our method. Finally, Ruel et al. (2014) found that
. However, in order to perform this transformation, they also assumed the same NFW density profile and the da Silva et al. (2004) mass-concentration relation as in our method. Finally, Ruel et al. (2014) found that
which is compatible with our result, except for its large error.
We would like to remark that we report the mass bias (Eq. (16) in Ruel et al. 2014) in Eq. (27), according to our definition of (1 − B) and after propagating the uncertainties.
7.2.2. Atacama Cosmology Telescope cluster sample
The second scaling relation, performed using dynamical masses, was obtained by Sifón et al. (2016). For their cosmological analysis, they used a subsample of ACT clusters composed of 21 objects detected with an S/N > 5.1 at redshifts 0.2 ≤ z ≤ 1.06 in a mass interval 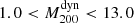 (in units of 1014 M⊙), which constitute their cosmological sample. The 21 GCs were observed spectroscopically using two different spectrographs: GMOS (Hoekstra et al. 2015) at the Gemini-South telescope (Chile), and RSS (Planck Collaboration XVI 2014) at the SALT telescope (South Africa). They obtained a median number of observed members of Ngal55. In this case, there are fewer differences between our method and the method of the ACT group. They used the same scaling relations Y500–M500 and σ200–M200, the pressure profile by Arnaud et al. (2010), and the AGN fit by Miyatake et al. (2019). The main difference is on the mass-concentration relation that was used to scale
(in units of 1014 M⊙), which constitute their cosmological sample. The 21 GCs were observed spectroscopically using two different spectrographs: GMOS (Hoekstra et al. 2015) at the Gemini-South telescope (Chile), and RSS (Planck Collaboration XVI 2014) at the SALT telescope (South Africa). They obtained a median number of observed members of Ngal55. In this case, there are fewer differences between our method and the method of the ACT group. They used the same scaling relations Y500–M500 and σ200–M200, the pressure profile by Arnaud et al. (2010), and the AGN fit by Miyatake et al. (2019). The main difference is on the mass-concentration relation that was used to scale 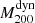 to
to 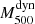 . While we used the da Silva et al. (2004) relation, they considered the Duffy et al. (2008) relation. In addition to the member selection algorithm, they also used the biweight as a velocity dispersion estimator. It is also important to remark that Sifón et al. (2016) applied an aperture correction to the velocity dispersion estimate and also took the Eddington bias into account when they corrected the Y500 estimation, as explained in Hartley et al. (2008). In this case, they did not fit for the relation Mdyn to MSZ, but they defined the mass bias as the ratio of the mean SZ and the mean dynamical mass. They obtained
. While we used the da Silva et al. (2004) relation, they considered the Duffy et al. (2008) relation. In addition to the member selection algorithm, they also used the biweight as a velocity dispersion estimator. It is also important to remark that Sifón et al. (2016) applied an aperture correction to the velocity dispersion estimate and also took the Eddington bias into account when they corrected the Y500 estimation, as explained in Hartley et al. (2008). In this case, they did not fit for the relation Mdyn to MSZ, but they defined the mass bias as the ratio of the mean SZ and the mean dynamical mass. They obtained
where βdyn is the bias of dynamical masses, defined as ⟨Mdyn⟩ = βdyn⟨Mtrue⟩. Our result (Eq. (24)) and that obtained by Sifón et al. (2016) are compatible within 1.7 − σ.
7.2.3. Planck PSZ2 sample
The most recent published scaling relation was obtained by Amodeo et al. (2017) using 17 low-redshift (z < 0.5) clusters from the PSZ2 catalogue in the mass interval 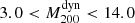 (units of 1014 M⊙) and with a median Ngal = 20. In this case, the SZ masses were estimated following the same prescription as we considered here. However, they selected a different velocity dispersion-mass relation. This choice was dictated by the method they used to determine the bias. Similarly to the Planck Collaboration, they decided not to compare the masses themselves, but to do the comparison with the σ200–M200 scaling relation normalisation parameter by assuming a self-similar slope (α = 1/3). To do this, they rescaled the Planck
(units of 1014 M⊙) and with a median Ngal = 20. In this case, the SZ masses were estimated following the same prescription as we considered here. However, they selected a different velocity dispersion-mass relation. This choice was dictated by the method they used to determine the bias. Similarly to the Planck Collaboration, they decided not to compare the masses themselves, but to do the comparison with the σ200–M200 scaling relation normalisation parameter by assuming a self-similar slope (α = 1/3). To do this, they rescaled the Planck 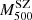 to
to 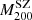 by assuming the mass-concentration relation by Duffy et al. (2008), and fitted the
by assuming the mass-concentration relation by Duffy et al. (2008), and fitted the 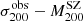 relation with a fixed slope α = 1/3. They obtained the normalisation parameter A = 1158 ± 61 in this way. They compared this result with the Eddington (1913) relation, which was constrained with an N-body DM-only simulation with a normalisation parameter ADM = 1082.9 ± 4.0, from which they obtained
relation with a fixed slope α = 1/3. They obtained the normalisation parameter A = 1158 ± 61 in this way. They compared this result with the Eddington (1913) relation, which was constrained with an N-body DM-only simulation with a normalisation parameter ADM = 1082.9 ± 4.0, from which they obtained
where bv, fEB, and fcorr are the velocity bias, the Eddington bias correction, and the correction for the correlated scatter between velocity dispersion and Planck masses, respectively. The velocity bias is defined as bv = Agal/ADM, which arises from assuming that the DM andhe galaxies of a cluster can have different velocities. Miyatake et al. (2019) used a hydrodynamical simulation and fitted the σ–M relation considering both the DM particles and galaxies. They obtained two different values for the normalisation parameters, which leads to a velocity bias bv = 1.08. In this paper, we accounted for the velocity bias using the AGN fit by Miyatake et al. (2019). Instead, the Eddington (1913) fit was made with DM-only simulations. The Eddington bias correction in this case is a global correction quantified in fEB = 0.84 ± 0.027 and the correlated scatter correction arises from the Stanek et al. (2010) study on the covariance between observables, which is estimated using the Millennium Gas Simulation (Ferragamo et al. 2020). Stanek et al. (2010) found a significant correlation between velocity dispersion and SZ signal due to non-gravitational processes in GCs. Amodeo et al. (2017) quantified this bias as fcorr = 1.01.
Comparing our result ((1−B) = 0.83 ± 0.07 ± 0.02) with Eq. (29), we see that they are consistent at ∼1.3 − σ.
7.3. Weak-lensing mass bias
Several research groups have studied the SZ mass bias, assuming the weak-lensing (WL) mass as the reference true mass. Here we describe seven of them.
7.3.1. WtG project
In 2014, the group of the Weighing the Giants (WtG) project studied the relation of the 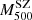 and the
and the 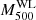 using a sample of 38 GCs in common with the PSZ1 catalogue (von der Linden et al. 2014). For a complete description of the WL mass estimate and for the GCs catalogue they used to constrain the scaling relation, see Applegate et al. (2014). von der Linden et al. (2014) found through a bootstrap realisation of the unweighted mean of the ratio between WL and SZ masses the following value:
using a sample of 38 GCs in common with the PSZ1 catalogue (von der Linden et al. 2014). For a complete description of the WL mass estimate and for the GCs catalogue they used to constrain the scaling relation, see Applegate et al. (2014). von der Linden et al. (2014) found through a bootstrap realisation of the unweighted mean of the ratio between WL and SZ masses the following value:
This result is compatible at 1.25 − σ with our estimate of the mass bias.
A sub-sample of 22 GCs of the WtG catalogue is part of the PSZ1 PlCS. Repeating the analysis with this sub-sample alone, they obtained
This result is slightly smaller than the previous one, but they are perfectly compatible with each other. This value was used by the Planck Collaboration in its 2015 cosmological analysis based on the PSZ2 catalogue as one of the priors on the value of the mass bias. The WtG group also performed the fit by letting the slope of the power law vary freely. By using the Bayesian linear regression method developed by Kay et al. (2012), they found
and
for the whole and the cosmological sample, respectively. Both results are compatible within the errors with our fit in Eq. (25).
7.3.2. Canadian Cluster Comparison Project
Hilton et al. (2018) presented the comparison between the WL masses, estimated by the Canadian Cluster Comparison Project (CCCP), and the masses from the PSZ1 catalogue of 37 GCs, 20 of them with S/N ≥ 7. Through a linear fit, they found
for the whole sample of 37 clusters and for the 20 with S/N ≥ 7, respectively. These two results are perfectly compatible with our estimate of (1−b).
During the comparison of their results with those of WtG, Hilton et al. (2018) fitted a power-law function to investigate whether the bias depended on the mass in their data as well. Using the entire sample, they found
The compatibility between the slope obtained by von der Linden et al. (2014), Hilton et al. (2018) and this paper supports the conclusion by von der Linden et al. (2014) that the bias of Planck masses might depend on the cluster mass.
7.3.3. Local Cluster Substructure Survey
Smith et al. (2016) analysed the mass bias with a sample of 44 clusters in common with the Local Cluster Substructure Survey (LoCuSS) and the PSZ2 catalogue. They obtained
The LoCuSS sample consists of clusters at redshift 0.15 ≤ z ≤ 0.3 with WL masses, estimated in Navarro et al. (1997), between 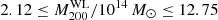 . In this case, the mass bias is defined as the weighted mean of the logarithmic ratio of SZ and WL masses, as
. In this case, the mass bias is defined as the weighted mean of the logarithmic ratio of SZ and WL masses, as
with weights defined by
This LoCuSS measurement (0.95 ± 0.04) is higher than our value of (1−B). Because no Eddington bias correction is cited in Smith et al. (2016) or in Navarro et al. (1997), we decided to repeat the fit by limiting our sample to the clusters within the range 0.15 ≤ z ≤ 0.3. As a result, we obtained (1−B) = 1.17 ± 0.11. However, this result might be biased by the clusters within the 0.11 ≤ z < 0.19 (see Table 3 and the discussion in Sect. 6).
7.3.4. Canada-France-Hawaii Telescope Stripe 82 Survey
The sample used by Battaglia et al. (2016) to determine the mass bias consists of 19 GCs from the ACT equatorial sample (Hartley et al. 2008) observed during the Canada-France-Hawaii Telescope Stripe 82 Survey (CS82). They divided their sample into two S/N bins. The first contains nine clusters with S/N > 5, 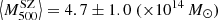 , and the second consists of ten clusters within the range 4 < S/N < 5, with
, and the second consists of ten clusters within the range 4 < S/N < 5, with 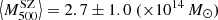 . The mass bias they found, defined as the ratio of the mean SZ and WL masses, is
. The mass bias they found, defined as the ratio of the mean SZ and WL masses, is
For a detailed description of the WL mass estimation, see Battaglia et al. (2016) and the references therein, and for SZ mass estimates, see Hartley et al. (2008). It is important to remark that the ACT SZ masses are corrected for Eddington bias as explained in Hartley et al. (2008). Furthermore, Battaglia et al. (2016) estimated that by comparing 31 clusters in common between ACT and Planck, the corrected ACT masses are lower by 0.89 times than those of Planck on average. These results are clearly compatible with our estimate of the bias.
7.3.5. PSZ2LenS
Sereno et al. (2017) used 32 clusters from the PSZ2LenS sample with a published SZ signal in Planck catalogues to estimate the (1−b) parameter. The PSZ2LenS sample consists of 35 GCs detected by Planck and within the sky coverage of the Canada France Hawaii Telescope Lensing Survey (CFHTLenS, Hasselfield et al. 2013) and the Red Cluster Sequence Lensing Survey (RCSLenS, Heymans et al. 2012). The PSZ2Lens clusters lie in a wide mass range, 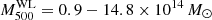 . SZ masses are taken from Planck catalogues (Planck Collaboration XXIX 2014; Planck Collaboration XXVII 2016), and were therefore calculated as in this paper. For a detailed description of the WL analysis, see Sereno et al. (2017) and references therein. The PSZ2LenS research group, after assuming the Eddington bias correction from Battaglia et al. (2016) and Sereno & Ettori (2015), found
. SZ masses are taken from Planck catalogues (Planck Collaboration XXIX 2014; Planck Collaboration XXVII 2016), and were therefore calculated as in this paper. For a detailed description of the WL analysis, see Sereno et al. (2017) and references therein. The PSZ2LenS research group, after assuming the Eddington bias correction from Battaglia et al. (2016) and Sereno & Ettori (2015), found
This value is statistically consistent with our result. They also used a sub-sample of 15 PSZ2LenS clusters within the Planck cosmological sample, finding (1−b) = 0.67 ± 0.09. This result is lower but still compatible with our result at 1.2 − σ.
7.3.6. Cluster Lensing And Supernova survey with Hubble
The WL masses of 21 GCs from the Cluster Lensing And Supernova survey with Hubble (CLASH, Postman et al. 2012)) were used by Okabe & Smith (2016) to compare with the respective SZ masses from Planck catalogues. They performed a Bayesian analysis to constrain the mass bias (1−b). After the correction of MSZ for Eddington bias from Battaglia et al. (2016), they found
which is fully compatible with our result.
7.3.7. Hyper Suprime-Cam Subaru Strategic Program
The Hyper Suprime-Cam Subaru Strategic Program (HSC-SSP, Aihara et al. 2018b,a) group published two studies for which they compared their WL masses with SZ masses from Planck PSZ2 and ACTPol (Atacama Cosmology Telescope Polarimeter experiment). In the first study, Mantz et al. (2010) used five clusters from the HSC-SSP first-year catalogue (Planck Collaboration XXVII 2016) in common with the PSZ2 catalogue. They chose the mean 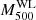 , defined as the weighted stack of the WL signal of these five clusters. The mean SZ mass is the weighted mean of the masses retrieved from the PSZ2 corrected for Eddington bias using the prescription given by Battaglia et al. (2016). The weight for the WL stack and for the SZ mean is the same and depends on the errors on the galaxy shape measurement for each cluster. The ratio of the mean WL and SZ mass is the bias
, defined as the weighted stack of the WL signal of these five clusters. The mean SZ mass is the weighted mean of the masses retrieved from the PSZ2 corrected for Eddington bias using the prescription given by Battaglia et al. (2016). The weight for the WL stack and for the SZ mean is the same and depends on the errors on the galaxy shape measurement for each cluster. The ratio of the mean WL and SZ mass is the bias
which is compatible with our result.
In a second study, Medezinski et al. (2018) used eight GCs in common with the ACTPol (Hildebrandt et al. 2016) sample. As in the previous analysis, the mean WL mass is the result of the weighted stack of all the clusters taken into account, whereas 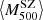 is the weighted mean of the corrected SZ masses from the ACTPol catalogue. The mass bias for this sample is
is the weighted mean of the corrected SZ masses from the ACTPol catalogue. The mass bias for this sample is
In this case, the value of the mass bias is also compatible with the value obtained in our analysis.
8. Conclusions
This is the third (and last) paper in a series describing the results of the ITP13 observational program, dedicated to the characterisation of the PSZ1 sources in the northern sky without known optical counterparts at the time the catalogue was published. Here we presented for the first time the velocity dispersion and mass estimates for 58 clusters in the PSZ1-North sample and for 35 clusters that are not associated with the PSZ1 sample.
Using SDSS archival data, we also studied 212 clusters with known counterparts, and we also extracted the velocity dispersion and mass estimation, using the same method as for the ITP sample. This paper presents dynamical masses for 270 s within the PSZ1-North sample.
A sub-sample of 207 clusters was used to explore the mass bias between the dynamical mass and the SZ mass estimates. Galaxy cluster number counts are extremely sensitive to Ωm and σ8 through the mass function. However, the cosmological analyses performed by the Planck Collaboration result in a tension between the constraints from the primordial CMB power spectrum and those derived from the cluster number counts (Penna-Lima et al. 2017; Planck Collaboration XXIV 2016). The main cause of this tension was originally ascribed to the value of the mass bias. The Planck Collaboration, through the joint analysis of SZ, X-ray data, and simulations, constrained this parameter to the value of 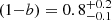 . In this paper, we used the largest sub-sample of PSZ1 clusters (207) observed both in microwave and optical wavelengths to date, and we obtained (1 − B) = 0.83 ± 0.07 (stat) ± 0.02 (syst). This measurement presents the lowest statistical error obtained so far using dynamical masses as reference, and it is statistically compatible with the Planck one.
. In this paper, we used the largest sub-sample of PSZ1 clusters (207) observed both in microwave and optical wavelengths to date, and we obtained (1 − B) = 0.83 ± 0.07 (stat) ± 0.02 (syst). This measurement presents the lowest statistical error obtained so far using dynamical masses as reference, and it is statistically compatible with the Planck one.
We have also compared our results with those in the literature. We find that although it is slightly higher than average, our measurement is compatible within 1 − σ in most cases, both with those obtained from dynamical mass analyses and those obtained from comparison with weak-lensing masses. The final mass bias from this study, as well as the mean value of all other previous results in the literature, is still higher than the value that is required to reconcile the tension between CMB and SZ number counts (Penna-Lima et al. 2017; Planck Collaboration XXIV 2016).
Acknowledgments
We thank R. van der Burg and J.-B. Melin for useful comments. This article is based on observations made with the Gran Telescopio Canarias operated by the Instituto de Astrofisica de Canarias, the Isaac Newton Telescope, and the William Herschel Telescope operated by the Isaac Newton Group of Telescopes, and the Italian Telescopio Nazionale Galileo operated by the Fundacion Galileo Galilei of the INAF (Istituto Nazionale di Astrofisica). All these facilities are located at the Spanish Roque de los Muchachos Observatory of the Instituto de Astrofisica de Canarias on the island of La Palma. Part of this research has been carried out with telescope time awarded by the CCI International Time Programme at the Canary Islands Observatories (programmes ITP13B-15A). Funding for the Sloan Digital Sky Survey (SDSS) has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Aeronautics and Space Administration, the National Science Foundation, the US Department of Energy, the Japanese Monbukagakusho, and the Max Planck Society. This work has been partially funded by the Spanish Ministry of Science and Innovation (MICINN) under the projects ESP2013-48362-C2-1-P, AYA2014-60438-P and AYA2017-84185-P. AS and RB acknowledge financial support from MICINN under the Severo Ochoa Programs SEV-2011-0187 and SEV-2015-0548. HL is supported by ETAg grants PUT1627 and PRG1006 and by EU through the ERDF CoE grant TK133.
References
- Aguado-Barahona, A., & Ferragamo, A. 2020, A&A, submitted [Google Scholar]
- Aihara, H., Allende Prieto, C., An, D., et al. 2011, ApJS, 193, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Aihara, H., Arimoto, N., Armstrong, R., et al. 2018a, PASJ, 70, S4 [NASA ADS] [Google Scholar]
- Aihara, H., Armstrong, R., Bickerton, S., et al. 2018b, PASJ, 70, S8 [NASA ADS] [Google Scholar]
- Akritas, M. G., & Bershady, M. A. 1996, ApJ, 470, 706 [Google Scholar]
- Allen, S. W., Evrard, A. E., & Mantz, A. B. 2011, ARA&A, 49, 409 [Google Scholar]
- Amodeo, S., Mei, S., Stanford, S. A., et al. 2017, ApJ, 844, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Applegate, D. E., von der Linden, A., Kelly, P. L., et al. 2014, MNRAS, 439, 48 [Google Scholar]
- Arnaud, M., Pratt, G. W., Piffaretti, R., et al. 2010, A&A, 517, A92 [CrossRef] [EDP Sciences] [Google Scholar]
- Barrena, R., & Ferragamo, A. 2020, A&A, 638, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barrena, R., Streblyanska, A., Ferragamo, A., et al. 2018, A&A, 616, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Battaglia, N., Bond, J. R., Pfrommer, C., & Sievers, J. L. 2012, ApJ, 758, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Battaglia, N., Leauthaud, A., Miyatake, H., et al. 2016, JCAP, 2016, 013 [NASA ADS] [CrossRef] [Google Scholar]
- Beers, T. C., Flynn, K., & Gebhardt, K. 1990, AJ, 100, 32 [Google Scholar]
- Burgh, E. B., Nordsieck, K. H., & Kobulnicky, H. A. 2003, in Instrument Design and Performance for Optical/Infrared Ground-based Telescopes, eds. M. Iye, & A. F. M. Moorwood, SPIE Conf. Ser., 4841, 1463 [NASA ADS] [CrossRef] [Google Scholar]
- da Silva, A. C., Kay, S. T., Liddle, A. R., & Thomas, P. A. 2004, MNRAS, 348, 1401 [Google Scholar]
- Duffy, A. R., Schaye, J., Kay, S. T., & Dalla Vecchia, C. 2008, MNRAS, 390, L64 [Google Scholar]
- Dutton, A. A., & Macciò, A. V. 2014, MNRAS, 441, 3359 [Google Scholar]
- Eddington, A. S. 1913, MNRAS, 73, 359 [Google Scholar]
- Evrard, A. E., Bialek, J., Busha, M., et al. 2008, ApJ, 672, 122 [Google Scholar]
- Ferragamo, A., Rubiño-Martín, J. A., Betancort-Rijo, J., et al. 2020, A&A, 641, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartley, W. G., Gazzola, L., Pearce, F. R., Kay, S. T., & Thomas, P. A. 2008, MNRAS, 386, 2015 [NASA ADS] [CrossRef] [Google Scholar]
- Hasselfield, M., Hilton, M., Marriage, T. A., et al. 2013, JCAP, 2013, 008 [Google Scholar]
- Heymans, C., Van Waerbeke, L., Miller, L., et al. 2012, MNRAS, 427, 146 [Google Scholar]
- Hildebrandt, H., Choi, A., Heymans, C., et al. 2016, MNRAS, 463, 635 [Google Scholar]
- Hilton, M., Hasselfield, M., Sifón, C., et al. 2018, ApJS, 235, 20 [Google Scholar]
- Hoekstra, H., Herbonnet, R., Muzzin, A., et al. 2015, MNRAS, 449, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Hook, I. M., Jørgensen, I., Allington-Smith, J. R., et al. 2004, PASP, 116, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Kay, S. T., Peel, M. W., Short, C. J., et al. 2012, MNRAS, 422, 1999 [NASA ADS] [CrossRef] [Google Scholar]
- Kelly, B. C. 2007, ApJ, 665, 1489 [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [Google Scholar]
- Krause, E., Pierpaoli, E., Dolag, K., & Borgani, S. 2012, MNRAS, 419, 1766 [NASA ADS] [CrossRef] [Google Scholar]
- Łokas, E. L., & Mamon, G. A. 2001, MNRAS, 321, 155 [CrossRef] [Google Scholar]
- Mamon, G. A., Biviano, A., & Murante, G. 2010, A&A, 520, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mantz, A., Allen, S. W., Rapetti, D., & Ebeling, H. 2010, MNRAS, 406, 1759 [NASA ADS] [Google Scholar]
- Medezinski, E., Battaglia, N., Umetsu, K., et al. 2018, PASJ, 70, S28 [NASA ADS] [Google Scholar]
- Miyatake, H., Battaglia, N., Hilton, M., et al. 2019, ApJ, 875, 63 [Google Scholar]
- Munari, E., Biviano, A., Borgani, S., Murante, G., & Fabjan, D. 2013, MNRAS, 430, 2638 [Google Scholar]
- Nagai, D. 2006, ApJ, 650, 538 [Google Scholar]
- Navarro, J. F., Frenk, C. S., & White, S. D. M. 1997, ApJ, 490, 493 [Google Scholar]
- Okabe, N., & Smith, G. P. 2016, MNRAS, 461, 3794 [Google Scholar]
- Penna-Lima, M., Bartlett, J. G., Rozo, E., et al. 2017, A&A, 604, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2014, A&A, 571, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIV. 2016, A&A, 594, A24 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXVII. 2016, A&A, 594, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXIX. 2014, A&A, 571, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXXII. 2015, A&A, 581, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXXVI. 2016, A&A, 586, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Postman, M., Coe, D., Benítez, N., et al. 2012, ApJS, 199, 25 [Google Scholar]
- Pratt, G. W., Arnaud, M., Biviano, A., et al. 2019, Space Sci. Rev., 215, 25 [Google Scholar]
- Reichardt, C. L., Stalder, B., Bleem, L. E., et al. 2013, ApJ, 763, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Ruel, J., Bazin, G., Bayliss, M., et al. 2014, ApJ, 792, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Saro, A., Mohr, J. J., Bazin, G., & Dolag, K. 2013, ApJ, 772, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Sehgal, N., Bode, P., Das, S., et al. 2010, ApJ, 709, 920 [NASA ADS] [CrossRef] [Google Scholar]
- Sembolini, F., Yepes, G., De Petris, M., et al. 2013, MNRAS, 434, 2718 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M., & Ettori, S. 2015, MNRAS, 450, 3633 [NASA ADS] [CrossRef] [Google Scholar]
- Sereno, M., Covone, G., Izzo, L., et al. 2017, MNRAS, 472, 1946 [Google Scholar]
- Sifón, C., Battaglia, N., Hasselfield, M., et al. 2016, MNRAS, 461, 248 [CrossRef] [Google Scholar]
- Smith, G. P., Mazzotta, P., Okabe, N., et al. 2016, MNRAS, 456, L74 [Google Scholar]
- Springel, V. 2005, MNRAS, 364, 1105 [Google Scholar]
- Stanek, R., Rasia, E., Evrard, A. E., Pearce, F., & Gazzola, L. 2010, ApJ, 715, 1508 [NASA ADS] [CrossRef] [Google Scholar]
- Sunyaev, R. A., & Zeldovich, Y. B. 1972, Comm. Astrophys. Space Phys., 4, 173 [Google Scholar]
- Tinker, J., Kravtsov, A. V., Klypin, A., et al. 2008, ApJ, 688, 709 [Google Scholar]
- Tremaine, S., Gebhardt, K., Bender, R., et al. 2002, ApJ, 574, 740 [NASA ADS] [CrossRef] [Google Scholar]
- van der Burg, R. F. J., Aussel, H., Pratt, G. W., et al. 2016, A&A, 587, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vanderlinde, K., Crawford, T. M., de Haan, T., et al. 2010, ApJ, 722, 1180 [CrossRef] [Google Scholar]
- Vikhlinin, A., Burenin, R. A., Ebeling, H., et al. 2009, ApJ, 692, 1033 [Google Scholar]
- von der Linden, A., Mantz, A., Allen, S. W., et al. 2014, MNRAS, 443, 1973 [NASA ADS] [CrossRef] [Google Scholar]
- Wainer, H., & Thissen, D. 1976, Psychometrika, 41, 9 [CrossRef] [Google Scholar]
- Williamson, R., Benson, B. A., High, F. W., et al. 2011, ApJ, 738, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H. Y. K., Bhattacharya, S., & Ricker, P. M. 2010, ApJ, 725, 1124 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Tables
In this appendix we present all the tables described in Sec. 2. The optical coordinates, the distance from the Planck ponting, the redshift, and the number of galaxy members (col. 4-8) were previously given in Planck Collaboration Int. XXXVI (2016) and Barrena et al. (2018), Barrena & Ferragamo (2020). We report the velocity dispersion and the dynamical mass of these GCs (col.9-10) for the first time. All these tables are only available at the CDS.
All Tables
Value of the mass bias before and after the Eddington bias correction for the S/N bins.
Value of the mass bias before and after correction for Eddigton bias for the redshift bins.
All Figures
 |
Fig. 1. Sky distribution of all the PSZ1 clusters studied in this paper. The figure uses a Mollweide projection in Galactic coordinates. The Galactic plane is horizontal and centred at longitude zero. Red circles and blue triangles represent ITP (Sect. 2.1) and SDSS (Sect. 2.2) clusters, respectively, and the symbol size is proportional to the cluster mass. The shaded grey area represents the union mask used to produce the CMB map in the first Planck data release (downloaded from the Planck Legacy Archive). This mask excludes 27% of the sky, mostly in the region of the Galactic plane, the Magellanic Clouds, and point sources. |
| In the text | |
 |
Fig. 2. Two examples of the velocity distribution of cluster members: PSZ1 G103.94+25.81 (top) and PSZ1 G123.55–10.34 (bottom). Both clusters have been observed within the ITP program. The histograms contain 17 and 30 members, respectively. In both cases, the red line corresponds to a Gaussian distribution centred in the mean cluster velocity, and with σ equal to the estimated velocity dispersion σv. |
| In the text | |
 |
Fig. 3. Projected phase-space and velocity histogram of the stack of all ITP clusters members (top) and all SDSS cluster members (bottom). In both cases, velocities are normalised to the cluster velocity dispersion. The dashed black lines indicate the 2.5 − σ clipping, and the dotted blue lines show the same clipping, but take the velocity dispersion radial profile as shown in Łokas & Mamon (2001) into account. The red line in the right panel represents a Gaussian fit of the stacked velocity histogram normalised to the total number of members. |
| In the text | |
 |
Fig. 4. Number of ITP clusters as a function of redshift (left panel) and the S/N of the SZ detection (right panel) we used, normalised to 88, which is the total number of ITP-validated clusters (for details, see Barrena & Ferragamo 2020). |
| In the text | |
 |
Fig. 5. Number of SDSS clusters as a function of redshift (left panel) and SZ S/N (right panel) we used, normalised to the total number of PSZ1 sources within the SDSS footprint (green). Red histograms correspond to the subsample of SDSS clusters within the Planck cosmological sample. |
| In the text | |
 |
Fig. 6. Distribution of the mass bias parameter estimates using the ODR method to fit Eq. (12) with the slope fixed to 1. The vertical dotted lines represent the mean (recovered) value and the simulated (input) value (1 − B) = 0.8 in blue and red, respectively. |
| In the text | |
 |
Fig. 7.
|
| In the text | |
 |
Fig. 8. Fit of the scaling relation |
| In the text | |
 |
Fig. 9. Scaling relation |
| In the text | |
 |
Fig. 10. Scaling relation between |
| In the text | |
 |
Fig. 11. Value of the mass bias from previous studies. In blue we show the result from Penna-Lima et al. (2017), using a scaling relation from X-ray observations; in green we plot the mass bias from Mdyn–MSZ scaling relations, and in red we show those from weak-lensing studies. All these values are listed in Table 4. The grey shaded region represents the mass bias values that reconciles the tension between CMB and SZ number counts from Penna-Lima et al. (2017). The green star represents the mass bias value we found here. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} \frac{\sigma }{\mathrm{km\,s^{-1}}} = A\left[\frac{h(z)\ M_{200}}{10^{15}\,{M}_{\odot }}\right]^{\alpha }, \end{aligned} $$](/articles/aa/full_html/2021/11/aa40382-21/aa40382-21-eq2.gif)
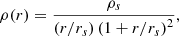
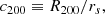
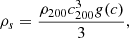
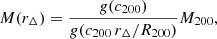
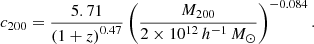
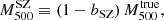
![$$ \begin{aligned} E^{-2/3}(z) \left[\frac{D_{A}^2\ Y_{500}^\mathrm{SZ}}{10^{-4}\ \mathrm {Mpc}^2} \right] = 10^{-0.19 \pm 0.02} \left[ \frac{M_{500}^\mathrm{SZ}}{6 \times 10^{14}\,M_{\odot }} \right] ^{1.79 \pm 0.08}, \end{aligned} $$](/articles/aa/full_html/2021/11/aa40382-21/aa40382-21-eq16.gif)
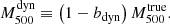
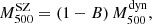
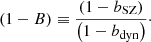
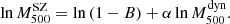
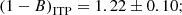
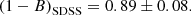
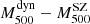
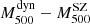
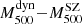
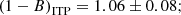
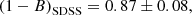
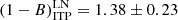
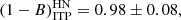
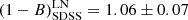
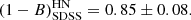
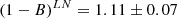
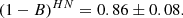
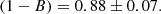
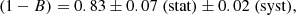
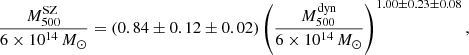
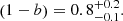
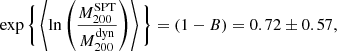
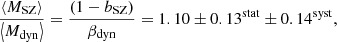
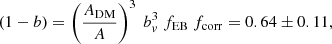
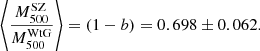
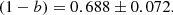
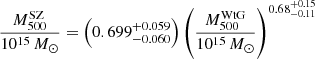
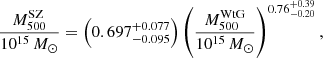
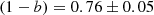
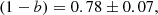
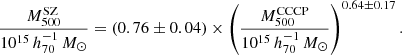
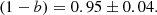
![$$ \begin{aligned} \left( 1-b \right) = \mathrm{exp} \left[ \frac{\sum _{i=1}^{n}\ \omega _i\ \mathrm{ln}\left( \frac{{ M}_{\mathrm{SZ},i}}{{ M}_{\mathrm{WL},i}} \right)}{\sum _{i=1}^{n}\ \omega _i} \right], \end{aligned} $$](/articles/aa/full_html/2021/11/aa40382-21/aa40382-21-eq77.gif)
![$$ \begin{aligned} \omega _i = \left[ \left( \frac{\delta M_{\mathrm{SZ},i}}{\langle \delta M_{\rm SZ} \rangle }\right)^2 + \left( \frac{\delta M_{\rm WL}}{\langle \delta M_{\mathrm{WL},i}\rangle } \right)^2 \right]^{-1}. \end{aligned} $$](/articles/aa/full_html/2021/11/aa40382-21/aa40382-21-eq78.gif)