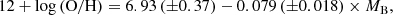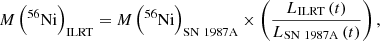EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 654 (October 2021) A&A, 654 (2021) A157 Full HTML
Free Access
Issue
A&A
Volume 654, October 2021
Article Number A157
Number of page(s) 30
Section Stellar structure and evolution
DOI https://doi.org/10.1051/0004-6361/202141078
Published online 27 October 2021

© ESO 2021

1. Introduction

Modern surveys are discovering new types of stellar transients. Some events show intermediate luminosities lying between classical novae and core-collapse (CC) supernovae (SNe), and are collectively named ‘gap transients’ (−10 mag < MV < −15 mag; e.g., Kulkarni et al. 2009; Kasliwal 2012; Pastorello & Fraser 2019) or even intermediate-luminosity optical transients (e.g., Berger et al. 2009a; Soker & Kashi 2012; Soker 2020; Soker & Kaplan 2021).

A fraction of these transients are called ‘SN impostors’, as they mimic some observational properties of H-rich interacting SNe, but deep late-time imaging reveals that the progenitor stars survived (see, e.g., Van Dyk et al. 2000). Their typical peak absolute magnitudes are between −13 and −15 mag, and their spectra show narrow emission lines similar to Type IIn SNe (Schlegel 1990; Filippenko 1997). Giant eruptions of luminous blue variables (LBVs) are considered a plausible interpretation for classical SN impostors. During giant eruptions, their luminosity increases by over 3 mag with respect to the quiescent phase, accompanied by severe mass loss, sometimes exceeding 1 M⊙ (Humphreys & Davidson 1994; Humphreys et al. 1999). Well-studied examples are the historical giant eruptions of two Galactic LBVs: η Carinae (e.g., Humphreys & Davidson 1994; Soker 2001a,b, 2003) and P Cygni (e.g., de Groot 1969a,b), whose physical parameters (including ejected mass, spatial geometry, and radiated energy) have been well constrained.

Another class of gap transients has double-peaked light curves and fast-evolving spectra, showing SN IIn-like spectra at early phases (e.g., blue continuum and narrow H emission lines) and spectra similar to M-type stars at late phases (i.e. a much redder continuum and molecular bands). They are conventionally designated as luminous red novae (LRNe; e.g., see Kochanek et al. 2014; Pejcha et al. 2016, 2017; Smith et al. 2016; Blagorodnova et al. 2017; Lipunov et al. 2017; MacLeod et al. 2017; Cai et al. 2019; Pastorello et al. 2019a,b, 2021a,b). The LRN phenomenon is usually interpreted as a post-common-envelope-ejection phase in a contact binary system, and may be followed by stellar coalescence (e.g., see Munari et al. 2002; Soker & Tylenda 2003, 2006; Tylenda et al. 2011; Soker & Kashi 2016; Smith et al. 2016; Lipunov et al. 2017; Mauerhan et al. 2018; Pastorello et al. 2019b; Soker 2021).

The third group of gap transients are named intermediate-luminosity red transients (ILRTs; Pastorello & Fraser 2019, and references therein). These show a slow rise time (≈2 weeks) to maximum (−11.5 mag < MV < −14.5 mag), followed by a linear decline or a plateau lasting about 2-4 months. When late-time light curves are observed, they decline following the expectation of 56Co decay. Their light curves resemble those of very faint SNe IIP/L. The spectra are similar to Type IIn SNe with narrow Balmer lines in emission, but are characterised by prominent Ca II lines (e.g., Ca H&K, [Ca II] doublet, and Ca II near-infrared triplet); in particular, the [Ca II] λλ 7291, 7324 doublet is always visible at all phases. ILRTs are linked to 8–15 M⊙ progenitors and are strong mid-infrared (MIR) emitters, suggesting their progenitors are embedded in dusty cocoons (see Prieto et al. 2008; Bond et al. 2009; Botticella et al. 2009; Berger et al. 2009b; Thompson et al. 2009). However, their origin remains mysterious and different scenarios are contemplated. These transients have been proposed to be LBV-like outbursts of moderate-mass stars (e.g., Smith et al. 2009; Andrews et al. 2020) or stellar mergers (e.g., Kasliwal et al. 2011). A third suggested scenario is that we are actually observing faint CC SN explosions triggered by electron captures in the core of super-asymptotic giant branch (S-AGB) stars, and these are therefore labelled electron-capture (EC) SNe (see, e.g., Botticella et al. 2009; Pumo et al. 2009). In recent years, a number of ILRTs have been studied, including SN 2008S (see, e.g., Prieto et al. 2008; Botticella et al. 2009; Smith et al. 2009; Kochanek 2011; Szczygieł et al. 2012; Adams et al. 2016), NGC 300-2008OT1 (NGC 300 OT hereafter) (e.g., Berger et al. 2009b; Bond et al. 2009; Prieto et al. 2009; Kashi et al. 2010; Humphreys et al. 2011), M85 OT2006-11 (Kulkarni et al. 2007; Pastorello et al. 2007; Rau et al. 2007), PTF10fqs (Kasliwal et al. 2011), AT 2017be (Stephens et al. 2017; Adams et al. 2018; Cai et al. 2018), and AT 2019abn (Jencson et al. 2019; Williams et al. 2020, Valerin et al., in prep.).

In this paper, we analyse a sample of five ILRTs2, including AT 2010dn, AT 2012jc, AT 2013la, AT 2013lb, and AT 2018aes. In general, they were initially classified as LBV-like outbursts or, more generically, SN impostors. Subsequent follow-up campaigns allowed us to confirm their classifications as ILRTs. In this work, we also compared ILRTs with other claimed EC SN candidates, such as SN 2018zd (Zhang et al. 2018, 2020; Arcavi et al. 2018; Hiramatsu et al. 2021; Kozyreva et al. 2021; Callis et al. 2021), SN 2018hwm (Reguitti et al. 2021), and SN 2015bf (Lin et al. 2021), as well as underluminous SNe IIP (i.e. SN 1999br, SN 2005cs; Pastorello et al. 2004, 2006, 2009).

The present paper is organised as follows: general information on the sampled ILRTs is given in Sect. 2. Photometric and spectroscopic analysis is reported in Sects. 3 and 4, respectively. The rate of ILRTs is estimated in Sect. 5. Finally, a discussion on the observational and theoretical properties of ILRTs is given in Sect. 6.

2. Basic sample information

2.1. Host galaxies: distance, reddening and metallicity

AT 2010dn was discovered by the amateur astronomer K. Itagaki in May 2010 at 31.523 UT (hereafter UT will be used throughout this paper) at an unfiltered magnitude 17.5 mag (CBAT3). The object was detected at RA = , Dec = +41° 26′28″.80 [J2000], 61″ north and 33″ east from the centre of NGC 3184. We adopt d = 14.40 ± 0.33 Mpc (μ = 30.79 ± 0.05 mag) as the distance to the host galaxy, as obtained from Cepheids (Ferrarese et al. 2000). The Galactic reddening E(B − V)Gal = 0.017 mag is from Schlafly & Finkbeiner (2011). The presence of narrow interstellar Na I D (λλ 5890, 5896) absorption in the transient spectra at the host galaxy redshift is usually considered as evidence for additional internal extinction (e.g., Munari & Zwitter 1997; Turatto et al. 2003; Pozzo et al. 2006; Sahu et al. 2006; Poznanski et al. 2011). In this case, the equivalent width (EW) of Na I D varies with time, suggesting that this dust is likely due to circumstellar material (CSM). For this reason, we neglect the possible host component of extinction and adopt a total reddening E(B − V)Total = E(B − V)Gal = 0.017 mag, in agreement with Smith et al. (2011).

AT 2012jc (also known as PSN J14535395+0334049, NGC 5775-2012OT1, SNhunt120 and LSQ12brd) was found by S. Howerton and the Catalina Real-Time Transient Survey (CRTS4) in March 2012 at 27.460 UT (Berger et al. 2012; Howerton et al. 2012). Its coordinates are: RA = , Dec = +03° 34′04″.90 [J2000], and it is located at 85″ north and 55″ west from the centre of NGC 5775. Based on the weighted average of several estimates using the Tully-Fisher method (e.g., Tully et al. 2013, 2016; Sorce et al. 2014) from the NASA/IPAC Extragalactic database (NED5), a distance of d = 18.62 ± 1.12 Mpc (hence μ = 31.35 ± 0.13 mag) can be estimated for NGC 5775. A Galactic reddening E(B − V)Gal = 0.037 mag (Schlafly & Finkbeiner 2011) is adopted. We measure a constant EW ≃ 0.9 Å for the Na I D absorption at the redshift of NGC 5775 in the early spectra of the transient. Following Turatto et al. (2003) and assuming RV = 3.1 (Cardelli et al. 1989), we obtain a host galaxy reddening of E(B − V)Host = 0.144 mag. Hence, the total reddening towards AT 2012jc is E(B − V)Total = 0.181 mag.

The discovery of AT 2013lb (PSN J15213475-0722183; NGC 5917-2013OT1) was announced by the CHilean Automatic Supernovas sEarch in January 2013 at 27.340 UT (CHASE6, Pignata et al. 2009; Margheim et al. 2013). The coordinates are RA = 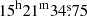, Dec = −07° 22′18″.30 [J2000], and 19″ north and 31″ east from the centre of NGC 5917. For this galaxy, we adopt a kinematic distance, assuming a standard cosmological model with H0 = 73 km s−1 Mpc−1, ΩM = 0.27, ΩΛ = 0.73 (Spergel et al. 2007), which is used throughout this paper. From the radial velocity corrected for Local Group infall onto the Virgo Cluster VVir = 2024 ± 7 km s−1 (see Sandage & Tammann 1990; Theureau et al. 1998; Terry et al. 2002, reported by HyperLeda7), we obtain a luminosity distance d = 27.73 ± 1.90 Mpc (μ = 32.21 ± 0.15 mag). A Galactic reddening E(B − V)Gal = 0.085 mag (Schlafly & Finkbeiner 2011) is reported for this object. Additionally, spectroscopy indicates a negligible host galaxy extinction based on non-detection of the Na I D absorption feature at the redshift of the host galaxy.

AT 2013la (also named PSN J13100734+3410514; PS1-14ln; UGC 8246-2013OT1) was discovered by B. Wang and X. Gao8 in December 2013 at 20.932 UT, at RA = 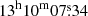, Dec = +34° 10′51″40 [J2000] (e.g., Tartaglia et al. 2014). The object is 0.8″ south and 32.7″ east from the centre of UGC 8246. Averaging several recent Tully-Fisher estimates (e.g., Tully et al. 2013, 2016; Sorce et al. 2014), we obtain d = 15.21 ± 0.11 Mpc (hence, μ = 30.91 ± 0.02 mag) for UGC 8246. We adopt the same line-of-sight reddening as Barsukova et al. (2014), that is, E(B − V)Total = 0.009 mag. We note that, in analogy to AT 2010dn, a variable EW of Na I D suggests the presence of additional circumstellar dust, which is not accounted for in this reddening estimate. We hence adopt E(B − V)Total = E(B − V)Gal.

AT 2018aes (Kait-18M) was discovered by the Lick Observatory Supernova Search (LOSS9) in March 2018 at 11.535 (Yunus et al. 2018). It was detected at RA = 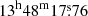, Dec = +03° 56′44″.20 [J2000], 18.9″ south and 25.7″ east of the nucleus of NGC 5300 (Andrews et al. 2018). We average a few recent Tully-Fisher distances estimates from NED (e.g., Tully et al. 2013, 2016; Sorce et al. 2014), obtaining a weighted average distance d = 18.02 ± 0.61 Mpc (μ = 31.28 ± 0.07 mag). As there is some persistent spectroscopic signatures of interstellar Na I D at the host galaxy redshift, following Turatto et al. (2003), we estimate an internal reddening E(B − V)Host = 0.160 mag, while we adopt a Milky Way contribution E(B − V)Gal = 0.020 mag (Schlafly & Finkbeiner 2011) for AT 2018aes. Hence, we obtain a total colour excess E(B − V)Total = 0.180 mag.

Although we did not perform precise estimates of metallicity at the locations of these ILRTs, an estimate of the characteristic oxygen abundance at 0.4R2510 can be done using a statistical approach and the following relation from Pilyugin et al. (2004):

(1)

which links the characteristic oxygen abundance to the absolute B-band magnitude (MB) of the galaxy. The oxygen abundances of the ILRT host galaxies span a very narrow range, from 8.2 to 8.6 dex, which is nearly solar or marginally subsolar (adopting a solar metallicity of 12 + log(O/H) = 8.69 dex; see e.g., Asplund et al. 2009; von Steiger & Zurbuchen 2016; Vagnozzi 2019). We note that the hosts are all spiral galaxies and the positions of the ILRTs are towards their outer edges.

A summary of the ILRTs and their host galaxy parameters is listed in Table 1, while in Fig. 1 we show the location of the transients in their host galaxies.

Table 1.

Basic information for the ILRT host galaxies.

thumbnail Fig. 1.

Top-left: AT 2010dn in one of the spiral arms of the host galaxy. Sloan r-band image taken in June 2010 at 19 with the 2m robotic Faulkes Telescope North (FTN) operated by Las Cumbres Observatory (LCO; Brown et al. 2013). Top-middle: AT 2012jc at the north edge of its host galaxy. Johnson-Cousins R-band image obtained in April 2012 at 06 with the 0.41m PROMPT5 telescope. Top-right: AT 2013lb in the outskirts of its host galaxy. Johnson-Cousins R-band image obtained in February 2013 at 20 with the 2m fully robotic Liverpool Telescope (LT) with RATCam. Bottom-left: AT 2013la at the east edge of its galaxy. A zoom-in of the transient position is shown in the lower-left corner. Sloan r-band image obtained in February 2014 at 12 with the LT equipped with IO:O. Bottom-right: AT 2018aes and its host galaxy. LT/IO:O Sloan r-band image obtained in May 2018 at 17 with a blow-up of the transient site in the lower-left inset.

2.2. Data reduction

Routine follow-up campaigns were triggered soon after the announcement of the ILRT discoveries, using the instruments available to our collaboration. Information on the instrumental configurations is reported in Table A.1. For some transients, additional early-time unfiltered data were collected from amateur astronomers. We also collected historical data available in public archives.

The raw images were first pre-reduced, applying overscan, bias and flat-field corrections through standard IRAF11 tasks (Tody 1986, 1993). When necessary, multiple-exposure frames were median-combined to increase the signal-to-noise ratio (S/N). Photometric measurements were performed through a dedicated pipeline, ecsnoopy12. ecsnoopy is a PYTHON-based script, which makes use of a series of packages for photometry and template subtraction (e.g., SEXTRACTOR13, DAOPHOT14, HOTPANTS15; Bertin & Arnouts 1996; Stetson 1987; Becker 2015). Individual instrumental magnitudes were measured with the point-spread function (PSF) fitting technique. We first subtracted the background contaminating the object using a low-order polynomial fit. A standard PSF template was constructed by fitting the profiles of several isolated stars (usually from 5 to 10 stars) in the SN frames. The PSF model was then fitted to the target source, and the goodness of the fit was evaluated by inspecting the residuals at the SN location. When the object was faint or had a complex background, we used the template-subtraction technique to remove the background contamination from our measurements. Specifically, we applied it to measurements of AT 2010dn, AT 2013la, and AT 2018aes. The errors were estimated via artificial star tests, in which several fake stars were placed close to the SN location. The fake stars were fitted with the PSF method, and the standard deviation of these measurements provided us the instrumental errors. These were combined in quadrature with the PSF-fit error, finally providing the total photometry error.

We applied the instrumental zero points (ZPs) and colour terms (CTs) to the instrumental magnitudes obtained through observations of standard fields obtained in photometric nights. Specifically, the Johnson-Cousins magnitudes were determined with reference to the Landolt (1992) catalogue, and Sloan-filter data were calibrated via the SDSS DR 13 catalogue (Albareti et al. 2017). In order to obtain an accurate calibration, a sequence of reference stars in the field of each ILRT was used to correct the ZPs in non-photometric nights. When available, the Sloan magnitudes of the reference stars in the ILRT field were directly taken from SDSS, while the Johnson-Cousins magnitudes were obtained from the SDSS data using the conversion relations of Chonis & Gaskell (2008).

Near-infrared (NIR) data reduction includes flat fielding, distortion correction and sky subtraction. We performed pre-reduction on NOT/NOTCam and NTT/SOFI raw images using dedicated pipelines for NOTCam (version 2.5) and SOFI (PESSTO pipeline, version 2.2.10; Smartt et al. 2015) respectively. Standard IRAF tasks were used to reduce LT/SupIRCam and TNG/NICS images. Instrumental magnitudes were measured via ecsnoopy, and then calibrated using the Two Micron All Sky Survey (2MASS16, Skrutskie et al. 2006) catalogue (assuming negligible colour corrections).

The Spitzer Space Telescope was equipped with the InfraRed Array Camera (IRAC; two channels: CH1 = 3.6 μm and CH2 = 4.5 μm). We used the Level 2 post-BCD (Basic Calibrated Data) images, which were reduced with the Spitzer pipeline17. These pBCD images are composed of a mosaic image, after rejection of most instrumental artefacts, an uncertainty image, and an associated coverage image which is the map of how many frames per position are available to generate the mosaic image. We note that AT 2010dn was targeted at 14 epochs by the Spitzer Space Telescope during 2010 – 2015 and the data are available from Spitzer Heritage Archive (SHA)18. We took the Spitzer images from 2019 September 14 as templates19, which were matched and transformed to each epoch of the observed images and then subtracted using HOTPANTS (Becker 2015). We performed aperture photometry on the subtracted images using a small (4×0.6″ pBCD pixel) aperture, and then applied an aperture correction and a conversion from MJy/sr to mJy/pix to get the fluxes. With this approach, we obtained ten detections for the CH1 and CH2 channels over a time-span of five years (from 2010 to 2015). For a few other epochs we have non-detections down to 3σ. The resulting magnitudes are reported in Table C.3.

3. Photometry

Our follow-up campaigns for each of the five transients started soon after their discovery, and lasted several months. The photometric measurements of the transients are reported in Tables C.1–C.10, while individual light curves are shown in Fig. 2. As a reference epoch, we selected the R/r-band maximum, obtained using a third-order polynomial fit to the observed light curves between about −20 and +20 days from maximum (see below).

thumbnail Fig. 2.

Multi-band light curves of AT 2010dn (top-left), AT 2012jc (top-right), AT 2013lb (middle-left), AT 2013la (middle-right), and AT 2018aes (bottom). The dashed vertical lines indicate the R/r-band maximum time. Upper limits are marked by empty symbols with arrows. The light curves are shifted with some constants for clarity and the shift amount is reported at the top. The errors of most magnitudes are smaller than the plotted symbol sizes.

3.1. Apparent light curves

In Fig. 2 we show the apparent light curves of the five events, which are similar to those of other ILRTs in the literature. Most of the objects have a rise time of about two weeks, but AT 2018aes has a longer rise of about 24.1 d. After maximum, the light curve evolution of the sample resembles that of SNe IIP/IIL. We divide the light curve evolution into three different phases: Phase I (γ1), Phase II (γ2), and Phase III (γ3), each with a different decline rate. The values obtained through linear fits are reported in Table 2. In general, ILRTs decline quite rapidly in all bands during Phase I, with the blue bands usually fading faster than the red bands. After Phase I, a sort of plateau (see AT 2012jc and AT 2013la) or a linear decline (see AT 2013lb and AT 2018aes) is observed in ILRTs. When late-time observations are available (i.e. AT 2013la, SN 2008S, and NGC 300 OT), a slow evolution is observed, consistent with that expected from the 56Co decay. We discuss the implications of this in Sect. 3.4.

Table 2.

Decline rates of the light curves of individual ILRTs (mag/100d), along with their uncertainties.

3.2. Colour evolution

The colour evolution of the five transients is shown in Fig. 3, along with those of other ILRTs and comparison objects from the literature. For the ILRTs, the B − V colour evolves steadily from ∼0.2–0.4 mag at early phases to ∼0.7–1.0 mag at around 100 days past maximum, suggesting that the temperature decreases with time (see panel a in Fig. 3). At the later phases (> 100 days), B − V becomes bluer again, from 0.8 to 0.5 mag. At similar epochs, the R − I/r − i colours increase from ∼0.1–0.3 mag to 0.5–1.0 mag (Fig. 3, panel b). Very late-time colours show a large dispersion. AT 2013la is somewhat discrepant, with the r − i colour becoming bluer (reaching ∼ − 0.2 mag) than at early epochs. The J − K colour usually shows a minimum at 30-70 days. The best-sampled NIR dataset is that of NGC 300 OT, which allows us to estimate a minimum value of ∼1.1 mag. Later, J − K rises to 3.0 mag at ∼230 days (Fig. 3, panel c). As shown in Fig. 3, the comparison objects are bluer (e.g., SN 2018zd and SN 2005cs: B − V ≈ −0.2 mag) at early phase and become redder (e.g., SN 2005cs: B − V ≈ 2.0 mag at tail phase) over time.

thumbnail Fig. 3.

Colour evolution of ILRTs, along with those of the comparison objects: SN 2018zd (Zhang et al. 2020), SN 2018hwm (Reguitti et al. 2021), SN 1999br (Pastorello et al. 2004), and SN 2005cs (Pastorello et al. 2006, 2009). (a) B − V colour curves of ILRTs; (b) R − I/r − i colour curves; (c) J − K colour curves; (d) and (e) show the same colours as panels a and b until +100 days without error bars for clarity. All phases are with respect to the R/r-band maximum.

3.3. Absolute light curves

The R/r-band absolute light curves of our ILRT sample, calibrated in the Vega system, are shown in Fig. 4. We used third-order polynomial fits to estimate the R/r-band peak absolute magnitudes20, and the resulting values are listed in Table 3. All transients have rise times to their maximum ≲2 weeks, apart from AT 2018aes, which reaches the light curve peak in ∼3 weeks. The peak absolute magnitudes span a range from ∼ − 11(±0.5) to −15(±0.5) mag, still within the range expected for gap transients (l − 10 <  M <  −15 mag; Pastorello & Fraser 2019). If we consider all objects in this study, we obtain an averaged absolute peak magnitude of MR = −13.04 ± 0.91 mag. As shown in Fig. 4, we compared the R/r-band absolute light curves of ILRTs with three proposed EC SN candidates: SN 2018zd, SN 2018hwm, and SN 2015bf; and two subluminous Type IIP SNe: SN 1999br and SN 2005cs. They show a wide range of peak magnitudes, with the faint SN 1999br (∼−13.8 mag), the relatively luminous SN 2018zd and SN 2015bf (∼−18.0 mag), and intermediate-luminosity SN 2018hwm and SN 2005cs (∼−15.5 mag). SN 1999br, SN 2018hwm, and SN 2005cs are characterised by long-lasting plateaus of above 100 days. At the end of the plateau, these comparison objects show a sudden drop in luminosity of 2.5–4.0 mag. Finally, they all settle onto the radioactive tails.

thumbnail Fig. 4.

Comparison of the R/r-band absolute light curves of ILRTs and SN 2018zd, SN 2018hwm, SN 1999br, and SN 2005cs. Reddenings and distance moduli of the comparison objects are taken from their respective papers (also see Table B.1). The dashed vertical line indicates the time of r-band maximum light. Upper limits are marked by empty symbols with down arrows.

3.4. Pseudo-bolometric light curves

The bolometric light curve is computed by integrating the spectral energy distribution (SED) over the whole electromagnetic spectrum. However, in most cases, observations at wavelengths shorter than the u band, and longer than I/i-band are not available. For this reason, to achieve meaningful comparisons among ILRTs, we computed pseudo-bolometric light curves including only the contribution from the B to the I/i band. We first converted the extinction-corrected magnitudes to flux densities, and finally integrated the SEDs at their effective wavelengths, assuming a negligible flux contribution outside of the integration region. The resulting pseudo-bolometric light curves are presented in Fig. 5, while peak luminosities are reported in Table 3. They show faint peak luminosities ranging from 0.5 × 1040 erg s−1 to 9.0 × 1040 erg s−1. For comparison, the claimed EC SNe SN 2018zd and SN 2015bf have peak luminosities of ∼3.7 × 1042 erg s−1 and the faint Type IIP SN 1999br is about 4.7 × 1040 erg s−1 (see Fig. 5). The pseudo-bolometric light curve shapes of ILRTs are broadly similar to Type IIP (in particular, PTF10fqs and AT 2017be) and/or Type IIL (SN 2008S and AT 2012jc) SNe, as demonstrated in Fig. 5. In analogy to Type IIP SNe, the light curves for ILRTs are influenced by a number of factors, such as the presence of a CSM, the H recombination timescale, and 56Ni distribution. Finally, we perform a non-parametric fit using the ReFANN21 code (Wang et al. 2020, 2021) to reconstruct the pseudo-bolometric light curve, and integrate it over the covered photometric evolution. The resulting radiated energies are in the range of (0.30–2.94) × 1047 erg, with values reported in Table 3. These values should be regarded as lower limits due to our incomplete wavelength coverage and limited temporal coverage. These observed ILRTs radiated energies are fractions of about 10−4–10−3 of the theoretical predictions for the explosion energy of EC SNe (about 1050 erg, Kitaura et al. 2006; Wanajo et al. 2009; Tominaga et al. 2013). Stritzinger et al. (2020b) pointed out that theoretical EC SN simulations may overpredict the explosion energy. Therefore, this discrepancy should be considered in future observations and modelling efforts.

thumbnail Fig. 5.

Pseudo-bolometric B to I/i light curves of ILRTs and comparison objects. The dashed vertical line indicates the time of R/r-band maximum light.

Table 3.

Light-curve parameters for ILRTs.

In order to provide reliable estimates for the ejected 56Ni masses, we need to compute the bolometric light curves. Unfortunately, most objects do not have MIR observations, and optical and/or NIR light-curve information is sometimes incomplete at late times. SN 2008S and NGC 300 OT are exceptions, as they were followed until late phases, and also have MIR coverage. Observations of these two objects revealed that the SEDs of ILRTs shift from the optical to the MIR domain, with the MIR being dominant at late phases (e.g., Botticella et al. 2009; Kochanek 2011). To mitigate the limited observational information available for other objects, we adopted SN 2008S as a template for other ILRTs, and assumed that all others share the same SED evolution. Hence, we used SN 2008S to determine the bolometric corrections for all ILRTs that had incomplete wavelength coverage. We estimated the optical and NIR luminosity contribution of SN 2008S, using the bolometric light curve model (Lbol = L0 × exp(−t/t0) + L1, with L0 ≃ 107.3 L⊙, L1 ≃ 105.8 L⊙ and t0 ≃ 48 days) from Kochanek (2011). We first computed the 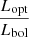, , 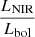and 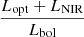ratios at late phases for SN 2008S. The Lopt, LNIR, and Lopt + LNIR contributions for other ILRTs at the same phases were then calculated, assuming the same ratios as for SN 2008S. Specifically, Lbol was computed starting from the measured Lopt + LNIR for AT 2010dn, from Lopt for AT 2013la, and LNIR for AT 2017be, and then by applying the adopted bolometric corrections.

Assuming that the late-time evolution of ILRTs are powered by the radioactive decay chain 56Ni → 56Co → 56Fe, the late-time luminosity of ILRTs can be used to constrain the synthesised 56Ni mass. We use the well-observed Type II SN 1987A as a reference (Catchpole et al. 1988, 1989; Whitelock et al. 1988) and estimate the ejected 56Ni mass of ILRTs using Equation 2:

(2)

where M(56Ni)SN 1987A ∼ 0.073 M⊙22 is the 56Ni mass synthesised by SN 1987A, and LILRT and LSN 1987A are late-time luminosities of an individual ILRT and SN 1987A, respectively. Hereafter, we only consider five ILRTs that have observations in the nebular phase. Because of the poor constraints on the explosion epoch of ILRTs, we use the last non-detection and the first detection to fix the earliest and the latest possible extremes for the explosion epochs. Hence, we obtain upper and lower limits of 56Ni masses for the ILRTs, reported in Table 3. SN 2008S ejected the largest amount of 56Ni (3.2–3.5 × 10−3 M⊙), while AT 2017be has the lowest 56Ni mass (6.7–7.2 × 10−4 M⊙). All inferred 56Ni masses are of the order of 10−4–10−3 M⊙, which, as discussed in Sect. 6, is in agreement with the predictions for EC SNe.

3.5. Evolution of the SED of ILRTs: the test case of AT 2010dn

It is well known that SN 2008S, NGC 300 OT, and AT 2012jc already showed an IR excess soon after their discovery (Botticella et al. 2009; Humphreys et al. 2011; Stritzinger et al. 2020b). If we assume their progenitors to be embedded in complex and extended dusty environments, we should expect such IR excesses to be frequently observed for ILRTs. This can be verified in the case of AT 2010dn, for which MIR observations are available. Using the light curves presented in Tables C.1, C.2, and C.3, we constructed the SEDs of AT 2010dn at different epochs using photometry from the optical to the MIR. The first optical to MIR SED is obtained at t ∼ 30.6 days after maximum, which clearly reveals an IR excess over a single black body (BB) model (see the top panel of Fig. 6). Hence, the SED was fitted with two-component (hot+warm components) BB functions instead of a single one. The hot component has a temperature Thot=5390 ± 70 K and a radius Rhot ≈ 2.87 × 1014 cm, while the warm component has Twarm ≈ 970 K and Rwarm ≈ 4.63 × 1015 cm. In comparison, SN 2008S had Thot= 8076 ± 150 K, Rhot = (2.1 ± 0.1) × 1014 cm, Twarm ≈ 585 K, Rwarm ≈ 9.9 × 1015 cm at maximum (Botticella et al. 2009), while AT 2012jc had a BB temperature of Thot ≈ 6430 K and Twarm ≈ 800 K at + 26.8 days (Stritzinger et al. 2020b). The hot-component estimates are consistent with emission from the photosphere, while the warm component peaking in the MIR domain is likely due to circumstellar dust. For AT 2010dn, additional epochs of SEDs along with the corresponding best-fit BB functions are shown in Fig. C.1, while the first BB parameters are reported in Table C.4. The Thot increases to ∼6490 K and, when the luminosity fades, Thot also declines to ∼3540 K at +199.2 d. The Rhot shows a slow evolution (from 2.4 to 2.9 × 1014 cm) until +21.5 d, and declines to 1.6 × 1014 cm at +199.2 d. Three epochs with K band data reveal a possible second warm component with an almost constant temperature of 1100–1200 K (see Fig. C.1).

thumbnail Fig. 6.

Top panel: two-component black body fits to the SED of AT 2010dn obtained from optical to MIR at the epoch of +30.6 days. Bottom panel: single black body fit for AT 2010dn in the MIR domain at very late phase of +1332.5 days. Although this fit could reproduce the late MIR data, the fitted temperature should be considered as an indicative value. The MIR measurements were obtained from the Spitzer Space Telescope + IRAC images at 3.6 μm and 4.5 μm.

We also measured the residual flux at the location of AT 2010dn in Spitzer MIR images taken more than 3 years (+1333 days) after the outburst, and constructed a very late-time SED. This SED can be reproduced by a single BB function with a characteristic temperature of 440 K (see the bottom panel of Fig. 6). We caution that this temperature should be regarded as an indicative value because of the limited coverage of MIR data. Similarly, AT 2012jc has very late-phase (+1155 days) Spitzer MIR photometric fluxes suggesting a BB temperature of about 600 K. Based on the similarity of these three cases, we suggest that this SED evolution seems to be typical of ILRTs. A plausible explanation is that a dusty environment has formed through mass-loss events prior to the ILRT outbursts, in analogy to what is frequently observed in a few CC SNe (e.g., SN 1995N, SN 1998S, SN 2010jl, SN 2014ab, SN 2015da; see Gerardy et al. 2002; Andrews et al. 2011; Fransson et al. 2014; Tartaglia et al. 2020; Moriya et al. 2020). The slowly declining IR flux lasting around 4 years suggests that the outer dust shell was not destroyed by the radiation field emitted by the luminous outburst (regardless of the physical mechanism that produced the ILRTs; Botticella et al. 2009).

4. Spectroscopy

Our spectral sequences for AT 2010dn, AT 2012jc, AT 2013lb, AT 2013la and AT 2018aes were obtained using multiple instrumental configurations, which are listed in Table A.1. Basic parameters for the spectra are reported in Table 4.

Table 4.

Log of spectroscopic observations of ILRTs.

The spectra were processed with the standard procedures in IRAF. The preliminary reduction steps included bias, overscan and flat-field corrections. We then extracted 1D spectra from the 2D frames using the task APALL. Wavelength calibration of the 1D spectra was performed with arc lamp spectra obtained with the same instrumental configuration as the science ones. The spectra of spectro-photometric standard stars were used to estimate a sensitivity function curve necessary to flux-calibrate the spectra of the transients. The accuracy of the flux calibration was then checked against coeval broadband photometry, and correction factors were applied in case of discrepancy. The spectra of the standard stars were also used to correct for the telluric absorption bands (e.g., O2 and H2O) from the ILRTs spectra. The resulting ILRT spectra are shown in Fig. 7.

thumbnail Fig. 7.

Spectral evolution of AT 2010dn (top-left), AT 2012jc (top-right), AT 2013lb (middle-left), AT 2013la (middle-right), and AT 2018aes (bottom). The epochs marked to the right of each spectrum are relative to the R/r-band maximum. The ⨁ symbols mark the position of the strongest telluric absorption bands. The spectra are only corrected for redshift.

4.1. Spectroscopic evolution and line identification

The five objects of our sample have spectra showing little evolution over the period of their spectral monitoring (from ∼ − 8 days to 1 year after maximum). At all epochs, the spectra have an almost featureless continuum, which is relatively blue at early phases, becoming redder with time. Narrow emission lines of the Balmer series are superposed on the continuum, with Hα and Hβ being the most prominent spectral features. Weak Fe II lines are also observed, along with Na I D and Ca H&K in absorption. Apart from the H lines, the most prominent spectral emissions are the [Ca II] doublet (λλ 7291, 7324) and the Ca NIR triplet (λλ 8498, 8542, 8662). In addition, O I, Fe II, Sc II and Ba II lines are also tentatively identified in some spectra with decent S/N and resolution (e.g., see a GTC/OSIRIS spectrum at +41.9 d of AT 2013la). Detailed line identification performed on the best-quality spectra of the five transients is given in Fig. 8. We note that the lines of the [Ca II] doublet are visible in all spectra with good S/N shown in this paper and are therefore considered a characteristic feature of ILRTs. In Fig. 9, all ILRTs share almost the same spectral features, supporting a remarkable overall homogeneity in their observables. However, as shown in Fig. 9, the spectra of the comparison objects show much bluer continuum than ILRTs. In addition, Hα has a classical broad P-Cygni profile and there is no obvious [Ca II] doublet feature.

thumbnail Fig. 8.

Line identification in the spectra of the five transients presented in this paper. The spectra have been corrected for redshift and reddening. Phases are relative to their R/r-band maximum.

thumbnail Fig. 9.

Spectral comparison of a sample of ILRTs and SN 2018zd, SN 2018hwm, SN 2015bf, SN 1999br, and SN 2005cs. The spectra of M85 OT, SN 2008S, PTF10fqs, AT 2017be, SN 2018zd, SN 2018hwm, SN 2015bf, SN 1999br, and SN 2005cs are taken from Kulkarni et al. (2007), Botticella et al. (2009), Kasliwal et al. (2011), Cai et al. (2018), Zhang et al. (2020), Reguitti et al. (2021), Lin et al. (2021), Pastorello et al. (2004), and Pastorello et al. (2006, 2009). The right panel shows the region of [Ca II], marked with the grey-shaded region in the left panel. All spectra were obtained at similar epochs from the R/r-band maxima, and were corrected for redshift and reddening.

During the follow-up campaign of AT 2013la, we collected spectra covering all the evolutionary phases. Hence, we take AT 2013la as a representative object to describe the spectral evolution of ILRTs. The spectral continuum evolves quite slowly, from initially blue (e.g., at phase ∼ +13.2 d) to much redder at late phases (+360.0 d). AT 2013la resembles other ILRT spectra in its continuum evolution and characteristic lines. However, we see additional strong He I (5876 Å) absorption feature in all GTC/OSIRIS spectra, most clearly at +42.2, +65.2, +202.9, +231.9, and +360.3 days (see middle right panel in Fig. 7). We note that narrow P-Cygni absorptions imposed on Hα lines are also detected in the highest resolution spectra (see e.g., the GTC/OSIRIS spectra of AT 2013la in Figs. 7 and 10). Such spectra allow us to infer the wind velocity via measurement of the position of the deep minimum of the P-Cygni profiles. This blueshifted absorption component on top of the Hα emission (see Fig. 10) has velocities of ∼360–410 km s−1, and may originate from a dense, slow-moving wind. This is discussed more widely in Sect. 4.2.

thumbnail Fig. 10.

Evolution of Hα and [Ca II] in ILRTs. The spectra of M85 OT, SN 2008S, PTF10fqs, and AT 2017be, downloaded from WISeREP archive (https://wiserep.weizmann.ac.il/) (Yaron & Gal-Yam 2012), were published by Kulkarni et al. (2007), Botticella et al. (2009), Kasliwal et al. (2011), and Cai et al. (2018). All spectra were corrected for redshift and reddening.

We assume that the SEDs of ILRTs in the optical domain covered by our spectra are approximated by black bodies. Therefore, we estimate the temperature through a black body fit to the spectral continuum. The inferred continuum temperatures are reported in Table 5, while the temperature evolution is shown in the top panel of Fig. 11. For all objects in our sample, the temperature rapidly declines from ∼7000–8500 K near maximum, to nearly 5000 K at ∼100 days. At late phases, the temperature decreases more slowly to ∼4200–4500 K at about 1 year after maximum. Overall, all our ILRTs show a similar temperature evolution. We note that the comparison objects show much higher temperatures than ILRTs at early phases, and this is consistent with their early-time bluer colours.

Table 5.

Physical parameters inferred from the optical spectra of the ILRTs sample.

thumbnail Fig. 11.

Evolution of the black body temperature (top) and the Hα luminosity (bottom) for a sample of ILRTs, and SN 2018zd (Zhang et al. 2020), SN 2018hwm (Reguitti et al. 2021), SN 2015bf (Lin et al. 2021), SN 1999br (Pastorello et al. 2004), and SN 2005cs (Pastorello et al. 2006, 2009).

4.2. Hα and Ca II line evolution

In order to understand the evolution of individual spectral features, we performed a detailed analysis of the spectra of our ILRT sample at three critical phases23: around 0, +30, and +70 days from maximum (see Fig. 10). We measure the full width at half maximum (FWHM) of Hα through a single Lorentzian function fit, as in general this type of fit accurately describes the line profiles of narrow-lined SNe (e.g., SNe IIn; see Taddia et al. 2013; Smith 2017; Nyholm et al. 2017). The Hα profile is dominated by a narrow component in the spectra of most objects (e.g., AT 2010dn, AT 2012jc, AT 2013lb, and

AT 2018aes). However, AT 2013la shows Hα with a more complex profile, with narrow, blueshifted P-Cygni absorption lines. For AT 2013la, we therefore fitted the Hα emission lines in our higher resolution spectra (i.e. at phases +65.2d, +202.9, +231.9 and +360.3d) via multiple components: an intermediate-width Lorentzian profile, a narrow Gaussian emission and a Gaussian absorption. We also fitted the Hα line at phase +42.2d with only a broader Lorentzian component plus a narrow Gaussian. The narrow component of Hα arises from the unshocked photoionised CSM, while the intermediate-width component likely originates from the shocked CSM. Finally, the broad component is produced by the faster ejecta. The FWHM velocities (vFWHM) of Hα, after correcting for instrumental resolution (vFWHM = ), are reported in Table 5 and plotted in Fig. 12. We note that most spectra of our sample have modest resolution. Hence, in most instances our measurements have to be considered upper limits for the expansion velocities. We also measured the Hα velocity for the comparison objects in Fig. 12, which were inferred from the minima of the broad P-Cygni absorptions. These show a remarkably large velocity evolution, ranging from ∼8000 km s−1 to ∼1000 km s−1. In contrast, ILRTs show a slow evolution in Hα velocity (< 1000 km s−1) over the entire monitoring campaigns. In Fig. 13, we show the temporal evolution of Hα profiles in the velocity space for AT 2013la, SN 2018zd, and SN 2005cs. AT 2013la shows a modest velocity evolution in Hα profile, while SN 2018zd and SN 2005cs experience significant velocity evolution along with the gradual emergence of broad P-Cygni features.

thumbnail Fig. 12.

Hα velocity evolution of a sample of ILRTs, SN 2018zd (Zhang et al. 2020), SN 2018hwm (Reguitti et al. 2021), SN 2015bf (Lin et al. 2021), SN 1999br (Pastorello et al. 2004), and SN 2005cs (Pastorello et al. 2006, 2009). The Hα velocities were estimated by measuring the FWHM for ILRTs, while those for SNe II were determined from the position of the minimum of the absorption component.

thumbnail Fig. 13.

Evolution of the Hα profile in selected spectra of the ILRT AT 2013la (left panel), SN 2018zd (Zhang et al. 2020, middle panel), and the underluminous Type IIP SN 2005cs (Pastorello et al. 2006, 2009, right panel). The Hα lines are shown in the velocity space, with zero velocity (rest wavelength) being marked by a grey dashed line.

The [Ca II] doublet and Ca II NIR triplet lines were fitted with Lorentzian functions. The [Ca II] doublet is produced by quadrupole transitions from 4s2S to the metastable 3d2D level, in which λ1 at 7291 Å and λ2 at 7324 Å are associated to 2S1/2−2D5/2 and 2S1/2−2D3/2 transitions, respectively (e.g., Osterbrock 1951; Lambert et al. 1969; Chevalier & Fransson 1994). The [Ca II] doublet likely originates from extremely low-density gas, possibly in a slow-moving circumstellar shell. The Ca II NIR triplet lines with λ1, 2, 3= 8498, 8542, 8662 Å are common features in many cool transients, and are produced by transitions from 4p2P1/2, 3/2 to 3d2D3/2, 5/2 levels (e.g., Mallik 1997, 1998; Andretta et al. 2005; Busà et al. 2007; Martin et al. 2017).

At early phases (see Fig. 10, left panel), the Hα FWHM velocities of the transients presented in this paper are 600-700 km s−1 (with upper limits up to 1000 km s−1 in cases of unresolved features), which are comparable to those of other ILRTs (e.g., ∼750 km s−1 and ∼600 km s−1 for SN 2008S and AT 2017be, respectively). We conclude that in all ILRTs the ejected material expands with similar velocities of several hundred km s−1. In most cases the FWHM of the [Ca II] doublet is below the resolution limits, and we do not have reliable estimates for the outflow velocity inferred from this feature. The doublet is resolved only in the spectra of AT 2010dn at −3.0 d, providing an FWHM velocity of 145 km s−1. The feature was also resolved in a spectrum of AT 2012jc at phase −6.2 d, where we measured vFWHM ∼ 220 km s−1. For AT 2018aes, a velocity of vFWHM ∼ 310 km s−1 was derived for the [Ca II] feature at phase −3.0 d. We conclude that the [Ca II] doublet originates in a slow-moving CSM (∼145–310 km s−1), while the broader Hα component forms in fast-expanding ejected gas.

At 3–5 weeks after maximum (Fig. 10, middle panel), the spectra become redder. We also see a strengthening of a narrow P-Cygni profile superimposed on Hα in AT 2013la, the minimum of which is blueshifted by about 360–410 km s−1. However, we cannot rule out that the non-detection of this feature in other objects is a mere resolution effect. The FWHM velocities of Hα are in the range 600–850 km s−1 for all objects, with M85 OT being the only outlier with vFWHM ∼ 350 km s−1. A resolved velocity of 115 km s−1 was reported at this phase for [Ca II] in AT 2017be (Cai et al. 2018).

At late phases (+70 to +80 d; Fig. 10, right panel), the Hα velocity does not change significantly, still ranging from 400 (in AT 2013la) up to 850 km s−1 (in the other objects). The spectra of AT 2013la also provide an averaged [Ca II] vFWHM ∼ 365 km s−1. In most cases, the low resolution or the low S/N of our spectra prevent us from probing the Ca II triplet lines in detail, with an exception being the Magellan spectrum of AT 2012jc obtained on 2012 June 23 (phase +77.7 d), where the triplet emission lines show a symmetric profile, with an average vFWHM ≃ 905 km s−1. The [Ca II] profile appears to show very little evolution in the FWHM until t∼ 70 days, and this is a further argument in favour of the hypothesis that these lines form in the circumstellar environment. We also note that none of the typical nebular lines, such as [O III] (λλ = 4959, 5007 Å) and [S II] (λλ = 6716, 6731 Å) lines (Lundqvist & Fransson 1996; Lundqvist et al. 2015, 2020), were detected in spectra. This implies that the wind density is high enough for those nebular lines to be collisionally de-excited, but that [Ca II] can exist at much higher density (e.g., critical density: ρ[S II] = 1 × 104 cm−3, ρ[Ca II] = 1 × 109 cm−3; Li & McCray 1993). In such a dense wind, the [Ca II] lines could also be broadened by Thomson scattering, albeit to a lesser extent than the Balmer lines because these latter are formed further out in the wind/CSM.

We use the few spectra with higher S/N to highlight the evolution of the Hα to [Ca II] luminosity ratio. The values for the different ILRTs are reported in Table 5 and shown in Fig. 14. The values for AT 2012jc and AT 2013lb show a faster decline (by a factor of three) from maximum (when Hα largely dominates) to one month later. However, for AT 2010dn and AT 2018aes, the above ratio shows a much flatter evolution (ratio from about 3 to 2) over the same temporal window. Interestingly, in these two ILRTs, the [Ca II] doublet is very luminous with respect to Hα. In addition, the Hα luminosity evolution is also shown in the bottom panel of Fig. 11.

thumbnail Fig. 14.

Ratio of Hα to [Ca II] (total profiles at λ ≈ 7300 Å) luminosities until phase ∼30 d.

5. Rate estimates for ILRTs

In the past 12 years (2008–2019), 12 objects have been confirmed to be ILRT events24; the observed rate of discoveries is 1.0 event per year, but this does not account for the luminosity distribution of ILRTs, or the efficiency or observing strategy of the surveys. The ILRTs in our sample are distributed in a radius of 30 Mpc, corresponding to a volume of 1.13 × 105 Mpc3. Hence, we obtain a volumetric rate of ILRTs of 0.09 × 10−4 Mpc−3 yr−1. In the same temporal window and volume, 147 CC SNe were discovered25 corresponding to a rate of 1.1 × 10−4 Mpc−3 yr−1. Therefore, assuming that the discovery of ILRTs suffers the same selection effects as all CC SNe, the rate of ILRTs is 8% that of CC SNe. We note that Thompson et al. (2009) estimated an EC SN rate of 2%–10% of CC SNe in 10 years (before 2008), while Poelarends et al. (2008) obtained an EC SN fraction of CC SNe of only about 6% based on a standard Salpeter initial mass function (IMF; Salpeter 1955) and an EC SN mass range of 9.00–9.25 v. Assuming a narrow mass range Δ ≈ 0.2 M⊙ and a metallicity range Z = 0.0001–0.02, Doherty et al. (2015, 2017) calculated that 2%–5% of CC SNe are EC SNe. However, theoretical estimates for EC SN rates are dependent on the uncertainties on the initial mass range, metallicity, and the details of stellar models. While theoretical calculations show some variations, they are roughly consistent with our rate estimate based on the observations. We note that we did not take into account the fact that ILRTs are on average fainter than CC SNe and surveys are incomplete up to 30 Mpc. Therefore, the true relative rate is larger than the current observed rate, and future advanced surveys could increase this estimate.

6. Discussion and conclusions

6.1. Observables and parameter correlations

In this paper, we systematically analyse a sample of ILRTs. They show relatively homogeneous spectrophotometric properties that can be summarised as follows:

  • I.

    They all show single-peaked light curves, resembling those of Type IIP/IIL SNe but scaled down in luminosity (see Fig. 4). The duration of the plateau is determined by the effective recombination time of the hydrogen envelope (e.g., see Grassberg et al. 1971; Eastman et al. 1994; Soma et al. 2010).

  • II.

    They show a homogeneous colour (hence temperature) evolution. The temperature evolution shows an initial fast decline (usually lasting < 30 days), followed by a much slower decline which is still ongoing at the end of the follow up. The temperature evolution of ILRTs is similar to what is observed in the hydrogen recombination of classical Type II SNe (e.g., see the Type IIP SN 2005cs in the top panel of Fig. 11). We note that ILRTs are usually redder than low-luminosity SNe IIP and other Type II events proposed to be EC SN candidates (see Fig. 3).

  • III.

    Their peak magnitudes range from −11(±0.5) to −15(±0.5) mag. Their quasi-bolometric (B to I) light curve peaks are in the range ∼5 × 1039 to ∼9 × 1040 erg s−1 and the radiated energies span from 0.30 × 1047 to 2.94 × 1047 erg. ILRTs are typically fainter than most SNe II, although they are comparable in luminosity to the most subluminous Type IIP SN 1999br (see Figs. 4 and 5).

  • IV.

    The SED of ILRTs with optical to MIR observations shows evidence of prominent IR excesses both at early and late phases. This is consistent with the expectation that the progenitors of ILRTs have dusty local environments. Furthermore, it corroborates the use of the nomenclature: ‘red’ transients. Another common feature in the SED evolution of ILRTs is the monotonic decrease of the photospheric radius, which could be a diagnostic tool to distinguish ILRTs from LRNe (see Fig. 4 of Cai et al. 2019.)

  • V.

    Their spectra experience relatively slow evolution. Prominent lines include the Balmer series, along with Ca II (e.g. Ca H&K, [Ca II] doublet, and Ca NIR triplet), Na I D, Fe II, and possibly O I. The [Ca II] doublet is normally visible during the entire monitoring campaign. However, the study of AT 2019abn challenges this paradigm with a barely detectable [Ca II] doublet at early phases (Jencson et al. 2019; Williams et al. 2020). In addition, this feature is never detected in SNe IIP at early phases (see Fig. 9), while it is always visible in the nebular phases.

  • VI.

    The ejecta velocities inferred from the Hα FWHM lie between about 400 and 800 km s−1. The measurements of the minimum of P-Cygni profiles indicate a modest wind velocity of about 360–410 km s−1. In addition, the [Ca II] feature width suggests the existence of slow-moving CSM with vFWHM ∼ 170–300 km s−1. In ILRTs, the Hα velocity is much lower than those inferred for SNe II at all phases (see Fig. 12).

In order to better characterise ILRTs, we looked for possible correlations among their physical parameters. In Fig. 15, we plot peak luminosity (Lpeak; reported in Table 3) against different physical parameters of ILRTs, namely the time (Δt0.5) for the luminosity to decline by a factor of two from maximum, the 56Ni mass, the Hα velocity, and the Hα luminosity at maximum. Unfortunately, several factors (e.g., poorly sampled light curve peaks; lack of late-time observations; low spectral resolution or modest S/N; incomplete wavelength coverage) limit the information available for the sample. More specifically, there seems to be no correlation between Lpeak and decline time Δt0.5, which is in the range of 20–50 days (Fig. 15, top-left panel). The lack of a correlation may point to variation in the progenitor mass loss or the strength of CSM-ejecta interaction. A trend may exist linking the peak luminosity to the ejected 56Ni mass (Fig. 15 top-right panel), although the lower limit for AT 2013la is somewhat discrepant with those of other ILRTs. We cannot rule out that the ejecta-CSM interaction significantly affects the late-time luminosity, therefore biasing the 56Ni mass estimates of the sampled objects. The limited range of 56Ni masses (∼1–5 × 10−3 M⊙) may be attributed to their progenitor masses lying within a narrow mass range (∼8–10 M⊙). As a comparison, both Type II and Type Ib/c SNe also show a similar correlation, but they have higher energies and wider 56Ni mass ranges than ILRTs (Hamuy 2001, 2003; Pastorello et al. 2005). 26, which was also proposed as a possible EC SN, has a significantly higher 56Ni mass (0.013–0.035 M⊙; Zhang et al. 2020), exceeding that of ILRTs (∼1–5 × 10−3 M⊙) by nearly one order of magnitude. In the bottom-left panel, the Hα velocity seems to be uncorrelated with Lpeak. The fact that v (Hα) = 600 ± 200 km s−1 for all objects suggests a common explosive or eruptive mechanism for all ILRTs, and again a relatively small range of progenitor masses. From this, the LBV giant eruption scenario appears less likely. The diagram showing bolometric versus Hα luminosity at peak reveals a trend, with ILRTs clustered along two different lines. In particular, we note that ILRTs along the lower line of the diagram (PTF10fqs, AT 2017be, and AT 2013la) show a clear plateau in their light curves. A wider sample of well-monitored ILRTs is necessary to confirm or rule out the putative trends mentioned above. Figure 15 shows how the different classes of objects discussed in this paper distribute in the Lpeak versus Δt0.5 and Hα velocity diagrams. The clear separation of ILRTs from the comparison SNe II suggests that they are a distinct class of transients.

thumbnail Fig. 15.

Peak luminosity (Lpeak) vs. decline time (Δt0.5) from Lpeak to 0.5Lpeak (top-left); Lpeak vs. 56Ni mass (top-right); Lpeak vs. vHα at peak (bottom-left); and Lpeak vs. Hα peak luminosity (bottom-right).

In Fig. 16, we also investigated the evolution of luminosity (L) against effective temperature (Teff) of ILRTs, and compared with giant eruptions of LBVs, claimed EC SNe, and some representative SNe II. The ILRTs tend to show a homogeneous evolution, and lie in a narrow strip in which the luminosity declines monotonically with temperature. SNe II lie in a region that is distinct from that where ILRTs and LBVs are found, and span a wide range of luminosities and temperatures. The physical homogeneity in this L-T diagram is suggestive of a common mechanism triggering the ILRTs and seems to exclude the LBV origin for ILRTs and enable us to distinguish ILRTs from traditional Type II SNe.

thumbnail Fig. 16.

Luminosity (L) vs. effective temperature (Teff). ILRTs are marked as solid lines with different colours, while the area where LBVs lie is marked in grey. Comparison SNe II lie in the upper part of the diagram and are labelled with dashed lines.

6.2. Plausible scenarios for ILRTs and conclusions

Although several plausible scenarios have been proposed to explain ILRTs, their nature is still debated. Possible scenarios include LBV-like eruptions, LRN-like events (stellar mergers), and EC-induced SN explosions.

Luminous blue variables originate from massive star (> 20 M⊙) eruptions, and show irregular light curves and SN IIn-like spectra27. A luminous progenitor is expected to be detected both in pre-outburst and post-outburst optical and NIR images. No 56Ni is expected to be produced. In addition, LBVs and ILRTs are distributed in two separate regions in the L-Teff diagram (see Fig. 16). Our observational arguments disfavour a LBV-like eruption scenario for ILRTs. However, we note that Andrews et al. (2020) proposed that a recent gap transient, AT 2019krl, was an unobscured ILRT eruption from a relatively massive star.

Luminous red novae are another subclass of gap transients, and show double-peaked (or triple-peaked) light curves and a remarkable spectral evolution. Specifically, the major drop in continuum temperature, the appearance of narrow metal lines in absorption, the dramatic change in the Hα strength and profile, and the emergence of molecular bands are typical spectral features of LRNe. In addition, the typical Hα FWHM velocities of LRNe are lower than 500 km s−1 (Pastorello et al. 2019b). Their colours become progressively redder; for example, the intrinsic B − V colour of an LRN can even reach 1.8 mag at late phases (see Fig. 4 of Pastorello et al. 2019b). The evolution of the SED and the radius of LRNe is markedly different from that of ILRTs (Cai et al. 2019; Stritzinger et al. 2020a). LRNe are likely produced by the coalescence of two stars, however we disfavour such a merging scenario for ILRTs.

Theory predicts that some stars with initial mass 8–10 M⊙ form a S-AGB star with a strongly degenerate oxygen-neon-magnesium (O-Ne-Mg) core surrounded by thin He and H envelopes (e.g., Nomoto 1984, 1987; Pumo et al. 2009; Takahashi et al. 2013; Moriya et al. 2014; Doherty et al. 2017; Nomoto & Leung 2017; Leung & Nomoto 2019; Leung et al. 2020). The final O-Ne-Mg core mass is determined by the competition between core increase from the He and H shell burning and mass loss through thermal pulses (Siess 2007; Langer 2012; Leung et al. 2020). Once the core reaches the Chandrasekhar mass (1.37 M⊙; Nomoto 1984), electron capture reactions on 20Ne and 24Mg take place, and eventually ignite an O-Ne deflagration that propagates outward. This type of CC explosion is referred to as an EC SN (Nomoto 1984; Zha et al. 2019; Leung et al. 2020). According to models, EC SNe are expected to explode with low energy, low ejected 56Ni mass, and typically in a dense and dusty CSM (e.g., Poelarends et al. 2008; Woosley & Heger 2015; Moriya & Eldridge 2016). Although Fe-core progenitors at the low-mass end of the CC SNe also explode with low energy (∼0.5 − 1.0 × 1050 erg) and small 56Ni mass (4–6 × 10−3 M⊙) (Stockinger et al. 2020), some of them (e.g., low-lominosity Type IIP SNe 2003gd, 2005cs, and 2008bk; Eldridge et al. 2007; Maund et al. 2014a,b) can be distinguished from EC SNe through the explosion mechanism, chemical composition, and nucleosynthesis (Jerkstrand et al. 2018). The possible correlations among physical parameters, the homogenous observational properties and the L-T evolution suggest that all ILRTs are regulated by the same mechanism, and the EC SN explosion is a plausible scenario. In particular, this scenario for ILRTs is supported by the following arguments:

  • The late-time light curves of SN 2008S and NGC 300 OT2008-1 decline approximately following the 56Co decay rate (i.e. ∼0.98 mag/100d). The 56Ni masses inferred from the bolometric light curve are of the order of 10−4–10−3 M⊙, consistent with the expected EC SN yields.

  • Investigation of archival optical and IR images of the transient locations obtained years before the explosion suggests that the ILRT progenitors are moderately massive, in the range between 8 and 15 M⊙. Their progenitors appear to be embedded in dusty cocoons (i.e. SN 2008S; Botticella et al. 2009; Prieto et al. 2009).

  • Inspection of the transient sites a few years after the explosion suggests that the objects are at least 15 times fainter than the quiescent progenitors (i.e. SN 2008S and NGC 300 OT; Adams et al. 2016). This supports the terminal SN explosion nature.

  • The estimated ILRT event rate is in fair agreement with EC SN theoretical predictions.

The observational properties described in this paper agree well with theoretical expectations, and we favour terminal EC SN explosions as the possible origin of ILRTs. Future facilities, such as the Vera C. Rubin Observatory28 and the Nancy Grace Roman Space Telescope29, will be essential for expanding the sample of ILRTs, and will be crucial in fine-tuning existing theoretical models.

1

For M85 OT2006-1 (hereafter M85 OT), the classification as ILRT or LRN is still controversial (Kulkarni et al. 2007; Pastorello et al. 2007; Rau et al. 2007).

2

International Astronomical Union (IAU) names for the sampled five ILRTs are used throughout this paper.

10

R25, also known as the de Vaucouleurs radius, is defined as the radius along the semi-major axis where the surface brightness in B-band is 25 magnitudes per square arcsecond (μB = 25 mag arcsec−2) (e.g., de Vaucouleurs et al. 1991; Corwin et al. 1994).

12

ecsnoopy is a package for SN photometry using PSF fitting and/or template subtraction developed by E. Cappellaro. A package description can be found at http://sngroup.oapd.inaf.it/snoopy.html

17

The IRAC Instrument Handbook is available on the website: https://irsa.ipac.caltech.edu/data/SPITZER/docs/irac/iracinstrumenthandbook/

19

Note that there were some images taken before AT 2010dn exploded, but as these were taken during the cryogenic phase of the Spitzer mission they would be less suitable for our data.

20

These fits were performed on the absolute light curves about −20 to +20 days from maximum.

21

ReFANN is a nonlinear interpolating tool based on Artificial Neural Networks that can reconstruct functions from data (see https://github.com/Guo-Jian-Wang/refann).

22

This value is computed through a weighted mean of values reported in Arnett & Fu (1989) and Bouchet et al. (1991).

23

These critical phases are fixed on the basis of relatively large changes in the colour evolution.

24

We note that we only include confirmed ILRTs prior to 2020, as systematic surveys and monitoring campaigns were almost globally suspended because of the Covid-19 pandemic in 2020. In addition to the objects listed in Table 1 (M85 OT was excluded in the rate estimate sample because of its controversial nature as discussed by Kulkarni et al. (2007), Pastorello et al. (2007), and Rau et al. (2007)), there are three confirmed ILRTs to be added in 2019: AT 2019abn (De et al. 2019; Nordin et al. 2019; Burke et al. 2019; Fremling et al. 2019), AT 2019ahd (Jha et al. 2019; Jha 2019; Tonry et al. 2019), and AT 2019udc (Malesani et al. 2019a,b; Siebert et al. 2019; Valenti et al. 2019).

25

Bright SNe archive: https://www.rochesterastronomy.org/ Asiago SN group archive: http://graspa.oapd.inaf.it/asnc.html

26

Hiramatsu et al. (2021) estimated a much lower 56Ni mass (∼8.6 × 10−3 M⊙) for SN 2018zd, adopting a very low distance obtained through the standard candle method (SCM). We note however that the SCM distance is discrepant with the significantly larger kinematic estimates (e.g., Zhang et al. 2020; Callis et al. 2021).

27

Although the [Ca II] doublet is sometimes visible in LBV spectra, no persistent signature of this feature has been observed in these events.

Acknowledgments

We thank the reviewer for his/her insightful comments that have improved the paper. Y.-Z. Cai thanks AP/AR/EC/MT/NER/SB for their training in the photometric and spectral reduction techniques. We are grateful to Han Lin (THU-THCA) and JuJia Zhang (CAS-YNAO) for providing the data of SN 2015bf and SN 2018zd, respectively. We thank F. Taddia and D. E. Wright for their few images taken with NOT/ALFOSC. We also thank M. Sullivan for his contribution in a spectrum observed with WHT/GB-GR. This work is funded by China Postdoctoral Science Foundation (grant no. 2021M691821). This work is supported by National Natural Science Foundation of China (NSFC grants 12033003, 11633002, 11325313, and 11761141001), National Program on Key Research and Development Project (grant no. 2016YFA0400803). DAH is supported by NSF grant AST-1911225. F. H. is supported by NSFC grant 11803021 and the Startup Fund for Youngman Research at SJTU. K. M. and S. J. P. are supported by H2020 ERC grant no. 758638. M.F. is supported by a Royal Society – Science Foundation Ireland University Research Fellowship. S. B., P. O., and M. T. are partially supported by PRIN-INAF 2017 of Toward the SKA and CTA era: discovery, localization, and physics of transient sources. E.C., N.E.R., L.T., F.O. acknowledge support from MIUR, PRIN 2017 (grant 20179ZF5KS) “The new frontier of the Multi-Messenger Astrophysics: follow-up of electromagnetic transient counterparts of gravitational wave sources”. L.Bo. acknowledges the funding support from Italian Space Agency (ASI) regulated by “Accordo ASI-INAF n. 2013-016-R.0 del 9 luglio 2013 e integrazione del 9 luglio 2015 CHEOPS Fasi A/B/C”. L. G. acknowledges financial support from the Spanish Ministry of Science, Innovation and Universities (MICIU) under the 2019 Ramón y Cajal program RYC2019-027683 and from the Spanish MICIU project PID2020-115253GA-I00. T. R. acknowledges the financial support of the Jenny and Antti Wihuri and the Vilho, Yrjö and Kalle Väisälä foundations. A.R. acknowledges support from ANID BECAS/DOCTORADO NACIONAL 21202412. M.G. is supported by the Polish NCN MAESTRO grant 2014/14/A/ST9/00121. M.S. is supported by generous grants from Villum FONDEN (13261,28021) and by a project grant (8021-00170B) from the Independent Research Fund Denmark. L. W. is sponsored (in part) by the Chinese Academy of Sciences (CAS) through a grant to the CAS South America Center for Astronomy (CASSACA) in Santiago, Chile. A.M.G. acknowledges financial support from the 2014–2020 ERDF Operational Programme and by the Department of Economy, Knowledge, Business and University of the Regional Government of Andalusia through the FEDER-UCA18-107404 grant. E.Co. acknowledges support from ANID project Basal AFB-170002. S.Mo. acknowledges the financial support of the Magnus Ehrnrooth Foundation. Research by S. V. is supported by NSF grants AST-1813176 and AST-2008108. This paper is partially based on observations obtained under the European supernova collaboration involved in ESO-NTT large programme 184.D-1140 led by Stefano Benetti and the ESO-NTT Large Program 188.D-3003 (the Public ESO Spectroscopic Survey for Transient Objects – PESSTO). Based on observations made with the Nordic Optical Telescope, operated by the Nordic Optical Telescope Scientific Association at the Observatorio del Roque de los Muchachos, La Palma, Spain, of the Instituto de Astrofisica de Canarias. Observations from the NOT were obtained through the NUTS and NUTS2 collaboration which are supported in part by the Instrument Centre for Danish Astrophysics (IDA). The data presented here were obtained in part with ALFOSC, which is provided by the Instituto de Astrofisica de Andalucia (IAA) under a joint agreement with the University of Copenhagen and NOTSA. The Liverpool Telescope is operated on the island of La Palma by Liverpool John Moores University in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias with financial support from the UK Science and Technology Facilities Council. The Italian Telescopio Nazionale Galileo (TNG) operated on the island of La Palma by the Fundación Galileo Galilei of the INAF (Istituto Nazionale di Astrofisica) at the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofísica de Canarias. Based on observations obtained with the Gran Telescopio Canarias (GTC), installed in the Spanish Observatorio del Roque de los Muchachos of the Instituto de Astrofisica de Canarias, in the island of La Palma. Based on observations collected at Copernico and Schmidt telescope (Asiago, Italy) of the INAF – Osservatorio Astronomico di Padova; and the Galilei Telescope of the Padova University in Asiago. Based on observations obtained at the international Gemini Observatory, a program of NSF’s NOIRLab, which is managed by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation. on behalf of the Gemini Observatory partnership: the National Science Foundation (United States), National Research Council (Canada), Agencia Nacional de Investigación y Desarrollo (Chile), Ministerio de Ciencia, Tecnología e Innovación (Argentina), Ministério da Ciência, Tecnologia, Inovações e Comunicações (Brazil), and Korea Astronomy and Space Science Institute (Republic of Korea). This work makes use of data from the Las Cumbres Observatory Network and the Global Supernova Project. This work is based on observations collected at the William Herschel Telescope (WHT), operated on the island of La Palma by the Isaac Newton Group of Telescope. This paper includes data gathered with the 6.5 meter Magellan Telescopes located at Las Campanas Observatory, Chile. Data for this study were gathered with the du Pont telescope at Las Campanas Observatory, Chile. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This work has made use of data from the Asteroid Terrestrial-impact Last Alert System (ATLAS) project. The Asteroid Terrestrial-impact Last Alert System (ATLAS) project is primarily funded to search for near earth asteroids through NASA grants NN12AR55G, 80NSSC18K0284, and 80NSSC18K1575; by products of the NEO search include images and catalogs from the survey area. This work was partially funded by Kepler/K2 grant J1944/80NSSC19K0112 and HST GO-15889, and STFC grants ST/T000198/1 and ST/S006109/1. The ATLAS science products have been made possible through the contributions of the University of Hawaii Institute for Astronomy, the Queen’s University Belfast, the Space Telescope Science Institute, the South African Astronomical Observatory, and The Millennium Institute of Astrophysics (MAS), Chile. The Pan-STARRS1 Surveys (PS1) and the PS1 public science archive have been made possible through contributions by the Institute for Astronomy, the University of Hawaii, the Pan-STARRS Project Office, the Max-Planck Society and its participating institutes, the Max Planck Institute for Astronomy, Heidelberg and the Max Planck Institute for Extraterrestrial Physics, Garching, the Johns Hopkins University, Durham University, the University of Edinburgh, the Queen’s University Belfast, the Harvard-Smithsonian Center for Astrophysics, the Las Cumbres Observatory Global Telescope Network Incorporated, the National Central University of Taiwan, the Space Telescope Science Institute, the National Aeronautics and Space Administration under Grant No. NNX08AR22G issued through the Planetary Science Division of the NASA Science Mission Directorate, the National Science Foundation Grant No. AST-1238877, the University of Maryland, Eotvos Lorand University (ELTE), the Los Alamos National Laboratory, and the Gordon and Betty Moore Foundation. The operation of Xingming Observatory was made possible by the generous support from the Xinjiang Astronomical Observatory of the Chinese Academy of Sciences. IRAF was distributed by the National Optical Astronomy Observatory, which was managed by the Association of Universities for Research in Astronomy (AURA) under a cooperative agreement with the National Science Foundation. This research has made use of the NASA/IPAC Extragalactic Database (NED), which is operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration.

References

  1. Adams, S. M., Kochanek, C. S., Prieto, J. L., et al. 2016, MNRAS, 460, 1645 [NASA ADS] [CrossRef] [Google Scholar]
  2. Adams, S. M., Blagorodnova, N., Kasliwal, M. M., et al. 2018, PASP, 130, 034202 [NASA ADS] [CrossRef] [Google Scholar]
  3. Albareti, F. D., Allende Prieto, C., Almeida, A., et al. 2017, ApJS, 233, 25 [Google Scholar]
  4. Andretta, V., Busà, I., Gomez, M. T., & Terranegra, L. 2005, A&A, 430, 669 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  5. Andrews, J. E., Clayton, G. C., Wesson, R., et al. 2011, AJ, 142, 45 [NASA ADS] [CrossRef] [Google Scholar]
  6. Andrews, J., Smith, N., & Van Dyk, S. D. 2018, ATel, 11441, 1 [NASA ADS] [Google Scholar]
  7. Andrews, J. E., Jencson, J. E., Van Dyk, S. D., et al. 2020, ApJ, 917, 63 [Google Scholar]
  8. Arcavi, I., Hosseinzadeh, G., Hiramatsu, D., et al. 2018, Transient Name Server Classification Report, 2018-2082, 1 [NASA ADS] [Google Scholar]
  9. Arnett, W. D., & Fu, A. 1989, ApJ, 340, 396 [NASA ADS] [CrossRef] [Google Scholar]
  10. Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
  11. Barsukova, E. A., Goranskij, V. P., Valeev, A. F., & Kaisin, S. S. 2014, Variable Stars [Google Scholar]
  12. Becker, A. 2015, HOTPANTS: High Order Transform of PSF ANd Template Subtraction [Google Scholar]
  13. Berger, E. 2010, ATel, 2655 [Google Scholar]
  14. Berger, E., Roth, K., Stubbs, C., et al. 2009a, Exotic Explosions and Eruptions: Exploring a New Transient Phase-Space with Pan-STARRS, NOAO Proposal [Google Scholar]
  15. Berger, E., Soderberg, A. M., Chevalier, R. A., et al. 2009b, ApJ, 699, 1850 [NASA ADS] [CrossRef] [Google Scholar]
  16. Berger, E., Marion, G. H., Hsiao, E., Foley, R., & Chornock, R. 2012, ATel, 4009 [Google Scholar]
  17. Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  18. Blagorodnova, N., Kotak, R., Polshaw, J., et al. 2017, ApJ, 834, 107 [NASA ADS] [CrossRef] [Google Scholar]
  19. Bond, H. E., Bedin, L. R., Bonanos, A. Z., et al. 2009, ApJ, 695, L154 [Google Scholar]
  20. Botticella, M. T., Pastorello, A., Smartt, S. J., et al. 2009, MNRAS, 398, 1041 [NASA ADS] [CrossRef] [Google Scholar]
  21. Bouchet, P., Danziger, I. J., & Lucy, L. B. 1991, AJ, 102, 1135 [NASA ADS] [CrossRef] [Google Scholar]
  22. Brown, T. M., Baliber, N., Bianco, F. B., et al. 2013, PASP, 125, 1031 [Google Scholar]
  23. Burke, J., Howell, D. A., Arcavi, I., et al. 2019, Transient Name Server Classification Report, 2019-328, 1 [NASA ADS] [Google Scholar]
  24. Busà, I., Aznar Cuadrado, R., Terranegra, L., Andretta, V., & Gomez, M. T. 2007, A&A, 466, 1089 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  25. Cai, Y.-Z., Pastorello, A., Fraser, M., et al. 2018, MNRAS, 480, 3424 [Google Scholar]
  26. Cai, Y. Z., Pastorello, A., Fraser, M., et al. 2019, A&A, 632, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  27. Callis, E., Fraser, M., Pastorello, A., et al. 2021, ArXiv e-prints [arXiv:2109.12943] [Google Scholar]
  28. Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [Google Scholar]
  29. Catchpole, R. M., Whitelock, P. A., Feast, M. W., et al. 1988, MNRAS, 231, 75 [Google Scholar]
  30. Catchpole, R. M., Whitelock, P. A., Menzies, J. W., et al. 1989, MNRAS, 237, 55 [Google Scholar]
  31. Chevalier, R. A., & Fransson, C. 1994, ApJ, 420, 268 [NASA ADS] [CrossRef] [Google Scholar]
  32. Chonis, T. S., & Gaskell, C. M. 2008, AJ, 135, 264 [NASA ADS] [CrossRef] [Google Scholar]
  33. Corwin, H. G. J., Buta, R. J., & de Vaucouleurs, G. 1994, AJ, 108, 2128 [NASA ADS] [CrossRef] [Google Scholar]
  34. De, K., Tartaglia, L., Andreoni, I., et al. 2019, ATel, 12433, 1 [NASA ADS] [Google Scholar]
  35. de Groot, M. 1969a, Bull. Astron. Inst. Netherlands, 20, 225 [NASA ADS] [Google Scholar]
  36. de Groot, M. 1969b, Commmun. Konkoly Obs. Hungary, 65, 203 [NASA ADS] [Google Scholar]
  37. de Vaucouleurs, G., de Vaucouleurs, A., Corwin, H. G. J., et al. 1991, Third Reference Catalogue of Bright Galaxies [Google Scholar]
  38. Doherty, C. L., Gil-Pons, P., Siess, L., Lattanzio, J. C., & Lau, H. H. B. 2015, MNRAS, 446, 2599 [Google Scholar]
  39. Doherty, C. L., Gil-Pons, P., Siess, L., & Lattanzio, J. C. 2017, PASA, 34 [CrossRef] [Google Scholar]
  40. Eastman, R. G., Woosley, S. E., Weaver, T. A., & Pinto, P. A. 1994, ApJ, 430, 300 [NASA ADS] [CrossRef] [Google Scholar]
  41. Eldridge, J. J., Mattila, S., & Smartt, S. J. 2007, MNRAS, 376, L52 [NASA ADS] [Google Scholar]
  42. Ferrarese, L., Mould, J. R., Kennicutt, R. C., Jr, et al. 2000, ApJ, 529, 745 [NASA ADS] [CrossRef] [Google Scholar]
  43. Filippenko, A. V. 1997, ARA&A, 35, 309 [NASA ADS] [CrossRef] [Google Scholar]
  44. Fransson, C., Ergon, M., Challis, P. J., et al. 2014, ApJ, 797, 118 [Google Scholar]
  45. Fremling, C., Dugas, A., & Sharma, Y. 2019, Transient Name Server Classification Report, 2019-2789, 1 [NASA ADS] [Google Scholar]
  46. Gerardy, C. L., Fesen, R. A., Nomoto, K., et al. 2002, ApJ, 575, 1007 [NASA ADS] [CrossRef] [Google Scholar]
  47. Grassberg, E. K., Imshennik, V. S., & Nadyozhin, D. K. 1971, Ap&SS, 10, 28 [Google Scholar]
  48. Hamuy, M. A. 2001, PhD Thesis, The University of Arizona, USA [Google Scholar]
  49. Hamuy, M. 2003, ApJ, 582, 905 [NASA ADS] [CrossRef] [Google Scholar]
  50. Heinze, A. N., Tonry, J. L., Denneau, L., et al. 2018, AJ, 156, 241 [Google Scholar]
  51. Hiramatsu, D., Howell, D. A., Van Dyk, S. D., et al. 2021, Nat. Astron., 5, 903 [NASA ADS] [CrossRef] [Google Scholar]
  52. Howerton, S., Prieto, J., Drake, A. J., et al. 2012, ATel, 4004 [Google Scholar]
  53. Humphreys, R. M., & Davidson, K. 1994, PASP, 106, 1025 [NASA ADS] [CrossRef] [Google Scholar]
  54. Humphreys, R. M., Davidson, K., & Smith, N. 1999, PASP, 111, 1124 [NASA ADS] [CrossRef] [Google Scholar]
  55. Humphreys, R. M., Bond, H. E., Bedin, L. R., et al. 2011, ApJ, 743, 118 [NASA ADS] [CrossRef] [Google Scholar]
  56. Jencson, J. E., Adams, S. M., Bond, H. E., et al. 2019, ApJ, 880, L20 [NASA ADS] [CrossRef] [Google Scholar]
  57. Jerkstrand, A., Ertl, T., Janka, H. T., et al. 2018, MNRAS, 475, 277 [Google Scholar]
  58. Jha, S. 2019, Transient Name Server Classification Report, 2019-1237, 1 [NASA ADS] [Google Scholar]
  59. Jha, S. W., Eweis, Y., Camacho-Neves, Y., et al. 2019, ATel, 12454, 1 [NASA ADS] [Google Scholar]
  60. Jordi, K., Grebel, E. K., & Ammon, K. 2006, A&A, 460, 339 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  61. Kashi, A., Frankowski, A., & Soker, N. 2010, ApJ, 709, L11 [NASA ADS] [CrossRef] [Google Scholar]
  62. Kasliwal, M. M. 2012, PASA, 29, 482 [NASA ADS] [CrossRef] [Google Scholar]
  63. Kasliwal, M. M., Kulkarni, S. R., Arcavi, I., et al. 2011, ApJ, 730, 134 [NASA ADS] [CrossRef] [Google Scholar]
  64. Kitaura, F. S., Janka, H. T., & Hillebrandt, W. 2006, A&A, 450, 345 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  65. Kochanek, C. S. 2011, ApJ, 741, 37 [NASA ADS] [CrossRef] [Google Scholar]
  66. Kochanek, C. S., Adams, S. M., & Belczynski, K. 2014, MNRAS, 443, 1319 [NASA ADS] [CrossRef] [Google Scholar]
  67. Kozyreva, A., Baklanov, P., Jones, S., Stockinger, G., & Janka, H.-T. 2021, MNRAS, 503, 797 [NASA ADS] [CrossRef] [Google Scholar]
  68. Kulkarni, S., & Kasliwal, M. M. 2009, in Astrophysics with All-Sky X-Ray Observations, eds. N. Kawai, T. Mihara, M. Kohama, & M. Suzuki, 312 [Google Scholar]
  69. Kulkarni, S. R., Ofek, E. O., Rau, A., et al. 2007, Nature, 447, 458 [NASA ADS] [CrossRef] [Google Scholar]
  70. Lambert, D. L., Mallia, E. A., & Warner, B. 1969, Sol. Phys., 7, 11 [NASA ADS] [CrossRef] [Google Scholar]
  71. Landolt, A. U. 1992, AJ, 104, 340 [Google Scholar]
  72. Langer, N. 2012, ARA&A, 50, 107 [CrossRef] [Google Scholar]
  73. Leung, S.-C., & Nomoto, K. 2019, PASA, 36, e006 [NASA ADS] [CrossRef] [Google Scholar]
  74. Leung, S.-C., Nomoto, K., & Suzuki, T. 2020, ApJ, 889, 34 [NASA ADS] [CrossRef] [Google Scholar]
  75. Li, H., & McCray, R. 1993, ApJ, 405, 730 [Google Scholar]
  76. Lin, H., Wang, X., Zhang, J., et al. 2021, MNRAS, 505, 4890 [NASA ADS] [CrossRef] [Google Scholar]
  77. Lipunov, V. M., Blinnikov, S., Gorbovskoy, E., et al. 2017, MNRAS, 470, 2339 [NASA ADS] [CrossRef] [Google Scholar]
  78. Lundqvist, P., & Fransson, C. 1996, ApJ, 464, 924 [NASA ADS] [CrossRef] [Google Scholar]
  79. Lundqvist, P., Nyholm, A., Taddia, F., et al. 2015, A&A, 577, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  80. Lundqvist, P., Lundqvist, N., Vlahakis, C., et al. 2020, MNRAS, 496, 1834 [NASA ADS] [CrossRef] [Google Scholar]
  81. MacLeod, M., Macias, P., Ramirez-Ruiz, E., et al. 2017, ApJ, 835, 282 [NASA ADS] [CrossRef] [Google Scholar]
  82. Malesani, D. B., Charalampopoulos, P., Angus, C., Izzo, L., & Yaron, O. 2019a, Transient Name Server Classification Report, 2019-2881, 1 [NASA ADS] [Google Scholar]
  83. Malesani, D. B., Charalampopoulos, P., Angus, C. R., et al. 2019b, Transient Name Server AstroNote, 123, 1 [NASA ADS] [Google Scholar]
  84. Mallik, S. V. 1997, A&AS, 124, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  85. Mallik, S. V. 1998, Bull. Astron. Soc. India, 26, 479 [NASA ADS] [Google Scholar]
  86. Margheim, S. J., Rest, A., & Smartt, S. J. 2013, ATel, 4798 [Google Scholar]
  87. Martin, J., Fuhrmeister, B., Mittag, M., et al. 2017, A&A, 605, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  88. Mauerhan, J. C., Van Dyk, S. D., Johansson, J., et al. 2018, MNRAS, 473, 3765 [NASA ADS] [CrossRef] [Google Scholar]
  89. Maund, J. R., Mattila, S., Ramirez-Ruiz, E., & Eldridge, J. J. 2014a, MNRAS, 438, 1577 [NASA ADS] [CrossRef] [Google Scholar]
  90. Maund, J. R., Reilly, E., & Mattila, S. 2014b, MNRAS, 438, 938 [NASA ADS] [CrossRef] [Google Scholar]
  91. Moriya, T. J., & Eldridge, J. J. 2016, MNRAS, 461, 2155 [NASA ADS] [CrossRef] [Google Scholar]
  92. Moriya, T. J., Tominaga, N., Langer, N., et al. 2014, A&A, 569, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  93. Moriya, T. J., Stritzinger, M. D., Taddia, F., et al. 2020, A&A, 641, A148 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  94. Munari, U., & Zwitter, T. 1997, A&A, 318, 269 [NASA ADS] [Google Scholar]
  95. Munari, U., Henden, A., Kiyota, S., et al. 2002, A&A, 389, L51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  96. Nomoto, K. 1984, ApJ, 277, 791 [NASA ADS] [CrossRef] [Google Scholar]
  97. Nomoto, K. 1987, ApJ, 322, 206 [NASA ADS] [CrossRef] [Google Scholar]
  98. Nomoto, K., & Leung, S.-C. 2017, in Electron Capture Supernovae from Super Asymptotic Giant Branch Stars, eds. A. W. Alsabti, & P. Murdin, 483 [Google Scholar]
  99. Nordin, J., Brinnel, V., Giomi, M., et al. 2019, Transient Name Server Discovery Report, 2019-141, 1 [NASA ADS] [Google Scholar]
  100. Nyholm, A., Sollerman, J., Taddia, F., et al. 2017, A&A, 605, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  101. Osterbrock, D. E. 1951, ApJ, 114, 469 [NASA ADS] [CrossRef] [Google Scholar]
  102. Pastorello, A., & Fraser, M. 2019, Nat. Astron., 3, 676 [Google Scholar]
  103. Pastorello, A., Zampieri, L., Turatto, M., et al. 2004, MNRAS, 347, 74 [Google Scholar]
  104. Pastorello, A., Ramina, M., Zampieri, L., et al. 2005, in 192: Cosmic Explosions, On the 10th Anniversary of SN1993J, eds. J. M. Marcaide, K. W. Weiler, et al., IAU Colloq., 99, 195 [CrossRef] [Google Scholar]
  105. Pastorello, A., Sauer, D., Taubenberger, S., et al. 2006, MNRAS, 370, 1752 [NASA ADS] [CrossRef] [Google Scholar]
  106. Pastorello, A., Della Valle, M., Smartt, S. J., et al. 2007, Nature, 449, 1 [Google Scholar]
  107. Pastorello, A., Valenti, S., Zampieri, L., et al. 2009, MNRAS, 394, 2266 [Google Scholar]
  108. Pastorello, A., Chen, T. W., Cai, Y. Z., et al. 2019a, A&A, 625, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  109. Pastorello, A., Mason, E., Taubenberger, S., et al. 2019b, A&A, 630, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  110. Pastorello, A., Fraser, M., Valerin, G., et al. 2021a, A&A, 646, A119 [EDP Sciences] [Google Scholar]
  111. Pastorello, A., Valerin, G., Fraser, M., et al. 2021b, A&A, 647, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  112. Pejcha, O., Metzger, B. D., & Tomida, K. 2016, MNRAS, 461, 2527 [NASA ADS] [CrossRef] [Google Scholar]
  113. Pejcha, O., Metzger, B. D., Tyles, J. G., & Tomida, K. 2017, ApJ, 850, 59 [NASA ADS] [CrossRef] [Google Scholar]
  114. Pignata, G., Maza, J., Antezana, R., et al. 2009, in Probing Stellar Populations Out to the Distant Universe: Cefalu 2008, Proceedings of the International Conference, eds. G. Giobbi, A. Tornambe, G. Raimondo, et al., Am. Inst. Phys. Conf. Ser., 1111, 551 [NASA ADS] [CrossRef] [Google Scholar]
  115. Pilyugin, L. S., Vílchez, J. M., & Contini, T. 2004, A&A, 425, 849 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  116. Poelarends, A. J. T., Herwig, F., Langer, N., & Heger, A. 2008, ApJ, 675, 614 [Google Scholar]
  117. Poznanski, D., Ganeshalingam, M., Silverman, J. M., & Filippenko, A. V. 2011, MNRAS, 415, L81 [NASA ADS] [CrossRef] [Google Scholar]
  118. Pozzo, M., Meikle, W. P. S., Rayner, J. T., et al. 2006, MNRAS, 368, 1169 [CrossRef] [Google Scholar]
  119. Prieto, J. L., Kistler, M. D., Thompson, T. A., et al. 2008, ApJ, 681, L9 [NASA ADS] [CrossRef] [Google Scholar]
  120. Prieto, J. L., Sellgren, K., Thompson, T. A., & Kochanek, C. S. 2009, ApJ, 705, 1425 [NASA ADS] [CrossRef] [Google Scholar]
  121. Pumo, M. L., Turatto, M., Botticella, M. T., et al. 2009, ApJ, 705, L138 [NASA ADS] [CrossRef] [Google Scholar]
  122. Rau, A., Kulkarni, S. R., Ofek, E. O., & Yan, L. 2007, ApJ, 659, 1536 [NASA ADS] [CrossRef] [Google Scholar]
  123. Reguitti, A., Pumo, M. L., Mazzali, P. A., et al. 2021, MNRAS, 501, 1059 [Google Scholar]
  124. Sahu, D. K., Anupama, G. C., Srividya, S., & Muneer, S. 2006, MNRAS, 372, 1315 [Google Scholar]
  125. Salpeter, E. E. 1955, ApJ, 121, 161 [Google Scholar]
  126. Sandage, A., & Tammann, G. A. 1990, ApJ, 365, 1 [NASA ADS] [CrossRef] [Google Scholar]
  127. Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [Google Scholar]
  128. Schlegel, E. M. 1990, MNRAS, 244, 269 [NASA ADS] [Google Scholar]
  129. Siebert, M. R., Dimitriadis, G., Kilpatrick, C. D., et al. 2019, Transient Name Server Classification Report, 2019-2287, 1 [NASA ADS] [Google Scholar]
  130. Siess, L. 2007, A&A, 476, 893 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  131. Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [Google Scholar]
  132. Smartt, S. J., Valenti, S., Fraser, M., et al. 2015, A&A, 579, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  133. Smith, N. 2017, Interacting Supernovae: Types IIn and Ibn, 403 [Google Scholar]
  134. Smith, N., Ganeshalingam, M., Chornock, R., et al. 2009, ApJ, 697, L49 [Google Scholar]
  135. Smith, N., Li, W., Silverman, J. M., Ganeshalingam, M., & Filippenko, A. V. 2011, MNRAS, 415, 773 [NASA ADS] [CrossRef] [Google Scholar]
  136. Smith, N., Andrews, J. E., Van Dyk, S. D., et al. 2016, MNRAS, 458, 950 [Google Scholar]
  137. Smith, K. W., Smartt, S. J., Young, D. R., et al. 2020, PASP, 132, 085002 [Google Scholar]
  138. Soker, N. 2001a, A&A, 377, 672 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  139. Soker, N. 2001b, MNRAS, 325, 584 [NASA ADS] [CrossRef] [Google Scholar]
  140. Soker, N. 2003, ApJ, 597, 513 [CrossRef] [Google Scholar]
  141. Soker, N. 2020, ApJ, 893, 20 [Google Scholar]
  142. Soker, N. 2021, Res. Astron. Astrophys., 21, 112 [Google Scholar]
  143. Soker, N., & Kaplan, N. 2021, Res. Astron. Astrophys., 21, 090 [Google Scholar]
  144. Soker, N., & Kashi, A. 2012, ApJ, 746, 100 [NASA ADS] [CrossRef] [Google Scholar]
  145. Soker, N., & Kashi, A. 2016, MNRAS, 462, 217 [NASA ADS] [CrossRef] [Google Scholar]
  146. Soker, N., & Tylenda, R. 2003, ApJ, 582, L105 [NASA ADS] [CrossRef] [Google Scholar]
  147. Soker, N., & Tylenda, R. 2006, MNRAS, 373, 733 [NASA ADS] [CrossRef] [Google Scholar]
  148. Soma, D., Baron, E., & Hauschildt, P. H. 2010, MNRAS, 401, 2081 [NASA ADS] [CrossRef] [Google Scholar]
  149. Sorce, J. G., Tully, R. B., Courtois, H. M., et al. 2014, MNRAS, 444, 527 [Google Scholar]
  150. Spergel, D. N., Bean, R., Doré, O., et al. 2007, ApJS, 170, 377 [CrossRef] [Google Scholar]
  151. Stephens, H. F., Zheng, W., & Filippenko, A. V. 2017, Transient Name Server Discovery Report, 33 [Google Scholar]
  152. Stetson, P. B. 1987, PASP, 99, 191 [Google Scholar]
  153. Stockinger, G., Janka, H. T., Kresse, D., et al. 2020, MNRAS, 496, 2039 [Google Scholar]
  154. Stritzinger, M. D., Taddia, F., Fraser, M., et al. 2020a, A&A, 639, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  155. Stritzinger, M. D., Taddia, F., Fraser, M., et al. 2020b, A&A, 639, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  156. Szczygieł, D. M., Prieto, J. L., Kochanek, C. S., et al. 2012, ApJ, 750, 77 [CrossRef] [Google Scholar]
  157. Taddia, F., Stritzinger, M. D., Sollerman, J., et al. 2013, A&A, 555, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  158. Takahashi, K., Yoshida, T., & Umeda, H. 2013, ApJ, 771, 28 [NASA ADS] [CrossRef] [Google Scholar]
  159. Tartaglia, L., Pastorello, A., Benetti, S., et al. 2014, ATel, 5737, 1 [NASA ADS] [Google Scholar]
  160. Tartaglia, L., Pastorello, A., Sollerman, J., et al. 2020, A&A, 635, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  161. Terry, J. N., Paturel, G., & Ekholm, T. 2002, A&A, 393, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  162. Theureau, G., Rauzy, S., Bottinelli, L., & Gouguenheim, L. 1998, A&A, 340, 21 [NASA ADS] [Google Scholar]
  163. Thompson, T. A., Prieto, J. L., Stanek, K. Z., et al. 2009, ApJ, 705, 1364 [NASA ADS] [CrossRef] [Google Scholar]
  164. Tody, D. 1986, in Instrumentation in astronomy VI, ed. D. L. Crawford, Proc. SPIE, 627, 733 [Google Scholar]
  165. Tody, D. 1993, in Astronomical Data Analysis Software and Systems II, eds. R. J. Hanisch, R. J. V. Brissenden, & J. Barnes, ASP Conf. Ser., 52, 173 [Google Scholar]
  166. Tominaga, N., Blinnikov, S. I., & Nomoto, K. 2013, ApJ, 771, L12 [NASA ADS] [CrossRef] [Google Scholar]
  167. Tonry, J. L., Denneau, L., Heinze, A. N., et al. 2018, PASP, 130, 064505 [Google Scholar]
  168. Tonry, J., Denneau, L., Heinze, A., et al. 2019, Transient Name Server Discovery Report, 2019-161, 1 [NASA ADS] [Google Scholar]
  169. Tully, R. B., Courtois, H. M., Dolphin, A. E., et al. 2013, AJ, 146, 86 [NASA ADS] [CrossRef] [Google Scholar]
  170. Tully, R. B., Courtois, H. M., & Sorce, J. G. 2016, AJ, 152, 50 [Google Scholar]
  171. Turatto, M., Benetti, S., & Cappellaro, E. 2003, in From Twilight to Highlight: The Physics of Supernovae, eds. W. Hillebrandt, & B. Leibundgut, 200 [Google Scholar]
  172. Tylenda, R., Hajduk, M., Kamiński, T., et al. 2011, A&A, 528, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  173. Vagnozzi, S. 2019, Atoms, 7, 41 [Google Scholar]
  174. Valenti, S., Sand, D. J., Wyatt, S., et al. 2019, Transient Name Server Discovery Report, 2019-2263, 1 [NASA ADS] [Google Scholar]
  175. Van Dyk, S. D., Peng, C. Y., King, J. Y., et al. 2000, PASP, 112, 1532 [NASA ADS] [CrossRef] [Google Scholar]
  176. von Steiger, R., & Zurbuchen, T. H. 2016, ApJ, 816, 13 [Google Scholar]
  177. Wanajo, S., Nomoto, K., Janka, H.-T., Kitaura, F. S., & Müller, B. 2009, ApJ, 695, 208 [NASA ADS] [CrossRef] [Google Scholar]
  178. Wang, G.-J., Ma, X.-J., Li, S.-Y., & Xia, J.-Q. 2020, ApJS, 246, 13 [NASA ADS] [CrossRef] [Google Scholar]
  179. Wang, G.-J., Ma, X.-J., & Xia, J.-Q. 2021, MNRAS, 501, 5714 [NASA ADS] [Google Scholar]
  180. Whitelock, P. A., Catchpole, R. M., Menzies, J. W., et al. 1988, MNRAS, 234, 5 [NASA ADS] [Google Scholar]
  181. Williams, S. C., Jones, D., Pessev, P., et al. 2020, A&A, 637, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  182. Woosley, S. E., & Heger, A. 2015, ApJ, 810, 34 [NASA ADS] [CrossRef] [Google Scholar]
  183. Yaron, O., & Gal-Yam, A. 2012, PASP, 124, 668 [Google Scholar]
  184. Yunus, S., Zheng, W., & Filippenko, A. V. 2018, Transient Name Server Discovery Report, 338 [Google Scholar]
  185. Zha, S., Leung, S.-C., Suzuki, T., & Nomoto, K. 2019, ApJ, 886, 22 [NASA ADS] [CrossRef] [Google Scholar]
  186. Zhang, J., Xu, L., & Wang, X. 2018, ATel, 11379, 1 [NASA ADS] [Google Scholar]
  187. Zhang, J., Wang, X., József, V., et al. 2020, MNRAS, 498, 84 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Basic information for observational facilities used

We report the basic information for observational facilities in Table A.1, which were used for the five ILRTs.

Table A.1.

Information on the instrumental setups.

Appendix B: Reddenings and distances adopted for SNe II

In this section, the reddenings and distances adopted for the comparison SNe II are reported in Table B.1, along with their respective references.

Table B.1.

Reddenings and distances of SN 2018zd, SN 2018hwm, SN 2015bf, SN 1999br, and SN 2005cs.

Appendix C: Photometric data of ILRTs

The photometric data of five ILRTs and associated errors are reported in this section. In addition, black body parameters and SED evolution of individual ILRT AT 2010dn are presented in Table C.4 and Figure C.1, respectively. Our observations will be made public via the Weizmann Interactive Supernova Data Repository (WISeREP; Yaron & Gal-Yam 2012).

Table C.1.

Optical (BVuriz) photometric measurements of AT 2010dn.

Table C.2.

NIR (JHK) photometric measurements of AT 2010dn.

Table C.3.

Spitzer IRAC photometry of AT 2010dn (AB mag). Uncertainties are given in parentheses.

Table C.4.

Parameters of blackbody fit to the uBVrizJHK bands of AT 2010dn. Uncertainties are given in parentheses.

thumbnail Fig. C.1.

SED evolution of AT 2010dn. The lines are the best-fit BBs, which are overplotted on each SED. Blue lines are the fits of the single BB, while red lines are the fits of the double BB. The epochs marked to the right of each SED are relative to the r-band maximum. Each SED has been sifted by an arbitrary constant for clarity.

Table C.5.

Optical (UBVRI) photometric measurements of AT 2012jc.

Table C.6.

Optical (UBVRI) photometric measurements of AT 2013lb.

Table C.7.

NIR (JHK) photometric measurements of AT 2013lb.

Table C.8.

Optical (BVugriz) photometric measurements of AT 2013la.

Table C.9.

Optical (BVgriz) photometric measurements of AT 2018aes.

Table C.10.

NIR (JHK) photometric measurements of AT 2018aes.

All Tables

Table 1.

Basic information for the ILRT host galaxies.

In the text
Table 2.

Decline rates of the light curves of individual ILRTs (mag/100d), along with their uncertainties.

In the text
Table 3.

Light-curve parameters for ILRTs.

In the text
Table 4.

Log of spectroscopic observations of ILRTs.

In the text
Table 5.

Physical parameters inferred from the optical spectra of the ILRTs sample.

In the text
Table A.1.

Information on the instrumental setups.

In the text
Table B.1.

Reddenings and distances of SN 2018zd, SN 2018hwm, SN 2015bf, SN 1999br, and SN 2005cs.

In the text
Table C.1.

Optical (BVuriz) photometric measurements of AT 2010dn.

In the text
Table C.2.

NIR (JHK) photometric measurements of AT 2010dn.

In the text
Table C.3.

Spitzer IRAC photometry of AT 2010dn (AB mag). Uncertainties are given in parentheses.

In the text
Table C.4.

Parameters of blackbody fit to the uBVrizJHK bands of AT 2010dn. Uncertainties are given in parentheses.

In the text
Table C.5.

Optical (UBVRI) photometric measurements of AT 2012jc.

In the text
Table C.6.

Optical (UBVRI) photometric measurements of AT 2013lb.

In the text
Table C.7.

NIR (JHK) photometric measurements of AT 2013lb.

In the text
Table C.8.

Optical (BVugriz) photometric measurements of AT 2013la.

In the text
Table C.9.

Optical (BVgriz) photometric measurements of AT 2018aes.

In the text
Table C.10.

NIR (JHK) photometric measurements of AT 2018aes.

In the text

All Figures

thumbnail Fig. 1.

Top-left: AT 2010dn in one of the spiral arms of the host galaxy. Sloan r-band image taken in June 2010 at 19 with the 2m robotic Faulkes Telescope North (FTN) operated by Las Cumbres Observatory (LCO; Brown et al. 2013). Top-middle: AT 2012jc at the north edge of its host galaxy. Johnson-Cousins R-band image obtained in April 2012 at 06 with the 0.41m PROMPT5 telescope. Top-right: AT 2013lb in the outskirts of its host galaxy. Johnson-Cousins R-band image obtained in February 2013 at 20 with the 2m fully robotic Liverpool Telescope (LT) with RATCam. Bottom-left: AT 2013la at the east edge of its galaxy. A zoom-in of the transient position is shown in the lower-left corner. Sloan r-band image obtained in February 2014 at 12 with the LT equipped with IO:O. Bottom-right: AT 2018aes and its host galaxy. LT/IO:O Sloan r-band image obtained in May 2018 at 17 with a blow-up of the transient site in the lower-left inset.
In the text
thumbnail Fig. 2.

Multi-band light curves of AT 2010dn (top-left), AT 2012jc (top-right), AT 2013lb (middle-left), AT 2013la (middle-right), and AT 2018aes (bottom). The dashed vertical lines indicate the R/r-band maximum time. Upper limits are marked by empty symbols with arrows. The light curves are shifted with some constants for clarity and the shift amount is reported at the top. The errors of most magnitudes are smaller than the plotted symbol sizes.
In the text
thumbnail Fig. 3.

Colour evolution of ILRTs, along with those of the comparison objects: SN 2018zd (Zhang et al. 2020), SN 2018hwm (Reguitti et al. 2021), SN 1999br (Pastorello et al. 2004), and SN 2005cs (Pastorello et al. 2006, 2009). (a) B − V colour curves of ILRTs; (b) R − I/r − i colour curves; (c) J − K colour curves; (d) and (e) show the same colours as panels a and b until +100 days without error bars for clarity. All phases are with respect to the R/r-band maximum.
In the text
thumbnail Fig. 4.

Comparison of the R/r-band absolute light curves of ILRTs and SN 2018zd, SN 2018hwm, SN 1999br, and SN 2005cs. Reddenings and distance moduli of the comparison objects are taken from their respective papers (also see Table B.1). The dashed vertical line indicates the time of r-band maximum light. Upper limits are marked by empty symbols with down arrows.
In the text
thumbnail Fig. 5.

Pseudo-bolometric B to I/i light curves of ILRTs and comparison objects. The dashed vertical line indicates the time of R/r-band maximum light.
In the text
thumbnail Fig. 6.

Top panel: two-component black body fits to the SED of AT 2010dn obtained from optical to MIR at the epoch of +30.6 days. Bottom panel: single black body fit for AT 2010dn in the MIR domain at very late phase of +1332.5 days. Although this fit could reproduce the late MIR data, the fitted temperature should be considered as an indicative value. The MIR measurements were obtained from the Spitzer Space Telescope + IRAC images at 3.6 μm and 4.5 μm.
In the text
thumbnail Fig. 7.

Spectral evolution of AT 2010dn (top-left), AT 2012jc (top-right), AT 2013lb (middle-left), AT 2013la (middle-right), and AT 2018aes (bottom). The epochs marked to the right of each spectrum are relative to the R/r-band maximum. The ⨁ symbols mark the position of the strongest telluric absorption bands. The spectra are only corrected for redshift.
In the text
thumbnail Fig. 8.

Line identification in the spectra of the five transients presented in this paper. The spectra have been corrected for redshift and reddening. Phases are relative to their R/r-band maximum.
In the text
thumbnail Fig. 9.

Spectral comparison of a sample of ILRTs and SN 2018zd, SN 2018hwm, SN 2015bf, SN 1999br, and SN 2005cs. The spectra of M85 OT, SN 2008S, PTF10fqs, AT 2017be, SN 2018zd, SN 2018hwm, SN 2015bf, SN 1999br, and SN 2005cs are taken from Kulkarni et al. (2007), Botticella et al. (2009), Kasliwal et al. (2011), Cai et al. (2018), Zhang et al. (2020), Reguitti et al. (2021), Lin et al. (2021), Pastorello et al. (2004), and Pastorello et al. (2006, 2009). The right panel shows the region of [Ca II], marked with the grey-shaded region in the left panel. All spectra were obtained at similar epochs from the R/r-band maxima, and were corrected for redshift and reddening.
In the text
thumbnail Fig. 10.

Evolution of Hα and [Ca II] in ILRTs. The spectra of M85 OT, SN 2008S, PTF10fqs, and AT 2017be, downloaded from WISeREP archive (https://wiserep.weizmann.ac.il/) (Yaron & Gal-Yam 2012), were published by Kulkarni et al. (2007), Botticella et al. (2009), Kasliwal et al. (2011), and Cai et al. (2018). All spectra were corrected for redshift and reddening.
In the text
thumbnail Fig. 11.

Evolution of the black body temperature (top) and the Hα luminosity (bottom) for a sample of ILRTs, and SN 2018zd (Zhang et al. 2020), SN 2018hwm (Reguitti et al. 2021), SN 2015bf (Lin et al. 2021), SN 1999br (Pastorello et al. 2004), and SN 2005cs (Pastorello et al. 2006, 2009).
In the text
thumbnail Fig. 12.

Hα velocity evolution of a sample of ILRTs, SN 2018zd (Zhang et al. 2020), SN 2018hwm (Reguitti et al. 2021), SN 2015bf (Lin et al. 2021), SN 1999br (Pastorello et al. 2004), and SN 2005cs (Pastorello et al. 2006, 2009). The Hα velocities were estimated by measuring the FWHM for ILRTs, while those for SNe II were determined from the position of the minimum of the absorption component.
In the text
thumbnail Fig. 13.

Evolution of the Hα profile in selected spectra of the ILRT AT 2013la (left panel), SN 2018zd (Zhang et al. 2020, middle panel), and the underluminous Type IIP SN 2005cs (Pastorello et al. 2006, 2009, right panel). The Hα lines are shown in the velocity space, with zero velocity (rest wavelength) being marked by a grey dashed line.
In the text
thumbnail Fig. 14.

Ratio of Hα to [Ca II] (total profiles at λ ≈ 7300 Å) luminosities until phase ∼30 d.
In the text
thumbnail Fig. 15.

Peak luminosity (Lpeak) vs. decline time (Δt0.5) from Lpeak to 0.5Lpeak (top-left); Lpeak vs. 56Ni mass (top-right); Lpeak vs. vHα at peak (bottom-left); and Lpeak vs. Hα peak luminosity (bottom-right).
In the text
thumbnail Fig. 16.

Luminosity (L) vs. effective temperature (Teff). ILRTs are marked as solid lines with different colours, while the area where LBVs lie is marked in grey. Comparison SNe II lie in the upper part of the diagram and are labelled with dashed lines.
In the text
thumbnail Fig. C.1.

SED evolution of AT 2010dn. The lines are the best-fit BBs, which are overplotted on each SED. Blue lines are the fits of the single BB, while red lines are the fits of the double BB. The epochs marked to the right of each SED are relative to the r-band maximum. Each SED has been sifted by an arbitrary constant for clarity.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.