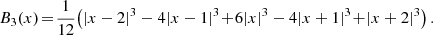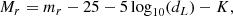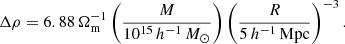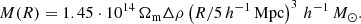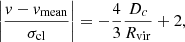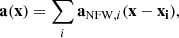| Issue |
A&A
Volume 649, May 2021
|
|
|---|---|---|
| Article Number | A51 | |
| Number of page(s) | 23 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/202040200 | |
| Published online | 12 May 2021 | |
The Corona Borealis supercluster: connectivity, collapse, and evolution
1
Tartu Observatory, University of Tartu, Observatooriumi 1, 61602 Tõravere, Estonia
e-mail: maret.einasto@ut.ee
2
Estonian Academy of Sciences, Kohtu 6, 10130 Tallinn, Estonia
3
ICRANet, Piazza della Repubblica 10, 65122 Pescara, Italy
4
Tuorla Observatory, Department of Physics and Astronomy, University of Turku, 20014 Turku, Finland
5
Biodiversity Unit, University of Turku, 20014 Turku, Finland
Received:
22
December
2020
Accepted:
23
February
2021
Context. Rich superclusters of galaxies represent dynamically active environments in which galaxies and their systems form and evolve.
Aims. We study the dynamical properties and connectivity of the richest galaxy clusters in the Corona Borealis (CB) supercluster and of the whole supercluster, and analyse star formation of galaxies in them with the aim to understand the evolution of the supercluster and the galaxies within it. We compare it with the supercluster SCl A2142.
Methods. We used the luminosity-density field to determine the high-density cores of the CB. We identified the richest galaxy clusters in them and studied the dynamical state of the clusters, analysed their substructure, and studied the star formation properties of galaxies in them using normal mixture modelling and the projected phase space diagram. We determined filaments in the supercluster to analyse the connectivity of clusters. To understand the possible future evolution of the CB, we compared the mass distribution in it with predictions from the spherical collapse model and analysed the gravitational acceleration field in the CB.
Results. The richest clusters in the high-density cores of the CB are the Abell clusters A2065, A2061 (together with A2067), A2089, and Gr2064. At a radius R30 around each cluster (corresponding to the density contrast Δρ ≈ 30), the galaxy distribution shows a minimum. The R30 values for individual clusters lie in the range of 3 − 6 h−1 Mpc. The radii of the clusters (splashback radii) lie in the range of Rcl ≈ 2 − 3 Rvir. The projected phase space diagrams and the comparison with the spherical collapse model suggest that R30 regions have passed turnaround and are collapsing, forming infall regions around each cluster. Galaxies in the richest cluster of the CB, A2065, and in its infall region have on average younger stellar populations than other clusters and their environment. The cluster A2061 has the highest fraction of galaxies with very old stellar populations, similar to those in A2142. The number of long filaments that begin near clusters vary from one near A2089 to five near A2061. The total connectivity of these clusters (the number of infalling groups and filaments) varies from two to nine.
Conclusions. During the future evolution, the clusters in the main part of the CB may merge and form one of the largest bound systems in the nearby Universe. Another part, with the cluster Gr2064, will form a separate system. Our study suggests that structures with a current characteristic density contrast Δρ ≈ 30 have passed turnaround and started to collapse at redshifts z ≈ 0.3 − 0.4. The comparison of the number and properties of the most massive collapsing supercluster cores from observations and simulations may serve as a test for cosmological models.
Key words: large-scale structure of Universe / galaxies: clusters: general / galaxies: groups: general
© ESO 2021
1. Introduction
The largest systems in the cosmic web that may eventually become gravitationally bound are galaxy superclusters or their high-density cores, which are defined as the high-density regions in the cosmic web that embed galaxies, galaxy groups, and clusters. They are connected by filaments (de Vaucouleurs 1953, 1958; Jõeveer et al. 1978; Einasto et al. 1980; Reisenegger et al. 2000; Luparello et al. 2011; O’Mill et al. 2015; Chon et al. 2015). Galaxy superclusters have been detected using various methods such as the clustering analysis (e.g., the friends-of-friends method), the luminosity density field, and the cosmological graph method (Zucca et al. 1993; Einasto et al. 1994, 2003a,b; Basilakos et al. 2001; Erdoǧdu et al. 2004; Luparello et al. 2011; Chow-Martínez et al. 2014; Hong et al. 2020). The study of superclusters, their dynamical state, and galaxy content helps us to understand the formation and evolution of different structures in the cosmic web, from individual galaxies to rich clusters and superclusters.
Tully et al. (2014) used data of the cosmic velocity field in the nearby Universe to show that galaxy flows from low-density regions around the local (Laniakea) supercluster are converging. In this study the whole volume with converging galaxy flows (the basin of attraction) and high-density region of galaxies is called the supercluster. Einasto et al. (2019) proposed to call the low-density regions around traditional, high-density regions in the cosmic web (superclusters) supercluster cocoons. Superclusters act as great attractors. They grow through the inflow of matter from surrounding cocoons.
Studies of superclusters have shown that rich superclusters have high-density cores that may contain one or several rich clusters (Einasto et al. 2007a,c, 2015, 2016b, 2020). Rich clusters in supercluster cores may be merging or be in pre-merger state, for example, in the Shapley supercluster, in the Corona Borealis supercluster, or in the Sloan Great Wall superclusters (Hanami et al. 1999; de Filippis et al. 2005; Belsole et al. 2005; Farnsworth et al. 2013; Einasto et al. 2016b). Merging clusters may also reside in poor superclusters (Donnelly et al. 2001; Reiprich et al. 2021; Einasto et al. 1997). Rich superclusters may have several cores with clusters away from each other, as in the Perseus-Pisces supercluster or in the Coma supercluster (Jõeveer et al. 1978; Malavasi et al. 2020b; Seth & Raychaudhury 2020).
The formation of the present-day structures in the cosmic web began with the growth of tiny density perturbations in the very early Universe when smaller structures merged and accrete (White & Rees 1978; Einasto et al. 1980; Bond et al. 1996). Rich galaxy clusters form where positive sections of medium- and large-scale density perturbations combine (Suhhonenko et al. 2011). Simulations show that present-day rich clusters have collected their galaxies along filaments from regions with comoving radii of at least 10 h−1 Mpc at redshift z ≥ 1 (Chiang et al. 2013; Overzier 2016). The sizes of these regions around the clusters depend on the cluster mass (Chiang et al. 2013) and also on the assembly history of the infalling systems themselves. Chiang et al. (2013) used these regions as one criterion to search for protoclusters in the high-redshift Universe (see also Ando et al. 2020). In the local Universe, Einasto et al. (2015, 2020) found a density minimum in the galaxy distribution around the high-density core of the supercluster SCl A2142. Einasto et al. (2020) found that within this region, all galaxy systems (groups and substructures of A2142) are falling into the cluster (see also Einasto et al. 2018a,b). They suggested that this region can be called the sphere of dynamical influence of the cluster, and the density minimum marks the border of this sphere around the main cluster of the supercluster in the supercluster high-density core.
Studies of superclusters and their high-density cores help us to understand the coevolution of clusters and superclusters, and also of galaxies and groups in them. For example, Einasto et al. (2003c) and Pompei & Iovino (2012) showed that poor groups of galaxies near rich clusters are themselves richer and more luminous than poor groups elsewhere. This environmental enhancement of groups near clusters is evidence of the coevolution of groups and clusters. The growth of clusters by infall of groups and galaxies is accompanied by the changes in star formation properties of galaxies (Haines et al. 2015; Chiang et al. 2017; Einasto et al. 2018b; Muldrew et al. 2018; Musso et al. 2018; Oteo et al. 2018; Kraljic et al. 2019; Maier et al. 2019; Shi et al. 2020; Trussler et al. 2020). Toshikawa et al. (2020) suggested that the evolution of protoclusters and protosuperclusters may have two stages, one accompanied by the changes in star formation dominated by the steady accretion of galaxies, and the other by the merging between group-size halos, perhaps depending on the surrounding large-scale environments.
The studies of supercluster properties have revealed that morphologically, superclusters can be divided into two classes: spider-type and filament-type superclusters (Einasto et al. 2007c, 2011a). Spider-type superclusters have a complicated inner structure with galaxy clusters and groups connected by a large number of filaments. In contrast, in superclusters with a filament morphology groups and clusters are connected by a small number of filaments. Einasto et al. (2014) and Cohen et al. (2017) showed that spider-type superclusters have a higher fraction of star-forming galaxies and clusters with more substructure than filament-type superclusters. This is again evidence of a coevolution of superclusters and galaxy groups and galaxies within them.
In this paper we focus on the study of the rich nearby Corona Borealis (CB) supercluster at redshift z ≈ 0.07. The richest clusters in the CB supercluster are A2065, A2061, A2067, and A2089. The CB supercluster is located at the crossing of three chains of rich superclusters, in the dominant supercluster plane (Einasto et al. 1997, 2011a). Morphologically, the CB supercluster is elongated and a clumpy supercluster of the multispider type (Einasto et al. 2011a).
The dynamics of the CB was first studied by Postman et al. (1988) who concluded that mass of the supercluster is probably sufficient to bind the system. Small et al. (1998) used data from the Norris Survey to show that the most prominent core region of the CB supercluster centred at A2065 may have started to collapse. Pearson et al. (2014) suggested that if the intercluster mass in the CB were sufficient, then it might be collapsing and forming an extended bound structure. The CB supercluster is listed among the future virialised structures by Luparello et al. (2011).
The interest in the study of the CB supercluster increased when it was found that the Cosmic Microwave Background (CMB) cold spots lie in the direction of the CB (Génova-Santos et al. 2008, 2010; Padilla-Torres et al. 2009, 2010). These studies found that the CB cold spot may be partly related to the warm-hot diffuse gas in the supercluster region between galaxy filaments, but it may also be related to some distant cluster or some other large structures.
The aim of this study is to understand the evolution of the CB supercluster and its components, the connections between clusters in the supercluster, and transformations of galaxies in it. We focus on the study of the high-density cores of the supercluster, which may be local centres of attraction. These centres evolve by infall of galaxies and galaxy groups and clusters. If the supercluster contains several high-density cores, then each of them may collapse at present or in the future. This means that the supercluster may be split into several systems in the future. It is also possible that cores will join to form massive bound object(s) in the future. Therefore one goal of our study is to distinguish between these future scenarios for the CB supercluster. We also wish to understand whether dynamical processes in clusters and in the supercluster scale are accompanied with the change in star formation properties of the galaxies in them.
We determine the high-density cores of the CB using the luminosity-density field based on galaxy data from the Sloan Digital Sky Survey (SDSS) and select the richest clusters from the high-density cores of the supercluster as possible centres of attraction. Next we analyse the distribution of galaxies around them to detect their regions of dynamical influence. We analyse the cluster substructure with normal mixture modelling and use the Projected Phase Space (PPS) diagrams to study the possible infall of galaxies, groups, and filaments into clusters. We use data of filaments to study the connectivity of clusters. We also study galaxy populations in clusters and between them, with an emphasis on the star formation properties of galaxies and on the galaxies in various stages of transformation, that is, red star-forming galaxies and recently quenched galaxies. Finally, to predict the evolution of clusters and the whole supercluster, we compare the mass distribution around them with the predictions from the spherical collapse model and analyse the acceleration field of the supercluster. A detailed study of galaxy populations in groups of the CB will be presented separately.
One aim of this paper is to compare the properties of the richest clusters in the CB with the properties of cluster A2142, which is the richest cluster in the supercluster SCl A2142 (Einasto et al. 2015, 2020). Munari et al. (2016) found that cluster A2142 has a very high number of luminous galaxies that are not reproduced in simulations. In addition, Einasto et al. (2018a) showed that cluster A2142 is an outlier in the mass – richness diagram for groups and clusters from the Tempel et al. (2014c) group catalogue at nearly the same distances. A2142 has a significantly higher fraction of red, passive galaxies than other rich clusters at the same distances. In this study we compare the galaxy content and dynamical properties, and the connectivity of A2142 and the richest clusters in the CB. A comparison of individual clusters may reveal details that are lost when an ensemble of clusters is compared, as in Einasto et al. (2018a).
We use the following cosmological parameters: the Hubble parameter H0 = 100 h km s−1 Mpc−1, the matter density Ωm = 0.27, and the dark energy density ΩΛ = 0.73 (Komatsu et al. 2011).
2. Data
2.1. Supercluster, group, and filament data
We used data from the supercluster, group, and filament catalogues by Liivamägi et al. (2012) and Tempel et al. (2012, 2014c,b, 2016). The initial data of galaxies with which these catalogues were generated were taken from the SDSS DR10 MAIN spectroscopic galaxy sample with apparent Galactic extinction-corrected r magnitudes r ≤ 17.77 and redshifts 0.009 ≤ z ≤ 0.200 (Aihara et al. 2011; Ahn et al. 2014). The catalogues of galaxy superclusters, groups, and filaments are available from the database of cosmology-related catalogues at1. Data of the galaxy properties were taken from the SDSS DR10 web page2. The same data were used by Einasto et al. (2018a, 2020) in the analysis of supercluster SCl A2142.
In the catalogue of galaxy superclusters by Liivamägi et al. (2012), superclusters are determined on the basis of the luminosity-density field. In this study, the luminosity-density field was calculated using a B3 spline kernel with a smoothing length 8 h−1 Mpc at a location x,
Superclusters were defined as the connected volumes above a threshold density D8 = 5.0 (in units of mean luminosity density, ℓmean = 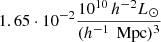 in the luminosity density field). The threshold density for determining superclusters was chosen as a result of the analysis of supercluster properties when the threshold density level was varied. This analysis showed that at high threshold densities, the method selects only the highest density regions as superclusters, which can be considered high-density cores of superclusters. If the threshold density level is low, then neighbouring superclusters are combined into huge complexes of superclusters, as was shown in the case of the Sloan Great Wall in Einasto et al. (2011b). For details of the luminosity density field and the supercluster definition, we refer to Liivamägi et al. (2012).
in the luminosity density field). The threshold density for determining superclusters was chosen as a result of the analysis of supercluster properties when the threshold density level was varied. This analysis showed that at high threshold densities, the method selects only the highest density regions as superclusters, which can be considered high-density cores of superclusters. If the threshold density level is low, then neighbouring superclusters are combined into huge complexes of superclusters, as was shown in the case of the Sloan Great Wall in Einasto et al. (2011b). For details of the luminosity density field and the supercluster definition, we refer to Liivamägi et al. (2012).
The data for the CB supercluster as defined in Liivamägi et al. (2012) are given in Table 1. The length of the supercluster is ≈55 h−1 Mpc, and its mass is M ≈ 4.3 × 1015 h−1 M⊙. In Fig. 1 we show the sky distribution of galaxy groups in the CB and its surrounding region, which also includes the supercluster SCl A2142. SCl A2142 is partly projected on the Gr2064 part of CB, and is connected with it by a filament through a void between superclusters (Kopylova & Kopylov 2007; Pillastrini 2019; Einasto et al. 2020).
 |
Fig. 1. Distribution of galaxy groups in a large region around the CB in the plane of the sky. The size of the circles is proportional to group size in the sky. Grey circles show the positions of groups in a low global density environment, D8 < 5. Orange circles correspond to groups in the CB supercluster, and red circles show groups in a high global density environment with D8 ≥ 8 that do not belong to the CB. These groups mostly lie in supercluster SCl A2142. In the sky projection, part of the CB supercluster is projected on SCl A2142, and some groups from these superclusters overlap in the figure. Large coloured circles indicate the location of the richest clusters with corresponding ID numbers. |
General properties of the CB supercluster.
We used data for flux-limited galaxy groups from the catalogue by Tempel et al. (2014c) to find groups and clusters that belong to the CB. Tempel et al. (2014c) determined galaxy groups using the friends-of-friends cluster analysis method (Zeldovich et al. 1982; Huchra & Geller 1982). In this method, a galaxy is considered a member of a group if at least one group member galaxy lies closer to this galaxy than a linking length. In a flux-limited sample, the density of galaxies slowly decreases with distance. To take this selection effect properly into account when a group catalogue was constructed, the linking length was rescaled with distance, calibrating the scaling relation by observed groups. As a result, the maximum sizes in the sky projection and the velocity dispersions of the groups are similar at all distances. The redshift-space distortions (also known as Fingers of God) for groups were supressed, as described in detail in Tempel et al. (2014c). Tempel et al. (2014c) reported details of the data reduction, the group finding procedure, and the description of the group catalogue. We determined the number of groups as at least four member galaxies and with two to three member galaxies in Table 1. In Table 1 we also list the number of single galaxies, that is, galaxies that do not have neighbours in the galaxy catalogue that are luminous enough to be included in the SDSS spectroscopic sample. In the flux-limited group catalogue, approximately 52% of all galaxies are single (Tempel et al. 2009). However, single galaxies are more common in the low-density environment outside superclusters. In superclusters, the fraction of single galaxies is lower, and in the CB, approximately 15% of all galaxies do not belong to any group. Tempel et al. (2009) also showed based on the luminosity functions of galaxies that especially in the supercluster environment, single galaxies may be the brightest galaxies of faint groups, and truly isolated galaxies may lie in low-density regions, but these are rare in superclusters. We note that one fossil group candidate is included in the groups in the CB, at the edge of the supercluster at approximately RA = 232.2° and Dec = 32.4°, with a magnitude gap between the brightest and second brightest galaxy |ΔM12| = 2.2. Groups with such large magnitude gaps are defined as possible fossil groups in X-ray studies (Ponman et al. 1994).
As candidates for the centres of attraction in the high-density cores of the supercluster, we chose the richest clusters above the global luminosity density level D8 ≥ 8. This threshold density level for high-density cores of CB was chosen on the basis of earlier studies of superclusters, which showed that rich superclusters contain high-density cores, while such cores are absent in poor superclusters (Einasto et al. 2007b,a, 2015, 2020). We searched for rich clusters from the group catalogue with D8 ≥ 8, and selected the richest of them as possible centres of attraction in the supercluster. This choice returned Abell clusters A2065, A2061, and A2089, and one rich cluster without an Abell ID, Gr2064 in the Tempel et al. (2014c) group catalogue. The data of the rich clusters are given in Table 2. In this table we also list the data of the low-mass cluster A2067, which, as we show in Sect. 4.2, forms a pair of merging clusters with A2061. The sky distribution of galaxies in the CB supercluster is shown in Fig. 2. In this figure galaxies are colour-coded according to the luminosity-density D8 value around them. The high-density cores have a threshold density D8 ≥ 8, and the outskirts region of the supercluster is defined as having 5 ≤ D8 < 8. Figure 2 shows that the CB supercluster consists of two parts, divided at RA ≈ 235°. The CB is commonly associated with the main part with RA < 235°. Another part of the CB is connected with the main part by a bridge of galaxies, and there are no Abell clusters in this part. The richest cluster there is Gr2064. In the following, we call these parts the main part and the Gr2064 part of the CB.
 |
Fig. 2. Distribution of galaxies in the CB supercluster region in the plane of the sky. The colour marks the global luminosity density D8. Red circles correspond to the galaxies in high-density cores with D8 ≥ 8, orange circles show galaxies in the outskirts of the supercluster with 5 ≤ D8 < 8, and grey symbols show galaxies in the low-density region around the supercluster with D8 < 5. The ID numbers of the richest clusters in the high-density cores of the supercluster are shown (Abell clusters A2065, A2061, and A2089, and cluster Gr2064 that does not belong to Abell). |
Data of rich galaxy clusters in the CB.
We also identified galaxy filaments in the CB. Tempel et al. (2014b, 2016) detected filaments by applying a marked point process to the galaxy distribution (the Bisous model). For each galaxy, a distance from the nearest filament axis was calculated. Galaxies were considered filament members when their distance from the nearest filament axis was within 0.5 h−1 Mpc (see Tempel et al. 2014b; Einasto et al. 2020, for details).
2.2. Galaxy populations
We used data of the galaxy properties from the SDSS DR10 web page3. From the available data for each galaxy, we used the magnitudes, colours, stellar masses M*, star formation rates (SFR), and the Dn(4000) index.
The absolute magnitudes of the galaxies were calculated as
where dL is the luminosity distance in units of h−1 Mpc and K is the k+e-correction, calculated as in Blanton & Roweis (2007) and Blanton et al. (2003) (see Tempel et al. 2014c, for details). To calculate the galaxy rest frame colour (g − r)0 and the concentration index, we used galaxy magnitudes from the SDSS photometric data. Red and blue galaxies are approximately separated by the colour index value (g − r)0 = 0.7; red galaxies have (g − r)0 ≥ 0.7 (Einasto et al. 2014).
Data of stellar masses M*, SFR, and the Dn(4000) index for galaxies were taken from the Max Planck for Astrophysics (MPA) and Johns Hopkins University (JHU) spectroscopic catalogue (Tremonti et al. 2004; Brinchmann et al. 2004). In this catalogue the properties of galaxies are calculated using the stellar population synthesis models and fitting SDSS photometry and spectra with Bruzual & Charlot (2003) models. The stellar masses of galaxies are calculated as described in Kauffmann et al. (2003a).
The Dn(4000) index is the ratio of the average flux densities in the band 4000 − 4100 Å and 3850 − 3950 Å. It is correlated with the time that has passed from the most recent star formation event in a galaxy. The Dn(4000) index can be used as a proxy for the age of stellar populations of galaxies and star formation rates. We used the Dn(4000) index of galaxies as calculated in Balogh et al. (1999). Kauffmann et al. (2003a) showed that the value Dn(4000) = 1.55 corresponds to a mean age of about 1.5 Gyr. This limit can be used to separate galaxies with old and young stellar populations (see Kauffmann et al. 2003b; Haines et al. 2017; Einasto et al. 2018b). Galaxies with young stellar populations have Dn(4000) ≤ 1.55. According to Kauffmann et al. (2003a), the value Dn(4000) = 1.75 corresponds to a mean age of about 4 Gyr (for solar metallicity) or older (for lower metallicities). At Dn(4000) = 1.75, the galactic star formation rate drops (see Fig. 27 in Brinchmann et al. 2004). The value Dn(4000) = 1.35 limits galaxies with very young stellar populations with a mean age of approximately 0.6 Gyr only (Kauffmann et al. 2003a).
In our study we divided galaxies into various populations according to their star formation properties. Galaxies with very old stellar populations (hereafter VO galaxies) are defined as those with Dn(4000) ≥ 1.75. Blue star forming (hereafter BSF) galaxies, red star forming (RSF), and recently quenched (RQ) galaxies are defined using parameter combinations. BSF galaxies are defined as galaxies with blue colours ((g − r)0 < 0.7) and a high star formation rate (logSFR ≥ −0.5). RSF galaxies are defined as galaxies with colour index (g − r)0 ≥ 0.7 and a star formation rate logSFR ≥ −0.5. RQ galaxies are defined as galaxies with low SFRs that have young stellar populations (low values of the Dn(4000) index, Dn(4000) ≤ 1.55 and logSFR < −0.5). The data of the galaxy populations are summarised in Table 3.
Data of galaxy populations.
Figure 3 shows galaxies from different populations in a Dn(4000) index versus stellar mass log M* diagram. Galaxies in transformation (RSF and RQ) form a sequence in this plot in which galaxies with higher stellar mass are red but are still forming their stars, while galaxies with lower stellar mass from the same Dn(4000) index range are already quenched. As discussed in Einasto et al. (2018b) and in Einasto et al. (2020), the location of RSF and RQ galaxies in the cosmic web is somewhat different, RSF galaxies follow the distribution of groups and inner parts of filaments more closely. RQ galaxies lie mostly in the infall regions of groups or in the outskirts of filaments. Galaxies below Dn(4000) = 1.35 line are almost all BSF galaxies with low stellar mass and very young stellar populations. Galaxies from the stellar mass range M* ≈ 1010 h−1 M⊙ − 1011 h−1 M⊙ may belong to any of these populations (Fig. 3). In what follows we examine where galaxies from different populations lie in the CB supercluster, and where galaxy transformations occur.
 |
Fig. 3. Dn(4000) index vs. stellar mass log M* for galaxies in the CB supercluster. Blue stars denote BSF galaxies, orange stars denote RSF galaxies, green triangles mark RQ galaxies, black dots show red galaxies with 1.55 ≤ Dn(4000) < 1.75, and red filled circles denote VO galaxies (see Table 3). The green ellipse approximately borders the area populated by RQ galaxies, and the orange ellipse shows the area populated by RSF galaxies. |
3. Methods
3.1. Spherical collapse model
The spherical collapse model describes the evolution of a spherical perturbation in an expanding universe (Peebles 1980, 1984; Lahav et al. 1991). In standard models with a cosmological constant, the acceleration of the expansion of the Universe began at the redshift z ≈ 0.5 by the influence of dark energy (Frieman et al. 2008). The formation of structure slowed down, and the largest bound structures just began forming. The evolution of a collapsing spherical shell is determined by the mass in its interior, and it can be characterised by several important epochs (Chon et al. 2015; Gramann et al. 2015).
For a spherical volume, the density ratio to the mean density (overdensity) Δρ = ρ/ρm can be calculated as
From Eq. (3), we determine the mass of a structure as
The spherical collapse model defines several epochs in the evolution of a perturbation as follows. Turnaround (T) corresponds to the epoch at which a spherical overdensity region decouples from expansion and its collapse begins, with Δρ = 13.1 (for the cosmological parameters used in this paper, see e.g., Gramann et al. 2015). Overdensity regions with Δρ = 8.73 will collapse in the future (FC for future collapse). The density contrast Δρ = 5.41 corresponds to so-called zero gravity (ZG), at which the radial peculiar velocity component of the test particle velocity equals the Hubble expansion, and gravitational attraction of the system and its expansion are equal. The density contrast Δρ = 1 corresponds to a linear mass scale or the Einstein-Straus radius at which the radial velocity around a system reaches the Hubble velocity, u = HR, and peculiar velocities vpec = 0 (Teerikorpi et al. 2015; Gramann et al. 2015). Around superclusters, the linear mass scale approximately follows the cocoon borders (Einasto et al. 2020).
3.2. Mass distribution in the CB supercluster
In our study we compared the density contrast around the richest galaxy clusters in the CB supercluster with the predictions of the spherical collapse model to understand the possible evolution of clusters and the whole supercluster. To calculate the density contrast, we calculated the distribution of mass around the rich clusters in the supercluster. The supercluster itself was determined as the overdensity region in the luminosity-density field, as described in Sect. 2.1. However, the analysis of the mass-to-light ratios of galaxy systems shows that the luminosity-density field is a biased tracer of the underlying mass field (Bahcall & Kulier 2014; Einasto et al. 2016b). Thus we cannot use the luminosity-density field directly to determine the mass distribution in the supercluster.
To determine the mass distribution in the supercluster, we therefore used the dynamical mass of galaxy groups from Tempel et al. (2014c). In the case of groups with at least four member galaxies, we directly used the masses from the Tempel et al. (2014c) group catalogue. For very poor groups with fewer than four member galaxies, the mass estimates from Tempel et al. (2014c) have a large scatter, which makes the masses of individual groups unreliable. Therefore we used the median mass of groups with two to three member galaxies to calculate the total mass of groups within a given clustercentric distance, M ≈ 1.6 × 1012 h−1 M⊙. The median mass was multiplied by the number of groups of this richness class to obtain the total mass in these groups at a given clustercentric distance interval around clusters. To estimate the mass related to single galaxies, we considered single galaxies as the brightest galaxies of faint groups with other group members being too faint to be included in the SDSS spectroscopic sample. To take the mass of these faint groups into account, we used the median mass of very poor groups with two to three member galaxies. We could also have applied the stellar mass – halo mass relation to determine the mass of dark matter haloes around single galaxies, as was done for example in Einasto et al. (2016b) and in Einasto et al. (2018a), using the stellar mass – halo mass relation from Moster et al. (2010), and drop the assumption about faint groups. However, as shown in Einasto et al. (2016b, 2018a), these two estimates agree well on average (within adopted mass errors), therefore we used the median mass of poor groups. The details of this method were described in Einasto et al. (2015) and in Einasto et al. (2018b), who applied the method to calculate the mass of supercluster SCl A2142. The mass distribution around each cluster was calculated by summing the masses of clusters and groups within a sphere of increasing radius. As in Einasto et al. (2018b), we used a 50% mass error. Superclusters also contain gas. The gas mass may form approximately 10% of the supercluster mass (Pompei et al. 2016). To obtain the total mass of the supercluster, we added this to the sum of the dynamical masses of groups. Rich groups with at least four member galaxies give approximately 75% of the total mass of the supercluster, and poor groups and single galaxies 10% and 5%, respectively.
The accuracy of the supercluster mass determination can be tested with simulations. For group dynamical masses comparison of group masses from the Tempel et al. (2014c) group catalogue and from the mock group catalogues from simulations showed that there is no clear bias between these masses (Old et al. 2014, 2015). The mass of a supercluster calculated using the dynamical masses of groups and the gas mass is biased relative to the total mass of the supercluster. This bias depends on the richness limit of the groups that are used in the calculations (Chon et al. 2014). Einasto et al. (2015) compared supercluster mass estimates for the A2142 supercluster and for simulated superclusters (Chon et al. 2014), and estimated that the bias factor may be of order of 1.8, which means that we are still underestimating the mass of the supercluster. If we only used rich groups with reliable mass estimations, the bias factor would be larger. We assume that the missing mass partly comes from unobserved faint galaxies and groups, which can be uncovered in simulated superclusters (Chon et al. 2014). If approximately 50% of all galaxies in the supercluster were faint single galaxies, then the total mass of the supercluser would increase by approximately 10%, which is within the adopted mass errors.
3.3. Substructure of clusters
We applied multidimensional normal mixture modelling to search for the 3D substructure of galaxy clusters. We also analysed whether the structures of clusters and their galaxy populations are related with (possibly infalling) groups and filaments near clusters. In this analysis we used the package mclust for classification and clustering (Fraley & Raftery 2006) from R statistical environment (Ihaka & Gentleman 19964). This package studies a finite mixture of distributions, in which each component is taken to correspond to a different subgroup of the cluster. With mclust we searched for an optimal model for the clustering of the data among the models with varying shape, orientation, and volume, and determined the optimal number of components in the data and the membership of components (classification of the data). mclust also calculates the uncertainty of the classification, which is defined as one minus the highest probability of a datapoint to belong to a component. It finds for each datapoint the probability to belong to a component. The mean uncertainty for the full sample is a statistical estimate of the reliability of the results. As input for mclust, we used the sky coordinates and line-of-sight velocities (calculated from their redshifts) of the cluster member galaxies. The velocity values were scaled to make them of the same order as the values of coordinates. The best solution for the components was chosen using the Bayesian information criterion (BIC).
3.4. Projected phase space diagram
To analyse the galaxy content and merging history of clusters, we employed the PPS. The PPS diagram shows line-of-sight velocities of galaxies with respect to the cluster mean velocity versus projected clustercentric distance. Simulations show that in the PPS diagram, galaxies at small clustercentric radii form an early infall (virialised) population with infall times τinf > 1 Gyr, and galaxies at large clustercentric radii form late or ongoing infall populations with τinf < 1 Gyr (Oman et al. 2013; Muzzin et al. 2014; Haines et al. 2015; Rhee et al. 2017; Pasquali et al. 2019; Smith et al. 2019). Early and late infall regions can be approximately separated with a line as follows (Oman et al. 2013):
where v are the velocities of the galaxies, σcl is the velocity dispersion of galaxies in the cluster, Dc is the projected clustercentric distance, and Rvir is the cluster virial radius. Oman et al. (2013) showed that in simulations a large percentage of galaxies on the left of the line at small clustercentric radii form an early infall (virialised) population with τinf > 1 Gyr. However, simulations show that galaxies with late infall time may populate areas of PPS diagram at all projected radii and velocities, which complicates the interpretation of the PPS diagram from observations (Haines et al. 2015).
In our study we used PPS diagrams to study the dynamical state of clusters, the distribution of galaxies with different star formation properties in them, and to detect possible infalling galaxies, groups, and filaments.
3.5. Cluster radii Rcl.
In order to help us to interpret the PPS diagrams, we additionally used the radius that we denote Rcl. This radius corresponds to the radius of a cluster for one-component clusters and to the radius of the main component in clusters with several components (for cluster A2142, see Einasto et al. 2018a). At this radius, the outer (infalling) components of the cluster enter the main cluster, and therefore this radius defines the infall zone at the cluster boundaries, which are part of the late infall region in the PPS diagram. The infall zone of the cluster is also the zone in which splashback galaxies are to be most likely found, that is, galaxies that entered the cluster a long time ago and might now be moving out of the cluster. The radius that we call Rcl is commonly known as the splashback radius of a cluster (Haines et al. 2015; More et al. 2015; Rhee et al. 2017; Bianconi et al. 2021). At this radius, the density profiles of clusters change (More et al. 2015; Bianconi et al. 2021). However, as we do not have direct information about galaxy orbits in clusters from observations (as can be obtained from simulations), we call this radius Rcl. How the virial radius Rvir and Rcl are related depends on the structure and merging history of a cluster (More et al. 2015). To mark the early infall zone in the PPS diagram, we applied Eq. (5), and used Rvir in calculations. We additionally show in the PPS diagrams the region, which is more likely to also include galaxies with late infall times. The borderline of this region is calculated with Eq. (5) and using Rcl. We also used additional information about galaxies (their star formation properties) to separate possible early and late infallers, members of infalling components, and possible interlopes.
3.6. Connectivity of clusters
The connectivity of a cluster is defined as the number of filaments connected to a cluster (see e.g., Colombi et al. 2000; Codis et al. 2018). The connectivity characterises the growth of clusters and depends on their mass and richness. The connectivity of poor clusters is lower than that for rich clusters (and groups) (Darragh Ford et al. 2019; Kraljic et al. 2020; Gouin et al. 2020). The determination of filaments connected to a cluster may not be easy. For example, in the high-density environment of superclusters, filaments may not be well defined. Especially short filaments may be spurious and are often excluded from an analysis (Malavasi et al. 2020a; Santiago-Bautista et al. 2020; Kuutma et al. 2020). In supercluster cores, clusters may be surrounded by various infalling structures, as discussed, for example, in the case of the cluster A2142 in Einasto et al. (2018a, 2020). These may include infalling substructures, groups, and filaments. To determine the connectivity of clusters in supercluster cores, it is therefore straightforward to analyse all possible infalling substructures of clusters, groups, and filaments near these clusters together. When we determined the connectivity of clusters, we accordingly took all possible infalling structures into account. Among all these structures, we separately searched for long filaments. We analysed the distance distribution of these structures from the cluster centre, the distribution of their member galaxies in the plane of the sky, in the sky – velocity plane, and in the PPS diagram.
3.7. Acceleration field in the supercluster
To complement the predictions for the dynamical state and future evolution of the supercluster based on the spherical collapse model, we calculated the acceleration field of the supercluster. In these calculations we treated the groups and clusters in the supercluster as a source of acceleration and analysed how the acceleration field would affect its further evolution. We wish to understand whether the acceleration is strong enough to overcome the Hubble expansion. Our observational data are limited to three coordinates for each object, the sky coordinates and the redshift, which is a mixture of distance and line-of-sight velocity. The dynamics of objects is fully calculable with six coordinates (an example of the inference of accelerations with all spatial coordinates is shown in Kipper et al. 2020). Because we do not have all six coordinates, we must compensate for missing information by making assumptions. The classical and most reliable assumption for this compensation is applied in the spherical collapse model. In this model, the spherically averaged radial velocity around a system in the shell of radius R can be written as u = HR − vpec, where vH = HR is the Hubble expansion velocity and vpec is the averaged radial peculiar velocity towards the centre of the system. The peculiar velocity at the turnaround vpec = HR and u = 0. If vpec < HR, the system expands, and if vpec > HR, the system begins to collapse (Gramann et al. 2015). When using data of supercluster cores, deviations from this model are expected as they are typically not spherical. In order to estimate the robustness of assuming spherical collapse model, we used the acceleration field as a test. This test was performed to make a competing estimate by swapping assumptions. Instead of spherical symmetry and assumable velocities, we discarded the assumption about the spherical symmetry in an observational distribution of groups and clusters in the supercluster. As the price of not knowing velocities, the present mean movements of groups and clusters were taken to be zero. We assumed that the dominant acceleration is caused by the most massive clusters in the supercluster. In order to show their effect most strongly, we selected a coordinate system that is located in the plane determined by the three richest clusters in the main part of the CB: A2065, A2089, and A0261. The x2 coordinate was determined by connecting A2089 and A2065, the y2 coordinate was defined to be perpendicular with x2 and to be in the same plane as determined by these three clusters. The third coordinate was determined to be perpendicular with both x2 and y2. The zero point of these is the mid-point between these clusters. This coordinate system was designed to keep the majority of the acceleration field in the plane of the figures, hence to show how the system may evolve in the clearest way. We illustrate the coordinate system used in these calculations in Fig. A.1. Errors in the calculation of the acceleration field come mostly from the assumption about cluster velocities.
We calculated the acceleration field based on the distribution of the clusters in the supercluster region. Each group or cluster had its Navarro-Frenk-White (NFW) profile determined from the Tempel et al. (2014c) group catalogue, which is sufficient to estimate the acceleration field caused by them. The acceleration field is estimated from
where the index i sums over the groups or clusters in the SC, and aNFW, i(⋅) is a function that calculates the acceleration field by group i at x assuming an NFW density profile. Single galaxies are taken into account as the possible brightest members of faint groups, and as above, we used the median mass of the poorest groups as their mass. Our acceleration field does not include the matter that is not bound to the clusters as a source of the acceleration field.
4. Results
In this section we present the analysis of the richest clusters in high-density cores of the CB. For each cluster we show the sky distribution of galaxies from different populations, the location of galaxies from various populations in the PPS diagrams and the Dn(4000) index versus clustercentric distance Dc plots, and give the radii Rcl in Table 6. We also show the sky distribution of galaxies in filaments that begin near clusters. We briefly analyse the location of galaxies from various populations, and compare galaxy populations in clusters and in their close environment. We summarise the results for the clusters in Sect. 4.6.
4.1. Cluster A2065
We start our analysis from the richest cluster in the CB, cluster A2065. In Fig. 4 (upper left panel) we plot the sky distribution of galaxies in the region of A2065. Here galaxies from different populations are marked with different symbols. To show the physical scale of the cluster, we add to Fig. 4 (upper left panel) a circle with radius of 1.5 h−1 Mpc. We also plot a circle with radius R30; we explain below why we use this notation. We show the distribution of galaxies from various populations in A2065 and around it using the PPS diagram and the Dn(4000) index versus clustercentric distance Dc plot (Fig. 4, right panels). We analyse possible infalling structures and filaments near the cluster to determine its connectivity (Fig. 4, lower left panel).
 |
Fig. 4. Left panels: distribution of galaxies in A2065 in the plane of the sky. The colours in the upper panel correspond to galaxies from different populations (BSF – blue, RSF – orange, RQ – green, and VO – dark red). Filled symbols denote galaxies in different components of the cluster. Empty circles show galaxies that are not cluster members. Grey crosses denote galaxies in the low-density region with D8 < 5. The inner black circle indicates the scale with a radius 1.5 h−1 Mpc. The outer red circle corresponds to the radius R30 (= 6 h−1 Mpc for A2065). A and B denote substructures that extend from the cluster (see text). The colour in the lower panel shows galaxies in long filaments with a length larger than 5 h−1 Mpc, and in green we plot galaxies in a short filament with a length of 3 h−1 Mpc, which connects the long filament with the cluster. The upper right panel shows the PPS diagram and the distribution of the clustercentric distances Dc for galaxies from different populations in A2065 and in its environment towards A2089. Filled circles represent A2065 members, and filled triangles (at clustercentric distances Dc > 6 h−1 Mpc) show A2089 members. Empty symbols mark galaxies that are not members of these two clusters. The blue region shows the early infall (E) region, and light blue shows late infall (L) region. The lower right panel presents the Dn(4000) index versus clustercentric distance Dc for galaxies from A2065 to A2089. Colours show the density of points at a given location in the plot. Vertical lines correspond to the infall zone of the cluster, Rcl, and to the radius R30. Horizontal lines show Dn(4000) index values Dn(4000) = 1.75, Dn(4000) = 1.55, and Dn(4000) = 1.35 (see Sect. 2.2). |
The sky distribution of galaxies at A2065 (Fig. 4, upper left panel) shows that this cluster is located at the intersection of galaxy systems connecting it with clusters A2061 in the north and with A2089 in the east. Substructures appear to extend from the cluster in both directions. The substructure analysis of A2065 revealed four components in the cluster. The first component is the cluster itself. Another component lies along the line of sight; in the sky projection, it is projected onto the main component. The other two components of A2065 are elongated and point towards clusters A2061 and A2089 (Fig. 4, upper left panel, denoted A and B).
Next we analysed the galaxy populations in and around A2065 using PPS diagrams. To avoid contamination due to projections, we calculated the PPS diagrams separately for the direction to clusters A2089 and A2061. To find the PPS diagram from A2065 to A2089, we used galaxies in the declination interval 26.8 − 28.8 degrees (Fig. 4, upper right panel). In order to not to overcrowd the text with figures, we do not show the PPS diagram for galaxies in the direction of A2061. In the upper panel of the PPS diagram, we show the distribution of clustercentric distances of galaxies from different populations. We complement the PPS diagram with a figure in which we plot the Dn(4000) index of galaxies versus clustercentric distances of galaxies, Dc, in the same region as shown in the PPS diagram (Fig. 4, lower right panel).
In the PPS diagram in the infall region of the line-of-sight component there are some blue star-forming and recently quenched galaxies, and also some VO galaxies (Fig. 4, upper right panel). The presence of star-forming and recently quenched galaxies is a signature that this component is probably a remnant of a group that is falling into the cluster. This conclusion is supported by X-ray and radio studies (Markevitch et al. 1999; Farnsworth et al. 2013). Markevitch et al. (1999) proposed using an analysis of X-ray data that a late-stage merger occurs here, perhaps well after a core passage. From the analysis of XMM-Newton observations data, Belsole et al. (2005) concluded that the data show signatures of an ongoing merger. Farnsworth et al. (2013) detected diffuse radio emission, which they identified as possible giant radio halo at the location of X-ray peak. We can also say this in another way: X-ray and radio studies have revealed a possible infalling group in A2065 that coincides with the line-of-sight component detected in A2065. Some galaxies of this component are recently quenched, they are visible on the PPS diagram as galaxies with high velocities and small clustercentric distances. Their quenching may be related to their infall into the cluster.
Comparison of galaxy populations in the main cluster and in the components shows that the main cluster is populated mostly by VO galaxies, as also shown in Fig. 4 (lower right panel, Dn(4000) index versus clustercentric distance Dc plot). Star-forming galaxies, both red and blue, populate the region between the early infall region and the boundaries of the cluster, up to Rcl h−1 Mpc. They may belong to late infallers, or they may be falling into the cluster now and not yet be quenched in the cluster environment. Some of these galaxies may be interlopers. The upper panel of the PPS diagram shows an excess of blue star-forming galaxies at Rcl, followed by a lower excess of red star-forming galaxies. Their star formation may be triggered by the infall into the cluster. At very small clustercentric distances lie VO galaxies with high peculiar velocities. These galaxies might belong to the part of an infalling cluster after a core passage, as suggested by X-ray data (Markevitch et al. 1999). RQ and star-forming galaxies may be at their first infall.
In the PPS diagram, galaxies with Dc > Rcl (up to clustercentric distances Dc ≈ 6 h−1 Mpc) are not yet members of the (main) cluster. They either belong to substructures or are falling into the cluster. Galaxies at this clustercentric distance interval with very large velocity differences may be there due to projection effects and do not belong to the infalling population. At clustercentric distances up to Dc ≈ 6 h−1 Mpc, individual maxima in the clustercentric distance distribution correspond to small groups and filaments near the cluster (we discuss them below). At clustercentric distances in the range Dc ≈ 6 − 7 h−1 Mpc, there is a minimum in the distance distribution of galaxies. This distance interval is populated by only a few star-forming galaxies. At higher clustercentric distances, close to cluster A2089, the number of galaxies increases again. In the PPS diagram, the radius Dc ≈ 6 h−1 Mpc marks the borders of the late infall region. We may assume that this radius marks the borders of the possible sphere of influence of cluster A2065. We denote the clustercentric distance at which the minimum occurs as the radius R30 and give the reasons of this notation in Sect. 5.
To determine the connectivity of A2065, we identified galaxy filaments within the sphere of influence of A2065, and galaxy groups and galaxies belonging to filaments. Then we analysed their properties and their location in the plane of the sky and in the PPS diagram. Filaments near clusters may be poorly defined by an automatic algorithm, and sometimes elongated groups may be included in a filament catalogue. Therefore we checked all the systems near the cluster, and excluded very short, spurious filaments with lengths shorter than 3 h−1 Mpc. The mean velocity dispersion of groups is ≈200 km s−1, and our automatic algorithm may confuse these groups with short filaments. Typically, filaments with a length in the range of 3 − 5 h−1 Mpc were associated with a group and a few galaxies near it. Filaments with lengths greater than 5 h−1 Mpc either connect two clusters (A2065 and A2089, or A2065 and A2061) or enter the low-density region around the supercluster.
As mentioned, A2065 has three infalling substructures. As in the case of cluster A2142 in Einasto et al. (2020), they were taken into account to determine the connectivity of A2065. In the region of influence of the cluster, two groups are associated with short filaments. Four filaments with length > 8 h−1 Mpc are also connected to A2065. One of these filaments connects clusters A2065 and A2089, another extends from A2065 to A2061. Two long filaments continue in the low-density region. When we count them all, the total connectivity 𝒞 of A2065 is 𝒞 = 9. In Table 6 we list the total number of different systems near the cluster and the number of long filaments.
In the lower right panel of Fig. 4 we show the value of the Dn(4000) index versus clustercentric distance Dc. This figure shows that VO galaxies populate the early infall region of A2065. This figure clearly shows that galaxies that probably have been falling into the cluster during its formation stopped their star formation and became VO galaxies in the cluster environment. Blue star-forming galaxies lie in the infall zone of A2065. The infall zone is also populated by galaxies in transition (RQ and RSF galaxies). The gap in the galaxy distribution at R30 is also visible, although this is not strong. This means that galaxy groups and filaments that extend from A2065 to A2089 are not continuous. In other words, they do not touch, but rather greet each other across a distance5.
In the A2065 sphere of influence, there is a local excess of red star forming galaxies at Dc ≈ 3 h−1 Mpc, and another local excess of blue star-forming galaxies at Dc ≈ 4 h−1 Mpc. We might witness the transformations of star-forming galaxies, in which at first the colour of galaxies changes.
4.2. A2061 to A2067 region
We show the distribution in the sky of galaxies in cluster A2061 in the left panel of Fig. 5. The PPS diagram up to clustercentric distances 5 h−1 Mpc and the Dn(4000) index versus Dc are given in the right panels of Fig. 5. Here galaxies from the low-mass cluster A2067 near A2061 are plotted with separate symbols. These figures show that clusters A2061 and A2067 form a close pair; in the distribution in the sky, they almost overlap. In the PPS diagram, galaxies from A2067 lie in the infall region of A2061. Interestingly, the galaxies from A2067 that are closest to A2061 all contain very old stellar populations, and they also include two red star-forming galaxies. There are also other RSF galaxies in both A2061 and A2067. In A2061, they may be just falling in, as they lie in and near boundaries of the late infall (light blue) zone (as seen also in the lower right panel of Fig. 5). The virialised part of the PPS diagram is populated mostly by VO galaxies. Blue star-forming galaxies lie in the late infall zone of A2067, giving the impression that this cluster may consist of two merging groups. These galaxies cause a maximum in the clustercentric distance distribution of BSF galaxies between Rvir and Rcl (upper panel of the PPS diagram). We might therefore witness several simultaneous mergers: two merging groups that form A2067, which in turn is falling into A2061. The upper panel of the PPS diagram shows a minimum in the galaxy distribution around A2061, followed by a small maximum, especially in the distribution of RFS galaxies. Some of these galaxies are members of A2067, and some of them belong to other groups. They include VO galaxies and also star-forming galaxies (Fig. 5, lower right panel). mclust identified three components in A2061, which may partly be due to its elongated shape.
 |
Fig. 5. Same as in Fig. 5 for A2061. Triangles in the upper panels denote galaxies from cluster A2067. |
Both X-ray and radio observations have demonstrated complicated and structure-rich X-ray and radio emission in the area of A2061 and A2067 (Farnsworth et al. 2013; Marini et al. 2004, and references therein). Farnsworth et al. (2013) showed that A2061 is elongated and has an elongated radio relict that form a diagonal from north-east to south-west in Fig. 5. Farnsworth et al. (2013) discussed the possibility that a filament of galaxies might connect A2061 and A2067. This filament is formed by the same galaxies that connect these clusters in Fig. 5. Marini et al. (2004) found from X-ray data that a group of galaxies may have been falling into A2061 along the axis that connects A2061 and A2067. Thus it is possible that several merging events in the past and at present have been occurred along this axis, and in the future, the whole cluster A2067 will merge with A2061. These mergers may affect the star-forming properties of galaxies in both clusters. We plan to study the A2061 and A2067 cluster pair in more detail in the future.
There is a minimum in the distance distribution of galaxies around A2061 at approximately 4 h−1 Mpc (Fig. 5, right panels). This radius, R30, defines the radius of the sphere of influence for A2061. Galaxies from A2067 are within this sphere. Near R30, at clustercentric distances of approximately 3.2 < Dc < 4 h−1 Mpc, most galaxies are with very young stellar populations (Fig. 5, right panels).
The analysis of groups and filaments in the sphere of influence of A2061 showed that this cluster has three short filaments near it, and one of them connects A2061 and A2065. All these short filaments are associated with infalling groups in the PPS diagram. A2061 also has five long filaments. One of them connects A2061 and A2065 and is related with the radio relict mentioned above (Farnsworth et al. 2013). Another filament is directed towards A2065 but does not extend to it. Three filaments that are longer than 10 h−1 Mpc are directed towards the low-density region around the supercluster. We thus obtain for A2061 a total connectivity 𝒞 = 8, with five long filaments (Table 2).
4.3. A2089 region
Cluster A2089 in Fig. 6 is elongated along the direction towards A2065. It has a tail of galaxies pointing towards A2065. However, normal mixture modelling showed that A2089 is a one-component cluster. Aryal et al. (2007) found that the galactic planes of the galaxies in A2089 tend to lie in the plane defined by the elongated shape of the cluster (and filaments, as our study shows). The central part of the cluster (early infall zone in the PPS diagram) is populated mostly by VO galaxies; there are blue and red star-forming galaxies in the late infall (light blue) zone and in the tail. Two RQ galaxies lie in the late infall zone of A2089. We may assume that the star formation properties of these galaxies are affected by the infall into the cluster. There are also galaxies with clustercentric distances smaller than Rcl and large velocity differences between these galaxies and the cluster centre. Some of them may be interlopers (due to their high velocities), but an RQ galaxy, for instance, may be falling into the cluster, and its star formation may be recently quenched because of this. Figure 6 (upper right panel) shows a minimum in galaxy distribution at Rcl, and another broad minimum in the clustercentric distance distribution at approximately 2.5 − 3 h−1 Mpc, where only a few BSF galaxies lie. In Fig. 6, the upper panel of the PPS diagram and the lower panel (Dn(4000) index versus clustercentric distance Dc plot) show that of the infalling galaxies at Dc > Rcl, the VO galaxies are closer to the cluster than the star-forming galaxies. It is possible that the star formation of these galaxies has been quenched because of the infall, but this may also be evidence of preprocessing of galaxies in groups before infall to the cluster. The overall density minimum at this clustercentric distance interval suggests that this distance defines the size of the sphere of influence for A2089, R30.
A2089 has only one infalling group and one outgoing filament. This filament extends from A2089 to A2065. According to the filament finder, galaxies in the tail that extends from A2089 also belong to this filament. Therefore the total connectivity of A2089 is only 𝒞 = 2, with one long filament (Table 2).
4.4. Gr2064 region
Figure 7 shows galaxies in cluster Gr2064 in the plane of the sky, in the PPS diagram, and in the Dn(4000) index versus Dc plot. Gr2064 is a multicomponent cluster, as shown in the results of normal mixture modelling. Gr2064 consists of the main cluster and two elongated substructures pointing towards neighbouring structures (Fig. 7, upper right panel). These substructures extend from the cluster up to a distance of approximately 4 h−1 Mpc. There is a rich group of 30 galaxies near Gr2064, and as the PPS diagram suggests, this group is falling into Gr2064. It may have already started to merge; the nearest galaxies from this group are closer than 1.5 h−1 Mpc to the centre of Gr2064. The right panels of Fig. 7 show an excess of star-forming galaxies (blue, with very young galaxy populations, and RSF galaxies) in the late infall region of the cluster at clustercentric distances Dc > Rvir h−1 Mpc. One recently quenched galaxy also lies in this region. No rich group near other clusters in the CB has such a high fraction of star-forming galaxies (Figs. 4–6; in Sect. 4.5 we compare galaxy populations in and around clusters in more detail). A minimum in galaxy distribution at clustercentric distances ≈4 h−1 Mpc is visible in the galaxy distribution in the sky and in the PPS diagram. Only a few (red and blue) star-forming galaxies lie there. This distance determines the size of the sphere of influence for Gr2064.
Cluster Gr2064 has two elongated substructures and one infalling group. Three long filaments start in the sphere of influence of Gr2064. Two of these extend in the direction of the low-density region around the cluster; they are longer than 10 h−1 Mpc. A filament with a length of 5 h−1 Mpc connects Gr2064 with the other nearby cluster, as shown in Fig. 7. Thus the total connectivity of Gr2064 is 𝒞 = 6, with three long filaments.
4.5. Galaxy populations in clusters and in the spheres of influence
In this section we compare galaxy populations in four clusters of the CB supercluster and in cluster A2142. The supercluster SCl A2142 has a high-density core with a clear gap in the galaxy distribution, which defines the boundary of the core. Within the high-density core, all galaxies and groups are falling into cluster A2142, thus it corresponds to the sphere of influence of A2142. Its radius is ≈5 h−1 Mpc (Einasto et al. 2020). Therefore we also compared the galaxy populations in clusters and in the spheres of influence of the clusters from the CB and in A2142. In the comparison we used data of the Dn(4000) index and stellar masses log M* of galaxies introduced in Sect. 2.2. The Dn(4000) index can be used to characterise the age of galactic stellar populations and star formation rates. The value Dn(4000) = 1.55 corresponds to a mean age of stellar populations of about 1.5 Gyr. We used this limit to separate galaxies with old and young stellar populations. Galaxies with young stellar populations have Dn(4000) ≤ 1.55. The value Dn(4000) ≥ 1.75 corresponds to a mean age of stellar populations of about 4 Gyr or older. The value Dn(4000) = 1.35 limits galaxies with very young stellar populations with a mean age of only approximately 0.6 Gyr (see references in Sect. 2.2). The galaxy populations are summarised in Table 3, and we briefly show them also in Table 4.
Galaxy populations as used in this paper.
The galaxy content in cluster A2142 and in supercluster SCl A2142 was analysed in Einasto et al. (2018a) and in Einasto et al. (2018b), and in the comparison, we use data from these papers. As in the present paper, Einasto et al. (2018a) and Einasto et al. (2018b) used SDSS data in their analysis of SCl A2142 and defined galaxy populations in the same way as they are defined here. In the following comparison we only include galaxies from the magnitude-limited complete sample from both superclusters, with a magnitude limit Mr = −19.6 mag. We used a Kolmogorov-Smirnov test to estimate the statistical significance of the differences between the galaxy populations. We considered that the differences between distributions are highly significant when the p – value (the estimated probability of rejecting the hypothesis that the distributions are statistically similar) p ≤ 0.01. We considered that the differences between distributions are significant when the p – value p ≤ 0.05.
Figure 8 shows the distributions of the Dn(4000) index (left panel) and stellar masses log M* (right panel) in clusters A2065, A2061, A2089, Gr2064, and A2142. In Fig. 9 we present these distributions for galaxies in the spheres of influence of these clusters. In Table 5 we give median values of Dn(4000) index and stellar masses log M* of the galaxies in the clusters and in their regions of influence, and the fractions of galaxies with Dn(4000) ≥ 1.75 (VO galaxies, f1.75), 1.35 < Dn(4000) ≤ 1.75 (RQ and RSF galaxies, and BSF galaxies in this Dn(4000) index interval, f1.55), and Dn(4000) ≤ 1.35 (galaxies with the youngest stellar populations, f1.35). In the Dn(4000) interval 1.35 < Dn(4000) ≤ 1.75 we do not separate RQ and RSF galaxies because they have been discussed briefly in Sect. 4 in the subsections about each individual cluster.
 |
Fig. 8. Distribution of Dn(4000) index of galaxies (left panel) and distribution of stellar masses of galaxies (right panel) in clusters A2065, A2061, A2089, Gr2064, and A2142. Vertical lines in the left panel show the limits Dn(4000) = 1.75, Dn(4000) = 1.55, and Dn(4000) = 1.35. |
Median values of the Dn(4000) index and stellar masses (log M*), and the fractions of galaxies with Dn(4000) ≥ 1.75 (f1.75), 1.35 < Dn(4000) ≤ 1.75 (f1.55), and Dn(4000) ≤ 1.35 (f1.35) for galaxies in the CB and SCl A2142 clusters and in their spheres of influence, R30.
In Fig. 8 the distributions of the Dn(4000) indexes show that clusters A2061 and Gr2064 have galaxies with a higher Dn(4000) index (higher value of f1.75, indicating that galaxies have older stellar populations) than clusters A2065 and A2089. The KS test shows that these differences are significant. The galaxy populations (according to Dn(4000) index) in A2061 and in Gr2064 are statistically similar, although the cluster Gr2064 has higher fraction of galaxies with intermediate values of the Dn(4000) index than A2061 (f1.55). The KS test shows that galaxy populations in A2065 and in A2089 are also statistically similar, although the fraction of galaxies with very young stellar populations is higher in A2065. Cluster A2089 has the highest fraction of galaxies with 1.35 < Dn(4000) ≤ 1.75. These are mostly red and blue star-forming galaxies (Fig. 6). As the connectivity of the cluster A2065 is as high as 𝒞 = 9 (Table 6) and the cluster contains infalling substructures and groups, we may conclude that A2065 is a dynamically active cluster, and this may explain the high fraction of star-forming galaxies in it.
Characteristic radii Rvir, Rcl, and R30, and connectivity 𝒞 of clusters.
We found that the galaxy populations in A2142 and in A2061 are statistically similar. In both clusters, the stellar populations are older than in A2065 and A2089, although A2061 has higher fraction of galaxies with young stellar populations with Dn(4000) ≤ 1.35 (11% in A2061 and 6% in A2142). These galaxies lie in the infall region of A2061 (Fig. 5).
The KS test shows that the stellar masses of the galaxies are statistically similar in all clusters. However, we note the lack of galaxies with low stellar masses in clusters A2142, A2061, and Gr2064, which also had galaxies with older stellar populations than other clusters. Cluster A2089 has a larger number of low stellar mass galaxies than other clusters.
In the spheres of influence, the fraction of galaxies with very old stellar populations is lower than in clusters. This is expected because as galaxies fall into clusters, they loose their gas and their star formation is suppressed. It is interesting to note that galaxies in the environment of A2065 and A2089 within R30 have lower values of the Dn(4000) index than galaxies in the spheres of influence of other clusters. This difference is statistically significant. The neighbourhood of Gr2064 is different from the neighbourhood of any other cluster in this study, with an excess of galaxies with Dn(4000) < 1.55, that is, galaxies with young and very young stellar populations. As we showed in Fig. 7, there is an infalling rich group near Gr2064 with a large number of star-forming galaxies, and this excess is partly due to galaxies in this group. We return to this in the discussion.
Figure 9 shows that in the environment of clusters, there is some lack of low stellar mass galaxies around A2061 and around A2089, in comparison with the environment of Gr2064 and A2065. However, the KS test shows that these differences are not significant. Einasto et al. (2018b) noted that there is a large variety in the galaxy content of individual structures falling into the cluster A2142, but on average, the galaxy content in the sphere of influence of A2142 is similar to that around the other clusters we studied.
 |
Fig. 9. Distribution of Dn(4000) index of galaxies (left panel) and distribution of stellar masses of galaxies (right panel) in the environment of clusters A2065, A2061, A2089, Gr2064, and A2142. Vertical lines in the left panel show the limits Dn(4000) = 1.75, Dn(4000) = 1.55, and Dn(4000) = 1.35. |
4.6. Summary of cluster properties
We analysed the dynamical state, connectivity, and galaxy populations of the richest clusters in the high-density cores of the CB supercluster. We show the 3D distribution of galaxies in the CB region in Fig. 10. In our study we found that at a certain clustercentric distance around each cluster, there is a minimum in the distributions of galaxies. According to the PPS diagrams, within this distance limit, galaxies and groups are falling into the central cluster. We may assume that the corresponding clustercentric distance marks the borders of the sphere of influence for clusters. We denoted this distance as the radius R30 (Table 6). The spheres of influence of three clusters touch each other, but they do not overlap (they overlap partly in Fig. 10 because of projections). Interestingly, a similar scale has been found in the distribution of galaxy groups along filaments (Tempel et al. 2014a). Einasto et al. (2020) noted a similar feature around the cluster A2142 in the high-density core of the SCl A2142 supercluster, where it corresponds to the density contrast around the cluster Δρ ≈ 30. To compare the density contrast around clusters from the CB and in SCl A2142, we calculate corresponding density contrasts for the CB clusters below, but first we briefly summarise the results for the clusters.
 |
Fig. 10. 3D distribution of galaxies in the CB and in the low-density region around it. Filled symbols denote galaxies in clusters A2065, A2061, A2089, and Gr2064. Empty circles show supercluster galaxies that are not members of these clusters. Grey dots denote galaxies in the low-density region with a global density D8 < 5. Blue circles denote BSF galaxies, orange circles denote RSF galaxies, turquoise green circles mark RQ galaxies, and red circles denote VO galaxies. Green circles mark galaxies in long filaments with a length larger than 5 h−1 Mpc. Large red circles show the circles with a radius R30, which partly overlap because of projections in the 3D view. |
A2065 is the richest and most massive cluster in the CB. It has the largest number of substructures, the highest connectivity and the second highest number of long filaments of the CB clusters. The star formation activity both in the cluster and in its sphere of influence may be triggered by the overall dynamical activity of the cluster. Infalls into A2065 occur from many directions: along the line of sight, and from north and east, where A2061 and A2089 lie.
A2061 is the second richest cluster in the CB. Its mass is close to the mass of Gr2064. A2061 forms a close pair with A2067, and these clusters have probably already started to merge. It has the largest number of long filaments that reach out of its sphere of influence. Relatively old stellar populations both in the cluster and in its sphere of influence suggest that it already passed its most active period of star formation or that the transition of galaxies is now ongoing, as indicated by the high fraction of (red) star-forming galaxies near it.
The cluster A2089 is the poorest and has the lowest mass of the clusters we studied. It also has the lowest connectivity value and the smallest R30. There is only one long filament near it that points towards the cluster A2065. A2089 itself is elongated in the direction of this filament. A2089 is dominated by galaxies with old stellar populations. We may assume that this cluster has already passed the active formation stage.
Cluster Gr2064 is the richest cluster in the high-density peak in an another part of the CB. Its mass is similar to the mass of A2061. It has three long filaments, one of which connects A2064 with the other rich groups in CB. Galaxy populations of galaxies in the sphere of influence of Gr2064 differ from those around any other rich cluster in the CB. This cluster has an infalling group with the highest fraction of star-forming galaxies of the infalling groups near the CB clusters. There are also RSF galaxies in the outskirts of GR2064.
In all clusters at Rcl there is a small minimum in the galaxy distribution followed by a local maximum. This is similar to the splashback feature detected in cluster profiles (More et al. 2015; Bianconi et al. 2021, and references therein). However, because we lack information about galaxy orbits, we call this the radius of the (main) cluster Rcl, where substructures and groups or clusters near clusters are falling into the cluster. We defined the radius Rcl for each cluster empirically as the radius at which the minimum in the galaxy distribution occurs. The values of Rcl lie between the virial radii of clusters and their maximum size in the sky, given in Table 2. They depend on the structure and merging history of clusters. Some galaxies here may actually be splashback galaxies, but we need to study them in more detail to test this. This could be a subject for future studies.
Several studies have found that dynamically active clusters have higher fraction of star-forming galaxies than relaxed clusters (see, for example, Einasto et al. 2010; Cohen et al. 2014; Deshev et al. 2017; Seth & Raychaudhury 2020; Sengupta et al. 2021). Star formation of galaxies in these clusters may be triggered by infall of galaxies and groups. In our study we found that clusters A2061 and A2065 have the largest number of infalling structures and long filaments near them, with connectivities 𝒞 = 8 and 𝒞 = 9, respectively, but their galaxy populations are different. Cluster A2061 has galaxies with older stellar populations than A2065. This suggests that the formation history of these clusters has been different.
Interestingly, the galaxy populations in A2142 and in A2061 are statistically similar. In both clusters the stellar populations are older than in A2065 and A2089. Einasto et al. (2018a) showed that on average, galaxies in A2142 are redder and have lower star formation rates than other rich clusters from the SDSS at the same distances. Our finding that the galaxy populations in A2142 and A2061 are similar shows that large sets of data need to be compared with caution: individual differences and possible large variations in the properties of the objects, in our case, the richest galaxy clusters in superclusters, might be washed out. Large variations in the galaxy populations of individual rich clusters in the same supercluster have been found before, for example, in the superclusters of the Sloan Great Wall and in the Coma supercluster (Einasto et al. 2010; Seth & Raychaudhury 2020). Moreover, variations in star formation properties of galaxies have been found in infalling systems near clusters A2142 and A963 (Einasto et al. 2010, 2018a; Deshev et al. 2017, 2020). This is probably related to the different history of these galaxies (Bahé et al. 2013; Seth & Raychaudhury 2020). These are interesting topics for the future studies that search for variations in cluster properties based on simulations.
We also found a certain cosmic concordance of the galaxy properties in clusters and in their spheres of influence in the main part of the CB. Clusters with a higher fraction of star-forming galaxies also have a higher fraction of star-forming galaxies in their neighbourhood. However, the environment of Gr2064 is different, with an infalling group with a very high fraction of star-forming galaxies. This is again evidence of large variations in galaxy populations of individual rich clusters and their spheres of influence, which shows that the clusters in the CB have different merging histories.
When we count all long filaments that extend from the CB supercluster to the low-density region around it (supercluster cocoon, see Einasto et al. 2020, for details and references), then we find that the connectivity of the CB is 𝒞 = 7 (here we did not count the long filaments between clusters inside the supercluster). Thus the connectivity of the CB is comparable with that of SCl A2142 with 𝒞 = 7.
5. Discussion
5.1. Spheres of influence R30 and the density contrast Δρ
In Fig. 11 we plot the sky distribution of galaxies in the main part of the CB with RA < 234 degrees and plot the circles around each cluster showing the spheres of influence of the corresponding cluster. This figure shows that spheres of influence do not overlap. This is expected from the evolution of protoclusters, where clusters grow by accretion of galaxies from surrounding region (Chiang et al. 2013; Overzier 2016). Each cluster is surrounded by a region from which galaxies fall towards the central cluster, as also seen in the PPS diagrams above. When we compare this figure with Fig. 2, we see that the borders of the regions of influence approximately correspond to the minima in the luminosity-density field in the CB (we discuss this in more detail in another study).
 |
Fig. 11. Distribution of galaxies in the main part of the CB in the plane of the sky. Filled symbols denote galaxies in clusters A2065, A2061, and A2089, and empty circles show other galaxies in the supercluster. Grey crosses denote galaxies in the low-density region with D8 < 5 (partly overlapping with the supercluster region due to projections). Large red circles show the circles with radius of R30 (Table 6). |
In Fig. 12 we show the acceleration field of the CB supercluster. Here arrows show how far galaxy groups in the CB may move during 2 Gyr. Coordinates (x, y) are rectangular coordinates in the plane containing the centres of all three main clusters. This is quite different from the plane of the sky, thus the sphere of influence around A2061, seen at a different angle, appears to be smaller than in Fig. 11. The spheres of influence around A2065 and A2089 touch, as in Fig. 11. In the acceleration field figure (Fig. 12), each cluster acts as a small attractor. The centre of the gravitational potential lies between clusters. The separation between the clusters, where the acceleration is lowest, is seen in the field between clusters. In calculations of the acceleration field, all four richest clusters in the CB have been taken into account. We do not show the cluster Gr2064 in Fig. 12 because it is difficult to project it onto the plane that is determined by the three other richest clusters in the CB without distortions.
 |
Fig. 12. Acceleration field of the CB supercluster. Here coordinates (x, y) are rectangular coordinates in the plane containing centres of all three main clusters. Colours show the values of the difference in z coordinate direction, and arrows show how far galaxy groups in the CB may move during 2 Gyr. |
We note that Einasto et al. (2020) showed that the A2142 supercluster has a high-density core with a radius of ≈5 h−1 Mpc, with a clear minimum in the galaxy distribution. This minimum separates it from the surrounding main body of the supercluster. Einasto et al. (2020) found that the minimum corresponds to the density contrast Δρ ≈ 30. It is interesting to analyse the density contrast around rich clusters in the CB and to compare it with that of the SCl A2142.
For this purpose, we compared the mass distribution around clusters with the predictions of the spherical collapse model. In our analysis we used the density contrast Δρ within spheres around clusters with increasing radius. To calculate the density contrast, we used the distribution of cluster and group masses calculated as described in Sect. 3.1. From the cumulative mass distribution, we calculated the corresponding density distributions.
In Figs. 13 and 14 we plot the density contrast Δρ with respect to the clustercentric distance for A2065, A2061, A2089, and for Gr2064. In the right panel of Fig. 13 we mark the location of A2067 from the centre of A2061. In these figures vertical red areas correspond to the borders of the spheres of influence, R30. It is interesting to note that they all approximately correspond to the density contrast Δρ ≃ 30 (or slightly higher). The same density contrast was found at the borders of the high-density core of the SCl A2142 (Einasto et al. 2020). Vertical blue, light blue, and grey areas in Figs. 13 and 14 mark borders of the turnaround, future collapse, and zero-gravity regions. The width of these areas is determined by the width of the mass error corridor. These regions were introduced in Sect. 3.1. The turnaround radius corresponds to the radius of a spherical shell around a cluster that is at the turnaround. Within this radius, the galaxy systems around clusters (between R30 and Rturn) are collapsing, that is, they fall into the clusters. Galaxy systems within the future collapse region will collapse in the future.
 |
Fig. 13. Density contrast Δρ = ρ/ρm vs. clustercentric distance for A2065 (left panel) and for A2061 (rich panel). The density contrast for the centre cluster is plotted with the red line. The golden area shows the error corridor from the mass errors. Characteristic density contrasts are denoted as follows: Δρ = 360 (virial), Δρ = 200 (r200), Δρ = 13.1 (turnaround, dashed blue line), Δρ = 8.73 (FC, dash-dotted violet line), and Δρ = 5.41 (ZG, solid light blue line). Blue, light blue, and grey areas mark the borders of the turnaround, FC, and ZG regions. The red area marks R30. The arrow in the right panel marks the average distance of cluster A2067 from the centre of A2061. |
 |
Fig. 14. Density contrast Δρ = ρ/ρm vs. clustercentric distance for cluster A2089 (left panel) and for Gr2064 (right panel). Notations are as in Fig. 13. |
The density contrast at the turnaround in the local Universe is Δρ = 13.1. The density contrast Δρ at the borders of the spheres of influence, Δρ ≃ 30, shows that the structures within R30 around clusters have already passed the turnaround some time ago, and they continue to contract. This might be a universal density contrast that characterises the evolution of clusters. To understand at which redshift the collapse may have begun if the current density contrast is Δρ ≃ 30, we analysed the evolution of the density perturbation and calculated the current density contrast for cases in which the turnaround occurs at redshifts in the range of z = 0.6 − 0.2. In our calculations we used formulae derived by Lee & Ng (2010). We show the results for two values of Ωm, Ωm = 0.27, as used in this paper, and Ωm = 0.4. The reason for this is that according to current observational data, the value of Ωm lies in a certain range around 0.3 (Heymans et al. 2021). For Ωm = 0.3 the turnaround density contrast value can be found, for example, in Gramann et al. (2015) and in Gramann & Suhhonenko (2002).
We show the results of these calculations in Fig. 15. This figure shows the density contrast Δρ at present, if the turnaround occurred at higher redshifts. Structures with a current value Δρ ≃ 30 passed the turnaround at redshifts z ≈ 0.37 for Ωm = 0.27, and at redshifts z ≈ 0.41 for Ωm = 0.40. The difference between the two Ωm values is very small, as was also concluded in Gramann et al. (2015). We may therefore assume that structures around clusters within the spheres of influence, R30, passed the turnaround in the redshift interval z ≈ 0.3 − 0.4. Galaxies closer to the clusters than this radius are falling into clusters, and this is probably the reason for the minimum in the galaxy distribution at R30. Protocluster simulations show that the clusters themselves probably already obtained their current sizes at redshifts z > 0.4 (Chiang et al. 2013). This agrees with the estimate about the formation of cluster A2142 by Einasto et al. (2018a).
 |
Fig. 15. Current density contrast Δρ for Ωm = 0.27 (solid red line) and for Ωm = 0.40 (dashed blue line) if the turnaround occurred at redshifts in the interval z = 0.56 − 0.2. |
Einasto et al. (2020) showed that the galaxy groups within the high-density core of A2142 are all falling into cluster A2142 (see Einasto et al. 2020, for details). We showed the same for the richest clusters in the CB. Therefore each cluster acts as a small attractor for galaxies within their sphere of influence with R30. The radii of the spheres of influence, R30, are proportional to the mass of the cluster and also to the mass inside the spheres of influence, but the scatter is large (Table 7). Tables 5 and 6 show that galaxy content and connectivity of clusters are not directly related to their masses or to radii R30. In other words, in the high-density cores of the CB, the richest clusters and their close environment show large variations in their dynamical properties, in addition to the variations in their galaxy content and connectivity.
Radii and masses of centre clusters within their spheres of influence at characteristic density contrasts Δρ = 30, 13.1, and 8.7.
5.2. Evolution of the CB
Next we discuss possible future evolution scenarios of the richest clusters in the CB and for the whole supercluster. For this we compare the density contrasts at various clustercentric distances in Figs. 13 and 14 and in Table 7 with the characteristic radii and density contrasts from the spherical collapse model.
Distancing scenario. Figures 13 and 14 and Table 7 demonstrate that the turnaround radius Rturn for each cluster is larger than the radius R30. This means that each cluster with its surrounding region has already passed turnaround.
One scenario for the future of the CB, which can be called the distancing scenario, therefore is that each of clusters will shrink into a separate system. These systems will move away from each other as the Universe expands. Unfortunately, as we lack distances for galaxies that are independent from Hubble expansion and we therefore also lack their peculiar velocities, we cannot directly determine whether this scenario really occurs. However, cluster Gr2064 lies far away from the clusters in the main part of the CB. Its distance from the nearest cluster in the main part of the CB, A2089, is ≈20 h−1 Mpc (Table 7). This value exceeds the values of the turnaround and future collapse for all clusters. For this cluster, the distancing scenario therefore probably correctly predicts its future.
This assumption is supported by the fact that this cluster and the whole part of the CB surrounding it is only weakly connected with another part of the CB by a bridge of galaxies in which the global density barely exceeds the global density limit for defining superclusters, D8 ≃ 5 (Sect. 2.1, and Figs. 2 and 10). Cluster Gr2064 is projected onto the supercluster SCl A2142 in the sky distribution. These two structures, the Gr2064 part of the CB supercluster and SCl A2142, are connected by a filament (see Fig. 7 and the figures in Einasto et al. 2020). This poses the question whether the Gr2064 region might be a part of SCl A2142. However, as the analysis in Einasto et al. (2020) showed, there is a density minimum in this filament that is characteristic of supercluster cocoon borders, and the Gr2064 region lies outside of the SCl A2142 cocoon. It is interesting to note that the Gr2064 region resembles the small Arrowhead supercluster that is embedded between the Laniakea, the Perseus-Pisces, and the Coma superclusters in the local Universe (Pomarède et al. 2015), and has approximately the same mass as the turnaround region around Gr2064 (Table 7). According to the distancing scenario, the Gr2064 region may in the future become a system similar to the Arrowhead supercluster.
The total collapse scenario. For clusters in the main part of the CB, the distances between A2065 and other clusters given in Table 7 are smaller than the radius of the future collapse region around A2065. A2089 lies within the turnaround region of A2065. The distance between the centres of A2065 and A2061 is approximately 9 h−1 Mpc, which is within the future collapse radius of A2065.
This suggests another scenario for the future evolution of the CB, which can be called the total collapse scenario. In this scenario, all three clusters will merge into one massive system. As a result, this scenario describes the formation of one of the largest bound systems in the local Universe. Cluster A2065, which has the highest mass of the rich clusters of the CB, will be closest to the centre of this new system. To illustrate the total collapse scenario, we calculated the density contrast versus distance from the possible new centre, shown in the left panel of Fig. 16. As in previous figures, we mark the regions of turnaround, future collapse, and zero gravity. In the right panel of Fig. 16 we show the sky distribution of galaxies in the CB, with circles corresponding to the turnaround and future collapse regions. In the main part of the CB, they are centred on the possible new centre of the CB, and in the Gr2064 part, they are centred on cluster Gr2064. This division is based on the previous results of the distancing scenario, which showed that most likely, the part of the CB with GR2064 will separate from the main part of the CB in the future.
 |
Fig. 16. Left panel: density contrast Δρ = ρ/ρm vs. clustercentric distance Dc for the possible new centre of the main part of the CB. Notations are as in Fig. 13. Arrows mark the distances of clusters A2065, A2061, and A2089 at which they join the possible new collapsing system. Right panel: sky distribution of galaxies in the CB. Filled circles mark turnaround (blue) and future collapse (light blue) zones in the supercluster, as shown in the left panel. Colours are as in Fig. 2. |
In this figure we mark the distances at which the clusters join this possible future system. The three richest clusters in the CB are within the turnaround radius of the possible new centre. This supports the scenario according to which the main part of the CB is already collapsing. Its outer parts will collapse in the future. This figure shows that the mass of the possible new system at the turnaround radius, Rturn ≈ 10 h−1 Mpc, is Mturn ≈ 4.5 × 1015 M⊙. The radius and mass of the future collapse region is RFC ≈ 12.5 h−1 Mpc and MFC ≈ 4.7 × 1015 M⊙. Comparison with the sizes and masses of turnaround and future collapse regions around individual clusters in Table 7 shows that if the centre of the possible new system is at the most massive cluster in the CB, cluster A2065, the total mass in the system that will collapse in the future is slightly lower (MFC ≈ 4.3 × 1015 M⊙), but all three clusters lie within the radius RFC from A2065. The lower mass comes from the fact that in this case, a larger part of the low-density region that surrounds the supercluster is included in the collapsing system. With the new centre, the collapsing region mostly includes the main part of the CB. The zero-gravity zone surrounds the whole main part of the CB. This is similar to what Einasto et al. (2020) found for the main body of the supercluster SCl A2142. The total collapse scenario suggests that different parts of the CB will separate in the future.
The right panel of Fig. 16 shows that the turnaround region around cluster Gr2064 includes a rich group that is infalling on Gr2064 (see Sect. 4.4). Interestingly, above we found that differently from the other clusters we studied, the infall zone of Gr2064 contains a large number of star-forming galaxies (Fig. 7, lower right panel). The star formation of galaxies in this group might be enhanced due to the joint effect of infall and collapse of this region. Similarly, there is an excess of star-forming galaxies in the turnaround region of supercluster SCl A2142 (Einasto et al. 2018b) that supports this assumption.
The total collapse scenario is similar to what Araya-Melo et al. (2009) described for the future evolution of superclusters. According to Araya-Melo et al. (2009), individual clusters and groups in superclusters will merge to form massive systems of low multiplicity. The shapes of future superclusters will be more spherical than the current shapes of superclusers, which are mostly elongated (Einasto et al. 2011a).
Our suggestions for the future evolution of the CB depend on how good our mass estimates for the supercluster are. Our mass estimates for the Corona Borealis supercluster high-density cores agree well with the lower limits of the mass estimates by Pearson et al. (2014). Pearson et al. (2014) reported that the A2065 region will form a bound system in the future if there is enough mass between the clusters. In Sect. 3.2 we showed that the mass of the supercluster may be underestimated, partly due to the faint, unobserved galaxies. Therefore we may conclude that at least we probably do not overestimate the supercluster mass, and this adds weight to our conclusions about the total collapse scenario.
The collapsing high-density cores have also been studied in other superclusters: in the Shapley supercluster, in superclusters of the Sloan Great Wall, in the Perseus-Pisces supercluster, and in the Hercules supercluster (Reisenegger et al. 2000; Rines et al. 2002; Chon et al. 2015; Teerikorpi et al. 2015; Einasto et al. 2016b). High-density collapsing cores of superclusters may inhabit several (merging) clusters, like in the Shapley supercluster. Rich superclusters may have several cores that may collapse and form separate systems in the future, like in the Sloan Great Wall superclusters (Einasto et al. 2016b). The CB supercluster is interesting among other rich superclusters as it embeds rich clusters at various stages of evolution, from single clusters to merging ones. This makes the CB supercluster especially interesting for studies of the coevolution of clusters in superclusters.
We may ask how large and massive the largest bound structures (collapsing cores of superclusters) in the local Universe are. Their sizes and masses are determined by the mass in clusters and groups, and by the intercluster matter within them. The mass and radius of the collapsing core at turnaround of supercluster SCl A2142 with one very massive cluster are M ≈ 2.3 × 1015 h−1 M⊙ and RT ≈ 8 h−1 Mpc (Einasto et al. 2018b). The total mass in the collapsing core is determined by the mass of the main cluster, A2142, and by the mass of galaxy groups and gas in the core. The mass and radius of the most massive collapsing core in the Sloan Great Wall superclusters with one very massive cluster are M ≈ 1.8 × 1015 h−1 M⊙ and RT ≈ 7.5 h−1 Mpc (Einasto et al. 2016b). In the Shapley supercluster, the mass and radius of the collapsing core with several merging clusters are M ≈ 1.3 × 1016 h−1 M⊙ and RT ≈ 12.4 h−1 Mpc (Reisenegger et al. 2000; Bardelli 2004; Chon et al. 2015). The collapsing core of the Shapley supercluster is the largest and most massive bound structure in the local Universe found so far, and the core of the CB is the second most massive. We found that the radius of the core of the CB, which may collapse in the future, is RFC ≈ 12.5 h−1 Mpc, with a mass of MFC ≈ 4.7 × 1015 M⊙, which is lower than that in the Shapley supercluster.
Even the most massive clusters in the local Universe are still growing, as shown by their merging and infalling structures. Collapsing cores in the CB supercluster, as well as in SCl A2142, are surrounded by the zero-gravity zone that borders the bound and unbound structures (Teerikorpi et al. 2015; Einasto et al. 2020). This suggests that the supercluster cores themselves have stopped growing. The masses and sizes of the most massive possibly collapsing supercluster cores are determined by the mass of structures within them, first of all, by the mass and number of the richest clusters. The masses of the most massive clusters in the local Universe and in simulations are of about M ≈ 1015 h−1 M⊙ (Andreon 2016; Kim et al. 2015). It would be an interesting task to further search for high-density cores of superclusters that embed several close and/or merging high-mass clusters, which could define the most massive bound structures in the Universe. It could also be interesting to compare the observed number of the most massive collapsing cores of superclusters with that from simulations. For example, Yaryura et al. (2011) and Park et al. (2012) showed that although the probability of finding in the local Universe as many very rich superclusters as in the ΛCDM model is very low, the number of these systems is still compatible with the predictions of the ΛCDM model. Sheth & Diaferio (2011) showed that having both the Shapley supercluster and the Sloan Great Wall in the local Universe is barely compatible with the initial Gaussian density fluctuations. The number of massive collapsing cores of superclusters may add another constraint on the ΛCDM model and on the nature of the primordial fluctuation field. Sheth & Diaferio (2011) estimated that the masses of these superclusters are about M ≈ 1.8 × 1016 h−1 M⊙ (the Shapley supercluster) and M ≈ 1.2 × 1017 h−1 M⊙ (the Sloan Grea Wall). Einasto et al. (2016b) estimated using the same supercluster mass estimation method as used in this paper that the total mass of the Sloan Great Wall is M ≈ 2.4 × 1016 h−1 M⊙, which is lower than the Sheth & Diaferio (2011) estimate. The total mass of the Corona Borealis supercluster, as found in this paper (M ≈ 4.7 × 1015 h−1 M⊙, mass of the future collapse region), is approximately 5–25 times lower than these estimates. The large differences in estimated supercluster masses show that we need to refine the methods for estimating supercluster masses. To strenghten the predictions by Sheth & Diaferio (2011), the CB supercluster alone is probably not massive enough in comparison with extreme superclusters and their complexes, such as the Shapley supercluster and the Sloan Great Wall. To test the predictions by Sheth & Diaferio (2011), we need to search for and analyse the properties of massive (collapsing cores of) superclusters, especially in the local Universe. This is an interesting task for future studies that will help us to test possible constraints for cosmological models.
5.3. Why the Corona Borealis?
Here we try to answer the question why the CB will probably become one of the most massive bound systems in the Local Universe. Galaxy clusters act as attractors that lie at the crossing of galaxy filaments. In the high-density cores of superclusters, clusters and groups are connected by a number of filaments, and therefore the number of connections is large and groups are typically richer there than elsewhere (see also Einasto et al. 2003c, 2005, about the environmental enhancement of galaxy groups near rich clusters). Thus the high-density cores of superclusters act as great attractors on supercluster scales. The CB is located in the dominant supercluster plane, at the crossing of three very rich supercluster chains that embed, among other superclusters, the Sloan Great Wall, and the structures of one of the shell-like structures detected in the nearby Universe (Einasto et al. 1997, 2011a, 2016a). This specific location might cause the CB to be so rich and massive, which will lead to the formation of very massive and large bound systems in the future.
Suhhonenko et al. (2011) showed that the density waves of different scales affect the formation of galaxy systems of different richness. Rich galaxy clusters and high-density cores of superclusters form in regions of high environmental density, where positive sections of medium- and large-scale density perturbations combine. The CB is an example of one of such region. Moreover, a 120 h−1 Mpc scale has been found in the cosmic web (Broadhurst et al. 1990; Einasto et al. 1994, 2016a). This scale is determined by the distribution of galaxy clusters and superclusters, but not necessarily by the distribution of the very rich clusters. To understand the formation of the richest clusters and supercluster cores better, it would be an interesting task on its own to search for possible characteristic scales in their distribution and for their possibly specific locations in the cosmic web.
6. Summary
We studied the galaxy content, substructure, and connectivity of the richest galaxy clusters and their spheres of influence in the Corona Borealis supercluster, and we predicted the future evolution of the supercluster. We found that the density contrast at the boundaries of the spheres of influence around the richest clusters in the CB is Δρ ≈ 30. This suggests that they passed the turnaround and started to collapse around redshifts of approximately z ≈ 0.4. Our main conclusions are listed below.
-
(1)
Rich clusters in the CB are dynamically active, as shown by their infalling and possibly merging subclusters, groups, and clusters near them.
-
(2)
The total connectivity of clusters varies from 2 to 9, and the number of long filaments that begin near clusters varies from 1 to 5.
-
(3)
The values of the cluster radii, Rcl (the radius of a cluster for a one-component cluster, and the radius of the main component in clusters with several components, usually called splashback radius) are Rcl ≈ 2 − 3 Rvir. At clustercentric distances Dc ≃ Rcl, there is a small maximum in the distribution of galaxies.
-
(4)
Around each cluster lies a sphere of influence with radius R30 that corresponds to the density contrast around the cluster, Δρ ≈ 30. Within this sphere, all galaxies and groups are falling into clusters. The high-density contrast shows that within the spheres of influence, galaxy systems are collapsing, and the collapse began at redshifts of approximately z ≈ 0.3 − 0.4.
-
(5)
Galaxy content in clusters and in their spheres of influence varies strongly. In the main part of the CB in the most massive cluster, A2065, and in its sphere of influence the fraction of galaxies with very old stellar populations is lower than in the other two clusters in this part of the CB. Cluster Gr2064 has a high fraction of star-forming galaxies in an infalling group in the turnaround region of the cluster. Star formation in galaxies in this group may be triggered by infall and collapse.
-
(6)
Galaxies in transformations, red star-forming galaxies and recently quenched galaxies, lie in the infall zones of clusters and in infalling groups.
-
(7)
The galaxy populations in clusters A2142 and in A2061 are statistically similar. In these clusters, the galaxies have older stellar populations than in A2065 and A2089.
-
(8)
During the future evolution, two parts of the CB will separate. The main part forms a collapsing region that will probably become one of the largest and most massive bound systems in the nearby Universe.
We found that the density contrast at the boundaries of the spheres of influence around the richest clusters in the CB is Δρ ≈ 30. To understand the formation and evolution of rich galaxy clusters, we need to continue to study the environment of clusters to determine whether the characteristic density contrast Δρ = 30 can be found around other clusters, and what the implications of this are for the understanding of cluster evolution. This finding suggests that they have passed turnaround and started to collapse around redshifts of approximately z ≈ 0.4. Simulations show that at redshift z = 0.5, galaxy clusters have half of their current mass (Kim et al. 2015). This means that studies of galaxy clusters and their environment at redshifts between z = 0 − 0.5 are especially important for understanding the evolution of galaxy clusters and galaxies within them. These data will be provided by future surveys, for example, the 4MOST cluster survey and 4-MOST Cosmology Redshift Survey (CRS) (de Jong et al. 2019; Finoguenov et al. 2019; Richard et al. 2019). The CRS survey can be extended with HI data from the SKA survey (Wolz et al. 2017).
The massive and large collapsing supercluster cores are the largest objects in the Universe to collapse now or in the future. It would be an interesting task on its own to search for similar structures from observations, and to compare the number and properties of these structures in observations and simulations. With data from the next generation of large galaxy redshift surveys, for instance, Euclid (Laureijs et al. 2011), DESI (Levi et al. 2013; DESI Collaboration 2016), and J-PAS (Benitez et al. 2014), it will become possible to study such systems over a reasonable span of the history of the Universe, enabling a direct comparison to the evolution seen in large-scale cosmological simulations. This comparison will serve as a test for cosmological models and may give valuable information about dark matter and dark energy.
Acknowledgments
We thank the referee for valuable comments and suggestions which helped us to improve the paper. We thank Changbom Park, Boris Deshev, Gayoung Chon, and Mirt Gramann for useful discussions. We are pleased to thank the SDSS Team for the publicly available data releases. Funding for the Sloan Digital Sky Survey (SDSS) and SDSS-II has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, the US Department of Energy, the National Aeronautics and Space Administration, the Japanese Monbukagakusho, and the Max Planck Society, and the Higher Education Funding Council for England. The SDSS website is http://www.sdss.org/. The SDSS is managed by the Astrophysical Research Consortium (ARC) for the Participating Institutions. The Participating Institutions are the American Museum of Natural History, Astrophysical Institute Potsdam, University of Basel, University of Cambridge, Case Western Reserve University, The University of Chicago, Drexel University, Fermilab, the Institute for Advanced Study, the Japan Participation Group, The Johns Hopkins University, the Joint Institute for Nuclear Astrophysics, the Kavli Institute for Particle Astrophysics and Cosmology, the Korean Scientist Group, the Chinese Academy of Sciences (LAMOST), Los Alamos National Laboratory, the Max-Planck-Institute for Astronomy (MPIA), the Max-Planck-Institute for Astrophysics (MPA), New Mexico State University, Ohio State University, University of Pittsburgh, University of Portsmouth, Princeton University, the United States Naval Observatory, and the University of Washington. The present study was supported by the ETAG projects PRG1006, PUT1627, PUTJD907, and by the European Structural Funds grant for the Centre of Excellence “Dark Matter in (Astro)particle Physics and Cosmology” (TK133). This work has also been supported by ICRAnet through a professorship for Jaan Einasto. We applied in this study R statistical environment (Ihaka & Gentleman 1996).
References
- Ahn, C. P., Alexandroff, R., Allende Prieto, C., et al. 2014, ApJS, 211, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Aihara, H., Allende Prieto, C., An, D., et al. 2011, ApJS, 193, 29 [Google Scholar]
- Ando, M., Shimasaku, K., & Momose, R. 2020, MNRAS, 496, 3169 [Google Scholar]
- Andreon, S. 2016, A&A, 587, A158 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Araya-Melo, P. A., Reisenegger, A., Meza, A., et al. 2009, MNRAS, 399, 97 [Google Scholar]
- Aryal, B., Paudel, S., & Saurer, W. 2007, MNRAS, 379, 1011 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, N. A., & Kulier, A. 2014, MNRAS, 439, 2505 [NASA ADS] [CrossRef] [Google Scholar]
- Bahé, Y. M., McCarthy, I. G., Balogh, M. L., & Font, A. S. 2013, MNRAS, 430, 3017 [NASA ADS] [CrossRef] [Google Scholar]
- Balogh, M. L., Morris, S. L., Yee, H. K. C., Carlberg, R. G., & Ellingson, E. 1999, ApJ, 527, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Bardelli, S. 2004, in 195: Outskirts of Galaxy Clusters: Intense Life in the Suburbs, ed. A. Diaferio, IAU Colloq., 71 [Google Scholar]
- Basilakos, S., Plionis, M., & Rowan-Robinson, M. 2001, MNRAS, 323, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Belsole, E., Sauvageot, J. L., Pratt, G. W., & Bourdin, H. 2005, Adv. Space Res., 36, 630 [Google Scholar]
- Benitez, N., Dupke, R., Moles, M., et al. 2014, ArXiv e-prints [arXiv:1403.5237] [Google Scholar]
- Bianconi, M., Buscicchio, R., Smith, G. P., et al. 2021, ApJ, 911, 136 [Google Scholar]
- Blanton, M. R., & Roweis, S. 2007, AJ, 133, 734 [Google Scholar]
- Blanton, M. R., Hogg, D. W., Bahcall, N. A., et al. 2003, ApJ, 592, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Bond, J. R., Kofman, L., & Pogosyan, D. 1996, Nature, 380, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Broadhurst, T. J., Ellis, R. S., Koo, D. C., & Szalay, A. S. 1990, Nature, 343, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, Y.-K., Overzier, R., & Gebhardt, K. 2013, ApJ, 779, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Chiang, Y.-K., Overzier, R. A., Gebhardt, K., & Henriques, B. 2017, ApJ, 844, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Chon, G., Böhringer, H., Collins, C. A., & Krause, M. 2014, A&A, 567, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chon, G., Böhringer, H., & Zaroubi, S. 2015, A&A, 575, L14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chow-Martínez, M., Andernach, H., Caretta, C. A., & Trejo-Alonso, J. J. 2014, MNRAS, 445, 4073 [NASA ADS] [CrossRef] [Google Scholar]
- Codis, S., Pogosyan, D., & Pichon, C. 2018, MNRAS, 479, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, S. A., Hickox, R. C., Wegner, G. A., Einasto, M., & Vennik, J. 2014, ApJ, 783, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, S. A., Hickox, R. C., Wegner, G. A., Einasto, M., & Vennik, J. 2017, ApJ, 835, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Colombi, S., Pogosyan, D., & Souradeep, T. 2000, Phys. Rev. Lett., 85, 5515 [NASA ADS] [CrossRef] [Google Scholar]
- Darragh Ford, E., Laigle, C., Gozaliasl, G., et al. 2019, MNRAS, 489, 5695 [CrossRef] [Google Scholar]
- de Filippis, E., Schindler, S., & Erben, T. 2005, A&A, 444, 387 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Jong, R. S., Agertz, O., Berbel, A. A., et al. 2019, Messenger, 175, 3 [Google Scholar]
- Deshev, B., Finoguenov, A., Verdugo, M., et al. 2017, A&A, 607, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deshev, B., Haines, C., Hwang, H. S., et al. 2020, A&A, 638, A126 [CrossRef] [EDP Sciences] [Google Scholar]
- DESI Collaboration (Aghamousa, A., et al.) 2016, ArXiv e-prints [arXiv:1611.00036] [Google Scholar]
- de Vaucouleurs, G. 1953, AJ, 58, 30 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G. 1958, Nature, 182, 1478 [NASA ADS] [CrossRef] [Google Scholar]
- Donnelly, R. H., Forman, W., Jones, C., et al. 2001, ApJ, 562, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, J., Jôeveer, M., & Saar, E. 1980, Nature, 283, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, M., Einasto, J., Tago, E., Dalton, G. B., & Andernach, H. 1994, MNRAS, 269, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, M., Tago, E., Jaaniste, J., Einasto, J., & Andernach, H. 1997, A&AS, 123, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, J., Einasto, M., Hütsi, G., et al. 2003a, A&A, 410, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, J., Hütsi, G., Einasto, M., et al. 2003b, A&A, 405, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Einasto, J., Müller, V., Heinämäki, P., & Tucker, D. L. 2003c, A&A, 401, 851 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Suhhonenko, I., Heinämäki, P., Einasto, J., & Saar, E. 2005, A&A, 436, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, J., Einasto, M., Saar, E., et al. 2007a, A&A, 462, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Saar, E., Liivamägi, L. J., et al. 2007b, A&A, 476, 697 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Einasto, J., Tago, E., et al. 2007c, A&A, 464, 815 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Tago, E., Saar, E., et al. 2010, A&A, 522, A92 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Liivamägi, L. J., Tago, E., et al. 2011a, A&A, 532, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Liivamägi, L. J., Tempel, E., et al. 2011b, ApJ, 736, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, M., Lietzen, H., Tempel, E., et al. 2014, A&A, 562, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Gramann, M., Saar, E., et al. 2015, A&A, 580, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Lietzen, H., Gramann, M., et al. 2016a, A&A, 595, A70 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Heinämäki, P., Liivamägi, L. J., et al. 2016b, A&A, 587, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Deshev, B., Lietzen, H., et al. 2018a, A&A, 610, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Gramann, M., Park, C., et al. 2018b, A&A, 620, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, J., Suhhonenko, I., Liivamägi, L. J., & Einasto, M. 2019, A&A, 623, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Deshev, B., Tenjes, P., et al. 2020, A&A, 641, A172 [CrossRef] [EDP Sciences] [Google Scholar]
- Erdoǧdu, P., Lahav, O., Zaroubi, S., et al. 2004, MNRAS, 352, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Farnsworth, D., Rudnick, L., Brown, S., & Brunetti, G. 2013, ApJ, 779, 189 [Google Scholar]
- Finoguenov, A., Merloni, A., Comparat, J., et al. 2019, Messenger, 175, 39 [Google Scholar]
- Fraley, C., & Raftery, A. E. 2006, Technical Report, Dep. of Statistics, University of Washington, 504, 1 [Google Scholar]
- Frieman, J. A., Turner, M. S., & Huterer, D. 2008, ARA&A, 46, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Génova-Santos, R., Rubiño-Martín, J. A., Rebolo, R., et al. 2008, MNRAS, 391, 1127 [NASA ADS] [CrossRef] [Google Scholar]
- Génova-Santos, R., Padilla-Torres, C. P., Rubiño Martín, J. A., Gutiérrez, C. M., & Rebolo, R. 2010, MNRAS, 403, 1531 [NASA ADS] [CrossRef] [Google Scholar]
- Gouin, C., Aghanim, N., Bonjean, V., & Douspis, M. 2020, A&A, 635, A195 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gramann, M., & Suhhonenko, I. 2002, MNRAS, 337, 1417 [NASA ADS] [CrossRef] [Google Scholar]
- Gramann, M., Einasto, M., Heinämäki, P., et al. 2015, A&A, 581, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haines, C. P., Pereira, M. J., Smith, G. P., et al. 2015, ApJ, 806, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Haines, C. P., Iovino, A., Krywult, J., et al. 2017, A&A, 605, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hanami, H., Tsuru, T., Shimasaku, K., et al. 1999, ApJ, 521, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Heymans, C., Tröster, T., Asgari, M., et al. 2021, A&A, 646, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hong, S., Jeong, D., Hwang, H. S., et al. 2020, MNRAS, 493, 5972 [CrossRef] [Google Scholar]
- Huchra, J. P., & Geller, M. J. 1982, ApJ, 257, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Ihaka, R., & Gentleman, R. 1996, J. Comput. Graphical Stat., 5, 299 [Google Scholar]
- Jõeveer, M., Einasto, J., & Tago, E. 1978, MNRAS, 185, 357 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003a, MNRAS, 341, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003b, MNRAS, 341, 54 [Google Scholar]
- Kim, J., Park, C., L’Huillier, B., & Hong, S. E. 2015, J. Korean Astron. Soc., 48, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Kipper, R., Tenjes, P., Tuvikene, T., Ganeshaiah Veena, P., & Tempel, E. 2020, MNRAS, 494, 3358 [Google Scholar]
- Komatsu, E., Smith, K. M., Dunkley, J., et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Kopylova, F. G., & Kopylov, A. I. 2007, Astron. Lett., 33, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Kovács, A., & García-Bellido, J. 2016, MNRAS, 462, 1882 [Google Scholar]
- Kraljic, K., Pichon, C., Dubois, Y., et al. 2019, MNRAS, 483, 3227 [NASA ADS] [CrossRef] [Google Scholar]
- Kraljic, K., Pichon, C., Codis, S., et al. 2020, MNRAS, 491, 4294 [CrossRef] [Google Scholar]
- Kuutma, T., Poudel, A., Einasto, M., et al. 2020, A&A, 639, A71 [CrossRef] [EDP Sciences] [Google Scholar]
- Lahav, O., Lilje, P. B., Primack, J. R., & Rees, M. J. 1991, MNRAS, 251, 128 [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Lee, S., & Ng, K.-W. 2010, JCAP, 2010, 028 [Google Scholar]
- Levi, M., Bebek, C., Beers, T., et al. 2013, ArXiv e-prints [arXiv:1308.0847] [Google Scholar]
- Liivamägi, L. J., Tempel, E., & Saar, E. 2012, A&A, 539, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luparello, H., Lares, M., Lambas, D. G., & Padilla, N. 2011, MNRAS, 415, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Maier, C., Ziegler, B. L., Haines, C. P., & Smith, G. P. 2019, A&A, 621, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malavasi, N., Aghanim, N., Tanimura, H., Bonjean, V., & Douspis, M. 2020a, A&A, 634, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Malavasi, N., Aghanim, N., Douspis, M., Tanimura, H., & Bonjean, V. 2020b, A&A, 642, A19 [CrossRef] [EDP Sciences] [Google Scholar]
- Marini, F., Bardelli, S., Zucca, E., et al. 2004, MNRAS, 353, 1219 [NASA ADS] [CrossRef] [Google Scholar]
- Markevitch, M., Sarazin, C. L., & Vikhlinin, A. 1999, ApJ, 521, 526 [Google Scholar]
- More, S., Diemer, B., & Kravtsov, A. V. 2015, ApJ, 810, 36 [Google Scholar]
- Moster, B. P., Somerville, R. S., Maulbetsch, C., et al. 2010, ApJ, 710, 903 [Google Scholar]
- Muldrew, S. I., Hatch, N. A., & Cooke, E. A. 2018, MNRAS, 473, 2335 [NASA ADS] [CrossRef] [Google Scholar]
- Munari, E., Grillo, C., De Lucia, G., et al. 2016, ApJ, 827, L5 [NASA ADS] [CrossRef] [Google Scholar]
- Musso, M., Cadiou, C., Pichon, C., et al. 2018, MNRAS, 476, 4877 [NASA ADS] [CrossRef] [Google Scholar]
- Muzzin, A., van der Burg, R. F. J., McGee, S. L., et al. 2014, ApJ, 796, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Old, L., Skibba, R. A., Pearce, F. R., et al. 2014, MNRAS, 441, 1513 [Google Scholar]
- Old, L., Wojtak, R., Mamon, G. A., et al. 2015, MNRAS, 449, 1897 [NASA ADS] [CrossRef] [Google Scholar]
- Oman, K. A., Hudson, M. J., & Behroozi, P. S. 2013, MNRAS, 431, 2307 [NASA ADS] [CrossRef] [Google Scholar]
- O’Mill, A. L., Proust, D., Capelato, H. V., et al. 2015, MNRAS, 453, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Oteo, I., Ivison, R. J., Dunne, L., et al. 2018, ApJ, 856, 72 [Google Scholar]
- Overzier, R. A. 2016, A&ARv, 24, 14 [NASA ADS] [CrossRef] [Google Scholar]
- Padilla-Torres, C. P., Gutiérrez, C. M., Rebolo, R., Génova-Santos, R., & Rubiño-Martin, J. A. 2009, MNRAS, 396, 53 [NASA ADS] [CrossRef] [Google Scholar]
- Padilla-Torres, C. P., Rebolo, R., Gutiérrez, C. M., Génova-Santos, R., & Rubiño-Martin, J. A. 2010, in Highlights of Spanish Astrophysics V, eds. J. M. Diego, L. J. Goicoechea, J. I. González-Serrano, & J. Gorgas, 329 [Google Scholar]
- Park, C., Choi, Y.-Y., Kim, J., et al. 2012, ApJ, 759, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Pasquali, A., Smith, R., Gallazzi, A., et al. 2019, MNRAS, 484, 1702 [NASA ADS] [CrossRef] [Google Scholar]
- Pearson, D. W., Batiste, M., & Batuski, D. J. 2014, MNRAS, 441, 1601 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1980, The Large-scale Structure of the Universe (Princeton University Press) [Google Scholar]
- Peebles, P. J. E. 1984, ApJ, 284, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Pillastrini, G. C. B. 2019, New Astron., 69, 1 [Google Scholar]
- Pomarède, D., Tully, R. B., Hoffman, Y., & Courtois, H. M. 2015, ApJ, 812, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Pompei, E., & Iovino, A. 2012, A&A, 539, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pompei, E., Adami, C., Eckert, D., et al. 2016, A&A, 592, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ponman, T. J., Allan, D. J., Jones, L. R., et al. 1994, Nature, 369, 462 [NASA ADS] [CrossRef] [Google Scholar]
- Postman, M., Geller, M. J., & Huchra, J. P. 1988, AJ, 95, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Reiprich, T. H., Veronica, A., Pacaud, F., et al. 2021, A&A, 647, A2 [EDP Sciences] [Google Scholar]
- Reisenegger, A., Quintana, H., Carrasco, E. R., & Maze, J. 2000, AJ, 120, 523 [Google Scholar]
- Rhee, J., Smith, R., Choi, H., et al. 2017, ApJ, 843, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Richard, J., Kneib, J. P., Blake, C., et al. 2019, Messenger, 175, 50 [Google Scholar]
- Rines, K., Geller, M. J., Diaferio, A., et al. 2002, AJ, 124, 1266 [NASA ADS] [CrossRef] [Google Scholar]
- Santiago-Bautista, I., Caretta, C. A., Bravo-Alfaro, H., Pointecouteau, E., & Andernach, H. 2020, A&A, 637, A31 [CrossRef] [EDP Sciences] [Google Scholar]
- Sengupta, A., Keel, W. C., Morrison, G., et al. 2021, ApJ, submitted [arXiv:2102.06612] [Google Scholar]
- Seth, R., & Raychaudhury, S. 2020, MNRAS, 497, 466 [Google Scholar]
- Sheth, R. K., & Diaferio, A. 2011, MNRAS, 417, 2938 [Google Scholar]
- Shi, K., Toshikawa, J., Cai, Z., Lee, K.-S., & Fang, T. 2020, ApJ, 899, 79 [Google Scholar]
- Small, T. A., Ma, C., Sargent, W. L. W., & Hamilton, D. 1998, ApJ, 492, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R., Pacifici, C., Pasquali, A., & Calderón-Castillo, P. 2019, ApJ, 876, 145 [CrossRef] [Google Scholar]
- Suhhonenko, I., Einasto, J., Liivamägi, L. J., et al. 2011, A&A, 531, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Teerikorpi, P., Heinämäki, P., Nurmi, P., et al. 2015, A&A, 577, A144 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tempel, E., Einasto, J., Einasto, M., Saar, E., & Tago, E. 2009, A&A, 495, 37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tempel, E., Tago, E., & Liivamägi, L. J. 2012, A&A, 540, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tempel, E., Tamm, A., Gramann, M., et al. 2014a, A&A, 566, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tempel, E., Stoica, R. S., Martínez, V. J., et al. 2014b, MNRAS, 438, 3465 [NASA ADS] [CrossRef] [Google Scholar]
- Tempel, E., Kipper, R., Saar, E., et al. 2014c, A&A, 572, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tempel, E., Stoica, R. S., Kipper, R., & Saar, E. 2016, Astron. Comput., 16, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Toshikawa, J., Malkan, M. A., Kashikawa, N., et al. 2020, ApJ, 888, 89 [CrossRef] [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Trussler, J., Maiolino, R., Maraston, C., et al. 2020, MNRAS, 491, 5406 [CrossRef] [Google Scholar]
- Tully, R. B., Courtois, H., Hoffman, Y., & Pomarède, D. 2014, Nature, 513, 71 [NASA ADS] [CrossRef] [Google Scholar]
- White, S. D. M., & Rees, M. J. 1978, MNRAS, 183, 341 [NASA ADS] [CrossRef] [Google Scholar]
- Wolz, L., Blake, C., & Wyithe, J. S. B. 2017, MNRAS, 470, 3220 [Google Scholar]
- Yaryura, C. Y., Baugh, C. M., & Angulo, R. E. 2011, MNRAS, 413, 1311 [Google Scholar]
- Zeldovich, I. B., Einasto, J., & Shandarin, S. F. 1982, Nature, 300, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Zucca, E., Zamorani, G., Scaramella, R., & Vettolani, G. 1993, ApJ, 407, 470 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Coordinate system used in acceleration field calculations.
To calculate the acceleration field for the main part of the CB supercluster, we assumed that the dominant acceleration is caused by the most massive clusters in it (A2065, A2061, and A2089). In order to show their effect most strongly, we used in the calculations a coordinate system that is located in the plane determined by these three clusters. The x2 coordinate is determined by connecting A2089 and A2065, the y2 coordinate is defined to be perpendicular to x2 and to be in the same plane as determined by these three clusters. The z2 coordinate is perpendicular to both x2 and y2. The zero point of this coordinate system is the mid-point between clusters. This coordinate system is designed to keep the majority of the acceleration field in the plane of the figures, hence to show how the system may evolve in the clearest manner. This coordinate system is shown in Fig. A.1.
 |
Fig. A.1. Coordinate system used in calculating the acceleration field of clusters in the plane of the sky. The blue plane shows the plane of the three clusters that define the coordinate system. The x2 coordinate direction connects A2089 and A2065, the y2 coordinate is perpendicular to x2 and is in the same plane as determined by the clusters. The z2 coordinate is perpendicular to both x2 and y2. |
All Tables
Median values of the Dn(4000) index and stellar masses (log M*), and the fractions of galaxies with Dn(4000) ≥ 1.75 (f1.75), 1.35 < Dn(4000) ≤ 1.75 (f1.55), and Dn(4000) ≤ 1.35 (f1.35) for galaxies in the CB and SCl A2142 clusters and in their spheres of influence, R30.
Radii and masses of centre clusters within their spheres of influence at characteristic density contrasts Δρ = 30, 13.1, and 8.7.
All Figures
 |
Fig. 1. Distribution of galaxy groups in a large region around the CB in the plane of the sky. The size of the circles is proportional to group size in the sky. Grey circles show the positions of groups in a low global density environment, D8 < 5. Orange circles correspond to groups in the CB supercluster, and red circles show groups in a high global density environment with D8 ≥ 8 that do not belong to the CB. These groups mostly lie in supercluster SCl A2142. In the sky projection, part of the CB supercluster is projected on SCl A2142, and some groups from these superclusters overlap in the figure. Large coloured circles indicate the location of the richest clusters with corresponding ID numbers. |
| In the text | |
 |
Fig. 2. Distribution of galaxies in the CB supercluster region in the plane of the sky. The colour marks the global luminosity density D8. Red circles correspond to the galaxies in high-density cores with D8 ≥ 8, orange circles show galaxies in the outskirts of the supercluster with 5 ≤ D8 < 8, and grey symbols show galaxies in the low-density region around the supercluster with D8 < 5. The ID numbers of the richest clusters in the high-density cores of the supercluster are shown (Abell clusters A2065, A2061, and A2089, and cluster Gr2064 that does not belong to Abell). |
| In the text | |
 |
Fig. 3. Dn(4000) index vs. stellar mass log M* for galaxies in the CB supercluster. Blue stars denote BSF galaxies, orange stars denote RSF galaxies, green triangles mark RQ galaxies, black dots show red galaxies with 1.55 ≤ Dn(4000) < 1.75, and red filled circles denote VO galaxies (see Table 3). The green ellipse approximately borders the area populated by RQ galaxies, and the orange ellipse shows the area populated by RSF galaxies. |
| In the text | |
 |
Fig. 4. Left panels: distribution of galaxies in A2065 in the plane of the sky. The colours in the upper panel correspond to galaxies from different populations (BSF – blue, RSF – orange, RQ – green, and VO – dark red). Filled symbols denote galaxies in different components of the cluster. Empty circles show galaxies that are not cluster members. Grey crosses denote galaxies in the low-density region with D8 < 5. The inner black circle indicates the scale with a radius 1.5 h−1 Mpc. The outer red circle corresponds to the radius R30 (= 6 h−1 Mpc for A2065). A and B denote substructures that extend from the cluster (see text). The colour in the lower panel shows galaxies in long filaments with a length larger than 5 h−1 Mpc, and in green we plot galaxies in a short filament with a length of 3 h−1 Mpc, which connects the long filament with the cluster. The upper right panel shows the PPS diagram and the distribution of the clustercentric distances Dc for galaxies from different populations in A2065 and in its environment towards A2089. Filled circles represent A2065 members, and filled triangles (at clustercentric distances Dc > 6 h−1 Mpc) show A2089 members. Empty symbols mark galaxies that are not members of these two clusters. The blue region shows the early infall (E) region, and light blue shows late infall (L) region. The lower right panel presents the Dn(4000) index versus clustercentric distance Dc for galaxies from A2065 to A2089. Colours show the density of points at a given location in the plot. Vertical lines correspond to the infall zone of the cluster, Rcl, and to the radius R30. Horizontal lines show Dn(4000) index values Dn(4000) = 1.75, Dn(4000) = 1.55, and Dn(4000) = 1.35 (see Sect. 2.2). |
| In the text | |
 |
Fig. 5. Same as in Fig. 5 for A2061. Triangles in the upper panels denote galaxies from cluster A2067. |
| In the text | |
 |
Fig. 6. Same as in Fig. 5 for A2089. |
| In the text | |
 |
Fig. 7. Same as in Fig. 5 for Gr2064. |
| In the text | |
 |
Fig. 8. Distribution of Dn(4000) index of galaxies (left panel) and distribution of stellar masses of galaxies (right panel) in clusters A2065, A2061, A2089, Gr2064, and A2142. Vertical lines in the left panel show the limits Dn(4000) = 1.75, Dn(4000) = 1.55, and Dn(4000) = 1.35. |
| In the text | |
 |
Fig. 9. Distribution of Dn(4000) index of galaxies (left panel) and distribution of stellar masses of galaxies (right panel) in the environment of clusters A2065, A2061, A2089, Gr2064, and A2142. Vertical lines in the left panel show the limits Dn(4000) = 1.75, Dn(4000) = 1.55, and Dn(4000) = 1.35. |
| In the text | |
 |
Fig. 10. 3D distribution of galaxies in the CB and in the low-density region around it. Filled symbols denote galaxies in clusters A2065, A2061, A2089, and Gr2064. Empty circles show supercluster galaxies that are not members of these clusters. Grey dots denote galaxies in the low-density region with a global density D8 < 5. Blue circles denote BSF galaxies, orange circles denote RSF galaxies, turquoise green circles mark RQ galaxies, and red circles denote VO galaxies. Green circles mark galaxies in long filaments with a length larger than 5 h−1 Mpc. Large red circles show the circles with a radius R30, which partly overlap because of projections in the 3D view. |
| In the text | |
 |
Fig. 11. Distribution of galaxies in the main part of the CB in the plane of the sky. Filled symbols denote galaxies in clusters A2065, A2061, and A2089, and empty circles show other galaxies in the supercluster. Grey crosses denote galaxies in the low-density region with D8 < 5 (partly overlapping with the supercluster region due to projections). Large red circles show the circles with radius of R30 (Table 6). |
| In the text | |
 |
Fig. 12. Acceleration field of the CB supercluster. Here coordinates (x, y) are rectangular coordinates in the plane containing centres of all three main clusters. Colours show the values of the difference in z coordinate direction, and arrows show how far galaxy groups in the CB may move during 2 Gyr. |
| In the text | |
 |
Fig. 13. Density contrast Δρ = ρ/ρm vs. clustercentric distance for A2065 (left panel) and for A2061 (rich panel). The density contrast for the centre cluster is plotted with the red line. The golden area shows the error corridor from the mass errors. Characteristic density contrasts are denoted as follows: Δρ = 360 (virial), Δρ = 200 (r200), Δρ = 13.1 (turnaround, dashed blue line), Δρ = 8.73 (FC, dash-dotted violet line), and Δρ = 5.41 (ZG, solid light blue line). Blue, light blue, and grey areas mark the borders of the turnaround, FC, and ZG regions. The red area marks R30. The arrow in the right panel marks the average distance of cluster A2067 from the centre of A2061. |
| In the text | |
 |
Fig. 14. Density contrast Δρ = ρ/ρm vs. clustercentric distance for cluster A2089 (left panel) and for Gr2064 (right panel). Notations are as in Fig. 13. |
| In the text | |
 |
Fig. 15. Current density contrast Δρ for Ωm = 0.27 (solid red line) and for Ωm = 0.40 (dashed blue line) if the turnaround occurred at redshifts in the interval z = 0.56 − 0.2. |
| In the text | |
 |
Fig. 16. Left panel: density contrast Δρ = ρ/ρm vs. clustercentric distance Dc for the possible new centre of the main part of the CB. Notations are as in Fig. 13. Arrows mark the distances of clusters A2065, A2061, and A2089 at which they join the possible new collapsing system. Right panel: sky distribution of galaxies in the CB. Filled circles mark turnaround (blue) and future collapse (light blue) zones in the supercluster, as shown in the left panel. Colours are as in Fig. 2. |
| In the text | |
 |
Fig. A.1. Coordinate system used in calculating the acceleration field of clusters in the plane of the sky. The blue plane shows the plane of the three clusters that define the coordinate system. The x2 coordinate direction connects A2089 and A2065, the y2 coordinate is perpendicular to x2 and is in the same plane as determined by the clusters. The z2 coordinate is perpendicular to both x2 and y2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.