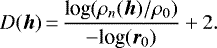| Issue |
A&A
Volume 649, May 2021
|
|
|---|---|---|
| Article Number | A33 | |
| Number of page(s) | 26 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/202039874 | |
| Published online | 05 May 2021 | |
Description of turbulent dynamics in the interstellar medium: multifractal-microcanonical analysis
I. Application to Herschel observations of the Musca filament
1
INRIA,
Geostat team, France
e-mail: hussein.yahia@inria.fr
2
I. Physik. Institut, University of Cologne,
Zülpicher Str. 77,
50937
Cologne, Germany
3
CNRS LAB, UMR 5804, Bordeaux University,
Bordeaux, France
4
ICM CSIC,
Barcelona, Spain
5
INAF,
Roma, Italy
6
Indian Institute of Technology,
Patna, India
7
CNRS, Univ. Lille, Univ. Littoral Cote d’Opale, UMR 8187, LOG,
62930
Wimereux, France
8
Univ. Grenoble Alpes, CNRS, IPAG,
38000
Grenoble, France
Received:
7
November
2020
Accepted:
16
February
2021
Observations of the interstellar medium (ISM) show a complex density and velocity structure, which is in part attributed to turbulence. Consequently, the multifractal formalism should be applied to observation maps of the ISM in order to characterize its turbulent and multiplicative cascade properties. However, the multifractal formalism, even in its more advanced and recent canonical versions, requires a large number of realizations of the system, which usually cannot be obtained in astronomy. We present a self-contained introduction to the multifractal formalism in a “microcanonical” version, which allows us, for the first time, to compute precise turbulence characteristic parameters from a single observational map without the need for averages in a grand ensemble of statistical observables (e.g., a temporal sequence of images). We compute the singularity exponents and the singularity spectrum for both observations and magnetohydrodynamic simulations, which include key parameters to describe turbulence in the ISM. For the observations we focus on the 250 μm Herschel map of the Musca filament. Scaling properties are investigated using spatial 2D structure functions, and we apply a two-point log-correlation magnitude analysis over various lines of the spatial observation, which is known to be directly related to the existence of a multiplicative cascade under precise conditions. It reveals a clear signature of a multiplicative cascade in Musca with an inertial range from 0.05–0.65 pc. We show that the proposed microcanonical approach provides singularity spectra that are truly scale invariant, as required to validate any method used to analyze multifractality. The obtained singularity spectrum of Musca, which is sufficiently precise for the first time, is clearly not as symmetric as usually observed in log-normal behavior. We claim that the singularity spectrum of the ISM toward Musca features a more log-Poisson shape. Since log-Poisson behavior is claimed to exist when dissipation is stronger for rare events in turbulent flows, in contrast to more homogeneous (in volume and time) dissipation events, we suggest that this deviation from log-normality could trace enhanced dissipation in rare events at small scales, which may explain, or is at least consistent with, the dominant filamentary structure in Musca. Moreover, we find that subregions in Musca tend to show different multifractal properties: While a few regions can be described by a log-normal model, other regions have singularity spectra better fitted by a log-Poisson model. This strongly suggests that different types of dynamics exist inside the Musca cloud. We note that this deviation from log-normality and these differences between subregions appear only after reducing noise features, using a sparse edge-aware algorithm, which have the tendency to “log-normalize” an observational map. Implications for the star formation process are discussed. Our study establishes fundamental tools that will be applied to other galactic clouds and simulations in forthcoming studies.
Key words: ISM: structure / ISM: individual objects: Musca / turbulence / ISM: clouds / magnetohydrodynamics (MHD)
© H. Yahia et al. 2021
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Stars form in the cold (~10 K) and dense (>104 cm−3) gas phase of the interstellar medium (ISM) which represents only a small percentage in mass (e.g., Tielens 2005; McKee & Ostriker 2007; Bergin & Tafalla 2007; Lada et al. 2010; André et al. 2014; Shimajiri et al. 2017). This rare occurrence of “fertile” gas in the ISM explains the low star formation rates of galaxies, and gets its origin from the global physics of the ISM from galactic down to star formation scales, including heating, cooling, magnetic fields, cosmic rays, and gravity. It is only by understanding the origin of this rare dense gas from the bulk of the predominantly diffuse and warm ISM that the initial conditions for star formation will be fully constrained and understood.
In the 1980s and 1990s, the star-forming ISM was generally described as being driven by a quasi-static evolution of clouds and clumps which could condense into dense collapsing cores (e.g., Mouschovias 1976; Shu et al. 1987). The importance of supersonic motions and dynamical processes have since then been recognized and better understood (e.g., Elmegreen 2000; Koyama & Inutsuka 2000; Mac Low & Klessen 2004), and a gravo-turbulent paradigm has emerged to explain how islands of quiet dense gas can emerge from a sea of turbulent low-density gas. More recently it has been realized, thanks the Herschel Space Telescope (Pilbratt et al. 2010), that the dense star-forming gas is located in filamentary structures (e.g., Myers 2009; André et al. 2010; Schneider et al. 2010, 2012; Bontemps et al. 2010; Molinari et al. 2010; Schisano et al. 2014; Könyves et al. 2015; Marsh et al. 2016; Rayner et al. 2017; Motte et al. 2018), which complicates the usually implied simple view of a mostly isotropic and thermal pressure like turbulence. In parallel to these observational results, the formation ofcoherent structures such as filaments and hubs (where filaments merge) has also been discerned in numerical simulations by many groups. These simulations take into account the role of one or several physical processes such as gravity, turbulence, magnetic fields, radiation, and thermodynamics; they also play a fundamental role in the evaluation of the statistics of intensive variables displaying a multifractal behavior (Mac Low 2000; Heitsch et al. 2005; Chappell & Scalo 2001; Klessen & Hennebelle 2010; Dib & Burkert 2005; Krumholz & McKee 2005; Krumholz 2014; Hull et al. 2017; Elia et al. 2018).
The turbulent nature of the ISM is well established by the extremely high values of Reynolds number (Elmegreen & Scalo 2004; Kowal et al. 2007; Burkhart et al. 2009a,b; Schneider et al. 2011; Seifried & Walch 2015; Kritsuk et al. 2017; Mocz et al. 2017; Elia et al. 2018; Lee & Lee 2019). The need to progress toward a more precise way to measure the properties of the turbulent motions led to fractal approaches. Self-similarity of the ISM was observed and described first with monofractal descriptors (by e.g., Stutzki et al. 1998; Falgarone et al. 1998; Bensch et al. 2001; Sanchez et al. 2006; Elia et al. 2014), but it was realized that the observations cannot be characterized as pure monofractals, which is in accordance with most advanced phenomenological descriptions of turbulence (Frisch 1995). Characteristic scales, mostly on the subparsec scale up to a few parsec, were found (Padoan et al. 2003; Hartmann 2002; Sun et al. 2006; Brunt et al. 2010; Schneider et al. 2011; Elia et al. 2018; Dib et al. 2020), breaking the premise of pure self-similarity. Moreover, the transition from incoherent to coherent structures is usually assumed to be related to the formation of dense structures and to the dissipation of turbulence. If coherent structures display a significant scale invariance, they are multifractal in nature, expressed and observed in power-law statistics for spatial and time correlation functions. This leads to the existence of critical manifolds as predicted in dynamical systems, especially those of turbulence (Arneodo et al. 1995; Venugopal et al. 2006a; Khalil et al. 2006; Turiel et al. 2008; Robitaille et al. 2019). In order to understand the turbulent mechanisms present in the ISM and to be able to discriminate between the effects of magnetic pressure and gravity on structureevolution the most recent advances in the analysis of multiscale and multifractal signals must be used.
Computational tools have been developed in order to obtain the most important fingerprints of multifractality from the data and to establish links with multiplicative processes and energy cascades in the case of turbulence (Chhabra et al. 1989; Meneveau & Sreenivasan 1991; Bacry et al. 1993; Muzy et al. 1993; Arneodo et al. 1995; Hosokawa 1997; Delour et al. 2001; Venugopal et al. 2006b,a; Turiel et al. 2006, 2008; Muzy & Baïle 2016; Leonarduzzi et al. 2016; Salat et al. 2017; Muzy 2019). In physical systems, multifractality is closely related to the existence of singular measures defined from the observables; for instance, in a turbulent 3D medium, if we denote by 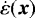 the rate of kinetic energy dissipation per unit volume, the total dissipation of energy E is a measure of density
the rate of kinetic energy dissipation per unit volume, the total dissipation of energy E is a measure of density 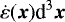 , which has a singular behavior around each point x with a particular singularity exponent h(x); this means that
, which has a singular behavior around each point x with a particular singularity exponent h(x); this means that  , the energy dissipation in a ball
, the energy dissipation in a ball  centered at point x and of radius r, behaves as rh(x) + o(rh(x)) when r → 0. The spatial intermittence of the support1 of energy transfer is directly related to the existence of critical manifolds defined by the geometrical distribution of the singularity exponents h(x), as it implies a complex partition of the energy at different scales and the power-law behavior observed in the statistics of physical variables (Frisch 1995).
centered at point x and of radius r, behaves as rh(x) + o(rh(x)) when r → 0. The spatial intermittence of the support1 of energy transfer is directly related to the existence of critical manifolds defined by the geometrical distribution of the singularity exponents h(x), as it implies a complex partition of the energy at different scales and the power-law behavior observed in the statistics of physical variables (Frisch 1995).
To apply multifractal analysis to the acquired signals, a canonical formalism is generally used (Arneodo et al. 1995; Venugopal et al. 2006b,a; Turiel et al. 2006, 2008). This formalism is based on statistical averages (moments of different orders, correlation, and structure functions) computed on grand ensembles of realizations, from which the singularity spectrum and singular values are obtained as mean values, through log-regression, of quantities usually defined from partition functions. In astronomy, this procedure is usually only applicable for magnetohydrodynamic (MHD) simulations since multi-epoch data are usually rare or not possible due to the long timescales of evolution. The canonical approach is ruled out to characterize turbulent behaviors from single realization observations (i.e., for typical astronomical images).
In this study, we go beyond the limitations of the canonical approach by using a “microcanonical” formulation of the multifractal signal analysis, in which individual microstates are evaluated in a single realization (Turiel et al. 2006, 2008). As a direct application of the method, we examine the turbulence properties of gas associated with the Musca filament observed with Herschel. This source (see Sect. 2 for details) is a prototypical example of a rather isolated filamentary structure in the Chamaeleon-Musca cloud complex (Cox et al. 2016), not affected by stellar feedback. Thanks to its sensitive access from space to thebulk of dust emission of nearby cloud complexes, the Herschel mission provides us with excellent datasets with unprecedented spatial and flux dynamical ranges to provide the required statistical significance to study the properties of the turbulent flows presumably leading to dense gas and star formation (e.g., André et al. 2010; Molinari et al. 2010; Elia et al. 2018). The spectral coverage of the Herschel photometric surveys is 70–500 μm at an angular resolution of 6″ to 36″ covering several square degrees per region.
Section 2 describes the Herschel data used in this study. The multifractal formalism, its relations with turbulence, intermittency, and the multiplicative cascade is presented in Sect. 3. We also explain in Sect. 3 the canonical and microcanonical approaches to multifractality. The scale invariance of an observation map is studied indetail in Sect. 4. In Sect. 5, we introduce a sparse filtering methodology designed to reveal the filaments hidden by background noise, and the 2D structure function approach. In Sect. 6, we present the MHD simulations used in this work. Section 7 presents the results obtained applying the multifractal analysis to our available data: the Herschel observation map of Musca and the MHD simulations. These results are discussed in Sect. 8, followed by the conclusions of this study in Sect. 9.
2 The Musca cloud: Herschel flux density map
Musca is a prominent filamentary structure, 6 pc in length, with a high aspect ratio at a distance of only 140–150 pc (Hacar et al. 2016; Cox et al. 2016; Kainulainen et al. 2016; Gaia Collaboration 2018). It has a low average column density N, with N(max) ~ 4–8 1021 cm−2 (Bonne et al. 2020b), and shows only one protostellar source located at the northern end of the filament (Juvela et al. 2012; Machaieie et al. 2017). Furthermore, Herschel observations reveal a network of striations orthogonal to the filament, which are thought to be indications of mass inflow along the magnetic field (Cox et al. 2016). An indication of continuous mass accretion from inflow toward the Musca filament was found by observed presence of low-velocity filament accretion shocks around the Musca filament (Bonne et al. 2020b). Hacar et al. (2016) conclude from individual 13CO and C18O pointings that the crest of the Musca filament is a single velocity-coherent structure. It was proposed (Tritsis & Tassis 2018) that the Musca filament is only a sheet viewed edge-on, but our detailed study using the APEX and SOFIA spectroscopic observations(Bonne et al. 2020a) shows that the data most closely fit the concept that the crest of Musca is a dense ( 104 cm−3) cylindrical structure and not a low-density sheet, and that the mass input for building up the crest is provided by large-scale flows, but there is no evidence that this inflow appears in the form of striations. The striations are then only the result of gas compressionby magnetosonic waves, which could fit what has been recently suggested by theoretical studies (Tritsis & Tassis 2016).
104 cm−3) cylindrical structure and not a low-density sheet, and that the mass input for building up the crest is provided by large-scale flows, but there is no evidence that this inflow appears in the form of striations. The striations are then only the result of gas compressionby magnetosonic waves, which could fit what has been recently suggested by theoretical studies (Tritsis & Tassis 2016).
The Herschel SPIRE 250 μm data of Musca (Fig. 1) used in this paper are part of the Herschel Gould Belt Survey (André et al. 2010) and are published inCox et al. (2016). We use here the same dataset that was obtained in parallel mode at a sampling at 10Hz and at high speed (60″ s−1), and reduced using modified pipeline scripts of HIPE version 10. The resulting Level 1 contexts for each scan direction (two maps taken in orthogonal directions) were then combined using the naive map maker in the de-striper module. The conversion of the maps into surface brightness (from Jy beam−1 into MJy sr−1) was done using the beam-areas obtained from measurements of Neptune (March 2013). The zeroPointCorrection task was used to absolutely calibrate the maps using information from the Planck satellite. The angular resolution of the maps at 250 μm is 18″. Here we use the 250 μm flux map for our studies and not the dust column density map used in Cox et al. (2016); Bonne et al. (2020b,a) because the latter has only an angular resolution of 36″. The 250 μm map can be considered a good proxy for the column density, but only in regions that are not strongly affected by stellar feedback (Miville-Deschênes et al. 2010) because it traces mostly cold dust that is mixed with the cold molecular gas.
3 Canonical and microcanonical approaches to multifractality
A number of Galactic studies using continuum data or emission lines of atomic hydrogen or molecules showed that the Fourier power spectrum of the observed line intensity was well fitted by a power law, at least over certain size scales, and which was commonly interpreted as a consequence of the scale-free and turbulent nature of the ISM (Scalo 1987; Green 1993; Elmegreen & Scalo 2004; Stutzki et al. 1998; Miville-Deschênes et al. 2010; Schneider et al. 2011; Robitaille et al. 2020). As mentioned since the introduction of the first phenomenological descriptions of hydrodynamic turbulence (Frisch 1995), the observed scale invariance suggests the existence of an energy cascade in which energy injected at large scales is transferred into smaller ones, hence providing a natural explanation for the complex structure of the ISM at each scale. The Fourier power spectrum with its single descriptive parameter (the slope of the spectrum), however, turned out to be too coarse to encode all turbulent and scale-free phenomena observed in the ISM and notably filamentary structures (Roy et al. 2015, 2019; Arzoumanian et al. 2019). The simplest models able to describe the partition of energy across the scales of a turbulent medium are monofractal: they rely on a single parameter, the fractal dimension, which characterizes the geometry of the sets between which the energy transfer is operated.
For modeling purposes in astronomy, monofractal signals can be generated using stochastic processes such as the fractional Brownian motion (fBm) (Mandelbrot & Ness 1968) and, more specifically, 2D fBMs (Heneghan et al. 1996; Stutzki et al. 1998; Robitaille et al. 2020). These fBms are parameterized by their Hurst exponent which defines their monofractal properties. In Khalil et al. (2006) a monofractal signature is found in atomic hydrogen data from the Canadian Galactic Plane Survey, while an anisotropic signature is also detected. The complex organization of the ISM can be fully described by the multifractal formalism, which is as necessary in magnetohydrodynamic turbulence as it is needed in hydrodynamic turbulence (Frisch 1995; Robitaille et al. 2020).
The multifractal formalism is already used in astronomy, for example in heliophysical turbulence (Movahed et al. 2006; McAteer et al. 2007; Salem et al. 2009; Kestener et al. 2010; Macek et al. 2014; Wu et al. 2015; Cadavid et al. 2016; Maruyama et al. 2017), the ISM (Elia et al. 2018), the large-scale structure of the Universe (Gaite 2007; Gaite & Domínguez 2007), galaxy mergers (De La Fuente Marcos & De La Fuente Marcos 2006), and gravitational wave detection (Eghdami et al. 2018). This formalism comes into two distinct presentations: canonical and microcanonical. The first is the most popular (Arneodo et al. 1995); it includes the Wavelet Transform Modulus Maxima (WTMM) method (Arneodo et al. 1995; Turiel et al. 2006) and the cumulant approach (Brillinger 1994; Delour et al. 2001; Wendt et al. 2006; Ciuciu et al. 2008; Venugopal et al. 2006b). Microcanonical approaches were developed first in less accurate versions such as the counting box and histogram methods, then in the efficient geometrico-statistical formulation (Turiel et al. 2008) that we use in this work. In the following, we review the most important aspects of the multifractal approach without being exhaustive.
In hydrodynamics or magnetohydrodynamic turbulence, as explained above, a very complex partition of the energy according to the scale is observed (She et al. 1990; Frisch 1995; Shivamoggi 2015), and it was understood that this complexity was an effect of intermittency, that is a consequence of the extremely complex geometrical organization, or partition, of the support of the energy at small scales. Observationally, this was supported by the detection of strong velocity-shears at subparsec scale (Falgarone et al. 2009). Multifractal models were introduced to describe this intermittency because they allow the fluctuations of a physical variable (such as the projection of velocity on a given fixed axis) to be related to the complex geometry of the points where such a physical variable changes abruptly. First, we consider a fluid evolving in a 2D or 3D medium, and denote by v (x) the velocity vector at a given point x inside the medium. We can then measure the values taken by v(x) either in time at a fixed point x or at a fixed time atmany different points x. Experimentally, some decades ago, it was much easier to measure the projection of the turbulent velocity field v in a specific fixed direction defined by a unitary vector u instead of the vector v(x) itself. Today, laser-mounted optical devices allow a direct measurement of the velocity vector field. Nevertheless, following the experimental setup described in Frisch (1995), measuring the velocity field in a fixed direction allows us to evaluate the statistical moments,
 (1)
(1)
of the turbulent velocity field v; depending on the experimental setup, in Eq. (1) the averages ⟨ ⋅ ⟩ can be computed either in time at a given point x or spatially over the domain. Then it is observed that the moments in Eq. (1) behave as rξ(q) when r is inside a well-defined interval of scale values [r1, r2] called the inertial range:
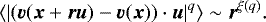 (2)
(2)
When ξ(q) is a linear function of q we are in the monofractal formalism. On the other hand, ξ(q) is observed experimentally to be nonlinearin q which means a multifractal behavior. The nonlinearity of ξ(q) as a function of q is thus interpreted as a consequence of intermittency; it has a geometric origin and the link between statistics and geometry is as follows. Let us denote with 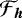 the set of points x whose velocity increments, measured in the unitary direction u as before, behave as rh for a certainh:
the set of points x whose velocity increments, measured in the unitary direction u as before, behave as rh for a certainh:
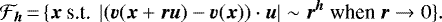 (3)
(3)
These sets  for small or even negative values of h feature a complex geometrical organization that is closely related to the nonlinear behavior of ξ(q). To quantify how the geometry of the sets
for small or even negative values of h feature a complex geometrical organization that is closely related to the nonlinear behavior of ξ(q). To quantify how the geometry of the sets  is related to the turbulent behavior of the velocity field, we can introduce a notion of dimension for these sets, called the Hausdorff fractal dimension (Falconer 1997), which is a positive real number describing the way they fill in the space. We come back to this point in Sect. 3.3, but let us denote for the moment D(h) the Hausdorff fractal dimension of the sets
is related to the turbulent behavior of the velocity field, we can introduce a notion of dimension for these sets, called the Hausdorff fractal dimension (Falconer 1997), which is a positive real number describing the way they fill in the space. We come back to this point in Sect. 3.3, but let us denote for the moment D(h) the Hausdorff fractal dimension of the sets  :
:
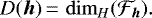 (4)
(4)
The link between geometrical complexity and statistical behavior is then given by the relation
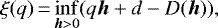 (5)
(5)
where d is the dimension of embedding space of the experiment (d = 2 in 2D turbulence, d = 3 in 3D turbulence); this means that for each fixed value of q, ξ(q) is the lower bound of the subset of real numbers qh + d − D(h) when h varies over the set of positive numbers. We note that ξ(q) is a Legendre transform. The mapping
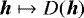 (6)
(6)
is called the singularity spectrum of the velocity field. In the monofractal formalism, ξ(q) is a linear function of q and the mapping (6) reduces to a single point in the graph of D(h). In the multifractal formalism Eq. (6) defines a distribution of fractal dimensions as a function of h. In general, 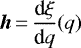 .
.
The notion applies to any signal s(x) or random process 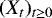 with values in
with values in 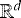 displaying a multiscale behavior (i.e., a nonlinear scaling of moments ⟨∥X(t)∥q⟩ = c(q)tξ(q) for a nonlinear mapping q↦ξ(q)) or to even more general multifractal random processes (Grahovac 2020). As we see in Sect. 3.3, it also applies to measures. The singularity spectrum thus contains a lot of information on the statistics of turbulence, but its computation is a fundamental problem of the multifractal formalism.
displaying a multiscale behavior (i.e., a nonlinear scaling of moments ⟨∥X(t)∥q⟩ = c(q)tξ(q) for a nonlinear mapping q↦ξ(q)) or to even more general multifractal random processes (Grahovac 2020). As we see in Sect. 3.3, it also applies to measures. The singularity spectrum thus contains a lot of information on the statistics of turbulence, but its computation is a fundamental problem of the multifractal formalism.
The intermittency of the velocity field, which is responsible for the observed scaling behavior and the partition of energy at different scales, has been the subject of a description in terms of random multiplicative cascades proposed by the Russian school (Kolmogorov 1941, 1962; Yaglom 1966; Novikov 1990, 1994). Denoting 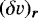 the longitudinal increments
the longitudinal increments 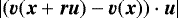 , it was proposed to model the cascade through the probability distribution for
, it was proposed to model the cascade through the probability distribution for 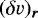 (Castaing 1996; Arneodo et al. 1998a)
(Castaing 1996; Arneodo et al. 1998a)
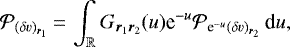 (7)
(7)
which expresses the change in scales of the probability distribution depending on a kernel measure 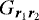 (r1 < r2). For instance if
(r1 < r2). For instance if 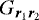 were a Dirac measure, then Eq. (7) implies that
were a Dirac measure, then Eq. (7) implies that 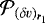 would have the same shape as
would have the same shape as 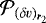 within a scaling factor in the velocity amplitudes. Equation (7) is satisfied if the kernel G satisfies the convolution law (for each monotonic sequence of scales r1 < r2 < ⋯ < rn)
within a scaling factor in the velocity amplitudes. Equation (7) is satisfied if the kernel G satisfies the convolution law (for each monotonic sequence of scales r1 < r2 < ⋯ < rn)
 (8)
(8)
which implies that the laws 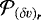 are indefinitely divisible. In turn, this can be physically interpreted in the form of the multiplicative cascade.
are indefinitely divisible. In turn, this can be physically interpreted in the form of the multiplicative cascade.
 |
Fig. 1 Musca flux density map from Herschel at 250 μm. The filamentary structure with a high aspect ratio is obvious. Perpendicular to the main ridge of emission are fainter hair-like structures (called striations in Cox et al. 2016) that are mostly attached to the main filament. |
3.1 log-normal and log-Poisson processes
There are only a few cases for which a singularity spectrum can be computed exactly. We give here two examples, well-known for their physical interpretation, that will also play a key role in this study: the log -normal and the log-Poisson processes.
The energy cascading model for intermittency in a turbulent medium mentioned previously implies a multiplicative form for the energy dissipation rate  (Vazquez-Semadeni 1994). An initial (cubic) volume of space is divided into eight cubes of equal size, whose sides are one-half the size of the initial volume. The energy dissipation rate is then multiplied by eight random variables, equally distributed. When this scheme is recursively repeated, the field
(Vazquez-Semadeni 1994). An initial (cubic) volume of space is divided into eight cubes of equal size, whose sides are one-half the size of the initial volume. The energy dissipation rate is then multiplied by eight random variables, equally distributed. When this scheme is recursively repeated, the field  at a given scale has a multiplicative form. Its logarithm is then a sum of random variables and, under the hypotheses of the central limit theorem, the energy dissipation rate can be approximated by a log -normal process. In this case, the space intermittency comes from the existence of a large number of regions with nearly equal dissipation rates. The log-normal model was introduced by N. Kolmogorov (Kolmogorov 1962).
at a given scale has a multiplicative form. Its logarithm is then a sum of random variables and, under the hypotheses of the central limit theorem, the energy dissipation rate can be approximated by a log -normal process. In this case, the space intermittency comes from the existence of a large number of regions with nearly equal dissipation rates. The log-normal model was introduced by N. Kolmogorov (Kolmogorov 1962).
There are, however, different intermittency models that depend on various assumptions about the energy dissipation rate (Hopkins 2013). In Gledzer et al. (1996) an energy cascade model of intermittency is introduced, involving rare localized regions of both large and weak energy dissipation areas, in the spirit of She & Leveque (1994), leading to log -Poisson statistics. It is a model with dissipatively active and passive localized regions, allowing the existence of “holes of dissipation”; log -Poisson processes are particularly interesting in this context for their potential ability to describe distribution of filaments, as we show in this work.
The singularity spectrum h↦D(h) can be computed in a closed form in the case of log-normal and log-Poisson processes. Precisely, a log-normal process in 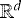 has a parabolic singularity spectrum
has a parabolic singularity spectrum
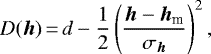 (9)
(9)
where 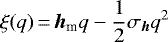 , hm is the mean singularity, and σh is the singularity dispersion. Meanwhile, a log-Poisson process in
, hm is the mean singularity, and σh is the singularity dispersion. Meanwhile, a log-Poisson process in 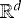 is a translationally invariant, indefinitely divisible process with a singularity spectrum given by
is a translationally invariant, indefinitely divisible process with a singularity spectrum given by
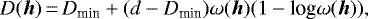 (10)
(10)
where 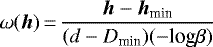 , hmin is the minimum value of singularities, Dmin is the associated dimension of set
, hmin is the minimum value of singularities, Dmin is the associated dimension of set 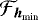 , and β is the dissipation parameter (0 < β < 1):
, and β is the dissipation parameter (0 < β < 1): 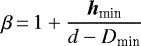 . Accordingly, ξ(q) = hminq + (d − Dmin)(1 − βq).
. Accordingly, ξ(q) = hminq + (d − Dmin)(1 − βq).
In general, for a wide class of processes, the singularity spectrum D(h), being the Legendre transform ofξ(q), has a concave shape (see left panel of Fig. 2). The same figure displays the singularity spectra of typical log -normal processes (middle panel), and log-Poisson processes (right panel). A log-normal singularity spectrum, being parabolic, is symmetric, while a log-Poisson process has a nonsymmetric singularity spectrum. The lack of symmetry is a strong indication of very different dynamic properties compared to those described by a log-normal model. In this work we focus on the log-normal and log-Poisson processes because they are associated with geometrical models. It should be noted, however, that there are other models, among which the log -α-stable that also has also a nonsymmetric spectrum (Schmitt & Huang 2016).
 |
Fig. 2 Singularity spectra of log-normal and log -Poisson stochastic processes. Left: general form of the singularity spectrum D(h), Legendre transform of ξ(q). See text for a definition of D(h), ξ(q), and |
3.2 Existing computational approaches
In this subsection, we summarize previous works done in astronomy that made use of the multifractal approach. We recapitulate previous introductions given in Elia et al. (2018) and Khalil et al. (2006), McAteer et al. (2007), Salem et al. (2009), Kestener et al. (2010), Macek et al. (2014), Robitaille et al. (2020), and combine them with more fundamental presentations given in Arneodo et al. (1995) and: Turiel et al. (2008) that describe general signal processing approaches.
Equation (3) defines the scaling exponents h from the true turbulent velocity field v(x), which is not directly accessible either in astronomy or in many other geophysical sciences. The basic information from which numerical computations are performed is one or more observational maps, which constitute an original signal denoted s in the following. Consequently, in signal processing, the multifractal formalism consists in defining and computing singularity exponents h (x) and other characteristics like the singularity spectrum from the data in s. This is done by considering, from the data in s, general positive measures, denoted μ instead of the unknown velocity field v(x). These can be, for instance, probability measures built out of the signal or some kind of additive quantity defined in the domain of the signal s.
If μ is a positive measure, and if 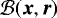 is a ball centered at point x and of radius r in the signal’s domain, we can evaluate the measure of that ball,
is a ball centered at point x and of radius r in the signal’s domain, we can evaluate the measure of that ball, 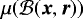 and, since the measure is supposed to be positive, we can consider the limit
and, since the measure is supposed to be positive, we can consider the limit
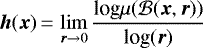 (11)
(11)
called the singularity exponent h(x) of μ at x (Arneodo et al. 1995; Venugopal et al. 2006a; Turiel et al. 2008). The singularity exponent h (x) appears as a power-law exponent in the limiting measures of the balls
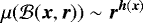 (12)
(12)
when r → 0. A singularity exponent h (x) encodes a limiting scaling information at every point x. It is a pointwise generalization of other scaling parameters often used by astrophysicists and defined globally, such as the power law of a power spectrum or the Δ-variance (Ossenkopf et al. 2008). If the singularity exponents h(x) can be computed at every point x in the signal’s domain, then we can generalize Eq. (3) and define the sets
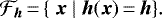 (13)
(13)
As in Eq. (4), the complex organization of the sets 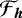 is measured by their fractal dimension. This implies that if we cover the support of the measure μ with balls of size r, the histogram Nh (r), or number of such balls that scale as rh for a given h, behaves as
is measured by their fractal dimension. This implies that if we cover the support of the measure μ with balls of size r, the histogram Nh (r), or number of such balls that scale as rh for a given h, behaves as
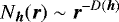 (14)
(14)
(see Arneodo et al. 1995). Hence, the singularity spectrum h ↦ D(h) is a distribution that represents the limiting behavior of the histograms Nh(r) when r → 0; it is one of the fundamental tools used to study complex and turbulent signals. The main problem in the analysis of observational maps in astronomy is to be able to compute the singularity spectrum for the whole map or parts of it.
The most direct approach, which consists in estimating the slope of 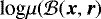 versus log r for various r (called the box-counting method), is known to be inefficient and can potentially lead to errors (Arneodo et al. 1995; Chappell & Scalo 2001). In Elia et al. (2018) the authors make use of the generalized fractal dimensions Dq : the support of the signal’s domain is covered with boxes
versus log r for various r (called the box-counting method), is known to be inefficient and can potentially lead to errors (Arneodo et al. 1995; Chappell & Scalo 2001). In Elia et al. (2018) the authors make use of the generalized fractal dimensions Dq : the support of the signal’s domain is covered with boxes 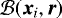 of size r (1 ≤ i ≤ N(r)), and μi (r) is defined as the proportion of signal values inside a ball
of size r (1 ≤ i ≤ N(r)), and μi (r) is defined as the proportion of signal values inside a ball 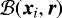 . In this case, the measure μ reduces to consider the signal a probability distribution. Then a partition function is defined:
. In this case, the measure μ reduces to consider the signal a probability distribution. Then a partition function is defined:
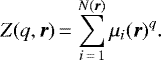 (15)
(15)
In the limit r → 0 we have, just as in Eq. (2),
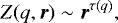 (16)
(16)
and the generalized dimensions are defined as
 (17)
(17)
Some of the quantities Dq can be interpreted: D0 is the box dimension of the support of μ (i.e., the dimension of the signal’s support as defined in Elia et al. 2018), D1 is the information dimension, and Dq encodes the scaling of correlation integrals for q ≥ 2. In Arneodo et al. (1995) it is shown that the relation between τ(q) = (q − 1)Dq and the singularity spectrum D(h) is
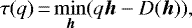 (18)
(18)
which is a Legendre transform. This leads to an interpretation of the multifractal formalism with thermodynamics: q is identified with a Boltzmann inverse temperature and the multifractal formalism allows the study of the self-similarity phases of the measure μ. The limit r → 0 is the thermodynamic limit at infinite volume (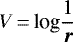 ) and
) and 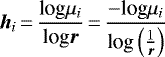 corresponds to Ei, the energy per unit volume of microstate i. The partition function Z(q, r) is rewritten in its usual form:
corresponds to Ei, the energy per unit volume of microstate i. The partition function Z(q, r) is rewritten in its usual form:
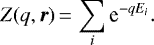 (19)
(19)
In this context the singularity spectrum h↦D(h) is the entropy per unit volume, so that the computation of the singularity spectrum is equivalent to the computation of the entropy per internal energy in a large multibody system. This is one microcanonical formulation of the multifractal formalism, which is correct only in the thermodynamic limit, because it corresponds to microcanonical ensembles of thermodynamics. It can be implemented numerically through the box-counting or the histogram method. This is the approach used in Chhabra et al. (1989), Chappell & Scalo (2001), Elia et al. (2018), and also in Movahed et al. (2006) with detrending in the context of solar data. This approach, however, gives poor results due to severe finite size effects (Arneodo et al. 1995). Very importantly, an essential criterion for verifying the quality of the results obtained with this or any other multifractal approach is to test the results on several rescaled versions of the same signal. The singularity spectrum, for example, must be the same for different scales by the very definition of scale invariance. This is not the case with the box-counting implementation, as we demonstrate in Sect. 4.
To cope with the difficulties of the microcanonical approach, canonical formulations have been introduced in the literature. They consist in evaluating the h values and D(h) as averages among many realizations, i.e., in a canonical ensemble. This approach supposes the availability of many realizations of a same system. The canonical approach to multifractal formalism is currently the most used when grand ensembles of a system’s realizations are available. The most advanced canonical numerical implementations include the WTMM technique (see Arneodo et al. 1995; Venugopal et al. 2006a; Khalil et al. 2006 for a detailed exposition); the cumulant analysis method, which we use in this work for analyzing log -correlations (Venugopal et al. 2006a); the wavelet leaders technique (Serrano & Figliola 2009); and the multifractal detrended fluctuation analysis (MDFA) (Kantelhardt et al. 2002).
As an example, the WTMM methodology applied on a signal s(x) from an observational map (so that x refers to the spatial coordinates in the signal) makes use of an analyzing wavelet ψ with sufficient vanishing moments to filter out spurious long-range correlations; the wavelet-projected signal 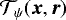 evaluated at position x and scale r; and a suitably chosen qth order partition function Z(q, r) built out of
evaluated at position x and scale r; and a suitably chosen qth order partition function Z(q, r) built out of 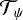 so that Z(q, r) ~rτ(q) when r → 0 (see Venugopal et al. 2006a for computationally effective choices of partition functions). The singularity spectrum is recovered as
so that Z(q, r) ~rτ(q) when r → 0 (see Venugopal et al. 2006a for computationally effective choices of partition functions). The singularity spectrum is recovered as 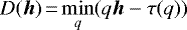 . This supposes the correct evaluation of τ(q) through log -log regression with large amounts of data coming from ensembles of realizations of the signal.
. This supposes the correct evaluation of τ(q) through log -log regression with large amounts of data coming from ensembles of realizations of the signal.
In the study of the ISM, in most of the cases, grand ensembles of observational maps of the same cloud are not available; this is the reason why Elia et al. (2018) favors a microcanonical computational approach over the canonical formulations. Using the box-counting or histogram method, however, does not produce satisfactory evaluations of the singularity spectrum. In this work we develop an alternative and much more reliable implementation of the microcanonical approach, which we introduce in the next section.
 |
Fig. 3 Increasing sequence of lattice nets Ω0 ⊂ Ω1 ⊂⋯ ⊂ Ωn ⊂⋯ inside the unit square. |
3.3 Singularity spectrum from microstates
One major goal of the microcanonical multifractal formalism is to evaluate precisely the quantities h (x) for a well-defined measure μ and to derive the singularity spectrum h↦D(h) in order to obtain information on the statistics of a complex and turbulent signal. We present in this section and Appendix A the determination of the singularity spectrum and the singularity exponents in a microcanonical formulation based on the theory of predictability in complex systems (Turiel et al. 2008), which overcomes the drawbacks of the box-counting and histogram methods.
In the case of observational maps in astronomy, but also in the analysis of general turbulence data, scaling is valid only within a certain inertial range of scales (Sect. 3) and we have to define a measure from a finite set of discrete acquisitions values in the map. Hence, we follow the exposition of the multifractal ansatz in the physics of disordered systems, which allows for a rigorous presentation of the multifractal formalism in the case of discrete signals (Fyodorov 2010; Fyodorov et al. 2012). First, we have to define a measure from the data of an observational map. In previous works (Chhabra et al. 1989; Chappell & Scalo 2001; Elia et al. 2018) the measure is often defined from the signal s itself. Following Turiel et al. (2008), it turns out that better accuracy is obtained when starting from discrete gradient information. Consequently we consider an inertial range in the image domain [r1, r2 ], which we identify for convenience with the unit square ![$[0,1]^2$](/articles/aa/full_html/2021/05/aa39874-20/aa39874-20-eq59.png) . We define a collection of refined lattice points as follows. For each
. We define a collection of refined lattice points as follows. For each 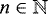 we consider the set Ωn of points whose coordinates are integer multiples of 2−n inside the unit square. We get an increasing sequence Ω0 ⊂ Ω1 ⊂⋯ ⊂ Ωn ⊂⋯ of lattice points, as shown in Fig. 3.
we consider the set Ωn of points whose coordinates are integer multiples of 2−n inside the unit square. We get an increasing sequence Ω0 ⊂ Ω1 ⊂⋯ ⊂ Ωn ⊂⋯ of lattice points, as shown in Fig. 3.
For each x ∈ Ωn, we define a finite set of neighboring points 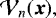 as shown in Fig. 4.
as shown in Fig. 4.
If x ∈ Ωn, we have the information of the signal data s(x) at point x together with the discrete gradient’s norms determined by the differences 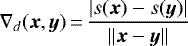 , with
, with 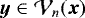 of vicinity points around x at scale 2−n (the subscript d in ∇d stands for discrete). We define a measure μn at that scale2−n from the discrete gradient information data. The exact definitions are given in Appendix A, and μn is seen as agradient measure associated with the observational map data at scale 2−n, which means that the μn-measure of a ball is the sum of discrete gradient’s norms information inside that ball.
of vicinity points around x at scale 2−n (the subscript d in ∇d stands for discrete). We define a measure μn at that scale2−n from the discrete gradient information data. The exact definitions are given in Appendix A, and μn is seen as agradient measure associated with the observational map data at scale 2−n, which means that the μn-measure of a ball is the sum of discrete gradient’s norms information inside that ball.
The application of the multifractal formalism to the signal s and its associated measure μn is valid only if the measure μn satisfies the scaling hypothesis shown in Eq. (A.9). In canonical implementations of the multifractal formalism, checking the scaling is a necessary first step before applying the numerical tools, and is generally done by log -regression performed on the chosen partition functions. In existing microcanonical implementations such as in Elia et al. (2018), the scaling is shown only for output simulations of fractional Brownian motion realizations. In Sect. 5.3, we make use of the 2D structure function methodology (Renosh et al. 2015) to check the scaling of the analyzed data.
The key idea in a computation of the singularity exponents in a microcanonical setting based on predictability is to relate the quantities h(x) to the signal’s reconstruction. In physical signals, the set of possible values taken by h (x) is bounded, and the lowest value of the singularity exponent h∞ = min{h(x)} corresponds to the sharpest transitions in a signal according to Eq. (12). The points x such that h (x) = h∞ form a particular subset  in the signal’s domain, of fractal nature, encoding the strongest transitions; in a 2D signal,
in the signal’s domain, of fractal nature, encoding the strongest transitions; in a 2D signal, 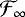 encodes the strongest edges, while the other sets
encodes the strongest edges, while the other sets 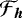 correspond to smoother edges and transitions as h increases. Under the assumption that
correspond to smoother edges and transitions as h increases. Under the assumption that 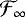 coincides with the set of most unpredictable points (in the sense of complex systems theory), it can be shown that the computation of h (x) at scale 2−n involves only immediate neighboring points around x. When these intuitive considerations are expressed rigorously into a more mathematical manner, as shown in Appendix B, we arrive to a computation of the singularity exponents h (x) using a correlation measure denoted
coincides with the set of most unpredictable points (in the sense of complex systems theory), it can be shown that the computation of h (x) at scale 2−n involves only immediate neighboring points around x. When these intuitive considerations are expressed rigorously into a more mathematical manner, as shown in Appendix B, we arrive to a computation of the singularity exponents h (x) using a correlation measure denoted 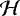 in Appendix B, which can be evaluated locally around any point x in the signal’s domain, leading to Eqs. (B.5) and (B.7), which we use as our fundamental methodology to compute the singularity exponents in a microcanonical formulation.
in Appendix B, which can be evaluated locally around any point x in the signal’s domain, leading to Eqs. (B.5) and (B.7), which we use as our fundamental methodology to compute the singularity exponents in a microcanonical formulation.
 |
Fig. 4 Discrete neighborhood sets |
4 Experimental comparison of microcanonical methodologies: scale invariance
In this section, we test the validity of the scaling hypothesis (Eq. (A.9)) by comparing the singularity spectra computed in a microcanonical formulation of the multifractal formalism using the two approaches mentioned previously: first, an enhanced version of the counting-box method presented in Sect. 3.2 called the gradient modulus wavelet projection method detailed in Turiel et al. (2006), and second, the method explained in Sect. 3.3. The experiment is performed on the Musca Herschel 250 μm observational map described in more detail in Sect. 2.
The scale invariance in Eq. (A.9) implies that singularity spectra computed from two scaled versions of an original observational map must coincide. Consequently, we performed the following experiment: we took the Musca map, generated out of it two downscaled versions of the map, computed the singularity spectrum with either method on the two downscaled versions of the map (see below), and checked if the resulting spectra coincide.
4.1 Gradient modulus wavelet projection method
The algorithm is described in detail in Turiel et al. (2006). It is an enhanced counting-box method that allows for the computation of the singularity exponents h(x) and the singularity spectrum h↦D(h) through a log-regression performed, not directly on the scaling hypothesis in Eq. (A.9), but rather over wavelet projections of the measure for better computational accuracy. This approach is allowed because if a measure μ scales with singularity exponents h (x), as in Eq. (A.9), wavelet projections of μ scale with the same exponents h(x) as long as the analyzing wavelet has n vanishing moments with n > h(x) (Venugopal et al. 2006a; Turiel et al. 2008): if r > 0 is a scale, μ a measure on 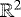 , ψ a real wavelet, and λr the measure
, ψ a real wavelet, and λr the measure 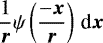 , the wavelet projection of μ at scale r is another measure denoted
, the wavelet projection of μ at scale r is another measure denoted 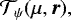 which is the convolution of the measures μ and λr:
which is the convolution of the measures μ and λr:
 (20)
(20)
If μ possesses a density, then 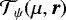 has a density given by the usual continuous wavelet transform of the original density with mother wavelet ψ. The measure μn considered here is the one defined by Eq. (A.1) with the neighboring set
has a density given by the usual continuous wavelet transform of the original density with mother wavelet ψ. The measure μn considered here is the one defined by Eq. (A.1) with the neighboring set 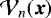 , corresponding to the left part of Fig. 4 (two neighboring points). To compute the singularity exponents, we take as an analyzing wavelet a β-Lorentzian defined as
, corresponding to the left part of Fig. 4 (two neighboring points). To compute the singularity exponents, we take as an analyzing wavelet a β-Lorentzian defined as
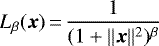 (21)
(21)
with β = 3, with its support scaled to adapt to the signal Nyquist frequency. The log -regression is performed over 30 scales.
To check the scaling of the measure we downscale the original signal on two consecutive scales less than the original signal maximum resolution using a standard discrete wavelet transform defined by the reverse bi-orthogonal projection of order 4.4. Then, for each of these two downscaled wavelet projections, we compute the singularity exponents through log -regression with the Lorentzian wavelet, as explained previously, to get two scalar fields of singularity exponents h (x) at the two consecutive resolutions. From each of these scalar fields, we compute a mapping h ↦ D(h) using Eq. (A.11). If the measure is scale invariant and the singularity exponents are correctly computed, then the two mappings corresponding to each resolution should be coincident. We show the result of the log -regression in Fig. 5. We observe in the figure that inside the most informative part of the mapping, corresponding to h ≤ 0, the two mappings do not coincide. Consequently, the log-regression method for computing the singularity exponents provide poor results in this case and the quantities computed through log -regression do not showthe scaling of the measure.
 |
Fig. 5 Checking scale invariance: gradient modulus wavelet projection method, log-regression. Top row: visualization of the singularity exponents computed through log-regression using a Lorentz wavelet of order 3 on the Musca 250 μm Herschel flux map presented in Sect. 2. The singularity exponents are computed with the gradient modulus wavelet projection method algorithm. The two upper images correspond to two consecutive downscaled wavelet projections of the original signal using a discrete wavelet projection. Bottom: resulting mappings h ↦ D(h) using the singularity exponents computed on the two consecutive scales (red: one-half scale of the original Musca 250 μm Herschel flux map; green: one-fourth scale of the original Musca 250 μm Herschel flux map). Inside the domain corresponding to h ≤ 0 the two mappings do not coincide. Consequently, the log-regression method for computing the singularity exponents provide poor result in this case. |
4.2 Local correlation measure of Sect. 3.3
In Fig. 6, we reiterate the previous experiment on the Musca 250 μm Herschel map, this time with the singularity exponents computed using Eqs. (B.7) and (B.5). The resulting maps h↦D(h) reveal much more satisfactorily the scaling behavior of the measure because they coincide very closely for the two consecutive scales over the range of singular values. This agreement is much stronger than that of the exponents previously computed from log -regression and displayed in Fig. 5. Consequently, the local correlation measure algorithm exhibits the scaling in a much better way. We also note that the resulting graphs differ notably from those computed using log -regression and shown in the bottom of Fig. 5: they are much less parabolic. It becomes obvious that the log -regression method (gradient modulus wavelet projection algorithm) tends to produce singularity spectra of the log -normal type in this case.
 |
Fig. 6 Checking scale invariance: local correlation measure. Top left and right: visualization of the singularity exponents computed with the local correlation measure described in Eqs. (B.7) and (B.5), respectively, on the Musca 250 μm Herschel flux map presented in Sect. 2. The two images correspond to two consecutive downscaled wavelet projections of the original signal using a discrete wavelet projection. Bottom: resulting mappings h ↦ D(h) using the singularity exponents computed on the two consecutive scales (red: one-half scale of the original Musca Herschel map; green: one-fourth scale of the original Musca Herschel map). The two mappings coincide much better than with the exponents computed from log -regression and displayed in Fig. 5. Consequently, the local correlation measure algorithm exhibits the scaling in a much betterway. |
 |
Fig. 7 Map of the singularity exponents computed on filtered Musca 250 μm data. The image is a magnification of the singularity map over the central part of the Musca observation map to better show how the singularity exponents reflect the complex distribution of filamentary coherent structures. |
5 Application to the Musca observation map, sparse filtering, and determination of the inertial range
5.1 Map of the singularity exponents
In Sect. 3, we introduced the multifractal formalism through the analysis of intermittency in the velocity field as this is the usual presentation in the turbulence literature. In this study the analysis is done on thermal continuum emission using the discrete gradient measures introduced in Sect. 3.3. In Fig. 7, we display the singularity exponents h (x) on the Herschel 250 μm map, computed using the local correlation measure defined by Eqs. (B.7) and (B.5). The computation has been done on a filtered version of the map, described in Sect. 5.2, to reduce some background noise. As we show in the following, background noise reduction is performed not only for better visualization, but also to compute more precise singularity spectra. The wedge used in the figure is such that most negative singularity exponents are brighter. We can see how the singularity exponents trace the transitions in the signal, particularly along the filamentary structures, which are very well rendered by negative values of h (x). We also note the thin dark region along the crest of the main filament: it follows a generatrix-like curve of a cylindrical structure, along which the flux appears constant. We observe the same phenomenon in MHD simulations. In the case of the Musca cloud, however, a close inspection of the crest shows that this thin dark region is filled with small elongated structures perpendicular to the crest, making the picture even more complex. In addition, there are small circular features distributed all over the map that are most likely background galaxies that were not eliminated.
5.2 Sparse filtering of an observational map
The Musca Herschel 250 μm flux map contains point-like sources, which are mostly galaxies, and the cosmic infrared background2 (CIB) and the cosmic microwave background (Padoan et al. 2001; Robitaille et al. 2019), which have isotropic low amplitude values very close to those of small-scale filamentary structures. As a consequence, reducing this noise is of primary importance in the multifractal analysis of the Musca gas. One possible method, presented in Robitaille et al. (2019), makes use of a filtering algorithm aiming at separating (and reconstructing) the large space-filling monofractal content of an image from the coherent structures that have a multifractal nature. This technique applies a threshold on the probability distribution function (PDF) of wavelet coefficients at different spatial scales and successfully identifies both the monofractal component signature of the noise and the turbulent component of the ISM. However, we do not employ this method here because thresholding a wavelet decomposition at small scales irremediably blurs the filamentary structures after reconstruction. Consequently, a multifractal analysis applied on the reconstruction can have substantial impact on the singularity spectrum. Instead, it is necessary to keep any coherent structure at low scales intact while reducing noise. For this reason it is preferable to use an edge-aware noise filtering approach (Badri 2015) for the multifractal analysis of astronomical data, which we present in the following.
We compute a filtered image sf(x) such that the result sf remains close to the original data s while having sparse gradients (i.e., we want to reduce the noise but keep coherent structures). Therefore, given a norm ∥ ⋅ ∥ promoting sparsity, the image sf is computedas the solution of the optimization problem:
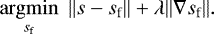 (22)
(22)
Candès et al. (2008) show that the L1 norm favors sparsity in a much better way than the L2 norm while remaining convex, which greatly facilitates the numerical implementation and guarantees the existence of a global minimum. Consequently, we make use of the L1 norm
 (23)
(23)
and solve the optimization problem 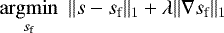 with λ > 0 being a tuning parameter. The first term ∥s − sf∥1 guarantees that the filtered image is very similar to the original (data fitting term), while the second term λ ∥∇sf∥1, when minimized, promotes the sparsity of the filtered gradients. Hence, the minimization of the two terms reduces noise, while keeping gradient information. The L1 minimization problem is solved using the half-quadratic splitting resolution method (Geman & Chengda Yang 1995; Schmidt & Roth 2014). We show the result of sparse filtering first on the original flux density data in Fig. 8, where it appears as standard noise reduction. However, turning to the visualization on the singularity exponents, as shown in Fig. 9, reveals the power of this sparse filtering with respect to the filamentary structures, as they are clearly enhanced with respect to the unfiltered version. We also observe that although the filtering does not eliminate many background galaxies, it sufficiently reduces the cosmic infrared background (CIB) and cosmic microwave background to significantly expose filamentary structures that were hidden by Gaussian noise in the original data. Figure 10 shows the image s − sf (i.e., the resulting noise suppressed by the edge-aware filtering). Figure 11 displays the results of applying filtering for the singularity spectrum on the Musca map, with and without background noise reduction. We note how the background noise leads to an overestimation of the low dimensional filamentary structures, and how the Gaussianity of background noise makes the unfiltered spectrum more parabolic than the filtered spectrum. Consequently, noise reduction is a necessary preprocessing step in a multifractal analysis of astronomical data for a better computation of the singularity spectrum.
with λ > 0 being a tuning parameter. The first term ∥s − sf∥1 guarantees that the filtered image is very similar to the original (data fitting term), while the second term λ ∥∇sf∥1, when minimized, promotes the sparsity of the filtered gradients. Hence, the minimization of the two terms reduces noise, while keeping gradient information. The L1 minimization problem is solved using the half-quadratic splitting resolution method (Geman & Chengda Yang 1995; Schmidt & Roth 2014). We show the result of sparse filtering first on the original flux density data in Fig. 8, where it appears as standard noise reduction. However, turning to the visualization on the singularity exponents, as shown in Fig. 9, reveals the power of this sparse filtering with respect to the filamentary structures, as they are clearly enhanced with respect to the unfiltered version. We also observe that although the filtering does not eliminate many background galaxies, it sufficiently reduces the cosmic infrared background (CIB) and cosmic microwave background to significantly expose filamentary structures that were hidden by Gaussian noise in the original data. Figure 10 shows the image s − sf (i.e., the resulting noise suppressed by the edge-aware filtering). Figure 11 displays the results of applying filtering for the singularity spectrum on the Musca map, with and without background noise reduction. We note how the background noise leads to an overestimation of the low dimensional filamentary structures, and how the Gaussianity of background noise makes the unfiltered spectrum more parabolic than the filtered spectrum. Consequently, noise reduction is a necessary preprocessing step in a multifractal analysis of astronomical data for a better computation of the singularity spectrum.
Nevertheless, a question can be raised. Does the edge-aware filtering defined by Eq. (22) introduce spurious new gradients, initially not present in the original data? The answer is no, as can be seen from the numerical implementation of the minimization algorithm, which is performed in two steps. First, low-level gradients are set to 0, and gradients whose norm is greater than a given threshold3 are kept. This operation does not introduce new gradients. In the second step, a new image is generated whose gradient is, at each point, a weighted sum of the original gradient image and the image obtained at the precedent step. This operation also does not introduce new gradients.
In Sect. 4 and Appendix B, we checked the scaling of the gradient measure by computing the singularity spectra at two consecutive scales in a wavelet projection of the signal. We observed from this experiment the scaling of the measurewhen the singularity spectra are derived from the computation of the singularity exponents using the method presented inAppendix B. These experiments were performed on the filtered Musca map with λ = 0.7. We show in Fig. 12 the result of the same test using the nonfiltered Musca map. The two scaled versions are generated, as before, using a reverse bi-orthogonal discrete wavelet transform of order 4.4. We see from the graphs that the presence of noise alters the scaling of the measure. This also advocates for the use of filtered observational maps.
Figure 13 displays the result of the computation of the function q↦ ζ(q) defined in the structure function method (see Sect. 5.3, Eq. (25)) on the unfiltered and filtered Musca map. The two graphs are clearly distinct, which adds to non-negligible effects of the background noise on the scaling properties of the observational map.
Since the singularity spectrum is estimated from the histogram of the singularity exponents (see Eq. (A.11)), it is possible to estimate the error bars in the spectrum. If we discretize the histogram of singularity exponents with a large number of bins, the probability pα that a singularity exponent belongs to bin Bα can be estimated by Nα∕N, where N is the total (large) number of realizations of the singularity exponents, and Nα is the number of samples falling in thebin indexed by α. Then, if N is large enough, Nα can be estimated by a Gaussian, and we can assign an error bar to the measurement by setting a 99% confidence interval. A computation using this hypothesis leads to the following values of the error bars (Turiel et al. 2006):
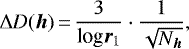 (24)
(24)
with Nh the number of events in the bin associated with singularity exponent h, and r1 as the minimum resolution of the inertial range. Figure 14 displays the singularity spectrum with its error bars of the edge-aware filtered Musca 250 μm map with a parameter value λ = 0.7.
 |
Fig. 8 Visualization of the filtering (computed with λ = 0.7) zoomed in on the central part of the Musca 250 μm map. The level was chosen to emphasize low values. The left panel shows the filtered data and the right the unfiltered data. The positive effect of the filtering on the flux density data becomes obvious. The visualization performed on the singularity exponents (see Fig. 9) demonstrates the importance of filtering on filamentary structures, which are oflow fractal dimensions. |
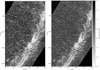 |
Fig. 9 Illustration of background noise reduction and enhancement of the filamentary structures in the Musca 250 μm map by edge-aware nonlinear filtering while promoting a signal’s gradient sparsity with L1 norm. The images show the singularity exponents of a region in Musca that is rich in filamentary structures. The right panel displays the singularity exponents derived from the unfiltered original map, while the left panel shows the singularity exponents after filtering the map with λ = 0.7 (Eq. (1)). The same grayscale wedge is used for both images. |
5.3 Inertial range and the 2D structure function method
In a canonical approach to multifractality, the determination of scaling laws is achieved by statistical analysis of the moments of wavelets projections of the signal over a large range of scales, and a grand ensemble of realizations (Venugopal et al. 2006a). As mentioned before, verifying the existence of scaling laws through the computation on grand ensembles of realizations cannot be achieved with our single Musca image.
We thushave to use a spatial approach, based on 2D structure functions, introduced in Renosh et al. (2015) to check the existence of a significant inertial range. If x1 and x2 are points in the 2D signal domain, the existence of scaling laws for a certain range of spatial distances is verified when
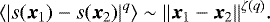 (25)
(25)
Consequently, the spatial moments ⟨|s(x1) − s(x2)|q⟩ are log −log plotted against the distances ∥x1 −x2∥ for a very large ensemble of couples (x1, x2). We carried out experiments on both original and edge-aware filtered data for 5 × 108 couples of points (x1, x2), chosen randomly in the Musca map. We also conducted the experiment on MHD simulation outputs presented in Sect. 6. In Fig. 15, we show the result of the structure function method for the Musca 250 μm map filtered data with λ = 0.7 (Eq. (22)). From left to right, the first image (top left) is the graph of a log −log plot with colors indicating some moment values q. The image also shows the graphs of linear regression fits (dotted lines) performed in an inertial range covering the interval [13, 160] pixels, corresponding to the range of distance [0.053, 0.65] pc. The middle image displays the resulting map q↦ζ(q). The two images on the right show the quality of linear regression, evaluated with the sum of squares due to error (sse) and with the classical Pearson correlation coefficient r.
We note that the derived inertial range is probably affected by the beam size (~ 3 pixels, 0.012 pc) for the lower boundary (0.05 pc) and by the sizes of the rectangular map (1786 pixels in the x-direction, or 7.144 pc, and 2135 pixels in the y-direction, or 8.54 pc) for the upper boundary (0.65 pc).
 |
Fig. 10 Visualization of noise reduction by the edge-aware noise filtering. The data displayed are s − sf in the same area as shown in Fig. 9. |
6 MHD simulation data
The simulations used in this work are presented in Dib et al. (2007, 2008). Here we recall their basic features. The ideal MHD equations are solved on a uniform 3D cubic grid using a total variation diminishing scheme (TVD), which is a second-order-accurate upwind scheme (Kim et al. 1999). The boundary conditions used in the three directions are periodic. The Poisson equation is solved to account for the self-gravity of the gas using a standard Fourier algorithm. In order to achieve second-order accuracy in time, an updated step of the momentum density due to the gravitational force is implemented, as in Truelove et al. (1998).
Following the method described in Stone et al. (1998), turbulence is continuously driven in the simulation box and the kinetic energy input rate is adjusted to maintain a constant specified rms sonic Mach number Ms = 10. Kinetic energy is injected at large scales, in the wave number range k = 1–2. When converted into physical units, the models correspond to a box size of 4 pc and an average number density of 500 cm−3. The corresponding column density is thus ~ 5 1021 cm−2, which is similar to that of many molecular clouds except for those associated with massive star formation. The temperature is 11.4 K, the sound speed 0.2 km s−1, and the initial rms velocity is 2 km s−1 (therefore the initial sonic Mach number is Ms = 10). The four simulations vary by the strength of the initial magnetic field ranging from a magnetically subcritical cloud model to a non-magnetic cloud. The strength of the initial magnetic field in the box for the subcritical, moderately supercritical, and strongly supercritical magnetized models are B0 = 45.8, 14.5, and 4.6μG, respectively. This corresponds to β plasma andmass-to-magnetic flux values of the box for these runs of β = 0.01, 0.1, and 1, and μbox = 0.9, 2.8, and 8.8, respectively. The simulations start with a uniform density field, and are evolved for one-half of a sound crossing time (the sound crossing time is ts = 20 Myr), equivalent to five turbulent crossing times (the turbulent crossing time is tc = 2 Myr), before self-gravity is turned on. This is a common practice in such simulations and a necessary step in order to allow for the full development of the turbulent cascade. The left-hand image of Fig. 17 displays the integrated column density maps of one snapshot corresponding to the hydrodynamical case with no magnetic field at a time t = 0.422 tc Myr after gravityis turned on.
In Fig. 16, we show the result of the determination of inertial range with the 2D structure function method (Sect. 5.3) applied over one MHD simulation output. We see considerable differences compared to the Musca 250 μm observational map results, notably in terms of the quality of the linear regression. The range of distances chosen for performing the linear regression fit is [0.18, 1.5] pc. Other outputs in the MHD simulation show similar plots. Hence, the scaling properties of MHD simulation outputs are different compared to real observation maps.
In the middle and right panels of Fig. 17, we also show the singularity exponents and the singularity spectrum, as described in Sect. 3.3. We note that the error bars display more uncertainty than those of the Musca 250 μm map displayed in Fig. 14. This larger uncertainty arises from the small number of samples; the image data is (256 × 256). In Fig. 18, we display both the singularity spectrum (in orange) and the computation of a fitted log -normal spectrum (in blue) 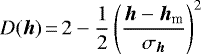 (Eq. (9)) for the data corresponding to time t = 0.62 tc Myr after gravity is turned on. The fitting is performed using the quasi-Newton minimization algorithm implementation available in Matlab. We obtain here hm = −0.0223, σh = 0.2037. Hence, in this case
(Eq. (9)) for the data corresponding to time t = 0.62 tc Myr after gravity is turned on. The fitting is performed using the quasi-Newton minimization algorithm implementation available in Matlab. We obtain here hm = −0.0223, σh = 0.2037. Hence, in this case 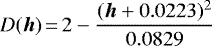 . The fit is very good, which indicates a good approximation by a log-normal process. This good fit was observed for all our simulation outputs. In comparison, looking at Figs. 14 and 19 we conclude that the singularity spectrum of the Musca 250 μm map does not fit a log-normal process so well. We discuss this point in the next sections.
. The fit is very good, which indicates a good approximation by a log-normal process. This good fit was observed for all our simulation outputs. In comparison, looking at Figs. 14 and 19 we conclude that the singularity spectrum of the Musca 250 μm map does not fit a log-normal process so well. We discuss this point in the next sections.
 |
Fig. 11 Singularity spectrum of the Musca 250 μm Herschel map, computed with and without edge-aware filtering. The orange curve shows the singularity spectrum computed on raw unfiltered data, while the blue curve displays the singularity spectrum computed on edge-aware filtered data using the filtering introduced in Sect. 5.2 with parameter
λ = 0.7. The horizontal axis gives the h-values of the scaling exponents, and the vertical axis gives the fractal dimension
|
 |
Fig. 12 Mappings h↦D(h) computed for two consecutive scales of the unfiltered Musca 250 μm Herschel observational map using a reverse bi-orthogonal discrete wavelet transform of order 4.4. The graphs show that the presenceof the noise alters the scaling of the measure. |
 |
Fig. 13 Plot of ζ(q) for the Musca 250 μm Herschel observational map with filtering (λ = 0.7, curve in red)and without filtering (curve in green); the mapping q↦ζ(q) is defined by the structure function method (Eq. (25)). This graph shows that the background noise does affect the statistics of scaling. |
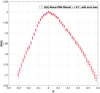 |
Fig. 14 Singularity spectrum of the Musca Herschel 250 μm map with error bars as defined by Eq. (24); the observational map is edge-aware filtered with a tuning parameter λ = 0.7. |
7 Multifractal analysis of data
7.1 Detection of a multiplicative cascade
The existence of a multiplicative cascade is of primary importance in phenomenological descriptions of turbulence (see Sect. 3). It has been shown, in a sufficiently general setting, that models built from a multiplicative cascade possess log -correlations 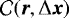 such that
such that 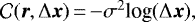 where σ2 = Var(log|W|) and W is the random variable generating the cascade (see Eq. (D.1) for a definition of the log -correlation). Moreover, if the cascade is log-normal, then
where σ2 = Var(log|W|) and W is the random variable generating the cascade (see Eq. (D.1) for a definition of the log -correlation). Moreover, if the cascade is log-normal, then  with c2 being the second cumulant associated with the log-normal process (Arneodo et al. 1998b). A summary of the tools used in this perspective can be found Appendix D. Consequently, to investigate the existence of a multiplicative cascade in the Musca map we first use the cumulant approach described in Appendix C. The cumulant analysis is performed over 1D signals that are extracted from columns of a 2D observational map, as shown in the left panel of Fig. 20. In this figure we display, as an example, a 1D signal that comes from a particular column in the Musca observation map; the column crosses low- and high-flux regimes (i.e., regions outside and inside the main filament). We perform the cumulant analysis using the Mexican hat as analyzing wavelet,
with c2 being the second cumulant associated with the log-normal process (Arneodo et al. 1998b). A summary of the tools used in this perspective can be found Appendix D. Consequently, to investigate the existence of a multiplicative cascade in the Musca map we first use the cumulant approach described in Appendix C. The cumulant analysis is performed over 1D signals that are extracted from columns of a 2D observational map, as shown in the left panel of Fig. 20. In this figure we display, as an example, a 1D signal that comes from a particular column in the Musca observation map; the column crosses low- and high-flux regimes (i.e., regions outside and inside the main filament). We perform the cumulant analysis using the Mexican hat as analyzing wavelet,
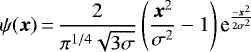 (26)
(26)
(second derivative of a Gaussian), with a deviation σ = 3.2 chosen for the data. If f(x) is a 1D signal, the continuous wavelet projection (CWT) of f at scale r > 0 is
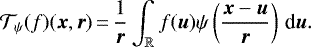 (27)
(27)
It should be noted that we use L1 normalization instead of L2; to study correlations the conservation of energy is not necessary, while L1 normalization better adapts to strong variations in the signal (Venugopal et al. 2006a). We use the Herschel 250 μm Musca dataset filtered with λ = 0.7 (Eq. (22) in Sect. 5.2). Figure 20 shows a selected column in the Musca map and the associated 1D signal f(x) with two of its wavelet projections 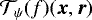 at two respective scales r1 and r2 with r2 < r1 (in red and blue, respectively).
at two respective scales r1 and r2 with r2 < r1 (in red and blue, respectively).
We apply this cumulant analysis on each 1D signal (columns) by computing the log -correlations  (Eq. (D.1)) and plot them against log(Δx). As explained in Appendix C, we look for the fingerprints of long-range correlations and the existence of a multiplicative cascade according to
(Eq. (D.1)) and plot them against log(Δx). As explained in Appendix C, we look for the fingerprints of long-range correlations and the existence of a multiplicative cascade according to 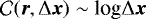 and Eq. (D.2). We use 500 scales from r = 1 to r = 500 and 400 values for Δx between 1 and 400. The slope c2 is computedthrough linear regression, according to Eq. (C.3). The linear regression used to compute c2 is performed for scales between 10 and 200. Our experiment shows that long-range correlations are found for all 1D columns, and that a multiplicative cascade does exist in the Musca cloud. The left panel of Fig. 21 displays an example, corresponding to Col. 970 in the Musca map, of a typical graph obtained in Musca: the log -correlations corresponding to different scales decrease in accordance with the equation of the line y = −c2log(Δx) for the computed c2 value, whichis an indication of the presence of a multiplicative cascade in the column. However, there is an interval of columns, corresponding to the rectangular area shown in Fig. 22 (left), for which the curves behave as shown in the right panel of Fig. 21. This does not imply the absence of a multiplicative cascade, but there is an area, inside this region that brings perturbations to the statistics; this is also an indication that different processes are at work inside the Musca cloud.
and Eq. (D.2). We use 500 scales from r = 1 to r = 500 and 400 values for Δx between 1 and 400. The slope c2 is computedthrough linear regression, according to Eq. (C.3). The linear regression used to compute c2 is performed for scales between 10 and 200. Our experiment shows that long-range correlations are found for all 1D columns, and that a multiplicative cascade does exist in the Musca cloud. The left panel of Fig. 21 displays an example, corresponding to Col. 970 in the Musca map, of a typical graph obtained in Musca: the log -correlations corresponding to different scales decrease in accordance with the equation of the line y = −c2log(Δx) for the computed c2 value, whichis an indication of the presence of a multiplicative cascade in the column. However, there is an interval of columns, corresponding to the rectangular area shown in Fig. 22 (left), for which the curves behave as shown in the right panel of Fig. 21. This does not imply the absence of a multiplicative cascade, but there is an area, inside this region that brings perturbations to the statistics; this is also an indication that different processes are at work inside the Musca cloud.
 |
Fig. 15 Result of the 2D structure function method for the determination of an inertial range of spatial scales. Computations are done on the Musca 250 μm map filtered data with λ = 0.7 (Eq. (22)). A total of 5 × 108 couples of points (x1, x2) are chosen uniformly in the spatial domain; moments q are between 0.1 and 5, with increment steps of 0.1 (for clarity, only some of the moments are shown). The left panel shows the graph of a log −log plot (Eq. (25)), with colors indicating some moment values, q. The image also shows the graphs of linear regression fits (dotted lines), performed in an inertial range covering the interval [13, 160] pixels, corresponding to the range of distance [0.053, 0.65] pc. The middle panel displays the resulting map q↦ζ(q). The two panels on the right show the quality of the linear regression: the sse and the r correlation coefficient. Hence, the quality of the fit decreases with the moment order q. |
 |
Fig. 16 Result of the 2D structure function method, applied over one of the MHD simulation outputs presented in Sect. 6, for the determination of an inertial range of spatial scales. A total of 5 × 108 couples of points (x1, x2) are chosen uniformly in the spatial domain; the moments q have values between 0.1 and 5, with increment steps of 0.1 (for clarity, only a few of the moments are shown). The first panel shows the graphs of the log − log plot (Eq. (25), with colors indicating some moment values, q). As in Fig. 15, the graphs show linear regression fits (dotted lines) performed in an inertial range covering the interval of distance [0.18, 1.5] pc. The second panel displays the map q↦ζ(q). The third and fourth panels show the quality of linear regression: sse and the r correlation coefficient. |
7.2 Musca spectrum: multifractality, log-normality
Our final singularity spectrum obtained for the whole Musca region is displayed in Fig. 14. In contrast to previously obtained singularity spectra for the ISM (e.g., Khalil et al. 2006; Elia et al. 2018), this improved spectrum is not very symmetrical with a clearly steep, almost linear descent on the h ≤ 0 side (left) and a rounder Gaussian shape on the h ≥ 0 side (right). We note that this clear asymmetric shape has been enhanced and clearly revealed thanks to the noise filtering (see Fig. 11). Despite this clear asymmetry, we fitted in Fig. 23 (left) the obtained spectrum with a parabolic curve that would represent a log-normal behavior of the turbulent fluctuations. We find hm = 0.0206, σh = 0.4564. The part of the singularity spectrum corresponding to h ≤ 0 shows a clear deviation between the spectrum computed in the microcanonical formalism (orange) and the parabolic (blue), which seems to strongly point to some non-log-normal process in the turbulent flow of Musca. We note that there is actually more resemblance with a log -Poisson spectrum, as shown by the fit displayed in Fig. 23, right panel. A log -Poisson spectrum is indeed asymmetric with a steep descent on the negative h side (see Fig. 2). These fit results can be compared with the bottom panel of Fig. 194, which corresponds to the non-filtered case. Given that the noise filtering mostly enhances the contrast of filamentary structures (which are otherwise merged in the noise data), it suggests that the asymmetry in the singularity spectrum and the log -Poisson behavior arerelated to 1D structures (i.e., filaments), as expected for the most singular structures in a turbulent cascade with intermittency (see She et al. 1990 and Sect. 3.1 below for a discussion). In the next section, we show that some regions of Musca are more log -normal than others.
Furthermore, in addition to the possible proxy of the whole spectrum by a log -Poisson curve a close inspection of Fig. 14 reveals at around h = −0.2 a slight non-convex area in the graph. This observation can be made only on the edge-aware filtered signal because the background noise smoothes the spectrum, as seen in the orange graph of Fig. 11. Consequently, the singularity spectrum in this case seems to present two local extrema. This might be an indication that at least two different processes can be present in the signal.
 |
Fig. 17 Multifractal analysis of MHD data. Left panel: one snapshot of the column density output of the MHD simulation data used in this work, integrated along one axis of the cube. The output shown here corresponds to the hydrodynamical case with no magnetic field at time t = 0.422 tc. Middle panel: map of the singularity exponents. Right panel: singularity spectrum with its error bars computed using Eq. (24). |
 |
Fig. 18 Log-normal fit of the singularity spectrum for the data corresponding to time t = 0.62tc Myr after gravityis turned on. Shown is the singularity spectrum computed in the microcanonical framework (orange) and a fitted quadratic log-normal singularity spectrum (blue). The fit is very good, which indicates a good approximation by a log -normal process. |
7.3 Distinct statistical properties observed in the data
To go one step further, we now compare the singularity spectra computed over different regions of interest (ROI) to reveal potential different turbulent behaviors inside the cloud. Figure 22 shows the geometric location of six ROIs inside the Musca cloud that were selected based on different physical properties. ROI1 is the northern end of the filament where a single protostellar object is located. ROI2 represents the eastern cloud area with prominent striations (weak filamentary structures perpendicular to the main crest of Musca filament). ROI3 and ROI4 are the highest density crest regions. We define two ROIs on the crest with ROI4 being the southern part with already signs of fragmentation, while in ROI3 the northern part, the crest is still homogeneous. ROI5 is the southern end of the filament which is less organized in filaments or striations. ROI6 is the western part of the embedding cloud with less prominent striations. For each ROI, we compute the following: the singularity spectrum and the values hm and σh of a fitted log -normal spectrum 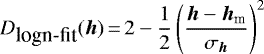 . The quality of the fit is estimated by the L2 error
. The quality of the fit is estimated by the L2 error 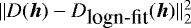 . The best-defined curves are those with the highest number of pixels: ROI2 and ROI5. Figure 24 and Table 1 show the results of the computations. The obtained graphs and values confirm that the processes inside each ROI can display strong deviation from a log-normal process. First, it becomes obvious that we can distinguish two classes of curves, those that are not too far from a log -normal fit, ROI1 and to a lesser extent ROI4 (with respective fit errors 0.028 and 0.19), and the remaining ones that deviate significantly from log -normality. ROI1 and ROI4 have the largest singularity dispersions σh of a fitted log-normal with σh = 0.62 and 0.44, respectively. Moreover, ROI1 and ROI4 feature the most symmetric singularity spectra among the ROIs. The other ROIs all show a steeper slope at negative h values than at positive ones, and ROI2 features the worst log-normal fit among the six ROIs; this result that can be put in relation with the high density of striations seen in ROI2, and with Fig. 22 and the discussion in Sect. 7.1: it is likely that the part of rectangle shown in Fig. 22 that intersects ROI2 is responsible for deviation also observed in the log -correlations
. The best-defined curves are those with the highest number of pixels: ROI2 and ROI5. Figure 24 and Table 1 show the results of the computations. The obtained graphs and values confirm that the processes inside each ROI can display strong deviation from a log-normal process. First, it becomes obvious that we can distinguish two classes of curves, those that are not too far from a log -normal fit, ROI1 and to a lesser extent ROI4 (with respective fit errors 0.028 and 0.19), and the remaining ones that deviate significantly from log -normality. ROI1 and ROI4 have the largest singularity dispersions σh of a fitted log-normal with σh = 0.62 and 0.44, respectively. Moreover, ROI1 and ROI4 feature the most symmetric singularity spectra among the ROIs. The other ROIs all show a steeper slope at negative h values than at positive ones, and ROI2 features the worst log-normal fit among the six ROIs; this result that can be put in relation with the high density of striations seen in ROI2, and with Fig. 22 and the discussion in Sect. 7.1: it is likely that the part of rectangle shown in Fig. 22 that intersects ROI2 is responsible for deviation also observed in the log -correlations  . For all ROIs except ROI1 and ROI4, the singularity spectrum is closer to the log -Poisson type than log-normal. This finding also applies to the singularity spectrum of the whole (edge-aware filtered) Musca observational map, as can be seen in Figs. 14, 19, and 23.
. For all ROIs except ROI1 and ROI4, the singularity spectrum is closer to the log -Poisson type than log-normal. This finding also applies to the singularity spectrum of the whole (edge-aware filtered) Musca observational map, as can be seen in Figs. 14, 19, and 23.
 |
Fig. 19 Results of a log-normal fit for the singularity spectrum of the full Musca 250 μm map (also called PSW), edge-aware filtered (top image, λ = 0.7), and unfiltered (bottom image). In each image, the singularity spectrum h↦D(h) is shown in orange, and the log-normal parabola in blue. The values obtained for the coefficients of the fit (Eq. (9)) are given in each case. The differences between the two fits shows the importance of the edge-aware filtering for multifractal analysis of astronomical observational maps. It appears that the background noise “log -normalizes” the data, while the filtered version, which takes fine filamentary structures into account better, deviates from log -normality. We note in the filtered version the change in the orange curve around h = −0.2. This is an indication that different types of turbulent processes are present in the Musca cloud, in particular those processes inside the main filament and the surrounding cloud. |
7.4 Application on data from simulations
Figure 18 shows a typical result of a log -normal fit applied on one projection of the MHD simulation data presented in Sect. 6; by projection we mean in one of the three spatial directions (X, Y, or Z) since the data is in the form of a 3D cubic volume. The fit is very good, in all directions, and this is true for all available simulation outputs. Consequently, we can say that the MHD simulation outputs are log -normal processes, and it is then possible to see the variation in time of the width of the log -normal fitted singularity spectrum (the coefficient σh of Eq. (9)). Figure 25 displays the graph of the dispersion of the fitted log -normal process, or σh of Eq. (9) as a function of time, in Myr, for the value β = 0.1. The dispersion becomes wider as gravitational effects become much more pronounced (more bound and collapsing structures), as was already stated in Elia et al. (2018), where the authors note that when gravity is present one gets a broader spectrum, and this is also the case when turbulence is driven with compressive modes. Compressive driving generates larger density contrasts in the simulations volume and in the resulting 2D maps. This effect mimics the presence of gravity. Accordingly, in the log -normal approximation, the dispersion σh can be used as an indication of the gravitational effects.
8 Discussion of results: musca turbulent dynamics and implication on star formation processes
As discussed, for instance, in Bonne et al. (2020a), several physical processes are presumably at work to explain the formation of the Musca filament in particular, as well as the global behavior of the ISM in this molecular cloud. We have to consider the turbulence injected from large scales, self-gravity presumably acting at small scales, magnetic field pressures and tensions at all scales, and possibly some local effects such as shocks. Our long-term goal is to seek for statistical signatures of these different processes thanks to the multifractal analysis, introduced in this paper, and profiting from the unprecedented depth and richness of Herschel maps. Facing the numerous difficulties in deriving such clean statistical probes, and in investigating the possible different signature of processes and the inherently complex situations of the real data, the present article should be seen as a first step toward this long-term ambitious goal. The following discussion thus only provides hints for new directions which will need confirmation and further interpretations thanks to extensive studies on simulations and on a large number of star-forming regions.
We clearly found a multiplicative cascade with a significant and large inertial range from at least 0.05–0.65 pc, which is an important step toward supporting the turbulence interpretation of the dust emission from Herschel toward a weak column density cloud surrounding the low-mass Musca filament. This result points to a dominance of turbulent motions, and confirms that this turbulent behavior originates from at least parsec scales.
With the help of this new microcanonical approach that does not require multiple realizations (single map), we could then derive for the first time a precise enough singularity spectrum of the observed flow to characterize its turbulent behavior. We verified thatwe have a good invariance of the singularity spectrum to a scale that was not obtained with box counting method, for instance.This is highly important as we believe this is the missing step to be able to derive the true, relatively precise singularity spectra of our datasets (real data and simulations) and to quantify some differences between regions and between observationsand simulations to make progress in the understanding of the physics leading to cloud and filament formation.
The obtained singularity spectrum confirms that the ISM toward Musca and its surroundings has a clear multifractal structure. It implies the existence of intermittency and non-Gaussian behavior which are believed to be critical to explain the formation of the densest and star-forming structures. Moreover, while the so-far derived singularity spectra were often found to have a log -normal behavior in previous works, here we clearly obtain a global singularity spectrum which strongly deviates from log -normality. The deviation from log-normality is apparent here as the singularity spectra are clearly nonsymmetric. Among the many multifractal processes having a nonsymmetric spectrum, here we discussed the simplest case, the log -Poisson behavior that has been extensively discussed in the literature on turbulence. According to Gledzer et al. (1996), for instance, log -Poisson behavior is expected for an energy cascading model of intermittency involving rare localized regions of large and/or weak energy dissipation (dynamical intermittency), while log-normal behavior is obtained for intermittency arising from widespread regions with nearly equal dissipation rates (space intermittency). The existence of such geometric models for the log-Poisson spectrum is interesting in astronomy, although further analysis must be done in order to relate the observed statistics with a particular type of process. In all the ROIs chosen in the Musca map, and even in the ROI1, we can see filamentary and linear structures of various sizes and orientations on the map of singularity exponents, Consequently, it could be the distribution of these structures that affects the log -normality of a singularity spectrum (see Fig. 26). According to She et al. (1990), the most intermittent structures in incompressible purely hydrodynamical turbulence have to be filamentary to be stable. In the case of compressible and magnetized turbulence, we can only expect that these filaments are more stable.
We therefore propose that the ISM associated with the Musca filament region shows a turbulent behavior which is better reproduced by a dynamical intermittency than by a space intermittency with localized enhanced dissipation locations. From the global view discussed in Bonne et al. (2020a), among others, and from the realistic view that most intermittent regions have to be filamentary (She et al. 1990; She & Leveque 1994) we can then speculate that these localized enhanced dissipations are associated with the formation of the Musca filament and with the striations in the surroundings, and could be related to the efficient guiding and focusing by the magnetic field (reducing the space dissipation) toward a region of strong accumulation of matter where dissipation could be enhanced in accretion events. Local (accretion) shocks, providing strong local turbulence dissipation may explain and complement our understanding of the particular statistics (log -Poisson type) of the large singularities of the map (large h values, i.e., the locations of large local gradients as imaged in white in the singularity map of Fig. 7). We find the most nonsymmetric (hence, possibly log-Poisson) singularity spectra toward the ROIs associated with the filaments of Musca, which reinforces the interpretation that the dynamical intermittency is associated with filament formation.
Interestingly enough, using the same microcanonical analysis we could not identify in simulated data a similar log -Poisson behavior. From simulated datasets we always obtain log-normal spectra. This behavior could perhaps reflect the fact that these simulations are run with a continuous injection of well-behaved turbulence at large scales. The fact that self-gravity is included does not seem to affect the singularity spectra. We clearly need to continue to investigate what is missing in the simulations to properly reproduce the observed data, but we note that we have found a statistical tool sensitive enough to make the difference between simulations and real datasets.
 |
Fig. 20 CWT analysis performed on a 1D signal extracted from the Musca 250 μm map. Left panel: Musca 250 μm map in which the white column defines a 1D signal. Right panel: original 1D signal (centered and rescaled) and CWT projections of the selected 1D signal with the Mexican hat wavelet at scales 5 (red) and 60 (blue). |
 |
Fig. 21 Plots of the log-correlations
|
 |
Fig. 22 Definition of areas. In the left panel, the statistics of the log-correlations are differentfrom those of the other parts of Musca in the rectangular area shown in the picture. In the right panel, a definition of six ROIs inside the Musca ISM are shown. |
 |
Fig. 23 log-normal and log -Poisson fitting of Musca singularity spectrum. Left: singularity spectrum of the filtered (λ = 0.7) Musca 250 μm observational map (in orange) fitted against a log-normal parabolic spectrum (blue) defined by Eq. (9). The fit is performed using the quasi-Newton minimization algorithm implementation available in Matlab. Right: singularity spectrum of the filtered (λ = 0.7) Musca 250 μm observational map (in orange) fitted against a log-Poisson singularity spectrum (blue) defined by Eq. (10). The minimization algorithm is the same. Both images display the values found by the minimization algorithm and the error fit. |
 |
Fig. 24 Singularity spectrum and log-normal fit for each ROI. Shown for each region of interest in the Musca cloud delimited in Fig. 22 are the singularity spectrum h↦D(h) of an ROI (in orange), a log-normal fitted approximation singularity spectrum (in blue; Eq. (9)), the obtained numerical values hm and σh, and the error of the fit. The various values of hm and σh for each ROI are also given in Table 1. |
 |
Fig. 25 Variation in time of the fitted σh of the log-normal singularity spectrum (Eq. (9)) for the simulation outputs described in Sect. 6. The value of the magnetic pressure β = 0.1. |
Parameters of the fitted log-normal process for each ROI.
9 Conclusion
In this work, we made use of a new computable multifractal formalism in a microcanonical formulation, based on ideas from predictability in complex systems, and we applied it to analyze the complex turbulent structure of the ISM for the case of a Musca Herschel observational map. We confirm that to be fully effective, the use of the multifractal formalism must be operated with important checks on an observational map: determination of the inertial range for which scaling laws apply, scale invariance must be checked by computing singularity spectra at different scales and checking their coincidence, background noise reduction must be operated with particular care in order to preserve low-dimensional weak coherent structures.
Our aim was to present a self-contained study with sufficient detail to help reproduce the experiments. Very importantly, we could make the check of scaling laws and the determination of the inertial range, as is usually done in canonical formulations, thanks to moments of the chosen partition functions achieved using a 2D structure function methodology. The microcanonical formulation is based on the direct computation of the singularity exponents. The singularity spectra are derived, and we check the invariance of the resulting spectra with respect to scale. Background noise has the tendency to log -normalize the signals by making their spectra parabolic. We propose a L1 denoising algorithm based on edge-aware filtering which preserves low-dimensional features. We use the theory of cumulants to determine the presence of a multiplicative cascade using log -correlations.
The results show a clear multiplicative cascade with a significant and large inertial range from at least 0.05–0.65 pc (larger scales might be affected by the ~4 pc width of the observed map, and smaller scales by the 0.012 pc beam size) pointing to a dominance of the turbulence originating from scales probably larger than a parsec. We show that a precise study of the intermittency can be achieved by the methodology introduced in this work. For the time in ISM studies, our data and analysis challenge the log -normality of the singularity spectrum of the turbulence. This is one of the major results of this work. It suggests that the turbulence associated with the Musca filament formation exhibits more a dynamical intermittency with localized, enhanced energy dissipation than a space intermittency. Some hints for different turbulent behavior in the region and for some missing physics in simulations shows that the work presented in this study is only a first step in our long-term goal to seek for statistical signatures of different turbulent, physical processes at work in the ISM.
 |
Fig. 26 Distribution of the singularity exponents in ROI1 (left) and in the southern region of Musca ROI5 (right). Both regions show complex linear structures, but of different sizes and organizations. |
Acknowledgements
This work is supported by the GENESIS project (GENeration and Evolution of Structure in the ISm), via the french ANR and the german DFG through grant numbers ANR-16-CE92-0035-01 and DFG1591/2-1. N. Schneider acknowledges support by the German Deutsche Forschungsgemeinschaft, DFG project number SFB 956. L. Bonne acknowledges support by the Région Nouvelle-Aquitaine, France.
Appendix A Definition of the measure
We keep the notations and conventions defined in Sect. 3.3. Let us begin by considering the set 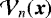 displayed on the left of Fig. 4. In this case, each
displayed on the left of Fig. 4. In this case, each 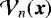 is made of two points, and we introduce the discrete measure noted μn on the unit square by
is made of two points, and we introduce the discrete measure noted μn on the unit square by
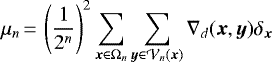 (A.1)
(A.1)
with δx: Dirac measure at x. For each n, μn can be written as a sum of local measures
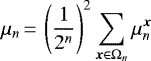 (A.2)
(A.2)
with 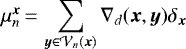 . We examine the behavior of the measures μn when n → +∞. Let us suppose first that s is differentiable. Then
. We examine the behavior of the measures μn when n → +∞. Let us suppose first that s is differentiable. Then
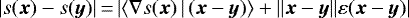 (A.3)
(A.3)
Consequently, if f is any continuous bounded function, then
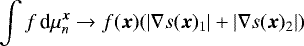 (A.5)
(A.5)
when n → +∞ with 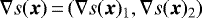 because
because 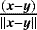 is a unitary vector, and because of the types of neighboring points considered in Fig. 4. Hence, when n → +∞ we have that
is a unitary vector, and because of the types of neighboring points considered in Fig. 4. Hence, when n → +∞ we have that 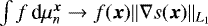 . If we want to obtain
. If we want to obtain 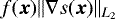 , then we must start from the measure
, then we must start from the measure
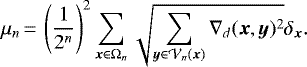 (A.6)
(A.6)
If we use the second set of  displayed on the right of Fig. 4, then we must use
displayed on the right of Fig. 4, then we must use
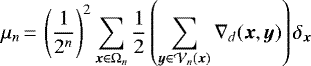 (A.7)
(A.7)
to ensure convergence toward 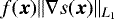 for
for 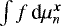 . Then, if f is any continuous bounded function as above then, when n → +∞, we get
. Then, if f is any continuous bounded function as above then, when n → +∞, we get
![\[ \int f \, \mbox{d}\mu_n \rightarrow \int f \| \nabla s \| \, \mbox{d}\lambda \]](/articles/aa/full_html/2021/05/aa39874-20/aa39874-20-eq111.png)
with λ = Lebesgue measure on the unit square because the points in each lattice set Ωn are regularly spaced with distance 2−n and as a classical theorem from the Lebesgue integration. Consequently, the measures μn converge vaguely toward the measure associated with the gradient’s norm when s is differentiable.
When s is any signal, differentiable or not, let us consider x ∈ Ω = ⋃n≥0Ωn so that x ∈ Ωn for a certain n; then x ∈ Ωk for all k ≥ n. Let 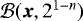 with n ≥ 1 a ball centered at x at resolution
with n ≥ 1 a ball centered at x at resolution 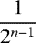 . Then
. Then
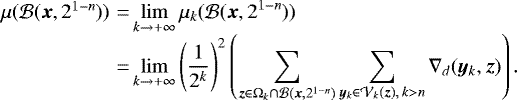 (A.8)
(A.8)
When n → +∞ the last term is a sum of discrete differences taken in the balls  . Consequently, we make the following scaling hypothesis
. Consequently, we make the following scaling hypothesis
 (A.9)
(A.9)
which expresses the scaling of the measure as n → +∞. This defines a scalar field of singularities on the dense subset Ω = ⋃n≥0Ωn of the unit square; consequently, h(x) possesses a unique continuous continuation over the whole unit square as long as the limit 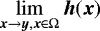 exists for all y in the unit square (Dieudonné 1969, Prop. (3.15.5)), which is a reasonable hypothesis also assumed.
exists for all y in the unit square (Dieudonné 1969, Prop. (3.15.5)), which is a reasonable hypothesis also assumed.
To count the sites x with same scaling behavior, we introduce the density of the exponents at resolution 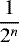 :
:
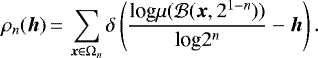 (A.10)
(A.10)
Here ρn(h) is the histogram of the singularity exponents. In the limit n → +∞ we have
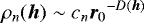 (A.11)
(A.11)
with cn > 0 and the mapping h↦D(h) is the singularity spectrum of the measure defined by the gradient’s norm density (i.e., d μ = ∥∇s∥ dx) when the signal is differentiable.
Let 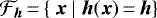 . There is a general physical argument showing that, for sufficient complex signals s such as the ones in fully developed turbulence, the sets
. There is a general physical argument showing that, for sufficient complex signals s such as the ones in fully developed turbulence, the sets 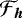 are dense. If there were an h such that the corresponding
are dense. If there were an h such that the corresponding  was not dense, then we could find an open ball in the signal’s domain such that no point in that ball has a singularity exponent h. In the differentiable case this means a particular gradient’s norm is forbidden in that ball.
was not dense, then we could find an open ball in the signal’s domain such that no point in that ball has a singularity exponent h. In the differentiable case this means a particular gradient’s norm is forbidden in that ball.
Appendix B Singularity exponents and predictability
In this appendix we describe a different methodology to evaluate the singularity exponents h (x) which leads to a much better evaluation of the singularity spectrum h↦D(h), as we show in the experiments. It is based on the notion of predictability in complex systems. In the theory of dynamical systems, there is a simple notion of predictability which consists of evaluating the “predictability time”. For an initial small perturbation of size δ, and an accepted tolerance error Δ, the predictability time is the quantity
 (B.1)
(B.1)
with λd the leading Lyapunov exponent. In Aurell et al. (1997), this elementary notion is extended to the case of fully developed turbulence with a formula that involves the singularity spectrum h ↦ D(h). Consequently, the singularity exponents, through the singularity spectrum, are related to predictability. As pointed out in Pont et al. (2006, 2013), Turiel et al. (2006, 2008) it is therefore proposed to relate the computation of singularity exponents to predictability, information content, and reconstructability. The most unpredictable points are considered to encode the information in the system, and they form a set from which the whole system can be completely reconstructed. However, it is necessary to specify this notion of reconstructability.
Given an observational map s(x), where x designates 2D spatial coordinates, a subset  is said to reconstruct the signal s if we have
is said to reconstruct the signal s if we have
 (B.2)
(B.2)
where  is a reconstruction functional and
is a reconstruction functional and  means the gradient operator restricted to the set
means the gradient operator restricted to the set  . In Turiel et al. (2008) it is shown, under the assumption that
. In Turiel et al. (2008) it is shown, under the assumption that  is deterministic, linear, translationally invariant, and isotropic, that Eq. (B.2) then implies the existence of a reconstruction kernel g, which leads to the following reconstruction formula in Fourier space
is deterministic, linear, translationally invariant, and isotropic, that Eq. (B.2) then implies the existence of a reconstruction kernel g, which leads to the following reconstruction formula in Fourier space
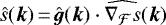 (B.3)
(B.3)
with k the frequency vector. This formula has the consequence that if a set 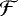 satisfies the reconstruction Eq. (B.3), then
satisfies the reconstruction Eq. (B.3), then
 (B.4)
(B.4)
Here  is complementary set of
is complementary set of  . Since the gradient and divergence operators are local, this means that the decision whether a point x belongs or not to
. Since the gradient and divergence operators are local, this means that the decision whether a point x belongs or not to  should be made only locally. From these considerations, Pont et al. (2006, 2013), Turiel et al. (2006, 2008) made the following assumption.
should be made only locally. From these considerations, Pont et al. (2006, 2013), Turiel et al. (2006, 2008) made the following assumption.
The set of most unpredictable points  is the one that gives a perfect reconstruction according to Eq. (B.3); the decision that a point
is the one that gives a perfect reconstruction according to Eq. (B.3); the decision that a point  can be made locally around x and the set
can be made locally around x and the set  is identical to the set of points that have the lowest singularity exponents in the signal (i.e.,
is identical to the set of points that have the lowest singularity exponents in the signal (i.e., 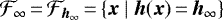 with h∞ being the minimum of the singularity exponents).
with h∞ being the minimum of the singularity exponents).
Under the previous assumption, the computation of the values of the singularity exponents can be made at the lowest scale r0 = 2−n of the acquisition signal instead of log-regression through scales.
To understand the type of relation existing between the singularity exponent h (x) at the point x and the local behavior of a multifractal measure μ satisfying the assumption (A.9), let us consider first the case where s is differentiable and possesses a well-defined gradient ∇s. At scale r0 = 2−n, supposed to be small enough, we have
![\[ \| \nabla s \| ({\bm x}) \sim {\bm r}_{0}^2\,\mu({\cal B}({\bm x}, 2^{1-n})) \sim \displaystyle A({\bm x}) \left(\frac{1}{2^n} \right)^{{\bm h}({\bm x}) + 2}\,{=}\,A({\bm x}) {\bm r}_0^{{\bm h}(\bf x) + 2}. \]](/articles/aa/full_html/2021/05/aa39874-20/aa39874-20-eq141.png)
By translational invariance, the ensemble average 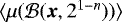 is a constant, denoted C. From this we obtain, after a short calculation,
is a constant, denoted C. From this we obtain, after a short calculation,
![\[ {\bm h}({\bm x}) + 2\,{=}\,\displaystyle \frac{\textrm{log} (\| \nabla s \| ({\bm x})/\langle \| \nabla s \| \rangle)}{\textrm{log} {\bm r}_{0}} - \frac{1}{\textrm{log} {\bm r}_{0}} \textrm{log} \left(\frac{A({\bm x})}{C} \right). \]](/articles/aa/full_html/2021/05/aa39874-20/aa39874-20-eq143.png)
It results that the quantity 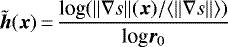 is a valuable estimate of the singularity exponent at x as long as r0 is small enough to make the variations of
is a valuable estimate of the singularity exponent at x as long as r0 is small enough to make the variations of 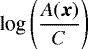 negligible. We then have
negligible. We then have 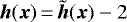 .
.
 |
Fig. B.1 Neighborhood system |
When the signal s of the observation map is arbitrary (not supposed differentiable), and r0 = 2−n is as before the at lowest scale, the singularity exponent h(x) is derived by a similar formula from the quantity,
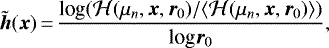 (B.5)
(B.5)
but now with 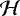 being a function of the input measure μn, which makes uses of local information around point x at scale r0. The term
being a function of the input measure μn, which makes uses of local information around point x at scale r0. The term  is the spatial average of
is the spatial average of  over the whole observational map, which lessens the relative amplitudes of the fluctuations of μn at scale r0. The function
over the whole observational map, which lessens the relative amplitudes of the fluctuations of μn at scale r0. The function  is defined as one of the simplest and most generic ways of measuring the local unpredictability: subtracting the signal value at a given point from the value inferred from its neighbor points. These values must be previously detrended to cancel any global offset influence. The result
is defined as one of the simplest and most generic ways of measuring the local unpredictability: subtracting the signal value at a given point from the value inferred from its neighbor points. These values must be previously detrended to cancel any global offset influence. The result 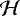 then measures local correlation. We now describe how
then measures local correlation. We now describe how  is computed.
is computed.
We consider a point x at which we compute h(x) and local neighborhood information around x at scale r0 = 2−n,  (see Fig. B.1).
(see Fig. B.1).
The vector (s(x), s(x1), s(x2), s(x3), s(x4)) is first properly detrended by considering the trend 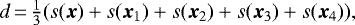 and generating from it the detrended vector (s(x) + d, s(x1) − d, s(x2) − d, s(x3) − d, s(x4) − d). Let us denote this detrended vector (p0(x), p1(x), p2(x), p3(x), p4(x)). We define
and generating from it the detrended vector (s(x) + d, s(x1) − d, s(x2) − d, s(x3) − d, s(x4) − d). Let us denote this detrended vector (p0(x), p1(x), p2(x), p3(x), p4(x)). We define
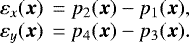 (B.6)
(B.6)
We note that the values of εx(x) and εy(x) are related to the cross neighboring sets  and
and  shown in red and green in Fig. B.1. The local correlation measure is then defined as
shown in red and green in Fig. B.1. The local correlation measure is then defined as
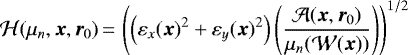 (B.7)
(B.7)
The value h(x) is then computed with Eq. (B.5) as 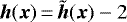 . Once the singularity exponents are determined, they define the collection of sets
. Once the singularity exponents are determined, they define the collection of sets 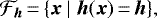 which are of particular importance in the description of a turbulent system (Frisch 1995). In Turiel et al. (2008) an argument for the case of log-Poisson processes is derived, which generalizes the work presented in She & Leveque (1994), and which describes the multiplicative cascade from the geometrical organization of the level-sets
which are of particular importance in the description of a turbulent system (Frisch 1995). In Turiel et al. (2008) an argument for the case of log-Poisson processes is derived, which generalizes the work presented in She & Leveque (1994), and which describes the multiplicative cascade from the geometrical organization of the level-sets  defined by the local singularity exponents. However a general justification valid for a large class of physical processes has not yet been realized.
defined by the local singularity exponents. However a general justification valid for a large class of physical processes has not yet been realized.
Algorithm for the computation of the singularity spectrum
Equation (A.11) shows that the singularity spectrum h ↦ D(h) is related to the logarithm of the histogram ρn(h), but in practical computation, we must determine the value cn which appears in Eq. (A.11). At this point, we make the physical observation that there exists, in all physical signals, a value h0 of the singularity exponents such that the corresponding set  has the dimension of the observational map (i.e., such that D(h0) = 2). Then, from (A.11) we obtain that
has the dimension of the observational map (i.e., such that D(h0) = 2). Then, from (A.11) we obtain that  . Since D(h) is always ≤ 2 by definition, the value h0 must correspond to the most probable singularity exponent, which is the one corresponding to the maximum of ρn (h) (or equivalently, corresponding to the maximum of
. Since D(h) is always ≤ 2 by definition, the value h0 must correspond to the most probable singularity exponent, which is the one corresponding to the maximum of ρn (h) (or equivalently, corresponding to the maximum of 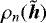 ). Then from Eq. (A.11), we get
). Then from Eq. (A.11), we get
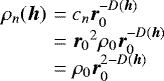 (B.8)
(B.8)
This leads to Algorithm 1 for the computation of the singularity spectrum.

Appendix C Cumulant analysis method
In this appendix we go back to the canonical description of multifractality, considering an advanced and powerful computational approach based on cumulants, which was introduced in Delour et al. (2001). It is used in this work as it provides a criterion for determining the existence of a multiplicative cascade (Arneodo et al. 1998a, 1999b) and the existence of long-range correlations. The reader is referred to Venugopal et al. (2006a) for a detailed and accurate description. If μ is a probability measure on the line, its characteristic function is 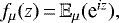 which can be expanded in a power series involving μ’s moments Mn:
which can be expanded in a power series involving μ’s moments Mn: 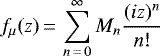 with Mn = ∫ xndμ(x). The cumulant generating function of μ, gμ (z), is the log of μ’s characteristic function: gμ(z) = logfμ(z). Since M0 = 1,
with Mn = ∫ xndμ(x). The cumulant generating function of μ, gμ (z), is the log of μ’s characteristic function: gμ(z) = logfμ(z). Since M0 = 1, 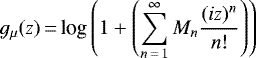 , which can in turn be expanded into a power series
, which can in turn be expanded into a power series 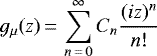 ; the Cn are called the cumulants of μ. The first cumulants are given by the relations
; the Cn are called the cumulants of μ. The first cumulants are given by the relations
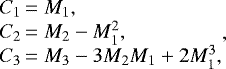 (C.1)
(C.1)
and the general recurrence relation is
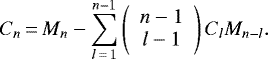 (C.2)
(C.2)
The most interesting part of the theory is the relation between the Cn and the multifractal spectrum when μ is a multifractal measure. We present the main results here.
As in Sect. 3, let s be a given signal, ψ an analyzing wavelet,  the wavelet-projected signal evaluated at position x and scale r, Z(q, r) a suitably chosen qth order partition function built out of
the wavelet-projected signal evaluated at position x and scale r, Z(q, r) a suitably chosen qth order partition function built out of  . Let us consider as the analyzing measure μ the one having density
. Let us consider as the analyzing measure μ the one having density 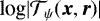 . Let Cn (r) be its cumulants. Then the evaluation of the slope of Cn(r) versus log(r) gives, when r → 0, coefficients
. Let Cn (r) be its cumulants. Then the evaluation of the slope of Cn(r) versus log(r) gives, when r → 0, coefficients
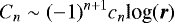 (C.3)
(C.3)
in such a way that τ(q) can be retrieved as τ(q) = −c0 + c1q − c2q2∕2! + c3q3∕3! + ⋯. For a 1D log-normal process, cn = 0 for n > 2 and we have
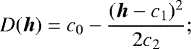 (C.4)
(C.4)
in other words, we get a parabolic spectrum as stated before, and comparing it with the previous general expression for the singularity spectrum of a log-normal process (Eq. (9) Sect. 3), we find in this case: c0 = 1 (dimension of the support of the measure), c1 = hm (average value of the singularity exponents), and 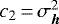 (variance).
(variance).
Appendix D Two-point magnitude statistical analysis and the multiplicative cascade
Using again the notation from the last section, we define the two-point correlation function for a given scale r and spatial interval Δx:
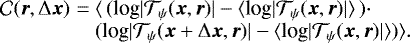 (D.1)
(D.1)
It is shown that if 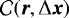 is logarithmic in Δx and independentof scale r provided Δx > r (i.e.,
is logarithmic in Δx and independentof scale r provided Δx > r (i.e., 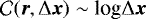 ) then a long-range dependence exists in the system (Arneodo et al. 1998a,b; Venugopal et al. 2006a). If there is a multiplicative cascade, then, in the case of a log-normal cascading process,
) then a long-range dependence exists in the system (Arneodo et al. 1998a,b; Venugopal et al. 2006a). If there is a multiplicative cascade, then, in the case of a log-normal cascading process,
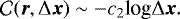 (D.2)
(D.2)
We note that some random processes can be self-similar without displaying a multiplicative cascade (Arneodo et al. 1999a,b; Venugopal et al. 2006a). This feature is often neglected in multifractal analysis of signals in astronomy, although it is of primary importance if we want to prove the existence of a multiplicative cascade in the ISM.
References
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, A102 [Google Scholar]
- André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, in Protostars and Planets VI, eds. H. Beuther, R. S. Klessen, C. P. Dullemond, & T. Henning, 27 [Google Scholar]
- Arneodo, A., Bacry, E., & Muzy, J. F. 1995, Physica A, 213, 232 [Google Scholar]
- Arneodo, A., Bacry, E., Manneville, S., & Muzy, J. F. 1998a, Phys. Rev. Lett., 80, 708 [CrossRef] [Google Scholar]
- Arneodo, A., Bacry, E., & Muzy, J. F. 1998b, J. Math. Phys., 39, 4142 [CrossRef] [MathSciNet] [Google Scholar]
- Arneodo, A., Manneville, S., Muzy, J., & Roux, S. 1999a, Philos. Trans. Roy. Soc. B: Biol. Sci., 357 [Google Scholar]
- Arneodo, A., Manneville, S., Muzy, J. F., & Roux, S. G. 1999b, Philosophical Transactions: Mathematical, Phys. Eng. Sci., 357, 2415 [Google Scholar]
- Arzoumanian, D., André, P., Könyves, V., et al. 2019, A&A, 621, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Aurell, E., Boffetta, G., Crisanti, A., Paladin, G., & Vulpiani, A. 1997, J. Phys. A: Math. Gen., 30, 1 [Google Scholar]
- Bacry, E., Muzy, J. F., & Arnéodo, A. 1993, J. Stat. Phys., 70, 635 [CrossRef] [MathSciNet] [Google Scholar]
- Badri, H. 2015, PhD thesis, Université de Bordeaux, France [Google Scholar]
- Bensch, F., Panis, J.-F., Stutzki, J., Heithausen, A., & Falgarone, E. 2001, A&A, 365, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bonne, L., Bontemps, S., Schneider, N., et al. 2020a, A&A, 644, A27 [EDP Sciences] [Google Scholar]
- Bonne, L., Schneider, N., Bontemps, S., et al. 2020b, A&A, 641, A17 [CrossRef] [EDP Sciences] [Google Scholar]
- Bontemps, S., André, P., Könyves, V., et al. 2010, A&A, 518, A85 [Google Scholar]
- Brillinger, D. R. 1994, in Advanced Signal Processing: Algorithms, Architectures, and Implementations V, eds. F. T. Luk, 2296, International Society for Optics and Photonics (SPIE), 2, 18 [Google Scholar]
- Brunt, C. M., Federrath, C., & Price, D. J. 2010, MNRAS, 403, 1507 [NASA ADS] [CrossRef] [Google Scholar]
- Burkhart, B., Falceta-Gonçalves, D., Kowal, G., & Lazarian, A. 2009a, ApJ, 693, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Burkhart, B., Stanimirović, S., Lazarian, A., & Kowal, G. 2009b, ApJ, 708, 1204 [Google Scholar]
- Cadavid, A. C., Rivera, Y. J., Lawrence, J. K., et al. 2016, ApJ, 831, 186 [Google Scholar]
- Candès, E. J., Wakin, M. B., & Boyd, S. P. 2008, J. Fourier Anal. Applic., 14, 877 [Google Scholar]
- Castaing, B. 1996, J. Phys. II France, 6, 105 [CrossRef] [EDP Sciences] [Google Scholar]
- Chappell, D., & Scalo, J. 2001, ApJ, 551, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Chhabra, A. B., Meneveau, C., Jensen, R. V., & Sreenivasan, K. R. 1989, Phys. Rev. A, 40, 5284 [CrossRef] [PubMed] [Google Scholar]
- Ciuciu, P., Abry, P., Rabrait, C., & Wendt, H. 2008, IEEE J. Sel. Top. Signal Process., 2, 929 [Google Scholar]
- Cox, N. L. J., Arzoumanian, D., André, P., et al. 2016, A&A, 590, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De La Fuente Marcos, R., & De La Fuente Marcos, C. 2006, MNRAS, 372, 279 [Google Scholar]
- Delour, J., Muzy, J. F., & Arneodo, A. 2001, Eur. Phys. J. B: Condensed Matter Complex Syst., 23, 243 [Google Scholar]
- Dib, S., & Burkert, A. 2005, ApJ, 630, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., Kim, J., Vazquez-Semadeni, E., Burkert, A., & Shadmehri, M. 2007, ApJ, 661, 262 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., Brandenburg, A., Kim, J., Gopinathan, M., & André, P. 2008, ApJ, 678, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Dib, S., Bontemps, S., Schneider, N., et al. 2020, The Structure and Characteristic Scales of Molecular Clouds [Google Scholar]
- Dieudonné, J. 1969, Foundations of Modern Analysis (Academic Press) [Google Scholar]
- Eghdami, I., Panahi, H., & Movahed, S. M. S. 2018, ApJ, 864, 162 [Google Scholar]
- Elia, D., Strafella, F., Schneider, N., et al. 2014, ApJ, 788, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Elia, D., Strafella, F., Dib, S., et al. 2018, MNRAS, 481, 509 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G. 2000, ApJ, 530, 277 [Google Scholar]
- Elmegreen, B. G., & Scalo, J. 2004, ARA&A, 42, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Falconer, K. 1997, Techniques in Fractal Geometry (John Wiley & Sons) [Google Scholar]
- Falgarone, E., Panis, J.-F., Heithausen, A., et al. 1998, A&A, 331, 669 [NASA ADS] [Google Scholar]
- Falgarone, E., Pety, J., & Hily-Blant, P. 2009, A&A, 507, 355 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frisch, U. 1995, Turbulence: The Legacy of A. N. (Kolmogorov: Cambridge University Press) [Google Scholar]
- Fyodorov, Y. V. 2010, Physica A, 389, 4229 [CrossRef] [Google Scholar]
- Fyodorov, Y. V., Le Doussal, P., & Rosso, A. 2012, J. Stat. Phys., 149, 898 [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaite, J. 2007, ApJ, 658, 11 [Google Scholar]
- Gaite, J., & Domínguez, A. 2007, J. Phys. A: Math. Theor., 40, 6849 [Google Scholar]
- Geman, D., & Chengda Yang. 1995, IEEE Trans. Image Process., 4, 932 [NASA ADS] [CrossRef] [Google Scholar]
- Gledzer, E., Villermaux, E., Kahalerras, H., & Gagne, Y. 1996, Phys. Fluids, 8, 3367 [Google Scholar]
- Grahovac, D. 2020, Chaos, Solitons Fractals, 134, 109735 [Google Scholar]
- Green, D. A. 1993, MNRAS, 262, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Hacar, A., Kainulainen, J., Tafalla, M., Beuther, H., & Alves, J. 2016, A&A, 587, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L. 2002, ApJ, 578, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Heitsch, F., Burkert, A., Hartmann, L. W., Slyz, A. D., & Devriendt, J. E. G. 2005, ApJ, 633, L113 [NASA ADS] [CrossRef] [Google Scholar]
- Heneghan, C., Lowen, S. B., & Teich, M. C. 1996, in Proceeding of Southwest Symposium on Image Analysis and Interpretation, 213 [Google Scholar]
- Hopkins, P. F. 2013, MNRAS, 430, 1880 [NASA ADS] [CrossRef] [Google Scholar]
- Hosokawa, I. 1997, Proc. Roy. Soc. London A: Math. Phys. Eng. Sci., 453, 691 [Google Scholar]
- Hull, C. L. H., Mocz, P., Burkhart, B., et al. 2017, ApJ, 842, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Juvela, M., Ristorcelli, I., Pagani, L., et al. 2012, A&A, 541, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Hacar, A., Alves, J., et al. 2016, A&A, 586, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kantelhardt, J. W., Zschiegner, S. A., Koscielny-Bunde, E., et al. 2002, Physica A, 316, 87 [Google Scholar]
- Kestener, P., Conlon, P. A., Khalil, A., et al. 2010, ApJ, 717, 995 [NASA ADS] [CrossRef] [Google Scholar]
- Khalil, A., Joncas, G., Nekka, F., Kestener, P., & Arneodo, A. 2006, ApJS, 165, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, J., Ryu, D., Jones, T. W., & Hong, S. S. 1999, ApJ, 514, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., & Hennebelle, P. 2010, A&A, 520, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kolmogorov, A. N. 1941, Proc.: Math. Phys. Sci., 434, 9 [Google Scholar]
- Kolmogorov, A. N. 1962, J. Fluid Mech., 13, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Könyves, V., André, P., Men’shchikov, A., et al. 2015, A&A, 584, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kowal, G., Lazarian, A., & Beresnyak, A. 2007, ApJ, 658, 423 [NASA ADS] [CrossRef] [Google Scholar]
- Koyama, H., & Inutsuka, S.-I. 2000, ApJ, 532, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Kritsuk, A. G., Ustyugov, S. D., & Norman, M. L. 2017, New J. Phys., 19, 065003 [CrossRef] [Google Scholar]
- Krumholz, M. R. 2014, Phys. Rep., 539, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Krumholz, M. R., & McKee, C. F. 2005, ApJ, 630, 250 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., & Alves, J. F. 2010, ApJ, 724, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, K. H., & Lee, L. C. 2019, Nat. Astron., 3, 154 [Google Scholar]
- Leonarduzzi, R., Touchette, H., Wendt, H., Abry, P., & Jaffard, S. 2016, in 2016 IEEE Statistical Signal Processing Workshop (SSP), 1 [Google Scholar]
- Macek, W. M., Wawrzaszek, A., & Burlaga, L. F. 2014, ApJ, 793, L30 [Google Scholar]
- Machaieie, D. A., Vilas-Boas, J. W., Wuensche, C. A., et al. 2017, ApJ, 836, 19 [CrossRef] [Google Scholar]
- Mac Low, M. M. 2000, in Stars, Gas and Dust in Galaxies: Exploring the Links, eds. D. Alloin, K. Olsen, & G. Galaz [Google Scholar]
- Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Mod. Phys., 76, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbrot, B. B., & Ness, J. W. V. 1968, SIAM Rev., 10, 422 [Google Scholar]
- Marsh, K. A., Kirk, J. M., André, P., et al. 2016, MNRAS, 459, 342 [Google Scholar]
- Maruyama, F., Kai, K., & Morimoto, H. 2017, Adv. Space Res., 60, 1363 [Google Scholar]
- McAteer, R. T. J., Young, C. A., Ireland, J., & Gallagher, P. T. 2007, ApJ, 662, 691 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, E. C. 2007, ARA&A, 45, 565 [Google Scholar]
- Meneveau, C.,& Sreenivasan, K. R. 1991, J. Fluid Mech., 224, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Miville-Deschênes, M. A., Martin, P. G., Abergel, A., et al. 2010, A&A, 518, L104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mocz, P., Burkhart, B., Hernquist, L., McKee, C. F., & Springel, V. 2017, ApJ, 838, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, A100 [Google Scholar]
- Motte, F., Bontemps, S., & Louvet, F. 2018, ARA&A, 56, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Mouschovias, T. C. 1976, ApJ, 206, 753 [NASA ADS] [CrossRef] [Google Scholar]
- Movahed, M. S., Jafari, G. R., Ghasemi, F., Rahvar, S., & Tabar, M. R. R. 2006, J. Stat. Mech.: Theory Exp., 2006, P02003 [Google Scholar]
- Muzy, J.-F. m. c. 2019, Phys. Rev. E, 99, 042113 [CrossRef] [Google Scholar]
- Muzy, J.-F. m. c., & Baïle, R. 2016, Phys. Rev. E, 93, 052305 [Google Scholar]
- Muzy, J. F., Bacry, E., & Arneodo, A. 1993, Phys. Rev. E, 47, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C. 2009, AJ, 700, 1609 [Google Scholar]
- Novikov, E. A. 1990, Phys. Fluids A: Fluid Dyn., 2, 814 [Google Scholar]
- Novikov, E. A. 1994, Phys. Rev. E, 50, R3303 [CrossRef] [Google Scholar]
- Ossenkopf, V., Krips, M., & Stutzki, J. 2008, A&A, 485, 917 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Padoan, P., Rosolowsky, E. W., & Goodman, A. A. 2001, ApJ, 547, 862 [Google Scholar]
- Padoan, P., Goodman, A. A., & Juvela, M. 2003, ApJ, 588, 881 [NASA ADS] [CrossRef] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pont, O., Turiel, A., & Pérez-Vicente, C. J. 2006, Phys. Rev. E, 74, 061110 [Google Scholar]
- Pont, O., Turiel, A., & Yahia, H. 2013, Int. J. Comput. Math., 90, 1693 [Google Scholar]
- Rayner, T., Griffin, M., Schneider, N., et al. 2017, VizieR Online Data Catalog: J/A+A/607/A22. [Google Scholar]
- Renosh, P. R., Schmitt, F. G., & Loisel, H. 2015, PLOS ONE, 10, 1 [CrossRef] [Google Scholar]
- Robitaille, J.-F., Motte, F., Schneider, N., Elia, D., & Bontemps, S. 2019, A&A, 628, A33 [CrossRef] [EDP Sciences] [Google Scholar]
- Robitaille, J.-F., Abdeldayem, A., Joncour, I., et al. 2020, A&A, 641, A138 [CrossRef] [EDP Sciences] [Google Scholar]
- Roy, A., André, P., Arzoumanian, D., et al. 2015, A&A, 584, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roy, A., André, P., Arzoumanian, D., et al. 2019, A&A, 626, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Salat, H., Murcio, R., & Arcaute, E. 2017, Physica A, 473, 467 [Google Scholar]
- Salem, C., Mangeney, A., Bale, S. D., & Veltri, P. 2009, ApJ, 702, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Sanchez, N., Alfaro, E. J., & Perez, E. 2006, ApJ, 641, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Scalo, J. M. 1987, Interstellar Processes, 134, 349 [Google Scholar]
- Schisano, E., Rygl, K. L. J., Molinari, S., et al. 2014, ApJ, 791, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, U., & Roth, S. 2014, in 2014 IEEE Conference on Computer Vision and Pattern Recognition, 2774 [Google Scholar]
- Schmitt, F. G., & Huang, Y. 2016, Stochastic Analysis of Scaling Time Series: From Turbulence Theory to Applications (Cambridge University Press) [Google Scholar]
- Schneider, N., Csengeri, T., Bontemps, S., et al. 2010, A&A, 520, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Bontemps, S., Simon, R., et al. 2011, A&A, 529, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Csengeri, T., Hennemann, M., et al. 2012, A&A, 540, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Seifried, D., & Walch, S. 2015, MNRAS, 452, 2410 [NASA ADS] [CrossRef] [Google Scholar]
- Serrano, E., & Figliola, A. 2009, Physica A, 388, 2793 [CrossRef] [Google Scholar]
- She, Z.-S., & Leveque, E. 1994, Phys. Rev. Lett., 72, 336 [Google Scholar]
- She, Z.-S., Jackson, E., & Orszag, S. 1990, Nature, 344, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Shimajiri, Y., André, P., Braine, J., et al. 2017, A&A, 604, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shivamoggi, B. K. 2015, Phys. Lett. A, 379, 1887 [Google Scholar]
- Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23 [Google Scholar]
- Stone, J. M., Ostriker, E. C., & Gammie, C. F. 1998, ApJ, 508, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Stutzki, J., Bensch, F., Heithausen, A., Ossenkopf, V., & Zielinsky, M. 1998, A&A, 336, 697 [NASA ADS] [Google Scholar]
- Sun, K., Kramer, C., Ossenkopf, V., et al. 2006, A&A, 451, 539 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tielens, A. G. G. M. 2005, The Physics and Chemistry of the Interstellar Medium (Cambridge University Press) [CrossRef] [Google Scholar]
- Tritsis, A., & Tassis, K. 2016, MNRAS, 462, 3602 [CrossRef] [Google Scholar]
- Tritsis, A., & Tassis, K. 2018, Science, 360, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Truelove, J. K., Klein, R. I., McKee, C. F., et al. 1998, ApJ, 495, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Turiel, A., Pérez-Vicente, C. J., & Grazzini, J. 2006, J. Comput. Phys., 216, 362 [Google Scholar]
- Turiel, A., Yahia, H., & Perez-Vicente, C. J. 2008, J. Phys. A: Math. Theor., 41, 015501 [Google Scholar]
- Vazquez-Semadeni, E. 1994, ApJ, 423, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Venugopal, V., Roux, S. G., Foufoula-Georgiou, E., & Arnéodo, A. 2006a, Water Resour. Res., 42, W06D14 [Google Scholar]
- Venugopal, V., Roux, S. G., Foufoula-Georgiou, E., & Arnéodo, A. 2006b, Phys. Lett. A, 348, 335 [Google Scholar]
- Wendt, H., Roux, S. G., & Abry, P. 2006, in 14th European Signal Processing Conference (EUSIPCO), Université de Pise. (Florence, Italy: European Association for Signal Processing (EURASIP)) [Google Scholar]
- Wu, N., Li, Q.-X., & Zou, P. 2015, New Astron., 38, 1 [Google Scholar]
- Yaglom, A. M. 1966, Sov. Phys. Dokl., 11, 26 [Google Scholar]
Throughout the article, the term “support” is applied to various types of objects. For a function or an observational map, the support is the domain (continuous or discrete) on which the function or the observational map is defined, while the support of a positive measure denotes the set of points x such that any open neighborhood containing x has a strictly positive measure.
All Tables
All Figures
 |
Fig. 1 Musca flux density map from Herschel at 250 μm. The filamentary structure with a high aspect ratio is obvious. Perpendicular to the main ridge of emission are fainter hair-like structures (called striations in Cox et al. 2016) that are mostly attached to the main filament. |
| In the text | |
 |
Fig. 2 Singularity spectra of log-normal and log -Poisson stochastic processes. Left: general form of the singularity spectrum D(h), Legendre transform of ξ(q). See text for a definition of D(h), ξ(q), and |
| In the text | |
 |
Fig. 3 Increasing sequence of lattice nets Ω0 ⊂ Ω1 ⊂⋯ ⊂ Ωn ⊂⋯ inside the unit square. |
| In the text | |
 |
Fig. 4 Discrete neighborhood sets |
| In the text | |
 |
Fig. 5 Checking scale invariance: gradient modulus wavelet projection method, log-regression. Top row: visualization of the singularity exponents computed through log-regression using a Lorentz wavelet of order 3 on the Musca 250 μm Herschel flux map presented in Sect. 2. The singularity exponents are computed with the gradient modulus wavelet projection method algorithm. The two upper images correspond to two consecutive downscaled wavelet projections of the original signal using a discrete wavelet projection. Bottom: resulting mappings h ↦ D(h) using the singularity exponents computed on the two consecutive scales (red: one-half scale of the original Musca 250 μm Herschel flux map; green: one-fourth scale of the original Musca 250 μm Herschel flux map). Inside the domain corresponding to h ≤ 0 the two mappings do not coincide. Consequently, the log-regression method for computing the singularity exponents provide poor result in this case. |
| In the text | |
 |
Fig. 6 Checking scale invariance: local correlation measure. Top left and right: visualization of the singularity exponents computed with the local correlation measure described in Eqs. (B.7) and (B.5), respectively, on the Musca 250 μm Herschel flux map presented in Sect. 2. The two images correspond to two consecutive downscaled wavelet projections of the original signal using a discrete wavelet projection. Bottom: resulting mappings h ↦ D(h) using the singularity exponents computed on the two consecutive scales (red: one-half scale of the original Musca Herschel map; green: one-fourth scale of the original Musca Herschel map). The two mappings coincide much better than with the exponents computed from log -regression and displayed in Fig. 5. Consequently, the local correlation measure algorithm exhibits the scaling in a much betterway. |
| In the text | |
 |
Fig. 7 Map of the singularity exponents computed on filtered Musca 250 μm data. The image is a magnification of the singularity map over the central part of the Musca observation map to better show how the singularity exponents reflect the complex distribution of filamentary coherent structures. |
| In the text | |
 |
Fig. 8 Visualization of the filtering (computed with λ = 0.7) zoomed in on the central part of the Musca 250 μm map. The level was chosen to emphasize low values. The left panel shows the filtered data and the right the unfiltered data. The positive effect of the filtering on the flux density data becomes obvious. The visualization performed on the singularity exponents (see Fig. 9) demonstrates the importance of filtering on filamentary structures, which are oflow fractal dimensions. |
| In the text | |
 |
Fig. 9 Illustration of background noise reduction and enhancement of the filamentary structures in the Musca 250 μm map by edge-aware nonlinear filtering while promoting a signal’s gradient sparsity with L1 norm. The images show the singularity exponents of a region in Musca that is rich in filamentary structures. The right panel displays the singularity exponents derived from the unfiltered original map, while the left panel shows the singularity exponents after filtering the map with λ = 0.7 (Eq. (1)). The same grayscale wedge is used for both images. |
| In the text | |
 |
Fig. 10 Visualization of noise reduction by the edge-aware noise filtering. The data displayed are s − sf in the same area as shown in Fig. 9. |
| In the text | |
 |
Fig. 11 Singularity spectrum of the Musca 250 μm Herschel map, computed with and without edge-aware filtering. The orange curve shows the singularity spectrum computed on raw unfiltered data, while the blue curve displays the singularity spectrum computed on edge-aware filtered data using the filtering introduced in Sect. 5.2 with parameter
λ = 0.7. The horizontal axis gives the h-values of the scaling exponents, and the vertical axis gives the fractal dimension
|
| In the text | |
 |
Fig. 12 Mappings h↦D(h) computed for two consecutive scales of the unfiltered Musca 250 μm Herschel observational map using a reverse bi-orthogonal discrete wavelet transform of order 4.4. The graphs show that the presenceof the noise alters the scaling of the measure. |
| In the text | |
 |
Fig. 13 Plot of ζ(q) for the Musca 250 μm Herschel observational map with filtering (λ = 0.7, curve in red)and without filtering (curve in green); the mapping q↦ζ(q) is defined by the structure function method (Eq. (25)). This graph shows that the background noise does affect the statistics of scaling. |
| In the text | |
 |
Fig. 14 Singularity spectrum of the Musca Herschel 250 μm map with error bars as defined by Eq. (24); the observational map is edge-aware filtered with a tuning parameter λ = 0.7. |
| In the text | |
 |
Fig. 15 Result of the 2D structure function method for the determination of an inertial range of spatial scales. Computations are done on the Musca 250 μm map filtered data with λ = 0.7 (Eq. (22)). A total of 5 × 108 couples of points (x1, x2) are chosen uniformly in the spatial domain; moments q are between 0.1 and 5, with increment steps of 0.1 (for clarity, only some of the moments are shown). The left panel shows the graph of a log −log plot (Eq. (25)), with colors indicating some moment values, q. The image also shows the graphs of linear regression fits (dotted lines), performed in an inertial range covering the interval [13, 160] pixels, corresponding to the range of distance [0.053, 0.65] pc. The middle panel displays the resulting map q↦ζ(q). The two panels on the right show the quality of the linear regression: the sse and the r correlation coefficient. Hence, the quality of the fit decreases with the moment order q. |
| In the text | |
 |
Fig. 16 Result of the 2D structure function method, applied over one of the MHD simulation outputs presented in Sect. 6, for the determination of an inertial range of spatial scales. A total of 5 × 108 couples of points (x1, x2) are chosen uniformly in the spatial domain; the moments q have values between 0.1 and 5, with increment steps of 0.1 (for clarity, only a few of the moments are shown). The first panel shows the graphs of the log − log plot (Eq. (25), with colors indicating some moment values, q). As in Fig. 15, the graphs show linear regression fits (dotted lines) performed in an inertial range covering the interval of distance [0.18, 1.5] pc. The second panel displays the map q↦ζ(q). The third and fourth panels show the quality of linear regression: sse and the r correlation coefficient. |
| In the text | |
 |
Fig. 17 Multifractal analysis of MHD data. Left panel: one snapshot of the column density output of the MHD simulation data used in this work, integrated along one axis of the cube. The output shown here corresponds to the hydrodynamical case with no magnetic field at time t = 0.422 tc. Middle panel: map of the singularity exponents. Right panel: singularity spectrum with its error bars computed using Eq. (24). |
| In the text | |
 |
Fig. 18 Log-normal fit of the singularity spectrum for the data corresponding to time t = 0.62tc Myr after gravityis turned on. Shown is the singularity spectrum computed in the microcanonical framework (orange) and a fitted quadratic log-normal singularity spectrum (blue). The fit is very good, which indicates a good approximation by a log -normal process. |
| In the text | |
 |
Fig. 19 Results of a log-normal fit for the singularity spectrum of the full Musca 250 μm map (also called PSW), edge-aware filtered (top image, λ = 0.7), and unfiltered (bottom image). In each image, the singularity spectrum h↦D(h) is shown in orange, and the log-normal parabola in blue. The values obtained for the coefficients of the fit (Eq. (9)) are given in each case. The differences between the two fits shows the importance of the edge-aware filtering for multifractal analysis of astronomical observational maps. It appears that the background noise “log -normalizes” the data, while the filtered version, which takes fine filamentary structures into account better, deviates from log -normality. We note in the filtered version the change in the orange curve around h = −0.2. This is an indication that different types of turbulent processes are present in the Musca cloud, in particular those processes inside the main filament and the surrounding cloud. |
| In the text | |
 |
Fig. 20 CWT analysis performed on a 1D signal extracted from the Musca 250 μm map. Left panel: Musca 250 μm map in which the white column defines a 1D signal. Right panel: original 1D signal (centered and rescaled) and CWT projections of the selected 1D signal with the Mexican hat wavelet at scales 5 (red) and 60 (blue). |
| In the text | |
 |
Fig. 21 Plots of the log-correlations
|
| In the text | |
 |
Fig. 22 Definition of areas. In the left panel, the statistics of the log-correlations are differentfrom those of the other parts of Musca in the rectangular area shown in the picture. In the right panel, a definition of six ROIs inside the Musca ISM are shown. |
| In the text | |
 |
Fig. 23 log-normal and log -Poisson fitting of Musca singularity spectrum. Left: singularity spectrum of the filtered (λ = 0.7) Musca 250 μm observational map (in orange) fitted against a log-normal parabolic spectrum (blue) defined by Eq. (9). The fit is performed using the quasi-Newton minimization algorithm implementation available in Matlab. Right: singularity spectrum of the filtered (λ = 0.7) Musca 250 μm observational map (in orange) fitted against a log-Poisson singularity spectrum (blue) defined by Eq. (10). The minimization algorithm is the same. Both images display the values found by the minimization algorithm and the error fit. |
| In the text | |
 |
Fig. 24 Singularity spectrum and log-normal fit for each ROI. Shown for each region of interest in the Musca cloud delimited in Fig. 22 are the singularity spectrum h↦D(h) of an ROI (in orange), a log-normal fitted approximation singularity spectrum (in blue; Eq. (9)), the obtained numerical values hm and σh, and the error of the fit. The various values of hm and σh for each ROI are also given in Table 1. |
| In the text | |
 |
Fig. 25 Variation in time of the fitted σh of the log-normal singularity spectrum (Eq. (9)) for the simulation outputs described in Sect. 6. The value of the magnetic pressure β = 0.1. |
| In the text | |
 |
Fig. 26 Distribution of the singularity exponents in ROI1 (left) and in the southern region of Musca ROI5 (right). Both regions show complex linear structures, but of different sizes and organizations. |
| In the text | |
 |
Fig. B.1 Neighborhood system |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



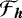
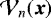
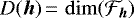
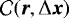
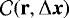
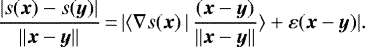

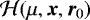
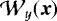
![\[ {\cal A}({\bm x}, {\bm r}_0)\,{=}\,\displaystyle \left | \varepsilon_x({\bm x}) \left (\sum_{{\bm y} \in {\cal W}({\bm x})} \varepsilon_x({\bm y}) \right) + \varepsilon_y({\bm x}) \left (\sum_{{\bm y} \in {\cal W}({\bm x})} \varepsilon_y({\bm y}) \right)\right |. \]](/articles/aa/full_html/2021/05/aa39874-20/aa39874-20-eq160.png)