| Issue |
A&A
Volume 649, May 2021
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202039704 | |
| Published online | 06 May 2021 | |
Kiloparsec view of a typical star-forming galaxy when the Universe was ∼1 Gyr old
I. Properties of outflow, halo, and interstellar medium⋆
1
Departamento de Astronomía, Universidad de Concepción, Barrio Universitario, Concepción, Chile
e-mail: rhc@astro-udec.cl
2
Max-Planck-Institut für Extraterrestische Physik (MPE), Giessenbachstr., 85748 Garching, Germany
3
Department of Astronomy, University of Maryland, College Park, MD 20742, USA
4
Centre for Astrophysics and Supercomputing, Swinburne Univ. of Technology, PO Box 218, Hawthorn, VIC 3122, Australia
5
ARC Centre of Excellence for All Sky Astrophysics in 3 Dimensions (ASTRO 3D), Australia
6
Max-Planck Institute for Astrophysics, Karl Schwarzschildstrasse 1, 85748 Garching, Germany
7
National Astronomical Observatory of Japan, 2-21-1 Osawa, Mitaka, Tokyo 181-8588, Japan
Received:
16
October
2020
Accepted:
4
January
2021
We present new Atacama Large Millimeter/Submillimeter Array observations of the [C II] 158 μm transition and the dust continuum in HZ4, a typical star-forming galaxy when the Universe was only ∼1 Gyr old (z ≈ 5.5). Our high ≈0.3″ spatial resolution allows us to study the relationships between [C II] line emission, star formation rate, and far-infrared emission on spatial scales of ∼2 kpc. In the central ∼4 kpc of HZ4, the [C II]/FIR is ∼3 × 10−3 on global scales as well as on spatially resolved scales of ∼2 kpc, comparable to the ratio observed in local moderate starburst galaxies such as M 82 or M 83. For the first time in an individual normal galaxy at this redshift, we find evidence for outflowing gas from the central star-forming region in the direction of the minor axis of the galaxy. The projected velocity of the outflow is ∼400 km s−1, and the neutral gas-mass outflow rate is ∼3 − 6 times higher than the star formation rate in the central region. Finally, we detect a diffuse component of [C II] emission, or [C II] halo, that extends beyond the star-forming disk and has a diameter of ∼12 kpc. The outflow, which has a velocity approximately half of the escape velocity of the system, most likely partly fuels the [C II] extended emission. Together with the kinematic analysis of HZ4 (presented in a forthcoming paper), the analysis supports the hypothesis that HZ4 is a typical star-forming disk at z ∼ 5 with interstellar medium conditions similar to present-day galaxies forming stars at a similar level, driving a galactic outflow that may already play a role in its evolution.
Key words: galaxies: high-redshift / galaxies: ISM / galaxies: structure
The reduced images and datacubes are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/649/A31
© ESO 2021
1. Introduction
The complex interplay between star formation, stellar feedback, and accretion from the circumgalactic medium (CGM), known as the baryon cycle, drives galaxy growth and evolution (e.g., Tumlinson et al. 2017). Understanding these competing processes requires observations of the stars and multiple phases of the gas throughout cosmic time. Here, the Atacama Large Millimeter/submillimeter Array (ALMA) has opened a window for exploring the cold neutral and molecular gas in early galaxies at an unprecedented level of detail.
This paper focuses on the study of a typical galaxy at z ≈ 5.5, when the Universe was only ∼1 billion years old. Observations of the cold gas based on CO lines for normal galaxies at this redshift are challenging (e.g., Pavesi et al. 2019; Neeleman et al. 2020). A powerful alternative tracer is the [C II] 157.74 μm fine-structure transition, which mostly traces the cold, neutral gas with a minor contribution from the ionized phase (e.g., Croxall et al. 2017; Díaz-Santos et al. 2017; Cormier et al. 2019). The [C II] line is tightly connected to the star formation activity because the far-ultraviolet (FUV) photons produced in star-forming regions heat the gas through the photoelectric effect on dust grains, which then cools mainly through the [C II] transition (e.g., Wolfire et al. 1995; De Looze et al. 2014; Herrera-Camus et al. 2015; Schaerer et al. 2020). Thus, the comparison between tracers of the gas heating such as the star formation rate (SFR) or the far-infrared luminosity (FIR) and the [C II] line luminosity can help to constrain the heating-cooling balance in the interstellar medium (ISM).
Recent ALMA observations of main-sequence (MS) galaxies at z ∼ 4 − 5 have revealed different aspects of the baryon cycle in action in these systems. On the one hand, stacking of [C II] spectra reveals signatures of outflows with velocities of ∼500 km s−1, and global mass-outflow rates comparable to the SFRs of their hosts (Gallerani et al. 2018; Ginolfi et al. 2020a). At similar redshift, Sugahara et al. (2019) also detected neutral gas outflows with median velocities of ∼400 km s−1 from the analysis of the stacked spectra of metal-absorption lines. As simulations suggest (e.g., Pizzati et al. 2020), these outflows are most likely connected to the observed presence of a diffuse component of [C II] emission around galaxies. These [C II] halos extend for scales of ∼5 − 10 kpc beyond the extent of the star-forming disk that is traced by the rest-frame UV-optical emission, and can be considered part of the CGM (Fujimoto et al. 2019, 2020; Ginolfi et al. 2020a).
The results discussed above are based on observations of large sample of galaxies at 4 ≲ z ≲ 6 from the ALMA Large Program to Investigate C+ at Early Times (ALPINE; Le Fèvre et al. 2020), and the earlier work by Capak et al. (2015). The spatial resolution achieved by these programs was modest, typically ∼5 − 9 kpc (for reference, the median UV effective radius of z ∼ 5 galaxies is ∼1 kpc; e.g., Shibuya et al. 2015). To date, the majority of the [C II] observations of early galaxies that achieved kiloparsec-scale resolution (or better) targeted bright, submillimeter galaxies (e.g., De Breuck et al. 2014; Neri et al. 2014; Díaz-Santos et al. 2016; Gullberg et al. 2018; Litke et al. 2019; Tadaki et al. 2020). The few cases that focused on normal (i.e., main-sequence) galaxies include the discovery of a regular, rotating disk in a neutral H I absorber (Neeleman et al. 2020), a system with a complex kinematic structure that could be the result of a triple merger (Riechers et al. 2014), and two Lyman break galaxies at z ∼ 7 that show disk-like velocity gradients (Smit et al. 2018).
Although progress is being made in the study of main-sequence galaxies at z ∼ 5, we still lack a detailed characterization of their ISM, the detection of outflow signatures in individual galaxies, and a deeper understanding of the effect of outflows on the star formation activity, and the existence and maintenance of the [C II] halos. Motivated by these open issues, in this paper we present new [C II] and dust continuum ALMA observations of HZ4, a typical star-forming galaxy at z = 5.5. The spatial resolution and sensitivity achieved by our observations (see Sects. 2 and 3) allow us to study the ISM (Sect. 3.2), outflow (Sect. 3.3), and [C II] extended emission properties (Sect. 3.4) at a kiloparsec scale level. The analysis of the kinematic properties of HZ4 will be discussed in a forthcoming paper (Paper II; Herrera-Camus et al., in prep.). Throughout this paper, we adopt a cosmology with H0 = 67.4 km s−1 Mpc−1 and ΩM = 0.315 (Planck Collaboration VI 2020), which results in a scale of 6.09 kpc/″ for a source at z = 5.54.
2. Observations and data reduction
Between November 2018 and April 2019 (Cycle 6), HZ4 (RA 9:58:28.5, Dec +2:03:06.7) was observed for 8.4 h in total (4.7 h on-source) using ALMA as part of project 2018.1.01605.S (PI Herrera-Camus). The observations were carried out in the C43-4 configuration. We centered one spectral window on the [C II] line (νrest = 1900.537 GHz), which for the source is redshifted to νobs = 290.386 GHz and falls in Band 7. The remaining three spectral windows were used to detect the dust continuum at rest-frame 160 μm, near the peak of the FIR spectral energy distribution in star-forming galaxies. The quasar J1058+0133 was used as the flux and bandpass calibrator, and the quasar J0948+0022 was used as the phase calibrator.
The data were processed using the Common Astronomy Software Applications package (CASA; McMullin et al. 2007) version 5.6.2. The cubes were cleaned using the CASA/tclean task with Briggs weighting (robust = +0.5) and down to the 1σ level using the auto-multithresh automasking algorithm (Kepley et al. 2020). We also adopted the Multi-Scale Clean algorithm (Cornwell 2008) to image both structures, which are compact and unresolved as well as extended. The resulting synthesized beam size was θbeam = 0.39″ × 0.34″ (2.3 × 2.0 kpc) at a position angle of PA = −72.4°. The maximum recoverable scale is 3.26″1, which is larger than the angular scale of the [C II] emission structures detected in our observations (see Sect. 3.4). The rms noise for the line cube is 0.15 mJy beam−1 in 16 km s−1 channels, and 8.5 μJy beam−1 in the continuum maps. All maps were primary beam corrected.
3. Results
3.1. [C II] line and dust continuum emission in the main-sequence star-forming galaxy HZ4
HZ4 is a Lyman break selected galaxy in the COSMOS field (Koekemoer et al. 2007) with a [C II]-based spectroscopic redshift of z = 5.54 (Capak et al. 2015; Hasinger et al. 2018; Béthermin et al. 2020). As Fig. 1 (left panel) shows, with a stellar mass of log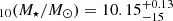 and a star formation rate of
and a star formation rate of 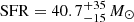 yr−1 (Faisst et al. 2020), HZ4 lies on the main sequence of star-forming galaxies at z ∼ 5 (e.g., Speagle et al. 2014). The gray circles show galaxies between 5 ≤ z ≤ 6 detected in [C II] line emission as part of the ALMA ALPINE Large Program (Le Fèvre et al. 2020; Béthermin et al. 2020). In contrast to our deep, high-resolution observation, ALPINE galaxies have typical on-source integration times of only t ∼ 15 − 25 min with angular resolution in the range θbeam ∼ 0.8 − 1.5″.
yr−1 (Faisst et al. 2020), HZ4 lies on the main sequence of star-forming galaxies at z ∼ 5 (e.g., Speagle et al. 2014). The gray circles show galaxies between 5 ≤ z ≤ 6 detected in [C II] line emission as part of the ALMA ALPINE Large Program (Le Fèvre et al. 2020; Béthermin et al. 2020). In contrast to our deep, high-resolution observation, ALPINE galaxies have typical on-source integration times of only t ∼ 15 − 25 min with angular resolution in the range θbeam ∼ 0.8 − 1.5″.
 |
Fig. 1. Left: star formation rate – stellar mass plane between 5 ≤ z ≤ 6 showing the position of the main sequence of star-forming galaxies (black line; Speagle et al. 2014) and the z ∼ 5 galaxies with [C II] detections in the ALPINE survey (gray circles; Le Fèvre et al. 2020; Faisst et al. 2020). HZ4, shown as an orange diamond, lies only ∼0.2 dex above the main sequence and can be considered a typical star-forming galaxy at this redshift (Faisst et al. 2020). Right: continuum-subtracted [C II] 158 μm spectrum of HZ4 extracted inside a circular aperture of 0.9″ radius (∼5.4 kpc). The best Gaussian fit is centered at an observed frequency of ν0 = 290.471 GHz, which corresponds to a redshift of z = 5.54. |
Figure 1 (right panel) shows the global [C II] spectrum of HZ4 extracted within a circular aperture of 0.9″ (∼5.4 kpc) radius centered at the peak of the [C II] emission (RA 09:58:28.5, Dec +02:03:06.6). The line is detected with a global signal-to-noise ratio of S/N ≈ 16. The best single-Gaussian fit is centered at an observed frequency of ν0 = 290.471 ± 2 × 10−3 GHz, which corresponds to a redshift of z = 5.543, consistent with previous measurements. The peak flux density and line width (full width at half maximum; FWHM) are 4.79 ± 0.22 mJy and 232 ± 8 km s−1, respectively. The total flux measured is S[CII] = 1.12 ± 0.07 Jy km s−1. This is similar to the flux measured by Capak et al. (2015) of S[CII] = 1.14 Jy km s−1 based on observations with an angular resolution of θbeam = 0.90″ × 0.48″, and about 20% higher than the total flux measured based on observations from the ALPINE survey (under the name DEIMOS_COSMOS_494057; Le Fèvre et al. 2020; Béthermin et al. 2020) with an angular resolution of θbeam = 1.01″ × 0.85″. Most likely due to the high S/N of our observations, we do not observe a lower [C II] global flux in our high angular resolution data as reported in other high-redshift galaxies, which is due to the effect of surface brightness dimming discussed by Carniani et al. (2020).
The left panel of Fig. 2 shows the [C II] line intensity map integrated in the velocity range between −300 and +300 km s−1, which corresponds to the orange region in the spectrum of Fig. 1. The galaxy morphology resembles an extended disk that looks slightly warped in the southwest region. A two-dimensional Gaussian fitting yields a deconvolved size (at FWHM) of 0.80″ × 0.47″ (±0.05″) (4.9 × 2.9 kpc) with the major axis at a PA of 17.7° ±5°.
 |
Fig. 2. Left: [C II] 158 μm integrated intensity of HZ4. The contours start at 2σ (dotted line) and then increase from 3σ to 17σ in steps of two (solid lines). The ALMA-synthesized beam (θ = 0.39″ × 0.34″) is shown in the bottom left corner. Center: dust continuum emission at rest-frame 160 μm. The contours level are 2 (dotted brown line), and 3, 3.5, and 4σ (solid brown lines). Right: contours of rest-frame UV emission as observed by HST WFC3 F160W (Barisic et al. 2017) overlaid on the [C II] integrated intensity map. The contour levels are 2 (dashed black line), 3, 5, 10, and 20σ (solid black lines). The contours are shifted in the direction of the black arrow from the original position marked by the black dot. The HST WFC3 F160W point-spread function is shown in black in the bottom left corner next to the ALMA beam in white. |
Together with the [C II] transition, we also detect the dust continuum of HZ4 at rest-frame 160 μm. The middle panel of Fig. 2 shows the integrated intensity map. The total dust continuum flux is Scont, 160 μm = 0.15 ± 0.03 mJy. The distribution of the dust emission is aligned with the morphological major axis of the [C II] line emission, but is significantly less extended in the direction of the minor axis, although this depends on the sensitivity of the observations. A two-dimensional Gaussian fitting yields a deconvolved size (at FWHM) of 0.93″ × 0.18″ (±0.20″) (5.6 × 1.1 kpc) with the major axis at a PA of 27.9° ±5°. In Sect. 3.2 we discuss that the differences in the spatial distribution of the dust and the [C II] line emission can shed light on the physical conditions of the gas, and in Sect. 3.4 we compare the light distribution from the [C II] and dust emission in more detail.
In the last panel of Fig. 2 we show the rest-frame UV emission observed with HST WFC3 (F160W; Barisic et al. 2017) overlaid on the [C II] line integrated emission. In principle, we expect the [C II] and UV emission to trace each other well as they correspond to important cooling and heating channels of the ISM (e.g., Wolfire et al. 2003). However, the original HST UV peak emission is centered at the position marked with a black dot, shifted with respect to the ALMA dust continuum and [C II] peak emission by ∼0.3″. Spatial offsets of this magnitude between Hα or UV and dust emission have been observed in z ∼ 2 − 3 submillimeter galaxies (SMGs; e.g., Hodge et al. 2016; Chen et al. 2017), and main-sequence galaxies at z ≳ 4 (e.g., Maiolino et al. 2015; Carniani et al. 2017; Ginolfi et al. 2020b). Fujimoto et al. (2020), for example, reported an average offset between the [C II] and UV emission of 23 ALPINE galaxies of ∼0.15″. The physical origin of these offsets could be related to dust obscuration or the ionization state of the gas (e.g., Katz et al. 2017), or to stellar feedback destroying molecular clouds around star-forming regions (Vallini et al. 2015).
Another possibility is that the ALMA and HST datasets show astromentric differences (e.g., Dunlop et al. 2017; Faisst et al. 2020). According to the Cycle 6 ALMA Technical Handbook (Eq. (10.7)), the astrometric precision of our ALMA observation is ∼0.01″. In the case of the HST observations of HZ4, the astrometric precision is at the subarcsecond level (Barisic et al. 2017). One alternative to confirm the precision of the HST astrometry is to compare the positions of stars in the HST field with those in the Gaia catalog (Gaia Collaboration 2016, 2018). We find a small offset of only 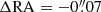 and
and 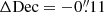 , which is not sufficient to explain the ∼0.3″ displacement between the [C II] and rest-frame UV disks. The reason for at least a 0.2″ (∼3 kpc) spatial offset therefore remains unclear at this point.
, which is not sufficient to explain the ∼0.3″ displacement between the [C II] and rest-frame UV disks. The reason for at least a 0.2″ (∼3 kpc) spatial offset therefore remains unclear at this point.
When we assume that the observed spatial offset between the HST and ALMA data is a problem of astrometric accuracy, we can use an alternative tracer of the stellar light to verify the position of the HST rest-frame UV map. For this we used a SUBARU/HSC i-band image (Aihara et al. 2019), which has an astrometric precision better than 0.1″. To match the peak emission in the HST and SUBARU data, we need to shift the former by ΔRA = −0.3″ and ΔDec = +0.05″. The shifted HST rest-frame UV contours are shown in the last panel of Fig. 2, and they agree far better with the spatial distribution of the ALMA [C II] and dust continuum data.
Together with the dust continuum emission in HZ4, we detect a strong continuum source in the northeast direction at a distance of ∼13″ from HZ4. This source has no apparent counterparts in the available HST/WFC3 images. We discuss the properties of this serendipitous source in Appendix A.
3.2. ISM properties: Relation of the [C II] line, the FIR continuum, and the SFR in HZ4
The ratio of the [C II] line to the FIR continuum is closely linked to the physical properties of the ISM in galaxies. A decrease in the [C II]/FIR can be driven by an increase in the ionization parameter of HII regions (e.g., Graciá-Carpio et al. 2011; Herrera-Camus et al. 2018b), the impact of active galactic nuclei (AGN) on the ionization state of the gas (e.g., Langer & Pineda 2015; Herrera-Camus et al. 2018b), and/or the increase in the ratio between the radiation field intensity and the neutral gas density, which leads to the destruction or charging of small dust grains (e.g., Kaufman et al. 1999; Malhotra et al. 2001; Díaz-Santos et al. 2017), among other factors. Typical [C II]/FIR ratios range from 0.1 − 1% in low-metallicity dwarfs and disks of star-forming galaxies (e.g., Cormier et al. 2015; Smith et al. 2017; Herrera-Camus et al. 2018a) to ∼0.01 − 0.1% in nuclear regions of starburst systems and AGNs (e.g., Malhotra et al. 2001; Díaz-Santos et al. 2013; Herrera-Camus et al. 2018a).
Figure 3 shows a map of the [C II]/FIR in HZ4. The FIR luminosity was calculated by fitting a modified single dust temperature graybody model to the rest-frame 160 μm continuum assuming a dust temperature of Tdust = 45 K and a dust emissivity index of β = 1.5. To the best of our knowledge, these assumptions seem appropriate for a typical star-forming galaxy at z ≈ 5 (e.g., Pavesi et al. 2016; Faisst et al. 2017).
 |
Fig. 3. Left: [C II]/FIR map of HZ4. We have considered only rest-frame ∼160 μm dust continuum emission above the 2σ level. The color bar indicates the [C II]/FIR value. Right: [C II]/FIR ratio as a function of ΣFIR in four kiloparsec-size regions extracted across the disk of HZ4 (orange circles and dashed black circles in the left panel). The error bars, mainly due to the uncertainty in the FIR luminosity, are shown in orange. For comparison, we show nearby star-forming and starburst galaxies from the SHINING sample (Herrera-Camus et al. 2018a), ∼100 pc scale regions in the central disk of M 82 in green (Contursi et al. 2013; Herrera-Camus et al. 2018a), and ∼400 pc scale regions in the central region of M 83 in purple. The solid gray line shows the best quadratic fit to the SHINING data (Herrera-Camus et al. 2018a). |
The right panel of Fig. 3 shows the [C II]/FIR measured along the major axis of HZ4 as a function of the FIR surface brightness. The error bars show the change in FIR luminosity when we vary our assumptions for the dust temperature and dust emissivity in the range 30 ≤ Tdust (K) ≤ 50 and 1 ≤ β ≤ 2. For comparison, we include the relatively tight (∼0.25 dex) relation observed in nearby star-forming galaxies and starbursts from the SHINING sample (Lutz et al. 2016; Herrera-Camus et al. 2018a). The four kiloparsec-scale regions in HZ4 follow this relation, with ΣFIR and [C II]/FIR ratios comparable to those observed in the central region of the starburst galaxy M 83 or the ∼700 pc disk around the nuclear region of M 82 (Contursi et al. 2013; Herrera-Camus et al. 2018a).
Interestingly, in the four apertures shown in Fig. 3 the distribution of the dust continuum emission is smooth, with variations in ΣFIR of only ∼30%. The [C II] emission, on the other hand, varies by a factor of ∼2 in the same area in which the dust continuum is detected. In the photodissociation region (PDR) models of Kaufman et al. (2006), a variation of [C II] emission for a fixed ΣFIR, and thus a fixed FUV (6 eV < hν < 13.6 eV) radiation field intensity (G0), can be explained by a change in the total neutral gas density (nH). For a fixed G0, if two regions have neutral gas densities below the critical density for collisions with H atoms (ncrit ≈ 3 × 103 cm−3; Goldsmith et al. 2015), then a lower [C II]/FIR implies a lower neutral gas density. Conversely, if two regions have neutral gas densities higher than the critical density, then a lower [C II]/FIR implies a higher neutral gas density. This is probably the case in the ISM of HZ4.
To independently constrain G0 and nH, it is unfortunately necessary to have observations of at least one additional PDR line (e.g., one of the [O I] transitions). With the available information, the one relevant physical quantity we can constrain is the ratio between G0 and nH. This parameter is a proxy for the charging of the dust grains, which in turn sets the [C II]/FIR: a higher dust grain charge implies that photoelectrons have to overcome a higher Coulomb barrier, resulting in a decrease in gas photoelectric heating efficiency (Tielens & Hollenbach 1985), and thus a decrease in [C II]/FIR. Following the relation between ΣFIR and G0/nH derived by Díaz-Santos et al. (2017), we estimate that the G0/nH ratio in HZ4 is ≈0.5. This value is comparable to those observed in nearby star-forming galaxies (G0/nH ∼ 0.5 − 1; e.g., Contursi et al. 2013; Croxall et al. 2013; Hughes et al. 2015), and at least one order of magnitude lower than the ratios measured in ultra-luminous infrared galaxies (ULIRGs) and high-z starbursts (G0/nH ∼ 10 − 100; e.g., Gullberg et al. 2015; Díaz-Santos et al. 2017).
An alternative way to study the heating and cooling properties of the neutral gas in HZ4 is by comparing the [C II] line emission to the star formation activity. If the gas is in thermal balance, and [C II] is the dominant coolant of the neutral gas, then the [C II] luminosity is a measure of the total energy that is put into the gas by different processes, including FUV photons through the photoelectric effect on dust grains and mechanical heating. This physical connection is behind the observed relation between the [C II] surface brightness (Σ[CII]) and the star formation rate surface density (ΣSFR) observed in the Milky Way (e.g., Pineda et al. 2014) and nearby galaxies (e.g., Boselli et al. 2002; De Looze et al. 2011, 2014; Sargsyan et al. 2012; Kapala et al. 2015; Herrera-Camus et al. 2015, 2018b).
Figure 4 shows the Σ[CII] − ΣSFR correlation observed in approximately kiloparsec-size regions of nearby galaxies from the KINGFISH sample (Herrera-Camus et al. 2015), spatially resolved starbursts (Herrera-Camus et al. 2018a), and the four approximately kiloparsec-size regions of HZ4 in which we detect the ALMA dust continuum (see Fig. 3). In the case of HZ4, we calculated ΣSFR based on the FIR luminosity using the calibration by Murphy et al. (2011), the rest-frame 160 μm luminosity following the calibration by Calzetti et al. (2010), the UV luminosity using the calibration by Murphy et al. (2011), and the combination of the UV and FIR luminosities following the calibration by Bell et al. (2005). All four estimates of the ΣSFR in HZ4 are consistent within a factor of ∼3. The values of ΣSFR shown in Fig. 4 correspond to those measured using the FIR luminosity.
 |
Fig. 4. [C II] surface brightness density vs. star formation rate surface density observed in regions from star-forming nearby galaxies from the KINGFISH sample (contours enclose 95%, 45%, and 25% of the 3846 regions; Herrera-Camus et al. 2015), nearby starbursts from the SHINING sample (gray circles; Herrera-Camus et al. 2018a), and the four regions in HZ4 in which we detect the dust continuum with ALMA (orange circles). The black line shows the best fit (and ±1σ scatter) to the KINGFISH regions (Herrera-Camus et al. 2015). |
The ratio between the FIR- and UV-based SFRs in HZ4, which is essentially a scaling of LFIR/LUV, is close to ≈1, as observed in other main-sequence galaxies at z ∼ 5 (e.g., Heinis et al. 2014; Capak et al. 2015; Bouwens et al. 2016; Fudamoto et al. 2020), and suggests that the observed offset between the ALMA dust continuum and HST rest-frame UV map is not caused by dust obscuration of the UV photons.
The Σ[CII] − ΣSFR relation observed in nearby star-forming galaxies, characterized in Fig. 4 by the linear relation derived by Herrera-Camus et al. (2015) (Eq. (2)), holds up to galaxies with ΣSFR ∼ 1 M⊙ yr−1 kpc−2. This includes the central regions in HZ4. At higher ΣSFR values, galaxies start to deviate from the local scaling relation, showing a deficit of [C II] emission relative to ΣSFR. The systems that show a [C II] deficit are typically dusty, dense starbursts characterized by strong radiation fields, high ionization parameters, and high neutral gas densities. As discussed above, all these factors play a role in driving the [C II] deficit (for a discussion, see, e.g., Malhotra et al. 2001; Graciá-Carpio et al. 2011; Smith et al. 2016; Herrera-Camus et al. 2018b). The combination of the analysis of the [C II]/FIR and [C II]/SFR suggests that the ISM conditions in the central region of HZ4 are more comparable to those observed in modest, nearby starbursts (e.g., M 82, M 83, or NGC 253) rather than in dense, dusty starbursts such as those found in luminous infrared systems.
3.3. Outflows: Evidence for an outflow along the minor axis
So far, the strongest evidence for neutral outflows in typical star-forming galaxies at z ∼ 5 comes from the stacking of [C II] spectra (Gallerani et al. 2018; Ginolfi et al. 2020a) or metal absorption lines (Sugahara et al. 2019). In the case of the analysis of the ALPINE galaxies, the stacked [C II] spectra of galaxies with SFR > 25 M⊙ yr−1 show a high-velocity tail that can be fit by a broad Gaussian component of FWHM ∼ 680 km s−1 (Ginolfi et al. 2020a). The mass outflow rate, although uncertain for reasons we discuss below, is comparable to the SFR of the stacked systems.
HZ4 has a total SFR of ∼40 M⊙ yr−1, comparable to the SFR in the group of stacked galaxies in Ginolfi et al. (2020a) that show evidence for outflows. Taking advantage of the high spatial resolution and sensitivity of our observations, we searched for outflow signatures in approximately kiloparsec-scale regions across the disk of HZ4. Figure 5 shows the distribution of seven circular apertures in which we search for outflow signatures in the spectrum. Spectra from regions 3 to 7 (Appendix B) appear to be symmetric. For each spectrum from region 3 to 7, a single-Gaussian fit was strongly preferred over fitting a double-Gaussian distribution based on the reduced chi-squared value. We also find that the residuals from the single-Gaussian fit do not show any clear evidence of flux excess over the entire velocity range. Spectra from apertures 1 and 2, on the other hand, require two Gaussian components for an optimal fit: a narrow component that can be associated with the star-forming disk, and a broad component associated with a potential outflow. The right panel of Fig. 5 shows the result of the double-Gaussian fit. The FWHM of the broad components of apertures 1 and 2 are 406 and 326 km s−1, respectively. These values are a factor ×1.6 − 2 lower than the FWHM of the broad component in the stacked [C II] spectrum of main-sequence galaxies at z ∼ 4 − 5 (Ginolfi et al. 2020a), QSOs at z ∼ 6 (Stanley et al. 2019), and about a factor of 5 lower than the FWHM in the powerful AGN-driven outflows detected in QSOs at z ≳ 5 (Maiolino et al. 2012; Bischetti et al. 2019).
 |
Fig. 5. Evidence for an outflow in HZ4. Left panel: [C II] line integrated intensity contours with S/N ≥ 3 (yellow). The spectra extracted from the seven apertures placed across the disk are shown in Appendix B, except for apertures 1 and 2 (in purple), for which the spectra are shown in the right panels. In these cases, the best Gaussian fit to the spectra involves two components: a narrow component that we associate with the disk (green), and a broad component that we associate with outflowing gas (purple). The purple arrow in the [C II] map shows the direction in the disk were we find evidence for outflowing gas, which is almost along the galaxy minor axis (gray arrow). |
It is interesting to note that the broad component features observed in regions 1 and 2 become diluted in the global [C II] spectrum shown in Fig. 1. This shows that it is only due to our ability to spatially resolve the [C II] emission with high sensitivity that we can detect the outflow signatures. Additional evidence in favor of the outflow interpretation of the broad component comes from two signatures that are also observed in nearby galaxy outflows: (1) the outflow in HZ4 is located near the peak of the gas velocity dispersion (see Paper II; Herrera-Camus et al., in prep.), and (2) the outflow extends nearly aligned with the minor axis (the path of least resistance through the disk; e.g., Chen et al. 2010; Leroy et al. 2015; Roberts-Borsani et al. 2020; Herrera-Camus et al. 2020).
To further explore the outflow scenario, we compared the properties of the potential outflow in HZ4 with those observed in the outflows of other local and high-z star-forming galaxies. We first estimated the projected maximum velocity of the outflowing gas following vout ∼ |Δv|+FW10%/2 (e.g., Lutz et al. 2020), where Δv is the shift of the centroid of the broad Gaussian line component for the outflow with respect to the systemic velocity, and FW10% is the full width at a tenth of the maximum of the broad outflow component. The projected outflow velocities we obtain for apertures 1 and 2 are vout, A1 ≈ 415 km s−1 and vout, A2 ≈ 320 km s−1, respectively. These velocities are most likely lower limits because we did not consider projection effects. Based on the axial ratio b/a of the deconvolved size of the [C II] image, we infer an inclination for HZ4 of approximately θ ≈ 45°. When we assume that the outflows are perpendicular to the disk, then the deprojected velocities are a factor 1/cos(45° ) ≈ 1.4 higher, that is, vout, A1 ≈ 590 km s−1 and vout, A2 ≈ 445 km s−1, respectively.
Next, we calculated the star formation rate surface density. For region 1, this can be done based on the FIR luminosity or the combination of the FIR and UV continuum emission. These two are comparable within the uncertainties. For region 2, which is not detected in the 160 μm continuum map, we estimated the SFR from the UV luminosity following the calibration by Murphy et al. (2011). On average, the star formation rate surface densities of regions 1 and 2 are in the range ΣSFR ≈ 0.3 − 1 M⊙ yr−1 kpc−2. This value is comparable to the threshold value found by Newman et al. (2012) for the occurrence of strong outflows in z ∼ 2 star-forming galaxies. Davies et al. (2019) expanded the work of Newman et al. (2012) by studying the ionized outflow properties of stacked ∼1 − 2 kpc star-forming regions in z ∼ 2 main-sequence galaxies (similar spatial scale as our ALMA observations). As Fig. 6 (left panel) shows, Davies et al. (2019) reported a positive correlation between the outflow velocities and ΣSFR consistent with trends from rest-UV absorption features tracing winds at z ∼ 1 − 3 (e.g., Weiner et al. 2009; Kornei et al. 2012). Regions 1 and 2 in HZ4 follow this relation within the uncertainties, which provides additional support for the outflow interpretation of the broad component in the [C II] spectra.
 |
Fig. 6. Left: outflow velocity vs. star formation rate surface density observed in apertures 1 and 2 of HZ4 (orange circles) and in the stacked approximately kiloparsec-scale star-forming regions in z ∼ 2 main-sequence galaxies (blue lines; Davies et al. 2019). Right: local neutral mass-loading factor as a function of ΣSFR for HZ4 (orange circle) and stacked galaxies from the MANGA survey based on the Na D λλ5889,5895 Å absorption doublet (green diamonds; Roberts-Borsani & Saintonge 2019). |
Another relevant quantity for studying in the outflow scenario is the mass outflow rate (Ṁout). For this, we first need to estimate the atomic gas mass in the outflow based on the [C II] luminosity of the broad Gaussian component. As we describe in detail in Appendix C, the conversion factor κ[CII] (MH = κ[CII] × L[CII]) depends on the neutral gas density, temperature, and metallicity of the gas. Figures C.1 and C.2 show the variation in the value of κ[CII] as a function of the neutral gas density (0.1 ≤ nH ≤ 105 cm−3), temperature (10 ≤ T ≤ 104 K), and metallicity (7 ≤ 12 + log10(O/H)≤9). Table 1 lists a subset of values relevant for the physical conditions that could be found in the outflowing gas of nearby and high-z galaxies. In the case of maximum excitation (T ≫ 91 K, n ≫ ncrit ∼ 103 cm−3) and gas with solar metallicity, the mass-to-light ratio is κ[CII] ≈ 1.5. This effectively represents a lower limit to the amount of gas in the outflow traced by the [C II] line emission (see also the discussion in Veilleux et al. 2020). When the metallicity of the gas decreases to half or one-tenth solar, then κ[CII] increases approximately by a factor ×3 or ×27, respectively.
κ[CII](n, T, Z): [C II] luminosity-to-mass conversion factor.
To estimate the outflow mass in HZ4, we followed a conservative approach and assumed κ[CII] ≈ 1.5 (i.e., maximum excitation and solar metallicity). This results in a neutral gas mass in the outflow of Mout, 1 ≈ 1.2 × 108 M⊙ and Mout, 2 ≈ 8.5 × 107 M⊙ for regions 1 and 2, respectively. It could be argued based on Spitzer color-based metallicities (Faisst et al. 2017), or the mass-metallicity relation at z ∼ 5, that the metallicity of HZ4 is about half solar or lower (e.g., Mannucci et al. 2009; Laskar et al. 2011; Torrey et al. 2018). This represents an additional reason to assume that these mass outflow estimates correspond to lower limits.
Based on the outflow mass, we estimated the mass outflow rate as Ṁout = Mout × vout/Rout. When we use the projected outflow velocity and extent of the outflow (Rout ∼ 2 kpc), the neutral mass outflow rates for regions 1 and 2 are Ṁout,1 ≈ 22 M⊙ yr−1 and Ṁout,2 ≈ 12 M⊙ yr−1, respectively. When we consider inclination effects, the mass outflow rates increase by tan(θ), so the values remain the same as tan(45° ) = 1. When the uncertainties and assumptions involved in the calculation are taken into account, these values are comparable to the neutral mass outflow rate of Ṁout ≈ 25 M⊙ yr−1 measured in the stacked [C II] spectra of the subgroup of ALPINE star-forming galaxies with median SFR similar to that of HZ4 (SFRmed ∼ 50 M⊙ yr−1; Ginolfi et al. 2020a)2. This implies that the ratio between the total neutral mass outflow rate and the total star formation rate, that is, the global neutral mass-loading factor, is ηglobal ≈ 0.5 for both HZ4 and the ALPINE stack. Our present ALMA observations offer the advantage, however, that they spatially resolve the regions where the outflow is located. Thus, compared to the star formation rate in regions 1 and 2, the local neutral mass outflow rates are around ηlocal ≈ 3 − 6, which are a factor of ∼6 − 12 higher than the global value. As the right panel in Fig. 6 shows, the local mass-loading factors measured in HZ4 are comparable with the neutral outflow properties of stacked MANGA z ∼ 0 galaxies with similar star formation rate surface densities (Roberts-Borsani & Saintonge 2019).
Compared to the modest global mass outflow rates measured in stacked z ∼ 5 galaxies, the ∼6 − 10 times higher local mass outflow rate measured in the central region of HZ4 highlights the effect that outflows can have in locally depleting the gas, potentially preventing or delaying future episodes of star formation at their launch sites. We emphasize the word “delay” because the bulk of the gas in the outflow is most likely not fast enough to escape the system. Following a similar approach as Fluetsch et al. (2019), and based on a dynamical mass of Mdyn ≈ 1010.5 M⊙ measured from the kinematic analysis (see Paper II; Herrera-Camus et al., in prep.), the escape velocity at a distance of one effective radius is vesc ≈ 2 × vout, A1. The fact that ejected gas remains bound to the galaxy is key for the formation and maintenance of the CGM. Evidence for this comes directly from the existence of extended [C II] halos around z ∼ 5 galaxies (e.g., Fujimoto et al. 2019, 2020), which we also detect in HZ4.
3.4. Morphology: Extended component (or halo) visible in [C II] line emission
One of the most exciting new results of ALMA observations of main-sequence galaxies at z ∼ 4 − 5 is the detection of an extended [C II] emission component or halo. These [C II] halos extend significantly beyond the stellar disk and are potentially part of the circumgalactic medium (e.g., Fujimoto et al. 2019, 2020; Ginolfi et al. 2020a).
To compare the light distribution in HZ4 of the ALMA [C II] and dust continuum with the HST rest-frame UV continuum, we first degraded the resolution of the latter to match the resolution of the ALMA images. This was done using a kernel constructed to match the HST WFC3 F160W point-spread function (PSF) to that of the ALMA data using the IRAF task PSFMATCH. The left panel of Fig. 7 shows the result, with the extent of the dust (green) and convolved UV rest-frame continuum (blue) emission with S/N ≥ 3 overlaid on the [C II] integrated intensity map. The detection of an extended [C II] component is evident from visual inspection.
 |
Fig. 7. Left: integrated intensity map of the [C II] line emission. The extent of the dust and convolved rest-frame UV continuum emission with S/N > 3 is shown in green and blue, respectively. Right: normalized radial intensity profile for the [C II] line (red), dust continuum (green), and convolved rest-frame UV continuum emission (blue). The common ALMA beam intensity profile is shown with a dashed gray line. The distance from the center is shown in arcseconds (bottom) and projected kiloparsec (top, not corrected for inclination). |
To better quantify the distribution of the [C II], dust, and convolved rest-frame UV continuum emission, we compared their azimuthally averaged radial intensity profiles calculated using the task casairing3. The right panel of Fig. 7 shows the results, with the surface brightness profile of the [C II] line extending to a radial distance of ∼6 kpc, an additional ∼3.5 kpc compared to the dust continuum, and ∼2 kpc farther than the convolved rest-frame UV emission.
Fitting an exponential function of the form e−r/h (where h is the scale length) reproduces the emission profiles well (goodness-of-fit parameter R2 ≳ 0.95), and yields scale lengths of h[CII] = 2.0 kpc, hdust = 1.6 kpc, and hUV = 1.7 kpc. In the exponential disk case, the effective radius is Reff = 1.678 h, which implies that the ratio between the [C II] and rest-frame UV effective radius is Reff, [CII]/Reff, UV = 1.2. This ratio increases by only 10% when we consider the radial profile along the major axis, or when we reduce the data using a natural weighting to maximize the surface brightness sensitivity.
The ratio Reff, [CII]/Reff, UV we measure in HZ4 is lower than the median value found in the ALPINE sample of Reff, [CII]/Reff, UV = 2.3, but comparable to the ratio of ∼1.3 measured in the two ALPINE galaxies with stellar masses slightly lower than HZ4 (Fujimoto et al. 2020). The good correspondence between the [C II], dust, and rest-frame UV continuum emission in the central R ∼ 3 kpc disk suggests that the main source of heating is the photoelectric effect on dust grains.
Fujimoto et al. (2020) classified ALPINE galaxies as having a [C II], dust, and/or UV halo when the integrated emission of the tracer is detected above a 4σ level outside the central area defined by the size of the synthesized beam (typically ∼0.8 − 1″ for ALPINE galaxies; Le Fèvre et al. 2020). HZ4, part of their sample, was not identified as having a [C II] halo, possibly because of comparatively shallower [C II] line and dust continuum observations.
The difficulty with the [C II]-halo definition in Fujimoto et al. (2020) is that it is purely observational and dependent on the galaxy size relative to the beam size. A more physically driven classification criteria would be to compare the extent of the [C II] emission relative to the stellar disk as traced by the UV emission, although this would still be dependent on the sensitivity achieved in the observations of each tracer. In the case of HZ4, our deep observations show that the [C II] emission is detected above a 4σ significance both outside the stellar disk and outside a circular aperture of 1″ in diameter. Thus, the extended [C II] line emission in HZ4 could be considered as a [C II] halo based on both criteria.
The sources of heating of the gas in the extended [C II] emission of high-z galaxies are still debated (e.g., see Fujimoto et al. 2020). In the case of HZ4, the existence of [C II] emission beyond the UV disk could imply that UV photons are able to travel far from the star-forming regions due to the low dust-to-gas ratio of the ISM. In addition to photoelectric heating, supernova-driven cooling outflows could contribute to the [C II] emission in the outer disk. In the one-dimensional models of Pizzati et al. (2020), a galaxy with a mass-loading factor of ∼3 and a dynamical mass of Mdyn ≈ 1011 M⊙ (similar to HZ4, see Paper II; Herrera-Camus et al., in prep.) can produce a [C II] halo with an extent comparable to that observed in HZ4. Finally, there could be the additional contribution to the extended [C II] emission of shock heating from inflowing gas, although this cannot be constrained by our data. More observations are clearly needed to explore the origin and physical conditions of the [C II]-halo, including tracers such as the [O III] 88 μm line, which might help to constrain the in situ star formation scenario, or deeper HST or James Webb Space Telescope images that could offer a less obscured view of the stellar population or reveal reveal the presence of satellite galaxies.
4. Summary and conclusions
We have obtained deep kiloparsec-scale resolution ALMA observations of the [C II] 158 μm transition and the dust continuum of HZ4, a main-sequence galaxy at z = 5.5 (Figs. 1 and 2). The results are presented in two papers. This first focuses on the properties of the ISM, outflow, and [C II] halo. The second paper will focus on the analysis of the spatially resolved kinematics of the source (Paper II; Herrera-Camus et al., in prep.). The main results are summarized below in three categories.
-
Interstellar medium properties: The [C II] transition is one of the main coolants of the cold neutral gas, and in combination with the FIR luminosity and/or the SFR, it can be used to constrain the heating-cooling balance in the ISM. Over the central ∼4 kpc region of HZ4, the [C II]/FIR is ∼3 × 10−3, which is comparable to the [C II]/FIR observed in nearby galaxies with similar FIR luminosity surface densities (Fig. 3). HZ4 also follows the Σ[CII] − ΣSFR correlation observed in nearby star-forming galaxies and starbursts (Fig. 4; Herrera-Camus et al. 2015, 2018b). In this sense, HZ4 does not show a [C II] deficit as observed in dense starbursts, submillimeter galaxies, or a number of z ≳ 7 low-metallicity systems. This suggests that the ISM properties of HZ4 are comparable to those observed in the central regions of modest starbursts, such as M 82 or M 83.
-
Outflows: Evidence for outflows in z ≈ 4 − 6 normal galaxies has previously been presented only from stacking of [C II] or metal absorption lines (e.g., Gallerani et al. 2018; Sugahara et al. 2019; Ginolfi et al. 2020a). Here we present the first evidence for a star formation driven outflow in an individual main-sequence galaxy at z ≈ 5. The outflow signatures are found in two connected regions with sizes of ∼2 kpc that extend from the central part of the galaxy in the direction of the minor axis (Fig. 5). These regions have ΣSFR ≈ 0.3 − 1 M⊙ yr−1 kpc−2, a known threshold for the launch of star formation driven outflows at z ∼ 2 (e.g., Newman et al. 2012). The projected velocity of the outflows is vout ≈ 320 − 420 km s−1, consistent with outflow velocities measured in z ∼ 2 main-sequence galaxies with comparable star formation activity (Fig. 6; Davies et al. 2019). Similar to studies based on stacking of the [C II] spectra, we measure a modest global neutral mass-loading factor of ηneutral ∼ 0.5. However, when we consider the star formation activity in the central region in which the outflow is launched, the mass-loading factor increases by an order of magnitude. This high mass-loading factor may contribute to suppressing or delaying the star formation activity in the central region of the galaxy.
-
[C II] extended emission or halo: The [C II] emission in HZ4 extends beyond the dust and UV continuum disk, forming an extended component or halo of emission of about ∼12 kpc in diameter (Fig. 7). The outflows detected in HZ4, which have maximum velocities that are roughly half the escape velocity of the system, belong to the most likely candidates for explaining the extended [C II] emission.
In summary, our new ALMA observations present one of the most detailed views on kiloparsec scales of a typical galaxy when the Universe was only ∼1 Gyr old. We show that the combination of the [C II] line, the dust continuum, and the rest-frame UV emission observed with HST (and in the future with the James Webb Space Telescope) offers an excellent opportunity to study different processes involved in the baryon cycle of galaxies. An important next step is to increase the number of spatially resolved observations of main-sequence galaxies at z ≳ 4, making sure to achieve enough sensitivity to detect the dust continuum and potential faint features associated with outflows and halos.
We note that Ginolfi et al. (2020a) assumed a similar value of κ[CII] for their calculations of the [C II] outflow mass.
This task is provided by the Nordic ALMA regional centre: https://www.oso.nordic-alma.se/software-tools.php
Acknowledgments
We thank the referee for very useful comments and suggestions that improved the manuscript. R.H.-C. would also like to deeply thank his wife Fares and daughter Olivia for their support, as this paper was written at home during lockdown due to the COVID-19 pandemic. R.H.-C. would also like to thank Guido Roberts-Borsani for kindly providing the data of the MANGA galaxies. This paper makes use of the following ALMA data: ADS/JAO.ALMA#2018.1.01605.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ. PACS has been developed by a consortium of institutes led by MPE (Germany) and including UVIE (Austria); KU Leuven, CSL, IMEC (Belgium); CEA, LAM (France); MPIA (Germany); INAF-IFSI/OAA/OAP/OAT, LENS, SISSA (Italy); IAC (Spain). This development has been supported by the funding agencies BMVIT (Austria), ESA-PRODEX (Belgium), CEA/CNES (France), DLR (Germany), ASI/INAF (Italy), and CICYT/MCYT (Spain).
References
- Aihara, H., AlSayyad, Y., Ando, M., et al. 2019, PASJ, 71, 114 [CrossRef] [Google Scholar]
- Barisic, I., Faisst, A. L., Capak, P. L., et al. 2017, ApJ, 845, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Bell, E. F., Papovich, C., Wolf, C., et al. 2005, ApJ, 625, 23 [NASA ADS] [CrossRef] [Google Scholar]
- Béthermin, M., Fudamoto, Y., Ginolfi, M., et al. 2020, A&A, 643, A2 [CrossRef] [EDP Sciences] [Google Scholar]
- Bischetti, M., Maiolino, R., Carniani, S., et al. 2019, A&A, 630, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Gavazzi, G., Lequeux, J., & Pierini, D. 2002, A&A, 385, 454 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bouwens, R. J., Aravena, M., Decarli, R., et al. 2016, ApJ, 833, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Calzetti, D., Wu, S.-Y., Hong, S., et al. 2010, ApJ, 714, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Capak, P. L., Carilli, C., Jones, G., et al. 2015, Nature, 522, 455 [NASA ADS] [CrossRef] [Google Scholar]
- Carniani, S., Maiolino, R., Pallottini, A., et al. 2017, A&A, 605, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Carniani, S., Ferrara, A., Maiolino, R., et al. 2020, MNRAS, 499, 5136 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y.-M., Tremonti, C. A., Heckman, T. M., et al. 2010, AJ, 140, 445 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, C.-C., Hodge, J. A., Smail, I., et al. 2017, ApJ, 846, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Contursi, A., Poglitsch, A., Grácia Carpio, J., et al. 2013, A&A, 549, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cormier, D., Madden, S. C., Lebouteiller, V., et al. 2015, A&A, 578, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cormier, D., Abel, N. P., Hony, S., et al. 2019, A&A, 626, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cornwell, T. J. 2008, IEEE J. Sel. Top. Signal Process., 2, 793 [Google Scholar]
- Crawford, M. K., Genzel, R., Townes, C. H., & Watson, D. M. 1985, ApJ, 291, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Croxall, K. V., Smith, J. D., Brandl, B. R., et al. 2013, ApJ, 777, 96 [Google Scholar]
- Croxall, K. V., Smith, J. D., Pellegrini, E., et al. 2017, ApJ, 845, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, R. L., Förster Schreiber, N. M., Übler, H., et al. 2019, ApJ, 873, 122 [NASA ADS] [CrossRef] [Google Scholar]
- De Breuck, C., Williams, R. J., Swinbank, M., et al. 2014, A&A, 565, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Looze, I., Baes, M., Bendo, G. J., Cortese, L., & Fritz, J. 2011, MNRAS, 416, 2712 [Google Scholar]
- De Looze, I., Cormier, D., Lebouteiller, V., et al. 2014, A&A, 568, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Díaz-Santos, T., Armus, L., Charmandaris, V., et al. 2013, ApJ, 774, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz-Santos, T., Assef, R. J., Blain, A. W., et al. 2016, ApJ, 816, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Díaz-Santos, T., Armus, L., Charmandaris, V., et al. 2017, ApJ, 846, 32 [Google Scholar]
- Dunlop, J. S., McLure, R. J., Biggs, A. D., et al. 2017, MNRAS, 466, 861 [Google Scholar]
- Faisst, A. L., Capak, P. L., Yan, L., et al. 2017, ApJ, 847, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Faisst, A. L., Schaerer, D., Lemaux, B. C., et al. 2020, ApJS, 247, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Fluetsch, A., Maiolino, R., Carniani, S., et al. 2019, MNRAS, 483, 4586 [NASA ADS] [Google Scholar]
- Fudamoto, Y., Oesch, P. A., Faisst, A., et al. 2020, A&A, 643, A4 [CrossRef] [EDP Sciences] [Google Scholar]
- Fujimoto, S., Ouchi, M., Ferrara, A., et al. 2019, ApJ, 887, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Fujimoto, S., Silverman, J. D., Bethermin, M., et al. 2020, ApJ, 900, 1 [CrossRef] [Google Scholar]
- Gaia Collaboration (Prusti, T., et al.) 2016, A&A, 595, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaia Collaboration (Brown, A. G. A., et al.) 2018, A&A, 616, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gallerani, S., Pallottini, A., Feruglio, C., et al. 2018, MNRAS, 473, 1909 [NASA ADS] [CrossRef] [Google Scholar]
- Gerin, M., Ruaud, M., Goicoechea, J. R., et al. 2015, A&A, 573, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginolfi, M., Jones, G. C., Béthermin, M., et al. 2020a, A&A, 633, A90 [CrossRef] [EDP Sciences] [Google Scholar]
- Ginolfi, M., Jones, G. C., Béthermin, M., et al. 2020b, A&A, 643, A7 [CrossRef] [EDP Sciences] [Google Scholar]
- Goldsmith, P. F., Yıldız, U. A., Langer, W. D., & Pineda, J. L. 2015, ApJ, 814, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Graciá-Carpio, J., Sturm, E., Hailey-Dunsheath, S., et al. 2011, ApJ, 728, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Gullberg, B., De Breuck, C., Vieira, J. D., et al. 2015, MNRAS, 449, 2883 [Google Scholar]
- Gullberg, B., Swinbank, A. M., Smail, I., et al. 2018, ApJ, 859, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Hailey-Dunsheath, S., Nikola, T., Stacey, G. J., et al. 2010, ApJ, 714, L162 [Google Scholar]
- Hasinger, G., Capak, P., Salvato, M., et al. 2018, ApJ, 858, 77 [Google Scholar]
- Heinis, S., Buat, V., Béthermin, M., et al. 2014, MNRAS, 437, 1268 [NASA ADS] [CrossRef] [Google Scholar]
- Herrera-Camus, R., Bolatto, A. D., Wolfire, M. G., et al. 2015, ApJ, 800, 1 [Google Scholar]
- Herrera-Camus, R., Sturm, E., Graciá-Carpio, J., et al. 2018a, ApJ, 861, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Herrera-Camus, R., Sturm, E., Graciá-Carpio, J., et al. 2018b, ApJ, 861, 95 [Google Scholar]
- Herrera-Camus, R., Janssen, A., Sturm, E., et al. 2020, A&A, 635, A47 [CrossRef] [EDP Sciences] [Google Scholar]
- Hodge, J. A., Swinbank, A. M., Simpson, J. M., et al. 2016, ApJ, 833, 103 [Google Scholar]
- Hughes, T. M., Foyle, K., Schirm, M. R. P., et al. 2015, A&A, 575, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kapala, M. J., Sandstrom, K., Groves, B., et al. 2015, ApJ, 798, 24 [Google Scholar]
- Katz, H., Kimm, T., Sijacki, D., & Haehnelt, M. G. 2017, MNRAS, 468, 4831 [NASA ADS] [CrossRef] [Google Scholar]
- Kaufman, M. J., Wolfire, M. G., Hollenbach, D. J., & Luhman, M. L. 1999, ApJ, 527, 795 [Google Scholar]
- Kaufman, M. J., Wolfire, M. G., & Hollenbach, D. J. 2006, ApJ, 644, 283 [Google Scholar]
- Kepley, A. A., Tsutsumi, T., Brogan, C. L., et al. 2020, PASP, 132, 024505 [Google Scholar]
- Koekemoer, A. M., Aussel, H., Calzetti, D., et al. 2007, ApJS, 172, 196 [NASA ADS] [CrossRef] [Google Scholar]
- Kornei, K. A., Shapley, A. E., Martin, C. L., et al. 2012, ApJ, 758, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Langer, W. D., & Pineda, J. L. 2015, A&A, 580, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Laskar, T., Berger, E., & Chary, R.-R. 2011, ApJ, 739, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Le Fèvre, O., Béthermin, M., Faisst, A., et al. 2020, A&A, 643, A1 [CrossRef] [EDP Sciences] [Google Scholar]
- Leroy, A. K., Walter, F., Martini, P., et al. 2015, ApJ, 814, 83 [NASA ADS] [CrossRef] [Google Scholar]
- Litke, K. C., Marrone, D. P., Spilker, J. S., et al. 2019, ApJ, 870, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Lutz, D., Berta, S., Contursi, A., et al. 2016, A&A, 591, A136 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lutz, D., Sturm, E., Janssen, A., et al. 2020, A&A, 633, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiolino, R., Gallerani, S., Neri, R., et al. 2012, MNRAS, 425, L66 [Google Scholar]
- Maiolino, R., Carniani, S., Fontana, A., et al. 2015, MNRAS, 452, 54 [NASA ADS] [CrossRef] [Google Scholar]
- Malhotra, S., Kaufman, M. J., Hollenbach, D., et al. 2001, ApJ, 561, 766 [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., et al. 2009, MNRAS, 398, 1915 [NASA ADS] [CrossRef] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [Google Scholar]
- Murphy, E. J., Condon, J. J., Schinnerer, E., et al. 2011, ApJ, 737, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Neeleman, M., Prochaska, J. X., Kanekar, N., & Rafelski, M. 2020, Nature, 581, 269 [Google Scholar]
- Neri, R., Downes, D., Cox, P., & Walter, F. 2014, A&A, 562, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Newman, S. F., Genzel, R., Förster-Schreiber, N. M., et al. 2012, ApJ, 761, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Nicholls, D. C., Sutherland, R. S., Dopita, M. A., Kewley, L. J., & Groves, B. A. 2017, MNRAS, 466, 4403 [Google Scholar]
- Pavesi, R., Riechers, D. A., Capak, P. L., et al. 2016, ApJ, 832, 151 [NASA ADS] [CrossRef] [Google Scholar]
- Pavesi, R., Riechers, D. A., Faisst, A. L., Stacey, G. J., & Capak, P. L. 2019, ApJ, 882, 168 [CrossRef] [Google Scholar]
- Pineda, J. L., Langer, W. D., & Goldsmith, P. F. 2014, A&A, 570, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pizzati, E., Ferrara, A., Pallottini, A., et al. 2020, MNRAS, 495, 160 [CrossRef] [Google Scholar]
- Planck Collaboration VI. 2020, A&A, 641, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riechers, D. A., Carilli, C. L., Capak, P. L., et al. 2014, ApJ, 796, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts-Borsani, G. W., & Saintonge, A. 2019, MNRAS, 482, 4111 [NASA ADS] [Google Scholar]
- Roberts-Borsani, G. W., Saintonge, A., Masters, K. L., & Stark, D. V. 2020, MNRAS, 493, 3081 [Google Scholar]
- Sargsyan, L., Lebouteiller, V., Weedman, D., et al. 2012, ApJ, 755, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Schaerer, D., Ginolfi, M., Béthermin, M., et al. 2020, A&A, 643, A3 [CrossRef] [EDP Sciences] [Google Scholar]
- Shibuya, T., Ouchi, M., & Harikane, Y. 2015, ApJS, 219, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Simón-Díaz, S., & Stasińska, G. 2011, A&A, 526, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Smit, R., Bouwens, R. J., Carniani, S., et al. 2018, Nature, 553, 178 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, K. L., Mushotzky, R. F., Vogel, S., Shimizu, T. T., & Miller, N. 2016, ApJ, 832, 163 [Google Scholar]
- Smith, J. D. T., Croxall, K., Draine, B., et al. 2017, ApJ, 834, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Stanley, F., Jolly, J. B., König, S., & Knudsen, K. K. 2019, A&A, 631, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sugahara, Y., Ouchi, M., Harikane, Y., et al. 2019, ApJ, 886, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Tadaki, K.-I., Iono, D., Yun, M. S., et al. 2020, ApJ, 889, 141 [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., & Hollenbach, D. 1985, ApJ, 291, 722 [Google Scholar]
- Torrey, P., Vogelsberger, M., Hernquist, L., et al. 2018, MNRAS, 477, L16 [NASA ADS] [CrossRef] [Google Scholar]
- Tumlinson, J., Peeples, M. S., & Werk, J. K. 2017, ARA&A, 55, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Vallini, L., Gallerani, S., Ferrara, A., Pallottini, A., & Yue, B. 2015, ApJ, 813, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Maiolino, R., Bolatto, A. D., & Aalto, S. 2020, A&ARv, 28, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Weiner, B. J., Coil, A. L., Prochaska, J. X., et al. 2009, ApJ, 692, 187 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., Hollenbach, D., McKee, C. F., Tielens, A. G. G. M., & Bakes, E. L. O. 1995, ApJ, 443, 152 [Google Scholar]
- Wolfire, M. G., McKee, C. F., Hollenbach, D., & Tielens, A. G. G. M. 2003, ApJ, 587, 278 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Serendipitous detection of a strong continuum source with no HST counterpart
While analyzing the ALMA Band 7 continuum map centered at an observed frequency of νobs = 285 GHz, we detected a strong continuum source at the very edge of the image in the northeast direction at a distance of ∼13″ at RA 09:58:29.19, Dec +2.03.15.39. The left panel of Fig. A.1 shows the source, which is detected at high significance. The source is barely resolved and has a size (deconvolved from beam) of 0.29″ × 0.17″. The integrated flux at 285 GHz is 0.67 mJy. We searched in vain for a counterpart in deep HST WFC3 images (see right panel of Fig. A.1).
 |
Fig. A.1. Left: ALMA Band 7 continuum source detected at the edge of the map in the northeast direction. The contours correspond to S/N = 2 (dashed), 3, 5, 10, 15, and 20. Right: contours of the ALMA continuum source (in white) overplotted on an HST WFC3 F160W image. There is no HST counterpart. |
Appendix B: [C II] spectra from apertures 3, 4, 5, 6, and 7
Figure B.1 shows [C II] spectra extracted from apertures 3 to 7. The spatial distribution of the apertures is shown in the left panel of Fig. 5. Different from the spectra extracted from apertures 1 and 2, which require a combination of a narrow and broad Gaussian component, these spectra are well fit by a single Gaussian.
 |
Fig. B.1. [C II] spectra extracted from apertures 3 to 7. The position of the apertures is shown in the left panel of Fig. 5. The solid black lines correspond to the best single-Gaussian fit to the spectrum. |
Appendix C: Using the [C II] luminosity in the outflow to estimate (a lower limit of) the outflow mass
As described in Crawford et al. (1985), for example, the integrated [C II] line intensity from collisional excitation in the optically thin limit and negligible background emission is given by
The ratio of the statistical weights of the upper and lower level is gu/gl = 2, the transition energy of the [C II] transition (νul = 1900.5369 GHz) is hνul = 1.26 × 10−14 ergs, and the Einstein coefficient for spontaneous emission is Aul = 2.36 × 10−6 s−1. NC+ (cm−2) is the column density of C+, n is the number density of the collisional partner, and ncrit(T) is the critical density defined as the ratio of Aul and the collision rate for de-excitation out of that state (Rul), which is a function of the temperature of the gas (e.g., Goldsmith et al. 2015).
Filling in the constants and replacing NC+ = χC+NH, where χC+(Z) is the carbon abundance (which is a function of the metallicity Z of the gas) and NH is the column density of hydrogen nuclei in the C+ region, we obtain
The gas mass traced by the [C II] line emission can be written as Mgas = κ[CII] × L[CII], where the mass-to-light conversion factor κ[CII] is (see also Hailey-Dunsheath et al. 2010; Veilleux et al. 2020)
κ[CII] is a function of the density of the collisional partner (n), the temperature (T), and metallicity (χC+(Z)) of the gas. We have assumed a standard composition for the gas of 36% helium (μ = 1.36).
We calculate κ[CII] as a function of n, T, and Z for gas where the collisional excitation of C+ is dominated by hydrogen atoms (H0). For this we substitute ncrit using the parameterization of Goldsmith et al. (2015),
For the carbon abundance χC+(Z), we assume that it changes as a function of the oxygen abundance following the analytic function from the MAPPINGS photoionization code (Nicholls et al. 2017):
This function was renormalized to obtain the measured local Galactic depleted ISM carbon abundance (χC+ = 1.5 × 10−4; Gerin et al. 2015) when we used the oxygen gas-phase abundance of the Orion nebula (12 + log(O/H) = 8.65; Simón-Díaz & Stasińska 2011).
Figure C.1 shows the results for κ[CII](H0) in the parameter space 0.1 ≤ n (cm−3)≤105 and 10 ≤ T (K)≤104 assuming solar metallicity. The dashed black line shows the critical density as a function of temperature (Eq. (C.4)). κ[CII](H0) varies from κ[CII] ∼ 1 in dense warm environments (maximum excitation; n ≈ 104 − 5 cm−3, T ≈ 300 − 104 K) to κ[CII](H0)∼10 − 300 in colder gas (T ≲ 100 K). As expected, at gas densities n > ncrit, the value of κ[CII](H0) varies only slightly with n.
 |
Fig. C.1. κ[CII](H0) as a function of neutral gas density n and temperature T. The value of the critical density as a function of T from Goldsmith et al. (2015) is shown as a dashed black line. The black contours represent |
Figure C.2 shows the dependence of κ[CII](H0) on metallicity as measured by the oxygen abundance 12 + log10(O/H). The right ordinate shows the carbon abundance dependence with metallicity from the parameterization in the MAPPINGS code. κ[CII](H0) increases by a factor ∼30 when we reduce the metallicity of the gas from solar to one-tenth solar.
 |
Fig. C.2. Variation of κ[CII](H0) calculated for six combinations of T and n as a function of metallicity as traced by the oxygen abundance. The vertical yellow line shows the assumed value for solar metallicity (12 + log(O/H) = 8.65; Simón-Díaz & Stasińska 2011). The right ordinate shows in red the dependence on the carbon abundance [C/H] as a function of metallicity from the MAPPINGS code (Nicholls et al. 2017). |
All Tables
All Figures
 |
Fig. 1. Left: star formation rate – stellar mass plane between 5 ≤ z ≤ 6 showing the position of the main sequence of star-forming galaxies (black line; Speagle et al. 2014) and the z ∼ 5 galaxies with [C II] detections in the ALPINE survey (gray circles; Le Fèvre et al. 2020; Faisst et al. 2020). HZ4, shown as an orange diamond, lies only ∼0.2 dex above the main sequence and can be considered a typical star-forming galaxy at this redshift (Faisst et al. 2020). Right: continuum-subtracted [C II] 158 μm spectrum of HZ4 extracted inside a circular aperture of 0.9″ radius (∼5.4 kpc). The best Gaussian fit is centered at an observed frequency of ν0 = 290.471 GHz, which corresponds to a redshift of z = 5.54. |
| In the text | |
 |
Fig. 2. Left: [C II] 158 μm integrated intensity of HZ4. The contours start at 2σ (dotted line) and then increase from 3σ to 17σ in steps of two (solid lines). The ALMA-synthesized beam (θ = 0.39″ × 0.34″) is shown in the bottom left corner. Center: dust continuum emission at rest-frame 160 μm. The contours level are 2 (dotted brown line), and 3, 3.5, and 4σ (solid brown lines). Right: contours of rest-frame UV emission as observed by HST WFC3 F160W (Barisic et al. 2017) overlaid on the [C II] integrated intensity map. The contour levels are 2 (dashed black line), 3, 5, 10, and 20σ (solid black lines). The contours are shifted in the direction of the black arrow from the original position marked by the black dot. The HST WFC3 F160W point-spread function is shown in black in the bottom left corner next to the ALMA beam in white. |
| In the text | |
 |
Fig. 3. Left: [C II]/FIR map of HZ4. We have considered only rest-frame ∼160 μm dust continuum emission above the 2σ level. The color bar indicates the [C II]/FIR value. Right: [C II]/FIR ratio as a function of ΣFIR in four kiloparsec-size regions extracted across the disk of HZ4 (orange circles and dashed black circles in the left panel). The error bars, mainly due to the uncertainty in the FIR luminosity, are shown in orange. For comparison, we show nearby star-forming and starburst galaxies from the SHINING sample (Herrera-Camus et al. 2018a), ∼100 pc scale regions in the central disk of M 82 in green (Contursi et al. 2013; Herrera-Camus et al. 2018a), and ∼400 pc scale regions in the central region of M 83 in purple. The solid gray line shows the best quadratic fit to the SHINING data (Herrera-Camus et al. 2018a). |
| In the text | |
 |
Fig. 4. [C II] surface brightness density vs. star formation rate surface density observed in regions from star-forming nearby galaxies from the KINGFISH sample (contours enclose 95%, 45%, and 25% of the 3846 regions; Herrera-Camus et al. 2015), nearby starbursts from the SHINING sample (gray circles; Herrera-Camus et al. 2018a), and the four regions in HZ4 in which we detect the dust continuum with ALMA (orange circles). The black line shows the best fit (and ±1σ scatter) to the KINGFISH regions (Herrera-Camus et al. 2015). |
| In the text | |
 |
Fig. 5. Evidence for an outflow in HZ4. Left panel: [C II] line integrated intensity contours with S/N ≥ 3 (yellow). The spectra extracted from the seven apertures placed across the disk are shown in Appendix B, except for apertures 1 and 2 (in purple), for which the spectra are shown in the right panels. In these cases, the best Gaussian fit to the spectra involves two components: a narrow component that we associate with the disk (green), and a broad component that we associate with outflowing gas (purple). The purple arrow in the [C II] map shows the direction in the disk were we find evidence for outflowing gas, which is almost along the galaxy minor axis (gray arrow). |
| In the text | |
 |
Fig. 6. Left: outflow velocity vs. star formation rate surface density observed in apertures 1 and 2 of HZ4 (orange circles) and in the stacked approximately kiloparsec-scale star-forming regions in z ∼ 2 main-sequence galaxies (blue lines; Davies et al. 2019). Right: local neutral mass-loading factor as a function of ΣSFR for HZ4 (orange circle) and stacked galaxies from the MANGA survey based on the Na D λλ5889,5895 Å absorption doublet (green diamonds; Roberts-Borsani & Saintonge 2019). |
| In the text | |
 |
Fig. 7. Left: integrated intensity map of the [C II] line emission. The extent of the dust and convolved rest-frame UV continuum emission with S/N > 3 is shown in green and blue, respectively. Right: normalized radial intensity profile for the [C II] line (red), dust continuum (green), and convolved rest-frame UV continuum emission (blue). The common ALMA beam intensity profile is shown with a dashed gray line. The distance from the center is shown in arcseconds (bottom) and projected kiloparsec (top, not corrected for inclination). |
| In the text | |
 |
Fig. A.1. Left: ALMA Band 7 continuum source detected at the edge of the map in the northeast direction. The contours correspond to S/N = 2 (dashed), 3, 5, 10, 15, and 20. Right: contours of the ALMA continuum source (in white) overplotted on an HST WFC3 F160W image. There is no HST counterpart. |
| In the text | |
 |
Fig. B.1. [C II] spectra extracted from apertures 3 to 7. The position of the apertures is shown in the left panel of Fig. 5. The solid black lines correspond to the best single-Gaussian fit to the spectrum. |
| In the text | |
 |
Fig. C.1. κ[CII](H0) as a function of neutral gas density n and temperature T. The value of the critical density as a function of T from Goldsmith et al. (2015) is shown as a dashed black line. The black contours represent |
| In the text | |
 |
Fig. C.2. Variation of κ[CII](H0) calculated for six combinations of T and n as a function of metallicity as traced by the oxygen abundance. The vertical yellow line shows the assumed value for solar metallicity (12 + log(O/H) = 8.65; Simón-Díaz & Stasińska 2011). The right ordinate shows in red the dependence on the carbon abundance [C/H] as a function of metallicity from the MAPPINGS code (Nicholls et al. 2017). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$$ \begin{aligned} I_{\rm [CII]} = \frac{h \nu _{\rm ul} A_{\rm ul}}{4\pi }\Bigg [\frac{g_{\rm u}/g_{\rm l} e^{-h\nu _{\rm ul}/kT}}{1+g_{\rm u}/g_{\rm l} e^{-h\nu _{\rm ul}/kT}+n_{\rm crit}(T)/n} \Bigg ]N_{\rm C^{+}}. \end{aligned} $$](/articles/aa/full_html/2021/05/aa39704-20/aa39704-20-eq5.gif)
![$$ \begin{aligned} I_{\rm [CII]}\,(\mathrm{erg\,s^{-1}\,cm^{-2}\,sr^{-1}}) =&2.36\times 10^{-21}\nonumber \\&\times \Bigg [\frac{2 e^{-91\,\mathrm{K}/T}}{1+2e^{-91\,\mathrm{K}/T}+n_{\rm crit}(T)/n} \Bigg ]\chi _{\rm C^{+}}(Z)N_{\rm H}. \end{aligned} $$](/articles/aa/full_html/2021/05/aa39704-20/aa39704-20-eq6.gif)
![$$ \begin{aligned} \kappa _{\rm [CII]}\,(M_{\odot }\,L_{\odot }^{-1}) =&0.98\Bigg (\frac{\mu }{1.36}\Bigg )\Bigg (\frac{1.5\times 10^{-4}}{\chi _{\rm C^{+}}(Z)}\Bigg )\nonumber \\&\times \Bigg [\frac{1+2e^{-91\,\mathrm{K}/T}+n_{\rm crit}(T)/n}{2e^{-91\,\mathrm{K}/T}} \Bigg ]\cdot \end{aligned} $$](/articles/aa/full_html/2021/05/aa39704-20/aa39704-20-eq7.gif)
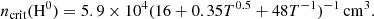
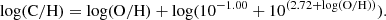
![$ \log_{10}(\kappa_{\mathrm{[CII]}}/M_{\odot}\,L_{\odot}^{-1})=0.25,0.5,1,2,3,4 $](/articles/aa/full_html/2021/05/aa39704-20/aa39704-20-eq10.gif)