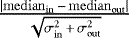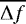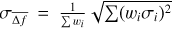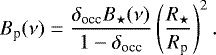| Issue |
A&A
Volume 640, August 2020
|
|
|---|---|---|
| Article Number | A112 | |
| Number of page(s) | 44 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201937392 | |
| Published online | 24 August 2020 | |
TRAPPIST-1: Global results of the Spitzer Exploration Science Program Red Worlds★
1
Astrobiology Research Unit, Université de Liège,
Alléee du 6 Aout 19C,
4000
Liège, Belgium
e-mail: educrot@uliege.be
2
Department of Earth Sciences, University of Cambridge,
Downing St,
Cambridge
CB2 3EQ, UK
3
Cavendish Laboratory,
JJ Thomson Avenue,
Cambridge,
CB3 0H3, UK
4
MRC Laboratory of Molecular Biology,
Cambridge Biomedical Campus,
Francis Crick Ave,
Cambridge
CB2 0QH, UK
5
Observatoire astronomique de l’Université de Genève,
51 chemin de Pégase,
1290
Sauverny, Switzerland
6
Department of Physics, and Kavli Institute for Astrophysics and Space Research, Massachusetts Institute of Technology,
Cambridge,
MA
02139, USA
7
University of Bern, Center for Space and Habitability,
Gesellschaftsstrasse 6,
3012
Bern, Switzerland
8
School of Physics & Astronomy, University of Birmingham,
Edgbaston,
Birmimgham
B15 2TT, UK
9
Astronomy Department, University of Washington,
Seattle,
WA
98195,
USA
10
Department of Earth, Atmospheric and Planetary Science, Massachusetts Institute of Technology,
77 Massachusetts Avenue,
Cambridge,
MA
02139, USA
11
Center for Astrophysics and Space Science, University of California San Diego,
La Jolla,
CA
92093, USA
12
IPAC, California Institute of Technology,
1200 E California Boulevard, Mail Code 314-6,
Pasadena,
CA
91125, USA
13
Space Sciences, Technologies and Astrophysics Research (STAR) Institute, Université de Liège,
Allée du 6 Août 19C,
4000 Liège, Belgium
11
Laboratoire d’astrophysique de Bordeaux, Univ. Bordeaux, CNRS, B18N, Allée Geoffroy Saint-Hilaire,
33615
Pessac, France
15
NASA Johnson Space Center,
2101 NASA Parkway,
Houston,
TX
77058, USA
Received:
21
December
2019
Accepted:
15
June
2020
Context. With more than 1000 h of observation from Feb. 2016 to Oct. 2019, the Spitzer Exploration Program Red Worlds (ID: 13067, 13175 and 14223) exclusively targeted TRAPPIST-1, a nearby (12 pc) ultracool dwarf star, finding that it is orbited by seven transiting Earth-sized planets. At least three of these planets orbit within the classical habitable zone of the star, and all of them are well-suited for a detailed atmospheric characterization with the upcoming JWST.
Aims. The main goals of the Spitzer Red Worlds program were (1) to explore the system for new transiting planets, (2) to intensively monitor the planets’ transits to yield the strongest possible constraints on their masses, sizes, compositions, and dynamics, and (3) to assess the infrared variability of the host star. In this paper, we present the global results of the project.
Methods. We analyzed 88 new transits and combined them with 100 previously analyzed transits, for a total of 188 transits observed at 3.6 or 4.5 μm. For a comprehensive study, we analyzed all light curves both individually and globally. We also analyzed 29 occultations (secondary eclipses) of planet b and eight occultations of planet c observed at 4.5 μm to constrain the brightness temperatures of their daysides.
Results. We identify several orphan transit-like structures in our Spitzer photometry, but all of them are of low significance. We do not confirm any new transiting planets. We do not detect any significant variation of the transit depths of the planets throughout the different campaigns. Comparing our individual and global analyses of the transits, we estimate for TRAPPIST-1 transit depth measurements mean noise floors of ~35 and 25 ppm in channels 1 and 2 of Spitzer/IRAC, respectively. We estimate that most of this noise floor is of instrumental origins and due to the large inter-pixel inhomogeneity of IRAC InSb arrays, and that the much better interpixel homogeneity of JWST instruments should result in noise floors as low as 10 ppm, which is low enough to enable the atmospheric characterization of the planets by transit transmission spectroscopy. Our analysis reveals a few outlier transits, but we cannot conclude whether or not they correspond to spot or faculae crossing events. We construct updated broadband transmission spectra for all seven planets which show consistent transit depths between the two Spitzer channels. Although we are limited by instrumental precision, the combined transmission spectrum of planet b to g tells us that their atmospheres seem unlikely to be CH4-dominated. We identify and model five distinct high energy flares in the whole dataset, and discuss our results in the context of habitability. Finally, we fail to detect occultation signals of planets b and c at 4.5 μm, and can only set 3-σ upper limits on their dayside brightness temperatures (611 K for b 586 K for c).
Key words: planets and satellites: terrestrial planets / planets and satellites: atmospheres / techniques: photometric
The data products for the figures are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/cat/J/A+A/640/A112
© ESO 2020
1 Introduction
Thanks to their small size, mass, and luminosity combined with their relatively large infrared brightness, the nearest ultracool dwarf stars (spectral types M7 and later) represent promising targets for the detailed study of potentially habitable transiting exoplanets with upcoming giant telescopes such as JWST or ELTs (Kaltenegger & Traub 2009; Malik et al. 2019; Mansfield et al. 2019; Koll 2019). This fact motivated the development of the new ground-based transit survey called the Search for habitable Planets EClipsing ULtra-cOOl Stars (SPECULOOS). SPECULOOS aims to explore the ~1000 nearest ultracool dwarf stars for transiting rocky planets as small as the Earth (Burdanov et al. 2018; Gillon 2018; Delrez et al. 2018a). While SPECULOOS only started its operations in 2019, a prototype version of the survey has been ongoing since 2011 on the TRAPPIST-South telescope (Gillon et al. 2013) in Chile. As of 2015, this prototype survey has initially detected three transiting temperate Earth-sized planets around an isolated M8 dwarf star at ≃ 12 parsecs from Earth, named the TRAPPIST-1 system (Gillon et al. 2016). The intensive ground-based photometricfollow-up of this system suggests that it hosted several other transiting planets, while leaving their actual number and orbital periods ambiguous. In this context, the Spitzer Exploration Science Program Red Worlds was initiated a 20-day long (i.e., 480 h) near-continuous monitoring of the system at 4.5 μm, which revealed that it hosted no less than seven planets (Gillon et al. 2017a). This was followed by intense, high-precision monitoring of the eclipses of the known planets at 3.6 and 4.5 μm from 2017 to 2018 (520 h). The initial 20-day observation campaign revealed only one transit of the outermost planet (h), making follow-up impossible due to the unknown orbital period until four additional transits were detected with the K2 spacecraft, which enabled further monitoring with Spitzer (Luger et al. 2017a).
One of the primary goals of this ambitious Spitzer program was to create a complete inventory of the transiting objects (planets, moons, Trojans) of the inner system of TRAPPIST-1, not only to constrain its dynamical properties, history, and stability, but also to identify more objects well-suited for detailed atmospheric characterization with next-generation telescopes. It also aimed to perform a thorough assessment of the infrared variability of the star. Finally, it aimed to determine the masses and constrain the orbital parameters of the planets through the transit timing variation method (TTV; Agol et al. 2005; Holman 2005). The precise and accurate determination of the masses and radii of the planets – and the resulting constraints on their bulk compositions – is indeed critical for their thorough characterization, notably for the optimal exploitation of future atmospheric observations (Morley et al. 2017).
Since its discovery, a large number of research investigations have been dedicated to the study of the TRAPPIST-1 system. While a fully comprehensive list of all observational and theoretical results published to date is not practical for this work, we overview several important characteristics of this system in the following paragraph.
First, the host star is an old M8V type star (7.6 ± 2.2 Gyr, Burgasser & Mamajek 2017) with a moderate flaring activity (about 1 or 2 flares per week, Gillon et al. 2017a) and its (putative) stellar rotation period derived from K2 observations by Luger et al. (2017a) is 3.30 ± 0.14 days. Recent study by Gonzales et al. (2019) presented a distance-calibrated SED for the star and found, from band-by-band comparisons, that TRAPPIST-1 exhibits a blend of field star and young star spectral features. Its XUV luminosity is similar to the Sun’s, which, when considering its past evolution – notably its ~2 Gyr-long premain sequence phase (Van Grootel et al. 2018) and the small orbital distances of the planets (between 0.01 and 0.06 au) – potentially drove extreme atmospheric erosion and water loss (Wheatley et al. 2016; Bolmont et al. 2016; Bourrier et al. 2017; Fleming et al. 2020). In short, if the habitable zone planets originally had primordial H ∕He envelopes, XUV evaporation may have rendered the planets habitable (Luger et al. 2015; Owen & Mohanty 2016). Three planets orbit within the habitable zone of the star (Gillon et al. 2017a), and planet e is the most likely to harbour liquid water on its surface (Wolf 2017, 2018; Turbet et al. 2018; Fauchez et al. 2019a).
The seven planets form the longest resonant chain known to date (Luger et al. 2017b; Papaloizou et al. 2018). Some works modeled the planet formation process from small dust grains to full-sized planets, while keeping track of their water content using pebble and planetesimal accretion mechanisms (Ormel et al. 2017; Schoonenberg et al. 2019; Coleman et al. 2019).
The planets are good potential targets for atmospheric characterization with JWST (Lustig-Yaeger et al. 2019; Lincowski et al. 2018, 2019; Wunderlich et al. 2019; Krissansen-Totton et al. 2018; Barstow & Irwin 2016; Fauchez et al. 2019b). Preliminary atmospheric prescreening was performed with HST/WFC3 and the resulting low-resolution transmission spectra acquired in the 1.1–1.7 μm spectral range made it possible to exclude clear hydrogen-dominated atmospheres for six of the seven planets (de Wit et al. 2016, 2018; Wakeford et al. 2018).
Lastly, some works have suggested that the heterogeneous photosphere of the host star could overwhelm planetary atmospheric absorption features in transit transmission spectra because of the so-called transit light source (a.k.a. stellar contamination) effect (Apai et al. 2018; Rackham et al. 2018). Associated models predict important spot and faculae covering fractions (Zhang et al. 2018 find faculae covering ≃ 50%, spots covering ≃ 40%, while Wakeford et al. 2018 find 5800 K hot spots covering <3% and 3000 K hot spots covering ≃35%) for TRAPPIST-1.
While the TRAPPIST system is gradually revealing its properties, some big questions still remain. For instance, we still can not explain why the rotational modulation seen in K2 data is not detected in Spitzer light curves (Delrez et al. 2018b; Luger et al. 2017b; Morris et al. 2018a). Neither do we know if the host star’s high-energy incident flux on the planets can jeopardize their habitability (Roettenbacher & Kane 2017; Vida et al. 2017) or if it can alternatively drive chemical processes needed for life’s origin, through, for example, CME-driven generation of prebiotically relevant molecules (Airapetian et al. 2016), and by increasing NUV flux for the production of life’s building blocks (Ranjan et al. 2017; Rimmer et al. 2018). We are also uncertain on the information content will we be able to retrieve from the planetary transmission spectra and how significant the impact of stellar contamination may be on their interpretation.
In this context, our work aims to meet the initial expectations of the Red Worlds Spitzer exploration program and present them within the framework of the most recent studies on stellar contamination, atmospheric retrieval, and habitability.
This paper is structured as follows. In Sect. 2, we present the observations, their reduction, and describe the data analysis. In Sect. 3, we discuss the results brought by the many analyses carried out, notably the evolution of the measured transit depths over time, the transmission spectra of the planets, their interpretation in terms of stellar contamination and atmospheric spectral features retrieval, the transit timing variations, the occultation signals and emission spectra, the impact of flares on the potential habitability of the planets, and finally the presence of orphan structures in the photometry. We summarize our results in Sect. 4.
 |
Fig. 1 Spitzer photometric measurements (sky blue) resulting from observations of the star from February 2016 to Oct 2019 cleanedof data gaps between the four campaigns. Colored diamonds show the positions of the transits of the different planets withtheir corresponding depth + a constant offset by planet for clarity. |
Number of transits monitored by Spitzer from early 2016 to late 2019 for each TRAPPIST-1 planet.
2 Observations and data analysis
2.1 Observations and data reduction
The dataset used in this work includes all time-series observations of TRAPPIST-1 carried out by Spitzer/IRAC since the discovery of its planetary system: 45 h of observations gathered within the DDT program 12126 in Feb and March 2016 (Gillon et al. 2017a, Delrez et al. 2018b, hereafter D2018), and all data (1080 h) taken within the Spitzer Exploration Science program Red Worlds (ID 13067) between Feb 2017 and Oct 2019 (see Fig. 1) including data from the DDT program 13175 (PI: L. Delrez) targeting occultations of the two inner planets and data from the DDT program 14223 (PI: E. Agol) taken in Oct 2019 to better constrain the masses of the planets and to tighten the ephemeris forecast for observations with JWST,see Agol et al. (2020). All these data can be accessed through the online Spitzer Heritage Archive database1. This extensive dataset includes 65, 47, 23, 18, 15, 13, and 7 transits of planets b, c, d, e, f, g, and h, respectively. Among these 188 transits, 88 are “new”, that is, they were observed in fall 2017 and fall 2019, and were not included in the analysis discussed in D2018 which presented data taken by Spitzer through March 2017. Our aim is to give an overview of the exploration of TRAPPIST-1 system with the Spitzer space telescope, we therefore did not include transits observed with other telescopes, but the results of the analysis of those additional observations can be found in existing papers: Luger et al. (2017b) and Grimm et al. (2018) for K2 observations, de Wit et al. (2016, 2018); Wakeford et al. (2018) for HST observations, Ducrot et al. (2018) for SPECULOOS and Liverpool telescope observations, Burdanov et al. (2019) for VLT, AAT and UKIRT observations. Nevertheless, we use those results later in the paper to constructed the transit transmission spectra of the planets, in Sect. 3.1.4
Back on the Spitzer dataset, we identified 29 blended transits (that is to say transits of multiple planets simultaneously) or partial transits (see Table 1) which were analyzed individually but not included in our global analysis presented in Sect. 3. Indeed, shapes of blended + partial transits are less constraining than well isolated full transits so we chose not to include them in our global analysis of all transits to have a better convergence. We also did not include them in our global planet by planet analyses for similar reasons when the transit was partial, and because we wished to deal with only one planet in these analyses.
Besides, we targeted 28 occultations of TRAPPIST-1b and 9 of TRAPPIST-1c with Spitzer/IRAC channel 2 with the aim to detect a signal or at least obtain an upper bound on the occultation depth and consequently derive the first empirical constraints on the planets’ thermal emission. Indeed, as the orbital planes of the seven TRAPPIST-1 planets are aligned to < 0.3° at 90% confidence (Luger et al. 2017b) their orbital tracks overlap over large fraction of their orbit (Luger et al. 2017a), hence we expect all planets to undergo secondary ecplise. Given the small size of the planets, our best chance to catch an occultation signal is to phase-fold several occultations, which is why focusing on the inner planets (with the smallest periods) is the wisest choice. Furthermore, an updated TTV analysis using all transits observed by Spitzer, HST, K2, and ground-based transits observed up to 2019 (Agol et al. 2020) confirms that the expected eccentricities are very small (eccentricity <0.01 for all planets). In this context, we note that we did not spot any sign of planet-planet eclipses in our analyses of the blended transits, and for none of them was a planet “caught up” by a more inner one during its crossing of the stellar disk.
As described by Gillon et al. (2017a), the star was observed nearly-continuously from 19 Sep to 10 Oct 2016 within the program 13067 (480 h). The rest of the dataset (1061 h) is composed of sequences of a few hours corresponding to the observations of one or several transit(s) and/or occultation(s). For all observations in both bandpasses, each frame is composed of 64 subexposures each of 1.92 s on the target plus an additional 0.8 s for read out, which gives a cadence of a point every 2.06 min.
All these observations were obtained with the Infrared Array Camera (IRAC) (Carey et al. 2004) of the Spitzer Space telescope in subarray mode (32 × 32 pixels windowing of the detector) with an exposure time of 1.92 s. No dithering was used (continuous staring), and the observations were all done using the “peak-up” mode (Ingalls et al. 2016) to maximize the accuracy in the position of the target on the detector’s sweet spot (as detailed in IRAC Instrument Handbook) to minimize the so-called “pixel phase effect” of IRAC detectors (e.g., Knutson et al. 2008). All the data were calibrated with the Spitzer pipeline S19.2.0, and delivered as cubes of 64 subarray images of 32 × 32 pixels (pixel scale = 1.2 arcsec).
All 2016 and 2019 data were obtained with the 4.5 μm IRAC detector. In 2017 and 2018, additional observations were obtained at 3.6 μm with the goal of further constraining the chromatic variability of the transit depths of the seven planets. The same method was used for the photometric extraction as that described by Gillon et al. (2017a) and D2018. We converted the fluxes from MJy sr−1 to photon counts, and then we used the IRAF/DAOPHOT2 software (Stetson 1987) to measure the flux of TRAPPIST-1 within a circular aperture of 2.3 pixels. For each subarray image, the aperture was centered on the star’s point-spread function (PSF) by fitting a 2D Gaussian profile, yielding measurements of the PSF width along the x- and y-axis in the process. We discarded subarray images corresponding to >10 σ discrepant measurements for the PSF center, target flux, and background flux, as described by Gillon et al. (2014). We then combined the measurements per cube of 64 images. The photometric error of each cube (which is the standard error on the mean) was taken as the error of its average flux measurement.
2.2 Data analysis
Our data analysis was divided in three distinct steps. First, we performed individual analyses of each transit light curve to select an optimal photometric model and assess the variability of the photometry, see Sect. 2.2.1. We also carried out an analysis aiming to refine the stellar parameters of TRAPPIST-1, see Sect. 2.2.2. Then, we performed several sets of global analyses: (a) one with the entire set of transits to refine the physical parameters of the system; (b) seven others (one for each planet)for which we allow the transit depths to vary in order to assess their stability; and (c) a repeat of the seven global analyses (planet by planet), this time to improve the errors on the timings, see Sect. 2.2.3. Finally, we carried out a global analysis of the light curves from program 13175 (PI: L. Delrez) obtained around the expected occultation times for planet b and c to search for occultation signals, see Sect. 3.2 for details.
2.2.1 Individual analyses
We used our adaptive Markov-chain Monte Carlo (MCMC) code (Gillon et al. 2010, 2012, 2014) to analyze each transit light curve individually (that is to say each individual transit). It uses the eclipse model of Mandel & Agol (2002) as a photometric time-series, multiplied by a baseline model to represent the other astrophysical and instrumental systematics that could produce photometric variations.
First, we select a model to represent each light curve through the minimization of the Bayesian Information Criteria (BIC; Schwarz 1978) which is given by the formula:
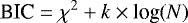 (1)
(1)
where k is the number of free parameters of the model, N is the number of data points, and χ2 is the best-fit chi-square. We tested a large range of baseline models to account for different types of external sources of flux variations/modulations (instrumental and stellar effects). This includes polynomials of variable orders in: PSF size and position on the detector (to account for the Spitzer “pixel-phase” effect and the breathing of its PSF; Gillon et al. 2017a); time (to correct for time dependent trends); and the logarithm of time (to represent the “ramp” effect, Knutson et al. 2008). For some light curves the “pixel-phase” effect was additionally corrected by complementing the position polynomial model with the bi-linearly-interpolated subpixel sensitivity (BLISS) mapping method presented by Stevenson et al. (2012). To do so, we sampled the detector area probed by the PSF center in several sub-pixel box such that at least five measurements fell within the same box. Further details of the implementation of BLISS mapping in our MCMC code can be found in Gillon et al. (2014). The details of the baseline model adopted for each transit light curve are given in Table A.1. Once the baseline was chosen, we ran a preliminary analysis with one Markov chain of 50 000 steps to evaluate the need for re-scaling the photometric errors through the consideration of a potential under- or over-estimation of the white noise of each measurement and the presence of time-correlated (red) noise in the light curve. The white noise is represented by the factor βw issued from the comparison of the rms of the residuals and the mean photometric errors. The red noise is represented by the scaling factor βr derived from the rms of the binned and unbinned residuals for different binning intervals ranging from 5 to 120 min, following the procedure detailed in Winn et al. (2009). The values of βw and βr derived for each light curve are listed in Table A.1.
The jump parameters that were randomly perturbed at each step of the Markov chains were:
-
the mass M⋆, the radius R⋆, the effective temperature Teff, and the metallicity [Fe/H] of the star, assuming the following prior probability distribution functions (PDFs) for these stellar parameters:
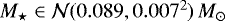 ,
,
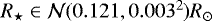 ,
,
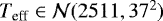 K and [Fe/H]
K and [Fe/H] 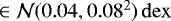 ;
; -
the planet/star area ratio
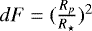 , where Rp
and R⋆
are the radius of the planet and the star, respectively;
, where Rp
and R⋆
are the radius of the planet and the star, respectively; -
the transit impact parameter b for the case of a circular orbit, defined as b = acos(ip)∕R⋆ where a and ip are, respectively, the semi-major axis and inclination of the orbit;
-
the mid-transit time (inferior conjunction) for which we assumed a noninformative uniform prior PDF;
-
the transit duration T14, assuming a circular orbit (justified by really small eccentricities for all planets, Luger et al. 2017a,b; Agol et al. 2020), defined as follow (Winn 2010):
![\begin{equation*} T_{14} = \frac{P}{\pi}\arcsin\left[\frac{R_{\star}}{a}\frac{\sqrt{\left(1+\frac{R_{p}}{R_{\star}}\right)^{2}-b^{2}}}{\sin i}\right] \end{equation*}](/articles/aa/full_html/2020/08/aa37392-19/aa37392-19-eq7.png) (2)
(2) -
the linear combinations of the quadratic limb darkening coefficients (u1, u2) in Spitzer’s 3.6 and 4.5 μm channels, defined as c1 = 2 × u1 + u2 and c2 = u1 − 2 × u2. Values and errors for u1 and u2 in a given band pass were interpolated from the tables of Claret et al. (2012, 2013) basing on the stellar parameters Teff = 2511 K ± 37 K, log(g[cm sec-2]) = 5.18 ± 0.06, and [Fe∕H] = 0.04 ± 0.08 dex, (Delrez et al. 2018b). The corresponding normal distributions were used as prior PDFs (for channel 1:
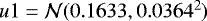 and
and 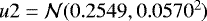 , for channel 2: u1 =
, for channel 2: u1 = 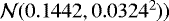 and
and 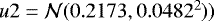 . In terms of combined limb darkening coefficients those value translates as: for channel 1: c1
. In terms of combined limb darkening coefficients those value translates as: for channel 1: c1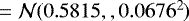 and
and 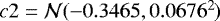 , for channel 2: c1 =
, for channel 2: c1 = 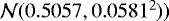 and
and 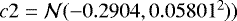 .
.
All of our priors come from the updated system parameters presented in D2018. We recognize that those values were derived from analyses carried out on a subset of the same data set, noting that in this section our intention is not to determine the physical parameters of the system but rather to assess the stability (or variability) of the transits parameters. This subset is sufficient for this assessment.
We then re-scaled the photometric errors by multiplying the error bars by the correction factor CF = βw * βr. Once the correction factor was applied, we ran two Markov chains of 100 000 steps each to sample the PDFs of the parameters of the model and the system’s physical parameters (Ford 2006), and assessed the convergence of the MCMC analysis with the Gelman & Rubin statistical test (Gelman & Rubin 1992). Our threshold for convergence was a Gelman-Rubin statistic lower than 1.1 for every jump parameter, measured across the two chains.
For all of the analyses, the resulting values and error bars for the jump and system parameters as well as the complete details on the assumed baseline and on the correction factor applied can be found in Table A.1, A.2, and A.3. In addition to setting the baseline to use for each light curve, proceeding to individual analyses is also a way to search for variability in the transits, notably spot/faculae crossing or flares events (see Sect. 3.1.3).
2.2.2 Stellar parameters
Stellar parameters
In this paper, we derived stellar parameters using 142 of the 171 TRAPPIST-1’s planets transits observed with Spitzer (the transits not included were either partial or multiple). We proceeded as follows: first we inferred the density of the star ρ⋆ and its error through a global MCMC analysis of all stacked transit (detailed in the following paragraph). Then we derived the mass of the star M⋆ following the empirical relationship between 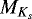 (magnitude in K band) and M⋆ (with M⋆ spanning from 0.075 M⊙ < M⋆ < 0.70 M⊙) derived from 62 nearby binaries by Mann et al. (2019). The mass and its error were estimated by taking the metallicity of the star (from Van Grootel et al. 2018) into account and through the use of the GitHub repository M− − MK− provided by Mann et al. (2019), which accounts for systematic errors. With this estimate of the mass of the star and its error, we derived the radius of the star R⋆ from our posterior probability distribution function (PDF) on the density:
(magnitude in K band) and M⋆ (with M⋆ spanning from 0.075 M⊙ < M⋆ < 0.70 M⊙) derived from 62 nearby binaries by Mann et al. (2019). The mass and its error were estimated by taking the metallicity of the star (from Van Grootel et al. 2018) into account and through the use of the GitHub repository M− − MK− provided by Mann et al. (2019), which accounts for systematic errors. With this estimate of the mass of the star and its error, we derived the radius of the star R⋆ from our posterior probability distribution function (PDF) on the density:
![\begin{equation*} R_{\star}=\Bigg[\frac{3M_{\star}}{4\pi \rho_{\star}}\Bigg]^{1/3}.\end{equation*}](/articles/aa/full_html/2020/08/aa37392-19/aa37392-19-eq17.png) (3)
(3)
Using the exquisite parallax value (d = 80.4512 ± 0.1211 pc) from Gaia DR2 (Lindegren et al. 2018) and the integrated flux derived from Filippazzo et al. (2015), we computed the luminosity of the star, with no correction for extinction:
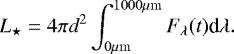 (4)
(4)
Finally, we derived the effective temperature of TRAPPIST-1 from its luminosity and its radius following the Stefan-Boltzmann Law:
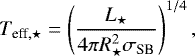 (5)
(5)
where σSB is the Stefan-Boltzmann constant.
We note that the computations of L⋆, R⋆ and Teff are straightforward, such that we don’t need to consider possible systematic errors. Their errors were then computed through error propagation on Eqs. (3)–(5).The stellar parameters derived from this approach are presented in Table 2.
Density inferred from individual planets
In the preceding paragraph we mentioned that we derived the stellar density through a global MCMC analysis of all stacked transit. This method uses the transits shapes and Kepler’s third law to constraint the stellar density (Seager & Mallen-Ornelas 2003). However, in this particular case, the TRAPPIST-1 system is composed of 7 planets, that is to say 7 different sets of transit parameters. Hence, it is legitimate to investigate whether there are noticeable differences between the stellar density value inferred from each individual planet’s analysis and the one inferred from all transits together. The level of agreement between the two values would allow us to justify the use of the globally derived stellar density. Figure 2 shows the stellar density value as obtained from individual planet analysis with its error bars and a color code for the number of transits used in each analysis. Table 3 presents the corresponding values. In those analysis, for the star, M⋆, R⋆, Teff,⋆, [Fe/H], and the linear combinations c1 and c2 of the quadratic limb-darkening coefficients (u1, u2) for each bandpass were jump parameter, with informative priors on M⋆, Teff,⋆, [Fe/H], u1 and u2. And for each the planet, the transit depth 4.5 μm, the impact parameter and the transit depth difference between Spitzer/IRAC 3.6 μm and Spitzer/IRAC 4.5 μm channels were jump parameters.
From Fig. 2, it appears that the inner planets prefer a lower stellar density than the outer ones. This could be translated as a correlation between period P and the inferred stellar density ρ⋆. We carried out a linear regression between ρ⋆ and P, and computed the Akaike information criterion (AIC) and Bayesian information criterion (BIC) to identify the best fit, see Fig. 3.
According to Fig. 3, it turns out that a linear relation between the period and the stellar density is slightly preferred over a constant density (with a functional form of ρ⋆ = 0.65 × P + 45.95). This suggests that a correlation may exist between density and orbital period (and therefore b and T14). However, the amplitude of this bias is smaller than the 1-σ error bars on the stellar density from the individual planet analyses, and therefore we conclude it is insignificant. On the origin of this weak trend in stellar density versus period, it could be the result of a trend of orbital eccentricity with orbital period. However, the eccentricities computed by Agol et al. (2020) do not seem to confirm this scenario. Another explanation could be that it is the consequence of an observational bias, as we have less transits for the outer planets (details on the number of transits per planets in Table 1). As a whole, this comparison shows the advantage of having a multiplanetary system where the planets sample different parts of the stellar disk. We conclude that using the stellar density derived from a global analysis of all transits, as we did in the previous paragraph, is appropriate.
Furthermore, in Fig. 2 we have added the stellar density computed by Agol et al. (2020) using a photodynamical model created with the mass-ratios and orbital parameters derived from a transit-timing analysis. We observe that the value derived from our global analysis is in excellent agreement with the one by Agol et al. (2020), which strengthens our confidence in using this value as the final one.
 |
Fig. 2 Coloured dots gives the stellar density derived from MCMC analyses of transits from a single planet, solid black line gives the density derived from a global analysis of all transits observed with its 1-σ uncertainty in gray shades. Colorbar shows the number of transits used in each analysis. Solid blue line give the stellar density value computed by Agol et al. (2020) using a photodynamical model created with the mass-ratios and orbital parameters derived from a transit-timing analysis, with its 1-σ uncertainty in blue shades. |
Stellar density from individual planets’s MCMC analyses with its 1-σ uncertainty.
 |
Fig. 3 Stellar density inferred from individual planet’s analysis versus period of the corresponding planet and its linear and constant fit with their corresponding AIC and BIC values. |
2.2.3 Global analyses
Once we selected a baseline model for each light curve (see Sect. 2.2.1), we continued to the next steps of our analysis. First, we carried out a global analysis of all the light curves together to refine the transit parameters. This is an update of the parameters presented in Table 1 of D2018 with the advantage that a global analysis with transits in both channels enables us to lift a part of the degeneracy between the transit parameters and the assumed limb-darkening coefficients. Second, we conducted 2 × 7 global analyses of transits for each planet to focus on computing first the transit timing variations and then the transit depth variations.
All light curves
This analysis consisted of a preliminary run of one 50 000 step Markov chain to estimate the correction factors CF that are applied to the photometric error bars (see Sect. 2.2.1) and a second run with two Markov chains of 500 000 steps for which we used the Gelman-Rubin test to assess the convergence. The relatively large number of steps for the two chains is necessary for a data set of this size. This method for analysis is identical to the one conducted by D2018, but includes an increased number of transits observed at 4.5 μm for all planets and newly observed transits at 3.6 μm for planets c, d, e, f, g, and h. The jump parameters were R⋆, M*, Teff, [Fe/H], the linear combinations c1 and c2 of the quadratic limb-darkening coefficients (u1, u2) for each bandpass. For each planet, parameters include:
the transit depth at 4.5 μm, dF4.5μm;
the impact parameter, b;
the transit depth difference between Spitzer/IRAC 3.6 μm and Spitzer/IRAC 4.5 μm channels, ddF = dF3.6μm − dF4.5μm;
the transit timing variation (TTV) of each transit with respect to the mean transit ephemeris derived from the individual analyses.
For the mass of the star, we used a normal prior PDF based on the value derived in Sect. 2.2.2 (M⋆ = 0.0898 ± 0.0024 M⊙). Then, for the metallicity and the limb-darkening coefficients in both channels we assumed the same normal prior PDFs as in Sect. 2.2.1. For the rest of the jump parameters, we assumed uniform noninformative prior distributions. We did not set the transit duration as a jump parameter because it is defined for each planet by its orbital period, transit depth, and impact parameter, combined with the stellar mass and radius (Seager & Mallen-Ornelas 2003). Furthermore, dynamical models predict rather small amplitudes of variation for the transit durations (Luger et al. 2017a). The convergence of the chains was checked with the Gelman-Rubin statistic (Gelman & Rubin 1992). The value of the statistic was less than 1.1 for every jump parameter, measured across the two chains, which indicates that the chains are converged. From the jump parameters the code deduced the physical parameters of the system at each step of the MCMC. In particular, the value of the effective temperature, Teff, was derived at each MCMC stepfrom the R⋆ and L⋆ values givenin Sect. 2.2.2. Then, for each planet, values for the radius of the planet Rp, its semi-major axis a, its inclination i, its irradiation Sp, and its equilibrium temperatureTeq were deduced from the values for the stellar and transit parameters. Table 4 presents the outputs from this analysis.
We note that prior to this paper different stellar parameters for TRAPPIST-1 were published. In 2019, Gonzales et al. (2019) presented a distance-calibrated SED of TRAPPIST-1 using a new NIR FIRE spectrum and parallax from the Gaia DR2 data release from which they derived updated fundamental parameters for the star. Back in 2018, Van Grootel et al. (2018) derived stellar parameters from two distinct approaches to compute the mass of the star, first via stellar evolution modeling, and second through an empirical derivation from dynamical masses of equivalently classified ultracool dwarfs in astrometric binaries. The stellar parameters we derived are in agreement with those from previous studies, as shown in Table 5.
Planet by planet
For each planet, the analysis itself was divided in three: a global analysis to extract the TTV of each transit, a global analysis with a free variation of the transit depth allowed to monitor its evolution with time, and finally an analysis of the occultation observationsfor planets b and c.
- (a)
Transit timing variations: we used nearly the same priors and jump parameters as in the individual analyses although we fixed the time of transit for epoch zero (T0) and period P for each planet, and set TTV as a jump parameter for each transit. The priors value for T0 and P are extracted from D2018. In this analysis, the same depth was assumed for all transits observed in the same bandpass. For each transit, we assumed the same baseline as the one obtained from its individual analysis. Then, after one 50 000 step Markov chain, we re-scaled our photometric errors with the resulting correction factor and ran two Markov chains of 100 000 steps. Transits timings and their corresponding TTVs are reported in Table A.6 and displayed in Fig. 4. From those, for each planet we performed a linear regression of the timings as a function of their epochs to derive an updated mean transit ephemeris, i.e., an updated value of the mid-transit time T0 and the orbital period P for each planet, see Table 4 (as done in D2018). Finally the median of the global MCMC posterior PDF of the transit depth in both channels are given in Table 6, those results are discussed in Sect. 3 and used to constructthe planetary transmission spectra in Sect. 3.1.4.
- (b)
Transit depth variations: here, we also used similar priors as in the individual analyses except that we fixed the values of transit timings and periods P but for jump parameters we set the TTV of each transit and δdF, the depth variations from one transit to another. Again we ran first a 50 000 steps Markov chain to get the CF, andthen two 100 000 steps chains. The evolution of the transit depths as a function of the epochs is presented for each planet in Fig. 5. For further comparison, these figures also display the mediansof the global MCMC PDFs as obtained by the previous global analysis with TTV and no δdF variations, values from Table 6. We compared the results obtained from the individual and global analyses of the transits and found them to be fully consistent. In Fig. 5 we chose to plot the depth values obtained from the global analysis with δdF variations allowed instead of the individual analyses because the global analysis should be less impacted by systematic errors due to the red noise (i.e., the response of the pixels to time-varying illumination) in Spitzer photometry.
- (c)
Occultations: we also used the eclipse model of Mandel & Agol (2002) to represent occultations of TRAPPIST-1b and c as photometric time-series, multiplied by a baseline model to represent external sources of photometric variations (either from astrophysical or instrumental mechanisms). The details of this analysis are given in Sect. 3.2, where we discuss the occultation observations and their interpretation. In this work, we analyzed29 occultations of planet b and 8 occultations of planet c. All windows were observed in channel 2 (4.5 μm) as part of the DDT program 13175 (PI: L. Delrez). Our aim was to constrain the day-side brightness temperature of the two inner planets from the occultation depths. For both planets, we performed a global analysis of the occultation light curves, assuming as priors the Gaussian PDFs corresponding to the values for the stellar parameters and for the planets’ transit depths, impact parameters, mid-transit-times, and orbital periods derived from our global analysis of all Spitzer transit light curves (Table 4). Circular orbits were assumed for both planets, andthe occultation depth was the only jump parameter of the analyses for which a uniform prior PDF [0, +∞) was assumed.Wejustify circular orbits assumption from the fact that in a system with planets that have migrated in Laplace resonances orbital, like TRAPPIST-1, eccentricity are expected to be very small. Indeed simulations carried out by Luger et al. (2017a) show that within a few Myr eccentricities of each planet damped to less than 0.01. In addition, recent results by Agol et al. (2020) from TTV and photodynamical model confirm that all planets eccentricities are most likely inferior to 0.01. Furthermore, when calculating the timing of secondary eclipse using the eccentricities given by Agol et al. (2020) and their 3-σ uncertainties we compute a shift in time of 0.28 and 0.27 h for planet b and c respectively. Considering that the out-of-secondary eclipse time is ≃2 h for each light curve of this DDT program, we can confidently state that we did not miss the time of secondary eclipse. As with the transit analysis reported above, we identified the most applicable baseline for each light curve and ran a first chain of 50 000 steps to get the CF coefficients, applied these coefficients to the photometric error bars, and then ran two MCMC chains of 100 000 steps. We ascertained the convergence of our analyses with the Gelman & Rubin test (less than 1.1 for all jump parameters, as recommended by Brooks & Gelman 1998; Andrew Gelman 2003). Unfortunately, no significant occultation signal was detected, Table 7 gives the occultation depth as output by the MCMC analysis with its 1 sigma and 3 sigma uncertainty. Those results are discussed in Sect. 3.2.
 |
Fig. 4 TTVs measured for the seven planets as obtained from our global planet by planet analyses (see Sect. 2.2.3) relative to the ephemeris (T0 and P) given in Table 4. |
Updated system parameters: median values and 1-σ limits of the posterior PDFs derived from our global MCMC analysis of all nonblended and partial transits of Trappist-1 planets observed by Spitzer.
Comparison of stellar parameters value from various studies.
Median of the global MCMC posterior PDF of the transit depth derived from global analyses of all transits, planet by planet, with no transit depth variations allowed.
Median of the occultation depths global MCMC posterior PDF + their 1-σ and 3-σ uncertainitiesas derived from the global analysis of 28 occultations of TRAPPIST-1b and 9 occultations of TRAPPIST-1c observed at 4.5 μm.
3 Results and discussion
3.1 Transits
3.1.1 Mean transit ephemeris
Our global analysis of the transits of the seven planets led to an updated mean ephemeris, given in Table 4. The mean ephemeris for each planet was derived from a linear regression of the timings derived in Sect. 2.2.3 – planet by planet – as a function of their epochs. The new ephemerides are consistent with the ones derived in D2018. They do not take into accountthe TTVs, but should be sufficiently precise to forecast transit observations with an accuracy of better than ~30 min (for theouter planets, and much better for the inner ones) within the next couple of years.
3.1.2 Noise floor
From the transit depths globally derived in each band (Table 6), and from the mean error on the depths of each transit given in Tables A.4 and A.5, we can estimate the amplitude of the noise floor of Spitzer transit monitoring of TRAPPIST-1. To do so, we compute the mean depth error 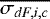 for the ith planet in each band, c, from Tables A.4 and A.5. Assuming a purely white noise, the expected error for n transits of planet i in band c should be
for the ith planet in each band, c, from Tables A.4 and A.5. Assuming a purely white noise, the expected error for n transits of planet i in band c should be 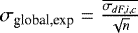 . We then subtract in quadrature this expected value from the globally derived transit depth to estimate the Spitzer noise floor:
. We then subtract in quadrature this expected value from the globally derived transit depth to estimate the Spitzer noise floor:
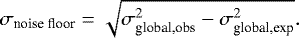 (6)
(6)
From Eq. (6) we calculate the noise floor for each planet and derive the mean noise floor in each channel. The resulting values are 36 ppm in channel 1 and 22 ppm in channel 2. These values are consistent – and even lower actually – than those derived for a sample of ~20 bright sun-like stars by Gillon et al. (2017b). Considering how small these values are, we can conclude that stacking dozens of transits of TRAPPIST-1 observed in the infrared does improve the precision nearly in a 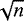 manner. This agrees well with the high photometric stabilty of TRAPPIST-1 observed during its Spitzer 20d continuous monitoring (Gillon et al. 2017a; Delrez et al. 2018b). Furthermore, the larger value of the noise floor at 3.6 μm – as observed by Gillon et al. (2017b) for brighter Sun-like stars – suggests that this floor is mostly of instrumental origin, as the pixel-phase effect is significantly larger in IRAC channel 1 than in channel 2 and requires more complex baseline models (see Table A.1).
manner. This agrees well with the high photometric stabilty of TRAPPIST-1 observed during its Spitzer 20d continuous monitoring (Gillon et al. 2017a; Delrez et al. 2018b). Furthermore, the larger value of the noise floor at 3.6 μm – as observed by Gillon et al. (2017b) for brighter Sun-like stars – suggests that this floor is mostly of instrumental origin, as the pixel-phase effect is significantly larger in IRAC channel 1 than in channel 2 and requires more complex baseline models (see Table A.1).
These results are particularly encouraging for the upcoming atmospheric characterization of the planets by transit transmission spectroscopy with JWST (Gillon et al. 2020). Indeed, the detectors of the JWST instruments (HgCdTe for all except SiAs for MIRI) should all have a much better intrapixel homogeneity than the IRAC InSb arrays, which should result in much less severe position-dependent effects in the JWST spectrophotometric light curves. This is supported by the results obtained by Kreidberg et al. (2014), who observed 15 transits of GJ1214b with HST/WFC3 (also an HgCdTe array, like NIRISS, NIRSPEC and NIRCAM) and obtained global transit depth errors consistent with a noise floor of ~ 10 ppm. Based on these considerations, noise floors in the 10–20 ppm range can thus be expected for JWST observations of TRAPPIST-1, low enough to enable the detection and characterization of compact atmospheres around the planets (e.g., Lustig-Yaeger et al. 2019).
 |
Fig. 5 Left: evolution of the measured transit depths from the planet- per- planet global analyses of transit light curves at 3.6 μm. The horizontal black lines show the medians of the global MCMC posterior PDFs from the planet- per- planet analyses with TTV and no transit depth variations allowed (with their 1-σ and 2-σ confidence intervals (see values in Table 6) in shades of gray). Events are ranked in order of capture, left to right (but not linearly in time). Right: similarly, but for transits observed at 4.5 μm. |
3.1.3 Time-dependent variations of the transit depths
One possible way to gain insight into the host star of a planetary system is to use transits as a scan of the stellar photosphere(Espinoza et al. 2018). By comparing the transit depths at different epochs we can identify unusual events that could inform us about the (in-)homogeneity of the star. Spot and faculae crossings are typically the kind of signatures detected with this method. For this purpose, we looked for unusually low or high depth values in the results from the global planet-by-planet analyses (Fig. 5). We identified one clear outlier at 3-σ lower than the other measurements for planet g (first point of the plot at 4.5 μm on Fig. 5, epoch 0). The corresponding light curve and the fit for this epoch obtained from the global analysis are displayed in Fig. 6.
Yet, when we look at the same light curve as modeled in the global planet-by-planet analysis assuming a constant transit depth (Fig. 6, bottom panel), the first part of the transit seems to be consistent with the global model, while the rest is affected by a significant flux increase as expected for a spot-crossing event (Espinoza et al. 2018).
The discrepancy between individual and global fits is explained by the fact that in the global analyses per planet the model tries to optimize the fit with free transit depth variations allowed so the MCMC favor an unusually small depth for planet g to fit the unusual structure (see Fig. 6). From the individual fit, Fig. 6 bottom panel, we see that the structure in transit is very large (almost as long as the transit duration). If it corresponds to a spot crossing event the latter must be very large and at quite a low latitude as planet g has an impact parameter of ≃ 0.42 from Table 4. To investigate the origin of this structure, first we checked all the planetary transits happening near the outlier, meaning several days before and several days after the event, and found no evidence of a similar structure in any of those transits including transits of TRAPPIST-1f, the planet with the closest impact parameter to planet g (see Table 4). Nevertheless, it is worth mentioning that the closest transit of planet h to the event(happening 3 days before the event at 2 457 662.55449 JD precisely) is one of the outliers shown in Fig. 8 (see below for details of this figure), yet this light curve is particularly noisy in- and out- of transit and therefore not reliable. Secondly, as this event was captured during the continuous observation of the system by Spitzer in 2016, we looked in the photometry for evidence of important variations in the amplitude of the stellar variability around this event as a sign of a sudden appearance of a massive spot that could explain the structure in planet g’s epoch 0 transit. To do so we applied a time rolling window (of fixed size equal to 20 min) on the residuals of the detrended light curve corresponding to several days before and after the event, and from this rolling window we calculated the standard deviation and amplitude of the residual in order to catch any significant increase. Unfortunately, there does not seem to be any correlation between the appearance of the structure in the transit light curve of g and the variability of TRAPPIST-1, and as the Spitzer space telescope underwent some tracking problems during this campaign, our interpretation is limited. In a nutshell, this event is most probably isolated, which weakens the spot-crossing hypothesis considering that a massive photospheric heterogeneity would be needed to explain the observations. Nevertheless, as this structure cannot be corrected with any detrending of the systematics,one could still hypothesize that planet g transited with a different stellar hemisphere facing Earth than the other planets, or at least compared with f and h (as they have similar transit chords), and that the expected changes in stellar variability for such a large spot is not significant enough in the near infrared to significantly influence the stellar variability. However, this hypothesis is ruled out by the monotonic increase in the planets’ transit duration and impact parameters with orbital period, which implies an extremely coplanar planet system (Luger et al. 2017b).
Based on this experience with planet g, we visually inspected all individual light curves associated with the other outlier values in the global analysis results of Fig. 5, but we did not find additional peculiar transits. To identify transit depth anomalies, we compute the median values and deviation of the photometric residuals in and out of transit (Table. A.7) as derived from the planet-by-planet global analyses (like in D2018). Figure 7 and Table A.7 present the standard deviations obtained for the in- and out of transit residuals. Such statistics allow us to investigate the localized spot/faculae population through the “in-transit” variations and the global stellar activity more generally through the “out-of-transit” variations. We deal specifically with stellar flares in Sect. 3.3.
Considering the scatter of the measurements throughout the observations, we choose to define outliers as measurements whose standard deviations of the residuals is above 769 ppm (median of deviation in- and out-of-transit + 3-σ, dashed gray line on Fig. 7). Then, a careful look at all the light curves allows us to understand the source of uncertainty of those measurements. We were particularly interested in cases where the standard deviation of the in-transit residuals is larger than the standard deviation of the out-of-transit residuals as this could correspond to spot or faculae crossing events. Yet, we kept in mind that a the standard deviation of the residuals in-transit has a lower precision because it is calculated with fewer points than the standard deviation of out-of-transit residuals as the planets spend more time out-of-transit than in-transit, limiting the amount of data that can be collected in-transit. In Fig. 7, we identify nine outliers, notably two transits of planet b which show a standard deviation of the in-transit residual of more than 1000 ppm and 900 ppm respectively. The corresponding light curves are presented in Fig. 8.
In Fig. 8, we observe that for some light curves the large value of the standard deviation of the in-transit residuals is explained by a structure that modifies the shapes of the transit. Such structures could indeed be due to the crossing of spots or faculae located within the transit chord of the planet at the time of transit. Light curves #1, #2, #4, #5, #6 and #9 could be interpreted as cases of bright spot crossing, while light curves #3, #7, and #8 could be interpreted as cases of dark spot crossing. The potential presence of spots could be worrisome for a precise derivation of the radius of the planets which is an essential step toward their detailed characterization (Roettenbacher & Kane 2017). To weight the relevance of those anomalies and leverage the statistical bias mentioned above, we calculated the significance of the difference between the median residual in- and out-of-transit which we define by the following formula:
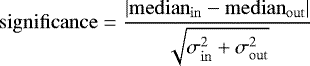 (7)
(7)
where medianin and medianout are the medians of the residuals in- and out-of- transit, and σin and σout are the absolute deviations of the residuals in- and out-of-transit, respectively. The results are presented in Table A.7 and in Fig. 9 for clarity.
We do not notice any significant difference between the in- and out-of-transit medians as they are comparable to within 1σ for all transits, see Fig. 9. Those results do not favor the spot/faculae crossing hypothesis to explain the variability in transit depths that we discussed earlier, but rather systematic effects or some high-frequency stellar variability equally affecting in- and out-of-transit data to explain those anomalies. In fact, most of the outliers identified previously belong to the second of the five campaigns, during which the Spitzer telescope had some known drifting issues due to the use of inaccurate pointing coordinates (Gillon et al. 2017a). We conclude that although it is hard to firmly discard this scenario, our results do not support the presence of stellar photospheric heterogeneities (spots and faculae affecting the transit shape at 3.6 and 4.5 μm). However, one could argue that the lower contrast expected in the mid-IR may explain why we do not firmly detect any spot/faculaecrossing event. Yet, recent results by Ducrot et al. (2018) failed to observe any spot crossing event in either the visible or the near-IR which favors a rather homogeneous stellar photosphere, at least for the portion transited by the seven planets. If numerous, spots would be expected to be relatively cool and small or out of the transits chords to agree with the very few events observed, see D2018, Ducrot et al. (2018), and Morris et al. (2018c). Nevertheless, it is still worth mentioning that some techniques are being developed to recover the true radii of planets transiting spotted stars with axisymmetric spot distributions from measurements of the ingress/egress duration, on the condition that the limb-darkening parameters are precisely known, see Morris et al. (2018b). The authors of the latter paper applied this technique to TRAPPIST-1 and concluded that active regions on the star seem small, low contrast, and/or uniformly distributed (Morris et al. 2018a). In any case, future JWST observations are expected to be more precise, less impacted by the limb darkening effect and therefore decisive for the confirmation of those conclusions, especially with an instrument like NIRSpec that will be able to cover a large spectral range (from 0.6 to 5.3 μm, Ferruit et al. 2014).
Figure 10 shows the period-folded photometric measurements for all transits in both bands, corrected for the measured TTVs as well as the corresponding best-fit baseline models. We observe no recurrent structure for all planets. The limb darkening effect is less important at those wavelengths than in the visible or near-IR (see Ducrot et al. 2018)and the difference between the two channels is hardly noticeable by eye in Fig. 10.
 |
Fig. 6 Top panel: detrended light curve of the first isolated transit of TRAPPIST-1g observed by Spitzer with, superimposed in red, the best-fit model resulting from the global per-planet analysis with variations of the transit depth allowed. Bottom panel: similar to top panel but with the best-fit model resulting from the individual analysis assuming a constant depth for all transits superimposed in darkblue. |
 |
Fig. 7 Standard deviation of the residuals (ppm) in- and out-of-transit for each planet (filled dots for in-transit data, empty dots for out-of-transit) such that for each transit’s epoch there is one empty dot and one filled dot. Each color is associated with a planet: purple for planet b, orange for c, yellow for d, olive for e, dark green for f, teal for g and turquoise for h. The dashed gray line show the limit value above we label the transits as outliers. |
3.1.4 Transmission spectra of the planets
Stellar contamination
As mentioned above, the TRAPPIST-1 planets are promising candidates for atmospheric characterization for several different reasons: the proximity of the system, the short periods of the planets, and their large sizes relative to their host. Yet, the host star itself might turn out to be an obstacle in characterizing the atmosphere of the planets if its photospheric inhomogeneity and evolution (formation, fading, and migration of spots/faculae) complicate the retrieval of atmospheric transmission signals. Consequently, a growing number of studies are dedicated to understanding the role played by the star’s activity and by the heterogeneity of its photosphere when studying exoplanets with the transit method (for studies of TRAPPIST-1, see Apai et al. 2018; Rackham et al. 2018; Zhang et al. 2018; Wakeford et al. 2018). To confirm the detection of atmospheric spectral features of terrestrial planets it is essential to optimize the disentanglement of signals of planetary and stellar origin. As stated before, intensive photometric follow up is an efficient way to probe the time-variable component of stellar activity of the host star. In the previous section we focused on the impact of the presence of stellar photospheric heterogeneities within the transits chords only. Here we discuss the potential impact of spectral contamination from out-of-transits spots & faculae on the chromatic variability of the transit depth through the transit light source effect (more details below) and how this can complicate the characterization of the planets. In particular, we construct the broadband transmission spectrum of each planet to estimate the amplitude of potential false spectral features introduced by star spots and faculae. In Fig. 11, we show the updated version of the transmission spectra of the seven planets presented by Burdanov et al. (2019). This update consists of an additional point at 3.6 μm for planets c–h, updated values at 4.5 μm, and updated weighted mean values for all planets (continuous lines in the plot). Figure 11 combines results from de Wit et al. (2016, 2018), Ducrot et al. (2018), Wakeford et al. (2018), and Burdanov et al. (2019) and shows transmission spectra with the largest number of experimental measurements to date for the TRAPPIST-1 planets. We have decided not to include HST measurements (de Wit et al. 2016, 2018; Wakeford et al. 2018) to compute the weighted mean depth for each planet (black continuous line). This choice is justified by the fact that, although the transit transmission spectra measured in HST/WFC3 spectra are certainly reliable in relative terms, the derived absolute value of the transit depths themselves can be questioned because HST/WFC3 spectrophotometric observationsare affected by orbit-dependent systematic effects which can result in diluted or amplified monochromatic transit depths, as implied by several previous studies (de Wit et al. 2016; Wakeford et al. 2018; Ducrot et al. 2018).
Concerning the Spitzer observations only, in Fig. 11 we observe that for all planets there are no significant differences between the 3.6 and 4.5 μm measurements (particularly in comparison with visible and near-IR variations), both agreeing with each other better than 2-σ for all planets (value given in Table 6). When we next consider all of the observational points, the depths measured at different wavelengths are all consistent with each other at better than 1-σ for planet b, and better than 2-σ for planets d and g. However, for planets c, e, f, and h the transmission spectra show a scatter larger than expected based on the measurement errors alone. For planet h, only one point exceeds the two sigma confidence, the one derived from the Liverpool Telescope (LT) dataset. But, it is worth mentioning that the effective wavelength for LT observations (0.9046 μm) is very close to that of SPECULOOS (0.9102 μm) and yet the SPECULOOS value is not discrepant with the others. Furthermore those data were obtained at the same period on SPECULOOS and LT. Therefore, the difference in depth measurements between those two facilities is probably more of a systematic rather than a physical origin. Yet, for planet c and e, the points that are the most inconsistent with the weighted mean value are the measurements obtained from observations carried out in the near-Infrared, with either UKIRT, VLT, AAT, or HST. Such spectroscopic transit depth variations could be the result of photospheric heterogeneity on the host star, such as unocculted active regions, which could alter the observed transit depths through the transit light source effect (Rackham et al. 2018). This effect refers to the case where a difference between the disk-averaged spectrum and the spectrum of the transit chord – which is the actual light source from the measurement – imprints spectral features on the observed transmission spectrum (Rackham et al. 2019). In that regard, Zhang et al. (2018) modeled the transit light source effect by adapting spots parameters to fit the empirical transit depth of theTRAPPIST-1 planets derived from K2, SPECULOOS, LT, HST, and previous Spitzer observations (Ducrot et al. 2018; de Wit et al. 2016, 2018; Wakeford et al. 2018, D2018). The new depths that we derived at 3.6 μm for planets c, d, e, f, g and the updated value at 4.5 μm for all planets allow us to compare two new observational values with the theoretical predictions of Zhang et al. (2018). Figure 12 shows the combined transmission spectrum for b+c+d+e+f+g+h and best-fitting contamination model formerly computed by Zhang et al. (2018) using K2+SSO+HST+Spitzer (IRAC channel2, D2018). We computed the χ2 statistic value of the best-fit contamination model published in Zhang et al. (2018) to our observational points (that contains updated and new points compared to the values used in Zhang et al. 2018). We obtain a χ2 of 17.5 with a p-value (Pearson 1900) of 0.29, indicating that the model is not ruled out by the data. The next step would be to see if those new data points could be better fitted with a new run of the model presented by Zhang et al. (2018) or with any other model, but this is out of the scope of this paper.
Based on their analysis, Zhang et al. (2018) concluded that TRAPPIST-1 should be covered at ≃ 50% with spots and ≃40% with faculae overall. Yet, their model predicted some location-dependent spot covering fraction over the star. For instance it favored a scenario where the region transited by the planets was less spotted than the whole disk, with a spot covering fraction of only ≃ 10% of the transit chord. The authors interpreted this mismatch as the presence of an active region left unprobed by the transit chords, suchas an active high-latitude or circumpolar spot. Similar structures had already been observed on fully convective M-dwarfs (Barnes et al. 2015, 2017). In light of the previous section which showed that neither our work nor D2018 nor Ducrot et al. (2018) detected clear spot/faculae crossing events, while the transit chords represent 56% of the hemisphere (D2018), and considering the results of Zhang et al. (2018), it could indeed be possible that spots appear at preferential latitudes, like the poles. As mentioned by Zhang et al. (2018), one way to confirm this could be to use Doppler tomography with the upcoming E-ELT/HIRES instrument, as has already been done for a few brighter stars (Barnes et al. 2005), or to use spectral template fitting to constrain spot sizes and population through molecular band observations (Vogt 1979). Meanwhile, analyses driven by Morris et al. (2018c) on the Spitzer dataset (observations carried out from 2016 up to 2017) using the self-contamination method from Morris et al. (2018b) suggest that the mean photosphere of TRAPPIST-1 was rather similar to the photosphere occulted by the planets, even if they could not rule out a scenario of small-scale magnetic activity analogous in size to the smallest sunspots present within (or outside) of the transit chords. Such a scenario could also agree with our empirical results but cannot be confirmed with the current photometric precision of the existing instruments. Last, it is important to mention that a method to separate the planetary transmission spectrum from stellar molecular features using the out-of-transit stellar spectra, planetary transit geometries, and planetary atmospheric models has been developed by Wakeford et al. (2018). After discarding several scenarios, Wakeford et al. (2018) concluded that a three component flux model composed of the photosphere, hotter spots (≃ 35%) and some faculae (<3%), with an additional small fraction of flux (1%) from magnetic activity would be the most likely scenario for TRAPPIST-1, and that the planetary transmission spectra were likely not contaminated by any stellar spectral features (Wakeford et al. 2018).
Considering next the transit spectra of planets c and e, it should be emphasized that, as mentioned in Sect. 3.1.3, de Wit et al. (2016, 2018) warned us that HST/WFC3 spectrophotometric observations are affected by orbit-dependent systematic effects, which can alter the monochromatic absolute transit depth values. Furthermore, concerning the measurements obtained from UKIRT, VLT and AAT, Burdanov et al. (2019) highlighted a few data gaps during some observations that could have influenced the derived transit depth values, and also emphasized how strong the influence of water vapor can be at those wavelengths for ground-based observations. Finally, those observations are also the least numerous ones, with less than 3 combined transits for all planets used to derive the values plotted in Fig. 11 in the corresponding bands. For these reasons, it is important to remain cautious about the relevance of our interpretation of planet c and e transmission spectra. For planet f, however, it is different as the dispersion of the measurements is even larger, with clear outliers in J band and in the visible. On one side, we could again argue for low statistics in the near-IR band to justify the large gap between UKIRT measurement and the weighted mean value, as only 3 transits were used to compute this value. But in the visible, K2’s surprisingly low depth value seems more robust as it was derived from the combined analysis of 6 transits. The transmission spectrum of planet f is really intriguing and more observations in the near-IR and visible are required to draw proper conclusions on the origin of its larger scatter.
All things considered, we can confidently state that the observed transmission spectra of the TRAPPIST-1 planets are not flat, but we cannot conclude on weather those variations could be attributed to stellar contamination or low statistic data. Nonetheless, these Spitzer observations provide unique statistics and show no discrepancy greater than 400 ppm peak-to-peak and consistency at better than 2-σ for all planets. Recent papers are converging toward a three spectral component TRAPPIST-1 photosphere as the most likely scenario (Rackham et al. 2018; Zhang et al. 2018; Wakeford et al. 2018), and authors are proposing different approaches to constrain this stellar photosphere, such as: time resolved spectral decomposition (Gully-Santiago et al. 2017); joint retrievals of stellar and planetary properties (Pinhas et al. 2018); visual transmission spectroscopy (Rackham et al. 2017); transit-crossing events (Espinoza et al. 2018); or the use of out-of-transit stellar spectra to reconstruct the stellar flux (Wakeford et al. 2018). The combination of multiple approaches toward the study of the star’s photosphere represents a promising path toward the disentangling of the planetary atmospheric features from the stellar signals and therefore the optimization of future transit transmission spectroscopy with the eagerly-awaited JWST.
 |
Fig. 8 Transit light curves and their residuals for the 9 outliers identified on Fig. 7. Each outlier was attributed anumber in chronological order from 1 to 9, and the corresponding transiting planet at the time is indicated within the brackets. |
 |
Fig. 9 Significance of the difference between the median of the residuals (ppm) in and out of transit for each planet computed as: significance = |
 |
Fig. 10 Left: period-folded photometric measurements obtained with Spitzer/IRAC channel 1 (at 3.6 μm) near thetransits of the seven planets, corrected for the measured TTVs. Colored dots show the unbinned measurements; open circles depict the measurements binned over 5 min for visual clarity. The best-fit transit models are shown as dark blue lines. The numbers of transits that were observed to produce these combined curves are written on the plot. Right: similarly at 4.5 μm. |
 |
Fig. 11 Updated version of the transit transmission spectra of the seven TRAPPIST-1 planets. In each subplot the continuous line is the weighted mean depth |
 |
Fig. 12 TRAPPIST-1 combined transmission spectra for planets b+c+d+e+f+g (blue points) constructed from individual spectra (see Fig. 11), over-plotted with the stellar contamination model (black solid line) derived by Zhang et al. (2018) from the fit of previously published K2 + SPECULOOS-South (Ducrot et al. 2018) + HST (de Wit et al. 2016, 2018; Wakeford et al. 2018) + Spitzer (D2018) data. The black squares are the integrated depth values as predicted by the stellar contamination model of Zhang et al. (2018) in each spectral band for which observationswere performed, and gray dashed lines is the flat model at the weighted mean value of the transit depth. Wavelength is in log scale. |
Comparison with atmospheric models
One of the most ambitious results that the exoplanet community wishes to achieve with the upcoming JWST is the first detection of an atmosphere around a terrestrial exoplanet (Madhusudhan 2019). For the reasons discussed earlier, the TRAPPIST-1 system is particularly favorable for the achievement of this goal via transit transmission spectroscopy (Barstow & Irwin 2016; Morley et al. 2017; Batalha et al. 2018; Krissansen-Totton et al. 2018; Lustig-Yaeger et al. 2019; Fauchez et al. 2019b), and offers the opportunity to probe atmospheres not only around terrestrial planets but also around temperate terrestrial planets within the habitable-zone of their host star. In the previous section, we discussed the impact of stellar contamination on the planet transmission spectra, and we concluded that several solutions are being developed to optimize the retrieval of planetary atmosphere features. In this section, we do not consider stellar contamination and only discuss potential detections of atmospheric features of the TRAPPIST-1 planets. Here, we limit our discussion to include only the cases of TRAPPIST-1b, c, e and g because (a) b and c have the smallest periods – that is to say the most transits and therefore the greatest precision on measurements, (b) planet e is arguably the most promising candidate for habitability, for the reasons given in Wolf (2017, 2018), Turbet et al. (2018) and Fauchez et al. (2019a), and (c) planet g was the most observed with HST/WFC3 (Wakeford et al. 2018).
Combining ground and space-based observations, we can construct the broadband transmission spectra obtained in various wavelengths for each planet and compare them to recent atmospheric models of the TRAPPIST-1 atmospheres computed by Lincowski et al. (2018), see Fig. 13. To construct this figure, we have added a vertical offset to Lincowski et al. (2018)’s models to optimally overlap the observations. These offsets correspond physically to the difference between the assumed radius for TRAPPIST-1b and the solid body radius assuming a model atmosphere and its associated absorbing radius above the surface (Lincowski et al. 2018). We have applied this offset such that the models crossed the measured transit depth at the value of the sum of the weighted mean depth of each planet (shown in black solid line on Fig. 11). For the reasons mentioned above we also applied an offset to adjust the mean level of each HST/WFC3spectra to the weighted mean depth for each planet. By doing this we can benefit from the trustful information given by HST/WFC3 measurements on relative depths and use it to better constrain atmospheric properties.
Those spectra illustrate our current knowledge of the transit transmission spectra gained from follow-up observations. The wavelength range that has been probed since the discovery of the system goes from ≃ 0.6 μm to ≃ 5 μm. In this spectral range the strongest molecular features that we could expect in the absence of clouds and haze – and in a plausible planetary environment – are CO2, CH4, H2 O and CO (Tennyson & Yurchenko 2012; Gordon et al. 2017; Morley et al. 2017). Considering the distribution of the effective wavelength of the different instruments we can only look for some localized, strong features: the CO2 4.3 μm spectral feature in the 4–5 μm channel of Spitzer/IRAC (width of the bandpass is 1.015 μm for that channel), the CO2 2.1 μm spectral feature in the VLT/HAWK-I’s NB-2090 filter bandpass (width of the bandpass is 0.020 μm for NB-2090 filter), and the CH4 3.3 μm spectral feature in the 3.15–3.9 μm channel of Spitzer/IRAC (width of the bandpass is 0.750 μm for that channel).
We deliberately did not consider models of hydrogen-dominated atmospheres as there is now plenty of evidence that all TRAPPIST-1 planets are unlikely to host this kind of atmospheres. First, transmission spectroscopy with HST/WFC3 has shown that most of the planets in the system are unlikely to have cloud-free H2-rich atmospheres (de Wit et al. 2016, 2018; Wakeford et al. 2018). Although transmission spectroscopy cannot rule out H2-dominated atmospherescontaining high-altitude aerosols (Moran et al. 2018), such configuration is in fact unlikely. This stems from the fact that any small variation of hydrogen content between planets, as expected from (1) variations in the hydrogen-rich gas accretion rates during the planet formation phase (Hori & Ogihara 2020) and from (2) variations in H2 escape rates (Owen & Mohanty 2016; Bolmont et al. 2017; Bourrier et al. 2017), are expected to produce large variations in density between planets (Turbet et al. 2020) that are not observed (Grimm et al. 2018; Agol et al. 2020).
The transmission spectrum of TRAPPIST-1b – HST/WFC3 measurements excluded – can be relatively well fit by the models. It contains the observational points with the best precision with an error bar as low as 58 ppm (Table 6) in Spitzer/IRAC channel 2 measurement (thanks to the combination of 28 transits). Yet, even with 28 transits combined the precision reached is still of same order as the expected amplitude for detectable atmospheric features on TRAPPIST-1b (≃ 100% Morley et al. 2017; Lustig-Yaeger et al. 2019. TRAPPIST-1c’s spectrum shows a greater scatter than the one of b with an apparently poor fit to the models, yet the uncertainties on the measurements are large (at least relatively to the expected atmospheric features) and those variations are not significant at more than 3-σ. Then, for planets e and g, the expected spectral features are even shallower than for b and c, and the observations are less precise because of the smaller number of transits analyzed; thus it is impossible to speculate on the presence of any molecular species.
One possibility to gain some precision in the measured transit depths is to study the combined transit transmission spectrum of several planets. Figure 14 shows a transmission spectrum constructed from the combination of planets b, c, d, e, f and g’s transmission spectra.
This figure is similar to Fig. 12, except from the fact that we have now put an offset on HST-measurements to adjust the mean level to the weighted mean depth calculated from the rest of the observations, and the have over-plotted several simulated combined transmission spectra from Lincowski et al. (2018) and Morley et al. (2017). For the reasons we mentioned earlier, we have added a vertical offset to the atmospheric models to optimally overlap the observations. The offset value is such that the models crossed the value of the sum of the weigthed mean depth of each planet (shown in black dotted line on Fig. 12). From the observations, only points derived from the Spitzer dataset analyses have a precision of comparable magnitude than the variations expected in presence of an atmosphere. Table 8 gives the reduced chi square  for each model if its aim was to fit the observations, with ν the number of degrees of freedom and χ2 is defined by:
for each model if its aim was to fit the observations, with ν the number of degrees of freedom and χ2 is defined by:
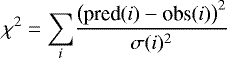 (8)
(8)
where obs(i) is the measured depth at wavelength i, σ(i) its error, and pred(i) is the depth predicted by the model for wavelength i.
In Fig. 14, Earth-like (Morley et al. 2017), Venus-like (Morley et al. 2017) and CO2-dominated (Lincowski et al. 2018) atmospheric scenarios seem to agree reasonably well with Spitzer experimental values, showing notably a larger depth in IRAC channel 2 than in channel 1 like the data suggest. In contrast, in a Titan-like (i.e., CH4-dominated) scenario thedepth measured in channel 1 is expected to be larger than the one measured in channel 2. This explains by the fact that a Titan-like atmospheres exhibit a strong, broad CH4 absorption feature centered at 3.3 μm that produces a deeper transit depth in the Spitzer channel 1 than in the channel 2. We note that the discrepancy between Titan-like atmospheres and the measured Spitzer channels 1–2 transit depths would be even greater if we assume that stellar contamination occurs at these wavelengths. Looking at the value reported in Table 8 we indeed confirm that a Titan like atmosphere appears to be the less likely considering our current observational points and their errors bars. As a very preliminary estimation, we could predict that, assuming high-mean-molecular weight atmospheres the TRAPPIST-1 planets, it is rather unlikely that most of the TRAPPIST-1 planets possess a CH4-dominated atmosphere.
Yet, what we can also note from Table 8 is that the most likely scenario, given the current observations, is a model with no atmosphere where the transit depth is equal to the sum of the weighted mean depth at all wavelengths. However, we cannot drawn any clear conclusion because as we mention before we are extremely limited by the precision on our each measurements, even for Spitzer/IRAC channel 1 and 2.
In conclusion, from Fig. 13 we can only lament that our current level of precision is unfortunately not high enough to draw proper conclusions about the existence of compact, high mean-molecular weight atmospheres around the TRAPPIST-1 planets. Even the combination of 22 transits of planet b at 4.5 μm and 28 transits at 3.6 μm with the Spitzer space telescope cannot reduce our error bars to sufficient precision. Nevertheless, the combined transmission spectrum of planets b to g presented in Fig. 14 tells us that the atmospheres of the TRAPPIST-1 planets are unlikely to be methane-dominated. Yet, this interpretation is made from only two observational points (Spitzer IRAC channels 1 and 2) and requires further investigation. A more rigorous study of the planets’ atmospheres will likely have to wait for JWST. In particular, the Prism mode of the NIRSPEC instrument shows a high potential to detect compact atmospheres around the planets (Batalha et al. 2018; Lincowski et al. 2018, 2019; Lustig-Yaeger et al. 2019; Fauchez et al. 2019b). Several independent simulations predict that it could take less than 10 transits for the seven planets to detect the dominant absorber (Morley et al. 2017; Krissansen-Totton et al. 2018; Lustig-Yaeger et al. 2019; Wunderlich et al. 2019; Batalha et al. 2018). This number may increase if clouds and/or photochemical hazes are present (Fauchez et al. 2019b). Moreover, more and more studies focus on understanding how JWST could provide us with insight into the planets’ potential habitability, either through the presence of biogenic oxygen in their atmospheres (Lincowski et al. 2018; Morley et al. 2017; Meadows et al. 2018), or via the detection of anoxic biosignatures such as CH4 + CO2 minus CO (Krissansen-Totton et al. 2018), while keeping in mind the importance of false positives/negatives (Harman et al. 2015; Reinhard et al. 2017).
 |
Fig. 13 Top left: transit transmission spectrum of TRAPPIST-1b from observations (similar Fig. 11, except for HST-measurement on which an offset has been applied) compared with simulated transit transmission spectra derived by Lincowski et al. (2018) for different terrestrial atmospheres. Each color is associated with a different scenario – gold stands for 10 or 100 bars CO2 -rich atmospheres, salmon stands for 10 or 100 bars O2-rich desiccated atmospheres, green stands for 10 or 100 bars O2-rich outgazing atmospheres, brown stands for 10 or 92 bars Venus-like atmospheres, and blue stands for an aqua planet with either clear or cloudy sky. Top right: similarly but for TRAPPIST-1c. Bottom left: similarly but for TRAPPIST-1e. Bottom right: similarly but for TRAPPIST-1g. |
Reduced χ2 values for different atmospheric models. The number of degrees of freedom used in calculating the reduced-chi-squared values listed here equal to the size of the observation sample – 1.
 |
Fig. 14 Similar to Fig. 12 with simulated combined transmission spectra. Observations and their error bars are in blue. Simulated combined transit transmission sp- ectra expected for CO2 dominated atmospheres is in red, for Earth-like atmospheres in blue-green, for Venus-like atmospheres in orange and for Titan-like atmospheres in brown. Corresponding colo- ured hexagons give the value expected from the models at the wavelengths of the observations. Wavelength is in log scale. |
3.1.5 Transit timing variations
While the near-infrared (nIR) spectropolarimeter / velocimeter for the Canada-France-Hawaii Telescope (CFHT) SPIRou (Donati et al. 2018) is expected to soon provide us with the first radial velocity detection of the TRAPPIST-1 planets (Klein & Donati 2019), transit timing variations (TTVs) are still the most useful tool for precisely estimating the masses of the planets. Combining the measured sizes (from transits) and masses (from TTVs) of the planets, we can deduce their densities and draw some inferences about their bulk compositions (Grimm et al. 2018; Dorn et al. 2018; Turbet et al. 2019). Furthermore, TTVs allow us to comprehend the complex dynamics that exists between those seven fast orbiting planets. Our measured timings as obtained from the global analysis (planet-by-planet) are presented in Table A.6, and will be used in a subsequent paper to improve the determination of the masses of the planets through the TTV method. For any future use of the transit timings of the TRAPPIST-1 planets from Spitzer observations, we recommend to use the ones derived from the global analyses planet by planet rather than from individual analysis as they are less impacted by systematic errors due to the red noise.
3.2 Occultations
In this work, we analyzed 29 predicted occultations of planet b and 8 predicted occultations of planet c, all observed in channel 2 (centered in 4.5 μm), hereafter indexed as c2. Our aim was to derive the dayside brightness temperature Tp,c2 of the two inner planets from their occultation depths. Unfortunately, we did not detect the occultation signal of either planet b or planet c (see Fig. 15), but we were able to estimate a 3-σ upper limit on their dayside brightness temperatures. No occultation observations were taken in channel 1.
To derive the brightness temperature Tp,c2 from the occultation depths we used the method described in Charbonneau et al. (2005) and Deming et al. (2005). Our starting point was to define the occultation depth as the ratio of the flux of the planet and the total flux outside of transit. This translates into Eq. (9), where Ωp is the solid angle subtended by the planet, Ω⋆ is the solid angle subtended by the star, Bp is the surface brightness of the planet and B⋆ is the surface brightness of the star,
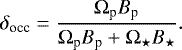 (9)
(9)
Then, assuming that the planet is a blackbody, its surface brightness Bp can be expressed with Planck’s blackbody law,
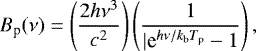 (10)
(10)
where ν is frequency, h is the Planck constant, c is the speed of light in vacuum, kb is the Boltzmann constant, and Tp is the brightness temperature. Equation (10) can be re-arranged as follows:
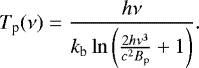 (11)
(11)
In addition, when we develop Eq. (9) we get the ratio 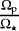 which we approximate as the ratio of the planet area with the star area, see Eq. (12), such that Eq. (10) becomes Eq. (13):
which we approximate as the ratio of the planet area with the star area, see Eq. (12), such that Eq. (10) becomes Eq. (13):
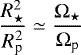 (12)
(12)
Finally, substituting Eq. (13) in Eq. (11) we obtain the brightness temperature Tp as a function of the occultation depth δocc, the surface brightness of the star B⋆, and the frequency of the observations, see Eq. (14):
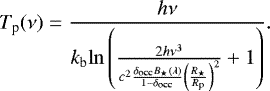 (14)
(14)
To obtain the value of the star surface brightness B⋆(ν), we followed two different approaches. First, we considered the host star as a blackbody and derive B⋆ (ν) from the value of the stellar temperature obtained in Table 4. Secondly, as TRAPPIST-1 is not an ideal blackbody we computed B⋆ directly from the flux measurements in Spitzer raw images. To do so, we measured the flux of the star in the Spitzer Basic Calibrated Data (BCDs) corrected from instrumental signatures and calibrated in physical units (MJy). We then followed the procedure described in the IRAC Instrument Handbook to obtain the absolute flux density of the star in Spitzer channel 2, such that we multiplied the measured counts by 2.3504 × 10−11 sr arcsec−2 × 1.222 arcsec2 pixel−1, and then divided by  to get the flux density in W m−2 Hz−1 sr−1, R⋆ being the radius of TRAPPIST-1 and d the distanceof the system from GAIA/DR2. Results from both approaches are presented in Table 9.
to get the flux density in W m−2 Hz−1 sr−1, R⋆ being the radius of TRAPPIST-1 and d the distanceof the system from GAIA/DR2. Results from both approaches are presented in Table 9.
Even though we did not significantly detect any occultation signal, we can compared the occultation depths outputs by the MCMC analysis and its 3-σ uncertainty with planetary thermal emission models. In Fig. 16, we compare the secondary eclipse spectrum models of TRAPPIST-1b and c for different simulated atmospheric models from Lincowski et al. (2018) with the values derived from our analysis. With Fig. 16 our intention is not to fit a model to the 3-sigma occultation depth measurement but rather to be informative on the level of signal that needs to be reached to draw conclusions from thermal occultations, and how our Spitzer occultation measurements compare to that. We observe that, for all atmospheric scenarios explored in Lincowski et al. (2018) for TRAPPIST-1b and c, the expected occultation depths are significantly smaller than the 3-σ precision that can be reached with existing Spitzer IRAC channel 2 measurements.
From Table 9 the 3-σ upper limit brightness temperatures derived from observations are ~ 750 and ~ 830 K for TRAPPIST-1b and c, respectively. By comparison, the equilibrium temperatures of TRAPPIST-1b and c are ~400 and ~340 K, respectively,assuming a null albedo. If we make the additional assumptions that the planets are (i) in synchronous rotation – which is one of their most likely spin state (Turbet et al. 2018; Makarov et al. 2018) – and (ii) that they are devoid of atmosphere, then we calculate that equilibrium temperatures on the dayside of TRAPPIST-1b and c are ~510 and ~430 K, respectively.In a thick atmosphere, the energy coming from the absorption of stellar radiation by the planet on a πR area is efficiently redistributed over the surface of the planet of 4πR
area is efficiently redistributed over the surface of the planet of 4πR area, leading to a dilution factor of 4. On an airless, synchronously rotating planet, the dilution factor is 1.5 due to the absence of heat redistribution combined with geometric factors. Koll (2019) provides an analytic framework to estimate this factor.
area, leading to a dilution factor of 4. On an airless, synchronously rotating planet, the dilution factor is 1.5 due to the absence of heat redistribution combined with geometric factors. Koll (2019) provides an analytic framework to estimate this factor.
As a result, our 3-σ confidence measurements of occultation depths for both planets are not sufficient to rule out the presence or absence of an atmosphere,and cannot be used to infer the spin states of the planets. They can be used in principle to set an upper limit on the tidal heat flux of the planet, but tidal calculations have shown it should be on the order of 0.1–40 W m−2 (Turbet et al. 2018; Barr et al. 2018; Papaloizou et al. 2018; Dobos et al. 2019), depending on the tidal dissipation factor assumed and eccentricity assumed and/or calculated. These tidal heat fluxes are more than two orders of magnitude lower than the irradiation received on TRAPPIST-1b and should thus not contribute in any way to the thermal infrared flux emitted by the planet.
From the results presented in Table 9, we can also speculate what kinds of atmosphere would theoretically induce brightness temperatures higher than our measured upper limit in order to eliminate those scenarios for planet b and c. To maximize thermal emission between 4 and 5 μm (i.e., in the Spitzer IRAC channel 2), we can build a virtual planet with a thick atmosphere that absorbs strongly at all wavelengths (specifically at wavelengths superior to 5 μm), except in the 4–5 μm spectral range. To be in agreement with our upper estimate measurements of occultation depths (see Table 9), we calculate (assuming a dilution factor of 4, because here the planet needs to have a thick atmosphere producing a strong greenhouse effect and which is likely to redistribute heat efficiently) that ~76% and ~114% of the total flux absorbed (assuming a null albedo) by TRAPPIST-1b and c, respectively, need to be thermally emitted in the 4–5 μm spectral range. It is very likely impossible for planet b (and virtually impossible for planet c) to build an atmosphere which would emit nearly 100% of its thermal flux in the 4–5 μm spectral range. This justifies a posteriori why we did not detect any occultation signal of planet b nor planet c.
The most likely yet plausible atmosphere to maximize thermal flux in the 4–5 μm spectral range is a thick H2O dominated atmosphere, due to a gap between two infrared absorption bands of H2 O near 4 μm (Miller-Ricci et al. 2009; Hamano et al. 2015; Katyal et al. 2019). This is one of the most likely scenarios for the atmospheres of the innermost planets of the TRAPPIST-1 system if the planets formed water-rich (rich enough that they survived atmospheric erosion) as supported by some planet formation scenarios (Coleman et al. 2019; Schoonenberg et al. 2019; Izidoro et al. 2019; Bitsch et al. 2019; Raymond et al. 2018) and density measurements (Grimm et al. 2018). This stems from the fact that TRAPPIST-1b and c have incident fluxes beyond the runaway greenhouse limit for which water has been shown to beunstable in condensed form and should rather form a thick H2O-dominated atmosphere (Turbet et al. 2019). Using the thermal emission spectra of Hamano et al. 2015 (e.g., their Figs. 1a and 3), we calculate that 15–30% of the thermal flux is emitted inthe 4–5 μm spectral range, depending on the assumption made on the total water content of the planet. For TRAPPIST-1b, this corresponds to a brightness temperature of 470–530 K. These brightness temperatures are similar in magnitude to those calculated for a synchronously rotating, airless planet (equilibrium temperature on the dayside of TRAPPIST-1b of ~510 K). This demonstrates how decisive JWST occultation observations of the two TRAPPIST-1 inner planets must be to be able to constrain different realistic scenarios about the nature of these planets.
Additional gases are also likely to quantitatively change these numbers (Marcq et al. 2017; Katyal et al. 2019). Specifically, there is a very strong CO2 absorption band around 4.3 μm which implies that even a small amount of CO2 in the atmospheres of both planets (if any) could mitigate their 4–5 μm brightness, which would limit the ability of the Spitzer/IRAC channel 2 to detect any signal. Again, the large spectral coverage of the various instruments of JWST (NIRSpec, MIRI) combined with their expected high sensitivity will be of great use to constrain these types of atmospheres.
 |
Fig. 15 Left: period-folded photometric measurements obtained by Spitzer IRAC/channel 2 (centered in 4.5 μm) near the 28 occultations of planets TRAPPIST-1b, corrected for the measured TTVs. Coloured dots show the unbinned measurements; open circles depict 20 min-binned measurements for visual clarity and solid gray line is simply an horizontal line centered in 1. Right: similarly but for 9 occultations of TRAPPIST-1c. |
 |
Fig. 16 Left: secondary eclipse spectrum models of TRAPPIST-1b for different assumptions on its atmospheric composition, as simulated by Lincowski et al. (2018), over-plotted with our empirical value, derived from the global analysis of 28 occultations observed with Spitzer IRAC/channel 2 (centered in 4.5 μm), the error barshown corresponds to the 3-σ confidence interval of the measurement. The y-axis has a logarithmic scale. The shade gray band stands for the zone where a spectral absorption from CO2 molecule – if present in the atmosphere – is expected. Right: similar but for TRAPPIST-1c. |
Output from the individual MCMC analyses of the light curves with the 5 highest energy flares.
3.3 Flares
The study of flares is essential to obtain insights into planetary evolution and the potential presence of life on extrasolar planets. On one hand, intense flare activity can induce strong atmospheric erosion and make the surface of a planet uninhabitable (Lammer et al. 2007), but on the other hand flares could be a key element to the emergence of life (Airapetian et al. 2016; Ranjan et al. 2017). Indeed, a minimum flaring activity seems beneficial to the formation of the ribonucleotides that will allow ribonucleic acid (RNA) synthesis and initiate prebiotic chemistry afterwards, as presented by Rimmer et al. (2018). This latter work outlines that further analyses of the frequencies of energetic flares around stars later than M4 are necessary to assess the habitability of temperate planets around the lowest-mass stars. Rimmer et al. (2018) also recommend concentrating on very energetic flares because of higher risks of uncertainties and contradictory findings with low energy flares. In this context, we looked for high energy flares in our extensive Spitzer data set and isolated the 5 largest-amplitude flares, 3 of them being caught during the continuous period of observations in 2016. This includes flares previously discussed by Davenport (2017) (flare #1, #2, #3) and two new flares (flare # 4 and # 5). We analyzed the corresponding light curves with the same MCMC code used to analyze the transits and occultations (see Sect. 2), as it also includes a flare model represented by a instantaneous flux increase followed by an exponential flux decrease. This flare model is embodied by Eq. (15):
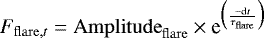 (15)
(15)
where dt = t − t0 (t0 being the time of the instantaneous flux increase), τflare is the flux decrease timescale, and Amplitudeflare is the flux increase amplitude.
The parameters resulting from our fits are presented in Table 10 and the corresponding light curves are displayed in Fig. 17. We estimated the quality of the fit through theGelman & Rubin test, and for all light curves the Gelman & Rubin coefficient was below 1.1.
Table 10 gives the flare parameters obtained from those fits. From those values we computed estimates of the bolometric luminosity of each flare. To do so we followed the procedure described by Shibayama et al. (2013), that is to say we estimated the total energy of each flare from its amplitude and duration combined to the stellar luminosity (see below), by assuming that the spectrum of a flare can be described by a black body function with an effective temperature of Tflare ≃ 9000 K. The justification for this assumption came from the observation of Kowalski et al. (2010), and was reinforced in other works like Kretzschmar (2011).
Assuming that the star is a blackbody radiator, the bolometric flare luminosity can be defined as equation:
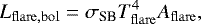 (16)
(16)
where σSB is the Stefan-Boltzmann constant, Tflare is the black-body temperatureof the flare, and Aflare is the area of the flare.
Then, to estimate Aflare, we used the observed luminosity of the star (L⋆), the luminosity of the flare (Lflare) defined by Eq. (17), where the integration is made for the 3.72–5.22 μm band pass (corresponding to IRAC/channel 2 spectral range in which all flares were observed):
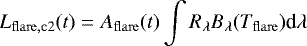 (17)
(17)
and the flare amplitude of the light curve 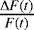 defined as Eq. (18):
defined as Eq. (18):
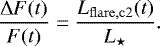 (18)
(18)
In Eq. (17), Rλ stands for the spectral response function of Spitzer/IRAC instrument and Bλ is the Planck function. From Eqs. (17) and (18), we can derive Aflare, see Eq. (19):
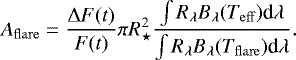 (19)
(19)
Finally, the total bolometric energy of the flare (Eflare) is defined as the integral of Lflare,bol over the flare duration, Eq. (20):
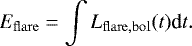 (20)
(20)
As underlined by Shibayama et al. (2013), since the star is not a blackbody radiator, such bolometric energy estimates may have errors of a few tens of percent, too small to affect our inferences described below. The results derived from those calculations are shown in Table 10.
The values that we obtained are consistent with flare energies amplitudes given by Paudel et al. (2018) and Vida et al. (2017) (energy range from (0.65–710) × 1030 erg). In Fig. 18, we compare the flare frequency distribution of TRAPPIST-1 from our measurements to the frequencies reported in those works. This figure is a log–log plot of cumulative frequency of flare energies; for instance, the cumulative frequency of flares with an energy E is the number of flares with energies superior or equal to E per day.
We noticed that the flare energy distribution of TRAPPIST-1 follows a power law as Eq. (21):
 (21)
(21)
where ν is the frequency, and β =−0.6303 ± 0.1358, fitted from our measurements. This value isconsistent with the β = −0.61 ± 0.02 derived by Paudel et al. (2018).
As TRAPPIST-1 is an ultracool dwarf star and its habitable zone planets are particularly close to their host, the question of whether those planets could harbour life in such radiation environments naturally arises (O’Malley-James & Kaltenegger 2017; Glazier et al. 2019). Within this context, we discuss the meaning of our results in terms of habitability; notably on how flares can promote the emergence of life. To do so, we based our discussion on the work of Rimmer et al. (2018), where the authors explain how the synthesis of pyrimidine ribonucleotides – part of the building blocks of RNA – from hydrogen cyanide and bisulfite in liquid water is likely driven by photochemical processes in the presence of ultraviolet (UV) light. From experiments, the authors defined the “abiogenesis zones” around stars of different stellar typesdepending on whether their UV fluxes provide sufficient energy to build a sufficiently large prebiotic inventory (Rimmer et al. 2018). Using the flare estimates of Rimmer et al. (2018), modified to account for the semi-major axes of the TRAPPIST-1 planets (Günther et al. 2020, their Eq. (10)), we derived the flare frequencies, ν, for which UV flux receivedby each TRAPPIST-1 planets would be sufficient for the planet to lie in the abiogenesis zone. Those frequencies are defined by the equation:
 (22)
(22)
where ν is a function of the flare’s U-band energy EU, the stellar radius, R⋆, and the stellar temperature, T⋆. To solve in Eq. (22), we need the U-band energy EU and the semi-major axis a. We took the semi-major axis from the refined parameters value (see Table 4 in Sect. 3.1) and we obtained the U-band energy from the bolometric energy through the integration of the flux density in the U-band spectral response function, like it was done by Günther et al. (2020) (see Eq. (23)). We assumed that the flux density of the flare could be expressed as a 9000 K blackbody. We estimate that 6.6788% of the flare’s bolometric energy belongs to the U-band, EU ≃ 6.7%Eflare.
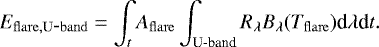 (23)
(23)
We over-plot the abiogenesis zone in terms of flare frequency and energy in Fig. 18 for planet TRAPPIST-1e; in other words, a zone where the inequality (Eq. (22)) is satisfied. We chose planets b and e because e is the planet that is the most likely to harbor liquid water on its surface (Wolf 2017, 2018; Turbet et al. 2018; Fauchez et al. 2019a) and b is the closest to the host star. We note that a planet could lie in the abiogenesis zone while not being in the classical habitable zone (Rimmer et al. 2018), yet, by choosing to study planet e we maximize the similarities with Earth.
In Fig. 18, if TRAPPIST-1’s power-law flare rates would have crossed the power law of inequality (Eq. (22)) – represented by the blue zone in the figure – it would have potentially meant that TRAPPIST-1e was located within the abiogenesis zone of its host star. However, we see that TRAPPIST-1’s power-law flare rates do not cross the blue zone. This means that TRAPPIST-1e currently does not receive enough UV flux to build up the prebiotic inventory photochemically. We note that the same interpretation can be made for planet b (the abiogenesis zone of b being the green patch in Fig. 18).
Nevertheless, TRAPPIST-1 is an old M8V type star (7.6 ± 2.2 Myr old according to Burgasser & Mamajek 2017) and empirical observations showed a decrease of the activity of ultracool dwarfs with age. Indeed, Paudel et al. (2019) compared the flare frequency distribution of 2M0837+2050 – a young ≃700 Myr old M8 typestar – with TRAPPIST-1, an old 7.6 Gyr old M8 type star, and found that the highest flare energy on 2M0837+2050 are ≃3 times larger than the ones on TRAPPIST-1, and that a flare of energy E = 1034erg has 10 times more chances to happen on 2M0837+2050 than on TRAPPIST-1. Considering that those two stars have a similar spectral type (M8 type) but different ages this argument could be used to hypothesize that TRAPPIST-1 used to show more energetic and more frequent flares in its youth. Both Ranjan et al. (2017) and Rimmer et al. (2018) discuss this scenario and argue that flares may be the only means to generate the building blocks of life via the pathways of Xu et al. (2018) and Patel et al. (2015). Furthermore, contrary to the classical habitable zone, it is not required that a planet remains in the abiogenesis zone of its star to maintain the presence of life. This would imply that planet e might have received enough UV flux in its history to drive the emergence of life’s building blocks.
Unfortunately, those interpretations are drawn from empirical studies and are limited by the number of flaring M8 type stars studied so far. Specifically, it remains to be seen whether there is a “golden mean” for flare rates, at which there are enough SEP’s to form feedstock molecules needed for prebiotic chemistry, and enough NUV light to drive that prebiotic chemistry, but not so much XUV light and SEP’s that the atmosphere is stripped (Garraffo et al. 2017; Dong et al. 2018), continually transformed (Vida et al. 2017; Tilley et al. 2019), or the planet desiccated (Luger & Barnes 2015). This “golden mean” for flare rates only applies for host planets outside the abiogenesis zone as delineated by quiescent stellar NUV flux. For those planets outside the abiogenesis zone, stellar activity would be the only means to generate sufficient NUV for this prebiotic chemistry. The Earth has resided well within the abiogenesis zone throughout its history.
It should be emphasized that the abiogenesis zones delineated by Rimmer et al. (2018) and Günther et al. (2020) and in this work are scenario-dependent. It may be that life’s building blocks can arise another way, either within hydrothermal vents (Rimmer & Shorttle 2019), in surface scenarios without ultraviolet light (Rimmer & Shorttle 2019), or that they may be delivered exogenously (Rimmer & Shorttle 2019). In addition, within the scenario explored by Rimmer et al. (2018), the threshold UV flux provides a necessary but not sufficient condition for the origins of life on a rocky planet. Hydrogen cyanide, bisulfite and phosphate must be present at high concentrations within liquid water, along with other chemical constituents (Patel et al. 2015; Xu et al. 2018). Given these added conditions, it is likely that each major category of life’s building blocks: amino acids, phospholipids, nucleotides, would be present in high concentrations, along with a mechanism for joining them together to form macromolecules: proteins, phospholipid membranes, RNA and DNA (Liu et al. 2019). The problem of how life arises from this system, or any complex molecular system, remains unsolved.
 |
Fig. 17 Light curves of the five highest amplitude flares found in our Spitzer time-series photometry. Some flares happened soon after/before a transit. The light curves are ranked in chronological order and a number is associated with each flare. |
 |
Fig. 18 Flare frequency distributions (FFD) in log–log scale. x-axis is the flare energy and y-axis is the cumulative rate of flares per day, that is to say how many flares of a corresponding energy E – or higher – happen per day. Solid lines represent the linear regressions defined by Eq. (21). The red solid line stands for the result from this work while the orange line stands for results from Paudel et al. (2018) and the green one from Vida et al. (2017). The green zone denotes the abiogenesis zone for planet TRAPPIST-1b, a zone where the inequality (Eq. (22)) is satisfied, the green bold line on the edge of the zone represent the minimum flare rate and energy required to trigger prebiotic chemistry on this planet (Rimmer et al. 2018), which corresponds mathematically to Eq. (22). The blue zone is similar to the green zone but for planet TRAPPIST-1e. |
 |
Fig. 19 Top panel: periodogram computed with the help of the Transit Least Squared (TLS) python package (Hippke & Heller 2019) applied to the time series made by the residuals of the entire Spitzer photometric (cleaned from all known transits). The x-axis is the period while the y-axis is the SignalDetection Efficiency (SDE) associated with each period. A steel-blue line indicates the harmonic for which the SED reached is the largest, here this output period is 15.74 days. Bottom panel: phase-folded transit signal for the most probable period output by the periodogram (blue dots) + transit model computed from the parameters output by the TLS algorithm (red solid line). |
3.4 Search for additional transiting objects
One of the primary goals of the Red Worlds program was to search for additional transiting planets. In this context, we ran a Transit Least Square analysis (TLS) with period spanning from 0.2 to 200 days on the residuals of the full photometric dataset corrected from all known transits. The TLS algorithm, presented by Hippke & Heller (2019), aims to detect transit-like features from time-series photometry while taking the stellar limb-darkening, the planetary ingress and egress into account. The TLS algorithm is particularly relevant here as it is optimized for small planets and was found more reliable than the Box least Square (BLS) algorithm in finding any kind of planets by Hippke & Heller (2019). We combined this with a visual inspection of all the light curves. Results are shown in Fig. 19, this figure was obtained using the Transit Least Squared (TLS) python package by Hippke & Heller (2019).
The periodogram peaks at 15.7397 days period, yet this result must be interpreted with care as the maximum value of the SDE for this period is only 6.767 whereas Pope et al. (2016) recommend to consider planetary candidate only for Signal Detection Efficiency (SDE) > 8. The SDE being define as SDE= max(power/stdpower). Besides, thedepth of the corresponding phase folded transit signal is relatively small (1487 ppm) and of the same order of magnitude as the dispersion of out-of-transit measurements (standard deviation ≃1987 ppm) (Fig. 19 bottom panel). In a nutshell, those results favors a non physical explanation (most probably systematics)for this periodic signal spotted at 15.7397 days by the TLS algorithm. We did not consider any other periods in the periodogram as their SDE were always inferior to 8 (Pope et al. 2016).
Howerver, one thing we can do is to compute the photometric precision that can be reach as a function of period, then inject planets withsignal-to-noise ratio (S/N) of 8 at each period and see if we recover them with TLS. Such results can help us define which kind of hypothetical ninth planet can be discarded from Spitzer’s photometry. Figure
20 shows the precision that we get from the photometry for a set of periods going from 0.2 to 200 days. To construct this figure we have folded the data on each period, for a set of transit timings such that the full period is covered, binned them and computed the standard deviation of this binned light curve, this standard deviation is what we refer to as the photometric precision reached on a given period. The minimum planet radius (hereafter Rp,min) was then derived from a depth equivalent to a S/N of 8. Where the S/N is expressed as 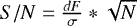 , with σ the precision at a given period and N the number of points in transit, as defined by Pont et al. (2006).
, with σ the precision at a given period and N the number of points in transit, as defined by Pont et al. (2006).
Assuming an hypothetical planets with circular orbit and null impact parameter, we observe that our precision on the dataset is good enough to detect any Mars-sized planet with period inferior to ≃45 days (with an S/N of 8), and good enough to detect any Earth sized planet that would have a period between 0.2 and 200 days (with an S/N of 8). We observe thatabove P ≃ 50 days the precision seems to stagnate, this is due to the fact that gaps exist in the dataset such that at some point only one event is used to construct the period-folded light curve for most of the periods. Yet, as the duration of the transit increases with the period and the precision stays more a less constant for P ≥ 50, the minimum planetary radius that we can detect with S∕N = 8 tends to decrease for P ≥ 50. To second those results we performed some transits injection/retrieval, the retrieval phase being essentially the capacity to find back the injected transits with an SDE > 8 when performing a TLS analysis on the residual + injected transits. The retrieval is obviously greatly dependent on the transit timing used as reference, as a scenario where no transits fall in the observations is likely. Therefore, we imposed this reference timing to be within Spitzer’s time series such that for all periods there is at least one transit in the data. The parameters of the injected transit are chosen as follow: its period P is the main variable, its depth dfp is such that S∕N = 8, with the S/N as defined above, its width T14,p is calculated analytically from dfp and P assuming a circular orbit and a null impact parameter.
As a result, TLS do recover all the injected planets with an SDE > 8 as long as at least 2 transits fall in the data, see Fig. 20. Hence, if present we should have detect any Mars-sized planet with period inferior to ≃50 days and all Earth sized planet with P < 200 days providing at least 2 of its transits happened during the observations.
To complement this analysis, we conducted a careful visual inspection of the light curves to catch any single occurrence event that could have been missed by the TLS. We found four orphan transit-like structures that did not correspond to any known planetary transit and that we could not model with any function of external parameters (e.g., x- and y-position of the star on the IRAC chip, fwhm variation and ramp effect). Therefore, we treated those events as possible transits of unknown transiting objects and tried to fit them with our MCMC code (see Sect. 2). We choose to freely vary the period and the impact parameter while assuming priors on the transit depth, the eclipse duration and the transit timing with large error bars that we estimated visually. For the stellar parameters, we used the same priors as for our individual transit analysis (see Sect. 2.2.1). The results from those analyses can be found in Table 11 and the visualization of the fits is shown in Fig. 21.
From Table 11, we note that if those events were associated with one or more transiting objects this object would be highly grazing as the impact parameters output from our fit are all larger than 0.6. Yet, we observe that the differences in duration and amplitude between events # 1, 2, 3 and # 4 tend to discard a common origin scenario. Event # 3 was caught in a particularly noisy AOR so even if the light curve structure can not be removed with any baseline detrending, we are doubtful this is a physicaltransit. As a general comment, event # 1, 2 and 3 were caught during the second campaigns which, as mentioned before, had some known drifting issues due to the use of inaccurate pointing coordinates, weakening our confidence in the detrending performed. Besides, none of the timings of those orphan transits are included in the transits timings associatedto the TLS most favored period of 15.74 days. Furthermore, at the time of event # 1, 2 and 3 we found out that some K2 observations were carried out simultaneously but the data do not confirm any of the structures we identifies, which strongly weaken any astrophysical origin scenario. Finally, event # 4 is rather shallow ≃ 0.2% and of similar order than the out-of-transit dispersion (≃0.12%), the event being significant at the 1.6σ level only.
In a nut shell, the 4 orphans structures identified seem to be emerging from a nonperfect correction of systematics effects rather than an eighth transiting object.
 |
Fig. 20 Evolution of the photometric precision and its corresponding planet radius for S∕N = 8 as a fun- ctionof the folding period. The number of injected tra- nsits for each period is given by the plot bar in gray. The blue patches show the periods for which the “injected planet” is recov- ered where as the red patches show the periods for which it is not. |
Outputs from the individual MCMC analysis of four transit-like structures found in Spitzer’s photometric observations of TRAPPIST-1.
 |
Fig. 21 Visualization of the fits of the light curve of the four transit-like structures found in Spitzer photometry. Gray dots show the unbinned measurements for Spitzer; green open circles depict 10 min-binned measurements for visual clarity. The best-fit transit models are shown as red solid lines. Events are ranked and assigned a number corresponding to their chronological order: Top left: event #1, top right: event #2, bottom left: event #3 and bottom right: event #4. When available K2 simultaneous measurements are over-plotted in blue dots with 10 min-binned measurements as blue open circles. |
4 Conclusion
The Spitzer Exploration Program Red Worlds is among the largest programs undertaken with the Spitzer Space Telescope and has gathered more than 1000 h of observation of the touchstone TRAPPIST-1 system. First, we emphasize that this program has largely met its expectations, notably through the discovery of 4 new planets orbiting the TRAPPIST-1 star, all well-suited for detailed atmospheric characterization with next-generation telescopes (Gillon et al. 2017a), as well as for the assessment of the variability of the host star (Delrez et al. 2018b), and the determination of planet masses and orbital parameters through the transit timing variations method (Grimm et al. 2018). In this work, we presented the analysis of all the transits of the TRAPPIST-1 planets observed with Spitzer/IRAC from February 2016 to March 2018 within the framework of the Red Worlds program. Our approach to analyze this exquisite data-set and our most relevant results are summarized as followed:
We refined both the stellar and transit parameters through global analyses of the entire dataset, which enabled us to revise the planets’ physical parameters (see Table 4).
We also performed a global analysis for each planet, and individual analyses of each transit, to search for signs of stellar contamination either of spectral or photometric nature. We did not find clear evidence of stellar contamination in the transit light curves, in agreement with Morris et al. (2018c).
Comparing our individual and global analyses of the transits, we estimate for TRAPPIST-1 transit depth measurements mean noise floors of ~35 and 25 ppm in channels 1 and 2 of Spitzer/IRAC, respectively. We estimate that most of this noise floor is of instrumental origins and due to the large inter-pixel inhomogeneity of IRAC InSb arrays, and that the much better inter-pixel homogeneity of JWST instruments should result in noise floors as low as 10 ppm, low enough to enable the atmospheric characterization of the planets by transit transmission spectroscopy.
On the spectral side, similarly to Ducrot et al. (2018) and Burdanov et al. (2019), we concluded that the transmission spectra of the TRAPPIST-1 planets are not flat and that Zhang et al. (2018)’s fit derived from the stellar contamination model from Rackham et al. (2018) agrees relatively well with the 7 planets’ combined observations, apart from the Spitzer observational point at 3.6 μm. Nevertheless, because of existing discrepancies in the near-IR between measurements from different instruments it is still too early to confirm that those spectral features originate from stellar contamination.
Then, we searched for an occultation signal but did not detect any, even with 28 occultations of b and 9 occultations of c. Yet, we were able to set an upper constraint on the dayside brightness temperature of b and c. Those upper limits on the temperatures were so high that it appears impossible for planet b and c to build virtual atmospheres that would be in agreement with our upper estimate measurements of occultation depths. This justifies a posteriori why we did not detect any occultation signal of either planet b or planet c.
We then compared realistic atmospheric models with our derived transmission/emission spectra and emphasized that even with a large number of transits observed with Spitzer/IRAC, interpretations are still limited by the current precision on the measurements. Only the combined transit transmission spectrum of several planets (b+c+d+e+f+g) lowered our error bars enough to open discussions on the presence/absence of certain molecular absorbers. This combined spectrum suggests that it is unlikely that most of the TRAPPIST-1 planets possess CH4-dominated atmospheres, yet this interpretation was made from only two observational points (Spitzer IRAC channels 1 and 2) and therefore requires further investigation. This observation highlights the even more crucial role of the future James Webb Space Telescope to shed light on the presence or absence of atmospheres around the TRAPPIST-1 planets, and their subsequent characterization.
We also computed the flare frequency distribution of the planets and observed that none of them currently lies in the abiogenenis zone of their host, meaning that the actual flaring activity is currently too weak to initiate prebiotic chemistry via the mechanism detailed in Xu et al. (2018) and Rimmer et al. (2018). However, TRAPPIST-1 is believed to be old and flaring activity is believed to decrease with star’s age meaning that the planets could have received the appropriate amount of UV energy in their past.
Last but not least, we identified four orphan transit structures in the dataset that we could not link to any known planet. However, three of those structures are not confirmed by simultaneous K2 data and the last one is not significant at more that the 2-σ level. These structure could be the result of unknown external systematical effect.
The most recent observations of the TRAPPIST-1 system with Spitzer were performed in October 2019, and will unfortunately be the last. But on a brighter note, the James Webb Space Telescope is on its way to take over and yield even more insight into this extraordinary system.
Acknowledgements
We thank Benjamin Rackham for useful discussions and the anonymous referee for very constructive remarks that improved the paper in a significant way. This work is based in part on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. The research leading to these results has received funding from the European Research Council under the FP/2007-2013 ERC Grant Agreement no. 336480, the European Union’s Horizon 2020 research and innovation programme (grant agreement n° 679030/WHIPLASH), and from the ARC grant for Concerted Research Actions, financed by the Wallonia-Brussels Federation. This project has received funding from the European Union’s Horizon 2020 research and innovation program under the Marie Sklodowska-Curie Grant Agreement n° 832738/ESCAPE. M.T. and L.D. acknowledge funding from the Gruber Foundation. M.G., E.J., and V.V.G. are F.R.S.-FNRS senior Research Associates. P.B.R. acknowledges support from the Simons Foundation (SCOL Grant #599634). M.N.G. acknowledges support from MIT’s Kavli Institute as a Juan Carlos Torres Fellow. This work has been carried out within the framework of the National Centre of Competence in Research PlanetS supported by the Swiss National Science Foundation. The authors acknowledge the financial support of the SNSF.
Appendix A Description of the data
Baseline for the individual analysis of each transit.
Transit timings and depths obtained from individual analyses of each transit.
Transit timings and depths obtained from individual analyses of each blended or partial transit.
Transit timings and depths obtained from global analyses of each transit with ddf variations allowed for 3.6 μm channel.
Transit timings and depths obtained from global analyses of each transit with ddf variations allowed for 4.5 μm channel.
Transit timings and transit timing variation calculated as the difference of the transit timing from the value given by the linear regression calculated with the reference timing, the period of the planet and the epoch of the transit.
Median values (medianin, medianout) and median absolute deviations (σin and σout) of the residuals in and out of transit, using the residuals from the global analyses planet-by-planet.
References
- Agol, E., Steffen, J., Sari, R., & Clarkson, W. 2005, MNRAS, 359, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Agol, E., Bolmont, E., Burgasser, A., et al. 2020, MNRAS [Google Scholar]
- Airapetian, V. S., Glocer, A., Gronoff, G., Hébrard, E., & Danchi, W. 2016, Nat. Geosci., 9, 452 [NASA ADS] [CrossRef] [Google Scholar]
- Apai, D., Rackham, B. V., Giampapa, M. S., et al. 2018, ArXiv e-prints [arXiv:1803.08708] [Google Scholar]
- Barnes, J. R., Cameron, A. C., Donati, J.-F., et al. 2005, MNRAS, 357, L1 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Barnes, J. R., Jeffers, S. V., Jones, H. R. A., et al. 2015, ApJ, 812, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J. R., Jeffers, S. V., Haswell, C. A., et al. 2017, MNRAS, 471, 811 [NASA ADS] [CrossRef] [Google Scholar]
- Barr, A. C., Dobos, V., & Kiss, L. L. 2018, A&A, 613, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barstow, J. K., & Irwin, P. G. J. 2016, MNRAS, 461, L92 [NASA ADS] [CrossRef] [Google Scholar]
- Batalha, N. E., Lewis, N. K., Line, M. R., Valenti, J., & Stevenson, K. 2018, ApJ, 856, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Bitsch, B., Raymond, S. N., & Izidoro, A. 2019, A&A, 624, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolmont, E., Selsis, F., Owen, J. E., et al. 2016, MNRAS, 464, 3728 [NASA ADS] [CrossRef] [Google Scholar]
- Bolmont, E., Gallet, F., Mathis, S., et al. 2017, A&A, 604, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bourrier, V., de Wit, J., Bolmont, E., et al. 2017, AJ, 154, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Brooks, S. P., & Gelman, A. 1998, J. Comput. Graph. Statist., 7, 434 [Google Scholar]
- Burdanov, A., Delrez, L., Gillon, M., & Jehin, E. 2018, Handbook of Exoplanets (Springer International Publishing AG), 130 [Google Scholar]
- Burdanov, A. Y., Lederer, S. M., Gillon, M., et al. 2019, MNRAS, 487, 1634 [CrossRef] [Google Scholar]
- Burgasser, A. J., & Mamajek, E. E. 2017, ApJ, 845, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Carey, S. J., Lacy, M. D., Laine, S. J., et al. 2004, Proc. SPIE, 5487 [Google Scholar]
- Charbonneau, D., Allen, L. E., Megeath, S. T., et al. 2005, ApJ, 626, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Claret, A., Hauschildt, P. H., & Witte, S. 2012, A&A, 546, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Claret, A., Hauschildt, P. H., & Witte, S. 2013, A&A, 552, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Coleman, G. A. L., Leleu, A., Alibert, Y., & Benz, W. 2019, A&A, 631, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davenport, J. R. A. 2017, Res. Notes AAS, 1, 2 [CrossRef] [Google Scholar]
- de Wit, J., Wakeford, H. R., Gillon, M., et al. 2016, Nature, 537, 69 [NASA ADS] [CrossRef] [Google Scholar]
- de Wit, J., Wakeford, H. R., Lewis, N. K., et al. 2018, Nat. Astron., 2, 214 [NASA ADS] [CrossRef] [Google Scholar]
- Delrez, L., Gillon, M., Queloz, D., et al. 2018a, Proc. SPIE, 10700, 446 [Google Scholar]
- Delrez, L., Gillon, M., Triaud, A. H. M. J., et al. 2018b, MNRAS, 475, 3577 [NASA ADS] [CrossRef] [Google Scholar]
- Deming, D., Seager, S., Richardson, L. J., & Harrington, J. 2005, Nature, 434, 740 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Dobos, V., Barr, A. C., & Kiss, L. L. 2019, A&A, 624, A2 [Google Scholar]
- Donati, J.-F., Kouach, D., Lacombe, M., et al. 2018, in Handbook of Exoplanets (Cham: Springer International Publishing), 903 [CrossRef] [Google Scholar]
- Dong, C., Jin, M., Lingam, M., et al. 2018, Proc. Natl. Acad. Sci., 115, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Dorn, C., Mosegaard, K., Grimm, S. L., & Alibert, Y. 2018, ApJ, 865, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Ducrot, E., Sestovic, M., Morris, B. M., et al. 2018, AJ, 156, 218 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Espinoza, N., Rackham, B. V., Jordán, A., et al. 2018, MNRAS, 482, 2065 [NASA ADS] [CrossRef] [Google Scholar]
- Fauchez, T., Turbet, M., Wolf, E. T., et al. 2019a, Geosci. Model Dev. Discuss., 2019, 1 [Google Scholar]
- Fauchez, T. J., Turbet, M., Villanueva, G. L., et al. 2019b, ApJ, 887, 2 [Google Scholar]
- Ferruit, P., Birkmann, S., Böker, T., et al. 2014, Proc. SPIE, 9143, 91430A [Google Scholar]
- Filippazzo, J. C., Rice, E. L., Faherty, J., et al. 2015, ApJ, 810, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Fleming, D. P., Barnes, R., Luger, R., & Vand erPlas, J. T. 2020, ApJ, 891, 155 [CrossRef] [Google Scholar]
- Ford, E. B. 2006, ApJ, 642, 505 [NASA ADS] [CrossRef] [Google Scholar]
- Garraffo, C., Drake, J. J., Cohen, O., Alvarado-Gómez, J. D., & Moschou, S. P. 2017, ApJ, 843, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Gelman, A., & Rubin, D. B. 1992, Stat. Sci., 7, 457 [Google Scholar]
- Gelman, A., Carlin. J. B., Stern, H. S., & Rubin, D. B. 2003, Bayesian Data Analysis, 2nd edn. (Boca Raton: CRC Press) [CrossRef] [Google Scholar]
- Gillon, M. 2018, Nat. Astron., 2, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Gillon, M., Deming, D., Demory, B.-O., et al. 2010, A&A, 518, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Triaud, A. H. M. J., Fortney, J. J., et al. 2012, A&A, 542, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Jehin, E., Fumel, A., Magain, P., & Queloz, D. 2013, Eur. Phys. J. Web Conf., 47, 03001 [CrossRef] [Google Scholar]
- Gillon, M., Demory, B.-O., Madhusudhan, N., et al. 2014, A&A, 563, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Jehin, E., Lederer, S. M., et al. 2016, Nature, 533, 221 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gillon, M., Triaud, A. H. M. J., Demory, B.-O., et al. 2017a, Nature, 542, 456 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Gillon, M., Demory, B. O., Lovis, C., et al. 2017b, A&A, 601, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gillon, M., Meadows, V., Agol, E., et al. 2020, ArXiv e-prints, [arXiv:2002.04798] [Google Scholar]
- Glazier, A., Howard, W. S., Corbett, H. T., et al. 2019, AAS Meeting Abstracts, 233, 247.05 [Google Scholar]
- Gonzales, E. C., Faherty, J. K., Gagné, J., et al. 2019, A Reanalysis of the Fundamental Parameters and Age of TRAPPIST-1 [Google Scholar]
- Gordon, I., Rothman, L., Hill, C., et al. 2017, J. Quant. Spectr. Rad. Transf., 203, 3 [Google Scholar]
- Grimm, S. L., Demory, B.-O., Gillon, M., et al. 2018, A&A, 613, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gully-Santiago, M. A., Herczeg, G. J., Czekala, I., et al. 2017, ApJ, 836, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Günther, M. N., Zhan, Z., Seager, S., et al. 2020, AJ, 159, 60 [CrossRef] [Google Scholar]
- Hamano, K., Kawahara, H., Abe, Y., Onishi, M., & Hashimoto, G. L. 2015, ApJ, 806, 216 [NASA ADS] [CrossRef] [Google Scholar]
- Harman, C. E., Schwieterman, E. W., Schottelkotte, J. C., & Kasting, J. F. 2015, ApJ, 812, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Hippke, M., & Heller, R. 2019, A&A, 623, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Holman, M. J. 2005, Science, 307, 1288 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Hori, Y., & Ogihara, M. 2020, ApJ, 889, 77 [CrossRef] [Google Scholar]
- Ingalls, J. G., Krick, J. E., Carey, S. J., et al. 2016, AJ, 152, 44 [CrossRef] [Google Scholar]
- Izidoro, A., Bitsch, B., Raymond, S. N., et al. 2019, A&A, submitted [arXiv:1902.08772] [Google Scholar]
- Kaltenegger, L., & Traub, W. A. 2009, ApJ, 698, 519 [NASA ADS] [CrossRef] [Google Scholar]
- Katyal, N., Nikolaou, A., Godolt, M., et al. 2019, ApJ, 875, 31 [CrossRef] [Google Scholar]
- Klein, B., & Donati, J.-F. 2019, MNRAS, 488, 5114 [NASA ADS] [CrossRef] [Google Scholar]
- Knutson, H. A., Charbonneau, D., Allen, L. E., Burrows, A., & Megeath, S. T. 2008, ApJ, 673, 526 [NASA ADS] [CrossRef] [Google Scholar]
- Koll, D. D. B. 2019, ApJ, submitted [arXiv:1907.13145] [Google Scholar]
- Kowalski,A. F., Hawley, S. L., Holtzman, J. A., Wisniewski, J. P., & Hilton, E. J. 2010, Proc. IAU, 6, 261 [CrossRef] [Google Scholar]
- Kreidberg, L., Bean, J. L., Désert, J.-M., et al. 2014, Nature, 505, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Kretzschmar, M. 2011, A&A, 530, A84 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krissansen-Totton, J., Garland, R., Irwin, P., & Catling, D. C. 2018, AJ, 156, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Lammer, H., Lichtenegger, H. I., Kulikov, Y. N., et al. 2007, Astrobiology, 7, 185 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lincowski, A. P., Meadows, V. S., Crisp, D., et al. 2018, ApJ, 867, 76 [CrossRef] [Google Scholar]
- Lincowski, A. P., Lustig-Yaeger, J., & Meadows, V. S. 2019, AJ, 158, 26 [CrossRef] [Google Scholar]
- Lindegren, L., Hernández, J., Bombrun, A., et al. 2018, A&A, 616, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liu, Z., Wu, L.-F., Xu, J., et al. 2019, http://doi.org/10.26434/chemrxiv.11210867.v1 [Google Scholar]
- Luger, R., & Barnes, R. 2015, Astrobiology, 15, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Luger, R., Barnes, R., Lopez, E., et al. 2015, Astrobiology, 15, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Luger, R., Lustig-Yaeger, J., & Agol, E. 2017a, ApJ, 851, 94 [NASA ADS] [CrossRef] [Google Scholar]
- Luger, R., Sestovic, M., Kruse, E., et al. 2017b, Nat. Astron., 1, 0129 [Google Scholar]
- Lustig-Yaeger,J., Meadows, V. S., & Lincowski, A. P. 2019, AJ, 158, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Madhusudhan, N. 2019, ARA&A, 57, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, V. V., Berghea, C. T., & Efroimsky, M. 2018, ApJ, 857, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Malik, M., Kempton, E. M.-R., Koll, D. D. B., et al. 2019, ApJ, 886, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Mandel, K., & Agol, E. 2002, ApJ, 580, L171 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, A. W., Dupuy, T., Kraus, A. L., et al. 2019, ApJ, 871, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Mansfield, M., Kite, E. S., Hu, R., et al. 2019, ApJ, 886, 141 [CrossRef] [Google Scholar]
- Marcq, E., Salvador, A., Massol, H., & Davaille, A. 2017, J. Geophys. Res. Planets, 122, 1539 [Google Scholar]
- Meadows, V. S., Reinhard, C. T., Arney, G. N., et al. 2018, Astrobiology, 18, 630 [CrossRef] [Google Scholar]
- Miller-Ricci, E., Meyer, M. R., Seager, S., & Elkins-Tanton, L. 2009, ApJ, 704, 770 [NASA ADS] [CrossRef] [Google Scholar]
- Moran, S. E., Hörst, S. M., Batalha, N. E., Lewis, N. K., & Wakeford, H. R. 2018, AJ, 156, 252 [Google Scholar]
- Morley, C. V., Kreidberg, L., Rustamkulov, Z., Robinson, T., & Fortney, J. J. 2017, ApJ, 850, 121 [Google Scholar]
- Morris, B. M., Agol, E., Davenport, J. R. A., & Hawley, S. L. 2018a, ApJ, 857, 39 [Google Scholar]
- Morris, B. M., Agol, E., Hebb, L., & Hawley, S. L. 2018b, AJ, 156, 91 [Google Scholar]
- Morris, B. M., Agol, E., Hebb, L., et al. 2018c, ApJ, 863, L32 [Google Scholar]
- O’Malley-James, J. T., & Kaltenegger, L. 2017, MNRAS, 469, L26 [Google Scholar]
- Ormel, C. W., Liu, B., & Schoonenberg, D. 2017, A&A, 604, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Owen, J. E., & Mohanty, S. 2016, MNRAS, 459, 4088 [Google Scholar]
- Papaloizou, J. C. B., Szuszkiewicz, E., & Terquem, C. 2018, MNRAS, 476, 5032 [Google Scholar]
- Patel, B. H., Percivalle, C., Ritson, D. J., Duffy, C. D., & Sutherland, J. D. 2015, Nat. Chem., 7, 301 [Google Scholar]
- Paudel, R. R., Gizis, J. E., Mullan, D. J., et al. 2018, ApJ, 858, 55 [Google Scholar]
- Paudel, R. R., Gizis, J. E., Mullan, D. J., et al. 2019, MNRAS, 486, 1438 [Google Scholar]
- Pearson, K. 1900, London Edinburgh Dublin Philos. Mag. J. Sci., 50, 157 [Google Scholar]
- Pinhas, A., Rackham, B. V., Madhusudhan, N., & Apai, D. 2018, MNRAS, 480, 5314 [Google Scholar]
- Pont, F., Zucker, S., & Queloz, D. 2006, MNRAS, 373, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Pope, B. J. S., Parviainen, H., & Aigrain, S. 2016, MNRAS, 461, 3399 [Google Scholar]
- Rackham, B., Espinoza, N., Apai, D., et al. 2017, ApJ, 834, 151 [Google Scholar]
- Rackham, B. V., Apai, D., & Giampapa, M. S. 2018, ApJ, 853, 122 [Google Scholar]
- Rackham, B., Pinhas, A., Apai, D., et al. 2019, BAAS, 51, 328 [Google Scholar]
- Ranjan, S., Wordsworth, R., & Sasselov, D. D. 2017, ApJ, 843, 110 [Google Scholar]
- Raymond, S. N., Boulet, T., Izidoro, A., Esteves, L., & Bitsch, B. 2018, MNRAS, 479, L81 [Google Scholar]
- Reinhard, C. T., Olson, S. L., Schwieterman, E. W., & Lyons, T. W. 2017, Astrobiology, 17, 287 [Google Scholar]
- Rimmer, P. B., & Shorttle, O. 2019, Origin of life’s building blocks in carbon and nitrogen rich surface hydrothermal vents [Google Scholar]
- Rimmer, P. B., Xu, J., Thompson, S. J., et al. 2018, Sci. Adv., 4, eaar3302 [Google Scholar]
- Roettenbacher, R. M., & Kane, S. R. 2017, ApJ, 851, 77 [Google Scholar]
- Schoonenberg,D., Liu, B., Ormel, C. W., & Dorn, C. 2019, A&A, 627, A149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schwarz, G. 1978, Ann. Stat., 6, 461 [Google Scholar]
- Seager, S., & Mallen-Ornelas, G. 2003, ApJ, 585, 1038 [Google Scholar]
- Shibayama, T., Maehara, H., Notsu, S., et al. 2013, ApJS, 209, 5 [Google Scholar]
- Stetson, P. B. 1987, PASP, 99, 191 [Google Scholar]
- Stevenson, K. B., Harrington, J., Fortney, J. J., et al. 2012, ApJ, 754, 136 [Google Scholar]
- Tennyson, J., & Yurchenko, S. N. 2012, MNRAS, 425, 21 [Google Scholar]
- Tilley, M. A., Segura, A., Meadows, V., Hawley, S., & Davenport, J. 2019, Astrobiology, 19, 64 [Google Scholar]
- Turbet, M., Bolmont, E., Leconte, J., et al. 2018, A&A, 612, A86 [CrossRef] [EDP Sciences] [Google Scholar]
- Turbet, M., Bolmont, E., Ehrenreich, D., et al. 2019, A&A, 638, A41 [Google Scholar]
- Turbet, M., Bolmont, E., Bourrier, V., et al. 2020, Space Sci. Rev., 216, 100 [Google Scholar]
- Van Grootel, V., Fernandes, C. S., Gillon, M., et al. 2018, ApJ, 853, 30 [Google Scholar]
- Vida, K., Kővári, Z., Pál, A., Oláh, K., & Kriskovics, L. 2017, ApJ, 841, 124 [Google Scholar]
- Vogt, S. S. 1979, PASP, 91, 616 [Google Scholar]
- Wakeford, H. R., Lewis, N. K., Fowler, J., et al. 2018, AJ, 157, 11 [Google Scholar]
- Wheatley, P. J., Louden, T., Bourrier, V., Ehrenreich, D., & Gillon, M. 2016, MNRAS, 465, L74 [Google Scholar]
- Winn, J. N. 2010, Exoplanets (Tucson, AZ: University of Arizona Press) [Google Scholar]
- Winn, J. N., Holman, M. J., Henry, G. W., et al. 2009, ApJ, 693, 794 [Google Scholar]
- Wolf, E. T. 2017, ApJ, 839, L1 [Google Scholar]
- Wolf, E. T. 2018, ApJ, 855, L14 [Google Scholar]
- Wunderlich, F., Godolt, M., Grenfell, J. L., et al. 2019, A&A, 624, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Xu, J., Ritson, D. J., Ranjan, S., et al. 2018, Chem. Commun., 54, 5566 [Google Scholar]
- Zhang, Z., Zhou, Y., Rackham, B. V., & Apai, D. 2018, AJ, 156, 178 [Google Scholar]
All Tables
Number of transits monitored by Spitzer from early 2016 to late 2019 for each TRAPPIST-1 planet.
Stellar density from individual planets’s MCMC analyses with its 1-σ uncertainty.
Updated system parameters: median values and 1-σ limits of the posterior PDFs derived from our global MCMC analysis of all nonblended and partial transits of Trappist-1 planets observed by Spitzer.
Median of the global MCMC posterior PDF of the transit depth derived from global analyses of all transits, planet by planet, with no transit depth variations allowed.
Median of the occultation depths global MCMC posterior PDF + their 1-σ and 3-σ uncertainitiesas derived from the global analysis of 28 occultations of TRAPPIST-1b and 9 occultations of TRAPPIST-1c observed at 4.5 μm.
Reduced χ2 values for different atmospheric models. The number of degrees of freedom used in calculating the reduced-chi-squared values listed here equal to the size of the observation sample – 1.
Output from the individual MCMC analyses of the light curves with the 5 highest energy flares.
Outputs from the individual MCMC analysis of four transit-like structures found in Spitzer’s photometric observations of TRAPPIST-1.
Transit timings and depths obtained from individual analyses of each blended or partial transit.
Transit timings and depths obtained from global analyses of each transit with ddf variations allowed for 3.6 μm channel.
Transit timings and depths obtained from global analyses of each transit with ddf variations allowed for 4.5 μm channel.
Transit timings and transit timing variation calculated as the difference of the transit timing from the value given by the linear regression calculated with the reference timing, the period of the planet and the epoch of the transit.
Median values (medianin, medianout) and median absolute deviations (σin and σout) of the residuals in and out of transit, using the residuals from the global analyses planet-by-planet.
All Figures
 |
Fig. 1 Spitzer photometric measurements (sky blue) resulting from observations of the star from February 2016 to Oct 2019 cleanedof data gaps between the four campaigns. Colored diamonds show the positions of the transits of the different planets withtheir corresponding depth + a constant offset by planet for clarity. |
| In the text | |
 |
Fig. 2 Coloured dots gives the stellar density derived from MCMC analyses of transits from a single planet, solid black line gives the density derived from a global analysis of all transits observed with its 1-σ uncertainty in gray shades. Colorbar shows the number of transits used in each analysis. Solid blue line give the stellar density value computed by Agol et al. (2020) using a photodynamical model created with the mass-ratios and orbital parameters derived from a transit-timing analysis, with its 1-σ uncertainty in blue shades. |
| In the text | |
 |
Fig. 3 Stellar density inferred from individual planet’s analysis versus period of the corresponding planet and its linear and constant fit with their corresponding AIC and BIC values. |
| In the text | |
 |
Fig. 4 TTVs measured for the seven planets as obtained from our global planet by planet analyses (see Sect. 2.2.3) relative to the ephemeris (T0 and P) given in Table 4. |
| In the text | |
 |
Fig. 5 Left: evolution of the measured transit depths from the planet- per- planet global analyses of transit light curves at 3.6 μm. The horizontal black lines show the medians of the global MCMC posterior PDFs from the planet- per- planet analyses with TTV and no transit depth variations allowed (with their 1-σ and 2-σ confidence intervals (see values in Table 6) in shades of gray). Events are ranked in order of capture, left to right (but not linearly in time). Right: similarly, but for transits observed at 4.5 μm. |
| In the text | |
 |
Fig. 6 Top panel: detrended light curve of the first isolated transit of TRAPPIST-1g observed by Spitzer with, superimposed in red, the best-fit model resulting from the global per-planet analysis with variations of the transit depth allowed. Bottom panel: similar to top panel but with the best-fit model resulting from the individual analysis assuming a constant depth for all transits superimposed in darkblue. |
| In the text | |
 |
Fig. 7 Standard deviation of the residuals (ppm) in- and out-of-transit for each planet (filled dots for in-transit data, empty dots for out-of-transit) such that for each transit’s epoch there is one empty dot and one filled dot. Each color is associated with a planet: purple for planet b, orange for c, yellow for d, olive for e, dark green for f, teal for g and turquoise for h. The dashed gray line show the limit value above we label the transits as outliers. |
| In the text | |
 |
Fig. 8 Transit light curves and their residuals for the 9 outliers identified on Fig. 7. Each outlier was attributed anumber in chronological order from 1 to 9, and the corresponding transiting planet at the time is indicated within the brackets. |
| In the text | |
 |
Fig. 9 Significance of the difference between the median of the residuals (ppm) in and out of transit for each planet computed as: significance = |
| In the text | |
 |
Fig. 10 Left: period-folded photometric measurements obtained with Spitzer/IRAC channel 1 (at 3.6 μm) near thetransits of the seven planets, corrected for the measured TTVs. Colored dots show the unbinned measurements; open circles depict the measurements binned over 5 min for visual clarity. The best-fit transit models are shown as dark blue lines. The numbers of transits that were observed to produce these combined curves are written on the plot. Right: similarly at 4.5 μm. |
| In the text | |
 |
Fig. 11 Updated version of the transit transmission spectra of the seven TRAPPIST-1 planets. In each subplot the continuous line is the weighted mean depth |
| In the text | |
 |
Fig. 12 TRAPPIST-1 combined transmission spectra for planets b+c+d+e+f+g (blue points) constructed from individual spectra (see Fig. 11), over-plotted with the stellar contamination model (black solid line) derived by Zhang et al. (2018) from the fit of previously published K2 + SPECULOOS-South (Ducrot et al. 2018) + HST (de Wit et al. 2016, 2018; Wakeford et al. 2018) + Spitzer (D2018) data. The black squares are the integrated depth values as predicted by the stellar contamination model of Zhang et al. (2018) in each spectral band for which observationswere performed, and gray dashed lines is the flat model at the weighted mean value of the transit depth. Wavelength is in log scale. |
| In the text | |
 |
Fig. 13 Top left: transit transmission spectrum of TRAPPIST-1b from observations (similar Fig. 11, except for HST-measurement on which an offset has been applied) compared with simulated transit transmission spectra derived by Lincowski et al. (2018) for different terrestrial atmospheres. Each color is associated with a different scenario – gold stands for 10 or 100 bars CO2 -rich atmospheres, salmon stands for 10 or 100 bars O2-rich desiccated atmospheres, green stands for 10 or 100 bars O2-rich outgazing atmospheres, brown stands for 10 or 92 bars Venus-like atmospheres, and blue stands for an aqua planet with either clear or cloudy sky. Top right: similarly but for TRAPPIST-1c. Bottom left: similarly but for TRAPPIST-1e. Bottom right: similarly but for TRAPPIST-1g. |
| In the text | |
 |
Fig. 14 Similar to Fig. 12 with simulated combined transmission spectra. Observations and their error bars are in blue. Simulated combined transit transmission sp- ectra expected for CO2 dominated atmospheres is in red, for Earth-like atmospheres in blue-green, for Venus-like atmospheres in orange and for Titan-like atmospheres in brown. Corresponding colo- ured hexagons give the value expected from the models at the wavelengths of the observations. Wavelength is in log scale. |
| In the text | |
 |
Fig. 15 Left: period-folded photometric measurements obtained by Spitzer IRAC/channel 2 (centered in 4.5 μm) near the 28 occultations of planets TRAPPIST-1b, corrected for the measured TTVs. Coloured dots show the unbinned measurements; open circles depict 20 min-binned measurements for visual clarity and solid gray line is simply an horizontal line centered in 1. Right: similarly but for 9 occultations of TRAPPIST-1c. |
| In the text | |
 |
Fig. 16 Left: secondary eclipse spectrum models of TRAPPIST-1b for different assumptions on its atmospheric composition, as simulated by Lincowski et al. (2018), over-plotted with our empirical value, derived from the global analysis of 28 occultations observed with Spitzer IRAC/channel 2 (centered in 4.5 μm), the error barshown corresponds to the 3-σ confidence interval of the measurement. The y-axis has a logarithmic scale. The shade gray band stands for the zone where a spectral absorption from CO2 molecule – if present in the atmosphere – is expected. Right: similar but for TRAPPIST-1c. |
| In the text | |
 |
Fig. 17 Light curves of the five highest amplitude flares found in our Spitzer time-series photometry. Some flares happened soon after/before a transit. The light curves are ranked in chronological order and a number is associated with each flare. |
| In the text | |
 |
Fig. 18 Flare frequency distributions (FFD) in log–log scale. x-axis is the flare energy and y-axis is the cumulative rate of flares per day, that is to say how many flares of a corresponding energy E – or higher – happen per day. Solid lines represent the linear regressions defined by Eq. (21). The red solid line stands for the result from this work while the orange line stands for results from Paudel et al. (2018) and the green one from Vida et al. (2017). The green zone denotes the abiogenesis zone for planet TRAPPIST-1b, a zone where the inequality (Eq. (22)) is satisfied, the green bold line on the edge of the zone represent the minimum flare rate and energy required to trigger prebiotic chemistry on this planet (Rimmer et al. 2018), which corresponds mathematically to Eq. (22). The blue zone is similar to the green zone but for planet TRAPPIST-1e. |
| In the text | |
 |
Fig. 19 Top panel: periodogram computed with the help of the Transit Least Squared (TLS) python package (Hippke & Heller 2019) applied to the time series made by the residuals of the entire Spitzer photometric (cleaned from all known transits). The x-axis is the period while the y-axis is the SignalDetection Efficiency (SDE) associated with each period. A steel-blue line indicates the harmonic for which the SED reached is the largest, here this output period is 15.74 days. Bottom panel: phase-folded transit signal for the most probable period output by the periodogram (blue dots) + transit model computed from the parameters output by the TLS algorithm (red solid line). |
| In the text | |
 |
Fig. 20 Evolution of the photometric precision and its corresponding planet radius for S∕N = 8 as a fun- ctionof the folding period. The number of injected tra- nsits for each period is given by the plot bar in gray. The blue patches show the periods for which the “injected planet” is recov- ered where as the red patches show the periods for which it is not. |
| In the text | |
 |
Fig. 21 Visualization of the fits of the light curve of the four transit-like structures found in Spitzer photometry. Gray dots show the unbinned measurements for Spitzer; green open circles depict 10 min-binned measurements for visual clarity. The best-fit transit models are shown as red solid lines. Events are ranked and assigned a number corresponding to their chronological order: Top left: event #1, top right: event #2, bottom left: event #3 and bottom right: event #4. When available K2 simultaneous measurements are over-plotted in blue dots with 10 min-binned measurements as blue open circles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.