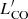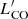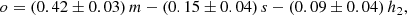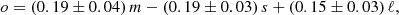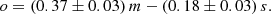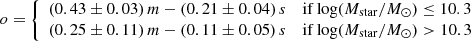| Issue |
A&A
Volume 638, June 2020
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 19 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201936304 | |
| Published online | 29 May 2020 | |
Scaling relations and baryonic cycling in local star-forming galaxies
I. The sample
1
Observatoire de Genève, Université de Genève, 51 Ch. des Maillettes, 1290 Versoix, Switzerland
e-mail: michele.ginolfi@unige.ch
2
INAF/Osservatorio Astrofisico di Arcetri, Largo Enrico Fermi 5, 50125 Firenze, Italy
3
Dipartimento di Fisica, Sapienza Università di Roma, Piazzale Aldo Moro 5, 00185 Roma, Italy
Received:
12
July
2019
Accepted:
6
April
2020
Metallicity and gas content are intimately related in the baryonic exchange cycle of galaxies, and galaxy evolution scenarios can be constrained by quantifying this relation. To this end, we have compiled a sample of ∼400 galaxies in the local Universe, dubbed “MAGMA” (Metallicity And Gas for Mass Assembly), which covers an unprecedented range in parameter space, spanning more than 5 orders of magnitude in stellar mass (Mstar), star-formation rate (SFR), and gas mass (Mgas), and it has a factor of ∼60 in metallicity [Z, 12 + log(O/H)]. Stellar masses and SFRs were recalculated for all of the galaxies using IRAC, WISE, and GALEX photometry, and 12 + log(O/H) was transformed, where necessary, to a common metallicity calibration. To assess the true dimensionality of the data, we applied multidimensional principal component analyses (PCAs) to our sample. We find that even with the vast parameter space covered by MAGMA, the relations between Mstar, SFR, Z, and Mgas (MHI + MH2) require only two dimensions to describe the hypersurface, which confirms the findings of previous work. To accommodate the curvature in the Mstar–Z relation, we applied a piecewise 3D PCA that successfully predicts observed 12 + log(O/H) to an accuracy of ∼0.1 dex. MAGMA is a representative sample of isolated star-forming galaxies in the local Universe, and it can be used as a benchmark for cosmological simulations and to calibrate evolutionary trends with redshift.
Key words: galaxies: evolution / galaxies: ISM / galaxies: general / galaxies: star formation / galaxies: statistics
© ESO 2020
1. Introduction
As long as star formation occurs in the gas reservoirs of galaxies, they evolve increasing their stellar mass (Mstar) and metal content, depending on the relative efficiency of inflows and outflows, dynamical interactions, and environmental processes. In other words, at any time, Mstar and the metallicity (Z) reflect the combined effect of both the integrated history of star formation and the degree of interaction with the surrounding environment. Not surprisingly, the causal links between gas mass (Mgas), the star formation rate (SFR), Mstar, and Z manifest in a number of observed correlations between these quantities, which are often referred to as “scaling relations”. Amongst the most notable examples are: (i) the correlation between Mstar and SFR (dubbed the “main sequence”, MS: e.g., Brinchmann et al. 2004; Noeske et al. 2007; Daddi et al. 2010; Elbaz et al. 2011; Renzini & Peng 2015); (ii) the correlation between Mgas and SFR (the “Schmidt-Kennicutt relation”, SK; e.g., Schmidt 1959; Kennicutt 1998; Bigiel et al. 2008; Leroy et al. 2009; Romeo 2020); and (iii) the “mass-metallicity relation”, MZR, between Mstar and Z (e.g., Lequeux et al. 1979; Tremonti et al. 2004; Maiolino et al. 2008). In star-forming galaxies, Z is typically measured by the abundance of oxygen, O/H, in the ionized gas, as it is the most abundant heavy element produced by massive stars.
These scaling relations among fundamental properties of galaxies are potentially insightful tools to explore demographics of galaxies and their evolution. In particular, the mutual correlations among physical properties in galaxies imply that the observed residuals from the main relations (in other words, their intrinsic scatters) could be correlated with other variables. Many studies have investigated such a notion, and this type of analysis has proved to be a powerful diagnostic, providing simple quantitative tests for analytical models and numerical simulations.
Only recently has it been possible to incorporate gas properties in studies of baryonic cycling thanks to the growing number of available gas measurements (atomic and molecular), including the Arecibo Legacy Fast ALFA survey (ALFALFA, Haynes et al. 2011, 2018), the Galaxy Evolution Explorer (GALEX) Arecibo SDSS Survey (GASS, Catinella et al. 2010, 2018), the COLD-GASS survey (Saintonge et al. 2011a, 2017), the Nearby Field Galaxy Survey (NFGS, Jansen & Kannappan 2001; Wei et al. 2010; Stark et al. 2013), the Herschel Reference Survey (HRS, Boselli et al. 2010, 2014a; Cortese et al. 2011), and the APEX Low-redshift Legacy Survey for MOlecular Gas (ALLSMOG, Bothwell et al. 2014; Cicone et al. 2017). These surveys have provided important new observations of HI and CO in order to derive H2 and compare gas content with other galaxy properties. Results suggest that the relation of atomic gas to Mstar and SFR drives a galaxy’s position relative to the MS (e.g., Huang et al. 2012; Gavazzi et al. 2013; Saintonge et al. 2016), and that HI gas fractions increase with decreasing Mstar and stellar mass surface density, at least down to log(Mstar/M⊙) = 9 (e.g., Cortese et al. 2011; Gavazzi et al. 2013; Catinella et al. 2018). Incorporating molecular gas H2 in the analysis suggests that the strongest correlations are between H2 content and SFR; in particular, molecular depletion time strongly depends on the specific SFR (sSFR ≡ SFR/Mstar) (e.g., Saintonge et al. 2011a,b, 2017; Boselli et al. 2014b; Hunt et al. 2015).
Important clues as to baryonic cycling also come from systematic studies of the intrinsic scatter of the MZR, which find that a fundamental metallicity relation (FMR) exists between Mstar, Z, and SFR that minimizes the scatter in the MZR (see e.g., Ellison et al. 2008; Mannucci et al. 2010). According to the FMR, galaxies lie on a tight, redshift-independent two-dimensional (2D) surface in 3D space defined by Mstar, Z, and SFR, where at a given Mstar, galaxies with a higher SFR have systematically lower gas-phase Z (see e.g., Hunt et al. 2012, 2016a; Lara-López et al. 2013; Hashimoto et al. 2018; Cresci et al. 2019). Many theoretical models have investigated this finding, explaining it in terms of an equilibrium between metal-poor inflows and metal-enriched outflows (e.g., Davé et al. 2012; Dayal et al. 2013; Lilly et al. 2013; Graziani et al. 2017). Observational results suggest that the FMR may be more strongly expressed via the gas mass rather than via the SFR (see e.g., Bothwell et al. 2013; Brown et al. 2018). In this light, the FMR might be interpreted as a by-product of an underlying relationship between the scatter of the MZR and the gas content (e.g., Zahid et al. 2014). In particular, Bothwell et al. (2016a), with an analysis that included Mstar, SFR, O/H, and molecular gas mass, MH2, suggest that the true FMR exists between Mstar, O/H, and MH2, which is linked to the SFR via the SK star-formation law.
Virtually all previous studies of gas scaling relations in galaxies have focused on galaxies that are more massive than 109 M⊙. In this paper, we extend previous studies to lower stellar masses, reporting the analysis of the mutual dependencies of physical properties in a sample of ∼400 local galaxies, with simultaneous availability of Mstar, SFR, MHI, MH2 (thus also total gas, Mgas), and O/H, spanning an unprecedented range in Mstar, from ∼105 M⊙ to 3 × 1011 M⊙. In Sect. 2, we first describe the individual subsamples, and then homogenize the stellar mass and SFR estimates by incorporating mid-IR (MIR) fluxes from the Wide-field Infrared Survey Explorer (WISE, Wright et al. 2010) and photometry from GALEX (Morrissey et al. 2007). With updated principle component analysis (PCA) techniques, Sect. 3 explores the correlations in the four- and three-dimensional (4D, 3D) parameter spaces defined by Mstar, SFR, O/H, and Mgas, together with the two separate gas components MHI and MH2. There is a particular focus, in Sect. 4, on the MZR scatter and the ramifications of including a significant population of low-mass galaxies in the sample.
2. Combined sample: MAGMA
We have compiled a sample of 392 local galaxies, with simultaneous availability of Mstar, SFR, gas masses (both atomic, MHI, and molecular, MH2, the latter was obtained by measurements of CO luminosity, 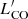 ), and metallicities [12 + log(O/H)]. We assembled our sample by combining a variety of previous surveys at z ∼ 0 with new observations of CO in low-mass galaxies. The details of the parent surveys, such as metallicity calibration, stellar-mass, and SFR determinations, are provided below. The following four selection criteria were adopted:
), and metallicities [12 + log(O/H)]. We assembled our sample by combining a variety of previous surveys at z ∼ 0 with new observations of CO in low-mass galaxies. The details of the parent surveys, such as metallicity calibration, stellar-mass, and SFR determinations, are provided below. The following four selection criteria were adopted:
1. Only galaxies with robust (≳3σ) detections of Mstar, SFR, 12 + log(O/H), MHI, and 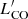 are considered;
are considered;
2. Galaxies were eliminated if they were thought to host active galactic nuclei (AGN) based on the BPT classifications1 provided by the original surveys;
3. When HI-deficiency measurements HI–def were available (e.g., Boselli et al. 2009, 2014a), following Boselli et al. (2014b), only galaxies with HI–def ≤ 0.4 were retained; and
4. The properties of galaxies that are common to two or more parent surveys were taken from the sample that provided more ancillary information (e.g., high quality spectra, resolved maps, uniform derivation of parameters).
HI-deficiency is defined as the logarithm of the ratio of the observed HI mass of a galaxy and the mean HI mass expected for an isolated galaxy with the same optical size and morphological type (e.g., Haynes & Giovanelli 1984). The H I-deficiency requirement was included to ensure that our sample is representative of isolated, field galaxies, which have not undergone potential stripping effects from residence in a cluster. Because we require metallicity and gas measurements, we have dubbed our compiled sample MAGMA (Metallicity And Gas in Mass Assembly). The final MAGMA sample was drawn from the following nine parent surveys and papers:
xGASS-CO. xGASS-CO is the overlap between the extended GALEX Arecibo SDSS survey (xGASS: Catinella et al. 2018) and the extended CO Legacy Database for GASS (xCOLD GASS: Saintonge et al. 2017). xGASS2 is a gas fraction-limited census of the HI gas content of ∼1200 local galaxies, spanning over two decades in stellar mass (Mstar = 109 − 1011.5 M⊙). The xCOLD GASS survey3 contains IRAM-30 m CO(1–0) measurements for 532 galaxies also spanning the entire SFR–Mstar plane at Mstar > 109 M⊙. Stellar masses are from the MPA-JHU4 catalog, where Mstar is computed from a fit to the spectral energy distribution (SED) obtained using SDSS broadband photometry (Brinchmann et al. 2004; Salim et al. 2007). SFRs are computed as described by Janowiecki et al. (2017) by combining NUV with mid-IR (MIR) fluxes from the Wide-field Infrared Survey Explorer (WISE; Wright et al. 2010). When these are not available, which is the case for ∼70% of the xGASS sample, SFRs are determined by using the “ladder” technique (Janowiecki et al. 2017; Saintonge et al. 2017). Data Release 7 (SDSS DR7, Abazajian et al. 2009) was calibrated by Saintonge et al. (2017) to the [NII]-based strong-line calibration by Pettini & Pagel (2004, PP04N2). In addition to omitting AGN and Seyferts (see above), we have also excluded galaxies in Saintonge et al. (2017) with an “undetermined” or “composite” classification, based on the BPT diagram; metallicities from PP04N2 for such galaxies tend to be highly uncertain. xGASS-CO, which illustrates the overlap between xGASS and xCOLDGASS, includes 477 galaxies with 221 non-AGN galaxies with robust CO detections. The subset of xGASS-CO that respects our selection criteria (i.e., with HI and CO detections and non ambiguous O/H calibration) consists of 181 galaxies.
HRS. The Herschel Reference Sample (Boselli et al. 2010) is a K-band selected, volume-limited sample that is comprised of 323 galaxies. HRS5 is a fairly complete description of the local Universe galaxy population, although it is underrepresented in low-mass galaxies (see Boselli et al. 2010). Stellar masses Mstar and SFRs were obtained from Boselli et al. (2015), where Mstar values were derived according to the precepts of Zibetti et al. (2009) using i-band luminosities and g − i colors, and SFRs are the mean of the four methods investigated by Boselli et al. (2015). These include radio continuum at 20 cm, Hα + 24 μm luminosities, FUV + 24 μm luminosities, and Hα luminosities corrected for extinction using the Balmer decrement6. We took 12 + log(O/H) from Hughes et al. (2013) based on the PP04N2 calibration, and gas quantities MHI and 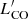 were taken from Boselli et al. (2014a). Eighty-six HRS galaxies have HI and CO detections, but 18 of these have HI–def > 0.4 (as given by Boselli et al. 2014a), so we are left with 68 HRS galaxies that satisfy our selection criteria.
were taken from Boselli et al. (2014a). Eighty-six HRS galaxies have HI and CO detections, but 18 of these have HI–def > 0.4 (as given by Boselli et al. 2014a), so we are left with 68 HRS galaxies that satisfy our selection criteria.
ALLSMOG. The APEX Low-redshift Legacy Survey of MOlecular Gas (Bothwell et al. 2014; Cicone et al. 2017) comprises 88 nearby, star-forming galaxies with stellar masses in the range of 108.5 < Mstar/M⊙ < 1010 and gas-phase metallicities of 12 + log(O/H) > 8.4. ALLSMOG is entirely drawn from the MPA-JHU catalog of spectral measurements and galactic parameters of SDSS DR7. Stellar mass and SFR values of ALLSMOG galaxies are taken from the MPA-JHU catalog, and the SFR is based on the, aperture- and extinction-corrected, Hα intrinsic line luminosity. We used the PP04N2 O/H calibration given by Cicone et al. (2017). To convert the ALLSMOG CO(2–1) values from Cicone et al. (2017) to the lower-J CO(1–0) available for the remaining samples, we assume R21 = 0.8 as they advocate. The subset of ALLSMOG that respects our selection criteria consists of 38 galaxies.
KINGFISH. The Key Insights on Nearby Galaxies: a Far-Infrared Survey with Herschel, KINGFISH7 (Kennicutt et al. 2011), contains 61 galaxies with metallicity in the range of 7.54 ≤ 12 + log(O/H) ≤ 8.77 and stellar masses in the range of [2 × 107 − 1.4 × 1011] M⊙. Stellar masses and SFRs are taken from Hunt et al. (2019). The Mstar values were computed from the SFR-corrected IRAC 3.6 μm luminosities according to the luminosity-dependent mass-to-light (M/L) ratio given by Wen et al. (2013), and they are within ∼0.1 dex of those derived by comprehensive SED fitting (see Hunt et al. 2019). SFRs are inferred from the far-ultraviolet (FUV) luminosity combined with total-infrared (TIR) luminosity following Murphy et al. (2011). Atomic gas masses MHI and CO measurements for MH2 are taken from Kennicutt et al. (2011), with refinements from Sandstrom et al. (2013) and Aniano et al. (2020). “Representative” metallicities evaluated at 0.4 times the optical radius Ropt from Moustakas et al. (2010) were converted from the Kobulnicky & Kewley (2004, KK04) calibration to the PP04N2 calibration according to the transformations given by Kewley & Ellison (2008); more details are given in Hunt et al. (2016a) and Aniano et al. (2020). After omitting NGC 2841 and NGC 5055 because their metallicities exceeded the valid regime for the Kewley & Ellison (2008) transformations, the required data are available for 38 KINGFISH galaxies. Three of these have HI–def > 0.4 (given by Boselli et al. 2014a) so we ultimately selected 35 galaxies from KINGFISH.
NFGS. The Nearby Field Galaxy Survey (Jansen et al. 2000; Kewley et al. 2005; Kannappan et al. 2009) consists of 196 galaxies spanning the entire Hubble sequence in morphological types, and a range in luminosities from low-mass dwarf galaxies to luminous massive systems. Stellar masses, Mstar, are given by Kannappan et al. (2013) and are based on NUV + ugrizJHK + IRAC 3.6 μm SEDs. We took (spatially) integrated SFR (based on Hα) and O/H values from Kewley et al. (2005) and transformed 12 + log(O/H) from their Kewley & Dopita (2002, KD02) calibration to PP04N2 according to the formulations by Kewley & Ellison (2008). Stark et al. (2013) provide CO and MH2 measurements, and MHI was tabulated by Wei et al. (2010) and Kannappan et al. (2013). After removing NGC 7077, which appears in the following dwarf sample, there are 26 galaxies that meet our selection criteria.
BCDs. The Blue Compact Dwarf galaxies (BCDs) were observed and detected in 12CO(1–0) with the IRAM 30 m single dish (Hunt et al. 2015, 2017). They were selected primarily from the primordial helium sample of Izotov et al. (2007), which is known to have reliable metallicities of 12 + log(O/H) that were measured through the direct electron-temperature (Te) method. An additional, similar set of BCDs has been detected in 12CO(1–0) (Hunt et al., in prep.) with analogous selection criteria. For both sets of BCDs, Mstar was derived as for KINGFISH galaxies, namely from IRAC 3.6 μm or WISE 3.4 μm luminosities, after correcting for free-free, line emission based on SFR, and dust continuum when possible (see also Hunt et al. 2015). This method has been shown to be consistent with full-SED derived Mstar values to within ≲0.1 dex (Hunt et al. 2019). For the galaxy in common with the NFGS, NGC 7077, the two Mstar estimates are the same to within 0.07 dex. SFRs are based on the Calzetti et al. (2010) combination of Hα and 24 μm luminosities. HI masses are given by Hunt et al. (2015, and in prep.). As mentioned above, 12 + log(O/H) is obtained from the direct Te method (for details see Hunt et al. 2016a). The subset of BCDs that respect our selection criteria with HI and CO [12CO(1–0)] detections comprises 17 galaxies with metallicities 12 + log(O/H) ranging from 7.7 to 8.4; to our knowledge, this is the largest sample of low-metallicity dwarf galaxies in the local Universe detected in CO.
DGS. The Dwarf Galaxy Survey, DGS8 (Madden et al. 2013, 2014), is a Herschel sample of 48 local metal-poor low-mass galaxies, with metallicities ranging from 12 + log(O/H) = 7.14 to 8.43 and stellar masses from 3 × 106 to ∼3 × 1010 M⊙. The DGS sample was originally selected from several deep optical emission line and photometric surveys, including the Hamburg/SAO survey and the first and second Byurakan surveys (e.g., Ugryumov et al. 1999, 2003; Markarian & Stepanian 1983; Izotov et al. 1991). Although stellar masses are given by Madden et al. (2013) with corrected values in Madden et al. (2014), these were calculated according to Eskew et al. (2012) using the Spitzer/IRAC luminosities at 3.6 μm and 4.5 μm. Hunt et al. (2016a) give Mstar for these same galaxies by first subtracting nebular continuum and line emission, known to be important in metal-poor star-forming dwarf galaxies (e.g., Smith & Hancock 2009); a comparison shows that the Mstar values in Madden et al. (2014) are, on average, 0.3 dex larger than those by Hunt et al. (2016a). Thus, in order to maximize consistency with the other samples considered here, such as for the KINGFISH, BCDs, and the Virgo star-forming dwarfs (see below), we used stellar masses based on WISE and/or IRAC 3.4−3.6 μm luminosities using the method by Wen et al. (2013) after subtracting off nonstellar emission estimated from the SFR (see also Hunt et al. 2012, 2015, 2019). Metallicities for the DGS are taken from De Vis et al. (2017), using their PP04N2 calibration. We also recalculated the SFRs using Hα and 24 μm luminosities as advocated by Calzetti et al. (2010) and reported in Hunt et al. (2016a). Of the 48 DGS galaxies discussed by Rémy-Ruyer et al. (2014), seven are included in the BCD sample observed in CO by Hunt et al. (2015, 2017), five have CO detections from Cormier et al. (2014), and nine are found elsewhere in the literature (Kobulnicky et al. 1995; Young et al. 1995; Greve et al. 1996; Walter et al. 2001; Leroy et al. 2005, 2006; Gratier et al. 2010; Schruba et al. 2012; Oey et al. 2017). However, one of these, UM 311, is a metal-poor HII region within a larger galaxy (see Hunt et al. 2010). There is a discrepancy between the Mstar values given by Madden et al. (2014) and Hunt et al. (2016a) of more than a factor of 100; this is roughly the difference between the larger UM 311 complex and the individual metal-poor HII regions, illustrating that the gas content of the individual HII regions is highly uncertain. We thus eliminate UM 311 from the DGS subset, and include the remaining 13 DGS galaxies that respect our selection criteria.
Virgo star-forming dwarfs. This sample of star-forming dwarf galaxies (SFDs) in Virgo is taken from a larger survey, namely the Herschel Virgo Cluster Survey, HeViCS9 (Davies et al. 2010). Here, to supplement the low-mass portion of our combined sample, we have included the dwarf galaxies in HeViCS studied by Grossi et al. (2015, 2016). They were selected from the larger sample by requiring a dwarf morphology (e.g., Sm, Im, BCD) and detectable far-infrared (FIR) emission with Herschel. We note that Mstar was estimated according to the WISE 3.4 μm luminosities, and SFRs were calculated using Hα luminosities and correcting for dust using WISE 22 μm emission as proposed by Wen et al. (2014). Both quantities are originally given with a Kroupa (2001) initial mass function (IMF), and, here, they have been corrected to a Chabrier (2003) IMF according to Speagle et al. (2014). Metallicities, 12 + log(O/H), were based on the SDSS spectroscopy and use the PP04N2 calibration reported by Grossi et al. (2016), with the exception of VCC 1686 for which O/H was derived using the mass-metallicity relation given in Hughes et al. (2013). Of 20 targets observed, 11 were detected in 12CO(1–0) with the IRAM 30 m (Grossi et al. 2016). Atomic hydrogen HI is detected in all of these targets (Grossi et al. 2016), but of the 11 galaxies with both HI and CO detections, four have HI–def > 0.4 (from Boselli et al. 2014a); thus seven Virgo SFDs satisfy our selection criteria.
Extra single sources. This subset includes individual galaxies that are not included in any survey, but for which our required data of Mstar, SFR, O/H, CO, and HI measurements exist. These include seven low-metallicity galaxies: DDO 53 and DDO 70 (Sextans B, Shi et al. 2016), NGC 3310 (Zhu et al. 2009), NGC 2537 (Gil de Paz et al. 2002), WLM (Elmegreen et al. 2013), Sextans A (Shi et al. 2015), and NGC 2403 (Schruba et al. 2012). For these sources, as previously mentioned above, we used Mstar and SFR from Hunt et al. (2016a) for consistency. We were able to compare global Mstar for one of these, WLM, which was once reported to a common distance scale; our value of Mstar agrees with that from Elmegreen et al. (2013) to within 0.1 dex. Metallicities for these objects are based on the direct Te method and are taken from Engelbracht et al. (2008), Marble et al. (2010), and Berg et al. (2012). In the following figures, the seven galaxies from these additional sources are labeled as “Extra”.
2.1. Galaxy parameters, data comparison, and potential selection effects
Because of potential systematics that could perturb our results, we first “homogenized” the MAGMA sample by recalculating Mstar and SFR in a uniform way. The following sections compare the newly-derived values with the original ones described above. We also analyze O/H, CO luminosities, and overall properties of the individual samples in order to assess any systematics that could affect the reliability of our results.
2.1.1. Stellar mass
To estimate Mstar, we used 3.4 − 3.6 μm luminosities together with a luminosity-dependent M/L. The photometry at 3.4 μm was acquired from the ALLWISE source catalog (e.g., Wright et al. 2010), taking the photometry measured in an elliptical aperture or within a circular aperture of a radius of 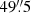 , whichever was larger. Galactic extinction was corrected for using the Schlafly & Finkbeiner (2011)AB values10 and the reddening curve by Draine (2003). Luminosities were calculated from the apparent magnitudes according to the zero points of Jarrett et al. (2013). They were then converted to masses using the M/L ratio for 3.4 − 3.6 μm luminosities given by Hunt et al. (2019), which were calibrated using the CIGALE (Boquien et al. 2019) stellar masses (see also Leroy et al. 2019):
, whichever was larger. Galactic extinction was corrected for using the Schlafly & Finkbeiner (2011)AB values10 and the reddening curve by Draine (2003). Luminosities were calculated from the apparent magnitudes according to the zero points of Jarrett et al. (2013). They were then converted to masses using the M/L ratio for 3.4 − 3.6 μm luminosities given by Hunt et al. (2019), which were calibrated using the CIGALE (Boquien et al. 2019) stellar masses (see also Leroy et al. 2019):
where νLν is the WISE (3.4 μm) or IRAC (3.6 μm) luminosities in units of erg s−1. Relative to the Mstar values obtained with detailed SED fitting, Eq. (1) gives a slightly lower scatter and offset relative to the formulation of Wen et al. (2013) and a negligible offset relative to constant M/L ratios at these wavelengths that are advocated by various groups (e.g., Eskew et al. 2012; Meidt et al. 2012, 2014; McGaugh & Schombert 2014, 2015).
When WISE photometry was unavailable, or had a low signal-to-noise ratio (mainly for the BCDs), we used IRAC 3.6 μm photometry from Engelbracht et al. (2008) or from Hunt et al. (in prep.). We have assumed that IRAC 3.6 μm and WISE 3.4 μm monochromatic luminosities are identical to within uncertainties as discussed in detail by Hunt et al. (2016a, 2019) (see also Leroy et al. 2019). All stellar masses were calculated according to a Chabrier (2003) IMF (for more details, see Hunt et al. 2019).
Figure 1 (left panel) compares the original Mstar values described in the preceding section and the new ones derived here. The mean differences (in log) are reported in Table 1. There are apparently no systematics among the different samples, given that the deviations reported in Table 1 are typically smaller or commensurate with their scatters. However, there is some tendency for the new WISE W1-derived Mstar to be larger than the originals, which were typically derived from optical SED fitting. The best agreement is for xGASS-CO, but none of the samples, except for KINGFISH, show a significant offset. Moreover, for virtually all of the samples, the scatter is good to within a factor of 2. This corresponds to an uncertainty of ∼0.3 dex, which is consistent with the overall uncertainty of mass-to-light ratios (e.g., Hunt et al. 2019). The KINGFISH galaxies show the same offset relative to SED fitting results found by Hunt et al. (2019). Here, we use the best-fit CIGALE-calibrated power-law slope with luminosity, and Wen et al. (2013) used the power-law dependence. In any case, the scatter is small because the same photometry (from Dale et al. 2017) was adopted in both cases.
 |
Fig. 1. Comparison of newly-derived Mstar (left) and SFR (right) with the original values. The individual samples are distinguished by different symbols as given in the legend. See text for more details on the derivations. |
Logarithmic differences of Mstar and SFR between the original description and adopted values.
There are four ALLSMOG galaxies that show particularly high discrepancies relative to our homogenized estimates of Mstar: 2MASXJ1336+1552, CGCG 058−066, UGC 02004, and VIII Zw 039. The previous stellar masses are roughly an order of magnitude smaller than the new values. We inspected the SDSS images of these galaxies, and they tend to be clumpy, with a series of brightness knots throughout their disks. In these cases, the stellar masses automatically estimated by SDSS tend to regard the clumps, rather than the galaxy as a whole. If these galaxies are eliminated from the comparison of the new homogenized values and the previous values for ALLSMOG, the mean difference (see Table 1) of old minus new log(Mstar) becomes −0.18 ± 0.16. These galaxies have been retained in our overall analysis.
2.1.2. SFR
Possibly the most difficult parameter is the SFR; the parent samples of MAGMA infer the SFR originally using many different methods, ranging from extinction-corrected Hα (e.g., ALLSMOG, NFGS: Cicone et al. 2017; Kannappan et al. 2013), to hybrid FUV + IR or Hα + IR (e.g., xGASS-CO, KINGFISH, BCDs, DGS, Virgo SFDs, “Extra”: Saintonge et al. 2017; Hunt et al. 2019, 2016a; Grossi et al. 2015) to the mean of different methods (e.g., HRS: Boselli et al. 2015). To calculate the SFR for MAGMA, we adopted the hybrid formulations of Leroy et al. (2019) based on linear combinations of GALEX and WISE luminosities, estimated for their sample of 15 750 galaxies within distances of ∼50 Mpc. Their expressions (see Table 7 in Leroy et al. 2019) are calibrated on the GALEX-SDSS-WISE Legacy Catalog (GSWLC) by Salim et al. (2016, 2018), which were, in turn, obtained by integrated population synthesis modeling relying on CIGALE fits to ∼700 000 low-redshift galaxies. Thus, they are consistent with, and on the same scale, as our CIGALE-calibrated stellar masses. Here, we have converted their Kroupa (2001) IMF to the Chabrier (2003) one used here, according to Speagle et al. (2014).
Leroy et al. (2019) give several “recipes” for the SFR in hybrid combinations: we have preferentially used the expression with the smallest scatter, namely luminosities of GALEX FUV combined with WISE W4. The W4 luminosities were calculated in the same apertures as the W1 luminosities used for Mstar. For GALEX, we adopted the magnitudes in the revised catalog of GALEX UV sources by Bianchi et al. (2017) that correspond to integrated values within elliptical apertures, and we checked to make sure that the aperture size was commensurate with the WISE apertures. As for the Mstar estimates, the GALEX and WISE luminosities were corrected for Galactic extinction using the Schlafly & Finkbeiner (2011)AB values and the reddening curve from Draine (2003). According to Leroy et al. (2019), the FUV + W4 formulation gives a mean scatter of ∼0.17 dex in log(SFR) for the ∼16 000 galaxies they analyzed. SFRs derived from FUV + W4 were available for 277 MAGMA galaxies (∼71% of the sample), but if not, we adopted NUV + W4 (available for 66 galaxies, ∼17%), which gives a slightly higher scatter (∼0.18 dex). Overall, these two formulations gave the lowest systematic uncertainties for the SFR, and they are available for ∼88% of the MAGMA galaxies. If GALEX was unavailable, we relied on W4 alone (for 32 galaxies, ∼9% of the sample) or, otherwise, on the hybrid recombination line (Hα) luminosity combined with 24 μm luminosities (for ten galaxies), as prescribed by Calzetti et al. (2010), or on the original SFR value (seven galaxies: 1 ALLSMOG, 1 NFGS, 1 Virgo SFD, Sextans A, DDO 154, and regions of DDO 53 and DDO 73). All SFRs were converted to the Chabrier (2003) IMF.
Overall, as shown in Fig. 1 (right panel), the original SFRs and the new values agree reasonably well, with small mean differences, and always zero to within the scatter (see Table 1). The agreement with the original SFRs from xGASS-CO and HRS is particularly good, with virtually zero offsets and scatters of ∼0.2 dex. Both of these samples derived a SFR using hybrid schemes, not unlike the ones reported by Leroy et al. (2019) used here. NFGS and the Virgo SFDs show the largest scatters; for NFGS, we attribute this to their use of Hα luminosities only, which were corrected for extinction (see Kewley et al. 2005). The original SFRs for the Virgo SFDs were derived following Wen et al. (2014), but the scatter is dominated by the galaxies with the lowest SFRs (and Mstar); this effect for low-mass, low-metallicity dwarfs was also noted by Wen et al. (2014), so it is not unexpected.
2.1.3. Metallicity
As mentioned above, all gas-phase metallicities in our combined sample are either direct Te methods or calibrated through the [NII]-based PP04N2 Pettini & Pagel (2004) calibration. When the original O/H calibration is not PP04N2, we converted it to PP04N2 according to Kewley & Ellison (2008). The PP04N2 calibration has been shown to be the most consistent with Te methods (see also Hunt et al. 2016a). Extinction corrections for this calibration are very small because the lines are very close in wavelength: λ[NII](a) = 6549.86 Å, λ[NII](b) = 6585.27 Å, and Hα = 6564.614 Å, so the extinction correction is negligible for a Cardelli et al. (1989) extinction curve. Even for visual extinction AV = 5 mag, the relative correction is on the order of 1%. This is well within the signal-to-noise ratio of the Hα flux itself.
Since metallicity is found to decline from galactic centers to the peripheries (e.g., Kewley et al. 2005; Pilyugin et al. 2014a,b; De Vis et al. 2019), such gradients represent a possible source of systematics; therefore it is worth examining their impact on our metallicity estimates. Some of the O/H for our sample are integrated (e.g., NFGS, HRS, xGASS-CO, ALLSMOG: Kewley et al. 2005; Boselli et al. 2013; Saintonge et al. 2017), some are “representative” and evaluated at 0.4 Ropt (e.g., KINGFISH: Moustakas et al. 2010), and some are nuclear (e.g., the dwarf samples: BCDs, DGS, Virgo SFDs, and “extra” sources). Kewley et al. (2005) quantified the difference among the global metallicities and the ones measured in the nuclear regions for a sample of 101 star-forming galaxies selected from the NFGS. Independent of the galaxy type, they find that such a difference amounts to ∼0.1 dex, a value which is similar to the typical statistical uncertainty of metallicities of 0.1–0.2 dex. Metallicity gradients in late-type dwarf irregulars or BCDs are generally negligible (e.g., Croxall et al. 2009) or at most comparable to those in more massive spirals (e.g., Pilyugin et al. 2015). Thus, we conclude that metallicity gradients should not markedly affect our conclusions.
2.1.4. Molecular gas mass
Like metallicity, molecular gas mass is another delicate issue. Except for ALLSMOG and some KINGFISH galaxies, we only used CO(1–0) in order to avoid excitation issues; as previously mentioned, to convert the CO(2–1) values to CO(1–0), a ratio of R21 = 0.8 was assumed (see also Leroy et al. 2009). Here, the molecular gas masses have been calculated from 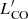 , using the conversion MH2,=
, using the conversion MH2,= 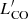 ,αCO (where αCO is the H2 mass-to-CO light conversion factor), and by adopting a metallicity-dependent calibration, following Hunt et al. (2015). Specifically, for galaxies with Z/Z⊙ < 1 (i.e., 12 + log(O/H) < 8.69, see Asplund et al. 2009), we applied αCO = αCO⊙(Z/Z⊙)−1.96; for metallicities Z/Z⊙ ≥ 1, we used a constant solar value of αCO = αCO⊙ = 3.2 M⊙ (K km s−1 pc2)−1.
,αCO (where αCO is the H2 mass-to-CO light conversion factor), and by adopting a metallicity-dependent calibration, following Hunt et al. (2015). Specifically, for galaxies with Z/Z⊙ < 1 (i.e., 12 + log(O/H) < 8.69, see Asplund et al. 2009), we applied αCO = αCO⊙(Z/Z⊙)−1.96; for metallicities Z/Z⊙ ≥ 1, we used a constant solar value of αCO = αCO⊙ = 3.2 M⊙ (K km s−1 pc2)−1.
As previously mentioned, for MAGMA O/H, we adopted either Te or the PP04N2 metallicity calibrations. However, for the calculation of αCO, we also investigated the effect of adopting an alternative strong-line calibration, namely the formulation by Kewley & Dopita (2002, KD02). To emulate Bothwell et al. (2016b,a), we also explored the αCO formulation from Wolfire et al. (2010) using KD02 metallicities. This assumes that the αCO varies exponentially with visual extinction, AV, with a weak metallicity dependence for AV (see Bolatto et al. 2013, for more details). These results are discussed in Sect. 4.1.
Aperture corrections for CO single-dish measurements are also a source of uncertainty because of the beam size compared to the dimensions of the galaxy. Because of the relatively large distances of the xGASS-CO galaxies (0.025 < z < 0.05 for Mstar ≥ 1010 M⊙), the median correction to total CO flux applied by Saintonge et al. (2017) is fairly small, that is, a factor of 1.17. Aperture corrections for the ALLSMOG galaxies (Cicone et al. 2017) are even smaller, corresponding to a median covering fraction of 0.98.
We compared the CO luminosities 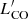 of the six galaxies that are common to HRS and KINGFISH. This is an interesting comparison because the KINGFISH galaxies were mapped in CO(2–1) with the HERA CO Line Extragalactic Survey (HERACLES, Leroy et al. 2009), and the HRS measurements were mostly single-dish CO(1–0) observations with few maps (Boselli et al. 2014a). The mean difference between the two datasets is 0.04 dex (larger luminosities for the HRS sample), with a standard deviation of 0.24 dex. Thus there is no systematic difference in
of the six galaxies that are common to HRS and KINGFISH. This is an interesting comparison because the KINGFISH galaxies were mapped in CO(2–1) with the HERA CO Line Extragalactic Survey (HERACLES, Leroy et al. 2009), and the HRS measurements were mostly single-dish CO(1–0) observations with few maps (Boselli et al. 2014a). The mean difference between the two datasets is 0.04 dex (larger luminosities for the HRS sample), with a standard deviation of 0.24 dex. Thus there is no systematic difference in 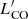 between these two samples, and, moreover, the spread is similar to the typical aperture corrections of ∼0.2 dex or less for xGASS-CO and ALLSMOG.
between these two samples, and, moreover, the spread is similar to the typical aperture corrections of ∼0.2 dex or less for xGASS-CO and ALLSMOG.
2.1.5. Overall properties
Finally, we compare median differences of each parent sample within MAGMA, relative to the sample as a whole. This is done in some detail in Appendix A where we show this comparison graphically. Our analysis shows that ultimately there are no significant systematic differences among the individual parent samples, despite the different criteria for their original selection. We therefore expect that MAGMA, as a whole, is representative of field galaxies in the local Universe and that it can be used to assess the gas scaling relations driving baryonic cycling.
The Mstar distributions of our combined sample are shown in Fig. 2, while sSFR, Z [measured in units of 12 + log(O/H)] gas fraction Mgas/(Mgas + Mstar) distributions are shown in Fig. 3. The combined MAGMA sample covers the following unprecedented ranges in parameter space, spanning more than 5 orders of magnitude in Mstar, SFR, and Mgas, and almost 2 orders of magnitude in metallicity11:
 |
Fig. 2. Distributions of Mstar for the MAGMA sample; the right panels illustrate the subdivisions in Mstar for the parent surveys. The red vertical dashed line in the left panel corresponds to the median Mstar for MAGMA, log(Mstar/M⊙) = 9.68. Also shown in the left panel is the SDSS10 sample, taken from Mannucci et al. (2010), consisting of 78579 galaxies. Here, it has been renormalized to show the Mstar distribution it would have if it contained the same number of galaxies (390) as MAGMA; the Mstar median of SDSS10 (shown as a blue vertical dashed line) is log(Mstar/M⊙) = 10.28. |
To demonstrate the general applicability of results obtained for MAGMA to the general (field) galaxy population in the local Universe, we have included in Figs. 2 and 3 the parameter distributions for the SDSS-DR7 catalog consisting of ∼79 000 galaxies from Mannucci et al. (2010); hereafter we refer to this sample as SDSS10. For a consistent comparison with MAGMA, like for the samples described above, we transformed the original O/H calibration from Maiolino et al. (2008) based on KD02 to PP04N2 according to the formulation of Kewley & Ellison (2008) (for more details, see also Hunt et al. 2016a); according to Kewley & Ellison (2008), this transformation has an accuracy of ∼0.05 dex. The distributions shown in Figs. 2 and 3 were renormalized to the number of galaxies in the MAGMA sample to be able to compare the number distributions directly. The SDSS10 has a relatively narrow spread in O/H; there are five MAGMA galaxies (∼1%) beyond the highest metallicities in SDSS10, and all are from the xGASS-CO sample, which also corresponds to some of the most massive galaxies. The MAGMA Mstar median is 0.6 dex lower than the one for SDSS10, and the sSFR median (Fig. 3) is ∼0.4 dex higher, illustrating that the MAGMA sample contains more low-mass galaxies than SDSS10. Interestingly, there are only 25 SDSS10 galaxies (0.03%) with log(Mstar/M⊙) > 11.5; thus because of the normalization in Fig. 2, they do not appear.
 |
Fig. 3. Distributions for combined sample of 392 galaxies for log (sSFR) (left panel), 12 + log(O/H) (middle), and log [Mgas/(Mstar + Mgas) ≡ Mgas/Mbaryonic] (right). The red vertical dashed lines in each panel correspond to the MAGMA medians: log(sSFR/yr−1) = −9.92; 12 + log(O/H) = 8.64 (Z⊙ would be 12 + log(O/H) = 8.69, see Asplund et al. 2009); and log(Mgas/Mbaryonic) = log(fbaryonic) = 0.39. The left and middle panels also include the SDSS10 sample, as in Fig. 2; the sSFR and O/H medians of SDSS10 are log(sSFR/yr−1) = −10.36 and 12 + log(O/H) = 8.69, respectively, and they are shown by blue vertical dashed lines. |
Both MAGMA and SDSS10 contain a high percentage of massive galaxies relative to local volume-limited samples, such as the Local Volume Legacy (e.g., LVL, Dale et al. 2009; Kennicutt et al. 2009) or galaxy-stellar mass functions (GSMF). For the z ∼ 0 GSMF determined by Baldry et al. (2012), we would expect ∼0.1% of the galaxies to be more massive than the break mass, M* = 5 × 1010; ∼14% of the galaxies in SDSS10 and ∼5% of those in MAGMA are more massive than this. The preponderance of massive galaxies in these two samples, relative to a volume-limited one, is due to flux limits and the necessity of accessing to spectroscopic measurements (for SDSS10) and CO measurements (for MAGMA). In any case, as shown in Figs. 2 and 3, the parameter coverage of MAGMA does not significantly deviate from SDSS10 at high Mstar and O/H, but it substantially extends the parameter space to lower Mstar and O/H values.
Given that we required that CO be detected, even at low metallicity, there could be a chance that the MAGMA sample is dominated by starbursts, that is, galaxies with SFRs significantly above the main sequence. We examine this possibility in Fig. 4, where we compare the distributions for MAGMA galaxies of SFR in different bins of Mstar with the SDSS10 data from Mannucci et al. (2010) as above. The main sequence of star formation given by fitting LVL and KINGFISH by Hunt et al. (2019) is also shown; here, it was approximated by a Gaussian distribution with a width of 0.3 dex (see also Renzini & Peng 2015). Except for possibly the lowest mass bins, log(Mstar/M⊙) ≤ 9, Fig. 4 demonstrates that the MAGMA sample is well approximated by main-sequence SFR distributions. Thus, it is not dominated by starbursts, and it can be considered to be a reliable diagnostic for gas processes in the local Universe.
 |
Fig. 4. Distributions of SFR for the MAGMA sample are shown as red-shaded regions in bins of Mstar; the SDSS10 sample in yellow-shaded regions and the fit to the SFMS (shown as a solid gray curve) reported by Hunt et al. (2019) are also shown. The close agreement of MAGMA with SDSS and the SFMS, except possibly for the lowest Mstar bin, suggests that starbursts do not dominate the galaxy population represented. |
2.2. Fundamental scaling relations
In Fig. 5, MAGMA galaxies are plotted in the Mstar–SFR plane, forming the SFMS; the lower panels of Fig. 5 show various forms of the correlation between SFR and Mgas, a global SK law. In particular we explore different gas phases (atomic, molecular, and total, i.e., MHI + MH2), and CO luminosity,  . The loci of the SDSS10 galaxies reported in previous figures are also shown in Fig. 5. The lowest level contour encloses 90% of the sample, illustrating the extension by MAGMA to lower Mstar and SFR. In Fig. 5, we have also included the parameters from the LVL sample as measured by Hunt et al. (2016a); most metallicities are from the direct Te method (Marble et al. 2010; Berg et al. 2012). This sample is the best approximation available for the number and types of galaxies present in the nearby Universe.
. The loci of the SDSS10 galaxies reported in previous figures are also shown in Fig. 5. The lowest level contour encloses 90% of the sample, illustrating the extension by MAGMA to lower Mstar and SFR. In Fig. 5, we have also included the parameters from the LVL sample as measured by Hunt et al. (2016a); most metallicities are from the direct Te method (Marble et al. 2010; Berg et al. 2012). This sample is the best approximation available for the number and types of galaxies present in the nearby Universe.
 |
Fig. 5. Upper panel: galaxies from the MAGMA sample plotted in the SFR–Mstar plane. The green line is the MS of star-forming galaxies derived from the SDSS (Brinchmann et al. 2004). Contours in this plane for the SDSS10 sample are shown as gray closed curves; the lowest level contour encloses 90% of the sample. The LVL sample (Dale et al. 2009; Kennicutt et al. 2009), as described in the text, is also shown in the upper panels. Lower panels: MAGMA galaxies in the SFR–Mgas (upper-left), MH2–SFR (upper-right), MHI–SFR (lower-left), and |
Figure 6 shows the mass-metallicity (Mstar–Z) relation of the MAGMA sample; although, with some scatter, galaxies lie along the MZR over > 4 dex in Mstar and a factor of ∼50 in Z (1.7 dex in 12 + log(O/H)). As in Fig. 5, we have also included SDSS10 and LVL; the MAGMA sample is consistent with both of them, implying that there are no significant selection effects from our gas detection requirements. The direct-Te calibration for the SDSS obtained by Andrews & Martini (2013) is also shown in Fig. 6 as a blue curve; the MAGMA PP04N2 + direct Te metallicities are in good agreement with this calibration, illustrating that PP04N2 is a good approximation for Te methods (see also Hunt et al. 2016a).
 |
Fig. 6. Upper panel: MAGMA sample in the Mstar–Z plane. Lower panel: MAGMA sample in the sSFR–Z plane. Metallicities are reported in PP04N2 (or Te) units of 12 + log(O/H). In both panels, as in previous figures, the SDSS10 sample is also plotted, with 90% of the galaxies enclosed within the lowest contours; both panels also show the LVL sample (Dale et al. 2009; Kennicutt et al. 2009) as described in the text. Upper panel: the MZR from the direct-Te determination by Andrews & Martini (2013) is also given, and its good agreement with the MAGMA PP04N2 (+Te) metallicities suggests that the calibrations are consistent. Symbols and colors refer to different parent surveys, as indicated in the legend. The black dashed line represents the median trend of the distribution, which was calculated at different bins (see black dots); the horizontal bars indicate the widths of the bins, while vertical bars indicate the standard deviation around median values of the galaxies in the bins. |
 |
Fig. 7. PCA coefficients for MAGMA log(Mstar) plotted against Mbreak for the division into the two PCAs. Right panel: magnification of the left panel, showing, more effectively, that the range of Mstar coefficients as the Mbreak mass is varied. The lower values of the Mstar coefficient toward higher Mbreak results from the flattening of the MZR at high Mstar. |
Figure 6 illustrates that the flattening of the MZR that frequently emerges at high Mstar is present in the MAGMA and SDSS10 samples. This curvature is clearly seen in the contours of SDSS10 where 90% of the SDSS10 galaxies are enclosed in the lowest contour. Again, the overall extension of MAGMA to lower Mstar and O/H is evident. In what follows, we focus on applying linear scaling relations to this curved MZR. A single linear relation is not altogether appropriate, given the flattening of the MZR at high Mstar. Indeed, as shown by the linear trend in the upper panel of Fig. 6, it can only roughly approximate the overall MAGMA distribution. In what follows, we investigate the best approach to approximate nonlinear trends in the data.
A combination of the scaling relations described above produce the result reported in the lower panel of Fig. 6, namely a tight correlation between the specific SFR (sSFR = SFR/Mstar) and metallicity over ∼2 dex in sSFR and ≳1.5 dex in 12 + log(O/H). Figure 6 demonstrates that galaxies more actively forming stars (i.e., with a high sSFR) are less metal-enriched (and also more gas-rich; see Mannucci et al. 2010; Cresci et al. 2012, 2019; Hunt et al. 2016b for a discussion).
In the next section, we focus on the MZR (Fig. 6), exploring its secondary and tertiary dependencies on SFR and MH2, MHI, and Mgas. Since Z is the only intensive12 quantity among the available integrated physical properties of our galaxies, the MZR is, among the others described above, the most sensitive to internal physical mechanisms.
3. Mutual correlations: A PCA analysis
Principal component analysis is a parameter transformation technique that diagonalizes the covariance matrix of a set of variables. Consequently, a PCA gives the linear combinations of observables, the eigenvectors, that define the orientations whose projections constitute a hyper-plane; these eigenvectors minimize the covariance and are, by definition, mutually orthogonal. In other words, a PCA performs a coordinate transformation that identifies the optimum projection of a dataset and the parameters that are most responsible for the variance in the sample. The most common use of PCA is to search for possible dimensionality reduction of the parameter space needed to describe a dataset. For instance, a PCA approach has shown that galaxies lie roughly on a 2D surface in the 3D parameter space defined by Mstar, SFR, and Z (e.g., Hunt et al. 2012, 2016a) or Mstar, MH2, and Z (e.g., Bothwell et al. 2016b).
We used the MAGMA sample to expand upon and re-examine previous trends found with PCAs of Mstar, SFR, metallicity, and gas. In addition to the “classical” algorithm for PCA (an unweighted matrix diagonalization), we also applied two additional PCA methods, which give the uncertainties associated with the best-fit parameters: the “bootstrap PCA” (BSPCA), which was first introduced by Efron (1979, 1982), and the “probablistic PCA” (PPCA) described by Roweis (1998). BSPCA is a specific example of more generic techniques that resample the original data set with replacement in order to construct “independent and identically distributed” observations. PPCA is an expectation-maximization (EM) algorithm which also accommodates missing information. For the PPCA, we randomly removed 5% of the individual entries for each galaxy; in practice, this means that we omitted the SFR for 5% of the galaxies, Mstar for a different 5%, and so on. For both methods, we generated several realizations of 100–1000 repetitions and calculated the means and standard deviations of the resulting PC coefficients. For all statistical analyses, we relied on the R statistical package13.
To estimate uncertainties, other groups have used Monte Carlo methods with resampling, injecting Gaussian noise into the nominal measurement values (e.g., Bothwell et al. 2016b,a). We performed several detailed tests using this technique and found that it introduces systematics in the results, depending on the amplitude of the noise as well as the Mstar and SFR distributions of the samples; hence we prefer resampling techniques in order to avoid potential unreliability in the results. This point is discussed further in Sect. 4.3 and Appendix C.
Thus, we performed three kinds of PCAs on the following: (1) a 4D parameter space defined by Mstar, SFR, Z, and a gas quantity (either Mgas, MH2, MHI, or  ); and (2) a 3D space defined by Mstar, SFR, and either metallicity Z or a gas quantity (as for 4D). We then assessed whether two, three, or four parameters are statistically necessary to describe the variance of these quantities in the MAGMA sample; this was decided by comparing the change in scatter produced by adding an additional variable. We note that
); and (2) a 3D space defined by Mstar, SFR, and either metallicity Z or a gas quantity (as for 4D). We then assessed whether two, three, or four parameters are statistically necessary to describe the variance of these quantities in the MAGMA sample; this was decided by comparing the change in scatter produced by adding an additional variable. We note that  was included as a separate gas quantity in order to separate the effects of true CO luminosity from the effects of a metallicity-dependent αCO; this point is discussed further below. We also performed a five-dimensional PCA on Mstar, SFR, Z, MHI, and
was included as a separate gas quantity in order to separate the effects of true CO luminosity from the effects of a metallicity-dependent αCO; this point is discussed further below. We also performed a five-dimensional PCA on Mstar, SFR, Z, MHI, and  (or MH2), but results do not significantly differ from the 4D case, so we do not discuss it here.
(or MH2), but results do not significantly differ from the 4D case, so we do not discuss it here.
3.1. 4D PCA
Results for the 4D PCA are given in Table 2; the coefficients of the PC with the least variance (by definition PC4) are reported, together with the fraction of variance contained in PC4, PC3, and the sum of PC1 + PC2. There are two separate rows for the PPCA and the BSPCA; these are the different methods used to infer uncertainties and they demonstrate that the coefficients of all the methods agree within the uncertainties. We find that the proportion of variance contained in only the first two eigenvectors, PC1 + PC2, is generally large, that is, ≳94%. Because most of the variance of the sample is contained within the first two eigenvectors, the dimensionality of the parameter space of the MAGMA galaxies is two-fold. They are distributed on a 2D plane in the 4D space; the remaining ≲6% of the variance (shared between PC3 and PC4) produces a scatter perpendicular to this plane.
4D PCA results for MAGMA.
It is important to note that PC4, the eigenvector with the least variance (∼1%), is always dominated by metallicity, Z (see Table 2). Because very little of the sample variance is contained in PC4, it can be set to zero and inverted to give a useful prediction for the dominant term, namely metallicity Z (see Hunt et al. 2012, 2016a, for a discussion). The estimate for the metallicity obtained by setting PC4 equal to zero is formally accurate to the 1–2% level, that is, the variance associated with PC4; however, a more robust assessment of the accuracy is obtained by fitting the residuals to a Gaussian as described below.
Interestingly, the contribution of MHI to PC4 is consistent with zero within the uncertainties, and the coefficients for MH2 and Mgas are small, which were determined to be nonzero only at a 2σ level or less. The PC4 coefficient for all gas components is less than that for the SFR. The only gas PC4 coefficient that is strongly different than 0 is 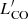 , which was determined at ∼5 − 7σ, and comparable in magnitude to the SFR coefficient. This result implies that the 2D plane does not significantly depend on gas properties, except for possibly CO luminosity
, which was determined at ∼5 − 7σ, and comparable in magnitude to the SFR coefficient. This result implies that the 2D plane does not significantly depend on gas properties, except for possibly CO luminosity 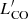 . The expression for 12 + log(O/H) obtained by inverting the expression based on MH2 is:
. The expression for 12 + log(O/H) obtained by inverting the expression based on MH2 is:
where h2, m, o, and s are defined as the centered variables, that is, log(MH2), log(Mstar), 12 + log(O/H), and log(SFR) minus their respective means in the MAGMA sample as given in Table 3. The accuracy of this expression is ∼0.12 dex, which was assessed by fitting a Gaussian to the residuals of this fit compared to the observations of 12 + log(O/H). Equation (2), in which the uncertainties from Table 2 have been propagated, tells us that:
MAGMA sample means.
– the gas-phase metallicity of galaxies in the MAGMA sample is primarily dependent on Mstar (a confirmation of the existence of the well-known MZR);
– there is a strong secondary dependence on the SFR, whose contribution in determining Z is ∼40% as strong as the dependence on Mstar;
– the tertiary dependence on MH2 is negligible, virtually zero, given that the accuracy with which the coefficient is determined is ≲2σ.
We explored the behavior of the other gas quantities and, as suggested by Table 2, it is similar to the behavior of H2; with the possible exception of 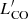 , the gas content does not influence metallicity Z. However, in the case of
, the gas content does not influence metallicity Z. However, in the case of 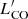 , the Mstar coefficient is significantly lower than those for the other gas quantities and the
, the Mstar coefficient is significantly lower than those for the other gas quantities and the 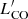 coefficient has the same sign. It seems that, in some sense, the CO content (not necessarily the H2 content which also depends on metallicity as we inferred in Sect. 2.1) is linked to Z, and can partially substitute the influence of Mstar. If we express 12 + log(O/H) in terms of
coefficient has the same sign. It seems that, in some sense, the CO content (not necessarily the H2 content which also depends on metallicity as we inferred in Sect. 2.1) is linked to Z, and can partially substitute the influence of Mstar. If we express 12 + log(O/H) in terms of 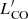 , as is done in Eq. (2), we obtain:
, as is done in Eq. (2), we obtain:
where o, m, and s are the same as in Eq. (2), and ℓ is the centered variable log(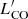 ). This expression is accurate to ∼0.11 dex, where this uncertainty was assessed, as above for MH2, by fitting a Gaussian to the residuals of the fit. In reality, this fit should not be interpreted rigorously since the gas content, rather than CO luminosity, is the quantity of interest. The relation between
). This expression is accurate to ∼0.11 dex, where this uncertainty was assessed, as above for MH2, by fitting a Gaussian to the residuals of the fit. In reality, this fit should not be interpreted rigorously since the gas content, rather than CO luminosity, is the quantity of interest. The relation between 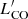 and the molecular gas content is almost entirely governed by metallicity (e.g., Hunt et al. 2015; Accurso et al. 2017); thus the strong dependence by
and the molecular gas content is almost entirely governed by metallicity (e.g., Hunt et al. 2015; Accurso et al. 2017); thus the strong dependence by 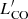 in Eq. (3) is a reflection of the strong metallicity dependence of the conversion factor αCO. We will explore this notion more in detail in a future paper.
in Eq. (3) is a reflection of the strong metallicity dependence of the conversion factor αCO. We will explore this notion more in detail in a future paper.
3.2. 3D PCA
Section 3.1 shows that the 4D parameter space can be approximated by a planar surface, with ≳94% of the variance contained in the first two eigenvectors, PC1 + PC2. Here we examine the 3D parameter space (in log space) by retaining Mstar and SFR as the two main observables as well as considering 12 + log(O/H) as one of the variables together with the following four gas quantities described above: MHI, MH2, Mgas, and 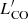 . The aim of this exercise is to assess whether any of the gas parameters can be described only by Mstar and SFR as well as to investigate the implication of our 4D PCAs that metallicity 12 + log(O/H) can be adequately described by Mstar and SFR alone.
. The aim of this exercise is to assess whether any of the gas parameters can be described only by Mstar and SFR as well as to investigate the implication of our 4D PCAs that metallicity 12 + log(O/H) can be adequately described by Mstar and SFR alone.
Using the same methodology as for the 4D PCA (“classic” PCA without uncertainties, PPCA and BSPCA with uncertainties), we performed 3D PCAs on the MAGMA sample, and obtain the results reported in Table 4. Similar to the 4D PCA, the 3D-PCA component with the least variance is dominated by the metallicity, 12 + log(O/H) (see Col. 4 in Table 4). By inverting the PC3 dominated by O/H, as before, for the 4D PCA, we find:
3D PCA results for MAGMA.
The coefficients multiplying log(Mstar) and log(SFR) in Eq. (4) are the same to within the uncertainties as those from the 4D PCA given in Eq. (2). This expression describes 12 + log(O/H) for the MAGMA sample with an accuracy of ∼0.12 dex, which was yet again obtained by fitting the residuals to a Gaussian. The scatter of this expression is comparable to the scatter obtained from the 4D PCA, leading to the conclusion that only Mstar and the SFR are necessary to describe metallicity. The MAGMA coefficient for log(Mstar) of 0.37 is the same as what was found by Hunt et al. (2016a).
There are two considerations here: one is that a PCA, by definition, must pass through the multivariable centroid of the dataset. That is why here, in contrast to Hunt et al. (2012, 2016a), we define the PCA results in terms of centered variables. This is important when applying a PCA determined with one sample to another sample; if the means of the two samples are significantly different, then the PCA does not pass through the barycenter of the data for the second sample, and it is apparently not a good fit. Thus a PCA must be applied using the centered variables associated with a particular data set. The second consideration is that despite the similarity in Mstar coefficients, the curvature of the MZR present in MAGMA (and SDSS10) is somewhat more pronounced than for the sample analyzed by Hunt et al. (2016a). Figure 7 shows the coefficient of Mstar for the subsample with Mstar ≤ Mbreak and Mstar > Mbreak, where Mbreak is the value of Mstar where one PCA ends and the other one starts. The slopes for Mstar are systematically smaller for increasing Mbreak because of the flattening of the MZR. In the following section, we explore a remedy for this using an approach that is more appropriate for data showing nonlinear relationships.
3.3. 3D PCA, a nonlinear approach
Several methods have been developed to assess mutual dependencies and dimensionality in a dataset that shows nonlinear behavior. In particular, curvature in a dataset can be first approximated by a piecewise linear approach (e.g., Hastie & Stuetzle 1989; Strange & Zwiggelaar 2015; Xianxi et al. 2017). In the case of the curved MZR and its relation with the SFR (e.g., Mannucci et al. 2010; Cresci et al. 2019), this is a fairly good approximation as we show below. The fit to the MZR given by Andrews & Martini (2013), shown in Fig. 6, consists of a mainly linear portion toward low Mstar, which is smoothly connected to a roughly flat regime at high Mstar (see also Curti et al. 2020). Thus, as a simplified solution to the problem of MZR curvature, we approximated its behavior with two linear segments, and performed a PCA separately on each. Such a procedure is a specific example of a more complex piecewise linear approach, and a more detailed analysis is reserved for a future paper.
The only “free parameter” in the piecewise linear PCA exercise is the break mass, Mbreak, namely the value of Mstar where we establish the transition from one PCA to the other. We investigated Mbreak between 3 × 109 M⊙ and 3 × 1010 M⊙ (see Fig. 7) and find an “optimal spot” around Mbreak = 2 × 1010 M⊙, where the overall variance is minimized. The best-fit piecewise 3D-PCA for MAGMA is as follows:
and the averages of the parameters in the two bins are given in Table 3.
Figure 8 shows the piecewise 3D-PCA results [hereafter “3DPCA2(OH)”] where we compare the predictions of 12 + log(O/H) from Eq. (5) and the means given above to the observed values (vertical axis). The parent samples of the individual MAGMA galaxies are given in the legend in the middle panel. The standard deviation of the PC3 component is slightly lower (0.11 dex versus ∼0.12 dex) than that in the metallicity-dominated 4D PCA for which, however, gas content was taken into account. The piecewise PC3 standard deviation of 0.11 dex is also slightly lower than the continuous 3D PCA result without gas, ∼0.12 dex. The Gaussian fit to the 3DPCA2(OH) residuals is shown in the right panel of Fig. 8. We expect that the degree to which the piecewise is better than the single PCA depends on the number of galaxies that are more massive than ∼2 × 1010 M⊙, that is, the amplitude of the curvature in the MZR.
 |
Fig. 8. Observed values of 12 + log(O/H) in the MAGMA sample compared to those predicted by the 3DPCA2(OH) given in Eq. (5). The parent sample of the individual MAGMA galaxies is given in the legend in the middle panel, and the right panel shows the residuals and the Gaussian fit; the 1σ dispersion of the Gaussian is 0.074 dex as discussed in the text. The MAGMA 3DPCA2(OH) applied to SDSS10 is also shown, and as before 90% of SDSS10 is enclosed within the contours. The median of the SDSS10 residuals relative to the 3DPCA2(OH) is 0.002 dex, with a standard deviation of ∼0.08 dex, showing that even when the MZR curvature is clearly evident in SDSS10, the MAGMA 3DPCA2(OH) does a good job of reproducing the metallicities (see text for more details). |
The SDSS10 sample is also reported in Fig. 8, to which we applied the 3DPCA2(OH) determined from MAGMA; the gray contours enclose 90% of the sample. The mean (median) SDSS10 residuals are 0.000 (0.002) dex with a standard deviation of 0.08 dex over 78579 galaxies. Thus the MAGMA 3DPCA2(OH) applied to SDSS10 represents the metallicities in that sample with an accuracy that is comparable to the scatter found for the new formulation of the FMR for SDSS by Curti et al. (2020), and with low systematics given the zero mean. For LVL, the scatter is slightly worse: mean (median) LVL residuals are 0.000 (−0.02) dex, with a standard deviation of ∼0.2 dex over 135 galaxies. Nevertheless, the small mean (median) residuals indicate that the LVL metallicities are also fairly well approximated by the MAGMA 3DPCA2(OH), even for the low masses in LVL, with a median log(Mstar/M⊙) of 8.1, and 25% of the galaxies are less massive than log(Mstar/M⊙) = 7.3.
Ultimately, comparing the 4D and 3D PCAs shows that there is no need to include gas content, either Mgas, MHI, or MH2, in the description of Z; it is statistically irrelevant since a similar scatter is obtained without any gas coefficients. This is a clear confirmation that metallicity in field galaxies in the local Universe can be determined to a ≲0.1 dex accuracy using only Mstar and SFR. However, this does not mean that metallicity is independent of gas content; on the contrary, in a companion paper, we describe how gas content shapes the MZR through star-formation-driven outflows. As we shall see below, the point is that gas content, similar to metallicity, can be described through Mstar and SFR dependencies.
4. Comparison with previous work
Our results are in stark contrast with those of Bothwell et al. (2016a) who, as mentioned above, in a 4D PCA found that H2 mass has a stronger link with metallicity than the SFR. Bothwell et al. (2016b) found a similar result based on a 3D PCA, namely that gas content drives the relation between Mstar and metallicity and that any tertiary dependence on the SFR is merely a consequence of the Schmidt-Kennicutt relation between gas mass and the SFR. In a similar vein, Brown et al. (2018), through stacking, and Bothwell et al. (2013) found that HI mass is strongly tied to Z, more than to the SFR, which is similar to later results for MH2. We conclude, instead, that metallicity is more tightly linked with stellar mass and the SFR than with either Mgas, MHI, or even MH2. There are several possible reasons for this disagreement, and we explore them here, with additional details appearing in Appendix B.
4.1. Metallicity calibration and CO luminosity-to-molecular gas mass conversion
We first examine how our results change if we use the same metallicity calibration as Bothwell et al. (2016b,a). This is potentially an important consideration because the KD02 O/H calibration used by Bothwell et al. tends to give metallicities that are too high (e.g., Kewley & Ellison 2008), relative to direct-Te estimates; as shown in Fig. 6, the PP04N2 is a better approximation of these (Andrews & Martini 2013; Hunt et al. 2016a; Curti et al. 2017). Together with using the KD02 calibration, we also assessed the effect of applying the αCO conversion factor used by Bothwell et al. The exponential metallicity dependence proposed by Wolfire et al. (2010) and Bolatto et al. (2013) depends more steeply on metallicity than the power-law dependence we use above, as formulated by Hunt et al. (2015). Thus it is possible that the effects of metallicity are enhanced for the molecular gas mass MH2 with this approach.
We thus applied these calibrations to the MAGMA sample, and performed a 4D PCA, as in Bothwell et al. (2016a). The results of this exercise are reported in the lower portion of Table 2. With the KD02 calibration and the exponential metallicity dependence of αCO, we find that the PCA4 coefficients are slightly altered: the Mstar and SFR coefficients are higher in amplitude and the O/H coefficient is lower. The H2 term is even smaller than with our original formulation, and it is zero within the uncertainties. In agreement with our original formulation, we would have concluded that H2 has a negligible impact relative to the SFR. Thus, the different approaches for αCO and the metallicity calibration are probably not the cause of the disagreement.
4.2. Differences in sample sizes and properties
Here we examine whether the larger MAGMA sample, its significant low-mass representation, and different SFR relations can influence PCA results. Our MAGMA sample of 392 galaxies is nominally twice as large as the sample studied by Bothwell et al. (2016b,a). However, if we only consider the CO detections in their low-z sample (141 galaxies), judging from Table 2 in Bothwell et al. (2016b), our sample is almost three times larger. Moreover, MAGMA contains a much higher fraction of low-mass galaxies, as it includes the HeViCs dwarf galaxies (Grossi et al. 2015), the DGS (Cormier et al. 2014), the BCDs not yet published by Hunt et al., and DDO 53, Sextans A, Sextans B, and WLM, the extremely metal-poor galaxies studied by Shi et al. (2015, 2016) and Elmegreen et al. (2013). The MAGMA mean log(Mstar/M⊙) = 9.7 is ∼3 times lower than the mean log(Mstar/M⊙) = 10.2 of the 158 (including high-z) detections in the Bothwell et al. (2016b) sample; while 24% (94) of the MAGMA galaxies have Mstar ≤ 109.3 M⊙, the same applies only for 7% (11) of the Bothwell et al. (2016b) galaxies and for ∼11% (18) of those in Bothwell et al. (2016a).
Nevertheless, the most important difference between the MAGMA sample and the Bothwell et al. sample(s) is the inclusion of galaxies at high redshift in the latter. As shown in Appendix B, the addition of these galaxies significantly increases the amplitude of the MH2 term in the 4D PCA and reduces that of the SFR. When the z ∼ 2 galaxies are not included, the results of a 4D PCA on the Bothwell et al. sample are ambiguous because the metal content is found to increase with the increasing SFR, similarly to the increase with Mstar. However the statistical significance of this result is low, and the sample is ill conditioned because of the behavior of the SFR with Mstar in the sample.
4.3. Methodology comparison and parameter uncertainties
In Appendix C, we assess the consequences of introducing Gaussian noise to an observing sample that is to be subject to a PCA. After constructing several sets of mock samples based on well-defined input scaling relations, we conclude that the accuracy with which the original relations can be retrieved depends on the amount of noise injected. It is fairly common to calculate uncertainties on fitted parameters by injecting noise in a sample and repeating the exercise several times (e.g., Bothwell et al. 2016b,a). However, our results show that this process skews the data because of the broader range in the parameter space and the relative importance of outliers in a PCA.
Another important consideration is the importance of the Mstar distribution of a sample, such as the one considered here. At a given level of noise injection σ, we found that the broader the range of Mstar, the more consistent the results are with the original “true” scaling relations.
In some sense, as we show in Appendix C, adding more noise to observing samples, such as MAGMA, that already contain noise skews results, thus compromising reliability. Ultimately, these are the reasons we chose to apply probabilistic PCA and boot-strap PCA with sample replacement, rather than perturb the parameters of the sample by injecting noise.
5. Summary and conclusions
With the aim of investigating the role of gas on the mass-metallicity relation, we compiled a new “MAGMA” sample of 392 galaxies covering unprecedented ranges in parameter space, spanning more than 5 orders of magnitude in Mstar, SFR, and Mgas, and almost 2 orders of magnitude in metallicity. Basic galaxy parameters, Mstar and SFR, were recalculated using available data from IRAC, WISE, and GALEX archives, and all O/H values were converted to a common metallicity calibration, PP04N2. All stellar masses and SFRs rely on a common Chabrier (2003) IMF, and the combined sample was carefully checked for potential systematics among the subsamples.
Applying 4D and piecewise 3D PCAs to MAGMA confirms previous results that O/H can be accurately (≲0.1 dex) described only using Mstar and the SFR. However, our findings contradict earlier versions of PCA dimension reduction on smaller samples, as we find that the O/H depends on the SFR more strongly than on either HI or H2. Thus, even though a PCA shows mathematically that only a 2D plane is necessary to describe metallicity Z or Mgas (or MH2), the dependence of Z on gas content is not well constrained with a PCA.
In Sect. 3.1, a 4D PCA shows that the four parameters Mstar, SFR, 12 + log(O/H), and MH2 or Mgas are related through a 2D planar relation, with metallicity as the main primary dependent variable. This implies that O/H primarily depends on Mstar and the SFR, but also that Mgas must primarily depend on these two variables because of the physical connection between the gas content and metallicity.
The observational scaling relations here for O/H are applicable to isolated (field) galaxies in the local Universe, over a wide range of stellar masses, SFR, and metallicities 12 + log(O/H) ≳ 7.6. They can be used as a local benchmark for cosmological simulations and to calibrate evolutionary trends with redshift. Future papers will consider relations among gas content, star formation, and metal-loading efficiencies, as well as provide a detailed comparison with evolutionary models.
The Baldwin-Philips-Terlevich (BPT) diagram classification (Baldwin et al. 1981) relies on the emission-line properties of galaxies, based on the [SII]/Hα versus [O III]/Hβ ratios.
The full xGASS representative sample is available on the xGASS website, http://xgass.icrar.org in digital format.
The full xCOLD GASS survey data products are available on the xCOLD GASS website http://www.star.ucl.ac.uk/xCOLDGASS/
A full description of the survey and the ancillary data can be found at https://hedam.lam.fr/HRS/
Boselli et al. (2015) do not publish the individual estimates, so we were unable to select the hybrid method based on 24 μm luminosities that would be more consistent with other samples discussed here.
An overview of the scientific strategy for KINGFISH and the properties of the galaxy sample can be found on the web page https://www.ast.cam.ac.uk/research/kingfish
Information on the DGS sample, as well as data products, can be found on the website http://irfu.cea.fr/Pisp/diane.cormier/dgsweb/publi.html
Information on HeViCS and public data can be found in http://wiki.arcetri.astro.it/HeViCS/WebHome
Intensive properties are physical properties of a system that do not depend on the system size or the amount of material in the system (e.g., the metallicity of a galaxy does not depend on its size). They differ from extensive properties, which are additive for subsystems. For instance, the total Mstar, Mgas, and SFR in a galaxy are the sums of the parts composing the galaxy; in other words, these quantities depend on the size of a galaxy.
R is a free software environment for statistical computing and graphics (https://www.r-project.org/).
Bothwell et al. (2016a) used a different technique to estimate Mstar, and they find roughly a factor of 3 times lower values, but there is no tabulation of their modified values.
This sample is not quite the same as the one analyzed by Bothwell et al. (2016a) because the eight galaxies from Hunt et al. (2015) were included with an arbitrary factor of 3 lower Mstar, since Bothwell et al. (2016a) recalculated their Mstar values but did not tabulate the new Mstar values. Moreover, the numbers of galaxies do not apparently match; here we only analyze the 158 + 8 CO detections given in Table 2 of Bothwell et al. (2016b) with eight BCDs (with Mstar/3 from Hunt et al. 2015).
Acknowledgments
We are grateful to the anonymous referee whose critical comments improved the paper. The authors would also like to thank A. Baker, F. Belfiore, S. Bisogni, C. Cicone, M. Dessauges-Zavadsky, Y. Izotov, S. Kannappan, R. Maiolino, P. Oesch, K. Sandstrom and D. Schaerer for helpful discussions. We acknowledge funding from the INAF PRIN-SKA 2017 program 1.05.01.88.04. We thank Yong Shi for passing us their results in digital form. We have benefited from the public available programming language Python, including the numpy, matplotlib and scipy packages. This research made extensive use of ASTROPY, a community-developed core Python package for Astronomy (Astropy Collaboration 2013), and glueviz, a Python library for multidimensional data exploration (Beaumont et al. 2015). This research has also made use of data from the HRS project; HRS is a Herschel key program utilizing Guaranteed Time from the SPIRE instrument team, ESAC scientists and a mission scientist. The HRS data was accessed through the Herschel Database in Marseille (HeDaM – http://hedam.lam.fr) operated by CeSAM and hosted by the Laboratoire d’Astrophysique de Marseille.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Accurso, G., Saintonge, A., Catinella, B., et al. 2017, MNRAS, 470, 4750 [NASA ADS] [Google Scholar]
- Andrews, B. H., & Martini, P. 2013, ApJ, 765, 140 [NASA ADS] [CrossRef] [Google Scholar]
- Aniano, G., Draine, B. T., Hunt, L. K., et al. 2020, ApJ, 889, 150 [NASA ADS] [CrossRef] [Google Scholar]
- Asplund, M., Grevesse, N., Sauval, A. J., & Scott, P. 2009, ARA&A, 47, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baldry, I. K., Driver, S. P., Loveday, J., et al. 2012, MNRAS, 421, 621 [NASA ADS] [Google Scholar]
- Baldwin, J. A., Phillips, M. M., & Terlevich, R. 1981, PASP, 93, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beaumont, C., Goodman, A., & Greenfield, P. 2015, in Astronomical Data Analysis Software an Systems XXIV (ADASS XXIV), eds. A. R. Taylor, & E. Rosolowsky, ASP Conf. Ser., 495, 101 [NASA ADS] [Google Scholar]
- Berg, D. A., Skillman, E. D., Marble, A. R., et al. 2012, ApJ, 754, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Bianchi, L., Shiao, B., & Thilker, D. 2017, ApJS, 230, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Bigiel, F., Leroy, A., Walter, F., et al. 2008, AJ, 136, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Bisigello, L., Caputi, K. I., Grogin, N., & Koekemoer, A. 2018, A&A, 609, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013, ARA&A, 51, 207 [Google Scholar]
- Boquien, M., Burgarella, D., Roehlly, Y., et al. 2019, A&A, 622, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Boissier, S., Cortese, L., et al. 2009, ApJ, 706, 1527 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Eales, S., Cortese, L., et al. 2010, PASP, 122, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Hughes, T. M., Cortese, L., Gavazzi, G., & Buat, V. 2013, A&A, 550, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Cortese, L., & Boquien, M. 2014a, A&A, 564, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Cortese, L., Boquien, M., et al. 2014b, A&A, 564, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boselli, A., Fossati, M., Gavazzi, G., et al. 2015, A&A, 579, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bothwell, M. S., Maiolino, R., Kennicutt, R., et al. 2013, MNRAS, 433, 1425 [NASA ADS] [CrossRef] [Google Scholar]
- Bothwell, M. S., Wagg, J., Cicone, C., et al. 2014, MNRAS, 445, 2599 [NASA ADS] [CrossRef] [Google Scholar]
- Bothwell, M. S., Maiolino, R., Peng, Y., et al. 2016a, MNRAS, 455, 1156 [NASA ADS] [CrossRef] [Google Scholar]
- Bothwell, M. S., Maiolino, R., Cicone, C., Peng, Y., & Wagg, J. 2016b, A&A, 595, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brinchmann, J., Charlot, S., White, S. D. M., et al. 2004, MNRAS, 351, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Brown, T., Cortese, L., Catinella, B., & Kilborn, V. 2018, MNRAS, 473, 1868 [Google Scholar]
- Calzetti, D., Wu, S.-Y., Hong, S., et al. 2010, ApJ, 714, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Catinella, B., Schiminovich, D., Kauffmann, G., et al. 2010, MNRAS, 403, 683 [NASA ADS] [CrossRef] [Google Scholar]
- Catinella, B., Saintonge, A., Janowiecki, S., et al. 2018, MNRAS, 476, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G. 2003, PASP, 115, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Cicone, C., Bothwell, M., Wagg, J., et al. 2017, A&A, 604, A53 [Google Scholar]
- Cormier, D., Madden, S. C., Lebouteiller, V., et al. 2014, A&A, 564, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cortese, L., Catinella, B., Boissier, S., Boselli, A., & Heinis, S. 2011, MNRAS, 415, 1797 [NASA ADS] [CrossRef] [Google Scholar]
- Cresci, G., Mannucci, F., Sommariva, V., et al. 2012, MNRAS, 421, 262 [NASA ADS] [Google Scholar]
- Cresci, G., Mannucci, F., & Curti, M. 2019, A&A, 627, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Croxall, K. V., van Zee, L., Lee, H., et al. 2009, ApJ, 705, 723 [NASA ADS] [CrossRef] [Google Scholar]
- Curti, M., Cresci, G., Mannucci, F., et al. 2017, MNRAS, 465, 1384 [NASA ADS] [CrossRef] [Google Scholar]
- Curti, M., Mannucci, F., Cresci, G., & Maiolino, R. 2020, MNRAS, 491, 944 [NASA ADS] [CrossRef] [Google Scholar]
- Daddi, E., Elbaz, D., Walter, F., et al. 2010, ApJ, 714, L118 [Google Scholar]
- Dale, D. A., Cohen, S. A., Johnson, L. C., et al. 2009, ApJ, 703, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Dale, D. A., Cook, D. O., Roussel, H., et al. 2017, ApJ, 837, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Davé, R., Finlator, K., & Oppenheimer, B. D. 2012, MNRAS, 421, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Davies, J. I., Baes, M., Bendo, G. J., et al. 2010, A&A, 518, L48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dayal, P., Ferrara, A., & Dunlop, J. S. 2013, MNRAS, 430, 2891 [NASA ADS] [CrossRef] [Google Scholar]
- De Vis, P., Gomez, H. L., Schofield, S. P., et al. 2017, MNRAS, 471, 1743 [NASA ADS] [CrossRef] [Google Scholar]
- De Vis, P., Jones, A., Viaene, S., et al. 2019, A&A, 623, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Draine, B. T. 2003, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Efron, B. 1979, Ann. Stat., 7, 1 [Google Scholar]
- Efron, B. 1982, The Jackknife, the Bootstrap and Other Resampling Plans (Philadelphia: Society for Industrial and Applied Mathematics) [Google Scholar]
- Elbaz, D., Dickinson, M., Hwang, H. S., et al. 2011, A&A, 533, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ellison, S. L., Patton, D. R., Simard, L., & McConnachie, A. W. 2008, ApJ, 672, L107 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., Rubio, M., Hunter, D. A., et al. 2013, Nature, 495, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Engelbracht, C. W., Rieke, G. H., Gordon, K. D., et al. 2008, ApJ, 678, 804 [NASA ADS] [CrossRef] [Google Scholar]
- Eskew, M., Zaritsky, D., & Meidt, S. 2012, AJ, 143, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, Y., & Solomon, P. M. 2004, ApJ, 606, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Gavazzi, G., Fumagalli, M., Fossati, M., et al. 2013, A&A, 553, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gil de Paz, A., Silich, S. A., Madore, B. F., et al. 2002, ApJ, 573, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Gratier, P., Braine, J., Rodriguez-Fernandez, N. J., et al. 2010, A&A, 512, A68 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Graziani, L., de Bennassuti, M., Schneider, R., Kawata, D., & Salvadori, S. 2017, MNRAS, 469, 1101 [NASA ADS] [CrossRef] [Google Scholar]
- Greve, A., Becker, R., Johansson, L. E. B., & McKeith, C. D. 1996, A&A, 312, 391 [NASA ADS] [Google Scholar]
- Grossi, M., Hunt, L. K., Madden, S. C., et al. 2015, A&A, 574, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grossi, M., Corbelli, E., Bizzocchi, L., et al. 2016, A&A, 590, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hashimoto, T., Goto, T., & Momose, R. 2018, MNRAS, 475, 4424 [NASA ADS] [CrossRef] [Google Scholar]
- Hastie, T., & Stuetzle, W. 1989, J. Am. Stat. Assoc., 84, 502 [CrossRef] [MathSciNet] [Google Scholar]
- Haynes, M. P., & Giovanelli, R. 1984, AJ, 89, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Haynes, M. P., Giovanelli, R., Martin, A. M., et al. 2011, AJ, 142, 170 [NASA ADS] [CrossRef] [Google Scholar]
- Haynes, M. P., Giovanelli, R., Kent, B. R., et al. 2018, ApJ, 861, 49 [Google Scholar]
- Huang, M.-L., & Kauffmann, G. 2014, MNRAS, 443, 1329 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, S., Haynes, M. P., Giovanelli, R., & Brinchmann, J. 2012, ApJ, 756, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Hughes, T. M., Cortese, L., Boselli, A., Gavazzi, G., & Davies, J. I. 2013, A&A, 550, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L. K., Thuan, T. X., Izotov, Y. I., & Sauvage, M. 2010, ApJ, 712, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L., Magrini, L., Galli, D., et al. 2012, MNRAS, 427, 906 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., García-Burillo, S., Casasola, V., et al. 2015, A&A, 583, A114 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hunt, L., Dayal, P., Magrini, L., & Ferrara, A. 2016a, MNRAS, 463, 2002 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L., Dayal, P., Magrini, L., & Ferrara, A. 2016b, MNRAS, 463, 2020 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., Weiß, A., Henkel, C., et al. 2017, A&A, 606, A99 [Google Scholar]
- Hunt, L. K., De Looze, I., Boquien, M., et al. 2019, A&A, 621, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Izotov, I. I., Guseva, N. G., Lipovetskii, V. A., Kniazev, A. I., & Stepanian, J. A. 1991, A&A, 247, 303 [NASA ADS] [Google Scholar]
- Izotov, Y. I., Thuan, T. X., & Stasińska, G. 2007, ApJ, 662, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Janowiecki, S., Catinella, B., Cortese, L., et al. 2017, MNRAS, 466, 4795 [NASA ADS] [Google Scholar]
- Jansen, R. A., & Kannappan, S. J. 2001, Ap&SS, 276, 1151 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, R. A., Fabricant, D., Franx, M., & Caldwell, N. 2000, ApJS, 126, 331 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Jarrett, T. H., Masci, F., Tsai, C. W., et al. 2013, AJ, 145, 6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kannappan, S. J., Guie, J. M., & Baker, A. J. 2009, AJ, 138, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Kannappan, S. J., Stark, D. V., Eckert, K. D., et al. 2013, ApJ, 777, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Jr., Hao, C.-N., Calzetti, D., et al. 2009, ApJ, 703, 1672 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Calzetti, D., Aniano, G., et al. 2011, PASP, 123, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Dopita, M. A. 2002, ApJS, 142, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., & Ellison, S. L. 2008, ApJ, 681, 1183 [NASA ADS] [CrossRef] [Google Scholar]
- Kewley, L. J., Jansen, R. A., & Geller, M. J. 2005, PASP, 117, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., & Kewley, L. J. 2004, ApJ, 617, 240 [NASA ADS] [CrossRef] [Google Scholar]
- Kobulnicky, H. A., Dickey, J. M., Sargent, A. I., Hogg, D. E., & Conti, P. S. 1995, AJ, 110, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Lara-López, M. A., Hopkins, A. M., López-Sánchez, A. R., et al. 2013, MNRAS, 434, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Lequeux, J., Peimbert, M., Rayo, J. F., Serrano, A., & Torres-Peimbert, S. 1979, A&A, 500, 145 [NASA ADS] [Google Scholar]
- Leroy, A., Bolatto, A. D., Simon, J. D., & Blitz, L. 2005, ApJ, 625, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A., Bolatto, A., Walter, F., & Blitz, L. 2006, ApJ, 643, 825 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Bigiel, F., et al. 2009, AJ, 137, 4670 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Sandstrom, K. M., Lang, D., et al. 2019, ApJS, 244, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Lilly, S. J., Carollo, C. M., Pipino, A., Renzini, A., & Peng, Y. 2013, ApJ, 772, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Madden, S. C., Rémy-Ruyer, A., Galametz, M., et al. 2013, PASP, 125, 600 [NASA ADS] [CrossRef] [Google Scholar]
- Madden, S. C., Rémy-Ruyer, A., Galametz, M., et al. 2014, PASP, 126, 1079 [CrossRef] [Google Scholar]
- Maiolino, R., Nagao, T., Grazian, A., et al. 2008, A&A, 488, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mannucci, F., Cresci, G., Maiolino, R., Marconi, A., & Gnerucci, A. 2010, MNRAS, 408, 2115 [NASA ADS] [CrossRef] [Google Scholar]
- Marble, A. R., Engelbracht, C. W., van Zee, L., et al. 2010, ApJ, 715, 506 [NASA ADS] [CrossRef] [Google Scholar]
- Markarian, B. E., & Stepanian, D. A. 1983, Astrofizika, 19, 639 [NASA ADS] [Google Scholar]
- McGaugh, S. S., & Schombert, J. M. 2014, AJ, 148, 77 [NASA ADS] [CrossRef] [Google Scholar]
- McGaugh, S. S., & Schombert, J. M. 2015, ApJ, 802, 18 [CrossRef] [Google Scholar]
- Meidt, S. E., Schinnerer, E., Knapen, J. H., et al. 2012, ApJ, 744, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Meidt, S. E., Schinnerer, E., van de Ven, G., et al. 2014, ApJ, 788, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Morrissey, P., Conrow, T., Barlow, T. A., et al. 2007, ApJS, 173, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Moustakas, J., Kennicutt, R. C., Jr., Tremonti, C. A., et al. 2010, ApJS, 190, 233 [NASA ADS] [CrossRef] [Google Scholar]
- Murphy, E. J., Condon, J. J., Schinnerer, E., et al. 2011, ApJ, 737, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Noeske, K. G., Faber, S. M., Weiner, B. J., et al. 2007, ApJ, 660, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Oey, M. S., Herrera, C. N., Silich, S., et al. 2017, ApJ, 849, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Pettini, M., & Pagel, B. E. J. 2004, MNRAS, 348, L59 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Grebel, E. K., & Kniazev, A. Y. 2014a, AJ, 147, 131 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Grebel, E. K., Zinchenko, I. A., & Kniazev, A. Y. 2014b, AJ, 148, 134 [NASA ADS] [CrossRef] [Google Scholar]
- Pilyugin, L. S., Grebel, E. K., & Zinchenko, I. A. 2015, MNRAS, 450, 3254 [NASA ADS] [CrossRef] [Google Scholar]
- Rémy-Ruyer, A., Madden, S. C., Galliano, F., et al. 2014, A&A, 563, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Renzini, A., & Peng, Y.-J. 2015, ApJ, 801, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Romeo, A. B. 2020, MNRAS, 491, 4843 [NASA ADS] [CrossRef] [Google Scholar]
- Roweis, S. 1998, Proceedings of the 1997 Conference on Advances in Neural Information Processing Systems 10, NIPS ’97 (Cambridge, MA, USA: MIT Press), 626 [Google Scholar]
- Saintonge, A., Kauffmann, G., Kramer, C., et al. 2011a, MNRAS, 415, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Saintonge, A., Kauffmann, G., Wang, J., et al. 2011b, MNRAS, 415, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Saintonge, A., Catinella, B., Cortese, L., et al. 2016, MNRAS, 462, 1749 [NASA ADS] [CrossRef] [Google Scholar]
- Saintonge, A., Catinella, B., Tacconi, L. J., et al. 2017, ApJS, 233, 22 [Google Scholar]
- Salim, S., Rich, R. M., Charlot, S., et al. 2007, ApJS, 173, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Lee, J. C., Janowiecki, S., et al. 2016, ApJS, 227, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Salim, S., Boquien, M., & Lee, J. C. 2018, ApJ, 859, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Sandstrom, K. M., Leroy, A. K., Walter, F., et al. 2013, ApJ, 777, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Sargent, M. T., Béthermin, M., Daddi, E., & Elbaz, D. 2012, ApJ, 747, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, M. 1959, ApJ, 129, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Schruba, A., Leroy, A. K., Walter, F., et al. 2012, AJ, 143, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, Y., Wang, J., Zhang, Z.-Y., et al. 2015, ApJ, 804, L11 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, Y., Wang, J., Zhang, Z.-Y., et al. 2016, Nat. Commun., 7, 13789 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, B. J., & Hancock, M. 2009, AJ, 138, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Speagle, J. S., Steinhardt, C. L., Capak, P. L., & Silverman, J. D. 2014, ApJS, 214, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, D. V., Kannappan, S. J., Wei, L. H., et al. 2013, ApJ, 769, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Strange, H., & Zwiggelaar, R. 2015, Intell. Data Anal., 19, 1213 [Google Scholar]
- Tremonti, C. A., Heckman, T. M., Kauffmann, G., et al. 2004, ApJ, 613, 898 [NASA ADS] [CrossRef] [Google Scholar]
- Ugryumov, A. V., Engels, D., Lipovetsky, V. A., et al. 1999, A&AS, 135, 511 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ugryumov, A. V., Engels, D., Pustilnik, S. A., et al. 2003, A&A, 397, 463 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walter, F., Taylor, C. L., Hüttemeister, S., Scoville, N., & McIntyre, V. 2001, AJ, 121, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Wei, L. H., Kannappan, S. J., Vogel, S. N., & Baker, A. J. 2010, ApJ, 708, 841 [NASA ADS] [CrossRef] [Google Scholar]
- Wen, X.-Q., Wu, H., Zhu, Y.-N., et al. 2013, MNRAS, 433, 2946 [NASA ADS] [CrossRef] [Google Scholar]
- Wen, X.-Q., Wu, H., Zhu, Y.-N., et al. 2014, MNRAS, 438, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Wolfire, M. G., Hollenbach, D., & McKee, C. F. 2010, ApJ, 716, 1191 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Xianxi, L., Li, S., Guoquan, L., Menghua, X., & Wei, W. 2017, 2017 36th Chinese Control Conference (CCC), 9665 [Google Scholar]
- Young, J. S., Xie, S., Tacconi, L., et al. 1995, ApJS, 98, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Zahid, H. J., Dima, G. I., Kudritzki, R.-P., et al. 2014, ApJ, 791, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Zhu, M., Papadopoulos, P. P., Xilouris, E. M., Kuno, N., & Lisenfeld, U. 2009, ApJ, 706, 941 [NASA ADS] [CrossRef] [Google Scholar]
- Zibetti, S., Charlot, S., & Rix, H.-W. 2009, MNRAS, 400, 1181 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Overall comparison of galaxy parameters in MAGMA
Figure A.1 shows the median differences of each individual parent sample in MAGMA relative to the sample as a whole as a function of the discrete Mstar bin; the error bars are the standard deviations of the estimate. The gray regions give the standard deviations of the entire MAGMA sample, and the horizontal dashed lines show the median difference, which is zero by definition. If there were any systematic differences as a function of the parent sample and/or Mstar, they should stand out in Fig. A.1. However, it is clear from the figure that there are no systematic differences in any of the parameters shown. The only exception could be the 12 + log(O/H) (bottom) panel, where the BCD, DGS, and Virgo SFDs have a lower O/H than would be expected; there is a similar corresponding excess, although within the spreads, in the SFR. There is a real, physical difference, among the samples, due to the anticorrelation between the SFR and O/H, the FMR (see, e.g., Mannucci et al. 2010). These dwarf samples at low Mstar are slightly starburst biased because of our requirement for CO detections. Thus, with this exception, we conclude that there are no apparent systematic differences among the parent samples in MAGMA.
 |
Fig. A.1. Comparison of SFR, 12 + log(O/H), MH2, and MHI in segregated Mstar bins for the MAGMA sample. The gray regions correspond to the standard deviations (±1σ), and the horizontal dashed line represents the zero difference (by definition) relative to the sample median. The nine different parent samples comprising MAGMA are shown by different symbols given in the legend in the upper right corner. The points and their error bars correspond to the median of the difference, relative to the median parameter of the MAGMA sample as a whole. |
Appendix B: Details of comparison with previous work: A cautionary tale
There are two salient differences between the MAGMA sample and the sample from Bothwell et al. (2016a). One is the significant low-mass coverage of the MAGMA sample, and the other is the SFRs. Both of these are illustrated in Fig. B.1 where the MS for the two samples are plotted; the median points only show those Mstar bins with ≥3 data points. The Bothwell et al. (2016a) sample is the same as that from Bothwell et al. (2016b), but with 8 BCDs from Hunt et al. (2015),; Bothwell et al. (2016a) altered the Mstar values, and to best approximate their sample, for the BCDs from Hunt et al. (2015) we have arbitrarily lowered the Mstar values by a factor of three14. Even with the addition of the BCDs from Hunt et al. (2015), the mass distribution is significantly more extended for MAGMA. The low-mass bin in the Bothwell et al. sample of Fig. B.1 is comprised of the galaxies from Hunt et al. (2015) that are not present in the sample used by Bothwell et al. (2016b), and the highest-mass bin is dominated by the high-z submillimeter galaxies (SMGs) and MS galaxies at z ∼ 2. MAGMA shows slight downward inflection associated with quiescent or passive high-mass galaxies (see also Fig. 5), while the Bothwell et al. (2016a) sample shows a steep upturn because of the inclusion of high-z massive galaxies with a consequently higher SFR.
 |
Fig. B.1. Log(SFR) versus Log(Mstar) for the MAGMA sample as in Fig. 5, but here we plotted also the galaxies from Bothwell et al. (2016b, see their Table 2), together with the eight galaxies from Hunt et al. (2015) (we used a reduced Mstar as described in the main text). Medians for both samples are also shown, but only medians with ≥3 points in the respective Mstar bins are plotted here. |
There are also differences in the SFRs: while MAGMA adopts COLDGASS galaxies with parameters from Saintonge et al. (2017), Bothwell et al. (2016b,a) use the COLDGASS parameters reported by Saintonge et al. (2011a,b). However, a subsequent study (Huang & Kauffmann 2014) showed that the SFRs in those papers are overestimated by ∼0.2 dex because of aperture effects from the CO single-dish IRAM beam. Roughly half (115 galaxies) of the Bothwell et al. sample is from COLDGASS, which means that these values are also discrepant with respect to MAGMA. This can be seen in Fig. B.1 where, at a given Mstar, the Bothwell et al. sample tends to have higher SFRs than MAGMA.
Possibly the most important difference in this context relative to MAGMA is the inclusion by Bothwell et al. of the 17 high-z galaxies (nine main-sequence galaxies and eight SMGs). These galaxies are at z ∼ 2 and have significantly higher SFRs than the local galaxies of similar stellar mass because of the increasing normalization of the star-formation main sequence with redshift (e.g., Speagle et al. 2014). The minimum Log(Mstar/M⊙) value in the high-z sample is 9.78, and the mean SFR is ∼274 M⊙ yr−1; for the low-z sample over the same mass range, the mean SFR is ∼2.4 M⊙ yr−1, which is more than 100 times smaller. A similar difference applies to the ratios of MH2 in the two samples, where the mean MH2 in the high-z sample is ∼85 times higher than in the low-z galaxies over the same range in Mstar. To assess the impact of these galaxies on the results by Bothwell et al. (2016b,a), we performed 4D PCAs on the Bothwell et al. (2016a) sample, both with and without the 17 high-z galaxies, using only the galaxies with CO detections in their Table 2 (Hunt et al. 2015). The results are reported in Table B.1.
4D PCA results for the Bothwell et al. (2016a) sample.
The upper part of Table B.1 shows the 4D PCA for H2 for the Bothwell et al. (2016a) sample including the 17 high-z MS galaxies and SMGs as well as the eight BCDs from Hunt et al. (2015). The results are in fairly good agreement15 with those of Bothwell et al. (2016a). The dependence of 12 + log(O/H) on MH2 is larger than that on the SFR; our probabilistic PCA estimates of the uncertainties show, however, that the coefficient for the MH2 dependence is determined with < 3σ significance.
The lower part of Table B.1 instead shows the 4D PCA result for the low-zBothwell et al. (2016b) sample, without the 17 high-z galaxies, but with the eight BCDs from Hunt et al. (2015). The Mstar dependence is significantly reduced, the SFR dependence is increased, and the MH2 dependence is consistent with 0.0 to within the errors. Interestingly, the SFR and Mstar coefficients have the same sign, implying that increasing both the SFR and Mstar increases Z; this is contrary to the “normal” 3DPCA1–OH behavior in which at a given Mstar, increasing the SFR tends to reduce Z. The comparison in Table B.1 of the two versions of the Bothwell et al. sample, including or omitting the high-z galaxies, shows that the PCA significantly changes and that the most probable driver of the lack of metallicity SFR dependence relative to MH2 is caused by the inclusion of z ∼ 2 galaxies which, at a given Mstar, have a significantly higher molecular gas content and SFR than galaxies in the local Universe.
Appendix C: Assessment of Monte Carlo error injection on PCA fits
To explore the effect of injecting Gaussian noise on a dataset subject to a PCA, we generated several “mock” samples of the 3DPCA1–OH for galaxies at z ∼ 0. To do this, we first distributed numbers of galaxies in Mstar bins with redshifts ranging from z = 0.0 to z = 0.02, according to either a constant Mstar distribution or one that resembles the GSMF given by Baldry et al. (2012). Within each mass and (small) redshift bin, we randomly selected Mstar in order to more or less reproduce the assumed distribution. Then, we derived a MS of star formation by imposing Speagle et al. (2014) at z = 0, or equivalently adopting the relation given by Hunt et al. (2019) for the KINGFISH sample. We added a small (realistic) fraction of starbursts using the formulation of Sargent et al. (2012); this approach separates galaxy populations according to sSFR and approximates the distribution with two Gaussians. Sargent et al. (2012) further assume that the starburst fraction is independent of mass and redshift, which may or may not be correct (see e.g., Bisigello et al. 2018). Finally, we related 12 + log(O/H) to Mstar and SFR via the 3DPCA1–OH (FPZ) reported by Hunt et al. (2016a). This means that the basic input parameter is Mstar, which defines the SFR through the MS with the addition of a small fraction of starbursts; then 12 + log(O/H) is calculated based on Mstar and the SFR. We adopted a total mock sample size for both Mstar distributions of ∼12 000 simulated galaxies.
This construction of the mock samples may seem arbitrary, but in truth the details are not important; we only want to compare what we get out versus what we put in, in the case of varying levels of noise injection. To this end, we took this initial “noiseless” sample and introduced varying degrees of Gaussian uncertainty, σ, to the SFR and 12 + log(O/H); for simplicity, we used the same value of σ for both the SFR and 12 + log(O/H). We repeated this procedure several times and applied a PCA to each of the noise-injected samples. The results are shown in Fig. C.1, where the 3D PCA coefficients are plotted against the injected noise level σ. The left-hand part of the curves for σ = 0 are the input values of the 3DPCA1–OH by which the mock sample was generated. There are seven separate curves in Fig. C.1 for each of the three PCs, corresponding to seven different realizations of the noise injection for the mock samples; the closeness of the curves evident in the figure indicates that the statistical results are quite stable. The discrepant curves for the constant Mstar case correspond to different lower-mass limits.
 |
Fig. C.1. 3D PCA coefficients for Log(Mstar) (in red), Log(SFR) (in orange), and 12 + log(O/H) (in blue) plotted against the injected noise level σ; different line types correspond to the two different Mstar distributions as described in the text and illustrated in the legend. The different curves for the constant Mstar case correspond to different lower-mass limits. The true input of 3DPCA2(OH) is shown by the transparent lines, with a thickness of ±0.025 dex. The data points, including error bars that are smaller than the symbols, report the PCA coefficients from the initial σ = 0.15 dex mock sample, but which has been in turn perturbed as described in the text. The aim of this subsequent exercise is to simulate a Monte Carlo perturbation of an observed sample. |
The idea here is to simulate an observed sample, such as MAGMA, and assess the accuracy of the resulting PCA, compared to the input “true” values. The implicit assumption is that MAGMA, or similar samples, are governed by an underlying 3DPCA1–OH or 2D plane, but they suffer from uncertainty in the measurement of the observables. We cannot know whether or not this is true; we can only ascertain how far the observed data set could differ from the underlying relation if it were present.
Also shown in Fig. C.1 are six data points corresponding to a PCA on the σ = 0.15 mock sample, but to which an additional perturbation has been applied. We have chosen σ = 0.15 dex as a starting point, in order to best approximate the behavior of the MAGMA sample, which shows a dispersion in 12 + log(O/H) of roughly this amplitude around the best-fit 3DPCA1–OH. While the original mock samples are intended to reproduce observed samples, this additional injection of Gaussian noise is aimed at simulating a Monte Carlo perturbation of an observed sample. Thus, we injected Gaussian noise of various amplitudes on the variables of our mock sample: Log(Mstar) was varied by 0.3 dex; the SFR was varied by 30% [corresponding to ∼0.2 dex on Log(SFR)]; and 12 + log(O/H) was varied by 0.1 dex. This is a similar technique as the one described by Bothwell et al. (2016b,a), and in principle it helps to establish uncertainties in the final PCA results. However, Fig. C.1 clearly shows that the injection of additional noise on the mock sample carries the PCA results even further from the input true 3DPCA1–OH. The amplitude of the noise injected σ already masks the 3DPCA1–OH that was the basis for the mock samples, but the additional perturbation exacerbates, even more, the capacity of the PCA to diagnose the underlying relation.
Figure C.2 illustrates in another way the process of this subsequent perturbation on the mock sample; the orthogonal projections of the PCs are shown in three different panels. The color maps show the original mock sample with σ = 0.15 injected Gaussian noise, while the contours show the same data as the individual points (with the GSMF from Baldry et al. 2012), but here the PCs were calculated according to the loadings of the original mock sample. This is done to highlight the change in orientation relative to the original sample, thus illustrating that the injection of additional noise alters the orientation of the components. This can be seen in particular in the upper right panel comparing PC3, which is dominated by O/H, to PC2, which is dominated by Mstar, and to a lesser extent the SFR; the contours are oriented at a different angle relative to the underlying color map.
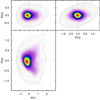 |
Fig. C.2. 3D PC components under various projections. The underlying color maps show the density distribution of data points with the PCA calculated from the original mock sample with σ = 0.15 dex and the contours of the density distribution of the perturbed sample but with the PCA loadings of the original one. The change of orientation of the PC decomposition introduced by the perturbation is evident, especially in the upper right panel. |
We conclude that:
-
The injection of Gaussian noise in a noiseless sample changes the PCA characteristics because of the resulting change of the orientation of the derived PCs (see the curves in Fig. C.1). Further injection of Gaussian noise moves the PCA even further from the input relation, as shown by the individual points in Fig. C.1. Even though the introduction of noise does not change the means of the parameters, it skews the orientation because PCAs consider the entire distribution of data, including outliers.
-
The distribution of Mstar in a sample also impacts the results of a PCA (see varying curves in Fig. C.1). This is because a PCA calculates the orthogonal distance from an orientation, and it requires a broad distribution in parameters in order to better take eventual outliers into account.
Ultimately, because of the mathematical nature of the PCA, the addition of noise to a sample for which a PCA is to be performed is deleterious to the reliability of the results. For this reason, here, we preferred using resampling techniques, rather than altering the noise characteristics of the sample.
All Tables
Logarithmic differences of Mstar and SFR between the original description and adopted values.
All Figures
 |
Fig. 1. Comparison of newly-derived Mstar (left) and SFR (right) with the original values. The individual samples are distinguished by different symbols as given in the legend. See text for more details on the derivations. |
| In the text | |
 |
Fig. 2. Distributions of Mstar for the MAGMA sample; the right panels illustrate the subdivisions in Mstar for the parent surveys. The red vertical dashed line in the left panel corresponds to the median Mstar for MAGMA, log(Mstar/M⊙) = 9.68. Also shown in the left panel is the SDSS10 sample, taken from Mannucci et al. (2010), consisting of 78579 galaxies. Here, it has been renormalized to show the Mstar distribution it would have if it contained the same number of galaxies (390) as MAGMA; the Mstar median of SDSS10 (shown as a blue vertical dashed line) is log(Mstar/M⊙) = 10.28. |
| In the text | |
 |
Fig. 3. Distributions for combined sample of 392 galaxies for log (sSFR) (left panel), 12 + log(O/H) (middle), and log [Mgas/(Mstar + Mgas) ≡ Mgas/Mbaryonic] (right). The red vertical dashed lines in each panel correspond to the MAGMA medians: log(sSFR/yr−1) = −9.92; 12 + log(O/H) = 8.64 (Z⊙ would be 12 + log(O/H) = 8.69, see Asplund et al. 2009); and log(Mgas/Mbaryonic) = log(fbaryonic) = 0.39. The left and middle panels also include the SDSS10 sample, as in Fig. 2; the sSFR and O/H medians of SDSS10 are log(sSFR/yr−1) = −10.36 and 12 + log(O/H) = 8.69, respectively, and they are shown by blue vertical dashed lines. |
| In the text | |
 |
Fig. 4. Distributions of SFR for the MAGMA sample are shown as red-shaded regions in bins of Mstar; the SDSS10 sample in yellow-shaded regions and the fit to the SFMS (shown as a solid gray curve) reported by Hunt et al. (2019) are also shown. The close agreement of MAGMA with SDSS and the SFMS, except possibly for the lowest Mstar bin, suggests that starbursts do not dominate the galaxy population represented. |
| In the text | |
 |
Fig. 5. Upper panel: galaxies from the MAGMA sample plotted in the SFR–Mstar plane. The green line is the MS of star-forming galaxies derived from the SDSS (Brinchmann et al. 2004). Contours in this plane for the SDSS10 sample are shown as gray closed curves; the lowest level contour encloses 90% of the sample. The LVL sample (Dale et al. 2009; Kennicutt et al. 2009), as described in the text, is also shown in the upper panels. Lower panels: MAGMA galaxies in the SFR–Mgas (upper-left), MH2–SFR (upper-right), MHI–SFR (lower-left), and |
| In the text | |
 |
Fig. 6. Upper panel: MAGMA sample in the Mstar–Z plane. Lower panel: MAGMA sample in the sSFR–Z plane. Metallicities are reported in PP04N2 (or Te) units of 12 + log(O/H). In both panels, as in previous figures, the SDSS10 sample is also plotted, with 90% of the galaxies enclosed within the lowest contours; both panels also show the LVL sample (Dale et al. 2009; Kennicutt et al. 2009) as described in the text. Upper panel: the MZR from the direct-Te determination by Andrews & Martini (2013) is also given, and its good agreement with the MAGMA PP04N2 (+Te) metallicities suggests that the calibrations are consistent. Symbols and colors refer to different parent surveys, as indicated in the legend. The black dashed line represents the median trend of the distribution, which was calculated at different bins (see black dots); the horizontal bars indicate the widths of the bins, while vertical bars indicate the standard deviation around median values of the galaxies in the bins. |
| In the text | |
 |
Fig. 7. PCA coefficients for MAGMA log(Mstar) plotted against Mbreak for the division into the two PCAs. Right panel: magnification of the left panel, showing, more effectively, that the range of Mstar coefficients as the Mbreak mass is varied. The lower values of the Mstar coefficient toward higher Mbreak results from the flattening of the MZR at high Mstar. |
| In the text | |
 |
Fig. 8. Observed values of 12 + log(O/H) in the MAGMA sample compared to those predicted by the 3DPCA2(OH) given in Eq. (5). The parent sample of the individual MAGMA galaxies is given in the legend in the middle panel, and the right panel shows the residuals and the Gaussian fit; the 1σ dispersion of the Gaussian is 0.074 dex as discussed in the text. The MAGMA 3DPCA2(OH) applied to SDSS10 is also shown, and as before 90% of SDSS10 is enclosed within the contours. The median of the SDSS10 residuals relative to the 3DPCA2(OH) is 0.002 dex, with a standard deviation of ∼0.08 dex, showing that even when the MZR curvature is clearly evident in SDSS10, the MAGMA 3DPCA2(OH) does a good job of reproducing the metallicities (see text for more details). |
| In the text | |
 |
Fig. A.1. Comparison of SFR, 12 + log(O/H), MH2, and MHI in segregated Mstar bins for the MAGMA sample. The gray regions correspond to the standard deviations (±1σ), and the horizontal dashed line represents the zero difference (by definition) relative to the sample median. The nine different parent samples comprising MAGMA are shown by different symbols given in the legend in the upper right corner. The points and their error bars correspond to the median of the difference, relative to the median parameter of the MAGMA sample as a whole. |
| In the text | |
 |
Fig. B.1. Log(SFR) versus Log(Mstar) for the MAGMA sample as in Fig. 5, but here we plotted also the galaxies from Bothwell et al. (2016b, see their Table 2), together with the eight galaxies from Hunt et al. (2015) (we used a reduced Mstar as described in the main text). Medians for both samples are also shown, but only medians with ≥3 points in the respective Mstar bins are plotted here. |
| In the text | |
 |
Fig. C.1. 3D PCA coefficients for Log(Mstar) (in red), Log(SFR) (in orange), and 12 + log(O/H) (in blue) plotted against the injected noise level σ; different line types correspond to the two different Mstar distributions as described in the text and illustrated in the legend. The different curves for the constant Mstar case correspond to different lower-mass limits. The true input of 3DPCA2(OH) is shown by the transparent lines, with a thickness of ±0.025 dex. The data points, including error bars that are smaller than the symbols, report the PCA coefficients from the initial σ = 0.15 dex mock sample, but which has been in turn perturbed as described in the text. The aim of this subsequent exercise is to simulate a Monte Carlo perturbation of an observed sample. |
| In the text | |
 |
Fig. C.2. 3D PC components under various projections. The underlying color maps show the density distribution of data points with the PCA calculated from the original mock sample with σ = 0.15 dex and the contours of the density distribution of the perturbed sample but with the PCA loadings of the original one. The change of orientation of the PC decomposition introduced by the perturbation is evident, especially in the upper right panel. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.