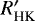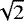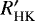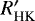| Issue |
A&A
Volume 628, August 2019
|
|
|---|---|---|
| Article Number | A125 | |
| Number of page(s) | 13 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201935347 | |
| Published online | 20 August 2019 | |
Activity time series of old stars from late F to early K
II. Radial velocity jitter and exoplanet detectability
Université Grenoble Alpes, CNRS, IPAG,
38000 Grenoble, France
e-mail: nadege.meunier@univ-grenoble-alpes.fr
Received:
22
February
2019
Accepted:
2
July
2019
Context. The effect of stellar activity on radial velocity (RV) measurements appears to be a limiting factor in detecting Earth-mass planets in the habitable zone of a star that is similar to the Sun in spectral type and activity level. It is crucial to estimate whether this conclusion remain true for other stars with current correction methods.
Aims. We built realistic time series in radial velocity and chromospheric emission for old main-sequence F6-K4 stars. We studied the effect of the stellar parameters we investigate on exoplanet detectability. The stellar parameters are spectral type, activity level, rotation period, cycle period and amplitude, latitude coverage, and spot constrast, which we chose to be in ranges that are compatible with our current knowledge of stellar activity.
Methods. This very large set of synthetic time series allowed us to study the effect of the parameters on the RV jitter and how the different contributions to the RV are affected in this first analysis of the data set. The RV jitter was used to provide a first-order detection limit for each time series and different temporal samplings.
Results. We find that the coverage in latitude of the activity pattern and the cycle amplitudes have a strong effect on the RV jitter, as has stellar inclination. RV jitter trends with B–V and Log R′HK are similar to observations, but activity cannot be responsible for RV jitter larger than 2–3 m s−1 for very quiet stars: this observed jitter is therefore likely to be due to other causes (instrumental noise or stellar or planetary companions, e.g.). Finally, we show that based on the RV jitter that is associated with each time series and using a simple criterion, a planet with one Earth mass and a period of one to two years probably cannot be detected with current analysis techniques, except for the lower mass stars in our sample, but very many observations would be required. The effect of inclination is critical.
Conclusions. The results are very important in the context of future RV follow-ups of transit detections of such planets. We conclude that a significant improvement of analysis techniques and/or observing strategies must be made to reach such low detection limits.
Key words: stars: activity / stars: magnetic field / stars: solar-type / convection / techniques: radial velocities / Sun: granulation
© N. Meunier and A.-M. Lagrange 2019
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
In the past few years, we undertook several steps to be able to produce realistic radial velocity (RV) time series for stars other than the Sun. After modeling the solar RV using observed magnetic structures (Lagrange et al. 2010; Meunier et al. 2010a), we developed a complex model in which we randomly generated the structures using our current knowledge of the Sun (Borgniet et al. 2015). This model allowed us to simulate complex patterns of activity for the Sun viewed from any point of view. We also computed other variables, such as brightness variations and astrometry. Finally, we adapted the model to other stars (different activity levels and spectral types) that we described in Meunier et al. (2019, hereafter Paper I). Other models considering complex activity patterns have been proposed by Herrero et al. (2016) to reproduce the contributions of spots and plages and by Santos et al. (2015) for spots alone. The simulations made in Dumusque (2016) include all effects for a few configurations.
In this paper we perform a first analysis based on the RV jitter. Although we know that using RV jitter remains a simple approach, it is widely used in the literature: simple models of activity (Saar & Donahue 1997; Hatzes 2002; Saar et al. 2003; Wright 2005) have been used to predict RV jitter from other data (e.g., Martínez-Arnáiz et al. 2010; Arriagada 2011). Therefore it is interesting to propose a first application of the RV jitter derived from the models to explore the limits of exoplanet detect- ability as a function of spectral type and activity level beyond the solar case. We consider a threshold in RV jitter that corresponds to the current status of correction methods derived from Dumusque (2016) and Dumusque et al. (2017) and apply it to derive an approximate detection limit as a function of spectral type and activity level.
The outline of the paper is the following. In Sect. 2 we recall the model principles, parameters, and the observables, which are produced for each set of parameters from Paper I. Section 3 describes the effect of the parameters on the RV jitter. We also studied the individual components due to magnetic activity of the whole RV signal and the effect of several parameters on the corresponding RV jitter. In Sect. 4 we compare the RV jitter we obtained in our simulations with observations, and we investigate the RV jitter at different scales. In Sect. 5 we propose a first application of these RV jitter to exoplanet detectability, and we conclude in Sect. 6.
2 Model and parameter grid
In this section we describe the model used throughout the paper. The parameters for stars with different spectral types and activity levels are then reviewed.
2.1 Simulation of magnetic structures and raw time series
The approach is described in detail in Borgniet et al. (2015) for the Sun and in Paper I for other stars. The solar chromospheric model proposed in Meunier (2018) is also extended to other stars (Paper I). This model is based on a large number of parameters (see next section) to produce spots, plages, and network structures in a consistent way. In this series of papers, we cover spectral types from F6 to K4 and relatively old main-sequence stars (maximum average Log  depending on spectral type, from −4.6 for F6 stars to −4.85 for K4 stars).
depending on spectral type, from −4.6 for F6 stars to −4.85 for K4 stars).
We recall here the time series used in the following analysis:
rvspot1 and rvspot2: RV due to the presence of spots, following two laws (see Sect. 2.2) for the spot temperature contrast (a lower and an upper limit, ΔTspot1 and ΔTspot2, respectively).
rvplage: RV due to plages and network.
rvconv: RV due to the inhibition of the convective blueshift in plages and in the network. In the following, “convection” refers to this process, which is related to both granulation properties and to magnetic activity. This is different from the granulation signal rvogs described below.
rvact1 and rvact2: sum of rvspot1 (rvspot2), rvplage, and rvconv.
rvogs: RV due to oscillation, granulation, and supergranulation (hereafter the OGS signal), either at the original temporal resolution (30 s) or averaged over one hour.
rvinst: RV due to instrumental white noise represented by a Gaussian noise with an amplitude of 0.6 m s−1.
Log
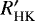 : chromospheric emission index derived from the S-index produced in the simulation (Harvey & White 1999; Meunier 2018).
: chromospheric emission index derived from the S-index produced in the simulation (Harvey & White 1999; Meunier 2018).
The temporal step is on average one day (with random departures up to four hours). The time series cover an integer number of cycles, with a maximum of 15 yr, the duration therefore varies between 3327 and 5378 days depending on the simulation. We also used a degraded sampling that is defined as follows: a four-month gap each year was introduced to simulate the fact that a star is not always visible from a given observatory; a maximum duration of 9 yr was imposed to degrade the duration, so that in some cases not a complete activity cycle was covered; the number of point Nobs was reduced to 100, 300, 500, 1000, or 2000 depending on the time series, with a random choice between these four values and a ramdom choice between 100 realizations of the sampling).
2.2 Parameter grid
We list here the parameters that we modified from the solar values. More details about the laws, justification, and references can be found in Paper I. Our basic sets of parameters depend on B–V and Log 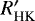 . For each point in this 2D (B–V, Log
. For each point in this 2D (B–V, Log 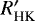 ) grid, the following parameters were adapted (from the solar values):
) grid, the following parameters were adapted (from the solar values):
Fundamental parameters (Teff, mass, radius). They depend on the spectral type (and therefore B− V).
Spot temperature contrast. We used two laws: a lower limit defined by the solar contrast in Borgniet et al. (2015), ΔTspot1, and an upper limit law depending on Teff from Berdyugina (2005), ΔTspot2. We assumed that star spots have contrasts within this range.
The plage contrast. It depends on B–V, but also on the size and position of each structure (Unruh et al. 1999; Meunier et al. 2010a; Borgniet et al. 2015; Norris 2018).
Convective blueshift and attenuation factor. They depend on B− V and Log
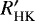 . We also scaled the diffusion coefficient to the convective blueshift amplitude (Meunier et al. 2017a).
. We also scaled the diffusion coefficient to the convective blueshift amplitude (Meunier et al. 2017a).The maximum average latitude at the beginning of the cycle θmax. It is not constrained observationally or from models, therefore we studied the effect of three values: the solar latitude θmax,⊙, θmax,⊙ + 10°, and θmax,⊙ + 20°. The two last values produce butterfly diagrams with a larger extent in latitude than in the Sun and were chosen arbitrarily in Paper I to study the effect of this important parameter.
The rotation period Prot. It depends on B−V and on the ave- rage Log
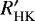 . We considered three laws: a median law, a lower limit law, and an upper limit law, assuming that the observed dispersion in the relationship between Prot and Log
. We considered three laws: a median law, a lower limit law, and an upper limit law, assuming that the observed dispersion in the relationship between Prot and Log 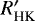 reflects an actual dispersion between stars (Mamajek & Hillenbrand 2008).
reflects an actual dispersion between stars (Mamajek & Hillenbrand 2008).The differential rotation. It depends on Teff, but also onthe rotation period (Reinhold & Gizon 2015), and on θmax.
The cycle period Pcyc. It depends on the rotation period (and therefore also on B−V and Log
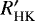 ). We considered three laws (median law, and two extreme laws), assuming that the observed dispersion in the relationship between the cycle period and Prot is real (Noyes et al. 1984; Baliunas et al. 1995; Saar & Brandenburg 1999; Böhm-Vitense 2007; Oláh et al. 2009, 2016; Lovis et al. 2011; Suárez Mascareño et al. 2016).
). We considered three laws (median law, and two extreme laws), assuming that the observed dispersion in the relationship between the cycle period and Prot is real (Noyes et al. 1984; Baliunas et al. 1995; Saar & Brandenburg 1999; Böhm-Vitense 2007; Oláh et al. 2009, 2016; Lovis et al. 2011; Suárez Mascareño et al. 2016).The cycle amplitude Acyc. It depends on B−V and Log
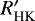 . We considered three laws: median law, and two extreme laws (Lovis et al. 2011; Radick et al. 1998).
. We considered three laws: median law, and two extreme laws (Lovis et al. 2011; Radick et al. 1998).OGS parameters. The typical frequencies and frequency width of the power spectra (for the oscillations), timescale, and exponent in the power spectra (granulation and supergranulation) as well as their amplitude depend on B− V (Kallinger et al. 2014; Kjeldsen & Bedding 1995; Samadi et al. 2007; Bedding & Kjeldsen 2003; Kippenhahn & Weigert 1990; Belkacem et al. 2013; Harvey 1984; Beeck et al. 2013; Meunier et al. 2015).
All other parameters were kept to our solar values as in Borgniet et al. (2015): meridional circulation (Komm et al. 1993), other plage and network properties (Borgniet et al. 2015; Schrijver 2001; Meunier et al. 2017a), and spot properties (Martinez Pillet et al. 1993; Baumann & Solanki 2005; Borgniet et al. 2015). The five parameters for which we tested several laws (spot contrast, θmax, Prot, Pcyc, and Acyc) were used to produce time series that correspond to the same (B−V, Log 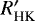 ) point. We study the effect of these parameters in Sect. 3.2. Finally, the inclination, although not an intrinsic parameter, strongly affects the RV jitter.
) point. We study the effect of these parameters in Sect. 3.2. Finally, the inclination, although not an intrinsic parameter, strongly affects the RV jitter.
3 Effect of parameters on the RV jitter
In this section, we study the effect of the parameters on the RV jitter to identify the most critical parameters. This is important because many parameters have complex dependencies, some of which produce strong geometrical effects.
3.1 Magnetic contributions to the RV jitter
We illustrate how the different components of magnetic activity (spots, plages, and inhibition of the convective blueshift in plages) listed in Sect. 2.1 depend on the stellar spectral type and Log 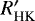 and how they relate to each other. We focus on the magnetic activity contributions without noise or OGS signal. Figure 1 shows a strong decrease in the RV jitter that is induced by spots and plages toward larger B− V and toward quiet stars. The main reason for the former result is likely to be the decrease in contrast (both for spot and plages). As expected, the RV jitter is larger for rvspot2 compared to rvspot1. The convective component first increases with B− V and then decreases again. There is an expected decrease in amplitude of the convective blueshift itself, but this is modulated by the amplitude of the cycle, which is dominating the trend. The RV jitter on the complete time series is slightly higher for the highest spot temperature contrast, but the difference between the final RV jitter for rvact1 and rvact2 is very small because rvconv often dominates. Finally, on average, the RV jitter (due to convection and total) is higher when seen edge-on compared to pole-on. This is mostly due to the rotational modulation effect and partly to the long-term variability (one-third). The ratio between the edge-on andpole-on RV jitter for rvconv strongly varies; it takes values between 0.1 and 1.1 for the most extreme cases.
and how they relate to each other. We focus on the magnetic activity contributions without noise or OGS signal. Figure 1 shows a strong decrease in the RV jitter that is induced by spots and plages toward larger B− V and toward quiet stars. The main reason for the former result is likely to be the decrease in contrast (both for spot and plages). As expected, the RV jitter is larger for rvspot2 compared to rvspot1. The convective component first increases with B− V and then decreases again. There is an expected decrease in amplitude of the convective blueshift itself, but this is modulated by the amplitude of the cycle, which is dominating the trend. The RV jitter on the complete time series is slightly higher for the highest spot temperature contrast, but the difference between the final RV jitter for rvact1 and rvact2 is very small because rvconv often dominates. Finally, on average, the RV jitter (due to convection and total) is higher when seen edge-on compared to pole-on. This is mostly due to the rotational modulation effect and partly to the long-term variability (one-third). The ratio between the edge-on andpole-on RV jitter for rvconv strongly varies; it takes values between 0.1 and 1.1 for the most extreme cases.
In the following we illustrate our results with ΔTspot2 unless indicated otherwise. We know that the signals from spots and plages partially compensate for each other because they are located at roughly the same positions (as shown in Meunier et al. 2010a). Spots have a much higher contrast than plages, but are also much smaller. The compensation is not strict, however, because there is a dispersion in plage-to-spot size ratio and because plages have a longer lifetime. To illustrate this, Fig. 2 shows how the root mean square (rms) of the RV jitter due tospots and plages separately varies with the RV jitter of the rvspot + rvplage time series. They both lie between thetwo straight lines (the lowest line corresponds to an exact compensation between plages and spots), indicating some compensation, although they do no compensate entirely. The compensation is slightly better with ΔTspot2.
The lower panel of Fig. 2 shows how the RV jitter due to spots and plages varies with the RV jitter due to rvconv. Although higher rvconv variability tends to be associated with high rvspot + rvplage variability, there is a high dispersion: for medium rvconv jitter, we observe the highest rvspot + rvplage jitter, for example. There is also a weak inclination effect. The solid line indicates the limit between RV jitter that is dominated by rvspot + rvplage (above the line) and by rvconv (below the line). For ΔTspot1, they correspond to less than 1% of the simulations, all for F6 stars. For ΔTspot2, the RV jitter in almost 5% of the simulations (all corresponding to F stars) is higher for rvspot + rvplage than for rvconv. This is illustrated in Fig. 3, which shows a version of the lower panel of Fig. 2 separately for each spectral type and after binning in rvconv.
 |
Fig. 1 RV jitter for the different magnetic activity components to the RV, vs. B–V (left) and Log |
 |
Fig. 2 Upper panel: root mean square of the RV jitter due to spot (rvspot1 in black and rvspot2 in red)) and plages separately vs. the RV jitter of rvspot + rvplage. The solid line indicates a y = x linear function and the dashed line has a slope of |
 |
Fig. 3 Upper panel: binned RV jitter of rvspot + rvplage vs. RV jitter from the attenuation of the convective blueshift rvconv for the 19 spectral types from F6 (yellow) to K4 (blue). Lower panel: same for ΔTspot2. |
3.2 Effect of cycle parameters (Acyc, Pcyc, θmax) and Prot on RV jitter
We now consider the time series including all contributions (magnetic, OGS averaged over one hour, and instrumental) for ΔTspot2. The results are very similar for ΔTspot1 and when rvact1 or rvact2 are considered alone (not shown here).
In the previous section, we have shown the dependence of the different components of the RV jitter on B− V and Log  and discussed the effect of ΔTspot. We now consider the four other laws for which we test different levels (see Sect. 2.2): θmax, Pcyc, Acyc, and Prot. Figure 4 shows a global view of the effect of these parameters after binning in B− V and Log
and discussed the effect of ΔTspot. We now consider the four other laws for which we test different levels (see Sect. 2.2): θmax, Pcyc, Acyc, and Prot. Figure 4 shows a global view of the effect of these parameters after binning in B− V and Log 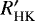 , providing one curve for each level. We note that the different choices of θmax do not depend on the other parameters (they take either the solar value or a value of +10° and +20°), while for the other three parameters, all laws (lower, medium, and higher) vary with the other parameters (mainly spectral type and activity level). Prot and Pcyc do not significantly affect the RV jitter, at least on average: this is not surprising because we expect them to strongly affect the frequency dependence of the variability, but not its global amplitude (the frequency analysis will be the subject of a future paper). On the other hand, θmax and Acyc strongly affect the RV jitter, the first because of geometrical effects (e.g., inclination), and the second naturally through the number of structures that are injected.
, providing one curve for each level. We note that the different choices of θmax do not depend on the other parameters (they take either the solar value or a value of +10° and +20°), while for the other three parameters, all laws (lower, medium, and higher) vary with the other parameters (mainly spectral type and activity level). Prot and Pcyc do not significantly affect the RV jitter, at least on average: this is not surprising because we expect them to strongly affect the frequency dependence of the variability, but not its global amplitude (the frequency analysis will be the subject of a future paper). On the other hand, θmax and Acyc strongly affect the RV jitter, the first because of geometrical effects (e.g., inclination), and the second naturally through the number of structures that are injected.
We therefore study the effect of θmax and Acyc in more detail in Figs. 5 and 6, respectively. These plots show the RV jitter separately for the three laws versus B−V and Log 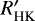 . They simultaneously show the inclination effect. We observe that the weak increase in RV jitter when θmax increases masks a larger diversity that is due to inclination because the interplay between θmax and inclination is strong. For the lower θmax values (upper panels), the RV jitter strongly increases with inclination. However, for higher θmax values, the effect of inclination is much weaker and remains strong only for F stars. Figure 6 shows similar plots for Acyc. On average, we observe higher RV jitter at high inclinations at all B−V, mostly for high-mass stars. The inclination effect is stronger for high cycle amplitudes.
. They simultaneously show the inclination effect. We observe that the weak increase in RV jitter when θmax increases masks a larger diversity that is due to inclination because the interplay between θmax and inclination is strong. For the lower θmax values (upper panels), the RV jitter strongly increases with inclination. However, for higher θmax values, the effect of inclination is much weaker and remains strong only for F stars. Figure 6 shows similar plots for Acyc. On average, we observe higher RV jitter at high inclinations at all B−V, mostly for high-mass stars. The inclination effect is stronger for high cycle amplitudes.
 |
Fig. 4 First line: average RV jitter (computed on rvact2 with no noise) in bins of B− V (left) and Log |
 |
Fig. 5 Upper panel: RV jitter (computed on rvact2 added to rvogs and rvinst) vs. B− V (right) and Log |
4 RV jitter versus B–V and Log 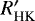
In this section, we compare RV with observations, first for the RV jitter, and then for the slope between RV and 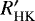 . Finally, we focus on the comparison between short-term and long-term correlations between RV and Log
. Finally, we focus on the comparison between short-term and long-term correlations between RV and Log  .
.
4.1 Comparison of the RV jitter with observations
In this section, we use the series we generated when the contribution from magnetic activity was taken into account, as well as the oscillations, granulation, and supergranulation signal (with no averaging to represent realistic short-term exposures). We do not include instrumental noise here because the observed RV jitter with which we compare our jitter is assumed to be corrected for them. Time exposures should be relatively short (and in any case much shorter than one hour), although they are not available. The RV jitter was computed on the whole time series, and therefore includes signal at all temporal scales. It is therefore not representative of what happens at a specific scale, but instead includes different contributions, which may vary in different proportions from one series to the other.
Figure 7 shows a comparison of our RV jitter with the jitter provided in three publications (Saar et al. 1998; Santos et al. 2000; Wright 2005) that all studied a large sample of F-G-K stars. For G and K stars, the trend versus Log 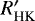 is similar between observations and simulations, with a higher RV jitter for high-activity level. The RV jitter also decreases toward lower mass stars in simulations and observations. The amplitudes are often smaller in our simulations, however, especially at low-activity level. We find that we cannot reproduce RV jitter higher than 2–3 m s−1 with activity, oscillation, granulation, and supergranulation combined for very quiet stars. At high-activity level the agreement is good, especially with the RV obtained by Wright (2005).
is similar between observations and simulations, with a higher RV jitter for high-activity level. The RV jitter also decreases toward lower mass stars in simulations and observations. The amplitudes are often smaller in our simulations, however, especially at low-activity level. We find that we cannot reproduce RV jitter higher than 2–3 m s−1 with activity, oscillation, granulation, and supergranulation combined for very quiet stars. At high-activity level the agreement is good, especially with the RV obtained by Wright (2005).
However, it is difficult to understand how a higher variability in RV due to these effects (spots, plages, inhibition of the convective blueshift, and OGS) could be significantly higher for such stars without increasing their average Log  . Our interpretation is that the discrepancy between simulations (lack of very quiet stars with RV jitter in the 5–10 m s−1 range) and observations (significantly higher RV jitter) could have three possible causes:
. Our interpretation is that the discrepancy between simulations (lack of very quiet stars with RV jitter in the 5–10 m s−1 range) and observations (significantly higher RV jitter) could have three possible causes:
The instrumental contribution has been underestimated in these publications. This is probably at least partially the case because depending on the reference, the RV jitter level is different. For example, Wright (2005) found a much lower RV jitter than the other references: it was lower by a factor 2–3. RV jitter has also been produced by Isaacson & Fischer (2010) for a large sample of stars that we do not show here. Their trend with activity level is less clear than for the three previous works, but the authors provide a lower bound that is also higher than our lower bound.
The observed RV jitter is not only caused by activity and short-term stellar variability, but also by other sources, for example, still-undetected planets and binaries. This is consistent with the HARPS data, which suggest that the RV jitter is overestimated due to activity in previous publications. We looked at a sample of stars observed with HARPS and with a low-activity level (Log
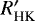 lower than −5). Out of a sample of 408 F-G-K stars with Log
lower than −5). Out of a sample of 408 F-G-K stars with Log 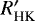 lower than −5.54 (to fit our range of parameters), 35 stars have an average Log
lower than −5.54 (to fit our range of parameters), 35 stars have an average Log  lower than −5.0 and an RV jitter (including instrumental noise) larger than 4 m s−1 (i.e., they lie outside our simulation results). A close examination of these 35 stars shows that this RV jitter is mostly due to binaries (21 stars) and to published planet(s) (9 stars). We examined the six remaining stars in detail. Four stars show long-term variations that might be due to one (or more) planet, although the PI of the observations did not published them yet (the RV signal at long period for three stars is not correlated with Log
lower than −5.0 and an RV jitter (including instrumental noise) larger than 4 m s−1 (i.e., they lie outside our simulation results). A close examination of these 35 stars shows that this RV jitter is mostly due to binaries (21 stars) and to published planet(s) (9 stars). We examined the six remaining stars in detail. Four stars show long-term variations that might be due to one (or more) planet, although the PI of the observations did not published them yet (the RV signal at long period for three stars is not correlated with Log 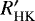 and is significantly above the false-alarm probability, while for the fourth the RV signal is not yet significant). For another star the dispersion in RV appears to occur mostly at very short timescales (minutes), for example, with a jump of 5 m s−1 over a few minutes, which is beyond the scope of our simulation and for which we have no explanation: the star is a G2 star and is expected to exhibit much smaller oscillations. The last star presents variations at the scale of a few dozen days for both RV and Log
and is significantly above the false-alarm probability, while for the fourth the RV signal is not yet significant). For another star the dispersion in RV appears to occur mostly at very short timescales (minutes), for example, with a jump of 5 m s−1 over a few minutes, which is beyond the scope of our simulation and for which we have no explanation: the star is a G2 star and is expected to exhibit much smaller oscillations. The last star presents variations at the scale of a few dozen days for both RV and Log 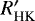 , with indeed relatively large RV variations, but there are also jumps at very short scales. In conclusion, HARPS data, which have a much better uncertainties than those of previous instruments, show that very few stars are expected to populate the domain with low-activity level and RV jitter higher than a few m s−1, in agreement with our simulations, except for companions or instrumental noise.
, with indeed relatively large RV variations, but there are also jumps at very short scales. In conclusion, HARPS data, which have a much better uncertainties than those of previous instruments, show that very few stars are expected to populate the domain with low-activity level and RV jitter higher than a few m s−1, in agreement with our simulations, except for companions or instrumental noise.The parameters of the simulations are not well adapted to the samples analyzed in these papers. Mostly three parameters might cause a significant increase in the RV jitter: the number of structures, the size of the structures, and their contrast (for the rvspot1, rvspot2, and rvplage components) or amplitude of the inhibition of the convective blueshift (for the rvconv component). It is extremely unlikely that the number of structures should be underestimated by such a large factor because the Sun, seen edge-on (i.e., with maximum variability), is well modeled, and although its Log
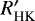 is well above −5, it does not have an rms larger than 3 m s−1 (Meunier et al. 2010a,b). The number of structures that would be required to reach more than a few m s−1 would then be incompatible with a very low Log
is well above −5, it does not have an rms larger than 3 m s−1 (Meunier et al. 2010a,b). The number of structures that would be required to reach more than a few m s−1 would then be incompatible with a very low Log 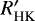 value. Similarly, the size of the structures, although not well constrained, is unlikely to be much larger than considered in our model because there is a trend to have larger spots for very active stars and conversely smaller spots for less active stars. Larger plages would lead to a larger Log
value. Similarly, the size of the structures, although not well constrained, is unlikely to be much larger than considered in our model because there is a trend to have larger spots for very active stars and conversely smaller spots for less active stars. Larger plages would lead to a larger Log 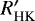 . Finally, the inhibition of the convective blueshift has been well determined in Meunier et al. (2017a) and again is in good agreement for the Sun, which is more active than the quiet stars we discussed here (Log
. Finally, the inhibition of the convective blueshift has been well determined in Meunier et al. (2017a) and again is in good agreement for the Sun, which is more active than the quiet stars we discussed here (Log 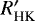 below −5). In addition, it would not be compatible with the slope we observe between RV and Log
below −5). In addition, it would not be compatible with the slope we observe between RV and Log 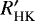 either, which agrees well with observations (see below).
either, which agrees well with observations (see below).
For F stars, the trend versus Log  we obtain is much flatter, and the discrepancy between the simulated and observed jitter is larger than for G and K stars. The reason might be that our computations did not take the possible trend in convective blueshift attenuation with Teff discussed in Sect. 3.2.1 into account. If this were included, the RV jitter would be slightly higher, although it would remain below the average found by Wright (2005). This shows that our simulations are quite robust with respect to the choice of parameters. As for the trend, the relatively flat curve is related to the fact that for F stars, cycle amplitudes are lower than for less massive stars, as discussed in Sect. 2.6.2: even for high-activity levels, the cycle amplitudes are therefore not as different from the lower activity level amplitudes. Therefore a much higher RV jitter at high-activity level is not compatible with such low cycle amplitudes. One possible explanation could be that the magnetic flux in quiet regions could depend differently on the activity level for G or K stars, which is unknown.
we obtain is much flatter, and the discrepancy between the simulated and observed jitter is larger than for G and K stars. The reason might be that our computations did not take the possible trend in convective blueshift attenuation with Teff discussed in Sect. 3.2.1 into account. If this were included, the RV jitter would be slightly higher, although it would remain below the average found by Wright (2005). This shows that our simulations are quite robust with respect to the choice of parameters. As for the trend, the relatively flat curve is related to the fact that for F stars, cycle amplitudes are lower than for less massive stars, as discussed in Sect. 2.6.2: even for high-activity levels, the cycle amplitudes are therefore not as different from the lower activity level amplitudes. Therefore a much higher RV jitter at high-activity level is not compatible with such low cycle amplitudes. One possible explanation could be that the magnetic flux in quiet regions could depend differently on the activity level for G or K stars, which is unknown.
 |
Fig. 7 First line: RV jitter for F stars (left) and G+K stars (right) vs. Log |
4.2 Comparison of the RV versus 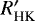 slope with observations
slope with observations
We now consider time series that are constituted by magnetic activity, OGS (averaged over one hour or not) and instrumental noise, with the original sampling and a degraded sampling. We compute the slope of RV versus 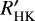 to compare with the results of Lovis et al. (2011). This slope can then be visualized as a function of other parameters, for example, Teff. Because the inhibition of the convective blueshift plays an important role and because both the chromospheric emission and this contributionto the RV are strongly related to the surface covered by plages (and network), we expect this slope to be significant and representative of the variability of these two variables.
to compare with the results of Lovis et al. (2011). This slope can then be visualized as a function of other parameters, for example, Teff. Because the inhibition of the convective blueshift plays an important role and because both the chromospheric emission and this contributionto the RV are strongly related to the surface covered by plages (and network), we expect this slope to be significant and representative of the variability of these two variables.
The slope is shown in Fig. 8 versus Teff. This slope was also computed on a large number of F-G-K stars observed with HARPS by Lovis et al. (2011), and we compare their trend with our results. They show a good agreement, both in average trend (green line) and dispersion (although the dispersion issmaller in the simulations). This means that both our RV model (as far as the inhibition of convection contributionis concerned) and the chromospheric emission model (for the part due to active regions) are consistent with each other. There is a small departure for stars with either a very high mass or a very low mass (in our range of parameters), however. There is a possibility for the inhibition of the convective blueshift to depend slightly on Teff (Meunier et al. 2017a), at least above 5400 K, but it does not explain the discrepancy, although the slope is increased. This comparison suggests that the trend (of the percentage of inhibition as a function of Teff) could be higher than expected from the results of Meunier et al. (2017a), but this is not the only possible explanation. For example, in Paper I, we considered a similar chromospheric emission for all spectral types (for a given structure size) because this is not constrained. A large chromospheric emission (for a given size) for F stars and a lower chromospheric emission forK stars (compared to the Sun) could also increase the slope to better match the results of Lovis et al. (2011).
Furthermore, even if all slopes are positive when the sampling is perfect, we occasionally observe negative slopes when the sampling is degraded. A few stars with a negative slope have been observed (Lovis et al. 2011). Lovis and collaborators have argued that these stars could present a reverse convection pattern (leading to a convective redshift instead of a convective blueshift), but this is unlikely to be the explanation because the convective properties of this same sample of stars have also been studied by Meunier et al. (2017a), and none showed any reversal. No such analysis was done by Lovis et al. (2011), whose objective was to concentrate on the variability derived from HARPS data, but Meunier et al. (2017a) derived the amplitude of the convective blueshift (including its sign). Their Fig. 9 also shows a few stars with a negative ΔRV for a positive ΔLog 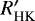 (similar to the results of Lovis et al. 2011), but their Fig. 3 shows that the convective blueshift of all these stars has the same sign, which is not compatible with a convection reversal. We propose that the few negative slopes that are observed might be an artifact due to poor sampling, although we cannot exclude that they are due to the presence of still-unidentified exoplanets.
(similar to the results of Lovis et al. 2011), but their Fig. 3 shows that the convective blueshift of all these stars has the same sign, which is not compatible with a convection reversal. We propose that the few negative slopes that are observed might be an artifact due to poor sampling, although we cannot exclude that they are due to the presence of still-unidentified exoplanets.
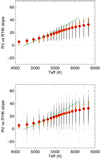 |
Fig. 8 Upper panel: slope of RV vs. |
4.3 Short-term and long-term contributions to RV jitter
The components rvspot1 (as well as rvspot2) and rvplage are relatively short-term signals, that is, around the rotational period and below (although the dispersion changes on long timescales), while rvconv presents variations both at these short timescales and on long timescale (cycle variations). The RV jitter includes all components, short and long term. Observationally, RV jitter also usually includes all components, hence the present study. We computed two cases of RV jitter, one on long timescales, hereafter LT (RV time series are smoothed over 100 days to eliminate most of the rotational modulation), and one on short timescales, hereafter ST (computed on the residuals after subtraction of the smoothed series). The LT RV jitter is mostly sensitive to rvconv, while the ST RV jitter is sensitive to all magnetic RV components (rvspot, rvplage, rvconv). We first illustrate the result with the series including the magnetic component (with ΔTspot2), OGS (averaged over one hour), and instrumental white noise in Fig. 9. Long- and short-term RV jitter both increases with inclination. This is expected because the rotational modulation becomes increasingly weaker from edge-on to pole-on. The long-term RV jitter is affected by projection effects, and when seen edge-on, the structures present a larger apparent area. The ratio between short- and long-term contributions is on average always above 1 (i.e., dominated by short-term RV jitter), but the dispersion is very high and both configurations exist (i.e., dominated by either short term or long term). Furthermore, the ratio increases with inclination for F stars, is flat for G stars, and decreases with inclination for K stars.
When we consider the magnetic component alone, the LT RV jitter is almost exactly the same (as expected), while the ST RV jitter is lower and is more strongly dependent on inclination because the OGS signal and instrumental noise do notdepend on inclination. As a consequence, the ratio between ST and LT RV jitter is quite different: it always increases with inclination, and is on average below one (except for F stars with inclinations higher than 40°). The inclination dependence therefore strongly depends on the other sources of signal (OGS and instrumental noise) that are superposed on the activity contribution.
We now focus on the long-term RV jitter, which is of interest for exoplanet detections in the habitable zone of the stars we consider. Figure 10 shows the long-term jitter separately for the three values of θmax. The jitter becomes flatter with inclination when θmax increases. For K stars and higher θmax, there is even a reversal in the trend as the RV jitter passes through a maximum for inclination around 40°. The effect of inclination becomes very small for the highest value of θmax. After binning, the RV jitter for F and G stars is not very different, and over all K stars are more suitable for exoplanet detection. The ratio between short- and long-term contributions depends on the spectral type: it is stronger for F stars when seen edge-on than for K stars. It is the opposite when seen pole-on.
We conclude that it is important to be careful in interpreting observed RV jitter because many configurations are present, depending on spectral type or inclination, for example. In addition, it is not possible to easily deduce a long-term variability from short-term observations, for example, and vice versa, because of the large diversity of configurations.
5 Exoplanet detectability
This section focuses on exoplanet detectability. We first describe the approach we have followed to derive mass detection limits. The criterion is then applied to derive typical planetary amplitudes and masses versus B− V and Log 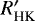 .
.
5.1 Approach
In this section, we use these simulations to predict exoplanet detectability in a simple way. Detailed and precise computations of detection limits, which request taking the frequency behavior of the time series into account, is beyond the scope of this paper and will be presented in a future study. To do so, we used the results of the fitting challenge performed by Dumusque (2016) and Dumusque et al. (2017). They proposed a criterion to establish a relation between the properties of a time series (jitter and number of observation namely) and the RV amplitude of a planet that can be detected assuming these properties. The criterion C is defined as 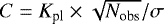 , where Kpl is the RV amplitude of the planet, Nobs is the number of observations, and σ is the rms of the RV signal after a correction using a linear dependence on Log
, where Kpl is the RV amplitude of the planet, Nobs is the number of observations, and σ is the rms of the RV signal after a correction using a linear dependence on Log 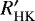 and a second-degree polynomial in time (the latter is often performed on observed RV time series to remove any far and not well-constrained companion, either stellar or substellar). The fitting challenge (Dumusque et al. 2017) shows that the rate of success in recovering injected planets depended on C, with a very rough limit around7.5: they showed that that current correction techniques were usually unsuccessful below this limit. We therefore considered C = 7.5, computed the RV jitter σ after the correction described above, and deduced the minimum Kpl for each time series, knowing the number of points. From this value of Kpl, a planet mass was derived for a given period (we assumed eccentricities of 0). This provides an approximate detection limit across our grid of parameters that is representative of the current status of correcting techniques.
and a second-degree polynomial in time (the latter is often performed on observed RV time series to remove any far and not well-constrained companion, either stellar or substellar). The fitting challenge (Dumusque et al. 2017) shows that the rate of success in recovering injected planets depended on C, with a very rough limit around7.5: they showed that that current correction techniques were usually unsuccessful below this limit. We therefore considered C = 7.5, computed the RV jitter σ after the correction described above, and deduced the minimum Kpl for each time series, knowing the number of points. From this value of Kpl, a planet mass was derived for a given period (we assumed eccentricities of 0). This provides an approximate detection limit across our grid of parameters that is representative of the current status of correcting techniques.
We considered several time series in this computation, either the full sample (the number of points then vary depending on the simulation), or subsamples of 100, 300, 500, 1000, or 2000 points, as described in Sect. 2.1. The computations were made on the time series with OGS (averaged over one hour) and the instrumental white noise.
 |
Fig. 9 Left column: long-term RV jitter vs. inclination (all simulations, black dots, and average, red points) for F stars (upper panel), G stars (middle panel), and K stars (lower panel) for activity and OGS contributions. The green points are the average values for activity alone. Middle column: same for the short-term RV jitter. Right column: same for the ratio between short-term RV jitter and long-term RV jitter. |
5.2 RV amplitude after correction
Figure 11 shows Kpl (i.e., after correction using the correlation with Log 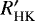 and a second-degree polynomial in time) versus B−V and Log
and a second-degree polynomial in time) versus B−V and Log 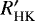 for various numbers of points and inclinations. The trends are naturally very similar to those of rvact1 or rvact2 shown in Fig. 1, but the amplitude was reduced compared to the original RV jitter due to the correction applied to the RV time series. Kpl can be higher than a few m s−1 in the less favorable cases, but often reaches values below 1 m s−1 for stars with a sufficient number of observations, even for relatively active stars.
for various numbers of points and inclinations. The trends are naturally very similar to those of rvact1 or rvact2 shown in Fig. 1, but the amplitude was reduced compared to the original RV jitter due to the correction applied to the RV time series. Kpl can be higher than a few m s−1 in the less favorable cases, but often reaches values below 1 m s−1 for stars with a sufficient number of observations, even for relatively active stars.
5.3 Planetary mass and detection percentage
From Kpl, we derived a planet mass for a period that corresponds to the middle of the habitable zone and no eccentricity. The habitable zone was computed from the relationship between luminosity L and stellar flux S at the boundaries  (Kasting et al. 1993), where the luminosity is derived from the effective temperature (Zaninetti 2008), as well as the flux at the boundaries (Jones et al. 2006). This leads to a distance from the star of 1.73 AU (0.83 AU) and a period of 759 days (327 days) for F6 (K4) stars. We then divided the mass by sin (i), assuming that the planetary orbit lies within the equatorial plane of the star. Naturally, there may occasionally be departures from this configuration, but very highly inclined orbits are unlikely. The RV signal due to activity indeed changes with inclination, as studied in the present paper, but the RV signal due to a planet will also change withinclination. This strongly affects the comparison with the RV jitter, which correspond to all types of inclinations.
(Kasting et al. 1993), where the luminosity is derived from the effective temperature (Zaninetti 2008), as well as the flux at the boundaries (Jones et al. 2006). This leads to a distance from the star of 1.73 AU (0.83 AU) and a period of 759 days (327 days) for F6 (K4) stars. We then divided the mass by sin (i), assuming that the planetary orbit lies within the equatorial plane of the star. Naturally, there may occasionally be departures from this configuration, but very highly inclined orbits are unlikely. The RV signal due to activity indeed changes with inclination, as studied in the present paper, but the RV signal due to a planet will also change withinclination. This strongly affects the comparison with the RV jitter, which correspond to all types of inclinations.
Figure 12 show the resulting minimum planet mass vs. B− V and Log 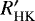 . Only a very large number of points (several thousands) allows reaching masses below 1 Mearth with the current status of correction techniques (as defined by a criterion C = 7.5, as discussed above), and this is only true for relatively quiet low-mass stars or stars with a medium activity level. A star like the Sun (G2, medium activity level) remains in a regime where the detection of planets with masses below 1 Mearth is expected to be very difficult, and possible only if there are a very large number of observations (several thousands) and if the star is seen close to edge-on. The lower limit can be much higher depending on the configuration. The mass is also very dependent on inclination because the RV jitter depends on inclination, and because low-inclination stars (assuming a planet orbiting in the equatorial plane) have planets with a lower RV amplitude. Figure 13 shows the effect of the parameters on the mass. Overall, they have a relatively weak effect on the results, probably because they do not strongly affect the RV jitter. The criterion used here, based on the RV jitter, is not necessarily the best metric to observe any effect because it does not take the temporal variability at different scales into account. More sophisticated methods must therefore be implemented to account for this. The lower bound for the planet mass versus B− V for a number of points that are representative of well-observed stars (100–500, because there are very few stars with a larger number of nights) are in good agreement with the lower bound in a similar plot for exoplanets that were found using RV in the exoplanet encyclopedia1.
. Only a very large number of points (several thousands) allows reaching masses below 1 Mearth with the current status of correction techniques (as defined by a criterion C = 7.5, as discussed above), and this is only true for relatively quiet low-mass stars or stars with a medium activity level. A star like the Sun (G2, medium activity level) remains in a regime where the detection of planets with masses below 1 Mearth is expected to be very difficult, and possible only if there are a very large number of observations (several thousands) and if the star is seen close to edge-on. The lower limit can be much higher depending on the configuration. The mass is also very dependent on inclination because the RV jitter depends on inclination, and because low-inclination stars (assuming a planet orbiting in the equatorial plane) have planets with a lower RV amplitude. Figure 13 shows the effect of the parameters on the mass. Overall, they have a relatively weak effect on the results, probably because they do not strongly affect the RV jitter. The criterion used here, based on the RV jitter, is not necessarily the best metric to observe any effect because it does not take the temporal variability at different scales into account. More sophisticated methods must therefore be implemented to account for this. The lower bound for the planet mass versus B− V for a number of points that are representative of well-observed stars (100–500, because there are very few stars with a larger number of nights) are in good agreement with the lower bound in a similar plot for exoplanets that were found using RV in the exoplanet encyclopedia1.
Finally, Fig. 14 shows the percentage of simulations providing masses below 1, 2, or 5 MEarth. This quantifies the performance of current techniques in a simple way for various spectral types and activity levels. We first consider all inclinations. For low-mass stars (B−V above 0.9) and low-activity levels (Log  below − 5.0), a small fraction (above 10%) of planets with 1 MEarth can be detected. For the same ranges, almost all 5 MEarth would be detected. However, the percentage falls to zero in the other ranges of B− V and Log
below − 5.0), a small fraction (above 10%) of planets with 1 MEarth can be detected. For the same ranges, almost all 5 MEarth would be detected. However, the percentage falls to zero in the other ranges of B− V and Log 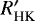 . These percentages are only indicative and should be taken with caution because the same probability is attributed to each point in the grid in this computation.
. These percentages are only indicative and should be taken with caution because the same probability is attributed to each point in the grid in this computation.
In the context of the follow-up programs of transit detections (TESS and PLATO) using RV techniques, it is interesting to consider simulations made edge-on only. The percentages, shown in red in Fig. 14, are higher and can be close to 100% for the lowest mass star in the grid and a threshold of 1 Mearth (dashed lines). This percentage is different from 0 for B−V higher than 0.8 only, however. The edge-on configuration is then the most suitable inclination for detecting such planets, with good performance mostly for K stars if the sampling is very good.
 |
Fig. 10 Rows1–3: binned long-term RV jitter vs. inclination (left) vs. B−V for various inclinations (middle) and vs. Log |
 |
Fig. 11 Kpl vs. B− V (left) and vs. Log |
 |
Fig. 12 Same as Fig. 11 for Mpla, after correction for sin(i) (simulations with i = 0 are not included in this plot due to the correction). |
 |
Fig. 14 Percentage of simulations with Mpla below 5 Mearth (solid line), below 2 Mearth (dashed line), and 1 Mearth (dotted line), vs. B−V (left) and vs. Log |
6 Conclusion
We simulated RV time series showing variability for a range of spectral types from F6 to K4. These time series are realistic in the sense that the set of stellar parameters is consistent over this range of stars with different typical activity levels and variability. They also exhibit complex activity patterns, which allowed us to retrieve a realistic complexity of the time series. We here studied the effect of the parameters on the RV jitter. We showed that θmax and Acyc strongly affect the RV jitter. We highlighted that the inclination of the star is a critical factor and that it leads to a wide diversity of configurations. The RV jitter is sensitive to the various contributions to the RV, but also to processes that operate at different timescales (we focused here on the rotation period and shorter periods on one hand, and on longer periods on the other): many configurations exist depending on these parameters. It is therefore crucial not to overinterpret observations because a local RV jitter is not entirely representative of the long-term variability, for example.
The trend of the RV jitter with B−V and Log 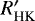 is similar tothe observed values (Saar et al. 1998; Santos et al. 2000; Wright 2005). However, the simulated RV jitter is lower. We estimate that such large jitter (e.g., between 5–10 m s−1 for stars with Log
is similar tothe observed values (Saar et al. 1998; Santos et al. 2000; Wright 2005). However, the simulated RV jitter is lower. We estimate that such large jitter (e.g., between 5–10 m s−1 for stars with Log 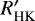 below −5) cannot be reached with stellar activity (even when stellar granulation or supergranulation is included). The high observed RV jitter in the literature for these quiet stars may be due to either an underestimation of the instrumental noise, and/or the presence of other sources of RV (e.g., still-undetected planets). Finally, the slope of RV versus
below −5) cannot be reached with stellar activity (even when stellar granulation or supergranulation is included). The high observed RV jitter in the literature for these quiet stars may be due to either an underestimation of the instrumental noise, and/or the presence of other sources of RV (e.g., still-undetected planets). Finally, the slope of RV versus 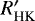 obtained in our simulation is in good agreement with the observations (Lovis et al. 2011), both in range and trend versus spectral type, showing that the models providing RV and Log
obtained in our simulation is in good agreement with the observations (Lovis et al. 2011), both in range and trend versus spectral type, showing that the models providing RV and Log  give coherent results. They suggest, however, that the trend in the attenuation of the convective blueshift with Teff observed by Meunier et al. (2017a) may be slightly stronger than estimated.
give coherent results. They suggest, however, that the trend in the attenuation of the convective blueshift with Teff observed by Meunier et al. (2017a) may be slightly stronger than estimated.
Using a simple approach based on the criterion proposed in Dumusque et al. (2017) and assuming a threshold that corresponds to the current performance of correction techniques, we showed that an Earth-mass planet in the middle of the habitable zone of these stars cannot be detected around the lower mass stars in our sample, and this is thought to be possible only with a very large number of observations. Better correction techniques must therefore be implemented in the future. New methods that have recently been proposed and are based on the fact that the convective blueshift depends on the line properties so that different sets of lines produce different RV time series or allow optimizing the RV (Meunier et al. 2017b; Dumusque 2018) may be better adapted to the search for Earth-mass planets around solar-type stars. In addition, further analysis of this large number of synthetic time series will greatly help us to find new paths to improve these correction methods. This will be done in Meunier & Lagrange (2019).
Acknowledgements
This work has been funded by the ANR GIPSE ANR-14-CE33-0018. We are very grateful to Charlotte Norris, who has provided us the plage contrasts we used in this work prior the publication of her thesis. This work was supported by the “Programme National de Physique Stellaire” (PNPS) of CNRS/INSU, which is cofunded by CEA and CNES. This work was supported by the Programme National de Planétologie (PNP) of CNRS/INSU, which is cofunded by CNES.
References
- Arriagada, P. 2011, ApJ, 734, 70 [NASA ADS] [CrossRef] [Google Scholar]
- Baliunas, S. L., Donahue, R. A., Soon, W. H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Baumann, I., & Solanki, S. K. 2005, A&A, 443, 1061 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bedding, T. R., & Kjeldsen, H. 2003, PASA, 20, 203 [Google Scholar]
- Beeck, B., Cameron, R. H., Reiners, A., & Schüssler, M. 2013, A&A, 558, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belkacem, K., Samadi, R., Mosser, B., Goupil, M.-J., & Ludwig, H.-G. 2013, in Progress in Physics of the Sun and Stars: A New Era in Helio- and Asteroseismology, eds. H. Shibahashi & A. E. Lynas-Gray, ASP Conf. Ser., 479, 61 [Google Scholar]
- Berdyugina, S. V. 2005, Liv. Rev. Sol. Phys., 2, 8 [Google Scholar]
- Böhm-Vitense, E. 2007, ApJ, 657, 486 [NASA ADS] [CrossRef] [Google Scholar]
- Borgniet, S., Meunier, N., & Lagrange, A.-M. 2015, A&A, 581, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X. 2016, A&A, 593, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X. 2018, A&A, 620, A47 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X., Borsa, F., Damasso, M., et al. 2017, A&A, 598, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Harvey, J. W. 1984, in Probing the Depths of a Star: the Study of Solar Oscillation from Space, eds. R. W. Noyes & E. J. Rhodes Jr., JPL, (Pasadena, CA: NASA Jet Propulsion Laboratory) 400, 327 [Google Scholar]
- Harvey, K. L., & White, O. R. 1999, ApJ, 515, 812 [Google Scholar]
- Hatzes, A. P. 2002, Astron. Nachr., 323, 392 [NASA ADS] [CrossRef] [Google Scholar]
- Herrero, E., Ribas, I., Jordi, C., et al. 2016, A&A, 586, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Isaacson, H., & Fischer, D. 2010, ApJ, 725, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, B. W., Sleep, P. N., & Underwood, D. R. 2006, ApJ, 649, 1010 [NASA ADS] [CrossRef] [Google Scholar]
- Kallinger, T., De Ridder, J., Hekker, S., et al. 2014, A&A, 570, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kasting, J. F., Whitmire, D. P., & Reynolds, R. T. 1993, Icarus, 101, 108 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Kippenhahn, R., & Weigert, A. 1990, Stellar Structure and Evolution (Berlin: Springer Science & Business Media), 192 [Google Scholar]
- Kjeldsen, H., & Bedding, T. R. 1995, A&A, 293, 87 [NASA ADS] [Google Scholar]
- Komm, R. W., Howard, R. F., & Harvey, J. W. 1993, Sol. Phys., 147, 207 [Google Scholar]
- Lagrange, A.-M., Desort, M., & Meunier, N. 2010, A&A, 512, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, ArXiv e-prints [arXiv:1107.5325] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Arnáiz, R., Maldonado, J., Montes, D., Eiroa, C., & Montesinos, B. 2010, A&A, 520, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martinez Pillet, V., Moreno-Insertis, F., & Vazquez, M. 1993, A&A, 274, 521 [Google Scholar]
- Meunier, N. 2018, A&A, 615, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., & Lagrange, A.-M. 2019, A&A, in press, https://doi.org/10.1051/0004-6361/201935651 [Google Scholar]
- Meunier, N., Desort, M., & Lagrange, A.-M. 2010a, A&A, 512, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Lagrange, A.-M., & Desort, M. 2010b, A&A, 519, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Lagrange, A.-M., Borgniet, S., & Rieutord, M. 2015, A&A, 583, A118 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Mignon, L., & Lagrange, A.-M. 2017a, A&A, 607, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Lagrange, A.-M., & Borgniet, S. 2017b, A&A, 607, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Lagrange, A.-M., Boulet, T., & Borgniet, S. 2019, A&A, 627, A56 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Norris, C. 2018, PhD Thesis, Imperial College London, London, UK [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Oláh, K., Kolláth, Z., Granzer, T., et al. 2009, A&A, 501, 703 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oláh, K., Kővári, Z., Petrovay, K., et al. 2016, A&A, 590, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Radick, R. R., Lockwood, G. W., Skiff, B. A., & Baliunas, S. L. 1998, ApJS, 118, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Reinhold, T., & Gizon, L. 2015, A&A, 583, A65 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saar, S. H., & Brandenburg, A. 1999, ApJ, 524, 295 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., & Donahue, R. A. 1997, ApJ, 485, 319 [NASA ADS] [CrossRef] [Google Scholar]
- Saar, S. H., Butler, R. P., & Marcy, G. W. 1998, ApJ, 498, L153 [Google Scholar]
- Saar, S. H., Hatzes, A., Cochran, W., & Paulson, D. 2003, in The Future of Cool-Star Astrophysics: 12th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. A. Brown, G. M. Harper, & T. R. Ayres (Boulder: University of Colorado), 12, 694 [NASA ADS] [Google Scholar]
- Samadi, R., Georgobiani, D., Trampedach, R., et al. 2007, A&A, 463, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, A. R. G., Cunha, M. S., Avelino, P. P., & Campante, T. L. 2015, A&A, 580, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Santos, N. C., Mayor, M., Naef, D., et al. 2000, A&A, 361, 265 [NASA ADS] [Google Scholar]
- Schrijver, C. J. 2001, ApJ, 547, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., & González Hernández, J. I. 2016, A&A, 595, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Unruh, Y. C., Solanki, S. K., & Fligge, M. 1999, A&A, 345, 635 [NASA ADS] [Google Scholar]
- Wright, J. T. 2005, PASP, 117, 657 [NASA ADS] [CrossRef] [Google Scholar]
- Zaninetti, L. 2008, Serb. Astron. J., 177, 73 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 RV jitter for the different magnetic activity components to the RV, vs. B–V (left) and Log |
| In the text | |
 |
Fig. 2 Upper panel: root mean square of the RV jitter due to spot (rvspot1 in black and rvspot2 in red)) and plages separately vs. the RV jitter of rvspot + rvplage. The solid line indicates a y = x linear function and the dashed line has a slope of |
| In the text | |
 |
Fig. 3 Upper panel: binned RV jitter of rvspot + rvplage vs. RV jitter from the attenuation of the convective blueshift rvconv for the 19 spectral types from F6 (yellow) to K4 (blue). Lower panel: same for ΔTspot2. |
| In the text | |
 |
Fig. 4 First line: average RV jitter (computed on rvact2 with no noise) in bins of B− V (left) and Log |
| In the text | |
 |
Fig. 5 Upper panel: RV jitter (computed on rvact2 added to rvogs and rvinst) vs. B− V (right) and Log |
| In the text | |
 |
Fig. 6 Same as Fig. 5 for Acyc. |
| In the text | |
 |
Fig. 7 First line: RV jitter for F stars (left) and G+K stars (right) vs. Log |
| In the text | |
 |
Fig. 8 Upper panel: slope of RV vs. |
| In the text | |
 |
Fig. 9 Left column: long-term RV jitter vs. inclination (all simulations, black dots, and average, red points) for F stars (upper panel), G stars (middle panel), and K stars (lower panel) for activity and OGS contributions. The green points are the average values for activity alone. Middle column: same for the short-term RV jitter. Right column: same for the ratio between short-term RV jitter and long-term RV jitter. |
| In the text | |
 |
Fig. 10 Rows1–3: binned long-term RV jitter vs. inclination (left) vs. B−V for various inclinations (middle) and vs. Log |
| In the text | |
 |
Fig. 11 Kpl vs. B− V (left) and vs. Log |
| In the text | |
 |
Fig. 12 Same as Fig. 11 for Mpla, after correction for sin(i) (simulations with i = 0 are not included in this plot due to the correction). |
| In the text | |
 |
Fig. 13 Effect of the parameters on Mpla, similar to Fig. 4. |
| In the text | |
 |
Fig. 14 Percentage of simulations with Mpla below 5 Mearth (solid line), below 2 Mearth (dashed line), and 1 Mearth (dotted line), vs. B−V (left) and vs. Log |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.