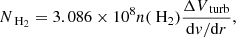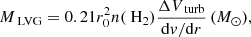EDP Sciences logo
Subscriber Authentication Point
Search
Menu
Home All issues Volume 628 (August 2019) A&A, 628 (2019) A23 Full HTML
Free Access
Issue
A&A
Volume 628, August 2019
Article Number A23
Number of page(s) 13
Section Extragalactic astronomy
DOI https://doi.org/10.1051/0004-6361/201935308
Published online 30 July 2019

© ESO 2019

1. Introduction

The study of dusty star-forming galaxies (DSFG) at high redshifts (z >  1; Casey et al. 2014) has become a relevant tool for understanding the evolution and growth of the most massive galaxies in the universe. These galaxies play a key role as nurseries of new stars, with star formation rates (SFRs) ranging from ∼500 to 1000 M⊙ yr−1 and far-infrared luminosities LFIR >  1012 L⊙ (Barger et al. 2012; Magnelli et al. 2012; Swinbank et al. 2014; da Cunha et al. 2015; Spilker et al. 2016; Miettinen et al. 2017; Michałowski et al. 2017). DSFGs are typically found to be at redshifts z = 2 − 4 (Barger et al. 1999; Ivison et al. 2002; Chapman et al. 2005; Aretxaga et al. 2007; Chapin et al. 2009; Wardlow et al. 2011; Yun et al. 2012; Smolčić et al. 2012; Weiß et al. 2013; Simpson et al. 2014; Chen et al. 2016; Brisbin et al. 2017), with a high-redshift tail extending out to z ∼ 6 − 7 (Riechers et al. 2013; Weiß et al. 2013; Strandet et al. 2016, 2017); they contribute significantly to the cosmic SFR history (e.g., Magnelli et al. 2012; Sargent et al. 2014). The high SFRs observed in DSFGs yield high stellar masses of M*​​ ∼ ​​1011 M⊙ in < 1 Gyr (Dye et al. 2008; Hainline et al. 2011; Michałowski et al. 2014; Ma et al. 2015) and can only be sustained by massive molecular gas reservoirs, with typical observed gas masses of Mgas​ ∼ ​3 − 5 × 1010 M⊙ (Frayer et al. 1998; Greve et al. 2005; Danielson et al. 2011; Bothwell et al. 2013; Sharon 2013; Riechers et al. 2013; Rawle et al. 2014; Aravena et al. 2016; Huynh et al. 2017). The main sources of radiation in these objects are thermal continuum emission from dust grains and line emission from molecular transitions within the interstellar medium (ISM).

Despite their high bolometric luminosities, the detection and study of DSFGs are made difficult not only due to the heavy dust obscuration that usually makes them inconspicuous at optical and near-IR wavelengths, but also due to the weakness of their spectral lines in the redshifted far-infrared regime. Here, gravitational lensing provides a solution to both these issues, acting as a natural cosmic telescope to magnify faint galaxies that would otherwise be too difficult to detect. Since gravitational lensing is a geometric effect, sources close in projection to the caustics are significantly more magnified than sources far from caustics. As a consequence the magnification (μ) of the background galaxy will be the same at all frequencies. However, because the lensed galaxy has a finite size, the magnification will vary across the galaxy (Blandford & Narayan 1992; Hezaveh et al. 2012; Serjeant 2012). This is known as differential lensing and can have consequences in the interpretation of the observed integrated properties of lensed galaxies (Serjeant 2012; Hezaveh et al. 2012).

The large-scale millimeter survey of the southern sky conducted with the South Pole Telescope (SPT; Carlstrom et al. 2011), covers 2500 square degrees of the sky, and has unveiled ∼100 millimeter-bright, gravitationally lensed DSFGs (Vieira et al. 2010, 2013). Follow-up with the Atacama Large Millimeter/submillimeter Array (ALMA) showed that these sources are located at very high redshifts, typically ranging from z = 2 − 6 (Weiß et al. 2013; Strandet et al. 2016). All of these sources are associated with intense starburst activity, and provide an ideal laboratory to study the conditions of galaxy build-up very early in the Universe (Spilker et al. 2015; Gullberg et al. 2015; Béthermin et al. 2016; Bothwell et al. 2016; Ma et al. 2015, 2016; Strandet et al. 2017; Marrone et al. 2018; Litke et al. 2019).

Line emission from the rotational transitions of the carbon monoxide (CO) molecule has been widely used to provide information about the ISM, particularly at high redshift (Solomon & Vanden Bout 2005; Carilli & Walter 2013). The CO line emission has been observed to trace the distribution and amount of molecular hydrogen in local star-forming regions and nearby galaxies (Omont 2007). Its multiple transitions trace a wide range of physical environments within the cold ISM, and therefore constitutes a useful tool for the study of the physical properties of the molecular gas in galaxies through modeling their CO spectral line energy distribution (CO SLED; e.g., Weiß et al. 2007). The CO excitation level depends on temperature and gas density, with mid-J to high-J CO lines tracing denser and warmer gas than low-J CO lines (Rosenberg et al. 2015). A complementary tracer of dense molecular gas is the H2O line emission. H2O transitions trace the dense, warm gas where the radiation produced by young stars or by active galactic nuclei (AGN) increases the temperature of the dust. Since most of the H2O lines fall at rest-frame far-infrared frequencies, ground-based observations of these lines in high-redshift galaxies have flourished in recent years, providing an excellent complement to CO studies (Omont et al. 2013; Yang et al. 2016).

In the last few years CO and H2O observations of high-redshift galaxies have increased dramatically. However, most studies are not able to accurately measure physical parameters from CO spectral line energy distribution (SLED) modeling in individual galaxies since this requires multiple CO transitions that trace the full range of excitation conditions. Even among studies that have many CO lines (e.g., Weiß et al. 2007; Riechers et al. 2013), spatially resolved observations of many transitions remain scarce (e.g., Bothwell et al. 2013; Spilker et al. 2014; Yang et al. 2019).

The millimeter-bright, gravitationally lensed galaxy SPT 0346-52 at z = 5.6556 is among the most distant and intrinsically luminous DSFGs known to date. This system seems to be forming stars close to the Eddington limit for a starburst, with a SFR surface density of ∑SFR = 1540 ± 130 M⊙ yr−1 kpc−2 using the IR–SFR relation described in Kennicutt (1998), Hezaveh et al. (2013), Spilker et al. (2015), and Ma et al. (2016). After correcting for lensing effects its far-IR luminosity yields LFIR = (3.6 ± 0.3)×1013 L⊙, and is thus one of the most luminous sources in the SPT DSFG sample (Spilker et al. 2015; Ma et al. 2015, 2016). Despite the highly concentrated star formation activity, Chandra observatory X-ray observations provide no evidence indicating the presence of AGN activity (Ma et al. 2016). Based on measurement of its CO (J = 2 − 1) line emission, SPT 0346-52 was found to have a large molecular gas reservoir of ∼8.2 × 1010 M⊙, necessary in sustaining its high IR luminosities (Spilker et al. 2015; Aravena et al. 2016).

To understand the gas and dust distribution of this source, Spilker et al. (2015) used observations of the 870 μm dust continuum emission (rest frame 130 μm) and the CO(2−1) line emission with angular resolution of ∼0.4″ from ALMA and the Australia Telescope Compact Array (ATCA), respectively. After modeling the effects of the gravitational lensing, these data yield an effective source-plane resolution of ∼1 kpc at the redshift of SPT 0346-52. Their observations suggest that dust has a significantly more compact distribution than the diffuse cold gas traced by the low-J CO emission. However, the modest sensitivity of the low-J CO observations did not allow them to study the velocity structure of the gas and thus the actual nature of this source. To understand the relationship between molecular gas and the star formation process it is necessary to directly trace the denser phases of the molecular gas, resolving the molecular gas both spatially and kinematically.

Litke et al. (2019) used a pixelated lensing reconstruction tool (Hezaveh et al. 2016) in SPT 0346-52 of ∼015 ALMA [CII] (λ = 157.74 μm) observations, where two spatially and kinematically separated components were found to be connected by a “bridge” of gas ∼1.6 kpc in size, which is consistent with a galaxy merger. Dong et al. (2019) observed and reconstructed the emission of CO(8−7) in this source with ALMA ∼04 data, obtaining an intrinsic CO circularized size of 0.73 kpc, clearly more compact than [CII].

In this work, we present the observation of CO(10−9) in addition to sensitive Jup = 6 − 9 CO and H2O(202 − 111 and 211 − 202) ALMA imaging of SPT 0346-52 at a source-plane resolution of ∼1 kpc and with a high S/N. These observations spatially and kinematically resolve both the bright 12CO and the H2O lines, as well as the cold dust continuum at the observed wavelengths of 2 mm and 3 mm (300 and 450 μm rest frame, respectively). Along with the previous resolved observations of CO(2−1) and dust continuum at 870 μm, our measurements allow us to (i) reconstruct the molecular gas emission in the source plane; (ii) derive their emitting sizes, resolve the gas distribution along the velocity axis, and make a comparison with previous observations; (iii) compare the spatial distributions of the cold and dense molecular gas and dust; and (iv) explore the physical conditions of the ISM in the source-plane through radiative transfer modeling. Hereafter, we adopt a WMAP9 ΛCDM cosmology with Ωm = 0.286, ΩΛ = 0.713, and H0 = 69.3 km s−1 Mpc−1 (Hinshaw et al. 2013).

2. Observations

In this section, we describe details of the molecular line observations of SPT 0346-52 at z = 5.7.

2.1. ALMA observations

Observations of SPT 0346-52 were performed with ALMA bands 3 and 4 as a part of projects 2013.1.00722.S and 2015.1.00117.S during ALMA cycles 2 and 3, respectively (PI: M. Aravena). Cycle 2 and 3 observations were conducted during April and May 2015, and during April 2016, respectively.

The observations were configured to cover the redshifted emission from faint molecular gas lines in the rest-frame far-IR SED (including HCN, HCO+, 13CO; see Spilker et al. 2014). However, in this study, we focus on the brighter, higher significance molecular lines detected of 12CO and H2O, which allow us to perform detailed lensing source reconstruction. Analysis of the fainter lines will be published elsewhere. A summary of the ALMA observations in this study is provided in Table 1.

Table 1.

Observational summary of data.

For each observing band (3 and 4), three frequency tunings were used. Each frequency tuning was observed using four spectral windows (SPWs) in frequency division mode (FDM) and a bandwidth of 1.875 GHz per SPW. We used online spectral averaging that led to a spectral resolution of 7.8125 MHz and 15.6250 MHz per channel for the band 3 and 4 frequency setups, respectively. They correspond to velocity resolutions of 23 and 31 km s−1 per channel at observing frequencies of 100 and 150 GHz, respectively. Following standard procedures, bright quasars and Mars were used for bandpass, flux, and phase calibration, including J0411−5149, J0334−401, and J0519−4546.

The data were reduced and imaged using the Common Astronomy Software Application package CASA (McMullin et al. 2007). We performed an independent reduction and calibration of the data; however, we did not see differences with respect to the ALMA pipeline calibration. Time ranges and antennas showing bad visibilities were flagged accordingly, following standard procedures. We created data cubes at different channel resolutions, averaging by two, four, and eight original channels. The visibilities were deconvolved using the CLEAN algorithm. Since our target is detected significantly (S/N >  20), we masked this source using a tight circular aperture around it with a radius of 5″, cleaning down to 2σ, where σ corresponds to the rms noise level of each channel of the data cube. We tested various weighting schemes, and finally used the Briggs weighting with a robustness factor of 0.5 to have a good trade-off between resolution and sensitivity. The resulting maps are shown in Fig. 1. We note that most of the results of this paper do not depend on the actual weighting scheme used or image resolution obtained, since most of our lens modeling was performed on the visibility plane.

thumbnail Fig. 1.

Maps of the line transitions detected in SPT 0346-52 obtained with ALMA observations, integrated over 4σvelocity km s−1 channels. For H2O 211 − 202 and H2O 202 − 111 red contours are the 2, 4, 6, 8σ intervals. For CO(6−5), CO(8−7), and CO(9−8) red contours are the 5, 10, 20, 30σ intervals. The synthesized beam is shown in the bottom left corner as a red ellipse. The orange cross shows the center of the lensing galaxy.

We performed aperture photometry using an aperture diameter of 7″ centered at the central lensing galaxy position, using the cubes averaged by four channels. We subtracted the continuum emission from the line profiles by fitting a power law to the extracted spectra.

2.2. APEX observations

We used the Atacama Pathfinder Experiment (APEX) single-dish telescope under Max-Planck Institute time (Programme ID: 099.F-9525B) and its Swedish–ESO PI receiver for APEX (SEPIA) band 5 receiver to observe the redshifted emission of the 12CO J = 10 − 9 in SPT 0346-52. Observations of this line were motivated by the bright detection of CO(9−8) obtained with ALMA. The APEX observations were tuned to a frequency of ∼173.077 GHz. SEPIA band 5 is a dual polarization sideband separating receiver, covering 4 GHz bandwidth for both sidebands. The observations were done in wobbler switching mode, with switching frequency of 1.5 Hz and a wobbler throw of 60 arcsec in azimuth, with a total observing time (including integration and overheads) of 34.1 h. The precipitable water vapor during the observations varied between 0.4 and 4.5 mm yielding system temperatures between 140 and 1050 K. Pointing was checked frequently and was found to be stable to within 2.5″. Calibration was done every ∼10 min using the standard hot- and cold-load absorber measurements. The beam size and antenna gain at the observing frequency are 31″ and 38.4 Jy K−1, respectively (Belitsky et al. 2018). Offline data calibration and flagging was performed using the CLASS software package, including baseline subtraction of polynomials of order 1 for individual scans and spectral averaging. Calibration flux uncertainties are conservatively estimated to be in the range 15 − 20%. The data were smoothed to velocity resolutions of ∼60 km s−1.

2.3. ATCA observations

We used previous ATCA observations of the 12CO J = 2 − 1 emission line toward SPT 0346-52 obtained and described in detail by Spilker et al. (2015). In short, these observations were centered at a frequency of 34.64 GHz, and obtained in three different array configurations (providing good uv coverage over baselines from 100 m to 6 km) integrating on source for 44.8 h. This led to an angular resolution of 0.45″ × 0.65″ down to 1σ sensitivities of 54 μJy beam−1 per 200 km s−1 channels.

3. Results

All the targeted 12CO and H2O lines and the dust continuum emission are significantly detected and spatially resolved. Figure 1 shows the integrated line maps, summed up over 1.7 times the line full width at half maximum (FWHM). As expected for a lensed source, each line map shows two lobes, which are multiple images of the same source and the line emission of the source. Spectra of each individual emission line are shown in Fig. 2.

thumbnail Fig. 2.

Spectra of the line transitions detected in SPT 0346-52 obtained with the ATCA and ALMA observations. Single Gaussian fits are represented by black lines, centered at the observed frequencies. The white line shows the intrinsic flux using the values of magnification described in Tables A.1 and A.2. The different channels used in the lens modeling are color-coded according to their velocity on whether the emission is receding (red) or approaching (blue). Each channel is 100 km s−1 wide, except for the edge channels which are 400 km s−1 to improve their low S/N.

The line FWHM and central frequency are computed from single, one-dimensional Gaussian fits to the emission line profiles. Fluxes are computed by directly integrating the continuum subtracted line profiles over the relevant velocity range. The continuum emission is measured using a 7″ diameter aperture around the source. Table 2 lists the observed measured line and continuum fluxes.

Table 2.

Observed parameters.

All the line profiles are consistent in width and central frequency within the uncertainties. However, in the case of CO(10 − 9), the single Gaussian fit yields an integrated flux of ∼17.3 ± 2.9 Jy km s−1, which is approximately two times brighter than that of CO(9−8). The line width of 560 ± 100 km s−1 is in agreement with the other CO lines. González-Alfonso et al. (2010) describes a blending between H2O 312 − 221 (νobs = 173.25 GHz) and CO(10−9) (νobs = 173.08 GHz) since both lines lie within ≈300 km s−1 of each other. From the H2O line ratios observed in NGC 253, NGC 4945, and Arp 220 (Liu et al. 2017), we estimate a possible contribution in the range 5.6 − 11.5 Jy km s−1 from H2O 312 − 221 to the detected feature, which would imply a flux density of 5.8 − 11.7 Jy km s−1 for CO(10−9). However, if this H2O line were blended with CO(10−9) we would expect some broadening of the detected line feature, which we do not see. This, however, can have been missed due to the moderate significance of the detection. We note that the expected calibration uncertainties (15%−20%) cannot account for the excess flux.

3.1. Lensed source reconstruction

To understand the intrinsic geometry of the background high-redshift galaxy in SPT 0346-52, we have performed source plane reconstructions through a strong lens model (VISILENS; Spilker et al. 2014). The method relies on modeling the visibilities instead of images and simultaneously determining self-calibration phases (Hezaveh et al. 2013). The emission regions have been assumed to have a circularly symmetric Gaussian light profile with four free parameters: flux density FS, scale radius RS, and position offsets from the lens center XS and YS. Since we are interested in the intrinsic sizes of emission regions, the choice of a Gaussian profile compared to Sérsic, for example, or other commonly used source profiles is justified in order to minimize the number of free source parameters.

The lensing mass distribution used was fixed to that obtained by Spilker et al. (2016) using ALMA 870 μm observations with a resolution of ∼0.5″. It is comprised of a singular isothermal ellipsoid (SIE) plus an external shear component. The fixed parameters that define the lens model are its Einstein radius θE,L, SIE position angle ϕL, ellipticity eL, external shear strength γ, and position angle θγ (see Table 3). The central position of the lens (a nuisance parameter) was fixed to that obtained through a lens model that used the highest S/N line while keeping the other parameter fixed to those of Spilker et al. (2016). Each of the lens-modeled lines in SPT 0346-52 was split into nine velocity bins with a width of 100 km s−1, ranging from −400 to 400 km s−1. The lensed emission from each one of these bins was de-projected into the source plane. Due to the lower S/N, in the case of the wings of the lines, the first and last velocity bin widths were increased by a factor of four (from −850 to −450 km s−1 and from 450 to 850 km s−1, respectively).

Table 3.

Fixed lens model parameters from Spilker et al. (2016).

The derived source plane arrangement is shown in Fig. 4. The radius of each circle is the half-light radius defined as 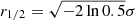, where σ is the Gaussian dispersion of the source light profile. The rest of the derived parameters are shown in Tables A.1 and A.2. Finally, we also performed a reconstruction of each line using a single, wide velocity channel (from −2σvel to 2σvel) as a benchmark for comparison. The obtained source parameters are shown in Table 4.

thumbnail Fig. 3.

Spectrum of the CO(10 − 9) line emission observed with APEX of SPT 0346-52. The red solid curve shows a Gaussian fit to the line profile. This line is about two times stonger than that of CO(9−8), suggesting contamination by a neighboring emission line.

thumbnail Fig. 4.

Reconstruction of the source plane in each velocity bin as described in the text. The velocity bins are color-coded, following the color bar to the right and as represented in Fig. 2. The circles represent the size of the reconstructed emission in each velocity bin, defined by the half-light radius (see text). The color-coded central dots show the reconstructed source position at the respective velocity bin. The dotted black line shows the lensing caustic curve from the lens model of Spilker et al. (2016).

Table 4.

Reconstruction parameters.

3.2. Intrinsic CO line emission regions

As seen in Fig. 4 and more evidently in Fig. 6, the size of the CO line emitting regions are more compact for higher rotational transitions, with CO(2−1) coming from a region of r1/2 = 1.15 kpc down to CO(9−8) coming from a region of r1/2 = 0.79 kpc. Even though this is expected and has been observed in other sources such as M 82, where the low-J CO is dominated by the diffuse outer regions, while transitions Jup >  5 are emitted from the central regions (Weiß et al. 2005b), it could not have been observed without the enhancement to the resolution produced by strong lensing in this system, giving us a picture of the different fluxes and also the variation in the CO sizes through the quantum number.

We observe some differences in the structure between different CO transitions with respect to both reconstructed size and position of each velocity bin. In CO(2−1) a trend of increasing emission region size is seen with decreasing radial velocity (see Table A.2 and Fig. 4): red wings of the lines appear to emit from regions three times more compact than those emitting the blue wings, with ranges 0.9 ≲ r1/2 ≲ 2.7 kpc. This trend is also hinted at in CO(6−5), but only in the highest velocity bins. Within the uncertainties, however, all CO (Jup >  2) are consistent with no size variation per velocity bin. We note that this variation, seen only in CO(2−1), may be due to the fact that this line has been observed with ATCA at a significantly lower significance than the rest of the lines.

Regarding relative position of the reconstructed emission regions per velocity bins, we see in Fig. 5 that CO(2−1) does not follow any specific trend. On the other hand, in the three higher CO transitions studied, a clear gradient is observed suggesting a rotating disk-like structure for these lines. The projected extension of this line-of-sight structure of the emission regions is largest for CO(6−5) (∼1.2 kpc) and smallest for CO(9−8) (∼0.4 kpc), consistent with the integrated lines reconstruction sizes (Fig. 6).

thumbnail Fig. 5.

Position relative to the center of the lens for each velocity bin. The color bar shows the normalized flux density of each transition line.

thumbnail Fig. 6.

Dependency of the reconstructed source size (half-light radius) of the line emission regions with transition or frequency. Black dots show reconstructed CO line emission regions as a function of the J transition and the observed frequency. Purple triangles show reconstructed H2O line emission as a function of the observed frequency. The dotted lines represent the size (r1/2) of the dust for different wavelengths, blue for 870 μm, red for 2 mm, and green for 3 mm continuum emission.

3.3. H2O lines

In the H2O transitions we also observe some differences in structure. As shown in Table A.2 and Fig. 4 the H2O (211 − 202) transition shows variation in reconstructed sizes per velocity bin, with no clear correlation (albeit with high uncertainty in reconstructed sizes), thus suggesting a merger scenario. On the other hand, much like the CO (Jup >  2) lines reconstruction, the rotational H2O (202 − 111) transition line reconstruction shows no size variation per velocity bin within the uncertainties.

As seen in Fig. 5 both H2O lines show line-of-sight structure with projected extensions of ∼2.3 kpc for H2O (211 − 202) and ∼0.5 kpc for H2O (202 − 111). We note that the lower S/N of the H2O (211 − 202) line coupled with the significantly larger reconstructed sizes of the regions implies less robust reconstructed center measurements, and thus the projected extension.

3.4. Size, magnification, and bias

Gravitational lensing is a geometrical effect: sources close in projection to the “infinite magnification” caustics are significantly more magnified than sources far from caustics and compact sources are magnified more than extended sources. As a direct consequence, the magnification and distortion of sources with non-isotropic morphologies has a strong correlation not only with their shape, but also with their projected positions relative to the lensing potential. These two (sometimes competing) effects are shown in Tables A.1 and A.2 where the most compact regions or the regions closest to the caustics are not necessarily the most magnified. This supports the idea that the intrinsic structure of lensed sources detected in submillimeter surveys may play a significant role in their detection (e.g., Hezaveh et al. 2012).

4. Discussion

4.1. CO ratios

Since our model are not able to capture the morphology of each line, and thus we cannot investigate the effects of differential magnification in the projected plane, we explore the variation in the magnification and CO line ratios as a function of velocity (i.e., along the line of sight).

Figure 7 shows the variation with velocity of the magnification and the ratio of each CO line with respect to CO(2 − 1). Also shown is the observed line luminosity for reference. We find that the magnification factor obtained for each CO line varies throughout the line profile (Fig. 7), showing a consistent behavior among all three lines. The magnifications seem to increase from −400 km s−1 to a peak at around 100 − 200 km s−1, decreasing at higher velocities.

thumbnail Fig. 7.

CO ratio of intrinsic (blue line) and observed emission line intensities (red line) across the line profile for CO(6 − 5)/CO(2 − 1) (left panel), CO(8 − 7)/CO(2 − 1) (middle panel), and CO(9 − 8)/CO(2 − 1) (right panel). The orange line represent the magnification factor across the line profile for CO(6 − 5), CO(8 − 7) (middle panel), and CO(9 − 8) (right panel).

Figure 7 also shows the CO ratios (ICOJ ≥ 6/ICO(2 − 1)) of the observed and intrinsic line fluxes, as a function of velocity. The magnifications vary significantly across velocities (a factor of two for CO(6 − 5)); however, the CO line ratios present milder differences for both observed and intrinsic measurements. While the observed line ratios show little variation with velocity, the intrinsic line ratios show non-negligible gradients along the line of sight. This behaviour is broadly consistent with the results presented by Dong et al. (2019), where fairly constant CO line ratios for this source across velocities are found, even though they use partially different datasets. We note, however, that Dong et al. (2019) study brightness temperature ratios with coarser velocity resolution, whereas here we show the intensity ratios (their Fig. 9). Neglecting the +400 km s−1 velocity bin, which has large uncertainties, there is a tendency for higher line ratios at v ∼ 0 − 200 km s−1, suggesting higher excitation in this velocity range. Conversely, for v <  0 we observe a roughly constant ratio with variations of less than 25% for I8 − 7/I2 − 1 and less than 17% for I9 − 8/I2 − 1.

It is interesting to note that neglecting the H2O(211 − 202) line, which has the higher uncertainties, the H2O line has a size compatible within the uncertainties with those of the CO(6 − 5) or CO(8 − 7) lines, and significantly higher than CO(9 − 8). This contrasts the results from low-z ultra-luminous infrared galaxies (ULIRGs), where the H2O emission arises from particularly dense, dust-obscured regions (González-Alfonso et al. 2010; König et al. 2017). One possible explanation for this could be that the high-J CO and H2O lines, which in general trace similarly dense star-forming regions, are essentially probing different physical mechanisms within the galactic environment. High-J CO lines trace collisionally excited molecular gas, whereas the H2O lines trace gas that is illuminated by IR photons (radiative IR pumping). Therefore, if the IR radiation extends beyond the collisionally excited regions (typically traced by CO), the H2O molecules located farther away could be excited, leading to larger sizes. Mapping other H2O transitions at high(-er) angular resolution will be able to solve this puzzle.

4.2. CO SLED

We study the physical conditions of the ISM in SPT 0346-52 by modeling the CO lines and continuum emission, using the method described in Weiß et al. (2007). This method is based on a spherical, multi-component, large velocity gradient (LVG) model. Here the dust continuum and the CO rotational transition line emission are linked via the gas column density NH2 which is defined by

(1)

where ΔVturb is the turbulence linewidth, n(H2) the gas density, and dv/dr the velocity gradient of the LVG model. From this we can obtain the total gas mass from the LVG model, using

(2)

where 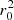is the equivalent source radius which depends on angular size distance to the source (DA) and the magnified solid angle (Ωapp).

We ran the model using the intrinsic flux densities of all CO lines and FIR continuum fluxes. We include our 2 mm and 3 mm ALMA continuum measurements, the ALMA 0.87 mm flux (Spilker et al. 2016), and the 250 μm, 350 μm, and 500 μm from Herschel/SPIRE observations (Ma et al. 2016). To correct the Herschel SPIRE fluxes, we use the magnifications obtained at 0.87 mm (Spilker et al. 2016). Since the CO line widths are relatively uniform, we assume a fixed CO line width, corresponding to the weighted average line width value (642 km s−1).

Figure 8 shows the CO spectral line energy distribution (SLED) and continuum measurements. The CO SLED shows a peak close to CO(8−7); however, it appears to stay roughly constant toward higher J transitions, indicating a highly excited gas component which could extend beyond J = 10 − 9. The ISM properties derived from the best-fit radiative transfer model are summarized in Table 5.

thumbnail Fig. 8.

Result of the fitting of the CO-SLED (left panel) and SED (right panel). The filled circles are the CO rotational lines and the open circles represent the continuum fluxes obtained in this work and from Spilker et al. (2016) and Ma et al. (2016). The blue line in both panels shows the best-fit model.

Table 5.

Summary of the radiative transfer model.

The kinetic temperature (Tkin ∼ 43 K) is higher than the dust temperature (Tdust ∼ 29 K). This could suggest that the ISM is being affected by an external mechanical energy input. This result is in agreement with the virial velocity gradient (κvir ∼ 3.4) obtained from the model, where the uncertainties are affected by the cloud geometry and the density profile. We note that most parameters in this model, including the CO abundance and intrinsic source sizes, are left as free parameters. Our model yields an intrinsic source size of 4.4 ± 2.4 kpc, a CO chemical abundance of 8 × 10−5, dv/dr = 220, and Δturb = 40.

Using Eq. (2), we derive a total intrinsic gas mass of ∼3.9 ± 2.2 × 1011 M⊙, which, despite the large uncertainties, is significantly higher than the molecular gas mass derived using the low-J CO line alone (Aravena et al. 2016), and even higher than the dynamical mass estimate of 1.5 × 1011 M⊙ obtained from the high-resolution CO(2 − 1) imaging (Spilker et al. 2015). This difference of the LVG-based molecular gas mass and the dynamical mass is 10% above the formal 1σ uncertainties of the LVG measurement. The latter are mostly driven by our inability to trace the peak of the CO SLED with our current observations, and thus our radiative transfer model is not fully constrained. We note that this discrepancy could also reflect uncertainties in the CO luminosity-to-gas mass conversion factor used to transform the low-J CO luminosities.

Figure 9 compares the integrated CO SLED normalized to CO(1 − 0) of SPT 0346-52 with the literature values. For this comparison, we normalize the CO SLED of SPT 0346-52 to the CO(1 − 0) line intensity by assuming a brightness temperature line ratio 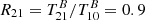(Carilli & Walter 2013), and using the measured CO(2 − 1) line intensity to obtain the CO(1 − 0) intensity from I10 = I21(ν21/ν10)2 .

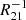thumbnail Fig. 9.

Comparison of the CO SLEDs normalized to the CO(1 − 0) flux density transition with different galaxies. Orange squares represent the obtained CO SLED of SPT 0356-52 taking the line flux described in Table 4. Black lines shows BR 1202−0725 (z = 4.69, (Carilli et al. 2002; Riechers et al. 2006), M 82 Center (Weiß et al. 2005b), NGC 253 Center (Güsten et al. 2006), SMM 16359 (z = 2.5, Weiß et al. (2005a)). The solid circles shows the Galactic center (Fixsen et al. 1999), diamonds shows average SLED of DSFGs (Bothwell et al. 2013), and triangles shows SLED of SPT DSFGs (Spilker et al. 2014). The inset shows the CO SLED normalized to the CO(1 − 0) for different velocities in SPT 0356-52.

SPT 0346-52 clearly has a higher CO excitation than local starburst galaxies, and even luminous quasars. Interestingly, SPT 0346-52 seems to be an extreme case when compared to most distant DSFGs (e.g., Bothwell et al. 2013; Spilker et al. 2014; Cañameras et al. 2018), with a CO SLED similar to that of HLFS-3 at z = 6.3 (Riechers et al. 2013). This is exemplified by the high gas density obtained through the radiative transfer model. Confirmation of this higher excitation nature will require observations of higher J CO transitions. The inset in Fig. 9 shows what could be interpreted as a dependency of the excitation with velocity; however, as shown by the uncertainties, it is consistent with no variation.

4.3. H2O line emission

Recent systematic observations of the H2O emission lines showed that these lines are among the most luminous in the far-infrared spectra of galaxies (e.g., Omont et al. 2013; Yang et al. 2013, 2016). Furthermore, the H2O line luminosities were found to correlate tightly with their total IR luminosities. This has been found to be an almost direct consequence of IR pumping (van der Werf et al. 2011; Yang et al. 2013, 2016), and thus the H2O emission likely traces the far-infrared radiation field generated in dense star-forming regions in galaxies. While some galaxies that host AGN show lower LH2O/LIR ratios, no real dependence has been found on the existence of AGN or lack thereof (Yang et al. 2013).

As previously shown, we significantly detected two H2O emission lines toward SPT 0346-52. This is one of the most distant objects in which H2O has been detected (see also: Riechers et al. 2013). Figure 10 shows the H2O and IR luminosities of SPT 0346-52 compared to other galaxies at low and high redshift in the literature. We find that our source closely follows the correlation between these two quantities, suggesting the presence of IR radiative pumping of the H2O molecules in the ISM. In addition, we find no signs of a signature pointing to the presence of AGN based on this correlation, in agreement with previous results from Ma et al. (2016). The close match of the spatial location of the reconstructed CO(6−5) and H2O lines in the source-plane (Fig. 4) and the agreement between the line widths of the H2O and the high-J CO transitions observed, supports the idea that H2O and the high-J CO are co-located, presumably in a region of intense star formation.

thumbnail Fig. 10.

Correlation between the H2O/FIR and FIR luminosities for a sample of galaxies in the literature, compared to SPT 0346-52. Green squares represent local starburst galaxies observed with Herschel (Liu et al. 2017), grey circles show local ULIRGS and blue circles show high-redshift Hy/ULIRGs (Yang et al. 2016). The large red square shows the location of SPT 0346-52. The uncertainties in some of these measurements are smaller than the size of each data point. SPT 0346-52 follows the trend, suggesting the presence of radiative pumping of the H2O molecules.

4.4. Gas tracers

The reconstruction results presented here are consistent with those presented in Litke et al. (2019) and Dong et al. (2019). The kinematics of our CO(6−5) reconstruction is similar to the [CII] reconstruction in Litke et al. (2019) (see Fig. 4), where the v >  0 part of the gas lies directly on the caustic line, while for v <  0 the emission shows a displacement of ∼1 kpc. Our CO(J = 8 − 7 and 9 − 8) and H2O(202−211) reconstruction indeed show a more compact structure with a separation of ∼0.5 kpc between the bluest and reddest part of the gas, near the bridge that Litke et al. (2019) found between the two [CII] lobes. Restricting the lines to the range with higher S/N (within ±450 km s−1), we observe that for these three lines the largest part of the flux comes from v ≥ 0, with 55 ± 4%, 54 ± 2%, and 57 ± 2% of the line emission coming from this range for the CO(9 − 8), CO(8 − 7), and H2O(202 − 111), respectively.

Conversely, the three remaining lines that have an extended structure (CO J = (2 − 1), (6−5) and H2O(211 − 202)), show a peak of the flux at ∼ − 200 km s−1, but with a second increment of the flux between ∼100 − 200 km s−1. It is important to note that a direct comparison between the reconstructed source shape with this work is not possible since in Dong et al. (2019) the ellipticity (and position angle) in the source plane reconstruction for each velocity bin in the line have been left free in the fit. Since magnification is defined exactly as image-to-source area ratios, complete freedom in ellipticity can result in differing fitted sizes and magnifications, making the contrast of recovered sizes per velocity not directly comparable. The magnifications and sizes measured by Dong et al. (2019) in each velocity bin are consistent, though systematically larger and smaller, respectively, than those presented here. Fitted central positions, on the other hand, are only mildly affected by this freedom and are indeed compatible with those shown here.

5. Summary and conclusions

We presented mid- to high-J CO and H2O transition lines in SPT 0346-52 using ALMA Band 3 and Band 4 observations. Using the VISILENS code and lens model parameters obtained in Spilker et al. (2016) we reconstructed the lensed galaxy in the source-plane, and analyzed its intrinsic ISM properties. The main results of this study are the following:

(i) We derived intrinsic sizes, positions, and fluxes of multiple CO lines (J = 6 − 5, 8 − 7, and 9 − 8) and H2O (202 − 111 and 211 − 202) in several velocity channels per line. Although there is in general a continuous gradient in the projected extension of the line-of-sight structure that would suggest a disk-like morphology, at least two emission lines (CO(2 − 1) and H2O(211 − 202)) show significant variations in their reconstructed sizes at resolved velocity bins. Even when these two lines have the largest uncertainties in the reconstructed sizes, it could be consistent with a more complicated structure such as a galaxy merger. This scenario is indeed consistent with that shown by Litke et al. (2019). Furthermore, the variation in the normalized flux along the velocity axis in all line transitions (CO and H2O) suggests evidence of a disturbed structure, which supports the scenario of a galaxy merger found by Litke et al. (2019).

(ii) The CO sizes show a clear trend of decreasing size with increasing J, and the CO sizes for all transitions appear larger than the dust continuum sizes (at rest frame 450, 300, and 130 μm).

(iii) Our observations suggest differential magnification in the CO lines along the velocity axis. While the observed CO line ratios appear roughly constant with velocity, we find that the intrinsic CO line ratios (CO(6 − 5)/CO(2 − 1), CO(8 − 7)/CO(2 − 1), and CO(9 − 8)/CO(2 − 1)) show a peak at ∼0 − 200 km s−1. This could argue for a more excited region within the galaxy.

(iv) CO SLED shows a peak at J = 8 − 7, indicating excited gas with a Tkin ∼ 43 K and Tdust ∼ 29 K. The intrinsic CO SLED seems to be more excited than local starburst and luminous quasars.

(v) H2O emission follows the correlation of 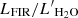in accordance with IR radiative pumping. The resemblance between CO and H2O of the linewidths and the structure of the source plane show that the emission is likely co-spatial, coming from regions of intense star formation.

The source plane reconstruction presented in this work, thus support a merger scenario in SPT 0346-52. This interpretation can explain the high SFR measured for the background galaxy. Deeper and higher-JCO observations will allow us to tighten our LVG model constraints and the source plane structure presented in this work.

Acknowledgments

Y.A. acknowledges support of Universidad Andrés Bello through a Graduate School Fellowship. Y.A. and T.A. acknowledge support from the Ministry for the Economy, Development, and Tourism’s Programa Inicativa Científica Milenio through grant IC 12009. This paper makes use of the following ALMA data: ADS/JAO.ALMA 2013.1.00722.S and 2015.1.00117.S. ALMA is a partnership of ESO (representing its member states), NSF (USA), and NINS (Japan), together with NRC (Canada), MOST and ASIAA (Taiwan), and KASI (Republic of Korea), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO, and NAOJ. The National Radio Astronomy Observatory is a facility of the National Science Foundation operated under cooperative agreement by Associated Universities, Inc. The Australia Telescope Compact Array is part of the Australia Telescope National Facility which is funded by the Australian Government for operation as a National Facility managed by CSIRO. This publication is based on data acquired with the Atacama Pathfinder Experiment (APEX). APEX is a collaboration between the Max-Planck-Institut fur Radioastronomie, the European Southern Observatory, and the Onsala Space Observatory. The SPT is supported by the NSF through grant PLR-1248097, with partial support through PHY-1125897, the Kavli Foundation, and the Gordon and Betty Moore Foundation grant GBMF 947. S.J., J.D.V., and D.P.M. acknowledge support from the US NSF under grants AST-1715213 and AST-1716127. S.J. acknowledges support from the US NSF NRAO under grant SOSPA5-001. J.D.V. acknowledges support from an A.P. Sloan Foundation Fellowship. The Flatiron Institute is supported by the Simons Foundation. D.N. was supported in part by NSF Award AST-1715206 and HST Theory Award 15043.0001.

References

  1. Aravena, M., Spilker, J. S., Bethermin, M., et al. 2016, MNRAS, 457, 4406 [NASA ADS] [CrossRef] [Google Scholar]
  2. Aretxaga, I., Hughes, D. H., Coppin, K., et al. 2007, MNRAS, 379, 1571 [NASA ADS] [CrossRef] [Google Scholar]
  3. Barger, A. J., Cowie, L. L., Smail, I., et al. 1999, AJ, 117, 2656 [NASA ADS] [CrossRef] [Google Scholar]
  4. Barger, A. J., Wang, W.-H., Cowie, L. L., et al. 2012, ApJ, 761, 89 [Google Scholar]
  5. Belitsky, V., Lapkin, I., Fredrixon, M., et al. 2018, A&A, 612, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  6. Béthermin, M., De Breuck, C., Gullberg, B., et al. 2016, A&A, 586, L7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  7. Blandford, R. D., & Narayan, R. 1992, ARA&A, 30, 311 [NASA ADS] [CrossRef] [Google Scholar]
  8. Bothwell, M. S., Smail, I., Chapman, S. C., et al. 2013, MNRAS, 429, 3047 [NASA ADS] [CrossRef] [Google Scholar]
  9. Bothwell, M. S., Maiolino, R., Peng, Y., et al. 2016, MNRAS, 455, 1156 [NASA ADS] [CrossRef] [Google Scholar]
  10. Brisbin, D., Miettinen, O., Aravena, M., et al. 2017, A&A, 608, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  11. Cañameras, R., Yang, C., Nesvadba, N. P. H., et al. 2018, A&A, 620, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  12. Carilli, C. L., & Walter, F. 2013, ARA&A, 51, 105 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  13. Carilli, C. L., Kohno, K., Kawabe, R., et al. 2002, AJ, 123, 1838 [NASA ADS] [CrossRef] [Google Scholar]
  14. Carlstrom, J. E., Ade, P. A. R., Aird, K. A., et al. 2011, PASP, 123, 568 [NASA ADS] [CrossRef] [Google Scholar]
  15. Casey, C. M., Narayanan, D., & Cooray, A. 2014, Phys. Rep., 541, 45 [NASA ADS] [CrossRef] [Google Scholar]
  16. Chapin, E. L., Pope, A., Scott, D., et al. 2009, MNRAS, 398, 1793 [NASA ADS] [CrossRef] [Google Scholar]
  17. Chapman, S. C., Blain, A. W., Smail, I., & Ivison, R. J. 2005, ApJ, 622, 772 [NASA ADS] [CrossRef] [Google Scholar]
  18. Chen, C.-C., Smail, I., Ivison, R. J., et al. 2016, ApJ, 820, 82 [NASA ADS] [CrossRef] [Google Scholar]
  19. da Cunha, E., Walter, F., Smail, I. R., et al. 2015, ApJ, 806, 110 [NASA ADS] [CrossRef] [Google Scholar]
  20. Danielson, A. L. R., Swinbank, A. M., Smail, I., et al. 2011, MNRAS, 410, 1687 [NASA ADS] [Google Scholar]
  21. Dong, C., Spilker, J. S., Gonzalez, A. H., et al. 2019, ApJ, 873, 50 [NASA ADS] [CrossRef] [Google Scholar]
  22. Dye, S., Eales, S. A., Aretxaga, I., et al. 2008, MNRAS, 386, 1107 [NASA ADS] [CrossRef] [Google Scholar]
  23. Fixsen, D. J., Bennett, C. L., & Mather, J. C. 1999, ApJ, 526, 207 [NASA ADS] [CrossRef] [Google Scholar]
  24. Frayer, D. T., Ivison, R. J., Scoville, N. Z., et al. 1998, ApJ, 506, L7 [NASA ADS] [CrossRef] [Google Scholar]
  25. González-Alfonso, E., Fischer, J., Isaak, K., et al. 2010, A&A, 518, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  26. Greve, T. R., Bertoldi, F., Smail, I., et al. 2005, MNRAS, 359, 1165 [NASA ADS] [CrossRef] [Google Scholar]
  27. Gullberg, B., De Breuck, C., Vieira, J. D., et al. 2015, MNRAS, 449, 2883 [NASA ADS] [CrossRef] [Google Scholar]
  28. Güsten, R., Philipp, S. D., Weiß, A., & Klein, B. 2006, A&A, 454, L115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  29. Hainline, L. J., Blain, A. W., Smail, I., et al. 2011, ApJ, 740, 96 [NASA ADS] [CrossRef] [Google Scholar]
  30. Hezaveh, Y. D., Dalal, N., Marrone, D. P., et al. 2016, ApJ, 823, 37 [NASA ADS] [CrossRef] [Google Scholar]
  31. Hezaveh, Y. D., Marrone, D. P., & Holder, G. P. 2012, ApJ, 761, 20 [NASA ADS] [CrossRef] [Google Scholar]
  32. Hezaveh, Y. D., Marrone, D. P., Fassnacht, C. D., et al. 2013, ApJ, 767, 132 [NASA ADS] [CrossRef] [Google Scholar]
  33. Hinshaw, G., Larson, D., Komatsu, E., et al. 2013, ApJS, 208, 19 [NASA ADS] [CrossRef] [Google Scholar]
  34. Huynh, M. T., Emonts, B. H. C., Kimball, A. E., et al. 2017, MNRAS, 467, 1222 [NASA ADS] [Google Scholar]
  35. Ivison, R. J., Greve, T. R., Smail, I., et al. 2002, MNRAS, 337, 1 [NASA ADS] [CrossRef] [Google Scholar]
  36. Kennicutt, Jr., R. C. 1998, ARA&A, 36, 189 [Google Scholar]
  37. König, S., Martín, S., Muller, S., et al. 2017, A&A, 602, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  38. Litke, K. C., Marrone, D. P., Spilker, J. S., et al. 2019, ApJ, 870, 80 [NASA ADS] [CrossRef] [Google Scholar]
  39. Liu, L., Weiß, A., Perez-Beaupuits, J. P., et al. 2017, ApJ, 846, 5 [NASA ADS] [CrossRef] [Google Scholar]
  40. Ma, J., Gonzalez, A. H., Spilker, J. S., et al. 2015, ApJ, 812, 88 [NASA ADS] [CrossRef] [Google Scholar]
  41. Ma, J., Gonzalez, A. H., Vieira, J. D., et al. 2016, ApJ, 832, 114 [CrossRef] [Google Scholar]
  42. Magnelli, B., Lutz, D., Santini, P., et al. 2012, A&A, 539, A155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  43. Marrone, D. P., Spilker, J. S., Hayward, C. C., et al. 2018, Nature, 553, 51 [NASA ADS] [CrossRef] [Google Scholar]
  44. McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, ASP Conf. Ser., 376, 127 [Google Scholar]
  45. Michałowski, M. J., Hayward, C. C., Dunlop, J. S., et al. 2014, A&A, 571, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  46. Michałowski, M. J., Dunlop, J. S., Koprowski, M. P., et al. 2017, MNRAS, 469, 492 [NASA ADS] [CrossRef] [Google Scholar]
  47. Miettinen, O., Delvecchio, I., Smolčić, V., et al. 2017, A&A, 597, A5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  48. Omont, A. 2007, Rep. Progr. Phys., 70, 1099 [Google Scholar]
  49. Omont, A., Yang, C., Cox, P., et al. 2013, A&A, 551, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  50. Rawle, T. D., Egami, E., Bussmann, R. S., et al. 2014, ApJ, 783, 59 [NASA ADS] [CrossRef] [Google Scholar]
  51. Riechers, D. A., Walter, F., Carilli, C. L., et al. 2006, ApJ, 650, 604 [NASA ADS] [CrossRef] [Google Scholar]
  52. Riechers, D. A., Bradford, C. M., Clements, D. L., et al. 2013, Nature, 496, 329 [Google Scholar]
  53. Rosenberg, M. J. F., van der Werf, P. P., Aalto, S., et al. 2015, ApJ, 801, 72 [NASA ADS] [CrossRef] [Google Scholar]
  54. Sargent, M. T., Daddi, E., Béthermin, M., et al. 2014, ApJ, 793, 19 [NASA ADS] [CrossRef] [Google Scholar]
  55. Serjeant, S. 2012, MNRAS, 424, 2429 [NASA ADS] [CrossRef] [Google Scholar]
  56. Sharon, C. E. 2013, PhD Thesis, Rutgers The State University of New Jersey, New Brunswick [Google Scholar]
  57. Simpson, J. M., Swinbank, A. M., Smail, I., et al. 2014, ApJ, 788, 125 [Google Scholar]
  58. Smolčić, V., Aravena, M., Navarrete, F., et al. 2012, A&A, 548, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  59. Solomon, P. M., & Vanden Bout, P. A. 2005, ARA&A, 43, 677 [NASA ADS] [CrossRef] [Google Scholar]
  60. Spilker, J. S., Aravena, M., Marrone, D. P., et al. 2015, ApJ, 811, 124 [NASA ADS] [CrossRef] [Google Scholar]
  61. Spilker, J. S., Marrone, D. P., Aguirre, J. E., et al. 2014, ApJ, 785, 149 [NASA ADS] [CrossRef] [Google Scholar]
  62. Spilker, J. S., Marrone, D. P., Aravena, M., et al. 2016, ApJ, 826, 112 [NASA ADS] [CrossRef] [Google Scholar]
  63. Strandet, M. L., Weiss, A., Vieira, J. D., et al. 2016, ApJ, 822, 80 [NASA ADS] [CrossRef] [Google Scholar]
  64. Strandet, M. L., Weiss, A., De Breuck, C., et al. 2017, ApJ, 842, L15 [NASA ADS] [CrossRef] [Google Scholar]
  65. Swinbank, A. M., Simpson, J. M., Smail, I., et al. 2014, MNRAS, 438, 1267 [Google Scholar]
  66. van der Werf, P. P., Berciano Alba, A., Spaans, M., et al. 2011, ApJ, 741, L38 [NASA ADS] [CrossRef] [Google Scholar]
  67. Vieira, J. D., Crawford, T. M., Switzer, E. R., et al. 2010, ApJ, 719, 763 [NASA ADS] [CrossRef] [Google Scholar]
  68. Vieira, J. D., Marrone, D. P., Chapman, S. C., et al. 2013, Nature, 495, 344 [NASA ADS] [CrossRef] [Google Scholar]
  69. Wardlow, J. L., Smail, I., Coppin, K. E. K., et al. 2011, MNRAS, 415, 1479 [NASA ADS] [CrossRef] [Google Scholar]
  70. Weiß, A., Downes, D., Neri, R., et al. 2007, A&A, 467, 955 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  71. Weiß, A., De Breuck, C., Marrone, D. P., et al. 2013, ApJ, 767, 88 [NASA ADS] [CrossRef] [Google Scholar]
  72. Weiß, A., Downes, D., Walter, F., & Henkel, C. 2005a, A&A, 440, L45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  73. Weiß, A., Walter, F., & Scoville, N. Z. 2005b, A&A, 438, 533 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  74. Yang, C., Gao, Y., Omont, A., et al. 2013, ApJ, 771, L24 [NASA ADS] [CrossRef] [Google Scholar]
  75. Yang, C., Omont, A., Beelen, A., et al. 2016, A&A, 595, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  76. Yang, C., Gavazzi, R., Beelen, A., et al. 2019, A&A, 624, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
  77. Yun, M. S., Scott, K. S., Guo, Y., et al. 2012, MNRAS, 420, 957 [NASA ADS] [CrossRef] [Google Scholar]

Appendix A: Additional tables

Table A.1.

H2O source reconstruction results.

Table A.2.

CO source reconstruction results.

All Tables

Table 1.

Observational summary of data.

In the text
Table 2.

Observed parameters.

In the text
Table 3.

Fixed lens model parameters from Spilker et al. (2016).

In the text
Table 4.

Reconstruction parameters.

In the text
Table 5.

Summary of the radiative transfer model.

In the text
Table A.1.

H2O source reconstruction results.

In the text
Table A.2.

CO source reconstruction results.

In the text

All Figures

thumbnail Fig. 1.

Maps of the line transitions detected in SPT 0346-52 obtained with ALMA observations, integrated over 4σvelocity km s−1 channels. For H2O 211 − 202 and H2O 202 − 111 red contours are the 2, 4, 6, 8σ intervals. For CO(6−5), CO(8−7), and CO(9−8) red contours are the 5, 10, 20, 30σ intervals. The synthesized beam is shown in the bottom left corner as a red ellipse. The orange cross shows the center of the lensing galaxy.
In the text
thumbnail Fig. 2.

Spectra of the line transitions detected in SPT 0346-52 obtained with the ATCA and ALMA observations. Single Gaussian fits are represented by black lines, centered at the observed frequencies. The white line shows the intrinsic flux using the values of magnification described in Tables A.1 and A.2. The different channels used in the lens modeling are color-coded according to their velocity on whether the emission is receding (red) or approaching (blue). Each channel is 100 km s−1 wide, except for the edge channels which are 400 km s−1 to improve their low S/N.
In the text
thumbnail Fig. 3.

Spectrum of the CO(10 − 9) line emission observed with APEX of SPT 0346-52. The red solid curve shows a Gaussian fit to the line profile. This line is about two times stonger than that of CO(9−8), suggesting contamination by a neighboring emission line.
In the text
thumbnail Fig. 4.

Reconstruction of the source plane in each velocity bin as described in the text. The velocity bins are color-coded, following the color bar to the right and as represented in Fig. 2. The circles represent the size of the reconstructed emission in each velocity bin, defined by the half-light radius (see text). The color-coded central dots show the reconstructed source position at the respective velocity bin. The dotted black line shows the lensing caustic curve from the lens model of Spilker et al. (2016).
In the text
thumbnail Fig. 5.

Position relative to the center of the lens for each velocity bin. The color bar shows the normalized flux density of each transition line.
In the text
thumbnail Fig. 6.

Dependency of the reconstructed source size (half-light radius) of the line emission regions with transition or frequency. Black dots show reconstructed CO line emission regions as a function of the J transition and the observed frequency. Purple triangles show reconstructed H2O line emission as a function of the observed frequency. The dotted lines represent the size (r1/2) of the dust for different wavelengths, blue for 870 μm, red for 2 mm, and green for 3 mm continuum emission.
In the text
thumbnail Fig. 7.

CO ratio of intrinsic (blue line) and observed emission line intensities (red line) across the line profile for CO(6 − 5)/CO(2 − 1) (left panel), CO(8 − 7)/CO(2 − 1) (middle panel), and CO(9 − 8)/CO(2 − 1) (right panel). The orange line represent the magnification factor across the line profile for CO(6 − 5), CO(8 − 7) (middle panel), and CO(9 − 8) (right panel).
In the text
thumbnail Fig. 8.

Result of the fitting of the CO-SLED (left panel) and SED (right panel). The filled circles are the CO rotational lines and the open circles represent the continuum fluxes obtained in this work and from Spilker et al. (2016) and Ma et al. (2016). The blue line in both panels shows the best-fit model.
In the text
thumbnail Fig. 9.

Comparison of the CO SLEDs normalized to the CO(1 − 0) flux density transition with different galaxies. Orange squares represent the obtained CO SLED of SPT 0356-52 taking the line flux described in Table 4. Black lines shows BR 1202−0725 (z = 4.69, (Carilli et al. 2002; Riechers et al. 2006), M 82 Center (Weiß et al. 2005b), NGC 253 Center (Güsten et al. 2006), SMM 16359 (z = 2.5, Weiß et al. (2005a)). The solid circles shows the Galactic center (Fixsen et al. 1999), diamonds shows average SLED of DSFGs (Bothwell et al. 2013), and triangles shows SLED of SPT DSFGs (Spilker et al. 2014). The inset shows the CO SLED normalized to the CO(1 − 0) for different velocities in SPT 0356-52.
In the text
thumbnail Fig. 10.

Correlation between the H2O/FIR and FIR luminosities for a sample of galaxies in the literature, compared to SPT 0346-52. Green squares represent local starburst galaxies observed with Herschel (Liu et al. 2017), grey circles show local ULIRGS and blue circles show high-redshift Hy/ULIRGs (Yang et al. 2016). The large red square shows the location of SPT 0346-52. The uncertainties in some of these measurements are smaller than the size of each data point. SPT 0346-52 follows the trend, suggesting the presence of radiative pumping of the H2O molecules.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.