| Issue |
A&A
Volume 623, March 2019
|
|
|---|---|---|
| Article Number | A136 | |
| Number of page(s) | 21 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201834788 | |
| Published online | 20 March 2019 | |
The CARMENES search for exoplanets around M dwarfs
Chromospheric modeling of M 2–3 V stars with PHOENIX
1
Hamburger Sternwarte, University of Hamburg,
Gojenbergsweg 112,
21029 Hamburg,
Germany
e-mail: dominik.hintz@hs.uni-hamburg.de
2
Institut für Astrophysik,
Friedrich-Hund-Platz 1,
37077 Göttingen,
Germany
3
Centro de Astrobiología (CSIC-INTA), ESAC,
Camino Bajo del Castillo s/n,
28692 Villanueva de la Cañada,
Madrid, Spain
4
Institut de Ciències de l’Espai (ICE, CSIC), Campus UAB, c/ de Can Magrans s/n,
08193 Bellaterra,
Barcelona, Spain
5
Institut d’Estudis Espacials de Catalunya (IEEC),
08034 Barcelona,
Spain
6
Instituto de Astrofísica de Andalucía (CSIC),
Glorieta de la Astronomía s/n,
18008 Granada, Spain
7
Landessternwarte,
Zentrum für Astronomie der Universität Heidelberg,
Königstuhl 12,
69117 Heidelberg, Germany
8
School of Physics and Astronomy, Queen Mary, University of London,
327 Mile End Road,
London, E1 4NS, UK
9
Instituto de Astrofísica de Canarias,
c/ Vía Láctea s/n,
38205 La Laguna,
Tenerife, Spain
10
Departamento de Astrofísica, Universidad de La Laguna,
38206 Tenerife,
Spain
11
Centro Astronómico Hispano-Alemán (MPG-CSIC),
Observatorio Astronómico de Calar Alto,
Sierra de los Filabres,
04550 Gérgal, Almería, Spain
12
Thüringer Landessternwarte Tautenburg,
Sternwarte 5,
07778 Tautenburg,
Germany
13
Max-Planck-Institut für Astronomie,
Königstuhl 17,
69117 Heidelberg,
Germany
14
Departamento de Física de la Tierra y Astrofísica and UPARCOS-UCM (Unidad de Física de Partículas y del Cosmos de la UCM), Facultad de Ciencias Físicas, Universidad Complutense de Madrid,
28040
Madrid, Spain
Received:
6
December
2018
Accepted:
31
January
2019
Chromospheric modeling of observed differences in stellar activity lines is imperative to fully understand the upper atmospheres of late-type stars. We present one-dimensional parametrized chromosphere models computed with the atmosphere code PHOENIX using an underlying photosphere of 3500 K. The aim of this work is to model chromospheric lines of a sample of 50 M2–3 dwarfs observed in the framework of the CARMENES, the Calar Alto high-Resolution search for M dwarfs with Exo-earths with Near-infrared and optical Echelle Spectrographs, exoplanet survey. The spectral comparison between observed data and models is performed in the chromospheric lines of Na I D2, Hα, and the bluest Ca II infrared triplet line to obtain best-fit models for each star in the sample. We find that for inactive stars a single model with a VAL C-like temperature structure is sufficient to describe simultaneously all three lines adequately. Active stars are rather modeled by a combination of an inactive and an active model, also giving the filling factors of inactive and active regions. Moreover, the fitting of linear combinations on variable stars yields relationships between filling factors and activity states, indicating that more active phases are coupled to a larger portion of active regions on the surface of the star.
Key words: stars: activity / stars: chromospheres / stars: late-type
© ESO 2019
1 Introduction
Magnetic stellar activity comprises a zoo of phenomena affecting different layers of stellar atmospheres. Magnetic activity is thought to be fundamental for the heating of the hot chromospheres and even hotter coronae of late-type stars, which produce all of their high-energy ultraviolet and X-ray fluxes observed from these stars. In addition, late-type stars are frequently planet hosts, and hence their activity is also recognized to have a crucial influence on the evolution of their planets, their atmospheric structure, and also possible life on their surfaces (e.g. Segura et al. 2010; France et al. 2016; O’Malley-James & Kaltenegger 2017).
In late-type stars, the chromosphere is the atmospheric layer between the photosphere and transition region. In the classical, one-dimensional picture, the atmospheric temperature reaches a minimum at the base of the chromosphere and then starts increasing outward. Several heating processes, such as acoustic heating (Wedemeyer et al. 2004), back warming from the corona lying above the chromosphere and the transition region, and magnetic heating, are likely operating in the chromosphere. The importance and magnitude of the individual proposed heating processes still remains unsettled even in the case of the Sun.
The chromosphere is the origin of a plethora of emission lines used to study its structure and physical conditions. Solar images show the chromosphere to be highly inhomogeneous and constantly evolving (e.g. Kuridze et al. 2015). In the stellar context, there is the concept of the so-called basal chromospheric emission, since all stars show some small extent of chromospheric activity which is referred to as basal chromospheric activity (Schrijver 1987; Schrijver et al. 1989; Mittag et al. 2013).
It is clear that a proper representation of such a chromosphere requires a dynamical three-dimensional approach. For example, Uitenbroek & Criscuoli (2011) give a thorough discussion about the limitations of one-dimensional modeling even of stellar photospheres. These authors concluded that the neglect of convective motions, nonlinearities of temperatures, and densities in computing the molecular equilibrium and level populations as well as the nonlinearities of the Planck function depending on the temperaturemay cause inaccurate interpretations of the calculated spectra. On the other hand, currently existing computer codes combining magnetohydrodynamic models with realistic radiative transfer for the chromosphere (and also for the photosphere) still remain computationally too costly to handle larger grids and cannot sensibly be juxtaposed to observations (De Gennaro Aquino 2016). Therefore, irrespective of its shortcomings, we consider the inferred chromospheric parameters from one-dimensional modeling useful, in particular, in a comparison among a sample of stars.
Fundamental insights into the chromospheric structure can, however, already be obtained based on static one-dimensional models with a parametrized temperature stratification. In the case of stars we are presumably looking simultaneously at the integrated emission of many, spatially unresolved “mini- chromospheres”, which may be described by a mean one-dimensional model; at least, such models can reproduce obser- ved stellar spectra well for M dwarfs (Fuhrmeister et al. 2005). On the other hand, the VAL C model by Vernazza et al. (1981) is often considered the classical model for the temperature structure in the photosphere, the chromosphere, and the transition region of the average quiet Sun. Up to now there are two approaches to model the chromospheres in late-type stars, viz., scaling the VAL C model (Mauas & Falchi 1994; Fontenla et al. 2016) or parameterizing the chromosphere (Short & Doyle 1997). Analyzing chromosphere models for a large stellar sample of homogeneous effective temperatures gives the opportunity to detect whether and how the chromospheres are distinguished.
In this study we use the state-of-the-art atmosphere code PHOENIX1 (Hauschildt 1992, 1993; Hauschildt & Baron 1999) to compute chromospheric model atmospheres based on a parametrized temperaturestratification and obtain the resulting spectra. These spectra are then compared to observed high-resolution spectra obtained with the CARMENES (Calar Alto high-Resolution search for M dwarfs with Exo-earths with Near-infrared and optical Echelle Spectrographs) spectrograph. Section 2 describes these observations and Sect. 3 highlights the model construction. We compare the computed model spectra to a stellar sample of M2.0, M2.5, and M3.0 dwarfs observed by CARMENES and search for the best-fit models to each star of the stellar sample in Sect. 4. Moreover, we also fit linear model combinations to the spectra to improve the modeling of the active stars where single models do not yield adequate fits. By calculating model combinations we obtain filling factors illustrating the coverage of inactive and active regions on the surfaces of the stars. In Sect. 5 we present our results and conclusions.
2 Observations
2.1 CARMENES
The CARMENES spectrograph (Calar Alto high-Resolution search for M dwarfs with Exo-earths with Near-infrared and optical Echelle Spectrographs; Quirrenbach et al. 2018) is a highly stabilized spectrograph attached to the 3.5 m telescope at the Calar Alto Observatory. The visual channel (VIS) operates in the wavelength range from 5200 to 9600 Å, and the infrared channel (NIR) covers the range between 9600 and 17 100 Å. The spectral resolution of the VIS channel is about R = 94 600 and that of the NIR channel is R = 80 400.
Since the start of the observations at the beginning of 2016, CARMENES regularly observes a sample of ~300 dM0 to dM9 stars in the context of its CARMENES survey (Alonso-Floriano et al. 2015; Reiners et al. 2018). The main goal of the survey is to find Earth-like planets in the habitable zone of M dwarfs by measuring periodic signals in the radial velocities of the stars with a precision on the order of 1 m s−1 and long-term stability (Reiners et al. 2018; Ribas et al. 2018). The CARMENES survey sample is only magnitude limited in each spectral type. Notably, no activity selection was applied.
The CARMENES spectra cover a wide range of chromospheric activity indicators except for the classical Ca II H and K lines. However, the Ca II infrared triplet (IRT) lines can be observed, which were recently shown to bea good substitute of the blue Ca II H and K lines (Martínez-Arnáiz et al. 2011; Martin et al. 2017). Additional chromospherically active lines covered by the CARMENES spectrograph are Hα, the Na I D lines, and the He I D3 line. The shape of the different lines is well resolved, including possible self-reversal in Hα (in case of emission lines) or the emission cores of Na I D. Traditionally, M dwarfs have been designated with spectral class identifiers dM, dM(e), and dMe depending on whether Hα is in absorption, not detectable, or in emission in low-resolution spectra. We mainly use the indices of the Ca II IRT lines as activity indicators, since they simply fill in and go into emission without showing a complicated line profile like Hα. Nevertheless, we refer to the traditional designations in Table 1 and examples of each class can be found in Fig. 4.
Basic information about the considered stars.
2.2 Stellar sample
This study focuses on simulations and observations of the chromospheric properties of dM-type stars with an effective temperature of about 3500 K, a surface gravity of logg = 5.0, and solar metallicity [Fe∕H] = 0.0 dex. These stars lie between the earliest M and the mid-M dwarfs. While the stellar parameters can be fixed in the modeling, we have to allow some margin in the selection of targets from the CARMENES sample. For this study, we selected all targets with stellar parameters fulfilling Teff = 3500 ± 50 K, log g = 5.0 ± 0.2 dex, and [Fe ∕H] = 0.0 ± 0.3 dex as measured by Passegger et al. (2018) using PHOENIX photospheric models and also given in the CARMENES input catalog Carmencita (Caballero et al. 2016a). Carmencita gathers information about the stars observed by CARMENES from different sources, including the effective temperature, gravity, and metallicity. We choose this range of effective temperature because it comprises a large number of M dwarfs, some of which show Hα in emission. Below this effective temperature range the number of observed dM-type stars quickly decreases. The stellar sample investigated in this work comprises 50 M dwarfs with spectral types between dM1.5 and dM3.5. According to Pecaut & Mamajek (2013)2, dM2 and dM3 stars typically have effective temperatures at 3550 and 3400 K. Table 1 gathers basic data about our stellar sample including Carmencita identifiers, names, spectral types, effective temperatures, surface gravities, and metallicities.
2.3 Data reduction
The spectra for our sample stars provided in the CARMENES archive are reduced by the CARMENES data reduction pipeline (Caballero et al. 2016b; Zechmeister et al. 2018); note that all wavelengths refer to vacuum. Typical exposure times of the spectra were 800, 900, 1200, and 1800 s, but there are also several spectra with integration times lower than 500 s. Since we want to compare line shapes to the model predictions we require a minimum of 300 s of integration time in order to exclude very noisy spectra.
To investigate the spectra, we corrected them for the barycentric velocity shift and also systematic radial velocity shifts of the individual stars. We did not apply a telluric correction since the chromospheric lines used in our study are usually only weakly affected (Hα and He I D3). However, spectra containing airglow signals in the cores of the Na I D lines are neglected in the modeling. Therefore, we inspected by eye the spectra exhibiting possible airglow contamination in the Na I D line cores (in the wavelength range of λNaD ± 0.4 Å) and excluded those affected; we only used spectra observed up until 21 December 2017. The number of available and used spectra of our sample stars are listed in Table 1; most of the excluded spectra contain airglow signals.
2.4 Activity characterization of the sample stars
The stars in the sample feature very different levels of stellar activity as can be easily seen qualitatively in the Hα line, which is an absorption line for most of our sample stars, but goes into emission for four stars. The state of activity can be characterized quantitatively by the line index of chromospheric emission lines. Following the method of Fuhrmeister et al. (2018) and Robertson et al. (2016), the line index Iline is defined by
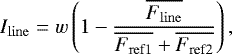 (1)
(1)
where w is the bandwidth of the spectral line, and 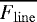 ,
, 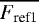 , and
, and 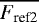 indicate the mean flux densities of the spectral line and reference bands. The line index corresponds to the pseudo-equivalent width.
indicate the mean flux densities of the spectral line and reference bands. The line index corresponds to the pseudo-equivalent width.
In this paper, we investigated the Na I D, Hα, and Ca II IRT lines. These lines represent the most widely used chromospheric indicators in our wavelength range. Another known chromospheric line covered by our wavelength range is the He I D3 line, which is seen in none of the spectra of our more inactive stars. Of the Na I D doublet and the Ca II IRT triplet lines, we only considered the bluest components because the remaining lines are influenced in the same manner by the chromospheric structure. For the Ca II IRT line we chose w = 0.5 Å to be the width of the line band centered at the (vacuum) wavelength of the line at 8500.35 Å. The reference band located at the blue side of the Ca line is centered at 8481.33 Å with a half-width of 5 Å, and the central wavelength of the red band is 8553.35 Å with a half-width of 1 Å to avoid telluric contamination for most radial and barycentric velocities. The center of the Hα line band is located at a wavelength of 6564.62 Å and we chose the width of the line band to be 1.6 Å. The reference bands are located at 6552.68 ± 5.25 and 6582.13 ± 4.25 Å. For the Na I D2 line at 5891.58 ± 0.2 Å the reference bands are 5872.3 ± 2.3 and 5912.0 ± 2.0 Å.
Figure 1 shows an overview of the activity levels and the spread in effective temperature of the stellar sample. Most of the stars are considered inactive indicated by the high Ca II IRT index above 0.6 Å, which should represent the average activity level of the star. The more active stars in our sample are GJ 360 and G 234-057 exhibiting line indices between 0.6 and 0.55 Å (further on also called semi-active), and even more active are LP 733-099 and TYC 3529-1437-1 with indices below 0.55 Å. There is a photospheric trend to higher indices for higher effective temperatures marked as the linear fit in Fig. 1. This trend can also be found for the photospheric models by Husser et al. (2013) varying the effective temperatures between 3400 and 3600 K ( log g = 5.0 dex, [Fe ∕H] = 0.0 dex and [α∕Fe] = 0.0 dex). We used the index of the Ca II IRT line to specify the different activity levels of the investigated stars, although in many studies, such as in Fuhrmeister et al. (2018), the line index of Hα is used to determine the activity state. While the Hα line is a strong line very sensitive to activity changes, the drawback in using the Hα line is its evolution with increasing stellar activity: this line first goes into absorption, then fills up the line core and eventually goes into emission (see, e. g. Cram & Mullan 1979). Thus more active stars can exhibit the same Hα line index as lessactive stars. The Ca II IRT line only fills in and goes into emission while the activity level increases, making its index easier to interpret in terms of the activity state.
In Fig. 2 we compare the average line indices of the Ca II IRT line and the Hα line that are given in Table 1. The plot exhibits a good correlation between the two indices with a Pearson correlation coefficient of 0.97, while the indices of the more inactive stars form an uncorrelated cloud. At the highest Ca II IRT line indices there are two stars, Ross 730 and HD 349726, exhibiting lower Hα indices; we interpret these to be the most inactive stars of the sample being located in the branch where increasing activity means increasing Hα line depth. As error bars we plot the standard deviation of the line indices derived from individual spectra of the respective stars. The scatter in the Hα line index is obviously larger than that in the Ca II IRT line. So the Hα line appearsto be more sensitive for activity variations in the whole observation period. This supports the choice for the Ca II IRT line index as a robust estimate of the mean activity level of a given star. For further insight into the variability of individual stars we show the time series of the three considered lines for TYC 3529-1437-1 in Fig. 3 as one of the stars with the largest amount of variations. Figure 3 demonstrates the typical temporal sampling of the spectral time series, which has been optimized for planet searches. The average sampling cadence is around 14 days. Also times of different levels of activity can be identified: the star was more active at the end of the time series. Since we do not want to average the variations of the lines or whole periods of enhanced activity, we do not co-add the observations. Co-adding would certainly boost the signal-to-noise ratio (S/N), but most stars also have S/Ns above 50 in single spectra, which is sufficient for our analysis. Therefore, we examine the spectrum with the median line index ICa IRT as a representation of the median activity level of the star. For the inactive stars the level of variation is much lower and an averaging would be possible in the sense of not mixing different activity states, but for consistency we treat these like the four active stars.
In Fig. 4 we show individual example spectra of one inactive (GJ 671) and two active stars (GJ 360, TYC 3529-1437-1). The inactive star exhibits absorption lines in Na I D2, Hα, and the bluest Ca II IRT line. For GJ 360 the spectral lines are in the transition from absorption to emission, while the lines in the spectrum of TYC 3529-1437-1 are clearly in emission. Thus we cover the bandwidth of rather inactive, semi-active, and very active M dwarfs in our sample.
 |
Fig. 1 Average Iline in the Ca II IRT line at 8500.35 Å against the Teff of the investigated stars. The error bars correspond to the standard deviations of the line indices of individual spectra of the respective stars. The red line is a linear fit for the inactive stars exceeding ICa IRT = 0.6 Å. The four active stars are highlighted by their names. |
 |
Fig. 2 Upper panel: average Iline in the Ca II IRT line at 8500.35 Å against the average Iline in the Hα line of the investigated stars. The error bars correspond to the standard deviations of the line indices of individual spectra of the respective stars. Lower panel: zoom of the range of the inactive stars without error bars (blue box in the upper panel). The black pluses indicate the stars best fit by model #079, red hexagons indicate best fit by model #080, blue circles by #042, green diamonds by #047, and magenta squares by #029 (see Sect. 4.2). The model numbers and properties are given in Table C.1. To improve clarity, the errors are faded out in the lower panel. |
 |
Fig. 3 Time series of the indices Iline of the Na I D2 (blue crosses), Hα (red pluses),and Ca II IRT line (green diamonds) of TYC 3529-1437-1. |
 |
Fig. 4 Example spectra of one inactive (GJ 671, blue line), one semi-active (GJ 360, red line), and one veryactive star (TYC 3529-1437-1, yellow line) in the stellar sample in the range between Na I D2, Hα, and the bluest Ca II IRT line. The peak right to the sodium line of TYC 3529-1437-1 is an airglow line. |
3 Model construction
The state-of-the-art PHOENIX code models atmospheres and spectra of a wide variety of objects such as novae, supernovae, planets, and stars (Hauschildt 1992, 1993; Hauschildt & Baron 1999). A number of PHOENIX model libraries covering M dwarfs have been published. For instance, Allard & Hauschildt (1995) used local thermodynamic equilibrium (LTE) calculations for dwarfs with effective temperatures of 1500 K ≤ Teff ≤ 4000 K and Hauschildt et al. (1999) computed an even wider model grid in the temperature range between 3000 and 10 000 K. A recent library of PHOENIX model atmospheres was presented by Husser et al. (2013).
3.1 Selection of a photospheric model
All of the above-mentioned libraries are exclusively concerned with the photospheres. The first model calculations that investigated the chromospheres using PHOENIX were carried out by Short & Doyle (1997) and Fuhrmeister et al. (2005). These models extend the atmospheric range up to the transition region, but are still rooted in the atmospheric structure of the photosphere, which therefore, provides the basis for our calculations.
In this paper, we adopt a photospheric model from the Husser et al. (2013) library as the underlying photosphere. This model was calculated under the assumptions of spherical symmetry and LTE using 64 atmospheric layers. The particular model atmosphere we adopted was computed for the parameters Teff= 3500 K, log g = 5.0 dex, [Fe ∕H] = 0.0 dex, and [α∕Fe] = 0.0 dex; in Fig. 5 (blue line) we show the temperature as a function of column mass for this model photosphere. Obviously, the temperature decreases continuously outward.
 |
Fig. 5 Photosphere model (blue solid line) at Teff = 3500 K,
log g =5.0 dex,
|
3.2 Chromospheric models
We now extend the photospheric model following the approach of Short & Doyle (1997) and Fuhrmeister et al. (2005). In particular, we add three sections of rising temperature to the model photosphere, which represent the lower and upper chromosphere and the transition region. To technically facilitate the extension, we increase the number of atmospheric layers in the model from originally 64 to 100 layers.
Our model chromosphere is described by a total of six free parameters. The column mass density at the onset of the lower chromosphere, mmin, defines the location of the temperature minimum. The column mass densities and temperatures of the end points of the lower ( log mmid, Tmid) and the upper chromosphere ( logmmax, Tmax), and the temperature gradient in the transition region, gradTR, given by
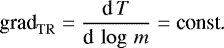 (2)
(2)
as introduced by Fuhrmeister et al. (2005). The maximum temperature of the transition region is fixed at TTR = 98 000 K. The temperature rise segments in the lower, upper chromosphere, and transition region are taken to be linear in the logarithm of the column mass density in our model. This is a rough approximation to the structure of the VAL C model. The meaning of the individual parameters is also illustrated in Fig. 5, where we show the temperature structure of the original photospheric model along with a modified structure including the photosphere, chromosphere, and transition region.
We used this modified temperature structure as a new starting point for the PHOENIX calculations. To account for the conditions in the chromosphere, the atomic species of H I, He I−II, C I−II, N I−V, O I−V, Na I−II, Mg I−II, K I−II, and Ca I−III are computed in non-LTE (NLTE) for all available levels taken from the database of Kurucz & Bell (1995)3 . This appliesto all species but He, for which we consulted CHIANTI v4 (Landi et al. 2006). The PHOENIX code iteratively adapts the electron pressure and mean molecular weight to reconcile these with the NLTE H I/HII ionization equilibrium. To that end, it is necessary that the population of all the states of the NLTE species are reiterated with the photoexciting and photoionizing radiation field, which is particularly important in the thin chromospheric and transition region layers. Moreover, the electron collisions have to be taken into account. A detailed comparison between LTE and NLTE atmospheric models is described by, for example, Short & Hauschildt (2003). Our calculations rely on the assumption of complete redistribution, as PHOENIX does not yet support partial redistribution, which would provide a more appropriate treatment in large parts of the chromosphere. However, its expected impact is largest for the Lyα line and resonance lines such as the Ca II H and K lines, which we also do not use in our study; the Na I D lines are much less affected (Mauas 2000).
3.3 Hidden parameters
Besides the six parameters describing the temperature structure introduced in Sect. 3.2, there are further aspects of the model that can be modified and influence the solution, most importantly, the microturbulence and the chosen set of NLTE lines.
While in our models the photospheric microturbulent velocity is set to 2 km s−1, in the chromosphere and the transition region the velocity is set to half the speed of sound in each layer, but is not allowed to exceed 20 km s−1 which may otherwise happen in the transition region. This follows the ansatz by Fuhrmeister et al. (2005). We do not smooth the microturbulent velocity transition between photosphere and chromosphere but the conditions in the model lead to quasi-smooth transitions with increases between two layers not exceeding 3 km s−1. Varying the microturbulent velocity leads to changes in the intensity as well as in the shape of the spectral lines (Jevremović et al. 2000). The considered NLTE set is practically restricted by the computational effort. While a more comprehensive NLTE set including, for example, higher O and Fe species would certainly be desirable to improve the synthetic spectra, we consider the here-adopted NLTE set sufficient to model the chromosphere in the context of the investigated lines.
3.4 The model set
Our chromospheric model is described by six free parameters, and as a result of the rather large NLTE sets, each model calculation requires several dozens of CPU hours. While it may seem most straightforward to obtain a model grid homogeneously covering typical ranges for all free parameters, already a very moderate sampling of ten grid points per free parameter results in a grid with 106 elements, which results in too high a computational demand. It is also clear that the large majority of the grid points are expected to result in spectra nowhere near the observations, which would be of little use in the subsequent analysis.
The challenge was therefore to identify reasonable parameter ranges and to explore these with a number of models. To that end, we firstcalculated limiting cases, such as models simultaneously showing all spectral lines in absorption or emission, in other words inactive or active chromosphere models. By visual comparison with the observed spectra, we subsequently identified the most promising parameter ranges to be explored further.
A particularly interesting comparison is between models with a steep temperature rise in the lower chromosphere and a plateau in the upper chromosphere, and models with a shallow temperature increase in the lower chromosphere and a steeper increase in the upper chromosphere. The first type of model is similar in structure to the VAL models used for the Sun.
The final set of models used in this study comprises 166 models with different model parameter configurations. The parameters are varied in the ranges listed in Table 2, and the properties of the individual models are given in Table C.1. The activity levels of the models are given by the line index ICa IRT but, as shown in Sects. 3.6 and 3.7, Hα can behave differently compared to the Ca II IRT. Figure 6 shows an excerpt of the model set. The models in the upper panel have steep gradients in the lower chromosphere and shallow gradients in the upper chromosphere, and it turns out these models represent more inactive states. The models in the lower panel have the shallow gradients in the lower and the steep gradients in the upper chromosphere and are rather characteristic of active chromospheres.
Parameter ranges for the chromosphere models.
 |
Fig. 6 Upper panel: temperature structure of the best single-component fits for the inactive stars as listed in Table A.1. Model #029 is shown by the red solid line, #042 by the blue dashed line, #047 by the yellow dash-dotted line, #079 by the green crossed line, and #080 by the magenta dotted line. Lower panel: same as in the upper panel for the active stars. Model #131 is plotted by the red solid line and #136 by the blue dashed line. The black solid diamond line shows the VAL C model for the Sun (Vernazza et al. 1981). |
3.5 Synthetic high-resolution spectra
To compare our models to stellar spectra, we need densely sampled synthetic spectra. We calculated the synthetic spectra in the spectral ranges of 3900–4000, 4830–4890, 5700–7000, and 8000–8800 Å with a sampling of Δλ = 0.005 Å per spectral bin. These ranges comprise the chromospheric lines covered by CARMENES as discussed in Sect. 2.4 and additionally the Ca II H and K, Hϵ, and Hβ lines to enable a comparison to spectra obtained by other instruments such as the High Accuracy Radial velocity Planet Searcher (HARPS; Mayor et al. 2003) in the context of further investigations. For the comparison to the CARMENES spectra, we lowered the model spectral resolution to that of CARMENES by folding with a Gaussian kernel of the approximated width. The stellar rotational velocities are neglected because none of the sample stars is a fast rotator with v sin i never exceeding 4 km s−1 (Reiners et al. 2017; Jeffers et al. 2018). Even for the most active stars in our sample, relatively long rotation periods are not in contradiction with their activity. Newton et al. (2017) found the threshold between active and inactive stars (Hα in emission or absorption) for early M dwarfs to be at a rotation period of about 30 days. For two of our active dwarfs we have rotation period measurements by Díez Alonso et al. (2019): GJ 360 has a period of 21 days and TYC 3529-1437-1 has a period of 15.8 days. These periods are consistent with the corresponding v sini values and there is no need to assume that they are seen pole-on.
3.6 Sequences modeling the evolution of the chromospheric lines
The interaction of the parameters determines whether the chromospheric lines are in absorption or emission and determines the strengths and shapes of the lines. In order to obtain an impression of how variations of a single parameter affect the line properties, we show in Fig. 7 the lines of Na I D2, Hα, and the blue Ca II IRT line of different models only varying in the parameter mtop from − 4.0 to − 3.5 dex (left-hand side) and in mmid from − 2.7 to − 2.0 dex (right-hand side). Changing a parameter of the upper chromosphere leads to stronger effects for Hα compared to Na I D and Ca II IRT, although the Ca II IRT is clearly more influenced than Na I D. The line indices illustrated in the lower panel confirm this impression with the gradients of the linear fits. However, the line core of Na I D2 is filled up while the peaks are increasing less. The Hα and Ca II IRT lines completely go from absorption to emission, and simultaneously the Hα self-absorption becomes even stronger.
While Hα is almost not influenced by the variation of mmid, the Ca II IRT emission peak is approximately four times higher above the continuum for mmid = −2.0 dex than for mmid = −2.7 dex. The variation of Na I D is also visible in the spectra, but not as strong as for the Ca II IRT line. The strong self-absorption of Na I D leads to a smaller variation of the line index than for the Ca II IRT. This sequence suggests a weak relationship of the Hα formation to the mid-chromosphere, while the other two lines clearly depend on the structure of the transition between lower and upper chromosphere.
Furthermore, we also found the location mmin of the temperature minimum of the chromosphere to be a decisive factor to determine whether lines appear in absorption or emission. More active lines are generated with a temperature minimum at higher density as found by Short & Doyle (1998) who calculated a model grid for the chromospheric lines of Hα and Na I D in five M dwarfs.
 |
Fig. 7 Top panels, left-hand side: sequence of model spectra varying only the parameter mtop from −4.0 to − 3.5 dex, the models are: #136 (black), #137 (blue), #138 (yellow), and #139 (red). Top panels, right-hand side: sequence for the parameter mmid varying from −2.7 to −2.0 dex, models: #121 (yellow), #126 (blue), #138 (red), and #153 (black). Bottom panels: corresponding values of Iline against mtop for Na I D (blue crosses), Hα (red pluses), and Ca II IRT (green diamonds) for the top panels. Additionally the linear fits are plotted: the Na I D fit is plotted by the blue dashed line, the Hα fit by the red dash-dotted line, and the Ca II IRT fit by the green dotted line. |
3.7 Flux contribution functions
Performing sequences indicates that modeling the chromospheric lines of Na I D2, Hα, and the bluest Ca II IRT line turns out to be a challenge mainly due to different formation heights of the line wings and cores in the chromosphere. Therefore, we investigated where the lines form in order to improve the understanding of the chromospheric structure and to make restrictions for the calculations of the chromospheres. The PHOENIX code is capable of computing flux contributionfunctions following the concept of Magain (1986) and Fuhrmeister et al. (2006). The intensity contribution function 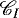 is defined by
is defined by
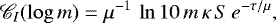 (3)
(3)
where m is the column mass density, κ the absorption coefficient, S the source function, τ the optical depth, and μ = cosθ, with θ as the angle between the considered direction and surface normal. The flux contribution function C is the intensity contribution function integrated over all μ and it gives information on where the flux density of every computed wavelength in the stellar atmosphere arises from. Figure 8 illustrates the flux contribution function of the line core (upper panel) and wing (mid-panel) of the bluest Ca II IRT line for model #080 (see Table C.1). Additionally, the source function Sν, Planck function Bν, and intensity Jν are given in the plots. The core is formed nearly at the center of the upper chromosphere at T = 6200 K. In the lower panel the temperature structure of the model is shown to visualize at which temperatures the lines are formed and the formation regions of Na I D2, Hα and the Ca II IRT line are given. The formation region is defined as the full width at half maximum around the maximum of the contribution function above the photosphere. The Na I D2 core is formed in the transition between the lower and upper chromosphere at T = 5800 K, while the Hα core is formed at the top of the chromosphere at T = 13700 K. This is in agreement with the results from the best-fit model by Fuhrmeister et al. (2005) for AD Leo in Na I D and Hα.
 |
Fig. 8 Upper and middle panels: scaled flux contribution function Cν (solid blue), source function Sν (dash-dotted red), Planck function Bν (dashed green), and intensity Jν (dotted cyan) for λ = 8500.36 Å representing the line core (upper panel) and λ = 8500.54 Å in the line wing (mid-panel) of the Ca II IRT line in model #080. The peak at high column mass in the contribution function of the line wing shows that the photospheric flux already dominates at this wavelength but there is still some chromospheric contribution. Lower panel: temperature structure of model #080 and the formation regions of Na I D2, Hα, and the bluest Ca II IRT line. |
4 Results and discussion
4.1 Comparing synthetic and observed spectra
To compare our synthetic spectra to observations we focus on the Na I D2, Hα, and the bluest Ca II IRT lines. Before carrying out the comparison, the flux densities of the observed and synthetic spectra were normalized to the mean value in the blue reference bands of the respective chromospheric line (see Sect. 2.4). For stars with several available spectra, we used the spectrum with the median value of the ICa IRT line index for comparison.
Our comparison is based on a least-squares-like minimization. In particular, we consider the difference between the observed and synthetic spectra simultaneously in the wavelength ranges λNaD ± 0.2 , λH α ± 0.8 and λCaIRT ± 0.25 . These line bands cover the chromospheric cores of the respective spectral lines. In Fig. 9 we show the best-fit models to the individual lines of TYC 3529-1437-1 irrespective of the other two lines. In the case of the Ca II IRT line, the best-fit model (yellow line) produces an almost perfect match to the observed line core, however, a comparison of this model to the shape of Na I D and Hα shows clear mismatches with regard to the data. While the predicted Hα line shows too strong an emission, the core of the associated Na I D line profile is strongly absorbed, which is clearly at odds with the observation. However, it is possible to obtain good fits for each of the three lines individually using appropriate models.
For physical reasons, the line band used for the Hα line is nearly three times as wide as that of the Ca II IRT line and four times wider than that of the Na I D2 line. Moreover, the observed (and modeled) amplitude of variation in these line profiles is by far largest for the Hα line. Both factors boost the weight of the Hα line profile in the minimization based on the summed χ2 values obtained in the three line bands as the objective. This reflects a relative overabundance of data in the Hα line and makes it the dominant component in such a fit. However, we intend to find the model that provides the most appropriate representation of all three considered chromospheric lines simultaneously.
Therefore, we constructed a dedicated statistic,  , which we use as the objective function in our minimization. Specifically, we define
, which we use as the objective function in our minimization. Specifically, we define
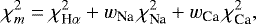 (4)
(4)
where 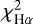 ,
, 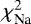 , and
, and 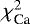 denote the sum of squared differences between model and observation obtained in the individual line bands. The weighting factors wNa and wCa were adapted to give approximately the same weight to all three lines in the minimization. To counterbalance the different widths of the line bands we increase the weighting of the Na I D2 and Ca II IRT line bands by a factor of 3. To account for the different flux density scales of variation in the Na I D2 and Ca II IRT lines, an additional factor of 4 is added to further increase their weight. The factor of 4 was estimated based on the observed amplitude of variation of the Hα line compared to the variation of the Na I D2 and Ca II IRT lines. We therefore end up with weighting factors of wNa = wCa = 12. The resulting
denote the sum of squared differences between model and observation obtained in the individual line bands. The weighting factors wNa and wCa were adapted to give approximately the same weight to all three lines in the minimization. To counterbalance the different widths of the line bands we increase the weighting of the Na I D2 and Ca II IRT line bands by a factor of 3. To account for the different flux density scales of variation in the Na I D2 and Ca II IRT lines, an additional factor of 4 is added to further increase their weight. The factor of 4 was estimated based on the observed amplitude of variation of the Hα line compared to the variation of the Na I D2 and Ca II IRT lines. We therefore end up with weighting factors of wNa = wCa = 12. The resulting 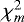 statistic establishes a relative order among the model fits, but cannot be used as a goodness-of-fit criterion.
statistic establishes a relative order among the model fits, but cannot be used as a goodness-of-fit criterion.
 |
Fig. 9 Comparison of the observed median activity spectrum of TYC 3529-1437-1 (black) as given by ICa IRT to the model spectrum fitting best in a single line. Best-fit models using only Na I D2 are denoted in red (model #078), using only Hα in blue (model #073), and Ca II IRT in yellow (model #157). |
4.2 Single-component fits
In a first attempt, we directly compare our set of synthetic spectra with the observations using the modified  criterion defined above. Since we normalize both the model and observation using the same reference band, no free parameters in this comparison remain; however, we compare every observed spectrum to all spectra from our set of models. Table A.1lists the results of the single model fits for the whole stellar sample, i. e., the models with the lowest modified
criterion defined above. Since we normalize both the model and observation using the same reference band, no free parameters in this comparison remain; however, we compare every observed spectrum to all spectra from our set of models. Table A.1lists the results of the single model fits for the whole stellar sample, i. e., the models with the lowest modified 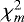 value. An inspection of Table A.1 shows that this approach yields reasonable fits with
value. An inspection of Table A.1 shows that this approach yields reasonable fits with  values between 1.8 and 4.04 for most stars, while four stars, the outliers in Fig. 1, show only poor fits with
values between 1.8 and 4.04 for most stars, while four stars, the outliers in Fig. 1, show only poor fits with 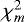 values in excess of 10.
values in excess of 10.
4.2.1 Inactive stars
For the inactive stars in our sample interestingly a small subset of five models provides the best fits, viz., the models #029 (2 cases), #042 (13 cases), #047 (12 cases), #079 (9 cases), and #080 (10 cases). In the lower panel of Fig. 2, the distribution of inactive stars is shown in the plane spanned by the Hα and Ca IRT activity indices. The color coding identifies the best-fitting models from Table A.1. While for most of the stars with ICa IRT < 0.625 model #080is the best from our set, the spectra of the majority of stars exceeding this value are best represented by model #042. The two stars Ross 730 and HD 349726, which we consider the most inactive in our sample (see Sect. 2.4), are best represented by model #029. The modified 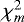 values range between 1.8 and 4.5 for the inactive stars.
values range between 1.8 and 4.5 for the inactive stars.
As an example, we juxtapose the best-fitting models and observed spectra of the two inactive stars GJ 671 and EW Dra in Fig. 10. In these models as well as in the observations all the considered lines appear in absorption. We note that the observation of the sodium line of GJ 671 shows some telluric emission, however, sufficiently offset from the line core. From our point of view, the #042 provides a reasonable fit to all considered lines in the case of GJ 671. Despite some shortcomings, such as a too deep Ca IRT line in the model and a somewhat too narrow sodium trough, all aspects of the data are appropriately reproduced by the model spectrum.
For the case of EW Dra, the overall situation is less comfortable. The strongest deviation of model #080 from the observed spectrum of EW Dra is the width of the central part of the Na I D2 line. The model clearly produces a too wide line with a signature of a central fill-in and self-absorption clearly more pronounced than in the observation. We emphasize, however, that despite these differences, the observation shows a similar structure in the line core, yet of course less pronounced. The line shapes of the Hα and the Ca II IRT line are well represented by this model although in particular the observed Hα line is deeper than that predicted by the model.
Although there are shortcomings, we conclude that the spectra of inactive stars can be appropriately represented by our models. Notably, all best-fit models for inactive stars are characterized by a temperature structure with a steeper temperature rise in the lower chromosphere and a more shallow rise in the upper chromosphere. This is in fact not very different from the VAL C model (Vernazza et al. 1981) for the Sun, which also shows a steeper temperature rise in the lower chromosphere and a plateau in the upper chromosphere.
 |
Fig. 10 Comparison of the best-fit model spectrum (red) to the observed spectrum (black) with median activity as defined by ICa IRT. Upper panels: GJ 671 and model #042. Lower panels: EW Dra and model #080. |
4.2.2 Active stars
For the active stars in our sample we only need two models that provide the best fits, viz., the models #131 (2 cases) and #136 (2 cases). In Fig. 11 we show the observed spectra and best-fit models for the more active stars GJ 360 and TYC 3529-1437-1, and clearly, in both cases the modified 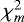 values are more than twice as high as for any inactive star in the sample. The observed Na I D line profiles show self-absorption in both stars, which is also predicted bythe model, but the width of the emission core is too broad for the models and the self-absorption is too strong. The observed Hα lines of both stars show clear self-absorption. This aspect is reproduced by the models, although for GJ 360 the model strongly overpredicts the self-absorption. The overall Hα line profile seems more appropriate for TYC 3529-1437-1, although the model yields a line that is too strong. The shape of the Ca II IRT line in the model is roughly reproduced in GJ 360; the model for TYC 3529-1437-1 shows considerable self-absorption, which is notobserved. In particular for the more active stars, it is hard to fit all three lines simultaneously by one model.
values are more than twice as high as for any inactive star in the sample. The observed Na I D line profiles show self-absorption in both stars, which is also predicted bythe model, but the width of the emission core is too broad for the models and the self-absorption is too strong. The observed Hα lines of both stars show clear self-absorption. This aspect is reproduced by the models, although for GJ 360 the model strongly overpredicts the self-absorption. The overall Hα line profile seems more appropriate for TYC 3529-1437-1, although the model yields a line that is too strong. The shape of the Ca II IRT line in the model is roughly reproduced in GJ 360; the model for TYC 3529-1437-1 shows considerable self-absorption, which is notobserved. In particular for the more active stars, it is hard to fit all three lines simultaneously by one model.
The column mass densities of the temperature minima mmin of the best-fit models of the active stars are obviously higher compared to the models of the inactive stars. Both models have a density of at least Δmmin = 0.5 dex higher than the found inactive models. In notable contrast to our results for the inactive stars, the best-fit models for the spectra of the more active stars tend to show a more shallow rise in the lower chromosphere and a steeper rise in the upper chromosphere. It is possible to increase the flux of the Hα and Na I D2 lines by only moving the chromosphere to increasing densities, but the shape of the chromosphere needs to be changed to reconcile a more active chromosphere with the Ca II IRT line. Although this result has to be viewed against the background of the shortcomings of the fit, we tentatively identify this reversal of gradients as a characteristic change in the chromospheric temperature structure associated with a change from an inactive to an active chromosphere.
 |
Fig. 11 Same as Fig. 10. Upper panels: GJ 360 and model #136. Lower panels: TYC 3529-1437-1 and model #131. |
4.3 Linear-combination fits
The solar chromospheric spectrum is well known for varying across the solar disk, in particular, when active regions and quiet regions are compared. To account for this fact, some studies using one-dimensional static models have combined models applying a filling factor. This method was first applied using models with a thermal bifurcation by Ayres (1981) to account for observations of molecular CO in the solar spectrum. However, it cannot be explained by chromospheric models alone, which have a temperature minimum well above a temperature allowing for CO. Such studies normally use linear combinations of a photospheric (or inactive chromospheric) and an active chromospheric model and have also been used for flare modeling (Fuhrmeister et al. 2010). Classically this treatment is also known as 1.5D modeling, since it tries to account for the inhomogeneity of the stellar atmospheres (Ayres et al. 2006). It relies on the assumption that the individual components are independent and influence each other neither radiatively nor collisionally via NLTE. This assumption would be satisfied if these regions were optically thick, which they are most probably not, but neither are they too optically thin. Therefore, we consider the assumption to be approximately satisfied.
We also adopt this approach in an attempt to improve especially the spectral fits of the more active dwarfs in our sample. In particular, we consider a linear combination of an inactive and an active spectral model, and determine a best-fit filling factor by again minimizing the modified 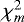 value. This analysis is done for the whole stellar sample from Table 1, and Table A.2 summarizes the results. The latter table contains the filling factors of the inactive and active component and the associated modified
value. This analysis is done for the whole stellar sample from Table 1, and Table A.2 summarizes the results. The latter table contains the filling factors of the inactive and active component and the associated modified  values. Although these values do not represent classical χ2 values, they can be compared with those of the single model fits (see Table A.1). As expected, the modified
values. Although these values do not represent classical χ2 values, they can be compared with those of the single model fits (see Table A.1). As expected, the modified 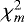 values improve for every star when a second component is added to the model. Table A.2 also lists the differences of the Ca II IRT line indices (ΔICa IRT) between the inactive and active model in the best combination fits giving an impression of the contrast in the respective combinations.
values improve for every star when a second component is added to the model. Table A.2 also lists the differences of the Ca II IRT line indices (ΔICa IRT) between the inactive and active model in the best combination fits giving an impression of the contrast in the respective combinations.
4.3.1 Inactive stars
In the spectral fits of the inactive sample stars, we start with the best-fit single-component model as the first component. We then add every model of our model set, determine a best-fit filling factor, and finally, choose the model combination providing the minimum modified 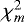 . The thus determined second model component mostly also exhibits the Na I D2, Hα and the Ca II IRT lines in absorption. Although the combination leads to better matching of the line shapes, the overall improvement obtained for the inactive stars remains moderate.
. The thus determined second model component mostly also exhibits the Na I D2, Hα and the Ca II IRT lines in absorption. Although the combination leads to better matching of the line shapes, the overall improvement obtained for the inactive stars remains moderate.
4.3.2 Active stars
The spectra of the active stars could not be reproduced well with our single-component fits. Therefore, we do not consider the best-fit single modelcomponent as a good starting point for the fit as for the inactive stars and, instead, apply the following procedure. As the inactive spectral model component, we subsequently tested the five models, which produced the best fits for the inactive stars in the single-component approach (see Sect. 4.2). These were then tentatively combined with all other models from our setand the filling factor determined. Again, we finally opted for that combination providing the minimum modified 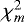 value.
value.
The best 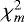 value is obtained by the combination with models with differences regarding the temperature structure in comparison to the found inactive models. The temperature gradient of the lower chromosphere is shallower and that of the upper chromosphere is steeper, which is thereverse case for the five best models of the inactive stars. While the active models of G 234-057 and GJ 360 have higher gradients in the upper than in the lower chromosphere, in the active model of LP 733-099 and TYC 3529-1437-1 the gradients of the lower and upper chromosphere are equal, meaning the chromosphere consists of only one linear section. Furthermore, in each of these active models the whole chromosphere is shifted inward about Δm= 0.5 dex compared to the inactive models. The width of the chromosphere nearly remains the same in every case, but the temperature at the top of the chromosphere increases at least by about 300 K. The interaction of the free parameters yields chromospheric emission lines in the corresponding synthetic spectra, i. e. varying only one parameter does not necessarily yield all the chromospheric lines in emission. In particular, the contribution function of PHOENIX can provide information about where the lines are formed, as discussed in Sect. 3.7.
value is obtained by the combination with models with differences regarding the temperature structure in comparison to the found inactive models. The temperature gradient of the lower chromosphere is shallower and that of the upper chromosphere is steeper, which is thereverse case for the five best models of the inactive stars. While the active models of G 234-057 and GJ 360 have higher gradients in the upper than in the lower chromosphere, in the active model of LP 733-099 and TYC 3529-1437-1 the gradients of the lower and upper chromosphere are equal, meaning the chromosphere consists of only one linear section. Furthermore, in each of these active models the whole chromosphere is shifted inward about Δm= 0.5 dex compared to the inactive models. The width of the chromosphere nearly remains the same in every case, but the temperature at the top of the chromosphere increases at least by about 300 K. The interaction of the free parameters yields chromospheric emission lines in the corresponding synthetic spectra, i. e. varying only one parameter does not necessarily yield all the chromospheric lines in emission. In particular, the contribution function of PHOENIX can provide information about where the lines are formed, as discussed in Sect. 3.7.
In these three active models all three investigated lines clearly appear in emission. In Fig. 12, we show the observed spectrum of TYC 3529-1437-1 with median activity as given by ICa IRT, the spectra of the inactive and active model, and the best linear-combination spectral fit of the two models to the observed spectrum. From the modified 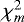 and in comparison to Fig. 11 it becomes obvious that the combination provides a better representation of the observation than the best-fit single model. In Fig. 12 we also show the linear-combination fit for the spectrum of GJ 360. Again the linear combination gives a better fit to the shape of the Na I D2 and Hα lines. However, reproducing the transition from absorption to emission in the Ca II IRT line also turns out to be hard with this method. While in the fit for TYC 3529-1437-1 the inactive model spectrum contributes 75%, the filling factors for the moderately more active LP 733-099 yields 68% for the inactive and 32% for the active component. The semi-active stars G 234-057 and GJ 360 exhibit filling factors of 90 and 82% for the inactive chromospheric model. We therefore conclude that the resulting filling factors of the active model component match the activity levels of the stars as determined from spectral indices.
and in comparison to Fig. 11 it becomes obvious that the combination provides a better representation of the observation than the best-fit single model. In Fig. 12 we also show the linear-combination fit for the spectrum of GJ 360. Again the linear combination gives a better fit to the shape of the Na I D2 and Hα lines. However, reproducing the transition from absorption to emission in the Ca II IRT line also turns out to be hard with this method. While in the fit for TYC 3529-1437-1 the inactive model spectrum contributes 75%, the filling factors for the moderately more active LP 733-099 yields 68% for the inactive and 32% for the active component. The semi-active stars G 234-057 and GJ 360 exhibit filling factors of 90 and 82% for the inactive chromospheric model. We therefore conclude that the resulting filling factors of the active model component match the activity levels of the stars as determined from spectral indices.
 |
Fig. 12 Comparison of the observed median activity spectrum to the best linear-combination fits for GJ 360 (upper panels, inactive model #080 and active model #132) and TYC 3529-1437-1 (lower panels, inactive model #079 and active model #149). The line of Na I D 2 and the bluest Ca II IRT line are weighted by a factor of 12, respectively, compared to Hα as describedin Sect. 4.1. |
4.4 Filling factor as a function of activity level
To study the relationship between the activity state and the filling factors in individual stars, we perform an analysis of a set of available CARMENES spectra, considering the restrictions described in Sect. 2.3, of a subsample of stars. This subsample consists of all active stars and those inactive stars from which we have used more than five spectra and that show variability in the flux density of the considered chromospheric lines. We determine filling factors based on fits to all used CARMENES spectra, following the same method as in Sect. 4.3, but fix the combination of models to the pair previously determined.
In Fig. 13 we show the filling factor of the inactive model component as listed in Table A.2 as a function of the ICa IRT. Our modeling yields a decrease in the filling factor of the inactive chromospheric component as the level of activity rises (i.e. ICa IRT decreases), but even for LP 733-099, the most active star in our sample, the filling factor of the inactive model component remains as high as ~65%. While this indicates that the major fraction of its surface is not covered with active chromosphere, we caution that our two-component approach remains a highly simplified description of the chromosphere. In the case of the inactive stars, the interpretation of the filling factor in Table A.2 is more complicated. In particular, combinations of two inactive chromospheric components possibly yield formally large filling factors for either component.
In the upper panel of Fig. 13 we show the relation between the Ca IRT index, ICa IRT, and the filling factor for the active stars LP 733-099, TYC 3529-1437-1, GJ 360, G 234-057. There is a clear relation between ICa IRT and the filling factor in all these stars, which can well be approximated by a linear trend (see Fig. 13). This trend can also be seen for most of the inactive stars considered in this study, some of these are plotted in the lower panel of Fig. 13. The filling factor of the inactive model decreases with increasing activity level.
Therefore linear regressions are performed to reveal the following linear trends:
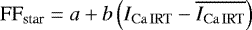 (5)
(5)
for the filling factor (FFstar) as a function of ICa IRT, where  is the mean ICa IRT of the respective star. The gradients are denoted by b and the intercepts by a, and the uncertainties on the coefficients (σb and σa) were estimated using the Jackknife method (Efron & Stein 1981). For example, the application of a linear regression for GJ 360 yields a = 0.83 ± 0.0015 and b = 5.59 ± 0.28 Å−1. Table B.1 lists the results of the linear regressions of our study. For nearly all of the subsample stars we obtain clear positive gradients. Ross 730 and Wolf 1014 show a slight negative trend that cannot be distinguished from noise as visible in the comparably high relative errors. The negative slope of Ross 730 is dominated by a single outlier data point. Therefore, GJ 793 is the only star for which we find a significant negative gradient. In this case model #080 is more active than model #112 according to ICa IRT, although it is the opposite for Hα. The variation of Hα in GJ 793 leads the linear-combination method to give model #112 a higher weight with increasing activity state of GJ 793. The particular model combination is the reason for the negative slope of GJ 793.
is the mean ICa IRT of the respective star. The gradients are denoted by b and the intercepts by a, and the uncertainties on the coefficients (σb and σa) were estimated using the Jackknife method (Efron & Stein 1981). For example, the application of a linear regression for GJ 360 yields a = 0.83 ± 0.0015 and b = 5.59 ± 0.28 Å−1. Table B.1 lists the results of the linear regressions of our study. For nearly all of the subsample stars we obtain clear positive gradients. Ross 730 and Wolf 1014 show a slight negative trend that cannot be distinguished from noise as visible in the comparably high relative errors. The negative slope of Ross 730 is dominated by a single outlier data point. Therefore, GJ 793 is the only star for which we find a significant negative gradient. In this case model #080 is more active than model #112 according to ICa IRT, although it is the opposite for Hα. The variation of Hα in GJ 793 leads the linear-combination method to give model #112 a higher weight with increasing activity state of GJ 793. The particular model combination is the reason for the negative slope of GJ 793.
Interestingly, the range of filling factors of the inactive part for the active stars shown in Fig. 13 is comparable irrespective of their activity level. However, with increasing ICa IRT the gradient of the relationship appears to increase except for G 234-057 from which we only used two spectra. Therefore, compared to an active star, the same change in filling factor in an inactive star produces only a comparably weak response in the Ca IRT line index, ICa IRT. In our modeling, this results from a stronger contrast between inactive and active chromospheric components in active stars, which is also indicated by the differences of the Ca II IRT line indices as given in Table A.2.
 |
Fig. 13 Upper panel: filling factors of the inactive models in the combination fits as a function of ICa IRT of the four active stars LP 733-099 (yellow dots), TYC 3529-1437-1 (blue crosses), GJ 360 (red pluses), and G 234-057 (magenta diamonds) are shown. Lower panel: same as in the upper panel for Ross 905 (blue crosses), EW Dra (red pluses), LP 743-031 (yellow dots), GJ 625 (magenta diamonds), BD+70 68 (black asterisks), Ross 730 (cyan triangles), and GJ 793 (green circles). The solid lines show the linear fits of the stars. To improve clarity, the errors of ICa IRT are not shown. |
5 Conclusions
We have calculated a set of one-dimensional parametrized chromosphere models for a stellar sample of M-type stars in the effective temperature range 3500 ± 50 K. The synthetic spectra of single models have turned out to be able to represent inactive stars in the lines of Na I D2, Hα, and a Ca II IRT line simultaneously, while a linear combination of at least two models is needed to simultaneously approach the chromospheric lines of active stars, suggesting that the enhanced activity originates only in parts of the stellar surface – as though the Sun is covered partially in active regions. The shape of the temperature structure of the models representing the inactive stars is comparable to the VAL C model for the Sun. A steep temperature gradient in the lower chromosphere is followed by a plateau-like structure in the upper chromosphere. Our best-fit inactive models resemble this general structure of the VAL C model, but the temperatures and column mass densities differ, of course.
Concerning the models representing the active regions of the four active stars in our sample, the temperature structure rather indicates a steeper temperature gradient in the upper chromosphere than a plateau-like structure. The deduced filling factors of inactive and active models correspond to the activity levels of the active stars under the constraint of the model combination. Furthermore, the variable stars revealed a linear relationship between the filling factors and the line index in the Ca II IRT line, i. e. the higher the activity state, the less the coverage of the inactive chromosphere. The gradients of the filling factors of the variable stars depend on the model combinations, hence the gradients are not evenly distributed, but they only vary in their absolute value. Moreover, the model combination analysis also indicates an increasing contrast between the inactive and active regions with increasing level of activity.
Acknowledgements
D.H. acknowledges funding by the DLR under DLR 50 OR1701. B.F. acknowledges funding by the DFG under Cz 222/1-1 and Schm 1032/69-1. S.C. acknowledges support through DFG projects SCH 1382/2-1 and SCHM 1032/66-1. CARMENES is an instrument for the Centro Astronómico Hispano-Alemán de Calar Alto (CAHA, Almería, Spain). CARMENES is funded by the German Max-Planck-Gesellschaft (MPG), the Spanish Consejo Superior de Investigaciones Científicas (CSIC), the European Union through FEDER/ERF FICTS-2011-02 funds, and the members of the CARMENES Consortium (Max-Planck-Institut für Astronomie, Instituto de Astrofísica de Andalucía, Landessternwarte Königstuhl, Institut de Ciències de l’Espai, Institut fürAstrophysik Göttingen, Universidad Complutense de Madrid, Thüringer Landessternwarte Tautenburg, Instituto de Astrofísica de Canarias, Hamburger Sternwarte, Centro de Astrobiología and Centro Astronómico Hispano-Alemán), with additional contributions by the Spanish Ministry of Science [through projects AYA2016-79425-C3-1/2/3-P, ESP2016-80435-C2-1-R, AYA2015-69350-C3-2-P, and AYA2018-84089], the German Science Foundation through the Major Research Instrumentation Programme and DFG Research Unit FOR2544 “Blue Planets around Red Stars”, the Klaus Tschira Stiftung, the states of Baden-Württemberg and Niedersachsen, and by the Junta de Andalucía. We thank J. M. Fontenla for providing us with the atmospheric structure of his chromospheric model for GJ 832 (Fontenla et al. 2016) for comparison purposes. CHIANTI is a collaborative project involving George Mason University, the University of Michigan (USA) and the University of Cambridge (UK).
Appendix A Best single-component fits and best linear-combination fits
Best single-component fits for the considered stars.
Best-fit models in a linear-combination fit with filling factors and the difference ΔICa IRT of the models.
Appendix B Linear regressions of the filling factors as a function of activity state
Appendix C Calculated model set
Calculated model set and parameters.
continued.
continued.
References
- Allard, F., & Hauschildt, P. H. 1995, ApJ, 445, 433 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Floriano, F. J., Morales, J. C., Caballero, J. A., et al. 2015, A&A, 577, A128 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ayres, T. R. 1981, ApJ, 244, 1064 [NASA ADS] [CrossRef] [Google Scholar]
- Ayres, T. R., Plymate, C., & Keller, C. U. 2006, ApJS, 165, 618 [NASA ADS] [CrossRef] [Google Scholar]
- Caballero, J. A., Cortés-Contreras, M., Alonso-Floriano, F. J., et al. 2016a, in 19th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun (CS19), 148 [Google Scholar]
- Caballero, J. A., Guàrdia, J., López del Fresno, M., et al. 2016b, in Observatory Operations: Strategies, Processes, and Systems VI, Proc. SPIE, 9910, 99100E [Google Scholar]
- Cram, L. E., & Mullan, D. J. 1979, ApJ, 234, 579 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Gennaro, I. 2016, Ph.D. Thesis, University of Hamburg, Hamburg, Germany [Google Scholar]
- Díez Alonso, E., Caballero, J. A., Montes, D., et al. 2019, A&A, 621, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Efron, B., & Stein, C. 1981, Ann. Stat., 9, 586 [CrossRef] [MathSciNet] [Google Scholar]
- Fontenla, J. M., Linsky, J. L., Witbrod, J., et al. 2016, ApJ, 830, 154 [NASA ADS] [CrossRef] [Google Scholar]
- France, K., Loyd, R. O. P., Youngblood, A., et al. 2016, ApJ, 820, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmeister, B., Schmitt, J. H. M. M., & Hauschildt, P. H. 2005, A&A, 439, 1137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmeister, B., Short, C. I., & Hauschildt, P. H. 2006, A&A, 452, 1083 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmeister, B., Schmitt, J. H. M. M., & Hauschildt, P. H. 2010, A&A, 511, A83 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmeister, B., Czesla, S., Schmitt, J. H. M. M., et al. 2018, A&A, 615, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauschildt, P. H. 1992, J. Quant. Spectr. Rad. Transf., 47, 433 [Google Scholar]
- Hauschildt, P. H. 1993, J. Quant. Spectr. Rad. Transf., 50, 301 [Google Scholar]
- Hauschildt, P. H., & Baron, E. 1999, J. Comput. Methods Appl. Math., 109, 41 [Google Scholar]
- Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jeffers, S. V., Schöfer, P., Lamert, A., et al. 2018, A&A, 614, A76 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jevremović, D., Doyle, J. G., & Short, C. I. 2000, A&A, 358, 575 [NASA ADS] [Google Scholar]
- Kuridze, D., Henriques, V., Mathioudakis, M., et al. 2015, ApJ, 802, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L., & Bell, B. 1995, Atomic Line List (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
- Landi, E., Del Zanna, G., Young, P. R., et al. 2006, ApJS, 162, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Lépine, S., Hilton, E. J., Mann, A. W., et al. 2013, AJ, 145, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Magain, P. 1986, A&A, 163, 135 [NASA ADS] [Google Scholar]
- Martin, J., Fuhrmeister, B., Mittag, M., et al. 2017, A&A, 605, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martínez-Arnáiz, R., López-Santiago, J., Crespo-Chacón, I., & Montes, D. 2011, MNRAS, 414, 2629 [NASA ADS] [CrossRef] [Google Scholar]
- Mauas, P. J. D. 2000, ApJ, 539, 858 [NASA ADS] [CrossRef] [Google Scholar]
- Mauas, P. J. D., & Falchi, A. 1994, A&A, 281, 129 [NASA ADS] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Mittag, M., Schmitt, J. H. M. M., & Schröder, K.-P. 2013, A&A, 549, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Newton, E. R., Irwin, J., Charbonneau, D., et al. 2017, ApJ, 834, 85 [NASA ADS] [CrossRef] [Google Scholar]
- O’Malley-James, J. T., & Kaltenegger, L. 2017, MNRAS, 469, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Passegger, V. M., Reiners, A., Jeffers, S. V., et al. 2018, A&A, 615, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pecaut, M. J.,& Mamajek, E. E. 2013, ApJS, 208, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Quirrenbach, A., Amado, P. J., Ribas, I., et al. 2018, SPIE Conf. Ser., 10702, 107020W [Google Scholar]
- Reid, I. N., Hawley, S. L., & Gizis, J. E. 1995, AJ, 110, 1838 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Ribas, I., Zechmeister, M., et al. 2017, VizieR Online Data Catalog: 360 [Google Scholar]
- Reiners, A., Zechmeister, M., Caballero, J. A., et al. 2018, A&A, 612, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riaz, B., Gizis, J. E., & Harvin, J. 2006, AJ, 132, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Ribas, I., Tuomi, M., Reiners, A., et al. 2018, Nature, 563, 365 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, P., Bender, C., Mahadevan, S., Roy, A., & Ramsey, L. W. 2016, ApJ, 832, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Scholz, R.-D., Meusinger, H., & Jahreiß, H. 2005, A&A, 442, 211 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schrijver, C. J. 1987, A&A, 172, 111 [NASA ADS] [Google Scholar]
- Schrijver, C. J., Dobson, A. K., & Radick, R. R. 1989, ApJ, 341, 1035 [NASA ADS] [CrossRef] [Google Scholar]
- Segura, A., Walkowicz, L. M., Meadows, V., Kasting, J., & Hawley, S. 2010, Astrobiology, 10, 751 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Short, C. I., & Doyle, J. G. 1997, A&A, 326, 287 [NASA ADS] [Google Scholar]
- Short, C. I., & Doyle, J. G. 1998, A&A, 336, 613 [NASA ADS] [Google Scholar]
- Short, C. I., & Hauschildt, P. H. 2003, ApJ, 596, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Uitenbroek, H., & Criscuoli, S. 2011, ApJ, 736, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Vernazza, J. E., Avrett, E. H., & Loeser, R. 1981, ApJS, 45, 635 [NASA ADS] [CrossRef] [Google Scholar]
- Wedemeyer, S., Freytag, B., Steffen, M., Ludwig, H.-G., & Holweger, H. 2004, A&A, 414, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zechmeister, M., Reiners, A., Amado, P. J., et al. 2018, A&A, 609, A12 [CrossRef] [Google Scholar]
The effective temperatures for the spectral subtypes are given in http://www.pas.rochester.edu/emamajek/EEM_dwarf_UBVIJHK_colors_Teff.txt
All Tables
Best-fit models in a linear-combination fit with filling factors and the difference ΔICa IRT of the models.
All Figures
 |
Fig. 1 Average Iline in the Ca II IRT line at 8500.35 Å against the Teff of the investigated stars. The error bars correspond to the standard deviations of the line indices of individual spectra of the respective stars. The red line is a linear fit for the inactive stars exceeding ICa IRT = 0.6 Å. The four active stars are highlighted by their names. |
| In the text | |
 |
Fig. 2 Upper panel: average Iline in the Ca II IRT line at 8500.35 Å against the average Iline in the Hα line of the investigated stars. The error bars correspond to the standard deviations of the line indices of individual spectra of the respective stars. Lower panel: zoom of the range of the inactive stars without error bars (blue box in the upper panel). The black pluses indicate the stars best fit by model #079, red hexagons indicate best fit by model #080, blue circles by #042, green diamonds by #047, and magenta squares by #029 (see Sect. 4.2). The model numbers and properties are given in Table C.1. To improve clarity, the errors are faded out in the lower panel. |
| In the text | |
 |
Fig. 3 Time series of the indices Iline of the Na I D2 (blue crosses), Hα (red pluses),and Ca II IRT line (green diamonds) of TYC 3529-1437-1. |
| In the text | |
 |
Fig. 4 Example spectra of one inactive (GJ 671, blue line), one semi-active (GJ 360, red line), and one veryactive star (TYC 3529-1437-1, yellow line) in the stellar sample in the range between Na I D2, Hα, and the bluest Ca II IRT line. The peak right to the sodium line of TYC 3529-1437-1 is an airglow line. |
| In the text | |
 |
Fig. 5 Photosphere model (blue solid line) at Teff = 3500 K,
log g =5.0 dex,
|
| In the text | |
 |
Fig. 6 Upper panel: temperature structure of the best single-component fits for the inactive stars as listed in Table A.1. Model #029 is shown by the red solid line, #042 by the blue dashed line, #047 by the yellow dash-dotted line, #079 by the green crossed line, and #080 by the magenta dotted line. Lower panel: same as in the upper panel for the active stars. Model #131 is plotted by the red solid line and #136 by the blue dashed line. The black solid diamond line shows the VAL C model for the Sun (Vernazza et al. 1981). |
| In the text | |
 |
Fig. 7 Top panels, left-hand side: sequence of model spectra varying only the parameter mtop from −4.0 to − 3.5 dex, the models are: #136 (black), #137 (blue), #138 (yellow), and #139 (red). Top panels, right-hand side: sequence for the parameter mmid varying from −2.7 to −2.0 dex, models: #121 (yellow), #126 (blue), #138 (red), and #153 (black). Bottom panels: corresponding values of Iline against mtop for Na I D (blue crosses), Hα (red pluses), and Ca II IRT (green diamonds) for the top panels. Additionally the linear fits are plotted: the Na I D fit is plotted by the blue dashed line, the Hα fit by the red dash-dotted line, and the Ca II IRT fit by the green dotted line. |
| In the text | |
 |
Fig. 8 Upper and middle panels: scaled flux contribution function Cν (solid blue), source function Sν (dash-dotted red), Planck function Bν (dashed green), and intensity Jν (dotted cyan) for λ = 8500.36 Å representing the line core (upper panel) and λ = 8500.54 Å in the line wing (mid-panel) of the Ca II IRT line in model #080. The peak at high column mass in the contribution function of the line wing shows that the photospheric flux already dominates at this wavelength but there is still some chromospheric contribution. Lower panel: temperature structure of model #080 and the formation regions of Na I D2, Hα, and the bluest Ca II IRT line. |
| In the text | |
 |
Fig. 9 Comparison of the observed median activity spectrum of TYC 3529-1437-1 (black) as given by ICa IRT to the model spectrum fitting best in a single line. Best-fit models using only Na I D2 are denoted in red (model #078), using only Hα in blue (model #073), and Ca II IRT in yellow (model #157). |
| In the text | |
 |
Fig. 10 Comparison of the best-fit model spectrum (red) to the observed spectrum (black) with median activity as defined by ICa IRT. Upper panels: GJ 671 and model #042. Lower panels: EW Dra and model #080. |
| In the text | |
 |
Fig. 11 Same as Fig. 10. Upper panels: GJ 360 and model #136. Lower panels: TYC 3529-1437-1 and model #131. |
| In the text | |
 |
Fig. 12 Comparison of the observed median activity spectrum to the best linear-combination fits for GJ 360 (upper panels, inactive model #080 and active model #132) and TYC 3529-1437-1 (lower panels, inactive model #079 and active model #149). The line of Na I D 2 and the bluest Ca II IRT line are weighted by a factor of 12, respectively, compared to Hα as describedin Sect. 4.1. |
| In the text | |
 |
Fig. 13 Upper panel: filling factors of the inactive models in the combination fits as a function of ICa IRT of the four active stars LP 733-099 (yellow dots), TYC 3529-1437-1 (blue crosses), GJ 360 (red pluses), and G 234-057 (magenta diamonds) are shown. Lower panel: same as in the upper panel for Ross 905 (blue crosses), EW Dra (red pluses), LP 743-031 (yellow dots), GJ 625 (magenta diamonds), BD+70 68 (black asterisks), Ross 730 (cyan triangles), and GJ 793 (green circles). The solid lines show the linear fits of the stars. To improve clarity, the errors of ICa IRT are not shown. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



![$\left[\mathrm{Fe}/\mathrm{H}\right] = 0\,\mathrm{dex,}$](/articles/aa/full_html/2019/03/aa34788-18/aa34788-18-eq29.png)
![$\left[\alpha/\mathrm{Fe}\right] = 0\,\mathrm{dex}$](/articles/aa/full_html/2019/03/aa34788-18/aa34788-18-eq30.png)