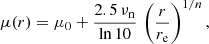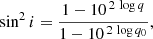| Issue |
A&A
Volume 622, February 2019
|
|
|---|---|---|
| Article Number | A132 | |
| Number of page(s) | 24 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201833932 | |
| Published online | 07 February 2019 | |
Dust emission profiles of DustPedia galaxies⋆,⋆⋆
1
Sterrenkundig Observatorium, Department of Physics and Astronomy, Universiteit Ghent, Krijgslaan 281 S9, 9000 Ghent, Belgium
e-mail: mosenkovAV@gmail.com
2
Central Astronomical Observatory of RAS, Pulkovskoye Chaussee 65/1, 196140 St. Petersburg, Russia
3
St. Petersburg State University, Universitetskij Pr. 28, 198504 St. Petersburg, Stary Peterhof, Russia
4
INAF-Osservatorio Astrofisico di Arcetri, Largo E. Fermi 5, 50125 Florence, Italy
5
INAF-Istituto di Radioastronomia, Via Piero Gobetti 101, 40129 Bologna, Italy
6
National Observatory of Athens, Institute for Astronomy, Astrophysics, Space Applications and Remote Sensing, Ioannou Metaxa and Vasileos Pavlou, 15236 Athens, Greece
7
School of Physics and Astronomy, Cardiff University, The Parade, Cardiff, CF24 3AA, UK
8
Department of Physics and Astronomy, University College London, Gower Street, London WC1E 6BT, UK
9
Institut d’Astrophysique Spatiale, CNRS, Univ. Paris-Sud, Université Paris-Saclay, Bât. 121, 91405 Orsay Cedex, France
10
Instituto de Radioastronomía y Astrofísica, UNAM, Campus Morelia, AP 3-72, CP 58089, Mexico
11
Laboratoire AIM, CEA/DSM – CNRS – Université Paris Diderot, IRFU/Service d’Astrophysique, CEA Saclay, 91191 Gif-sur-Yvette, France
12
Department of Astrophysics, Astronomy & Mechanics, Faculty of Physics, University of Athens, Panepistimiopolis, 15784 Zografos, Athens, Greece
13
Centre for Astrophysics Research, University of Hertfordshire, College Lane, Hatfield AL10 9AB, UK
Received:
23
July
2018
Accepted:
19
November
2018
Most radiative transfer models assume that dust in spiral galaxies is distributed exponentially. In this paper our goal is to verify this assumption by analysing the two-dimensional large-scale distribution of dust in galaxies from the DustPedia sample. For this purpose, we have made use of Herschel imaging in five bands, from 100 to 500 μm, in which the cold dust constituent is primarily traced and makes up the bulk of the dust mass in spiral galaxies. For a subsample of 320 disc galaxies, we successfully performed a simultaneous fitting with a single Sérsic model of the Herschel images in all five bands using the multi-band modelling code GALFITM. We report that the Sérsic index n, which characterises the shape of the Sérsic profile, lies systematically below 1 in all Herschel bands and is almost constant with wavelength. The average value at 250 μm is 0.67 ± 0.37 (187 galaxies are fitted with n250 ≤ 0.75, 87 galaxies have 0.75 < n250 ≤ 1.25, and 46 – with n250 > 1.25). Most observed profiles exhibit a depletion in the inner region (at r < 0.3−0.4 of the optical radius r25) and are more or less exponential in the outer part. We also find breaks in the dust emission profiles at longer distances (0.5−0.6) r25 which are associated with the breaks in the optical and near-infrared. We assumed that the observed deficit of dust emission in the inner galaxy region is related to the depression in the radial profile of the HI surface density in the same region because the atomic gas reaches high enough surface densities there to be transformed into molecular gas. If a galaxy has a triggered star formation in the inner region (for example, because of a strong bar instability, which transfers the gas inwards to the centre, or a pseudobulge formation), no depletion or even an excess of dust emission in the centre is observed.
Key words: galaxies: ISM / submillimeter: ISM / galaxies: structure
DustPedia is a project funded by the EU under the heading “Exploitation of space science and exploration data”. It has the primary goal of exploiting existing data in the Herschel Space Observatory and Planck Telescope databases.
The tables with the results are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/622/A132
© ESO 2019
1. Introduction
Dust is one of the several constituents of galaxies which holds a major role in the interstellar medium (ISM). First, it acts as a catalyst in the transformation of the atomic hydrogen into molecular hydrogen from which stars form (Wolfire et al. 1995). Thus, the dust is an important element in the chemical evolution of the ISM. Second, it allows the gas to cool and condense to form new stars (Draine 1978; Dwek 1986; Hollenbach & Tielens 1997). Third, it absorbs some fraction of the emitted starlight and re-emits it in the infrared (IR) domain, where the thermal emission by dust grains dominates in the spectral energy distribution (SED) of galaxies between ≈10 and 1000 μm (Popescu & Tuffs 2002; Viaene et al. 2016). Dust is thus an effective tracer of the star formation activity. Because of the important role of dust in the ISM and its tight link to the other components of galaxies, the study of dust emission is mandatory to have a better understanding of all of the processes at play.
Spiral galaxies have cold and warm dust, as first suggested by de Jong et al. (1984), and confirmed by the Infrared Space Observatory (ISO, Kessler et al. 1996; see review of Sauvage et al. 2005). The cold dust component (Td = 10−20 K) is associated with molecular and atomic hydrogen clouds, which are heated mostly by the general interstellar radiation field (ISRF, Cox & Mezger 1989; Bendo et al. 2015). Since most of the total interstellar dust mass of a galaxy resides in its cold phase (see review of Galliano et al. 2018 and references therein), the cold dust component can therefore be used to estimate the total dust distribution over the galaxy.
Radiative transfer (RT) modelling serves as a good tool to study the dust distribution by the observed dust attenuation in edge-on galaxies. To retrieve structural parameters of the dust component, optical and near-infrared (NIR) observations are used to create monochromatic (i.e. based on one photometric band, see e.g. Xilouris et al. 1997, 1998, 1999; Bianchi 2007; De Looze et al. 2012a; De Geyter et al. 2013) or oligochromatic (based on several bands, see e.g. Baes et al. 2010; De Geyter et al. 2014, 2015a; Mosenkov et al. 2016, 2018; Peters et al. 2017) models. In the optical, the dust attenuation in the edge-on view is severe and can be observed in many edge-on galaxies as a prominent dust lane which corresponds to an absorbing dust disc. The dust surface density of this disc is usually represented by a double-exponential model, and from the fitting its main free parameters (the total dust mass, the dust disc scalelength and scaleheight) can be recovered. Despite the fact that the model of a double exponential disc is plausible for most galaxies, few attempts were made to fit the dust component with a different dust model, for example, a dust ring (De Looze et al. 2012a; De Geyter et al. 2015a; Schechtman-Rook & Bershady 2014; Viaene et al. 2015). However, a model of a non-exponential dust disc has not ever been adopted in RT modelling. In face-on galaxies RT modelling has been also successfully used (see e.g. De Looze et al. 2014; Viaene et al. 2017).
Apart from RT fitting of the observed dust attenuation in edge-on galaxies, a more straightforward way to study dust distribution in galaxies is by mapping the radial distribution of dust emission in the far-infrared (FIR). First studies of dust discs in galaxies were performed with the Infrared Astronomical Satellite (IRAS, Neugebauer et al. 1984; Moshir et al. 1990; Sanders et al. 2003; Lisenfeld et al. 2007) and the ISO, and later with the Spitzer Space Telescope (Werner et al. 2004).
Often, to study the radial distribution of dust emission in galaxies, a 1D azimuthally averaged or 2D profile is used. Below we briefly list some studies in which the large-scale distribution of dust was traced.
In Alton et al. (1998), eight nearby galaxies observed with the ISO at 200 μm were studied. Based on these observations, the exponential scalelengths of the dust emission were estimated and compared with those determined in the IRAS bands and the optical B band.
Muñoz-Mateos et al. (2009) carried out a detailed analysis of the radial distributions of stars, gas, and dust in the Spitzer Infrared Nearby Galaxies Survey (SINGS, Kennicutt et al. 2003). They found that the dust density profiles are exponential. However, in S0/a and Sab galaxies the dust profiles usually present a central depletion.
In recent years, the Herschel Space Observatory (Pilbratt et al. 2010) offered a unique opportunity to study the FIR/submm spectral domain (from 55 to 672 μm, thus covering wavelengths beyond the peak of thermal dust emission). Thanks to the Herschel telescope, we are able to map the distribution of the cold dust component in a large number of nearby objects in an unprecedented way.
In Hunt et al. (2015), radial surface brightness (SB) profiles of 61 galaxies from the KINGFISH (Key Insights into Nearby Galaxies: Far-Infrared Survey with Herschel, Kennicutt et al. 2011) sample were fitted with an exponential function in order to compare stellar and cool-dust disc scalelengths, as measured at 3.6 μm and 250 μm.
In Smith et al. (2016), combining FIR emission of 110 galaxies from the Herschel Reference Survey (HRS, Boselli et al. 2010), an exponential distribution for the dust was recovered. However, the average SB profile at 250 μm for a subsample of 45 large galaxies clearly shows evidence for a shallower slope at large radii than in the inner part (a broken- or double-exponential model was adopted in this case). Combining signal has the advantage that very large radii of the SB profile can be probed. On the other hand, some individual galaxy features are obviously washed out, with a general smooth profile created.
In most of the studies mentioned above the azimuthally averaged (1D) distribution of the galaxy SB was used to present the radial distribution of dust emission in galaxies. However, as was first shown by Byun & Freeman (1995), while being simple to implement, the 1D approach has some serious drawbacks. As noticed by Peng et al. (2010), “for compact galaxies, 1D profile fitting cannot properly correct for image smearing by the point spread function (PSF) because 1D profile convolution is not mathematically equivalent to convolution in a 2D image”. 2D fitting is more beneficial than 1D profile analysis when a multi-component decomposition is required (see e.g. Simard 1998; Peng et al. 2002, 2010; de Souza et al. 2004; Erwin 2015). Furthermore, the radial distribution of dust is usually a priori approximated by an exponential law. Often, the inner part of the galaxy, which exhibits some deviation from this unified function, is not taken into account when fitting the radial profile. To this day, no 2D fitting with a non-exponential disc model (e.g. with a general Sérsic law, Sérsic 1968) in the FIR/submm has yet been done.
The aim of this paper is to study the 2D distribution of dust for a large sample of galaxies using the Sérsic law where the shape of the profile is controlled by the Sérsic index n (see Sect. 3). The advantage of using this law is that setting n = 0.5 gives a Gaussian, for n = 1 it converts into an exponential law, and for n = 4 we get a de Vaucouleurs profile. Therefore, in this work we verify whether the dust distribution in disc galaxies is truly exponential as was assumed earlier, mostly based on analysing 1D profiles. We apply the Sérsic law for describing the 2D distribution of dust emission in exactly the same way as it is done for the stellar emission. To the best of our knowledge, this is done here for the first time.
In this paper we focus our attention on the spatial distribution of cold dust in galaxies by exploiting five Herschel bands, from 100 μm to 500 μm. It is the distribution of the emission of the diffuse dust disc which we investigate in this paper. In addition, we trace old stellar populations using the NIR imaging (3.4 μm) available due to the WISE space observatory (Wright et al. 2010). We make use of the DustPedia sample, which aims at characterising the dust in the Local Universe using a series of robust and homogeneous modelling and analysis tools. We apply a unified approach for fitting the Sérsic model to both the NIR and FIR/submm sets of observations. From this, we are able to draw conclusions about the shape of the radial distribution (given by the Sérsic index) and the effective radius of the dust component, as well as about the change of these parameters with wavelength.
This paper is structured as follows. In Sect. 2, we briefly describe the DustPedia sample and define a subsample of galaxies, on which we focus our analysis. We also provide a description of the data preparation we use in our study. The procedure for performing the fitting of galaxy images is presented in Sect. 3. We provide the results of our fitting in Sect. 4. The discussion of the obtained results is presented in Sect. 5. Finally, our conclusions are summarised in Sect. 6. In the Appendix we provide some details and results of an additional analysis which is important for our study. Throughout this paper, we assume regression in the form y = k x + b with the Spearman rank-order correlation coefficient ρ (lying between −1 and +1).
2. The sample and data
The DustPedia sample, which we use in our study, was originally selected to fulfil the following criteria. It includes galaxies with a radial velocity v < 3000 km s−1. The selected galaxies are large, with an optical diameter larger than 1′. They are detected at 3.4 μm (signal-to-noise ratio (S/N) > 5σ) and have Herschel Photoconductor Array Camera and Spectrometer (PACS, Poglitsch et al. 2010) or Spectral and Photometric Imaging Receiver (SPIRE, Griffin et al. 2010) observations. The total number of the selected galaxies is 875 and, at the moment, it is the most representative sample of galaxies built upon the Herschel legacy; it spans a wide range of galaxy masses and morphologies.
The imagery and photometry for the DustPedia sample was specially prepared by Clark et al. (2018, hereafter C18) and can be freely retrieved from the DustPedia database1. Below, we use the DustPedia sample and its imagery to select galaxies for our subsequent analysis.
To study the cold dust distribution in galaxies, we make use of the Herschel observations which have the best spatial resolution in the FIR/submm to date. We consider five Herschel wavebands: PACS 100 μm, PACS 160 μm, SPIRE 250 μm, SPIRE 350 μm, and SPIRE 500 μm. We do not exploit PACS 70 data as they are available for only 244 galaxies of the DustPedia sample. On top of that, in this band emission from stochastically heated warm dust can be substantial and, therefore, could potentially bias our current study.
In order to select galaxies for a Sérsic modelling of their Herschel images, we impose the following criteria. If a galaxy has a measured flux density lower than 3σ in any Herschel band, then this galaxy is removed from the subsequent consideration. Also, we rejected galaxies which have a major flag associated with the Herschel flux due to contamination, artefacts, or insufficient sky coverage in this band (flags “C”, “A”, “N”, respectively, given in the aperture photometry table from C18). This results in a sample of 344 galaxies. After a visual inspection of the selected galaxies, we additionally rejected five galaxies (IC 3521, IC 3611, NGC 2992, PGC 166077, and UGC 7249) which appeared to be too small to be fitted. The final subsample thus consists of 339 DustPedia galaxies. Our sample comprises only one early-type galaxy, NGC 2974, which has a morphological type code in HyperLeda (Makarov et al. 2014) of −4.3 ± 1.2. However, more careful investigation of this galaxy reveals a spiral structure: Naim et al. (1995) classified this galaxy as Sa. Therefore, we can consider our subsample as consisting entirely of disc galaxies.
Herschel imagery for all PACS 100–SPIRE 500 μm wavebands is taken completely from the DustPedia archive (see details in Davies et al. 2017 and C18 on how the images were reduced), including the flux density maps and the error-maps. The maps have pixel sizes of 3″ (PACS 100), 4″ (PACS 160), 6″ (SPIRE 250), 8″ (SPIRE 350), and 12″ (SPIRE 500), with a corresponding FWHM of 10″, 13″, 18″, 25″, and 36″. For PACS 100 and PACS 160, we retrieved the extended PSF kernels provided in Bocchio et al. (2016) which were created by combining Vesta (central part of the PSFs) and Mars (wings) dedicated observations. For SPIRE 250, SPIRE 350, and SPIRE 500, we adopted the kernels which were used in Smith et al. (2016) (created by means of SPIRE calibration observations of Neptune). These extended PSFs are mandatory to have correct fits of the SB profiles.
Complementary NIR data were also used to trace the old stellar population (see e.g. Elmegreen & Elmegreen 1984; Rix & Zaritsky 1995; Grosbol 1993). The WISE observatory scanned the whole sky in the W1 band (3.4 μm), and so we make use of its observations for the entire sample of 875 DustPedia galaxies. We do this to obtain some important general characteristics of these galaxies (e.g. galaxy inclination, see Appendix D), as well as some galaxy structural properties. These quantities are used in the current study and in the papers to follow.
Since no error-maps are provided for the WISE data in the DustPedia database, we applied the same scripts used by C18 to retrieve the WISE W1 intensity maps and the related pixel-uncertainty maps from the NASA/IPAC Infrared Science Archive (IRSA2). These maps store the 1σ uncertainty per pixel corresponding to the co-added intensity values in the AllWISE data release Image Atlas. The final WISE cutouts retain the standard AllWISE Image Atlas pixel size of 1.375″ and the FWHM of 6.1″. The PSF image for WISE W1 is taken from Section IV.4.c.viii of the WISE All-Sky Data Release Explanatory Supplement3, which is constructed from co-added mosaics of the deep Ecliptic Pole observations, and rescaled to match the pixel size and resolution of the WISE cutouts.
In order to prepare galaxy images in the WISE W1 and Herschel bands, we used the following steps which are described in full detail in Appendix A. For each galaxy, its image in each band was rebinned to PACS 100 μm (except for WISE W1), background subtracted, and cropped to encompass the whole galaxy body and some free space. We also masked out contaminating objects (stars and galaxies), which should not be taken into account in the process of fitting. The extended PSF in each band was also specially treated to match the corresponding cutout.
Once these routines were run, the final images are ready to be processed with our special fitting tool. The detailed description of our fitting technique is given in the next section.
3. Single Sérsic modelling technique
In order to quantitatively describe the SB distribution in galaxies in a chosen waveband (which traces the stellar density distribution of a stellar population or highlights a mixture of different populations with intrinsic dust attenuation), two-dimensional (2D, Byun & Freeman 1995; de Jong 1996; Emsellem et al. 1994; Cappellari 2002) profiles are usually fitted with an analytic function or a superposition of functions which represent different structural components of the galaxy. This is the so-called parametric method, which, if used appropriately, gives reliable results on the galaxy structure, and, at the same time, can be considered as a useful indicator of galaxy morphology.
A simple way to fit the light radial profile of a galaxy is by using a Sérsic model (Sérsic 1968), with several free parameters: the effective radius re (the radius which encompasses half of the total luminosity of the system), the Sérsic index n (which controls the degree of curvature of the profile), and the effective SB μe (in units of Jy arcsec−2) at the radius re (equivalently, the total luminosity of the model or its central SB μ0 can be used):
where νn ≃ ln10 (0.868 n−0.142) (Caon et al. 1993). To distinguish the designations of the same Sérsic parameters fitted in different bands, we use an upper index for denoting the passband (or wavelength), for example, for WISE W1 the Sérsic index is written as n3.4.
Since the Sérsic law has several free parameters, which control the view of the profile, a large variety of the observed galaxy profiles can be approximated by this function very well (Caon et al. 1993, 2005; Caldwell 1999; D’Onofrio 2001; Aguerri et al. 2005; Venhola et al. 2017). Single Sérsic fitting was applied to large samples of galaxies to study how their parameters change with morphological type and other general properties of galaxies (see e.g. Häussler et al. 2007; La Barbera et al. 2010; Hoyos et al. 2011; Kelvin et al. 2012; Häußler et al. 2013; Méndez-Abreu et al. 2017).
The Sérsic index shows how far the light profile is from being exponential. n = 1 shows that a galaxy consists of a single exponential disc. n < 2 is an efficient criterion for selecting disc-dominated galaxies, whereas n > 2 is likely to be related to an early-type galaxy or a spiral galaxy with a bright bulge (see e.g. Ravindranath et al. 2004 and Sect. 4). In other words, the general Sérsic index is sensitive to the presence of a central component (a bulge or a bar). Thus, this unified function serves as a good first step in describing the multi-component structure of galaxies (see e.g. Andredakis et al. 1995; de Jong 1996; Möllenhoff 2004; Laurikainen et al. 2005; Amorín et al. 2007; Reese et al. 2007; Gadotti 2008, 2009; Mosenkov et al. 2010).
In this paper we apply single Sérsic modelling to describe 2D stellar and dust emission of the selected galaxies. Apart from the parameters in Eq. (1), the free parameters of the 2D model include the coordinates of the galaxy centre, its apparent flattening, and position angle. The applicability of this fitting method to the Herschel observations and its robustness is discussed in Appendix B.
In this study we implement the GALFIT and GALFITM software to fit a Sérsic profile to the galaxy light profile. GALFIT performs a Levenberg-Marquardt minimisation of the χ2 residual between a galaxy image and its PSF-convolved model by modifying the free parameters. The final model is found when χ2 reaches a minimum. The calculation of χ2 is weighted by a sigma map, which is provided for each galaxy in our sample. This code has been successfully applied to individual galaxies with a diverse morphology (Gabor et al. 2009; Huang et al. 2013; Reshetnikov & Combes 2015) and to large samples of galaxies consisting of thousands of objects (Häussler et al. 2007; Hoyos et al. 2011; Salo et al. 2015).
Recently, a new fitting code GALFITM (Bamford et al. 2011; Häußler et al. 2013; Vika et al. 2013, 2014, 2015) has been created (as an extension of GALFIT) to fit a wavelength-dependent model by using multiple images of the same galaxy in a simultaneous and consistent manner. Rather than fitting the parameter values at the wavelength of each band, GALFITM fits the coefficients of a smooth function describing the wavelength dependence of each parameter. It has been shown that multi-band modelling significantly improves the extraction of information, particularly from bands with low S/N when combined with higher S/N images (Vika et al. 2013, 2014; Vulcani et al. 2014; Kennedy et al. 2016). Using such a multi-band approach, one can obtain a more reliable model based on several observations of the same galaxy at different wavelengths.
For the purpose of this work, we make use of the GALFIT wrapper DECA written in Python (we refer the reader to Mosenkov 2014 for a complete description of the initial version of the package). We constructed 2D photometric models of the light profiles for each galaxy, selected in Sect. 2, using a general Sérsic model (Eq. (1)). In addition, the GALFITM code is also incorporated in DECA for a simultaneous fitting of galaxy images in different bands.
DECA is especially suitable for a large sample of galaxies, when a modelling of each individual galaxy by hand is problematic. It can work in a fully automated regime if we use a unified Sérsic model for all galaxies selected. Sérsic fitting assumes that each galaxy has a light distribution which can be satisfactorily described by a Sérsic function. Of course, since galaxies are quite complex systems, using this single component can be a rather coarse approximation of the observed 2D profile in some galaxies (for example, in grand-design galaxies, galaxies with strong bars or ring structures, i.e. where different components have different geometry and/or position and orientation towards the observer). Nevertheless, to trace the general distribution of both stars and dust in a unified way, our single-model approach should be applicable to the statistically large sample of DustPedia galaxies.
For the Herschel images, we use first GALFIT and then GALFITM: DECA first performs modelling in all five Herschel bands separately running GALFIT and then uses the output results as an input, first-guess model for GALFITM five-band fitting. For GALFIT, we do not put any constraints on the fit parameters, however, for GALFITM we perform a multi-wavelength modelling where the parameters are replaced with functions of wavelength (Chebyshev polynomials). With these polynomials the user is allowed to control how the structural parameters of the model will vary as a function of wavelength. For the total galaxy magnitude we set the maximum polynomial order (for which the coefficients are free to vary in the fitting process) to be 5 (as the number of bands is five, i.e., in essence, they are considered as unconstrained). The Sérsic index and re are allowed to vary parabolically with wavelength (this degree of freedom is based on the previous results of gradual increase of the scalelength of the dust emission profile with wavelength, see Introduction). All other parameters (centre position, axis ratio, and position angle) are selected to be constant with wavelength, that is the same in all bands.
As GALFITM significantly improves the extraction of information, particularly from bands with low S/N when combined with higher S/N images, the use of this approach is justified for the Herschel observations. In addition, it allows us to link models of the same galaxy in different bands, so that, for example, the fit models would have the same centre, position angle, and axis ratio in all five fitted bands. We found this very convenient when fitting galaxy images in different wavebands.
If there are other sources within the fitting region, they are either masked or, if close enough to the main source to cause significant photometric blending, are included in the fit. In the case of severe foreground Galactic cirrus in some Herschel images (as, for instance, for NGC 6946), the sky component is also fitted simultaneously with the target galaxy.
In Fig. 1 we show an example of a GALFIT fitting in the WISE W1 band for one of the typical DustPedia galaxies, the Sbc-type galaxy NGC 3686. An example of the azimuthally averaged profile with the overimposed model in the SPIRE 250 μm band (both created using the IRAF’s ELLIPSE task4) is shown in Fig. 2. The profiles in all Herschel bands look similar and, therefore, we only show here (and to the end of the paper) the profiles for the SPIRE 250 μm band. We note that for this galaxy the Sérsic index of the dust component n250 = 0.52 (i.e. it has a Gaussian profile), in comparison with n3.4 = 1.15 (an exponential profile) for the SB distribution of the old stellar population. The results of a GALFITM fitting in all five Herschel bands for the same galaxy are presented in Fig. 3.
 |
Fig. 1. Results of the fitting for NGC 3686 in the WISE W1 band: the WISE W1 image (left panel), the best fitting image (middle panel), and the residual image (right panel) which indicates the relative deviation between the fit and the image in absolute values, i.e. |data-model|/model. The right colour bar shows the scaling of the residual image. The masked objects are highlighted by the white colour (left and right panels) or are transparent areas (middle panel). The galaxy and model images are given in a logarithmic scale. All images cover a field-of-view of 6.5′ × 6.5′. |
 |
Fig. 2. Azimuthally averaged profile for NGC 3686 (grey circles), its convolved (red solid line) and unconvolved (orange dashed line) model, and the PSF kernel (green dotdash line) in the SPIRE 250 μm band. |
 |
Fig. 3. Results of the GALFITM modelling for NGC 3686: the Herschel images from 100 to 500 μm (left panels), the models (middle panels), and the relative residual images (right panels, in the same units as presented in Fig. 1). The righthand colour bar shows the scaling of the residual images. Any masked objects are highlighted with a white colour. The galaxy and model images are given in a logarithmic scale. All images cover a field-of-view of 6.75′ × 8.35′. |
4. Results
DECA was applied to the WISE W1 images for all 875 DustPedia galaxies, as well as to the selected subsample of 339 galaxies with available Herschel observations in all five bands. Below we present results of the fitting and discuss them in Sect. 5.
In Appendix C we provide the robustness of our fitting results by comparing them with the literature. This comparison shows that the model parameters are recovered well using our DECA fitting. We also show that 865 galaxies (98.86% of the whole DustPedia sample) have successful single Sérsic fits in the WISE W1 band.
Based on the GALFITM results for the Herschel data, we found that 320 galaxies (94% out of the selected subsample of 339 galaxies) are large enough to have a plausible Sérsic model. The minimum value of the semimajor axis (measured for all DustPedia galaxies in C18) for this subsample is 63″, whereas the mean value is 3.2′ ± 1.5′. Out of them, we also define a subsample (and call it the reference sample) of 71 “good” galaxies which have a smooth SB distribution in all five bands and a reduced χ2 which yields 0.8 ≤ χ2 ≤ 1.2, an arbitrary criterion of the goodness of the fit. To the end of the paper we restrict our analysis to the 320 galaxies (as those for which a single Sérsic fit is reliable in the WISE W1 as well as in all five Herschel bands). We also consider the reference sample to make sure that the results for both samples are compatible and our findings are not affected by the effects of resolution and the presence of a complex dust structure which can be observed in well-resolved galaxies.
Because neither GALFIT, neither GALFITM provide errors of the retrieved parameters, we decided to estimate them for a randomly selected, typical spiral galaxy, NGC 3622, using a genetic algorithm (Goldberg 1989). We applied it ten times and took the scatter in the fitted parameters as their uncertainties. Unfortunately, this operation is very time consuming, therefore we only did it for one galaxy. We found the Sérsic index n250 for this galaxy to be 0.79 ± 0.22, which means that the estimated uncertainty is approximately 25% of the retrieved parameter. For the effective radius we found 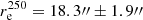 , i.e. its uncertainty is within 10% of the parameter value.
, i.e. its uncertainty is within 10% of the parameter value.
The tables with the results can be accessed from the DustPedia database and from the CDS. The final pipeline product includes separate tables with the model results for the WISE W1 band and for the Herschel bands. For the WISE W1 band, we also provide some supplementary information described in Appendix D, for instance, the estimated galaxy inclinations and stellar masses.
Additionally, in Appendix B we describe galaxy simulations which we performed to test the fitting technique described in Sect. 3 and for comparing them with real observations. In our simulations we essentially used a well-defined model of the galaxy IC 2531, varying its inclination angle and the distance to it (i.e. its spatial resolution). Two models for the dust component, an exponential disc and a Sérsic disc, are adopted to show if we can see a difference between the fitted dust emission profiles in these mock galaxies. IC 2531 is a typical Sc galaxy. Sc is one of the most numerous types in our sample (see Table 2), and, therefore, by doing these simulations we strive to reproduce some characteristic view for the intermediate late-type galaxies in our sample. Of course, these mock galaxies cannot be completely compared to the selected sample which exhibit a large variety of morphological types, masses, environment, and other properties. Nevertheless, the behaviour of the fit parameters from the simulations can be easily compared to those for the real galaxies, from which we can conclude if our models are consistent with what we see in practice. On top of that, as shown below, the fitted parameters barely depend on galaxy morphology.
4.1. Distributions of the parameters
In Fig. 4 we show different distributions of the retrieved structural parameters. We also show distributions of the fitted parameters for the mock galaxies from Appendix B: for the exponential dust disc (the black solid line) and the Sérsic dust disc with nd = 0.6 (the dark blue dashed line).
 |
Fig. 4. Distributions of different parameters over wavelength. Left panel: ratio of the effective radius in each Herschel band to the effective radius in the WISE W1 band; middle panel: distribution of the Sérsic index in each Herschel band; right panel: ratio of the Sérsic index in each Herschel band to the Sérsic index in the WISE W1 band. By the lilac colour we show the subsample of 320 galaxies with reliable fitting results, whereas the dark lilac corresponds to the reference sample of 71 galaxies. The black solid and dark blue dashed lines refer to the simulations from Appendix B with an exponential and Sérsic disc, respectively. |
Table 1 lists the mean and median values with the standard deviations of the retrieved parameters. We can see that, for example, the average Sérsic index at 250 μm is 0.67 ± 0.37. 187 galaxies in our sample are fitted with n250 ≤ 0.75 (⟨n250⟩ = 0.44 ± 0.19), 87 galaxies have 0.75 < n250 ≤ 1.25 (⟨n250⟩ = 0.96 ± 0.14), and 46 – with n250 > 1.25 (⟨n250⟩ = 2.17 ± 0.79). Here we use the border values 0.75 and 1.25 as the typical error for determining the Sérsic index of 1.0 in this band is 0.25 (25%). From these numbers we can see that more than half of the sample galaxies exhibit significantly non-exponential discs. This fact will be discussed in Sect. 5.
Distributions of the fit parameters (mean value, median value (inside the parentheses), and standard deviation).
We decided to verify that our results are not affected by the effects of inclination and angular resolution. For all Herschel bands we analysed if the Sérsic index correlates with the galaxy radius sma, galaxy flux density (both taken from C18), and galaxy inclination (computed in Appendix D). As one can see for SPIRE 250 (all other bands show similar results) in Fig. 5, no correlations between these quantities are found. Therefore, we are confident that our results are not influenced by any of these effects.
 |
Fig. 5. Dependences of the Sérsic index on the radius (left panel), flux density (middle panel), and galaxy inclination computed in Appendix D (right panel). The black filled circle with the bar corresponds to NGC 3622 (see text). |
4.2. Dependence of the parameters on wavelength
The dependence of the retrieved parameters on wavelength is shown in Fig. 6. Here we notice that one should always keep in mind that we do not expect to recover the effective radius of the dust density profile because there is always an IR colour gradient (i.e. dust is warmer in the centre), and, hence, at any IR wavelength the monochromatic light distribution will be more centrally concentrated (i.e. will have a smaller effective radius) than the actual dust distribution. As to the Sérsic index, our simulations indicate that the dust emission profiles in the SPIRE bands follow the dust mass density profiles very well, i.e. they should have the same Sérsic index.
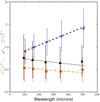 |
Fig. 6. Dependences of three different parameters on wavelength: the orange filled circles – for the ratio of the Sérsic index in each Herschel band to the Sérsic index in the WISE W1, the black filled triangles – for the Sérsic index, the lilac filled stars – for the effective radius in each Herschel band to the effective radius in the WISE W1 band. |
In the left panel of Fig. 4 we presented the ratio of the effective radius in each Herschel band to the effective radius in the WISE W1 band. For the sample galaxies, we can see a gradual increase of this ratio with wavelength, from 0.90 ± 0.27 in PACS 100 to 1.41 ± 0.43 in SPIRE 500. The view of the distributions for the mock galaxies is similar for both the exponential and Sérsic discs. From the comparison of the distributions for the real and mock galaxies one fact is obvious: the increase of the effective radius with wavelength is steeper for the real galaxies than for the simulated galaxies. Though the ratio 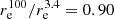 for the observations is close to the simulations (0.91–0.94), the ratio
for the observations is close to the simulations (0.91–0.94), the ratio 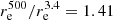 is underestimated in our simulations by 20–25%. This can be explained by several reasons. First, the dust temperature gradient of the model for the prototype edge-on galaxy IC 2531 may differ from what we observe in the other galaxies, with different inclination angles. Second, the dust energy balance problem, observed in nearby edge-on galaxies (see Popescu et al. 2000, 2011; Misiriotis et al. 2001; Alton et al. 2004; Dasyra et al. 2005; Baes et al. 2010; De Looze et al. 2012b; De Geyter et al. 2015b; Mosenkov et al. 2016 and recent study by Mosenkov et al. 2018), may be responsible for the observed steeper increase of the effective radius in the real galaxies: in the FIR/submm, the dust emission derived from RT calculations underestimates the real observations by a factor 1.5–4. The dust heating mechanisms (Law et al. 2011; Boquien et al. 2011; Bendo et al. 2012, 2015; Hunt et al. 2015) and the complex large- and small-scale dust structure (Popescu et al. 2000; Misiriotis et al. 2001; Bianchi 2008; Bianchi & Xilouris 2011; MacLachlan et al. 2011; De Looze et al. 2012b; Holwerda et al. 2012; Mosenkov et al. 2018), observed in galaxies, are among the possible explanations for this problem.
is underestimated in our simulations by 20–25%. This can be explained by several reasons. First, the dust temperature gradient of the model for the prototype edge-on galaxy IC 2531 may differ from what we observe in the other galaxies, with different inclination angles. Second, the dust energy balance problem, observed in nearby edge-on galaxies (see Popescu et al. 2000, 2011; Misiriotis et al. 2001; Alton et al. 2004; Dasyra et al. 2005; Baes et al. 2010; De Looze et al. 2012b; De Geyter et al. 2015b; Mosenkov et al. 2016 and recent study by Mosenkov et al. 2018), may be responsible for the observed steeper increase of the effective radius in the real galaxies: in the FIR/submm, the dust emission derived from RT calculations underestimates the real observations by a factor 1.5–4. The dust heating mechanisms (Law et al. 2011; Boquien et al. 2011; Bendo et al. 2012, 2015; Hunt et al. 2015) and the complex large- and small-scale dust structure (Popescu et al. 2000; Misiriotis et al. 2001; Bianchi 2008; Bianchi & Xilouris 2011; MacLachlan et al. 2011; De Looze et al. 2012b; Holwerda et al. 2012; Mosenkov et al. 2018), observed in galaxies, are among the possible explanations for this problem.
In the middle panel of Fig. 4 we showed the distribution of the Sérsic index in each band. As we can see, the distributions look similar in all bands, though we can definitely distinguish an asymmetry of the nλ-histograms: a vast majority of galaxies are concentrated near nλ ∼ 0.5, whereas a flat distribution of galaxies with nλ > 1 is also present. The similar distributions by nλ in all Herschel bands (this is seen well in Fig. 6) implies that the dust emission has an essentially identical profile in the whole FIR/submm domain. However, according to our simulations, the fitted profile of the dust emission has a systematically lower Sérsic index with increasing wavelength. From this comparison we can conclude that the Sérsic model for the dust density distribution with a Sérsic index of about 0.5–0.7 fits the observations much better than the model with an exponential profile, which lies significantly off the peaks for the observations in all Herschel bands. This is also seen well when we consider the ratio nλ/n3.4 (see the right panel of Fig. 4). We can see that the observed distributions in all five bands are rather broad (σ = 0.3), with a mean value of approximately 0.5. However, we should notice that this ratio is overestimated (by 10–20%) in our simulations as compared to the real galaxies. This can be explained by the fact that our simulations include only one prototype galaxy with a fixed bulge-to-total ratio, whereas galaxies in the selected sample may have a different bulge contribution, i.e. have a different morphological type and, consequently, different general Sérsic index in the WISE W1 band (see Fig. 9).
4.3. Dependence of the parameters on morphology
We also studied the dependence of the fitted parameters on morphological type. The distributions are shown in Table 2. As the number of early-type galaxies in the selected sample of 320 galaxies is not enough to consider them in a bin of 1 numerical Hubble stage T separately, for them we use the broad bin (−4,0), i.e. we consider them as a single type of lenticulars. As to Sdm (T = 8) and Sm (T = 9) galaxies, we combine them in one type Sdm for the same reason.
Numbers of galaxies in each bin (T − 0.5, T + 0.5) for a subsample of 320 galaxies with reliable fitting results.
The dependence of the effective radius as a function of morphological type is shown in Fig. 7, the left and middle panels. In general, the scatter is large and the apparent trend in each band is feeble, within the scatter. In all bands, we can see an increase of the effective radius with wavelength up to T ≈ 4−5: on average, the most extended dust components, as well as stellar discs, are found in galaxies of these morphological types. For galaxies with T > 5, we observe a decrease of the effective radius to the smallest discs in Sm galaxies (we note that this decrease becomes sharper with increasing wavelength). However, for our selected sample a clear bump is seen for galaxies with T = 1. A closer look at these galaxies revealed that many of them are viewed edge-on and possess prominent stellar haloes (e.g. NGC 4235, NGC 4260, NGC 4300, NGC 4424, NGC 4506), similar to the Sombrero galaxy. Thus, the large effective radius of the single Sérsic model for these galaxies can be reasonably explained by their extended haloes. By the dashed line in the left plot we also show the distribution for the whole sample and can see a similar behaviour as for our subsample of 320 galaxies but without a bump at T = 1. This means that the bump at T = 1 for the subsample is likely a selection effect.
 |
Fig. 7. Dependence of the effective radius measured in the WISE W1 band on the Hubble stage (left panel), the dependences of the effective radius measured in the five Herschel bands on the Hubble stage (middle panel), and the dependences of the ratio of the effective radius in each Herschel band to the effective radius in the WISE W1 band on the Hubble stage (right panel). Each dependence is plotted for the averaged data for the subsample of 320 galaxies (except for the lilac line in the left plot which refers to the sample of 865 DustPedia galaxies) within a bin of 1 T, with 15 and 85 percentiles shown. All lenticular galaxies (T ≤ 0) are combined together and shown by T = −2. Sm and Sdm galaxies are joined together in one type T = 8. |
The right panel of Fig. 7 shows the ratio 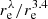 . We can see that this ratio is almost constant with type in all Herschel bands, with a tendency of decreasing
. We can see that this ratio is almost constant with type in all Herschel bands, with a tendency of decreasing 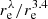 for late-type spirals. In the SPIRE bands, lenticular galaxies exhibit slightly more extended cold dust discs, as compared to their stellar discs, than spiral galaxies (see also Smith et al. 2012). The same tendency is observed in irregular galaxies which often show intensive star formation over the whole galaxy.
for late-type spirals. In the SPIRE bands, lenticular galaxies exhibit slightly more extended cold dust discs, as compared to their stellar discs, than spiral galaxies (see also Smith et al. 2012). The same tendency is observed in irregular galaxies which often show intensive star formation over the whole galaxy.
In Figs. 8 (top panel) and 9, we present the distribution of the Sérsic index over Hubble stage. For the Herschel data, we do not see a statistical difference of nλ for all morphological types, except that lenticular galaxies exhibit a large difference between the Sérsic index in all five bands, reaching values larger than 3 in PACS 100 and going down to approximately 0.9 in SPIRE 500. We interpret this steep change of the Sérsic index by a possible bias in their fitting. The selected lenticular galaxies are rather small and often exhibit a complex morphology, with rings (e.g. NGC 4324 and NGC 5701), lenses (e.g. NGC 3626), and different peculiarities (e.g. ESO 495–021 and NGC 2685). Two lenticular galaxies (IC 691 and NGC 7465) are classified as blue compact galaxies (Thuan & Martin 1981). Going from PACS 100 to SPIRE 500, these features can be washed out because of the increasing beam size. Nevertheless, we can discern that typical profiles of the selected lenticular galaxies in SPIRE 250 often have extended wings (NGC 5145), some galaxies show rather abrupt profiles with n250 < 0.5 (NGC 4531).
 |
Fig. 8. Dependences of the Sérsic index on the type (top panel) and the ratio of the Sérsic index in each Herschel band to the Sérsic index in the WISE W1 band on the type (bottom panel). The dependences are plotted for the averaged data for the subsample of 320 galaxies in each bin of 1 T with 15 and 85 percentiles shown. All lenticular galaxies (T ≤ 0) are combined together and shown by T = −2. Sm and Sdm galaxies are joined together in one type T = 8. |
 |
Fig. 9. Relationship between the Sérsic index in the WISE W1 band and the Hubble stage for the sample of 865 DustPedia galaxies. The median average and the 15 and 85 percentiles are shown by the black colour for each bin of 1 T. The orange dashed line refers to n3.4 = 2, the border value to split galaxies into bulgeless (n3.4 < 2) and bulge-dominated galaxies (n3.4 > 2). |
For the WISE W1 band (Fig. 9), we can see that late-type galaxies (T > 0) have n3.4 < 2. Notice also that bulgeless galaxies with T > 5 have a Sérsic index close to 1, which means that, indeed, an exponential profile is a good approximation for describing SB distribution in stellar discs. On the contrary, early-type galaxies with a spheroidal dominance have more extended profiles with n3.4 > 2.
We found that 218 galaxies with a morphological type between 3 and 7 (late-type spirals), which constituent the majority of the sample galaxies, have the mean value ⟨n250⟩ = 0.67 ± 0.34.
The bottom panel in Fig. 8 depicts the ratio of the Sérsic index in each Herschel band to that in the WISE W1 band. Galaxies with T < 0 and T ≥ 3 demonstrate an essentially constant ratio of approximately 0.56 ± 0.11, whereas for the remaining galaxies of S0a–Sab types this ratio drops to 0.25 ± 0.06. A closer look at these galaxies revealed that many of them have a bright ring (for example, NGC 1808 and NGC 4772) or a grand-design structure (for example, NGC 4260 and NGC 5691) which are less apparent in the NIR and very prominent in the FIR. 28 out of 56 galaxies with 0 < T < 3 have bright ring structures. This leads to a small Sérsic index (nλ ≤ 0.3) in the FIR/submm and a potentially lower ratio nλ/n3.4 than observed in later spiral galaxies without such bright features in the FIR/submm. In its turn, n3.4 decreases with type, and since nλ is almost constant for late-type spirals, we observe a gradual increase of nλ/n3.4 with Hubble type.
5. Discussion
In the previous section, we presented the main results from our structural analysis of the DustPedia galaxies. In discussing these results, we comment here on some of the more noteworthy issues regarding our study, and concentrate on interpreting the parameter distributions obtained in this work.
5.1. On our simple dust emission modelling
The results of our fitting are obtained for a large sample of DustPedia galaxies, with a diverse morphology and structural features. For the reference sample of 71 galaxies, where each galaxy have a smooth, regular distribution of dust emission, the results are essentially the same as for the subsample of 320 galaxies. We compared the distributions of the structural parameters in Fig. 4 for both samples and verified that they show similar statistical features (e.g. the mean, median and standard deviation values). According to the Kolmogorov–Smirnov test, we cannot reject the hypothesis that the distributions of the two samples are the same since the p-value is high (>0.3) for all pairs of distributions presented in Fig. 4.
For the Herschel bands, there are a few galaxies (about 30 in each band) with a very low or large Sérsic index (nλ < 0.3 or nλ > 10). This indicates that a contrast bar, a ring, or a highly asymmetric structure (e.g. spirals) is present. In the case of a ring, the formal Sérsic index appears to be very small (for example, for the ring galaxy NGC 1436, nλ ≈ 0.05). In this case the code is trying to fit the ring structure by a Sérsic function with such a low Sérsic index which corresponds to a flat profile in the central part and abrupt at the edge of the ring.
5.2. Change of the effective radius with wavelength
Since in our study we derived the geometrical scale 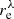 of the dust parameter using the Sérsic profile for the first time, it is impossible to directly compare it with the literature where an exponential law was fitted to the observed galaxy profiles. However, if from our sample we select galaxies with nλ ≈ 1 (e.g. in the SPIRE 250 μm band, approximately 50 galaxies demonstrate exponential profiles), we can compute the disc scalelength as
of the dust parameter using the Sérsic profile for the first time, it is impossible to directly compare it with the literature where an exponential law was fitted to the observed galaxy profiles. However, if from our sample we select galaxies with nλ ≈ 1 (e.g. in the SPIRE 250 μm band, approximately 50 galaxies demonstrate exponential profiles), we can compute the disc scalelength as 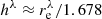 . For these galaxies we find h160/h100 = 1.16 ± 0.05, h250/h100 = 1.33 ± 0.07, h350/h100 = 1.51 ± 0.15, and h500/h100 = 1.64 ± 0.26. These are well-consistent with the results from Casasola et al. (2017) for a sample of 18 face-on spiral galaxies from the DustPedia sample: h160/h100 = 1.10 ± 0.01, h250/h100 = 1.30 ± 0.03, h350/h100 = 1.45 ± 0.05, and h500/h100 = 1.60 ± 0.01. The comparison with Smith et al. (2016) for h500/h250 gives 1.23 versus their 1.15 (and 1.25 from Casasola et al. 2017).
. For these galaxies we find h160/h100 = 1.16 ± 0.05, h250/h100 = 1.33 ± 0.07, h350/h100 = 1.51 ± 0.15, and h500/h100 = 1.64 ± 0.26. These are well-consistent with the results from Casasola et al. (2017) for a sample of 18 face-on spiral galaxies from the DustPedia sample: h160/h100 = 1.10 ± 0.01, h250/h100 = 1.30 ± 0.03, h350/h100 = 1.45 ± 0.05, and h500/h100 = 1.60 ± 0.01. The comparison with Smith et al. (2016) for h500/h250 gives 1.23 versus their 1.15 (and 1.25 from Casasola et al. 2017).
As Alton et al. (1998) and Casasola et al. (2017), we attribute the steady increase of the effective radius of the dust emission with radius to the cold-warm dust temperature gradient. The dust heating in turn is consistent with the FIR colour gradient observed in the disc. This suggests that part of the FIR emission arises from grains heated by the diffuse ISRF gradually decreasing with galactocentric distance.
5.3. Non-exponentiality of dust discs: comparison with the literature
Muñoz-Mateos et al. (2009) studied dust surface density profiles for the SINGS galaxies and concluded that in most cases they show an exponential behaviour. They also pointed out that the dust profiles in S0/a and Sab spirals usually have central depressions. Our results confirm their conclusion regarding early-type spirals – as was shown in Fig. 8, many early-type spirals in our sample have a Sérsic index close to 0.4–0.5 in the FIR/submm domain. Because of the flatness of the SB profile in the central region in these galaxies, the Sérsic index appears to be typically lower than 0.5. We should notice, however, that if we carefully look at the de-projected dust mass surface density profiles in their Fig. 8, we can find many profiles with a central depletion or, vice versa, an excess of dust density among galaxies of Sb-Sd types and irregular galaxies. Similarly, in our sample galaxies we observe a large scatter of the Sérsic index – profiles with a deficit or excess in the centre are present. The average profiles, which they provide in the same figure, obviously wash out the details for each individual galaxy and do not reflect the diversity of dust mass density profiles in the galaxies under consideration. For example, by averaging two profiles with a deficit and excess of dust mass density in the centre, we might obtain a fairly exponential decline in both the inner and outer parts of the profile.
The same explanation might be applicable to the conclusion by Smith et al. (2016) who reported that “the distribution of dust is consistent with an exponential at all radii”. This result was obtained for an average SB profile by combining the signal of 110 spiral galaxies from the Herschel Reference Survey (Boselli et al. 2010). A closer look at their Figs. 2 and 3, indeed, does not reveal a deficiency in the central regions of their SB profiles. On the contrary, we can see a little excess in the centre (within r/r25 < 0.1, where r25 is defined as the radius of the isophotal level 25 mag arcsec−2 in the B band) at 250 μm and 350 μm. Using their subsample of 45 large galaxies (r25 > 1.5′), we found 27 common galaxies with our sample. This number is almost two times smaller than the number of the selected HRS galaxies because in our subsample only galaxies with all five PACS 100–SPIRE 500 observations were selected. Some galaxies (for example, NGC 4298 and NGC 5363) have the “C”, “R” or “N” flags in the DustPedia database, and, therefore, we did not include them in our subsample. For the 27 common galaxies we computed the following average Sérsic indices: 0.67 ± 0.37 (SPIRE 250), 0.62 ± 0.29 (SPIRE 350), and 0.58 ± 0.26 (SPIRE 500). Thus, for these common galaxies the results of our Sérsic fitting confirm the conclusion drawn for the larger sample – the FIR dust emission has a distribution which is closer to a Gaussian rather than to an exponent.
In another work, Casasola et al. (2017) made use of the DustPedia data to analyse SB profiles in the FIR and to accurately create dust mass density profiles for 18 face-on spiral galaxies. In their Fig. A.2 we can see examples of galaxies where surface density profiles for the mass of dust have an obvious depletion in the inner galaxy region (NGC 300, NGC 628, NGC 3031, NGC 3521, NGC 3621, NGC 4725, NGC 4736, and NGC 7793). Most of these galaxies are present in our subsample, and for them the mean Sérsic index in the SPIRE 250 μm band is 0.62 ± 0.35.
We should point here that if we do not take into account the depression in the inner galaxy region and the truncation in the galaxy outskirts, which are often observed in galaxies, the dust emission and dust mass density profiles look more or less exponential (see further).
5.4. Non-exponentiality of dust discs: possible reasons
One of the most striking results of the present work is a non-exponential profile of the dust distribution in galaxies. Unlike the stellar distribution, the dust emission profile for many galaxies in our sample is close to Gaussian. Although our sample is incomplete in any sense due to selection restrictions, the representativity of the DustPedia sample, covering a wide range of morphological types and physical conditions within the interstellar medium of galaxies, should not affect the main finding of this study – non-exponentiality of dust discs. The presence of the substantial number of galaxies with Gaussian dust discs, whereas their stellar distribution has an exponential decline or close to it, is an interesting fact by itself and needs an interpretation.
In Fig. 10 we show some typical examples of galaxies with different types of SB profiles in the SPIRE 250 μm band which are discussed below.
 |
Fig. 10. Some typical galaxies in our sample with different features in their SB profiles (no correction for the galaxy inclination has been done). The grey circles represent the azimuthally averaged galaxy profile in the SPIRE 250 μm band. The model (convolved with the respecting PSF which is shown by the green dotdash line) is represented by the red solid line. The blue dashed line shows a break (if applicable) in the profile at some characteristic radius rc (see text). The two images in each plot are a coloured SDSS snapshot (left created with the Aladin sky atlas, http://aladin.u-strasbg.fr/, Bonnarel et al. 2000; Boch & Fernique 2014) and a SPIRE 250 μm band image (right). Both images have the same scale and orientation. |
 |
Fig. 10. continued. |
5.4.1. The presence of spiral arms
Sauvage et al. (2010) pointed out regarding the FIR SB profiles for the three galaxies M 81, M 99, M 100: the result that “some of the disc profiles prefer a Gaussian to an exponential must not be overinterpreted because the presence of prominent spiral arms can create a distinctive bump in the disc part of the profile that is represented by a Gaussian better than by an exponential”. We agree that the spiral structure is indeed a very bright feature in many galaxies in our sample, and might potentially influence the fitting results. However, as has been shown in Sect. 4, galaxies of different morphology (i.e. from bright to very dim flocculent spirals to S0 galaxies without a spiral structure at all) may have a Gaussian profile. Moreover, a clear, rather extended dust depletion in the centre (sometimes, a plato or even a decrease of dust emission while going closer to the centre) with a more or less exponential profile in the periphery (see below) suggests that this cannot be related to the spiral structure, or, at least, that this cannot be regarded as the main reason for the observed overall Gaussian profile in galaxies.
5.4.2. Depression of the HI surface density in the galaxy central region
Since most SB profiles of the galaxies under study show downbending (in Fig. 10 see panels for the galaxies IC 3102, NGC 3938, NGC 5300, and NGC 4411A), we estimated a radius where a prominent break takes place and can be unmistakably detected by the following approach. Using the IRAF task ellipse, we created azimuthally averaged profiles for the sample galaxies in the SPIRE 250 μm band. Then we fitted a piecewise two-side linear function to each of the created profiles. Using this function, we can fit the SB profile in the inner and outer parts of a galaxy with two linear functions simultaneously, which intersect at a characteristic radius rc. We use the term “characteristic radius” following Wang et al. (2014), who described the HI galaxy profiles with a depression at the centre where the profile transitions to the inner flat region. In total, we fitted 178 galaxy profiles where we observe a distinct inner break. We show the distributions by the rc in Fig. 14 expressed in different units: kpc, optical radius r25, and effective radius 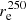 . One can see that the galaxies have a mean characteristic radius of 3.89 ± 1.79 kpc, and the distribution is asymmetric in shape. If we normalise the characteristic radius by the galaxy optical radius (taken from HyperLeda) or the effective radius found for the same SPIRE 250 μm band, we can see that the created distributions are broad (the mean values are 0.52 ± 0.19 r25 and
. One can see that the galaxies have a mean characteristic radius of 3.89 ± 1.79 kpc, and the distribution is asymmetric in shape. If we normalise the characteristic radius by the galaxy optical radius (taken from HyperLeda) or the effective radius found for the same SPIRE 250 μm band, we can see that the created distributions are broad (the mean values are 0.52 ± 0.19 r25 and 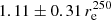 , respectively) and obviously have two peaks. This points to a bimodal distribution of the characteristic radius. We observe galaxies where a break may appear at rather long distances from the galaxy centre, as well as galaxies with shorter characteristic radii. Therefore, we fitted two Gaussian functions to these two distributions and found the following parameters of the observed dichotomy. For the optical radius: rc = 0.38 ± 0.08 r25 and rc = 0.60 ± 0.12 r25. For the effective radius:
, respectively) and obviously have two peaks. This points to a bimodal distribution of the characteristic radius. We observe galaxies where a break may appear at rather long distances from the galaxy centre, as well as galaxies with shorter characteristic radii. Therefore, we fitted two Gaussian functions to these two distributions and found the following parameters of the observed dichotomy. For the optical radius: rc = 0.38 ± 0.08 r25 and rc = 0.60 ± 0.12 r25. For the effective radius: 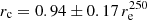 and
and 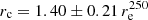 . If we compute the ratios between the short and long characteristic radii expressed in the units of optical and effective radius, we will receive 0.64 and 0.67, respectively, which are very close (taking into account that the effective radius was derived from the fitting whereas the optical radius was taken from HyperLeda). This bimodality suggests that the physical nature of these two types of characteristic radii is different. Below, we show that the short characteristic radius is related to the characteristic radius of the gas, whereas the long characteristic radius is, in fact, a break in the SB profile in the optical and NIR, which manifests a change in the stellar population.
. If we compute the ratios between the short and long characteristic radii expressed in the units of optical and effective radius, we will receive 0.64 and 0.67, respectively, which are very close (taking into account that the effective radius was derived from the fitting whereas the optical radius was taken from HyperLeda). This bimodality suggests that the physical nature of these two types of characteristic radii is different. Below, we show that the short characteristic radius is related to the characteristic radius of the gas, whereas the long characteristic radius is, in fact, a break in the SB profile in the optical and NIR, which manifests a change in the stellar population.
 |
Fig. 11. Distributions by the characteristic radius expressed in kpc (top panel), and in units r25 (grey colour) and |
As has been shown in many studies (see e.g. Wevers et al. 1984; Swaters et al. 2002; Wang et al. 2014), in nearby spiral galaxies their HI radial profiles decline exponentially in the outer regions and flatten or even decline near the galaxy centre. This is in contrast to the stellar surface density, which is peaked in the centre of the galaxy and drops steeply with radius. Bigiel & Blitz (2012) found for a sample of 32 nearby spiral galaxies that the combined HI and H2 gas profiles exhibit a universal exponentially declining radial distribution if the radius is scaled to r25. To describe the shape of a two-component HI radial profile and to obtain the deconvolved shape of it, Wang et al. (2014) developed a model which is an exponential function of radius in the outer regions and shows a depression towards the centre.
Wang et al. (2014) considered semi-analytic models to form a disc galaxy in a Λ Cold Dark Matter universe with proper treating the conversion of atomic into molecular gas. They concluded that the depression in the inner HI surface density profile arises because the gas reaches high enough surface densities in this region to be transformed into molecular gas. Because the level of star formation activity in the galaxy depends on its molecular gas content (Kennicutt 1998), correlations between star formation rate (and, hence, dust mass density) and HI surface density arise consequently.
The second type of breaks, which is mostly detected at longer distances with respect to the galaxy optical radius (or the effective radius of the dust component), is related to the breaks in the SB profiles observed in galaxies in the optical. We discuss this below.
5.4.3. Discs with different stellar populations
Poglitsch et al. (2010) studied radial distribution of gas and dust in the two spiral galaxies M 99 and M 100 and concluded that the dust shows the same breaks in the radial profiles as seen in the optical. Both of these galaxies exhibit a radial break in the profile at approximately 0.6 × r25. This is very close to the second peak of the distribution for the characteristic radius found above in this section.
In the optical, such a type of breaks in the SB profiles is frequent. The scheme for classifying breaks in galaxy profiles was proposed in several studies (Erwin et al. 2005, 2008; Pohlen & Trujillo 2006), which are grouped according to the specific behaviour of the declining brightness in the outer disc. The Type I profile is associated with a single exponentially declining disc with no signs of truncation within the optical radius. The Type II profile has a truncation with a steeper outer exponential (downbending profile). According to this classification, the breaks in the SB profile, which we observe in some galaxies of our sample, are of Type II. As was shown by Pohlen & Trujillo (2006), Erwin et al. (2008) and Gutiérrez et al. (2011), these breaks are often found at a radius of approximately 2.5 disc scalelengths, or 0.5–0.6×r25 (again, this is very close to the longer characteristic radius found above). The frequency of this type is estimated to be 50–60%. The Type III profile shows untitrancation in the periphery of the galaxy disc, i.e. has a shallower outer profile (upbending profile).
We found ten common galaxies with the sample from Pohlen & Trujillo (2006) and compared our profiles plotted for these galaxies in the SPIRE 250 μm band with the ones presented in their study in the optical (see their Appendix A). In Fig. 12 we show SPIRE 250 profiles for these galaxies, along with the marked characteristic radii measured in this study and the break radii taken from Pohlen & Trujillo (2006) for both the g and r bands. For two galaxies, NGC 450 and NGC 5584, the break and characteristic radii are close (for NGC 450, 79″ versus 90″ and for NGC 5584, 84″ versus 80″, respectively). For the remaining galaxies, our characteristic radius is, on average, two-times smaller than their break radius (⟨rc⟩ = 4.60 ± 1.50 kpc and ⟨rbr⟩ = 9.65 ± 3.67 kpc). Comparing the profiles in the optical and FIR for these galaxies, we found a depletion in the centre of the dust emission profiles (which is absent in the optical profiles). Obviously, what we measure in the FIR is the short characteristic radius.
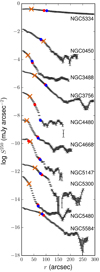 |
Fig. 12. SPIRE 250 profiles for the 10 common galaxies with Pohlen & Trujillo (2006). No correction for the galaxy inclination has been done. The orange cross is related to the characteristic radius found in this paper, the blue and red circles represent the break radii from Pohlen & Trujillo (2006) in the g and r bands, respectively. Each profile is shifted down relative to the previous one by 1.6 mJy arcsec−2. |
For the galaxies NGC 3488 and NGC 3756, there are no apparent breaks of Type II at longer distances from the galaxy centre which are detected in the optical profiles.
The three galaxies NGC 4668, NGC 5147, and NGC 5480 exhibit Type III profiles: the up-bending profiles start at approximately the same break radius both in the optical and FIR. NGC 5300 and NGC 5334 have, apparently, both short and long characteristic radii – the short radius is measured in the FIR, while the long radius (the break) can be detected both in the optical and FIR. To summarise, in general, the dust shows the same breaks not only of Type II, but of Type III in the radial profiles as seen in the optical. The depletion in the centre is only seen in dust emission.
We also performed the same analysis of measuring the break radius for the WISE W1 azimuthally averaged profiles. We did this only for those galaxies which have a downbending profile with a prominent break in the SPIRE 250 μm band profile. The total number of galaxies for which both the characteristic and break radii were measured is 55. We show the comparison for both radii in Fig. 13. As one can see, they compare very well. The mean value of the characteristic radius in this sample is 0.54 ± 0.18 r25 which signifies that this is the long characteristic radius associated with the Type II break in the NIR.
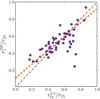 |
Fig. 13. Comparison between the break radius measured in the WISE W1 band and the characteristic radius in the SPIRE 250 μm band. The black dotdash line shows the one-to-one relation, whereas the orange line represents the regression line with k = 0.82, b = 0.11, and ρ = 0.83. |
Azzollini et al. (2008) and Bakos et al. (2008) studied Type II breaks and found that they usually show a minimum in their colour profile (the so-called U-shaped colour profile) at the break, or very near to it: the colour gets bluer out to the break radius, as one would expect from an inside-out formation scenario, and then becomes redder past the break radius. As shown by Radburn-Smith et al. (2012), the strength of the break decreases towards longer wavelengths (i.e. for older stellar populations). These and other studies (e.g. Bakos et al. 2008; Yoachim et al. 2010, 2012) suggest that Type II breaks are attributed to changes on the stellar populations at the break position rather than to drops in the number density of stars. Several mechanisms have been proposed to explain this fact: star formation thresholds (Kennicutt 1989); stellar migration (de Jong et al. 2007; Radburn-Smith et al. 2011; Yoachim et al. 2010, 2012), confirmed by numerical simulations (see Roškar et al. 2008; Sánchez-Blázquez et al. 2009); or stellar migration induced by resonances produced by strong bars (Debattista et al. 2006; Foyle et al. 2008; Muñoz-Mateos et al. 2013).
Antitruncations of stellar discs, which are also observed in the corresponding dust emission profiles, are connected to activity in the outer galaxy parts which can be related to the disc (interactions with other galaxies triggering outer star formation, see Elmegreen & Hunter 2006) or the galaxy spheroid (minor merging/smooth gas accretion, see Younger et al. 2007; Minchev et al. 2012).
Obviously, the observed breaks in the dust discs should have the same origin as proposed for explaining the breaks in the stellar discs.
5.4.4. Triggered star formation in the galaxy inner region
Interestingly, in some galaxies of the same morphological type the Sérsic index of the dust emission profile is Gaussian, whereas in others we can see a profile close to exponential or even with a Sérsic index much larger than 1 (see Fig. 10 for the galaxies NGC 3631, NGC 4030, and NGC 4214). A careful investigation of this fact showed that when a triggered star formation in the central region takes place, in the FIR we do not see a depletion in the centre of the SB profile, and often, on the contrary, we observe a “bump” of dust emission in the centre. This star formation activity in the inner region can be caused by several reasons.
Sauvage et al. (2010) studied a bright central component in three nearby spiral galaxies. They noticed that the rising profile in the inner part of M 100 is related to the more prominent bulge, bar, or inner-disc component, whereas in M 81 a small AGN boosts the emission from transiently heated dust grains.
Using the NED database, we selected galaxies which are classified as “Sy” or “LINER”, meaning that with these galaxies some activity in the centre is associated. The total number of such galaxies in the DustPedia sample is 90, from which 34 galaxies have determined Sérsic models. For these galaxies, we found their average Sérsic index in the SPIRE 250 μm band to be 1.29 ± 0.47. The large scatter can be explained by the fact that the activity (power) of the AGN is different in these galaxies. In some, the AGN does not contribute much emission in the FIR (NGC 613), whereas in others it is the most luminous component (for example, NGC 7465).
For seven NED-classified starburst galaxies out of 320 galaxies in our sample, we found that their profiles show particularly high Sérsic indices which decrease with wavelength from PACS 100 to SPIRE 500: 2.93 ± 1.97, 2.64 ± 1.60, 2.22 ± 1.79, 1.73 ± 1.38, and 1.20 ± 0.62. Six starburst galaxies (NGC 3049, NGC 3504, NGC 4123, NGC 4416, NGC 4779, and NGC 4904) have an apparent bar structure and a relatively bright nucleus. As was shown in Mihos & Hernquist (1994), and Di Matteo et al. (2007, 2008), through the bar instability, which may be triggered by interaction with other galaxies or a minor merging event, gas can be effectively funneled towards the galactic nucleus. This ignites bursts of star formation near the galaxy centre, which, in its turn, leads to efficient dust producing. The star formation burst heats the dust in the inner galaxy region and increases the fraction of warm dust emission in the FIR domain of the galaxy SED. This leads to increasing the Sérsic index in these galaxies, with its dependence on wavelength, as the contribution of the warm dust emission to the total emission decreases with wavelength.
Another reason which explains the steeper profile in the inner region in some galaxies is the presence of a pseudobulge. There exist at least two families of bulges in galaxies (see reviews by Kormendy & Kennicutt 2004; Kormendy 2013): pseudobulges (bulges made through secular evolution) and classical bulges (bulges made through hierarchical mergers). Pseudobulges can be identified by the presence of a disc-like structure in the centre of the galaxy (nuclear spirals, nuclear bars, and high ellipticity in bulge) and classical bulges with smooth isophotes that are round compared to the outer disc and show no discy structure in their bulge. Fisher (2006) showed that pseudobulges have significantly higher specific SFRs than classical bulges. Also, the PAH emission profiles of pseudobulges are brighter and more centrally concentrated without a transition in star formation properties from the outer disc to the central pseudobulge. On the contrary, classical bulges exhibit remarkably regular star formation profiles in the inner region with a sharp change (decline) in star formation rate towards the galaxy centre. In addition, it was shown that galaxies with bars or ovals, on average, have brighter central PAH emission than galaxies without strong drivers of secular evolution (see also Sakamoto et al. 1999; Sheth et al. 2005).
To verify that the bulge type and the bar strength have impact on dust emission, we selected galaxies with available multi-component decomposition in the S4G database.
Fisher et al. (2009) showed that more massive pseudobulges have higher SFR density. In Fig. 14, left plot, we show the correlation between the bulge fraction to the total galaxy luminosity (mass) in the 3.6 μm band and the Sérsic index in SPIRE 250 (which is related to the central SFR density), for classical bulges and pseudobulges (we identify them by the Sérsic index 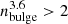 for classical bulges and
for classical bulges and 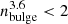 for pseudobulges, see Fisher & Drory 2010). One can see that for the pseudobulges there exists a correlation between these two quantities, whereas for the classical bulges without a prominent star formation this correlation does not exist. This correlation indicates that the more luminous/massive the pseudobulge is as compared to the total galaxy luminosity/mass, the steeper the dust emission profile in the inner region.
for pseudobulges, see Fisher & Drory 2010). One can see that for the pseudobulges there exists a correlation between these two quantities, whereas for the classical bulges without a prominent star formation this correlation does not exist. This correlation indicates that the more luminous/massive the pseudobulge is as compared to the total galaxy luminosity/mass, the steeper the dust emission profile in the inner region.
 |
Fig. 14. Correlations between the bulge (left plot) and bar (right plot) fraction to the total galaxy model, based on the S4G decomposition, and the Sérsic index in the SPIRE 250 μm band. The black dashed lines in each plot represent the regression lines: log n250 = 0.68 fbulge + 0.65 (ρ = 0.78) and log n250 = 0.82 fbar + 0.81 (ρ = 0.60). |
We also studied a similar correlation but for the bar fraction to the total galaxy luminosity (Fig. 14, right plot). This correlation is weaker but still we can see that galaxies with stronger bars (defined as having a higher fraction to the total galaxy luminosity at 3.6 μm) have dust emission profiles with a larger Sérsic index. However, the situation here is complicated by the fact that bars may have some inner structures with a triggered star formation: from pseudobulge to AGN galaxy-scale (see also Vera et al. 2016).
In our sample we have a few irregular galaxies (T = 9 − 10) which do not have a distinct well-organised structure, though most of them feature a patchy disc with some trace of a bar and/or spiral arms. Among them we can find a large variety of structural features which are typical for irregular galaxies: a starburst nucleus (NGC 4194), a pseudobulge structure (NGC 4214, Fisher & Drory 2011), an elongated bar (NGC 3846A), a ring (NGC 1427A), and a faint spiral pattern (NGC 4032). UGC 5720 is also classified as a blue compact dwarf galaxy (Thuan & Martin 1981; Gil de Paz et al. 2003). In the optical, in almost all of these galaxies we observe multiple blue “beads” of starforming regions, which in the FIR are associated with bright dust emission features. As shown in Fig. 8, the mean Sérsic index for irregular galaxies is close to 1, however there are Irr galaxies with a very small Sérsic index (e.g. for NGC 3846A n250 = 0.37), as well as with a large Sérsic index (for NGC 4214 n250 = 3.40). Galaxies with a large Sérsic index demonstrate intensive star formation in the central region which naturally results in a higher Sérsic index. The inner region in irregular galaxies with a Gaussian profile does not show a high star formation and this explains their small Sérsic index.
5.4.5. Dust heating
The continuum emission from dust depends both on the column-density and temperature of the dust. The dust is heated by starlight, coming from both sites of the hot young stars in star-formation regions and from more evolved (old) stellar populations, as well as from the presence of AGN (e.g. Draine & Li 2007). FIR/submm wavelengths give information on the dominant heating mechanism of dust, though no clear picture about the exact fraction of dust heating contributed by each stellar population has been created (e.g. Law et al. 2011; Boquien et al. 2011; Bendo et al. 2012, 2015; Hunt et al. 2015): it depends on the intrinsic SED of the stellar populations, the dust mass and optical properties, as well as the relative dust-star geometry. For example, the heating of dust in the galaxy centre can be initiated by the old stellar population of the luminous bulge in S0-Sb galaxies and AGN galaxies (dust torus?). This might be the reason for the higher Sérsic index in the FIR wavebands observed in these galaxies.
In this study we do not analyse the dust-density but only dust emission profiles of galaxies. Therefore, formally, our conclusions relate to the dust emission profiles and cannot be extended to the dust density profiles automatically. To create the dust mass density distribution in a galaxy some additional modelling should be done (see e.g. Muñoz-Mateos et al. 2009; Smith et al. 2016; Casasola et al. 2017), which is beyond the scope of this paper and will be done in a subsequent DustPedia study. However, the comparison with the other works (see above), where such dust mass density distributions have been analysed, and for our simulations in Appendix B showed that the dust emission in the FIR/submm region generally follows the dust mass density distribution. Therefore, this suggests that the conclusions of this study should work for the mass density distribution of dust in galaxies as well.
6. Conclusions
We have studied the two-dimensional distribution of stellar and dust tracers in galaxies selected from the DustPedia sample. For this purpose we used WISE W1 and Herschel (from PACS 100 to SPIRE 500) observations gathered in the DustPedia database. All galaxy images have been homogeneously treated and prepared for fitting. Using a new version of the Python wrapper DECA, we fitted the 2D SB distribution of the galaxies with a single Sérsic profile and determined their best-fit structural parameters. For the galaxy images in the WISE W1 band, we used the GALFIT code, whereas for the Herschel observations, both GALFIT and GALFITM were applied. Using DECA, we were able to properly fit even those galaxies which reside in a close pair or interact, and most of the galaxies where a bright foreground star contaminates the light from the target galaxy.
Our main results can be summarised as follows:
-
We derived structural parameters for the whole DustPedia sample based on their WISE W1 images. These parameters are the overall Sérsic index (related to galaxy morphology), the effective radius (which is an indication of the galaxy’s size), and its total luminosity, upon which the stellar mass was computed.
-
For 320 DustPedia galaxies we obtained reliable 2D Sérsic models based on the available Herschel images in all five FIR bands.
-
The obtained set of the parameters puts constrains on the structural properties of the dust component. We found that there is no significant change in the Sérsic index at 100–500 μm. This indicates that the dust emission profile is essentially the same in the fitted Herschel bands. The average value at 250 μm is 0.67 ± 0.37 (187 galaxies are fitted with n250 ≤ 0.75, 87 galaxies have 0.75 < n250 ≤ 1.25, and 46 – with n250 > 1.25). This signifies that, formally, cold dust in galaxies is distributed by a non-exponential law. Plenty of galaxies in our sample demonstrate a Gaussian dust emission profile – with a depression in the central region up to the characteristic radius rc ≈ 0.4 r25 and a rather exponential decline in the outer region. We suggest that this is related to the depletion in the inner region of the HI surface density profiles. In this region the atomic gas reaches high enough surface densities to be transformed into molecular form. When a triggered star formation in the central region takes place (e.g. because of a bar instability, formation of a pseudobulge, AGN activity etc.), we observe a SB profile of the cold dust emission with a steeper decline in this region (no depression in the centre). We confirm the result by Pohlen et al. (2010) that the dust mostly shows the same breaks of Type II in the radial profiles as seen in the optical and NIR at rbr ≈ 0.6 r25. The Type III breaks are seen in the FIR and optical as well.
-
The effective radius of the dust SB profile steadily increases with wavelength, from 0.90 ± 0.27 in PACS 100 to 1.41 ± 0.43 in SPIRE 500, most likely because of the cold-dust temperature gradient with galactocentric distance.
The fit results for the WISE W1 and Herschel data are available on the DustPedia database.
Our future follow-up studies will be focused on a detailed decomposition of well-resolved DustPedia galaxies, by taking into account several dust components which are associated with different galaxy substructures.
See the photometry files at http://dustpedia.astro.noa.gr/Photometry
Acknowledgments
A.V.M. expresses gratitude for the grant of the Russian Foundation for Basic Researches number mol_a 18-32-00194. IDL gratefully acknowledges the support of the Flemish Fund for Scientific Research (FWO-Vlaanderen). The DustPedia project is funded by the European Union, as a European Research Council (ERC) 7th Framework Program (FP7) project (PI Jon Davies, proposal 606824). JF acknowledges the financial support from UNAM-DGAPA-PAPIIT IA104015 grant, México. This research made use of MONTAGE (http://montage.ipac.caltech.edu/), which is funded by the National Science Foundation under Grant Number ACI-1440620, and was previously funded by the National Aeronautics and Space Administration’s Earth Science Technology Office, Computation Technologies Project, under Cooperative Agreement Number NCC5-626 between NASA and the California Institute of Technology. This research has made use of the NASA/IPAC Infrared Science Archive (IRSA; http://irsa.ipac.caltech.edu/frontpage/), and the NASA/IPAC Extragalactic Database (NED; https://ned.ipac.caltech.edu/), both of which are operated by the Jet Propulsion Laboratory, California Institute of Technology, under contract with the National Aeronautics and Space Administration. This research has made use of the HyperLEDA database (http://leda.univ-lyon1.fr/; Makarov et al. 2014). This research makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, and NEOWISE, which is a project of the Jet Propulsion Laboratory/California Institute of Technology. WISE and NEOWISE are funded by the National Aeronautics and Space Administration. This work is based in part on observations made with the Spitzer Space Telescope, which is operated by the Jet Propulsion Laboratory, California Institute of Technology under a contract with NASA. Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA. The Herschel spacecraft was designed, built, tested, and launched under a contract to ESA managed by the Herschel/Planck Project team by an industrial consortium under the overall responsibility of the prime contractor Thales Alenia Space (Cannes), and including Astrium (Friedrichshafen) responsible for the payload module and for system testing at spacecraft level, Thales Alenia Space (Turin) responsible for the service module, and Astrium (Toulouse) responsible for the telescope, with in excess of a hundred subcontractors. This research has made use of “Aladin sky atlas” developed at CDS, Strasbourg Observatory, France.
References
- Aguerri, J. A. L., Iglesias-Páramo, J., Vílchez, J. M., Muñoz-Tuñón, C., & Sánchez-Janssen, R. 2005, AJ, 130, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Alton, P. B., Trewhella, M., Davies, J. I., et al. 1998, A&A, 335, 807 [NASA ADS] [Google Scholar]
- Alton, P. B., Xilouris, E. M., Misiriotis, A., Dasyra, K. M., & Dumke, M. 2004, A&A, 425, 109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Amorín, R. O., Muñoz-Tuñón, C., Aguerri, J. A. L., Cairós, L. M., & Caon, N. 2007, A&A, 467, 541 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Andredakis, Y. C., Peletier, R. F., & Balcells, M. 1995, MNRAS, 275, 874 [NASA ADS] [CrossRef] [Google Scholar]
- Astropy Collaboration (Robitaille, T. P., et al.) 2013, A&A, 558, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Azzollini, R., Trujillo, I., & Beckman, J. E. 2008, ApJ, 684, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Baes, M., Fritz, J., Gadotti, D. A., et al. 2010, A&A, 518, L39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bakos, J., Trujillo, I., & Pohlen, M. 2008, ApJ, 683, L103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bamford, S. P., Häußler, B., Rojas, A., & Borch, A. 2011, in Astronomical Data Analysis Software and Systems XX, eds. I. N. Evans, A. Accomazzi, D. J. Mink, & A. H. Rots, ASP Conf. Ser., 442, 479 [NASA ADS] [Google Scholar]
- Bendo, G. J., Boselli, A., Dariush, A., et al. 2012, MNRAS, 419, 1833 [NASA ADS] [CrossRef] [Google Scholar]
- Bendo, G. J., Baes, M., Bianchi, S., et al. 2015, MNRAS, 448, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S. 2007, A&A, 471, 765 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S. 2008, A&A, 490, 461 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bianchi, S., & Xilouris, E. M. 2011, A&A, 531, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bigiel, F., & Blitz, L. 2012, ApJ, 756, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Bocchio, M., Bianchi, S., & Abergel, A. 2016, A&A, 591, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boch, T., & Fernique, P. 2014, in Astronomical Data Analysis Software and Systems XXIII, eds. N. Manset, & P. Forshay, ASP Conf. Ser., 485, 277 [NASA ADS] [Google Scholar]
- Bonnarel, F., Fernique, P., Bienaymé, O., et al. 2000, A&AS, 143, 33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boquien, M., Calzetti, D., Combes, F., et al. 2011, AJ, 142, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Boselli, A., Eales, S., Cortese, L., et al. 2010, PASP, 122, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Byun, Y. I., & Freeman, K. C. 1995, ApJ, 448, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Caldwell, N. 1999, AJ, 118, 1230 [NASA ADS] [CrossRef] [Google Scholar]
- Caon, N., Capaccioli, M., & D’Onofrio, M. 1993, MNRAS, 265, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Caon, N., Cairós, L. M., Aguerri, J. A. L., & Muñoz-Tuñón, C. 2005, ApJS, 157, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M. 2002, MNRAS, 333, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Casasola, V., Cassarà, L. P., Bianchi, S., et al. 2017, A&A, 605, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clark, C. J. R., Verstocken, S., Bianchi, S., et al. 2018, A&A, 609, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cox, P., & Mezger, P. G. 1989, A&ARv, 1, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Dasyra, K. M., Xilouris, E. M., Misiriotis, A., & Kylafis, N. D. 2005, A&A, 437, 447 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davies, J. I., Baes, M., Bianchi, S., et al. 2017, PASP, 129, 044102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Geyter, G., Baes, M., Fritz, J., & Camps, P. 2013, A&A, 550, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Geyter, G., Baes, M., Camps, P., et al. 2014, MNRAS, 441, 869 [NASA ADS] [CrossRef] [Google Scholar]
- De Geyter, G., Baes, M., Camps, P., Fritz, J., & Viaene, S. 2015a, in Galaxies in 3D across the Universe, eds. B. L. Ziegler, F. Combes, H. Dannerbauer, & M. Verdugo, IAU Symp., 309, 309 [NASA ADS] [Google Scholar]
- De Geyter, G., Baes, M., De Looze, I., et al. 2015b, MNRAS, 451, 1728 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, R. S. 1996, A&AS, 118, 557 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Jong, T., Clegg, P. E., Soifer, B. T., et al. 1984, ApJ, 278, L67 [NASA ADS] [CrossRef] [Google Scholar]
- de Jong, R. S., Seth, A. C., Radburn-Smith, D. J., et al. 2007, ApJ, 667, L49 [NASA ADS] [CrossRef] [Google Scholar]
- De Looze, I., Baes, M., Bendo, G. J., et al. 2012a, MNRAS, 427, 2797 [NASA ADS] [CrossRef] [Google Scholar]
- De Looze, I., Baes, M., Fritz, J., & Verstappen, J. 2012b, MNRAS, 419, 895 [NASA ADS] [CrossRef] [Google Scholar]
- De Looze, I., Fritz, J., Baes, M., et al. 2014, A&A, 571, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Souza, R. E., Gadotti, D. A., & dos Anjos, S. 2004, ApJS, 153, 411 [NASA ADS] [CrossRef] [Google Scholar]
- Debattista, V. P., Mayer, L., Carollo, C. M., et al. 2006, ApJ, 645, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, P., Combes, F., Melchior, A.-L., & Semelin, B. 2007, A&A, 468, 61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Di Matteo, P., Bournaud, F., Martig, M., et al. 2008, A&A, 492, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Onofrio, M. 2001, MNRAS, 326, 1517 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Li, A. 2007, ApJ, 657, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Dwek, E. 1986, ApJ, 302, 363 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, D. M., & Elmegreen, B. G. 1984, ApJS, 54, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., & Hunter, D. A. 2006, ApJ, 636, 712 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Monnet, G., & Bacon, R. 1994, A&A, 285, 723 [NASA ADS] [Google Scholar]
- Erwin, P. 2015, ApJ, 799, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Erwin, P., Beckman, J. E., & Pohlen, M. 2005, ApJ, 626, L81 [Google Scholar]
- Erwin, P., Pohlen, M., & Beckman, J. E. 2008, AJ, 135, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Fazio, G. G., Hora, J. L., Allen, L. E., et al. 2004, ApJS, 154, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, D. B. 2006, ApJ, 642, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, D. B., & Drory, N. 2010, ApJ, 716, 942 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, D. B., & Drory, N. 2011, ApJ, 733, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Fisher, D. B., Drory, N., & Fabricius, M. H. 2009, ApJ, 697, 630 [NASA ADS] [CrossRef] [Google Scholar]
- Foyle, K., Courteau, S., & Thacker, R. J. 2008, MNRAS, 386, 1821 [NASA ADS] [CrossRef] [Google Scholar]
- Gabor, J. M., Impey, C. D., Jahnke, K., et al. 2009, ApJ, 691, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Gadotti, D. A. 2008, MNRAS, 384, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Gadotti, D. A. 2009, MNRAS, 393, 1531 [NASA ADS] [CrossRef] [Google Scholar]
- Galliano, F., Galametz, M., & Jones, A. P. 2018, ARA&A, 56, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Gil de Paz, A., Madore, B. F., & Pevunova, O. 2003, ApJS, 147, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Giovanelli, R., Haynes, M. P., Salzer, J. J., et al. 1994, AJ, 107, 2036 [NASA ADS] [CrossRef] [Google Scholar]
- Goldberg, D. E. 1989, Genetic Algorithms in Search, Optimization and Machine Learning (Addison-Wesley) [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Grosbol, P. 1993, PASP, 105, 651 [NASA ADS] [CrossRef] [Google Scholar]
- Gutiérrez, L., Erwin, P., Aladro, R., & Beckman, J. E. 2011, AJ, 142, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Häussler, B., McIntosh, D. H., Barden, M., et al. 2007, ApJS, 172, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Häußler, B., Bamford, S. P., Vika, M., et al. 2013, MNRAS, 430, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D. J., & Tielens, A. G. G. M. 1997, ARA&A, 35, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Holwerda, B. W., Bianchi, S., Böker, T., et al. 2012, A&A, 541, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hoyos, C., den Brok, M., Verdoes Kleijn, G., et al. 2011, MNRAS, 411, 2439 [NASA ADS] [CrossRef] [Google Scholar]
- Huang, S., Ho, L. C., Peng, C. Y., Li, Z.-Y., & Barth, A. J. 2013, ApJ, 766, 47 [NASA ADS] [CrossRef] [Google Scholar]
- Hubble, E. P. 1926, ApJ, 64 [Google Scholar]
- Hunt, L. K., Draine, B. T., Bianchi, S., et al. 2015, A&A, 576, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kelvin, L. S., Driver, S. P., Robotham, A. S. G., et al. 2012, MNRAS, 421, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Kennedy, R., Bamford, S. P., Häußler, B., et al. 2016, MNRAS, 460, 3458 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1989, ApJ, 344, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C. 1998, ApJ, 498, 541 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr., R. C., Armus, L., Bendo, G., et al. 2003, PASP, 115, 928 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., Calzetti, D., Aniano, G., et al. 2011, PASP, 123, 1347 [NASA ADS] [CrossRef] [Google Scholar]
- Kessler, M. F., Steinz, J. A., Anderegg, M. E., et al. 1996, A&A, 315, L27 [NASA ADS] [Google Scholar]
- Kettlety, T., Hesling, J., Phillipps, S., et al. 2018, MNRAS, 473, 776 [NASA ADS] [CrossRef] [Google Scholar]
- Kormendy, J. 2013, in Secular Evolution in Disk Galaxies, eds. J. Falcón-Barroso, & J. H. Knapen, 1 [Google Scholar]
- Kormendy, J., & Kennicutt, Jr., R. C. 2004, ARA&A, 42, 603 [NASA ADS] [CrossRef] [Google Scholar]
- La Barbera, F., de Carvalho, R. R., de La Rosa, I. G., et al. 2010, MNRAS, 408, 1313 [NASA ADS] [CrossRef] [Google Scholar]
- Laurikainen, E., Salo, H., & Buta, R. 2005, MNRAS, 362, 1319 [NASA ADS] [CrossRef] [Google Scholar]
- Law, K.-H., Gordon, K. D., & Misselt, K. A. 2011, ApJ, 738, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Lisenfeld, U., Verdes-Montenegro, L., Sulentic, J., et al. 2007, A&A, 462, 507 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- MacLachlan, J. M., Matthews, L. D., Wood, K., & Gallagher, J. S. 2011, ApJ, 741, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Makarov, D., Prugniel, P., Terekhova, N., Courtois, H., & Vauglin, I. 2014, A&A, 570, A13 [CrossRef] [EDP Sciences] [Google Scholar]
- Méndez-Abreu, J., Ruiz-Lara, T., Sánchez-Menguiano, L., et al. 2017, A&A, 598, A32 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mihos, J. C., & Hernquist, L. 1994, ApJ, 425, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Minchev, I., Famaey, B., Quillen, A. C., et al. 2012, A&A, 548, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Misiriotis, A., Popescu, C. C., Tuffs, R., & Kylafis, N. D. 2001, A&A, 372, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Möllenhoff, C. 2004, A&A, 415, 63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosenkov, A. V. 2014, Astrophys. Bull., 69, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Mosenkov, A. V., Sotnikova, N. Y., & Reshetnikov, V. P. 2010, MNRAS, 401, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Mosenkov, A. V., Sotnikova, N. Y., Reshetnikov, V. P., Bizyaev, D. V., & Kautsch, S. J. 2015, MNRAS, 451, 2376 [NASA ADS] [CrossRef] [Google Scholar]
- Mosenkov, A. V., Allaert, F., Baes, M., et al. 2016, A&A, 592, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosenkov, A. V., Allaert, F., Baes, M., et al. 2018, A&A, 616, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moshir, M., Kopan, G., Conrow, T., et al. 1990, BAAS, 22, 1325 [Google Scholar]
- Muñoz-Mateos, J. C., Gil de Paz, A., Boissier, S., et al. 2009, ApJ, 701, 1965 [NASA ADS] [CrossRef] [Google Scholar]
- Muñoz-Mateos, J. C., Sheth, K., Gil de Paz, A., et al. 2013, ApJ, 771, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Naim, A., Lahav, O., Buta, R. J., et al. 1995, MNRAS, 274, 1107 [NASA ADS] [Google Scholar]
- Neugebauer, G., Habing, H. J., van Duinen, R., et al. 1984, ApJ, 278, L1 [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2002, AJ, 124, 266 [NASA ADS] [CrossRef] [Google Scholar]
- Peng, C. Y., Ho, L. C., Impey, C. D., & Rix, H.-W. 2010, AJ, 139, 2097 [NASA ADS] [CrossRef] [Google Scholar]
- Peters, S. P. C., de Geyter, G., van der Kruit, P. C., & Freeman, K. C. 2017, MNRAS, 464, 48 [NASA ADS] [CrossRef] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pohlen, M., & Trujillo, I. 2006, A&A, 454, 759 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pohlen, M., Cortese, L., Smith, M. W. L., et al. 2010, A&A, 518, L72 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Popescu, C. C., & Tuffs, R. J. 2002, MNRAS, 335, L41 [NASA ADS] [CrossRef] [Google Scholar]
- Popescu, C. C., Misiriotis, A., Kylafis, N. D., Tuffs, R. J., & Fischera, J. 2000, A&A, 362, 138 [NASA ADS] [Google Scholar]
- Popescu, C. C., Tuffs, R. J., Dopita, M. A., et al. 2011, A&A, 527, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Querejeta, M., Meidt, S. E., Schinnerer, E., et al. 2015, ApJS, 219, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Radburn-Smith, D. J., de Jong, R. S., Seth, A. C., et al. 2011, ApJS, 195, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Radburn-Smith, D. J., Roškar, R., Debattista, V. P., et al. 2012, ApJ, 753, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Ravindranath, S., Ferguson, H. C., Conselice, C., et al. 2004, ApJ, 604, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Reese, A. S., Williams, T. B., Sellwood, J. A., Barnes, E. I., & Powell, B. A. 2007, AJ, 133, 2846 [NASA ADS] [CrossRef] [Google Scholar]
- Reshetnikov, V., & Combes, F. 2015, MNRAS, 447, 2287 [NASA ADS] [CrossRef] [Google Scholar]
- Rix, H.-W., & Zaritsky, D. 1995, ApJ, 447, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Roškar, R., Debattista, V. P., Stinson, G. S., et al. 2008, ApJ, 675, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, K., Okumura, S. K., Ishizuki, S., & Scoville, N. Z. 1999, ApJ, 525, 691 [NASA ADS] [CrossRef] [Google Scholar]
- Salo, H., Laurikainen, E., Laine, J., et al. 2015, ApJS, 219, 4 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez-Blázquez, P., Courty, S., Gibson, B. K., & Brook, C. B. 2009, MNRAS, 398, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Mazzarella, J. M., Kim, D.-C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [Google Scholar]
- Sauvage, M., Tuffs, R. J., & Popescu, C. C. 2005, Space Sci. Rev., 119, 313 [NASA ADS] [CrossRef] [Google Scholar]
- Sauvage, M., Sacchi, N., Bendo, G. J., et al. 2010, A&A, 518, L64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schechtman-Rook, A., & Bershady, M. A. 2014, ApJ, 795, 136 [NASA ADS] [CrossRef] [Google Scholar]
- Sérsic, J. L. 1968, Atlas de Galaxias Australes (Cordoba, Argentina: Observatorio Astronomico) [Google Scholar]
- Sheth, K., Vogel, S. N., Regan, M. W., Thornley, M. D., & Teuben, P. J. 2005, ApJ, 632, 217 [NASA ADS] [CrossRef] [Google Scholar]
- Sheth, K., Regan, M., Hinz, J. L., et al. 2010, PASP, 122, 1397 [NASA ADS] [CrossRef] [Google Scholar]
- Simard, L. 1998, in Astronomical Data Analysis Software and Systems VII, eds. R. Albrecht, R. N. Hook, & H. A. Bushouse, ASP Conf. Ser., 145, 108 [NASA ADS] [Google Scholar]
- Smith, M. W. L., Gomez, H. L., Eales, S. A., et al. 2012, ApJ, 748, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, M. W. L., Eales, S. A., De Looze, I., et al. 2016, MNRAS, 462, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Swaters, R. A., van Albada, T. S., van der Hulst, J. M., & Sancisi, R. 2002, A&A, 390, 829 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Thuan, T. X., & Martin, G. E. 1981, ApJ, 247, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Venhola, A., Peletier, R., Laurikainen, E., et al. 2017, A&A, 608, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vera, M., Alonso, S., & Coldwell, G. 2016, A&A, 595, A63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verstappen, J., Fritz, J., Baes, M., et al. 2013, A&A, 556, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viaene, S., De Geyter, G., Baes, M., et al. 2015, A&A, 579, A103 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viaene, S., Baes, M., Bendo, G., et al. 2016, A&A, 586, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Viaene, S., Baes, M., Tamm, A., et al. 2017, A&A, 599, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vika, M., Bamford, S. P., Häußler, B., et al. 2013, MNRAS, 435, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Vika, M., Bamford, S. P., Häußler, B., & Rojas, A. L. 2014, MNRAS, 444, 3603 [NASA ADS] [CrossRef] [Google Scholar]
- Vika, M., Vulcani, B., Bamford, S. P., Häußler, B., & Rojas, A. L. 2015, A&A, 577, A97 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vulcani, B., Bamford, S. P., Häußler, B., et al. 2014, MNRAS, 441, 1340 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, J., Fu, J., Aumer, M., et al. 2014, MNRAS, 441, 2159 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, M. W., Roellig, T. L., Low, F. J., et al. 2004, ApJS, 154, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wevers, B. M. H. R., Appleton, P. N., Davies, R. D., & Hart, L. 1984, A&A, 140, 125 [NASA ADS] [Google Scholar]
- Wolfire, M. G., Hollenbach, D., McKee, C. F., Tielens, A. G. G. M., & Bakes, E. L. O. 1995, ApJ, 443, 152 [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Xilouris, E. M., Kylafis, N. D., Papamastorakis, J., Paleologou, E. V., & Haerendel, G. 1997, A&A, 325, 135 [NASA ADS] [Google Scholar]
- Xilouris, E. M., Alton, P. B., Davies, J. I., et al. 1998, A&A, 331, 894 [NASA ADS] [Google Scholar]
- Xilouris, E. M., Byun, Y. I., Kylafis, N. D., Paleologou, E. V., & Papamastorakis, J. 1999, A&A, 344, 868 [NASA ADS] [Google Scholar]
- Yoachim, P., Roškar, R., & Debattista, V. P. 2010, ApJ, 716, L4 [NASA ADS] [CrossRef] [Google Scholar]
- Yoachim, P., Roškar, R., & Debattista, V. P. 2012, ApJ, 752, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Younger, J. D., Cox, T. J., Seth, A. C., & Hernquist, L. 2007, ApJ, 670, 269 [Google Scholar]
Appendix A: Data preparation
We exploited the aperture photometry analysis which had been carried out in C18. For each galaxy, C18 determined a photometric master aperture ellipse5, which is described by the semimajor axis (sma) and ellipticity (ϵ). Also, carefully calculated total fluxes and their uncertainties over a large set of wavelengths are provided.
First, for each galaxy, we rebinned its Herschel images to the PACS 100 μm band image which has the best resolution among all chosen PACS and SPIRE bands. The corresponding sigma- and PSF-images were rebinned as well, to match their rebinned flux density maps.
To properly estimate background emission, we masked out all objects on the images which lie outside of the aperture ellipse. The masking was performed using a combined mask created by SEXTRACTOR (Bertin & Arnouts 1996) and the Astropy (Astropy Collaboration 2013) Python library6, the routine Findpeaks.
After masking background and foreground sources, a 2D 5th-order polynomial sky model was fitted to remove large-scale background emission. It was estimated within an annulus with the inner semimajor axis 1.250 sma, the outer semimajor axis 1.601 sma, and the ellipticity ϵ (see C18). For galaxies without enough empty space for a robust determination of the background emission in this way, we fitted the background simultaneously with the galaxy (see Sect. 3). Also, the same approach is applied to galaxies which have some bright glow in the WISE W1 band from close saturated stars.
After removing background emission, we used the same routine, as previously, to mask objects overlapping with the primary galaxy, with the revision of the created masks and fixing incorrect detections if needed. In this step, foreground stars, bright clumpy details (e.g. bright starforming and HII regions), and small satellite galaxies, which overlap the body of the galaxy, were masked out. Obviously, all these features cannot be described by a single Sérsic function, see Sect. 3. However if the contamination of a non target source was too high (from a foreground star or an extended object), this source was not included in the final mask and, instead, was fitted simultaneously with the primary galaxy (see Sect. 3).
To match the final WISE W1 galaxy image, the WISE W1 PSF image was rotated by some angle. This position angle was found using the following approach. First, in each retrieved WISE W1 map, we selected 5 point-like sources (unsaturated, non-overlapping stars with a high S/N). Then we fitted the selected stars with a PSF function (available in GALFIT) multiple times, rotating each time the PSF image by an angle from 0° to 360°, with a step of 1°. The PSF position angle with the smallest χ2 value was then chosen to be the correct angle. After that, we found an average angle for all five stars and rotated the original PSF image for each galaxy frame by the corresponding position angle.
As to the FIR/submm observations, all Herschel PSF images were rotated by an average angle (the average of the list with PSFs, which are the scanning directions for all obsIDs used in the image) between the scanning direction of the telescope and the north direction.
The final step is to cut out the galaxy by cropping the galaxy images (if possible) to encompass the ellipse with a semimajor axis of 2 sma and an ellipticity ϵ. We insure that all images have sufficient empty background space included. For the Herschel images, if an original image, provided in the DustPedia database for a galaxy, is smaller than the size of the required cut-out image for this galaxy, than no cropping was done.
Appendix B: The fitting of mock galaxy images
To verify the robustness of our fitting method (see Sect. 3) in its ability to recover the properties of the dust distribution in galaxies, we apply the following approach. Mosenkov et al. (2016) performed a consistent fitting of the stellar and dust structural components and obtained a plausible complex model of one of the galaxies from the HEROES (HERschel Observations of Edge-on Spirals, Verstappen et al. 2013) sample, IC 2531. Despite the fact that for this galaxy they found the dust energy balance problem, we adopted their results in the current study to create realistic galaxy simulations and then estimate the dust distribution parameters in the FIR/submm for these galaxy images using the technique described in Sect. 3. Potentially, the dust energy balance problem in IC 2531 might affect the reliability of our simulations (as compared to real galaxies). However, as no commonly accepted solution to the dust energy problem has yet been proposed, we decided to consider this simplified galaxy model to merely test our fitting method and to study the dependence of the retrieved dust distribution parameters on wavelength. We should point out that this problem is unlikely to be related to the observed depression in the dust emission profile discovered in many DustPedia galaxies (see Sect. 5.4 for possible explanations of this fact). If we used a dust density profile with a depression in the centre (e.g. a Sérsic profile with n ≈ 0.5−0.7), then the dust energy problem would be even worse as less emission would be radiated in the central region as compared to the exponential profile.
The model of IC 2531, adopted from Mosenkov et al. (2016) consists of several stellar components (a superthin young disc, a thin disc, a thick disc, and a bulge) and a dust disc. The model parameters, as well as some other quantities, which we use in our panchromatic RT modelling, are listed in Table B.1.
Using the model of IC 2531, we created a set of RT simulations at the wavelengths 3.4 μm, 100 μm, 160 μm, 250 μm, 350 μm, and 500 μm, which correspond to the WISE W1 and Herschel bands. We used the RT code SKIRT to create the mock galaxy images. In our simulations, we varied the galaxy inclination angle i and the distance to it D using the normal distributions for the these parameters (⟨i⟩=57°, σi = 22° and ⟨D⟩ = 21.6 Mpc, σD = 11.1 Mpc – these are the average values for the DustPedia sample). By doing so, we created a sample of 300 galaxies: for each galaxy we tried both an exponential and Sérsic disc to describe the dust component (see Table B.1). The output mock galaxy images in each band were then rebinned and convolved (the details of the pixel size and the PSF in each band are provided in Sect. 2) to match the corresponding WISE W1 and Herschel bands. Also, the following Gaussian noise was added to the created frames, estimated from the real observations of IC 2531: 0.00035 mJy pix−1 (in WISE W1), 0.51 mJy pix−1 (in PACS 100), 0.68 mJy pix−1 (in PACS 160), 0.91 mJy pix−1 (in SPIRE 250), 1.31 mJy pix−1 (in SPIRE 350), and 1.47 mJy pix−1 (in SPIRE 500).
Structural parameters of the multi-component decomposition model for IC 2531 adopted from Mosenkov et al. (2016), with an originally used double-exponential dust disc or an alternative Sérsic dust disc (not used in Mosenkov et al. 2016).
Results of the fitting for the mock galaxy images with a double-exponential and Sérsic dust disc.
Using our code DECA (see Sect. 3), we performed a single Sérsic fitting of the created mock galaxy images in the WISE W1 and Herschel bands. The results of our fitting are summarised in Table B.2. Here we concentrate on the distributions by the Sérsic index, whereas we comment on the other parameters (for example, the effective radius) in Sect. 4. As one can see, the Sérsic index of the dust emission profile, recovered by DECA, is approximately 0.9–1.0 if the dust mass density distribution is given by an exponential law. If the dust density is given by a Sérsic law with nd = 0.6, then for the PACS bands the retrieved Sérsic index appeared to be somewhat higher (nd = 0.7−0.8), as compared to the Sérsic index of the dust density profile. However, for the SPIRE bands, it is approximately 0.6–0.7, i.e. the Sérsic index of the dust emission is almost the same as the Sérsic index of the dust mass density profile. Thus, we can conclude that the distribution of dust emission in the SPIRE bands should be very close to the real dust density distribution. It is no surprise since the 500 μm flux serves as a proxy of the dust mass. Also, the adopted fitting technique is able to recover the dust emission profiles fairly well. The histograms for these parameters are plotted in Figs. 4–8.
Appendix C: Robustness of the results and comparison with the literature
To verify how robust our fitting is, we applied the following test. The border value 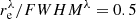 (see e.g. Peng et al. 2010 and comments to the GALFIT code7) separates galaxies with a reliable Sérsic fitting (with a larger effective radius) and galaxies which are too small for recovering their structural parameters. Below we consider the WISE W1 and Herschel bands separately.
(see e.g. Peng et al. 2010 and comments to the GALFIT code7) separates galaxies with a reliable Sérsic fitting (with a larger effective radius) and galaxies which are too small for recovering their structural parameters. Below we consider the WISE W1 and Herschel bands separately.
C.1. WISE W1
In the WISE W1 band, for only 5 galaxies (PGC 2807061, ESO 434–040, IC 0691, NGC 4194, and PGC 40819) our results cannot be considered as reliable by any means since these galaxies are too small to be fitted. The WISE W1 images for another 5 galaxies (ESO 116–012, UGC 4684, PGC 28759, UGC 6566, and UGC 7636) contain a very bright saturated star, therefore for these galaxies our analysis failed to compute realistic parameters of the Sérsic model, even when a simultaneous fitting of the star and the target galaxy was performed. Thus, in total, 865 galaxies (98.86% of the whole DustPedia sample) have reliable single Sérsic fits in the sense that they are sufficiently resolved to be fitted. We should stress, however, that for a small fraction of these galaxies their Sérsic models are meaningless because of a quite complex geometry of their structure (see Sect. 5).
 |
Fig. C.1. Comparison between our results (x-axis) and the same parameter from the literature (y-axis): between the single Sérsic model and aperture flux from C18 (panel a), between the model flux in WISE W1 and the one from the S4G single Sérsic modelling (panel b), between the effective radius in WISE W1 and the one from the S4G single Sérsic modelling (panel c), between the Sérsic index in WISE W1 and the one from the S4G single Sérsic modelling (panel d), between the model flattening in WISE W1 and the one from the S4G single Sérsic fitting (panel e), between our estimate of the galaxy inclination and the one taken from HyperLeda (panel f). The clustering dots at 90° for both estimates are either galaxies for which an edge-on model in the S4G modelling pipeline was adopted, or for which the apparent flattening was less then the intrinsic one (see Appendix D). The black dotdash lines show the one-to-one relationship and the orange dashed lines refer to the regression lines. |
We compared the retrieved model fluxes with the aperture fluxes from C18 (see Fig. C.1a). One can see that the fluxes compare very well (k = 0.967, b = −0.010, ρ = 0.97), except for some outliers which appeared to be interacting galaxies (for example, NGC 2480, IC 2163, ESO 491–021) or galaxies with bright foreground stars (for example, ESO 411–013, NGC 2974, ESO 377–039).
539 galaxies in our sample are common with the sample from the Spitzer Survey of Stellar Structure in Galaxies (S4G, Sheth et al. 2010; Muñoz-Mateos et al. 2013; Querejeta et al. 2015). The WISE W1 and the Spitzer (Werner et al. 2004) IRAC 3.6 μm passbands (Fazio et al. 2004) are overlapping enough to make a reliable comparison. In the frame of the S4G project, a single Sérsic fitting has already been performed (see Table 6 in Salo et al. 2015) using the same fitting code GALFIT. Therefore, we compared the results of the fitting for the WISE W1 and S4G IRAC 3.6 μm data (see Fig. C.1, panels b, c, d, and e). As one can see, the comparison is very good (ρ = 0.92−1.0 in all panels), and, despite the different resolution and deepness of the WISE W1 and IRAC 3.6 μm observations, the results of the Sérsic modelling compare well.
In Fig. C.1f, we show the comparison between the HyperLeda inclinations and those found in Appendix D. One can see a large scatter in this correlation which can be explained by a large scatter in the correlation between the apparent flattening logr25 from HyperLeda (this is the axis ratio of the galaxy isophote of 25 mag arcsec−2 in the B band) and the apparent flattening fitted in this work. Also, we can clearly see a systematic overestimation of the inclination in HyperLeda as compared to the inclination based on our results (ρ = 0.75, k = 1.10) – this is especially apparent for the highly-inclined galaxies. It can be explained by the fact that we used the intrinsic disc flattening ⟨q0⟩≈0.14 (see Appendix D), whereas in HyperLeda ⟨q0⟩≈0.23. According to the formula for calculating galaxy inclination (see Eq. (D.1)), the number of galaxies with 90° inclinations is larger in the latter case than if we imply a lower intrinsic flattening.
C.2. Herschel
As for WISE W1, we built the distribution of the ratio of the effective radius to the PSF FWHM in each Herschel band. We found that 320 galaxies (94% out of the subsample of 339 galaxies) are large enough to have a plausible Sérsic model, i.e. their  in each band.
in each band.
 |
Fig. C.2. Comparison between the single Sérsic model (x-axis) and the aperture (y-axis) taken from C18. The lilac filled circles refer to all galaxies with reliable models, while the dark-blue filled triangles correspond to the reference sample. The black dotdash line shows the one-to-one relationship and the orange dashed line depicts the fit for all galaxies shown. |
In Fig. C.2 we present the comparison between the aperture fluxes from C18 and the GALFITM model fluxes. For PACS 100 and PACS 160, we can see that the observed and model fluxes are not completely consistent (k = 1.13 and b = −0.11 for PACS 100 and k = 1.04 and b = −0.04 for PACS 160). However, for SPIRE 250–SPIRE 500 the consistency is much better (k ≈ 1.02 and b ≈ −0.01). This discrepancy may be explained, as above, by the better resolution in the PACS bands than in the SPIRE bands: bright emission details, which are seen in PACS, are smeared out in SPIRE. However, in general our models follow the observations fairly well, taking into account that our simple Sérsic model cannot adequately describe the complex geometry of the dust component in some cases (see discussion in Sect. 5).
Appendix D: Inclinations and stellar masses
In addition to the single Sérsic modelling, which was done for all DustPedia galaxies in the WISE W1 band, we used results of the multi-component modelling for the 539 galaxies common with S4G. The models were taken from the S4G pipeline 4 (Salo et al. 2015)8.
For galaxies with the bulge-to-total luminosity ratio B/T less than 1 (i.e. for disc galaxies), we estimated the disc inclination angle i towards the observer using the relation (Hubble 1926)
in which q is the ratio between the apparent minor and major axes of a galaxy outer disc (retrieved from our 2D fitting) and q0 is the intrinsic disc flattening.
To estimate the inner flattening q0 of disc galaxies, we selected a sub-sample of edge-on galaxies from the S4G sample. We used the multi-component decomposition results from Salo et al. (2015), where at least one component of an edge-on (isothermal) disc is present.
In order to calculate the intrinsic disc flattening q0 = hz/hR, we used the computed disc scaleheight z0 ≈ 2 hz (here hz is the disc scaleheight of the exponential disc) and the disc scalelength hR for the outer disc (if the model consists of two stellar discs) or the single disc. Both values hz and hR were taken from the S4G decomposition. We estimated the dependence of the disc flattening on the Hubble type T from HyperLeda (see Fig. D.1). As one can see, the dependence of q0 on T is very poor, however, we split up galaxies by their T and found an average trend (the red dashed line) separately for T ≤ 7 ( logq0 = −0.026 T − 0.774) and T > 7 (logq0 = 0.107 T − 1.705), similar to what is done in HyperLeda to compute their inner flattening of galaxies (for T ≤ 7, logq0 = −0.43−0.053 T and for T > 7, logq0 = −0.38, both the trends are shown with the blue dashed line). As one can see, the estimated flattening is ≈1.6 times lower than from HyperLeda taken for the same T. According to our estimation, the average value for late-type galaxies is ⟨q0⟩≈0.14, consistent with Giovanelli et al. (1994) and Mosenkov et al. (2015).
 |
Fig. D.1. Intrinsic disc flattening versus Hubble stage (see text). The black dashed line represents the HyperLeda piecewise formula from http://leda.univ-lyon1.fr/leda/param/incl.html, the black solid line is an approximation for the S4G edge-on galaxies. |
Having the derived dependence of the intrinsic disc flattening q0 on Hubble stage, we computed the galaxy inclination for all DustPedia galaxies using Eq. (D.1). If a galaxy has an edge-on disc model in S4G, we count it as viewed edge-on with i ≡ 90°. For the other galaxies common with S4G, we used the fitted disc flattening q. For the remaining galaxies, we use the galaxy flattening q taken from the single Sérsic fitting in WISE W1. Although such inclination estimates are inhomogeneous since they are taken from the two different sources, this seems to be the best solution to measure the galaxy inclinations for the given sample as precisely as possible. The regression analysis shows that iHL = 1.10 i and ρ = 0.75 (see Fig. C.1f), i.e. there is a systematic overestimation of the galaxy inclination in HyperLeda, mainly because their intrinsic flattening is 1.6 times larger than found here. Also notice that the scatter in this correlation is quite large, which might be explained by a large scatter in the correlation q versus r25 (ρ = 0.78, not shown here), where r25 is taken from HyperLeda. Since r25 is the galaxy (not disc) axis ratio and it was measured in the B band (while we consider the WISE W1 band with a drastically reduced contamination of dust), our inclination estimates should be more precise.
To properly estimate WISE W1 total fluxes of the galaxies, we used the following method. For the frames with more than one fitted object, where apart from the target galaxy some other objects (interacting galaxies or background stars) are present, we subtracted the models of the non-target (contaminating) objects from the given galaxy image. For the obtained residual frames and for the frames of galaxies with only one fitted object (the galaxy), we filled the masked pixels with the model pixels and then measured the total flux within the master aperture from C18. By so doing, we were able to reliably reconstruct the direct flux coming from the target galaxy taking into account the light from the detected contaminants. The extracted fluxes were then converted to Vega magnitudes9 and then to AB magnitudes10. Extended-source correction needs to be applied when performing aperture photometry upon WISE maps11, to account for the fact that the calibration of WISE data is based upon profile fitting of point sources. To convert the calculated AB-magnitudes into stellar masses, we computed the total galaxy luminosities using the “best” distances tabulated in C18 and applied the mass-to-light luminosity ratio from Kettlety et al. (2018)M*/L3.4 = 0.65, which was recently estimated in the WISE W1 band for non-star forming galaxies.
All Tables
Distributions of the fit parameters (mean value, median value (inside the parentheses), and standard deviation).
Numbers of galaxies in each bin (T − 0.5, T + 0.5) for a subsample of 320 galaxies with reliable fitting results.
Structural parameters of the multi-component decomposition model for IC 2531 adopted from Mosenkov et al. (2016), with an originally used double-exponential dust disc or an alternative Sérsic dust disc (not used in Mosenkov et al. 2016).
Results of the fitting for the mock galaxy images with a double-exponential and Sérsic dust disc.
All Figures
 |
Fig. 1. Results of the fitting for NGC 3686 in the WISE W1 band: the WISE W1 image (left panel), the best fitting image (middle panel), and the residual image (right panel) which indicates the relative deviation between the fit and the image in absolute values, i.e. |data-model|/model. The right colour bar shows the scaling of the residual image. The masked objects are highlighted by the white colour (left and right panels) or are transparent areas (middle panel). The galaxy and model images are given in a logarithmic scale. All images cover a field-of-view of 6.5′ × 6.5′. |
| In the text | |
 |
Fig. 2. Azimuthally averaged profile for NGC 3686 (grey circles), its convolved (red solid line) and unconvolved (orange dashed line) model, and the PSF kernel (green dotdash line) in the SPIRE 250 μm band. |
| In the text | |
 |
Fig. 3. Results of the GALFITM modelling for NGC 3686: the Herschel images from 100 to 500 μm (left panels), the models (middle panels), and the relative residual images (right panels, in the same units as presented in Fig. 1). The righthand colour bar shows the scaling of the residual images. Any masked objects are highlighted with a white colour. The galaxy and model images are given in a logarithmic scale. All images cover a field-of-view of 6.75′ × 8.35′. |
| In the text | |
 |
Fig. 4. Distributions of different parameters over wavelength. Left panel: ratio of the effective radius in each Herschel band to the effective radius in the WISE W1 band; middle panel: distribution of the Sérsic index in each Herschel band; right panel: ratio of the Sérsic index in each Herschel band to the Sérsic index in the WISE W1 band. By the lilac colour we show the subsample of 320 galaxies with reliable fitting results, whereas the dark lilac corresponds to the reference sample of 71 galaxies. The black solid and dark blue dashed lines refer to the simulations from Appendix B with an exponential and Sérsic disc, respectively. |
| In the text | |
 |
Fig. 5. Dependences of the Sérsic index on the radius (left panel), flux density (middle panel), and galaxy inclination computed in Appendix D (right panel). The black filled circle with the bar corresponds to NGC 3622 (see text). |
| In the text | |
 |
Fig. 6. Dependences of three different parameters on wavelength: the orange filled circles – for the ratio of the Sérsic index in each Herschel band to the Sérsic index in the WISE W1, the black filled triangles – for the Sérsic index, the lilac filled stars – for the effective radius in each Herschel band to the effective radius in the WISE W1 band. |
| In the text | |
 |
Fig. 7. Dependence of the effective radius measured in the WISE W1 band on the Hubble stage (left panel), the dependences of the effective radius measured in the five Herschel bands on the Hubble stage (middle panel), and the dependences of the ratio of the effective radius in each Herschel band to the effective radius in the WISE W1 band on the Hubble stage (right panel). Each dependence is plotted for the averaged data for the subsample of 320 galaxies (except for the lilac line in the left plot which refers to the sample of 865 DustPedia galaxies) within a bin of 1 T, with 15 and 85 percentiles shown. All lenticular galaxies (T ≤ 0) are combined together and shown by T = −2. Sm and Sdm galaxies are joined together in one type T = 8. |
| In the text | |
 |
Fig. 8. Dependences of the Sérsic index on the type (top panel) and the ratio of the Sérsic index in each Herschel band to the Sérsic index in the WISE W1 band on the type (bottom panel). The dependences are plotted for the averaged data for the subsample of 320 galaxies in each bin of 1 T with 15 and 85 percentiles shown. All lenticular galaxies (T ≤ 0) are combined together and shown by T = −2. Sm and Sdm galaxies are joined together in one type T = 8. |
| In the text | |
 |
Fig. 9. Relationship between the Sérsic index in the WISE W1 band and the Hubble stage for the sample of 865 DustPedia galaxies. The median average and the 15 and 85 percentiles are shown by the black colour for each bin of 1 T. The orange dashed line refers to n3.4 = 2, the border value to split galaxies into bulgeless (n3.4 < 2) and bulge-dominated galaxies (n3.4 > 2). |
| In the text | |
 |
Fig. 10. Some typical galaxies in our sample with different features in their SB profiles (no correction for the galaxy inclination has been done). The grey circles represent the azimuthally averaged galaxy profile in the SPIRE 250 μm band. The model (convolved with the respecting PSF which is shown by the green dotdash line) is represented by the red solid line. The blue dashed line shows a break (if applicable) in the profile at some characteristic radius rc (see text). The two images in each plot are a coloured SDSS snapshot (left created with the Aladin sky atlas, http://aladin.u-strasbg.fr/, Bonnarel et al. 2000; Boch & Fernique 2014) and a SPIRE 250 μm band image (right). Both images have the same scale and orientation. |
| In the text | |
 |
Fig. 10. continued. |
| In the text | |
 |
Fig. 11. Distributions by the characteristic radius expressed in kpc (top panel), and in units r25 (grey colour) and |
| In the text | |
 |
Fig. 12. SPIRE 250 profiles for the 10 common galaxies with Pohlen & Trujillo (2006). No correction for the galaxy inclination has been done. The orange cross is related to the characteristic radius found in this paper, the blue and red circles represent the break radii from Pohlen & Trujillo (2006) in the g and r bands, respectively. Each profile is shifted down relative to the previous one by 1.6 mJy arcsec−2. |
| In the text | |
 |
Fig. 13. Comparison between the break radius measured in the WISE W1 band and the characteristic radius in the SPIRE 250 μm band. The black dotdash line shows the one-to-one relation, whereas the orange line represents the regression line with k = 0.82, b = 0.11, and ρ = 0.83. |
| In the text | |
 |
Fig. 14. Correlations between the bulge (left plot) and bar (right plot) fraction to the total galaxy model, based on the S4G decomposition, and the Sérsic index in the SPIRE 250 μm band. The black dashed lines in each plot represent the regression lines: log n250 = 0.68 fbulge + 0.65 (ρ = 0.78) and log n250 = 0.82 fbar + 0.81 (ρ = 0.60). |
| In the text | |
 |
Fig. C.1. Comparison between our results (x-axis) and the same parameter from the literature (y-axis): between the single Sérsic model and aperture flux from C18 (panel a), between the model flux in WISE W1 and the one from the S4G single Sérsic modelling (panel b), between the effective radius in WISE W1 and the one from the S4G single Sérsic modelling (panel c), between the Sérsic index in WISE W1 and the one from the S4G single Sérsic modelling (panel d), between the model flattening in WISE W1 and the one from the S4G single Sérsic fitting (panel e), between our estimate of the galaxy inclination and the one taken from HyperLeda (panel f). The clustering dots at 90° for both estimates are either galaxies for which an edge-on model in the S4G modelling pipeline was adopted, or for which the apparent flattening was less then the intrinsic one (see Appendix D). The black dotdash lines show the one-to-one relationship and the orange dashed lines refer to the regression lines. |
| In the text | |
 |
Fig. C.2. Comparison between the single Sérsic model (x-axis) and the aperture (y-axis) taken from C18. The lilac filled circles refer to all galaxies with reliable models, while the dark-blue filled triangles correspond to the reference sample. The black dotdash line shows the one-to-one relationship and the orange dashed line depicts the fit for all galaxies shown. |
| In the text | |
 |
Fig. D.1. Intrinsic disc flattening versus Hubble stage (see text). The black dashed line represents the HyperLeda piecewise formula from http://leda.univ-lyon1.fr/leda/param/incl.html, the black solid line is an approximation for the S4G edge-on galaxies. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.