| Issue |
A&A
Volume 620, December 2018
The XXL Survey: second series
|
|
|---|---|---|
| Article Number | A9 | |
| Number of page(s) | 20 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201832931 | |
| Published online | 20 November 2018 | |
The XXL Survey
XXIV. The final detection pipeline
1
AIM, CEA, CNRS, Université Paris-Saclay, Université Paris Diderot, Sorbonne Paris Cité,
91191
Gif-sur-Yvette,
France
e-mail: lorenzo.faccioli@cea.fr
2
Argelander Institut für Astronomie, Universität Bonn,
53121
Bonn,
Germany
3
INAF, IASF Milano,
via Bassini 15,
20133
Milano,
Italy
4
IRAP, Université de Toulouse, CNRS, CNES, UPS,
Toulouse,
France
Received:
1
March
2018
Accepted:
18
July
2018
Aims. A well characterised detection pipeline is an important ingredient for X-ray cluster surveys.
Methods. We present the final development of the XXL Survey pipeline. The pipeline optimally uses X-ray information by combining many overlapping observations of a source when possible, both for its detection and its characterisation. It can robustly detect and characterise several types of X-ray sources: AGNs (point-like), galaxy clusters (extended), galaxy clusters contaminated by a central AGN, and pairs of AGNs close on the sky. We perform a thorough suite of validation tests via realistic simulations of XMM-Newton images and we introduce new selection criteria for various types of sources that will be detected by the survey.
Results. We find that the use of overlapping observations allows new clusters to be securely identified that would be missed or less securely identified by using only one observation at a time. We also find that, with the new pipeline we can robustly identify clusters with a central AGN that would otherwise have been missed, and we can flag pairs of AGNs close on the sky that might have been mistaken for a cluster.
Key words: galaxies: clusters: general / X-rays: galaxies: clusters / large-scale structure of Universe / methods: numerical
© ESO 2018
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The XXL survey is a large-scale survey of the X-ray sky carried out with the XMM-Newton satellite and designed both to derive competitive constraints on cosmological parameters, especially for the Dark Energy equation of state, see Pierre et al. (2011), and to provide a rich legacy data set. The survey has observed two ≈25deg2 patches of sky with good coverage across multiple wave bands. The rationale for such a survey is thoroughly explained in Pierre et al. (2016; hereafter XXL Paper I), to which we refer for details; here, we recall two facts from XXL Paper I relevant to the present paper. First, the survey flux sensitivity in [0.5−2] keV, the band most relevant to cluster studies and the one which we use to test our pipeline, is 6 × 10−15 erg cm−2 s−1 (90% completeness limit) for point sources (Chiappetti et al. 2018, XXL Paper XXVII). Second, the survey layout is made up of XMM-Newton observations (hereafter referred to as “pointings”) separated both in right ascension (RA) and declination (DEC) by 20′ so as to have good overlap among them given that the XMM field of view (FoV) is ≈30′ in diameter. This tiling ensures good sensitivity over the whole survey footprint, one of the strengths of XXL.
In the context of such a survey, it is imperative to have a dedicated pipeline for the identification of extended sources, as the default XMM-Newton software developed for such purposes is not really optimised for the relatively faint clusters which XXL mostly observed with shallow exposures. The need for such a pipeline was recognised early on in the course of the XMM-LSS survey (Pierre et al. 2004), the forerunner to XXL, and Pacaud et al. (2006, hereafter P06) introduce a dedicated survey pipeline, called XAmin in P06 and hereafter referred to as XAminP06. P06 provide a thorough description of XAminP06 and of the rationale behind its development, extensively test it via simulations, and use it to define the XMM-LSS selection function. Since its introduction XAminP06 has been successfully used by the XMM-LSS project to assemble their cluster sample (Pierre et al. 2006; Pacaud et al. 2007; Willis et al. 2013; Clerc et al. 2014) and the survey source catalogues, both point-like and extended (Pierre et al. 2007; Chiappetti et al. 2013). In the XXL project, XAminP06 has been so far used to define the brightest 100 cluster sample (Pacaud et al. 2016, XXL Paper II) and the 1000 brightest point source sample (Fotopoulou et al. 2016, XXL Paper VI), as well as the catalogue of 365 clusters (Adami et al. 2018, XXL Paper XX), and the newer source catalogue (XXL Paper XXVII). The pipeline was also used by the X-CLASS project (Clerc et al. 2012) to perform a complete reprocessing of the whole XMM-Newton archive with the aim of building a cosmologically useful sample of serendipitous X-ray galaxy clusters.
The major shortcoming of the otherwise very satisfying XAminP06 is that it works on each XMM-Newton pointing separately; it is possible for a source not to be detected, or to be badly measured, simply because it lies at a large off-axis angle in that observation, where the sensitivity of the X-ray telescopes is sharply degraded. It is therefore necessary to address this weakness, as it would prevent us from making optimal use of the carefully designed XXL survey layout. As a concrete example, let us consider the case (relevant for the survey: we recall that the centres of the pointings are spaced by 20′ on the sky) of a source lying halfway between two such pointings. This source would be at an off-axis angle of 10′ from the centres of both pointings, where the XMM-Newton telescopes sensitivity is degraded by about ≈ 50%; therefore, with two observations the number of counts collected would be about the same as the counts collected by a single observation on-axis (for the same exposure time) but distributed over the two pointings. By analysing each of these twopointings separately, as done by XAminP06, there is the risk that the source will not be detected at all or, even if it is detected, there will be too few counts to securely classify it. However, by combining both observations(thus using all the counts from all the pointings at the same time) the source may be clearly detected and characterised. We have therefore completely rewritten the pipeline to allow it to optimally use all X-ray information by using all the available pointings at the same time; as this new pipeline is largely new we will refer to it as XAminF18.
The paper is organised as follows: Sect. 2 describes the XAminF18 pipeline; Sect. 3 describes how to identify different types of sources; Sect. 4 describes the suite of simulations we use to test XAminF18; Sect. 5 describes our results; Sect. 6 describes a new selection for an almost pure sample of point sources (the P1 selection) and summarises all selection criteria we introduce for the different sources considered in the paper; and Sect. 7 presents our conclusions. In the following, we use the terms “point source” and “AGN” interchangeably as virtually all extra galactic X-ray point sources are indeed AGNs. For the same reason we use the terms “extended source” and “cluster” interchangeably.
2 The XAminF18 pipeline: general description
Pacaud et al. (2006) provide a thorough introduction to XAminP06; however, we repeat here several points for the sake of being self-contained.
2.1 Event lists
Calibrated event lists are created from raw observation data files (ODFs) using SAS tasks emchain and epchain, and are then filtered for solar soft proton flares. Photon flares are filtered using the light curves of high-energy events; the band used for filtering differs for each EPIC detector: 10− 12 keV for the MOS1 and MOS2 detectors (Turner et al. 2001) and 12−14 keV for the pn detector (Strüder et al. 2001). Histograms of these light curves are created, binned by 104 s, and fitted to a Poisson law of mean λ, and intervals where emission exceeds 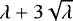 are discarded; this method is described by Pratt & Arnaud (2002). Soft proton cleaned lists are then used to produce images of 2.5′′ /pixel to correctly sample the XMM-Newton point spread function (PSF ≈ 6′′ on-axis) using the SAS task evselect.
are discarded; this method is described by Pratt & Arnaud (2002). Soft proton cleaned lists are then used to produce images of 2.5′′ /pixel to correctly sample the XMM-Newton point spread function (PSF ≈ 6′′ on-axis) using the SAS task evselect.
One image for each EPIC detector (MOS1, MOS2, and pn) is then created for each energy band of interest: [0.3− 0.5], [0.5−2], [2−10] keV; all these steps are unchanged from XAminP06 and more details are given in P06. In the following, we consider only [0.5− 2] keV images as this is the most important band for cluster detections and characterisation, especially for the faint clusters typically observed by XXL.
2.2 Tile creation
Next, mosaicked images of the XXL sky, hereafter referred to as “tiles” (the term “mosaic” is reserved for combined images, tiles, or single pointings of more than one EPIC instrument), are created, one per EPIC instrument. These tiles, which are 68′ × 68′ images pixelized at 2.5′′, are obtainedby re-projecting the event lists pertaining to each tile to a common frame in the sky using SAS task attcalc. Tiles are spaced by 60′ each in RA and Dec; the 68′ length allows for a 4′ overlap across tiles.
As the XXL coverage is rather dense (we recall that 30′ diameter pointings are separated by 20′ in RA and Dec), on average ≈20−25 pointings are included in one deg2, most of which only partially overlap with the tile; conversely, each pointing may in general fall across tile borders and therefore can be used in many tiles. For each 68′ × 68′ region of sky covered by the survey, we now have three tiles (one for each instrument); these three tiles are co-added to have a single MOS1+MOS2+pn 68′ × 68′ tile which is then wavelet smoothed as the first stage of source detection. Combined exposure maps and detector masks for each tile are also created at this stage. This step is new in XAminF18.
2.3 Preliminary source detection
We are now ready to perform preliminary source detection using the mosaicked MOS1+MOS2+pn 68′ × 68′ tiles to take advantage of the many overlapping pointings in a tile.
We use the mixed approach introduced by Valtchanov et al. (2001, hereafter V01) and used in P06; it consists of first filtering the input X-ray image and then performing source detection on the smoothed image, taking advantage of the many well-developed source detection procedures developed for optical images. The validity of this approach is demonstrated via extensive simulations in V01, who show that it gives the best results compared to the other approaches they test for detecting and characterising both point-like and extended objects when used on XMM-Newton images. Filtering an image through wavelets is a popular choice and many techniques have been introduced. Starck & Pierre (1998, hereafter SP98) show via simulations that the best filtering method for images containing Poisson noise with few photons like X-ray images is the method based on the auto-convolutions of the histogram of the wavelet function. SP98 show in particular that the method is effective at recovering extended sources with only few photons which is the case of XXL clusters. They also note that one strong point of the method is that it does not need a background model, and they show how an input cluster can be successfully retrieved with different background levels. We refer to SP98 for the relevant formulas and we only briefly recall the main features of the method in Sect. 2.3.2.
Starck et al. (1998) describe their implementation of the method in the MR/1 software; we chose to develop our own IDL implementation of MR/1 (the rest of XAminF18 is written in Python), based on the latest implementation kindly provided by Jean-Luc Starck, to make it easier to perform two additional steps, not executed in XAminP06, before smoothing; these steps are detailed below.
2.3.1 File preparation
As a first step, a model of particle background, obtained by simulating very long XMM-Newton exposures with closed filter wheel, is subtracted from the tiles. This is necessary because the background component is unvignetted (the probability of a particle being mistakenly detected as a photon is independent of off-axis angle) so there is an excess of photons due to particle background in regions ofoverlap with respect to the centre of the pointings. This excess, if not corrected, may bias source detection; the problem is absent when using images of single pointings as in XAminP06. To model the particle background, we use the same procedure used to add particle background, on simulated images, but using an exposure time of 1 Ms to ensure a good sampling of all pixels, a nominal XXL 10 ks exposure time would have left many pixels empty. We then re-scale the pixel values to the nominal XXL exposure time 10 ks.
The second step consists in correcting for the different exposure time across a tile by dividing it by a tiled, combined exposure map; this step was not performed by XAminP06, but we found that it improves overall performance. The combined exposure map is obtained by adding together the tiled exposure maps of the three EPIC detectors. We compensate for the fact that the effective area of the pn detector is ≈3.1 times the effective area of the MOS detectors in the energy range of interest ([0.5−2] keV) by multiplying the pn tiled exposure map by 3.1 before adding it to the MOS ones. This last step is useful because it returns a lower estimate of the count rate of a candidate source than would be obtained by simply adding the three exposure maps, since the exposure time is longer. This lowers the risk that the fit will go wrong because SEXtractor returns an initial count rate estimate that is too high, a problem that sometimes occurs. Figure 1, left panel, shows an example of particle background model for a simulated 68′ × 68′ tile reproducing the real XXL tiling; we note the strong spatial variation due to the fact that this background component is unvignetted so it is much more prominent in regions of overlap. In the right panel of Fig. 1, the tiled combined (MOS1+MOS2 + 3.1×pn) exposure map is shown of the same simulated region of sky assuming the nominal exposuretime 10 ks for each instrument. The map is given in MOS units: we correct for the larger effective area of the pn detector by multiplying it by 3.1 so at the centre of each pointing the total exposure time is ≈50 ks. This is roughly the time needed to reach the nominal XXL sensitivity in the [0.5− 2] keV band with a single MOS detector.
 |
Fig. 1 Left panel: example of particle background model subtracted from a 68′ × 68′ tile. Right panel: tiled combined exposure map (MOS1+MOS2 + 3.1×pn) of the same region. A nominal XMM-LSS exposure time 10 ks for each instrument is assumed. The map is in MOS units: the pn exposure map is corrected for the larger pn effective area by multiplying it by 3.1 (see text) so the combined exposure map has an exposure time ≈50 ks at the pointing centres. The exposure time is even larger (≈60 ks) in areas where three pointings overlap. |
2.3.2 Wavelet smoothing
After performing the first two steps detailed above we are ready to wavelet smooth the tile. The wavelet smoothing procedure is applied to (I − P)∕Expo, where I is the input MOS1+MOS2+pn tile, P is the particle background model image (see the left panel of Fig. 1), and Expo is the combined tile exposure map (see the right panel of Fig. 1).
The MR/1 algorithm computes a smoothed image from an input image as the sum of a predefined number of scale-dependent wavelet coefficients; each coefficient is computed from the input image using a chosen wavelet function ψ(x, y), in our case a B3-spline. A wavelet coefficient wj(x, y) at position (x, y) and scale j (the total number of scales is fixed) carries information about whether or not there is signal in the image at that position and scale; only coefficients that contain signal, according to the criteria detailed below, are included in the final smoothed image. Many different choices of wj (x, y) have been considered in the literature; SP98 review several of them and show that for the Poisson regime typical of X-ray images, a good choice of wj (x, y) is the one introduced by Slezak et al. (1993) and Bury (1995) in the context of galaxy clustering; its expression is given by Eq. (6) of SP98 which we reproduce here:
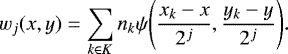 (1)
(1)
In Eq. (1), K is the support of the wavelet function ψ, i.e. the box where ψ≠0, and nk is the number of photons at position (xk, yk); we note thatψ is dilated by a factor 2j for scale j and is centred at the coefficient position (x, y).
It is easy to understand from Eq. (1) why this choice is appropriate for the Poisson regime: nk can take any value, including 0, and no assumption, e.g. of Gaussianity, needs to be made. If the coefficient wj (x, y) is due to noise, it can be considered the sum of n independentrandom variables, each corresponding to one count and having a distribution given by the histogram H1 of the wavelet function ψ. The distribution of the sum of n such independent variables is given by n auto-convolutions of H1:
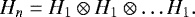 (2)
(2)
So, a simple and rigorous way of assessing the significance of wj (x, y) is to compare it to a threshold expressed as a pre-defined multiple (denoted by σ) of the standard deviation of Hn. Only coefficients found to be significant according to this criterion are included in the smoothed image. Hn converges to a Gaussian distribution in the limit of large n.
Equation (1) shows that each scale is twice as large as the previous one (each scale j corresponds to 2j−1 pixels); as in P06 we consider eight scales (scales 2−9; scale 1 is not used) with dimensions varying from 2 to 256 pixels. We impose a set of eight thresholds with values σ = 3, 3, 3, 3, 4, 4, 3, and 3 for the eight scales used. We choose a 3σ threshold for most scales; however, for scales 6 and 7 (which correspond to 32− 64 pixels =80′′-160′′, roughly the scale of the largest clusters observed by XXL) we demand a higher threshold for significance.
We found that doing so improves overall performance and allows us to reduce the number of sources mistakenly identified as clusters because their photons are spread out to a large area by the strong XMM-Newton PSF distortion at large off-axis angles.
Our choice of thresholds differs somewhat from that of P06: they define a P value such that, if the probability for a wavelet coefficient wj(x, y) being due to noise (computed from the cumulative distribution of Hn) is < P, the coefficient is considered significant; P06 choose P = 0.001 for all scales, which, in the limit of large n, corresponds to σ ≈ 3.09.
It is important to note that the MR/1 wavelet filtering removes noise already in the wavelet filtering stage, thanks to the thresholdingscheme adopted; the result is a smoothed image in which most of the noise is already almost completely removed and the background has been smoothed; this justifies the use of SEXtractor in source detection described in Sect. 2.3.3.
2.3.3 Identifying sources on the smoothed image using SEXtractor
To identify candidate sources in the smoothed image we use SEXtractor (Bertin & Arnouts 1996); the suitability of this package is demonstrated by V01 who use it in conjunction with MR/1 to successfully recover point and extended sources in simulated XMM-Newton images. V01 present detailed statistics of missed or false source detections for their simulations in which they show that the MR/1+SEXtractor combination is the best overall of the many approaches they study; in particular, they show that it works better than all the other methods in recovering high-z clusters, an important concern for XXL.
Valtchanov et al. (2001) also present a detailed discussion of the many possible choices of SEXtractor parameters, identifying the choices that give the best results and which are adopted in P06. SEXtractor parameters are unchanged from P06 except that we use a larger box (512 pixels instead of 64) to estimate the background. V01 point out that the choice of a good background box size is a tricky one, implying a trade-off between bad photometry (small box) and the risk of missing faint sources (large box); they advocate boxes of 32− 64 pixels, and P06 adopt 64 pixels. We found however that choosing a background box as large as 512 pixels helps to reduce the number of false cluster detections when using tiles and does not provoke the loss of faint sources, but instead improves things a bit. In our simulations, we find for 25 deg2 that using a 512 pixel box leads to recovering ≈ 8200 genuine point sources, whereas using 64 pixels leads to recovering ≈7800 genuine ones. We conclude that using a 512 pixel background box does not have an adverse effect on pipeline performance regarding point sources and is beneficial regarding extended ones. See Sect. 2.5 for the criteria to decide whether a detection is genuine or due to background, and Sect. 4 for details on simulations.
Table 1 reproduces Table 1 of P06 and reports the values of the parameters used for the detection stage; most parameters are unchanged from P06; the cases where they are not explicitly noted.
2.4 Likelihood fit: models and parameters
After SEXtractor has found the list of candidate sources for each 68′ × 68′ tile, each candidate source is characterised by performing a maximum likelihood fit based on the C-statistic (Cash 1979), appropriate for the Poisson regime, using raw photon images; all images that cover the candidate are used, whereas with XAminP06 images were used one by one.
It is essential to understand that for the likelihood fit tiles cannot be used because when fitting it is necessary to correctly account for the strong PSF distortion introduced by the XMM-Newton telescopes, which depends on off-axis and position angles and so is different for each individual pointing, as detailed below. Each source is fit to the following:
- 1.
a PSF model (PNT fit);
- 2.
a β model (Cavaliere & Fusco-Femiano 1976; EXT fit);
- 3.
a β model superposed to a central PSF (EPN fit);
- 4.
two PSFs (DBL fit);
the β model is also convolved with the XMM-Newton PSF.
All PSFmodels used in all fits are computed at the source position on each different pointing; since these positions are in general different from pointing to pointing, a different PSF model must be used for each different pointing, preventing the use of a single tile where photons from different pointings, differently affected by the PSF distortion, are grouped together.
In all cases, a local background is estimated by subtracting the total number of photons expected from the model from the total number of photons in the fit region. A model in which all photons are assumed to be due to background is also considered; we refer to it as the BKG model and it is used in assessing the significance of each fit in connection with Eq. (9).
The PNT and the EXT fits are present in XAminP06; the EPN and the DBL fits are new to XAminF18 and will be described in more detail in Sect. 2.6.
The β profile is described by
![\begin{equation*}S_{\mathrm{X}}(r)\propto\bigg[1+\bigg(\frac{r}{\textsc{ext}}\bigg)^2\bigg]^{-3\beta+1/2}, \end{equation*}](/articles/aa/full_html/2018/12/aa32931-18/aa32931-18-eq4.png) (3)
(3)
where the core radius EXT is measured in inches and β = 2∕3. Different values of β may be specified at the start of the fit, but its value is then kept fixed as, in general, XXL clusters have too few counts to robustly constrain it.
Fit parameters always include count rates CRmos and CRpn; MOS1 and MOS2 are assumed to be identical and only one count rate for them is introduced. In the EXT fit the core radius EXT is also a fit parameter; in the EPN and DBL additional parameters are introduced as explained in Sect. 2.6. A total count rate CR can be estimated from CRmos and CRpn as
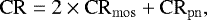 (4)
(4)
and a total count rate CRMOSNORM normalised to the MOS effective area can also be estimated as
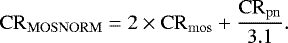 (5)
(5)
Equation (5) allows us to compensate for the difference in sensitivity between the MOS and pn detectors; in the following when quoting values for derived count rates we use Eq. (4). All fit parameters are forced to be the same across all pointings: there is only one CRmos, one CRpn, one EXT, and so on. In principle, the source position may be fitted in all fits; however, unlike P06 where it was fitted in the EXT fit and kept fixed in the PNT fit, we do not fit for it in any case but we always keep it fixed at the value found by SEXtractor.
2.5 Likelihood fit: the C- and E-statistics
The validity of each model in the Poisson regime can be estimated using the Cash C-statistic (Cash 1979)
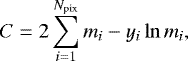 (6)
(6)
where yi is the number of observed photons andmi is the number of photons expected from the model in pixel i. Introducing Npix (the number of pixels used in the fit), 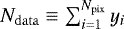 (the total number of observed photons used in the fit), and
(the total number of observed photons used in the fit), and 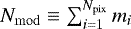 (the overall model normalisation), we can express the value of each model pixel mi as mi = Nmod × di with
(the overall model normalisation), we can express the value of each model pixel mi as mi = Nmod × di with 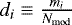 , and we can rewrite Eq. (6) as
, and we can rewrite Eq. (6) as
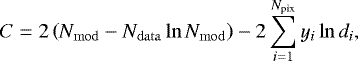 (7)
(7)
which has the advantage of explicitly factoring out Ndata and Nmod. Minimising Eq. (7) with respect to Nmod yields Nmod = Ndata and we choose to fix Nmod = Ndata and use the simplified E-statistic
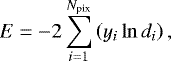 (8)
(8)
to assess the validity of each model (convolved with the XMM-Newton PSF) used in the fit.
We use the E-statistic because it allows us to have one fewer parameter in the fit, since the model normalisation Nmod is now fixed at Ndata; since XXL observations do not have many photons it is important to reduce the number of parameters when possible.
The E-statistic is equivalent to the C-statistic for parameter estimation, but not for uncertainty estimation; as we are not interested in uncertainty estimation (see Sect. 2.7) this is not a serious problem. It should be noted that the C- and E-statistics are not really likelihood functions but are related to the likelihood function L by C = −2logL + const. (and similarly for E). It is insteadmore appropriate to think of them as the Poisson distribution equivalent of the χ2 statistic appropriate to the Gaussian distribution (recall that χ2 = −2logL + const as well) and, like χ2, C, and E reach a minimum atthe optimum.
The significance of a detection is assessed by evaluating the increase in E between its best fit value EBF and a modelcontaining only background (the BKG model introduced above); this allows us to define the detection statistic
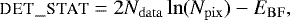 (9)
(9)
used by P06to show via simulations that a good criterion for discriminating real detections from chance background fluctuations is given by
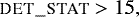 (10)
(10)
these sources were referred to in P06 and subsequent papers as “point sources”.
This criterion is also valid for XAminF18 and we use Eq. (10) to discriminate between real detections and chance background fluctuations. Applying the cut of course leads to several faint real sources to be found by SEXtractor and then discarded. In our simulations we find that for 25 deg2 this happens for ≈ 1400 input sources out of every ≈10 000 found by SEXtractor. In Sect. 6, we give more information about the selection of point sources.
All these considerations apply to each of the four fits we perform, and we derive one value of DET_STAT for each of them; we must then compare different fits to one another to decide which best describes the source. To assess the significance of an EXT fit over a PNT fit, P06 introduce an extent statistic defined as
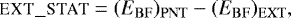 (11)
(11)
which continues to be used in XAminF18; EXT_STAT plays a crucial role in cluster identification. The issue of selecting a best fit model among the four models we consider is very important and is described in more detail in Sect. 3, after introducing the EPN and DBL fits.
2.6 Likelihood fit: the EPN and DBL fits
Although the EXT and PNT fits are unchanged from XAminP06, apart from the above-mentioned improvements in wavelet smoothing, and other improvements described in Sect. 2.9, the EPN and DBL fits are new and are described here.
The EPN is introduced to allow the recovery of clusters with a strong contamination by a central AGN; in Sect. 5.2, we show how, in this case, a real cluster can be missed by the EXT fit, which means that it is necessary to introducea more sophisticated fit to recover it. The fit can also be used to flag clusters which, though being identified assuch by the EXT fit, are nevertheless contaminated by central AGN; these clusters may be interesting in themselves.
In the EPN fit, we fit the source to a superposition of a β profile (always convolved with the XMM-Newton PSF) and the PSF itself, placed at the cluster centre to model the effect of the central contaminating AGN. Again, the value of β can be specified in advance and we choose β = 2∕3, but it is then kept fixed during the fit. The fit parameters are CRmos and CRpn, the cluster core radius, called EPN_EXT to distinguish it from the core radius ext computed by the ext fit, and the relative count rate between cluster and AGN, indicated by EPN_RATIO, which is the same for the MOS and pn detectors; we do not fit for any offset between the AGN and the cluster as in general we do not have enough counts to constrain it. The count rates for the cluster and the AGN can be computed from the total count rate CR given by Eq. (4) and EPN_RATIO as
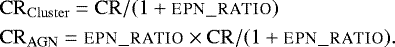 (12)
(12)
The DBL fit is introduced to account for the frequent case where two or more AGNs are close in the sky and their combined X-ray emission can be mistakenly classified as a single extended emission in the EXT; the fit is used in conjunction with the cluster classification criteria in Sect. 3.1 to flag such cases since we obviously do not want to include them in any subsequent cluster catalogue. The DBL fit is performed in a manner similar to that of the EPN fit: the source is fit to a superposition of two XMM-Newton PSFs; the fit parameters are CRmos and CRpn, the relative count rate between the PSFs DBL_RATIO, which again is the same for the MOS and pn detectors, and the separation between the PSFs DBL_SEP. We fit only the separation DBL_SEP; the midpoint of the line joining the PSFs is always the source SEXtractor position, which we keep fixed. The position angle between the PSFs is computed in advance by first smoothing the MOS1+MOS2+pn image of each pointing using a Gaussian filter with σ = 2 pixels and then computing its second moments. We note that in doing so we estimate a different position angle for each pointing. Unlike DBL_SEP, the position angle is then kept fixed at the value computed from its second moments and it is not a fit parameter because in general we do not have enough counts to constrain it. The relative count rate of the two point sources can be computed from an equation similar to Eq. (12).
2.7 Parameter uncertainties
We have not said anything about the uncertainty in the recovered parameters. The reason is that XAminF18 is primarily a detection pipeline to identify sources as real and securely classify them according to their type (point or extended); it is not meant primarily to derive accurate values of source parameters and their associated uncertainties for the cluster candidates. More accurate parameter estimation is carried out in successive steps by other means such as growth curve analysis for count rates, as done by e.g. Clerc et al. (2012), and in the XXL project, in XXL Paper II, and by Giles et al. (2016, XXL Paper III). It is still possible, however, to use the pipeline in either version to derive uncertainties using simulations: Pierre et al. (2007) and Chiappetti et al. (2013) derive estimates of the positional accuracy of the sources in the first and second version of the XMM source catalogue, respectively, as a function of the countrate derived by the pipeline and off-axis angle, by running XAminP06 on simulated XMM-Newton images. Flux uncertainties, on the other hand, are currently estimated, as explained in XXL Paper XXVII, by calculating the Poisson error on gross photons according to the formula of Gehrels (1986). Gross photons, in turn, are reconstructed by adding net photons and background photons in the fitting region, as computed by XAminF18.
2.8 Choosing the fitting region
SEXtractor returns an estimate of the source extent via the ellipse parameters cea_a and cea_b, the semi-major and semi-minor axes, in arcseconds, of the ellipse that best describes the source. We choose an initial fitting region as three times the mean semi-axis (cea_a + cea_b)∕2, and if there are no photons in it we take a region three times as large; we always impose the constraint that the region must be > 35′′ and < 200′′. Within this region we flag pixels belonging to different sources according to the SEXtractor pixel segmentation mask; these pixels are excluded from the fit which is then not affected by neighbouring sources.
2.9 Other improvements
Other important improvements are the following:
1. XAminF18 uses the latest XMM-Newton PSF model, described in Read et al. (2011), whereas XAminP06 used the older “Medium” model composed of a set of images, the same for each of the three XMM-Newton telescopes, which did not take into account the strong azimuthal dependence of the PSF shape.
2. XAminP06 was not optimised for detection of bright point sources and sometimes it missed them; XAminF18 corrects this and is able to detect bright point sources more reliably. It should be noted that since cluster identification is based on the computation of the extent statistic (Eq. (11)), which requires the results of the PNT fit, a failure of the PNT fit may cause a failure to recognise a candidate source as a cluster; as a consequence, several bright clusters in the XXL images were missed by XAminP06 which are now detected by XAminF18.
3 Identifying different types of sources
XAminF18 performs four fits on each candidate source and computes a detection statistic EXT_DET for each of them (see Sect. 2.4). We indicate these statistics by PNT_DET_STAT, EXT_DET_STAT, EPN_DET_STAT, DBL_DET_STAT; all the statistics are dimensionless.
Intuitively, a source will be flagged as point, extended, extended+point, or double depending on which of its detection statistics mentioned above is highest and by how much. To do this rigorously, we must first introduce the appropriate statistics, the analogue of EXT_LIKE in the EXT fit, and then we must derive quantitative criteria of source classification based upon these statistics by using simulations. The relevant statistics are introduced in Sects. 3.1 and 3.2.
The criteria for cluster selection, the C1 and C2 selections introduced in P06, are reported in Sect. 3.1 and are shown to be still valid for XAminF18 (see Sect. 5.1). The criteria for recovering clusters contaminated by a central AGN are defined and tested via simulations in Sect. 5.2. The criteria for flagging double sources that may be misidentified as extended ones are introduced and tested via simulations in Sect. 5.3. The criteria for selecting an almost pure sample of point sources (the P1 selection) are introduced and tested via simulations in Sect. 6. Finally, in Table 8, we summarise all the criteria we introduce. These criteria are usually defined by several conditions; if more than one condition is specified all conditions must be used unless explicitly stated otherwise.
3.1 Selecting clusters
To select clusters, as explained in P06 and restated in Sect. 2.4, we introduce an extent statistic (EXT_STAT), defined in Eq. (11) as the difference between the best fit detection statistics of the PNT and EXT fits. In principle, EXT_STAT can have either sign, and we expect that for a point source it should be negative; if XAminF18 finds a negative value of EXT_STAT it forces it to 0, so we expect a point source to have EXT_STAT = 0 in the EXT fit and in most cases this is true. In certain cases, however, a point source will have EXT_STAT > 0 and we must establish a threshold to decide whether a certain value of EXT_STAT is high enough for a source to be considered extended; this can only be done by simulations. P06 show via simulations that a threshold EXT_STAT > 33 allows us to robustly distinguish between extended and point sources, and to introduce the C1 selection:
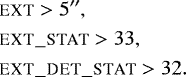 (13)
(13)
The C1 selection is shown in P06 to be almost pure; this continues to be true with XAminF18. P06 introduce a second selection, the C2 selection, composed of fainter clusters and with a ≈50% probability of contamination, defined as
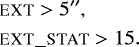 (14)
(14)
We show in Sect. 5.1 that the C1∕C2 selections asdefined in Eqs. (13) and (14) are still appropriate for XAminF18.
3.2 Recovering AGN contaminated clusters and flagging double sources
For the DBL fit we introduce, in the same vein, a double statistic (DBL_STAT) defined as the difference between the best fit detection statistics of the PNT and DBL fits (see Eq. (15)):
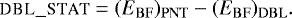 (15)
(15)
This statistic allows us to flag sources that may be initially identified as extended (i.e. they pass the C1 or C2 criteria), but which are actually a double, as is explained in Sect. 5.3.
For the extended+point (EPN) fit, we need two statistics as we need to quantify the likelihood of an EPN fit with respect to a simple extended fit (EXT), and the likelihood of an EPN fit with respect to a point fit (PNT). The first statistic, which we refer to as EPN_STAT_EXT, is necessary in order to classify a cluster contaminated by a central AGN as a cluster. The second statistic, which we refer to as EPN_STAT_PNT, is necessary in order to distinguish an AGN contaminated cluster from a simple AGN; it may happen that, for an AGN, an EPN fit is better than an EXT fit (revealed by a high value of EPN_STAT_EXT), but not as good as a PNT fit (revealed by a low or zero value of EPN_STAT_PNT). To classify a source as a cluster contaminated by a central AGN we require significant values of both statistics (defined in Sect. 5.2 via simulations), whose equations are
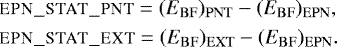 (16)
(16)
Table 2 summarises the fit parameters and the statistics we introduce.
Again, we expect a point source to have a 0 value or lowvalues (to be defined) of EPN_STAT_DET, EPN_STAT_PNT, and DBL_STAT.
4 Testing XAminF18 with simulations
We use a dedicated suite of simulations to test XAminF18 performance; all simulations are carried out in [0.5−2] keV; details of the simulation (count rate, core radii of input clusters, and so on) are given in Tables A.1–A.3.
Relevant parameters of the XXL pipeline detection stage.
Main fit parameters and statistics.
4.1 Simulated sources
Creating images of simulated clusters consist of the following steps. We start by creating simulated ideal 5 × 5 deg photon images, without any background, resolved AGNs, and instrumental effect, of clusters: the images represent a perfect X-ray sky observed with an infinite exposure time, where only the sources of interest are present. In practice, this is achieved by using a very large exposure time, 106 s, to have enoughphotons in the image, and re-scaling the image by this exposure time so that each pixel represents the number of photons per second in a 2.5′′ × 2.5′′ region of sky seen by a 1 cm2 perfect detector. The number of actual photons for each cluster in the image is drawn from a Poisson distribution with mean given by the cluster count rate × 106 s. We assume input clusters to be described bya β model (Cavaliere & Fusco-Femiano 1976) with β = 2∕3; so they are specified by their core radius in inches and their count rates in count s-1.
Input clusters are placed on a 5 × 5deg image; we build oneimage per core radius−count rate combination. These images are tiled with the same tiling scheme of the XXL survey (XXL Paper I), with pointings displaced by 20′ from each other; clusters are placed either at the geometrical centre of a pointing or at 10′ from it, so that a large fraction of them is covered by more than one pointing (see Fig. 3). It is important to note that the geometrical centre of a pointing is not the same as its centre of optics, i.e. the point of maximum telescope sensitivity; these two points may be displaced from one another by as much as 1′, so the space distribution of the input sources samples the 0′ –1′ and 9′ –11′ off-axis range.
Count rates of 0.005, 0.01, 0.05, and 0.1 count s-1 are used; core radii of 10, 20, and 50′′ are used; for 0.05 count s-1 we also consider 40′′ for the reasons explained in Sect. 5.1.3.
Double sources and clusters contaminated by a central AGN are simulated in a similar way. For contaminated clusters, the AGN is just put in the central pixel of the cluster; although this is a very simplified model, as in real clusters the AGN may not be at the centre, it is sufficient for our purpose, and testing XAminF18 with more realistic simulations will be left to another paper. For double sources, the AGNs are put at two pixels separated by a prescribed distance. For contaminated clusters, the AGN has a count rate that is double that of the cluster; for double sources, the AGNs have the same count rates and are placed at 6′′ and 12′′ (we recall that the XMM-Newton PSF on-axis is ≈ 6′′). The AGNs at the centre of the clusters and those in pairs close on the sky are in addition to those which constitute the resolved AGN background described in Sect. 4.2.
The choice of count rates and core radii for simulated clusters is driven by the need to conveniently bracket the corresponding values of observed XXL clusters: a count rate range [0.005−0.1] count s-1 translates to [50−1000] counts on-axis for a nominal XXL 10 000 s exposure time and is appropriate since typical XXL clusters have at most a few hundred photons (XXL Paper I); a core radius range [10−50]′′ is appropriate as the typical core radius of XXL clusters is ≈ 20′′ (XXL PaperII).
The features of these simulated sources are summarised in Tables A.1–A.3.
4.2 Realistic background model
The background needed by the simulated images consists of four components.
The first componenent is the particle background (unvignetted): it comes from the spectrum accumulated in 200 ks exposures with the EPIC filter wheel in closed position so as to not have X-ray photons pass through and selected not to have flares. The background is then created with a uniform spatial distribution over each CCD and the energy distribution follows that spectrum.
The second component is the resolved AGN background (vignetted): it is taken from the log (N)−log(S) relation of Moretti et al. (2003); AGNs are uniformly distributed in a 25deg2 FoV and hence they may fall near clusters or close to each other. The flux limit is 10−16 erg cm−2 s−1 which gives 80536 AGNs; photons are distributed in [0.5−2] keV according to a power law with index 1.9 and with Poisson noise. The flux is corrected for Galactic absorption according to Morrison & McCammon (1983).
The third component is the diffuse photon background (vignetted): the model adopted is taken from Snowden et al. (2008). Galactic photon background is described by two MEKAL models (Mewe et al. 1985, 1986; Liedahl et al. 1995)for the Local Hot Bubble (LHB) and the cold halo, respectively, both with a plasma temperature of 0.1 keV, and one MEKAL model for the hot halo with a plasma temperature of 0.25 keV. Unresolved extra-galactic sources are modelled by a power law index 1.46. All diffuse photon background components except the LHB are corrected for Galactic absorption assuming a column density 1.2 × 1020 cm2. Calculations are performed with XSPEC, described in Arnaud (1996).
The fourth component is the residual contamination from soft protons (SP; Read & Ponman 2003; De Luca & Molendi 2004; Leccardi & Molendi 2008; Snowden et al. 2008) (vignetted): it is due to interactions between particles accelerated in the Earth’s magnetosphere that reach the detector and simulate the effect of a photon. Although the most severe episodes can be easily identified and removed, some residual contamination may remain in supposedly “clean” observations and must be taken into account. To model residual SP contamination we again follow Snowden et al. (2008) who model it as a single power law with index ≈ 0.9, although other parameterizations are possible (Leccardi & Molendi 2008 adopt a double power law broken at 5 keV).
The relative normalisations of the different diffuse photon background components are taken from Table 2 of Snowden et al. (2008); we checked, by generating 100 simulated pointings containing only backgrounds (both photon and particle) that the mean background per pixel is ≈ 10−5photons s-1 pixel-1, compatible with the measured XXL background level (Fig. 7 of XXL Paper I). We note that our background modelling is not entirely realistic as it is neither time nor position dependent (as real X-ray background is); however, we think that it is sufficient for our purposes of validating XAminF18 using simplified analytical simulations.
4.3 Making realistic simulated XMM-Newton images
We simulate images as follows.
– Each XMM pointing is simulated independently.
– For both the simulated clusters and three of the background components described in Sect. 4.2 (the particle background is included at a successive time), a perfect event list is created and fed to a dedicated IDL routine, which creates a realistic XMM-Newton image introducing the relevant instrumental effects.
– In all cases an exposure time of 10 ks and THIN filters are assumed so as to reproduce the real XXL observing conditions.
– For the photons in the perfect event lists which come from the simulated clusters, an energy of 1 keV (appropriate for the low-mass clusters preferentially observed by XXL) is assumed.
– Other photons from resolved AGNs, diffuse photon background, and soft protons are distributed in energy according to the models described in Sect. 4.2.
– Galactic absorption is corrected for according to Morrison & McCammon (1983).
– The routine assumes as input an ideal event list coming from a perfect detector with an effective area 1387.71 cm2, appropriate for pn THIN filtersat ≈1.5 keV, where the XMM-Newton sensitivity is maximum.
– “Blurred” event lists are created from the perfect input event lists, one for each EPIC detector; they include instrumental effects such as vignetting and blurring in energy and position.
– To create these blurred event lists, input photons are reshuffled in position and energy and/or thrown away according to their initial position and energy. This reshuffling takes into account the different effective areas and PSF distortions, both strongly energy and position dependent, of the three EPIC detectors.
– Particle background is added according to the model described in Sect. 4.2.
– Images in [0.5−2] keV at 2.5′′ /pixel (one for each EPIC detector), to oversample the XMM-Newton PSF, are then created along with the corresponding exposure maps; the format is the same as the real XMM-Newton images.
– Images are created so as to reproduce the real XXL tiling with pointings are spaced by 20′ (XXL Paper I). To cover 25 deg2 of sky with this tiling 256 overlapping pointings are needed. Exposure maps and detector masks are created as well.
– After creating an event list for each pointing, event lists from neighbouring pointings are re-projected to a common point on the sky to make a 68′ × 68′ tile per detector; exposure maps are also re-projected and 68′ × 68′ tiled exposure maps are created.
Figure 2 shows an example of a simulated 68′ × 68′ MOS1+MOS2+pn tile of several bright simulated clusters (all with count rate 0.1 count s-1 and core radius 20′′) and its corresponding tiled exposure map. The tile includes ≈22 overlapping pointings; the red crosses in the right panel show the cluster positions; the wavelet smoothed image of the same area is shown in Fig. 3.
Figure 3 shows a 68′ × 68′ tile smoothed with the MR/1 wavelet smoothing code on which preliminary source detection with SEXtractor has been run; the figure is the smoothed version of the X-ray raw tile shown in the left panel of Fig. 2.
 |
Fig. 2 Examples of a simulated tile and its corresponding tiled exposure map. Left panel: mosaic (MOS1+MOS2+pn) raw X-ray tile, comprising ≈25 overlapping pointings. Sources in the tile include both clusters (larger sources regularly spaced by 10′) all with count rates of 0.1 count s-1 and core radius 20′′, and resolved AGNs inserted at random positions; background is added. A wavelet smoothed image of the same area is shown in Fig. 3. Right panel: combined (MOS1+MOS2 + 3.1×pn) tiled exposure map of the same region. Red crosses show the cluster positions. A nominal XMM-LSS exposure time 10 ks for each instrument is assumed in both panels. The exposure map is in MOS units: the pn exposure map is corrected for the larger pn effective area by multiplying it by 3.1 (see text) so the combined exposure map has an exposure time ≈50 ks at the pointing centres. The area is the same as that shown in Fig. 1 and the exposure maps in the right panels of both figures are the same. |
 |
Fig. 3 68′ × 68′ combined (MOS1+MOS2+pn) tile smoothed with MR/1 on which preliminary source detection with SEXtractor has been run. The figure is the smoothed version of the left panel of Fig. 2. Green circles indicate sources tentatively identified by SEXtractor. Detected sources include clusters (larger sources regularly spaced by 10′) with count rates of 0.1 count s-1 and core radius 20′′, and resolved AGNs inserted at random positions (smaller sources irregularly spaced). The exposure time is 10 ks and background is added. Cyan circles represent the XMM pointings and are 15′ in radius; the pointing geometrical centres at which the circles are drawn are not the same as the centres of the optics (points of maximum telescope sensitivity). |
4.4 PSF model
Our PSF model is the latest ELLBETA model for XMM-Newton described in Read et al. (2011). More specifically we use the SAS task psfgen to generate PSF images at 1.1′′ /pixel and at a range of energies, off-axis angles, and azimuthal angles for each EPIC detector. These images are stored together in a FITS file and our program computes a random shift from its nominal position for each event, first by interpolating between the images according to the event energy and position and then sampling a random shift from the interpolated image; PSF images for the appropriate detector are used each time. An example is shown for the MOS2 detector in Fig. 4; the figure shows how a point source with a 1 keV energy put at 0′, 5′, 10′, and 13′ from the centre of the image and at several azimuthal angles is distorted by the XMM-Newton optics. No blurring in energy or vignetting was introduced in making the figure to show more clearly the effects of PSF distortion (but of course they are introduced in the simulated images).
Similar figures could be drawn for MOS1 and pn and they would show equally strong off-axis and azimuthal dependent distortions, though the shapes of the distortions would be different in each detector.
 |
Fig. 4 PSF distortion of the MOS2 detector for a point source with a 1 keV energy put at 0′, 5′, 10′, and 13′ from the centre of the image. No blurring in energy or vignetting is introduced here to show more clearly the effects of PSF distortion. |
5 Results
5.1 Recovering clusters
In the following we compare the relative performance of using single pointings and using all available overlapping pointings. We will loosely speak of “tiles vs. pointings” but it should be remembered that 68′ × 68′ tiles are used only for source detection by SEXtractor and that multiple overlapping pointings are used for the actual fit. In addition, even in the case of single pointings, fits have been performed with the new XAminF18 incorporating all other improvements (new PSF model, new fits, etc.), so the results are not exactly the same as those that would be obtained by XAminP06.
5.1.1 Tiles vs. single pointings
Figure 5 shows the recovered core radius (EXT) vs. the extent statistic (EXT_STAT) of the EXT fit for recovered clusters (red points) and AGNs (blue points). The panels in the figure all show cluster detections within 37.5′′ of an input cluster (except for clusters with input core radius 40′′ where the correlation radius is 50′′, and clusters with input core radius 50′′ where the correlation radius is 60′′). If the same input cluster is detected more than once because it falls on more than one tile or one pointing, the detection with the highest value of EXT_STAT is shown. AGN detections are taken from a 25 deg2 simulation containing only AGNs randomly distributed in the field and with a flux distributed according to a Moretti et al. (2003) log (N)−log(S) relation; detections from these simulations within 6′′ of an input AGNs are reported. The figure shows all detections (top panels) and only the detections of input clusters placed at off-axis angle >9′ measured from the centre of the optics, not the geometrical centre, from all pointings that cover them (bottom panels). We chose > 9′ even though clusters are either at the centre or displaced by > 10′ from the geometrical centre because the centre of the optics can be offset from it by as much as ≈ 1′. In both cases in Fig. 5, the left panels pertain to the case where only single pointings are used and the right panels pertain to the case where tiles are used. The lines show the C1∕C2 selection criteria defined in P06. The figure shows that the separation between clusters (red points), on the one hand, and AGNs (blue points), on the other, is very clear; the main point is that the C1∕C2 selection criteria defined by P06 are still valid and do not need to be revised in view of the changes intervened in both the PSF model and the wavelet smoothing program between XAminP06 and XAminF18, currently not tested beyond 10 ks.
Other trends are apparent in Fig. 5. Comparing the two left panels, i.e. the detections using single pointings (top, all detections; bottom, only detections of sources at off-axis angle > 9′ from all pointings) we see that the three red clouds at the top, corresponding to the highest values of EXT_STAT, disappear at the bottom; these are the detections of the sources on-axis, which are detected with the highest significance. Comparing the two right panels, i.e. detections using tiles (top, all detections; bottom, only detections of sources at off-axis angle > 9′ from all pointings); however, we see that the shapes of the red clouds are similar. This means that sources on-axis and at large off-axisare recovered at the same level of significance, which is not the case with single pointings. There is also an overall trend toward higher values of EXT_STAT moving from single pointings to tiles (compare left and right panels in Fig. 5). Comparing the two top panels we see that the isolated clouds on the left disappear on the right, and that the distribution of EXT_STAT becomes more uniform: sources detected at lower EXT_STAT in single pointings migrate toward higher values of EXT_STAT. This is not surprising: we expect that using, on average, two pointings instead of one would lead to a doubling, on average, of EXT_STAT for sources at large off-axis angles. The effect is demonstrated in Fig. 6 which shows EXT_STAT using tiles vs. EXT_STAT using single pointings. The figure shows the line of equality (EXT_STATTiles = EXT_STAT Pointings) where sources on-axis fall, and the line EXT_STATTiles = 2 × EXT_STATPointings where the bulk of the off-axis sources fall, which means that the level of significance roughly doubles using tiles.
Figure 5 shows several clouds of red points both in the case of tiles and of single pointings; their presence is just due to fact that count rates and core radii of input clusters take a few values and are not continuously distributed. This is easy to see for the clouds at ext = [10, 20, 50]′′ in all panels of Fig. 5, and is further seen in Fig. 7 which shows again the EXT vs. EXT_STAT plane, using tiles, of recovered clusters where clusters have been separated by input count rate.
 |
Fig. 5 EXT vs. EXT_STAT plane for recovered clusters (red) and AGNs (blue). The continuous line in each panel at EXT_STAT = 33 shows the cut for the C1 selection and the dashed line at EXT_STAT = 15 shows the cut for the C2 selection. The continuous line at ext =5′′ shows the cut in extent for both the C1 and C2 selections. If a source is found in more than one tile or pointing, the detection with the highest value of EXT_STAT is shown. Panel a: single pointings; all sources. Panel b: tiles; all sources. Panel c: single pointings; off-axis angle > 9′. Panel d: tiles; off-axis angle >9′. |
 |
Fig. 6 EXT_STAT using tiles vs. EXT_STAT using single pointings. The lines at EXT_STAT = 33 show the C1 selection criterion, the dashed lines at EXT_STAT = 15 the C2 selection criterion. Also, shown are the line of equality, where on-axis sources fall, and the line EXT_STATTiles = 2 ×EXT_STATPointings, where most sources off-axis fall, showing the EXT_STATTiles ≈ 2 EXT_STATPointings. |
 |
Fig. 7 EXT vs. EXT_STAT plane for recovered clusters where clusters have been separated by input count rate. The continuous line at EXT_STAT = 33 shows the cut for the C1 selection and the dashed line at EXT_STAT = 15 shows the cut for the C2 selection. The continuous line at ext =5′′ shows the cut in extent for both the C1 and C2 selections. If a source is found in more than one tile, the detection with the highest value of EXT_STAT is shown. Panel a: tiles; input count rate 0.1 count s-1. Panel b: tiles; input count rate 0.05 count s-1. Panel c: tiles; input count rate 0.01 count s-1. Panel d: tiles; input count rate 0.005 count s-1. |
5.1.2 Detection probabilities
We now show the detection probabilities of our simulated clusters. Detection probabilities are computed, for each count rate−core radius combination, by dividing the number of detected C1 or C2 clusters by the number of input clusters. Detected clusters are found by matching a detection (C1 or C2) to the nearest input cluster using correlation radii [37.5,37.5,50.0,60.0]′′ for input core radii [10,20,40,50]′′; unmatched detections are not considered. If an input cluster is found in more than one tile or pointing, only the detection with the highest value of EXT_STAT is considered; therefore, if an input cluster is found both as a C1 and a C2, only the C1 detection is considered. In computing the probabilities we have removed input clusters and detections which were too close to the border of the simulated 25deg2 sky patch to avoid border effects; this removal reduces the number of input cluster from 841 to 784. Tables 3–6list the C1 and C2 detection probabilities for simulated clusters as a function of input count rate and core radius both using tiles and using single pointings. Tables 3 and 5 list the probabilities across the whole XMM FoV and Tables 4 and 6 list the probabilities for input clusters which fall at an off-axis angle > 9′ on all pointings that cover them to better asses the benefits of using tiles for sources at large off-axis angles.
The most important message from these numbers is that using tiles greatly enhances the detection probability of the weakest clusters, which constitute the bulk of the XXL population; for example, the detection probability of a cluster with count rate 0.01 count s-1 and core radius 10′′ doubles from 0.094 to 0.204. Even more impressive is the performance increase at large off-axis angle; in this case, for the same values of count rate and core radius, the probability increases from 0.017 to 0.173. This is important since XXL is a blind survey so a cluster is more likely to fall at large off-axis angles from all XXL pointings than near the centre of one pointing.
For example, since the XMM FoV is 15′, the probability of a cluster falling at off-axis angle > 10′ is (152−102)∕152 = 0.56 whereas the probability of falling within 10′ of a pointing is just 102∕152 = 0.44
Therefore, we expect that the upcoming reprocessing of the XXL data with XAminF18 will yield a substantial increase in new, secure cluster detections. It is also interesting to note that using tiles the sensitivity at large off-axis angles is not much lower than the sensitivity across the whole FoV; the detection probability of a cluster with count rate 0.01 count s-1 and core radius 10′′ is 0.173 at off-axis > 9′′ and 0.204 across the whole FoV. Therefore, we conclude that we manage to do almost as well at large off-axis angles as on-axis. This should be contrasted with the single pointing case where the detection probability drops from 0.094 to 0.017 for the same values of count rate and core radii. For larger values of count rate (> 0.05 count s-1) the improvement is less impressive since these clusters already have enough photons to be securely detected even at large off-axis angles in single pointings; however, these clusters will not constitute the majority of the XXL population.
From Table 3, we see that we detect 5300 C1 clusters; in addition, we find a total of 288 false detections after excluding detections too close to the border of the simulations and detections likely to be double sources (see Sect. 5.3 for more details), so the fraction of false detections in comparison with the total number of C1 clusters detected is ≈ 3.9%, confirming the high purity of the C1 selection.
C1 detections for all sources.
C1 detections for sources with input off-axis angle >9′.
C2 detections for all sources.
C2 detections for sources with input off-axis angle >9′.
5.1.3 Poor performance of XAminF18 for 0.05 count s−1 – 50′′
We must justify the poorer performance using tiles with respect to using single pointings in the case of count rate 0.05 count s-1 and core radius 50′′. We attribute this degradation to the large value of the box chosen to estimate the background in SEXtractor (see Table 1): 512 pixels instead of 64, as used in P06, which in turn was necessary because we found that using 64 pixels led, in the case of tiles, to too many false C1 detections; using a larger box therefore increases sample purity. This choice may negatively affect the detection of sources with low photon density. A cluster with count rate 0.05 count s-1 and core radius 50′′ produces 500 counts (or less if not on-axis) at the nominal XXL 10 ks exposure time, spread over a large area (50′′ in radius), so the surface brightness is low; instead, using a large box to estimate the background may lead SEXtractor to miss these sources as their contrast above the background is too low. However, we do not expect this to be a serious problem as clusters with core radius ≈ 50′′ are rare in the first place, and in general have higher count rates than 0.05 count s-1 as we now show using a realistic cosmological hydro-dynamical simulation. We used the cosmoOWLS simulation (McCarthy et al. 2010; Le Brun et al. 2014), for which X-ray fluxes, R500c, and θ500c for the input halos were available; for one of its ten realisations we found, after applying a flux cut > 5 × 10−16 erg cm−2 s−1 (roughly the XXL flux limit for extended sources in [0.5−2] keV), 14 260 input halos. Count rates were measured for these simulated halos from their X-ray fluxes by adopting a conversion factor from flux to count rate 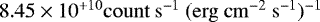 , computed with WebSpec. The value is appropriate for a z = 0.5, T = 2 keV plasma (typical values for XXL clusters) described by an APEC model and for XMM-Newton THIN filters used in XXL observations. Core radii ext were measured for the same halos by their θ500c by assuming a constant ratio ext ∕θ500c = 0.24 (Pierre et al. 2017). We found that only 189 halos had count rate < 0.05 count s-1 and core radius > 50′′, that is ≈1.3% We conclude that the poorer performance in this regime of the pipeline will not negatively impact its overall performance too severely and the improvement in sample purity we obtain is worth the price. We finally note that for count rate 0.05 count s-1 and core radius 40′′ using tiles still leads to a significant improvement in C1 detections probability: 0.977 compared to 0.903 across the whole field of view and 0.976 compared to 0.881 for the >9′ region, so the degradation affects only the very largest and fainter clusters. Again the use of tiles allowed us to perfectly compensate for the decrease in detector sensitivity: the detection probabilities across the whole FoV and at > 9′ are almost identical.
, computed with WebSpec. The value is appropriate for a z = 0.5, T = 2 keV plasma (typical values for XXL clusters) described by an APEC model and for XMM-Newton THIN filters used in XXL observations. Core radii ext were measured for the same halos by their θ500c by assuming a constant ratio ext ∕θ500c = 0.24 (Pierre et al. 2017). We found that only 189 halos had count rate < 0.05 count s-1 and core radius > 50′′, that is ≈1.3% We conclude that the poorer performance in this regime of the pipeline will not negatively impact its overall performance too severely and the improvement in sample purity we obtain is worth the price. We finally note that for count rate 0.05 count s-1 and core radius 40′′ using tiles still leads to a significant improvement in C1 detections probability: 0.977 compared to 0.903 across the whole field of view and 0.976 compared to 0.881 for the >9′ region, so the degradation affects only the very largest and fainter clusters. Again the use of tiles allowed us to perfectly compensate for the decrease in detector sensitivity: the detection probabilities across the whole FoV and at > 9′ are almost identical.
5.1.4 Sample purity
We now check the purity of the sample of recovered C1 detections. We look, in all simulations, for sources detected as C1 that are too far froman input clusters to be considered legitimate detections of an input source; as usual, our correlation radius is 50′′ for clusters with input core radius 40′′, 60′′ for clusters with input core radius 50′′, and 37.5′′ in all other cases; C1 detections outside these radii are considered spurious. We exclude spurious C1 detections too close to the border of the 25deg2 simulated sky patch to avoid border effects; we also exclude spurious C1 detections which are probably pairs of AGNs close on the sky as these can be effectively flagged as such (see explanation in Sect. 5.3). We find that for all count rate−core radius combinations, the contamination rate defined as the fraction of spurious C1 detections divided by the number of input clusters is at most ≈3% confirming the P06 finding that the C1 selection is indeed very pure and remains so when using tiles. This depends, of course, on the count rate−core radius sampling used in the simulation, which may not be the real one; we also avoided projection effects.
5.1.5 Example
As an example of the power of using tiles, we show in Fig. 8a simulated weak cluster with count rate 0.01 count s-1 and core radius 10′′ observed by two pointings. The cluster is securely recovered as a C1 using tiles, but is not recognised as such when using single pointings separately. In the top panel are shown, on the left, the combined photon map of the two pointings (which is not used in the fit) and, at the centre and on the right, the individual photon images of the two separate pointings. In the bottom panel are shown the corresponding wavelet smoothed images. As can be seen in the figure, the emission in either pointing is very weak as the sources are at a large off-axis angle (≈ 10′) and are not bright enough to reliably identify the source as a cluster. However, when both are used the source is securely identified as a C1 cluster (at the position indicated by the cyan cross) with a value of EXT_STAT ≈ 47, more than enough for a secure identification as a cluster.
 |
Fig. 8 Using tiles allows us to recover a cluster that would be missed using separatepointings. In all images a green circle indicates an extended source (C1 or C2 detection) and a green square a source that is significant (PNT_DET_STAT > 15) but which cannot be securely identified as point-like or extended; the cyan cross shows the position of the recovered cluster and the black squares in the left panels the position of the input AGNs; X-ray contours are also shown. Panel a: combined photon image. Panel b: photon image of one of the pointings. Panel c: photon image of the other pointing. Panel d: combined wavelet image. Panel e: wavelet image of one of the pointings. Panel f: wavelet image of the other pointing. |
5.2 Recovering clusters with central AGN contamination (AC)
Figure 9 shows the EXT vs. EXT_STAT plane for recovered clusters contaminated by a central AGN where the contaminating AGN has twice the count rate as the cluster. The continuous line at EXT_STAT = 33 shows the cut for the C1 selection and the dashed line at EXT_STAT = 15 shows the cut for the C2 selection. The figure shows that many clusters are not identified as C1, or even as C2, because of the central AGN contamination.
Figure 10 shows the EPN_STAT_PNT vs. EPN_STAT_EXT plane for clusters contaminated by a central AGN (red) and AGNs (blue). The figure shows that the region (epn_stat_pnt = 20 AND epn_stat_ext = 20) OR (epn_stat_ext = 100) is almost empty of recovered AGNs, and can be used to identify AC clusters.
 |
Fig. 9 EXT vs. EXT_STAT plane for recovered clusters contaminated by a central AGN (AC). The continuous line at EXT_STAT = 33 shows the cut for the C1 selection, and the dashed line at EXT_STAT = 15 shows the cut for the C2 selection. The figure shows that many clusters are no longer identified as C1, or even as C2, because of the central AGN contamination. |
 |
Fig. 10 EPN_STAT_PNT vs. EPN_STAT_EXT plane for clusters contaminated by a central AGN (red) and AGNs (blue). The continuous lines show the cuts for the AC selection. The figure shows that AC clusters may be recovered by applying the AC selection. |
5.3 Distinguishing clusters from double sources.
We finally introduce a criterion to flag pairs of point sources appearing close in projection on the sky (double sources or doubles); this is necessary as point sources that are so close (in projection) may sometimes be misidentified as an extended source. These sources may be easily flagged by considering the DBL_STAT statistic, defined in Eq. (15). This is shown in Fig. 11 showing the DBL_STAT vs. EXT_STAT plane for recovered clusters (red) and double sources (blue) where the continuous line at EXT_STAT = 33 shows the cut for the C1 selection; the condition DBL_STAT > EXT_STAT does a good job of separating these double sources from real C1s. The blue line at DBL_STAT = 1.5 in Fig. 11 pertains to double sources for which DBL_STAT = 0; although some of these sources have EXT_STAT > 33, almost all such cases also have EXT <5′′ so there is no risk for them to be classified as C1s.
 |
Fig. 11 DBL_STAT vs. EXT_STAT plane for recovered clusters (red) and double sources (blue). The continuous line at EXT_STAT = 33 shows the cut for the C1 selection The figure shows that most double sources have DBL_STAT > EXT_STAT. |
6 P1 selection
In the same way as done for the C1/C2/AC selection, it is interesting to investigate selection criteria for point sources that will yield samples with high purity down to a flux limit that isas small as possible; we refer to this new selection as P1. As stated in Sect. 2.4, a cut PNT_DET_STAT > 15 works well in distinguishing real sources from chance background fluctuations. As the criterion PNT_DET_STAT > 15 was derived using only simulations of point sources, there is the concern that weak, extended sources which do not pass the C1∕C2 selections but were detected with PNT_DET_STAT > 15 can be mistakenly classified as “point sources” in the sense of P06. In the following we refer to sources with PNT_DET_STAT > 15 as “significant detections” (SD). We use the simulations of clusters introduced above to check the validity of this assumption; we want to find how many input clusters in our simulations are detected with PNT_DET_STAT > 15 but do not pass the C1∕C2 selection. It might be argued that since the number of AGNs in the sky is so much higher than the number of clusters, possible contamination of AGN samples from clusters flagged as SD and therefore regarded as point sources should not be a concern. However, this is not so as there is a correlation between clusters and AGNs: many clusters are known to harbour a central AGN; we think it is important to have a selection that yields a sample of point sources that is as pure as possible, down to a flux limit that is as low as possible. We have therefore introduced the class P1 for point sources with the aim of selecting a sample of point sources, defined only in terms of instrumental variables, that has a high degree of purity and is complete down to a count rate that is as low as possible. The P1 class is defined by the following criteria in the [0.5−2] keV band:
- 1.
PNT_DET_STAT > 30
- 2.
ext < 3′′ OR EXT_STAT = 0.
Figure 12 shows the EXT vs. EXT_STAT plane recovered clusters (red) and AGNs (blue); the figure shows the C1∕C2 selection box and the P1 selection box, mutually exclusive. Sources classified as C1∕C2 or P1 are shown with larger points than the others.
Table 7 shows that for the P1 selection the fraction of input clusters that are classified as P1 sources is quite low (≈3% or less) for almost all combinations of count rates and core radii; therefore, the P1 selection wehave introduced is expected to give virtually pure samples of point sources, first because AGNs greatly outnumber clusters, and second because a small fraction of clusters is mistakenly classified as P1 for any realistic combination of count rates and core radii. To test the validity of the P1 selection criteria we have simulated four patches of sky of 5 × 5deg each containing only randomly distributed AGNs; each 5 × 5deg patch of sky contains ≈80 000 AGNs with flux distribution from Moretti et al. (2003) and down to a flux limit 10−16 erg cm−2 s−1, exactly as done for the other simulations. Figure 13 shows the cumulative distribution of the input AGNs, (log (N(> CR))−log(CR), with
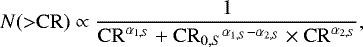 (17)
(17)
with α1,CR = 1.851, α2,CR = 0.607, and CR0,CR = 0.014 count s-1, appropriate for the [0.5−2] keV band, from Moretti et al. (2003)1.
Figure 14 shows the differential distribution (non-cumulative) log (N(CR)−log(CR)) both for significant detections (PNT_DET_STAT > 15) and for P1 sources. The left panel shows that the P1 selection is virtually complete down to CR ≈ 0.006 count s-1; the right panel shows a blow up of the plot at CR ≈ 0.006 count s-1 making it clearer. Table 8 lists the selection criteria we have introduced.
 |
Fig. 12 EXT vs. EXT_STAT plane for recovered clusters (red) and AGNs (blue). The boxes indicate the C1∕C2 and P1 selection regions, respectively. Sources identified as either C1∕C2 or P1 are shown with larger points than the others. |
 |
Fig. 13 log(N(> CR))−log(CR) of input simulated point sources. |
 |
Fig. 14 Differential log(N(CR))−log(CR) for recoveredsources. Blue line: all significant detections; red line: P1 detections. The figure shows that the P1 selection is complete down to CR ≈ 0.006 count s-1. Panel a: overall view. Panel b: blow up of the regime where P1 selection becomes incomplete. |
7 Conclusions
We presented XAminF18, the newest and final pipeline for the XXL survey, we detailed the main improvements with respect to the older pipeline XAminP06, and we validated it through an extensive set of simulations. The need for an updated version, even though XAminP06 already works very well, stems mostly from the need to make optimal use of the available X-ray information, using multiple observations of the same source when available.
Using 68′ × 68′ tiles for source detection and all available observations when fitting a candidate source we showed that we can significantly increase the number of detected clusters; clusters that are too faint in either observations and would be missed (or found as C2 at best) can be reliably found. This is particularly important for the low-mass, low-luminosity systems which are the bulk of the XXL population.
Another major improvement we introduced is the capability to detect clusters contaminated by a central AGN by simultaneously fitting for an extended and a point source. The presence of an AGN at the centre of a cluster severely degrades the performanceof the simple extended source fit, causing the cluster to be missed in many cases, especially where the AGN count rate is close to or higher than the cluster rate. We have shown that the introduction of the EPN fit allows us to recover the contaminated cluster in many cases.
We also introduced the capability of fitting two point sources, useful for flagging pairs of AGNs seen close in projection that may otherwise be incorrectly identified as a cluster; we were able to define, through simulations, a criterion for flagging double sources based again on purely instrumental variables.
Although we have shown that XAminF18 is an excellent pipeline for the XXL survey, and in principle could be adapted to other X-ray surveys, more work remains to be done. In an upcoming paper we will test the XAminF18 performance using more realistic hydrodynamic simulations where the shape of clusters is not circular and using a more realistic population of AGNs; we will also consider different exposure times and the consequences of adopting different values of β. All this will be necessary to allow the XXL survey to achieve its ultimate goal of precision cosmology with X-ray selected clusters of galaxies.
Simulated clusters recovered as P1.
Summary of the various types of source and their selection criteria.
Acknowledgements
XXL is an international project based around an XMM Very Large Programme surveying two 25 deg2 extra-galactic fields at a depth of ≈ 5 × 10−15 erg cm−2 s−1 in the [0.5 − 2] keV band for point-like sources. The XXL website is http://irfu.cea.fr/xxl. Multi-band information and spectroscopic follow-up of the X-ray sources are obtained through a number of survey programmes, summarised at http://xxlmultiwave.pbworks.com/. We thank Ian McCarthy for making available the X-ray fluxes of the input halos in the cosmoOWLS simulation. The Saclay group acknowledges long-term support from the Centre National d’Études Spatiales (CNES). L.F. thanks CEA for a long-term research contract. E.K. thanks CNES and CNRS for support during his post-doctoral research. We thank Jean-Luc Starck for supplying us with an improved version of MR/1 from which our IDL implementation was derived.
Appendix A Summary of simulations of different types of sources
A summary of all the simulations of clusters used is given in Table A.1. A summary of all the simulations of clusters with a central AGN used is given in Table A.2. A summary of all the simulations of double sources used is given in Table A.3.
Summary of simulated clusters.
Summary of simulated clusters with central AGN.
Summary of simulated double sources.
References
- Adami, C., Giles, P., Koulouridis, E., et al. 2018, A&A, 620, A5 (XXL Survey, XX) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arnaud, K. A. 1996, in Astronomical Data Analysis Software and Systems V, eds. G. H. Jacoby, & J. Barnes, ASP Conf. Ser., 101, 17 [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bury, P. 1995, PhD Thesis, University of Nice-Sophia Antipolis, France [Google Scholar]
- Cash, W. 1979, ApJ, 228, 939 [NASA ADS] [CrossRef] [Google Scholar]
- Cavaliere, A., & Fusco-Femiano, R. 1976, A&A, 49, 137 [NASA ADS] [Google Scholar]
- Chiappetti, L., Clerc, N., Pacaud, F., et al. 2013, MNRAS, 429, 1652 [NASA ADS] [CrossRef] [Google Scholar]
- Chiappetti, L., Fotopoulou, S., Lidman, C., et al. 2018, A&A, 620, A12 (XXL Survey, XXVII) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Clerc, N., Sadibekova, T., Pierre, M., et al. 2012, MNRAS, 423, 3561 [NASA ADS] [CrossRef] [Google Scholar]
- Clerc, N., Adami, C., Lieu, M., et al. 2014, MNRAS, 444, 2723 [NASA ADS] [CrossRef] [Google Scholar]
- De Luca, A., & Molendi, S. 2004, A&A, 419, 837 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fotopoulou, S., Pacaud, F., Paltani, S., et al. 2016, A&A, 592, A5 (XXL Survey, VI) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehrels, N. 1986, ApJ, 303, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Giles, P. A., Maughan, B. J., Pacaud, F., et al. 2016, A&A, 592, A3 (XXL Survey, III) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Brun, A. M. C., McCarthy, I. G., Schaye, J., & Ponman, T. J. 2014, MNRAS, 441, 1270 [NASA ADS] [CrossRef] [Google Scholar]
- Leccardi, A., & Molendi, S. 2008, A&A, 486, 359 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liedahl, D. A., Osterheld, A. L., & Goldstein, W. H. 1995, ApJ, 438, L115 [NASA ADS] [CrossRef] [Google Scholar]
- McCarthy, I. G., Schaye, J., Ponman, T. J., et al. 2010, MNRAS, 406, 822 [NASA ADS] [Google Scholar]
- Mewe, R., Gronenschild, E. H. B. M., & van den Oord, G. H. J. 1985, A&AS, 62, 197 [NASA ADS] [Google Scholar]
- Mewe, R., Lemen, J. R., & van den Oord, G. H. J. 1986, A&AS, 65, 511 [NASA ADS] [Google Scholar]
- Moretti, A., Campana, S., Lazzati, D., & Tagliaferri, G. 2003, ApJ, 588, 696 [NASA ADS] [CrossRef] [Google Scholar]
- Morrison, R., & McCammon, D. 1983, ApJ, 270, 119 [NASA ADS] [CrossRef] [Google Scholar]
- Pacaud, F., Pierre, M., Refregier, A., et al. 2006, MNRAS, 372, 578 (P06) [NASA ADS] [CrossRef] [Google Scholar]
- Pacaud, F., Pierre, M., Adami, C., et al. 2007, MNRAS, 382, 1289 [NASA ADS] [CrossRef] [Google Scholar]
- Pacaud, F., Clerc, N., Giles, P. A., et al. 2016, A&A, 592, A2 (XXL Survey, II) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierre, M., Valtchanov, I., Altieri, B., et al. 2004, JCAP, 9, 011 [NASA ADS] [CrossRef] [Google Scholar]
- Pierre, M., Pacaud, F., Duc, P.-A., et al. 2006, MNRAS, 372, 591 [NASA ADS] [CrossRef] [Google Scholar]
- Pierre, M., Chiappetti, L., Pacaud, F., et al. 2007, MNRAS, 382, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Pierre, M., Pacaud, F., Juin, J. B., et al. 2011, MNRAS, 414, 1732 [NASA ADS] [CrossRef] [Google Scholar]
- Pierre, M., Pacaud, F., Adami, C., et al. 2016, A&A, 592, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pierre, M., Valotti, A., Faccioli, L., et al. 2017, A&A, 607, A123 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pratt, G. W., & Arnaud, M. 2002, A&A, 394, 375 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Read, A. M., & Ponman, T. J. 2003, A&A, 409, 395 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Read, A. M., Rosen, S. R., Saxton, R. D., & Ramirez, J. 2011, A&A, 534, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Slezak, E., de Lapparent, V., & Bijaoui, A. 1993, ApJ, 409, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Snowden, S. L., Mushotzky, R. F., Kuntz, K. D., & Davis, D. S. 2008, A&A, 478, 615 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starck, J.-L., & Pierre, M. 1998, A&AS, 128, 397 (SP98) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Starck, J.-L., Murtagh, F. D., & Bijaoui, A. 1998, Image Processing and Data Analysis (Cambridge: Cambridge University Press) [Google Scholar]
- Strüder, L., Briel, U., Dennerl, K., et al. 2001, A&A, 365, L18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Turner, M. J. L., Abbey, A., Arnaud, M., et al. 2001, A&A, 365, L27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valtchanov, I., Pierre, M., & Gastaud, R. 2001, A&A, 370, 689 (V01) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willis, J. P., Clerc, N., Bremer, M. N., et al. 2013, MNRAS, 430, 134 [NASA ADS] [CrossRef] [Google Scholar]
Moretti et al. (2003) work with physical fluxes; we work with instrumental count rates and adopt a conversion factor 1.086 × 10−12 erg cm−2 s−1∕(count s-1), computed from WebSpec and appropriate for a power law spectral model with index 1.7 and THIN XMM filters.
All Tables
All Figures
 |
Fig. 1 Left panel: example of particle background model subtracted from a 68′ × 68′ tile. Right panel: tiled combined exposure map (MOS1+MOS2 + 3.1×pn) of the same region. A nominal XMM-LSS exposure time 10 ks for each instrument is assumed. The map is in MOS units: the pn exposure map is corrected for the larger pn effective area by multiplying it by 3.1 (see text) so the combined exposure map has an exposure time ≈50 ks at the pointing centres. The exposure time is even larger (≈60 ks) in areas where three pointings overlap. |
| In the text | |
 |
Fig. 2 Examples of a simulated tile and its corresponding tiled exposure map. Left panel: mosaic (MOS1+MOS2+pn) raw X-ray tile, comprising ≈25 overlapping pointings. Sources in the tile include both clusters (larger sources regularly spaced by 10′) all with count rates of 0.1 count s-1 and core radius 20′′, and resolved AGNs inserted at random positions; background is added. A wavelet smoothed image of the same area is shown in Fig. 3. Right panel: combined (MOS1+MOS2 + 3.1×pn) tiled exposure map of the same region. Red crosses show the cluster positions. A nominal XMM-LSS exposure time 10 ks for each instrument is assumed in both panels. The exposure map is in MOS units: the pn exposure map is corrected for the larger pn effective area by multiplying it by 3.1 (see text) so the combined exposure map has an exposure time ≈50 ks at the pointing centres. The area is the same as that shown in Fig. 1 and the exposure maps in the right panels of both figures are the same. |
| In the text | |
 |
Fig. 3 68′ × 68′ combined (MOS1+MOS2+pn) tile smoothed with MR/1 on which preliminary source detection with SEXtractor has been run. The figure is the smoothed version of the left panel of Fig. 2. Green circles indicate sources tentatively identified by SEXtractor. Detected sources include clusters (larger sources regularly spaced by 10′) with count rates of 0.1 count s-1 and core radius 20′′, and resolved AGNs inserted at random positions (smaller sources irregularly spaced). The exposure time is 10 ks and background is added. Cyan circles represent the XMM pointings and are 15′ in radius; the pointing geometrical centres at which the circles are drawn are not the same as the centres of the optics (points of maximum telescope sensitivity). |
| In the text | |
 |
Fig. 4 PSF distortion of the MOS2 detector for a point source with a 1 keV energy put at 0′, 5′, 10′, and 13′ from the centre of the image. No blurring in energy or vignetting is introduced here to show more clearly the effects of PSF distortion. |
| In the text | |
 |
Fig. 5 EXT vs. EXT_STAT plane for recovered clusters (red) and AGNs (blue). The continuous line in each panel at EXT_STAT = 33 shows the cut for the C1 selection and the dashed line at EXT_STAT = 15 shows the cut for the C2 selection. The continuous line at ext =5′′ shows the cut in extent for both the C1 and C2 selections. If a source is found in more than one tile or pointing, the detection with the highest value of EXT_STAT is shown. Panel a: single pointings; all sources. Panel b: tiles; all sources. Panel c: single pointings; off-axis angle > 9′. Panel d: tiles; off-axis angle >9′. |
| In the text | |
 |
Fig. 6 EXT_STAT using tiles vs. EXT_STAT using single pointings. The lines at EXT_STAT = 33 show the C1 selection criterion, the dashed lines at EXT_STAT = 15 the C2 selection criterion. Also, shown are the line of equality, where on-axis sources fall, and the line EXT_STATTiles = 2 ×EXT_STATPointings, where most sources off-axis fall, showing the EXT_STATTiles ≈ 2 EXT_STATPointings. |
| In the text | |
 |
Fig. 7 EXT vs. EXT_STAT plane for recovered clusters where clusters have been separated by input count rate. The continuous line at EXT_STAT = 33 shows the cut for the C1 selection and the dashed line at EXT_STAT = 15 shows the cut for the C2 selection. The continuous line at ext =5′′ shows the cut in extent for both the C1 and C2 selections. If a source is found in more than one tile, the detection with the highest value of EXT_STAT is shown. Panel a: tiles; input count rate 0.1 count s-1. Panel b: tiles; input count rate 0.05 count s-1. Panel c: tiles; input count rate 0.01 count s-1. Panel d: tiles; input count rate 0.005 count s-1. |
| In the text | |
 |
Fig. 8 Using tiles allows us to recover a cluster that would be missed using separatepointings. In all images a green circle indicates an extended source (C1 or C2 detection) and a green square a source that is significant (PNT_DET_STAT > 15) but which cannot be securely identified as point-like or extended; the cyan cross shows the position of the recovered cluster and the black squares in the left panels the position of the input AGNs; X-ray contours are also shown. Panel a: combined photon image. Panel b: photon image of one of the pointings. Panel c: photon image of the other pointing. Panel d: combined wavelet image. Panel e: wavelet image of one of the pointings. Panel f: wavelet image of the other pointing. |
| In the text | |
 |
Fig. 9 EXT vs. EXT_STAT plane for recovered clusters contaminated by a central AGN (AC). The continuous line at EXT_STAT = 33 shows the cut for the C1 selection, and the dashed line at EXT_STAT = 15 shows the cut for the C2 selection. The figure shows that many clusters are no longer identified as C1, or even as C2, because of the central AGN contamination. |
| In the text | |
 |
Fig. 10 EPN_STAT_PNT vs. EPN_STAT_EXT plane for clusters contaminated by a central AGN (red) and AGNs (blue). The continuous lines show the cuts for the AC selection. The figure shows that AC clusters may be recovered by applying the AC selection. |
| In the text | |
 |
Fig. 11 DBL_STAT vs. EXT_STAT plane for recovered clusters (red) and double sources (blue). The continuous line at EXT_STAT = 33 shows the cut for the C1 selection The figure shows that most double sources have DBL_STAT > EXT_STAT. |
| In the text | |
 |
Fig. 12 EXT vs. EXT_STAT plane for recovered clusters (red) and AGNs (blue). The boxes indicate the C1∕C2 and P1 selection regions, respectively. Sources identified as either C1∕C2 or P1 are shown with larger points than the others. |
| In the text | |
 |
Fig. 13 log(N(> CR))−log(CR) of input simulated point sources. |
| In the text | |
 |
Fig. 14 Differential log(N(CR))−log(CR) for recoveredsources. Blue line: all significant detections; red line: P1 detections. The figure shows that the P1 selection is complete down to CR ≈ 0.006 count s-1. Panel a: overall view. Panel b: blow up of the regime where P1 selection becomes incomplete. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


