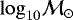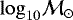| Issue |
A&A
Volume 615, July 2018
|
|
|---|---|---|
| Article Number | A68 | |
| Number of page(s) | 24 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201731425 | |
| Published online | 16 July 2018 | |
Dependence of Type Ia supernova luminosities on their local environment★
1
Sorbonne Université, Université Paris Diderot, CNRS/IN2P3, Laboratoire de Physique Nucléaire et de Hautes Energies, LPNHE,
4 Place Jussieu,
75252
Paris, France
e-mail: mroman@lpnhe.in2p3.fr
2
European Southern Observatory (ESO),
Karl-Schwarzschild Strasse 2,
85748
Garching, Germany
3
Department of Physics and Astronomy, University College London,
Gower Street,
London
WC1E 6BT, UK
4
NRC Herzberg Institute for Astrophysics,
5071 West Saanich Road,
Victoria
V9E 2E7,
British Columbia, Canada
5
Department of Physics, Lancaster University, Lancaster,
Lancs,
LA1 4YB, UK
6
Las Cumbres Observatory Global Telescope Network,
6740 Cortona Dr., Suite 102,
Goleta,
CA
93117, USA
7
Physics Department, University of California,
Santa Barbara,
CA
93106, USA
8
Australian Astronomical Observatory,
PO Box 915, North Ryde,
NSW
1670, Australia
9
Research School of Astronomy and Astrophysics, Australian National University,
Canberra, Australia
10
ARC Centre of Excellence for All-sky Astrophysics (CAASTRO),
Canberra, Australia
11
CENTRA e Departamento de Física, Instituto Superior Técnico, ULisboa, Avenida Rovisco Pais,
1049-001
Lisboa, Portugal
12
LAL, Univ. Paris-Sud, CNRS/IN2P3, Université Paris-Saclay,
Orsay, France
13
IRFU, CEA, Université Paris-Saclay,
91191
Gif-sur-Yvette, France
14
Department of Physics and Astronomy, University of Victoria,
Victoria
BC V8T 1M8, Canada
15
Sorbonne Université, Institut Lagrange de Paris (ILP),
98 bis Boulevard Arago,
75014
Paris, France
16
Department of Physics and Astronomy, University of Southampton,
Southampton
SO17 1BJ, UK
Received:
23
June
2017
Accepted:
30
January
2018
We present a fully consistent catalog of local and global properties of host galaxies of 882 Type Ia supernovæ (SNIa) that were selected based on their light-curve properties, spanning the redshift range 0.01 < z < 1. This catalog corresponds to a preliminary version of the compilation sample and includes Supernova Legacy Survey (SNLS) 5-year data, Sloan Digital Sky Survey (SDSS), and low-redshift surveys. We measured low- and moderate-redshift host galaxy photometry in SDSS stacked and single-epoch images and used spectral energy distribution fitting techniques to derive host properties such as stellar mass and U − V rest-frame colors; the latter are an indicator of the luminosity-weighted age of the stellar population in a galaxy. We combined these results with high-redshift host photometry from the SNLS survey and thus obtained a consistent catalog of host stellar masses and colors across a wide redshift range. We also estimated the local observed fluxes at the supernova location within a proper distance radius of 3 kpc, corresponding to the SNLS imaging resolution, and transposed them into local U − V rest-frame colors. This is the first time that local environments surrounding SNIa have been measured at redshifts spanning the entire Hubble diagram. Selecting SNIa based on host photometry quality, we then performed cosmological fits using local color as a third standardization variable, for which we split the sample at the median value. We find a local color step significance of − 0.091 ± 0.013 mag (7σ), which effect is as significant as the maximum mass step effect. This indicates that the remaining luminosity variations in SNIa samples can be reduced with a third standardization variable that takes the environment into account. Correcting for the maximum mass step correction of − 0.094 ± 0.013 mag, we find a local color effect of − 0.057 ± 0.012 mag (5σ), which shows that additional information is provided by the close environment of SNIa. Departures from the initial choices were investigated and showed that the local color effect is still present, although less pronounced. We discuss the possible implications for cosmology and find that using the local color in place of the stellar mass results in a change in the measured value of the dark energy equation-of-state parameter of 0.6%. Standardization using local U − V color in addition to stretch and color reduces the total dispersion in the Hubble diagram from 0.15 to 0.14 mag. This will be of tremendous importance for the forthcoming SNIa surveys, and in particular for the Large Synoptic Survey Telescope (LSST), for which uncertainties on the dark energy equation of state will be comparable to the effects reported here.
Key words: supernovae: general / techniques: image processing / techniques: photometric / dark energy / methods: data analysis / galaxies: photometry
Data on supernovae are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/615/A68
© ESO 2018
1 Introduction
The first Hubble diagrams that were constructed using both high- and low-redshift Type Ia supernovæ (SNIa) revealed that the expansion of the Universe recently entered a phase of acceleration (Perlmutter et al. 1999; Riess et al. 1998; Schmidt et al. 1998), which is inconsistent with a matter-dominated Universe, and which in the simplest cosmology model requires the existence of a now dominant, supplementary component that is dubbed “dark energy”.
The past decade saw the confirmation of this effect by the combination of different cosmological probes based on large-scale structures, at the recombination epoch, or later on through cosmic microwave background (CMB) emission, baryonic acoustic oscillations (BAO), and lensing measurements. The deeper, better-quality supernova samples of increasing size still provide the most sensitive probe for the nature of dark energy, which is phenomenologically described as a perfect fluid with the equation of state w = p∕(ρc2).
The Supernova Legacy Survey (SNLS) has regularly published constraints on the dark energy fluid characterization as it updated both its data sample and analysis methods (Astier et al. 2006; Guy et al. 2010; Sullivan et al. 2011; Conley et al. 2011). The latest such release was a joint analysis between the SNLS and “Sloan Digital Sky Survey” (SDSS) teams that is called the “Joint Light-curve Analysis” (JLA, Betoule et al. 2014), which provided a 6% measurement of the dark energy equation-of-state parameter.
The success of the Type Ia supernovæ as a cosmological probe is based on them being standardizable candles. The standardization process relies on correcting the supernova rest-frame B-peak magnitude using the empirical light-curve width (brighter-slower effect, or stretch), with relations shown by Pskovskii (1977, 1984), Rust (1974) and Phillips (1993). Later on, color-dependence laws (brighter-bluer relation) were established by Hamuy et al. (1996b) and Tripp (1998). This correction process, as well as similar approaches, reduces the standard SNIa peak magnitude dispersion to ~ 0.15 mag. However, the remaining dispersion in the SNIa population reflects the fact that the standardization procedure does not entirely capture the physical processes at play during the explosion and leaves room for at least one more variable that correlates with supernova brightness. Our theoretical understanding suggests that a thermonuclear explosion of a carbon-oxygen white dwarf that accretes mass from a companion star or from another white dwarf and reaches the Chandrasekhar limit gives rise to SNIa (Iben & Tutukov 1984; Whelan & Iben 1973). The exact mechanism for how the progenitor system accretes mass is still poorly known and could be different between galaxy types or local stellar populations.
Lately, numerous studies on a few individual Type Ia supernovæ gave birth to different conclusions regarding the type of stellar progenitor. Hubble Space Telescope (HST) imaging of an SNIa remnant in the Large Magellanic Cloud (Schaefer & Pagnotta 2012) strongly favored a progenitor system consisting of two white dwarf stars. This is known as the double-degenerate scenario (Iben & Tutukov 1984). It has received further support by recent simulations (Pakmor et al. 2012; Sim et al. 2012) and by various analyses. The recent nearby SNIa 2011fe observed in M101 (Nugent et al. 2011) fits this scenario. The analysis of archival HST imaging ruled out any kind of main-sequence companion star. However, it has been established that other individual SNIa have interacted with circumstellar material (for example, González Hernández et al. 2012), thus favoring the single-degenerate scenario of a low-mass main-sequence star accompanying a white dwarf star (Whelan & Iben 1973). In reality, it is probable that a large variety of explosion mechanisms exists that defines a continuum between the single- and double-degenerate models.
This debate on the progenitor type and explosion mechanism for a few individual supernovæ is one of the concerns calling for further investigations of the luminosity dependence of SNIa. Other concerns include metallicity effects through the nickel mass that is synthesized in the explosion (Höflich et al. 1998; Domínguez et al. 2001; Timmes et al. 2003; Moreno-Raya et al. 2016; Piersanti et al. 2017) or the varying properties of the dust surrounding the explosion region. One way to answer the question of the progenitor type is a statistical study of host galaxy properties, such as stellar age or metallicity, in order to address the question of the progenitor influence on the SNIa luminosity (e.g., Foley et al. 2013). Although the evidence of cosmic acceleration is not questioned, this might affect the cosmological parameters measurement and bias the estimation of the dark energy equation-of-state w and its redshift evolution.
All this strongly motivates the search for correlations between SNIa characteristics and the properties of their parent galaxies. The SNIa progenitor system and explosion scenarii can be constrained by studying the supernova environment: Mannucci et al. (2005); Sullivan et al. (2006b) showed evidence that Type Ia supernovæ explosions occur more often in young environments. Early studies also found significant evidence that the SNIa intrinsic luminosity could vary with galaxy morphology. Hamuy (2000) confirmed this trend for a sample of 44 galaxies that hosted the best observed low-redshift (z < 0.1) SNIa. With a larger sample spanning a wider range of redshifts, Sullivan et al. (2006b) supported this result. Significant correlations were soon brought to evidence between SNIa light-curve parameters and luminosities and the properties of their hosts (Hamuy et al. 1996a; Hamuy 2000; Gallagher et al. 2005, 2008; Howell et al. 2009; Neill et al. 2009): bluer, more slowly declining, and thus intrinsically brighter supernovæ occurred in galaxies with a lower mass, and also in bluer galaxies, in galaxies with a stronger star formation or in galaxies with a lower metallicity. These results have been confirmed as the SNIa sample increased in size and quality.
SNIa spectroscopic properties were also studied regarding the host photometric and/or spectroscopic properties: in the framework of the SNLS survey, Bronder et al. (2008) and Balland et al. (2009) pointed out the correlation between the equivalent width of the SiII feature at ~ 4000 Å and the host type, which is similar at low and high redshift. Correlations of low-redshift SNIa properties with host spectroscopic properties were studied in Pan et al. (2015), showing evidence that high-velocity SNIa preferably explode in more massive galaxies and in the inner region of their host galaxies. SNIa with a stronger high-velocity component of the Ca IInear-IR absorption are located in low-mass star-forming hosts, which suggests a young progenitor population.
The observed differences in SNIa intrinsic luminosities with respect to the host caracteristics, however, was thought to be captured bythe slower-brighter relations, so that the standardized supernova-corrected luminosity – and the use of these supernovae as standard candle – remained unaffected (Perlmutter et al. 1999; Riess 1999; Sullivan et al. 2003). By refining the analysis techniques and increasing the size and quality of their data sample, various studies were finally able to address the question of the variation of the standardized SNIa luminosity. Hicken et al. (2009) exploited the CfAIII sample to highlight that the standardized SNIa luminosity when corrected for stretch and color dependence is brighter in elliptical galaxies than those in spiral galaxies at the 2σ level. Note that SNIa are on the whole fainter in elliptical galaxies because their stretch is smaller. Using a sample of about 166 nearby SNIa, Neill et al. (2009), hereafter N09, found evidence that events exploding in star-forming galaxies decline more slowly and are thus intrinsically brighter, and that fainter, faster declining SNIa preferentially occur in more massive hosts with presumably higher metallicity, which confirmed the results of Hamuy (2000) and Sullivan et al. (2006b). N09 also demonstrated that when the supernovæ peak brightnesses were corrected for stretch and color, the standardized SNIa in older hosts were brighter. This observed residual trend corroborates the conclusions of Hicken et al. (2009). Similar behaviors have also been obtained with the whole SDSS-II supernova survey (Lampeitl et al. 2010). Concerning the low-redshift restricted SDSS-II subset, Konishi et al. (2011) and D’Andrea et al. (2011) obtained that after correction for stretch and color, the standardized SNIa are ~ 0.1 magnitude brighter in hosts with higher metallicity. In these analyses, SNIa are also found to be fainter in passive hosts before any brightness correction, but a residual trend suggests that they are fainter in active hosts after corrections for stretch and color at a significance of between 2 and 3σ.
Several analyses also tried to correlate SNIa luminosities with other properties of their host galaxies, such as the galaxy stellar mass, which was directly estimated as a function of the galaxy luminosity. Considering nearby SNIa, Kelly et al. (2010) computed a positive correlation at 2.5σ significance between the observed supernova magnitude residuals on the Hubble diagram (where the laws for color and stretch correction were fitted along with the cosmological model) and the stellar masses of the hosts: the corrected luminosity was 10% brighter for SNIa that were located in massive parent galaxies. Furthermore, for the first time, a sample that included distant SNIa observed by the SNLS after a three-year survey and intermediate-redshift events has been gathered and analyzed by Sullivan et al. (2010). Completing the sample with nearby SNIa from N09, this work found at a 4σ confidence level that SNIa exploding in massive and passive galaxies are on average brighter after stretch and color correction are applied. A similar trend has been observed using the SDSS-II supernova survey for SNIa at intermediate redshift (Gupta et al. 2011). The most recent release of dark energy equation-of-state parameter constraints using SNIa in Betoule et al. (2014), simultaneously obtained with distant (SNLS), intermediate (SDSS), and nearby events, showed a non-zero correlation at 5σ confidence level between observed Hubble diagram residuals and the stellar mass of host galaxies. Based on a complete SDSS-II Supernova Survey of 345 SNIa, Wolf et al. (2016) recovered the now well-known relation between Hubble residuals and host-galaxy mass and found a 3.6σ significance of a non-zero linear slope. They also confirmed the correlations between Hubble residuals and host-galaxy gas-phase metallicity and specific star formation rate, estimated through spectroscopy of the host galaxy.
The galaxy stellar mass is strongly correlated with many other properties of the stellar population (age, stellar formation rate and history, metallicity, and color) and is likely to act as a proxy for other local galactic characteristics. This idea has been exploited with SNIa located in the local Universe by Childress et al. (2013). Examining the different physical effects that could drive the observed trend of Hubble diagram residuals with host properties, they showed that metallicity and progenitor age are the most probable factors. A direct hint was provided by results from Rigault et al. (2013), hereafter R13, which were obtained using observations from the Nearby Supernova Factory: they showed evidence that SNIa standardized magnitudes depend on the star formation of the supernova environment within a radius of 1 kpc, as traced by Hα surface brightness. This study established that SNIa exploding in locally passive environments are on average brighter, after correction, than in locally active star-forming regions at 3σ significance. Rigault et al. (2015), hereafter R15, exploited the nearby SNIa from the Constitution data set compiled by Hicken et al. (2009) and the Far Ultra-Violet (FUV) flux measured by the Galaxy Evolution Explorer satellite (GALEX) as a star formation indicator within a few kiloparsec of SNIa positions: they upheld their conclusion that SNIa from locally star-forming environments are fainter after standardization than those from locally passive environments. Conversely, however, with a significant increase of the SNIa sample based on a mixture of hosts whose distances come from both JLA and HST and using different selection criteria, Jones et al. (2015) found little evidence for a star-formation bias.
Studying the dependence of SNIa luminosities on their local environment involves a difficult measurement that depends on the resolution and quality of the available galaxy data and is subject to systematic errors whose characterization is challenging. As cosmological consequences are important (measurement of the present expansion rate of the Universe, nature of dark energy), it is fundamental to shed new light on the environmental dependence of supernova luminosity.
We here report on measuring the local environment of a large sample of SNIa over the whole Hubble diagram and compare theresults with the properties of the host galaxies as a whole. We demonstrate, as claimed by R13, that local information is crucial and constitutes an important systematic effect that needs to be taken into account in on-going and future surveys. Our study is based on a composite sample of about 900 classified Type Ia supernovæ that all have high-quality multiband light curves and spectroscopic redshift spanning a wide range (0.01< z < 1.1). We were able togather accurate photometry of both host galaxies and local SNIa environment of the whole sample. For the high-redshift end, we took advantage of the good image quality of the Canada-France-Hawaï Telescope (CFHT) imaging that yieldedthe SNLS sample. We first describe our supernova sample and the global and local photometry of associated host galaxies and environments in Sects. 2 and 3. The conversion of the raw photometric measurements into rest-frame quantities and global host galaxy properties is detailed in Sect. 4, together with the presentation of our host property catalog and a direct comparison with published results. We then proceed to extend previous analyses of correlations between Hubble residuals and environment properties using our diverse and larger sample in Sect. 5. In Sect. 6 we assess the robustness of the results. Finally, we summarize our results and discuss cosmological implications in Sect. 7.
2 Type Ia supernovæ and host galaxy data
2.1 Supernova sample
The discovery and follow-up of nearby and distant events requires different instruments and survey strategies. We base this work on a compilation of data from two low-redshift surveys, the Carnegie Supernova Project (CSP) and the Center for Astrophysics Supernova survey (CfA), the intermediate-redshift SDSS supernova survey, and the high-redshift SNLS survey. This compilation has been assembled as part of an effort to derive cosmological constraints from the full SNLS spectroscopic sample. In all cases, the Spectral Adaptive Light curve Template (SALT2) model (Guy et al. 2007) was adjusted to the available multiband photometry, and consistent selection requirements were applied to the whole sample in order to obtain the results that are listed in the first column of Table 3.
A few modifications were applied compared to the most recent SNIa compilation from JLA (Betoule et al. 2014). First, all supernovæ whose photometry was not measured in the natural system were discarded. This corresponds to historical nearby supernovæ and SNIa observed by the CfAI and CfAII programs. In our SNLS5 sample, CfAIV SNIa are included, as is the full SNLS spectroscopic sample. Compared to JLA, a slightly different selection procedure was applied to obtain the SNLS5 sample. In JLA, some SNIa from SDSS and low-redshift surveys were discarded by a requirement on the quality of the SALT2 fit. This selection cut affects SNIa differently as a function of their reported signal-to-noise ratio (S/N). It is thus sensitive to the accuracy of the reported uncertainties and to the remaining dispersion around the SALT2 model. Most cosmological analyses additionally require a minimum light-curve fit quality (Betoule et al. 2014; Scolnic et al. 2018). Applying such a requirement to our sample, for example, imposing that the probability of the SALT2 fit is better than 0.001, would discard 132 of our 994 remaining supernovæ, which is more than the statistically expected one event, approximately. This discrepancy could have three different origins, either underestimated measurement uncertainties, underestimated intrinsic variability of supernovæ around the light-curve model as modeled in the SALT2 framework, or very many peculiar SNIa in the spectroscopic sample. It is noticeable that most of the very high S/N events are discarded by this cut (e.g., 14/28 CSP SNIa). To distinguish between these assumptions, we gathered the residuals to the blinded Hubble fit and compared statistics for the subsample of 132 SNIa that were rejected by the fit probability cut and the entire sample. We found that the dispersion of Hubble residuals in the rejected sample is smaller than in the entire sample (0.161/0.185), while their reduced χ2 is similar (1.054/1.033). In addition, the rejected sample displays no evidence for bias: its mean residual is − 0.021 ± 0.014. We thus concluded that the main origin of the large number of SNIa that were rejected by the fit probability cut was a slight underestimation of the intrinsic variability of the SNIa population in the current SALT2. While forthcoming cosmological analyses will have to consider this modeling issue properly, preferentially by improving the modeling of the SNIa population, we did not apply this cut to our sample because it discarded some of the best-measured events without preventing any visible bias in the analysis.
The sample presented in this work is very similar to the sample that will be used to derive cosmological constraints. However, a new calibration awaits the current measurement of SNLS filters. It is therefore probable that the cosmological sample differs from the sample used in this paper. A similar approach regarding environmental effects will also be presented together with the cosmological publication.
The data were blinded with respect to the cosmology by warping the fluxes with a smooth function of the redshift f(z) while photometric calibration and supernova evolution issues were investigated. Cosmological parameters measurements are extremely sensitive to the relative calibration of flux measurements in the different bands. In contrast, the results presented here are essentially insensitive to calibration issues or other systematics, as discussed in Sect. 6, so that we do not expect them to be altered by any of the calibration adjustments.
2.1.1 Low-redshift SNIa
The low-redshift part of the compilation is dominated by SNIa from the third and fourth releases of photometric data acquired at the F. L. Whipple Observatory of the Harvard-Smithsonian Center for Astrophysics (Hicken 2009, 2012, hereafter CfA3 and CfA4). The data were acquired between 2001 and 2011 using three different CCD cameras (Keplercam, Minicam, and 4Shooter2). We also included high-quality photometric data from the first and second release of the Carnegie Supernova Project (Contreras et al. 2010; Stritzinger et al. 2011, hereafter CSP1 and CSP2). These data were acquired in each of the six photometric bands ugriBV of the Swope instrument at the Las Campanas Observatory, with a typical two-day cadence.
In both cases, we used the photometry available in the natural system of the photometric instrument. We did not consider photometric data that were color-transformed, because this procedure, ill-suited to supernovæ, introduces significant scatter and bias in the measurement (e.g., Betoule et al. 2014, Appendix B).
2.1.2 SDSS survey
The intermediate-redshift part of our sample is provided by the SDSS-II supernova survey (Sako et al. 2018, hereafter S14), which scanned a 300 deg2 region during three months (September, October and November) in each of three years (2005–2007). It delivered light curves for 10 258 variable and transient sources, as well as host galaxy identification for thousands of transients, photometric classifications for the candidates with good multicolor light curves, dedicated spectroscopic observations for a subset of 889 transients, and host galaxy redshifts obtained using spectra from the original SDSS spectrograph, the SDSS-III BOSS spectrograph, and the telescopes used to obtain SDSS SN spectra. The survey used the SDSS camera (Gunn et al. 1998) on the SDSS 2.5 m telescope (York et al. 2000; Gunn et al. 2006) at the Apache Point Observatory (APO) to provide simultaneous light curves in the five broad passbands, ugriz (Fukugita et al. 1996; Doi et al. 2010), with a typical cadence of observations of once every four nights. These observations resulted in the largest sample of supernova candidates ever compiled, with 4607 likely supernovæ, about 500 of which have been confirmed as SNIa by the spectroscopic follow-up. We restrict our analysis to SNIa in this spectroscopically confirmed subsample.
The SNIa photometry for SDSS is based on the scene modeling photometry (SMP) described in Holtzman et al. (2008). The basic approach of the SMP is to simultaneously model the ensemble of survey images covering an SNIa candidate location as a time-varying point source (the SN) and sky background plus a time-independent galaxy background and nearby calibration stars, all convolved with a time-varying point-spread function (PSF). The fitted parameters are the SN position, the SN flux for each epoch and passband, and the host galaxy intensity distribution in each passband. The galaxy model for each passband is a 20 × 20 grid of CCD pixels (approximately 8′′ × 8′′), and each of the 15 × 15(pixels) × 5(passbands) = 1125 galaxy intensities is an independent fit parameter. As there is no pixel resampling or convolution of the observed images, the procedure yields reliable statistical error estimates.
The complete data release of SDSS supernova light curves, spectra, host galaxy identification, and estimate of their properties are described in S14.
Central coordinates of the CFHT Deep Survey fields.
Total integration time of the deep survey in different bands, for each field, that is, the total time allocated to the survey is four times as long as what is shown.
2.1.3 SNLS survey
Our sample includes spectroscopically confirmed high-redshift SNIa from the full five-year SNLS survey, built from the deep component of the CFHT Legacy Survey, which covers four patches of sky, called D1, D2, D3, and D4, corresponding to a single pointing of the 1 deg2 MegaCam camera on the 3.6 m CFHT. The patches are located high over the galactic plane so as to minimize local extinction of the incoming light (see Table 1). They are also chosen such that at least two of them are visible to the CFHT at any given time of the year. Images were taken in four passbands similar to those used by the SDSS: gM, rM, iM, zM, where the subscript M denotes the MegaCam system. Each field and passband was repeatedly imaged four or five times per lunation, with exposure times of ~ 1 h (the total observing time for each band is provided in Table 2, see Sullivan et al. 2006a for details). About 1000 supernovæ were discovered in the redshift range 0.2 < z < 1, and 427 of them were confirmed as SNIa with their redshift measured by massive spectroscopic follow-up programs (Howell et al. 2005; Bronder et al. 2008; Ellis et al. 2008; Balland et al. 2009, 2018; Walker et al. 2011). In July 2007, the CFHT iM filter broke and was replaced by a new filter a few months later. Since this corresponds to the end of the survey, we did not include images from the new filter in the coadded images.
In the same spirit as for the method developed for the SDSS survey, the SNLS supernova photometry consists of fitting a time-variable point source in addition to a time-independent galaxy image to the SNLS image series, without resampling the images before the fit. This method delivers unbiased SN magnitudes at the mmag accuracy level, with systematic uncertainty less than 1.5 mmag (Astier et al. 2013).
2.2 Available host photometric data
For the purpose of the analysis presented in this paper, we need to distinguish between the number of available SNIa in our sample and the supernovæ for which we can perform our own host photometry. We relied on SNLS data for the corresponding SNIa sample and on available SDSS imaging for the SDSS and nearby SNIa samples. This requirement defined the number of supernovæ for this analysis. In Table 3 we list the corresponding numbers for each survey. For the high-redshift SNIa from SNLS, we gathered the host galaxy photometry for the whole available sample. The details describing host identification and photometric techniques used for the SNLS sample are presented in more detail in Sect. 3.1.1 and also in our companion paper (Hardin et al., in prep.).
Redshift, position, and magnitudes (among others) of intermediate-redshift supernovæ observed with the ugriz filters of the SDSS instrument and for their parent galaxies are found in the catalogs produced by S14. In this redshift range and for this specific study, we find host galaxy photometry in S14 for approximately 80% of the total SDSS sample. This enables us to compute and compare local and global properties of host galaxies for the SNLS and SDSS surveys.
The situation is more complex for low-redshift surveys. The low-redshift SNIa total sample includes events from CSP and the CfAIII and CfAIV SNIa surveys (see Sect. 2.1.1), which amounts to 156 supernovæ. To determine which SNIa is included in the SDSS footprint, we checked in the SIMBAD database1 for events with SDSS ugriz data associated with their host. We also checked for JHK photometry from the Two Micron All-Sky Survey catalogs (2MASS, Skrutskie et al. 2006) because we used the K magnitude as a stellar mass proxy (see Sect. 4.2). Only a fraction (35%) of the nearby SNIa from the CSP survey are SDSS supernovæ, and about 60% of those from the CfAIII and CfAIV surveys are located in the SDSS footprint. When they were not recovered in the SDSS footprint, we nonetheless retained the K-magnitude photometry information from 2MASS for to study the host galaxy properties.
As a result, we used the number of supernovæ described in Table 3 to study the local environment around the supernova explosion and to strictly compare local and global properties. For the global properties, we used additional information from the 2MASS catalog.
3 Global and local photometry of the SNIa hosts
The photometry of the whole host galaxy and of the region close to the SNIa explosion traces information on the age and evolution of their stellar population. We present in this section a reliably calibrated photometric method from which the host properties, both local and global, are derived. This provides a consistent measurement across the wide redshift range of the supernova sample for the global photometry of the host galaxy and for the photometry at the supernova location (local photometry).
3.1 Global photometry
3.1.1 Host galaxies in SNLS images
The SNLS host galaxy photometry was performed on deep stacked images in the ugriz filters. The CFHT-LS ugriz observations of the Deep fields were pre-processed through the Elixir pipeline to correct for the instrumental effects that affect the pixel flux. More information on the Elixir pipeline can be found in Magnier & Cuillandre (2004) or on the CFHT website2. It includes flat-fielding and fringe correction in i and z data.
Individual CCD images were then processed through the SNLS pipeline (Astier et al. 2013). A weight map was generated that incorporates bad pixels information (set to a zero-value weight) and was normalized with the image sky-variance. Each CCD image catalog was built using SExtractor (Bertin & Arnouts 1996), and a smooth sky-background map was subtracted. Each image was calibrated by performing a large-diameter (D =15 × σseeing) aperture photometry on the tertiary stars catalog from Regnault et al. (2009) and computing a Vega photometric zero-point. The astrometric calibration was derived using the SNLS internal astrometric catalog.
The ugriz 36-CCDs frames were selected using cuts on the photometric zero-point, the mean seeing (FWHM < 1.1′′ for griz bands, 1.3′′ in u), the sky variance, the mean star shapes, the number of saturated stars, and the amount of fringing. The cut was performed solely on the central CCD of each frame. About 60% of the best-quality images were kept in griz, which corresponds to 300–400 36-CCDs frames. For the u-band, only 8% of the data were rejected.
The selected 36-CCDs frames then enter the stacking procedure. Each field was observed during a season of six consecutive months. Depending on the field, between five to six observing seasons were available. The selected 36-CCDs frames were combined on a per-season basis to construct 1-square-degree griz “per-season”deep stacked images.
Individual CCD images, rescaled to a common photometric zero-point zp = 30, were co-added using the SWarp V2.17.1 package3 with the median-filter option. This permitted us to reject remaining satellite trails and cosmic rays. A total weight map was also produced.
To avoid supernova light contamination, the supernova host photometry was performed on the “excluded-season” stacked images. They were obtained by coadding all seasons except for the supernova season stacks through a weighted average, using the per-season stack weight map scaled with the sky variance and the image quality: 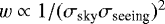 .
.
For the u-band, all season stacks were produced and used because the supernova light contamination is reduced in the SNLS redshift range z > 0.2. For the D2 field, the Terapix T0006 D2-u stack was used because it incorporates COSMOS CFHT-MegaCam u data that were overlapping the D2 field.
The detection of the sources and the related photometry were performed using SExtractor in the dual-image mode, with a detection threshold level of 2.5σ for 3 contiguous pixels. The detection was realized on the i frame and the photometry on the ugriz frames.
Magnitudes were estimated within SExtractor Kron (Kron 1980) elliptical-aperture magnitudes (AUTO-magnitudes), which provided a measurement of the total galaxy flux. Then, flux uncertainties were modeled by a two-component (added in quadrature) model: δf = af ⊕ eempty. The first term a corresponds to the magnitude uncertainty for bright sources, which is about 0.01–0.015 mag depending on the band. The second term eempty denotes the RMS of the “empty” flux, that is, the aperture flux measured at random positions on each frame, in regions without sources. The local residual background variation, correlated at the aperture spatial scale, provided the major contribution to the “empty-flux” dispersion.
The reproducibility of the magnitude measurement and the flux error model parametrization were tested on computed on-purpose stacked frames, combining the first two seasons S0 and S1 images, and the two following seasons S2 and S3. At the limiting magnitude i ≃ 24.8, this corresponds to a magnitude uncertainty of 0.12 mag.
Number of available supernovæ for the whole SNLS five-year release and the corresponding amount of host photometry.
3.1.2 Host galaxies in SDSS images
We used the Sloan Digital Sky Survey DR12 legacy, which provides uniform, well-calibrated images in ugriz bands of more than 31600 square degrees in the sky, comprising the North Galactic Cap and three stripes in the South Galactic Cap (Alam et al. 2015). The DR12 release observed about 940 000 individual fields separated into images of size 1361 × 2048 with a pixel scale of 0.396 square arcseconds on the sky and with a median PSF FWHM of 1.3 arcsecond. These images are dubbed single-epoch images in the following. Astrometry is specified at a level of 70 mas at the limit of r = 16, with systematic errors smaller than 30 mas.
The Sloan Digital Sky Survey DR7 release (Abazajian et al. 2009) also includes all images from the Stripe 82 (S82) along the Celestial Equator in the Southern Galactic Cap. It contains a coaddition of 47 South strip and 55 North strip scans into a pair of SDSS runs in which objects are detected at about 2 magnitudes deeper than in any individual Stripe 82 scan. The 270 square degrees area of Stripe 82, between − 50° < RA < 59° and − 1.25° < Dec < 1.25°, has been covered approximately 80 times (Jiang et al. 2014). The corresponding images are referred to as stacks in the following. In Fig. 1 we present examples of the two types of images that show the observation of the same portion of the sky. It is clear from that figure and from comparing the two panels that stacked images from Stripe 82 are deeper and allow the detection of more objects.
As stack images are much deeper than single-epoch images, we used them whenever possible, that is, for all supernovæ exploding in the S82 footprint outside the time range of the stack images (in practice, after December 2005; see Table 4 for the exact survey repartition). As expected, we mostly found SDSS host galaxies in the coadded images, except for those that were contaminated by the supernovæ. Conversely, a large majority of host galaxies from low-redshift surveys were found in single-epoch images since the SNIa included in them exploded at random places in the sky and were not necessarily found in the Stripe 82 footprint.
The sources were detected with SExtractor, with a detection threshold level of 2.5σ for single-epoch images (4σ for stacked images) with at least three contiguous pixels. Each time an object was extracted, the connected pixels passed through a filter, which split them into components that might overlap. At low redshift (z < 0.05) and at SDSS imaging resolution, larger galaxies appear as extended and sometimes clumpy objects, so that their outer and central regions might be erroneously identified as separate sources. On the other hand, at higher redshift (z ≃ 0.2) and for a locally denser area, neighboring objects should be identified as distinct sources. This can be handled with the SExtractor deblending parameter DEBLEND_MINCOUNT, which governs the way in which local flux maxima are identified as individual overlapping sources, or conversely, merged into an extended single object. This parameter reaches from 0, where even the faintest peaks in the detection profile are considered as single independent objects (high-deblending), to 1 (no deblending).
We thusproduced two different source catalogs: a highly deblended catalog (corresponding to a deblending parameter of 2 × 10−6, the high-deblend configuration), so that galaxies at higher redshift are well identified; and a catalog with a deblending parameter of 0.05 (the low-deblend configuration), so that large, nearby galaxies below z = 0.05 are not broken up into sub-regions. In the top row of Fig. 2, the red dashed ellipse corresponds to the low-deblending configuration, while the white solid ellipse represents the high-deblending case. For the vast majority of host galaxies, both extraction configurations yield similar host characteristics. Examples of low-redshift bright galaxies for which the two configurations give different results are displayed in Fig. 3. Using field galaxies from SDSS images, we find that the magnitude difference using the two extraction configurations is significant for objects below z = 0.04. Therefore, the limit we set for the transition at z = 0.05 is reasonable.
For each image, a zero-point was estimated by computing the difference between magnitudes of field stars inside a radius of 4 arcseconds and their reference magnitudes in the SDSS catalog. We estimated the measurement errors in two different ways, depending on the available type of image.
-
For SNIain single-epoch images I: the sky image Isky, the dark current ND , and the gain G are available. We therefore constructed a variance map defined as
 (1)
(1)
and we measured the error by integration inside the corresponding photometric ellipse:
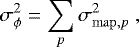 (2)
(2)
going from flux error to magnitude error by computing
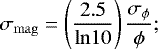 (3)
(3)
where ϕ is the measured flux.
-
For SNIa in stacks: since the available weight image is a relative weight map, we resorted to building a σϕ = f(ϕ) relation, or equivalently, a σmag = f(mag) relation, using the magnitude errors published in the SDSS stack catalogs for the field galaxies to compute the errors for the global photometry of the host galaxy.
In the following, the global photometry corresponds to the flux integrated in the SExtractor ellipse that is associated with the host galaxy using the Python tool aperture_photometry from the photutils module of Astropy. This allows us to remain consistent throughout the analysis since the same tool is used for local photometry.
Repartition of SNIa host galaxies in the different SDSS images.
 |
Fig. 1 Examples of the two types of SDSS images on the same portion of the sky in the g band. The DR12 single-epoch image is shown in the top panel, and the Stripe 82 coadded image is illustrated in the bottom panel. |
3.2 Local photometry
The local photometry was performed at the SN location, inside a radius with a proper size of 3 kpc. This corresponds to the smallest achievable physical size for high-redshift SNIa. Because the true FWHM seeing of SNLS images is about 0.85′′, we defined the smallest physical sizeas 1σ seeing in radius (0.364′′, equivalent to 2 SNLS pixels) at the highest redshifts. At z ~ 0.7, where mostof SNLS SNIa are located, the radius is greater than 1.12σ. The integrated flux within a 1σ radius is ~ 40%, so that local information can still be extracted. Figure 4 illustrates the evolution of the local photometric radius with redshift. It varies from ~ 1.9 pixel for SNLS supernovæ at the highest redshifts to ~26 pixels for very low redshift SNIa. The corresponding 1σ seeing for the different surveys is displayed as dashed lines. We discuss the results we obtained when probing smaller areas in a limited redshift range in Sect. 5.4. For intermediate and low redshifts, the local radius is always greater than 1.3σ.
The SNLS local photometry was performed within these apertures using the SNLS data C++ analysis tool, which handles fractional pixels. The flux error was computed using the error model described in Sect. 3.1.1. We also performed our own local photometry on SDSS images for host galaxies with low and intermediate redshift. The local photometry was computed with the Python tool aperture_photometry from the photutils module of Astropy. The errors for the local photometry were estimated in the same way as for global photometry, as described in Sect. 3.1. After the variance map was built starting from single-epoch images, we measured the error byintegrating inside the local photometric radius. As an example, a few image tiles are presented in Fig. 2, centered on the positions of the SNLS and SDSS host galaxies. The global photometry ellipse aperture and the local photometry circular aperture are indicated. In the SDSS cases, the high-deblend and low-deblend configuration ellipses are shown in white and red, respectively. The examples illustrate the redshift range that each survey achieves. A more quantitative comparison between local and global quantities is presented in Sect. 5.2.
 |
Fig. 2 Examples of eight g-band images of SNIa host galaxies ordered in redshift. The top row corresponds to SDSS images with sn2006gr, sn2003kc, sn2005hc, and sn2006hr. For this survey, the dashed red and solid white ellipses represent the region where the global photometry is measured for a low and high level of deblending. The solid red circle symbolizes the 3 kpc region where the local photometry is computed. The second row displays SNLS images corresponding to 04D2bt, 03D3bl, 03D1bf, and 05D3ht, using one single SExtractor configuration. This illustrates the great variety of cases, from SNIa exploding in the inner galaxy core to SNIa observed far away from the center, in the galactic arms. |
 |
Fig. 3 Examples of nearby bright galaxies for which the low-deblending mode (red dashed ellipse) gives much better results than the high-deblending mode (white solid ellipse). The solid red circle represents the local photometric radius described in Sect. 3.2. |
3.3 Host identification
For the SNLS survey, the supernova host was identified using two criteria: the minimum distance to the supernova location, and the match between the photometric redshift of the galaxy (see Sect. 3.5) and the spectroscopic redshift of the supernova (Howell et al. 2005; Bronder et al. 2008; Ellis et al. 2008; Balland et al. 2009, 2018; Walker et al. 2011).
A normalized elliptical distance d was computed using the SExtractor shape parameters and Kron elliptical radius, so that d < 1 defines the photometry elliptic aperture of the galaxy. The supernova host galaxy was identified as the galaxy that lay closest to the distance d. When the closest galaxy lay at d > 1.8, the supernova was declared to have no host. To unambiguously identify the host, we also required that the photometricredshift of the closest galaxy was consistent with the spectroscopic redshift of the supernova: Δz∕(1 + z) < 0.15. When morethan one galaxy was detected close to the supernova location within d < 1.8, the galaxy with the closest photometric redshift was selected as the host. Ambiguous cases were flagged as problematic, for instance, when more than one of these close galaxies met the criterion Δz∕(1 + z) < 0.15. We also rejected SNIa for which the identified host might be polluted by a nearby bright star. These criteria ensure a secure host galaxy identification. We identified a host galaxy for ~87% of SNLS SNIa and did not detect a host for 6%. The remaining 7% SNIa were either dubious or problematic cases.
For the SDSS and low-redshift surveys, we identified the host galaxies with a different algorithm, which yielded similar results: the galaxy with the largest overlap between a circle surrounding the SNIa location and the SExtractor segmentation map was defined as the parent galaxy of the supernova. When there was no overlap between the SNIa region and a galaxy, we selected the closest object from the segmentation map, as for SNLS. Figure 2 illustrates the difficulties encountered when identifying the host galaxies. sn2006hr (top right) seems to be occurring in a merger, and 05D3ht (bottom right) is just below the normalized elliptic distance limit from its assumed host. In these cases, the local color is more reliably related to the SNIa environment than to the stellar mass, which requires a rigorous definition of the host galaxy area.
Host galaxy photometry from SDSS has also been published in S14, with a more sophisticated host identification algorithm. When comparing our own SDSS host ID number, obtained from the SDSS database by matching objects found in single-epoch images, with the number from S14 for the host galaxies that we share, we find that 11% of them do not match. In appearance, more than 20% of the hosts do not match S14. The ID numbers are different only because the association with the SDSS database has been made using single-epoch images. As a result, no change is needed for the corresponding hosts. The large majority of them occur in configurations where the host galaxy is faint (g ~ 21.5), with a relatively high spectroscopic redshift (z ~ 0.26). About 70% of the non-matching cases correspond to configurations where the stacked images are not available, and the host identification was thus performed using single-epoch images. The identification even fails for the remaining 30% host galaxies that are found in stacked images. This corresponds to only 13 hosts. For all non-matching hosts, we selected hosts properties (stellar mass and U − V color) with the identification method S14. For more details about comparing host properties with S14, see Sect. 4.3.2. The efficiency of host identification methods has been described by Gupta et al. (2016), where normalized elliptical distances were found to be more accurate. Machine-learning algorithms were also studied in the context of future large SN surveys.
 |
Fig. 4 Evolution of the local photometric radius with a size of 3 kpc with redshift in arcseconds for host galaxies of SNIa observed by the SNLS (blue), SDSS (red), and low-redshift surveys (green points). The 1σ seeing of SNLS and SDSS images is illustrated with dashed lines using the same color code. A 1σ seeing corresponds to a diameter of about 85% of the FWHM. |
3.4 Comparison with SDSS DR12 photometry
Since we estimated the photometry of hundreds of host galaxies form SDSS images in order to infer their color and stellar masses, we checked that our measurement was consistent with published data from SDSS DR12 for all field galaxies detected by SExtractor in those images. As described in Sect. 3.1, we used SExtractor in two different configuration modes. After building the low-deblending and the high-deblending catalogs based on SDSS single images (see Sect. 3.1), we matched every source with the SDSS database, restricted to primary objects identified as galaxies with a valid spectroscopic redshift. To ensure that the comparison was made for the same objects on both sides, we required an association distance shorter than one pixel together with the clean photometry flag from the SDSS database. The magnitude comparison presented here was then performed for 2676 field galaxies using the high-deblending configuration, and 2624 field galaxies using the low-deblending case. These galaxy populations that contain our host galaxies are thus representative of them.
Using the same technique as for the host galaxies, we computed the aperture photometry of all field galaxies in ugriz bands using a circular aperture for point-like objects (i.e., detected with a zero Kron radius by SExtractor) and an elliptical aperture for extended sources (i.e., detected with a non-zero Kron radius) with the same photometric tool. Here, we compare our photometry with different SDSS magnitude definitions. We chose the model magnitudes to compute the magnitude difference for objects identified as point-like objects by SExtractor that corresponded to a fixed circular aperture for our photometry.On the other hand, we took the SDSS petrosian magnitudes when comparing objects seen as extended and corresponding to our elliptical aperture photometry. Petrosian magnitudes are indeed better adapted for a comparison of extended source photometry since galaxy fluxes are measured within a circular aperture whose radius is defined by the shape of the azimuthally averaged light profile. The overall result is presented in Fig. 5.
For the g-band and taking into account the SDSS magnitude definitions described above, we find a good agreement between thetwo magnitude estimates. For the high-deblending configuration mode, we obtain Δg = 0.008 ± 0.080. For the low-deblending configuration, we have Δg = 0.007 ± 0.079, in which error bars represent one standard deviation of the distribution. In this sample of field galaxies, we can find the subsample corresponding to host galaxies of our SDSS and low-redshift surveys SNIa. Because the magnitude comparison was computed in the same way as for the whole sample, we obtain a good overall agreement with Δg = −0.001 ± 0.076 using the high-deblending mode and Δg = 0.014 ± 0.074 using the low-deblending mode.
When we split these results into different magnitude regions, we find that in the lowest magnitude bin, the two different deblending settings differ by more than 1σ. This means that the low-blending case is less consistent with SDSS magnitudes than the first configuration (see the two leftmost bins in Fig. 5). This can be explained by the fact that for bright (hence large and nearby) galaxies, a higher deblending threshold should indeed be chosen so that galaxies are not separated into multiple portions. This corresponds to our low-deblending configuration. In Sect. 3.1.2 we illustrated the phenomenon in Fig. 3 with the white and red ellipses around nearby host galaxies. Since we focus on primary galaxies for the purpose of a direct photometry comparison, on occasion we do not consider SDSS parents for some objects, but objects flagged as child (in principle, subparts of the parent image). For example, a parent object can be a bright star, while an object flagged as its child is a galaxy a few arcseconds away. In the framework of this comparison, we selected only primary galaxies and thus find a slight magnitude difference for the brighter galaxies.
Table 5 lists the offsets we find between our observed magnitudes and the DR12 magnitudes for the five optical bands for all field galaxies and our subsample of SNIa hosts using the low-deblending configuration. In the comparison, we distinguish between extended and point-like sources from the SDSS point of view, as explained above.
Except for the u- and z-band showing higher dispersion than the other three, the consistency between SDSS magnitudes and our photometry for field galaxies and parent galaxies of our SNIa sample is good overall. The remaining differences lie in the method details of the object extraction. In the following, we use our own measurement for the galaxy photometry in order to remain consistent for all surveys.
 |
Fig. 5 Density of points (blue hexagonal bins) representing the absolute difference between observed aperture magnitudes and SDSS DR12 magnitudes in the g optical bandfor all field galaxies detected in the low-deblending configuration. Although the dispersion is relatively high, the overall agreement between the two photometries is good (see text). When split into magnitude bins for host galaxies (pink and purple bins for high- and low-deblending modes, respectively), the two configurations are similar, except for the first bin, where the low-deblending case shows less consistency with SDSS. |
Mean value and standard deviation for the difference between our observed magnitudes and magnitudes from the single-epoch SDSS catalogs for field galaxies and the subsample of the SNIa hosts.
3.5 Spectral energy distribution (SED) fitting
All our surveys benefit from precise multiband photometry, from which we may estimate the galaxy global properties, such as metallicity, age, color, stellar mass, or star formation rate.
These quantities were derived by fitting a series of template galaxy SEDs to the ugriz fluxes available for each galaxy. The SED series was computed using the synthetic evolutive optical galaxies spectra code PEGASE.2 (Fioc & Rocca-Volmerange 1997, 1999). Eight scenarii were provided to PEGASE, as published in Le Borgne & Rocca-Volmerange (2002), corresponding to a star formation history and an evolution of the gas content corresponding, at z = 0 for a given age, to the morphological types E, S0, and spirals from Sa to Sd. We assumed a Rana & Basu (1992) initial mass function. The synthetic SEDS were computed at 68 different ages from 0 to 15 Gyr, and the galaxy properties such as the star formation rate (SFR) or the stellar mass were provided by the code.
The relevant SED was selected via a χ2 minimization performed with our own package, which takes into account the extinction from the Milky Way as estimated using the E(B − V) map from Planck Collaboration XI (2014) and allowing for an additional extinction described by the Cardelli et al. (1989) extinction law. Galaxy properties were then obtained from the best-fitting SED. The stellar mass was estimated in units of 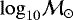 to a precision better than 11% for SNLS, better than 23% for the SDSS survey, and better than 7% for the fraction of hosts of the low-redshift sample for which we have ugriz photometry.
to a precision better than 11% for SNLS, better than 23% for the SDSS survey, and better than 7% for the fraction of hosts of the low-redshift sample for which we have ugriz photometry.
To provide rest-frame colors as closely interpolated from the observer frame data as possible, we used a spectral template library developed for this purpose, EGALITE (Empirical GALactic InTErpolator). As described in Kronborg et al. (2010), the building of this library is a two-step procedure. We first computed a series of eight spectra using PEGASE, specifying eight SFR laws proportional to (t∕τ) × exp(−t∕τ) and a given galaxy age a(τ). The eight synthetic spectra were indexed using a single parameter that is equivalent to the mean age of their stellar population a⋆ and then interpolated to obtain a continuous spectral sequence indexed by a⋆.
The continuous spectral sequence was then optimized to refine the data description. For this, the library was trained using the magnitudes of ~6000 galaxies in the D3 field catalog, with known spectroscopic redshift from the DEEP-2 spectroscopic survey (Davis et al. 2003, 2007). The training procedure corrects the initial templates by as much as 30%. Therefore, the galaxy parameters provided by PEGASE for each of the eight initial templates, such as the star formation rate or the stellar mass, are no longer relevant. The interpolated colors, however, are expected to be closer to the truth because the spectral sequence is specifically trained to describe the data better.
The accuracy of the obtained photometric redshifts was estimated using spectroscopic data from the VIMOS VLT Deep Survey (VVDS Le Fèvre et al. 2004) and the Cosmic Evolution Survey (COSMOS, Scoville et al. 2007): at limiting magnitude i < 24, the rate of catastrophic error Δz∕(1 + z) > 0.15 is 3.15%, and the precision is σ[Δz∕(1 + z)] = 0.030. Photometricredshifts are not used in this analysis.
We fit the host galaxies photometry using EGALITE via a χ2 minimization performed with our own package involving the ugriz photometricfluxes that we measured for each galaxy. As described above, we took the Milky Way extinction into account, and we allowed for an additional extinction. Observed fluxes 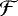 should be modified compared to the initial fluxes f that we measured with a given measured zero-point zp as
should be modified compared to the initial fluxes f that we measured with a given measured zero-point zp as
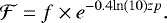 (4)
(4)
Rest-frame U − V galaxy colors were measured with a mean precision of 13%, 14%, and 9.7% for SNLS, the SDSS survey, and the nearby SNIa sample, respectively. In the following, the spectral sequence EGALITE is used as a photometry interpolator in order to compute photometricredshifts and rest-frame local and global colors. Stellar masses are estimated using the PEGASE spectral sequence.
4 Consistent catalog of stellar mass estimates
We present here the derivation of the supernova host galaxy stellar masses. Depending on the SNIa sample, stellar masses were derived using different methods applied on different sets of global photometric measurements: SED fitting on ugriz magnitudes measured on SDSS and SNLS imaging data, or the mass from the Two Micron All Sky Survey near-infrared (NIR) K band. To ensure a consistent host mass catalog, we intercalibrated these different methods using overlapping data of the surveys. We finally compare the mass catalog to published values for the corresponding host subset.
4.1 Intercalibration of mass estimates
We computed the possible bias existing between galaxy stellar mass estimates from ugriz photometry given by the MegaCam instrument on the CFHT, and the same mass estimates from similar filters on the SDSS instrument. For this purpose, we used the spectral sequence PEGASE and our own fitting code to derive the galaxy stellar mass as described in Sect. 3.5. We considered the D3 deep field of the SNLS survey, located between 214.04° and 215.52° in right ascension and between 52.16° and 53.21° in declination, which has a large overlap with the SDSS footprint. We find about 2400 galaxies in common among the ~ 6000 galaxies with a spectroscopic redshift in the SNLS D3 catalog and the ~20 000 objects found in the same right-ascension and declination area in the SDSS database4 by imposing that galaxy coordinates should match below 10−4 degrees, or 0.36′′. We applied selection cuts to the outcome of our query to improve its quality in the following way.
-
We kept galaxies that satisfied 0.1 < z < 0.8.
-
We removed galaxies for which the u-band magnitude was not properly measured by the SNLS.
-
We discarded all galaxies that lay more than 5σ away from the mean of the distribution in g and r bands (i.e., Δg∕σg < 5 and Δr∕σr < 5).
After these cuts, the sample consisted of about 1700 elements for which we obtained two different mass estimates based on SNLS and SDSS photometries. The estimates are displayed in Fig. 6 as red points in the top panel. By fitting a linear function to the logarithmic stellar mass distribution, we obtained a slope of 1.017 ± 0.072 and a y-intercept at − 0.146 ± 0.227. The corresponding fit is drawn as a black dashed line in Fig. 6. As a consequence of the outcome of the fit, we can equally use SNLS or SDSS photometries to compute galaxy stellar masses, or any other galactic information. We checked that the redshift dependence of the difference between stellar masses from SNLS and SDSS was not significant (see the bottom panel of Fig. 6). Moreover, we verified the good correlation between the rest-frame color U − V estimated from SNLS and SDSS observed magnitudes with the EGALITE spectral sequence.
 |
Fig. 6 Top: distribution of galaxy stellar masses obtained from two different photometries from the SNLS and the SDSS surveys. All galaxies are located in the D3 deep SNLS field. Stellar masses are drawn as red points in the top panel; the resulting weighted linear fit is shown as the dashed black line. Bottom: redshift dependence of the stellar mass difference. The median rms is 0.21 dex. |
4.2 Massestimates from the 2MASS survey
As described in more detail in Sect. 2.2, some nearby host galaxies are not located in the SDSS footprint and have no corresponding photometry in ugriz bands. Thirty-nine of these have photometry in the 2MASS All-Sky Data Release from the Two Micron All Sky Survey, in particular, in the NIR K band. The NIR luminosity traces the emission from low-mass stars that best represents the build-up of stellar material and thus provides a reliable estimate of the stellar mass of a galaxy because the NIR mass-to-light ratio is nearly independentof star formation history (Bell et al. 2003). Following the method described in Appendix C of Betoule et al. (2014), we can take advantage of the existing NIR data to infer the host galaxy stellar mass when the galaxy lacks ugriz photometry.
In order to calibrate the relation between galaxy stellar mass and K absolute magnitude, we completed part of the ugriz background galaxy catalog we built on SDSS images as described (see Sect. 3.4), with K-band photometry extracted from the SDSS database. We selected objects with a valid spectroscopic redshift and restricted the sample at z < 0.15. This calibration sample comprises 349 galaxies and has a median redshift of 0.07. We then estimated the stellar mass  for each galaxy from the ugriz magnitudes we measured on SDSS images with the PEGASE template fit described in Sect. 3.5.
for each galaxy from the ugriz magnitudes we measured on SDSS images with the PEGASE template fit described in Sect. 3.5.
The K absolute magnitude is defined as
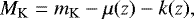 (5)
(5)
where mK is the 2MASS Kron elliptical-aperture magnitude in the K band, μ(z) is the distance modulus computed using the galaxy redshift and H0 = 70 km s−1 Mpc−1. The K-correction is defined by k(z) ~–2.1z as in Bell et al. (2003). Given the stellar mass estimated from the same PEGASE fit based on ugriz magnitudes, we adjusted a weighted linear fit to the MK-stellar mass distribution 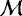 and obtained
and obtained
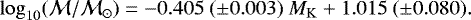 (6)
(6)
We recovered the slope of ~–0.4 expected from the model of the stellar mass-luminosity ratio from Bell et al. (2003). Because we know the masses of these calibration objects from two different estimators, we compared the two estimated values and obtained a dispersion around the fit of 0.121 dex. The relationship between the galaxy mass essentially depends on its absolute K magnitude, but also on its rest-frame U − V color, therefore we observed a color dependence of the fit residuals proportional to ~ 0.3(U − V). We also observed a residual redshift dependence proportional to z, which mightbe due to the limiting K magnitude of the surveye. As a consequence, we added in quadrature to the residuals of 0.121 dex a term that takes the redshift bias (0.1) into account, and another that included the color bias (0.2). The total uncertainty is then about 0.25 dex, and this calibration is precise enough for the purpose of this analysis. With this calibrated relation between stellar mass and K absolute magnitude in hand, we are able to infer the stellar mass of host galaxies that lack ugriz photometry and complete our catalog of stellar mass estimates in a consistent way.
In our low-redshift sample, we found 69 parent galaxies from low-redshift SNIa surveys with photometry from both SDSS and 2MASS, which we completed with 15 additional intermediate-redshift hosts from the SDSS that are also listed in the 2MASS extended source catalog. Thus, we can compare stellar mass estimates from PEGASE fits with ugriz observed magnitudes using the low-deblend (see Sect. 3.1), and stellar mass estimated with K-band absolute magnitudes for this subsample of 84 hosts. The subsample mainly consists of nearby galaxies with a median redshift of 0.031, of which 80% were observed in single-epoch images. We derived the host stellar masses from Eq. (6). Computing the absolute stellar mass difference, we found a good overall consistency of 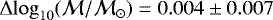 dex. Thus, we can estimate the galaxy stellar mass from our host catalog either using SDSS observed magnitudes, or with the K-band absolute magnitude, when available.
dex. Thus, we can estimate the galaxy stellar mass from our host catalog either using SDSS observed magnitudes, or with the K-band absolute magnitude, when available.
4.3 Comparison with public mass catalogs
4.3.1 Nearby host galaxies from N09
A catalog of parent galaxy properties of 168 low-redshift SNIa has been published by N09, and it has been used in many other analyses (Kelly et al. 2010; Sullivan et al. 2010; Betoule et al. 2014). The authors used UV imaging with measurements from the homogeneous magnitude-limited sample Galaxy Evolution Explorer survey (GALEX, Martin et al. 2005). Observed magnitudes in the UV range were obtained by performing surface photometry in elliptical apertures on sky-subtracted images. For optical photometry, they considered RC3 integrated Johnson UBV magnitudes (de Vaucouleurs et al. 1991) obtained from the NASA/IPAC Extragalactic Database (NED) and/or SDSS images in the ugriz bands. For larger hosts, the SDSS catalog was found to be inaccurate, thus elliptical-aperture photometry was performed on coadded SDSS images. Forty-one host galaxies belong to our catalog and the N09 catalog. As the photometry is not public, we directly compared the host masses and distinguished between our two methods to infer stellar masses (from SED fitting based on ugriz SDSS elliptical aperture magnitudes or from the K optical band magnitude). The result is shown in Fig. 7. Of the 41 common hosts
-
8 only have SDSS ugriz photometry;
-
8 only have K-band photometry in the 2MASS survey. One of these corresponds to interacting galaxies and was not identified as the same host in N09. Consequently, the corresponding point does not appear in the figure;
-
25 have both SDSS ugriz magnitudes and K-band magnitude. It is thus equivalent to fit the spectral series PEGASE to our ugriz magnitudes or the relation written in Eq. (6), as demonstrated in Sect. 4.2 We used stellar masses derived from ugriz photometry.
For the 40 common host galaxies, we find that N09 tends to underestimate stellar masses by about 0.18± 0.14 dex on average compared to our mass values.
4.3.2 Intermediate-redshift host galaxies from S14
The data release of the SDSS-II supernova survey has been compiled by S14 and corresponds to the period between 2005 and 2007. Thus, the overlap with our SNLS 5 year SNIa catalog is relatively extensive. With their own host identification algorithm and using a similar SED-fitting code based on a PEGASE spectral template library to obtain galaxy properties, the authors published magnitudes, redshifts, stellar masses, specific star-formation rates, and ages for more than 400 host galaxies. The goal now is to compare the common host galaxy properties derived by S14 with our own estimates that were directly measured in SDSS images. When we compared our stellar mass estimates, we focused on objects for which the host ID was identical to the ID in our sample (see Sect. 3.3), and for which the global photometry was correctly measured (i.e., we removed galaxies for which the photometry in the u-band was not measured). This permits a comparison of 252 objects.
The differences between the two stellar mass estimates are represented as red points in Fig. 8, and they are distributed as a function of redshift. We obtain a mean absolute difference of 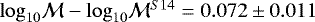 dex, which illustrates the good agreement with a reasonable dispersion (0.17 dex) between the masses obtained from different host identification algorithms and distinct photometric tools. We nonetheless find that the S14 mass values are slightly lower than those we obtained with our own photometric method in SDSS images. The difference is not very significant and well below what is required for the analysis presented here.
dex, which illustrates the good agreement with a reasonable dispersion (0.17 dex) between the masses obtained from different host identification algorithms and distinct photometric tools. We nonetheless find that the S14 mass values are slightly lower than those we obtained with our own photometric method in SDSS images. The difference is not very significant and well below what is required for the analysis presented here.
 |
Fig. 7 Redshift evolution of the differences in common host stellar mass between N09 and our sample. Galaxies with only SDSS-like photometry are represented in orange. Their masses are estimated by fitting the spectral series PEGASE to our observed ugriz magnitudes.Galaxies presenting photometry in the 2MASS survey alone are drawn in dark red, their masses are derived from K-band absolute magnitude through Eq. (6). Stellar mass differences of objects with both types of photometry are displayed in purple. For these galaxies, we present masses derived from ugriz observed magnitudes. The dashed black line corresponds to the mean difference, with the rms represented by the gray area. |
5 Environmental dependence of supernova luminosity
We have measured the photometry and local photometry of the host galaxy inside a 3 kpc radius around the SNIa explosion region. The photometry was transposed into U − V rest-frame color. This section presents the construction of a clean sample using selection requirements based on the local and global measurement quality and then compares local and global information. Finally, we try to use the local environment as a third standardization variable.
5.1 Selection requirements
To be included in the sample, supernovæ and results of the local photometry of our host galaxies must satisfy several conditions.
First, we required that host galaxy stellar masses were available, which means that the quantity had to be properly derived through the SED-fitting process. In practice, this requirement discards some high-redshift SNIa in the SNLS survey with bad host identification (discrepant photometric redshift between the SNIa and the host, or contamination by a bright star). Second, we only selected well-measured host stellar masses and removed the 10% fraction of SNIa with the largest mass error. This corresponds to a limit of about 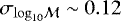 , where
, where 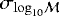 is the host mass dispersion. Finally, we ensured that the local U − V color was well measured by removing the 10% fraction of SNIa with the largest error on this parameter. This corresponds to a limit of about
is the host mass dispersion. Finally, we ensured that the local U − V color was well measured by removing the 10% fraction of SNIa with the largest error on this parameter. This corresponds to a limit of about 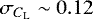 , where
, where 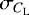 is the dispersion of the local color measurement.
is the dispersion of the local color measurement.
Applying these three requirements together, we retained about 74% of the 397 parent galaxy photometries of the SNLS survey, and 293 of them remained in the analysis sample. Of the 389 hosts from S14 with photometry measured in SDSS images, we retained a large fraction (~74%) of the sample, and 288 elements remained. Of the hosts belonging to low-redshift surveys, we discarded 11, thus keeping most of the sample for the analysis. In total, the correlations with Hubble diagram residuals presented in the following sections include 666 host galaxies of Type Ia supernovæ out of 882, which represents about 76% of the original sample. They span a wide redshift range of between z = 0.01 and z = 1.03, with a median redshift of 0.25. More details on the selection requirements for each survey are listed in Table 6. The initial selection requirement for the SALT2 fit quality described in Sect. 2.1 does not affect our results because the additional SNIa we included are equally distributed in terms of high and low U − V local color.
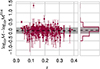 |
Fig. 8 Redshift evolution of stellar mass differences in common hosts between S14 and our sample for objects with the same identification number (dark red points). This corresponds to intermediate-redshift galaxies detected in the SDSS survey. We find a good agreement between the two mass estimates, with a slight mean overestimation of stellar masses of about 0.07 dex compared to S14 (dashed black line; the gray area represents the rms). |
5.2 Comparison of global and local variables
Next, we compare local and global quantities after the selection cuts described in Sect. 5.1. In the top panel of Fig. 9 we displayed the difference between the U − V rest-frame color of the host galaxy as a whole (named U − V global) and the U − V rest-frame color estimated within a region of 3 kpc around the supernova explosion as a function of redshift (U − V local). The low-redshift (SNLS and SDSS) surveys are respectively represented by the green (blue and red) points. As expected, we find a good correlation between the two quantities on average, and we checked that the difference between global and local rest-frame colors converges to zero when the ratio between the parent galaxy size and thelocal circle area is close to one. However, we also note that the difference between the global and local rest-frame colors is different from zero for a significant number of our host galaxies (40% of them are more than 2σ different from the zero difference between global and local colors). These differences indicate that probing the local environment and the host galaxy as a whole do not convey the same physical information. This can be explained by situations where, for example, a supernova explodes in the old passive bulge of an active spiral galaxy, or in an active region of an old spiral galaxy. We find that the color difference is on average different from zero, that it evolves with redshift, and finally, that there is a systematic trend to measure SNIa in locally red regions compared to the host galaxy. This result can partly be explained by a distance effect to the galactic center, represented in the bottom panel of Fig. 9. For a supernova exploding in the outskirts of the host galaxy, the explosion area is seen bluer than its host (positive difference between global and local U − V colors). Conversely, if the explosion region is close to the galactic center, then the local rest-frame color is redder than the galaxy as a whole (negative difference between global and local U − V colors). As for the top panel, we observe that the majority of our sample contains SNIa that explode close to the center of their host galaxy.
In numerous cases, the rest-frame local and global colors measurements are significantly different (i.e., points departing from the zero line in the two panels of Fig. 9). In some redshift bins, the difference between global and local colors departs from zero with a significance of about 4σ. This shows that different information might be accessible through the study of local environment, and this has to be accounted for, as suggested in R13.
The relation between local U − V rest-frame color and the host galaxy stellar mass is drawn in Fig. 10 for the three different survey categories. As expected, we find the most massive galaxies to be those for which the close environment of the SNIa explosion is seen as red. This confirms the general trend that massive galaxies are more passive in terms of star formation than low-mass galaxies (Kennicutt 1998; Kauffmann et al. 2003). The dashed gray lines in Fig. 10 illustrate the bin separation, assuming that both local color and stellar mass distributions are bimodal (see Sect. 5.3 for more details). A significant proportion of our sample (~ 20%) belongs to the lower right and upper left parts of the figure (second and fourth quadrants). These specific host galaxies belong to the same mass bin as hosts in the other quadrants, but they will belong to different local color bins. Hence, the observed difference between local environment and host properties as a whole derives from this fraction of our sample. Investigating these differences is the purpose of the next section.
Selection requirements for the analysis focusing on local and global properties of the host.
 |
Fig. 9 Top: difference between U − V rest-frame color of the whole host galaxy and local U − V rest-frame color in a region of 3 kpc around the supernova location for SNLS (blue dots), SDSS (red dots), and low-redshift survey (green dots) hosts. The difference is displayed as a function of redshift. The observed redshift dependence (black bins) indicates that the cosmology is affected when local effects are included. Bottom: difference between U − V rest-frame color of the whole host galaxy and local U − V rest-frame color as a function of projected distance to the galactic center in kiloparsec. The color code is the same as for the top plot. The general trend shows that local regions that appear bluer than the host galaxy are located far from the center, whereas locally redder regions are close to the galactic center. |
5.3 Third parameter and correlations with Hubble diagram residuals
At this stage, we can estimate distance moduli and Hubble diagram residuals, defined as the difference between the observed distances and the distances predicted by the best-fit cosmology (while simultaneously fitting and applying the brighter-slower and brighter-bluer relations). The distance estimator assumes that supernovæ with identical color, shape, and galactic environmenton average have the same intrinsic luminosity at all redshifts. This yields a standardized distance modulus μ = 5log10(dL∕10 pc)
 (7)
(7)
where 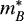 is the observed peak magnitude in rest-frame B band, and α, β, and MB are nuisance parameters. Hubble diagram residuals thus represent the difference between this quantity and the cosmological model prediction μmodel(dL(z;Ωm)) = 5log10(dL(z;Ωm)∕10 pc) computed for a fixed value of H0 = 70 km s −1Mpc−1, assuming a Friedmann-Lemaître-Robertson-Walker geometry. Ωm is defined as the total matter density in the Universe. As a result, the residuals reflect the intrinsic luminosity scatter of the supernova sample. However, the following results do not depend on the cosmological model, as explained in Sect. 6.4.
is the observed peak magnitude in rest-frame B band, and α, β, and MB are nuisance parameters. Hubble diagram residuals thus represent the difference between this quantity and the cosmological model prediction μmodel(dL(z;Ωm)) = 5log10(dL(z;Ωm)∕10 pc) computed for a fixed value of H0 = 70 km s −1Mpc−1, assuming a Friedmann-Lemaître-Robertson-Walker geometry. Ωm is defined as the total matter density in the Universe. As a result, the residuals reflect the intrinsic luminosity scatter of the supernova sample. However, the following results do not depend on the cosmological model, as explained in Sect. 6.4.
In practice, we performed a cosmological fit that computes distances based on blinded fluxes allowing for a third variable that standardizes SNIa and minimizes the function
![\begin{equation*} \chi^2=\left[\hat{\mu}-\mu_{\mathrm{model}}(d_L(z;{\rm{\Omega}}_m))\right]^{\dagger}\mathcal{C}^{-1}\left[ \hat{\mu}-\mu_{\mathrm{model}}(d_L(z;{\rm{\Omega}}_m))\right] ,\end{equation*}](/articles/aa/full_html/2018/07/aa31425-17/aa31425-17-eq20.png) (8)
(8)
where 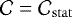 is the covariance matrix of
is the covariance matrix of 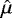 rewritten in matrix notation. It is obtained from the error propagation of light-curve fit uncertainties.
rewritten in matrix notation. It is obtained from the error propagation of light-curve fit uncertainties.
The third variable was taken into account in the cosmological fit through a step function for the absolute magnitude MB, assuming a bimodal distribution for all types of host properties (local color, host global color, and stellar mass of the host). Hence SNIa were divided into two groups of locally red regions or locally blue regions, but also red host galaxies or blue host galaxies and low-mass hosts or high-mass hosts. We followed the procedure described in Sullivan et al. (2010), which defines a magnitude step written as
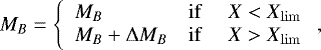 (9)
(9)
where X is any type of variable related to host galaxy properties and Xlim is the bimodal distribution limit.
For each variable, the separation between the groups, Xlim, corresponds to the median value of the sample. SNIa were then separated in half between locally red and blue regions for U − V ~ 0.63. Equivalently, SNIa were found in two groups of red and blue host galaxies with a separation estimated at U −V ~ 0.62. We find the bin limit for the stellar mass of the host at 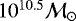 , which is different from previous studies, for which the separation was arbitrarily chosen at
, which is different from previous studies, for which the separation was arbitrarily chosen at 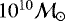 . In Figs. 13 and 11 we display the Hubble diagram residuals corrected for stretch and color as a function of stellar mass of the host and local U − V color for SNIa detected by the SNLS (blue), SDSS (red), and low-redshift surveys (green). Figure 12 is the same as Fig. 13, but only considering the second and fourth quadrants of Fig. 10. We separated the final sample into two bins at the median. The separation is represented by the dotted black lines, and the bin positions by black points with error bars corresponding to the dispersion in the given bin, divided by the square root of the number of elements in it. A linear evolution of Hubble diagram residuals with our local and global variables were also computed and are shown as the purple dashed line (see Sect. 6.1). Next, we interpret the observed Hubble diagram dependence on color or mass as environmental effects that can be absorbed in the cosmological fit as a third standardization variable.
. In Figs. 13 and 11 we display the Hubble diagram residuals corrected for stretch and color as a function of stellar mass of the host and local U − V color for SNIa detected by the SNLS (blue), SDSS (red), and low-redshift surveys (green). Figure 12 is the same as Fig. 13, but only considering the second and fourth quadrants of Fig. 10. We separated the final sample into two bins at the median. The separation is represented by the dotted black lines, and the bin positions by black points with error bars corresponding to the dispersion in the given bin, divided by the square root of the number of elements in it. A linear evolution of Hubble diagram residuals with our local and global variables were also computed and are shown as the purple dashed line (see Sect. 6.1). Next, we interpret the observed Hubble diagram dependence on color or mass as environmental effects that can be absorbed in the cosmological fit as a third standardization variable.
When we performed a cosmological fit using the stellar mass of the host as a third variable, we find
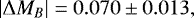 (10)
(10)
which corresponds to a significance of 5.5σ. This value is consistent with the most recent results obtained by Betoule et al. (2014) with different samples and different selection criteria. Applying the same method to the host galaxy U − V color, we obtain
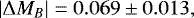 (11)
(11)
thus a change in ΔMB at the 5.3σ confidence level. Considering the local U − V color as the third standardization parameter, we obtain
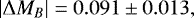 (12)
(12)
which means that the change in MB magnitude with a color step is at a significance of about 7.0σ. Its amplitude is compatible with similar local age-bias measurements from R13 and R15.
The details of this study for the different surveys and for various redshift ranges are shown in Table 7. We observe a general increase in significance when the local U − V rest-frame color is considered as a third standardization parameter compared to the host global color or stellar mass. The physical meaning can be understood when we assume that galaxy color can be related to other properties (star formation rate, metallicity, or age), and that the galaxy stellar mass is very likely a proxy for these properties. The local U − V color is the most highly correlated variable for high- and intermediate-redshift surveys, whereas global color is slightly more significant for low-redshift surveys. When we split the sample into redshift bins below z = 0.1, between z = 0.1 and z = 0.5, and above z = 0.5, we find that the local color is the most significant third variable for all redshift intervals, and that it is comparable to the host stellar mass variable at high redhsifts. The local signal is particularly stronger at intermediate redshifts, where we see a departure from the zero line in the top panel of Fig. 9. We note that for each of the significance calculations, we considered the median value of the total sample as a separation between the bins. Last but not least, when all redshifts are combined, a clear preference for local color is visible, as described above.
In Sect. 3 we described the high quality of the photometry we derived in detail, which leads to precise measurements of the stellar masses and local U − V colors of the hosts. As a result, a small fraction of SNIa are likely to change bin within errors. Of the SNIa that constitute the basic sample, 7.8% are within 1σ of the local color bin separation, and 5.6% are within 1σ of the mass bin separation. To precisely characterize the effect of SNIa changing bin, we randomly drew Gaussian-distributed local colors (or host stellar masses). With 1000 realizations, the local (mass) step amplitude is shifted at 1σ significance by 0.00391 mag (0.00383 mag). This variation is approximately three times less important than the errors that are due to uncertainties on the distance measurement.
When we restrict the SNIa from our basic sample to the SNIa that are in common with the SNIa of the JLA analysis (Betoule et al. 2014), we find 589 matches (see Sect. 2.1 for the difference between the two samples). Without applying any selection requirement on the common sample and cutting the sample in half with respect to the stellar masses of the hosts and local U − V colors, we measure a local color step of − 0.075 ± 0.012 when this variable is considered as a third standardization parameter. If the stellar mass of the host is used instead, the mass step is found to be − 0.077 ± 0.012. These values are consistent with the step amplitudes reported in Table 7.
As expected from the relation between x1 and the absolute magnitude, values of the cosmological fit nuisance parameters depend on the method that is used to estimate the magnitude steps. The covariance of the nuisance parameter associated with the stretch factor (α) with the magnitude step ΔMB is shown in Fig. 14. The central value when the stellar mass of the host is used as a third-parameter standardization is α = 0.16301 ± 0.0075, and α = 0.16788 ± 0.0076 when the local U − V color is chosen. These values are higher when they are compared to JLA estimates because different initial selection cuts, validated onsimulations, were used in our analysis (see Sect. 2.1). However, this difference in α between our sample and JLA has little effect (≪1σ) on the amplitude of both local color and mass steps when α is a free fit parameter.
In Fig. 15 we display the correlations between SNIa properties (stretch and color) as a function of local U − V color and stellar mass of the host galaxy. As has been noted in R13, R15, and in previous studies, we find a strong correlation of the two variables with the stretch factor x1 (Branch et al. 1996; Howell et al. 2009; Neill et al. 2009; Sullivan et al. 2006b), and a small color dependence on local environment and host mass (Sullivan et al. 2010; Childress et al. 2013). Although we note a strong dependence of light-curve decline rate with environment variables, this cannot explain the significance of a third SALT2 parameter that takes local color into account because the cosmological fit was performed after correcting for stretch.
 |
Fig. 10 Local U − V rest-frame color of SNLS (blue dots), SDSS (red dots), and low-redshift survey (green dots) hosts in a region of 3 kpc around the supernova location as a function of the stellar mass of the host galaxy (in |
 |
Fig. 11 Correlation of host galaxy stellar mass (in units of |
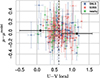 |
Fig. 12 Correlation of local U − V rest-frame colors (in a region of 3 kpc around the supernova location) with Hubble diagram residuals corrected for stretch and color for the SNLS (blue dots), SDSS (red dots), and low-redshift (green dots) surveys for SNIa lying in the second and fourth quadrants of Fig. 10. |
 |
Fig. 13 Correlation of local U − V rest-framecolors (in a region of 3 kpc around the supernova location) with Hubble diagram residuals corrected for stretch and color for the SNLS (blue dots), SDSS (red dots), and low-redshift (green dots) surveys. The separation between the two local color bins at U − V ~ 0.63, corresponding to the median value of the sample, is shown as the black vertical dash-dotted line. The bins are drawn in black, with the weighted mean values as black dots and their dispersion, divided by the square root of the number of elements in the bin. The purple dashed line shows the weighted linear fit for the entire color distribution. The top histogram displays the repartition of the 441 elements in terms of local color, together with the fit to a bimodal distribution represented by the solid red line. The histogram on the right draws the Hubble diagram residual distribution of blue SNIa regions (for local color values below the separation in U − V), associated with star-forming regions, together with the equivalent distribution of red regions (for local color values above the separation in U − V), associated with more passive areas. |
Significance of the third parameter in the cosmological fit standardizing light-curves of SNIa as a function of survey type and redshift range for the different galactic properties, assuming a bimodal distribution.
 |
Fig. 14 Covariance of α and the absolute magnitude step when three standardization parameters are used (blue contours for local color correction, and red contours for host stellar mass correction). The green rectangle corresponds to the case where two standardization parameters are used. Contours correspond to 68% and 95% confidence levels. |
5.4 Varying the local radius
The basis ofthis work has been chosen so that the local probed physical size remains 3 kpc in radius at all redshifts. Therefore, the obtained results are consistent. For redshifts that are low enough for the local photometric radius to be still larger than the resolution ofa given survey, however, we can probe smaller physical sizes and check whether it increases the significance of the local color as a third standardization parameter. In practice, we measured photometry in a circle with a radius of 2 kpc for z < 0.4 in SNLS. In the SDSS and low-redshift surveys, we probed a physical size of 2 kpc for 0.16< z < 0.26 and of 1.5 kpc when the redshift verified the condition z < 0.16 (see Fig. 16, the equivalent of Fig. 4). Performing the same cosmological fit using the new local colors as a third variable on 620 events (the selection requirements cause a slight change), we find |ΔM| = 0.087 ± 0.014. We conclude that the standardized supernova brightness still displays a dependence on local environment at the 6.2σ confidence level. This is very similar to the significance we find using a 3 kpc local radius at all redshifts. A comparable size test has been performed in R15 and yielded similar results.
We modified values of the local radius from 3 kpc to 2, 4, 8, 16, 32, and 64 kpc and analyzed the local color step effect as a function of radius. The local step radius dependence is represented in Fig. 17, where points are colored as a function of the number of SNIa in the corresponding samples. For each radius, we applied the selection requirements described in Sect. 5.1, and to compute the local step, we used the method explained in Sect. 5.3. Within the cosmological fit, we split the obtained local U − V colors into two bins using the basic sample median as a separation. Between radii of 3 and 32 kpc, we find a smooth transition from local to global, with values compatible with mass or global U − V steps. When the radius is smaller than 3 kpc, the regions have a physical size smaller than 1σ seeing. This means that local U − V are measured with larger error bars than in the basic case, and the selection requirement on local color (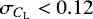 ) removes more SNIa. The local step is less important in this configuration. As a result, we cannot probe regions smaller than 3 kpc at all redshifts without significantly decreasing the sample. For large radii (r = 64 kpc), the flux errors increase and prevent EGALITE from finding good U − V colors. Since fewer SNIa are present in this situation, the local step is also less important. It is thus important to note that the error bars for dark blue points are correlated (the sample contains the same objects), whereas the error bars for r = 2 kpc and r = 64 kpc are estimated with different SNIa in the sample.
) removes more SNIa. The local step is less important in this configuration. As a result, we cannot probe regions smaller than 3 kpc at all redshifts without significantly decreasing the sample. For large radii (r = 64 kpc), the flux errors increase and prevent EGALITE from finding good U − V colors. Since fewer SNIa are present in this situation, the local step is also less important. It is thus important to note that the error bars for dark blue points are correlated (the sample contains the same objects), whereas the error bars for r = 2 kpc and r = 64 kpc are estimated with different SNIa in the sample.
 |
Fig. 15 Correlations between supernova properties (stretch and color) as a function of local U − V color (first row) and host galaxy stellar mass (second row). The bins are drawn in black, with the weighted mean central values as black dots and the bin dispersion. Linear fits of the data are shown as dashed purple lines. |
6 Reliability tests
6.1 Alternative methods for estimating correlations
In the basic analysis, we studied the significance of a magnitude step for a cosmological fit including a three-variable standardization with host properties. Alternatively, we might also estimate Hubble diagram residuals corrected for stretch and color, and verify the correlation with any other variable related to host properties. Therefore, we have access to correlations between Hubble diagram residuals and host properties a posteriori and can verify whether the conclusions we drew beforehand are still valid. Assuming a bimodal behavior of the local U − V color and of the stellar mass distribution of the host, we can split each distribution into two bins and thus estimate the a posteriori statistical significance of Hubble diagram residuals with respect to these two variables. In practice, this corresponds to the significance of the difference between the two black bins in Figs. 11 and 13. With this other method, we find a 7.1σ significance for the correlation between Hubble diagram residuals computed with the regular standardization and the local color, which confirms the result obtained with a three-parameter standardization in the cosmological fit. When the stellar mass of the host is chosen instead, the correlation is present at a significance level of 5.4σ. The stellar mass of the host is still less strongly correlated to the Hubble diagram residuals than the color inside the area around the supernova explosion.
With this technique, it is also possible to obtain the remaining signal after the Hubble diagram residuals are estimated using a standardization with three variables. In particular, the correlation between the residuals corrected using the stellar mass of the host as a third variable and the local color shows a δμ difference that is significant at 4.6σ. This means that correcting for the stellar mass of the host does not capture all the physical information, as expected. On the other hand, when we correct distance moduli with local color in addition to stretch and color effects, we find a correlation between the corresponding Hubble diagram residuals and the stellar mass of the host that is half as significant (2.3σ). This shows that more information is taken into account when distance moduli are corrected using the local environment of Type Ia supernovæ.
Until now, correlations were computed assuming that the stellar mass of the host or the local U − V color distributions are separated into two distinct bins. This was taken into account in the cosmological fit computing Hubble diagram residuals with a step function for the absolute magnitude (see Eq. (9)). Alternatively, the importance of an additional variable that standardizes SNIa light curves by computing weighted linear fits for the Hubble diagram residuals can be described as corresponding to a two-variable standardization, rather than a step function. The weighted linear regressions are represented as the dashed purple line in Figs. 11 and 13. We find a slope of − 0.107 ± 0.046 when the Hubble diagram residuals are distributed against local color, and a slope of − 0.056 ± 0.033 for the host mass. Therefore, the deviation from a zero slope is not highly significant (2.3σ for local color and 1.7σ for the stellar mass of the host). Since slopes can be biased by outliers, we also used the Theil-Sen estimator, which is minimally affected by them (Theil 1992; Sen 1968). We found better constraints on slopes with compatible central values than for the least-squares estimator: − 0.093 ± 0.015 for the local color, and − 0.055 ± 0.009 for the stellar mass of the host. We can still conclude that studying weighted linear fits to the data also tends to prove that a stronger dependence of the Hubble diagram residuals on local color is observed. Moreover, the step function appears to describe the effect better.
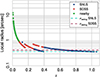 |
Fig. 16 Evolution of the local photometric radius of 1.5, 2, and 3 kpc with redshift in arcseconds for host galaxies of SNIa observed by the SNLS (blue), SDSS (red), and low-redshift surveys (green points). The 1σ seeing size of SNLS and SDSS images are illustrated with dashed lines using the same color code. A 1σ seeing corresponds to a diameter of about 85% of the FWHM. |
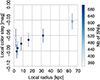 |
Fig. 17 Evolution of the local step amplitude (in magnitude) as a function of the local radius size (in kpc). Points with error bars are colored as a function of the number of SNIa that belong to the corresponding samples. |
6.2 Removing supernovæ from the sample
As a reliability test, we aimed to verify that the signal we observed with local color and stellar mass of the host was not due to the presence of a subsample of Type Ia supernovæ that drives this effect and pushes toward high significance.In order to test this, we randomly selected 100, 200, and 300 SNIa and removed them from the sample. Then we computed the significance of a third variable in the cosmological fit with a magnitude step ΔMB. We repeated the random process a thousand times in total for the three configurations and the two variables. The corresponding significance histograms are shown in Fig. 18.
First, the observed signal that shows a correlation between the Hubble diagram residuals and local color (or stellar mass of the host) is still present when part of the initial sample is missing, thus proving that the results are not dependent on the number of events and are reliable regarding the random disappearance of some supernovæ. Moreover, the histograms are compatible with the significance we expect with a sample containing 100, 200, and 300 fewer events (dashed lines in Fig. 18). These expected values were estimated assuming that the significance scales as the square root of the number of events in the sample. Considering that we obtained a 7σ confidence level for the basic case with local color as a third standardization parameter using 666 events, we then expect 6.4σ, 5.9σ, and 5.2σ with only 566, 466, and 366 events, respectively, provided that the change in significance is only due to the decrease in statistics and not to another effect that decreases the local color signal itself. Since the histograms are consistent with the expected significances, we are confident that the signal we obtain is reliable and does not disappear when part of the sample is removed. We also note that within each subsample, the local color step is on average more significant than the mass step. Removing very many SNIa (half of the sample) enlarges the overlap between step significances for local color and stellar mass of the host.
 |
Fig. 18 Histograms of the step significance of the local U − V color (dark red) and stellar mass of the host (dark blue) used as a third standardization parameterin the cosmological fit. Correlations are estimated by removing 100 (top panel), 200 (middle panel), and 300 (bottom panel) random supernovæ from the initial sample of events and repeating the process a thousand times. The expected significances, assuming that it scales with
|
Selection requirements when we use EGALITE as an SED fitting code taking observed magnitudes into account.
6.3 Local environment from SED fitting in magnitudes
As explained in Sect. 3.5, we fit a series of template galaxy SEDs using interpolated fluxes from EGALITE codes in order to obtain the local U − V rest-frame color. This ensures higher precision on colors, since objects with low surface brightness are easily handled. On the other hand, globalproperties such as color and stellar masses of the host are derived with EGALITE and PEGASE starting from observed magnitudes. For the purpose of a consistency check, we used EGALITE as an SED fitting code, taking as inputs observed magnitudes and estimating local galactic properties by finding the best-fit spectrum (through a χ2 minimization).
After verifying that the local U − V colors were consistent with those obtained when the SED fit was performed using observed fluxes, we built a new analysis sample. We discarded from our basic sample the few events for which the local measurement error was below the limit defined in Sect. 5.1 for local colors that were directly estimated by interpolating fluxes, but above the limit when magnitudes were used. Thus we obtain in Table 8 the equivalent of Table 6, using the same definition for the selection requirements.
We then performed the same cosmological fit using the local U − V color as a third variable. We find that its significance is 6.9σ with ΔMB = −0.090 ± 0.013 (5.6σ for the stellar mass), which is compatible with the results we obtained by interpolating fluxes to fit local galactic properties. Furthermore, using the SED fitting code considering magnitudes, we also computed the local colors estimated inside 2 kpc for the SNLS and SDSS surveys and 1.5 kpc for the SDSS (see details in Sect. 5.4). We obtained a similar significance of 6.5σ (with ΔMB = −0.081 ± 0.013) for the local color step.
This shows that using a flux interpolator to derive local environment effects around the SNIa location is a comparable approach to the approach that uses observed magnitudes as inputs of the estimation of local galactic properties. Both methods yield similar results, although fitting in flux allows including the uncertainties better.
6.4 Effect of calibration uncertainties, blinding, and cosmological assumptions
Calibration uncertainties are not expected to have a strong influence on the results presented above because the two considered populations (locally red/blue, massive/light host) are present in all redshift bins. All of the information thus comes from the comparison of SNIa in the same redshift bin, that is, brightness measurements conducted with the same instrument and in the same effective filters.
For the same reason, we do not expect an effect of the blinding and of the assumed cosmological model. In our analysis, and in particular, in the cosmological fit producing Hubble diagram residuals corrected for a third variable in addition to stretch and color, we assumed a model with a flat Universe including evolving dark energy w(z). Even when we are blind to the cosmological parameters, we can still verify whether the color step significance is independentof the cosmological model, as it should be. For a model with time-independent dark energy (w(z) is constant), we obtain an increase in ΔMB of 1%, thusraising the color step significance by 1.1%. When using the ΛCDM concordance model with dark energy as a cosmological constant (w = −1), the increase in ΔMB is also at the 1% level. The significance of the color step will then be on the same order of magnitude. Assuming the basic cosmological model, variations in ΔMB can be found when additional cosmological priors are used. Considering the most recent constraints on dark energy from Planck and BOSS (Planck Collaboration XIV 2016; Anderson et al. 2014), we note an increase in absolute magnitude of 0.6%, which corresponds to a significance modification of 0.8%. Therefore, we can conclude that cosmological assumptions do not affect our analysis.
6.5 Interplay with the selection bias
Concerns have been raised in Scolnic & Kessler (2016) that selection bias affects supernovæ with different brightnesses differently. Specifically, caution must be exerted when dividing supernovæ into two groups with a priori different mean brightness because selection effects will affect the mean brightness of each group differently. In the present case, such an effect is expected because x1 is strongly correlated to both local color and stellar mass of the host. As a consequence, segregation into two bins according to one of the latter variables forms two groups with different x1 distributions and hence different effective brightnesses, which are differently affected by selection bias. We computed a worst-case estimate of this effect using a simulation of the SNLS survey, based on the rate measurement of Perrett et al. (2012), color and stretch intrinsic distribution measured in Scolnic & Kessler (2016), and assuming a selection function giving the probability of a supernova of true app- arent magnitude m to be selected as p(m) = max(0.4 * (0.5 + arctan((24.3 − m)∕0.2)), 0). We found that the difference in selection bias that would affect the perfectly segregated x1 < 0 and x1 > 0 bins is negligibly small (2 ± 1 × 10−4 mag). Therefore, we did not consider correcting for it.
6.6 Inclusion of SNIa with faint hosts
The selection requirements are described in details in Sect. 5.1. We imposed that a stellar mass needs to be properly measured and that our sample keeps the 90% best measured host stellar masses and local U − V rest-frame colors. As another consistency check, we aimed at including more diverse situations in the analysis sample, for which the host is faint and the host properties not easily measurable. However, the local measurement was still possible. In Table 9 we present the numbers in each survey, using a single requirement on the quality of the local color measurement derived through flux interpolation with EGALITE. The new sample includes more than 60 SNIa, which correspond to negative local fluxes or local fluxes close to zero. With 737 SNIa in total, we performed a cosmological fit using three standardization parameters and found a significance of 6.6σ for the local U − V color variable (with ΔMB = −0.083 ± 0.013) and 5.8σ for the host stellar mass variable (ΔMB = −0.071 ± 0.012). In this configuration where faint hosts are included, we also found that local color is the most significant third parameter. Without any selection cut (the whole SNIa sample was used), we found ΔMB = −0.075 ± 0.012 with the local U − V color and ΔMB = −0.077 ± 0.012 with the host mass.
Unique selection requirement imposed when we include events with faint host galaxies in the sample.
 |
Fig. 19 Top: evolution of local color step significance as a function of the position of the local U − V color cut. The position of the sample median, chosen for the basic analysis, is shown as the dashed black line. Bottom: same as the top panel, but for the stellar mass of the host. |
6.7 Look-elsewhere effect
In the entireanalysis, we presented magnitude step significances assuming a bimodal distribution of the third standardization parameter (stellar mass or color of the host, or local color) with a separation corresponding to the median of this distribution. Therefore, we did not aim at maximizing the step significance. When we changed the local color bin separation in order to maximize the significance of the color step, the limit in local color was slightly larger than the median value at U −V ~ 0.65 with a magnitude step significant at 7.4σ. On the other hand, maximizing the mass step significance led to a mass limit of about 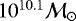 , corresponding to a magnitude step of 7.2σ significance.In this case, the separation does not lie close to the median value, since 31% of our sample is found below the new mass limit, and 69% above. This new limit is closer to the mass bin separation of
, corresponding to a magnitude step of 7.2σ significance.In this case, the separation does not lie close to the median value, since 31% of our sample is found below the new mass limit, and 69% above. This new limit is closer to the mass bin separation of 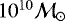 , chosen in allprevious studies on host galaxies. In particular, Childress et al. (2013) found an apparent Hubble residual transition between 109.8 and
, chosen in allprevious studies on host galaxies. In particular, Childress et al. (2013) found an apparent Hubble residual transition between 109.8 and 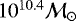 . Choosing this mass separation yields comparably significant mass and color steps. The top and bottom panels of Fig. 19 show the evolution of step significance as a function of the cut position when local U − V colors and host stellar masses are used as a third standardization parameter. The sample median lies close to the maximum local color step significance, whereas the most significant mass step implies a bin separation at
. Choosing this mass separation yields comparably significant mass and color steps. The top and bottom panels of Fig. 19 show the evolution of step significance as a function of the cut position when local U − V colors and host stellar masses are used as a third standardization parameter. The sample median lies close to the maximum local color step significance, whereas the most significant mass step implies a bin separation at 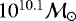 .
.
However, the correlations between the Hubble diagram residuals derived from a three-parameter standardization and our host variables yield additional information. When residuals are corrected for local U − V color, the remaining maximum mass step significance is of 3.8σ (i.e., the maximum correlation between stellar mass and corrected Hubble diagram residuals using the most significant local step). Conversely, the remaining maximum local color step after mass correction as a third variable is of 5σ (i.e., the maximum correlation between local U − V color and corrected Hubble diagram residuals using the most significant mass step). Hence, maximizing the significance still shows that scatter in the Hubble diagram is better accounted for when the supernova brightness is corrected for local environment. It is also worth noting that the local U − V color does not fully account for the remaining scatter either. A better proxy, or a combination of proxies, linked to properties of the local environment of SNIa, is yet to be found.
Summary of all tests performed throughout the paper with the corresponding number of SNIa in the sample, the local U − V color step, the host stellar mass step, and step values when corrected for one or the other effect.
7 Summary and perspectives
As elaborated in Sect. 1, many studies in the literature have found compelling proof of a dependence of Type Ia supernovæ properties on their close or distant environment, concerning a few hundred events at most that exploded in the nearby Universe. In this work, we measured the photometry of the host galaxy and local fluxes in regions with a radius a 3 kpc for 882 supernovæ that are distributed in a wide redshift range, from z = 0.01 to z = 1.1. We consistently measured photometry from SNLS and SDSS images, and gathered additional photometry from the 2MASS catalog when needed, in order to complete our sample of host galaxy properties. On SDSS images, we used a single method to find hosts and define the region where galaxy photometry should be estimated, and we applied the same technique for all supernovæ discovered by SDSS or low-redshift surveys and all field galaxies corresponding to images where these supernovæ are found. With this new set of measurements, we find good consistency with public SDSS galaxy photometry.
As a consequence, we publish here a consistent and large catalog of host properties of supernovæ spanning this redshift range. This catalog contains intercalibrated stellar masses of the hosts, U − V colors of the host galaxies, and the local U − V color estimated with radii of 1.5, 2, and 3 kpc around the location of the supernova explosion. When we compared the global and local properties of our sample of host galaxies, we found a correlation between the color of the whole galaxy and the color measured ina more local region. At high, intermediate, and low redshift, a significant fraction of the sample deviates from a null difference between local and global color. We note that SNIa locations situated in the outskirts of their host galaxy tend on average to be locally bluer than their host, and that SNIa exploding regions that lie close to the galactic center show redder local colors than the host itself. This means that the global properties of host galaxies do not capture all the information, and that local effects that are due to stellar population evolution need to be taken into account to constrain cosmology with Type Ia supernovæ, as has first been claimed in R13 and R15.
The remaining dispersion in the sample luminosity of about 0.15 magnitude after a two-step standardization, although rather low considering that these extremely energetic events occur at different moments of the history of the Universe, needs to be reduced in order to set new competitive constraints on the nature of dark energy. For many years, it was established that Hubble diagram residuals also correlate with SNIa environment. In this work we envisage the possibility that in addition to stretch and color, a third variable related to the close environment of supernovæ must be used in light-curve cosmological fitters. After selecting SNIa based on their data quality (light curve and host photometry), we find that the local U − V color is well suited to be chosen as a third standardization parameter. When the sample is split at the median local U − V color, the corresponding magnitude step is significant at 7σ. Using a global variable instead, such as the stellar mass or the U − V color of the host with the same cut location, leads to a statistically less significant magnitude step. When we probed larger galactic regions, the color step effect was still present, although less significant. This adds evidence that local host galaxy information might be the key parameter for reducing dispersions in the Hubble diagram. In order to verify the reliability of the observed signal, we performed a variety of tests that are summarized in Table 10, and we investigated all possible modifications of our initial choices. First, we randomly reshuffled part of the sample and randomly removed a significant part of it. In all cases, we found that the local environment and the mass steps were still present. We also used magnitudes instead of interpolating fluxes to derive the properties of the host galaxies and noted no meaningful change in the significance of the third parameter needed for the light-curve standardization. Then, we checked alternative methods that did not rely on the assumption of a bimodal distribution for local color and stellar masses of the host, which led to the same conclusions, and we still obtained a high significance of local environment effects. Moreover, when we corrected distance moduli with a mass step, we still found room for an additional local effect at the 4.6σ confidence level. The opposite exercise proved that this statement is not reciprocal. When the mass or color bin separation was modified in order to maximize the step significance, we found similar effects when the mass separation was chosen far from the median value. However, this other approach also confirmed that more information is taken into account when standardizing with the local color. Moreover, a posteriori linear fits of color and stellar mass distribution point in the same direction and also highlight the dependence of Hubble diagram residuals on SNIa local environment. We also demonstrated that calibration uncertainties, cosmology, and selection cuts do not have a major influence on the conclusions we draw in this work. Moreover, a study focusing on SNIa spectra from SNLS also mentions an effect on host stellar mass that is seen even stronger using local U − V color (Balland et al. 2018). Therefore, spectroscopic analyses of the SNIa environment are also very promising for on-going and future surveys.
After the correlation with either the mass or the local color of the host galaxy was taken into account, the correlation with the other parameter remained significant. This might indicate that neither the mass nor the local color of the host galaxy is the key parameter for modeling supernovæ luminosity in addition to stretch and color. While it seems logical that supernova physics depends on local galactic characteristics, it should be emphasized that the mass and the rest-frame color are themselves related to several features of the stellar history of the galaxy (metallicity, past star formation rate, etc.). It therefore needs to be considered that this key standardization parameter, if it exists, is in this sense multi-factorial.
Although this analysis is blind to the actual values of cosmological parameters, using Planck survey priors on the dark energy equation of state, we have access to the expected order of magnitude of the change in w and Ωm when correcting for local color. The change is Δw ~ 0.01 and ΔΩm ~ 0.003 when compared to a two-parameter standardization, considering a varying equation-of-state parameter. A comparison of the local color correction and the host mass correction yields Δw ~ 0.006 and ΔΩm ~ 0.002. This is important enough to be taken into account in current and future surveys, since their expected statistic precision is close to the parameter shift we estimate. When cosmological constraints using the SNLS five-year sample are unblinded and published, it will be possible to characterize the exact change and improvement in the measurement of the dark energy equation-of-state parameter and the total matter density. For the SNLS five-year analysis, the local U − V color should be taken into account in the standardization, using only a selection requirement on the local color measurement quality. The numberof SNIa in the SNLS five-year cosmological sample is then expected to be larger than the number published in this work, since we constructed our sample by applying quality cuts for both local color and stellar mass in order to show comparative results.
With ongoing SNIa surveys such as the DES and future surveys such as the LSST, larger SNIa samples will be obtained (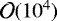 for the LSST, depending on the efficiency of spectroscopic follow-up and of supernova classification), with increasing precision. In order to derive competitive constraints and shed new light on the nature of the dark energy that drives the accelerated expansion of the Universe, it will be crucial to measure and include effects of the local environment of Type Ia supernovæ: the local U − V color, or any better proxy of the stellar population age; this will provide further insights on the progenitor type.
for the LSST, depending on the efficiency of spectroscopic follow-up and of supernova classification), with increasing precision. In order to derive competitive constraints and shed new light on the nature of the dark energy that drives the accelerated expansion of the Universe, it will be crucial to measure and include effects of the local environment of Type Ia supernovæ: the local U − V color, or any better proxy of the stellar population age; this will provide further insights on the progenitor type.
Acknowledgements
This paper is based on observations obtained with MegaPrime/MegaCam, a joint project of CFHT and CEA/DAPNIA, at the Canada-France-Hawaii Telescope (CFHT) which is operated by the National Research Council (NRC) of Canada, the Institut National des Sciences de l’Univers of the Centre National de la Recherche Scientifique (CNRS) of France, and the University of Hawaii. It is based on observations obtained at the Gemini Observatory, which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (United States), the Science and Technology Facilities Council (United Kingdom), the National Research Council (Canada), CONICYT (Chile), the Australian Research Council (Australia), Ministério da Ciência, Tecnologia e Inovacão (Brazil) and Ministerio de Ciencia, Tecnología e Innovación Productiva (Argentina). Observations were also obtained with FORS1 and FORS2 at the Very Large Telescope on Cerro Paranal, operated by the European Southern Observatory, Chile (ESO Large Programs 171.A-0486 and 176.A-0589). This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the U.S. Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University. Parts of this research were conducted by the Australian Research Council Centre of Excellence for All-sky Astrophysics (CAASTRO), through project number CE110001020. We thank Mickaël Rigault, Adam Riess, Dan Scolnic, and David Jones for useful discussions.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Alam, S., Albareti, F. D., Allende Prieto, C., et al. 2015, ApJS, 219, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, L., Aubourg, É., Bailey, S., et al. 2014, MNRAS, 441, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Astier, P., Guy, J., Regnault, N., et al. 2006, A&A, 447, 31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Astier, P., El Hage, P., Guy, J., et al. 2013, A&A, 557, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balland, C., Baumont, S., Basa, S., et al. 2009, A&A, 507, 85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Balland, C., Cellier-Holzem, F., Lidman, C., et al. 2018, A&A, 614, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bell, E. F., McIntosh, D. H., Katz, N., & Weinberg, M. D. 2003, ApJS, 149, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Bertin, E., & Arnouts, S. 1996, A&AS, 117, 393 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Betoule, M., Kessler, R., Guy, J., et al. 2014, A&A, 568, A22 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Branch, D., Romanishin, W., & Baron, E. 1996, ApJ, 465, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Bronder, T. J., Hook, I. M., Astier, P., et al. 2008, A&A, 477, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cardelli, J. A., Clayton, G. C., & Mathis, J. S. 1989, ApJ, 345, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Childress, M., Aldering, G., Antilogus, P., et al. 2013, ApJ, 770, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Conley, A., Guy, J., Sullivan, M., et al. 2011, ApJS, 192, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Contreras, C., Hamuy, M., Phillips, M. M., et al. 2010, AJ, 139, 519 [NASA ADS] [CrossRef] [Google Scholar]
- D’Andrea, C. B., Gupta, R. R., Sako, M., et al. 2011, ApJ, 743, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Davis, M., Faber, S. M., Newman, J., et al. 2003, in Proc. SPIE Conf. Ser., ed. P. Guhathakurta, 4834, 161 [Google Scholar]
- Davis, M., Guhathakurta, P., Konidaris, N. P., et al. 2007, ApJ, 660, L1 [NASA ADS] [CrossRef] [Google Scholar]
- de Vaucouleurs, G., de Vaucouleurs, A., Corwin, Jr. H. G., et al. 1991, Third Reference Catalogue of Bright Galaxies. Volume I: Explanations and references. Volume II: Data for galaxies between 0h and 12h. Volume III: Data for galaxies between 12h and 24h. [Google Scholar]
- Doi, M., Tanaka, M., Fukugita, M., et al. 2010, AJ, 139, 1628 [NASA ADS] [CrossRef] [Google Scholar]
- Domínguez, I., Höflich, P., & Straniero, O. 2001, ApJ, 557, 279 [NASA ADS] [CrossRef] [Google Scholar]
- Ellis, R. S., Sullivan, M., Nugent, P. E., et al. 2008, ApJ, 674, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 1997, A&A, 326, 950 [NASA ADS] [Google Scholar]
- Fioc, M., & Rocca-Volmerange, B. 1999, ArXiv e-prints [arXiv:astrop-ph/9912179] [Google Scholar]
- Foley, R. J., Challis, P. J., Chornock, R., et al. 2013, ApJ, 767, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Fukugita, M., Ichikawa, T., Gunn, J. E., et al. 1996, AJ, 111, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, J. S., Garnavich, P. M., Berlind, P., et al. 2005, ApJ, 634, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, J. S., Garnavich, P. M., Caldwell, N., et al. 2008, ApJ, 685, 752 [NASA ADS] [CrossRef] [Google Scholar]
- González Hernández, J. I., Ruiz-Lapuente, P., Tabernero, H. M., et al. 2012, Nature, 489, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Carr, M., Rockosi, C., et al. 1998, AJ, 116, 3040 [NASA ADS] [CrossRef] [Google Scholar]
- Gunn, J. E., Siegmund, W. A., Mannery, E. J., et al. 2006, AJ, 131, 2332 [NASA ADS] [CrossRef] [Google Scholar]
- Gupta, R. R., D’Andrea, C. B., Sako, M., et al. 2011, ApJ, 741, 127 [CrossRef] [Google Scholar]
- Gupta, R. R., Kuhlmann, S., Kovacs, E., et al. 2016, AJ, 152, 154 [CrossRef] [Google Scholar]
- Guy, J., Astier, P., Baumont, S., et al. 2007, A&A, 466, 11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guy, J., Sullivan, M., Conley, A., et al. 2010, A&A, 523, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hamuy, M. 2000, AJ, 120, 1479 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Phillips, M. M., Suntzeff, N. B., et al. 1996a, AJ, 112, 2391 [NASA ADS] [CrossRef] [Google Scholar]
- Hamuy, M., Phillips, M. M., Suntzeff, N. B., et al. 1996b, AJ, 112, 2398 [NASA ADS] [CrossRef] [Google Scholar]
- Hicken, M. 2009, ApJ, 700, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Hicken, M. 2012, ApJS, 200, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Hicken, M., Wood-Vasey, W. M., Blondin, S., et al. 2009, ApJ, 700, 1097 [NASA ADS] [CrossRef] [Google Scholar]
- Höflich, P., Wheeler, J. C., & Thielemann, F. K. 1998, ApJ, 495, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Holtzman, J. A., Marriner, J., Kessler, R., et al. 2008, AJ, 136, 2306 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, D. A., Sullivan, M., Perrett, K., et al. 2005, ApJ, 634, 1190 [NASA ADS] [CrossRef] [Google Scholar]
- Howell, D. A., Sullivan, M., Brown, E. F., et al. 2009, ApJ, 691, 661 [NASA ADS] [CrossRef] [Google Scholar]
- Iben, Jr. I., & Tutukov, A. V. 1984, ApJS, 54, 335 [NASA ADS] [CrossRef] [Google Scholar]
- Jiang, L., Fan,X., Bian, F., et al. 2014, ApJS, 213, 12 [CrossRef] [Google Scholar]
- Jones, D. O., Riess, A. G., & Scolnic, D. M. 2015, ApJ, 812, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Kauffmann, G., Heckman, T. M., White, S. D. M., et al. 2003, MNRAS, 341, 54 [Google Scholar]
- Kelly, P. L., Hicken, M., Burke, D. L., Mandel, K. S., & Kirshner, R. P. 2010, ApJ, 715, 743 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, Jr. R. C. 1998, ARA&A, 36, 189 [Google Scholar]
- Konishi, K., Cinabro, D., Garnavich, P. M., et al. 2011, ArXiv e-prints: [arXiv:1101.4269] [Google Scholar]
- Kron, R. G. 1980, ApJS, 43, 305 [NASA ADS] [CrossRef] [Google Scholar]
- Kronborg, T., Hardin, D., Guy, J., et al. 2010, A&A, 514, A44 [CrossRef] [EDP Sciences] [Google Scholar]
- Lampeitl, H., Smith, M., Nichol, R. C., et al. 2010, ApJ, 722, 566 [NASA ADS] [CrossRef] [Google Scholar]
- Le Borgne, D., & Rocca-Volmerange, B. 2002, A&A, 386, 446 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Le Fèvre, O., Mellier, Y., McCracken, H. J., et al. 2004, A&A, 417, 839 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Magnier, E. A., & Cuillandre, J.-C. 2004, PASP, 116, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Mannucci, F., Della Valle, M., Panagia, N., et al. 2005, A&A, 433, 807 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Martin, D. C., Fanson, J., Schiminovich, D., et al. 2005, ApJ, 619, L1 [Google Scholar]
- Moreno-Raya, M. E., López-Sánchez, Á. R., Mollá, M., et al. 2016, MNRAS, 462, 1281 [CrossRef] [Google Scholar]
- Neill, J. D., Sullivan, M., Howell, D. A., et al. 2009, ApJ, 707, 1449 [NASA ADS] [CrossRef] [Google Scholar]
- Nugent, P. E., Sullivan, M., Cenko, S. B., et al. 2011, Nature, 480, 344 [NASA ADS] [CrossRef] [Google Scholar]
- Pakmor, R., Kromer, M., Taubenberger, S., et al. 2012, ApJ, 747, L10 [Google Scholar]
- Pan, Y.-C., Sullivan, M., Maguire, K., et al. 2015, MNRAS, 446, 354 [CrossRef] [Google Scholar]
- Perlmutter, S., Aldering, G., Goldhaber, G., et al. 1999, ApJ, 517, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Perrett, K., Sullivan, M., Conley, A., et al. 2012, AJ, 144, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, M. M. 1993, ApJ, 413, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Piersanti, L., Bravo, E., Cristallo, S., et al. 2017, ApJ, 836, L9 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIV. 2016, A&A, 594, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pskovskii, I. P. 1977, Soviet Ast., 21, 675 [Google Scholar]
- Pskovskii, Y. P. 1984, Soviet Ast., 28, 658 [Google Scholar]
- Rana, N. C., & Basu, S. 1992, A&A, 265, 499 [NASA ADS] [Google Scholar]
- Regnault, N., Conley, A., Guy, J., et al. 2009, A&A, 506, 999 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riess, A. G. 1999, AJ, 117, 707 [Google Scholar]
- Riess, A. G., Filippenko, A. V., Challis, P., et al. 1998, AJ, 116, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Rigault, M., Copin, Y., Aldering, G., et al. 2013, A&A, 560, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rigault, M., Aldering, G., Kowalski, M., et al. 2015, ApJ, 802, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Rust, B. W. 1974, PhD Thesis, Oak Ridge National Lab., USA [Google Scholar]
- Sako, M., Bassett, B., Becker, A. C., et al. 2018, PASP, 130, 064002 [NASA ADS] [CrossRef] [Google Scholar]
- Schaefer, B. E., & Pagnotta, A. 2012, Nature, 481, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, B. P., Suntzeff, N. B., Phillips, M. M., et al. 1998, ApJ, 507, 46 [NASA ADS] [CrossRef] [Google Scholar]
- Scolnic, D., & Kessler, R. 2016, ApJ, 822, L35 [CrossRef] [Google Scholar]
- Scolnic, D. M., Jones, D. O., Rest, A., et al. 2018, ApJ, 859, 101 [NASA ADS] [CrossRef] [Google Scholar]
- Scoville, N., Abraham, R. G., Aussel, H., et al. 2007, ApJS, 172, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Sen, P. K. 1968, J. Am. Stat. Assoc., 63, 1379 [Google Scholar]
- Sim, S. A., Fink, M., Kromer, M., et al. 2012, MNRAS, 420, 3003 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Stritzinger, M. D., Phillips, M. M., Boldt, L. N., et al. 2011, AJ, 142, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, M., Ellis, R. S., Aldering, G., et al. 2003, MNRAS, 340, 1057 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, M., Howell, D. A., Perrett, K., et al. 2006a, AJ, 131, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, M., Le Borgne, D., Pritchet, C. J., et al. 2006b, ApJ, 648, 868 [NASA ADS] [CrossRef] [Google Scholar]
- Sullivan, M., Conley, A., Howell, D. A., et al. 2010, MNRAS, 406, 782 [NASA ADS] [Google Scholar]
- Sullivan, M., Guy, J., Conley, A., et al. 2011, ApJ, 737, 102 [NASA ADS] [CrossRef] [Google Scholar]
- Theil, H. 1992, A Rank-Invariant Method of Linear and Polynomial Regression Analysis, eds. B. Raj & J. Koerts (Dordrecht: Springer Netherlands), 345 [Google Scholar]
- Timmes, F. X., Brown, E. F., & Truran, J. W. 2003, ApJ, 590, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Tripp, R. 1998, A&A, 331, 815 [NASA ADS] [Google Scholar]
- Walker, E. S., Hook, I. M., Sullivan, M., et al. 2011, MNRAS, 410, 1262 [NASA ADS] [CrossRef] [Google Scholar]
- Whelan, J., & Iben, Jr. I. 1973, ApJ, 186, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Wolf, R. C., D’Andrea, C. B., Gupta, R. R., et al. 2016, ApJ, 821, 115 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr. J. E., et al. 2000, AJ, 120, 1579 [CrossRef] [Google Scholar]
We used the SDSS CasJobs server at http://skyserver.sdss.org/CasJobs with the following SQL command: SELECT str(p.ra,13,8) as ra, str(p.[dec],13,8) as dec, p.modelMagu, p.modelMagg, p.modelMagr, p.modelMagi, p.modelMagz, p.modelMagErru, p.modelMagErrg, p.modelMagErrr, p.modelMagErri, p.modelMagErrz FROM dr8.PhotoObj AS p JOIN dbo.fGetObjFromRect(214.042448, 215.519408, 52.160128, 53.20855) AS b ON p.objID = b.objID WHERE (p.type = 3 OR p.type = 6)
All Tables
Total integration time of the deep survey in different bands, for each field, that is, the total time allocated to the survey is four times as long as what is shown.
Number of available supernovæ for the whole SNLS five-year release and the corresponding amount of host photometry.
Mean value and standard deviation for the difference between our observed magnitudes and magnitudes from the single-epoch SDSS catalogs for field galaxies and the subsample of the SNIa hosts.
Selection requirements for the analysis focusing on local and global properties of the host.
Significance of the third parameter in the cosmological fit standardizing light-curves of SNIa as a function of survey type and redshift range for the different galactic properties, assuming a bimodal distribution.
Selection requirements when we use EGALITE as an SED fitting code taking observed magnitudes into account.
Unique selection requirement imposed when we include events with faint host galaxies in the sample.
Summary of all tests performed throughout the paper with the corresponding number of SNIa in the sample, the local U − V color step, the host stellar mass step, and step values when corrected for one or the other effect.
All Figures
 |
Fig. 1 Examples of the two types of SDSS images on the same portion of the sky in the g band. The DR12 single-epoch image is shown in the top panel, and the Stripe 82 coadded image is illustrated in the bottom panel. |
| In the text | |
 |
Fig. 2 Examples of eight g-band images of SNIa host galaxies ordered in redshift. The top row corresponds to SDSS images with sn2006gr, sn2003kc, sn2005hc, and sn2006hr. For this survey, the dashed red and solid white ellipses represent the region where the global photometry is measured for a low and high level of deblending. The solid red circle symbolizes the 3 kpc region where the local photometry is computed. The second row displays SNLS images corresponding to 04D2bt, 03D3bl, 03D1bf, and 05D3ht, using one single SExtractor configuration. This illustrates the great variety of cases, from SNIa exploding in the inner galaxy core to SNIa observed far away from the center, in the galactic arms. |
| In the text | |
 |
Fig. 3 Examples of nearby bright galaxies for which the low-deblending mode (red dashed ellipse) gives much better results than the high-deblending mode (white solid ellipse). The solid red circle represents the local photometric radius described in Sect. 3.2. |
| In the text | |
 |
Fig. 4 Evolution of the local photometric radius with a size of 3 kpc with redshift in arcseconds for host galaxies of SNIa observed by the SNLS (blue), SDSS (red), and low-redshift surveys (green points). The 1σ seeing of SNLS and SDSS images is illustrated with dashed lines using the same color code. A 1σ seeing corresponds to a diameter of about 85% of the FWHM. |
| In the text | |
 |
Fig. 5 Density of points (blue hexagonal bins) representing the absolute difference between observed aperture magnitudes and SDSS DR12 magnitudes in the g optical bandfor all field galaxies detected in the low-deblending configuration. Although the dispersion is relatively high, the overall agreement between the two photometries is good (see text). When split into magnitude bins for host galaxies (pink and purple bins for high- and low-deblending modes, respectively), the two configurations are similar, except for the first bin, where the low-deblending case shows less consistency with SDSS. |
| In the text | |
 |
Fig. 6 Top: distribution of galaxy stellar masses obtained from two different photometries from the SNLS and the SDSS surveys. All galaxies are located in the D3 deep SNLS field. Stellar masses are drawn as red points in the top panel; the resulting weighted linear fit is shown as the dashed black line. Bottom: redshift dependence of the stellar mass difference. The median rms is 0.21 dex. |
| In the text | |
 |
Fig. 7 Redshift evolution of the differences in common host stellar mass between N09 and our sample. Galaxies with only SDSS-like photometry are represented in orange. Their masses are estimated by fitting the spectral series PEGASE to our observed ugriz magnitudes.Galaxies presenting photometry in the 2MASS survey alone are drawn in dark red, their masses are derived from K-band absolute magnitude through Eq. (6). Stellar mass differences of objects with both types of photometry are displayed in purple. For these galaxies, we present masses derived from ugriz observed magnitudes. The dashed black line corresponds to the mean difference, with the rms represented by the gray area. |
| In the text | |
 |
Fig. 8 Redshift evolution of stellar mass differences in common hosts between S14 and our sample for objects with the same identification number (dark red points). This corresponds to intermediate-redshift galaxies detected in the SDSS survey. We find a good agreement between the two mass estimates, with a slight mean overestimation of stellar masses of about 0.07 dex compared to S14 (dashed black line; the gray area represents the rms). |
| In the text | |
 |
Fig. 9 Top: difference between U − V rest-frame color of the whole host galaxy and local U − V rest-frame color in a region of 3 kpc around the supernova location for SNLS (blue dots), SDSS (red dots), and low-redshift survey (green dots) hosts. The difference is displayed as a function of redshift. The observed redshift dependence (black bins) indicates that the cosmology is affected when local effects are included. Bottom: difference between U − V rest-frame color of the whole host galaxy and local U − V rest-frame color as a function of projected distance to the galactic center in kiloparsec. The color code is the same as for the top plot. The general trend shows that local regions that appear bluer than the host galaxy are located far from the center, whereas locally redder regions are close to the galactic center. |
| In the text | |
 |
Fig. 10 Local U − V rest-frame color of SNLS (blue dots), SDSS (red dots), and low-redshift survey (green dots) hosts in a region of 3 kpc around the supernova location as a function of the stellar mass of the host galaxy (in |
| In the text | |
 |
Fig. 11 Correlation of host galaxy stellar mass (in units of |
| In the text | |
 |
Fig. 12 Correlation of local U − V rest-frame colors (in a region of 3 kpc around the supernova location) with Hubble diagram residuals corrected for stretch and color for the SNLS (blue dots), SDSS (red dots), and low-redshift (green dots) surveys for SNIa lying in the second and fourth quadrants of Fig. 10. |
| In the text | |
 |
Fig. 13 Correlation of local U − V rest-framecolors (in a region of 3 kpc around the supernova location) with Hubble diagram residuals corrected for stretch and color for the SNLS (blue dots), SDSS (red dots), and low-redshift (green dots) surveys. The separation between the two local color bins at U − V ~ 0.63, corresponding to the median value of the sample, is shown as the black vertical dash-dotted line. The bins are drawn in black, with the weighted mean values as black dots and their dispersion, divided by the square root of the number of elements in the bin. The purple dashed line shows the weighted linear fit for the entire color distribution. The top histogram displays the repartition of the 441 elements in terms of local color, together with the fit to a bimodal distribution represented by the solid red line. The histogram on the right draws the Hubble diagram residual distribution of blue SNIa regions (for local color values below the separation in U − V), associated with star-forming regions, together with the equivalent distribution of red regions (for local color values above the separation in U − V), associated with more passive areas. |
| In the text | |
 |
Fig. 14 Covariance of α and the absolute magnitude step when three standardization parameters are used (blue contours for local color correction, and red contours for host stellar mass correction). The green rectangle corresponds to the case where two standardization parameters are used. Contours correspond to 68% and 95% confidence levels. |
| In the text | |
 |
Fig. 15 Correlations between supernova properties (stretch and color) as a function of local U − V color (first row) and host galaxy stellar mass (second row). The bins are drawn in black, with the weighted mean central values as black dots and the bin dispersion. Linear fits of the data are shown as dashed purple lines. |
| In the text | |
 |
Fig. 16 Evolution of the local photometric radius of 1.5, 2, and 3 kpc with redshift in arcseconds for host galaxies of SNIa observed by the SNLS (blue), SDSS (red), and low-redshift surveys (green points). The 1σ seeing size of SNLS and SDSS images are illustrated with dashed lines using the same color code. A 1σ seeing corresponds to a diameter of about 85% of the FWHM. |
| In the text | |
 |
Fig. 17 Evolution of the local step amplitude (in magnitude) as a function of the local radius size (in kpc). Points with error bars are colored as a function of the number of SNIa that belong to the corresponding samples. |
| In the text | |
 |
Fig. 18 Histograms of the step significance of the local U − V color (dark red) and stellar mass of the host (dark blue) used as a third standardization parameterin the cosmological fit. Correlations are estimated by removing 100 (top panel), 200 (middle panel), and 300 (bottom panel) random supernovæ from the initial sample of events and repeating the process a thousand times. The expected significances, assuming that it scales with
|
| In the text | |
 |
Fig. 19 Top: evolution of local color step significance as a function of the position of the local U − V color cut. The position of the sample median, chosen for the basic analysis, is shown as the dashed black line. Bottom: same as the top panel, but for the stellar mass of the host. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.