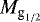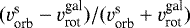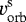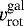| Issue |
A&A
Volume 613, May 2018
|
|
|---|---|---|
| Article Number | A4 | |
| Number of page(s) | 26 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201629007 | |
| Published online | 15 May 2018 | |
Caught in the rhythm
I. How satellites settle into a plane around their central galaxy
1
ICRAR, The University of Western Australia,
Crawley,
Perth 6009,
WA, Australia
e-mail: charlotte.welker@uwa.edu.au
2
CNRS and UPMC Univ. Paris 06, UMR 7095, Institut d’Astrophysique de Paris,
98bis boulevard Arago,
75014 Paris, France
3
Institute of Astronomy, University of Cambridge,
Madingley Road,
Cambridge CB3 0HA, UK
4
Sub-department of Astrophysics, University of Oxford,
Keble Road,
Oxford OX1 3RH, UK
5
Observatoire de Lyon, UMR 5574,
9 avenue Charles André,
69561
Saint-Genis-Laval, France
Received:
26
May
2016
Accepted:
22
August
2017
Context. The anisotropic distribution of satellites around the central galaxy of their host halo is both well-documented in observations and predicted by the ΛCDM model. However its amplitude, direction and possible biases associated to the specific dynamics of such satellite galaxies are still highly debated.
Aims. Using the cosmological hydrodynamics simulation Horizon-AGN, we aim to quantify the anisotropy of the spatial distribution of satellite galaxies relative to their central counterpart and explore its connexion to the local cosmic web, in the redshift range between 0.3 and 0.8.
Methods. Haloes and galaxies were identified and their kinematics computed using their dark matter and stellar particles respectively. Sub-haloes were discarded and galaxies lying within 5 Rvir of a given halo are matched to it. The filamentary structure of the cosmic web was extracted from the density field – smoothed over a 3 h−1 Mpc typical scale – as a network of contiguous segments. We then investigated the distribution function of relevant angles, most importantly the angle α between the central-to-satellite separation vector and the group’s nearest filament, aside with the angle between this same separation and the central minor axis. This allowed us to explore the correlations between filamentary infall, intra-cluster inspiralling and the resulting distribution of satellites around their central counterpart.
Results. We find that, on average, satellites tend to be located on the galactic plane of the central object. This effect is detected for central galaxies with a stellar mass larger than 1010 M⊙ and found to be strongest for red passive galaxies, while blue galaxies exhibit a weaker trend. For galaxies with a minor axis parallel to the direction of the nearest filament, we find that the coplanarity is stronger in the vicinity of the central galaxy, and decreases when moving towards the outskirts of the host halo. By contrast, the spatial distribution of satellite galaxies relative to their closest filament follows the opposite trend: their tendency to align with them dominates at large distances from the central galaxy, and fades away in its vicinity. In that redshift range, we find hints that massive red centrals with a spin perpendicular to their filament also have corotating satellites well aligned with both the galactic plane and the filament. On the other hand, lower-mass blue centrals with a spin parallel to their filament have satellites flowing straight along this filament, and hence orthogonally to their galactic plane. The orbit of these satellites is then progressively bent towards a better alignment with the galactic plane as they penetrate the central region of their host halo.
Conclusions. The kinematics previously described are consistent with satellite infall and spin build-up via quasi-polar flows, followed by a re-orientation of the spin of massive red galaxies through mergers.
Key words: methods: numerical / galaxies: clusters: general / galaxies: groups: general / galaxies: statistics / large-scale structure of Universe / galaxies: interactions
© ESO 2018
1 Introduction
The complex interactions between central galaxies and their satellites in dark matter haloes have received a great deal of attention from both theorists and observers over the past decades. Numerous questions regarding the precise distribution of satellites around their central counterparts – noticeably their orientation with respect to the central galactic plane and the connection of this latter with the surrounding cosmic web – have been investigated in both observational and numerical works. Although a few observational studies have claimed to observe polar alignment of satellites around centrals (the so-called Holmberg effect, Holmberg 1969; Zaritsky et al. 1997) or none at all (Hawley & Peebles 1975; Phillips et al. 2015), most of these studies show that satellite galaxies are distributed within the galactic plane of their central galaxy (Brainerd 2005; Yang et al. 2006; Sales & Lambas 2009; Wang et al. 2010; Nierenberg et al. 2012; Smith et al. 2016), and possibly corotating with it (Ibata et al. 2013). Those findings are in fair agreement with predictions from N-body (Aubert et al. 2004; Zentner et al. 2005) and hydrodynamical cosmological simulations (Dong et al. 2014), although it is still debated whether these models predict planes of satellites as thin as those observed around the Milky-Way and Andromeda (Bahl & Baumgardt 2014; Pawlowski et al. 2014; Gillet et al. 2015). The analysis of galaxy groups in the Sloan Digital Sky Survey (SDSS; Abazajian et al. 2009) has confirmed this trend and established that the signal is stronger for massive red central galaxies, especially in the inner regions of the halo (Yang et al. 2006).
The interest in the distribution of satellites stems in part from their expected ability to trace the underlying dark matter density of their host halo. In the standard picture, progenitors of satellite galaxies end up orbiting around their host with a distribution tracing its potential well, hence the geometry of the underling dark matter density. A robust consequenceof this scenario (Wang et al. 2005; Agustsson & Brainerd 2010) is therefore that the perceived concentration of satellites in the rotation plane of their host halo is a direct tracer of its triaxiality (Barnes & Efstathiou 1987; Warren et al. 1992; Yoshida et al. 2000; Meneghetti et al. 2001; Jing & Suto 2002) inherited from its hierarchical build-up within an anisotropic cosmic web. Moreover, there is evidence that alignment trends of brightest cluster galaxies, luminous red galaxies and groups and clusters are also preserved on large scales (up to 100 h −1 Mpc, Binggeli 1982; Plionis & Basilakos 2002; Hopkins et al. 2005; Mandelbaum et al. 2006; Hirata et al. 2007; Okumura & Jing 2009; Niederste-Ostholt et al. 2010; Joachimi et al. 2011; Paz et al. 2011; Smargon et al. 2012; Li et al. 2013; Singh et al. 2015) as a consequence of hierarchical structure formation, stretching and re-orientation from tidal interactions (Croft & Metzler 2000; Lee & Pen 2000; Crittenden et al. 2001; Catelan et al. 2001; Hirata & Seljak 2004, 2010; Blazek et al. 2011, 2015; Schaefer & Merkel 2015; Codis et al. 2015b).
The anisotropic distribution of satellites is thus a prediction of the Λ cold dark matter (CDM) model but its amplitude and the possible additional biases arising from the specific dynamics of satellite galaxies are still highly debated. Numerical simulations have in particular pointed out a possible degeneracy regarding the anisotropic distribution of satellites arising from the effect of halo ellipticity and the ongoing – unrelaxed – anisotropic cosmic infall (Aubert et al. 2004; Pichon et al. 2011). Massive halos have a spin preferentially orthogonal to their host filament (van Haarlem & van de Weygaert 1993; Tormen et al. 1997; Bailin et al. 2008; Paz et al. 2011; Codis et al. 2012; Zhang et al. 2013) since they are the product of multiple mergers between pairs of objects drifting along the cosmic web, hence with orbital angular momentum is preferentially perpendicular to filaments along which they flow (Dubois et al. 2014; Welker et al. 2014).
As a consequence, the elongation of the halo and filamentary infall share a unique direction. The tendency of satellites to orbit in the central galactic plane is therefore not a mere tracer of the halo triaxiality, but is also naturally enhanced by the continuing infall of satellites (Aubert et al. 2004; Knebe et al. 2004; Wang et al. 2005; Zentner et al. 2005). Recent observationsof planes of satellites for M 31 or the Milky Way (Ibata et al. 2013; Libeskind et al. 2015) and the detection of alignment trends in the SDSS by Paz et al. (2008; see also Tempel et al. 2015) strongly support this claim.
However, it is still unclear how strongly sustained anisotropic cosmic infall of satellites impacts their observed angular distribution compared to the possibly more relaxed diffuse dark matter component. It may however be important to make a distinction between a dynamical angular bias (sustained polar accretion of satellites, gravitational torques from the central disc and halo) specific to the dense baryonic substructures, and a purely geometrical angular anisotropy related to the elongation of the halo and affecting the diffuse dark matter component likewise. Getting a better understanding of how satellite galaxies flow along the host filament and sink into their host halo, how this process depends on the orientations of infall relative to that of the central galaxy, and how it affects their statistical distribution, is, thus, of major importance.
Beyond the goal of understanding galactic accretion, intrinsic alignments of galaxy shapes are widely regarded as a contaminant to weak gravitational lensing measurements (Croft & Metzler 2000; Crittenden et al. 2001; Catelan et al. 2001; Bernstein & Norberg 2002; Hirata et al. 2004; Mandelbaum et al. 2006; Hui & Zhang 2008; Schneider & Bridle 2010; Joachimi & Bridle 2010; Kirk et al. 2015). They could play a particularly important role in upcoming cosmic shear measurements, potentially biasing constraints on the evolution of the dark energy equation of state (Kirk et al. 2010; Krause et al. 2016). The need to access information on the nonlinear scales of the cosmic shear power spectrum to constrain dark energy makes numerical hydrodynamical simulations useful to study the mechanisms that lead to alignments (Tenneti et al. 2015; Codis et al. 2015a; Velliscig et al. 2015a,b; Chisari et al. 2015), to build a halo model to describe them (Schneider & Bridle 2010) and to constrain alignment bias parameters (Blazek et al. 2015). Indeed, the coplanarity of satellites in the vicinity of a central massive galaxy could lead to an alignment signal that would contaminate such lensing measurements. It would induce a correlation between the shape of the central and the location of the satellites. In particular, coherent alignments of galaxies with the filaments that define the large-scale structure of the Universe could also produce a contamination to cosmic shear and galaxy-galaxy lensing. A complementary analysis to the work presented in this paper is given in Chisari et al. (2015), which relates the shapes of galaxies in the simulation and their correlations to currently available models for intrinsic alignments. In the present study, we analyse the distribution of galaxy satellites around their central galaxy in the cosmological hydrodynamics simulation Horizon-AGN (Dubois et al. 2014) primarily between redshift z = 0.8 and z = 0.3, and how this distribution is reconfigured as satellites approach the central galaxy.
This paper is structured as follows: after a short review of the numerical setup and methods used in Sects. 2 and 3 focuses on the description of alignment trends measured in Horizon-AGN. Section 4 presents a more detailed kinematic analysis of the corotation features found for satellites of massive halos at various stages of evolution. Mock observations are presented in Sect. 5, where the impact of various parameters, such as the shape of the central galaxy, on the alignment trends are further studied. Finally, Sect. 6 discusses these results in the scope of recent observations and Sect. 7 summarizes our main results.
2 Numerical, methods and definitions
Let us first briefly review the numerical setup and methods used to produce virtual data sets and analyse galaxy orientations.
2.1 The Horizon-AGN simulation
The details of the Horizon-AGN1 simulation, that we only briefly describe here, can be found in Dubois et al. (2014). The Horizon-AGN simulation is run in a Lbox = 100 h−1 Mpc cube with a ΛCDM cosmology with total matter density Ωm = 0.272, dark energy density ΩΛ = 0.728, amplitude of the matter power spectrum σ8 = 0.81, baryon density Ωb = 0.045, Hubble constant H0 = 70.4 km s−1 Mpc−1, and ns = 0.967 compatible with the WMAP-7 data (Komatsu 2011). The total volume contains 10243 dark matter (DM) particles, corresponding to a DM mass resolution of MDM, res = 8 × 107 M⊙, and initial gas resolution of Mgas,res = 1 × 107 M⊙. It is run with the RAMSES code (Teyssier 2002), and the initially coarse 10243 grid is adaptively refined down to Δx = 1 proper kpc, with refinement triggered in a quasi-Lagrangian manner: if the number of DM particles in a cell becomes greater than 8, or if the total baryonic mass reaches eight times the initial baryonic mass resolution in a cell. It results in a typical number of 7 × 109 gas resolution elements (leaf cells) in the Horizon-AGN simulation at z = 0.
Heating of the gas from a uniform UV background takes place after redshift zreion = 10 following Haardt & Madau (1996). Gas can cool down to 104 K through H and He collisions with a contribution from metals using rates tabulated by Sutherland & Dopita (1993). Star formation occurs in regions of gas number density above n0 = 0.1 H cm−3 following a Schmidt law: 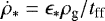 , where
, where 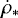 is the star formation rate mass density, ρg the gas mass density, ϵ* = 0.02 the constant star formation efficiency, and tff the local free-fall time of the gas. Feedback from stellar winds, supernovae type Ia and type II are included into the simulation with mass, energy and metal release, assuming a Salpeter initial mass function. The formation of black holes (BHs) is also taken into account. They can grow by gas accretion at a Bondi-capped-at-Eddington rate and coalesce when they form a tight enough binary. BHs release energy in a heating or jet mode (respectively “quasar” and “radio” mode) when the accretion rate is respectively above and below one per cent of Eddington, with efficiencies tuned to match the BH-galaxy scaling relations at z = 0 (see Dubois et al. 2012, for details).
is the star formation rate mass density, ρg the gas mass density, ϵ* = 0.02 the constant star formation efficiency, and tff the local free-fall time of the gas. Feedback from stellar winds, supernovae type Ia and type II are included into the simulation with mass, energy and metal release, assuming a Salpeter initial mass function. The formation of black holes (BHs) is also taken into account. They can grow by gas accretion at a Bondi-capped-at-Eddington rate and coalesce when they form a tight enough binary. BHs release energy in a heating or jet mode (respectively “quasar” and “radio” mode) when the accretion rate is respectively above and below one per cent of Eddington, with efficiencies tuned to match the BH-galaxy scaling relations at z = 0 (see Dubois et al. 2012, for details).
2.2 Galaxies and haloes: detection and matching
Galaxies were identified using the most massive sub-node method (Tweed et al. 2009) of the AdaptaHOP halo finder (Aubert et al. 2004) operating on the distribution of star particles with the same parameters than in Dubois et al. (2014). Unless specified otherwise, only structures with a minimum of Nmin = 50 star particles were considered, which typically selected objects with masses larger than 1.7 ×108 M⊙. Catalogues containing up to ~350 000 haloes and ~180 000 galaxies were produced for each redshift output analysed in this paper (0.3 < z < 0.8). This study focused on a rather low redshift range z = 0.3−0.8, accessible to current observations. This detection threshold in terms of number of particles might seem low with respect to possible lack of convergence of shape tracers for poorly defined centrals, however, weapplied a higher threshold to select central galaxies afterwards: galaxies with a stellar mass Mg < 109 M⊙ were systematically excluded from the central galaxy sample. Unless specified otherwise, results were stacked over the whole range of redshifts 0.3 < z < 0.8 (all pairs found were stacked).
To match central galaxies with their host halo, we associated each galaxy with the halo located at the shortest distance from it (measured as the distance between their respective centres of mass). In case of multiple galaxies associated with the same halo, we identified the central galaxy as the most massive galaxy contained within a sphere of radius R = 0.25 Rvir with Rvir the virial radiusof the halo. This criterium on distance AND mass – as opposed to only distance – reduced the number of misidentifications due to strong interactions between an infalling satellite and the central galaxy. Indeed, in such cases, mutual interactions between the two galaxies – combined to uncertainties on the centres of mass of haloes and the galaxies – can lead to deviations between the galaxy centre of mass and that of the host halo, leading to lower mass satellites being temporarily identified as the “central”. Our two parameter criterium not only corrected for that, but it also mimicked the identification of BCGs in groups and clusters, which are not necessarily the most central galaxy and around which satellite alignments trends are usually established in observations.
Unless otherwise specified, sub-haloes were not considered as able to host central galaxies. The satellite galaxies of a halo were defined as all the galaxies – excluding the central – situated within a sphere of radius R = 5 Rvir. This includes galaxies belonging to sub-haloes of the host halo, but also to sub-haloes of neighbouring haloes. This seemingly too large a scale was chosen so as to ensure that incomplete randomisation of walls and grid periodicity on the largest scales of the simulated volume did not affect the 3D angular statistics presented in our analysis. Further cuts in distance to the central galaxy can be performed afterwards and will be specified in each case. Let us stress the fact that above 2 Rvir, galaxies neighbouring a halo are not necessarily bound to this halo and can therefore also be centrals of another halo. Since our aim was precisely to show the continuity between motion of galaxies in the cosmic web and the orientation of satellites in the outer parts of the haloes they enter, we chose to consider a 2− 5Rvir bin in our analysis to investigate the continuity of some alignment trends from extra- to intra-halo scales.
At z = 0.3, approximately 16 000 main haloes are inhabited. The richest one hosts 678 galaxies; 263 haloes contain more than 30 galaxies; 2220, haloes more than 10; and 6622 host at least two galaxies. This distribution does not show strong variations across the redshift range analysed in this work.
2.3 Synthetic colours
For each galaxy, the absolute AB magnitudes and rest-frame colours were computed using single stellar population models from Bruzual & Charlot (2003) assuming a Salpeter initial mass function. Each star particle contributes to a flux per frequency that depends on its mass, age, and metallicity. Contributions to the reddening of spectra from internal (interstellar medium) or external (intergalactic medium) dust extinction were not taken into account. Computing the spectrum of all star particles and convolving with the u, g, r, and i filters from the SDSS, we then built two-dimensional projected maps of each galaxy (satellites are excised using the galaxy finder) and computed their luminosities in these wavebands.
2.4 Galaxy morphologies and kinematics
We computed stellar particle kinematics for all central galaxies and satellites in the sample. All quantities were computed in the half mass radius of the galaxy, defined as the radius that contains half the mass of the galaxy, noted Mg. The angular momentum – or spin – of a galaxy was defined as the total angular momentum of the star particles it contains and is measured with respect to the densest star particle (which proves a more robust estimator of the galaxy centre than its centre of mass in cases were the central galaxy is in the process of merging):
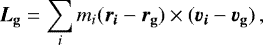 (1)
(1)
with ri, mi and vi the position, mass and velocity of particle i, rg the position of the centre of the galaxy and vg its centre of mass velocity. The notation Lg is hereafter used for the angular momentum of the central galaxy while 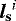 denotes the intrinsic angular momentum of its ith satellite.
denotes the intrinsic angular momentum of its ith satellite.
The separation vector, or position vector of each satellite in the rest frame of its central galaxy was defined as rgs = rs − rg with rs the position of the satellite. Its norm is the separation Rgs = ||rgs||.
The inertia tensor of each galaxy was computed from the star particle masses (ml ) and positions (xl) (in the barycentric coordinate system of the galaxy):
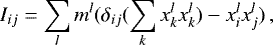 (2)
(2)
where δij is the Kronecker symbol. This inertia tensor was diagonalised, with its eigenvalues λ1 > λ2 > λ3 the moments of the tensor relative to the basis of principal axes e1, e2 and e3. The lengths of the semi-principal axes (with a1 < a2 < a3) were derived from the moments of inertia:
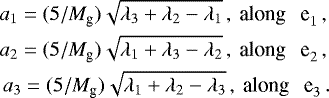
This allowed for an easy estimation of the galactic shape using the tri-axiality ratio τ = (a2 − a1)∕(a3 − a2). Oblate structures (disc-shaped) have τ > 1 while prolate structures (cigar-shaped) have τ < 1.
For comparison with observations, we also defined the corresponding projected quantities along the x-axis of the grid (labeled “X”). Definitions are similar for the positions and inertia tensor with summations restricted to the projected coordinates (y, z). This led to the eigenvalues 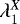 and
and 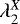 , from which we derived the axis
, from which we derived the axis 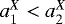 .
.
As we were interested in studying the corotation of satellites, that is their tendency to align their orbital momentum with the spin of the central galaxy and synchronise their rotation with that of the central disc, we also computed the total orbital angular momentum of satellite systems as 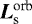 with similar definitions as previously used to derive spins, but applied to the velocities and positions of satellites. Average circular velocities (for the central galaxy or its orbiting system of satellites) were defined as
with similar definitions as previously used to derive spins, but applied to the velocities and positions of satellites. Average circular velocities (for the central galaxy or its orbiting system of satellites) were defined as
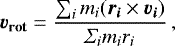 (3)
(3)
with mi, ri and vi the masses, radius and velocities of structures considered: star particles for the central galaxy, satellites for a system of satellites.
We chose to use the notation 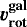 for the average rotational velocity of the stellar material within the central galaxy, and
for the average rotational velocity of the stellar material within the central galaxy, and 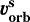 for the average orbital rotational velocity of the system of satellites.
for the average orbital rotational velocity of the system of satellites.
Each satellite has an individual orbital plane defined by eρ = rgs∕Rgs, the direction to the central, and eθ = vortho∕||vortho||, the direction of the component of its velocity orthogonal to rgs. The intersections, D1 and D3, of such a plane with the planes P1 = (e1, e2) and P3 = (e1, e3) of the central galaxy allowed us to compute two orientation angles ζ1 between D1 and e1, and ζ3 between D3 and e3, respectively. An illustration of these angles can be found in Fig. 1.
Averaging angles ζ1 and ζ3 for all the satellites in the system, we obtained two angles that define their mean orbital plane. This allowed us to compute the dispersion ratio: 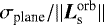 with
with 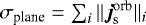 and
and 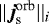 the norm of the projected orbital momentum of satellite i on the mean orbital plane of all satellites. This measures the dispersion of the orientation of the angular momentum of the satellites around the mean rotation plane. This parameter drops to zero if satellites are all rotating in the same plane. Similarly, we measured the corotation ratio:
the norm of the projected orbital momentum of satellite i on the mean orbital plane of all satellites. This measures the dispersion of the orientation of the angular momentum of the satellites around the mean rotation plane. This parameter drops to zero if satellites are all rotating in the same plane. Similarly, we measured the corotation ratio: 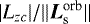 , where Lzc is the projection of the total orbital momentum on the spin axis of the central galaxy.
, where Lzc is the projection of the total orbital momentum on the spin axis of the central galaxy.
Table 1 summarises the definitions of all the angles used in this paper to follow alignment trends and the amount of corotation of satellites relative to their central galaxy.
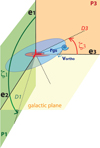 |
Fig. 1 Sketch representation of the angles ζ1 and ζ3 used to describe the orientation of the orbital plane of a satellite (in blue) around its central galaxy (in red), that are used to compute the average orbital plane of satellites and their dispersion ratio (see the text for details). Dashed lines illustrate the intersections between the central galaxy principal planes and the satellite orbital plane. |
2.5 Characterization of the cosmic web
In order to quantify the orientation of galaxies relative to the cosmic web, we used a geometric three-dimensional ridge extractor called the SKELETON (Sousbie et al. 2009) computed from the full volume DM density distribution sampled on a 5123 Cartesian grid. This density distribution was smoothed with a Gaussian kernel of length 3 h −1 comoving Mpc. The orientation and distribution of galaxies could be measured relative to the direction of the closest filament segment. It is important to notice that such filaments are defined as ridge lines of the density field and therefore have no thickness. The closest filament of a given galaxy is thus simply the segment whose distance to the galaxy is the shortest. However, allcentral galaxies in the sample are separated from their nearest filament by less than 1 Mpc, and the vast majority of them by less than 0.5 Mpc (the peak of the galaxy distance-to-filament distribution lies around 0.2 Mpc).
2.6 Grid-locking effects
A common caveat of Cartesian based Poisson solvers is the numerical anisotropy that arises in the force calculation. On smallest mass scales, this can lead to spurious alignments of spins with the Cartesian grid. This effect was explicitly tested in Horizon-AGN in Dubois et al. (2014). We summarise main results here: the spins of less massive galaxies Mg < 5 × 109 show some preferential spin alignments with the grid while no obvious alignment is seen for the high-mass galaxies. Low-mass galaxies are preferentially locked with the grid because they are composed of very few grid elements, this disappears for more massive galaxies due to the larger number of resolution elements to describe those objects. Cosmic filaments were found not to be subject to grid-locking, coherently with their large-scale nature.
In the present study, the threshold chosen for central galaxies and the scales considered ensured that most of our results are not subject to grid-locking. There is however a possibility that grid-locking add some noise to the measurements in Sect. 4.2 as we computed in that case the spin of satellites, which can be low-mass. However, given that structures they were tested against for alignment (central galaxies and filaments) are not subject to grid-locking, this numerical artefact cannot account for the alignment trends found, nor can it explain the corotation features described. A detailed analysis of those effects in Horizon-AGN can also be found in Chisari et al. (2015).
3 Orientation of satellites
We investigate the alignment of satellites galaxies in the redshift range 0.3 < z < 0.8. We characterise two distinct trends:
-
The tendency of satellites to lie on the galactic plane of their central galaxy: the coplanar trend. This can be analysed computing either μ = cos θ, the cosine of the angle between the satellite’s position vector and the spin of the central, or μ1 = cos θ1, with the minor axis of the central (see Fig. 4). In this paper, we mostly focus on the latter, because it is more closely related to observational methods (see Yang et al. 2006; Tempel et al. 2015).
-
The tendency of satellites to align within the nearest filament: the filamentary trend. To quantify it, we compute ν = cos α the cosine of the angle between the satellite’s position vector and the direction of the closest filament. The filamentary trend is detected when there is an excess probability ξ > 0 for cos α = 1.
3.1 Mass dependence of in-plane alignments
3.1.1 Results
Let us first study the coplanar trend. The top panel of Fig. 2 shows the probability density function (or PDF ≡ 1 + ξ, with ξ the excess of probability) of μ1 = cos θ1, where θ1 is the unsigned angle in [0, π∕2] between the minor axis of the central galaxy and rgs for central galaxies in different stellar mass bins. As previously mentioned, we stack results from the satellite distribution around central galaxies over six Horizon-AGN outputs in the redshift range 0.3 < z < 0.8 equally spaced in redshift and consider only satellites within 5Rvir of the central galaxy. The main effect of this stacking is a smoothing of the signal. It was checked that results for individual snapshots are fully consistent with the stacked results, although with larger error bars.
On average, satellites have a tendency to lie on the galactic plane of the central galaxy, or equivalently, their direction is preferentially perpendicular to the minor axis of the galaxy as shown by the excess PDF, ξ, at μ1 = 0 (see Aubert et al. 2004, for DM sub-halos). However, this conclusion does not hold equally for all central galaxies: while the distribution of satellites around their central is mostly random for low-mass centrals with 109 < Mg < 1010 M⊙, the alignment strengthens as the central mass increases. For the most massive centrals, galaxy satellites clearly tend to be preferentially distributed in the plane of the central galaxy. For central galaxies with stellar mass Mg > 1010.5 M⊙, the excess PDF at μ1 = 0 is ξ = 40%, with 52% of satellites lying outside of a 66° (cos θ1 < 0.4) double cone of axis perpendicular to the galactic plane, as opposed to 40% for the uniform PDF (dashed line). For intermediate central masses (1010 < Mg < 1010.5 M⊙), the excess PDF at μ1 = 0 is ξ = 13%, and 45% of satellites lie outside of the 66° inverted bicone. No substantial excess is found for lower masses (ξ < 2% at μ1 = 0). Thus the tendency of satellites to lie on the galactic plane of their central galaxy is directly correlated to this latter’s mass.
Let us now investigate the tendency of satellites to be distributed along filaments. In the bottom panel of Fig. 2, we show the excess PDF of ν = cos α, the angle between the direction of the central galaxy nearest filament axis and rgs. Satellite galaxies tend to align with the direction of the closest filament associated with the central galaxy at the level of ξ ≃ 30%, mostly independently of the central galaxy mass (though we see a slight increase of ξ with Mg ). Here 27% of the satellites are contained within a 37° cone with axis parallel to the filament (cos α > 0.8), as opposed to 20% for angles uniformly distributed on the sphere. This effect holds even for the smallest central masses with a decrease in amplitude of less than 1%.
 |
Fig. 2 Top panel: excess PDF ξ of μ1 = cos θ1, the angle between the minor axis of the central galaxy and the direction towards the centre of mass of its satellites, for different central galaxy stellar mass bins, between redshift 0.3 < z < 0.8. Satellites tend to be distributed on the galactic plane of the central and this trend is stronger with the increasing mass of the central. Bottom panel: excess PDF of ν = cos α, the cosine of the angle between the direction of the central’s nearest filament axis and the direction towards the centre of mass of its satellites. Satellites tend to be strongly distributed along filaments. Error bars are 1− σ Poissonian error bars. |
3.1.2 Interpretation
Satellites live preferentially in the nearest filament, which suggests that their tendency to align within the galactic plane may be linked to whether the central galaxy is also aligned with the filament or not. We can connect this trend to the findings of Codis et al. (2012); Dubois et al. (2014); Welker et al. (2014); Laigle et al. (2015). These papers found that massive centrals – formed through mergers – display a spin orthogonal to their nearest filament. As a consequence, their galactic plane will be parallel to the filament and we thus expect an excess of satellites in the plane of the central. In other words, this mass-dependent trend for satellites seems directly connected to the already known mass dependent spin orientation of centrals. However, one should bear in mind that the scenario developed in the above mentioned papers also advocates that low-mass central galaxies, caught in the winding of the cosmic flows within a filament, are more likely to develop a spin parallel to this filament. Hence, one would expect an excess of satellites orthogonal to the galactic plane of these low-mass centrals. At first glance, this does not happen: we find that satellites tend to be randomly distributed around low mass centrals. Several reasons lead to this discrepancy (see Appendix A for detail):
-
The spin alignment trend for low mass centrals was actually detected at higher redshift (z > 1) and wasshown to decrease with cosmic time, while the perpendicular orientation trend for higher mass galaxies is expected to strengthen. As a consequence, the satellite orientation on the galactic plane is much weaker around low-mass centrals in our redshift range.
-
The combined effect of the threshold we use for galaxy detection and of our choice to use the minor axis rather than the spinto quantify alignments on the galactic plane. Indeed, because we only detect structures with mass above 108.5 M⊙, systems of low-mass centrals with satellites in Horizon-AGN are most often pairs of galaxies (85% of the low-mass sample, or 97% countingthree-body systems) – the most massive one being labelled as central – with a mass ratio close to unity. This implies that the satellite and the central are actually interacting galaxies: they mutually affect each other’s spin orientation and shape significantly. The shape – as traced by the minor axis – is especially impacted by the interaction while the spin is slightly more resilient.
Consequently, even though low-mass central galaxies tend to display an orientation of spin parallel to the filament on average, thiseffect is weak and the alignment signal is strongly suppressed for the subsample of these centrals interacting with a close neighbour, and even further suppressed when traced using the minor axis, for satellites in the vicinity of the central galaxy. This latter effect is analysed in greater detail in Appendix A, where we show that the alignment of satellites orthogonally to the galactic plane of low mass centrals is actually recovered either using μ =cos θ (central spin-separation angle) rather than μ1 = cos θ1, or focusing on μ1 = cos θ1 for a sub-sample of more distant satellites and/or lower mass ratio central/satellite pairs.
As a conclusion, after careful analysis these trends seem fully consistent with the statistical measurements of the orientation of the spin of galaxies in the cosmic web highlighted in previous works: low-mass young galaxies fed in vorticity rich regions in the vicinity of filaments (Laigle et al. 2015) have their spin parallel to the filament they are embedded in, while older galaxies, more likely to be the products of mergers, are also more likely to display a spin flipped orthogonally to the filament by a transfer of orbital angular momentum (Dubois et al. 2014; Welker et al. 2014). Figure 3 illustrates this idea that the trends measured in Fig. 2 can therefore be explained by the preferred distribution of satellite galaxies within the filament closest to the central galaxy. It depicts an “ideal” evolved massive central galaxy and a low-mass galaxy.
Those alignments are consistent with observational results of Yang et al. (2006) and numerical results of Dong et al. (2014) which found a clear alignment of satellites on the galactic plane around red (hence more massive) central galaxies. At the extreme mass end, brightest cluster galaxies are also known to be elongated in the direction of their neighbours; this is the “Binggeli effect” (Binggeli 1982; Niederste-Ostholt et al. 2010), and possibly of their closest filament (Paz et al. 2011). Moreover, our results concerning the filamentary trend are also supported by recent observational studies by Tempel et al. (2015) and Libeskind et al. (2015) who studied the orientation of plane of satellites in the Local Group and in the SDSS with respect to observationally detected filaments.
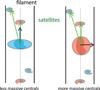 |
Fig. 3 Sketch of the expected results for the filamentary trend. Satellite galaxies tend to be aligned within the nearest filament. Consequently, they are distributed orthogonally to the spin/minor axis of older red central galaxies, and more often aligned with the spin/minor axis of young blue central galaxies. |
3.2 Satellite alignments versus distance to central
While massive central galaxies are overall more likely to show a galactic plane aligned with the nearest filament (or equivalently a spin orthogonal to it), this does not mean however that central galaxies whose spin is aligned with the filament (angle smaller than 37°) constitute a negligible population, even in the higher mass ranges. In fact, they still represent 17% of all central galaxies with Mg > 1010 M⊙, and moderately misaligned ones (angle between 37° and 45°) account for 23% of the same sample.
Such misalignments between central galaxy planes and nearby filaments imply the existence of galaxy populations for which the filamentary and coplanar trends are best described as mutually exclusive (when the spin of the central is well-aligned with the filament) while for “well-behaved” massive centrals (with a galactic plane aligned to the filament) they would lead to qualitatively similar effects. Understanding whether the coplanar trend can be reduced to being mostly consequence of the filamentary trend requires further analysis of cases in which both trends might compete. To better comprehend where and how this competition occurs, Fig. 5 focuses on two sub-samples, which we select so as to preserve statistics:
-
central galaxies with minor axis parallel/aligned with the filament axis, that is their minor axis direction lies within a 37° double cone (cos αg > 0.8) whose axis of revolution direction coincides with that of the filament,
-
central galaxies with minor axis perpendicular/misaligned to/with the filament axis, that is their minor axis direction lies outside the double cone with opening angle of 66° whose axis of revolution direction coincides with that of the filament (cos αg < 0.4).
The definitions of these two sub-samples is illustrated on Fig. 4.
3.2.1 Results
Figure 5 shows the excess PDF ξ of μ1 = cos θ1 (coplanar trend) and ν = cos α (filamentarytrend) for both samples and different ranges of central galaxy mass. In the first case (top row), the coplanarity and filamentary trends are mutually exclusive, while in the second case they affect the distribution of satellites in similar waysand become reinforced. Recall that the coplanar trend is detected when there is an excess probability ξ > 0 for cos θ1 = 0, while the filamentary trend is detected when ξ > 0 for cos α = 1. Looking at the first sample of centrals, we see that the coplanar trend dominates for the most massive galaxies (Mg > 1010.5 M⊙) with 43% of satellites found on the galactic plane – that is outside the 66° double cone whose axis coincides with the central minor axis – (40% for random), even though the filamentary trend has vanished: satellites tend to lie preferentially orthogonally to the nearest filament.
However, the coplanar trend disappears as the central mass decreases (Mg < 1010.5 M⊙) and as it gets replaced by a polar trend, compatible in this case with the filamentary trend. Indeed, the filamentary trend is in contrast recovered for central galaxies with mass Mg < 1010.5 M⊙, which show a greater degree of alignment to the filament (24% in the filament 37° double cone instead of 20% for random). This investigation reveals that the coplanar trend is not a mere consequence of the filamentary trend as they both exhibit complementary transitional patterns with respect to the mass of the central galaxy for centrals of similar spin orientation. This suggests that dissipation in the halo and torques from the central galaxy also strongly impact the orientation of satellites around the most massive centrals, independently from the filamentary infall.
Focusing on the second sample of central galaxies whose minor axis is more perpendicular to the filament axis, coplanarity and filamentary trends co-exist in all stellar mass bins (excess in cos θ1 = 0 for the solid line, and in cos α = 1 for the dashed line). Both trends are strengthened for the most massive central galaxies (Mg > 1010.5 M⊙), which confirms the distinct role played by galactic plane and filament in orienting satellites. The strength of the alignment for this sample are significantly higher than that obtained when the trends compete. The corresponding satellite fractions in the highest mass bin (centrals with masses Mg > 1010.5 M⊙) are: 46% located on the galactic plane, – that is outside the 66° double cone revolving around central the minor axis direction – and 32% located within the 37° double cone whose axis is aligned with the filament axis (20% for random).
In a nutshell, these findings suggest that when the minor axis is orthogonal to the filament, regardless of the mass of the central, satellites always preferentially lie on the galactic plane, which coincides with the direction of the filament. However, when the minor axis is parallel to the filament, the coplanar trend can trump the filamentary trend if the mass of the central galaxy is large enough. It implies that, for these massive galaxies, satellites will preferentially lie on the galactic plane irrespective of the direction of the filament, which in turn suggests that gravitational torques that act on satellite trajectories play a more dominant role in this case.
Quantifying the relative influence of the filament and the joint effect of dissipation angular momentum in the halo and central galaxy torques (which also influence the inner halo shape) is best achieved noticing that these processes operate on different radial scales (Danovich et al. 2015). Far enough from the central galaxy, the filamentary trend should be recovered for all host systems, and we therefore expect a transition from filamentary to coplanar trend as satellites are plunging into haloes hosting misaligned centrals.
Analysis of the scale segregation inherent to this competition between coplanarity and filamentary trends can be found in Fig. 6. This figure shows the excess PDF of μ1 and ν for different satellite-to-central galaxy separations restricted to the first sample, for which trends are mutually exclusive, as seen in the top panels of Fig. 5. The transition between the filamentary trend far from the central galaxy and the coplanar trend in its vicinity is striking, with a 50% excess of satellites within the 37° double cone around the filament axis (30% of satellites instead of 20% for random) at Rgs > 2 Rvir – and no detectable coplanarity with the central at that distance – that progressively decreases and turns to a 20% excess outside of the corresponding 66° bicone for Rgs < 0.25 Rvir, associated to a ξ = 70% excess at μ1 = 0. In other words, 59% of satellites are located outside the 66° bicone revolving around the central minor axis (40% for random).
The investigation of satellite alignment with distance to the central galaxy carried out in this subsection shows that the coplanar trend is not a mere consequence of the filamentary trend as satellites transition from one trend to the other, with coplanarity dominant inthe vicinity of the central galaxy and filamentary more prominent in the outskirts of the halo. Hence, the dynamical bias introduced by the filamentary trend can reach an amplitude comparable to that of the coplanar trend for satellites within Rvir < R < 2 Rvir from their central galaxy, an effect also seen when the same analysis is performed on the full sample of centrals, regardless of orientation (see Appendix B).
An illustration of the satellite alignment evolution as a function of distance to the central is shown in Fig. 7. The transition between the coplanar and filamentary trends may represent a real source of angular bias in the distribution of satellites. In other words, inferring the anisotropy of the DM halo from the distribution of satellite galaxies assuming this distribution is unbiased may lead to significant errors. Effects of such errors will then strongly depend on the orientation of the central galaxy: whether its minor axis is aligned or not with the closest filament.
As a consequence, the transition between coplanar and filamentary trends for centrals with misaligned spin significantly impacts the statistics of the orientation of satellites around all centrals, as can be seen in Fig. B.1, which displays the excess PDF of μ1 and ν for different satellite-to-central galaxy separations for the full sample irrespectively of the orientation of the central spin. Further analysis of this transition for different central stellar mass bins can be found in Appendix B which highlights specific features that confirm the overall transition between filamentary infall and realignment of satellites through torquing deeper into the halo.
We note that these results suggest that the contradictory findings from observations since Holmberg (1969)’s are mass and scale dependent, as Zaritsky et al. (1997) suggested.
 |
Fig. 4 Sketch of the main angles used in our analysis. Left Panel: definition of α, θ1 and αg, used to describe the relative orientation of the satellite and the filament, the satellite and the central galaxy, and the central galaxy and the filament respectively. Middle panel and right panel: illustration of the solid angle sectors used to define the “aligned central minor axis” sample (within the 37° cone) and “perpendicular central minor axis” sample (outside the 66° cone) respectively. We note that similar angular sectors can be defined for α and θ1 to describe the orientation of satellites. |
3.2.2 Interpretation
The main results of this section suggest a dynamical scenario in which satellites flow along filaments and plunge into the halo where their orbits/spins are progressively deflected from alignment with the filament by gravitational torquing from the central galaxy, so as to preferentially lie in the central galactic plane. In effect, their fate is reminiscent of that of the cold gas at higher redshift (z > 1), which slithers as cold streams down to the core of central galaxies in formation (Pichon et al. 2011; Codis et al. 2012; Tillson et al. 2015; Danovich et al. 2015). High-redshift gas inflow in the frame of the galaxy is qualitatively double helix-like along its spin axis (Pichon et al. 2011). Generated via the same winding/folding process as the protogalaxy, it represents the dominant source of filamentary infall at redshift z ≃ 2 − 3 which feeds the galaxy with gas with well aligned angular momentum (Pichon et al. 2011; Stewart et al. 2013; Danovich et al. 2015).
Here, we argue that the distribution of satellites at z < 0.8 traces that of the cold gas at z > 1, directly correlated with the fact that satellites have progressively formed within these gas streams. This is not completely obvious a priori, as the gas, unlike the satellites, can shock in the circumgalactic medium. In this picture, satellites initially aligned with the filaments in the vicinity of the halo end up corotating in the central galactic plane, in agreement with Danovich et al. (2015) who argue that central gravitational torques dominate even for the cold gas. To test this scenario, we investigate possible kinematic signatures of such a trend in the next section.
 |
Fig. 5 Evolution of the filamentary trend (dashed line) and the coplanar trend (solid line) for either the central galaxy’s minor axis aligned to the filament axis within a 37° cone (toppanels), or the central galaxy’s minor axis perpendicular to the filament axis within a 37° cone (bottom panels). From left to right panel, three different central galaxy stellar mass bins Mg are shown asindicated in each panel. Results are stacked for 0.3 < z < 0.8. In the top panels, the two trends are mutually exclusive. This reveals a transitional pattern: coplanar trend takes over for massive centrals while the filamentary trend is dominant for low mass centrals, consistently with the limited influence of the central torques in this case. In the bottom panels, the two trends reinforce each other. Expectedly, the trends are strengthened for the most massive centrals. |
 |
Fig. 6 Same as Fig. 2 but binning the sample in distance, Rgs, from satellite to central, and restricting it to satellites hosted by halos whose central galaxy’s minor axis is aligned to the nearest filament within a 37° double cone, for which the coplanar and filamentary trends compete. Results are stacked for 0.3 < z < 0.8 for different radius Rgs bins. Satellites close to their central tend to be distributed on the galactic plane, hence orthogonally to the filament, while satellites in the outskirts of the halo are strongly aligned with the filament and the coplanarity with the central is lost. |
 |
Fig. 7 Sketch of the evolution of the alignment trends with distance to the centre of the halo. In the outskirts of the halo, satellite galaxies are strongly aligned with the nearest filament. Probing deeper into the halo this trend weakens as the alignment of satellites with the galactic plane strengthens. |
4 Kinematics of satellites
Let us now quantify the tendency for satellites to corotate with their central galaxy, that is their tendency to align their orbital momentum (direction and polarity) with the intrinsic angular momentum of this central galaxy and synchronize their circular velocity with its velocity.
4.1 Corotation with the central galaxy
To test the importance of the intrinsic torques of the central galaxy on its orbiting satellites, we first study their rotation around the central galaxy. Figure 8 shows twice the PDF, 1 + 2ξ, of cos ϕ, the cosine of the angle between the spin of the central galaxy and the total orbital momentum of its satellites calculated in its rest-frame, for 0.3 < z < 0.8. We note that in this case the PDF is 0.5 + ξ, not 1 + ξ, due to renormalization on the interval [−1, 1] rather than [0, 1]. Indeed, we plot here the cosine of the angle, not its absolute value, as we are interested in the orientation and not only the alignment between both spins. We therefore choose to plot 1 + 2ξ to allow for straightforward comparison with other signals. We study rotation evolution with mass in the left panel, but also rotation evolution as a function of distance to the central, Rgs, in the middle panel.
Evolution as a function of mass and radius confirms the tendency of satellites to rotate on the galactic plane of their central with a circular velocity of the same sign as the central galaxy. This trend is observed for satellites of massive centrals (Mg > 1010M⊙) and within 2 Rvir, and is all the more pronounced as the mass of the central increases and the distance Rgs decreases. More massive central galaxies, and therefore host haloes, influence the orbital angular momentum of satellites more strongly: the excess probability at cos ϕ = 1 is 3 times higher for centrals with Mg > 1010.5M⊙ than for centrals with Mg < 1010M⊙.
Focusing on evolution as a function of distance to the central galaxy, we observe that 21.5% of satellites within a Rgs < 0.5 Rvir sphere around their central display an orbital angular momentum that remains within a 40° double conearound its spin and rotate in the same direction (to be contrasted to 12.5% for a random distribution). In contrast, counter-rotation is more unlikely in the vicinity of the central galaxy, with only 8% of the sample counter-rotating within a double cone of 40° (12.5% for random). The relative orientation of the satellite’s orbital angular momentum and the spin of the central galaxy is close to a random distribution outside the halo of the central galaxy, where satellites motions are governed by the filamentary flow.
These results are consistent with a transfer of satellite orbital angular momentum to the intrinsic angular momentum of their host halo and central galaxy, through dynamical friction and gravitational torques. This exchange of angular momentum drives the evolution of the orbital angular momentum satellites, which end up corotating on the galactic plane, as they are dragged deeper into the halo. This dynamical effect is what drives the coplanar trend in the central regions of the halo. As such, it is a kinematic signature of the distinction between the coplanar trend at small distance and the filamentary trend at large distance.
To confirm this dynamical picture, we study the evolution of three quantities derived from definitions given in Sect. 2.4:
-
The velocity contrast
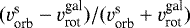 with
with 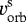 and
and 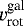 corresponding to the angular orbital velocities of the system of satellites and to the rotational velocity of the central galaxy respectively. This quantity measures the tendency of satellites to synchronize their orbital velocity with the stellar material of the central galaxy.
corresponding to the angular orbital velocities of the system of satellites and to the rotational velocity of the central galaxy respectively. This quantity measures the tendency of satellites to synchronize their orbital velocity with the stellar material of the central galaxy. -
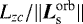 , with Lzc, the component of the orbital angular momentum of satellites aligned with the spin of the central galaxy and
, with Lzc, the component of the orbital angular momentum of satellites aligned with the spin of the central galaxy and
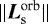 , the norm of the total orbital angular momentum. This quantity measures the tendency of systems of satellites to align their mean rotation plane with the central galactic plane.
, the norm of the total orbital angular momentum. This quantity measures the tendency of systems of satellites to align their mean rotation plane with the central galactic plane. -
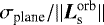 , with σplane
the dispersion component. This quantity measures the dispersion of satellites’ orbits around the mean orbit of the system for a given central, and, therefore, quantifies the tendency of satellites to be located in a thin rotation plane.
, with σplane
the dispersion component. This quantity measures the dispersion of satellites’ orbits around the mean orbit of the system for a given central, and, therefore, quantifies the tendency of satellites to be located in a thin rotation plane.
The right panel of Fig. 8 shows the PDF of 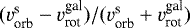 for different distance bins (with same colour-coding as in the middle panel). The vertical dashed line separates the left side of the panel where the satellite orbital velocity is lower than the central rotation velocity, and the right side where satellites orbit faster. In the outer region of the halo, Rgs > 0.5 Rvir, the average orbital velocity of satellites around their central galaxy is found to be lower than the rotation velocity of the central galaxy but
for different distance bins (with same colour-coding as in the middle panel). The vertical dashed line separates the left side of the panel where the satellite orbital velocity is lower than the central rotation velocity, and the right side where satellites orbit faster. In the outer region of the halo, Rgs > 0.5 Rvir, the average orbital velocity of satellites around their central galaxy is found to be lower than the rotation velocity of the central galaxy but 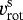 increases in the inner part of the halo. Therefore, satellites increase their orbital velocity, synchronize with their central galaxy as they reach the inner part of the halo and achieve corotation.
increases in the inner part of the halo. Therefore, satellites increase their orbital velocity, synchronize with their central galaxy as they reach the inner part of the halo and achieve corotation.
Two effects are competing: conservation of angular momentum tends to increase the amount of orbital velocity as satellites goes deeper in the halo, but the dynamical friction forces the orbital motions of satellites to synchronize with the rest of the matter in the halo, and this effect is stronger in the densest regions of the halo.
As expected from dissipation of angular momentum via dynamical friction in the halo, the strength of the average specific orbital angular momentum of systems of satellites 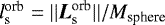 , with Msphere, the total mass of satellites enclosed within a sphere of radius Rmax from the central galaxy, (represented in the left panel in Fig. 9) decreases for satellites closer to the central galaxy (by a factor three between satellites within Rgs < 5 Rvir and those within Rgs < 0.5 Rvir). Comparing between the ratios of
, with Msphere, the total mass of satellites enclosed within a sphere of radius Rmax from the central galaxy, (represented in the left panel in Fig. 9) decreases for satellites closer to the central galaxy (by a factor three between satellites within Rgs < 5 Rvir and those within Rgs < 0.5 Rvir). Comparing between the ratios of 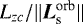 (in the middle panel of Fig. 9) and of
(in the middle panel of Fig. 9) and of 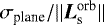 (in the right panel of Fig. 9), we see that the relative importance of the aligned angular momentum component increases for satellites closer to the central galaxy (from 60% to 70%), while the relative amplitude of the dispersion between satellite orbits drops from 120% to 20% between 2 Rvir and 0.25 Rvir. This behaviour once again indicates that orbits of satellites progressively become coplanar due to torques. On average, satellites lose orbital angular momentum as they are dragged deeper into the halo (decrease in
(in the right panel of Fig. 9), we see that the relative importance of the aligned angular momentum component increases for satellites closer to the central galaxy (from 60% to 70%), while the relative amplitude of the dispersion between satellite orbits drops from 120% to 20% between 2 Rvir and 0.25 Rvir. This behaviour once again indicates that orbits of satellites progressively become coplanar due to torques. On average, satellites lose orbital angular momentum as they are dragged deeper into the halo (decrease in  ) but this trend is different along the different components of the orbital angular moment: the component aligned with the spin of the central galaxy is better preserved (even slightly increased) as satellites reach the inner parts of the halo than the unaligned components. As a result, the dispersion in the distribution of satellites orbital planes as they approach the central galaxy shrinks.
) but this trend is different along the different components of the orbital angular moment: the component aligned with the spin of the central galaxy is better preserved (even slightly increased) as satellites reach the inner parts of the halo than the unaligned components. As a result, the dispersion in the distribution of satellites orbital planes as they approach the central galaxy shrinks.
 |
Fig. 8 Twice the PDF of cos ϕ, the cosine of the angle between the spin of the central galaxy and the total orbital momentum of its satellites for 0.3 < z < 0.8 for different mass (left panel) and radius Rgs bins (middle panel). For massive central galaxies, the orbital angular momentum of satellites tends to align with the galactic spin of the central, especially in its vicinity. Right panel: excess PDF of |
4.2 Satellite spin swings into the halo
As can be seen in Fig. 10, we also find that satellites not only align their orbital plane with the plane of the central galaxy, but also align their spin (intrinsic angular momentum) with that of the central galaxy as they reach the inner parts of the halo (see also Aubert et al. 2004). In fact, cuts in mass and distance to the central galaxy lead to similar results as for cos ϕ, when applied to cos χ, the cosine of the angle between the central galaxy spin and the satellite spin, though the signal is weaker and rapidly decreasing with distance to the central. Nonetheless, within a 0.5 Rvir sphere around the central, satellites have a ξ = 9% excess probability to stay within a 37° double cone around the spin of their central (22% of the satellites). This effect is weaker than the previous trends but this excess was also found to reach 18% for satellites within 0.25 Rvir, and even 20% for the most massive central galaxies with Mg > 1011 M⊙). We note that this particular measurement is at least partially sensitive to grid-locking (that is tendency of spins to align with the grid on which the gas fluxes are computed). Such effects are discussed in a companion paper, Chisari et al. (2015), which analyses the impact of grid-locking on intrinsic alignment measurements in more detail.
Such satellite swings are confirmed by the measurement of the PDF of cos χs, the cosine of the angle between the spin of the satellite and its position vector relative to the central galaxy for different separation bins (see Fig. 11). We find that outer satellites have a spin preferentially aligned with their position vector. This is consistent with low-mass infalling galaxies having their spin aligned with the filament they are flowing from (Dubois et al. 2014). Conversely inner satellites have a spin more likely to be perpendicular to their position vector, hence a rotation plane aligned with it. We note that this result holds for the full sample of central galaxies with Mg > 1010 M⊙, irrespective of the fact that it is dominated by centrals with a galactic plane well aligned or moderately misaligned with the nearest filament. Satellites progressively swing their rotation plane to align with that of the central as they reach the inner parts of the halo.
These results statistically confirm the importance of torquing from the massive central as a driving mechanism for satellite alignment. Such torques are in agreement with theoretical predictions derived from linear response theory by Colpi (1998). This author interpreted the orbital decay as triggered not by the surrounding halo, but by the central galaxy (stellar material) itself on its external satellites, via near resonance energy and angular momentum transfers. This mechanism noticeably leads to a circularization of orbits, and an alignment between the major axis of the satellite with rgs, a result also found for dark haloes in N-body simulations by Aubert et al. (2004) and Faltenbacher et al. (2008). We show below in Sect. 5.3 that the evolution of the age of satellites as traced by colours also lends support to this interpretation of our results.
Several observational works have looked for signs of satellite alignment from their shapes. Schneider et al. (2013) find a weak signal of radial alignment of satellites in observations from the “Galaxy And Mass Assembly” survey. This 3σ detection is obtained when projected galaxy shapes are modeled using Sérsic profiles. The significance decreases to 2σ when up-weighting the inner parts of galaxies (as for weak lensing shape measurements). Sifón et al. (2015) and Chisari et al. (2014) recently looked at projected ellipticity alignments around stacked clusters at low redshift (0.05 < z < 0.5) and did not find any significant alignment. This may suggest that satellite alignments in most massive clusters are mostly damped by nonlinear evolution or projection effects, at least in the local Universe. In contrast Singh et al. (2015) found a significant one-halo component to the alignment signal of luminous red galaxies in the SDSS survey. The discrepancy between these works could be caused by a luminosity dependence of the alignment signal, along with the use of different radial weights for recovering galaxy ellipticities. In comparison, our shape estimation is un-weighted, and thus it is presumably more sensitive to tidal features in the outskirts of galaxies. Also, we have relied up to now on three-dimensional galaxy shapes, while projection is known to damp the alignment signal, as we will see in the next section.
 |
Fig. 9 Left panel: average strength of the total specific orbital angular momentum |
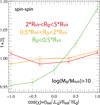 |
Fig. 10 Twice the PDF of cos χ, the cosine of the angle between the spin of the central galaxy and the spin of the satellite for 0.3 < z < 0.8 for different bins of distance to the central galaxy. Satellites align their intrinsic angular momentum to that of the central galaxies in the inner part of the halo. |
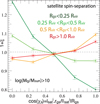 |
Fig. 11 PDF of cos χs, the cosine ofthe angle between the spin of the satellite and its position vector relative to the central galaxy as a function of distance to the central (radius bins are indicated on the figure). |
 |
Fig. 12 Distribution of rest frame colours in Horizon-AGN. Coloured areas indicate the colour bins used throughout the analysis in this section of the paper. |
5 Comparison with existing observations
In this section, we provide further insight into how the alignment signal can be traced in observations and how our trends compare to what is found in existing surveys.
5.1 Colours in Horizon-AGN
In most observational studies, the mass of galaxies and satellites is traced by their rest-frame colours. It is therefore of interest to recover the previously described variation of the satellite alignment trends with the mass of the central galaxy, using central galaxy rest-frame colours.
To trace in the observations the dynamical scenario previously described, we need to make a distinction between young outer satellites and old(er), quenched, inner satellites. To estimate the age of satellites we rely on their rest-frame colours computed from AB magnitudes in SDSS filters. Figure 12 shows this distribution for three rest-frame colours, g − r, r − i and u − r in Horizon-AGN for all galaxies with Mg > 109 M⊙ at different redshifts. We note that these colours do not take into account dust extinction. Although the blue cloud-red sequence bimodality is not as clear in the simulation as it is in observed colour-mass diagrams, the simulated galaxy population reveals a noticeable increase in the fraction of red galaxies as redshift decreases (more galaxies are passively evolving). The cuts used in the remainder of the paper to split the galaxy population into “blue” (star-forming), “intermediate” (green valley) and “red” (quenched) galaxies are represented in Fig. 12 (left panel) and correspond to g − r < 0.4, 0.4 < g − r < 0.55 and g − r > 0.55. They are defined in this way as a compromise between isolating the two peaks present in the colour distribution and selecting large enough galaxy samples. We use the same colour cuts to split central and satellite galaxies.
5.2 Alignment trends with colour selection
5.2.1 Results in three-dimensions
Figure 13 shows two plots very similar to the mass-dependent plots presented in the previous sections (e.g. Fig. 2), albeit where stellar mass bins are replaced by g − r colour bins for the central galaxy. As red central galaxies are older and more massive their blue counterparts, we expect to observe an increase in the coplanar trend as g − r increases. This is indeed the case, as can be seen in the first panel of the figure, which displays the PDF of μ1 = cos θ1 for three different central galaxy colour bins, and for all satellites within a sphere of radius 5 Rgs centred on these centrals. Red centrals with g − r > 0.55 tend to have their satellites aligned in their galactic plane, with 54% of satellites outside the 66° bi-cone revolving around the central minor axis, an amount which falls down to 46% for blue centrals with g − r < 0.4 (by comparison the value expected for a uniform distribution is 40%). The filamentary trend is also observed in the right panel, with an excess of probability similar to that when the trend is broken down in mass instead of colour. The fact that blue centrals are more likely to be young galaxies with a spin parallel to the filament explains why blue centrals are subject to a slight decrease in the filamentary trend compared to their red counterparts: they are more likely to be found in a situation where both trends compete.
As a conclusion, colour selection proves as efficient as mass selection to identify and quantify both trends, which is consistent with a steady evolution of the average mass in each colour bin for all galaxies with Mg > 1010 M⊙: red galaxies have an average mass of 8.8 × 1010 M⊙, while it falls down to 4.2 × 1010 M⊙ for the intermediate bin and 2.9 × 1010 M⊙ for the blue galaxies.
Additionally, the PDF of μ = cos θ, (central spin-separation angle) can be found in Appendix C. While using the spin rather than the minor axis does not change our results qualitatively, the amplitude of the spin signal is significantly lower. The discrepancy between those two signals is highly dependent on the shape of the central galaxy, which can induce significant misalignments between the minor axis and the spin, as suggested in the next section.
Finally, in Fig. 14 we perform a detailed analysis of the alignments of galaxies as a function of the colours of both satellites and centrals so as reproduce the similar analysis by Yang et al. (2006) in observations and by Dong et al. (2014) for simulations. We find that:
-
The coplanar trend is stronger for red centrals, especially when they have bluer satellites (although this distinction is quite minor). We attribute this to more efficient torques exerted by massive central galaxies, as the mass ratio
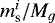 is smaller on average for blue satellites. It is important to remember that trends are more likely to reinforce in this case, as red centrals are often dominated by mergers in their stellar mass budget as opposed to in situ star formation (Oser et al. 2010; Dubois et al. 2013), and hence have a higher chance of maintaining a spin orthogonal to their filament. Therefore, the distance to the filament is not crucial in this case, as satellites fall directly from the filament into the galactic plane.
is smaller on average for blue satellites. It is important to remember that trends are more likely to reinforce in this case, as red centrals are often dominated by mergers in their stellar mass budget as opposed to in situ star formation (Oser et al. 2010; Dubois et al. 2013), and hence have a higher chance of maintaining a spin orthogonal to their filament. Therefore, the distance to the filament is not crucial in this case, as satellites fall directly from the filament into the galactic plane. -
Blue centrals, younger and less massive, are more likely to have a spin parallel to their filament – which induces a competition between the filamentary and the coplanar trends – and less likely to efficiently torque satellites to line them up in their rotation plane. Expectedly, the coplanar signal is weaker than that for their red counterparts. Consequently, the signal is then slightly stronger for red satellites of blue centrals which are more evolved and closer on average to their central than blue satellites.
Those results are consistent with those of Yang et al. (2006) who report a significant alignment of satellites along the major axis of their projected central. Although these authors found a red-red signal higher than the red-blue one, their study focused on Rgs < Rvir which potentially left aside an important number of blue satellites in alignment with the filament (recall that we use all satellites up to 5 Rvir separation). However, their general colour and mass trends for the central galaxy are in good agreement with our results, as detailed in the next section.
 |
Fig. 13 Left panel: PDF of μ1 = cos θ1, the angle between the minor axis of the central galaxy and the vector separating it from its satellites, at 0.3 < z < 0.8 and for different colour bins. Right panel: PDF of ν = cos α, the angle between the satellite separation vector and the direction of the nearest filament. The average central galaxy mass in each colour bin is also indicated. For massive red central galaxies, the satellites tend to be distributed on the galactic plane. The filamentary trend is also recovered although degraded by projection for the bluest central colour range. |
5.2.2 Alignments in projection
Figure 15 shows alignments projected along the x-axis of the grid. The left panel shows the PDF of θx the angle between the major axis of the projected central galaxy and the projected rgs, at 0.3 < z < 0.8 for different colour bins. The right panel displays the PDF of αx, the angle between the projected direction of the filament and the projected rgs. Results are in good agreement with the observed signal found in the SDSS by Yang et al. (2006; overplotted as blue dots and red squares in Fig. 15), although alignment trends seem to be slightly stronger in our case, when accounting for the fact that our mass range is biased towards smaller masses. Average values for θx in each colour bin are given in the left panel and confirm the steady evolution of the trend with g − r. This increase is sharper than that found in Yang et al. (2006), however we believe the results remain consistent given that we do not model dust extinction, which likely impacts our estimation of galaxy colours.
Extinction notwithstanding, it is interesting to notice that the projected estimation follows very closely the 3D results, although it leads to a systematic slight underestimate of the alignment trends.
Repeating the measurement of Fig. 14 in projection along the x-axis of the grid, we also recover similar alignments that result in a mean angle variation detailed in Table 2. This mean angle is presented for satellites within two different maximum separation from their central galaxy: Rvir and 5 Rvir, and systematically compared to values found in Yang et al. (2006). Colour variations are qualitatively preserved and suggest that the transition between the coplanar and filamentary trend with separation can be recovered in projection, although the effects are weak and an analysis of the central spin’s orientation might be necessary.
Mean values (in degrees) for θx in different colour bins for both satellites and central galaxies, and within two different radius from their central galaxy.
 |
Fig. 14 Same as Fig. 13 but splitting both the central galaxies and the satellites in different colour bins. Blue galaxies are identified as objects with g − r < 0.4 and red galaxies as objects with g − r > 0.55. The mass cut is a compromise between statistics and comparability to existing observations. |
 |
Fig. 15 PDF of θx and αx, the angles between the x-projected major axis of, respectively, the central galaxy (left panel), and direction of the filament (right panel) and the x-projected rgs, at 0.3 < z < 0.8 for differentcolour bins. For massive red central galaxies, the satellites tend to be distributed on the galactic plane. The projected signal is qualitatively comparable to results in 3D. Observational results from Yang et al. (2006) are overplotted for red centrals (red squares) and blue centrals (blue dots). The agreement is good. |
5.3 Evolution of satellites within the halo
Let us now focus on the satellite dynamical transition from a filamentary to a coplanar distribution as they plunge into their host halo.
Figure 16 shows the PDF of cos ϕ, the angle between the spin of the central galaxy and the total orbital angular momentum of its satellites for 0.3 < z < 0.8 and for different satellite g − r colour bins. We see that red satellites, on average, have an orbital plane better aligned with the central galactic plane than blue satellites (24% of the sample within the 37° double cone around the spin of the central for g − r > 0.55, and 21.5% for g − r < 0.4). Moreover, Fig. 17 presents the average distance of satellites to the central as a function of their colour for satellites within 5 Rvir: red galaxies are closer to the central (≃1.3 Rvir) than blue galaxies (≃0.9 Rvir). Therefore, red satellites are more clustered around the central galaxies than blue satellites, as an effect of ram-pressure stripping and strangulation which gradually remove gas from satellites and prevent further accretion onto them as they evolve in the hot pressurised atmosphere of the host halo.
Hence, using colours, we also recover the trend that satellite orbits achieve better coplanarity with the central galaxy as they get closer to it and get more and more deprived of star forming gas. To confirm the satellite rotation plane swings, we plot in Fig. 18 the PDF of cos χs, the cosine of the angle between the spin of the satellite and its position vector for different colour bins. We find that blue (outer) satellites have a spin preferentially aligned with their position vector, in accordance with their spins being aligned with the filament they are flowing from, while red (inner) satellites have a spin more likely to be perpendicular to their position vector, hence a rotation plane aligned with it.
In Fig. 19, we consider the orientation of the minor axis rather than that of the spin of the satellite for different distance and colour bins. This static geometrical parameter is more sensitive to limited resolution (recall that the minimum number of stellar particles is lower for satellites than for centrals), stripping and friction than the orientation of the satellite spin and we do not detect a flip as clear as the one found for the spin, but the evolution is globally similar and the tendency to display a minor axis orthogonal to the galactic plane for redder satellites in the inner parts of the halo is strengthened. It confirms the dynamical mechanism that bends the rotation plane of satellites to align it with their orbital plane. As this latter progressively aligns itself with the central galactic plane, the rotation plane of satellites also ends up aligned.
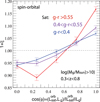 |
Fig. 16 PDF of |cos ϕ|, the cosine of the angle between the spin of the central galaxy and the total orbital momentum of its satellites (measured in the rest frame of their central) for 0.3 < z < 0.8 and for different g − r satellite colour bins. For red quenched satellites, the orbital momentum tends to be aligned with the central galactic spin. The effect is much weaker for blue star forming satellites, consistent with their preferential orientation along the filament. |
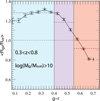 |
Fig. 17 Evolution of the mean (rescaled) central-satellite separation as a function of the satellite g − r colour (for all satellites within Rgs < 5 Rvir). Our colour bins are overplotted as coloured areas and the average separation in each bin is indicated by a dashed line. |
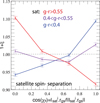 |
Fig. 18 PDF of cos χs, the cosine of the angle between satellite spin and position vector for different satellites in g − r colour bins. Blue (outer) satellites have a spin preferentially aligned with their position vector, while red (inner) satellites have a rotation plane aligned with it. |
5.4 Shape effects
A full understanding of the amplitude of the alignment signal requires to take into account its dependence on the shape of the central galaxy, as trends display different features for oblate (“disky”) and prolate (“spheroidal”) structures. Figure 20 shows the evolution of the PDF of μ1 = cos θ1 (minor axis/separation angle) for oblate and prolate central galaxies in the intermediate mass range for which the deviation between both samples is maximal. The satellite orthogonality to the minor axis is more pronounced for prolate structures. However, one should not deduce that it corresponds to a better alignment on the galactic plane, as such a plane for prolate structures is poorly defined. For prolate galaxies, the rotation plane is more likely to be orthogonal to the major axis, hence not coinciding with the plane of maximal elongation. Prolate structures show a significant amount of misalignment between their spin and minor axis, with more than 30% displaying a spin aligned with the major axis.
The evolution of the PDF of μ1 = cos θ1 and ν = cos α for satellitesof central galaxies with a spin aligned to the filament (not represented here) confirmed that the alignment of satellites along the minor axis of their central galaxy and along the filament cannot be straightforwardly deduced from the orientation of the spin for such prolate structures. In this case, only the filamentary trend is clearly detected, while other alignments are strongly dependent on the proxy used to define the galactic plane (shape or rotation plane) and how it correlates to the filament direction.
Finally, focusing on the correlations with the central shape, Fig. 21 shows the PDF of μ3 = cos θ3 the cosine of the angle between rgs and the major axis of the central galaxy for oblate (dashed line) and prolate (solid line) centrals. While oblate centrals display a certain degree of satellite alignment along their major axis, prolate centrals have their satellites more strongly aligned with their major axis. This is consistent with a distribution of satellites tracing the underlying triaxiality of their host halo but is also consistent with the fact that the major axis is more often aligned with the spin in the prolate case, since prolate galaxies are very likely to be dispersion-dominated systems (a.k.a. ellipticals).
 |
Fig. 19 PDF of cos χ1, the cosine of the angle between the minor axis of the satellite and its position vector for 0.3 < z < 0.8 for different radius (left panel), satellite colour (middle panel) and mixed (right panel). Satellites align their minor axis with that of the central galaxy as they reach the inner regions of the halo. |
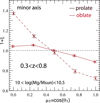 |
Fig. 20 PDF of μ1 = cos θ1 similar to that in Fig. 2 for oblate (solid line) and prolate (dashed line) central galaxies, restricted to the intermediate mass range. Tendency to lie orthogonal to the minor axis is stronger for prolate structures, as in this case the minor axis is most often orthogonal to the filament direction and the galactic plane is poorly defined. |
 |
Fig. 21 PDF of μ3 = cos θ3 the cosine of the angle between rgs and the major axis of the central galaxy for oblate (dashed line) and prolate (solid line) centrals. Prolate centrals have their satellites aligned along their major axis, which is consistent with the fact that this axis is more often aligned with the spin in this case. Oblate centrals display a certain degree of satellite alignment too, which is consistent with the distribution of satellites tracing the underlying triaxiality of their host halo. |
6 Discussion
In this paper, we have compared the alignment trends identified in Horizon-AGN with observational constraints obtained mainly from the SDSS. We have found good agreement with the work of Yang et al. (2006), who confirmed the tendency of satellite galaxies to align on the galactic plane of their central galaxy and found this trend to be mass and colour dependent (for both centralgalaxies and satellites), and Zaritsky et al. (1997) who found it to be also separation (distance) dependent. Our results also confirm the satellite galaxies’ tendency to align with their host’s closest filament. This trend is found to be independent of the orientation of the central galactic plane at large separations, as established in recent observations by Tempel et al. (2015) (see also Paz et al. 2011). Closer kinematic analysis reveals a transition for satellites from filamentary infall at large separations to orbit alignment in the central galactic plane in the vicinity of their central, when such a plane is misaligned with the closest filament. This dynamical behaviour is very similar to that of the cold gas in high-redshift zoom simulations (Tillson et al. 2015; Danovich et al. 2015) and suggests a tight connection between the dynamics of cold gas accretion in the early Universe and the alignment trends of satellites in clusters in the Local Universe.
The development of models to quantify such trends is crucial for upcoming imaging surveys to achieve their goals of constraining the equation of state of dark energy and modifications to General Relativity, such as Euclid2 (Laureijs et al. 2011), the Large Synoptic Survey Telescope3 (Ivezic et al. 2008) and WFIRST4 (Spergel et al. 2013). Hydrodynamical cosmological simulations are a promising tool to quantify intrinsic alignments in the nonlinear regime and provide estimates of contamination to future surveys (Tenneti et al. 2014, 2015; Chisari et al. 2015; Velliscig et al. 2015a,b). The results of simulations can be used to inform the parameters of an intrinsic alignment “halo model” (Schneider & Bridle 2010), or nonlinear models that rely on perturbation theory power spectra (Blazek et al. 2015).
However, our work shows that alignments of galaxies on small scales are the result of a complex dynamical interplay between the central galaxy, the satellites and the surrounding filamentary structure. In short, alignment trends depend on the evolutionary stage of a galaxy (as probed by e.g. its colour) as well as on the orientation of the central with respect to the nearest filament. We have also shown that alignments can transition between two regimes as satellites move from the surrounding filament into the gravitational zone of influence of the central galaxy. The filamentary trend implies a tangential alignment of discs around centrals, resulting in a tangential shear signal that adds to the galaxy-lensing in projection. The coplanar trend represents a net radial orientation of satellites and their central, suggesting that galaxy-lensing could be suppressed on the small scales in projection. Both trends would contribute to a cosmic shear measurement through correlation of intrinsic shapes and weak lensing (the “GI” term Hirata et al. 2004).
A companion paper, Chisari et al. (2015), studies projected correlations of intrinsic shapes in the language of lensing measurements, including the case of a two-halo term (the correlation between centrals). These authors studied alignments on scales > 100 h−1 kpc, finding an overall tendency for discs to align their rotation planes tangentially around spheroidals, which we now re-interpret as consequence of the filamentary trend. They also found a tendency for spheroidals to be elongated towards other spheroidals, which can be a consequence of this type of galaxies being elongated following the direction of the filament, which connects them to other spheroidals. In comparison, Chen et al. (2015) also found evidence for alignment of the major axis of massive galaxies in the direction of the nearest filament (also, nearest group) in the MassiveBlackII smoothed-particle-hydrodynamics cosmological simulation. However, no evidence has been found for tangential alignment of discs in that simulation nor in the moving-mesh Illustris simulation (Tenneti et al. 2016); a discrepancy that will require further investigation. Finally, Chisari et al. (2015) suggested that the spin and the shape of a spheroidal are poorly correlated, a conclusion that we validated for prolate galaxies in Sect. 5.4.
 |
Fig. 22 Summary of the orientation trends that drive the fate of satellites in their host halo. Alignment trends are distance dependent: filamentary trend dominates in the outskirt of the halo (for bluer satellites on average), while coplanar trend takes over inthe vicinity of the central (redder satellites on average). These trends may bias the standard expectation that the satellitesdistribution traces the overall shape of the diffuse dark matter halo (orange ellipses). More probably, specific populations of satellites (selected in mass, colour and separation) trace specific parts of the halo and the embedding cosmic web. |
7 Conclusion and prospects
We investigated the alignment of satellites galaxies in the redshift range 0.3 < z < 0.8. We found alignments on the galactic plane consistent with previous investigations (both observational and numerical), but we also unraveled an interesting dynamical interplay between this known alignment and the tendency of satellites to be aligned with the filament from which they flow into the halo. Noticeably, we find that, although most massive central galaxies display some coplanarity among their satellites, this effect is enhanced when the galactic plane lies parallel to the direction of the filament. Conversely, it can be weakened or even canceled when the galactic plane is misaligned with its filament. Satellites are then found to lie preferentially along the filament far from the central galaxy, and on the galactic plane in its vicinity.
The main results of this work are sketched in Fig. 22, where we illustrate the fact that the distribution of satellites in their host halo and around their central galaxy arises from the superposition of at least two different effects, represented in addition to the common expectation that they should trace the tri-axiality of the halo:
- i)
the polar flow from the filament, which mostly affects young blue satellites in the outskirt of the halo;
- ii)
the dissipation in the halo and torques from the central galaxy, which bend older inner redder satellite orbits close to coplanarity with the galactic plane.
The analysis of the radial evolution of those processes in Horizon-AGN strongly suggests that:
- 1.
The leading effect in the orientation of satellites is the tendency to align with the nearest filament. While stronger for satellites in the outskirts of the halo, this tendency decreases as the satellites are dragged deeper into the halo – where they exchange angular momentum via gravitational torques from the central galaxy – but not to the point where it becomes negligible, unless a strong misalignment (>45°) exists beforehand between the central galaxy minor axis and the filament direction.
- 2.
A secondary effect that becomes dominant in the inner parts of the halo is the tendency of satellites to align with the central galactic plane. This effect can either compete or strengthen the alignment with the filament, depending on the orientation of the plane. As expected, the signal is stronger for red massive centrals which are already more likely to have a spin orthogonal to the filament, and therefore a galactic plane aligned with the filament. The two effects reinforce in this case. On the contrary, low mass blue centrals with a minor axis aligned with their filament have satellites predominantly aligned with their filament and so orthogonal to the galactic plane.
- 3.
The alignment of satellites in both the filament and the galactic plane is consistently stronger for red central galaxies, as these correspond to massive centrals. The dependence of this coplanar trend on the g − r colour ofsatellites is kinematically consistent with a dynamical scenario in which young (blue) satellites flowing from the filament progressively bend their orbits towards the central galactic plane (under its tidal influence). As they reach the inner parts of the halo and they progressively get deprived of more of their gas and stars through tidal (and ram pressure) stripping, becoming redder in the process. We predict this trend is likely to be observable.
- 4.
Around 40% of massive centrals with Mg > 1010 M⊙ display significant deviations from the spin-filament orthogonality (>30°) and are therefore subject to competing alignment trends between the two processes, with the alignment along the filament predominant for blue satellites in the outskirts of the halo, and coplanarity with the central galaxy taking over for older red satellites in the inner regions of the halo.
- 5.
The tendency for systems of satellites to align on the galactic plane is accompanied with a tendency to align and synchronize their orbital momentum with the angular momentum of the central galaxy. We also find hints that satellites align their intrinsic angular momentum with that of their central as they reach the inner regions of their host halo.
In conclusion, this investigation has shown that the distribution of satellites in host halos is dynamically biased first by the filamentary anisotropic flow from which they originate and second by the gravitational torques of the central galaxy which bend them close to the galactic plane. This evolution closely resembles that of the cold gas, even though the satellite population does not shock in the circumgalactic medium. Given that such flows were identified at high redshift, it is remarkable that it has a stellar counterpart at low redshift in the possibly observable colour variation of the satellite distribution. The anisotropy of the infall and realignment within the virial radius as characterized in this paper could have an impact on building up thick discs, turning discs into ellipticals and producing either fast or slow rotators (Emsellem et al. 2011). A natural question that arise from these trends is whether such a satellite distribution is still in good correspondence with the triaxiality of the host halo, and how it might affect estimations of the halo triaxiality on specific scales. This will be investigated in a follow-up study.
Acknowledgements
This work was granted access to the HPC resources of CINES (Jade and Occigen) under the allocation 2013047012, c2014047012 and c2015047012 made by GENCI. This research is part of the Spin(e) (ANR-13-BS05-0005, http://cosmicorigin.org) and Horizon-UK projects. Let us thank D. Munro for freely distributing his YORICK programming language and opengl interface (available at http://yorick.sourceforge.net/). We warmly thank S. Rouberol for running the Horizon cluster on which the simulation was post-processed. Part of the analysis was also performed using the DiRAC facility jointly funded by BIS and STFC. The research of JD is supported by Adrian Beecroft, The Oxford Martin School and STFC. CP thanks Churchill college for hospitality while this work was finalized.
Appendix A Low-mass centrals
We stated in Sect. 3.1 that the overall anisotropic distribution of satellites around central galaxies is, for a good part, inherited from filamentary infall and from the mass-dependent orientation of central galaxy planes relative to the nearby filament. However, this naively implies that satellites of low-mass centrals (Mg < 1010 M⊙) should preferentially be orthogonal to the central plane, while the distribution of alignments we find for this mass range is closer to random, see Fig. 2. In this Appendix, we detail the reasons for this apparent discrepancy.
In Sect. 3.1, Fig. 2 we opted for a comparison with the direction of the minor axis of the central galaxy to quantify alignment on the galactic plane. This is a well justified method for high-mass galaxies, sufficiently well resolved to neglect errors due to a lack of convergence of the shape estimator with the number of particles, as it gives a stronger and smoother signal: many of them have little rotation relative to their dispersion support, often displaying strong variations between the inner and outer shells of the galaxy as a result of their on-going merging activity. Moreover, most of these massive centrals have satellites of comparatively smaller mass which have little impact on the shape of the central prior to merger.
However, this statistics is more questionable for less resolved low-mass centrals as such systems of centrals with satellites are often pairs (or triplets) of interacting galaxies (85% of the sample, 97% including systems with two satellites). As we define a threshold around 108.5 M⊙ for structure detection and a threshold Mg = 109 M⊙ for centrals, low-mass centrals have by construction fewer satellites. Consequently, these pairs have mass ratios close to one (pre-major merger systems). Therefore, galaxies in such pairs strongly impact each other’s shape through tidal interactions, which results in stronger and faster variations of their central minor axis direction than what is expected for a reference sample of galaxies with Mg < 1010 M⊙ without satellites. Comparatively, the spin direction, which somehow probes better the inner rounder parts of galaxies that do not weight much in the calculation of the inertia tensor, and must also remain consistent with the conservation of the total angular momentum of the pair proves more robust.
While previous studies of the Horizon-AGN simulation from Dubois et al. (2014) and Welker et al. (2014) were performed at 1 < z < 3, we focus on a lower redshift range: 0.3 < z < 0.8. As a result, the tendency of massive galaxies to display a spin/minor axis perpendicular to their nearest filament is expected to increase with cosmic time due to the cumulative effect of mergers. In a similar vein, the parallel orientation trend of young, low mass galaxies is expected to decrease at lower redshift as a result of the disappearance of the cold and vorticity rich gas inflows that feed them. To illustrate these effects, Fig. A.1 displays the PDF of νg = cos αg, with αg the angle between the spin of the central and the direction of the nearest filament, and νg1 = cos αg1, with αg1 the angle between the minor axis of the central and the direction of the nearest filament, for two mass ranges of central galaxies: 109 < Mg < 1010 M⊙ and Mg > 1010 M⊙. The solid lines on the figure lend support to the claim that galactic planes of low-mass centrals are preferentially oriented orthogonally to the nearest filament, but that this alignment is better traced with the spin-filament angle than with the minor axis-filament angle (for which the signal is strongly damped and compatible with a random distribution). Conversely, when tracing the (parallel) orientation of the galactic plane of massive centrals with respect to the filament minor axis yields a stronger signal than spin. However, we emphasize that the signal for low-mass galaxies remains weak using either the spin or the minor axis to compute the plane orientation, with a maximum amplitude ξ = 5% for the excess probability.
 |
Fig. A.1 PDF of νg1 = cos αg1, the cosine ofthe angle between the minor axis of the central galaxy and the direction of the nearest filament (brown lines) and νg = cos αg, the angle between the spin of the central galaxy and the direction of the nearest filament (blue lines). Distributions are plotted for central galaxies in two different mass ranges: 109 < Mg < 1010 M⊙ (solid lines) and Mg > 1010 M⊙ (blue lines). The transition for the galactic plane orientation is recovered, but the signal is stronger using the spin for low-mass centrals. The opposite is true for high mass centrals: the minor axis estimator yields an increased amplitude in the excess probability ξ. |
Figure A.2 shows the PDF of μ1 = cos θ1 and of μ = cos θ for the satellites of three different samples of centrals: Γ1, which includes all the satellites around centrals in the lower mass range: 109 < Mg < 1010 M⊙, Γ2 which focuses on centrals with low mass ratio satellites (Ms∕Mg < 0.4): 5 × 109 < Mg < 1010 M⊙ irrespective of their distance to the central and Ms < 2 × 109 M⊙, and Γ3 which focuses on centrals with low mass ratio, outer satellites only: 5 × 109 < Mg < 1010 M⊙, Ms < 2 × 109 M⊙ and Rgs > Rvir. Focusing on sample Γ1, Fig. A.2 confirms the lack of a clear detection for satellites to be oriented orthogonally to their central galactic plane. Although a weak signal is detected when computing the spin-separation angle, using the minor axis-separation angle yields an opposite signal of similar amplitude, that is a weak tendency for satellites to lie on the galactic plane of such centrals. However, when focusing on Γ2 and Γ3, that is centrals with no massive satellites and centrals with neither massive nor close satellites, the perpendicular orientation of satellites is progressively recovered for both θ (for Γ2 and Γ3 ) and θ1 (for Γ3 ). This result supports the idea that the damping of the low-mass central trend results from their greater sensitivity to interaction with satellites, amplified by their excess probability of having satellites of similar mass.
This effect is perhaps best emphasized when focusing on the PDF of νg1 = cos αg1, the cosine of the angle between the minor axis of the central galaxy and the direction of its nearest filament, for different subsets of centrals depending on whether or not their halo hosts a close satellite. The results of this analysis are presented in Fig. A.3 which displays this PDF for centrals with 109 < Mg < 1010.25 M⊙. This threshold corresponds to the lower limit for the transition mass where galaxy spins switch between preferentially aligned and preferentially perpendicular to the closest filament, as estimated in Dubois et al. (2014). Such a choice of threshold allows us to preserve a decent statistics for each subsample. These centrals are further divided in three subsets: those whose closest satellite is found within 0.5 Rvir, those whose closest satellite is found between 0.5 Rvir and Rvir, and those whose closest satellite is more distant than Rvir. One clearly sees that the presence of a satellite in the vicinity of a low-mass central clearly impacts the orientation of its spin, damping its tendency to align with the nearest filament. This effect is increased for closer satellites.
 |
Fig. A.2 Leftpanel: PDF of μ1 = cos θ1, the angle between the minor axis of the central galaxy and the satellite separation vector rgs. Right panel: PDF of μ = cos θ, the angle between the spin of the central galaxy and the separation vector. Distributions are plotted for three different subsets of low-mass centrals with varying types of satellites (green and blue shades): Γ1: 109 < Mg < 1010 M⊙, Γ2: 5 × 109< Mg < 1010 M⊙ and Ms < 2 × 109 M⊙, Γ3: 5 × 109< Mg < 1010 M⊙, Ms < 2× 109 M⊙ and Rgs > Rvir. Satellites oflow-mass centrals tend to align with their central’s spin/minor axis, consistently with the fact that they tend to align with the nearest filament. However, the signal is limited in amplitude and tends to vanish when traced with the minor axis for centrals with massive satellites and/or with satellites in their close vicinity. In this mass range for the central, the satellite is often of comparable mass and both galaxies equally impact the orientation and shape of one another prior to merger. |
 |
Fig. A.3 PDF of νg1 = cos αg1, the cosine of the angle between the minor axis of the central galaxy and the direction of the nearest filament, for three subsets of low-mass centrals (109 < Mg < 1010.25 M⊙, upper threshold corresponds to the lower limit for the galactic plane orientation transition mass as estimated in Dubois et al. 2014) depending on the distance of their closest satellite: Rgs < 0.5 Rvir, 0.5 Rvir < Rgs < Rvir and Rgs > Rvir. The presence of a close satellite impacts the orientation of the central spin and damps its tendency to align to the nearest filament. The closer the satellite, the stronger the effect. |
This explains why the alignment of satellites orthogonally to the galactic plane of low-mass centrals is not measured in Fig. 2, even though they do follow the filamentary trend.
Appendix B Distance to the central galaxy
Let us investigate here the effect of alignment change as a function of distance to the central for the full sample of galaxies, that is without specific mass cuts.
B.1 Full sample
Quantifying the relative influence of the filament and the joint effect of angular momentum dissipation via dynamical friction in the halo and central galaxy torques (which also alter the inner halo shape) is best achieved by noticing that these processes operate on different radial scales (as shown by Danovich et al. 2015, for cold flows). We presented results for a sub-sample of centrals in Fig. 6. We now measure the distribution of satellite galaxies around their central as a function of distance for the full sample of central-satellites pair, with no further consideration on the spin orientation of the central galaxy.
Figure B.1 shows the excess PDF of μ1 = cos θ1 (central galaxy minor axis) and ν = cos α (filament axis) for different bins of Rgs, the distance from the satellite to the central galaxy. We see that, as the distance increases, the alignment with the galactic plane weakens progressively while the alignment with the filament is strengthened. For satellites in the vicinity of their central, within a sphere of radius Rgs= 0.25 Rvir, the coplanar trend is highly dominant with ξ = 80% at μ1 = 0, and with 60% of the satellites outside a 66° double cone around the minor axis. (40% for random), while the filamentary trend is reduced to a 12% excess within a 37° double cone around the filament axis, which hosts 23% of the satellites (20% for random). In contrast, for satellites in the outskirts of the halo with Rgs > Rvir the filamentary trend dominates with this same excess, soaring to 41% at ν= 1 and hosting 28% of the satellites in a 37° double cone around the filament axis (20% for random). The amount of satellites outside the 66° double cone around the minor axis falls down to 48% that case (40% for random).
 |
Fig. B.1 Same as Fig. 2 where samples are binned in distance, Rgs, from satellite to central. Satellites close to the central galaxy tend to be distributed on the galactic plane and exhibit onlymarginal alignment with the filament, while satellites in the outskirts of the host halo of the central are strongly aligned with the filament, while their coplanarity with the central galaxy is weakened. Results are stacked for 0.3 < z < 0.8. |
Thus, in this “full-sample” analysis we recover the evolution with distance characteristic of a transition between both alignment trends for satellites around centrals whose spin is aligned to the nearest filament. However, in the present case, contrary to the results discussed in the main body of the paper, centrals both with aligned and misaligned spin are analysed together, which leads to an overall persistence of the filamentary trend at any distance from the central galaxy.
B.2 Evolution for different central stellar mass bins
In order to further confirm this transition from filamentary to coplanar trend, Fig. B.2 reproduces the analysis of Fig. B.1 for three different central stellar mass bins: 109 < Mg < 1010 M⊙, 1010 < Mg < 1010.5 M⊙ and Mg > 1010.5 M⊙. The evolution of both trends with respect to the mass of the central is consistent with the idea that more massive centrals should exert stronger torques and with their average mass-dependent orientation within the cosmic web.
This confirms the general tendency already observed for all central galaxies with Mg > 1010 M⊙ in Fig. B.1: satellites in the outskirts of the halo are aligned with the nearest filament. As they reach the inner parts of the halo they deviatefrom the filament to align with the galactic plane of their central. Specific features in each mass bin tend to confirm this general scenario:
-
For low mass centrals, the coplanar trend is significantly weaker than for centrals with Mg > 1010 M⊙ (for satellites within 0.25 Rvir: ξ = 30% at cos θ1 = 0 instead of ξ ≃ 100% for the two highest mass ranges). This is consistent with a weaker torquing of lower mass centrals. However, the flip from the filamentary trend to the coplanar trend is more distinctive than for higher stellar mass bins, which is directly related to the fact that those small mass centrals are under the swing transition mass evaluated in Dubois et al. (2014), and therefore are more likely to have a minor axis aligned with the filament, in which case both trends compete.
-
The filamentary trend in the outskirts of the halo is mildly affected by the mass of the centrals. As expected, it undergoes a little increase and persists at shorter distances from the central for high mass centrals for which filamentary and coplanar trends are more likely to reinforce each other.
-
For mostmassive central galaxies, the coplanar trend shows a general evolution very similar to that observed for lower masses but experiences a new increase, although somewhat limited, for satellites in the most outer parts of the halo (Rgs > 2 Rvir). Satellites so distant can actually be satellites of a neighbouring cluster. Thus, this trend is consistent with the Binggeli effect (Binggeli 1982) that applies to massive clusters, which tend to align their rotation plane with that of their neighbours and is a hint of the importance of the two-halo term discussed in further detail by Chisari et al. (2015).
B.3 Evolution for different satellite mass ratios
In this section, we investigate the impact of the satellite-to-central stellar mass ratio on the radial alignment trends described in this study. Figure B.3 reproduces the analysis of Fig. B.1 for four different satellite-to-central stellar mass ratios Mg ∕Ms < 0.05 (top panels), 0.05 < Mg∕Ms < 0.1 (upper intermediate panels), 0.1 < Mg∕Ms < 0.2 (lower intermediate panels) and Mg∕Ms > 0.2 (bottom panels). These cuts are chosen to be directly relatable to the definitions of minor and major mergers and to sample the mass ratio distribution in Horizon-AGN. Indeed in our simulation, the median satellite-to-central mass ratio is of order 0.05, while the average is 0.12. To focus on the transition between the filamentary and the coplanar trends, we restrict the sample to centrals with a minor axis aligned with the nearest filament (within a 37 degree cone) that is to the case where both trends compete.
 |
Fig. B.2 Same as Fig. 2 where samples are binned in distance, Rgs, from satellite to central. This is plotted for three different central stellar mass bins: 109 < Mg < 1010 M⊙ (top panels),1010 < Mg < 1010.5 M⊙ (middle panels) and Mg > 1010.5 M⊙ (bottom panels). The amplitude of the signal for the lowest mass bin (109 < Mg < 1010 M⊙) is represented as a grey area in the plots obtained for higher stellar mass bins. Satellites close to the central galaxy tend to be distributed on the galactic plane with marginal alignment to the filament, while satellites in the outskirt of the host halo of the central are strongly aligned with the filament but the coplanarity with the central galaxy is weakened. Results are stacked for 0.3 < z < 0.8. |
Both trends are consistent with those found in Fig. B.1 across all stellar mass ratio bins, with second order variations of the amplitude with the satellite-to-central mass ratio. Let us discuss them in further details
Focusing on the coplanar trend represented on left panels, we find that the tendency of innermost satellites (Rgs < 0.5 Rvir) to align in the plane of their central galaxy strongly increases with the satellite-to-central mass ratio. This effect is comparable to what we discussed for low-mass centrals: in the case of a high mass ratio satellite, both galaxies in the pair are in strong interaction and both tend to align in the plane of one another, which strengthens the alignment signal and allows it to be detected at larger distances. However, it is important to notice that even in the lowest mass ratio bin, the coplanar trend is strong (systematically stronger than the corresponding trend with the filament) and detectable up to 2 Rvir from the central galaxy, while in that case the alignment cannot be artificially enhanced by any disturbance of the central galaxy morphology due to the interaction.
 |
Fig. B.3 Same as Fig. 2 where samples are binned in distance, Rgs, from satellite to central. We restrict the sample to centrals with a minor axis aligned with the nearest filament (within a 37 degree cone).This is plotted for four different satellite-to-central stellar mass ratios Mg ∕Ms < 0.05 (top panels),0.05 < Mg∕Ms < 0.1 (upper intermediate panels), 0.1 < Mg∕Ms < 0.2 (lower intermediate panels) and Mg∕Ms > 0.2 (bottom panels). To help the eye, the maximal amplitude of the alignment signals across the four mass bins are represented as dotted blue lines in the plots obtained for stellar mass bins with weaker signal. The minimal amplitude of the orthogonality signal across the four mass bins is represented as a dotted pink line in the plots obtained for stellar mass bins with stronger signals. Results are stacked for 0.3 < z < 0.8. |
 |
Fig. C.1 Left panel: PDF of μ1 = cos θ1, the angle between the minor axis of the central galaxy and the vector separating it from its satellites, at 0.3 < z < 0.8 and for different colour bins. Right panel: PDF of μ = cos θ, the angle between the spin of the central galaxy and the satellite separation vector. For massive red central galaxies, the satellites tend to be distributed on the galactic plane. The amplitude of the signal is stronger when using the minor axis rather than the spin. |
In the outskirt of haloes (Rgs > Rvir), the coplanar trend rapidly fades away with distance to the central galaxy, being progressively replaced by the filamentary trend. The filamentary trend is found to be very similar across all mass ratio bins but the lowest one, where the signal is noticeably weaker. This last result is consistent with the fact that, on halo scales, the infall of low mass satellites tend grow more isotropic as their mass decreases, the anisotropy being undetectable for Mg ∕Ms < 0.02 in Horizon-AGN.
Appendix C Spin versus minor axis: effect on satellite alignment
Additionally, the right panel of Fig. C.1 shows the PDF of μ =cos θ, the angle between the spin of the central galaxy and the satellite separation vector. While replacing the alignment with the minor axis by the alignment with the galactic spin does not change our results qualitatively, one can see that the amplitude of the spin signal is significantly lower than that of the axis signal, with the previously mentioned 54% fraction of satellites within a solid angle sector around the midplane falling to less than 45%.
This is a general trend that we observed for several PDFs presented in this paper, which suggests a significant impact of torquing from the central galaxy on the motion of satellites entering the halo. It also suggests that the spin can be significantly misaligned with both the minor axis of the central galaxy and the spin of the host halo. The discrepancy between those two signals is highly dependent on the shape of the central galaxy, which can induce significant misalignments between the minor axis and the spin, especially for prolate structures.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Agustsson, I., & Brainerd, T. G. 2010, ApJ, 709, 1321 [NASA ADS] [CrossRef] [Google Scholar]
- Aubert, D., Pichon, C., & Colombi, S. 2004, MNRAS, 352, 376 [NASA ADS] [CrossRef] [Google Scholar]
- Bahl, H., & Baumgardt, H. 2014, MNRAS, 438, 2916 [NASA ADS] [CrossRef] [Google Scholar]
- Bailin, J., Power, C., Norberg, P., Zaritsky, D., & Gibson, B. K. 2008, MNRAS, 390, 1133 [NASA ADS] [CrossRef] [Google Scholar]
- Barnes, J., & Efstathiou, G. 1987, ApJ, 319, 575 [NASA ADS] [CrossRef] [Google Scholar]
- Bernstein, G. M., & Norberg, P. 2002, AJ, 124, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Binggeli, B. 1982, A&A, 107, 338 [NASA ADS] [Google Scholar]
- Blazek, J., McQuinn, M., & Seljak, U. 2011, JCAP, 5, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Blazek, J., Vlah, Z., & Seljak, U. 2015, JCAP, 08, 015 [CrossRef] [Google Scholar]
- Brainerd, T. G. 2005, ApJ, 628, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Catelan, P., Kamionkowski, M., & Blandford, R. D. 2001, MNRAS, 320, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, Y.-C., Ho, S., Tenneti, A., et al. 2015, MNRAS, 454, 3341 [Google Scholar]
- Chisari, N. E., Mandelbaum, R., Strauss, M. A., Huff, E. M., & Bahcall, N. A. 2014, MNRAS, 445, 726 [NASA ADS] [CrossRef] [Google Scholar]
- Chisari, N. E., Codis, S., Laigle, C., et al. 2015, MNRAS, 454, 2736 [NASA ADS] [CrossRef] [Google Scholar]
- Codis, S., Pichon, C., Devriendt, J., et al. 2012, MNRAS, 427, 3320 [NASA ADS] [CrossRef] [Google Scholar]
- Codis, S., Gavazzi, R., Dubois, Y., et al. 2015a, MNRAS, 448, 3391 [Google Scholar]
- Codis, S., Pichon, C., & Pogosyan, D. 2015b, MNRAS, 452, 3369 [Google Scholar]
- Colpi, M. 1998, ApJ, 502, 167 [NASA ADS] [CrossRef] [Google Scholar]
- Crittenden, R. G., Natarajan, P., Pen, U.-L., & Theuns, T. 2001, ApJ, 559, 552 [NASA ADS] [CrossRef] [Google Scholar]
- Croft, R. A. C., & Metzler, C. A. 2000, ApJ, 545, 561 [NASA ADS] [CrossRef] [Google Scholar]
- Danovich, M., Dekel, A., Hahn, O., Ceverino, D., & Primack, J. 2015, MNRAS, 449, 2087 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, X. C., Lin, W. P., Kang, X., et al. 2014, ApJ, 791, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Dubois, Y., Devriendt, J., Slyz, A., & Teyssier, R. 2012, MNRAS, 420, 2662 [NASA ADS] [CrossRef] [Google Scholar]
- Dubois, Y., Gavazzi, R., Peirani, S., & Silk, J. 2013, MNRAS, 433, 3297 [NASA ADS] [CrossRef] [Google Scholar]
- Dubois, Y., Pichon, C., Welker, C., et al. 2014, MNRAS, 444, 1453 [NASA ADS] [CrossRef] [Google Scholar]
- Emsellem, E., Cappellari, M., Krajnović, D., et al. 2011, MNRAS, 414, 888 [NASA ADS] [CrossRef] [Google Scholar]
- Faltenbacher, A., Jing, Y. P., Li, C., et al. 2008, ApJ, 675, 146 [NASA ADS] [CrossRef] [Google Scholar]
- Gillet, N., Ocvirk, P., Aubert, D., et al. 2015, ApJ, 800, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Haardt, F., & Madau, P. 1996, ApJ, 461, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, D. L., & Peebles, P. J. E. 1975, AJ, 80, 477 [NASA ADS] [CrossRef] [Google Scholar]
- Hirata, C. M., & Seljak, U. 2004, Phys. Rev. D, 70, 063526 [NASA ADS] [CrossRef] [Google Scholar]
- Hirata, C. M., & Seljak, U. 2010, Phys. Rev. D, 82, 049901 [NASA ADS] [CrossRef] [Google Scholar]
- Hirata, C. M., Mandelbaum, R., Seljak, U., et al. 2004, MNRAS, 353, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Hirata, C. M., Mandelbaum, R., Ishak, M., et al. 2007, MNRAS, 381, 1197 [NASA ADS] [CrossRef] [Google Scholar]
- Holmberg, E. 1969, Arkiv för Astronomi, 5, 305 [NASA ADS] [Google Scholar]
- Hopkins, P. F., Bahcall, N. A., & Bode, P. 2005, ApJ, 618, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Hui, L., & Zhang, J. 2008, ApJ, 688, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Ibata, R. A., Lewis, G. F., Conn, A. R., et al. 2013, Nature, 493, 62 [CrossRef] [Google Scholar]
- Ivezic, Z., Tyson, J. A., et al., & the LSST Collaboration. 2008, ArXiv e-prints [arXiv:0805.2366] [Google Scholar]
- Jing, Y. P., & Suto, Y. 2002, ApJ, 574, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Joachimi, B., & Bridle, S. L. 2010, A&A, 523, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Joachimi, B., Mandelbaum, R., Abdalla, F. B., & Bridle, S. L. 2011, A&A, 527, A26 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kirk, D., Bridle, S., & Schneider, M. 2010, MNRAS, 408, 1502 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, D., Brown, M. L., Hoekstra, H., et al. 2015, Space Sci. Rev., 193, 139 [NASA ADS] [CrossRef] [Google Scholar]
- Knebe, A., Gill, S. P. D., Gibson, B. K., et al. 2004, ApJ, 603, 7 [NASA ADS] [CrossRef] [Google Scholar]
- Komatsu, E. et al. 2011, ApJS, 192, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, E., Eifler, T., & Blazek, J. 2016, MNRAS, 456, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Laigle, C., Pichon, C., Codis, S., et al. 2015, MNRAS, 446, 2744 [NASA ADS] [CrossRef] [Google Scholar]
- Laureijs, R., Amiaux, J., Arduini, S., et al. 2011, ArXiv e-prints [arXiv:1110.3193] [Google Scholar]
- Lee, J., & Pen, U.-L. 2000, ApJ, 532, L5 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Li, C., Jing, Y. P., Faltenbacher, A., & Wang, J. 2013, ApJ, 770, L12 [NASA ADS] [CrossRef] [Google Scholar]
- Libeskind, N. I., Hoffman, Y., Tully, R. B., et al. 2015, MNRAS, 452, 1052 [NASA ADS] [CrossRef] [Google Scholar]
- Mandelbaum, R., Hirata, C. M., Ishak, M., & Seljak, U. 2006, in Amer. Astron. Soc. Meet. Abstr., BAAS, 38, 1001 [NASA ADS] [Google Scholar]
- Meneghetti, M., Bartelmann, M., & Moscardini, L. 2001, ArXiv e-prints [arXiv:0109250] [Google Scholar]
- Niederste-Ostholt, M., Strauss, M. A., Dong, F., Koester, B. P., & McKay, T. A. 2010, MNRAS, 405, 2023 [NASA ADS] [Google Scholar]
- Nierenberg, A. M., Auger, M. W., Treu, T., et al. 2012, ApJ, 752, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Okumura, T., & Jing, Y. P. 2009, ApJ, 694, L83 [NASA ADS] [CrossRef] [Google Scholar]
- Oser, L., Ostriker, J. P., Naab, T., Johansson, P. H., & Burkert, A. 2010, ApJ, 725, 2312 [NASA ADS] [CrossRef] [Google Scholar]
- Pawlowski, M. S., Famaey, B., Jerjen, H., et al. 2014, MNRAS, 442, 2362 [NASA ADS] [CrossRef] [Google Scholar]
- Paz, D. J., Stasyszyn, F., & Padilla, N. D. 2008, MNRAS, 389, 1127 [NASA ADS] [CrossRef] [Google Scholar]
- Paz, D. J., Sgró, M. A., Merchán, M., & Padilla, N. 2011, MNRAS, 414, 2029 [NASA ADS] [CrossRef] [Google Scholar]
- Phillips, J. I., Cooper, M. C., Bullock, J. S., & Boylan-Kolchin, M. 2015, MNRAS, 453, 3839 [NASA ADS] [CrossRef] [Google Scholar]
- Pichon, C., Pogosyan, D., Kimm, T., et al. 2011, MNRAS, 418, 2493 [NASA ADS] [CrossRef] [Google Scholar]
- Plionis, M., & Basilakos, S. 2002, MNRAS, 329, L47 [NASA ADS] [CrossRef] [Google Scholar]
- Sales, L., & Lambas, D. G. 2009, MNRAS, 395, 1184 [NASA ADS] [CrossRef] [Google Scholar]
- Schaefer, B. M., & Merkel, P. M. 2015, MNRAS, submitted, [arXiv:1506.07366] [Google Scholar]
- Schneider, M. D., & Bridle, S. 2010, MNRAS, 402, 2127 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, M. D., Cole, S., Frenk, C. S., & Kelvin, L. a. 2013, MNRAS, 433, 2727 [NASA ADS] [CrossRef] [Google Scholar]
- Sifón, C., Hoekstra, H., Cacciato, M., et al. 2015, A&A, 575, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Singh, S., Mandelbaum, R., & More, S. 2015, MNRAS, 450, 2195 [NASA ADS] [CrossRef] [Google Scholar]
- Smargon, A., Mandelbaum, R., Bahcall, N., & Niederste-Ostholt, M. 2012, MNRAS, 423, 856 [Google Scholar]
- Smith, R., Duc, P.-A., Bournaud, F., & Yi, S. K. 2016, ApJ, 818, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Sousbie, T., Colombi, S., & Pichon, C. 2009, MNRAS, 393, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D., Gehrels, N., Breckinridge, J., et al. 2013, ArXiv e-prints [arXiv:1305.5425] [Google Scholar]
- Stewart, K. R., Brooks, A. M., Bullock, J. S., et al. 2013, ApJ, 769, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Sutherland, R. S., & Dopita, M. A. 1993, ApJS, 88, 253 [NASA ADS] [CrossRef] [Google Scholar]
- Tempel, E., Guo, Q., Kipper, R., & Libeskind, N. I. 2015, MNRAS, 450, 2727 [NASA ADS] [CrossRef] [Google Scholar]
- Tenneti, A., Mandelbaum, R., Di Matteo, T., Feng, Y., & Khandai, N. 2014, MNRAS, 441, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Tenneti, A., Singh, S., Mandelbaum, R., et al. 2015, MNRAS, 448, 3522 [NASA ADS] [CrossRef] [Google Scholar]
- Tenneti, A., Mandelbaum, R., & Di Matteo T. 2016, MNRAS, 462, 2668 [NASA ADS] [CrossRef] [Google Scholar]
- Teyssier, R. 2002, A&A, 385, 337 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tillson, H., Devriendt, J., Slyz, A., Miller, L., & Pichon, C. 2015, MNRAS, 449, 4363 [NASA ADS] [CrossRef] [Google Scholar]
- Tormen, G., Bouchet, F. R., & White, S. D. M. 1997, MNRAS, 286, 865 [NASA ADS] [CrossRef] [Google Scholar]
- Tweed, D., Devriendt, J., Blaizot, J., Colombi, S., & Slyz, A. 2009, A&A, 506, 647 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Haarlem, M., & van de Weygaert, R. 1993, ApJ, 418, 544 [NASA ADS] [CrossRef] [Google Scholar]
- Velliscig, M., Cacciato, M., Schaye, J., et al. 2015a, MNRAS, 453, 721 [NASA ADS] [CrossRef] [Google Scholar]
- Velliscig, M., Cacciato, M., Schaye, J., et al. 2015b, MNRAS, 454, 3328 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, H. Y., Jing, Y. P., Mao, S., & Kang, X. 2005, MNRAS, 364, 424 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, Y., Park, C., Hwang, H. S., & Chen, X. 2010, ApJ, 718, 762 [NASA ADS] [CrossRef] [Google Scholar]
- Warren, M. S., Quinn, P. J., Salmon, J. K., & Zurek, W. H. 1992, ApJ, 399, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Welker, C., Devriendt, J., Dubois, Y., Pichon, C., & Peirani, S. 2014, MNRAS, 445, L46 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, X., van den Bosch, F. C., Mo, H. J., Mao, S., & Kang, X. 2006, MNRAS, 369, 1293 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshida, N., Springel, V., White, S. D. M., & Tormen, G. 2000, ApJ, 535, L103 [NASA ADS] [CrossRef] [Google Scholar]
- Zaritsky, D., Smith, R., Frenk, C. S., & White, S. D. M. 1997, ApJ, 478, L53 [NASA ADS] [CrossRef] [Google Scholar]
- Zentner, A. R., Kravtsov, A. V., Gnedin, O. Y., & Klypin, A. A. 2005, ApJ, 629, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, Y., Yang, X., Wang, H., et al. 2013, ApJ, 779, 160 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Mean values (in degrees) for θx in different colour bins for both satellites and central galaxies, and within two different radius from their central galaxy.
All Figures
 |
Fig. 1 Sketch representation of the angles ζ1 and ζ3 used to describe the orientation of the orbital plane of a satellite (in blue) around its central galaxy (in red), that are used to compute the average orbital plane of satellites and their dispersion ratio (see the text for details). Dashed lines illustrate the intersections between the central galaxy principal planes and the satellite orbital plane. |
| In the text | |
 |
Fig. 2 Top panel: excess PDF ξ of μ1 = cos θ1, the angle between the minor axis of the central galaxy and the direction towards the centre of mass of its satellites, for different central galaxy stellar mass bins, between redshift 0.3 < z < 0.8. Satellites tend to be distributed on the galactic plane of the central and this trend is stronger with the increasing mass of the central. Bottom panel: excess PDF of ν = cos α, the cosine of the angle between the direction of the central’s nearest filament axis and the direction towards the centre of mass of its satellites. Satellites tend to be strongly distributed along filaments. Error bars are 1− σ Poissonian error bars. |
| In the text | |
 |
Fig. 3 Sketch of the expected results for the filamentary trend. Satellite galaxies tend to be aligned within the nearest filament. Consequently, they are distributed orthogonally to the spin/minor axis of older red central galaxies, and more often aligned with the spin/minor axis of young blue central galaxies. |
| In the text | |
 |
Fig. 4 Sketch of the main angles used in our analysis. Left Panel: definition of α, θ1 and αg, used to describe the relative orientation of the satellite and the filament, the satellite and the central galaxy, and the central galaxy and the filament respectively. Middle panel and right panel: illustration of the solid angle sectors used to define the “aligned central minor axis” sample (within the 37° cone) and “perpendicular central minor axis” sample (outside the 66° cone) respectively. We note that similar angular sectors can be defined for α and θ1 to describe the orientation of satellites. |
| In the text | |
 |
Fig. 5 Evolution of the filamentary trend (dashed line) and the coplanar trend (solid line) for either the central galaxy’s minor axis aligned to the filament axis within a 37° cone (toppanels), or the central galaxy’s minor axis perpendicular to the filament axis within a 37° cone (bottom panels). From left to right panel, three different central galaxy stellar mass bins Mg are shown asindicated in each panel. Results are stacked for 0.3 < z < 0.8. In the top panels, the two trends are mutually exclusive. This reveals a transitional pattern: coplanar trend takes over for massive centrals while the filamentary trend is dominant for low mass centrals, consistently with the limited influence of the central torques in this case. In the bottom panels, the two trends reinforce each other. Expectedly, the trends are strengthened for the most massive centrals. |
| In the text | |
 |
Fig. 6 Same as Fig. 2 but binning the sample in distance, Rgs, from satellite to central, and restricting it to satellites hosted by halos whose central galaxy’s minor axis is aligned to the nearest filament within a 37° double cone, for which the coplanar and filamentary trends compete. Results are stacked for 0.3 < z < 0.8 for different radius Rgs bins. Satellites close to their central tend to be distributed on the galactic plane, hence orthogonally to the filament, while satellites in the outskirts of the halo are strongly aligned with the filament and the coplanarity with the central is lost. |
| In the text | |
 |
Fig. 7 Sketch of the evolution of the alignment trends with distance to the centre of the halo. In the outskirts of the halo, satellite galaxies are strongly aligned with the nearest filament. Probing deeper into the halo this trend weakens as the alignment of satellites with the galactic plane strengthens. |
| In the text | |
 |
Fig. 8 Twice the PDF of cos ϕ, the cosine of the angle between the spin of the central galaxy and the total orbital momentum of its satellites for 0.3 < z < 0.8 for different mass (left panel) and radius Rgs bins (middle panel). For massive central galaxies, the orbital angular momentum of satellites tends to align with the galactic spin of the central, especially in its vicinity. Right panel: excess PDF of |
| In the text | |
 |
Fig. 9 Left panel: average strength of the total specific orbital angular momentum |
| In the text | |
 |
Fig. 10 Twice the PDF of cos χ, the cosine of the angle between the spin of the central galaxy and the spin of the satellite for 0.3 < z < 0.8 for different bins of distance to the central galaxy. Satellites align their intrinsic angular momentum to that of the central galaxies in the inner part of the halo. |
| In the text | |
 |
Fig. 11 PDF of cos χs, the cosine ofthe angle between the spin of the satellite and its position vector relative to the central galaxy as a function of distance to the central (radius bins are indicated on the figure). |
| In the text | |
 |
Fig. 12 Distribution of rest frame colours in Horizon-AGN. Coloured areas indicate the colour bins used throughout the analysis in this section of the paper. |
| In the text | |
 |
Fig. 13 Left panel: PDF of μ1 = cos θ1, the angle between the minor axis of the central galaxy and the vector separating it from its satellites, at 0.3 < z < 0.8 and for different colour bins. Right panel: PDF of ν = cos α, the angle between the satellite separation vector and the direction of the nearest filament. The average central galaxy mass in each colour bin is also indicated. For massive red central galaxies, the satellites tend to be distributed on the galactic plane. The filamentary trend is also recovered although degraded by projection for the bluest central colour range. |
| In the text | |
 |
Fig. 14 Same as Fig. 13 but splitting both the central galaxies and the satellites in different colour bins. Blue galaxies are identified as objects with g − r < 0.4 and red galaxies as objects with g − r > 0.55. The mass cut is a compromise between statistics and comparability to existing observations. |
| In the text | |
 |
Fig. 15 PDF of θx and αx, the angles between the x-projected major axis of, respectively, the central galaxy (left panel), and direction of the filament (right panel) and the x-projected rgs, at 0.3 < z < 0.8 for differentcolour bins. For massive red central galaxies, the satellites tend to be distributed on the galactic plane. The projected signal is qualitatively comparable to results in 3D. Observational results from Yang et al. (2006) are overplotted for red centrals (red squares) and blue centrals (blue dots). The agreement is good. |
| In the text | |
 |
Fig. 16 PDF of |cos ϕ|, the cosine of the angle between the spin of the central galaxy and the total orbital momentum of its satellites (measured in the rest frame of their central) for 0.3 < z < 0.8 and for different g − r satellite colour bins. For red quenched satellites, the orbital momentum tends to be aligned with the central galactic spin. The effect is much weaker for blue star forming satellites, consistent with their preferential orientation along the filament. |
| In the text | |
 |
Fig. 17 Evolution of the mean (rescaled) central-satellite separation as a function of the satellite g − r colour (for all satellites within Rgs < 5 Rvir). Our colour bins are overplotted as coloured areas and the average separation in each bin is indicated by a dashed line. |
| In the text | |
 |
Fig. 18 PDF of cos χs, the cosine of the angle between satellite spin and position vector for different satellites in g − r colour bins. Blue (outer) satellites have a spin preferentially aligned with their position vector, while red (inner) satellites have a rotation plane aligned with it. |
| In the text | |
 |
Fig. 19 PDF of cos χ1, the cosine of the angle between the minor axis of the satellite and its position vector for 0.3 < z < 0.8 for different radius (left panel), satellite colour (middle panel) and mixed (right panel). Satellites align their minor axis with that of the central galaxy as they reach the inner regions of the halo. |
| In the text | |
 |
Fig. 20 PDF of μ1 = cos θ1 similar to that in Fig. 2 for oblate (solid line) and prolate (dashed line) central galaxies, restricted to the intermediate mass range. Tendency to lie orthogonal to the minor axis is stronger for prolate structures, as in this case the minor axis is most often orthogonal to the filament direction and the galactic plane is poorly defined. |
| In the text | |
 |
Fig. 21 PDF of μ3 = cos θ3 the cosine of the angle between rgs and the major axis of the central galaxy for oblate (dashed line) and prolate (solid line) centrals. Prolate centrals have their satellites aligned along their major axis, which is consistent with the fact that this axis is more often aligned with the spin in this case. Oblate centrals display a certain degree of satellite alignment too, which is consistent with the distribution of satellites tracing the underlying triaxiality of their host halo. |
| In the text | |
 |
Fig. 22 Summary of the orientation trends that drive the fate of satellites in their host halo. Alignment trends are distance dependent: filamentary trend dominates in the outskirt of the halo (for bluer satellites on average), while coplanar trend takes over inthe vicinity of the central (redder satellites on average). These trends may bias the standard expectation that the satellitesdistribution traces the overall shape of the diffuse dark matter halo (orange ellipses). More probably, specific populations of satellites (selected in mass, colour and separation) trace specific parts of the halo and the embedding cosmic web. |
| In the text | |
 |
Fig. A.1 PDF of νg1 = cos αg1, the cosine ofthe angle between the minor axis of the central galaxy and the direction of the nearest filament (brown lines) and νg = cos αg, the angle between the spin of the central galaxy and the direction of the nearest filament (blue lines). Distributions are plotted for central galaxies in two different mass ranges: 109 < Mg < 1010 M⊙ (solid lines) and Mg > 1010 M⊙ (blue lines). The transition for the galactic plane orientation is recovered, but the signal is stronger using the spin for low-mass centrals. The opposite is true for high mass centrals: the minor axis estimator yields an increased amplitude in the excess probability ξ. |
| In the text | |
 |
Fig. A.2 Leftpanel: PDF of μ1 = cos θ1, the angle between the minor axis of the central galaxy and the satellite separation vector rgs. Right panel: PDF of μ = cos θ, the angle between the spin of the central galaxy and the separation vector. Distributions are plotted for three different subsets of low-mass centrals with varying types of satellites (green and blue shades): Γ1: 109 < Mg < 1010 M⊙, Γ2: 5 × 109< Mg < 1010 M⊙ and Ms < 2 × 109 M⊙, Γ3: 5 × 109< Mg < 1010 M⊙, Ms < 2× 109 M⊙ and Rgs > Rvir. Satellites oflow-mass centrals tend to align with their central’s spin/minor axis, consistently with the fact that they tend to align with the nearest filament. However, the signal is limited in amplitude and tends to vanish when traced with the minor axis for centrals with massive satellites and/or with satellites in their close vicinity. In this mass range for the central, the satellite is often of comparable mass and both galaxies equally impact the orientation and shape of one another prior to merger. |
| In the text | |
 |
Fig. A.3 PDF of νg1 = cos αg1, the cosine of the angle between the minor axis of the central galaxy and the direction of the nearest filament, for three subsets of low-mass centrals (109 < Mg < 1010.25 M⊙, upper threshold corresponds to the lower limit for the galactic plane orientation transition mass as estimated in Dubois et al. 2014) depending on the distance of their closest satellite: Rgs < 0.5 Rvir, 0.5 Rvir < Rgs < Rvir and Rgs > Rvir. The presence of a close satellite impacts the orientation of the central spin and damps its tendency to align to the nearest filament. The closer the satellite, the stronger the effect. |
| In the text | |
 |
Fig. B.1 Same as Fig. 2 where samples are binned in distance, Rgs, from satellite to central. Satellites close to the central galaxy tend to be distributed on the galactic plane and exhibit onlymarginal alignment with the filament, while satellites in the outskirts of the host halo of the central are strongly aligned with the filament, while their coplanarity with the central galaxy is weakened. Results are stacked for 0.3 < z < 0.8. |
| In the text | |
 |
Fig. B.2 Same as Fig. 2 where samples are binned in distance, Rgs, from satellite to central. This is plotted for three different central stellar mass bins: 109 < Mg < 1010 M⊙ (top panels),1010 < Mg < 1010.5 M⊙ (middle panels) and Mg > 1010.5 M⊙ (bottom panels). The amplitude of the signal for the lowest mass bin (109 < Mg < 1010 M⊙) is represented as a grey area in the plots obtained for higher stellar mass bins. Satellites close to the central galaxy tend to be distributed on the galactic plane with marginal alignment to the filament, while satellites in the outskirt of the host halo of the central are strongly aligned with the filament but the coplanarity with the central galaxy is weakened. Results are stacked for 0.3 < z < 0.8. |
| In the text | |
 |
Fig. B.3 Same as Fig. 2 where samples are binned in distance, Rgs, from satellite to central. We restrict the sample to centrals with a minor axis aligned with the nearest filament (within a 37 degree cone).This is plotted for four different satellite-to-central stellar mass ratios Mg ∕Ms < 0.05 (top panels),0.05 < Mg∕Ms < 0.1 (upper intermediate panels), 0.1 < Mg∕Ms < 0.2 (lower intermediate panels) and Mg∕Ms > 0.2 (bottom panels). To help the eye, the maximal amplitude of the alignment signals across the four mass bins are represented as dotted blue lines in the plots obtained for stellar mass bins with weaker signal. The minimal amplitude of the orthogonality signal across the four mass bins is represented as a dotted pink line in the plots obtained for stellar mass bins with stronger signals. Results are stacked for 0.3 < z < 0.8. |
| In the text | |
 |
Fig. C.1 Left panel: PDF of μ1 = cos θ1, the angle between the minor axis of the central galaxy and the vector separating it from its satellites, at 0.3 < z < 0.8 and for different colour bins. Right panel: PDF of μ = cos θ, the angle between the spin of the central galaxy and the satellite separation vector. For massive red central galaxies, the satellites tend to be distributed on the galactic plane. The amplitude of the signal is stronger when using the minor axis rather than the spin. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.