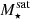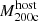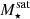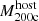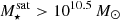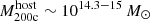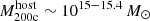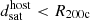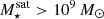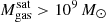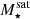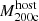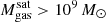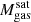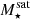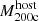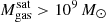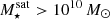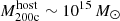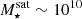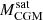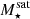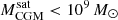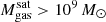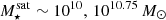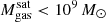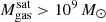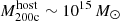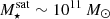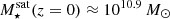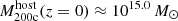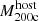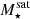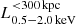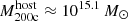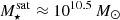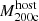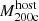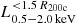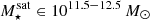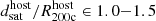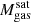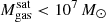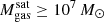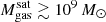© The Authors 2024

1. Introduction

Since the 1950s, astronomers have been observing absorption lines in the spectra of background sources due to gas along the line of sight, including in the gaseous halos of intervening galaxies. This circumgalactic medium (CGM) is an enigmatic component of the baryonic Universe, and a necessary element for a comprehensive picture of galaxy evolution (see Tumlinson et al. 2017; Faucher-Giguère et al. 2023, for recent reviews). The CGM is the interface between gas that is expelled from the galaxy due to stellar and active galactic nucleus (AGN) feedback, and gas flowing into the halo from the intergalactic medium (IGM), as well as from satellite galaxies (hereafter satellites).

To first approximation, the CGM is a thermally pressure-supported atmosphere in rough hydrostatic equilibrium (Rees & Ostriker 1977; Silk 1977; White & Rees 1978). With increasing halo mass and virial temperature, the CGM also becomes hotter and emits at progressively higher energies. Inflowing gas is expected to be shock-heated to approximately the same virial temperature or, depending on galaxy mass and redshift, to penetrate toward the inner regions (Kereš et al. 2005; Dekel & Birnboim 2006; Faucher-Giguere et al. 2011; Nelson et al. 2016). However, outflows, inflows, and the quasi-static CGM are all multiphase, and can contain cold, molecular components as well as hot, virialized phases. As a result, the CGM is a complex component of the galactic ecosystem that is shaped by the complex interplay of physical processes including gas cooling, magnetic fields, galactic feedback, filamentary inflows, and galaxy mergers and satellites (e.g., Sarazin 2002; Voit 2005; Peeples et al. 2019; Nelson et al. 2020; Ramesh et al. 2023). Within the current cosmological paradigm, all massive central galaxies (hereafter centrals) are expected to be surrounded by a gaseous halo or CGM, embedded within a halo of cold dark matter. The picture for satellites orbiting within the halo of a more massive central galaxy is, however, less clear. It is unknown if satellites can retain their own CGM after they begin interacting with their host halo.

Satellite and central galaxies differ in many respects. Observationally, satellites have higher elliptical and S0 fractions, higher quenched fractions, lower (specific) star formation rates (SFRs), redder colors, lower neutral and molecular gas fractions, elevated gas metallicities, reduced X-ray emission, and suppressed AGN activity compared to centrals of the same mass (e.g., Dressler 1980; Giovanelli et al. 1985; Wetzel et al. 2013; Peng et al. 2010, 2012; Brown et al. 2016; Maier et al. 2019a,b; Cortese et al. 2021; Boselli et al. 2022). A number of physical mechanisms have been invoked to explain these differences (see Cortese et al. 2021, for a recent review), many of which are related to the hydrodynamical interaction between the gas of the satellites and the ambient gaseous halo of their hosts.

Starting from the outermost scales and working inward, satellites are thought to be cut off from the intergalactic medium (IGM), removing a source of gas replenishment (Larson et al. 1980). Satellite gas is vulnerable to ram pressure stripping (RPS), which directly removes gas preferentially from the outside in (Gunn & Gott 1972; McCarthy et al. 2008; Boselli et al. 2022, for a recent review). First, the gaseous halo of the satellite is stripped, after which it is no longer able to accrete from its own CGM (Balogh & Morris 2000). Moreover, gas accretion from the ambient medium is expected to be strongly suppressed (van de Voort et al. 2017; Wright et al. 2020). Finally, ram pressure can also directly remove the interstellar medium (ISM) of satellites, likely in an outside in fashion as inferred by observations of truncated disks (e.g., Warmels 1988; Cayatte et al. 1990, 1994; Vollmer et al. 2001; Lee et al. 2022). Consequently, RPS deposits the CGM and ISM of satellites into the gaseous halos of their hosts (e.g., Rohr et al. 2023; Roy et al. 2024).

Simultaneously with these environmental effects, the ISM and CGM gas of satellites is subject to internal stellar and AGN feedback processes. These feedback processes increase the effectiveness of RPS (e.g., Bahé & McCarthy 2015; Ayromlou et al. 2021a; Kulier et al. 2023). Several observations suggest that ram pressure may compress the ISM and temporarily enhance star formation (e.g., Gavazzi et al. 2001; Vulcani et al. 2018; Roberts et al. 2022) and AGN activity (e.g., Poggianti et al. 2017; Peluso et al. 2022, contra: Roman-Oliveira et al. 2018) before eventually removing most satellite gas. This ram pressure driven increase in ISM gas density has also been seen in some idealized simulations of individual satellites (Lee et al. 2020; Choi et al. 2022; Zhu et al. 2024) and to cause bursts of star formation also in cosmological volume galaxy simulations (Göller et al. 2023).

The effectiveness of RPS increases with host mass. Furthermore, at fixed host mass, ram pressure stripping is expected to become more important with decreasing satellite stellar mass, since the satellite stellar body acts as the gravitationally restoring force opposing ram pressure (e.g., Wright et al. 2022; Zinger et al. 2024). However at galaxy stellar masses ≳10^10.5 M_⊙ AGN feedback is expected and inferred to become more efficient at ejecting gas and quenching galaxies (e.g., Silk & Rees 1998; Schawinski et al. 2007; Fabian 2011), both in centrals and satellites (e.g., Bluck et al. 2020; Joshi et al. 2020; Donnari et al. 2021a). After the ISM has been largely ejected, it becomes more susceptible to ram pressure removal. As a result, the retention of hot CGM and cold ISM gas reservoirs, on timescales of Myr to Gyr, depends sensitively on both satellite mass as well as host halo mass.

The low density and surface brightness of the CGM have made it difficult to directly observe in emission, but recent instrumentation and surveys have detected the CGM of single and stacked galaxies in the optical/UV (e.g., Hayes et al. 2013; Leclercq et al. 2022; Dutta et al. 2023), X-ray (e.g., Bogdan et al. 2013; Comparat et al. 2022; Chadayammuri et al. 2022), and even the radio (Chen et al. 2024). For satellites, the first detection of a gaseous corona in emission was the Large Magellanic Cloud (LMC) using Hubble Space Telescope spectra (Wakker et al. 1998; Krishnarao et al. 2022). Using Chandra, Sun et al. (2007) detect X-ray galactic coronae with temperatures kT ≈ 0.5 − 1.1 keV in ≈60% of super-L_* galaxies residing in clusters, implying CGM stripping timescales of several Gyr. Goulding et al. (2016) detect X-ray emission within the stellar effective radius of 33 early-type systems in the MASSIVE survey, a fraction of which are not the central of their group or cluster. Babyk et al. (2018) extract X-ray scaling relations out to five times the stellar effective radius of 94 early-type galaxies in the local Universe, many of which are satellites of nearby groups and clusters. Zhang et al. (2019) find in stacked SDSS spectra suppressed Hα + [N II] emission from the CGM of ∼L_⋆ galaxies that are in denser environments (see also Burchett et al. 2018). Lastly, Hou et al. (2024) and Zhang et al. (2024) find X-ray emission around satellites in stacked Chandra and eROSITA observations (see also Hou et al. 2021). However, it remains unclear what percentage of satellites today retain hot gas reservoirs, and to what extent their CGM have been damaged by the environment of their hosts, especially if these are massive groups and clusters of galaxies.

Despite the relatively low number statistics for detected CGM gas around satellites, its existence is consequential. For example, Lucchini et al. (2020) find that such a satellite CGM is necessary to reproduce the observed kinematics and mass of the Large and Small Magellanic Cloud system. Moreover, the high surviving HI fractions of a Hydra galaxy cluster subgroup suggest a surviving intragroup medium actually shields the group members from the hotter intracluster medium (ICM; Hess et al. 2022). Lastly, Churazov et al. (2012) infer that the largest fluctuations in resolved X-ray maps of the Coma cluster are due to cluster members.

The stripping and loss of gas from satellites have been studied with cosmological hydrodynamical galaxy simulations. For example, using the GIMIC simulations, Bahé et al. (2013) find that group and cluster hosts with total mass ∼10^{13 − 15.2} M_⊙ are able to strip infalling galaxies of their CGM already when the latter are at distances of 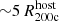$\sim 5R_{200\mathrm{c}}^{\mathrm{host}}$. More recently, Wright et al. (2022) study the orbital histories of EAGLE satellites around groups and clusters, finding that satellites begin to lose their CGM at 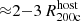$\approx 2-3R_{200\mathrm{c}}^{\mathrm{host}}$, while gas removal is more efficient for clusters and lower-mass satellites. The emerging phenomenology of diverse satellite CGM properties and removal timescales depends on satellite-host configurations (e.g., Kawata & Mulchaey 2008; McCarthy et al. 2008; Bekki 2009; Zinger et al. 2018; Kulier et al. 2023). This has also led to the revision of simplified assumptions previously adopted in semi-analytical models. Typically, these models have only accounted for gas stripping in satellites within the virial radius (e.g., Henriques et al. 2015), with some even removing the entire satellite CGM gas once a satellite crosses into the halo boundary (e.g., Lacey et al. 2016; Lagos et al. 2018). Updated semi-analytical models, which include both the stripping of satellites and centrals beyond the halo boundary, as well as a gradual approach to gas stripping, demonstrate improved alignment with observational data (e.g., Ayromlou et al. 2021b). However, the majority of the theoretical analyses so far focus on galaxy groups and low-mass clusters rather than the largest clusters in the Universe, where environmental effects are maximal. Moreover, no previous simulation work has connected the possible survival of the CGM around satellites and its observability.

In this work, we use the new TNG-Cluster simulation suite (Nelson et al. 2024; Pillepich et al., in prep.) to address the question: do z = 0 satellites in massive galaxy clusters retain, or not, their CGM. We specifically target the massive end of the host distribution to focus on the harshest environments and to maximize the mass range of satellite galaxies. TNG-Cluster includes 352 galaxy clusters with total mass 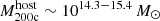$M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{14.3-15.4}{M}_{\odot }$ and over 90 000 satellites with stellar mass larger than ∼10⁹ M_⊙ at z = 0. It therefore provides an unprecedented sample size of satellites, including thousands of satellites more massive than our own Milky Way and Andromeda. These are simulated with the well-tested IllustrisTNG galaxy formation model (TNG hereafter) within a full ΛCDM cosmological context, and with competitive spatial and mass resolution. Despite important simplifications (such as no explicit modeling of the multiphase ISM, influencing results related to the cold gas – see Zinger et al. 2018; Kukstas et al. 2022), the TNG model returns satellite quenched fractions and gas contents that are broadly consistent with observations (e.g., Stevens et al. 2019, 2021; Donnari et al. 2021a).

Moreover, as shown in a series of companion papers that showcase first results from TNG-Cluster, the simulated halos exhibit X-ray luminosity scaling relations and other global properties of the ICM (Nelson et al. 2024), fractions of cool cores (Lehle et al. 2024), gas kinematics (Ayromlou et al. 2023a), levels of turbulence in the cores (Truong et al. 2024), and morphologically diverse radio relics (Lee et al. 2024) that are all broadly consistent with observations.

The goals of this work are: (a) to quantify the predictions from TNG-Cluster for the population of cluster satellites and their hot and cold gas reservoirs; by doing so, we aim to (b) provide interpretation for current X-ray observations of cluster galaxies and their spatial extent; (c) suggest an experiment to constrain the physics of satellites in massive hosts, beyond X-ray observations of individual systems; and (d) quantify the covering fraction of the CGM of satellites versus the ICM of the host.

We begin by describing the new simulation suite, sample selection, and our methods (Sect. 2). In Sect. 3, we present the clusters and their satellite demographics, the gaseous content of the satellites, the spatial extent of the satellite CGM, and the causes of satellite-to-satellite variations. We discuss details and caveats of our results in Sects. 4 and 4.1 we present a statistical stacking experiment to detect the soft X-ray emission from satellite CGM. We discuss implications of our findings in Sects. 4.2 and 4.3 and summarize our main results in Sect. 5.

2. Methods

2.1. TNG-Cluster

TNG-Cluster¹ is a suite of 352 massive galaxy cluster simulations, spanning halo masses M_200c ≈ 10^{14.3 − 15.4} M_⊙ (Nelson et al. 2024; Pillepich et al., in prep.). These halos were chosen from a ≈1 Gpc box-size parent dark matter only simulation, TNG-Cluster-Dark. The 352 halos chosen for re-simulation are based only on z = 0 halo mass such that: (i) all ∼100 halos with mass > 10¹⁵ M_⊙ are included; and (ii) halos with mass 10^{14.3 − 15.0} M_⊙ were randomly selected in bins of 0.1 dex such that the halo mass distribution is flat over this mass range (see Nelson et al. 2024, for details).

The TNG-Cluster simulation employs the well-tested TNG galaxy formation model (Weinberger et al. 2017; Pillepich et al. 2018a). The baryon mass resolution of TNG-Cluster is m_bar = 1.1 × 10⁷ M_⊙, the same resolution as TNG300 from the original TNG simulation suite (Pillepich et al. 2018b; Nelson et al. 2018; Naiman et al. 2018; Marinacci et al. 2018; Springel et al. 2018). We note that the TNG galaxy formation model at the TNG-Cluster mass resolution (the same as TNG300) has already been at least partially validated in the low-mass cluster regime (e.g., Nelson et al. 2018; Donnari et al. 2021a,b; Truong et al. 2020). Here we briefly summarize the model.

The TNG simulations, including TNG-Cluster, evolve gas, cold dark matter, stars, and super massive black holes (SMBHs) within an expanding universe, based on a self-gravity + magneto-hydrodynamic framework (Pakmor et al. 2011; Pakmor & Springel 2013) using the AREPO code (Springel 2010). The fluid dynamics employ a dynamic, moving Voronoi tessellation of space. Gas has a cooling floor at 10⁴ K, and the relationship between temperature and density for star-forming gas is determined via a two-phase sub-grid pressurization model (Springel & Hernquist 2003). For this analysis, we manually set the temperature of star-forming gas to 10³ K, its cold-phase value. The TNG galaxy evolution model includes: gas heating and cooling; star formation; stellar population evolution and chemical enrichment from AGB stars and type Ia + II supernovae; supernova driven outflows and winds (Pillepich et al. 2018a); the formation, merging, and growth of SMBHs; and two main SMBH hole feedback modes: a thermal “quasar” mode, and a kinetic “wind” mode (Weinberger et al. 2017).

Catalogs contain halos as well as galaxies. Dark matter halos are identified using the Friends-of-Friends (FoF) algorithm with a linking length b = 0.2, run only using the dark matter particles (Davis et al. 1985). Then the baryonic components are connected to the same halos as their closest dark matter particle. Throughout this paper, we use “FoF”, “group”, “FoF group”, and “halo” synonymously. Galaxies are then identified using the SUBFIND algorithm, which identifies gravitationally bound sets of particles and cells (Springel et al. 2001; Dolag et al. 2009). We use the terms “subhalo” and “galaxy” synonymously even though, in general, SUBFIND objects may contain no stars and/or gas whatsoever. Typically, the most massive subhalo within a halo is the “main” or “primary subhalo”, also called the “central galaxy”; all other subhalos within a halo are “satellites”. We follow the evolution of galaxies using SUBLINK_GAL, which constructs merger trees for subhalos by searching for descendants with common stellar particles and star-forming gas cells (Rodriguez-Gomez et al. 2015). The TNG simulations are publicly available in their entirety, and TNG-Cluster will likewise be released in 2024 (Nelson et al. 2019a, 2024). Our analyses adopt the same ΛCDM cosmology as TNG, consistent with the Planck Collaboration XIII (2016) results: Ω_Λ, 0 = 0.6911, Ω_m, 0 = Ω_bar, 0 + Ω_dm, 0 = 0.3089, Ω_bar, 0 = 0.0486, σ₈ = 0.8159, n_s = 0.9667, and h = H₀/(100 km s⁻¹ Mpc⁻¹) = 0.6774, where H₀ is the Hubble parameter.

2.2. Halo and satellite galaxy sample selection

In this work, we exclusively focus on the 352 primary zoom targets from the TNG-Cluster simulation². Moreover, we only consider satellite galaxies with stellar mass 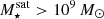$M_{\star }^{\mathrm{sat}}>{10}^9{M}_{\odot }$, corresponding to ≳100 stellar particles each.

As is common practice with TNG, we define galaxy stellar mass M_⋆ as the total SUBFIND stellar mass within twice the stellar half mass radius M_⋆ ≡ M_⋆(< 2 R_half, ⋆). For galaxy gas mass M_gas, we take the total gravitationally bound SUBFIND gas mass, regardless of galactic-centric distance. At times, we consider only cold ≤10^4.5 K, hot > 10^4.5 K, ISM (< 2 R_half, ⋆), or CGM (> 2 R_half, ⋆) gas, where all star-forming gas is cold by definition. The median (10th, 90th percentiles) gas cell size in the satellite CGM is 5.2 (3.0, 8.6) kpc. Table 1 summarizes all quantities and definitions.

Unless noted otherwise, we consider galaxies as satellites based on their Friends-of-Friends membership, and do not enforce any explicit restriction on the cluster-centric distance. In some analyses, we rather consider satellites as all galaxies within a 2D projected cluster-centric distance, to mimic observational samples (see Sect. 4.1 for more details). In all cases, we only consider subhalos of cosmological origin as defined by the SubhaloFlag in Nelson et al. (2019a). All FoF satellite galaxies considered are uncontaminated at z = 0, meaning that they contain zero dark matter low resolution elements. However, in general, it is possible that low resolution gas, stars, or dark matter are present, particularly at large distances away from clusters, but this is not expected to influence our results.

3. The circumgalactic medium of cluster satellites according to TNG-Cluster

3.1. Clusters and their satellite demographics

TNG-Cluster provides an unprecedentedly large set of simulated massive cluster galaxies whose basic demographics are consistent with observations of cluster richness. In particular, in Fig. 1 we plot the 2D histogram of all well-resolved satellites with M_⋆ > 10⁹ M_⊙ across the 352 clusters in the z = 0 satellite stellar 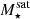$M_{\star }^{\mathrm{sat}}$ – host halo 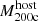$M_{200\mathrm{c}}^{\mathrm{host}}$ mass plane (main panel). The color shows the number of galaxies in each bin, which span 0.1 dex in each axis, with 1D histograms for host halo and satellite stellar mass on the top and right subpanels, respectively.

Fig. 1. Cluster and satellite demographics in TNG-Cluster. Top panels: we plot the number of satellite galaxies of the 352 clusters in bins of satellite stellar $M_{\star }^{\mathrm{sat}}$ and host halo $M_{200\mathrm{c}}^{\mathrm{host}}$ mass at z = 0. The one-dimensional histograms for $M_{\star }^{\mathrm{sat}}$ and $M_{200\mathrm{c}}^{\mathrm{host}}$ are included in the right and top panels. The number of satellites per stellar mass bin decreases with satellite stellar mass, where there is a sharp decrease in the number of super-L⋆ galaxies $M_{\star }^{\mathrm{sat}}>{10}^{10.5}{M}_{\odot }$. The number of satellites per host mass bin increases at lower cluster masses $M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{14.3-15}{M}_{\odot }$, and then decreases for the most massive clusters $M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{15-15.4}{M}_{\odot }$, which reflects the TNG-Cluster halo mass function (see text and Nelson et al. 2024 for details). Bottom panels: for each of the 352 hosts, we plot the number of FoF satellites above given stellar masses (left), where the medians and 16th and 84th percentiles are the solid curves and shaded regions respectively. Additionally, we qualitatively compare the TNG-Cluster results to spectroscopic (GalWCat19; Abdullah et al. 2020, 2023) and photometric (redMaPPer; Costanzi et al. 2019) SDSS observations, considering all galaxies brighter than rmag < −20.4 and within a projected distance $d_{\mathrm{sat}}^{\mathrm{host}}<R_{200\mathrm{c}}$ as satellites (right panel; see text for details). The TNG-Cluster mass-richness relation is qualitatively consistent with observations.

The 352 galaxy clusters spanning 1 dex in host mass contain a total of ≈90 000 satellites, covering 3.5 dex in stellar mass. The maximum satellite stellar mass increases with halo mass, as no satellite galaxy may be more massive than its brightest cluster galaxy (BCG) by definition. For example, the BCG stellar mass within a 10^14.5 (10¹⁵) M_⊙ cluster is ≈10¹² (10^12.2) M_⊙. This is, for example, visible in the 2D histogram (central panel) as a triangular region lacking satellites in the upper left corner. Throughout this work, we refer to satellites 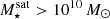$M_{\star }^{\mathrm{sat}}>{10}^{10}{M}_{\odot }$ as massive, and focus primarily on these systems.

It should be kept in mind that the TNG-Cluster (+TNG300) halo mass function is approximately flat at masses 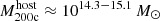$M_{200\mathrm{c}}^{\mathrm{host}}\approx {10}^{14.3-15.1}{M}_{\odot }$, whereas there is a sharp decrease in the number of halos at the highest-mass end 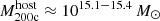$M_{200\mathrm{c}}^{\mathrm{host}}\approx {10}^{15.1-15.4}{M}_{\odot }$, where the sample is volume limited (see Fig. 1 from Nelson et al. 2024). As a consequence, in TNG-Cluster, the number of satellites per host mass bin increases with halo mass for lower-mass clusters to then decrease again toward the most massive systems in our sample: this is because more massive clusters on average host more satellites, but more massive clusters are also rarer. On the other hand, the TNG-Cluster satellite stellar mass function (top right subpanel) exhibits the typical shape characteristic also of central galaxies, with a slow decrease for 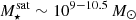$M_{\star }^{\mathrm{sat}}\sim {10}^{9-10.5}{M}_{\odot }$, and a fast drop-off for massive super-L_⋆ satellites 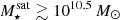$M_{\star }^{\mathrm{sat}}\gtrsim {10}^{10.5}{M}_{\odot }$ (e.g., Baldry et al. 2012).

In Fig. 1 (bottom left panel), we show a theoretical richness-mass relation, that is, the average number of satellites per host above a given stellar mass threshold, as a function of host mass 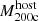$M_{200\mathrm{c}}^{\mathrm{host}}$. Solid curves represent medians across the cluster sample, with the 16th and 84th percentiles as shaded regions. As expected, the number of satellites per host above any given stellar mass increases with host mass. For example, at a mass 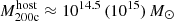$M_{200\mathrm{c}}^{\mathrm{host}}\approx {10}^{14.5}({10}^{15})M_{\odot }$, each cluster hosts ≈100 (300) satellite galaxies of mass 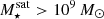$M_{\star }^{\mathrm{sat}}>{10}^9{M}_{\odot }$ (light orange). Also as expected, at a fixed halo mass, the number of galaxies above a given stellar mass threshold increases as the mass threshold decreases. In TNG-Cluster, nearly all clusters host a few extremely massive satellite galaxies M_⋆ > 10¹¹ M_⊙ (dark orange).

Finally, in Fig. 1 (bottom right panel), we qualitatively compare the richness-mass relation predicted by TNG-Cluster with spectroscopic (GalWCat19; Abdullah et al. 2020, 2023) and photometric (redMaPPer; Costanzi et al. 2019) SDSS observations. In particular, we plot the number of satellites per host brighter than r < −20.4 mag, corresponding to 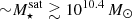$\sim M_{\star }^{\mathrm{sat}}\gtrsim {10}^{10.4}{M}_{\odot }$. Here by satellites we mean all galaxies within the high-resolution zoom region of depth 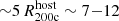$\sim 5R_{200\mathrm{c}}^{\mathrm{host}}\sim 7-12$ Mpc and within a projected distance 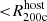$<R_{200\mathrm{c}}^{\mathrm{host}}$, regardless of the FoF membership. Even though we do not create synthetic observations to match the SDSS data and hence even though these comparisons are at face value, the result is encouraging: the TNG-Cluster richness-mass relation is qualitatively consistent with SDSS (see also Nelson et al. 2024, and their Fig. 16).

3.2. The gas content of cluster satellites

Of the ≈90 000 TNG-Cluster satellites with 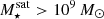$M_{\star }^{\mathrm{sat}}>{10}^9{M}_{\odot }$, only ≈10 000 (10%) retain at least some gas today. Throughout the paper, by this we mean at least 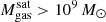$M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ of gravitationally bound gas reservoirs, that is,a well resolved amount of gas. We motivate this choice in Appendix A and, we have checked that adding an additional criterion on the gas mass fraction 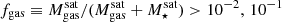$f_{\mathrm{gas}}\equiv M_{\mathrm{gas}}^{\mathrm{sat}}/(M_{\mathrm{gas}}^{\mathrm{sat}}+M_{\star }^{\mathrm{sat}})>{10}^{-2},{10}^{-1}$ would remove an unimportant subset of galaxies, that is, 40 (0.4%), 777 (7.7%) of the gaseous satellites.

In Fig. 2 (top left panel), we explore how this fraction of gas-rich satellites varies with satellite stellar 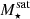$M_{\star }^{\mathrm{sat}}$ and host cluster 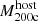$M_{200\mathrm{c}}^{\mathrm{host}}$ mass. At a fixed satellite stellar mass (a given row), the fraction of gas-rich satellites tends to decrease with increasing host mass, broadly consistent with expectations from RPS. Namely, ram pressure increases with host mass, thereby driving down the fraction of gas-rich satellites. Moreover, at a fixed halo mass (a given column), the fraction of gas-rich satellites increases with satellite stellar mass, and this trend exists at all considered stellar masses. The restorative gravitational pull from the stellar body acts as the primary foil to ram pressure, thereby increasing the fraction of gas-rich satellites with increasing satellite mass (e.g., Wright et al. 2022; Rohr et al. 2023; Kulier et al. 2023).

Fig. 2. How the TNG-Cluster satellite gas mass varies with the satellite stellar and host halo mass. Top left panel: for the ≈90 000 TNG-Cluster satellites with $M_{\star }^{\mathrm{sat}}>{10}^9{M}_{\odot }$, the fraction of satellites that retain gas reservoirs $M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ today as satellites is shown in bins of satellite stellar $M_{\star }^{\mathrm{sat}}$ and cluster $M_{200\mathrm{c}}^{\mathrm{host}}$ mass. Top right panel: only 10 000 (10%) of the TNG-Cluster satellites retain gas masses $M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ today. For these gaseous satellites, we show the median satellite gas mass $M_{\mathrm{gas}}^{\mathrm{sat}}$ in bins of satellite stellar $M_{\star }^{\mathrm{sat}}$ and host halo $M_{200\mathrm{c}}^{\mathrm{host}}$ mass. Bottom panels: we show the fractions (left panel) and numbers (right panel) of satellites with all (purple, solid, filled), hot (red, dashed, “\” hatched), and cold (blue, dashed-dotted, “/” hatched) gas masses > 109 M⊙ within a given stellar mass bin at z = 0. We mark 100% and the global average of 10% with black lines, and include the total number of gaseous satellites in the legend. While a given satellite is more likely to retain gas if it has a higher stellar mass, a given gaseous satellite is more likely to have a lower stellar mass because there are simply more lower-mass satellites.

In Fig. 2 (top right panel), we further show that, for the ≈10 000 gas-rich satellites, the average satellite gas mass generally increases with satellite stellar mass. In fact, this applies to the most massive satellites and is not the case for those with mass 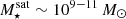$M_{\star }^{\mathrm{sat}}\sim {10}^{9-11}{M}_{\odot }$, which all exhibit a rather uniform 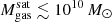$M_{\mathrm{gas}}^{\mathrm{sat}}\lesssim {10}^{10}{M}_{\odot }$ of gas reservoir³. Indeed, about 100 TNG-Cluster satellites retain gas masses 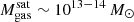$M_{\mathrm{gas}}^{\mathrm{sat}}\sim {10}^{13-14}{M}_{\odot }$ today: these are the most massive satellites in the simulation, and would be in general some of the most massive galaxies in the Universe. We note that these could in fact be considered merging sub clusters (see the companion paper by Lehle et al. 2024). Interestingly, for all gas-rich satellites, the average gas mass does not depend on host mass across the TNG-Cluster mass range. We speculate two origins for the null-trend of median (gas-rich) satellite gas mass with cluster mass. First, and only applying to satellites of mass 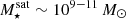$M_{\star }^{\mathrm{sat}}\sim {10}^{9-11}{M}_{\odot }$, the average satellite gas mass 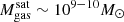$M_{\mathrm{gas}}^{\mathrm{sat}}\sim {10}^{9-10}{M}_{\odot }$ is just above our threshold for being considered gas-rich 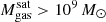$M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ (see Appendix A for more details). Many of these satellites are likely undergoing environmental processes en route toward becoming gas-poor; they have not yet been cluster-members long enough to have been stripped of their gas. Second and related, these satellites may have had their gas reservoirs first preprocessed by other groups before falling into their current cluster hosts (e.g., Jung et al. 2018; Donnari et al. 2021b).

With this intuition that gas retention is primarily determined by satellite mass, in Fig. 2 (bottom panels), we show how the fraction (bottom left panel) and number (bottom right panel) of satellites that retain significant gas reservoirs at z = 0 vary with satellite stellar mass. We split the gas (purple, solid, filled) into hot (red, dashed, “/” hatch) and cold (blue, dash-dotted, “\” hash) phases. Across all stellar masses considered, ≈91% of the gaseous satellites retain at least some cold gas. For the hot gas, this only applies to ≈70% of the gaseous satellites.

At low stellar masses 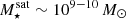$M_{\star }^{\mathrm{sat}}\sim {10}^{9-10}{M}_{\odot }$ the fraction (left) and number (right) of gas-rich satellites increases with stellar mass for all, hot, and cold gas. Nearly all gas-rich satellites retain cold gas at these stellar masses, and the fraction of gas-rich satellites that retain hot gas increases rapidly with stellar mass. This is consistent with ram pressure removing hot, spatially extended gas preferentially first, while the cold ISM gas tends to be more resistant to these environmental effects (e.g., Wright et al. 2022; Rohr et al. 2023, Fig. 3).

Fig. 3. Spatial extent of satellite gas in TNG-Cluster. Of the ≈5000 gas-rich $M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ massive satellites $M_{\star }^{\mathrm{sat}}>{10}^{10}{M}_{\odot }$ at z = 0, we examine the spatial extent of all (hot and cold) gas at a fixed host cluster mass $M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{15}{M}_{\odot }$ and at three stellar masses $M_{\star }^{\mathrm{sat}}\sim {10}^{10}$, 1010.75,  1011.5 M⊙ (top panels, left to right respectively). Moreover, we compare the total gas density (purple) at z = 0 of cluster members as satellites with that at infall as centrals (black). All curves show the median profiles of all galaxies in the bin; see Fig. 4 for the individual profiles to see the galaxy-to-galaxy variation. We define all gas outside > 2 Rhalf, ⋆ as the circumgalactic medium (CGM). We then plot total CGM mass $M_{\mathrm{CGM}}^{\mathrm{sat}}$ as a function of galaxy stellar mass $M_{\star }^{\mathrm{sat}}$ (bottom panel) at infall as centrals (black), and at z = 0 as satellites (pink). The curves are the medians of the CGM masses (only the galaxies with nonzero CGM mass for the satellites), and for the most massive galaxies we plot the individual objects (circles) and the median stacks (squares). We manually place the ≈28 000 CGM-poor $M_{\mathrm{CGM}}^{\mathrm{sat}}<{10}^9{M}_{\odot }$ satellites at masses ∼107 − 8 M⊙. All stacks use stellar, host, and gas masses at z = 0, and the radial profiles are normalized to Rhalf, ⋆ at the considered time (infall or today). More than 5000 cluster satellites retain a CGM despite residing in harsh cluster environments.

At intermediate stellar masses 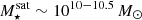$M_{\star }^{\mathrm{sat}}\sim {10}^{10-10.5}{M}_{\odot }$, the fraction of gas-rich satellites (left panel) slightly decreases from ≈16 to ≈13%, where the fraction with cold gas (blue, dashed-dotted) drops to ≈12%. The decrease in gas retention at these stellar masses is likely due to the onset of the kinetic-mode of AGN feedback (Weinberger et al. 2017; Nelson et al. 2018; Zinger et al. 2020; Truong et al. 2020; Ayromlou et al. 2021b, see below: Figs. 3 and 4 right panels). At high stellar masses 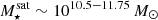$M_{\star }^{\mathrm{sat}}\sim {10}^{10.5-11.75}{M}_{\odot }$, the fraction of (cold) gaseous satellites increases with stellar mass to a maximum of ≈60% (≈30%). More massive galaxies retain more gas as they (i) have deeper gravitational potential wells; and (ii) tend to be later infallers (into any host; see Table 1 for details), thereby decreasing the amount of time they have been experiencing environmental effects.

Fig. 4. How ram pressure and SMBHs affect the gas contents of TNG-Cluster satellite galaxies. For the gas-rich $M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ satellites at a fixed cluster $M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{15}{M}_{\odot }$ and satellite $M_{\star }^{\mathrm{sat}}\sim {10}^{10},{10}^{10.75}{M}_{\odot }$ (top versus bottom panels) mass, we show total gas density radial profiles colored by current ram pressure (left column) and SMBH mass (right column). The thick curves show the medians of the top and bottom quartiles of ram pressure and SMBH mass, and the thin curves are the profiles of the individual satellites. Ram pressure tends to truncate the gas profiles at large distances and slightly compress the ISM gas, while SMBH feedback tends to eject and decrease the density of the ISM gas for more massive satellites.

While the fraction of gaseous satellites generally increases with mass (top panel), the total number of gaseous satellites decreases with stellar mass (bottom panel), because that the total number of satellites decreases with stellar mass (Fig. 1). Thus, while a given satellite is more likely to retain gas if it has a higher stellar mass, a given gas-rich satellite is more likely to have a lower stellar mass, because there are in general many more low-mass satellites.

3.3. The spatial extent of the satellite gas: The case for the satellite circumgalactic medium

To assess the extent of and understand how various physical processes reshape the multiphase gas reservoirs in and around satellites, we turn to the gas radial profiles of the ≈10 000 gas-rich satellites in TNG-Cluster. In Fig. 3 (top panels), we show the median gas radial profiles (see Fig. 4 for the individual profiles to see the galaxy-to-galaxy variation) separated into all (purple), hot (red), and cold (blue) phases at z = 0 as satellites at a fixed host cluster mass 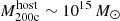$M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{15}{M}_{\odot }$ and at fixed satellite stellar masses 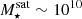$M_{\star }^{\mathrm{sat}}\sim {10}^{10}$, 10^10.75, 10^11.5 M_⊙ (left to right, respectively). All stacks and 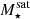$M_{\star }^{\mathrm{sat}}$ measurements are at z = 0. For comparison, we include the total gas profile at infall when the galaxies were centrals (black). We consider all gas within 2 R_half, ⋆ as the interstellar medium (ISM) and all gas at > 2 R_half, ⋆ as the circumgalactic medium (CGM).

Across all considered stellar masses and at all galactic-centric distances, galaxies have higher gas densities at infall as centrals, compared to today as satellites. As a result, satellites have lower gas masses and higher quenched fractions than their central counterparts (e.g., Stevens et al. 2019; Donnari et al. 2021b, for TNG). In detail, the differences between the gas density at infall and z = 0 vary both with galactic-centric distance and satellite stellar mass. Moreover, the most prevalent gas phase (hot, red; or cold, blue) today also depends on these two quantities. Complicating the issue, at higher stellar masses 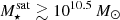$M_{\star }^{\mathrm{sat}}\gtrsim {10}^{10.5}{M}_{\odot }$, nearly all galaxies in the TNG model experience strong AGN kinetic-mode feedback. That is, high-mass satellites are subject to both external and internal processes that impact their gas reservoirs.

At lower stellar masses 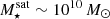$M_{\star }^{\mathrm{sat}}\sim {10}^{10}{M}_{\odot }$ (left panel), the total gas density today is composed primarily of cold gas, especially within the ISM. Only at large distances ≳5 R_half, ⋆ does the hot gas begin to contribute significantly to the total gas density. Within the ISM, the total gas density is largely unchanged for central versus satellite status. However, at the outskirts ≳10 R_half, ⋆, there is a clear truncation in gas profiles. These differences are consistent with expectations from ram pressure removal, where the spatially extended gas is removed preferentially earlier than the tightly bound ISM (Balogh & Morris 2000).

At intermediate stellar masses 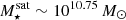$M_{\star }^{\mathrm{sat}}\sim {10}^{10.75}{M}_{\odot }$ (middle panel), the total gas density today is composed of similar amounts of hot and cold gas at all distances. Unlike lower-mass galaxies, these have experienced episodes of AGN feedback which partially ejects nearby, mostly cold, ISM gas (Nelson et al. 2019b), reducing its density. At large distances in the CGM > 2R_half, ⋆, the total gas density both at infall and z = 0 extend to farther distances than at smaller stellar masses. The higher-mass satellites retain sizeable gas reservoirs at large distances up to ≳30 R_half, ⋆.

This trend continues to the highest stellar mass bin 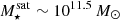$M_{\star }^{\mathrm{sat}}\sim {10}^{11.5}{M}_{\odot }$ (right panel). Here, the gas density is comprised almost entirely of hot gas at all distances. In fact, there is little to no cold gas within the ISM, that is, galaxies at these masses are largely quenched, regardless of central or satellite status (Donnari et al. 2021b). The differences between the total gas density profiles as centrals versus as satellites are roughly constant at all distances. The CGM density is highest for these high-mass galaxies, and this satellite CGM gas extends to larger physical distances.

In the bottom panel of Fig. 3, we provide one of the key quantitative findings of this analysis: the CGM mass 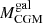$M_{\mathrm{CGM}}^{\mathrm{gal}}$ of satellites as a function of stellar mass 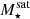$M_{\star }^{\mathrm{sat}}$ (pink), and at infall as centrals (black). The curves are the medians of the CGM masses (only the galaxies with nonzero CGM mass for the satellites), and for the most massive galaxies we plot the individual objects (circles) and the median stacks (squares). Here by CGM we mean the gas reservoir that extends beyond the main stellar body of a galaxy. According to TNG-Cluster, more than 5000 massive 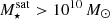$M_{\star }^{\mathrm{sat}}>{10}^{10}{M}_{\odot }$ satellites retain their own CGM or gaseous atmosphere despite the harsh cluster environments. Further, on average, the retained CGM mass increases with satellite stellar mass, while the differences between infall and z = 0 decrease. higher-mass satellites are more resistant to environmental effects and are able to retain spatially extended gas reservoirs. Beyond the average trends, however, there remains a large galaxy-to-galaxy variation in the ability of retaining CGM mass, and we study exactly this diversity next.

3.4. The diversity of satellite circumgalactic media

We now consider individual galaxies to explore the diversity of satellite CGM. In Fig. 4 we plot the total gas density radial profiles for all gas-rich 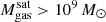$M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ satellites at a fixed host halo 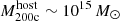$M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{15}{M}_{\odot }$ and satellite stellar mass 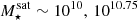$M_{\star }^{\mathrm{sat}}\sim {10}^{10},{10}^{10.75}$. We color the profiles by their instantaneous ram pressure⁴ (left column) and supermassive black hole (SMBH) mass (right column), and we overplot the medians of the top and bottom quartiles of ram pressure and SMBH mass. We also examine the effect of time since infall, a proxy for the integrated environmental effects, on the radial profiles and find similar results that of the instantaneous ram pressure (not shown).

At lower stellar masses 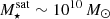$M_{\star }^{\mathrm{sat}}\sim {10}^{10}{M}_{\odot }$, satellites experiencing more ram pressure have lower CGM densities, and their spatial extent is truncated (top left panel). This result also holds for higher satellite masses (lower left panel). In the ISM < 2 R_half, ⋆, gas densities tend to increase with ram pressure, but the effect is small. At higher stellar masses 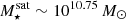$M_{\star }^{\mathrm{sat}}\sim {10}^{10.75}{M}_{\odot }$ (bottom left panel), this effect is stronger. Recent simulations and radio observations predict and infer that ram pressure can compress a satellite’s ISM (e.g., Vulcani et al. 2018; Roberts et al. 2022; Kulier et al. 2023), and our results qualitatively agree.

To examine the effect of SMBH feedback we use SMBH mass as a proxy. This is the integral of the SMBH accretion history, and so it is a proxy of and proportional to the total feedback energy ever released. At lower stellar masses 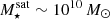$M_{\star }^{\mathrm{sat}}\sim {10}^{10}{M}_{\odot }$ (top left panel), SMBHs do not seem to have an impact on satellite gas densities. Within the TNG model, the SMBHs in these galaxies are largely in the quasar mode, where the corresponding feedback couples poorly to the gas, and is thus not ejected (Weinberger et al. 2018).

At higher stellar masses 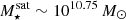$M_{\star }^{\mathrm{sat}}\sim {10}^{10.75}{M}_{\odot }$ (bottom right panel), SMBHs are more important. At these masses and by z = 0, most of these satellites have experienced episodes of kinetic AGN feedback. Those with lower SMBH masses have higher ISM densities by ∼1 − 2 dex than those with higher-masses. This effect extends into the CGM, to ∼10 R_half, ⋆. When SMBHs begin accreting at low rates, exerting wind mode feedback and expelling the ISM gas, they partially remove their own source of fuel for gas accretion. Without a supply of nearby cold gas, SMBHs grow more slowly. As a result, finding SMBHs in satellites that are much more massive is rare, although in central galaxies they can continue to grow via mergers (Joshi et al. 2020). At large radii ≳10 R_half, ⋆ there is little impact from SMBH feedback. So, in summary, SMBH feedback tends to eject and decrease the density of the ISM gas for more massive, gas-rich satellites M_⋆ ≳ 10¹¹ M_⊙, which are typically quenched as a result but can still hold on to their CGM.

Now as seen in the previous sections, while many massive satellites manage to retain their own CGM today, at stellar masses 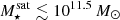$M_{\star }^{\mathrm{sat}}\lesssim {10}^{11.5}{M}_{\odot }$ a majority of TNG-Cluster satellites have actually lost their gas reservoirs due to combinations of secular and environmental processes. Moreover, among the gas-rich massive satellites, the retained CGM mass can vary by 2 or 3 orders of magnitude (Fig. 3, main panel).

For high-mass satellites 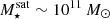$M_{\star }^{\mathrm{sat}}\sim {10}^{11}{M}_{\odot }$, we therefore study why most (∼80%; Fig. 2, bottom left panel) end up gas-poor at z = 0. Figure 5 shows the probability distribution functions (PDFs) of infall times for satellites at a fixed host halo 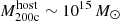$M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{15}{M}_{\odot }$ and satellite stellar 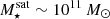$M_{\star }^{\mathrm{sat}}\sim {10}^{11}{M}_{\odot }$ (total, black), split into those that are gas-poor 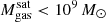$M_{\mathrm{gas}}^{\mathrm{sat}}<{10}^9{M}_{\odot }$ (red), and those that are gas-rich 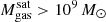$M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ (blue) today. The infall time is the first infall into any host, regardless if the galaxy has been preprocessed or not. Gas-rich satellites tend to be late-infallers, experiencing environmental effects for a shorter period of time than gas-poor satellites.

Fig. 5. Gas-rich satellites today are typically late infallers. We plot the probability distribution functions (PDFs) of the infall times of all (black), gas-poor $M_{\mathrm{gas}}^{\mathrm{sat}}<{10}^9{M}_{\odot }$ (red), and gas-rich $M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ (blue) TNG-Cluster satellites at a fixed host halo $M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{15}{M}_{\odot }$ and satellite stellar $M_{\star }^{\mathrm{sat}}\sim {10}^{11}{M}_{\odot }$ mass. We mark the medians and errors of the distributions as hashes on the top x-axis. The infall time is the first infall into any host, regardless if the galaxy has been preprocessed or not. At a fixed host halo and satellite stellar mass, the infall time is the primary driver determining whether satellites remain gas-rich or gas-poor today: more recent infallers are more likely to retain large gas reservoirs.

We further explore the cumulative environmental effects in Fig. 6, where we show the time-evolution since infall (τ_FirstInfall ≈ 8.6 Gyr, i.e., look-back time ≈5 Gyr ago) of the gas radial profiles for an example gas-poor satellite today (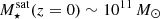$M_{\star }^{\mathrm{sat}}(z=0)\sim {10}^{11}{M}_{\odot }$ in a cluster of mass 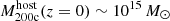$M_{200\mathrm{c}}^{\mathrm{host}}(z=0)\sim {10}^{15}{M}_{\odot }$). As the time since infall increases, the gas density at a fixed galacto-centric distance decreases, and the maximum extent of the CGM truncates, approximately following the direction of arrow. After sufficient time in the cluster environment, subject to ram pressure from its passage through the ICM, the galaxy loses all of its gas, becoming a gas-poor, quenched satellite today.

Fig. 6. How the environment removes gas from an example satellite. For an example gas-poor satellite today of mass $M_{\star }^{\mathrm{sat}}(z=0)\approx {10}^{10.9}{M}_{\odot }$ in a cluster of mass $M_{200\mathrm{c}}^{\mathrm{host}}(z=0)\approx {10}^{15.0}{M}_{\odot }$, we study the time evolution of the gas radial profiles since first infall (τFirstInfall ≈ 8.6 Gyr i.e., look-back time ≈5 Gyr) until it becomes gas-poor today. The cumulative environmental effects, namely the integrated ram pressure since infall, and secular processes, namely feedback from the SMBH, remove the satellite’s gas, leaving a gas-poor, quenched satellite today.

4. Implications of satellite CGM in clusters

As we have seen in the previous sections, massive satellite galaxies can retain a spatially extended, mostly hot CGM, and each cluster hosts a few to tens such massive satellites. One would then expect the satellite CGM to emit in the X-ray and to contribute to the total X-ray flux from galaxy clusters. Moreover, satellite CGM could contribute to absorption lines on background quasar spectra in the near UV. We thereby study the possibility to statistically detect this satellite CGM in observations.

These results and the following discussion depend on a number of assumptions: the TNG galaxy formation model, the Friends-of-Friends halo finder for defining the halos and their members, the SUBFIND algorithm for determining the galaxies’ bound resolution elements, the TNG-Cluster halo sample, and the numerical resolution of TNG-Cluster itself (see Appendix A for more details on the gas resolution).

4.1. Detecting extended soft X-ray emission around satellites

We now turn to answer the following question: can the hot CGM retained by satellites be detected, above the background ICM (Schuecker et al. 2001). This hot satellite gas emits thermally via bremsstrahlung in the X-ray, similarly to the ICM. However the gas temperature is much lower for satellite CGM gas ≈0.5 − 2 keV compared to the ICM at ≈5 − 10 keV (see also Truong et al. 2024). We therefore focus on the soft X-ray 0.5 − 2 keV emission, computed using the collisional ionization tables of AtomDB from the Astrophysical Plasma Emission Code (Smith et al. 2001, following Nelson et al. 2023).

In Fig. 7 we show examples of broad-band soft X-ray emission around 16 TNG-Cluster satellite galaxies. These galaxies are necessarily within a projected distanced 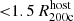$<1.5R_{200\mathrm{c}}^{\mathrm{host}}$ of one of the 352 TNG-Cluster BCGs. Each image is 600 × 600 kpc² in size, and we include information about each galaxy and its host in the panels. The X-ray emission around these galaxies is clearly visible against the background ICM, even without a background subtraction. The X-ray morphologies are diverse; while many examples are roughly circular, many also show asymmetries and filamentary features. These morphologies could be caused by both internal (for example, SMBH feedback, such as for SubfindIDs 256830, 4373716, 7596594) and/or external processes (for example, ram pressure, such as for SubfindIDs 7596594, 7929001). These are some of the most prominent spatially extended X-ray emission around satellites, but each cluster hosts several such examples⁵ (Nelson et al. 2024).

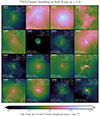Fig. 7. Poster of the diversity of TNG-Cluster satellites in soft X-ray emission. We show the soft X-ray (0.5−2.0 keV) surface brightness for 16 example TNG-Cluster satellite galaxies at z = 0. Each image is 600 × 600 kpc2 in size (scale bar in the upper left). These galaxies are necessarily within a projected distance of 1.5 R200c of their host. We include information about the galaxy and its host in the upper right and lower left corners; the units of the cluster $M_{200\mathrm{c}}^{\mathrm{host}}$ and satellite $M_{\star }^{\mathrm{sat}}$ mass are [log10 M⊙], and the soft X-ray luminosity $L_{0.5-2.0\mathrm{keV}}^{<300\mathrm{kpc}}$ is the total X-ray luminosity within a projected aperture of 300 kpc in units of [log10 erg s−1]. Many of the maps display morphological signatures of SMBH feedback, with dome-like inflated bubbles and/or ram pressure, with gas tails extending in specific directions.

We now quantify the spatial extent of the X-ray emitting gas compared to the ambient background for all > 30 000 massive satellite galaxies around TNG-Cluster hosts. Figure 8 displays a schematic of our methodology. We start with the projected soft X-ray map of an entire cluster (top left panel; this example has mass 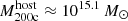$M_{200\mathrm{c}}^{\mathrm{host}}\approx {10}^{15.1}{M}_{\odot }$), where the image is 3 R_200c (≈6.9 Mpc) in size in each direction and the white circle marks R_200c. We include all gas in the simulation in this projection, with a depth of ∼5 R_200c ∼ 10 Mpc. We then smooth the X-ray map using a Gaussian kernel with a fixed physical width of 300 kpc (top center panel). This choice of smoothing length enables us to detect excesses and deficits compared to the background on scales smaller than 300 kpc. On larger scales, the signal is smoothed out and tends toward the background medium. We vary this smoothing scale between 100 and 1000 kpc, finding qualitatively similar results. The projected soft X-ray surface brightness radial profile (top right panel) decreases with halo-centric radius, where the dashed line marks the halo radius. This radial profile itself does not provide a good background estimate, as the ICM can be far from spherically symmetric (e.g., Truong et al. 2021).

Fig. 8. Schematic detailing how we detected satellites’ circumgalactic media and measured their radial profiles. For a given halo (halo mass $M_{200\mathrm{c}}^{\mathrm{host}}\approx {10}^{15.1}{M}_{\odot }$) at z = 0, we compute the soft X-ray (0.5 − 2.0 keV) continuum surface brightness (SB) on 5 × 5 kpc2 pixels (top left). We then smooth the image using a Gaussian kernel of standard deviation 300 kpc (top center). The white circles indicate the virial radius. We include the azimuthally averaged radial profile, where the dashed line marks the virial radius (top right). We compute the soft X-ray surface brightness excess as the ratio of all the gas in the image to the smoothed model (bottom left), and zoom in on an individual example satellite (bottom center; stellar mass $M_{\star }^{\mathrm{sat}}\approx {10}^{10.5}{M}_{\odot }$ at projected cluster-centric distance $d_{\mathrm{sat}}^{\mathrm{host}}\approx 1.0R_{200\mathrm{c}}^{\mathrm{host}}$). We include the contours of {1, 2, 5} times the background on the zoom-in and on the satellite’s excess radial profile (bottom right). In this satellite we detect a soft X-ray surface brightness excess out to ≈200 kpc from the satellite’s center, and the morphology suggests the satellite’s X-ray emitting gas is experiencing environmental effects. The soft X-ray excess profile for this example satellite is similar to others of the same stellar mass and cluster-centric distance (see Fig. 9 and text).

We compute the soft X-ray surface brightness excess map (bottom left) as the normal X-ray map divided by the smoothed model. In this map the perturbations – both excess (green-blue) and deficits (orange-red) – are clearly visible. Satellites and their CGM produce many of these perturbations, both point-like and extended excess sources. Here, we zoom in on one example satellite of mass 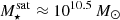$M_{\star }^{\mathrm{sat}}\approx {10}^{10.5}{M}_{\odot }$ and at projected host-centric distance 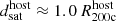$d_{\mathrm{sat}}^{\mathrm{host}}\approx 1.0R_{200\mathrm{c}}^{\mathrm{host}}$ (bottom center panel), where the zoom region is 600 kpc per side. The contours mark where the X-ray surface brightness reaches {1, 2, 5} times the smoothed background. The region of excess X-ray emission (inside the outermost contour) extends to large distances and has a complex morphology. The inner, brighter regions show signs of ram pressure removal. We show the projected radial profile (lower right panel), and find that the excess X-ray emission decreases with satellite-centric distance, reaching the background value at ≈200 kpc. This example X-ray excess profile is similar to the average of all satellites of this mass and distance, although the maximum excess at small satellite-centric distances for this example is lower than average (see text below and Fig. 9, bottom right panel).

Fig. 9. Stack of the z = 0 satellite soft X-ray surface brightness excess radial profiles around all 352 TNG-Cluster halos. We compute the soft X-ray (0.5−2.0 keV) surface brightness (SB) excess around all ≈37 000 galaxies with $M_{\star }^{\mathrm{sat}}>{10}^{10}{M}_{\odot }$ and within a projected distance $d_{\mathrm{sat}}^{\mathrm{host}}<1.5R_{200\mathrm{c}}^{\mathrm{host}}$ of the 352 hosts. We then mean-stack these radial profiles in bins of satellite stellar mass $M_{\star }^{\mathrm{sat}}$ (top panel), and within a fixed stellar mass bin, we further stack in bins of host cluster mass $M_{200\mathrm{c}}^{\mathrm{host}}$ (bottom left) and cluster-centric distance (bottom right). In all panels, the control sample represents the same measurement, at random locations such that the distributions of cluster-centric distances match that of the satellites. Across all satellites, the X-ray excess extends to ∼20 − 100 kpc, although individual satellites or specific stacks may exhibit excesses out to ≈300 kpc from the satellites.

We next consider all massive galaxies 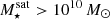$M_{\star }^{\mathrm{sat}}>{10}^{10}{M}_{\odot }$ within a projected cluster-centric distance 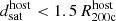$d_{\mathrm{sat}}^{\mathrm{host}}<1.5R_{200\mathrm{c}}^{\mathrm{host}}$, ignoring the FoF membership. This yields ≈37 000 satellites around the 352 clusters. We zoom-in on the positions of each of these satellites and compute the soft X-ray surface brightness excess radial profile. Figure 9 shows the mean-stacked profiles in bins of satellite stellar mass 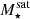$M_{\star }^{\mathrm{sat}}$ (top center), host halo mass 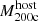$M_{200\mathrm{c}}^{\mathrm{host}}$ (bottom left), and cluster-centric distance (bottom right). As a reminder, ≈85% of these satellites are gas-poor and do not contribute to the total emission, but we still include them in stacks⁶. Some of these galaxies lie in projection near other X-ray excesses (deficits) and would still contribute (negatively) to the stacked profile. It is not clear a priori if the excesses and deficits cancel each other out. We therefore construct a control sample stack that matches the distribution of cluster-centric distances. While we construct control samples for each stack (in satellite mass, host mass, and cluster-centric distance), the differences between the controls of each stack are negligible, and all show a surface brightness excess of ≈1. We simplify by plotting the total control sample (black curves) in each panel.

In Fig. 9 (top center), all three stellar mass 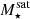$M_{\star }^{\mathrm{sat}}$ bins display X-ray excesses compared to the control. The most massive satellites 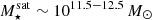$M_{\star }^{\mathrm{sat}}\sim {10}^{11.5-12.5}{M}_{\odot }$ (dark orange), have an excess of nearly ≈10× the background at small satellite-centric distances ≲10 kpc, and the excess extends out to ≈300 kpc. The intermediate 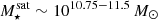$M_{\star }^{\mathrm{sat}}\sim {10}^{10.75-11.5}{M}_{\odot }$ (orange) and lower 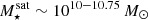$M_{\star }^{\mathrm{sat}}\sim {10}^{10-10.75}{M}_{\odot }$ (light orange) bins also display extended X-ray excesses out to ≈100 and ≈30 kpc respectively. The satellites in the lower-mass bin have a higher peak X-ray excess at small distances than those in the intermediate mass bin. As shown in Fig. 3 (top panels), the hot gas density at small distances ≲R_half, ⋆ is higher for lower-mass satellites 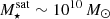$M_{\star }^{\mathrm{sat}}\sim {10}^{10}{M}_{\odot }$ than for intermediate-mass satellites 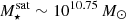$M_{\star }^{\mathrm{sat}}\sim {10}^{10.75}{M}_{\odot }$. Using hot gas density as a proxy for soft X-ray luminosity, we would then expect these lower-mass satellites (light orange) to be brighter at small distances than intermediate-mass satellites (orange). We speculate that the lower hot gas density in the centers of high-mass satellites could be caused by the AGN feedback redistributing gas to larger distances (e.g., Ayromlou et al. 2023b).

To distinguish from the effects of satellite mass, we now further stack the X-ray excess radial profiles by host mass 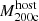$M_{200\mathrm{c}}^{\mathrm{host}}$ (bottom left) and cluster-centric distance 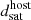$d_{\mathrm{sat}}^{\mathrm{host}}$ (bottom right) only for the satellites in the lowest-mass bin 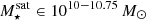$M_{\star }^{\mathrm{sat}}\in {10}^{10-10.75}{M}_{\odot }$. In the X-ray excess radial profiles stacked by host mass 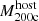$M_{200\mathrm{c}}^{\mathrm{host}}$ (bottom left), all three halo mass bins display similar maximum excess of ≈10× the background at small distances and similar extents to ≈50 − 100 kpc. There are no significant differences between different host masses, in agreement with our earlier result that the gas mass of gas-rich satellites 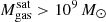$M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ does not vary with halo mass (Fig. 2, top right panel).

Lastly, in the stack by projected cluster centric distance 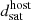$d_{\mathrm{sat}}^{\mathrm{host}}$ (bottom right), satellites at larger projected cluster-centric distances have both higher peak X-ray excesses and extend to farther satellite-centric distances. Satellites at projected distances 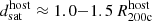$d_{\mathrm{sat}}^{\mathrm{host}}\approx 1.0-1.5R_{200\mathrm{c}}^{\mathrm{host}}$ (dark green) have maximum excesses of ≳30× the background and extend out to ≈50 kpc from the satellite. Greater excesses at large distances arise because these satellites retain more of their CGM. They likely consist of mostly first infallers into the clusters, and so have not been experiencing the cluster-environment effects for as long as other satellites. Since the satellites at the closest projected distances 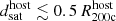$d_{\mathrm{sat}}^{\mathrm{host}}\lesssim 0.5R_{200\mathrm{c}}^{\mathrm{host}}$ (light green) are, and have been, experiencing stronger ram pressure removal of their gas, it is natural that they have no significant excess X-ray emission compared to the control.

According to our theoretical experiment and on the outcome of TNG-Cluster, stacking the soft X-ray excess emission around the positions of optically selected satellites can yield a clear signal of the satellite CGM emission. We expect these results to qualitatively hold in X-ray surveys, and such an experiment could be conducted with the eROSITA all sky survey, albeit only for a sample of nearby clusters (e.g., Comparat et al. 2022; Zhang et al. 2024). Recently, Hou et al. (2024) stack the archival Chandra observations (0.5−2.0 keV) of 21 star-forming, edge-on, late-type galaxies in the Virgo cluster. They find three detections without the need for stacking, and, when stacking by satellite SFR, they detect a signal for the highest SFR bin, with an X-ray luminosity L_X ∼ 10³⁸ erg s⁻¹ per galaxy. While all of the brightest example TNG-Cluster satellites exceed this luminosity (Fig. 7), we speculate that many of the fainter TNG-Cluster satellites would emit at approximately this luminosity. Finally, although we have focused on the broad-band soft X-ray as an example for satellite CGM detectability, we also expect the CGM to be detectable in SZ, by using, for example, X-ray hardness (e.g., Truong et al. 2021), and in ratios of X-ray emission lines using XRISM or LEM (Kraft et al. 2022).

4.2. Implications of satellite CGM for ICM emission studies

Considering that each cluster hosts tens to hundreds of massive satellites and that many can retain their own CGM, we turn to the covering fraction of satellite CGM on a cluster by cluster basis. While the overall luminosity and mass fractions of satellite CGM compared to the total ICM may be small, it may be an important component of observable soft X-ray emission from the ICM.

In Fig. 10, we split the total (left column) soft X-ray emission of four example clusters into its two main components: gas gravitationally bound to the main halo or BCG (second column); gas gravitationally bound to satellite galaxies (third column). We consider all galaxies within the projected field of view as satellites, regardless of stellar mass or FoF membership. A majority of the TNG-Cluster soft X-ray emission within R_200c (circles) comes from the gas bound to the BCG, but there are also many satellites with their hot CGM that contribute. We compute and show the fractional contribution from satellites to the total soft X-ray emission (rightmost column).

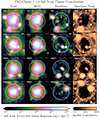Fig. 10. Separating cluster soft X-ray emission into its main sources, for four clusters in TNG-Cluster. We break down the total soft X-ray emission (Total) of an example cluster into its main components: gas that is gravitationally bound to the main halo, i.e., brightest central galaxy (BCG), and gas bound to the satellite galaxies (Satellites). Here, satellites are all galaxies besides the BCG that lie within the field of view of the image 3 R200c × 3 R200c. We include the haloID and mass $M_{200\mathrm{c}}^{\mathrm{host}}$ in units of [log10 M⊙] in the lower left in the Total image, and the soft X-ray luminosity $L_{0.5-2.0\mathrm{keV}}^{<1.5R_{200\mathrm{c}}}$ within a projected aperture 1.5 R200c in units of [log10 erg s−1] in the top right of each panel. We compute the fractional contribution from satellites to the total soft X-ray emission (Satellites/Total), and include both the total soft X-ray contribution from satellites and the mean satellite contribution per pixel in the upper right corner. In all panels the circles denote R200c. The satellite contributions vary from halo-to-halo, but in general satellites contribute ∼10% of the total soft X-ray flux within ≲1.5 R200c of the clusters.

In the cluster centers, satellites do not contribute significantly to the total X-ray flux, except for, locally, around the positions of particularly bright satellites. In the outskirts, however, satellites contribute more significantly to the total X-ray. In each cluster here there are at least a few satellites with bright, spatially extended CGM, and all clusters host many satellites with visible CGM emission.

We quantify the projected covering fraction of soft X-ray emission from bound satellite gas in Fig. 11. We compute the projected covering fraction of satellite soft X-ray (0.5−2.0 keV) emission within a given aperture for the 352 clusters at z = 0 in two ways: (a) above a given surface brightness threshold (left panel) or satellite-to-total fractional threshold – that is above a given threshold of local satellite-to-total fractional emission on a pixel by pixel basis (right panel). Thick curves are the medians, shaded regions enclose the 16th and 84th percentiles, and points are the individual clusters.

Fig. 11. Covering fraction of X-ray emission from satellite circumgalactic media in TNG-Cluster. We measure the projected covering fraction of satellites soft X-ray (0.5−2.0 keV) emission to total for the 352 clusters at z = 0 for two cases: above a given fixed satellite surface brightness threshold (left panel) and above a given satellite-to-total fractional local threshold (right panel). The fiducial threshold choices are shown for varying cluster-centric apertures. Thick curves are the medians across all clusters, shaded regions enclose the 16th and 84th percentiles, and points are the individual clusters, where we manually place clusters with satellite covering fractions < 10−2 between 10−2 and 10−2.5. In both panels when varying the minimum threshold we use the fiducial aperture of < 1.0 R200c, and when varying the aperture we use the intermediate threshold (> 1035 erg s−1 kpc−2 in the left panel; > 10% contribution in the right panel). The collection of satellite CGM can contribute to a significant portion of the cluster’s projected area, and at larger surface brightness or satellite-to-total fractional thresholds there is more halo to halo variation.

Above any of the considered physical surface brightness thresholds (left panel, different colors), the satellite covering fractions increase with cluster mass. As the cluster mass increases, the number of satellites and average satellite mass increase, while higher-mass satellites are also more likely to retain larger, brighter CGM. At a surface brightness above 10³⁴ erg s⁻¹ kpc⁻² (blue), nearly all clusters have a satellite covering fraction of ≈0.7 − 1, suggesting that with deep enough X-ray observations a majority of cluster-sightlines intercept some satellite circumgalactic gas. That is, while the current eROSITA all sky survey (eRASS:4) can detect X-ray surface brightness down to ∼10³⁵ erg s⁻¹ kpc⁻² (at least via stacking; Zhang et al. 2024), we speculate that at ∼1 dex deeper imaging more than of pixels would contain emission from satellites. Detecting this satellite contribution would depend on the signal to noise, or using X-ray spectra to distinguish the satellite CGM from the ICM emission.

Above 10³⁵ erg s⁻¹ kpc⁻² (green; the level currently achievable in eRASS:4), the satellite covering fraction increases from ≈3% at 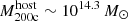$M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{14.3}{M}_{\odot }$ to ≈30% at 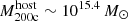$M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{15.4}{M}_{\odot }$. Above 10³⁶ erg s⁻¹ kpc⁻² (pink) the median satellite covering fraction is ≲10⁻¹ for halo masses ≲10¹⁵ M_⊙ (not shown). There are however a number of individual clusters at all masses with high covering fractions, that is,> 0.1 within 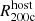$R_{200\mathrm{c}}^{\mathrm{host}}$. Finally, at a surface brightness threshold of > 10³⁵ erg s⁻¹ kpc⁻², the covering fractions are similar within 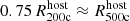$0.75R_{200\mathrm{c}}^{\mathrm{host}}\approx R_{500\mathrm{c}}^{\mathrm{host}}$ (dashed-dotted) and 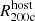$R_{200\mathrm{c}}^{\mathrm{host}}$ (solid), decreasing at larger radii 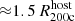$\approx 1.5R_{200\mathrm{c}}^{\mathrm{host}}$ (dashed).

Roughly half the cluster project area within the virial radius has > 1% contribution from satellites (Fig. 11, black line). Only ≈10% of the pixels have satellite contributions above the fiducial 10% threshold. At the highest satellite-to-total threshold of > 50%, meaning that at least half of the total soft X-ray flux per pixel originates from satellites, only ≈3% of clusters have significant satellite covering fractions > 10%. As can been seen from the images in Fig. 10, the X-ray emission in cluster cores is dominated by the gas bound to the BCG. In the outskirts however, satellites contribute more significantly to the total flux. Considering the region from 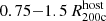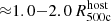$0.75-1.5R_{200\mathrm{c}}^{\mathrm{host}}$ ($\approx 1.0-2.0R_{500\mathrm{c}}^{\mathrm{host}}$), the covering fractions above the fiducial > 10% satellite contribute are the highest at ≈0.75. Overall, satellites contribute ≳10% of the total soft X-ray emission to cluster outskirts $\approx 0.75-1.5R_{200\mathrm{c}}^{\mathrm{host}}$.

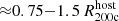4.3. Implications for satellite galaxy evolution

The presence of a CGM, or not, affects the evolution of a given satellite galaxy and how the satellite interacts with its surrounding medium. From the perspective of the satellites themselves, the presence of an extended CGM gaseous halo and reservoir will modify their evolution in high-density environments, versus if they were directly exposed to the cluster environment (Li et al. 2023). Conversely, from the perspective of the cluster-satellite interactions, feedback from the satellites will have different effects on the surrounding host medium if they have their own CGM (Bahé et al. 2012). Finally, from the perspective of the CGM and/or ICM of massive haloes, whether satellites are surrounded by their own gas will affect the interpretation of the ICM itself also via, for example, absorption line studies (Anand et al. 2022).

Satellites that have already had their CGM removed have lost their barrier or protection against the ICM. If there is continued star formation or black hole accretion, then the ensuing outflows would interact with the ICM, heating up and becoming unbound from the satellite, that is being directly deposited into and mixed with the ICM (McGee et al. 2014). As a majority of satellites in TNG-Cluster are gas-poor today, many satellites have deposited their CGM and ISM into cluster atmospheres, and these satellites could potentially act as a source of metals in cluster outskirts (see Nelson et al. 2024).

Satellites that still retain their CGM behave differently. First, the CGM will roughly co-move with the satellite, shielding it from ram pressure stripping. To an extent, satellites with a spatially extended, roughly spherical CGM may continue evolving similarly to central galaxies of the same mass, that is forming stars, growing their central SMBHs, and even accreting cold gas from their own CGM. However, there remain key differences between these massive satellites and their central counterparts (e.g., Engler et al. 2020). For example, in TNG100 massive satellites 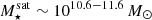$M_{\star }^{\mathrm{sat}}\sim {10}^{10.6-11.6}{M}_{\odot }$ that quench as satellites tend to have reduced SMBH accretion rates compared to centrals (Joshi et al. 2020). This could be caused by lower gas accretion rates from a disturbed or partially stripped CGM. The existence of the CGM for satellite galaxies modulates not only their secular evolution but also the impact of environment, as well as the strength and nature of interactions with the parent cluster ICM.

5. Summary and main conclusions

In this work we study the gas content, circumgalactic medium retention, and observability of ≈90 000 satellite galaxies in and around 352 host clusters from the new TNG-Cluster simulation (Nelson et al. 2024; Pillepich et al., in prep.). This simulation provides statistical and representative samples of satellites at high resolution m_bar ∼ 10⁷ M_⊙ with the well-validated TNG galaxy formation model (Weinberger et al. 2017; Pillepich et al. 2018a). We focus on satellites with stellar mass 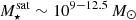$M_{\star }^{\mathrm{sat}}\sim {10}^{9-12.5}{M}_{\odot }$ around clusters with total mass 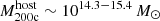$M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{14.3-15.4}{M}_{\odot }$ at z = 0. Our main results are:

• The number of satellites per cluster above a given stellar mass threshold increases with cluster mass such that a cluster of mass 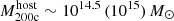$M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{14.5}({10}^{15})M_{\odot }$ hosts ∼100 (300) satellites today (Fig. 1, Sect. 3.1). Of these satellites, ∼40 (100) are massive 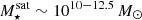$M_{\star }^{\mathrm{sat}}\sim {10}^{10-12.5}{M}_{\odot }$. Each cluster hosts at least a few extremely massive satellites 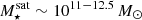$M_{\star }^{\mathrm{sat}}\sim {10}^{11-12.5}{M}_{\odot }$, that is as or more massive than Andromeda. The TNG-Cluster satellite-richness relation broadly agrees with SDSS observations.

• Across all studied stellar and host masses, only a minority (10%) of satellites retain significant gas reservoirs 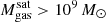$M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ at z = 0. The fraction of gas-rich satellites increases with satellite stellar mass (Fig. 2, Sect. 3.2), where more massive satellites have higher gas masses. There is little trend with host cluster mass.

• Lower-mass satellites 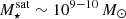$M_{\star }^{\mathrm{sat}}\sim {10}^{9-10}{M}_{\odot }$ are more likely to retain, if at all, a mostly cold interstellar medium (ISM) as opposed to a hot CGM, as ram pressure preferentially removes the CGM first (Figs. 3 and 4, Sects. 3.2 and 3.4). Higher-mass satellites 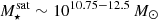$M_{\star }^{\mathrm{sat}}\sim {10}^{10.75-12.5}{M}_{\odot }$ are more likely to retain a mostly hot, spatially extended CGM because of their stronger self-gravity, and the ejective impact of AGN feedback on ISM gas (Figs. 3 and 4).

• With a sample of over 5000 satellites that retain a sizeable amount of their CGM gas, we find that CGM gas mass increases with satellite stellar mass (Fig. 3). More massive satellites lose less CGM mass since infall, reflecting their resistance to environmentally driven gas-removal processes.

• We predict that many gas-rich TNG-Cluster satellites should be visible in the soft X-ray (0.5−2.0 keV), even without a background subtraction (Fig. 7, Sect. 4.1).

• We quantify the soft X-ray excess around satellites by subtracting a smoothed model from the total X-ray surface brightness maps (Fig. 8). When mean-stacking all 37 000 satellites of mass 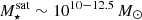$M_{\star }^{\mathrm{sat}}\sim {10}^{10-12.5}{M}_{\odot }$ within a projected distance 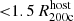$<1.5R_{200\mathrm{c}}^{\mathrm{host}}$, there is an excess in the X-ray surface brightness up to ≈10× the background, extending to ≈50 − 100 kpc (Fig. 9). The excess is the largest for satellites with high masses and large cluster-centric distances.

• We contrast the soft X-ray contribution from satellites to the total ICM emission (Figs. 10 and 11; Sect. 4.2). Satellites can contribute significantly to the X-ray emission over large portions of the projected areas of clusters, that is they have a high covering fraction. Approximately 10% of the soft X-ray emission in cluster outskirts ≈0.75 − 1.5 R_200c originates from satellite galaxies.

In conclusion, massive satellite galaxies are able to retain at least some of their hot, spatially extended, X-ray emitting CGM, despite living in harsh cluster environments. The gaseous atmospheres around some of these satellites should be visible in the soft X-ray, sometimes without a background subtraction. These results have numerous implications related to the evolution of satellite galaxies and interpretation of X-ray surveys and background quasar absorption studies. The presence or not of a satellite CGM affects how the ICM can remove the ISM of the satellite, how the outflows from the satellite interact with the surrounding medium, and to what extent the satellite is able to accrete from the surrounding medium. We predict a fraction of satellites do in fact retain a sizeable amount of their CGM, and these extended gas reservoirs contribute to the X-ray flux of their host clusters. The average cluster has a high covering fraction of satellite CGM, especially in the outskirts, and these CGM contribute absorbers along the line of sight to background quasars. Future studies can model the TNG-Cluster satellite CGM to compute quantitatively the column densities of specific ions, also in the UV, such as Mg II or O VI, whose absorbing strength depend on the thermodynamic properties of the gas. As we expect these properties to differ between the gas in the satellite CGM and that in the ICM, the absorption features could be dominated by the interloping satellite CGM rather than the ICM. Future observational studies of both quasar absorption features and X-ray clusters should consider the possible influences from the satellite population.

Acknowledgments

We thank the anonymous referee for the detailed suggestions that improved the quality of the manuscript. E.R. is a fellow of the International Max Planck Research School for Astronomy and Cosmic Physics at the University of Heidelberg (IMPRS-HD). E.R. would like to acknowledge the following (in alphabetical order) for useful comments and discussions that improved the quality of the manuscript: Chris Byrohl, Anna de Graaff, Morgan Fouesneau, Maximilian Häberle, Noa Hoffmann, Katrin Lehle, Joseph S. W. Lewis, Iva Momcheva, M. Selina Nitschai, Hans-Walter Rix, Nhut Truong, Nico Winkel, and Zhang-Liang Xie. D.N. and M.A. acknowledge funding from the Deutsche Forschungsgemeinschaft (DFG) through an Emmy Noether Research Group (grant number NE 2441/1-1). Moreover, this work is co-funded by the European Union (ERC, COSMIC-KEY, 101087822, PI: Pillepich). Views and opinions expressed are however those of the author(s) only and do not necessarily reflect those of the European Union or the European Research Council. Neither the European Union nor the granting authority can be held responsible for them. The TNG-Cluster simulation suite has been executed on several machines: with compute time awarded under the TNG-Cluster project on the HoreKa supercomputer, funded by the Ministry of Science, Research and the Arts Baden-Württemberg and by the Federal Ministry of Education and Research; the bwForCluster Helix supercomputer, supported by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant INST 35/1597-1 FUGG; the Vera cluster of the Max Planck Institute for Astronomy (MPIA), as well as the Cobra and Raven clusters, all three operated by the Max Planck Computational Data Facility (MPCDF); and the BinAC cluster, supported by the High Performance and Cloud Computing Group at the Zentrum für Datenverarbeitung of the University of Tübingen, the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no INST 37/935-1 FUGG. Data Availability: The IllustrisTNG simulations themselves are publicly available and accessible at https://www.tng-project.org/data, as described in Nelson et al. (2019a), where the TNG-Cluster simulation will also be made public in 2024. Data directly related to this publication is available on request from the corresponding author. All codes used to analyze the TNG-Cluster data and to produce the figures in this manuscript are publicly available at https://github.com/ecrohr/TNG_RPS. Software used: PYTHON (Van Der Walt et al. 2011); IPYTHON (Pérez & Granger 2007); NUMPY (Van Der Walt et al. 2011; Harris et al. 2020); SCIPY (Virtanen et al. 2020); MATPLOTLIB (Hunter 2007); JUPYTER (Kluyver et al. 2016). This work made extensive use of the NASA Astrophysics Data System and arXiv (https://arxiv.org/) preprint server.

References

Appendix A: Defining a gas mass threshold for gas-rich satellites

Figure A.1 shows the number of satellites per host, as a function of host halo mass, with a gas mass above a given threshold. Halos with mass 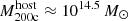$M_{200\mathrm{c}}^{\mathrm{host}}\approx {10}^{14.5}{M}_{\odot }$ host ≈100 satellites (Fig. 1 bottom left panel), but only ≈10 (≈10 percent) of those galaxies retain gas masses above our resolution limit at z = 0. In fact, the majority of satellites have negligible gas masses 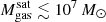$M_{\mathrm{gas}}^{\mathrm{sat}}\lesssim {10}^7{M}_{\odot }$. The curves for the numbers of satellites with 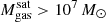$M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^7{M}_{\odot }$ (light purple) and 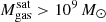$M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ (purple) are remarkably similar: there are only ≈10 percent more of the former. This suggests that satellites with nonzero gas content 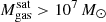$M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^7{M}_{\odot }$ (that is, at least one gas cell, or above the TNG-Cluster resolution limit) are reasonably resolved and relatively gas rich 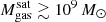$M_{\mathrm{gas}}^{\mathrm{sat}}\gtrsim {10}^9{M}_{\odot }$ (≳100 gas cells).

Fig. A.1. Similar to Fig. 1 (bottom left panel) except we show the number of satellites per host with a given gas mass $M_{\mathrm{gas}}^{\mathrm{sat}}$ or higher. The medians and 16th and 84th percentiles are the solid curves and shaded regions respectively. The number of satellites per host above a given gas mass increases with host mass. While ≈90 percent of satellites have gas masses $M_{\mathrm{gas}}^{\mathrm{sat}}<{10}^7{M}_{\odot }$, 90 percent of those with gas mass $M_{\mathrm{gas}}^{\mathrm{sat}}\ge {10}^7{M}_{\odot }$ (∼1 gas cell) actually have $M_{\mathrm{gas}}^{\mathrm{sat}}\gtrsim {10}^9{M}_{\odot }$ (≈100 gas cells), suggesting that the gaseous TNG-Cluster satellites are sufficiently resolved.

As a result, we consider satellites with 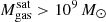$M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ gas-rich and those with 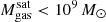$M_{\mathrm{gas}}^{\mathrm{sat}}<{10}^9{M}_{\odot }$ gas-poor. We check that adding an additional criterion that the gas fraction 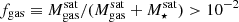$f_{\mathrm{gas}}\equiv M_{\mathrm{gas}}^{\mathrm{sat}}/(M_{\mathrm{gas}}^{\mathrm{sat}}+M_{\star }^{\mathrm{sat}})>{10}^{-2}$, 10⁻¹ removes 40 (0.4 percent), 777 (7.7) percent of the gaseous satellites, and excising these galaxies does not significantly affect the results.

Moreover, the difference between these two 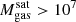$M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^7$, 10⁹ M_⊙ (light purple, purple) populations is much smaller than between the 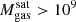$M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9$, 10¹⁰ M_⊙ (purple, dark purple) populations. This well-defined difference suggests that the processes removing gas from satellites are spatially and temporarily resolved at gas masses M_gas ∼ 10^9 − 10 M_⊙, but perhaps not at lower gas masses 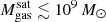$M_{\mathrm{gas}}^{\mathrm{sat}}\lesssim {10}^9{M}_{\odot }$. That is, once a gas reservoir drops to ∼ a few ×10² cells, it quickly becomes gas-poor. A resolution convergence study with the IllustrisTNG boxes can quantitatively assess possible numerical effects on satellite gas contents and physical properties (e.g., Joshi et al. 2020; Donnari et al. 2021a; Stevens et al. 2021).

All Tables

All Figures

Fig. 1. Cluster and satellite demographics in TNG-Cluster. Top panels: we plot the number of satellite galaxies of the 352 clusters in bins of satellite stellar $M_{\star }^{\mathrm{sat}}$ and host halo $M_{200\mathrm{c}}^{\mathrm{host}}$ mass at z = 0. The one-dimensional histograms for $M_{\star }^{\mathrm{sat}}$ and $M_{200\mathrm{c}}^{\mathrm{host}}$ are included in the right and top panels. The number of satellites per stellar mass bin decreases with satellite stellar mass, where there is a sharp decrease in the number of super-L⋆ galaxies $M_{\star }^{\mathrm{sat}}>{10}^{10.5}{M}_{\odot }$. The number of satellites per host mass bin increases at lower cluster masses $M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{14.3-15}{M}_{\odot }$, and then decreases for the most massive clusters $M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{15-15.4}{M}_{\odot }$, which reflects the TNG-Cluster halo mass function (see text and Nelson et al. 2024 for details). Bottom panels: for each of the 352 hosts, we plot the number of FoF satellites above given stellar masses (left), where the medians and 16th and 84th percentiles are the solid curves and shaded regions respectively. Additionally, we qualitatively compare the TNG-Cluster results to spectroscopic (GalWCat19; Abdullah et al. 2020, 2023) and photometric (redMaPPer; Costanzi et al. 2019) SDSS observations, considering all galaxies brighter than rmag < −20.4 and within a projected distance $d_{\mathrm{sat}}^{\mathrm{host}}<R_{200\mathrm{c}}$ as satellites (right panel; see text for details). The TNG-Cluster mass-richness relation is qualitatively consistent with observations.

In the text

Fig. 2. How the TNG-Cluster satellite gas mass varies with the satellite stellar and host halo mass. Top left panel: for the ≈90 000 TNG-Cluster satellites with $M_{\star }^{\mathrm{sat}}>{10}^9{M}_{\odot }$, the fraction of satellites that retain gas reservoirs $M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ today as satellites is shown in bins of satellite stellar $M_{\star }^{\mathrm{sat}}$ and cluster $M_{200\mathrm{c}}^{\mathrm{host}}$ mass. Top right panel: only 10 000 (10%) of the TNG-Cluster satellites retain gas masses $M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ today. For these gaseous satellites, we show the median satellite gas mass $M_{\mathrm{gas}}^{\mathrm{sat}}$ in bins of satellite stellar $M_{\star }^{\mathrm{sat}}$ and host halo $M_{200\mathrm{c}}^{\mathrm{host}}$ mass. Bottom panels: we show the fractions (left panel) and numbers (right panel) of satellites with all (purple, solid, filled), hot (red, dashed, “\” hatched), and cold (blue, dashed-dotted, “/” hatched) gas masses > 109 M⊙ within a given stellar mass bin at z = 0. We mark 100% and the global average of 10% with black lines, and include the total number of gaseous satellites in the legend. While a given satellite is more likely to retain gas if it has a higher stellar mass, a given gaseous satellite is more likely to have a lower stellar mass because there are simply more lower-mass satellites.

In the text

Fig. 3. Spatial extent of satellite gas in TNG-Cluster. Of the ≈5000 gas-rich $M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ massive satellites $M_{\star }^{\mathrm{sat}}>{10}^{10}{M}_{\odot }$ at z = 0, we examine the spatial extent of all (hot and cold) gas at a fixed host cluster mass $M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{15}{M}_{\odot }$ and at three stellar masses $M_{\star }^{\mathrm{sat}}\sim {10}^{10}$, 1010.75,  1011.5 M⊙ (top panels, left to right respectively). Moreover, we compare the total gas density (purple) at z = 0 of cluster members as satellites with that at infall as centrals (black). All curves show the median profiles of all galaxies in the bin; see Fig. 4 for the individual profiles to see the galaxy-to-galaxy variation. We define all gas outside > 2 Rhalf, ⋆ as the circumgalactic medium (CGM). We then plot total CGM mass $M_{\mathrm{CGM}}^{\mathrm{sat}}$ as a function of galaxy stellar mass $M_{\star }^{\mathrm{sat}}$ (bottom panel) at infall as centrals (black), and at z = 0 as satellites (pink). The curves are the medians of the CGM masses (only the galaxies with nonzero CGM mass for the satellites), and for the most massive galaxies we plot the individual objects (circles) and the median stacks (squares). We manually place the ≈28 000 CGM-poor $M_{\mathrm{CGM}}^{\mathrm{sat}}<{10}^9{M}_{\odot }$ satellites at masses ∼107 − 8 M⊙. All stacks use stellar, host, and gas masses at z = 0, and the radial profiles are normalized to Rhalf, ⋆ at the considered time (infall or today). More than 5000 cluster satellites retain a CGM despite residing in harsh cluster environments.

In the text

Fig. 4. How ram pressure and SMBHs affect the gas contents of TNG-Cluster satellite galaxies. For the gas-rich $M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ satellites at a fixed cluster $M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{15}{M}_{\odot }$ and satellite $M_{\star }^{\mathrm{sat}}\sim {10}^{10},{10}^{10.75}{M}_{\odot }$ (top versus bottom panels) mass, we show total gas density radial profiles colored by current ram pressure (left column) and SMBH mass (right column). The thick curves show the medians of the top and bottom quartiles of ram pressure and SMBH mass, and the thin curves are the profiles of the individual satellites. Ram pressure tends to truncate the gas profiles at large distances and slightly compress the ISM gas, while SMBH feedback tends to eject and decrease the density of the ISM gas for more massive satellites.

In the text

Fig. 5. Gas-rich satellites today are typically late infallers. We plot the probability distribution functions (PDFs) of the infall times of all (black), gas-poor $M_{\mathrm{gas}}^{\mathrm{sat}}<{10}^9{M}_{\odot }$ (red), and gas-rich $M_{\mathrm{gas}}^{\mathrm{sat}}>{10}^9{M}_{\odot }$ (blue) TNG-Cluster satellites at a fixed host halo $M_{200\mathrm{c}}^{\mathrm{host}}\sim {10}^{15}{M}_{\odot }$ and satellite stellar $M_{\star }^{\mathrm{sat}}\sim {10}^{11}{M}_{\odot }$ mass. We mark the medians and errors of the distributions as hashes on the top x-axis. The infall time is the first infall into any host, regardless if the galaxy has been preprocessed or not. At a fixed host halo and satellite stellar mass, the infall time is the primary driver determining whether satellites remain gas-rich or gas-poor today: more recent infallers are more likely to retain large gas reservoirs.

In the text

Fig. 6. How the environment removes gas from an example satellite. For an example gas-poor satellite today of mass $M_{\star }^{\mathrm{sat}}(z=0)\approx {10}^{10.9}{M}_{\odot }$ in a cluster of mass $M_{200\mathrm{c}}^{\mathrm{host}}(z=0)\approx {10}^{15.0}{M}_{\odot }$, we study the time evolution of the gas radial profiles since first infall (τFirstInfall ≈ 8.6 Gyr i.e., look-back time ≈5 Gyr) until it becomes gas-poor today. The cumulative environmental effects, namely the integrated ram pressure since infall, and secular processes, namely feedback from the SMBH, remove the satellite’s gas, leaving a gas-poor, quenched satellite today.

In the text

Fig. 7. Poster of the diversity of TNG-Cluster satellites in soft X-ray emission. We show the soft X-ray (0.5−2.0 keV) surface brightness for 16 example TNG-Cluster satellite galaxies at z = 0. Each image is 600 × 600 kpc2 in size (scale bar in the upper left). These galaxies are necessarily within a projected distance of 1.5 R200c of their host. We include information about the galaxy and its host in the upper right and lower left corners; the units of the cluster $M_{200\mathrm{c}}^{\mathrm{host}}$ and satellite $M_{\star }^{\mathrm{sat}}$ mass are [log10 M⊙], and the soft X-ray luminosity $L_{0.5-2.0\mathrm{keV}}^{<300\mathrm{kpc}}$ is the total X-ray luminosity within a projected aperture of 300 kpc in units of [log10 erg s−1]. Many of the maps display morphological signatures of SMBH feedback, with dome-like inflated bubbles and/or ram pressure, with gas tails extending in specific directions.

In the text

Fig. 8. Schematic detailing how we detected satellites’ circumgalactic media and measured their radial profiles. For a given halo (halo mass $M_{200\mathrm{c}}^{\mathrm{host}}\approx {10}^{15.1}{M}_{\odot }$) at z = 0, we compute the soft X-ray (0.5 − 2.0 keV) continuum surface brightness (SB) on 5 × 5 kpc2 pixels (top left). We then smooth the image using a Gaussian kernel of standard deviation 300 kpc (top center). The white circles indicate the virial radius. We include the azimuthally averaged radial profile, where the dashed line marks the virial radius (top right). We compute the soft X-ray surface brightness excess as the ratio of all the gas in the image to the smoothed model (bottom left), and zoom in on an individual example satellite (bottom center; stellar mass $M_{\star }^{\mathrm{sat}}\approx {10}^{10.5}{M}_{\odot }$ at projected cluster-centric distance $d_{\mathrm{sat}}^{\mathrm{host}}\approx 1.0R_{200\mathrm{c}}^{\mathrm{host}}$). We include the contours of {1, 2, 5} times the background on the zoom-in and on the satellite’s excess radial profile (bottom right). In this satellite we detect a soft X-ray surface brightness excess out to ≈200 kpc from the satellite’s center, and the morphology suggests the satellite’s X-ray emitting gas is experiencing environmental effects. The soft X-ray excess profile for this example satellite is similar to others of the same stellar mass and cluster-centric distance (see Fig. 9 and text).

In the text

Fig. 9. Stack of the z = 0 satellite soft X-ray surface brightness excess radial profiles around all 352 TNG-Cluster halos. We compute the soft X-ray (0.5−2.0 keV) surface brightness (SB) excess around all ≈37 000 galaxies with $M_{\star }^{\mathrm{sat}}>{10}^{10}{M}_{\odot }$ and within a projected distance $d_{\mathrm{sat}}^{\mathrm{host}}<1.5R_{200\mathrm{c}}^{\mathrm{host}}$ of the 352 hosts. We then mean-stack these radial profiles in bins of satellite stellar mass $M_{\star }^{\mathrm{sat}}$ (top panel), and within a fixed stellar mass bin, we further stack in bins of host cluster mass $M_{200\mathrm{c}}^{\mathrm{host}}$ (bottom left) and cluster-centric distance (bottom right). In all panels, the control sample represents the same measurement, at random locations such that the distributions of cluster-centric distances match that of the satellites. Across all satellites, the X-ray excess extends to ∼20 − 100 kpc, although individual satellites or specific stacks may exhibit excesses out to ≈300 kpc from the satellites.

In the text

Fig. 10. Separating cluster soft X-ray emission into its main sources, for four clusters in TNG-Cluster. We break down the total soft X-ray emission (Total) of an example cluster into its main components: gas that is gravitationally bound to the main halo, i.e., brightest central galaxy (BCG), and gas bound to the satellite galaxies (Satellites). Here, satellites are all galaxies besides the BCG that lie within the field of view of the image 3 R200c × 3 R200c. We include the haloID and mass $M_{200\mathrm{c}}^{\mathrm{host}}$ in units of [log10 M⊙] in the lower left in the Total image, and the soft X-ray luminosity $L_{0.5-2.0\mathrm{keV}}^{<1.5R_{200\mathrm{c}}}$ within a projected aperture 1.5 R200c in units of [log10 erg s−1] in the top right of each panel. We compute the fractional contribution from satellites to the total soft X-ray emission (Satellites/Total), and include both the total soft X-ray contribution from satellites and the mean satellite contribution per pixel in the upper right corner. In all panels the circles denote R200c. The satellite contributions vary from halo-to-halo, but in general satellites contribute ∼10% of the total soft X-ray flux within ≲1.5 R200c of the clusters.

In the text

Fig. 11. Covering fraction of X-ray emission from satellite circumgalactic media in TNG-Cluster. We measure the projected covering fraction of satellites soft X-ray (0.5−2.0 keV) emission to total for the 352 clusters at z = 0 for two cases: above a given fixed satellite surface brightness threshold (left panel) and above a given satellite-to-total fractional local threshold (right panel). The fiducial threshold choices are shown for varying cluster-centric apertures. Thick curves are the medians across all clusters, shaded regions enclose the 16th and 84th percentiles, and points are the individual clusters, where we manually place clusters with satellite covering fractions < 10−2 between 10−2 and 10−2.5. In both panels when varying the minimum threshold we use the fiducial aperture of < 1.0 R200c, and when varying the aperture we use the intermediate threshold (> 1035 erg s−1 kpc−2 in the left panel; > 10% contribution in the right panel). The collection of satellite CGM can contribute to a significant portion of the cluster’s projected area, and at larger surface brightness or satellite-to-total fractional thresholds there is more halo to halo variation.

In the text

Fig. A.1. Similar to Fig. 1 (bottom left panel) except we show the number of satellites per host with a given gas mass $M_{\mathrm{gas}}^{\mathrm{sat}}$ or higher. The medians and 16th and 84th percentiles are the solid curves and shaded regions respectively. The number of satellites per host above a given gas mass increases with host mass. While ≈90 percent of satellites have gas masses $M_{\mathrm{gas}}^{\mathrm{sat}}<{10}^7{M}_{\odot }$, 90 percent of those with gas mass $M_{\mathrm{gas}}^{\mathrm{sat}}\ge {10}^7{M}_{\odot }$ (∼1 gas cell) actually have $M_{\mathrm{gas}}^{\mathrm{sat}}\gtrsim {10}^9{M}_{\odot }$ (≈100 gas cells), suggesting that the gaseous TNG-Cluster satellites are sufficiently resolved.

In the text