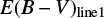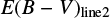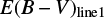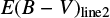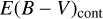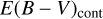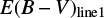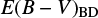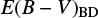| Issue |
A&A
Volume 610, February 2018
|
|
|---|---|---|
| Article Number | A31 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201731963 | |
| Published online | 22 February 2018 | |
What makes red quasars red?
Observational evidence for dust extinction from line ratio analysis★
1
Center for the Exploration of the Origin of the Universe (CEOU), Astronomy Program, Department of Physics and Astronomy, Seoul National University,
1 Gwanak-ro, Gwanak-gu,
Seoul 151-742,
South Korea
2
Astronomy Program, Department of Physics and Astronomy, Seoul National University,
1 Gwanak-ro,
Gwanak-gu,
Seoul 151-742,
South Korea
e-mail: dohyeong@astro.snu.ac.kr;mim@astro.snu.ac.kr
Received:
18
September
2017
Accepted:
4
November
2017
Red quasars are very red in the optical through near-infrared (NIR) wavelengths, which is possibly due to dust extinction in their host galaxies as expected in a scenario in which red quasars are an intermediate population between merger-driven star-forming galaxies and unobscured type 1 quasars. However, alternative mechanisms also exist to explain their red colors: (i) an intrinsically red continuum; (ii) an unusual high covering factor of the hot dust component, that is, CFHD = LHD∕Lbol, where the LHD is the luminosity from the hot dust component and the Lbol is the bolometric luminosity; and (iii) a moderate viewing angle. In order to investigate why red quasars are red, we studied optical and NIR spectra of 20 red quasars at z ~ 0.3 and 0.7, where the usage of the NIR spectra allowed us to look into red quasar properties in ways that are little affected by dust extinction. The Paschen to Balmer line ratios were derived for 13 red quasars and the values were found to be ~10 times higher than unobscured type 1 quasars, suggesting a heavy dust extinction with AV > 2.5 mag. Furthermore, the Paschen to Balmer line ratios of red quasars are difficult to explain with plausible physical conditions without adopting the concept of the dust extinction. The CFHD of red quasars are similar to, or marginally higher than, those of unobscured type 1 quasars. The Eddington ratios, computed for 19 out of 20 red quasars, are higher than those of unobscured type 1 quasars (by factors of 3−5), and hence the moderate viewing angle scenario is disfavored. Consequently, these results strongly suggest the dust extinction that is connected to an enhanced nuclear activity as the origin of the red color of red quasars, which is consistent with the merger-driven quasar evolution scenario.
Key words: quasars: general / quasars: emission lines / quasars: supermassive black holes / galaxies: evolution / galaxies: active
Full Table A.1 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/610/A31
© ESO, 2018
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Large area surveys in X-ray, ultraviolet (UV), optical, and radio wavelengths have uncovered nearly a half million quasars to date (Grazian et al. 2000; Becker et al. 2001; Anderson et al. 2003; Croom et al. 2004; Risaliti & Elvis 2005; Schneider et al. 2005; Véron-Cetty & Véron 2006; Im et al. 2007; Lee et al. 2008; Young et al. 2009; Pâris et al. 2014; Kim et al. 2015c). In the UV to optical wavelength range, the spectra of quasars show a blue power-law continuum with broad and narrow emission lines or a host galaxy continuum with only narrow emission lines, which are classified as type 1 and 2 quasars, respectively. The unification model (Urry & Padovani 1995) has been proposed to explain different types of quasars. In the model, a quasar is composed of a black hole (BH), accretion disk, dust torus, broad line regions (BLRs), and narrow line regions (NLRs). Under the unification model, the type 1 and 2 quasars are physically the same, but an obscuring dust torus prevents us from seeing the accretion disk and the BLR in a certain line-of-sight direction for type 2 quasars.
However, our knowledge about quasars is still incomplete, especially with a population of quasars called red quasars, which have been identified in recent infrared surveys (Webster et al. 1995; Benn et al. 1998; Cutri et al. 2001; Glikman et al. 2007, 2012, 2013; Urrutia et al. 2009; Banerji et al. 2012; Stern et al. 2012; Assef et al. 2013; Fynbo et al. 2013; Lacy et al. 2013). Red quasars typically indicate quasars with red continua from UV or optical through NIR (e.g., r′− K > 5 mag and J − K > 1.3 mag in Urrutia et al. 2009; g − r > 0.5 in Young et al. 2008), red mid-infrared (MIR) colors (Lacy et al. 2004), or detections in X-rays while being obscured in UV and optical wavelengths (Norman et al. 2002; Anderson et al. 2003; Risaliti & Elvis 2005; Young et al. 2009; Brusa et al. 2010).
Interestingly, red quasars are expected in simulations where merger-driven galaxy evolution is stressed (Menci et al. 2004; Hopkins et al. 2005, 2006, 2008). In such simulations, major mergers of galaxies trigger both star formation and quasar activity, often appearing as ultra-luminous infrared galaxies (ULIRGs; Sanders et al. 1988; Sanders & Mirabel 1996). After that, the central BH grows rapidly but it is still obscured by the remaining dust in their host galaxies. Finally, the obscured quasar evolves to an unobscured quasar after the feedback from the central BH sweeps away cold gas and dust. In this picture, red quasars should appear during the intermediate stage between ULIRGs and unobscured quasars. These quasars are red owing to dust extinction by the remaining dust and gas in their host galaxies. So far, observational signatures of red quasars tend to support thispicture. For example, red quasars have (i) higher BH accretion rates than unobscured type 1 quasars by factors of 4 to 5 (Urrutia et al. 2012; Kim et al. 2015b), (ii) enhanced star formation activities (Georgakakis et al. 2009), (iii) a high fraction of merging features (Urrutia et al. 2008; Glikman et al. 2015), and (iv) young radio jets (Georgakakis et al. 2012).
However, several studies have proposed varying explanations for the red continuum of red quasars. Wilkes et al. (2002) and Rose et al. (2013) suggested that the red J − K colors (J − K > 2) of red quasars come from a moderate viewing angle in the unification model when the photons from the accretion disk and the BLR are blocked by the dust torus and not by the dust in host galaxies. Other studies suggest that some (~40%; Young et al. 2008) red quasars have intrinsically red continuum (Puchnarewicz & Mason 1998; Whiting et al. 2001; Young et al. 2008; Rose et al. 2013; Ruiz et al. 2014) or an unusual covering factor of hot dust (Rose 2014). Also a synchrotron emission peak at NIR wavelength from radio jet (Whiting et al. 2001) has been proposed as a possible reason for the intrinsically red continuum of red quasars.
The hydrogen line ratios can be used to infer the amount of dust extinction over the BLRs. Rose et al. (2013) showed that 2MASS selected (J − K > 2) red quasars have higher LH α /LHβ ratios than unobscured type 1 quasars. However, the difference is modest (4.9 ± 0.5 vs. 3.2 ±0.4 for red and unobscured type 1 quasars, respectively) and the modest difference could originate from not only the dust extinction but also different physical condition in the BLRs.
In this study, we use Pβ and Pα lines with Balmer lines to investigate the red colors of red quasars that are shown to have broad emission lines (i.e., type 1). The use of the line ratios over a wide range of wavelength makes it easier to understand if the red colors are due to dust extinction or other mechanisms. Additionally, the use of AGN NIR diagnostics (e.g., Kim et al. 2010)allows us to measure black hole masses and bolometric luminosities in a way that is almost dust free. This fact is very advantageous when trying to distinguish several plausible mechanisms for red colors. For example, in a simple viewing angle scenario, we expect to find red quasars to have Eddington ratios similar to ordinary type 1 quasars, but not so in the intermediate population scenario. Throughout this paper, we use a standard ΛCDM cosmological model of H0 = 70 km s−1 Mpc−1, Ωm = 0.3, and ΩΛ = 0.7, supported by previous observations (e.g., Im et al. 1997).
2 Sample and data
In this work, we used 20 red quasars at 0.186 < z < 0.842 that are composed of 16 red quasars (z > 0.5 and Lbol > 1046 erg s−1) studied in Kim et al. (2015b) and four additional red quasars (z < 0.5 and Lbol ~ 1046 erg s−1). These 20 red quasars are a subsample of ~80 spectroscopically confirmed red quasars in Glikman et al. (2007) and Urrutia et al. (2009), which were selected to be red quasars based on their broadband colors (R − K > 4 and J − K > 1.7 mag in Glikman et al. 2007; r′− K > 5 and J − K > 1.3 mag in Urrutia et al. 2009) from radio-detected 2MASS point sources. In this work, “radio-detected” means the detection of the object in the FIRST radio catalog (Becker et al. 1995). We note that radio-detected AGNs are not necessarily radio-loud. We define radio-loudness as Ri = log(f(1.4 GHz)∕f(7480 Å)) (Ivezić et al. 2002). In our red quasars sample, we find that only one-third are radio-loud (e.g., Ri > 2; Karouzos et al. 2014) and the remaining two-thirds are in the radio-intermediate regime (1 < Ri < 2). Additionally, these quasars are chosen to be at z ~ 0.3 or z ~ 0.7 so that we can sample both the Balmer and Paschen lines.
In this study, we compare several properties of red quasars to those of unobscured type 1 quasars. We used 623 unobscured type 1 quasars at z ~ 0.3 and 0.7, both selected from Sloan Digital Sky Survey (SDSS) in an approach similar to the red quasars (also see Sect. 5.3), and 37 unobscured type 1 quasars at z < 0.5 for which Paschen line information is available from Kim et al. (2010). The 37 unobscured type 1 quasars are relatively bright (K < 14.5 mag). The unobscured type 1 quasars cover a wide range in the K band luminosities (− 30.0 < K mag < −21.3), which overlaps well with the K-band luminosities of our red quasars (− 30.3 < K mag < −25.7). Although the unobscured type 1 quasars from Kim et al. (2010) include six faint (K mag > −24) sources, the host galaxy contamination is negligible (<8%) due to a narrow slit width (Glikman et al. 2006; Kim et al. 2010).
Figure 1 indicates the redshifts and absolute K-band magnitudes of the 20 red quasars and the comparison quasar sample. The absolute K-band magnitudes are K-corrected using a composite spectrum of unobscured type 1 quasars (NIR: Glikman et al. 2006; MIR: Kim et al. 2015a). Here, we do not apply the dust extinction correction, and we note that the amount of extinction is rather small for K band. The mean E(B − V) of red quasars is 0.88 (AK = 0.45 mag).
For 13 of the 20 red quasars, both the optical and NIR spectra are available and the remaining objects have only NIR spectra. The optical spectra of the red quasars come from Glikman et al. (2007, 2012) while the NIR spectra are from Glikman et al. (2007, 2012) and Kim et al. (2015b). Additionally, new NIR spectra were obtained for two red quasars (0036−0113 and 1307+2338) using the SpeX instrument (Rayner et al. 2003) on the NASA Infrared Telescope Facility (IRTF). The observation was performed with a set of the short cross-dispersion mode (SXD; 0.8–2.5 μm) and a 0.′′8 slit width to achieve a resolution of R ~ 750 (400 km s−1 in FWHM) under clear weather and good seeing conditions of ~0.′′7. In order to get fully reduced spectra, we used the Spextool software (Vacca et al. 2003; Cushing et al. 2004). The spectrophotometric calibration was carried out using the standard star spectra taken before or after the spectrum of each quasar was obtained. These flux-calibrated spectra were matched with a K-band photometry from 2MASS and additional flux scaling was performed when necessary. The fully reduced and calibrated NIR spectra of the two red quasars are provided in Table A.1 by a machine readable table form.
Among our sample, we detected Pβ in 19 and Pα in two red quasars (only one red quasar is detected in both Pβ and Pα lines) at signal-to-noise ratios (S/N) of >5. Among 13 red quasars with optical spectra, we detected Hβ in 11 and Hα in 3 red quasars at S/N of >5. For 2 red quasars (0817+4354 and 1656+3821), we derived upper limits of their Hβ line luminosities. For the remainder, the spectra at Hβ and Hα lines are not readily available.
For the lines with no detection, we set upper limits. For the upper limits of the Hβ line luminosity, we assume the full width at half maximum (FWHM) of typical red quasars of 3000 km s−1 (Kim et al. 2015b). Then, the 5-sigma limit of the integrated luminosity density within the wavelength width of the FWHM value is adopted.
As summarized in Table 1, 12 red quasars have both Hβ and Pβ detections or upper limits, while only Pβ line is detected for 7 red quasars. A few red quasars have Hα or Pα line detected.
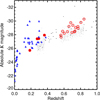 |
Fig. 1 Redshifts and absolute K-band magnitudes of red quasars and unobscured type 1 quasars. The 20 red quasars used in this study are denoted by red open circles, and the black dots indicate the red quasars listed in Glikman et al. (2007) and Urrutia et al. (2009) from which our sample is drawn. Four red quasars (0036−0113, 0817+4354, 1209−0107, and 1307+2338), which were not used in Kim et al. (2015b), are denoted by filled red circles. The comparison sample is made of 37 unobscured type 1 quasars from Kim et al. (2010; blue open triangles), and 623 SDSS unobscured type 1 quasars at 0.275 < z < 0.363 and 0.562 < z < 0.842 (gray dots). |
3 Analysis
We corrected the spectra for the Galactic extinction by adopting the reddening map of Schlafly & Finkbeiner (2011), and the extinction curve with RV = 3.1 of Fitzpatrick (1999). Then, we shifted the corrected spectra to the rest frame. In order to estimate the Hβ luminosity, first we determined the continuum spectrum around the Hβ line. Spectrum of type 1 quasar around the Hβ line is generally complex, which contains a power-law continuum component, a host galaxy component, blended Fe II multiplets, and several narrow emission lines (e.g., [O II] λ3726, Hγ λ4340, and [O III] λλ4959, 5007 doublet).
We fit the continuum of the red quasars with the power-law component and Fe template (Boroson & Green 1992). To avoid contamination from the several narrow emission lines around the Hβ line, the continuum-fitting regions were chosen as 4150–4280 Å, 4400–4750 Å, 4910–4945 Å, and 5070–5400 Å. For the fit, a MPFIT (Markwardt 2009) code based on an interactive data language (IDL) procedure was used to determine the power-law continuum and Fe blends. The Fe blends were determined by broadening and scaling the Fe template from the spectrum of IZw1 (Boroson & Green 1992). Figure 2 shows the optical spectrum of 2339−0912 with the fitted continuum model (the power-law continuum and Fe blends) and the continuum-subtracted spectrum.
We omitted the host galaxy component from the fit for two reasons. First, among the 11 Balmer line measurable red quasars, the measured rest-frame 5100 Å continuum luminosities (L5100 = λLλ at 5100 Å) of 6 red quasars (0825+ 4716, 1113+1244, 1227+5053, 1434+0935, 1720+6156, and 2339−0912) are very luminous (extinction-corrected L5100 = Lbol∕9.2 > 1045 erg, s−1; Table 2). For type 1 AGNs as luminous as the red quasars in L5100 (after the extinction correction), the host galaxy contamination is known to be well below 1% (Shen et al. 2011), and we assume the same for the red quasars. Then, even if we assume that the dust extinction occurs only in the nuclear part1 with E(B − V) = 1, the host contamination would be <30% at 5100 Å. Second, we measured the equivalent width (EW) of Ca II K λ3934 absorption line for the remaining 5 red quasars, since an EW of 1.5 Å for Ca II K corresponds to the host galaxy contribution of ~10% (Greene & Ho 2005; Kim et al. 2006). We could not detect the Ca II K absorption line for 3 red quasars, and for the remaining 2, we measured EWs of 3.8 Å, which corresponds to the host galaxy contribution of ~25% (0036−0113 and 1307+2338), by scaling the results of Greene & Ho (2005) and Kim et al. (2006). Even if the host galaxy contamination of red quasars is bigger than 25%, we stress that it will not affect the line luminosity and width measurements much since the continuum is well subtracted for each object.
After the continuum subtraction, we fit the narrow component of Hβ line using [O III] line at 5007 Å as a template when possible. The [O III] line was fitted with a double Gaussian function to reproduce both the symmetric component and asymmetric outflow component (Greene & Ho 2005), and the fitted result was used as the template. This was possible for nine red quasars.
Among the nine [O III]-fitted red quasars, the Hβ line of four red quasars (0036−0113, 0915+2418, 1307+2338, and 1532+2415) is well fitted by the narrow component only, although 0036−0113 and 1307+2338 were reported to have a broad Hβ component (Glikman et al. 2007). For these four red quasars, we estimated the upper limit of the Hβ line luminosities. In order to estimate the upper limit of the Hβ line luminosities, we performed the same procedures (see Sect. 2) in the narrow component subtracted spectra.
For the remaining five [O III]-fitted red quasars (0825+4716, 1113+1244, 1227+5053, 1434+0935, and 2325−1052), the Hβ line is fitted by a composition of the broad and narrow component. For the fit, we set the central wavelength, line width, and line flux of the broad component as free parameters. We set the lower limit of FWHM of broad component as 800 km s−1 that is twice of the typical FWHM of narrow emission line (400 km s−1; Schneider 2006) and the FWHMs of the fitted broad component are bigger than 800 km s−1.
For the [O III]-unfitted three red quasars (1309+6042, 1720+6156, and 2339−0912), we fit broad Hβ line with a single (1309+6042) or double (1702+6156 and 2339−0912) Gaussianfunction, and the fit is performed by the MPFIT. Similar to the procedure above, the central wavelength, line width, and line flux are set to be free parameters. The FWHMs of the fitted components of the three red quasars are bigger than 800 km s−1 and this result means that the fitted component represent the broad components. The flux of the Hβ line is taken to be the sum of the two broad components for 1704+6156 and 2339−0912, while only the flux of the single broad component is taken to be the broad line flux for 1309+6042. Figure 3 shows theHβ line-fitting results.
To fit the Hα line, we used a similar procedure as for Hβ line fitting. However, for the fitting the continuum, we use a single power-law component only because of the negligible contribution of the Fe blends around the Hα line. After the continuum subtraction, fitting the Hα is somewhat more complicated than fitting the Hβ line because the Hα line is blended with a [N II] λλ 6548, 6583 doublet. For Hα line measurable red quasars 0036−0113, 0817+4354, and 1307+2338, we constructed a model for narrow component of Hα and [N II] doublet using nearby [S II] λλ 6716, 6731 doublet. Using the model of narrow component, we simultaneously fit the Hα line and [N II] doublet. The [N II] doublet is also fitted by two single Gaussian functions, but the central wavelength and flux ratio (2.96; Kim et al. 2006) are fixed. For two red quasars (0817+4354 and 1307+2338), the Hα line is fitted by a composition of broad and narrow component, and the narrow component is from the model of the [S II] doublet. For the other red quasar (0036−0113), the Hα line is fitted by double broad components. Only the flux of the broad component is taken to be the broad Hα flux for 0817+4354 and 1307+2338, but the sum of the fluxes from the two broad components is taken to be the broad component flux of Hα line for 0036−0113. We show the fitting results of the Hα lines in Fig. 4.
The Pβ and Pα lines are detected for 19 and 2 red quasars, respectively. Among these, the Pβ luminosities of 16 red quasars are adopted from Kim et al. (2015b). The Paschen line luminosities of the other red quasars are newly measured, following the procedure in Kim et al. (2010). Figure 5 shows the fitting of the Paschen lines.
This procedure fits the line with a single or double Gaussian functions, neglecting the NLR component, since the S/N and the resolution ofthe spectra do not allow us to measure the NLR component. The measured line luminosities and line widths are taken as the values for the broad line. Hence, the derived broad line luminosities and widths can be somewhat biased. To correct for the bias we applied the mean correction factors that are derived from well-resolved Balmer lines of 26 local unobscured type 1 quasars (Kim et al. 2010). They measured the fluxes and FWHMs of the well-resolved Balmer lines with a single, double, and multiple Gaussian functions, and derived the correction factors by comparing the measured properties. The mean correction factors are fluxmulti/fluxdouble = 1.05 and fluxmulti/fluxsingle = 1.06 for correcting the luminosities and FWHMmulti/FWHMdouble = 0.85 and FWHMmulti/FWHMsingle = 0.91 for correcting FWHM values. For more details, see Sect. 2.3 of Kim et al. (2010).
When no Hβ line is detected (0817+4354 and 1656+3821), we estimated the upper limit of the Hβ line luminosity. In order to estimate the upper limit of the Hβ line luminosity, we used the same procedure mentioned above. The measured upper limits of Hβ line luminosities of the two red quasars are provided in Table 1.
In total, we obtained the broad line luminosities of eight Hβ, three Hα, 19 Pβ, and two Pα lines. The line luminosities and FWHMs are summarized in Table 1. We note that all the values in Table 1 are only corrected for Galactic extinction.
Luminosities and FWHMs of BLRs for red quasars.
 |
Fig. 2 Top: optical spectrum of 2339−0912 (the black solid line) and its model spectrum components. The optical spectrum includes several emission lines such as Hγ, Hβ, and [O III]. The red dashed line indicates the fitted continuum spectrum that is composed of a power-law component (green dotted line) and a component for the Fe blends (blue dot-dashed line). Bottom: the continuum-subtracted spectrum showing broad Balmer emission lines. The continuum-subtracted spectra are used for fitting the lines. |
4 Results
In order to investigate the factor leading to the red color of red quasars, we compared the luminosity ratios of the Pβ/Hβ, Pβ/Hα, Pα/Hβ, and Pα/Hα of red quasars to those of unobscured type 1 quasars. For a typical red quasar with the E(B − V) = 2 mag, its Hα and Hβ luminosities would be suppressed by a factor of 100 and 1000, respectively, but the Pα and Pβ fluxes are suppressed by a factor of only 2.3 and 4.7, respectively. Therefore, the analysis using optical to NIR emission lines is a useful way to investigate the dust obscuration, where the Paschen lines can serve as a good measure of the unobscured light.
For this analysis, the line luminosity ratios of unobscured type 1 quasars are adopted from Kim et al. (2010). Although several faint (LPaschen < 1042 erg s^-1) unobscured type 1 quasars are included in this comparison, the line luminosity ratios are insensitive to the luminosity (see Fig. 6 in Kim et al. 2010). Figure 6 compares line luminosities of the red quasars and unobscured type 1 quasars. We find that the observed Balmer line luminosity for a given Paschen line luminosity is 1.5–290 (~12 on average) times weaker for the red quasars than for unobscured type 1 quasars.
Figure 7 shows the distributions of the Pβ/Hβ luminosity ratios of the red quasars and unobscured type 1 quasars. We find that red quasars have the log (LPβ∕LHβ) values much higher than those of the unobscured type 1 quasars; median log (LPβ∕LHβ) of the red quasars are 0.27 ± 0.53, in contrast to that of unobscured type 1 quasars (− 0.49 ± 0.17). The Kolmogorov-Smirnov (K-S) test confirms this significant difference in the line luminosity ratios between the two quasar populations. We performed the K-S test using the KSTWO code based on the IDL. The maximum deviation between the cumulative distributions of these two Pβ/Hβ luminosity ratios, D, is 1.0, and the probability of the result given the null hypothesis, p, is only 9.22 × 10−7.
If red quasars are dust-reddened, we expect the dust-corrected line luminosity ratios of the red quasars to be consistent with those of unobscured type 1 quasars. For this test, we adopted the E(B − V) values from previous studies (Glikman et al. 2007; Urrutia et al. 2009) and applied the extinction correction assuming the Galactic extinction curve with RV = 3.1 (Schultz & Wiemer 1975). Glikman et al. (2007) and Urrutia et al. (2009) provide two types of E(B − V) values derived from the continuum shape and the Balmer decrement. In this study, we used the E(B − V) values from the continuum shape because the E(B − V) values from the continuum shape are available for all objects in the sample. The extinction-corrected line luminosities ratios of red quasars are indicated in Figs. 6 and 7.
The extinction-corrected median log(LPβ∕LHβ) of the red quasars is − 0.63 ± 0.81, that is almost the same as that of unobscured type 1 quasars. Furthermore, our K-S test for the histogram of the extinction-corrected Pβ/Hβ luminosity ratios show that the measured D and p values of the K-S statistic are 0.44 and 0.12, respectively, against unobscured type 1 quasars. For this K-S test, we broadened the Pβ/Hβ luminosity ratios distribution of unobscured type 1 quasars by adding scatters to Pβ/Hβ luminosity ratios through a Monte Carlo simulation by the amount that could be produced during dereddening of Pβ/Hβ luminosity ratios of red quasars assuming a typical scatter in E(B − V) of 0.5 (Glikman et al. 2007). Therefore, we conclude that, on average, both the continuum colors and the line ratios of red quasars can be explained by dust extinction.
One interesting question is whether we can accurately determine E(B − V) values of red quasars. In an attempt to make this determination, we compared E(B − V) values from the Paschen and Balmer line luminosity ratios ( ) vs. E(B − V) values from the continuum shape (
) vs. E(B − V) values from the continuum shape (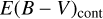 ). In this study, the
). In this study, the  is composed of the two values
is composed of the two values 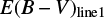 and
and 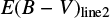 . The
. The 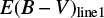 is derived by finding a proper value of E(B − V) that brings the observed LP β /LHβ ratio to the observed mean of unobscured type 1 quasars, where the Galactic extinction curve and RV = 3.1 are assumed. On the other hand, the
is derived by finding a proper value of E(B − V) that brings the observed LP β /LHβ ratio to the observed mean of unobscured type 1 quasars, where the Galactic extinction curve and RV = 3.1 are assumed. On the other hand, the 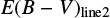 is determined by using the ratios of LPβ (0817+4354 and 1307+2338) or LPα (0036−0113) to LH α. The measured
is determined by using the ratios of LPβ (0817+4354 and 1307+2338) or LPα (0036−0113) to LH α. The measured 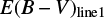 and
and 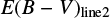 values are listed in Table 2. In Fig. 8, we compare
values are listed in Table 2. In Fig. 8, we compare  vs.
vs. 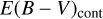 . The Pearson correlation coefficient between the two quantities is −0.21 and a rms scatter of 0.68 with respect to a one-to-one correlation. The result can be considered as no correlation or a one-to-one correlation with a very large scatter of 0.72 in E(B − V). On the same plot, we also compare
. The Pearson correlation coefficient between the two quantities is −0.21 and a rms scatter of 0.68 with respect to a one-to-one correlation. The result can be considered as no correlation or a one-to-one correlation with a very large scatter of 0.72 in E(B − V). On the same plot, we also compare  vs. E(B − V) from the Balmer decrement (
vs. E(B − V) from the Balmer decrement (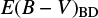 ). The
). The 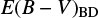 values are taken from Glikman et al. (2007) and determined using the ratios between the LH α and LH β. We note that the
values are taken from Glikman et al. (2007) and determined using the ratios between the LH α and LH β. We note that the 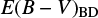 values were determined using total line intensity or broad component luminosity. Among the two types of
values were determined using total line intensity or broad component luminosity. Among the two types of 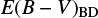 , we use the
, we use the 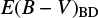 from the broad component luminosity except for 1227+5053 for which
from the broad component luminosity except for 1227+5053 for which 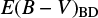 from the broad line is not available. For the comparison between the
from the broad line is not available. For the comparison between the 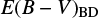 and
and  , only four data points are available, but we find a reasonably good agreement between
, only four data points are available, but we find a reasonably good agreement between  and
and 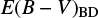 . The Pearson correlation coefficient between the two quantities is 0.80.
. The Pearson correlation coefficient between the two quantities is 0.80.
The large scatter between 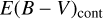 and
and  is likely due to the wide range of continuum slopes that quasars can have and the difficulty in estimating the intrinsic continuum shape in advance. Another possible reason is that the dust obscuration region varies between the continuum emitting and line emitting regions. We suggest that E(B − V) estimated through the continuum shape contains a large scatter (~0.72 in E(B − V)). This agrees with what we saw in Fig. 7, where the histogram of LP β /LHβ after the extinction correction with
is likely due to the wide range of continuum slopes that quasars can have and the difficulty in estimating the intrinsic continuum shape in advance. Another possible reason is that the dust obscuration region varies between the continuum emitting and line emitting regions. We suggest that E(B − V) estimated through the continuum shape contains a large scatter (~0.72 in E(B − V)). This agrees with what we saw in Fig. 7, where the histogram of LP β /LHβ after the extinction correction with 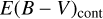 is much broader than the same histogram for unobscured type 1 quasars and the two histograms are virtually indistinguishable after taking into account this broadening effect.
is much broader than the same histogram for unobscured type 1 quasars and the two histograms are virtually indistinguishable after taking into account this broadening effect.
Values of MBH, Lbol, and E(B − V) for red quasars.
 |
Fig. 3 Results of the fitting of the Hβ lines. The continuum is already subtracted. The black and red solid lines indicate the observed spectra and best-fit model, respectively. The narrow component of Hβ line is fitted by using the nearby [O III] line at 5007 Å as a template, and the fitted narrow component is represented by the green dash-dotted line. The dashed blue lines represent the broad component (FWHM > 800km s−1) of the Hβ line. |
 |
Fig. 4 Results of the fitting of the Hα lines. The black and red solid lines indicate the continuum subtracted spectra and best-fit model, respectively. The blue dashed and purple dotted lines are the best-fit models for the broad and narrow component of the Hα line, respectively, and the green dot-dashed lines indicate the best-fit models for the [N II] doublet. |
 |
Fig. 5 Fitting results of the Pβ and Pα lines. The black solid lines are the continuum subtracted spectra. The blue and red solid lines are the best-fit models for the Pβ and Pα lines, respectively. |
5 Discussion
5.1 Physical condition as a cause for high line luminosity ratio
Here, we test a hypothesis that the observed LPaschen/LBalmer of red quasars are due to a different physical condition of broad emission line regions (BELRs) without dust extinction. To do so, we explore what physical conditions of BELRs can reproduce the observed line luminosity ratios by computing theoretically expected line luminosity ratios under different physical conditions using the CLOUDY code (version 13.03; Ferland et al. 1998).
We set the plausible ranges of input parameters as the following. Quasars do not show any broad forbidden lines (e.g., see Glikman et al. 2007; Urrutia et al. 2009). The absence of the broad forbidden lines implies that the hydrogen density (nH) in the BELR is higher than the critical density of the forbidden lines, which gives us the lower limit of nH = 107 cm−3. The upper limit of nH is set to 1014 cm−3 considering the existence of strong Fe blends (~1012 cm−3; Collin-Souffrin et al. 1982; Rees et al. 1989). For the other parameters, we vary the values of the shape of the ionizing continuum (α = −2−2) and the ionization parameter (U = 10−5−105) to cover various physical conditions.
Line luminosity ratios of LP α/LHβ, LP β /LHβ, and LH α/LHβ are sensitive to nH and U. The line luminosity ratios decrease when the nH and U values are increased, which is indicated in the B and C panels of Fig. 9.
Figure 9 shows the line luminosity ratios as a function of wavelength for red quasars and those from the CLOUDY calculation. The line luminosity ratios of unobscured type 1 quasars can be successfully reproduced by the CLOUDY calculation with a set of parameters, α = −1.0, U = 10−1.5, and nH = 109 cm−3 (Kim et al. 2010), which is represented by the dotted line in Fig. 9. For the Balmer lines, although the Hα/Hβ luminosity ratios of red quasars are not measured in this study, these luminosity ratios of local red AGNs are only moderately different from those of unobscured type 1 quasars (Rose et al. 2013).
However, the line luminosity ratios start to demand unusual physical conditions when Paschen lines are included. The median log (LPβ∕LHβ) is 0.43± 0.53 for red quasars, while it is only − 0.48 ± 0.17 for unobscured type 1 quasars. Among the eight LP β /LHβ ratios measured red quasars, five (63%) red quasars have higher line ratios than the maximum line luminosity ratios in the CLOUDY calculation (log (LPβ∕LHβ) ≤ 0.18). In other words, the LP β /LHβ ratios of the five red quasars are much higher than the line luminosity ratios from all the plausible physical parameters for BLR. For the remaining three (38%) red quasars, the LP β /LHβ ratios can beexplained with a condition of low nH = 107 cm−3, low U = 10−3, and α =2. The parameters are found by minimizing χ2, which is a function of the line luminosity ratios
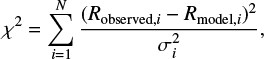 (1)
(1)
where N is the number of line luminosity ratios, and two types of Ri are the line luminosity ratios either from observation or the CLOUDY model, and σi is the uncertainty in the measured line luminosity ratio. However, this physical condition, that is, low nH and low U, is somewhat similar to that of NLRs (e.g., ne = 103.5−107.5 cm−3 and U ~10^-2; Osterbrock 1991; Netzer 2013), rather than the broad lines that we are studying here (FWHM > 800 km s−1), and this disfavors the physical condition as a reason for the observed line luminosity ratios.
 |
Fig. 6 Comparison between the Paschen and Balmer line luminosities of red quasars and unobscured type 1 quasars (gray squares). The dashed red lines mean the best-fit lines between the Paschen and Balmer line luminosities of unobscured type 1 quasars. The blue stars and red circles indicate the dust-corrected and uncorrected luminosities of the red quasars, respectively. The blue and red arrows represent the upper limits of dust corrected and uncorrected LH β vs. LP β of 0036−0113, 0915+2418, 1307+2338, 1532+2415, and 1656+3821, respectively, and LHβ vs. LP α of 0817+4354 and 1307+2338, respectively. The left two panels show the comparison of the Pβ and Balmer line luminosities, and the right two panels compare the Pα with the Balmer line luminosities. Before extinction correction and at a given Paschen line luminosity, the Balmer line luminosities of red quasars are much weaker than those of unobscured type 1 quasars, while extinction corrections bring the red quasars close to the unobscured type 1 quasars. |
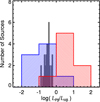 |
Fig. 7 Distributions of the Pβ/Hβ luminosityratios of the red quasars (color-hatched histogram) and unobscured type 1 quasars (gray histogram). The blue and red histograms indicate the distributions of the extinction corrected and uncorrected Pβ/Hβ luminosity ratios of the red quasars, respectively. After applying the extinction correction, the Pβ/Hβ distributionof red quasars agree broadly with that of unobscured type 1 quasars, but with a much larger scatter suggesting that the extinction-correction prescription is not perfect. |
5.2 High hot dust covering factor as a cause for redness
Rose et al. (2013) suggested that some of AGNs with red J − K colors are red owing to a relatively large hot dust covering factor (CFHD = LHD∕Lbol; Maiolino et al. 2007; Kim et al. 2015a). We address this point here with our sample.
For the comparison between the CFHD of red quasars and unobscured type 1 quasars, we used 37 unobscured type 1 quasars from Kim et al. (2010). The unobscured type 1 quasars are bright (K < 14.5 mag and Mi < −23 mag) and located at z < 0.5.
Because the Lbol and LHD are easily under- or overestimated from the spectral energy distribution (SED) model fitting depending on a set of the dust extinction value and extinction law, we used the Paschen line luminosities and NIR continuum luminosities (L2 and L3.5; λLλ at 2 μm and 3.5 μm in the rest-frame) as proxies for the Lbol and LHD, respectively. Considering previous results that found, first, the temperature of hot dust torus is ~1000−1500 K (Barvainis 1987; Glikman et al. 2006; Kim et al. 2015a; Hernán-Caballero et al. 2016) and, second, 2 μm and 3.5 μm are closed to the peak wavelengths of blackbody radiation from the hot dust component, L2 and L3.5 can represent LHD (Glikman et al. 2006; Kim et al. 2015a). Although the stellar emission can peak at 1.6 μm, the hot dust component can be a dominant component with its peak at 2–3.5 μm. This is supportedby J − K colors of redquasars that are significantly different from those of normal galaxies and star-forming galaxies (e.g., see Fig. 1 in Glikman et al. 2012). Although the NIR continuum luminosities of red quasars have a possibility to be overestimated by the stellar emission contamination, the NIR contribution of the stellar emission is known to be ≤10% for quasars, when NIR continuum luminosity is over than 1043.5 erg s−1 (Hernán-Caballero et al. 2016). There is no plausible reason to believe that the hot and warm dust emission should be much weaker for red quasars than type 1 quasars. If red quasars are red due to unusually high CFHD, this would make the host galaxy contribution to the NIR continuum luminosities even smaller. The Paschen line luminosities are used as a tracer for the Lbol (Kim et al. 2015b) by employing the excellentcorrelation between LP, LH α, L5100, and Lbol (Kim et al. 2010; Shen et al. 2011; Jun et al. 2015). The wavelengths of 2 μm and 3.5 μm are not too far from the Paschen lines (Pβ: 1.2818 μm and Pα: 1.8751 μm) and so the L2 /LP and L3.5/LP are rather insensitive to the exact values of dust extinction.
The NIR continuum luminosities are measured by interpolating the 2MASS (Skrutskie et al. 2006) and WISE (Wright et al. 2010) photometric data. The Pβ and Pα luminosities are adopted from Kim et al. (2010) for 37 and 27 unobscured type 1 quasars, respectively.
In this study, we do not consider the Baldwin effect because the Baldwin effect in the Balmer lines is weak (Dietrich et al. 2002), and the Paschen lines have a strong correlation with the Balmer lines (Kim et al. 2010).
Figures 10 and 11 show the comparisons between the NIR continuum luminosities vs. Paschen line luminosities of the red quasars and unobscured type 1 quasars. The unobscured type 1 quasars have the mean log (L2/LPβ) and log (L3.5/LPβ) of 2.58 ± 0.01 and 2.64 ± 0.01 with dispersions of 0.55 and 0.51, respectively. The measured luminosity ratios are only slightly smaller than those of red quasars (3.06 ± 0.01 and 3.21 ± 0.01 with dispersions of 0.27 and 0.28). Moreover, the mean log (L2/LPα) and log (L3.5/LPα) of the unobscured type 1 quasars are 2.51 ± 0.01 and 2.56 ± 0.01 with dispersions of 0.64 and 0.60, respectively, and those of red quasars (2.72 ± 0.02 and 2.97 ± 0.02 with dispersions of 0.32 and 0.35) are almost same.
The result indicates that the covering factor of red quasars are not much different from type 1 quasars, and an unusually large covering factor is not the reason for their red colors. This result is consistent with the viewing angle or torus obscuration scenario, but we address this scenario below.
 |
Fig. 8 Left: comparison between the continuum-based and the line ratio-based E(B − V) values of red quasars. The |
5.3 Viewing angle as a cause for redness
Wilkes et al. (2002) suggested that the redness of red quasars arises from a moderate viewing angle in the quasar unification model when the accretion disk and the BLR are viewed through a dust torus. If so, red quasars should show properties very similar to unobscured type 1 quasars.
However, previous studies (Urrutia et al. 2012; Kim et al. 2015b) showed that red quasars have significantly higher accretion rates than unobscured type 1 quasars, which cannot be explained by the viewing angle scenario. Among the 19 Pβ luminosity measured red quasars in our sample, the Eddington ratios of 16 red quasars at z ~ 0.7 were already studied in Kim et al. (2015b). We have three additional Pβ measured red quasars at z ~ 0.3 (0036−0113, 1209−0107, and 1307+2338). Below, we first examine the Eddington ratios of the three additional quasars and then compare the Eddington ratios of 16 red quasars at z ~ 0.7 to the Lbol matched unobscured type 1 quasars.
As a comparison sample, we select unobscured type 1 quasars from the quasar catalog (Schneider et al. 2010) of the SDSS seventh data release (DR7; Abazajian et al. 2009). In order to avoid the sample selection bias, the unobscured type 1 quasars are selected by the same selection criteria as red quasars as follows: (i) the same redshift range of the three red quasars (0.275 < z < 0.363), (ii) radio detection in Faint Images of the Radio Sky at Twenty-Centimeters (FIRST) survey (Becker et al. 1995), and (iii) photometric detection in 2MASS. This selection yields 213 unobscured type 1 quasars as the comparison sample.
In order to estimate the BH masses of red quasars, we corrected the Pβ luminosities by adopting E(B − V) values from previous studies (Glikman et al. 2007; Urrutia et al. 2009). The E(B − V) values were determined using their continuum shape. After then, we used the Pβ based MBH estimator from Eq. (1) of Kim et al. (2015b), which is modified from the Pβ scaling relation (Kim et al. 2010) by adopting a recent virial coefficient of log f = 0.05 (Woo et al. 2015). For the MBH of unobscured type 1 quasars, we used L5100 and FWHMHβ values from Shen et al. (2011) and the MBH estimator of Eq. (2) in Kim et al. (2015b).
The Hβ-based MBH values are lower than the Pβ-based MBH values by 0.45 dex before the extinction correction. No offset can be seen after the Hβ-based MBH values are derived by taking the extinction effect into account, but this introduces a large scatter (rms ~ 0.56 dex) in MBH values from the two methods, justifying the use of Pβ-based MBH here.
To obtain Lbol values of the red quasars, we translated the LPβ using the relationship between the Lbol and LP β of Eq. (4) in Kim et al. (2015b). The Lbol values of the unobscured type 1 quasars are converted from the L5100 values with a bolometric correction factor of 9.26 (Shen et al. 2011). We note that the measured MBH and Lbol values of the red quasars are summarized in Table 2.
The Lbol values of the red quasars (1045.50 erg s−1 < Lbol < 1046.51 erg s−1) and the comparison sample of unobscured type 1 quasars (1045.04 erg s−1 < Lbol < 1046.55 erg s−1) are similar but not identical. For that reason, we also performed the comparison of the two populations using Lbol-matched samples too.
To estimate the Eddington ratio, the Pβ is used as both an indicator of Lbol and MBH. Although these two different quantities are derived from the Pβ line and include the same line luminosity term, the MBH has a larger uncertainty than Lbol because the MBH values include FWHM square term and the square-rooted line luminosity term. The median uncertainties of the Pβ based Lbol and MBH are 0.03 and 0.08 dex, respectively. The Eddington ratio is proportional to L0.5 /FWHM2 and this gives the combined uncertainty of 0.08 dex2.
We compared the Eddington ratios (Lbol/LEdd, where LEdd is the Eddington luminosity) of red quasars and unobscured type 1 quasars in Fig. 12. The median Eddington ratios of unobscured type 1 quasars is 0.12 with an rms scatter of 0.34. Meanwhile, the measured Eddington ratios of three red quasars are 0.83, 0.30, and 0.52 for 0036−0113, 1209−0107, and 1307+2338, respectively. Among 213 unobscured type 1 quasars, only 55 unobscured type 1 quasars have higher Eddington ratios than 0.30. The probability is only 1.7% that three randomly chosen unobscured type 1 quasars from the comparison sample have the Eddington ratios higher than 0.30. No systematic bias is expected between Lbol/LEdd from Pβ (red quasars) and L5100 with FWHMHβ (unobscured type 1 quasars), except for an added scatter of 0.36 dex that comes from the scatter in the correlation of different quantities (Kim et al. 2015b).
Since several works suggest that the Eddington ratios are dependent on Lbol (e.g., Lusso et al. 2012; Suh et al. 2015), we also show the Eddington ratio distribution of the sample in a narrow Lbol range that matches the Lbol of red quasars. The objects 0036−0113 and 1307+2338 have similar Lbol of 1045.79 erg s−1 and 1045.50 erg s−1, respectively, but 1209−0107 has a much higher Lbol of 1046.51 erg s−1. For comparison, we selected 48 unobscured type 1 quasars with the same Lbol range (1045.50 < Lbol < 1045.79 erg s−1) of the 2 red quasars 0036−0113 and 1307+2338. The median Eddington ratio of the 48 unobscured type 1 quasars changes to 0.15 ± 0.33, but this is still much lower than those of the red quasars. Among the 48 unobscured type 1 quasars, only 9 unobscured type 1 quasars have higher Eddington ratios than the minimum Eddington ratio, 0.52, of 0036−0113 and 1307+2338. The probability is only 3.2% that 2 randomly chosen unobscured type 1 quasars from the comparison sample have the Eddington ratios higher than 0.52.
Previous studies (Urrutia et al. 2012; Kim et al. 2015b) showed red quasars at different redshift have higher Eddington ratios than unobscured type 1 quasars. Kim et al. (2015b) measured Eddington ratios for 16 red quasars at z ~ 0.7 and the 16 red quasars are included in our 20 red quasars. Kim et al. (2015b) compared the Eddington ratios of the 16 red quasars to those of unobscured type 1 quasars that are matched in MBH. We show how the Eddington ratios of 16 red quasars compare with those of Lbol-matched unobscured type 1 quasars. The unobscured type 1 quasars are selected from the SDSS DR7 quasar catalog (Schneider et al. 2010) with the same redshift range of the 16 red quasars (0.56 < z < 0.84). We note that the selection method of the comparison sample is identical to Kim et al. (2015b) and the details of the comparison sample selection are described in Sect. 2.1 of Kim et al. (2015b).
We divided the red quasars and the unobscured type 1 quasars into two luminosity bins. Figure 13 shows the comparisonof the Eddington ratio distributions and our results show that the Eddington ratios of 16 red quasars at z ~ 0.7 are significantly higher (factors of ~3 to 4) than those of unobscured type 1 quasars. Even if we assume a maximal amount of 35% contamination on the Paschen line flux by a narrow line (see Sect. 3), the Eddington ratio decreases by only ~15% or 0.07 dex, and we find that the analysis result does not change.
For the low luminosity sample, 9 red quasars and 246 unobscured type 1 quasars are selected, and their log (MBH∕M⊙) values have ranges of 7.98–9.07 and 7.71–10.27 for the red quasars and the unobscured type 1 quasars, respectively. The median Eddington ratios of the red quasars and the unobscured type 1 quasars are 0.62 and 0.15, respectively. The D and p values from a K-S test between these two distributions are 0.64 and 7.6 × 10−4. The high luminosity sample includes 7 red quasars and 36 unobscured type 1 quasars. The log (MBH∕M⊙) values have ranges of 8.26–9.09 and 8.58–10.18 for the red quasars and unobscured type 1 quasars, respectively. The median Eddington ratios of the red quasars and unobscured type 1 quasars are 0.97 and 0.35, respectively. The measured D and p values between these two distributions are 0.66 and 5.6 × 10−3.
Overall, the additional analysis of the three red quasars and the re-analysis of the luminosity matched 16 red quasars in Kim et al. (2015b) strengthens the previous results of Urrutia et al. (2012) and Kim et al. (2015b) that red quasars tend to have higher Eddington ratios than unobscured type 1 quasars. Therefore, we suggest that many of the red quasars, if not all, are not seen as red simply because of the viewing angle (also see Onori et al. 2017).
 |
Fig. 9 Line luminosity ratios of Hα, Pβ, and Pα with respect to Hβ of red quasars. The Pβ/Hβ luminosity ratios of eight red quasars are indicated by the open triangles, and the yellow stars are the Hα/Hβ luminosity ratios of the local red AGNs from Rose et al. (2013). The green arrows indicate the lower limits. Thedotted line is the line luminosity ratio reproduced by the CLOUDY code with a set of parameters (α = −1.0, U = 10−1.5, and nH= 109 cm−3), which is consistent with the line luminosity ratios of unobscured type 1 quasars from Hβ to Pα (Kim et al. 2010). Panel A: the five colored solid lines represent the line luminosity ratios from the CLOUDY code with nH = 1010 cm−3, U = 100, and various α from − 2 to 2. The various α is represented by color, i.e., the purple, blue, green, yellow, and red lines indicate α is − 2, − 1, 0, 1, and 2, respectively. Panel B: the meanings of the symbols and lines are identical to panel A, but the five colored lines are the line luminosity ratios with nH = 1010 cm−3, α = 0, and various U from 10−5 to 103. Panel C: the meanings of the symbols and lines are identical to panel A, but the five colored lines are the line luminosity ratios with α = 0, U = 100, and various nH from 107 to 1014 cm−3. Panel D: the meanings of the symbols and the dotted line are identical to panel A, and the gray lines represent the line luminosity ratios computed from the CLOUDY code with various physical conditions, within α = −2 to 2, nH = 107−1014 cm−3, and U = 10−5−105. |
 |
Fig. 10 Left: values of L2 vs. LP β of red quasars (the red filled squares) and unobscured type 1 quasars (the blue filled circles). Right: the L2 values vs. the LPα values. The meanings of the symbols are identical. This figure shows that red quasars do not have unusual hot dust emission that is much stronger (> 1 dex) than that of unobscured type 1 quasars, although their NIR emission may be a bit stronger (~ 0.3 dex) than unobscured type 1 quasars. |
 |
Fig. 11 Comparisons between L3.5 values vs. Paschen line luminosities. The meanings of the symbols are identical to Fig. 10. |
 |
Fig. 12 Panel A: eddington ratios of three red quasars (0036−0113, 1209−0107, and 1307+2338; red lines) and unobscured type 1 quasars z ~ 0.3 (blue histograms). The gray dashed and dotted lines represent the Eddington ratio distributions for red quasars and unobscured type 1 quasars at z ~ 0.7, respectively, where results are adopted from Kim et al. (2015b). Panel B: the same figure as above, except that unobscured type 1 quasars have bolometric luminosities similar to the two red quasars (0036−0113 and 1307+2338; 45.50 < log(Lbol∕erg s−1) < 45.79). |
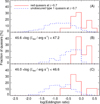 |
Fig. 13 Panel A: eddington ratio distributions of red quasars and unobscured type 1 quasars at z ~ 0.7. The red solid and blue dashed histograms represent red quasars and unobscured type 1 quasars, respectively. The Eddington ratios of red quasars at z ~ 0.7 are adopted from Kim et al. (2015b). Panel B: eddington ratio distributions for high-luminous quasars (46.6 <log(Lbol∕erg s−1) < 47.2). Panel C: eddington ratio distributions for low-luminous quasars (46.0 < log(Lbol∕erg s−1) < 46.6). |
6 Conclusions
So far, several explanations for the red colors of red quasars have been suggested; for example, (i) there is dust in their host galaxy, (ii) these quasars are intrinsically red, (iii) the redness is attributable to high CFHD, and (iv) the red color can be attributed to a moderate viewing angle. In order to investigate the origin of the red colors of red quasars, we used 20 red quasars at z ~ 0.3 and 0.7 in this study.
We compared the luminosity ratios from hydrogen Balmer to Paschen lines of red quasars to those of unobscured type 1 quasars adopted from Kim et al. (2010). We find that the line luminosity ratios of red quasars are almost six times higher than those of unobscured type 1 quasars, and the extinction correction based on E(B − V) estimated from the continuum shape can bring the similar mean Pβ/Hβ luminosity ratio to that of unobscured type 1 quasars (albeit with a large scatter). This result suggests that dust extinction is responsible for the red colors of red quasars.
Moreover, we examined if the characteristics of red quasars can be explained by other reasons. We examined whether the unusual line luminosity ratios of red quasars can be explained without the dust extinction effects. We compared the observed line luminosity ratios of red quasars to the theoretically expected line luminosity ratios computed from CLOUDY code. However, the observed line luminosity ratios of ~ 63% (5 out of 8) red quasars cannot be explained by any physical conditions of BELRs. We also examined whether red quasars have unusually higher CFHD than unobscured type 1 quasars, but we do not find clear evidence of NIR excess for a given Paschen line luminosity. Finally, using a dust-insensitive diagnostic Pβ line, we find that 19 red quasars – three at z ~ 0.3 (new measurements) and 16 at z ~ 0.7 (Kim et al. 2015b) – have Eddington ratios that are significantly (~ 5 times) higher than those of unobscured type 1 quasars. This result disfavors the scenario in which the red colors of red quasars are caused by a moderate viewing angle that passes though dust torus.
Our results and previous results from studies of red quasars have found that these quasars have (i) high luminosity ratios from Balmer to Paschen lines, (ii) high BH accretion rates (Kim et al. 2015b), (iii) enhanced star formation activities (Georgakakis et al. 2009), (iv) a high fraction of merging features (Urrutia et al. 2009; Glikman et al. 2015), and (v) young radio jets (Georgakakis et al. 2012). Based on these findings, we conclude that red quasars are dust-extincted quasars in the intermediate stage galaxies between ULIRGs and unobscured type 1 quasars and the dust extinction is caused by the remaining dust in their host galaxies.
Acknowledgements
This work was supported by the Creative Initiative Program of the National Research Foundation of Korea (NRF), No. 2017R1A3A3001362, funded by the Korea government. D.K. acknowledges support by the National Research Foundation of Korea to the Fostering Core Leaders of the Future Basic Science Program, No. 2017-002533. M.I. and D.K. are Visiting Astronomers at the Infrared Telescope Facility, which is operated by the University of Hawaii under Cooperative Agreement No. NNX-08AE38A with the National Aeronautics and Space Administration, Science Mission Directorate, Planetary Astronomy Program. We thank Eilat Glikman for sharing spectra of the red quasars listed in Glikman et al. (2007).
Appendix A Near-infrared spectra of red quasars
We provide 0.8–2.5 μm spectra of two red quasars (0036−0113 and 1307+2338) taken with NASA IRTF. Table A.1 is an example spectrum of 0036−0113, and the full version of the spectra is available in machine readable table form.
Spectrum of 0036−0113.
References
- Abazajian, K. N., Adelman-McCarthy, J. K., Agüeros, M. A., et al. 2009, ApJS, 182, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, S. F., Voges, W., Margon, B., et al. 2003, AJ, 126, 2209 [NASA ADS] [CrossRef] [Google Scholar]
- Assef, R. J., Stern, D., Kochanek, C. S., et al. 2013, ApJ, 772, 2 [Google Scholar]
- Banerji, M., McMahon, R. G., Hewett, P. C., et al. 2012, MNRAS, 427, 2275 [NASA ADS] [CrossRef] [Google Scholar]
- Barvainis, R. 1987, ApJ, 320, 537 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, R. H., White, R. L., Gregg, M. D., et al. 2001, ApJS, 135, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Benn, C. R., Vigotti, M., Carballo, R., Gonzalez-Serrano, J. I., & Sánchez, S. F. 1998, MNRAS, 295, 451 [NASA ADS] [CrossRef] [Google Scholar]
- Boroson, T. A., & Green, R. F. 1992, ApJS, 80, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Brusa, M., Civano, F., Comastri, A., et al. 2010, ApJ, 716, 348 [NASA ADS] [CrossRef] [Google Scholar]
- Bruzual, G., & Charlot, S. 2003, MNRAS, 344, 1000 [NASA ADS] [CrossRef] [Google Scholar]
- Canalizo, G., Wold, M., Hiner, K. D., et al. 2012, ApJ, 760, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Collin-Souffrin, S., Dumont, S., & Tully, J. 1982, A&A, 106, 362 [NASA ADS] [Google Scholar]
- Croom, S. M., Smith, R. J., Boyle, B. J., et al. 2004, MNRAS, 349, 1397 [NASA ADS] [CrossRef] [Google Scholar]
- Cushing, M. C., Vacca, W. D., & Rayner, J. T. 2004, PASP, 116, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Nelson, B. O., Kirkpatrick, J. D., Huchra, J. P., & Smith, P. S. 2001, A&AAS, 198, 3317 [NASA ADS] [Google Scholar]
- Dietrich, M., Hamann, F., Shields, J. C., et al. 2002, ApJ, 581, 912 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J., Korista, K. T., Verner, D. A., et al. 1998, PASP, 110, 761 [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [NASA ADS] [CrossRef] [Google Scholar]
- Fynbo, J. P. U., Krogager, J.-K., Venemans, B., et al. 2013, ApJS, 204, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Georgakakis, A., Clements, D. L., Bendo, G., et al. 2009, MNRAS, 394, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Georgakakis, A., Grossi, M., Afonso, J., & Hopkins, A. M. 2012, MNRAS, 421, 2223 [NASA ADS] [CrossRef] [Google Scholar]
- Glikman, E., Helfand, D. J., & White, R. L. 2006, ApJ, 640, 579 [NASA ADS] [CrossRef] [Google Scholar]
- Glikman, E., Helfand, D. J., White, R. L., et al. 2007, ApJ, 667, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Glikman, E., Urrutia, T., Lacy, M., et al. 2012, ApJ, 757, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Glikman, E., Urrutia, T., Lacy, M., et al. 2013, ApJ, 778, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Glikman, E., Simmons, B., Mailly, M., et al. 2015, ApJ, 806, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Grazian, A., Cristiani, S., D’Odorico, V., Omizzolo, A., & Pizzella, A. 2000, AJ, 119, 2540 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., & Ho, L. C. 2005, ApJ, 630, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Hernán-Caballero, A., Hatziminaoglou, E., Alonso-Herrero, A., & Mateos, S. 2016, MNRAS, 463, 2064 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2005, ApJ, 630, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2006, ApJS, 163, 1 [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., & Kereš D. 2008, ApJS, 175, 356 [NASA ADS] [CrossRef] [Google Scholar]
- Im, M., Griffiths, R. E., & Ratnatunga, K. U. 1997, ApJ, 475, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Im, M., Lee, I., Cho, Y., et al. 2007, ApJ, 664, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Ivezić, Ž., Menou, K., Knapp, G. R., et al. 2002, AJ, 124, 2364 [NASA ADS] [CrossRef] [Google Scholar]
- Jun, H. D., Im, M., Lee, H. M., et al. 2015, ApJ, 806, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Karouzos, M., Im, M., Kim, J.-W., et al. 2014, ApJ, 797, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, M., Ho, L. C., & Im, M. 2006, ApJ, 642, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., Im, M., & Kim, M. 2010, ApJ, 724, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., Im, M., Kim, J. H., et al. 2015a, ApJS, 216, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., Im, M., Glikman, E., Woo, J.-H., & Urrutia, T. 2015b, ApJ, 812, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, Y., Im, M., Jeon, Y., et al. 2015c, ApJ, 813, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Lacy, M., Storrie-Lombardi, L. J., Sajina, A., et al. 2004, ApJS, 154, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Lacy, M., Ridgway, S. E., Gates, E. L., et al. 2013, ApJS, 208, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, I., Im, M., Kim, M., et al. 2008, ApJS, 175, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Lusso, E., Comastri, A., Simmons, B. D., et al. 2012, MNRAS, 425, 623 [NASA ADS] [CrossRef] [Google Scholar]
- Maiolino, R., Shemmer, O., Imanishi, M., et al. 2007, A&A, 468, 979 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Markwardt, C. B. 2009, Astronomical Data Analysis Software and Systems XVIII, 411, 251 [NASA ADS] [Google Scholar]
- Menci, N., Cavaliere, A., Fontana, A., et al. 2004, ApJ, 604, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Mor, R., & Trakhtenbrot, B. 2011, ApJ, 737, L36 [NASA ADS] [CrossRef] [Google Scholar]
- Netzer, H. 2013, The Physics and Evolution of Active Galactic Nuclei, ed. Hagai Netzer (Cambridge, UK: Cambridge University Press) [Google Scholar]
- Norman, C., Hasinger, G., Giacconi, R., et al. 2002, ApJ, 571, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Onori, F., Ricci, F., La Franca, F., et al. 2017, MNRAS, 468, L97 [Google Scholar]
- Osterbrock, D. E. 1991, Rep. Prog. Phys., 54, 579 [CrossRef] [Google Scholar]
- Pâris, I., Petitjean, P., Aubourg, É., et al. 2014, A&A, 563, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puchnarewicz, E. M., & Mason, K. O. 1998, MNRAS, 293, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Rayner, J. T., Toomey, D. W., Onaka, P. M., et al. 2003, PASP, 115, 362 [NASA ADS] [CrossRef] [Google Scholar]
- Rees, M. J., Netzer, H., & Ferland, G. J. 1989, ApJ, 347, 640 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Lacy, M., Storrie-Lombardi, L. J., et al. 2006, ApJS, 166, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Risaliti, G., & Elvis, M. 2005, ApJ, 629, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Rose, M. 2014, American Astronomical Society Meeting Abstracts #223, 223, #321.03 [Google Scholar]
- Rose, M., Tadhunter, C. N., Holt, J., & Rodríguez Zaurín J. 2013, MNRAS, 432, 2150 [NASA ADS] [CrossRef] [Google Scholar]
- Ruff, A. J., Floyd, D. J. E., Webster, R. L., Korista, K. T., & Landt, H. 2012, ApJ, 754, 18 [NASA ADS] [CrossRef] [Google Scholar]
- Ruiz, A., Della Ceca, R., Caccianiga, A., Severgnini, P., & Carrera, F. 2014, The X-ray Universe 2014, 314 [Google Scholar]
- Sanders, D. B., & Mirabel, I. F. 1996, ARA&A, 34, 749 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Soifer, B. T., Elias, J. H., et al. 1988, ApJ, 325, 74 [NASA ADS] [CrossRef] [Google Scholar]
- Schlafly, E. F., & Finkbeiner, D. P. 2011, ApJ, 737, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, P. 2006, Extragalactic Astronomy and Cosmology, ed. P. Schneider (Berlin: Springer) [Google Scholar]
- Schneider, D. P., Hall, P. B., Richards, G. T., et al. 2005, AJ, 130, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, D. P., Richards, G. T., Hall, P. B., et al. 2010, AJ, 139, 2360 [NASA ADS] [CrossRef] [Google Scholar]
- Schultz, G. V., & Wiemer, W. 1975, A&A, 43, 133 [NASA ADS] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, D., Assef, R. J., Benford, D. J., et al. 2012, ApJ, 753, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Suh, H., Hasinger, G., Steinhardt, C., Silverman, J. D., & Schramm, M. 2015, ApJ, 815, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Urrutia, T., Lacy, M., & Becker, R. H. 2008, ApJ, 674, 80 [NASA ADS] [CrossRef] [Google Scholar]
- Urrutia, T., Becker, R. H., White, R. L., et al. 2009, ApJ, 698, 1095 [NASA ADS] [CrossRef] [Google Scholar]
- Urrutia, T., Lacy, M., Spoon, H., et al. 2012, ApJ, 757, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Vacca, W. D., Cushing, M. C., & Rayner, J. T. 2003, PASP, 115, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Véron-Cetty,M.-P., & Véron, P. 2006, A&A, 455, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Webster, R. L., Francis, P. J., Petersont, B. A., Drinkwater, M. J., & Masci, F. J. 1995, Nature, 375, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Whiting, M. T., Webster, R. L., & Francis, P. J. 2001, MNRAS, 323, 718 [NASA ADS] [CrossRef] [Google Scholar]
- Wilkes, B. J., Schmidt, G. D., Cutri, R. M., et al. 2002, ApJ, 564, L65 [NASA ADS] [CrossRef] [Google Scholar]
- Woo, J.-H., Yoon, Y., Park, S., Park, D., & Kim, S. C. 2015, ApJ, 801, 38 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [NASA ADS] [CrossRef] [Google Scholar]
- Young, M., Elvis, M., & Risaliti, G. 2008, ApJ, 688, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Young, M., Elvis, M., & Risaliti, G. 2009, ApJS, 183, 17 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Redshifts and absolute K-band magnitudes of red quasars and unobscured type 1 quasars. The 20 red quasars used in this study are denoted by red open circles, and the black dots indicate the red quasars listed in Glikman et al. (2007) and Urrutia et al. (2009) from which our sample is drawn. Four red quasars (0036−0113, 0817+4354, 1209−0107, and 1307+2338), which were not used in Kim et al. (2015b), are denoted by filled red circles. The comparison sample is made of 37 unobscured type 1 quasars from Kim et al. (2010; blue open triangles), and 623 SDSS unobscured type 1 quasars at 0.275 < z < 0.363 and 0.562 < z < 0.842 (gray dots). |
| In the text | |
 |
Fig. 2 Top: optical spectrum of 2339−0912 (the black solid line) and its model spectrum components. The optical spectrum includes several emission lines such as Hγ, Hβ, and [O III]. The red dashed line indicates the fitted continuum spectrum that is composed of a power-law component (green dotted line) and a component for the Fe blends (blue dot-dashed line). Bottom: the continuum-subtracted spectrum showing broad Balmer emission lines. The continuum-subtracted spectra are used for fitting the lines. |
| In the text | |
 |
Fig. 3 Results of the fitting of the Hβ lines. The continuum is already subtracted. The black and red solid lines indicate the observed spectra and best-fit model, respectively. The narrow component of Hβ line is fitted by using the nearby [O III] line at 5007 Å as a template, and the fitted narrow component is represented by the green dash-dotted line. The dashed blue lines represent the broad component (FWHM > 800km s−1) of the Hβ line. |
| In the text | |
 |
Fig. 4 Results of the fitting of the Hα lines. The black and red solid lines indicate the continuum subtracted spectra and best-fit model, respectively. The blue dashed and purple dotted lines are the best-fit models for the broad and narrow component of the Hα line, respectively, and the green dot-dashed lines indicate the best-fit models for the [N II] doublet. |
| In the text | |
 |
Fig. 5 Fitting results of the Pβ and Pα lines. The black solid lines are the continuum subtracted spectra. The blue and red solid lines are the best-fit models for the Pβ and Pα lines, respectively. |
| In the text | |
 |
Fig. 6 Comparison between the Paschen and Balmer line luminosities of red quasars and unobscured type 1 quasars (gray squares). The dashed red lines mean the best-fit lines between the Paschen and Balmer line luminosities of unobscured type 1 quasars. The blue stars and red circles indicate the dust-corrected and uncorrected luminosities of the red quasars, respectively. The blue and red arrows represent the upper limits of dust corrected and uncorrected LH β vs. LP β of 0036−0113, 0915+2418, 1307+2338, 1532+2415, and 1656+3821, respectively, and LHβ vs. LP α of 0817+4354 and 1307+2338, respectively. The left two panels show the comparison of the Pβ and Balmer line luminosities, and the right two panels compare the Pα with the Balmer line luminosities. Before extinction correction and at a given Paschen line luminosity, the Balmer line luminosities of red quasars are much weaker than those of unobscured type 1 quasars, while extinction corrections bring the red quasars close to the unobscured type 1 quasars. |
| In the text | |
 |
Fig. 7 Distributions of the Pβ/Hβ luminosityratios of the red quasars (color-hatched histogram) and unobscured type 1 quasars (gray histogram). The blue and red histograms indicate the distributions of the extinction corrected and uncorrected Pβ/Hβ luminosity ratios of the red quasars, respectively. After applying the extinction correction, the Pβ/Hβ distributionof red quasars agree broadly with that of unobscured type 1 quasars, but with a much larger scatter suggesting that the extinction-correction prescription is not perfect. |
| In the text | |
 |
Fig. 8 Left: comparison between the continuum-based and the line ratio-based E(B − V) values of red quasars. The |
| In the text | |
 |
Fig. 9 Line luminosity ratios of Hα, Pβ, and Pα with respect to Hβ of red quasars. The Pβ/Hβ luminosity ratios of eight red quasars are indicated by the open triangles, and the yellow stars are the Hα/Hβ luminosity ratios of the local red AGNs from Rose et al. (2013). The green arrows indicate the lower limits. Thedotted line is the line luminosity ratio reproduced by the CLOUDY code with a set of parameters (α = −1.0, U = 10−1.5, and nH= 109 cm−3), which is consistent with the line luminosity ratios of unobscured type 1 quasars from Hβ to Pα (Kim et al. 2010). Panel A: the five colored solid lines represent the line luminosity ratios from the CLOUDY code with nH = 1010 cm−3, U = 100, and various α from − 2 to 2. The various α is represented by color, i.e., the purple, blue, green, yellow, and red lines indicate α is − 2, − 1, 0, 1, and 2, respectively. Panel B: the meanings of the symbols and lines are identical to panel A, but the five colored lines are the line luminosity ratios with nH = 1010 cm−3, α = 0, and various U from 10−5 to 103. Panel C: the meanings of the symbols and lines are identical to panel A, but the five colored lines are the line luminosity ratios with α = 0, U = 100, and various nH from 107 to 1014 cm−3. Panel D: the meanings of the symbols and the dotted line are identical to panel A, and the gray lines represent the line luminosity ratios computed from the CLOUDY code with various physical conditions, within α = −2 to 2, nH = 107−1014 cm−3, and U = 10−5−105. |
| In the text | |
 |
Fig. 10 Left: values of L2 vs. LP β of red quasars (the red filled squares) and unobscured type 1 quasars (the blue filled circles). Right: the L2 values vs. the LPα values. The meanings of the symbols are identical. This figure shows that red quasars do not have unusual hot dust emission that is much stronger (> 1 dex) than that of unobscured type 1 quasars, although their NIR emission may be a bit stronger (~ 0.3 dex) than unobscured type 1 quasars. |
| In the text | |
 |
Fig. 11 Comparisons between L3.5 values vs. Paschen line luminosities. The meanings of the symbols are identical to Fig. 10. |
| In the text | |
 |
Fig. 12 Panel A: eddington ratios of three red quasars (0036−0113, 1209−0107, and 1307+2338; red lines) and unobscured type 1 quasars z ~ 0.3 (blue histograms). The gray dashed and dotted lines represent the Eddington ratio distributions for red quasars and unobscured type 1 quasars at z ~ 0.7, respectively, where results are adopted from Kim et al. (2015b). Panel B: the same figure as above, except that unobscured type 1 quasars have bolometric luminosities similar to the two red quasars (0036−0113 and 1307+2338; 45.50 < log(Lbol∕erg s−1) < 45.79). |
| In the text | |
 |
Fig. 13 Panel A: eddington ratio distributions of red quasars and unobscured type 1 quasars at z ~ 0.7. The red solid and blue dashed histograms represent red quasars and unobscured type 1 quasars, respectively. The Eddington ratios of red quasars at z ~ 0.7 are adopted from Kim et al. (2015b). Panel B: eddington ratio distributions for high-luminous quasars (46.6 <log(Lbol∕erg s−1) < 47.2). Panel C: eddington ratio distributions for low-luminous quasars (46.0 < log(Lbol∕erg s−1) < 46.6). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.