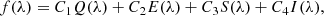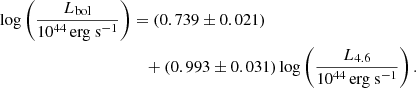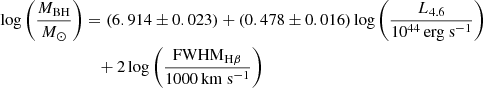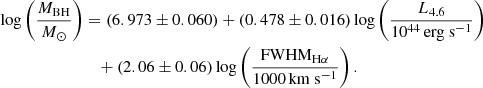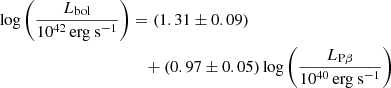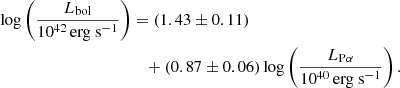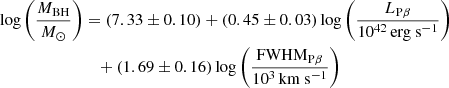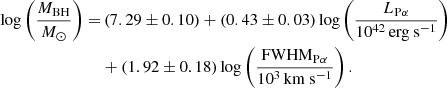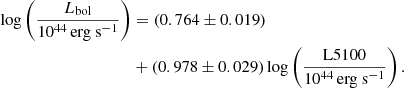| Issue |
A&A
Volume 690, October 2024
|
|
|---|---|---|
| Article Number | A283 | |
| Number of page(s) | 14 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/202450290 | |
| Published online | 17 October 2024 | |
Eddington ratios of dust-obscured quasars at z ≲ 1: Evidence supporting dust-obscured quasars as young quasars
1
Department of Earth Sciences, Pusan National University, Busan 46241, Republic of Korea
2
Korea Astronomy and Space Science Institute, Daejeon 34055, Republic of Korea
3
SNU Astronomy Research Center (SNU ARC), Astronomy Program, Dept. of Physics & Astronomy, Seoul National University, Seoul 08826, Republic of Korea
4
Department of Physics, Middlebury College, Middlebury, VT 05753, USA
5
Department of Astronomy and Atmospheric Sciences, College of Natural Sciences, Kyungpook National University, Daegu 41566, Republic of Korea
6
Leibniz-Institut für Astrophysik, Potsdam (AIP), An der Sternwarte 16, 14482 Potsdam, Germany
Received:
8
April
2024
Accepted:
6
August
2024
Dust-obscured quasars have been suspected of being the intermediate-stage galaxies between merger-driven star-forming galaxies and unobscured quasars. This merger-driven galaxy evolution scenario suggests that dust-obscured quasars exhibit higher Eddington ratios (λEdd) than those of unobscured quasars. However, their high dust obscuration poses challenges to accurately measuring their λEdd using commonly employed bolometric luminosity (Lbol) and black hole mass (MBH) estimators based on the ultraviolet or optical luminosity. Recently, new estimators for Lbol and MBH based on mid-infrared continuum luminosity (LMIR) were established, which are less affected by dust obscuration. These estimators enable the study of a large number of dust-obscured quasars across a wide redshift range. In this study, we measure the λEdd values of 30 dust-obscured quasars at z ≲ 1, the largest sample size to date, using the LMIR-based Lbol and MBH estimators. Our findings reveal that dust-obscured quasars exhibit significantly higher λEdd values compared to unobscured quasars. Moreover, we confirm that the enhanced λEdd values of dust-obscured quasars maintain consistency across the redshift span of 0 to 1. Our results strongly support the picture that dust-obscured quasars are in an earlier stage than unobscured quasars on the merger-driven galaxy evolutionary track.
Key words: galaxies: active / galaxies: evolution / quasars: emission lines / quasars: general / quasars: supermassive black holes / infrared: galaxies
© The Authors 2024
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1. Introduction
Quasars are some of the most energetic and luminous objects in the Universe, and they emit enormous energy at all wavelengths, from gamma ray to radio. The energy of quasars is powered by the accretion of surrounding materials onto supermassive black holes (SMBHs). These SMBHs are found at the centers of massive spheroidal galaxies, and the black hole (BH) masses have correlations with several properties of host galaxies (e.g., Ferrarese & Merritt 2000; Gebhardt et al. 2000).
To date, almost million quasars have been found based on X-ray, ultraviolet (UV), optical, and radio surveys (Grazian et al. 2000; Becker et al. 2001; Anderson et al. 2003; Croom et al. 2004; Risaliti & Elvis 2005; Schneider et al. 2005; Véron-Cetty & Véron 2006; Young et al. 2009; Pâris et al. 2014; Kim et al. 2015c, 2019, 2020b; Lyke et al. 2020; Shin et al. 2020, 2022). However, some previous studies (e.g., Comastri et al. 2001; Tozzi et al. 2006; Polletta et al. 2008) reported that soft X-ray, UV, and optical quasar surveys may overlook a substantial number of quasars, which have red colors caused by the dust extinction from intervening dust and gas in their host galaxies (Webster et al. 1995; Cutri et al. 2002) or our galaxy (Im et al. 2007; Lee et al. 2008). In this paper, we refer to the quasars with dust extinction from their host galaxies as dust-obscured quasars. Some previous studies (e.g., Polletta et al. 2008) expected these dust-obscured quasars to make up ∼50% of the whole quasar population, and even optical quasar surveys include a considerable number of dust-obscured quasars (e.g., ∼15%; Kim et al. 2023).
Dust-obscured quasars have been found through various methods, but the use of their red colors is a notably useful technique. In particular, the colors in the near-infrared (NIR; e.g., J − K > 2 mag; Cutri et al. 2001, 2002) and optical through NIR (e.g., R − K > 5 mag and J − K > 1.3 mag; Glikman et al. 2007; Urrutia et al. 2009) have been widely used. The quasars found by these red colors are called red quasars, and using these red colors proves to be an effective way to find dust-obscured quasars, since the red colors of most red quasars originate from the dust extinction (Kim & Im 2018). However, Kim et al. (2018) claimed that using only NIR color is not effective in selecting dust-obscured quasars.
Although our knowledge about dust-obscured quasars is still incomplete, the emergence of dust-obscured quasars is commonly associated with a merger-driven galaxy evolution scenario, extensively explored in previous simulation studies (Menci et al. 2004; Hopkins et al. 2005, 2006, 2008). In this merger-driven galaxy evolution scenario, major mergers between gas-rich galaxies can trigger both star formation and BH activities, and these phase galaxies are often seen as ultraluminous infrared galaxies (ULIRGs; Sanders et al. 1988; Sanders & Mirabel 1996). After this phase, these galaxies can have merging features and star formation activities. Furthermore, since gas flows onto the SMBHs are related to galaxy-scale disturbances caused by galaxy merger-driven torques (Di Matteo et al. 2005; Hopkins et al. 2008; Alexander & Hickox 2012), it is expected that their BH activities increase dramatically, resulting in them emitting enormous amounts of energy with a high λEdd. However, their BH activities are still obscured owing to the remaining dust and gas in their host galaxies. Finally, these galaxies evolve into normal unobscured quasars after sweeping away the remaining dust and gas by quasar-driven winds. Figure 1 shows a schematic outline of this merger-driven galaxy evolution scenario.
 |
Fig. 1. Schematic outline of merger-driven galaxy evolution scenario. |
In this scenario, it is believed that dust-obscured quasars can occur as the intermediate-stage galaxies between the merger-driven star-forming galaxies and unobscured quasars. Several theoretical studies (e.g., Hopkins et al. 2008) have suggested that dust-obscured quasars exhibit high BH accretion rates, which appear to be prevalent. This scenario has been supported by several pieces of observational evidence. For example, dust-obscured quasars have (i) high λEdd values (Urrutia et al. 2012; Kim et al. 2015a, 2018, 2024a), (ii) high fractions of merging features in their host galaxies (Urrutia et al. 2008; Glikman et al. 2015), (iii) dusty red colors (Kim & Im 2018), (iv) merging SMBH systems (Kim et al. 2020a), and (v) enhanced star formation activities (Georgakakis et al. 2009). It should be noted, however, that even in the merger-driven galaxy evolution scenario, the properties of dust-obscured quasars remain controversial. Recently, Lansbury et al. (2020) showed that the dust-obscured quasar phase lasts a few 105 years, which is significantly shorter than quasar lifetime of ∼107 years (e.g., Hopkins et al. 2006; Khrykin et al. 2021). Considering this significantly short dusty phase, some unobscured quasars might have SMBHs as active as those in dust-obscured quasars. However, these lifetimes are sensitive to several properties (e.g., Lbol and stellar mass; Hopkins et al. 2006), and hence more extensive observational studies on the quasar lifetimes are necessary to obtain a conclusive understanding of the BH activities of dust-obscured quasars. Moreover, some recent studies (e.g., Jun et al. 2021; Glikman et al. 2024) showed that outflows slowly sweeping away the dust and gas in host galaxies could result in luminous dust-obscured quasars with enhanced BH activities.
An alternative explanation for dust-obscured quasars is that they are obscured by a dust torus. The unification model suggests that the differences in emission lines between type 1 and 2 active galactic nuclei are due to the viewing angle (Antonucci 1993; Urry & Padovani 1995). Some previous studies (e.g., Wilkes et al. 2002; Rose et al. 2013; Ananna et al. 2022a,b) proposed that the red colors could be a result of the moderate viewing angle in the unification model, whereby the dust torus blocks the photons from the accretion disk and broad line region (BLR), instead of the dust and gas in their host galaxies. In this scenario, dust-obscured quasars appear solely due to the viewing angle, so their BH accretion rates should not differ from those of unobscured quasars. Even when considering the dust torus evolution with BH accretion rates (Ananna et al. 2022a,b), a significant number of dust-obscured quasars are expected to exhibit lower BH accretion rates than unobscured quasars.
Another possible explanation for dust-obscured quasars is that strong outflows play a crucial role in transporting the obscuring medium (Calistro Rivera et al. 2021). Several observational studies have shown that dust-obscured quasars exhibit strong outflows (e.g., Lansbury et al. 2020; Stacey et al. 2022; Glikman et al. 2024), which supports this explanation. However, that strong outflows are also expected to occur in the intermediate-stage galaxies of the merger-driven galaxy evolution scenario, indicating that it cannot be considered a completely separate explanation from the merger-driven galaxy evolution scenario. Furthermore, some previous studies (e.g., Puchnarewicz & Mason 1998; Whiting et al. 2001; Rose 2014) suggested that red quasars have intrinsic red colors, instead of the dust extinction. Additionally, Georgantopoulos et al. (2023) demonstrated that red quasars reside in the galaxies located between the young and old galaxy populations, in contrast to expectations from the merger-driven galaxy evolution scenario.
One of the ways to confirm if dust-obscured quasars are the intermediate population under the merger-driven galaxy evolution scenario is to examine whether dust-obscured quasars have high λEdd values. However, the λEdd values of dust-obscured quasars remain a topic of debate due to most of bolometric luminosity and BH mass estimators being established based on UV or optical luminosity (Kaspi et al. 2000; Vestergaard 2002; McLure & Dunlop 2004; Greene & Ho 2005), in which the UV- and optical-based estimators are easily affected by the dust extinction. For example, if a dust-obscured quasar is obscured by a color excess of E(B − V) = 2 mag, its fluxes at 1450 Å and 5100 Å are suppressed by factors of 4.3 × 106 and 500, respectively, which is obtained from a reddening law (Fitzpatrick 1999) with RV = 3.1 (Weingartner & Draine 2001). Furthermore, to determine the E(B − V) values for dust-obscured quasars is also uncertain; the differences in E(B − V) estimates can vary by as much as 1–2 mag, depending on the method used (Glikman et al. 2007; Urrutia et al. 2012; Kim et al. 2018). If a dust-obscured quasar with a color excess of E(B − V) = 1 mag is measured as having E(B − V) = 2 mag, then its fluxes at 1450 Å and 5100 Å are overestimated by ∼2000 and ∼20 times, respectively, after correcting the dust extinction. Recently, Calistro Rivera et al. (2021) measured the λEdd values of ∼300 dust-obscured quasars using UV and optical luminosities and found no significant difference from those of unobscured quasars. However, Calistro Rivera et al. (2021) used UV and optical luminosities to measure the BH properties, which are sensitive to accuracy in E(B − V) measurements.
To overcome the limitations of the UV- and optical-based estimators, several infrared (IR)-based estimators have been established. If a dust-obscured quasar with E(B − V) = 1 mag is incorrectly measured as E(B − V) = 2 mag, then the dust extinction corrected fluxes of Pα (1.87 μm) and Brα (4.05 μm) lines would be overestimated by only a factor of 1.48 and 1.16, respectively. For this advantage, Paschen and Brackett hydrogen line based estimators were derived (e.g., Kim et al. 2010, 2015b, 2022a). However, despite the advantage, these IR-based estimators need IR spectroscopic observation, and applying them to a large number of dust-obscured quasars has been a tough task due to the difficulty in obtaining IR spectroscopic data.
Consequently, while several previous studies (Kim et al. 2015a, 2018; Kim & Im 2018) have shown that the λEdd values of dust-obscured quasars are higher than those of unobscured quasars using these IR-based estimators, they used a limited sample size (≲15), yielding results that are (i) not statistically robust and (ii) not confirmed for a wide redshift range.
Recently, Kim et al. (2023) established bolometric luminosity and BH mass estimators based on LMIR using 129 unobscured (E(B − V) < 0.1) Sloan Digital Sky Survey (SDSS; York et al. 2000) quasars at z ≲ 0.5.
The LMIR values can be derived via spectral energy distribution (SED) fitting using various photometric data, such as SDSS (York et al. 2000), the Two Micron All-Sky Survey (2MASS; Skrutskie et al. 2006), and the Wide-field Infrared Survey Explorer (WISE; Wright et al. 2010). The bolometric luminosity can be measured from the LMIR with a root mean square (rms) scatter of ∼0.1 dex, while the BH mass can be derived with an rms scatter of ≲0.2 dex using the LMIR with the full width at half maximum (FWHM) of Balmer lines.
Since the measurement of the FWHM of Balmer lines is not significantly affected by the dust extinction, the LMIR-based estimators allow for the determination of Lbol and MBH without the need for IR spectroscopic data and relatively unaffected by the dust extinction. Hence, these LMIR-based estimators can be applied for a large number of dust-obscured quasars, and they are expected to yield the statistically robust result of the λEdd values of dust-obscured quasars.
In this paper, we measure the λEdd values of 30 dust-obscured quasars at z ≲ 1 using the LMIR-based estimators (Kim et al. 2023), and compare them to unobscured quasars selected from the SDSS quasars. Throughout this work, we use a standard ΛCDM model of H0 = 70 km s−1 Mpc−1, Ωm = 0.3, and ΩΛ = 0.7. This model has been supported by observational studies in previous decades (e.g. Im et al. 1997; Planck Collaboration XIII 2016).
2. Sample
Our sample is drawn from 120 dust-obscured quasars listed in Glikman et al. (2012), and these dust-obscured quasars were selected via the following procedures. First, they selected dust-obscured quasar candidates using (i) detections in NIR (2MASS Point Source Catalog [PSC]; Cutri et al. 2003) and radio (Faint Images of the Radio Sky at Twenty-centimeters [FIRST]; Becker et al. 1995); and (ii) red colors in NIR (J − K > 1.7 mag) and optical through NIR (R − K > 4 mag). Through this process, a total of 395 dust-obscured quasar candidates were selected. Second, Glikman et al. (2012) obtained the optical and/or NIR spectra of ∼300 dust-obscured quasar candidates for (i) object identification; (ii) redshift determination; and (iii) dust-reddening determination. Finally, of the ∼300 candidates, they found 120 dust-obscured quasars that have E(B − V) > 0.1, and provided their optical and/or NIR spectra.
Among the 120 dust-obscured quasars, we selected 30 dust-obscured quasars at z ≲ 1 by following conventions. First, the broad component of the Hβ or Hα line is broader than 2000 km s−1 (see Sect. 3.1 for more details). Second, the E(B − V) measured from the SED fitting is greater than 0.1, and the details of the SED fitting procedure are described in Sect. 3.2. Third, quasar fractions at 3.4 μm and 4.6 μm determined by the SED fitting exceed 0.5. The definition of the quasar fraction is also provided in Sect. 3.2.
The selected 30 dust-obscured quasars span wide ranges of the BH mass (108.15 M⊙ < MBH < 109.22 M⊙), bolometric luminosity (1044.94 erg s−1 < Lbol < 1047.07 erg s−1), and redshift (0.137 < z < 0.957), where the BH masses and bolometric luminosities were derived using LMIR-based estimators (Kim et al. 2010, 2023). Their basic properties are shown in Fig. 2.
 |
Fig. 2. (a) Redshift versus L4.6 luminosity. Red circles and blue dots denote the selected dust-obscured quasars and SDSS quasars, respectively. Among the blue dots, 300 blue dots with black edges represent the L4.6–z matched SDSS quasars, which were used as unobscured quasars. (b) Redshift distributions of the two kinds of quasars. Red and blue histograms represent the dust-obscured quasars and the unobscured quasars, respectively. |
In order to compare the dust-obscured quasars to the unobscured ones, we selected unobscured quasars from the SDSS Data Release 14 (DR14) quasar catalog (Pâris et al. 2018). This catalog contains 526 265 quasars, and their spectral properties were measured (Rakshit et al. 2020) by performing multicomponent fitting with the PyQSOFit code (Guo et al. 2019; Shen et al. 2019). To avoid sample bias effects, we chose the SDSS quasars with the same selection criteria of the dust-obscured quasars: (i) a redshift range of 0.137 < z < 0.957; (ii) a FIRST radio detection; (iii) detections in the J, H, and K bands from 2MASS PSC; and (iv) quasar fractions at 3.4 μm and 4.6 μm from the SED fitting exceeding 0.5.
Moreover, while SDSS quasars are generally known to have negligible dust extinction, Kim et al. (2023) and Kim et al. (2024b) have shown that a significant fraction (∼10–15%) of SDSS quasars are affected by dust extinction. Therefore, we performed the SED fitting (see Sect. 3.2) on SDSS quasars and include only those samples with the measured E(B − V) < 0.1. These SDSS quasars with E(B − V) < 0.1 can be classified as unobscured quasars. Kim et al. (2023) showed that the low E(B − V) SDSS quasars exhibit similar Balmer decrement of unobscured quasars (Dong et al. 2008), supporting the classification of these SDSS quasars with low E(B − V) as unobscured.
Using these selection criteria, 614 SDSS quasars were chosen. Figure 2 shows the L4.6–z distributions of the dust-obscured quasars and the selected SDSS quasars. The dust-obscured quasars tend to be slightly brighter than the SDSS ones at a given redshift, which may cause a sample bias. To eliminate this effect, we selected the ten closest SDSS quasars to each dust-obscured quasar using a two-dimensional metric in the L4.6 and redshift space. If an SDSS quasar was already selected for another nearby dust-obscured quasar, we excluded it and selected the next-closest SDSS quasar. Finally, 300 SDSS quasars with similar L4.6 values and redshifts to the selected 30 dust-obscured quasars were found and used as unobscured quasars. The unobscured quasars have a wide range of BH mass (107.76 M⊙ < MBH < 1010.03 M⊙), bolometric luminosity (1044.79 erg s−1 < Lbol < 1047.12 erg s−1), and redshift (0.154 < z < 0.954). Naturally, their K-band magnitudes and redshift distributions are comparable to those of the dust-obscured quasars, as is shown in Fig. 2.
3. Analysis
3.1. Spectral fitting of Balmer lines
In this subsection, we describe how Hβ and Hα lines of the dust-obscured quasars were fit to measure FWHM values for broad components of the Balmer lines, and the FWHM values were used to estimate the BH masses of the dust-obscured quasars. For this analysis, we used the optical and/or NIR spectra provided by Glikman et al. (2012). However, the FWHM values of the unobscured quasars were adopted from Rakshit et al. (2020).
To fit the Balmer lines of the dust-obscured quasars, we used the PyQSOFit code for consistency in methodology, which is identical to the procedure for the unobscured quasars (Rakshit et al. 2020). Using the PyQSOFit code, we decomposed several components of host galaxy, power-law continuum, and Fe II emissions from the spectra. After that, we fit the Balmer lines. We fit the Hβ and Hα line complexes separately, while all of the emission lines in each line complex were fit simultaneously. The Hβ line complex includes Hβ (broad and narrow components) and [O III] λλ 4959, 5007 doublet (core and wing components), and the Hα line complex comprises Hα (broad and narrow components), [N II] λλ 6549, 6585 doublet, and [S II] λλ 6718, 6732 doublet. Although the flux ratios of these doublets are fixed, we fit the Balmer line complexes without fixing the flux ratios due to low signal-to-noise and partially truncated spectra. We find that not fixing the flux ratios has a negligible effect on the FWHM measurements of the broad components of the Balmer lines.
During the fitting, the broad components of the Balmer lines were fit with a single- or multiple-Gaussian model. However, the FWHM values estimated by the single-Gaussian model are systematically different from the FWHM values from the multi-Gaussian model (Kim et al. 2010; Shen et al. 2011). Thus, we applied correction factors (Kim et al. 2010) to remove the model bias, which were derived from well-resolved Balmer lines of 26 unobscured bright quasars at low z. For the broad components, we set a lower limit of the FWHM as 2000 km s−1, and this FWHM criterion for the broad components has been widely used (e.g., Suh et al. 2019; Xu et al. 2007). The FWHM criterion, broader than that used in Glikman et al. (2012), was set to exclude narrow line Seyfert 1 galaxies (e.g., FWHM ≲ 2000 km s−1; Zhou et al. 2006) that may have systematically different λEdd values (Boroson 2002). Moreover, we only used the FWHM values that were measured reliably, selecting those with an FWHM /FWHMfit_err greater than 3, where FWHMfit_err represents the error in FWHM from the fitting.
Through this process, we fit the spectra of 120 dust-obscured quasars in Glikman et al. (2012), ultimately selecting 30 objects with reliably measured FWHM values. Figure 3 shows the line-fitting results. The fit provides the FWHM values of the broad components of the Balmer lines, but we used the FWHM values after correcting instrumental wavelength dispersion as 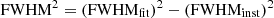 , where FWHMfit and FWHMinst denote the FWHM provided from the fit and the wavelength dispersion due to the instrumental spectral resolution, respectively. In this work, we used the corrected FWHM values of the Balmer lines, and they are summarized in Table 1. To avoid the effects of correction bias, the same instrumental wavelength dispersion correction was also applied to the FWHM values of unobscured quasars adopted from Rakshit et al. (2020), and the corrected FWHM values have been used in this study.
, where FWHMfit and FWHMinst denote the FWHM provided from the fit and the wavelength dispersion due to the instrumental spectral resolution, respectively. In this work, we used the corrected FWHM values of the Balmer lines, and they are summarized in Table 1. To avoid the effects of correction bias, the same instrumental wavelength dispersion correction was also applied to the FWHM values of unobscured quasars adopted from Rakshit et al. (2020), and the corrected FWHM values have been used in this study.
 |
Fig. 3. Fitting results of the Hβ and Hα lines for the dust-obscured quasars. The solid black lines denote the continuum-subtracted spectra in the rest-frame. The dash-dotted red lines are the best-fit model, and the dashed blue and dotted green lines represent the broad and narrow components of the each line complex, respectively. |
 |
Fig. 3. continued. |
Line and SED fitting results of dust-obscured quasars.
We validated the accuracy of our FWHM measurements through two methods: (i) by comparing them with the well-established relationship between Balmer lines; and (ii) by cross-referencing them with individual measurements from previous studies. Among the 30 dust-obscured quasars, the fit provides the FWHM values for both the Hβ and Hα lines in six objects. Our FWHM measurements for the Balmer lines are consistent with the well-known relationship, 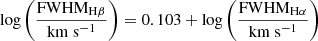 , established by Bisogni et al. (2017), as is shown in Fig. 4. Additionally, seven dust-obscured quasars were studied in Urrutia et al. (2012), and their Balmer line FWHM values were measured. Among these objects, three have had their FWHMHβ values measured in both this work and Urrutia et al. (2012), while another three objects have had FWHMHα values measured in both studies. For the remaining object, FWHMHα is measured in this work, whereas Urrutia et al. (2012) measured FWHMHβ. For this object, we converted FWHMHβ to FWHMHα using the relationship established by Bisogni et al. (2017) for comparison. Comparing the FWHM values measured in both studies reveals that, although not perfectly aligned, they closely match for most objects, with only a few exceptions. Upon selecting only those samples for which both FWHM measurements are over 2000 km s−1, the rms scatter between the FWHM measurements is 0.12 dex, which is taken as the average FWHM error (FWHMavg_err). The total error in FWHM (FWHMtot_err) is taken as the square root of the quadratic sum of the fitting error and average error as
, established by Bisogni et al. (2017), as is shown in Fig. 4. Additionally, seven dust-obscured quasars were studied in Urrutia et al. (2012), and their Balmer line FWHM values were measured. Among these objects, three have had their FWHMHβ values measured in both this work and Urrutia et al. (2012), while another three objects have had FWHMHα values measured in both studies. For the remaining object, FWHMHα is measured in this work, whereas Urrutia et al. (2012) measured FWHMHβ. For this object, we converted FWHMHβ to FWHMHα using the relationship established by Bisogni et al. (2017) for comparison. Comparing the FWHM values measured in both studies reveals that, although not perfectly aligned, they closely match for most objects, with only a few exceptions. Upon selecting only those samples for which both FWHM measurements are over 2000 km s−1, the rms scatter between the FWHM measurements is 0.12 dex, which is taken as the average FWHM error (FWHMavg_err). The total error in FWHM (FWHMtot_err) is taken as the square root of the quadratic sum of the fitting error and average error as 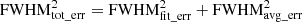 . However, the measured rms scatter is significantly affected by a few samples with large discrepancies in FWHM measurements, raising the possibility that the rms scatter could be overestimated. The exceptions are related to the FWHMHα measurements, which implies that the possibility of inaccuracy in the FWHMHα measurements cannot be ruled out. These comparisons of the FWHM values are shown in Fig. 4, suggesting the reliability of our FWHM measurements.
. However, the measured rms scatter is significantly affected by a few samples with large discrepancies in FWHM measurements, raising the possibility that the rms scatter could be overestimated. The exceptions are related to the FWHMHα measurements, which implies that the possibility of inaccuracy in the FWHMHα measurements cannot be ruled out. These comparisons of the FWHM values are shown in Fig. 4, suggesting the reliability of our FWHM measurements.
 |
Fig. 4. (a) Comparison of FWHM values of broad components of Hβ and Hα lines. The dashed line denotes a line where the FWHM values of the Balmer lines are identical, and dash-dotted line is a well-known relationship between the FWHM values of the Balmer lines (Bisogni et al. 2017). (b) Comparison of Balmer line FWHM values measured from this work and Urrutia et al. (2012). Red circles denote the comparison of FWHMHβ measurements, and blue squares mean the comparison of FWHMHα measurements. Green triangles represent the FWHMHα measurement comparison, but the FWHMHβ measured in Urrutia et al. (2012) was converted to FWHMHα using the relationship established in Bisogni et al. (2017). The meaning of the dashed line is identical to that of panel (a). |
3.2. Spectral energy distribution fitting for mid-infrared continuum luminosities
In order to measure Lbol and MBH values of the dust-obscured and unobscured quasars using LMIR-based estimators (Kim et al. 2023), we estimated the monochromatic continuum luminosity, λLλ, at 3.4 μm and 4.6 μm (hereafter, L3.4 and L4.6, respectively) in the rest-frame. Although Kim et al. (2023) show that host galaxy contaminations at 3.4 μm and 4.6 μm are negligible (< 20%), we measured the L3.4 and L4.6 values after subtracting the host galaxy light by an SED fitting with optical to mid-infrared (MIR) photometric data of SDSS, 2MASS PSC, and WISE. For these photometric data, the intrinsic fluctuation (σm = 0.035 mag) of the spectrum with respect to a simple power-law spectrum found in Kim et al. (2015b) was added in quadrature to the original photometric error in each band. We additionally used B- and R-band photometry (Lasker et al. 2008) adopted from Glikman et al. (2012) for only the dust-obscured quasars.
The SED fitting was implemented using the method described in Kim et al. (2023). The photometric data, denoted as f(λ), were fit with an SED model that combines quasar (Q(λ)), elliptical galaxy (E(λ)), spiral galaxy (S(λ)), and irregular galaxy (I(λ)) spectra through a weighted sum, as
where C1, C2, C3, and C4 are the normalization constants. Q(λ), E(λ), S(λ), and I(λ) are reddened spectra of Q0(λ), E0(λ), S0(λ), and I0(λ), respectively. The Q0(λ) spectrum was adopted from Krawczyk et al. (2013), while the E0(λ), S0(λ), and I0(λ) spectra were taken from Assef et al. (2010). The intrinsic quasar spectrum of Krawczyk et al. (2013) is not significantly different from other quasar spectral templates (e.g., Richards et al. 2006; Assef et al. 2010) in the optical-to-MIR wavelength range (Kim et al. 2023).
For the dust reddening, we adopted a reddening law of Fitzpatrick (1999) based on the average Galactic extinction curve with an assumption of RV = 3.1 (e.g., Weingartner & Draine 2001). The reddening law is significantly different from other reddening laws (e.g., Calzetti et al. 2000) in the UV region, particularly due to the presence or absence of a UV bump at 2175 Å, which can alter the SED fitting results depending on the reddening law used. Therefore, the UV region (< 4000 Å) was excluded from our SED fitting.
For the SED fitting, an interactive data language procedure, MPFIT (Markwardt 2009), was used. Figures 5 and 6 show examples of the best-fit SED models with the photometric data of unobscured and dust-obscured quasars, respectively. Through the SED fitting, we obtained the E(B − V) values and extinction-corrected L3.4 and L4.6 values, and these properties of the dust-obscured quasars are presented in Table 1. Moreover, since Kim et al. (2023) found that the measured L3.4 and L4.6 values based on the quasar spectrum of Krawczyk et al. (2013) are ∼5% higher than those from Assef et al. (2010), the discrepancy was added as an uncertainty in quadrature to their original uncertainties obtained from the fit. Furthermore, through the SED fitting, we can measure quasar fractions, defined as C1Q(λ)/f(λ), at 3.4 μm and 4.6 μm. Since quasar activities of the dust-obscured and the unobscured quasars are dominant, we only used the SED fitting results for the sample with the measured quasar fractions exceeding 0.5.
 |
Fig. 5. Best-fit SED models and photometric data of four randomly selected unobscured quasars. Blue triangles, green squares, and red circles denote the photometric data points of SDSS, 2MASS PSC, and WISE, respectively. Dashed red and dotted blue lines mean the reddened spectra of quasar and host galaxy, respectively, and solid black lines represent the best-fit SED models. The name of the randomly selected sample and their E(B − V) values measured from the SED fitting are presented on the top left and top right side of each panel, respectively. |
 |
Fig. 6. Best-fit SED models and photometric data of four randomly selected dust-obscured quasars. The meanings of the symbols and lines are identical to those in Fig. 5, but B- and R-band photometry are additionally shown as yellow stars. |
3.3. Lbol and MBH values
In this subsection, we estimate bolometric luminosities and BH masses for both the dust-obscured and unobscured quasars. However, given that dust-obscured quasars are heavily obscured, it is necessary to use Lbol and MBH estimators that are immune to the dust extinction. Therefore, we used the LMIR-based Lbol and MBH estimators (Kim et al. 2023) that can measure these properties without the effects of dust extinction.
To estimate the Lbol values, we used the extinction-corrected L4.6 values measured from the SED fitting with the L4.6-based Lbol estimator (Kim et al. 2023). The L4.6-based Lbol estimator used was
The measured Lbol values of the dust-obscured quasars are listed in Table 2.
BH properties of dust-obscured quasars.
To obtain the MBH values, we used the LMIR-based MBH estimators (Kim et al. 2023), which are
and
For objects for which both FWHMHβ and FWHMHα measurements are available, we used the MBH values derived from FWHMHα. This is because, in the case of the dust-obscured quasars, some objects exhibit a broad component in the Hα line, while the broad component of the Hβ line is absent, suggesting that the FWHMHβ could be affected by dust extinction in extreme cases. The measured MBH values of the dust-obscured quasars are summarized in Table 2.
Similar to the dust-obscured quasars, we estimated the MBH values of the unobscured quasars using Eqs. (3) and (4). Among the 614 unobscured quasars selected in Sect. 2, 93 lack Balmer line measurements but exhibit Mg II line properties.
We converted their FWHMMg II to FWHMHβ using the relationship presented in Bisogni et al. (2017). These FWHMHβ values were used to measure their MBH values.
4. Eddington ratios
Using the Lbol and MBH values, we measured λEdd (Lbol/LEdd, where LEdd is the Eddington luminosity) values of the dust-obscured and unobscured quasars. The measured λEdd values of the dust-obscured quasars are also listed in Table 2.
A comparison of the Lbol and MBH values of the dust-obscured and the unobscured quasars is shown in Figs. 7 and 8 shows distributions of the λEdd values. The median log(λEdd) values of the dust-obscured and the unobscured quasars are −0.61 ± 0.38 and −0.98 ± 0.49, respectively, which shows that the λEdd values of the dust-obscured quasars are significantly higher than those of the unobscured quasars. In order to quantify how these λEdd values are significantly different, we performed a Kolmogorov-Smirnov test (K-S test) using the SciPy package (Virtanen et al. 2020) on Python. The maximum deviation between the cumulative distribution of these two λEdd values, D, is 0.36, and the probability of the result given the null hypothesis, p, is 0.001, indicating that they have different distributions.
 |
Fig. 7. Bolometric luminosities versus BH masses of dust-obscured and unobscured quasars. The dust-obscured quasars are open circles, with the colors representing their E(B − V) values, and the unobscured quasars are blue dots. The dashed, dash-dotted, and dotted lines denote λEdd values of 1.0, 0.1, and 0.01, respectively. |
 |
Fig. 8. Distribution of λEdd values of dust-obscured and unobscured quasars. The solid red and dashed blue histograms refer to the dust-obscured and unobscured quasars, respectively. |
Since λEdd values can vary with redshift due to sample bias effects or cosmological evolution, we have compared the λEdd values of the two kinds of quasars across their redshifts. The comparison is shown in Fig. 9. For the comparison, we divided the two kinds of quasars into six redshift bins: 0.10 ∼ 0.25, 0.25 ∼ 0.40, 0.40 ∼ 0.55, 0.55 ∼ 0.70, 0.70 ∼ 0.85, and 0.85 ∼ 1.00. The log(λEdd) values of the dust-obscured quasars in the six redshift bins are −1.10 ± 0.21, −0.61 ± 0.33, −0.83 ± 0.34, −0.50 ± 0.18, −0.44 ± 0.38, and −0.26 ± 0.39, and those of the unobscured quasars are −1.30±0.45, −1.27 ± 0.42, −1.07 ± 0.49, −0.75 ± 0.38, −0.67 ± 0.41, and −0.82 ± 0.44. This comparison reveals that the λEdd values of the dust-obscured quasars are significantly higher than those of the unobscured quasars for a wide redshift range (0 ≲ z ≲ 1).
 |
Fig. 9. log λEdd values vs. redshifts. The meanings of open circles and blue dots are identical to Fig. 7. Red and blue polygons represent the log λEdd values and their standard deviations of dust-obscured and unobscured quasars, respectively, which are divided into six subsamples by redshifts. |
Furthermore, given that λEdd can be affected by BH mass (e.g., Shen et al. 2011; Kim et al. 2015a), we have also compared the λEdd distributions of four subsamples divided by BH mass and redshift to mitigate the effects of BH mass and redshift on the λEdd distribution. First, we divided the dust-obscured quasars and the unobscured quasars into low-z (0.137 ≤ z ≤ 0.5) and high-z (0.5 < z ≤ 0.957) samples. For the low-z sample, we divided them into low-z and low-mass (108.15 M⊙ ≤ MBH ≤ 108.50 M⊙) and low-z and high-mass (108.50 M⊙ < MBH ≤ 109.22 M⊙) subsamples. For the low-z and low-mass subsample, seven dust-obscured quasars and 32 unobscured quasars were selected; their log(λEdd) values are −0.99 ± 0.31 and −0.94 ± 0.36, respectively. The λEdd values of the dust-obscured and unobscured quasars are similar, with a considerable overlap due to large uncertainties. However, in other subsamples, more significant differences are found. For the low-z and high-mass subsample, seven dust-obscured quasars and 74 unobscured quasars were selected; their log(λEdd) values are −0.61 ± 0.38 and −1.33 ± 0.35, respectively. After that, for the high-z sample, we also divided them into high-z and low-mass (108.15 M⊙ ≤ MBH ≤ 108.90 M⊙) and high-z and high-mass (108.90 M⊙ < MBH ≤ 109.22 M⊙) subsamples. For the high-z and low-mass subsample, eight dust-obscured quasars and 65 unobscured quasars were chosen; their log(λEdd) values are −0.38 ± 0.24 and −0.52 ± 0.31, respectively. Moreover, for the high-z and high-mass subsample, we obtained eight dust-obscured quasars and 43 unobscured quasars; their log(λEdd) values are −0.56 ± 0.36 and −0.82 ± 0.28, respectively. Overall, the λEdd of the dust-obscured quasars are significantly higher than those of the unobscured quasars in the limited redshift and MBH range. These comparisons are shown in Fig. 10.
 |
Fig. 10. (a) λEdd distributions for low-z and low-mass quasars. The solid red and dashed blue histograms denote the dust-obscured and the unobscured quasars, respectively. (b) λEdd distributions for low-z and high-mass quasars. (c) λEdd distributions for high-z and low-mass quasars. (d) λEdd distributions for high-z and high-mass quasars. |
5. Discussion
5.1. Comparisons of Lbol and MBH values of dust-obscured quasars from different estimators
The Lbol and MBH values of dust-obscured quasars have been measured using various methods (Kim & Im 2018; Urrutia et al. 2012). In this subsection, we examine the consistency between the Lbol and MBH values measured with the LMIR-based estimators and those obtained from the different methods used in Kim & Im (2018) and Urrutia et al. (2012).
Nine and four of our dust-obscured quasars overlap with the dust-obscured quasars studied in Kim & Im (2018) and Urrutia et al. (2012), respectively. Using these objects, we compared the Lbol and MBH values from our method with those from other methods. First, for the nine dust-obscured quasars, we compared their Lbol and MBH values from the LMIR-based estimators to those from Paschen line-based estimators (Kim et al. 2010, 2022a). Kim & Im (2018) measured their Pβ or Pα line properties, luminosity, and FWHM, and their Lbol and MBH values can be measured with the Paschen line-based estimators established in Kim et al. (2022a) and Kim et al. (2010), respectively. The Paschen line-based Lbol estimators (Kim et al. 2022a) are
and
Moreover, the Paschen line-based MBH estimators (Kim et al. 2010) are
and
The FWHM and luminosity of both the Pβ and Pα lines for 1307+2338 were measured in Kim & Im (2018), and its Lbol and MBH values from both lines were used in this comparison. The measured Lbol and MBH values based on the Paschen lines are summarized in Table 3.
BH properties of dust-obscured quasars from different estimators.
Second, Urrutia et al. (2012) measured the monochromatic luminosities, λLλ, at 15 μm (hereafter, L15) and FWHM values of Balmer lines for the four dust-obscured quasars. Their L15 values can be converted to the L4.6 values by applying the ratio of L15 to L4.6 in the quasar template of Krawczyk et al. (2013), and the Lbol values can be measured with Eq. (2) using the converted L4.6 values. Additionally, the MBH values can be measured with Eqs. (3) and (4) after converting the L15 values to L4.6 values using the ratio. The measured Lbol and MBH values from the L15 are listed in Table 3.
 |
Fig. 11. (a) Comparison of Lbol values from this work and different estimators. Red circles, blue squares, and green triangles denote the Lbol values derived by using Pβ, Pα, and L15, respectively. The dashed line denotes a line where the Lbol values are identical. (b) MBH values from this work versus those from different methods. Red circles and blue squares represent the MBH values measured with Pβ and Pα lines, respectively. Green triangles denote the MBH values estimated from L15 and the Balmer line width. The dashed line represents a line for which the MBH values are identical. |
Figure 11a presents a comparison of the Lbol values, showing a reasonable agreement between the two independent estimations; their Pearson correlation coefficient is 0.831. Overall, the Lbol values derived in this work are slightly overestimated compared to the Lbol values obtained through the different methods, yet there is no clear tendency.
Furthermore, a comparison of the MBH values is also presented in Fig. 11b. Compared to the Lbol comparison, there is a far less substantial agreement between the MBH values, and their Pearson correlation coefficient is only 0.257. This weak agreement might be due to their limited MBH range, but the impact of the less robust line widths between Paschen and Balmer lines (e.g., Landt et al. 2013) as a contributing factor cannot be ruled out.
5.2. Validity of LMIR-based Lbol estimators up to z = 2.5
In this subsection, we explore the applicability of the LMIR estimators up to z = 2.5, which were established using only SDSS quasars at z ≲ 0.5 (Kim et al. 2023). To determine whether there is any significant deviation between the LMIR-based Lbol values and those derived from other estimators up to z = 2.5, we compare the Lbol values from the L4.6-based estimator to those measured from UV- and optical-based estimators (Kim et al. 2023; Runnoe et al. 2012) that were established with continuum luminosities, λLλ, at 3000 Å and 5100 Å (hereafter, L3000 and L5100, respectively).
For the comparison, we selected 1046 SDSS quasars at z < 2.5 among the SDSS DR14 quasars (Pâris et al. 2018), following the selection method for unobscured quasars described in Sect. 2. Rakshit et al. (2020) measured the L3000 and L5100 values for 959 and 563 SDSS quasars, respectively. Their Lbol values can be estimated with the L3000- and L5100-based Lbol estimators. The L3000-based Lbol estimator (Runnoe et al. 2012) is
and the L5100-based Lbol estimator (Kim et al. 2023) is
Figure 12a shows the comparison of Lbol derived from L4.6 with those from L3000 and L5100, exhibiting a Pearson correlation coefficient of 0.952.
 |
Fig. 12. (a) Comparison of Lbol values from L4.6 and those obtained using different estimators. Red circles mean the Lbol values derived from L5100, while blue circles denote those derived from L3000. The dashed line is a line for which the Lbol values are identical. (b) MBH values measured based on L4.6 versus those from different methods. Red circles represent the comparison of MBH values measured using L4.6 and FWHMH, compared to those derived from L5100 and FWHMH. Meanwhile, blue circles denote the MBH values derived using L4.6 and FWHMMg II, versus those from L3000 and FWHMMg II. The dashed line denotes a line for which the MBH values are identical. |
Moreover, we investigated whether there is a redshift dependence for the Lbol values measured from L4.6 compared to those from other methods, as shown in Fig. 13. However, we found no evidence of redshift dependence. Thus, although the L4.6-based Lbol estimator was established using the SDSS quasars at z ≲ 0.5, our results demonstrate that the L4.6-based estimator accurately measures Lbol for quasars up to z = 2.5.
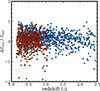 |
Fig. 13. Redshift versus ΔLbol/Lbol, where ΔLbol means the discrepancy between Lbol measured from L4.6 and that from either L3000 or L5100. Red and blue circles denote that the Lbol values have been derived from L5100 and L3000, respectively. |
Additionally, we compare MBH derived from L4.6 to those measured from other estimators. Among the 1046 SDSS quasars at z < 2.5, Rakshit et al. (2020) measured MBH values for 190 and 557 SDSS quasars using the L5100 combined with FWHMHα and FWHMHβ, respectively. Furthermore, Rakshit et al. (2020) also estimated MBH values for 804 SDSS quasars using L3000 and FWHMMg II. For the comparison, we determined MBH values based on L4.6 using Eq. (3) or (4) for objects with measurements of FWHMHβ or FWHMHα, respectively. For objects with FWHMMg II measurements, we estimated their MBH values using Eq. (3) after converting FWHMMg II to FWHMHβ, based on the relationship described by Bisogni et al. (2017). Figure 12b presents the comparison of MBH derived from L4.6 against those from L3000 and L5100, demonstrating the reliability of the L4.6-based MBH estimators up to z = 2.5. The Pearson correlation coefficient between the two quantities is 0.984. In this comparison, we used the FWHM values measured from the same line, and thus did not account for the relationships and distributions between FWHM values of different lines (e.g., Kim et al. 2010; Landt et al. 2013; Bisogni et al. 2017).
Although only some dust-obscured quasars at high z have been found to date (e.g., Banerji et al. 2015), it is expected that a significant number of high-z dust-obscured quasars will be discovered through future IR surveys, such as Spectro-Photometer for the History of the Universe, Epoch of Reionization, and Ices Explorer (SPHEREx; Doré et al. 2014). As a result, the LMIR-based estimators are expected to play an important role in unveiling the intrinsic properties of these high-z dust-obscured quasars.
6. Conclusions
In the merger-driven galaxy evolution scenario presented in Fig. 1, dust-obscured quasars are expected to occur as the intermediate-stage galaxies between ULIRGs and unobscured quasars. This scenario is supported by the higher λEdd values of dust-obscured quasars compared to those of unobscured quasars (Kim et al. 2015a; Kim & Im 2018). Although the BH activities of dust-obscured quasars are obscured, the previous studies used IR spectroscopic data to minimize the effects of dust extinction. However, the previous studies used a limited number of samples owing to (i) the considerable expense associated with obtaining the IR spectroscopic data; (ii) the limited IR wavelength window in the atmosphere. As a result, only a limited number of dust-obscured quasars have been studied, yielding statistics that are not robust and that are confined to narrow redshift ranges.
In order to overcome these limitations of the previous studies, we estimated the λEdd values of 30 dust-obscured quasars at z ≲ 1 using the L4.6-based Lbol and MBH estimators (Kim et al. 2023) that have the advantages of being widely applicable. Compared to the control sample of unobscured quasars, we found that the λEdd values of the dust-obscured quasars are significantly higher than those of the unobscured ones. This result was consistent across a wide redshift range (z ≲ 1), and identical outcomes were yielded even when the analysis was constrained by MBH or redshift.
Including our results, several observational studies have found that dust-obscured quasars have (i) high λEdd values (Urrutia et al. 2012; Kim et al. 2015a, 2018), (ii) high fractions of merging features in their host galaxies (Urrutia et al. 2008; Glikman et al. 2015), (iii) dusty red colors (Kim & Im 2018), (iv) merging SMBH systems (Kim et al. 2020a), and (v) enhanced star formation activities (Georgakakis et al. 2009). These findings strongly support the picture that dust-obscured quasars are the intermediate-stage galaxies between ULIRGs and unobscured quasars, as is outlined in Fig. 1.
Acknowledgments
D.K. acknowledges the support of the National Research Foundation of Korea (NRF) grant (Nos. 2021R1C1C1013580 and 2022R1A4A3031306) funded by the Korean Government (MSIT). Y. K. was supported by the National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. 2021R1C1C2091550). M.I. acknowledge the support from the National Research Foundation of Korea (NRF) grants, No. 2020R1A2C3011091, and No. 2021M3F7A1084525, funded by the Korea government (MSIT). M.K. acknowledges the support by the National Research Foundation of Korea (NRF) grant (No. 2022R1A4A3031306). G.L. acknowledges support from the Basic Science Research Program through NRF funded by MSIT (No.2022R1A6A3A01085930).
References
- Alexander, D. M., & Hickox, R. C. 2012, New Astron. Rev., 56, 93 [Google Scholar]
- Ananna, T. T., Urry, C. M., Ricci, C., et al. 2022a, ApJ, 939, L13 [NASA ADS] [CrossRef] [Google Scholar]
- Ananna, T. T., Weigel, A. K., Trakhtenbrot, B., et al. 2022b, ApJS, 261, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, S. F., Voges, W., Margon, B., et al. 2003, AJ, 126, 2209 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Assef, R. J., Kochanek, C. S., Brodwin, M., et al. 2010, ApJ, 713, 970 [NASA ADS] [CrossRef] [Google Scholar]
- Banerji, M., Alaghband-Zadeh, S., Hewett, P. C., et al. 2015, MNRAS, 447, 3368 [NASA ADS] [CrossRef] [Google Scholar]
- Becker, R. H., White, R. L., & Helfand, D. J. 1995, ApJ, 450, 559 [Google Scholar]
- Becker, R. H., White, R. L., Gregg, M. D., et al. 2001, ApJS, 135, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Bisogni, S., di Serego Alighieri, S., Goldoni, P., et al. 2017, A&A, 603, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boroson, T. A. 2002, ApJ, 565, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Calistro Rivera, G., Alexander, D. M., Rosario, D. J., et al. 2021, A&A, 649, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Calzetti, D., Armus, L., Bohlin, R. C., et al. 2000, ApJ, 533, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Comastri, A., Fiore, F., Vignali, C., et al. 2001, MNRAS, 327, 781 [CrossRef] [Google Scholar]
- Croom, S. M., Smith, R. J., Boyle, B. J., et al. 2004, MNRAS, 349, 1397 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Nelson, B. O., Kirkpatrick, J. D., Huchra, J. P., & Smith, P. S. 2001, The New Era of Wide Field Astronomy, 232, 78 [NASA ADS] [Google Scholar]
- Cutri, R. M., Nelson, B. O., Francis, P. J., & Smith, P. S. 2002, IAU Colloq. 184: AGN Surveys, 284, 127 [NASA ADS] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, The IRSA 2MASS All-Sky Point Source Catalog, NASA/IPAC Infrared Science Archive [Google Scholar]
- Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [Google Scholar]
- Dong, X., Wang, T., Wang, J., et al. 2008, MNRAS, 383, 581 [NASA ADS] [Google Scholar]
- Doré, O., Bock, J., Ashby, M., et al. 2014, ArXiv e-prints [arXiv:1412.4872] [Google Scholar]
- Ferrarese, L., & Merritt, D. 2000, ApJ, 539, L9 [Google Scholar]
- Fitzpatrick, E. L. 1999, PASP, 111, 63 [Google Scholar]
- Gebhardt, K., Bender, R., Bower, G., et al. 2000, ApJ, 539, L13 [Google Scholar]
- Georgakakis, A., Clements, D. L., Bendo, G., et al. 2009, MNRAS, 394, 533 [Google Scholar]
- Georgantopoulos, I., Pouliasis, E., Mountrichas, G., et al. 2023, A&A, 673, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Glikman, E., Gregg, M. D., Lacy, M., et al. 2004, ApJ, 607, 60 [NASA ADS] [CrossRef] [Google Scholar]
- Glikman, E., Helfand, D. J., White, R. L., et al. 2007, ApJ, 667, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Glikman, E., Urrutia, T., Lacy, M., et al. 2012, ApJ, 757, 51 [Google Scholar]
- Glikman, E., Simmons, B., Mailly, M., et al. 2015, ApJ, 806, 218 [Google Scholar]
- Glikman, E., LaMassa, S., Piconcelli, E., et al. 2024, MNRAS, 528, 711 [NASA ADS] [CrossRef] [Google Scholar]
- Grazian, A., Cristiani, S., D’Odorico, V., Omizzolo, A., & Pizzella, A. 2000, AJ, 119, 2540 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., & Ho, L. C. 2005, ApJ, 630, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Guo, H., Liu, X., Shen, Y., et al. 2019, MNRAS, 482, 3288 [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2005, ApJ, 630, 705 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., et al. 2006, ApJS, 163, 1 [Google Scholar]
- Hopkins, P. F., Hernquist, L., Cox, T. J., & Kereš, D. 2008, ApJS, 175, 356 [Google Scholar]
- Im, M., Griffiths, R. E., & Ratnatunga, K. U. 1997, ApJ, 475, 457 [NASA ADS] [CrossRef] [Google Scholar]
- Im, M., Lee, I., Cho, Y., et al. 2007, ApJ, 664, 64 [NASA ADS] [CrossRef] [Google Scholar]
- Jun, H. D., Assef, R. J., Carroll, C. M., et al. 2021, ApJ, 906, 21 [Google Scholar]
- Kaspi, S., Smith, P. S., Netzer, H., et al. 2000, ApJ, 533, 631 [Google Scholar]
- Khrykin, I. S., Hennawi, J. F., Worseck, G., et al. 2021, MNRAS, 505, 649 [CrossRef] [Google Scholar]
- Kim, D., & Im, M. 2018, A&A, 610, A31 [EDP Sciences] [Google Scholar]
- Kim, D., Im, M., & Kim, M. 2010, ApJ, 724, 386 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., Im, M., Glikman, E., et al. 2015a, ApJ, 812, 66 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., Im, M., Kim, J. H., et al. 2015b, ApJS, 216, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, Y., Im, M., Jeon, Y., et al. 2015c, ApJ, 813, L35 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., Im, M., Canalizo, G., et al. 2018, ApJS, 238, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, Y., Im, M., Jeon, Y., et al. 2019, ApJ, 870, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., Im, M., Kim, M., et al. 2020a, ApJ, 894, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, Y., Im, M., Jeon, Y., et al. 2020b, ApJ, 904, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., Lee, D., & Im, M. 2022a, MNRAS, 509, 1147 [Google Scholar]
- Kim, Y., Im, M., Jeon, Y., et al. 2022b, AJ, 164, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., Im, M., Kim, M., et al. 2023, ApJ, 954, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Kim, D., Im, M., Lim, G., et al. 2024a, J. Kor. Astron. Soc., 57, 95 [NASA ADS] [Google Scholar]
- Kim, Y., Kim, D., Im, M., et al. 2024b, ApJ, 972, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Krawczyk, C. M., Richards, G. T., Mehta, S. S., et al. 2013, ApJS, 206, 4 [Google Scholar]
- Lacy, M., Storrie-Lombardi, L. J., Sajina, A., et al. 2004, ApJS, 154, 166 [Google Scholar]
- Landt, H., Ward, M. J., Peterson, B. M., et al. 2013, MNRAS, 432, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Lansbury, G. B., Banerji, M., Fabian, A. C., et al. 2020, MNRAS, 495, 2652 [CrossRef] [Google Scholar]
- Lasker, B. M., Lattanzi, M. G., McLean, B. J., et al. 2008, AJ, 136, 735 [Google Scholar]
- Lee, I., Im, M., Kim, M., et al. 2008, ApJS, 175, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Lyke, B. W., Higley, A. N., McLane, J. N., et al. 2020, ApJS, 250, 8 [NASA ADS] [CrossRef] [Google Scholar]
- Markwardt, C. B. 2009, ASP Conf. Ser., 411, 251 [Google Scholar]
- McLure, R. J., & Dunlop, J. S. 2004, MNRAS, 352, 1390 [NASA ADS] [CrossRef] [Google Scholar]
- Menci, N., Cavaliere, A., Fontana, A., et al. 2004, ApJ, 604, 12 [Google Scholar]
- Pâris, I., Petitjean, P., Aubourg, É., et al. 2014, A&A, 563, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pâris, I., Petitjean, P., Aubourg, É., et al. 2018, A&A, 613, A51 [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Polletta, M., Weedman, D., Hönig, S., et al. 2008, ApJ, 675, 960 [NASA ADS] [CrossRef] [Google Scholar]
- Puchnarewicz, E. M., & Mason, K. O. 1998, MNRAS, 293, 243 [NASA ADS] [CrossRef] [Google Scholar]
- Rakshit, S., Stalin, C. S., & Kotilainen, J. 2020, ApJS, 249, 17 [Google Scholar]
- Richards, G. T., Lacy, M., Storrie-Lombardi, L. J., et al. 2006, ApJS, 166, 470 [Google Scholar]
- Risaliti, G., & Elvis, M. 2005, ApJ, 629, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Rose, M. 2014, Am. Astron. Soc. Meeting Abstr., 223, 32103 [NASA ADS] [Google Scholar]
- Rose, M., Tadhunter, C. N., Holt, J., & Rodríguez Zaurín, J. 2013, MNRAS, 432, 2150 [Google Scholar]
- Runnoe, J. C., Brotherton, M. S., & Shang, Z. 2012, MNRAS, 422, 478 [Google Scholar]
- Sanders, D. B., & Mirabel, I. F. 1996, ARA&A, 34, 749 [Google Scholar]
- Sanders, D. B., Soifer, B. T., Elias, J. H., et al. 1988, ApJ, 325, 74 [Google Scholar]
- Schneider, D. P., Hall, P. B., Richards, G. T., et al. 2005, AJ, 130, 367 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [Google Scholar]
- Shen, Y., Hall, P. B., Horne, K., et al. 2019, ApJS, 241, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Shin, S., Im, M., Kim, Y., et al. 2020, ApJ, 893, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Shin, S., Im, M., Kim, Y., et al. 2022, J. Kor. Astron. Soc., 55, 131 [NASA ADS] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Stacey, H. R., Costa, T., McKean, J. P., et al. 2022, MNRAS, 517, 3377 [NASA ADS] [CrossRef] [Google Scholar]
- Suh, H., Civano, F., Hasinger, G., et al. 2019, ApJ, 872, 168 [Google Scholar]
- Tozzi, P., Gilli, R., Mainieri, V., et al. 2006, A&A, 451, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urrutia, T., Lacy, M., & Becker, R. H. 2008, ApJ, 674, 80 [Google Scholar]
- Urrutia, T., Becker, R. H., White, R. L., et al. 2009, ApJ, 698, 1095 [Google Scholar]
- Urrutia, T., Lacy, M., Spoon, H., et al. 2012, ApJ, 757, 125 [Google Scholar]
- Urry, C. M., & Padovani, P. 1995, PASP, 107, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Vestergaard, M. 2002, ApJ, 571, 733 [NASA ADS] [CrossRef] [Google Scholar]
- Vestergaard, M., & Peterson, B. M. 2006, ApJ, 641, 689 [Google Scholar]
- Véron-Cetty, M.-P., & Véron, P. 2006, A&A, 455, 773 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Virtanen, P., Gommers, R., Oliphant, T. E., et al. 2020, Nat. Methods, 17, 261 [Google Scholar]
- Webster, R. L., Francis, P. J., Petersont, B. A., Drinkwater, M. J., & Masci, F. J. 1995, Nature, 375, 469 [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [Google Scholar]
- Whiting, M. T., Webster, R. L., & Francis, P. J. 2001, MNRAS, 323, 718 [Google Scholar]
- Wilkes, B. J., Schmidt, G. D., Cutri, R. M., et al. 2002, ApJ, 564, L65 [Google Scholar]
- Wright, E. L., Eisenhardt, P. R. M., Mainzer, A. K., et al. 2010, AJ, 140, 1868 [Google Scholar]
- Xu, D., Komossa, S., Zhou, H., et al. 2007, ApJ, 670, 60 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, J. E., et al. 2000, AJ, 120, 1579 [Google Scholar]
- Young, M., Elvis, M., & Risaliti, G. 2009, ApJS, 183, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, H., Wang, T., Yuan, W., et al. 2006, ApJS, 166, 128 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1. Schematic outline of merger-driven galaxy evolution scenario. |
| In the text | |
 |
Fig. 2. (a) Redshift versus L4.6 luminosity. Red circles and blue dots denote the selected dust-obscured quasars and SDSS quasars, respectively. Among the blue dots, 300 blue dots with black edges represent the L4.6–z matched SDSS quasars, which were used as unobscured quasars. (b) Redshift distributions of the two kinds of quasars. Red and blue histograms represent the dust-obscured quasars and the unobscured quasars, respectively. |
| In the text | |
 |
Fig. 3. Fitting results of the Hβ and Hα lines for the dust-obscured quasars. The solid black lines denote the continuum-subtracted spectra in the rest-frame. The dash-dotted red lines are the best-fit model, and the dashed blue and dotted green lines represent the broad and narrow components of the each line complex, respectively. |
| In the text | |
 |
Fig. 3. continued. |
| In the text | |
 |
Fig. 4. (a) Comparison of FWHM values of broad components of Hβ and Hα lines. The dashed line denotes a line where the FWHM values of the Balmer lines are identical, and dash-dotted line is a well-known relationship between the FWHM values of the Balmer lines (Bisogni et al. 2017). (b) Comparison of Balmer line FWHM values measured from this work and Urrutia et al. (2012). Red circles denote the comparison of FWHMHβ measurements, and blue squares mean the comparison of FWHMHα measurements. Green triangles represent the FWHMHα measurement comparison, but the FWHMHβ measured in Urrutia et al. (2012) was converted to FWHMHα using the relationship established in Bisogni et al. (2017). The meaning of the dashed line is identical to that of panel (a). |
| In the text | |
 |
Fig. 5. Best-fit SED models and photometric data of four randomly selected unobscured quasars. Blue triangles, green squares, and red circles denote the photometric data points of SDSS, 2MASS PSC, and WISE, respectively. Dashed red and dotted blue lines mean the reddened spectra of quasar and host galaxy, respectively, and solid black lines represent the best-fit SED models. The name of the randomly selected sample and their E(B − V) values measured from the SED fitting are presented on the top left and top right side of each panel, respectively. |
| In the text | |
 |
Fig. 6. Best-fit SED models and photometric data of four randomly selected dust-obscured quasars. The meanings of the symbols and lines are identical to those in Fig. 5, but B- and R-band photometry are additionally shown as yellow stars. |
| In the text | |
 |
Fig. 7. Bolometric luminosities versus BH masses of dust-obscured and unobscured quasars. The dust-obscured quasars are open circles, with the colors representing their E(B − V) values, and the unobscured quasars are blue dots. The dashed, dash-dotted, and dotted lines denote λEdd values of 1.0, 0.1, and 0.01, respectively. |
| In the text | |
 |
Fig. 8. Distribution of λEdd values of dust-obscured and unobscured quasars. The solid red and dashed blue histograms refer to the dust-obscured and unobscured quasars, respectively. |
| In the text | |
 |
Fig. 9. log λEdd values vs. redshifts. The meanings of open circles and blue dots are identical to Fig. 7. Red and blue polygons represent the log λEdd values and their standard deviations of dust-obscured and unobscured quasars, respectively, which are divided into six subsamples by redshifts. |
| In the text | |
 |
Fig. 10. (a) λEdd distributions for low-z and low-mass quasars. The solid red and dashed blue histograms denote the dust-obscured and the unobscured quasars, respectively. (b) λEdd distributions for low-z and high-mass quasars. (c) λEdd distributions for high-z and low-mass quasars. (d) λEdd distributions for high-z and high-mass quasars. |
| In the text | |
 |
Fig. 11. (a) Comparison of Lbol values from this work and different estimators. Red circles, blue squares, and green triangles denote the Lbol values derived by using Pβ, Pα, and L15, respectively. The dashed line denotes a line where the Lbol values are identical. (b) MBH values from this work versus those from different methods. Red circles and blue squares represent the MBH values measured with Pβ and Pα lines, respectively. Green triangles denote the MBH values estimated from L15 and the Balmer line width. The dashed line represents a line for which the MBH values are identical. |
| In the text | |
 |
Fig. 12. (a) Comparison of Lbol values from L4.6 and those obtained using different estimators. Red circles mean the Lbol values derived from L5100, while blue circles denote those derived from L3000. The dashed line is a line for which the Lbol values are identical. (b) MBH values measured based on L4.6 versus those from different methods. Red circles represent the comparison of MBH values measured using L4.6 and FWHMH, compared to those derived from L5100 and FWHMH. Meanwhile, blue circles denote the MBH values derived using L4.6 and FWHMMg II, versus those from L3000 and FWHMMg II. The dashed line denotes a line for which the MBH values are identical. |
| In the text | |
 |
Fig. 13. Redshift versus ΔLbol/Lbol, where ΔLbol means the discrepancy between Lbol measured from L4.6 and that from either L3000 or L5100. Red and blue circles denote that the Lbol values have been derived from L5100 and L3000, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.