| Issue |
A&A
Volume 607, November 2017
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 28 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201629627 | |
| Published online | 30 October 2017 | |
H i anisotropies associated with radio-polarimetric filaments
Steep power spectra associated with cold gas
1 Argelander-Institut für Astronomie, Auf dem Hügel 71, 53121 Bonn, Germany
e-mail: pkalberla@astro.uni-bonn.de
2 Tartu Observatory, 61602 Tõravere, Tartumaa, Estonia
3 Department of Astrophysics/IMAPP, Radboud University Nijmegen, PO Box 9010, 6500 GL Nijmegen, The Netherlands
Received: 31 August 2016
Accepted: 18 July 2017
Context. LOFAR detected toward 3C 196 linear polarization structures which were found subsequently to be closely correlated with cold filamentary H i structures. The derived direction-dependent H i power spectra revealed marked anisotropies for narrow ranges in velocity, sharing the orientation of the magnetic field as expected for magneto-hydrodynamical (MHD) turbulence.
Aims. Using the Galactic portion of the Effelsberg-Bonn H i Survey (EBHIS) we continue our study of such anisotropies in the H i distribution in direction of two WSRT fields, Horologium and Auriga; both are well known for their prominent radio-polarimetric depolarization canals. At 349 MHz the observed pattern in total intensity is insignificant but polarized intensity and polarization angle show prominent ubiquitous structures with so far unknown origin.
Methods. Apodizing the H i survey data by applying a rotational symmetric 50% Tukey window, we derive average and position angle dependent power spectra. We fit power laws and characterize anisotropies in the power distribution. We used a Gaussian analysis to determine relative abundances for the cold and warm neutral medium.
Results. For the analyzed radio-polarimetric targets significant anisotropies are detected in the H i power spectra; their position angles are aligned to the prominent depolarization canals, initially detected by WSRT. H i anisotropies are associated with steep power spectra. Steep power spectra, associated with cold gas, are detected also in other fields.
Conclusions. Radio-polarimetric depolarization canals are associated with filamentary H i structures that belong to the cold neutral medium (CNM). Anisotropies in the CNM are in this case linked to a steepening of the power-spectrum spectral index, indicating that phase transitions in a turbulent medium occur on all scales. Filamentary H i structures, driven by thermal instabilities, and radio-polarimetric filaments are associated with each other. The magneto-ionic medium that causes the radio-polarimetric filaments is probably wrapped around the H i.
Key words: turbulence / ISM: structure / ISM: magnetic fields
© ESO, 2017
1. Introduction
A significant fraction of the cold neutral medium (CNM) filamentary structures is aligned with filamentary structures in polarized dust emission, both elongated along the mean magnetic field (Clark et al. 2014; Planck Collaboration Int. XXXII 2016; Kalberla et al. 2016). The correlation is well defined over large areas. Constructing a dust model by incorporating CNM column density maps from the Galactic All Sky Survey (GASS, Kalberla & Haud 2015) as tracers of the dust intensity structures and using a phenomenological description of the mean Galactic magnetic field, Ghosh et al. (2017) were able to reproduce the Planck dust observations at 353 GHz for the southern Galactic cap.
LOFAR radio-polarimetric observations in a field toward 3C 196 show striking filamentary structures in polarized intensity. This is one of three primary fields of the LOFAR-Epoch of Reionization key science project. It shows many degrees long filamentary structures, the most striking of which is remarkably straight, at a Faraday depth of +0.5 rad m-2, oriented in equatorial coordinates in an approximately north-south direction and parallel to the Galactic plane (Jelić et al. 2015). If this filament is assumed to lie within the Local Bubble (Lallement et al. 2014), it shows an excess in thermal electron density compared to its surroundings. Radio-polarimetric depolarization canals appear to define boundaries around this filamentary structure, and are most probably the result of beam depolarization due to discontinuities in polarization angle orientation (Jelić et al. 2015, Sect. 5). These filamentary structures are surprisingly well correlated with the magnetic field orientation, probed by the Planck satellite (Zaroubi et al. 2015).
Characteristic for a radio-polarimetric depolarization canal is that the observed polarized intensity falls to zero; the polarization angle changes by 90° across the canal which is observed to be only a telescope beam wide. In case of the fields studied here and in (Kalberla & Kerp 2016, Paper I), many of the observed radio-polarimetric depolarization canals are rather straight with well defined preferential directions.
Radio-polarimetric depolarization canals are believed to have heterogeneous causes. Canals can be created by a boundary between two magneto-ionized regions with different properties and-or strong rotation measure (RM) gradients, that cause a 90-degree polarization angle change between the regions (Haverkorn & Heitsch 2004). These canals are characterized by a location-independence as a function of frequency and trace lines of constant RM gradient. The canals around the straight filaments in the LOFAR 3C 196 observations are likely caused by this effect.
Radio-polarimetric depolarization canals due to fortuitous properties of the magneto-ionized medium completely nulling polarization along the line of sight (differential Faraday rotation) have been called Faraday ghosts (Shukurov & Berkhuijsen 2003). These should only occur in very homogeneous media, change location with frequency, and trace lines of constant RM. In a turbulent, ionized medium in which synchrotron emission and Faraday rotation are mixed, the situation is more complex. Fletcher & Shukurov (2007) argue that straighter canals may arise from RM discontinuities in the diffuse ISM, in particular shocks, and the twisting canals have a different origin such as differential Faraday rotation.
We recently explored filamentary structures and anisotropies in the power distribution in H i gas on scales of arcminutes to a few degrees in the field toward 3C 196 (Paper I). There, we reported on strong anisotropies in the H i distribution that are best described as anisotropies in the power distribution for narrow ranges in velocity. For a narrow range in position angle, oriented perpendicular to the filamentary structures and the mean magnetic fields, the spectral power (measured in the Fourier plane) is on average more than an order of magnitude higher than parallel. These observational results are consistent with predictions by Goldreich & Sridhar (1995); the scale dependent anisotropy of the turbulence increases with spatial frequency but the spectral power distribution orthogonal to the filamentary structures is left nearly unaffected.
With respect to some aspects however, the observational findings do not agree with the theoretical expectations. Kandel et al. (2016) extended recently the velocity channel analysis (VCA), introduced by Lazarian & Pogosyan (2000), and found that for magneto-hydrodynamical (MHD) turbulence anisotropies should increase proportional to the thickness of the velocity slice. This proposal could not be confirmed by observations (Paper I), anisotropies tend to be best defined for narrow velocity intervals. The observations show in general that the strongest anisotropies are associated with rather cold filamentary H i structures.
Absorption measurements against continuum background sources are required to determine the temperature of the CNM (Dickey & Lockman 1990; Kalberla & Kerp 2009). In practice the number of available sufficiently strong continuum sources is however rather limited for a complete census of the CNM (e.g., Heiles & Troland 2003). But in case that the optical depth of the CNM is not too high (τ ≲ 0.5) it is possible to use alternative methods to determine upper limits of the kinetic temperature from line widths. The H i emission data are first filtered by unsharp masking (USM)1, afterwards Doppler temperatures TD are derived from line widths, see Sects. 3, 5.8 and 5.9 of Kalberla et al. (2016) for details. Typical Doppler temperatures, upper limit to the kinetic or excitation temperature of the H i gas, are TD ~ 223 K. At typical turbulent CNM Mach numbers of Mt ~ 3.7, such Doppler temperatures are characteristic for a thermal CNM gas temperature of T ~ 52 K (Heiles & Troland 2005; Kalberla et al. 2016). Consequently, radial velocity channel maps (velocity slices) that are separated by more the 3 km s-1 are uncorrelated and anisotropies are traceable for a very limited number of subsequent velocity channels only. Increasing the velocity slice thickness in such a situation does not necessarily improve the signal-to-noise ratio (S/N) of the anisotropic power distribution but may lead to the opposite result.
It is also striking to find filamentary CNM structures associated with the magneto-ionic medium. MHD simulations of the interstellar medium (ISM) by Choi & Stone (2012, their Fig. 8) showed that thermal conduction can play an important role in shaping structures formed by thermal instabilities (TI). Anisotropic conduction in the presence of a regular magnetic field can strongly affect the shapes and sizes of cold clouds, possibly leading to thin filamentary H i structures as reported first by McClure-Griffiths et al. (2006) and later on larger scales by Clark et al. (2014) and Kalberla et al. (2016). However, even without magnetic fields the formation of thin CNM sheets is considered to be feasible (Vázquez-Semadeni et al. 2006).
Anisotropies in the power distribution of the H i, analyzed in Paper I, are associated with CNM. Saury et al. (2014) have shown that turbulent motions of the H i cannot provoke the phase transition from warm neutral medium (WNM) to CNM. An increase of the WNM density by at least a factor two to four is needed to induce phase transitions. Based on the morphology of the CNM clouds it was argued in Paper I that these anisotropies must have been caused by shocks. As a follow-up of this conjecture we consider the case whether thermal instabilities might cause filamentary H i structures, associated with ionized gas layers which are in the presence of a magnetic field responsible for the linear polarization structures.
We study in detail two fields with prominent radio-polarimetric depolarization canals aligned with polarized intensity filaments, located in the constellations of Horologium and Auriga (Haverkorn et al. 2003a,b,c). Observations and data processing are presented in Sect. 2. In Sects. 3 and 4 respectively we derive power spectra and power anisotropies for the Horologium and Auriga fields. For several H i components we find dominant anisotropies and compare the corresponding filamentary H i structures with images of the radio-polarimetric Westerbork Synthesis Radio Telescope (WSRT) data. Anisotropies and power spectral indices show significant variations, depending on velocity. In Sect. 5 we demonstrate that the spectral index is related to the temperature of the H i gas and the column density ratio between CNM and WNM. We conclude that phase transitions must be responsible for a steepening of the power spectra and use in Sect. 6 a heuristic description for the changes in the turbulent power distribution caused by thermal instabilities. Section 7 discusses several possible explanations for the observed filamentary structures. We conclude in Sect. 8 that regular magnetic fields may play a significant role for phase transitions of compressed cold H i gas in a sheet-like geometry.
2. Data
We compare data from WSRT continuum polarization observations with H i data from the Effelsberg-Bonn H i Survey (EBHIS) and describe here the observations and basics of the data reduction.
2.1. Continuum polarization observations: Horologium and Auriga
For the multi-frequency radio-polarimetric observations of the Galactic radio background in Horologium and Auriga the WSRT was used. These fields were observed in 8 frequency bands between 325 and 390 MHz simultaneously, each with a band width of 5 MHz. To obtain a large field of view, and to reduce off-axis instrumental polarization, the mosaicking technique was used. In each case six 12 h periods were observed, resulting in baseline increments of 12 m with baselines between 36 m and 2700 m. The resulting resolution is 1′ but a Gaussian taper was applied later to the (u, v)-data to increase the S/N. The derived maps of linearly polarized intensities Stokes Q and U were used to compute the polarized intensity and polarization angle, for details see Haverkorn et al. (2003a–c).
The Horologium field is a ~5° × 7° field centered at (l ~ 137°, b ~ 7°), and Auriga is ~5° × 7° in size, centered at (l ~ 161°, b ~ 16°). So both fields are located not far off the Galactic plane in the second Galactic quadrant, in the Fan Region. The Fan Region is a large region in the sky, in the range ℓ ~ [120°,170°] and b ~ [−5°, + 20°] with remarkably high polarized intensity and regular polarization angle, interpreted as an especially regular magnetic field structure in that direction (Spoelstra 1984). The Fan Region has long thought to be a local structure, although recent work suggests that Fan Region emission may come from a range of distances out to the Perseus Arm (Wolleben et al. 2006; Hill et al. 2017). Over much of the Fan Region the electric vectors are perpendicular to the Galactic plane, indicating that the mean magnetic field is aligned with the plane.
Both the Horologium and the Auriga field show conspicuous linear structures in polarized intensity at frequencies around 349 MHz. These filaments are not present in total (synchrotron) intensity, indicating that they are caused by Faraday rotation creating small-scale structure in Stokes parameters Q and U, and not by enhanced filamentary synchrotron emission. The Auriga field is dominated by linearly polarized filaments up to 4° in length, dominated by two directions one of which is parallel to the Galactic plane. The most conspicuous feature in the Horologium field is a ring-like structure (not discussed here), crossed by long linear polarized filaments, again directed along the Galactic plane. Both fields show long and narrow depolarized filaments, always one resolution element wide, called depolarization canals (Haverkorn et al. 2000).
2.2. H I Survey data and processing
For the H i distribution in direction to these WSRT fields we use the first data release of the Galactic portion of the Effelsberg-Bonn H i Survey (EBHIS, Winkel et al. 2016a). This survey covers the northern sky for declinations grater than −5° at a velocity resolution of ΔvLSR = 1.44 km s-1. From the original EBHIS data base, corrected for instrumental baselines, radio interference and stray radiation, we extract FITS data cubes with an effective rotational symmetric Gaussian beam-size of 10.́8 FWHM (Winkel et al. 2016b). The brightness temperatures of individual velocity channel maps at this resolution have rms uncertainties of 90 mK.
To derive the spectral power distribution we use the same data processing as described in detail in Paper I. We first apodize the data with a rotational symmetric 50% cosine taper (Tukey) window (Harris 1978). The tapered distribution is Fourier transformed, the amplitudes are then squared and corrected for the beam response. We use polar coordinates k,Φ to determine dependencies in the u,v plane with a position angle Φ = atan2(v,u). This, also the definition in Paper I, differs from the standard north through east definition but we do not expect conflicts since Φ is not used for comparison with published position angles.
H i observations are here as usual processed as position-position-velocity (PPV) data cubes. Individual channels represent brightness temperatures (or column densities) at constant velocities with a bandwidth of ΔvLSR. This bandwidth can be increased by integrating several channel maps. Power spectra, calculated from such channel maps, provide the so-called 2D power distribution from which a 2D spectral index γ can be fit. Throughout this paper we provide without further notification observed 2D power distributions and accordingly 2D spectral indices.
We derive the average power spectrum P(k) by integrating the 2D power distribution in annuli of constant spatial frequencies 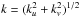 , fitting the power distribution with a power law of the form
, fitting the power distribution with a power law of the form 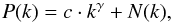 (1)here c is an arbitrary scaling factor, γ is the spectral index and N(k) the contribution due to instrumental noise. Subsequently we correct for the contribution N(k) to the power spectrum by subtracting the matched noise template N(k) as described in Paper I. The noise stability of the EBHIS is excellent, it is not necessary to derive position or time dependent templates.
(1)here c is an arbitrary scaling factor, γ is the spectral index and N(k) the contribution due to instrumental noise. Subsequently we correct for the contribution N(k) to the power spectrum by subtracting the matched noise template N(k) as described in Paper I. The noise stability of the EBHIS is excellent, it is not necessary to derive position or time dependent templates.
The derived normalized power spectrum P(k) ∝ kγ is noise limited for high spatial frequencies k; the limit depends on the S/N of the observations but reflects also the limited spatial sensitivity of the 100-m telescope. We interpret only data with a S/N of three or better, comparing the noise corrected power P(k) with the matched noise template N(k). This limit, typically close to k< 0.07 arcmin-1, is marked in all plots by a vertical line. The lowest spatial frequency that we can use for our analysis depends on the field of view and is k ~ 1.2 × 10-3 arcmin-1.
To quantify anisotropies, we average data within sectors Φ ± ΔΦ to measure the position angle dependent power P(Φ,k); we use ΔΦ = 4°. In case of significant anisotropies, P(Φ,k) shows well defined maxima in the u,v plane at similar position angles Φ⊥ over a range of spatial frequencies (Fig. 7 of Paper I). Since the power spectrum is defined in the u,v plane, Φ⊥ is oriented perpendicular to the position angle of filamentary structures in the image plane (Paper I, Figs. 3 to 5). In presence of a magnetic field the propagation of turbulence is affected by the field direction and eddies are elongated along the magnetic field lines at Φ∥ (Goldreich & Sridhar 1995).
As a measure of the local anisotropies we define the ratio between maximum and minimum power, at position angles Φ⊥ and Φ∥, 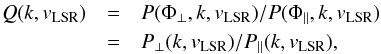 (2)where Φ∥ = Φ⊥ + 90°.
(2)where Φ∥ = Φ⊥ + 90°.
There are two different ways to derive characteristic power anisotropies, the average Qaver, defined as the geometrical mean anisotropy over a range in spatial frequencies and alternatively Qpeak, the peak anisotropy at a particular spatial frequency. Both anisotropy measures should result in similar position angles. The magnitude of Qaver is arbitrary since it depends on the spatial frequency range used. We use Qaver for an automated identification of velocity channels with significant anisotropies according to Eq. (2). Based on this we search then for peak anisotropies at particular interesting velocity channels.
Our data processing methods, outlined above and in Paper I, are discussed in more detail and compared with robust methods in Appendix A.
3. Horologium
In this section we derive parameters for the local H i distribution in the Horologium region (RA = 48°, Dec = 66°(B1950.0), l ~ 137°, b ~ 7°) that may be compared with observations of the linearly polarized component of the diffuse Galactic radio background (Haverkorn et al. 2003b,c). We analyze EBHIS data within a diameter of 13.̊7 (at 100% taper).
 |
Fig. 1 Comparison between average brightness temperature TB aver (red), anisotropy factor Qaver (blue) for 0.002 <k< 0.015 arcmin-1, and spectral index γ (green) for the Horologium field. The upper horizontal black dotted line indicates the Kolmogorov spectral index of γ = −8 / 3, the lower dash-dotted line Qaver = 0. |
3.1. Average H I properties
Figure 1 gives an overview over global properties of the H i gas in this region. The weighted mean brightness temperature TB aver (see Paper I, Eq. (4)), averaged after apodization, shows for the local gas a broad emission line with several components, peaking at a velocity of vLSR = −10.2 km s-1.
From the rotation curve of the Milky Way we may map velocities to distances (e.g., Kalberla & Dedes 2008)2. The galactocentric distance is R ~ 13 kpc, its height above mid-plane z ~ 0.7 kpc. In addition there is a faint high velocity component at vLSR ~ −100 km s-1. Using a dynamical distance estimate from Kalberla & Dedes (2008), this gas is located beyond the outer arm at a distance of 19 kpc with a galactocentric radius of 26 kpc (Levine et al. 2006). The anisotropies at high velocities are discussed in Appendix B.
In Fig. 1 we show the average (position angle independent) spectral index γ of the power distribution according to Eq. (1). For the local emission at vLSR = 2.7 km s-1 we find a well defined minimum at γ = −3.25 ± 0.03. The derivation of the anisotropy factor Qaver is explained in Sect. 3.2
 |
Fig. 2 Average position angles Φaver calculated for 0.002 < k < 0.015 arcmin-1 and associated one σ rms scatter for the Horologium field. The position angle Φ = −58.5°, perpendicular to the position angle of the radio-polarimetric depolarization canals that are aligned parallel to the Galactic plane, is indicated with a horizontal line. |
3.2. Position angle dependencies on vLSR
Local anisotropies and average position angles Φaver(vLSR), defined as averages over Φ⊥(vLSR), were determined as described in Sect. 3.2 of Paper I, see there Fig. 73. In spatial frequencies we used the range 0.007 <k < 0.07 arcmin-1, corresponding to angular scales of 140′ ≳ 1 /k ≳ 14′. In the velocity range −120 < vLSR < −35 km s-1 we found anisotropies predominantly at low spatial frequencies, corresponding to large scale features. We repeated therefore the determination within a range 0.002 < k < 0.015 arcmin-1. This choice resulted in better defined position angles with lower dispersion at high velocities but left the results for the local gas nearly unchanged. Figure 2 displays the average position angles Φaver and the associated standard deviation. For −20 < vLSR < 20 km s-1 the position angle is essentially constant, Φaver ~ −55°, indicated in Fig. 2 with a horizontal line. Φ = −55° is oriented perpendicular to the position angle of the WSRT depolarization canals and the Galactic plane (Haverkorn et al. 2003c, Fig. 3). This implies that filamentary structures in the image plane over this velocity range are elongated predominantly parallel to the Galactic plane, see Figs. 5 and 7.
 |
Fig. 3 Average power spectrum observed for vLSR = 2.7 km s-1 (black dots) and fit power law with γ = −3.25 ± 0.03 for k< 0.07 arcmin-1 (vertical line). In addition the power spectrum for 118° < Φ < 133° (red) and 28° < Φ < 43° (green) is given. The average anisotropy factor for 0.002 <k< 0.015 arcmin-1 is Qaver = 7.7. |
 |
Fig. 4 Anisotropies Q(k) for the channels at vLSR = 2.7 km s-1 (red) and vLSR = 1.4 km s-1 (blue). |
From the position angles Φaver(vLSR) we derive average anisotropies Qaver. The result is plotted in Fig. 1. The Horologium field shows moderate anisotropies with Qaver ~ 7.7 at vLSR = 2.7 km s-1. The anisotropies appear to increase for vLSR ≳ 0 km s-1, possibly related to a CNM component with a steep spectral index.
3.3. Anisotropies at vLSR = 2.7 km s-1
The H i distribution at vLSR = 2.7 km s-1 is of particular interest since the uncertainties in the average position angle are low and the spectral index γ = −3.25 ± 0.03 is quite steep. Anisotropic power spectra for this channel map are plotted in Fig. 3. We find frequently that anisotropies can change significantly from one velocity channel to another, although some of the structures may be preserved. We therefore compare the anisotropies of two neighbor channels (in comparing, please take the logarithmic scale into account). Figure 4 shows for comparison the anisotropies Q at vLSR = 2.7 km s-1 and vLSR = 1.4 km s-1.
The velocity channel at vLSR = 2.7 km s-1 has the best defined position angle with the lowest dispersion and we expect accordingly that the H i distribution should show filamentary structures. Small scale structures are best visualized from USM maps, as introduced by Kalberla et al. (2016) and demonstrated in Paper I. In Fig. 5 we compare the USM filamentary H i structures at vLSR = 2.7 km s-1, using isophotes, with the color coded map of the polarized intensity observed at 349 MHz. The filamentary H i structures are preferentially oriented parallel to the Galactic plane, in excellent agreement with the orientation obtained from power anisotropies. The ring-like structure close to the center of the WSRT map is missing in the H i data and not discussed here.
3.4. Anisotropies at vLSR = –16.6 km s-1
All channel maps at velocities −23.1 <vLSR< 5.25 km s-1 show filamentary structures that are aligned approximately parallel to the Galactic plane. At velocities vLSR = −16.6 km s-1 we found particular interesting features. We display in Fig. 6 the average power spectrum, the fit resulting in γ = −2.87 ± 0.02 arcmin-1, and the associated anisotropic power spectra. Figure 7 compares the USM H i distribution at this velocity (contours) with the polarized intensity observed at 349 MHz with the WSRT (color coded intensities). Near the field center (at RA = 3h, Dec = 66°) we observe a filamentary H i structure extending over a length of 4° along one of the radio-polarimetric depolarization canals and parallel to the Galactic plane.
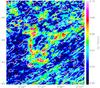 |
Fig. 5 Polarized intensity map of Horologium in equatorial coordinates (B1950.0), observed at 349 MHz with the WSRT. The filamentary features from an H i USM map at vLSR = 2.7 km s-1 are overlaid with contours of 0.1, 1, 2.5 and 5 K. The dashed lines are parallel to the Galactic plane, in steps of Δb = 1°. |
 |
Fig. 6 Average power spectrum observed for vLSR = −16.6 km s-1 (black dots) and fit power law with γ = −2.87 ± 0.02 arcmin-1 for k< 0.07 (vertical line). In addition the power spectrum for 108° < Φ < 123° (red) and 18° < Φ < 33° (green) is given. The average anisotropy factor for 0.002 <k< 0.015 arcmin-1 is Qaver = 5.1. |
 |
Fig. 7 Polarized intensity map of Horologium in equatorial coordinates (B1950.0), observed at 349 MHz with the WSRT. The filamentary features from an H i USM map at vLSR = −16.6 km s-1 are overlaid with contours of 0.1, 1, 2.5 and 5 K. The dashed lines are parallel to the Galactic plane, in steps of Δb = 1°. |
4. Auriga
This section deals with the analysis of the Auriga region (Haverkorn et al. 2003a,b) at RA = 92.̊5, Dec = 52.̊5 (B1950.0), l ~ 161°,b ~ 16°. We used again the EBHIS to generate a fits data cube with a diameter of 13.̊8 (at 100% taper).
 |
Fig. 8 Comparison between the average apodized brightness temperature profile TB aver (red) for the Auriga field, derived average anisotropy factor Qaver for 0.007 <k< 0.07 arcmin-1 (blue), and spectral index γ (green). The upper horizontal black dotted line indicates the Kolmogorov spectral index of γ = −8 / 3, the lower dash-dotted line Qaver = 0. |
4.1. Average H I properties
Figure 8 displays the global properties of the H i gas in this region. The weighted mean brightness temperature TB aver, averaged after apodization, shows two major components, peaking at velocities of vLSR = 1.4 and vLSR = −12.8 km s-1 respectively, with a long extended wing to more negative velocities. For comparison we give the average (position angle independent) spectral index γ of the power distribution for individual velocity channels according to Eq. (1). For the main emission line we find at vLSR = 1.4 km s-1, γ = −3.22 ± 0.03 while γ ~ −2.85 ± 0.03 at the secondary peak.
 |
Fig. 9 Average position angles Φaver calculated for 0.007 <k< 0.07 arcmin-1 and associated one σ rms scatter for the Auriga field. The blue asterisks denote peak anisotropies of the three CNM filamentary structures that we study in detail. |
4.2. Position angle dependencies on vLSR
To determine position angle dependencies of the power distribution on the radial velocity, we calculate for each channel the average anisotropy Qaver in the range 0.007 <k< 0.07 arcmin-1 as well as the associated position angle Φaver and its standard deviation.
Φaver is shown in Fig. 9, the corresponding Qaver is displayed in Fig. 8. The Φaver distribution differs significantly from Fig. 2. For Horologium we found little changes of Φaver over the main emission line. In Auriga we have distinct different Φaver for individual H i components. Φaver is ill-defined with large uncertainties for positive velocities. The best defined position angle with the lowest uncertainty is Φaver = −25° ± 12° at vLSR = −2.5 km s-1 and is marked in Fig. 9. The second feature that we will discuss is defined by a pronounced deviation from the vicinity with Φaver = 19° ± 22° at vLSR = −19.1 km s-1. The peak anisotropy at this velocity channel is at Φpeak = 25°, also marked. From the Galactic rotation curve this component may be at a distance of 3.5 kpc. The third feature at vLSR = −30.8 km s-1 shows a marked anisotropy with Φaver = −40° ± 16° although the emission is low, TB aver = 3.2 K. According to the rotation curve this gas may be at a distance of 7.5 kpc.
4.3. Anisotropies at vLSR = –2.5 km s-1
Figure 10 shows the H i power spectra at vLSR = −2.5 km s-1 with the power law fit to the average (isotropic) power spectrum. We fit γ = −2.97 ± 0.03 for 0.003 <k< 0.07 arcmin-1. The position dependent power spectra at the position angle with the most significant anisotropies appear in logarithmic presentation well displaced from the isotropic distribution. The spectral shape for k< 0.003 arcmin-1 is unusual and not understood but will be discussed in Sect. 5.5. Instrumental problems of the EBHIS in this range are unexpected and should be three orders of magnitude below the observed power (Paper I, Fig. 6). Furthermore the most important instrumental errors due to radio frequency interference, baseline defects or stray radiation problems should be strongly anisotropic but this is not observed.
 |
Fig. 10 Average power spectrum observed for vLSR = −2.5 km s-1 (black dots) and fit power law with γ = −2.97 ± 0.03 for k< 0.07 arcmin-1 (vertical line). In addition the power spectrum for 148° < Φ < 163° (red) and 58° < Φ < 73° (green) is given. The average anisotropy factor for 0.007 <k< 0.07 arcmin-1 is Qaver = 6. |
 |
Fig. 11 Anisotropies Q(k) for the channels at vLSR = −2.5 km s-1 (red) and vLSR = −3.76 km s-1 (blue). |
 |
Fig. 12 Polarized intensity map of Auriga in equatorial coordinates (B1950.0), observed at 349 MHz with the WSRT. The filamentary features from an H i USM map at vLSR = −2.5 km s-1 are overlaid with contours of 0.1, 1, 2.5 and 5 K. The dashed lines are parallel to the Galactic plane, in steps of Δb = 1°. |
Figure 11 displays the derived power anisotropies Q(k) for vLSR = −2.5 km s-1 at a position angle Φ = −25°. We find significant fluctuations of Q(k) that are common for our analysis. The scatter in Q is significant, by far larger than instrumental uncertainties that can be evaluated from the data points located to the right of the vertical line for k ≳ 0.07 arcmin-1. For comparison we plot Q(k) for the neighbor channel at vLSR = −3.76 km s-1 which shows the best agreement to the vLSR = −2.5 km s-1 channel also at a similar well defined position angle, see Fig. 9. Peak anisotropies differ in spatial frequencies and are in the range 20 ≲ Q(k) ≲ 30.
We conclude that the velocity channel at vLSR = −2.5 km s-1 has well defined anisotropies and expect accordingly that the H i distribution should show well defined filamentary structures. In Fig. 12 we compare USM structures, using contours, with the color coded map of the polarized intensity observed at 349 MHz with the WSRT. The filamentary H i structures are preferentially oriented parallel to the Galactic plane at a position angle of 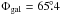 , in excellent agreement with the angle Φ∥ = 65° obtained from power anisotropies. The WSRT maps show that also one arm of the prominent X-shaped structure is oriented in this direction and partly well aligned with filamentary H i structures.
, in excellent agreement with the angle Φ∥ = 65° obtained from power anisotropies. The WSRT maps show that also one arm of the prominent X-shaped structure is oriented in this direction and partly well aligned with filamentary H i structures.
 |
Fig. 13 Average power spectrum observed for vLSR = −19.2 km s-1 (black dots) and fit power law with γ = −2.63 ± 0.03 for k< 0.07 arcmin-1 (vertical line). In addition the power spectrum for 18° < Φ < 33° (red) and 108° < Φ < 123° (green) is given. The average anisotropy factor for 0.007 <k< 0.07 arcmin-1 is Qaver = 2.3. |
4.4. Anisotropies at vLSR = –19.2 km s-1
The second feature, annotated in Fig. 9, is at a velocity of vLSR = −19.2 km s-1. Figure 13 displays the average power spectrum, fit with a power law γ = −2.63 ± 0.03 for k< 0.07 arcmin-1 (vertical line). Figure 8 shows that this H i gas belongs to the second prominent TB aver component at vLSR = −12.8 km s-1 and we safely may assume that this H i gas is not associated with the first component at vLSR = −2.5 km s-1.
 |
Fig. 14 Anisotropies Q(k) for the channel at vLSR = −19.2 km s-1 (red) and at vLSR = −17.9 km s-1 (blue). |
 |
Fig. 15 Polarized intensity map of Auriga in equatorial coordinates (B1950.0), observed at 349 MHz with the WSRT. The filamentary features from an H i USM map at vLSR = −19.2 km s-1 are overlaid with contours of 0.1, 1, 2.5 and 5 K. The dashed lines are parallel to the Galactic plane, in steps of Δb = 1°. |
Calculating average anisotropies Qaver, we derived the position angle Φaver = 19° ± 22°, see Fig. 9. The peak in the power anisotropy however was found after a more detailed analysis at Φpeak = 25°. Figure 13 displays the power spectra in this direction and perpendicular. We plot in Fig. 14 the power anisotropies Q at vLSR = −19.2 km s-1 together with the anisotropies of the neighbor channel at vLSR = −17.9 km s-1.
Most of the anisotropies appear to be weak, Q(k) ≲ 10 but Fig. 14 shows several narrow spikes with large anisotropies. At k = 0.0049 arcmin-1 we determine Q = 32 for vLSR = −19.2 km s-1. Interestingly, there are significant changes in Q for both neighbor channels. We conclude that this anisotropy must be associated with a rather cold H i feature. The formal Doppler temperature corresponding to the velocity resolution of ΔvLSR = 1.44 km s-1 is TD ~ 50 K. Figure 19 in Sect. 5.2 shows a geometric mean Doppler temperature of TD ~ 150 K, implying that the gas at this spatial frequency must be super-sonic.
An other remarkable structure in Fig. 14 is the anisotropy Q ~ 0.16 at k ~ 0.017 arcmin-1. There is a sharp cross-over of the anisotropies at this spatial frequency, implying a local anisotropy up to Q ~ 6 in perpendicular direction.
Figure 15 compares USM H i structures, using contours, with the color coded map of the polarized intensity observed at 349 MHz with the WSRT. The strongest filamentary H i structures are in this case well aligned with the other arm of the X-shape structure in polarized intensity. However we find also a few weaker filamentary H i structures that are roughly aligned parallel to the Galactic plane.
 |
Fig. 16 Average power spectrum observed for vLSR = −30.8 km s-1 (black dots) and fit power law with γ = −2.72 ± 0.03 for k< 0.07 arcmin-1 (vertical line). In addition the power spectrum for 133° < Φ < 148° (red) and 43° < Φ < 58° (green) is given. The average anisotropy factor for 0.007 <k< 0.07 arcmin-1 is Qaver = 10.6. |
4.5. Anisotropies at vLSR = –30.8 km s-1
 |
Fig. 17 Anisotropies Q(k) for the channel at vLSR = −30.8 km s-1 (red) and vLSR = −29.5 km s-1 (blue). |
 |
Fig. 18 Polarized intensity map of Auriga in equatorial coordinates (B1950.0), observed at 349 MHz with the WSRT. The filamentary features from an H i USM map at vLSR = −30.8 km s-1 are overlaid with contours of 0.1, 1, 2.5 and 5 K. |
A third weak H i feature does not stand out in the position angle distribution in Fig. 9 but shows up with a significant anisotropy Qaver = 10.6 at vLSR = −30.8 km s-1 in Fig. 8. This structure is located in the wing of the main H i emission component. This component has a mean Doppler temperature of TD ~ 700 K, implying that it is somewhat warmer than the typical CNM, close to the upper limit of the typical CNM temperature range (Wolfire et al. 2003; Kalberla et al. 2016). Its position angle is Φaver = −40° ± 16°.
Figure 16 displays the derived power spectra. The spectra are shallow, we fit γ = −2.72 ± 0.03 for the isotropic case. Figure 17 shows the anisotropies for two neighbor channels at vLSR = −30.8 and vLSR = −29.5 km s-1. Strong anisotropies up to Q ~ 60 are found around k ~ 0.02 arcmin-1 but else both channels share similar features.
In Fig. 18 we compare the corresponding H i structures at this velocity, using contours, with the color coded map of the polarized intensity observed at 349 MHz. Except for a few structures, the agreement between both data-sets is less obvious. The EBHIS data indicate that the H i distribution in the Auriga field is dominated by two independent H i layers which can also be traced in polarized intensity at 349 MHz. To distinguish a third weaker H i layer is quite problematic.
5. Spectral index dependencies
The power spectrum of a two-phase H i gas layer can be described as the sum of three individual power spectra for WNM, CNM, and a spectrum that describes the correlation between WNM and CNM components (Lazarian & Pogosyan 2000, their Sect. 4.3). Unfortunately none of these power spectra is directly observable. The H i gas is a mixture of WNM and CNM gas and emission lines are usually dominated by the WNM. The accurate CNM column density fraction has to be determined from absorption data. Continuum sources for such an analysis are sparse and, as demonstrated by Heiles & Troland (2003, Fig. 7), the CNM column density fraction has a very broad distribution. Accordingly it is not possible to derive from observations meaningful power spectra, characteristic either for WNM or CNM. We found however significant fluctuations of the spectral index and consider here the question whether the spectral index might depend on the WNM or CNM composition. Similar to Lazarian & Pogosyan (2000) we consider the idealized case of a two-phase medium without distinguishing whether or not the WNM belongs to a stable phase or lies in the thermally unstable region for temperatures of 500 to 5000 K (Heiles & Troland 2003).
5.1. Spectral indices from 2D images versus 3D turbulence
Turbulence is a 3D phenomenon and under certain conditions 2D power spectra can be converted to 3D power spectra in density and velocity. One of the most important preliminaries for an easy translation of 2D to 3D turbulent properties is that the extension of the observed optical thin H i gas layer along the line of sight is larger than the observed perpendicular extension. For our fields we have no reliable information about distances and extensions, but usually the H i gas layer is considered to be extended (Dickey & Lockman 1990; Kalberla & Kerp 2009).
For details about the 2D to 3D conversion we refer to Lazarian & Pogosyan (2000) or Miville-Deschênes et al. (2003) but we will give later a few applications. This is an observational paper and we consider in general 2D power spectra, regardless whether an unambiguous conversion to 3D is possible or not.
5.2. Spectral index versus Doppler temperature
 |
Fig. 19 Comparison between the geometric mean Doppler temperature TD (black) and the spectral index γ (green dashed) for Horologium (bottom) and Auriga (top). The horizontal lines indicate the velocity ranges used for the determination of the spectral steepening discussed in Sect. 6. |
We use USM maps to derive Doppler temperatures for filamentary CNM structures and characterize the temperature distribution of the CNM by its geometric mean Doppler temperatures TD, see Fig. 19. The minima for the derived values, TD ≳ 100 K for Auriga (top) and TD ≳ 160 K for Horologium (bottom), are low compared to the median value TD = 223 K for filamentary structures at high and intermediate latitudes, determined by Kalberla et al. (2016). For both targets Doppler temperatures tend to be the lowest at those velocities where the spectral index γ is the steepest.
The derivation of TD at low Galactic latitudes is affected by confusion. USM channel maps show there in general a wealth of filamentary structures. A reliable determination of Doppler temperatures is however only possible for H i structures that are isolated in 3D. We only can observe projections in the position-velocity space. Multiple filamentary features along the line of sight may blend, causing an unknown overestimation of the derived geometrical mean TD. Hence differences in geometric mean Doppler temperatures between Auriga (TD ≳ 100 K) and Horologium (TD ≳ 160 K) are probably not significant since Horologium is at a lower Galactic latitude with larger confusion.
Doppler temperatures are upper limits to the thermal (excitation or spin) temperatures of the filamentary CNM structures. Strong background sources are needed to derive this. The continuum source 3C 147 is located outside the Auriga field but nearby at RA = 84.̊7, Dec = 49.̊8 (B1950.0), l = 161.7°,b = 10.3° and strong enough to allow a determination of accurate spin temperatures Tspin. Kalberla et al. (1985) derived for small scale H i clumps temperatures between 37 and 74 K for the observed absorption components. For vLSR = 0.2 km s-1, Tspin = 37 ± 24 K was obtained, allowing to assign a typical turbulent CNM Mach number of MT ~ 2.7 at vLSR = 0.2 km s-1. For such CNM optical depth and self absorption may affect observed emission features at a few positions, however our data do not allow to correct such effects reliably. We find that power spectra for individual velocity channels tend to be steepest at velocities with low TD and Tspin, at the same time coincident with the velocity at the peak of the average H i emission (Fig. 8).
Continuum point sources, suitable for a determination of spin temperatures in the Horologium field, are unfortunately not available. The strongest point source has there only a flux density of 400 mJy at 1.4 GHz.
5.3. Spectral index and the TWNM/TWNM + CNM ratio
We find clear indications that the distributions of spectral indices derived from single velocity channels, have well defined narrow minima for velocities with strong H i emission lines (Figs. 1, 8 and in Paper I Figs. 12 and 18). The associated CNM, derived from USM data, shows also pronounced filamentary structures with low Doppler temperatures that depend strongly on the observed radial velocity (Fig. 19).
Since in general most of the observed H i emission data are dominated by the WNM, we determine in the following the velocity dependence of the WNM fraction, defined as the average brightness temperature ratio in the observed field, TB WNM(vLSR) /TB WNM + CNM(vLSR). We use a Gaussian analysis for an estimate TG WNM(vLSR) /TG WNM + CNM(vLSR) of this ratio. For the decomposition we use mostly the same approach which was described by Haud (2000) and applied earlier to the Leiden/ Argentine/Bonn (LAB, Kalberla et al. 2005) and the Galactic All Sky Survey (Kalberla & Haud 2015), see also Haud (2013). A similar analysis was applied to the EBHIS and used by Kalberla et al. (2016).
Each H i profile on a HEALPix nside = 1024 grid (Górski et al. 2005) within the apodized region was decomposed into Gaussian components. For each velocity channel we calculated the average brightness temperature contribution from the CNM and the WNM. To distinguish between the two H i phases we select Gaussians representing the CNM by applying a limit of TD< 1100 K to the Doppler temperatures of the Gaussian components. All remaining components were assigned to the WNM. According to Kalberla et al. (2016, Sect. 5.1) this limit corresponds for a typical turbulent CNM Mach number MT = 3.7 (Heiles & Troland 2003) and a typical thermal temperature T = 52 K to a maximum temperature of T = 258 K for a stable CNM phase (Wolfire et al. 2003). Increasing the TD threshold leads to a general decrease of the WNM fraction TG WNM(vLSR) /TG WNM + CNM(vLSR) at all velocities, as shown in Fig. 20 with the example TD< 3900 K. Alternatively we obtain a general increase of the WNM fraction for a lower TD threshold. The minima of TG WNM(vLSR) /TG WNM + CNM(vLSR) do not depend on the TD threshold.
 |
Fig. 20 Bottom: Horologium, top: Auriga. Spectral index γ(vLSR) (green) compared with the WNM fraction TWNM(vLSR) /TWNM + CNM(vLSR) derived from LAB (pink) and EBHIS Gaussians (red). An upper limit for the Doppler temperature of the CNM of TD< 1100 K, corresponding to a turbulent CNM Mach number of MT = 3.7 was applied. For comparison we display the WNM fraction TWNM(vLSR) /TWNM + CNM(vLSR) for a Doppler temperature of TD< 3900 K, corresponding to a turbulent CNM Mach number of MT = 7.7 (blue). |
Figure 20 displays a comparison of the spectral index γ(vLSR) with WNM fraction TG WNM(vLSR) /TG WNM + CNM(vLSR) derived from LAB and EBHIS Gaussians. We find that the minimum of the spectral index is mirrored by a well defined minimum of the WNM fraction. This minimum is associated with rather low Doppler temperatures and a maximum for TG CNM(vLSR) (not shown).
The separation of WNM and CNM components by a Gaussian analysis is based on the model assumption that the observed H i spectrum can be decomposed in a meaningful way into Gaussian components. There may be systematic biases, for example separate narrow emission lines at similar radial velocities can be blended in a way that the Gaussian decomposition results in a single broader component. This bias, leading usually to an underestimation of CNM lines, is more serious for weak emission lines and observations from telescopes with a broader beam. We therefore compare in Fig. 20 the results of two independent decompositions, using LAB and EBHIS data. Discrepancies in the WNM fraction are most probably caused by line blending but such problems appear unimportant in regions with well defined CNM components (see also Haud 2010, 2013).
The WNM fraction depends critically on the turbulent Mach number of the H i gas. In addition to the CNM Mach number MT = 3.7 (Heiles & Troland 2003; Kalberla et al. 2016), we plot the WNM fraction for a very high CNM Mach number MT = 7.7 as determined by Chepurnov et al. (2010). In this case the WNM fraction decreases significantly but location and shape of the minima of the WNM fraction are still in good agreement with the minima of γ. The case MT = 7.7 is for comparison only, in the following we will use the TG WNM(vLSR) /TG WNM + CNM(vLSR) for a CNM Mach number MT = 3.7 (thick line in Fig. 20) for discussion. The investigations by Heiles & Troland (2003) have shown that Mach numbers as high as 7.7 can exist but these are not frequent.
5.4. Velocity field analysis: VCA and velocity centroids
For an understanding of the observed systematic changes in the spectral power distribution we consider first theoretical investigations. Lazarian & Pogosyan (2000, 2004) have introduced an analytic relation for the change of the spectral index of velocity channel maps with the thickness of the velocity slice. They have shown that the integration over the full velocity dispersion provides the statistics that depends only on the density field. Hence, to determine the 3D H i density spectrum one needs to consider power spectra for thick velocity slices while properties of the 3D turbulent velocity spectrum can be derived from thin velocity slices.
A slice is defined to be thin if the velocity width of the investigated H i distribution is small compared to the FWHM velocity width of the gas, alternatively a thick slice needs to be larger than the H i velocity width. Typical numbers for the width of the WNM lines are considered to be ΔvLSR = 17 km s-1 and ΔvLSR = 2.6 km s-1 for the CNM respectively Lazarian & Pogosyan (2000). For comparison, the instrumental velocity resolution of the EBHIS is Δv = 1.44 km s-1 and such a velocity channel represents a thin slice.
Alternatively to VCA, velocity centroids have been used to characterize the 3D velocity field of a turbulent medium (Lazarian & Esquivel 2003; Miville-Deschênes et al. 2003). In the image plane the (normalized and restricted) centroid velocity VC(x,y) is for the velocity interval v1<vLSR<v2 defined as 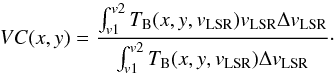 (3)The application of a velocity window v1<vLSR<v2 is necessary to restrict the centroid to a particular emission line feature since we usually observe multiple emission lines along the line of sight with different anisotropies, blending partly in velocity. To avoid biases from unrelated components, the velocity window should be restricted to velocities with significant line emission. Also it should be symmetric with TB(v1) ~ TB(v2) to avoid biases from the wings of the line.
(3)The application of a velocity window v1<vLSR<v2 is necessary to restrict the centroid to a particular emission line feature since we usually observe multiple emission lines along the line of sight with different anisotropies, blending partly in velocity. To avoid biases from unrelated components, the velocity window should be restricted to velocities with significant line emission. Also it should be symmetric with TB(v1) ~ TB(v2) to avoid biases from the wings of the line.
 |
Fig. 21 Anisotropies Q(k) for the velocity centroid (red) and average emission (blue), both calculated for the velocity range −23.1 <vLSR< 5.25 km s-1. |
As an application of the VCA we calculate power spectra, integrating for the Horologium field the H i emission over the velocity range −23.1 <vLSR< 5.2 km s-1. This is a thick slice. Figure 21 displays the derived anisotropies that can be attributed to the 3D density distribution. For comparison we plot also anisotropies derived from the velocity centroid over the same velocity interval. In both cases, anisotropies at k ~ 0.007 arcmin-1 are remarkable high with 80 ≲ Q ≲ 110. For higher spatial frequencies this plot confirms essentially the result from Fig. 4 but anisotropies for centroid and thick slice velocity average in Fig. 21 are there less pronounced.
Figure 22 shows power spectra for the same velocity interval. For the average emission from the thick velocity slice (bottom) we determine an average spectral index γ = −3.41 ± 0.05, derived for spatial frequencies k< 0.07 arcmin-1. Lazarian & Pogosyan (2000, Sect. 4.2) caution that one should use very thick slices for a reliable determination of the 3D spectral index in density. We took this into account and repeated the analysis, integrating over larger ranges in velocity. The derived spectral index did not change, thus the velocity range −23.1 <vLSR< 5.2 km s-1 can be considered as sufficiently broad under the very thick slice condition (we note that the strong H i emission in Fig. 1 originates from regions with similar position angle as shown in Fig. 2). Accordingly the power index, derived from the thick slice emission over this velocity range, may be considered as the power law exponent γn = −3.4 of the 3D density field. Such an index is considered to indicate the case of a steep power spectrum (Lazarian & Pogosyan 2000).
Power spectra derived from the velocity centroid are shown in Fig. 22 at the top. The fit average power distribution with γ = −3.35 ± 0.05 agrees within the uncertainties with γ = −3.41 ± 0.05 from the thick slice. The power spectra displayed in both panels of Fig. 22 are very similar. The implication from Lazarian & Pogosyan (2000) and Lazarian & Esquivel (2003) is that the 3D turbulent density and velocity fields in Horologium share similar properties.
 |
Fig. 22 Power spectrum (black dots) calculated for the velocity centroid (top) and the thick slice emission (bottom) over the velocity range −23.1 <vLSR< 5.2 km s-1. An average power law γ = −3.35 ± 0.05 for the centroid and respectively γ = −3.41 ± 0.05 for the thick velocity slice was fit for k< 0.07 arcmin-1 (vertical line). The power law fits for the restricted ranges 0.001 <k< 0.01 arcmin-1 in spatial frequency are indicated with blue dotted lines. In case of the centroid (top) γ = −4.5 ± 0.1 and γ = −4.9 ± 0.1 for the average emission respectively. In addition the power spectra for 118° < Φ < 133° (red) and 28° < Φ < 43° (green) are given. The average anisotropy factor for 0.007 <k< 0.07 arcmin-1 is Qaver = 2.1 for the centroid and Qaver = 4.1 for the average emission. |
 |
Fig. 23 Power spectrum (black dots) calculated for the velocity centroid (top) and the thick slice emission (bottom) over the velocity range −10.2 < vLSR < 11.7 km s-1. For the velocity centroid a power law with γ = −2.78 ± 0.03 was fit and respectively γ = −3.28 ± 0.04 for the average emission (black lines), in both cases for k< 0.07 arcmin-1 (vertical line). In addition the power spectra for 148° < Φ < 163° (red) and 58° < Φ < 73° (green) are plotted. The average anisotropy factor for 0.007 < k < 0.07 arcmin-1 is Qaver = 3.2 for the centroid and Qaver = 2.6 for the average emission. |
According to VCA in case of steep power spectra, thin velocity slices can be used for a determination of the velocity power index. For velocity fluctuations, described by a slope m, the expected 2D power index for a thin velocity slice is γ = −3 + m/ 2. Here m is restricted to 0 <m< 2 and m = 2 / 3 is distinct since it is the Kolmogorov index (Lazarian & Pogosyan 2000, Sect. 2.4). In case of dominant large-scale density fluctuations, the observed spectral slope is equal to −8/3 if the observed velocity slice is thin and steepens to −10/3 for thicker slices (Lazarian & Pogosyan 2000, Sect. 4.2). We note that in this case in absence of a velocity shear caused by Galactic rotation turbulent fluctuations will also produce a −8/3 spectrum in a thin slice. We observe spectral indices close to this value for many thin velocity channels when the H i gas is dominated by WNM, see Fig. 20.
 |
Fig. 24 Power spectrum (black dots) calculated for the average emission over the velocity range −3.8 <vLSR< 10.4 km s-1. In addition the power spectra for 118° < Φ < 133° (red) and 28° < Φ < 43° (green) are given. An average power law γ = −3.39 ± 0.05 was fit for k< 0.07 arcmin-1 (vertical line). For reference the power law fit for −10.2 <vLSR< 11.7 km s-1 at a restricted range 0.001 <k< 0.01 arcmin-1 in spatial frequency from Fig. 22 (bottom) is reproduced with the blue dotted line. |
Unfortunately the VCA is only partly applicable to our targets. An inspection of Fig. 20 (bottom) shows that m is ill-defined for −15.4 <vLSR< 6.5 km s-1 since γ< −3 in this range. Interestingly, this is the velocity range where we observe strong anisotropies and where we expect phase transitions; the H i gas is cold and the WNM fraction is low, typically TG WNM(vLSR) /TG WNM + CNM(vLSR) ≲ 0.6 for TD< 1100 K. For a larger WNM ratio TG WNM(vLSR) /TG WNM + CNM(vLSR) ≳ 0.7, the 3D power index for velocity fluctuations can be derived as m = 0.6 ± 0.1, consistent with the Kolmogorov index.
As pointed out in Sect. 5.1, the interpretation of the observed 2D spectral power may be affected by unknown distances and extensions of the observed H i gas layer. For Horologium the H i gas at velocities around vLSR = −16.6 km s-1 may be according to the rotation curve at a distance of 1.5 kpc (Sect. 3.1). The gas at vLSR = 0 km s-1 and (according to the rotation curve forbidden) more positive velocities should be local. To test whether the thick slice power spectrum, derived for −23.1 <vLSR< 5.2 km s-1 and displayed in Fig. 22 could be biased from distance problems we recalculated the thick slice power spectrum for a restricted velocity range −3.8 <vLSR< 10.4 km s-1. The result with the fit γ = −3.39 ± 0.05 is shown in Fig. 24. This result is consistent with that derived for −23.1 <vLSR< 5.2 km s-1. We conclude that for Horologium both velocity components share similar properties, regardless of their distances.
Discrepancies between VCA predictions and observed spectral indices have been noted previously by Dickey et al. (2001). They observed significant changes in spectral indices between regions that are considered to be dominated by WNM or CNM. The question arises whether in our case the Horologium field is special. But checking Fig. 20 (top) for the Auriga field it is obvious that m is also in this case ill-defined for −3.8 <vLSR< 5.3 km s-1. Again we find a low WNM fraction, TG WNM(vLSR) /TG WNM + CNM(vLSR) ≲ 0.6, also strong anisotropies. For the remaining velocity channels with a larger WNM ratio TG WNM(vLSR) /TG WNM + CNM(vLSR) ≳ 0.7, the power index for velocity fluctuations is consistent with m = 0.6 ± 0.1.
5.5. Local deviations from the exponential power distribution
Turbulent power spectra consist typically of three ranges, the forcing range, reflecting the energy input, the inertial range, reflecting the turbulent decay, and the dissipation range. The isotropic (average) power spectra derived by us belong to the inertial part and can usually be fit well by a constant power law with indices that are compatible with Kolmogorov turbulence. Our data cover a broad range in spatial frequencies but we find no indications for a turn-over of the power spectra at high spatial frequencies to the dissipation range. Such a turn-over may also indicate that the observed H i distribution has a limited depth along the line of sight (Miville-Deschênes et al. 2003, Fig. 8).
However in case of the power spectra for velocity centroid and thick slice emission in the Horologium field (Fig. 22) we observe the opposite. We find a significant systematic steepening for spatial frequencies 0.001 <k< 0.01 arcmin-1 only. This remains valid if we restrict the velocity range used for the thick slice, see Fig. 24. The power index fit to the thick slice emission in this range is γ = −4.9 ± 0.1, for the velocity centroid it is γ = −4.5 ± 0.1. In both cases there is a step like feature at k ~ 0.01 arcmin-1 that is linking the steep part of the power spectrum to the Kolmogorov type power law relation at higher spatial frequencies. A similar effect, but less obvious, is visible in the power spectrum for the average emission for Auriga, Fig. 23 (bottom). The power spectra derived from the velocity centroid (top) are rather straight with a shallower spectral index.
Thin slice power spectra do not show a steep power law signature for 0.001 <k< 0.01 arcmin-1, however we find in nearly all cases a significant local increase of the power at k ~ 0.001 arcmin-1, sometimes up to k ~ 0.002 arcmin-1. This effect is best visible in Fig. 10.
A steepening of the power distribution, indicating dissipative processes, occurs usually at high spatial frequencies at the end of the inertial range. This does not happen in our case. In summary, we observe the steepening at low spatial frequencies as a tilt that recovers with a step at k ~ 0.01 arcmin-1. This change is strongest for the density distribution (using thick velocity slices), less for the velocity centroid, and least for thin velocity slice power spectra (Fig 10). A more detailed discussion of velocity centroids is given in Appendix C.
6. Phase transitions and changes in spectral power
We interpret the steepening of the thin velocity slice power spectra in a narrow velocity range, associated with a decrease of the WNM fraction and the coexistence of cold anisotropic CNM filamentary structures as caused by phase transitions.
For a better understanding of the composition of the bi-stable H i gas and dependencies of the power distribution at the line center and adjacent velocities we compare similar to the analysis of absorption lines ON and OFF data. We define the power spectrum Pon at the velocity von of the steepest thin slice power spectrum. For the OFF data we use close-by velocities voff where the WNM fraction is significantly larger. The selection of voff is somewhat arbitrary but does not affect the results significantly since we can in any case only determine changes over a limited range of the WNM fraction. We pick two velocities at the wings of γ and TG WNM(vLSR) /TG WNM + CNM(vLSR), see Fig. 20. The characteristic OFF power spectrum Poff is derived then as the geometric mean of both OFF power spectra.
For the power spectra Poff(k) and Pon(k) we define Pon(k) = Poff(k)·T(k) and accordingly 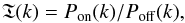 (4)where T(k) is the transfer function that describes changes of the power distribution between ON and OFF. We understand T(k) as an approximation to the transfer of the power distribution caused by thermal instabilities. We note that we use in Eq. (4) power spectra Pon and Poff without normalization.
(4)where T(k) is the transfer function that describes changes of the power distribution between ON and OFF. We understand T(k) as an approximation to the transfer of the power distribution caused by thermal instabilities. We note that we use in Eq. (4) power spectra Pon and Poff without normalization.
 |
Fig. 25 Changes in the spectral power distribution, most probably associated with phase transitions. Data points are derived according to Eq. (4), the solid black line indicates the change δ of the fit spectral indices. The blue dashed line represents a local fit for 0.002 <k< 0.015 arcmin-1. |
 |
Fig. 26 Changes in the spectral power distribution, most probably associated with phase transitions. Data points are derived according Eq. (4), the solid line indicates the change δ of the fit spectral indices. |
To characterize the Horologium field we select power spectra at von = 2.7 km s-1 and voff = −20.5 and 13.0 km s-1. Figure 25 displays T(k). The change of the average power law index is δ = −0.6. For 0.002 <k< 0.015 arcmin-1 we find significant deviations from the average slope, reflecting the local deviations from the power spectrum displayed in Fig. 22. This part can be fit by an index δ = −1.6, the excess local steepening is comparable to the steepening observed for the velocity centroid (Fig. 22). The transition from the steep part of the T(k) spectrum is at k ~ 0.01 arcmin-1, associated with strong power anisotropies, see also Fig. 21.
Remarkable is that we observe T(k) > 1. Extrapolating T we find T(k) = 1 for k ~ 0.3 arcmin-1. Interferometer observations would be necessary to observe such spatial frequencies. Equal power for ON and OFF power spectra may indicate a lower limit for the scale of eddies affected by phase transitions.
The excess power can be explained with the observational finding that absorption lines, indicating phase transitions, are frequently observed close to the peaks of the H i emission. The power at low spatial frequencies is there typically strongest. Consistently Fig. 1 shows that the H i emission is the strongest at von. We found also that the CNM signal, derived from the Gaussian decomposition, has a peak at this velocity.
To derive T(k) for Auriga we use von = 1.38 km s-1 and voff = −5.05 and 6.54 km s-1. Figure 26 displays T(k) as well as the average change in the power spectral index, δ = −0.3. For Auriga the transfer function T(k) is on average well represented by a power law, although there is quite some scatter, in addition to a strong deviation at k ~ 0.015 arcmin-1.
We supplement here the discussion with data from Paper I, see their Fig. 12 for the spectral index variation in the 3C 196 field. We use von = −2.47 km s-1. Since in this case the emission lines from the filamentary structures are affected by line blending at positive velocities, we use only a single offset channel at voff = −11.5 km s-1 to estimate the spectral power distribution. Figure 27 shows the result. There is a general trend for a steepening of the spectral index, but a closer look indicates that T(k) is approximately constant for k ≳ 0.02 arcmin-1. This is the spatial frequency range where we observed in Paper I little anisotropies, see there Fig. 25. T(k) in Fig. 27 shows a significant gradient for 0.003 ≲ k ≲ 0.02, this is the range where strong anisotropies were detected, see Fig. 24 of Paper I.
We conclude that all three fields discussed here show significant gradients in T(k) over a broad range in spatial frequencies. We interpret this as an indication that turbulent phase transitions affect a range of scales.
 |
Fig. 27 Changes in the spectral power distribution in direction to 3C 196, most probably associated with phase transitions. Data points are derived according to Eq. (4), the solid line indicates the change δ of the fit spectral indices. The blue dashed line represents a local fit for 0.003 <k< 0.02 arcmin-1. |
7. Discussion
7.1. Sheets or filaments, along the mean local magnetic field
The H i maps in the Horologium field show numerous crowded filamentary structures for −23.1 <vLSR< 5.2 km s-1, almost all of them are running parallel to the Galactic plane, see Figs. 5, 7 and D.1. This is also the orientation of the radio-polarimetric depolarization canals and the mean magnetic field according to Planck Collaboration Int. XIX (2015, Fig. 5). Auriga is a different case since we have two or three H i features at different radial velocities with different position angles that match to the radio-polarimetric depolarization canals. The dominating H i structure at vLSR = −2.5 km s-1 that matches the polarized filaments well is parallel to the Galactic plane. This is also the observed mean direction of the magnetic field (Planck Collaboration Int. XIX 2015, Fig. 5). In the case of 3C 196 (Paper I), H i anisotropies share clearly the orientation of the magnetic field (Zaroubi et al. 2015). In summary, the best defined H i filamentary structures are all within a scatter of ~6 parallel to the Galactic plane and anisotropies in the spectral power distribution are oriented along the observed mean magnetic field direction.
parallel to the Galactic plane and anisotropies in the spectral power distribution are oriented along the observed mean magnetic field direction.
While radio continuum observations in polarization map the Stokes parameters I, Q, and U and rotation measures integrated along the line of sight, H i observations are sensitive to the velocity distribution. Each individual velocity channel reflects the average properties at a particular velocity interval. Distinct features at different velocities are expected to be spatially separated if the differences in radial velocity are large enough. Hence H i observations potentially allow to disentangle different H i layers along the line of sight. This property can be exploited for polarized filaments correlated with the H i. For example, the H i filaments at vLSR = −19.2 km s-1 that align with the polarized filaments have an orientation not parallel to the Galactic plane. This indicates that along this line of sight some magnetic field components are on average directed along the Galactic plane, while others are not. The correspondence between H i and polarized filaments, pioneered by Clark et al. (2014), thus yields (under the assumption of perfect alignment between H i filamentary structures and magnetic fields) a method to differentiate the different polarized filaments in distance, based on H i velocity measurements.
However, projection effects are not easy to disentangle. Filamentary structures in H i, associated with magnetic fields, are sheets observed edge-on, according to Heiles & Troland (2005) and Kalberla et al. (2016), which can be uniquely identified only if they are predominantly stretched out along the line of sight, see Appendix D. However, filamentary H i structures may also be organized in fibers (Clark et al. 2014). Correspondingly phase transitions may occur in these fibers (Inoue & Inutsuka 2016) or sheets (Vázquez-Semadeni et al. 2006), possibly even on angular scales of eddies embedded in a thermally bistable turbulent medium as discussed by Vázquez-Semadeni (2012).
All of the most dominant H i anisotropies observed by us are limited to narrow velocity intervals, covering typically only two channels or ΔvLSR ~ 3 km s-1. Associated Doppler temperatures are TD ≲ 200 K, spin temperatures may be as low as Tspin ~ 50 K. For a broader range in velocity we find in the TB and USM data filamentary structures that are approximately parallel to the prominent filaments displayed in Figs. 5, 7, 12 and 15 (also Fig. 2 of Paper I). Changing the velocity of the H i channel maps causes for these filamentary structures apparent position shifts perpendicular to the filaments hence also perpendicular to the orientation of the mean magnetic field projected on the plane of the sky, see Appendix D.
Such systematic velocity channel gradients are expected in the framework of the Heiles & Troland (2005) sheet model and are according to Kalberla et al. (2016) frequently observed. H i sheets are coherent structures in position-velocity space. From observations it is not possible to disentangle the turbulent 3D density and velocity field structure. We emphasize that these sheets must be very cold and thin to be observed in projection as filamentary structures.
7.2. The correlation between H I and polarized filaments
In both Horologium and Auriga fields, the directional correspondence between polarized filaments and H i filaments is striking. The correspondence in direction can be explained by the alignment of both H i and polarized filaments with the mean local Galactic magnetic field, mostly directed along the Galactic plane. However, the tight correspondence between the widths of the filaments is more puzzling. In particular, Figs. 5, 7, 12 and 15 seem to show an anti-correlation between H i and polarized intensity along a filament, usually bordered by a radio-polarimetric depolarization canal.
According to Heiles & Haverkorn (2012), the electron density in the CNM is insufficient to produce a measurable Faraday rotation along the line of sight for the extent of the filamentary CNM structure. This implies that the filamentary H i structures need to be almost co-located with ionized gas which gives rise to the observed Faraday rotation from the magneto-ionic medium.
If the correlation can be explained by CNM filaments wrapped in an ionized envelope, the envelope needs to have substantial width and electron density to explain the observed RMs in these polarized filaments which are typically a few radians m-2 (Haverkorn et al. 2003a,b). (However, we note that care should be taken in interpreting mixed synchrotron-emitting and Faraday-rotating gas in terms of traditional RMs, see Brentjens & de Bruyn 2005.) These low RMs could be explained by a line-of-sight through the ionized gas of ~1 pc, combined with an electron density of ~1 cm-3 and a mean magnetic field of a few microgauss, which are very reasonable values.
On the other hand, the anti-correlation between H i and ionized gas within a filament may indicate that these filaments are the locations of phase transitions from warm ionized gas to neutral medium. Heiles & Haverkorn (2012) argue for an intermediate gaseous phase, the warm partially ionized medium (WPIM), producing and perhaps dominating the ISM’s Faraday Rotation. It appears promising to explore the relations between filamentary CNM structures and magneto-ionic structures in more detail but this is beyond the scope of the current paper.
7.3. Comparison to earlier observations of the 3C 147 field
Our analysis is based on EBHIS data with a moderate resolution of 10.́8. It is worth to revisit observations of 3C 147, making use of combined data from the Effelsberg and WSRT telescopes at a resolution of 1 to 3 arcmin (Kalberla et al. 1985). The WSRT observations on 3C 147 sampled the UV plane completely without tapering and needed no cleaning of the data. After self-calibration a dynamical range of 38 dB was obtained. For a field of view of 36′Kalberla & Mebold (1983) have determined a spectral index of γ = −2.5 ± 0.3 for −2 <vLSR< 3 km s-1, the velocity of the main emission line. Other results from this data set, which are unpublished, are γ = −2.75 ± 0.3 for −14 <vLSR< −11 km s-1, γ = −3 ± 0.3 for −9 <vLSR< −7 km s-1. In all of these cases the H i gas is cold and has a considerable optical depth. All thin slice power spectra are steeper than the thick velocity slice power spectrum for −14 <vLSR< 4 km s-1 with γ = −2.33 ± 0.3.
The H i with the steepest spectral index at a velocity of vLSR = −8.1 km s-1 is organized in a weak but well defined filamentary structure that is aligned parallel to the Galactic plane (Kalberla et al. 1985, their Figs. 2d and 4d). EBHIS data show that this H i component is clearly associated with a minimum in the WNM fraction. The determination of the WNM fraction from TG WNM(vLSR) /TG WNM + CNM(vLSR) depends critically on the Doppler temperature of TD< 1100 K that we have chosen for a selection of CNM components, but this assumption leads in case of 3C 147 to consistent results. The spin temperature of this H i component with an optical depth τ = 0.87 ± 0.01 was determined to Tspin = 32 ± 18 K from Gaussian decomposition of WSRT data, and to Tclump = 34 ± 17 K taking self-absorption in a clumpy medium into account. This is in good agreement with the EBHIS data, which indicate for the CNM at this velocity a brightness temperature of TG = 30 K.
VLBI observations show for this feature with the highest optical depth the most significant structures in column densities, with strong temporal and spatial fluctuations at spatial frequencies corresponding to scales as low as 10 AU (Diamond et al. 1989; Faison & Goss 2001; Lazio et al. 2009). The high resolution H i data at vLSR = −8.1 km s-1 in direction to 3C 147 are consistent with the power spectra for our EBHIS targets on scales of 10′. A more detailed discussion on 3C 147 is beyond the scope of this publication but “mysterious” optical depth structures at AU scales (Deshpande 2000) may find a simple explanation if MHD anisotropies in presence of a magnetic field are taken into account.
The steepening of the 3C 147 power spectrum, γ = −3 ± 0.3 for −9 <vLSR< −7 km s-1, relative to the power spectra at other velocities implies a decrease of turbulent fluctuations in the source structure at high spatial frequencies, hence a low VLBI signal is expected. Yet, observations by Diamond et al. (1989), Faison & Goss (2001), Lazio et al. (2009) show significant opacity and column density fluctuations that are apparently in conflict with such an assumption. Deshpande (2000) explains small scale structure at AU scales with a single constant power law over all observed scales. Highly over-dense H i small-scale structures are proposed not to be real but a misinterpretation of a turbulent source distribution. For this argumentation anisotropies have not been taken into account.
H i opacity fluctuations on AU scales are observed perpendicular to the direction of the filamentary structure observed with the WSRT. According to Goldreich & Sridhar (1995) the power of the turbulence spectrum is strongest in direction perpendicular to the observed mean magnetic field direction, one or two orders of magnitude are possible, much in favor of high VLBI visibilities.
7.4. Possible physical explanations
7.4.1. The McKee and Ostriker (1977) model
The McKee & Ostriker (1977) model of the ISM predicts an association between cold H i gas and ionized medium: “whenever there is a cold cloud along a given line of sight, at a given velocity, there should be warm ionized material as well at the same velocity4”. Around CNM cores they sketch an onion skin structure for the transitions between CNM, WNM and surrounding ionized gas (McKee & Ostriker 1977, Fig. 1). In case of a regular magnetic field anisotropies are expected and onion-skins should get deformed. For the model of cold H i sheets, proposed by Heiles & Troland (2005) and advocated by Kalberla et al. (2016), we should obtain instead of onion-skins flattened and elongated structures, observed nearly edge-on. “Edge-on sheets should be edge-on shocks in which the field is parallel to the sheet” (Heiles & Crutcher 2005). Then, the McKee & Ostriker (1977, Fig. 1) model remains valid if we replace the simplified spherical clouds with scale dependent anisotropic eddies, see Figs. 2, 28 and 29 of Paper I.
Such a geometry is complicated and line-of-sight effects are important. One should not expect always to observe a clear association between H i and Faraday depth structures. However, a close alignment of anisotropies is mandatory and such anisotropies are observed by us. H i channel maps at other velocities show some more cases with alignments but we can demonstrate here only the most prominent cases. A detailed modeling of EBHIS against LOFAR or WSRT data is not available but we believe that our results are consistent with the McKee & Ostriker (1977) model with a sheet geometry as proposed by Heiles & Troland (2005), see Appendix D.
7.4.2. Ideal MHD turbulence
Postulates for ideal 3D MHD turbulence are quite different. Density and velocity fields are assumed to be Gaussian and independent. “H i data cubes exhibit a lot of small-scale emissivity structure. The question is what part of them is real, i.e., is associated with density enhancements in Galactic coordinates, and what part is produced by velocity fluctuations” (Lazarian & Pogosyan 2000, Sect. 6.3.5). Accordingly density fluctuations with Gaussian distribution and power spectra result in filamentary structures that do not need to be “real”. To our understanding neither the observed H i structures, nor the polarized structures, are random or independent in density and velocity, see Appendix D. H i sheets are coherent structures in position-velocity space with distinct velocity gradients orthogonal to the observed orientation of filament and mean magnetic field. Steep thin slice power spectra reflect that the usual model assumptions of independent Gaussian distributions in density and velocity are in our case not applicable. In our case the VCA is not useful for a determination of the spectral power distribution of the turbulent velocity field.
7.4.3. Anisotropies according to Goldreich-Sridhar
A turbulence model allowing directional anisotropies is the Goldreich & Sridhar (1995) model, based on the assumption of a critically balanced shear Alfvénic cascade. It is questionable whether in case of shocks and induced thermal instabilities such a balance can develop. The predicted systematic increase of anisotropies with spatial frequency (Goldreich & Sridhar 1995) is only observed at a few velocity channels in the 3C 196 field. Anisotropies appear to have considerable fluctuations, with local enhancements at different spatial frequencies. The balance depends on the Alfvén velocity, 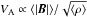 , usually defined as the average over the field of view. In case of phase transitions the density ρ can change by orders of magnitude (Wolfire et al. 2003). The magnetic field strength may also be affected but according to Crutcher et al. (2010) the magnetic field in the diffuse ISM does not scale with density for ρ< 300 cm-3. Thus turbulent anisotropy in the H i may be more complex than indicated by these models. However, more advanced MHD turbulence simulations are able to reproduce, at least qualitatively, the observed filamentary H i and polarized structures, see for example Mallet & Schekochihin (2017).
, usually defined as the average over the field of view. In case of phase transitions the density ρ can change by orders of magnitude (Wolfire et al. 2003). The magnetic field strength may also be affected but according to Crutcher et al. (2010) the magnetic field in the diffuse ISM does not scale with density for ρ< 300 cm-3. Thus turbulent anisotropy in the H i may be more complex than indicated by these models. However, more advanced MHD turbulence simulations are able to reproduce, at least qualitatively, the observed filamentary H i and polarized structures, see for example Mallet & Schekochihin (2017).
Here we do not analyze velocity anisotropies. But such anisotropies are predicted by Goldreich & Sridhar (1995) and have been analyzed for example by Heyer et al. (2008). They identify a velocity anisotropy that is aligned within 10° of the mean local magnetic field direction derived from optical polarization measurements.
7.4.4. Filamentary structures from colliding flows
Recent simulations of molecular cloud formation by Gómez & Vázquez-Semadeni (2014) have demonstrated that filaments can develop self-consistently by colliding flows. The WNM, affected by thermal instabilities, initially forms planar structures (or sheets) which become later Jeans-unstable and break into filamentary structures. Thus the collapse occurs as a cascade where structures at different scales have different morphologies: from sheets to filaments and from filaments to clumps. As discussed by Hartmann et al. (2001, their Fig. 5) clouds tend to form at bends or “kinks” in the magnetic field and are also associated with rapid changes in the field direction. Similar, along the filamentary structures there are rapid changes in the velocity field. Thus changes in density, velocity, and magnetic field direction are found to be correlated. The compression of the parallel magnetic field in such a configuration can cause a delay, but cannot prevent post-shock gas from compressing to high densities with phase transitions. This scenario fits well to our observations, provided that the filamentary CNM structures are associated with ionized gas, giving rise to the observed Faraday polarization filaments.
7.4.5. Filaments from turbulent velocity strain
In incompressible turbulence, some structures tend to be filamentary and it was shown by Moisy & Jiménez (2004, Figs. 6 and 7) that those structures with the highest rate-of-strain and dissipation are in the form of sheets or ribbons.
Hennebelle (2013) performed a series of numerical simulations to study the formation of clumps in a turbulent ISM. The result was that clumps in MHD simulations tend to be more filamentary than clumps in hydrodynamical simulations which are preferentially sheet-like. Such linear filamentary structures result from the stretch induced by turbulence and the filaments are in general preferentially aligned with the strain. As the filaments are getting stretched, the magnetic field is amplified and becomes largely parallel to the filament.
Inoue & Inutsuka (2016) study the formation of CNM in a shock-compressed layer. A magnetized thermally unstable gas layer develops behind the shock wave. Thermal instabilities cause fragments of filamentary CNM structures which align with the magnetic field if the shear flow is strong enough. For a weak shear strain along the magnetic field they observe an increase of the number of linear structures that lie perpendicular to the magnetic field.
7.4.6. Thermal instabilities and shocks
An other possibility for the formation of filamentary magneto-ionic structures is through thermal instabilities, as was previously discussed by Jelić et al. (2015). According to Choi & Stone (2012) the evaporation of cold gas from the surfaces of dense structures is strongly suppressed in regions where the field is parallel to the interface. This attenuates turbulence generated by thermal instabilities and supports the alignment between filamentary CNM and associated ionized structures.
Finally, we consider the possibility of low-Mach number shocks as cause for the filaments. For all of our velocity channel maps with anisotropies we observe a series of CNM filaments, roughly parallel and structured similar to washboard waves. Fletcher & Shukurov (2007) consider the case that radio-polarimetric depolarization canals are produced by a series of shocks with low Mach numbers, M ~ 1.2. As the primary source of shocks they assume supernovae. When these shocks encounter gas clouds they will be reflected, generating a population of secondary shocks. For such a foreground Faraday screen they estimate discontinuities to have an average distance of 15′, corresponding to a spatial frequency of k ~ 0.07 arcmin-1. We find for Horologium peak anisotropies at the same spatial frequency, for Auriga at k ~ 0.09 arcmin-1, and for 3C 196 at k ~ 0.06 arcmin-1. This is a reasonable agreement and a series of shock waves may according to Saury et al. (2014) explain the observed filamentary H i structures. Such shocks must lead in the presence of a magnetic field to the observed strong anisotropies (Goldreich & Sridhar 1995).
A steepening of the slope of the power spectrum implies that the power distribution is predominantly affected by dissipative events at small scales although we do not find any significant break in the power distribution. The filamentary CNM structures at low Doppler temperatures imply recent phase transitions. Saury et al. (2014) have shown that for typical values of the density, pressure and velocity dispersion of the WNM turbulent motions of the H i cannot provoke the phase transition from WNM to CNM. This is found to be valid regardless of amplitude and distribution for turbulent motions in solenoidal and compressive modes and implies that the WNM must be pressurized for phase transitions. Such a model is consistent with the observed shell structure (see Appendix D) but Saury et al. (2014, Figs. 18 and 19) find shallow spectral indices after phase transition from WNM to CNM.
7.5. MBM 16 – shear flow and thermal instabilities
Our comparison field MBM 16, see Appendix A, differs from the targets with a filamentary radio-polarimetric structure. In radio-continuum this source does not show any structure of particular interest. MBM 16 contains molecular gas but there are no indications for star formation (Pingel et al. 2013). Furthermore, this field has an almost perfect isotropic H i column density distribution. Some filamentary structure of the molecular gas does exist but the orientation of the mean magnetic field direction, determined from optical polarization data (Gomez de Castro et al. 1997), is aligned in perpendicular direction. The steepest spectral index for MBM 16 is found at a velocity which is close to the peak of the average CO line emission (Pingel et al. 2013, Fig. 2).
From H2CO observations Magnani et al. (1993) suggest that the molecular gas is caused by a large-scale shear instability. We observe that the velocity for the coldest H i gas, containing the least amount of WNM, is shifted systematically with respect to the velocity of the gas with the steepest spectral index. LaRosa et al. (1999) argue that coherent molecular gas structures may originate from an externally driven turbulent shear flow, causing both MHD and fluid turbulence on small scales. Our observations give some evidence for dynamical interactions and support this proposal.
8. Summary and conclusions
Using methods introduced in Paper I, we study here two WSRT fields with well defined straight polarization filaments and associated radio-polarimetric depolarization canals, named Horologium and Auriga (Haverkorn et al. 2003a–c).
EBHIS H i observations show H i filaments aligned with the polarized filaments in both fields. Figures 5, 12, 15, and in particular Fig. 7 show H i features that are well aligned with the polarized filaments. A similar good alignment was found in Paper I, see there Fig. 2. The H i power spectra in both fields discussed here show significant anisotropy, with the steepest power spectra aligned along the polarized filaments. Most prominent filaments are aligned with the Galactic plane, which is presumed to be the direction of the mean (local) Galactic magnetic field. In Auriga, one prominent H i filament aligns with a polarized filament but not with the Galactic plane, taken to indicate a mean local Galactic magnetic field direction which deviates from parallel to the Galactic plane.
The anisotropic filamentary H i structures are cold. For the Auriga field the spin temperature can be estimated from 3C 147, at vLSR = −8.1 and 0.2 km s-1, to be Tspin = 34 ± 17 or 37 ± 24 K respectively. In case of 3C 196 (Paper I) Tspin = 80.9 K. No spin temperature can be derived for the Horologium field but also here the derived geometrical mean Doppler temperature, an upper limit to the spin temperature, is low, Tspin<TD ~ 167 K. Anisotropies in H i power-spectra tend in all cases to be strongest for velocity channels with low Doppler temperatures.
We find that local minima in TD are associated with minima in the WNM ratio TG WNM(vLSR) /TG WNM + CNM(vLSR), determined from a Gaussian analysis. We conclude that H i anisotropies must be associated with phase transitions. We also find evidence for a distinct steepening of the average spectral power distribution.
To our best knowledge, steep thick slice H i power spectra with indices as low as γ = −4.9 and associated steep thin velocity slice power spectra with indices γ ≲ −3.2 have not been reported before. To study this steepening in more detail, we compared the steepest power spectra with more shallow power spectra at velocities close-by where the WNM fraction is significantly larger. We define the power transfer function T(k) (Eq. (4)) to characterize spatial changes in the power distribution between the coldest H i gas with the least WNM content and its environment.
T(k) shows a steepening over a broad range in spatial frequencies and we interpret this as an indication that also a broad range of scales in the image plane must be affected by phase transitions. Model calculations by Hennebelle (2013) indicate that phase transitions occur predominantly at scales around 1 pc. The strong steepening on scales k ≲ 0.01 or 0.02 arcmin-1 imply that phase transitions are most dominant on larger scales. Phase transitions obviously do not occur locally in isolated spots but rather simultaneously in a correlated way on larger scales, perhaps in larger eddies. Heiles & Troland (2005) propose transitions in sheets, Appendix D supports such structures. This is consistent with Hennebelle (2013), who found that the primary cause of the existence of filaments (or elongated clumps) is the stretching of the fluid particles induced by turbulent motions. He argues that the magnetic field helps to keep filamentary structures coherent and is playing a determining role in the formation of filamentary structures.
Steep power spectra for thin velocity slices were detected also for two other targets that are not associated with radio-polarimetric depolarization canals. Firback North 1 (FN1, Dole et al. 2001) was studied in Paper I. Steep thin velocity slice power spectra in FN1 are associated with anisotropies and cold CNM at a Doppler temperature TD ~ 250 K. For MBM 16, discussed in detail in Appendix A, we find no significant anisotropies but the steep spectral index is associated with molecular gas at a similar velocity. Remarkable is that the cold CNM with TD ~ 120 K is offset from that in velocity by a few km s-1, indicating dynamical interactions.
The radio-polarimetric targets discussed here, Horologium and Auriga, but also 3C 147 are located within the Fan Region. Here the mean field is remarkably well aligned with the Galactic plane, as indicated by both the dust polarization maps from Planck Collaboration Int. XIX (2015, Fig. 5) and the synchrotron polarization known from much earlier work since Brouw & Spoelstra (1976). We find a qualitative agreement of the mean magnetic field direction with anisotropies in the H i distribution, caused by filamentary H i structures that are associated with magneto-ionic structures (canals). We can not provide a proof that these structures are physically related to each other. However, coincidences exist for several targets: Horologium at vLSR = 2.7 and –16.6 km s-1, Auriga at vLSR = −2.6 km s-1, also 3C 196 at vLSR = −3.8 km s-1, and 3C 147 at vLSR = −8.1 km s-1 (only H i data available). Together, all these cases suggest that an ordered magnetic field, giving rise to polarized filamentary structures and associated anisotropic H i emission may play a significant role for phase transitions of compressed cold H i gas in a sheet-like geometry. We find H i gas with steep thin slice power spectra that is associated with cold gas. For our targets this coincidence is detected on scales between 10 AU (3C 147) up to tens of pc.
A simple tool is available at https://www.astro.uni-bonn.de/hisurvey/euhou/LABprofile/. The H i components with −18 ≲ vLSR ≲ 0 km s-1 can accordingly be at distances up to 1.5 kpc. In addition to the local gas we observe a component at a velocity of vLSR = −54 km s-1. This gas is according to the rotation curve located at a distance of 5.5 kpc and belongs probably to the Perseus arm.
Angles are circular quantities, for the processing see e.g., https://en.wikipedia.org/wiki/Mean_of_circular_quantities. When calculating the dispersion, the nearest of both possible angular distance needs to be taken.
The data analysis of the 3C 147 observations followed the same approach. Figure 1 of Kalberla & Mebold (1983) shows at high spatial frequencies the instrumental noise of the WSRT.
Acknowledgments
We acknowledge the referee for careful reading, concise and constructive criticism. P.K. thanks A. Lazarian for discussions at the ISM 2017 conference in Cologne. B. Winkel helped us with the generation of EBHIS maps in 1950.0 equatorial coordinates. We thank C. Heiles for stimulating comments. J.K. thanks the Deutsche Forschungsgemeinschaft (DFG) for support under grant numbers KE757/7–1, KE757/7–2, KE757/7–3, and KE757/11–1. U.H. acknowledges the support by the Estonian Research Council grant IUT26-2, and by the European Regional Development Fund (TK133). M.H. acknowledges the support of the research program 639.042.915, which is (partly) financed by the Netherlands Organisation for Scientific Research (NWO). This research has made use of NASA’s Astrophysics Data System. EBHIS is based on observations with the 100-m telescope of the MPIfR (Max-Planck-Institut für Radioastronomie) at Effelsberg.
References
- Blagrave, K., Martin, P. G., Joncas, G., et al. 2017, ApJ, 834, 126 [NASA ADS] [CrossRef] [Google Scholar]
- Brentjens, M. A., & de Bruyn, A. G. 2005, A&A, 441, 1217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brouw, W. N., & Spoelstra, T. A. T. 1976, A&AS, 26, 129 [NASA ADS] [Google Scholar]
- Burkhart, B., Lazarian, A., Leão, I. C., de Medeiros, J. R., & Esquivel, A. 2014, ApJ, 790, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Bykov, A. M., & Toptygin, I. N. 1987, Ap&SS, 138, 341 [Google Scholar]
- Chepurnov, A., Lazarian, A., Stanimirović, S., Heiles, C., & Peek, J. E. G. 2010, ApJ, 714, 1398 [NASA ADS] [CrossRef] [Google Scholar]
- Choi, E., & Stone, J. M. 2012, ApJ, 747, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Clark, S. E., Peek, J. E. G., & Putman, M. E. 2014, ApJ, 789, 82 [NASA ADS] [CrossRef] [Google Scholar]
- Crutcher, R. M., Wandelt, B., Heiles, C., Falgarone, E., & Troland, T. H. 2010, ApJ, 725, 466 [NASA ADS] [CrossRef] [Google Scholar]
- Deshpande, A. A. 2000, MNRAS, 317, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Diamond, P. J., Goss, W. M., Romney, J. D., et al. 1989, ApJ, 347, 302 [NASA ADS] [CrossRef] [Google Scholar]
- Dickey, J. M., & Lockman, F. J. 1990, ARA&A, 28, 215 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dickey, J. M., McClure-Griffiths, N. M., Stanimirović, S., Gaensler, B. M., & Green, A. J. 2001, ApJ, 561, 264 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Dole, H., Gispert, R., Lagache, G., et al. 2001, A&A, 372, 364 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ehlerová, S., & Palouš, J. 2005, A&A, 437, 101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ehlerová, S., & Palouš, J. 2013, A&A, 550, A23 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ehlerová, S., Palous, J., Theis, C., & Hensler, G. 1997, A&A, 328, 121 [NASA ADS] [Google Scholar]
- Esquivel, A., & Lazarian, A. 2005, ApJ, 631, 320 [NASA ADS] [CrossRef] [Google Scholar]
- Faison, M. D., & Goss, W. M. 2001, AJ, 121, 2706 [NASA ADS] [CrossRef] [Google Scholar]
- Fletcher, A., & Shukurov, A. 2007, EAS Pub. Ser., 23, 109 [CrossRef] [EDP Sciences] [Google Scholar]
- Ghosh, T., Boulanger, F., Martin, P. G., et al. 2017, A&A, 601, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Goldreich, P., & Sridhar, S. 1995, ApJ, 438, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, G. C., & Vázquez-Semadeni, E. 2014, ApJ, 791, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Gomez de Castro, A. I., Pudritz, R. E., & Bastien, P. 1997, ApJ, 476, 717 [NASA ADS] [CrossRef] [Google Scholar]
- Górski, K. M., Hivon, E., Banday, A. J., et al. 2005, ApJ, 622, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Green, D. A. 1993, MNRAS, 262, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Harris, F. J. 1978, IEEE Proc., 66, 51 [Google Scholar]
- Hartmann, L., Ballesteros-Paredes, J., & Bergin, E. A. 2001, ApJ, 562, 852 [NASA ADS] [CrossRef] [Google Scholar]
- Haud, U. 2000, A&A, 364, 83 [NASA ADS] [Google Scholar]
- Haud, U. 2010, A&A, 514, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haud, U. 2013, A&A, 552, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haverkorn, M., & Heitsch, F. 2004, A&A, 421, 1011 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haverkorn, M., Katgert, P., & de Bruyn, A. G. 2000, A&A, 356, L13 [NASA ADS] [Google Scholar]
- Haverkorn, M., Katgert, P., & de Bruyn, A. G. 2003a, A&A, 403, 1031 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haverkorn, M., Katgert, P., & de Bruyn, A. G. 2003b, A&A, 403, 1045 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Haverkorn, M., Katgert, P., & de Bruyn, A. G. 2003c, A&A, 404, 233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiles, C. 1979, ApJ, 229, 533 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C. 1984, ApJS, 55, 585 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., & Crutcher, R. 2005, in Cosmic Magnetic Fields, Lect. Notes Phys., 664, 137 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., & Haverkorn, M. 2012, Space Sci. Rev., 166, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heiles, C., & Troland, T. H. 2003, ApJ, 586, 1067 [NASA ADS] [CrossRef] [Google Scholar]
- Heiles, C., & Troland, T. H. 2005, ApJ, 624, 773 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P. 2013, A&A, 556, A153 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heyer, M., Gong, H., Ostriker, E., & Brunt, C. 2008, ApJ, 680, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, A. S., Landecker, T. L., Carretti, E., et al. 2017, MNRAS, 467, 4631 [NASA ADS] [CrossRef] [Google Scholar]
- Inoue, T., & Inutsuka, S.-I. 2016, ApJ, 833, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Jaynes, E. T. 2007, Probability Theory: The Logic of Science (Cambridge Univ. Press) [Google Scholar]
- Jelić, V., de Bruyn, A. G., Pandey, V. N., et al. 2015, A&A, 583, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., & Dedes, L. 2008, A&A, 487, 951 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., & Haud, U. 2015, A&A, 578, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., & Kerp, J. 2009, ARA&A, 47, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., & Kerp, J. 2016, A&A, 595, A37 (Paper I) [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., & Mebold, U. 1983, Mitteilungen der Astronomischen Gesellschaft Hamburg, 58, 101 [Google Scholar]
- Kalberla, P. M. W., Schwarz, U. J., & Goss, W. M. 1985, A&A, 144, 27 [NASA ADS] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., Kerp, J., Haud, U., et al. 2016, ApJ, 821, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Kandel, D., Lazarian, A., & Pogosyan, D. 2016, MNRAS, 461, 1227 [NASA ADS] [CrossRef] [Google Scholar]
- Kornreich, P., & Scalo, J. 2000, ApJ, 531, 366 [NASA ADS] [CrossRef] [Google Scholar]
- Lallement, R., Vergely, J.-L., Valette, B., et al. 2014, A&A, 561, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- LaRosa, T. N., Shore, S. N., & Magnani, L. 1999, ApJ, 512, 761 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., & Esquivel, A. 2003, ApJ, 592, L37 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., & Pogosyan, D. 2000, ApJ, 537, 720 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., & Pogosyan, D. 2004, ApJ, 616, 943 [NASA ADS] [CrossRef] [Google Scholar]
- Lazarian, A., & Pogosyan, D. 2006, ApJ, 652, 1348 [NASA ADS] [CrossRef] [Google Scholar]
- Lazio, T. J. W., Brogan, C. L., Goss, W. M., & Stanimirović, S. 2009, AJ, 137, 4526 [NASA ADS] [CrossRef] [Google Scholar]
- Levine, E. S., Blitz, L., & Heiles, C. 2006, Science, 312, 1773 [NASA ADS] [CrossRef] [Google Scholar]
- Magnani, L., Larosa, T. N., & Shore, S. N. 1993, ApJ, 402, 226 [NASA ADS] [CrossRef] [Google Scholar]
- Mallet, A., & Schekochihin, A. A. 2017, MNRAS, 466, 3918 [NASA ADS] [CrossRef] [Google Scholar]
- Martin, P. G., Blagrave, K. P. M., Lockman, F. J., et al. 2015, ApJ, 809, 153 [NASA ADS] [CrossRef] [Google Scholar]
- McClure-Griffiths, N. M., Dickey, J. M., Gaensler, B. M., & Green, A. J. 2002, ApJ, 578, 176 [NASA ADS] [CrossRef] [Google Scholar]
- McClure-Griffiths, N. M., Dickey, J. M., Gaensler, B. M., Green, A. J., & Haverkorn, M. 2006, ApJ, 652, 1339 [NASA ADS] [CrossRef] [Google Scholar]
- McKee, C. F., & Ostriker, J. P. 1977, ApJ, 218, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Pingel, N. M., Stanimirović, S., Peek, J. E. G., et al. 2013, ApJ, 779, 36 [NASA ADS] [CrossRef] [Google Scholar]
- Miville-Deschênes, M.-A., Lagache, G., & Puget, J.-L. 2002, A&A, 393, 749 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Miville-Deschênes, M.-A., Levrier, F., & Falgarone, E. 2003, ApJ, 593, 831 [NASA ADS] [CrossRef] [Google Scholar]
- Miville-Deschênes, M.-A., & Martin, P. G. 2007, A&A, 469, 189 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moisy, F., & Jiménez, J. 2004, J. Fluid Mech., 513, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration Int. XIX. 2015, A&A, 576, A104 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XXXII. 2016, A&A, 586, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saury, E., Miville-Deschênes, M.-A., Hennebelle, P., Audit, E., & Schmidt, W. 2014, A&A, 567, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shukurov, A., & Berkhuijsen, E. M. 2003, MNRAS, 342, 496 [NASA ADS] [CrossRef] [Google Scholar]
- Spoelstra, T. A. T. 1984, A&A, 135, 238 [NASA ADS] [Google Scholar]
- Vázquez-Semadeni, E. 2012, EAS Pub. Ser., 56, 39 [Google Scholar]
- Vázquez-Semadeni, E., Ryu, D., Passot, T., González, R. F., & Gazol, A. 2006, ApJ, 643, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Vorobyov, E. I., & Basu, S. 2005, A&A, 431, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vorobyov, E. I., Klein, U., Shchekinov, Y. A., & Ott, J. 2004, A&A, 413, 939 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winkel, B., Kerp, J., Flöer, L., et al. 2016a, A&A, 585, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Winkel, B., Lenz, D., & Flöer, L. 2016b, A&A, 591, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolleben, M., Landecker, T. L., Reich, W., & Wielebinski, R. 2006, A&A, 448, 411 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolfire, M. G., McKee, C. F., Hollenbach, D., & Tielens, A. G. G. M. 2003, ApJ, 587, 278 [NASA ADS] [CrossRef] [Google Scholar]
- Zaroubi, S., Jelić, V., de Bruyn, A. G., et al. 2015, MNRAS, 454, L46 [NASA ADS] [Google Scholar]
Appendix A: Processing of power spectra: apodization versus median
Our data processing methods, introduced in Paper I, were developed with the aim to allow an unbiased derivation of anisotropies in the H i spectral power distribution. Usually the analyzed region has a rectangular shape. The response of the window function is recognizable as a strong central cross in the power distribution (see Fig. 4 left in Paper I or Fig. 6 in Pingel et al. 2013). The observing process implies further that the data are convolved by the beam function, in addition instrumental noise is added to the genuine signal. To avoid observational biases we apodize the data by a circular taper, deconvolve for the beam function and subtract the statistical noise bias N(k), see Eq. (1), Paper I, Sect. 4 and there the presentation in Figs. 3 to 6. When fitting spectral indices we use a cut-off at high spatial frequencies to ensure that data below a S/N of three are excluded.
According to the convolution theorem apodization leads to a smoothing of the data in the Fourier transformed domain. This process is equivalent to the smoothing caused by the primary beam of a synthesis telescope (Green 1993) but in our case the equivalent “apodization beam” is defined by the observed region. The formal FWHM diameter of the apodization function is in our case 10° for the Auriga and Horologium fields and 9° for the MBM 16 field considered below. In the UV plane this smoothing function has 20 dB sidelobes however we do not expect a significant degradation of the derived power spectra since we matched the sampling in the UV plane to the FWHM diameter of the smoothing function. Binning of the power spectra in spatial frequencies was chosen to limit the FWHM size of the smoothing function to 70% (80% in case of MBM 16) of the selected bin. The smoothing in the UV plane, caused by apodization, is independent of k. Accordingly we have chosen a constant sampling and all k samples of the power spectra may be considered as nearly independent. In case of position dependent power spectra there is an exception. For sectors with a width of 15° samples at k< 0.003 arcmin-1 are not independent. This is only important for the derivation of anisotropies and we do not interpret anisotropies for such values.
When deriving power spectra we find significant changes in the derived spectral indices, see Figs. 12, 13, and 18 in Paper I, also Figs. 1, 8 and the discussion in Sect. 5. Such a steepening was not observed before and could therefore be related to a systematic effect in our methodology. For clarification we use here a case study and compare results from our data processing with recently published results obtained from more “standard” data processing methods that are so far considered to be robust against systematic effects, for discussion see for example Martin et al. (2015), Blagrave et al. (2017). These methods rely on median filtering and the results are assumed to be equivalent to those using apodization for power distributions with azimuthal symmetry in the UV plane (e.g., Miville-Deschênes et al. 2002).
To evaluate differences in data processing we consider the starless molecular cloud MBM 16 (suggested by the referee) and compare our results with those of Pingel et al. (2013). These authors used the Arecibo telescope to derive the turbulent properties of H i in this region for the range 42.̊5 < RA < 56.̊25 and 4°< Dec < 16°(J2000). We select EBHIS observations for the same region.
The data processing is identical to that for the targets described in Sects. 3 and 4. Figure A.1 displays the average brightness temperature TB aver, the anisotropy factor Qaver for 0.007 <k< 0.06 arcmin-1, and the derived spectral index γ for the MBM 16 field. Figure A.2 shows the corresponding average position angles for Qaver. The scatter of Qaver is large and a visual inspection of the data cube confirms that, except for velocities v ≳ 14 km s-1, anisotropies are insignificant. Complications from source anisotropies are thus not expected and we conclude that the MBM 16 field is an ideal case for a comparison of different data processing methods.
 |
Fig. A.1 Average brightness temperature TB aver (red), anisotropy factor Qaver (blue) for 0.007 <k< 0.06 arcmin-1, and spectral index γ (green) for the MBM 16 field as derived from EBHIS observations. The upper horizontal black dotted line indicates the Kolmogorov spectral index of γ = −8 / 3, the lower dash-dotted line Qaver = 0. |
 |
Fig. A.2 Average position angles Φaver calculated for 0.007 < k < 0.06 arcmin-1 and associated one σ rms scatter for the MBM 16 field. |
Using the procedures introduced in Paper I (apodization, beam deconvolution and noise bias correction) we derive mean power spectra for the MBM 16 field and fit the spectral indices γ. To avoid biases from instrumental noise we usually restrict the least square fits to the power spectra by applying a constant three sigma limit km at high spatial frequencies. To demonstrate the effect of such an upper limit we consider here several cases in the range 0.01 <km < 0.06 arcmin-1. The results are shown in Fig. A.3. With the horizontal line we indicate the expected Kolmogorov spectral index, γ = −8 / 3, the vertical lines bracket the velocity range with average brightness temperatures TB aver > 0.5 K. We consider derived spectral indices for lower TB aver values as very uncertain and possibly systematically biased despite the fact that the formal uncertainties from the least squares fit do not change significantly for lower TB aver.
 |
Fig. A.3 Comparison of results according to the method proposed in Paper I (using apodization, beam correction, and noise subtraction) obtained from fits with different upper limits 0.01 <km < 0.06 arcmin-1 in spatial frequency. Error bars are given in two cases to provide an impression of formal uncertainties of the least square fits. The horizontal black dotted line indicates the Kolmogorov spectral index γ = −8 / 3, the solid vertical lines bracket the velocity range with average brightness temperatures TB aver > 0.5 K. |
 |
Fig. A.4 The thick red line represents results obtained after apodization, beam correction, and noise subtraction. The other graphs show results obtained without apodization by fitting the median power distribution. km is in each case the upper limit for the spatial frequencies used for the fit. Error bars are given in three cases to provide an impression of formal uncertainties of the least square fits. The horizontal black dotted line represents the expected Kolmogorov index γ = −8 / 3. The vertical solid black lines bracket the velocity range analyzed by Pingel et al. (2013), the horizontal solid black line gives the weighted average slope γ = −3.58 ± 0.09 obtained by them for this velocity range. |
We repeat the derivation of spectral indices but use this time a processing similar to Pingel et al. (2013). No apodization, beam correction or noise bias correction is applied to the data and we determine for each annulus in the UV plane the median power instead of the mean power before we fit the spectrum. The different cases in Fig. A.4 are as before results obtained for upper limits 0.01 <km< 0.06 arcmin-1 in spatial frequencies. For comparison we plot the spectral index distribution from Fig. A.3 obtained by our method for km = 0.05 arcmin-1.
Comparing Fig. A.4 with A.3 it is obvious that for our apodization method the upper limit km is not a critical parameter5. For 0.04 <km< 0.06 arcmin-1 the spectral index profiles in Fig. A.3 are similar with systematic deviations close to the formal uncertainties of the least square fits for km = 0.05 arcmin-1. In particular, Fig. A.3 shows that the steep spectral index near vLSR ~ 9.1 km s-1 is well defined and within the errors identical for all km values used.
For the processing without apodization, beam deconvolution, and noise bias correction (Fig. A.4) the spectral index profiles depend strongly on the applied spatial frequency cutoff km. The weighted average slope for the six panels in Fig. 9 of Pingel et al. (2013) is γ = 3.58 ± 0.09, compatible with our result for the median fit with km = 0.05 arcmin-1 but is incompatible with the apodized fit from Fig. A.3, using the same constraint km = 0.05 arcmin-1.
 |
Fig. A.5 Unnormalized thick velocity slice power spectra for MBM 16, integrating over −1.1 <vLSR< 15.6 km s-1 and spectral indices from least squares fits. High spatial frequency limits km< 0.06 arcmin-1, corresponding to a linear size of 0.39 pc were applied and are indicated by the vertical black line. Black dots represent data derived after apodization, beam correction, and noise subtraction. In this case we fit γ = −3.63 ± 0.04. The red triangles show results obtained without apodization and beam correction by fitting the median power distribution. Here we fit γ = −3.88 ± 0.04. |
We continue our comparison of different data processing methods by deriving spectral indices for thick velocity slices. To calculate the spectral indices we select the velocity range −1.1 <vLSR< 15.6 km s-1 as defined by Pingel et al. (2013). We apply in both cases high spatial frequency limits corresponding to a linear size of 0.39 pc (at a source distance of 80 pc), to exclude instrumental noise for km> 0.06 arcmin-1. The results are shown in Fig. A.5. For the data derived after our apodization, beam correction, and noise bias correction, we fit γ = −3.63 ± 0.04. The triangles represent results obtained without apodization by fitting the median power distribution. We fit γ = −3.88 ± 0.04 (to be compared with γ = −3.63 ± 0.04 from apodization) and below we will argue that the median is biased.
Pingel et al. (2013) derived γ = −3.7 ± .2, within the errors consistent with our result of γ = −3.63 ± 0.04. We repeat our analysis (with apodization) for the full velocity range −30 <vLSR< 30 km s-1. Within the errors we get the same result, γ = −3.63, with only slightly lower uncertainties. For the normalized velocity centroid over −30 <vLSR< 30 km s-1 we determine γ = −3.65 ± 0.03. This result indicates that the turbulent density and velocity fields share within the uncertainties similar properties, compatible with a 3D Kolmogorov −11/3 slope expected for incompressible turbulence. For comparison with Pingel et al. (2013, Fig. 10) we calculate the variation of the 2D power spectrum slope, γ(ΔvLSR), with velocity slice thickness ΔvLSR. Figure A.6 shows the change in spectral index for the H i gas centered at vLSR = 9.1 km s-1. The slice may be considered as thick for ΔvLSR ≳ 15 km s-1 but the H i emission extends over a total range of ΔvLSR ~ 30 km s-1, see Fig. A.1.
 |
Fig. A.6 Spectral index changes with velocity slice thickness for the MBM 16 H i gas centered at vLSR = 9.1 km s-1. A high spatial frequency limit km = 0.06 arcmin-1, corresponding to a linear size of 0.39 pc, was applied when fitting the spectral index. The bars indicate uncertainties of the power law indices. |
Controversial results, apodization versus median, need to get explained but we do not intend to discuss subtle differences between the Arecibo and Effelsberg telescopes, nor differences in the data processing pipeline. A major difference is however the sampling in spatial frequencies. Pingel et al. (2013) use 13 samples with equal spacings in log (k). We use approximately ten times more samples with linear spacing in k. The main reason for our choice is that it allows a simple but reliable determination of the noise bias N(k), demonstrated with Fig. 6 of Paper I. The noise bias depends on the S/N, the fine grain linear spacing allows an accurate determination and subsequent correction for this noise bias, see Sect. 4 of Paper I. This correction, however, is a statistical correction for the average power level and does not result in “noise-free” power distributions as erroneously assumed by Green (1993). Uncertainties remain and are amplified by the beam correction (see Figs. 5 and 6 in Paper I). It is therefore necessary to restrict the interpretation of the power spectra to those spatial frequencies where the signal is stronger than the instrumental noise. For this purpose we use a three sigma upper limit km.
It is important to realize that for any reasonable instrumental setup the power at the highest spatial frequencies is dominated by instrumental noise. The transition from the genuine astrophysical signal to instrumental noise depends on the S/N and the telescope beam function. Without beam correction instrumental effects remain hidden. Accordingly the uncorrected signal in Fig. A.5 does not give the slightest hint where the transition from astrophysical signal to instrumental noise takes place. Figure 6 of Paper I shows that this transition is sharp and well defined in spatial frequency.
 |
Fig. A.7 Comparison between the geometric mean Doppler temperature TD (black) and the spectral index γ (green dashed) for MBM 16. |
 |
Fig. A.8 Spectral index γ(vLSR) (green) compared with the WNM fraction TWNM(vLSR) /TWNM + CNM(vLSR) derived from LAB (pink) and EBHIS Gaussians (red) for the MBM 16 field. An upper limit for the Doppler temperature of the CNM of TD< 1100 K, corresponding to a turbulent CNM Mach number of MT = 3.7 was applied. We display also with a blue dotted line the WNM fraction TWNM(vLSR) /TWNM + CNM(vLSR) derived from EBHIS, using TD< 1100 K, for a central position l = 171°,b = −37° within a radius of 1.̊5. This corresponds to the region with CO emission observed by LaRosa et al. (1999, Fig. 1). |
Our approach leads to power spectra that are on average straight as expected for the inertial range of turbulence spectra. Power spectra without correction for beam and noise bias have a concave shape, caused by the response to the telescope beam as demonstrated by Dickey et al. (2001, their Figs. 3, 4, and 6). Such a concave bending is visible in Fig. A.5. It was already demonstrated with Fig. 22 of Paper I that the missing beam correction, together with the missing noise bias removal, leads to such a bending. In turn the spectral index is biased. We notice that all of the power spectra in Figs. 7 and 8 of Pingel et al. (2013) are concave, similar to Figs. 3, 4, and 6 of Dickey et al. (2001). Fitting such spectra with a straight power law is difficult, in particular without a detailed evaluation of the significance of the data. Biases and uncertainties in derived spectral indices are unavoidable, the results depend on selection effects, such as details of the sampling method.
 |
Fig. A.9 Thick velocity slice power distributions for MBM 16, integrating over −1.1 <vLSR< 15.6 km s-1. Left: apodized distribution, corrected for the beam function. Right: the same data without apodization and beam correction. The scales are logarithmic in dB. The circle indicates the 3σ spatial frequency limit km = 0.06 arcmin-1, corresponding to a linear size of 0.39 pc. Data for higher spatial frequencies are dominated by the instrumental noise. |
When deriving and comparing thin with thick slice power spectra, changes in the noise bias must be taken into account. Pingel et al. (2013) used for this comparison channel widths between ΔvLSR = 0.18 and ΔvLSR = 18 km s-1. This implies that the noise power bias for the corresponding power spectra changes by a factor of 10. Disregarding this effect must lead to biases in the spectral index but it is difficult to estimate such an effect quantitatively (EBHIS does not provide data at a bandwidth of ΔvLSR< 1.44 km s-1).
The data processing has also consequences on the interpretation of power spectral distribution. Pingel et al. (2013) considered primarily velocities −1 <vLSR< 16 km s-1 but mention in their Sect. 3 that the results remain valid for the full velocity range −20 <vLSR< 20 km s-1. Within the uncertainties they find little fluctuations for the spectral index (γ = 3.58 ± 0.09). We interpret the full velocity range with TB aver> 0.5 K and get significant spectral index fluctuations in the range −2.7 >γ> −3.35.
We demonstrate in Sect. 5 that the steepest part of the spectral index distribution for the Horologium and Auriga fields is associated with cold gas at low Doppler temperatures with a low fraction of the WNM (Figs. 19 and 20). In Fig. A.7 we compare for the MBM 16 field the spectral index distribution with the geometric mean Doppler temperature TD. In Fig. A.8 we show how γ is related to the WNM fraction TWNM(vLSR) /TWNM + CNM(vLSR). Consistent with Sect. 5 we use for the CNM an upper limit for the Doppler temperature of TD< 1100 K and plot the results for LAB and EBHIS.
Similar to Horologium and Auriga, the steepest part of the spectral index distribution in the MBM 16 field is found to be associated with low values in TD and TWNM(vLSR)/ TWNM + CNM(vLSR) but in both cases there is for MBM 16 a shift for the minima by about 3 to 4 km s-1. Cold gas is also found at vLSR ~ −10 km s-1 but interestingly the spectral index is here less steep and only little molecular gas is associated with this part of the H i distribution.
The MBM 16 field, used by Pingel et al. (2013), is offset from the field center observed by (LaRosa et al. 1999). We repeat the EBHIS calculation of TWNM(vLSR) /TWNM + CNM(vLSR) for a center position of l = 171°,b = −37° within a limited radius of 1.̊5. This covers most of the region with CO as observed by LaRosa et al. (1999, Fig. 1). The result is shown in Fig. A.8. The positive wing of the double horned distribution for TWNM(vLSR) /TWNM + CNM(vLSR) has shifted somewhat closer to the velocity of the steepest spectral index. The negative part peaks now at vLSR = −9 km s-1, consistent with a weak secondary peak of the CO distribution (Pingel et al. 2013, Fig. 2) at this velocity. TWNM(vLSR) /TWNM + CNM(vLSR) contains now a central component (originating from H i gas at low Galactic latitudes). From the almost symmetrical shape of this distribution relative to the central component we suspect that some dynamical interactions are responsible for the TWNM(vLSR) /TWNM + CNM(vLSR) and TD distribution.
CO observations in the MBM 16 field suggest that the molecular gas is driven by an external shear flow (LaRosa et al. 1999). The velocity shifts observed by us may imply systematical internal motions in the H i gas, with shock induced phase transitions, leading to a separation of cold and warm gas. Whether there is a detailed relation to the velocity structure of the CO gas is an interesting question but far beyond the scope of this Appendix.
To summarize this part of the Appendix, we prefer a Bayesian approach over the so-called robust processing using the median. We exclude instrumental biases by apodization and beam correction and eliminate outliers caused by the system noise, using only data above a S/N of three6. The probability that data with significant instrumental biases belong to the true power distribution is close to zero, hence these data should be corrected and excluded from the analysis, see Jaynes (2007) for detailed discussions of Bayesian and robust approaches in probability theory.
Figure A.9 compares the data used for our Bayesian approach (left) with those from the robust data analysis (right). Obviously, both distributions are very different. The image displayed on the right hand side contains in comparison to the apodized distribution excess power from the source distribution outside the apodized region. Discontinuities in the H i column density distribution at the rectangular field boundaries cause the prominent cross structure in the Fourier transformed domain. The second problem with the power distribution on the right hand side is that the attenuation caused by the beam function of the telescope remained uncorrected. Quite surprisingly, the power spectra, given in Fig. A.5, show a remarkable good agreement between both methods. However without apodization the power at intermediate spatial frequencies (scales corresponding to 0.8–8 pc) is too high and the power at the smallest scales (below 0.5 pc) is too low.
Appendix B: Horologium anisotropies at high velocities
Searching for anisotropies in the H i component at a velocity of vLSR = −54 km s-1 we found also a position angle of Φ ~ −55°, corresponding to an alignment parallel to the Galactic plane. Figure B.1 displays for three velocity channels moderate anisotropies up to Q ~ 10 at k ~ 0.01 arcmin-1, corresponding to a linear scale of 175 pc at a distance of 6 kpc.
Figure 1 displays a local minimum in the spectral index distribution γ at vLSR = −76 km s-1. This feature is associated with a well defined position angles Φ = −65° ± 8° in Fig. 2 although there is no obvious emission component visible in the average brightness temperature profile from Fig. 1. An inspection of the EBHIS H i maps shows a bright (up to 66 K peak brightness temperature) but segregated filamentary structure at low latitudes with a length of ~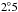 . This feature is part of a more extended structure outside the field of view, parallel to the Galactic plane. The kinematic distance for this H i gas is about 10 kpc, the Galactocentric distance 17 kpc. This feature fits well to arm 1 of the four-armed logarithmic spiral proposed by Levine et al. (2006, Fig. 4a).
. This feature is part of a more extended structure outside the field of view, parallel to the Galactic plane. The kinematic distance for this H i gas is about 10 kpc, the Galactocentric distance 17 kpc. This feature fits well to arm 1 of the four-armed logarithmic spiral proposed by Levine et al. (2006, Fig. 4a).
Figure B.2 displays anisotropies for three channels, at vLSR = −77.2,−75.9, and vLSR = −74.6 km s-1. For two of the channels we find strong anisotropies of Q ~ 210 at k = 0.0064 arcmin-1. These anistropies with a scale length of about 450 pc appear to decay with a well defined steep slope of γ = −3.71. For comparison, the spectral index of the average power spectrum is here γ = −2.89 ± 0.07.
 |
Fig. B.1 Anisotropies Q(k) in the Perseus arm at velocities vLSR = −50.1 km s-1 (green), vLSR = −54.0 km s-1 (blue), and vLSR = −57.9 km s-1 (red). |
 |
Fig. B.2 Anisotropies Q(k) in the outer arm at velocities vLSR = −77.2 km s-1 (green), vLSR = −75.9 km s-1 (blue), and vLSR = −74.6 km s-1 (red). The blue line reproduces a fit to 20 data points at vLSR = −75.9 km s-1, tentatively indicating the decay of the strong local anisotropy with Q = 209. |
Appendix C: Velocity centroids
Comparison of fit spectral indices.
Appendix C.1: Normalized velocity centroid (VC)
Using fractional Brownian motion simulations, Miville-Deschenes et al. (2003) used normalized velocity centroids (VC) according to Eq. (3). They demonstrated that the power spectrum of the velocity centroid map has in case of an isotropic and optically thin distribution the same spectral index as that of the velocity field. Esquivel & Lazarian (2005), using MHD simulations, confirm these results but caution that the results may get questionable for high turbulent Mach numbers MT ≳ 2.5. For 3C 147 we derived MT ~ 2.7, else we assume MT ~ 3.7. Thus, an application of the velocity centroid method may be somewhat questionable with our assumptions but it is certainly not applicable in case of MT = 7.7 (Chepurnov et al. 2010). In comparison with VCA or the velocity coordinate spectrum (VCS) method (Lazarian & Pogosyan 2006), Esquivel & Lazarian (2005) report advantages for velocity centroids in case that velocity statistics is not a straight power law. They mention that velocity centroids can better pick up the dissipation and injection energy scales.
Observed H i line profiles at low and intermediate latitudes are usually complex since they contain several independent components. It is then necessary to restrict the observations to the velocity range dominated by the H i cloud or H i layer under investigation (Eq. (3)). For velocity centroids an appropriate window is easily applicable. For the VCS method on the other hand the velocity window causes unwanted side effects which need to be taken into account. Such an elaborate analysis is beyond the scope of this paper.
VCA is not applicable for steep thin velocity slice power spectra observed by us, we therefore calculate the Horologium velocity centroid over the velocity range −23.1 <vLSR< 5.2 km s-1 (see Fig. 1), the same range as applied for the determination of the spectral index for the density field. Figure 22 (top) shows the result, the derived average spectral power index for the Horologium velocity field is within the errors identical to the index γ = −3.4 ± 0.05 for the density field.
For comparison, in case of Auriga (Fig. 23 bottom) we derive a thick slice spectral index of γ = −3.28 ± 0.04 for the density field and from the velocity centroid γ = −2.78 ± 0.03 (top) for k< 0.07 arcmin-1. In both cases we used a velocity range of −10.2 <vLSR< 11.7 km s-1 (see Fig 8). The width of the velocity window of 22 km s-1 fits formally to VCA thick slice condition ΔvLSR> 17 km s-1. In this case we have however at least two H i layers along the line of sight, blending may cause unwanted contributions and the thick slice window −10.2 <vLSR< 11.7 km s-1 does probably not match the criteria of a very thick slice. The derived spectral indices may suffer from such contributions.
Appendix C.2: Unnormalized velocity centroid (UVC)
For normalized velocity centroids the denominator in Eq. (3) introduces an algebraic complication for the analytical treatment of turbulence spectra or power distributions, we refer to the discussion by Esquivel & Lazarian (2005). To allow a better comparison of our results with model calculations we calculate UVCs in parallel to VCs, using also the prescription given in Esquivel & Lazarian (2005, Eq. (33)) to verify that the velocity centroids trace the turbulent velocity statistics, 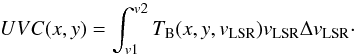 (C.1)A visual comparison of centroid maps shows that both methods are nearly equivalent, except that UVC images look slightly more diffuse. Correspondingly UVC spectral indices are slightly shallower than VC indices, see Table C.1.
(C.1)A visual comparison of centroid maps shows that both methods are nearly equivalent, except that UVC images look slightly more diffuse. Correspondingly UVC spectral indices are slightly shallower than VC indices, see Table C.1.
Appendix C.3: v2 centroid (VVC)
This centroid is analogous to Eq. (3), but replacing v with v2 and was introduced by Burkhart et al. (2014) for anisotropy studies. The VVC measures the second moment, making the isotropy degree more sensitive to velocity and less sensitive to density. Alternatively VVC may be considered as the first moment of the line width distribution, hence telling us about turbulent fluctuations of Doppler temperatures, 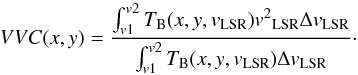 (C.2)
(C.2)
Appendix C.4: Comparing VC, UVC, and VVC spectral slopes
Table C.1 lists spectral indices for thick slices, centroids and also indices for the steepest thin slice power spectra. We include 3C 196 and FN1 from Paper I. MBM 16 and FN1 are reference fields and therefore not considered in the following discussion.
It is easy to verify from Table C.1 that VC and UVC are similar but have slight systematic differences. VVC spectral slopes tend to be steep, in case of Auriga and Horologium with a spectral index that is comparable to the steepest thin slice spectral index. Anisotropies in the VVC maps were found in all cases to be relatively weak, only slightly less than those of the VC or UVC maps and restricted to limited ranges in spatial frequency. We confirm the model calculations by Burkhart et al. (2014) who found that VVC anisotropies are similar to the VC case.
The VVC maps represent the spatial distribution of squared line widths, hence Doppler temperatures, and the inspection of these maps shows that they are dominated by broad WNM lines and correspondingly by high Doppler temperatures. The relative steep VVC power spectra imply that line widths and Doppler temperatures decrease strongly with increasing spatial frequency, compatible with the low geometric mean Doppler temperatures determined previously. However steep VVC power spectra are not associated with anisotropies. As pointed out by Burkhart et al. (2014), VVC was introduced to enhance the sensitivity of centroids with respect to the velocity field. Enhanced anisotropies are not observed by us and correspondingly there is no evidence that anisotropies are driven by the velocity field.
Along with this interpretation is our finding that anisotropies for the coldest gas components increase with decreasing velocity width of the slices under investigation. VC, UVC, and VVC maps show intermediate anisotropies. This is exactly opposite to the results reported by Kandel et al. (2016). Last, but not least, our observations contradict VCA results as proposed by Lazarian & Pogosyan (2000, 2004). All these theoretical investigations are based on the assumption that turbulent velocity and density fields can be represented by independent Gaussian fields. In Appendix D we demonstrate that the filamentary H i structures are caused by projection effects. The observed thin slice column densities depend on velocity and direction of the mean magnetic field. We find a well defined velocity gradient perpendicular to the magnetic field.
Appendix D: Anatomy of a filament
In common language the term filament is used to describe “a single thread or a thin flexible threadlike object” (Merriam-Webster). In this paper we use “filamentary structure” to describe such an object. But what is the 3D distribution of the H i gas that gives rise to the observed filamentary structure, projected onto the plane of the sky? Referring to Heiles & Crutcher (2005), Heiles & Troland (2005), Kalberla et al. (2016) we argue for sheets, seen almost edge-on. A different geometry is proposed by Clark et al. (2014), they interpret filamentary structures as fibers.
We intend to disclose here as an example the structure of one of the CNM filaments that appears to be associated with radio-polarimetric depolarization canals, the feature observed in the Horologium field at RA = 3h, Dec = 66° (B1950.0) with a velocity vLSR = −16.6 km s-1, see Fig. 7.
 |
Fig. D.1 Top: color coded brightness temperature distribution for the filamentary structure in the Horologium field at vLSR = −16.6 km s-1. The white isophotes display the USM temperatures at the same velocity. Bottom: the brightness temperature distribution at vLSR = −11.5 km s-1 is shown in color, the white isophotes are USM temperatures at the same velocity while black isophotes are at vLSR = −16.6 km s-1 for comparison with the top panel. Isophote levels are 1, 2.5, and 5 K Galactic coordinates are used, the black lines indicate longitudes of the velocity-position plots in Fig. D.2. |
This filamentary feature is oriented parallel to the Galactic plane. To determine details of the large scale structure we calculate EBHIS maps in Galactic coordinates. Figure D.1 shows at the top the brightness temperature distribution at vLSR = −16.6 km s-1. USM temperatures at the same velocity, emphasizing filamentary structures in the CNM, are overlayed with isophotes at 1, 2.5, and 5 K. The feature from Fig. 7 is located at 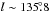 , b ~ 6.̊7 as part of an arc with a total length of at least 6°. In the bottom panel of Fig. D.1 we display the observed distribution similar to the top panel but now at vLSR = −11.5 km s-1. For comparison we replicate the USM structure from the top panel at vLSR = −16.6 km s-1 with black isophotes. It is obvious that the large scale filamentary structure has shifted to lower latitudes and is broken in several fragments.
, b ~ 6.̊7 as part of an arc with a total length of at least 6°. In the bottom panel of Fig. D.1 we display the observed distribution similar to the top panel but now at vLSR = −11.5 km s-1. For comparison we replicate the USM structure from the top panel at vLSR = −16.6 km s-1 with black isophotes. It is obvious that the large scale filamentary structure has shifted to lower latitudes and is broken in several fragments.
In Fig. D.2 we display four velocity-position cuts through this arc-like feature at constant longitudes indicated in Fig. D.1. In all cases we can trace coherent features that span a range of approximately 20 km s-1, shifting in latitude by roughly 1°. Hence we observe a velocity gradient of 20 km s-1/degree perpendicular to the mean magnetic field direction. For individual velocity channels the observed filamentary USM structures like that from Fig. D.1 may be modeled as fibers. The length of each fiber depends on the observed fragmentation. However, continuity in velocity-position space with well defined velocity gradients (Figs. D.1 and D.2) inhibits an interpretation as 1D structures for most of the observed filamentary structures. They need to be described as sheets, 2D structures, tilted in velocity with distinct gradients. Sheets are often warped and broken.
 |
Fig. D.2 Velocity-position diagrams, brightness temperatures (color coded) for cuts at constant longitudes l = 136.̊534, 135.̊277, 134.̊397, and 131.̊403 (top left to bottom right), indicated in Fig. D.1 by black lines. Radial velocities are in m s-1, isophotes are USM temperatures of 1, 2.5, and 5 K. |
 |
Fig. D.3 Position-velocity diagrams, color coded brightness temperatures for cuts at constant latitudes b = 8.̊0 to 4.̊5 in steps of −0.̊5 (top left to bottom right), overlaid with isophotes displaying USM temperatures of 1, 2.5, and 5 K. Radial velocities are in m s-1. |
The arc (Fig. D.1) is well defined on large scales but was not cataloged previously. Features like this are usually classified as expanding HI shells (Heiles 1979, 1984; McClure-Griffiths et al. 2002; Ehlerová & Palouš 2005, 2013). An expanding shell, originating from supernova explosions in the Galactic plane, is affected by the planar density distribution (Ehlerova et al. 1997; Vorobyov et al. 2004; Vorobyov & Basu 2005). In case of the filamentary feature displayed in Fig. D.1, the upper part of the shell is expanding toward us while the lower part in latitude is decelerated and fragmented by the stratified distribution of the ISM close to the Galactic plane.
The shell has a dominant main feature. Other structures, offset in latitude, are less intense and may represent secondary shocks. Bykov & Toptygin (1987) developed a model for the interstellar turbulence where shocks, produced by supernovae, are reflected by interstellar clouds. Associated structures in the magneto-ionic medium are expected (Fletcher & Shukurov 2007). Kornreich & Scalo (2000) argue that Galactic shocks propagating through interstellar density fluctuations may act as “shock pumps”, providing a mechanism for a turbulent cascade mechanism and explaining the fractal-like structure of the cool ISM.
Our data support these proposals, there are many filamentary features that may be interpreted as secondary shocks,
mostly parallel to the Galactic plane at different latitudes. We find indications for dynamic interactions between primary and secondary shock structures, including position-velocity structures that might be caused by curls in the turbulent flow, see Fig. D.3.
All Tables
All Figures
 |
Fig. 1 Comparison between average brightness temperature TB aver (red), anisotropy factor Qaver (blue) for 0.002 <k< 0.015 arcmin-1, and spectral index γ (green) for the Horologium field. The upper horizontal black dotted line indicates the Kolmogorov spectral index of γ = −8 / 3, the lower dash-dotted line Qaver = 0. |
| In the text | |
 |
Fig. 2 Average position angles Φaver calculated for 0.002 < k < 0.015 arcmin-1 and associated one σ rms scatter for the Horologium field. The position angle Φ = −58.5°, perpendicular to the position angle of the radio-polarimetric depolarization canals that are aligned parallel to the Galactic plane, is indicated with a horizontal line. |
| In the text | |
 |
Fig. 3 Average power spectrum observed for vLSR = 2.7 km s-1 (black dots) and fit power law with γ = −3.25 ± 0.03 for k< 0.07 arcmin-1 (vertical line). In addition the power spectrum for 118° < Φ < 133° (red) and 28° < Φ < 43° (green) is given. The average anisotropy factor for 0.002 <k< 0.015 arcmin-1 is Qaver = 7.7. |
| In the text | |
 |
Fig. 4 Anisotropies Q(k) for the channels at vLSR = 2.7 km s-1 (red) and vLSR = 1.4 km s-1 (blue). |
| In the text | |
 |
Fig. 5 Polarized intensity map of Horologium in equatorial coordinates (B1950.0), observed at 349 MHz with the WSRT. The filamentary features from an H i USM map at vLSR = 2.7 km s-1 are overlaid with contours of 0.1, 1, 2.5 and 5 K. The dashed lines are parallel to the Galactic plane, in steps of Δb = 1°. |
| In the text | |
 |
Fig. 6 Average power spectrum observed for vLSR = −16.6 km s-1 (black dots) and fit power law with γ = −2.87 ± 0.02 arcmin-1 for k< 0.07 (vertical line). In addition the power spectrum for 108° < Φ < 123° (red) and 18° < Φ < 33° (green) is given. The average anisotropy factor for 0.002 <k< 0.015 arcmin-1 is Qaver = 5.1. |
| In the text | |
 |
Fig. 7 Polarized intensity map of Horologium in equatorial coordinates (B1950.0), observed at 349 MHz with the WSRT. The filamentary features from an H i USM map at vLSR = −16.6 km s-1 are overlaid with contours of 0.1, 1, 2.5 and 5 K. The dashed lines are parallel to the Galactic plane, in steps of Δb = 1°. |
| In the text | |
 |
Fig. 8 Comparison between the average apodized brightness temperature profile TB aver (red) for the Auriga field, derived average anisotropy factor Qaver for 0.007 <k< 0.07 arcmin-1 (blue), and spectral index γ (green). The upper horizontal black dotted line indicates the Kolmogorov spectral index of γ = −8 / 3, the lower dash-dotted line Qaver = 0. |
| In the text | |
 |
Fig. 9 Average position angles Φaver calculated for 0.007 <k< 0.07 arcmin-1 and associated one σ rms scatter for the Auriga field. The blue asterisks denote peak anisotropies of the three CNM filamentary structures that we study in detail. |
| In the text | |
 |
Fig. 10 Average power spectrum observed for vLSR = −2.5 km s-1 (black dots) and fit power law with γ = −2.97 ± 0.03 for k< 0.07 arcmin-1 (vertical line). In addition the power spectrum for 148° < Φ < 163° (red) and 58° < Φ < 73° (green) is given. The average anisotropy factor for 0.007 <k< 0.07 arcmin-1 is Qaver = 6. |
| In the text | |
 |
Fig. 11 Anisotropies Q(k) for the channels at vLSR = −2.5 km s-1 (red) and vLSR = −3.76 km s-1 (blue). |
| In the text | |
 |
Fig. 12 Polarized intensity map of Auriga in equatorial coordinates (B1950.0), observed at 349 MHz with the WSRT. The filamentary features from an H i USM map at vLSR = −2.5 km s-1 are overlaid with contours of 0.1, 1, 2.5 and 5 K. The dashed lines are parallel to the Galactic plane, in steps of Δb = 1°. |
| In the text | |
 |
Fig. 13 Average power spectrum observed for vLSR = −19.2 km s-1 (black dots) and fit power law with γ = −2.63 ± 0.03 for k< 0.07 arcmin-1 (vertical line). In addition the power spectrum for 18° < Φ < 33° (red) and 108° < Φ < 123° (green) is given. The average anisotropy factor for 0.007 <k< 0.07 arcmin-1 is Qaver = 2.3. |
| In the text | |
 |
Fig. 14 Anisotropies Q(k) for the channel at vLSR = −19.2 km s-1 (red) and at vLSR = −17.9 km s-1 (blue). |
| In the text | |
 |
Fig. 15 Polarized intensity map of Auriga in equatorial coordinates (B1950.0), observed at 349 MHz with the WSRT. The filamentary features from an H i USM map at vLSR = −19.2 km s-1 are overlaid with contours of 0.1, 1, 2.5 and 5 K. The dashed lines are parallel to the Galactic plane, in steps of Δb = 1°. |
| In the text | |
 |
Fig. 16 Average power spectrum observed for vLSR = −30.8 km s-1 (black dots) and fit power law with γ = −2.72 ± 0.03 for k< 0.07 arcmin-1 (vertical line). In addition the power spectrum for 133° < Φ < 148° (red) and 43° < Φ < 58° (green) is given. The average anisotropy factor for 0.007 <k< 0.07 arcmin-1 is Qaver = 10.6. |
| In the text | |
 |
Fig. 17 Anisotropies Q(k) for the channel at vLSR = −30.8 km s-1 (red) and vLSR = −29.5 km s-1 (blue). |
| In the text | |
 |
Fig. 18 Polarized intensity map of Auriga in equatorial coordinates (B1950.0), observed at 349 MHz with the WSRT. The filamentary features from an H i USM map at vLSR = −30.8 km s-1 are overlaid with contours of 0.1, 1, 2.5 and 5 K. |
| In the text | |
 |
Fig. 19 Comparison between the geometric mean Doppler temperature TD (black) and the spectral index γ (green dashed) for Horologium (bottom) and Auriga (top). The horizontal lines indicate the velocity ranges used for the determination of the spectral steepening discussed in Sect. 6. |
| In the text | |
 |
Fig. 20 Bottom: Horologium, top: Auriga. Spectral index γ(vLSR) (green) compared with the WNM fraction TWNM(vLSR) /TWNM + CNM(vLSR) derived from LAB (pink) and EBHIS Gaussians (red). An upper limit for the Doppler temperature of the CNM of TD< 1100 K, corresponding to a turbulent CNM Mach number of MT = 3.7 was applied. For comparison we display the WNM fraction TWNM(vLSR) /TWNM + CNM(vLSR) for a Doppler temperature of TD< 3900 K, corresponding to a turbulent CNM Mach number of MT = 7.7 (blue). |
| In the text | |
 |
Fig. 21 Anisotropies Q(k) for the velocity centroid (red) and average emission (blue), both calculated for the velocity range −23.1 <vLSR< 5.25 km s-1. |
| In the text | |
 |
Fig. 22 Power spectrum (black dots) calculated for the velocity centroid (top) and the thick slice emission (bottom) over the velocity range −23.1 <vLSR< 5.2 km s-1. An average power law γ = −3.35 ± 0.05 for the centroid and respectively γ = −3.41 ± 0.05 for the thick velocity slice was fit for k< 0.07 arcmin-1 (vertical line). The power law fits for the restricted ranges 0.001 <k< 0.01 arcmin-1 in spatial frequency are indicated with blue dotted lines. In case of the centroid (top) γ = −4.5 ± 0.1 and γ = −4.9 ± 0.1 for the average emission respectively. In addition the power spectra for 118° < Φ < 133° (red) and 28° < Φ < 43° (green) are given. The average anisotropy factor for 0.007 <k< 0.07 arcmin-1 is Qaver = 2.1 for the centroid and Qaver = 4.1 for the average emission. |
| In the text | |
 |
Fig. 23 Power spectrum (black dots) calculated for the velocity centroid (top) and the thick slice emission (bottom) over the velocity range −10.2 < vLSR < 11.7 km s-1. For the velocity centroid a power law with γ = −2.78 ± 0.03 was fit and respectively γ = −3.28 ± 0.04 for the average emission (black lines), in both cases for k< 0.07 arcmin-1 (vertical line). In addition the power spectra for 148° < Φ < 163° (red) and 58° < Φ < 73° (green) are plotted. The average anisotropy factor for 0.007 < k < 0.07 arcmin-1 is Qaver = 3.2 for the centroid and Qaver = 2.6 for the average emission. |
| In the text | |
 |
Fig. 24 Power spectrum (black dots) calculated for the average emission over the velocity range −3.8 <vLSR< 10.4 km s-1. In addition the power spectra for 118° < Φ < 133° (red) and 28° < Φ < 43° (green) are given. An average power law γ = −3.39 ± 0.05 was fit for k< 0.07 arcmin-1 (vertical line). For reference the power law fit for −10.2 <vLSR< 11.7 km s-1 at a restricted range 0.001 <k< 0.01 arcmin-1 in spatial frequency from Fig. 22 (bottom) is reproduced with the blue dotted line. |
| In the text | |
 |
Fig. 25 Changes in the spectral power distribution, most probably associated with phase transitions. Data points are derived according to Eq. (4), the solid black line indicates the change δ of the fit spectral indices. The blue dashed line represents a local fit for 0.002 <k< 0.015 arcmin-1. |
| In the text | |
 |
Fig. 26 Changes in the spectral power distribution, most probably associated with phase transitions. Data points are derived according Eq. (4), the solid line indicates the change δ of the fit spectral indices. |
| In the text | |
 |
Fig. 27 Changes in the spectral power distribution in direction to 3C 196, most probably associated with phase transitions. Data points are derived according to Eq. (4), the solid line indicates the change δ of the fit spectral indices. The blue dashed line represents a local fit for 0.003 <k< 0.02 arcmin-1. |
| In the text | |
 |
Fig. A.1 Average brightness temperature TB aver (red), anisotropy factor Qaver (blue) for 0.007 <k< 0.06 arcmin-1, and spectral index γ (green) for the MBM 16 field as derived from EBHIS observations. The upper horizontal black dotted line indicates the Kolmogorov spectral index of γ = −8 / 3, the lower dash-dotted line Qaver = 0. |
| In the text | |
 |
Fig. A.2 Average position angles Φaver calculated for 0.007 < k < 0.06 arcmin-1 and associated one σ rms scatter for the MBM 16 field. |
| In the text | |
 |
Fig. A.3 Comparison of results according to the method proposed in Paper I (using apodization, beam correction, and noise subtraction) obtained from fits with different upper limits 0.01 <km < 0.06 arcmin-1 in spatial frequency. Error bars are given in two cases to provide an impression of formal uncertainties of the least square fits. The horizontal black dotted line indicates the Kolmogorov spectral index γ = −8 / 3, the solid vertical lines bracket the velocity range with average brightness temperatures TB aver > 0.5 K. |
| In the text | |
 |
Fig. A.4 The thick red line represents results obtained after apodization, beam correction, and noise subtraction. The other graphs show results obtained without apodization by fitting the median power distribution. km is in each case the upper limit for the spatial frequencies used for the fit. Error bars are given in three cases to provide an impression of formal uncertainties of the least square fits. The horizontal black dotted line represents the expected Kolmogorov index γ = −8 / 3. The vertical solid black lines bracket the velocity range analyzed by Pingel et al. (2013), the horizontal solid black line gives the weighted average slope γ = −3.58 ± 0.09 obtained by them for this velocity range. |
| In the text | |
 |
Fig. A.5 Unnormalized thick velocity slice power spectra for MBM 16, integrating over −1.1 <vLSR< 15.6 km s-1 and spectral indices from least squares fits. High spatial frequency limits km< 0.06 arcmin-1, corresponding to a linear size of 0.39 pc were applied and are indicated by the vertical black line. Black dots represent data derived after apodization, beam correction, and noise subtraction. In this case we fit γ = −3.63 ± 0.04. The red triangles show results obtained without apodization and beam correction by fitting the median power distribution. Here we fit γ = −3.88 ± 0.04. |
| In the text | |
 |
Fig. A.6 Spectral index changes with velocity slice thickness for the MBM 16 H i gas centered at vLSR = 9.1 km s-1. A high spatial frequency limit km = 0.06 arcmin-1, corresponding to a linear size of 0.39 pc, was applied when fitting the spectral index. The bars indicate uncertainties of the power law indices. |
| In the text | |
 |
Fig. A.7 Comparison between the geometric mean Doppler temperature TD (black) and the spectral index γ (green dashed) for MBM 16. |
| In the text | |
 |
Fig. A.8 Spectral index γ(vLSR) (green) compared with the WNM fraction TWNM(vLSR) /TWNM + CNM(vLSR) derived from LAB (pink) and EBHIS Gaussians (red) for the MBM 16 field. An upper limit for the Doppler temperature of the CNM of TD< 1100 K, corresponding to a turbulent CNM Mach number of MT = 3.7 was applied. We display also with a blue dotted line the WNM fraction TWNM(vLSR) /TWNM + CNM(vLSR) derived from EBHIS, using TD< 1100 K, for a central position l = 171°,b = −37° within a radius of 1.̊5. This corresponds to the region with CO emission observed by LaRosa et al. (1999, Fig. 1). |
| In the text | |
 |
Fig. A.9 Thick velocity slice power distributions for MBM 16, integrating over −1.1 <vLSR< 15.6 km s-1. Left: apodized distribution, corrected for the beam function. Right: the same data without apodization and beam correction. The scales are logarithmic in dB. The circle indicates the 3σ spatial frequency limit km = 0.06 arcmin-1, corresponding to a linear size of 0.39 pc. Data for higher spatial frequencies are dominated by the instrumental noise. |
| In the text | |
 |
Fig. B.1 Anisotropies Q(k) in the Perseus arm at velocities vLSR = −50.1 km s-1 (green), vLSR = −54.0 km s-1 (blue), and vLSR = −57.9 km s-1 (red). |
| In the text | |
 |
Fig. B.2 Anisotropies Q(k) in the outer arm at velocities vLSR = −77.2 km s-1 (green), vLSR = −75.9 km s-1 (blue), and vLSR = −74.6 km s-1 (red). The blue line reproduces a fit to 20 data points at vLSR = −75.9 km s-1, tentatively indicating the decay of the strong local anisotropy with Q = 209. |
| In the text | |
 |
Fig. D.1 Top: color coded brightness temperature distribution for the filamentary structure in the Horologium field at vLSR = −16.6 km s-1. The white isophotes display the USM temperatures at the same velocity. Bottom: the brightness temperature distribution at vLSR = −11.5 km s-1 is shown in color, the white isophotes are USM temperatures at the same velocity while black isophotes are at vLSR = −16.6 km s-1 for comparison with the top panel. Isophote levels are 1, 2.5, and 5 K Galactic coordinates are used, the black lines indicate longitudes of the velocity-position plots in Fig. D.2. |
| In the text | |
 |
Fig. D.2 Velocity-position diagrams, brightness temperatures (color coded) for cuts at constant longitudes l = 136.̊534, 135.̊277, 134.̊397, and 131.̊403 (top left to bottom right), indicated in Fig. D.1 by black lines. Radial velocities are in m s-1, isophotes are USM temperatures of 1, 2.5, and 5 K. |
| In the text | |
 |
Fig. D.3 Position-velocity diagrams, color coded brightness temperatures for cuts at constant latitudes b = 8.̊0 to 4.̊5 in steps of −0.̊5 (top left to bottom right), overlaid with isophotes displaying USM temperatures of 1, 2.5, and 5 K. Radial velocities are in m s-1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


