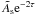| Issue |
A&A
Volume 607, November 2017
|
|
|---|---|---|
| Article Number | A95 | |
| Number of page(s) | 27 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201629504 | |
| Published online | 20 November 2017 | |
Planck intermediate results
LI. Features in the cosmic microwave background temperature power spectrum and shifts in cosmological parameters
1 APC, AstroParticule et Cosmologie, Université Paris Diderot, CNRS/IN2P3, CEA/lrfu, Observatoire de Paris, Sorbonne Paris Cité, 10 rue Alice Domon et Léonie Duquet, 75205 Paris Cedex 13, France
2 African Institute for Mathematical Sciences, 6-8 Melrose Road, Muizenberg, 7945 Cape Town, South Africa
3 Agenzia Spaziale Italiana Science Data Center, via del Politecnico snc, 00133 Roma, Italy
4 Agenzia Spaziale Italiana, via del Politecnico snc, 00133 Roma, Italy
5 Aix Marseille Univ., CNRS, LAM, Laboratoire d’Astrophysique de Marseille, 13013 Marseille, France
6 Astrophysics Group, Cavendish Laboratory, University of Cambridge, J J Thomson Avenue, Cambridge CB3 0HE, UK
7 Astrophysics & Cosmology Research Unit, School of Mathematics, Statistics & Computer Science, University of KwaZulu-Natal, Westville Campus, Private Bag X54001, Durban 4000, South Africa
8 CITA, University of Toronto, 60 St. George St., Toronto, ON M5S 3H8, Canada
9 CNRS, IRAP, 9 Av. colonel Roche, BP 44346, 31028 Toulouse Cedex 4, France
10 California Institute of Technology, Pasadena, California, CA 91125, USA
11 Centre for Theoretical Cosmology, DAMTP, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
12 Computational Cosmology Center, Lawrence Berkeley National Laboratory, Berkeley, California, CA 94720, USA
13 DTU Space, National Space Institute, Technical University of Denmark, Elektrovej 327, 2800 Kgs. Lyngby, Denmark
14 Département de Physique Théorique, Université de Genève, 24 Quai E. Ansermet, 1211 Genève 4, Switzerland
15 Departamento de Astrofísica, Universidad de La Laguna (ULL), 38206 La Laguna, Tenerife, Spain
16 Departamento de Física, Universidad de Oviedo, Avda. Calvo Sotelo s/n, 33007 Oviedo, Spain
17 Department of Astrophysics/IMAPP, Radboud University, PO Box 9010, 6500 GL Nijmegen, The Netherlands
18 Department of Mathematics, University of Stellenbosch, Stellenbosch 7602, South Africa
19 Department of Physics & Astronomy, University of British Columbia, 6224 Agricultural Road, Vancouver, British Columbia, Canada
20 Department of Physics and Astronomy, Dana and David Dornsife College of Letter, Arts and Sciences, University of Southern California, Los Angeles, CA 90089, USA
21 Department of Physics and Astronomy, University of Sussex, Brighton BN1 9QH, UK
22 Department of Physics, Gustaf Hällströmin katu 2a, University of Helsinki, 00014 Helsinki, Finland
23 Department of Physics, Princeton University, Princeton, New Jersey, NJ 08544, USA
24 Department of Physics, University of California, Berkeley, California, CA 94607, USA
25 Department of Physics, University of California, One Shields Avenue, Davis, California, CA 95616, USA
26 Department of Physics, University of California, Santa Barbara, California, CA 93106, USA
27 Department of Physics, University of Illinois at Urbana-Champaign, 1110 West Green Street, Urbana, Illinois, IL 61820, USA
28 Dipartimento di Fisica e Astronomia G. Galilei, Università degli Studi di Padova, via Marzolo 8, 35131 Padova, Italy
29 Dipartimento di Fisica e Astronomia, Alma Mater Studiorum, Università degli Studi di Bologna, Viale Berti Pichat 6/2, 40127 Bologna, Italy
30 Dipartimento di Fisica e Scienze della Terra, Università di Ferrara, via Saragat 1, 44122 Ferrara, Italy
31 Dipartimento di Fisica, Università La Sapienza, P.le A. Moro 2, 00185 Roma, Italy
32 Dipartimento di Fisica, Università degli Studi di Milano, via Celoria, 16, 20133 Milano, Italy
33 Dipartimento di Fisica, Università degli Studi di Trieste, via A. Valerio 2, 34127 Trieste, Italy
34 Dipartimento di Fisica, Università di Roma Tor Vergata, via della Ricerca Scientifica, 1, 00133 Roma, Italy
35 European Space Agency, ESAC, Planck Science Office, Camino bajo del Castillo, s/n, UrbanizaciónVillafranca del Castillo, 28692 Villanueva de la Cañada, Madrid, Spain
36 European Space Agency, ESTEC, Keplerlaan 1, 2201 AZ Noordwijk, The Netherlands
37 Gran Sasso Science Institute, INFN, viale F. Crispi 7, 67100 L’ Aquila, Italy
38 HGSFP and University of Heidelberg, Theoretical Physics Department, Philosophenweg 16, 69120 Heidelberg, Germany
39 Haverford College Astronomy Department, 370 Lancaster Avenue, Haverford, Pennsylvania, PA 19041, USA
40 Helsinki Institute of Physics, Gustaf Hällströmin katu 2, University of Helsinki, 00014 Helsinki, Finland
41 INAF–Osservatorio Astronomico di Padova, Vicolo dell’Osservatorio 5, 35122 Padova, Italy
42 INAF–Osservatorio Astronomico di Trieste, via G.B. Tiepolo 11, 40127 Trieste, Italy
43 INAF/IASF Bologna, via Gobetti 101, 40129 Bologna, Italy
44 INAF/IASF Milano, via E. Bassini 15, 20133 Milano, Italy
45 INFN – CNAF, viale Berti Pichat 6/2, 40127 Bologna, Italy
46 INFN, Sezione di Bologna, viale Berti Pichat 6/2, 40127 Bologna, Italy
47 INFN, Sezione di Ferrara, via Saragat 1, 44122 Ferrara, Italy
48 INFN, Sezione di Roma 2, Università di Roma Tor Vergata, via della Ricerca Scientifica, 1, 00185 Roma, Italy
49 INFN/National Institute for Nuclear Physics, via Valerio 2, 34127 Trieste, Italy
50 Imperial College London, Astrophysics group, Blackett Laboratory, Prince Consort Road, London, SW7 2AZ, UK
51 Institut d’Astrophysique Spatiale, CNRS, Univ. Paris-Sud, Université Paris-Saclay, Bât. 121, 91405 Orsay Cedex, France
52 Institut d’Astrophysique de Paris, CNRS (UMR 7095), 98bis Boulevard Arago, 75014 Paris, France
53 Institute Lorentz, Leiden University, PO Box 9506, Leiden 2300 RA, The Netherlands
54 Institute of Astronomy, University of Cambridge, Madingley Road, Cambridge CB3 0HA, UK
55 Institute of Theoretical Astrophysics, University of Oslo, Blindern, 0371 Oslo, Norway
56 Instituto de Astrofísica de Canarias, C/Vía Láctea s/n, La Laguna, 38205 Tenerife, Spain
57 Instituto de Física de Cantabria (CSIC-Universidad de Cantabria), Avda. de los Castros s/n, 39005 Santander, Spain
58 Istituto Nazionale di Fisica Nucleare, Sezione di Padova, via Marzolo 8, 35131 Padova, Italy
59 Jet Propulsion Laboratory, California Institute of Technology, 4800 Oak Grove Drive, Pasadena, California, CA 91125, USA
60 Jodrell Bank Centre for Astrophysics, Alan Turing Building, School of Physics and Astronomy, The University of Manchester, Oxford Road, Manchester, M13 9PL, UK
61 Kavli Institute for Cosmological Physics, University of Chicago, Chicago, IL 60637, USA
62 Kavli Institute for Cosmology Cambridge, Madingley Road, Cambridge, CB3 0HA, UK
63 LAL, Université Paris-Sud, CNRS/IN2P3, 91898 Orsay, France
64 LERMA, CNRS, Observatoire de Paris, 61 Avenue de l’Observatoire, 75014 Paris, France
65 Laboratoire Traitement et Communication de l’Information, CNRS (UMR 5141) and Télécom ParisTech, 46 rue Barrault, 75634 Paris Cedex 13, France
66 Laboratoire de Physique Subatomique et Cosmologie, Université Grenoble-Alpes, CNRS/IN2P3, 53, rue des Martyrs, 38026 Grenoble Cedex, France
67 Laboratoire de Physique Théorique, Université Paris-Sud 11 & CNRS, Bâtiment 210, 91405 Orsay, France
68 Lawrence Berkeley National Laboratory, Berkeley, California, USA
69 Low Temperature Laboratory, Department of Applied Physics, Aalto University, Espoo, 00076 Aalto, Finland
70 Max-Planck-Institut für Astrophysik, Karl-Schwarzschild-Str. 1, 85741 Garching, Germany
71 Mullard Space Science Laboratory, University College London, Surrey RH5 6NT, UK
72 Nicolaus Copernicus Astronomical Center, Polish Academy of Sciences, Bartycka 18, 00-716 Warsaw, Poland
73 Nordita (Nordic Institute for Theoretical Physics), Roslagstullsbacken 23, 106 91 Stockholm, Sweden
74 Purple Mountain Observatory, Chinese Academy of Sciences, Nanjing 210008, PR China
75 SISSA, Astrophysics Sector, via Bonomea 265, 34136 Trieste, Italy
76 San Diego Supercomputer Center, University of California, San Diego, 9500 Gilman Drive, La Jolla, CA 92093, USA
77 School of Chemistry and Physics, University of KwaZulu-Natal, Westville Campus, Private Bag X54001, Durban, 4000, South Africa
78 School of Physics and Astronomy, Cardiff University, Queens Buildings, The Parade, Cardiff, CF24 3AA, UK
79 School of Physics and Astronomy, Sun Yat-Sen University, 135 Xingang Xi Road, Guangzhou, 510006, PR China
80 School of Physics and Astronomy, University of Nottingham, Nottingham NG7 2RD, UK
81 School of Physics, Indian Institute of Science Educationand Research Thiruvananthapuram (IISER-TVM), Trivandrum 695016, Kerala, India
82 Simon Fraser University, Department of Physics, 8888 University Drive, Burnaby BC, Canada
83 Sorbonne Université-UPMC, UMR 7095, Institut d’Astrophysique de Paris, 98bis Boulevard Arago, 75014 Paris, France
84 Sorbonne Universités, Institut Lagrange de Paris (ILP), 98bis Boulevard Arago, 75014 Paris, France
85 Space Sciences Laboratory, University of California, Berkeley, California, CA 94720, USA
86 The Oskar Klein Centre for Cosmoparticle Physics, Department of Physics, Stockholm University, AlbaNova, 106 91 Stockholm, Sweden
87 UPMC Univ. Paris 06, UMR 7095, 98bis Boulevard Arago, 75014 Paris, France
88 Université de Toulouse, UPS-OMP, IRAP, 31028 Toulouse Cedex 4, France
89 University of Granada, Departamento de Física Teórica y del Cosmos, Facultad de Ciencias, 18071 Granada, Spain
90 Warsaw University Observatory, Aleje Ujazdowskie 4, 00-478 Warszawa, Poland
⋆
Corresponding authors: Silvia Galli, e-mail: gallis@iap.fr; Marius Millea, e-mail: millea@iap.fr
Received: 8 August 2016
Accepted: 10 September 2017
The six parameters of the standard ΛCDM model have best-fit values derived from the Planck temperature power spectrum that are shifted somewhat from the best-fit values derived from WMAP data. These shifts are driven by features in the Planck temperature power spectrum at angular scales that had never before been measured to cosmic-variance level precision. We have investigated these shifts to determine whether they are within the range of expectation and to understand their origin in the data. Taking our parameter set to be the optical depth of the reionized intergalactic medium τ, the baryon density ωb, the matter density ωm, the angular size of the sound horizon θ∗, the spectral index of the primordial power spectrum, ns, and Ase− 2τ (where As is the amplitude of the primordial power spectrum), we have examined the change in best-fit values between a WMAP-like large angular-scale data set (with multipole moment ℓ < 800 in the Planck temperature power spectrum) and an all angular-scale data set (ℓ < 2500Planck temperature power spectrum), each with a prior on τ of 0.07 ± 0.02. We find that the shifts, in units of the 1σ expected dispersion for each parameter, are { Δτ,ΔAse− 2τ,Δns,Δωm,Δωb,Δθ∗ } = { −1.7,−2.2,1.2,−2.0,1.1,0.9 }, with a χ2 value of 8.0. We find that this χ2 value is exceeded in 15% of our simulated data sets, and that a parameter deviates by more than 2.2σ in 9% of simulated data sets, meaning that the shifts are not unusually large. Comparing ℓ < 800 instead to ℓ> 800, or splitting at a different multipole, yields similar results. We examined the ℓ < 800 model residuals in the ℓ> 800 power spectrum data and find that the features there that drive these shifts are a set of oscillations across a broad range of angular scales. Although they partly appear similar to the effects of enhanced gravitational lensing, the shifts in ΛCDM parameters that arise in response to these features correspond to model spectrum changes that are predominantly due to non-lensing effects; the only exception is τ, which, at fixed Ase− 2τ, affects the ℓ> 800 temperature power spectrum solely through the associated change in As and the impact of that on the lensing potential power spectrum. We also ask, “what is it about the power spectrum at ℓ < 800 that leads to somewhat different best-fit parameters than come from the full ℓ range?” We find that if we discard the data at ℓ < 30, where there is a roughly 2σ downward fluctuation in power relative to the model that best fits the full ℓ range, the ℓ < 800 best-fit parameters shift significantly towards the ℓ < 2500 best-fit parameters. In contrast, including ℓ < 30, this previously noted “low-ℓ deficit” drives ns up and impacts parameters correlated with ns, such as ωm and H0. As expected, the ℓ < 30 data have a much greater impact on the ℓ < 800 best fit than on the ℓ < 2500 best fit. So although the shifts are not very significant, we find that they can be understood through the combined effects of an oscillatory-like set of high-ℓ residuals and the deficit in low-ℓ power, excursions consistent with sample variance that happen to map onto changes in cosmological parameters. Finally, we examine agreement between PlanckTT data and two other CMB data sets, namely the Planck lensing reconstruction and the TT power spectrum measured by the South Pole Telescope, again finding a lack of convincing evidence of any significant deviations in parameters, suggesting that current CMB data sets give an internally consistent picture of the ΛCDM model.
Key words: cosmology: observations / cosmic background radiation / cosmological parameters / cosmology: theory
© ESO, 2017
1. Introduction
Probably the most important high-level result from the Planck satellite1 (Planck Collaboration I 2016) is the good agreement of the statistical properties of the cosmic microwave background anisotropies (CMB) with the predictions of the six-parameter standard ΛCDM cosmological model (Planck Collaboration XV 2014; Planck Collaboration XVI 2014; Planck Collaboration XI 2016; Planck Collaboration XIII 2016). This agreement is quite remarkable, given the very significant increase in precision of the Planck measurements over those of prior experiments. The continuing success of the ΛCDM model has deepened the motivation for attempts to understand why the Universe is so well-described as having emerged from Gaussian adiabatic initial conditions with a particular mix of baryons, cold dark matter (CDM), and a cosmological constant (Λ).
Since the main message from Planck, and indeed from the Wilkinson Microwave Anisotropy Probe (WMAP; Bennett et al. 2013) before it, has been the continued success of the six-parameter ΛCDM model, attention naturally turns to precise details of the values of the best-fit parameters of the model. Many cosmologists have focused on the parameter shifts with respect to the best-fit values preferred by pre-Planck data. Compared to the WMAP data, for example, Planck data prefer a somewhat slower expansion rate, higher dark matter density, and higher matter power spectrum amplitude, as discussed in several Planck Collaboration papers (Planck Collaboration XV 2014; Planck Collaboration XVI 2014; Planck Collaboration XI 2016; Planck Collaboration XIII 2016), as well as in Addison et al. (2016). These shifts in parameters have increased the degree of tension between CMB-derived values and those determined from some other astrophysical data sets, and have thereby motivated discussion of extensions to the standard cosmological model (e.g. Verde et al. 2013; Marra et al. 2013; Efstathiou 2014; Wyman et al. 2014; Beutler et al. 2014; MacCrann et al. 2015; Seehars et al. 2016; Hildebrandt et al. 2016). However, none of these extensions are strongly supported by the Planck data themselves (e.g. see discussion in Planck Collaboration XIII 2016).
Despite the interest that the shifts in best-fit parameters has generated, there has not yet been an identification of the particular aspects of the Planck data, and their differences from WMAP data, that give rise to the shifts. The main goal of this paper is to identify the aspects of the data that lead to the shifts, and to understand the physics that drives ΛCDM parameters to respond to these differences in the way they do. We chose to pursue this goal with analysis that is entirely internal to the Planck data. In carrying out this Planck-based analysis, we still shed light on the WMAP-to-Planck parameter shifts, because when we restrict ourselves to modes that WMAP measures at high signal-to-noise ratio, the WMAP and Planck temperature maps agree well (e.g. Kovács et al. 2013; Planck Collaboration XXXI 2014). The qualitatively new attribute of the Planck data that leads to the parameter shifts is the high-precision measurement of the temperature power spectrum in the 600 ≲ ℓ ≲ 2000 range2. Restricting our analysis to be internal to Planck has the advantage of simplicity, without altering the main conclusions.
We also investigated the consistency of the differences in parameters inferred from different multipole ranges with expectations, given the ΛCDM model and our understanding of the sources of error. The consistency of such parameter shifts has been previously studied in Planck Collaboration XI (2016), Couchot et al. (2015), and Addison et al. (2016). In studying the consistency of parameters inferred from ℓ < 1000 with those inferred from ℓ> 1000Addison et al. (2016) claim to find significant evidence for internal inconsistencies in the Planck data. Our analysis improves upon theirs in several ways, mainly through our use of simulations to account for covariances between the pair of data sets being compared, as well as the “look elsewhere effect”, and the departure of the true distribution of the shift statistics away from a χ2 distribution.
Much has already been demonstrated about the robustness of the Planck parameter results to data processing, data selection, foreground removal, and instrument modelling choices Planck Collaboration XI (2016). We will not revisit all of that here. However, having identified the power spectrum features that are causing the shifts in cosmological parameters, we show that these features are all present in multiple individual frequency channels, as one would expect from the previous studies. The features in the data therefore appear to be cosmological in origin.
The Planck polarization maps, and the TE and EE polarization power spectra determinations they enable, are also new aspects of the Planck data. These new data are in agreement with the TT results and point to similar shifts away from the WMAP parameters (Planck Collaboration XIII 2016), although with less statistical weight. In order to focus on the primary driver of the parameter shifts, namely the temperature power spectrum, we have ignored polarization data except for the constraint on the value of the optical depth τ coming from polarization at the largest angular scales, which in practice we folded in with a prior on τ.
Our primary analysis is of the shift in best-fit cosmological parameters as determined from: (1) a prior on the value of τ (as a proxy for low-ℓ polarization data) and PlanckTT3 data restricted to ℓ < 8004; and (2) the same τ prior and the full ℓ-range (ℓ < 2500) of PlanckTT data. Taking the former data set as a proxy for WMAP, these are the parameter shifts that have been of great interest to the community. There is of course a degree of arbitrariness in the particular choice of ℓ = 800 for defining the low-ℓ data set. One might argue for a lower ℓ, based on the fact that the WMAP temperature maps reach a signal-to-noise ratio of unity by ℓ ≃ 600, and thus above 600 the power spectrum error bars are at least twice as large as the Planck ones. However, we explicitly selected ℓ = 800 for our primary analysis because it splits the weight on ΛCDM parameters coming from Planck so that half is from ℓ < 800 and half is from ℓ> 8005. Addressing the parameter shifts from ℓ < 800 versus ℓ> 800 is a related and interesting issue, and while our main focus is on the comparison of the full-ℓ results to those from ℓ < 800, we computed and showed the low-ℓ versus high-ℓ results as well. Additionally, as described in Appendix A, we performed an exhaustive search over many different choices for the multipole at which to split the data.
In addition to the high-ℓPlanck temperature data, inferences of the reionization optical depth obtained from the low-ℓPlanck polarization data also have an important impact on the determination of the other cosmological parameters. The parameter shifts that have been discussed in the literature to date have generally assumed a constraint on τ coming from Planck LFI polarization data (Planck Collaboration XI 2016; Planck Collaboration XIII 2016). During the writing of this paper, new and tighter constraints on τ were released using improved Planck HFI polarization data (Planck Collaboration Int. XLVI 2016; Planck Collaboration Int. XLVII 2016). These are consistent with the previous ones, shrinking the error by approximately a factor of two and moving the best fit to slightly lower values of τ. To make our work more easily comparable to previous discussions, and because the impact of this updated constraint is not very large, we have chosen to write the main body of this paper assuming the old τ prior. This also allows us to more cleanly isolate and discuss separately the impact of the new prior, which we do in a later section of this paper.
Our focus here is on the results from Planck, and so an in-depth study comparing the Planck results with those from other cosmological data sets is beyond our scope. Nevertheless, there do exist claims of internal inconsistencies in CMB data (Addison et al. 2016; Riess et al. 2016), with the parameter shifts we discuss here playing an important role, since they serve to drive the PlanckTT best fits away from those of the two other CMB data sets, namely the Planck measurements of the φφ lensing potential power spectrum (Planck Collaboration XVII 2014; Planck Collaboration XV 2016) and the South Pole Telescope (SPT) measurement of the TT damping tail (Story et al. 2013). Thus, we also briefly examine whether there is any evidence of discrepancies that are not just internal to the PlanckTT data, but also when comparing with these other two probes.
The features we identify that are driving the changes in parameters are approximately oscillatory in nature, a part of them with a frequency and phasing such that they could be caused by a smoothing of the power spectrum, of the sort that is generated by gravitational lensing. We thus investigate the role of lensing in the parameter shifts. The impact of lensing in PlanckTT parameter estimates has previously been investigated via use of the parameter “AL” that artificially scales the lensing power spectrum (as discussed on p. 28 of Planck Collaboration XVI 2014; and p. 24 of Planck Collaboration XIII 2016). Here we introduce a new method that more directly elucidates the impact of lensing on cosmological parameter determination.
Given that we regard the ℓ < 2500Planck data as providing a better determination of the cosmological parameters than the ℓ < 800Planck data, it is natural to turn our primary question around and ask: what is it about the ℓ < 800 data that makes the inferred parameter values differ from the full ℓ-range parameters? Addressing this question, we find that the deficit in low-multipole power at ℓ ≲ 30, the “low-ℓ deficit”6, plays a significant role in driving the ℓ < 800 parameters away from the results coming from the full ℓ-range.
The paper is organized as follows. Section 2 introduces the shifts seen in parameters between using Planckℓ < 800 data and full-ℓ data. Section 3 describes the extent to which the observed shifts are consistent with expectations; we make some simplifying assumptions in our analysis and justify their use here. Section 4 represents a pedagogical summary of the physical effects underlying the various parameter shifts. We then turn to a more detailed characterization of the parameter shifts and their origin. The most elementary, unornamented description of the shifts is presented in Sect. 5.1, followed by a discussion of the effects of gravitational lensing in Sect. 5.2 and the role of the low-ℓ deficit in Sect. 5.3. In Sect. 5.4 we consider whether there might be systematic effects significantly impacting the parameter shifts and in Sect. 5.5 we add a discussion of the effect of changing the τ prior. Finally, we comment on some differences with respect to other CMB experiments in Sect. 6 and conclude in Sect. 7.
Throughout we work within the context of the six-parameter, vacuum-dominated, cold dark matter (ΛCDM) model. This model is based upon a spatially flat, expanding Universe whose dynamics are governed by general relativity and dominated by cold dark matter and a cosmological constant (Λ). We shall assume that the primordial fluctuations have Gaussian statistics, with a power-law power spectrum of adiabatic fluctuations. Within that framework the usual set of cosmological parameters used in CMB studies is: ωb ≡ Ωbh2, the physical baryon density; ωc ≡ Ωch2, the physical density of cold dark matter (or ωm for baryons plus cold dark matter plus neutrinos); θ∗, the ratio of sound horizon to angular diameter distance to the last-scattering surface; As, the amplitude of the (scalar) initial power spectrum; ns, the power-law slope of those initial perturbations; and τ, the optical depth to Thomson scattering through the reionized intergalactic medium. Here the Hubble constant is expressed as H0 = 100 h km s-1 Mpc-1. In more detail, we follow the precise definitions used in Planck Collaboration XVI (2014) and Planck Collaboration XIII (2016).
Parameter constraints for our simulations and comparison to data use the publicly available CosmoSlik package (Millea 2017), and the full simulation pipeline code will be released publicly pending acceptance of this work. Other parameter constraints are determined using the Markov chain Monte Carlo package cosmomc (Lewis & Bridle 2002), with a convergence diagnostic based on the Gelman and Rubin statistic performed on four chains. Theoretical power spectra are calculated with CAMB (Lewis et al. 2000).
 |
Fig. 1 Cosmological parameter constraints from PlanckTT+τprior for the full multipole range (orange) and for ℓ < 800 (blue) – see the text for the definitions of the parameters. We note that the constraints are generally in good agreement, with the full Planck data providing tighter limits on the parameters; however, the best-fit values certainly do shift. It is these shifts that we seek to explain in this paper. A prior τ = 0.07 ± 0.02 has been used here as a proxy for the effect of the low-ℓ polarization data (with the impact of a different prior discussed later). As a comparison, we also show results for WMAP TT data combined with the same prior on τ (grey). |
2. Parameters from low-ℓ versus full-ℓPlanck data
Figure 1 compares the constraints on six parameters of the base-ΛCDM model from the PlanckTT+τprior data for ℓ < 2500 with those using only the data at ℓ < 800. We have imposed a specific prior on the optical depth, τ = 0.07 ± 0.02, as a proxy for the Planck LFI low-ℓ polarization data, in order to make it easier to compare the constraints, and to restrict our investigation to the TT power spectrum only. As mentioned before, we will discuss the impact of the newer HFI polarization results in Sect. 5.5. The constraints shown are one-dimensional marginal posterior distributions of the cosmological parameters given the data, obtained using the cosmomc code (Lewis & Bridle 2002), as described in Sect. 1, and applying exactly the same priors and assumptions for the Planck likelihoods as detailed in Planck Collaboration XIII (2016).
We see that the constraints from the full data set are tighter than those from using only ℓ < 800, and that the peaks of the distributions7 are slightly shifted. It is these shifts that we seek to explain in the later sections. Figure 1 also shows constraints from the WMAP TT spectrum. As already mentioned, these constraints are qualitatively very similar to those from Planckℓ < 800, although not exactly the same, since WMAP reaches the cosmic variance limit closer to ℓ = 600. Nevertheless, as was already shown by Kovács et al. (2013), Larson et al. (2015), the CMB maps themselves agree very well, and thus the small differences in parameter inferences (the largest of which is a roughly 1σ difference in θ∗) are presumably due to small differences in sky coverage and WMAP instrumental noise. We see that the dominant source of parameter shifts between Planck and WMAP is the new information contained in the ℓ> 800 modes, and that by discussing parameter shifts internal to Planck we are also directly addressing the differences between WMAP and Planck.
Figure 1 shows the shifts for some additional derived parameters, as well as the basic six-parameter set. In particular, one can choose to use the conventional cosmological parameter H0, rather than the CMB parameter θ∗, as part of a six-parameter set. Of course neither choice is unique, and we could have also focused on other derived quantities in addition to six that span the space; for the amplitude, we have presented results for the usual choice As, but added panels for the alternative choices Ase− 2τ (which will be important later in this paper) and σ8 (the rms density variation in spheres of size 8 h-1 Mpc in linear theory at z = 0). The shifts shown in Fig. 1 are fairly representative of the sorts of shifts that have already been discussed in previous papers (e.g. Planck Collaboration XVI 2014; Planck Collaboration XI 2016; Addison et al. 2016), despite different choices of τ prior and ℓ ranges.
To simplify the analysis as much as possible, throughout most of this paper we will choose our parametrization of the six degrees of freedom in the ΛCDM model so that we reduce the correlations between parameters, and also so that our choice maps onto the physically meaningful effects that will be described in Sect. 4. While a choice of six parameters satisfying both criteria is not possible, we have settled on θ∗, ωm, ωb, ns, As e− 2τ, and τ. Most of these choices are standard, but two are not the same as those focused on in most CMB papers: we have chosen ωm instead of ωc, because the former governs the size of the horizon at the epoch of matter-radiation equality, which controls both the potential-envelope effect and the amplitude of gravitational lensing (see Sect. 4); and we have chosen to use As e− 2τ in place of As, because the former is much more precisely determined and much less correlated with τ. Physically, this arises because at angular scales smaller than those that subtend the horizon at the epoch of reionization (ℓ ≃ 10) the primary impact of τ is to suppress power by e− 2τ (again, see Sect. 4).
As a consequence of this last fact, the temperature power spectrum places a much tighter constraint on the combination As e− 2τ than it does on τ or As. Due to the strong correlation between these two parameters, any extra information on one will then also translate into a constraint on the other. For this reason, a change in the prior we use on τ will be mirrored by a change in As, given a fixed As e− 2τ combination. Conversely, the extra information one obtains on As from the smoothing of the small-scale power spectrum due to gravitational lensing will be mirrored by a change in the recovered value of τ (and this will be important, as we will show later). As a result, since we will mainly focus on the shifts of As e− 2τ and τ, we will often interpret changes in the value of τ as a proxy for changes in As (at fixed As e− 2τ), and thus for the level of lensing observed in the data (see Sect. 5.2).
3. Comparison of parameter shifts with expectations
In light of the shifts in parameters described in the previous section, we would of course like to know whether they are large enough to indicate a failure of the ΛCDM model or the presence of systematic errors in the data, or if they can be explained simply as an expected statistical fluctuation arising from instrumental noise and sample variance. The aim of this section is to give a precise determination based on simulations, in particular one that avoids several approximations used by previous analyses.
One of the first attempts to quantify the shifts was performed in Appendix A of Planck Collaboration XVI (2014), and was based on a set of Gaussian simulations. More recent studies using the Planck 2015 data have generally compared posteriors of disjoint sets of Planck multipole ranges (e.g. Planck Collaboration XI 2016; Addison et al. 2016). There, the posterior distribution of the parameters shifts given the data is 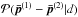 , with
, with 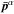 being the vector of parameter-marginalized means estimated from the multipole range α = 1,2. This posterior distribution is assumed to be a Gaussian with zero mean and covariance Σ = C(1) + C(2), where C(α) are the parameter posterior covariances of the two data sets and both
being the vector of parameter-marginalized means estimated from the multipole range α = 1,2. This posterior distribution is assumed to be a Gaussian with zero mean and covariance Σ = C(1) + C(2), where C(α) are the parameter posterior covariances of the two data sets and both 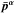 and C(α) are estimated from MCMC runs. Therefore, there it is assumed that, if one excludes from the parameter vector the optical depth τ for which prior information goes into both sets, the remaining five cosmological parameters are independent random variables. Additionally, to quantify the overall shift in parameters, a χ2 statistic is computed,
and C(α) are estimated from MCMC runs. Therefore, there it is assumed that, if one excludes from the parameter vector the optical depth τ for which prior information goes into both sets, the remaining five cosmological parameters are independent random variables. Additionally, to quantify the overall shift in parameters, a χ2 statistic is computed, 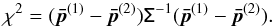 (1)The probability to exceed χ2 is then calculated assuming that it has a χ2 distribution with degrees of freedom equal to the number of parameters (usually five since τ is ignored).
(1)The probability to exceed χ2 is then calculated assuming that it has a χ2 distribution with degrees of freedom equal to the number of parameters (usually five since τ is ignored).
There are assumptions, both explicit and implicit, in previous analyses which we avoid with our procedure. We take into account the covariance in the parameter errors from one data set to the next, and do not assume that the parameter errors are normally distributed. Additionally our procedure allows us to include τ in the set of compared parameters. As we will see, our more exact procedure shows that consistency is somewhat better than would have appeared to be the case otherwise.
3.1. General outline of the procedure
We schematically outline here the steps of the procedure that we apply, with more details being provided in the following section.
First, we choose to quantify the shifts between parameters estimated from different multipole ranges as differences in best-fit values 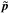 , that is, the values that maximize their posterior distributions, rather than differences in the mean values
, that is, the values that maximize their posterior distributions, rather than differences in the mean values 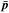 of their marginal distributions. We adopt this choice because best-fit values are much faster to compute (they are determined with a minimizer algorithm, while the means require full MCMC chains). We justify this choice by the fact that the posterior distributions of cosmological parameters in the ΛCDM model are very closely Gaussian, so that their means and maxima are very similar. Furthermore, we will consistently compare the shifts in best-fit parameters measured from the data with their probability distribution estimated from the simulations. Therefore we are confident that this choice should not affect our final results.
of their marginal distributions. We adopt this choice because best-fit values are much faster to compute (they are determined with a minimizer algorithm, while the means require full MCMC chains). We justify this choice by the fact that the posterior distributions of cosmological parameters in the ΛCDM model are very closely Gaussian, so that their means and maxima are very similar. Furthermore, we will consistently compare the shifts in best-fit parameters measured from the data with their probability distribution estimated from the simulations. Therefore we are confident that this choice should not affect our final results.
Next, we wish to determine the probability distribution of the parameter shifts given the data, that is, 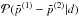 . Since when estimating
. Since when estimating 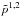 we use the same Gaussian prior on τ,
we use the same Gaussian prior on τ, 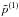 and
and 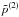 are correlated. Therefore, we use simulations to numerically build this distribution. The idea is to draw simulations from the Planck likelihoods
are correlated. Therefore, we use simulations to numerically build this distribution. The idea is to draw simulations from the Planck likelihoods 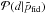 , where
, where 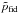 is a fiducial model. For each of these simulations, we estimate the best-fit parameters
is a fiducial model. For each of these simulations, we estimate the best-fit parameters 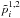 for each of the multipole ranges considered. This allows us to build the probability distribution of the shifts in parameters given a fiducial model,
for each of the multipole ranges considered. This allows us to build the probability distribution of the shifts in parameters given a fiducial model, 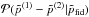 .
.
The fiducial model we use is the best-fit (the maximum of the posterior distribution) ΛCDM model for the full ℓ = 2–2500 PlanckTT data, with τ fixed to 0.07, and the Planck calibration parameter, yP, fixed to one (see details, for example about treatment of foregrounds, in the next section; yP is a map-level rescaling of the data as defined in Planck Collaboration XI (2016)). More explicitly, we use { Ase− 2τ,ns,ωm,ωb,θ∗,τ,yP } = { 1.886,0.959,0.1438,0.02206,1.04062,0.07,1 }. The reason for fixing τ and the calibration in obtaining the fiducial model is that for the analysis of each simulation, priors on these two parameters are applied, centred on 0.07 and 1, respectively; if our fiducial model had different values, the distribution of best-fits across simulations for those and all correlated parameters would be biased from their fiducial values, and one would need to recentre the distributions; our procedure is more straightforward and clearer to interpret. In any case, our analysis is not very sensitive to the exact fiducial values and we have checked that for a slightly different fiducial model with τ = 0.055, the significance levels of the shifts given in Sect. 3.3 change by <0.1σ8. This allows us to take the final step, which assumes that the distribution of the shifts in parameters is weakly dependent on the fiducial model in the range allowed by its probability distribution given the data, 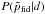 , so that we can estimate the posterior distribution of the parameter differences given the data from
, so that we can estimate the posterior distribution of the parameter differences given the data from 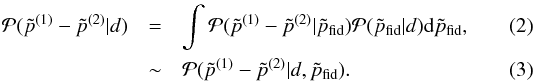 In fact, the uncertainty on the fiducial model estimated from the data, encoded in
In fact, the uncertainty on the fiducial model estimated from the data, encoded in 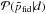 , is small (at the percent level for most of the parameters), and we explicitly checked in the τ = 0.055 case that its value does not change our results. Moreover, since we are interested in the distribution of the differences of the parameter best-fits, and not in the absolute values of the best-fits themselves, we expect that this difference essentially only depends on the scatter of the data as described by the Planck likelihood from which we generate the simulations. Since this likelihood is assumed to be weakly dependent on the fiducial model, again roughly in the range allowed by
, is small (at the percent level for most of the parameters), and we explicitly checked in the τ = 0.055 case that its value does not change our results. Moreover, since we are interested in the distribution of the differences of the parameter best-fits, and not in the absolute values of the best-fits themselves, we expect that this difference essentially only depends on the scatter of the data as described by the Planck likelihood from which we generate the simulations. Since this likelihood is assumed to be weakly dependent on the fiducial model, again roughly in the range allowed by 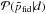 , we expect the distribution of the differences to have a weak dependence on the fiducial model.
, we expect the distribution of the differences to have a weak dependence on the fiducial model.
3.2. Detailed description of the simulations
We now turn to describe these simulations in more detail. The goal of these simulations is to be as consistent as possible with the approximations made in the real analysis (as opposed to, for example, the suite of end-to-end simulations described in Planck Collaboration XI 2016, which aim to simulate systematics not directly accounted for by the real likelihood). In this sense, our simulations are a self-consistency check of Planck data and likelihood products. We will now describe these simulations in more detail.
For each simulation, we draw a realization of the data independently at ℓ < 30 and at ℓ > 309. At ℓ < 30 we draw realizations directly at the map level, whereas for ℓ > 30 we use the plik_lite CMB covariance (described in Planck Collaboration XI 2016) to draw power spectrum realizations. For both ℓ < 30 and ℓ > 30, each realization is drawn assuming a fiducial model.
For ℓ> 30, we draw a random Gaussian sample from the plik_lite covariance and add it to the fiducial model. This, along with the covariance itself, forms the simulated likelihood. The plik_lite covariance includes in it uncertainties due to foregrounds, beams, and inter-frequency calibration, hence these are naturally included in our analysis. We note that the level of uncertainty from these sources is determined from the Planck ℓ < 2500 data themselves (extracted via a Gibbs-sampling procedure, assuming only the frequency dependence of the CMB). Thus, we do not expect exactly the same parameters from plik and plik_lite when restricted to an ℓmax below 2500 because plik_lite includes some information, mostly on foregrounds, from ℓmax < ℓ < 250010. For our purposes, this is actually a benefit of using plik_lite, since it lets us put well-motivated priors on the foregrounds for any value of ℓmax in a way that does not double count any data. Regardless of that, the difference between plik and plik_lite is not very large. For example, the largest of any parameter difference at ℓmax = 1000 is 0.15σ (in the σ of that parameter for ℓmax = 1000), growing to 0.35σ at ℓmax = 1500, and of course back to effectively zero by ℓmax = 2500. Regardless, since our simulations and analyses of real data are performed with the same likelihood, our approach is fully self-consistent.
At ℓ < 30, so as to simulate the correct non-Gaussian shape of the Cℓ posteriors, we draw a map-level realization of the fiducial CMB power spectrum. In doing so, we ignore uncertainties due to foregrounds, inter-frequency calibration, and noise; we will show below that this is a sufficient approximation. For the likelihood, rather than compute the Commander (Planck Collaboration IX 2016; Planck Collaboration X 2016) likelihood for each simulation (which in practice would be computationally prohibitive), we instead use the following simple but accurate analytic approximation. With no masking, the probability distribution of (2ℓ + 1)Ĉℓ/Cℓ is known to be exactly a χ2 distribution with 2ℓ + 1 degrees of freedom (here Ĉℓ is the observed spectrum and Cℓ is the theoretical spectrum). Our approximation posits that, for our masked sky, fℓ(2ℓ + 1)Ĉℓ/Cℓ is drawn from χ2 [fℓ(2ℓ + 1)], with fℓ an ℓ-dependent coefficient determined for our particular mask via simulations, and with Ĉℓ being the mask-deconvolved power spectrum. Approximations very similar to this have been studied previously by Benabed et al. (2009) and Hamimeche & Lewis (2008). Unlike some of those works, our approximation here does not aim to be a general purpose low-ℓ likelihood, rather just to work for our specific case of assuming the ΛCDM model and when combined with data up to ℓ ≃ 800 or higher. While it is not a priori obvious that it is sufficient in these cases, we can perform the following test. We run parameter estimation on the real data, replacing the full Commander likelihood with our approximate likelihood using Ĉℓ and fℓ as derived from the Commander map and mask. We note that this also tests the effect of fixing the foregrounds and inter-frequency calibrations, since we are using just the best-fit Commander map, and it also tests the effect of ignoring noise uncertainties, since our likelihood approximation does not include them. We find that, for both an ℓ < 800 and an ℓ < 2500 run11, no parameter deviates from the real results by more than 0.05σ, with several parameters changing much less than that; hence we find that our approximation is good enough for our purposes. Additionally, in Appendix B we describe a complementary test that scans over many realizations of the CMB sky as well, also finding the approximation to be sufficient.
The likelihood from each simulation is combined with a prior on τ of 0.07 ± 0.02 (with other choices of priors discussed in Sect. 5.5). It is worth emphasizing that the exact same prior is imposed on every simulation, and hence implicitly we are not drawing realizations of different polarization data to go along with the realizations of temperature data that we have discussed above. This is a valid choice because the polarization data are close to noise dominated and therefore largely uncorrelated with the temperature data. We have chosen to do this because our aim is to examine parameter shifts between different subsets of temperature data, rather than between temperature versus polarization, and thus we regard the polarization data as a fixed external prior. Had we sampled the polarization data, the significance levels of shifts would have been slightly smaller because the expected scatter on τ and correlated parameters would be slightly larger. We have explicitly checked this fact by running a subset of the simulations (ones for ℓ < 800 and ℓ < 2500) with the mean of the τ prior randomly draw from its prior distribution for each simulation, that is, we have implicitly drawn realizations of the polarization data. We find that the significance levels of the different statistics discussed in the following section are reduced by 0.1σ or less. We note that this same subset of simulations is described further in Appendix B, where it is used as an additional verification of our low-ℓ approximation.
 |
Fig. 2 Differences in best-fit parameters between ℓ < 800 and ℓ < 2500 as compared to expectations from a suite of simulations. The cloud of blue points and the histograms are the distribution from simulations (discussed in Sect. 3), while the orange points and lines are the shifts found in the data. Although the shifts may appear to be generally large for this particular choice of parameter set, it is important to realise that this is not an orthogonal basis, and that there are strong correlations among parameters; when this is taken into account, the overall significance of these shifts is 1.4σ, and the significance of the biggest outlier (Ase− 2τ), after accounting for look-elsewhere effects, is 1.7σ. Figure 3 shows these same shifts in a more orthogonal basis that makes judging these significance levels easier by eye. Choosing a different multipole at which to split the data, or comparing low ℓs versus high ℓs alone, does not change this qualitative level of agreement. We note that the parameter mode discussed in Sect. 3.3 is not projected out here, since it would correspond to moving any data point by less than the width of the point itself. |
3.3. Results
With the simulated data and likelihoods in hand, we now numerically maximize the likelihood for each of the realizations to obtain best-fit parameters. The maximization procedure uses “Powell’s method” from the SciPy package (Jones et al. 2001–2016) and has been tested to be robustby running it on the true data at all ℓ splits, beginning from several different starting points, and ensuring convergence to the same minimum. We find in all cases that convergence is sufficient to ensure that none of the significance values given in this section change by more than 0.1σ, which we consider a satisfactory level.
Using the computational power provided by the volunteers at Cosmology@Home12, whose computers ran a large part of these computations, we have been able to run simulations not just for ℓ < 800 and ℓ < 2500, but for roughly 100 different subsets of data, with around 5000 realizations for each. We discuss some of these results in this section, with a more comprehensive set of tests given in Appendix A.
Figure 2 shows the resulting distribution of parameter shifts expected between the ℓ < 800 and ℓ < 2500 cases, compared to the shift seen in the real data. To quantify the overall consistency, we pick a statistic, compute its value on the data as well as on the simulations, then compute the probability to exceed (PTE) the data value based on the distribution of simulations. We then turn this into the equivalent number of σ, such that a 1-dimensional Gaussian has the same 2-tailed PTE. We use two particular statistics:
-
the χ2 statistic, computing χ2 = Δp Σ-1 Δp, where Δp is the vector of shifts in parameters between the two data sets and Σ is the covariance of these shifts from the set of simulations;
-
the max-param statistic, where we scan for max( | Δp/σp |), that is, the most deviant parameter from the set { θ∗, ωm, ωb, Ase− 2τ, ns, τ }, in terms of the expected shifts from the simulations, σp.
 |
Fig. 3 Visually it might seem that the data point in the six-parameter space of Fig. 2 is a much worse outlier than only 1.4σ. One way to see that it really is only 1.4σ is to transform to another parameter space, as shown in this figure. Linear transformations leave the χ2 unaffected, and while ours here are not exactly linear, the shifts are small enough that they can be approximated as linear and the χ2 is largely unchanged (in fact it is slightly worse, 1.6σ). We have chosen these parameters so the shifts are more decorrelated while still using physical quantities. The parameter |
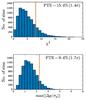 |
Fig. 4 Distribution of two different statistics computed on the simulations (blue histogram) and on the data (orange line). The first is the χ2 statistic, where we compute χ2 for the change in parameters between ℓ < 800 and ℓ < 2500, with respect to the covariance of the expected shifts. The second is a “biggest outlier” statistic, where we search for the parameter with the largest change, in units of the standard deviation of the simulated shifts. We give the probability to exceed (PTE) on each panel. For both statistics, we find that the observed shifts are largely consistent with expectations from simulations. |
In the case of the χ2 statistic, and when one is comparing two nested sets of data (by “nested” we mean that one data set contains the other, that is, ℓ < 800 is part of ℓ < 2500), there is an added caveat. In cases like this, there is the potential for the existence of one or more directions in parameter space for which expected shifts are extremely small compared to the posterior constraint on the same mode. These correspond to parameter modes where very little new information has been added, and hence one should see almost no shift. It is thus possible that the χ2 statistic is drastically altered by a change to the observed shifts that is in fact insignificant at our level of interest. Such a mode can be excited by any number of things, such as systematics, effects of approximations, minimizer errors, etc., but at a very small level. These modes can be enumerated by simultaneously diagonalizing the covariance of expected shifts and the covariance of the posteriors, and ordering them by the ratio of eigenvalues. For the case of comparing ℓ < 800 and ℓ < 2500, we find that the worst offending mode corresponds to altering the observed shifts in { H0, ωm, ωb, Ase− 2τ, ns, τ } by { 0.02, −0.01, 0.02, −0.003, 0.04, 0.01 } in units of the 1σ posteriors from ℓ < 2500. This can change the significance of the χ2 statistic by an amount that corresponds to 0.6σ, despite no cosmological parameter nor linear combination of them having changed by more than a few percent of each σ. To mitigate this effect and hence to make the χ2 statistic more meaningful for our desired goal of assessing consistency, we quote significance levels after projecting out any modes whose ratio of eigenvalues is greater than 10 (which in our case is just the aforementioned mode). We emphasize that removal of this mode is not meant to, nor does it, hide any problems; in fact, in some cases the χ2 becomes worse after removal. The point is that without removing it we would be sensitive to shifts in parameters at extremely small levels that we do not care about. In any case, this mode removal is only necessary for the case of the χ2 statistic and nested data sets, which is only a small subset of the tests performed in this paper.
Results for several data splits are summarized in Table 1, with the comparison of ℓ < 800 to ℓ < 2500 given in the first row and shown more fully in Fig. 4. In this case, we find that the parameter shifts are in fairly good agreement with expectations from simulations, with significance levels of 1.4σ and 1.7σ from the two statistics, respectively. We also note that the qualitative level of agreement is largely unchanged when considering ℓ < 800 versus ℓ> 800 or when splitting at ℓ = 1000.
Of the other data splits shown in Table 1, the ℓ < 1000 versus ℓ> 1000 case may be of particular interest, since it is discussed extensively in Addison et al. (2016). Although not the main focus in their paper, those authors find 1.8σ as the level of the overall agreement by applying the equivalent of our Eq. (1) to the shifts in five parameters, namely { θ∗,ωc,ωb,log As,ns }. This is similar to our result, although higher by 0.2σ. There are three main contributors to this difference. Firstly, although Addison et al. drop τ in the comparison to try to mitigate the effect of the prior on τ having induced correlations in the two data sets, they keep log As as a parameter, which is highly correlated with τ. This means that their comparison fails to remove the correlations, nor does it take them into account. One could largely remove the correlation by switching to Ase− 2τ (which is much less correlated with τ); this has the effect of reducing the significance of the shifts by 0.3σ. Secondly, the Addison et al. analysis puts no priors on the foreground parameters, which is especially important for the ℓ> 1000 part. For example, fixing the foregrounds to their best-fit levels from ℓ < 2500 reduces the significance by an additional 0.2σ. Finally, our result uses six parameters as opposed to five (since we are able to correctly account for the prior on τ); this increases the significance back up by around 0.3σ.
There is an additional point that Addison et al. (2016) fail to take into account when quoting significance levels – and the same issue arises in some other published claims of parameter shifts that focus on a single parameter. This is that one should not pick out the most extreme outlying parameter without assessing how large the largest expected shift is among the full set of parameters. In other words, one should account for what are sometimes called “look elsewhere” effects (see Planck Collaboration XVI 2016, for a discussion of this issue in a different context). Our simulations allow us to do this easily. For example, in the ℓ < 1000 versus ℓ> 1000 case, the biggest change in any parameter is a 2.3σ shift in ωm; however, the significance of finding a 2.3σ outlier when searching through six parameters with our particular correlation structure is only 1.6σ, which is the value we quote in Table 1.
To summarize this section, we do not find strong evidence of inconsistency in the parameter shifts from ℓ < 800 to those from ℓ < 2500, when compared with expectations, nor from any of the other data splits shown in Table 1. We also find that the results of Addison et al. (2016) somewhat exaggerate the significance of tension, for a number of reasons, as discussed above.
As a final note, we show in Table 2 the consistency of various data splits as in Table 1, but using data and simulations that have a prior of τ = 0.055 ± 0.010 instead of τ = 0.07 ± 0.02. In general the agreement between different splits changes by between −0.1 and 0.3σ, thus slightly worse. A detailed discussion of these results will be presented in Sect. 5.5.
Consistency of various data splits, as determined from two statistics computed on data and simulations.
 |
Fig. 5 Response of |
4. Physical explanation of the power spectrum response to changing ΛCDM parameters
Having studied the question of the magnitude of the parameter shifts relative to expectations, we now turn to an analysis of why the best-fit model parameters change in the particular way that they do. Understanding this requires reviewing exactly how changes to ΛCDM parameters affect the CMB power spectrum, so that these can be matched with the features in the data that drive the changes. The material in this section is meant as background for the narrative that will come later, and readers may want to skip it on a first reading; nevertheless, the information collected here is not available in any single source elsewhere, and will be important for understanding the relationship between parameters and power spectrum features. The key information is the response of the angular power spectrum to changes in parameters, shown in Fig. 5. In Sect. 5 we will close the loop on how the physics embodied in the curves of Fig. 5 interacts with the residual features in the power spectrum to give the parameter shifts we see in Fig. 1.
The structure in the CMB anisotropy spectrum arises from gravity-driven oscillations in the baryon-photon plasma before recombination (e.g. Peebles & Yu 1970; Zel’dovich et al. 1972). Fortunately our understanding of the CMB spectrum has become highly developed, so we are able to understand the physical causes (see Fig. 5) of the shifts already discussed as arising from the interaction of gravitational lensing, the early integrated Sachs-Wolfe (ISW, Sachs & Wolfe 1967) effect, the potential envelope, and diffusion damping. In this section we review the physics behind the 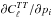 curves and clarify some interesting interactions by “turning off” various effects. The reader is referred to Peacock (1999), Liddle & Lyth (2000), and Dodelson (2003) for basic textbook treatments of the physics of CMB anisotropies.
curves and clarify some interesting interactions by “turning off” various effects. The reader is referred to Peacock (1999), Liddle & Lyth (2000), and Dodelson (2003) for basic textbook treatments of the physics of CMB anisotropies.
4.1. The matter density: ωm
We begin by considering how changes in the matter density affect the power spectrum, leading to the rising behaviour seen in the top left panel of Fig. 5. We note that here we have plotted the linear response in the quantity 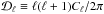 rather than Cℓ.
rather than Cℓ.
Since much of the relevant action occurs near horizon crossing, a description of the physics is best accomplished by picking a gauge; we choose the Newtonian gauge here and focus primarily on the potentials Φ and Ψ and the density. Within this picture, the impact of the matter density comes from the “early integrated Sachs-Wolfe effect” (i.e., the evolution of the potentials immediately after last scattering) and from the “potential envelope”. The effect of main interest to us is the latter – the enhancement of power above ℓ ≃ 100 arising due to the near-resonant driving of the acoustic oscillations by decaying potentials as they cross the horizon near, or earlier than, the epoch of matter-radiation equality (Hu & White 1996a, 1997; Hu et al. 1996). Overdense modes that enter the horizon during radiation domination (ρm/ρrad ≪ 1) cannot collapse rapidly enough into their potential wells (due to the large pressure of the radiation) to prevent the potentials from decaying due to the expansion of the Universe. The time it takes the potential to decay is closely related to the time at which the photons reach their maximal compression and hence maximal energy density perturbation. The near-resonant driving of the oscillator, and the fact that the photons do not lose (as much) energy climbing out of the potential well (as they gained falling in), leads to a large increase in observed amplitude of the temperature perturbation over its initial value. For modes that enter the horizon later, the matter density perturbations contribute more to the potentials, which are (partially) stabilized against decay by the contribution of the CDM. This reduces the amplitude enhancement. The net result is an ℓ-dependent boost to the power spectrum amplitude, transitioning from unity at low ℓ to a factor of over ten in the high-ℓ limit. This boost is known as the “potential envelope”. It is not immediately apparent in the power spectrum, due to the effects of damping at high ℓ, but it imprints a large dependence on ωm and can be uncovered if the effects of damping and line-of-sight averaging are removed (e.g. Fig. 7 of Hu & White 1997).
The characteristic scale of the power boost is set by the angular scale, θeq, which is the comoving size of the horizon at the epoch of matter-radiation equality projected from the last-scattering surface. Thus the CMB spectra are sensitive to θeq. In the ΛCDM model θeq depends almost solely on the redshift of matter-radiation equality, zeq (with an additional, very weak, dependence on Ωm). Higher ωm means higher zeq and thus θeq is smaller; the rise in power from low ℓ (modes that entered at z <zeq) to high ℓ (modes that entered at z>zeq) gets shifted to higher ℓ. This shifting of the transition to higher ℓ results in a decrease in power in the region of the transition and thus the shape of the change in 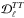 shown in Fig. 5. As we will see in Sect. 5.1, an oscillatory decrease in lower ℓ power (from increasing ωm) will be a key part of our explanation for the parameter shifts. Indeed, once the impact of the low multipoles is reduced by the addition of high-ℓ data, the increase in power near the first peak from a redder spectrum must be countered by a higher ωm (and other shifts, see Sect. 5.3).
shown in Fig. 5. As we will see in Sect. 5.1, an oscillatory decrease in lower ℓ power (from increasing ωm) will be a key part of our explanation for the parameter shifts. Indeed, once the impact of the low multipoles is reduced by the addition of high-ℓ data, the increase in power near the first peak from a redder spectrum must be countered by a higher ωm (and other shifts, see Sect. 5.3).
Additional dependence on ωm comes from the change in the damping scale and how recombination proceeds. The damping scale is the geometric mean of the horizon and the mean free path at recombination, and changing the expansion rate changes this scale (Silk 1968; Hu & Sugiyama 1995b). An increase in ωm corresponds to a decrease in the physical damping scale (which corresponds to a decreased angular scale at fixed distance to last scattering). However, within the range of variation in ωm allowed by Planck, changes in damping are a sub-dominant effect.
Finally, the anisotropies we observe are modified from their primordial form due to the effects of lensing by large-scale structure along the line of sight. One effect of lensing is to “smear” the acoustic peaks and troughs, reducing their contrast (Seljak 1996). The peak smearing by lensing depends on ωm through the decay of small-scale potentials between horizon crossing and the epoch of equality (see e.g. Pan et al. 2014). While ωm is an important contributor to the lensing effect, we will see in Sect. 5.2 that lensing will primarily drive shifts in τ and Ase− 2τ.
4.2. The baryon density: ωb
For the nearly scale-invariant, adiabatic perturbations of interest to us, the presence of baryons causes a modulation in the heights of the peaks in the power spectrum and a change in the damping scale due to the change in the mean free path. Physically a non-zero baryon-photon momentum density ratio, R = 3ρb/ (4ργ), alters the zero-point of the acoustic oscillations away from zero effective temperature (Θ0 + Ψ = 0) to Θ0 + (1−R)Ψ = 0 (see e.g. Seljak 1994; Hu & Sugiyama 1995a; Hu et al. 1997). For non-zero RΨ this leads to a modulation of even and odd peak heights, enhancing the odd peaks (corresponding to compression into a potential well) with RΨ < 0 and reducing the even peaks (corresponding to rarefactions in potential wells). Given only low-ℓ data, such as for WMAP, the relative heights of the first and second peaks, in particular, are important for determining R and therefore ωb. An increase in ωb boosts the first peak relative to the second, as is apparent in the ωb panel of Fig. 5. We will see in Sect. 5.1 that the inclusion of the high-ℓ data will lead to a decrease in ωb, which will be required to better match the ratio of the first and second peaks once the other parameters have shifted.
A change in ωb also changes the mean free path of photons near recombination, and the process of recombination itself, thus affecting the diffusion damping scale. As with an increase in ωm, an increase in ωb decreases the physical damping scale. The angular scale which this corresponds to depends on the distance to last scattering, which can be altered by changing ωb, depending on what other quantities are held fixed. For the choice shown in Fig. 5, we find that the angular scale decreases as well, leading to less damping and the excess of power seen at high ℓ in the ωb panel.
4.3. The optical depth: τ
Reionization in the late Universe recouples the CMB photons to the matter field, but not as tightly as before recombination (since the matter density has dropped by over six orders of magnitude in the intervening period). Scattering of photons off electrons in the ionized intergalactic medium suppresses the power in the primary anisotropies on scales smaller than the horizon at reionization (ℓ ≳ 10) by e− 2τ (Kaiser 1984; Efstathiou 1988; Sugiyama et al. 1993; Hu & White 1996b). Because of this, increasing τ at fixed As e− 2τ keeps the power spectrum at ℓ ≫ 10 nearly constant. The small wiggles in the τ panel are entirely from the increased gravitational lensing power, due to the increase in As necessary to keep As e− 2τ constant. At very low ℓ this increase in As directly boosts anisotropies.
Increasing As e− 2τ at fixed τ results in changes to 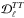 that are almost exactly proportional to
that are almost exactly proportional to 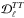 , with small corrections due to the second-order effect of gravitational lensing.
, with small corrections due to the second-order effect of gravitational lensing.
4.4. The spectral index, ns, and acoustic scale, θ∗
The final two effects are very easy to understand. A change in the spectral index of the primordial perturbations yields a corresponding change to the observed CMB power spectrum (e.g. Knox 1995). Increasing ns with the amplitude fixed at the pivot point k = k0 = 0.05 Mpc-1, increases (decreases) power at ℓ ≳ ( ≲ ) 550, since modes with k = k0 project into angular scales near ℓ = 550. We will see in Sect. 5.1 that a tilt towards redder spectra (i.e. a decrease in high-ℓ power) will be necessary to best fit the high-ℓ data. Alternatively, as discussed in Sect. 5.3, when not tightly constrained by the ℓ> 1000 data, a higher ns allows a better fit to the “deficit” of power at ℓ < 30.
The predominant effect of altering θ∗ (which, with the other parameters held fixed, is performed by modifying ωΛ) is to stretch the spectrum in the ℓ direction, causing large changes in the rapidly-varying regions of the spectrum between peaks and troughs. We note that the high sensitivity of the power spectrum to this scaling parameter (e.g. Kosowsky et al. 2002) means that small variations in θ∗ can swamp those of other parameters. In Sect. 5.1 we will see that one of the differences between the ℓ < 800 best-fit model and that for ℓ < 2500 is a variation in θ∗ that shifts the third peak in the angular power spectrum slightly to the right, removing some oscillatory residuals.
4.5. The Hubble constant, H0
With these effects in hand it is easy to understand how changes in other parameters, such as H0, impact 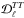 . As discussed in Planck Collaboration XVI (2014, Sect. 3.1), the characteristic angular size of fluctuations in the CMB (θ∗) is exceptionally well and robustly determined (better than 0.1%). Within the ΛCDM model this angle is a ratio of the sound horizon at the time of last scattering and the angular diameter distance to last scattering. The sound horizon is determined by the redshift of recombination, ωm, and ωb, so the constraint on θ∗ translates into a constraint on the distance to last scattering, which in turn becomes a constraint on the 3-dimensional subspace ωm–ωb–h. Marginalizing over ωb gives a strong degeneracy between ωm and h, which can be approximately expressed as Ωmh3 = constant (as will be important in Sect. 5.3). For example, an increase in ωm decreases the sound horizon as
. As discussed in Planck Collaboration XVI (2014, Sect. 3.1), the characteristic angular size of fluctuations in the CMB (θ∗) is exceptionally well and robustly determined (better than 0.1%). Within the ΛCDM model this angle is a ratio of the sound horizon at the time of last scattering and the angular diameter distance to last scattering. The sound horizon is determined by the redshift of recombination, ωm, and ωb, so the constraint on θ∗ translates into a constraint on the distance to last scattering, which in turn becomes a constraint on the 3-dimensional subspace ωm–ωb–h. Marginalizing over ωb gives a strong degeneracy between ωm and h, which can be approximately expressed as Ωmh3 = constant (as will be important in Sect. 5.3). For example, an increase in ωm decreases the sound horizon as 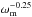 (softened by the influence of radiation) and hence the distance to last scattering must decrease, to hold θ∗ fixed. This distance is an integral of 1 /H(z), with H2(z) ∝ {ωm[(1 + z)3−1] + h2} for the dominant contribution from z ≪ zeq. Thus h must decrease in order for the distance to last scattering not to decrease too much.
(softened by the influence of radiation) and hence the distance to last scattering must decrease, to hold θ∗ fixed. This distance is an integral of 1 /H(z), with H2(z) ∝ {ωm[(1 + z)3−1] + h2} for the dominant contribution from z ≪ zeq. Thus h must decrease in order for the distance to last scattering not to decrease too much.
4.6. Lensing
As mentioned earlier, the anisotropies we observe are modified from their primordial form by several secondary processes, among them the deflection of CMB photons by the gravitational lensing associated with large-scale structure (see e.g. Lewis & Challinor 2006, for a review). These deflections serve to “smear” the last scattering surface, leading to a smoothing of the peaks and troughs in the angular power spectrum, as well as generating excess power on small scales, B-mode polarization, and non-Gaussian signatures. Our focus is on the first effect.
Gradients in the gravitational potential bend the paths of photons by a few arcminutes, with the bend angles coherent over degree scales, leading to a pattern of distortion and magnification on the initially Gaussian CMB sky. In magnified regions the power is shifted to lower ℓ, while in demagnified regions it is shifted to higher ℓ. Across the whole sky this reduces the contrast of the peaks and troughs in the power spectrum (while conserving the total power), and generates an almost power-law tail to very high ℓ. The amplitude of the peak smearing is set by (transverse gradients of) the (projected) gravitational potential and this is sensitive to parameters (such as As and ωm), which change its amplitude or shape. The separate topic of CMB lensing through the 4-point functions (to derive 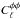 ) is discussed in Sect. 6.3.
) is discussed in Sect. 6.3.
5. Connecting parameter shifts to data to physics
With an understanding of the different ways in which the ΛCDM model parameters can adjust the TT spectrum, we can now begin to try to explain the parameter shifts of main interest for this paper. We start in Sect. 5.1 by showing how the best-fit model has adjusted from its ℓ < 800 solution to match the new data at ℓ> 800. This story tracks more or less chronologically how our best understanding of the ΛCDM model has progressed, since the modes at ℓ ≲ 800 had mostly been measured first with WMAP. Additionally, it highlights the features of the Planck data that are important for driving parameter shifts with respect to the ℓ < 800 best-fit model.
The question answered in Sect. 5.1 is “what caused the parameters to shift from their ℓ < 800 values to their ℓ < 2500 ones?” A different, and also useful, question is “what causes there to be shifts at all, that is, where do the differences come from?”. This puts the ℓ < 800 and ℓ> 800 data on more equal footing, allowing us to pick aspects of each that generate most of the difference between the two. Although the resulting story is not unique, we find that the particular choice we have made results in a helpful explanation. It leads us to identify the connection with gravitational lensing, which we discuss in Sect. 5.2, and of the low-ℓ deficit, which we discuss in Sect. 5.3.
 |
Fig. 6 Shifts in the best-fit values of parameters when one considers the multipole range either below or above different values of ℓsplit. This uses the PlanckTT+τprior data combination, with ℓ> 30 computed using plik_lite. The different lines correspond to restricting the data to ℓ <ℓsplit (blue), 30 <ℓ <ℓsplit (green), and ℓ>ℓsplit (orange). These shifts are described in Sect. 5.1. One can see here that excising the ℓ < 30 region moves the low-ℓ parameters closer to the high-ℓ parameters, as discussed in detail in Sect. 5.3. Error bands are the ± 1 and ± 2σ scatter in the simulations away from the input fiducial model. We have chosen to plot this quantity as opposed to posterior constraints on these parameters (which is different because of our prior on τ) because it is these bands that are appropriate for comparing the blue and orange lines against each other. We note that this has the perhaps counter-intuitive effect of having the error bands in the τ panel increase as more data are added. None of the local “spikes” are found to be significant, as can be seen from the bottom panel of Fig. A.1. |
 |
Fig. 7 How the best-fit ℓ <ℓmax PlanckTT+τprior ΛCDM model adjusts as ℓmax is increased from 800 to 2500 (going from the top panels to the bottom panels). Left column: all panels show residuals relative to the ℓ < 800 model. Planck power spectrum binned estimates and ± 1σ errors on the CMB spectrum, as extracted with plik_lite, are shown as grey boxes. Note the change in y-axis scale at ℓ = 500, indicated by the vertical dotted line. The solid black line is the best-fit model for ℓ <ℓmax, where ℓmax is different for each panel, as indicated by which of the boxes are shaded darker. The various coloured lines indicate the linear response to the shift in individual parameters between their ℓ < 800 best-fit value and their ℓ <ℓmax one. Right column: identical to the left column, except that the contribution from θ∗ (i.e., the blue line from the corresponding left panel) has been subtracted from the sums, as well as from the actual model and from the data. For reference, the arrows in the top and bottom panels show the locations of the peaks in the power spectrum. |
5.1. From ℓ < 800 to ℓ < 2500
We begin by examining how parameters shift as we increase ℓmax from 800 to 2500. The best-fit parameters from the range ℓ <ℓmax are shown by the solid blue curve in Fig. 6 (where ℓsplit is, in this case, ℓmax). Although eight parameters are displayed in this figure, for the purpose of explaining shifts it is important to consider only six parameters at a time (since there are only six degrees of freedom in the ΛCDM model). We will use the set of six discussed in Sect. 2, for the reasons described there. As a reminder, they are θ∗, ωm, ωb, ns, As e− 2τ, and τ. Focusing on these parameters, one can see in Fig. 6 the following changes:
-
a sharp drop in θ∗ between ℓmax = 800 and 1000;
-
a highly correlated gradual drop in ωb, drop in ns, increase in ωm, and increase in Ase− 2τ across the whole multipole range;
-
an increase in τ between ℓmax = 1000 and 1500.
Figure 7 illustrates even more explicitly how these different multipole ranges cause the parameter shifts. This figure compresses a large amount of information into a combination of ten panels, the full understanding of which requires a slow stepwise explanation. Each of the panels in the left column shows residuals of the data relative to the best-fit ℓ < 800 model. The thick black line is the best-fit model for ℓ <ℓmax, with ℓmax increased in each subsequent panel and represented by the darker data points (varying from ℓmax = 800 in the top panels to ℓmax = 2500 in the bottom panels).
In panel 1a of Fig. 7 we have ℓmax = 800 and thus we see directly the residuals in the ℓ> 800 data with respect to the ℓ < 800 model that cause the parameter shifts of main interest for this work. We will sometimes refer to these features as the “oscillatory residuals”; for definiteness, we are referring to the upward trends at ℓ ≃ { 900,1300,1600,1800 } and downward ones at ℓ ≃ { 1100,1400,1700 }. We note that these oscillations are (roughly) out of phase with the CMB peaks themselves, a point which will be important for future discussion.
In Sect. 3, we have been discussing the significance of these residuals at the parameter level, but we can also assess the significance at the power-spectrum level. With the same Δℓ = 50 bins as in Fig. 7, we find that the χ2 of the ℓ < 800 model against the ℓ> 800 data is 36.4 for 34 bins, equivalent to a 0.6σ Gaussian fluctuation. The fact that this is smaller than at parameter level is a consequence of the fact that these power spectrum differences evidently happen to project well onto a relatively small number of modes that are well represented by the cosmological parameters. Finally, we point out that these residuals are of course not inherent to the ℓ> 800 data themselves, rather to the difference with the best-fit model predicted from the ℓ < 800 data; in Sect. 5.3 we will comment on how the ℓ < 30 data can be viewed as having played a significant role in “throwing off” this model and pulling it away from the best estimate coming from the full ℓ range.
Beginning now to increase ℓmax up to 1000, in panel 2a we see the model adjusting to match the data in the 800 to 1000 region. We would also like to understand why and how the various parameters have shifted to incorporate these data, which we can do in the following way. Under the approximation of linear response, it is possible to break apart the total change in the model into the contribution from each individual parameter. This is given by the quantity Δpi dCℓ/ dpi, where pi represents each of the parameters and Δpi is the shift in each parameter’s value between the two cases being compared. If the linear approximation were perfect, the sum of the contributions from each parameter would give exactly the total shift; here we find that the approximation is accurate to 10% of the total shift, which is sufficient for our discussion here. We have computed these derivatives for the best-fit ℓ < 800 model. Because these are linear responses, the model can only change their amplitudes.
Panel 2a of Fig. 7 shows that the only response with significant support on the 800–1000 region is θ∗, which indeed shifts to almost perfectly pick up the difference there. The effect is essentially that the third peak has shifted slightly to the right. With the other parameters held fixed, this change in θ∗ alone is responsible for lowering H0 by 0.5 km s-1 Mpc-1. An additional decrease in H0, by about the same amount, can be ascribed to an increase of the matter density, which, in combination with an increased Ase− 2τ, better fits the position of the second trough at ℓ ≃ 650.
Because no further increase in ℓmax changes θ∗ by much (and because Planck’s measurement of θ∗ is so sensitive that the oscillation caused by changing θ∗ can be accommodated by only a small shift in its value), we subtract its effect from the model and data to better see the effects of the other parameters and we plot the result in the right column of Fig. 7. With this shift in θ∗ subtracted, panel 2b shows that qualitatively this makes the oscillatory features that we have already seen become slightly more pronounced.
The first way in which the parameters adjust to fit the remaining data is via movement along a parameter direction involving ωb, ωm, Ase− 2τ, and ns. Although this is a fairly complicated combination, the biggest change in the spectrum comes from the increase in primordial power that results in an oscillatory increase in the CMB spectrum, and an increase in the matter density that results in an oscillatory decrease in power. This leaves an oscillatory pattern oscillating about zero when we consider ℓmax = 1000. As we increase ℓmax between panels 2b and 5b, this same parameter mode grows in amplitude. Furthermore, the effect of the change in the primordial power spectrum, both the increase in amplitude and tilt towards redder spectra, is also necessary to match the oscillations. This combination of parameters, and in particular the decrease in ns, also drives disagreement with the very lowest bin in this figure, ℓ < 30 (as we discuss in Sect. 5.3).
Finally, we observe an increase in τ and a corresponding increase in As, which, although barely visible in Fig. 7, does also track the same oscillatory features. We discuss this shift further in Sect. 5.2.
To summarize, the features in the ℓ> 800 data that are primarily responsible for the shifts in parameters are largely oscillatory, as seen in for example panel 1a of Fig. 7. After an initial shift in θ∗ to pick up the excess between ℓ = 800 and 1000, the remaining residuals are tracked by two directions in parameter space, namely an increase in τ and a movement along the Ase− 2τ–ns–ωb–ωm degeneracy direction, both of which serve to increase the amplitude of the oscillations.
 |
Fig. 8 Power spectrum residuals for a few additional cases, in the same format as Fig. 7. We note that for the bottom panel, the fiducial model is the best-fit from 30 <ℓ < 800, as opposed to from ℓ < 800, as is the case in Fig. 7 and in the top two panels of this figure. In all cases the black line is the best-fit ΛCDM model in the range indicated by the shaded data boxes. The coloured lines are the linear responses to the shifts in parameters between these two best-fit solutions. Top: same as panel 5a of Fig. 7, but with an additional free parameter, AL, shown in yellow. This added degree of freedom tracks reasonably well the oscillatory residuals, leaving smaller shifts for the other parameters and a reduced low-ℓ deficit. Middle: same as panel 5a of Fig. 7, but with dashed lines showing the responses with the gravitational potential fixed. Bottom: the way in which the best-fit model from 30 <ℓ < 800 is “thrown off” by inclusion of ℓ < 30 data. We note that although visually the ℓ> 800 data appears to be a better fit with ℓ < 30, the χ2 is worse by Δχ2 = 3.2. |
5.2. Gravitational lensing
Having described the shifts fairly pragmatically, we now turn to trying to understand what, physically, is driving them. It is clear that the oscillatory residuals are important, and qualitatively we can see that they look like extra smoothing of the peaks and hence resemble the effects of gravitational lensing. Indeed, along with the parameter shifts themselves, much attention has been given in the literature to the fact that the Planck high-ℓ data appear to favour an overly enhanced gravitational lensing potential with respect to that expected from ΛCDM (Planck Collaboration XIII 2016; Couchot et al. 2015; Addison et al. 2016). Given this, and noting that the parameters shift to increase As and ωm (both of which increase the gravitational lensing potential) it may be tempting to think that the parameter shifts are dominantly driven by a desire to increase lensing and hence increase peak smoothing at high ℓ. We will see, however, that this only explains about a third of the total shifts and instead most of the change in the best-fit model spectrum is related to non-lensing effects such as changing the matter envelope (Sect. 4.1) and the primordial tilt (Sect. 4.4).
The effect of lensing of the TT spectrum has traditionally been studied by introducing an additional phenomenological parameter, AL, which artificially scales the lensing potential power spectrum used to calculate the lensed CMB spectra. By definition AL = 1 corresponds to ΛCDM. The Planckℓ < 2500 data prefer a value higher than unity, AL = 1.22 ± 0.10Planck Collaboration XIII (2016). The top panel of Fig. 8 shows the same power spectrum residual and linear responses of Fig. 7, now with AL as an additional free parameter. As we see, the response from increasing AL on its own does a somewhat good job of fitting the data, particularly at ℓ> 1000, leaving smaller shifts in the other parameters. We do note, however, that although some of the other cosmological parameters shift closer to the values preferred by the ℓ < 800 case13, differences remain. For example, as shown in Fig. 9, about half of the shifts (in e.g. ωm and H0) remain even in the ΛCDM+AL case. Thus, the shift in parameters between ℓ < 800 and ℓ < 2500 cannot be entirely explained through an extra peak-smoothing effect at high ℓ; other aspects of the data are also independently pointing to similar shifts.
In terms of understanding physically how the features in the ℓ> 800 data are fit by the ΛCDM model, the AL test is, however, not entirely useful. The ΛCDM model, unlike ΛCDM+AL, is of course not free to arbitrarily increase the lensing potential; it must do so through other parameters that also have non-lensing related effects. Thus the particular way in which ΛCDM chooses to optimally fit the features will be a balance between lensing and non-lensing effects. It is now useful to define more exactly the question we are seeking to answer. Ascertaining what aspects of the data “are lensing” is an ill-defined question; conversely, ascertaining which parts of the change between two model power spectra come from lensing is perfectly well defined because we can theoretically calculate the two spectra with and without lensing included. This is what is shown in the middle panel of Fig. 8. Here we plot the same power spectrum linear responses as in Fig. 7, but additionally (as the dashed lines) we remove the contribution from changing the lensing potential; more precisely, the dashed lines are dCℓ/ dpσp, with Cℓ being the unlensed power spectrum. Thus, even without affecting the lensing potential, the shifts in parameters we have been discussing cause the spectrum to largely match the oscillatory features we see in the data.
 |
Fig. 9 Marginalized mean and 68% error bars on cosmological parameters estimated with different data choices, assuming the ΛCDM model (unless otherwise labelled), derived from MCMC chains. We use the PlanckTT likelihood in combination with a prior τ = 0.07 ± 0.02. Excising the low multipoles, that is, ℓ < 30, substantially improves the agreement between the parameters from ℓ < 800 and the ℓ < 2500 range. Further agreement is then achieved when removing the effect of gravitational lensing. |
In terms of cosmological parameters, we can verify that most of the shifts are still there even in the absence of changes to the gravitational lensing potential with the following test. We again look at shifts between ℓ < 800 and ℓ < 2500, but for the ℓ < 2500 case we fix the lensing potential to its own best-fit from ℓ < 2500. In doing so, the cosmological parameters no longer impact the amplitude of the lensing potential, which is already at the value favoured by the full ℓ-range fit. Any remaining shifts must reflect features in the data that are not accounted for by the change to the lensing potential alone, and are instead fit by non-lensing effects of changing the cosmological parameters. We find, as shown in Fig. 9, that the majority of the shifts are still present. For example, H0 still moves from (70.0 ± 1.9) with ℓ < 800 to (68.4 ± 1.1) km s-1 Mpc-1 with ℓ < 2500 and fixed lensing. Roughly speaking, about two thirds of the shift in the Hubble constant and other parameters comes from non-lensing effects.
The only exception to lensing being a sub-dominant part of the shifts is τ and the corresponding change in As, whose entire shift is explained by lensing. This confirms what we might expect, since at ℓ> 100 the only effect of changing τ (at fixed Ase− 2τ) is via lensing effects, and if the non-lensing effect of τ at ℓ < 100 would have been driving its shift, it is clear from Fig. 7 that it would have shifted in the other direction. We have gone further and also investigated whether the part of shifts in As and ωm that are related to lensing are due to the fact that both of these parameters directly impact the lensing amplitude, or whether this is rather through the correlation between the two due to non-lensing effects in the power spectrum. We checked this by fixing the lensing potential to the 30 <ℓ < 800 best-fit case, and letting only As change its amplitude. We find that in this case, As and τ are forced to values even higher than in the standard 30 <ℓ < 2500 case, while the posterior of ωm remains very close to the best-fit of the 30 <ℓ < 800 case. We thus conclude that it is indeed the direct impact of both ωm and As on the lensing amplitude that is important.
One reason the sub-dominant impact of lensing discussed in this section is subtle is because of a coincidental parameter degeneracy. As discussed in the previous section, fitting the oscillatory features increases ωm and Ase− 2τ. By coincidence, these shifts both increase the lensing potential and increase the amplitude of the peak smoothing via non-lensing effects, but it is the latter that is more important.
Comparison of the expected dispersion (“Exp.”) and observed (“Obs.”) parameter shifts between pairs of datasets.
5.3. The low-ℓ deficit
With part of the shifts explained by a preference, albeit sub-dominant, for an increased lensing potential, we now seek to explain the rest of the differences. If we are free to attribute the variations to specific multipoles in either of the two data sets we are comparing, there is not a unique way to tell this story. For example, one could look further at the ℓ > 800 data and isolate what, aside from the lensing piece we have just described, is causing the shifts. We choose here a different path, which we believe is more elucidating and attributes the remaining difference to the ℓ < 800 data instead. It also has the advantage that it likely explains, chronologically, why the parameters have shifted (since, again, these modes were measured first with WMAP). The specific explanation is that a large remaining part of the differences is due to multipoles at ℓ < 30 having “thrown off” the ℓ < 800 result.
In the previous section, it was noted that as the model adjusted to fit the data in the 1000 <ℓ < 1500 region, the fit at ℓ < 30 became much worse. This is evidence that the ℓ < 30 region might play a major role in driving disagreement between the low and high multipoles. Indeed, “anomalies” related to the low-ℓ’s have been discussed extensively in the literature, for example the low quadrupole or the localized “dip” near ℓ ≃ 20 (Bennett et al. 1996; Hinshaw et al. 2003; Spergel et al. 2003; Peiris et al. 2003; Mortonson et al. 2009; Cai et al. 2015b). Here we are interested mainly in the overall deficit in power across the entire ℓ ≲ 30 region (which does of course gain some contributions from the low quadrupole and the ℓ ≃ 20 dip, but also from other multipoles); we refer to this as the “low-ℓ deficit”. This is exactly the same deficit in power discussed previously in Planck Collaboration XV (2014), Planck Collaboration XVI (2014), Planck Collaboration XIII (2016), and others papers, where it is sometimes called the “low-ℓ anomaly”. We explicitly call it a “power deficit” here to avoid confusion with any other “anomalies” at low-ℓ, and because it is a more appropriate name for a feature of only moderate significance. Indeed, if one models the deficit simply as an overall power rescaling at ℓ < 30 with respect to the ΛCDM model, its significance is 1.1σ when considering the ℓ < 800 data, growing to 1.6σ for the full-ℓ range (since the ΛCDM model prediction is moved higher)14. Assuming ΛCDM, the low-ℓ deficit is thus most likely a sample-variance fluctuation in Cℓ that happens to be concentrated at the lowest multipoles. Despite interpretation of the deficit from different perspectives (e.g. Contaldi et al. 2003; Piao et al. 2004; Iqbal et al. 2015; Chen & Lin 2016; Cai et al. 2015a), up until now, its effect on the parameter shifts has not been thoroughly explored.
Indeed, when excising the range ℓ < 30, we observe a relatively large, correlated shift in parameters, as shown in Fig. 9. For example, H0 shifts from (70.0 ± 1.9) km s-1 Mpc-1 when using ℓ < 800 to (68.0 ± 2.2) km s-1 Mpc-1 when using 30 <ℓ < 800, much closer to the value preferred by the full multipole Planck cosmology, which is (67.3 ± 1.0) km s-1 Mpc-1. This shift is 1.8 times larger than the 1-σ expected shift from simulations for the two data sets, in line with its somewhat anomalous nature. Although the deviations induced by these low multipoles are not statistically very significant, they are one of the main sources of difference between the ℓ < 800 and ℓ < 2500 parameters, as also shown in Table 3. Furthermore, if one considers this “deficit” as a mere statistical fluctuation in the power spectrum, the fact that it happens to occur at the lowest multipoles gives it greater weight in shifting parameter like ns than if it had occurred elsewhere. In detail we find that the shifts between the two ranges { ΔAse− 2τ,Δns,Δωm,Δωb,ΔH0,Δτ } in units of the 1σ expected shifts are {−2.2,1.2,−2.0,1.1,1.8,−1.7 }; without ℓ < 30 in either data set, they become {−1.3,0.0,−0.9,−0.0,0.6,−1.9 }.
We now turn to understanding in more detail the way that the low-ℓ deficit sources these parameter differences. This discussion follows closely the bottom panel of Fig. 8, which shows how one goes from the 30 <ℓ < 800 best-fit (the fiducial model against which the points in the figure are differenced) to the ℓ < 800 best-fit (the black line). Here we see how the low amplitude of the first 30 multipoles can be fit by a correlated change in ns, ωb, ωm, and As e− 2τ. In particular, with the 30 <ℓ < 800 best-fit as a starting point, the model needs to decrease power at ℓ < 30 to fit the low-ℓ deficit; this can be achieved with an increase in ns, which tilts the spectrum and decreases power at the lowest multipoles. However, this has three additional effects that trigger the response of the other cosmological parameters. Firstly, since the increase in ns reduces power not just at ℓ < 30 but over the entire ℓ ≲ 550 part of the power spectrum (because our pivot scale corresponds to ℓ ≃ 550), ωm decreases to compensate by shifting the matter envelope and increasing the early ISW effect (see Sect. 4.1). The change in ωm in turn raises the value of H0 due to the angular diameter distance degeneracy discussed in Sect. 4.5. Secondly, the increase in ns increases the amplitude of the power spectrum at ℓ ≳ 550; this can be compensated by a lower value of As e− 2τ. Thirdly, this shift in As e− 2τ also reduces power around the first peak, and so yields an increase in ωb, which increases the amplitude to partially compensate (through the modulation effect described in Sect. 4.2). Finally, some further adjustments are achieved by selecting a larger value of θ∗, which shifts the position of the peaks to the left. Comparatively speaking, excising ℓ < 30 from ℓ < 2500 leads to shifts that are similar to those just described but of smaller amplitude, since the excised region is a smaller fraction of the data. Hence, the parameter shifts are smaller without ℓ < 30, as can be seen in Fig. 9.
As a final check, we have tested the degeneracy between the low-ℓ deficit and the peak smoothing effect. The purpose of this test is to verify that these are two different effects, and that one cannot be explained with the other through degeneracies among cosmological parameters. In order to perform this test, we use an additional parameter Alow that multiplies the amplitude of the power spectrum at ℓ < 30. This parametrization does not fully capture the feature at low-ℓ, but should be enough for our purpose here, since we verified that the results we obtain in the ΛCDM + Alow case overlap those from excising completely the ℓ < 30 region. We then estimate parameters for a ΛCDM + AL+Alow case. Figure 10 shows the results of this exercise. As expected, we find a moderate degeneracy between AL and Alow, at the level of 30%, which reduces the deviations of both these parameters. Therefore, when looking at parameter shifts due to one of these two effects, one has to keep in mind that they are somewhat correlated. At the same time, since in Fig. 10 both parameters remain deviant at more than about the 1σ level, this test suggests that both effects are present and cannot mutually explain each other.
 |
Fig. 10 Posterior distributions for Alow (which phenomenologically parametrizes the low-ℓ deficit by multiplying the amplitude of the power spectrum at multipoles smaller than ℓ < 30) and for AL (which parametrizes the peak smoothing effect), derived from MCMC chains. We show the results for a ΛCDM+ Alow + AL model (black solid line), for ΛCDM+ Alow (blue) and for ΛCDM+ AL (red). Although a degeneracy is present between the two parameters, small deviations with respect to the ΛCDM expectations remain even when varying both parameters at the same time. |
5.4. Robustness tests
A large number of tests were performed in Planck Collaboration XI (2016) in order to validate the robustness of the Planck likelihood against possible systematics (for more details, see Sect. 5 in that paper). We recall here briefly the tests performed on the high-ℓTT likelihood, and describe an additional one that has been added specifically for this work.
The Planck likelihood was tested against methodological (e.g. incorrect likelihood approximations), instrumental (e.g. incorrect instrument characterization) and astrophysical (e.g. incorrect foreground modelling) systematics, through specific tests and the use of simulations. These three sources were shown, to the best of our knowledge, to introduce a possible bias on cosmological parameters smaller than about 0.2σ.
More specifically, a number of tests were performed to assess the impact of the use of: “detset”15 cross-spectra in place of “half-mission” ones (the former are less affected by systematics that are uncorrelated between detectors, the latter by systematics with timescales shorter than half of the mission length); smaller Galactic masks (less contaminated by foregrounds); Galactic dust template and amplitude priors; beam uncertainties; and frequency cross-spectra. All of these showed consistent results.
The latter test is particularly interesting. The baseline Plik likelihood at ℓ> 30 uses half-mission cross-spectra from the 100, 143, and 217-GHz frequency channels. Consistent results are obtained if one takes out one frequency at a time. For example, using two frequencies at a time with ℓ> 30, a prior on τ = 0.07 ± 0.02, and leaving foregrounds free to vary, for the Hubble parameter we obtain: (67.0 ± 1.1) km s-1 Mpc-1 for 100 and 143 GHz; (67.1 ± 1.1) km s-1 Mpc-1 for 100 and 217 GHz; and (66.9 ± 1.0) km s-1 Mpc-1 for 143 and 217 GHz. These are in excellent agreement with the final result using all three frequencies, (66.9 ± 0.95) km s-1 Mpc-1. This indicates that if the Planck results are affected by systematic effects, then all the main CMB channels must be affected in a similar way.
Another consistency check comes from the comparison of the results from the TT spectrum with those obtained from the high-ℓ polarization power spectra. Although known to be affected by small levels of residual systematics, both TE and EE provide cosmological parameters that are consistent with those from TT. We discuss this point further in Sect. 6.1.
We also present here an additional test to verify that the shifts analysed in the previous sections are consistently present in different frequency channels. In order to do this, we estimated cosmological parameters from ℓ < 800 and ℓ > 800 using one frequency spectrum at a time, that is, the 143 × 143, 143 × 217, or 217 × 217 combinations. Due to the low resolution of the 100 × 100 data, for this case we only estimate parameters for ℓ < 800 . We only use the Plik likelihood at ℓ > 30 in combination with a prior on τ. As shown in Fig. 11 we find very good agreement between the different cases, suggesting that the shifts are not induced by one particular frequency. This confirms the findings of Planck Collaboration XI (2016).
In Fig. 12 we also show the frequency residuals with respect to the best fit of the ℓ < 800 case. We find that the features identified in Sect. 5 to be driving the shifts are present in all frequency channels. This also confirms the findings of Sect. 5 of Planck Collaboration XI (2016), which showed good agreement in the comparison of the inter-frequency residuals.
 |
Fig. 11 Constraints on cosmological parameters from data derived from individual frequencies. The data used is 30 < ℓ < 2500 unless otherwise labelled, and in combination with a prior on τ. The reference case combines all frequencies. The constraints for 30 <ℓ < 800 and ℓ > 800 are obtained with foreground parameters fixed to the best fit of the reference case. The grey band shows the ± 1σ expected shifts in cosmological parameters with respect to the reference case (calculated as in Eq. (53) of Planck Collaboration XI 2016). For this test we use the PlikTT likelihood, as described in Planck Collaboration XI (2016). Results from individual frequencies are in very good agreement. |
5.5. Impact of the τ prior
While this paper was being prepared, an updated analysis of Planck HFI large-scale polarization data was released (Planck Collaboration Int. XLVI 2016). These results give somewhat smaller values of the optical depth to reionization, with smaller uncertainties than from previous results. The tightest constraint derived is τ = 0.055 ± 0.009, with slightly different values resulting from other choices of data combination and treatment, for example τ = 0.058 ± 0.012 in Planck Collaboration Int. XLVII (2016). By comparison, the prior we have been using is τ = 0.07 ± 0.02 (which was picked to correspond roughly to previous Planck LFI results). This tightening of the error bar and change in the central value affects the significance of the parameter shifts we have been discussing. Although this paper could have been written from the beginning with this updated constraint on τ, we chose not to and instead discuss its impact separately here because: (1) it does not have a very big impact on the main results of this paper; (2) the parameter shifts that have been discussed extensively to this point in the community were the ones coming from the earlier τ constraint; and (3) we can more clearly isolate and discuss the effect of the new prior in this way.
 |
Fig. 12 Residuals for different frequency combinations with respect to the ℓ = 2–800 best-fit model. For each frequency we only show the ℓ range used in the Planck likelihood. Although these data subsets are noisy, the oscillatory-like feature seems consistent across frequencies. |
As discussed in Planck Collaboration Int. XLVI (2016), the lower value of τ leads to some shifts in ΛCDM parameters from the full ℓ-range. At fixed Ase− 2τ, the main effect of lowering τ is to reduce As and hence reduce the gravitational lensing potential and associated smoothing of the peaks. A secondary effect of changing τ at very low ℓ’s (e.g. see Fig. 5) is too small with respect to the error bars at these these multipoles to have an appreciable effect. The ℓ < 800 data are largely insensitive to the peak smoothing, so no other parameters besides τ and As are affected (and we note that As alone is not one of the six parameters with which we compute the significance of the shifts). Conversely, the ℓ> 800 data do have sensitivity to gravitational lensing, hence other parameters try and shift to compensate for the decreased smoothing of the peaks. The way that they do this is exactly along the degeneracy direction discussed in Sect. 5.2, which gives extra peak smoothing and involves increasing ωm and Ase− 2τ, while reducing ns and ωb. This leads to, for example, a decrease in H0 of about 0.5 km s-1 Mpc-1. This is in the direction of making the shifts slightly more significant.
The exact level of agreement when using the updated constraint on τ is summarized in Table 2. These numbers come from running simulations identical to those which led to Table 1 except that we use a prior on τ of 0.055 ± 0.010 instead. In practice this means that the prior applied to each simulation is different, as well as the fiducial model from which the simulations are drawn, since this model is obtained with τ fixed to the mean of the prior (as discussed in Sect. 3.2). Generally, the effective agreement changes by between −0.1 and 0.3σ, thus slightly worse. In any case, the differences due to the lower value of τ do not qualitatively alter the main conclusions from this paper, and Table 2 should be considered our best estimate of the level of agreement.
Given that we have seen a lower τ prior increase the significance of the shifts, we might also ask if a higher τ prior can reduce them. Indeed, the PlanckTT data alone do prefer a higher value of τ (Planck Collaboration II 2016; Couchot et al. 2015), so one might be tempted to think that perhaps the parameter shifts reflect a tension between the values of τ from PlanckTT and from large scale polarization. To some extent this is true, and we have checked the significance of the shifts between ℓ < 800 and ℓ < 2500 with a prior of τ = 0.10 ± 0.02, finding that they are reduced from 1.4σ to 1.0σ. This is consistent with the results of Addison et al. (2016), who also showed that a higher value of τ can reduce the size of the shifts. Ultimately, however, the improved consistency is not very dramatic, and the tightest and most model-independent constraints on τ coming from Planck-HFI polarization rule out such high values of τ in any case, so it is unclear whether this can be a viable way to “explain” the parameter shifts.
 |
Fig. 13 Constraints on ΛCDM parameters from: SPT data from Story et al. (2013) in pink; PlanckTT ℓ> 800 in green; and WMAP in blue. Except for the latter data set, which has no sensitivity to τ, all others have been combined with a prior τ = 0.07 ± 0.02. The significance of parameter shifts between these three approximately uncorrelated data sets can be roughly calculated using Eq. (1). We find no strong evidence of discrepancies, with SPT and WMAP agreeing at the 1.7σ level, Planck ℓ > 800 and WMAP agree even better at 1.1σ, while Planck ℓ> 800 and SPT agree with each other at 2.1σ. Also plotted in orange is Planckφφ with θ∗, ωb, and ns fixed to the Planck best-fit values. This data set, across the two parameters it constrains, is also not in significant tension with the others. Sect. 6 discusses these comparisons in more detail. |
6. Comparison with other data sets
Having considered the internal consistency of the PlanckTT data themselves, as well as implicitly considering the comparison with WMAP, we now extend our discussion to a number of other CMB data sets. Although many measurements and analyses of the CMB have been made that have a bearing on agreement with Planck (e.g. Calabrese et al. 2013; Story et al. 2013; Das et al. 2014; Louis et al. 2014; Naess et al. 2014; George et al. 2015), it is impossible here to discuss them all in detail. We thus limit ourselves only to those that are the most constraining on ΛCDM parameters and therefore have the power to test the level of consistency most stringently. We will specifically consider the PlanckTE, EE, and φφ power spectra, as well as measurements of the TT damping tail from Story et al. (2013).
6.1. Comparison with Planck polarization
The first analysis of Planck high-ℓTE and EE spectra was presented in Planck Collaboration XI (2016). Consistency between parameters obtained from TE and EE with those obtained from TT was discussed in Planck Collaboration XIII (2016), which showed that error bars on ΛCDM parameters obtained from TE alone are of similar magnitude to those from TT, and the best-fit values are generally within 0.5σ. For example, from PlikTE+τprior we find H0 = (67.9 ± 0.93) km s-1 Mpc-1 as compared to (66.9 ± 0.95) km s-1 Mpc-1 from PlikTT+τprior. The EE constraints are considerably noisier, but generally within 1σ, with PlikEE+τprior giving H0 = (70.0 ± 2.8) km s-1 Mpc-1, for example. Because cosmic variance partially correlates the TE and EE constraints with those from TT, determining the exact level of consistency requires simulations. This study was discussed in Appendix C.3.6 of Planck Collaboration XI (2016), where it was found that the cosmological parameters obtained from EE and TE are in agreement with those obtained with TT. Given that there are still some residual systematic effects in the polarization spectra, which prevented them from being used for the baseline parameters for the 2015 Planck release (Planck Collaboration XI 2016), we stop at this point, rather than performing any more sophisticated tests. Further comparisons will be made following the next Planck data release.
6.2. Comparison with SPT
The tightest constraints on ΛCDM parameters obtained from the TT damping tail with a single experiment other than Planck come from the South Pole Telescope (SPT, as presented in Story et al. 2013). As such, assessment of the level of consistency between the two is of great interest. Disagreement between the two data sets has been claimed as an argument that the parameter shifts we have been discussing are not of cosmological origin (Addison et al. 2016). Although a more detailed comparison is outside of the scope of this paper, we perform a few basic tests of compatibility here, showing that any tension between Planck and SPT is not very statistically significant.
On their own, the SPT data are not very constraining on ΛCDM parameters because the sky coverage is about a factor of ten times smaller than Planck’s. If we limit Planck to ℓ > 800, roughly the same multipoles measured by SPT, the errors on all ΛCDM parameters are twice as large or more, as can be seen by comparing the green and pink contours in Fig. 13. Combining SPT with WMAP yields somewhat tighter ΛCDM constraints, although still larger than Planck’s full-ℓ range. It is not straightforward to compare Planck and WMAP+SPT because both Planck and WMAP are cosmic variance limited at low multipoles and hence very correlated. Instead, we will limit ourselves to data sets that are uncorrelated and use Eq. (1), which we will apply to the five parameters shown in Fig. 13. This will suffer from all of the problems mentioned in Sect. 3, but will still give us a rough idea of the level of agreement. For WMAP+SPT versus Planck ℓ > 800 we find χ2 = 12.0, which is equivalent to a 2.1σ fluctuation. SPT alone compared to Planck ℓ > 800 yields χ2 = 11.9, also equivalent to 2.1σ. We can additionally compare SPT to the Planck full multipole range, which gives χ2 = 12.3, equivalent to 2.2σ. Although we cannot compare WMAP+SPT and Planck directly, we already know from Kovács et al. (2013) that WMAP and Planck agree extremely well over the common multipole range. Therefore, we would expect WMAP+SPT and Planck parameters to be consistent to a similar level as the numbers just quoted.
Additionally, we point out that despite the impression sometimes given, both implicitly and explicitly, that the Planck high-ℓ’s are “anomalous” with respect to parameters derived from WMAP, the same and more can be said of the SPT parameters. Again using Eq. (1) and the five ΛCDM parameters shown in Fig. 13, WMAP and SPT agree to within 1.7σ, while WMAP and Planck ℓ > 800 are in better agreement, 1.1σ. Of course, given the significances we have seen in this section, the point is that we find no strong evidence for disagreement between any of these different CMB data sets.
6.3. Comparison with Planck lensing
Finally, we consider the level of agreement with the power spectrum of the gravitational lensing reconstruction from Planck data, hereafter referred to as Planckφφ. It has previously been noted that there is some tension between this data set and PlanckTT (Planck Collaboration XIII 2016; Planck Collaboration XV 2016; Addison et al. 2016).
One way to quantify agreement is via constraints on the AL parameter. As described in Sect. 5.2, this scales the gravitational lensing potential used in the calculation of the TT spectrum. A similar parameter, usually called Aφφ, can be introduced when computing constraints from PlanckTT+Planckφφ. In this case, Aφφ scales the gravitational lensing potential, which is passed to the Planckφφ likelihood, but does not scale the one passed to PlanckTT; essentially it offers a reasonable way to use the TT data to constrain the shape of  while allowing the lensing reconstruction to constrain its amplitude independently. We find AL = 1.21 ± 0.10 from PlanckTT, compared to Aφφ = 0.95 ± 0.04, a difference of 2.6σ. This comparison, however, is somewhat misleading because Aφφ and AL are a rescaling of the lensing potential with respect to two different models, mainly the models given by the best-fit ΛCDM parameters in the Aφφ and AL cases. More directly, we can instead just compare the lensing power preferred by the two data sets, for example
while allowing the lensing reconstruction to constrain its amplitude independently. We find AL = 1.21 ± 0.10 from PlanckTT, compared to Aφφ = 0.95 ± 0.04, a difference of 2.6σ. This comparison, however, is somewhat misleading because Aφφ and AL are a rescaling of the lensing potential with respect to two different models, mainly the models given by the best-fit ΛCDM parameters in the Aφφ and AL cases. More directly, we can instead just compare the lensing power preferred by the two data sets, for example  at ℓ = 100. In this case, the difference between Planckφφ and PlanckTTdrops to 2.3σ.
at ℓ = 100. In this case, the difference between Planckφφ and PlanckTTdrops to 2.3σ.
Another way to compare these data sets, which has the further advantage that it assumes ΛCDM unlike the previous case, is to simply analyse each data set independently given the ΛCDM model and compare constraints on parameters. These constraints are shown in Fig. 13, in orange for PlanckTT and in green for lensing (the lensing data assume a fixed θ∗, although are largely insensitive to the exact value). The parameter most often compared is 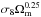 because it is a good proxy for the amplitude of the lensing potential and is most tightly constrained by the lensing data. Here, we find
because it is a good proxy for the amplitude of the lensing potential and is most tightly constrained by the lensing data. Here, we find 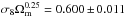 from Planckφφ and 0.623 ± 0.013 from PlanckTT, a difference of 1.3σ. We note that this agreement becomes even better with the addition of the lower prior on τ discussed in Sect. 5.5.
from Planckφφ and 0.623 ± 0.013 from PlanckTT, a difference of 1.3σ. We note that this agreement becomes even better with the addition of the lower prior on τ discussed in Sect. 5.5.
As pointed out by Addison et al. (2016), despite this good agreement over the full ℓ-range, the constraint on 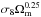 from just the ℓ > 1000 data is in tension with lensing at 2.4σ. Unlike for the full ℓ-range, however, constraints from ℓ> 1000 on a second parameter, ωm, are now comparable to those from lensing, hence it makes sense to include this in the comparison. This slightly reduces the tension to 2.2σ.
from just the ℓ > 1000 data is in tension with lensing at 2.4σ. Unlike for the full ℓ-range, however, constraints from ℓ> 1000 on a second parameter, ωm, are now comparable to those from lensing, hence it makes sense to include this in the comparison. This slightly reduces the tension to 2.2σ.
Addison et al. (2016) further pointed out that the quantity 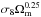 is internally inconsistent within the Planck temperature data themselves at a level of 2.9σ between ℓ < 1000 and ℓ > 1000. We find instead 2.5σ. The most likely source of difference is that we use plik_lite, which we believe gives the more correct result, since it imposes more reasonable priors on the foreground parameters and thus reflects more realistically our knowledge of foreground contamination.
is internally inconsistent within the Planck temperature data themselves at a level of 2.9σ between ℓ < 1000 and ℓ > 1000. We find instead 2.5σ. The most likely source of difference is that we use plik_lite, which we believe gives the more correct result, since it imposes more reasonable priors on the foreground parameters and thus reflects more realistically our knowledge of foreground contamination.
To conclude this section, although it is possible to single out specific parameter differences, overall we find no significant evidence of any strong discrepancies between the PlanckTT and Planckφφ data.
7. Conclusions
The main goals of this paper have been threefold: (i) to isolate the features in the Planckℓ > 800 temperature power spectrum that cause the shifts in parameters away from the ℓ < 800 (or similarly WMAP) parameters; (ii) to assess the consistency of these shifts with expectations; and (iii) to provide an explanation of the physics behind why the parameters are shifting. In our view, such a physical explanation serves to assuage some of the concern that one might initially have about the apparently unlikely nature of some of the shifts, and hence increases the confidence one places in the Planck data. While some discussions of points (i) and (ii) have already appeared in the literature, we have greatly expanded and clarified them here.
In particular, we have made extensive use of numerical simulations in order to evaluate the consistency of the results obtained from a large number of different multipole ranges. This allowed us to properly account for the correlations between the different ℓ ranges and compute the exact posterior distribution of the expected parameter shifts, avoiding the use of a Gaussian approximation, contrary to what was done in previous studies. In evaluating the probability of a shift in the most deviant parameter out of the six ΛCDM ones, we also pointed out the importance of taking into account look-elsewhere effects (i.e., accounting for having searched across several parameters).
We have found that the cosmological parameters inferred from ℓ < 800 versus the full multipole range ℓ < 2500 in the context of the ΛCDM model are consistent with each other within approximately 10% PTE. We find similar significance levels when evaluating the probability of shifts in the most deviant parameters, when comparing high-ℓ data with low-ℓ, or when splitting at multipoles other than ℓ = 800. Table 1 and Fig. A.1 summarize these results. In light of the recent Planck results on the reionization optical depth (Planck Collaboration Int. XLVI 2016; Planck Collaboration Int. XLVII 2016), we find that using a lower and tighter prior of τ = 0.055 ± 0.010 has a mild impact on the significance levels of the parameter shifts, increasing them by about 0.3σ, or equivalently reducing the PTE by around 0.05.
The discussion of point (iii), that is, explaining the physics underlying the shifts, has not previously existed at all. While we point out that the interpretation of the shifts is not unique, we provide one possible explanation by connecting features in the spectra with shifts in parameters. We find that when reducing the lever arm of the data by only using the larger angular scales (ℓ < 800), cosmological parameters are more strongly affected by the low-ℓ deficit, that is, the apparent lack of power at ℓ < 30. To decrease power at ℓ < 30, ns increases, Ase−2τ is then lowered to reduce power at ℓ ≳ 500, ωm decreases to compensate the induced change of power below ℓ ≃ 500, while ωb increases to reduce the amplitude of the second peak (which was raised by the decrease in ωm). The Hubble constant is in turn pulled high to keep the angular size of the horizon unchanged.
On the other hand, we find that the small-scale results are influenced by the preference for a larger smoothing of the power spectrum peaks and troughs at ℓ ≳ 1000. While at face value it might seem like this smoothing is the sign of an excess amplitude of gravitational lensing, we find that most of the shifts in the ΛCDM parameters serve not to increase the lensing potential, but rather to fit these features through non-lensing related effects. While neither the peak smoothing nor low-ℓ features are statistically very significant, and could just be statistical fluctuations in the data, we show that they can explain a large part of the observed parameter shifts.
In summary, we have identified the main features of the data leading to the observed parameter shifts and explained the physics of why the parameters of the ΛCDM model adjust in the way they do to fit these features. Further, we find that these shifts are not in strong disagreement with expectations for the size of such differences among a set of parameters; thus there is no requirement to explain such shifts with either systematic effects or new physics.
Planck (http://www.esa.int/Planck) is a project of the European Space Agency (ESA) with instruments provided by two scientific consortia funded by ESA member states and led by Principal Investigators from France and Italy, telescope reflectors provided through a collaboration between ESA and a scientific consortium led and funded by Denmark, and additional contributions from NASA (USA).
Although the South Pole Telescope and Atacama Cosmology Telescope had already measured the CMB TT power spectrum over this multipole range (e.g. Story et al. 2013; Das et al. 2014), Planck’s dramatically increased sky coverage leads to a much more precise power spectrum determination.
More precisely, the product of eigenvalues of the two Fisher information matrices (see e.g. Schervish 1996, for a definition) – one for ℓ < 800 and the other for ℓ > 800 – is approximately equal at this multipole split.
This is the same feature that has sometimes previously been called the “low-ℓ anomaly”. We choose to use the name “low-ℓ deficit” throughout this work to avoid ambiguity with other large scale “anomalies” and because it is more appropriate for a feature of only moderate significance. See Sect. 5.3 for further discussion.
We loosely refer here to the “peaks of the distributions”. In the next sections, we will more carefully specify whether we quantify the shifts in terms of difference in the best-fit values (i.e., the maximum of the full-dimensional posterior distribution of the parameters) or in terms of the marginalized means. Choosing one or the other should not significantly change our conclusions, since the posterior distributions of the parameters are nearly Gaussian, and therefore these two quantities are very close to each other.
We thus ignore ℓ-to-ℓ correlations across this multipole, consistent with what is assumed in the real likelihood (Planck Collaboration XI 2016).
Of course, the two likelihoods are identical when ℓmax = 2500, as demonstrated in Planck Collaboration XI (2016).
See Sects. 8 and 9 of Planck Collaboration XX (2016) for alternative investigations of the significance of the power deficit using P(k) reconstruction and parameterized model fits. Inflationary models with features are not found to give sufficiently improved fits (compared to a featureless power spectrum) to justify adding the additional parameters.
This is the short form of “detector sets” and indicates subsets of maps built from single detectors for the HFI’s spider-web bolometers (SWBs) and maps built from quadruplets of detectors for HFI’s polarization-sensitive bolometers (PSBs); see Planck Collaboration VIII (2016).
Acknowledgments
The Planck Collaboration acknowledges the support of: ESA; CNES, and CNRS/INSU-IN2P3-INP (France); ASI, CNR, and INAF (Italy); NASA and DoE (USA); STFC and UKSA (UK); CSIC, MINECO, JA, and RES (Spain); Tekes, AoF, and CSC (Finland); DLR and MPG (Germany); CSA (Canada); DTU Space (Denmark); SER/SSO (Switzerland); RCN (Norway); SFI (Ireland); FCT/MCTES (Portugal); ERC and PRACE (EU). A description of the Planck Collaboration and a list of its members, indicating which technical or scientific activities they have been involved in, can be found at http://www.cosmos.esa.int/web/planck/planck-collaboration. Part of the analysis for this paper was run on computers operated by WestGrid (www.westgrid.ca) and Compute Canada (www.computecanada.ca). This work was also supported by the Labex ILP (reference ANR-10-LABX-63). We thank all of the users of Cosmology@Home for donating computing time in support of this work, and in particular the top contributors, MaDcCow (Thomas Wooton), 25000ghz (Roberto Piantoni), Rally1965, Mumps, UofS-Computer-Science, and Bryan, as well as the top teams, BOINC.Italy and SETI.USA.
References
- Addison, G. E., Huang, Y., Watts, D. J., et al. 2016, ApJ, 818, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Benabed, K., Cardoso, J.-F., Prunet, S., & Hivon, E. 2009, MNRAS, 400, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Banday, A. J., Gorski, K. M., et al. 1996, ApJ, 464, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Bennett, C. L., Larson, D., Weiland, J. L., et al. 2013, ApJS, 208, 20 [Google Scholar]
- Beutler, F., Saito, S., Brownstein, J. R., et al. 2014, MNRAS, 444, 3501 [NASA ADS] [CrossRef] [Google Scholar]
- Cai, Y., Wang, Y.-T., & Piao, Y.-S. 2015a, Phys. Rev. D, 92, 023518 [NASA ADS] [CrossRef] [Google Scholar]
- Cai, Y.-F., Ferreira, E. G. M., Hu, B., & Quintin, J. 2015b, Phys. Rev. D, 92, 121303 [NASA ADS] [CrossRef] [Google Scholar]
- Calabrese, E., Hlozek, R. A., Battaglia, N., et al. 2013, Phys. Rev. D, 87, 103012 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, P., & Lin, Y.-H. 2016, Phys. Rev. D, 93, 023503 [NASA ADS] [CrossRef] [Google Scholar]
- Contaldi, C. R., Peloso, M., Kofman, L., & Linde, A. 2003, J. Cosmol. Astropart. Phys., 7, 002 [NASA ADS] [CrossRef] [Google Scholar]
- Couchot, F., Henrot-Versillé, S., Perdereau, O., et al. 2015, A&A, 594, A24 [Google Scholar]
- Das, S., Louis, T., Nolta, M. R., et al. 2014, J. Cosmol. Astropart. Phys., 4, 014 [NASA ADS] [CrossRef] [Google Scholar]
- Dodelson, S. 2003, Modern cosmology (Academic Press) [Google Scholar]
- Efstathiou, G. 1988, in Large-Scale Motions in the Universe: A Vatican study Week, eds. V. C. Rubin, & G. V. Coyne, 299 [Google Scholar]
- Efstathiou, G. 2014, MNRAS, 440, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- George, E. M., Reichardt, C. L., Aird, K. A., et al. 2015, ApJ, 799, 177 [Google Scholar]
- Hamimeche, S., & Lewis, A. 2008, Phys. Rev. D, 77, 103013 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrandt, H., Viola, M., Heymans, C., et al. 2016, MNRAS, 465, 1454 [NASA ADS] [CrossRef] [Google Scholar]
- Hinshaw, G., Spergel, D. N., Verde, L., et al. 2003, ApJS, 148, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W., & Sugiyama, N. 1995a, ApJ, 444, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W., & Sugiyama, N. 1995b, Phys. Rev. D, 51, 2599 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W., & White, M. 1996a, ApJ, 471, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W., & White, M. 1996b, A&A, 315, 33 [NASA ADS] [Google Scholar]
- Hu, W., & White, M. 1997, ApJ, 479, 568 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, W., Sugiyama, N., & Silk, J. 1996, ArXiv e-prints [arXiv:astro-ph/9604166] [Google Scholar]
- Hu, W., Sugiyama, N., & Silk, J. 1997, Nature, 386, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Iqbal, A., Prasad, J., Souradeep, T., & Malik, M. A. 2015, J. Cosmol. Astropart. Phys., 6, 014 [NASA ADS] [CrossRef] [Google Scholar]
- Jones, E., Oliphant, T., Peterson, P., et al. 2001–2016, SciPy: Open source scientific tools for Python (Online; version 0.14.0) [Google Scholar]
- Kaiser, N. 1984, ApJ, 282, 374 [NASA ADS] [CrossRef] [Google Scholar]
- Knox, L. 1995, Phys. Rev. D, 52, 4307 [NASA ADS] [CrossRef] [Google Scholar]
- Kosowsky, A., Milosavljevic, M., & Jimenez, R. 2002, Phys. Rev. D, 66, 063007 [NASA ADS] [CrossRef] [Google Scholar]
- Kovács, A., Carron, J., & Szapudi, I. 2013, MNRAS, 436, 1422 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, D., Weiland, J. L., Hinshaw, G., & Bennett, C. L. 2015, ApJ, 801, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., & Bridle, S. 2002, Phys. Rev. D, 66, 103511 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, A., & Challinor, A. 2006, Phys. Rep., 429, 1 [Google Scholar]
- Lewis, A., Challinor, A., & Lasenby, A. 2000, ApJ, 538, 473 [Google Scholar]
- Liddle, A. R., & Lyth, D. H. 2000, Cosmological Inflation and Large-Scale Structure (Cambridge University Press) [Google Scholar]
- Louis, T., Addison, G. E., Hasselfield, M., et al. 2014, J. Cosmol. Astropart. Phys., 2014, 016 [NASA ADS] [CrossRef] [Google Scholar]
- MacCrann, N., Zuntz, J., Bridle, S., Jain, B., & Becker, M. R. 2015, MNRAS, 451, 2877 [NASA ADS] [CrossRef] [Google Scholar]
- Marra, V., Amendola, L., Sawicki, I., & Valkenburg, W. 2013, Phys. Rev. Lett., 110, 241305 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Millea, M. 2017, Astrophysics Source Code Library [record ascl:1701.004] [Google Scholar]
- Mortonson, M. J., Dvorkin, C., Peiris, H. V., & Hu, W. 2009, Phys. Rev. D, 79, 103519 [NASA ADS] [CrossRef] [Google Scholar]
- Naess, S., Hasselfield, M., McMahon, J., et al. 2014, J. Cosmol. Astropart. Phys., 2014, 007 [NASA ADS] [CrossRef] [Google Scholar]
- Pan, Z., Knox, L., & White, M. 2014, MNRAS, 445, 2941 [NASA ADS] [CrossRef] [Google Scholar]
- Peacock, J. A. 1999, Cosmological Physics (Cambridge University Press) [Google Scholar]
- Peebles, P. J. E., & Yu, J. T. 1970, ApJ, 162, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Peiris, H. V., Komatsu, E., Verde, L., et al. 2003, ApJS, 148, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Piao, Y.-S., Feng, B., & Zhang, X. 2004, Phys. Rev. D, 69, 103520 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XV. 2014, A&A, 571, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVI. 2014, A&A, 571, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVII. 2014, A&A, 571, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XXXI. 2014, A&A, 571, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration I. 2016, A&A, 594, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration II. 2016, A&A, 594, A2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration VIII. 2016, A&A, 594, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration IX. 2016, A&A, 594, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration X. 2016, A&A, 594, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2016, A&A, 594, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XIII. 2016, A&A, 594, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XV. 2016, A&A, 594, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XVI. 2016, A&A, 594, A16 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XX. 2016, A&A, 594, A20 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLVI. 2016, A&A, 596, A107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration Int. XLVII. 2016, A&A, 596, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riess, A. G., Macri, L. M., Hoffmann, S. L., et al. 2016, ApJ, 826, 56 [NASA ADS] [CrossRef] [Google Scholar]
- Sachs, R. K., & Wolfe, A. M. 1967, ApJ, 147, 73 [NASA ADS] [CrossRef] [Google Scholar]
- Schervish, M. 1996, Theory of Statistics, Springer Series in Statistics (New York: Springer) [Google Scholar]
- Seehars, S., Grandis, S., Amara, A., & Refregier, A. 2016, Phys. Rev. D, 93, 103507 [NASA ADS] [CrossRef] [Google Scholar]
- Seljak, U. 1994, ApJ, 435, L87 [NASA ADS] [CrossRef] [Google Scholar]
- Seljak, U. 1996, ApJ, 463, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J. 1968, ApJ, 151, 459 [NASA ADS] [CrossRef] [Google Scholar]
- Spergel, D. N., Verde, L., Peiris, H. V., et al. 2003, ApJS, 148, 175 [NASA ADS] [CrossRef] [Google Scholar]
- Story, K. T., Reichardt, C. L., Hou, Z., et al. 2013, ApJ, 779, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Sugiyama, N., Silk, J., & Vittorio, N. 1993, ApJ, 419, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Verde, L., Protopapas, P., & Jimenez, R. 2013, Physics of the Dark Universe, 2, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Wyman, M., Rudd, D. H., Vanderveld, R. A., & Hu, W. 2014, Phys. Rev. Lett., 112, 051302 [NASA ADS] [CrossRef] [Google Scholar]
- Zel’dovich, Y. B.,Rakhmatulina, A. K., & Syunyaev, R. A. 1972, Radiophys. Quant. Electron., 15, 121 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: A more exhaustive set of tests
The main focus of this paper has been on shifts between parameters derived from ℓ < 800 data and those from ℓ < 2500 data. We considered this the most interesting choice because ℓ = 800 evenly splits the Fisher information on ΛCDM parameters in the PlanckTTdata; additionally, we focused on low-ℓ parameters versus full-ℓ parameters (as opposed to low-ℓ versus high-ℓ), since this is most directly relevant for the issue of WMAP versus Planck parameter shifts.
Despite this decision, we would like to know if our particular choice of ℓsplit = 800 greatly affected results, either making them seem more or less consistent than otherwise. Additionally, in terms of a generic test of the Planck data, there are many other data splits that one might consider to test the consistency even more stringently. We present results from a more exhaustive set of such tests in this appendix. More specifically, we look at three different ways of splitting the data:
-
1.
ℓ < ℓsplit vs. ℓ < 2500;
-
2.
ℓ < ℓsplit vs. ℓ > ℓsplit;
-
3.
ℓ < ℓsplit vs. ℓ > ℓsplit + 50.
We do this at several different values of ℓsplit across the range allowed by our simulations. For each case, we compute the χ2 and max-param statistics.
Of course, since we are now explicitly scanning over statistical tests, we need to account for a posteriori corrections to interpret the significance of any outliers we find. This is the same effect already discussed in the context of searching for a maximally discrepant parameter, but now for finding a maximally discrepant partitioning of the data. It is straightforward to calculate
these corrections based on the suite of simulations. For each realization, we search for the most discrepant result as a function of ℓsplit. We then compare the result on the real data against this distribution and compute a PTE as before.
We have computed results varying ℓsplit between 650 and 2500 with a step size Δℓ = 50. The results are shown in Fig. A.1. The blue line shows the raw (so-called “local”) significance for each case, computed exactly as described in Sect. 3.3. The significance shows considerable scatter, as one might expect due to noise, with no outlier above roughly 2.5σ. We see that any other choice of ℓsplit in the vicinity of 800 would have given the same qualitative results that we have focused in the main body of this paper.
If we search for the ℓsplit which gives the largest local significance, we need to account for the look-elsewhere effect to interpret the true significance of this outlier. This is given by the orange line and labelled “global”. For example, if for some ℓsplit we find a local significance of 2σ, then the global significance is the fraction of simulations for which we find a shift at any ℓsplit with a local significance exceeding 2σ. Generally speaking, this marginalization lowers the significance of any outliers we find by around 1σ. To be clear, we are not claiming the actual significance of the shifts presented in the main body of the paper are lower by 1σ, since we did not choose ℓsplit = 800 based on finding a most discrepant data split. Nevertheless, if we now look through Fig. A.1 for outliers (for example the roughly 2.5σ outlier in the top right panel at ℓsplit = 1100), it is clear that the true significance is somewhat lower. The conclusion after this wider set of tests is that we find no evidence for any inconsistency in the data that was hidden by our specific choice of data partitioning.
 |
Fig. A.1 Significance levels (in units of effective σ) of the parameter shifts between two multipole ranges, according to a given statistic, as a function of ℓsplit. The specific choice of the two multipole ranges and the statistic used are labelled on each panel. The blue line is the “local” significance, calculated as described in Sect. 3.3. The orange line is the “global” significance which should be used to interpret the significance of any outliers we find (see Appendix A for further description). |
Appendix B: The low-ℓ approximation
The simulations used in this paper make use of an approximate low-ℓ likelihood, as discussed in Sect. 3.2. Our main check of this approximation, as described in that section, is to estimate parameters from ℓ < 800 with the actual Commander likelihood swapped out for our approximate likelihood applied to the Commander CMB map. The ℓ < 800 case is important because it gives more weight to the low multipoles than, for example, ℓ < 2500; hence it is a more stringent test of the approximation. In either case, we find that all ΛCDM parameters are within 0.05σ and thus that the approximation is good enough.
Of course, this test relies on one particular realization of the CMB (namely, our actual CMB sky), and it is technically possible that this realization randomly conspired to make our approximation seem better than it actually is. In this appendix we therefore describe a further test that looks at many different realizations.
If our low-ℓ approximation is correct, it should be the case that the mean of the best-fit values from the simulations recovers the input fiducial parameters, and the scatter in the simulations should be the same as the posterior constraints from an MCMC chain run with the Commander likelihood. An error in the approximation at low ℓ, even just in the error bars, could manifest itself as both a bias in the mean of the best-fit parameters and a scatter that does not match the true posterior.
In Fig. B.1 we show a distribution of the best-fit values from simulations for the ℓ < 800 case, along with the input fiducial values and the posteriors from a chain (which have been re-centred on the fiducial values). However, there is one detail different about these simulations than the ones used in the main body of the paper. Whereas those all have the same prior on τ applied (so as to be consistent with what is done to the real data), these simulations have a different prior for each realization; the prior
is still Gaussian with a width of 0.02, but its mean has been randomly sampled from 0.07 ± 0.02 itself. This is akin to having drawn realization of the low-ℓ polarization data, and although it has no bearing on the accuracy of the low-ℓ approximation, it is necessary in order that the scatter actually matches the posterior. We find then, as expected, that the simulations are centred on the fiducial values to within the scatter expected from the finite number of simulations, and the distribution does indeed track the posterior constraint. We therefore conclude that our low-ℓ approximation is sufficient and our previous determination of its accuracy on the real data was not affected by our particular realization of the CMB. We stress that this is not an easy test to pass; for example, we have checked that had we used the traditional fsky approximation this test would have failed noticeably.
 |
Fig. B.1 Histograms showing the distribution of best-fit ℓ < 800 parameters from simulations performed using our low-ℓ approximation. The vertical line is the input fiducial model and the contours show the posteriors from an ℓ < 800 chain using the actual Commander likelihood at low ℓ. The unbiased recovery of the fiducial parameters and agreement with the posteriors is a stringent test of the validity of our low-ℓ approximation. We note that these simulations, unlike the ones used in the main body of the paper to determine significance levels, have the prior on τ handled slightly differently, so as to allow us to use them as a test of the low-ℓ approximation (see Appendix B for discussion). |
All Tables
Consistency of various data splits, as determined from two statistics computed on data and simulations.
Comparison of the expected dispersion (“Exp.”) and observed (“Obs.”) parameter shifts between pairs of datasets.
All Figures
 |
Fig. 1 Cosmological parameter constraints from PlanckTT+τprior for the full multipole range (orange) and for ℓ < 800 (blue) – see the text for the definitions of the parameters. We note that the constraints are generally in good agreement, with the full Planck data providing tighter limits on the parameters; however, the best-fit values certainly do shift. It is these shifts that we seek to explain in this paper. A prior τ = 0.07 ± 0.02 has been used here as a proxy for the effect of the low-ℓ polarization data (with the impact of a different prior discussed later). As a comparison, we also show results for WMAP TT data combined with the same prior on τ (grey). |
| In the text | |
 |
Fig. 2 Differences in best-fit parameters between ℓ < 800 and ℓ < 2500 as compared to expectations from a suite of simulations. The cloud of blue points and the histograms are the distribution from simulations (discussed in Sect. 3), while the orange points and lines are the shifts found in the data. Although the shifts may appear to be generally large for this particular choice of parameter set, it is important to realise that this is not an orthogonal basis, and that there are strong correlations among parameters; when this is taken into account, the overall significance of these shifts is 1.4σ, and the significance of the biggest outlier (Ase− 2τ), after accounting for look-elsewhere effects, is 1.7σ. Figure 3 shows these same shifts in a more orthogonal basis that makes judging these significance levels easier by eye. Choosing a different multipole at which to split the data, or comparing low ℓs versus high ℓs alone, does not change this qualitative level of agreement. We note that the parameter mode discussed in Sect. 3.3 is not projected out here, since it would correspond to moving any data point by less than the width of the point itself. |
| In the text | |
 |
Fig. 3 Visually it might seem that the data point in the six-parameter space of Fig. 2 is a much worse outlier than only 1.4σ. One way to see that it really is only 1.4σ is to transform to another parameter space, as shown in this figure. Linear transformations leave the χ2 unaffected, and while ours here are not exactly linear, the shifts are small enough that they can be approximated as linear and the χ2 is largely unchanged (in fact it is slightly worse, 1.6σ). We have chosen these parameters so the shifts are more decorrelated while still using physical quantities. The parameter |
| In the text | |
 |
Fig. 4 Distribution of two different statistics computed on the simulations (blue histogram) and on the data (orange line). The first is the χ2 statistic, where we compute χ2 for the change in parameters between ℓ < 800 and ℓ < 2500, with respect to the covariance of the expected shifts. The second is a “biggest outlier” statistic, where we search for the parameter with the largest change, in units of the standard deviation of the simulated shifts. We give the probability to exceed (PTE) on each panel. For both statistics, we find that the observed shifts are largely consistent with expectations from simulations. |
| In the text | |
 |
Fig. 5 Response of |
| In the text | |
 |
Fig. 6 Shifts in the best-fit values of parameters when one considers the multipole range either below or above different values of ℓsplit. This uses the PlanckTT+τprior data combination, with ℓ> 30 computed using plik_lite. The different lines correspond to restricting the data to ℓ <ℓsplit (blue), 30 <ℓ <ℓsplit (green), and ℓ>ℓsplit (orange). These shifts are described in Sect. 5.1. One can see here that excising the ℓ < 30 region moves the low-ℓ parameters closer to the high-ℓ parameters, as discussed in detail in Sect. 5.3. Error bands are the ± 1 and ± 2σ scatter in the simulations away from the input fiducial model. We have chosen to plot this quantity as opposed to posterior constraints on these parameters (which is different because of our prior on τ) because it is these bands that are appropriate for comparing the blue and orange lines against each other. We note that this has the perhaps counter-intuitive effect of having the error bands in the τ panel increase as more data are added. None of the local “spikes” are found to be significant, as can be seen from the bottom panel of Fig. A.1. |
| In the text | |
 |
Fig. 7 How the best-fit ℓ <ℓmax PlanckTT+τprior ΛCDM model adjusts as ℓmax is increased from 800 to 2500 (going from the top panels to the bottom panels). Left column: all panels show residuals relative to the ℓ < 800 model. Planck power spectrum binned estimates and ± 1σ errors on the CMB spectrum, as extracted with plik_lite, are shown as grey boxes. Note the change in y-axis scale at ℓ = 500, indicated by the vertical dotted line. The solid black line is the best-fit model for ℓ <ℓmax, where ℓmax is different for each panel, as indicated by which of the boxes are shaded darker. The various coloured lines indicate the linear response to the shift in individual parameters between their ℓ < 800 best-fit value and their ℓ <ℓmax one. Right column: identical to the left column, except that the contribution from θ∗ (i.e., the blue line from the corresponding left panel) has been subtracted from the sums, as well as from the actual model and from the data. For reference, the arrows in the top and bottom panels show the locations of the peaks in the power spectrum. |
| In the text | |
 |
Fig. 8 Power spectrum residuals for a few additional cases, in the same format as Fig. 7. We note that for the bottom panel, the fiducial model is the best-fit from 30 <ℓ < 800, as opposed to from ℓ < 800, as is the case in Fig. 7 and in the top two panels of this figure. In all cases the black line is the best-fit ΛCDM model in the range indicated by the shaded data boxes. The coloured lines are the linear responses to the shifts in parameters between these two best-fit solutions. Top: same as panel 5a of Fig. 7, but with an additional free parameter, AL, shown in yellow. This added degree of freedom tracks reasonably well the oscillatory residuals, leaving smaller shifts for the other parameters and a reduced low-ℓ deficit. Middle: same as panel 5a of Fig. 7, but with dashed lines showing the responses with the gravitational potential fixed. Bottom: the way in which the best-fit model from 30 <ℓ < 800 is “thrown off” by inclusion of ℓ < 30 data. We note that although visually the ℓ> 800 data appears to be a better fit with ℓ < 30, the χ2 is worse by Δχ2 = 3.2. |
| In the text | |
 |
Fig. 9 Marginalized mean and 68% error bars on cosmological parameters estimated with different data choices, assuming the ΛCDM model (unless otherwise labelled), derived from MCMC chains. We use the PlanckTT likelihood in combination with a prior τ = 0.07 ± 0.02. Excising the low multipoles, that is, ℓ < 30, substantially improves the agreement between the parameters from ℓ < 800 and the ℓ < 2500 range. Further agreement is then achieved when removing the effect of gravitational lensing. |
| In the text | |
 |
Fig. 10 Posterior distributions for Alow (which phenomenologically parametrizes the low-ℓ deficit by multiplying the amplitude of the power spectrum at multipoles smaller than ℓ < 30) and for AL (which parametrizes the peak smoothing effect), derived from MCMC chains. We show the results for a ΛCDM+ Alow + AL model (black solid line), for ΛCDM+ Alow (blue) and for ΛCDM+ AL (red). Although a degeneracy is present between the two parameters, small deviations with respect to the ΛCDM expectations remain even when varying both parameters at the same time. |
| In the text | |
 |
Fig. 11 Constraints on cosmological parameters from data derived from individual frequencies. The data used is 30 < ℓ < 2500 unless otherwise labelled, and in combination with a prior on τ. The reference case combines all frequencies. The constraints for 30 <ℓ < 800 and ℓ > 800 are obtained with foreground parameters fixed to the best fit of the reference case. The grey band shows the ± 1σ expected shifts in cosmological parameters with respect to the reference case (calculated as in Eq. (53) of Planck Collaboration XI 2016). For this test we use the PlikTT likelihood, as described in Planck Collaboration XI (2016). Results from individual frequencies are in very good agreement. |
| In the text | |
 |
Fig. 12 Residuals for different frequency combinations with respect to the ℓ = 2–800 best-fit model. For each frequency we only show the ℓ range used in the Planck likelihood. Although these data subsets are noisy, the oscillatory-like feature seems consistent across frequencies. |
| In the text | |
 |
Fig. 13 Constraints on ΛCDM parameters from: SPT data from Story et al. (2013) in pink; PlanckTT ℓ> 800 in green; and WMAP in blue. Except for the latter data set, which has no sensitivity to τ, all others have been combined with a prior τ = 0.07 ± 0.02. The significance of parameter shifts between these three approximately uncorrelated data sets can be roughly calculated using Eq. (1). We find no strong evidence of discrepancies, with SPT and WMAP agreeing at the 1.7σ level, Planck ℓ > 800 and WMAP agree even better at 1.1σ, while Planck ℓ> 800 and SPT agree with each other at 2.1σ. Also plotted in orange is Planckφφ with θ∗, ωb, and ns fixed to the Planck best-fit values. This data set, across the two parameters it constrains, is also not in significant tension with the others. Sect. 6 discusses these comparisons in more detail. |
| In the text | |
 |
Fig. A.1 Significance levels (in units of effective σ) of the parameter shifts between two multipole ranges, according to a given statistic, as a function of ℓsplit. The specific choice of the two multipole ranges and the statistic used are labelled on each panel. The blue line is the “local” significance, calculated as described in Sect. 3.3. The orange line is the “global” significance which should be used to interpret the significance of any outliers we find (see Appendix A for further description). |
| In the text | |
 |
Fig. B.1 Histograms showing the distribution of best-fit ℓ < 800 parameters from simulations performed using our low-ℓ approximation. The vertical line is the input fiducial model and the contours show the posteriors from an ℓ < 800 chain using the actual Commander likelihood at low ℓ. The unbiased recovery of the fiducial parameters and agreement with the posteriors is a stringent test of the validity of our low-ℓ approximation. We note that these simulations, unlike the ones used in the main body of the paper to determine significance levels, have the prior on τ handled slightly differently, so as to allow us to use them as a test of the low-ℓ approximation (see Appendix B for discussion). |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.