| Issue |
A&A
Volume 602, June 2017
|
|
|---|---|---|
| Article Number | A105 | |
| Number of page(s) | 62 | |
| Section | Atomic, molecular, and nuclear data | |
| DOI | https://doi.org/10.1051/0004-6361/201628742 | |
| Published online | 23 June 2017 | |
Photodissociation and photoionisation of atoms and molecules of astrophysical interest
Leiden Observatory, Leiden University, PO Box 9513, 2300 RA Leiden, The Netherlands
e-mail: heays@strw.leidenuniv.nl
Received: 19 April 2016
Accepted: 1 January 2017
A new collection of photodissociation and photoionisation cross sections for 102 atoms and molecules of astrochemical interest has been assembled, along with a brief review of the basic physical processes involved. These have been used to calculate dissociation and ionisation rates, with uncertainties, in a standard ultraviolet interstellar radiation field (ISRF) and for other wavelength-dependent radiation fields, including cool stellar and solar radiation, Lyman-α dominated radiation, and a cosmic-ray induced ultraviolet flux. The new ISRF rates generally agree within 30% with our previous compilations, with a few notable exceptions. Comparison with other databases such as PHIDRATES is made. The reduction of rates in shielded regions was calculated as a function of dust, molecular and atomic hydrogen, atomic C, and self-shielding column densities. The relative importance of these shielding types depends on the atom or molecule in question and the assumed dust optical properties. All of the new data are publicly available from the Leiden photodissociation and ionisation database. Sensitivity of the calculated rates to variation of temperature and isotope, and uncertainties in measured or calculated cross sections, are tested and discussed. Tests were conducted on the new rates with an interstellar-cloud chemical model, and find general agreement (within a factor of two) in abundances obtained with the previous iteration of the Leiden database assuming an ISRF, and order-of-magnitude variations assuming various kinds of stellar radiation. The newly parameterised dust-shielding factors makes a factor-of-two difference to many atomic and molecular abundances relative to parameters currently in the UDfA and KIDA astrochemical reaction databases. The newly-calculated cosmic-ray induced photodissociation and ionisation rates differ from current standard values up to a factor of 5. Under high temperature and cosmic-ray-flux conditions the new rates alter the equilibrium abundances of abundant dark cloud abundances by up to a factor of two. The partial cross sections for H2O and NH3 photodissociation forming OH, O, NH2 and NH are also evaluated and lead to radiation-field-dependent branching ratios.
Key words: photon-dominated region (PDR) / cosmic rays / dust, extinction / ISM: molecules / molecular data / atomic data
© ESO, 2017
1. Introduction
Ultraviolet (UV) photons play a critical role in interstellar and circumstellar chemistry. The realisation that photodissociation and photoionisation processes control the abundances of atoms and small molecules in diffuse interstellar clouds dates back nearly a century (Eddington 1928; Kramers & Ter Haar 1946; Bates & Spitzer 1951). Similarly, photodissociation of parent species by UV radiation from the Sun has long been known to explain the existence of small molecules in cometary comae (Haser 1957; Crovisier et al. 1997). Nowadays, photodissociation processes are found to be important for modelling the chemistry of nearly every type of astrophysical region, from the edges of dense clouds close to bright young stars to the surface layers of protoplanetary disks, envelopes around evolved stars and giant molecular clouds on galactic scales (e.g., Glassgold 1996; Hollenbach & Tielens 1999; Tielens 2013; van Dishoeck et al. 2006; Glover & Clark 2012). Such clouds of gas and dust in which photodissociation is the dominant molecular destruction path are termed photodissociation or photon-dominated regions (PDRs), although the term PDRs originally referred mostly to high density regions close to bright O and B stars such as found in Orion (Tielens & Hollenbach 1985).
The abundant UV photons in these regions photodissociate and photoionise the main hydrogen, carbon, oxygen and nitrogen-containing species, controlling the H+ → H → H2, C+ → C → CO, O → O2 and N → N2 transitions (Tielens & Hollenbach 1985; van Dishoeck & Black 1988; Li et al. 2013). Photoprocesses thus affect the abundance of the main cooling species in the interstellar medium, and they also generate chemically-reactive ions and radicals, opening pathways to the formation of larger species (Sternberg & Dalgarno 1995; Lee et al. 1996; Jansen et al. 1996; Li et al. 2014). The gas-phase abundance of more complex molecules formed in this way is simultaneously limited by their own photodestruction (Teyssier et al. 2004; van Hemert & van Dishoeck 2008; Guzman et al. 2014). The photoionisation of atoms and molecules also leads to a significant speed up of PDR chemistry due to the enhanced reaction rates of ions compared with neutral species (Tielens 2013; van Dishoeck 2014).
The quantitative modelling of chemical evolution in clouds, envelopes and disks is a prerequisite for the full interpretation of observations of their emitting molecular lines and dust continuum. Such models consider many physical regimes (e.g., Le Petit et al. 2006; Walsh et al. 2013) and involve many classes of chemical reactions (Wakelam et al. 2012; McElroy et al. 2013). By quantitatively constraining the rates of photoprocesses, as is done in this paper, other chemical and physical parameters processes affecting observations can be more reliably determined.
The fundamental quantities governing photodissociation and ionisation are the wavelength-dependent flux of incident UV radiation, discussed in Sect. 2, and the wavelength-dependent photoabsorption, photodissociation, and photoionisation cross sections of each atom or molecule, introduced in Sects. 3 and 4. Historically, the complete and unabridged specification of these quantities contained too much information to be included in astrochemical models, and is actually in many cases unnecessary given the scale of uncertainties in observations and other model parameters. Tabulated pre-integrations of the full wavelength dependence into a process rate (or lifetime) for different species in different kinds of UV-irradiated environments are useful to speed up modelling. We calculated such rates in Sect. 5. Such tabulations must necessarily include the column-density-dependent effect of radiation shielding by dust, H and H2 inside interstellar and circumstellar clouds. The wavelength dependence of such shielding is frequently presented by a simplified parameterisation and is discussed further in Sect. 6.
Astrochemical models can also use the full molecular and atomic cross sections as functions of wavelength, and consider the dissociation of species and shielding by H and H2 line-by-line, to compute the photodestruction of molecules as functions of depth into a PDR (e.g., van Dishoeck & Black 1988; Viala et al. 1988; Jansen et al. 1995; Le Petit et al. 2006; Woitke et al. 2009; Walsh et al. 2013; Li et al. 2013). Furthermore, astrochemical programs that employ simplified rates for photodestruction may require precomputing many of these when exploring, for example, a range of possible dust grain ultraviolet extinction properties (e.g., van Dishoeck et al. 2006; Röllig et al. 2013). Fundamental atomic and molecular cross sections such as those presented here are then required.
Even deep inside dark clouds well shielded from external radiation, a weak UV flux is maintained. This is induced by the interaction of cosmic rays with hydrogen. The resulting spectrum is highly structured (Prasad & Tarafdar 1983; Gredel et al. 1987) and incorporation of this process into astrochemical models also benefits from a reduction of the full wavelength dependence into a conveniently tabulated rate. The most-recent tabulation of these rates is by Gredel et al. (1989). Since that time there have been updates for many of the photodissociation cross sections of astrophysically relevant molecules. Here we update these rates in Sect. 7.
In Sect. 8, we discuss the potential variability of our collected cross sections and calculated rates given their dependence on: interstellar dust optical properties, temperature, spectrally unresolved cross sections, and isotopic substitution. We also make a special case of studying distinct fragment branching ratios from the photodissociation of H2O and NH3, and assess the significance of our new rates by means of a physically simple but chemically complex toy astrochemical model.
All cross sections and calculated rates are available from the Leiden Observatory database of “photodissociation and photoionisation of astrophysically relevant molecules”1, and any future updates will be available there. Some of these cross sections are carried over from the previous iteration of the Leiden database (van Dishoeck 1988; van Dishoeck et al. 2006); many species are updated where new experimental or theoretical data has become available, especially using the MPI Mainz UV/Vis database2. The list of molecules in the database has been extended by new additions of complex-organic species that have recently been detected in the interstellar medium3.
2. Radiation fields
The photodissociation or photoionisation rate (molec. atom-1 s-1) of a molecule (or atom) exposed to an ultraviolet radiation field is 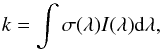 (1)where σ(λ) is the appropriate photodissociation or photoionisation cross section, to be discussed in Sect. 3, and I(λ) is the photon-based radiation intensity summed over all incidence angles. A photon-counting intensity was used for calculations in this paper because of the discrete nature of photodestruction events, but is directly related to the volumetric radiation energy density according to U(λ) = hI(λ) /λ where h is the Planck’s constant. An angularly-differential radiation intensity may be appropriate if the incident radiation is non-isotropic.The integration limits in Eq. (1) are defined by the wavelength range corresponding to the nonzero photodissociation or ionisation cross section and radiation intensity.
(1)where σ(λ) is the appropriate photodissociation or photoionisation cross section, to be discussed in Sect. 3, and I(λ) is the photon-based radiation intensity summed over all incidence angles. A photon-counting intensity was used for calculations in this paper because of the discrete nature of photodestruction events, but is directly related to the volumetric radiation energy density according to U(λ) = hI(λ) /λ where h is the Planck’s constant. An angularly-differential radiation intensity may be appropriate if the incident radiation is non-isotropic.The integration limits in Eq. (1) are defined by the wavelength range corresponding to the nonzero photodissociation or ionisation cross section and radiation intensity.
 |
Fig. 1 Wavelength dependence of some astrophysically-relevant ultraviolet radiation fields. Inset: radiation intensity in the solar neighbourhood estimated by Draine (1978; solid, modified according to van Dishoeck & Black 1982), Mathis et al. (1983; dashed), and Habing (1968; dotted). |
The average intensity of the interstellar radiation field (ISRF) can be estimated from the number and distribution of hot stars in the Galaxy, combined with a model for the dust distribution and its extinction of the stellar radiation (Habing 1968; Draine 1978; Mathis et al. 1983; Parravano et al. 2003). The various estimates of the mean UV energy density at a typical point in the local galaxy agree to within a factor of two. Variations in this energy density of a factor between two and three are expected throughout the galactic plane and on time scales of a few Gyr, as massive O and B star clusters form and die. In addition, the intensity ratio of short-wavelength photons capable of dissociating H2, CO and N2 and ionising atomic C (λ< 110 nm) and the broader far-ultraviolet range (91.2 <λ< 200 nm) may vary by a factor of two in location and time (Parravano et al. 2003).
The wavelength dependent UV intensity as defined by Draine (1978) is often adopted in astrochemical models, and given by the formula 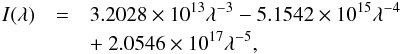 (2)where the wavelength, λ, has units of nm and the radiation intensity, I, has units of photons cm-2 s-1 nm-1. This formula was intended for application within the 91.2 to 200 nm wavelength range.An angularly-differential Draine field, I(λ)/4π, has units of photons cm-2 s-1 nm-1 sr-1; and a scaled version of the radiation intensity may be adopted, χI(λ), to describe regions with greater or lesser UV flux than the mean intensity defined by Draine.
(2)where the wavelength, λ, has units of nm and the radiation intensity, I, has units of photons cm-2 s-1 nm-1. This formula was intended for application within the 91.2 to 200 nm wavelength range.An angularly-differential Draine field, I(λ)/4π, has units of photons cm-2 s-1 nm-1 sr-1; and a scaled version of the radiation intensity may be adopted, χI(λ), to describe regions with greater or lesser UV flux than the mean intensity defined by Draine.
The form of Eq. (2) is shown in Fig. 1 and is reminiscent of a 20 000 K black-body radiation field (B-type star) with some excess at shorter wavelengths. There is assumed to be zero flux shortwards of 91.2 nm due to the ionisation continuum of atomic H that populates the interstellar medium with a high column density for all sight lines. An extension proposed by van Dishoeck & Black (1982) simulates the interstellar flux at longer wavelengths than considered by the Draine model, and fits a range of observed intensities between 200 and 2000 nm to within about 50%. This extension is given by the formula: 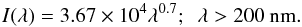 (3)We combine the full wavelength range of the Draine (1978) and van Dishoeck & Black (1982) fields into a “standard” ISRF for the following calculations of photodissociation and ionisation rates.
(3)We combine the full wavelength range of the Draine (1978) and van Dishoeck & Black (1982) fields into a “standard” ISRF for the following calculations of photodissociation and ionisation rates.
The energy intensity of the Draine field integrated between 91.2 and 200 nm is, 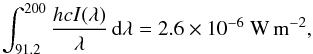 (4)where h is the Planck’s constant, and c the speed of light. This integrated value is a factor of 1.7 higher than the integrated flux of the Habing (1968) field, which is taken as the reference with scaling factor G0 in some models (Tielens & Hollenbach 1985). Thus, the standard Draine field has G0 = 1.7.
(4)where h is the Planck’s constant, and c the speed of light. This integrated value is a factor of 1.7 higher than the integrated flux of the Habing (1968) field, which is taken as the reference with scaling factor G0 in some models (Tielens & Hollenbach 1985). Thus, the standard Draine field has G0 = 1.7.
An independent estimate of the Galactic radiation field is made by Mathis et al. (1983), and its magnitude and wavelength dependence for the case of 10 kpc Galactocentric distance (the local Galaxy) is compared in Fig. 1 with the ISRF standard we adopted. The Mathis et al. UV flux is generally about 35% weaker, and photodissociation rates will be similarly reduced for all atoms and molecules, apart from those that are photodestroyed at wavelengths longer than 300 nm, at which point the Mathis radiation becomes stronger than our standard ISRF.
The ultraviolet field near to a star is dominated by its black body radiation and atomic emission or absorption lines, principally the H I Lyman-α emission line at 121.6 nm. We model several such radiation fields as pure black-body emitters in the following calculations. Special attention to the Lyman-α emission spectrum is warranted because of the known high intensity of this feature in some astrophysical situations, including fast shocks (Neufeld & Dalgarno 1989), the active Sun (Lammer et al. 2012), and young stars (Valenti et al. 2000; Yang et al. 2012). Indeed, around some T Tauri stars, up to 90% of the total far-ultraviolet flux is emitted in the Lyman-α band (Bergin et al. 2003; Schindhelm et al. 2012). Also, the propagation of Lyman-α radiation into a disk is significantly enhanced by scattering from the disk surface (Bethell & Bergin 2011), where a 121.6 nm photon absorbed by an H atom will be ultimately re-radiated in a random direction, including into the disk. Thus, we also treat a pure Lyman-α line in our calculations. A 200 km s-1 Doppler broadening is added to the Lorentzian natural linewidth of the Lyman-α transition. This broadening is a typical value from the observationally-constrained photospheric emission of a sample of T-Tauri stars (France et al. 2014).
In reality, stellar spectra are not black bodies but contain many emission or absorption lines (e.g., Ardila et al. 2002a,b; Leitherer et al. 2010). As an example of a structured stellar flux, we consider a combination of continuum and atomic emission simulating the photosphere of the classical T-Tauri star TW-Hydra, as deduced from UV telescope observations (France et al. 2014). This observationally-derived spectrum is extrapolated to shorter and longer wavelengths using the derived black body and accretion-induced short wavelength excess, respectively, proposed by Nomura & Millar (2005). This includes an additional nonblack-body ultraviolet excess due to the accretion of material onto the still-forming star.
The solar ultraviolet flux is measured directly in the series of SOHO-SUMER observations (Curdt et al. 2001) for λ< 160 nm and also by the UARS SOLSTICE mission (Woods et al. 1996), including longer wavelengths. We adopt a spectrum compiled from these two data sets corresponding to a quiet period in the Sun’s radiance. The activity level of the Sun makes little difference for λ> 160 nm but can induce variation of a factor of two or more at shorter wavelengths, including enhanced Lyman-α radiation. More detailed studies of the dependence of molecular photodissociation rates on solar activity are made by Huebner et al. (1992) and Huebner & Mukherjee (2015).
All stellar radiation fields were normalised to match the energy intensity of the Draine field integrated between 91.2 and 200 nm, that is, 2.6×10 W m-2. The photodissociation and ionisation rates calculated hereafter due to exposure of molecules and atoms to these radiation field should subsequently be scaled to match the flux in an astrophysical environment, which may differ by multiple orders of magnitude. Our normalisation scheme is selected to emphasise the wavelength-dependent effects induced by substituting radiation fields. A scale factor of 37 700 should be used to increase the solar photodissociation and photoionisation rates calculated here to values appropriate for the approximate solar intensity at 1 au, assuming an integrated solar flux between 91.2 and 200 nm of 0.098 W m-2.
For the cases of the solar and TW-Hydra radiation fields, intensity at wavelengths shorter than the ionisation threshold of atomic H, 91.2 nm, is included. This is certainly appropriate for studies of planetary atmospheres and cometary comae in the H-deprived solar system. There are also several known cases of highly-evolved, hydrogen gas-poor debris disks supporting some amount of CO (Mathews et al. 2014). The origin of this gas is unknown but may arise from evaporation of solids in collisions of planetesimals, allowing for relatively low amounts of gas-phase hydrogen relative to other species and the free transmission of short-wavelength radiation (Dent et al. 2014).
A cosmic-ray induced UV-emission spectrum is taken from the calculations of Gredel et al. (1989). The energetic electrons produced from cosmic-ray ionisation of hydrogen excite H2 into excited electronic states. Spontaneous emission back to the electronic ground state produces a rich spectrum of UV lines, from 91.2 to 170 nm, as well as a weak continuum between 150 and 170 nm. The precise spectral details depend on the initial population of H2 ro-vibrational levels and the ortho-to-para ratio of H2. Usually H2 is assumed to be in its vibrational and rotational ground state in the cold interiors of dark clouds.
3. Cross sections
3.1. General properties
The critical data needed to describe gas-phase molecular or atomic photoprocesses is the wavelength-dependent photoabsorption cross section, σ(λ). This differential quantity describes the expected rate of photoabsorption per spectral unit of an isolated molecule or atom, ABC, in a photon-intensity normalised radiation field, bringing it into an excited electronic state ABC∗, and (oddly) has dimension of area. The optical depth of the absorption at a certain wavelength is given by τ = N × σ. Thus, a cloud of molecules with cross section σ(λ) = 10 cm2 and column density N = 10 cm-2 has an optical depth of 1, and a 1 /e probability of absorbing a photon with wavelength λ.
A photo-excited molecule ABC∗ may decay by several channels, and the probability of each of them needs to be taken into account. This includes dissociation (e.g., forming A + BC), ionisation (ABC+ + e−), or non-destructive emission (ABC + photon). Their respective partial photodissociation, photoionisation, and photoemission cross sections σd(λ), σi(λ), and σe(λ), are the product of the photoabsorption cross section and a decay probability, ηd(λ), ηi(λ), and ηe(λ); respectively. We generally neglected further division of the photoabsorption cross section into decay channels leading to distinct dissociation products (e.g., A + BC, AB + C, or A + B + C) or dissociative-ionisation fragments (e.g., ABC+ or AB+ + C) because of limited branching-ratio data in the literature, although this is a very relevant issue for chemical models. In general, multiple fragments are energetically possible and participate distinctly in ongoing chemistry, for example, CH4 dissociating to form significant amounts of CH3 and CH2 in Titan’s atmosphere (Romanzin et al. 2005), or H2O dissociating into OH + H or O + H2, with a wavelength-dependent relative likelihood. As an exception, in Sect. 8.6 we undertake to characterise the photodissociation branching of H2O into OH and H products, and NH3 into NH2 and NH.
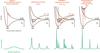 |
Fig. 2 Schematic cross sections for photodissociation and their associated dynamical pathway (arrows) through ground and excited state potential-energy curves. For polyatomic molecules these curves represent a cross section through a multidimensional energy surface. We note that the integrated values of the various cross sections may be similar, leading to orders-or-magnitude greater peak magnitudes for indirect mechanisms. Modified from van Dishoeck & Visser (2015). |
The wavelength dependence of a molecular cross section can be schematically associated with the structure of its electronically-excited states and categorised by its dissociation mechanism. These mechanisms are depicted in Fig. 2 by potential-energy curves. For small molecules absorption into an excited state whose potential is repulsive along 1 or more nuclear coordinates results in 100%-efficient direct dissociation of the molecule on sub-picosecond time scales (see Sect. 3.3 and Fig. 3 for a description and example of potential energy curves). The corresponding cross section has a broad wavelength distribution, covering several nm decades and peaking at the energy corresponding to vertical excitation from the ground-state equilibrium nuclear distance to the excited repulsive curve of AB∗. Typical peak values range from a few × 10-18 to a few × 10-17 cm2.
In contrast, the cross sections for the predissociation and indirect predissociation processes are highly structured, consisting of sharp peaks at discrete wavelengths. In these cases, the initial absorption occurs into a bound excited electronic state, which subsequently interacts non-radiatively with a nearby repulsive electronic state. The predissociation rate, and inversely-proportional linewidth, depends strongly on the details of this interaction and may vary from level to level, particularly in the indirect case where further intermediate states are involved. A non-unity dissociation probability will result from competitive rates for predissociation, kpre, and spontaneous emission, A; so that ηd = kpre/ (kpre + A). An excited molecule decaying by emission may follow multiple competing pathways involving multiple photons of different wavelengths in a de-excitation cascade through excited and ground electronic states, and result in a super-thermal population of ground state rotational and vibrational levels. Only the total emissive decay rate, A, is considered in this paper. CO and N2 are the best known astrophysical examples of molecules for which predissociation is dominant.
The fourth process is spontaneous radiative dissociation, in that an excited bound state radiates back into the vibrational continuum of a lower state with a line-dependent probability. For H2, this is the dominant photodissociation pathway (Stecher & Williams 1967), but not for any other interstellar molecule. Peak cross sections for discrete lines may reach 10-14 cm2 over a width of <0.1 nm.
Even though the peak cross sections may differ greatly for the various dissociation mechanisms depicted in Fig. 2, the integrated cross sections ∫σ(λ)dλ are often comparable. Further discussion and details of these phenomena may be found in van Dishoeck (1988) and van Dishoeck & Visser (2015).
As a real example, Fig. 3 illustrates that both direct continuous and discrete dissociation channels are available for a molecule like O2. The appearance of continuum absorption between 180 and 130 nm in Fig. 3 is consistent with an upward projection of the ground-state vibrational wavefunction to its intersection with the lowest-energy unbound excited state. The line absorption at shorter wavelengths occurs through the predissociation of multiple bound states above 9.2 eV.
 |
Fig. 3 Potential energy curves for the ground and excited state of O2 (red curves) (Guberman 1977; Lewis et al. 1998, 2001), and the O2 photoabsorption section from Sect. 4.3.35 (blue curve). Shown on equivalent energy and wavelength scales. The energy scale is relative to the minimum of the ground-state electronic potential curve, shown here shifted upwards by 4 eV. The shaded area shows the vertical excitation region. |
Large molecules such as polycyclic aromatic hydrocarbons (PAHs) are much more stable against photodissociation than the small species considered here because the absorptions are followed by non-radiative decay to the ground state (so-called internal conversion) from which there is only a small probability that the molecule finds a path to dissociation. In clouds exposed to very intense UV radiation, such as protoplanetary disks or near active galactic nuclei, photodissociation may however become significant on astronomical time scales, and small PAHs (less than about 50 carbon atoms) cannot survive. Photodissociation of these large molecules was not taken into account for this database but is discussed most recently by Le Page et al. (2003) and Visser et al. (2007; see also summary in van Dishoeck & Visser 2015). New experimental data on the photofragmentation and ionisation probabilities of PAHs is becoming available (Zhen et al. 2015, 2016).
In general, the key characteristics of a photoabsorption cross section are:
-
The long-wavelength dissociation threshold: usually this isgiven by the dissociation energy of the ground electronic state.The cross section at this threshold is often orders of magnitudesmaller than at shorter wavelengths. However, radiationintensity decreases rapidly with shortening wavelength forradiation fields dominated by cool stars, so even a low crosssection near threshold can dominate the photodissociation rate.
-
The ionisation threshold: this affects the relative importance of photodissociation and photoionisation. No ionisation will occur in most astrophysical environments if this threshold occurs at wavelengths shorter than 91.2 nm.
-
The wavelengths of absorption lines: maxima in the cross section can influence the total absorption rate if they correspond to emission lines, such as occur in the simulated TW-Hydra radiation field, or in cosmic-ray induced radiation.
-
The cross section corresponding to the Lyman-α emission line at 121.3 nm, that can singularly dominate the ultraviolet flux.
-
The characteristic width of absorption features: the precise linewidths, that can range from 0.001 to several 10 s of nm has a strong effect on their ability to self-shield (Sect. 6).
Further background information and descriptions of the collected data sources and cross sections for all updated and new species relative to van Dishoeck et al. (2006) are given in Sect. 4. In the following subsections, more background information on experimental and theoretical determinations of cross sections is given, since this is relevant for assessing the inherent uncertainty of the various data we used, and motivating our choices of adopted cross sections.
3.2. Experimental cross sections
Photoabsorption cross sections are most frequently recorded directly, by observing the transmission of an ultraviolet continuum through a gas sample, with radiation generated by discharge lamps (e.g., Ogawa & Ogawa 1975; Dehmer & Chupka 1976) or synchrotrons (e.g., Yoshino et al. 1996; Cheng et al. 2011), and dispersed by diffraction gratings or interferometry (Yoshino et al. 2006). Laser-generated ultraviolet radiation is sometimes used in photoabsorption experiments and provides the highest spectral resolution (Gao et al. 2013; Niu et al. 2014), but generally cannot be tuned over a large wavelength range or provide controllable intensity. Special techniques are required to record ultraviolet photoabsorption spectra for wavelengths shorter than 105 nm due to the lack of transmitting material for use as windows or beam splitters. For example, utilising frequency-multiplied lasers (e.g., Ubachs 2005; Stark et al. 1999), synchrotron radiation sources (e.g., Yoshino et al. 2006) and, recently, the vacuum-ultraviolet Fourier transform spectrometer at the SOLEIL synchrotron (de Oliveira et al. 2011; Eidelsberg et al. 2012), or occasionally the interstellar laboratory (e.g., Federman et al. 2001).
The interpretation of experimental photoabsorption spectra is generally straight-forward except where the instrumental spectral resolution is insufficient to resolve detailed structure of molecules with non-continuum absorption (cf., N2 as opposed to CH4 in Sect. 4). In this case, care needs to be taken not to underestimate the integrated cross section, potentially by more than an order of magnitude (Hudson & Carter 1968). Due to this issue, for some molecules (e.g., H2, N2, and CO) the recorded absorption spectra must be analysed line-by-line and the true cross section reconstructed without the limitation of experimental broadening (Eidelsberg et al. 1992; Heays et al. 2011; Glass-Maujean et al. 2013c).
Another difficulty concerns the calibration of absolute cross section values, which rely on precise knowledge of the absorbing sample gas column density and distribution of the ground-state rovibrational population. Neither quantity is generally diagnosable in photoabsorption experiments involving transient radical species. The uncertainty of directly-measured photoabsorption cross sections is usually between 10 to 20% for stable species, and typically a factor of 2 to 5 for the case of radicals, if it is known at all.
A photoabsorption cross section can also be estimated at relatively-low resolution by electron-energy-loss spectroscopy (e.g., Chan et al. 1992; Heays et al. 2012), where monoenergetic electrons are scattered from a low density of molecules and their final energy spectrum mimics the resonant energy structure of the scatterer. The correspondence of photoabsorption to the energy loss of scattered electrons relies on the incident beam being sufficiently energetic and the energy-loss spectrum being recorded at small scattering angles (Inokuti 1971). The lack of spectral resolution in this kind of experiment does not lead to an underestimate of unresolved features, in contrast to direct photoabsorption measurements, because of the linear relation between cross section and the signal from the analysed electrons. Electron-energy-loss cross sections can be recorded for energy-losses spanning the entire photoabsorbing wavelength range and then absolutely calibrated according to the Thomas-Reiche-Kuhn sum rule (Backx et al. 1976) without detailed knowledge of the sample column density. These kinds of experiments typically yield an uncertainty of 30% or better but can not resolve the detailed wavelength structure of many molecules. They provide a useful comparison to benchmark the accuracy of higher-spectral-resolution direct absorption cross sections.
The absorption of a photon with energy greater than the ionisation energy of a molecule can produce charged fragments. The resultant photoions and photoelectrons can be experimentally manipulated with electric fields and detected with high-efficiency, possibly simultaneously (e.g., Backx et al. 1976; Holland et al. 1993; Edvardsson et al. 1999). When all fragments are simultaneously detected, it is possible to spectroscopically examine the initial neutral species and produced ions. The simultaneous recording of photoion or photoelectron, and photoabsorption spectra provides a direct measurement of the fraction of excited molecules that decay via ionisation versus dissociation. Most molecules are ionised with near-100% efficiency by photons more than about 2 eV above their ionisation thresholds.
The branching to different dissociative-ionisation channels follows from the discrimination of photofragments with different charge-to-mass ratios. Less commonly, experimenters count neutral photofragments (e.g., Morley et al. 1992; Walter et al. 1993; Gao et al. 2013) or detect their fluorescence following dissociation into excited states (e.g., Lee 1984; Biehl et al. 1994). The emission of photoexcited molecules has is sometimes recorded (e.g., Jonas et al. 1990; Heays et al. 2014a) and provides further information on the decay branching of excited states.
3.3. Theoretical cross sections
3.3.1. General considerations
Quantum-chemical calculations of the excited electronic states of atoms and small molecules can be used to simulate photoabsorption, dissociation, and ionisation cross sections, and are particularly useful for species that are difficult to measure in the laboratory, such as radicals and ions (see Kirby & van Dishoeck 1988; van Dishoeck 1988; van Dishoeck & Visser 2015, for reviews).
For molecules, such calculations require knowledge of the ground state, one or more excited states, and the transition dipole moment connecting them. Ground and excited states are frequently summarised by potential energy curves describing the electrostatic interaction energy of the electrons as a function of the nuclear configuration. Some of these are plotted in Fig. 3 for the 1-dimensional case of a diatomic molecule, O2. These states are labelled by their symmetry and a numerical label increasing with excitation energy. For example, the 2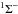 state denotes the second state of
state denotes the second state of 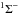 symmetry. If this state has been observed experimentally, it often also has an alphabetic label, with the letters; A, B, C, ...; mostly increasing with excitation energy. For polyatomic molecules, the notation becomes
symmetry. If this state has been observed experimentally, it often also has an alphabetic label, with the letters; A, B, C, ...; mostly increasing with excitation energy. For polyatomic molecules, the notation becomes 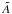 ,
, 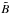 ,
, 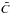 ...
...
The ground state potential energy of a stable molecule must form a well, leading to a quantised spectrum of bound states with increasing vibrational excitation. Electronically-excited states may be bound or repulsive, that is, possess no minimum energy (see Figs. 2 and 3). As discussed above, this distinction dramatically affects the structure of the resultant photoabsorption spectrum. The example in Fig. 3 reproduces the most important ultraviolet-excited states of O2 (Lewis et al. 1998, 2001) alongside its photoabsorption cross section. The strength of the cross section into each excited state depends on its specific transition moment with the ground state, and the size of the overlap of ground and excited vibrational wavefunctions. Within the Born-Oppenheimer approximation, this second factor requires a separate calculation considering the movement (vibration) of nuclei in a precomputed potential-energy environment.
The effects of nonzero molecular rotation are not usually explicitly included in ab initio cross section calculations, but can be simulated by assigning standard rotational-line strength factors (Larsson 1983) and assuming a population distribution of ground state rotational levels. These factors are not always accurate if centrifugal effects significantly alter the vibrational overlap of ground and excited states or the dissociation efficiency (e.g,. Lewis et al. 2005; Heays et al. 2011).
The spectral width of absorption features is characteristic of the lifetime of the excited state. The 135 to 180 nm absorption of O2 is rapidly followed by dissociative decay into O atoms, after less than 1 ps. The bound states at higher energy survive longer, but still dissociate because of a second-order interaction induced by the shown curve-crossing with the dissociative state (Lewis et al. 2002). States that take sufficiently long to dissociate, greater than typical Einstein A coefficients of about 1 ns, will have time to decay radiatively by spontaneous emission. Strong interactions lead to dissociation rates faster than 1012 s-1, implying a 100% dissociation efficiency. Detailed studies of the time evolution of nuclear motion may then provide an estimate of the dissociation branching ratio of photoexcited states (e.g., van Dishoeck et al. 1984; Kroes et al. 1997; Lewis et al. 2002; Heays et al. 2011).
The intrinsic linewidths of absorption features are given by the inverse of the sum of the predissociation and spontaneous decay rates, 1/(kpre + A). A predissociation rate kpre as large as 1011 s-1 corresponds to a linewidth of 5×10 nm FWHM (full-width half-maximum) at a wavelength of 100 nm. In velocity units, this amounts to 1 km s-1, which is comparable or less than the typical turbulent Doppler broadening of an interstellar clouds. Intrinsic widths seen in experimental data can vary greatly, from Doppler-broadening dominated (e.g., N2) to greater than 1 nm (e.g., NH3 and C2H2), obscuring all rotational structure when strongly predissociated. Such accurate knowledge of absorption line profiles is however only needed (i) to determine overlap with specific lines that dominate the radiation field in some astrophysical environments such as Lyman-α; (ii) to compute optical depth and self-shielding capacity.
For polyatomic molecules, the calculation of multidimensional excited-state potential-energy surfaces including all degrees of freedom, and subsequent nuclear dynamics on those surfaces, becomes computationally prohibitive. Moreover, such detail is often not needed to compute accurate photodestruction rates since the necessary absorption strengths are largely determined by one or a few excited states and, for cold molecules, the relevant nuclear motion only probes a small region of coordinate space around the ground state equilibrium geometry. Therefore, a simpler alternative is to only compute vertical excitation energies and transition dipole moments defined at the equilibrium geometry, and assume a dissociation probability for the excited state. This reduces the photoabsorption cross section of an entire electronic transition to a single wavelength, whereas the real cross section may be very broad. This approximation is quite sufficient for the case of photodissociation in a continuum-like radiation field, for example, the ISRF.
Our database includes vertical-excitation cross sections computed for a number of molecules and summarised in van Dishoeck (1988), van Dishoeck et al. (2006) and van Hemert & van Dishoeck (2008), based on our work and that of other groups (e.g., Kirby & van Dishoeck 1988; Roueff et al. 2014). These results are based on high-level configuration interaction calculations (see van Dishoeck & Visser 2015, for a top level overview of such calculations). In the latest calculations by van Hemert & van Dishoeck (2008), up to 9 electronic states per symmetry are considered, including diffuse (Rydberg) states. For the lower-energy states, comparisons with independent calculations and experiments indicate that the deduced excitation energies are accurate to better than 0.3 eV and that oscillator strengths connecting them to the ground state agree within 30% or better. For the higher states, typically the 5th root and higher per symmetry, the accuracy decreases because many states and orbitals can mix. Such calculations still provide a good indication of the location of those states and their combined strengths, typically within a factor of 2.
Only states above the ground-state dissociation limit and below the ionisation potential of the molecule need be taken into account for photodissociation calculations. The dissociation efficiency, ηd, of all calculated excited states in this range and presented here is assumed to be unity, that is, they are purely repulsive and dissociate directly, or have resonant levels and decay by predissociation (exceptions are H2, CO and N2 for which level-specific probabilities are available). For larger molecules (i.e., three or more atoms) dissociation rates assuming unity efficiency should be regarded as upper limits, given that internal conversion to a lower (dissociative) electronic state is usually much more rapid than radiative decay, because of their high density of states (e.g., Leger et al. 1989; Jochims et al. 1994). Above the ionisation potential, all absorption is assumed to lead to photoionisation (dissociative or not). Also, only states lying below the Lyman limit of 13.6 eV are included.
Even after computing a full potential-energy surface the wavelengths and absorption oscillator strengths of known bound vibrational levels, their predissociation lifetimes and widths may still be unknown. Additionally, the real photoabsorption cross section into a bound vibrational level may involve multiple rotational transitions, effectively increasing the width of its photoabsorption envelope. We assumed a Gaussian profile to encompass these phenomena for theoretical predissociated levels used in our cross section database, and uniformly assumed a width of 1 nm FWHM, where our following calculation of interstellar photodissociation rates is not sensitive to the precise value of this width.
The accuracy of cross sections derived from ab initio calculations can be remarkably high, within 20% or better, for diatomic molecules (e.g., OH van Dishoeck & Dalgarno 1983; van Dishoeck & Dalgarno 1984a) and sometimes for polyatomic cases (e.g., H2O in Sect. 4.3.33). The wavelengths of absorption lines exciting predissociated bound levels may be significantly in error where non-Born-Oppenheimer interactions shift energy levels and redistribute oscillator strengths between excited states (e.g., van Dishoeck et al. 1984). However, inaccuracies introduced by these effects are much reduced in the calculation of interstellar photodissociation rates that average over many states (e.g., C3H in Sects. 4.3.25 and 4.3.26). The largest uncertainty in ab initio photodissociation cross sections then arises, in most cases, from inaccurately-calculated or neglected states lying close to the ionisation threshold, which are numerous and difficult to calculate or measure.
Empirical corrections can resolve some of the uncertainty of theoretical cross sections, either by shifting absorption features to their experimentally known wavelengths, or adjusting the underlying excited state potential-energy surfaces to produced cross sections in better agreement with experiment (e.g., Heays et al. 2014a). For a few molecules in our database, we added a guessed wavelength and integrated cross section to approximate the influence of neglected high-lying states, with an associated order-of-magnitude uncertainty (in general, these additions contribute a small amount to the overall cross section and its uncertainty). For reference, inclusion of a hypothetical state at 9 eV with an oscillator strength of 0.1 would increase the ISRF photodissociation rates by 3.5 × 10-10 s-1. In general, no corrections were made for possibly-neglected states above the ionisation limit and below 13.6 eV. This is because the lowest Rydberg members are generally computed explicitly, and the oscillator strengths of higher Rydberg states converging to the ionisation threshold decrease roughly as 1/n3 (n is the principal quantum number) and do not contribute much.
For all theoretical cross sections in our database, a minimum photodissociation cross section of 5×10 cm2 was assumed between the dissociation threshold and Lyman-limit at 91.2 nm. This weak continuum negligibly increases the integrated cross section but ensures a low but nonzero cross section overlaps the strong emission lines present in some interstellar radiation fields.
3.3.2. Atomic photoionisation
Atomic photoionisation cross sections have long been an object of theoretical study due to their influence on the interpretation of spectroscopic observations of astrophysical plasmas in ionised interstellar gas as found around stars, active galactic nuclei, and elsewhere (Seaton 1951; Osterbrock 1979; Ferland 2003; Tielens 2013). We used theoretical cross sections here for the photoionisation of some neutral atoms. These are generally the result of R-matrix calculations (Seaton 1985; Mendoza 1996; McLaughlin 2001; Zatsarinny & Bartschat 2013), and produce continuum cross sections that are generally accurate to within 20%. The specification of resonant structure evident in most atomic cross sections presents more difficulty for this method, although the uncertainties are diminished for photoionisation rates calculated following integration over many resonances.
3.4. Cross section databases
There are various public databases of photoabsorption, dissociation, and ionisation cross sections, and some data from these were incorporated into our assessment of molecular and atomic cross sections. A comprehensive set of laboratory photoabsorption cross sections and a smaller amount of data concerning photofragment branching ratios is contained in the MPI Mainz UV/VIS Spectral Atlas4. Earlier compilations are given by Calvert & Pitts (1966), Okabe (1978), Lee (1984), Gallagher et al. (1988), Ashfold et al. (2006). The TOPbase5 database of photoionisation cross sections (Mendoza 1996) includes R-matrix calculations for many atoms, including their highly-charged states. A collation of molecular and atomic cross sections from multiple sources is contained in the PHIDRATES database6 (Huebner et al. 1992; Huebner & Mukherjee 2015) as well as calculations of their photodissociation and photoionisation rates in the ISRF and solar radiation fields. Our compilation differs somewhat from Huebner & Mukherjee (2015) for molecules in common, due to different choices of cross section data and a larger focus on highly excited electronic states in our work that are more important for the ISRF than for the solar radiation field.
More specialised databases containing cross sections of astrochemical interest are the MOLAT and SESAM databases of vacuum-ultraviolet (VUV) spectroscopy7, including CO, H2, and N2; the Harvard CfA VUV database8 including primary data on many small molecules including wavelengths as short as 80 nm; and the UGA Opacity Project database9. The VAMDC virtual portal10 integrates some of these data.
 |
Fig. 4 Compiled atomic photoionisation cross sections. The ionisation thresholds of H and C are indicated by vertical lines. |
 |
Fig. 5 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
 |
Fig. 6 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
 |
Fig. 7 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
 |
Fig. 8 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
 |
Fig. 9 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
 |
Fig. 10 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
 |
Fig. 11 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
 |
Fig. 12 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
 |
Fig. 13 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
 |
Fig. 14 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
4. Compiled cross sections
In this section the cross sections of atoms and molecules in our database are presented. All cross sections are plotted in Figs. 4 to 14 and have some summarised properties listed in Table 1. Complete descriptions of the source material for most cross section are given in Sects. 4.3.1 to 4.3.72. For some species, we did not exhaustively reappraise the literature and instead give a reference to its cross section in Table 1. There are dissociation and ionisation thresholds listed in Table 1 for all species where these are relevant. In some cases the listed molecular dissociation limits correspond to greater photon energies (shorter wavelengths) than the dissociation energies of their ground electronic states, due to the lack of accessible excited states for photoabsorption at these energies.
Some summary properties of atomic and molecular cross sections.
4.1. Cross section uncertainties
We assigned uncertainties to each overall molecular and atomic cross section according to estimates within their source material, where available, or based on the general accuracy of the various experimental and theoretical methods used, as discussed in Sects. 3.2 and 3.3.
We limited our estimated uncertainties to four broad categories for simplicity and in view of the ubiquity of large uncertainties in many other key parameters in astrophysical modelling. These categories are:
-
A+:
accurate to within 20%;
-
A:
accurate to within 30%;
-
B:
accurate within a factor of 2;
-
C:
accurate within a factor of 10.
For the purposes of programs requiring uncertainties in terms of log-normal standard deviations, our rating system corresponds approximately to 2σ uncertainties.
For some molecules, the compilation of data sources into a single best estimated cross section introduces clear wavelength-dependence into the cross section uncertainty, which we weighted according to the wavelength dependence of the ISRF to give the estimates in Table 1. Then, a greater uncertainty at the shortest wavelengths will not contribute as much to our uncertainty estimate as near the long-wavelength threshold.
The uncertainty of photodestruction rates calculated according to Eq. (1) will potentially differ for non-ISRF radiation fields. This is most significant for the case of a Lyman-α dominated radiation field, where the cross section uncertainty at 121.6 nm is most important. For molecules with weak and uncertain continua at this wavelength, or sharply resonant structure that may be experimentally under-resolved, recorded at an inappropriate temperature, or calculated with a line position error, the uncertainty may be significantly larger than for the overall cross section. For this reason we provide a separate uncertainty rating applicable to the Lyman-α wavelength.
The comparison of independent cross section measurements and calculations allows for testing their claimed uncertainties. An example is H2O in Sect. 8.4, where we find that the ISRF photodissociation rate obtained with cross section data from four independent experiments with quite different methodologies agrees within 10%.
4.2. Cross section database format
The collected cross sections, with references, are available for download from the Leiden Observatory database11. The data files are given in two alternative formats for convenient utilisation, in text files listing the continuum and line absorption of each cross section separately, and in binary format encoding the full wavelength dependence of absorption lines.
The first case provides for a concise data format and rapid calculation of the photodissociation rates for line absorption in a continuum field. This is at the cost of information regarding their shapes and its overlap with a structured radiation field. The strengths of discrete absorption lines are represented by their integrated cross section; related to the well-known (dimensionless) oscillator strength, fuℓ for a transition between upper state u and lower state ℓ; and defined as follows, 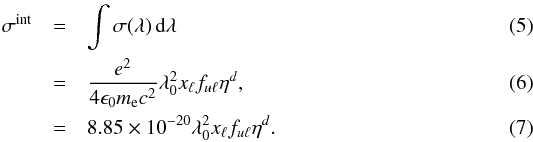 Here, the final form is appropriate for case of σ and λ in units of cm2 and nm, respectively. The integration domain for the cross sections is the wavelength range of an absorption feature, whether it is an individual ro-vibrational transition, or an entire electronic-state transition containing many rotational-vibrational levels. Here, e, me, c, and ϵ0 are the electron charge and mass, the speed of light, and permittivity of free space, respectively, and λ0 is the central wavelength of the transition. Finally, ηd is the dissociation probability of the upper level and xℓ is a ground-state fractional population. The latter is 1 for oscillator strengths describing transitions between entire electronic states but will depend on the ground state excitation temperature when individual rotational or vibrational transitions are considered.
Here, the final form is appropriate for case of σ and λ in units of cm2 and nm, respectively. The integration domain for the cross sections is the wavelength range of an absorption feature, whether it is an individual ro-vibrational transition, or an entire electronic-state transition containing many rotational-vibrational levels. Here, e, me, c, and ϵ0 are the electron charge and mass, the speed of light, and permittivity of free space, respectively, and λ0 is the central wavelength of the transition. Finally, ηd is the dissociation probability of the upper level and xℓ is a ground-state fractional population. The latter is 1 for oscillator strengths describing transitions between entire electronic states but will depend on the ground state excitation temperature when individual rotational or vibrational transitions are considered.
Then, the photodissociation or ionisation rate defined in Eq. (1) is substituted by the equation, 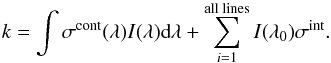 (8)
(8)
As an example the photodissociation cross section of the CH2 radical is available as the data file ch2.pd with contents:
CH2 P.D. cf. van Dishoeck et~al. (’96)
17
1 1187.6 0.100E-16
2 1227.6 0.800E-19
3 1240.0 0.240E-15
4 1267.7 0.460E-16
5 1276.9 0.490E-16
(more data)
13 1433.3 0.540E-16
14 1504.7 0.920E-16
15 1585.5 0.620E-17
16 1595.7 0.450E-18
17 1680.0 0.200E-16
306
-2750.
1 1427.6 0.100E-20
2 1516.3 0.100E-18
3 1555.7 0.499E-18
4 1564.1 0.684E-18
5 1572.6 0.870E-18
(more data)
302 2388.4 0.733E-21
303 2408.2 0.707E-21
304 2428.4 0.173E-21
305 2448.9 0.361E-21
306 2750.0 0.000E+00
This file can be serially decoded as follows:
-
Line 1:
describes the contents of the data file, provides the mainliterature reference.
-
Line 2:
number of discrete lines through which photodissociation occurs for this molecule, nl.
-
Line 3 to 3 + nl:
-
Field 1:
index of a line;
-
Field 2:
wavelength of the line centre (Å);
-
Field 3:
integrated cross section of this line (cm2 Å).
-
Field 1:
-
Line 3 + nl + 1:
number of continuum points defined, nc.
-
Line 3 + nl + 2:
long wavelength threshold for the continuum data, if set to -1 or blank the last explicitly listed wavelength is used.
-
Line 3 + nl + 3 to 3 + nl + 3 + nc:
-
Field 1:
index of this point;
-
Field 2:
wavelength (Å);
-
Field 3:
cross section (cm2).
-
Field 1:
All cross sections are also provided as data files in an alternative format including a full specification of their wavelength dependence. This may require tens or hundreds of thousands of wavelength points to capture the cross section of highly-structured molecules. To facilitate the handling of such large datasets we provide them in the hdf5 binary format12. For the case of CH2 with file name CH2.hdf5, this contains a dataset labelled README, providing a description of the file contents, literature references, and uncertainty estimate; a binary array labelled wavelength in units of nm; and multiple molecular cross sections in units of cm2, labelled photoabsorption, photodissociation, and photoionisation. The discrete lines listed with integrated cross sections in the text-formatted files are included in the continuum-only binary files with Gaussian profiles of 1 nm FWHM. Astrophysically-important rates calculated in the following are not sensitive to the precise value of this assumed width.
4.3. Photodissociation and photoionisation of atoms and molecules
In the following, the cross sections of atoms and molecules are discussed and summarised. These subsections (and various tables in the paper) are ordered by chemical type, for example, atoms, hydro-carbon species, and oxygen-, nitrogen-, sulphur- and metal-containing molecules. A summary of dissociation and ionisation thresholds, cross sections at the Lyman-α wavelength, and the estimated uncertainty of these cross sections is provided in Table 1. The ordering of the following subsections follows the row ordering of Table 1.
4.3.1. H – hydrogen
The hydrogen photoionisation continuum, 91.2 nm and shorter, is calculated for the TOPbase database (Mendoza 1996) and agrees very well with an experimental measurement (Palenius et al. 1976) where they overlap. We simulate the longer-wavelength Lyman-series line absorption from a list of transition wavelengths and oscillator strengths from the NIST atomic database13 (Kramida 2010). We adopted a Gaussian-shaped Doppler broadening of 1 km s-1 to accompany the Lorentzian natural linewidths of the H lines in the simulated photoabsorption cross section.
4.3.2. C – carbon
The calculated cross section for C was taken from the TOPbase database (Mendoza 1996; Nahar & Pradhan 1997).
4.3.3. N – nitrogen
The long-wavelength photoionisation threshold of atomic nitrogen, 85 nm, is shorter than the Lyman-limit, 91.2 nm, and its photoionisation in the interstellar medium is then suppressed. The cross section adopted here is taken from the absolute experimental data of Samson & Angel (1990), apart from the resonant region between 61.8 and 71.5 nm where the relative-magnitude high-resolution measurement of Dehmer et al. (1974) was used, after scaling this to match the Samson & Angel value at 67 nm, in a continuum region.
4.3.4. O – oxygen
A theoretical calculation of the oxygen photoionisation cross section (Cantu & Parkinson 1988; Huebner & Mukherjee 2015) was used and is in good agreement with an absolute photoionisation yield (Angel & Samson 1988) that lacks the spectral resolution to reveal the majority of calculated photoionisation resonances.
4.3.5. Mg – magnesium
The experimental photoabsorption cross section of Yih et al. (1998) was adopted for the photoionisation cross section of Mg for wavelengths between 120 and 163 nm. At shorter wavelengths the calculated TOPbase cross section (Mendoza 1996) was used after rescaling by a factor of 1.14 to match the integrated value of Yih et al. (1998) where they overlap.
4.3.6. Al – aluminium
The calculated cross section for Al was taken from the TOPbase database (Mendoza 1996) and is in reasonable agreement with an absolutely-calibrated experimental measurement (Kohl & Parkinson 1973).
4.3.7. Si – silicon
There are multiple R-matrix calculations of Si photoionisation (Mendoza & Zeippen 1988; Nahar & Pradhan 1993) that are broadly in agreement. Here, we adopt a cross section from the TOPbase database (Mendoza 1996; Huebner & Mukherjee 2015).
4.3.8. P – phosphorus
The photoionisation cross section determined by Tayal (2004) from R-matrix calculations is adopted between 62 and 118 nm.
4.3.9. S – sulphur
The recent R-matrix calculation of Barthel et al. (2015) is adopted for the atomic-S photoionisation cross section for wavelengths shorter than 93 nm, and an experimental measurement for longer wavelengths (Gibson et al. 1986). This non-absolute experiment includes the correct energy location of many resonances appearing in this cross section, including some that arise from excited fine-structure components of the S ground state and may not be populated under all astrophysical conditions. The experiment was scaled to match the calculated cross section after integrating over the range 96 to 121 nm.
4.3.10. Cl – chlorine
Two experimental Cl photoionisation cross sections are connected spanning from the Cl+ ionisation threshold (95.6 nm) to 60 nm. We adopt the measurement of Cantu & Parkinson (1988) for wavelengths longer than 75 nm, and Ruscic & Berkowitz (1983) at shorter wavelengths.
4.3.11. K – potassium
The most recent experimental measurement of the potassium photoionisation cross section (Sandner et al. 1981) covers the wavelengths region between 238 and 285 nm. We supplemented this between 120 and 238 nm with a recent R-matrix calculation (Zatsarinny & Tayal 2010), and adopted a linearly-decreasing cross section at still shorter wavelengths.
4.3.12. Ca – calcium
A recent high-resolution measurement of the calcium photoabsorption cross section is measured by Yih et al. (1998) from 160 nm to the ionisation threshold at 202 nm, and adopted here as a photoionisation cross section. This was combined with a further measurement that better resolves the two dominant resonant features at 176.5 and 188 nm (Carter et al. 1971), over the regions 176.3 to 176.8 nm and 187.1 to 189.6 nm. The R-matrix calculation from the TOPbase database (Mendoza 1996) was used for wavelengths shorter than 160 nm.
4.3.13. Fe – iron
Multiple measurements were combined into a single Fe photoionisation cross section file. An absolute cross section measured at 154 nm (Lombardi et al. 1978) was used to scale the wavelength-dependent relative photoionisation cross section of Hansen et al. (1977). In turn, this was used to calibrate the measurements of Reed et al. (2009) and Tondello (1975) by comparing integrated values over their overlapping ranges. For the case of Reed et al. (2009) separate calibration factors were used for the ranges 125 to 145 nm and 145 to 158 nm to account for an apparent wavelength dependence of laser power in their experiment. For wavelengths shorter than those covered by the various experiments the R-matrix calculation of Bautista (1997) was used, and at the shortest wavelengths the fitting formulate of Verner et al. (1996). The relevant scaling factors and wavelength ranges are listed in Table 2.
References and wavelength ranges of concatenated Fe cross sections.
4.3.14. Zn – zinc
There are two measurements of the Zn photoabsorption cross section between 110 nm and the photoionisation threshold at 132 nm (Marr & Austin 1969; Yih et al. 1998) that disagree by a factor of two. We used an average of these two measurements where they coincide, the measurement of Marr & Austin (1969) between 91 and 110 nm and the relative-photoionisation cross section of Harrison et al. (1969) at shorter wavelengths, after scaling its integrated magnitude to match the continuum level of an R-matrix calculation (Huebner & Mukherjee 2015).
4.3.15. H2 – hydrogen
Molecular hydrogen has a line-dominated spectrum beginning at 112 nm with absorption into the Lyman (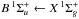 ) and Werner (
) and Werner (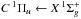 ) bands, and retains its resonant character even beyond the ionisation threshold at 80.3 nm. The excited rovibrational lines and their tendency to partially predissociate or autoionise is well studied experimentally and theoretically by the group of Abgrall and Glass-Maujean et al. (Abgrall et al. 1993c,a,b, 1994; Abgrall & Roueff 2006; Abgrall et al. 2000; Glass-Maujean et al. 2010, 2013a,b,c), culminating in a detailed experimental and theoretical database of absorption and emission lines14, as well as by other groups (e.g., Dehmer & Chupka 1976; Chan et al. 1992; Samson & Haddad 1994; Jonin et al. 2000; Philip et al. 2004; Hollenstein et al. 2006; Dickenson & Ubachs 2014; Holland & Shaw 2014).
) bands, and retains its resonant character even beyond the ionisation threshold at 80.3 nm. The excited rovibrational lines and their tendency to partially predissociate or autoionise is well studied experimentally and theoretically by the group of Abgrall and Glass-Maujean et al. (Abgrall et al. 1993c,a,b, 1994; Abgrall & Roueff 2006; Abgrall et al. 2000; Glass-Maujean et al. 2010, 2013a,b,c), culminating in a detailed experimental and theoretical database of absorption and emission lines14, as well as by other groups (e.g., Dehmer & Chupka 1976; Chan et al. 1992; Samson & Haddad 1994; Jonin et al. 2000; Philip et al. 2004; Hollenstein et al. 2006; Dickenson & Ubachs 2014; Holland & Shaw 2014).
Spontaneous emission from photoexcited 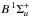 and
and 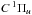 states into ground state vibrational levels produces a spectrum of vacuum- and far-ultraviolet emission lines. Emission into the ground state continuum is also possible and provides a dissociation mechanism at wavelengths below the direct-photodissociation threshold of 84 nm (Field et al. 1966; Stecher & Williams 1967; Abgrall et al. 1997, 1999). This spontaneous radiative dissociation mechanism is experimentally and theoretically verified (Dalgarno et al. 1970; Stephens & Dalgarn 1972). The overall H2 dissociation efficiency assuming several of the radiation fields discussed in Sect. 2 is listed in Table 3 and varies between 5 and 15% for continuum interstellar radiation fields. This efficiency is somewhat larger (up to 25%) for the solar and simulated TW-Hydra radiation fields because these include flux shorter than the Lyman limit at 91.2 nm and the dissociation fraction of the H2 cross section increases with decreasing wavelength.
states into ground state vibrational levels produces a spectrum of vacuum- and far-ultraviolet emission lines. Emission into the ground state continuum is also possible and provides a dissociation mechanism at wavelengths below the direct-photodissociation threshold of 84 nm (Field et al. 1966; Stecher & Williams 1967; Abgrall et al. 1997, 1999). This spontaneous radiative dissociation mechanism is experimentally and theoretically verified (Dalgarno et al. 1970; Stephens & Dalgarn 1972). The overall H2 dissociation efficiency assuming several of the radiation fields discussed in Sect. 2 is listed in Table 3 and varies between 5 and 15% for continuum interstellar radiation fields. This efficiency is somewhat larger (up to 25%) for the solar and simulated TW-Hydra radiation fields because these include flux shorter than the Lyman limit at 91.2 nm and the dissociation fraction of the H2 cross section increases with decreasing wavelength.
H2 integrated photodissociation efficiency assuming several radiation field types.
 |
Fig. 15 H2 photoabsorption cross section. The under-resolved experimental measurement of (Chan et al. 1992), and a model spectrum before and after smoothing to the experimental resolution. Also shown is a correction to the model accounting for neglected excitation mechanisms. |
Measured and calculated transition frequencies, strengths, and predissociation efficiencies of individual rovibrational transitions from the database of Abgrall and Glass-Maujean et al. were employed to reconstruct the temperature-dependent photoabsorption cross sections for H2 line-by-line, including excitation to 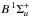 ,
, 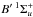 ,
, 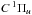 , and
, and 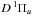 excited valence states, and many npπ and npσ Rydberg levels. The completeness of this database for wavelengths longer than 80 nm is evidenced by the agreement within 10% over this region of its integrated cross section with the low-resolution electron-energy-loss-derived absolute cross section of Chan et al. (1992). This comparison is shown in Fig. 15 after smoothing the line-by-line model spectrum to the under resolved experimental spectrum. The deficit of the model cross section relative to Chan et al. (1992) for wavelengths shorter than 80 nm was assumed to arise from direct ionisation to H2+ or autoionising highly-excited H2 levels that are neglected in the line-by-line model. This deficit is then added to the line-by-line model forming a continuum shortwards of 80 nm. The cross section of Backx et al. (1976) was adopted at the shortest wavelengths, <62 nm. The use of a line-absorption model permits calculation of cross sections with a range of ground-state excitation states and Doppler profiles.
excited valence states, and many npπ and npσ Rydberg levels. The completeness of this database for wavelengths longer than 80 nm is evidenced by the agreement within 10% over this region of its integrated cross section with the low-resolution electron-energy-loss-derived absolute cross section of Chan et al. (1992). This comparison is shown in Fig. 15 after smoothing the line-by-line model spectrum to the under resolved experimental spectrum. The deficit of the model cross section relative to Chan et al. (1992) for wavelengths shorter than 80 nm was assumed to arise from direct ionisation to H2+ or autoionising highly-excited H2 levels that are neglected in the line-by-line model. This deficit is then added to the line-by-line model forming a continuum shortwards of 80 nm. The cross section of Backx et al. (1976) was adopted at the shortest wavelengths, <62 nm. The use of a line-absorption model permits calculation of cross sections with a range of ground-state excitation states and Doppler profiles.
H2 photodissociation rate in the interstellar radiation field of Draine (1978).
There is a great deal of previous work done on H2 photodissociation due to its importance to the balance of atomic and molecular hydrogen in the Universe. This subject is well reviewed and state-of-the-art calculations made in Sternberg et al. (2014) and references therein. The correctness of our simulated H2 photodissociation cross section is verified by comparing an ISRF dissociation rate with the calculations of Sternberg et al. (2014), listed in Table 4. Two calculations are made, for an ortho:para ratio of H2 ground state levels of 3:1 and 0:1. The increased rate for the 3:1 case is due to increased population of rotationally-excited H2 levels that are more likely to decay dissociatively.
4.3.16. H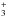 – trihydrogen cation
– trihydrogen cation
The electronic excitation of cold H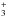 has not been measured in the laboratory, due to the difficult of cooling the highly-symmetric radical ions that must be formed in situ, although its photodissociation from excited ground state rotational-vibrational levels is studied in some detail (e.g., Carrington & Kennedy 1984). Calculations of its excited states find no allowed transitions with wavelength longer than about 70 nm (Talbi & Saxon 1988), well above its 283 nm ground state dissociation threshold (Kulander & Bottcher 1978). Equilibrium potential-energies and transition moments for the ground state accessible by photoabsorption are calculated by Talbi & Saxon (1988) and van Dishoeck (unpublished), leading to very similar cross sections. The cross section of van Dishoeck was adopted for our photodissociation database.
has not been measured in the laboratory, due to the difficult of cooling the highly-symmetric radical ions that must be formed in situ, although its photodissociation from excited ground state rotational-vibrational levels is studied in some detail (e.g., Carrington & Kennedy 1984). Calculations of its excited states find no allowed transitions with wavelength longer than about 70 nm (Talbi & Saxon 1988), well above its 283 nm ground state dissociation threshold (Kulander & Bottcher 1978). Equilibrium potential-energies and transition moments for the ground state accessible by photoabsorption are calculated by Talbi & Saxon (1988) and van Dishoeck (unpublished), leading to very similar cross sections. The cross section of van Dishoeck was adopted for our photodissociation database.
4.3.17. CH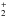 – methylene cation
– methylene cation
According to the calculations of Theodorakopoulos & Petsalakis (1991) this ion has many dipole-allowed excited states below 13.6 eV. The 1, 2 and 32B2, 2, 3 and 4 2A1 and 22B1 states were included in our cross section with f = 0.008, 0.0001, 0.02, 0.01, 0.06, 0.05 and 0.03, respectively, and ηd = 1 assumed.
4.3.18. CH3 – methyl radical
References and wavelength ranges of concatenated CH3 cross sections.
Several CH3 absorption bands are photographically observed between 120 and 230 nm by Herzberg & Shoosmith (1956) revealing predissociation-broadened bands with widths of around 1 nm, and very roughly estimated strengths. Higher-resolution absolutely-calibrated photoabsorption measurements of the longest-wavelength absorption features (Cameron et al. 2002; Khamaganov et al. 2007; 200 nm to the photoabsorption threshold at 220 nm) allow for a rough calibration of the other photographic features based on their apparent saturation.
An absolute photoionisation cross section is recorded in the neighbourhood of the 126 nm ionisation threshold (Gans et al. 2010), which was extrapolated here to shorter wavelengths. A summary of cross sectional data sources is given in Table 5.
4.3.19. CH4 – methane
CH4 photoabsorbs significantly at wavelengths shorter than 140 nm with an unstructured cross section that peaks at 90 nm, indicating mostly direct photodissociation. Here, the experimental cross section of Kameta et al. (2002) between 52 and 124 nm was used, and the slightly-lower resolution data of Au et al. (1993) outside this range. The cross sections of Kameta et al. (2002) was scaled down by a factor or 0.95 in order to agree with other more reliably calibrated overlapping measurements (Au et al. 1993; Lee 2009).
Many neutral and ionised fragments are observed following CH4 photodissociation and these data are well summarised elsewhere (Backx & Vanderwiel 1975; Huebner et al. 1992; Gans et al. 2011; Blitz & Seakins 2012; Huebner & Mukherjee 2015). Here, the wavelength-dependent branching ratios of Kameta et al. (2002) were used to decompose photoabsorption into ionisation and dissociation cross sections, assuming zero branching to fluorescence.
4.3.20. CH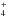 – methane cation
– methane cation
This ion is subject to detailed theoretical studies indicating several dissociative excited states (van Dishoeck et al. 1980). Oscillator strengths into the 2, 3 2A1 and 22B1 states are taken to be f = 0.04, 0.04 and 0.08, respectively, with ηd = 1.
4.3.21. C2H – ethynyl radical
Absorption into the 5 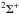 state lying around 10 eV dominates the interstellar photodissociation of this molecule. The higher 2Π states in the 8.5 to 10.5 eV range can also contribute significantly as far as the C2H ionization potential of 11.4 eV. The oscillator strengths listed in Table 1 of the calculations of van Hemert & van Dishoeck (2008) are used with ηd = 1.
state lying around 10 eV dominates the interstellar photodissociation of this molecule. The higher 2Π states in the 8.5 to 10.5 eV range can also contribute significantly as far as the C2H ionization potential of 11.4 eV. The oscillator strengths listed in Table 1 of the calculations of van Hemert & van Dishoeck (2008) are used with ηd = 1.
4.3.22. C2H2 – acetylene
References and wavelength ranges of concatenated C2H2 cross sections.
The C2H2 photoabsorption cross section is compiled from a collection of measurements (Wu et al. 1989; Xia et al. 1991; Cooper et al. 1995; Vattulainen et al. 1997; Cheng et al. 2011) over the wavelength ranges listed in Table 6, which extend beyond 200 nm and are strongest shortward of 153 nm. A strong absorption line of C2H2 coincides very nearly with the hydrogen Lyman-α line.
The longest C2H2 photodissociation threshold, forming C2H + H, occurs at 217 nm and the dissociation efficiency at shorter wavelengths was studied several times (e.g., Okabe 1983; Seki & Okabe 1993; Läuter et al. 2002; Kovács et al. 2010), as well as the probability of forming an H2 product. Läuter et al. (2002) convincingly determined a 100% efficiency for H-atom formation by 121.6 and 193.3 nm radiation after detecting these atoms through laser-induced fluorescence, and a 100% dissociation efficiency was assumed for all wavelengths shorter than the 217 nm threshold.
4.3.23. C2H6 – ethane
The photoabsorption cross section of C2H6 is measured between 120 and 150 nm by Chen & Wu (2004) and their 150 K measurement was adopted here (the temperature variation measured in this experiment was slight however). At shorter wavelengths, the cross section measured by Kameta et al. (1996) was used after scaling this down to match the overlapping region of Chen & Wu (2004) (a factor of 0.83). The ionisation fraction for C2H6 is also measured by Kameta et al. (1996) and adopted here.
4.3.24. C3 – tricarbon
The photoabsorption cross section of C3 is difficult to measure due to its radical nature. Vertical excitation energies are calculated by van Hemert & van Dishoeck (2008) for absorption into 5 highly-excited states as well as vertical oscillator strengths. We combine these transitions into a photodissociation cross section after assigning all states a Gaussian band profile of full-width half-maximum 18 nm. This width was selected to match the width of the strong C3 electronic transition near 160 nm (corresponding to the 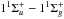 transition among the calculations of van Hemert & van Dishoeck 2008) observed in a matrix-isolation experiment (Monninger et al. 2002). Here, all bands were assumed to be 100% dissociative, since they lie well above the C3 dissociation limit.
transition among the calculations of van Hemert & van Dishoeck 2008) observed in a matrix-isolation experiment (Monninger et al. 2002). Here, all bands were assumed to be 100% dissociative, since they lie well above the C3 dissociation limit.
There is no absolute measurement of the photoionisation cross section of C3 shorter than its 11.6 eV threshold (Belau et al. 2007). The onset of ionisation and its wavelength dependence is measured by Nicolas et al. (2006). This wavelength dependence was adopted as a photoionisation cross section after scaling it to the typical molecular value of 2×10 cm2 at 91.2 nm.
4.3.25. l–C3H – linear propynylidyne
The photodissociation of this linear molecule is dominated by the high-lying 2Π states around 7.8 eV. The f-values given in Table 3 of van Hemert & van Dishoeck (2008) are to simulate the l–C3H spectrum, assuming ηd = 1.
4.3.26. c–C3H – cyclic propynylidyne
In contrast with its linear counterpart, many different electronic states in the 5 to 7.5 eV range can contribute to the photodissociation of cyclic C3H. The f-values given in Table 4 of van Hemert & van Dishoeck (2008) are used with ηd = 1.
4.3.27. HC3H – propargylene
Three isomers of H2C3 are treated in the calculations of van Hemert & van Dishoeck (2008). In this section, HC3H refers to the HCCCH linear form, with the alternative linear excited isomer (H2CCC or l-C3H2) and cyclic ground isomer (c-C3H2) discussed below. The photodissociation of HC3H is dominated by three excited 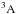 levels, with vertical excitations of 4.23, 6.29, and 7.52 eV above the ground state.
levels, with vertical excitations of 4.23, 6.29, and 7.52 eV above the ground state.
4.3.28. l-C3H2 – linear propenylidene
The strongest absorptions of this molecule are into the higher 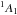 Rydberg states around 9 eV, below the ionization potential at 10.4 eV. The f-values given in Table 7 of van Hemert & van Dishoeck (2008) are used, with ηd = 1. The low-lying
Rydberg states around 9 eV, below the ionization potential at 10.4 eV. The f-values given in Table 7 of van Hemert & van Dishoeck (2008) are used, with ηd = 1. The low-lying 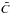 (2)
(2) state is taken into account, even though it is not clear how efficient predissociation is for this state. The linear HC3H isomer has a very different electronic structure from l-C3H2 with a triplet ground state. This molecule is included as a separate species in the database, following Table 5 of van Hemert & van Dishoeck (2008).
state is taken into account, even though it is not clear how efficient predissociation is for this state. The linear HC3H isomer has a very different electronic structure from l-C3H2 with a triplet ground state. This molecule is included as a separate species in the database, following Table 5 of van Hemert & van Dishoeck (2008).
4.3.29. c-C3H2 – cyclic propenylidene
This molecule has only a few low-lying dipole-allowed electronic states. The largest oscillator strengths are found to transitions in the 9 to 11 eV range, which is above the ionization potential of c-C3H2 at 9.15 eV. The current version of the database, based on Table 6 of van Hemert & van Dishoeck (2008) with ηd = 1, assumes that these transitions lead to ionization rather than dissociation. If they would lead to dissociation, the interstellar photodissociation rate would be increased by a factor of 2.
4.3.30. l-C4 – linear tetracarbon
The strongest absorption occurs into the 2 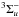 state around 6.95 eV, which, like a similar state for C3, has a huge oscillator strength of 1.6. This state, together with other states listed in Table 8 of van Hemert & van Dishoeck (2008), are included with ηd = 1. Rhombic C4, which is almost isoenergetic with ℓ-C4, is not considered and may well have a significantly different photodissociation rate.
state around 6.95 eV, which, like a similar state for C3, has a huge oscillator strength of 1.6. This state, together with other states listed in Table 8 of van Hemert & van Dishoeck (2008), are included with ηd = 1. Rhombic C4, which is almost isoenergetic with ℓ-C4, is not considered and may well have a significantly different photodissociation rate.
4.3.31. l-C4H – butadiynyl
Of the dipole-allowed transitions below the ionization potential at 9.6 eV, the higher 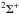 states at 7 to 9 eV have orders of magnitude larger oscillator strengths than other states and thus dominate the interstellar photodissociation. The values used in Table 9 of van Hemert & van Dishoeck (2008) are used with ηd = 1.
states at 7 to 9 eV have orders of magnitude larger oscillator strengths than other states and thus dominate the interstellar photodissociation. The values used in Table 9 of van Hemert & van Dishoeck (2008) are used with ηd = 1.
4.3.32. l-C5H – pentynylidyne
The higher 2Π states in the 4 to 6 eV range dominate the photodissociation of this molecule, using the values in Table 10 of van Hemert & van Dishoeck (2008) with ηd = 1.
4.3.33. H2O – water
References and wavelength ranges of concatenated H2O cross sections.
Measurements of the H2O photoabsorption cross section as a function of wavelength date back many decades (see van Dishoeck et al. (2013, Sect. 3.1.3)). Several measurements were concatenated into a single cross section file, as detailed in Table 7. Some of these data were rescaled to agree with the integrated cross section of more-reliable absolute measurements.
An absolutely-calibrated low-resolution cross section measured by electron-energy loss spectroscopy (Chan et al. 1993b), including the entire ultraviolet range from its onset at 190 nm, was combined with several higher-resolution direct photoabsorption measurements covering various portions of the spectrum (Smith et al. 1981; Yoshino et al. 1996, 1997; Parkinson & Yoshino 2003; Fillion et al. 2003, 2004; Mota et al. 2005, and others). Some of these resolve temperature-dependent rotational structure. Fillion et al. (2003) record the photoionisation yield of H2O that was used to partition the experimental photoabsorption cross section between ionisation and dissociation.
 |
Fig. 16 Photoabsorption cross section of H2O. Divided into channels producing O (green), OH (red), and ionisation (blue). |
The large abundance of water observed in interstellar space (van Dishoeck et al. 2013) means that its photodissociation products, either O or OH, are significant participants in the ongoing chemistry. A special case was made of further dividing the water photodissociation cross section into cross sections producing O or OH radicals. The product branching ratios are accurately measured at the Lyman-α wavelength (Slanger & Black 1982; Mordaunt et al. 1994) and some information is available at other wavelengths (Ung 1974; Stief et al. 1975). A coupled-states quantum mechanical wavepacket simulation of H2O photodissociation is carried out by van Harrevelt & van Hemert (2008) on multidimensional potential-energy surfaces describing its ground state and two excited states. This calculation agrees with the experimental O and OH branching ratios at 121.6 nm within 10% and the calculated wavelength dependence between 118 and 146 nm was adopted here. This ratio was linearly extrapolated to zero at the threshold O-atom production, 177 nm (Mordaunt et al. 1994). For wavelengths shorter than 118 nm, an equal production of OH and H radicals was assumed. The resulting partial cross sections are plotted in Fig. 16. van Harrevelt & van Hemert (2008) also calculated significant branching between the pair of products and excitations states O(3P) + 2H and O(3D) + H2, as well as OH(X2Π) + H and OH(X2Σ) + H.
4.3.34. H2O+ – water ion
This molecule is remarkably transparent at ultraviolet wavelengths: calculations show that there are no dipole-allowed dissociative electronic states below 13.6 eV so that the interstellar H2O+ photodissociation rate is negligible (van Dishoeck et al. 2006).
4.3.35. O2 – oxygen
References and wavelength ranges of concatenated O2 cross sections.
There are many laboratory studies of O2 photoabsorption. The cross section adopted here is compiled from several sources listed in Table 8. The photoionisation efficiency of Holland et al. (1993) was used to partition the photoabsorption cross section between dissociative and ionising branches shortwards of the ionisation threshold at 103 nm.
4.3.36. O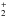 – oxygen ion
– oxygen ion
This molecule has no dissociative electronic states below 13.6 eV (Honjou et al. 1978). The only dipole-allowed states below 13.6 eV and above the O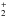 dissociation limit are the A
dissociation limit are the A and 2
and 2 states. Their oscillator strengths are only f = 0.005 each and, since they are bound, ηd = 0 is assumed.
states. Their oscillator strengths are only f = 0.005 each and, since they are bound, ηd = 0 is assumed.
4.3.37. H2O2 – hydrogen peroxide
References and wavelength ranges of concatenated H2O2 cross sections.
The combined experimental photoabsorption cross sections of Lin et al. (1978) and Suto & Lee (1983) extend from 105 to 195 nm, with the absorption at the longest wavelength being very small (less than 10 cm2) and likely to be temperature dependent. A photoionisation cross section was assembled by combining absolute and relative measurements of H2O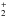 production (Dodson et al. 2015; Litorja & Ruscic 1998) and assuming a low production of fragmented ions.
production (Dodson et al. 2015; Litorja & Ruscic 1998) and assuming a low production of fragmented ions.
4.3.38. O3 – ozone
References and wavelength ranges of concatenated O3 cross sections.
The O3 photoabsorption cross section is compiled from a selection of many measurements and includes all wavelengths between 53 and 1100 nm, with the cross section longwards of 325 nm never exceeding 1×10 cm-2. The references and ranges of concatenated cross sections are give in Table 10. The binding energy of the O3 ground state corresponds to a wavelength of 1180 nm and all excited states decay dissociatively, even those absorbing weakly in the near-infrared (Grebenshchikov et al. 2007). The photoionisation threshold is 99 nm and a total photoionisation cross sections is generated by Berkowitz (2008) from reanalysis of the photoionisation yields of O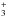 , O
, O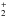 , and O+ ions measured by Mocellin et al. (2001).
, and O+ ions measured by Mocellin et al. (2001).
4.3.39. CO – carbon monoxide
The photodissociation of the strongly bound CO molecule starts shortward of 110 nm and occurs exclusively by predissociation. A detailed model of the completely line-dominated CO photodissociation cross section is constructed by Visser et al. (2009) based on wavelengths, oscillator strengths, and predissociation probabilities for individual lines and from a variety of experimental sources (e.g., Eidelsberg & Rostas 1990; Ubachs et al. 1994; Eidelsberg et al. 2006; Cacciani et al. 2001). Synthetic spectra were then constructed by summing the profile of all lines and including the effects of predissociation broadening, Doppler broadening, and alternative excitation temperatures. Visser et al. considered all of the important isotopologues in their analysis and proceeded to detailed calculations of photodissociation rates and shielding-functions, estimating the uncertainty of their cross sections to be 20%.
For the line-dominated part of the CO spectrum between 91 and 110 nm, a simulated photoabsorption and dissociation cross sections was constructed from the line parameters of Visser et al. This spectrum is shown in Fig. 8 assuming an excitation temperature of 100 K and a Doppler broadening of 1 km s-1. These values are also used in the various calculations involving CO later in the paper. The shorter wavelength part of the spectrum, <91 nm, is taken from the electron-energy loss measurement of Chan et al. (1993a) that does not resolve the CO band structure between 80 and 91.2 nm. The non-dissociative part of the spectrum longer than 108 nm is also taken from the measurement of Chan et al. (1993a) and does not include the full rotational structure of these bands.
4.3.40. CO+ – carbon monoxide ion
Like CO, CO+ has a deep potential well with a dissociation energy of 8.34 eV. The higher excited D2Π, G, E and F 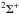 states are likely to be (pre-)dissociated, however, with oscillator strengths to the D and G states computed to be f = 0.01 and 0.02, respectively (Lavendy et al. 1993). Similar values were assumed for the higher states, with ηd = 1.
states are likely to be (pre-)dissociated, however, with oscillator strengths to the D and G states computed to be f = 0.01 and 0.02, respectively (Lavendy et al. 1993). Similar values were assumed for the higher states, with ηd = 1.
4.3.41. CO2 – carbon dioxide
CO2 is an important atmospheric molecule and thus well studied. A compilation representing its photodissociation cross section is made by Huestis & Berkowitz (2010), and was used here after being updated between 87 and 109 nm with a more recent higher-resolution photoabsorption cross section (Archer et al. 2013). The photoionisation cross section of (Shaw et al. 1995) was adopted.
4.3.42. HCO+ – isoformyl
The photodissociation of this ion is studied in detail theoretically (Koch et al. 1995a,b). The only dipole-allowed dissociative state is the 11Π state around 11.5 eV with a small cross section.
4.3.43. H2CO – formaldehyde
References and wavelength ranges of concatenated photoabsorption H2CO cross sections.
The electron-energy loss derived cross section of Cooper et al. (1996) was combined with the VUV photoabsorption spectra of Mentall et al. (1971) and Meller & Moortgat (2000), as listed in Table 11. The weak UV absorption between 240 and 360 nm is just shortwards of the effective threshold resulting from an internal barrier for dissociation to H2 and CO (Hopkins et al. 2007).
The highly-structured H2CO spectrum between 115 and 160 nm consists of predissociated Rydberg series, including some showing rotational structure (Brint et al. 1985), and presents the risk of cross sections deduced from under-resolved photoabsorption spectra being underestimated. However, the integrated cross section of an absolutely-calibrated medium-resolution photoabsorption cross section (Suto et al. 1986) agrees with the resolution-independent electron-energy loss measurement (Cooper et al. 1996) within 4%, negating this possibility. The 225 to 360 nm photodissociation cross section is also under resolved, but high-resolution data (e.g., Pope et al. 2005; Ernest et al. 2012) will not affect H2CO’s astrophysical photodestruction properties.
The photoionisation cross section is measured near threshold by Dodson et al. (2015) and at shorter wavelengths the photoabsorption cross section was scaled by the ionisation efficiency of Cooper et al. (1996). This ionisation efficiency approaches 100% at longer wavelengths than that measured by Mentall et al. (1971), which suffers from an estimated 30% uncertainty.
4.3.44. NH – imidogen
Experimental data on photoabsorption cross sections for NH exist only for the lower nondissociative excited states (Krishnamurty & Narasimham 1969) and via two-photon transitions (de Beer et al. 1991; Clement et al. 1992). The direct dissociation of NH into its first two excited repulsive curves is calculated by Kirby & Goldfield (1991) from ab initio potential-energy curves and electronic transition moments, and we adopt their theoretical cross sections. An additional broad feature at 100 nm with integrated cross section 10 cm2 nm was added to this cross section to roughly account for photoabsorption and dissociation into electronic states of higher energy than those calculated.
Predissociation of the v = 0, 1, and 2 bound levels of the low-lying  state contributes negligibly to the NH photodissociation rate in an ISRF (Kirby & Goldfield 1991), but are at sufficiently long wavelengths, greater than 250 nm, that they may influence this rate in cool radiation fields. These three bound levels were included int our cross section database without simulating their rotational structure by adopting the wavelengths of (Huber & Herzberg 1979), band oscillator strengths (the recommended values calculated by Kirby & Goldfield 1991), and predissociation efficiencies. The latter are assumed to be 0, 0, and 0.5 for the v = 0, 1, and 2 levels, respectively, in line with their ratios of radiative and dissociative lifetimes deduced by Patel-Misra et al. (1991), and assuming rotational excitation is limited to below J = 10, appropriate for astrophysical environments. The combined uncertainty in the excitation and dissociation of the
state contributes negligibly to the NH photodissociation rate in an ISRF (Kirby & Goldfield 1991), but are at sufficiently long wavelengths, greater than 250 nm, that they may influence this rate in cool radiation fields. These three bound levels were included int our cross section database without simulating their rotational structure by adopting the wavelengths of (Huber & Herzberg 1979), band oscillator strengths (the recommended values calculated by Kirby & Goldfield 1991), and predissociation efficiencies. The latter are assumed to be 0, 0, and 0.5 for the v = 0, 1, and 2 levels, respectively, in line with their ratios of radiative and dissociative lifetimes deduced by Patel-Misra et al. (1991), and assuming rotational excitation is limited to below J = 10, appropriate for astrophysical environments. The combined uncertainty in the excitation and dissociation of the  v = 2 level is an order of magnitude. The addition of this level increases the photodissociation rate of NH in a 4000 K black body radiation field by 20%. This contribution is less than the uncertainties associated with shorter-wavelength stronger-absorbing states.
v = 2 level is an order of magnitude. The addition of this level increases the photodissociation rate of NH in a 4000 K black body radiation field by 20%. This contribution is less than the uncertainties associated with shorter-wavelength stronger-absorbing states.
A theoretical photoionisation cross section was taken from Wang et al. (1990) that has significant magnitude, 7.4×10 cm2, at the Lyman-α wavelength.
4.3.45. NH2 – amidogen
There are two ab initio calculations of the dissociative excited states, transition moments, and photodissociation cross sections of this radical. Here, a photodissociation cross section file was composed, from data for the very weak 1 2A′′ → 2 2A′ transition between 150 and 210 nm (Saxon et al. 1983) added to the shorter-wavelength cross sections due to stronger transitions to various excited states calculated by Koch (1997) based on potential energy surfaces calculated by Vetter et al. (1996). An additional 2 nm FWHM Gaussian line of integrated cross section 10 cm2 nm was added to the photodissociation cross section at 110 nm to account for excitation into states not considered in the two calculations.
A photoionisation yield of NH2 is recorded by Gibson et al. (1985) from the ionisation threshold at 111 nm. We arbitrarily adopt a photoionisation cross section of 2×10 cm2 at 80 nm, in line with other molecules in the database, in order to place this onto an absolute scale.
4.3.46. NH3 – ammonia
References and wavelength ranges of concatenated NH3 cross sections.
The results of two high-resolution optical experiments (Wu et al. 2007; Liang et al. 2007) were supplemented by an electron energy-loss measurement (Samson et al. 1987) over the wavelength ranges listed in Table 12 to determine a best photoabsorption cross section for NH3. Since the cross section is broad and continuous, 100% dissociation efficiency is assumed below the ionisation threshold.
Two measurements of the NH3 ionisation efficiency were used to divide the cross section between photoionisation and photoabsorption above the ionisation limit, Samson et al. (1987) between 8 and 105 nm and Xia et al. (1991) between 106 and 124 nm. Samson et al. (1987) also determined the branching ratios of various dissociative photoionisation products with NH being the only ion product for wavelengths longer than 79 nm.
being the only ion product for wavelengths longer than 79 nm.
 |
Fig. 17 Photoabsorption cross section of NH3. Divided into channels producing NH (green), NH2 (red), and ionisation (blue). |
NH3 is an abundant species in many astrophysical environments (e.g., Ho & Townes 1983; Choi et al. 2010; Shinnaka et al. 2011), and the product branching of its dissociation may have a significant affect on the total abundance of astrochemical molecules NH2 and NH. As for H2O, a special case was made of determining the wavelength dependence of this branching.
A measurement of NH3 photolysis at 121.6 nm was made by Slanger & Black (1982), and previous experiments reviewed therein, finding a 1.89 quantum yield of H-atom production. This requires the formation of NH + H + H fragments with a branching ratio of 95% and the remaining 5% of photoabsorption events was assumed to produce NH2 + H. No further constraining information on these dissociation channels exists at shorter wavelengths and so the same 95 and 5% branching was adopted. At longer wavelengths, the observed threshold for NH fluorescence following NH3 dissociation is 132 nm (Leach et al. 2005), and 100% NH2 production was assumed for all longer wavelengths. The branching ratios between 121.6 and 132 nm were linearly interpolate between experimental constraints. The resulting partial cross sections are plotted in Fig. 17.
4.3.47. N2 – nitrogen
Detailed studies of the astrophysical photodissociation of N2 and its isotopic consequences can be found in Li et al. (2013) and Heays et al. (2014b), and are based on a large body of work, both experimental (e.g., Carroll & Collins 1969; Sprengers et al. 2003; Stark et al. 2008; Lewis et al. 2008; Heays et al. 2014a) and theoretical (e.g., Dressler 1969; Stahel et al. 1983; Lewis et al. 2005; Heays 2011).
The photoabsorption and dissociation cross sections of Heays et al. (2014b) between 85 and 100 nm were used. These are the product of a coupled-channels model (e.g., Gibson & Lewis 1996) defined by excited-state potential-energy curves that are experimentally-optimised (Heays et al. 2011). These cross sections reproduce the full ro-vibrationally resolved spectrum of the molecule, including its temperature dependence, and have an uncertainty of 10% over the wavelength relevant to the ISRF. The simulation used here assumes a thermal excitation of 100 K and a Doppler broadening of 1 km s-1.
N2 does not absorb significantly at longer wavelengths than 100 nm. Some highly-excited Rydberg states appearing at wavelengths shorter than 85 nm are missing in the coupled-channels formulation. The low-resolution electron-energy-loss-deduced cross sections of Chan et al. (1993d) and Shaw et al. (1992) were used over the wavelength ranges 79.5 <λ< 85 and λ< 79.5 nm, respectively. The cross section of Chan et al. (1993d) was scaled down by a factor of 0.7 in order to maintain continuity with the adjoining measurement.
4.3.48. NO – nitric oxide
The NO photoabsorption spectrum is well measured by low-resolution electron-energy-loss spectroscopy (Iida et al. 1986; Chan et al. 1993c) and at higher resolution by photoabsorption spectroscopy utilising He and H2 discharge sources to generate ultraviolet continua (Watanabe et al. 1967).
A further series of Fourier-transform spectroscopy measurements (Yoshino et al. 2006, and references therein) principally employing synchrotron radiation resolved many absorption lines between 166 and 196 nm, and reduced them to a list of wavelengths and oscillator strengths. These data were used to simulate this part of the spectrum with a line-by-line model capable of reproducing a range of excitation temperatures. As illustrated by various experiments, not all lines in this range dissociate completely (e.g., Brzozowski et al. 1976).
Assumed dissociation fraction of NO excited-state vibrational levels.
The predissociation fraction of the various excited levels was estimated from several studies (Brzozowski et al. 1974, 1976; Hikida & Mori 1978; Hart & Hepburn 1987; Luque & Crosley 2000) and the assumed values are listed in Table 13 for excited levels appearing in our line-by-line simulation. Some of the lowest-excited rotational transitions were not observed in the room temperature spectrum of Yoshino et al. (2006) but are important in the interstellar medium. The various line parameters for these transitions were extrapolated from higher levels.
The fraction of NO photoabsorption below the 134 nm threshold resulting in ionisation was estimated from the photoion spectroscopy of Watanabe et al. (1967). The cross section plotted in Fig. 10 and used later in various calculations is simulated assuming a 100 K ground state excitation and 1 km s-1 Doppler width.
4.3.49. CN – cyanide radical
 |
Fig. 18 Photodissociation cross section for CN. Presently calculated cross section and those of Lavendy et al. (1987) and el-Qadi & Stancil (2013). |
The photodissociating states of CN have not been experimentally observed. Ab initio configuration-interaction calculations (Lavendy et al. 1984, 1987) have identified high-lying valence states (the fourth and fifth members of  and
and 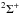 symmetry) to be responsible for its ultraviolet photodissociation cross section, and calculated its onset to occur near 105 nm. A further cross section is calculated by el-Qadi & Stancil (2013) adopting the potential-energy curves and transition moments published by Lavendy et al. (1987) but finds an approximately factor-of-three discrepancy compared with the earlier work, as shown in Fig. 18. To resolve this, we recomputed the potential-energy curves of
symmetry) to be responsible for its ultraviolet photodissociation cross section, and calculated its onset to occur near 105 nm. A further cross section is calculated by el-Qadi & Stancil (2013) adopting the potential-energy curves and transition moments published by Lavendy et al. (1987) but finds an approximately factor-of-three discrepancy compared with the earlier work, as shown in Fig. 18. To resolve this, we recomputed the potential-energy curves of 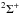 and
and 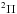 states and their transition moments with respect to photoexcitation from the ground state. This analysis included all states dissociating to form excited N(
states and their transition moments with respect to photoexcitation from the ground state. This analysis included all states dissociating to form excited N( S) atoms and ground state C(
S) atoms and ground state C( P), or to lower energy limits, and some states leading to more highly-excited atoms.
P), or to lower energy limits, and some states leading to more highly-excited atoms.
Full details of the ab initio calculation using the MOLPRO software will be given in a later publication but adopts similar methods as other recent calculations of CN excited states (Kulik et al. 2009; Shi et al. 2011) and as in van Hemert & van Dishoeck (2008). These calculated potential-energy curves are in good agreement with the ground state and first excited 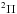 and
and 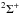 states of previous work (Lavendy et al. 1987; Kulik et al. 2009), but find the highly-excited photodissociating states to be more bound than in the previous calculations, by as much as 1 eV. This lowering arises from a larger basis set provided to the ab initio potential-energy curve calculation.
states of previous work (Lavendy et al. 1987; Kulik et al. 2009), but find the highly-excited photodissociating states to be more bound than in the previous calculations, by as much as 1 eV. This lowering arises from a larger basis set provided to the ab initio potential-energy curve calculation.
A photodissociation cross section was generated from the calculated curves and transition moments by reflecting the ground state vibrational wavefunction through each excited-state potential and onto the energy axis (Condon 1928). Scaling this reflection with the R-dependent transition moments and converting the potential-energy scale to wavelength generates the cross section in Fig. 18. The integrated calculated cross section is one quarter that determined by Lavendy et al. (1987) but in approximate agreement with the reanalysis of el-Qadi & Stancil (2013), however, the increased binding of the 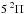 state in our calculation leads to a 10 nm longwards shift of its peak cross section, to 110 nm. The photodissociation rate assuming ISRF radiation is half of the value calculated assuming the cross section of Lavendy et al. (1987; see Sect. 5). The new rate would a factor of two smaller still without the 10 nm shift described.
state in our calculation leads to a 10 nm longwards shift of its peak cross section, to 110 nm. The photodissociation rate assuming ISRF radiation is half of the value calculated assuming the cross section of Lavendy et al. (1987; see Sect. 5). The new rate would a factor of two smaller still without the 10 nm shift described.
There are no strong ultraviolet-absorbing excited states of CN that dissociate to form C( P)+N(
P)+N( S) ground state atoms, or the excited pair C(
S) ground state atoms, or the excited pair C( D)+N(
D)+N( S) (with 140 nm dissociation threshold). We then assumed all bound
S) (with 140 nm dissociation threshold). We then assumed all bound 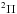 and
and 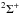 levels dissociate with efficiency ηd = 1 for energies above the C(
levels dissociate with efficiency ηd = 1 for energies above the C( P) + N(
P) + N( D) dissociation limit (with a 120 nm threshold) and all lower-energy levels have ηd = 0. It is also possible that the lower-energy bound levels are actually predissociated through spin-orbit interaction with quartet states dissociating to the C(
D) dissociation limit (with a 120 nm threshold) and all lower-energy levels have ηd = 0. It is also possible that the lower-energy bound levels are actually predissociated through spin-orbit interaction with quartet states dissociating to the C( P)+N(
P)+N( S) limit, with a corresponding 160 nm threshold. Even a moderate dissociation efficiency and low cross section at such long wavelengths could increase the dissociation rate of CN in a cool radiation field by an order of magnitude.
S) limit, with a corresponding 160 nm threshold. Even a moderate dissociation efficiency and low cross section at such long wavelengths could increase the dissociation rate of CN in a cool radiation field by an order of magnitude.
4.3.50. HCN – hydrogen cyanide
References and wavelength ranges of concatenated HCN cross sections.
HCN absorbs strongly at wavelengths shorter than 150 nm with a 100% yield of H and CN photodissociation products and two experimental cross sections for this process Lee (1980), Nuth & Glicker (1982) were combined, as listed in Table 14. There are weaker absorption bands longwards of 150 nm that appear in high-resolution spectra with broadened lineshapes suggestive of predissociation-dominated lifetimes (Herzberg & Innes 1957; Hsu et al. 1984; Jonas et al. 1990). The absorption cross section of West & Berry (1974) was adopted for wavelengths greater than 157 nm, and shows good agreement with the cross section of Lee (1980) where they overlap. Absorption at these long wavelengths contributes 50% of the total HCN photodissociation rate in a 4000 K black-body radiation field (see Sect. 5) but is not significant for hotter ultraviolet radiation fields.
HCN begins to photoionise to HCN+ shortward of 92 nm and is assumed to have a 100% ionisation yield by 83 nm. The intervening branching to dissociation and ionisation was calculated by comparing the wavelength dependence of the absorption cross section and a measured photoionisation yield (Dibeler & Liston 1967).
4.3.51. HC3N – cyanoacetylene
References and wavelength ranges of concatenated HC3N cross sections.
A combination of three HC3N experimental photoabsorption cross sections provide good coverage from its threshold at 255 nm to 80 nm, with sources listed in Table 15. Additionally, a total photoionisation cross section is recorded by Leach et al. (2014) and here the remaining photoabsorption cross section was attributed to neutral photodissociation.
4.3.52. CH3OH – methanol
References and wavelength ranges of concatenated CH3OH cross sections.
The photoabsorption cross section of methanol is well known and the sources of data used in our compilation are listed in Table 16. The photoabsorption and photoionisation cross sections measured by Burton et al. (1992) were used to determine the dissociation versus ionisation branching ratio shortwards of the 113 nm ionisation limit.
4.3.53. CH3CN – acetonitrile
The photoabsorption cross section of Eden et al. (2003) is adopted between 140 and 182 nm and the absorption coefficient of Nuth & Glicker (1982) between 61 and 140 nm. The latter was multiplied by 4.05×10 to match the former over their 25 nm overlapping range. The photoionisation yield measured by Schwell et al. (2008) was used to determine partial ionisation and neutral dissociation cross sections.
4.3.54. CH3CHO – acetaldehyde
The photoabsorption cross section of CH3CHO is recorded at high-resolution between 116 and 350 nm by Limão Vieira et al. (2015). This measurement shows a weak long-wavelength absorption peak between 250 and 350 nm as well as a stronger and more structured region appearing between 184 nm and the first ionisation limit, 121.5 nm.
The cross section at shorter wavelengths is not well constrained. Hurzeler et al. (1958) record the wavelength-dependent signal of mass 44 (CH3CHO+) and dehydrogenated mass 43 photoionisation fragments between 109 and 125 nm. To place this measurement on an absolute scale the threshold CH3CHO+ ionisation cross section calculated by Vega et al. (2010) was assumed. We extrapolate the photoion signal of Hurzeler et al. (1958) to shorter wavelengths by assuming the same fall-off for both mass 44 and 43 fragments as calculated by Vega et al. (2010). Photoionisation data between 110 and 122 nm are missing from the laboratory measurement and a linear extrapolation to the peak of the ionisation signal at 110 nm is used to approximate this. All absorption not accounted for by the deduced photoionisation cross section is assumed to result in dissociation.
The cross section put together in this way, and plotted in Fig. 11, is uncertain around the ionisation threshold though physically plausible, and is superior to completely neglecting wavelengths shorter than those studied by Limão Vieira et al. (2015).
4.3.55. CH3NH2 – methylamine
Methylamine photoabsorbs and dissociates at wavelengths shorter than 250 nm. A cross section was constructed from the photoabsorption measurements of Hubin-Franskin et al. (2002) (138 to 249 nm), combined with their simultaneously-recorded electron-energy-loss-derived cross section (83 to 138 nm) and another lower-resolution electron-energy loss measurement (Burton et al. 1994) shorter than 83 nm. Some information on branching ratios to various products is available at a few wavelengths (Michael & Noyes 1963; Gardner & McNesby 1982).
A relative photoionisation yield is measured by Hu et al. (2002) between 121 and 135 nm. This was absolutely calibrated with respect to the photoabsorption cross section by assuming a 100% ionisation yield at 121 nm. This may well be an overestimate of the yield, in that case the photoionisation rates calculated here will be overestimated and the non-ionising rates too low. Hu et al. (2002) also measured the branching of photoionisation products into fragments.
4.3.56. NH2CHO – formamide
The photoabsorption cross section of NH2CHO is measured for wavelengths greater than 89 nm by Gingell et al. (1997), who combined a direct measurement with electron energy-loss spectroscopy. This cross section begins around 215 nm and peaks around 168 nm with some resonant structure.
The ionisation threshold of NH2CHO occurs just shortwards of the 121.3 nm Lyman-α transition. The photoion spectra of Leach et al. (2010) was converted into dissociation and ionisation cross sections by assuming 100% ionisation shorter than 89 nm and scaling to match the photoabsorption cross section of (Gingell et al. 1997) at this wavelength.
4.3.57. C2H5OH – ethanol
A C2H5OH photoabsorption cross section measured by electron-energy loss spectroscopy (Feng & Brion 2002) agrees well with several less-complete direct photoabsorption measurements available from the MPI Mainz UV/VIS database, and is adopted here. All absorption events are assumed to lead to dissociation.
An absolute ionisation cross section determined by photoion spectroscopy (Cool et al. 2005) was adopted between 105 nm and the photoionisation threshold at 120 nm. For shorter wavelengths, 55 to 90.5 nm, a cross section was calculated from the measured photoionisation efficiency of Hatano (1999). The photoionisation cross section was linearly interpolated between these two wavelength ranges.
4.3.58. C3H7OH – 1-propanol
Two measurements spanning the wavelength ranges 120 to 208 nm (Salahub & Sandorfy 1971) and 30 to 120 nm (Koizumi et al. 1986) were combined into a single photoabsorption cross section. An absolute ionisation cross section between 125 and 107 nm is measured by ion mass-spectroscopy (Cool et al. 2005), and a photoionisation cross section constructed by supplementing this with a measured photoionisation efficiency between 76 and 92 nm (Hatano 1999). The ionisation cross section for intervening wavelengths was linearly interpolated, and linearly extrapolated to shorter wavelengths assuming a photoionisation fraction of 1 shortwards of 60 nm, in line with similar molecules (Hatano 1999).
4.3.59. OCS – carbonyl sulphide
The photoabsorption of OCS is studied extensively in view of its importance to atmospheric chemistry (e.g., Limão Vieira et al. 2015, and references therein). Here, the recent high-resolution measurement of its cross section by Limão Vieira et al. (2015) was adopted, and supplemented with photoabsorption and ionisation cross sections deduced form electron-energy loss spectroscopy for wavelengths shorter than 115 nm (Feng et al. 2000b,a).
4.3.60. CH3SH – methanethiol
Two experimental cross sections (Vaghjiani 1993; Tokue et al. 1987) were combined to describe CH3SH photoabsorption from its long-wavelength threshold at 330 nm (Wilson et al. 1994) to the ionisation threshold at 131 nm (Morgan et al. 1995). For shorter wavelengths, a photodissociation cross section linearly extrapolated to zero at 100 nm (30 nm below the ionisation threshold) was adopted, and a photoionisation cross section using the measured efficiency for CH3SH+ production of Kutina et al. (1982) after scaling its maximum value to 5×10 cm2. The various assumptions used in the shorter wavelength region were selected in a broad analogy to the photodissociation and ionisation properties of CH3OH.
4.3.61. CS – carbon monosulphide
There are no absolute measurements of the CS cross section for photoabsorption into pre- or directly-dissociative excited states. Here, the cross section simulated and discussed by van Dishoeck (1988) was retained. This uses the measured wavelengths of transitions to the 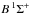 states (Stark et al. 1987) and vertical excitation energies of higher-lying states calculated by Bruna et al. (1975). The strengths of these electronic transitions are estimated.
states (Stark et al. 1987) and vertical excitation energies of higher-lying states calculated by Bruna et al. (1975). The strengths of these electronic transitions are estimated.
4.3.62. CS2 – carbon disulphide
References and wavelength ranges of concatenated CS2 cross sections.
Multiple experiments were combined into a single CS2 photoabsorption cross section spanning 20 to 370 nm, with details given in Table 17. The ionisation and ground-state dissociation thresholds are at 123 and 277 nm, respectively (Fischer et al. 1993; Okabe 1972). A photoionisation cross section was deduced by scaling the photoionisation efficiency measured by Dibeler & Walker (1967) to match the photoabsorption cross section of Wu & Judge (1983) for wavelengths sufficiently shorter than the ionisation threshold that non-ionising decay is negligible.
4.3.63. SO2 – sulphur dioxide
The photoabsorption cross section of SO2 was measured numerous times and a consolidation of these into a single spectrum between 106 and 403 nm was generated by Manatt & Lane (1993). This was modified by inserting a higher-resolution measured cross section between 172 and 289 nm, including the important photodissociating absorption bands between 170 nm and the photodissociation threshold at 218.7 nm (Becker et al. 1995). A measured fluorescence yield (Katagiri et al. 1997) was used to estimate the dissociation fraction near this threshold. Even-higher resolution measurements of these bands are available (e.g., Blackie et al. 2011; Endo et al. 2015) but were deemed unnecessary for our purposes.
A combination of photoionisation efficiency and short-wavelength photoabsorption cross sections measured by electron-impact and photoion spectroscopy (Feng et al. 1999c; Holland et al. 1995) were used to determine the absorption and ionisation cross sections for wavelengths shorter than compiled by Manatt & Lane (1993).
4.3.64. SH+ – mercapto ion
The direct photodissociation cross section of SH+ is calculated ab initio by McMillan et al. (2016) including transitions to several excited states. Their calculation from the v = 0 and J = 0 ground-state level was adopted here and added to this additional absorption into the longer-wavelength bound-levels of the 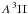 state, which is known to predissociate for v ≥ 1 (Gustafsson et al. 1988; Brites et al. 2008). Oscillator strength of transitions into the vibrational levels of
state, which is known to predissociate for v ≥ 1 (Gustafsson et al. 1988; Brites et al. 2008). Oscillator strength of transitions into the vibrational levels of 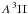 were calculated here using the potential-energy curves and transition dipole moments of McMillan et al. (2016) and the methods of Sect. 4.3.49, but did not include details of their rotational structure.
were calculated here using the potential-energy curves and transition dipole moments of McMillan et al. (2016) and the methods of Sect. 4.3.49, but did not include details of their rotational structure.
4.3.65. SO – sulphur monoxide
The predissociated  absorption bands of SO, appearing shortward of 235 nm, are measured by Phillips (1981). The short wavelength absorption between 116 and 135 nm measured by Nee & Lee (1986) was added to this and a relative photoionisation yield shortwards of 121 nm (Norwood & Ng 1989) that we arbitrarily scaled to give a peak value of 5×10 cm2.
absorption bands of SO, appearing shortward of 235 nm, are measured by Phillips (1981). The short wavelength absorption between 116 and 135 nm measured by Nee & Lee (1986) was added to this and a relative photoionisation yield shortwards of 121 nm (Norwood & Ng 1989) that we arbitrarily scaled to give a peak value of 5×10 cm2.
4.3.66. S2 – disulphur
The photodissociation and ionisation cross section of the S2 radical is not well known, but is important for understanding S-bearing molecular abundances evident in comets (de Almeida & Singh 1986). Photodissociating transitions occur into the 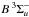 state, which is predissociated for levels v ≥ 10 (Kato & Baba 1995). Transition wavelengths for B(v′) ← X(0) photoabsorption bands were calculated using the molecular constants of Wheeler et al. (1998) and adopted oscillator strengths for v′ = 0 to 20 bands from the calculations of Pradhan et al. (1991). These oscillator strengths to v′ = 26 were extrapolated using Franck-Condon factors calculated for the B ← X transition by Smith & Liszt (1971). According to these factors, vibrational levels with v′> 26 will contribute less than 6% to the total absorption into the B state, and the continuum absorption shorter than the 224 nm direct dissociation limit will be weak. The photoabsorption and photodissociation cross sections simulated here neglect rotational structure of the individual vibrational bands (e.g., Wheeler et al. 1998).
state, which is predissociated for levels v ≥ 10 (Kato & Baba 1995). Transition wavelengths for B(v′) ← X(0) photoabsorption bands were calculated using the molecular constants of Wheeler et al. (1998) and adopted oscillator strengths for v′ = 0 to 20 bands from the calculations of Pradhan et al. (1991). These oscillator strengths to v′ = 26 were extrapolated using Franck-Condon factors calculated for the B ← X transition by Smith & Liszt (1971). According to these factors, vibrational levels with v′> 26 will contribute less than 6% to the total absorption into the B state, and the continuum absorption shorter than the 224 nm direct dissociation limit will be weak. The photoabsorption and photodissociation cross sections simulated here neglect rotational structure of the individual vibrational bands (e.g., Wheeler et al. 1998).
The photoionisation efficiency of S2 is measured (Liao & Ng 1986) and a typical absolute magnitude for this was arbitrarily assumed here. Additional bound and unbound states exist between the 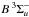 and ionisation continuum (e.g., Donovan et al. 1970; Xing et al. 2013) but no quantitative information on their photoabsorption cross sections is available. It is likely that the longer-wavelength absorption of
and ionisation continuum (e.g., Donovan et al. 1970; Xing et al. 2013) but no quantitative information on their photoabsorption cross sections is available. It is likely that the longer-wavelength absorption of 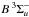 will dominate the photodissociation rate for S2 in most interstellar radiation fields.
will dominate the photodissociation rate for S2 in most interstellar radiation fields.
Foreshadowing Sect. 5, we calculate the photodissociation rate of S2 in the solar radiation field at 1 AU distance from the Sun to be 0.0079 s-1, that is with a lifetime of 130 s, which is a significant reduction from the 250 s lifetime calculated by de Almeida & Singh (1986). This difference is likely due to the larger number of predissociating 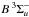 vibrational levels considered in the present work, leading to a larger total photodissociation rate.
vibrational levels considered in the present work, leading to a larger total photodissociation rate.
4.3.67. SH – mercapto radical
Several ab initio calculations of the SH ground and excited states have been made (Bruna & Hirsch 1987; Resende & Ornellas 2001; Lee et al. 2001), and there is one absolute absorption measurement, providing the oscillator strength of the predissociative X2Π(v′′ = 0) to A2Σ+(v′ = 0) transition. This measurement was combined with calculated Franck-Condon factors for transition to higher-v′′A2Σ+ levels (Resende & Ornellas 2001) and experimental spectroscopic constants (Johns & Ramsay 1961) to estimate the cross section of A−X transitions (neglecting their rotational structure). Furthermore, a “reflection” cross section to simulate continuum absorption into the lowest-energy repulsive 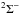 state was added, using the potential-energy curves and electronic transition moment of Lee et al. (2001), and the methods described in Sect. 4.3.49. Higher lying bound and repulsive states were included as vertical transitions according to their calculated equilibrium energies and transition moments (Bruna & Hirsch 1987). Finally, the unknown photoionisation cross section of SH was arbitrarily simulated by including an absorption feature of integrated cross section 5×10 cm2 shortwards of the 119 nm photoionisation threshold (Hsu et al. 1994).
state was added, using the potential-energy curves and electronic transition moment of Lee et al. (2001), and the methods described in Sect. 4.3.49. Higher lying bound and repulsive states were included as vertical transitions according to their calculated equilibrium energies and transition moments (Bruna & Hirsch 1987). Finally, the unknown photoionisation cross section of SH was arbitrarily simulated by including an absorption feature of integrated cross section 5×10 cm2 shortwards of the 119 nm photoionisation threshold (Hsu et al. 1994).
4.3.68. H2S – hydrogen sulphide
There are several measurements of the photoabsorption of H2S, and data from Lee et al. (1987) (240 to 118.8 nm), Xia et al. (1991) (118.8 to 106 nm), and Feng et al. (1999a) (106 to 41 nm), was compiled here into a single cross section. It is likely that some of the absorption features between 120 and 160 nm are not fully resolved by these measurements. It was assumed that all absorption leads to dissociation or ionisation, with the branching between these two determined from the photoionisation cross sections of Xia et al. (1991), Feng et al. (1999b).
4.3.69. SiO – silicon monoxide
This molecule has a similar electronic structure to that of CO, but with a lower dissociation energy, 8.26 eV vs. 11 eV. Thus, even the lower 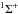 Rydberg states can contribute to SiO photodissociation whereas they are bound for CO (e.g., its B and C v = 0 levels). Another difference between the two molecules are quite distinct ionisation potentials: 11.4 eV for SiO and 14 eV for CO, putting the latter above the Lyman-limit. The oscillator strengths to the 3
Rydberg states can contribute to SiO photodissociation whereas they are bound for CO (e.g., its B and C v = 0 levels). Another difference between the two molecules are quite distinct ionisation potentials: 11.4 eV for SiO and 14 eV for CO, putting the latter above the Lyman-limit. The oscillator strengths to the 3 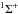 and 2, 3, 4 and 5 1Π states are taken to be f = 0.10, 0.32, 0.03, 0.11 and 0.10, respectively, with ηd = 1 as deduced by ab initio calculations (van Dishoeck et al. 2006).
and 2, 3, 4 and 5 1Π states are taken to be f = 0.10, 0.32, 0.03, 0.11 and 0.10, respectively, with ηd = 1 as deduced by ab initio calculations (van Dishoeck et al. 2006).
4.3.70. HCl – hydrogen chloride
The HCl photoabsorption cross section was adopted from the combination of a direct measurement (Bahou et al. 2001) and electron-energy loss spectroscopy (Brion et al. 2005) over the 5 to 135, and 135 to 230 nm wavelength regions, respectively. A photoionisation cross section is recorded by Frohlich & Glass-Maujean (1990). The HCl spectrum spans a region of continuous absorption into the repulsive  state between 135 and 250 nm, many bound excited Rydberg and valence levels between 100 and 135 nm, and an ionisation continuum shortwards of 97.2 nm.
state between 135 and 250 nm, many bound excited Rydberg and valence levels between 100 and 135 nm, and an ionisation continuum shortwards of 97.2 nm.
The most recent ab initio calculation of the HCl cross section by Engin et al. (2012) identifies 13 photoabsorbing electronically excited states of  and
and 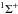 symmetry below 12.2 eV, and is excellent in agreement with the previous computation of van Dishoeck et al. (1982) for those states absorbing longer than 120 nm. Comparing the integrated cross section of Engin et al. (2012) and the experimental data between 102 and 200 nm leads to agreement within 4%. The excited states responsible for the significant HCl absorption between 91.6 and 102 nm are not well known. Many bands are observed and assigned to Rydberg-type excited states in this region (Ginter & Ginter 1981; Green et al. 1991) but without quantification of their absorption cross sections. An independent measurement of the HCl photoabsorption spectrum below 110 nm is warranted.
symmetry below 12.2 eV, and is excellent in agreement with the previous computation of van Dishoeck et al. (1982) for those states absorbing longer than 120 nm. Comparing the integrated cross section of Engin et al. (2012) and the experimental data between 102 and 200 nm leads to agreement within 4%. The excited states responsible for the significant HCl absorption between 91.6 and 102 nm are not well known. Many bands are observed and assigned to Rydberg-type excited states in this region (Ginter & Ginter 1981; Green et al. 1991) but without quantification of their absorption cross sections. An independent measurement of the HCl photoabsorption spectrum below 110 nm is warranted.
All photoabsorbing states were here assumed to be completely dissociative (ηd = 1), despite their sometimes unbroadened linewidths. This is based on the weakness of the fluorescence cross section from these states (Nee et al. 1986) and the strong coupling of Rydberg levels and unbound valence states in theoretical studies (e.g., van Dishoeck et al. 1982; Alexander et al. 1998).
Shorter than the 96 nm ionisation limit, a small signal of H+ or Cl+ dissociative-photoionisation products is measured (Daviel et al. 1984), as well as a small cross section for decay into neutral products (Frohlich & Glass-Maujean 1990).
4.3.71. HCl+ – hydrogen chloride ion
Ab initio calculation of potential-energy curves for the HCl+ ground and lowest-excited states, and the transition moments connecting them, permitted a calculation of the molecule’s wavelength-dependent photodissociation cross section (Pradhan et al. 1991). The dominant dissociation pathway determined by this calculation produces H and Cl+.
4.3.72. AlH – alumane
Potential-energy curves for the 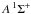 and
and 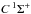 states of AlH are calculated by Matos et al. (1987) as well as electric-dipole transition moments with respect to the
states of AlH are calculated by Matos et al. (1987) as well as electric-dipole transition moments with respect to the 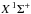 ground state. Vertical transitions calculated from this data at the equilibrium geometry give absorption at 430 and 230 nm with oscillator strengths of 0.0022 and 0.090, respectively. This however represents an upper limit for photodissociation because unbroadened emission lines from the v = 0 and 1 levels of both the A and C states is observed (Szajna & Zachwieja 2010; Szajna et al. 2011). The predissociation of higher energy vibrational structure for both states may be possible however if they are able to tunnel through maxima predicted for both potential-energy curves (Matos et al. 1987; Bauschlicher & Langhoff 1988). Given this uncertainty, two absorption features were assumed here to represent the AlH spectrum with oscillator strengths of 0.05, one at 200 nm to represent all photodissociating states, and another at 130 nm to for photoionisation, the photoionisation threshold occurs at approximately 160 nm (Matos et al. 1987). The ISRF rate is a factor of 10 smaller than previously given in the Leiden database because of the lack of dissociation via the v = 0 and 1 levels.
ground state. Vertical transitions calculated from this data at the equilibrium geometry give absorption at 430 and 230 nm with oscillator strengths of 0.0022 and 0.090, respectively. This however represents an upper limit for photodissociation because unbroadened emission lines from the v = 0 and 1 levels of both the A and C states is observed (Szajna & Zachwieja 2010; Szajna et al. 2011). The predissociation of higher energy vibrational structure for both states may be possible however if they are able to tunnel through maxima predicted for both potential-energy curves (Matos et al. 1987; Bauschlicher & Langhoff 1988). Given this uncertainty, two absorption features were assumed here to represent the AlH spectrum with oscillator strengths of 0.05, one at 200 nm to represent all photodissociating states, and another at 130 nm to for photoionisation, the photoionisation threshold occurs at approximately 160 nm (Matos et al. 1987). The ISRF rate is a factor of 10 smaller than previously given in the Leiden database because of the lack of dissociation via the v = 0 and 1 levels.
Photodissociation rates of molecules and parameterised dust shielding.
5. Photodestruction due to stellar and interstellar radiation
5.1. Results
Photodestruction rates were calculated according to Eq. (1) using the cross sections discussed in Sect. 4 and assuming several of the radiation fields detailed in Sect. 2, selected to represent a range of astrochemical environments. Tables 18 and 19 summarise the calculated rates for photodissociation and photoionisation, respectively. The photodissociation and photoionisation rates in the ISRF have uncertainties listed in Table 1 and described in Sect. 4.1. These can be incorporated into chemical rate networks to perform sensitivity analyses of model abundances (Wakelam et al. 2012). For cool radiation fields, such as a 4000 K black body or the solar radiation field, low-lying molecular states just above the dissociation limit dominate the photodissociation rate and uncertainty. For example, the interstellar rate of OH is dictated by three direct and continuous channels in the 190 to 91.2 nm range, whereas the rate assuming 4000 K black-body radiation proceeds primarily by predissociation through the 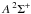 state around 300 nm (van Dishoeck & Dalgarno 1984b; van Dishoeck et al. 1984).
state around 300 nm (van Dishoeck & Dalgarno 1984b; van Dishoeck et al. 1984).
We also computed photodestruction rates assuming the radiation field of Mathis et al. (1983) (10 kpc Galactocentric distance). These are consistently 30 to 40% smaller than for our standard ISRF due to the differing magnitudes but similar shape of the two radiation fields over the range 100 to 300 nm. For the species (about 15%) that are primarily photodestroyed at wavelengths between the Lyman-limit and 100 nm (e.g., dissociation for many diatomics or ionisation of many species) the Mathis 1983 rates are more similar or occasionally greater.
Photoionisation rates of atoms and molecules and parameterised dust.
The photodissociation and photoionisation rates for all atoms and molecules in our database are compared in Figs. 19 and 20 assuming exposure to three different wavelength-dependent radiation fields. These are plotted in order of decreasing ISRF rate and with varying vertical scales. The largest ISRF photodissociation rate is 8.5×10 s-1 and occurs for ℓ-C4, while the smallest rate is 5.4×10 s-1 for HCO+. These extremes correspond to lifetimes against photodissociation of 4 to 6000 years, respectively. The lowest rates occur mostly for small ions, while neutral molecules mostly fall between 0.5 and 4×10 s-1.
The photoionisation rates of most molecules exposed to the ISRF are between 2 and 10 times smaller than their respective photodissociation rates, but can be many times smaller still. This provides some reassurance that the dominant photodestruction pathway is included in our database for those molecules where we evaluated a photodissociation rate but neglected the corresponding photoionisation cross section and rate because of a lack of reliable information. For two molecules, C2 and CH3NH2, that have particularly large cross section and long wavelength thresholds for photoionisation the ISRF photoionisation rate is actually larger than for photodissociation, by factors of 1.7 and 2.2, respectively.
The response of the various molecules to alternative radiation fields is highly variable and largely controlled by the qualitative properties of their wavelength-dependent cross sections. Comparative rates are plotted in Figs. 19 and 20. We note that these are calculated assuming radiation fields with equal integrated energy intensity between 91.2 and 200 nm, while the intensity in real astrochemical environments of interest varies by orders of magnitude. With this normalisation, molecules with relatively long-wavelength photodissociation thresholds show massively increased rates when irradiated by a 4000 K black body and sometimes supersede the scales of our figures by orders of magnitude. This effect is illustrated in Fig. 21 for four molecules with successively shorter-wavelength dissociation thresholds, in the order SiH+, NH3, HC3N, and N2, and with respective ratios between 4000 K and ISRF photodissociation rates of 1800, 2.5, 0.09, 2×10. The rapid increase of black body intensity longwards of 170 nm is responsible for this variation. The 4000 K photodissociation of CH3 and NH3 is dominated by absorption longer than 170 nm into their lowest-lying electronic states. In contrast, the very-short wavelength threshold of N2 makes it completely immune to 4000 K radiation. Figure 22 illustrates this point further by plotting the photodissociation or ionisation thresholds of all species versus their 4000 K and ISRF rate ratios, showing a sharp drop shortwards of 170 nm. According to this figure, these ratios vary by more than an order of magnitude due to other details of each atomic or molecular cross section.
Figures 19 and 20 also show rates assuming a Lyman-α dominated radiation field, most of which are smaller than in the ISRF case (under our normalisation scheme) or zero if there is no significant cross section at 121.6 nm. Most molecules and atoms have photoionisation thresholds at similar or shorter wavelengths than this (as listed in Table 1), explaining the general disappearance or lowering of photoionisation rates for Lyman-α radiation.
For molecules with line-dominated cross sections the Lyman-α cross section is sensitive to the positions of these lines. For example, Fig. 23 shows why the photodissociation rate of C2H2 increases by a factor of three when substituting the ISRF with a Lyman-α emission line, while HC3N decreases by a factor 2. In this case the respective overlap and non-overlap of resonances is responsible.
5.2. Comparison with previous rates
The new ISRF photodissociation and ionisation rates are compared with those calculated from cross sections taken from the previous version of the Leiden database (van Dishoeck 1988; van Dishoeck et al. 2006) and the PHIDRATES database (Huebner et al. 1992; Huebner & Mukherjee 2015) in Fig. 24. Not all species are included in all databases. We generally find agreement within 30% with the molecular rates from the previous Leiden database with exceptional cases being the photodissociation of CH3, HCl and the photoionisation of C2H2. All of these processes have larger rates in the updated database, by factors between 1.6 and 2.3, and this is due to the availability of new theoretical and experimental data, especially at shorter wavelengths, leading to increased cross sections.
More disagreement follows from comparison with the PHIDRATES database, with differences spanning factors of 0.15 to 3.8, and the extreme case of CH3CHO photodissociation for which the PHIDRATES cross section is based on somewhat incomplete information. In general PHIDRATES molecular cross sections were collated originally by Huebner et al. (1992) and in previous studies, and the subsequent availability of new experimental and theoretical information explains the different ISRF photodestruction rates.
It is important to note the differing intentions of the Leiden and PHIDRATES databases. The former considers cross sections important to interstellar chemistry, so that metastable dissociation products generally have time to decay before they can react, and the Lyman-limit at 91.2 nm provides a hard short-wavelength limit to the radiation field in most cases. Conversely, the PHIDRATES cross sections are intended for studying photochemistry in the solar system, including high-density environments like planetary atmospheres and cometary comae. Then, partial cross sections for many more dissociation and dissociative-ionisation fragments are considered, including metastable species, and with a stronger emphasis on the solar radiation field, favouring lower-lying states.
 |
Fig. 19 Unshielded photodissociation rates of molecules. Rates are shown assuming three different radiation fields with ultraviolet intensity matching the standard of Draine (1978). |
 |
Fig. 20 Unshielded photoionisation rates of molecules and atoms. Rates are shown assuming different radiation fields with ultraviolet intensity matching the standard of Draine (1978). |
6. Shielding functions
6.1. General formulation
Substantial molecular abundances cannot exist in the unshielded interstellar medium because of their short dissociation lifetimes. Instead, observed molecules are found embedded inside interstellar clouds, protoplanetary disks, or similar objects that are at least partially shielded from radiation. The unattenuated photodissociation and photoionisation rates given in Sect. 5 must then be recalculated taking into account the intervening material, according to, for example, ![\begin{eqnarray} \label{eq:shielded dissoc rate} k &=& \int \sigma^\text{pd}(\lambda) \exp\bigg[ - \tau_\text{dust}(\lambda,N_{{\rm H}+2{\rm H}_2}) \notag \\ &&\quad - \sum_{X={\rm H},{\rm H}_2,\text{self}} N_X\sigma_X^\text{abs}(\lambda) \bigg] I(\lambda)\,\text{d}\lambda. \end{eqnarray}](/articles/aa/full_html/2017/06/aa28742-16/aa28742-16-eq206.png) (9)The first exponentiated term in Eq. (9) models the attenuation of ultraviolet radiation due to dust as a function of wavelength and the column density of hydrogen nuclei (assuming this is proportional to the dust column). The non-absorbing scattering of UV photons by dust significantly alters their radiative transfer in a shielded region so that τdust(λ,NH + 2H2) is not simply proportional to column density. Additionally, the form of this term is dependent on the dust-cloud shape and nature of the incident radiation: isotropic, normal, or otherwise.
(9)The first exponentiated term in Eq. (9) models the attenuation of ultraviolet radiation due to dust as a function of wavelength and the column density of hydrogen nuclei (assuming this is proportional to the dust column). The non-absorbing scattering of UV photons by dust significantly alters their radiative transfer in a shielded region so that τdust(λ,NH + 2H2) is not simply proportional to column density. Additionally, the form of this term is dependent on the dust-cloud shape and nature of the incident radiation: isotropic, normal, or otherwise.
The summation term in Eq. (9) considers shielding by atomic and molecular species, where the most important cases are photoabsorption by H and H2, and self shielding for a few abundant species. The column density of species X is represented by NX.
The rate reduction due to dust, molecules, and atoms is characterised by a shielding function: 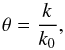 (10)where, k0 is the photoprocess rate at the irradiated edge of the shielded region. For an infinite-slab interstellar cloud in a region of space conforming to a standard isotropic ISRF, k0 will be slightly greater than half of the rates in Tables 18 and 19, due to the restriction of incident radiation to 2π sr and the occurrence of back-scattered radiation from the shielded region.
(10)where, k0 is the photoprocess rate at the irradiated edge of the shielded region. For an infinite-slab interstellar cloud in a region of space conforming to a standard isotropic ISRF, k0 will be slightly greater than half of the rates in Tables 18 and 19, due to the restriction of incident radiation to 2π sr and the occurrence of back-scattered radiation from the shielded region.
We calculated shielding functions according to Eqs. (9) and (10) for the photodissociation and ionisation of all atomic and molecular species in our database. These results are discussed below and are also available from the Leiden database15 in tabulated form. These tables contain values of θ as a function of column density for each bracketed term in Eq. (9) treated independently.
 |
Fig. 21 Photodissociation cross sections of four molecules. These are averaged into 2 nm intervals for clarity and compared with the wavelength-dependence of two radiation fields from Sect. 2. |
A demonstration of the relative importance of shielding terms in Eq. (9) is given by Fig. 25, which simulates the transmittance of ultraviolet radiation to a depth of AV = 1 into an interstellar cloud. The column densities of intervening atomic and molecular species are the result of a particular diffuse-cloud chemical model run by Heays et al. (2014b), but their magnitudes are typical in an interstellar PDR. For wavelengths shorter than about 130 nm multiple sources contribute to ultraviolet shielding in this model. The combined shielding in this case is approximately a product of these, e.g., θtotal = θdust·θH2·θH... This factorisation is somewhat inaccurate for multiple shielding species with overlapping and line-dominated cross sections. Additionally, the shielding functions calculated here are appropriate for infinite-slab geometries only. For more sophisticated astrochemical models the explicit simulation of ultraviolet radiative transfer using our database of cross sections may be required.
6.2. Shielding by dust
We calculated dust-shielding-dependent photodissociation and ionisation rates using the optical properties of a dust population assuming one particular composition and size distribution. These were taken from the mixed grain-size and composition model developed by Draine et al. (Draine & Lee 1984; Li & Draine 2001; Weingartner & Draine 2001; Draine 2003a,b,c). We used their “RV = 3.1” model published online16, with important optical properties plotted in Fig. 26. We also adopt a (gas mass)/(dust mass) ratio of 124 in line with the Draine et al. dust grain model. The interstellar variation of these parameters and their possible effects on shielding functions is discussed in Sect. 8.1.
 |
Fig. 22 Ratio of photodissociation and photoionisation rates. Calculated assuming two radiation fields from Sect. 2 as a function of their dissociation or ionisation thresholds. |
 |
Fig. 23 Comparing the wavelength dependence of the photodissociation cross sections of C2H2 and HC3N between 117 and 126 nm with Lyman-α radiation. |
The normal observationally-relevant extinction cross section is larger than the absorption cross section shown in Fig. 26 by a factor of 1/(1−ω), where ω is the grain albedo, to account for photons scattered out of the line of sight. These photons are however still available for photodestruction and their radiative transfer through an interstellar cloud must be considered. We did this for the case of an interstellar cloud with infinite-slab geometry and extending to large enough AV that it is effectively illuminated from one side only, and assume this illumination is incident isotropically. The radiative transfer equations were solved according to the method of Roberge et al. (1991) and van Dishoeck et al. (2006) that takes into account the dust absorption cross section, dust albedo, and the averaged fraction of forward-scattered photons. All of these properties are significantly wavelength dependent in the ultraviolet spectral region, as shown in Fig. 26. The transmission through a dust thickness corresponding to 1 AV, including scattered photons is shown in Fig. 25 and is largely wavelength independent longwards of about 120 nm. At shorter-wavelength dust absorption rapidly becomes more effective.
The calculated wavelength-dependent penetration of ultraviolet photons was used to calculate depth-dependent photodestruction rates for each molecule and atom in our database. These are summarised as shielding functions in Fig. 27. The alternative AV and H-nuclei column density scales are related by the standard proportionality (Savage et al. 1977) 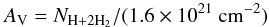 (11)and assuming a gas-mass to dust-mass ratio of 124. The differences between curves arise from the varying wavelength dependencies of atomic and molecular cross sections and the dust grain optical properties. All of the plotted shielding functions lie below the visual extinction curve, exp(−AV), despite the inclusion of forward scattering, which acts to increase the penetration depth. This is because of the larger dust absorption cross section at shorter wavelengths, which also explains the faster shielding of photoionisation than photodissociation, due to the shorter-wavelength thresholds of ionisation.
(11)and assuming a gas-mass to dust-mass ratio of 124. The differences between curves arise from the varying wavelength dependencies of atomic and molecular cross sections and the dust grain optical properties. All of the plotted shielding functions lie below the visual extinction curve, exp(−AV), despite the inclusion of forward scattering, which acts to increase the penetration depth. This is because of the larger dust absorption cross section at shorter wavelengths, which also explains the faster shielding of photoionisation than photodissociation, due to the shorter-wavelength thresholds of ionisation.
 |
Fig. 24 ISRF photodissociation and ionisation rates for atoms and molecules. The present calculations are compared with the PHIDRATES database (Huebner et al. 1992; Huebner & Mukherjee 2015) and the previous version of the Leiden database (van Dishoeck 1988; van Dishoeck et al. 2006). |
 |
Fig. 25 Possible wavelength-dependent transmittance (shaded region edges) of the highest-column density (N) species at AV = 1 depth into a semi-infinite one-sided interstellar cloud. |
Curves like those in Fig. 27 are sometimes approximated as simple functions of AV for easier utilisation. Either, as one-parameter exponential curves, 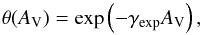 (12)(e.g., van Dishoeck et al. 2006) or 2nd-order exponential integrals,
(12)(e.g., van Dishoeck et al. 2006) or 2nd-order exponential integrals, 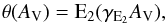 (13)(e.g., Neufeld & Wolfire 2009; Roueff et al. 2014), or bi-exponential functions (e.g. Roberge et al. 1991). We calculated values of γexp and γE2 in Eqs. (12) and (13) that best fit the results of our radiative transfer model, with an example fit for the shielded photodissociation of CH4 shown in Fig. 28. Calibrated exponential-integral functions were found to reproduce the shielding effects of dust absorption within 25% over the range of 1 ≥ θ> 10, while the exponential function deviate by up to a factor of 3 over the same range. Given the superior parameterisation of exponential-integral functions, we listed γE2 coefficients for all species in our database in Tables 18 and 19, along with updated values of the normal-exponential γexp parameters that are adopted in previous iterations of the Leiden database (van Dishoeck et al. 2006).
(13)(e.g., Neufeld & Wolfire 2009; Roueff et al. 2014), or bi-exponential functions (e.g. Roberge et al. 1991). We calculated values of γexp and γE2 in Eqs. (12) and (13) that best fit the results of our radiative transfer model, with an example fit for the shielded photodissociation of CH4 shown in Fig. 28. Calibrated exponential-integral functions were found to reproduce the shielding effects of dust absorption within 25% over the range of 1 ≥ θ> 10, while the exponential function deviate by up to a factor of 3 over the same range. Given the superior parameterisation of exponential-integral functions, we listed γE2 coefficients for all species in our database in Tables 18 and 19, along with updated values of the normal-exponential γexp parameters that are adopted in previous iterations of the Leiden database (van Dishoeck et al. 2006).
A further reduction of shielding functions is demonstrated in Fig. 28, whereby, an exponential-decay parameter γfit is adopted along with an effective unshielded rate, 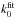 , so that the depth-dependent photodestruction rates are:
, so that the depth-dependent photodestruction rates are: 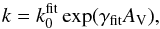 (14)leading to shielding functions
(14)leading to shielding functions 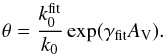 (15)The values of these parameters were selected to best fit the radiative-transfer calculation between AV = 0.1 and 3 (a range of extinction where the details of ISRF photodestruction has most influence on PDR chemistry), and provide a better approximation of this range than Eq. (12), but a poorer fit in general than Eq. (13). Fitted parameters of this modified exponential form are provided in the Leiden database for all atoms and molecules and may be useful for astrochemical codes where exponential-form dust shielding is required, but with improved accuracy over an intermediate range of AV.
(15)The values of these parameters were selected to best fit the radiative-transfer calculation between AV = 0.1 and 3 (a range of extinction where the details of ISRF photodestruction has most influence on PDR chemistry), and provide a better approximation of this range than Eq. (12), but a poorer fit in general than Eq. (13). Fitted parameters of this modified exponential form are provided in the Leiden database for all atoms and molecules and may be useful for astrochemical codes where exponential-form dust shielding is required, but with improved accuracy over an intermediate range of AV.
 |
Fig. 26 Solid lines: optical properties of interstellar dust grains according to Draine et al. (Draine & Lee 1984; Draine 2003b)17. Dashed lines: optical properties simulating grain growth in a protoplanetary disk. Upper: photoabsorption and photoextinction cross sections. Middle: grain albedo. Lower: probability of forward scattering. |
 |
Fig. 27 Shielding of photodissociation (red) and photoionisation (green) in the ISRF. For all molecules in our database by an amount of dust parameterised by H-nucleus column density. Cases are shown for interstellar dust and a population of larger dust grains (see text). An additional curve traces exp(−Av), the visual extinction (blue). |
 |
Fig. 28 Dust shielding function for CH4 photodissociation (solid red curve) in the ISRF. Calculated by means of an infinite-slab radiative transfer model. Also shown are some simple parameterisations of this curve according to three formulations. |
The quantitative shielding discussion in this section is appropriate for use in single-sided isotropically-irradiated infinite-slab interstellar cloud models. The modelling of dust-shielding effects in other geometries would require specific radiative-transfer calculations.
Previously, van Dishoeck et al. (2006) compared dust-shielding effects ad γexp parameters for a range of radiation field types and dust grain properties, a point that is discussed further in Sect. 8.1.
6.3. Shielding by H2, H, and C
 |
Fig. 29 Shielding functions for photodissociation (red curves) and photoionisation (blue curves) by a column of H2. Assumes an impinging ISRF or simulation of the TW-Hydra circumstellar radiation. A few extreme cases have their identity labelled. The shaded-region edge describes a typical ultraviolet-extinction curve due to interstellar dust, according to exp−3AV. |
The shielding of most molecules found in PDRs is dominated by dust extinction, assuming a standard amount of gas and dust. In some cases, additional terms in Eq. (9) must be considered.
The shielding effect on our database of molecules was calculated for a one-dimensional column of H2 while neglecting scattering in the molecular lines. Shielding functions calculated according by means of Eqs. (9) and (10) are summarised in Fig. 29 for two cases: the ISRF and TW-Hydra radiation fields. For these calculations, the H2 photoabsorption cross section was composed from a list of individual line parameters, as described in Sect. 4.3.15, and assumed an excitation temperature of 100 K and Gaussian Doppler broadening width b = 3 km s-1.
Significant H2 shielding only occurs in the ISRF for column densities of more than about 10 cm-2. Larger columns are required for some molecules that photoabsorb at wavelengths greater than 110 nm, outside the range of H2 line absorption. The shaded region in Fig. 29 shows a typical ultraviolet dust-shielding curve for comparison. The influence of H2-shielding in the ISRF is overshadowed by dust extinction in many cases, assuming a standard gas and dust mass ratio, and can safely be neglected. In a few cases it is of comparable importance. For instance, CO and N2, investigated in detail by Visser et al. (2009) and Li et al. (2013). The extreme case of H2 shielding itself is discussed in the following section.
Figure 29 also shows H2 shielding functions assuming a radiation field simulating the TW-Hydra emission spectrum. The resulting changes with respect to the ISRF follow from the inclusion of radiation shorter than 91.2 nm, so that the continuum absorption of H2 can rapidly reduce the photoionisation rate of some species. The shielding of longer-wavelength photodissociation remains dust dominated apart from the case of H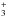 , whose cross section occurs entirely at short wavelengths (Kulander & Bottcher 1978).
, whose cross section occurs entirely at short wavelengths (Kulander & Bottcher 1978).
 |
Fig. 30 Shielding of CN photodissociation in the ISRF by H2 assuming various values for the H2 rotational excitation temperature, T, and Doppler broadening, b. Also shown is a typical shielding function due to interstellar dust, exp(−3AV) (shaded region edge). |
An increase in the rotational temperature and turbulent broadening of H2 increases its shielding effectiveness, due to the larger filling factor of its photoabsorption spectrum when more and broader rotational lines are included. This effect is quite small, for molecules and atoms that primarily absorb longwards of 110 nm. In some extreme cases the effect can be significant, as illustrated for CN photodissociation in Fig. 30. Here, increasing the temperature or Doppler width over astrophysically relevant ranges, from 30 to 300 K or 1 to 3 km s-1, respectively, leads to about twice the H2 shielding between 0.1 and 3 AV. Increasing these further to 1000 K and 10 km s-1 (conditions perhaps still relevant to some interstellar shocks or in some atmospheres) results in an order of magnitude increase in H2 shielding effectiveness. The effect of H2 temperature and broadening are studied by Visser et al. (2009) and Li et al. (2013) for the cases of CO and N2, respectively.
Shielding by the atomic H photoionisation continuum is implicit in calculations with radiation fields having a 91.2 nm Lyman-limit cut-off. In principle, column-density-dependent H-shielding occurs where UV radiation includes shorter wavelengths, although this detail is often negligible in view of the greater shielding effect of H2 and dust. Atomic-H shielding functions are discussed in Appendix A and may be important in dust-depleted environments near the edge of a PDR. Another species that potentially contributes to the exponential term in Eq. (9) is atomic C (Rollins & Rawlings 2012), present near the boundary layer of a PDR, and we computed shielding functions for this species also, discussed further in Appendix A.
We did not evaluate the scattering of photons by H2 and H, whereby photoabsorption into electronically-excited levels is followed by resonant photoemission (e.g., Black & van Dishoeck 1987). This is shown to significantly modify the UV spectrum in embedded regions (Le Petit et al. 2006), as well as for Lyman-α photons scattered by atomic-H (Neufeld 1991; Bethell & Bergin 2011). For H2, more than 80% of absorbed UV photons are re-emitted, mostly to ground state levels with v> 0 and at longer wavelengths. Ultimately, all photons will be absorbed by dust grains, but determining the influence of H2 resonant scattering on the photodestruction rates calculated here would be a worthwhile future project.
6.4. Self-shielding of molecules
 |
Fig. 31 Self-shielding of photodissociation in the ISRF. |
Self-shielding is also important for some photodissociating species. Shielding functions describing this phenomenon independently of other mechanisms are plotted in Fig. 31. The three prominent cases where self-shielding is effective at relatively low column densities are H2, CO, and N2. The most recent treatments of these three molecules are given in Sternberg et al. (2014), Visser et al. (2009), and Li et al. (2013), Heays et al. (2014b); respectively. The common cause is the line-like photoabsorption cross sections of all three molecules, leading to almost complete attenuation of ultraviolet radiation at their line centres for modest column densities, about 1015 cm-2. The column density of CO and N2 relative to H in the molecule-forming region of a PDR is typically high enough that their self-shielding competes with the simultaneous effect of dust extinction.
Atoms and molecules that absorb predominantly through continua may still be susceptible to self-shielding if their column densities are large enough. Three candidates for this phenomenon are highlighted in Fig. 31, H2O, OH, and C, where the minimum column density for effective self-shielding is approximately 1017 cm-2 in all cases. Such large columns of atomic C are actually found as discussed in the previous section, and some models of the inner regions of protoplanetary disks find sufficient H2O and OH columns (Bethell & Bergin 2009; Ádámkovics et al. 2014). These phenomena may be particularly relevant in shocked media where densities are abnormally high, for example, C in supernova remnants and (White 1994) protoplanetary disks (Tsukagoshi et al. 2015), or H2O in protostellar outflows (Mottram et al. 2014). All other molecular species have too low abundance or insufficiently peaked cross sections to effectively self-shield in space.
7. Photodestruction due to cosmic rays
7.1. Cosmic ray induced UV spectrum
Cosmic rays penetrate deeper into an interstellar cloud, protostellar envelope, protoplanetary disk or planetary atmosphere than ultraviolet photons and ionise H2 there. This primary process and resultant cascade of re-scattered electrons proceeds to excite further H2 and generate excited H-atoms (Cravens & Dalgarno 1978; Gredel & Dalgarno 1995), whose radiative decay generates a ultraviolet flux with a line-dominated structure (Prasad & Tarafdar 1983; Gredel et al. 1987; Cecchi-Pestellini & Aiello 1992). The photolysis of molecules due to this flux is quantified several times previously (Sternberg et al. 1987; Gredel et al. 1987, 1989; Heays et al. 2014b) but the last major summary of rates dates back to Gredel et al. (1989). Here all rates are recomputed with updated cross sections. Also, the effects of grain growth, such as appropriate for protoplanetary disks, are considered.
 |
Fig. 32 The cosmic-ray induced radiation field. Upper: the spectral density of photons generated per primary cosmic-ray ionisation event. Lower: a cumulative integration of this distribution. |
The cosmic-ray induced ultraviolet flux is modelled here as a rate of photons generated per unit spectral density per hydrogen nucleus: 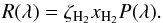 (16)Here, and below, xX = n(X)/ [n(H) + 2n(H2)] is the relative abundance of species X with respect to total hydrogen nuclei and ζH2 is the rate at which an H2 molecule is ionised by cosmic ray collisions. In the context of diffuse interstellar clouds (e.g., Oka 2013; Indriolo et al. 2015) it is atomic-H that is being ionised, and the appropriate ζ will then be per H atom.
(16)Here, and below, xX = n(X)/ [n(H) + 2n(H2)] is the relative abundance of species X with respect to total hydrogen nuclei and ζH2 is the rate at which an H2 molecule is ionised by cosmic ray collisions. In the context of diffuse interstellar clouds (e.g., Oka 2013; Indriolo et al. 2015) it is atomic-H that is being ionised, and the appropriate ζ will then be per H atom.
We used the wavelength-dependent probability distribution of generated photons, P(λ), of Gredel et al. (1989). This distribution is plotted in Fig. 32 and consists of many H2 and H emission lines between 80 and 170 nm as well as some continuum emission between 122 and 300 nm. The modelled photoemission mostly occurs between 90 and 170 nm, as shown by the rapid increase of the cumulative distribution in Fig. 32 over this range, with a single step at 121.6 nm constituting 15% of the integrated flux due to Lyman-α emission. The cumulative distribution attains a total value of only 0.36 because not every H2 ionisation event results in an ultraviolet photon being generated.
The value of ζH2 is uncertain due to the unknown origin and flux of cosmic rays and its energy spectrum, as well as the attenuation due to matter and magnetic fields (Dalgarno 2006; Grenier et al. 2015). Earlier values are indirectly deduced from observations of the HD and OH abundances (e.g., Hartquist et al. 1978; van Dishoeck & Black 1986) and H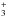 abundances (e.g., van der Tak & van Dishoeck 2000; Hezareh et al. 2008) in diffuse and dense interstellar clouds, and favoured a value of about 3×10 s-1 H2-1, although rates up to 2 × 10-16 s-1 are inferred for some diffuse clouds. Subsequent observations towards more lines of sight and of other tracers like OH+ and H2O+ are interpreted with updated H
abundances (e.g., van der Tak & van Dishoeck 2000; Hezareh et al. 2008) in diffuse and dense interstellar clouds, and favoured a value of about 3×10 s-1 H2-1, although rates up to 2 × 10-16 s-1 are inferred for some diffuse clouds. Subsequent observations towards more lines of sight and of other tracers like OH+ and H2O+ are interpreted with updated H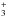 dissociative recombination rate coefficients generally and require a higher rate in diffuse clouds, 1 to 4 × 10-15 s-1 H2-1 (Indriolo & McCall 2012; Rimmer et al. 2012; Vaupré et al. 2014; Indriolo et al. 2015), and higher still in the Galactic centre. A reduction of the ionisation rate likely occurs in dark clouds and protoplanetary disks because of the shielding effects of the surrounding material (Padovani et al. 2009) or stellar winds and magnetic fields (Cleeves et al. 2013, 2015).
dissociative recombination rate coefficients generally and require a higher rate in diffuse clouds, 1 to 4 × 10-15 s-1 H2-1 (Indriolo & McCall 2012; Rimmer et al. 2012; Vaupré et al. 2014; Indriolo et al. 2015), and higher still in the Galactic centre. A reduction of the ionisation rate likely occurs in dark clouds and protoplanetary disks because of the shielding effects of the surrounding material (Padovani et al. 2009) or stellar winds and magnetic fields (Cleeves et al. 2013, 2015).
We adopt a primary ionisation rate for Eq. (16) of ζH2 = 10 s-1 H2-1. All molecular photodissociation rates can be adapted to an alternative ζH2 by simple scaling.
Most cosmic-ray generated photons are eventually eliminated through absorption by dust grains inside an interstellar cloud but some excite atoms and molecules. The fraction of photons that lead to the photodissociation or ionisation of an atom or molecule, X, is given by 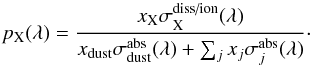 (17)Here,
(17)Here, 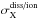 is the photodissociation or ionisation cross section of species X, and the denominator sums the photoabsorption cross section of all dust and gas species. The probability of a cosmic-ray generated ultraviolet photon being absorbed by a dust grain, H2 molecule, or some other gas-phase species depends on its wavelength through the various cross sections in Eq. (17).
is the photodissociation or ionisation cross section of species X, and the denominator sums the photoabsorption cross section of all dust and gas species. The probability of a cosmic-ray generated ultraviolet photon being absorbed by a dust grain, H2 molecule, or some other gas-phase species depends on its wavelength through the various cross sections in Eq. (17).
The rate of a particular photodestruction process for species X (per X) due to cosmic-ray-induced photons is then 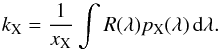 (18)The photolysis rates calculated by Gredel et al. (1989) and McElroy et al. (2013) are presented as efficiencies with the H2 ionisation rate and grain albedo factored out from Eq. (18). This is not possible if the summation terms in Eq. (17) are significant (Gredel et al. 1987; Heays et al. 2014b), and for the sake of generality we did not make this reduction. Our calculated rates divided by a factor of 2×10 are approximately comparable with the efficiencies given in Gredel et al. (1989), and a factor of 10 is required when comparing with McElroy et al. (2013).
(18)The photolysis rates calculated by Gredel et al. (1989) and McElroy et al. (2013) are presented as efficiencies with the H2 ionisation rate and grain albedo factored out from Eq. (18). This is not possible if the summation terms in Eq. (17) are significant (Gredel et al. 1987; Heays et al. 2014b), and for the sake of generality we did not make this reduction. Our calculated rates divided by a factor of 2×10 are approximately comparable with the efficiencies given in Gredel et al. (1989), and a factor of 10 is required when comparing with McElroy et al. (2013).
The spectrum shown in Fig. 32 and used in our rate calculations assumes an ortho-H2:para-H2 ratio of 0:1, that is, with H2 in its J = 0 rotational state. This is appropriate for excitation temperatures corresponding to the low temperatures of a molecular cloud because only 10% of equilibrated H2 is excited above J = 0 at, for example, 50 K. Even for cases where significant quantities of super-thermally excited H2 are inferred in interstellar clouds their influence on cosmic-ray induced ultraviolet photodissociation is unlikely to be large. This is because an altered distribution of emission lines is largely washed out in rate calculation by the integration in Eq. (18). Indeed, after testing J = 0:J = 1 populations with the two ratios 1:0 and 1:3 we find calculated-rate differences of less than 20% for most species in our database, in line with previous work (Gredel et al. 1989). Larger differences are found for the case of CO and N2, which are studied in more detail previously (Gredel et al. 1987; Heays et al. 2014b).
Gredel et al. (1989) considered the possibility of H2 bound levels absorbing the cosmic-ray induced ultraviolet flux and subsequently re-emitting photons of the same wavelength or longer (following emission into excited ground state vibrational levels). Their calculated rates are altered by up to 35% by considering this phenomenon, with most species being altered by less than 5%, and this effects is neglected here.
For the case of dust absorption, the wavelength-dependent mixed-grain absorption cross section of Draine et al. (Draine & Lee 1984; Li & Draine 2001; Weingartner & Draine 2001; Draine 2003b,c) were used, as discussed in Sect. 5 and plotted in Fig. 26. This absorption cross section is somewhat different from the wavelength-independent dust properties adopted previously (Gredel et al. 1987; Heays et al. 2014b) that converted an observationally-estimated dust extinction cross section, 2×10 cm-1 H-1, to an absorption cross section by assuming an effective grain albedo between 0 and 0.8. It is clear from Fig. 26 that consideration of the wavelength dependence of dust absorption can affect the deduced shielding of molecular photodestruction by, at most, a factor of about two, depending on the wavelength-dependence of the molecular photoabsorption cross section.
Cosmic ray photodestruction rates (× 10-16 s-1).
7.2. Results
Photodissociation and ionisation rates in a cosmic-ray induced ultraviolet field were calculated for all molecules in our database after adopting the following set of parameters:
| Cosmic-ray ionisation rate (ζH2): | 10-16 s-1 H2-1; |
| Doppler broadening (b): | 1 km s-1; |
| ortho-H2:para-H2: | 0:1; |
| x(H): | 10-4; |
| xN2 and xCO: | 10-5; |
where x is the abundance relative to H-nuclei.
The integration in Eq. (18) was performed on a wavelength grid with 0.001 nm (or finer) resolution, in order to capture full details of the cross section structure of absorbing species. The calculated photodissociation and photoionisation rates are presented in Table 20. The ISRF-weighted uncertainties listed in Table 1 provide a reasonable uncertainty estimate for these rates.
 |
Fig. 33 Molecular photodissociation and ionisation rates due to cosmic-ray-induced radiation. Shown for all species common to this data base and Gredel et al. (1989). Full dust and lines: including all available shielding cross sections. Simple dust only: no molecular or atomic shielding, wavelength independent dust extinction cross section 2×10 cm2 H-1 and an albedo of 0.5. Gredel et al.: rates computed from the efficiencies of Gredel et al. (1989; Table 1, column “a”, ignoring reabsorption) following multiplication by 10. |
A comparison of rates for molecules common to our database and that of Gredel et al. (1989) is plotted in Fig. 33. Also shown are rates calculated while neglecting the shielding of radiation by H2 and H, and assuming a constant dust absorption cross section, 10 cm2 H-1. These changes alter the rates in our database by factors between 0.5 and 5, the increase occurring for species absorbing mostly shortwards of 110 nm where the H2 photoabsorption is greatest and the wavelength-dependent dust absorption cross section is also greater than its average. These “simple dust” rates in Fig. 33 are in line with the assumption adopted by Gredel et al. (1989), assuming a dust grain albedo of 0.5. Then, any further differences between rates is due to the change in our photodissociation cross sections relative to the previous work.
Overall, agreement is within a factor of two, with some exceptions. The largest rate we find is for the dissociation of C3, with a 5-fold increase relative to Gredel et al. (1989), due to the addition of a previously-unknown and strong C3 absorption channel at 160 nm as computed by van Hemert & van Dishoeck (2008) and seen in the laboratory by Monninger et al. (2002). The new CH3OH dissociation and ionisations rates are 2.5 times smaller than that calculated by Gredel et al. (1989), who employed very similar cross sectional data (Harrison et al. 1959; Salahub & Sandorfy 1971) over the range 120 to 215 nm. Additional information described in Sect. 4.3.52 has permitted us to extend this cross section shortwards to 66 nm, without which our cosmic-ray photodestruction rates would actually be substantially smaller. The difference between our calculation and Gredel et al. is therefore unresolved. The new HC3N rate is 3 times larger than that calculated by Gredel et al. employing the cross section of Connors et al. (1974), which is nonetheless very similar to the data collected here, which we also are unable to immediately explain.
The three-times-increased HCl rate is due to the addition of higher-lying photodissociating transitions (described in Sect. 4.3.70) than included in the calculation of van Dishoeck et al. (1982), adopted previously. A similar explanation leads to the large change in the estimated NH2 dissociation and ionisation rates. Finally, the CN photodissociation rate was reduced by more than 10 times relative to Gredel et al., who adopted a earlier theoretical cross section (Lavendy et al. 1984) for this molecule that has since been updated (see Sect. 4.3.49 and Lavendy et al. 1987).
Similar to the conclusions of Sect. 6, self-shielding of the cosmic-ray flux was only found to be important for species with highly-structured cross sections and high abundance, that is, N2 and CO (Heays et al. 2014b; Gredel et al. 1987). The photodissociation rates of these species are reduced through self-shielding by about 50% after assuming abundances relative to H-nuclei of 10, as is typical for diffuse and dense interstellar clouds and prestellar cores (Tielens 2013), as long as the dust temperature is sufficiently high to prevent condensation of CO and N2 onto dust grains, that is greater than about 25 and 20 K, respectively.
A relative abundance of about 10 is predicted for H2O, OH, CO2, NH3, and CH4 in some specific models of prestellar cores and dense clouds, for example, Tielens (2013), with the abundance all other species being 10 or below. No species in our database achieves a self-shielding effect of more than 4% at the 10 abundance level.
The assumed H, CO, and N2 abundances contribute to line-shielding of the cosmic ray induced UV flux and subsequent reduction of the photoabsorption rates of other species. These abundances are, however, dependent on the cosmic-ray ionisation rate itself through the induced chemistry and other dynamical factors like temperature and evolutionary age. The rates calculated here should then be considered conditional on the assumed abundances. To test the severity of this assumption, neglecting line shielding entirely in favour of pure dust absorption increased the calculated photodissociation and ionisation rates by less than a factor of 2, apart from the self-shielding cases of N2 and CO that are treated in detail elsewhere (Gredel et al. 1987; Heays et al. 2014b).
8. Further discussion
8.1. Effect of dust-grain properties on ultraviolet shielding
The dominant absorber of ultraviolet radiation from interstellar, stellar, or cosmic-ray sources is dust. More radiation will be available for gas-phase photodestruction if the dust mass is reduced. The ratio of gas-mass to dust-mass adopted in our calculations, 124, is taken in line with the Milky Way dust model of Draine et al.18 (Draine 2003a), and is somewhat larger than the frequently-used value of 100. This parameter is also estimated from observations of local group Galaxies, and found to vary between about 50 and 500 (Draine et al. 2007; Leroy et al. 2011), and on small scales within the Milky Way, in one case falling to 88 and rising above 200 within one star-forming region (Liseau et al. 2015), although any such determinations have large inherent uncertainties. Finally, low “metallicity” (using astronomical terminology) galaxies such as the Magellanic Clouds have higher gas-to-dust ratios by up to an order of magnitude (Roman-Duval et al. 2014).
The ultraviolet opacity of dust is also reduced by its coagulation into larger sizes (Mathis et al. 1977; Draine & Lee 1984; van Dishoeck et al. 2006). This phenomena is observed (e.g., Li & Lunine 2003; Kessler-Silacci et al. 2006; Testi et al. 2014) and predicted (e.g., Birnstiel et al. 2010) to occur in protoplanetary disks, at least up to cm-sized grains, with the larger grains settling to the midplane and drifting towards the central star. Disks also show additional complex spatial structures seen in small and large grains being influenced by planetary bodies or dynamical instabilities (e.g., Johansen et al. 2007; Andrews et al. 2011; Muto et al. 2012; van der Marel et al. 2013; Pinilla et al. 2015).
The dust shielding functions plotted in Figs. 27 are shifted to higher gas column densities when their ultraviolet opacity is reduced by grain growth. The scaling between 550 nm visual extinction, AV, and ultraviolet extinction also changes due to the wavelength-dependent variation of all dust grain optical properties when their size distribution and composition is modified (Mathis et al. 1977). van Dishoeck et al. (2006) simulated the dust optical properties of a large-grain populated protoplanetary disk, designed to best reproduce observations of the dust disk around HD 141569A (Li & Lunine 2003; Jonkheid et al. 2006; van Dishoeck et al. 2006). This required the presence of dust grains as large as a few μm in diameter. Figure 26 compares the optical properties of this large-grain population with standard interstellar grains, showing a significantly-reduced ultraviolet absorption cross section (which matches interstellar grains at 550 nm) and a somewhat increased albedo and forward scattering probability. These changes all act to increase the penetration of photodestructive radiation through the disk. We computed alternative shielding functions assuming a HD 141569A dust population and compare these with the interstellar dust case in Fig. 27. The larger grains require nearly an order-of-magnitude greater column of dust mass before shielding effectively. This leads to correspondingly smaller γE2-factors in Eq. (13), about 0.5 for most molecules, as listed in Tables 18 and 19, as opposed to values of about 1.5 assuming interstellar type dust.
Grain growth will also increase photodissociation and ionisation rates in a cosmic-ray induced UV field. This may be significant in the midplane of a protoplanetary disk due to aggregation of dust in the high-density environment and the gravitational settling of large grains (D’Alessio et al. 2001). The reduced competitiveness of dust grains in the absorption of UV photons will then affect the chemistry of gas-phase molecules (Chaparro Molano & Kamp 2012).
8.2. Effect of temperature on molecular cross sections
Most laboratory measurements are recorded at room temperature, whereas many theoretical calculations do not include any ground state excitation whatsoever, simulating a low temperature of <10 K with v = 0 and J = 0. Fortunately, the difference between cross sections appropriate for interstellar or atmospheric excitation temperatures (10 to about 1000 K) and the available measurements and calculations is largely obliterated by the wavelength integration of Eq. (1). At temperatures up to a few hundred K, multiple rotational levels besides J = 0 will be excited, in most cases broadening the cross section slightly without changing its integrated value (e.g., Wu et al. 2000; Miyake et al. 2011; Li et al. 2013). At higher temperatures, such as encountered in protoplanetary disks and exoplanet atmospheres, vibrational levels of the ground electronic state start to be excited but as long as v ≤ 2 this again only results in a small wavelength redistribution of the integrated cross section. Such a change in cross section shape is unlikely to affect ISRF photodestruction rates but could significantly alter rates in a cool stellar radiation field if the cross section shifts in or out of the maximum of the stellar flux. This effect is particularly prominent for the case of CO2 at long wavelengths, as demonstrated by Venot et al. (2013).
Li et al. (2013) find the 1000 K ISRF photodissociation rate of N2 to be only 15% larger than at 10 K but a large temperature dependence for its self-shielding and shielding by H2, with factor-of-10 decreases of shielding effectiveness between 10 and 1000 K. A factor-of-two temperature variability of the N2 cosmic-ray induced photodissociation rate was also noted (Heays et al. 2014b) between 10 and 300 K. The temperature sensitivity of N2, and also CO (Visser et al. 2009) and H2 (Sternberg et al. 2014), arises from their rotational-line dominated spectra where linewidths are set mostly by the Doppler broadening. A higher kinetic temperature leads to more Doppler broadening and a lesser cross section at the line centres, reducing the effectiveness of self-shielding. And, a higher excitation temperature spreads the cross section over a greater number of rotational lines, also impeding self-shielding. A more subtle effect occurs for some predissociating molecules where the dissociation efficiency, ηd, increases with excitation temperature (this can happen because of increased centrifugal mixing of excited states for faster rotation molecules, e.g., Lewis et al. 2005; Eidelsberg et al. 2014).
8.3. Uncertainty of calculated line positions and widths
As noted in Sect. 3.3, theoretical cross sections are sometimes calculated as vertical excitations from the ground to one or more excited states, with each electronic transition summarised by a single line (e.g., van Hemert & van Dishoeck 2008). Then the assumption of a linewidth is required. The ISRF photodestruction rates calculated in Sect. 5 are not sensitive to the precise choice of width, however, the rates of cosmic-ray induced processes in Sect. 7 as well as rates for highly structured radiation fields such as Lyman-α are somewhat sensitive. For the cosmic-ray induced case, experimentation with synthetic lines suggests that calculated rates averaged over 10 lines and assuming 1 nm linewidths will be accurate to within about a factor of 2 should the real linewidths fall in the range 0.1 to 10 nm.
 |
Fig. 34 Distribution of Monte Carlo simulated cosmic-ray-induced photodissociation rates of three molecules. Normalised to the mean of the distribution. |
Another test was performed to determine the sensitivity of cosmic-ray induced photodissociation rates to uncertain vertical excitation energies. Rates were calculated for all molecules in our database that include vertical transitions (primarily those calculated by van Hemert & van Dishoeck 2008) in a Monte Carlo simulation. For this, the wavelength positions of all transitions were repeatedly and independently adjusted by an amount falling within a uniform probability distribution bounded by the assumed vertical-transition energy uncertainty ± 0.2 eV (± 3.6 nm at 150 nm). Each line has an assumed intrinsic FWHM of 1 nm. In this way, the possible range of overlap between absorption features and cosmic-ray induced emission lines was sampled. The resultant distribution of photodissociation rates for three molecules showing quite different sensitivities is shown in Fig. 34. Line-position uncertainty does not affect the photodissociation rate for l–C4 because the calculated absorption for this molecule occurs longwards of 170 nm and in the continuum part of the cosmic-ray induced spectrum. Whereas, the photodissociation of l–C3H is sensitive to the overlap of several of its transitions near to the strong H2 emission lines around 160 nm. The proximity of C2H vertical transition to the Lyman-α wavelength means a small uncertainty in this transition energy leads to a large variation in photodissociation rate. All other molecules tested have distributions with widths falling within the range of Fig. 34, and these were considered when assigning the rate uncertainties listed in Table 20.
8.4. Effect of unresolved structure on molecular cross sections
The spectral resolution of laboratory equipment used to record photoabsorption cross sections is sometimes insufficient to completely resolve molecular vibrational-rotational structure. For example, our assembly of H2O data incorporates very high-resolution measurements of Fillion et al. (2003), Fillion et al. (2004) and taken from the CfA VUV database19, with others that do not resolve the rotational spectrum (Chan et al. 1993b; Mota et al. 2005).
 |
Fig. 35 H2O photoabsorption cross section measured by low-resolution electron energy-loss spectroscopy and by direct higher-resolution photoabsorption measurements. |
A comparison of H2O spectra is plotted in Fig. 35, all recorded at room temperature. The apparent changes between spectra are significant despite their integrated cross sections being essentially the same. For example, the apparent peak cross section of the vibrational band near 111.5 nm, whose assignment is discussed in Fillion et al. (2004), varies by an order of magnitude. This peak-value difference is still a factor of three when comparing the two highest resolution cross sections available, CfA spectra with FWHM 0.0015 nm and those recorded by Fillion et al. (2004) with resolution 0.0025 to 0.005 nm FWHM.
In Table 21 we list photodissociation rates for H2O calculated using the highest-resolution data and neglecting this in favour of less-resolved cross sections (which still cover the entire wavelength range). In most cases, any difference is negated by the smoothing effect of wavelength integration and because the continuum part of the H2O cross section dominates the combined cross section of lines, despite their large maxima. The photodissociation rate due to Lyman-α dominated radiation is sharply reduced, however, when only the lowest resolution data set is used, because of the under resolution of a vibrational band near the Lyman-α wavelength.
Photodissociation rate of H2O.
The photodissociation cross sections of CO, N2, and H2 have no continuum absorption at all and will be sensitive to insufficient experimental resolving power. For this reason, these molecules are treated here with models that recreate each absorption line and its lineshape from experimental data, but without the influence of experimental instrumental broadening (Visser et al. 2009; Li et al. 2013; Abgrall et al. 1993c). We can then directly test their sensitivity to the resolution-dependent phenomenon of self-shielding by broadening their cross sections though convolution with Gaussian functions of increasingly greater width.
 |
Fig. 36 ISRF self-shielding factors. Shown for four molecules after convolution of their photodissociation cross sections by Gaussian functions of increasing width (equivalent Doppler widths are also shown). For these calculations, a column density of 10 cm-2 was assumed for N2, CO and H2; and 10 cm-2 for H2O. |
The results of such a test are shown in Fig. 36, the shielding effect decreases significantly (shielding function approaches unity) when absorption lines of N2, CO, and H2 are artificially broadened. From this figure, even the use of a 0.005 nm resolution cross section may incompletely-resolves and underestimate the self-shielding effect for a line-dominated molecular cross section spectrum.
Most species in our database are sufficiently continuum-dominated that any under-resolution will not influence their calculated photodestruction rates. For example, we also systematically broaden the highest-resolution experimental spectrum of H2O and find a negligible effect in Fig. 36. The experimentally-determined cross section of NO may benefit from the measurement of a higher resolution cross section between 130 to 165 nm, particular if this molecule can attain a high column density in an atmosphere. Some radical species, for example, NH2 or C2, likely also have unquantified sharply resonant features.
Turbulent Doppler broadening will actually reduce self-shielding in the way that experimental under-resolution mimics. This is shown in Fig. 36 where a Doppler width of 10 kms-1 is significant at least for the case of H2. Larger Doppler widths are unlikely to occur in astrochemical environments except in locally shocked regions.
8.5. Isotopic effects
Isotopic substitutions of one or more atoms within a molecule alter its rotational inertia and the reduced masses of its vibrational modes (e.g., Herzberg 1989). The resultant shifts in rotational-vibrational energy levels may be different for ground and excited states so that the wavelengths of lines in its photoabsorption spectrum also shift.
For diatomic molecules, the largest shifts are expected when deuterating H2 to form HD, a reduced mass (in atomic units) increase from (1 × 1)/(1 + 1) to (1 × 2)/(1 + 2). The resulting vibrational-level shifts for the astrophysically-important  and
and 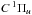 states of H2 can be as large as 1300 cm-1, equivalent to a 0.8 nm difference between the absorption line wavelengths of H2 and HD. This shift is large enough that H2 no longer shields HD, so that the photodissociation rate of HD with depth into a cloud is much larger than that of H2 (Spitzer et al. 1973; Black & Dalgarno 1977). Isotopic substitution of a heavier element leads to smaller shifts. For example, the substitution of the minor isotope 15N into molecular nitrogen, N2, leads to changes in energy levels and absorption line wavelengths of at most 200 cm-1 and 0.15 nm, respectively. This is still more than enough to maintain the self-shielding phenomenon for N2, but reduce the mutual shielding of 14N 15N by 14N2 (Heays et al. 2014b).
states of H2 can be as large as 1300 cm-1, equivalent to a 0.8 nm difference between the absorption line wavelengths of H2 and HD. This shift is large enough that H2 no longer shields HD, so that the photodissociation rate of HD with depth into a cloud is much larger than that of H2 (Spitzer et al. 1973; Black & Dalgarno 1977). Isotopic substitution of a heavier element leads to smaller shifts. For example, the substitution of the minor isotope 15N into molecular nitrogen, N2, leads to changes in energy levels and absorption line wavelengths of at most 200 cm-1 and 0.15 nm, respectively. This is still more than enough to maintain the self-shielding phenomenon for N2, but reduce the mutual shielding of 14N 15N by 14N2 (Heays et al. 2014b).
 |
Fig. 37 Long-wavelength and near-Lyman-α parts of the NH3 and NH2D photoabsorption cross sections. The source of the NH3 cross section is discussed in Sect. 4.3.46 and the NH2D data are taken from two sources (Wu et al. 2007; Cheng et al. 2006). Also indicated is the wavelength of Lyman-α emission and the vibrational progression of absorption into the excited |
Photodissociation branching of H2O and NH3.
The deuteration of NH3 to NH2D leads to wavelength shifts of its 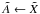 absorption bands, shown in Fig. 37, with larger shifts for higher vibrational levels of the
absorption bands, shown in Fig. 37, with larger shifts for higher vibrational levels of the 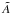 state. Most important is the isotope-induced shift of higher-energy excited states into resonance with the Lyman-α emission line. The nearly two-times larger cross section of NH2D at 121.6 nm leads directly to an increased photodissociation rate of this species in a Lyman-α dominated radiation field.
state. Most important is the isotope-induced shift of higher-energy excited states into resonance with the Lyman-α emission line. The nearly two-times larger cross section of NH2D at 121.6 nm leads directly to an increased photodissociation rate of this species in a Lyman-α dominated radiation field.
The Lyman-α resonance of C2H2 is even more critical than for NH3, as shown in Fig. 23. A small isotopic shift following deuteration will lower the dissociation rate of C2HD in a Lyman-α dominated radiation field by a factor of 10. This reduction is in fact indicated from laboratory action spectroscopy of C2H2 and C2HD (Löffler et al. 1996; Wang et al. 1997).
The photodissociation efficiency or branching may also be sensitive to isotopic substitution. For example, the deuteration of water to form HDO introduces the possibility of preferential branching to form OH or OD photodissociation fragments and imposing a significant influence on the ratios of H2O, HDO, and D2O found in interstellar space, comets, and terrestrially (Caselli & Ceccarelli 2012; van Dishoeck et al. 2013). The propensity for H-OD fission is determined in laboratory measurements at a few UV wavelengths (e.g., Shafer et al. 1989; Plusquellic et al. 1998) and theoretical calculations (e.g., Engel & Schinke 1988; Zhang et al. 1989; Zhou & Xie 2015), together indicating a wavelength and temperature dependent ratio of OD or OH fragments between 2 and 16 (or higher).
8.6. Photodissociation branching of H2O and NH3
We estimated the wavelength dependent branching ratios of H2O and NH3 into their main astrochemically-significant photodissociation products OH and O, and NH2 and NH, respectively. A discussion of these cross sections is given in Sects. 4.3.33 and 4.3.46, and the wavelength dependent partial cross sections shown in Figs. 16 and 17. We calculated the partial photodissociation rates generating these products when exposed to various kinds of interstellar and cosmic-ray-generated radiation fields, with results given in Table 22. The uncertainty estimates provided in this table are a combination of the overall cross section uncertainties of Table 1 and an estimate of the branching-ratio accuracy. Consideration was also made that minor branching channels will have larger fractional uncertainties than major ones.
The product branching ratios of both H2O and NH3 are well known at the Lyman-α wavelength, reasonably constrained at longer wavelengths, but poorly known shortwards of 121.6 nm. Then, their ISRF and cosmic-ray-induced photodissociation rates are assigned a larger uncertainty than for other stellar radiation fields because these are approximately 40% controlled by radiation shorter than Lyman-α. All other stellar rates are controlled by product branching ratios at Lyman-α or longwards.
The partial rates calculated here are in line with the previous version of the Leiden database for NH3 but lead to significantly greater production of atomic-O following the dissociation of H2O in the ISRF, 23% versus 6%. This is due to the product branching calculations of (van Harrevelt & van Hemert 2008) prompting the estimation of a higher O branching for wavelengths shorter than Lyman-α. This assumption is however quite uncertain. The ratio of partial rates of NH3 products due to cosmic ray photodissociation is NH2/NH = 0.6 and has decreased relative to the calculation of Gredel et al. (1989), finding a ratio of 2.4.
 |
Fig. 38 Fractional change of chemical abundances in a translucent cloud model when substituting photodestruction rates of the RATE12 network with the newly-calculated rates. A comparison is made with updated models including the same γexp parameterisation as RATE12 for dust shielding, and with dust shielding calculated explicitly for each molecule. The plotted species are those listed in Tielens (2013, Table II). |
 |
Fig. 39 Comparing the chemical abundances in a translucent cloud model assuming non-ISRF radiation fields. The plotted species are those listed in Tielens (2013, Table II). |
 |
Fig. 40 Fractional change of chemical abundances in the dark-cloud model when substituting photodestruction rates of the RATE12 network with the newly-calculated rates. A comparison is made for models assuming increasing ionisation rate, ζ. The plotted species are those listed in Tielens (2013, Table II). |
9. Updated astrochemical reaction network
The significance of the new and updated rates listed in Tables 18–20 are investigated by trialling a set of astrochemical models. These single-point time-dependent gas-phase models use the integration program of Walsh et al. (2009, 2010) to trace the chemical evolution of a range of atoms and molecules assuming a constant temperature, density, and visual extinction; and a set of initial abundances. For simplicity, these models are restricted to pure gas-phase chemistry, apart from the inclusion of grain-surface-mediated H2 formation, and neglect the self-shielding of CO and N2.
We adopt the RATE12 reaction network (McElroy et al. 2013) in a fiducial model, and then modify it by substituting or adding our newly-calculated photodissociation and photoionisation rates. This required the updating of 111 ISRF photodissociation and ionisation rates, and 82 cosmic-ray induced rates; and adding 40 new rates for species in the network that lacked one or more photodestruction processes. Alternative networks were also constructed that replace the ISRF rates with those appropriate for black-body fields of various temperatures, and the simulated flux from TW-Hydra, described in Sect. 2.
Two kinds of models were run, with their important parameters listed in Table 23. The translucent cloud model is useful for evaluating the effect of the updated ISRF photodestruction rates, and the dark cloud model for isolating the effects of the new cosmic-ray induced rates. We integrated the models until reaching chemical equilibrium, requiring about 10 years of model time.
The effects of the updated rates on model abundances at AV = 1 in a translucent cloud exposed to the ISRF are modest, with no abundance changes relative to the RATE12 model exceeding a factor of two. Trialling additional pairs of models after making order-of-magnitude variations of the temperature, density, and AV in the translucent cloud model resulted in similar differences.
An explicit radiative transfer (or improved parameterisation) of dust shielding is as important as the new photodestruction rates in altering the chemical model output. The RATE12 network incorporates the k0exp(−γexpAV) depth-dependent photodestruction rates of van Dishoeck et al. (2006). The effect on model abundances of updating all photodestruction rates while retaining the RATE12 γexp parameters is demonstrated in Fig. 38 for a selection of atoms and molecules with AV = 1. Also shown is a model with updated rates and an explicit radiative-transfer calculation simulating their reduction at a depth of 1 AV (as in Sect. 6). The addition of updated dust shielding leads to an increased abundance for most species by up to a factor of two after chemical equilibrium is reached.
The γexp parameters used in RATE12 generally underestimate the shielding effect of a semi-infinite slab of dust at an extinction of 1, and overestimate it at higher extinction, as exampled in Fig. 28. The explicit radiative transfer calculation then results in lower photodestruction rates and generally-higher abundances of molecules and neutral atoms at 1 AV. The disadvantages of the γexp parameterisation can be largely avoided while retaining its computational efficiency by adopting the more realistic exponential-integral formulation (with γE2 parameters in Sect. 6.2).
Physical parameters of interstellar cloud point models.
Some species shown in Fig. 38 are affected by the updated rates and dust shielding but are not included in our current database of wavelength-dependent cross sections, for example, N2H+ or HC5N. The modelled changes are then due to chemical formation and destruction routes involving species that we updated. The sensitivity of a chemical network to its input rates and the propagating influence of specific rates to unrelated model species is studied in the context of interstellar and atmospheric chemistry (e.g., Wakelam et al. 2010; Loison et al. 2015).
The wavelength dependence of our collected cross sections significantly alters the model output for non-ISRF ultraviolet radiation fields. Figure 39 summarises the equilibrium abundances calculated for 31 species known to compose interstellar clouds (Tielens 2013, Table II). The variation of these abundances with radiation field is plotted relative to the abundances calculated in the ISRF. Substitution with a cooler 10 000 K black-body radiation field increases the abundance of CO and N2 by factors of 4 and 20, respectively, because these molecules photodissociate at relatively short wavelengths only. The reduced occurrence of reactive C-atoms then lowers the abundance of small carbon-containing molecules by a similar factor. On the other hand, nitrogen-containing species, for example, NH2 and N2H+, have increased abundances. This is due to their increased lifetime in the cooler ultraviolet flux and a formation route reliant on ion-molecule reactions with N2 and not its photodissociation (Walsh et al. 2015). Similar effects with somewhat larger magnitude follow from assuming the TW-Hydra radiation field, and with multiple-order-of-magnitude changes when assuming the extremely long-wavelength biased 4000 K black-body field. An extreme example is the increased abundance of H3O+, even though we did not include a direct photodestruction mechanism for this molecule in our model. The modelled increase is due to the decreased photoionisation of other species in the black-body radiation field, and a lowered electron abundance slowing the rate of H3O+ dissociative recombination.
These differences are strongly-dependent on the total integrated flux of each radiation field, which we artificially normalised as is described in Sect. 2. However, an alternative scaling of the integrated flux will result in similarly divergent chemical abundances as pictured in Fig. 39 whenever photodissociation dominates molecular destruction, due to the wavelength-dependence of atomic and molecular cross sections: the abundances of small carbon-bearing molecules are reduced in cool radiation fields whereas nitrogen-containing species are enhanced.
Re-running the model while assuming weaker shielding from larger dust grains (with optical properties shown in Fig. 26) leads to significantly more photodestruction and a reduced population of stable molecules, for example, the abundance of CO is reduced by a factor of 30, and CN by a factor of 10. A very similar effect is achieved in our single-point steady-state model by retaining an interstellar dust opacity but reducing the model AV from 1 to 0.2. More sophisticated 1- or multi-dimensional astrochemical models would likely distinguish between these effects, and could include the effects of H2-shielding and self-shielding, necessary for computing a self-consistent PDR model.
The dark cloud model was used to assess the effect of the new rates on cosmic-ray induced photodissociation and ionisation. After comparing models using the RATE12 network and updated cosmic-ray induced photodestruction rates, and assuming a primary ionisation rate of 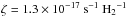 , no change greater than a factor of 2 was found for any species with abundance greater than 10 relative to H2. Alternative models were run with the comic-ray induced ionisation rates of H2 and H and ultraviolet flux increased by a common factor. Model results corresponding to ζ = 10-16 and
, no change greater than a factor of 2 was found for any species with abundance greater than 10 relative to H2. Alternative models were run with the comic-ray induced ionisation rates of H2 and H and ultraviolet flux increased by a common factor. Model results corresponding to ζ = 10-16 and 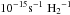 are also shown in Fig. 40. Under the extreme model of cosmic-ray influence the effects of the updated rates calculated here are somewhat increased for some species, particularly CH3OH, CS, SO, and NH3. Even in this case other sources of uncertainty in dark cloud chemical models may overshadow the abundance changes engendered by our updated rates.
are also shown in Fig. 40. Under the extreme model of cosmic-ray influence the effects of the updated rates calculated here are somewhat increased for some species, particularly CH3OH, CS, SO, and NH3. Even in this case other sources of uncertainty in dark cloud chemical models may overshadow the abundance changes engendered by our updated rates.
10. Summary
A new collection of photodissociation and photoionisation cross sections was assembled for atoms and molecules of astrochemical interest, with uncertainty estimates. These data are used to calculate photodissociation and photoionisation rates in the ISRF and other radiation fields, including Lyman-α dominated radiation and a cosmic-ray induced ultraviolet flux. The majority of photodissociation and ionisation rates agree within 30% when compared with other recent compilations (van Dishoeck et al. 2006; Huebner & Mukherjee 2015; Gredel et al.1989; where these include comparable cross sections), with some important differences. The reduction of these rates in shielded regions was calculated as a function of the dust, molecular and atomic hydrogen, neutral C, and self-shielding columns. Dust opacity is generally the most important shielding effect but a comparable influence from other forms of shielding was found for some molecules, particularly if grain growth has reduced the ultraviolet absorption cross section of the dust population.
Various sensitivities of the calculated rates to the experimental and theoretical data they are derived from, or the astrophysical environments where they are applied, is given. For most molecules, the under-resolution of resonant photoabsorption lines in experimental cross sections, small errors in the excitation electronic energies and linewidths in theoretical calculations, changes in excitation temperature, or isotopic substitution will not dramatically affect their astrochemical photodestruction. Exceptions occur for some molecules that show a high degree of sensitivity to these details, particularly when their cross sections feature a maximum near the Lyman-α wavelength.
Some tests of the new rates in simple astrochemical models show sensitivity to the updated rates up to a factor of two for molecules important in translucent and dark interstellar clouds. Additional sensitivity was shown to an improved dust-shielding parameterisation scheme that better matches the attenuation of absorbed and scattered UV light through a slab-model interstellar cloud.
The intention is to provide, along with precomputed rates and shielding functions, as detailed as possible wavelength-dependent cross sections that are suitable for use in astrochemical models of interstellar and circumstellar material that require specific treatments of photodissociation and photoionisation. That is, due to spatial and time variance of the ultraviolet radiation flux, temperature, density, turbulence, and dust optical properties, which cannot be easily or comprehensively parameterised.
The cross sections and derived data for a total of 102 molecules and atoms are available from the Leiden database20. These are provided in both a binary format, explicitly including all cross section features on a dense wavelength grid, and sparser text format that is more suitable for rapid calculation in a continuum radiation field like the ISRF. This new database extends its previous version by the addition of 9 new species and cross sections updates for 60 more.
A community supported list of interstellar molecules: http://wikipedia.org/wiki/List_of_interstellar_and_circumstellar_molecules
Model RV = 3.1′ from www.astro.princeton.edu/~draine/dust/dustmix.html
Acknowledgments
Thanks to Roland Gredel for provision of his cosmic-ray induced UV spectrum, Catherine Walsh for the use of her single-point astrochemical model program, and Marc van Hemert for ab initio calculations of CN. Astrochemistry in Leiden is supported by the European Union A-ERC grant 291141 CHEMPLAN, by The Netherlands Research School for Astronomy (NOVA), by a Royal Netherlands Academy of Arts and Sciences (KNAW) professor prize, and the Dutch astrochemistry network (DAN) from The Netherlands Organisation for Scientific Research (NWO) under grant 648.000.002. Thanks also to the anonymous referee for many useful comments, particularly regarding the use of exponential-integral functions to represent UV-shielding by dust grains.
References
- Abgrall, H., & Roueff, E. 2006, A&A, 445, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Abgrall, H., Roueff, E., Launay, F., Roncin, J. Y., & Subtil, J. 1993a, A&AS, 101, 273 [NASA ADS] [Google Scholar]
- Abgrall, H., Roueff, E., Launay, F., Roncin, J. Y., & Subtil, J. 1993b, A&AS, 101, 323 [NASA ADS] [Google Scholar]
- Abgrall, H., Roueff, E., Launay, F., Roncin, J. Y., & Subtil, J. L. 1993c, J. Mol. Spectr., 157, 512 [NASA ADS] [CrossRef] [Google Scholar]
- Abgrall, H., Roueff, E., Launay, F., & Roncin, J.-Y. 1994, Can. J. Phys., 72, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Abgrall, H., Roueff, E., Liu, X., & Shemansky, D. E. 1997, ApJ, 481, 557 [NASA ADS] [CrossRef] [Google Scholar]
- Abgrall, H., Roueff, E., Liu, X., Shemansky, D. E., & James, G. K. 1999, J. Phys. B, 32, 3813 [NASA ADS] [CrossRef] [Google Scholar]
- Abgrall, H., Roueff, E., & Drira, I. 2000, A&AS, 141, 297 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ackerman, M. 1971, in Mesospheric models and related experiments, ed. G. Fiocco, Astrophys. Space Sci. Lib., 25, 149 [Google Scholar]
- Ádámkovics, M., Glassgold, A. E., & Najita, J. R. 2014, ApJ, 786, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Alexander, M. H., Li, X., Liyanage, R., & Gordon, R. J. 1998, Chem. Phys., 231, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Andrews, S. M., Wilner, D. J., Espaillat, C., et al. 2011, ApJ, 732, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Angel, G. C., & Samson, J. A. R. 1988, Phys. Rev. A, 38, 5578 [NASA ADS] [CrossRef] [Google Scholar]
- Archer, L., Stark, G., Smith, P., et al. 2013, J. Quant. Spectr. Radiat. Transf., 117, 88 [NASA ADS] [CrossRef] [Google Scholar]
- Ardila, D. R., Basri, G., Walter, F. M., Valenti, J. A., & Johns-Krull, C. M. 2002a, ApJ, 566, 1100 [NASA ADS] [CrossRef] [Google Scholar]
- Ardila, D. R., Basri, G., Walter, F. M., Valenti, J. A., & Johns-Krull, C. M. 2002b, ApJ, 567, 1013 [NASA ADS] [CrossRef] [Google Scholar]
- Ashfold, M. N. R., Nahler, N. H., Orr-Ewing, A. J., et al. 2006, Phys. Chem. Chem. Phys., 8, 26 [CrossRef] [Google Scholar]
- Au, J., Cooper, G., Burton, G., Olney, T., & Brion, C. 1993, Chem. Phys., 173, 209 [NASA ADS] [CrossRef] [Google Scholar]
- Babb, J. F. 2015, ApJS, 216, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Backx, C., & Vanderwiel, M. 1975, J. Phys. B, 8, 3020 [NASA ADS] [CrossRef] [Google Scholar]
- Backx, C., Wight, G. R., & der Wiel, M. J. V. 1976, J. Phys. B, 9, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Bahou, M., Chung, C.-Y., Lee, Y.-P., et al. 2001, ApJ, 559, L179 [NASA ADS] [CrossRef] [Google Scholar]
- Baltayan, P., & Nedelec, O. 1979, J. Chem. Phys., 70, 2399 [NASA ADS] [CrossRef] [Google Scholar]
- Barthel, M., Flesch, R., Rühl, E., & McLaughlin, B. M. 2015, Phys. Rev. A, 91, 013406 [NASA ADS] [CrossRef] [Google Scholar]
- Bates, D. R., & Spitzer, Jr., L. 1951, ApJ, 113, 441 [NASA ADS] [CrossRef] [Google Scholar]
- Bauschlicher, C. W., & Langhoff, S. R. 1988, J. Chem. Phys., 89, 2116 [NASA ADS] [CrossRef] [Google Scholar]
- Bauschlicher, C. W., & Partridge, H. 1995, Chem. Phys. Lett., 239, 246 [NASA ADS] [CrossRef] [Google Scholar]
- Bautista, M. 1997, A&AS, 122, 167 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Becker, S., Braatz, C., Lindner, J., & Tiemann, E. 1995, Chem. Phys., 196, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Belau, L., Wheeler, S. E., Ticknor, B. W., et al. 2007, J. Am. Chem. Soc., 129, 10229 [CrossRef] [PubMed] [Google Scholar]
- Benedikt, J., Eijkman, D., Vandamme, W., Agarwal, S., & van de Sanden, M. 2005, Chem. Phys. Lett., 402, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Bénilan, Y., Bruston, P., Raulin, F., Cossart-Magos, C., & Guillemin, J.-C. 1994, J. Geophys. Res. – Planet., 99, 17069 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E., Calvet, N., D’Alessio, P., & Herczeg, G. J. 2003, ApJ, 591, L159 [NASA ADS] [CrossRef] [Google Scholar]
- Berkowitz, J. 1962, J. Chem. Phys., 36, 2533 [NASA ADS] [CrossRef] [Google Scholar]
- Berkowitz, J. 2008, Int. J. Mass Spectr., 271, 8 [CrossRef] [Google Scholar]
- Berkowitz, J., & Cho, H. 1989, J. Chem. Phys., 90, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Bethell, T., & Bergin, E. 2009, Science, 326, 1675 [NASA ADS] [CrossRef] [Google Scholar]
- Bethell, T. J., & Bergin, E. A. 2011, ApJ, 739, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Biehl, H., Schönnenbeck, G., Stuhl, F., & Staemmler, V. 1994, J. Chem. Phys., 101, 3819 [NASA ADS] [CrossRef] [Google Scholar]
- Birnstiel, T., Dullemond, C. P., & Brauer, F. 2010, A&A, 513, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Black, J. H., & Dalgarno, A. 1977, ApJS, 34, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Black, J. H., & van Dishoeck, E. F. 1987, ApJ, 322, 412 [NASA ADS] [CrossRef] [Google Scholar]
- Black, J. H., Weisheit, J. C., & Laviana, E. 1972, ApJ, 177, 567 [NASA ADS] [CrossRef] [Google Scholar]
- Blackie, D., Blackwell-Whitehead, R., Stark, G., et al. 2011, J. Geophys. Res., 116, E12099 [NASA ADS] [CrossRef] [Google Scholar]
- Blitz, M. A., & Seakins, P. W. 2012, Chem. Soc. Rev., 41, 6318 [CrossRef] [Google Scholar]
- Brint, P., Connerade, J.-P., Mayhew, C., & Sommer, K. 1985, J. Chem. Soc. Farad. T. 2, 81, 1643 [CrossRef] [Google Scholar]
- Brion, C., Dyck, A., & Cooper, G. 2005, J. Electron Spectr. Relat. Phenom., 144, 127 [Google Scholar]
- Brites, V., Hammoutène, D., & Hochlaf, M. 2008, J. Phys. B, 41, 045101 [NASA ADS] [CrossRef] [Google Scholar]
- Bruna, P. J., & Hirsch, G. 1987, Mol. Phys., 61, 1359 [NASA ADS] [CrossRef] [Google Scholar]
- Bruna, P., Kammer, W., & Vasudevan, K. 1975, Chem. Phys., 9, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Bruna, P. J., Buenker, R. J., & Peyerimhoff, S. D. 1976, J. Mol. Spectr., 32, 217 [NASA ADS] [Google Scholar]
- Bruna, P. J., Hirsch, G., Peyerimhoff, S. D., & Buenker, R. J. 1981, Mol. Phys., 42, 875 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Brzozowski, J., Elander, N., & Erman, P. 1974, Phys. Scr., 9, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Brzozowski, J., Erman, P., & Lyyra, M. 1976, Phys. Scr., 14, 290 [NASA ADS] [CrossRef] [Google Scholar]
- Burton, G. R., Chan, W. F., Cooper, G., & Brion, C. 1992, Chem. Phys., 167, 349 [NASA ADS] [CrossRef] [Google Scholar]
- Burton, G. R., Chan, W. F., Cooper, G., et al. 1994, Can. J. Chem., 72, 529 [CrossRef] [Google Scholar]
- Cacciani, P., Brandi, F., Velchev, I., et al. 2001, Eur. J. Phys. D, 15, 47 [Google Scholar]
- Calvert, J., & Pitts, J. 1966, in Photochemistry (Wiley) [Google Scholar]
- Cameron, M., Sivakumaran, V., Dillon, T. J., & Crowley, J. N. 2002, Phys. Chem. Chem. Phys., 4, 3628 [CrossRef] [Google Scholar]
- Cantu, A. M., & Parkinson, W. H. 1988, Phys. Scr., 37, 336 [NASA ADS] [CrossRef] [Google Scholar]
- Carmona-Novillo, E., Moccia, R., & Spizzo, P. 1996, Chem. Phys., 210, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Carnovale, F., White, M., & Brion, C. 1981, J. Electron Spectr. Relat. Phenom., 24, 63 [CrossRef] [Google Scholar]
- Carrington, A., & Kennedy, R. A. 1984, J. Chem. Phys., 81, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Carroll, P. K., & Collins, C. P. 1969, Can. J. Phys., 47, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, V. L., Hudson, R. D., & Breig, E. L. 1971, Phys. Rev. A, 4, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., & Ceccarelli, C. 2012, A&ARv, 20, 56 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Cecchi-Pestellini, C., & Aiello, S. 1992, MNRAS, 258, 125 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, W., Cooper, G., & Brion, C. 1992, Chem. Phys., 168, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, W., Cooper, G., & Brion, C. 1993a, Chem. Phys., 170, 123 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, W., Cooper, G., & Brion, C. 1993b, Chem. Phys., 178, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, W. F., Cooper, G., & Brion, C. E. 1993c, Chem. Phys., 170, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Chan, W. F., Cooper, G., Sodhi, R., & Brion, C. E. 1993d, Chem. Phys., 170, 81 [NASA ADS] [CrossRef] [Google Scholar]
- Chaparro Molano, G., & Kamp, I. 2012, A&A, 537, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chen, F., & Wu, C. 2004, J. Quant. Spectr. Rad. Transf., 85, 195 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, B.-M., Chew, E. P., Hung, W.-C., Eberhard, J., & Lee, Y.-P. 1998, J. Synchrotron Radiat., 5, 1041 [CrossRef] [Google Scholar]
- Cheng, B.-M., Bahou, M., Lee, Y.-P., & Lee, L. C. 2002, J. Geophys. Res., 107, A8 [CrossRef] [Google Scholar]
- Cheng, B.-M., Lu, H.-C., Chen, H.-K., et al. 2006, ApJ, 647, 1535 [NASA ADS] [CrossRef] [Google Scholar]
- Cheng, B.-M., Chen, H.-F., Lu, H.-C., et al. 2011, ApJS, 196, 1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Choi, M., Tatematsu, K., & Kang, M. 2010, ApJ, 723, L34 [NASA ADS] [CrossRef] [Google Scholar]
- Chupka, W. A., & Berkowitz, J. 1967, J. Chem. Phys., 47, 2921 [NASA ADS] [CrossRef] [Google Scholar]
- Clauberg, H., Minsek, D. W., & Chen, P. 1992, J. Am. Chem. Soc., 114, 99 [CrossRef] [Google Scholar]
- Cleeves, L. I., Adams, F. C., & Bergin, E. A. 2013, ApJ, 772, 5 [NASA ADS] [CrossRef] [Google Scholar]
- Cleeves, L. I., Bergin, E. A., Qi, C., Adams, F. C., & Öberg, K. I. 2015, ApJ, 799, 204 [NASA ADS] [CrossRef] [Google Scholar]
- Clement, S. G., Ashfold, M. N. R., Western, C. M., Johnson, R. D., & Hudgens, J. W. 1992, J. Chem. Phys., 97, 7064 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, E. U. 1928, Phys. Rev., 32, 858 [Google Scholar]
- Connors, R. E., Roebber, J. L., & Weiss, K. 1974, J. Chem. Phys., 60, 5011 [NASA ADS] [CrossRef] [Google Scholar]
- Cook, G. R., & Ogawa, M. 1969, J. Chem. Phys., 51, 2419 [NASA ADS] [CrossRef] [Google Scholar]
- Cool, T. A., Wang, J., Nakajima, K., Taatjes, C. A., & Mcllroy, A. 2005, Int. J. Mass Spectrom., 247, 18 [CrossRef] [Google Scholar]
- Cooper, G., Burton, G. R., & Brion, C. 1995, J. Electron Spectr. Relat. Phenom., 73, 139 [Google Scholar]
- Cooper, G., Anderson, J. E., & Brion, C. 1996, Chem. Phys., 209, 61 [NASA ADS] [CrossRef] [Google Scholar]
- Coppens, P., & Drowart, J. 1995, Chem. Phys. Lett., 243, 108 [NASA ADS] [CrossRef] [Google Scholar]
- Cosby, P., & Helm, H. 1988, Chem. Phys. Lett., 152, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Cravens, T. E., & Dalgarno, A. 1978, ApJ, 219, 750 [NASA ADS] [CrossRef] [Google Scholar]
- Crovisier, J., Leech, K., Bockelee-Morvan, D., et al. 1997, Science, 275, 1904 [CrossRef] [Google Scholar]
- Curdt, W., Brekke, P., Feldman, U., et al. 2001, A&A, 375, 591 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- D’Alessio, P., Calvet, N., & Hartmann, L. 2001, ApJ, 553, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Dalgarno, A. 2006, Pro. Nat. Acad. Sci., 103, 12269 [NASA ADS] [CrossRef] [Google Scholar]
- Dalgarno, A., Herzberg, G., & Stephens, T. L. 1970, ApJ, 162, L49 [NASA ADS] [CrossRef] [Google Scholar]
- Daviel, S., Iida, Y., Carnovale, F., & Brion, C. 1984, Chem. Phys., 83, 391 [Google Scholar]
- Davis, D. D., & Okabe, H. 1968, J. Chem. Phys., 49, 5526 [NASA ADS] [CrossRef] [Google Scholar]
- Day, R. L., Suto, M., & Lee, L. C. 1982, J. Phys. B, 15, 4403 [NASA ADS] [CrossRef] [Google Scholar]
- de Almeida, A. A., & Singh, P. D. 1986, Earth Moon and Planets, 36, 117 [NASA ADS] [CrossRef] [Google Scholar]
- de Beer, E., Born, M., de Lange, C., & Westwood, N. 1991, Chem. Phys. Lett., 186, 40 [NASA ADS] [CrossRef] [Google Scholar]
- de Oliveira, N., Roudjane, M., Joyeux, D., et al. 2011, Nature Photonics, 5, 149 [CrossRef] [Google Scholar]
- Dehmer, P. M., & Chupka, W. A. 1976, J. Chem. Phys., 65, 2243 [NASA ADS] [CrossRef] [Google Scholar]
- Dehmer, P. M., Berkowitz, J., & Chupka, W. A. 1974, J. Chem. Phys., 60, 2676 [NASA ADS] [CrossRef] [Google Scholar]
- Dent, W. R. F., Wyatt, M. C., Roberge, A., et al. 2014, Science, 343, 1490 [Google Scholar]
- Dibeler, V. H. 1967, J. Chem. Phys., 47, 2191 [NASA ADS] [CrossRef] [Google Scholar]
- Dibeler, V. H., & Liston, S. K. 1967, J. Chem. Phys., 47, 4548 [NASA ADS] [CrossRef] [Google Scholar]
- Dibeler, V. H., & Walker, J. A. 1967, J. Opt. Soc. Amer., 57, 1007 [NASA ADS] [CrossRef] [Google Scholar]
- Dickenson, G. D., & Ubachs, W. 2014, Mol. Phys., 112, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Dodson, L. G., Shen, L., Savee, J. D., et al. 2015, J. Phys. Chem. A, 119, 1279 [CrossRef] [Google Scholar]
- Donovan, R. J., Husain, D., & Stevenson, C. D. 1970, Trans. Faraday Soc., 66, 1 [CrossRef] [Google Scholar]
- Draine, B. T. 1978, ApJS, 36, 595 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. 2003a, ARA&A, 41, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003b, ApJ, 598, 1017 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2003c, ApJ, 598, 1026 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T., & Lee, H. M. 1984, ApJ, 285, 89 [Google Scholar]
- Draine, B. T., Dale, D. A., Bendo, G., et al. 2007, ApJ, 663, 866 [NASA ADS] [CrossRef] [Google Scholar]
- Dressler, K. 1969, Can. J. Phys., 47, 547 [NASA ADS] [CrossRef] [Google Scholar]
- Dunn, G. H. 1968, Phys. Rev., 172, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Eddington, A. S. 1928, MNRAS, 88, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Eden, S., Limão-Vieira, P., Kendall, P., et al. 2003, Eur. J. Phys. D, 26, 201 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Edvardsson, D., Baltzer, P., Karlsson, L., et al. 1999, J. Phys. B, 32, 2583 [Google Scholar]
- Eidelsberg, M., & Rostas, F. 1990, A&A, 235, 472 [NASA ADS] [Google Scholar]
- Eidelsberg, M., Benayoun, J., Viala, Y., et al. 1992, A&A, 265, 839 [NASA ADS] [Google Scholar]
- Eidelsberg, M., Sheffer, Y., Federman, S. R., et al. 2006, ApJ, 647, 1543 [NASA ADS] [CrossRef] [Google Scholar]
- Eidelsberg, M., Lemaire, J. L., Federman, S. R., et al. 2012, A&A, 543, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eidelsberg, M., Lemaire, J. L., Federman, S. R., et al. 2014, A&A, 566, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- el-Qadi, W. H., & Stancil, P. C. 2013, ApJ, 779, 97 [NASA ADS] [CrossRef] [Google Scholar]
- Endo, Y., Danielache, S. O., Ueno, Y., et al. 2015, J. Geophys. Res.: Atmos., 120, 2546 [NASA ADS] [CrossRef] [Google Scholar]
- Engel, V., & Schinke, R. 1988, J. Chem. Phys., 88, 6831 [NASA ADS] [CrossRef] [Google Scholar]
- Engin, S., Sisourat, N., & Carniato, S. 2012, J. Chem. Phys., 137 [Google Scholar]
- Ernest, C. T., Bauer, D., & Hynes, A. J. 2012, J. Phys. Chem. A, 116, 5910 [CrossRef] [Google Scholar]
- Federman, S. R., Fritts, M., Cheng, S., et al. 2001, ApJS, 134, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Feller, D., & Sordo, J. A. 2000, J. Chem. Phys., 113, 485 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, R., & Brion, C. 2002, Chem. Phys., 282, 419 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, R., Cooper, G., & Brion, C. 1999a, Chem. Phys., 244, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, R., Cooper, G., & Brion, C. 1999b, Chem. Phys., 249, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, R., Cooper, G., Burton, G. R., Brion, C., & Avaldi, L. 1999c, Chem. Phys., 240, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, R., Cooper, G., & Brion, C. E. 2000a, Chem. Phys., 252, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Feng, R., Cooper, G., Sakai, Y., & Brion, C. 2000b, Chem. Phys., 255, 353 [NASA ADS] [CrossRef] [Google Scholar]
- Ferland, G. J. 2003, ARA&A, 41, 517 [NASA ADS] [CrossRef] [Google Scholar]
- Ferradaz, T., Bénilan, Y., Fray, N., et al. 2009, Planet. Space Sci., 57, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Field, G. B., Somerville, W. B., & Dressler, K. 1966, ARA&A, 4, 207 [NASA ADS] [CrossRef] [Google Scholar]
- Fillion, J.-H., Dulieu, F., Baouche, S., et al. 2003, J. Phys. B, 36, 2767 [Google Scholar]
- Fillion, J.-H., Ruiz, J., Yang, X.-F., et al. 2004, J. Chem. Phys., 120, 6531 [NASA ADS] [CrossRef] [Google Scholar]
- Fischer, I., Lochschmidt, A., Strobel, A., et al. 1993, Chem. Phys. Lett., 202, 542 [NASA ADS] [CrossRef] [Google Scholar]
- France, K., Schindhelm, E., Bergin, E. A., Roueff, E., & Abgrall, H. 2014, ApJ, 784, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Frederix, P. W. J. M., Yang, C.-H., Groenenboom, G. C., et al. 2009, J. Phys. Chem. A, 113, 14995 [CrossRef] [Google Scholar]
- Frerking, M. A., Keene, J., Blake, G. A., & Phillips, T. G. 1989, ApJ, 344, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Fridh, C., & Asbrink, L. 1975, J. Electron Spectr. Relat. Phenom., 7, 119 [CrossRef] [Google Scholar]
- Frohlich, H., & Glass-Maujean, M. 1990, Phys. Rev. A, 42, 1396 [NASA ADS] [CrossRef] [Google Scholar]
- Gallagher, J. W., Brion, C. E., Samson, J. A. R., & Langhoff, P. W. 1988, J. Phys. Chem. Ref. Data, 17, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Gans, B., Mendes, L. A. V., Boyé-Péronne, S., et al. 2010, J. Phys. Chem. A, 114, 3237 [CrossRef] [Google Scholar]
- Gans, B., Boye-Peronne, S., Broquier, M., et al. 2011, Phys. Chem. Chem. Phys., 13, 8140 [CrossRef] [Google Scholar]
- Gao, Y., & Gao, T. 2014, Spectrochim. Acta. A, 118, 308 [NASA ADS] [CrossRef] [Google Scholar]
- Gao, H., Song, Y., Chang, Y.-C., et al. 2013, J. Phys. Chem. A, 117, 6185 [CrossRef] [Google Scholar]
- Garcia, G. A., Tang, X., Gil, J.-F., et al. 2015, J. Chem. Phys., 142 [Google Scholar]
- Gardner, E. P., & McNesby, J. R. 1982, J. Phys. Chem., 86, 2646 [CrossRef] [Google Scholar]
- Gibson, S. T., & Lewis, B. R. 1996, J. Electron Spectr. Relat. Phenom., 80, 9 [CrossRef] [Google Scholar]
- Gibson, S. T., Greene, J. P., & Berkowitz, J. 1985, J. Chem. Phys., 83, 4319 [NASA ADS] [CrossRef] [Google Scholar]
- Gibson, S. T., Greene, J. P., Ruscic, B., & Berkowitz, J. 1986, J. Phys. B, 19, 2825 [NASA ADS] [CrossRef] [Google Scholar]
- Gingell, J., Mason, N., Zhao, H., Walker, I., & Siggel, M. 1997, Chem. Phys., 220, 191 [NASA ADS] [CrossRef] [Google Scholar]
- Ginter, D. S., & Ginter, M. L. 1981, J. Mol. Spectr., 90, 177 [NASA ADS] [CrossRef] [Google Scholar]
- Glass-Maujean, M., Jungen, C., Reichardt, G., et al. 2010, Phys. Rev. A, 82, 062511 [NASA ADS] [CrossRef] [Google Scholar]
- Glass-Maujean, M., Jungen, C., Schmoranzer, H., et al. 2013a, J. Mol. Spectr., 293, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Glass-Maujean, M., Jungen, C., Schmoranzer, H., et al. 2013b, J. Mol. Spectr., 293, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Glass-Maujean, M., Jungen, C., Spielfiedel, A., et al. 2013c, J. Mol. Spectr., 293, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Glassgold, A. E. 1996, ARA&A, 34, 241 [NASA ADS] [CrossRef] [Google Scholar]
- Glover, S. C. O., & Clark, P. C. 2012, MNRAS, 421, 116 [NASA ADS] [Google Scholar]
- Grebenshchikov, S. Y., Qu, Z.-W., Zhu, H., & Schinke, R. 2007, Phys. Chem. Chem. Phys., 9, 2044 [CrossRef] [Google Scholar]
- Gredel, R., & Dalgarno, A. 1995, ApJ, 446, 852 [NASA ADS] [CrossRef] [Google Scholar]
- Gredel, R., Lepp, S., & Dalgarno, A. 1987, ApJ, 323, L137 [NASA ADS] [CrossRef] [Google Scholar]
- Gredel, R., Lepp, S., Dalgarno, A., & Herbst, E. 1989, ApJ, 347, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Green, D. S., Bickel, G. A., & Wallace, S. C. 1991, J. Mol. Spectr., 150, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Grenier, I. A., Black, J. H., & Strong, A. W. 2015, ARA&A, 53, 199 [NASA ADS] [CrossRef] [Google Scholar]
- Grosch, H., Fateev, A., & Clausen, S. 2015, J. Quant. Spectr. Rad.. Transf., 154, 28 [Google Scholar]
- Guberman, S. L. 1977, J. Chem. Phys., 67, 1125 [NASA ADS] [CrossRef] [Google Scholar]
- Gustafsson, O., Larsson, M., & Sigray, P. 1988, Z. Phys. D, 7, 373 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Guyon, P. M., Chupka, W. A., & Berkowitz, J. 1976, J. Chem. Phys., 64, 1419 [NASA ADS] [CrossRef] [Google Scholar]
- Guzman, V. V., Pety, J., Gratier, P., et al. 2014, Faraday Discuss., 168, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Habing, H. J. 1968, Bull. Astron. I. Neth., 19, 421 [Google Scholar]
- Halpern, J., Miller, G., Okabe, H., & Nottingham, W. 1988, J. Photoch. Photobio. A, 42, 63 [CrossRef] [Google Scholar]
- Hansen, J. E., Ziegenbein, B., Lincke, R., & Kelly, H. P. 1977, J. Phys. B, 10, 37 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, A. J., Cederholm, B. J., & Terwilliger, M. A. 1959, J. Chem. Phys., 30, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, H., Schoen, R., & Cairns, R. 1969, J. Chem. Phys., 50, 3930 [NASA ADS] [CrossRef] [Google Scholar]
- Hart, D. J., & Hepburn, J. W. 1987, J. Chem. Phys., 86, 1733 [NASA ADS] [CrossRef] [Google Scholar]
- Hartquist, T. W., Black, J. H., & Dalgarno, A. 1978, MNRAS, 185, 643 [NASA ADS] [CrossRef] [Google Scholar]
- Hasegawa, T. I., & Kwok, S. 2003, ApJ, 585, 475 [NASA ADS] [CrossRef] [Google Scholar]
- Haser, L. 1957, Bull. Soc. R. Sci. Liege, 43, 740 [Google Scholar]
- Hatano, Y. 1999, Phys. Rep., 313, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Heays, A. N. 2011, Ph.D. Thesis, The Australian National University [Google Scholar]
- Heays, A. N., Dickenson, G. D., Salumbides, E. J., et al. 2011, J. Chem. Phys., 135, 244301 [CrossRef] [PubMed] [Google Scholar]
- Heays, A. N., Lewis, B. R., Gibson, S. T., et al. 2012, Phys. Rev. A, 85, 012705 [NASA ADS] [CrossRef] [Google Scholar]
- Heays, A. N., Ajello, J. M., Aguilar, A., Lewis, B. R., & Gibson, S. T. 2014a, ApJS, 211, 28 [NASA ADS] [CrossRef] [Google Scholar]
- Heays, A. N., Visser, R., Gredel, R., et al. 2014b, A&A, 562, A61 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heazlewood, B. R., Rowling, S. J., Maccarone, A. T., Jordan, M. J. T., & Kable, S. H. 2009, J. Chem. Phys., 130 [Google Scholar]
- Herzberg, G. 1966, Molecular spectra and molecular structure, Vol. 3, Electronic spectra of polyatomic molecules (New York: van Nostrand) [Google Scholar]
- Herzberg, G. 1989, in Molecular Spectra and Molecular Structure I: Spectra of Diatomic Molecules, 2nd edn. (Krieger Publishing Company) [Google Scholar]
- Herzberg, G., & Innes, K. K. 1957, Can. J. Phys., 35, 842 [NASA ADS] [CrossRef] [Google Scholar]
- Herzberg, G., & Shoosmith, J. 1956, Can. J. Phys., 34, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Hezareh, T., Houde, M., McCoey, C., Vastel, C., & Peng, R. 2008, ApJ, 684, 1221 [NASA ADS] [CrossRef] [Google Scholar]
- Hikida, T., & Mori, Y. 1978, J. Chem. Phys., 69, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Ho, P. T. P., & Townes, C. H. 1983, ARA&A, 21, 239 [NASA ADS] [CrossRef] [Google Scholar]
- Holland, D. M. P., & Shaw, D. A. 2014, J. Phys. B, 47, 025101 [NASA ADS] [CrossRef] [Google Scholar]
- Holland, D., Shaw, D., McSweeney, S., et al. 1993, Chem. Phys., 173, 315 [NASA ADS] [CrossRef] [Google Scholar]
- Holland, D., Shaw, D., & Hayes, M. 1995, Chem. Phys., 201, 299 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenbach, D., & Tielens, A. 1999, Rev. Mod. Phys., 71, 173 [Google Scholar]
- Hollenbach, D. J., Takahashi, T., & Tielens, A. G. G. M. 1991, ApJ, 377, 192 [NASA ADS] [CrossRef] [Google Scholar]
- Hollenstein, U., Reinhold, E., de Lange, C., & Ubachs, W. 2006, J. Phys. B, 39, L195 [CrossRef] [Google Scholar]
- Holt, R. B., McLane, C. K., & Oldenberg, O. 1948, J. Chem. Phys., 16, 225 [NASA ADS] [CrossRef] [Google Scholar]
- Honjou, N., Tanaka, K., Ohno, K., & Taketa, H. 1978, Mol. Phys., 35, 1569 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, W. S., Loock, H.-P., Cronin, B., et al. 2007, J. Chem. Phys., 127, 064301 [NASA ADS] [CrossRef] [Google Scholar]
- Hotop, H., Hübler, G., & Kaufhold, L. 1975, Int. J. Mass Spectrom., 17, 163 [NASA ADS] [Google Scholar]
- Hsu, Y.-C., Smith, M. A., & Wallace, S. C. 1984, Chem. Phys. Lett., 111, 219 [NASA ADS] [CrossRef] [Google Scholar]
- Hsu, C., Baldwin, D. P., Liao, C., & Ng, C. Y. 1994, J. Chem. Phys., 100, 8047 [NASA ADS] [CrossRef] [Google Scholar]
- Hu, Z., Wang, Z., Kong, X., et al. 2002, Acta. Phys. Sin., 51, 235 [Google Scholar]
- Huang, Y., Barts, S. A., & Halpern, J. B. 1992, J. Phys. Chem., 96, 425 [CrossRef] [Google Scholar]
- Huber, K. P., & Herzberg, G. 1979, in Molecular spectra and molecular structure IV: Constants of diatomic molecules (New York: Van Nostrand) [Google Scholar]
- Hubin-Franskin, M.-J., Delwiche, J., Giuliani, A., et al. 2002, J. Chem. Phys., 116, 9261 [NASA ADS] [CrossRef] [Google Scholar]
- Hudson, R. D., & Carter, V. L. 1968, J. Opt. Soc. Amer., 58, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Huebner, W., & Mukherjee, J. 2015, Planet. Space Sci., 106, 11 [Google Scholar]
- Huebner, W., Keady, J., & Lyon, S. 1992, Astrophys. Space. Sci, 195, 1 [Google Scholar]
- Huestis, D. L., & Berkowitz, J. 2010, in BAAS, 42, AAS/Division for Planetary Sciences Meeting Abstracts #42, 972 [Google Scholar]
- Hurzeler, H., Inghram, M. G., & Morrison, J. D. 1958, J. Chem. Phys., 28, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Iida, Y., Carnovale, F., Daviel, S., & Brion, C. 1986, Chem. Phys., 105, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Indriolo, N., & McCall, B. J. 2012, ApJ, 745, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Indriolo, N., Neufeld, D. A., Gerin, M., et al. 2015, ApJ, 800, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Inokuti, M. 1971, Rev. Mod. Phys., 43, 297 [NASA ADS] [CrossRef] [Google Scholar]
- Jansen, D. J., van Dishoeck, E. F., Black, J. H., Spaans, M., & Sosin, C. 1995, A&A, 302, 223 [NASA ADS] [Google Scholar]
- Jansen, D. J., van Dishoeck, E. F., Keene, J., Boreiko, R. T., & Betz, A. L. 1996, A&A, 309, 899 [NASA ADS] [Google Scholar]
- Jochims, H. W., Ruhl, E., Baumgärtel, H., Tobita, S., & Leach, S. 1994, ApJ, 420, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Johansen, A., Oishi, J. S., Mac Low, M.-M., Klahr, H., & Henning, T. 2007, Nature, 448, 1022 [Google Scholar]
- Johns, J. W. C., & Ramsay, D. A. 1961, Can. J. Phys., 39, 210 [NASA ADS] [CrossRef] [Google Scholar]
- Jonas, D. M., Zhao, X., Yamanouchi, K., et al. 1990, J. Chem. Phys., 92, 3988 [NASA ADS] [CrossRef] [Google Scholar]
- Jonin, C., Liu, X., Ajello, J., James, G., & Abgrall, H. 2000, ApJS, 129, 247 [NASA ADS] [CrossRef] [Google Scholar]
- Jonkheid, B., Kamp, I., Augereau, J.-C., & van Dishoeck, E. F. 2006, A&A, 453, 163 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kameta, K., Machida, S., Kitajima, M., et al. 1996, J. Electron Spectr. Relat. Phenom., 79, 391 [CrossRef] [Google Scholar]
- Kameta, K., Kouchi, N., Ukai, M., & Hatano, Y. 2002, J. Electron Spectr. Relat. Phenom., 123, 225 [CrossRef] [Google Scholar]
- Katagiri, H., Sako, T., Hishikawa, A., et al. 1997, J. Mol. Struct., 413, 589 [NASA ADS] [CrossRef] [Google Scholar]
- Kato, H., & Baba, M. 1995, Chem. Rev., 95, 2311 [CrossRef] [Google Scholar]
- Kelly, R. 1987a, J. Phys. Chem. Ref. Data, 16, 1 [CrossRef] [Google Scholar]
- Kelly, R. 1987b, J. Phys. Chem. Ref. Data, 16, 651 [Google Scholar]
- Kessler-Silacci, J., Augereau, J.-C., Dullemond, C. P., et al. 2006, ApJ, 639, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Khamaganov, V., Karunanandan, R., Rodriguez, A., & Crowley, J. N. 2007, Phys. Chem. Chem. Phys., 9, 4098 [CrossRef] [Google Scholar]
- Kim, S. G., Lee, Y. H., Nordlander, P., & Tománek, D. 1997, Chem. Phys. Lett., 264, 345 [NASA ADS] [CrossRef] [Google Scholar]
- Kinghorn, D. B., & Adamowicz, L. 1997, J. Chem. Phys., 106, 4589 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, K., & Dalgarno, A. 1978, ApJ, 224, 444 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, K. P., & Goldfield, E. M. 1991, J. Chem. Phys., 94, 1271 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, K., & van Dishoeck, E. 1988, Adv. At. Mol. Phys., 25, 437 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, K., Saxon, R. P., & Liu, B. 1979, ApJ, 231, 637 [NASA ADS] [CrossRef] [Google Scholar]
- Kirby, K., Roberge, W. G., Saxon, R. P., & Liu, B. 1980, ApJ, 239, 855 [NASA ADS] [CrossRef] [Google Scholar]
- Klynning, L., & Pages, P. 1982, Phys. Scr., 25, 543 [NASA ADS] [CrossRef] [Google Scholar]
- Knowles, D. J., & Nicholson, A. J. C. 1974, J. Chem. Phys., 60, 1180 [NASA ADS] [CrossRef] [Google Scholar]
- Koch, A. 1997, J. Phys. Chem. A, 101, 1460 [CrossRef] [Google Scholar]
- Koch, A., van Dishoeck, E. F., & van Hemert, M. C. 1995a, Ber. Bunsen-Ges. Phys. Chem., 99, 393 [CrossRef] [Google Scholar]
- Koch, A., van Hemert, M. C., & van Dishoeck, E. F. 1995b, J. Chem. Phys., 103, 7006 [NASA ADS] [CrossRef] [Google Scholar]
- Kohl, J. L., & Parkinson, W. H. 1973, ApJ, 184, 641 [NASA ADS] [CrossRef] [Google Scholar]
- Koizumi, H., Hironaka, K., Shinsaka, K., et al. 1986, J. Chem. Phys., 85, 4276 [NASA ADS] [CrossRef] [Google Scholar]
- Kovács, T., Blitz, M. A., & Seakins, P. W. 2010, J. Phys. Chem. A, 114, 4735 [CrossRef] [Google Scholar]
- Kramers, H. A., & Ter Haar, D. 1946, Bull. Astron. I. Neth., 10, 137 [NASA ADS] [Google Scholar]
- Kramida, A. 2010, At. Dat. Nucl. Tabl., 96, 586 [NASA ADS] [CrossRef] [Google Scholar]
- Krishnamurty, G., & Narasimham, N. 1969, J. Mol. Spectr., 29, 410 [NASA ADS] [CrossRef] [Google Scholar]
- Kroes, G.-J., van Hemert, M. C., Billing, G., & Neuhauser, D. 1997, Chem. Phys. Lett., 271, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Kulander, K. C., & Bottcher, C. 1978, Chem. Phys., 29, 141 [NASA ADS] [CrossRef] [Google Scholar]
- Kulik, H. J., Steeves, A. H., & Field, R. W. 2009, J. Mol. Spectr., 258, 6 [NASA ADS] [CrossRef] [Google Scholar]
- Kutina, R. E., Edwards, A. K., Goodman, G. L., & Berkowitz, J. 1982, J. Chem. Phys., 77, 5508 [NASA ADS] [CrossRef] [Google Scholar]
- Lammer, H., Güdel, M., Kulikov, Y., et al. 2012, Earth Planets Space, 64, 179 [NASA ADS] [CrossRef] [Google Scholar]
- Langhoff, P. 1985, in Molecular astrophysics (Springer) [Google Scholar]
- Larsson, M. 1983, A&A, 128, 291 [NASA ADS] [Google Scholar]
- Läuter, A., Lee, K., Jung, K., et al. 2002, Chem. Phys. Lett., 358, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Lavendy, H., Gandara, G., & Robbe, J. 1984, J. Mol. Spectr., 106, 395 [NASA ADS] [CrossRef] [Google Scholar]
- Lavendy, H., Robbe, J. M., & Gandara, G. 1987, J. Phys. B, 20, 3067 [Google Scholar]
- Lavendy, H., Robbe, J. M., & Flament, J. P. 1993, Chem. Phys. Lett., 205, 456 [NASA ADS] [CrossRef] [Google Scholar]
- Le Page, V., Snow, T. P., & Bierbaum, V. M. 2003, ApJ, 584, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Le Petit, F., Nehmé, C., Le Bourlot, J., & Roueff, E. 2006, ApJS, 164, 506 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leach, S., Jochims, H.-W., & Baumgärtel, H. 2005, Phys. Chem. Chem. Phys., 7, 900 [CrossRef] [Google Scholar]
- Leach, S., Jochims, H.-W., & Baumgärtel, H. 2010, J. Phys. Chem. A, 114, 4847 [CrossRef] [Google Scholar]
- Leach, S., Garcia, G. A., Mahjoub, A., et al. 2014, J. Chem. Phys., 140 [Google Scholar]
- Lee, L. C. 1980, J. Chem. Phys., 72, 6414 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, L. C. 1984, ApJ, 282, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, L. C., & Chiang, C. C. 1982, J. Chem. Phys., 76, 4462 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, S.-H. 2009, J. Chem. Phys., 131, 11138 [Google Scholar]
- Lee, L. C., Wang, X., & Suto, M. 1987, J. Chem. Phys., 86, 4353 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, H.-H., Herbst, E., Pineau des Forets, G., Roueff, E., & Le Bourlot, J. 1996, A&A, 311, 690 [NASA ADS] [Google Scholar]
- Lee, S., Sun, H., Kim, B., & Freed, K. F. 2001, J. Chem. Phys., 114, 5537 [NASA ADS] [CrossRef] [Google Scholar]
- Leger, A., D’Hendecourt, L., Boissel, P., & Desert, F. X. 1989, A&A, 213, 351 [NASA ADS] [Google Scholar]
- Leitherer, C., Otálvaro, P. A. O., Bresolin, F., et al. 2010, ApJS, 189, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Bolatto, A., Gordon, K., et al. 2011, ApJ, 737, 12 [NASA ADS] [CrossRef] [Google Scholar]
- Levin, J., Hechtfischer, U., Knoll, L., et al. 2000, Hyperfine Interactions, 127, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Lewerenz, M., Bruna, P. J., Peyerimhoff, S. D., & Buenker, R. J. 1983, Mol. Phys., 49, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, B. R., Gibson, S. T., Torop, L. W., & McCoy, D. 1998, Geophys. Res. Lett., 25, 2457 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, B. R., England, J. P., Gibson, S. T., Brunger, M. J., & Allan, M. 2001, Phys. Rev. A, 63, 022707 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, B. R., Gibson, S. T., England, J. P., Stark, G., & West, J. B. 2002, J. Chem. Phys., 116, 3286 [NASA ADS] [CrossRef] [Google Scholar]
- Lewis, B. R., Gibson, S. T., Sprengers, J. P., et al. 2005, J. Chem. Phys., 123, 236101 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Lewis, B. R., Baldwin, K. G. H., Sprengers, J. P., et al. 2008, J. Chem. Phys., 129, 164305 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Li, A., & Draine, B. 2001, ApJ, 554, 778 [Google Scholar]
- Li, A., & Lunine, J. I. 2003, ApJ, 590, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Li, X., Heays, A. N., Visser, R., et al. 2013, A&A, 555, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Li, X., Millar, T. J., Walsh, C., Heays, A. N., & van Dishoeck, E. F. 2014, A&A, 568, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Liang, M.-C., Cheng, B.-M., Lu, H.-C., et al. 2007, ApJ, 657, L117 [NASA ADS] [CrossRef] [Google Scholar]
- Liao, C. L., & Ng, C. Y. 1986, J. Chem. Phys., 84, 778 [NASA ADS] [CrossRef] [Google Scholar]
- Limão Vieira, P., Ferreira da Silva, F., Almeida, D., et al. 2015, J. Chem. Phys., 142 [Google Scholar]
- Lin, C. L., Rohatgi, N. K., & DeMore, W. B. 1978, Geophys. Res. Lett., 5, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Liseau, R., Larsson, B., Lunttila, T., et al. 2015, A&A, 578, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Litorja, M., & Ruscic, B. 1998, J. Electron Spectr. Relat. Phenom., 97, 131 [CrossRef] [Google Scholar]
- Löffler, P., Lacombe, D., Ross, A., et al. 1996, Chem. Phys. Lett., 252, 304 [NASA ADS] [CrossRef] [Google Scholar]
- Loison, J., Hébrard, E., Dobrijevic, M., et al. 2015, Icarus, 247, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, G. G., Smith, P. L., & Parkinson, W. H. 1978, Phys. Rev. A, 18, 2131 [NASA ADS] [CrossRef] [Google Scholar]
- Lu, H.-C., Chen, H.-K., Chen, H.-F., Cheng, B.-M., & Ogilvie, J. F. 2010, A&A, 520, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luque, J., & Crosley, D. 2000, J. Chem. Phys., 112, 9411 [NASA ADS] [CrossRef] [Google Scholar]
- Manatt, S. L., & Lane, A. L. 1993, J. Quant. Spectr. Rad. Transf., 50, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Marinelli, F., & Allouche, A. 1982, Theor. Chim. Acta, 62, 175 [CrossRef] [Google Scholar]
- Marr, G. V., & Austin, J. M. 1969, J. Phys. B, 2, 107 [NASA ADS] [CrossRef] [Google Scholar]
- Mason, N. J., Gingell, J. M., Davies, J. A., et al. 1996, J. Phys. B, 29, 3075 [NASA ADS] [CrossRef] [Google Scholar]
- Mathews, B., Krivov, A., Wyatt, M., Bryden, G., & Eiroa, C. 2014, in Protostars and planets VI (University of Arizona Press) [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Mathis, J. S., Mezger, P. G., & Panagia, N. 1983, A&A, 128, 212 [NASA ADS] [Google Scholar]
- Matos, J. M. O., Malmqvist, P.-A., & Roos, B. O. 1987, J. Chem. Phys., 86, 5032 [NASA ADS] [CrossRef] [Google Scholar]
- Matsunaga, F. M., & Watanabe, K. 1967, Sci. Light, 16, 31 [Google Scholar]
- Mayer, E., & Grant, E. R. 1995, J. Chem. Phys., 103, 10513 [NASA ADS] [CrossRef] [Google Scholar]
- McAdam, K., Veyret, B., & Lesclaux, R. 1987, Chem. Phys. Lett., 133, 39 [NASA ADS] [CrossRef] [Google Scholar]
- McElroy, D., Walsh, C., Markwick, A. J., et al. 2013, A&A, 550, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McGuire, E. J. 1968, Phys. Rev., 175, 20 [NASA ADS] [CrossRef] [Google Scholar]
- McLaughlin, B. M. 2001, in Spectroscopic Challenges of Photoionized Plasmas, eds. G. Ferland & D. W. Savin, ASP Conf. Ser., 247 [Google Scholar]
- McMillan, E. C., Shen, G., McCann, J. F., McLaughlin, B. M., & Stancil, P. C. 2016, J. Phys. B, 49, 084001 [Google Scholar]
- Mebel, A. M., Jackson, W. M., Chang, A. H. H., & Lin, S. H. 1998, J. Am. Chem. Soc., 120, 5751 [CrossRef] [Google Scholar]
- Meller, R., & Moortgat, G. K. 2000, J. Geophys. Res. – Atmos., 105, 7089 [NASA ADS] [CrossRef] [Google Scholar]
- Mendoza, C. 1996, Phys. Scr., 1996, 198 [CrossRef] [Google Scholar]
- Mendoza, C., & Zeippen, C. J. 1988, J. Phys. B, 21, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Mentall, J. E., Gentieu, E. P., Krauss, M., & Neumann, D. 1971, J. Chem. Phys., 55, 5471 [NASA ADS] [CrossRef] [Google Scholar]
- Metzger, P. H., & Cook, G. R. 1964, J. Chem. Phys., 41, 642 [NASA ADS] [CrossRef] [Google Scholar]
- Michael, J., & Noyes, W. 1963, J. Am. Chem. Soc., 85, 1228 [CrossRef] [Google Scholar]
- Miyake, S., Gay, C. D., & Stancil, P. C. 2011, ApJ, 735, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Mocellin, A., Wiesner, K., Burmeister, F., Björneholm, O., & Naves de Brito, A. 2001, J. Chem. Phys., 115, 5041 [NASA ADS] [CrossRef] [Google Scholar]
- Molina, L. T., Lamb, J. J., & Molina, M. J. 1981, Geophys. Res. Lett., 8, 1008 [NASA ADS] [CrossRef] [Google Scholar]
- Monninger, G., Forderer, M., Gurtler, P., et al. 2002, J. Phys. Chem. A, 106, 5779 [CrossRef] [Google Scholar]
- Mordaunt, D. H., Ashfold, M. N. R., & Dixon, R. N. 1994, J. Chem. Phys., 100, 7360 [NASA ADS] [CrossRef] [Google Scholar]
- Morgan, R. A., Puyuelo, P., Howe, J. D., et al. 1995, J. Chem. Soc. Farad. Trans., 91, 2715 [CrossRef] [Google Scholar]
- Morley, G. P., Lambert, I. R., Ashfold, M. N. R., Rosser, K. N., & Western, C. M. 1992, J. Chem. Phys., 97, 3157 [NASA ADS] [CrossRef] [Google Scholar]
- Mota, R., Parafita, R., Giuliani, A., et al. 2005, Chem. Phys. Lett., 416, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Mottram, J. C., Kristensen, L. E., van Dishoeck, E. F., et al. 2014, A&A, 572, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Muto, T., Grady, C. A., Hashimoto, J., et al. 2012, ApJ, 748, L22 [NASA ADS] [CrossRef] [Google Scholar]
- Nahar, S. N., & Pradhan, A. K. 1993, J. Phys. B, 26, 1109 [NASA ADS] [CrossRef] [Google Scholar]
- Nahar, S. N., & Pradhan, A. K. 1997, ApJS, 111, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Nee, J. B., & Lee, L. C. 1986, J. Chem. Phys., 84, 5303 [NASA ADS] [CrossRef] [Google Scholar]
- Nee, J., Suto, M., & Lee, L. 1985, Chem. Phys., 98, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Nee, J. B., Suto, M., & Lee, L. C. 1986, J. Chem. Phys., 85, 719 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A. 1991, ApJ, 370, L85 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., & Dalgarno, A. 1989, ApJ, 344, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Neufeld, D. A., & Wolfire, M. G. 2009, ApJ, 706, 1594 [NASA ADS] [CrossRef] [Google Scholar]
- Nicolas, C., Shu, J., Peterka, D., et al. 2006, J. Am. Chem. Soc., 128, 220 [CrossRef] [Google Scholar]
- Niu, M. L., Salumbides, E. J., Dickenson, G. D., Eikema, K. S. E., & Ubachs, W. 2014, J. Mol. Spectr., 300, 44 [NASA ADS] [CrossRef] [Google Scholar]
- Nomura, H., & Millar, T. J. 2005, A&A, 438, 923 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Norwood, K., & Ng, C. 1989, Chem. Phys. Lett., 156, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Nuth, J. A., & Glicker, S. 1982, J. Quant. Spectr. Rad. Transf. 28, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Ogawa, M., & Cook, G. R. 1958, J. Chem. Phys., 28, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Ogawa, S., & Ogawa, M. 1975, Can. J. Phys., 53, 1845 [NASA ADS] [CrossRef] [Google Scholar]
- Oka, T. 2013, Chem. Rev., 113, 8738 [CrossRef] [PubMed] [Google Scholar]
- Okabe, H. 1972, J. Chem. Phys., 56, 4381 [NASA ADS] [CrossRef] [Google Scholar]
- Okabe, H. 1978, in Photochemistry of small molecules (New York: Wiley-Interscience) [Google Scholar]
- Okabe, H. 1983, Can. J. Phys., 61, 850 [Google Scholar]
- Ortiz, J. V. 1993, J. Chem. Phys., 99, 6716 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E. 1979, ApJ, 84, 901 [NASA ADS] [CrossRef] [Google Scholar]
- Padovani, M., Galli, D., & Glassgold, A. E. 2009, A&A, 501, 619 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Page, R. H., Larkin, R. J., Shen, Y. R., & Lee, Y. T. 1988, J. Chem. Phys., 88, 2249 [NASA ADS] [CrossRef] [Google Scholar]
- Palenius, H., Kohl, J., & Parkinson, W. 1976, Phys. Rev. A, 13, 1805 [NASA ADS] [CrossRef] [Google Scholar]
- Parkinson, W., & Yoshino, K. 2003, Chem. Phys., 294, 31 [NASA ADS] [CrossRef] [Google Scholar]
- Parravano, A., Hollenbach, D. J., & McKee, C. F. 2003, ApJ, 584, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Patel-Misra, D., Parlant, G., Sauder, D. G., Yarkony, D. R., & Dagdigian, P. J. 1991, J. Chem. Phys., 94, 1913 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, L. R., & Marshall, P. 2002, J. Chem. Phys., 117, 3132 [NASA ADS] [CrossRef] [Google Scholar]
- Petrank, A., Iraqi, M., Dotan, I., & Lifshitz, C. 1992, Int. J. Mass Spectrom., 117, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Philip, J., Sprengers, J., Pielage, T., et al. 2004, Can. J. Chem., 82, 713 [Google Scholar]
- Phillips, L. F. 1981, J. Phys. Chem., 85, 3994 [NASA ADS] [CrossRef] [Google Scholar]
- Pinilla, P., de Juan Ovelar, M., Ataiee, S., et al. 2015, A&A, 573, A9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Plusquellic, D. F., Votava, O., & Nesbitt, D. J. 1998, J. Chem. Phys., 109, 6631 [NASA ADS] [CrossRef] [Google Scholar]
- Pope, F. D., Smith, C. A., Ashfold, M. N. R., & Orr-Ewing, A. J. 2005, Phys. Chem. Chem. Phys., 7, 79 [CrossRef] [Google Scholar]
- Pouilly, B., Robbe, J. M., Schamps, J., & Roueff, E. 1983, J. Phys. B, 16, 437 [Google Scholar]
- Pradhan, A. D., Kirby, K. P., & Dalgarno, A. 1991, J. Chem. Phys., 95, 9009 [NASA ADS] [CrossRef] [Google Scholar]
- Prasad, S. S., & Tarafdar, S. P. 1983, ApJ, 267, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Reddy, R., Ahammed, Y., Gopal, K., Azeem, P., & Rao, T. 2000, J. Quant. Spectr. Rad. Transf., 66, 501 [NASA ADS] [CrossRef] [Google Scholar]
- Reed, B., Lam, C.-S., Chang, Y.-C., et al. 2009, ApJ, 693, 940 [NASA ADS] [CrossRef] [Google Scholar]
- Reilman, R. F., & Manson, S. T. 1979, ApJS, 40, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Resende, S. M., & Ornellas, F. R. 2001, J. Chem. Phys., 115, 2178 [NASA ADS] [CrossRef] [Google Scholar]
- Rimmer, P. B., Herbst, E., Morata, O., & Roueff, E. 2012, A&A, 537, A7 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roberge, W. G., Jones, D., Lepp, S., & Dalgarno, A. 1991, ApJS, 77, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Röllig, M., Szczerba, R., Ossenkopf, V., & Glück, C. 2013, A&A, 549, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rollins, R. P., & Rawlings, J. M. C. 2012, MNRAS, 427, 2328 [NASA ADS] [CrossRef] [Google Scholar]
- Roman-Duval, J., Gordon, K. D., Meixner, M., et al. 2014, ApJ, 797, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Romanzin, C., Gazeau, M.-C., Bénilan, Y., et al. 2005, Adv. Space Res., 36, 258 [NASA ADS] [CrossRef] [Google Scholar]
- Roncin, J. Y., Launay, F., & Yoshino, K. 1989, J. Mol. Spectr., 134, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Roueff, E., Alekseyev, A. B., & Le Bourlot, J. 2014, A&A, 566, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ruscic, B., & Berkowitz, J. 1983, Phys. Rev. Lett., 50, 675 [NASA ADS] [CrossRef] [Google Scholar]
- Salahub, D., & Sandorfy, C. 1971, Chem. Phys. Lett., 8, 71 [NASA ADS] [CrossRef] [Google Scholar]
- Samson, J. A. R., & Angel, G. C. 1990, Phys. Rev. A, 42, 1307 [NASA ADS] [CrossRef] [Google Scholar]
- Samson, J. A. R., & Haddad, G. N. 1994, J. Opt. Soc. Am. B, 11, 277 [NASA ADS] [CrossRef] [Google Scholar]
- Samson, J. A. R., Haddad, G. N., & Kilcoyne, L. D. 1987, J. Chem. Phys., 87, 6416 [NASA ADS] [CrossRef] [Google Scholar]
- Sandner, W., Gallagher, T. F., Safinya, K. A., & Gounand, F. 1981, Phys. Rev. A, 23, 2732 [NASA ADS] [CrossRef] [Google Scholar]
- Sansonetti, J. E. 2006, J. Phys. Chem. Ref. Data, 35, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Savage, B. D., Bohlin, R. C., Drake, J. F., & Budich, W. 1977, ApJ, 216, 291 [NASA ADS] [CrossRef] [Google Scholar]
- Sawyer, D. T. 1989, J. Phys. Chem., 93, 7977 [CrossRef] [Google Scholar]
- Saxon, R. P., & Liu, B. 1986, J. Chem. Phys., 85, 2099 [NASA ADS] [CrossRef] [Google Scholar]
- Saxon, R. P., Lengsfield, B. H., & Liu, B. 1983, J. Chem. Phys., 78, 312 [NASA ADS] [CrossRef] [Google Scholar]
- Schindhelm, E., France, K., Herczeg, G. J., et al. 2012, ApJ, 756, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Schulenburg, A. M., Alcaraz, C., Grassi, G., & Merkt, F. 2006, J. Chem. Phys., 125, 104310 [NASA ADS] [CrossRef] [Google Scholar]
- Schwell, M., Jochims, H.-W., Baumgärtel, H., & Leach, S. 2008, Chem. Phys., 344, 164 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J. 1951, MNRAS, 111, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Seaton, M. J. 1985, J. Phys. B, 18, 2111 [NASA ADS] [CrossRef] [Google Scholar]
- Seki, K., & Okabe, H. 1993, J. Phys. Chem., 97, 5284 [CrossRef] [Google Scholar]
- Seki, K., He, M., Liu, R., & Okabe, H. 1996, J. Phys. Chem., 100, 5349 [CrossRef] [Google Scholar]
- Serdyuchenko, A., Gorshelev, V., Weber, M., Chehade, W., & Burrows, J. P. 2014, Atm. Meas. Tech., 7, 625 [CrossRef] [Google Scholar]
- Shafer, N., Satyapal, S., & Bersohn, R. 1989, J. Chem. Phys., 90, 6807 [NASA ADS] [CrossRef] [Google Scholar]
- Shaw, D. A., Holland, D. M. P., MacDonald, M. A., et al. 1992, Chem. Phys., 166, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Shaw, D., Holland, D., Hayes, M., et al. 1995, Chem. Phys., 198, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Shi, D., Li, W., Sun, J., & Zhu, Z. 2011, J. Quant. Spectr. Rad. Transf., 112, 2335 [NASA ADS] [CrossRef] [Google Scholar]
- Shiell, R. C., Hu, X. K., Hu, Q. J., & Hepburn, J. W. 2000, J. Phys. Chem. A, 104, 4339 [CrossRef] [Google Scholar]
- Shinnaka, Y., Kawakita, H., Kobayashi, H., et al. 2011, ApJ, 729, 81 [Google Scholar]
- Silver, J. A., Worsnop, D. R., Freedman, A., & Kolb, C. E. 1986, J. Chem. Phys., 84, 4378 [NASA ADS] [CrossRef] [Google Scholar]
- Slanger, T. G., & Black, G. 1982, J. Chem. Phys., 77, 2432 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, W., & Liszt, H. 1971, J. Quant. Spectr. Rad. Transf., 11, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, P. L., Yoshino, K., Griesinger, H. E., & Black, J. H. 1981, ApJ, 250, 166 [NASA ADS] [CrossRef] [Google Scholar]
- Sohl, J. E., Zhu, Y., & Knight, R. D. 1990, J. Opt. Soc. Amer. B, 7, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Song, Y., Gao, H., Chang, Y. C., et al. 2014, Phys. Chem. Chem. Phys., 16, 563 [CrossRef] [Google Scholar]
- Sorensen, S., Karawajczyk, A., Strömholm, C., & Kirm, M. 1995, Chem. Phys. Lett., 232, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Spitzer, L., Drake, J. F., Jenkins, E. B., et al. 1973, ApJ, 181, L116 [NASA ADS] [CrossRef] [Google Scholar]
- Sprengers, J. P., Ubachs, W., Baldwin, K. G. H., Lewis, B. R., & Tchang-Brillet, W.-Ü. L. 2003, J. Chem. Phys., 119, 3160 [NASA ADS] [CrossRef] [Google Scholar]
- Stahel, D., Leoni, M., & Dressler, K. 1983, J. Chem. Phys., 79, 2541 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, G., Yoshino, K., & Smith, P. 1987, J. Mol. Spectr., 124, 420 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, G., Lewis, B. R., Gibson, S. T., & England, J. P. 1999, ApJ, 520, 732 [NASA ADS] [CrossRef] [Google Scholar]
- Stark, G., Lewis, B. R., Heays, A. N., et al. 2008, J. Chem. Phys., 128, 114302 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Stecher, T. P., & Williams, D. A. 1967, ApJ, 149, L29 [NASA ADS] [CrossRef] [Google Scholar]
- Stephens, T., & Dalgarno, A. 1972, J. Quant. Spectr. Rad. Transf., 12, 569 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sternberg, A., & Dalgarno, A. 1995, ApJS, 99, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Sternberg, A., Dalgarno, A., & Lepp, S. 1987, ApJ, 320, 676 [NASA ADS] [CrossRef] [Google Scholar]
- Sternberg, A., Petit, F. L., Roueff, E., & Bourlot, J. L. 2014, ApJ, 790, 10 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Stief, L. J., Payne, W. A., & Klemm, R. B. 1975, J. Chem. Phys., 62, 4000 [NASA ADS] [CrossRef] [Google Scholar]
- Suemitsu, H., & Samson, J. A. R. 1983, Phys. Rev. A, 28, 2752 [NASA ADS] [CrossRef] [Google Scholar]
- Sunanda, K., Shastri, A., Das, A. K., & Sekhar, B. R. 2015, J. Quant. Spectr. Rad. Transf., 151, 76 [NASA ADS] [CrossRef] [Google Scholar]
- Suto, M., & Lee, L. 1983, Chem. Phys. Lett., 98, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Suto, M., Wang, X., & Lee, L. C. 1986, J. Chem. Phys., 85, 4228 [NASA ADS] [CrossRef] [Google Scholar]
- Szajna, W., & Zachwieja, M. 2010, J. Mol. Spectr., 260, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Szajna, W., Zachwieja, M., Hakalla, R., & Kepa, R. 2011, Acta Phys. Pol. A, 120, 417 [CrossRef] [Google Scholar]
- Taatjes, C. A., Klippenstein, S. J., Hansen, N., et al. 2005, Phys. Chem. Chem. Phys., 7, 806 [CrossRef] [Google Scholar]
- Talbi, D., & Saxon, R. P. 1988, J. Chem. Phys., 89, 2235 [NASA ADS] [CrossRef] [Google Scholar]
- Tarroni, R., Palmieri, P., Mitrushenkov, A., Tosi, P., & Bassi, D. 1997, J. Chem. Phys., 106, 10265 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Tayal, S. S. 2004, J. Phys. B, 37, 3593 [NASA ADS] [CrossRef] [Google Scholar]
- Tchang-Brillet, W.-Ü. L., Julienne, P., Robbe, J., Letzelter, C., & Rostas, F. 1992, J. Chem. Phys., 96, 6735 [NASA ADS] [CrossRef] [Google Scholar]
- Testi, L., Birnstiel, T., Ricci, L., et al. 2014, in Protostars & Planets VI (Tucson: Univ. Arizona Press) [Google Scholar]
- Teyssier, D., Fossé, D., Gerin, M., et al. 2004, A&A, 417, 135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Theodorakopoulos, G., & Petsalakis, I. 1991, J. Mol. Struct., 76, 205 [CrossRef] [Google Scholar]
- Tielens, A. G. G. M. 2013, Rev. Mod. Phys., 85, 1021 [NASA ADS] [CrossRef] [Google Scholar]
- Tielens, A. G. G. M., & Hollenbach, D. 1985, ApJ, 291, 747 [NASA ADS] [CrossRef] [Google Scholar]
- Tokue, I., Hiraya, A., & Shobatake, K. 1987, Chem. Phys., 116, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Tondello, G. 1975, Mem. Soc. Astron. Ital., 46, 113 [NASA ADS] [Google Scholar]
- Tsukagoshi, T., Momose, M., Saito, M., et al. 2015, ApJ, 802, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Ubachs, W. 2005, J. Electron Spectr. Relat. Phenom., 144, 97 [CrossRef] [Google Scholar]
- Ubachs, W., Eikema, K. S. E., Levelt, P. F., et al. 1994, ApJ, 427, L55 [NASA ADS] [CrossRef] [Google Scholar]
- Ung, A.-M. 1974, Chem. Phys. Lett., 28, 603 [NASA ADS] [CrossRef] [Google Scholar]
- Uzer, T., & Dalgarno, A. 1978, Chem. Phys., 32, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Vaghjiani, G. L. 1993, J. Chem. Phys., 99, 5936 [NASA ADS] [CrossRef] [Google Scholar]
- Valenti, J. A., Johns-Krull, C. M., & Linsky, J. L. 2000, ApJS, 129, 399 [NASA ADS] [CrossRef] [Google Scholar]
- van der Marel, N., van Dishoeck, E. F., Bruderer, S., et al. 2013, Science, 340, 1199 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van der Tak, F. F. S., & van Dishoeck, E. F. 2000, A&A, 358, L79 [NASA ADS] [Google Scholar]
- van Dishoeck, E. F. 1987, J. Chem. Phys., 86, 196 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F. 1988, in Rate coefficients in astrochemistry, eds. T. J. Millar, & D. A. Williams (Dordrecht: Kluwer Academic Publishers), 49 [Google Scholar]
- van Dishoeck, E. F. 2014, Faraday Discuss., 168, 9 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Dishoeck, E. F., & Black, J. H. 1982, ApJ, 258, 533 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., & Black, J. H. 1986, ApJS, 62, 109 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., & Black, J. H. 1988, ApJ, 334, 771 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., & Dalgarno, A. 1983, J. Chem. Phys., 79, 873 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., & Dalgarno, A. 1984a, J. Chem. Phys., 277, 576 [Google Scholar]
- van Dishoeck, E. F., & Dalgarno, A. 1984b, J. Chem. Phys., 277, 576 [Google Scholar]
- van Dishoeck, E. F., & Visser, R. 2015, in Laboratory astrochemistry: From molecules through nanoparticles to grains (Weiheim: Wiley-VCH) [Google Scholar]
- van Dishoeck, E. F., van der Hart, W. J., & van Hemert, M. 1980, Chem. Phys., 50, 45 [CrossRef] [Google Scholar]
- van Dishoeck, E. F., van Hemert, M. C., & Dalgarno, A. 1982, J. Chem. Phys., 77, 3693 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., van Hemert, M. C., Allison, A. C., & Dalgarno, A. 1984, J. Chem. Phys., 81, 5709 [NASA ADS] [CrossRef] [Google Scholar]
- van Dishoeck, E. F., Beaerda, R. A., & van Hemert, M. C. 1996, A&A, 307, 645 [NASA ADS] [Google Scholar]
- van Dishoeck, E. F., Jonkheid, B., & van Hemert, M. C. 2006, Faraday Discuss., 133, 231 [Google Scholar]
- van Dishoeck, E. F., Herbst, E., & Neufeld, D. A. 2013, Chem. Rev., 113, 9043 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- van Harrevelt, R., & van Hemert, M. C. 2008, J. Phys. Chem. A, 112, 3002 [CrossRef] [Google Scholar]
- van Hemert, M. C., & van Dishoeck, E. F. 2008, Chem. Phys., 343, 292 [NASA ADS] [CrossRef] [Google Scholar]
- van Mourik, T., Dunning, T. H., & Peterson, K. A. 2000, J. Phys. Chem. A, 104, 2287 [CrossRef] [Google Scholar]
- Vane, C. R., Bahati, E. M., Bannister, M. E., & Thomas, R. D. 2007, Phys. Rev. A, 75, 052715 [NASA ADS] [CrossRef] [Google Scholar]
- Vattulainen, J., Wallenius, L., Stenberg, J., Hernberg, R., & Linna, V. 1997, App. Spectr., 51, 1311 [NASA ADS] [CrossRef] [Google Scholar]
- Vaupré, S., Hily-Blant, P., Ceccarelli, C., et al. 2014, A&A, 568, A50 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vega, M. V., Lavin, C., Velasco, A. M., & Martin, I. 2010, Theor. Chem. Acc., 127, 411 [CrossRef] [Google Scholar]
- Venot, O., Fray, N., Bénilan, Y., et al. 2013, A&A, 551, A131 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Verner, D. A., Ferland, G. J., Korista, K. T., & Yakovlev, D. G. 1996, ApJ, 465, 487 [NASA ADS] [CrossRef] [Google Scholar]
- Vetter, R., Zülicke, L., Koch, A., van Dishoeck, E. F., & Peyerimhoff, S. D. 1996, J. Chem. Phys., 104, 5558 [NASA ADS] [CrossRef] [Google Scholar]
- Viala, Y. P., Letzelter, C., Eidelsberg, M., & Rostas, F. 1988, A&A, 193, 265 [NASA ADS] [Google Scholar]
- Visser, R., Geers, V. C., Dullemond, C. P., et al. 2007, A&A, 466, 229 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Visser, R., van Dishoeck, E. F., & Black, J. H. 2009, A&A, 503, 323 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wakelam, V., Herbst, E., Loison, J.-C., et al. 2012, ApJS, 199, 21 [NASA ADS] [CrossRef] [Google Scholar]
- Wakelam, V., Smith, I. W. M., Herbst, E., et al. 2010, Space Sci. Rev., 156, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, C., Harada, N., Herbst, E., & Millar, T. J. 2009, ApJ, 700, 752 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, C., Millar, T. J., & Nomura, H. 2010, ApJ, 722, 1607 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, C., Millar, T. J., & Nomura, H. 2013, ApJ, 766, L23 [NASA ADS] [CrossRef] [Google Scholar]
- Walsh, C., Nomura, H., & van Dishoeck, E. 2015, A&A, 582, A88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Walter, C. W., Cosby, P. C., & Helm, H. 1993, J. Chem. Phys., 99, 3553 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, L., Reutt, J., Lee, Y., & Shirley, D. 1988, J. Electron Spectr. Relat. Phenom., 47, 167 [CrossRef] [Google Scholar]
- Wang, J.-H., Hsu, Y.-T., & Liu, K. 1997, J. Phys. Chem. A, 101, 6593 [CrossRef] [Google Scholar]
- Wang, K., Stephens, J. A., & McKoy, V. 1990, J. Chem. Phys., 93, 7874 [NASA ADS] [CrossRef] [Google Scholar]
- Watanabe, K., Matsunaga, F. M., & Sakai, H. 1967, Appl. Opt., 6, 391 [NASA ADS] [CrossRef] [Google Scholar]
- Weingartner, J. C., & Draine, B. T. 2001, ApJ, 548, 296 [NASA ADS] [CrossRef] [Google Scholar]
- Weisheit, J. C. 1972, Phys. Rev. A, 5, 1621 [NASA ADS] [CrossRef] [Google Scholar]
- Weiss, M. J., Lawrence, G. M., & Young, R. A. 1970, J. Chem. Phys., 52, 2867 [NASA ADS] [CrossRef] [Google Scholar]
- Werner, M. W. 1970, ApJ, 6, 81 [Google Scholar]
- West, G. A., & Berry, M. J. 1974, J. Chem. Phys., 61, 4700 [NASA ADS] [CrossRef] [Google Scholar]
- Wheeler, M. D., Newman, S. M., & Orr-Ewing, A. J. 1998, J. Chem. Phys., 108, 6594 [NASA ADS] [CrossRef] [Google Scholar]
- White, G. J. 1994, A&A, 283, L25 [NASA ADS] [Google Scholar]
- Willitsch, S., Innocenti, F., Dyke, J. M., & Merkt, F. 2005, J. Chem. Phys., 122, 024311 [NASA ADS] [CrossRef] [Google Scholar]
- Willitsch, S., Merkt, F., Kállay, M., & Gauss, J. 2006, Mol. Phys., 104, 1457 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, S. H. S., Ashfold, M. N. R., & Dixon, R. N. 1994, J. Chem. Phys., 101, 7538 [NASA ADS] [CrossRef] [Google Scholar]
- Wishart, A. W. 1979, J. Phys. B, 12, 3511 [NASA ADS] [CrossRef] [Google Scholar]
- Woitke, P., Kamp, I., & Thi, W.-F. 2009, A&A, 501, 383 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wolniewicz, L. 1995, J. Chem. Phys., 103, 1792 [NASA ADS] [CrossRef] [Google Scholar]
- Woods, T. N., Prinz, D. K., Rottman, G. J., et al. 1996, J. Geophys. Res. – Atmos., 101, 9541 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, C. Y. R., & Judge, D. L. 1983, J. Chem. Phys., 78, 2180 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, C. Y. R., Chien, T. S., Liu, G. S., Judge, D. L., & Caldwell, J. J. 1989, J. Chem. Phys., 91, 272 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, C. R., Yang, B., Chen, F., et al. 2000, Icarus, 145, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Wu, Y.-J., Lu, H.-C., Chen, H.-K., et al. 2007, J. Chem. Phys., 127, [Google Scholar]
- Wu, Y.-J., Lin, M.-Y., Chou, S.-L., et al. 2010, ApJ, 721, 856 [NASA ADS] [CrossRef] [Google Scholar]
- Xia, T., Chien, T., Wu, C., & Judge, D. 1991, J. Quant. Spectr. Rad. Transf., 45, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Xing, W., Shi, D., Sun, J., Liu, H., & Zhu, Z. 2013, Mol. Phys., 111, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, H., & Joens, J. A. 1993, Geophys. Res. Lett., 20, 1035 [NASA ADS] [CrossRef] [Google Scholar]
- Yang, H., Herczeg, G. J., Linsky, J. L., et al. 2012, ApJ, 744, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Yih, T., Wu, H., Chu, C., et al. 1998, J. Korean. Phys. Soc., 32, 405 [EDP Sciences] [Google Scholar]
- Yoshino, K., Cheung, A.-C., Esmond, J., et al. 1988, Planet. Space Sci., 36, 1469 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshino, K., Esmond, J., Cheung, A.-C., Freeman, D., & Parkinson, W. 1992, Planet. Space Sci., 40, 185 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshino, K., Esmond, J., Parkinson, W., Ito, K., & Matsui, T. 1996, Chem. Phys., 211, 387 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshino, K., Esmond, J., Parkinson, W., Ito, K., & Matsui, T. 1997, Chem. Phys., 215, 429 [NASA ADS] [CrossRef] [Google Scholar]
- Yoshino, K., Thorne, A. P., Murray, J. E., et al. 2006, J. Chem. Phys., 124, 054323 [NASA ADS] [CrossRef] [Google Scholar]
- Yu, H. T., Sevin, A., Kassab, E., & Evleth, E. M. 1984, J. Chem. Phys., 80, 2049 [NASA ADS] [CrossRef] [Google Scholar]
- Zatsarinny, O., & Bartschat, K. 2013, J. Phys. B, 46, 112001 [NASA ADS] [CrossRef] [Google Scholar]
- Zatsarinny, O., & Tayal, S. S. 2010, Phys. Rev. A, 81, 043423 [NASA ADS] [CrossRef] [Google Scholar]
- Zeiri, Y., & Balint-Kurti, G. 1983, J. Mol. Spectr., 99, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Zelikoff, M., & Watanabe, K. 1953, J. Opt. Soc. Amer., 43, 756 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J., Imre, D. G., & Frederick, J. H. 1989, J. Phys. Chem., 93, 1840 [CrossRef] [Google Scholar]
- Zhao, Y., Cao, M., Li, Y., et al. 2014, J. Electron Spectr. Relat. Phenom., 196, 181, Advances in Vacuum Ultraviolet and X-ray Physics, 38th Int. Conf. Vacuum Ultraviolet and X-ray Physics (VUVX2013), University of Science and Technology of China [CrossRef] [Google Scholar]
- Zhen, J., Castellanos, P., Paardekooper, D. M., et al. 2015, ApJ, 804, L7 [NASA ADS] [CrossRef] [Google Scholar]
- Zhen, J., Castillo, S. R., Joblin, C., et al. 2016, ApJ, 822, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Zhou, L., & Xie, D. 2015, J. Phys. Chem. A, 119, 12062 [CrossRef] [Google Scholar]
Appendix A: Shielding by atomic H and C
 |
Fig. A.1 Shielding of photodissociation and photoionisation by atomic H in the simulated TW-Hydra radiation field. |
 |
Fig. A.2 Shielding of photodissociation and ionisation in the ISRF by atomic C. |
Our simulated TW-Hydra radiation field, and other potential ultraviolet radiation environments, include shorter wavelengths than 91.2 nm and photoprocesses there may be sensitive to shielding by atomic H. A collection of functions for H-shielding in the TW-Hydra radiation field are shown in Fig. A.1. The photoionisation shielding by H for some molecular species (and photodissociation in the case of H ) is significant for H columns as low as 10 cm-2.
) is significant for H columns as low as 10 cm-2.
Photoabsorption lines of H longwards of its ionisation limit were also included and contribute to the shielding of molecules that dissociate predominantly between 91.2 nm and the Lyman-α wavelength, 121.6 nm. Of the entire series of Lyman-lines converging on the H ionisation limit, some of which are shown in Fig. 25, the Lyman-α transition absorbs more photons than all others combined. It should be noted that the extinction of Lyman-α wavelength radiation is complicated by its re-radiation and forward scattering from dust grains (e.g., Bethell & Bergin 2011).
The 110 nm-threshold ionisation continuum of C will significantly reduce the photodissociation and ionisation rates of atomic and molecular species with cross sections biased to shorter wavelengths, assuming a column density of at least 10 cm-2. Shielding functions for the ISRF are shown in Fig. A.2 as functions of C column density and clearly demonstrate this critical density. The requisite amount of C is observed and modelled to exist in some kinds of photodissociation regions (Werner 1970; Frerking et al. 1989; Hollenbach et al. 1991; Hasegawa & Kwok 2003). For molecules with photodissociation cross sections predominantly longwards of 110 nm an extremely unlikely C column density of at least 10 cm-2 is required for shielding. In this case, photoabsorption of non-ionising photoabsorption into excited C levels eventually provides the necessary opacity.
All Tables
H2 integrated photodissociation efficiency assuming several radiation field types.
References and wavelength ranges of concatenated photoabsorption H2CO cross sections.
All Figures
 |
Fig. 1 Wavelength dependence of some astrophysically-relevant ultraviolet radiation fields. Inset: radiation intensity in the solar neighbourhood estimated by Draine (1978; solid, modified according to van Dishoeck & Black 1982), Mathis et al. (1983; dashed), and Habing (1968; dotted). |
| In the text | |
 |
Fig. 2 Schematic cross sections for photodissociation and their associated dynamical pathway (arrows) through ground and excited state potential-energy curves. For polyatomic molecules these curves represent a cross section through a multidimensional energy surface. We note that the integrated values of the various cross sections may be similar, leading to orders-or-magnitude greater peak magnitudes for indirect mechanisms. Modified from van Dishoeck & Visser (2015). |
| In the text | |
 |
Fig. 3 Potential energy curves for the ground and excited state of O2 (red curves) (Guberman 1977; Lewis et al. 1998, 2001), and the O2 photoabsorption section from Sect. 4.3.35 (blue curve). Shown on equivalent energy and wavelength scales. The energy scale is relative to the minimum of the ground-state electronic potential curve, shown here shifted upwards by 4 eV. The shaded area shows the vertical excitation region. |
| In the text | |
 |
Fig. 4 Compiled atomic photoionisation cross sections. The ionisation thresholds of H and C are indicated by vertical lines. |
| In the text | |
 |
Fig. 5 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
| In the text | |
 |
Fig. 6 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
| In the text | |
 |
Fig. 7 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
| In the text | |
 |
Fig. 8 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
| In the text | |
 |
Fig. 9 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
| In the text | |
 |
Fig. 10 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
| In the text | |
 |
Fig. 11 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
| In the text | |
 |
Fig. 12 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
| In the text | |
 |
Fig. 13 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
| In the text | |
 |
Fig. 14 Cross sections of molecules. Red: photodissociation. Blue: photoionisation. Some photofragmentation thresholds are also labelled. |
| In the text | |
 |
Fig. 15 H2 photoabsorption cross section. The under-resolved experimental measurement of (Chan et al. 1992), and a model spectrum before and after smoothing to the experimental resolution. Also shown is a correction to the model accounting for neglected excitation mechanisms. |
| In the text | |
 |
Fig. 16 Photoabsorption cross section of H2O. Divided into channels producing O (green), OH (red), and ionisation (blue). |
| In the text | |
 |
Fig. 17 Photoabsorption cross section of NH3. Divided into channels producing NH (green), NH2 (red), and ionisation (blue). |
| In the text | |
 |
Fig. 18 Photodissociation cross section for CN. Presently calculated cross section and those of Lavendy et al. (1987) and el-Qadi & Stancil (2013). |
| In the text | |
 |
Fig. 19 Unshielded photodissociation rates of molecules. Rates are shown assuming three different radiation fields with ultraviolet intensity matching the standard of Draine (1978). |
| In the text | |
 |
Fig. 20 Unshielded photoionisation rates of molecules and atoms. Rates are shown assuming different radiation fields with ultraviolet intensity matching the standard of Draine (1978). |
| In the text | |
 |
Fig. 21 Photodissociation cross sections of four molecules. These are averaged into 2 nm intervals for clarity and compared with the wavelength-dependence of two radiation fields from Sect. 2. |
| In the text | |
 |
Fig. 22 Ratio of photodissociation and photoionisation rates. Calculated assuming two radiation fields from Sect. 2 as a function of their dissociation or ionisation thresholds. |
| In the text | |
 |
Fig. 23 Comparing the wavelength dependence of the photodissociation cross sections of C2H2 and HC3N between 117 and 126 nm with Lyman-α radiation. |
| In the text | |
 |
Fig. 24 ISRF photodissociation and ionisation rates for atoms and molecules. The present calculations are compared with the PHIDRATES database (Huebner et al. 1992; Huebner & Mukherjee 2015) and the previous version of the Leiden database (van Dishoeck 1988; van Dishoeck et al. 2006). |
| In the text | |
 |
Fig. 25 Possible wavelength-dependent transmittance (shaded region edges) of the highest-column density (N) species at AV = 1 depth into a semi-infinite one-sided interstellar cloud. |
| In the text | |
 |
Fig. 26 Solid lines: optical properties of interstellar dust grains according to Draine et al. (Draine & Lee 1984; Draine 2003b)17. Dashed lines: optical properties simulating grain growth in a protoplanetary disk. Upper: photoabsorption and photoextinction cross sections. Middle: grain albedo. Lower: probability of forward scattering. |
| In the text | |
 |
Fig. 27 Shielding of photodissociation (red) and photoionisation (green) in the ISRF. For all molecules in our database by an amount of dust parameterised by H-nucleus column density. Cases are shown for interstellar dust and a population of larger dust grains (see text). An additional curve traces exp(−Av), the visual extinction (blue). |
| In the text | |
 |
Fig. 28 Dust shielding function for CH4 photodissociation (solid red curve) in the ISRF. Calculated by means of an infinite-slab radiative transfer model. Also shown are some simple parameterisations of this curve according to three formulations. |
| In the text | |
 |
Fig. 29 Shielding functions for photodissociation (red curves) and photoionisation (blue curves) by a column of H2. Assumes an impinging ISRF or simulation of the TW-Hydra circumstellar radiation. A few extreme cases have their identity labelled. The shaded-region edge describes a typical ultraviolet-extinction curve due to interstellar dust, according to exp−3AV. |
| In the text | |
 |
Fig. 30 Shielding of CN photodissociation in the ISRF by H2 assuming various values for the H2 rotational excitation temperature, T, and Doppler broadening, b. Also shown is a typical shielding function due to interstellar dust, exp(−3AV) (shaded region edge). |
| In the text | |
 |
Fig. 31 Self-shielding of photodissociation in the ISRF. |
| In the text | |
 |
Fig. 32 The cosmic-ray induced radiation field. Upper: the spectral density of photons generated per primary cosmic-ray ionisation event. Lower: a cumulative integration of this distribution. |
| In the text | |
 |
Fig. 33 Molecular photodissociation and ionisation rates due to cosmic-ray-induced radiation. Shown for all species common to this data base and Gredel et al. (1989). Full dust and lines: including all available shielding cross sections. Simple dust only: no molecular or atomic shielding, wavelength independent dust extinction cross section 2×10 cm2 H-1 and an albedo of 0.5. Gredel et al.: rates computed from the efficiencies of Gredel et al. (1989; Table 1, column “a”, ignoring reabsorption) following multiplication by 10. |
| In the text | |
 |
Fig. 34 Distribution of Monte Carlo simulated cosmic-ray-induced photodissociation rates of three molecules. Normalised to the mean of the distribution. |
| In the text | |
 |
Fig. 35 H2O photoabsorption cross section measured by low-resolution electron energy-loss spectroscopy and by direct higher-resolution photoabsorption measurements. |
| In the text | |
 |
Fig. 36 ISRF self-shielding factors. Shown for four molecules after convolution of their photodissociation cross sections by Gaussian functions of increasing width (equivalent Doppler widths are also shown). For these calculations, a column density of 10 cm-2 was assumed for N2, CO and H2; and 10 cm-2 for H2O. |
| In the text | |
 |
Fig. 37 Long-wavelength and near-Lyman-α parts of the NH3 and NH2D photoabsorption cross sections. The source of the NH3 cross section is discussed in Sect. 4.3.46 and the NH2D data are taken from two sources (Wu et al. 2007; Cheng et al. 2006). Also indicated is the wavelength of Lyman-α emission and the vibrational progression of absorption into the excited |
| In the text | |
 |
Fig. 38 Fractional change of chemical abundances in a translucent cloud model when substituting photodestruction rates of the RATE12 network with the newly-calculated rates. A comparison is made with updated models including the same γexp parameterisation as RATE12 for dust shielding, and with dust shielding calculated explicitly for each molecule. The plotted species are those listed in Tielens (2013, Table II). |
| In the text | |
 |
Fig. 39 Comparing the chemical abundances in a translucent cloud model assuming non-ISRF radiation fields. The plotted species are those listed in Tielens (2013, Table II). |
| In the text | |
 |
Fig. 40 Fractional change of chemical abundances in the dark-cloud model when substituting photodestruction rates of the RATE12 network with the newly-calculated rates. A comparison is made for models assuming increasing ionisation rate, ζ. The plotted species are those listed in Tielens (2013, Table II). |
| In the text | |
 |
Fig. A.1 Shielding of photodissociation and photoionisation by atomic H in the simulated TW-Hydra radiation field. |
| In the text | |
 |
Fig. A.2 Shielding of photodissociation and ionisation in the ISRF by atomic C. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


