| Issue |
A&A
Volume 600, April 2017
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 15 | |
| Section | Planets and planetary systems | |
| DOI | https://doi.org/10.1051/0004-6361/201527078 | |
| Published online | 20 March 2017 | |
Magnetic activity in the HARPS M dwarf sample⋆
The rotation-activity relationship for very low-mass stars through R'HK
1 Univ. Grenoble Alpes, IPAG, 38000 Grenoble, France
2 CNRS, IPAG, 38000 Grenoble, France
3 Observatoire de Genève, Université de Genève, 51 ch. des Maillettes, 1290 Sauverny, Switzerland
e-mail: nicola.astudillo@unige.ch
4 Département de Physique, Université de Montréal, CP 6128 Succ. Centre-Ville, Montréal, QC H3C 3J7, Canada
Received: 29 July 2015
Accepted: 17 November 2016
Context. Atmospheric magnetic fields in stars with convective envelopes heat stellar chromospheres, and thus increase the observed flux in the Ca ii H and K doublet. Starting with the historical Mount Wilson monitoring program, these two spectral lines have been widely used to trace stellar magnetic activity, and as a proxy for rotation period (Prot) and consequently for stellar age. Monitoring stellar activity has also become essential in filtering out false-positives due to magnetic activity in extra-solar planet surveys. The Ca ii emission is traditionally quantified through the R'HK-index, which compares the chromospheric flux in the doublet to the overall bolometric flux of the star. Much work has been done to characterize this index for FGK-dwarfs, but M dwarfs – the most numerous stars of the Galaxy – were left out of these analyses and no calibration of their Ca ii H and K emission to an R'HK exists to date.
Aims. We set out to characterize the magnetic activity of the low- and very-low-mass stars by providing a calibration of the R'HK-index that extends to the realm of M dwarfs, and by evaluating the relationship between R'HK and the rotation period.
Methods. We calibrated the bolometric and photospheric factors for M dwarfs to properly transform the S-index (which compares the flux in the Ca ii H and K lines to a close spectral continuum) into the R'HK. We monitored magnetic activity through the Ca ii H and K emission lines in the HARPS M dwarf sample.
Results. The R'HK index, like the fractional X-ray luminosity LX/Lbol, shows a saturated correlation with rotation, with saturation setting in around a ten days rotation period. Above that period, slower rotators show weaker Ca ii activity, as expected. Under that period, the R'HK index saturates to approximately 10-4. Stellar mass modulates the Ca ii activity, with R'HK showing a constant basal activity above 0.6 M⊙ and then decreasing with mass between 0.6 M⊙ and the fully-convective limit of 0.35 M⊙. Short-term variability of the activity correlates with its mean level and stars with higher R'HK indexes show larger R'HK variability, as previously observed for earlier spectral types.
Key words: stars: activity / stars: late-type / stars: rotation / planetary systems / techniques: spectroscopic
Full Table A.2 is only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/600/A13
© ESO, 2017
1. Introduction
“Stellar activity” generically describes the various observational consequences of enhanced magnetic fields, whether those appear on the stellar photosphere, in the chromosphere, or in the corona. In low-mass stars, magnetic fields are in turn believed to originate from dynamo processes (e.g., Parker 1955). Stellar activity is thus used as a diagnostic of the dynamo over a wide range of stellar ages, masses, and rotational periods.
 |
Fig. 1 Median HARPS rest-frame spectrum of a representative mid-M dwarf (Gl 699) with overlays of the V, K (top panel), and H, R (middle panel) filters of the Mount Wilson system and of the photometric V band (bottom panel). |
It is well established that a larger fraction of M dwarfs exhibit evidence of magnetic activity than their more massive Sun-like siblings. The fraction of stars showing Hα chromospheric emission (Delfosse et al. 1998) or frequent flare (Hawley & Pettersen 1991; Schmidt et al. 2014a; Hawley et al. 2014) increase when the mass decreases, for two reasons. On the one hand, lower-mass stars have much longer rotational braking times (Delfosse et al. 1998; Barnes 2003; Delorme et al. 2011) and on the other, lower-mass stars show stronger chromospheric and coronae emission for a given rotation period (e.g., Kiraga & Stepien 2007). Spectropolarimetric observations demonstrate that the more massive (M⋆> 0.5 M⊙) M dwarfs with reconstructed magnetic topologies have magnetic fields with a strong toroidal component, reminiscent of those of active K and G dwarfs, whereas the lowest-mass M dwarfs exhibit magnetic fields that are mainly poloidal (Morin et al. 2008; Donati et al. 2008). This transition takes place slightly above the theoretical full-convection threshold (M ~ 0.35 M⊙), suggesting that the dynamo mechanism might change when the tachocline can no longer play a major role as the radiative core becomes negligibly small (Chabrier & Baraffe 2000). Recent theoretical works successfully reproduce such large-scale and small-scale field properties of magnetic fields in fully convective stars (e.g. Yadav et al. 2015).
Large-scale radial velocity searches for extra-solar planets have helped rejuvenate studies of stellar activity, both because they provide extensive time series of high-resolution spectra for large samples of stars and because characterizing the activity of a star is essential to avoid confusing symptoms of that activity with a planetary signal. Magnetic inhibition of surface convection, spots, plages, and other inhomogeneities of the stellar surface, indeed all affect the shape of spectral lines, shifting their centroids, and consequently biasing the measured radial velocity. This unwanted signal is often handled as random noise, part of the so-called RV-jitter, and added in quadrature to the known noise sources such as photon noise and instrumental instabilities. It can, however, be coherent over the ~months-long time-scale of the stellar rotation, or over the ~years-long time-scale of a stellar activity cycle, and can thus be mistaken for the signature of a planetary companion (e.g., Queloz et al. 2001; Bonfils et al. 2007; Robertson et al. 2014). This has stimulated extensive work to model the effect, identify proxies for its source, and filter it out of the RV time series (Dumusque et al. 2011b,a; Boisse et al. 2011, 2012; Lagrange et al. 2010; Meunier et al. 2010; Meunier & Lagrange 2013; Tuomi et al. 2014).
Emission in the core of the Ca ii H and K resonance lines (396.8 nm and 393.4 nm) reflects non-thermal heating in the chromosphere that produces bright plages, and is perhaps the most widely used of these activity diagnostics. The historical Mount Wilson program (Vaughan et al. 1978) intensively monitored this activity proxy for approximately sixty solar-type stars and quantified stellar activity through the so-called S-index. That index is the ratio between the flux through two triangular band-passes (with 1.09 Å full width at half maximum (FWHM)) centered on the Ca ii H and K lines and the flux through two 20 Å-wide rectangular pseudo-continuum band-passes on the violet (V, centered at 3901 Å) and red (R, centered at 4001 Å) sides of the lines (Fig. 1).
The S-index is akin to an equivalent width, and well matched to its initial purpose of quantifying variations in the activity of a given star. It can also be used to compare activity levels within a narrow spectral type bin, but is poorly suited to comparing stars of different spectral types. To account for the variation of the continuum level with spectral type, Middelkoop (1982) and Rutten (1984) introduced the Ccf factor, which is the ratio between the fraction of the stellar luminosity emitted in the Ca ii H and K lines and the S-index (alternatively, Ccf can be thought of as a bolometric correction for a photometric filter defined by the two pseudo-continuum bands of the Mount Wilson system). Ccf can be estimated from a broad-band color index, and then used to convert the S-index into the fractional luminosity on the Ca ii filters. Calibrations of the Ccf factor against a broad-band color have, to date, focused on FGK-dwarfs, with poor coverage of the M dwarfs. Furthermore, these calibrations tend to use B−V as their color index, which happens to be a poor choice for M dwarfs: these stars emit little flux in the B band, and their V-flux is also sensitive to metallicity (e.g., Delfosse et al. 2000; Bonfils et al. 2005). As a consequence, Ccf plotted against B−V has a large scatter for B−V> 1.2 (late-K) (Vaughan & Preston 1980, Fig. 3).
The two triangular band-passes of the Mount Wilson system centered on the Ca ii H and K lines measure a combination of chromospheric and photospheric emissions. RHK is consequently a fractional luminosity in the Ca ii lines, rather than a fractional chromospheric luminosity in those lines. Corrections for the photospheric contribution were first proposed by Blanco et al. (1974) and Linsky & Ayres (1978), but Hartmann et al. (1984) has become the standard reference. They compute an S-index from the spectrum of the photosphere, Sphot, which the Middelkoop (1982) color-dependent calibration transforms into a RHK for the photosphere, Rphot.  then results as
then results as 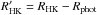 . The activity index
. The activity index  is thus the fraction of the stellar bolometric luminosity which the chromosphere emits in the Ca ii H and K lines. Full details on the conversion of the S-index into
is thus the fraction of the stellar bolometric luminosity which the chromosphere emits in the Ca ii H and K lines. Full details on the conversion of the S-index into  are given in the Appendix of Noyes et al. (1984).
are given in the Appendix of Noyes et al. (1984).
The  index is well characterized for the FGK-dwarfs (Henry et al. 1996; Santos et al. 2000; Wright et al. 2004; Hall et al. 2007; Isaacson & Fischer 2010; Lovis et al. 2011), and some authors (Strassmeier et al. 2000; Tinney et al. 2002; Jenkins et al. 2006) extrapolated the corresponding Ccf and Rphot conversion factors to later dwarfs. The validity of such extrapolations to redder colors is questionable, however. Two further, recent studies proposed better grounded calibrations of the Ca ii H and K emission of M dwarfs. Browning et al. (2010) determined LCa/Lbol from the Ca ii H and K equivalent widths of a sample of M dwarfs, but they chose not to anchor their index on the Mount Wilson
index is well characterized for the FGK-dwarfs (Henry et al. 1996; Santos et al. 2000; Wright et al. 2004; Hall et al. 2007; Isaacson & Fischer 2010; Lovis et al. 2011), and some authors (Strassmeier et al. 2000; Tinney et al. 2002; Jenkins et al. 2006) extrapolated the corresponding Ccf and Rphot conversion factors to later dwarfs. The validity of such extrapolations to redder colors is questionable, however. Two further, recent studies proposed better grounded calibrations of the Ca ii H and K emission of M dwarfs. Browning et al. (2010) determined LCa/Lbol from the Ca ii H and K equivalent widths of a sample of M dwarfs, but they chose not to anchor their index on the Mount Wilson  , complicating comparisons with solar-type stars. Mittag et al. (2013) used synthetic spectra computed to provide conversions from S to
, complicating comparisons with solar-type stars. Mittag et al. (2013) used synthetic spectra computed to provide conversions from S to  , but their use of B−V as the color index is, as discussed above, less than ideal for M dwarfs. Recently, Suárez Mascareño et al. (2015) analyzed the stellar rotation against activity for F-type to mid-M dwarfs; there they provide extended relationships for the Ccf and Rphot factors obtained following the classical works of Middelkoop (1982), Rutten (1984), and Hartmann et al. (1984), respectively.
, but their use of B−V as the color index is, as discussed above, less than ideal for M dwarfs. Recently, Suárez Mascareño et al. (2015) analyzed the stellar rotation against activity for F-type to mid-M dwarfs; there they provide extended relationships for the Ccf and Rphot factors obtained following the classical works of Middelkoop (1982), Rutten (1984), and Hartmann et al. (1984), respectively.
In the present work, we calibrate the Ccf and Rphot factors as a function of B−V, V−I, and I−K for the early to mid-M dwarfs. Sections 3–5 describe our alternative methodology to calibrate such factors. In Sect. 7, we then use the resulting  for the HARPS M dwarf sample to examine how magnetic activity depends on stellar rotation, while Sect. 8 analyses how
for the HARPS M dwarf sample to examine how magnetic activity depends on stellar rotation, while Sect. 8 analyses how  varies with the overall stellar parameters.
varies with the overall stellar parameters.
2. Observations and data reduction
2.1. HARPS spectra
We used spectra observed with the high accuracy radial velocity planets searcher (HARPS) installed on the ESO 3.6 m telescope at La Silla observatory in Chile. HARPS is a fiber-fed cross-dispersed echelle spectrograph covering the 380–690 nm spectral range with a resolving power of 115 000. The stellar light is injected into a science fiber and a second fiber can be illuminated either by a ThAr lamp for simultaneous calibration or by the sky for subtraction of its emission (Mayor et al. 2003).
In order to obtain a measurement of the fraction of luminosity that M dwarfs emit from the Ca ii H and K line we make a spectrophotometric analysis in using the HARPS spectra.
Since our spectra of M dwarfs are not flux-calibrated, we need to reference them to those of better characterized stars to calibrate Ccf and Rphot, and we use spectra of GK-dwarfs for that role. Both the GK and the M stars were originally observed to search for exoplanets through high-precision RV monitoring (Lovis et al. 2011; Bonfils et al. 2012, 2013), with selection criteria described in detail in the above papers. Briefly, the GK-dwarfs are within 50 pc and have low projected rotational velocity vsini< 3−4km s-1; their spectra usually have a signal-to-noise (S/N) ratio above 100 per pixel at 550 nm. Our M dwarfs sample includes ~300 M dwarfs closer than 20 pc, brighter than V = 12 mag and southward of δ = 15°, as well as ~40 fainter stars kept from the initial GTO sample (V< 14 mag; d< 11 pc; δ< 15°; vsini ≤ 6.5 km s-1).
The HARPS pipeline (Lovis & Pepe 2007) automatically reduces the spectroscopic images to spectra, making use of calibrations obtained during day time. It then extracts the radial velocity from the cross-correlation (CCF) of the spectrum and a binary mask, which also provides a FWHM, a contrast, and a bisector-span. In this work, we start from order-merged and background-subtracted spectra corrected from the motion of the observatory relative to the barycenter of the solar system. We used the stellar radial velocity provided by the pipeline to re-center those spectra to the stellar rest-frame. Finally, we corrected from the instrumental transmittance (normalized to unity) using the ratio between a BT-settle (Allard 2014) theoretical spectrum for the bright (V = 6.88) G-dwarf HD 223171 and the average of 20 observed spectra of that star. This correction therefore assumes that the transmittance does not vary and is consequently approximate. This, however, is of little consequence since, as described below, our Ccf and Rphot of M dwarfs are anchored on those of solar-type stars having these two parameters well-calibrated and observed under very similar conditions.
2.2. Literature photometry, parallaxes, and physical parameters
We obtained BVIK photometry of the M dwarfs from Leggett (1992), Gaidos et al. (2014) and Cutri et al. (2003); and of the GK-dwarf calibrators from Ducati et al. (2001) and Cutri et al. (2003). When needed, we used the transformations of Carpenter (2001) to homogenize this photometry to the Johnson-Cousins-CIT system. We adopted parallaxes (π) from van Leeuwen (2007), van Altena et al. (1995), Perryman & ESA (1997), Hawley et al. (1997) and the research consortium on nearby stars (RECONS) parallax program (e.g., Riedel et al. 2010; Jao et al. 2011).
For the GK-dwarfs, we adopt the effective temperature, radii, masses, and metallicities listed in Sousa et al. (2008). For the M dwarfs we obtained the metallicities from Neves et al. (2013), computed effective temperatures and radii using the Boyajian et al. (2012)V−K/metallicity relations, and the stellar masses using the Delfosse et al. (2000) mass vs. K-band absolute magnitude relation. The later relation is valid between 0.09 M⊙ and 0.7 M⊙, and the few masses between 0.7 M⊙ and 0.8 M⊙ are therefore based on a slight extrapolation.
3. Scaling the S-index from HARPS observations
 |
Fig. 2 Median HARPS S-index against the Wright et al. (2004)S-index for the 31 targets in common. The solid line represents the linear least-square fit (Eq. (3)) between the two data sets, which we use to bring our S measurements onto the Mount Wilson scale. |
The definition of the S-index traces back to the Mount Wilson stellar activity program, and modern measurements are traditionally brought onto the scale defined by that program to ease inter-comparisons. The long-term Mount Wilson program started with a Coudé scanner of the 100-inch telescope (HKP-1; Wilson 1968, 1978) and later transitioned to a photometer on the 60-inch telescope (HKP-2; Vaughan et al. 1978).
S is defined as  (1)where fH,fK,fV, and fR are the total counts in the four pass-bands described above (Sect. 1 and Fig. 1) and α = 2.4 is a calibration constant that brings the 100-inch and 60-inch activity indices into approximate agreement.
(1)where fH,fK,fV, and fR are the total counts in the four pass-bands described above (Sect. 1 and Fig. 1) and α = 2.4 is a calibration constant that brings the 100-inch and 60-inch activity indices into approximate agreement.
To compute an S-index with HARPS we chose to follow Lovis et al. (2011): instead of working with integrated flux in each passband, we used the mean flux per wavelength interval 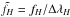 ,
, 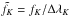 ,
, 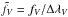 and
and 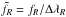 . To be coherent with the Mount Wilson one, our S relationship must be normalized by the ratio of the effective bandpass width ΔλH = ΔλK = 1.09 Å and ΔλV = ΔλR = 20 Å. In addition, we must account for the Mount Wilson program’s exposing eight times as long in its narrow H and K bands than in its broader V and R bands, versus our using. The HARPS calibration constant αH is therefore
. To be coherent with the Mount Wilson one, our S relationship must be normalized by the ratio of the effective bandpass width ΔλH = ΔλK = 1.09 Å and ΔλV = ΔλR = 20 Å. In addition, we must account for the Mount Wilson program’s exposing eight times as long in its narrow H and K bands than in its broader V and R bands, versus our using. The HARPS calibration constant αH is therefore
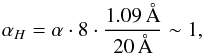 and the S-index can be written as:
and the S-index can be written as: 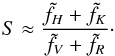 (2)We have no target in common with the Mount Wilson program to directly verify the consistency of our S values with its scale, but Wright et al. (2004) scaled their Keck and Lick S-indices to Mount Wilson measurements. We have 31 targets in common with them1 (Fig. 2), which we use to assess the consistency of the HARPS S-indices with the Mount Wilson scale. The best linear fit between between the two datasets is
(2)We have no target in common with the Mount Wilson program to directly verify the consistency of our S values with its scale, but Wright et al. (2004) scaled their Keck and Lick S-indices to Mount Wilson measurements. We have 31 targets in common with them1 (Fig. 2), which we use to assess the consistency of the HARPS S-indices with the Mount Wilson scale. The best linear fit between between the two datasets is  (3)The uncertainties in the slope and the intercept from the covariance matrix are 0.0025 and 0.0024, respectively, while the root-mean square deviation of the residuals from that fit, 0.080, is consistent with that expected from variations of the stellar activity between the two non-contemporaneous measurements as illustrated by the dispersion on the S-index obtained by Wright et al. (2004) or those listed in our Table A.2. Furthermore, the residuals from our fits are higher for large values of the S-index, which is an expected behavior since more active stars show the largest intrinsic variability of the S-index. The small 1.053 factor most likely accounts for minor mismatches between our synthetic filters and the original physical Mount Wilson bandpasses. We use Eq. (3) to bring our S measurements onto the Mount Wilson scale.
(3)The uncertainties in the slope and the intercept from the covariance matrix are 0.0025 and 0.0024, respectively, while the root-mean square deviation of the residuals from that fit, 0.080, is consistent with that expected from variations of the stellar activity between the two non-contemporaneous measurements as illustrated by the dispersion on the S-index obtained by Wright et al. (2004) or those listed in our Table A.2. Furthermore, the residuals from our fits are higher for large values of the S-index, which is an expected behavior since more active stars show the largest intrinsic variability of the S-index. The small 1.053 factor most likely accounts for minor mismatches between our synthetic filters and the original physical Mount Wilson bandpasses. We use Eq. (3) to bring our S measurements onto the Mount Wilson scale.
 derives from an S-index on the Mount Wilson scale through
derives from an S-index on the Mount Wilson scale through  (4)where Rphot and Sphot stand for the photospheric contribution to R and S, Ccf is the bolometric factor described in Sect. 1, σ is the Stefan-Boltzmann constant, and 10-14 is a scaling factor. K converts the surface fluxes from arbitrary units to physical fluxes on the stellar surface (for a detailed description see, e.g., Rutten 1984, Sect. 2.d). Middelkoop (1982), Rutten (1984), and Hall et al. (2007) respectively find K = 0.76 × 106, 1.29 × 106, 1.07 × 106 [erg cm-2 s-1]. We use the later value, which is referenced to more recent solar data, hence, K·σ-1·10-14 = 1.887 × 10-4.
(4)where Rphot and Sphot stand for the photospheric contribution to R and S, Ccf is the bolometric factor described in Sect. 1, σ is the Stefan-Boltzmann constant, and 10-14 is a scaling factor. K converts the surface fluxes from arbitrary units to physical fluxes on the stellar surface (for a detailed description see, e.g., Rutten 1984, Sect. 2.d). Middelkoop (1982), Rutten (1984), and Hall et al. (2007) respectively find K = 0.76 × 106, 1.29 × 106, 1.07 × 106 [erg cm-2 s-1]. We use the later value, which is referenced to more recent solar data, hence, K·σ-1·10-14 = 1.887 × 10-4.
As discussed in Sect. 1, Ccf and Rphot were previously poorly constrained in the M dwarfs domain.
4. The bolometric factor Ccf
The bolometric factor is: 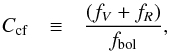 (5)where fV and fR are defined in Eq. (1), and fbol is the apparent bolometric flux of the star. Previous works directly applied Eq. (5) to FGK-dwarfs to derive a Ccf-color-dependent relation (Middelkoop 1982; Rutten 1984).
(5)where fV and fR are defined in Eq. (1), and fbol is the apparent bolometric flux of the star. Previous works directly applied Eq. (5) to FGK-dwarfs to derive a Ccf-color-dependent relation (Middelkoop 1982; Rutten 1984).
Our HARPS M dwarf spectra are not flux calibrated, and chromatic variations in both seeing (hence fiber injection efficiency) and atmospheric transmission therefore prevent the absolute spectro-photometric computation of fV, fR and fbol. However, Ccf being a flux ratio, its empirical determination is only important for the variation of the transmission (atmospheric and instrumental) in function of the wavelength, which can be corrected using a differential method discussed below.
Since our spectra were often observed close in time, and in similar condition to G-K dwarfs, they can be used to bootstrap the computation through the ratio of the Ccfs for the M dwarf and its G or K standard: 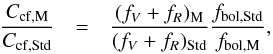 (6)where the chromatic components of both atmospheric absorption and injection efficiency cancel out as long as the M dwarf and its standard star were observed under even moderately similar atmospheric conditions. We stress that the use of
(6)where the chromatic components of both atmospheric absorption and injection efficiency cancel out as long as the M dwarf and its standard star were observed under even moderately similar atmospheric conditions. We stress that the use of  or fV,fR (defined above) in Eq. (6) is equivalent.
or fV,fR (defined above) in Eq. (6) is equivalent.
Since HARPS only observes a small fraction of the spectral energy distribution (SED) of our targets, we express fbol as the flux through a standard photometric band covered by the HARPS spectra scaled by a bolometric correction. We choose the standard visual band and write 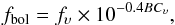 (7)where BCυ is the bolometric correction for the visual band, which is well determined by Flower (1996) for G-K dwarfs and by Leggett et al. (2001) for M dwarfs, the two relationships adopted in this work.
(7)where BCυ is the bolometric correction for the visual band, which is well determined by Flower (1996) for G-K dwarfs and by Leggett et al. (2001) for M dwarfs, the two relationships adopted in this work.
Combining Eqs. (7) and (6), one obtains:  (8)To ensure that the G or K spectra are observed under similar atmospheric conditions as the M spectra they are used to pseudo-calibrate, we select pairs of M dwarf and G or K spectra that were observed;
(8)To ensure that the G or K spectra are observed under similar atmospheric conditions as the M spectra they are used to pseudo-calibrate, we select pairs of M dwarf and G or K spectra that were observed;
-
within 30 min;
-
at an airmass less than 1.4 for both stars and with an airmass difference of less than 0.05;
-
on a good night, as evaluated by a ratio between the measured and synthetic fluxes in the visual band ( Σ = fυ/ [texp10− 0.4mυ] ) such that ΣStd/ ΣM−1 ≤ 0.2.
The HARPS M dwarf database contains 14 M dwarfs that fulfill those criteria. For each target, we adopt the median to take extra precaution allowing us to filter-out eventually imperfectly matched atmospheric conditions despite our selection procedure, and protect against the occasional stellar flare. Table A.3 lists the resulting median log Ccf, together with the B−V, I−K, and V−K colors.
Figure 3 shows the Ccf derived with Eq. (8) against B−V, I−K, and V−K, as well as third order polynomial least-square fits to these data: 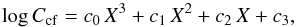 (9)where X is one of the color indexes. Table 1 lists the solution for the coefficients of Eq. (9), the number of data points used for the fit, the rms, and the range of validity for each color index. This range of validity corresponds to spectral classes G0 to M6. From the rms values, we highlight that the V−K and I−K relations are preferred, but we stress that V−K measurements are generally more available than I−K.
(9)where X is one of the color indexes. Table 1 lists the solution for the coefficients of Eq. (9), the number of data points used for the fit, the rms, and the range of validity for each color index. This range of validity corresponds to spectral classes G0 to M6. From the rms values, we highlight that the V−K and I−K relations are preferred, but we stress that V−K measurements are generally more available than I−K.
 |
Fig. 3 The Ccf bolometric factor against B−V (top panel), I−K (middle panel), and V−K (bottom panel). Black dots represent the Ccf, M median, while crosses represent Ccf, Std. Solid lines represent the least-square fits of Eq. (9) for each color index. The top panel omits the 125 Ccf, Std(B−V) data points to more clearly display the Middelkoop (1982) and Rutten (1984) fits, represented by dashed and dotted lines. The validity ranges of these previous relationships are 0.45 <B−V< 1.50 and 0.3 <B−V< 1.6, respectively, and, for comparison, are extrapolated in this figure up to the color index of M dwarfs. |
Solutions for coefficients for the log Ccf-color and Rphot-color relationships.
Jenkins et al. (2006) extrapolated the Middelkoop (1982) beyond its B−V< 0.9 stated validity range to compute RHK for M dwarfs. The top panel of Fig. 3 demonstrates that such an extrapolation becomes increasingly invalid for B−V> 1.5 and overestimates RHK by up to a factor of three. Our updated Ccf-color relation matches the latest main sequence stars in Rutten (1984) quite well and allows us to properly compute RHK from S.
5. The photospheric factor Rphot
 |
Fig. 4 Spectrum of Gl 205 around the Ca II K line. The thin black and bold gray lines respectively represent the observed spectrum and a BT-Settl theoretical spectrum with Teff = 3800 [K], log (g [cm/s] ) = 4.5, and Fe/H = 0.0. The dotted curve depicts the K filter. The bold black line represents part of the spectral contribution through the triangular K filter used to estimate the photospheric contribution in a previous study (Hartmann et al. 1984). |
RHK represents the sum of the photospheric and chromospheric fluxes through the two triangular pass-bands (Fig. 1) of the Mount Wilson system. Separating the chromospheric contribution of interest,  , therefore requires careful estimation of the photospheric flux, Rphot. Hartmann et al. (1984) and Noyes et al. (1984) discussed an empirical method for determining Rphot for the G-K-dwarfs from observed spectra. They use several alternative approaches; all of them consider the photospheric contribution as the flux outside the wavelength domain between the two minimum points in the line profiles of the H and K lines (see Fig. 4 for the K line profile). They conclude that arbitrariness in a number of choices limits the accuracy of the resulting photospheric correction to ~10%. More importantly, Noyes et al. (1984) pointed out that the photospheric correction becomes unimportant for the coolest stars (B−V ≳ 1.0) because the reversal emission is very much stronger than the photospheric contribution.
, therefore requires careful estimation of the photospheric flux, Rphot. Hartmann et al. (1984) and Noyes et al. (1984) discussed an empirical method for determining Rphot for the G-K-dwarfs from observed spectra. They use several alternative approaches; all of them consider the photospheric contribution as the flux outside the wavelength domain between the two minimum points in the line profiles of the H and K lines (see Fig. 4 for the K line profile). They conclude that arbitrariness in a number of choices limits the accuracy of the resulting photospheric correction to ~10%. More importantly, Noyes et al. (1984) pointed out that the photospheric correction becomes unimportant for the coolest stars (B−V ≳ 1.0) because the reversal emission is very much stronger than the photospheric contribution.
Measured stellar parameters, and stellar parameters for the BT-Settl model, which best matches the observed spectrum around the Ca II H and K lines.
Like previous authors (e.g., Walkowicz & Hawley 2009; Mittag et al. 2013), we therefore elect to use a theoretical grid of photospheric model, (here BT-Settl/CIFIST2011bc Allard 2013)2 to evaluate the photospheric contribution. Figure 4 illustrates an example of the match between one of these models and the observed spectra of an early-M dwarf around the Ca ii K line.
For each target, we compute log g from the mass and radius that we obtain from the relations of Delfosse et al. (2000) and Boyajian et al. (2012), respectively. We obtain Teff from Boyajian et al. (2012) and [Fe/H] from Neves et al. (2013). We then inspect the model spectra for grid points within Teff ± 200 [K] and log (g) ± 0.5 [cm s-1] and select that which visually best matches the average observed spectrum of the star between 3880 and 4022 Å. Table 2 lists our computed stellar parameters as well as those of the model that best matches the average spectrum of each star.
We then return to the individual observed spectra and normalize the model spectrum to match them over the wings of (separately) the Ca II H and K lines, which are free of chromospheric emission (Fig. 4). We then replace the central 2 Å region of each Ca ii H and K line with the normalized synthetic spectrum (Fig. 4), to obtain a hybrid spectrum that contains no chromospheric emission, from which we compute Sphot using Eqs. (2) and (3). Using Eq. (9) for V−K, we obtain the photospheric contribution Rphot in Eq. (4) as: 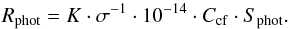 (10)As explained in Sect. 3: K·σ-1·10-14 = 1.887 × 10-4. Table A.3 lists the median of the individual Rphot measurements for each M dwarf and Table A.1 gives this value for our GK-dwarf calibrators.
(10)As explained in Sect. 3: K·σ-1·10-14 = 1.887 × 10-4. Table A.3 lists the median of the individual Rphot measurements for each M dwarf and Table A.1 gives this value for our GK-dwarf calibrators.
Figure 5 shows the median Rphot obtained against B−V, I−K, and V−K, as well as least-square third order polynomial fits: 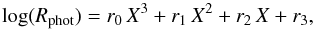 (11)where X stands for one of the color indexes. The values for the coefficients are tabulated in Table 1, in the same format as described in Sect. 4 for the bolometric factor Ccf. The Rphot vs. V−K relationship shows the lowest dispersion.
(11)where X stands for one of the color indexes. The values for the coefficients are tabulated in Table 1, in the same format as described in Sect. 4 for the bolometric factor Ccf. The Rphot vs. V−K relationship shows the lowest dispersion.
 |
Fig. 5 The photospheric factor as a function of, from top to bottom, B−V, I−K, and V−K. Dots and crosses represent Rphot for M and GK-dwarfs, respectively. The solid lines are from Eq. (11) for each one of the color indexes. In the top panel, we compare our relationship for the B−V colors to the ones of Hartmann et al. (1984), Noyes et al. (1984), and Mittag et al. (2013, only from synthetic spectra) in dotted, dashed, and dash-dotted lines, respectively. Their range of validity is 0.44 <B−V< 0.82 for Hartmann et al. (1984) and Noyes et al. (1984), and 0.44 <B−V< 1.6 for Mittag et al. (2013). |
We note a systematic offset between our measurements and the Hartmann et al. (1984) or Noyes et al. (1984)Rphot fits, with their Rphot being systematically lower. We suspect that the offset reflects low-level errors in the extrapolation that is intrinsic to a purely empirical estimation of the photospheric flux under a chromospheric line, but it could, in principle, instead reflect systematics in the theoretical spectra that we use. We note, however, that our approach is more correct from a physical point of view.
6. Accuracy of the R calibration
calibration
The  comes from, as expressed in Eq. (4), the product of a constant (K·σ-1·10-14) and of two factors: Ccf and (S−Sphot). Accuracy and precision of the
comes from, as expressed in Eq. (4), the product of a constant (K·σ-1·10-14) and of two factors: Ccf and (S−Sphot). Accuracy and precision of the  calibration is then directly connected to both.
calibration is then directly connected to both.
6.1. The log Ccf accuracy
Our updated log Ccf relationship, that includes M dwarfs, is purely empirically determined as the product of the Ccf of G-K dwarf calibrators of the flux ratio between M dwarfs and G-K dwarf calibrators in the two-wavelength domain of our HARPS spectra (V and R calcium pseudo-continuum and standard visual bands), and of a bolometric correction. The internal precision of log Ccf is given in Table 1, with a dispersion of approximately 0.06 dex. We discuss here the source of possible systematic errors generating bias.
The log Ccf of G-K dwarf calibrators is computed with the Middelkoop (1982) relationship whose origins are the Mount Wilson measurements in the 1960s and 1970s. It is probable that such a factor is too poorly flux calibrated (see the discussion of Mittag et al. 2013) to be considered as an accurate bolometric factor for the V and R calcium pseudo-continuum band. However, that does not impact our study since our goal is to obtain  for M dwarf that can be compared to the ones of G-K dwarfs. Therefore if we define our Ccf relationship as a calibration anchored on its equivalent for G-K dwarfs, this step does not create a bias.
for M dwarf that can be compared to the ones of G-K dwarfs. Therefore if we define our Ccf relationship as a calibration anchored on its equivalent for G-K dwarfs, this step does not create a bias.
We compute the ratio of fluxes3 passing through different bands when deriving the bolometric factor. As described in Sect. 4, we ensure that the G-K standards are observed under similar atmospheric conditions as the M dwarfs. Thus, if the signal-to-noise of spectra is sufficient, this step can only contribute to the dispersion of the Ccf. However, under low signal-to-noise conditions, an imperfect background subtraction can occur for HARPS reduced spectra and may generate an instrumental systematic error. This effect may impact the flux measurements in the V and R calcium pseudo-continuum band and then our Ccf calibration. This could be particularly significant for M dwarfs, due to their low flux at the blue wavelengths of the Ca ii H and K lines. Lovis et al. (2011) examine systematic errors in the HARPS spectrum in this wavelength domain and found that  measurements from HARPS spectra hit an instrumental noise floor only when the S-index photon uncertainty becomes smaller than ~0.007 dex. To confirm this behavior, for M dwarfs, we plotted the
measurements from HARPS spectra hit an instrumental noise floor only when the S-index photon uncertainty becomes smaller than ~0.007 dex. To confirm this behavior, for M dwarfs, we plotted the  standard deviation of our sample normalized to the
standard deviation of our sample normalized to the  mean value against the average of the S/N ratio (per pixel) in the V and R calcium pseudo-continuum bands (S/NVR, pix), and observe that its lower envelope rises systematically for S/NVR, pix ≲ 5. We attribute this rise to systematic error, including imperfect background subtraction. To ensure that our Ccf calibration is not affected by this effect, we only retain spectra with S/NVR, pix ≥ 5. The average signal-to-noise of the 14 M dwarfs and of their comparison G-K-dwarfs that we use is approximately 30 (ranging from 7.5 to 57.6). At such a level of flux, the effect of the background subtraction is negligible.
mean value against the average of the S/N ratio (per pixel) in the V and R calcium pseudo-continuum bands (S/NVR, pix), and observe that its lower envelope rises systematically for S/NVR, pix ≲ 5. We attribute this rise to systematic error, including imperfect background subtraction. To ensure that our Ccf calibration is not affected by this effect, we only retain spectra with S/NVR, pix ≥ 5. The average signal-to-noise of the 14 M dwarfs and of their comparison G-K-dwarfs that we use is approximately 30 (ranging from 7.5 to 57.6). At such a level of flux, the effect of the background subtraction is negligible.
 being, in theory, the ratio between the chromospheric emission in the Ca H and K lines and the bolometric flux, we have to use a bolometric correction. For that, we use two different bolometric correction relationships: Flower (1996) for G-K dwarf calibrators and Leggett et al. (2001) for M dwarfs. Both relations are obtained from flux distribution measurements that are completed by synthetic spectra when certain wavelength domains are uncovered. They use similar zero points (respectively Mbol, ⊙ = 4.73 and 4.75). As demonstrated by Flower (1996), Torres (2010) for G-K dwarfs and by Schmidt et al. (2014b), Mann et al. (2015) for M dwarfs, for example, the agreement among different bolometric corrections is usually better than 0.1 mag. We therefore do not expect that this step introduces systematic error higher that 0.1 mag on log Ccf.
being, in theory, the ratio between the chromospheric emission in the Ca H and K lines and the bolometric flux, we have to use a bolometric correction. For that, we use two different bolometric correction relationships: Flower (1996) for G-K dwarf calibrators and Leggett et al. (2001) for M dwarfs. Both relations are obtained from flux distribution measurements that are completed by synthetic spectra when certain wavelength domains are uncovered. They use similar zero points (respectively Mbol, ⊙ = 4.73 and 4.75). As demonstrated by Flower (1996), Torres (2010) for G-K dwarfs and by Schmidt et al. (2014b), Mann et al. (2015) for M dwarfs, for example, the agreement among different bolometric corrections is usually better than 0.1 mag. We therefore do not expect that this step introduces systematic error higher that 0.1 mag on log Ccf.
To conclude, we are confident that systematic error in our log Ccf for M dwarfs is negligible.
6.2. Accuracy on (S – Sphot)
It is more difficult to estimate the systematic error on Sphot, since we use synthetic spectra to reproduce the core of the photospheric Ca ii H and K absorption lines. Such line cores cannot be measured directly, being always hidden by the chromospheric emission. If the synthetic model does not reproduce them correctly, it will introduce a bias in our Rphot relationship. The log Rphot has a dispersion of approximately 0.05 dex (Table 1).
 |
Fig. 6
|
We make sure that the wings of photospheric Ca ii H and K lines are well reproduced by using theoretical spectra (see Fig. 4). If, however, the core of the photospheric line is not as well reproduced as the wings, we point out that this part of the photospheric contribution covers approximately 25% of the wavelength domain of the triangular spectrum used to measure S. The model of the photospheric flux used is intermediate between two extreme solutions: assuming that photospheric flux is 0 under the chromospheric line or that it is constant and at the level of the reversal points at the basis of the emission line. Therefore, our estimation will not differ by more than ~15% from these two extreme solutions. Hartmann et al. (1984) come to the same conclusion on the effect of different methods to estimate Sphot. We stress that the use of theoretical spectra is today the most physically motivated approach to address this issue.
Furthermore, the factor involved in the error budget is (S−Sphot). In our study the quietest (with lowest Ca ii H and K emission) M dwarf used in the calibration has a S 42% higher than Sphot, minimizing the impact of the systematic error on Sphot to less than 10%. Taking everything into account, we estimate that the effect of such systematic error is below 0.1 mag on  .
.
7. R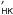 versus rotation
versus rotation
For low-mass stars the magnetic field is generated by a combination of (i) αΩ dynamo (e.g., Parker 1955) taking place under the presence of a radiative core separated from a convective envelope by a strongly sheared thin layer (the tachocline), and (ii) a fully convective dynamo (later than M4V; e.g., Bercik et al. 2005) showing similarities with a planetary one (Gastine et al. 2013; Schrinner et al. 2014). Stars later than M4V become fully convective (Bercik et al. 2005) and only the second type of dynamo is at work.
On the one hand, Zeeman Doppler Imaging of active M dwarfs indicates that the topology of the large-scale component of their magnetic field changes when they approach the full-convection limit (Donati et al. 2008; Morin et al. 2008). On the other, no obvious change at the fully-convective transition is noticeable in the relationship between the rotational period and the average field strength (Reiners & Basri 2007; Reiners et al. 2009), or its proxies such as magnetic activity (e.g., LXKiraga & Stepien 2007).
Here we analyze how  varies with stellar rotation around the fully convective limit. We use 38 M1 to M6 dwarfs with known stellar rotation periods, inferred from either photometric periodicities or periodic modulation of the S-index. The majority of periods are obtained from the literature (Table 3), but those for 7 M dwarfs are inferred from strong peaks (above 0.3% FAP) in the respective periodogram (e.g., Zechmeister & Kürster 2009) of our measurements of its Ca ii H and K emission (GJ 3138, Gl 654, Gl 752A, Gl 876, Gl 880, Gl 382, Gl 514). Both Ccf and Rphot correlate with a similar level of dispersion with either V−K or I−K (Table 1). The dispersion is superior in the correlation with B−V. To compute
varies with stellar rotation around the fully convective limit. We use 38 M1 to M6 dwarfs with known stellar rotation periods, inferred from either photometric periodicities or periodic modulation of the S-index. The majority of periods are obtained from the literature (Table 3), but those for 7 M dwarfs are inferred from strong peaks (above 0.3% FAP) in the respective periodogram (e.g., Zechmeister & Kürster 2009) of our measurements of its Ca ii H and K emission (GJ 3138, Gl 654, Gl 752A, Gl 876, Gl 880, Gl 382, Gl 514). Both Ccf and Rphot correlate with a similar level of dispersion with either V−K or I−K (Table 1). The dispersion is superior in the correlation with B−V. To compute  , we use, hereafter, log Ccf(V−K) and log Rphot(V−K) relationships, because, in general, V−K photometry is more available than I−K.
, we use, hereafter, log Ccf(V−K) and log Rphot(V−K) relationships, because, in general, V−K photometry is more available than I−K.
For solar type stars, 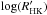 correlates better with the Rossby number (Ro = Pobs/τc, where τc is the convective overturn time) than with Prot alone (Noyes et al. 1984). This matches the theoretical expectation that the strength of an αΩ dynamo process is proportional to Ro-2. Ro is therefore widely used when relating magnetic activity with rotation, though some authors argue that Prot should be prioritized (Stepien 1993; Reiners et al. 2014). τc can be determined either empirically (e.g., Noyes et al. 1984) or theoretically (e.g., Ventura et al. 1998), with both approaches giving uncertain results for M dwarfs.
correlates better with the Rossby number (Ro = Pobs/τc, where τc is the convective overturn time) than with Prot alone (Noyes et al. 1984). This matches the theoretical expectation that the strength of an αΩ dynamo process is proportional to Ro-2. Ro is therefore widely used when relating magnetic activity with rotation, though some authors argue that Prot should be prioritized (Stepien 1993; Reiners et al. 2014). τc can be determined either empirically (e.g., Noyes et al. 1984) or theoretically (e.g., Ventura et al. 1998), with both approaches giving uncertain results for M dwarfs.
Figure 6 demonstrates that log (Prot) correlates closely with 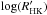 for stellar masses between 0.1 M⊙ and 0.8 M⊙. Above a ~10-day rotation period, activity decreases with slower rotation, while below that period it no longer depends on rotation. The
for stellar masses between 0.1 M⊙ and 0.8 M⊙. Above a ~10-day rotation period, activity decreases with slower rotation, while below that period it no longer depends on rotation. The 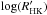 –log (Prot) relationship is well described by:
–log (Prot) relationship is well described by: ![\begin{equation} \label{eq:R_Prot_relation} \log(R^\prime_{\rm HK}) = \left\{ \begin{array}{ll} -1.509 \cdot \log(P_{\rm rot})-2.550 &\mbox{ if }P_{\rm rot}[d]>10 \\ -4.045 &\mbox{ if }P_{\rm rot}[d]<10\!\! \!\! \end{array} \right. \!\!\! , \end{equation}](/articles/aa/full_html/2017/04/aa27078-15/aa27078-15-eq156.png) (12)where the
(12)where the 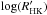 average for the saturated regime does not account for the three stars with masses below 0.2 M⊙ (GJ 3379, Gl 729, G141-29; see justification below), and Gl 551 is not considered for the non-saturated fit as it shows flares with a significantly higher cadence than their siblings with approximately the same age or rotational period (e.g., Davenport et al. 2016). The
average for the saturated regime does not account for the three stars with masses below 0.2 M⊙ (GJ 3379, Gl 729, G141-29; see justification below), and Gl 551 is not considered for the non-saturated fit as it shows flares with a significantly higher cadence than their siblings with approximately the same age or rotational period (e.g., Davenport et al. 2016). The 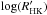 uncertainty is ± 0.093 if Prot [d] < 10. For Prot [d] > 10, the slope and the y-intercept uncertainties from the fit are ± 0.007 and ± 0.020, respectively. The rms of the non-saturated regime in Eq. (12) is 7.68 d, while the median relative uncertainty for our period estimation is 8.7%.
uncertainty is ± 0.093 if Prot [d] < 10. For Prot [d] > 10, the slope and the y-intercept uncertainties from the fit are ± 0.007 and ± 0.020, respectively. The rms of the non-saturated regime in Eq. (12) is 7.68 d, while the median relative uncertainty for our period estimation is 8.7%.
Activity saturation in fast M dwarf rotators is a well known behavior observed in many proxies LHα/Lbol, LX/Lbol, or Bf (e.g., Delfosse et al. 1998; Kiraga & Stepien 2007; Reiners et al. 2009, 2012), and is interpreted either as a physical saturation of the dynamo process or as active regions completely covering the stellar surface while the magnetic field continues to grow. For M dwarfs,  saturates at Ro ≈ 0.1 (adopting here τc = 70 d, following Reiners et al. 2009). LX/Lbol and Bf similarly saturate for Ro ≈ 0.1 (Kiraga & Stepien 2007; Reiners et al. 2009). Above 10 d and up to ~100 d,
saturates at Ro ≈ 0.1 (adopting here τc = 70 d, following Reiners et al. 2009). LX/Lbol and Bf similarly saturate for Ro ≈ 0.1 (Kiraga & Stepien 2007; Reiners et al. 2009). Above 10 d and up to ~100 d, 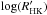 varies linearly with log (Prot), as also observed for FGK-dwarfs (Noyes et al. 1984; Mamajek & Hillenbrand 2008).
varies linearly with log (Prot), as also observed for FGK-dwarfs (Noyes et al. 1984; Mamajek & Hillenbrand 2008).
11 of our 38 M dwarfs have masses under the 0.35 M⊙ full convection limit. They therefore have no tachocline and consequently cannot operate an αΩ dynamo. Figure 6 demonstrates that the 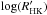 vs. log (Prot) relationship does not markedly change at this transition, and that stellar rotation continue to drive activity in fully convective stars. We note that the three lowest-mass stars in the saturated half of Fig. 6 have lower
vs. log (Prot) relationship does not markedly change at this transition, and that stellar rotation continue to drive activity in fully convective stars. We note that the three lowest-mass stars in the saturated half of Fig. 6 have lower 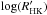 than their more massive counterparts. These three M dwarfs were not considered for the saturated fit as we suspect that they may follow a different regime. However, a larger sample will be needed to confirm if the
than their more massive counterparts. These three M dwarfs were not considered for the saturated fit as we suspect that they may follow a different regime. However, a larger sample will be needed to confirm if the 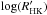 level in the saturated regime is correlated with stellar mass for mid- to late-M dwarfs.
level in the saturated regime is correlated with stellar mass for mid- to late-M dwarfs.
The 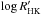 (fourth column) and rotation periods (fifth column) of the 38 M dwarfs for which both are known.
(fourth column) and rotation periods (fifth column) of the 38 M dwarfs for which both are known.
8. R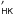 for the HARPS M dwarf sample
for the HARPS M dwarf sample
We computed  for 403 M dwarfs observed by HARPS for planet searches (Bonfils et al. 2012, 2013). To estimate Ccf and Rphot, we used the V−K relation for Eqs. (9) and (11) when a measurement of that color index was available in the literature, and we backed up to using the B−V relation for Eqs. (9) and (11) when only the color was available.
for 403 M dwarfs observed by HARPS for planet searches (Bonfils et al. 2012, 2013). To estimate Ccf and Rphot, we used the V−K relation for Eqs. (9) and (11) when a measurement of that color index was available in the literature, and we backed up to using the B−V relation for Eqs. (9) and (11) when only the color was available.
Table A.2 lists the median of the individual  measurements for each star, which was used for the following analysis. The most active M dwarfs are fast rotators and, as such, were rejected from the planet search programs by the projected rotational velocity cut mentioned in Sect. 2. Our sample is thus biased against the most active M dwarfs (but it nevertheless includes some of them) and representative of quiet and moderately active M dwarfs. Accordingly, our sample cannot be used to estimate the fraction of active stars among the M dwarfs. This is not, however, a limitation to study the correlation between stellar parameters and stellar activity.
measurements for each star, which was used for the following analysis. The most active M dwarfs are fast rotators and, as such, were rejected from the planet search programs by the projected rotational velocity cut mentioned in Sect. 2. Our sample is thus biased against the most active M dwarfs (but it nevertheless includes some of them) and representative of quiet and moderately active M dwarfs. Accordingly, our sample cannot be used to estimate the fraction of active stars among the M dwarfs. This is not, however, a limitation to study the correlation between stellar parameters and stellar activity.
8.1. R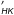 and metallicity
and metallicity
 |
Fig. 7
|
We first examined  against metallicity (Fig. 7). Metallicity affects
against metallicity (Fig. 7). Metallicity affects  measurements of the warmer solar-type stars, because, at a given Teff, metal-poor stars have weaker fluxes in the V and R pseudo-continuum pass-bands, and therefore higher S values for the same Ca ii H and K flux; metallicity also affects the Ccf factor, which is derived from the flux in the visual band, which in turn is sensitive to metallicity. Lovis et al. (2011) noticed from a linear trend in the lower envelope of a
measurements of the warmer solar-type stars, because, at a given Teff, metal-poor stars have weaker fluxes in the V and R pseudo-continuum pass-bands, and therefore higher S values for the same Ca ii H and K flux; metallicity also affects the Ccf factor, which is derived from the flux in the visual band, which in turn is sensitive to metallicity. Lovis et al. (2011) noticed from a linear trend in the lower envelope of a  versus Fe/H diagram that
versus Fe/H diagram that  systematically decreases as Fe/H increases, and find that taking into account the variation of the bolometric flux as a function of Fe/H eliminates that trend (their Fig. 3). Figure 7 demonstrates that the lower envelope of the M dwarf diagram shows no such trend, and we therefore include no metallicity term in our
systematically decreases as Fe/H increases, and find that taking into account the variation of the bolometric flux as a function of Fe/H eliminates that trend (their Fig. 3). Figure 7 demonstrates that the lower envelope of the M dwarf diagram shows no such trend, and we therefore include no metallicity term in our  calibration. One can also note that the active M dwarfs cluster in the metal-rich side of the diagram, as qualitatively expected from combination of the age-metallicity correlation and the decreasing chromospheric activity of older stars. Solar-metallicity M dwarfs of our sample nonetheless show
calibration. One can also note that the active M dwarfs cluster in the metal-rich side of the diagram, as qualitatively expected from combination of the age-metallicity correlation and the decreasing chromospheric activity of older stars. Solar-metallicity M dwarfs of our sample nonetheless show 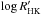 ranging from –6.0 to –4.25 while their FGK counterparts are less dispersed with
ranging from –6.0 to –4.25 while their FGK counterparts are less dispersed with 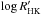 ranging from –5.1 to –4.65. Knowing that the most active stars have been rejected in our M dwarfs sample, the
ranging from –5.1 to –4.65. Knowing that the most active stars have been rejected in our M dwarfs sample, the 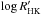 dispersion for these stars might even be stronger. This could originate from the longer spin-down timescales of M dwarfs and, therefore, it takes a longer time for all the stars to converge to the sequence of the lower rotators.
dispersion for these stars might even be stronger. This could originate from the longer spin-down timescales of M dwarfs and, therefore, it takes a longer time for all the stars to converge to the sequence of the lower rotators.
8.2. Dispersion of the R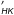 epoch measurements
epoch measurements
The dispersion of the individual  measurements of a star contains contributions from true stellar variability, instrumental systematic error, and noise. As discussed in Sect. 6, the latter can often be dominant for M dwarfs, due to their low flux at the blue wavelengths of the Ca ii H and K. To minimize this effect, we restrict discussion on variability to stars for which at least six
measurements of a star contains contributions from true stellar variability, instrumental systematic error, and noise. As discussed in Sect. 6, the latter can often be dominant for M dwarfs, due to their low flux at the blue wavelengths of the Ca ii H and K. To minimize this effect, we restrict discussion on variability to stars for which at least six  measurement have S/NVR, pix ≥ 5 (see Sect. 6 for more details).
measurement have S/NVR, pix ≥ 5 (see Sect. 6 for more details).
Figure 8 displays the median  against its dispersion and shows that the more active stars are more variable, as is also true for GK-dwarfs (e.g., Lovis et al. 2011). Many of the most active stars in Fig. 8 are known flare-stars, including Gl 551 (Proxima Centauri), Gl 54.1, Gl 729, GJ 3379, GJ 234AB, and GJ 3148A. The most likely
against its dispersion and shows that the more active stars are more variable, as is also true for GK-dwarfs (e.g., Lovis et al. 2011). Many of the most active stars in Fig. 8 are known flare-stars, including Gl 551 (Proxima Centauri), Gl 54.1, Gl 729, GJ 3379, GJ 234AB, and GJ 3148A. The most likely  dispersion for an M dwarf is 1.2 × 10-6, while the peak of the distribution is located at 0.6 × 10-6, three times higher than the 0.2 × 10-6 for G-K-dwarfs, and the M dwarf histogram is also broader. This may stem from the slower spin-down of the M dwarfs, although residual instrumental effects could perhaps contribute.
dispersion for an M dwarf is 1.2 × 10-6, while the peak of the distribution is located at 0.6 × 10-6, three times higher than the 0.2 × 10-6 for G-K-dwarfs, and the M dwarf histogram is also broader. This may stem from the slower spin-down of the M dwarfs, although residual instrumental effects could perhaps contribute.
Such strong intrinsic variability of the M dwarfs activity has often been pointed out, but few have been quantified until now. Such variability also concerns quiet M dwarfs.
 |
Fig. 8 Average |
8.3. Activity as a function of stellar mass
We now turn our attention to the relationship between magnetic activity and stellar mass, restricting the discussion to stars with a well measured parallax (δπ/π< 0.1) and for which a mass can therefore be inferred from the Delfosse et al. (2000) mass vs. MK relation. We first consider three mass bins, M/M⊙ ≤ 0.4, 0.4 <M/M⊙ ≤ 0.6, and 0.6 <M/M⊙< 0.8. Figure 9 presents histograms of the median 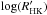 for each bin, and shows that activity level most likely decreases with stellar mass. The histogram for the highest mass bin peaks at
for each bin, and shows that activity level most likely decreases with stellar mass. The histogram for the highest mass bin peaks at 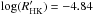 , slightly higher than the –4.95 observed for G-K dwarfs Lovis et al. (2011), that for the intermediate mass bin peaks at approximately –5.19, while that for the lowest-mass bin peaks at –5.47 but displays a strong tail of more active stars retained from our sample selection.
, slightly higher than the –4.95 observed for G-K dwarfs Lovis et al. (2011), that for the intermediate mass bin peaks at approximately –5.19, while that for the lowest-mass bin peaks at –5.47 but displays a strong tail of more active stars retained from our sample selection.
For an unbinned view, Fig. 10 displays  as a function of stellar mass. Both the lower envelope and the mode of the
as a function of stellar mass. Both the lower envelope and the mode of the  distribution are approximately flat above ~ 0.6 M⊙, decrease with mass between ~0.6 M⊙ and ~0.35 M⊙, and flatten again below ~0.35 M⊙. The later break approximately coincides with the transition from partially to fully convective stars (Chabrier & Baraffe 2000), and could potentially reflect a change at this transition where the αΩ dynamo vanishes and a change is observed in the topology of the large-scale component of their magnetic field (Donati et al. 2008; Morin et al. 2008).
distribution are approximately flat above ~ 0.6 M⊙, decrease with mass between ~0.6 M⊙ and ~0.35 M⊙, and flatten again below ~0.35 M⊙. The later break approximately coincides with the transition from partially to fully convective stars (Chabrier & Baraffe 2000), and could potentially reflect a change at this transition where the αΩ dynamo vanishes and a change is observed in the topology of the large-scale component of their magnetic field (Donati et al. 2008; Morin et al. 2008).
 |
Fig. 9 Histograms of the median |
For the earlier spectral types, our findings are consistent with those of Mittag et al. (2013). They found that Ca ii activity rises over 1.1 ≤ B−V ≤ 1.3 (K5 to K7-dwarfs) and decreases over 1.3 ≤ B−V ≤ 1.5 (M0 to M3-dwarfs), but could not establish whether or not that decrease continues to later spectral types since their sample does not extend beyond M3. Figure 5 in Browning et al. (2010) shows a similar behavior of LCa/LBol against spectral type for M dwarfs, albeit less clearly.
Hα shows a similar behavior although the decline starts at mid-M dwarfs. LHα/Lbol remains approximately constant for spectral types M0 to M5 and only starts to decline at M5-M6 (West et al. 2004). This is not inconsistent, since Ca ii H and K and Hα trace different chromospheric heights. Their emissions do positively correlate for very active stars, but not for intermediate or weak activity stars (Rauscher & Marcy 2006; Walkowicz & Hawley 2009).
 |
Fig. 10 Median |
9. Conclusions and summary
We use high-resolution spectra of M dwarfs observed in HARPS planet-search programs to analyze their Ca ii H and K magnetic activity and examine how it varies with stellar rotation period, stellar mass, and color. For this purpose, we extend the B−V photometric calibrations of the bolometric Ccf and photospheric Rphot factors used in the computation of the  -index to B−V = 1.90 (spectral type M6). We also derive alternative, and preferred, I−K and V−K calibrations of these two factors.
-index to B−V = 1.90 (spectral type M6). We also derive alternative, and preferred, I−K and V−K calibrations of these two factors.
We calibrated the Ccf relationship in a purely empirical way, without the use of synthetic spectra, through the integrated flux in the V and R control bands, and the bolometric flux determined by the integrated flux in the visual band and the bolometric correction (Flower 1996; Leggett et al. 2001). On the contrary, the Rphot relationship is calibrated in using a synthetic spectrum that replaces a narrow window (2 Å) around Ca ii H and K lines of observed spectra (chromosphere+photosphere). While an extrapolation of the Rutten (1984)Ccf vs. B−V relation agrees reasonably well with our new relation for B−V< 1.6, we find that extrapolating the Middelkoop (1982) or Noyes et al. (1984), as done by Tinney et al. (e.g. 2002), Jenkins et al. (e.g. 2006) overestimates  values by factors of two to three for mid- to late-M dwarfs.
values by factors of two to three for mid- to late-M dwarfs.
The 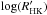 vs. log (Prot) diagram of M0-M6 dwarfs displays two distinct regimes, with
vs. log (Prot) diagram of M0-M6 dwarfs displays two distinct regimes, with 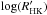 saturated for P< 10 d (or a Rossby number of ≈0.1 for an assumed τc = 70 d convective turnover timescale) and then decreasing as a linear function of log (Prot) for longer rotational periods. These two regimes similarly appear in other tracers of magnetic activity (such as LX/Lbol or Bf, Kiraga & Stepien 2007; Reiners et al. 2009).
saturated for P< 10 d (or a Rossby number of ≈0.1 for an assumed τc = 70 d convective turnover timescale) and then decreasing as a linear function of log (Prot) for longer rotational periods. These two regimes similarly appear in other tracers of magnetic activity (such as LX/Lbol or Bf, Kiraga & Stepien 2007; Reiners et al. 2009).  , LX/Lbol, and Bf all depend similarly on stellar rotation in the unsaturated regime, as expected if rotation drives all magnetic activity. The stellar rotation can be estimated from LX/Lbol (e.g., Kiraga & Stepien 2007), although
, LX/Lbol, and Bf all depend similarly on stellar rotation in the unsaturated regime, as expected if rotation drives all magnetic activity. The stellar rotation can be estimated from LX/Lbol (e.g., Kiraga & Stepien 2007), although  has the potential to derive PRot for quieter stars, where X emission is eventually not detected.
has the potential to derive PRot for quieter stars, where X emission is eventually not detected.
The lower envelope of the Ca ii H and K activity varies with mass over the M dwarf range. The basal level of the  distribution decreases with the lower envelope and mode of the
distribution decreases with the lower envelope and mode of the  distribution decreases with stellar mass down to M ~ 0.35 M⊙ and flattens below that mass, which coincides with the transition from partially to fully convective stars. It will be difficult to confirm if another basal coronae and chromosphere emission decrease with mass for M dwarfs, LHα/LBOL or LX/LBOL not being determined for the quietest stars.
distribution decreases with stellar mass down to M ~ 0.35 M⊙ and flattens below that mass, which coincides with the transition from partially to fully convective stars. It will be difficult to confirm if another basal coronae and chromosphere emission decrease with mass for M dwarfs, LHα/LBOL or LX/LBOL not being determined for the quietest stars.
Besides insight into surface magnetic fields, Eq. (12) provides information on Prot (with a typical accuracy of 8 d) from a measurement of  that can be obtained from a single high-resolution spectrum. This has significant practical importance in the context of extra-solar planet searches, where stellar activity modulated by rotational visibility is an important source of false-positives (e.g., Bonfils et al. 2007; Robertson et al. 2014). A good estimate of Prot from Eq. (12) can thus retire false positive worries when the potential signal is sufficiently removed from the estimated stellar-rotation period and its harmonics (Boisse et al. 2011), and will intensify such worries when it is not.
that can be obtained from a single high-resolution spectrum. This has significant practical importance in the context of extra-solar planet searches, where stellar activity modulated by rotational visibility is an important source of false-positives (e.g., Bonfils et al. 2007; Robertson et al. 2014). A good estimate of Prot from Eq. (12) can thus retire false positive worries when the potential signal is sufficiently removed from the estimated stellar-rotation period and its harmonics (Boisse et al. 2011), and will intensify such worries when it is not.
Ccf ∝ [(fV + fR)M/ (fV + fR)Std] / [fυ,Std/fυ,M]; from Eq. (8).
Acknowledgments
Based on observations made with the HARPS instrument on the ESO 3.6 m telescope under program IDs 072.C-0488(E), 183.C-0437(A), 072.C-0488, 183.C-0972 and 083.C-1001 at Cerro La Silla (Chile). The authors acknowledge Nadège Meunier and Eduardo Martín for theirs precious comments. N.A.-D. acknowledges support from CONICYT Becas-Chile 72120460. X.B., X.D., and T.F. acknowledge the support of the French Agence Nationale de la Recherche (ANR), under the program ANR-12-BS05-0012 Exo-atmos and of PNP (Programme national de planétologie). This work has been partially supported by the Labex OSUG@2020. X.B. acknowledges funding from the European Research Council under the ERC Grant Agreement n. 337591-ExTrA.
References
- Allard, F. 2013, in Exploring the Formation and Evolution of Planetary Systems, Proc. IAU, 8, 271 [CrossRef] [Google Scholar]
- Allard, F. 2014, in IAU Symp. 299, eds. M. Booth, B. C. Matthews, & J. R. Graham, 271 [Google Scholar]
- Astudillo-Defru, N., Bonfils, X., Delfosse, X., et al. 2015, A&A, 575, A119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Barnes, S. A. 2003, ApJ, 586, 464 [NASA ADS] [CrossRef] [Google Scholar]
- Bercik, D. J., Fisher, G. H., Johns-Krull, C. M., & Abbett, W. P. 2005, ApJ, 631, 529 [NASA ADS] [CrossRef] [Google Scholar]
- Blanco, C., Catalano, S., Marilli, E., & Rodonò, M. 1974, A&A, 33, 257 [NASA ADS] [Google Scholar]
- Boisse, I., Bouchy, F., Hébrard, G., et al. 2011, A&A, 528, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boisse, I., Bonfils, X., & Santos, N. C. 2012, A&A, 545, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2005, A&A, 442, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Mayor, M., Delfosse, X., et al. 2007, A&A, 474, 293 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Gillon, M., Udry, S., et al. 2012, A&A, 546, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boyajian, T. S., von Braun, K., van Belle, G., et al. 2012, ApJ, 757, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Browning, M. K., Basri, G., Marcy, G. W., West, A. A., & Zhang, J. 2010, AJ, 139, 504 [NASA ADS] [CrossRef] [Google Scholar]
- Carpenter, J. M. 2001, AJ, 121, 2851 [NASA ADS] [CrossRef] [Google Scholar]
- Chabrier, G., & Baraffe, I. 2000, ARA&A, 38, 337 [NASA ADS] [CrossRef] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, VizieR Online Data Catalog: II/246 [Google Scholar]
- Davenport, J. R. A., Kipping, D. M., Sasselov, D., Matthews, J. M., & Cameron, C. 2016, ApJ, 829, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Delfosse, X., Forveille, T., Perrier, C., & Mayor, M. 1998, A&A, 331, 581 [NASA ADS] [Google Scholar]
- Delfosse, X., Forveille, T., Ségransan, D., et al. 2000, A&A, 364, 217 [NASA ADS] [Google Scholar]
- Delorme, P., Collier Cameron, A., Hebb, L., et al. 2011, MNRAS, 413, 2218 [NASA ADS] [CrossRef] [Google Scholar]
- Donati, J.-F., Morin, J., Petit, P., et al. 2008, MNRAS, 390, 545 [NASA ADS] [CrossRef] [Google Scholar]
- Ducati, J. R., Bevilacqua, C. M., Rembold, S. B., & Ribeiro, D. 2001, ApJ, 558, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Dumusque, X., Santos, N. C., Udry, S., Lovis, C., & Bonfils, X. 2011a, A&A, 527, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dumusque, X., Udry, S., Lovis, C., Santos, N. C., & Monteiro, M. J. P. F. G. 2011b, A&A, 525, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Flower, P. J. 1996, ApJ, 469, 355 [NASA ADS] [CrossRef] [Google Scholar]
- Gaidos, E., Mann, A. W., Lépine, S., et al. 2014, MNRAS, 443, 2561 [NASA ADS] [CrossRef] [Google Scholar]
- Gastine, T., Morin, J., Duarte, L., et al. 2013, A&A, 549, L5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hall, J. C., Lockwood, G. W., & Skiff, B. A. 2007, AJ, 133, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Soderblom, D. R., Noyes, R. W., Burnham, N., & Vaughan, A. H. 1984, ApJ, 276, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, S. L., & Pettersen, B. R. 1991, ApJ, 378, 725 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, S. L., Gizis, J. E., & Reid, N. I. 1997, AJ, 113, 1458 [NASA ADS] [CrossRef] [Google Scholar]
- Hawley, S. L., Davenport, J. R. A., Kowalski, A. F., et al. 2014, ApJ, 797, 121 [NASA ADS] [CrossRef] [Google Scholar]
- Henry, T. J., Soderblom, D. R., Donahue, R. A., & Baliunas, S. L. 1996, AJ, 111, 439 [NASA ADS] [CrossRef] [Google Scholar]
- Irwin, J., Berta, Z. K., Burke, C. J., et al. 2011, ApJ, 727, 56 [Google Scholar]
- Isaacson, H., & Fischer, D. 2010, ApJ, 725, 875 [NASA ADS] [CrossRef] [Google Scholar]
- Jao, W.-C., Henry, T. J., Subasavage, J. P., et al. 2011, AJ, 141, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. S., Jones, H. R. A., Tinney, C. G., et al. 2006, MNRAS, 372, 163 [NASA ADS] [CrossRef] [Google Scholar]
- Kiraga, M., & Stepien, K. 2007, Acta Astron., 57, 149 [NASA ADS] [Google Scholar]
- Lagrange, A.-M., Desort, M., & Meunier, N. 2010, A&A, 512, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Leggett, S. K. 1992, ApJS, 82, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Leggett, S. K., Allard, F., Geballe, T. R., Hauschildt, P. H., & Schweitzer, A. 2001, ApJ, 548, 908 [NASA ADS] [CrossRef] [Google Scholar]
- Lépine, S., & Gaidos, E. 2011, AJ, 142, 138 [Google Scholar]
- Linsky, J. L., & Ayres, T. R. 1978, ApJ, 220, 619 [NASA ADS] [CrossRef] [Google Scholar]
- Lovis, C., & Pepe, F. 2007, A&A, 468, 1115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lovis, C., Dumusque, X., Santos, N. C., et al. 2011, ArXiv e-prints [arXiv:1107.5325] [Google Scholar]
- Mamajek, E. E., & Hillenbrand, L. A. 2008, ApJ, 687, 1264 [NASA ADS] [CrossRef] [Google Scholar]
- Mann, A. W., Feiden, G. A., Gaidos, E., Boyajian, T., & von Braun, K. 2015, ApJ, 804, 64 [CrossRef] [Google Scholar]
- Mayor, M., Pepe, F., Queloz, D., et al. 2003, The Messenger, 114, 20 [NASA ADS] [Google Scholar]
- Meunier, N., & Lagrange, A.-M. 2013, A&A, 551, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N., Desort, M., & Lagrange, A.-M. 2010, A&A, 512, A39 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Middelkoop, F. 1982, A&A, 107, 31 [NASA ADS] [Google Scholar]
- Mittag, M., Schmitt, J. H. M. M., & Schröder, K.-P. 2013, A&A, 549, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Morin, J., Donati, J.-F., Petit, P., et al. 2008, MNRAS, 390, 567 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Neves, V., Bonfils, X., Santos, N. C., et al. 2013, A&A, 551, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Noyes, R. W., Hartmann, L. W., Baliunas, S. L., Duncan, D. K., & Vaughan, A. H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Parker, E. N. 1955, ApJ, 122, 293 [NASA ADS] [CrossRef] [Google Scholar]
- Perryman, M. A. C., & ESA 1997, The Hipparcos and Tycho catalogues, Astrometric and photometric star catalogues derived from the ESA Hipparcos Space Astrometry Mission, ESA SP, 1200 [Google Scholar]
- Queloz, D., Henry, G. W., Sivan, J. P., et al. 2001, A&A, 379, 279 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rauscher, E., & Marcy, G. W. 2006, PASP, 118, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., & Basri, G. 2007, ApJ, 656, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Basri, G., & Browning, M. 2009, ApJ, 692, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Joshi, N., & Goldman, B. 2012, AJ, 143, 93 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., Schüssler, M., & Passegger, V. M. 2014, ApJ, 794, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Riedel, A. R., Subasavage, J. P., Finch, C. T., et al. 2010, AJ, 140, 897 [NASA ADS] [CrossRef] [Google Scholar]
- Robertson, P., Mahadevan, S., Endl, M., & Roy, A. 2014, Science, 345, 440 [NASA ADS] [CrossRef] [Google Scholar]
- Rutten, R. G. M. 1984, A&A, 130, 353 [NASA ADS] [Google Scholar]
- Santos, N. C., Mayor, M., Naef, D., et al. 2000, A&A, 361, 265 [NASA ADS] [Google Scholar]
- Schmidt, S. J., Prieto, J. L., Stanek, K. Z., et al. 2014a, ApJ, 781, L24 [NASA ADS] [CrossRef] [Google Scholar]
- Schmidt, S. J., West, A. A., Bochanski, J. J., Hawley, S. L., & Kielty, C. 2014b, PASP, 126, 642 [NASA ADS] [Google Scholar]
- Schrinner, M., Petitdemange, L., Raynaud, R., & Dormy, E. 2014, A&A, 564, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sousa, S. G., Santos, N. C., Mayor, M., et al. 2008, A&A, 487, 373 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [Google Scholar]
- Stepien, K. 1993, in The Cosmic Dynamo, eds. F. Krause, K. H. Radler, & G. Rudiger, IAU Symp., 157, 141 [Google Scholar]
- Strassmeier, K., Washuettl, A., Granzer, T., Scheck, M., & Weber, M. 2000, A&AS, 142, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., GonzálezHernández, J. I., & Esposito, M. 2015, MNRAS, 452, 2745 [NASA ADS] [CrossRef] [Google Scholar]
- Tinney, C. G., McCarthy, C., Jones, H. R. A., et al. 2002, MNRAS, 332, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G. 2010, AJ, 140, 1158 [NASA ADS] [CrossRef] [Google Scholar]
- Tuomi, M., Anglada-Escude, G., Jenkins, J. S., & Jones, H. R. A. 2014, MNRAS, submitted [arXiv:1405.2016] [Google Scholar]
- van Altena, W. F., Lee, J. T., & Hoffleit, E. D. 1995, The general catalogue of trigonometric [stellar] parallaxes (New Haven, CT: Yale University Observatory) [Google Scholar]
- van Leeuwen, F. 2007, A&A, 474, 653 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaughan, A. H., & Preston, G. W. 1980, PASP, 92, 385 [NASA ADS] [CrossRef] [Google Scholar]
- Vaughan, A. H., Preston, G. W., & Wilson, O. C. 1978, PASP, 90, 267 [NASA ADS] [CrossRef] [Google Scholar]
- Ventura, P., Zeppieri, A., Mazzitelli, I., & D’Antona, F. 1998, A&A, 334, 953 [Google Scholar]
- Walkowicz, L. M., & Hawley, S. L. 2009, AJ, 137, 3297 [NASA ADS] [CrossRef] [Google Scholar]
- West, A. A., Hawley, S. L., Walkowicz, L. M., et al. 2004, AJ, 128, 426 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, O. C. 1968, ApJ, 153, 221 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, O. C. 1978, ApJ, 226, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Wright, J. T., Marcy, G. W., Butler, R. P., & Vogt, S. S. 2004, ApJS, 152, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Yadav, R. K., Christensen, U. R., Morin, J., et al. 2015, ApJ, 813, L31 [NASA ADS] [CrossRef] [Google Scholar]
- Zechmeister, M., & Kürster, M. 2009, A&A, 496, 577 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
Appendix A: Additional tables
Ccf and median Rphot for standards.
The Ca II H and K analysis for the HARPS M dwarf sample (minimal; full version available at the CDS).
Median values for Ccf and for Rphot for M dwarfs.
All Tables
Measured stellar parameters, and stellar parameters for the BT-Settl model, which best matches the observed spectrum around the Ca II H and K lines.
The 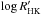 (fourth column) and rotation periods (fifth column) of the 38 M dwarfs for which both are known.
(fourth column) and rotation periods (fifth column) of the 38 M dwarfs for which both are known.
The Ca II H and K analysis for the HARPS M dwarf sample (minimal; full version available at the CDS).
All Figures
 |
Fig. 1 Median HARPS rest-frame spectrum of a representative mid-M dwarf (Gl 699) with overlays of the V, K (top panel), and H, R (middle panel) filters of the Mount Wilson system and of the photometric V band (bottom panel). |
| In the text | |
 |
Fig. 2 Median HARPS S-index against the Wright et al. (2004)S-index for the 31 targets in common. The solid line represents the linear least-square fit (Eq. (3)) between the two data sets, which we use to bring our S measurements onto the Mount Wilson scale. |
| In the text | |
 |
Fig. 3 The Ccf bolometric factor against B−V (top panel), I−K (middle panel), and V−K (bottom panel). Black dots represent the Ccf, M median, while crosses represent Ccf, Std. Solid lines represent the least-square fits of Eq. (9) for each color index. The top panel omits the 125 Ccf, Std(B−V) data points to more clearly display the Middelkoop (1982) and Rutten (1984) fits, represented by dashed and dotted lines. The validity ranges of these previous relationships are 0.45 <B−V< 1.50 and 0.3 <B−V< 1.6, respectively, and, for comparison, are extrapolated in this figure up to the color index of M dwarfs. |
| In the text | |
 |
Fig. 4 Spectrum of Gl 205 around the Ca II K line. The thin black and bold gray lines respectively represent the observed spectrum and a BT-Settl theoretical spectrum with Teff = 3800 [K], log (g [cm/s] ) = 4.5, and Fe/H = 0.0. The dotted curve depicts the K filter. The bold black line represents part of the spectral contribution through the triangular K filter used to estimate the photospheric contribution in a previous study (Hartmann et al. 1984). |
| In the text | |
 |
Fig. 5 The photospheric factor as a function of, from top to bottom, B−V, I−K, and V−K. Dots and crosses represent Rphot for M and GK-dwarfs, respectively. The solid lines are from Eq. (11) for each one of the color indexes. In the top panel, we compare our relationship for the B−V colors to the ones of Hartmann et al. (1984), Noyes et al. (1984), and Mittag et al. (2013, only from synthetic spectra) in dotted, dashed, and dash-dotted lines, respectively. Their range of validity is 0.44 <B−V< 0.82 for Hartmann et al. (1984) and Noyes et al. (1984), and 0.44 <B−V< 1.6 for Mittag et al. (2013). |
| In the text | |
 |
Fig. 6
|
| In the text | |
 |
Fig. 7
|
| In the text | |
 |
Fig. 8 Average |
| In the text | |
 |
Fig. 9 Histograms of the median |
| In the text | |
 |
Fig. 10 Median |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


