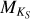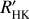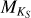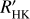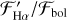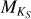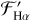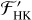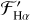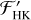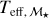| Issue |
A&A
Volume 671, March 2023
|
|
|---|---|---|
| Article Number | A162 | |
| Number of page(s) | 26 | |
| Section | Stellar atmospheres | |
| DOI | https://doi.org/10.1051/0004-6361/201937306 | |
| Published online | 22 March 2023 | |
Absolute Ca II H & K and H-alpha flux measurements of low-mass stars: Extending R′HK to M dwarfs
1
Universität Göttingen, Institut für Astrophysik und Geophysik,
Friedrich-Hund-Platz 1,
37077
Göttingen, Germany
e-mail: chris.j.marvin@gmail.com
2
School of Physics and Astronomy, Queen Mary, University of London,
327 Mile End Rd.
London, UK
3
Instituto de Astrofísica de Andalucía,
Glorieta de la Astronomía 1,
18008
Granada, Spain
4
University of Vienna, Department of Astrophysics,
Türkenschanzstrasse 17,
1180
Vienna, Austria
5
Max-Planck-Institut für Sonnensystemforschung,
Justus-von-Liebig-Weg-3,
37077
Goettingen, Germany
Received:
12
December
2019
Accepted:
25
September
2022
Context. With the recent surge of planetary surveys focusing on detecting Earth-mass planets around M dwarfs, it is becoming more important to understand chromospheric activity in M dwarfs. Stellar chromospheric calcium emission is typically measured using the R′HK calibrations of Noyes et al. (1984), which are only valid for 0.44 ≤ B – V ≤ 0.82. Measurements of calcium emission for cooler dwarfs B – V ≥ 0.82 are difficult because of their intrinsic dimness in the blue end of the visible spectrum.
Aims. We measure the absolute Ca II H & K and Hα flux of a sample of 110 HARPS M dwarfs and also extend the calibration of R′HK to the M dwarf regime using PHOENIX stellar atmosphere models.
Methods. We normalized a template spectrum with a high signal-to-noise ratio that was obtained by coadding multiple spectra of the same star to a PHOENIX stellar atmosphere model to measure the chromospheric Ca II H & K and Ha flux in physical units. We used three different Teff calibrations and investigated their effect on Ca II H & K and Hα activity measurements. We performed conversions of the Mount Wilson S index to R′HK as a function of effective temperature for the range 2300 K ≤ Teff ≤ 7200 K. Last, we calculated continuum luminosity χ values for Ca II H & K and Hα in the same manner as West & Hawley (2008) for –1.0 ≤ [Fe/H] ≤ + 1.0 in steps of Δ [Fe/H] = 0.5.
Results. We compare different Teff calibrations and find ΔΤeff ~ several 100 K for mid- to late-M dwarfs. Using these different Teff calibrations, we establish a catalog of log R′HK and ℱ′Hα/ℱbol measurements for 110 HARPS M dwarfs. The difference between our results and the calibrations of Noyes et al. (1984) is Δ log R′HK = 0.01 dex for a Sun-like star. Our χ values agree well with those of West & Hawley (2008). We confirm that the lower boundary of chromospheric Ca II H and K activity does not increase toward later-M dwarfs: it either stays constant or decreases, depending on the Teff calibration used. We also confirm that for Ha, the lower boundary of chromospheric flux is in absorption for earlier -M dwarfs and fills into the continuum toward later M dwarfs.
Conclusions. We confirm that we can effectively measure R′HK in M dwarfs using template spectra with a high signal-to-noise ratio. We also conclude that our calibrations are a reliable extension of previous R′HK calibrations, and effective temperature calibration is the main source of error in our activity measurements.
Key words: stars: activity / stars: low-mass / stars: late-type / stars: chromospheres
© The Authors 2023
 Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Open Access article, published by EDP Sciences, under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This article is published in open access under the Subscribe to Open model. Subscribe to A&A to support open access publication.
1 Introduction
M dwarfs comprise the majority of the stellar population, but their fundamental properties present challenges in measuring some of the most common activity indicators in the optical wavelength region, in particular, Ca II H and K, which lie in the bluer part of the visible spectrum. The cooler temperatures of M dwarfs imply that the bulk of their radiation lies toward longer wavelengths than for their FGK counterparts. M dwarfs are also intrinsically dimmer, which either decreases the signal-to-noise ratio (S/N) of observations or requires longer exposure times. Figure 1 demonstrates the differences in brightness and spectral energy distribution between a Sun-like G2 dwarf and a typical M4 dwarf. Additionally, telescope transmission and detector sensitivity are often higher in the redder wavelengths, which further exacerbates the problem of comparing their calcium flux with FGK stars in a consistent manner.
In what is known as the de facto standard of stellar activity surveys, Baliunas et al. (1995) monitored Ca II H and K lines of 111 main-sequence FGKM stars for several decades using the dimensionless measure called the Mount Wilson S index, or SMWO. This S index is a ratio of the Ca II H and K line core fluxes normalized to nearby continuum bands. However, the fluxes of the nearby continuum bands are not constant across spectral types (Vaughan & Preston 1980; Hartmann et al. 1984), which makes the comparison of stellar activity of different spectral types difficult with SMWO. To mitigate the color-dependence, SMWO is usually transformed into a physical quantity known as RHK, which is the ratio of the Ca II H and K surface flux to bolometric flux. A more desirable measure, known as 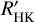 , subtracts the photospheric contribution RHK,phot, leaving only the chromospheric flux excess. Here, the prime denotes that the flux measurement is solely of chromospheric origin. The most common method of calculating
, subtracts the photospheric contribution RHK,phot, leaving only the chromospheric flux excess. Here, the prime denotes that the flux measurement is solely of chromospheric origin. The most common method of calculating 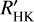 is the prescription derived by Noyes et al. (1984), which requires only SMWO and B – V to obtain
is the prescription derived by Noyes et al. (1984), which requires only SMWO and B – V to obtain 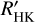 . However, this method is only valid for 0.44 ≤ B – V ≤ 0.82, which means that M dwarfs lie outside of this
. However, this method is only valid for 0.44 ≤ B – V ≤ 0.82, which means that M dwarfs lie outside of this 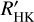 calibration range.
calibration range.
Despite these difficulties, measurements of Ca II H and K and Hα flux in M dwarfs have been performed before. Walkowicz & Hawley (2009) measured Ca II H and K equivalent widths for a sample of M3 dwarfs with the spectral subtraction method, using a stellar atmosphere model to correct for the photospheric flux contribution. The same technique was used by Montes et al. (1995b), who coined the term “spectral subtraction technique” and that has been performed as far back as Barden (1985) and Herbig (1985). In these studies, a synthetic spectral line profile is used as the photospheric contribution of a given star and is subtracted from an observed spectrum, resulting in a measurement of the chromospheric flux excess. Montes et al. (1995a) used the spectral subtraction technique to measure the chromospheric Ca II H and K flux excess in 28 FGK stars. Instead of using a photospheric spectrum, Cincunegui et al. (2007) measured the surface flux FHK of main-sequence stars from early-F down to M5 spectral types, and extrapolated the Noyes et al. (1984) photospheric contribution for the M dwarfs. To measure the fractional surface flux to bolometric flux of Ca II H and K, West & Hawley (2008) used the χ method, where multiplying an equivalent width by a factor χ, a continuum measurement nearby the calcium line, results in LCa II HK/Lbol. This study provided χ factors of Ca II H and K for the spectral range M0–M8. However, it did not provide a correction for the photospheric contribution. To extend the photospheric flux relation down to B – V = 1.6 with the spectral subtraction technique, Martínez-Arnáiz et al. (2011) used a synthetic template photospheric spectrum obtained by adding together spectra of nonactive stars of similar spectral type, and measured excess surface fluxes of 298 main-sequence stars ranging from F to M. Mittag et al. (2013) used PHOENIX model atmospheres to update the relations of Noyes et al. (1984) and measured 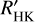 for 2133 main-sequence stars. Instead of using stellar models, Suárez Mascareño et al. (2015) used HARPS spectra of main-sequence FGKM dwarfs to derive their own
for 2133 main-sequence stars. Instead of using stellar models, Suárez Mascareño et al. (2015) used HARPS spectra of main-sequence FGKM dwarfs to derive their own 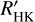 relations down to B – V ~ 1.9, and measured
relations down to B – V ~ 1.9, and measured 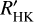 for 48 late-F to mid-M type stars. Scandariato et al. (2017) used the spectral subtraction technique with BT-Settl models as photospheric spectra for 71 early-M dwarfs and measured Ca II H, K, and Hα. Astudillo-Defru et al. (2017) formulated their own S-index calibration using HARPS spectra and used their own conversion from S-index to
for 48 late-F to mid-M type stars. Scandariato et al. (2017) used the spectral subtraction technique with BT-Settl models as photospheric spectra for 71 early-M dwarfs and measured Ca II H, K, and Hα. Astudillo-Defru et al. (2017) formulated their own S-index calibration using HARPS spectra and used their own conversion from S-index to 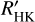 for 403 M dwarfs. Newton et al. (2017) found LHα/Lbol for 270 nearby M dwarfs using recomputed χΗα values of West & Hawley (2008).
for 403 M dwarfs. Newton et al. (2017) found LHα/Lbol for 270 nearby M dwarfs using recomputed χΗα values of West & Hawley (2008).
The relation between Ca II H, K, and Ha emission (or absorption) is also of much interest. Measuring the line profiles of 147 K7-M5 main-sequence stars, Rauscher & Marcy (2006) showed that Ca II H and K lines form at slightly different heights in the chromosphere, and that the equivalent width of Hα only correlates with Ca II H and K high widths. They also reported a possible threshold above which the lower and upper chromospheres become thermally coupled. Cincunegui et al. (2007) found a clear correlation between averaged Ca II H, K, and Hα with the strongest correlation for stars with the strongest emission. Conversely, studying stars individually and at different time intervals, Cincunegui et al. (2007) found no clear indication of how Hα varies with Ca II, with stars showing correlation, anti-corellation, or no correlation. Also observing individual time measurements for a sample of 30 M dwarfs, Gomes da Silva et al. (2011) found a positive correlation for the most active stars, and a tendency for a low or negative correlation in the least active stars. Walkowicz & Hawley (2009) found an initial deepening of Hα absorption for the stars that are least active in Ca II H and K before line filling and going into emission. Scandariato et al. (2017) found this same nonlinear relation between Ca II H, K, and Hα in 71 early-M dwarfs. Maldonado et al. (2017) separated older stars from younger and more active stars using the distinction of two branches identified by Martínez-Arnáiz et al. (2011). They found that the log-fluxes of Ca II H, K, and Hα relatively follow the same linear relation for stars spectral type F to M, which they identify as being the inactive branch, and found that stars deviating from this tend to be more active and younger, and thus lie on the active branch. More recently, Reiners et al. (2022) reported relations between chromospheric Ca II H, K, and magnetic flux, and also Hα emission and magnetic flux. Combining these relations, a relation between Ca II H, K, and Hα might be derived.
Many calibrations for 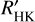 exist for the main sequence from early-F to late-M spectral type. Very few studies have used high S/N coadded spectra with the spectral subtraction technique (Boro Saikia et al. 2018; Perdelwitz et al. 2021). In fact, our work in this paper provided the M18 template-model method and measurements of Boro Saikia et al. (2018, see Sects. 2 and 3.2.2 of the aforementioned work). In this work, we measure Ca II H, K, and Hα activity with the spectral subtraction technique in a sample of 110 M dwarfs using high S/N template spectra that are flux-calibrated to PHOENIX stellar atmosphere models. The main difference of this study is that instead of taking the mean value of Ca II H and K flux measurements, we combine all available spectra and coadd them together before the flux measurement. This allows us to not just scale the Ca II H and K measurement to an absolute flux unit, but to fit the spectral energy distribution (SED) of the calcium line to a PHOENIX stellar atmosphere, and similarly for Hα. We compare three different effective temperature calibrations, and investigate their effect on Ca II H, K, and Hα activity measurements. We extend the
exist for the main sequence from early-F to late-M spectral type. Very few studies have used high S/N coadded spectra with the spectral subtraction technique (Boro Saikia et al. 2018; Perdelwitz et al. 2021). In fact, our work in this paper provided the M18 template-model method and measurements of Boro Saikia et al. (2018, see Sects. 2 and 3.2.2 of the aforementioned work). In this work, we measure Ca II H, K, and Hα activity with the spectral subtraction technique in a sample of 110 M dwarfs using high S/N template spectra that are flux-calibrated to PHOENIX stellar atmosphere models. The main difference of this study is that instead of taking the mean value of Ca II H and K flux measurements, we combine all available spectra and coadd them together before the flux measurement. This allows us to not just scale the Ca II H and K measurement to an absolute flux unit, but to fit the spectral energy distribution (SED) of the calcium line to a PHOENIX stellar atmosphere, and similarly for Hα. We compare three different effective temperature calibrations, and investigate their effect on Ca II H, K, and Hα activity measurements. We extend the 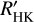 calibrations to 2300 K ≤ Teff ≤ 7200 K using PHOENIX stellar atmosphere models. We also provide a table of
calibrations to 2300 K ≤ Teff ≤ 7200 K using PHOENIX stellar atmosphere models. We also provide a table of 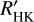 calibrations in this effective temperature range for different metallicities and surface gravities of main-sequence stars. Last, we compute the χ values of West & Hawley (2008) for Ca II H, K, and Hα for different metallicities from the PHOENIX model atmospheres.
calibrations in this effective temperature range for different metallicities and surface gravities of main-sequence stars. Last, we compute the χ values of West & Hawley (2008) for Ca II H, K, and Hα for different metallicities from the PHOENIX model atmospheres.
This paper is organized as follows: in Sect. 2 we briefly review the definition of Ca II H and K and Hα activity. In Sect. 3 we discuss the sample of stars, and we calibrate Teff using three different methods. We discuss the technique of measuring Ca II H, K, and Hα in M dwarfs with the subtraction method, using coadded template spectra and model photospheres. In Sect. 4 we discuss our Ca II H, K, and Hα measurements, provide extended 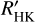 calibrations, and compare our calibrations with previous works. In Sect. 6 we summarize our work.
calibrations, and compare our calibrations with previous works. In Sect. 6 we summarize our work.
 |
Fig. 1 Model G2V spectra (yellow) and model M4V spectra (red). The flux scale of the G2V is displayed on the left, and the flux scale of the M4V is given on the right. The blue shaded area indicates the region of the Ca II H and K lines. |
2 Overview of the measurement equations
2.1 Mount Wilson S-index
The HKP-2 spectrophotometer installed at the Mount Wilson Observatory measures the Ca II H and K line cores with a triangular 1.09 Å full width at half maximum (FWHM) bandpass while simultaneously measuring two 20 Å wide bands; R, centered on 4001.07 Å, and V, centered on 3901.07 Å. To mimic the response of this instrument, Duncan et al. (1991) prescribed the following S index formula:
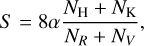 (1)
(1)
where NH, NK, NR, and NV are the counts in their respective bands, and α is a proportionality constant equating measurements made by the HKP-2 spectrophotometer to those made with HKP-1; Duncan et al. (1991) adopted the value α = 2.4. The factor of 8 arises from the 8:1 duty cycle between the line core and continuum bandpasses. Since its inception, the S-index has been the most widely used activity indicator for FGK stars.
2.2 Chromospheric Ca II H and K ratio
To convert the dimensionless SMWO into arbitrary surface flux FHK, Middelkoop (1982) and Rutten (1984) derived a continuum conversion factor Ccf. The arbitrary surface flux is defined as
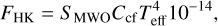 (2)
(2)
and its conversion into absolute units is given by
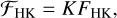 (3)
(3)
where ℱHK and K are in units of erg cm−2 s−1.
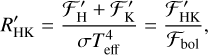 (4)
(4)
where 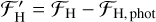 and
and 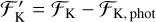 . Here,
. Here, 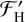 and
and 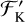 are the chromospheric fluxes, ℱH and ℱK are the surface fluxes, and ℱHphot and ℱKphot are the photospheric fluxes of the Ca II H and K lines, respectively. From a slight rearranging, Eq. (4) can be written as
are the chromospheric fluxes, ℱH and ℱK are the surface fluxes, and ℱHphot and ℱKphot are the photospheric fluxes of the Ca II H and K lines, respectively. From a slight rearranging, Eq. (4) can be written as
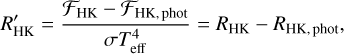 (5)
(5)
with the surface flux ratio given by
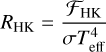 (6)
(6)
and the photospheric flux ratio given by
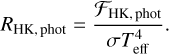 (7)
(7)
Typically, 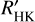 is measured through a conversion from the Mount Wilson S-index. The method pioneered by Noyes et al. (1984) calculates RHK using the equation
is measured through a conversion from the Mount Wilson S-index. The method pioneered by Noyes et al. (1984) calculates RHK using the equation
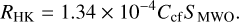 (8)
(8)
The quantity Ccf is a color-dependent conversion factor to remove the color-dependence of the SMWO, and Noyes et al. (1984) used the Middelkoop (1982) relation,
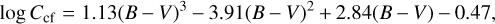 (9)
(9)
for 0.45 ≤ (B – V) ≤ 1.50. To calculate Rphot, Noyes et al. (1984) used the following relation:
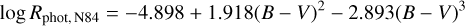 (10)
(10)
for 0.44 ≤ (B – V) ≤ 0.82. Equations (8) and (10) are then combined to obtain the chromospheric flux excess,
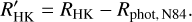 (11)
(11)
2.3 H-alpha
Hα can be measured in a similar way to RHK in Eq. (4), but substituting Hα for Ca II H and K. The chromospheric flux ratio of Hα might be defined as the surface flux subtracted by the photospheric flux, divided by the bolometric flux so that
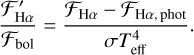 (12)
(12)
In brief, we measure the surface flux of each line, ℱline by integrating the flux of the template spectrum, normalized to a stellar atmosphere model, inside an integration window centered on the line core. We measure the photospheric flux, ℱline,phot, by integrating the flux of the stellar atmosphere model, with the same integration window centered on the line core. The bolometric flux ℱbol is determined from Teff, which is needed to obtain a proper stellar atmosphere model for a given star. We provide more detail in Sect. 3.
3 Case study: HARPS M dwarf sample
We used high-resolution archival spectra obtained with the HARPS spectrograph (Pepe et al. 2002) installed on ESO’s 3.6 m telescope in La Silla, Chile. The sample mainly consists of 102 targets from the HARPS GTO M dwarf sample (Bonfils et al. 2013)1. We also used data obtained for the Cool Tiny Beats survey (Anglada-Escudé et al. 2014; Berdinas et al. 2015)2, which adds the following four stars to the sample: GJ 160.2, GJ 180, GJ 570B, and GJ 317. Last, the following six M dwarfs with published planetary systems, and that are available in the ESO HARPS public archive, were added: GJ 676A, GJ 1214, HIP 12961, GJ 163, GJ 3634, and GJ 3740. Photometry values, mean radial velocities, proper motions, and parallaxes were acquired from SIMBAD (Wenger et al. 2000; see Table D.1).
PHOENIX grid parameter space.
3.1 High S/N template spectra
We used the HARPS-TERRA software (Anglada-Escudé & Butler 2012) for all available spectra on all stars in the sample. HARPS-TERRA is a sophisticated tool that matches individual spectra to a high S/N “template spectrum” using a least-squares fit to compute high-precision radial velocities. The high S/N template spectrum is obtained by coadding all individual spectra of a given star using the highest S/N spectrum as a basis spectrum. Pixel weighting, telluric masking, and outlier filtering are all implemented in the algorithm to assess and reduce systematic biases (see Sect. 2 in Anglada-Escudé & Butler 2012 for a much more detailed explanation). Because of this technique, the template spectrum for a star is essentially an averaged spectrum with median clipping. For each star, we obtained a high S/N template spectrum of each spectral order. We then used the corresponding spectral order that contains the chromospheric line of interest as the stellar observation spectrum.
After the initial run of HARPS-TERRA on all spectra of each target, we ran HARPS-TERRA a second time, excluding spectra that matched any of the following criteria: (1) program ID 60.A-9036(A), where spectra were acquired under nonoptimal conditions (an engineering run), (2) spectra reduced with cross-correlation function (CCF) masks earlier than M2 (the HARPS DRS pipeline uses an M2 mask for all M stars), and (3) spectra with radial velocity (RV) outliers determined by inspection. In general, looking at the RV time-series, spurious observation differences on the order of 1–10 km s−1 with respect to most observations are considered outliers. All three of the above criteria could negatively influence the resulting template spectra in a suboptimal way. After the second run of HARPS-TERRA, we corrected for the blaze function by running HARPS-TERRA a third time with the -useblaze option and the blaze file given by the ESO DRS BLAZE FILE keyword in the template spectrum file header. Finally, we obtained a blaze-corrected high S/N template spectrum for each star.
3.2 Photospheric flux from stellar atmosphere models
To calculate photospheric fluxes, we used a grid of PHOENIX-ACES stellar atmosphere models from the Göttingen Spectral Library3 (Husser et al. 2013). The parameters and step sizes of the grid are listed in Table 1. We calculated ℱHK, phot by setting a 1.09 Å FWHM triangular bandpass centered on the Ca II H and K lines and summing the flux. The triangular bandpass mimics the response of the H and K bands of the HKP-2 Mount Wilson spectrograph (Duncan et al. 1991: see Sect. 2.1). To measure the fractional chromospheric flux 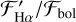 , we used a 5.0 Å wide rectangular bandpass centered on Hα.
, we used a 5.0 Å wide rectangular bandpass centered on Hα.
3.3 Surface flux from a high S/N template spectum
For a given star, the surface flux is measured from the high S/N template spectrum computed in Sect. 3.1. In the left panel of Fig. 2, we plot a single HARPS observation of the Ca II K line of an M 1.5 star. Because HARPS has a high resolution of R ~ 110 000, the S/N in the region near the calcium line is low, as shown in the figure. The right panel of Fig. 2 shows the same line of the same star, but this time, with 47 observations coadded together. This demonstrates the considerable S/N improvement obtained by coadding spectra.
For a single chromospheric line of a given star, the entire template order spectrum is normalized to a PHOENIX model spectrum via a first-degree polynomial least-squares fit, namely ℱ(λ) = af (λ) + b. The PHOENIX spectra were bilinearly interpolated to a precision of ΔTeff = 1K and Δ[Fe/H] = 0.01 dex using the stellar parameters chosen by the methods outlined in Sect. 3.5 and listed in Table D.2. For the Ca II K line, we used order 6, for the Ca II H line, we used order 8, and for Hα, we used order 68. Before normalizing the template spectrum to the PHOENIX spectrum, we converted counts into energy, shifted the spectrum to rest wavelengths, and then transformed wavelengths to vacuum wavelengths. We masked the active lines, as well as Hϵ at 3971.2 Å. To reduce the influence of low S/N at the spectral order edges from the blaze function, we also masked the outer 10% of each order. We took the sum of the line flux in the same manner as in Sect. 3.2.
Figure 3 demonstrates this normalization of a high S/N template spectrum of an early-M dwarf normalized to a PHOENIX atmosphere model around the Ca II K line. The high S/N template spectrum consists of all available spectra coadded and flux-calibrated to the PHOENIX model atmosphere. Similarly, Fig. 4 shows this normalization of an M dwarf with Hα in absorption, while Fig. 5 shows another M dwarf with Hα in emission.
 |
Fig. 2 Ca II K line of an M1.5 star. Left: spectrum of a single HARPS observation. Right: template spectrum consisting of 47 coadded spectra of the same star. |
 |
Fig. 3 High S/N template spectrum of an early-M dwarf normalized to a PHOENIX atmosphere model. The solid red line is the high S/N template spectrum, while the dashed black line is the PHOENIX model atmosphere. The blue shaded region shows the chromospheric emission. The dotted lines indicate the 1.09 Å FWHM triangular bandpass used to integrate the Ca II H and K lines. |
 |
Fig. 4 High S/N template spectrum of an M dwarf with Hα in absorption normalized to a PHOENIX atmosphere model. The solid red line is the high S/N template spectrum, while the dashed black line is the PHOENIX model atmosphere. The vertical dotted lines indicate a 5.0 Å integration region. |
 |
Fig. 5 High S/N template spectrum of an active M dwarf with Hα in emission normalized to a PHOENIX atmosphere model. The solid red line is the high S/N template spectrum, while the dashed black line is the PHOENIX model atmosphere. The vertical dotted lines indicate the 5.0 Å integration region of Hα. |
3.4 S-index comparison
As a sanity check, we compared the S -index values of our sample (for their values, we refer to Boro Saikia et al. 2018 and for the treatment of how they were calculated) with those of Astudillo-Defru et al. (2017) in Fig. 6. Although it agrees, the linear fit slightly overestimates the values of Astudillo-Defru et al. (2017) compared to Boro Saikia et al. (2018) for S values below 2,
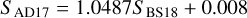 (13)
(13)
3.5 Stellar parameters
For an accurate stellar atmosphere model to normalize a template spectrum to, we must first determine a set of stellar parameters for each star in a self-consistent manner. Here we describe the different calibrations we used to determine effective temperature and how we determined metallicity.
 |
Fig. 6 SAD17 of Astudillo-Defru et al. (2017) vs our work SBS18 (Boro Saikia et al. 2018). Top: entire range of the sample. Bottom: same sample with zoomed in axes. The dotted line shows the 1:1 relation. |
Effective temperature
For each star in the sample, we estimated Teff using three different calibrations. The first and second calibration used the combined relation of spectral type, effective temperature, mass, and radius from Kenyon & Hartmann (1995) and Golimowski et al. (2004). This same combination of calibrations was used by Reiners & Basri (2007), Shulyak et al. (2011), and Reiners & Mohanty (2012). The first method simply converts spectral type into effective temperature. We denote effective temperatures obtained from this method with Teff, SpT. The second method uses the 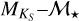 calibration of Delfosse et al. (2000) to first obtain a mass ℳ⋆ from the absolute
calibration of Delfosse et al. (2000) to first obtain a mass ℳ⋆ from the absolute 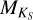 magnitude, and then uses the former relation to convert ℳ⋆ into Teff. We denote effective temperatures obtained from this method with
magnitude, and then uses the former relation to convert ℳ⋆ into Teff. We denote effective temperatures obtained from this method with 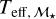 . The third method adopts Teff values obtained by Maldonado et al. (2015) of 53 stars in the HARPS M dwarf GTO sample. We denote effective temperatures from this study with Teff, M15.
. The third method adopts Teff values obtained by Maldonado et al. (2015) of 53 stars in the HARPS M dwarf GTO sample. We denote effective temperatures from this study with Teff, M15.
Metallicity
Maldonado et al. (2015) also calculated metal-licities of the same 53 targets using the pseudo-equivalent width (PEW) technique of Neves et al. (2014), who also calculated metallicities for the entire HARPS GTO M dwarf sample. Maldonado et al. (2015) reported that their results agreed well overall with those of Neves et al. (2014), and we therefore adopted the metallicities of Neves et al. (2014) for the sample completeness. Although effective temperatures were also calculated, the authors noted that their Teff values are systematically underestimated compared with other works; therefore, we did not adopt the Teff values of Neves et al. (2014). For two stars not listed in Neves et al. (2014, GJ 570B and GJ 180), we used the conversion of 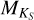 and V – K to [Fe/H] in Neves et al. (2012). We note that the difference in metallicities between Neves et al. (2012) and Maldonado et al. (2015) can be up to Δ[Fe/H] ± 0.2. However, this difference is much smaller than the resolution of our grid of models, Δ[Fe/H] ± 0.5. For stars with no
and V – K to [Fe/H] in Neves et al. (2012). We note that the difference in metallicities between Neves et al. (2012) and Maldonado et al. (2015) can be up to Δ[Fe/H] ± 0.2. However, this difference is much smaller than the resolution of our grid of models, Δ[Fe/H] ± 0.5. For stars with no 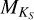 or V – KS measurements, we assumed solar metallicity. For all stars in the sample, we constrained the surface gravity to log(ɡ) = 5.0, which is a typical value for M dwarfs. The stellar parameters we used are listed in Table D.2.
or V – KS measurements, we assumed solar metallicity. For all stars in the sample, we constrained the surface gravity to log(ɡ) = 5.0, which is a typical value for M dwarfs. The stellar parameters we used are listed in Table D.2.
The top panel of Fig. 7 shows Teff of the three methods we used as a function of 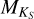 , with their metallicity represented by color. For Teff,SpT, we were able to calibrate 110 stars. With
, with their metallicity represented by color. For Teff,SpT, we were able to calibrate 110 stars. With 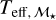 , we were able to calibrate 99 stars, and for Teff,M15, there are 49 stars. Temperatures of the same star are connected with a solid vertical line. In the lower panel of Fig. 7, we show the residuals of the different sources of Teff. As is evident from both panels, the Teff determined by different methods disagrees to some extent, and this becomes much more pronounced for stars with
, we were able to calibrate 99 stars, and for Teff,M15, there are 49 stars. Temperatures of the same star are connected with a solid vertical line. In the lower panel of Fig. 7, we show the residuals of the different sources of Teff. As is evident from both panels, the Teff determined by different methods disagrees to some extent, and this becomes much more pronounced for stars with 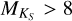 . The mean of all ΔTeff values is 176 K. For ΔTeff values with
. The mean of all ΔTeff values is 176 K. For ΔTeff values with 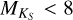 , the mean difference drops to 122 K. The mean of ΔTeff values for
, the mean difference drops to 122 K. The mean of ΔTeff values for 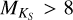 increases to 363 K. Most of these values with
increases to 363 K. Most of these values with 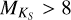 belong to
belong to  .
.
We note that metallicity has an effect on the Teff determination. The largest scatter in ΔTeff is between Teff,SpT and Teff,M15. The determination of the spectral type depends on line ratios that are sensitive to both Teff and [Fe/H]. Moreover, Maldonado et al. (2015) determined Teff simultaneously with metallicity, However, metallicity does not have much impact when determining Teff from 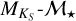 , as infrared absolute magnitudes are less sensitive to metallicity (Delfosse et al. 2000). For
, as infrared absolute magnitudes are less sensitive to metallicity (Delfosse et al. 2000). For 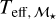 , since ℳ⋆ is determined from a polynomial as a function of
, since ℳ⋆ is determined from a polynomial as a function of 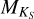 , we expect to see a clear relation between Teff and
, we expect to see a clear relation between Teff and 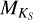 . Whether
. Whether 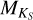 actually is such a precise indicator of Teff is beyond the context of this study. Regardless, accurate effective temperatures of M dwarfs remain elusive; see Mann et al. (2015) and Passegger et al. (2016) for more thorough analyses of the current state of M dwarf stellar parameter determination.
actually is such a precise indicator of Teff is beyond the context of this study. Regardless, accurate effective temperatures of M dwarfs remain elusive; see Mann et al. (2015) and Passegger et al. (2016) for more thorough analyses of the current state of M dwarf stellar parameter determination.
 |
Fig. 7 Effective temperature Teff of the stellar sample using different Teff determination methods, which are shown by different plot symbols. Top: effective temperature Teff as a function of absolute magnitude |
4 Results
4.1 Chromospheric Ca II H and K flux
We plot the chromospheric Ca II H and K flux normalized to bolometric flux, log 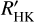 , as a function of absolute magnitude
, as a function of absolute magnitude 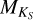 in Fig. 8. log
in Fig. 8. log 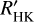 was calculated using the spectral subtraction technique outlined in Sect. 3, following Eq. (4). We estimated Teff using the three different methods described in Sect. 3.5 and for each Teff, calculated log
was calculated using the spectral subtraction technique outlined in Sect. 3, following Eq. (4). We estimated Teff using the three different methods described in Sect. 3.5 and for each Teff, calculated log 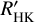 . The plot legend contains the colors of each Teff calibration. We connect log
. The plot legend contains the colors of each Teff calibration. We connect log 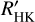 measurements of the same star but different effective temperatures with a solid vertical line. Additionally, we plot stars with known planetary systems with open symbols, and stars without known planetary systems with closed symbols. Stars without Hα in emission are plotted with a circle and stars exhibiting Hα emission with a triangle.
measurements of the same star but different effective temperatures with a solid vertical line. Additionally, we plot stars with known planetary systems with open symbols, and stars without known planetary systems with closed symbols. Stars without Hα in emission are plotted with a circle and stars exhibiting Hα emission with a triangle.
4.1.1 Teff,SpT calibration
For 110 stars we have spectral type information and are able to measure log 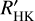 using the spectral type to Teff conversion, Teff,SpT. Of these stars, 13 exhibit Hα emission, and 19 have known planetary systems. The earliest-M dwarfs with
using the spectral type to Teff conversion, Teff,SpT. Of these stars, 13 exhibit Hα emission, and 19 have known planetary systems. The earliest-M dwarfs with 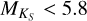 have higher values of log
have higher values of log 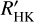 , between –4.8 and –4.5. There is a drop in the lower boundary of activity levels near
, between –4.8 and –4.5. There is a drop in the lower boundary of activity levels near 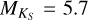 , where values range from –5.3 < log
, where values range from –5.3 < log 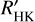 . After this drop, the sequence of lower-activity stars has no apparent drop, and log
. After this drop, the sequence of lower-activity stars has no apparent drop, and log 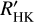 stays between –5.5 and –4.9. Stars exhibiting Hα emission tend to have much higher log
stays between –5.5 and –4.9. Stars exhibiting Hα emission tend to have much higher log 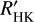 values than those that do not exhibit Hα emission. Their measured activity levels are log
values than those that do not exhibit Hα emission. Their measured activity levels are log 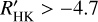 and can be as high as log
and can be as high as log 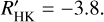 .
.
4.1.2 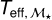 calibration
calibration
For 99 stars, we have 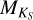 measurements and can measure log
measurements and can measure log 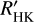 using the
using the 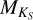 to mass to Teff calibration
to mass to Teff calibration 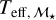 . Of these stars, 13 exhibit Hα emission, and 16 have known planetary systems. Unlike log
. Of these stars, 13 exhibit Hα emission, and 16 have known planetary systems. Unlike log 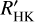 measured with Teff, SpT, the lower boundary of activity for
measured with Teff, SpT, the lower boundary of activity for 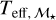 decreases with
decreases with 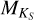 . This relation is expected because in this case,
. This relation is expected because in this case, 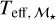 is calibrated using
is calibrated using 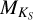 . This does not have a dramatic effect on log
. This does not have a dramatic effect on log 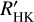 values until
values until 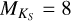 . At higher
. At higher 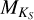 , the difference in log
, the difference in log 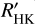 can be as high as 1.3 dex, and this arises from the large differences in Teff seen in Fig. 7. However, even though the measured values of log
can be as high as 1.3 dex, and this arises from the large differences in Teff seen in Fig. 7. However, even though the measured values of log 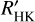 using
using 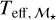 are much lower, stars with Hα in emission still have significantly higher log
are much lower, stars with Hα in emission still have significantly higher log 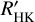 values than their counterparts.
values than their counterparts.
4.1.3 Teff,M15 calibration
For 49 stars with adopted values from Maldonado et al. (2015), we are able to measure log 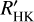 using Teff,M15. Of these stars, 4 exhibit Hα emission, and 9 have known planetary systems. Similar with the other Teff calibrations, the lower level of log
using Teff,M15. Of these stars, 4 exhibit Hα emission, and 9 have known planetary systems. Similar with the other Teff calibrations, the lower level of log 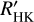 decreases from −4.5 to −5.4 between
decreases from −4.5 to −5.4 between 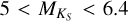 . There are only three stars with
. There are only three stars with 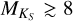 , and they tend to agree more with Teff,SpT values than
, and they tend to agree more with Teff,SpT values than 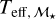 .
.
We list the individual log 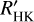 measurements in Table D.3. The largest differences of log
measurements in Table D.3. The largest differences of log 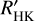 values occur at the latest spectral types where it is difficult to determine a consistent Teff using a color, magnitude, or spectral type relation. For the entire sequence of stars, the mean of
values occur at the latest spectral types where it is difficult to determine a consistent Teff using a color, magnitude, or spectral type relation. For the entire sequence of stars, the mean of 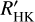 is 0.17 dex. At
is 0.17 dex. At 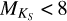 , the mean of
, the mean of 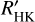 is only 0.10 dex, however for
is only 0.10 dex, however for 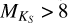 , the mean is 0.56 dex. The star with the highest difference in log
, the mean is 0.56 dex. The star with the highest difference in log 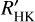 is GJ 1002, which has
is GJ 1002, which has 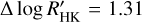 dex. This is because of its wide range of Teff calibrations, with ΔTeff = 534 K.
dex. This is because of its wide range of Teff calibrations, with ΔTeff = 534 K.
 |
Fig. 8 Fractional chromospheric Ca II H and K flux normalized to bolometric flux on a logarithmic scale, log |
 |
Fig. 9 Fractional chromospheric Ha flux, |
4.2 Chromospheric H-alpha flux
In Fig. 9, we correct for the photospheric contribution and plot the chromospheric flux ratio of Hα, 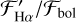 . This is not on a logarithmic scale, unlike how we plot log
. This is not on a logarithmic scale, unlike how we plot log 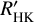 . This is because the sign of
. This is because the sign of 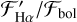 indicates whether the line is in emission or absorption. Values of
indicates whether the line is in emission or absorption. Values of 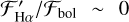 indicate that Ha is filled to the continuum. Values
indicate that Ha is filled to the continuum. Values 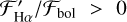 indicate that Ha is in emission, as in Fig. 5, while values
indicate that Ha is in emission, as in Fig. 5, while values 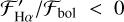 indicate that Hα is in absorption as in Fig. 4. The plotting colors and symbols are the same as used in Fig. 8.
indicate that Hα is in absorption as in Fig. 4. The plotting colors and symbols are the same as used in Fig. 8.
For stars with Ha in absorption, 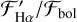 increases toward a filling-in of the continuum toward larger
increases toward a filling-in of the continuum toward larger 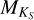 . The stars in which Hα is in emission tend to have significantly higher
. The stars in which Hα is in emission tend to have significantly higher 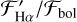 than stars for which Hα is near the continuum level. We note that the absorption of Ha stays in a relatively narrow range. Values of
than stars for which Hα is near the continuum level. We note that the absorption of Ha stays in a relatively narrow range. Values of 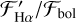 are
are 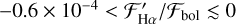 . However, for stars in which Hα is in emission, the range of
. However, for stars in which Hα is in emission, the range of 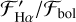 is on the order of several 10−4. larger
is on the order of several 10−4. larger 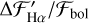 due to the different Teff calibrations. Stars for which Hα is in emission also have significantly higher values of
due to the different Teff calibrations. Stars for which Hα is in emission also have significantly higher values of 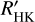 than those in which Hα is not in emission.
than those in which Hα is not in emission.
4.3 H-alpha versus calcium II H and K flux
We plot chromospheric flux values of Hα against Ca II H and K in Figs. 10 and 11. Figure 10 contains flux in absolute flux units, and therefore contains negative values of Hα that correspond to absorption. Figure 11 shows flux on a log-scale and excludes inactive stars with Hα in absorption. Symbols and markers are the same as in Figs. 8 and 9.
Figure 10 shows Hα only in absoprtion 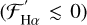 , and a decreasing trend is apparent where it goes deeper into absorption with increasing
, and a decreasing trend is apparent where it goes deeper into absorption with increasing 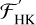 . The trend appears to be linear from
. The trend appears to be linear from 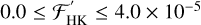 erg cm−2 s−1. When Hα is in emission, the trend of
erg cm−2 s−1. When Hα is in emission, the trend of 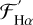 increases with increasing
increases with increasing 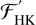 . This deepening of the Hα line before filling-in and going into emission was reported by Walkowicz & Hawley (2009) and Scandariato et al. (2017). Scandariato et al. (2017) only observed a decreasing trend from
. This deepening of the Hα line before filling-in and going into emission was reported by Walkowicz & Hawley (2009) and Scandariato et al. (2017). Scandariato et al. (2017) only observed a decreasing trend from 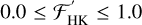 . In Fig. 11, we overplot as a dashed red line a linear fit that we find to be
. In Fig. 11, we overplot as a dashed red line a linear fit that we find to be
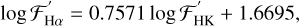 (14)
(14)
with R2 = 0.706.
 |
Fig. 10 Fractional chromospheric Hα flux, |
 |
Fig. 11 Fractional chromospheric Hα flux, |
4.4 Ca II H and K surface flux calibrations
We compared calibrations of the continuum conversion factor Ccf (used for measuring FHK) of other studies with Ccf calibrations using the PHOENIX model grid. To derive our Teff dependent conversion factor Ccf, we combined Eqs. (2), (3), and 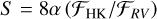 , to arrive at
, to arrive at
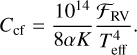 (15)
(15)
Using values of α = 2.4 and K = 1.07 × 106 erg cm−2 s−1 (Hall et al. 2007), we then obtained
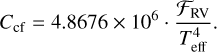 (16)
(16)
The top panel of Fig. 12 shows our computed log Ccf as a function of Teff. Different values of [Fe/H] are shown as a function of color, and different values of log(ɡ) are plotted with different symbols. For Teff > 5000 K, we used log(ɡ) values of 4.0 and 4.5, and for Teff ≤ 5000 K, we used log(ɡ) values of 4.5 and 5.0. A fifth-order polynomial,
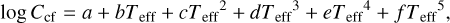 (17)
(17)
was fit to all of the points and overplotted as a solid red line. The coefficients of this polynomial are listed in Table 2. We provide the computed PHOENIX stellar atmosphere log Ccf values in Table D.4 for the entire model grid.
Even for the wide range of metallicity values, the spread of log Ccf is not too wide for Teff > 3400 K. For these higher temperatures, log Ccf varies by 0.25 dex at most. At Teff < 3100 K, metallicity begins to contribute to a larger spread of log Ccf values, around 0.5 dex. This spread of log Ccf increases to 1.4 dex as Teff decreases to 2300 K.
The bottom panel of Fig. 12 compares the polynomial fit in the upper panel with previously published log Ccf-Teff relations (see Appendix A for details about the relations).
For the relations of the other authors, we plot the range for which the relations are calibrated. Our log Ccf values agree well with those from other studies for Teff ≳ 4100 K to ~0.1 dex. At temperatures cooler than 4100 K, our log Ccf values start to deviate from those of Middelkoop (1982); Rutten (1984); Cincunegui et al. (2007); Suárez Mascareño et al. (2015); and Astudillo-Defru et al. (2017); our values are higher for cooler temperatures. For temperatures cooler than Teff = 4100 K, log Ccf diverges by more than 0.2 dex. The difference between our relation and Cincunegui et al. (2007) increases to 0.4 dex at Teff = 3100 K, while the difference between our relation and both Suárez Mascareño et al. (2015) and Astudillo-Defru et al. (2017) increases to 0.8 dex at Teff = 3000 K. This discrepency in log Ccf might be attributed to the use of empirical calibrations with these studies as opposed to this work using stellar models (see Sect. 5).
As an example, when we take for the Sun B – V = 0.642 and SMWO = 0.164, the Noyes et al. (1984) calibration of RHK will give us log RHK = −4.62. Our calibration using Eq. (17) results in log RHK = −4.60. This means that for a Sun-like star, Δ log RHK = 0.02.
 |
Fig. 12 Different log Ccf calibrations as a function of Teff. The approximate spectral type is shown on the top axis. Top: PHOENIX stellar atmosphere models with different [Fe/H] and log(ɡ), where [Fe/H] is indicated by color and log(ɡ) indicated by symbol. The solid red line indicates a fifth-order polynomial fit. Bottom: calibrations of log Ccf from other works where only the valid calibration region is plotted. Overplotted in red is the same fifth-order polynomial fit from the top panel. |
log Ccf vs. Teff fifth-order polynomial fit coefficients.
4.5 Ca II H and K photospheric flux calibrations
In the top panel of Fig. 13, we plot log RHK,phot as a function of Teff, computed as described in Sect. 3.2. The colors and symbols are assigned in the same manner as in Fig. 12. A fifth-order polynomial fit
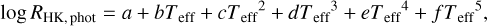 (18)
(18)
is overplotted as a solid red line, and coefficients of this polynomial are listed in Table 3. Similarly as with log Ccf, metallicity has an effect on the spread of log RHK,phot values. The spread increases at 4000 ≤ Teff ≤ 5100 K and Teff ≤ 3800 K. At Teff > 5100 K, the spread of log RHK,phot values is lower than 0.2 dex. The spread increases from Teff = 5100 K to Teff = 4200 K, where it is about 0.4 dex. At Teff = 3100 K, the spread of log RHK,phot is 0.6 dex. Here, a change in metallicity of ±0.5 dex can result in a Δ log RHK,phot ~ 0.1 dex. At Teff < 3300 K, the spread continually increases with lower temperatures to almost 1.6 dex at Teff = 2400 K. At Teff = 2400 K., a change in metal-licity of ±0.5 can result in a Δ log RHK,phot ~ 0.5 dex. We provide the computed PHOENIX stellar atmosphere log RHK,phot values in Table D.4 for the entire model grid.
In the bottom panel of Fig. 13, we compare our log RHK,phot-Teff polynomial fit with previous literature relations (see Appendix B for details about the relations). The higher log RHK,phot values of both Mittag et al. (2013) and our work in comparison with Noyes et al. (1984) and Suárez Mascareño et al. (2015) are clear. The difference between Mittag et al. (2013) and Noyes et al. (1984) is ~0.3 dex, and the difference between our work and Noyes et al. (1984) ranges from 0.4 to 0.5 dex. The difference between our work and Suárez Mascareño et al. (2015) can be as large as 1.3 dex at Teff = 3000 K. Our values of log RHK,phot agree very well with those of Astudillo-Defru et al. (2017), with the largest difference being 0.12 dex at Teff = 4800 K, and other differences on the order of 0.1 dex at Teff = 3500,3400, and 3100 K.
Our log RHK,phot calibration has much higher values than the calibration used by Noyes et al. (1984). This systematic offset was also observed by Astudillo-Defru et al. (2017), who also used synthetic spectra to obtain an RHK,phot calibration. While the exact reason for this offset is not known (see the discussion in Astudillo-Defru et al. 2017), an offset correction can be applied to scale our log RHK,phot calibration to Noyes et al. (1984),
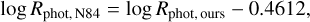 (19)
(19)
where 0.4612 is the offset correction. This simple offset correction scales our log RHK phot values to Noyes et al. (1984) values in their valid calibration region, so that our calibration can be used to obtain comparable results to Noyes et al. (1984), and also to extend the calibration to later-type stars. We note that although they are widely used, the Noyes et al. (1984) calibrations are only calibrated in the range 5300 K ≲ Teff ≲ 6300 K.
If we take the same B – V and SMWO values as in Sect. 4.4, the Noyes et al. (1984) calibration of RHK phot will give us log RHK phot = −4.92. This will give us an activity measurement of log 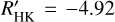 . Our calibration using Eq. (19) results inlog RHK, phot = −4.89, which gives us log
. Our calibration using Eq. (19) results inlog RHK, phot = −4.89, which gives us log 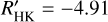 . Then, for a Sun-like star, Δ log RHK phot = 0.03 and
. Then, for a Sun-like star, Δ log RHK phot = 0.03 and 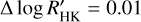 .
.
 |
Fig. 13 Different log RHK,phot as a function of Teff. The approximate spectral type is shown on the top axis. Top: PHOENIX stellar atmosphere models with different [Fe/H] and log(ɡ), where [Fe/H] is indicated by color and log(ɡ) indicated by symbol. The solid red line indicates a fifth-order polynomial fit. Bottom: calibrations of log RHK,phot from other works where only the valid calibration region is plotted. Overplotted in red is the same fifth-order polynomial fit from the top panel. |
log RHK,phot vs. Teff fifth-order polynomial fit coefficients.
4.6 χ-factor
The χ-factor provides a method to convert the equivalent width of Ca II H and K into RHK and Ha indto 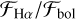 in M dwarfs. Walkowicz et al. (2004) define the χ factor as the ratio of the Hα line continuum luminosity to bolometric luminosity, namely
in M dwarfs. Walkowicz et al. (2004) define the χ factor as the ratio of the Hα line continuum luminosity to bolometric luminosity, namely
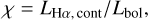 (20)
(20)
where LHα,cont is the luminosity of a selected continuum region near Hα. West & Hawley (2008) extend the selection of χ values to higher-order Balmer lines and Ca II H and K. When multiplied by the equivalent width of the respective line, we can obtain the ratio of the line luminosity to the bolometric luminosity,
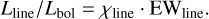 (21)
(21)
For both Ca II H and K and Hα, we calculated the χ values of West & Hawley (2008) of the PHOENIX model grid for M dwarf Teff values and different metallicities, constraining log(ɡ) = 5.0. For Ca II H and K, we used the continuum regions given by Walkowicz & Hawley (2009), and for Hα, we used the continuum regions given by West & Hawley (2008). We plot these with the values listed in West & Hawley (2008) in Fig. 14, with Ca II H and K in the top panel and Hα in the lower panel. We provide the computed χline values in Table D.5.
Similar to Fig. 12, the continuum values diverge as Teff decreases for different metallicities. For χCaIIHK, a metallicity of [Fe/H] = −0.5 agrees best with West & Hawley (2008). We note that all of our χCaIIHK values are higher for M3 and M4 spectral types. However, this difference is very small (on the order of 10−7), and the error bars of West & Hawley (2008) are much smaller than the spread of χCaIIHK by metallicity. Our χ Hα values also agree well with West & Hawley (2008), especially for [Fe/H] = 0.0. Our χ Hα values deviate from West & Hawley (2008) at spectral types M4 and earlier. However, like with χCaIIHK the difference is small, on the order of 10−6.
4.7 Proxima Centauri
Proxima Centauri, or GJ 551, is the only star in this study that exhibits Hα emission and is a known planet host (Anglada-Escudé et al. 2016). This indicator of high activity is consistent with the findings of Ribas et al. (2016), who reported that Proxima b receives ten times more far-UV flux than the current Earth.
Except for the Teff,M15 calibration of Proxima Centauri (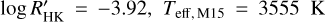 ), we did not measure log
), we did not measure log 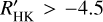 for any planet hosts. However, this particular value may be overestimated. For example, for Proxima Centauri, Boyajian et al. (2012) reported Teff ~ 3050 K, and the calibration of Teff,SpT = 2900 K, which has log
for any planet hosts. However, this particular value may be overestimated. For example, for Proxima Centauri, Boyajian et al. (2012) reported Teff ~ 3050 K, and the calibration of Teff,SpT = 2900 K, which has log 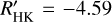 . The similarities between these two temperatures mean that log
. The similarities between these two temperatures mean that log 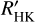 of Proxima Centauri probably sits closer to approximately −4.5 than −3.9.
of Proxima Centauri probably sits closer to approximately −4.5 than −3.9.
 |
Fig. 14 Top: continuum flux normalized to bolometric flux of Ca II H and K, χ Ca II HK, as a function of Teff using PHOENIX stellar atmospheres with log(ɡ) = 5.0 and different metallicities. Values from West & Hawley (2008) are plotted in gray. Bottom: continuum flux normalized to bolometric flux of Hα, χHα, as a function of Teff using PHOENIX stellar atmospheres with log(ɡ) = 5.0 and different metallicities. Values from West & Hawley (2008) are plotted in gray. |
5 Discussion
With the exception of Proxima Centauri, which exhibits Hα in emission, the remaining known planet hosts exhibit low activity. This is expected as activity can mimic planetary signals and cause incorrect planet detections, so that stars with lower activity stars are preferred for planet searches.
There is a divergence of log Ccf values between our work and other works that begins at the start of the M dwarf sequence near 4000 K. Middelkoop (1982); Rutten (1984); Cincunegui et al. (2007); Suárez Mascareño et al. (2015), and Astudillo-Defru et al. (2017) used observational data to calibrate log Ccf as a function of B – V, while we used stellar models as a function of Teff. The discrepency might be due to an insufficient (B – V) – Teff relation in this region. However, our χ Ca II HK values agree with those of West & Hawley (2008), whose relations were also derived from observational data. This gives us confidence that the PHOENIX models are accurate in the continuum near the Ca II H and K lines, although the continuum region of χ Ca II HK differs from the region used in log Ccf.
Our log RHK,phot values remain higher than log RHK,phot values obtained using observational data (Noyes et al. 1984; Suárez Mascareño et al. 2016). As noted by Mittag et al. (2013), this difference arises from the integration region of the calcium line. Our work and Mittag et al. (2013) both integrated the entire photospheric line. The log RHK,phot relation used by Noyes et al. (1984) is that of Hartmann et al. (1984), who only estimated the flux outside of the line core exterior to the H1 and K1 points: they assumed the flux of the line core to be zero. The log RHK,phot relation derived by Suárez Mascareño et al. (2015) also masks the line core: 0.7 Å for FGK stars, and 0.4 Å for M stars. For this reason, we provide the correction factor in Eq. (19) to keep the calculated 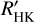 values consistent with historical published measurements based on Noyes et al. (1984). Moreover, although both use PHOENIX models, our log RHK phot values are still higher than those of Mittag et al. (2013). One reason for this difference might be the models that were used; Mittag et al. (2013) used models computed in non-local thermo-dynamic equilibrium, while we used models computed in local thermodynamic equilibrium.
values consistent with historical published measurements based on Noyes et al. (1984). Moreover, although both use PHOENIX models, our log RHK phot values are still higher than those of Mittag et al. (2013). One reason for this difference might be the models that were used; Mittag et al. (2013) used models computed in non-local thermo-dynamic equilibrium, while we used models computed in local thermodynamic equilibrium.
Astudillo-Defru et al. (2017) measured 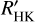 of 403 stars of the HARPS M dwarf sample. They extended the technique of Noyes et al. (1984) by calibrating their own log Ccf using 14 G or K and M dwarf pairs and use BT-Settl models to arrive at RHK,phot through an S-index conversion. Although we used different methods to arrive at the measurement of
of 403 stars of the HARPS M dwarf sample. They extended the technique of Noyes et al. (1984) by calibrating their own log Ccf using 14 G or K and M dwarf pairs and use BT-Settl models to arrive at RHK,phot through an S-index conversion. Although we used different methods to arrive at the measurement of 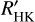 in M dwarfs, we find our results to be consistent with Astudillo-Defru et al. (2017). Namely, our Fig. 8 exhibits a very similar lower envelope of
in M dwarfs, we find our results to be consistent with Astudillo-Defru et al. (2017). Namely, our Fig. 8 exhibits a very similar lower envelope of 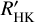 values to their Fig. 10. For brighter
values to their Fig. 10. For brighter 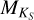 values (earlier-M dwarf types), we find a relatively constant lower envelope of
values (earlier-M dwarf types), we find a relatively constant lower envelope of 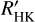 values (see Fig. 8), while Astudillo-Defru et al. (2017) also reported a constant lower envelope of
values (see Fig. 8), while Astudillo-Defru et al. (2017) also reported a constant lower envelope of 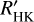 for the higher M dwarf masses (see their lower Fig. 10). As
for the higher M dwarf masses (see their lower Fig. 10). As 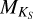 increases and M dwarf types move to later types, the lower envelope of
increases and M dwarf types move to later types, the lower envelope of 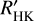 values begins to decrease. Finally, this lower envelope flattens out again for lower masses, or later spectral types. Mittag et al. (2013) similarly reported that the initially constant lower envelope was followed by a decreasing lower envelope. We note a key difference in our findings in that the technique used to derive Teff influences the extent of the decreasing lower envelope and then the level of the constant envelope for the lowest masses. However, each method individually still exhibits this behavior.
values begins to decrease. Finally, this lower envelope flattens out again for lower masses, or later spectral types. Mittag et al. (2013) similarly reported that the initially constant lower envelope was followed by a decreasing lower envelope. We note a key difference in our findings in that the technique used to derive Teff influences the extent of the decreasing lower envelope and then the level of the constant envelope for the lowest masses. However, each method individually still exhibits this behavior.
Surveys that focus on determining stellar parameters (e.g., Maldonado et al. 2015) would be the more reliable source of stellar parameters if the given star were included in that survey. Moreover, when the S-index of a given star is the sole measurement and no access to any spectra is possible, then we recommend the use of Eqs. (17) and (18) to calculate 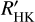 .
.
6 Summary and conclusions
In this work, we have measured Ca II H and K and Hα activity in a large sample of HARPS M dwarf spectra using high S/N template spectra and PHOENIX model atmospheres. We compared three different Teff calibrations and find ΔTeff ~ several 100 K for mid- to late-M dwarfs. This uncertainty in Teff contributes up to Δ log 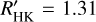 dex and Δ log
dex and Δ log 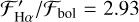 dex. We have extended
dex. We have extended 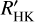 calibrations to the M dwarf regime using PHOENIX model spectra. We compared these new
calibrations to the M dwarf regime using PHOENIX model spectra. We compared these new 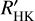 calibrations with previous calibrations. Our log Ccf calibration agrees very well with previous calibrations within 0.2 dex, and extends the calibration from 3100 K ≤ Teff ≤ 6800 K to 2300 K ≤ Teff ≤ 7200 K. Our log RHK,phot calibration overstimates the Noyes et al. (1984) calibration by 0.46 dex. However, our calibration extends log RHK,phot to 2300 K ≤ Teff ≤ 7200 K, and a simple offset correction can be applied to scale our log RHK,phot to that of Noyes et al. (1984). We have provided a grid of log Ccf and log RHK,phot values as functions of Teff, [Fe/H], and log(ɡ). This grid can be used to compute
calibrations with previous calibrations. Our log Ccf calibration agrees very well with previous calibrations within 0.2 dex, and extends the calibration from 3100 K ≤ Teff ≤ 6800 K to 2300 K ≤ Teff ≤ 7200 K. Our log RHK,phot calibration overstimates the Noyes et al. (1984) calibration by 0.46 dex. However, our calibration extends log RHK,phot to 2300 K ≤ Teff ≤ 7200 K, and a simple offset correction can be applied to scale our log RHK,phot to that of Noyes et al. (1984). We have provided a grid of log Ccf and log RHK,phot values as functions of Teff, [Fe/H], and log(ɡ). This grid can be used to compute 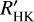 from S-index values using either polynomial fits to or an interpolation of the grid, and can be further beneficial when constraints on the stellar parameters of the targets are established. We have calculated χCaIIHK and χHα for −1.0 ≤ [Fe/H] ≤ +1.0 in steps of Δ [Fe/H] = 0.5 for the entire M dwarf Teff range. We find that our χ values from PHOENIX models agree well with the χ values of West & Hawley (2008).
from S-index values using either polynomial fits to or an interpolation of the grid, and can be further beneficial when constraints on the stellar parameters of the targets are established. We have calculated χCaIIHK and χHα for −1.0 ≤ [Fe/H] ≤ +1.0 in steps of Δ [Fe/H] = 0.5 for the entire M dwarf Teff range. We find that our χ values from PHOENIX models agree well with the χ values of West & Hawley (2008).
We find that the lower boundary of log 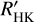 either stays constant or decreases with later-M dwarfs depending on the Teff calibration used. Because of conflicting Teff measurements toward later-M dwarfs, an accurate determination of
either stays constant or decreases with later-M dwarfs depending on the Teff calibration used. Because of conflicting Teff measurements toward later-M dwarfs, an accurate determination of 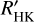 cannot be made beyond
cannot be made beyond 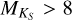 . For
. For 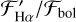 , the lower boundary of inactive stars begins with early-M dwarfs in deeper absorption, and fills in to the continuum towards later-M dwarfs. Stars with known planetary systems do not exhibit unexpected or peculiar levels of Ca II H, K, and Hα activity in relation to stars of similar spectral type or absolute magnitude.
, the lower boundary of inactive stars begins with early-M dwarfs in deeper absorption, and fills in to the continuum towards later-M dwarfs. Stars with known planetary systems do not exhibit unexpected or peculiar levels of Ca II H, K, and Hα activity in relation to stars of similar spectral type or absolute magnitude.
Our surface flux calibration of log Ccf agrees very well with that of Middelkoop (1982) for FGK stars, and our surface flux calibrations of χCaIIHK and χHα also agree well with those of West & Hawley (2008) for M stars. Our 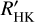 calibrations agree very well with those of Noyes et al. (1984) to within Δ log
calibrations agree very well with those of Noyes et al. (1984) to within Δ log 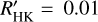 dex for the Sun. We conclude that our calibrations are a reliable extension to previous
dex for the Sun. We conclude that our calibrations are a reliable extension to previous 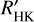 calibrations, provide a consistent way to measure
calibrations, provide a consistent way to measure 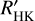 across spectral types early F to late M, and allow the comparison of activity of Sun-like stars to M dwarfs.
across spectral types early F to late M, and allow the comparison of activity of Sun-like stars to M dwarfs.
Acknowledgements
We thank Tim-Oliver Husser for fruitful discussions and providing us with recalculated PHOENIX models. The authors acknowledge research funding by the Deutsche Forschungsgemeinschaft (DFG) under the grant SFB 963, project A04. SVJ acknowledges the support of the DFG priority program SPP 1992 “Exploring the Diversity of Extrasolar Planets” (JE 701/5-1). SBS acknowledges the support of the Austrian Science Fund (FWF) Lise Meitner project M2829-N. This work is based on data products from observations made with ESO Telescopes at the La Silla Observatory (Chile) under the program IDs 60.A-9036, 072.C-0488, 074.C-0364, 075.C-0202, 075.D-0614, 076.C-0155, 077.C-0364, 078.C-0044, 082.C-0718, 085.C-0019, 086.C-0284, 087.C-0831, 089.C-0050, 089.C-0732, 090.C-0395, 090.C-0421, 091.C-0034, 180.C-0886, 183.C-0437, 183.C-0972, 185.D-0056, 191.C-0505, 192.C-0224, and 283.C-5022. We acknowledge the effort of all the observers of the aforementioned ESO projects whose data we have used.
Appendix A Ca II H and K surface flux calibrations
Measuring log Ccf of 85 main-sequence stars from the Vaughan & Preston (1980) survey of the solar neighborhood, Middelkoop (1982) fit a polynomial to log Ccf as a function of B – V,
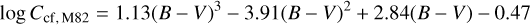 (A.1)
(A.1)
for 0.45 ≤ (B – V) ≤ 1.50.
Rutten (1984) extended the relation further by measuring 30 additional main-sequence stars and also 27 subgiants and giants,
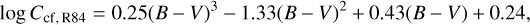 (A.2)
(A.2)
which is valid for main-sequence stars with 0.3 ≤ (B – V) ≤ 1.6.
Cincunegui et al. (2007) extended the calibration using 109 stars ranging from spectral type F6 to M5,
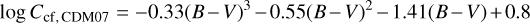 (A.3)
(A.3)
for 0.45 ≤ (B – V) ≤ 1.81. Middelkoop (1982), Rutten (1984), and Cincunegui et al. (2007) all made use of the relation of Noyes et al. (1984) to convert B – V into Teff.
Instead of using observational spectra, Mittag et al. (2013) used PHOENIX stellar atmosphere models to measure ℱRV directly in absolute flux units,
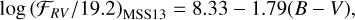 (A.4)
(A.4)
where 0.44 ≤ (B – V) ≤ 1.60. They transformed this to log Ccf using
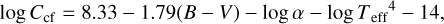 (A.5)
(A.5)
where α = 19.2, and used the B – V to Teff relation of Gray (2005).
Similarly, Pérez Martínez et al. (2014) also used PHOENIX models to derive a conversion factor
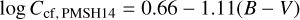 (A.6)
(A.6)
for 0.44 ≤ (B – V) ≤ 1.33. Pérez Martínez et al. (2014) used the B – V to Teff tables of Schmidt-Kaler (1982) (which they also included in their publication).
Using HARPS spectra of FGKM stars, Suárez Mascareño et al. (2015) derived a continuum correction factor
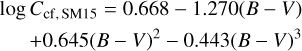 (A.7)
(A.7)
for 0.4 ≲ (B – V) ≲ 1.9.
Astudillo-Defru et al. (2017) empirically determine a continuum correction factor,
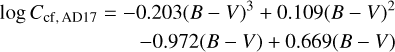 (A.8)
(A.8)
for 0.54 ≤ (B – V) ≤ 1.9.
Appendix B Ca II H and K photospheric flux calibrations
In their publication, Noyes et al. (1984) also provided an alternative, simpler form of Eq. 10 and obtained similar results within the valid calibration range,
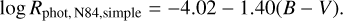 (B.1)
(B.1)
Mittag et al. (2013), using PHOENIX stellar atmosphere models, reported two linear dependences of log RHK phot on B – V with for two B – V ranges:
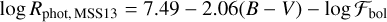 (B.2)
(B.2)
for 0.44 ≤ B – V ≤ 1.28, and
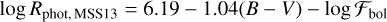 (B.3)
(B.3)
for 1.28 ≤ B – V ≤ 1.60.
Using HARPS spectra and a 0.7 Å rectangular mask of the line core for the most inactive FGK stars and a 0.4 Å rectangular mask for the most inactive M stars, Suárez Mascareño et al. (2015) fit a photospheric flux relation,
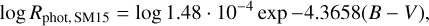 (B.4)
(B.4)
for 0.4 ≲ (B – V) ≲ 1.9.
Astudillo-Defru et al. (2017) determined a photospheric flux relation using a synthetic spectrum, resulting in,
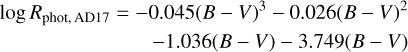 (B.5)
(B.5)
for 0.54 ≤ (B – V) ≤ 1.9.
Appendix C Effective temperature comparison with other calibrations
In Section 3.5 we presented three different Teff calibrations that we used as stellar parameters in this study (see Fig. 7). Here in this appendix we present the Teff measurements of common targets by Mann et al. (2015) to show agreement and the degree of agreement with the different Teff calibration techniques.
 |
Fig. C.1 Teff of Mann et al. (2015) vs Teff,SpT. The dotted line shows the 1:1 relation. |
 |
Fig. C.2 Teff of Mann et al. (2015) vs |
 |
Fig. C.3 Teff of Mann et al. (2015) vs Teff,M15. The dotted line shows the 1:1 relation. |
Appendix D Tables
Astronomical measurements of the sample of stars.
Stellar parameters
Results
PHOENIX−ACES grid calibrations
Chi values of PHOENIX model atmospheres
References
- Anglada-Escudé, G., & Butler, R.P. 2012, ApJS, 200, 15 [CrossRef] [Google Scholar]
- Anglada-Escudé, G., Arriagada, P., Tuomi, M., et al. 2014, MNRAS, 443, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Anglada-Escudé, G., Amado, P.J., Barnes, J., et al. 2016, Nature, 536, 437 [CrossRef] [Google Scholar]
- Astudillo-Defru, N., Delfosse, X., Bonfils, X., et al. 2017, A&A, 600, A13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baliunas, S.L., Donahue, R.A., Soon, W.H., et al. 1995, ApJ, 438, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Barden, S.C. 1985, ApJ, 295, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Berdinas, Z.M., Amado, P.J., & Anglada-Escude, G. 2015, in 18th Cambridge Workshop on Cool Stars, Stellar Systems, and the Sun, eds. G.T. van Belle, & H.C. Harris, 18, 723 [NASA ADS] [Google Scholar]
- Bonfils, X., Delfosse, X., Udry, S., et al. 2013, A&A, 549, A109 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boro Saikia, S., Marvin, C.J., Jeffers, S.V., et al. 2018, A&A, 616, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boyajian, T.S., von Braun, K., van Belle, G., et al. 2012, ApJ, 757, 112 [NASA ADS] [CrossRef] [Google Scholar]
- Cincunegui, C., Díaz, R.F., & Mauas, P.J.D. 2007, A&A, 469, 309 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Delfosse, X., Forveille, T., Ségransan, D., et al. 2000, A&A, 364, 217 [NASA ADS] [Google Scholar]
- Duncan, D.K., Vaughan, A.H., Wilson, O.C., et al. 1991, ApJS, 76, 383 [NASA ADS] [CrossRef] [Google Scholar]
- Golimowski, D.A., Henry, T.J., Krist, J.E., et al. 2004, AJ, 128, 1733 [NASA ADS] [CrossRef] [Google Scholar]
- Gomes da Silva, J., Santos, N.C., Bonfils, X., et al. 2011, A&A, 534, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gray, D.F. 2005, The Observation and Analysis of Stellar Photospheres (Cambridge: Cambridge University Press) [CrossRef] [Google Scholar]
- Hall, J.C., Lockwood, G.W., & Skiff, B.A. 2007, AJ, 133, 862 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Soderblom, D.R., Noyes, R.W., Burnham, N., & Vaughan, A.H. 1984, ApJ, 276, 254 [NASA ADS] [CrossRef] [Google Scholar]
- Herbig, G.H. 1985, ApJ, 289, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Husser, T.-O., Wende-von Berg, S., Dreizler, S., et al. 2013, A&A, 553, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kenyon, S.J., & Hartmann, L. 1995, ApJS, 101, 117 [NASA ADS] [CrossRef] [Google Scholar]
- Maldonado, J., Affer, L., Micela, G., et al. 2015, A&A, 577, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maldonado, J., Scandariato, G., Stelzer, B., et al. 2017, A&A, 598, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mann, A.W., Feiden, G.A., Gaidos, E., Boyajian, T., & von Braun, K. 2015, ApJ, 804, 64 [CrossRef] [Google Scholar]
- Martínez-Arnáiz, R., López-Santiago, J., Crespo-Chacón, I., & Montes, D. 2011, MNRAS, 414, 2629 [CrossRef] [Google Scholar]
- Middelkoop, F. 1982, A&A, 107, 31 [NASA ADS] [Google Scholar]
- Mittag, M., Schmitt, J.H.M.M., & Schröder, K.-P. 2013, A&A, 549, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montes, D., de Castro, E., Fernandez-Figueroa, M.J., & Cornide, M. 1995a, A&AS, 114, 287 [NASA ADS] [Google Scholar]
- Montes, D., Fernandez-Figueroa, M.J., de Castro, E., & Cornide, M. 1995b, A&A, 294, 165 [NASA ADS] [Google Scholar]
- Neves, V., Bonfils, X., Santos, N.C., et al. 2012, A&A, 538, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Neves, V., Bonfils, X., Santos, N.C., et al. 2014, A&A, 568, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Newton, E.R., Irwin, J., Charbonneau, D., et al. 2017, ApJ, 834, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Noyes, R.W., Hartmann, L.W., Baliunas, S.L., Duncan, D.K., & Vaughan, A.H. 1984, ApJ, 279, 763 [NASA ADS] [CrossRef] [Google Scholar]
- Passegger, V.M., Wende-von Berg, S., & Reiners, A. 2016, A&A, 587, A19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pepe, F., Mayor, M., Rupprecht, G., et al. 2002, The Messenger, 110, 9 [NASA ADS] [Google Scholar]
- Perdelwitz, V., Mittag, M., Tal-Or, L., et al. 2021, A&A, 652, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pérez Martínez, M.I., Schröder, K.-P., & Hauschildt, P. 2014, MNRAS, 445, 270 [CrossRef] [Google Scholar]
- Rauscher, E., & Marcy, G.W. 2006, PASP, 118, 617 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., & Basri, G. 2007, ApJ, 656, 1121 [NASA ADS] [CrossRef] [Google Scholar]
- Reiners, A., & Mohanty, S. 2012, ApJ, 746, 43 [Google Scholar]
- Reiners, A., Shulyak, D., Käpylä, P.J., et al. 2022, A&A, 662, A41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ribas, I., Bolmont, E., Selsis, F., et al. 2016, A&A, 596, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rutten, R.G.M. 1984, A&A, 130, 353 [NASA ADS] [Google Scholar]
- Scandariato, G., Maldonado, J., Affer, L., et al. 2017, A&A, 598, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shulyak, D., Seifahrt, A., Reiners, A., Kochukhov, O., & Piskunov, N. 2011, MNRAS, 418, 2548 [NASA ADS] [CrossRef] [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., González Hernández, J.I., & Esposito, M. 2015, MNRAS, 452, 2745 [CrossRef] [Google Scholar]
- Suárez Mascareño, A., Rebolo, R., & González Hernández, J.I. 2016, A&A, 595, A12 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vaughan, A.H., & Preston, G.W. 1980, PASP, 92, 385 [CrossRef] [Google Scholar]
- Walkowicz, L.M., & Hawley, S.L. 2009, AJ, 137, 3297 [NASA ADS] [CrossRef] [Google Scholar]
- Walkowicz, L.M., Hawley, S.L., & West, A.A. 2004, PASP, 116, 1105 [CrossRef] [Google Scholar]
- Wenger, M., Ochsenbein, F., Egret, D., et al. 2000, A&AS, 143, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- West, A.A., & Hawley, S.L. 2008, PASP, 120, 1161 [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Model G2V spectra (yellow) and model M4V spectra (red). The flux scale of the G2V is displayed on the left, and the flux scale of the M4V is given on the right. The blue shaded area indicates the region of the Ca II H and K lines. |
| In the text | |
 |
Fig. 2 Ca II K line of an M1.5 star. Left: spectrum of a single HARPS observation. Right: template spectrum consisting of 47 coadded spectra of the same star. |
| In the text | |
 |
Fig. 3 High S/N template spectrum of an early-M dwarf normalized to a PHOENIX atmosphere model. The solid red line is the high S/N template spectrum, while the dashed black line is the PHOENIX model atmosphere. The blue shaded region shows the chromospheric emission. The dotted lines indicate the 1.09 Å FWHM triangular bandpass used to integrate the Ca II H and K lines. |
| In the text | |
 |
Fig. 4 High S/N template spectrum of an M dwarf with Hα in absorption normalized to a PHOENIX atmosphere model. The solid red line is the high S/N template spectrum, while the dashed black line is the PHOENIX model atmosphere. The vertical dotted lines indicate a 5.0 Å integration region. |
| In the text | |
 |
Fig. 5 High S/N template spectrum of an active M dwarf with Hα in emission normalized to a PHOENIX atmosphere model. The solid red line is the high S/N template spectrum, while the dashed black line is the PHOENIX model atmosphere. The vertical dotted lines indicate the 5.0 Å integration region of Hα. |
| In the text | |
 |
Fig. 6 SAD17 of Astudillo-Defru et al. (2017) vs our work SBS18 (Boro Saikia et al. 2018). Top: entire range of the sample. Bottom: same sample with zoomed in axes. The dotted line shows the 1:1 relation. |
| In the text | |
 |
Fig. 7 Effective temperature Teff of the stellar sample using different Teff determination methods, which are shown by different plot symbols. Top: effective temperature Teff as a function of absolute magnitude |
| In the text | |
 |
Fig. 8 Fractional chromospheric Ca II H and K flux normalized to bolometric flux on a logarithmic scale, log |
| In the text | |
 |
Fig. 9 Fractional chromospheric Ha flux, |
| In the text | |
 |
Fig. 10 Fractional chromospheric Hα flux, |
| In the text | |
 |
Fig. 11 Fractional chromospheric Hα flux, |
| In the text | |
 |
Fig. 12 Different log Ccf calibrations as a function of Teff. The approximate spectral type is shown on the top axis. Top: PHOENIX stellar atmosphere models with different [Fe/H] and log(ɡ), where [Fe/H] is indicated by color and log(ɡ) indicated by symbol. The solid red line indicates a fifth-order polynomial fit. Bottom: calibrations of log Ccf from other works where only the valid calibration region is plotted. Overplotted in red is the same fifth-order polynomial fit from the top panel. |
| In the text | |
 |
Fig. 13 Different log RHK,phot as a function of Teff. The approximate spectral type is shown on the top axis. Top: PHOENIX stellar atmosphere models with different [Fe/H] and log(ɡ), where [Fe/H] is indicated by color and log(ɡ) indicated by symbol. The solid red line indicates a fifth-order polynomial fit. Bottom: calibrations of log RHK,phot from other works where only the valid calibration region is plotted. Overplotted in red is the same fifth-order polynomial fit from the top panel. |
| In the text | |
 |
Fig. 14 Top: continuum flux normalized to bolometric flux of Ca II H and K, χ Ca II HK, as a function of Teff using PHOENIX stellar atmospheres with log(ɡ) = 5.0 and different metallicities. Values from West & Hawley (2008) are plotted in gray. Bottom: continuum flux normalized to bolometric flux of Hα, χHα, as a function of Teff using PHOENIX stellar atmospheres with log(ɡ) = 5.0 and different metallicities. Values from West & Hawley (2008) are plotted in gray. |
| In the text | |
 |
Fig. C.1 Teff of Mann et al. (2015) vs Teff,SpT. The dotted line shows the 1:1 relation. |
| In the text | |
 |
Fig. C.2 Teff of Mann et al. (2015) vs |
| In the text | |
 |
Fig. C.3 Teff of Mann et al. (2015) vs Teff,M15. The dotted line shows the 1:1 relation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.