| Issue |
A&A
Volume 594, October 2016
|
|
|---|---|---|
| Article Number | A81 | |
| Number of page(s) | 12 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201628875 | |
| Published online | 14 October 2016 | |
High-velocity extended molecular outflow in the star-formation dominated luminous infrared galaxy ESO 320-G030⋆
1 Centro de Astrobiología (CSIC/INTA), Ctra de Torrejón a Ajalvir, km 4, 28850, Torrejón de Ardoz, Madrid, Spain
2 ASTRO-UAM, UAM, Unidad Asociada CSIC, 28049 Madrid, Spain
3 Department of Physics, University of Oxford, Keble Road, Oxford, OX1 3RH, UK
e-mail: miguel.pereira@physics.ox.ac.uk
4 Observatorio Astronómico Nacional (OAN-IGN)-Observatorio de Madrid, Alfonso XII, 3, 28014 Madrid, Spain
5 Universidade Federal do Rio Grande do Sul, Instituto de Física, CP 15051, 91501-970 Porto Alegre, RS, Brazil
Received: 8 May 2016
Accepted: 12 July 2016
We analyze new high spatial resolution (~60 pc) ALMA CO(2−1) observations of the isolated luminous infrared galaxy ESO 320-G030 (d = 48 Mpc) in combination with ancillary Hubble Space Telescope optical and near infrared (IR) imaging, as well as VLT/SINFONI near-IR integral field spectroscopy. We detect a high-velocity (~450 km s-1) spatially resolved (size~2.5 kpc; dynamical time ~3 Myr) massive (~107 M⊙; Ṁ ~ 2−8 M⊙ yr-1) molecular outflow that has originated in the central ~250 pc. We observe a clumpy structure in the outflowing cold molecular gas with clump sizes between 60 and 150 pc and masses between 105.5 and 106.4 M⊙. The mass of the clumps decreases with increasing distance, while the velocity is approximately constant. Therefore, both the momentum and kinetic energy of the clumps decrease outwards. In the innermost (~100 pc) part of the outflow, we measure a hot-to-cold molecular gas ratio of 7 × 10-5, which is similar to that measured in other resolved molecular outflows. We do not find evidence of an ionized phase in this outflow. The nuclear IR and radio properties are compatible with strong and highly obscured star-formation (Ak ~ 4.6 mag; star formation rate ~ 15 M⊙ yr-1). We do not find any evidence for the presence of an active galactic nucleus. We estimate that supernova explosions in the nuclear starburst (νSN ~ 0.2 yr-1) can power the observed molecular outflow. The kinetic energy and radial momentum of the cold molecular phase of the outflow correspond to about 2% and 20%, respectively, of the supernovae output. The cold molecular outflow velocity is lower than the escape velocity, so the gas will likely return to the galaxy disk. The mass loading factor is ~0.1−0.5, so the negative feedback owing to this star-formation-powered molecular outflow is probably limited.
Key words: galaxies: ISM / galaxies: kinematics and dynamics / galaxies: starburst / galaxies: nuclei / radio lines: galaxies
The reduced images and datacubes (FITS files) are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/594/A81
© ESO, 2016
1. Introduction
Theoretical models predict that massive gas outflows, driven by starbursts or active galactic nuclei (AGN), are fundamental actors in shaping the observed properties of galaxies (e.g., galaxy mass function, mass-metallicity relation). This is because massive outflows can regulate both the accretion rate of the central supermassive black hole and the star-formation (SF) activity, but also because they can redistribute dust and metals over kpc scales (e.g., Veilleux et al. 2005; Narayanan et al. 2008; Hopkins et al. 2012).
Gas outflows have a multiphase (ionized, neutral atomic, and molecular) structure (Veilleux et al. 2005; Hopkins et al. 2012). The ionized and neutral atomic phases have been studied over the past 25 years using optical and ultraviolet spectral features (e.g., Heckman et al. 1990; Veilleux et al. 1995; Rupke et al. 2008; Arribas et al. 2014; Heckman et al. 2015; Cazzoli et al. 2016). Just recently, thanks to improved capabilities of millimeter observatories, many works have focused on the molecular phase of the outflow, which dominates the outflowing gas mass, energy, and momentum in most cases (e.g., Feruglio et al. 2010; Tsai et al. 2012; Bolatto et al. 2013a; Cicone et al. 2014; García-Burillo et al. 2014, 2015). These studies show that massive molecular outflows are ubiquitous in AGN and starbursts and that they might have an important impact in the evolution of their host galaxies.
Multi-transition and multi-species studies of the molecular phase of the outflow shed some light on the poorly known physical and chemical properties of this phase. For instance, the isotopic O abundance measured using the far-IR OH absorption in the outflow of Mrk 231 suggests that the outflowing gas has been processed by advanced starbursts (Fischer et al. 2010). In addition, the HCN, HNC, and HCO+ emissions indicate that the molecular gas in that outflow can be chemically differentiated while being compressed and fragmented by shocks (Aalto et al. 2012; Lindberg et al. 2016). Actually, the analysis of cold and hot molecular gas tracers (e.g., CO and near-IR H2 transitions) in various objects indicates that the outflowing molecular gas is continuously heated by shocks (Dasyra et al. 2014; Emonts et al. 2014).
Similarly, spatially resolved observations of outflows at sub-kpc scales (e.g., Bolatto et al. 2013a; Emonts et al. 2014; Sakamoto et al. 2014; García-Burillo et al. 2014; Salak et al. 2016) are essential to study the outflowing molecular gas. The clumpy distribution of the molecular gas in the outflow, as shown in this work, and the physical properties of these clumps provide a benchmark for models and simulations to establish how the molecular gas evolves in the outflow (e.g., Nath & Silk 2009; Zubovas & Nayakshin 2014) and also to better constrain the global effect of the outflow in the host galaxy.
Many of these outflow studies analyze local luminous and ultraluminous infrared galaxies (LIRGs and ULIRGs respectively) because they are the most extreme examples of starbursts (and AGN) in the local Universe. LIRGs have infrared (IR) luminosities >1011 L⊙, while ULIRGs have LIR> 1012 L⊙. These IR luminosities, if produced solely by SF, are equivalent to star formation rates (SFR) of >15 and >150 M⊙ yr-1 , respectively (see Table 1 of Kennicutt & Evans 2012). These local U/LIRGs are considered as local counterparts of high-z starburst with similar or higher IR luminosities (e.g., Muzzin et al. 2010). Therefore, they are perfect targets for detailed studies at high spatial resolution of the processes, for example outflows, that take place in their high-z counterparts.
In this paper, we analyze new Atacama Large Millimeter/submillimeter Array (ALMA) CO(2−1) high spatial resolution (~60 pc) observations of the local (d = 48 Mpc; scale of 240 pc arcsec-1) LIRG ESO 320-G030 (log LIR/L⊙ = 11.3; also known as IRAS F11506-3851). We combine the CO(2−1) data (cold molecular gas tracer) with available near-IR integral field spectroscopy (IFS) to trace the hot molecular gas, as well as the ionized gas (Piqueras López et al. 2012). This galaxy is an isolated spiral galaxy with an ordered velocity field (Bellocchi et al. 2013, 2016) hosting a strong starburst (Alonso-Herrero et al. 2006). Its nuclear activity is classified as H ii from optical spectroscopy (van den Broek et al. 1991; Pereira-Santaella et al. 2011) and there is no evidence of an AGN in this galaxy based on its mid-IR and X-ray emissions (Pereira-Santaella et al. 2010b, 2011). It also hosts an OH megamaser (Norris et al. 1986), which is associated with compact starbursts most of the time (Baan & Klöckner 2006; Zhang et al. 2014). In addition, a massive outflow of neutral atomic gas is already detected in this object using optical IFS (Cazzoli et al. 2014, 2016).
This paper is organized as follows: we describe the observations and data reduction in Sect. 2. The analysis of the gas and stellar morphology and kinematics is presented in Sects. 3 and 4. In Sect. 5, we describe the structure and physical properties of the resolved molecular outflow. In Sect. 6, we investigate the nature of the compact central source of this galaxy. The main results are discussed in Sect. 7 and, finally, in Sect. 8, we summarize the main findings of the paper.
2. Observations and data reduction
 |
Fig. 1 Top row: ALMA 12CO(2−1), VLT/SINFONI H2 1−0 S(1) 2.12 μm, and ALMA 233 GHz continuum (rest frequency) maps of ESO 320-G030. The contours in all the images correspond to the CO(2−1) emission in logarithmic steps (1, 2, 4, 8, 16, 32, 64) × 0.43 Jy km s-1 beam-1. Lower panels: HST/NICMOS F160W and continuum subtracted Paα maps and the HST F814W to F160W ratio to highlight obscured regions (red colors indicate more obscured regions). In the last panel we added an extra contour level at 0.5 × 0.43 Jy km s-1 beam-1. The red hatched ellipses indicate the beam size of each image. For the ALMA CO(2−1) and the 233 GHz continuum images, the beam size is 0.̋25 × 0.̋23, PA 89°. For the SINFONI H2 1−0 S(1) image, the beam FWHM is 0.̋6, and for the HST/NICMOS data, the beam is ~0.̋15. |
2.1. 12CO(2−1) ALMA data
Band 6 ALMA observations of ESO 320-G030 were obtained on 8 December 2014 and 18 July 2015 using compact and extended array configurations with 35 and 39 antennas, respectively, as part of the project 2013.1.00271.S (PI: L. Colina). On-source integration times were 8 and 17 min, respectively. Both observations were single pointing centered at the nucleus of ESO 320-G030. The extended configuration had baselines between 15.1 m and 1.6 km while for the compact configuration the baselines ranged between 15.0 m and 348 m. For these configurations the maximum recoverable scales are ~10′′.
Two spectral windows of 1.875 GHz bandwidth (0.49 MHz ~ 0.6 km s-1 channels) were centered at the sky frequencies of 12CO(2−1) (228.2 GHz) and CS(5−4) (242.4 GHz). In addition, two continuum spectral windows were set at 230.4 and 245.2 GHz (~1.3 mm). We excluded the CS(5−4) transition from our analysis because its redshifted frequency coincides with a variable atmospheric feature.
The two datasets were calibrated using the standard ALMA reduction software CASA (v4.2.2; McMullin et al. 2007). For the amplitude calibration we used J1147-3812, assuming a flux density of 0.817 Jy at 236.5 GHz, and Ganymede, using the Butler-JPL-Horizons 2012 model, for the extended and compact configurations, respectively. The uv visibilities of each observation were converted to a common frequency reference frame (kinematic local standard of rest; LSRK) and then combined. We checked that the amplitudes of the baselines in common for both array configurations were in good agreement. For the CO(2−1) data, the continuum was fitted with a constant using the line free channels and subtracted in the uv plane. In the final data cubes, we used 4 MHz channels (~5 km s-1) to increase the signal-to-noise ratio and 256 × 256 pixels of 0.̋06. For the cleaning of both the CO(2−1) and continuum data, we used the Briggs weighting with a robustness parameter of 0.5 (Briggs 1995) which provided a beam with a full-width half-maximum (FWHM) of 0.̋25 × 0.̋23 (~60 pc × 55 pc) with a position angle (PA) of 89°. A mask derived from the observed CO(2−1) emission in each channel was used during the clean process. The achieved 1σ sensitivity is ~1 mJy beam-1 in the CO(2−1) cube for the 4 MHz channels and ~100 μJy beam-1 in the continuum images. We applied the primary beam (FWHM = 27′′) correction to the data.
The integrated CO(2−1) flux in the analyzed ALMA field of view (15′′× 15′′) is 640 Jy km s-1 with a flux calibration uncertainty about 15%. To our knowledge, no single dish CO(2−1) observations of this galaxy exist. A CO(1−0) flux of 180 Jy km s-1 was reported by Mirabel et al. (1990) using the 15 m SEST telescope (44′′ beam size). Assuming an r21 ratio of 0.9 (Bolatto et al. 2013b), the expected CO(2−1) flux would be ~650 Jy km s-1, which is slightly higher than our measured flux. Although the single dish data covers a larger area and the r21 ratio is somewhat uncertain, this similarity suggests that we recover the majority of the CO(2−1) flux combining both the compact and the extended ALMA array configurations.
2.2. Ancillary data
2.2.1. Optical and near-IR Hubble Space Telescope imaging
We used the continuum subtracted narrow-band Paα and the broad-band F160W (λc = 1.60 μm, FWHM = 0.34 μm) images obtained with the NICMOS camera on the Hubble Space Telescope (HST) presented by Alonso-Herrero et al. (2006) to trace the SFR and the distribution of the stellar mass, respectively. From the Mikulski Archive for Space Telescopes (MAST), we downloaded the HST/ACS reduced images obtained with the filter F814W (λc = 8012 Å, FWHM = 1539 Å) and the ramp filter FR656N centered at 6634 Å (redshifted wavelength of Hα for this object) with a bandwidth of 46 Å. We used these images to map the global morphology of ESO 320-G030.
2.2.2. Near-IR VLT/SINFONI IFS
We observed this galaxy with the near-IR VLT/SINFONI integral field spectrograph in the J and K bands. These observations have been analyzed by Piqueras López et al. (2012, 2016) and Cazzoli et al. (2014). They cover a field of view of 8′′× 8′′ centered at the nucleus of the galaxy with a seeing limited angular resolution of ~0.̋6. From these observations, we use the Brγ to Brδ ratio maps to derive the extinction, the H2 1−0 S(1) 2.12 μm transition to trace the presence of hot molecular gas, and the [Fe ii]1.64 μm as a supernovae tracer.
2.2.3. Far-IR Herschel imaging
Far-IR Herschel imaging of ESO 320-G030 was available in the Herschel archive. We downloaded the PACS (Poglitsch et al. 2010) 70, 100, and 160 μm images, as well as the SPIRE (Griffin et al. 2010) 250, 350, and 500 μm images. We processed the data using the standard Herschel pipeline environment software (HIPE) and created the maps using Scanamorphos (Roussel 2013). The angular resolution of the images varies from 6′′ to 35′′ depending on the wavelength. More details on the data reduction can be found in Pereira-Santaella et al. (2015).
2.2.4. Image alignment
Figure 1 shows the ALMA, HST/NICMOS, and SINFONI maps of ESO 320-G030. Since the absolute positioning, i.e., astrometry, of the HST images and SINFONI cubes is in general not known to better than ~1′′, the alignment of the different datasets required several steps. First, we took the ALMA position as reference. The CO(2−1) spiral arms closely resemble the dust lanes observed in the optical F814W and FR656N images, so we used these features to align these two optical images with the ALMA maps. Next, we used the stars in the field of view of both the F814W and F160W images to align the NICMOS images (F160W and Paα). Finally, the SINFONI maps (H2 1−0 S(1) and Brγ) were aligned by matching the Brγ map (see Piqueras López et al. 2012) with the NICMOS Paα image. The uncertainty of the alignment is around 0.̋15 (~pixel size of SINFONI).
3. Global morphology
 |
Fig. 2 Deprojected F814W image of ESO 320-G030 assuming an inclination of 43° and a PA of 133°. In the left panel, the central region is saturated to make visible the primary bar and the external spiral arms (pseudoring). The right panel shows the secondary bar and spiral structure present in the central 5 kpc. The contours represent the deprojected CO(2−1) emission. The diagonal white line in the left panel corresponds to the gap between the two HST/ACS detectors. |
ESO 320-G030 is an isolated barred spiral galaxy (Buta 1986; Greusard et al. 2000). In the left panel of Fig. 2, we show the deprojected1 optical image where a large-scale primary bar (semi-major axis a ~ 9 kpc) and the outer pseudoring are clearly visible. A secondary stellar bar (a ~ 1.2 kpc) within the primary bar was observed in the near-IR with an internal spiral structure starting from it (Greusard et al. 2000; see F160W panel in Fig. 1). Greusard et al. (2000) measured a PA difference between the primary and secondary stellar bars of 35° using near-IR K-band images. However, the high-angular resolution HST and ALMA data (right panel of Fig. 2) show that this secondary stellar bar and the elongated molecular structure associated with it are approximately perpendicular to the primary bar. This difference in the measured PA could be due to the lower angular resolution of their near-IR images (seeing >1.̋2) and the effect of the strong dust lanes on those images.
Almost 60% of the CO(2−1) emission in the field of view is concentrated within the central 500 pc (see Fig. 1). This accumulation of gas in the nuclear region is likely driven by the inward gravity torques due to the decoupled secondary bar, since most of it is inside corotation. This is the common scenario reproduced by n-body numerical simulations (Hunt et al. 2008), including gas dissipation, which predict the secondary bar decoupling and the gas inflow to the inner Lindblad resonance of the secondary bar.
The hot molecular gas traced by the H2 1−0 S(1) emission follows remarkably well the morphology of CO(2−1) emission. The observed H2 1−0 S(1) emission is less concentrated in the nucleus than the CO(2−1) emission (~25% of the integrated emission is produced in the central 500 pc vs ~60% for the CO), but this can be due to the large extinction of the nuclear region (see Sect. 6.2). On the contrary, the SF traced by Paα is dominated by the emission from the internal spiral arms. We also note that most of the H ii regions do not exactly coincide with the CO(2−1) emitting regions. This agrees with our previous findings in another LIRG, IC 4687 (Pereira-Santaella et al. 2016), where ALMA observations suggest that the CO and Paα emitting regions do not generally coincide at 100−200 pc scales, and therefore the SF law breaks down on these sub-kpc scales. Similar results are obtained for spiral (e.g., Schruba et al. 2010) and interacting galaxies (e.g., Zaragoza-Cardiel et al. 2014) as well as for irregular galaxies (e.g., Kawamura et al. 2009).
We used the ratio between the F814W and the F160W images to obtain a qualitative measurement of the extinction. The bottom right panel of Fig. 1 shows the good agreement of this ratio with the CO(2−1) emission.
Finally, the 233 GHz continuum comes from a slightly resolved source (0.̋34 × 0.̋30) located at the nucleus of this object. We discuss the properties of the nucleus in detail in Sect. 6.
4. Global kinematics
 |
Fig. 3 CO(2−1) isovelocity contours in steps of 50 km s-1 from v(lsrk) = 2800 to 3300 km s-1. The dotted and the dashed lines indicate the major and minor kinematic axes. |
 |
Fig. 4 Left panel: CO(2−1) velocity field after excluding those pixels with complex line profiles. Middle panel: best fitting model (see Sect. 4). In these two panels, the contour levels are set in steps of 50 km s-1 from v(lsrk) = 2800 to 3300 km s-1. Right panel: residuals (data − model) and the CO(2−1) emission contours as in Fig. 1. The dotted and the dashed lines indicate the major and minor kinematic axes. |
The Hα velocity field of this object (~1′′ resolution) was studied by Bellocchi et al. (2013, 2016). It shows a very regular pattern with a centrally peaked velocity dispersion which these authors classify as a pure rotating disk. This regular pattern is also observed using the near-IR Brγ and H2 1−0 S(1) emission lines (Piqueras López et al. 2012).
In Fig. 3, we show the velocity field obtained from the first moment of the CO(2−1) emission. It also presents a regular rotating disk pattern, although some deviations are present (see also Bellocchi et al. 2013, 2016; and Cazzoli et al. 2014). To quantify them, we modeled the velocity field using a simple kinematic model (e.g., Mihalas & Binney 1981) 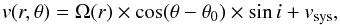 (1)where r and θ are the galactocentric distance and azimuthal angle, respectively, Ω(r) is the azimuthal velocity, θ0 is the PA of the major kinematic axis, i the inclination angle of the galaxy, and vsys the systemic velocity.
(1)where r and θ are the galactocentric distance and azimuthal angle, respectively, Ω(r) is the azimuthal velocity, θ0 is the PA of the major kinematic axis, i the inclination angle of the galaxy, and vsys the systemic velocity.
In the central region, the CO(2−1) emission has complex profiles (see Sect. 5) indicating that the gas kinematic there will not be well reproduced by our simple model. To exclude these regions, we fitted the CO(2−1) profiles pixel by pixel using a Gaussian and rejected all those pixels where the quality of the fit was poor (reduced χ2> 1.4). The left panel of Fig. 4 shows the velocity field used for the kinematic model fit with the central pixels excluded.
For the fit, all the parameters were left free to vary, except the inclination that was fixed at the value derived from the elliptical isophote fitting (43°; see Sect. 3). The resulting model (middle panel of Figs. 4 and 5) reproduces well the overall structure of the velocity field. The residuals standard deviation is 14 km s-1 (right panel of Fig. 4). The largest deviations (~±70 km s-1) occur at the tips of the secondary bar. If we assume that the spiral arms are trailing, from the velocity field, we can conclude that the NE tip of the bar is the most distant from us. The negative (positive) velocity of the residuals at the NE (SW) tip of the bar indicate the presence of non-circular motions. Similar structures found in low-z Seyfert galaxies have been interpreted as gas inflows (Diniz et al. 2015; Schnorr-Müller et al. 2016; see also van de Ven & Fathi 2010). However, these non-circular motions can also be associated with the elliptical orbits followed by the gas in the bar (Wada 1994). Therefore, these radial velocities can only be considered as an upper limit, and the contribution from elliptical orbits to the observed velocity amplitude must be evaluated before estimating the gas inflow rate.
From this fit, we also obtained the PA of the major kinematic axis (133 ± 2°) and the systemic velocity (3080 ± 4 km s-1 in the LSRK frame). This is in agreement with the CO(1−0) velocity reported by Mirabel et al. (1990).
Figure 5 shows the rotation curve along the major kinematic axis using the first moment map (Fig. 3) and the uncertainty associated with it. From this figure, we obtain that the amplitude of the rotation curve corrected for inclination is ~270 km s-1.
 |
Fig. 5 Rotation curve corrected for inclination (i = 43°) along the major axis (PA = 133°) for the cold molecular gas traced by the CO(2−1) transition (red circles). The error bars of the CO(2−1) points are 1−2 km s-1. The solid black line is the best fit model to the CO(2−1) data (see Sect. 4). |
5. Resolved molecular outflow
 |
Fig. 6 Left panels: CO(2−1) integrated emission between 2650 and 2850 km s-1 in blue contours and between 3370 and 3530 km s-1 in red contours. The contours correspond to 3, 4, 5, 6, 8, and 12σ levels in their respective bands (the 3σ contour level is not plotted in the top left panel for clarity). The background of the top left panel is the HST/ACS F814W image which shows the internal spiral arms. The background of the bottom left panel is the HST/ACS FR656N image to maximize the contrast of the dust lanes. The dashed line indicates the minor kinematic axis and the dotted lines indicate the approximate opening angle of the outflowing gas. The orange cross marks the position of the 233 GHz continuum peak. Right panels: CO(2−1) spectra of the regions marked in the bottom left panel. The blue and red shaded areas indicate the velocity ranges used to construct the blue and red contours, respectively. The vertical dashed line corresponds to the velocity derived in Sect. 4 assuming a rotating disk model. To increase the signal-to-noise ratio, we binned the spectra in channels of 60, 20, 15, 5, 15, 20, and 20 km s-1from top to bottom. |
Properties of the outflow regions.
In the ALMA data cube, we identified some regions with secondary CO(2−1) emission separated by >200 km s-1 from the local modeled velocity in Sect. 4. This deviation is considerably higher than the largest residual (~70 km s-1; see Fig. 4) found for the rotating disk model. In Fig. 6, we show the location of these seven regions and their spectra. The blue- and red-shifted regions are located to the NE and SW of the nucleus, respectively, and approximately symmetric with respect to the nucleus with a PA ~ 23° and an opening angle ~30°. Both the spatial distribution approximately along the minor kinematic axis and the high velocities of the molecular gas in these regions are compatible with a molecular outflow almost perpendicular to the rotating disk and with origin at the nucleus of this galaxy. Alternatively, these blue- and red-shifted regions could be due to coplanar non-circular motions. Since they are approximate aligned with the minor kinematic axis, these motions would be mainly radial motions. However, the high velocity of this gas (comparable to the rotation curve half amplitude) is much higher than that expected for density-wave-driven gas flows (García-Burillo et al. 2015).
In addition, there are two regions which also show high blue- and red-shifted velocities close to the nucleus and aligned approximately perpendicular (PA ~ 125°) to the outflow. We excluded them from the analysis because the rotation and high velocity dispersion of the gas in the inner 400 pc (see line profiles in Fig. 6) can explain their location approximately along the major kinematic axis.
In the optical HST images, there is a prominent dust lane that originates at the nucleus in a radial direction close to the positions of the blueshifted regions A, B, C, and D. This is also visible in the F814W/F160W ratio (Fig. 1 and also in the near-IR color map presented in Alonso-Herrero et al. 2006) where the most obscured region (in red in that ratio map) coincides approximately with region D. These observables also support the hypothesis of a molecular dusty outflow originating in the nucleus which produces a screen obscuration over the galaxy disk in our line of sight. As expected in this scenario, we do not find a clear correlation between the optical obscuration and the redshifted part of the outflow (which would be behind the disk in our line of sight).
Figure 6 shows that the dust lane associated with the outflow is more or less uniform while the CO(2−1) emission is concentrated in few clumps along the lane. With the ALMA configurations used to obtain these data, we should be able to recover structures with angular scales up to ~10′′. Thus, it is not likely that diffuse emission from this ~3′′ region is completely filtered out. On the other hand, we detect weak (3−4σ) blueshifted CO(2−1) emission between regions C and D, but closer in velocity to the rotation disk model (Δv ~ 120 km s-1) and not included in the velocity range considered in Fig. 6. This suggests that molecular gas associated with the outflow exists between the selected regions, but with lower velocities and/or lower surface brightness and representing just a small fraction of the total CO(2−1) emission of the outflow. Therefore, the observed clumpy structure of the molecular gas in the outflow agrees with the predictions of numerical simulations where these clumps of cold molecular gas dominates the outflowing molecular gas mass (Zubovas & King 2014; Nayakshin & Zubovas 2012).
5.1. Physical properties of the clumps
The PA of the outflow, between 50° and 80°, is relatively close to the minor kinematic axis, (43 ± 2)°, and the opening angle is low (30°). Therefore, for simplicity, we assume that the outflow is perpendicular to the galaxy disk when we calculate the deprojected distances and velocities of the outflow regions. The CO-to-H2 conversion factor for outflows is poorly known. Therefore, we used the ULIRG-like factor (αCO ~ 0.78 M⊙ (K km s-1 pc-2)-1), which is ~5 times lower than the Galactic conversion factor and also the ULIRG-like ratio r21 = 0.9 (Bolatto et al. 2013b). The molecular gas masses were calculated using Eqs. (3) and (4) of Solomon & Vanden Bout (2005) which account for the He mass. The uncertainty in the mass determination is dominated by the factor of ~5 systematic uncertainty in the CO-to-H2 conversion factor. However, the adopted approach probably provides robust lower limits to the molecular gas mass of the outflow.
The properties of the regions are summarized in Table 1. The total size of the outflow is ~2.5 kpc and the velocities of the molecular gas with respect to the systemic velocity are ~370−540 km s-1 with no clear dependence on the distance from the nucleus (Fig. 7). This implies that the dynamical times required for the gas to reach its current locations are 0.2−3 Myr.
The sizes of the selected clumps are 60−150 pc and their masses are in the range 105.5−106.4 M⊙. Being more massive those clumps closer to the nucleus (top panel of Fig. 7). Likewise, the kinetic energy of the clumps, calculated as 1/2 Mmol(v × seci)2, and the momentum (p = Mmolv × seci) also decrease with increasing distances (bottom panels of Fig. 7). Although, these correlations are slightly worse than the mass vs distance relation. We ignored the kinetic energy associated with turbulence since for those clumps with a well defined σ it represents less than 2% of the total kinetic energy.
 |
Fig. 7 Logarithm of the molecular mass (first), velocity (second), kinetic energy (third), and momentum (fourth) of the outflowing clumps as a function of the deprojected distance from the nucleus. Blue and red points are blueshifted and redshifted clumps, respectively. The dotted line is the best fit. The parameters of the best fit and the Pearson correlation coefficients are indicated in each panel. The error bars correspond to the statistical uncertainties. |
5.2. Hot molecular, ionized, and neutral atomic gas
Both observations (e.g., Dasyra et al. 2014; Emonts et al. 2014) and numerical simulations (e.g., King & Pounds 2015) indicate that outflows have a multiphase structure. So far, we have focused our analysis on the new ALMA CO(2−1) data, but we have observed ESO 320-G030 using near-IR and optical IFS (Piqueras López et al. 2012; Cazzoli et al. 2014). Therefore, it is interesting to use these data to analyze other phases of the outflowing gas.
We used the near-IR K-band SINFONI to study the hot molecular phase traced by the H2 1−0 S(1) 2.12 μm transition. K-band presents numerous stellar continuum features that can be confused with broad wings of the emission lines. For this reason, we subtracted the stellar continuum spaxel by spaxel using the penalized pixel-fitting method (Cappellari & Emsellem 2004) with the NASA Infrared Telescope Facility (IRTF) spectral library (Cushing et al. 2005; Rayner et al. 2009).
In the channel maps, we found H2 1−0 S(1) emission that can be associated with region D. The rest of near-IR H2 transitions are not detected in this region, probably because they are too weak to be detected with these SINFONI observations. The angular resolution of the SINFONI data is two times worse than the ALMA data and the spectral resolution is ~80 km s-1. However, both the velocity range and the location to the NE of the nucleus of the hot H2 emitting region are similar to those of the CO(2−1) region (see Fig. 8). Therefore, we consider that they are likely produced in the same physical region.
We measure an H2 1−0 S(1) flux in this region of (2.5 ± 0.4) × 10-17 erg cm-2 s-1. Similar to Emonts et al. (2014), we assume that the hot molecular gas is thermalized to derive the hot molecular gas mass. The extinction maps presented by Piqueras López et al. (2013) indicate that the nuclear extinction is high. Here, we assume that Ak = 4.6 mag in the nucleus (Sect. 6.2). With these numbers, we derive a hot molecular gas mass of 190 M⊙. However, it is uncertain whether the extinction affecting the hot molecular gas is the same affecting the ionized gas traced by the nuclear Brγ. If the extinction is lower, the hot molecular gas mass can be up to tens of times lower.
The ratio of hot-to-cold molecular gas is 7 × 10-5, which is similar to the ratio observed in the AGN powered outflow detected in the LIRG NGC 3256 (Emonts et al. 2014), and is higher than most of the ratios measured in the integrated spectra of local objects including Seyfert galaxies and starbursts (10-8−10-5; Dale et al. 2005). The enhanced hot-to-cold ratio in NGC 3256 is associated with H2 being heated through shocks or X-rays. In ESO 320-G030, since there is no AGN (see Sect. 6), the observed hot-to-cold ratio could be due to shocks in the outflowing gas.
We do not detect near-IR H2 emission in the other clumps of the outflow, but, assuming that the hot-to-cold ratio is also ~1 × 10-4 in those clumps, their hot H2 emission would be below the sensitivity of these VLT/SINFONI observations.
To study the ionized component of the outflow, we analyzed the Brγ emission line in the SINFONI IFS data by inspecting the individual channel emission maps. However, we did not find any hint of emission at the locations and velocities of the molecular outflow.
Neutral atomic outflowing gas was detected in this object by Cazzoli et al. (2014) analyzing the NaD kinematics in the VIMOS data. A blueshifted NaD absorption component was found to the NE of the nucleus, coincident with the blueshifted molecular gas detected in the ALMA data. Although the morphologies of the neutral atomic and molecular outflowing gas are similar, the velocity range of the neutral atomic gas (30−150 km s-1) is lower than that of the molecular gas. However, it is also likely that outflowing gas has a wide distribution of velocities, from few tens of km s-1 to >1000 km s-1 as predicted by numerical simulations (e.g., Hopkins et al. 2012). The derived neutral atomic gas mass of the outflow is 108.5±0.9 M⊙.
 |
Fig. 8 Comparison between the hot (left) and cold (right) molecular gas phases of the outflow region D. The hot molecular gas is traced by the H2 1−0 S(1) 2.12 μm transition observed with SINFONI, while the cold molecular gas is traced by CO(2−1). The background images are the integrated emission in the channels shaded in the bottom panels. The contours represent the total emission of the corresponding transition at peak ×0.9, ×0.6, and ×0.3 levels. The orange hatched circles represent the FWHM of the beam of each image (0.̋6 and ~0.̋25, respectively). The bottom panels are the spectra extracted from the regions located to the NE of the nucleus in the top panels. |
6. Nature of the central source
The nuclear region of this object is highly obscured (Ak> 2.3 mag derived from the 9.7 μm silicate absorption; Pereira-Santaella et al. 2010a) and even in the near-IR it is not clear where the nucleus is located (see Fig. 1 and also Alonso-Herrero et al. 2006). To identify the nucleus, we used the ALMA 230 GHz continuum image where most of the emission is produced by a barely resolved source (observed size 0.̋34 × 0.̋30) whose location is compatible with the kinematic center derived from the CO(2−1) velocity field (Sect. 4). This continuum source is also coincident with the peak of the cold and hot molecular gas emissions (CO(2−1) and H2 1−0 S(1)).
The nuclear activity of ESO 320-G030 is classified as H ii from optical spectroscopy (Appendix B of Pereira-Santaella et al. 2011). Similarly, its X-ray emission is that expected in a starburst (Pereira-Santaella et al. 2011). The mid-IR high-ionization transitions of [Ne v]15.6 μm and [O iv]25.9 μm, which can be used to identify obscured AGNs, are not detected in this object (Pereira-Santaella et al. 2010b). Moreover, the spectral decomposition of the mid-IR Spitzer/IRS spectrum of this object did not reveal the presence of an AGN component (Alonso-Herrero et al. 2012). Therefore, there is no evidence for an AGN in this object.
6.1. Spectral energy distribution
To further study the power source of the nucleus of ESO 320-G030, we analyzed its spectral energy distribution (SED). In Tables 2 and 3, we list the IR and radio measurement used to construct the SED. In addition, to the radio and IR data already published, we measured the ALMA continuum fluxes at 230 and 242 GHz (~1.3 mm), as well as the far-IR fluxes from Herschel/PACS and SPIRE images (see Sect. 2). In all these images, the emission of ESO 320-G030 is barely resolved at their corresponding angular resolutions (from 6 to 35′′; see Table 2). This indicates that the IR emission is dominated by the nucleus and not by the circumnuclear SF regions (see Fig. 1), at least for λ< 100 μm where the angular resolutions are <7″. This galaxy was recently observed with the Australia Telescope Compact Array (ATCA) at 36 GHz (B. Emonts, priv. comm.) and we also include this measurement in our SED.
6.1.1. Radio emission
First, we fitted with a power-law model (Sν ~ ν− α) the observed radio emission (ν ≤ 36 GHz). The spectral index, α, is 0.7 ± 0.1, which is the value expected for pure synchrotron emission. It is also similar to the values of α found in normal galaxies (Condon 1992). Therefore, the radio emission of ESO 320-G030 does not suggest the presence of an AGN. Using only the VLA fluxes, Baan & Klöckner (2006) estimated a flatter spectral index of ~0.6, although they also consider this object as a starburst.
Infrared photometry of the nucleus.
Radio photometry of the nucleus.
 |
Fig. 9 Far-IR and radio SED of ESO 320-G030. Tables 2 and 3 list the wavelength (or frequency), flux, and instrument of the plotted measurements. The cyan line is the best gray body fit to the far-IR photometry (Sect. 6.1.2), the dashed dark blue line the best power-law fit to the radio (ν ≤ 36 GHz) emission after subtracting the thermal radio continuum (dot-dash green line) to the observed data (Sect. 6.1.1). The solid red line is the sum of the three components (gray body, thermal radio continuum, and synchrotron). The error bars are smaller than the symbols. |
To avoid any bias, in the previous paragraph we ignored the thermal radio continuum that would be produced by the nuclear SF. Since the presence of an AGN in this object seems unlikely, we can estimate the nuclear SFR (15 M⊙ yr-1; see Sect. 6.2) and derive the associated thermal radio continuum using Eq. (3) of Condon (1992). First, we derive the equivalent Hα flux for the nuclear SFR using the Kennicutt & Evans (2012) calibration. From this flux, F(Hα) = 1.1 × 10-11 erg s-1 cm-2 and assuming Te = 10 000 K, we obtain that Sthermal = 13.5(ν/ GHz)-0.1mJy. This thermal continuum coincides with the 36 GHz observed flux, and it represents ~40% and ~25% of the 4.8 and 1.4 GHz VLA fluxes, respectively. Therefore, after subtracting the thermal continuum, the spectral index is even stepper, α = 1.0 ± 0.1 (Fig. 9).
If we extrapolate this model at the ALMA continuum frequencies, we obtain that the thermal radio continuum contribution is 8 mJy, that is, ~30% of the observed ALMA fluxes at 230 and 242 GHz.
6.1.2. Far-IR continuum
Following Kovács et al. (2010), we fitted the far-IR emission between 70 and 500 μm using a single temperature gray body  (2)where S is the observed flux density, Ω the physical solid angle, τ the optical depth, and Bν the Planck’s blackbody law for a temperature T. We assume that the optical depth follows the relation τν = τ0(ν/ν0)β, with β = 1.8 (Planck Collaboration XXV 2011). The best fit parameters are T = 49 ± 2 K, τ350 μm = 0.30 ± 0.04, and Ω = (2.4 ± 0.3) × 10-11 sr. This corresponds to an IR luminosity of 1011.12 L⊙ and an emitting area with a diameter of 260 pc (assuming an uniform disk). Using Eq. (2) of Kovács et al. (2010), we derive a dust mass of 107.4 M⊙, assuming κ350 μm = 1.92 cm2 g-1 (Li & Draine 2001).
(2)where S is the observed flux density, Ω the physical solid angle, τ the optical depth, and Bν the Planck’s blackbody law for a temperature T. We assume that the optical depth follows the relation τν = τ0(ν/ν0)β, with β = 1.8 (Planck Collaboration XXV 2011). The best fit parameters are T = 49 ± 2 K, τ350 μm = 0.30 ± 0.04, and Ω = (2.4 ± 0.3) × 10-11 sr. This corresponds to an IR luminosity of 1011.12 L⊙ and an emitting area with a diameter of 260 pc (assuming an uniform disk). Using Eq. (2) of Kovács et al. (2010), we derive a dust mass of 107.4 M⊙, assuming κ350 μm = 1.92 cm2 g-1 (Li & Draine 2001).
The model predicts a flux at 230 GHz ~ 30% higher than the measurement and indicates that the emitting area is larger than the area derived from the ALMA continuum map (~50 pc), so it is likely that part of the more spatially extended continuum emission is filtered in the ALMA data.
The predicted flux at 24 μm is 4 times lower than the observed flux. This indicates that dust with T> 49 K exists in the nucleus of this galaxy as expected in a SF object (Rieke et al. 2009).
To calculate the total IR luminosity, we must include this contribution from warm dust. From the analysis of the SED of local LIRGs, the fraction of the IR luminosity produced by dust with T< 50 K is ~80% (Pereira-Santaella et al. 2015; da Cunha et al. 2010). In addition, the IR emission from polycyclic aromatic hydrocarbons (PAH) is ~10% of the total IR luminosity in LIRGs (Pereira-Santaella et al. 2015). Taking into account these two contributions, we derive a total nuclear IR luminosity of 1011.26 L⊙. This value is in very good agreement with the 8−1000 μm IR luminosity derived using the IRAS fluxes and our adopted luminosity distance (1011.28 L⊙; Sanders et al. 2003).
6.2. Nuclear and circumnuclear star-formation
The SFR of the circumnuclear regions (1.5′′< r < 5′′) can be directly estimated from the Paα or Brγ maps (Alonso-Herrero et al. 2006; Piqueras López et al. 2016). In particular, we use the Brγ map corrected for extinction using the spatially resolved Brγ/Brδ ratio (Piqueras López et al. 2016). The average Ak in the circumnuclear region is 1.4 mag and the total Brγ luminosity excluding the central 3′′ is (2.4 ± 0.1) × 1040 erg s-1. Using the Kennicutt & Evans (2012) SFR calibration for Hα (their Eq. (12)) and that Hα/Brγ = 104 for case B conditions, T = 10 000 K, and ne = 103 cm-3 (Hummer & Storey 1987), we derive a circumnuclear SFR of 13 ± 1 M⊙ yr-1. This is similar to the value derived by Rodríguez-Zaurín et al. (2011) using the optical Hα emission, 11 ± 3 M⊙ yr-1.
The nucleus is almost completely obscured in the Brγ map, so we use an indirect method to derive the nuclear SFR. The SFR from the total IR luminosity is 28 M⊙ yr-1 using the Kennicutt & Evans (2012) calibration. Therefore, we estimate that the nuclear SFR is the difference between the total SFR from the IR luminosity and the circumnuclear SFR, that is, 15 ± 2 M⊙ yr-1. We note, that the total IR emission is dominated by the nucleus (see Sect. 6.1), so it is reasonable that it also dominates the total SFR.
We can now calculate the extinction affecting the nucleus by comparing the observed Brγ flux with the expected one from a region with SFR of ~15 M⊙ yr-1. This gives an extinction of AK = 4.6 mag (AV = 40 mag). Due to this extreme extinction level, the nucleus is almost indistinguishable in the Paα and Brγ maps.
In this scenario, the cm radio emission is mainly due to nonthermal emission from supernovae remnants (Condon 1992). In particular, the 4.85 GHz (~6 cm) emission is related to the SN rate (νSN) according to 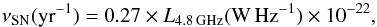 (3)assuming that the nonthermal spectral index is 0.8 (Condon 1992; Colina & Perez-Olea 1992). Taking into account that 40% of the nuclear 4.85 GHz emission is produced by thermal radio emission (Sect. 6.1.1), we derive a SN rate of 0.14 ± 0.02 yr-1. Another SN rate indicator is the near-IR [Fe ii]1.64 μm emission (e.g., Colina 1993; Alonso-Herrero et al. 2003). We measured the nuclear [Fe ii]1.64 μm flux from the SINFONI data and corrected it for extinction assuming the AK derived for the ionized gas. The derived SN rate is 1.2 ± 0.1 yr-1 using Eq. (3) of Alonso-Herrero et al. (2003). Although, as for the hot molecular gas, it is uncertain if this value of AK applies to the shocked gas traced by the [Fe ii].
(3)assuming that the nonthermal spectral index is 0.8 (Condon 1992; Colina & Perez-Olea 1992). Taking into account that 40% of the nuclear 4.85 GHz emission is produced by thermal radio emission (Sect. 6.1.1), we derive a SN rate of 0.14 ± 0.02 yr-1. Another SN rate indicator is the near-IR [Fe ii]1.64 μm emission (e.g., Colina 1993; Alonso-Herrero et al. 2003). We measured the nuclear [Fe ii]1.64 μm flux from the SINFONI data and corrected it for extinction assuming the AK derived for the ionized gas. The derived SN rate is 1.2 ± 0.1 yr-1 using Eq. (3) of Alonso-Herrero et al. (2003). Although, as for the hot molecular gas, it is uncertain if this value of AK applies to the shocked gas traced by the [Fe ii].
The SN rate is directly determined by the SFR. For the assumed Kroupa (2001) initial mass function, νSN(yr-1) = 0.012 × SFR(M⊙ yr-1). Therefore, the expected SN rate is 0.18 ± 0.02 yr-1, which is in agreement with the rate derived from the radio emission, but it is 7 lower than that derived from the [Fe ii] emission. Because of the extreme nuclear obscuration in this object, the latter is highly dependent on the assumed extinction, so this comparison suggests that the nuclear [Fe ii] emission is less affected by extinction than the ionized gas (AK = 3 mag for the [Fe ii] emission would reconcile the three SN rate estimates).
To determine the SF efficiency, we estimate the molecular gas in the nucleus from the CO(2−1) ALMA data. The CO(2−1) emission is more extended than the 232 GHz continuum (0.̋74 × 0.̋65, 180 pc × 160 pc). This size is more similar to that derived from the far-IR SED (260 pc; Section 6.1.2), so it seems likely that the nuclear SF occurs in a region with a diameter between 170 and 260 pc. Therefore, to measure the nuclear CO(2−1) flux, we use an aperture with 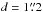 (~290 pc). The resulting flux is 202.6 ± 0.1 Jy km s-1, that corresponds to a molecular gas mass of 109.1 M⊙ using the Galactic CO-to-H2 conversion factor which is appropriate for SF regions in LIRGs (Pereira-Santaella et al. 2016). Therefore, the gas-to-dust ratio in the nucleus is ~50−60, which lies at the lower end of the observed ratios in U/LIRGs (Wilson et al. 2008). The depletion time (tdep = MH2/SFR) of the nucleus is ~80 Myr. This tdep is much shorter than those measured in normal spiral and Seyfert galaxies (~1 Gyr; Leroy et al. 2013; Casasola et al. 2015), but we found similar tdep values in individual regions of another LIRG (IC 4687) observed at a similar spatial resolution (Pereira-Santaella et al. 2016). Therefore, the nucleus of ESO 320-G030 is not particularly extreme in terms of SF efficiency.
(~290 pc). The resulting flux is 202.6 ± 0.1 Jy km s-1, that corresponds to a molecular gas mass of 109.1 M⊙ using the Galactic CO-to-H2 conversion factor which is appropriate for SF regions in LIRGs (Pereira-Santaella et al. 2016). Therefore, the gas-to-dust ratio in the nucleus is ~50−60, which lies at the lower end of the observed ratios in U/LIRGs (Wilson et al. 2008). The depletion time (tdep = MH2/SFR) of the nucleus is ~80 Myr. This tdep is much shorter than those measured in normal spiral and Seyfert galaxies (~1 Gyr; Leroy et al. 2013; Casasola et al. 2015), but we found similar tdep values in individual regions of another LIRG (IC 4687) observed at a similar spatial resolution (Pereira-Santaella et al. 2016). Therefore, the nucleus of ESO 320-G030 is not particularly extreme in terms of SF efficiency.
However, the molecular gas surface density is 104.4 M⊙ pc-2, which is ~20 times higher than the highest surface densities observed in local objects and also ~10 times higher than in the regions of IC 4687 (see Fig. 7 of Pereira-Santaella et al. 2016). Similarly, the SFR surface density is 102.5 M⊙ kpc-2, which is ~2 orders of magnitude higher than in normal galaxies and 3 times higher than the most extreme value of IC 4687. To find similar values of molecular gas and SFR surface densities, we need to go to merger LIRGs and ULIRGs (e.g., Xu et al. 2015).
7. Discussion
In this section, we discuss several aspects of the massive molecular outflow detected in ESO 320-G030.
7.1. Physical properties and kinematics
We measured a molecular gas mass of 106.8 M⊙ in the outflow clumps. Using the Galactic CO-to-H2 conversion factor, this mass would be 5 times higher, so this number is a lower limit. Moreover, it is possible that diffuse emission exists between these clumps, although, according to models, most of the gas of outflows is in fragmented clouds (Nath & Silk 2009).
On average, the molecular mass outflow rate is Ṁout = 1.7 M⊙ yr-1 (assuming a 3 Myr dynamical time). This corresponds to a loading factor (Ṁout/SFR) ~ 0.1 (or 0.5 using the Galactic CO conversion factor). Loading factors about 0.2−3 are often observed in starbursts (Salak et al. 2016; Cicone et al. 2014), so the observed loading factor is compatible with a SF origin as suggested by the nuclear activity. Although, this low loading factor indicates that SF quenching is not efficient in this object.
The velocity of the outflowing gas is ~370−540 km s-1 (see Sect. 5) and the escape velocity at 1.5 kpc for this object is 530 km s-1 (see Cazzoli et al. 2016). Therefore, this suggests that most of this outflowing molecular gas will return to the disk after several Myr. This recycling of material is also compatible with the slowly rotation thick disk of neutral atomic gas found in this object (Cazzoli et al. 2014).
7.2. Origin and evolution of the clumpy structure
In Sect. 5, we showed that the properties of the clumps change with the distance from the nucleus. Two possibilities can explain the presence of molecular gas in outflows: (1) it forms in overdensities in the outflowing neutral/ionized gas (e.g., Zubovas & Nayakshin 2014); or (2) the molecular gas is dragged from the molecular phase of the interstellar medium (ISM; e.g., Hopkins et al. 2012). In the first case, despite the clumpy structure of the outflow, the outflow rate can be relatively constant with time, while in the second case, the clumps might correspond to peaks of the outflow rate.
From Fig. 7, we see that the mass of the clumps decreases with the distance from the nucleus, but the velocity remains approximately constant. If the clumps appear in neutral atomic gas overdensities, this indicates that, further from the outflow origin, these overdensities are less common or that the formation of the molecular gas is less efficient. The volume occupied by the outflow increases proportionally to d3, so both the larger volume of the outflow and the lower gas density at higher distances from the origin would agree with this possibility. On the other hand, if the clumps were originally part of the ISM, they would be losing mass, energy, and momentum as they move. The loss of energy and momentum is expected due to turbulence and the effect of the gravity potential of the galaxy. The mass loss can be due to the clump evaporation in a hot gas outflow environment (Cowie & McKee 1977).
7.3. Power source and energetics
Outflows are produced in starbursts due to supernova explosions, stellar winds, and radiation pressure (Hopkins et al. 2012). Here, we investigate if SNe alone could power the molecular outflow of ESO 320-G030 by comparing the kinetic energy and momentum provided by SNe and those measured in the outflowing clumps.
The kinetic energy of the molecular gas clumps is ~1055 erg s-1, or ~4 × 1048 erg s-1 yr-1 averaged over the dynamical time. For the SN rate of the nucleus (~0.2 yr-1) and assuming an energy of 1051 erg per SN, the kinetic energy associated with this molecular outflow is ~2% of the total available energy. Similarly, the total momentum is 3 × 109 M⊙ km s-1 and the momentum rate ~103 M⊙ km s-1 yr-1. The radial momentum per SN is 2.8 × 104 M⊙ km s-1 (Walch & Naab 2015), so about 20% of the momentum due to SNe is deposited in the outflowing molecular gas. Therefore, the observed outflow can be powered by SNe, although stellar winds and radiation pressure might contribute as well.
8. Conclusions
We present high spatial resolution (~60 pc) ALMA CO(2−1) observations of the local spiral LIRG ESO 320-G030. We study the morphology and kinematics of the cold molecular gas traced by the CO(2−1) emission and combine these data with ancillary HST optical and near-IR imaging, as well as VLT/SINFONI near-IR IFS. The main goals of this work are: characterize the resolved massive molecular outflow detected in this object and establish the nature of the extremely obscured nucleus which produces the massive molecular outflow. The main results are the following:
-
1.
The global kinematics is well represented by a regular rotating disk, although we find non-circular molecular gas motions related to the secondary bar. This can be the signature of inflowing gas motions, which might explain the extreme concentration of molecular gas in the central 500 pc of ESO 320-G030 (60% of the total CO(2−1) emission and 104.4 M⊙ pc-2).
-
2.
We spatially resolve a high velocity (~450 km s-1) outflow containing 106.8 M⊙ of molecular gas (assuming the ULIRG conversion factor) originating in the central ~250 pc. The size of the outflow is ~±1.2 kpc, which corresponds to a dynamical time of ~2.8 Myr. The opening angle is ~30°.
-
3.
We measure the properties of 7 clumps in the outflow. Their sizes are 60−150 pc and they have molecular gas masses between 105.5 and 106.4 M⊙(assuming an ULIRG-like conversion factor). The mass, kinetic energy, and momentum of the clumps decrease with increasing distances while the velocity is approximately constant.
-
4.
The hot molecular gas component of the outflow, as probed by the near-IR H2 transitions, is detected in the innermost (~100 pc) part of the outflow with a hot-to-cold molecular gas ratio of 7 × 10-5. This ratio is similar to that measured by Emonts et al. (2014) in another resolved molecular outflow.
-
5.
We find that the nuclear IR and radio emission of the nucleus (d ~ 250 pc) are compatible with highly obscured intense SF (Ak ~ 4.6 mag; SFR ~ 15 M⊙ yr-1). No evidence for the presence of an AGN is found. The outflow rate and loading factor are Ṁout = 2−8 M⊙ yr-1 and ~0.1−0.5, respectively, and depending on the CO conversion factor assumed. This low loading factor indicates that SF quenching due to the molecular outflow is not efficient in this object.
-
6.
We find that SN explosions in the nuclear starburst (νSN ~ 0.2 yr-1) can power the observed molecular outflow. The kinetic energy and radial momentum of the outflow represent ~2% and 20%, respectively, of the SNe output.
-
7.
The velocity of the outflowing clumps is lower than the escape velocity, so it is likely that most of this molecular gas will return to the disk after several Myr. This is compatible with the thick neutral atomic gas disk found in this object.
The origin of this outflowing molecular gas (either formed in overdensities in the outflowing ionized/neutral gas or dragged from the nuclear ISM) is not clear from the available data. New high-spatial resolution observations of the different phases of this outflow will help to establish the formation and evolution of the observed molecular gas.
Acknowledgments
We thank the anonymous referee for useful comments and suggestions. We acknowledge support from the Spanish Plan Nacional de Astronomía y Astrofísica through grants AYA2010-21161-C02-01 and AYA2012-32295. A.A.-H. acknowledges financial support from the Spanish Ministry of Economy and Competitiveness through grant AYA2015-64346-C2-1-P. B.E. acknowledges funding through the European Union FP7-PEOPLE-2013-IEF grant 624351 This paper makes use of the following ALMA data: ADS/JAO.ALMA#2013.1.00271.S. ALMA is a partnership of ESO (representing its member states), NSF (USA) and NINS (Japan), together with NRC (Canada) and NSC and ASIAA (Taiwan), in cooperation with the Republic of Chile. The Joint ALMA Observatory is operated by ESO, AUI/NRAO and NAOJ.
References
- Aalto, S., Garcia-Burillo, S., Muller, S., et al. 2012, A&A, 537, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Alonso-Herrero, A., Rieke, G. H., Rieke, M. J., & Kelly, D. M. 2003, AJ, 125, 1210 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., Rieke, G. H., Rieke, M. J., et al. 2006, ApJ, 650, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Alonso-Herrero, A., Pereira-Santaella, M., Rieke, G. H., & Rigopoulou, D. 2012, ApJ, 744, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Arribas, S., Colina, L., Bellocchi, E., Maiolino, R., & Villar-Martín, M. 2014, A&A, 568, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Baan, W. A., & Klöckner, H.-R. 2006, A&A, 449, 559 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellocchi, E., Arribas, S., Colina, L., & Miralles-Caballero, D. 2013, A&A, 557, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellocchi, E., Arribas, S., & Colina, L. 2016, A&A, 591, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bolatto, A. D., Warren, S. R., Leroy, A. K., et al. 2013a, Nature, 499, 450 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Bolatto, A. D., Wolfire, M., & Leroy, A. K. 2013b, ARA&A, 51, 207 [Google Scholar]
- Briggs, D. S. 1995, Ph.D. Thesis, New Mexico Institute of Mining and Technology [Google Scholar]
- Buta, R. 1986, ApJS, 61, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Cappellari, M., & Emsellem, E. 2004, PASP, 116, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Casasola, V., Hunt, L., Combes, F., & García-Burillo, S. 2015,A&A, 577, A135 [Google Scholar]
- Cazzoli, S., Arribas, S., Colina, L., et al. 2014, A&A, 569, A14 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cazzoli, S., Arribas, S., Maiolino, R., & Colina, L. 2016, A&A, 590, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cicone, C., Maiolino, R., Sturm, E., et al. 2014, A&A, 562, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Colina, L. 1993, ApJ, 411, 565 [NASA ADS] [CrossRef] [Google Scholar]
- Colina, L., & Perez-Olea, D. 1992, MNRAS, 259, 709 [NASA ADS] [CrossRef] [Google Scholar]
- Condon, J. J. 1992, ARA&A, 30, 575 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Cowie, L. L., & McKee, C. F. 1977, ApJ, 211, 135 [NASA ADS] [CrossRef] [Google Scholar]
- Cushing, M. C., Rayner, J. T., & Vacca, W. D. 2005, ApJ, 623, 1115 [NASA ADS] [CrossRef] [Google Scholar]
- da Cunha, E., Charmandaris, V., Díaz-Santos, T., et al. 2010,A&A, 523, A78 [Google Scholar]
- Dale, D. A., Sheth, K., Helou, G., Regan, M. W., & Hüttemeister, S. 2005, AJ, 129, 2197 [NASA ADS] [CrossRef] [Google Scholar]
- Dasyra, K. M., Combes, F., Novak, G. S., et al. 2014, A&A, 565, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Diniz, M. R., Riffel, R. A., Storchi-Bergmann, T., & Winge, C. 2015, MNRAS, 453, 1727 [NASA ADS] [CrossRef] [Google Scholar]
- Emonts, B. H. C., Piqueras-López, J., Colina, L., et al. 2014, A&A, 572, A40 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Feruglio, C., Maiolino, R., Piconcelli, E., et al. 2010, A&A, 518, L155 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, J., Sturm, E., González-Alfonso, E., et al. 2010, A&A, 518, L41 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Combes, F., Usero, A., et al. 2014, A&A, 567, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Burillo, S., Combes, F., Usero, A., et al. 2015, A&A, 580, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Greusard, D., Friedli, D., Wozniak, H., Martinet, L., & Martin, P. 2000, A&AS, 145, 425 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Heckman, T. M., Armus, L., & Miley, G. K. 1990, ApJS, 74, 833 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Alexandroff, R. M., Borthakur, S., Overzier, R., & Leitherer, C. 2015, ApJ, 809, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Hopkins, P. F., Quataert, E., & Murray, N. 2012, MNRAS, 421, 3522 [Google Scholar]
- Hummer, D. G., & Storey, P. J. 1987, MNRAS, 224, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Hunt, L. K., Combes, F., García-Burillo, S., et al. 2008, A&A, 482, 133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kawamura, A., Mizuno, Y., Minamidani, T., et al. 2009, ApJS, 184, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Kennicutt, R. C., & Evans, N. J. 2012, ARA&A, 50, 531 [NASA ADS] [CrossRef] [Google Scholar]
- King, A., & Pounds, K. 2015, ARA&A, 53, 115 [Google Scholar]
- Kovács, A., Omont, A., Beelen, A., et al. 2010, ApJ, 717, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Kroupa, P. 2001, MNRAS, 322, 231 [NASA ADS] [CrossRef] [Google Scholar]
- Leroy, A. K., Walter, F., Sandstrom, K., et al. 2013, AJ, 146, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Li, A., & Draine, B. T. 2001, ApJ, 554, 778 [Google Scholar]
- Lindberg, J. E., Aalto, S., Muller, S., et al. 2016, A&A, 587, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McMullin, J. P., Waters, B., Schiebel, D., Young, W., & Golap, K. 2007, in Astronomical Data Analysis Software and Systems XVI, eds. R. A. Shaw, F. Hill, & D. J. Bell, ASP Conf. Ser., 376, 127 [Google Scholar]
- Mihalas, D., & Binney, J. 1981, Galactic astronomy: Structure and kinematics, 2nd edn. (San Francisco: W.H. Freeman & Co.) [Google Scholar]
- Mirabel, I. F., Booth, R. S., Johansson, L. E. B., Garay, G., & Sanders, D. B. 1990, A&A, 236, 327 [NASA ADS] [Google Scholar]
- Muzzin, A., van Dokkum, P., Kriek, M., et al. 2010, ApJ, 725, 742 [NASA ADS] [CrossRef] [Google Scholar]
- Narayanan, D., Cox, T. J., Kelly, B., et al. 2008, ApJS, 176, 331 [NASA ADS] [CrossRef] [Google Scholar]
- Nath, B. B., & Silk, J. 2009, MNRAS, 396, L90 [NASA ADS] [Google Scholar]
- Nayakshin, S., & Zubovas, K. 2012, MNRAS, 427, 372 [NASA ADS] [CrossRef] [Google Scholar]
- Norris, R. P., Whiteoak, J. B., Gardner, F. F., Allen, D. A., & Roche, P. F. 1986, MNRAS, 221, 51P [NASA ADS] [CrossRef] [Google Scholar]
- Pereira-Santaella, M., Alonso-Herrero, A., Rieke, G. H., et al. 2010a, ApJS, 188, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira-Santaella, M., Diamond-Stanic, A. M., Alonso-Herrero, A., & Rieke, G. H. 2010b, ApJ, 725, 2270 [NASA ADS] [CrossRef] [Google Scholar]
- Pereira-Santaella, M., Alonso-Herrero, A., Santos-Lleo, M., et al. 2011, A&A, 535, A93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira-Santaella, M., Alonso-Herrero, A., Colina, L., et al. 2015, A&A, 577, A78 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pereira-Santaella, M., Colina, L., García-Burillo, S., et al. 2016, A&A, 587, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piqueras López, J., Colina, L., Arribas, S., Alonso-Herrero, A., & Bedregal, A. G. 2012, A&A, 546, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piqueras López, J., Colina, L., Arribas, S., & Alonso-Herrero, A. 2013, A&A, 553, A85 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Piqueras López, J., Colina, L., Arribas, S., Pereira-Santaella, M., & Alonso-Herrero, A. 2016,A&A, 590, A67 [Google Scholar]
- Planck Collaboration XXV. 2011, A&A, 536, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rayner, J. T., Cushing, M. C., & Vacca, W. D. 2009, ApJS, 185, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Rieke, G. H., Alonso-Herrero, A., Weiner, B. J., et al. 2009, ApJ, 692, 556 [NASA ADS] [CrossRef] [Google Scholar]
- Rodríguez-Zaurín, J., Arribas, S., Monreal-Ibero, A., et al. 2011, A&A, 527, A60 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Roussel, H. 2013, PASP, 125, 1126 [Google Scholar]
- Rupke, D. S. N., Veilleux, S., & Baker, A. J. 2008, ApJ, 674, 172 [NASA ADS] [CrossRef] [Google Scholar]
- Sakamoto, K., Aalto, S., Combes, F., Evans, A., & Peck, A. 2014, ApJ, 797, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Salak, D., Nakai, N., Hatakeyama, T., & Miyamoto, Y. 2016, ApJ, 823, 68 [NASA ADS] [CrossRef] [Google Scholar]
- Sanders, D. B., Mazzarella, J. M., Kim, D.-C., Surace, J. A., & Soifer, B. T. 2003, AJ, 126, 1607 [Google Scholar]
- Schnorr-Müller, A., Storchi-Bergmann, T., Robinson, A., Lena, D., & Nagar, N. M. 2016, MNRAS, 457, 972 [NASA ADS] [CrossRef] [Google Scholar]
- Schruba, A., Leroy, A. K., Walter, F., Sandstrom, K., & Rosolowsky, E. 2010, ApJ, 722, 1699 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., & Van den Bout, P. A. 2005, ARA&A, 43, 677 [NASA ADS] [CrossRef] [Google Scholar]
- Tsai, A.-L., Matsushita, S., Kong, A. K. H., Matsumoto, H., & Kohno, K. 2012, ApJ, 752, 38 [NASA ADS] [CrossRef] [Google Scholar]
- van de Ven, G., & Fathi, K. 2010, ApJ, 723, 767 [NASA ADS] [CrossRef] [Google Scholar]
- van den Broek, A. C., van Driel, W., de Jong, T., et al. 1991, A&AS, 91, 61 [NASA ADS] [Google Scholar]
- Veilleux, S., Kim, D.-C., Sanders, D. B., Mazzarella, J. M., & Soifer, B. T. 1995, ApJS, 98, 171 [NASA ADS] [CrossRef] [Google Scholar]
- Veilleux, S., Cecil, G., & Bland-Hawthorn, J. 2005, ARA&A, 43, 769 [Google Scholar]
- Wada, K. 1994, PASJ, 46, 165 [NASA ADS] [Google Scholar]
- Walch, S., & Naab, T. 2015, MNRAS, 451, 2757 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, C. D., Petitpas, G. R., Iono, D., et al. 2008, ApJS, 178, 189 [NASA ADS] [CrossRef] [Google Scholar]
- Xu, C. K., Cao, C., Lu, N., et al. 2015, ApJ, 799, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Zaragoza-Cardiel, J., Font, J., Beckman, J. E., et al. 2014, MNRAS, 445, 1412 [NASA ADS] [CrossRef] [Google Scholar]
- Zhang, J. S., Wang, J. Z., Di, G. X., et al. 2014, A&A, 570, A110 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zubovas, K., & King, A. R. 2014, MNRAS, 439, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Zubovas, K., & Nayakshin, S. 2014, MNRAS, 440, 2625 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Top row: ALMA 12CO(2−1), VLT/SINFONI H2 1−0 S(1) 2.12 μm, and ALMA 233 GHz continuum (rest frequency) maps of ESO 320-G030. The contours in all the images correspond to the CO(2−1) emission in logarithmic steps (1, 2, 4, 8, 16, 32, 64) × 0.43 Jy km s-1 beam-1. Lower panels: HST/NICMOS F160W and continuum subtracted Paα maps and the HST F814W to F160W ratio to highlight obscured regions (red colors indicate more obscured regions). In the last panel we added an extra contour level at 0.5 × 0.43 Jy km s-1 beam-1. The red hatched ellipses indicate the beam size of each image. For the ALMA CO(2−1) and the 233 GHz continuum images, the beam size is 0.̋25 × 0.̋23, PA 89°. For the SINFONI H2 1−0 S(1) image, the beam FWHM is 0.̋6, and for the HST/NICMOS data, the beam is ~0.̋15. |
| In the text | |
 |
Fig. 2 Deprojected F814W image of ESO 320-G030 assuming an inclination of 43° and a PA of 133°. In the left panel, the central region is saturated to make visible the primary bar and the external spiral arms (pseudoring). The right panel shows the secondary bar and spiral structure present in the central 5 kpc. The contours represent the deprojected CO(2−1) emission. The diagonal white line in the left panel corresponds to the gap between the two HST/ACS detectors. |
| In the text | |
 |
Fig. 3 CO(2−1) isovelocity contours in steps of 50 km s-1 from v(lsrk) = 2800 to 3300 km s-1. The dotted and the dashed lines indicate the major and minor kinematic axes. |
| In the text | |
 |
Fig. 4 Left panel: CO(2−1) velocity field after excluding those pixels with complex line profiles. Middle panel: best fitting model (see Sect. 4). In these two panels, the contour levels are set in steps of 50 km s-1 from v(lsrk) = 2800 to 3300 km s-1. Right panel: residuals (data − model) and the CO(2−1) emission contours as in Fig. 1. The dotted and the dashed lines indicate the major and minor kinematic axes. |
| In the text | |
 |
Fig. 5 Rotation curve corrected for inclination (i = 43°) along the major axis (PA = 133°) for the cold molecular gas traced by the CO(2−1) transition (red circles). The error bars of the CO(2−1) points are 1−2 km s-1. The solid black line is the best fit model to the CO(2−1) data (see Sect. 4). |
| In the text | |
 |
Fig. 6 Left panels: CO(2−1) integrated emission between 2650 and 2850 km s-1 in blue contours and between 3370 and 3530 km s-1 in red contours. The contours correspond to 3, 4, 5, 6, 8, and 12σ levels in their respective bands (the 3σ contour level is not plotted in the top left panel for clarity). The background of the top left panel is the HST/ACS F814W image which shows the internal spiral arms. The background of the bottom left panel is the HST/ACS FR656N image to maximize the contrast of the dust lanes. The dashed line indicates the minor kinematic axis and the dotted lines indicate the approximate opening angle of the outflowing gas. The orange cross marks the position of the 233 GHz continuum peak. Right panels: CO(2−1) spectra of the regions marked in the bottom left panel. The blue and red shaded areas indicate the velocity ranges used to construct the blue and red contours, respectively. The vertical dashed line corresponds to the velocity derived in Sect. 4 assuming a rotating disk model. To increase the signal-to-noise ratio, we binned the spectra in channels of 60, 20, 15, 5, 15, 20, and 20 km s-1from top to bottom. |
| In the text | |
 |
Fig. 7 Logarithm of the molecular mass (first), velocity (second), kinetic energy (third), and momentum (fourth) of the outflowing clumps as a function of the deprojected distance from the nucleus. Blue and red points are blueshifted and redshifted clumps, respectively. The dotted line is the best fit. The parameters of the best fit and the Pearson correlation coefficients are indicated in each panel. The error bars correspond to the statistical uncertainties. |
| In the text | |
 |
Fig. 8 Comparison between the hot (left) and cold (right) molecular gas phases of the outflow region D. The hot molecular gas is traced by the H2 1−0 S(1) 2.12 μm transition observed with SINFONI, while the cold molecular gas is traced by CO(2−1). The background images are the integrated emission in the channels shaded in the bottom panels. The contours represent the total emission of the corresponding transition at peak ×0.9, ×0.6, and ×0.3 levels. The orange hatched circles represent the FWHM of the beam of each image (0.̋6 and ~0.̋25, respectively). The bottom panels are the spectra extracted from the regions located to the NE of the nucleus in the top panels. |
| In the text | |
 |
Fig. 9 Far-IR and radio SED of ESO 320-G030. Tables 2 and 3 list the wavelength (or frequency), flux, and instrument of the plotted measurements. The cyan line is the best gray body fit to the far-IR photometry (Sect. 6.1.2), the dashed dark blue line the best power-law fit to the radio (ν ≤ 36 GHz) emission after subtracting the thermal radio continuum (dot-dash green line) to the observed data (Sect. 6.1.1). The solid red line is the sum of the three components (gray body, thermal radio continuum, and synchrotron). The error bars are smaller than the symbols. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


