| Issue |
A&A
Volume 594, October 2016
|
|
|---|---|---|
| Article Number | A39 | |
| Number of page(s) | 31 | |
| Section | Catalogs and data | |
| DOI | https://doi.org/10.1051/0004-6361/201628337 | |
| Published online | 07 October 2016 | |
Activity indicators and stellar parameters of the Kepler targets
An application of the ROTFIT pipeline to LAMOST-Kepler stellar spectra ⋆,⋆⋆
1 INAF–Osservatorio Astrofisico di Catania, via S. Sofia, 78, 95123 Catania, Italy
e-mail: antonio.frasca@oact.inaf.it
2 Astronomical Institute of the University of Wrocław, ul. Kopernika 11, 51-622 Wrocław, Poland
3 Department of Astronomy, New Mexico State University, Las Cruces, NM 88003, USA
4 Royal observatory of Belgium, Ringlaan 3, 1180 Brussel, Belgium
5 Department of Astronomy, Beijing Normal University, 19 Avenue Xinjiekouwai, 100875 Beijing, PR China
6 Key Lab for Optical Astronomy, National Astronomical Observatories, Chinese Academy of Sciences, 100012 Beijing, PR China
Received: 18 February 2016
Accepted: 23 June 2016
Aims. A comprehensive and homogeneous determination of stellar parameters for the stars observed by the Kepler space telescope is necessary for statistical studies of their properties. As a result of the large number of stars monitored by Kepler, the largest and more complete databases of stellar parameters published to date are multiband photometric surveys. The LAMOST-Kepler survey, whose spectra are analyzed in the present paper, was the first large spectroscopic project, which started in 2011 and aimed at filling that gap. In this work we present the results of our analysis, which is focused on selecting spectra with emission lines and chromospherically active stars by means of the spectral subtraction of inactive templates. The spectroscopic determination of the atmospheric parameters for a large number of stars is a by-product of our analysis.
Methods. We have used a purposely developed version of the code ROTFIT for the determination of the stellar parameters by exploiting a wide and homogeneous collection of real star spectra, namely the Indo US library. We provide a catalog with the atmospheric parameters (Teff, log g, and [Fe/H]), radial velocity (RV), and an estimate of the projected rotation velocity (vsini). For cool stars (Teff≤ 6000 K), we also calculated the Hα and Ca ii-IRT fluxes, which are important proxies of chromospheric activity.
Results. We have derived the RV and atmospheric parameters for 61 753 spectra of 51 385 stars. The average uncertainties, which we estimate from the stars observed more than once, are about 12 km s-1, 1.3%, 0.05 dex, and 0.06 dex for RV, Teff, log g, and [Fe/H], respectively, although they are larger for the spectra with a very low signal-to-noise ratio. Literature data for a few hundred stars (mainly from high-resolution spectroscopy) were used to peform quality control of our results. The final accuracy of the RV is about 14 km s-1. The accuracy of the Teff, log g, and [Fe/H] measurements is about 3.5%, 0.3 dex, and 0.2 dex, respectively. However, while the Teff values are in very good agreement with the literature, we noted some issues with the determination of [Fe/H] of metal poor stars and the tendency, for log g, to cluster around the values typical for main-sequence and red giant stars. We propose correction relations based on these comparisons and we show that this does not have a significant effect on the determination of the chromospheric fluxes. The RV distribution is asymmetric and shows an excess of stars with negative RVs that are larger at low metallicities. Despite the rather low LAMOST resolution, we were able to identify interesting and peculiar objects, such as stars with variable RV, ultrafast rotators, and emission-line objects. Based on the Hα and Ca ii-IRT fluxes, we found 442 chromospherically active stars, one of which is a likely accreting object. The availability of precise rotation periods from the Kepler photometry allowed us to study the dependency of these chromospheric fluxes on the rotation rate for a very large sample of field stars.
Key words: surveys / techniques: spectroscopic / stars: fundamental parameters / stars: kinematics and dynamics / stars: activity / stars: chromospheres
Based on observations collected with the Large Sky Area Multi-Object Fiber Spectroscopic Telescope (LAMOST) located at the Xinglong observatory, China.
Full Tables A.3 and A.4 are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/594/A39
© ESO, 2016
1. Introduction
Large databases of astronomical observations have been constructed since the dawn of astronomy. Even though the content of the early catalogs was relatively simple and the observations reported there suffered from low precision and various systematic errors, careful analysis of those data led to discoveries that are now considered to be milestones in our understanding of the structure and evolution of the Universe (see, e.g., Kepler 1609; Shapley & Curtis 1921; Hubble 1942).
Also in modern astronomy, projects like Optical Gravitational Lensing Experiment (OGLE; Udalski et al. 1992), All Sky Automated Survey (ASAS; Pojmański 1997), Sloan Digital Sky Survey (SDSS; York et al. 2000), Radial Velocity Experiment (RAVE; Steinmetz et al. 2006), Apache Point Observatory Galactic Evolution Experiment (APOGEE; Allende Prieto et al. 2008), Gaia-ESO (Gilmore et al. 2012), Large sky Area Multi-Object fiber Spectroscopic Telescope (LAMOST) Spectral Survey (Zhao et al. 2012), and many others provide vast databases of photometric and spectroscopic observations that aim at detailed investigations of the Galaxy and beyond and that also open the possibility for discoveries that are not predicted by the original scientific concept.
Apart from those systematic projects that aim to cover large portions of the sky, including different components of the Galaxy (bulge, thin and thick disk, open and globular clusters), there are also more specific observing projects that observe smaller sky areas and/or are conceived to give support to space missions. Among these, it is worth mentioning the ground-based, follow-up observations of Kepler asteroseismic targets coordinated by the Kepler Asteroseismic Science Consortium (KASC; see Uytterhoeven, et al. 2010) or the Kepler Community Follow-up Observing Program (CFOP), which associates individuals interested in providing ground-based observational support to the Kepler space mission1. Other large projects that aim to derive parameters for large samples of the Kepler sources are the SAGA (Casagrande et al. 2014, 2016) and the APOKASC (Pinsonneault et al. 2014) surveys. The former is based on Strömgren photometry, while the latter, which is still running, relies on intermediate-resolution infrared spectra taken in the framework of the APOGEE survey.
The LAMOST-Kepler project (hereafter the LK project) is part of the activities realized in the framework of the KASC. It aims at deriving the effective temperature (Teff), the surface gravity (log g), the metallicity ([Fe / H]), the radial velocity (RV), and the projected rotational velocity (vsini) of tens of thousands of stars, which fall in the field of view of the Kepler space telescope (hereafter the Kepler field), as described in detail by De Cat et al. (2015; hereafter Paper I). The purpose of those measurements is multifarious. First, the atmospheric parameters yielded by the LK project complement and can serve as a test-bench for the content of the Kepler Input Catalog (KIC, Brown et al. 2011) and, as such, they provide firm bases for asteroseismic and evolutionary modeling of stars in the Kepler field. Second, our data enables us to flag interesting objects as it allows us to identify fast-rotating stars and those for which the variability in radial velocity exceeds ~20 km s-1. Similarly, stars that show strong emission in their spectral lines or display other relevant spectral features can be identified and used for further research reaching beyond asteroseismic analysis. The analysis of the spectra obtained in the framework of the LK project is performed by three analysis teams with different methodologies. The American team uses the MKCLASS code to produce an MK spectral classification (Gray et al. 2016), the Asian team derives the atmospheric parameters and radial velocities by means of the LASP pipeline (Wu et al. 2014; Ren et al. 2016), the European team, whose results are presented in the present paper, adopt the code ROTFIT for deriving the atmospheric parameters, radial velocity, projected rotational velocity, and activity indicators.
As the selection of the targets and technical details of observations and reductions have been described in detail in Paper I, we focus in the present paper on the results we obtained with the code ROTFIT, developed by Frasca et al. (2003, 2006), and discussed in detail in Molenda-Żakowicz et al. (2013). This code has been adapted to the LAMOST data as described in Sect. 3. Here, we present the catalog containing the products of our analysis (the spectral type SpT, Teff, log g, [Fe/H], RV, vsini, and the activity indicators EWHα, EW8498, EW8542, and EW8662) and discuss the precision and accuracy of the stellar parameters derived with ROTFIT. This is achieved by carrying out detailed comparisons between the results produced by that code and those available in the literature for the stars in common.
This paper is organized as follows. In Sect. 2 we briefly describe the observations. Sect. 3 presents the methods of analysis and discusses the accuracy of the data. This section includes a brief description of the ROTFIT pipeline, the procedure for the measure of the activity indicators, and a comparison of the RVs and atmospheric parameters derived in this work with values from the literature. The results from the activity indicators are presented in Sect. 4. We summarize the main findings of this work in Sect. 5.
2. Observations
Located at the Xinglong observatory (China), LAMOST is a unique astronomical instrument that combines a large aperture (3.6-4.9 m) with a wide field of view (circular with a diameter of 5°), which is covered with 4000 optical fibers connected to 16 multiobject optical spectrometers with 250 fibers each (Wang et al. 1996; Xing et al. 1998). For the LK project, we selected 14 LAMOST fields of view (FOVs) to cover the Kepler field. The data that are analyzed in this paper are those acquired with the LAMOST during the first round of observations. For a detailed description of these observations, we refer to Paper I. A total of 101 086 spectra for objects in the Kepler field were gathered during 38 nights from 30 May 2011 to 29 September 2014. The spectra were reduced and calibrated with the LAMOST pipeline as described by Luo et al. (2012, 2015). The integration times of individual exposures were set according to the typical magnitude of the selected subset of targets and to the weather conditions. These exposures range between 300 to 1800 s (see Table 2 of De Cat et al. 2015). In general, the observation of a plate, which denotes a unique configuration of the fibers, consists of a combination of several of such individual exposures of the same subset of targets. Therefore, the total integration times of the observed plates reaches values between 900 and 4930 s.
Since the exposure time is the same for all stars observed within a plate, the signal-to-noise ratio (S/N) of the acquired spectra varies significantly from target to target, which is mainly a reflection of their magnitude distribution. Because the number of available LAMOST spectra is huge, we decided to semiautomate the process of selection of high- and low-quality spectra using the information yielded by the LAMOST pipeline, namely, the values of S/N at the effective wavelengths of the Sloan DSS filters ugriz (Fukugita et al. 1996; Tucker et al. 2006) and the spectral type given either in the Harvard system or in a free, descriptive system of classification used in the LAMOST pipeline (e.g., carbon or flat). For targets classified by the LAMOST pipeline as A, F, G, or K-type, we rejected spectra with S/N< 10 in the r filter. Spectra of targets classified to the other types were checked by eye to find and reject those that contain only noise. In Fig. 1, we show histograms of S/N at the ugriz filters for the LAMOST spectra for which we derived the atmospheric parameters. In Table 1, we give an overview of the analyzed LAMOST spectra. In total, the atmospheric parameters were derived from 61,753 LAMOST spectra, which correspond to 51 385 unique targets, including 30 213 stars that were observed by Kepler. For 8832 objects, more than one LAMOST spectrum was analyzed.
 |
Fig. 1 Histograms of the S/N of the spectra from which we derived the atmospheric parameters with the ROTFIT code measured at the effective wavelengths of the Sloan DSS filters ugriz. The left and right panels show the S/N range [0, 100] with bin size 10 and the S/N range [100, 600] with bin size 100, respectively. |
Statistical overview of the analyzed LAMOST spectra that have been obtained before the end of the 2014 observation season for the Kepler FOV.
3. Data analysis
3.1. Radial velocity
Templates adopted for the cross-correlation.
The radial velocity was measured by means of the cross-correlation between the target spectrum and a template chosen among a list of 20 spectra of stars with different spectral types (Table 2) taken from the Indo US library (Valdes et al. 2004). We chose stars with vsini as low as possible to minimize the enlargement of the cross-correlation function (CCF). However, given the low resolution of the LAMOST spectra (R ≃ 1800 with the slit width at 2/3 of the fiber size) and the coarse grid of spectral points, where the spacing corresponds to about 70 km s-1, only stars that are rotating faster than about 120 km s-1 can have an appreciable effect on the CCF (see Sect. 3.2).
The Indo-US spectra are suitable RV templates, since they are in the laboratory frame, i.e., the barycentric correction was already applied and the RV of the star subtracted. We only had to handle the continuum normalization.
Each LAMOST spectrum was split into eight spectral segments centered at about 4000, 4500, 5000, 5500, 6200, 6700, 7900, and 8700 Å, and, for each segment, the CCF with each template listed in Table 2 was computed. We therefore developed an ad hoc code in the IDL2 environment. The best template was selected based on the height of the peak. To evaluate the centroid and full width at half maximum (FWHM) of the CCF peak, we fitted it with a Gaussian. For each spectral segment, the RV error, σi, was estimated by the fitting procedure curvefit (Bevington 1969), taking the CCF noise into account, which was evaluated far from the peak (|ΔRV| > 4000 km s-1). The final RV for each star was obtained as the weighted mean of the values of all the analyzed spectral segments, using as weights 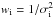 , and applying a sigma clipping algorithm to reject outliers. The standard error of the weighted mean was adopted as the estimate of the RV uncertainty, σRV. The resulting RV and σRV values are given in columns 15 and 16 of Table A.3.
, and applying a sigma clipping algorithm to reject outliers. The standard error of the weighted mean was adopted as the estimate of the RV uncertainty, σRV. The resulting RV and σRV values are given in columns 15 and 16 of Table A.3.
 |
Fig. 2 Scatter plots with the errors of RV, Teff, log g, and [Fe/H] (from top to bottom) as a function of the S/N in the r band. The following color coding is used: blue for 2011–2012, black for 2013, and red for 2014. The full green line, in each box, is the median value as a function of S/N. |
The RV errors are typically in the range 10–30 km s-1 with an average value of about 20 km s-1. These errors are in line with what is expected on the basis of the LAMOST resolution and data sampling. In particular, less than 0.03% of the stars have an error σRV ≤ 10 km s-1, while 10 ≤ σRV < 20 km s-1 for 66% of the full sample, 20 ≤ σRV < 30 km s-1 for 29% , 30 ≤ σRV < 40 km s-1 for about 3.5%, and σRV ≥ 40 km s-1 for about 1.5% of the sample. The behavior of these errors as a function of SNRr is shown in Fig. 2. The median value ranges from about 18 km s-1 to 27 km s-1as a function of S/N.
An empirical determination of the measurement uncertainty, however, can be performed by comparing repeated measurements of RV for the same star in different spectra (e.g., Yanny et al. 2009; Jackson et al. 2015). The distribution of the RV differences is plotted in Fig. 3a. This distribution shows broad tails and it is best fitted by a double-exponential (Laplace) function (see, e.g., Norton 1984) rather than by a normal distribution (Gaussian). The standard deviation of the Laplace fit is 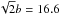 km s-1, where b is the dispersion parameter of the Laplace function. Considering that this distribution is for RV differences of couples of measures, we must divide by
km s-1, where b is the dispersion parameter of the Laplace function. Considering that this distribution is for RV differences of couples of measures, we must divide by 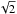 to obtain an estimate of the average error on each individual measure (e.g., Jackson et al. 2015), which is b = 11.7 km s-1. This may suggest a slightly better RV precision than that indicated by the individual RV errors reported in Table A.3 and plotted in Fig. 2.
to obtain an estimate of the average error on each individual measure (e.g., Jackson et al. 2015), which is b = 11.7 km s-1. This may suggest a slightly better RV precision than that indicated by the individual RV errors reported in Table A.3 and plotted in Fig. 2.
 |
Fig. 3 Distributions of the differences of RV, Teff, log g, and [Fe/H] for the stars with repeated observations (histograms). In each box, the full line is the double-exponential (Laplace) fit, while the dotted line is the Gaussian fit. |
For 104 of the stars that we analyzed, we found RV values in the literature that come from high- or mid-resolution spectra. We discarded the stars known to be spectroscopic binaries (SB) and those with large pulsation amplitudes, for example, Mira-type variables, even if their RV variations are small compared to the typical LAMOST RV errors. To validate the RV determinations and to evaluate their external accuracy, we compared our measurements with those from the literature. The results are shown in Fig. 4. The RV values and errors are also reported in Table A.1 together with those from the literature for these stars. For most of these objects we have only one LAMOST spectrum, but for some of them we have from two to four different spectra with a total of 133 RV values. As it appears in Fig. 4, our values of RV are consistent with the literature values within 3σ. There is only one star for which we found at least one discrepant RV value; this star is indicated with a filled circle enclosed in an open square in Fig. 4. We considered an RV value as discrepant when 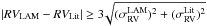 , i.e., when the RV difference is larger than three times the quadratic sum of the errors. This object is KIC 7599132 (=HD 180757), which has been classified as a rotationally variable star by McNamara et al. (2012). We inserted this star in our ongoing campaign at the Catania Astrophysical Observatory aimed at a spectroscopic monitoring of newly discovered binary systems. As a very preliminary result, we can confirm its RV variations. The full results of this spectroscopic monitoring will be presented in a forthcoming paper.
, i.e., when the RV difference is larger than three times the quadratic sum of the errors. This object is KIC 7599132 (=HD 180757), which has been classified as a rotationally variable star by McNamara et al. (2012). We inserted this star in our ongoing campaign at the Catania Astrophysical Observatory aimed at a spectroscopic monitoring of newly discovered binary systems. As a very preliminary result, we can confirm its RV variations. The full results of this spectroscopic monitoring will be presented in a forthcoming paper.
This example shows that the LAMOST RVs are accurate enough to detect pulsating stars or single-lined spectroscopic binary systems (SB1) with a large variation amplitude (ΔRV > 50 km s-1 when σRV ≤ 20 km s-1) among the stars with multiple observations. To this purpose, for stars with multiple observations, we calculated the reduced χ2 and probability P(χ2) that the RV variations have a random occurrence (e.g., Press et al. 1992). The values of P(χ2) are quoted in column 19 of Table A.3.
On average, the offset between the LAMOST and literature RVs is only +5 km s-1 and the rms scatter of our data around the bisector is ≃14 km s-1, which confirms the reliability of our RV measurements and their errors. In any case, if we take into account that some of these stars, especially those with only one LAMOST RV value, could indeed be undetected SBs, the dispersion of 14 km s-1 can be considered an upper limit for the accuracy of our RV determinations.
The procedure for the measurement of RV was run inside the code for the determination of the atmospheric parameters (see Sect. 3.2), since the RV was needed to align in wavelength the reference spectra with the observed one.
 |
Fig. 4 Top panel: comparison between the RV measured on LAMOST spectra (Table A.1) with literature values based mainly on high-resolution spectra (open circles). Filled circles refer to stars with multiple LAMOST observations. The continuous line is the one-to-one relationship. The differences, shown in the bottom panel, show a mean value of ≃+5 km s-1 (dashed line) and a standard deviation of about 14 km s-1 (dotted lines). Discrepant values are indicated with filled circles enclosed in squares in both panels. |
3.2. Projected rotation velocity and atmospheric parameters
We estimated the projected rotation velocity, vsini, and the atmospheric parameters (APs), Teff, log g, and [Fe/H] with a version of the ROTFIT code (e.g., Frasca et al. 2003, 2006), which we adapted to the LAMOST spectra. We adopted, as templates, the low-resolution spectra of the Indo-US Library of Coudé Feed Stellar Spectra (Valdes et al. 2004) whose parameters were recently revised by Wu et al. (2011). This library has the advantage of containing a large number of spectra of different stars, which sufficiently cover the space of the atmospheric parameters, even if the density of templates is not uniform and is rather low in the very metal poor regime. Although the small number of metal-poor templates is a limit for the determination of the APs, the use of spectra of real stars is beneficial for spectral subtraction, as the synthetic spectra are more prone to problems in the cores of Hα and Ca ii-IRT lines (see, e.g., Linsky et al. 1979; Montes et al. 1995).
The resolution of ≈1 Å and the sampling of 0.44 Å pixel-1 are both higher than the LAMOST resolution and sampling, and allow us to properly degrade the Indo-US spectra to match the LAMOST resolution and to resample them on the same wavelength scale as the LAMOST spectra. Furthermore, the wavelength range covered by these spectra (from 3465 to 9470 Å) is larger than the wavelength range of the LAMOST spectra (from 3700 to 9000 Å), which allows us to exploit all the information contained in the LAMOST spectra for our analysis. We discarded those stars for which some parts of the spectrum were missing from the full library and kept 1150 templates.
In the first step, the reference spectra were aligned onto the target spectrum as a result of the radial velocity measured as described in Sect. 3.1. In the second step, each template was broadened by the convolution with a rotational profile of increasing vsini (in steps of 5 km s-1) until a minimum of the residuals was reached. This can provide us with an estimate of vsini. However, given the low resolution of the LAMOST spectra, R ≃ 1800, which corresponds to about 170 km s-1, and the spectra sampling of about 70 km s-1, this parameter is badly defined. We were only able to use it to unambiguously identify the very fast rotators in our sample. We ran Monte Carlo simulations with LAMOST spectra of a few stars, known to be slow rotators from the literature, with the aim of estimating the minimum vsini that can be measured with our procedure. These spectra were artificially broadened by convolution with a rotation profile of increasing vsini (in steps of 30 km s-1) and a random noise was added, similar to Frasca et al. (2015). We found that the rotational broadening is unresolved up to 90 km s-1 and we start to resolve it when vsini ≥ 120 km s-1. We therefore can only trust vsini values above 120 km s-1. For stars with a resulting vsini value below 120 km s-1, the calculated value was replaced by <120 km s-1 and flagged as an upper limit in Table A.3.
 |
Fig. 5 Comparison between the atmospheric parameters measured on LAMOST spectra with literature values. The continuous lines in the top panels represent one-to-one relationships, as in Fig. 4. The dash-dotted line in the [Fe/H] plot (panel c)) is a linear fit to the data with [Fe/H]Lit > −1.5. The differences are shown in the bottom panels along with their average values and standard deviations. |
As for the RV, we split the spectrum into eight spectral segments that were analyzed independently. The templates were then sorted in a decreasing order of the residuals, giving the highest score to the best-fitting template. The spectral type of the template with the highest total score, summing up the results of the individual spectral regions, was assigned to the target star. An example of the fit of an early A-type star, in five spectral segments, is shown in Fig. A.1. Two other examples are shown in Figs. A.2 and A.3 for an F5 V and a K0 III star, respectively.
For each segment we derived values of Teff, log g, and [Fe/H] and their standard errors, which were based on the parameters of the ten best matching templates. The final APs were obtained as the weighted mean of those of the individual segments and are reported in Cols. 9, 11, and 13 of Table A.3, respectively. We adopted as uncertainties for Teff, log g, and [Fe/H] the standard errors of the weighted means to which the average uncertainties of the APs of the templates (±50 K, ±0.1 dex, ±0.1 dex, respectively) were added in quadrature. Scatter plots of APs errors as a function of the S/N in the r band are shown in Fig. 2.
We also considered the stars with two or more spectra for the evaluation of the AP uncertainties, as we did for the RV. The distributions of Teff, log g, and [Fe/H] differences are indicated with the histograms in Figs. 3b, c, and d, respectively. All these distributions are best fitted by a double-exponential function whose dispersion parameter b indicates an average uncertainty of about 66 K or 1.3% for Teff, 0.046 dex for log g, and 0.055 dex for [Fe/H]. These values are all significantly smaller than the average errors (full lines in Fig. 2), which are likely slightly overestimated.
Both these evaluations of uncertainties are internal to the procedure and do not reveal the accuracy of the APs derived with ROTFIT and the templates’ grid of choice. To this aim we compared the parameters that were derived in the present work with those available for some stars from the literature. The literature values were mainly derived from high-resolution optical spectra and, in some cases, with asteroseismic techniques. The APs derived from LAMOST spectra, together with those found in the literature (468 stars with Teff data, of which 352 and 350 also have log g and [Fe/H] values, respectively), are listed in Table A.2. The results of the comparison are shown in Fig. 5.
We note the very good agreement between the Teff values with an average offset of only + 30 K and an rms of 150 K in the temperature range 3000–7000 K (FGKM spectral types). As the errors of Teff determinations usually grow with the temperature, we preferred to plot the logarithm of temperature in Fig. 5, whose dispersion, σlog (Teff) = 0.4343σln(Teff) ≃ 0.4343σTeff/Teff, is a measure of the relative accuracy of temperature. This turns out to be σTeff/Teff ≃ 3.5% with no significant systematic offset with respect to the literature values.
The log g values display instead a larger scatter, which amounts to about 0.30 dex and a tendency for our values to cluster around 2.5 (the typical log g of the K stars in the red giant branch) and 4–4.5 (main-sequence stars). This is likely the result of the different density of templates as a function of log g that, at any given Teff, are more frequent at log g ≃ 4.5 and log g ≃ 2.5, giving rise to a possible bias toward MS or red-giant gravities in the average log g. We note that our analysis code derives a correct log g for several stars with literature values of log g that are intermediate between MS and giants or lower than 2.5. This comparison shows that the log g values are not very accurate, but we are still able to distinguish between luminosity classes I, III, and V, which, together with an accurate Teff determination unaffected by interstellar extinction, was one of the main aims of this analysis. Indeed, this is the requirement for performing a trustworthy spectral subtraction and flux calibration of the chromospheric EWs (see Sect. 3.4) because the surface continuum flux depends mainly on Teff and exhibits only a second-order dependence on log g that is properly considered with our gravity estimates (see Appendix C).
The [Fe/H] values are only in good agreement with the literature values around the solar metallicity, i.e., between −0.3 and +0.2. We tend to overestimate [Fe/H] when it is lower than −0.3 and to underestimate it for values higher than + 0.2. Although the data scatter could be due to the low resolution of the spectra, the systematic trend is likely an effect of the relative scarcity of metal poor and super metal rich stars among our templates. Interestingly, the very low value of metallicity for KIC 9206432 ([Fe/H] = −2.23) has been correctly found by ROTFIT in the LAMOST spectrum, which indicates a negligible contamination by metal richer templates. A linear fit to the values with [Fe/H]Lit > −1.5 (dashed line in Fig. 5c) gives a slope of m = 0.428 ± 0.029.
 |
Fig. 6 Comparison between the atmospheric parameters of red giants in the APOKASC catalog and in our database of LAMOST spectra. The meaning of symbols and lines is the same as in Fig. 5. The open diamonds in the bottom box of panel c) refer to [Fe/H] values corrected according to Eq. (1). |
 |
Fig. 7 Comparison between the atmospheric parameters in the SAGA catalog and in our database of LAMOST spectra. The meaning of symbols and lines is the same as in Fig. 5. |
A large and very recent data set of APs for red giants in the Kepler field is given in the APOKASC catalog (Pinsonneault et al. 2014). They analyzed APOGEE near-IR spectra, complemented with asteroseismic surface gravities. We found 787 stars in common. The comparison of the APs for these stars is shown in Fig. 6. Even if the ranges of Teff and log g values are smaller than those of Fig. 5, these plots show the same general trends as in Fig. 5. In particular, the agreement of Teff is rather good with an rms dispersion of 127 K and only two outliers that we denoted with open squares.
The log g values display a systematic deviation from the one-to-one relation, which is similar to that shown by the giant stars in Fig. 5 with the LAMOST gravities clustered around the average value of red giants (~2.5). This behavior is clearly shown by the differences plotted in the lower box. The outliers of the Teff plot show also discrepant log g values; these values are indicated with red dots enclosed in open squares in Fig. 6b and the properties of these objects are described in Appendix B.
The plot of [Fe/H] comparison is very similar to that of Fig. 5. In this case the systematic trend of the LAMOST versus APOKASC metallicity is even more evident and best fitted with a linear relation in the range of [Fe/H]APOKASC > −1.5, which roughly corresponds to [Fe/H]LAMOST > −1.0. We find a slope m = 0.464 ± 0.017, which is close to that of the fit of Fig. 5. We thus propose a correction relation for the LAMOST metallicity, based on this linear fit, which can be expressed as ![\begin{equation} {\rm [Fe/H}]_{\rm corr} = 2.16\cdot{\rm [Fe/H]} + 0.17, \label{Eq:FeH} \end{equation}](/articles/aa/full_html/2016/10/aa28337-16/aa28337-16-eq58.png) (1)applicable in the range [Fe/H] > −1.0. The LAMOST values of [Fe/H] corrected with the above equation are plotted in the bottom panel of Fig. 6 as green open diamonds. As shown in the figure, the trend has disappeared at the cost of a greater dispersion of the data. However, we prefer to report, in Table A.3, the [Fe/H] values as derived by our code without applying any correction to them, but these raw values should be corrected with Eq. (1) (or with purposely developed relations in their proper range of validity) before they are used.
(1)applicable in the range [Fe/H] > −1.0. The LAMOST values of [Fe/H] corrected with the above equation are plotted in the bottom panel of Fig. 6 as green open diamonds. As shown in the figure, the trend has disappeared at the cost of a greater dispersion of the data. However, we prefer to report, in Table A.3, the [Fe/H] values as derived by our code without applying any correction to them, but these raw values should be corrected with Eq. (1) (or with purposely developed relations in their proper range of validity) before they are used.
Another large set of atmospheric parameters for stars in the Kepler field is represented by the SAGA catalog (Casagrande et al. 2014), which is based on asteroseismic data and Strömgren photometry. Currently, this catalog contains parameters for about 1000 objects, 287 of which have been analyzed in the present paper. The results of the comparison of LAMOST and SAGA parameters are shown in Fig. 7, where symbols and lines have the same meaning as in Figs. 5 and 6. The comparison with SAGA data displays behaviors similar to those already found with the other data sets. Some outliers were also detected and indicated with open squares in Fig. 7. These outliers are briefly discussed in Appendix B.
Similar to what we did for [Fe/H], we made an attempt to find a correction relation for log g. For this purpose we considered all the stars with log g values in the literature (Fig. 5b) from the APOKASC (Fig. 6b) and the SAGA (Fig. 7b) catalogs. These data are shown together, using different symbols, in Fig. 8. As the log g values are basically grouped into two separate regions, we performed two different linear fits for log g < 3.3 and log g ≥ 3.3, which are shown in Fig. 8 by the dash-dotted and dashed lines, respectively, and are given by the following equations: 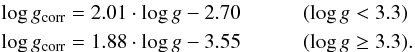 (2)This correction removes much of the nearly linear trends that appear in the bottom panel of Fig. 8, although the scatter is enhanced. As with [Fe/H], we report only the original values, without any correction, in Table A.3.
(2)This correction removes much of the nearly linear trends that appear in the bottom panel of Fig. 8, although the scatter is enhanced. As with [Fe/H], we report only the original values, without any correction, in Table A.3.
 |
Fig. 8 Comparison between our log g values and those from the literature (blue dots), the APOKASC (red dots), and the SAGA (green asterisks) catalogs. Linear fits to the data with log g < 3.3 and log g ≥ 3.3 are shown with the dash-dotted and dashed lines, respectively. The open diamonds in the bottom panel refer to values corrected according to Eq. (2). |
3.3. Statistical properties of the LAMOST-Kepler sample
 |
Fig. 9 [Fe/H] distribution (red filled histogram) for the LAMOST-Kepler subsample of stars in common with the Huber et al. (2014) catalog (blue hatched histogram). The metallicities from the KIC catalog are shown with the empty histogram. |
Figure 9 shows a comparison of the metallicity distributions of the LAMOST-Kepler targets derived in the present work (where [Fe/H] has been corrected according to Eq. (1)) with those from the KIC catalog and from the work of Huber et al. (2014). For a meaningful comparison, we selected all the stars in common between these three catalogs (30 104 stars). The different distributions of LAMOST and KIC metallicities is apparent. The mean and median for the LAMOST data are −0.05 and + 0.02 dex, respectively, while for the KIC data they are −0.17 and −0.13 dex, respectively. This result is in close agreement with the finding of Dong et al. (2014), which strengthens the validity of the correction expressed by Eq. (1), at least in a statistical sense. The Huber et al. metallicities are distributed in a very similar way to that of the KIC catalog (mean = −0.19 dex; median = −0.16 dex). This is not surprising because the majority of these values are not spectroscopic and are mostly derived from the KIC photometry. Indeed, if we only consider the spectroscopic data in Huber et al. (2014), we find a mean of −0.02 dex and a median of −0.01 dex, which are much closer to those of the LAMOST data.
 |
Fig. 10 RV distribution for the full sample of spectra (empty histogram) and for the subsamples in specific metallicity ranges, as indicated in the legend. A bin size of 20 km s-1 was used. |
The RV distribution for the full sample of LAMOST spectra is shown in Fig. 10, in which we also overplot the RV distributions for the subsamples in three different metallicity ranges. The distribution is far from symmetric and displays a tail toward negative radial velocities. The asymmetry of the distribution is clearly enhanced with the decrease of metallicity, as expected from the higher percentage of high-velocity stars among the metal poor stars.
 |
Fig. 11 Upper panel: spatial distribution of the SEGUE targets (dots) in the Kepler field. Lower panel: RV distribution for the SEGUE targets. A bin size of 20 km s-1 was used. |
As a further test on our results, we built the RV distribution obtained with the SEGUE data (Yanny et al. 2009) in the Kepler field. We selected stars with coordinates in the range 275° ≤ RA ≤ 305° and 35.5° ≤ Dec ≤ 52.5°. Because of the different selection criteria (mainly the limiting magnitude) for the Kepler-LAMOST and SEGUE surveys, only 13 stars are in common in the two samples. Nevertheless, the SEGUE sample is composed of 3039 stars, which are spatially distributed as in Fig. 11a. Therefore it is statistically significant. As seen in Fig. 11b, its RV distribution shows a shape that is very similar to that of LAMOST RVs. These data also display the larger contribution of stars with negative velocity at low metallicities.
3.4. Activity indicators and spectral peculiarities
Despite the rather low resolution, which prevents a detailed study of individual spectral lines, the LAMOST spectra are also very helpful to identify objects with spectral peculiarities such as emission lines ascribable, for example, to magnetic activity for late-type stars or to the circumstellar environment and winds in hot stars.
The most sensitive diagnostics of chromospheres in the range covered by the LAMOST spectra are the Ca ii H and K lines that lie, however, in a spectral region where the instrument efficiency is very low, compared to the red wavelengths. Moreover, the flux emitted by cool stars at the Ca ii H and K wavelengths is very low and, with the exception of the brightest targets, is dominated by the noise in the LAMOST spectra.
 |
Fig. 12 Upper panel: LAMOST spectrum of KIC 4637336 (black dotted line), a late G-type star with the Hα totally filled in by emission. The inactive template is overplotted with a thin red line. The difference between target and template spectrum, plotted in the bottom of the panel (blue line), shows only a residual Hα emission (hatched area). The integration range for the residual equivalent width, |
We have therefore used the Balmer Hα line to identify late-type or early-type objects with emission, which can be produced by various physical mechanisms. We subtracted the Indo-US template that best matches the final APs from each LAMOST spectrum. This template has been aligned to the target RV and resampled on its spectral points. The residual Hα emission, 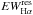 , was integrated over a wavelength interval of 35 Å around the line center (see Fig. 12, upper panel). The stars with a residual Hα equivalent width
, was integrated over a wavelength interval of 35 Å around the line center (see Fig. 12, upper panel). The stars with a residual Hα equivalent width 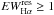 Å were selected as emission-line candidates. A visual inspection of their spectra allowed us to reject several false positives, which are the result of (i) a mismatch in the line wings between target and template; (ii) a spurious emission inside the Hα integration range, which derives from a residual cosmic ray spike; and (iii) problems occurring in spectra with a very low signal. This selection criterion can be too strict for some stars, such as K and M dwarfs, with a filled-in profile or an intrinsically narrow Hα emission of moderate intensity that can be smeared by the low resolution to a signature with an
Å were selected as emission-line candidates. A visual inspection of their spectra allowed us to reject several false positives, which are the result of (i) a mismatch in the line wings between target and template; (ii) a spurious emission inside the Hα integration range, which derives from a residual cosmic ray spike; and (iii) problems occurring in spectra with a very low signal. This selection criterion can be too strict for some stars, such as K and M dwarfs, with a filled-in profile or an intrinsically narrow Hα emission of moderate intensity that can be smeared by the low resolution to a signature with an 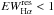 Å. For this reason we scrutinized all the spectra for which we found a Teff< 5000 K and a log g> 3.0 integrating the residual Hα profile over a smaller range (16 Å) and adopting 0.3 Å as the minimum
Å. For this reason we scrutinized all the spectra for which we found a Teff< 5000 K and a log g> 3.0 integrating the residual Hα profile over a smaller range (16 Å) and adopting 0.3 Å as the minimum 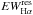 value for keeping a star as a candidate. This allowed us to select, after a visual inspection of the results, additional stars that are likely to be active. As an example, we show in Fig. 13 the spectrum of KIC 4929016, which we classified as a K7V star (Teff = 4035 K). This star displays a weak Hα emission feature with an equivalent width of about 0.90 Å. This star has an RV (Table A.1) derived from the APOGEE survey of M dwarfs (Deshpande et al. 2013) and is known to display a strong and nearly continuous flare activity from the Kepler light curves analyzed by Walkowicz et al. (2011).
value for keeping a star as a candidate. This allowed us to select, after a visual inspection of the results, additional stars that are likely to be active. As an example, we show in Fig. 13 the spectrum of KIC 4929016, which we classified as a K7V star (Teff = 4035 K). This star displays a weak Hα emission feature with an equivalent width of about 0.90 Å. This star has an RV (Table A.1) derived from the APOGEE survey of M dwarfs (Deshpande et al. 2013) and is known to display a strong and nearly continuous flare activity from the Kepler light curves analyzed by Walkowicz et al. (2011).
We selected a total of 577 spectra of 547 stars displaying Hα in emission or filled in by a minimum amount as defined above. The values of EWHα, along with their errors, are quoted in Table A.4. We also report whether the line is observed as a pure emission feature and whether the measure is uncertain as a result of the low S/N or other possible spectral issues.
For these stars we also investigated the behavior of the Ca ii IRT by subtracting the same inactive template used for the Hα (see lower panels of Figs. 12 and 13). For late-type active stars, the emission, which fills the cores of the Ca ii lines, originates from a chromosphere. The equivalent widths of the residual Ca ii IRT emission lines, 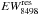 ,
, 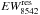 , and
, and 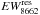 , are also given in Table A.4.
, are also given in Table A.4.
 |
Fig. 14 Example of a star where the Hα line is dominated by nebular sky emission superimposed on the stellar spectrum. The forbidden nitrogen lines at the two sides of Hα appear both in the original and subtracted spectrum. |
In some cases we saw two emission lines at the two sides of the Hα emission that are, without any doubt, the forbidden lines [N ii] at λ 6548 and λ 6584 Å. This pattern is best observed in the residual spectrum (see Fig. 14). These lines are normally observed in ionization nebulae. We think that these emission features can be the result of nebular emission that has not been fully removed by the sky subtraction. Indeed, the intensity of nebular emission was observed to be strongly variable over small spatial scales, from arcminutes down to a few arcseconds (e.g., O’Dell et al. 2003; Hillenbrand et al. 2013), and the sky fibers cannot reproduce the actual nebular emission around each star in the LAMOST field of view. We also flagged these stars in Table A.4.
4. Chromospheric activity
For stars cooler than about 6500 K, for which the sub-photospheric convective envelopes are deep enough to permit an efficient dynamo action, the Hα and Ca ii cores are suitable diagnostics of magnetic activity. The best indicators of chromospheric activity, rather than the EW of a chromospheric line, are the surface line flux, F, and the ratio between the line luminosity and bolometric luminosity, R′, which are calculated, for the Hα, as 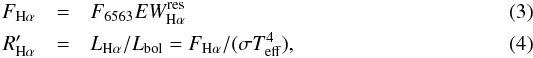 where F6563 is the continuum surface flux at the Hα center, which has been evaluated from the NextGen synthetic low-resolution spectra (Hauschildt et al. 1999) at the stellar temperature and surface gravity of the target. The line fluxes in the three Ca ii IRT lines were calculated with similar relations, where the continuum flux at the center of each line was also evaluated from the NextGen spectra. For each line, the flux error includes both the EW error and uncertainty in the continuum flux at the line center, which is obtained by propagating the Teff and log g errors.
where F6563 is the continuum surface flux at the Hα center, which has been evaluated from the NextGen synthetic low-resolution spectra (Hauschildt et al. 1999) at the stellar temperature and surface gravity of the target. The line fluxes in the three Ca ii IRT lines were calculated with similar relations, where the continuum flux at the center of each line was also evaluated from the NextGen spectra. For each line, the flux error includes both the EW error and uncertainty in the continuum flux at the line center, which is obtained by propagating the Teff and log g errors.
 |
Fig. 15 Left panel: Hα flux vs. Teff. Right panel: |
The Hα fluxes and 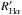 of our targets are plotted as a function of the effective temperature in Fig. 15, along with the boundary between the accreting objects (mostly located above this line) and the chromospherically active stars, as defined by Frasca et al. (2015). Different symbols are used for stars with solid measures of
of our targets are plotted as a function of the effective temperature in Fig. 15, along with the boundary between the accreting objects (mostly located above this line) and the chromospherically active stars, as defined by Frasca et al. (2015). Different symbols are used for stars with solid measures of 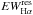 (blue dots) and those where the detection of the Hα core filling is less secure (green asterisks) either because of a low S/N, problems in the spectrum, or the presence of nebular emission lines. This figure clearly shows a different lower level of fluxes and R′ for stars with Teff< 5000 K and Teff> 5000 K, which is the result of the two thresholds adopted for selecting active stars in the two Teff domains.
(blue dots) and those where the detection of the Hα core filling is less secure (green asterisks) either because of a low S/N, problems in the spectrum, or the presence of nebular emission lines. This figure clearly shows a different lower level of fluxes and R′ for stars with Teff< 5000 K and Teff> 5000 K, which is the result of the two thresholds adopted for selecting active stars in the two Teff domains.
We point out that only one star is located in the region occupied by accreting stars. This object, KIC 8749284, is denoted with “1” in Fig. 15b. It was classified by ROTFIT as K1 V and it is the star with the highest value of 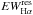 (13 Å). In the only spectrum acquired by LAMOST there is no clear evidence of lithium absorption, which is normally observed in young accreting objects. Alternatively, this object could be an active close binary (SB2 or SB1) composed of main-sequence or evolved stars. Nevertheless, a young age is supported by the infrared (IR) colors, which place KIC 8749284 in the domain of Class II objects in the 2MASS and WISE color-color diagrams (e.g., Koenig et al. 2012). Besides, the spectral energy distribution (SED) clearly shows an IR excess starting from the H band, which is compatible with an evolved circumstellar disk of a Class II source (see Fig. 16). The fit of the SED has been performed as in Frasca et al. (2015) from the B to J band, adopting the effective temperature found by ROTFIT for the photospheric model and letting the interstellar extinction AV free to vary. This star displays rotational modulation in the Kepler photometry with a period of about 3.2 days (Debosscher et al. 2011). Follow-up spectroscopic observations with a higher resolution would help to unveil its nature.
(13 Å). In the only spectrum acquired by LAMOST there is no clear evidence of lithium absorption, which is normally observed in young accreting objects. Alternatively, this object could be an active close binary (SB2 or SB1) composed of main-sequence or evolved stars. Nevertheless, a young age is supported by the infrared (IR) colors, which place KIC 8749284 in the domain of Class II objects in the 2MASS and WISE color-color diagrams (e.g., Koenig et al. 2012). Besides, the spectral energy distribution (SED) clearly shows an IR excess starting from the H band, which is compatible with an evolved circumstellar disk of a Class II source (see Fig. 16). The fit of the SED has been performed as in Frasca et al. (2015) from the B to J band, adopting the effective temperature found by ROTFIT for the photospheric model and letting the interstellar extinction AV free to vary. This star displays rotational modulation in the Kepler photometry with a period of about 3.2 days (Debosscher et al. 2011). Follow-up spectroscopic observations with a higher resolution would help to unveil its nature.
The star labeled “2”, which lies close to the dividing line in Fig. 15, is KIC 8991738. Its SED does not show any IR excess (Fig. 16). Although it is included in the KIC, it has never been observed by Kepler. The target “3”, KIC 4644922 (=V677 Lyr), has an anomalously high level of chromospheric activity for such a hot star. It was previously classified as a semiregular variable (e.g., Pigulski et al. 2009). Indeed, according to Gorlova et al. (2012), KIC 4644922 is a candidate post-AGB star surrounded by a dusty disk for which the Hα emission originates in the circumstellar environment. The spectra of star “4” (KIC 8722673) and “5” (KIC 9377946) show the clear pattern of nebular emission with the two forbidden nitrogen lines at the two sides of Hα (see Fig. 14 for KIC 9377946). We think that, for these two stars, the strong Hα flux does not have a chromospheric origin but is mostly the result of sky line emission that overlaps the stellar spectrum.
In Fig. 17 we compare the Hα and Ca ii chromospheric fluxes. The latter, FCaII−IRT, is the sum of the flux in each line of the triplet. We limited our analysis to the GKM stars (Teff< 6000 K) to minimize the contamination by sources for which the emission does not have a chromospheric origin. However, this subsample (442 stars) is a large portion of the sample of active objects that were selected as described in Sect. 3.4. The two fluxes are clearly correlated, as indicated by the Spearman’s rank correlation coefficient ρ = 0.62 with a significance of σ = 4.35 × 10-24 (Press et al. 1992). A least-squares regression yields the following relation: 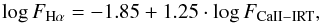 (5)where we took the bisector of the two least-squares regressions (X on Y and Y on X). A power law with an exponent larger than 1 for this flux–flux relationship is in agreement with previous results (see, e.g., Martínez-Arnáiz et al. 2011, and reference therein).
(5)where we took the bisector of the two least-squares regressions (X on Y and Y on X). A power law with an exponent larger than 1 for this flux–flux relationship is in agreement with previous results (see, e.g., Martínez-Arnáiz et al. 2011, and reference therein).
 |
Fig. 16 Spectral energy distribution of the two stars cooler than 5500 K with the highest |
 |
Fig. 17 Flux–flux relationship between Hα and Ca ii IRT. The meaning of the symbols is as in Fig. 15. The dashed line is the least-squares regression. |
For about 200 stars we found the rotation periods in the literature (Debosscher et al. 2011; Nielsen et al. 2013; Reinhold et al. 2013; McQuillan et al. 2013, 2014; Mazeh et al. 2015). We found that, besides the scatter, the Hα flux increases with decreasing rotation period, Prot, as shown in Fig. 18. The correlation with Prot is an expected result, based on the αΩ dynamo mechanism, and it is widely documented in the literature for several diagnostics of chromospheric and coronal activity (e.g., Frasca & Catalano 1994; Montes et al. 1995; Pizzolato et al. 2003; Cardini & Cassatella 2007; Reiners et al. 2015, and references therein). The Spearman rank correlation analysis, which is limited to the stars with solid measures of Hα emission (blue dots in Fig. 18) and Teff< 6000 K, yields a correlation coefficient ρ = −0.59 with a significance of σ = 2.5 × 10-11, which means a highly significant correlation between FHα and Prot. A similar behavior, albeit with a lower degree of correlation (ρ = −0.18; σ = 0.07), is displayed by the Ca ii-IRT flux. We think that the low resolution of the spectra, which gives rise to rather large flux errors, and the heterogeneous sample, which includes stars with very different properties, are mainly responsible for the large data scatter. The latter prevents us, for example, from clearly distinguishing the saturated and unsaturated activity regimes.
 |
Fig. 18 Hα and Ca ii-IRT flux vs. Prot. |
5. Summary
We are carrying out a large spectroscopic survey of the stars in the Kepler field using the LAMOST spectrograph. In this paper we present the results of the analysis of the spectra obtained during the first round of observations (2011–2014), which are mainly based on the code ROTFIT.
We selected spectra with Hα emission and chromospherically active stars by means of the spectral subtraction of inactive templates chosen in a large grid of real-star spectra. Because of the low resolution and rather low S/N for most of the surveyed stars, we set an EW threshold that minimizes the contamination with false positive detections. For cool stars (Teff< 6000 K) we also calculated the Hα and Ca ii-IRT fluxes, which are important proxies of chromospheric activity.
In total, we analyzed 61 753 spectra of 51 385 stars performing an MK spectral classification, evaluating their atmospheric parameters (Teff, log g, and [Fe/H]) and deriving their radial velocity (RV). Our code also allows us to measure the projected rotation velocity (vsini) that, because of the low resolution of the LAMOST spectra, is possible only for fast-rotating stars (vsini> 120 km s-1).
To check the data quality, we searched in the literature for values of the parameters derived from high- or intermediate-resolution spectra. The comparison of the LAMOST Teff values with those from the literature (468 stars in the range 3000–20 000 K) shows a very good agreement and indicates an accuracy of about 3.5%. The comparison with literature values for log g (352 stars) displays a larger scatter and the tendency of LAMOST values to cluster around the average log g of main-sequence stars (~4.5) and red giants (~2.5). Similarly, for [Fe/H] we found a systematic trend, which is best observed when our data are compared with those from the APOKASC catalog (787 stars in common). We proposed a correction relation for the metallicities derived with ROTFIT from the LAMOST spectra, which is based on these comparisons. These effects are likely the result of both the low resolution and the uneven distributions of the spectral templates in the space of parameters. Anyway, the accuracy of the log g and [Fe/H] measurements is sufficient to perform a discrete luminosity classification and to sort the stars in bins of metallicity. This allows us to get a safe flux calibration of the lines EWs.
Our RV measurements agree with literature data within 14 km s-1 , which we consider the external accuracy. Despite the rather low LAMOST resolution, we could identify interesting and peculiar objects, such as stars with variable RV (SB or pulsating star candidates), ultrafast rotators, and stars in particular evolutionary stages.
Our data display a different metallicity distribution compared to that obtained from the Sloan photometry, with a median value that is higher by about 0.15 dex. This result is in agreement with previous findings based on smaller data samples, supporting the validity of the correction relation for [Fe/H] that we proposed.
The RV distribution is asymmetric and shows an excess of stars with negative RVs which is larger at low metallicities. This results is in agreement with the data of the SEGUE survey in the Kepler field.
Based on the Hα and Ca ii-IRT fluxes, we have found 442 chromospherically active stars, one of which is a likely accreting object, as indicated by the strong and broad Hα emission and by the relevant infrared excess. The availability of precise rotation periods from the Kepler photometry has allowed us to study the dependency of these chromospheric fluxes on the rotation rate for a very large sample of field stars. We found that both the Hα and Ca ii-IRT fluxes are correlated with the rotation period, with the former diagnostic showing the largest decrease with the increasing Prot.
Acknowledgments
The authors are grateful to the anonymous referee for very useful suggestions. Guoshoujing Telescope (the Large Sky Area Multi-Object Fibre Spectroscopic Telescope LAMOST) is a National Major Scientific Project built by the Chinese Academy of Sciences. Funding for the project has been provided by the National Development and Reform Commission. lamost is operated and managed by the National Astronomical Observatories, Chinese Academy of Sciences. We thank Katia Biazzo and Gijs Mulders for helpful discussions and suggestions. Support from the Italian Ministero dell’Istruzione, Università e Ricerca (MIUR) is also acknowledged. J.M.-Ż. acknowledges the funding received from the European Community’s Seventh Framework Programme (FP7/2007–2013) under grant agreement No. 269194 and grant number NCN 2014/13/B/ST9/00902. J.N.F. and A.N.R. acknowledge the support of the Joint Fund of Astronomy of National Natural Science Foundation of China (NSFC) and Chinese Academy of Sciences through the Grant U1231202, and the National Basic Research Program of China (973 Program 2014CB845700 and 2013CB834900). Y.W. acknowledges the National Science Foundation of China (NSFC) under grant 11403056. This research made use of SIMBAD and VIZIER databases, operated at the CDS, Strasbourg, France. This publication makes use of data products from the Two Micron All Sky Survey, which is a joint project of the University of Massachusetts and the Infrared Processing and Analysis Center/California Institute of Technology, funded by the National Aeronautics and Space Administration and the National Science Foundation. This publication makes use of data products from the Wide-field Infrared Survey Explorer, which is a joint project of the University of California, Los Angeles, and the Jet Propulsion Laboratory/California Institute of Technology, funded by the National Aeronautics and Space Administration.
References
- Abt, H. A., & Morrel, N. I. 1995, ApJS, 99, 135 [Google Scholar]
- Abt, H. A., Levato, H., & Grosso, M. 2002, ApJ, 573, 359 [NASA ADS] [CrossRef] [Google Scholar]
- Allende Prieto, C., et al. 2008, Astron. Nachr., 329, 1018 [Google Scholar]
- Balona, L. A., Pigulski, A., De Cat, P., et al. 2011, MNRAS, 413, 2043 [Google Scholar]
- Barbier-Brossat, M., Petit, M., & Figon, P. 1994, A&AS, 108, 603 [NASA ADS] [Google Scholar]
- Batalha, N. M., Rowe, J. F., Bryson, S. T., et al. 2013, ApJS, 204, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Bevington, P. 1969, in Data Reduction and Error Analysis for the Physical Sciences (New York: Mc Graw-Hill), 237 [Google Scholar]
- Brown, T. M., Latham, D. W., Everett, M. E., & Esquerdo, G. A. 2011, AJ, 144, 24 [Google Scholar]
- Bruntt, H., Frandsen, S., & Thygesen, A. O. 2011, A&A, 528, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruntt, H., Basu, S., Smalley, B., et al. 2012, MNRAS, 423, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Buchhave, L. A., Latham, D. W., Johansen, A., et al. 2012, Nature, 486, 375 [NASA ADS] [Google Scholar]
- Cardini, D., & Cassatella, A. 2007, ApJ, 666, 393 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Schönrich, R., Asplund, M., et al. 2011, A&A, 530, A138 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Casagrande, L., Silva Aguirre, V., Stello, D., et al. 2014, ApJ, 787, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Silva Aguirre, V., Schlesinger, K. J., et al. 2016, MNRAS, 455, 987 [NASA ADS] [CrossRef] [Google Scholar]
- Catanzaro, G., Frasca, A., Molenda-Żakowicz, J., & Marilli, E. 2010, A&A, 517, A3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Catanzaro, G., Ripepi, V., Bernabei, S., et al. 2011, MNRAS, 411, 1167 [NASA ADS] [CrossRef] [Google Scholar]
- Debosscher, J., Blomme, J., Aerts, C., & De Ridder, J. 2011, A&A, 529, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- De Cat, P., Fu, J. N., Ren, A. B., et al. 2015, ApJS, 220, 19 (Paper I) [NASA ADS] [CrossRef] [Google Scholar]
- Delfosse, X., Forveille, T., Perrier, C., & Mayor, M. 1998, A&A, 331, 581 [NASA ADS] [Google Scholar]
- Deshpande, R., Blake, C. H., Bender, C. F., et al. 2013, AJ, 146, 156 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- de Medeiros, J. R., & Mayor, M. 1999, A&AS, 139, 433 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dong, S., Zheng, Z., Zhu, Z., et al. 2014, ApJ, 789, L3 [NASA ADS] [CrossRef] [Google Scholar]
- Famaey, B., Jorissen, A., Luri, X., et al. 2005, A&A, 430, 165 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fehrenbach, C., Duflot, M., Mannone, C., Burnage, R., & Genty, V. 1997, A&AS, 124, 255 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fekel, F. C. 1997, PASP, 109, 514 [NASA ADS] [CrossRef] [Google Scholar]
- Frasca, A., & Catalano, S. 1994, A&A, 284, 883 [NASA ADS] [Google Scholar]
- Frasca, A., Alcalá, J. M., Covino, E., et al. 2003, A&A, 405, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frasca, A., Guillout, P., Marilli, E., et al. 2006, A&A, 454, 301 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frasca, A., Fröhlich, H.-E., Bonanno, A., et al. 2011, A&A, 523, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frasca, A., Biazzo, K., Lanzafame, A. C., et al. 2015, A&A, 575, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frinchaboy, P. M., & Majewski, S. R. 2008, AJ, 136, 118 [NASA ADS] [CrossRef] [Google Scholar]
- Fröhlich, H.-E., Frasca, A., Catanzaro, G., et al. 2011, A&A, 543, A146 [Google Scholar]
- Fukugita, M., Ichikawa, T., Gunn, J. E., et al. 1996, AJ, 111, 1748 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G., et al. 2012, Messenger, 147, 25 [Google Scholar]
- Gontcharov, G. A. 2006, Astron. Lett., 32, 759 [NASA ADS] [CrossRef] [Google Scholar]
- Gorlova, N., Van Winckel, H., & Jorissen, A. 2012, Balt. Astron., 21, 165 [NASA ADS] [Google Scholar]
- Gray, D. F., & Toner, C. G. 1987, ApJ, 322, 360 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, R. O., Corbally, C. J., De Cat, P., et al. 2016, AJ, 151, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Grenier, S., Baylac, M.-O., Rolland, L., et al. 1999, A&AS, 137, 451 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauck, B., & Mermilliod, M. 1998, A&AS, 129, 431 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauschildt, P. H., Allard, F., & Baron, E. 1999, ApJ, 512, 377 [NASA ADS] [CrossRef] [Google Scholar]
- Hillenbrand, L. A., Hoffer, A. S., & Herczeg, G. J. 2013, AJ, 146, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Howarth, I. D., Siebert, K. W., Hussain, G. A. J., & Prinja, R. K. 1997, MNRAS, 284, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Hubble, E. 1942, Science, 95, 212 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Chaplin, W. J., Christensen-Dalsgaard, J., et al. 2013, ApJ, 767, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Silva Aguirre, V., Matthews, J. M., et al. 2014, ApJS, 211, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Jackson, R. J., Jeffries, R. D., Lewis, J., et al. 2015, A&A, 580, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kepler, J. 1609, Astronomia nova [Google Scholar]
- Kharchenko, N. V., Scholz, R.-D., Piskunov, A. E., Röser, S., & Schilbach, E. 2007,Astron. Nachr., 328, 889 [Google Scholar]
- Koenig, X. P., Leisawitz, D. T., Benford, D. J., et al. 2012, ApJ, 744, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Lehmann, H., Tkachenko, A., Semaan, T., et al. 2011, A&A, 526, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Linsky, J. R., Hunten, D. M., Sowell, R., Glackin, D. L., & Kelch, W. L. 1979, ApJS, 41, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Luo, A.-L., Zhang, H.-T., Zhao, Y.-H., et al. 2012, RA&A, 12, 1243 [Google Scholar]
- Luo, A.-L., Zhao, Y.-H., Zhao, G., et al. 2015, RA&A, 15, 1095 [Google Scholar]
- Mann, A. W., Gaidos, E., Lépine, S., & Hilton, E. J. 2012, ApJ, 753, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Marcy, G. W., Isaacson, H., Howard, A. W., et al. 2014, ApJS, 210, 20 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez-Arnáiz, R., López-Santiago, J., Crespo-Chacón, I., & Montes, D., MNRAS, 414, 2629 [Google Scholar]
- Mazeh, T., Perets, H. B., McQuillan, A., & Goldstein, E. S. 2015, ApJ, 801, 3 [NASA ADS] [CrossRef] [Google Scholar]
- McNamara, B. J., Jackiewicz, J., & McKeever, J. 2012, AJ, 143, 101 [NASA ADS] [CrossRef] [Google Scholar]
- McQuillan, A., Mazeh, T., & Aigrain, S. 2013, ApJ, 775, L11 [NASA ADS] [CrossRef] [Google Scholar]
- McQuillan, A., Mazeh, T., & Aigrain, S. 2014, ApJS, 211, 24 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Mermilliod, J. C., Mayor, M., & Udry, S. 2008, A&A, 485, 303 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meszaros, Sz., Holtzman, J., Garcia Perez, A. E., et al. 2013, AJ, 146, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Molenda-Żakowicz, J., Frasca, A., Latham, D. W., & Jerzykiewicz, M. 2007, Acta Astron., 57, 301 [NASA ADS] [Google Scholar]
- Molenda-Żakowicz, J., Frasca, A., & Latham, D. W. 2008, Acta Astron., 58, 419 [NASA ADS] [Google Scholar]
- Molenda-Żakowicz, J., Latham, D. W., Catanzaro, G., Frasca, A., & Quinn, S. N. 2011, MNRAS, 412, 1210 [NASA ADS] [Google Scholar]
- Molenda-Żakowicz, J., Sousa, S. G., Frasca, A., et al. 2013, MNRAS, 434, 1422 [NASA ADS] [CrossRef] [Google Scholar]
- Molenda-Żakowicz, J., Brogaard, K., Niemczura, E., et al. 2014, MNRAS, 445, 2446 [NASA ADS] [CrossRef] [Google Scholar]
- Montes, D., Fernández-Figueroa, M. J., De Castro, E., & Cornide, M. 1995, A&A, 294, 165 [NASA ADS] [Google Scholar]
- Nidever, D. L., Marcy, G. W., Butler, R. P., Fischer, D. A., & Vogt, S. S. 2002, ApJS, 141, 503 [NASA ADS] [CrossRef] [Google Scholar]
- Nielsen, M. B., Schunker, H., Gizon, L., & Ball, W. H. 2015, A&A, 582, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Niemczura, E., Murphy, S. J., Smalley, B., et al. 2015, MNRAS, 450, 2764 [NASA ADS] [CrossRef] [Google Scholar]
- Nordström, B., Mayor, M., Andersen, J., et al. 2004, A&A, 418, 989 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Norton, R. M. 1984,The American Statistician (American Statistical Association), 38, 135 [Google Scholar]
- O’Dell, C. R., Peimbert, M., & Peimbert, A. 2003, AJ, 125, 2590 [NASA ADS] [CrossRef] [Google Scholar]
- Pakhomov, Yu. V., Antipova, L. I., Boyarchuk, A. A., Zhao, G., & Liang, Ya. 2009, Astron. Rep., 53, 685 [NASA ADS] [CrossRef] [Google Scholar]
- Petigura, E. A., Marcy, G. W., & Howard, A. W. 2013, ApJ, 770, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Pigulski, A., Pojmański, G., Pilecki, B., & Szczygieł, D. M. 2009, Acta Astron., 59, 33 [NASA ADS] [Google Scholar]
- Pinsonneault, M. H., Elsworth, Y., Epstein, C., et al. 2014, ApJS, 215, [Google Scholar]
- Pizzolato, N., Maggio, A., Micela, G., Sciortino, S., & Ventura, P. 2003, A&A, 397, 147 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pojmański, G. 1997, Acta Astron., 47, 467 [NASA ADS] [Google Scholar]
- Press, W. H., Teukolsky, S. A., Vetterling, W. T., & Flannery, B. P. 1992, Numerical Recipes in Fortran 2nd edn. (Cambridge: Cambridge Univ. Press) [Google Scholar]
- Queloz, D., Allain, S., Mermilliod, J.-C., Bouvier, J., & Mayor, M. 1998, A&A, 335, 183 [NASA ADS] [Google Scholar]
- Reiners, A., Schüssler, M., & Passegger, V. M. 2014, ApJ, 794, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Reinhold, T., Reiners, A., & Basri, G. 2013, A&A, 560, A4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ren, A. B., Fu, J. N., De Cat, P., et al. 2016, ApJS, submitted [Google Scholar]
- Royer, F., Grenier, S., Baylac, M.-O., Gómez, A. E., & Zorec, J. 2002, A&A, 393, 897 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Saar, S. H., & Osten, R. A. 1997, MNRAS, 284, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Shapley, H., & Curtis, H. D. 1921, Bulletin of the National Research Council, 2, 171 [Google Scholar]
- Steinmetz, M., et al. 2006, AJ, 132, 1645 [NASA ADS] [CrossRef] [Google Scholar]
- Thygesen, A. O., Frandsen, S., Bruntt, H., et al. 2012, A&A, 543, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tkachenko, A., Lehmann, H., Smalley, B., Debosscher, J., & Aerts, C. 2012, MNRAS, 422, 2960 [NASA ADS] [CrossRef] [Google Scholar]
- Torres, G., Fischer, D. A., Sozzetti, A., et al. 2012, ApJ, 757, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Tucker, D. L., Kent, S., Richmond, M. W., et al. 2006, Astron. Nachr., 327, 821 [NASA ADS] [CrossRef] [Google Scholar]
- Udalski, A., Szymanski, M., Kałużny, J., Kubiak, M., & Mateo, M. 1992, Acta Astron., 42, 253 [NASA ADS] [Google Scholar]
- Uytterhoeven, K., Briquet, M., Bruntt, H., et al. 2010, Astron. Nachr., 331, 993 [NASA ADS] [CrossRef] [Google Scholar]
- Uytterhoeven, K., Moya, A., Grigahcène, et al. 2011, A&A, 534, A125 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Valdes, F., Gupta, R., Rose, J. A., Singh, H. P., & Bell, D. J., 2004. ApJS, 152, 251 [NASA ADS] [CrossRef] [Google Scholar]
- Walkowicz, L. M., Basri, G., Batalha, N., et al. 2011, AJ, 141, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Wang, S.-G., Su, D.-Q., Chu, Y.-Q., Cui, X., & Wang, Y.-N. 1996, Apl. Opt., 35, 5155 [Google Scholar]
- Wang, J., Fischer, D. A., Barclay, T., et al. 2013, ApJ, 776, 10 [NASA ADS] [CrossRef] [Google Scholar]
- Wilson, R. E. 1953, in General Catalogue of Stellar Radial Velocities (Carnegie Inst. Washington D.C. Publ.), 601 [Google Scholar]
- Wu, Y., Singh, H. P., Prugniel, P., Gupta, R., & Koleva, M. 2011, A&A, 525, A71 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wu, Y., Du, B., Luo, A., Zhao, Y., & Yuan, H. 2014, in Statistical Challenges in 21st Century Cosmology, Proc. IAU Symp., 306, 340 [CrossRef] [Google Scholar]
- Xing, X., Zhai, C., Du, H., et al. 1998, Proc. SPIE, 3352, 839 [NASA ADS] [CrossRef] [Google Scholar]
- Yanny, B., Rockosi, C., Newberg, H. J., et al. 2009, AJ, 137, 4377 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., et al. 2000, AJ, 120, 1579 [Google Scholar]
- Zhao, G., Zhao, Y.-H., Chu, Y.-Q., Jing, Y.-P., & Deng, L.-C. 2012, RA&A, 12, 723 [Google Scholar]
Appendix A: Additional data
 |
Fig. A.1 Example of the continuum-normalized LAMOST spectrum of an early A-type star in five spectral regions (dots). The best template found by ROTFIT is overplotted with a thin red line. The difference between the two spectra is shown in the bottom of each panel with a blue full line. |
Stars with radial velocity in the literature.
Stars with atmospheric parameters in the literature.
Stellar parameters for the whole sample of LAMOST spectra.
Activity indicators.
Appendix B: Stars with discrepant Teff and log g compared to APOKASC and SAGA
 |
Fig. B.1 Example of the continuum-normalized LAMOST spectrum of KIC 9542218 in three spectral regions (dots). The best template found by ROTFIT for each spectral region is overplotted with a thin red line. The difference between the two spectra is shown in the bottom of each panel with a blue full line. We note the large residual of the fit in the first region where a mid-F type template (HD 150453) is not able to reproduce either the Balmer lines or narrower absorptions, such as the Fe i λ 4057 Å lines. The spectrum at red wavelengths is instead well reproduced by a cool giant template. |
 |
Fig. B.2 Example of the continuum-normalized LAMOST spectrum of KIC 7273199 in three spectral regions (dots). The best template found by ROTFIT for each spectral region is overplotted with a thin red line. The difference between the two spectra is shown in the bottom of each panel with a blue full line. The spectrum is clearly reminiscent of a warm (F-type) star. However, the asymmetry in the red wings of the Balmer Hγ and Hβ lines, can be due to a spectroscopic companion. |
The two stars with very discrepant Teff and log g values, compared with those listed in the APOKASC catalog, are KIC 9542218 and KIC 8936084 from left to right of Fig. 6a, respectively. KIC 8936084, although correctly classified as K1 III, displays very broad spectral features, which have been fitted by our code in most of the analyzed spectral segments with a giant star template with a vsini≃ 205 km s-1. We cannot exclude that the large vsini is instead the effect of an unresolved SB. The values of Teff and log g and their errors are affected by those of main-sequence templates that have been selected together with giant star templates, particularly in some spectral regions. We think that this is the result of the large line broadening or binarity. The other discrepant star, KIC 9542218, is the most interesting case because its spectrum shows clear signatures of a hot star (Balmer Hδ, Hϵ and H8 lines) superimposed on a cool star in the bluest spectral segment (3850–4200 Å), while it is reminiscent of a normal red giant in the red part of the spectrum (see Fig. B.1). This explains why the LAMOST Teff and log g values are higher than those in the APOKASC catalog. The contribution of the hot component could be so small in the near-IR to make it undetectable with APOGEE, but the observed near-IR spectrum of this star could be still slightly contaminated and the parameters reported in the APOKASC catalog could have been affected. The large wavelength coverage of the LAMOST from the near UV to the near-IR is suitable to detect composite spectra with very different stars.
Four stars appear as outliers in Fig. 7. The most noticeable case is that of KIC 7273199, which displays very discrepant values for all the parameters. We found a temperature Teff = 6190 K and a metallicity [Fe/H] = −2.05 dex, while the SAGA catalog reports 4917 K and −0.59 dex, respectively. The spectrum of this star, which is reminiscent of a warm (F-type) star, shows asymmetries in the wings of the Balmer Hγ and Hβ lines that can be due to a spectroscopic companion. This could have given rise to this large discrepancy of atmospheric parameters derived with very different methods and suggests to consider them as highly unreliable. KIC 5373233 and KIC 8212479 display strong discrepancies only for log g, given our values of 3.6 ± 0.5 and 3.4 ± 0.5 dex for the two stars, respectively, i.e., more than 1 dex higher than the values of SAGA that are more typical of giant stars. The former star is a fast rotator (vsini≃ 220 km s-1), which can explain a rather inaccurate value. The second star has instead a projected rotation velocity that is not detectable with the LAMOST resolution (vsini≤ 120 km s-1). The last object, KIC 8145677, has both log g and [Fe/H] that is much different than the SAGA values. The latter catalog reports a gravity log g = 2.41 and a metallicity [Fe/H] = −1.77 dex. The LAMOST spectrum (see Fig. B.3), however, does not seem that of a very metal poor star, but it rather resembles a mildly metal poor giant or subgiant, in agreement with the value of [Fe/H] = −0.53 that we found.
Appendix C: Continuum surface fluxes as a function of atmospheric parameters
The continuum flux at 6563 Å (Hα center) and in the centers of the Ca ii-IRT lines as a function of the APs (Teff,log g, and [Fe/H]) was measured in the NextGen synthetic spectra. We took the average continuum flux in two regions at the two sides of the aforementioned lines. We plot the continuum flux at 6563 Å as a function of Teff for different values of log g and [Fe/H] in Fig. C.1. The continuum flux at the line center of the Ca ii λ 8542 Å line, F8542, is shown in Fig. C.2. It is worth noticing that the dependence of these continuum fluxes on log g and [Fe/H] is negligible for Teff ≥ 4000 K. The flux differences as a function of log g are more pronounced at lower temperatures, mostly when Teff ≤ 3500 K, which is likely due to the strengthening of molecular bands. Anyway, this dependence is a second-order effect, compared to the Teff dependence, and it is properly taken into account when we convert the EWs into line fluxes using the log g and [Fe/H] values that we derived, although their accuracy is not as high as that of Teff determinations.
 |
Fig. B.3 Example of the continuum-normalized LAMOST spectrum of KIC 8145677 in three spectral regions (dots). The best template found by ROTFIT for each spectral region is overplotted with a thin red line. The difference between the two spectra is indicated in the bottom of each panel with a blue full line. |
 |
Fig. C.1 Left panel: continuum flux at the Hα wavelength, as derived from the NextGen spectra for a solar metallicity, vs. Teff. Different log g are coded with different colors. Right panel: the same continuum flux at log g = 4.0 for three values of metallicity. |
All Tables
Statistical overview of the analyzed LAMOST spectra that have been obtained before the end of the 2014 observation season for the Kepler FOV.
All Figures
 |
Fig. 1 Histograms of the S/N of the spectra from which we derived the atmospheric parameters with the ROTFIT code measured at the effective wavelengths of the Sloan DSS filters ugriz. The left and right panels show the S/N range [0, 100] with bin size 10 and the S/N range [100, 600] with bin size 100, respectively. |
| In the text | |
 |
Fig. 2 Scatter plots with the errors of RV, Teff, log g, and [Fe/H] (from top to bottom) as a function of the S/N in the r band. The following color coding is used: blue for 2011–2012, black for 2013, and red for 2014. The full green line, in each box, is the median value as a function of S/N. |
| In the text | |
 |
Fig. 3 Distributions of the differences of RV, Teff, log g, and [Fe/H] for the stars with repeated observations (histograms). In each box, the full line is the double-exponential (Laplace) fit, while the dotted line is the Gaussian fit. |
| In the text | |
 |
Fig. 4 Top panel: comparison between the RV measured on LAMOST spectra (Table A.1) with literature values based mainly on high-resolution spectra (open circles). Filled circles refer to stars with multiple LAMOST observations. The continuous line is the one-to-one relationship. The differences, shown in the bottom panel, show a mean value of ≃+5 km s-1 (dashed line) and a standard deviation of about 14 km s-1 (dotted lines). Discrepant values are indicated with filled circles enclosed in squares in both panels. |
| In the text | |
 |
Fig. 5 Comparison between the atmospheric parameters measured on LAMOST spectra with literature values. The continuous lines in the top panels represent one-to-one relationships, as in Fig. 4. The dash-dotted line in the [Fe/H] plot (panel c)) is a linear fit to the data with [Fe/H]Lit > −1.5. The differences are shown in the bottom panels along with their average values and standard deviations. |
| In the text | |
 |
Fig. 6 Comparison between the atmospheric parameters of red giants in the APOKASC catalog and in our database of LAMOST spectra. The meaning of symbols and lines is the same as in Fig. 5. The open diamonds in the bottom box of panel c) refer to [Fe/H] values corrected according to Eq. (1). |
| In the text | |
 |
Fig. 7 Comparison between the atmospheric parameters in the SAGA catalog and in our database of LAMOST spectra. The meaning of symbols and lines is the same as in Fig. 5. |
| In the text | |
 |
Fig. 8 Comparison between our log g values and those from the literature (blue dots), the APOKASC (red dots), and the SAGA (green asterisks) catalogs. Linear fits to the data with log g < 3.3 and log g ≥ 3.3 are shown with the dash-dotted and dashed lines, respectively. The open diamonds in the bottom panel refer to values corrected according to Eq. (2). |
| In the text | |
 |
Fig. 9 [Fe/H] distribution (red filled histogram) for the LAMOST-Kepler subsample of stars in common with the Huber et al. (2014) catalog (blue hatched histogram). The metallicities from the KIC catalog are shown with the empty histogram. |
| In the text | |
 |
Fig. 10 RV distribution for the full sample of spectra (empty histogram) and for the subsamples in specific metallicity ranges, as indicated in the legend. A bin size of 20 km s-1 was used. |
| In the text | |
 |
Fig. 11 Upper panel: spatial distribution of the SEGUE targets (dots) in the Kepler field. Lower panel: RV distribution for the SEGUE targets. A bin size of 20 km s-1 was used. |
| In the text | |
 |
Fig. 12 Upper panel: LAMOST spectrum of KIC 4637336 (black dotted line), a late G-type star with the Hα totally filled in by emission. The inactive template is overplotted with a thin red line. The difference between target and template spectrum, plotted in the bottom of the panel (blue line), shows only a residual Hα emission (hatched area). The integration range for the residual equivalent width, |
| In the text | |
 |
Fig. 13 Hα emission in the LAMOST spectrum of KIC 4929016. Lines and symbols are as in Fig. 12. |
| In the text | |
 |
Fig. 14 Example of a star where the Hα line is dominated by nebular sky emission superimposed on the stellar spectrum. The forbidden nitrogen lines at the two sides of Hα appear both in the original and subtracted spectrum. |
| In the text | |
 |
Fig. 15 Left panel: Hα flux vs. Teff. Right panel: |
| In the text | |
 |
Fig. 16 Spectral energy distribution of the two stars cooler than 5500 K with the highest |
| In the text | |
 |
Fig. 17 Flux–flux relationship between Hα and Ca ii IRT. The meaning of the symbols is as in Fig. 15. The dashed line is the least-squares regression. |
| In the text | |
 |
Fig. 18 Hα and Ca ii-IRT flux vs. Prot. |
| In the text | |
 |
Fig. A.1 Example of the continuum-normalized LAMOST spectrum of an early A-type star in five spectral regions (dots). The best template found by ROTFIT is overplotted with a thin red line. The difference between the two spectra is shown in the bottom of each panel with a blue full line. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1 but for an F5 V star. |
| In the text | |
 |
Fig. A.3 Same as Fig. A.1 but for a K0 III star. |
| In the text | |
 |
Fig. B.1 Example of the continuum-normalized LAMOST spectrum of KIC 9542218 in three spectral regions (dots). The best template found by ROTFIT for each spectral region is overplotted with a thin red line. The difference between the two spectra is shown in the bottom of each panel with a blue full line. We note the large residual of the fit in the first region where a mid-F type template (HD 150453) is not able to reproduce either the Balmer lines or narrower absorptions, such as the Fe i λ 4057 Å lines. The spectrum at red wavelengths is instead well reproduced by a cool giant template. |
| In the text | |
 |
Fig. B.2 Example of the continuum-normalized LAMOST spectrum of KIC 7273199 in three spectral regions (dots). The best template found by ROTFIT for each spectral region is overplotted with a thin red line. The difference between the two spectra is shown in the bottom of each panel with a blue full line. The spectrum is clearly reminiscent of a warm (F-type) star. However, the asymmetry in the red wings of the Balmer Hγ and Hβ lines, can be due to a spectroscopic companion. |
| In the text | |
 |
Fig. B.3 Example of the continuum-normalized LAMOST spectrum of KIC 8145677 in three spectral regions (dots). The best template found by ROTFIT for each spectral region is overplotted with a thin red line. The difference between the two spectra is indicated in the bottom of each panel with a blue full line. |
| In the text | |
 |
Fig. C.1 Left panel: continuum flux at the Hα wavelength, as derived from the NextGen spectra for a solar metallicity, vs. Teff. Different log g are coded with different colors. Right panel: the same continuum flux at log g = 4.0 for three values of metallicity. |
| In the text | |
 |
Fig. C.2 Same as Fig. C.1 for the continuum flux at the Ca ii-IRT wavelengths. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


