| Issue |
A&A
Volume 594, October 2016
|
|
|---|---|---|
| Article Number | A44 | |
| Number of page(s) | 25 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201527992 | |
| Published online | 10 October 2016 | |
Large-scale outflows in luminous QSOs revisited
The impact of beam smearing on AGN feedback efficiencies
1 European Southern Observatory, Karl-Schwarzschild-Str. 2, 85748 Garching b. München, Germany
e-mail: bhuseman@eso.org
2 LERMA, Observatoire de Paris, PSL, CNRS, Sorbonne Universités, UPMC, 75014 Paris, France
3 Gemini Observatory, Northern Operations Center, 670 North A’ohoku Place, Hilo, HI 96720, USA
4 Physics Department, California Polytechnic State University, San Luis Obispo, CA 93407, USA
5 Department of Physics and Astronomy, Seoul National University, 151-742 Seoul, Korea
Received: 17 December 2015
Accepted: 26 May 2016
Context. Feedback from active galactic nuclei (AGN) is thought to play an important role in quenching star formation in galaxies. However, the efficiency with which AGN dissipate their radiative energy into the ambient medium remains strongly debated.
Aims. Enormous observational efforts have been made to constrain the energetics of AGN feedback by mapping the kinematics of the ionized gas on kpc scale. We study how the observed kinematics and inferred energetics are affected by beam smearing of a bright unresolved narrow-line region (NLR) due to seeing.
Methods. We re-analyse optical integral-field spectroscopy of a sample of twelve luminous unobscured quasi-stellar objects (QSOs) (0.4 <z< 0.7) previously presented in the literature. The point-spread function (PSF) for the observations is directly obtained from the light distribution of the broad Hβ line component. Therefore, we are able to compare the ionized gas kinematics and derived energetics of the total, truly spatially extended, and unresolved [O iii] emission.
Results. We find that the spatially resolved [O iii] line width on kpc scales is significantly narrower than the one before PSF deblending. The extended NLRs (ENLRs) appear intrinsically offset from the QSO position or more elongated which can be interpreted in favour of a conical outflow on large scales while a spherical geometry cannot be ruled out for the unresolved NLR. We find that the kinetic power at 5 kpc distance based on a spherical model is reduced by two orders of magnitude for a conical outflow and one order of magnitude for the unresolved NLR after PSF deblending. This reduced kinetic power corresponds to only 0.01−0.1 per cent of the bolometric AGN luminosity. This is smaller than the 5−10% feedback efficiency required by some cosmological simulations to reproduce the massive galaxy population. The injected momentum fluxes are close or below the simple radiation-pressure limit Lbol/c for the conical outflow model for the NLR and ENLR when beam smearing is considered.
Conclusions. Integral-field spectroscopy is a powerful tool to investigate the energetics of AGN outflows, but the impact of beam smearing has to be taken into account in the high contrast regime of QSOs. For the majority of observations in the literature, this has not been addressed carefully so that the incidence and energetics of presumed kpc-scale AGN-driven outflows still remain an unsolved issue, from an observational perspective.
Key words: ISM: jets and outflows / galaxies: active / quasars: emission lines / techniques: imaging spectroscopy
© ESO, 2016
1. Introduction
Feedback from active galactic nuclei (AGN) has become a key ingredient in numerical simulations and semi-analytic models of galaxy evolution to suppress star formation at the highest stellar masses, which appears necessary to recover the properties of the local galaxy population (e.g. Di Matteo et al. 2005; Bower et al. 2006; Croton et al. 2006; Somerville et al. 2008; Schaye et al. 2015). However, the mechanism(s) with which the released energy of AGN is dissipated to the surrounding interstellar medium of the host galaxy is poorly constrained by observations so far. One popular scenario for AGN feedback is a large-scale outflow where the AGN energy is sufficient to expel a large fraction of the gas from the host galaxy (e.g. Silk & Rees 1998). Thereby, the AGN is reducing the available gas reservoir and the star formation activity becomes greatly suppressed.
The existence of high-velocity AGN-driven gas outflows has been confirmed by X-ray observations of ultra-fast outflowing material in the circumnuclear region (e.g. Tombesi et al. 2010; Gofford et al. 2015). Also, broad-absorption line (BAL) AGN display outflowing gas with velocities of a few 1000 km s-1 in UV absorption lines like [C iv] and Mg ii (e.g. Reichard et al. 2003; Trump et al. 2006; Gibson et al. 2009). The extent of the outflows is usually not directly constrained from those observation due to a lack of spatial resolution. A remedy to this dilemma is provided through the (extended) narrow-line region (E)NLR, which corresponds to the gas ionized by the AGN on tens of pc to tens of kpc scales (e.g. Pogge 1988; Capetti et al. 1996; Bennert et al. 2002; Schmitt et al. 2003; Hainline et al. 2014; Keel et al. 2015). The demarcation between NLR and ENLR is arbitrary given that the ionization mechanism is the same, but a transition radius at ~1 kpc has been used (e.g. Unger et al. 1987). The bright [O iii] λλ4960,5007 doublet line ([O iii] hereafter) is mainly used at optical wavelengths to trace the kinematics in the NLR close to the AGN. It is well-known that this line tends to be systematically asymmetric with a blue wing that is interpreted as a genuine signature for an extended outflow (e.g. Heckman et al. 1981; Boroson 2005; Komossa et al. 2008; Mullaney et al. 2013). These high-velocity outflows are well resolved in very nearby Seyfert galaxies on < 1 kpc scales (e.g. Crenshaw & Kraemer 2000; Rice et al. 2006; Storchi-Bergmann et al. 2010; Fischer et al. 2013).
Currently, great efforts are being made to investigate the properties of large-scale high-velocity outflows in the most luminous AGN, that is quasi-stellar objects (QSOs). They are expected to show the strongest outflows if these are driven by the AGN radiation (e.g. Silk & Rees 1998; King 2003; Hopkins et al. 2010; Faucher-Giguère & Quataert 2012). With the advent of optical and near-IR long-slit or integral-field unit (IFU) spectrographs on 8 m class telescopes, the ENLR kinematics has been mapped on kpc scale for luminous QSOs at low redshift z< 1 (e.g. Fu & Stockton 2009; Greene et al. 2011, 2012; Rupke & Veilleux 2011; Villar-Martín et al. 2011; Husemann et al. 2013b; Liu et al. 2013b, 2014, 2015; Harrison et al. 2014; McElroy et al. 2015; Humphrey et al. 2015; Villar-Martín et al. 2016; Karouzos et al. 2016) and high redshift z> 1 (e.g. Cano-Díaz et al. 2012; Harrison et al. 2012; Brusa et al. 2015; Cresci et al. 2015; Carniani et al. 2015). The majority of those studies report outflows on several kpc scales in almost all QSOs as indicated by broad and/or blue-shifted [O iii] emission lines.
Many of the spectroscopic QSO observations are focussed on obscured (type II) QSOs. Obscured QSOs lack the bright point-like power-law continuum of the accretion disc and the emission of the broad-line region (BLR) that are prominent in unobscured (type I) QSOs. This difference has been explained by the inclination of a toroidal-like obscuring structure with respect to our line-of-sight in the unification model of AGN (e.g. Antonucci 1993). In this model the NLR is located outside the obscuring structure and can be seen in both types of QSOs. Given the high gas density and radiation field close to the AGN, the [O iii] emission lines from the NLR on scales of ≪1 kpc can outshine the ENLR on host galaxy scales by a factor of a few depending on the size of the ENLR and physical resolution of the observation. Therefore, for the purpose of our study we define the NLR and ENLR as the spatially unresolved and resolved emission, respectively.
It is therefore crucial to characterize the point-spread function (PSF) for QSO observations in order to separate the emission from the compact NLR and the contributions from the ENLR. The ability to achieve such a separation depends strongly on the spatial resolution. Characterizing the PSF is particularly challenging for spectroscopic observations of obscured QSOs, because the slit or IFU usually do not simultaneously cover a star. In these cases, an approximation of the PSF and its shape may be obtained from acquisition images (e.g. Hainline et al. 2013, 2014; Humphrey et al. 2015) or standard star observations (e.g. Liu et al. 2013a, 2014) taken close in time to the science observations. However, the actual PSF for the science observation can still be different due to time variability of the seeing and the tracking error of the telescope for significantly longer science exposures.
IFU spectroscopy of unobscured QSOs provides a way to reconstruct the PSF directly from the science data assuming that broad Balmer lines from the BLR are intrinsically unresolved (e.g. Jahnke et al. 2004). This technique was applied to various IFU observations of unobscured QSOs (Sánchez et al. 2004; Christensen et al. 2006; Husemann et al. 2008, 2013b, 2014; Carniani et al. 2015; Herenz et al. 2015; Liu et al. 2015) enabling the study of line diagnostics and kinematics across the host galaxy without the apparent contamination of the bright unresolved NLR. Based on a large sample of luminous unobscured QSOs at z< 0.3 and luminous obscured QSOs, Husemann et al. (2013b), Villar-Martín et al. (2016), and Karouzos et al. (2016) reported a lack of high-velocity outflows on kpc scales after deblending the unresolved NLR and ENLR. This appears to be in direct contradiction to the result of various other groups for luminous obscured QSOs (e.g. Greene et al. 2011; Liu et al. 2013a, 2014; Harrison et al. 2014; McElroy et al. 2015). However, those studies did not separate kinematics of the NLR and ENLR given the difficulty of constraining the PSF. It is therefore unclear whether beam smearing, differences in the QSO feedback efficiency or even differences in the unobscured and obscured QSOs sample selection are causing these discrepant conclusions.
In this paper, we systematically investigate the effect of the beam smearing on the measured kpc-scale kinematics of the [O iii] lines. In particular, Liu et al. (2013b) reported very large mass-outflow rates and kinetic power from IFU spectroscopy of the [O iii] line for a sample of luminous obscured QSOs at redshift 0.4 <z< 0.7 . While the PSF for these observations cannot be reconstructed, the authors also presented a matched sample of unobscured QSOs in Liu et al. (2014) for which the BLR can be used as a PSF tracer. Here, we re-reduce and re-analyse the dataset of luminous unobscured QSOs from Liu et al. (2014) and compare the results with and without deblending the contribution from the unresolved NLR and ENLR. Thereby, we can verify how much the results on the ENLR geometry, the large-scaled ionized gas kinematics and associated AGN feedback efficiency are affected by beam smearing.
The paper is organized as follows. In Sect. 2 we describe the IFU data reduction and analysis including our QSO-host galaxy deblending scheme and emission-line measurements. This is followed by a comparison of various parameters on the extended ionized gas measurements before and after deblending the point-like and extended emission (Sect. 3). From the measured quantities we compute outflow energetics for two different outflow models in Sect. 4. We then discuss our results with previous observations and expectations for AGN feedback scenarios (Sect. 5). Finally, we close with a summary and our main conclusions in Sect. 6. Throughout the paper we assume a concordance cosmological model with H0 = 70 km s-1 Mpc-1, Ωm = 0.3, and ΩΛ = 0.7.
Basic sample characteristics.
2. Integral-field spectroscopy of luminous QSOs
2.1. The QSO sample and IFU data reduction
The QSO sample and optical integral-field observation we focus on in this paper are presented by Liu et al. (2014); here we briefly recap the main characteristics of the sample. The 12 QSOs were selected from the Shen et al. (2011) catalogue to have (i) a minimum [O iii] luminosity of L[O iii]> 1042.7 erg s-1 to be comparable with the unobscured QSO selection in Liu et al. (2013a); (ii) a redshift range of 0.4 <z< 0.7; (iii) a 1.4 GHz radio flux not exceeding f1.4 GHz< 10 mJy in the NVSS or FIRST radio surveys to exclude radio-loud QSOs; and (iv) a high [O iii] equivalent width. In Table 1, we list some characteristic parameters of the sample mainly taken from Liu et al. (2014), but we also compute additional parameters from the data itself, that is the broad Hβ line luminosity (LHβ) and the continuum luminosity at 5100 Å (L5100).
Observations of the QSO sample were taken with the Gemini multi-object spectrograph (GMOS: Allington-Smith et al. 2002) in IFU-mode at the Gemini-north telescope as part of programme GN-2012B-Q-29 (PI: G. Liu). We retrieved the raw data and corresponding calibrations from the GEMINI science archive after the data became publicly available. The two-slit mode of the GMOS IFU provides a 5″ × 7″ target field-of-view (FoV) that is contiguously sampled with 1000 hexagonal lenslets of 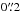 in diameter. Additionally, 500 lenslets are packed into a 5′′ × 3.5′′ FoV about 1′ offset from the primary IFU field to simultaneously monitor the sky. The spectral range was chosen such that Hβ and [O iii] lines are simultaneously covered. Two different setups with the R400-G5305 grism (R ~ 2000) in the i band are necessary to capture those important lines considering the redshift range in the sample and to avoid that lines falling in one of the gaps between the three charged-coupled devices (CCDs). Two 1620 s exposure were obtained for each QSO in the sample.
in diameter. Additionally, 500 lenslets are packed into a 5′′ × 3.5′′ FoV about 1′ offset from the primary IFU field to simultaneously monitor the sky. The spectral range was chosen such that Hβ and [O iii] lines are simultaneously covered. Two different setups with the R400-G5305 grism (R ~ 2000) in the i band are necessary to capture those important lines considering the redshift range in the sample and to avoid that lines falling in one of the gaps between the three charged-coupled devices (CCDs). Two 1620 s exposure were obtained for each QSO in the sample.
 |
Fig. 1 Comparison of the GMOS 3′′ aperture spectra (black line) with the corresponding SDSS spectrum (red line). The wavelength range is limited to the rest-frame wavelength range between 4500 and 5500 Å. An absolute photometric calibration of the GMOS data based on the median of the ratio of spectra over the common wavelength range. The spectra are normalized in flux density so that the peak in the [O iii] λ5007 line is set to one in the SDSS spectrum. A large part of the SDSS spectrum of SDSS J0304+0022 is masked as bad, as seen as the linear interpolated region. In general, the relative GMOS flux calibration across the wavelength range is consistent with the SDSS spectra at a <10% level. |
For the data reduction, we use the IFU data reduction package developed and extensively tested for the Calar Alto large integral field area (CALIFA) survey (Sánchez et al. 2012; Husemann et al. 2013a; García-Benito et al. 2015). Since CALIFA uses the fibre-based IFU spectrograph PMAS (Roth et al. 2005), all reduction steps are almost identical except that the GMOS IFU samples the FoV contiguously and that the data is spread over three independent CCDs. The data reduction work-flow consists of standard tasks such as bias subtraction, cosmic-ray masking with PyCosmic (Husemann et al. 2012), fibre tracing and fibre profile fitting using the continuum lamp exposure, flexure correction, optimal fibre extraction, wavelength calibration using the attached arc lamp exposure, and relative wavelength-dependent fibre transmission correction using a continuum lamp. One important difference with respect to the data reduction of Liu et al. (2014) is that we re-sample the data into a datacube with 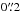 rectangular spaxels. Over-sampling the native data resolution with just two exposures does not provide additional information and would degrade the S/N per final spaxel. For the re-sampling, we assume that the hexagons effectively collect light within a circular aperture of 0.2′′ diameter and apply the “drizzle” resampling scheme (Fruchter & Hook 2002) to construct the final datacubes. During this re-sampling step, we simultaneously correct for the effect of atmospheric dispersion by shifting the sample grid to account for the continuous shift in the relative position along wavelength.
rectangular spaxels. Over-sampling the native data resolution with just two exposures does not provide additional information and would degrade the S/N per final spaxel. For the re-sampling, we assume that the hexagons effectively collect light within a circular aperture of 0.2′′ diameter and apply the “drizzle” resampling scheme (Fruchter & Hook 2002) to construct the final datacubes. During this re-sampling step, we simultaneously correct for the effect of atmospheric dispersion by shifting the sample grid to account for the continuous shift in the relative position along wavelength.
Standard star observations are reduced in the same way as the science data to perform a relative spectrophotometric flux calibration along wavelength. Following Liu et al. (2014), we retrieve Sloan digital sky survey (SDSS, York et al. 2000) spectra from DR10 (Ahn et al. 2014) and compare the GMOS spectra with the SDSS ones to anchor our absolute flux calibration. Here, we simply extract spectra within a 3′′ diameter centred on the QSO and compare it directly with the SDSS DR10 spectra since they were already re-scaled in flux to account for the aperture fibre losses. Then we determine the photometric scale factor compared to the SDSS spectra as the median of the ratio between the two spectra. We show the SDSS and the matched aperture GMOS spectra in Fig. 1. Although the spectrophotometric calibration of SDSS spectra are considered very accurate, the GMOS and SDSS data are taken a few years apart so that intrinsic variability of AGN in the continuum and broad lines will lead to systematic uncertainties in our adopted absolute photometric calibration.
 |
Fig. 2 Example of the broad Hβ and Fe ii emission-line subtraction without QSO-host deblending for SDSS J0924+0642. The observed spectrum (black line) and our best-fit model (red line) are shown in the upper panel. The best-fit model consisting of the broad Hβ and Fe ii λλ4948,5017 plus continuum is represented by the blue line with the corresponding residual spectrum of the narrow Hβ and [O iii] λλ4960,5007 indicated by the green line. The residuals of the total model are shown in the panel below. Details of the assumed model are given in the main text. |
 |
Fig. 3 Upper panel: example PSF estimated from the intensity of the broad Hβ line for SDSS J0924+0642. The white circle indicates the FWHM of the seeing. We highlight two spaxels with a black and red square for which we show the spectra from the datacube in the lower panels. The red spaxel is |
 |
Fig. 4 Upper panel: intensity profile for various seeing conditions assuming a Gaussian shape. The region of the central spaxel (core) and the adjacent host galaxy spaxel (host) are indicated by shaded areas for the GMOS sampling. Lower panel: corresponding scale factors for a point-source as a function seeing is shown by the black line. Higher scale factors would imply surface brightness distributions steeper than point-like sources (red shaded area). |
2.2. Spatially-resolved [O III] emission-line analysis
The first analysis step is usually to create emission-line maps and parameters from the individual spaxel of the datacube. A generic feature of ground-based observations is that the signal from the source is spatially smeared due to the seeing, so that the spaxels may not be independent in their information content. In particular, luminous unobscured QSOs are subject to this effect since the light from the accretion disc and BLR are emitted from a very compact region but which can be as bright as the entire host galaxy. Nevertheless, the beam smearing affects the bright narrow lines like the [O iii] λλ4960,5007 lines in unobscured and obscured QSOs in exactly the same way. The reason for this is that the classical compact NLR on ≪ 1 kpc scales seen for both types of AGN becomes quickly unresolved with increasing redshift and can outshine any ionized gas emission of the ENLR, which extends over several kpc for luminous QSOs (e.g. Bennert et al. 2002; Husemann et al. 2014; Hainline et al. 2014; Keel et al. 2015), depending on the size and contrast ratio.
Here, we specifically want to test how much the light from the unresolved NLR blends with the ENLR in IFU observations, altering the spatially resolved line profiles and biasing the derived quantities. Unobscured QSOs are ideal for this purpose since the broad emission-lines from the unresolved BLR provide an intrinsic measurement for the PSF of a given observation (e.g., Jahnke et al. 2004). This allows us to accurately deblend spatially unresolved, NLR or QSO, and resolved, ENLR or host galaxy emission, in an empirical way. We will refer to this process as a NLR-ENLR deblending or QSO-host galaxy deblending. To make a fair comparison, we characterize the [O iii] λλ4960,5007 doublet line profile spaxel by spaxel in a consistent way before and after applying NLR-ENLR deblending as described below.
2.2.1. Mapping the total [O III] line profile
To characterize the spatially resolved [O iii] emission-line profile, we follow the algorithm of Liu et al. (2013b) which consists of three basic steps: 1) removal of Fe ii and broad Hβ emission; 2) multi-component modelling of the [O iii] doublet line; and 3) non-parametric line shape measurements based on the best-fit model. The first step is achieved by modelling the QSO spectrum with a set of Gaussian profiles to separate the various emission line components in the spectral range (see Fig. 2). Then, we create a best-fit model only for the broad Hβ and Fe ii line components as well as the local AGN power-law continuum. This template spectrum is subtracted from each spaxel after proper matching in flux. The residual is a pure narrow Hβ plus [O iii] emission-line datacube. According to Liu et al. (2013b), we model the [O iii] doublet lines as a superposition of up to three independent Gaussian systems coupled in their intrinsic flux ratio (1:3, Storey & Zeippen 2000), redshift and line dispersion. A Levenberg-Marquardt minimization algorithm with reasonable starting values is applied to determine the best-fit parameters per spaxel. Any model with an increased number of free parameters will provide a better fit. Based on a statistical F-test we decide whether the increased number of free parameters significantly improved the χ2 in excess of what is expected from statistical fluctuations. From the [O iii] line shape of the best-fit model we directly compute non-parametric parameters such as the integrated flux f[O iii], the median line velocity vmed, the line width at the 80 per cent quantile of the line flux (W80), the line asymmetry (A) and line kurtosis (K) following the formula presented in Liu et al. (2013b).
2.2.2. Mapping the ENLR [O III] line profile
We repeat the entire analysis process again, but now replacing step 1) with a spectral QSO-host galaxy deblending scheme to separate the apparently unresolved (NLR) and resolved (ENLR) [O iii] line emission. The explicit modelling and subtraction of the broad Hβ and Fe ii emission lines is not necessary, because those emission lines originate from the BLR and are intrinsically unresolved emission associated with the QSO spectrum and automatically subtracted during QSO-host galaxy deblending process as shown in Fig. 3. For the QSO-host deblending we adopt an iterative algorithm implemented in the public software package qdeblend (Husemann et al. 2013b, 2014).
(Husemann et al. 2013b, 2014).
qdeblend first re-constructs the PSF of the observations from the strength of the broad emission line, the Hβ line in this case. In the first iteration, the brightest spaxel which is dominated by the QSO light is scaled according to the PSF and subtracted from each spaxel. The central spaxel contains not only spatially unresolved emission from the QSO, but also a fraction of host galaxy emission including the ENLR. The algorithm iteratively removes the host galaxy contribution based on the average surface brightness of the residual host galaxy emission (Σhost) in the spaxels around the central QSO spaxel (Σcore) after each iteration. A scale factor Σcore/ Σhost is applied to scale the brightness towards the centre, which clearly depends on the intrinsic surface brightness profile of the extended host galaxy/ENLR emission. It can reasonably vary only between a factor of one (constant surface brightness) and a factor corresponding to purely unresolved emission depending on the PSF and GMOS sampling (see Fig. 4).
first re-constructs the PSF of the observations from the strength of the broad emission line, the Hβ line in this case. In the first iteration, the brightest spaxel which is dominated by the QSO light is scaled according to the PSF and subtracted from each spaxel. The central spaxel contains not only spatially unresolved emission from the QSO, but also a fraction of host galaxy emission including the ENLR. The algorithm iteratively removes the host galaxy contribution based on the average surface brightness of the residual host galaxy emission (Σhost) in the spaxels around the central QSO spaxel (Σcore) after each iteration. A scale factor Σcore/ Σhost is applied to scale the brightness towards the centre, which clearly depends on the intrinsic surface brightness profile of the extended host galaxy/ENLR emission. It can reasonably vary only between a factor of one (constant surface brightness) and a factor corresponding to purely unresolved emission depending on the PSF and GMOS sampling (see Fig. 4).
We choose a factor very close to the scale factor in the limit of a point-like emission, because we have no ancillary information on the exact surface brightness distribution of the extended emission on small scales. For all sources we assume a scale factor of about 70% between the point-like and constant surface brightness value. This is a conservative choice that avoids significant over-subtraction of extended emission. It also ensures that the process actually converges because the scale factors are below the point-like limit in all cases, otherwise the QSO spectrum would be oversubtracted. The process usually converges after a few iterations and we choose five iterations for all objects. We then repeat the [O iii] line modelling and the non-parametric measurements in the QSO-subtracted data. The uncertainties of the line profile measurements increase after the QSO-host deblending process due to additional uncertainties in the PSF reconstruction and the noise of the subtracted QSO spectrum. In Fig. 5 we present the resulting [O iii] line parameter maps for all the QSOs from the total line profile and from the ENLR only after applying the QSO-host deblending.
3. Quantifying the impact of an unresolved NLR on ENLR measurements
Basic parameters inferred for the ENLR before and after the deblending process.
3.1. Comparison with the original measurements
 |
Fig. 5 Example for the spatially resolved emission-line maps before and after applying the QSO-host galaxy deblending for SDSS J0304+0022. Similar figures for all QSOs are moved to the Appendix. |
 |
Fig. 6 Comparison of the total [O iii] line width (W80, upper left panel), maximum velocity range (Δv, upper right panel), size of the ENLR (Rint, lower right panel), and the power-law slope of the total [O iii] surface brightness profile (η, lower left panel) from the QSO as measured by Liu et al. (2014) and our re-analysis. We find good agreement between measurements with only a weak systematic offset and a scatter consistent with the intrinsic accuracy of measurements. The surface brightness profile slope η shows the greatest scatter because the actual range of the outer profile to measure η is not clearly specified in Liu et al. (2014), so that our measurements are likely not exactly matching their methodology. For the ENLR we measure the isophotal radius at a surface brightness (corrected for cosmological dimming) of Σ[O iii] = 10-15 erg s-1 cm-2 arcsec-2 (black circles) and the maximum projected distance to spaxels which exhibit the same threshold surface brightness locally (grey symbols). |
Since we performed a completely independent re-analysis, from the data reduction to the data analysis, compared to the work by Liu et al. (2014), we first want to test whether we recover their measurements if we follow their methods as closely as possible. In Fig. 6, we show a comparison of the [O iii] line width (W80), maximum velocity range (Δv), the size of the ENLR (Rint) and the power-law slope of the total [O iii] surface brightness profile (I[O iii](R) ~ R− η) over the range 1″−2.5″ from the QSO as measured by Liu et al. (2014) and our own measurement from total [O iii] line maps before deblending.
We find that our measurements are in good agreement with the values reported by Liu et al. (2014). Systematic differences are less than 20% in all cases. Our measurements for W80 are slightly smaller by 13 ± 10% and also the maximum velocity range Δv is smaller by 15 ± 17 per cent. For the latter, the rms is significant, which is caused by the systematic uncertainties on the measurements of the radial velocities given that we have independently re-reduced the entire dataset. The most significant scatter is found for the outer radial [O iii] surface brightness profile η. The reason for this is that the radius over which the slope is measured is not clearly defined in Liu et al. (2014). The arbitrary fitting range of 1″−2.5″ along the major axis of the ENLR that we adopt here may simply not reflect the original prescription to measure this parameter. However, our mean value of ⟨ η ⟩ = 3.5 ± 0.6 is consistent with the measurements for the unobscured and obscured QSOs by Liu et al. (2014).
We can almost exactly reproduce the isophotal radius of the ENLR, based on the surface brightness of concentric annuli, with a rather small deviation of 5 ± 5%. However, when the surface brightness of individual spaxels is concerned we can also define a ENLR size based on the largest projected distance from the QSO position to a single spaxel above the same threshold surface brightness. These ENLR sizes can be significantly larger than the azimuthally averaged isophotal radii reported by Liu et al. (2014) and may explain the apparent flattening of the ENLR size – QSO luminosity relation at high QSO luminosities (Liu et al. 2014; Hainline et al. 2014). It is beyond the scope of this paper to investigate this in detail.
In the following, we study how much the measurements change after separating the compact unresolved NLR from the ENLR. After the tests discussed above, any difference we find can be unambiguously attributed to the effect of beam smearing. Given the high S/N of the data we do not report uncertainties on measured quantities in Table 2 which exhibits measurement errors of less than 0.1 dex. Systematic uncertainties on the derived quantities will dominate the error budget by more than an order of magnitude so that we can safely ignore the measurement errors.
 |
Fig. 7 Comparison of the total and ENLR [O iii] line measurements for the centroid distance from the QSO (dQSO), maximum size out to a fixed surface brightness limit (Rint), the median [O iii] line width within the central 1′′ (W80), the ellipticity of the central [O iii] emitting region (e) and the outer power-law radial surface brightness slope (η). The 1:1 relations are shown as a dashed line in each panel. The colour of each data point corresponds to the contrast ratio C as indicated by the colour bar which is defined as the fraction of resolved to the total [O iii] emission. |
3.2. Surface brightness distribution
We observe some subtle but important differences between the [O iii] surface distribution for some objects, after subtracting the compact unresolved NLR contribution. Here, we quantify the changes by means of a few important parameters. From the flux maps, we compute the total and ENLR [O iii] flux (f[O iii]) within the GMOS FoV from which we define a contrast ratio as C = fENLR/ (fNLR + fENLR); the fraction of the ENLR to the total flux. In addition, we compute the flux-weighted centroid and ellipticity within a 2″ × 2″ sub-frame centred on the QSO position. From the flux-weighted centroid, we infer the apparent distance to the QSO position (dQSO), defined as the flux-weighted centre of the broad Hβ distribution. All those measurements are summarized in Table 2.
We find that the contrast ratio C spans a large range across the sample. In four QSOs the ENLR contributes more than 50% to the total [O iii] emission, whereas the ENLR contributes less than 10% in the most extreme case. As expected, the changes in the ENLR surface brightness distribution appear marginal if C > 0.5. Remarkably, the distance between the peak in the surface brightness distribution and the QSO position dQSO is generally higher for pure resolved emission (ENLR) than for the total light as shown in Fig. 7 (upper left panel). The ratio between the offsets also increases with with decreasing contrast ratio C. Those offsets of up to ~ 0.2′′ correspond to about 1−2 kpc at the redshift of the QSOs and imply that the ENLR is highly asymmetric. They appear much smaller in the total [O iii] light which is clearly attributed to the bright unresolved NLR almost centred on the QSO. Only in two cases, SDSS J0412−0511 and SDSS J0753+3153, we can detect neither a large offset (d < 0.4 kpc) nor a strong elongation of the ENLR (e ≤ 0.1).
Something that is not strongly affected by the beam smearing is the size of the ENLR up to an intrinsic [O iii] surface brightness threshold of Σ[O iii] > 10-15/ (1 + z)4 erg s-1 cm-1, corrected for cosmological surface brightness dimming, which was defined in Liu et al. (2013a) and is an arbitrary choice. As we discussed before, we simply measure the distance to all the spaxels that are above the surface brightness threshold. Among those spaxels, the one with the greatest distance defines the ENLR size. Apparently, the ENLR dominates the emission at large radii sufficiently well, so that we find that no significant change of Rint as a function of contrast ratio (Fig. 7). This is consistent with the studies of Hainline et al. (2013, 2014) who find that the ENLR maybe at most 0.1−0.2 dex smaller after a full PSF convolution of the [O iii] surface brightness distribution. Only for SDSS J0924+0624 do we recover a substantially smaller ENLR size by 40% (0.4 dex). Here, the the total emission is dominated by unresolved emission (C < 0.2) and is most strongly affected by the beam smearing.
If we look at the power-law slope of the outer surface brightness profile between 1′′−2.5′′ away from the QSO, we find that the slope becomes flatter with decreasing contrast ratio. Although we measure the slope outside the formal seeing disc, the wings of the PSF still contribute to the surface brightness beyond 1′′ making the profile steeper. At the lowest contrast ratio, SDSS J0924+0624 stands out again, because the size of the ENLR is much smaller than 2.5′′ after subtracting the unresolved emission. In this case, the slope actually does not make sense as it is dominated by noise over most of the range. Therefore, we think that the power-law slope of the surface brightness is an ill-defined quantity if the beam smearing is not taken into account for data at the given spatial resolution.
3.3. Spatially resolved kinematics
In Table 2, we also report the characteristic ENLR [O iii] line width W80 as the median of all individual spaxel measurements within <0.̋6 around the QSO position. Three QSOs in the sample appear to show an [O iii] line width of W80 > 1000 km s-1 on kpc scales consistent with Liu et al. (2014). We find that in all those cases, the unresolved NLR is at least as bright as the entire ENLR with C < 0.5 and that the [O iii] line width in the ENLR reduces significantly to W80 < 800 km s-1 after the deblending of the NLR. The most extreme difference between NLR and ENLR kinematics is observed for the QSO SDSS J0304+0022 with W80 ~ 1500 km s-1 for the NLR and almost completely quiescent kinematics for the ENLR with W80 ~ 400 km s-1. The opposite happens for QSO SDSS J2214+2115 for which we detect significantly broader lines in the ENLR after removing the NLR contribution. In all the other cases the line widths are either fully consistent with each other or slightly smaller by 100−200 km s-1.
Depending on the contrast ratio, we see more detailed structure in the velocity field after the QSO-host deblending. An extreme case is SDSS J0924+0642 (C< 0.2) where we see a symmetric velocity gradient across the nucleus with an amplitude of ± 230 km s-1. The velocity field in the total light appears flat, because the velocity of the unresolved NLR dominates over a significant area due to the seeing. The signature for symmetric velocity gradients is also clearly enhanced in the case of SDSS J0304−0707, SDSS J0753+3153 and SDSS J2214+2115. Whether those gradients are due to ordered rotation of a gas disc, or indicate bipolar outflows is unclear at this point.
Another special case is SDSS J0304+0022 for which we detect a huge offset of >500 km s-1 in the radial velocity close to the QSO position after subtracting the unresolved emission. The [O iii] line in this QSO has an exceptionally broad blue-shifted component, but only the narrow [O iii] component is actually spatially resolved. Thus, the radial velocity measured from the total light is dominated by the unresolved emission up to the radius where the ENLR emission starts to dominate the [O iii] line shape.
3.4. Spatially-resolved line ratios
A key diagnostic for the ionization conditions of the ENLR is the [O iii]/Hβ line ratio. Liu et al. (2013a) measured the line ratio across the ENLR for their sample of obscured QSOs as a function of [O iii] surface brightness and distance from the QSO. They reported an almost constant ratio [O iii]/Hβ ~ 10 up to a characteristic radius of R ~ 7 kpc after which the line ratio drops continuously. Here, we present the same analysis for the unobscured QSOs that was not presented in Liu et al. (2014). In Fig. 8, we show the [O iii]/Hβ line ratio for all the spaxels with a S/N > 5 before and after subtracting the unresolved emission contribution. The imposed S/N condition leads to a detection limit for the line ratio that varies with the [O iii] surface brightness given the fixed depth of the given dataset.
 |
Fig. 8 Example of the [O iii]/Hβ emission-line ratio distribution for SDSS J0233-0743. The line ratio is shown as a function of [O iii] surface brightness, distance from the QSO, and its 2D distribution before (black points) and after performing the QSO-host galaxy deblending (red points). Similar figures for all QSOs are moved to the Appendix. |
In contrast with Liu et al. (2013a), we do not detect a strong break in the line ratio, which remains flat close to log ([O iii] /Hβ) ~ 1 across the entire range of Σ[O iii] and D. The deblending of the NLR and ENLR does not change the line ratios in most cases and confirms that the ENLR is photoionized by the AGN out to large distances. Exceptions from the flat distributions are SDSS J0233-0743 and SDSS J2214+2115, which show a systematic decrease of [O iii] /Hβ at low surface brightness. This decrease can be explained either by ionization of young stars in star forming regions, slow shocks < 500 km s-1 in the ISM or if photoionization by the AGN changes from the “ionization” to the “matter-bounded” region. The latter scenario has been favoured by Liu et al. (2013a) as an explanation for the strong decrease in log ([O iii] /Hβ) after a well-defined break radius.
One important aspect to consider here are the actual detection limits for the lines. When Σ[O iii] decreases, the Hβ line may already be below the detection limit depending on the intrinsic line ratio. Since only spaxels are considered for which both lines are detected with > 3σ confidence, a bias is introduced towards low [O iii]/Hβ line ratios with decreasing Σ[O iii] if low line ratios are present in the data. It is unclear at this point which role this effect plays in the analysis of the corresponding obscured QSOs sample (Liu et al. 2013a,b).
4. AGN outflow energetics
The estimation of the ionized gas outflow energetics and mass outflow rate is a difficult task and usually depends on assumption on parameters that are not directly constrained by the data. In particular, the lack of spatial resolution usually does not allow us to directly constrain the geometry of the ionized gas outflows. This is even worse for high-redshift AGN where the spatial resolution is limited to a few kpc per resolution element. Here, we primarily focus on the comparison of estimates from different models and evaluate how strongly they are affected by contributions from an unresolved source owing to beam smearing.
4.1. Ionized gas mass and kinetic energy
The amount of ionized gas is set by the amount of ionized hydrogen which can be estimated from the photons emitted by the recombination lines. Adopting “case B” recombination for the low-density limit and a gas temperature of 10 000 K, we expect an intrinsic Balmer line decrement of Hα/Hβ = 2.85 (Osterbrock & Ferland 2006). The ionized gas mass can then be approximated from the Hβ luminosity following (Osterbrock & Ferland 2006) as 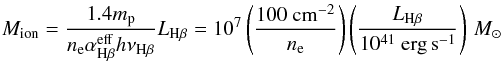 (1)where mp is the proton mass, ne is the electron density and h is the Planck constant. Although Hβ is covered in the observed wavelength range, it suffers from a much lower S/N per resolution element. We therefore use the bright [O iii] as a surrogate for Hβ with a line ratio of [O iii]/Hβ ~ 10. Adopting this fixed line-ratio is accurate within ± 0.2 dex for all objects as verified by the line ratio distribution (Fig. 8). In fact this provides a lower limit for the ionized gas mass as we do not apply any correction for internal dust extinction.
(1)where mp is the proton mass, ne is the electron density and h is the Planck constant. Although Hβ is covered in the observed wavelength range, it suffers from a much lower S/N per resolution element. We therefore use the bright [O iii] as a surrogate for Hβ with a line ratio of [O iii]/Hβ ~ 10. Adopting this fixed line-ratio is accurate within ± 0.2 dex for all objects as verified by the line ratio distribution (Fig. 8). In fact this provides a lower limit for the ionized gas mass as we do not apply any correction for internal dust extinction.
The greatest uncertainty in our case is the unconstrained electron density ne. We cannot infer it from the data itself because no density-sensitive lines are in the covered wavelength range. For the following calculations, we adopt an electron density of ne ~ 100 cm-2 as a reference. This value is a typical value observed in the ENLR around luminous QSOs (e.g. Husemann et al. 2016). However, the density has a large range since it is decreasing with distance (e.g. Bennert et al. 2006b,a) from ne ~ 1000 cm-2 in the NLR on 100 pc scales (e.g. Vaona et al. 2012) and ne ~ 10 cm-2 in the very extended and diffuse medium on kpc scale (e.g. Liu et al. 2013b).
The total kinetic energy of the ionized nebulae is split into bulk motion vg and the turbulent motion σg of the gas as measured from the emission lines. With the assumption of constant electron density we can simply integrate the localized kinetic energy per spatial pixel at position x and y leading to 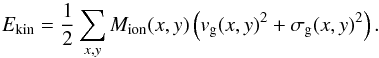 (2)The results for the estimated ionized gas mass and the kinetic energy are listed in Table 3. The total ionized gas mass is in the range of 0.6–10 × 108M⊙ with a mean of 2 × 108M⊙. Although Liu et al. (2014) did not estimate the ionized gas mass for this unobscured QSO sample, they reported a similar ionized gas mass of 6 × 108M⊙ for their obscured QSO sample (Liu et al. 2013b) following the same assumptions.
(2)The results for the estimated ionized gas mass and the kinetic energy are listed in Table 3. The total ionized gas mass is in the range of 0.6–10 × 108M⊙ with a mean of 2 × 108M⊙. Although Liu et al. (2014) did not estimate the ionized gas mass for this unobscured QSO sample, they reported a similar ionized gas mass of 6 × 108M⊙ for their obscured QSO sample (Liu et al. 2013b) following the same assumptions.
Here, we derive the kinetic energy from the kinematics of the total and the ENLR [O iii] line profile distribution across the field separately. We note that in the majority of cases the kinematic energies do not change significantly. Only QSOs with a lower contrast ratio C show a clear difference which is caused by a lower ionized gas mass in the ENLR and a lower line width on kpc scales which reduces the turbulent energy term. We obtain a mean kinetic energy of 10 × 1055 erg and 6 × 1055 erg, for the total and the ENLR energy, respectively. This is about 1 dex lower than reported by Liu et al. (2013b) for the unobscured QSOs, because they assumed a constant outflow velocity of 760 km s-1 across the entire nebulae.
Assuming a timescale τ for the kinetic energy injection one can roughly estimate a kinetic power Ėkin = Ekin/τ. Usually a timescale of about 107 yr is assumed for the life time of a luminous QSO phase, but Schawinski et al. (2015) recently suggested a much shorter timescale of 105 yr. This yields kinetic powers of 2 × 1041 erg s-1 and 2 × 1043 erg s-1, respectively, for the two timescales.
As argued in many studies (e.g. Nesvadba et al. 2006; Cicone et al. 2014), these estimates are lower limits to the actual kinetic energy, because the geometry and projection effect are not taken into account. Therefore, models for the outflow have been used to improve the estimates. Below we describe the results we obtain for a spherical symmetric outflow Liu et al. (2013b) and a conical outflow model (e.g., Cano-Díaz et al. 2012; Cresci et al. 2015).
Derived outflow energetics for different models.
4.2. Kinetic power and mass outflow rate
4.2.1. Spherical symmetric outflow model
Liu et al. (2013b) adopted a spherical and symmetric outflow geometry to estimate the energetics and outflow rate for the ionized gas around luminous obscured QSOs. They argued that a spherical geometry is strongly supported by the apparently round ENLR with almost constant broad lines out to kpc distances. They define a shell at distance D through which they estimate the current kinetic power (Ėkin) and mass outflow rate Ṁ. They set D to be the radius at which they observed a break in the [O iii]/Hβ line ratio as a function of radius which they associate with the transition from ionization- to matter-bounded clouds, which occurs at D ~ 7 kpc for their sample of QSOs. Based on the assumptions of matter-bounded and pressure-confined clouds, spherical symmetry and ionization equilibrium, Liu et al. (2013a) derived the following relations 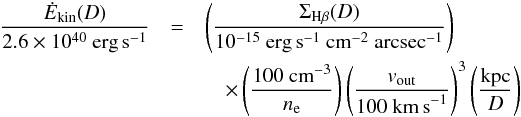 (3)where ΣHβ(D) is the Hβ surface brightness, corrected for the surface brightness dimming with redshift, at distance D from the QSO, vout is the outflow velocity and ne is the electron density. The corresponding mass outflow is then defined as
(3)where ΣHβ(D) is the Hβ surface brightness, corrected for the surface brightness dimming with redshift, at distance D from the QSO, vout is the outflow velocity and ne is the electron density. The corresponding mass outflow is then defined as 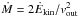 which corresponds to
which corresponds to 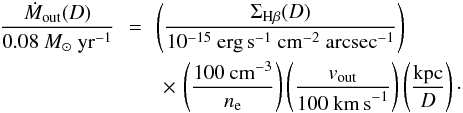 (4)Since the maximum ENLR size drops to Rmax = 6 kpc after subtracting the unresolved emission for SDSS J0924+0642 and no clear break radius in the line ratios is detected for any of the objects, we adopt a fixed radius of D = 5 kpc for which we compute the energetics. In this way we can consistently measure the mean [O iii] surface brightness within 4 kpc <R< 6 kpc for all objects and therefore achieve comparable estimates among the sample considering the similar luminosity of all QSOs. Given the low spatial resolution of the data there is no objective criterion to adjust the radius on an object-by-object basis for a comparative study.
(4)Since the maximum ENLR size drops to Rmax = 6 kpc after subtracting the unresolved emission for SDSS J0924+0642 and no clear break radius in the line ratios is detected for any of the objects, we adopt a fixed radius of D = 5 kpc for which we compute the energetics. In this way we can consistently measure the mean [O iii] surface brightness within 4 kpc <R< 6 kpc for all objects and therefore achieve comparable estimates among the sample considering the similar luminosity of all QSOs. Given the low spatial resolution of the data there is no objective criterion to adjust the radius on an object-by-object basis for a comparative study.
In the spherical symmetric outflow model, Liu et al. (2013b) predicted the line shape to vary across the field as a function of the distance from the QSO and measured radial velocity vz and adopted a power-law function for the radial luminosity distribution in [O iii] with slope α = η + 1, 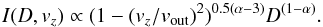 (5)Such a line shape parametrization implies that W80 ~ 1.3 × vout for a power-law slope η ~ 3.5 and W80 ~ 1.5 × vout for a power-law slope η ~ 2.6 which are the mean slopes for the total and ENLR radial profiles, respectively. In Table 3 we report the computed kinetic powers and mass outflow rates based on the prescription above and adopting an electron density of ne = 100 cm-3. We find a mean kinetic power of Ėkin(D = 5 kpc) = 1045 erg s-1 and mass outflow rate of Ṁout(D = 5 kpc) = 450 M⊙ yr-1 for the initial values and Ėkin(D = 5 kpc) = 6 × 1043 erg s-1 and mass outflow rate of Ṁout(D = 5 kpc) = 100 M⊙ yr-1 for the ENLR after subtracting the unresolved emission contribution, respectively. Thus, the difference is more than an order of magnitude for the kinetic power and a factor of four in the mass outflow rate, but strongly depends on the contrast ratio for each individual source. In the extreme case, the kinetic power drops by more than 2 dex and 1 dex in the mass outflow rate.
(5)Such a line shape parametrization implies that W80 ~ 1.3 × vout for a power-law slope η ~ 3.5 and W80 ~ 1.5 × vout for a power-law slope η ~ 2.6 which are the mean slopes for the total and ENLR radial profiles, respectively. In Table 3 we report the computed kinetic powers and mass outflow rates based on the prescription above and adopting an electron density of ne = 100 cm-3. We find a mean kinetic power of Ėkin(D = 5 kpc) = 1045 erg s-1 and mass outflow rate of Ṁout(D = 5 kpc) = 450 M⊙ yr-1 for the initial values and Ėkin(D = 5 kpc) = 6 × 1043 erg s-1 and mass outflow rate of Ṁout(D = 5 kpc) = 100 M⊙ yr-1 for the ENLR after subtracting the unresolved emission contribution, respectively. Thus, the difference is more than an order of magnitude for the kinetic power and a factor of four in the mass outflow rate, but strongly depends on the contrast ratio for each individual source. In the extreme case, the kinetic power drops by more than 2 dex and 1 dex in the mass outflow rate.
The changes in the energetics we state above are only valid for the kinetic power and mass outflow rate going through a sphere at a distance of D = 5 kpc. The lower rates are expected because of subtraction of the point-like component which leads to a lower mass and smaller outflow velocity at that radius. However, the decomposition into unresolved and resolved emission also implies that outflow power and mass outflow rate may change with time/distance from the nucleus in particular on scales smaller than 1 kpc. Therefore, it would be important to estimate also the outflow power in the unresolved component. By design this is impossible for this specific spherical outflow model as it requires to compute the emission-line surface brightness at a given radius. We therefore explore this difference between the NLR and ENLR energetics details based on a simple bi-conical outflow model below.
4.2.2. Simple conical outflow model
In nearby Seyfert galaxies, the NLR and associated outflows were often reported to have a (bi-)conical geometry (e.g. Mulchaey et al. 1996; Schmitt et al. 2003; Crenshaw et al. 2010; Müller-Sánchez et al. 2011). The frequency of conical outflows, however, is still a matter of debate. In a recent study Fischer et al. (2013) could detect conical outflows in only ~1/3 of nearby AGN based on HST long-slit spectroscopy. It is not clear at this point if this is due to misaligned slits, weak/small outflows or a different geometry. On one hand, a conical outflow geometry is a natural outcome of the unified AGN model that can be easily resolved and confirmed for many nearby AGN with HST, if present. On the other hand, the opening angle is expected to increase with AGN luminosity so that for luminous QSOs a quasi-spherical outflow cannot be ruled out.
The spatial resolution of these luminous AGN at higher redshift does not allow us to directly constrain the geometrical parameters for this model. Cano-Díaz et al. (2012) and Cresci et al. (2015) preferred a conical outflow geometry and adopted a simple model for their high-z QSOs. The authors assumed a conical geometry with opening angle Ω, uniformly distributed clouds with the same density and a constant outflow velocity. With the assumption of constant density clouds, the kinetic power and mass outflow rate become independent of the opening angle and the filling factor of the clouds within the cone and one derives the following relations:  Assuming case B recombination with an electron temperature of T ~ 104 K, we can replace Mion with Eq. (1) which leads to
Assuming case B recombination with an electron temperature of T ~ 104 K, we can replace Mion with Eq. (1) which leads to 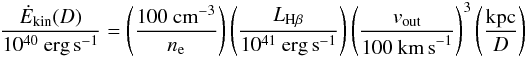 (8)
(8)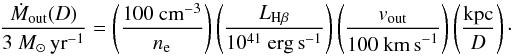 (9)To be consistent with the estimates based on the spherical outflow model, we measure the [O iii] luminosity within D = 5 kpc converted to Hβ luminosity with a factor of 0.1 and assume again an electron density of ne = 100 cm-3. The outflow velocities are assumed to be maximum velocities in the works of Cano-Díaz et al. (2012) and Cresci et al. (2015) so that we assume W80 to be the representative outflow velocity. In this case, we obtain kinetic powers and mass outflow rates as reported in Table 3 with a mean kinetic power of Ėkin(D = 5 kpc) = 3 × 1043 erg s-1 and mass outflow rate of Ṁout(D = 5 kpc) = 85 M⊙ yr-1 for the initial values and Ėkin(D = 5 kpc) = 2 × 1042 erg s-1 and mass outflow rate of Ṁout(D = 5 kpc) = 16 M⊙ yr-1 for the ENLR after subtracting the contribution of unresolved emission, respectively. The change owing to the beam smearing of the unresolved NLR is again about 1 dex for the kinetic power and a factor of five in mass outflow rate. Furthermore, the mean kinetic power and outflow rate is almost two orders of magnitude lower in the conical compared to the spherical outflow model.
(9)To be consistent with the estimates based on the spherical outflow model, we measure the [O iii] luminosity within D = 5 kpc converted to Hβ luminosity with a factor of 0.1 and assume again an electron density of ne = 100 cm-3. The outflow velocities are assumed to be maximum velocities in the works of Cano-Díaz et al. (2012) and Cresci et al. (2015) so that we assume W80 to be the representative outflow velocity. In this case, we obtain kinetic powers and mass outflow rates as reported in Table 3 with a mean kinetic power of Ėkin(D = 5 kpc) = 3 × 1043 erg s-1 and mass outflow rate of Ṁout(D = 5 kpc) = 85 M⊙ yr-1 for the initial values and Ėkin(D = 5 kpc) = 2 × 1042 erg s-1 and mass outflow rate of Ṁout(D = 5 kpc) = 16 M⊙ yr-1 for the ENLR after subtracting the contribution of unresolved emission, respectively. The change owing to the beam smearing of the unresolved NLR is again about 1 dex for the kinetic power and a factor of five in mass outflow rate. Furthermore, the mean kinetic power and outflow rate is almost two orders of magnitude lower in the conical compared to the spherical outflow model.
In the same way, we can roughly estimate the kinetic power and mass outflow rate at smaller distances from the unresolved NLR component. Consequently, we adopt the assumptions for the unresolved NLR of a cone with a size of 1 kpc, a slightly higher density of ne ~ 600 cm-3 and a corresponding outflow velocity based on the [O iii] line width in the unresolved QSO spectrum. Given that the assumed simple conical model is independent of the opening angle by design, we also consider it valid for an approximation for a spherical model given that we cannot constrain the outflow geometry for the unresolved NLR. Under these assumptions we obtain up to an order of magnitude higher kinetic power and outflow rates in the compact NLR than in the ENLR (see Table 3). While this may indicate much more powerful outflows close to the nucleus these values have to be taken skeptically. The assumption of constant-density clouds across the cone is expected to be strongly violated on these small scales and can vary by orders of magnitude up to several 1000 cm-3. Without spatially resolving the electron density via density-sensitive emission-lines, like done for local Seyfert galaxies with HST (e.g. Crenshaw & Kraemer 2000; Rice et al. 2006; Storchi-Bergmann et al. 2010; Fischer et al. 2013), no firm conclusions can be made. However, it is certainly possible that a high mass outflow rate is still confined to a region less than 1 kpc and has not travelled throughout the host galaxy yet.
5. Discussion
5.1. Morphology and incidence of kpc scale outflows
A major result of the work by Liu et al. (2013b, 2014) is that the ENLR appears round with a constant line width of W80 ~ 1000 km s-1 on kpc scales around luminous QSOs at redshift z ~ 0.6 irrespective of their type. This notion would naturally imply large opening angles for the escape of the AGN radiation out to large distances and therefore favour an almost spherical outflow geometry. This is in stark contrast with the results of Husemann et al. (2013b) who reported rather elongated or even one-sided shapes of the ENLR around unobscured QSOs at z< 0.3. One big difference in the analysis of Husemann et al. (2013b) is the deblending of an unresolved NLR and the ENLR based on the PSF reconstructed from the broad Hβ emission line.
Here, we have resolved this issue and performed a consistent analysis of the unobscured QSO sample of Liu et al. (2014) with the same deblending technique used by Husemann et al. (2013b) to allow a fair comparison. In many cases, we recover one-sided or elongated structures in the ENLR close to the nucleus that was previously hidden underneath. The dominant emission of a bright unresolved NLR necessarily produces round structure caused by the seeing. In addition, the obtained offsets in the peak intensity of the ENLR about 1−2 kpc is a striking feature and implies that the ionization has a preferred direction which disfavours a wide-angle ionization/outflow scenario on kpc scales. Nevertheless, we cannot rule out that the outflow associated with the compact unresolved NLR has a very different geometry, spherical or something completely different, and that only the radiation field on large scales appears conical or asymmetric.
Hainline et al. (2013, 2014) carefully considered the beam-smearing effect on the ENLR in deep long-slit observations for a large sample of obscured QSOs. They reported a small overestimation of the ENLR size by 0.1−0.2 dex if the beam smearing by the seeing is not considered. This is also consistent with the results of our analysis except for SDSS J0924+0642 where the difference reaches even 0.3 dex due to a very low contrast ratio. Hainline et al. assumed a Sersić or Voigt profile for the ENLR light distribution, but enforcing azimuthal symmetry. Thus, they are not sensitive to asymmetries in the [O iii] light distribution that can only be mapped using 3D spectroscopy or narrow-band imaging. Furthermore, with just a single slit it is impossible to measure the elongation of the ENLR and a reliable maximum extension. Very extended emission on >20 kpc scales can be easily missed, as in in case of SDSS J0809+0743, if the slit is not aligned with these structures.
It is well known that the forbidden lines, in particular the [O iii] lines, are systematically asymmetric with a blue wing caused by a broad and blue-shifted emission line component (e.g. Heckman et al. 1981; Whittle 1985; Mullaney et al. 2013; Shen et al. 2015; Woo et al. 2016). This is usually interpreted as a signature of a fast bipolar AGN outflow were the receding side is obscured by the dust screen from the host galaxy. There is an increasing number of studies which report broad emission lines with line widths of 1000 km s-1 on kpc scale in luminous QSO at low (Greene et al. 2011; Liu et al. 2013b; Harrison et al. 2014; Liu et al. 2014; McElroy et al. 2015) and high redshift (Cano-Díaz et al. 2012; Carniani et al. 2015; Cresci et al. 2015; Brusa et al. 2015; Perna et al. 2015). However, all those studies lack a proper discussion of the impact of beam smearing on the observed light intensity profile of the broad [O iii] line component to verify the real size of the outflows.
Based on our re-analysis of the unobscured QSO sample of Liu et al. (2014), we find that the line width of [O iii] is significantly broader in the unresolved NLR than in the ENLR on kpc scales. In particular the cases where the [O iii] line appears broader than 1000 km s-1 (FWHM) on kpc scales reduces by several 100 km s-1 down to 400 km s-1 in the most extreme case of SDSS J0304+0022 when the spatially unresolved component is removed. From the twelve QSOs in the Liu et al. (2014) sample, eight have a line width W80> 900 km s-1 in the NLR of which only three QSOs show a line width of ~800 km s-1 on kpc scales. There is only one case, SDSS J2214+2115, where we find an increase in the line width on kpc scales which indicates a very powerful extended outflow. However, in general our analysis strongly favours outflows that slow down as they expand from the ≪1 kpc scales of the NLR.
 |
Fig. 9 Bolometric AGN luminosity (Lbol) versus kinetic power (Ėkin) and momentum outflow rate (voutṀout) for the spherical and conical outflow model at kpc-scale distances (D = 5 kpc). The black and red data points correspond to the measurements from the total and extended [O iii] line profile maps, respectively. In addition we also plot the corresponding values from the spatially unresolved [O iii] line from the NLR as blue data points. This is based on the conical formula but also applies to the spherical case as described in the main text. The dashed lines correspond to various AGN feedback efficiencies (ϵf) and outflow covering factors (Ω) as labelled in the corresponding panels. The error bars on Ėkin correspond to the range in electron densities 10 <ne< 1000. The uncertainty on Lbol is assumed to be 0.3 dex taking into account the photometric calibration of the data and the error on the bolometric correction factor. In the right panels, we show the change of the kinetic power and the momentum outflow rate from the total and extended [O iii] measurements as a function of contrast ratio (C). |
The asymmetric light distribution of [O iii] emission together with the smaller line width on large scales questions the primary outflow mechanisms for these QSOs. While Liu et al. (2013b) proposed a wide-angle high-velocity outflow driven by the QSO radiation for these objects, Mullaney et al. (2013) and Villar Martín et al. (2014) argued that the power of the radio jets is more strongly correlated with the line width than the AGN luminosity for a large sample of AGN from the SDSS (see, however, Woo et al. 2016, for a different interpretation). Given the enhanced asymmetry in the [O iii] light distribution it is unlikely that the proposed wide-angle radiation-driven outflow scenario is still valid for these QSOs. The ENLR morphologies that we recover rather support a conical geometry which is consistent with a preferred outflow axis as required by a radio-jet scenario. Given the redshift of the sample, the upper limits on the radio fluxes imply radio luminosities of 2 × 1024 W Hz-1. Although the QSOs are considered radio-quiet, these radio luminosities are consistent with those of low-redshift Seyferts and QSOs where broad emission lines on 100−1000 pc scales could be directly associated with the hotspots of radio jets (e.g. Fu & Stockton 2009; Müller-Sánchez et al. 2011; Husemann et al. 2013b; Harrison et al. 2015). This matches with our findings that the very broad lines must be emitted on scales <1 kpc that cannot be resolved with the seeing-limited optical observations at z ~ 0.6. However, an alternative interpretation of the radio emission is that is generated by the shock front of an AGN-driven outflow itself (Faucher-Giguère & Quataert 2012; Zakamska & Greene 2014).
Whether the impact of an unresolved NLR is similarly strong on the morphology of the ENLR and the outflow kinematics for the obscured QSOs is unclear. The similarity of the uncorrected maps inferred of the obscured and unobscured QSOs as discussed in Liu et al. (2014) suggests that the beam smeared emission of an unresolved NLR affects both types similarly. However, a reliable deblending and estimation of the contrast between resolved and unresolved emission is difficult for the obscured QSOs without a simultaneous characterization of the PSF. Thus, we are not able to directly verify that effect for obscured QSOs directly with the existing observations, but Villar-Martín et al. (2016) and Karouzos et al. (2016) have recently also reported very compact outflow sizes of < 1−2 kpc after correction for a sample of luminous obscured QSOs at z< 0.6. While a consistent picture of the systematic effects is appearing, we cannot entirely rule out that the ionized gas properties on kpc scales are intrinsically different in obscured and unobscured AGN given the different selection criteria used for the obscured QSO samples.
5.2. Implications for the AGN feedback efficiency
A major goal of this study is to explore the impact of the beam smearing on the derived outflow energetics and mass outflow rates on large scales. We have shown that the kinetic power on kpc scales can drop up to two orders of magnitudes and the outflow rate up to one order of magnitude (see Table 3), since the outflow velocity and line flux on kpc scales can be severely overestimated. Furthermore, we find a large difference in the results inferred for two popular outflow models that have frequently been used to infer AGN-driven large scale outflow energetics from integral-field spectroscopy data. This has significant impact on the AGN feedback efficiency ϵf, i.e. Ėkin = ϵfLbol, which we show in Fig. 9 (upper left panels) for the spherical and the conical outflow model. Here, we use the continuum luminosity at 5100 Å as a proxy for Lbol with a bolometric correction factor of Lbol ~ 10 L5100, following Richards et al. (2006). Errors are dominated by systematics in both cases and we adopt an order of magnitude error on the kinetic power due to the unknown electron density (10 < ne/ cm-3 < 1000) and an uncertainty of 0.3 dex on the bolometric luminosity.
We find that the spherical outflow model reaches values up to ϵf ~ 0.3 in the most extreme cases, when beam smearing is ignored. This decreases to a maximum value of ϵf ~ 0.01, with a range of 0.001 < ϵf < 0.01 after taking into account beam smearing from the unresolved NLR. Since the kinetic energies are much lower in the conical outflow model, we also compute lower AGN feedback efficiencies in the range of 10-5 <ϵf< 10-4 after beam smearing correction. Similar feedback efficiencies have been inferred for outflows in nearby lower luminosity AGN that can be properly resolved (e.g. Barbosa et al. 2009; Liu et al. 2015). The difference between the spherical and conical outflow models is important because current cosmological simulations including radiative QSO feedback predict or assume a feedback efficiency of ϵf ~ 0.005–0.05 (e.g. Di Matteo et al. 2005; Hopkins et al. 2010). On the contrary, dedicated radiation-hydrodynamical simulations reported much lower feedback efficiencies in the range of ϵf ~ 10-8–10-4 (Kurosawa et al. 2009), but were computed on much smaller scales of 1−10 pc and therefore do not quite match our spatial resolution. Thus, the answer to the question if AGN feedback is consistent with theoretical predictions depends strongly on the assumed theoretical model and outflow model as well as whether beam smearing is taken into account during the data analysis.
To further check the reliability of the prediction of both models, we compute the momentum outflow rate Ṗ = Ṁvout based on our measurements provided in Tables 2 and 3. In the simple picture of a radiation-pressure driven wind, an upper limit is set by Ṗ < ΩLbol/c where Ω is the covering factor and c is the speed of light. In Fig. 9 (lower left panels), we compare the estimated momentum outflow rate with the corresponding limit based on the AGN bolometric luminosity of the QSO. We find that Ω > 1 in the spherical outflow model, even if beam smearing is considered. A covering factor larger than one can only be explained if the wind is not momentum conservative, or it is not radiatively driven in the first place, or the AGN luminosity has dropped on timescales much shorter than the dynamical timescale of the wind. For the conical outflow model, the observations including beam smearing correction are below the limit, with covering factors between 0.01 < Ω < 1 as required for a simple radiatively driven QSO wind (e.g. Zubovas & King 2012; Stern et al. 2016). Thus, there would not need to be an additional momentum boost to explain previous observations with Ω ≫ 1 (e.g. Faucher-Giguère & Quataert 2012) as beam-smearing effects alone are able to solve this issue from the observational side. Recent observations of circum-nuclear winds that suggest Ṗ ~ ΩLbol/c (e.g Tombesi et al. 2015; Feruglio et al. 2015) support our notion of an outflow that remains within the limit of radiation pressure. Overall it is clear from Fig. 9 (right panels) that the overestimation of kinetic power and momentum outflow rate due to the beam-smearing effect is strongly increasing with lower contrast ratio C independent of the assumed model on the order of magnitude level.
The effect of beam smearing on the unresolved region NLR is the opposite as the light is spread out to large angular distances and the line width is slightly reduce by the blending from the large-scale quiescent kinematics. Thus, the associated energetics would be artificially reduced if simple aperture photometry is applied. It is therefore possible that most of the kinetic power and momentum outflow rate is actually confined to the unresolved NLR on scales < 1 kpc. This would imply a significant discontinuity of the mass outflow rate as function of radius, which may be a natural consequence of the finite outflow velocity combined with the finite life time of the bright AGN phase, of invalid assumptions for the physical conditions in the unresolved NLR, or of potential miss-interpretation of the unresolved NLR kinematics. Nevertheless, the estimated outflow rates in Table 3 for the unresolved NLR are still an order of magnitude smaller than the estimates for the large-scale wide-angle spherical outflow model of Liu et al. (2013b) when beam smearing is not taken into account.
Besides a radiatively driven wind, it is also possible that a radio jet provides sufficient mechanical energy for powering a wind on galactic scales. Several studies have shown that high-velocity outflows seen as broad extended emission lines are co-spatial with kpc-scale jets even for radio-quiet AGN (e.g. Fu & Stockton 2009; Müller-Sánchez et al. 2011; Husemann et al. 2013b). Here, we compute an upper limit for the mechanical power of the putative radio jets from the upper limit in the 1.4 GHz radio luminosity. The relation between jet (Pjet) and mechanical power (Pcav) by Cavagnolo et al. (2010), 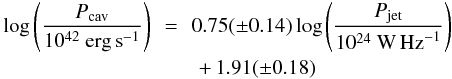 (10)yields an upper limit on the mechanical power of Pcav ≲ 8 × 1043 erg s-1 based on the upper limit of Pjet ≲ 1024 W Hz-1 valid for almost all QSOs in the sample. This limit is about an order of magnitude higher than the estimated kinetic power of the conical outflow model corrected for the beam-smearing effect. Therefore, it is also possible, within the current observational limits, that the outflow in these QSOs is powered by low-luminosity radio jets inflating a cavity along the jet axis. If confirmed by deep high-resolution radio imaging, it would support the observation by Mullaney et al. (2013) that the strength of the broad [O iii] emission line component in stacked SDSS spectra of AGN is most strongly correlated with radio luminosity.
(10)yields an upper limit on the mechanical power of Pcav ≲ 8 × 1043 erg s-1 based on the upper limit of Pjet ≲ 1024 W Hz-1 valid for almost all QSOs in the sample. This limit is about an order of magnitude higher than the estimated kinetic power of the conical outflow model corrected for the beam-smearing effect. Therefore, it is also possible, within the current observational limits, that the outflow in these QSOs is powered by low-luminosity radio jets inflating a cavity along the jet axis. If confirmed by deep high-resolution radio imaging, it would support the observation by Mullaney et al. (2013) that the strength of the broad [O iii] emission line component in stacked SDSS spectra of AGN is most strongly correlated with radio luminosity.
In any case, the revised outflow energetics for this particular QSO sample suggest significantly weaker outflows than previously thought. With an ionized gas mass outflow rate of about Ṁ ~ 10−100 M⊙ yr-1 the QSOs would be able to expel the entire ionized gas content over a life time of 1–10 Myr. Given that the total gas mass of the QSOs hosts and the mass-loading factor of the ionized gas outflows are unknown, it remains unclear whether QSO feedback in these cases is efficient enough to expel enough gas to significantly suppress star formation on short timescales. Furthermore, the question remains open over whether the outflows are able to effect the entire host galaxies since the mass outflow rates in the unresolved compact NLR appear to be an order of magnitude higher than on kpc scales of the conical model.
5.3. Are the results applicable also to obscured QSOs?
Liu et al. (2014) reported that the surface brightness distributions and kinematics are similar for the unobscured QSO and their matched obscured QSOs presented in Liu et al. (2013a,b). Specifically, the ENLR morphology appeared to be round out to kpc scales with a high velocity dispersion in [O iii] over a large region in both cases. This is already a surprising result as the AGN unification model (Antonucci 1993) predicts that the inclination of the torus is different for unobscured and obscured QSOs and so we would expect the ionization cones oriented more perpendicular to our line-of-sight for obscured QSOs and pointing more towards us for unobscured QSOs. This projection effect should lead to different apparent morphologies of the ENLR from bi-conical for obscured and more round for unobscured QSOs.
 |
Fig. 10 Comparison of various AGN luminosity indicators are shown for the unobscured QSO samples of Husemann et al. (2013b, 2014), and Liu et al. (2014), and for the obscured QSO sample of Liu et al. (2013a) in the upper panels. Here we consider the continuum luminosity at 8 μm (L8 μm), total [O iii] luminosity (L[O iii]), broad Hβ luminosity (Lbroad Hβ) and continuum luminosity at 5100 Å (L5100) as independent AGN luminosity indicators. The corresponding distributions in the luminosity ratios are shown in the lower panels. For obscured QSOs only L[O iii] and L8 μm can be measured because the broad lines from the BLR and the continuum from the accretion disc are obscured and unobservable. |
The outflow energetics inferred by Liu et al. (2013b) for the obscured QSOs is in agreement with our estimates for the matched unobscured QSO sample consistently assuming the spherical outflow geometry before corrected for the beam-smearing effect of a compact NLR. Since we show that the beam-smearing effect is prominent for the unobscured QSOs to recover the true morphology and kinematics of the ENLR on kpc scales, there are two possibilities to interpret the similarities reported by Liu et al. (2014): (i) the obscured QSOs are similarly affected by the beam smearing of a bright unresolved NLR outshining the ENLR; or (ii) the compact NLR close the nucleus is fainter or more strongly obscured by dust from the host galaxy in obscured QSOs compared to unobscured ones so that the beam smearing would be less problematic.
To test whether the [O iii] line in obscured QSOs is more strongly suppressed by dust obscuration we compare various AGN bolometric luminosities indicators for the different samples. In Fig. 10, we compare the [O iii] luminosity (L[O iii]) to the 8 μm continuum luminosity (L8 μm), the broad Hβ luminosity (Lbroad Hβ), and the continuum luminosity at 5100 Å (L5100) for the unobscured QSO sample discussed in this paper with the matched obscured QSO sample of Liu et al. (2013a), and the large sample of 50 unobscured QSOs at 0.04 <z< 0.3 (Husemann et al. 2013b, 2014). Here ,we use the [O iii] luminosity as the primary AGN luminosity reference given that the obscured and unobscured QSOs samples of Liu et al. (2013a, 2014) were selected from the SDSS catalogue based on [O iii] luminosity (Reyes et al. 2008). The use of the [O iii] luminosity as a bolometric luminosity indicator has been established over several order of magnitude (e.g. Zakamska et al. 2003; Heckman et al. 2004) which is the basis for the selection.
The unobscured QSOs studied in Husemann et al. (2013b) and Husemann et al. (2014) were selected from the Hamburg/ESO QSO survey (Wisotzki et al. 2000) and the Palomar Bright QSO survey (Schmidt & Green 1983) based on their continuum luminosity which is not obscured by the torus around the nucleus. For those QSOs, the continuum luminosity from the accretion disc and the broad Hβ luminosity from the surrounding BLR are well calibrated AGN luminosity indicators that were shown to be directly linked through reverberation mapping (e.g. Kaspi et al. 2000; Peterson et al. 2004). We find that all unobscured QSOs follow a clear correlation with the [O iii] luminosity and that the unobscured QSOs have a similar distribution in the ratio with L5100 and Lbroad Hβ as verified by a Kolmogorov-Smirnov test.
Since the nucleus is obscured by the torus we cannot measure those quantities for the obscured QSOs. Thus, we use the infrared luminosity at ~8 μm as a measure for the AGN luminosity (e.g. Ramos Almeida et al. 2007; Horst et al. 2008; Gandhi et al. 2009; Mateos et al. 2015) as it is assumed to be the re-radiated dust emission from the AGN-heated torus. Indeed, we find the infrared luminosity to be closely correlated with the [O iii] luminosity for the unobscured QSOs samples shown in Fig. 10 (left panel). However, we find a significantly different distribution of L8 μm/L[O iii] for the obscured QSO sample of Liu et al. (2013a) compared to the unobscured QSO samples including the one matched in the [OIII] luminosity selection (Liu et al. 2014). There appears to be an excess in [O iii] compared to the AGN luminosity only for the obscured QSOs. This is likely a selection effect given that the sample is specifically selected to be the most luminous [O iii] emitters at a given redshift picking up preferentially outliers.
Therefore, it is very unlikely that the NLR in the obscured QSOs is much weaker compared to the unobscured one. The opposite may even be true and the NLR is brighter relative to the ENLR in the obscured QSOs compared to the unobscured ones. Thus, a correct handling of the beam-smearing effect seems to be at least as important for obscured as for unobscured QSOs. The recent long-slit observations of obscured QSOs by Humphrey et al. (2015) indeed confirm that a large fraction of the [O iii] emission originates from a spatially unresolved component supporting our claim. We conclude that it is very likely that the effect of the beam smearing will need to be taken into account for the obscured QSOs and that the outflow energetics reported by Liu et al. (2013b) are likely overestimated as well.
6. Summary and conclusions
In this paper, we have presented an independent re-analysis of GMOS IFU spectroscopy of 12 luminous unobscured QSO at 0.4 <z< 0.7 initially presented by Liu et al. (2014). We focus on the beam-smearing effect associated with the spatially unresolved [O iii] emission and its impact on the apparent large scale kinematics over several kpc and corresponding measures of AGN outflow energetics and feedback efficiencies. Our findings can be summarized as follows.
-
We find a large range in contrast ratios 0.2 <C< 1 between the spatially resolved and total [O iii] emission among the sample. The contrast ratio has a significant impact on the measured properties of the spatially extended [O iii] emission on kpc scales. The radial surface brightness gradient has an intrinsically shallower power-law slope when the contribution from the unresolved component is removed.
-
While the estimated size of the ENLR is only overestimated at the lowest contrast ratios, we find an increasing asymmetry in the distribution of the truly extended [O iii] emission which is indicated by an offset in the flux-weighted centre with respect to the QSO position. More importantly, we notice that the [O iii] line width (W80) on kpc scales significantly decreases with decreasing contrast ratio after subtraction of the spatially unresolved [O iii] component.
-
We do not detect a clear break radius in the [O iii]/Hβ ratio for this unobscured QSO sample which is in stark contrast to the results for the obscured QSO sample presented by (Liu et al. 2013a). Together with the intrinsically asymmetric ENLR light distribution our observations provide evidence against the proposed spherical outflow model as the best interpretation of the observations.
-
The inferred AGN outflow energetics and feedback efficiencies on kpc scales dramatically decrease with decreasing contrast ratio by up to approximately two orders of magnitude in the in the most extreme case, when the unresolved emission of the QSO is taken into account. In addition, there is also a significant difference in the AGN feedback efficiency between the spherical and conical outflow model by 1−2 orders of magnitude. The (bi-)conical model seems to better match energetic constraints.
-
The AGN outflow energetics and feedback efficiencies for the unresolved NLR may carry most of the outflow power confined to a sub-kpc region with mass outflow rates of up to 100 M⊙ yr-1. This is still an order of magnitude lower than in the spherical model without correction for beam smearing.
-
After correction for beam smearing the AGN feedback efficiencies reduce in all considered models to 0.01−0.1 per cent which are lower efficiencies than assumed in many cosmological simulations to reproduce the galaxy population at high stellar masses. This could mean that either the kinetic coupling of the energy is small compared to thermal feedback or that current model assumptions have to be adjusted. In addition, we find that the momentum injection rate close or below the limit of Lbol/c for a radiatively-driven outflow in the conical case when beam smearing is taken into account.
Overall our investigation implies that a proper handling of the beam-smearing effect is crucial for interpreting and quantifying the energetics of AGN-driven outflows around luminous QSOs. This is particularly important for data providing low spatial resolution (>1 kpc). The overestimation of AGN efficiencies is probably not just restricted to this specific QSO sample studied here, but may apply to other unobscured QSO studies at low and high redshift, in which beam smearing is not properly addressed yet. For example, it has not yet been discussed which role beam smearing plays in high-redshift QSOs showing signatures of kpc-scale broad [O iii] lines (e.g. Cano-Díaz et al. 2012; Cresci et al. 2015; Brusa et al. 2015). Of course, there are also individual examples of truly extended AGN outflows in objects where the light distribution of the broad [O iii] line is clearly asymmetric on kpc scales (Harrison et al. 2015; Greene et al. 2012). While broad components in the [O iii] line seem to be quite common for luminous AGN, which can be interpreted as AGN outflow, the beam-smearing effect needs to be carefully evaluated to robustly quantify the large-scale kinematics on a case-by-case basis.
Our results also imply that a significant part of the kinetic power and mass outflow rate may be confined to small scales (< 1 kpc) given the prominence of the unresolved NLR. It is difficult to verify these estimates without being able to verify if the assumption of constant-density clouds for the conical model actually holds or not. In any case, even with our conservative assumptions our estimates are more than an order of magnitude lower than in the case of the spherical outflow model if beam smearing is not taken into account.
Consequently, the AGN energetics can change drastically depending on the contrast ratio between the unresolved and resolved [O iii] emission and its associated kinematics. Estimated AGN energetics depend strongly on (i) the measurements itself, given the contamination of extended emission by an unresolved component and (ii) assumptions made in the model, such as the outflow geometry and the electron density, if not measurable. For the QSO sample presented here, it means that the inferred kinematic power for the conical outflow model yields 1.5 to 3 orders of magnitude lower outflow energies compared to the spherical outflow model taking the unresolved emission contribution into account.
The beam-smearing effect may therefore partially explain the discrepancy between the claim for ubiquitous kpc-scale outflows in obscured QSOs (Liu et al. 2013a) and the contrary result for unobscured QSO by Husemann et al. (2013b). However, it remains unclear whether the observation of unobscured and obscured QSOs are equally affected. A direct study of beam-smearing effects for obscured QSOs is often infeasible but Villar-Martín et al. (2016) and Karouzos et al. (2016) have taken the beam smearing into account when analysing a sample of obscured QSOs and also report rather compact outflows size of 1–2 kpc. Given that we find [O iii] luminosity in obscured QSOs slightly enhanced compared to the AGN luminosity, the compact NLR region is not more obscured than in unobscured QSOs and makes the beam-smearing effect as important as for unobscured QSOs.
Therefore, we conclude that the question whether powerful kpc-scale outflows are ubiquitous in all AGN above a certain luminosity remains open. Given that there is also necessarily a time evolution in the size of the outflow and its properties, there should be a population of luminous QSOs where the size of the outflow is still small and appears barely resolved. Such scenarios can only be studied when the beam-smearing effect, ubiquitous for observational data, is taken into account.
Acknowledgments
We appreciate the valuable comments and suggestions of the referee that greatly improved the clarity and quality of the article. We thank Kevin Hainline for providing his measurements of the 8 μm luminosity for the QSO sample presented in Husemann et al. (2013b) and Dominika Wylezalek for helping to retrieve the GMOS data from the Gemini archive. J.S. acknowledges the European Research Council for the Advanced Grant Program 267399-Momentum. V.N.B. acknowledges assistance from a National Science Foundation (NSF) Research at Undergraduate Institutions (RUI) grant AST-1312296 and support for program number HST-AR-12625.11-A, provided by NASA through a grant from the Space Telescope Science Institute, which is operated by the Association of Universities for Research in Astronomy, Incorporated, under NASA contract NAS5-26555. J.H.W. acknowledges support by the National Research Foundation of Korea to the Center for Galaxy Evolution Research (2010-0027910). Based on observations (Program ID: GN-2012B-Q-29) obtained at the Gemini Observatory acquired through the Gemini Science Archive, which is operated by the Association of Universities for Research in Astronomy, Inc., under a cooperative agreement with the NSF on behalf of the Gemini partnership: the National Science Foundation (United States), the National Research Council (Canada), CONICYT (Chile), the Australian Research Council (Australia), Ministério da Ciência, Tecnologia e Inovação (Brazil) and Ministerio de Ciencia, Tecnología e Innovación Productiva (Argentina). Funding for SDSS-III has been provided by the Alfred P. Sloan Foundation, the Participating Institutions, the National Science Foundation, and the US Department of Energy Office of Science. The SDSS-III web site is http://www.sdss3.org/. SDSS-III is managed by the Astrophysical Research Consortium for the Participating Institutions of the SDSS-III Collaboration including the University of Arizona, the Brazilian Participation Group, Brookhaven National Laboratory, Carnegie Mellon University, University of Florida, the French Participation Group, the German Participation Group, Harvard University, the Instituto de Astrofisica de Canarias, the Michigan State/Notre Dame/JINA Participation Group, Johns Hopkins University, Lawrence Berkeley National Laboratory, Max Planck Institute for Astrophysics, Max Planck Institute for Extraterrestrial Physics, New Mexico State University, New York University, Ohio State University, Pennsylvania State University, University of Portsmouth, Princeton University, the Spanish Participation Group, University of Tokyo, University of Utah, Vanderbilt University, University of Virginia, University of Washington, and Yale University.
References
- Ahn, C. P., Alexandroff, R., Allen de Prieto, C., et al. 2014, ApJS, 211, 17 [NASA ADS] [CrossRef] [Google Scholar]
- Allington-Smith, J., Murray, G., Content, R., et al. 2002, PASP, 114, 892 [NASA ADS] [CrossRef] [Google Scholar]
- Antonucci, R. 1993, ARA&A, 31, 473 [Google Scholar]
- Barbosa, F. K. B., Storchi-Bergmann, T., Cid Fernandes, R., Winge, C., & Schmitt, H. 2009, MNRAS, 396, 2 [NASA ADS] [CrossRef] [Google Scholar]
- Bennert, N., Falcke, H., Schulz, H., Wilson, A. S., & Wills, B. J. 2002, ApJ, 574, L105 [NASA ADS] [CrossRef] [Google Scholar]
- Bennert, N., Jungwiert, B., Komossa, S., Haas, M., & Chini, R. 2006a, A&A, 459, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bennert, N., Jungwiert, B., Komossa, S., Haas, M., & Chini, R. 2006b, A&A, 456, 953 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boroson, T. 2005, AJ, 130, 381 [NASA ADS] [CrossRef] [Google Scholar]
- Bower, R. G., Benson, A. J., Malbon, R., et al. 2006, MNRAS, 370, 645 [NASA ADS] [CrossRef] [Google Scholar]
- Brusa, M., Bongiorno, A., Cresci, G., et al. 2015, MNRAS, 446, 2394 [NASA ADS] [CrossRef] [Google Scholar]
- Cano-Díaz, M., Maiolino, R., Marconi, A., et al. 2012, A&A, 537, L8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Capetti, A., Axon, D. J., Macchetto, F., Sparks, W. B., & Boksenberg, A. 1996, ApJ, 469, 554 [NASA ADS] [CrossRef] [Google Scholar]
- Carniani, S., Marconi, A., Maiolino, R., et al. 2015, A&A, 580, A102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cavagnolo, K. W., McNamara, B. R., Nulsen, P. E. J., et al. 2010, ApJ, 720, 1066 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen, L., Jahnke, K., Wisotzki, L., & Sánchez, S. F. 2006, A&A, 459, 717 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cicone, C., Maiolino, R., Sturm, E., et al. 2014, A&A, 562, A21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Crenshaw, D. M., & Kraemer, S. B. 2000, ApJ, 532, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Crenshaw, D. M., Kraemer, S. B., Schmitt, H. R., et al. 2010, AJ, 139, 871 [NASA ADS] [CrossRef] [Google Scholar]
- Cresci, G., Mainieri, V., Brusa, M., et al. 2015, ApJ, 799, 82 [Google Scholar]
- Croton, D. J., Springel, V., White, S. D. M., et al. 2006, MNRAS, 365, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Di Matteo, T., Springel, V., & Hernquist, L. 2005, Nature, 433, 604 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Faucher-Giguère, C.-A., & Quataert, E. 2012, MNRAS, 425, 605 [NASA ADS] [CrossRef] [Google Scholar]
- Feruglio, C., Fiore, F., Carniani, S., et al. 2015, A&A, 583, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fischer, T. C., Crenshaw, D. M., Kraemer, S. B., & Schmitt, H. R. 2013, ApJS, 209, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Fruchter, A. S., & Hook, R. N. 2002, PASP, 114, 144 [NASA ADS] [CrossRef] [Google Scholar]
- Fu, H., & Stockton, A. 2009, ApJ, 690, 953 [NASA ADS] [CrossRef] [Google Scholar]
- Gandhi, P., Horst, H., Smette, A., et al. 2009, A&A, 502, 457 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- García-Benito, R., Zibetti, S., Sánchez, S. F., et al. 2015, A&A, 576, A135 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gibson, R. R., Jiang, L., Brandt, W. N., et al. 2009, ApJ, 692, 758 [NASA ADS] [CrossRef] [Google Scholar]
- Gofford, J., Reeves, J. N., McLaughlin, D. E., et al. 2015, MNRAS, 451, 4169 [Google Scholar]
- Greene, J. E., Zakamska, N. L., Ho, L. C., & Barth, A. J. 2011, ApJ, 732, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Greene, J. E., Zakamska, N. L., & Smith, P. S. 2012, ApJ, 746, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Hainline, K. N., Hickox, R., Greene, J. E., Myers, A. D., & Zakamska, N. L. 2013, ApJ, 774, 145 [NASA ADS] [CrossRef] [Google Scholar]
- Hainline, K. N., Hickox, R. C., Greene, J. E., et al. 2014, ApJ, 787, 65 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, C. M., Alexander, D. M., Swinbank, A. M., et al. 2012, MNRAS, 426, 1073 [NASA ADS] [CrossRef] [Google Scholar]
- Harrison, C. M., Alexander, D. M., Mullaney, J. R., & Swinbank, A. M. 2014, MNRAS, 441, 3306 [Google Scholar]
- Harrison, C. M., Thomson, A. P., Alexander, D. M., et al. 2015, ApJ, 800, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Miley, G. K., van Breugel, W. J. M., & Butcher, H. R. 1981, ApJ, 247, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Heckman, T. M., Kauffmann, G., Brinchmann, J., et al. 2004, ApJ, 613, 109 [NASA ADS] [CrossRef] [Google Scholar]
- Herenz, E. C., Wisotzki, L., Roth, M., & Anders, F. 2015, A&A, 576, A115 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hopkins, P. F., Bundy, K., Croton, D., et al. 2010, ApJ, 715, 202 [NASA ADS] [CrossRef] [Google Scholar]
- Horst, H., Gandhi, P., Smette, A., & Duschl, W. J. 2008, A&A, 479, 389 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Humphrey, A., Villar-Martín, M., Ramos Almeida, C., et al. 2015, MNRAS, 454, 4452 [NASA ADS] [CrossRef] [Google Scholar]
- Husemann, B., Wisotzki, L., Sánchez, S. F., & Jahnke, K. 2008, A&A, 488, 145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Husemann, B., Kamann, S., Sandin, C., et al. 2012, A&A, 545, A137 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Husemann, B., Jahnke, K., Sánchez, S. F., et al. 2013a, A&A, 549, A87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Husemann, B., Wisotzki, L., Sánchez, S. F., & Jahnke, K. 2013b, A&A, 549, A43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Husemann, B., Jahnke, K., Sánchez, S. F., et al. 2014, MNRAS, 443, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Husemann, B., Bennert, V. N., Scharwächter, J., Woo, J.-H., & Choudhury, O. S. 2016, MNRAS, 455, 1905 [NASA ADS] [CrossRef] [Google Scholar]
- Jahnke, K., Wisotzki, L., Sánchez, S. F., et al. 2004, Astron. Nachr., 325, 128 [NASA ADS] [CrossRef] [Google Scholar]
- Karouzos, M., Woo, J.-H., & Bae, H.-J. 2016, ApJ, 819, 148 [NASA ADS] [CrossRef] [Google Scholar]
- Kaspi, S., Smith, P. S., Netzer, H., et al. 2000, ApJ, 533, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Keel, W. C., Maksym, W. P., Bennert, V. N., et al. 2015, AJ, 149, 155 [NASA ADS] [CrossRef] [Google Scholar]
- King, A. 2003, ApJ, 596, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Komossa, S., Xu, D., Zhou, H., Storchi-Bergmann, T., & Binette, L. 2008, ApJ, 680, 926 [NASA ADS] [CrossRef] [Google Scholar]
- Kurosawa, R., Proga, D., & Nagamine, K. 2009, ApJ, 707, 823 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, G., Zakamska, N. L., Greene, J. E., Nesvadba, N. P. H., & Liu, X. 2013a, MNRAS, 430, 2327 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, G., Zakamska, N. L., Greene, J. E., Nesvadba, N. P. H., & Liu, X. 2013b, MNRAS, 436, 2576 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, G., Zakamska, N. L., & Greene, J. E. 2014, MNRAS, 442, 1303 [NASA ADS] [CrossRef] [Google Scholar]
- Liu, G., Arav, N., & Rupke, D. S. N. 2015, ApJS, 221, 9 [NASA ADS] [CrossRef] [Google Scholar]
- Mateos, S., Carrera, F. J., Alonso-Herrero, A., et al. 2015, MNRAS, 449, 1422 [NASA ADS] [CrossRef] [Google Scholar]
- McElroy, R., Croom, S. M., Pracy, M., et al. 2015, MNRAS, 446, 2186 [NASA ADS] [CrossRef] [Google Scholar]
- Mulchaey, J. S., Wilson, A. S., & Tsvetanov, Z. 1996, ApJS, 102, 309 [NASA ADS] [CrossRef] [Google Scholar]
- Mullaney, J. R., Alexander, D. M., Fine, S., et al. 2013, MNRAS, 433, 622 [NASA ADS] [CrossRef] [Google Scholar]
- Müller-Sánchez, F., Prieto, M. A., Hicks, E. K. S., et al. 2011, ApJ, 739, 69 [NASA ADS] [CrossRef] [Google Scholar]
- Nesvadba, N. P. H., Lehnert, M. D., Eisenhauer, F., et al. 2006, ApJ, 650, 693 [NASA ADS] [CrossRef] [Google Scholar]
- Osterbrock, D. E., & Ferland, G. J. 2006, Astrophysics of gaseous nebulae and active galactic nuclei, 2nd. edn. (Sausalito, CA: University Science Books) [Google Scholar]
- Perna, M., Brusa, M., Cresci, G., et al. 2015, A&A, 574, A82 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Peterson, B. M., Ferrarese, L., Gilbert, K. M., et al. 2004, ApJ, 613, 682 [NASA ADS] [CrossRef] [Google Scholar]
- Pogge, R. W. 1988, ApJ, 332, 702 [NASA ADS] [CrossRef] [Google Scholar]
- Ramos Almeida, C., Pérez García, A. M., Acosta-Pulido, J. A., & Rodríguez Espinosa, J. M. 2007, AJ, 134, 2006 [NASA ADS] [CrossRef] [Google Scholar]
- Reichard, T. A., Richards, G. T., Schneider, D. P., et al. 2003, AJ, 125, 1711 [NASA ADS] [CrossRef] [Google Scholar]
- Reyes, R., Zakamska, N. L., Strauss, M. A., et al. 2008, AJ, 136, 2373 [NASA ADS] [CrossRef] [Google Scholar]
- Rice, M. S., Martini, P., Greene, J. E., et al. 2006, ApJ, 636, 654 [NASA ADS] [CrossRef] [Google Scholar]
- Richards, G. T., Lacy, M., Storrie-Lombardi, L. J., et al. 2006, ApJS, 166, 470 [NASA ADS] [CrossRef] [Google Scholar]
- Roth, M. M., Kelz, A., Fechner, T., et al. 2005, PASP, 117, 620 [NASA ADS] [CrossRef] [Google Scholar]
- Rupke, D. S. N., & Veilleux, S. 2011, ApJ, 729, L27 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Garcia-Lorenzo, B., Mediavilla, E., González-Serrano, J. I., & Christensen, L. 2004, ApJ, 615, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez, S. F., Kennicutt, R. C., Gil de Paz, A., et al. 2012, A&A, 538, A8 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schawinski, K., Koss, M., Berney, S., & Sartori, L. F. 2015, MNRAS, 451, 2517 [NASA ADS] [CrossRef] [Google Scholar]
- Schaye, J., Crain, R. A., Bower, R. G., et al. 2015, MNRAS, 446, 521 [Google Scholar]
- Schmidt, M., & Green, R. F. 1983, ApJ, 269, 352 [NASA ADS] [CrossRef] [Google Scholar]
- Schmitt, H. R., Donley, J. L., Antonucci, R. R. J., Hutchings, J. B., & Kinney, A. L. 2003, ApJS, 148, 327 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Richards, G. T., Strauss, M. A., et al. 2011, ApJS, 194, 45 [NASA ADS] [CrossRef] [Google Scholar]
- Shen, Y., Greene, J. E., Ho, L. C., et al. 2015, ApJ, 805, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Silk, J., & Rees, M. J. 1998, A&A, 331, L1 [NASA ADS] [Google Scholar]
- Somerville, R. S., Hopkins, P. F., Cox, T. J., Robertson, B. E., & Hernquist, L. 2008, MNRAS, 391, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Stern, J., Faucher-Giguère, C.-A., Zakamska, N. L., & Hennawi, J. F. 2016, ApJ, 819, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Storchi-Bergmann, T., Lopes, R. D. S., McGregor, P. J., et al. 2010, MNRAS, 402, 819 [NASA ADS] [CrossRef] [Google Scholar]
- Storey, P. J., & Zeippen, C. J. 2000, MNRAS, 312, 813 [Google Scholar]
- Tombesi, F., Cappi, M., Reeves, J. N., et al. 2010, A&A, 521, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tombesi, F., Meléndez, M., Veilleux, S., et al. 2015, Nature, 519, 436 [Google Scholar]
- Trump, J. R., Hall, P. B., Reichard, T. A., et al. 2006, ApJS, 165, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Unger, S. W., Pedlar, A., Axon, D. J., et al. 1987, MNRAS, 228, 671 [NASA ADS] [CrossRef] [Google Scholar]
- Vaona, L., Ciroi, S., Di Mille, F., et al. 2012, MNRAS, 427, 1266 [NASA ADS] [CrossRef] [Google Scholar]
- Villar-Martín, M., Humphrey, A., Delgado, R. G., Colina, L., & Arribas, S. 2011, MNRAS, 418, 2032 [NASA ADS] [CrossRef] [Google Scholar]
- Villar Martín, M., Emonts, B., Humphrey, A., Cabrera Lavers, A., & Binette, L. 2014, MNRAS, 440, 3202 [NASA ADS] [CrossRef] [Google Scholar]
- Villar-Martín, M., Arribas, S., Emonts, B., et al. 2016, MNRAS, 460, 130 [NASA ADS] [CrossRef] [Google Scholar]
- Whittle, M. 1985, MNRAS, 213, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Wisotzki, L., Christlieb, N., Bade, N., et al. 2000, A&A, 358, 77 [NASA ADS] [Google Scholar]
- Woo, J.-H., Bae, H.-J., Son, D., & Karouzos, M. 2016, ApJ, 817, 108 [NASA ADS] [CrossRef] [Google Scholar]
- York, D. G., Adelman, J., Anderson, Jr., J. E., et al. 2000, AJ, 120, 1579 [Google Scholar]
- Zakamska, N. L., & Greene, J. E. 2014, MNRAS, 442, 784 [NASA ADS] [CrossRef] [Google Scholar]
- Zakamska, N. L., Strauss, M. A., Krolik, J. H., et al. 2003, AJ, 126, 2125 [NASA ADS] [CrossRef] [Google Scholar]
- Zubovas, K., & King, A. 2012, ApJ, 745, L34 [Google Scholar]
Appendix A: Additional figures
 |
Fig. A.1 Comparison of spatially resolved emission-line parameters across the GMOS FoV before (upper panels) and after (lower panels) applying the QSO-host galaxy deblending for each QSO. From left to right we present the [O iii] surface brightness distribution (Σ[O iii]), the median line velocity (vmedian), the line width covering 80 per cent of the line flux (W80), the line asymmetry parameter (A), and the kurtosis parameter (K). |
 |
Fig. A.1 continued. |
 |
Fig. A.1 continued. |
 |
Fig. A.2 Left panel: emission-line ratio of [O iii]/Hβ as a function of [O iii] surface brightness for the original data after removing the broad Hβ line (black data points) and after performing the QSO-host galaxy deblending (red data points). The shaded area indicates the rms of line ratios within a given bin. The dashed line indicates the 3σ detect limit for Hβ for a given [O iii]/Hβ ratio given the estimated noise in the unblended data. Middle panel: line ratios as a function of distance D from the QSOs. Right panel: line ratio maps before and after the QSO-host galaxy deblending. |
 |
Fig. A.2 continued. |
 |
Fig. A.2 continued. |
All Tables
All Figures
 |
Fig. 1 Comparison of the GMOS 3′′ aperture spectra (black line) with the corresponding SDSS spectrum (red line). The wavelength range is limited to the rest-frame wavelength range between 4500 and 5500 Å. An absolute photometric calibration of the GMOS data based on the median of the ratio of spectra over the common wavelength range. The spectra are normalized in flux density so that the peak in the [O iii] λ5007 line is set to one in the SDSS spectrum. A large part of the SDSS spectrum of SDSS J0304+0022 is masked as bad, as seen as the linear interpolated region. In general, the relative GMOS flux calibration across the wavelength range is consistent with the SDSS spectra at a <10% level. |
| In the text | |
 |
Fig. 2 Example of the broad Hβ and Fe ii emission-line subtraction without QSO-host deblending for SDSS J0924+0642. The observed spectrum (black line) and our best-fit model (red line) are shown in the upper panel. The best-fit model consisting of the broad Hβ and Fe ii λλ4948,5017 plus continuum is represented by the blue line with the corresponding residual spectrum of the narrow Hβ and [O iii] λλ4960,5007 indicated by the green line. The residuals of the total model are shown in the panel below. Details of the assumed model are given in the main text. |
| In the text | |
 |
Fig. 3 Upper panel: example PSF estimated from the intensity of the broad Hβ line for SDSS J0924+0642. The white circle indicates the FWHM of the seeing. We highlight two spaxels with a black and red square for which we show the spectra from the datacube in the lower panels. The red spaxel is |
| In the text | |
 |
Fig. 4 Upper panel: intensity profile for various seeing conditions assuming a Gaussian shape. The region of the central spaxel (core) and the adjacent host galaxy spaxel (host) are indicated by shaded areas for the GMOS sampling. Lower panel: corresponding scale factors for a point-source as a function seeing is shown by the black line. Higher scale factors would imply surface brightness distributions steeper than point-like sources (red shaded area). |
| In the text | |
 |
Fig. 5 Example for the spatially resolved emission-line maps before and after applying the QSO-host galaxy deblending for SDSS J0304+0022. Similar figures for all QSOs are moved to the Appendix. |
| In the text | |
 |
Fig. 6 Comparison of the total [O iii] line width (W80, upper left panel), maximum velocity range (Δv, upper right panel), size of the ENLR (Rint, lower right panel), and the power-law slope of the total [O iii] surface brightness profile (η, lower left panel) from the QSO as measured by Liu et al. (2014) and our re-analysis. We find good agreement between measurements with only a weak systematic offset and a scatter consistent with the intrinsic accuracy of measurements. The surface brightness profile slope η shows the greatest scatter because the actual range of the outer profile to measure η is not clearly specified in Liu et al. (2014), so that our measurements are likely not exactly matching their methodology. For the ENLR we measure the isophotal radius at a surface brightness (corrected for cosmological dimming) of Σ[O iii] = 10-15 erg s-1 cm-2 arcsec-2 (black circles) and the maximum projected distance to spaxels which exhibit the same threshold surface brightness locally (grey symbols). |
| In the text | |
 |
Fig. 7 Comparison of the total and ENLR [O iii] line measurements for the centroid distance from the QSO (dQSO), maximum size out to a fixed surface brightness limit (Rint), the median [O iii] line width within the central 1′′ (W80), the ellipticity of the central [O iii] emitting region (e) and the outer power-law radial surface brightness slope (η). The 1:1 relations are shown as a dashed line in each panel. The colour of each data point corresponds to the contrast ratio C as indicated by the colour bar which is defined as the fraction of resolved to the total [O iii] emission. |
| In the text | |
 |
Fig. 8 Example of the [O iii]/Hβ emission-line ratio distribution for SDSS J0233-0743. The line ratio is shown as a function of [O iii] surface brightness, distance from the QSO, and its 2D distribution before (black points) and after performing the QSO-host galaxy deblending (red points). Similar figures for all QSOs are moved to the Appendix. |
| In the text | |
 |
Fig. 9 Bolometric AGN luminosity (Lbol) versus kinetic power (Ėkin) and momentum outflow rate (voutṀout) for the spherical and conical outflow model at kpc-scale distances (D = 5 kpc). The black and red data points correspond to the measurements from the total and extended [O iii] line profile maps, respectively. In addition we also plot the corresponding values from the spatially unresolved [O iii] line from the NLR as blue data points. This is based on the conical formula but also applies to the spherical case as described in the main text. The dashed lines correspond to various AGN feedback efficiencies (ϵf) and outflow covering factors (Ω) as labelled in the corresponding panels. The error bars on Ėkin correspond to the range in electron densities 10 <ne< 1000. The uncertainty on Lbol is assumed to be 0.3 dex taking into account the photometric calibration of the data and the error on the bolometric correction factor. In the right panels, we show the change of the kinetic power and the momentum outflow rate from the total and extended [O iii] measurements as a function of contrast ratio (C). |
| In the text | |
 |
Fig. 10 Comparison of various AGN luminosity indicators are shown for the unobscured QSO samples of Husemann et al. (2013b, 2014), and Liu et al. (2014), and for the obscured QSO sample of Liu et al. (2013a) in the upper panels. Here we consider the continuum luminosity at 8 μm (L8 μm), total [O iii] luminosity (L[O iii]), broad Hβ luminosity (Lbroad Hβ) and continuum luminosity at 5100 Å (L5100) as independent AGN luminosity indicators. The corresponding distributions in the luminosity ratios are shown in the lower panels. For obscured QSOs only L[O iii] and L8 μm can be measured because the broad lines from the BLR and the continuum from the accretion disc are obscured and unobservable. |
| In the text | |
 |
Fig. A.1 Comparison of spatially resolved emission-line parameters across the GMOS FoV before (upper panels) and after (lower panels) applying the QSO-host galaxy deblending for each QSO. From left to right we present the [O iii] surface brightness distribution (Σ[O iii]), the median line velocity (vmedian), the line width covering 80 per cent of the line flux (W80), the line asymmetry parameter (A), and the kurtosis parameter (K). |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.1 continued. |
| In the text | |
 |
Fig. A.2 Left panel: emission-line ratio of [O iii]/Hβ as a function of [O iii] surface brightness for the original data after removing the broad Hβ line (black data points) and after performing the QSO-host galaxy deblending (red data points). The shaded area indicates the rms of line ratios within a given bin. The dashed line indicates the 3σ detect limit for Hβ for a given [O iii]/Hβ ratio given the estimated noise in the unblended data. Middle panel: line ratios as a function of distance D from the QSOs. Right panel: line ratio maps before and after the QSO-host galaxy deblending. |
| In the text | |
 |
Fig. A.2 continued. |
| In the text | |
 |
Fig. A.2 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.