| Issue |
A&A
Volume 591, July 2016
|
|
|---|---|---|
| Article Number | A139 | |
| Number of page(s) | 11 | |
| Section | Astrophysical processes | |
| DOI | https://doi.org/10.1051/0004-6361/201628264 | |
| Published online | 30 June 2016 | |
A model for the non-thermal emission of the very massive colliding-wind binary HD 93129A
1 Instituto Argentino de
Radioastronomía (CCT La Plata, CONICET), C.C.5, (1894) Villa Elisa,
Buenos Aires,
Argentina
e-mail:
sdelpalacio@iar-conicet.gov.ar;romero@iar-conicet.gov.ar
2 Facultad de Ciencias Astronómicas y
Geofísicas, Universidad Nacional de La Plata, Paseo del Bosque, B1900 FWA La Plata,
Argentina
3 Departament d’Astronomia i
Meteorologia, Institut de Ciènces del Cosmos (ICCUB), Universitat de Barcelona
(IEEC-UB), Martí i Franquès 1,
08028 Barcelona, Catalonia, Spain
e-mail: vbosch@am.ub.es
Received:
5
February
2016
Accepted:
20
April
2016
Context. Recently, the colliding-wind region of the binary stellar system HD 93129A was resolved for the first time using Very Large Baseline Interferometry. This system, one of the most massive known binaries in our Galaxy, presents non-thermal emission in the radio band, which can be used to infer the physical conditions in the system, and make predictions for the high-energy band.
Aims. We intend to constrain some of the unknown parameters of HD 93129A through modeling the non-thermal emitter. We also aim to analyse the detectability of this source in hard X-rays and γ-rays. Finally, we want to predict how the non-thermal emission will evolve in the future, when the stars approach periastron.
Methods. A broadband radiative model for the wind-collision region (WCR) has been developed taking into account the evolution of the accelerated particles streaming along the shocked region, the emission by different radiative processes, and the attenuation of the emission propagating through the local matter and radiation fields. We reproduce the available radio data, and make predictions of the emission in hard X-rays and γ-rays under different assumptions.
Results. From the analysis of the radio emission, we find that the binary HD 93129A is more likely to have a low inclination and a high eccentricity, with the more massive star being currently closer to the observer. The minimum energy of the non-thermal electrons seems to be between ~20–100 MeV, depending on the intensity of the magnetic field in the WCR. The latter can be in the range ~20–1500 mG.
Conclusions. Our model is able to reproduce the observed radio emission, and predicts that the non-thermal radiation from HD 93129A will increase in the near future. With instruments such as NuSTAR, Fermi, and CTA, it will be possible to constrain the relativistic particle content of the source, and other parameters such as the magnetic field strength in the WCR which, in turn, can be used to obtain upper-limits of the magnetic field on the surface of the very massive stars, thereby inferring whether magnetic field amplification is taking place in the particle acceleration region.
Key words: stars: massive / radiation mechanisms: non-thermal / acceleration of particles / stars: winds, outflows
© ESO, 2016
1. Introduction
Stars of type O and early B and their evolved counterparts, Wolf-Rayet (WR) stars, are very massive and luminous. These stars possess powerful stellar winds with mass-loss rates Ṁ ~ 10-7−10-5M⊙ yr-1 and wind terminal velocities up to v∞ ~ 1000−3000 km s-1. If two massive stars, of types OB+OB or OB+WR, form a binary system, their winds will collide. These systems are known as massive colliding-wind binaries (CWBs). The stars in CWBs can be of various luminosity classes, from main-sequence to supergiants and WRs, and thus have different chemical abundances, mass-loss rates, and wind terminal velocities. The periods of CWBs also span a wide range. These systems, therefore, occupy a quite large region in the parameter space. In this work we focus on the subgroup of CWBs capable of accelerating relativistic particles (particle-accelerating colliding-wind binaries or PACWBs; De Becker & Raucq 2013).
The radio emission from PACWBs is made up of three contributions: two thermal, namely one from the individual stellar winds and one from the thermal plasma in the wind-collision region (WCR); and the other one non-thermal (NT), from the relativistic particles in the WCR. The latter is of synchrotron nature. An adequate interpretation of the radio spectral information requires the separation and analysis of both thermal and non-thermal components. The steady thermal radio emission from a single stellar wind is due to the free-free process, and presents a flux density at a frequency ν of the form Sν ∝ να, with a spectral index α ~ 0.6 (Wright & Barlow 1975). The thermal emission from the WCR is optically thick in radiative WCR shock systems, for which α ~ 2, whereas it is optically thin in adiabatic WCR shock systems, leading to α ~ −0.1. This kind of emission generally presents orbital modulation, depending on the viewing angle (Pittard 2010). In contrast, the features of NT radio emission are a spectral index much lower (often negative) than the typical 0.6 value for single stars, variable radiation and/or spectral index, and a flux density at relatively low frequencies that are much higher than the thermal component (Dougherty & Williams 2000). In a few cases, VLBI observations have resolved the NT emission region associated with the WCR (see, e.g., O’Connor et al. 2005; Benaglia et al. 2010).
Typically, the radio spectrum of a PACWB can be separated into three regions:
-
At ν> 10 GHz, the thermal component of the winds is dominant. The flux density depends mostly on Ṁ and v∞. In principle, constraints on these kinds of parameters can be obtained by the study of the spectrum at high frequencies. However, there are some caveats owing to the uncertainties in the clumpiness of the winds (e.g., Blomme 2011). The thermal emission from the WCR can also contribute significantly to the total flux in compact binary systems.
-
Approximately for 2 <ν< 10 GHz, the NT component is dominant. The flux density is determined by the NT particle energetics and the B-field strength in the WCR. No appreciable absorption features are expected unless the binary is rather compact.
-
At ν< 2 GHz, the absorption effects on the emission become significant. Through the spectral turn-over frequency and the steepness of the radiation below the cut-off, it is possible to infer whether the suppression of the low energy emission is generated either by free-free absorption (FFA) in the stellar wind, synchrotron self-absorption (SSA) within the emitter, attenuation owing to the Razin-Tsytovich effect (R-T), or because of a low-energy cut-off in the electron energy distribution (Melrose 1980). If FFA is dominant, it is possible to constrain the electron number density (ne) in the wind, and therefore the Ṁ of the star. If R-T dominates, it is possible to constrain the value of B/ne in the WCR. Finally, if there is a low-energy cut-off in the electron distribution, it provides insight into the physics of particle acceleration processes in dense and highly energetic environments. In these dense environments, unless the radio emitter is very compact, SSA is likely to be negligible (e.g. Marcote et al. 2015).
The synchrotron radio emission is explained by the presence of relativistic electrons and a local magnetic field (Ginzburg & Syrovatskii 1964; De Becker 2007). The detection of NT radio emission from many massive binaries, as well as hard X-rays (see Leyder et al. 2010; Sugawara et al. 2015, for a detection in η-Carinae and a possible NT component in WR 140, respectively) and γ-rays (see below) in a few of them, leads to the conclusion that relativistic particle acceleration is taking place in these systems; electrons, protons, and heavier nuclei can be efficiently accelerated to high energies (HE) through first-order diffusive shock acceleration (DSA) in the strong shocks produced by the collision of the supersonic stellar winds (Eichler & Usov 1993; Benaglia & Romero 2003; Reimer et al. 2006; Pittard & Dougherty 2006).
The data at radio-frequencies enable a characterization of the injection spectrum of the relativistic particles responsible for this emission which, in turn, can be extrapolated to model the broadband spectral energy distribution (SED). The NT emission from IR to soft X-rays is completely overcome by the thermal emission from the stars and/or the WCR, but beyond this range we can use the information gathered at radio frequencies to predict the behavior of the systems in the HE domain, where the NT radiation dominates the spectrum again. The same population of particles (electrons) producing synchrotron radiation also interacts with the stellar UV field, producing HE photons through IC scattering (Eichler & Usov 1993; Benaglia & Romero 2003; Reitberger et al. 2014a). We note that the changing physical conditions in the WCR along the orbit, together with the geometrical dependence of some of the most relevant HE processes, lead to a periodic variability in the spectrum. The relevant HE processes are anisotropic IC and γ-γ absorption in the stellar radiation field. The role of proton-proton (p-p) interactions in radio emission may also be considered under some circumstances.
In this work, we develop a model that enables us to derive physical information of a binary stellar system and the NT emitting region using the available radio data. With this model, we can also determine under which conditions the system HD 93129A, one of the earliest, hottest, most massive and luminous binary stellar systems in the Galaxy, is most suitable for being detected at γ-rays. So far only η-Carinae (Tavani et al. 2009; Farnier et al. 2011) and (presumably) WR 11 (Pshirkov 2016; Benaglia 2016) are seen in γ-rays. In this paper we discuss whether HD 93129A is a promising candidate to join the family of γ-ray emitting, massive-star binaries.
2. Model
Stellar winds collide forming an interaction region bound on either side by the reverse shocks of the winds. The shocked winds are separated by a surface called the contact discontinuity (CD), which is located where the ram pressure components that are perpendicular to this surface are in equilibrium: 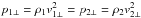 , where ρ1,2 and v1,2 ⊥ are the density and velocity of the two winds at the CD. The stellar winds follow a β-velocity law in the radial direction, vw(r) = v∞(1 − R/r)β, but here we have simply considered vw(r) = v∞ since the system we are studying is sufficiently extended. The azimuthal component of the wind velocity is also neglected.
, where ρ1,2 and v1,2 ⊥ are the density and velocity of the two winds at the CD. The stellar winds follow a β-velocity law in the radial direction, vw(r) = v∞(1 − R/r)β, but here we have simply considered vw(r) = v∞ since the system we are studying is sufficiently extended. The azimuthal component of the wind velocity is also neglected.
A complete broadband radiative model of the WCR must take into account the (magneto)hydrodynamics of the wind interaction zone, the acceleration of relativistic particles, the emission owing to these particles, and the possible attenuation of radiation through different processes. Some detailed models for the NT particle evolution (Reimer et al. 2006; Reitberger et al. 2014a) and the NT emission (Dougherty et al. 2003; Pittard et al. 2006; Pittard & Dougherty 2006; Reitberger et al. 2014b) have been developed in recent years.
One-zone models (i.e., punctual emitter) have been argued as being inadequate to represent CWBs because the free-free opacity varies along the extended region of synchrotron emission (Dougherty et al. 2003). Thus, we develop a two-dimensional (2D) model for the WCR approximating it as an axisymmetric shell with a very small width, which effectively allows a 1D description for the emitter along which NT particles evolve. The shocked flows stream frozen to the magnetic field, which is not dynamically dominant, starting at their injection/acceleration locations along the WCR, from the apex to the periphery of the binary. A schematic picture is shown in Fig. 1.
 |
Fig. 1 Sketch (not to scale) of the model considered in this work. The primary is located at (0,0) and the secondary at (D,0). The dashed line represents the contact discontinuity (CD) and, on either side, the shocked winds S1 and S2 are shown. The two solid lines with arrows entering the WCR from both sides are representative of the different streamlines that make up the emitter. Photons produced in the WCR travel towards the observer through the unshocked stellar winds. |
To compute the position of the CD, we use Eq. (6) prescribed in Antokhin et al. (2004). As both shocks, S1 and S2, have different properties because they depend on the conditions of the respective incoming wind (Bednarek & Pabich 2011), we apply an analytic hydrodynamical (HD) model to characterize the values of the relevant thermodynamical quantities for each side of the CD, which implies that there are actually two overlapped emitters at the CD. The WCR is formed by a sum of these 1D-emitters (linear-emitters hereafter) that are symmetrically distributed around the two-star axis in a 3D space: each discrete emission cell is first defined in the XY-plane, and the full 3D structure of the wind interaction zone is then obtained via rotation around the X-axis. The hydrodynamics and particle distribution have azimuthal symmetry neglecting orbital effects. The dependence with the azimuthal angle arises only for some emission and absorption processes that also depend on the position of the observer.
A more detailed description of the source, the hydrodynamic aspects of the model, and the acceleration, emission, and absorption processes, is provided in the following subsections.
2.1. Characteristics of HD 93129A
The system HD 93129A is formed of an O2 If* star (the primary) and a likely O3.5 V star (the secondary). The primary is among the earliest, hottest, most massive, luminous, and with the highest mass-loss rate, O stars in the Galaxy. The astrometric analysis in Benaglia et al. (2015) indicates that the two stars in HD 93129A form a gravitationally bound system. Furthermore, the LBA data from 2008 presented in Benaglia et al. (2015) reveals an extended arc-shaped NT source between the two stars, indicative of a WCR.
Parameters of the system HD 93129A for the primary (sub-index 1) and the secondary (sub-index 2).
Benaglia et al. (2006) show that the flux density of HD 93129A diminished with frequency, and point out a putative spectral turnover at ν< 1.4 GHz, which is indicated by the slight decrease in the ratio between the 1.4 GHz and the 2.4 GHz flux. Archival ATCA data show a point source with a change in flux level between 2003 and 2008. The emission is consistent with an NT spectral index α from −1.2 to −1, which corresponds to an injection index of p = −2α + 1 ~ 3.2. At frequencies above 15 GHz, the thermal wind contribution dominates, as seen in Fig. 5. The thermal emission, either from the stellar wind or the WCR, has a positive spectral index (e.g. Pittard 2010, Fig. 1, middle panel), and therefore a thermal contribution in the observed emission from HD 93129A would only imply an even steeper (i.e., more negative) intrinsic non-thermal spectral index. For simplicity we assume here that the steep emission from HD 93129A is non-thermal in nature (which, given the hardness of thermal radiation, is surely the case at the lowest frequencies).
Using the radio data, both the total fluxes and the wind momentum ratio, Benaglia et al. (2015) derived mass-loss rates in the range 2−5 × 10-5M⊙ yr-1, which are consistent with estimates obtained by other authors. However, these values might be overestimated because of wind clumping. Cohen et al. (2011) analysed Chandra observations of HD 93129A and showed that the intrinsically hard emission from the WCR contributes less than 10% to the total X-ray flux. The spectrum is dominated by thermal (kT = 0.6 keV) emission along with significant wind absorption. The broadband wind absorption and the line profiles provided two independent measurements of the wind mass-loss rate, Ṁ = (5.2−6.8) × 10-6M⊙ yr-1, which are ~3–10 times smaller than the values derived from radio observations. The X-ray line-profile diagnostic of the mass-loss rate can be complementary to that in radio as it is not affected by small-scale clumping, as long as the individual clumps are optically thin to X-rays. Previous X-ray observations with XMM-Newton also showed a thermal spectrum (Benaglia et al. 2006).
Benaglia et al. (2015) estimate some orbital parameters, although the binary has a very long period of more than 50 years (Benaglia & Koribalski 2007), and thus the orbit is still poorly sampled and the fitting errors are large. A high orbital inclination angle (i ~ 77°) was favoured (nearly edge-on), with a relatively small eccentricity, although a highly eccentric orbit, along with a small inclination angle (nearly face-on), could not be ruled out. The angular separation between the components was Dproj = 55 mas in 2003, and it shortened to 36 mas in 2008 and 27 mas in 2013 (Sana et al. 2014). According to the estimates of the orbital parameters, the binary system should go through periastron in the next few years. An unpublished analysis by Maiz Apellaniz (2007) also indicates that the system may approach periastron in ~2020 (Gagné et al. 2011). In Table 1, the known system parameters, as well as others derived for the model described in Sect. 2, are listed.
Previous estimates from Benaglia & Koribalski (2007) indicate that the equipartition magnetic field at the WCR could be ~20 mG, and the surface stellar magnetic field B∗ ~ 500 G, whereas in Benaglia et al. (2006) a smaller value of B∗ = 50 G was derived, assuming an initial toroidal component of the wind velocity of vrot = 0.2v∞, an Alfvén radius of rA = 3R∗, and a stellar radius of R∗ = 20 R⊙. The analysis presented in this work for two representative cases of low and high stellar magnetic fields gives consistent results (Sect. 3), with values of B∗ in the range 20−1000 G.
For the two unshocked winds, we assume the same molecular weight, μw1 = μw2 = 1.3, an rms ionic charge of Zw1 = Zw2 = 1.0, and an electron-to-ion ratio of γw1 = γw2 = 1.0 (Leitherer et al. 1995). For the WCR, the adopted stellar wind abundances are X = 0.705, Y = 0.275, and Z = 0.02, considering complete ionization, which yields μ1 = μ2 = 0.62, Z1 = Z2 = 1.23, and γ1 = γ2 = 1.34.
We are left with only a few free parameters: the value of B in the WCR, the acceleration efficiency, the spectrum of relativistic particles, and the inclination of the orbit, whose fit has large uncertainty. As we show in the following sections, it is possible to constrain B, the low-energy particle spectrum, and i by using the radio fluxes measured for different epochs, and the morphological information from the resolved NT emission region. A list, including the available radio data for different epochs and frequencies, is presented in Table 3 of Benaglia et al. (2015).
2.2. Hydrodynamics
The hydrodynamics of the wind interaction in the adiabatic regime, and close enough to the binary to avoid orbital effects, is characterized to a large extent by the secondary-to-primary wind momentum ratio 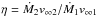 . If the wind shocks are adiabatic, the WCR thickness will be larger than in cases when the shocks are radiative, although for simplicity we assume that they are thin enough to neglect their width. Adiabatic wind shocks are convenient because the shocked two-wind structure is more stable so a stationary approximation is more valid. A cooling parameter Ξ can be introduced as a characteristic measure of the importance of cooling in the shocked region. Using Eq. (8) in Stevens et al. (1992), we obtain Ξ = trad/tesc ~ (v8)4D12/Ṁ-7 ≳ 100 ≫ 1, and therefore we can consider that the shocked gas is adiabatic (see, e.g., Zabalza et al. 2011). The value of Ξ is computed assuming that vw and Ṁ are similar for both stars, and that the shock is farther than 8 AU from any of the stars, roughly the distance at periastron.
. If the wind shocks are adiabatic, the WCR thickness will be larger than in cases when the shocks are radiative, although for simplicity we assume that they are thin enough to neglect their width. Adiabatic wind shocks are convenient because the shocked two-wind structure is more stable so a stationary approximation is more valid. A cooling parameter Ξ can be introduced as a characteristic measure of the importance of cooling in the shocked region. Using Eq. (8) in Stevens et al. (1992), we obtain Ξ = trad/tesc ~ (v8)4D12/Ṁ-7 ≳ 100 ≫ 1, and therefore we can consider that the shocked gas is adiabatic (see, e.g., Zabalza et al. 2011). The value of Ξ is computed assuming that vw and Ṁ are similar for both stars, and that the shock is farther than 8 AU from any of the stars, roughly the distance at periastron.
Following the approach of Antokhin et al. (2004), we assume that the flow along the WCR is laminar, neglecting any possible effect owing to mixing of the fluid streamlines. We also suppose that the velocity of the fluid at a given position of the WCR is equal to the projected tangential component of the stellar wind velocity. The particles are followed until they travel a distance ~4D, where D is the linear separation between the stars. We note that, at large scales, the Coriolis effect associated with the orbital motion breaks the azimuthal symmetry of the WCR, but this effect can be neglected for scales smaller than ~(vw/vorb) D, which is far enough for the emitting region considered, even close to periastron.
Each streamline coming from each star reaches the WCR at a different position (see Fig. 1). We consider a discrete number of streamlines and that the j-streamline enters the WCR at the point (xj,yj), where the jth linear-emitter begins. For simplicity, in our model, the magnetohydrodynamic quantities at a cell i are determined solely by the j = i streamline and are identical for all streamlines with j<i. To characterize the thermodynamical quantities in the WCR, we consider the fluid as behaving like an ideal gas and we apply Rankine-Hugoniot jump conditions in the strong shocks.
Explicitly, the set of equations describing the fluid is as follows: ![\begin{eqnarray} \label{eq:hydro} \rho(i) &=& 4\rho_{\mathrm{wind}}(i) = \dot{M} \left[ \pi d(i)^2 v_{\mathrm{wind}} \right]^{-1}, \\ P(i) &=& 0.75\left( \rho_{\mathrm{wind}} v_{\mathrm{wind}\perp}^2 \right), \\ v(i) &=& \vec{v}_{\mathrm{wind}}(i) \cdot \vec{u}(i)_\parallel \,, \\ T(i) &=& \frac{P(i) m_p \mu}{\rho(i)k}, \\ B(i) &=& \zeta^{1/2} B_{\mathrm{eq}} = \left[\zeta \, 8\pi \gamma_\mathrm{ad} P(i) \right]^{1/2}. \end{eqnarray}](/articles/aa/full_html/2016/07/aa28264-16/aa28264-16-eq94.png) In these equations, i represents the position of the i-cell along the WCR (see Fig. 2), d is the distance to the respective star (i.e., to the primary for S1 and to the secondary for S2), γad = 5/3 is the adiabatic coefficient, P is the pressure, T is the temperature, v is the fluid velocity, u∥ is a versor tangent to the WCR (see Fig. 2), mp is the proton mass, μ is the mean molecular weight, and ζ the magnetic-to-thermal energy density ratio, umag/uth (with uth = γadP), at the shock. The parameter ζ is set to reproduce the observed radio fluxes, as described in Sect. 3. Finally, an upper limit for the stellar surface magnetic field can be estimated, assuming that the magnetic field in the WCR comes solely from the adiabatic compression of the stellar field lines. Then, assuming an Alfvén radius rA ~ R∗, we get the expression B∗ = 0.25B(1)[(D − x(1)) /R∗](v∞/vrot). We note that it is possible that the magnetic fields are generated, or at least strongly amplified in situ, and therefore the values of the upper-limits for the stellar surface magnetic field we derive could be well above the actual field values.
In these equations, i represents the position of the i-cell along the WCR (see Fig. 2), d is the distance to the respective star (i.e., to the primary for S1 and to the secondary for S2), γad = 5/3 is the adiabatic coefficient, P is the pressure, T is the temperature, v is the fluid velocity, u∥ is a versor tangent to the WCR (see Fig. 2), mp is the proton mass, μ is the mean molecular weight, and ζ the magnetic-to-thermal energy density ratio, umag/uth (with uth = γadP), at the shock. The parameter ζ is set to reproduce the observed radio fluxes, as described in Sect. 3. Finally, an upper limit for the stellar surface magnetic field can be estimated, assuming that the magnetic field in the WCR comes solely from the adiabatic compression of the stellar field lines. Then, assuming an Alfvén radius rA ~ R∗, we get the expression B∗ = 0.25B(1)[(D − x(1)) /R∗](v∞/vrot). We note that it is possible that the magnetic fields are generated, or at least strongly amplified in situ, and therefore the values of the upper-limits for the stellar surface magnetic field we derive could be well above the actual field values.
 |
Fig. 2 Illustration of the model for the spatial distribution of NT particles in the WCR. On the left side we show different linear-emitters, named as j = 1,2,3, coming from each star. On the right side we represent a set of linear-emitters, obtained from summing the contributions from the different linear-emitters at each location (see text). |
Numerical results of hydrodynamical simulations can also be used to obtain the conditions in which NT particles evolve and radiate (Reitberger et al. 2014a,b). For simplicity, at this stage, we use simple hydrodynamical prescriptions (Eqs. (1)–(5)) because it eases the treatment. To first order, we do not expect significant differences from using more accurate fluid descriptions, as long as instabilities are not relevant in shaping the WCR. Nevertheless, in future works we plan to use numerical results to characterize the hydrodynamics of the emitter.
2.3. Particle distribution
The WCR presents hypersonic, non-relativistic adiabatic shocks, where NT particles of energy E and charge qe are expected to accelerate via DSA on a timescale tacc ≈ 2πE(c/v∞)2(Bcqe)-1 s (see, e.g., Drury 1983, for a review on non-relativistic DSA), where we have assumed diffusion in the Bohm regime. To derive the maximum particle energy, tacc is compared with the relevant cooling and escape timescales. These particles are responsible for the observed NT radio emission. Radio observations indicate that the particle energy distribution of electrons that emit at 3–10 GHz has a power-law index of p ~ 3.2. The corresponding electron energy distribution seems particularly soft when compared with the observed spectral indices in other NT CWBs (De Becker & Raucq 2013), and considering that the expected index for DSA in a strong shock is p = 2. This type of soft energy distribution of the radio-emitting particles might be related to the wide nature of the orbit, which could imply a stronger toroidal magnetic field component that may soften the particle distribution by quickly dragging the particles away from the shock, at least at low energies. At this stage, we just take the radio spectrum as a constraint for the radio-emitting particles, and we do not discuss the details of their acceleration. The particles accelerated in each cell of the WCR cool through various processes although, except for the most energetic particles, advection dominates the particle energy loss. Under these conditions, the evolved particle distribution has the same spectral index as the injected distribution, as seen in Fig. 3, because cooling cannot modify the distribution of the particles as they move along the WCR (see Eq. (6) below). The energy distribution of the accelerated particles at injection is taken as Q(E) ∝ E− p.
 |
Fig. 3 Examples of the electron energy distribution for a set of linear-emitters assuming a constant spectral index (top), and a hardening at higher energies (bottom). The color bar corresponds to different positions along the line, with higher values meaning farther from the apex. Both cases correspond to a low ambient magnetic field (ζ ≪ 1). |
Radio observations do not provide any information of the electron distribution above the corresponding electron energies. On the other hand, the DSA process for the less energetic particles could be affected by small-scale irregularities in the shock precursor, magnetic field geometry (already mentioned), energy-dependent compression ratios, non-linear effects in the shocks, etc. (see, e.g., Drury 1983). Moreover, other acceleration processes might also operate in addition to DSA, such as magnetic reconnection (Falceta-Gonçalves & Abraham 2012), affecting the particle distribution as well. Therefore, the resulting particle distribution could be softer at low energies (see, e.g., Berezhko et al. 2009, for similar conclusions in SN 1006), and harder at high energies. To explore the possibility of a harder distribution of the accelerated particles at high energies, two different cases are investigated here (see Sects. 3.2 and 3.4); in Fig. 3, the two different models of the electron energy distribution are shown.
Radio observations also show that radio emission is strongly reduced below 1–2 GHz. Our analysis below (Sect. 3) shows that statistically this reduction is best explained in terms of a low-energy cut-off in the electron energy distribution. The determination of the origin of such a low-energy cut-off is out of the scope of this work, but this may again be related to the peculiarities of particle acceleration in HD 93129A. An electron with a Lorentz factor γ, in presence of a magnetic field of intensity B, emits mostly at a frequency 0.29νc ~ 106Bγ2. Therefore, to obtain a cut-off around ν ~ 1 GHz, one needs 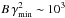 . For BWCR ~ 1 G, this leads to γmin ~ 30, whereas for BWCR ~ 10 mG it leads to γmin ~ 280.
. For BWCR ~ 1 G, this leads to γmin ~ 30, whereas for BWCR ~ 10 mG it leads to γmin ~ 280.
The normalization of the evolved particle distribution depends on the amount of kinetic energy flux perpendicular to the shock surface, and on the fraction of that flux that goes to NT particles (fNT). The luminosity associated with this flux is only 1−6% of the total wind luminosity, and the explored range of fNT is ~0.01–100%, which yields a NT luminosity LNT ~ 1032−1036 erg s-1. We note that secondary particles produced in p-p interactions (e.g., Ohm et al. 2015) are not expected to play a dominant role; a brief analysis of this scenario is discussed in Sect. 3.5.
2.4. Numerical treatment
We apply the following scheme to each of the two shocks:
-
We integrate numerically Eq. (6) fromAntokhin et al. (2004) to obtain thelocation of the CD on the XY-plane in discrete points (xi,yi). We characterize the position of the particles in their trajectories along the WCR through 1D cells located at those points.
-
We compute the thermodynamical variables at each position in the trajectory from Eqs. (1)–(5). Those quantities at a point (xi,yi) only depend on the position characterized by the value of i alone.
-
The wind magnetic field lines reach the wind shocks at different locations, from where they are advected along the WCR. We simulate the different trajectories by taking different values of imin: the case in which imin = 1 corresponds to a line starting in the apex of the WCR, whereas imin = 2 corresponds to a line that starts a bit farther out in the WCR, etc. The axisymmetry enables us to compute the trajectories only for the 1D emitters with y> 0.
-
Relativistic particles are injected in only one cell per linear-emitter (the corresponding imin), and each linear-emitter is independent from the rest. For a given linear-emitter, particles are injected at a location (ximin,yimin), where we estimate the particle maximum energy E0max and the cooling
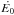 . Adiabatic cooling is included as tadi ≈ R(i) /v(i), where R(i) is the distance from the i-cell to the closest star. In the Bohm regime, the diffusion coefficient is DBohm = rgc/ 3, where rg = E/ (qB) is the gyro-radius of the particle. The diffusion timescale tdif ≈ 0.5R(i)2/DBohm is much larger than the radiative cooling timescale, and therefore diffusion losses are negligible. We calculate the advection time, i.e., the time taken by the particles to go from one cell to the next, as tadv = d(i) /v(i), where
. Adiabatic cooling is included as tadi ≈ R(i) /v(i), where R(i) is the distance from the i-cell to the closest star. In the Bohm regime, the diffusion coefficient is DBohm = rgc/ 3, where rg = E/ (qB) is the gyro-radius of the particle. The diffusion timescale tdif ≈ 0.5R(i)2/DBohm is much larger than the radiative cooling timescale, and therefore diffusion losses are negligible. We calculate the advection time, i.e., the time taken by the particles to go from one cell to the next, as tadv = d(i) /v(i), where 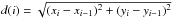 is the size of that cell. We obtain the distribution at the injection point, N0(E,imin), as N0(E,imin) = Q(E) tadv. In the next step in the trajectory of the HE particles, which are attached to the flow through the chaotic B-component, we calculate Emax(i) and Ė(i) to obtain the version of the injected distribution evolved under the relevant energy losses (IC scattering, synchrotron, and relativistic Bremsstrahlung for relativistic electrons; proton-proton interactions, adiabatic losses, and diffusion for relativistic protons):
is the size of that cell. We obtain the distribution at the injection point, N0(E,imin), as N0(E,imin) = Q(E) tadv. In the next step in the trajectory of the HE particles, which are attached to the flow through the chaotic B-component, we calculate Emax(i) and Ė(i) to obtain the version of the injected distribution evolved under the relevant energy losses (IC scattering, synchrotron, and relativistic Bremsstrahlung for relativistic electrons; proton-proton interactions, adiabatic losses, and diffusion for relativistic protons): 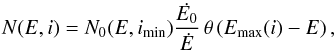 (6)where θ is the Heaviside function and Emax is the evolved maximum energy of the particles streaming away from the injection point with i = imin. The particle energy distribution in the injection cell is normalized according to the NT luminosity deposited in that cell. The normalization depends both on the size of the cell, as lines are not equi-spatially divided, and on the angle between the direction perpendicular to the CD and the unshocked wind motion, which varies along the CD.
(6)where θ is the Heaviside function and Emax is the evolved maximum energy of the particles streaming away from the injection point with i = imin. The particle energy distribution in the injection cell is normalized according to the NT luminosity deposited in that cell. The normalization depends both on the size of the cell, as lines are not equi-spatially divided, and on the angle between the direction perpendicular to the CD and the unshocked wind motion, which varies along the CD. -
We repeat the same procedure varying imin, which represents different line emitters in the XY-plane.
-
Finally we calculate Ntot(E,i), summing the distributions N(E,i) obtained before. The number of sums depends on the value of i: for i = 1 there is only one population; for i = 2 we have the evolved version of the particles injected at imin = 1, and those injected at imin = 2 (two streamlines total); for i = 3 there is the evolved version of the particles injected at imin = 1 and imin = 2 (two streamlines), and those injected at imin = 3 (giving a total of three streamlines crossing the point i = 3), and so on. We recall that along the CD there are actually two overlapping sets of linear-emitters that correspond to S1 and S2. An illustration of the linear-emitters and the sets of linear-emitters is shown in Fig. 2.
2.5. Emission and absorption
Once the particle distribution for each cell (xi,yi) is known, it is possible to calculate the total emission corrected for absorption as follows:
-
We rotate the set of linear-emitters around the axis joining thetwo stars, ending up with many sets of linear-emitters, each with adifferent value of the azimuthal angle φ. The particle energy distribution is normalized accounting for the number of sets of linear-emitters with different φ-values (i.e., for mφ sets of linear-emitters, each one has a luminosity LNT/mφ, as we are assuming azimuthal symmetry). In this way, we have the evolved particle energy distribution for each position (xi,yi,zi) of the CD surface in a 3D geometry.
-
At each position (xi,yi,zi), we calculate the total opacity τ in the direction of the observer for γ-γ (e.g., Dubus 2006) and free-free (e.g., Rybicki & Lightman 1986) absorption. We note that the FFA coefficient in the limit hν ≪ kT is αff ∝ neniT− 3/2, where ne and ni are the electron and ion number density, respectively. From Eqs. (1)–(4), it follows that the free-free opacity is much larger in the wind than in the WCR (see Fig. 5 from Pittard & Dougherty 2006, for numerical estimates of this effect). Thus, our consideration of a thin shock is not an impairment when calculating the impact of FFA.
-
At each position (xi,yi,zi), we calculate the emission of the various relevant radiative processes, IC, synchrotron, p-p, and relativistic Bremsstrahlung (see, e.g., Bosch-Ramon & Khangulyan 2009, and references therein), and then take into account the absorption when necessary. Except for the IC, which depends on the star-emitter-observer geometry, the other radiative processes can be regarded as isotropic. This is related to the fact that the magnetic field is expected to be highly tangled in the shocked gas. In these cases, i.e., excepting IC, the only dependence with the azimuthal angle appears through absorption effects.
-
The total emission from each location for both S1 and S2, accounting for absorption if needed, is summed to obtain the SED of the source.
3. Results
The particle energy distribution and the NT emission through IC, synchrotron, and relativistic Bremsstrahlung are computed for different scenarios and epochs. The p-p interactions are also discussed to assess their potential importance in HD 93129A.
3.1. Inclination of the orbit
We revisit a previous estimation of the inclination of the orbit (i) of HD 93129A obtained by Benaglia et al. (2015) based on the reconstruction of the observed orbit. In this work, we explore the different possibilities for i under two constraints: the first is the total flux intensity, and the second is the morphology of the emission map. As for the first, if i is high (say, i> 60°), it is hard to explain the low-energy cut-off in the SED by means of FFA in the stellar wind (see the forthcoming Sect. 3.2.1). This is reflected by the high value (>10) of the reduced χ2 (3 d.o.f.) of the fit at radio frequencies. In principle, it could still be possible to have χ2< 10, reproducing better the low-energy cut-off, by assuming that the stellar wind is much denser, but this type of scenario would be in tension with the observational X-ray data. The only possibility remaining is to assume a low-energy cutoff in the particle distribution, which yields χ2 ≳ 1. This leads us to the second point: we explored various values of i and the subsequent emission maps (see Sect. 3.2.1 below). In Fig. 4, we show that a high i (>60°) leads to synthetic maps inconsistent with the source radio morphology. We conclude that scenarios with a low i are, therefore, strongly favored, and we restrict our further analysis to them. For values of i ~ 15°, the linear separation of the stars at the epoch of observation is D ≈ 85 UA.
We note that a small improvement in the fit is obtained if the secondary is in front of the system, since its wind is slightly slower and therefore its column density is slightly higher, thereby increasing slightly the role of FFA in the generation of the low-energy cut-off seen in radio. In all the remaining calculations (including the maps presented in Fig. 4), we consider the secondary to be closer to the observer. However, as the winds of both stars have similar characteristics and this effect is small, this should not be taken as a tight restriction.
 |
Fig. 4 Comparison between the observed radio emission map at 2.3 GHz (top, adapted from Benaglia et al. 2015) and our synthetic maps for the same binary separation as in the epoch of LBA observations. The two observed maps have different synthesized beams: the one on the left has a better resolution but a poorer sensitivity, whereas the one on the right has a poorer resolution but a higher sensitivity. In the synthetic maps, different values of the inclination of the orbit, ranging from 0° to 75°, are considered. The color bar represents the flux in units of mJy beam-1. The contours from the observed map start at 0.4 mJy beam-1 and increase in steps of 0.1 mJy beam-1, with a maximum value of 1.6 mJy beam-1 (right). In the synthetic maps, along with these contours, we show the contours at 0.1, 0.2 and 0.3 mJy beam-1 (below the 3σ threshold of the observations) in red, and the contours at 1.8, 2.0 and 2.2 mJy beam-1 (above the observed values) in green. Cases where i> 60° completely fail to reproduce the observed maps. The best fit is achieved for low inclinations (i< 30°). |
3.2. Low magnetic field scenario
We apply the model described in Sect. 2 to a scenario with a low magnetic field (i.e., ζ ≪ 1). To reproduce the 2008 radio observations, we fix the values of the following parameters: i = 15°, motivated by the discussion in Sec. 3.1; fNT = 0.11, which represents an optimistic case, yet more conservative than assuming fNT = 1; ζ = 2. × 10-4, which leads to BWCR ~ 24 mG, and B∗< 30 G; and electron minimum energy given by γmin = 100, which is needed to obtain the low-energy cut-off in the synchrotron spectrum (we note that this value is constrained by the value of BWCR as described in Sect. 2.3). We also consider equipartition of energy between electrons and protons. We note that, since it is statistically favored, the case with a high Emin is adopted even when FFA is significant for low i values. A constant value of p = 3.2, the one suitable for fitting the radio data, is adopted for the particle energy distribution at injection, Q(E).
We calculate the radio emission of the system for various epochs. First, when the distance between the two stars was D (roughly the epoch of the 2008–2009 observations), achieving a good fit with a reduced χ2 = 1.9 (3 d.o.f.). To check whether our results are consistent in time, we calculate the expected radio emission for the previous epoch of observation, 2003–2004, when the distance between the components was 1.5 D; we achieve a poor fit with a reduced χ2 = 17 (4 d.o.f.), which shows that an error in the fluxes of ~25% arises from assuming that ζ, γmin, α, and fNT remain constant in time. Finally, we repeat the calculations for closer distances, D/ 3 (roughly the present time), and D/ 10 (roughly the periastron passage). The slight departure of our predictions from the 2003–2004 observational points implies that the constant parameter assumption does not strictly apply, although the qualitative conclusions we arrive at should be quite robust. In Fig. 5 we present the time evolution of the radio emission. The flux at 2.3 GHz is gets fainter with time owing to increased FFA, since photons have to travel through denser regions of the winds. This effect is not so significant at 8.6 GHz but for D/ 10, so the flux at 8.6 GHz increases until D ~ D/ 3, and then drops considerably for D ~ D/ 10. We conclude that in the near future (i.e., close to periastron), the low-frequency turnover in the spectrum will be due to FFA. Comparing past and future observations can show whether the evolution of the low-frequency radio spectrum is consistent with two different hardening mechanisms (low-energy cutoff in the electron distribution and FFA), or just one (FFA). For such purposes, sensitive observations at frequencies below 1 GHz are recommended, since the steepness of the turnover will clarify the nature of the suppression mechanism that affects the radio emission (being steeper if FFA dominates).
 |
Fig. 5 Modeled emission for a distance between the componentes of 1.5 D (green solid line), D (orange long-dashed line), D/ 3 (blue intermediate-dashed), and D/ 10 (magenta short-dashed). The goodness of the fit is given by χ2 ~ 17 (3 d.o.f.) for the 2003–2004 observations, and χ2 ~ 1.9 (4 d.o.f.) for the 2008–2009 observations. |
The broadband SEDs for different epochs are shown in Fig. 6, along with some instrument sensitivities1. As the stars get closer, the density of the stellar photon field becomes higher. The IC cooling time decreases in consequence, leading to an increase in the IC luminosity and a slight decrease in the electron maximum energy. We predict that the system will be detectable in hard X-rays and HE γ-rays close to periastron passage, even if fNT is an order of magnitude below the assumed 0.2 value. The production of TeV photons will be low and undetectable with the current or near-future instruments.
 |
Fig. 6 Broadband SEDs for the epoch of radio observations (top), roughly the present epoch (middle), and roughly the periastron passage (bottom). For the epoch of radio observations, we show the ATCA data from 2008–2009, and upper-limits in the X-ray flux derived from Benaglia et al. (2006). Dashed lines indicate contributions from synchrotron (brown), IC (cyan), relativistic Bremsstrahlung (olive), and p-p (green); the filled red curve is the total emission. We show instrument sensitivity curves for 1-Ms NuSTAR (gray), 4-yr Fermi (dark gray), and 50-h CTA (black). |
3.2.1. Synthetic maps
The full information from the spatially resolved radio observations is only partially contained in the SEDS. Therefore we compare the morphology predicted by our model with the observed one (Benaglia et al. 2015). For this purpose, we produce synthetic radio maps at two frequencies, 2.3 GHz and 8.6 GHz, and for different epochs. To produce the radio maps, we first project the 3D emitting structure in the plane of the sky, obtaining a two-dimensional distribution of flux at a certain frequency. Then we cover the plane, adjusting at each location of the map an elliptic Gaussian that simulates the synthesized (clean) beam. If the observational synthesized beam has an angular size a × b, each Gaussian has 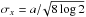 and
and 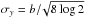 . At each pointing we sum the emission from every location weighted by the distance between its projected position and the Gaussian center. The LBA observations at 2.3 GHz from Benaglia et al. (2015) had a synthesized beam of 15 × 11 mas2; at 8.6 GHz, we adopt a synthesized beam of ~4 × 3 mas2.
. At each pointing we sum the emission from every location weighted by the distance between its projected position and the Gaussian center. The LBA observations at 2.3 GHz from Benaglia et al. (2015) had a synthesized beam of 15 × 11 mas2; at 8.6 GHz, we adopt a synthesized beam of ~4 × 3 mas2.
As seen in Fig. 4, for a high orbital inclination, the angular size of the WCR is much larger, and the resultant image is completely different from the one in the maps obtained from observations (Benaglia et al. 2015). This can be explained as follows: the projected distance between the stars is Dproj = 36 mas, so for a source at 2.3 kpc the linear distance is D ~ 83cos (i)-1 AU. A large (>60°) value of i leads to D> 150 AU. The impact of FFA is also very much reduced in this case. The linear size of the dominant WCR radio-emitting region is of a few D, and as the wind density drops as r-2, the FFA is very small except for photons coming from a region close to the apex of the WCR. This results in a small region of the whole WCR being affected by absorption. In contrast, Fig. 4 shows that, for a low inclination (i< 30°), the morphology and flux levels in the synthetic map are consistent with the observations. The emission maps at 2.3 GHz (not shown) for future epochs simply indicate that the radiation will come from a much compact (unresolved) region, with a faint signal that is hardly detectable above the noise level. Nevertheless, the maps at 8.6 GHz presented in Fig. 7 show that future observations at this frequency should be able to track the evolution of the WCR, since it is bright enough.
 |
Fig. 7 Synthetic radio maps at 8.6 GHz for the same binary separation as in the epoch of the LBA observations (top), for roughly the present epoch (middle), and for roughly the periastron passage (bottom) for the model described in Sect. 3.2. In all images, the red contours are at 0.1 mJy beam-1 and 0.3 mJy beam-1. In the top image the black contours are 0.5 mJy beam-1 and 1.0 mJy beam-1, in the middle image they start at 0.5 mJy beam-1 and increase in 2.0 mJy beam-1, and in the bottom one, there is only one contour at 0.5 mJy beam-1. |
3.3. Equipartition magnetic field scenario
We apply the same model as in Sect. 3.2, but with a different value of ζ to analyze a scenario with an extremely high magnetic field. We explore the case ζ = 1, which corresponds to equipartition between the magnetic field and the thermal energy densities in the WCR (Eq. (5)). We note that under these conditions the magnetic field could be dynamically relevant, i.e., the magnetic pressure could be a significant fraction of the total pressure in the post-shock region. Nonetheless, we do not alter our prescription of the flow properties, since we adopt a phenomenological model for them only to get a rough approximation of the gas properties in the shock. Moreover, our intentions are just to give a semi-qualitative description of this extreme scenario, not to make a precise modeling of the emission, and to obtain a rough estimate of some relevant physical parameters. Fixing ζ = 1 yields B ~ 1 G in the WCR and, if the magnetic field in the WCR is solely due to adiabatic compression of the stellar magnetic field lines, then we get B∗ 1 ~ 1.3 kG and B∗ 2 ~ 2.2 kG on the stellar surface of each star. We note that such high values of B∗ have never been measured in PACWBs (Neiner et al. 2015), something that suggests that in this scenario the magnetic field in the WCR should be generated or amplified in situ. In this case, owing to the stronger magnetic field, electrons with Lorentz factor γe ≈ 20 emit synchrotron radiation at ν ≈ 1 GHz and, in accordance, the electron energy distribution cut-off is set to γmin = 20. Setting fNT ≈ 10-4 leads to a spectral fit of the 2009 observed radio fluxes with χ2 = 2.1, and the obtained synthetic radio maps are very similar to the ones obtained in Sect. 3.2. However, such a small value of fNT seems suspicious. The synchrotron cooling time is tsy ≈ tIC for Ee< 10 GeV, when IC interactions occur in the Thomson regime, and tsy<tIC for Ee> 10 GeV, when IC interactions occur in the Klein-Nishina regime. Therefore the bulk of the NT emission is produced in the form of low-energy photons, and little luminosity goes into γ-ray production. The value of Lγ ≲ 1031 erg s-1 obtained is ~104 times smaller than the one obtained in Sect. 3.2. Considering that we are using a value 104 times larger for ζ, this result is expected since it follows the relation LIC/Lsy ∝ B-2 ∝ ζ-1 (see, e.g., White & Chen 1995). In this scenario HD 93129A is not detectable with the current (or in progress) HE observatories.
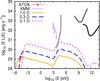 |
Fig. 8 Same as Fig. 6, but considering an equipartition magnetic field in the WCR. The solid orange curve represents the modeled SED for the epoch of radio observations, the long-dashed blue line is the SED for roughly the present epoch (middle), and the short-dashed magenta line is the SED for roughly the periastron passage. |
3.4. Best-case scenario
In this case we fix the HE particle spectrum to optimize the NT outcome. We maximize the HE outcome by assuming essentially the same parameters as in the scenario presented in Sect. 3.2, but also that electrons with Lorentz factors >7 × 103 are accelerated with p = 2. This may be a reasonable assumption, as discussed in Sect. 2.3. The emission at radio frequencies is therefore similar to the one in Sect. 3.2; the major difference is the stronger IC emission of γ-rays, as seen in the SEDs presented in Fig. 9. At energies close to 10 GeV, the source would be well within the detection capability of Fermi when the binary is close to periastron. At energies >100 GeV the source should be detectable by CTA. We note that the specific value of the turnover in the particle energy distribution has been chosen just to illustrate a case in which the chances of high-energy detection are enhanced.
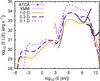 |
Fig. 9 Same as Fig. 6, but considering a possible hardening in the electron distribution. The solid orange curve represents the modeled SED for the epoch of radio observations, the long-dashed blue line is the SED for roughly the present epoch (middle), and the short-dashed magenta line is the SED for roughly the periastron passage. |
3.5. Hadronic scenario
The secondary e± pairs from p-p interactions could account for a significant part of the radio emission (e.g., Orellana et al. 2007). To explore this possibility, we consider the most favorable scenario in which the totality of the wind kinetic energy injected in the WCR goes into accelerating NT particles (i.e., fNT = 1), from which almost 100% goes into NT protons. For this NT proton energetics and under the density values of the shocked wind, the γ-ray luminosity from pp interactions is Lpp ~ 3 × 1030−7 × 1031 erg s-1, for p ~ 3.2−2 for protons (the higher luminosity corresponds to a higher ζ). Taking into account that the luminosity from pp interactions to secondary e± pairs is κLpp, with κ ≈ 0.25−0.5, depending on p (Kelner et al. 2006), the synchrotron luminosity of the secondary pairs in the radio band can be estimated as 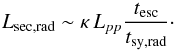 (7)The secondary e± energy distribution at creation will be similar to that of the primary protons and, given that it should have a cut-off around 10−50 MeV to explain the radio data, a cut-off in the proton energy distribution should also be introduced. For the escape time, we can derive tesc = D∗/vesc ~ 3 × 106 s, where D∗ is the shock distance to the closest star, and vesc is the typical shocked wind velocity. The synchrotron cooling time of the secondary e± pairs depends on their energy and the local magnetic field. For the pairs that produce synchrotron emission at the observed frequencies, we get tsy ~ 1010 s if B ~ 0.01 Beq, and tsy ~ 106 s for B ~ Beq. Therefore, if the magnetic field is below 0.1 Beq, we get Lsec,sy< 1029 erg s-1 = Lsy,obs, which is too low to account for the observed luminosity. If, instead, the magnetic field is above 0.1 Beq, then Lsec,sy ≳ Lsy,obs. However, this type of strong magnetic field leads to an excessively high synchrotron luminosity of the primary electrons, unless only a tiny amount <10-3 (<10-4 if B ~ Beq) of the injected NT luminosity goes into these particles.
(7)The secondary e± energy distribution at creation will be similar to that of the primary protons and, given that it should have a cut-off around 10−50 MeV to explain the radio data, a cut-off in the proton energy distribution should also be introduced. For the escape time, we can derive tesc = D∗/vesc ~ 3 × 106 s, where D∗ is the shock distance to the closest star, and vesc is the typical shocked wind velocity. The synchrotron cooling time of the secondary e± pairs depends on their energy and the local magnetic field. For the pairs that produce synchrotron emission at the observed frequencies, we get tsy ~ 1010 s if B ~ 0.01 Beq, and tsy ~ 106 s for B ~ Beq. Therefore, if the magnetic field is below 0.1 Beq, we get Lsec,sy< 1029 erg s-1 = Lsy,obs, which is too low to account for the observed luminosity. If, instead, the magnetic field is above 0.1 Beq, then Lsec,sy ≳ Lsy,obs. However, this type of strong magnetic field leads to an excessively high synchrotron luminosity of the primary electrons, unless only a tiny amount <10-3 (<10-4 if B ~ Beq) of the injected NT luminosity goes into these particles.
We have shown qualitatively that, even if we adopt an extreme case of fNT = 1, which is probably far from realistic, we cannot satisfactorily explain the observed radio emission with a hadronic scenario unless the B ≳ 0.1 Beq and for the primary electrons fNTe< 10-3 in the WCR. Nevertheless, a small contribution of secondary e± pairs to radio emission cannot be ruled out.
4. Conclusions
In this work we studied in detail the information provided by the observations of the colliding-wind binary HD 93129A. We developed a leptonic model that reproduces reasonably well the radio observations, and we showed that it is possible to explain the low-energy cut-off in the SED by means of a combination of FFA in the stellar winds and a low-energy cut-off in the electron energy distribution. We also provide radio morphological arguments to favor a low i for the system, implying a high eccentricity but also a not far-in-the-future periastron passage. Unfortunately, the limited knowledge on the physical parameters of the source, some model degeneracy in the amount of energy that goes into accelerating non-thermal particles versus the magnetic field intensity in the wind-collision region and limited observations make it difficult to fully constrain the properties of the non-thermal processes in HD 93129A. In any case, the results presented in this work provide a good insight for future observational campaigns in the radio and γ-ray range. In particular, we showed that future observations of the system HD 93129A at 0.5−10 GHz radio frequencies can confirm the nature of the radio absorption/suppression mechanism by comparing them with our predictions of the cut-off frequency and the steepness of the turnover. Observations in the hard X-ray range (10−100 keV), moreover, would provide tighter constraints to the free parameters in our model, such as the injected particle energy distribution at low energies, and the magnetic field strength, through comparison of the synchrotron and IC emission, constraining then the acceleration efficiency. We have shown that moderate values of the stellar surface magnetic field (B∗< 50 G) are sufficient to account for the synchrotron emission, even if there is no amplification of the magnetic field besides adiabatic compression; however, if the magnetic field in the wind-collision region is high (as seems to be the case if the source remains undetected in hard X-rays and γ-rays), then magnetic field amplification is likely to occur. We predict that this source is a good candidate to be detected during the periastron passage by Fermi in HE, and even possibly by CTA in VHE, although it is not expected to be a strong and persistent γ-ray emitter.
The electron energy distribution spectral index is poorly constrained, specially at high energies. However, even for a soft index p = 3.2 the γ-ray emission could still be detected by Fermi. Considering that slightly smaller values of p ≈ 3 are also derived from some radio observations, and that a possible hardening of the particle energy distribution cannot be discarded, the detection of HD 93129A in γ-rays in the near future seems feasible, as long as fNT ≳ 10-2 and ζ ≲ 10-3. Given the very long period of the binary HD 93129A, we strongly suggest dedicating observing time to this source in γ-rays, but also in the radio and X-ray band, in the next few years, since this will provide very valuable information of non-thermal processes in massive colliding-wind binaries.
The sensitivity curve of NuSTAR is adapted from Koglin et al. (2005), whereas the Fermi one is from http://fermi.gsfc.nasa.gov, and the CTA one from Takahashi et al. (2013).
Acknowledgments
We want to thank the referee for his/her constructive and useful comments and suggestions that helped us to improve our work and its presentation. This work is supported by ANPCyT (PICT 2012-00878). V.B-R. acknowledges financial support from MICINN and European Social Funds through a Ramón y Cajal fellowship. V.B-R. acknowledges support by the MDM-2014-0369 of ICCUB (Unidad de Excelencia María de Maeztu). This research has been supported by the Marie Curie Career Integration Grant 321520. V.B-R. and G.E.R. acknowledges support by the Spanish Ministerio de Economía y Competitividad (MINECO) under grant AYA2013-47447-C3-1-P. The acknowledgment extends to the whole GARRA group.
References
- Antokhin, I. I., Owocki, S. P., & Brown, J. C. 2004, ApJ, 611, 434 [NASA ADS] [CrossRef] [Google Scholar]
- Bednarek, W., & Pabich, J. 2011, A&A, 530, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benaglia, P. 2016, PASA, 33, e017 [NASA ADS] [CrossRef] [Google Scholar]
- Benaglia, P., & Koribalski, B. 2007, in Massive Stars in Interactive Binaries, eds. N. St.-Louis, & A. F. J. Moffat, ASP Conf. Ser., 367, 179 [Google Scholar]
- Benaglia, P., & Romero, G. E. 2003, A&A, 399, 1121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benaglia, P., Koribalski, B., & AlbaceteColombo, J. F. 2006, PASA, 23, 50 [NASA ADS] [CrossRef] [Google Scholar]
- Benaglia, P., Dougherty, S. M., Phillips, C., Koribalski, B., & Tzioumis, T. 2010, in Rev. Mex. Astron. Astrofis. Conf. Ser., 38, 41 [Google Scholar]
- Benaglia, P., Marcote, B., Moldón, J., et al. 2015, A&A, 579, A99 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berezhko, E. G., Ksenofontov, L. T., & Völk, H. J. 2009, A&A, 505, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blomme, R. 2011, Bull. Soc. Roy. Sci. Liège, 80, 67 [NASA ADS] [Google Scholar]
- Bosch-Ramon, V., & Khangulyan, D. 2009, Int. J. Mod. Phys. D, 18, 347 [NASA ADS] [CrossRef] [Google Scholar]
- Cohen, D. H., Gagné, M., Leutenegger, M. A., et al. 2011, MNRAS, 415, 3354 [NASA ADS] [CrossRef] [Google Scholar]
- De Becker, M. 2007, A&ARv, 14, 171 [NASA ADS] [CrossRef] [Google Scholar]
- De Becker, M., & Raucq, F. 2013, A&A, 558, A28 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dougherty, S. M., & Williams, P. M. 2000, MNRAS, 319, 1005 [NASA ADS] [CrossRef] [Google Scholar]
- Dougherty, S. M., Pittard, J. M., Kasian, L., et al. 2003, A&A, 409, 217 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drury, L. O. 1983, Rep. Prog. Phys., 46, 973 [NASA ADS] [CrossRef] [Google Scholar]
- Dubus, G. 2006, A&A, 451, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eichler, D., & Usov, V. 1993, ApJ, 402, 271 [NASA ADS] [CrossRef] [Google Scholar]
- Falceta-Gonçalves, D., & Abraham, Z. 2012, MNRAS, 423, 1562 [NASA ADS] [CrossRef] [Google Scholar]
- Farnier, C., Walter, R., & Leyder, J.-C. 2011, A&A, 526, A57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gagné, M., Fehon, G., Savoy, M. R., et al. 2011, ApJS, 194, 5 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ginzburg, V. L., & Syrovatskii, S. I. 1964, The Origin of Cosmic Rays (New York: Macmillan) [Google Scholar]
- Kelner, S. R., Aharonian, F. A., & Bugayov, V. V. 2006, Phys. Rev. D, 74, 034018 [NASA ADS] [CrossRef] [Google Scholar]
- Koglin, J. E., Christensen, F. E., Craig, W. W., et al. 2005, in Optics for EUV, X-Ray, and Gamma-Ray Astronomy II, eds. O. Citterio, & S. L. O’Dell, SPIE Conf. Ser., 5900, 266 [Google Scholar]
- Leitherer, C., Chapman, J. M., & Koribalski, B. 1995, ApJ, 450, 289 [NASA ADS] [CrossRef] [Google Scholar]
- Leyder, J.-C., Walter, R., & Rauw, G. 2010, A&A, 524, A59 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maiz Apellaniz, J. 2007, The orbit of the most massive known astrometric binary, HST Proposal [Google Scholar]
- Maíz Apellániz, J., Walborn, N. R., Morrell, N. I., et al. 2008, in Rev. Mex. Astron. Astrofis. Conf. Ser., 33, 55 [Google Scholar]
- Marcote, B., Ribó, M., Paredes, J. M., & Ishwara-Chandra, C. H. 2015, MNRAS, 451, 59 [NASA ADS] [CrossRef] [Google Scholar]
- Melrose, D. B. 1980, Plasma astrophysics. Nonthermal processes in diffuse magnetized plasmas – Vol. 1: The emission, absorption and transfer of waves in plasmas, Vol. 2: Astrophysical applications (New York: Gordon and Breach) [Google Scholar]
- Muijres, L. E., Vink, J. S., de Koter, A., Müller, P. E., & Langer, N. 2012, A&A, 537, A37 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mullan, D. J. 1984, ApJ, 283, 303 [NASA ADS] [CrossRef] [Google Scholar]
- Neiner, C., Grunhut, J., Leroy, B., De Becker, M., & Rauw, G. 2015, A&A, 575, A66 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- O’Connor, E. P., Dougherty, S. M., Pittard, J. M., & Williams, P. M. 2005, in Proc. Massive Stars and High-Energy Emission in OB Associations, eds. G. Rauw, Y. Nazé, R. Blomme, & E. Gosset, 81 [Google Scholar]
- Ohm, S., Zabalza, V., Hinton, J. A., & Parkin, E. R. 2015, MNRAS, 449, L132 [NASA ADS] [CrossRef] [Google Scholar]
- Orellana, M., Bordas, P., Bosch-Ramon, V., Romero, G. E., & Paredes, J. M. 2007, A&A, 476, 9 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pittard, J. M. 2010, MNRAS, 403, 1633 [NASA ADS] [CrossRef] [Google Scholar]
- Pittard, J. M., & Dougherty, S. M. 2006, MNRAS, 372, 801 [NASA ADS] [CrossRef] [Google Scholar]
- Pittard, J. M., Dougherty, S. M., Coker, R. F., O’Connor, E., & Bolingbroke, N. J. 2006, A&A, 446, 1001 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Prinja, R. K., Barlow, M. J., & Howarth, I. D. 1990, ApJ, 361, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Pshirkov, M. S. 2016, MNRAS, 457, L99 [NASA ADS] [CrossRef] [Google Scholar]
- Reimer, A., Pohl, M., & Reimer, O. 2006, ApJ, 644, 1118 [NASA ADS] [CrossRef] [Google Scholar]
- Reitberger, K., Kissmann, R., Reimer, A., & Reimer, O. 2014a, ApJ, 789, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Reitberger, K., Kissmann, R., Reimer, A., Reimer, O., & Dubus, G. 2014b, ApJ, 782, 96 [NASA ADS] [CrossRef] [Google Scholar]
- Repolust, T., Puls, J., & Herrero, A. 2004, A&A, 415, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rybicki, G. B., & Lightman, A. P. 1986, Radiative Processes in Astrophysics (Wiley-VCH) [Google Scholar]
- Sana, H., Le Bouquin, J.-B., Lacour, S., et al. 2014, ApJS, 215, 15 [NASA ADS] [CrossRef] [Google Scholar]
- Stevens, I. R., Blondin, J. M., & Pollock, A. M. T. 1992, ApJ, 386, 265 [NASA ADS] [CrossRef] [Google Scholar]
- Sugawara, Y., Maeda, Y., Tsuboi, Y., et al. 2015, PASJ, 67, 121 [NASA ADS] [Google Scholar]
- Takahashi, T., Uchiyama, Y., & Stawarz, Ł. 2013, Astropart. Phys., 43, 142 [NASA ADS] [CrossRef] [Google Scholar]
- Taresch, G., Kudritzki, R. P., Hurwitz, M., et al. 1997, A&A, 321, 531 [NASA ADS] [Google Scholar]
- Tavani, M., Sabatini, S., Pian, E., et al. 2009, ApJ, 698, L142 [Google Scholar]
- Walborn, N. R., Howarth, I. D., Lennon, D. J., et al. 2002, AJ, 123, 2754 [NASA ADS] [CrossRef] [Google Scholar]
- White, R. L., & Chen, W. 1995, in Wolf-Rayet Stars: Binaries; Colliding Winds, Evolution, eds. K. A. van der Hucht, & P. M. Williams, IAU Symp., 163, 438 [Google Scholar]
- Wright, A. E., & Barlow, M. J. 1975, MNRAS, 170, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Zabalza, V., Bosch-Ramon, V., & Paredes, J. M. 2011, ApJ, 743, 7 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Parameters of the system HD 93129A for the primary (sub-index 1) and the secondary (sub-index 2).
All Figures
 |
Fig. 1 Sketch (not to scale) of the model considered in this work. The primary is located at (0,0) and the secondary at (D,0). The dashed line represents the contact discontinuity (CD) and, on either side, the shocked winds S1 and S2 are shown. The two solid lines with arrows entering the WCR from both sides are representative of the different streamlines that make up the emitter. Photons produced in the WCR travel towards the observer through the unshocked stellar winds. |
| In the text | |
 |
Fig. 2 Illustration of the model for the spatial distribution of NT particles in the WCR. On the left side we show different linear-emitters, named as j = 1,2,3, coming from each star. On the right side we represent a set of linear-emitters, obtained from summing the contributions from the different linear-emitters at each location (see text). |
| In the text | |
 |
Fig. 3 Examples of the electron energy distribution for a set of linear-emitters assuming a constant spectral index (top), and a hardening at higher energies (bottom). The color bar corresponds to different positions along the line, with higher values meaning farther from the apex. Both cases correspond to a low ambient magnetic field (ζ ≪ 1). |
| In the text | |
 |
Fig. 4 Comparison between the observed radio emission map at 2.3 GHz (top, adapted from Benaglia et al. 2015) and our synthetic maps for the same binary separation as in the epoch of LBA observations. The two observed maps have different synthesized beams: the one on the left has a better resolution but a poorer sensitivity, whereas the one on the right has a poorer resolution but a higher sensitivity. In the synthetic maps, different values of the inclination of the orbit, ranging from 0° to 75°, are considered. The color bar represents the flux in units of mJy beam-1. The contours from the observed map start at 0.4 mJy beam-1 and increase in steps of 0.1 mJy beam-1, with a maximum value of 1.6 mJy beam-1 (right). In the synthetic maps, along with these contours, we show the contours at 0.1, 0.2 and 0.3 mJy beam-1 (below the 3σ threshold of the observations) in red, and the contours at 1.8, 2.0 and 2.2 mJy beam-1 (above the observed values) in green. Cases where i> 60° completely fail to reproduce the observed maps. The best fit is achieved for low inclinations (i< 30°). |
| In the text | |
 |
Fig. 5 Modeled emission for a distance between the componentes of 1.5 D (green solid line), D (orange long-dashed line), D/ 3 (blue intermediate-dashed), and D/ 10 (magenta short-dashed). The goodness of the fit is given by χ2 ~ 17 (3 d.o.f.) for the 2003–2004 observations, and χ2 ~ 1.9 (4 d.o.f.) for the 2008–2009 observations. |
| In the text | |
 |
Fig. 6 Broadband SEDs for the epoch of radio observations (top), roughly the present epoch (middle), and roughly the periastron passage (bottom). For the epoch of radio observations, we show the ATCA data from 2008–2009, and upper-limits in the X-ray flux derived from Benaglia et al. (2006). Dashed lines indicate contributions from synchrotron (brown), IC (cyan), relativistic Bremsstrahlung (olive), and p-p (green); the filled red curve is the total emission. We show instrument sensitivity curves for 1-Ms NuSTAR (gray), 4-yr Fermi (dark gray), and 50-h CTA (black). |
| In the text | |
 |
Fig. 7 Synthetic radio maps at 8.6 GHz for the same binary separation as in the epoch of the LBA observations (top), for roughly the present epoch (middle), and for roughly the periastron passage (bottom) for the model described in Sect. 3.2. In all images, the red contours are at 0.1 mJy beam-1 and 0.3 mJy beam-1. In the top image the black contours are 0.5 mJy beam-1 and 1.0 mJy beam-1, in the middle image they start at 0.5 mJy beam-1 and increase in 2.0 mJy beam-1, and in the bottom one, there is only one contour at 0.5 mJy beam-1. |
| In the text | |
 |
Fig. 8 Same as Fig. 6, but considering an equipartition magnetic field in the WCR. The solid orange curve represents the modeled SED for the epoch of radio observations, the long-dashed blue line is the SED for roughly the present epoch (middle), and the short-dashed magenta line is the SED for roughly the periastron passage. |
| In the text | |
 |
Fig. 9 Same as Fig. 6, but considering a possible hardening in the electron distribution. The solid orange curve represents the modeled SED for the epoch of radio observations, the long-dashed blue line is the SED for roughly the present epoch (middle), and the short-dashed magenta line is the SED for roughly the periastron passage. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


