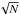| Issue |
A&A
Volume 584, December 2015
|
|
|---|---|---|
| Article Number | A36 | |
| Number of page(s) | 14 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201526527 | |
| Published online | 17 November 2015 | |
Squeezed between shells? The origin of the Lupus I molecular cloud
APEX/LABOCA, Herschel, and Planck observations⋆,⋆⋆,⋆⋆⋆
1 Universitäts-Sternwarte München, Ludwig-Maximilians-Universität, Scheinerstr. 1, 81679 München, Germany
e-mail: bengac@usm.uni-muenchen.de
2 ESO, Karl-Schwarzschild-Strasse 2, 85748 Garching bei München, Germany
3 Max-Planck-Institut für extraterrestrische Physik, Postfach 1312, 85741 Garching, Germany
4 Excellence Cluster Universe, Technische Universität München, Boltzmannstrasse 2, 85748 Garching, Germany
Received: 13 May 2015
Accepted: 21 September 2015
Context. The Lupus I cloud is found between the Upper Scorpius (USco) and the Upper Centaurus-Lupus (UCL) subgroups of the Scorpius-Centaurus OB association, where the expanding USco H I shell appears to interact with a bubble currently driven by the winds of the remaining B-stars of UCL.
Aims. We want to study how collisions of large-scale interstellar gas flows form and influence new dense clouds in the ISM.
Methods. We performed LABOCA continuum sub-mm observations of Lupus I that provide for the first time a direct view of the densest, coldest cloud clumps and cores at high angular resolution. We complemented these data with Herschel and Planck data from which we constructed column density and temperature maps. From the Herschel and LABOCA column density maps we calculated probability density functions (PDFs) to characterize the density structure of the cloud.
Results. The northern part of Lupus I is found to have, on average, lower densities, higher temperatures, and no active star formation. The center-south part harbors dozens of pre-stellar cores where density and temperature reach their maximum and minimum, respectively. Our analysis of the column density PDFs from the Herschel data show double-peak profiles for all parts of the cloud, which we attribute to an external compression. In those parts with active star formation, the PDF shows a power-law tail at high densities. The PDFs we calculated from our LABOCA data trace the denser parts of the cloud showing one peak and a power-law tail. With LABOCA we find 15 cores with masses between 0.07 and 1.71 M⊙ and a total mass of ≈8 M⊙. The total gas and dust mass of the cloud is ≈164 M⊙ and hence ~5% of the mass is in cores. From the Herschel and Planck data we find a total mass of ≈174 M⊙ and ≈171 M⊙, respectively.
Conclusions. The position, orientation, and elongated shape of Lupus I, the double-peak PDFs and the population of pre-stellar and protostellar cores could be explained by the large-scale compression from the advancing USco H I shell and the UCL wind bubble.
Key words: stars: formation / stars: protostars / ISM: bubbles / ISM: clouds / dust, extinction
The Atacama Pathfinder Experiment (APEX) is a collaboration between the Max-Planck-Institut für Radioastronomie (MPIfR), the European Southern Observatory (ESO), and the Onsala Space Observatory (OSO).
Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
Final APEX cube and Herschel N and T maps as FITS files are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/584/A36
© ESO, 2015
1. Introduction
In the current picture of the dynamic interstellar medium (ISM), molecular cloud formation is attributed to collisions of large-scale flows in the ISM (see review by Dobbs et al. 2014, and references within). Such flows can be driven by stellar feedback processes (e.g. UV-radiation and winds) and supernovae. Compression, cooling, and fragmentation of the diffuse atomic medium produces cold sheets and filaments at the interface of the colliding flows that may later become molecular and self-gravitating and dominate the appearance of the ISM as observed today (see review by André et al. 2014). In this picture the fast formation (and dispersion) of molecular clouds and the often simultaneous onset of star formation within (see Hartmann et al. 2001; Vázquez-Semadeni et al. 2007; Banerjee et al. 2009; Gómez & Vázquez-Semadeni 2014) appears plausible.
One example of such a large-scale flow is an expanding shell or super-shell around, for example, an OB association or in general driven by multiple stellar feedback of a star cluster or association (see review by Dawson 2013). Molecular clouds may then either form inside the wall of such a shell (Dawson et al. 2011) or at the interface region when two such shells collide with each other. The latter case has recently been investigated by Dawson et al. (2015) for a young giant molecular cloud (GMC) at the interface of two colliding super-shells. From the comparison of CO observations with high-resolution 3D hydrodynamical simulations they found that the GMC assembled into its current form by the action of the shells.
The Scorpius-Centaurus OB association (Blaauw 1964; de Zeeuw et al. 1999; Preibisch et al. 2002; Preibisch & Mamajek 2008, Sco-Cen) is the closest site of recent massive star formation to us and it consists of three subgroups with different ages and well-known stellar populations down to 2 M⊙ (de Bruijne 1999). The oldest one is the Upper Centaurus-Lupus (UCL) subgroup with an age of ~17 Myr harboring 66 B-stars. With an age of ~15 Myr the Lower Centaurus Crux (LCC) subgroup is somewhat younger and contains 42 B-stars. The youngest subgroup is Upper-Scorpius (USco) with an age of ~5 Myr and consisting of 49 B-stars.
The feedback of the numerous massive stars in Sco-Cen probably cleared the inner region of the association from diffuse matter creating expanding loop-like H I shells around each of the subgroups of the association (de Geus 1992). At the edge of the USco shell several dense molecular clouds with very young (≤1−2 Myr) stellar populations are found. Of those the most prominent ones are the Lupus I cloud (near the western edge of the shell) and the ρ Oph cloud (near the eastern edge).
The Lupus I molecular cloud complex (for an overview see Comerón 2008) is found at a distance of 150 pc and consists of a ≈2.6° × 0.6° (corresponds to a physical size of ≈6.8 × 1.6 pc) main filament extending in a north to south direction (Galactic coordinates) and a ring-like structure of ~0.6° in diameter west of the main filament (towards UCL; see Tothill et al. 2009). Recently Matthews et al. (2014) also noted two smaller secondary filaments one of which is about half a degree long and runs perpendicular to the main filament and seems to connect with it in the south. The other is about a degree long and lies southwest of the main filament extending from the southern end of the main filament to the ring-like structure.
In this work we concentrate our analysis on the main filament commonly seen in all observations. We refer to it as Lupus I or the Lupus I filament.
The cloud is found between the USco and the UCL subgroups at a location where the expanding USco shell appears to interact with a bubble currently powered by the winds of the remaining B-stars of UCL. Because it is close, Lupus I is a good candidate to study how such a collision process forms and how it influences new dense clouds in the ISM.
Lupus I has been mapped as part of several large surveys like the Herschel Gould-belt survey (André et al. 2010; Rygl et al. 2013) and the Spitzer Legacy Program “From molecular clouds to planet-forming disks” (c2d; Chapman et al. 2007; Merín et al. 2008). These near-infrared to far-infrared surveys revealed the population of young stellar objects (YSOs) within the cloud showing that it is dominated by pre-stellar and protostellar cores indicating an on-going star formation event. Rygl et al. (2013) found that the star formation rate (SFR) has been increasing over the past 0.5−1.5 Myr and Merín et al. (2008) estimated a SFR of 4.3 M⊙ Myr-1 for Lupus I from their Spitzer data.
Extinction maps of Lupus I have been created by various authors using different methods. Cambrésy (1999) created an extinction map based on optical star counts with a resolution of a few arc-minutes. Using 2MASS data Chapman et al. (2007) created a visual extinction map with a 2′ resolution. Lombardi et al. (2008) also used 2MASS data for a wide-field extinction map of Lupus I. It allowed extinction measurements down to AK = 0.05 mag, but had a resolution of 3′. Merín et al. (2008) created extinction maps from their Spitzer data by estimating the visual extinction towards each source classified as a background star, based on their spectral energy distribution (SED) from 1.25 to 24 μm. Their maps had a resolution of 2−5′. Rygl et al. (2013) created a column density map of dust emission in Lupus I from their Herschel data by making a modified blackbody fit for each pixel in the four bands from 160−500 μm. The resulting resolution was 36″.
Here we present a far-infrared and sub-mm analysis of the Lupus I cloud based on newly obtained APEX/LABOCA sub-mm continuum data at 870 μm and complementing those with Herschel and Planck archival data. In Sect. 2 we briefly describe the observations used and their data reduction process. Section 3 gives an overview of the methods used to create column density maps and probability distribution functions (PDFs) from the observations. We present and discuss our results in Sect. 4. In Sect. 5 we consider the surroundings of Lupus I and the influence of large-scale processes on the cloud. Finally, we summarize and conclude our paper in Sect. 6.
2. Observations and data reduction
2.1. LABOCA data
The sub-mm continuum observations of Lupus I were performed with the APEX 12 m telescope located in the Chilean Atacama desert (Güsten et al. 2006). We used the LArge APEX BOlometer CAmera (LABOCA, Siringo et al. 2009) which operates in the atmospheric window at 870 μm (345 GHz). The angular resolution is 19.2′′ (HPBW1), and the total field of view is 11.4′. At the distance of Lupus I (150 pc) the angular resolution corresponds to a spatial scale of ~2800 AU (~0.01 pc). This is sufficient to resolve the structure of molecular cores.
The LABOCA observations of Lupus I were obtained in Max-Planck and ESO Periods 91 and 92, on 24th March, 31st August, 12th, 13th September 2013, and 31st March 2014 (PI: B. Gaczkowski; Program IDs: M-091.F-0005-2013and E-092.C-0131A-2013). They were performed in the on-the-fly (OTF) mode, scanning perpendicularly and along the filament’s major axis with a random position angle to the axis for each scan to reduce striping effects and improve the sampling. The total observing time was 11.3 h and the weather conditions were good to average.
 |
Fig. 1 Lupus I LABOCA 870 μm map with square-root intensity scaling in units of Jy/21.2″-beam. The positions of the 15 cores that were found by Clumpfind are marked with white crosses. The white polygon indicates the common area within which the mass of the cloud was calculated from the LABOCA and Herschel column density maps (see Sect. 4.4). |
Data reduction included standard steps for submillimeter bolometer data, using the BoA software package (Schuller 2012). First, data were converted from instrumental count values to a Jansky scale using a standard conversion factor, then a flat-field correction (derived from scans of bright, compact sources) was applied. Corrections for atmospheric opacity were derived from skydips taken every 1−2 h, and finally residual correction factors were determined from observations of planets and secondary calibrator sources. Data at the turning points of the map were flagged, as were spikes. The data from the individual bolometers were then corrected for slow amplitude drifts due to instrumental effects and atmosphere by subtracting low-order polynomials from the time-stream data. Short timescale sky brightness variations (sky-noise) was corrected by removing the correlated signal (over a large number of bolometers) in an iterative fashion. Then the time-stream data were converted into sky-brightness maps for each scan, and finally all scans combined into one map.
The removal of the correlated sky variations is also known to filter out astronomical emission from extended sources, usually leading to negative artifacts surrounding bright emission structures. In order to recover some of the extended emission, an iterative source modeling procedure was applied, using the result from the previous iteration to construct an input model for the following iteration. To construct the model the previous map was smoothed, all pixels below a pixel value of 0 set to 0, and the map smoothed again. In the following iteration, the model is subtracted from the time-stream data before de-spiking, baseline subtraction, and sky-noise removal, and then added back to the data stream before the new map is created. This procedure effectively injects artificial flux into the mapped area and is prone to creating runaway high surface brightness areas especially in regions without significant astronomical signal and low signal-to-noise. For that reason, the model image was set entirely to 0 in areas of the map with poor coverage below a certain threshold in rms (basically the map edges), and the procedure was stopped after 25 iterations. Typically, structures on scales on the order of 3−4′ can be recovered, while larger scales get more and more filtered out (see simulations done by Belloche et al. 2011). The gridding was done with a cell size of 6.1″ and the map was smoothed with a Gaussian kernel of size 9″ (FWHM). The angular resolution of the final map is 21.2″ (HPBW) and the rms noise level is 23 mJy/21.2″-beam (hereafter the notation per beam in context of LABOCA will mean per 21.2″-beam). The resulting map is shown in Fig. 1.
In order to determine the total sub-mm flux of the entire LABOCA map, we integrated all pixel values above the 3σ noise level of 69 mJy/beam. This yielded a total flux value of 476 Jy. Our peak intensity in the map is 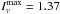 Jy/beam.
Jy/beam.
2.2. Herschel archival data
The Lupus I cloud complex was observed by the Herschel far-infrared observatory (Pilbratt et al. 2010) in January 2011 as part of the Gould-belt survey (André et al. 2010; Rygl et al. 2013). The Photodetector Array Camera and Spectrometer (PACS, Poglitsch et al. 2010) and the Spectral and Photometric Imaging Receiver (SPIRE, Griffin et al. 2010) were used to map an area of ≈2° × 2.3°. We retrieved these data from the Herschel science archive and reduced them using HIPE v12.1 (Ott 2010) for the calibration and the deglitching of the Level 0 PACS and SPIRE data. The Level 1 data of both instruments were then used to produce the final maps with the Scanamorphos package v24 (Roussel 2013, /parallel and /galactic options were switched on in both cases to preserve extended structures in complex, bright Galactic fields). The pixel-sizes for the five maps at 70, 160, 250, 350, and 500 μm were chosen as 3.2″, 4.5″, 6″, 8″, and 11.5″, respectively.
The absolute calibration of the Herschel data was done following the approach described in Bernard et al. (2010). Using the Planck and the IRAS data of the same field as the Herschel data the expected fluxes to be observed by Herschel are calculated at each band and from that the zero-level offsets are computed (see Table 1). These are then added to the Herschel maps to create the final mosaics.
Zero-level offsets for the Herschel maps obtained from the cross-correlation with Planck and IRAS.
For the dust properties and temperatures considered in our analysis the color corrections for both PACS and SPIRE are on the order of 1−2% and so are negligible.
2.3. Planck archival data
We retrieved the all-sky maps of the High Frequency Instrument (HFI) in the 353, 545, and 857 GHz bands (corresponding to the FIR and sub-mm wavelengths of 850, 550, and 350 μm) from the Planck legacy archive (release PR1 21.03.2013). From these data cubes in HEALPix2 format, we extracted the area covering the Lupus I region separately for each wavelength and created gnomonic projected maps. The resolution in each of the three bands is 5′ and the pixel size was chosen as 1.7′.
3. Data analysis
3.1. Column density and temperature maps of Lupus I
From our three data sets of LABOCA, Herschel, and Planck we calculated column density maps to characterize the cloud in a multi-wavelength approach. Additionally, we constructed a temperature map from the Herschel data.
3.1.1. Column density and temperature map from Herschel SED fit with all SPIRE bands
The standard and often practiced way to derive column density and temperature maps from the Herschel data is to fit an SED to the observed fluxes of the Herschel bands for each pixel of the maps (see e.g. Alves de Oliveira et al. 2014; Lombardi et al. 2014; ?). Here we fit the SED to the three SPIRE bands 250, 350, and 500 μm. We did not include the two PACS 70 and 160 μm bands, because these observations were corrupted by stray moonlight and hence are not reliable for an analysis of large-scale structures.
Because Lupus I is optically thin to the dust emission at the considered densities and wavelengths we can model its emission as a modified blackbody. We assume that the long wavelength emission (λ ≥ 250 μm) of a pixel [i, j] comes from a unique species of grains being all at the same equilibrium temperature, and having a power-law wavelength dependent opacity. If 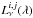 is the monochromatic luminosity of pixel [i, j] at wavelength λ, then it can be expressed as
is the monochromatic luminosity of pixel [i, j] at wavelength λ, then it can be expressed as 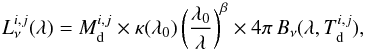 (1)where κ is the dust opacity, β the emissivity index, Bν(λ,Td) the blackbody spectral flux density for a dust temperature Td. The two free parameters
(1)where κ is the dust opacity, β the emissivity index, Bν(λ,Td) the blackbody spectral flux density for a dust temperature Td. The two free parameters 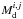 and
and 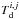 are the dust mass and temperature per pixel of the material along the line of sight. Here we adopt a typical κ(λ0) = 5.91 cm2 g-1 with λ0 = 350 μm for dust grains with thin ice mantels and gas densities <105 cm-3 (Ossenkopf & Henning 1994). Using the available information about β from the Planck data, we found that the emissivity index within the Lupus I cloud lies between ~1.6 and ~1.7. Therefore, we fixed its value to β = 1.65 as an average value within the cloud. Considering the low resolution of the β map of 30′, this is a reasonable approximation. In this way we also limit the number of free parameters in the fit making it more stable.
are the dust mass and temperature per pixel of the material along the line of sight. Here we adopt a typical κ(λ0) = 5.91 cm2 g-1 with λ0 = 350 μm for dust grains with thin ice mantels and gas densities <105 cm-3 (Ossenkopf & Henning 1994). Using the available information about β from the Planck data, we found that the emissivity index within the Lupus I cloud lies between ~1.6 and ~1.7. Therefore, we fixed its value to β = 1.65 as an average value within the cloud. Considering the low resolution of the β map of 30′, this is a reasonable approximation. In this way we also limit the number of free parameters in the fit making it more stable.
After convolving the 250 and 350 μm maps to the resolution of the 500 μm band using the kernels from Aniano et al. (2011), the modified blackbody fit was performed pixel-by-pixel. From the dust mass 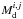 in each pixel the total column density for both dust and gas was then calculated as
in each pixel the total column density for both dust and gas was then calculated as 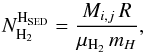 (2)where R = 100 is the gas-to-dust mass ratio, μH2 = 2.8 the molecular weight per hydrogen molecule, and mH the hydrogen atom mass. The resulting dust temperature values
(2)where R = 100 is the gas-to-dust mass ratio, μH2 = 2.8 the molecular weight per hydrogen molecule, and mH the hydrogen atom mass. The resulting dust temperature values 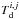 from the fit at each pixel give the temperature map of Lupus I (shown in Fig. 2a) at the resolution of the 500 μm band, i.e. FWHM500 = 36″.
from the fit at each pixel give the temperature map of Lupus I (shown in Fig. 2a) at the resolution of the 500 μm band, i.e. FWHM500 = 36″.
Since the composition of the dust grains and their density is unknown, the choice of a particular dust model and thus a specific opacity law introduces an uncertainty of the dust opacity and thus of the resulting column density. In order to estimate it, we took different κ(λ0) values at 350 μm for grains with and without ice mantles and the three initial gas densities of <105, 105, and 106 cm-3 in the online table of Ossenkopf & Henning (1994). They vary between 3.64 cm2 g-1 (MRN3 without ice mantles and ρ< 105 cm-3) and 11.3 cm2 g-1 (MRN with thin ice mantles and ρ = 106 cm-3). Hence, our chosen value of κ(λ0) might still vary by a factor of about 2.
The statistical error on both the final column density map and the temperature map consists of errors in the calibration, the photometry, and the SED fitting process. We conservatively estimated the sum of these uncertainties to be ~20% for both maps.
 |
Fig. 2 Left: temperature map of Lupus I from the Herschel SPIRE SED fit. Right: histogram of the dust temperature for the whole cloud (purple), in the north part (orange), and in the center-south (green). |
3.1.2. Column density map from Herschel SPIRE 250 μm map
To obtain a column density map with the resolution of the SPIRE 250 μm band (i.e. FWHM250 = 18″), we followed the technique described in Juvela et al. (2013). Using the intensity map of the SPIRE 250 μm band and the previously calculated temperature map (at the lower resolution) to compute the Planck function Bν(Td), it is possible to gain an additional factor of two in resolution compared to the SED fitting (to all three SPIRE bands) case. In this way the column density is simply 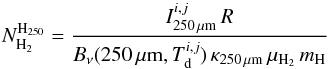 (3)with
(3)with 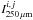 the intensity of the SPIRE 250 μm band. We used this higher resolution Herschel column density map for our further analysis of Lupus I.
the intensity of the SPIRE 250 μm band. We used this higher resolution Herschel column density map for our further analysis of Lupus I.
3.1.3. Column density map from the LABOCA data
Lupus I is sufficiently far away from ionizing UV sources to exclude significant amounts of free-free emission. We may therefore assume the sub-mm fluxes to be entirely due to thermal dust emission. To determine whether the cloud is optically thin in this wavelength regime one can look at the peak intensity in the LABOCA map, which is 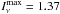 Jy/beam. The corresponding optical depth can be calculated via Eq. (3) in Schuller et al. (2009),
Jy/beam. The corresponding optical depth can be calculated via Eq. (3) in Schuller et al. (2009), ![\begin{equation} \tau_{870~\mu\mathrm{m}}=-\ln\left[1-\frac{I_\nu}{\Omega\,B_\nu(T_\mathrm{d})}\right] , \end{equation}](/articles/aa/full_html/2015/12/aa26527-15/aa26527-15-eq89.png) (4)where Ω is the beam solid angle. In the case of Lupus I this yields values of τ870 μm ≤ 0.01 for temperatures Td ≥ 10 K and thereore the cloud is clearly optically thin in this wavelength regime. Therefore, the 870 μm intensities are directly proportional to the column densities of the interstellar dust and the line-of-sight extinction. They can be converted to the beam-averaged hydrogen molecule column density via Eq. (3).
(4)where Ω is the beam solid angle. In the case of Lupus I this yields values of τ870 μm ≤ 0.01 for temperatures Td ≥ 10 K and thereore the cloud is clearly optically thin in this wavelength regime. Therefore, the 870 μm intensities are directly proportional to the column densities of the interstellar dust and the line-of-sight extinction. They can be converted to the beam-averaged hydrogen molecule column density via Eq. (3).
We again assume a gas-to-dust mass ratio of R = 100 and for consistency extrapolate our dust model used for the Herschel analysis to the LABOCA wavelength, which yields a value of κ870 μm = 1.32 cm2 g-1. Because the assumption of a constant dust temperature throughout the cloud is not valid, we used the temperature map from the Herschel analysis to calculate the blackbody function at each pixel of the map. In this way a column density map is obtained at the original resolution of the LABOCA map (i.e. FWHM870 = 21.2″).
3.1.4. Column density and temperature map from the Planck data
The thermal emission of interstellar dust over the whole sky was captured by the HFI-instrument of Planck at its six available wavelengths between 350 μm and 3 mm. Together with the IRAS 100 μm data the emission can be modeled well by a modified blackbody. The details of the model and the fitting procedure are described in Planck Collaboration XI (2014). The resulting maps of temperature and optical depth (at 850 μm) can be downloaded from the Planck archive4. We extracted the part covering Lupus I from both maps to get gnomonic projected maps. The column density map was then computed from the optical depth map using the relation 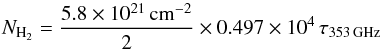 (5)suggested in Planck Collaboration XI (2014) for regions with higher column density than the diffuse ISM, i.e. molecular clouds.
(5)suggested in Planck Collaboration XI (2014) for regions with higher column density than the diffuse ISM, i.e. molecular clouds.
3.2. Column density PDFs
Probability distribution functions of the column density are a widely used way to characterize the evolution and state of molecular clouds. Both simulators (see e.g. Federrath & Klessen 2012; Ward et al. 2014; Girichidis et al. 2014) and observers (see e.g. Kainulainen et al. 2009, 2011; Palmeirim et al. 2013; Tremblin et al. 2014; Schneider et al. 2015; Roccatagliata et al. 2015) use them in their studies and they are a good tool for comparing both simulations and observations with each other.
As Lupus I is close to us and lies at a high Galactic latitude far away from the Galactic plane, we expect the contamination of the map by overlaying foreground or background emission to be small. We normalize the PDFs to the dimensionless η = ln(NH2/ ⟨ NH2 ⟩ ), which gives the opportunity of comparing different regions of different column density, as well as the same cloud, but observed with different instruments. For similar observations of the Orion clouds Schneider et al. (2013) showed that the effect of varying the resolution of the maps within 18″ and 36″ did not significantly affect the main features of the PDFs (shape, width, etc.). The Lupus I cloud is much closer, yielding a much finer physical resolution and the tests we performed on our maps smoothing them with a grid of Gaussians with different FWHM and rebinning them to several different pixel sizes confirmed their findings. If the difference, however, is as big as the one, for example, in angular resolution between Herschel and Planck, it is no longer possible to maintain the features of the PDF unchanged when degrading the Herschel map by a factor of ≈8 (from 500 μm) to ≈17 (from 250 μm). But in our case, both the angular resolution and the pixel size of the Herschel and the LABOCA column density map are almost the same. Therefore, both maps have sufficiently large numbers of pixels to have a high statistic.
 |
Fig. 3 Column density maps of Lupus I from a) the Herschel 250 μm map; b) LABOCA; and c) Planck. |
The basic shape of the PDF in the low column density regime can be described by a lognormal distribution. In more complicated cases the PDF might also be the combination of two lognormals, 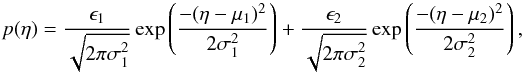 (6)where ϵi is the norm, and μi and σi are the mean logarithmic column density and dispersion of each lognormal. In the high column density regime one often finds a deviation from the lognormal. This can be modeled with a power-law of slope s, which is equivalent to the slope of a spherical density profile ρ(r) ∝ r− α with α = −2 /s + 1 (see ?Schneider et al. 2013).
(6)where ϵi is the norm, and μi and σi are the mean logarithmic column density and dispersion of each lognormal. In the high column density regime one often finds a deviation from the lognormal. This can be modeled with a power-law of slope s, which is equivalent to the slope of a spherical density profile ρ(r) ∝ r− α with α = −2 /s + 1 (see ?Schneider et al. 2013).
Using a least-squares method (Levenberg Marquardt algorithm; Poisson weighting)5 we derived the characteristic values of the distributions by fitting the PDFs with either one lognormal to the distribution around the single peak and where applicable a power-law to the high density tail, or with two lognormals to the distributions around the first and second peak, respectively, and a possible power-law tail. We checked the robustness of the fits by performing it on four different bin sizes for the histograms (0.05, 0.1, 0.15, 0.2) and looking at the variation of the resulting fit parameters, which was on the order of 2%−8%. We took the final parameters from the fits for a bin size of 0.1 (see Schneider et al. 2015) and conservatively adopted an error of 10% for all fit parameters. The results are summarized in Table 2.
4. Results
4.1. Column density and temperature maps
The Herschel column density map of Lupus I is shown in Fig. 3a. The average column density is ⟨ NH2 ⟩ = 1.44 × 1021 cm-2. The map reveals two distinct regions within the filament (see also Fig. 4), the north where the column densities are lowest (⟨ NH2 ⟩ = 1.10 × 1021 cm-2) and just one dense core can be seen (Rygl et al. 2013) and the center-south where several cores with high column densities above 1022 cm-2 are found and the average column density (⟨ NH2 ⟩ = 1.72 × 1021 cm-2) is about 60% higher than in the north.
Comparing our map to the one derived by Rygl et al. (2013) we note that our values are lower by a factor of about 2−2.5. This can be explained by the use of a different dust model (opacity and dust spectral index) and the inclusion of the PACS 160 μm band in their work. The extinction maps created from 2MASS and Spitzer data (see Chapman et al. 2007; Lombardi et al. 2008; Merín et al. 2008) have a resolution that is lower by a factor of about 7−30. Nevertheless, there is a clear resemblance between those maps and our column density map.
The column density map of Lupus I that we obtained from LABOCA (see Fig. 3b) is dominated by the dozen cores in the center-south and the denser dust in the central part of the filament. The average column density is ⟨ NH2 ⟩ = 1.47 × 1021 cm-2.
The Planck column density map of Lupus I with a resolution of 5′ reveals the basic structure of the cloud that agrees well with the column density maps from LABOCA and Herschel. This is consistent with what is shown by the other two maps when smoothed to the resolution of Planck and thus smoothing out the highest column density peaks.
The temperature map obtained from the Herschel SED fit (see Fig. 2a) shows an anti-correlation of the temperature with the column density. The densest parts are the coldest and the less dense the material is, the warmer it becomes. In addition, a difference between the northern and the center-south parts of the cloud can be seen again. In the north dust temperatures between ≈15−23 K with a mean and median of ≈19 K are found, but only in the dense pre-stellar core and slightly north of it does the temperature drop down to ≈15 K. The maximum temperature in the center-south is ≈22 K at the edges of the filament. The inner part of the filament has an average temperature of ≈17 K, but it drops down to even 11 K in the densest cores. The histogram of the dust temperatures (see Fig. 2b) shows that most of the dust in the north (orange histogram) ranges between ≈18−20 K, whereas in the center-south (green) it is between ≈16−18 K. This means that the dust in the center-south is on average 2 K colder than in the north.
 |
Fig. 4 3D surface plot of the Herschel 250 μm column density map. The cores in the center-south of Lupus I can be identified and the average lower column density in the northern part of the cloud can be seen. The red dashed boxes mark the two regions that we distinguish in this work. |
4.2. Column density PDFs
We derived PDFs of the Lupus I cloud from the Herschel and LABOCA column density maps for the two distinct parts of the cloud (north and center-south; see Fig. 4), and for the whole cloud. They are shown in Fig. 5. For a correct interpretation of the PDFs the completeness limit of the underlying column density map must be considered; here we adopted the lowest closed contour, which is 1.1 × 1021 and 2 × 1021 cm-2 for the Herschel and LABOCA map, respectively. It is marked by the vertical dashed line in the plots in Fig. 5.
 |
Fig. 5 Column density PDFs of Lupus I and their model fits for the north and the center-south parts of the cloud, and for the entire cloud. The error bars show the |
Looking at the entire cloud the Herschel PDF is very complex with clear deviations from a simple lognormal distribution which would be expected for a cloud that is dominated by isothermal, hydrodynamic turbulence (e.g. Klessen et al. 2000). The distribution shows two peaks in the low column density regime and a power-law tail in the high density end. The first peak at NH2,peak1 = 8.66 × 1020 cm-2 falls below our completeness limit, so it might just be reflecting the drop of observational sensitivity and will not be used for interpretation. However, the distribution above the limit can be represented well by a fit of two lognormals around the first and second peak, which is at NH2,peak2 = 2.57 × 1021 cm-2. The width of the first component is σ1 = 0.56, but could also be broader due to the possible underestimate of the column densities below the completeness limit. Nevertheless, it is more than twice as broad as the width of the second lognormal (σ2 = 0.26) and larger than in other nearby clouds like Maddalena, Auriga (Schneider et al. 2013), or Aquila (Schneider et al. 2015). This can be a sign of broadening by turbulence and external compressive forcing (see Federrath et al. 2010; Tremblin et al. 2012; ?). The power-law tail follows a slope of s = −2.55 or corresponding α = 1.78 for a spherical density distribution. The deviation from the lognormal into the power-law occurs near NH2,dev = 3.6 × 1021 cm-2, which is slightly below the recent values by Schneider et al. (2015) who found the transition into the power-law tail to be at AV ~ 4−5 mag6 in their investigation of four low-mass and high-mass star forming regions, although it is higher than the result of Roccatagliata et al. (2015) who find the deviation to occur at AV ~ 1.2−2 mag in the Serpens Core region.
From the Herschel data the center-south part of the cloud shows a PDF very similar to that of the entire cloud. Here again two peaks are present and the distribution above the completeness limit can be fitted by a double lognormal and a power-law tail. The width of the first fitted lognormal is narrower, the width of the second broader than those of the entire cloud with values of σ1 = 0.46 and σ2 = 0.35. The slope of the power-law is slightly flatter with s = −2.43, but leading to a comparable exponent α = 1.82.
In the northern part of the cloud the double-peak lognormal profile of the PDF from Herschel is found again, but now there is no excess above the second lognormal at higher densities. The peak position of the first lognormal is lower (NH2,peak1 = 7.94 × 1020 cm-2) than in the center-south and in the whole cloud, but with similar width (σ1 = 0.55). The peak position of the second lognormal (NH2,peak2 = 2.23 × 1021 cm-2) is lower than that of the whole cloud and its width (σ2 = 0.18) is approximately half as broad.
Although it is not possible to strictly constrain the shape of the PDF below the completeness limit, one can say that the distribution above does not show just two components (lognormal and a power-law), but at least three because of the second peak that appears before the deviation into the power-law. This shape could be attributed to an initial turbulent cloud which was later compressed by an external driving agent. This agent can either be an ionization front, an expanding shell driven by winds, and/or supernovae or colliding flows. The initial lognormal form of the PDF of the cloud develops a second component caused by the dense compressed gas. This behavior was found in simulations by Tremblin et al. (2012) of an initial turbulent medium that is ionized and heated by an ionization source. They concluded that a double peak is present when the ionized gas pressure dominates over the turbulent ram pressure of the cloud. Matsumoto et al. (2015) studied the evolution of turbulent molecular clouds swept by a colliding flow. They found that the PDF exhibits two peaks in the case when the Mach numbers of the initial turbulence and the colliding flow are of the same order M = 10 (model HT10F10; see their Fig. 11b) and the line of sight is perpendicular to the colliding flow. Then the low column density peak represents the colliding flow and the higher column density peak the sheet cloud, respectively. Observationally, double-peak PDFs have been reported and recently studied by Schneider et al. (2012), Harvey et al. (2013), and Tremblin et al. (2014) for several nearby clouds exposed to an ionization source. Areas of the cloud close to the ionization front did show the predicted second peak in the PDF due to the compression induced by the expansion of the ionized gas into the molecular cloud. In the case of Lupus I the source of the compression is very likely the expanding H I shell around the USco subgroup of Sco-Cen (possibly together with a supernova that exploded within USco) and the wind bubble of the remaining B-stars of UCL pushing from the eastern and western side of the cloud, respectively. This scenario is discussed in more detail in Sect. 5.
Lognormal PDFs indicate shock waves (Kevlahan & Pudritz 2009) or turbulence (e.g. Vazquez-Semadeni 1994; Federrath et al. 2010). Tremblin et al. (2012) have shown in a simulation of Stroemgren spheres advancing into turbulent regions that the region compressed by the ionization front also has a lognormal density PDF, but shifted to higher density due to the compression. A PDF of a region that includes compressed and undisturbed parts of the cloud will thus show a double-peak PDF.
The power-law tail that is seen in our PDFs could be explained by active star formation and the transition to a gravity dominated density regime represented by the star forming cores. This can be shown by comparing the PDFs of the two regions in the north and the center-south. In the north where there is almost no star formation and just one pre-stellar core and ≈20 unbound cores can be found (Rygl et al. 2013), the PDF shows no power-law tail in the high density regime. In the center-south instead where almost all the star formation activity takes place with plenty of very young bound cores, the PDF shows the power-law tail very clearly. Numerical studies have also shown that the PDF for an actively star forming region develops a clear deviation from the lognormal in the form of a power-law tail (Ballesteros-Paredes et al. 2011; Girichidis et al. 2014).
With LABOCA the PDF of Lupus I can be modeled as one lognormal with a power-law tail at high densities (NH2,dev = 6.0 × 1021 cm-2). The peak of the lognormal distribution lies at NH2,peak = 1.43 × 1021 cm-2, which is below the completeness limit of the LABOCA column density map. The width of the lognormal is broad (σ = 0.56), but uncertain due to the peak position and thus possibly even broader. The power-law slope (s = −2.66, α = 1.75) is very similar to the value of the Herschel PDF indicating the star formation activity in the cloud.
The PDF of the center-south region shows the same behavior as the one for the whole cloud. The lognormal part is slightly broader (σ = 0.60), but the power-law slope (s = −2.59, α = 1.77) and the deviation point (6.0 × 1021 cm-2) are almost the same as in the whole cloud. In the northern part only the now narrower lognormal is seen instead (σ = 0.52), indicating the lack of star formation activity and the dominance by the turbulence induced trough the compression. In all three cases the positions of the peaks are very close to each other.
As was already seen in the column density map from LABOCA, its PDF shows only the dense cores and the intercore medium. The instrument is not sensitive to all the material that can still be probed with Herschel. With LABOCA we thus sample the second lognormal of the Herschel PDF and the power-law tail.
4.3. Core distribution
For the core analysis in the LABOCA map we used the Clumpfind package (Williams et al. 1994). It decomposes the emission of the map into a set of clumps or cores contouring the data at given threshold levels. The results can be found in Table 3 and the distribution of the cores (represented by the white crosses) is shown in Fig. 1. The algorithm identified 15 different cores with masses between 0.07 and 1.71 M⊙. Their total mass is 8.37 M⊙ and their total flux is 25.39 Jy. This corresponds to ≈5% of the total mass of Lupus I (see Sect. 4.4) and ≈5% of the total flux of the LABOCA map. For the computation of the core masses, we derived their temperatures from the Herschel SPIRE SED fit temperature map as a mean temperature within the ellipse representing the core. With this temperature the mass of the cores was calculated following Schuller et al. (2009)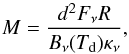 (7)where d is the distance to Lupus I, Fν the total flux of the core, R = 100 the dust-to-gas ratio, and κν = 1.32 cm2 g-1 (see Sect. 3.1.3). Interestingly, all but one core are found in the center-south part of Lupus I. This confirms our interpretation of the column density maps, i.e. that active star formation is taking place in this part of Lupus I.
(7)where d is the distance to Lupus I, Fν the total flux of the core, R = 100 the dust-to-gas ratio, and κν = 1.32 cm2 g-1 (see Sect. 3.1.3). Interestingly, all but one core are found in the center-south part of Lupus I. This confirms our interpretation of the column density maps, i.e. that active star formation is taking place in this part of Lupus I.
The distribution of the cores from the Herschel data (Rygl et al. 2013) agrees with this picture and the core distribution from our LABOCA map. The northern part of Lupus I is mainly populated by unbound cores and just one pre-stellar core, whereas the center-south is dominated by pre-stellar cores, many of which coincide with our LABOCA cores. However, a direct assignment is not easily possible since the Herschel coordinates can only be estimated from the source images in the paper of Rygl et al. (2013) and in some cases several Herschel sources seem to be on the position of one LABOCA source or vice versa.
Benedettini et al. (2012) found eight dense cores in Lupus I using high-density molecular tracers at 3 and 12 mm with the Mopra telescope (red diamonds in Fig. 6), seven of which have one or more counterparts in our LABOCA map. The matches are given in Table 3. They classify five of their cores as very young protostars or pre-stellar cores (Lup1 C1-C3, C5, and C8) and the remaining three also as very likely to be protostellar or pre-stellar. For three of their cores (Lup1 C4, C6, and C7) they calculated a kinetic temperature of ≈12 K. This agrees within 20% with the core temperatures derived from the Herschel SPIRE SED fit temperature map.
Of the 17 young stellar objects found in Lupus I by the Spitzer c2d near-infrared survey (Chapman et al. 2007; Merín et al. 2008), 11 lie within the boundaries of the LABOCA map (blue boxes in Fig. 6), but only one object (IRAS 15398–3359) clearly matches one of our LABOCA cores (#1). This is the well-known low-mass class 0 protostar IRAS 15398–3359 (inside the B228 core), which has a molecular outflow (see e.g. Oya et al. 2014; Dunham et al. 2014). Two other objects of the c2d survey are close, but offset by ≈0.5′ to the center of our cores #3 and #5, respectively. Nevertheless, each of these two objects still lies within the boundaries of the corresponding ellipse representing the LABOCA core (see Table 3). Most of the LABOCA cores are potentially at a very early evolutionary stage, i.e. without a protostar inside to heat it and eventually destroy the surrounding dust envelope to allow near-infrared radiation to escape. The only cores with a 70 μm counterpart, which is a good proxy for a protostar inside a core, are #1 and #3. Therefore, we do not expect to find many Spitzer counterparts.
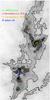 |
Fig. 6 Herschel column density map of the center-south region with contour levels of 1.1, 4, 7, and 10 × 1021 cm-2. The different symbols mark the center positions of the cores found with LABOCA and of objects found in other studies as discussed in Sect. 4.3. |
Vilas-Boas et al. (2000) found 15 (14) condensations in C18O (13CO) with the 15 m SEST telescope. Eight cores lie within our LABOCA map (orange crosses in Fig. 6), three of which (Lu7, Lu10, B228) coincide with LABOCA detected cores (#12, #5, and #1). Their C18O excitation temperatures are 9, 11, and 10 K, respectively. This is ≈20−40% lower than the temperatures from the Herschel map. For cores Lu7 and Lu10 they calculated a mass from C18O of 11.7 and 3.1 M⊙, respectively. This is a factor of ≈20 and ≈7 higher than the LABOCA masses. But the sizes of their condensations were on average larger than at least three times their beam size of 48″.
Figure 6 shows the Herschel column density map of the center-south region with contour levels of 1.1, 4, 7, and 10 × 1021 cm-2. Overplotted are the LABOCA cores found in this study (green circles), as well as the above mentioned cores and YSOs found by Benedettini et al. (2012; red diamonds), Vilas-Boas et al. (2000; orange crosses), and the Spitzer c2d survey (blue boxes), respectively.
Our findings confirm that Lupus I harbors a population of very young cores that are forming stars right now and probably have ages below 1 Myr. This could support the idea of an external shock agent, like the USco shell, sweeping up the cloud and triggering the simultaneous formation of new stars within the cloud.
 |
Fig. 7 Surroundings of Lupus I in X-rays (ROSAT 3/4 keV, left) and dust emission (Planck 850 μm, right). There are two X-ray bubbles on either side of the Lupus I ridge and both Lupus I and ρ Ophiuchus, as well as the little cloudlets north of them seen in dust emission, have X-ray shadows. The yellow dashed circles in the right image give the position of the inner and outer edge of the USco H I shell determined from our preliminary analysis of the GASS H I data. The center lies at l = 347°, b = 25° and the inner and outer radius is 12° and 15°, respectively. |
4.4. Total mass estimates of Lupus I
To derive the total mass of the cloud from the three different column density maps we defined a polygon around the filament (shown in Fig. 1 on the LABOCA map) to derive the total mass always in the same area (≈1 deg2). The total gas and dust mass was then calculated via the formula 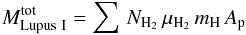 (8)with Ap the area of a pixel in cm2. As the common lower level we chose NH2> 1021 cm-2, which corresponds to AV> 1 mag. The resulting total mass for Lupus I is
(8)with Ap the area of a pixel in cm2. As the common lower level we chose NH2> 1021 cm-2, which corresponds to AV> 1 mag. The resulting total mass for Lupus I is 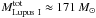 , ≈174 M⊙, and ≈164 M⊙ for the Planck, Herschel, and LABOCA data. This means that the total masses calculated from the three data sets agree with each other. Comparing the total mass of the cloud to the total mass in cores from LABOCA (≈8 M⊙) it can be seen that only about 5% of the mass is concentrated in the densest condensations. Most of the dust and gas is in more diffuse components.
, ≈174 M⊙, and ≈164 M⊙ for the Planck, Herschel, and LABOCA data. This means that the total masses calculated from the three data sets agree with each other. Comparing the total mass of the cloud to the total mass in cores from LABOCA (≈8 M⊙) it can be seen that only about 5% of the mass is concentrated in the densest condensations. Most of the dust and gas is in more diffuse components.
The most recent literature value for the total mass of Lupus I is from the Herschel data by Rygl et al. (2013). They calculated the total mass in a much bigger area than this work (≈4.5 deg2 compared to our ≈1 deg2) and used a different method to create their column density map as mentioned already in Sect. 4.1. Therefore, a difference of about a factor of 4−5 arises between their value of M = 830 M⊙ (for AV> 2 mag) and our findings.
Other literature values cover a wide range of total masses for Lupus I, depending on the tracer used and the size of the area that was considered. Merín et al. (2008) determined a total mass of 479 M⊙ for AV> 3 from the Spitzer c2d near-infrared extinction maps. Various CO measurements (e.g. Tachihara et al. 1996; Hara et al. 1999; Tothill et al. 2009) yielded values of ≈280−880 M⊙. Direct comparisons with our values are not always possible since all maps cover different parts of the Lupus I cloud complex and the material is not homogeneously distributed to allow scaling of the mass with the area. We note, however, that our values agree with most of the literature values within a factor of 2−3, which is expected considering the uncertainties in the choice of the dust model, the dust-to-gas ratio, and the CO-to-H2 conversion factors.
 |
Fig. 8 Surroundings of Lupus I seen in dust emission (Planck 350 μm). The white contours mark the X-ray emission (ROSAT 0.8 keV) from 0.27−1 × 10-3 counts/s. The cyan dots mark the positions of the B1-B3 stars of UCL from the Hipparcos catalog. Labels are given in green. |
5. Surroundings of Lupus I and the interaction with USco and UCL
The Planck data are best suited to looking at the dust surroundings of Lupus I (see Figs. 7 and 8). These observations at 350, 550, and 850 μm cover the whole sky at a resolution of 5′. Lupus I lies on the eastern edge (Galactic coordinates) of a ring-like dust ridge (labeled in Fig. 8) that extends from about b = + 10° to b = + 25° in Galactic latitude with a center at about l = + 345°, b = 17.5°. The ridge is ~5° wide, which corresponds to ~13 pc at the distance of Lupus I. In addition to Lupus I it consists of several small molecular clouds extending north of Lupus I and then bending towards the east connecting with the ρ Ophiuchus molecular cloud on the opposite site of Lupus I. No dust emission is seen in the Planck maps farther west of Lupus I. The same is true for the inside of the dust ridge. Between ρ Ophiuchus and Lupus I a roundish dust void is seen. However, these two dust voids on either side of Lupus I are filled with hot X-ray gas that can be seen with ROSAT (left in Fig. 7). Figure 8 shows the dust emission seen by Planck in 350 μm. Overlayed in white are the contours of the ROSAT diffuse X-ray emission at 3/4 keV7. Inside USco the contours follow the edge of the dust ridge indicating that the hot X-ray gas might be in contact with the cold dust. On the western side of Lupus I the contours mark the outline of the second roundish X-ray emission seen in ROSAT. The cyan dots mark the remaining early B-type stars of UCL. Both contours seem to wrap around Lupus I, which might be a sign that the cloud is embedded in hot ISM.
These dust voids and the observed X-ray gas might be explained by the cumulative feedback of the massive stars in the USco and UCL subgroups of Sco-Cen. Their creation has been interpreted in a scenario of propagating molecular cloud formation and triggered cloud collapse and star formation taking place within the last 17 Myr in the UCL and USco subgroups of Scorpius-Centaurus (see de Geus 1992; Preibisch & Zinnecker 2007). The expansion of the UCL H I shell that started ~10 Myr ago and was driven by winds of the massive stars and supernovae explosions has probably cleared out almost all the dust and molecular material west of Lupus I; however, the observed X-ray gas on that side is probably not related to the supernova explosions because the X-ray luminosity of supernova-heated superbubbles dims via expansion losses and mixing with entrained gas on a timescale of typically less than a million years (Krause et al. 2014). The shell today has a radius of ~110 pc (as seen from H I data; de Geus 1992), generally consistent (compare, e.g. ?Krause et al. 2013) with the inferred age of the stellar group, about 17 million years. Therefore, this X-ray gas is probably currently heated by the remaining B-stars of UCL. Six of the stars southwest of Lupus I (325° <l< 335° and 10° <b< 15°; see Fig. 8) lie at positions that makes it likely that they are the sources of this wind bubble.
The USco H I shell has started its expansion ~5 Myr ago powered by the winds of the OB-stars and quite possibly a recent supernova explosion, about 1.5 Myr ago, as suggested by the detection of the 1.8 MeV gamma-ray line towards the USco subgroup and the detection of the pulsar PSR J1932+1059 (Diehl et al. 2010, and references therein). What now forms the above-mentioned dust ridge is probably the remaining material of the USco parental molecular cloud that was swept up by the advancing USco shell leaving the dust void filled with X-ray gas. From simulations, we expect large-scale oscillations of the hot, X-ray emitting gas (Krause et al. 2014) because the energy source is never exactly symmetric.
It seems that the UCL wind bubble could be colliding with the USco H I shell right at the position of Lupus I, squeezing it in between. This wind bubble might have provided a counter-pressure to the expanding USco shell and thus favored this position for an additional compression of the shell material. In this way a new molecular cloud could have been created there and it might explain why we do not see more very young star forming clouds (except ρ Oph) distributed within the wall of the USco shell. With its distance of 150 pc, the cloud is neither in the foreground of the B-stars of UCL that have an average distance of ~140 pc (de Zeeuw et al. 1999) nor in front of USco (~145 pc; Preibisch et al. 2002). To rule out shadow effects completely, however, a more comprehensive analysis of the X-ray data would be required.
From our preliminary analysis of the GASS H I data (McClure-Griffiths et al. 2009; Kalberla et al. 2010) we see that Lupus I is indeed embedded within the expanding shell around USco (Kroell et al., in prep.). The shell has an expansion velocity of ≈7 km s-1 and a thickness of ≈6 pc. We estimate the current outer radius to be ≈36 pc (both inner and outer radius of the USco shell from our H I model are indicated in Fig. 7).
These findings complement previous suggestions of an interaction of Lupus I (and ρ Oph) with the two subgroups of Sco-Cen that were originally proposed by de Geus (1992). From the spatial and velocity structure of 12CO observations Tachihara et al. (2001) also found evidence for an interaction. In their analysis of 13CO and CO(4-3), Tothill et al. (2009) found enhanced line widths at the western end of Lupus I and a velocity gradient across the filament, i.e. in the direction of the USco shell expansion, of ~1 km s-1, which they conclude to be consistent with a dynamical interaction between Lupus I and the USco H I shell. Matthews et al. (2014) have found that the large-scale magnetic field is perpendicular to the Lupus I filament, i.e. it points in the direction of the USco shell expansion. This might have favored the accumulation of cold, dense atomic gas along the field lines and promoted faster molecule formation (Hartmann et al. 2001; Vázquez-Semadeni et al. 2011).
These results suggest the scenario that Lupus I was affected by large-scale external compressing forces coming from the expansion of the USco H I shell and the UCL wind bubble. This might explain its position, orientation and elongated shape, the appearance of a double peak in the PDF, and the large population of very young pre-stellar cores that are seen with both LABOCA and Herschel.
6. Summary and conclusions
From our LABOCA observations of Lupus I and from archival Herschel and Planck data we created column density maps of the cloud. In addition, we calculated a temperature map from an SED fit using the three SPIRE bands of Herschel. All maps suggest that the cloud can be divided into two distinct regions. The northern part, which has – on average – lower densities, higher temperatures and no active star formation, and the center-south part with dozens of pre-stellar cores where density and temperature reach their maximum and minimum, respectively.
From the LABOCA and Herschel maps we derived column density PDFs for the entire cloud and separately for the two above-mentioned regions. The Herschel PDF of Lupus I showed a double-peak profile with a power-law tail. The power-law can be attributed to the star formation activity in the center-south part of the cloud since it disappears in the PDF of the northern part. However, the double-peak profile is maintained throughout the cloud and possibly arises from the large-scale compressions from the cumulative massive star feedback of the Sco-Cen subgroups. Such a sign for compression in the PDF was previously found in both observations and simulations of advancing ionization fronts, also supported by simulations of colliding turbulent flows. With LABOCA we probe the denser parts of Lupus I and find one lognormal and the power-law tail for the whole cloud and the center-south. The PDF of the northern part shows only the lognormal behavior.
The distribution of the 15 cores that were found in our LABOCA map confirms that only the center-south part of Lupus I is actively forming stars, whereas the north is quiescent. The cores have masses between 0.07 and 1.71 M⊙ and a total mass of ≈8 M⊙. As the cloud has a total gas and dust mass of ≈164 M⊙ (from LABOCA for NH2> 1021 cm-2) this means that ~5% of the mass is in cores. All of these cores are pre-stellar or protostellar confirming that we are witnessing a large star formation event (see e.g. Benedettini et al. 2012; Rygl et al. 2013). The total mass from Herschel and Planck for NH2> 1021 cm-2 was ≈174 M⊙ and ≈171 M⊙, respectively.
We argue that the main driving agents in the formation process of Lupus I are the advancing USco H I shell, which most likely contains the cloud, and the UCL wind bubble interacting with the USco shell and hence squeezing Lupus I in between these two shells in a complex manner. The age of the population of young stellar objects suggests a compression event ~1−2 Myr ago, which could be the interaction between the two shells, and possibly a supernova explosion as suggested by the gamma ray data (Diehl et al. 2010). This large-scale compression might be the reason for the position, orientation, and elongated shape of Lupus I, and the reason for the double-peak PDFs and the population of very young pre-stellar cores that we found.
In future work we will analyze our newly performed high-resolution APEX CO line observations to study the kinematics of the Lupus I cloud. We will also compare our observational findings with dedicated numerical simulations and search for signs in the theoretical PDF that will allow us to distinguish between different scenarios of molecular cloud formation.
Mathis-Rumpl-Nordsieck size distribution of interstellar grains (Mathis et al. 1977).
N(H2)/Av = 0.94 × 1021 cm-2 mag-1 (Bohlin et al. 1978).
Acknowledgments
We would like to thank our anonymous referee for his constructive comments which helped to improve this paper. This work was supported by funding from Deutsche Forschungsgemeinschaft under DFG project number PR 569/10-1 in the context of the Priority Program 1573 “Physics of the Interstellar Medium”. Additional support came from funds from the Munich Cluster of Excellence “Origin and Structure of the Universe”. We thank Jean-Philippe Bernard for computing the Planck offsets for the Herschel maps. The Herschel spacecraft was designed, built, tested, and launched under a contract to ESA managed by the Herschel/Planck Project team by an industrial consortium under the overall responsibility of the prime contractor Thales Alenia Space (Cannes), and including Astrium (Friedrichshafen) responsible for the payload module and for system testing at spacecraft level, Thales Alenia Space (Turin) responsible for the service module, and Astrium (Toulouse) responsible for the telescope, with in excess of a hundred subcontractors. Based on observations obtained with Planck (http://www.esa.int/Planck), an ESA science mission with instruments and contributions directly funded by ESA Member States, NASA, and Canada. HIPE is a joint development by the Herschel Science Ground Segment Consortium, consisting of ESA, the NASA Herschel Science Center, and the HIFI, PACS and SPIRE consortia. This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France. We acknowledge the use of NASA’s SkyView facility (http://skyview.gsfc.nasa.gov) located at NASA Goddard Space Flight Center.
References
- Alves de Oliveira, C., Schneider, N., Merín, B., et al. 2014, A&A, 568, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, Protostars and Planets VI, 27 [Google Scholar]
- Aniano, G., Draine, B. T., Gordon, K. D., & Sandstrom, K. 2011, PASP, 123, 1218 [NASA ADS] [CrossRef] [Google Scholar]
- Ballesteros-Paredes, J., Vázquez-Semadeni, E., Gazol, A., et al. 2011, MNRAS, 416, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Banerjee, R., Vázquez-Semadeni, E., Hennebelle, P., & Klessen, R. S. 2009, MNRAS, 398, 1082 [NASA ADS] [CrossRef] [Google Scholar]
- Battersby, C., Bally, J., Dunham, M., et al. 2014, ApJ, 786, 116 [NASA ADS] [CrossRef] [Google Scholar]
- Baumgartner, V., & Breitschwerdt, D. 2013, A&A, 557, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Belloche, A., Schuller, F., Parise, B., et al. 2011, A&A, 527, A145 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benedettini, M., Pezzuto, S., Burton, M. G., et al. 2012, MNRAS, 419, 238 [Google Scholar]
- Bernard, J.-P., Paradis, D., Marshall, D. J., et al. 2010, A&A, 518, L88 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Blaauw, A. 1964, in The Galaxy and the Magellanic Clouds, ed. F. J. Kerr, IAU Symp., 20, 50 [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Cambrésy, L. 1999, A&A, 345, 965 [NASA ADS] [Google Scholar]
- Chapman, N. L., Lai, S.-P., Mundy, L. G., et al. 2007, ApJ, 667, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Comerón, F. 2008, Handbook of Star Forming Regions, Vol. II, ed. B. Reipurth, 295 [Google Scholar]
- Dawson, J. R. 2013, PASA, 30, 25 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, J. R., McClure-Griffiths, N. M., Dickey, J. M., & Fukui, Y. 2011, ApJ, 741, 85 [NASA ADS] [CrossRef] [Google Scholar]
- Dawson, J. R., Ntormousi, E., Fukui, Y., Hayakawa, T., & Fierlinger, K. 2015, ApJ, 799, 64 [NASA ADS] [CrossRef] [Google Scholar]
- de Bruijne, J. H. J. 1999, MNRAS, 310, 585 [NASA ADS] [CrossRef] [Google Scholar]
- de Geus, E. J. 1992, A&A, 262, 258 [NASA ADS] [Google Scholar]
- de Zeeuw, P. T., Hoogerwerf, R., de Bruijne, J. H. J., Brown, A. G. A., & Blaauw, A. 1999, AJ, 117, 354 [NASA ADS] [CrossRef] [Google Scholar]
- Diehl, R., Lang, M. G., Martin, P., et al. 2010, A&A, 522, A51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dobbs, C. L., Krumholz, M. R., Ballesteros-Paredes, J., et al. 2014, Protostars and Planets VI, 3 [Google Scholar]
- Dunham, M. M., Arce, H. G., Mardones, D., et al. 2014, ApJ, 783, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., & Klessen, R. S. 2012, ApJ, 761, 156 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., & Klessen, R. S. 2013, ApJ, 763, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., Roman-Duval, J., Klessen, R. S., Schmidt, W., & Mac Low, M.-M. 2010, A&A, 512, A81 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Girichidis, P., Konstandin, L., Whitworth, A. P., & Klessen, R. S. 2014, ApJ, 781, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Gómez, G. C., & Vázquez-Semadeni, E. 2014, ApJ, 791, 124 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Güsten, R., Nyman, L. Å., Schilke, P., et al. 2006, A&A, 454, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hara, A., Tachihara, K., Mizuno, A., et al. 1999, PASJ, 51, 895 [NASA ADS] [Google Scholar]
- Hartmann, L., Ballesteros-Paredes, J., & Bergin, E. A. 2001, ApJ, 562, 852 [NASA ADS] [CrossRef] [Google Scholar]
- Harvey, P. M., Fallscheer, C., Ginsburg, A., et al. 2013, ApJ, 764, 133 [NASA ADS] [CrossRef] [Google Scholar]
- Juvela, M., Malinen, J., & Lunttila, T. 2013, A&A, 553, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Henning, T., & Plume, R. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Banerjee, R., Federrath, C., & Henning, T. 2011, A&A, 530, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kalberla, P. M. W., McClure-Griffiths, N. M., Pisano, D. J., et al. 2010, A&A, 521, A17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kevlahan, N., & Pudritz, R. E. 2009, ApJ, 702, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., Heitsch, F., & Mac Low, M.-M. 2000, ApJ, 535, 887 [NASA ADS] [CrossRef] [Google Scholar]
- Krause, M., Diehl, R., Böhringer, H., Freyberg, M., & Lubos, D. 2014, A&A, 566, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krause, M., Fierlinger, K., Diehl, R., et al. 2013, A&A, 550, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Lada, C. J., & Alves, J. 2008, A&A, 489, 143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Bouy, H., Alves, J., & Lada, C. J. 2014, A&A, 566, A45 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, J. S., Rumpl, W., & Nordsieck, K. H. 1977, ApJ, 217, 425 [NASA ADS] [CrossRef] [Google Scholar]
- Matsumoto, T., Dobashi, K., & Shimoikura, T. 2015, ApJ, 801, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Matthews, T. G., Ade, P. A. R., Angilè, F. E., et al. 2014, ApJ, 784, 116 [NASA ADS] [CrossRef] [Google Scholar]
- McClure-Griffiths, N. M., Pisano, D. J., Calabretta, M. R., et al. 2009, ApJS, 181, 398 [NASA ADS] [CrossRef] [Google Scholar]
- Merín, B., Jørgensen, J., Spezzi, L., et al. 2008, ApJS, 177, 551 [NASA ADS] [CrossRef] [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Ott, S. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 139 [Google Scholar]
- Oya, Y., Sakai, N., Sakai, T., et al. 2014, ApJ, 795, 152 [NASA ADS] [CrossRef] [Google Scholar]
- Palmeirim, P., André, P., Kirk, J., et al. 2013, A&A, 550, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Preibisch, T., Brown, A. G. A., Bridges, T., Guenther, E., & Zinnecker, H. 2002, AJ, 124, 404 [NASA ADS] [CrossRef] [Google Scholar]
- Preibisch, T., & Mamajek, E. 2008, Handbook of Star Forming Regions, Vol. II, ed. B. Reipurth, 235 [Google Scholar]
- Preibisch, T., & Zinnecker, H. 2007, in IAU Symp. 237, eds. B. G. Elmegreen, & J. Palous, 270 [Google Scholar]
- Roccatagliata, V., Dale, J. E., Ratzka, T., et al. 2015, A&A, in press DOI: 10.1051/0004-6361/201425253 [Google Scholar]
- Roussel, H. 2013, PASP, 125, 1126 [Google Scholar]
- Rygl, K. L. J., Benedettini, M., Schisano, E., et al. 2013, A&A, 549, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Csengeri, T., Hennemann, M., et al. 2012, A&A, 540, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., André, P., Könyves, V., et al. 2013, ApJ, 766, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Ossenkopf, V., Csengeri, T., et al. 2015, A&A, 575, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuller, F. 2012, in SPIE Conf. Ser., 8452 [Google Scholar]
- Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Siringo, G., Kreysa, E., Kovács, A., et al. 2009, A&A, 497, 945 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tachihara, K., Dobashi, K., Mizuno, A., Ogawa, H., & Fukui, Y. 1996, PASJ, 48, 489 [NASA ADS] [CrossRef] [Google Scholar]
- Tachihara, K., Toyoda, S., Onishi, T., et al. 2001, PASJ, 53, 1081 [NASA ADS] [Google Scholar]
- Tothill, N. F. H., Löhr, A., Parshley, S. C., et al. 2009, ApJS, 185, 98 [NASA ADS] [CrossRef] [Google Scholar]
- Tremblin, P., Audit, E., Minier, V., Schmidt, W., & Schneider, N. 2012, A&A, 546, A33 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tremblin, P., Schneider, N., Minier, V., et al. 2014, A&A, 564, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vazquez-Semadeni, E. 1994, ApJ, 423, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez-Semadeni, E., Gómez, G. C., Jappsen, A. K., et al. 2007, ApJ, 657, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez-Semadeni, E., Banerjee, R., Gómez, G. C., et al. 2011, MNRAS, 414, 2511 [NASA ADS] [CrossRef] [Google Scholar]
- Vilas-Boas, J. W. S., Myers, P. C., & Fuller, G. A. 2000, ApJ, 532, 1038 [NASA ADS] [CrossRef] [Google Scholar]
- Ward, R. L., Wadsley, J., & Sills, A. 2014, MNRAS, 445, 1575 [NASA ADS] [CrossRef] [Google Scholar]
- Williams, J. P., de Geus, E. J., & Blitz, L. 1994, ApJ, 428, 693 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
Zero-level offsets for the Herschel maps obtained from the cross-correlation with Planck and IRAS.
All Figures
 |
Fig. 1 Lupus I LABOCA 870 μm map with square-root intensity scaling in units of Jy/21.2″-beam. The positions of the 15 cores that were found by Clumpfind are marked with white crosses. The white polygon indicates the common area within which the mass of the cloud was calculated from the LABOCA and Herschel column density maps (see Sect. 4.4). |
| In the text | |
 |
Fig. 2 Left: temperature map of Lupus I from the Herschel SPIRE SED fit. Right: histogram of the dust temperature for the whole cloud (purple), in the north part (orange), and in the center-south (green). |
| In the text | |
 |
Fig. 3 Column density maps of Lupus I from a) the Herschel 250 μm map; b) LABOCA; and c) Planck. |
| In the text | |
 |
Fig. 4 3D surface plot of the Herschel 250 μm column density map. The cores in the center-south of Lupus I can be identified and the average lower column density in the northern part of the cloud can be seen. The red dashed boxes mark the two regions that we distinguish in this work. |
| In the text | |
 |
Fig. 5 Column density PDFs of Lupus I and their model fits for the north and the center-south parts of the cloud, and for the entire cloud. The error bars show the |
| In the text | |
 |
Fig. 6 Herschel column density map of the center-south region with contour levels of 1.1, 4, 7, and 10 × 1021 cm-2. The different symbols mark the center positions of the cores found with LABOCA and of objects found in other studies as discussed in Sect. 4.3. |
| In the text | |
 |
Fig. 7 Surroundings of Lupus I in X-rays (ROSAT 3/4 keV, left) and dust emission (Planck 850 μm, right). There are two X-ray bubbles on either side of the Lupus I ridge and both Lupus I and ρ Ophiuchus, as well as the little cloudlets north of them seen in dust emission, have X-ray shadows. The yellow dashed circles in the right image give the position of the inner and outer edge of the USco H I shell determined from our preliminary analysis of the GASS H I data. The center lies at l = 347°, b = 25° and the inner and outer radius is 12° and 15°, respectively. |
| In the text | |
 |
Fig. 8 Surroundings of Lupus I seen in dust emission (Planck 350 μm). The white contours mark the X-ray emission (ROSAT 0.8 keV) from 0.27−1 × 10-3 counts/s. The cyan dots mark the positions of the B1-B3 stars of UCL from the Hipparcos catalog. Labels are given in green. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.