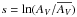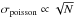| Issue |
A&A
Volume 581, September 2015
|
|
|---|---|---|
| Article Number | A74 | |
| Number of page(s) | 33 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424959 | |
| Published online | 07 September 2015 | |
Relationship between the column density distribution and evolutionary class of molecular clouds as viewed by ATLASGAL⋆
Max-Planck-Institut für Astronomie (MPIA), Königstuhl 17, 69117 Heidelberg, Germany
e-mail: abreu@mpia-hd.mpg.de
Received: 11 September 2014
Accepted: 23 June 2015
We present the first study of the relationship between the column density distribution of molecular clouds within nearby Galactic spiral arms and their evolutionary status as measured from their stellar content. We analyze a sample of 195 molecular clouds located at distances below 5.5 kpc, identified from the ATLASGAL 870 μm data. We define three evolutionary classes within this sample: starless clumps, star-forming clouds with associated young stellar objects, and clouds associated with H ii regions. We find that the N(H2) probability density functions (N-PDFs) of these three classes of objects are clearly different: the N-PDFs of starless clumps are narrowest and close to log-normal in shape, while star-forming clouds and H ii regions exhibit a power-law shape over a wide range of column densities and log-normal-like components only at low column densities. We use the N-PDFs to estimate the evolutionary time-scales of the three classes of objects based on a simple analytic model from literature. Finally, we show that the integral of the N-PDFs, the dense gas mass fraction, depends on the total mass of the regions as measured by ATLASGAL: more massive clouds contain greater relative amounts of dense gas across all evolutionary classes.
Key words: ISM: clouds / evolution / ISM: structure / dust, extinction / stars: formation / infrared: ISM
Appendices are available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Molecular clouds (MCs) are the densest regions of the interstellar medium and the birth sites of stars. Nevertheless, despite this important role in star formation, the key aspects of MC evolution remain unclear: what are the key parameters in determining the star-forming activity of MCs? How do these parameters change with MC evolution? The column density distribution of MCs has been found to be sensitive to the relevant physical processes (Hennebelle & Falgarone 2012). The study of the density structure of clouds that are at different evolutionary stages can therefore help to understand which physical processes are dominating the cloud structure at those stages.
Column density probability density functions (N-PDFs) are useful tools for inferring the role of different physical processes in shaping the structure of molecular clouds. Observations have shown that non-star-forming molecular clouds show bottom-heavy1N-PDFs, while the star-forming molecular clouds show top-heavy2N-PDFs (Kainulainen et al. 2009, 2011b, 2014; Kainulainen & Tan 2013; Schneider et al. 2013). It is generally accepted that the top-heavy N-PDFs are well described by a power-law function in their high-column density regimes. The description of the shapes of the low-column density regimes of both kinds of N-PDFs is still a matter of debate. The papers cited above describe the low-column density regimes as log-normal functions. In contrast, Alves et al. (2014) and Lombardi et al. (2015) argue that a power-law function fits the observed N-PDFs throughout their range. The origin of these differences is currently unclear.
Simulations predict that turbulence-dominated gas develops a log-normal N-PDF (Federrath & Klessen 2013); such a form is predicted for the volume density PDF (hereafter ρ-PDF) of isothermal, supersonic turbulent, and non-self-gravitating gas (Vazquez-Semadeni 1994; Padoan et al. 1997; Scalo et al. 1998; Ostriker et al. 2001; Padoan & Nordlund 2011; Ballesteros-Paredes et al. 2011; Federrath & Klessen 2013). Log-normal ρ-PDFs can, however, result also from processes other than supersonic turbulence such as gravity opposed only by thermal-pressure forces or gravitationally-driven ambipolar diffusion (Tassis et al. 2010).
The log-normal N-PDF is defined as: 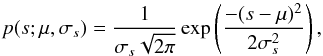 (1)where
(1)where 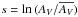 is the mean-normalized visual extinction (tracer of column density, see Sect. 2.3), and μ and σs are respectively the mean and standard deviation of the distribution. The log-normal component that is used to describe low column densities has typically the width of σs = 0.3−0.4 (Kainulainen et al. 2009). It has been suggested that the determination of the width can be affected by issues such as unrelated dust emission along the line of sight to the cloud (Schneider et al. 2015b). Practically all star-forming clouds in the Solar neighborhood show an excess to this component at higher column densities, following a power-law, or a wider log-normal function (Kainulainen et al. 2009; Kainulainen & Tan 2013; Schneider et al. 2013), especially reflecting their ongoing star formation activity (Kainulainen et al. 2014; Sadavoy et al. 2014; Stutz & Kainulainen 2015). Such behavior is suggested by the predictions that develope top-heavy ρ-PDFs for self-gravitating systems (Klessen 2000; Klessen & Burkert 2000; Kritsuk et al. 2011; Girichidis et al. 2014).
is the mean-normalized visual extinction (tracer of column density, see Sect. 2.3), and μ and σs are respectively the mean and standard deviation of the distribution. The log-normal component that is used to describe low column densities has typically the width of σs = 0.3−0.4 (Kainulainen et al. 2009). It has been suggested that the determination of the width can be affected by issues such as unrelated dust emission along the line of sight to the cloud (Schneider et al. 2015b). Practically all star-forming clouds in the Solar neighborhood show an excess to this component at higher column densities, following a power-law, or a wider log-normal function (Kainulainen et al. 2009; Kainulainen & Tan 2013; Schneider et al. 2013), especially reflecting their ongoing star formation activity (Kainulainen et al. 2014; Sadavoy et al. 2014; Stutz & Kainulainen 2015). Such behavior is suggested by the predictions that develope top-heavy ρ-PDFs for self-gravitating systems (Klessen 2000; Klessen & Burkert 2000; Kritsuk et al. 2011; Girichidis et al. 2014).
Another interesting measure of the density structure of molecular clouds is the dense gas mass fraction (DGMF) that describes the mass enclosed by regions with M(AV ≥ A′V), relative to the total mass of the cloud, Mtot. 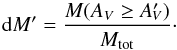 (2)The DGMF has been recently linked to the star-forming rates of molecular clouds: Heiderman et al. (2010) and Lada et al. (2010, 2012) showed, using samples of nearby molecular clouds and external galaxies, that there is a relation between the mean star-forming rate (SFR) surface density (ΣSFR) and the mean mass surface density (Σmass) of MCs:
(2)The DGMF has been recently linked to the star-forming rates of molecular clouds: Heiderman et al. (2010) and Lada et al. (2010, 2012) showed, using samples of nearby molecular clouds and external galaxies, that there is a relation between the mean star-forming rate (SFR) surface density (ΣSFR) and the mean mass surface density (Σmass) of MCs: 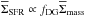 , where
, where 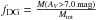 . Furthermore, in a sample of eight molecular clouds within 1 kpc, a correlation
. Furthermore, in a sample of eight molecular clouds within 1 kpc, a correlation 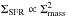 was reported by Gutermuth et al. (2011). Combining these two results suggests fDG ∝ Σmass.
was reported by Gutermuth et al. (2011). Combining these two results suggests fDG ∝ Σmass.
Despite their utility, a complete, global understanding of the N-PDFs and DGMFs of molecular clouds is still missing. One of the main problems arises from the fact that the dynamic ranges of different observational techniques sample the N-PDFs and DGMFs differently. Previous works have employed various methods: CO line emission only samples N-PDFs between AV ≈ 3−8 mag (Goodman et al. 2009). NIR extinction traces column density at wider, but still narrow, dynamic range, AV ≈ 1−25 mag (Lombardi & Alves 2001). Kainulainen & Tan (2013) and Kainulainen et al. (2013a) used a novel extinction technique that combines NIR and MIR data, considerably increasing the observable dynamic range, AV = 3−100 mag. Schneider et al. (2013) and Lombardi et al. (2015) used Herschel FIR data to sample N-PDFs at AV< 100 mag.
Another observational hindrance arises from the limited spatial resolution of observations. The high-column densities typically correspond to small spatial scales in molecular clouds; to probe the N-PDFs at high-column densities requires spatial resolution that approaches the scale of dense cores in the clouds (~0.1 pc). Herschel reaches resolution of ~36″ that corresponds to 0.17 pc at 1 kpc distance. Extinction mapping using both NIR and MIR wavelengths can reach arcsecond-scale resolution, but only about ten clouds have been studied so far with that technique (Kainulainen & Tan 2013; Kainulainen et al. 2013b).
Born out of the observational limitations above, the most important weakness in previous studies is that they only analyze relatively nearby molecular clouds (d ≲ 1.5 kpc). Thus, they probe only a very limited range of Galatic environments, which prohibits the development of a global picture of the factors that control N-PDFs across different Galactic environments. Extending N-PDF studies to larger distances is imperative for three principal reasons. First, studying the more massive and distant MCs will allow us to sample the entire MC mass range present in the Galaxy. Second, larger numbers of MCs over all masses provide statistically meaningful samples. Finally, extending to larger distances is necessary to study the possible effect of the Galactic structure on the mass distribution statistics.
In this paper, we employ the ATLASGAL (Schuller et al. 2009; Csengeri et al. 2014) survey to study a large sample of molecular clouds in the Galaxy. The ATLASGAL survey traces submillimeter dust emission at 870 μm. Submillimeter dust emission is an optically thin tracer of interstellar dust, and hence a direct tracer of gas if a canonical dust-gas mass ratio is assumed. The submillimeter observing technique employed in the ATLASGAL survey filters out diffuse emission on spatial scales greater than 2.5′, hence making the survey most sensitive to the densest material of the interstellar medium in which star formation occurs. With this data set we can observe the cold dense interiors of molecular clouds in both the near and far sides of the Galactic plane. With an angular resolution of 19.2″, ATLASGAL improves by almost a factor of two the resolution of Herschel observations, thus providing a more detailed view of the dense material inside molecular clouds. We will use this data sample to study the N-PDFs and DGMFs of molecular clouds at different evolutionary classes.
2. Data and methods
We used continuum maps at 870 μm from ATLASGAL to identify MCs in the Galactic plane region between l ∈ [9°,21°] and | b | ≤ 1°, where the rms of the survey is 50 mJy/beam. We selected this area, because extensive auxiliary data sets were available for it, and specifically, starless clumps have already been identified by Tackenberg et al. (2012). We classified the identified molecular cloud regions in three groups based on their evolutionary classes: starless clumps (SLCs), star-forming clouds (SFCs), and H ii regions. In the following, we describe how each class was defined and how we estimated the distance to each region.
2.1. Source selection
We identified molecular cloud regions based primarily on ATLASGAL dust emission data. As a first step, we defined objects from ATLASGAL data simply by using 3σ emission contours (0.15 Jy/beam) to define the region boundaries. Then, we used distances available in literature (see Sect. 2.2) to group together neighbouring objects located at similar distances (within the assumed distance uncertainty of 0.5 kpc), i.e., those that are likely associated with the same molecular cloud. As a next step, we expanded the boundaries of the regions down to their 1σ level in the cases in which they show close contours at 1σ. Finally, each region created in this manner was classified either as a SLC, SFC, or H ii region using information about their stellar content available in literature. An example of the region definition is shown in Fig. 1 (see also Appendix C). We identify a total of 615 regions, 330 of them with known distances and classified either as SLC, SFC, or H ii regions (Fig. 2). Throughout this paper we refer to each of the ellipses shown in Fig. 1 with the term region. In the following we explain the definition of the three evolutionary classes in detail.
H ii regions are defined as regions hosting previously cataloged H ii regions. We used the catalogues Wood & Churchwell (1989), Lockman (1989), Garay et al. (1993), Bronfman et al. (1996), Lockman et al. (1996), Forster & Caswell (2000), and Urquhart et al. (2013). We identified 114 H ii regions in the considered area. Distances are known for 84 of them (74%). Two thirds (57) of the H ii regions with distance estimates lie at near distances (d< 5.5 kpc). If we assume the same distribution for the 30 H ii regions with unknown distances, 20 of them would be located at near distances. Nevertheless, we exclude these regions from our analysis. We summarize the number of regions with and without known distances in Table 1 (see Sect. 2.2).
 |
Fig. 1 MIPSGAL 24 μm map of the Galactic plane between 9deg <l< 10.5deg. Yellow contours indicate the 3σ (0.15 Jy/beam) emission level of the ATLASGAL data. Red and blue ellipses show the H ii regions and SFCs, respectively. SLCs are shown with green filled diamonds. Similar maps for the Galactic plane between 10.5deg <l< 21deg and | b | ≤ 1deg are shown in Appendix C. |
 |
Fig. 2 Distance distribution of the molecular cloud regions. Black solid line shows the total number of regions. Red dotted line shows the HII regions, the blue dashed line the SFCs, and green filled area the SLCs. Black dashed vertical line at 5 kpc shows the common distance to which we have smoothed the data. |
Completeness of each evolutionary class.
The star-forming clouds (SFCs) are defined as the subset of regions devoid of H ii regions but containing young stellar objects (YSOs) and protostars. Here the presence of YSOs and protostars is assumed to be a clear indication of ongoing star formation. For this purpose, we used the YSO catalogues of Dunham et al. (2011) and Tóth et al. (2014). The former search signs of active star formation in the Bolocam Galactic Plane Survey (Aguirre et al. 2011, BGPS) using the GLIMPSE Red Source catalogue (Robitaille et al. 2008), the EGO catalogue (Cyganowski et al. 2008), and the rms catalogue (Lumsden et al. 2013). They found 1341 YSOs in the area l ∈ [9°,21°] and | b | ≤ 0.5° and it is >98% complete at the 0.4 Jy level (Dunham et al. 2011). Tóth et al. (2014) present a catalog of 44 001 YSO candidates, 2138 in the area l ∈ [9°,21°] and | b | ≤ 1°, with a reliability of 90% in the YSO classification. All the regions showing spatially coincident YSOs were classified as SFCs. We only require one YSO to classify a region as SFC, but our SFCs have more than one. The probability of classifying a SFC as a region without YSOs due to completeness issues in the YSOs catalogues is therefore very low. We identified 184 SFCs, 126 of them with known distances. The 80% (99) of the SFCs with known distances lie at d< 5.5 kpc and are therefore studied in this paper. Assuming the same SFC distribution for the SFCs with unknown distances, we estimate that the 80% (46) of the SFCs with no distance estimates would be located at near distances.
Finally, we adopted the starless clump catalog from Tackenberg et al. (2012) to define our sample of SLCs. They present a SLC sample with peak column densities N> 1023 cm-2. The properties of this SLC sample were specifically chosen in order to detect potential high-mass star progenitors. Tackenberg et al. (2012) used uniform criteria to classify their SLC sample: absence of GLIMPSE and/or 24μm MIPSGAL sources. Tackenberg et al. (2012) identified 120 SLCs with known distances3 in the Galactic plane area studied. All SLCs are located inside our previously defined H ii regions or SFCs (see Fig. 1).
Literature sources from which distances were obtained.
We note a caveat in the above evolutionary class definition scheme. Our scheme makes an effort to capture the dominant evolutionary phase of the region, but it is clear that not all the regions are straightforward to classify. In principle, the distinction between H ii regions and SFCs is well defined; it depends on whether the regions host an H ii region or not. However, eight regions harbor only UCH ii regions whose extent is tiny compared to the full extent of those regions (#34, #54, #192, #195, #233, #246, #247 and #390). Since our aim is to capture the dominant evolutionary phase, we classified these regions as SFCs.
We also note that our evolutionary class definition is based only on the stellar content of the regions. The SLCs exhibit no indications of star-forming activity, SFCs have star-forming sources, H ii region have formed massive stars. However, we emphasize that we cannot assume that all the SLCs will definitely form stars. Similarly, we cannot assume that all the star-forming content within SFCs will become massive enough to create H ii regions, although some of them will. Therefore we do not aim to draw a sequential evolutionary link between these three classes of regions. Instead, the estimated time-scales for each class instead aim to identify independent evolutionary time-scales for each observational class.
2.2. Distance estimates and convolution to a common spatial resolution
We adopted distances to each region from literature. The two main literature sources used were Ellsworth-Bowers et al. (2013) and Wienen et al. (2012). The former catalog measures kinematic distances of molecular clumps identified with sub-mm dust emission. They solve the kinematic distance ambiguity (KDA) using Bayesian distance probability density functions. They use previous data sets to establish the prior distance probabilities to be used in the Bayesian analysis. This method has a 92% agreement with Galactic Ring Survey based distances. In total, 68 out of 330 regions have counterparts in Ellsworth-Bowers et al. (2013). Wienen et al. (2012) measured the kinematic distances to dense clumps in the ATLASGAL survey using ammonia observations. We obtained distance estimates for 80 regions from this catalog. We also used other catalogs based on kinematic distances (Walsh et al. 1997; Simon et al. 2006; Rudolph et al. 2006; Roman-Duval et al. 2009; Urquhart et al. 2013; Tackenberg et al. 2012), and in a three-dimensional model of interstellar extinction (Marshall et al. 2009). A detailed discussion on the methods for distance estimates is beyond the scope of this paper. We therefore refer to the cited papers for a detailed discussion on them. Table 2 shows the number of distance estimates adopted from each literature source. In regions with more than one distance estimate, we estimated the distance averaging the different values. For all but six of the studied regions (~96%) the distance ambiguity was solved in at least one of the cited papers. Regions with different KDA solutions in literature (i.e. with several clouds along the same line-of-sight) were removed from our sample to avoid line-of-sight contamination. For the remaining six regions we used maps from the GLIMPSE and MIPS surveys to search for dark shadows against background emission (e.g. Stutz et al. 2009; Ragan et al. 2012). The near distance was adopted for regions associated with IRDCs.
Since all the SLCs of our sample are embedded in H ii regions or SFCs (see Sect. 2.1), we compared the distance estimates for the SLCs and for their hosting regions. In every but one case, the distance estimates of the SLCs and their hosting SFCs or H ii regions were in good agreement. In the only inconsistent case, the SLC was located at the far distance in (Tackenberg et al. 2012) and its hosting SFC was located at the near distance. Since the KDA solutions of the SLC and its hosting SFC differ, we removed out both regions from the final sample (see also previous paragraph).
Figure 2 shows the distance distribution of our sample. A vast majority (~80%) of our regions is located within 5 kpc distance. There is a gap between 6 and 10 kpc, coinciding with the central hole of the Galactic molecular ring (Solomon & Rivolo 1989)4. At the far side of the Galaxy, there are three density enhancements that coincide with the Sagittarius, Norma, and Perseus spiral arms (Fig. 3).
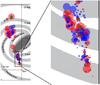 |
Fig. 3 Artist impression of face-on view of the Milky Way (R. Hurt, SSC-Caltech, MPIA graphic, Tackenberg et al. 2012). H ii regions are shown as red circles, star-forming clouds as blue circles and starless clumps as green circles. Circle sizes are proportional to region sizes. The right panel shows a zoom to the region enclosed by the black rectangle in the left panel, where the source density is highest. |
We study only regions within 5 kpc since the highest source density of our sample is located there. Assuming an error in distance determination of about 0.5 kpc, we also included regions located between 5 kpc and 5.5 kpc. We convolved the ATLASGAL data of all closer regions to a common 5 kpc distance resolution using a Gaussian kernel of 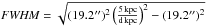 . This convolution was done for each region individually. At the distance of 5 kpc, the 19.2″ resolution of the ATLASGAL translates to about 0.5 pc. We therefore do not resolve the dense cores ultimately linked to star formation that have typically a size of ~0.1 pc (Motte & Hennebelle 2009; Ragan et al. 2013).
. This convolution was done for each region individually. At the distance of 5 kpc, the 19.2″ resolution of the ATLASGAL translates to about 0.5 pc. We therefore do not resolve the dense cores ultimately linked to star formation that have typically a size of ~0.1 pc (Motte & Hennebelle 2009; Ragan et al. 2013).
When smoothing maps to a common distance, some of the smaller SLCs were washed out by strong emission gradients likely associated with nearby strong sources. This artificially increases the SLCs column densities. To minimize the effect, we inspected each SLC by eye, discarding those that were significantly affected by strong gradients. Appendix D shows the SLCs included in the final sample.
The total number of regions studied in this paper, and the number of regions in each evolutionary class, are listed in Table 1.
2.3. Column density and mass estimation
Column densities of molecular gas were calculated via ![\begin{equation} \label{eq:NH2} N_{\mathrm{H_{2}}} [\mathrm{cm^{-2}}] = \frac{RF_{\lambda}}{B_{\lambda}(T_{\rm Dust})\mu m_{\mathrm{H}}\kappa\Omega}, \end{equation}](/articles/aa/full_html/2015/09/aa24959-14/aa24959-14-eq44.png) (3)where Fλ and Bλ(T) are respectively the flux and the blackbody radiation as a function of temperature, T, at 870 μm. The quantity μ is the mean molecular weight (assumed to be 2.8) of the interstellar medium per hydrogen molecule, mH is the mass of the hydrogen atom, Ω is the beam solid angle, and R = 154 is the gas-to-dust ratio (Draine 2011). We used a dust absorption coefficient κ = 1.85 cm2 g-1 at 870 μm, which was calculated by interpolation of the Ossenkopf & Henning (1994) dust model of grains with thin ice mantles and a mean density of n = 106 cm-3. We assumed T = 15 K for SLCs and SFCs (Wienen et al. 2012), in agreement with previous dust temperature estimations within infrared dark clouds (Peretto & Fuller 2010, IRDCs) and in envelopes of star-forming cores (Stutz et al. 2010; Launhardt et al. 2013). For H ii regions we assumed T = 25 K. This dust temperature is in agreement with the average dust temperatures in PDR regions surrounding H ii regions (T = 26 K), where most of the FIR-submm dust emission of these objects comes from (Anderson et al. 2012). It also agrees with the mean temperature found in the central region of NGC 6334 (T ~ 24 K), that is an expanding H ii region (Russeil et al. 2013). For a better comparison with previous works, we present the column density data also in units of visual extinction using a conversion: NH2 = 0.94 × 1021AV cm-2 mag-1 (Bohlin et al. 1978). The rms noise of the ATLASGAL data (50 mJy) corresponds to AV = 4.5 mag for both the SFCs and SLCs and 2.2 mag5 for H ii regions. No saturation problems were found in the ATLASGAL survey. The optical depth is ≪1, therefore our measurements do not suffer from optical depth effects in the high-column density regime (Schuller et al. 2009).
(3)where Fλ and Bλ(T) are respectively the flux and the blackbody radiation as a function of temperature, T, at 870 μm. The quantity μ is the mean molecular weight (assumed to be 2.8) of the interstellar medium per hydrogen molecule, mH is the mass of the hydrogen atom, Ω is the beam solid angle, and R = 154 is the gas-to-dust ratio (Draine 2011). We used a dust absorption coefficient κ = 1.85 cm2 g-1 at 870 μm, which was calculated by interpolation of the Ossenkopf & Henning (1994) dust model of grains with thin ice mantles and a mean density of n = 106 cm-3. We assumed T = 15 K for SLCs and SFCs (Wienen et al. 2012), in agreement with previous dust temperature estimations within infrared dark clouds (Peretto & Fuller 2010, IRDCs) and in envelopes of star-forming cores (Stutz et al. 2010; Launhardt et al. 2013). For H ii regions we assumed T = 25 K. This dust temperature is in agreement with the average dust temperatures in PDR regions surrounding H ii regions (T = 26 K), where most of the FIR-submm dust emission of these objects comes from (Anderson et al. 2012). It also agrees with the mean temperature found in the central region of NGC 6334 (T ~ 24 K), that is an expanding H ii region (Russeil et al. 2013). For a better comparison with previous works, we present the column density data also in units of visual extinction using a conversion: NH2 = 0.94 × 1021AV cm-2 mag-1 (Bohlin et al. 1978). The rms noise of the ATLASGAL data (50 mJy) corresponds to AV = 4.5 mag for both the SFCs and SLCs and 2.2 mag5 for H ii regions. No saturation problems were found in the ATLASGAL survey. The optical depth is ≪1, therefore our measurements do not suffer from optical depth effects in the high-column density regime (Schuller et al. 2009).
We estimated the total gas mass of each region from dust continuum emission, assuming that emission is optically thin: 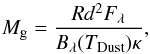 (4)where d is the distance to the region. We assume the same values for the other listed quantities as we assume for the column density determination (Eq. (3)). Masses of the regions cover three orders of magnitude (Fig. 4). The masses of the SLCs span 0.2−4 × 103M⊙, the SFCs 0.3−15 × 103M⊙, and the H ii regions 0.2−200 × 103M⊙. Larger masses for H ii regions and SFCs are expected since both have much larger sizes than SLCs (Fig. 1).
(4)where d is the distance to the region. We assume the same values for the other listed quantities as we assume for the column density determination (Eq. (3)). Masses of the regions cover three orders of magnitude (Fig. 4). The masses of the SLCs span 0.2−4 × 103M⊙, the SFCs 0.3−15 × 103M⊙, and the H ii regions 0.2−200 × 103M⊙. Larger masses for H ii regions and SFCs are expected since both have much larger sizes than SLCs (Fig. 1).
 |
Fig. 4 Mass distribution of the molecular cloud regions. Filled green area shows mass for starless clumps, dashed blue line shows star-forming clouds and red dashed line shows H ii regions. Masses are given in solar mass units. |
The derived mass and column density values depend on the assumed dust properties, specifically on κ870 μm, R and TDust. Both κ870 μm and R are subject to uncertainties: κ870 μm values differ by ~1 dex in different dust models (Shirley et al. 2005, 2011). Equations (3) and (4) assume isothermal clouds. This is clearly an oversimplification, increasing the uncertainty in the derived masses. Mass depends also on d2, making uncertainties in distance a major contributor to the absolute uncertainties. If we adopt Δd ~ 0.5 kpc, nearby regions will be more affected by distance uncertainties (50% at 1 kpc) than the most distant regions (10% at 5 kpc). This assumption agrees with the distance uncertainties reported by Roman-Duval et al. (2009). We note that the absolute uncertainty in our derived column densities is very large, potentially larger than a factor 10. The relative uncertainties between the evolutionary classes can be influenced by the different temperature assumptions or intrinsic differences in the dust properties. The isothermal assumption introduces differences in the low-column density regime of the N-PDFs, but it has negligible effect in shaping the column density distribution at high-column densities (see Appendix B). In the case of dust properties, we have no knowledge about any observational-based study suggesting changes in them in molecular clouds at different evolutionary phases. We therefore assume that the dust properties do not introduce relative uncertainties between the three molecular cloud classes defined.
2.4. Physical properties of the evolutionary classes
We define and analyze in this work three distinctive evolutionary classes of objects: SLCs, SFCs and H ii regions. The objects in these classes are different in their physical characteristics. These differences originate dominantly from the fact that the H ii regions and SFCs are typically extended regions (i.e., molecular clouds or even cloud complexes), while SLCs are smaller, “clump-like” structures. We quantify here the basic physical properties of the objects in our three evolutionary classes. The properties are also listed in Table 3.
Figure 4 shows the mass distribution of our regions. The mass distribution of H ii regions spans 3 dex from 102−105M⊙. SFCs have masses of 102−104M⊙, and SLCs show the most narrow mass range, 102−103M⊙.
The spread of the distribution of mean column densities is 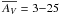 mag and it peaks at
mag and it peaks at 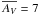 mag (see Fig. 5). The
mag (see Fig. 5). The 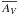 distribution differs in each evolutionary class. While most SFCs and SLCs have
distribution differs in each evolutionary class. While most SFCs and SLCs have 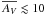 mag, a considerable number of H ii regions show
mag, a considerable number of H ii regions show 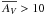 mag. We note that the mean column densities of our sample are overestimated due to the spatial filtering of ATLASGAL, and so is the peak of the
mag. We note that the mean column densities of our sample are overestimated due to the spatial filtering of ATLASGAL, and so is the peak of the 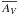 distribution. This effect is more important in H ii regions and SFCs since they have larger areas and hence larger fraction of diffuse material that is filtered out than the SLCs.
distribution. This effect is more important in H ii regions and SFCs since they have larger areas and hence larger fraction of diffuse material that is filtered out than the SLCs.
Figure 5 also shows the size distribution of each class and of the total sample. The SLCs have the smallest sizes of the sample with a mean size of 1.4 pc and a range of sizes between 1 pc and 2.5 pc. The range of sizes of the SFCs is 2−15 pc, with a mean of 5.3 pc. The H ii regions have the largest mean size of the three evolutionary classes, 7 pc, and also the largest spread, 2−18 pc.
 |
Fig. 5 Mean column density, |
Mean physical properties of the evolutionary classes.
3. Results
3.1. Column density distribution
We use the column density data to study the column density distributions of the regions. In the following, we first analyze the N-PDFs and DGMFs. We then examine the relationship between the total mass and the column density distribution of the regions.
 |
Fig. 6 Total mean normalized column density PDFs of H ii regions (left), SFCs (center) and SLCs (right). All panels: horizontal axis show mean normalized column densities, |
3.1.1. N-PDFs
We first analyze the total N-PDFs of the three evolutionary classes. To construct the N-PDFs, we used the mean normalized column densities 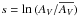 (see Eq. (1)) of each region. We calculated
(see Eq. (1)) of each region. We calculated 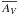 as the mean column density of all the pixels of each region. The resulting N-PDFs were then stacked together to form the total N-PDFs, shown in Fig. 6 as the black histogram. The three classes show clearly different N-PDFs: the H ii regions have the widest (or shallowest) N-PDF, followed by a slightly narrower (or steeper) N-PDF of SFCs. The SLCs have the narrowest N-PDF.
as the mean column density of all the pixels of each region. The resulting N-PDFs were then stacked together to form the total N-PDFs, shown in Fig. 6 as the black histogram. The three classes show clearly different N-PDFs: the H ii regions have the widest (or shallowest) N-PDF, followed by a slightly narrower (or steeper) N-PDF of SFCs. The SLCs have the narrowest N-PDF.
Interpreting the low-column density shape of the N-PDFs requires taking into account two issues. First, ideally the N-PDF should not be affected by how exactly the field-of-view toward an individual region is cropped, i.e., it must include all column density values above a given level. Second, one must ascertain that the pixels are not dominated by noise or contamination from neighbouring regions. To fold these two limitations into one, we define a ”reliability limit” of the N-PDFs as the minimum column density value above which all regions of the evolutionary class are well defined by a closed emission iso-contour (see Appendices D, E and F). These levels are s = −1.5, −0.75, and 0 for H ii regions, SFCs, and SLCs, respectively. These levels correspond typically to AV = 2,4, and 9 mag, all at least 1σ above the noise level (50 mJy; see Sect. 2.3). The larger reliability limit in SLCs originates from the fact that they are embedded in H ii regions and SFCs, being surrounded by emission levels higher than the map noise. The total number of pixels above these limits are 20 × 104, 9 × 104, and 104 for H ii regions, SFCs, and SLCs, respectively. We note that this definition of the reliability limit is very conservative; it is set by the lowest iso-contour above which all regions of the evolutionary class show a closed contour. Most regions, however, have this limit at lower s values. We also note that systematic uncertainties such as the dust opacity uncertainty do not affect (or, are unlikely to affect) the relative shapes of the three classes with respect to each others.
To quantify the shapes of the N-PDFs shown in Fig. 6, we fit them, equally sampled in the log space, with a combination of log-normal (see Eq. (1)) and power-law (p(s) ∝ csp) functions. We used five free parameters in the fit: the width (σs) and mean (μ) of the log-normal function, the slope (p) and constant (c) of the power-law, and the break point between both functions (st). Furthermore, molecular cloud masses should be recovered when integrating the fitted function, representing an extra boundary condition to the fit. The fitting range was defined as all s values larger than the reliability limit. We weighted the data points by their Poisson noise. We obtained the uncertainties of the fitted parameters by fitting the N-PDFs using different bin sizes (Sadavoy et al. 2014). Results are summarized in Table 4.
SLCs are well described by a log-normal N-PDF (σs,SLC = 0.5 ± 0.1). Even though the peak of the N-PDFs is below the reliability limit, it is well constrained by the fit because of the normalization factor in Eq. (1). The N-PDFs of H ii regions and SFCs are inconsistent with a single log-normal function; they are better described by a combination of a log-normal function at low column densities and a power-law function at high column densities. The low-column density log-normal portion of H ii regions is wider (σs,H ii = 0.9 ± 0.09) than that of SFCs (σs,SFC = 0.5 ± 0.05). The mean-normalized column densities at which the N-PDFs transition from log-normal to power-law is similar in both classes, H ii regions and SFCs: st = 1.0 ± 0.2. We also find differences in the power-law slopes of the N-PDFs. The power-law slope is clearly shallower for H ii regions (p = −2.1 ± 0.1) than for SFCs (p = −3.8 ± 0.3).
Results of the best-fit parameters to the total N-PDFs and DGMFs.
 |
Fig. 7 Mean DGMFs of H ii regions (left), SFCs (center) and SLCs (right). Solid colored lines show mean normalized DGMFs. DGMFs were normalized to the reliability limit of each evolutionary class: AV = 2, 4, 9 mag for H ii regions, SFCs and SLCs, respectively. Colored dashed lines show the fit of the DGMFs with exponential functions. Dashed-dotted colored lines show fits with power-law tails in the higher AV range. Grey shaded regions show statistical poisson errors of the DGMFs. Small box in left panel shows the whole mean DGMF of H ii regions up to AV = 1000 mag. |
 |
Fig. 8 Mass-binned average DGMFs for each evolutionary class. Each line shows the DGMF for each of the mass intervals listed in the corresponding panel and defined in Table 5. Dotted lines, dotted-dashed lines, dashed lines, and solid lines progress from less to most massive bins, respectively. The DGMFs were normalized following the procedure described in Sect. 3.1.2 and shown in Fig. 7. |
3.1.2. Dense Gas Mass Fraction
In Sect. 1 we defined the DGMFs as the fraction of gas mass enclosed by regions with M(AV ≥ A′V), relative to the total mass of the cloud (see Eq. (2)). Figure 7 shows the mean DGMFs of each evolutionary class. Generally, H ii regions exhibit larger reservoirs of high-column density gas than the SLC and SFC regions.
We quantified the shapes of the mean DGMFs by fitting them with a combination of exponential (∝eαAV) and power-law (∝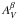 ) functions, leaving both exponents and the breaking point as free parameters and weighting each point by the Poisson standard deviation. Fit errors were calculated as in Sect. 3.1.1, resulting in parameter value uncertainties of 10−15%. While the mean DGMF of the SLCs is well fitted by an exponential, H ii regions and SFCs transition from an exponential to a power-law shape at AV ≥ 20 mag. This change is evidently linked to the change from log-normal to power-law shape in the N-PDF because the DGMFs are an integral of the N-PDF. H ii regions show the shallowest mean DGMF (α = −0.06), followed by SLCs (α = −0.11) and SFCs (α = −0.14). In the power-law portion of the DGMFs, H ii regions are also shallower (β = −1.0) than SFCs (β = −2.1). The amount of mass enclosed by the power-law DGMF is 30% of the total mass in H ii regions, almost a factor of three lower, 10%, for the SFCs.
) functions, leaving both exponents and the breaking point as free parameters and weighting each point by the Poisson standard deviation. Fit errors were calculated as in Sect. 3.1.1, resulting in parameter value uncertainties of 10−15%. While the mean DGMF of the SLCs is well fitted by an exponential, H ii regions and SFCs transition from an exponential to a power-law shape at AV ≥ 20 mag. This change is evidently linked to the change from log-normal to power-law shape in the N-PDF because the DGMFs are an integral of the N-PDF. H ii regions show the shallowest mean DGMF (α = −0.06), followed by SLCs (α = −0.11) and SFCs (α = −0.14). In the power-law portion of the DGMFs, H ii regions are also shallower (β = −1.0) than SFCs (β = −2.1). The amount of mass enclosed by the power-law DGMF is 30% of the total mass in H ii regions, almost a factor of three lower, 10%, for the SFCs.
The mean DGMF of H ii regions above AV = 300 mag is dominated by regions #4, #55 and #122 (see Table F.1). This flat tail is built up by less than 1% of the pixels in each of the mentioned regions, and hence, is not representative of the whole H ii sample.
3.1.3. Relationship between the region’s mass and column density distribution
Does the dense gas mass fraction of a region depend on its mass and from therein, affect the SFR – cloud mass relation presented by Lada et al. (2012)? We analyze the DGMFs of each evolutionary class divided in five mass intervals (listed in Table 5) that have at least 9 regions each to answer this question.
Figure 8 shows the mean DGMFs of each mass interval for the three evolutionary classes. In all evolutionary classes, most massive regions have shallower DGMFs than those of less massive regions. We fit the mean DGMFs with exponential and power-law functions as described in Sect. 3.1.2. Most DGMFs could not be fitted well with the combination of both functions over their entire column density range. Only the DGMFs of the most massive SFCs and H ii regions required two component functions; DGMFs of less massive regions are well described by an exponential alone. Exponents derived from this analysis are shown in Table 6.
In all evolutionary classes, the exponent of the exponential function, α, increases with mass (see Table 6). In order to further investigate this correlation, we repeated the same fitting procedure for each individual region. Results are shown in Fig. 9. Top panel of Fig. 9 shows the relationship between α and the mass of each region: α ∝ M− 0.43 ± 0.05, that has a correlation coefficient r = 0.64 and a significance value p = 0.18. The fit parameters and their errors were obtained from a Monte-Carlo simulation of 106 cycles. On each cycle we selected a random sample of points and fitted the resulting data set. We adopt the average of the best fit parameters obtained on each cycle as the best fit values and their standard deviation as the error of the fit. It could be argued that the correlation between α and mass is dominated by the most massive (M> 3 × 104M⊙) H ii regions. To establish whether the correlation strength depends strongly on these few massive clouds we also explored this correlation without those extreme points. The correlation coefficient is somewhat lower in this case r = 0.56 and a significant value p = 0.21. However, there is no significant difference in the resulting fit (α ∝ M− 0.40 ± 0.08). Power-law exponents of DGMFs also exhibit a correlation with mass: β ∝ M− 0.16 ± 0.03 (see middle panel of Fig. 9). The larger scatter seen in the data from the exponential fits relative to that seen in power-law fits may indicate that the power-law regimes of DGMFs are much better constrained than the exponential regimes.
 |
Fig. 9 Top: relationship between the mass of the regions [M⊙] and the exponent of the exponential fit to the DGMFs (αexp). Black solid line shows the best fit to the data and the shaded region shows its σ error. The dotted and dashed lines show the best fit when the most massive H ii regions are removed. Colors indicate the evolutionary class of each point as indicated. Middle: relationship between mass of the regions and the slope of the power-law range of the DGMFs. Black line shows the best fit to the data and the shaded region shows its σ error. Bottom: relationship between the mean gas mass surface density of the MCs, Σmass, and the dense gas mass fraction of gas, |
4. Discussion
4.1. N-PDFs as a measure of the evolutionary stage of objects
The total N-PDFs of different evolutionary classes exhibit clear differences; these differences can be linked to differences in the mechanisms that drive the evolution of objects within the various classes. The N-PDF of SLCs is well described by a single log-normal function (see Fig. 6). This agrees with previous observations of starless low-mass clouds (Kainulainen et al. 2009) or starless regions of star-forming clouds (Schneider et al. 2012, 2013; Russeil et al. 2013). In particular, this simple log-normal form agrees with predictions for turbulence-dominated media from numerical simulations (Padoan et al. 1997; Vázquez-Semadeni & García 2001).
In contrast, the total N-PDFs of star-forming clouds, i.e., H ii regions and SFCs, show two components that can be described by log-normal and power-law functions. The power-law components of the N-PDFs of the H ii regions are shallower than those of the SFCs. Previous studies have found that the power-law slopes are within p = [−1.5,−3.3], with shallower slopes related to most active star-forming regions. In the only study with a resolution similar to ours, Russeil et al. (2013) found a non-star-forming region in NGC 6334 to have a steep N-PDF slope6 (p = −5.7), moderately star-forming regions to have shallower slopes (p = −3.3,−3.0), and an H ii region to have the shallowest slope (p = −1.5). Their trend to have shallower N-PDF in a cloud region that contains an H ii region is similar to what we find in our work.
Theories and simulations that consider turbulent gas under the influence of gravity predict power-law-like tails for N-PDFs with exponents comparable to what is observed (Kritsuk et al. 2011; Federrath & Klessen 2013), possibly featuring flattening of the power-law over time-scales relevant for star formation (Ballesteros-Paredes et al. 2011; Federrath & Klessen 2013; Girichidis et al. 2014). Kritsuk et al. (2011) showed that a collapsing spherical cloud with a power-law density distribution, ρ ∝ r− κ, will have a power-law N-PDF with a slope of p = −2/(κ−1). The power-law slopes that we observe (see Table 4) indicate κ = 1.9 and 1.5 for the H ii regions and SFCs, respectively. The former is very close to the value κ = 2 of a collapsing isothermal sphere (Shu et al. 1987), suggesting that the density distribution of H ii regions may be dominated by self-gravity. The value of κ = 1.5 we find for SFCs can also be indicative of a collapse slowed down by turbulence-driving effects (Girichidis et al. 2014). We note a caveat in this analysis. Our SFCs and H ii regions are unlikely to be close to spheres and their large sizes make them unlikely to be under general free-fall collapse. However, these regions are composed of numerous smaller ATLASGAL clumps (see Fig. 1) that may be closer to spherical symmetry, and we are averaging the emission of all these smaller clumps. Indeed, the density profile exponent of our SFCs is similar to that found by Beuther et al. (2002) in a sample of small high mass star-forming objects, which correspond to our definition of SFCs.
Recent works based on Herschel observations have explored possible effects of other processes (e.g. ionising radiation or shock compression) on the N-PDFs of H ii regions (Schneider et al. 2012, 2013; Tremblin et al. 2014). Tremblin et al. (2014) report N-PDFs with two log-normal components. They relate the log-normal component at low column-densities to the turbulent motions of the gas and the component at high-column densities to ionization pressure. They also suggest that the presence of these double-peaked N-PDFs depends on the relative importance of ionizing and turbulent pressures. The total N-PDFs of our H ii regions, composed of 60 individual regions, does not exhibit such behavior. This could originate from a combination of several factors: i) the low-column density component detected by Tremblin et al. (2014) is at column densities of Av ≲ 6 mag. These column densities are generally filtered out from the ATLASGAL data; ii) the size-scales of the molecular clouds studied in Tremblin et al. (2014) and this work are different and it may happen that the ionisation front of the H ii regions is not spatially resolved in our observations.
The above models offer an attractive possibility to link the observed N-PDF tails to self-gravitating gas in molecular clouds. However, it has not yet been shown observationally that the power-law parts would be definitely caused by self-gravity; an alternative interpretation has been proposed by Kainulainen et al. (2011a) who suggested that the overall pressure conditions in the clouds may play a role in producing the observed power-law-like behavior in low-mass molecular clouds.
4.2. Dense gas mass fraction in molecular clouds
With our cloud sample, we are able to study the DGMFs of molecular clouds over a relatively wide dynamic range of column densities and separately in various evolutionary classes. The continuous DGMF functions (Eq. (2)) allow for a more complete census of the dense gas in the clouds than the analysis of the ratios of two tracers, e.g., of CO emission and dust emission. We find that the DGMFs of H ii regions are shallower than those of SFCs and SLCs. This suggests a direct relation between the star-forming activity of molecular clouds and their relative dense gas mass fraction. Similar results have also been previously found in nearby regions (Lada et al. 2009, 2010; Kainulainen et al. 2009; Kainulainen & Tan 2013) and filmentary clouds (André et al. 2010).
We detect a clear correlation between the DGMF slope and cloud mass (see Fig. 8). Previously, Battisti & Heyer (2014) found no correlation between molecular cloud mass and the dense gas fraction in a large sample of molecular clouds. They defined the dense gas fraction as the ratio of dust emission-derived mass, traced with 1 mm flux, above AV = 9.5 mag to CO-derived mass: 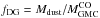 . Their result imply that there is no correlation between the mass of CO-traced gas (AV ~ 3−8 mag) and the mass of gas at column densities AV> 9 mag. Unfortunately, we do not measure the CO mass of our MCs and therefore we cannot directly compare our results with those of Battisti & Heyer (2014). The correlation we find between the molecular cloud masses and the slope of DGMFs suggests that the dense gas fraction depends on the mass of moderately dense gas (AV ≳ 10 mag) rather than the CO mass of the clouds.
. Their result imply that there is no correlation between the mass of CO-traced gas (AV ~ 3−8 mag) and the mass of gas at column densities AV> 9 mag. Unfortunately, we do not measure the CO mass of our MCs and therefore we cannot directly compare our results with those of Battisti & Heyer (2014). The correlation we find between the molecular cloud masses and the slope of DGMFs suggests that the dense gas fraction depends on the mass of moderately dense gas (AV ≳ 10 mag) rather than the CO mass of the clouds.
Lada et al. (2010, 2012) suggested that star formation rates depend linearly on the amount of dense gas in molecular clouds: ΣSFR ∝ fDGΣmass, with fDG = M(AV> 7 mag) /Mtot. Combining this relation with Gutermuth et al. (2011), who derived the relation 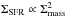 , suggests fDG ∝ Σmass. We find that this correlation indeed exists in the range Σmass = 50−200 M⊙ pc-2 (see Fig. 9). At higher surface densities the relationship flattens at fDG ≅ 0.8, suggesting that the maximum amount of dense gas that a MC can harbor is around 80% of its total mass. Consequently, the maximum ΣSFR of a molecular cloud is reached at fDG ≅ 0.8. This value depends on the definition of the column density threshold (
, suggests fDG ∝ Σmass. We find that this correlation indeed exists in the range Σmass = 50−200 M⊙ pc-2 (see Fig. 9). At higher surface densities the relationship flattens at fDG ≅ 0.8, suggesting that the maximum amount of dense gas that a MC can harbor is around 80% of its total mass. Consequently, the maximum ΣSFR of a molecular cloud is reached at fDG ≅ 0.8. This value depends on the definition of the column density threshold (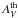 ) of the dense gas becoming lower for higher values of
) of the dense gas becoming lower for higher values of 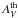 . The spatial filtering of ATLASGAL data (see Appendix A) results in overestimated fDG values. We therefore propose fDG ≅ 0.8 as an upper limit to the actual maximum fDG of a MC. The overestimation of the fDG values derived above can be studied using DGMFs. In general, DGMFs have been shown to follow an exponential function, ∝eαAV, down to low column densities (Kainulainen et al. 2009; Kainulainen & Tan 2013). We adopted the α values calculated in Sect. 3.1.3 and integrated the exponential DGMF in the range AV = 0−7 mag to obtain an estimate of fDG. The result is shown with crosses in bottom panel of Fig. 9. The mean overestimation of fDG in SFCs and H ii regions is 2 and ~1.3 respectively. We did not include the SLCs in this experiment because their reliability limit is AV = 9 mag and therefore they have fDG = 1 (i.e. all its mass is enclosed in regions AV> 7 mag).
. The spatial filtering of ATLASGAL data (see Appendix A) results in overestimated fDG values. We therefore propose fDG ≅ 0.8 as an upper limit to the actual maximum fDG of a MC. The overestimation of the fDG values derived above can be studied using DGMFs. In general, DGMFs have been shown to follow an exponential function, ∝eαAV, down to low column densities (Kainulainen et al. 2009; Kainulainen & Tan 2013). We adopted the α values calculated in Sect. 3.1.3 and integrated the exponential DGMF in the range AV = 0−7 mag to obtain an estimate of fDG. The result is shown with crosses in bottom panel of Fig. 9. The mean overestimation of fDG in SFCs and H ii regions is 2 and ~1.3 respectively. We did not include the SLCs in this experiment because their reliability limit is AV = 9 mag and therefore they have fDG = 1 (i.e. all its mass is enclosed in regions AV> 7 mag).
Our data can also help to understand the SFR – dense gas mass relation suggested by Lada et al. (2012). The SFR – dense gas mass relation shows significant scatter of star formation rates for a given dense gas mass, about 0.6 dex (see Fig. 2 Lada et al. 2012 and Fig. 10). This scatter shows that not all clouds with the same amount of dense gas form stars with the same rate. To gain insight into this, we calculated the dense gas mass fractions and star formation rates for our regions as defined by Lada et al. (2012), i.e., SFR = 4.6 × 10-8fDGMtotMsun yr-1. Figure 10 shows the SFR – dense gas mass relation with data points from Lada et al. (2010). The figure also shows the mean SFR of our regions in six mass bins, with error bars showing the relative standard deviation of fDG. The standard deviations are also listed in Table 7. The relative standard deviation of fDG over the entire mass range of our regions is 0.71, which is slightly higher than the relative scatter of SFR in Lada et al. (2012), fDG = 0.56. We conclude that the scatter in star formation rates for a given dense gas mass can originate from differences in dense gas fractions, i.e., in the total masses of clouds for a given dense gas mass. This, in turn, suggests that the dense gas mass is not the only ingredient affecting the star formation rate, but the lower-density envelope of the cloud also plays a significant role. However, we note the caveat that ATLASGAL filters out low-column densities, which may make the dense gas fractions we derive not comparable with those in Lada et al. (2012), derived using dust extinction data.
 |
Fig. 10 SFR as defined in Lada et al. (2012) for different mass ranges of SFCs and H ii regions. Red crosses show data from Lada et al. (2012). Solid black vertical lines show the standard deviation, σ, for each mass bin for our study. Black dashed line shows the constant value fDG = 1. |
Statistics of fDG in this work and in Lada et al. (2012).
4.3. Evolutionary time-scales of the evolutionary classes as indicated by their N-PDFs
If N-PDFs evolve during the lives of molecular clouds, could they give us information about the evolutionary timescales of the clouds in the three classes we have defined? Girichidis et al. (2014) have developed an analytical model which predicts the evolution of the ρ-PDFs of a system in free-fall collapse. They estimate the relative evolution time-scale, tE, from the free-fall time at the mean density, 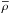 , of the molecular cloud,
, of the molecular cloud, 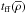 , and the density at which the ρ-PDFs begin to show a power-law shape, ρtail
, and the density at which the ρ-PDFs begin to show a power-law shape, ρtail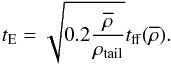 (5)The model also predicts the mass fraction of gas in regions with ρ>ρtail. We denote this mass as Mdense.
(5)The model also predicts the mass fraction of gas in regions with ρ>ρtail. We denote this mass as Mdense.
Since our work is based on column densities instead of volume densities, we need to write Eq. (5) in terms of column densities. To this aim, we assume a ratio between 2D and 3D variances, 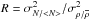 . This relation is also valid for the ratios
. This relation is also valid for the ratios 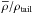 and
and 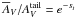 , where
, where 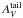 is the column density value at which the N-PDF becomes a power-law and st is the mean normalized
is the column density value at which the N-PDF becomes a power-law and st is the mean normalized 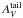 . Then, Eq. (5) can be written as
. Then, Eq. (5) can be written as 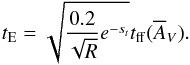 (6)This equation allows us to estimate the evolutionary time-scale of a molecular cloud using two observable quantities, namely
(6)This equation allows us to estimate the evolutionary time-scale of a molecular cloud using two observable quantities, namely 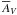 and
and 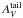 . The factor R is still not well constrained. Kainulainen et al. (2014) obtained observationally a value of R ~ 0.4 while Brunt et al. (2010) obtained R = [0.03,0.15] in MHD turbulence simulations without gravity. In the following we use the observationally derived value, R = 0.4, to estimate the time-scales of our three evolutionary classes. We estimate the uncertainty in the time-scales as the relative uncertainty between R = 0.4 and R = 0.15, which is roughly 30%.
. The factor R is still not well constrained. Kainulainen et al. (2014) obtained observationally a value of R ~ 0.4 while Brunt et al. (2010) obtained R = [0.03,0.15] in MHD turbulence simulations without gravity. In the following we use the observationally derived value, R = 0.4, to estimate the time-scales of our three evolutionary classes. We estimate the uncertainty in the time-scales as the relative uncertainty between R = 0.4 and R = 0.15, which is roughly 30%.
We find that our H ii and SFCs classes have evolutionary time-scales tE,H ii = tE,SFC = 0.4 ± 0.1tff and their relative mass of gas in regions with s>st are Mdense,H ii ~ 30 ± 0.05% and Mdense,SFC ~ 10 ± 0.06% where the uncertainties were obtained from the 1σ uncertainties in st (see Sect. 3.1.1). Since the N-PDF of the SLCs has no power-law tail, we calculated an upper limit of their evolutionary time-scale by using the largest extinction in their N-PDFs as a lower limit, st> 1.2. We obtained tE,SLC< 0.3 ± 0.1tff.
Evolutionary time-scales.
The above relative time-scales can be used to estimate absolute time-scales if the free-fall time is known. We estimate the free-fall time of each evolutionary class as 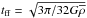 . The mean density of each class was estimated using their mean masses and effective radii7 and assuming spherical symmetry. We find that the mean evolutionary time-scale for our H ii regions is tE,H ii = 0.7 ± 0.2 Myr, and the time-scale of SFCs is tE,SFC = 0.3 ± 0.1 Myr. SLCs have the shortest time-scales, tE,SLC< 0.1 ± 0.03 Myr. We note that the absolute time-scales are measured using the onset of the gravitational collapse in the molecular cloud as t = 0 and that they were specifically estimated independently for each of the three classes of clouds defined in this work.
. The mean density of each class was estimated using their mean masses and effective radii7 and assuming spherical symmetry. We find that the mean evolutionary time-scale for our H ii regions is tE,H ii = 0.7 ± 0.2 Myr, and the time-scale of SFCs is tE,SFC = 0.3 ± 0.1 Myr. SLCs have the shortest time-scales, tE,SLC< 0.1 ± 0.03 Myr. We note that the absolute time-scales are measured using the onset of the gravitational collapse in the molecular cloud as t = 0 and that they were specifically estimated independently for each of the three classes of clouds defined in this work.
Do the above results agree with previous time-scale estimations? The evolutionary time-scale of our SLC sample is within the range of collapse life-times derived in other studies. For example, Tackenberg et al. (2012) derived a life-time of 6 × 104 yr and Ragan et al. (2013), 7−17 × 104 yr for the starless core phase. Furthermore, Csengeri et al. (2014) found a time-scale of 7.5 ± 2.5 × 104 yr for massive starless clumps in the Galaxy using ATLASGAL data. In all these studies, as well as in the present paper, the starless clumps are massive enough to be able to harbor high-mass star-forming activity. Similar evolutionary time-scales have also been found in regions that are more likely to only form low-mass stars, e.g., in Perseus (Walker-LaFollette et al. 2014). The SFC evolutionary time-scale is close to recent age estimates of Class 0+1 protostars, ~0.5−0.4 Myr (Dunham et al. 2014, Table 1). H ii regions are subject to other physical processes apart from gravity, such as Rayleigh-Taylor (RT) instabilities involved in the expansion of the H ii regions and shocks due to stellar feedback. These processes make this simple evolutionary model hardly applicable to them and we therefore do not discuss the evolutionary time obtained for H ii regions further.
Finally, we mention several caveats associated with the time-scales derived above. The mean column density used in Eq. (6) corresponds only to the mean observed column density and not necessarily to the actual mean column density that should be used in Eq. (6). In addition, the factor, R, relating 2D and 3D variances of mean normalized densities is still not well constrained. Furthermore, this model assumes a single cloud undergoing free-fall collapse. While this assumption can be true for the SLCs, it is unlikely to be the case in SFCs. As mentioned in Sect. 4.1, we assume that the smaller ATLASGAL clumps which compose each SFC region are close to spherical symmetry. With these caveats, we only aim to study the evolutionary time-scales in terms of orders of magnitude. Considering these caveats, we conclude that the method of estimating evolutionary time-scale presented agrees with independently derived typical ages for SLCs and SFCs.
5. Conclusions
We have used ATLASGAL 870 μm dust continuum data to study the column density distribution of 330 molecular clouds molecular clouds that we divide in three evolutionary classes: starless clumps (SLCs), star-forming clouds (SFCs), and H ii regions. Our large sample of molecular clouds allows us to study their column density distributions at Galactic scale for the first time. We study the column density distributions of the clouds over a wide dynamic range AV ~ 3−1000 mag, spanning a wide range of cloud masses (102−105M⊙). In the following we summarize the main results obtained.
-
The total N-PDFs of SLCs is well described by a log-normal function with a width of about σs ~ 0.5. The total N-PDF of SFCs and H ii regions show power-law tails at high column densities, with H ii regions having a shallower slope. These observations agree with a picture in which the density distribution of SLCs is dominated by turbulent motions. The SFCs are significantly affected by gravity, although turbulence may still play a role in structuring the clouds. The density distributions of H ii regions are consistent with gravity-dominated media. Our statistical sample shows that this picture, earlier observed in clouds of the Solar neighborhood, is relevant also at Galactic scale.
-
DGMFs of SLCs are well described by exponential functions with exponent αexp = −0.1. The DGMFs of H ii regions and SFCs are better described by power-laws with exponents of β = −1.0 and β = −2.1 respectively. The DGMF shape depends on cloud mass, being shallower for the most massive clouds and steeper for the less massive clouds. This dependence exists in all evolutionary classes.
-
We find an approximately linear correlation fDG ∝ Σmass for Σmass = 50−200 M⊙ pc-2, valid for all evolutionary classes. This relation flatens at fDG ≅ 0.8 in MCs, suggesting that the maximum star-forming activity in MCs is reached at fDG ≅ 0.8. We also find that the intrinsic scatter of fDG is (~0.7 dex) is similar to the scatter seen in the relation SFR – dense gas mass of Lada et al. (2010, 2012). This suggests that both, the dense gas mass and the lower-density envelope of the cloud, play a significant role in affecting the star formation rate.
-
We estimate the evolutionary time-scales of our three classes using an analytical model which predicts the evolution of the PDF of a cloud in free-fall collapse (Girichidis et al. 2014). We found tE ≲ 0.1 Myr, tE ~ 0.3 Myr, and tE ≲ 0.7 Myr for SLCs, SFCs, and H ii regions, respectively. Both time-scales agree with previous, independent age estimates of corresponding objects, suggesting that molecular cloud evolution may indeed be imprinted into the observable N-PDF functions. H ii regions show a complexity of physical processes that make this model hard to apply to them.
Online material
Appendix A: Comparing ATLASGAL and Herschel
Every observational technique to estimate N-PDFs has its own limitations. The ATLASGAL data reduction process filters out extended emission from the maps in scales larger than 2.5′ (Schuller et al. 2009). The FIR emission observed by Herschel (Pilbratt et al. 2010) is very likely to be contaminated by emission from dust unrelated to the cloud of interest (Schneider et al. 2015b). We explore now how the N-PDFs derived with Herschel and ATLASGAL differ. We do this for one example object of each evolutionary class using the H ii region M17 (#248), the SFC IRDC G11.11-0.12 (#54) and the SLC (#54c).
The Herschel data of the SFC the SLC were taken as part of the Herschel guaranteed time key program Earliest Phases of Star formation (Henning et al. 2010; Ragan et al. 2012, EPOS). The data of M17 was obtained from the Herschel program Hi-GAL (Molinari et al. 2010). We used the three SPIRE (Griffin et al. 2010) wavelengths (250 μm, 350 μm and 500 μm), reduced using scanamorphos v23 (Roussel 2013), and PACS 160 μm (Poglitsch et al. 2010), reduced using HIPE v12 (Ott 2010). In the flux calibration process, the Planck zero-point correction was applied only to the M17 data.
We derived the column density and temperature maps for each of the three selected regions through a pixel-to-pixel modified greybody fit to the four Herschel continuum maps, all of them smoothed to a resolution of 36″. For consistency with the ATLASGAL data analysis, we adopted the dust opacity by interpolation of the Ossenkopf & Henning (1994) dust model of grains with thin ice mantles and a mean density of n = 106 cm-3. The mean uncertainty obtained in our greybody fitting technique for the temperature maps is ~2.5 K. The relative uncertainty of the column density maps is ~40%. The column density maps are shown in Fig. A.1.
The area over which a molecular cloud shows significant emission is different in ATLASGAL and Herschel column density maps. We face this issue by comparing the N-PDFs over two different areas: the area over which ATLASGAL shows significant emission, which we will refer to as dense gas area (white contours in Fig. A.1 and panels in the mid row in the same figure). We also compare the N-PDFs derived from the entire areas shown in Fig. A.1.
We now describe how the N-PDFs derived from Herschel and ATLASGAL data look like. In the SFC and the H ii region Herschel-derived N-PDFs show a clear log-normal and power-law combination. This combination is seen in both cases of area selection: dense gas area and whole map. The ATLASGAL-derived N-PDFs of the SFC and the H ii region also have power-law tails at high column densities but they do not show a log-normal distribution at low column densities. In both cases, Herschel-derived N-PDFs do not probe regions with AV ≲ 10 mag. Both, the ATLASGAL-derived and Herschel-derived N-PDFs of the SLC are unfortunately dominated by noise, making a comparison impossible. At 36″ of resolution the SLCs do not have enough pixels for an analysis.
The absence of column densities AV ≲ 10 mag in the Herschel data-set is very likely related to the line-of-sight contamination. To compare N-PDFs of the datasets without this contamination, we subtracted the background emission from the Herschel column density maps. We estimated the magnitude of the line-of-sight contamination averaging the Herschel-derived column densities inside the white boxes shown in the top row of Fig. A.1. We found 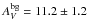 mag in the SFC and SLC regions and
mag in the SFC and SLC regions and 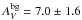 mag in the H ii region. The background-subtracted N-PDFs are shown in the fourth and fifth rows of Fig. A.1 for the whole map and the dense gas area. The background subtraction significantly widens the Herschel-derived N-PDFs in the low column density regime. It has, however, very small effect in the high column-density regime, which is slightly flattened.
mag in the H ii region. The background-subtracted N-PDFs are shown in the fourth and fifth rows of Fig. A.1 for the whole map and the dense gas area. The background subtraction significantly widens the Herschel-derived N-PDFs in the low column density regime. It has, however, very small effect in the high column-density regime, which is slightly flattened.
To estimate the difference between the fitted parameters in the datasets we fitted the power-law tails of the N-PDFs, following the same procedure as in Sect. 3.1.1. The fits were performed in the column density regimes AV> 30 mag and AV> 40 mag in the SFC and H ii region respectively. In all cases, the power-law portion of ATLASGAL is somewhat shallower (pHII,AG = −1.2, pSFC,AG = −2.0) than that obtained for Herschel (pHII,H = −1.6, pSFC,H = −2.3). The power-law slopes obtained in this work for the SFC are shallower than those reported by Schneider et al. (2015a). The difference is probably caused by the different column density ranges used to fit the power-law in the works. When the background component of Herschel is removed, the power-law tails flatten and become much more similar to those observed by ATLASGAL (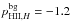 ,
, 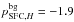 ). Using only the ATLASGAL emission area (middle row of Fig. A.1) or the whole map (bottom row of Fig. A.1) makes no significant difference in the slope of the power-law tails obtained. We conclude that the high-column density power-law parts of the N-PDFs are in good agreement between ATLASGAL and Herschel. The agreement is even better when the background contamination component of Herschel is removed. Note that a background correction to the Herschel column densities is usually necessary, as the diffuse Galactic dust component is significant at the Galactic plane. Therefore, one should consider the background subtracted N-PDF as a better estimate of the N-PDF of the cloud.
). Using only the ATLASGAL emission area (middle row of Fig. A.1) or the whole map (bottom row of Fig. A.1) makes no significant difference in the slope of the power-law tails obtained. We conclude that the high-column density power-law parts of the N-PDFs are in good agreement between ATLASGAL and Herschel. The agreement is even better when the background contamination component of Herschel is removed. Note that a background correction to the Herschel column densities is usually necessary, as the diffuse Galactic dust component is significant at the Galactic plane. Therefore, one should consider the background subtracted N-PDF as a better estimate of the N-PDF of the cloud.
We identify the absence of log-normal components in the ATLASGAL-derived N-PDFs as an effect associated to the spatial filtering in the data reduction process. This effect is significant in both H ii regions and SFCs, being less important in denser regions of molecular clouds where SLC objects lie. Spatial filtering is clearly seen at column densities AV ~ 10−20 mag in Fig. A.1, where the Herschel-derived N-PDFs shows a clear excess compared to the ATLASGAL-derived N-PDFs. Despite the significant differences shown by the N-PDFs derived at low column density regimes, the power-law tails at high column densities are in good agreement, showing the ATLASGAL-derived N-PDFs marginally flatter distributions than the Herschel-derived N-PDFs. Similar results are obtained when the ATLASGAL-derived and Herschel-derived DGMFs are compared.
 |
Fig. A.1 Top row: Herschel-derived column density maps of M17 (H ii region), G11 (SFC) and #53c (SLC), in units of AV. The white contours show the dense gas area (AV> 2 mag, 4.5 mag and 9 mag for the H ii region, SFC and SLC respectively). The white dashed boxes show the regions where the background contamination of Herschel has been calculated. Second row: N-PDFs as seen by Herschel (blue) and ATLASGAL (black) in the maps shown in the top row. The vertical error bars show the Poison standard deviation. The solid lines show the best fit to the power-law tail. Third row: ATLASGAL-derived and Herschel-derived N-PDFs in the dense gas area. Fourth row: background corrected ATLASGAL-derived and Herschel-derived N-PDFs in the whole map area of the top row. The background emission was estimated as the mean column density in the dashed boxes of the first row, seen by Herschel. Bottom row: background corrected N-PDFs evaluated in the dense gas area. |
Appendix B: Effects of the isothermal assumption on the N-PDFs
Obtaining column densities via dust emission maps at sub-mm wavelengths requires the use of the dust temperature (see Eq. (3)). When only one wavelength is available, as in the case of this paper, the most simple assumption is that the dust is isothermal. However, molecular clouds are not isothermal and the isothermal assumption can therefore generate artificial features in the column density distributions of the maps derived with this method. When several wavelengths are available, as in the case of Herschel observations, the line-of-sight averaged temperature and column density distributions can be simultaneously obtained via modified blackbody fitting to the FIR/sub-mm spectral energy distribution.
To study the temperature effects on the resulting N-PDFs we used the Herschel derived temperature distributions in the previous section to reconstruct the ATLASGAL column density maps of the same three regions. The results of this experiment are shown in Fig. B.1. In the H ii region, the isothermal
assumption underestimates the low column density regimes of the N-PDF, which remain practically unaffected at AV> 40 mag. The isothermal N-PDF of the SFC overestimates the low column density regime and remain similar to the N-PDF of the Herschel-derived temperature distribution at AV = 10−90 mag. The isothermal N-PDF in the SLC is shifted to lower column densities.
The isothermal assumption is therefore valid in the high column density regime (i.e. in the power-law tail) of the H ii region and the SFC examples shown here. We note that the relative temperature uncertainties are larger in the coldest regions (T ~ 12−15 K) of molecular clouds (i.e. in the densest regions) and these uncertainties could also result in the underestimate of the N-PDF observed at AV> 90 mag in the SFC. Unfortunately, we cannot quantify the possible differences in the shape of the isothermal and the Herschel-derived temperature distribution N-PDFs of the SLC. The isothermal N-PDF therefore offers a more accurate reproduction of the Herschel-derived temperature distribution N-PDF in the column density regime of the power-law tail than at low-column densities.
 |
Fig. B.1 Isothermal ATLASGAL-derived N-PDFs (black) and N-PDFs derived using ATLASGAL emission maps together with Herschel-derived temperature maps (red). From left to right, H ii region, SFC and SLC. The vertical error bars show the Poison standard deviation. The solid lines show the power-law fit to the data in the column density range covered by the lines. |
Appendix C: MIPSGAL 24 μm maps with ATLASGAL contours and regions
 |
Fig. C.1 Greyscale MIPSGAL 24 μm map of the Galactic plane region comprised between Galactic longitudes l = 10.5−13.5deg. Overlayed yellow contours show 3σ level (0.15 Jy/beam) isocontours of ATLASGAL survey. Red circles and ellipses show our defined H ii regions while molecular cloud regions are shown in blue. Starless clumps are shown as green filled circles. In all cases, size of region markers matches their sizes. |
Appendix D: ATLASGAL maps from starless clumps
 |
Fig. D.1 Dust emission, in Jy/beam, of the starless clumps studied. |
 |
Fig. D.1 continued. |
Appendix E: H II regions
 |
Fig. E.1 Dust emission, in Jy/beam, of the H ii regions studied. |
 |
Fig. E.1 continued. |
 |
Fig. E.1 continued. |
Appendix F: Star-forming clouds
 |
Fig. F.1 Dust emission, in Jy/beam, of the SFC regions studied. |
 |
Fig. F.1 continued. |
 |
Fig. F.1 continued. |
 |
Fig. F.1 continued. |
 |
Fig. F.1 continued. |
Regions studied in this paper.
We note that the existence of the Galactic ring has recently been questioned by Dobbs & Burkert (2012), who proposed a two symmetric spiral arm pattern for the Milky Way as an explanation of observations.
Russeil et al. (2013) quote the equivalent radial density profile (κ), which can be related with the slope of the power-law tail of the N-PDF via p = −2/(κ−1).
Acknowledgments
The work of J.A. is supported by the Sonderforschungsbereich (SFB) 881 “The Milky Way System” and the International Max-Planck Research School (IMPRS) at Heidelberg University. The work of J.K. and A.S. was supported by the Deutsche Forschungsgemeinschaft priority program 1573 (“Physics of the Interstellar Medium”). This research has made use of the SIMBAD database, operated at CDS, Strasbourg, France.
References
- Aguirre, J. E., Ginsburg, A. G., Dunham, M. K., et al. 2011, ApJS, 192, 4 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Alves, J., Lombardi, M., & Lada, C. J. 2014, A&A, 565, A18 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Anderson, L. D., Zavagno, A., Deharveng, L., et al. 2012, A&A, 542, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ballesteros-Paredes, J., Vázquez-Semadeni, E., Gazol, A., et al. 2011, MNRAS, 416, 1436 [NASA ADS] [CrossRef] [Google Scholar]
- Battisti, A. J., & Heyer, M. H. 2014, ApJ, 780, 173 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beuther, H., Schilke, P., Menten, K. M., et al. 2002, ApJ, 566, 945 [NASA ADS] [CrossRef] [Google Scholar]
- Bohlin, R. C., Savage, B. D., & Drake, J. F. 1978, ApJ, 224, 132 [NASA ADS] [CrossRef] [Google Scholar]
- Bronfman, L., Nyman, L.-A., & May, J. 1996, A&AS, 115, 81 [NASA ADS] [Google Scholar]
- Brunt, C. M., Federrath, C., & Price, D. J. 2010, MNRAS, 403, 1507 [NASA ADS] [CrossRef] [Google Scholar]
- Csengeri, T., Urquhart, J. S., Schuller, F., et al. 2014, A&A, 565, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cyganowski, C. J., Whitney, B. A., Holden, E., et al. 2008, AJ, 136, 2391 [NASA ADS] [CrossRef] [Google Scholar]
- Dobbs, C. L., & Burkert, A. 2012, MNRAS, 421, 2940 [NASA ADS] [CrossRef] [Google Scholar]
- Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press) [Google Scholar]
- Dunham, M. K., Robitaille, T. P., Evans, II, N. J., et al. 2011, ApJ, 731, 90 [NASA ADS] [CrossRef] [Google Scholar]
- Dunham, M. M., Stutz, A. M., Allen, L. E., et al. 2014, Protostars and Planets VI, 195 [Google Scholar]
- Ellsworth-Bowers, T. P., Glenn, J., Rosolowsky, E., et al. 2013, ApJ, 770, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Federrath, C., & Klessen, R. S. 2013, ApJ, 763, 51 [NASA ADS] [CrossRef] [Google Scholar]
- Forster, J. R., & Caswell, J. L. 2000, ApJ, 530, 371 [NASA ADS] [CrossRef] [Google Scholar]
- Garay, G., Rodriguez, L. F., Moran, J. M., & Churchwell, E. 1993, ApJ, 418, 368 [NASA ADS] [CrossRef] [Google Scholar]
- Girichidis, P., Konstandin, L., Whitworth, A. P., & Klessen, R. S. 2014, ApJ, 781, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Pineda, J. E., & Schnee, S. L. 2009, ApJ, 692, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Gutermuth, R. A., Pipher, J. L., Megeath, S. T., et al. 2011, ApJ, 739, 84 [NASA ADS] [CrossRef] [Google Scholar]
- Heiderman, A., Evans, II, N. J., Allen, L. E., Huard, T., & Heyer, M. 2010, ApJ, 723, 1019 [NASA ADS] [CrossRef] [Google Scholar]
- Hennebelle, P., & Falgarone, E. 2012, A&ARv, 20, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Henning, T., Linz, H., Krause, O., et al. 2010, A&A, 518, L95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., & Tan, J. C. 2013, A&A, 549, A53 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Henning, T., & Plume, R. 2009, A&A, 508, L35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Alves, J., Beuther, H., Henning, T., & Schuller, F. 2011a, A&A, 536, A48 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Beuther, H., Banerjee, R., Federrath, C., & Henning, T. 2011b, A&A, 530, A64 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Federrath, C., & Henning, T. 2013a, A&A, 553, L8 [Google Scholar]
- Kainulainen, J., Ragan, S. E., Henning, T., & Stutz, A. 2013b, A&A, 557, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kainulainen, J., Federrath, C., & Henning, T. 2014, Science, 344, 183 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S. 2000, ApJ, 535, 869 [NASA ADS] [CrossRef] [Google Scholar]
- Klessen, R. S., & Burkert, A. 2000, ApJS, 128, 287 [NASA ADS] [CrossRef] [Google Scholar]
- Kritsuk, A. G., Norman, M. L., & Wagner, R. 2011, ApJ, 727, L20 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., & Alves, J. F. 2009, ApJ, 703, 52 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Lombardi, M., & Alves, J. F. 2010, ApJ, 724, 687 [NASA ADS] [CrossRef] [Google Scholar]
- Lada, C. J., Forbrich, J., Lombardi, M., & Alves, J. F. 2012, ApJ, 745, 190 [NASA ADS] [CrossRef] [Google Scholar]
- Launhardt, R., Stutz, A. M., Schmiedeke, A., et al. 2013, A&A, 551, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lockman, F. J. 1989, ApJS, 71, 469 [NASA ADS] [CrossRef] [Google Scholar]
- Lockman, F. J., Pisano, D. J., & Howard, G. J. 1996, ApJ, 472, 173 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., & Alves, J. 2001, A&A, 377, 1023 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lombardi, M., Alves, J., & Lada, C. J. 2015, A&A, 576, L1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lumsden, S. L., Hoare, M. G., Urquhart, J. S., et al. 2013, ApJS, 208, 11 [NASA ADS] [CrossRef] [Google Scholar]
- Marshall, D. J., Joncas, G., & Jones, A. P. 2009, ApJ, 706, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, PASP, 122, 314 [NASA ADS] [CrossRef] [Google Scholar]
- Motte, F., & Hennebelle, P. 2009, in EAS PS 34, eds. L. Pagani, & M. Gerin, 195 [Google Scholar]
- Ossenkopf, V., & Henning, T. 1994, A&A, 291, 943 [NASA ADS] [Google Scholar]
- Ostriker, E. C., Stone, J. M., & Gammie, C. F. 2001, ApJ, 546, 980 [NASA ADS] [CrossRef] [Google Scholar]
- Ott, S. 2010, in Astronomical Data Analysis Software and Systems XIX, eds. Y. Mizumoto, K.-I. Morita, & M. Ohishi, ASP Conf. Ser., 434, 139 [Google Scholar]
- Padoan, P., & Nordlund, Å. 2011, ApJ, 730, 40 [NASA ADS] [CrossRef] [Google Scholar]
- Padoan, P., Jones, B. J. T., & Nordlund, A. P. 1997, ApJ, 474, 730 [NASA ADS] [CrossRef] [Google Scholar]
- Peretto, N., & Fuller, G. A. 2010, ApJ, 723, 555 [NASA ADS] [CrossRef] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Poglitsch, A., Waelkens, C., Geis, N., et al. 2010, A&A, 518, L2 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ragan, S., Henning, T., Krause, O., et al. 2012, A&A, 547, A49 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ragan, S. E., Henning, T., & Beuther, H. 2013, A&A, 559, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Robitaille, T. P., Meade, M. R., Babler, B. L., et al. 2008, AJ, 136, 2413 [NASA ADS] [CrossRef] [Google Scholar]
- Roman-Duval, J., Jackson, J. M., Heyer, M., et al. 2009, ApJ, 699, 1153 [Google Scholar]
- Roussel, H. 2013, PASP, 125, 1126 [Google Scholar]
- Rudolph, A. L., Fich, M., Bell, G. R., et al. 2006, ApJS, 162, 346 [NASA ADS] [CrossRef] [Google Scholar]
- Russeil, D., Schneider, N., Anderson, L. D., et al. 2013, A&A, 554, A42 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sadavoy, S. I., Di Francesco, J., André, P., et al. 2014, ApJ, 787, L18 [NASA ADS] [CrossRef] [Google Scholar]
- Scalo, J., Vazquez-Semadeni, E., Chappell, D., & Passot, T. 1998, ApJ, 504, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Csengeri, T., Hennemann, M., et al. 2012, A&A, 540, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., André, P., Könyves, V., et al. 2013, ApJ, 766, L17 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, N., Csengeri, T., Klessen, R. S., et al. 2015a, A&A, 578, A29 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schneider, N., Ossenkopf, V., Csengeri, T., et al. 2015b, A&A, 575, A79 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schuller, F., Menten, K. M., Contreras, Y., et al. 2009, A&A, 504, 415 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shirley, Y. L., Nordhaus, M. K., Grcevich, J. M., et al. 2005, ApJ, 632, 982 [NASA ADS] [CrossRef] [Google Scholar]
- Shirley, Y. L., Huard, T. L., Pontoppidan, K. M., et al. 2011, ApJ, 728, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Shu, F. H., Adams, F. C., & Lizano, S. 1987, ARA&A, 25, 23 [Google Scholar]
- Simon, R., Jackson, J. M., Rathborne, J. M., & Chambers, E. T. 2006, ApJ, 639, 227 [NASA ADS] [CrossRef] [Google Scholar]
- Solomon, P. M., & Rivolo, A. R. 1989, ApJ, 339, 919 [NASA ADS] [CrossRef] [Google Scholar]
- Stutz, A. M., & Kainulainen, J. 2015, A&A, 577, L6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Stutz, A., Launhardt, R., Linz, H., et al. 2010, A&A, 518, L87 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tackenberg, J., Beuther, H., Henning, T., et al. 2012, A&A, 540, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tassis, K., Christie, D. A., Urban, A., et al. 2010, MNRAS, 408, 1089 [NASA ADS] [CrossRef] [Google Scholar]
- Tóth, L. V., Marton, G., Zahorecz, S., et al. 2014, PASJ, 66, 17 [NASA ADS] [Google Scholar]
- Tremblin, P., Schneider, N., Minier, V., et al. 2014, A&A, 564, A106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Urquhart, J. S., Thompson, M. A., Moore, T. J. T., et al. 2013, MNRAS, 435, 400 [NASA ADS] [CrossRef] [Google Scholar]
- Vazquez-Semadeni, E. 1994, ApJ, 423, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez-Semadeni, E., & García, N. 2001, ApJ, 557, 727 [NASA ADS] [CrossRef] [Google Scholar]
- Walker-LaFollette, A., Shirley, Y. L., Amaya, H., et al. 2014, Amer. Astron. Soc. Meet. Abstracts, 223, 454.33 [Google Scholar]
- Walsh, A. J., Hyland, A. R., Robinson, G., & Burton, M. G. 1997, MNRAS, 291, 261 [NASA ADS] [CrossRef] [Google Scholar]
- Wienen, M., Wyrowski, F., Schuller, F., et al. 2012, A&A, 544, A146 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wood, D. O. S., & Churchwell, E. 1989, ApJS, 69, 831 [NASA ADS] [CrossRef] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 MIPSGAL 24 μm map of the Galactic plane between 9deg <l< 10.5deg. Yellow contours indicate the 3σ (0.15 Jy/beam) emission level of the ATLASGAL data. Red and blue ellipses show the H ii regions and SFCs, respectively. SLCs are shown with green filled diamonds. Similar maps for the Galactic plane between 10.5deg <l< 21deg and | b | ≤ 1deg are shown in Appendix C. |
| In the text | |
 |
Fig. 2 Distance distribution of the molecular cloud regions. Black solid line shows the total number of regions. Red dotted line shows the HII regions, the blue dashed line the SFCs, and green filled area the SLCs. Black dashed vertical line at 5 kpc shows the common distance to which we have smoothed the data. |
| In the text | |
 |
Fig. 3 Artist impression of face-on view of the Milky Way (R. Hurt, SSC-Caltech, MPIA graphic, Tackenberg et al. 2012). H ii regions are shown as red circles, star-forming clouds as blue circles and starless clumps as green circles. Circle sizes are proportional to region sizes. The right panel shows a zoom to the region enclosed by the black rectangle in the left panel, where the source density is highest. |
| In the text | |
 |
Fig. 4 Mass distribution of the molecular cloud regions. Filled green area shows mass for starless clumps, dashed blue line shows star-forming clouds and red dashed line shows H ii regions. Masses are given in solar mass units. |
| In the text | |
 |
Fig. 5 Mean column density, |
| In the text | |
 |
Fig. 6 Total mean normalized column density PDFs of H ii regions (left), SFCs (center) and SLCs (right). All panels: horizontal axis show mean normalized column densities, |
| In the text | |
 |
Fig. 7 Mean DGMFs of H ii regions (left), SFCs (center) and SLCs (right). Solid colored lines show mean normalized DGMFs. DGMFs were normalized to the reliability limit of each evolutionary class: AV = 2, 4, 9 mag for H ii regions, SFCs and SLCs, respectively. Colored dashed lines show the fit of the DGMFs with exponential functions. Dashed-dotted colored lines show fits with power-law tails in the higher AV range. Grey shaded regions show statistical poisson errors of the DGMFs. Small box in left panel shows the whole mean DGMF of H ii regions up to AV = 1000 mag. |
| In the text | |
 |
Fig. 8 Mass-binned average DGMFs for each evolutionary class. Each line shows the DGMF for each of the mass intervals listed in the corresponding panel and defined in Table 5. Dotted lines, dotted-dashed lines, dashed lines, and solid lines progress from less to most massive bins, respectively. The DGMFs were normalized following the procedure described in Sect. 3.1.2 and shown in Fig. 7. |
| In the text | |
 |
Fig. 9 Top: relationship between the mass of the regions [M⊙] and the exponent of the exponential fit to the DGMFs (αexp). Black solid line shows the best fit to the data and the shaded region shows its σ error. The dotted and dashed lines show the best fit when the most massive H ii regions are removed. Colors indicate the evolutionary class of each point as indicated. Middle: relationship between mass of the regions and the slope of the power-law range of the DGMFs. Black line shows the best fit to the data and the shaded region shows its σ error. Bottom: relationship between the mean gas mass surface density of the MCs, Σmass, and the dense gas mass fraction of gas, |
| In the text | |
 |
Fig. 10 SFR as defined in Lada et al. (2012) for different mass ranges of SFCs and H ii regions. Red crosses show data from Lada et al. (2012). Solid black vertical lines show the standard deviation, σ, for each mass bin for our study. Black dashed line shows the constant value fDG = 1. |
| In the text | |
 |
Fig. A.1 Top row: Herschel-derived column density maps of M17 (H ii region), G11 (SFC) and #53c (SLC), in units of AV. The white contours show the dense gas area (AV> 2 mag, 4.5 mag and 9 mag for the H ii region, SFC and SLC respectively). The white dashed boxes show the regions where the background contamination of Herschel has been calculated. Second row: N-PDFs as seen by Herschel (blue) and ATLASGAL (black) in the maps shown in the top row. The vertical error bars show the Poison standard deviation. The solid lines show the best fit to the power-law tail. Third row: ATLASGAL-derived and Herschel-derived N-PDFs in the dense gas area. Fourth row: background corrected ATLASGAL-derived and Herschel-derived N-PDFs in the whole map area of the top row. The background emission was estimated as the mean column density in the dashed boxes of the first row, seen by Herschel. Bottom row: background corrected N-PDFs evaluated in the dense gas area. |
| In the text | |
 |
Fig. B.1 Isothermal ATLASGAL-derived N-PDFs (black) and N-PDFs derived using ATLASGAL emission maps together with Herschel-derived temperature maps (red). From left to right, H ii region, SFC and SLC. The vertical error bars show the Poison standard deviation. The solid lines show the power-law fit to the data in the column density range covered by the lines. |
| In the text | |
 |
Fig. C.1 Greyscale MIPSGAL 24 μm map of the Galactic plane region comprised between Galactic longitudes l = 10.5−13.5deg. Overlayed yellow contours show 3σ level (0.15 Jy/beam) isocontours of ATLASGAL survey. Red circles and ellipses show our defined H ii regions while molecular cloud regions are shown in blue. Starless clumps are shown as green filled circles. In all cases, size of region markers matches their sizes. |
| In the text | |
 |
Fig. C.2 Same as Fig. C.1 for Galactic longitudes l = 13.5−16.5deg. |
| In the text | |
 |
Fig. C.3 Same as Fig. C.1 for Galactic longitudes l = 16.5−19.5deg. |
| In the text | |
 |
Fig. C.4 Same as Fig. C.1 for Galactic longitudes l = 19.5−21deg. |
| In the text | |
 |
Fig. D.1 Dust emission, in Jy/beam, of the starless clumps studied. |
| In the text | |
 |
Fig. D.1 continued. |
| In the text | |
 |
Fig. E.1 Dust emission, in Jy/beam, of the H ii regions studied. |
| In the text | |
 |
Fig. E.1 continued. |
| In the text | |
 |
Fig. E.1 continued. |
| In the text | |
 |
Fig. F.1 Dust emission, in Jy/beam, of the SFC regions studied. |
| In the text | |
 |
Fig. F.1 continued. |
| In the text | |
 |
Fig. F.1 continued. |
| In the text | |
 |
Fig. F.1 continued. |
| In the text | |
 |
Fig. F.1 continued. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.