| Issue |
A&A
Volume 580, August 2015
|
|
|---|---|---|
| Article Number | A94 | |
| Number of page(s) | 21 | |
| Section | Extragalactic astronomy | |
| DOI | https://doi.org/10.1051/0004-6361/201424815 | |
| Published online | 07 August 2015 | |
Multi-frequency properties of synthetic blazar radio light curves within the shock-in-jet scenario⋆
1
Max-Planck-Institut für Radioastronomie, Auf dem Hügel 69, 53121
Bonn, Germany
e-mail: cfromm@mpifr.de; lfuhrmann@mpifr.de
2
Departament d’Astronomia i Astrofisica, Universitat de Valencia
C/Dr. Moliner 50, 46100
Burjassot, Valencia, Spain
e-mail:
perucho@uv.es
3
Observatori Astronòmic, Parc Científic, Universitat de
València, C/ Catedràtic José
Beltrán 2, 46980
Paterna ( València), Spain
Received: 15 August 2014
Accepted: 16 December 2014
Context. Blazars are among the most powerful extragalactic objects as a sub-class of active galactic nuclei. They launch relativistic jets and their emitted radiation shows strong variability across the entire electro-magnetic spectrum. The mechanisms producing the variability are still controversial, and different models have been proposed to explain the observed variations in multi-frequency blazar light curves.
Aims. We investigate the capabilities of the classical shock-in-jet model to explain and reconstruct the observed evolution of flares in the turnover frequency – turnover flux density (νm–Sm) plane and their frequency dependent light curve parameters. With a detailed parameter space study, we provide the framework for future, detailed comparisons of observed flare signatures with the shock-in-jet scenario.
Methods. Based on the shock model, we compute synthetic single-dish light curves at different radio frequencies (2.6 to 345 GHz) and for different physical conditions in a conical jet (e.g. magnetic field geometry and Doppler factor). From those we extract the slopes of the different energy loss stages within the (νm–Sm) plane and deduce the frequency dependence of different light curve parameters, such as flare amplitude, time scale, and cross-band delays.
Results. The evolution of the Doppler factor along the jet has the strongest influence on the evolution of the flare and on the frequency dependent light curve parameters. The synchrotron stage can be hidden in the Compton or in the adiabatic stage, depending mainly on the evolution of the Doppler factor, which makes it difficult to detect its signature in observations. In addition, we show that the time lags between different frequencies can be used as an efficient tool to better constrain the physical properties of these objects.
Key words: galaxies: active / quasars: general / galaxies: jets / radiation mechanisms: non-thermal / methods: analytical
Appendix A is available in electronic form at http://www.aanda.org
© ESO, 2015
1. Introduction
Blazars (flat-spectrum radio quasars and BL Lacertae objects) are a sub-class of powerful active galactic nuclei (AGN). They exhibit extreme phenomenological characteristics mostly attributed to small viewing angles with respect to their jet axis (≲20°). Among those, rapid broad-band flux density and polarisation variability, fast superluminal motion, a high degree of polarisation, and a broad-band, double-humped spectral energy distribution (SED) are commonly observed (e.g. Urry 1999).
The origin of the rapid (time scales of days to weeks or months to years) variability in the synchrotron and high-energy branch of blazar SEDs is still a matter of debate. The observed rapid variability probes spatial scales that are often inaccessible even to interferometric imaging and has been explained in terms for example, relativistic shock-in-jet models (e.g. Marscher & Gear 1985; Valtaoja et al. 1992a,b; Stevens et al. 1994; Türler et al. 2000) or colliding relativistic plasma shells (e.g. Spada et al. 2001; Guetta et al. 2004; Mimica et al. 2007; Rueda-Becerril et al. 2014). Quasi-periodicities on time scales of months to years indicate systematic changes in the beam orientation (Camenzind & Krockenberger 1992), possibly related to binary black hole systems, magneto-hydrodynamic instabilities in the accretion disks and/or helical/precessing jets (e.g. Begelman et al. 1980; Villata & Raiteri 1999). Perucho et al. (2012) and Lister et al. (2013) have suggested that the radio emission from jets could be emitted from a portion of the jet cross-section that is brighter owing to instability structures within the jet. Lister et al. (2013) also point out that radio-components that could be associated to shocks travelling through the jet are generally non-ballistic. This fact is revealed at parsec scales, and there is no evidence of this behaviour being extended to more compact scales, where the flares are bright at higher frequencies. If that is the case, the changes in the direction of propagation of the bright features associated to flares would translate into variable flux associated to variations in the Doppler factor.
Different variability models predict different frequency dependencies for various observables in the time domain, such as variability amplitudes, characteristic time scales, or cross-band delays. According to these predictions, different spectral characteristics and evolution are expected for quantities, such as the radio spectral index and the turnover frequency, νm, and turnover flux density, Sm. Previous detailed studies support shocks as the origin of the observed radio variability in cm to mm band blazar light curves: individual source and flare studies in the time and/or spectral domain (e.g. Marscher & Gear 1985; Türler et al. 2000; Fromm et al. 2011; Orienti et al. 2013; Rani et al. 2013), as well as studies of larger samples and/or many individual flares (e.g. Valtaoja et al. 1992b; Stevens et al. 1994; Hovatta et al. 2008; Angelakis et al. 2011; Fuhrmann et al. 2015) often show overall good agreement of the observed flare signatures with the shock-in-jet scenario. However, in order to test the different variability models and their multi-frequency predictions in detail, broad-band radio AGN/blazar monitoring programmes of larger samples are of uttermost importance in providing the necessary constraints for understanding the origin of variability and energy production. The Fermi-GST AGN Multi-frequency Monitoring Alliance (F-GAMMA Program)1 (Fuhrmann et al. 2007, 2014; Angelakis et al. 2010), for instance, has been providing such detailed data sets and observational parameters since 2007, monitoring contemporaneously the total flux density, polarisation and spectral evolution of about 60 Fermi γ-ray blazars at three radio observatories with a cadence of about one month. The overall frequency range spans from 2.64 to 345 GHz (110 mm to 0.8 mm) using the Effelsberg 100-m, IRAM 30-m, and APEX 12-m telescopes at a total of 11 frequency bands.
To provide the framework for future, detailed comparisons of theoretical models and F-GAMMA radio monitoring data, we focus in the current work on the shock-in-jet scenario and study its predictions of frequency dependent light curve parameters as a function of different physical conditions. We perform a parameter space study for conical jets within the shock-in-jet model, where we use different scenarios for the evolution of the magnetic field with the jet radius R, B ∝ R−b, the spectral slope, s, of the relativistic electron distribution with energy E, N ∝ E−s, and the Doppler factor along the jet, δ ∝ R−d. For each set of jet conditions given by b, s, and d, we compute the slopes of the different energy loss stages, namely the Compton, synchrotron, and adiabatic stage and based on these slopes, we calculate synthetic single-dish light curves. From the synthetic light curves we extract frequency dependent single-dish light curve parameters, i.e. flare amplitudes, time scales, and cross-band delays (Marscher & Gear 1985; Fromm et al. 2011). Moreover, we investigate in an additional model the impacts of second-order Compton scattering on those parameters (Björnsson & Aslaksen 2000).
The paper is structured as follows. In Sect. 2 we review the standard shock-in-jet model, the parameter space for the physical conditions in the jet, and our analysis applied to the synthetic light curves. We present the results of this analysis in Sect. 3, Sect. 4 includes the discussion, and in Sect. 5 we list the main conclusions and outlook of this paper.
2. The shock model
We used the classical shock-in-jet model to compute the spectral evolution during a flare within the mm- to cm-wavelength regime (Marscher & Gear 1985; Türler et al. 2000; Fromm et al. 2011). This model assumes that a shock wave is propagating through a conical jet (direct proportionality between the jet radius R and the distance along the jet r, R ∝ rρ, with ρ = 1) and accelerates relativistic particles at the shock front. These particles travel behind the shock front and lose their energy because of different energy loss mechanisms, namely Compton, synchrotron, and adiabatic losses. The energy distribution of the relativistic electrons is assumed to be a power law N(E) = KE−s, with K the normalisation coefficient, E the energy, and s the spectral slope. The evolution of the physical parameters, e.g. the magnetic field, B, the normalisation coefficient K, and the Doppler factor, δ, in the bulk flow are parameterised by power laws 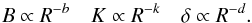 (1)Given these dependencies and the standard synchrotron self-absorption (SSA) theory, the evolution of the turnover-frequency, νm, and the turnover flux density, Sm, can be written as a power law:
(1)Given these dependencies and the standard synchrotron self-absorption (SSA) theory, the evolution of the turnover-frequency, νm, and the turnover flux density, Sm, can be written as a power law: 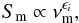 (2)where the exponent ϵi = fi/ni is given below, and the subscript i = 1 corresponds to the Compton, i = 2 to the synchrotron and i = 3 to the adiabatic stage, with:
(2)where the exponent ϵi = fi/ni is given below, and the subscript i = 1 corresponds to the Compton, i = 2 to the synchrotron and i = 3 to the adiabatic stage, with: ![\begin{eqnarray} \label{an1}n_1&=&-(b+1)/4-d(s+3)/(s+5) \\ n_2&=&-[2k+b(s-1)+d(s+3)]/(s+5)\\ \label{n3}n_3&=&-[2(k-1)+(b+d)(s+2)]/(s+4)\\ f_1&=&[(11-b)/8]-[d(3s+10)/(s+5)]\\ f_2&=&2-[5k+b(2s-5)+d(3s+10)]/(s+5)\\ \label{f3}f_3&=&[2s+13-5k-b(2s+3)-d(3s+7)]/(s+4). \end{eqnarray}](/articles/aa/full_html/2015/08/aa24815-14/aa24815-14-eq27.png) In the following, we label ϵ1 = ϵC(ompton), ϵ2 = ϵS(ynchrotron) and ϵ3 = ϵA(diabatic).
In the following, we label ϵ1 = ϵC(ompton), ϵ2 = ϵS(ynchrotron) and ϵ3 = ϵA(diabatic).
In addition to the evolution of the flare in the turnover frequency-turnover flux density 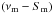 plane, the temporal evolution of the turnover frequency and the turnover flux density can be computed:
plane, the temporal evolution of the turnover frequency and the turnover flux density can be computed:  where ξ = (2dρ + 1) /ρ (see, e.g. Fromm et al. 2011, for a detailed derivation). The proportionality constants in Eqs. (2), (9), and (10) can be calculated by using the turnover frequency and the turnover flux density at the end of the Compton stage (νm,c,Sm,c), the duration of the Compton stage, tc2, and a given set of exponents (s, b, k, d, and ρ). Some estimates for the end of the Compton stage could be, for example, extracted from blazar single-dish monitoring data of the F-GAMMA Program.
where ξ = (2dρ + 1) /ρ (see, e.g. Fromm et al. 2011, for a detailed derivation). The proportionality constants in Eqs. (2), (9), and (10) can be calculated by using the turnover frequency and the turnover flux density at the end of the Compton stage (νm,c,Sm,c), the duration of the Compton stage, tc2, and a given set of exponents (s, b, k, d, and ρ). Some estimates for the end of the Compton stage could be, for example, extracted from blazar single-dish monitoring data of the F-GAMMA Program.
Once the temporal evolution of the turnover frequency and the turnover flux density is given, we can compute the single-dish light curves using an approximation for the SSA spectrum: 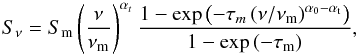 (11)where τm ≈ 3/2 [ (1−8α0/ 3αt)1/2−1 ] is the optical depth at the turnover frequency, Sm is the turnover flux density, νm is the turnover frequency, and αt and α0 are the spectral indices for the optically thick and optically thin parts of the spectrum, respectively.
(11)where τm ≈ 3/2 [ (1−8α0/ 3αt)1/2−1 ] is the optical depth at the turnover frequency, Sm is the turnover flux density, νm is the turnover frequency, and αt and α0 are the spectral indices for the optically thick and optically thin parts of the spectrum, respectively.
The spectral shape is determined by two additional break frequencies, one at low frequencies, νl, and a high frequency break, νh. For frequencies lower than νl the optically thick spectral index is given by αt = 5/2 whereas at higher frequencies the value for the optically thick spectral index is computed from the shock parameters of the adiabatic stage (αt = f3/n3). This low frequency break is motivated by the superposition of individual spectra with αt = 5/2 emitted from regions close to the shock front which leads to a flattening of the overall spectrum. Throughout the temporal evolution of the flare, νl is set as a constant fraction, ζ, of the turnover frequency, νm (see Türler et al. 2000). Since we are not fitting the model to the flare of an individual blazar, we assume ζ = 0.6 throughout the paper.
At frequencies higher than νh the optically thin spectral index, α0 steepens by −0.5 due to synchrotron losses (see, e.g. Marscher & Gear 1985). This break frequency depends on the energy of the relativistic electron distribution and on the magnetic field. Using the parameterisation of the energy and the magnetic field in terms of the jet radius, the evolution of the break frequency can be written as: 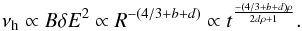 (12)Throughout the paper we assume that the break frequency is initially around 1012–1013 Hz and evolves according the above stated relation.
(12)Throughout the paper we assume that the break frequency is initially around 1012–1013 Hz and evolves according the above stated relation.
Following Türler et al. (2000) we include an additional flattening of the optically thin spectral index, α0, from −s/ 2 to −(s−1)/2. This transition occurs usually during the transition from the synchrotron to the adiabatic stage and is modelled by 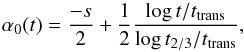 (13)where t2/3 is the transition time from the synchrotron to the adiabatic stage and ttrans is the time for the start of the spectral flattening, assuming ttrans<t2/3. Since t2/3 depends on the conditions in the jet, the transfer time is dynamically obtained in our model in order to obey the conditions above. See the top panel of Fig. 1 as an example for the influence of the break frequencies and the flattening of α0 on the spectral shape.
(13)where t2/3 is the transition time from the synchrotron to the adiabatic stage and ttrans is the time for the start of the spectral flattening, assuming ttrans<t2/3. Since t2/3 depends on the conditions in the jet, the transfer time is dynamically obtained in our model in order to obey the conditions above. See the top panel of Fig. 1 as an example for the influence of the break frequencies and the flattening of α0 on the spectral shape.
 |
Fig. 1 Evolution of the turnover frequency, νm, and the turnover flux density, Sm, for a model with b = 1.5, s = 2.5, ρ = 1, k = 3.0, and d = 0. The top panel shows the evolution of the flare in the (νm–Sm) plane (the time evolution is from the bottom right, to the centre and to the bottom left). The black dashed line indicates the path along which νm and Sm (red dots) evolve. The slopes of the different stages are given in the plot. The red lines correspond to SSA spectra computed for different times (position along the spectral evolution path). The middle panel shows the temporal evolution of νm, and the bottom panel displays the temporal evolution of Sm. |
2.1. Shock-in-jet parameters
It is generally assumed that the flare spectrum is superimposed on top of a steady, quiescent spectrum (see Fromm et al. 2011). We model this underlying spectrum using a SSA spectrum with an optically thick spectral index, αt = 5/2. In Table 1 we present the parameters used for both, the quiescent and the flare spectrum. To reduce the amount of free parameters in our analysis, we assume a conical jet (ρ = 1) and a normalisation coefficient of the relativistic electron distribution decreasing adiabatically, which leads to k = 2(s + 2)/3.
Parameters used for the modelling of the spectral evolution.
The remaining free parameters in Eqs. (3)–(8) are related to the evolution of the magnetic field and the Doppler factor with distance, given by b and d, respectively (see Eqs. (3)–(8)), and the spectral slope of the relativistic electron distribution, s. Parameter b gives also information about the structure of the magnetic field in the flow: if the magnetic field is toroidal and if we assume an ideal plasma (implying that the magnetic field is frozen to the particles), b is equal to 1. Similarly, a poloidal magnetic field leads to b = 2. Consequently, the exponent for the evolution of the magnetic field varies between 1 <b< 2. In the case of the spectral slope we study values between 2 <s< 3 (and thus 2.7 <k< 3.3), which gives the range of observed spectral slopes. Finally, the influence of the Doppler factor δ on the spectral evolution is studied for values between d = −0.45 to d = 0.45.This range is motivated by the assumption that the flux density should decrease with frequency in the Compton stage (ϵCompton< 0). Solving the expression for ϵCompton (ϵC, hereafter) for the maximum allowed value of d that gives ϵC = 0, we obtain d = 0.45. For the lower limit of d, we use a value of d = −0.45 leading to a symmetric parameter range for d. According to our definition (Eq. (1)), we thus investigate Doppler factors increasing along the jet for −0.45 <d< 0 and decreasing for 0 <d< 0.45, whereas d = 0 denotes constant Doppler boosting along the jet.
The range for the exponents and the values of the relevant parameters at the end of the Compton stage, as observed by the F-GAMMA Program, are summarised in Table 1. The latter are obtained from the variability and spectral analysis of the first 2.5 years of F-GAMMA monitoring data at 2.6 to 228 GHz demonstrating that maximum flux variations usually occur at mm wavelengths (Fuhrmann et al. 2014). Based on the results of the F-GAMMA monitoring, we compute the variability amplitude for all monitored sources. The peak of the variability amplitude is typically placed at frequencies between 43 GHz and 142 GHz. Therefore, we use 86 GHz as a reasonable estimate for the end of the Compton stage. For the end of the Compton stage, tc, we use the typical flare rise time (on-set of the flare to peak of the flare) at mm-wavelength which is roughly around 0.05 yr. For most of the sources, the peak of the quiescent spectrum is out of the frequency range of the F-GAMMA monitoring. Therefore, we assume a low turnover frequency (νm,q = 0.1 GHz) and turnover flux density of Sm,q = 5.4 Jy and a spectral index, αq = −0.5. The reported values are first order estimates and could be improved by detailed modelling of the individual sources within the F-GAMMA monitoring which is out of the scope of this paper.
In Fig. 1 we present an example of a flare using d = 0 (constant Doppler factor), b = 1.5 (helical field), s = 2.5, k = 3.0 (fixed by s following the assumption of adiabatic expansion), and ρ = 1.0 (conical jet). The top panel displays the evolution of the flare in the turnover frequency – turnover flux density (νm − Sm) plane. Some example SSA spectra at different times during the flare are shown, including the low and high frequency spectral breaks.
 |
Fig. 2 Example for the analysis of the synthetic single-dish light curves. Top panel: the single-dish multi-frequency light curves (2.6 to 345 GHz) computed for b = 1.5, s = 2.5, k = 3.0, ρ = 1.0, and d = 0 (see also Fig. 1). Bottom panels, from left to right: flare amplitudes, flare time scales and cross-band delays. The solid lines correspond to power law fits and the exponent is given in the plots. |
The middle and bottom panels show the temporal evolution of the turnover frequency, νm, and the turnover flux density, Sm, respectively. The flare evolution along the three different energy loss stages can be best seen in the (νm–Sm) plane (red circles along the dashed line in Fig. 1, top). The flare starts at high turnover frequency and low turnover flux density, and, as long as Compton losses are the dominant energy loss mechanism, the turnover frequency decreases while the flux density increases (see middle and bottom panels for t< 0.05 yr). In the synchrotron stage (0.05 yr <t< 0.1 yr) the turnover flux density is constant (only for certain sets of parameters, see Appendix) and the turnover frequency continues decreasing, this leads to a plateau in the (νm–Sm) plane. In the final stage of the shock evolution, the main losses are due to the adiabatic expansion of the jet and both, turnover frequency and turnover flux density decrease (t> 0.1 yr).
2.2. Synthetic light curve analysis
We produced synthetic total flux density light curves at different radio frequencies by sweeping through the parameter space of exponents b, s, and d, as given in Table 1. These light curves are similar to those typically acquired by multi-frequency single-dish blazar monitoring programmes (the F-GAMMA Program for instance). In total we calculated light curves for twelve “standard” radio frequency bands, namely 2.6 GHz, 4.8 GHz, 8.3 GHz, 10.5 GHz, 14.6 GHz, 23 GHz, 32,GHz, 43 GHz, 86.2 GHz, 142.3 GHz, 228.9 GHz, and 345 GHz. In addition, we extracted a series of multi-frequency parameters from each set of light curves that could be compared to single-dish observations. Our aim was to produce a catalogue of spectral evolution types that could be used as patterns to derive jet parameters from observed light curves. The parameters that we propose are the following:
-
flare amplitudes: in order to characterise the frequency dependent strength of the synthetic flares, we compute the light curve standard deviations σs from the ground values in Fig. 2 and apply a power law fit with frequency σ(S) ∝ νϵflare amp.. Since the flare amplitudes show a rising and a decaying part, we apply a power law fit to each part separately;
-
flare time scales: the time scale of a flare can be obtained from the rising and/or from the decaying edge of the individual light curves. The rising time scale of a given flare is obtained as Δt = tmax − tmin,r (see also Fig. 2), with the time between the start of flux density increase (tmin,r) and the time at the flare maximum (tmax). Whereas the decaying time scale is computed as Δt = tmin,d − tmax, with tmin,d>tmax the time required to obtain quiescent flux density (see Fig. 2). We extract these two time scales from the light curves and fit the obtained data with a power law, Δt ∝ νϵflare time;
-
cross-band delays: in general, there is a delay between the flux density peaks at different frequencies. In order to quantify these multi-frequency delays, we compute the time difference between the flux density peak at our highest frequency (345 GHz) and the flux density peaks of the other frequencies. The growth of the cross-band delays with decreasing frequency was approximated with a power law fit (τ345 − νi ∝ νϵdelay).
2.3. An example
In Fig. 2 we show the analysis of the synthetic light curves computed for the set of parameters also used in Fig. 1: b = 1.5, s = 2.5, k = 3.0, ρ = 1.0, and d = 0. While Fig. 1 shows the evolution of νm and Sm as well as example spectra during the evolution of the flare, the upper panel of Fig. 2 presents the computed single-dish light curves from 2.6 GHz to 345 GHz. In this panel, the measure of the light curve parameters (flare amplitudes, time scales and cross-band delays) is indicated. The high-frequency light curves (ν ≥ 86 GHz) show a rapid rise and reach their peak flux density nearly simultaneously. The increase in the time delay between the highest frequency (here 345 GHz) and the lower frequency light curves (ν< 86 GHz) is clearly visible. The amplitude of the flux density peak first increases towards lower frequencies, peaks around ν = 86 GHz, and then decreases, while the time required for obtaining the flux density peak at each frequency increases with decreasing frequency (best visible at 2.6 GHz). The analysis of these trends can be found in the bottom panelsof Fig. 2, which show, from left to right, the flare amplitudes σs, time scales Δt, and cross-band delays Δt345 − νi versus frequency. The solid line in each of those panels corresponds to a power law fit (see Sect. 2.2) and the exponents are given in the plots. Notice that for frequencies higher than 43 GHz no delays are obtained for this example.
3. Results
In this Section we present the results for the variation of the slopes of the different energy loss stages in the (νm − Sm) plane, and the corresponding changes of the light curve parameters, as a function of b, s, and d (we recall that ρ = 1 and k = 2(s + 2)/3). Since the range of possibilities given by the different combinations of the parameters is large, we only show the results for selected models where we fixed either b = 1.5 (helical magnetic field) or s = 2.5 (a typical value of a spectral slope), while varying parameter d, which controls the evolution of the Doppler factor. This is motivated by the results being most sensitive to changes in this parameter, as we show below. The results for the entire parameter space can be found in the Appendix.
 |
Fig. 3 Evolution of the flare in the turnover frequency – turnover flux density plane for three different values of d while keeping b = 1.5, s = 2.5, ρ = 1, and k = 3.0 fixed. The slopes of the different stages are given in the plot and are colour-coded. |
 |
Fig. 4 Exponents for the different energy loss stages from left to right: compton (A, D), synchrotron (B, E) and adiabatic stage (C, F). The top panels (A–C) show the variation of the slopes using a fixed spectral slope of s = 2.5 and the bottom panels (D–F) present the changes in the slopes for a fixed helical magnetic field (b = 1.5). The different values for d are colour-coded and can be found in the plot legend. |
3.1. Slopes of the energy loss stages
The results of our modelling show that the evolution of the Doppler factor along the jet, which is controlled by parameter d, has the strongest impact on the variation of the slopes for the different energy loss mechanisms in the (νm − Sm) plane (see the Appendix). Figure 3 shows the changes in the slopes that characterise the different stages, for three values of d (d = −0.3, d = 0, and d = 0.3) while keeping b = 1.5, s = 2.5, and k = 3.0 fixed. We remind the reader that the definition of d in Eq. (1) results into an increasing Doppler factor with distance for d< 0 and a decreasing Doppler factor for d> 0. The slopes of the Compton (ϵCompton, ϵC hereafter) and the adiabatic stage (ϵAdiabatic, ϵA hereafter) increase with d, i.e. the Compton stage flattens while the adiabatic stage steepens for increasing values of d (see Fig. 3). Interestingly, there is a change in the sign of the synchrotron stage (ϵSynchrotron, ϵS hereafter): the slope is positive for d> 0 and negative for d< 0. This implies that the difference between the slopes of the Compton and the synchrotron stage decreases for d< 0 (red line in Fig. 3), which can cause an identification of the latter within the former, while for d> 0 the same happens with the slopes of the synchrotron and the adiabatic stages (blue line in Fig. 3). Consequently, the synchrotron stage could be difficult to identify in single-dish observations. Another important conclusion is that, assuming that the viewing angle to the flaring flow does not change during this time, acceleration of the flow would produce a synchrotron stage with negative slope, whereas a decelerating flow would result into a positive slope.
 |
Fig. 5 High-frequency (86 to 345 GHz) light curves computed for three different values of d while keeping b = 1.5, s = 2.5, ρ = 1, and k = 3.0 fixed. The dashed lines correspond to 345 GHz, the solid ones to 140 GHz and the dot-dashed ones to 86 GHz. See text for more details. |
The dependence of the slopes of the different energy loss stages in the (νm − Sm) plane with parameters b and s, for different values of d (−0.45 <d< 0.45), is presented in Fig. 4. The upper panels show the variation of the slopes with b (1 <b< 2), taking s = 2.5, whereas the bottom panels show the variation of the slopes with s (2 <s< 3), taking b = 1.5. The results can be summarised as follows:
Compton stage (ϵC):
the slope of the Compton stage is not sensitive to changes in b for values larger than about 1.5 (panel A in Fig. 4) or positive values of d, while for (large) negative values of d the Compton stage steepens strongly for values b ≲ 1.5. ϵC also shows little sensitivity with respect to the spectral slope s (panel D in Fig. 4).
Synchrotron stage (ϵS):
while b increases, the slope of the synchrotron stage decreases for jets with d> 0 and increases for jets with d< 0 (panel B in Fig. 4). The slope of this stage increases with increasing s (panel E in Fig. 4).
Adiabatic stage (ϵA):
the slope of the final stage increases with b and s, being slightly more sensitive to the former (see panel C and F in Fig. 4).
 |
Fig. 6 Light curve parameters obtained from synthetic light curves with three different values of d while keeping b = 1.5, s = 2.5, ρ = 1, and k = 3.0 fixed. The panels show from left to right the flare amplitude, the flare time scale and the cross-band delays with respect to the peak of the 345 GHz light curve. The solid lines correspond to the power law fits and the exponents are given in the plots. The values in brackets correspond to the exponents of a power law fit to the decaying regime of flare amplitude and flare time scale. |
 |
Fig. 7 Exponents of the light curve parameters obtained from the synthetic light curves from left to right: flare amplitude, flare time scale and cross band delay exponent. The top panels (A–C) show the variation in the light curve parameters using a fixed spectral slope of s = 2.5 and the bottom panels (D–F) present the changes in the parameters for a fixed helical magnetic field (b = 1.5). The different values for d are colour-coded and can be found in the plot legend. |
 |
Fig. 8 Cross-band delays between 345 GHz and three selected frequencies (from left to right 5 GHz, 15 GHz and 86 GHz). The top panels (A−C) show the variation in the cross-band delays using a fixed spectral slope of s = 2.5 and the bottom panels (D–F) present the changes in the cross-band delays for a fixed helical magnetic field (b = 1.5). The different values used for d are colour-coded and can be found in the plot legend. |
3.2. Light curve parameters
To better understand the results of our analysis with respect to the synthetic single-dish light curves it is necessary to investigate the influence of the shock parameters on the shape of the light curves, especially above 86 GHz. In Fig. 5 we present light curves at 345 GHz (dashed lines), 140 GHz (solid lines), and 86 GHz (dot-dashed lines) for d = 0 (black lines), d = 0.3 (blue lines) and d = −0.3 (red lines) while keeping b = 1.5, s = 2.5 and k = 3.0. For d = 0 the shape of these high-frequency light curves is basically the same and the flare peak is reached simultaneously (black lines). For d> 0, a time delay between the peaks in the light curves is observed. For d ≥ 0, the shape of the curves changes with frequency: the light curves steepen after the peak as the frequency is decreasing (black and blue lines). In the case of d< 0, the 86 and 142 GHz flares peak at the same time but delayed w.r.t. the reference frequency (345 GHz), i.e. a constant delay between the peaks at ν = 86 GHz and ν = 140 GHz and 345 GHz is observed. This behaviour can be explained by the rising turnover flux density during the synchrotron stage (see Fig. 3), which brings the peaks at high-frequencies (those to the right of the one giving the maximum flux-density of the flare) to occur at the same time, and the cut-off frequency, which limits the peak flux-density at 345 GHz to the time when the cut-off crosses it (see Fig. 1).
Parameter d has a stronge impact on the light curve parameters, too. As an example, we show in Fig. 6 the computed light curve parameters for the three different values of d while fixing b = 1.5, s = 2.5, ρ = 1, and k = 3.0. The panels show, from left to right, the flare amplitude, flare time scale and the cross-band delay relative to the peak of the 345 GHz light curve. The solid and dashed lines in each panel correspond to power law fits as described in Sect. 2.2. The slope of the flare amplitude for the rising and decaying edge (left panel in Fig. 6), given by the exponent ϵflare amp., increases with d (The values in brackets correspond to the decaying edge). For d< 0, the flare time-scale (middle panel in Fig. 6) approaches a constant value for all frequencies, as opposed to d> 0, in which case it continues decreasing with frequency (blue dots in the panel). This translates into a decrease of the flare time scale exponent with d, which implies that the flare time scale is steepening with d. We only find for d> 0 an increasing time delay between all frequencies (see right panel in Fig. 6). In the case of d< 0, we observe a constant delay among frequencies ν> 86 GHz and an increase for smaller frequencies. If d = 0, there is no delay between the frequencies ν> 86 GHz. The exponent obtained from a power law fit to the time-lags decreases with increasing d.
The influence of b and s on the frequency dependent light curve parameters are presented in Fig. 7. As in Fig. 4, the upper panels show the variation of the slopes with b, taking s = 2.5, whereas the bottom panels show the variation of the slopes with s, taking b = 1.5. The results can be summarised as follows:
The flare amplitude exponent (ϵvar. amp):
the values for the flare amplitude exponent increase while the magnetic field configuration is changing from toroidal (b = 1) to poloidal (b = 2) and with s. The variation in ϵvar. amp is slightly larger with b than with s (see panel E of Fig. 7). The influence of b and of s on ϵvar. amp decreases with d (see panel A and E in Fig. 7).
The flare time scale exponent (ϵvar. time scale):
exponent ϵvar. time scale increases while b changes from b = 1 (toroidal field) to b = 2 (poloidal field) (panel C of Fig. 7). Finally, we observe only a minor variation of ϵvar. time scale with increasing s for d< 0, and an increase when d> 0 (panel F of Fig. 7).
The cross-band delay exponent (ϵdelay):
the distribution of values for the delay exponent strongly depends on the value of d. The exponent is strongly increasing with b for d> 0 and only a minor increase is obtained for d< 0 (see panel C of Fig 7). The delay exponent increases with s, except for d = 0 and d = −0.15, where the delay exponent decreases with increasing s. The variation in the cross-band delay exponent is smaller than for b (see panel F of Fig 7 and decrease with d)
Time lags with respect to 345 GHz:
in Fig. 8 we present time lags for the peak fluxes at 5 GHz, 15 GHz, and 86 GHz, with respect to 345 GHz. The top panels show the variation of the time lag for a constant spectral slope, s = 2.5, while changing b from 1 to 2, whereas the bottom panels show these variations for b = 1.5 (helical magnetic field), and spectral slope ranging from s = 2 to s = 3. The general trend for ν< 86 GHz can be described as follows: The time lags increase with increasing d, as expected from Fig. 6. Regarding the influence of b, the time lags significantly decrease with increasing b. Finally, there is only a minor decrease in the time lags with increasing s. The obtained time lags at high frequencies, panels C and F, are very small <18 days. The general trend for the variation of the time lags can be summarised as follows: for d> 0 the time lags are nearly constant and decrease with s and b for d< 0.
3.3. The effects of second order Compton scattering
Björnsson & Aslaksen (2000) re-evaluated the spectral evolution within the Compton stage of the classical shock-in-jet model of Marscher & Gear (1985) by including second order Compton scattering and showed that this leads to flatter slopes in the (νm–Sm) plane. Within our model this is obtained by replacing n1 and f1, as given by Eqs. (3) and (6) with: ![\begin{eqnarray} n_{1,\mathrm{mod}}&=&-(4s+8+3bs+12b)/[3(s+12)]\\ f_{1,\mathrm{mod}}&=&[-4(s-13)-6b(s+2)]/[3(s+12)]. \end{eqnarray}](/articles/aa/full_html/2015/08/aa24815-14/aa24815-14-eq138.png) The Compton stage for d = 0 and the results for the slopes are presented in the first row of Fig. A.9. The range of the slope varies between −0.6 <ϵC< 0.3. The positive value of ϵC indicates an increase of the flux density with frequency in the Compton stage, which is opposed to the observed evolution during flares. We thus find that this model is only valid for a limited range of shock parameters (1 <b< 1.4 and 2 <s< 3) (see Fig. A.9). In contrast to the standard shock-in-jet model with d = 0, this model results into non-zero time delays between the highest frequencies (see right panel in the third row in Fig. A.9).
The Compton stage for d = 0 and the results for the slopes are presented in the first row of Fig. A.9. The range of the slope varies between −0.6 <ϵC< 0.3. The positive value of ϵC indicates an increase of the flux density with frequency in the Compton stage, which is opposed to the observed evolution during flares. We thus find that this model is only valid for a limited range of shock parameters (1 <b< 1.4 and 2 <s< 3) (see Fig. A.9). In contrast to the standard shock-in-jet model with d = 0, this model results into non-zero time delays between the highest frequencies (see right panel in the third row in Fig. A.9).
4. Discussion
4.1. Emission, absorption and expansion
Overall, the different exponents and light curve parameters depend on the delicate interplay between emission and absorption that controls the spectral evolution of the flares. To discuss this we will restrict ourselves to Figs. 3 to 8, as the argumentation remains valid for the global picture drawn by Figs. A.1−A.6. During the Compton stage the main energy-loss mechanism is inverse Compton scattering. The radio spectrum is thus conformed to the synchrotron emission and the amount of high-energy electrons/positrons available to up-scatter the photons. The slope ϵC of this stage depends on the delay of the passage of the spectral peak through the different frequencies. The smaller the delay, the steeper the slope. The radio emission rises within this stage due to a decrease in the opacity owing to a drop of the amount of available high-energy electrons/positrons. For d< 0 (increasing Doppler factor with distance) the slope becomes steeper, i.e. the rise in Sm faster: assuming a constant viewing angle, the acceleration brings the flare to faster expansion and cooling and a consequent loss of high-energy pairs, whereas if the velocity is constant, a decreasing viewing angle implies an increase in the observed emission while the flow expands and the loss of high-energy pairs also occurs, although at a slower rate. Both possibilities make ϵC steeper. The exponent that controls the evolution of the magnetic field intensity has a role, although secondary, in the value of ϵC. The smaller the parameter b is, the slower is the decrease of the intensity and the higher the synchrotron emissivity remains along the evolution of the flare. This gives a fast increase in Sm as the density of absorbing high-energy particles falls with distance. The spectral index does not play a significant role, other than increasing the relative amount of available high-energy particles for smaller values of s. This, in addition, decreases the emissivity at lower frequencies, thus having a negligible overall effect on the development of this stage.
During the synchrotron and adiabatic stages, the spectral peak is basically controlled by synchrotron self-absorption. An accelerated expansion or a decrease of the viewing angle produces a further increase in Sm while the peak frequency decreases within the synchrotron stage, owing to the faster drop in non-thermal particle density (i.e. a drop in the absorption coefficient) or larger boosting, respectively, while the intrinsic emissivity at those frequencies is still high. Flow deceleration or an increase of the viewing angle would have the contrary effect. We only obtain in the case of d = 0 a flat slope in the (νm − Sm) plane. The electron distribution s plays a more important role than during the Compton stage, with flatter electron distributions reducing the steepness of positive slopes (ϵS> 0) and increasing the steepness of negative slopes (ϵS< 0). In the former case, a flatter distribution of electrons results into a more important loss of absorbing electrons at the highest energy end of the spectrum (they cool-down faster), implying a faster drop in the peak frequency relative to that in the peak flux, thus giving a flatter ϵS. In the latter, the same loss of absorbing electrons implies a continued increase of received flux and, thus, a steeper negative slope. The evolution of the magnetic field is less important to this stage because, on the one hand, a faster drop in the field implies a decrease in the emissivity but, on the other hand, also a smaller absorption coefficient. The adiabatic stage shows a very similar trend relative to the relevant parameters. However, ϵA is more sensitive to the evolution of the magnetic field intensity: smaller values of b imply a smaller change in Sm relative to the drop in νm, because the emissivity decrease with distance is slower than for larger values of b.
Regarding the light curve parameters (Fig. 7), an increasing Doppler factor with distance (d< 0) results into flatter values of ϵflare amp.. This slope is slightly steepening with increasing b and s. The same trend with Doppler factor evolution applies to ϵvar. time, but this parameter does not change significantly with s or b, other than a minor increase (implying a flattening of the slope). Finally, the same result is valid for ϵtime lag, including some irregular behaviours for d = 0 and d = −0.15 at the edges of the studied parameter space, i.e. for s ~ 2.0 and b ~ 2 or for s ~ 3 and b ~ 2, see Fig. A.3. The general trend is that faster changes in the spectral evolution of the flare during the Compton stage, as given by d< 0 or b → 1 (see Fig. 4), result into smaller cross-band delays and flare time-scales for the highest frequencies. For the low-frequency range the time lags and differences in flare time-scales are also smaller for d< 0 (as it gives a flatter slope, ϵtime lag). However, in this case the slopes are flatter for b → 2, which gives a flatter ϵtime lag, too, because of steeper slopes during the relevant stage at low frequencies (i.e. the adiabatic stage, see Fig. 4). Therefore, again, faster changes, i.e. a steeper slope in the adiabatic stage, results into flatter light curve parameters because of a faster passage of the peak emission through the observing frequencies. On the contrary, slower changes in the flare evolution along the jet provide more differences among frequencies and thus, steeper light curve parameters.
4.2. General trends
Our modelling of flares with the shock-in-jet model shows that the evolution of the Doppler factor along the jet, d, has the strongest influence on the slopes of the different energy loss mechanisms. Based on the assumption that the slope of the Compton stage has to be ϵC ≤ 0 (i.e. increasing turnover flux density with decreasing turnover frequency) as obtained from the observed spectral evolution of these flares, we derive an upper limit for d = 0.45. With this upper boundary for d we obtain a large range of slopes (0 <ϵC< −14) for the initial stage of the shock-in-jet model (assuming a symmetric lower limit of d = −0.45). Therefore, jets with increasing Doppler factor along the jet (δ ∝ R−d → d< 0) can explain observed steep Compton stages (see, e.g. Rani et al. 2013). Such steep slopes, if considered as a general trend, can correspond to acceleration of the bulk flow. The alternative explanation implies that the flares in different jets approach the line of sight as they evolve. The first option is favoured by the hypothesis of homogeneity, which excludes privileged directions. We also find that jets with purely toroidal magnetic field (b = 1) develop steeper Compton stages in the (νm − Sm) plane than jets with a purely poloidal field (b = 2) (see panel A of Fig. 4). The spectral index of the electron distribution does not play a crucial role on the slope of the Compton stage.
In some single-dish observations of blazar flares the synchrotron stage is not clearly visible or apparently missing (e.g. Türler 2011; Stevens et al. 1996) and some authors claim that this stage may not even exist (Björnsson & Aslaksen 2000). However, we find that for d ≠ 0 the slope of the synchrotron stage, ϵS can be similar to either the slope of the Compton stage (d< 0) or the slope of the adiabatic stage (d> 0) (see Fig. 3). Due to the usually limited frequency sampling of single-dish monitoring observations it is well possible that a difference in the slopes between these two energy loss stages is not detected and the synchrotron stage is just “hidden” in the Compton or adiabatic stage. The slope of the synchrotron stage in the (νm − Sm) plane does not change significantly with the magnetic field, but it grows with the spectral index of the electron distribution, becoming flatter for negative values of ϵS, and steeper for positive values.
Exponent d also has a strong influence on the variation of the light curve parameters. The time lag between any observed frequency and a given reference frequency (345 GHz in this work) can be used to distinguish decelerating jets (d> 0) from accelerating jets (d< 0), assuming constant viewing angle, ϑ = const. We only obtain for d> 0 time lags between the reference frequency of 345 GHz and frequencies ν ≤ 86 GHz which are in reach of typical cadence of single-dish monitoring programmes (>10 days). This behaviour can be explained by the slope of the Compton stage and the shape of the observed spectrum: the optically thin flux density is given by 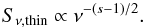 (16)If the slope of the Compton stage, ϵC, is steeper(i.e. steeper) than −(s − 1)/2, the optically thin flux densityat a given frequency νi is still increasing after νm = νi. This behaviour is usually obtained for d< 0 (accelerating jets, assuming constant viewing angle). However, if ϵC ~ −(s − 1)/2 the flux density peakat a given frequency is equal to theturnover point (νm,Sm).
(16)If the slope of the Compton stage, ϵC, is steeper(i.e. steeper) than −(s − 1)/2, the optically thin flux densityat a given frequency νi is still increasing after νm = νi. This behaviour is usually obtained for d< 0 (accelerating jets, assuming constant viewing angle). However, if ϵC ~ −(s − 1)/2 the flux density peakat a given frequency is equal to theturnover point (νm,Sm).
The cross-band delay exponent, ϵdelay, is a measure of the opacity variations along the jet(e.g. Lobanov 1998, Kudryavtseva et al. 2011, Fuhrmann et al. 2014). For a conical jet with b=1 the expected value is ϵdelay = 1, assuming equipartition between the magnetic energy density and the energy density of relativistic particles (Lobanov 1998). We obtain ϵdelay = 1 for jets with d ≥ 0, b< 1.4 and 2.0 <s< 3.0 (see panel A of Fig. 7, and Fig. A.3). Those shock-models have large time lags between low frequencies (ν< 5 GHz) and the reference frequency (here 345 GHz) and show flat Compton stages (ϵC> −2.0). If we assume a fixed viewing angle those jets could be classified as constant velocity or decelerating flows.
Both the standard shock-in-jet model for d> 0 and the modified Compton stage of Björnsson & Aslaksen (2000) give flat Compton stages. This could be used to additionally distinguish between d> 0 and d< 0. However, second order Compton scattering could produce non-zero time delays between the highest frequencies, too.
4.3. A guide to identify shock parameters
The work presented here can serve as (i) a guide to identify the jet flow properties from the observed spectral evolution of flares in blazar jets and (ii) as a test for the validity of the shock-in-jet model (including or excluding second-order Compton scattering). Making use of our results and the previous discussion, we provide here a short recipe for the extraction of shock parameters from multi-frequency, single-dish light curves. The frequency dependent light curve parameters, flare amplitude, flare time scale, and the cross-band delays can be obtained from well sampled light curves at any given frequency. If the flare of a blazar is observed by more than two frequencies, the exponents of the light curve parameters can be derived by fitting a power law or a broken power law (see, e.g. the flare amplitude for a broken power law) to the light curve parameters. Given at least five frequencies and a relatively dense time sampling it is possible to extract the spectral evolution of a flare in the (νm − Sm) plane. Depending on the observing frequency range the entire spectral evolution can be obtained, i.e. covering the Compton, synchrotron, and adiabatic stages, or in the case of a low frequency range only the synchrotron or the adiabatic stage. However, even in the case of only extracting one stage, based on its slope the evolution of the physical condition in the jet can be obtained. The frequency dependent light curve parameters (Sect. 2.2) can be estimated by different methods, for instance, using τ = tmax,νi − tmax,ref (see Sect. 2.2) or a discrete cross-correlation function analysis (e.g. Edelson & Krolik 1988; Larsson 2012) to obtain flare time lags. Flare amplitudes can be obtained using e.g. light curve standard deviations (see Sect. 2.2) or directly the minimum/maximum flux density of the flare (ΔS = Smax − Smin), or using the intrinsic modulation index following Richards et al. (2011) The flare rise/decay times Δtr,d can be extracted using the times between the start, the maximum and the end of the flare (see Sect. 2.2). Alternatively, each individual (“isolated”) and well sampled flare in multi-frequency single dish light curves could be approximated by 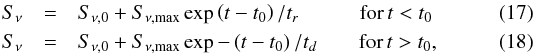 where Sν,0 is the quiescent flux for a given frequency, Sν,max is the maximum flux density for a given frequency, t0 is the time at which the maximum flux density is obtained, and tr and td characterise the rise and decay times of the flare, respectively (see, e.g. Hovatta et al. 2008; Rani et al. 2013). After modelling the flare at each frequency by Eq. (17) and (18), the frequency dependent parameters are computed as described in Sect. 2.2.
where Sν,0 is the quiescent flux for a given frequency, Sν,max is the maximum flux density for a given frequency, t0 is the time at which the maximum flux density is obtained, and tr and td characterise the rise and decay times of the flare, respectively (see, e.g. Hovatta et al. 2008; Rani et al. 2013). After modelling the flare at each frequency by Eq. (17) and (18), the frequency dependent parameters are computed as described in Sect. 2.2.
By fitting a power law to the obtained frequency dependent light curve parameters, the exponents ϵtime lag, ϵflare amp, and ϵflare time scale are obtained. The shock parameters d, s, and b can be estimated by comparing the exponents ϵtime lag, ϵflare amp, and ϵflare time scale with those provided in Figs. A.3 or A.4.
The relevant parameters can also be obtained from studying the spectral evolution of the flare in the (νm − Sm)-plane. This additional analysis requires (quasi-) simultaneous broad-band spectra, constructed from (quasi-) simultaneous multi-frequency flux densities and/or an interpolation between observed data points. In this work we assumed that the total flux density is the superposition of a quiescent and a flaring spectrum. Therefore it is necessary to re-construct the quiescent spectrum from the available or archival data. This quiescent spectrum could be modelled by a simple power law Sν,q ∝ ναq or by the full expression for a SSA spectrum (see Eq. (11)), depending on the frequency sampling and the quality of the data. The evolution of the turnover frequency, νm, the turnover flux density, Sm, and the optically thin spectral index, α0, are derived by fitting Eq. (11) to the quiescent spectrum corrected flare spectra.
The different energy loss stages can be identified in the (νm − Sm)-plane by their slopes, as described in Sect. 2. After identifying the energy loss stages and extracting the slopes by means of a power law fit 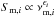 (see, Fromm et al. 2011, for details on the spectral analysis of single dish light curves), the shock parameters can be derived by comparing the obtained slopes for the different stages with the ones provided in Figs. A.1 and A.2.
(see, Fromm et al. 2011, for details on the spectral analysis of single dish light curves), the shock parameters can be derived by comparing the obtained slopes for the different stages with the ones provided in Figs. A.1 and A.2.
5. Conclusions and outlook
In this paper we used the shock-in-jet model and computed single-dish light curves for different jet configurations. From the synthetic light curves we extracted the slopes of the different energy loss stages, the frequency dependent light curve parameters which can be used to distinguish different jet models and constrain the jet parameters, e.g. d, b, and s.
Our results can be used to constrain the physical properties of jets and their evolution within the collimation and acceleration regions, by comparison with detailed multi-frequency monitoring observations of blazar radio flares. As an example, a first comparison between our analysis and observational results (see, e.g. Rani et al. 2013) could point towards bulk flow acceleration during the initial Compton stage. Taking advantage of the broad-band (2.6 to 345 GHz), F-GAMMA monitoring Program, we plan to apply this model to a large number of blazar flares to constrain the jet and/or flare properties. The parameters obtained can be used as initial conditions in more advanced shock models, including the relativistic magneto-hydrodynamic nature of jets to further investigate the physics of blazars. An additional study for a parabolic jet geometry should be performed to consider possible differences with conical jets that can be relevant for the jet collimation region.
Online material
Appendix A
Here we present the results for the frequency dependent light curve parameters including the entire range of shock parameters (see Table 1). The plots in this Appendix provide a global view of the changes in the slopes of the different stages in the (νm − Sm) plane and the light curve parameters.
A.1. Slopes of the energy loss stages
Figures A.1 and A.2 show the maps of the values obtained for the slopes of the different energy loss stages as a function of d, b, and s, indicating some colour levels (black, solid lines) in the plot to help identifying the values, and providing also a dashed line that separates the case of evolution towards a magnetically dominated from evolution towards particle dominated flows. This line is derived as follows: Taking into account that the magnetic energy density is uB ∝ B2 and using B ∝ R− b, we obtain uB ∝ R−2b. For particles, ue ∝ ∫n(γ)γdγ using n(γ) ∝ Kγ−s. Neglecting the evolution of γ with distance, we can assume ue ∝ K, and using K ∝ R−k and k = 2(s + 2)/3 if the jet expands adiabatically, we have uB/ue ∝ R−2b + 2(s + 2)/3. Imposing independence with distance brings the exponent to zero, which requires b = (s + 2)/3. If b< (s + 2)/3, the ratio grows with distance, whereas for b> (s + 2)/3 the ratio decreases with distance. Each panel shows the variation of ϵi (i = 1 Compton, i = 2 synchrotron, and i = 3 adiabatic) for 2 <s< 3 and 1 <b< 2 and a fixed value of d. The value of d is changing from top to bottom from d = −0.45 to d = 0.45 (see also the figure captions). The left column in both plots shows the maps of values of ϵC as a function of b and d. The vertical levels indicate that this slope is fairly independent of s for any values of b and d, and that it mainly changes with these two parameters. In the case of ϵS, the slope of the synchrotron stage, the situation is different, and s and d appear to be the most relevant parameters to determine it, although there is also a smooth gradient of this slope in the direction of b for the extreme values of d. Finally, the third column shows the maps of ϵA, which is most sensitive to d and b, and only shows a smooth variation with s.
A.2. Slopes of the frequency dependent light curve parameters
Figures A.3–A.6 show maps of the exponents of the frequency dependent light curve parameters as a function of s and b for different values of d. As mentioned earlier, the exponents for the flare amplitude and the flare time scale can be obtained either from the rising edge or the decaying edge of the light curve. In Figs. A.3 and A.4 we present these parameters obtained from the
rising edge and in Figs. A.5 and A.6 for the decaying edge of the light curves. In Figs. A.3 and A.4, each panel shows, from left to right, the variation in the flare amplitude exponent, ϵflare amp., the flare time scale exponent ϵflare time scale and the cross-band delay exponent, ϵdelay, for 2 <s< 3 and 1 <b< 2 and a fixed value of d. The value of d is changing from top to bottom from d = 0.45 to d = −0.45 (see also the figure captions). The amplitude of the flare undergoes a stronger variation with frequency for decreasing Doppler factors with distance (Fig. A.3) than for the increasing (Fig. A.4), as indicated by the colour-scales. In all cases, the slope grows with increasing s and b. The time lapse between the onset of the flare and the peak at each frequency is more sensitive to changes in frequency for decreasing Doppler factors with distance. This time lapse is more sensitive to b than to s, and the difference among frequencies becomes larger (smaller ϵflare time scale) for values of b closer to 1. Finally, the time lag between the peaks at different frequencies and a reference one has a similar behaviour with respect to the relevant parameters to the time lapse between onsets and peaks. The main difference is that there is not a large difference in the slopes between positive and negative values of d and that there are clear discontinuities in the values of the ϵtime lag for increasing Doppler factors, at certain values of s.
 |
Fig. A.1 Parameter space plots for the variation of the slopes, ϵi as function of b and s while keeping the d parameter fixed. The columns show from left to right, the slope of the Compton stage, ϵC, the slope of the synchrotron stage, ϵS, and the slope of the adiabatic stage, ϵA. The exponent for the evolution of the Doppler factor, d, is from top to bottom d = −0.45, d = −0.30, d = −0.15, and d = 0. The black dashed line corresponds to a constant uB/ue ratio with distance (beq = (s + 2)/3)), i.e. to the left of this line the jet flow tends to be magnetically dominated with distance and to the right the jet tends to be particle energy dominated with distance. |
In Figs. A.5 and A.6 we show the variation of the exponent for the flare amplitude and the flare time scale obtained from the decaying edge of the light curve. The exponent for the flare amplitude ϵflare amp. decay decreases with d. For d< 0 the absolute value of the exponent increases with s and b. However, for d> 0 the distribution of ϵflare amp. decay changes: The exponents still increase with s but larger values are obtained towards b = 1. The exponent for the flare time scale derived from the decaying edge of the light curve, ϵflare time decay is small, typically <0.05. The value and its distribution depend strongly on d. For d< 0 the distribution is smooth and the values decrease with s and b. Nearly no variation in ϵflare time. decay is obtained for d> 0 (see second column in Figs. A.5 and A.6).
Figures A.7 and A.8 show the expected time lags (in years) between the peaks at 5 GHz, 15 GHz, and 140 GHz and our reference frequency, 345 GHz (left, central and right columns, respectively), for different values of d (different rows), as a function of s and b. The cross-band delays become shorter for increasing Doppler factor with distance as indicated by the colour scales at the top of the panels. The time lags between the reference frequency and low frequencies are typically more sensitive to b increasing as this parameter tends to 1, whereas the time lags between 140 GHz and 345 GHz show significant values only for decreasing Doppler factor with distance and higher sensitivity to the spectral slope s.
 |
Fig. A.3 Parameter space plots for the variation of frequency dependent single-dish light curve parameters obtained from the rising edge of the light curves as function of b and s while keeping the d parameter fixed. The columns show from left to right the exponent for the variability amplitude, ϵflare amp., the exponent for the variability time scale, ϵflare time scale, and the exponent for the time lag, ϵdelay. The exponent for the evolution of the Doppler factor, d, is from top to bottom d = −0.45, d = −0.30, d = −0.15, and d = 0. The black dashed line corresponds to a constant uB/ue ratio with distance (beq = (s + 2)/3)), i.e. to the left of this line the jet flow tends to be magnetically dominated with distance and to the right the jet tends to be particle energy dominated with distance. |
 |
Fig. A.5 Parameter space plots for the variation of frequency dependent single-dish light curve parameters obtained from the decaying edge of the light curves as function of b and s while keeping the d parameter fixed. The columns show from left to right, the exponent for the variability amplitude, ϵvar. amp., the exponent for the variability time scale, ϵvar. time scale, and the exponent for the cross-band delay, ϵdelay. The exponent for the evolution of the Doppler factor, d, is from top to bottom d = −0.45, d = −0.30, d = −0.15, and d = 0. The black dashed line corresponds to a constant uB/ue ratio with distance (beq = (s + 2)/3)), i.e. to the left of this line the jet flow tends to be magnetically dominated with distance and to the right the jet tends to be particle energy dominated with distance. |
 |
Fig. A.7 Parameter space plots for the for the time lag between three selected frequencies as function of b and s while keeping the d parameter fixed. The columns show from left to right, the (345−5) GHz time lag, the (345−15) GHz time lag, and the (345−86) GHz time lag. The exponent for the evolution of the Doppler factor, d, is from top to bottom d = −0.45, d = −0.30, d = −0.15, and d = 0. The black dashed line corresponds to a constant uB/ue ratio with distance (beq = (s + 2)/3)), i.e. to the left of this line the jet flow tends to be magnetically dominated with distance and to the right the jet tends to be particle energy dominated with distance. |
 |
Fig. A.9 Modified Compton stage model using d = 0. The top row shows the slopes for the different energy loss stages from left to right: compton, synchrotron, and adiabatic stage. The delay between selected frequencies with respect to 345 GHz in years is plotted in the second row from left to right: delay to 5 GHz, delay to 15 GHz and delay to 86 GHz. The third row presents the frequency dependent light curve parameters obtained from the rising edge of the light curve from left to right: flare amplitude, flare time scale and cross frequency delay. The bottom row shows the exponent for the flare amplitude and the flare time scale as derived from the decaying edge of the light curve. The black dashed line corresponds to a constant uB/ue ratio with distance (beq = (s + 2)/3)), i.e. to the left of this line the jet flow tends to be magnetically dominated with distance and to the right the jet tends to be particle energy dominated with distance. |
Acknowledgments
We thank E. Ros for careful reading and useful comments on the manuscript. M.P. acknowledges financial support by the Spanish “Ministerio de Ciencia e Innovación” (MICINN) grants AYA2010-21322-C03-01, AYA2010-21097-C03-01. MP is a member of the work team of projects AYA2013-40979-P and AYA2013-48226-C3-2-P.
References
- Angelakis, E., Angelakis, E., Fuhrmann, L., et al. 2010, in Accretion and Ejection in AGN: a Global View, eds. L. Maraschi, G. Ghisellini, R. Della Ceca, & F. Tavecchio, ASP Conf. Ser., 427, 289 [Google Scholar]
- Angelakis, E., Fuhrmann, L., Nestoras, I., et al. 2011, 2011 Fermi Symp. Proc., eConf C110509 [arXiv:1111.6992] [Google Scholar]
- Begelman, M. C., Blandford, R. D., & Rees, M. J. 1980, Nature, 287, 307 [NASA ADS] [CrossRef] [Google Scholar]
- Björnsson, C.-I., & Aslaksen, T. 2000, ApJ, 533, 787 [NASA ADS] [CrossRef] [Google Scholar]
- Camenzind, M., & Krockenberger, M. 1992, A&A, 255, 59 [NASA ADS] [Google Scholar]
- Edelson, R. A., & Krolik, J. H. 1988, ApJ, 333, 646 [NASA ADS] [CrossRef] [Google Scholar]
- Fromm, C. M., Perucho, M., Ros, E., et al. 2011, A&A, 531, A95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Fuhrmann, L., Zensus, J. A., Krichbaum, T. P., Angelakis, E., & Readhead, A. C. S. 2007, AIP Conf. Proc., 921, 249 [Google Scholar]
- Fuhrmann, L., Larsson, S., Chiang, J., et al. 2014, MNRAS, 441, 1899 [NASA ADS] [CrossRef] [Google Scholar]
- Fuhrmann, L., Angelakis, E., Zensus, J. A., & et al. 2015, MNRAS, submitted [Google Scholar]
- Guetta, D., Ghisellini, G., Lazzati, D., & Celotti, A. 2004, A&A, 421, 877 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hovatta, T., Nieppola, E., Tornikoski, M., et al. 2008, A&A, 485, 51 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kudryavtseva, N. A., Gabuzda, D. C., Aller, M. F., & Aller, H. D. 2011, MNRAS, 415, 1631 [NASA ADS] [CrossRef] [Google Scholar]
- Larsson, S. 2012, 2012 Fermi & Jansky Proc., eConf C1111101 [arXiv:1207.1459] [Google Scholar]
- Lister, M. L., Aller, M. F., Aller, H. D., et al. 2013, AJ, 146, 120 [NASA ADS] [CrossRef] [Google Scholar]
- Lobanov, A. P. 1998, A&A, 330, 79 [NASA ADS] [Google Scholar]
- Marscher, A. P., & Gear, W. K. 1985, ApJ, 298, 114 [NASA ADS] [CrossRef] [Google Scholar]
- Mimica, P., Aloy, M. A., & Müller, E. 2007, A&A, 466, 93 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Orienti, M., Koyama, S., D’ammando, F., et al. 2013, MNRAS, 428, 2418 [Google Scholar]
- Perucho, M., Kovalev, Y. Y., Lobanov, A. P., Hardee, P. E., & Agudo, I. 2012, ApJ, 749, 55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rani, B., Krichbaum, T. P., Fuhrmann, L., et al. 2013, A&A, 552, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Richards, J. L., Max-Moerbeck, W., Pavlidou, V., et al. 2011, ApJS, 194, 29 [NASA ADS] [CrossRef] [Google Scholar]
- Rueda-Becerril, J. M., Mimica, P., & Aloy, M. A. 2014, MNRAS, 438, 1856 [NASA ADS] [CrossRef] [Google Scholar]
- Spada, M., Ghisellini, G., Lazzati, D., & Celotti, A. 2001, MNRAS, 325, 1559 [NASA ADS] [CrossRef] [Google Scholar]
- Stevens, J. A., Litchfield, S. J., Robson, E. I., et al. 1994, ApJ, 437, 91 [NASA ADS] [CrossRef] [Google Scholar]
- Stevens, J. A., Litchfield, S. J., Robson, E. I., et al. 1996, ApJ, 466, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Türler, M. 2011, Mem. Soc. Astron. Italiana, 82, 104 [Google Scholar]
- Türler, M., Courvoisier, T. J. L., & Paltani, S. 2000, A&A, 361, 850 [NASA ADS] [Google Scholar]
- Urry, C. M. 1999, Astropart. Phys., 11, 159 [NASA ADS] [CrossRef] [Google Scholar]
- Valtaoja, E., Terasranta, H., Urpo, S., et al. 1992a, A&A, 254, 80 [NASA ADS] [Google Scholar]
- Valtaoja, E., Terasranta, H., Urpo, S., et al. 1992b, A&A, 254, 71 [NASA ADS] [Google Scholar]
- Villata, M., & Raiteri, C. M. 1999, A&A, 347, 30 [NASA ADS] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Evolution of the turnover frequency, νm, and the turnover flux density, Sm, for a model with b = 1.5, s = 2.5, ρ = 1, k = 3.0, and d = 0. The top panel shows the evolution of the flare in the (νm–Sm) plane (the time evolution is from the bottom right, to the centre and to the bottom left). The black dashed line indicates the path along which νm and Sm (red dots) evolve. The slopes of the different stages are given in the plot. The red lines correspond to SSA spectra computed for different times (position along the spectral evolution path). The middle panel shows the temporal evolution of νm, and the bottom panel displays the temporal evolution of Sm. |
| In the text | |
 |
Fig. 2 Example for the analysis of the synthetic single-dish light curves. Top panel: the single-dish multi-frequency light curves (2.6 to 345 GHz) computed for b = 1.5, s = 2.5, k = 3.0, ρ = 1.0, and d = 0 (see also Fig. 1). Bottom panels, from left to right: flare amplitudes, flare time scales and cross-band delays. The solid lines correspond to power law fits and the exponent is given in the plots. |
| In the text | |
 |
Fig. 3 Evolution of the flare in the turnover frequency – turnover flux density plane for three different values of d while keeping b = 1.5, s = 2.5, ρ = 1, and k = 3.0 fixed. The slopes of the different stages are given in the plot and are colour-coded. |
| In the text | |
 |
Fig. 4 Exponents for the different energy loss stages from left to right: compton (A, D), synchrotron (B, E) and adiabatic stage (C, F). The top panels (A–C) show the variation of the slopes using a fixed spectral slope of s = 2.5 and the bottom panels (D–F) present the changes in the slopes for a fixed helical magnetic field (b = 1.5). The different values for d are colour-coded and can be found in the plot legend. |
| In the text | |
 |
Fig. 5 High-frequency (86 to 345 GHz) light curves computed for three different values of d while keeping b = 1.5, s = 2.5, ρ = 1, and k = 3.0 fixed. The dashed lines correspond to 345 GHz, the solid ones to 140 GHz and the dot-dashed ones to 86 GHz. See text for more details. |
| In the text | |
 |
Fig. 6 Light curve parameters obtained from synthetic light curves with three different values of d while keeping b = 1.5, s = 2.5, ρ = 1, and k = 3.0 fixed. The panels show from left to right the flare amplitude, the flare time scale and the cross-band delays with respect to the peak of the 345 GHz light curve. The solid lines correspond to the power law fits and the exponents are given in the plots. The values in brackets correspond to the exponents of a power law fit to the decaying regime of flare amplitude and flare time scale. |
| In the text | |
 |
Fig. 7 Exponents of the light curve parameters obtained from the synthetic light curves from left to right: flare amplitude, flare time scale and cross band delay exponent. The top panels (A–C) show the variation in the light curve parameters using a fixed spectral slope of s = 2.5 and the bottom panels (D–F) present the changes in the parameters for a fixed helical magnetic field (b = 1.5). The different values for d are colour-coded and can be found in the plot legend. |
| In the text | |
 |
Fig. 8 Cross-band delays between 345 GHz and three selected frequencies (from left to right 5 GHz, 15 GHz and 86 GHz). The top panels (A−C) show the variation in the cross-band delays using a fixed spectral slope of s = 2.5 and the bottom panels (D–F) present the changes in the cross-band delays for a fixed helical magnetic field (b = 1.5). The different values used for d are colour-coded and can be found in the plot legend. |
| In the text | |
 |
Fig. A.1 Parameter space plots for the variation of the slopes, ϵi as function of b and s while keeping the d parameter fixed. The columns show from left to right, the slope of the Compton stage, ϵC, the slope of the synchrotron stage, ϵS, and the slope of the adiabatic stage, ϵA. The exponent for the evolution of the Doppler factor, d, is from top to bottom d = −0.45, d = −0.30, d = −0.15, and d = 0. The black dashed line corresponds to a constant uB/ue ratio with distance (beq = (s + 2)/3)), i.e. to the left of this line the jet flow tends to be magnetically dominated with distance and to the right the jet tends to be particle energy dominated with distance. |
| In the text | |
 |
Fig. A.2 Same as Fig .A.1 for d = 0.15, d = 0.30, and d = 0.45. |
| In the text | |
 |
Fig. A.3 Parameter space plots for the variation of frequency dependent single-dish light curve parameters obtained from the rising edge of the light curves as function of b and s while keeping the d parameter fixed. The columns show from left to right the exponent for the variability amplitude, ϵflare amp., the exponent for the variability time scale, ϵflare time scale, and the exponent for the time lag, ϵdelay. The exponent for the evolution of the Doppler factor, d, is from top to bottom d = −0.45, d = −0.30, d = −0.15, and d = 0. The black dashed line corresponds to a constant uB/ue ratio with distance (beq = (s + 2)/3)), i.e. to the left of this line the jet flow tends to be magnetically dominated with distance and to the right the jet tends to be particle energy dominated with distance. |
| In the text | |
 |
Fig. A.4 Same as Fig. A.3 for d = 0.15, d = 0.30, and d = 0.45. |
| In the text | |
 |
Fig. A.5 Parameter space plots for the variation of frequency dependent single-dish light curve parameters obtained from the decaying edge of the light curves as function of b and s while keeping the d parameter fixed. The columns show from left to right, the exponent for the variability amplitude, ϵvar. amp., the exponent for the variability time scale, ϵvar. time scale, and the exponent for the cross-band delay, ϵdelay. The exponent for the evolution of the Doppler factor, d, is from top to bottom d = −0.45, d = −0.30, d = −0.15, and d = 0. The black dashed line corresponds to a constant uB/ue ratio with distance (beq = (s + 2)/3)), i.e. to the left of this line the jet flow tends to be magnetically dominated with distance and to the right the jet tends to be particle energy dominated with distance. |
| In the text | |
 |
Fig. A.6 Same as Fig. A.3 for d = 0.15, d = 0.30, and d = 0.45. |
| In the text | |
 |
Fig. A.7 Parameter space plots for the for the time lag between three selected frequencies as function of b and s while keeping the d parameter fixed. The columns show from left to right, the (345−5) GHz time lag, the (345−15) GHz time lag, and the (345−86) GHz time lag. The exponent for the evolution of the Doppler factor, d, is from top to bottom d = −0.45, d = −0.30, d = −0.15, and d = 0. The black dashed line corresponds to a constant uB/ue ratio with distance (beq = (s + 2)/3)), i.e. to the left of this line the jet flow tends to be magnetically dominated with distance and to the right the jet tends to be particle energy dominated with distance. |
| In the text | |
 |
Fig. A.8 Same as Fig. A.7 for d = 0.15, d = 0.30, and d = 0.45. |
| In the text | |
 |
Fig. A.9 Modified Compton stage model using d = 0. The top row shows the slopes for the different energy loss stages from left to right: compton, synchrotron, and adiabatic stage. The delay between selected frequencies with respect to 345 GHz in years is plotted in the second row from left to right: delay to 5 GHz, delay to 15 GHz and delay to 86 GHz. The third row presents the frequency dependent light curve parameters obtained from the rising edge of the light curve from left to right: flare amplitude, flare time scale and cross frequency delay. The bottom row shows the exponent for the flare amplitude and the flare time scale as derived from the decaying edge of the light curve. The black dashed line corresponds to a constant uB/ue ratio with distance (beq = (s + 2)/3)), i.e. to the left of this line the jet flow tends to be magnetically dominated with distance and to the right the jet tends to be particle energy dominated with distance. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


