| Issue |
A&A
Volume 574, February 2015
|
|
|---|---|---|
| Article Number | A104 | |
| Number of page(s) | 17 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424576 | |
| Published online | 02 February 2015 | |
Chains of dense cores in the Taurus L1495/B213 complex⋆,⋆⋆,⋆⋆⋆
1
Observatorio Astronómico Nacional (IGN),
Alfonso XII 3,
28014
Madrid,
Spain
e-mail:
m.tafalla@oan.es
2
Institute for Astrophysics, University of Vienna,
Türkenschanzstrasse 17,
1180
Vienna,
Austria
e-mail:
alvaro.hacar@univie.ac.at
Received: 9 July 2014
Accepted: 18 November 2014
Context. Cloud fragmentation into dense cores is a critical step in the process of star formation. A number of recent observations show that it is connected to the filamentary structure of the gas, but the processes responsible for core formation remain mysterious.
Aims. We studied the kinematics and spatial distribution of the dense gas in the L1495/B213 filamentary region of the Taurus molecular cloud with the goal of understanding the mechanism of core formation.
Methods. We mapped the densest regions of L1495/B213 in N2H+(1–0) and C18O(2–1) with the IRAM 30 m telescope, and complemented these data with archival dust-continuum observations from the Herschel Space Observatory.
Results. The dense cores in L1495/B213 are significantly clustered in linear chain-like groups about 0.5 pc long. The internal motions in these chains are mostly subsonic and the velocity is continuous, indicating that turbulence dissipation in the cloud has occurred at the scale of the chains and not at the smaller scale of the individual cores. The chains also present an approximately constant abundance of N2H+ and radial intensity profiles that can be modeled with a density law that follows a softened power law. A simple analysis of the spacing between the cores using an isothermal cylinder model indicates that the cores have likely formed by gravitational fragmentation of velocity-coherent filaments.
Conclusions. Combining our analysis of the cores with our previous study of the large-scale C18O emission from the cloud, we propose a two-step scenario of core formation in L1495/B213. In this scenario, named “fray and fragment”, L1495/B213 originated from the supersonic collision of two flows. The collision produced a network of intertwined subsonic filaments or fibers (fray step). Some of these fibers accumulated enough mass to become gravitationally unstable and fragment into chains of closely-spaced cores.
Key words: stars: formation / ISM: abundances / ISM: kinematics and dynamics / ISM: molecules / radio lines: ISM
Based on observations carried out with the IRAM 30 m Telescope. IRAM is supported by INSU/CNRS (France), MPG (Germany), and IGN (Spain).
Herschel is an ESA space observatory with science instruments provided by European-led Principal Investigator consortia and with important participation from NASA.
The final IRAM FITS cubes are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/574/A104
© ESO, 2015
1. Introduction
Star formation requires a high degree of cloud fragmentation. A typical dark cloud is tens of parsecs in size, but the cores that undergo gravitational collapse and form stars are less than 0.1 pc in diameter. Understanding how a large-scale cloud of gas fragments into a small number of dense cores remains a critical challenge in the field of star formation (di Francesco et al. 2007; Ward-Thompson et al. 2007; Bergin & Tafalla 2007).
A clue to understanding fragmentation comes from cloud morphology. Molecular clouds are known to present complex filamentary distributions over multiple size scales, and a connection between this filamentary structure and the process of cloud fragmentation has long been proposed (Schneider & Elmegreen 1979; Larson 1985; Hartmann 2002; Myers 2009). Interest on this connection has been boosted by the large-scale cloud images from the Herschel Space Observatory, which display a striking prevalence of filamentary structures in the distribution of cloud material (André et al. 2010; Molinari et al. 2010). These new Herschel images show that dense cores often lie along large-scale filaments like beads in a string, and leave little doubt that some type of filamentary fragmentation must be responsible for their condensation (see André et al. 2014, for a recent review).
While filamentary fragmentation appears to produce cores, the exact manner in which this process operates is far from clear. Filamentary structures are often as large as the clouds themselves and involve most of the cloud mass, but core and star formation have an efficiency of only a few percent (Evans et al. 2009). Filaments therefore cannot completely fragment into cores, and some process must prevent most mass in a filament to end up forming cores and stars. What limits fragmentation is still a mystery, especially considering that many of the observed filaments have estimated mass-per-unit-lengths that greatly exceed the limit of gravitational stability (Arzoumanian et al. 2011; Hennemann et al. 2012; Palmeirim et al. 2013)
In a previous study of the filamentary region L1495/B213 in Taurus (Hacar et al. 2013), we used velocity information derived from the C18O emission to decompose what looks like a single filament in optical and continuum images into a complex network of 35 smaller filamentary structures. These structures, referred to as “fibers” to distinguish them from the large-scale filament, present properties that differ significantly from those of the 10 pc-long L1495/B213 region. The fibers, for example, have typical sizes around 0.5 pc, coherent velocity fields, and mass-per-unit-lengths that lie within uncertainties in the expected range of gravitational equilibrium values. These fibers seem to represent a size scale intermediate between the large filamentary cloud and the smaller dense cores, and have likely formed by some type of fragmentation process associated with the dissipation of turbulence (Hacar et al. 2013).
When the C18O data of L1495/B213 were complemented with N2H+ observations, which highlight the dense cores, the fibers were found to divide into two groups. Most fibers did not contain embedded cores, and were referred to as “sterile,” but a small group of fibers contained the totality of the cores and were classified as “fertile”. This difference between sterile-fertile fibers was significant. Sterile fibers did not contain cores, but fertile fibers contained around three cores on average. As a result, most cores in the L1495/B213 were found to be located in characteristic closely-packed linear groups.
The low angular resolution observations of Hacar et al. (2013), made with the 14 m FCRAO telescope, limited the study of the closely-packed cores to only the most basic global properties. To remedy this, we carried out higher-resolution observations using the IRAM 30 m telescope. These new observations allow us to resolve the internal structure of the core linear groups and to study the connection between the different cores formed from a single fiber. In the following sections we present the analysis of the core emission with emphasis on the kinematics of the gas. In the last section, we present a simple scenario of core formation that combines the large-scale analysis of Hacar et al. (2013) with the results from the new IRAM 30 m data.
2. Observations
We observed selected regions of the L1495/B213 cloud with the IRAM 30 m telescope during one session in February–March 2013 and another one the following June. In both sessions we used the EMIR heterodyne receiver (Carter et al. 2012) in frequency-switching mode together with the VESPA autocorrelator.
The observations consisted of simultaneous on-the-fly maps in the lines of N2H+(1–0) (93.17 GHz) and C18O(2–1) (219.56 GHz) in dual polarization mode. The maps covered the regions identified by Hacar et al. (2013) as bright in N2H+(1–0) and therefore indicative of dense core formation. To resolve the lines in velocity, the VESPA autocorrelator was set to a frequency resolution of 20 kHz, which corresponds to 0.063 km s-1 at the frequency of N2H+(1–0) and to 0.027 km s-1 at the frequency of C18O(2–1)
The data were calibrated by observing a combination of ambient and cold loads plus the blank sky every 10 min approximately. The resulting 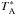 scale was converted into main beam brightness temperature Tmb using the facility-recommended main beam efficiencies of 0.8 and 0.6 for N2H+ and C18O, respectively. All intensities in this paper are reported in Tmb scale and have an estimated uncertainty of 10−15%.
scale was converted into main beam brightness temperature Tmb using the facility-recommended main beam efficiencies of 0.8 and 0.6 for N2H+ and C18O, respectively. All intensities in this paper are reported in Tmb scale and have an estimated uncertainty of 10−15%.
Additional off-line data processing was carried out using the GILDAS program CLASS1, and included convolving the data with a Gaussian kernel to resample the observations into a regular spatial grid (Mangum et al. 2007), folding the spectra to correct for frequency switching, and subtracting a polynomial to flatten the baseline. In some steps of the analysis, the data, which have an original angular resolution of 26′′ and 12′′ for N2H+ and C18O, were further convolved with a Gaussian of full with half maximum (FWHM) of 20′′ to enhance the sensitivity. These convolved data have an angular resolution of 33′′ (N2H+) and 23′′ (C18O).
To complement the IRAM 30 m observations, we used archival data from the Herschel Space Observatory (Pilbratt et al. 2010). These data consisted of dust continuum maps of the L1495/B213 region observed with the SPIRE instrument at 250, 350, and 500 μm (Griffin et al. 2010). They were obtained as part of the Herschel Gould Belt Survey (HGBS, André et al. 2010), and have been previously presented by Palmeirim et al. (2013) and Kirk et al. (2013). The data used here (OBSID 1342202254) were obtained through the Herschel Science Archive and correspond to level 2.5 as reduced with version 9.1.0 of the Standard Product Generation (SPG) software.
 |
Fig. 1 Large-scale view of the L1495/B213 complex. The grey scale shows the Herschel-SPIRE 250 μm emission mapped by Palmeirim et al. (2013), and the red contours represent the N2H+(1–0) emission mapped by Hacar et al. (2013) with the FCRAO telescope. The black dashed lines show the limits of the FCRAO observations, and the blue solid lines enclose the regions newly mapped with the IRAM 30 m telescope. |
3. Results
3.1. Large-scale distribution of the gas in L1495/B213
Figure 1 presents a large-scale view of the L1495/B213 complex. The grey background represents the Herschel-SPIRE 250 μm dust continuum emission mapped by Palmeirim et al. (2013), which traces the distribution of material in the region. As can be seen, this emission delineates a ≈10 pc long filament that has L1495 at its northern end and runs almost diagonally towards the south-east, becoming weaker and more fragmented along the way. This filamentary geometry seen with Herschel is in good agreement with previous maps of the large-scale dust extinction, both in the optical (Gaida et al. 1984; Cernicharo et al. 1985) and the NIR (Schmalzl et al. 2010).
 |
Fig. 2 Integrated intensity maps of the N2H+(1–0) emission showing how the dense cores in L1495/B213 form linear chain-like structures (IRAM 30 m data). All maps have the same linear and intensity scales, and the first contour and contour interval are 0.5 K km s-1. The star symbols indicate the position of the YSOs in the compilation of Luhman et al. (2010), with solid symbols representing Class 0/I objects. The central positions, in (α(J2000), δ(J2000)) coordinates are (04:19:42.5, +27:13:36) for B213, (04:18:05.0, +27:35:16) for B211, (04:28:02.0, +26:19:32) for B218, (04:18:32.2, +28:27:18) for B7, and (04:18:04.0, +28:08:14) for B10. |
While striking for its prominence, the L1495/B213 region is not the only large-scale filamentary structure in the Taurus dark cloud. Images of Taurus using both molecules and dust reveal that most of the material in the cloud is distributed in a network of crisscrossing filaments of different sizes and orientations (Barnard 1907; Dobashi et al. 2005; Lombardi et al. 2010; Goldsmith et al. 2008; Kirk et al. 2013). In this sense, the L1495/B213 region is a prominent but still representative part of the Taurus molecular cloud.
Figure 1 also shows the N2H+(1–0) emission mapped by Hacar et al. (2013) using the FCRAO telescope with an angular resolution of about 60′′ (red contours). This N2H+ emission traces the denser, chemically-evolved gas that has condensed out of the more diffuse material in the cloud. This gas occupies only a small fraction of the total cloud area and forms linear structures with typical length of ≈0.5 pc and generally aligned with the large-scale direction of the cloud. The higher resolution IRAM 30 m observations presented here cover the regions indicated by blue lines in the figure.
3.2. High-resolution N2H+ maps
Figure 2 shows the new IRAM 30 m maps of N2H+(1–0) integrated intensity toward the regions with significant emission, each labeled with a Barnard cloud name following the convention of Hacar et al. (2013). The figure also shows the location of the young stellar objects (YSOs) identified by the Spitzer survey of Luhman et al. (2010; see Rebull et al. 2010, for a similar compilation).
The new IRAM 30 m maps agree with the lower resolution FCRAO maps of Hacar et al. (2013), and with maps of some of the individual regions previously presented by Lee et al. (2001) and Tatematsu et al. (2004). These new maps provide a sharper and more sensitive view of the dense cores, and highlight the tendency of the cores to lie in elongated structures, which we will refer to as “chains” due to their linear appearance and the presence of multiple peaks.
Many N2H+ peaks in Fig. 2 correspond to dense cores in the sense used by previous studies of NH3 or N2H+ emission, like those of Benson & Myers (1989) and Caselli et al. (2002). This is the case of the peaks in the B218 chain and those in the northern part of B213. These N2H+ peaks have a strong degree of central concentration and typical sizes of 0.05−0.1 pc, implying that the emitting gas is self-gravitating and likely evolving toward star formation. Indeed, several of these peaks contain embedded Class 0 or Class I YSOs indicating that star formation has already taken place.
Not all the N2H+ peaks in Fig. 2 however have the distinct central concentration that we normally associate with dense cores. Most peaks in the B10 chain, for example, are true emission maxima, but they barely stand out above the extended filamentary emission that surrounds them. This lack of contrast and central concentration makes the nature of these peaks unclear. They seem to represent pockets of dense gas that are still connected to their surroundings, and that therefore have not yet evolved into gravitationally decoupled objects similar to the standard dense cores. If so, these N2H+ peaks must correspond to an evolutionary stage earlier than the dense core phase, but that is more evolved than the extended material traced with C18O by Hacar et al. (2013) since the gas is chemically evolved. The variety of peak contrasts in Fig. 2 therefore implies that the N2H+ data cover an almost complete sequence of core evolutionary stages that goes from the barely-discernible peak near Δδ = 200′′ in B10 to the highly compact peak near the origin of the B213 map, which is associated with the well-known outflow source IRAS 04166+2706 (Bontemps et al. 1996; Tafalla et al. 2004b; Santiago-García et al. 2009).
The ambiguous classification of some of the N2H+ peaks is likely a consequence of the continuous transition between the ambient and core regimes, and implies that distinguishing between “true” dense cores and precursors of dense cores is an impossible (or arbitrary) task. For this reason, here we will not attempt to distinguish between N2H+ peaks that we consider to be “cores” and those that we consider as not having reached the core phase yet, and we will treat them equally in our analysis. The lack of a clear distinction between cores and pre-cores, however, seems not enough reason to stop using the term “core”. It is just a reminder that when studying core formation, some intermediate structures will unavoidably end up having an ambiguous nature.
3.3. Mean surface density of companions
Hacar et al. (2013) used the mean surface density of companions (MSDC) to quantify the clustering of dense cores in L1495/B213. The MSDC measures the average number of neighbors per unit area that one object has as a function of angular separation. It has often been used, together with its equivalent the two-point correlation function, to determine the degree of clustering of stars in Taurus (Gomez et al. 1993; Larson 1995; Simon 1997; Hartmann 2002). Studying the distribution of low-density condensations identified from from NIR extinction measurements, Schmalzl et al. (2010) found an excess of power in the MSDC at small angular separations. Hacar et al. (2013) found also an excess of nearby companions, but in a different type of structures: the dense cores derived from N2H+ observations.
The new IRAM 30 m data provide an improved description of the N2H+ emission in L1495/B213, especially at small angular scales. Thus, as a first step in our analysis, we have re-evaluated the MSDC of dense cores in the cloud. To do this, we have determined the location of all the N2H+ emission peaks in the maps of Fig. 2. We have counted 22 distinct peaks, which are three more than the 19 found by Hacar et al. 2013 because the new data identify additional peaks in the B10 region. Using the position of these N2H+ peaks, we have calculated the MSDC following the procedure described in Hacar et al. (2013). To extend the MSDC to the largest angular separations, we have used the large-scale information from the FCRAO data, since the new 30 m observations do not recover new peaks in regions with no FCRAO detection, but only separate better the regions already known to have bright N2H+ emission.
 |
Fig. 3 Mean surface density of companions as a function of angular separation for the 22 cores identified in L1495/B213. The red squares represent observed data. The black line and the blue-shaded region represent the mean and the ±rms interval from 100 Monte Carlo simulations of a random distribution of 22 cores. The departure of the red squares from the shaded region at small angles indicates a significant level of clustering at scales less than 700′′. |
 |
Fig. 4 Correlation between observed N2H+(1–0) integrated intensity and H2 column density derived from SPIRE dust-continuum data. Points within 45′′ of an embedded YSO have been excluded to avoid effects of stellar heating. The open squares in the B7/L1495 panel indicate points likely affected by V892 Tau (see text). The black lines represent the analytic expression discussed in the text. |
The new MSDC determined from the IRAM 30 m data is shown in Fig. 3 with red squares. This MSDC has a finer sampling than that determined with the FCRAO data due to the higher sensitivity and resolution of the new observations, but apart from that, the two MSDCs are consistent with each other. Also shown in Fig. 3 is the expected MSDC for a uniformly random distribution of cores. This distribution was determined using a set of 100 Monte Carlo simulations in which 22 dense cores were assigned random coordinates inside a rectangular region of dimensions approximately equal to those of L1495/B213. The mean value of this model MSDC is indicated by the black line, and its rms interval is contained in the blue-shaded region.
As Fig. 3 shows, the MSDC for the cores in L1495/B213 has a significant excess over the random distribution for angular separations smaller than about 700′′ (0.5 pc for a Taurus distance of 140 pc, Elias 1978). This excess means that for a given core, the probability of having a neighbor closer than about 0.5 pc is higher than it would be if the cores were distributed randomly over the cloud. The excess confirms the visual impression from Fig. 1 that the N2H+ peaks in L1495/B213 tend to cluster in small chains, and that the chains have a typical length of 0.5 pc. The chains, therefore, are true physical structures, and not mere chance groupings of dense cores in the cloud.
The clustering of dense cores into chains implies that core formation in L1495/B213 is a highly correlated process. A number of authors have previously emphasized that core formation results from the fragmentation of filamentary clouds (Schneider & Elmegreen 1979; Larson 1985; Hartmann 2002; Myers 2009; André et al. 2010; Molinari et al. 2010). Our observations of L1495/B213 go further than that by showing that fragmentation does not occur equally distributed along the length of a filament, but that it favors special locations where multiple cores are formed in chains. The reason for this selectivity is likely associated with the multiplicity of fibers found by Hacar et al. (2013), who argued that the L1495/B213 large-scale filament is in fact a collection of 35 intertwined velocity-coherent fibers. If most of these fibers are “sterile” and do not form cores, while a small minority are “fertile” and form multiple cores, a clustering of the cores into a few elongated chains is naturally expected. In Sect. 4 we will discuss in more detail the implications of this result to our understanding of core and star formation.
3.4. Comparison with SPIRE data and N2H+ abundance
While N2H+ is a tracer of choice for dense core gas due to its resistance to freeze out, its formation is enhanced by the disappearance of CO from the gas phase, so it can suffer systematic abundance variations during the evolution of a core (Caselli et al. 1999; Bergin et al. 2002; Tafalla et al. 2002; Aikawa et al. 2005). To quantify possible N2H+ abundance variations in the chains of L1495/B213, we need to compare the N2H+ data with data from a different tracer that is insensitive to freeze out. As mentioned before, observations of the dust emission and absorption provide an independent estimate of the gas column density, and therefore represent the ideal counterpart to the molecular line data presented here.
The Herschel Gould Belt Survey (HGBS) used the Herschel Space Observatory to produce very high quality images of the dust continuum emission from the Taurus molecular cloud (André et al. 2010; Palmeirim et al. 2013; Kirk et al. 2013). These publicly-available images are an excellent counterpart to the N2H+ line data, since they have high angular resolution, cover multiple wavelengths, and trace optically thin emission. As a first step in our analysis, we compared the dust and the N2H+ data by superposing the N2H+(1–0) maps of Fig. 2 with the 250, 350, and 500 μm maps made by the HGBS team with the SPIRE instrument. These SPIRE maps cover the longest wavelengths observable with Herschel, and provide the highest sensitivity to cold dust emission.
The SPIRE-N2H+ comparison showed that in places with significant N2H+(1–0) emission (≥0.5 K km s-1), the dust continuum flux and the N2H+(1–0) integrated intensity have similar spatial distributions. This implies that in N2H+-bright places, most of the dust continuum emission arises from the component emitting N2H+ (in N2H+-weak places, the dust emission traces the extended cloud). As a result, we can use the dust continuum emission from the chains to estimate an associated H2 column density, and with it, an N2H+ abundance. To carry out this estimate, we first convolved the 250 μm map to match the 35.̋2 angular resolution of the 500 μm map, which is also similar to the 33′′ resolution of the convolved N2H+ data (Sect. 2). We then followed standard practice and assumed that the dust emitted as an optically thin grey body with an emissivity that varies with frequency as ν2 (Hildebrand 1983), and used the fluxes at the two wavelengths to derive a dust temperature and an H2 column density for each position.
Our choice of the 500 μm dust opacity was κ500 μm = 0.03 cm2 g-1, based on the matching between our SPIRE-derived H2 column densities with the extinction-derived column densities of Schmalzl et al. (2010), which were kindly provided by Markus Schmalzl. This choice is only 20% lower than the value assumed by the HGBS team (André et al. 2010; Könyves et al. 2010; Arzoumanian et al. 2011; Palmeirim et al. 2013; Kirk et al. 2013), and lies within the range of values used or derived by other authors from Herschel data (Henning et al. 2010; Juvela et al. 2011; Launhardt et al. 2013; Suutarinen et al. 2013). Still, it should be noted that the dust opacity has an uncertainty of at least 50%, and that it could suffer variations with density, as shown by the detailed analysis of Juvela et al. (2011), Suutarinen et al. (2013), and Ysard et al. (2013). The uncertainty in the dust opacity represents the largest source of uncertainty in our H2 column density estimate.
Figure 4 compares the SPIRE-derived H2 column density with the N2H+(1–0) integrated intensity in all the regions with N2H+ emission. The B213 data have been split into two panels to distinguish the region two main components (labeled SE and NW), and the southern part of B7/L1495 has been treated separately from the north one (and labeled with open squares), due to its anomalous N2H+ abundance further discussed below. As the figure shows, the N2H+(1–0) integrated intensity and the H2 column density appear to be correlated in all regions. An estimate of the Pearson’s r coefficient confirms this impression and returns values that range from 0.81 in B213-NW (lowest) to 0.94 in B218 (highest), all indicative of a significant degree of correlation.
While significant, the correlation in the panels of Fig. 4 presents a non-negligible level of scatter. Part of it appears to arise from the contribution of gas with either low density or low N2H+ abundance (or likely both). This gas does not contribute to the N2H+ intensity, but increases the H2 column density and shifts some of the points along the x-axis, broadening the distribution in the plots. An extreme example of this effect can be seen in the B213-NW panel, where in addition to the main diagonal band of points there is a secondary band that has weaker N2H+ emission and is shifted horizontally by about 1022 cm-3. This band is associated with a small condensation near Δα = −200′′ seen in Fig. 2. A less extreme example occurs in B218, where the broad diagonal band of points is in fact the superposition of two slightly shifted and narrower bands, each one due to one of the bright cores in the chain. In contrast, the B211 region presents only a single dense core in the N2H+ maps, and its distribution of points presents the narrowest correlation of the sample.
If the scatter in the panels of Fig. 4 results from additional gas components along the line of sight, the slope is an indicator of the N2H+ abundance in the dense gas. This is expected because the N2H+ integrated intensity represented in the y-axis is proportional to the N2H+ column density (assuming that the emission is optically thin, see below), and as a result, the slope of the correlation equals the ratio between the N2H+ and H2 column densities, which is an estimate of the N2H+ abundance. A detailed radiative transfer model presented in the next section to fit the radial profiles of N2H+ emission confirms this interpretation, and shows that there is an almost linear relation between the N2H+ integrated intensity and the H2 column density. This is illustrated in Fig. 4 with a series of black lines that represent the predictions from the radiative transfer model assuming that all chains have the same N2H+ abundance of 5 × 10-10 with the exception of B7/L1495-south, where the abundance is 1.5 × 10-10. To fit the data in Fig. 4, we added small horizontal offsets of 7 × 1021 cm-3, 6 × 1021 cm-3, and 3 × 1021 cm-3 to the fits of B211, B7/L1495-north, and B10, respectively. The offset in B211 is in fact expected, since this region contains two additional C18O components (numbers 9 and 12 in the decomposition of Hacar et al. 2013) that do not emit in N2H+ and clearly contribute to the H2 column density (see Fig. 7 below). The offsets in B7/L1495 and B10 are also likely related to the presence of lower-density gas toward these two regions.
While uncertain, the N2H+ abundance in B7/L1495-south is much lower than in other chains (by a factor of 3), and is the only one that deviates from a pattern of almost constant abundance. To investigate its origin, we have inspected the SPIRE images of B7/L1495 at different wavelengths. These images show that B7/L1495-south lies inside a region of bright and extended far-infrared emission in the vicinity of V892 Tau, a Herbig Ae/Be star first identified by Elias (1978) and with a total luminosity of ≈400 L⊙ (Sandell et al. 2011; Mooley et al. 2013) that lies about 300′′ (0.2 pc) in projection from B7/L1495-south. A grey body analysis of the SPIRE emission, indicates that the dust temperature in the region is elevated, and that it gradually increases toward V892 Tau, where it reaches about 15 K, or 50% higher than in B7/L1495-north. In addition, the C18O maps of Fig. 7 (discussed below) show that B7/L1495-south coincides with a region of bright C18O emission. This is in contrast with the other N2H+-bright regions, which coincide with weak C18O emission due to CO freeze out. Thus, it appears that molecular depletion, and its resulting N2H+ enhancement, are anomalously low in the dense gas of B7/L1495-south. The low N2H+ abundance in B7/L1495-south seems therefore a result from the action of V892 Tau. Whether this is a consequence of simple dust heating or of a different energetic process requires a more detailed investigation.
 |
Fig. 5 Radial profiles of N2H+(1–0) integrated intensity in log-log scale. The red squares represent the data and the black lines are our models. B7/L1495 north data and model have been shifted by a factor of two to ease visibility. |
3.5. Density structure of the chains
In the maps, the core chains appear irregular in shape and different from each other. A closer inspection of the emission, however, shows that they have a similar internal structure. This can be seen in the radial profiles of N2H+ emission presented in Fig. 5. These profiles were created by following the emission of each chain in the map with a cursor and defining the line of relative maxima as the axis of the chain. Using this axis, the radial distance of each observed position was calculated, and the intensity of the emission was plotted as a function of it.
As Fig. 5 shows, the emission from each chain follows a radial profile that consists of a flat inner region and a power-law tail, similar to that often found in filamentary clouds (Arzoumanian et al. 2011; Hacar & Tafalla 2011; Palmeirim et al. 2013). The B213 and B218 chains present a larger level of dispersion near the axis because they contain bright cores separated by regions of weak emission, so points with the same axial radius can have a large range of intensities. The B10 and B7/L1495-north chains, on the other hand, present a less clumpy and more pristine appearance, and their radial profiles have a lower dispersion near the axis (as in Fig. 4, the emission from B7/L1495 has been separated into north and south components).
The combination of clumpiness due to the embedded cores and comparable radial profiles implies that the chains started their evolution with a similar density structure, and that later events added different fragmentation patterns to each one. Our goal in this section is to determine this common underlying structure, since it represents the initial conditions of core formation. For this, we have modeled the N2H+ radial profiles assuming that the chains are cylindrically symmetric, and that they have a density profile of the form 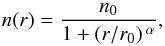 (1)where n0 is the central density, r0 the half-density radius, and α the asymptotic power index. This type of radial profile has previously been used to fit the density structure of both starless cores (Tafalla et al. 2002) and filamentary clouds (Arzoumanian et al. 2011; Hacar & Tafalla 2011; Palmeirim et al. 2013; Ysard et al. 2013).
(1)where n0 is the central density, r0 the half-density radius, and α the asymptotic power index. This type of radial profile has previously been used to fit the density structure of both starless cores (Tafalla et al. 2002) and filamentary clouds (Arzoumanian et al. 2011; Hacar & Tafalla 2011; Palmeirim et al. 2013; Ysard et al. 2013).
 |
Fig. 6 Histogram of the N2H+(1–0) mean optical depth for all chain positions used in the radiative transfer analysis. |
To compare the model with the observations, we have solved the equations of radiative transfer and predicted the radial profile of N2H+ intensity. Lacking a 2D model for the radiation transfer in a cylinder, we have instead used a spherically symmetric model that has the same density radial profile. This model properly accounts for the radial drop of collisional excitation caused by the density law, although it likely underestimates the excitation due to photon trapping because photons escape more easily from a sphere that from a cylinder. The effect of this difference in the trapping, however, is likely to be very small, since the optical depth of the N2H+(1–0) emission is low. This is illustrated in Fig. 6 with a histogram of the mean N2H+(1–0) optical depth estimated from the data of all bright positions in our survey (4947 spectra in total). The mean optical depth was defined by dividing the total optical depth of the N2H+(1–0) transition (determined with the HFS hyperfine analysis in the CLASS program) between seven, which is the number of components. It therefore represents the average optical depth of an individual N2H+(1–0) component.
As can be seen, the histogram of mean optical depths is dominated by low values. In all regions but B7/L1495, ~90% of the points have a mean optical depth lower than 1, and less than 1% of the points have a mean optical depth larger than 2. The cluster-forming B7/L1495 region is significantly more opaque and is responsible for the small group of points between optical depths 1 and 2 in the histogram. Still, 56% of its positions have a mean optical depth lower than 1, and no point exceeds a value of 2. Under these conditions, using spherical geometry to simulate the radiative excitation in a cylinder appears to be an acceptable approximation, especially considering that the assumption of cylindrical symmetry is itself a large simplification of the true geometry of the chains.
To solve the radiative transfer equations we used the Monte Carlo code of Bernes (1979) previously applied to analyze the emission from starless cores (Tafalla et al. 2002, 2004a). This code was implemented with the molecular parameters of N2H+ from the LAMDA web site (Schöier et al. 2005), which include the collision rates of Daniel et al. (2005). These rates include the individual hyperfine components of each rotational transition (up to J = 6), which were treated as independent lines whose flux was later combined to simulate the observed integrated intensity.
Our radiative transfer calculation also assumed a constant gas kinetic temperature of 10 K. This assumption is based on the analysis of ammonia, a molecule that coexists with N2H+ in the dense gas and whose emission in Taurus cores indicates a median temperature of 9.5 K (which little dispersion, Jijina et al. 1999). Recent large-scale ammonia mapping of the L1495/B213 complex by Seo et al. (in prep.) confirms this assumption, and indicates that while there are small local variations of 1−2 K in some cores, there are no global temperature gradients in the chains. Even the lower-density gas that surrounds the core chains appears to have a similar temperature, since the CO-based estimate of Goldsmith et al. (2008) indicates that the majority of points in this region (their Mask 2) have temperatures that lie in the 6−12 K range. This constant temperature of the gas in the density range of interest (105−104 cm-3, see below) is expected from detailed modeling of the gas heating and cooling, and contrasts with the well-measured temperature gradient of the dust component found by Palmeirim et al. (2013), which is expected from heating by the interstellar radiation field (Evans et al. 2001; Galli et al. 2002).
Additional assumptions of the model were a non-thermal FWHM linewidth of 0.25 km s-1, as suggested by the analysis of Sect. 3.7.2, and a maximum radius of 400 arcsec (0.27 pc), although the comparison with the data is restricted to the central 100 arcsec due to limited signal to noise (the exact size has only a small effect on the result). Following our experience with the analysis of dense cores, we divided the cloud model into 200 shells, used 2000 photons, and iterated the calculation 40 times. To simulate the IRAM 30 m observations, plus the additional 20′′ Gaussian smoothing applied to the data to enhance its signal to noise, the emerging intensity distribution was convolved with a Gaussian of 33′′ FWHM. Finally, the data were scaled up by a factor of 1.4 to simulate a 45 degree inclination angle of the model with respect to the line of sight. The L1495/B213 cloud appears as a relatively long filament in the sky (≈10 pc), so it is unlikely to be highly inclined; using a moderate angle of 45 seems like a reasonable assumption that is unlikely to introduce a large error.
Best-fit chain parameters.
To find the best fit to the data, we explored different values of the N2H+ abundance and the density law. As discussed in the previous section, the choice of N2H+ abundance has a direct effect on the slope of correlation between the N2H+ intensity and the H2 column density, and the plots of Fig. 4 were used to derive a constant value of 5 × 10-10 for all chains but B7/L1495-south (were the best fit is 1.5 × 10-10). To fit the density law, we used the radial profiles of N2H+(1–0) intensity and explored the effect of each of the three free parameters. The power law index is only weakly constrained, since the radial profile only approaches this asymptotic behavior at large radius, where the data have a low signal to noise ratio. Reasonable fits were achieved with values close to 3 (as found for the filaments in L1517, Hacar & Tafalla 2011), so this parameter was fixed to 3 in all the chains. The remaining two parameters, central density and half-maximum radius, are somewhat correlated, since both contribute linearly to the central column density, and they need to be distinguished by fitting the profiles at large radii (with the already mentioned problem of low signal to noise and certain dependence on the power-law index). After exploring a number of combinations, we determined as best fit values those given in Table 1, which produce the radial profiles shown with black lines in Fig. 5. Since we were interested in the density structure of the chains as possible indicator of the initial conditions of core formation, the fits were purposely chosen to fit the points with lowest intensity near the axis and to avoid the brighter points that arise from the dense cores.
As can be seen in Table 1, both the central density and the half-maximum radius vary little over the sample of chains (6−7 × 104 cm-3 and 35′′−50′′, respectively). This small variation agrees with our expectation of a common internal density structure based on the similarity of the radial profiles, and strengthens the idea that the different chains may have formed in a similar manner. The fit values, however, have a significant level of uncertainty due to the uncertainty in the the dust opacity discussed before. Also, the large scatter in the radial profiles is a remainder that cylindrical symmetry is an over-simplification of the 3D geometry of the chains. For this reason, the best-fit parameters in Table 1 should be considered only as a first-order approximation to the true parameters of the chain gas, which likely have an uncertainty level of a factor of 2.
Even if approximate, the parameters of Table 1 can be used to explore the physical state and gravitational stability of the core chains. To do this, we compare our best fit models with the classical solution of an isothermal cylinder in equilibrium, first studied by Stodólkiewicz (1963) and Ostriker (1964). This solution has an asymptotic power-law index of −4, while our best fit models are slightly flatter and have a power-law index of −3. More importantly, the isothermal cylinder has an equilibrium mass per unit length of 16.6 M⊙ pc-1, assuming a gas kinetic temperature of 10 K. Table 1 shows that the mass per unit length values of our best-fit models are systematically larger, although only by at most a factor of 2. Palmeirim et al. (2013) also found a larger-than-equilibrium mass per unit length in the B213/B211 filament as a whole using dust continuum measurements, although these authors treated the region as a single object and ignored the presence of multiple velocity components. Whether this larger mass per unit length means that the chains are significantly out of equilibrium is unclear, especially considering the uncertainty in the dust opacity and that additional support mechanisms, such as magnetic fields or temperature gradients can increase the equilibrium mass per unit length (Stodólkiewicz 1963; Nakamura et al. 1993; Recchi et al. 2013). Further understanding of the physical state of the chains requires the analysis of their internal kinematics, which is the topic of the next two sections.
3.6. Cloud kinematics from C18O data: multiple components
The C18O molecule freezes out rapidly onto the dust grains at densities typical of the cores and the chains, so it is a poor tracer of the dense gas kinematics. It is however a faithful tracer of the motions in the lower-density gas that surrounds the chains, since in this regime C18O is chemically stable, easily thermalized, and does not suffer appreciably from saturation due to its low abundance. Hacar et al. (2013) showed that in the L1495/B213 region, the velocity fields of C18O and N2H+ are similar, indicating that the dense cores and their surrounding environment are closely coupled kinematically. Before studying the kinematics of the dense gas with N2H+ in the next section, it is therefore convenient to use the C18O emission to determine the properties of the velocity field in the vicinity of the chains. These properties provide important context and help solve some of the ambiguities that affect the more selective N2H+ emission.
As analyzed in detail by Hacar et al. (2013), the C18O velocity field in L1495/B213 is complex. It consists of about 35 intertwined filamentary components (or fibers) that appear in the spectra as multiple velocity peaks. To disentangle these components, Hacar et al. (2013) used a combination of Gaussian fits to the spectra and the Friends In VElocity (FIVE) algorithm, which connects spatially the velocity components from nearby positions. The IRAM 30 m maps discussed here are less extended than the FCRAO maps of Hacar et al. (2013), and the focus of our analysis is limited to the C18O emission related to the dense gas in the chains. For this reason, we have carried out a simplified analysis of the velocity structure of the C18O emission based on the inspection of the spectra and the use of velocity-integrated maps.
An inspection of the C18O data reveals that each mapped region contains at least several positions where the spectrum has two peaks separated by more than one full linewidth. These double-peaked spectra do not originate from self-absorption, since, when detected, the optically thin isolated component of N2H+(1–0) matches the velocity of one of the two C18O components, instead of appearing at the intermediate velocity that would be expected in the case of self-absorption. The double peaks therefore arise from the multiple velocity components studied by Hacar et al. (2013) when they overlap along some lines of sight. Examples of these double-peaked spectra can be seen in the top panel of Fig. 7 for each of the five regions associated with dense gas.
To determine the spatial distribution of the C18O velocity components in the vicinity of the core chains, we have divided the emission into two velocity intervals centered approximately on each of the C18O peaks. The resulting maps, presented in the bottom panels of Fig. 7, show that in each chain, the two C18O components differ markedly in spatial distribution. In B213, the blue component extends to the NW of the mapped region and is unrelated to the chain of N2H+ cores, that has a different velocity and spatial distribution. This blue C18O component corresponds to component number 18 in the cloud decomposition of Hacar et al. (2013). The red component, on the other hand, is associated with the chain of dense cores, and its velocity and large-scale orientation are similar to those of the chain. In contrast with N2H+, the C18O emission presents strong evidence of large-scale freeze out. It misses some of the brightest N2H+ and continuum peaks, such as the core around IRAS 04166+2706 and the starless core SE of it, and only presents bright emission toward some embedded YSOs. C18O freeze out in this region seems therefore not limited to the dense cores, but occurs at the scale of the full chain, and is only reversed locally in the vicinity of some YSOs.
 |
Fig. 7 Velocity structure of the C18O(2–1) emission in L1495/B213. Top: C18O(2–1) spectra from selected positions illustrating the presence of multiple velocity components along the line of sight. The selected positions are indicated with red circles in the maps below. Bottom: maps of C18O(2–1) emission integrated in two velocity intervals that approximately coincide with the components in the top spectra. All maps have the same physical scale, color code (shown in the B7/L1495 panel), and contour scale (first contour and interval are 0.3 K km-1). Coordinate centers and star symbols as in Fig. 2. |
In the single-core region B211, also the red component is associated with the N2H+ dense core, since it has the same velocity and a similar spatial distribution. The unrelated blue component arises from a long diagonal filament that is in fact the superposition of the parallel components 9 and 12 in the velocity decomposition of Hacar et al. (2013).
The more complex B10 region appears in the N2H+ maps of Fig. 2 as consisting of two roughly parallel chains plus an isolated core in the south. The C18O spectrum and maps in Fig. 7 show now that the western chain of B10 coincides with a region where two velocity components that are separated by 1 km s-1 spatially overlap. These two components seem to be responsible for the apparent velocity jump of about 1 km s-1 seen in N2H+ (Sect. 3.7.1), indicating that the western chain of B10 is in fact the overlap of two separate structures. This interpretation is in agreement with the decomposition of the large-scale C18O emission by Hacar et al. (2013), who divided this region into two components labeled 6 and 8.
The C18O maps of Fig. 7 also show that chain-wide CO freeze out has also taken place in B10, since the eastern chain is very prominent in N2H+ but only marginally visible in C18O. As mentioned before, this eastern chain shows little fragmentation. This indicates that CO depletion precedes the fragmentation of the chain into cores.
In the B7/L1495 region, the blue C18O velocity component is associated with the isolated N2H+ core to the SW, while the red component is associated with the N2H+ chain of cores. As can be seen in Fig. 7, the blue C18O brightens significantly toward the south end of the map, which coincides with the region where the dust temperature increases due to heating by V892 Tau. This brightening of the C18O emission implies that CO depletion may be lower closer to V892 Tau, and this may explain the anomalously low N2H+ abundance inferred from the comparison with the SPIRE data.
Finally, in B218, the two C18O components present anticorrelated spatial distributions. The blue component peaks toward the NE and SW of IRAS 04248+2612, and is associated with the two N2H+ starless cores at each side of the YSO because they match both in position and velocity. The red C18O component, on the other hand, peaks toward the IRAS source and extends slightly toward the NW. The nature of this component is unclear due to its limited extent. A likely possibility is that it is caused by the action of the YSO on its surrounding gas, since IRAS 04248+2612 powers a molecular outflow that has a dominant red wing (although mostly towards the SE, see Narayanan et al. 2012), and is associated with a chain of HH objects directed opposite to the red C18O emission (Gomez et al. 1997). In this interpretation, the B218 region would consists of a single C18O velocity component that corresponds to the blue C18O regime. Further observations of this region are needed to clarify its kinematics.
To summarize, the C18O data show that the presence of multiple velocity components in the vicinity of the chains is common. These components are separated by supersonic speeds and do not seem to be interacting, since they are forming dense cores at their own systemic velocity, and not at the intermediate velocity that would be expected if core formation occurred through collisions. The components in each region, however, are not completely unrelated. In B10 and B7/L1495, for example, the two components have produced cores in close proximity, which given the strong clustering of cores in the cloud seems an unlikely random event. In other regions, like B213 and B211, different filamentary components are almost parallel, suggesting that they have some type of relation or common origin. From their large-scale study of the C18O emission, Hacar et al. (2013) found that indeed, most velocity components in L1495/B213 belong to groups or bundles with a common origin, and proposed that some type of turbulent fragmentation process was responsible for their origin. A number of recent hydrodynamical simulations have shown that bundles of filamentary components like those in L1495/B213 arise naturally from the combination of turbulent motions and self gravity (Kritsuk et al. 2013; Smith et al. 2013; Moeckel & Burkert 2014; Myers et al. 2014). This implies that the formation of dense cores and chains is preceded by a step of fragmentation whose product are the C18O components shown in Fig. 7. Thus, the multiplicity of components in the C18O spectra near the core chains is not a mere superposition coincidence, but a natural consequence of the hierarchical fragmentation required to form dense cores. Further discussion on this topic is presented below after the analysis of the N2H+ kinematics.
 |
Fig. 8 Velocity structure of the N2H+ emission as determined from hyperfine fits to the spectra. For each region, the first panel shows (in km s-1) the spatial distribution of the velocity centroid, and the second panel shows (also in km s-1) the distribution of non-thermal linewidth (FWHM). The black contours show the distribution of integrated emission to help identify the main dense gas features. All plots use the same spatial scale and color code, which is indicated by wedges in the maps of B213. Coordinate centers, contour levels, and star symbols as in Fig. 2. |
3.7. Chain kinematics from N2H+ data
The velocity structure of the N2H+ emission is simpler than that of C18O due to the more selective nature of this tracer. In general, the N2H+(1–0) spectra present a single velocity component, although split into seven features due to hyperfine structure. A few spectra show hints of two velocity components, like near B213 (900′′, −650′′), but the components are so weak that is not possible to analyze them using multiple fits. For this reason, we have fitted the N2H+(1–0) spectra assuming a single velocity component, using for this the CLASS program and the numerical parameters of the hyperfine structure derived by Caselli et al. (1995). This single-component fit analysis determines both the line center velocity and the full width at half maximum (FWHM) corrected for optical depth broadening. Subtracting the thermal contribution of a gas at 10 K, the FWHM can be converted into an estimate of the non-thermal velocity dispersion in the gas.
Figure 8 shows in color the distribution of N2H+ line center velocity and non-thermal FWHM as derived from the hyperfine analysis. To ensure the quality of the data, the figure only presents results from fits that appear reliable under visual inspection, which approximately corresponds to an intensity threshold of 0.5 K km s-1. As can be seen, the line center velocity changes smoothly over each chain, with a typical size scale for the changes of the order of a core diameter. The accompanying linewidth maps also show a smooth behavior, although there are several regions of high dispersion that we discuss in more detail below. Since the sound speed FWHM corresponds to 0.45 km s-1, the maps in Fig. 8 indicate that the gas in the chains is mostly subsonic, and that only a few locations have supersonic linewidths.
 |
Fig. 9 Velocity structure of the N2H+ emission along the axis of the core chains. For each chain, the plot shows the velocity centroid in the top panel (blue symbols), the non-thermal FWHM in the middle panel (red symbols), and the integrated intensity in the bottom panel (black symbols). Only points within 30′′ of the chain axis are shown to ensure proximity. The horizontal dashed line indicates the FWHM-equivalent of the sound velocity. Note the smooth oscillations in the velocity centroid and the predominance of subsonic values in the non-thermal linewidth. |
While the maps in Fig. 8 provide a good representation of the gas velocity field in two dimensions, they provide limited quantitative information on the gas kinematics. This information is better appreciated in the velocity profiles of Fig. 9. These profiles represent, as a function of distance along the axis of each chain, the line center velocity (blue), the non-thermal FWHM (red), and for reference, the N2H+(1–0) integrated intensity (black). To ensure physical proximity between the points, the figure only shows data from positions within 30 arcsec from each chain axis. All panels use the same linear scale, and as a result, the figure is dominated by the data from the B213 region, which has a length almost as large as the rest of the chains combined.
3.7.1. Line center velocity
We first study the line-center velocity, which is represented with blue squares in the top panels of Fig. 9. As can be seen, this parameter presents little dispersion and an almost oscillatory behavior in most panels. In the longest B213 chain, the line center velocity oscillates repeatedly without deviating by more than about 0.3 km s-1 from the mean value over its full length of almost 1.5 pc. The smaller B10-E (eastern branch of B10) and B7/L1495 chains also show smooth velocity oscillations, again with close-to-constant mean values and amplitudes of the order of 0.2 km s-1.
In contrast with the other chains, the western branch of B10 presents a jump in velocity of about 1 km s-1 near D = 300′′. This jump most likely results from the presence in B10-W of two separate chains. As discussed in Sect. 3.6 and evidenced by the double-peaked C18O spectrum of Fig. 7, two cloud components with velocities around 6 and 7 km s-1 coexist and overlap in B10-W. The blue C18O component lies mostly toward the NW, and the red component lies mostly toward the SW. This is also the distribution of the N2H+ line center velocities, which also match the velocities of the two C18O components. Since the N2H+ center velocity remains almost constant toward each side of the jump, and the jump coincides with a sharp drop of N2H+ emission (as shown in the 2D map of Fig. 8), the most natural interpretation of the velocity jump in B10-W is that it represents the transition between the two C18O components. This implies that B10-W is not a single chain of cores, but the chance alignment of two different velocity components. The recent numerical simulations of turbulent molecular clouds by Moeckel & Burkert (2014) show that this type of chance alignment is expected in regions like the L1495/B213 cloud.
Another discontinuity in the velocity profiles of Fig. 9 occurs in B218 near D = 400′′. As shown in Fig. 2, the B218 chain consists of three N2H+ cores, two of them starless and located at each end of the chain and a weaker one located near the center and associated with the Class I object IRAS 04248+2612. Figure 9 shows that the two starless cores have the same line center velocity within 0.1 km s-1, but that the region between them, where the N2H+ emission weakens and the IRAS source lies, presents a rapid shift in velocity towards the red. This reddening of the N2H+ emission coincides with the reddening of the C18O emission discussed in Sect. 3.6, and is highly localized toward the vicinity of the YSO (see Fig. 8). As discussed in Sect. 3.6 this reddening of the emission likely results from the interaction of the YSO with the surrounding cloud, and does not represent a remnant of the pre-stellar motions in the chain.
The velocity oscillations in Fig. 9 are similar to those found in L1517, also in the Taurus complex, by Hacar & Tafalla (2011). In L1517, several filaments presented a sinusoidal velocity pattern that was approximately shifted by λ/ 4 from the also sinusoidal pattern of column density. Such a shift was interpreted as possible evidence of core-forming gas motions along the filament axis, since analytic theory predicts a λ/ 4 offset between density and velocity in the case of an unstable (core-forming) perturbation (Gehman et al. 1996; Hacar & Tafalla 2011). The core chains in L1495/B213 provide an ideal place to search for similar core-forming motions, since the multiplicity of cores provides a strong constraint in the displacement between the velocity and column density profiles. The B213-NW chain, for example, contains 4 almost equally-spaced cores, while the filaments in L1517 contained only two cores. For this reason, we have fitted the N2H+ intensity profiles in Fig. 9 with simple sinusoidal functions (after subtracting a mean value), and we have compared the velocity profiles with shifted versions of the intensity sinusoids. While occasional matches for individual cores can be found, no chain presents a systematic displacement between its velocity and intensity profiles that applies to all cores and that could be interpreted unambiguously as evidence of core-forming motions along the chain axis. This lack of a systematic shift between the velocity and column density patterns implies that the velocity oscillations in the chains are not entirely due to the core-forming motions predicted by the analytic theory.
There are several possible origins for the velocity oscillations seen in N2H+. One possibility is that they still arise from core-forming motions, but that the motions are more complex than what the simple analytic model assumes. Most chains contain a mixture of starless cores and cores with embedded YSOs, and this indicates that the contraction history of the chain must have been more irregular than what is assumed by the simple model, in which all cores are formed simultaneously through the exponential growth of a single sinusoidal perturbation. Another possibility is that the oscillations arise from motions that pre exist the formation of the chains and the cores. Hacar et al. (2013) found that most C18O filamentary components in the cloud present oscillations in their velocity field irrespectively of their core-forming status. In this case, the chains must start their evolution with an already perturbed velocity field, and identifying any core-forming motions in such conditions may require a more complex analysis. Numerical simulations of the formation and fragmentation of realistic filamentary structures are needed to clarify this issue.
3.7.2. Non-thermal velocity component
The non-thermal N2H+ component of the velocity field is represented with red squares in the middle panels of Fig. 9. Like the line center velocity, the non-thermal component presents both a smooth oscillatory behavior along each of the chains and a very low level of dispersion, except for a few regions of moderate scatter. The great majority of points lie below the sonic threshold of 0.45 km s-1, indicating that subsonic gas motions dominate the chains. For the data presented in the figure, which consists of points with separations of less than 30′′ from the chain axis, the fraction of supersonic points is only 2.1%. Increasing the separation threshold to 90′′ adds more weak points, but only increases the fraction of supersonic points to 3.7%. Subsonic points are therefore the norm, and supersonic positions are rare.
In addition to being rare, the supersonic points tend to lie in small groups, implying that they result from localized causes. Feedback from outflows is one of them, as illustrated by the points in the vicinity of IRAS 04169+2702, which lies in B213-NW, near D = 1600′′. This Class I source powers a well-known bipolar outflow previously studied in CO by Moriarty-Schieven et al. (1992), Bontemps et al. (1996), and Narayanan et al. (2012). As Fig. 8 shows, the points of supersonic N2H+ linewidth lie north and south of IRAS 04169+2702 and approximately match the bipolar distribution of the CO outflow lobes (see Fig. 10 in Narayanan et al. 2012).
Other regions with supersonic N2H+ linewidths of possible outflow origin are the vicinity of the three low-mass sources near D = 400′′ in B213 SE, which appears to have already been evacuated of dense gas, and the already-mentioned vicinity of IRAS 04248+2612 in B218. A few additional points with enhanced linewidth close to the supersonic limit are associated with IRAS 04166+2706 in B213-NW near D = 1950′′. This is another outflow source of low luminosity that has evacuated a cavity in the surrounding dense core (Bontemps et al. 1996; Tafalla et al. 2004b; Santiago-García et al. 2009).
Not all regions with supersonic linewidth result from outflow feedback. A group of supersonic points in B10-NW coincide with the region of double-peaked C18O spectra shown in Fig. 7, and their enhanced linewidth likely results from this multi-component kinematics. Indeed, some N2H+(1−0) spectra in this region show two velocity components, and confusion between these components and the hyperfine structure seems to cause the larger linewidths seen in this region. A similar mixing between components is likely to occur toward the western part of B213-SE (D ≈ 650′′ in Fig. 9), where two velocity components at 6.7 and 7.0 km s-1 seem to coexist.
While we cannot exclude that some of the remaining supersonic N2H+ linewidths correspond to positions with intrinsically supersonic motions, the overwhelming dominance of subsonic positions (>95%) indicates that subsonic motions are a main characteristic of the chain gas.
 |
Fig. 10 Structure function of the dense-gas velocity field. The color–coded solid squares show the structure function as a function of lag in B213 (black), B10 (red), B218 (green), and B7/L1495 (blue). The blue dashed line represents the classical relation from Larson (1981), and the red dashed line represents the recently-determined core-velocity difference of Qian et al. (2012). |
 |
Fig. 11 Fray and fragment scenario of core formation. The three panels represent three different stages in the evolution of a large-scale filament like L1495/B213. In the first stage (left panel), two gas flows collide and produce a filamentary density enhancement. With time (middle panel), a combination of residual turbulent motions and gravity splits the gas into a series of intertwined velocity-coherent fibers. Finally (right panel), some fibers accumulate sufficient mass to reach the limit for gravitational fragmentation and form chains of dense cores. |
3.7.3. Structure function
The combination of subsonic motions and large-scale continuity in the velocity field of the B213 gas filaments led Hacar et al. (2013) to refer to these structures as “velocity coherent” (see also Hacar & Tafalla 2011). This term stresses the quiescent state of the filaments compared to the cloud as a whole, which is characterized by a Kolmogoroff-type relation between size and velocity indicative of turbulent motions (Larson 1981). To further compare the kinematics of the gas in the chains with that of the large-scale cloud, we have carried out a structure-function analysis of the N2H+ line-center velocities. The structure function measures the mean difference in velocity between positions separated by a distance l, and is defined as 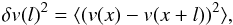 where v(x) is the gas velocity at an arbitrary position x and the brackets represent a spatial average over all positions separated by l. This function is commonly used as a descriptor of the velocity field in a cloud, where it is systematically found to depend on l as a power law (Elmegreen & Scalo 2004; Heyer & Brunt 2004).
where v(x) is the gas velocity at an arbitrary position x and the brackets represent a spatial average over all positions separated by l. This function is commonly used as a descriptor of the velocity field in a cloud, where it is systematically found to depend on l as a power law (Elmegreen & Scalo 2004; Heyer & Brunt 2004).
To estimate the structure function of the gas in the L1495/B213 chains, we have used the N2H+ line-center velocities derived in Sect. 3.7 from hyperfine fits. These velocities measure the radial component of the velocity field, so our estimate of the structure function refers only to this radial component. Figure 10 shows in colored squares the structure function for all the chains but B10-W, which was found to be the superposition of two different gas components. As can be seen, the structure functions of B213, B10E, and B7/L1495 are approximately flat or present only smooth oscillations as a function of l. The structure function of B218 (green squares) presents a spike near l = 0.15 pc, but this feature is caused by the strong reddening of the emission near the YSO, which we saw is likely due to outflow feedback. At larger distances, corresponding to the separation between the starless cores at each side of the YSO, the structure function of B218 converges to a low value comparable to that of the other chains.
The flat structure functions of the chains contrast with the power-law functions of the extended gas indicative of turbulent motions (Larson 1981; Elmegreen & Scalo 2004; Heyer & Brunt 2004). This is illustrated in Fig. 10 with two dashed lines. The blue line represents the classical Larson (1981) relation, and the red line is the structure function estimated by Qian et al. (2012) for Taurus using a large-scale map of the 13CO emission (Goldsmith et al. 2008). As seen in the figure, both dashed lines follow a similar power-law increase with l and deviate systematically from the flat structure functions of the chains. While the deviation between chains and cloud is most prominent in the B213 chain due to its larger length, it is also significant in the other three chains due to the consistency of their behavior.
The flatness of the structure functions in Fig. 10 adds evidence to the suggestion by Hacar et al. (2013), from C18O data, that the gas in the velocity-coherent filaments has decoupled from the turbulent velocity field that dominates the cloud as a whole. The observations, therefore, imply that turbulence does not dissipate at the ≈0.1 pc scale of the dense cores (Goodman et al. 1998), but at a larger scale of approximately 0.5 pc that corresponds to the C18O velocity-coherent fibers. As a result of this dissipation of the turbulence at larger scales, the condensation of the cores out of the chain gas must involve little kinematic change, which is in agreement with the smooth oscillations seen in the radial profiles of velocity. Thus, while turbulence dominates the motions of the cloud gas at large scales, it appears to have been dissipated before the gas condenses into close-to-spherical dense cores.
4. Implications for core and star formation
We now combine our analysis of the internal structure of the N2H+ chains with the study of the large-scale C18O emission by Hacar et al. (2013) and a number of arguments from analytic theory and numerical simulations to present a scenario of core and star formation in the L1495/B213 region. A schematic view of this scenario is shown in Fig. 11 with a three-step time sequence of the gas evolution in the cloud. For reasons that should be clear below, we refer to this scenario as “fray and fragment”.
The first step in the scenario consists of the formation of the 10 pc-long L1495/B213 region. This event, like the formation of the rest of the Taurus molecular cloud, most likely resulted from the collision between two large-scale flows of gas, as proposed by a number authors and implied by numerical simulations (Ballesteros-Paredes et al. 1999; Hartmann et al. 2001; Padoan & Nordlund 2002; Mac Low & Klessen 2004; Vázquez-Semadeni et al. 2007; Heitsch et al. 2008). A lower limit to the velocity of this collision can be estimated using the velocity spread of the gas in the L1495/B213 filament. The C18O data of Hacar et al. (2013) show some spectra containing multiple velocity components that range in LSR centroid velocity between 4.8 and 7.0 km s-1 (their Fig. 8). This spread implies that the relative velocity of the converging flows was at least 2.2 km s-1.
Since the velocity spread of 2.2 km s-1 refers to C18O-emitting gas, which has a typical temperature of 10 K, it corresponds to a Mach number of about 11. This implies that the internal motions in the large-scale filament of L1495/B213 definitely belong to the supersonic regime.
The second step in the scenario of Fig. 11 is the generation of substructure inside the 10 pc-long L1495/B213 filamentary cloud. This substructure was studied in detail by Hacar et al. (2013), who analyzed the C18O emission from the cloud with the Friends In VElocity (FIVE) algorithm and identified 35 distinct velocity-coherent fibers. These fibers run approximately parallel to the 10 pc-long L1495/B213 cloud and criss-cross each other like the threads of a frayed rope.
While the relative velocity between fibers spans the full 2.2 km s-1 range, the velocity dispersion of the gas inside each fibers is much lower and lies in the subsonic or slightly transonic regime. Such combination of low internal velocity dispersion and large-scale continuity of the velocity implies that these fibers have already decoupled from the large-scale turbulent velocity field of the cloud, and that therefore represent a critical scale of velocity dissipation. The recent numerical simulations of cloud turbulence by Moeckel & Burkert (2014) seem to confirm this. The simulations show that large-scale filamentary structures quickly evolve into bundles of intertwined fibers like those of L1495/B213 due to the combined effect of vorticity and self gravity (see also Kritsuk et al. 2013; Smith et al. 2013; and Myers et al. 2014).
The final step of the scenario shown in Fig. 11 is the formation of dense cores out of the velocity-coherent fibers. Hacar et al. (2013) showed that only a few of these fibers are responsible for the formation of all dense cores cores in L1495/B213, and referred to them as “fertile”. These fertile fibers preferentially form multiple cores, so they seem to have an intrinsic predisposition to core formation along most of their length. A natural origin for this predisposition is gravitational instability, as implied by the higher value of the mass-per-unit-length in these fibers.
 |
Fig. 12 Distance to the nearest neighbor among the N2H+ cores in L1495/B213 (no projection correction applied). Note how most values lie below 0.2 pc. |
To test this interpretation, we have studied the typical separation between dense cores along the chains. This has been done using the core positions determined in Sect. 2 and calculating the distribution of distance to the nearest neighbor. Figure 12 shows a histogram with the results. As can be seen, the distribution is dominated by values smaller than 0.2 pc, with 3/4 of the points lying below this length. The median of the distribution is 0.14 pc and the mean is 0.2 pc, although this latter value is biased due to the the large contribution from the isolated core in B211.
Since the observed distances represent measures in the plane of the sky, they have to be corrected for inclination. As discussed in Sect. 3.5, the inclination angle of the chains is unknown, but it is unlikely to be very large due to the already long appearance of the L1495/B213 complex. Thus, we have assumed a moderate inclination angle of 45 degrees, which implies a foreshortening factor of only 1.4. With this correction, the true median distance between cores is estimated to be approximately 0.2 pc.
To compare the above inter-core distance with the expectation from gravitational fragmentation, we use as a guide the self-gravitating isothermal cylinder model. This model can only represent a first-order approximation to the chains, since we have seen that their mass per unit length likely exceed the model prediction. In addition, the turbulent origin of the fibers and chains makes it unlikely that the gas in them has had sufficient time to fully relax to an isothermal equilibrium configuration, or even to acquire the axial symmetry required for a cylindrical geometry. Still, the deviations from equilibrium are unlikely to be very large, since the prevalence of subsonic linewidths in the spectra indicates an absence of shocks. Under these conditions, the isothermal cylinder model must provide a reasonable approximation, especially considering that the characteristics of gravitational fragmentation are robust with respect to changes in geometry and contributions from rotation and magnetic fields (Larson 1985).
As shown by Stodólkiewicz (1963), an isothermal cylinder with an equilibrium mass per unit length is unstable to sinusoidal perturbations that have a wavelength larger than a critical value of 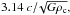 where ρc is the central density of the filament. These perturbations fragment the cylinder into a a series of equally-spaced condensations whose separation is given by the wavelength of the perturbation applied to the system, or if no single-wavelength perturbation is imposed, by the wavelength of the fastest-growing unstable mode, which is twice the critical wavelength (Nagasawa 1987, also Larson 1985; Inutsuka & Miyama 1997; Fischera & Martin 2012). In Sect. 3.5 we estimated that the core chains have a typical pre-fragmentation central density of ≈0.65 × 105 cm-3. For the isothermal cylinder model, this density implies a critical wavelength of 0.14 pc, and a fastest-growing mode wavelength of 0.28 pc, assuming the gas is at 10 K. These values are in reasonable agreement with our estimate of a typical inter-core distance of 0.2 pc. Strictly speaking, an inter-core value closer to 0.3 pc would have been expected, but it is also possible that the initial central density of the fibers has been underestimated, and that this has led to an overestimate of the expected critical wavelength and the separation between the cores. Given all the uncertainties in our estimates of the chain physical parameters, it appears that gravitational fragmentation is the likely mechanism responsible for the formation of the dense cores inside the chains.
where ρc is the central density of the filament. These perturbations fragment the cylinder into a a series of equally-spaced condensations whose separation is given by the wavelength of the perturbation applied to the system, or if no single-wavelength perturbation is imposed, by the wavelength of the fastest-growing unstable mode, which is twice the critical wavelength (Nagasawa 1987, also Larson 1985; Inutsuka & Miyama 1997; Fischera & Martin 2012). In Sect. 3.5 we estimated that the core chains have a typical pre-fragmentation central density of ≈0.65 × 105 cm-3. For the isothermal cylinder model, this density implies a critical wavelength of 0.14 pc, and a fastest-growing mode wavelength of 0.28 pc, assuming the gas is at 10 K. These values are in reasonable agreement with our estimate of a typical inter-core distance of 0.2 pc. Strictly speaking, an inter-core value closer to 0.3 pc would have been expected, but it is also possible that the initial central density of the fibers has been underestimated, and that this has led to an overestimate of the expected critical wavelength and the separation between the cores. Given all the uncertainties in our estimates of the chain physical parameters, it appears that gravitational fragmentation is the likely mechanism responsible for the formation of the dense cores inside the chains.
If correct, the picture of core formation by gravitational fragmentation has several important consequences. In first place, fragmentation can only occur if an isothermal cylinder has sufficient mass per unit length. Since core formation in L1495/B213 is restricted to a small number of fertile fibers, it appears that only fertile fibers reach the required mass-per-unit-length, and that the rest of the fibers remain sterile because they never accumulate enough mass (this is supported by the analysis of Hacar et al. 2013). This interpretation suggests that core formation in L1495/B213 is regulated by how much mass the fibers can accumulate, and that inability to reach the critical mass is a main bottleneck in the core and star formation process. Given the turbulent state of the large-scale cloud, early dissipation of sterile fibers by shocks is the most likely mechanism to limit their growth. Star formation is thus limited, not by failed cores, but by failed (or sterile) fibers.
Another consequence of the gravitational fragmentation scenario is that dense cores may not be equilibrium structures, since they originate from an instability that cannot be reversed without external energy injection. This conclusion may seem to contradict the idea that cores are in gravitational equilibrium, as implied by the good fit of their radial density profiles with models of isothermal (Bonnor-Ebert) equilibrium (Alves et al. 2001). Equilibrium density profiles, however, are not a guarantee of true hydrostatic equilibrium, since they are expected to occur also during the first stages of gravitational collapse (Kandori et al. 2005). Evidence of (subsonic) gas contraction in starless cores is in fact often found when combining observations of optically thick and thin tracers (Lee et al. 1999).
While cylindrical models represent useful tools to understand core formation in the chains, they can only represent a first order approximation. As seen in the N2H+ maps, the chains have a typical full length of 0.5 pc, which is only about twice the wavelength of the fastest-growing mode. The chains therefore hardly qualify as “infinitely long”, and their fragmentation is likely to have been affected by edge effects. Chain edges, however, are unlikely to be sharp, since this would favor the rapid production of condensations near the boundaries (Burkert & Hartmann 2004), which is not seen in the maps. More likely, the edges of the chains are characterized by a smooth density decrease, which is expected to favor fragmentation in the chain interior (Nelson & Papaloizou 1993). Other deviations from the idealized infinite cylinder model include the natural bending of some of the chains, like B10, and the likely presence of significant initial perturbations in the density profile as a result of their turbulent environment. These additional elements are likely responsible for the already-discussed irregular pattern of fragmentation in the chains, by which cores that have already formed stars are intermixed with starless cores at an earlier stage of evolution. Numerical simulations of bundles of filaments, like those presented by Moeckel & Burkert (2014), are needed to explore how gravitational fragmentation occurs under more realistic conditions.
We finish by noting that the fray and fragment scenario proposed here has been inspired by the analysis of L1495/B213, but that it could apply to other regions of core and star formation. The analysis of the N2H+ emission from the NGC 1333 cluster-forming region by Hacar et al. (in prep.), for example, shows that the dense gas in this region forms a network of velocity-coherent fibers very similar to those found in L1495/B213, although with a higher density of fibers per unit volume, as it would be expected for a cluster-forming region. In addition, a number of large-scale dust-continuum images of clouds show that what initially appears as a single large-scale filament, on close inspection is resolved into a network of closely-aligned, small-scale fibers containing dense cores and embedded young stars. This is noticeable in some of the SPIRE images of the Herschel Gould Belt Survey, and is especially prominent in the APEX image of Orion presented by the ESO press release eso13212 (see also Stanke et al. 2013). Velocity-resolved observations of these filamentary structures are needed to test whether a fray and fragment scenario can explain core formation in other regions and in more massive environments.
5. Conclusions
We have presented new N2H+(1–0) and C18O(2–1) observations of the dense regions of L1498/B213 in Taurus made with the IRAM 30 m telescope and complemented with archival dust-continuum observations from the Herschel Space Observatory. From the analysis of the combined dataset, we have reached the following main conclusions.
-
1.
The dense cores in L1498/B213 tend to cluster in linear groups of three cores on average, which we call chains. This clustering is evident in the maps of integrated emission, and produces a significant peak in the mean surface density of companions for separations smaller than about 500′′ (≈0.3 pc). Only 3 cores out of 22 have no neighbor within 300′′ (0.2 pc).
-
2.
The N2H+ integrated intensities are correlated with the H2 column densities estimated from the SPIRE-Herschel data. This correlation is approximately linear, and in some chains it has a small threshold of H2 column density that seems to arise from additional gas components. The linear correlation indicates that towards the chains, the N2H+ emission traces most of the material seen in the Herschel images, and therefore provides velocity information to the continuum data. It also indicates that the N2H+ abundance is approximately uniform with a value of 5 × 10-10.
-
3.
A simplified Monte Carlo model of the N2H+ radial profiles indicates that the density of the chains decreases with radius as a softened power law. Typical central densities are 6−7 × 104 cm-3 and half-maximum diameters are 0.05 pc.
-
4.
While the C18O emission reveals the presence of multiple velocity components separated by supersonic speeds (analyzed in detail by Hacar et al. 2013), the N2H+ emission shows that the dense gas is overwhelmingly subsonic and continuous in velocity. This gas appears to have decoupled from the turbulent velocity field of the cloud and does not follow the standard Larson relation despite extending for up to 1 pc in length.
-
5.
When combined with the analysis of the C18O emission from Hacar et al. (2013), our observations suggest a scenario of core formation which we refer to as fray and fragment. In this scenario, a collision between two supersonic gas flows has created the large-scale L1498/B213 filament. Due to a combination of turbulence and self-gravity, the large-scale filament has split into a network of smaller and intertwined filamentary structures or fibers (fray step). Some of these fibers have accumulated enough material to exceed the mass-per-unit-length limit of gravitational instability and to fragment forming chains of dense cores. Although this scenario is motivated by L1498/B213, additional observations suggest that it may apply to other regions.
Acknowledgments
We thank the IRAM staff for support during the observations, and Markus Schmalzl for generously providing us with his extinction data and for information on the relation between NIR extinction and SPIRE 500 μm emission. We also thank Joaquín Santiago-García for his rendering of the fray and fragment scenario shown in Fig. 11. This research was performed in part thanks to financial support from projects FIS2012-32096 and AYA2012-32032 of Spanish MINECO and from the MICINN program CONSOLIDER INGENIO 2010, grant “Molecular Astrophysics: The Herschel and ALMA era – ASTROMOL” (ref.: CSD2009-00038). A.H. acknowledges support from the Austrian Science Fund (FWF). This research has made use of NASA’s Astrophysics Data System Bibliographic Services together with the SIMBAD database and the VizieR catalogue access tool operated at CDS, Strasbourg, France.
References
- Aikawa, Y., Herbst, E., Roberts, H., & Caselli, P. 2005, ApJ, 620, 330 [NASA ADS] [CrossRef] [Google Scholar]
- Alves, J. F., Lada, C. J., & Lada, E. A. 2001, Nature, 409, 159 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- André, P., Men’shchikov, A., Bontemps, S., et al. 2010, A&A, 518, L102 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- André, P., Di Francesco, J., Ward-Thompson, D., et al. 2014, in Protostars and Planets VI (University of Arizona Press), eds. H. Beuther et al., in press [arXiv:1312.6232] [Google Scholar]
- Arzoumanian, D., André, P., Didelon, P., et al. 2011, A&A, 529, L6 [Google Scholar]
- Ballesteros-Paredes, J., Vázquez-Semadeni, E., & Scalo, J. 1999, ApJ, 515, 286 [NASA ADS] [CrossRef] [Google Scholar]
- Barnard, E. E. 1907, ApJ, 25, 218 [NASA ADS] [CrossRef] [Google Scholar]
- Benson, P. J., & Myers, P. C. 1989, ApJS, 71, 89 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Bergin, E. A., Alves, J., Huard, T., & Lada, C. J. 2002, ApJ, 570, L101 [NASA ADS] [CrossRef] [Google Scholar]
- Bernes, C. 1979, A&A, 73, 67 [NASA ADS] [Google Scholar]
- Bontemps, S., Andre, P., Terebey, S., & Cabrit, S. 1996, A&A, 311, 858 [NASA ADS] [Google Scholar]
- Burkert, A., & Hartmann, L. 2004, ApJ, 616, 288 [NASA ADS] [CrossRef] [Google Scholar]
- Carter, M., Lazareff, B., Maier, D., et al. 2012, A&A, 538, A89 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Caselli, P., Myers, P. C., & Thaddeus, P. 1995, ApJ, 455, L77 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Walmsley, C. M., Tafalla, M., Dore, L., & Myers, P. C. 1999, ApJ, 523, L165 [NASA ADS] [CrossRef] [Google Scholar]
- Caselli, P., Benson, P. J., Myers, P. C., & Tafalla, M. 2002, ApJ, 572, 238 [NASA ADS] [CrossRef] [Google Scholar]
- Cernicharo, J., Bachiller, R., & Duvert, G. 1985, A&A, 149, 273 [NASA ADS] [Google Scholar]
- Daniel, F., Dubernet, M.-L., Meuwly, M., Cernicharo, J., & Pagani, L. 2005, MNRAS, 363, 1083 [NASA ADS] [CrossRef] [Google Scholar]
- di Francesco, J., Evans, N. J., II, Caselli, P., et al. 2007, Protostars and Planets V, 17 [Google Scholar]
- Dobashi, K., Uehara, H., Kandori, R., et al. 2005, PASJ, 57, 1 [Google Scholar]
- Elias, J. H. 1978, ApJ, 224, 857 [NASA ADS] [CrossRef] [Google Scholar]
- Elmegreen, B. G., & Scalo, J. 2004, ARA&A, 42, 211 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. J., II, Rawlings, J. M. C., Shirley, Y. L., & Mundy, L. G. 2001, ApJ, 557, 193 [NASA ADS] [CrossRef] [Google Scholar]
- Evans, N. J., II, Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321 [NASA ADS] [CrossRef] [Google Scholar]
- Fischera, J., & Martin, P. G. 2012, A&A, 542, A77 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gaida, M., Ungerechts, H., & Winnewisser, G. 1984, A&A, 137, 17 [NASA ADS] [Google Scholar]
- Galli, D., Walmsley, M., & Gonçalves, J. 2002, A&A, 394, 275 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Gehman, C. S., Adams, F. C., & Watkins, R. 1996, ApJ, 472, 673 [NASA ADS] [CrossRef] [Google Scholar]
- Goldsmith, P. F., Heyer, M., Narayanan, G., et al. 2008, ApJ, 680, 428 [NASA ADS] [CrossRef] [Google Scholar]
- Gomez, M., Hartmann, L., Kenyon, S. J., & Hewett, R. 1993, AJ, 105, 1927 [NASA ADS] [CrossRef] [Google Scholar]
- Gomez, M., Whitney, B. A., & Kenyon, S. J. 1997, AJ, 114, 1138 [NASA ADS] [CrossRef] [Google Scholar]
- Goodman, A. A., Barranco, J. A., Wilner, D. J., & Heyer, M. H. 1998, ApJ, 504, 223 [NASA ADS] [CrossRef] [Google Scholar]
- Griffin, M. J., Abergel, A., Abreu, A., et al. 2010, A&A, 518, L3 [Google Scholar]
- Hacar, A., & Tafalla, M. 2011, A&A, 533, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hacar, A., Tafalla, M., Kauffmann, J., & Kovács, A. 2013, A&A, 554, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hartmann, L. 2002, ApJ, 578, 914 [NASA ADS] [CrossRef] [Google Scholar]
- Hartmann, L., Ballesteros-Paredes, J., & Bergin, E. A. 2001, ApJ, 562, 852 [NASA ADS] [CrossRef] [Google Scholar]
- Heitsch, F., Hartmann, L. W., Slyz, A. D., Devriendt, J. E. G., & Burkert, A. 2008, ApJ, 674, 316 [NASA ADS] [CrossRef] [Google Scholar]
- Hennemann, M., Motte, F., Schneider, N., et al. 2012, A&A, 543, L3 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Henning, T., Linz, H., Krause, O., et al. 2010, A&A, 518, L95 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Heyer, M. H., & Brunt, C. M. 2004, ApJ, 615, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Hildebrand, R. H. 1983, QJRAS, 24, 267 [NASA ADS] [Google Scholar]
- Inutsuka, S.-i., & Miyama, S. M. 1997, ApJ, 480, 681 [NASA ADS] [CrossRef] [Google Scholar]
- Jijina, J., Myers, P. C., & Adams, F. C. 1999, ApJS, 125, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Juvela, M., Ristorcelli, I., Pelkonen, V.-M., et al. 2011, A&A, 527, A111 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kandori, R., Nakajima, Y., Tamura, M., et al. 2005, AJ, 130, 2166 [NASA ADS] [CrossRef] [Google Scholar]
- Kirk, J. M., Ward-Thompson, D., Palmeirim, P., et al. 2013, MNRAS, 432, 1424 [NASA ADS] [CrossRef] [Google Scholar]
- Könyves, V., André, P., Men’shchikov, A., et al. 2010, A&A, 518, L106 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kritsuk, A. G., Lee, C. T., & Norman, M. L. 2013, MNRAS, 436, 3247 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1981, MNRAS, 194, 809 [NASA ADS] [CrossRef] [Google Scholar]
- Larson, R. B. 1985, MNRAS, 214, 379 [NASA ADS] [Google Scholar]
- Larson, R. B. 1995, MNRAS, 272, 213 [NASA ADS] [Google Scholar]
- Launhardt, R., Stutz, A. M., Schmiedeke, A., et al. 2013, A&A, 551, A98 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lee, C. W., Myers, P. C., & Tafalla, M. 1999, ApJ, 526, 788 [NASA ADS] [CrossRef] [Google Scholar]
- Lee, C. W., Myers, P. C., & Tafalla, M. 2001, ApJS, 136, 703 [NASA ADS] [CrossRef] [Google Scholar]
- Lombardi, M., Lada, C. J., & Alves, J. 2010, A&A, 512, A67 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luhman, K. L., Allen, P. R., Espaillat, C., Hartmann, L., & Calvet, N. 2010, ApJS, 186, 111 [NASA ADS] [CrossRef] [Google Scholar]
- Mac Low, M.-M., & Klessen, R. S. 2004, Rev. Modern Phys., 76, 125 [Google Scholar]
- Mangum, J. G., Emerson, D. T., & Greisen, E. W. 2007, A&A, 474, 679 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Moeckel, N., & Burkert, A. 2014, ApJ, submitted [arXiv:1402.2614] [Google Scholar]
- Molinari, S., Swinyard, B., Bally, J., et al. 2010, A&A, 518, L100 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mooley, K., Hillenbrand, L., Rebull, L., Padgett, D., & Knapp, G. 2013, ApJ, 771, 110 [NASA ADS] [CrossRef] [Google Scholar]
- Moriarty-Schieven, G. H., Wannier, P. G., Tamura, M., & Keene, J. 1992, ApJ, 400, 260 [NASA ADS] [CrossRef] [Google Scholar]
- Myers, P. C. 2009, ApJ, 700, 1609 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Myers, A. T., Klein, R. I., Krumholz, M. R., & McKee, C. F. 2014, MNRAS, 439, 3420 [NASA ADS] [CrossRef] [Google Scholar]
- Nagasawa, M. 1987, Prog. Theoret. Phys., 77, 635 [Google Scholar]
- Nakamura, F., Hanawa, T., & Nakano, T. 1993, PASJ, 45, 551 [NASA ADS] [Google Scholar]
- Narayanan, G., Snell, R., & Bemis, A. 2012, MNRAS, 425, 2641 [NASA ADS] [CrossRef] [Google Scholar]
- Nelson, R. P., & Papaloizou, J. C. B. 1993, MNRAS, 265, 905 [NASA ADS] [Google Scholar]
- Ostriker, J. 1964, ApJ, 140, 1056 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Padoan, P., & Nordlund, Å. 2002, ApJ, 576, 870 [Google Scholar]
- Palmeirim, P., André, P., Kirk, J., et al. 2013, A&A, 550, A38 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pilbratt, G. L., Riedinger, J. R., Passvogel, T., et al. 2010, A&A, 518, L1 [CrossRef] [EDP Sciences] [Google Scholar]
- Qian, L., Li, D., & Goldsmith, P. F. 2012, ApJ, 760, 147 [NASA ADS] [CrossRef] [Google Scholar]
- Rebull, L. M., Padgett, D. L., McCabe, C.-E., et al. 2010, ApJS, 186, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Recchi, S., Hacar, A., & Palestini, A. 2013, A&A, 558, A27 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sandell, G., Weintraub, D. A., & Hamidouche, M. 2011, ApJ, 727, 26 [NASA ADS] [CrossRef] [Google Scholar]
- Santiago-García, J., Tafalla, M., Johnstone, D., & Bachiller, R. 2009, A&A, 495, 169 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Schmalzl, M., Kainulainen, J., Quanz, S. P., et al. 2010, ApJ, 725, 1327 [NASA ADS] [CrossRef] [Google Scholar]
- Schneider, S., & Elmegreen, B. G. 1979, ApJS, 41, 87 [NASA ADS] [CrossRef] [Google Scholar]
- Schöier, F. L., van der Tak, F. F. S., van Dishoeck, E. F., & Black, J. H. 2005, A&A, 432, 369 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Simon, M. 1997, ApJ, 482, L81 [NASA ADS] [CrossRef] [Google Scholar]
- Smith, R. J., Shetty, R., Beuther, H., Klessen, R. S., & Bonnell, I. A. 2013, ApJ, 771, 24 [NASA ADS] [CrossRef] [Google Scholar]
- Stanke, T., Stutz, A., Megeath, T., & HOPS Team 2013, Protostars and Planets VI Posters, 4 [Google Scholar]
- Stodólkiewicz, J. S. 1963, Acta Astron., 13, 30 [NASA ADS] [Google Scholar]
- Suutarinen, A., Haikala, L. K., Harju, J., et al. 2013, A&A, 555, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., Walmsley, C. M., & Comito, C. 2002, ApJ, 569, 815 [NASA ADS] [CrossRef] [Google Scholar]
- Tafalla, M., Myers, P. C., Caselli, P., & Walmsley, C. M. 2004a, A&A, 416, 191 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tafalla, M., Santiago, J., Johnstone, D., & Bachiller, R. 2004b, A&A, 423, L21 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tatematsu, K., Umemoto, T., Kandori, R., & Sekimoto, Y. 2004, ApJ, 606, 333 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez-Semadeni, E., Gómez, G. C., Jappsen, A. K., et al. 2007, ApJ, 657, 870 [NASA ADS] [CrossRef] [Google Scholar]
- Ward-Thompson, D., André, P., Crutcher, R., et al. 2007, Protostars and Planets V, 33 [Google Scholar]
- Ysard, N., Abergel, A., Ristorcelli, I., et al. 2013, A&A, 559, A133 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
All Figures
 |
Fig. 1 Large-scale view of the L1495/B213 complex. The grey scale shows the Herschel-SPIRE 250 μm emission mapped by Palmeirim et al. (2013), and the red contours represent the N2H+(1–0) emission mapped by Hacar et al. (2013) with the FCRAO telescope. The black dashed lines show the limits of the FCRAO observations, and the blue solid lines enclose the regions newly mapped with the IRAM 30 m telescope. |
| In the text | |
 |
Fig. 2 Integrated intensity maps of the N2H+(1–0) emission showing how the dense cores in L1495/B213 form linear chain-like structures (IRAM 30 m data). All maps have the same linear and intensity scales, and the first contour and contour interval are 0.5 K km s-1. The star symbols indicate the position of the YSOs in the compilation of Luhman et al. (2010), with solid symbols representing Class 0/I objects. The central positions, in (α(J2000), δ(J2000)) coordinates are (04:19:42.5, +27:13:36) for B213, (04:18:05.0, +27:35:16) for B211, (04:28:02.0, +26:19:32) for B218, (04:18:32.2, +28:27:18) for B7, and (04:18:04.0, +28:08:14) for B10. |
| In the text | |
 |
Fig. 3 Mean surface density of companions as a function of angular separation for the 22 cores identified in L1495/B213. The red squares represent observed data. The black line and the blue-shaded region represent the mean and the ±rms interval from 100 Monte Carlo simulations of a random distribution of 22 cores. The departure of the red squares from the shaded region at small angles indicates a significant level of clustering at scales less than 700′′. |
| In the text | |
 |
Fig. 4 Correlation between observed N2H+(1–0) integrated intensity and H2 column density derived from SPIRE dust-continuum data. Points within 45′′ of an embedded YSO have been excluded to avoid effects of stellar heating. The open squares in the B7/L1495 panel indicate points likely affected by V892 Tau (see text). The black lines represent the analytic expression discussed in the text. |
| In the text | |
 |
Fig. 5 Radial profiles of N2H+(1–0) integrated intensity in log-log scale. The red squares represent the data and the black lines are our models. B7/L1495 north data and model have been shifted by a factor of two to ease visibility. |
| In the text | |
 |
Fig. 6 Histogram of the N2H+(1–0) mean optical depth for all chain positions used in the radiative transfer analysis. |
| In the text | |
 |
Fig. 7 Velocity structure of the C18O(2–1) emission in L1495/B213. Top: C18O(2–1) spectra from selected positions illustrating the presence of multiple velocity components along the line of sight. The selected positions are indicated with red circles in the maps below. Bottom: maps of C18O(2–1) emission integrated in two velocity intervals that approximately coincide with the components in the top spectra. All maps have the same physical scale, color code (shown in the B7/L1495 panel), and contour scale (first contour and interval are 0.3 K km-1). Coordinate centers and star symbols as in Fig. 2. |
| In the text | |
 |
Fig. 8 Velocity structure of the N2H+ emission as determined from hyperfine fits to the spectra. For each region, the first panel shows (in km s-1) the spatial distribution of the velocity centroid, and the second panel shows (also in km s-1) the distribution of non-thermal linewidth (FWHM). The black contours show the distribution of integrated emission to help identify the main dense gas features. All plots use the same spatial scale and color code, which is indicated by wedges in the maps of B213. Coordinate centers, contour levels, and star symbols as in Fig. 2. |
| In the text | |
 |
Fig. 9 Velocity structure of the N2H+ emission along the axis of the core chains. For each chain, the plot shows the velocity centroid in the top panel (blue symbols), the non-thermal FWHM in the middle panel (red symbols), and the integrated intensity in the bottom panel (black symbols). Only points within 30′′ of the chain axis are shown to ensure proximity. The horizontal dashed line indicates the FWHM-equivalent of the sound velocity. Note the smooth oscillations in the velocity centroid and the predominance of subsonic values in the non-thermal linewidth. |
| In the text | |
 |
Fig. 10 Structure function of the dense-gas velocity field. The color–coded solid squares show the structure function as a function of lag in B213 (black), B10 (red), B218 (green), and B7/L1495 (blue). The blue dashed line represents the classical relation from Larson (1981), and the red dashed line represents the recently-determined core-velocity difference of Qian et al. (2012). |
| In the text | |
 |
Fig. 11 Fray and fragment scenario of core formation. The three panels represent three different stages in the evolution of a large-scale filament like L1495/B213. In the first stage (left panel), two gas flows collide and produce a filamentary density enhancement. With time (middle panel), a combination of residual turbulent motions and gravity splits the gas into a series of intertwined velocity-coherent fibers. Finally (right panel), some fibers accumulate sufficient mass to reach the limit for gravitational fragmentation and form chains of dense cores. |
| In the text | |
 |
Fig. 12 Distance to the nearest neighbor among the N2H+ cores in L1495/B213 (no projection correction applied). Note how most values lie below 0.2 pc. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


