| Issue |
A&A
Volume 573, January 2015
|
|
|---|---|---|
| Article Number | A35 | |
| Number of page(s) | 16 | |
| Section | Interstellar and circumstellar matter | |
| DOI | https://doi.org/10.1051/0004-6361/201424391 | |
| Published online | 12 December 2014 | |
The Gaia-ESO Survey: Extracting diffuse interstellar bands from cool star spectra⋆,⋆⋆
DIB-based interstellar medium line-of-sight structures at the kpc scale
1 GEPI, Observatoire de Paris, CNRS UMR8111, Université Paris Diderot, Place Jules Janssen, 92190 Meudon, France
e-mail: lucky.puspitarini@obspm.fr; rosine.lallement@obspm.fr
2 Institute of Astronomy, National Central University, Chungli, Taiwan
3 Zentrum für Astronomie der Universität Heidelberg, Landessternwarte, Königstuhl 12, 69117 Heidelberg, Germany
4 Millennium Institute of Astrophysics, Av. Vicuña Mackenna 4860, 782-0436 Macul, Santiago, Chile
5 Pontificia Universidad Católica de Chile, Av. Vicuña Mackenna 4860, 782-0436 Macul, Santiago, Chile
6 Laboratoire Lagrange (UMR7293), Université de Nice Sophia Antipolis, CNRS, Observatoire de la Côte d’Azur, Bd. de l’Observatoire, BP 4229, 06304 Nice Cedex 4, France
7 LESIA, Observatoire de Paris, CNRS UMR8109, Université Pierre et Marie Curie (Paris 6), 5 Place Jules Janssen, 92190 Meudon, France
8 Centre for Astrophysics Research, STRI, University of Hertfordshire, College Lane Campus, Hatfield AL10 9AB, UK
9 Dipartimento di Fisica e Chimica, Universita’ di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
10 INAF – Osservatorio Astronomico di Palermo, Piazza del Parlamento 1, 90134 Palermo, Italy
11 S. D. Astronomia y Geodesia, Facultad de Ciencias Matematicas, Universidad Complutense de Madrid, 28040 Madrid, Spain
12 Instituto de Astrofísica de Andalucía-CSIC, Apdo. 3004, 18080 Granada, Spain
13 Lund Observatory, Department of Astronomy and Theoretical Physics, Box 43, 221 00 Lund, Sweden
14 INAF – Osservatorio Astronomico di Bologna, via Ranzani 1, 40127 Bologna, Italy
15 Dipartimento di Fisica e Astronomia, Sezione Astrofisica, Università di Catania, via S. Sofia 78, 95123 Catania, Italy
16 ASI Science Data Center, Via del Politecnico snr, 00133 Roma, Italy
17 Department for Astrophysics, Nicolaus Copernicus Astronomical Center, ul. Rabiańska 8, 87-100 Toruń, Poland
18 Astrophysics Research Institute, Liverpool John Moores University, 146 Brownlow Hill, Liverpool L3 5RF, UK
19 Faculty of Mathematics and Physics, University of Ljubljana, Jadranska 19, 1000 Ljubljana, Slovenia
Received: 12 June 2014
Accepted: 5 October 2014
Aims. We study how diffuse interstellar bands (DIBs) measured toward distance-distributed target stars can be used to locate dense interstellar (IS) clouds in the Galaxy and probe a line-of-sight (LOS) kinematical structure, a potentially useful tool when gaseous absorption lines are saturated or not available in the spectral range. Cool target stars are numerous enough for this purpose.
Methods. We devised automated DIB-fitting methods appropriate for cool star spectra and multiple IS components. The data were fitted with a combination of a synthetic stellar spectrum, a synthetic telluric transmission, and empirical DIB profiles. The initial number of DIB components and their radial velocity were guided by HI 21 cm emission spectra, or, when available in the spectral range, IS neutral sodium absorption lines. For NaI, radial velocities of NaI lines and DIBs were maintained linked during a global simultaneous fit. In parallel, stellar distances and extinctions were estimated self-consistently by means of a 2D Bayesian method from spectroscopically-derived stellar parameters and photometric data.
Results. We have analyzed Gaia-ESO Survey (GES) spectra of 225 stars that probe between ~2 and 10 kpc long LOS in five different regions of the Milky Way. The targets are the two CoRoT fields, two open clusters (NGC 4815 and γ Vel), and the Galactic bulge. Two OGLE fields toward the bulge observed before the GES are also included (205 target stars). Depending on the observed spectral intervals, we extracted one or more of the following DIBs: λλ 6283.8, 6613.6, and 8620.4. For each field, we compared the DIB strengths with the Bayesian distances and extinctions, and the DIB Doppler velocities with the HI emission spectra.
Conclusions. For all fields, the DIB strength and the target extinction are well correlated. For targets that are widely distributed in distance, marked steps in DIBs and extinction radial distance profiles match each other and broadly correspond to the expected locations of spiral arms. For all fields, the DIB velocity structure agrees with HI emission spectra, and all detected DIBs correspond to strong NaI lines. This illustrates how DIBs can be used to locate the Galactic interstellar gas and to study its kinematics at the kpc scale, as illustrated by Local and Perseus Arm DIBs that differ by ≳30 km s-1, in agreement with HI emission spectra. On the other hand, if most targets are located beyond the main absorber, DIBs can trace the differential reddening within the field.
Key words: ISM: general / dust, extinction / ISM: lines and bands / Galaxy: general
Based on observations made with the ESO/VLT at Paranal Observatory, under programs 188.B-3002 (The Gaia-ESO Public Spectroscopic Survey) and 079.B-0662.
Tables with the basic data and observed parameters for the 429 stars are only available at the CDS via anonymous ftp to cdsarc.u-strasbg.fr (130.79.128.5) or via http://cdsarc.u-strasbg.fr/viz-bin/qcat?J/A+A/573/A35
© ESO, 2014
1. Introduction
About 500 diffuse interstellar bands (DIBs) have been detected in the optical domain between 4400 and 8600 Å (Hobbs et al. 2008, 2009; McCall & Griffin 2013; Maíz Apellániz et al. 2014), and their number in the infrared and ultraviolet windows is still growing (Joblin et al. 1990; Geballe et al. 2011). Identifying the carriers of these irregular features that appear in absorption in stellar spectra has been a subject of active research for many years (see reviews by Herbig 1995; Sarre 2006; Friedman et al. 2011; Cami & Cox 2014, and references therein). Much effort has been extended to extract the most precise information on the DIBs from high-resolution, high-signal stellar spectra and derive their various properties, in particular their fine structure and the way they react to the radiation field (see, e.g. Jenniskens & Desert 1994; Krelowski et al. 1995; Galazutdinov et al. 2000; Tuairisg et al. 2000; Cox et al. 2005; Welty et al. 2006; Hobbs et al. 2009; Vos et al. 2011). In these spectral studies, DIBs were extracted from hot (early-type) stars because of their smooth, easily fitted continuum. This introduces a limitation on the number of potential target stars that can be used to study DIBs. For nearby stars, it favors highly variable conditions in irradiation and in subsequent DIB carrier destruction or ionization state changes (e.g., Vos et al. 2011).
Recently, progress was made on extracting DIBs from cool (late-type) star spectra, in particular with a method devised by Chen et al. (2013) that is using synthetic stellar models. This technique has the advantage of enormously increasing the number of potential targets, probing average conditions in the interstellar medium (ISM) far away from the strong radiation field of UV stars, and simultaneously providing some feedback to improve both the synthetic stellar spectrum and the DIB detection (Monreal-Ibero et al., in prep.). Other methods have been applied to cool stars, such as using comparisons with unreddened star spectra (Kos et al. 2013), or interpolations within a grid of models (Zasowski & Ménard 2014).
Independently of the search for their carriers, our goal here is to study how DIBs can be used to trace the ISM at the Galactic scale, both its distribution and kinematics (see previous works in this direction by van Loon et al. 2013; van Loon 2014; Zasowski & Ménard 2014). In particular, DIBs used as an interstellar (IS) tracer may potentially help building 3D ISM maps by means of inversion methods, similar to the inversion of neutral sodium or extinction data (Vergely et al. 2001, 2010; Lallement et al. 2014). Thanks to the Gaia mission, which was launched 19 December 2013, parallax distances will become available for a huge number of Milky Way stars, which will allow us to build more accurate maps. One of the observational advantages of DIBs over gaseous lines is that they are spread over a wide wavelength interval (from optical to IR), and, more importantly, the absence of saturation for distant or particularly opaque sightlines. Another strong advantage over the use of photometric extinction is that kinematic information can be derived, that is, the radial velocities of the IS clouds.
All of the individual IS clouds that are present along a line-of-sight (LOS) imprint a specific DIB absorption whose strength and Doppler shift reflect the IS matter content and cloud radial velocity, respectively. This is why measuring DIB equivalent widths in a single-component approach becomes inappropriate when the radial velocity interval that is spanned by all cloud motions is not negligible with respect to the DIB spectral width, which means that it is an unsuitable technique for narrow DIB and/or distant sight-lines. However, the extraction of multicomponent DIBs together with their kinematics has rarely been attempted. Cox et al. (2005) used the convolution of a template DIB profile and the multicomponent KI absorption profile, while Cordiner et al. (2008) (resp. Cordiner et al. 2011) separately fitted the Milky Way and M31 (resp. M33) DIBs using Gaussian profiles. Here, we present improved fitting methods allowing for multicomponent DIBs. The methods are fully automated. Automated here means that no intervention by the user is needed during the series of fittings that are launched in a unique run for a large number of spectra. More precisely, no spectral interval selection for continuum fitting is needed, nor are there any manual “guesses” (most profile-fitting methods are only partly automated and require these “manual” steps). Each component has a pre-determined shape derived from high-resolution spectra of hot nearby stars. The methods are suitable for any type of stars as long as their stellar parameters have been determined and their synthetic spectra can be computed.
 |
Fig. 1 Distribution of the selected fields, numbered as in Table 1. The distribution is superimposed on the HI 21 cm brightness temperature map (Kalberla et al. 2005) in the radial velocity interval −100 km s-1≤ vLSR ≤ 100 km s-1. The map is in Galactic coordinates, centered on l = −60°. |
Selected fields with FLAMES observations.
We applied these new fitting techniques to a series of spectra of cool target stars for which stellar atmospheric parameters and estimated distances have been determined spectroscopically. Part of the data are taken from the Gaia-ESO Spectroscopic Survey (GES; Gilmore et al. 2012), a public spectroscopic survey that started in 2011 and aims at recording VLT/FLAMES spectra of ~100 000 stars in our Galaxy down to magnitude 19, systematically covering all the major components of the Milky Way and the selected open clusters. This survey will provide a wealth of precise radial velocity and abundance determinations. The other data are part of an earlier program devoted to the study of the inner disk (Hill et al. 2012, Hill et al., in prep.). Deducing properties of the ISM is a by-product of these stellar-oriented programs.
Seven FLAMES fields were selected for their wide distribution in Galactic longitudes, to probe very different interstellar cloud complexes, and because they are located close to the Galactic plane, to ensure significant absorptions. They were chosen totally independently of the primary objectives (i.e., open-cluster studies, bulge star properties, etc, and of the target star properties themselves). We also gave priority to fields with targets that are widely distributed in distance. Our goal is (i) to test our interstellar absorption fitting methods; (ii) to study the variation of the DIBs as a function of the distance along the LOS and show the potential of the DIBs for 3D mapping purposes; and (iii) to study the DIB-extinction relationship in different regions of the Milky Way disk.
Section 2 presents the data and some general properties of the selected DIBs. Section 3 describes the spectral analysis method for multicomponent DIB extraction and illustrates how it is applied. Section 4 describes the results and the observed DIB properties. In this section we compare the DIB equivalent widths with the estimated extinctions and draw LOS profiles of DIBs in the various directions. Section 5 discusses future improvements and the mapping potential.
2. Data and choice of DIBs
Of the seven fields, five fields are GES data. We complemented the GES data with previously recorded spectra from two fields toward the bulge. Along with one of the GES LOS, this allows comparisons between DIBs in directions that differ by a few degrees. Overall, we tried to probe a variety of cases to test our methods. All of the selected spectra are characterized by a good signal-to-noise ratio (S/N), S/N≳50, which ensures good results.
Figure 1 shows the distribution of the fields in the sky, superimposed on a HI 21 cm emission map. The projections on the Galactic plane are also shown in Fig. 20. All targets were observed with the FLAMES multi-object spectrograph at the VLT-UT2. We used both GIRAFFE (R ≃ 17 000) and UVES (R ≃ 47 000) observations (see Dekker et al. 2000, for UVES). The UVES spectra cover the 5822 to 6831 Å spectral range, which contains the classical NaI (D2-D1 5889.9−5895.9 Å) IS lines as well as some rather strong DIBs, such as the 6283.8 (hereafter called 6283) and 6613.6 (6614) Å bands. Depending on the observed field, the GIRAFFE observations were made with the H665 (HR15N) setting (spectral range 6444−6816 Å), which allows studying the 6614 Å DIB at a lower resolution than UVES, and with the H875 (HR21) setting (spectral range 8475−8982 Å), which includes the 8620.4 (8620) Å DIB (informally known as the Gaia DIB, since it is contained in the spectral interval of the Radial Velocity Spectrometer (RVS) onboard the satellite). The additional inner disk bulge data was observed with GIRAFFE H13 setting (spectral range 6170−6309 Å). The GES UVES and GIRAFFE reduced spectra are issued from the dedicated pipeline (Sacco et al. 2014), while the two OGLE field spectra were reduced by means of using our dedicated GIRAFFE tool based on the ESO pipeline.
Table 1 lists the selected fields, the number of targets in each field, the field center coordinates, the observing modes, and the whole range of estimated stellar distances and extinctions (see the next section). The full list of target stars along with their coordinates, estimated extinction, and distances can be found at the CDS. There are 429 target stars, from which about half (224) have been observed as part of GES. A majority of those GES target stars are within the GES-CoRoT (COnvection ROtation et Transits planétaires) fields (172 stars).
We focus on the 6614 and 6283 Å DIBs that are strong enough to ensure a detection in most targets. When recorded, we also analyzed the shallower 8620 Å DIB. The 6614 Å DIB is a widely studied, strong and narrow DIB and has a good correlation with E(B − V) (see Sonnentrucker et al. 1997; Friedman et al. 2011; Vos et al. 2011; Puspitarini et al. 2013; Kos & Zwitter 2013, etc). The broader 6283 Å DIB is a strong, broad DIB that was also widely studied and is known for being significantly influenced by the radiation field (Vos et al. 2011). The 8620 Å DIB is a rather weak band that has recently been studied as part of the RAVE Spectroscopic Survey (see Munari et al. 2008; Kos et al. 2013) and is of particular interest in the frame of Gaia. It seems to be quite well correlated with the reddening, although the number of studies is still limited.
3. Data analysis
3.1. Description of the fitting method
The principles of the fitting method are essentially the same as in Chen et al. (2013), the main difference being that we allow here for multicomponent DIBs and subsequently extract kinematic information. As the length of LOS increases, differences in cloud radial velocities may become similar to or larger than the DIB width, making the use of a multicomponent fit necessary. We modeled the observed spectrum as the product of a synthetic stellar spectrum (Sλ), a synthetic telluric transmission (Tλ), and a DIB model that is itself the product of several DIB profiles, each one representing one absorbing cloud complex. When the telluric absorption is very weak or negligible, Tλ ≃ 1. Finally, to take into account the local slope of the unnormalized spectrum, we allowed for a continuum that is simply represented by a linear polynomial with A and B as the coefficients. This appears to be sufficient for our limited wavelength interval around each DIB. The model spectrum (M) can be therefore written as ![\begin{eqnarray} M(_{\lambda})&=& S_{\lambda} [V_{\rm star}] \hspace{0.2cm}\times\hspace{0.2cm} T_{\lambda} [V_{\rm tell}]^{\alpha_{\rm tell}} \nonumber \\ &&\quad \times \Pi^{i}(DIB^{i}_{\lambda} \hspace{0.05cm}[vel^{i}]^{\hspace{0.05cm}\alpha^{i}}) \times ([A]+[B]\times\lambda) . \end{eqnarray}](/articles/aa/full_html/2015/01/aa24391-14/aa24391-14-eq25.png) (1)Vstaris the stellar radial velocity, Vtell is the Earth motion, and veli is the interstellar cloud radial velocity. These various terms are detailed below, as well as the coefficients αtell and αi.
(1)Vstaris the stellar radial velocity, Vtell is the Earth motion, and veli is the interstellar cloud radial velocity. These various terms are detailed below, as well as the coefficients αtell and αi.
The computation of the stellar model Sλ requires the preliminary knowledge of the stellar parameters. For each of our target stars, the effective temperature, gravity, metallicity, and micro-turbulence have been determined previously: (i) for the GES targets we used the stellar parameters jointly determined by the GES team members (Smiljanic et al. 2014; Lanzafame et al. 2014, Recio-Blanco et al., in prep.); (ii) for the additional archival data, see Hill et al. (2012). Based on the stellar parameters, a synthetic stellar model was computed for each target star using an ATLAS 9 model atmosphere and the SYNTHE suite (Kurucz 2005; Sbordone et al. 2004; Sbordone 2005). For GES targets, this may yield a synthetic spectrum that is not exactly the same as the one of the synthetic spectral library used in GES. Similarly, inner disk spectra may be slightly different from those used in the first analysis. However, in both cases the differences probably are too small to influence the determinations of the DIBs, see Sect. 5.
The synthetic telluric transmissions Tλ were computed by means of the LBLRTM code (Line-By-Line Radiative Transfer Model, Clough et al. 2005), using the molecular database HITRAN (HIgh-resolution TRANsmission molecular absorption (Rothman et al. 2009). This telluric transmission model is available online from the TAPAS web-based service (Bertaux et al. 2014). Telluric lines are strong in the 6283 Å spectral region and negligible for the 6614 Å band. We make use of the same telluric models to derive of the fitting of neutral sodium lines. The coefficient αtell is proportional to the optical depth of the telluric lines.
 |
Fig. 2 NaI doublet/6614 Å DIB global, multicomponent analysis, here for the GES star 12574905-6458511 (field 3). The NaI region is shown in the top panel and the DIB region in the lower panel. The entire fitted spectral interval is shown in the left panels, while the right panels display enlarged the NaI-D2 region (top) and the DIB region (lower). In each figure the red line shows the stellar spectrum (lower plot) and the fitting residuals (upper plot). The dotted lines are the models: stellar (orange), telluric (green), and interstellar components (blue). The thick blue line is the final adjustment. The radial velocities of the NaI and DIB components are linked throughout (see the black vertical line). Velocities are heliocentric. |
The models for the 6614 and 6283 Å bands are empirical profiles that have been determined previously from high S/N spectra of nearby stars (Puspitarini et al. 2013). Since the laboratory wavelengths for the DIBs are currently unknown and their profiles are irregular, the choice of rest wavelengths that correspond to a null Doppler shift of the absorbing matter is somewhat arbitrary. Throughout this work, we used for these first two DIBs the wavelength values derived by Hobbs et al. (2008), who cross-calibrated the DIB profiles and interstellar KI absorption lines. We assumed that the rest wavelength corresponds to the deepest point in the profile. Because our model profiles may slightly differ from the profiles of Hobbs et al. (2008), a small offset may exist between the rest wavelengths, about a few km s-1, which we neglect here. On the other hand, it is well established that the 6614 Å DIB has substructures and that these substructures may slightly vary from one LOS to the other (Galazutdinov et al. 2002). This results in small changes of the overall profile. In our case, the GIRAFFE and UVES spectral resolutions do not allow these subtle changes to be distinguished. We ignored the profile variability to simplify the modeling. For at least the 6614 Å DIB, it has been shown that in very rare, extreme conditions for the radiation field, the DIB profile may evolve and be characterized by a redward wing (Oka et al. 2013). We neglected this possibility here, which is a reasonable assumption because our LOS do not target particular strong infrared sources. The model for the 8620 Å DIB is also an empirical model, obtained by averaging DIB profiles from several spectra based on the data analysis reported by Chen et al. (2013). For this band the rest wavelength is chosen to be the one defined by Munari et al. (2008). The three empirical DIB profiles are defined over the λλ 6609−6619 Å, 6263−6303 Å, and 8612−8628 Å intervals. Finally, αi is an adjustable coefficient that is the ratio between the optical depth of the absorber that produces the DIB and the optical depth of the reference.
The fitting procedure adjusts the convolution of this product by the instrumental function (here represented by a Gaussian G) to the data. During the adjustment of the composite stellar-DIB-telluric model, we allowed Doppler shifting of the stellar model by a free quantity Vstar to take into account the stellar radial velocity, of the telluric transmission model by a free quantity Vtell to take into account the Earth motion, and of the DIB profile i by a radial velocity veli to take into account the ISM kinematics. We might have used the star radial velocity that comes out from the stellar spectrum analysis and is derived over a much wider wavelength range, and we might also use of the telluric information linked to the observing conditions. However, a cross-correlation operation has been integrated into our code to make a first estimate of these offset values, which is convenient for handling any spectroscopic data and allows fine-tuning them during the adjustment. Our derived values conform to the expected values. We allowed for changes of the αtell parameter and αi to adjust the telluric lines and DIB strength.
The DIB equivalent width (EW) was derived in two different ways: (i) by using the best-fit DIB strength αi and the EW of the DIB model, which provides a first result we refer to as the fitted EW (EWf), or (ii) by measuring the true area of the absorption band with respect to the continuum, which provides a second result that is independent of the DIB model; we name this the continuum-integrated EW (EWci). The EWci is obtained after subtracting the other components (stellar and telluric lines) in the normalized spectrum. In the multiple-component case, the EW for each absorbing cloud can be independently derived using the EWf method. The total intervening matter corresponds to the sum of the fitted EWs from each DIB component. In contrast, the EWci method does not detect the individual components, but only measures the total absorption. The spectral interval used for computing the DIB EW is the same as that of Friedman et al. (2011); for the 8620 Å DIB it was taken from −7 to +7 Å from the DIB center.
In principle, sky emission lines disappear after background subtraction, but there are potential residuals. The spectral ranges we considered here for the DIB extraction are free of strong sky emission lines: OI at 6300 Å for instance, does not overlap with the 6283 Å DIB. The red wing of the 8620 Å DIB is an exception: here emission line residuals may influence the DIB fitting (see next sections). Similarly, there may be features within strong stellar lines that are not accounted for by stellar atmosphere models, such as circumstellar Hα emissions or interstellar permitted and forbidden emissions, but they do not overlap with our selected DIBs.
3.2. Fitting strategies and adjustment examples
For all multicomponent adjustments, it is necessary to start with initial parameters that are as close as possible to the actual solutions to avoid secondary minima and to converge more rapidly toward the final solution. Here, the initial guesses for the number of required velocity components, their radial velocities, and their strengths come either from interstellar NaI lines as for UVES spectra, or, in the absence of any absorption line, from a simplified decomposition of the HI emission spectrum, taken from the spectral HI cube in the direction of the target star as for GIRAFFE spectra. Before using these guesses we performed profile-fitting tests without any such initial parameters, and compared this with the subsequent results. We did not find any negative influence of the guesses such as biases toward an unrealistic solution, instead we always found the expected positive effects of fast convergence toward the primary minimum.
3.2.1. Using NaI absorption lines
NaI lines are not only used as sources of the first guesses of the cloud parameters, but also enter in the global analysis of lines and DIBs, which means that they are simultaneously measured together with the DIB components. Their radial velocities are linked so that they remain identical throughout the adjustment, component by component. This method is justified by the fact that any NaI line must have a (strong or weak) DIB counterpart. From the previous observations, we know that all of the detected DIBs were found to be associated with strong neutral sodium lines. There may be a small Doppler shift between the DIB and interstellar NaI line center due to the preferential presence of the DIBs carriers in a particular phase, for example at the cloud periphery or in the core. However, these shifts remain small compared with the DIB widths, and we neglected this effect. On the other hand, this global fitting method is particularly tractable here because the initial guesses for the parameters can be determined quite precisely, especially if the interstellar lines used are not saturated.
The automated global analysis procedure is developed in the frame of the software and environment Igor Pro (2009), which allows fitting multiple datasets simultaneously while linking some of their parameters. Initial-guess values for the radial velocities of the interstellar NaI components were preliminarily determined from the observed spectrum on the basis of the main absorption peaks. The sodium lines were modeled by Voigt profiles with three free parameters: opacity, radial velocity, and apparent temperature. In normal, realistic profile fitting of NaI lines, the apparent temperature (combination of thermal broadening and turbulence) is constrained to be T< 10 000 K, since NaI is negligible in warmer gas. However, here we are interested only in the first-order kinematics, and neither the actual number of clouds nor the NaI columns need to be known in detail. To avoid having too many interstellar components, we therefore extended the line broadening and allowed for a significantly higher apparent temperature (T< 100 000 K). In turn, we only listed EWs, and omitted NaI column densities that are too imprecise. Figure 2 illustrates the global analysis of the NaI- D2/D1 lines and the 6614 Å DIB. In all cases the fitting results for the DIB/NaI radial velocities and the main HI 21 cm velocities agree well. Figure 3 is a similar illustration for the 6283 Å DIB.
3.2.2. Using HI 21 cm emission profiles
In the second case, when no NaI lines are available and HI emission spectra (Kalberla et al. 2005) are used instead, the fitting scheme is different. Since the HI emission spectrum represents the totality of the IS clouds, both in front of and beyond the target star, a global analysis based on all main HI components is inappropriate. The HI emission spectrum was therefore used to construct a table of velocity guesses (vrHI) and provide upper and lower limits to the velocity range. Then, the DIBs were fitted independently of the actual HI measurement, using the hierarchical sequence of velocity prior values described below. Another significant difference in this second case is that the initial values of the cloud Doppler shifts are much less precise than for the sodium lines, and the cloud velocity profiles strongly overlap (for the same gas temperature the Doppler width is about five times wider than for sodium). Finally, the HI map has a spatial resolution of ~0.6°, which is higher than the FLAMES field of view. Still, the emission spectra provide an appropriate starting point for the fitting and initial parameters of the interstellar cloud components.
However, the 6614 and 8620 Å DIBs have very different widths, and only the 6614 Å DIB is narrow enough to distinguish multicomponents with velocity differences on the order of 10 km s-1 in an automated way. Figure 4 shows an example of such a fitting of this DIB based on the HI initial guesses. The first adjustment involves a single component vrHI and uses as a guess the lowest absolute value of the HI velocities, which in all cases corresponds to local gas. When the single-component velocity derived from the fit is significantly different from vrHI, the second velocity component from the vrHI table is included and a fit with these two prior values is performed, and so on. Using two components gives a significantly better fit, see the red part of the DIB.
The very broad 8620 Å band does not react with enough sensitivity to changes on the order of 10−20 km s-1 to guide the fit to multivelocity solutions, at least for our present dataset. Moreover, many spectra are contaminated by sky emission residuals, which make the fitting even more difficult. For these reasons and after several negative tests, we chose to keep the monocloud procedure, that is, we considered only the first step (see Fig. 5), and the prior was the velocity that corresponds to the lowest absolute value (the local value). Still, the DIB EW was derived with a rather good precision, as tests made with one or more components have shown, again due to the large width of this absorption band. Very rarely, we used the velocity results from the 6614 Å DIB fitting as the initial guesses of the 8620 Å DIB fitting to avoid the artificial effects of the sky emission contamination.
 |
Fig. 4 Multicomponent 6614 Å DIB fitting: GIRAFFE field 1, GES target 06441034-0048254. The red line shows the stellar spectrum. The dotted lines are the models: stellar (orange), telluric (green), empirical DIBs (gray). The thick blue line is the best model adjustment. The initial guesses for the DIB velocity centroids are 24, 40, and 50 km s-1 and are based on the HI spectrum in the same direction (see top plot). Middle: an example of a preliminary adjustment with a unique DIB component. The DIB velocity is found to be ~33 km s-1. The large difference from the initial guess (24 km s-1) demonstrates the need for a second cloud component. Bottom: an example of a subsequent adjustment with two DIB components. The two fitted velocities are now close to the first two HI emission peaks. |
 |
Fig. 5 Same as Fig. 4 (middle), but for 8620 Å (GES target 06441034-0048254). There are sky residuals in the red wing of the DIB. For this broad DIB a single velocity component is used (see text). |
3.3. Deriving the DIB equivalent width and error estimate
As previously discussed, the DIB EW can be derived using two different ways: the EWf and the EWci. The results and figures that are presented in this article all correspond to the first method. As already said, it allows for the distribution into separate components, but it has also the additional advantage of being less influenced by the potential errors in the computed stellar lines. The reason why both EWs are computed in each case is that their comparisons acts as a flag for the quality of the fit and reveals poor quality spectra. For all data we present, the two EWs are found to agree within the observational and model uncertainties.
The errors on the EW have three distinct sources: errors on the stellar continuum determination, statistical noise, and errors on the stellar model: 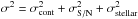 . The error on the stellar continuum placement is mainly linked to the statistical noise and both errors are estimated in a joined manner. To obtain a first estimate of these combined errors, we performed a preliminary study that is a series of simulations with varying random noise. For each simulation, we fitted the DIB and then compared all resulting EWs. For a random noise representative of the typical S/N of the spectra (S/N ≃ 100), we obtained a typical relative error of about 5% on the EW (more specifically, a deviation of ~5 mÅ when the EW is 100 mÅ). This gives an estimate of the contribution of the first two errors. For the third error linked to the stellar model, we already know that the data-model residuals are higher than average for some specific stellar lines and depend mainly on the stellar effective temperature and metallicity (see Chen et al. 2013). Figures A.1 and A.2 show the stacked residual of the DIB fitting for the 6614 Å and 8620 Å bands for ~ 160 GIRAFFE stars, and examples of dependence on the stellar effective temperature. To study the order of magnitude of the contribution of the stellar model to the error, we extracted all of the residuals and estimated their highest level at the center of the DIB. This corresponds to the most contaminated cases for which the stellar line falls close to the DIB center. Then we again performed a random noise simulation with this new variance instead of the measurement noise and obtained a new error estimation on the order of 13% and 15% for the 6614 and 8620 Å DIBs respectively. We estimate that this gives us a realistic estimate of the largest total error from the three sources. Although our final estimate for individual spectra is based on another method, described below, this range for the errors linked to the signal and the model illustrates the gain in precision we can expect in future by improving the stellar model. Applying this method to each of individual targets would be too time-consuming. Instead, we used a different approximation. For the first two errors, we used the following formulation:
. The error on the stellar continuum placement is mainly linked to the statistical noise and both errors are estimated in a joined manner. To obtain a first estimate of these combined errors, we performed a preliminary study that is a series of simulations with varying random noise. For each simulation, we fitted the DIB and then compared all resulting EWs. For a random noise representative of the typical S/N of the spectra (S/N ≃ 100), we obtained a typical relative error of about 5% on the EW (more specifically, a deviation of ~5 mÅ when the EW is 100 mÅ). This gives an estimate of the contribution of the first two errors. For the third error linked to the stellar model, we already know that the data-model residuals are higher than average for some specific stellar lines and depend mainly on the stellar effective temperature and metallicity (see Chen et al. 2013). Figures A.1 and A.2 show the stacked residual of the DIB fitting for the 6614 Å and 8620 Å bands for ~ 160 GIRAFFE stars, and examples of dependence on the stellar effective temperature. To study the order of magnitude of the contribution of the stellar model to the error, we extracted all of the residuals and estimated their highest level at the center of the DIB. This corresponds to the most contaminated cases for which the stellar line falls close to the DIB center. Then we again performed a random noise simulation with this new variance instead of the measurement noise and obtained a new error estimation on the order of 13% and 15% for the 6614 and 8620 Å DIBs respectively. We estimate that this gives us a realistic estimate of the largest total error from the three sources. Although our final estimate for individual spectra is based on another method, described below, this range for the errors linked to the signal and the model illustrates the gain in precision we can expect in future by improving the stellar model. Applying this method to each of individual targets would be too time-consuming. Instead, we used a different approximation. For the first two errors, we used the following formulation: 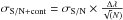 ; Δλ is width of DIB and N is number of data points covering this width. The S/N was estimated for each spectrum based on a linear fit in a clean area. Secondly, to obtain the third error, σstellar, we performed two consecutive fits without, then with masking of the strong stellar lines that fall in the DIB interval. The number of masked lines depends on the DIB and on the stellar radial velocity (it varies between one and three lines). The difference between the two calculated EWs (when stellar lines are not masked and when they are masked) gives us an estimate of σstellar, σstellar = ΔEWf = EWf − EWf masked. Finally, the total error is
; Δλ is width of DIB and N is number of data points covering this width. The S/N was estimated for each spectrum based on a linear fit in a clean area. Secondly, to obtain the third error, σstellar, we performed two consecutive fits without, then with masking of the strong stellar lines that fall in the DIB interval. The number of masked lines depends on the DIB and on the stellar radial velocity (it varies between one and three lines). The difference between the two calculated EWs (when stellar lines are not masked and when they are masked) gives us an estimate of σstellar, σstellar = ΔEWf = EWf − EWf masked. Finally, the total error is 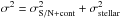 . This method gives errors that agree with those from the preliminary study described above.
. This method gives errors that agree with those from the preliminary study described above.
For the 8620 Å DIB, we have an additional complication because the right wing of the DIB region is sometimes contaminated by sky emission residual σsky. Correcting for this emission is beyond the scope of this work and its effects cannot be estimated in the same way as for the two other DIBs because the contamination results in a bumpy feature that changes the absorption shape and produces an unrealistic runaway shift from the true DIB radial velocity. Instead, we calculated the error as the sum of four terms: 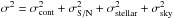 . The term σsky was obtained by calculating the variance in the region of sky contamination and multiplying by the full width at half maximum (FWHM) of the DIB profile. We plan to incorporate the pixel-by-pixel estimated uncertainties provided by the pipeline in the future.
. The term σsky was obtained by calculating the variance in the region of sky contamination and multiplying by the full width at half maximum (FWHM) of the DIB profile. We plan to incorporate the pixel-by-pixel estimated uncertainties provided by the pipeline in the future.
3.4. Distance and reddening estimates
To estimate the distance and extinction of the GES data, we used the 2D Bayesian method described in Babusiaux et al. (2014) (see also Burnett & Binney 2010). All our targets have 2MASS NIR photometry (Cutri et al. 2003) as well as V magnitude from different sources: from OGLE-II photometry as reported by Udalski et al. (2002) for the bulge directions, from Deleuil et al. (2009) for the CoRoT fields, and from Bragaglia et al. (in prep.) for the open clusters. We used here the V − K color, which is more sensitive to the extinction than the J − K color used in Babusiaux et al. (2014).
We used the isochrones reported by Bressan et al. (2012) (PARSEC 1.1) with a step of 0.05 in log(Age) between [6.6, 10.13] and a step of 0.05 dex in [M/H] between [−2.15, 0.5]. Each isochrone point i, corresponding to a metallicity [M/H]i, age τi and mass ℳi, has a weight associated to it P(i) according to the Initial Mass Function (IMF) ξ(ℳ) and Star Formation Rate (SFR) ψ(τ). We used here the lognormal IMF (integrated over the mass interval between isochrone points) following Chabrier (2001) and a constant SFR (considering that we have a grid sampled in log(Age) this means that the weight associated with the SFR is proportional to the age), and we did not introduce any age-metallicity correlation.
We computed the probability of a star with the observed parameters 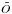 (
(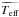 ,
, 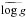 ,
, 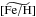 ,
, 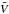 ,
, 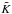 ) to have the physical parameters of the isochrone point i (Teffi, log gi, [Fe/H] i, τi, ℳi,
) to have the physical parameters of the isochrone point i (Teffi, log gi, [Fe/H] i, τi, ℳi, 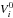 ,
, 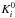 ),
), 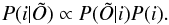 (2)To compute
(2)To compute 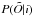 , we assumed Gaussian (
, we assumed Gaussian (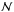 ) observational errors ϵO on the atmospheric parameters and the magnitudes. Assuming a distance d and an extinction A0 for the isochrone point i, we have
) observational errors ϵO on the atmospheric parameters and the magnitudes. Assuming a distance d and an extinction A0 for the isochrone point i, we have 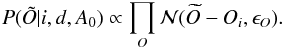 (3)However, the atmospheric parameters derived from spectroscopy (
(3)However, the atmospheric parameters derived from spectroscopy (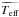 ,
, 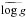 ,
, 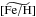 ) are not independent. For the inner disk fields we derived correlation coefficients that we applied in the above equation using a multivariate normal distribution. For the GES UVES parameters, the GES Consortium provides the individual node values, so instead of using only the recommended value, we used all nodes individual values (in general about 5 nodes provide parameters for the same star), which mimic the correlation we want to introduce on a star-by-star basis. For the GES GIRAFFE parameters we have no information about the correlations available.
) are not independent. For the inner disk fields we derived correlation coefficients that we applied in the above equation using a multivariate normal distribution. For the GES UVES parameters, the GES Consortium provides the individual node values, so instead of using only the recommended value, we used all nodes individual values (in general about 5 nodes provide parameters for the same star), which mimic the correlation we want to introduce on a star-by-star basis. For the GES GIRAFFE parameters we have no information about the correlations available.
The apparent magnitude mi derived from the isochrone i is a function of the absolute magnitude 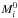 , the extinction Am, and the distance d:
, the extinction Am, and the distance d: 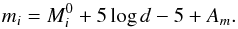 (4)We therefore derived
(4)We therefore derived 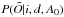 for a very thin 2D grid of distances d and extinction A0. A0 is the absorption at 5500 Å and is roughly equivalent to AV (e.g., Bailer-Jones 2011). To derive the extinction in the different photometric bands Am, we used the extinction law Eλ = 10− 0.4kλ of Fitzpatrick & Massa (2007). We used a typical red clump SED
for a very thin 2D grid of distances d and extinction A0. A0 is the absorption at 5500 Å and is roughly equivalent to AV (e.g., Bailer-Jones 2011). To derive the extinction in the different photometric bands Am, we used the extinction law Eλ = 10− 0.4kλ of Fitzpatrick & Massa (2007). We used a typical red clump SED 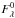 from Castelli & Kurucz (2003) ATLAS9 models. With Tλ the photometric total instrumental transmission we have
from Castelli & Kurucz (2003) ATLAS9 models. With Tλ the photometric total instrumental transmission we have 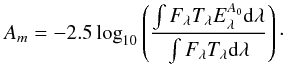 (5)To take the nonlinearity of this equation into account, we used a discrete table of Am as a function of A0. We did not add a prior on the distance or the extinction.
(5)To take the nonlinearity of this equation into account, we used a discrete table of Am as a function of A0. We did not add a prior on the distance or the extinction.
We seek the distance probability 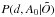 , which we obtained by marginalization over the isochrone points:
, which we obtained by marginalization over the isochrone points: 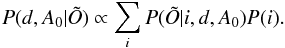 (6)Marginalization over the extinction leads to
(6)Marginalization over the extinction leads to 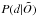 , and marginalization over the distance leads to
, and marginalization over the distance leads to 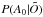 . The resulting distance and extinction estimates used hereafter correspond to the mode of the distribution, and the errors corresponds to the 68% highest Bayesian confidence interval (or highest density interval, HDI).
. The resulting distance and extinction estimates used hereafter correspond to the mode of the distribution, and the errors corresponds to the 68% highest Bayesian confidence interval (or highest density interval, HDI).
 |
Fig. 6 Results for target stars in field 1 (CoRoT anticenter). 6614 Å DIB EW (top), 8620 Å DIB EW (middle) and extinction A0 (bottom) vs. the estimated distance. Circles show GIRAFFE observations. Triangles show UVES observations. Colors in the top panel correspond to the number of IS components used to fit the IS line or band. All nearby targets (D ≤ 1 kpc) have only one IS component, or, for three targets, a very weak, negligible second component. Distant targets have more than one velocity component, in agreement with the crossing of at least one external arm (see the text). The outlier star 06441428-0057447 marked by a red star has stellar spectroscopic parameters that strongly disagree with stellar seismology information, which indicates that their distance and extinction are inaccurate for this target. |
 |
Fig. 7 6283, 6614, and 8620 Å DIB EWs as a function of the extinction for CoRoT ANTI CENTER field targets. |
4. Results
The first subsection discusses the measurements of the two CoRoT fields, while the second subsection discusses the measurements of the five other fields that have less targets.
4.1. CoRoT fields
The DIBs in these sightlines were derived following the fitting strategy described above. All of the measured EWs, uncertainties, and NaI/DIB velocities are listed in the Appendix A.
For the CoRoT anticenter field, the target stars are located about the Galactic plane and are widely distributed in distances (from 0 to 7 kpc from the Sun). This allows us to probe not only the local arm, but we also expect to cross external Galactic arms. As the distance of the target star increases, the LOS intersects a greater part of the ISM and therefore the EW of the DIB is expected to increase, with abrupt increases corresponding to crossings of dense clouds and plateaus to interclouds or interarms. Figure 6 shows the 6614 and 8620 bands DIB strength and the estimated extinction A0 as a function of the target distance. We do not show the 6283 band profile because of the very limited distance range of the measurements. The DIBs and A0 profiles, that is three quantities that are totally independently derived, agree well. They all show a clear increasing trend, which is expected for a field of view as narrow as that of FLAMES, and they also show the same overall pattern. There is an increase between distances 0 and 1 kpc, and a second increase beyond 2.5 kpc, up to 6 kpc. These two ramps correspond to two distinct interstellar cloud complexes, which we identify as the local and Perseus arms. The plateau from 1 to 2.5 kpc most likely corresponds to the gap between the two Galactic arms. In this distance range there are two groups of stars with EWs that differ by about 30%. They seem to correspond to two different regions within the field of view and most likely, the two groups do not intersect the same parts of the densest clouds, which is expected because the targets are distributed over ~30 arcmin. Better precisions on distances and extinctions, which will be provided by Gaia, may help refine this point. We note a very discrepant point in the A0-distance curve, lower panel), with no corresponding anomalously small DIBs. Interestingly, this target star has seismological parameters that markedly disagree with the spectrophotometric determinations (R.A. Peralta, priv. comm.), and for this reason its distance and extinction determination may be incorrect. It is encouraging that our most discrepant result points to this contradiction. At large distance, it is unclear whether the strong increase beyond 4 kpc corresponds to the Outer Arm. Its location agrees well with a crossing of the Outer Arm internal part as it appears in the schematic Galactic map of Churchwell et al. (2009) (see Fig. 20). Moreover, the total reddening E(B − V) from the Planck map (Planck Collaboration XI 2014) varies between 0.5 and 0.9 across the field covered by the targets (~20 × 25 arcmin wide), and the spectrophotometric extinction (or the similar DIB-based extinction) for the most distant stars is found to reach the Planck integrated value (the highest value is even slightly above the Planck value in the direction of the corresponding target). However, we do not detect clearly a corresponding distinct and strong shift in radial velocity (see the discussion about the kinematics below).
Figure 7 displays the variations of the three DIBs as a function of the estimated extinction A0 based on all of the target stars in the field. The figure clearly shows that the three DIBs appear to be linearly correlated with the extinction. Our three selected DIBs are among those that are reasonably well correlated with extinction in average conditions. However, previous studies based on early-type stars have revealed a strong dispersion about the mean relationship and in particular many outliers that correspond to the bright UV stars. Here we note that there are no equivalent outliers, which is probably due to our cool target stars and our integrations over large distances. This corresponds to a less severely modulated character of the sightline, or the ISM varies more moderately (see the combined results in Sect. 4.3).
 |
Fig. 8 Evolution of the DIB profile with target distance. Left: the 6614Å DIB absorption spectral profile up to stars at increasing distances along the CoRoT anticentre direction (l, b = 213°, −2°). We show the average of stacked extracted, normalized absorption spectra sorted by stellar distances (an offset of 0.5 in y-axis separates the two spectra). The continuum on the blue side of the DIB is affected by strong stellar lines that are insufficiently corrected for. The first (top) spectrum corresponds to the first kpc, the last (bottom) spectrum to distances between 4 and 6 kpc. Right: comparisons between one- and two-DIB component adjustments for close and distant stars. Distant stars require at least two DIBs separated by more than 20 km s-1 (see text). |
The need for a multicomponent analysis for the CoRoT AC field and the narrow 6614 Å band is illustrated in Fig. 8. For each star we derived the full absorption attributable to the DIB in the following manner: the full profile-fitting (whose results are described below) was performed first. The fitted continuum and the adjusted stellar spectrum were used to subtract the modeled stellar lines from the normalized spectrum, leaving solely the DIB. Within stellar line residuals, this provides the full DIB absorption independently of its assumed intrinsic shape and the number of components. After sorting the targets by increasing distance, we averaged the absorption profiles over groups of eight stars each. The resulting profiles for each distance bin are displayed in Fig. 8 as a function of the heliocentric velocity. The figure shows that the DIB depth increase with distance is accompanied by a significant velocity shift toward higher positive values, as expected from the rotation curves in this direction. The value of the strongest shift, on the order of 20 km s-1, is not negligible w.r.t. the DIB width for a single cloud and requires a multi-cloud fitting procedure. We show how this need for at least two shifted DIBs is a function of the LOS extent by fitting with one and then two components the mean profiles obtained from stars located between 1 and 1.3 kpc on one hand, and from stars located beyond 5 kpc on the other hand. For the most distant stars there is a strong, highly visible discrepancy between the observed profile and the adjustment with a single DIB, while the adjustment with two DIBs separated by about 30 km s-1 is acceptable. For the closer stars the differences between the two adjusted models are smaller and not easily detected by-eye. We performed several statistical tests to derive the reliability of the two-DIB model using standard deviations derived from the continuum outside the DIB for both narrow or broad spectral intervals. The standard deviation varies depending on whether spectral regions that are the most contaminated by stellar line residuals are included or not. We also caution that because of these stellar lines residuals, errors on the continuum are not regularly distributed and such statistical tests are approximate, but they provide some first-order useful indications. For the distant stars the reduced chi-square increases by more than a factor of 2 from two components to one component, which means that this second component is statistically extremely probable and confirms the discrepancy between the observed profile and the single-DIB shape. A second test based on the Bayesian Information Criterion (BIC) similarly shows that a second, shifted DIB is also extremely likely (ΔBIC is always high above 10). For the stars located between 1 and 1.3 kpc (middle curve in Fig. 8) the reduced chi-square increases by at least 20%, showing that the measured profile is also very likely broadened, which is confirmed by the BIC test. This is expected because within the Local Arm the velocity dispersion may reach 20 km s-1. For the closest stars (top curve in Fig. 8), stellar residuals in the DIB area become half of the DIB itself, and a better correction of those residuals is necessary to conclude unambiguously, as confirmed by all tests.
 |
Fig. 9 Comparison between the fitted DIB radial velocities and EWs and the HI 21 cm emission spectra. Black (red) markers and lines are GIRAFFE results and HI spectra from field 1 (field 2). Error bars on the velocities are based on the full covariance matrix for the various parameters. For the narrow 6614 Å DIB (GIRAFFE observations) a significant number of spectra require two velocity components, which very likely correspond to the Local and Perseus arms. Small EWs and large error bars on velocities correspond to marginal results in low S/N spectra. UVES target results are displayed with triangles (yellow and blue for fields 1 and 2). At variance with GIRAFFE, UVES velocities are linked to the strong sodium lines through global fitting. Their agreement with the velocity structure derived from the GIRAFFE targets shows the link between NaI and DIB velocities. |
 |
Fig. 10 CoRoT CENTER FIELD field. Left: DIB/A0 vs. distance profile. Right: DIB vs. A0: 6283 and 6614. |
We represent in Fig. 9 the velocities of the detected components that result from the automated fitting following the strategy described in the previous section. For all individual stars standard deviations including the measurement uncertainties and the stellar line residuals were estimated from the best adjustments, and new adjustments were performed using these standard deviations. The errors on the free parameters were estimated using the full covariance matrix and take into account all correlations between the parameters. Resulting errors are displayed in Fig 9. The resulting DIB velocities belong to two groups centered on vhel ≃ 15−32 and vhel ≃ 40 − 55 km s-1 (or vLSR ≃ −2−15 and vLSR ≃ 23−38). Velocity results for targets for which the DIB velocities were determined by global fitting and which are consequently linked to the strong sodium absorptions are marked by triangles. They agree with the main groups of radial velocities, showing a general agreement between the main HI, NaI, and DIB structures. The first velocity group is tightly associated with the first HI peak, which corresponds to the Local Arm. The second group corresponds to the second or blended second and third HI components at ~35−45 km s-1, which correspond to Perseus. Interestingly, none of our targets requires absorption at around +65 km s-1, the heliocentric radial velocity of the reddest, strong HI emission peak (see Fig. 9). It is unclear whether this highest velocity component seen in HI corresponds to the Perseus or a more distant arm, in this case the Outer (or Cygnus) Arm. In their synthetic Fig. 3, Dame et al. (2001) are attributing a heliocentric velocity interval vhel = 37 − 67 km s-1 (vlsr = 20−50 km s-1) to the Perseus Arm in the direction of the CoRoT anti-center field, while lower velocities are predicted by Vallée (2008). If the higher HI velocity corresponds to the Outer Arm, then apparently none of our targets is beyond a significant column of gas or dust belonging to this arm, and all the detected IS matter is from Perseus, even though (i) the target estimated distances reach at least 4.8 kpc (6.8 kpc is the most probable distance); (ii) there is a strong and coherent increase of DIBs and extinction with distance found for the six most distant targets; and (iii) as discussed above, the Planck integrated reddening is on the same order as the reddening toward our most distant targets. In this case, the fastest HI arises beyond 5−6 kpc and is too poor in dust to produce a significant additional reddening. Conversely, if the faster gas belongs to Perseus, a potential explanation is that the ensemble of distant targets may miss these clouds. HI maps have a lower resolution than Planck, the Perseus Arm is highly fragmented, and the distant targets are distributed across ~15 arcmin. If there is a strong inhomogeneity within the field, the path to the distant targets may not cross the higher velocity matter. More data are needed and more accurate distances will help in answering this question.
 |
Fig. 11 NGC 4815 field: (left) DIB and A0 distance profiles. Stars identified by Friel et al. (2014) as cluster members correspond to blue, nonmembers to red markers. Right: 6283 (top) and 6614 (lower panel) Å DIB EW vs the estimated extinction A0. The black “0" sign indicates the unique star with a single DIB velocity, for all other targets the adjustment to the data requires two velocity components. |
For the CoRoT center field, the target stars are also widely distributed in distance, but its higher latitude (b = −7°) has a strong impact on the results. For this field, the 8620 Å DIB was not extracted because of significant sky emission line residuals. Figure 10 displays the DIBs and the extinctions as a function of the target distance. Although distributed over large distances, we do not detect any EW increase (ramp) in addition to the one associated with the Local Arm. Instead, the DIB strength appears to form a plateau. This shows that the LOS do not intersect inner arms because the distant target stars are significantly below the Galactic plane. The measured profile implies that most of the absorbing matter is closer than 1.5 kpc. The relationships between the DIB strength and the extinction is shown in Fig. 10. As a result of the quite small DIB and extinction interval covered by the targets in this field, all of the data points are clustered. Still, an increasing trend is clearly observed. For this field, the kinematics is also rather simple (Fig. 9). There was no need for more than one IS component, all velocities fall close to each other, in agreement with the peak of the HI emission spectrum at vhel ≃ − 14 km s-1.
4.2. Fields 3 to 7
For the field3/NGC 4815 direction (see Friel et al. 2014; Magrini et al. 2014), we analyzed 14 red clump stars that were observed with UVES. Only six are open cluster members. We simultaneously fitted the NaI lines and the 6283 Å DIB (respectively the 6614 Å DIB). The NaI absorption is characterized by two velocity components at vhel ≃ − 25 and −5 km s-1 (see Fig. 12) that are well separated, and it was useful to test our multicomponent technique. The results are displayed in Fig. 11. The extinctions and DIB strengths are on the same order for most stars, showing that at their distances on the order of 2 kpc, they are located beyond the main, nearby absorber, in agreement with the 3D ISM map (Lallement et al. 2014). The two stars with lower extinction are not cluster members and must be foreground stars. Their most probable distances are 1.7 and 1.9 kpc, which shows that not all the absorption is local and pinpoints another absorber between 1.9 kpc and 2.5 kpc (cluster distance). According to the results of the most distant target, there is no significant additional IS absorption between 2 and 4 kpc. The comparison between the DIBs and the estimated extinctions shows they are well correlated (Fig. 11 right). Radial velocities of the NaI lines and DIBs correspond to two strong peaks in the HI spectrum. These cloud complexes also appear in the CO survey of Dame et al. (1987) and probably correspond to the Coalsack complex and another dense cloud. In none of the spectra do we detect velocities above +10 km s-1, which implies that these HI structures at higher velocity are located beyond 4 kpc.
 |
Fig. 12 NGC 4815 field: kinematics. Top: the 6283 Å DIB. Bottom: the 6614 Å DIB. The black line represents the HI 21 cm emission spectrum (LAB Survey). The dashed blue lines are an example of the fitted IS NaI lines (here from star 12581939-6453533) and triangles are the velocities of the DIB components derived from the global fit for all targets. |
For the γ Vel direction (field 4) (see Jeffries et al. 2009, 2014; Spina et al. 2014), the most significant difference from the other directions is the distribution of targets over a wider area (1° × 1°). We show in Fig. 13 that this has a strong impact on the star-to-star variability, especially for this region which is well-known for its complex interstellar density and ionization structure, partly under the strong influence from the Wolf-Rayet (WR) star. For the 6614 Å DIB the profile is also significantly contaminated by strong stellar line residuals, which produces large relative errors. The HI spectrum presents a strong peak at vhel 35 km s-1, a velocity that agrees well with the NaI and DIB absorptions (see Fig. 14). The second component in the HI spectrum at vhel 50 km s-1 is found to be very weak or null, while the HI component at ≃ 100 km s-1 is not detected in any of the spectra and corresponds to more distant clouds.
 |
Fig. 13 γ Vel field. Left: DIB EW and estimated extinction as a function of target distance. Two star groups are present that probe different regions of the foreground cloud. Right: the relation between EWs and extinction. There is a significant scatter, the largest of the 7 fields. Several outliers have stronger DIBs than the averaged relation. These departures from linearity are very likely linked to the influence of the Wolf-Rayet star environment. |
 |
Fig. 14 γ Vel field: kinematics. Top: the 6283 Å DIB. Bottom: the 6614 Å DIB. Line and markers are the same as in Fig. 12. |
The last three fields lie in the direction of the Galactic bulge. The first field corresponds to the commonly used, low-extinction direction at (l,b) ≃ (1°, −4°), the Baade’s window (BW). Figure 15 (left) shows the extinction, and the 6283 and 6614 EWs along this LOS. As for the previous field, the 6614 Å profile is consistent with the two others, but much less precisely defined because the absorption is weaker and the stellar line residuals have a stronger impact. Figure 16 shows the HI emission spectrum in this bulge direction; the spectrum is characterized by a dominant emission peak at −5 km s-1 (heliocentric frame). Here again, the comparison with the DIB velocity that results from the automated fitting agrees well with HI, with a dispersion of a few km s-1 around the central velocity.
 |
Fig. 15 Baade’s window direction: DIB vs. distance and A0 vs. distance |
 |
Fig. 16 Baade’s window direction: kinematics. All DIB velocities are found to be consistent with the local HI, around 5 km s-1. The second velocity component allowed by the fitting procedure is found to be unnecessary or negligible. Note that the discrepant data point at +15 km s-1 for the 6283 Å DIB (lower panel) is due to the effect of a strongly discrepant stellar line and disappears when the fitting is repeated after masking the corresponding region (the total EW is found to be unchanged). |
For the next two fields (INNERDISK O and W), IS absorptions are expected to be confined within a narrow interstellar radial velocity range, which is confirmed by the HI emission spectra, and the DIBs were analyzed by means of the single-component method. We checked for several stars that allowing for more than one component results in EW values that are fully compatible with those from the single-component method, within our estimated uncertainties. Figures 17 and 18 show the radial profiles of the DIB strength and the estimated extinction. They both gradually increase. The profiles agree with the profiles derived by Marshall et al. (2006) from 2MASS and the Besanon model in adjacent directions. We used AKs/A0 = 0.11 for the conversion. The DIB-extinction correlation is shown in lower panel and is compatible with a linear relationship within the measurements and the model uncertainties. The Pearson coefficients are found to be 0.55 and 0.76 for INNERDISK O and W.
 |
Fig. 17 6283 DIB EW and estimated extinction as a function of distance (top) and DIB extinction relationship (lower panel) for the OGLE BUL_SC24 (INNERDISK O) field. We compare our estimated extinction with the profiles from Marshall et al. (2006) (see text) for the closest directions. |
 |
Fig. 18 INNERDISK W field: DIB vs. distance, A0 vs. distance, and DIB vs. A0. The EW vs. A0 linear relationship (lower panel) has a slope of 567 ± 7 mA per magnitude (forcing the intercept to be 0). The Pearson correlation coefficient is 0.76. |
4.3. All fields: correlation with extinction
As discussed in Sect. 1, many studies were devoted to the correlation between the DIBs and extinction. Our results provide an opportunity to study this relation in more detail, with a large selection of DIBs in very different regions of the Galaxy for the first time. Figure 19 shows the whole set of 6283 and 6614 Å DIB EWs as a function of extinction. We also display the DIB-extinction relations obtained from previous studies using early-type star data (Puspitarini et al. 2013; Vos et al. 2011). To convert the color excess values E(B-V) listed in the previous works into extinction values A0, we assumed that A0/E(B − V) = 3.2882 + 0.04397 × E(B − V) in all directions. We fitted the DIB-extinction relationship independently of the error bars, and also using both errors (in extinction and EW) using the orthogonal distance regression (ODR) method (Boggs et al. 1989).
We compared our correlation coefficients with those obtained from previous studies based on early-type target stars, characterized by well-known extinctions and excellent spectra. It is remarkable that despite the complexity of the global adjustment and the stellar lines, the correlation between the 6283 Å DIB and the reddening is found to be tighter, as shown by the error-independent Pearson correlation coefficient of 0.91. This value is above most previous determinations, for example the coefficient of 0.82 reported by Friedman et al (2011). Using late-type stars is probably the main reason for a generally decreased dispersion, because we avoided the radiation field effects on the DIB carriers that arise around hot stars. Instead, our LOS mainly cross clouds that are far from these radiation sources. This conclusion agrees with the results of Chen et al. (2013).
For the weaker and narrower 6614 DIB, our correlation coefficient is 0.83, which is on the same order as the coefficient reported by Friedman et al (2011). Here, the absence of a correlation increase is probably due to the strong impact of the residual stellar features. This impact is much stronger than on the 6283 DIB because of the smaller DIB width, which is closer to the stellar line width. Better synthetic stellar models will help in reducing this source of uncertainty.
Figure 19 shows that our measured EWs are overall higher than what has generally been derived from early-type stars. This is especially clear for the inner disk and CoRoT anticenter fields and may be explained by the fact that we avoided some of the strong DIB suppressions that arise in the environment of UV-bright stars. For other sight lines such as the one toward NGC 4815 there are no significant differences from the DIB-color excess relations based on early-type stars. Finally, we note that more dispersion seems to be present for the local clouds, which may be explained by averaging effects along large distances.
 |
Fig. 19 DIB vs. A0, all fields. |
4.4. Spatial distribution
Figure 20 shows the projections of the target stars onto the Galactic plane, superimposed on a face-on map of the Milky Way. The color represents the 6283 DIB EW when it is measured, and a 6283-equivalent value deduced by simply scaling the 6614 or 8620 DIBs based on the mean ratios of 6614 to 6283 and of 8620 to 6283. When the LOS is along the Galactic plane, the EW reflects the spiral arm crossings. This is no longer the case when the latitude increases, as can be seen in the figure where the latitudes are indicated for each LOS.
 |
Fig. 20 Projections of the target stars onto the face-on map of the Galaxy (image from Churchwell et al. 2009). Units are parsecs, counted from the Sun, with dSun ≃ 8 kpc. The color-coding corresponds to the equivalent of the 6283 Å DIB, either directly measured, or, when not measured, estimated from the other DIB measurements using the average EW(6283)/EW(8620) or EW(6283)/EW(6614) ratios computed from the whole dataset. The black asterisk and small arrow mark bulge field 5 (Baade’s window direction) for which the X coordinate has been multiplied by 4 to avoid confusion with the other directions. The Galactic latitude of each field is indicated at the extremity of the sightline. |
5. Discussion and perspectives
We have developed and applied automated methods for extracting multicomponent DIBs from stellar spectra. These methods can be applied to any kind of stellar spectrum as long as the stellar parameters are known. In particular, it can handle cool star spectra despite their complex continua. Here we have presented the results of our automated adjustments when they are applied to ESO/FLAMES high-resolution spectra of red giants and F, G, K dwarfs that are part of the GES first data release and about the same number of FLAMES spectra from a previous program about the inner disk. We extracted three DIBs and studied their strengths and velocity shifts.
The comparison between the DIB strengths and spectro-photometric estimated extinctions reveals a significant correlation and demonstrates that we successfully extracted the DIB EWs despite the stellar and telluric absorptions. This correlation suggests that the link between the DIB strength and the extinction does not vary by much among regions of the Galaxy that span galactocentric radii from 2.5 to 13 kpc. This dataset shows a broad consistency between the DIB distance profiles and the estimated locations or extents of the Local and Perseus arms. The LOS velocity structure deduced from the HI 21 cm emission spectra and the DIBs velocities also agree. This shows that on large scales DIBs may be a kinematical tool in the same way as IS gaseous lines are commonly used. This opens perspectives for studying the most external arms for which very few measurements of the DIB abundance exist to date.
Altogether, these results show how DIBs can be used to reconstruct the large-scale distribution of the ISM in the Galaxy, and may be especially useful for distant clouds because in this case they are strong enough, but not saturated. In addition, DIBs in more distant clouds (such as Perseus) are found to be more tightly correlated with the extinction and less spatially or angularly variable than in the local clouds, which we interpret as an effect of distance-averaging. It also confirms that when using cool (or cool and distant) stars, the effects of a strong radiation field on the DIB abundance and/or ionization are minimized (or minimized and averaged out), and DIBs follow the extinction more closely. This latter aspect is quantitatively confirmed by the correlation coefficients we obtained when assembling all measurements. For the broad 6283 Å DIB, the Pearson coefficient is 0.91, significantly above previous determinations that were based on early-type stars despite the extremely large distances between the probed areas and the stellar lines. This implies that DIBs can be used as a first prior for the extinction in the absence of any other information. However, we note that for one field, the γ Vel cluster direction, the relationship between DIBs and extinction estimates is more complex. The proximity of the absorber and the presence of bright UV stars is probably responsible for this complexity and the departures from the average conditions. Finally, we note that for two sightlines the measured DIBs are slightly stronger than previous relationships based on early-type targets have predicted. This is probably also due to the absence of strong environmental effects. This deserves a more detailed study because the data presented here are still too limited to permit drawing definitive conclusions.
There is still room for a number of improvements of the synthetic stellar spectrum computations, and subsequent DIB measurements. Here we used the most probable values of the stellar parameters, and did not allow for any uncertainty. Moreover, we did not make any use of individual abundances, although most of them are determined for the GES spectra. One reason is our choice of a homogenous treatment of both GES spectra and other data for which the individual abundance measurements were not available. The second reason is, as previously developed by Chen et al. (2013), that the main source of poor quality adjustments of the stellar synthetic spectra to the data is clearly linked to specific spectral lines that are systematically under- or overestimated, or simply missing (see Figs. A.1, A.2), and allowing for small changes of the parameters would not solve for those discrepancies. Work is in progress to correct for these systematics, which must be done before fine-tuning of the parameters within the GES error bars or individual abundances are used. This should result in a better accuracy of the DIB strength and allow us to proceed in the kinematical analysis, which is still limited to the detection of velocity shifts above 5 to 10 km s-1 depending on DIBs and the signal. Improvements of the fitting strategy are also in progress, in particular the simultaneous adjustment of NaI lines and all measurable DIBs is expected to provide more reliable results. There is also room for an improved strategy for choosing the number of velocity components. We explored criteria based on the DIB velocity shift, but other methods need also to be developed and tested. This will be the subject of future studies based on larger datasets. Finally, residuals from sky emission removal are still significantly limiting the DIB extraction in some cases, and special attention must be devoted to this problem.
In general, these results pave the way to three-dimensional mapping of the Galactic ISM based on DIB absorption measurements from current or future stellar spectroscopic surveys. Like all three-dimensional maps, future DIB-based maps are expected to gain in accuracy in a considerable way when Gaia parallax measurements will be available. Finally, as illustrated by the CoRoT anticenter LOS, a very promising aspect that is specific to these DIB spectroscopic measurements is the potential detailed comparison, sight line by sight line, between the distance-limited absorption measurements and emission spectra that trace the gas at all distances. This comparison by means of the radial velocities will bring interesting information on the location of the poorly known dust-poor distant gas in the outer parts of the spiral arms.
Acknowledgments
R.L, L. P., C. B., F. A., and A.M-I. acknowledge support from the French National Research Agency (ANR) through the STILISM project. L. S. and S. D. acknowledge the support of Sonderforschungsbereich SFB 881 “The Milky Way system” (subprojects A4 and A5) of the German Research Foundation (DFG), and of Project IC120009 “Millennium Institute of Astrophysics (MAS)” of Iniciativa Cientfica Milenio del Ministerio de Economa, Fomento y Turismo de Chile. E. C. is grateful to the FONDATION MERAC for funding her fellowship. This work was partly supported by the European Union FP7 programme through ERC grant number 320360 and by the Leverhulme Trust through grant RPG-2012-541. We acknowledge the support from INAF and Ministero dell’ Istruzione, dell’ Università’ e della Ricerca (MIUR) in the form of the grant “Premiale VLT 2012”. The results presented here benefit from discussions held during the Gaia-ESO workshops and conferences supported by the ESF (European Science Foundation) through the GREAT Research Network Programme.
References
- Babusiaux, C., Katz, D., Hill, V., et al. 2014, A&A, 563, A15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bailer-Jones, C. A. L. 2011, MNRAS, 411, 435 [NASA ADS] [CrossRef] [Google Scholar]
- Bertaux, J. L., Lallement, R., Ferron, S., Boonne, C., & Bodichon, R. 2014, A&A, 564, A46 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Boggs, P. T., Byrd, R. H., Donaldson, J. R., & Schnabel, R. B. 1989, ACM Transactions on Mathematical Software, 15, 348 [CrossRef] [Google Scholar]
- Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127 [NASA ADS] [CrossRef] [Google Scholar]
- Burnett, B., & Binney, J. 2010, MNRAS, 407, 339 [NASA ADS] [CrossRef] [Google Scholar]
- Cami J., & Cox, N. L. J. 2013, Diffuse interstellar bands, Proc. IAU 297 Symp. [Google Scholar]
- Castelli, F., & Kurucz, R. L. 2003, Modelling of Stellar Atmospheres, 210, 20 [Google Scholar]
- Chabrier, G. 2001, ApJ, 554, 1274 [NASA ADS] [CrossRef] [Google Scholar]
- Chen, H.-C., Lallement, R., Babusiaux, C., et al. 2013, A&A, 550, A62 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Churchwell, E., Babler, B. L., Meade, M. R., et al. 2009, PASP, 121, 213 [NASA ADS] [CrossRef] [Google Scholar]
- Clough, S. A., Shephard, M. W., & Mlawer, E. J. 2005, J. Quant. Spectr. Rad. Transf., 91, 233 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Cordiner, M. A., Cox, N. L. J., Trundle, C., et al. 2008, A&A, 480, L13 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cordiner, M. A., Cox, N. L. J., Evans, C. J., et al. 2011, ApJ, 726, 39 [NASA ADS] [CrossRef] [Google Scholar]
- Cox, N. L. J., Kaper, L., Foing, B. H., & Ehrenfreund, P. 2005, A&A, 438, 187 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Cutri, R. M., Skrutskie, M. F., van Dyk, S., et al. 2003, ViZieR Online Data Catalog: II/246 [Google Scholar]
- Dame, T. M., Ungerechts, H., Cohen, R. S., et al. 1987, ApJ, 322, 706 [NASA ADS] [CrossRef] [Google Scholar]
- Dame, T. M., Hartmann, D., & Thaddeus, P. 2001, ApJ, 547, 792 [NASA ADS] [CrossRef] [Google Scholar]
- Dekker, H., D’Odorico, S., Kaufer, A., Delabre, B., & Kotzlowski, H. 2000, Proc. SPIE, 4008, 534 [Google Scholar]
- Deleuil, M., Meunier, J. C., Moutou, C., et al. 2009, AJ, 138, 649 [NASA ADS] [CrossRef] [Google Scholar]
- Fitzpatrick, E. L., & Massa, D. 2007, ApJ, 663, 320 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Friedman, S. D., York, D. G., McCall, B. J., et al. 2011, ApJ, 727, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Friel, E. D., Donati, P., Bragaglia, A., et al. 2014, A&A, 563, A117 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Galazutdinov, G. A., Musaev, F. A., Krełowski, J., & Walker, G. A. H. 2000, PASP, 112, 648 [NASA ADS] [CrossRef] [Google Scholar]
- Galazutdinov, G., Moutou, C., Musaev, F., & Krełowski, J. 2002, A&A, 384, 215 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Geballe, T. R., Najarro, F., Figer, D. F., Schlegelmilch, B. W., & de La Fuente, D. 2011, Nature, 479, 200 [NASA ADS] [CrossRef] [Google Scholar]
- Gilmore, G., Randich, S., Asplund, M., et al. 2012, The Messenger, 147, 25 [NASA ADS] [Google Scholar]
- Herbig, G. H. 1995, ARA&A, 33, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Hill, V., Babusiaux, C., Gómez, A., et al. 2012, Eur. Phys. J. Web Conf., 19, 6001 [CrossRef] [EDP Sciences] [Google Scholar]
- Hobbs, L. M., York, D. G., Snow, T. P., et al. 2008, ApJ, 680, 1256 [NASA ADS] [CrossRef] [Google Scholar]
- Hobbs, L. M., York, D. G., Thorburn, J. A., et al. 2009, ApJ, 705, 32 [NASA ADS] [CrossRef] [Google Scholar]
- IGOR Pro 2009. WaveMetrics Inc., Lake Oswego, OR, USA, http:www.wavemetrics.com [Google Scholar]
- Jeffries, R. D., Naylor, T., Walter, F. M., Pozzo, M. P., & Devey, C. R. 2009, MNRAS, 393, 538 [NASA ADS] [CrossRef] [Google Scholar]
- Jeffries, R. D., Jackson, R. J., Cottaar, M., et al. 2014, A&A, 563, A94 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jenniskens, P., & Desert, F.-X. 1994, A&AS, 106, 39 [NASA ADS] [Google Scholar]
- Joblin, C., D’Hendecourt, L., Leger, A., & Maillard, J. P. 1990, Nature, 346, 729 [NASA ADS] [CrossRef] [Google Scholar]
- Kalberla, P. M. W., Burton, W. B., Hartmann, D., et al. 2005, A&A, 440, 775 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kos, J., & Zwitter, T. 2013, ApJ, 774, 72 [NASA ADS] [CrossRef] [Google Scholar]
- Kos, J., Zwitter, T., Grebel, E. K., et al. 2013, ApJ, 778, 86 [NASA ADS] [CrossRef] [Google Scholar]
- Krelowski, J., Sneden, C., & Hiltgen, D. 1995, Planet. Space Sci., 43, 1195 [NASA ADS] [CrossRef] [Google Scholar]
- Kurucz, R. L. 2005, Mem. Soc. Astron. It. Suppl., 8, 14 [Google Scholar]
- Lallement, R., Vergely, J.-L., Valette, B., et al. 2014, A&A, 561, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Lanzafame, A. C., Frasca, A., Damiani, F., et al. 2014, A&A, submitted [Google Scholar]
- Magrini, L., Randich, S., Romano, D., et al. 2014, A&A, 563, A44 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Maíz Apellániz, J., Sota, A., Barbá, R. H., et al. 2014, IAU Symp., 297, 117 [NASA ADS] [Google Scholar]
- Marshall, D. J., Robin, A. C., Reylé, C., Schultheis, M., & Picaud, S. 2006, A&A, 453, 635 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- McCall, B. J, & Griffin, R. E. 2013, Proc. R. Soc. A, 469, 2151 [Google Scholar]
- Munari, U., Tomasella, L., Fiorucci, M., et al. 2008, A&A, 488, 969 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Oka, T., Welty, D. E., Johnson, S., et al. 2013, ApJ, 773, 42 [NASA ADS] [CrossRef] [Google Scholar]
- Planck Collaboration XI. 2014, A&A, 571, A11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Puspitarini, L., Lallement, R., & Chen, H.-C. 2013, A&A, 555, A25 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rothman, L. S., Gordon, I. E., Barbe, A., et al. 2009, J. Quant. Spec. Radiat. Transf., 110, 533 [Google Scholar]
- Sacco, G. G., Morbidelli, L., Franciosini, E., et al. 2014, A&A, 565, A113 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sarre, P. J. 2006, J. Mol. Spectr., 238, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Sbordone, L. 2005, Mem. Soc. Astron. It. Suppl., 8, 61 [Google Scholar]
- Sbordone, L., Bonifacio, P., Castelli, F., & Kurucz, R. L. 2004, Mem. Soc. Astron. It. Suppl., 5, 93 [Google Scholar]
- Smiljanic, R., Korn, A. J., Bergemann, M., et al. 2014, A&A, 570, A122 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spina, L., Randich, S., Palla, F., et al. 2014, A&A, 567, A55 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sonnentrucker, P., Cami, J., Ehrenfreund, P., & Foing, B. H. 1997, A&A, 327, 1215 [NASA ADS] [Google Scholar]
- Tuairisg, S. Ó., Cami, J., Foing, B. H., Sonnentrucker, P., & Ehrenfreund, P. 2000, A&AS, 142, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Udalski, A., Szymanski, M., Kubiak, M., et al. 2002, Acta Astron., 52, 217 [NASA ADS] [Google Scholar]
- Vallée, J. P. 2008, AJ, 135, 1301 [NASA ADS] [CrossRef] [Google Scholar]
- van Loon, J. T. 2014, IAU Symp., 297, 79 [NASA ADS] [Google Scholar]
- van Loon, J. T., Bailey, M., Tatton, B. L., et al. 2013, A&A, 550, A108 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vergely, J.-L., Freire Ferrero, R., Siebert, A., & Valette, B. 2001, A&A, 366, 1016 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vergely, J.-L., Valette, B., Lallement, R., & Raimond, S. 2010, A&A, 518, A31 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vos, D. A. I., Cox, N. L. J., Kaper, L., Spaans, M., & Ehrenfreund, P. 2011, A&A, 533, A129 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Welty, D. E., Federman, S. R., Gredel, R., Thorburn, J. A., & Lambert, D. L. 2006, ApJS, 165, 138 [NASA ADS] [CrossRef] [Google Scholar]
- Zasowski, G., & Ménard, B. 2014, IAU Symp., 297, 68 [NASA ADS] [Google Scholar]
- Zhang, B., Reid, M. J., Menten, K. M., et al. 2013, ApJ, 775, 79 [NASA ADS] [CrossRef] [Google Scholar]
Appendix A: Estimate of the error on the DIB equivalent width
 |
Fig. A.1 Left: fit residuals (the difference between the data spectrum and the fitted model) for all of target stars in the CoRoT fields observed by GIRAFFE (6613.6 Å DIB). The left axis is the star stacking axis and the top axis is the wavelength (after spectra have all been shifted to their respective stellar frames). The color shows the residual intensity. Zero value (green) corresponds to well-fitted spectra. The residual (red and blue for positive and negative residuals) is due to imperfect stellar modeling. Right: the residuals at chosen wavelengths: at ~6605 Å (shown as red marks) and at ~6614 Å (shown in green). The ~6605 Å region shows higher positive residuals because the model overestimates the stellar line in this area. At 6614 Å, we have fit residuals about 0. |
 |
Fig. A.2 Same as Fig. A.1, but for 8620 DIB. Left: fit residuals for all of target stars over the entire wavelength range. Right: the residuals at chosen wavelengths. The 8611 Å region shows higher negative residuals because the model underestimates the stellar line in this area. |
All Tables
All Figures
 |
Fig. 1 Distribution of the selected fields, numbered as in Table 1. The distribution is superimposed on the HI 21 cm brightness temperature map (Kalberla et al. 2005) in the radial velocity interval −100 km s-1≤ vLSR ≤ 100 km s-1. The map is in Galactic coordinates, centered on l = −60°. |
| In the text | |
 |
Fig. 2 NaI doublet/6614 Å DIB global, multicomponent analysis, here for the GES star 12574905-6458511 (field 3). The NaI region is shown in the top panel and the DIB region in the lower panel. The entire fitted spectral interval is shown in the left panels, while the right panels display enlarged the NaI-D2 region (top) and the DIB region (lower). In each figure the red line shows the stellar spectrum (lower plot) and the fitting residuals (upper plot). The dotted lines are the models: stellar (orange), telluric (green), and interstellar components (blue). The thick blue line is the final adjustment. The radial velocities of the NaI and DIB components are linked throughout (see the black vertical line). Velocities are heliocentric. |
| In the text | |
 |
Fig. 3 Same as Fig. 2 (except for the enlarged figure) for the 6283 Å DIB. |
| In the text | |
 |
Fig. 4 Multicomponent 6614 Å DIB fitting: GIRAFFE field 1, GES target 06441034-0048254. The red line shows the stellar spectrum. The dotted lines are the models: stellar (orange), telluric (green), empirical DIBs (gray). The thick blue line is the best model adjustment. The initial guesses for the DIB velocity centroids are 24, 40, and 50 km s-1 and are based on the HI spectrum in the same direction (see top plot). Middle: an example of a preliminary adjustment with a unique DIB component. The DIB velocity is found to be ~33 km s-1. The large difference from the initial guess (24 km s-1) demonstrates the need for a second cloud component. Bottom: an example of a subsequent adjustment with two DIB components. The two fitted velocities are now close to the first two HI emission peaks. |
| In the text | |
 |
Fig. 5 Same as Fig. 4 (middle), but for 8620 Å (GES target 06441034-0048254). There are sky residuals in the red wing of the DIB. For this broad DIB a single velocity component is used (see text). |
| In the text | |
 |
Fig. 6 Results for target stars in field 1 (CoRoT anticenter). 6614 Å DIB EW (top), 8620 Å DIB EW (middle) and extinction A0 (bottom) vs. the estimated distance. Circles show GIRAFFE observations. Triangles show UVES observations. Colors in the top panel correspond to the number of IS components used to fit the IS line or band. All nearby targets (D ≤ 1 kpc) have only one IS component, or, for three targets, a very weak, negligible second component. Distant targets have more than one velocity component, in agreement with the crossing of at least one external arm (see the text). The outlier star 06441428-0057447 marked by a red star has stellar spectroscopic parameters that strongly disagree with stellar seismology information, which indicates that their distance and extinction are inaccurate for this target. |
| In the text | |
 |
Fig. 7 6283, 6614, and 8620 Å DIB EWs as a function of the extinction for CoRoT ANTI CENTER field targets. |
| In the text | |
 |
Fig. 8 Evolution of the DIB profile with target distance. Left: the 6614Å DIB absorption spectral profile up to stars at increasing distances along the CoRoT anticentre direction (l, b = 213°, −2°). We show the average of stacked extracted, normalized absorption spectra sorted by stellar distances (an offset of 0.5 in y-axis separates the two spectra). The continuum on the blue side of the DIB is affected by strong stellar lines that are insufficiently corrected for. The first (top) spectrum corresponds to the first kpc, the last (bottom) spectrum to distances between 4 and 6 kpc. Right: comparisons between one- and two-DIB component adjustments for close and distant stars. Distant stars require at least two DIBs separated by more than 20 km s-1 (see text). |
| In the text | |
 |
Fig. 9 Comparison between the fitted DIB radial velocities and EWs and the HI 21 cm emission spectra. Black (red) markers and lines are GIRAFFE results and HI spectra from field 1 (field 2). Error bars on the velocities are based on the full covariance matrix for the various parameters. For the narrow 6614 Å DIB (GIRAFFE observations) a significant number of spectra require two velocity components, which very likely correspond to the Local and Perseus arms. Small EWs and large error bars on velocities correspond to marginal results in low S/N spectra. UVES target results are displayed with triangles (yellow and blue for fields 1 and 2). At variance with GIRAFFE, UVES velocities are linked to the strong sodium lines through global fitting. Their agreement with the velocity structure derived from the GIRAFFE targets shows the link between NaI and DIB velocities. |
| In the text | |
 |
Fig. 10 CoRoT CENTER FIELD field. Left: DIB/A0 vs. distance profile. Right: DIB vs. A0: 6283 and 6614. |
| In the text | |
 |
Fig. 11 NGC 4815 field: (left) DIB and A0 distance profiles. Stars identified by Friel et al. (2014) as cluster members correspond to blue, nonmembers to red markers. Right: 6283 (top) and 6614 (lower panel) Å DIB EW vs the estimated extinction A0. The black “0" sign indicates the unique star with a single DIB velocity, for all other targets the adjustment to the data requires two velocity components. |
| In the text | |
 |
Fig. 12 NGC 4815 field: kinematics. Top: the 6283 Å DIB. Bottom: the 6614 Å DIB. The black line represents the HI 21 cm emission spectrum (LAB Survey). The dashed blue lines are an example of the fitted IS NaI lines (here from star 12581939-6453533) and triangles are the velocities of the DIB components derived from the global fit for all targets. |
| In the text | |
 |
Fig. 13 γ Vel field. Left: DIB EW and estimated extinction as a function of target distance. Two star groups are present that probe different regions of the foreground cloud. Right: the relation between EWs and extinction. There is a significant scatter, the largest of the 7 fields. Several outliers have stronger DIBs than the averaged relation. These departures from linearity are very likely linked to the influence of the Wolf-Rayet star environment. |
| In the text | |
 |
Fig. 14 γ Vel field: kinematics. Top: the 6283 Å DIB. Bottom: the 6614 Å DIB. Line and markers are the same as in Fig. 12. |
| In the text | |
 |
Fig. 15 Baade’s window direction: DIB vs. distance and A0 vs. distance |
| In the text | |
 |
Fig. 16 Baade’s window direction: kinematics. All DIB velocities are found to be consistent with the local HI, around 5 km s-1. The second velocity component allowed by the fitting procedure is found to be unnecessary or negligible. Note that the discrepant data point at +15 km s-1 for the 6283 Å DIB (lower panel) is due to the effect of a strongly discrepant stellar line and disappears when the fitting is repeated after masking the corresponding region (the total EW is found to be unchanged). |
| In the text | |
 |
Fig. 17 6283 DIB EW and estimated extinction as a function of distance (top) and DIB extinction relationship (lower panel) for the OGLE BUL_SC24 (INNERDISK O) field. We compare our estimated extinction with the profiles from Marshall et al. (2006) (see text) for the closest directions. |
| In the text | |
 |
Fig. 18 INNERDISK W field: DIB vs. distance, A0 vs. distance, and DIB vs. A0. The EW vs. A0 linear relationship (lower panel) has a slope of 567 ± 7 mA per magnitude (forcing the intercept to be 0). The Pearson correlation coefficient is 0.76. |
| In the text | |
 |
Fig. 19 DIB vs. A0, all fields. |
| In the text | |
 |
Fig. 20 Projections of the target stars onto the face-on map of the Galaxy (image from Churchwell et al. 2009). Units are parsecs, counted from the Sun, with dSun ≃ 8 kpc. The color-coding corresponds to the equivalent of the 6283 Å DIB, either directly measured, or, when not measured, estimated from the other DIB measurements using the average EW(6283)/EW(8620) or EW(6283)/EW(6614) ratios computed from the whole dataset. The black asterisk and small arrow mark bulge field 5 (Baade’s window direction) for which the X coordinate has been multiplied by 4 to avoid confusion with the other directions. The Galactic latitude of each field is indicated at the extremity of the sightline. |
| In the text | |
 |
Fig. A.1 Left: fit residuals (the difference between the data spectrum and the fitted model) for all of target stars in the CoRoT fields observed by GIRAFFE (6613.6 Å DIB). The left axis is the star stacking axis and the top axis is the wavelength (after spectra have all been shifted to their respective stellar frames). The color shows the residual intensity. Zero value (green) corresponds to well-fitted spectra. The residual (red and blue for positive and negative residuals) is due to imperfect stellar modeling. Right: the residuals at chosen wavelengths: at ~6605 Å (shown as red marks) and at ~6614 Å (shown in green). The ~6605 Å region shows higher positive residuals because the model overestimates the stellar line in this area. At 6614 Å, we have fit residuals about 0. |
| In the text | |
 |
Fig. A.2 Same as Fig. A.1, but for 8620 DIB. Left: fit residuals for all of target stars over the entire wavelength range. Right: the residuals at chosen wavelengths. The 8611 Å region shows higher negative residuals because the model underestimates the stellar line in this area. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


