| Issue |
A&A
Volume 568, August 2014
|
|
|---|---|---|
| Article Number | A13 | |
| Number of page(s) | 23 | |
| Section | The Sun | |
| DOI | https://doi.org/10.1051/0004-6361/201423892 | |
| Published online | 06 August 2014 | |
Comparison of solar photospheric bright points between Sunrise observations and MHD simulations
1 Max-Planck-Institut für Sonnensystemforschung (MPS), Justus-von-Liebig-Weg 3, 37077 Göttingen, Germany
e-mail: riethmueller@mps.mpg.de
2 School of Space Research, Kyung Hee University, Yongin, 446-701 Gyeonggi, Republic of Korea
3 Kiepenheuer-Institut für Sonnenphysik (KIS), Schöneckstr. 6, 79104 Freiburg, Germany
4 National Solar Observatory (NSO), Sunspot NM 88349, USA
Received: 27 March 2014
Accepted: 30 May 2014
Bright points (BPs) in the solar photosphere are thought to be the radiative signatures (small-scale brightness enhancements) of magnetic elements described by slender flux tubes or sheets located in the darker intergranular lanes in the solar photosphere. They contribute to the ultraviolet (UV) flux variations over the solar cycle and hence may play a role in influencing the Earth’s climate. Here we aim to obtain a better insight into their properties by combining high-resolution UV and spectro-polarimetric observations of BPs by the Sunrise Observatory with 3D compressible radiation magnetohydrodynamical (MHD) simulations. To this end, full spectral line syntheses are performed with the MHD data and a careful degradation is applied to take into account all relevant instrumental effects of the observations. In a first step it is demonstrated that the selected MHD simulations reproduce the measured distributions of intensity at multiple wavelengths, line-of-sight velocity, spectral line width, and polarization degree rather well. The simulated line width also displays the correct mean, but a scatter that is too small. In the second step, the properties of observed BPs are compared with synthetic ones. Again, these are found to match relatively well, except that the observations display a tail of large BPs with strong polarization signals (most likely network elements) not found in the simulations, possibly due to the small size of the simulation box. The higher spatial resolution of the simulations has a significant effect, leading to smaller and more numerous BPs. The observation that most BPs are weakly polarized is explained mainly by the spatial degradation, the stray light contamination, and the temperature sensitivity of the Fe i line at 5250.2 Å. Finally, given that the MHD simulations are highly consistent with the observations, we used the simulations to explore the properties of BPs further. The Stokes V asymmetries increase with the distance to the center of the mean BP in both observations and simulations, consistent with the classical picture of a production of the asymmetry in the canopy. This is the first time that this has been found also in the internetwork. More or less vertical kilogauss magnetic fields are found for 98% of the synthetic BPs underlining that basically every BP is associated with kilogauss fields. At the continuum formation height, the simulated BPs are on average 190 K hotter than the mean quiet Sun, the mean BP field strength is found to be 1750 G, and the mean inclination is 17°, supporting the physical flux-tube paradigm to describe BPs. On average, the synthetic BPs harbor downflows increasing with depth. The origin of these downflows is not yet understood very well and needs further investigation.
Key words: Sun: magnetic fields / Sun: photosphere / Sun: UV radiation / techniques: polarimetric / techniques: spectroscopic
© ESO, 2014
1. Introduction
Magnetic fields in the network and in active region plage are often concentrated into strong kilogauss field elements (Stenflo 1973; Solanki et al. 2006; Ishikawa et al. 2007). At high spatial resolution these elements appear as bright points (BPs; Berger & Title 2001) owing to the inflow of radiation from their walls into their evacuated interiors (Spruit 1976; Deinzer et al. 1984). Many features of magnetic elements are known (see Solanki 1993, for an overview) and various aspects of the underlying model of magnetic flux tubes have been tested, but such tests have generally suffered from the fact that the data were not able to spatially resolve magnetic elements.
This situation has changed with the availability of data recorded by the Sunrise balloon-borne observatory, which have allowed magnetic elements even in the internetwork quiet Sun to be spatially resolved (Lagg et al. 2010) and have allowed the internal structure of network magnetic features to be probed (Martínez González et al. 2012) providing a good opportunity to revisit BPs and to compare their observational properties with predictions from state-of-the-art radiation magnetohydrodynamic (MHD) simulations.
One motivation to study BPs is their contribution to variations in the total solar irradiance (TSI). Around the maximum of the solar activity cycle, the reduction of solar irradiance owing to dark sunspots and pores is overcompensated by an increased brightness of the BPs (Fröhlich 2013; Solanki et al. 2013). As a result, the TSI, i.e., the irradiance integrated over all wavelengths, is on average higher during maximum solar activity than during minimum (Willson & Hudson 1988). The TSI variations are only weak over the solar cycle, but because 60% (Krivova et al. 2006) or even more (Harder et al. 2009) of the variations in TSI are produced at wavelengths shorter than 4000 Å, the variations in the ultraviolet (UV) can be much more relevant. From recent stratospheric observations we know that the BP contrasts are particularly high in the UV (Riethmüller et al. 2010), i.e., the radiative properties of BPs possibly play an important role in influencing the Earth’s climate. A variation of the UV irradiance changes the chemistry of the stratosphere, which can propagate into the troposphere and finally influence the climate (London 1994; Larkin et al. 2000; Gray et al. 2010; Haigh et al. 2010; Ermolli et al. 2012).
In addition, there are reasons intrinsic to solar physics why BPs are of interest. First, BPs are the most easily visible signatures of strong-field magnetic elements and hence have been widely observed (e.g., Muller & Roudier 1984; Berger et al. 1995; Berger & Title 2001; Utz et al. 2009). Such magnetic elements carry much of the magnetic energy, even if they harbor only a small fraction of the magnetic flux. Second, the flux tubes guide MHD waves, which could contribute to coronal heating (Roberts 1983; Choudhuri et al. 1993) and may be related to the waves found to run along spicules (De Pontieu et al. 2007). Additionally, flux-tube motions can lead to field-line braiding and the build up of energy, which may be released through nanoflares (Parker 1988).
The first science flight of the Sunrise observatory revealed the very high contrasts of BPs in the UV (Riethmüller et al. 2010). Here we follow up on this work by carrying out a more in-depth analysis of a quiet-Sun region as observed by Sunrise and by comparing the data with numerical simulations of three-dimensional radiative magnetoconvection. Hence, we further explore the interplay between observation and simulation which has been so fruitful in the past. The MHD simulation data were degraded with known instrumental effects that were present during the Sunrise observations so that they can be compared directly with the observational data. We extend existing studies by considering many more observational quantities (intensity at multiple wavelengths, line-of-sight (LOS) velocity, spectral line width, and polarization degree) when comparing observational data and MHD simulations, which allowed us to test the realism of the MHD simulations far more stringently than by simply comparing intensities. We carried out these comparisons in two steps, first for all pixels in the images and later restricted to just the pixels identified as lying within BPs. After we were satisfied that the simulations give a reasonable representation of the observations, we used the original, undegraded simulations to learn more about the BPs and their underlying magnetic features.
2. Observations, simulations, and degradation
2.1. Observations
The data we used in this study were acquired with the balloon-borne 1 m aperture Sunrise telescope that flew from Kiruna in northern Sweden to Somerset Island in northern Canada in June 2009 (Barthol et al. 2011; Solanki et al. 2010). At the flight altitude of roughly 35 km, 99% of the air mass was below the observatory, so that the disturbing influence of the Earth’s atmosphere (seeing) was minimized. A fast tip-tilt mirror, which was controlled by a correlating wavefront sensor, reduced the residual pointing jitter and the on-board adaptive optics system corrected the images for low order wavefront aberrations (Berkefeld et al. 2011). Two instruments were operated simultaneously: the Sunrise Filter Imager (SuFI; Gandorfer et al. 2011) and the Imaging Magnetograph eXperiment (IMaX; Martínez Pillet et al. 2011).
During the time series considered herein, recorded from 23:00 to 24:00 UT on 2009 June 10, the telescope pointed to a quiet-Sun region close to the center of the solar disk (μ = 0.99). The SuFI instrument observed the Sun at the wavelengths 2995 Å (33 Å FWHM, 325 ms exposure time, mainly atomic spectral lines), 3118 Å (8.5 Å FWHM, 300 ms exposure time, part of an OH band), 3877 Å (5.6 Å FWHM, 65 ms exposure time, CN band), and 3973 Å (1.8 Å FWHM, 750 ms exposure time, Ca ii H line). Dark-current and flat-field corrections were applied to the SuFI data. The images were phase-diversity (PD) reconstructed using the wavefront errors retrieved from the in-flight PD measurements via a PD prism in front of the camera. The reconstructed data are referred to as level 2 data (see Hirzberger et al. 2010, 2011). Here we concentrated on the 3118 Å and the 3877 Å bands. The spectra in these bands, taken from the NSO spectral atlas of Kurucz et al. (1984) are plotted in the upper two panels of Fig. 1 (black lines) along with the filter profiles (green lines).
The IMaX instrument scanned the Fe i line at 5250.2 Å (Landé factor g = 3) in its L12-2 mode, i.e., only Stokes I and V were measured, at twelve scan positions with two accumulations. The twelve scan positions were set to λ − λ0 = −192.5,..., + 192.5 mÅ relative to the center of the average quiet-Sun profile of the line, in steps of 35 mÅ. The effective spectral resolution of IMaX was 85 mÅ (full width half maximum (FWHM) value). The data were corrected for dark current and flat field and interference fringes were removed with a manually designed Fourier filter. The IMaX data were then reconstructed with the help of the phase diversity technique. Additionally, the instrumental polarization and the residual cross talk with intensity was removed. Stray light was not removed from either data set. All intensity images were divided by the mean quiet-Sun value, IQS, that was defined as the average of the image.
Finally, the Stokes I profiles were fitted with a Gaussian function to retrieve the spectral line parameters: LOS velocity and line width. The increased reliability of the retrieved parameters for more scanned line positions was the main motivation for using data with twelve scan positions instead of five as in the so-called V5-6 mode of IMaX, which was employed in our previous study (Riethmüller et al. 2010). Since we were studying BPs, thought to be associated with strong-field relatively vertical magnetic features, the Stokes Q and U profiles were considered to be less important for the present work. This assumption is supported by the analysis of Jafarzadeh et al. (2014b), who found that BPs extend nearly vertically in height. Figure 1 shows the relevant parts of the solar spectrum taken from an NSO spectral atlas (Kurucz et al. 1984). The spectrum centered on the Fe i line at 5250.2 Å is plotted in the bottom panel. A simulated profile of the 5250.2 Å line (see Sect. 2.2) in the presence of an upflow of 5 km s-1 is overplotted as a dotted red line in order to demonstrate that even strong upflows (or downflows) can be safely identified with the L12-2 mode of IMaX (see the blue arrows marking the wavelengths sampled by IMaX in L12-2 mode), but can be missed or misidentified with only five scan positions (see red arrows). The image quality of the Sunrise data depended on the gondola’s varying pointing stability. The L12-2 data were recorded over only a relatively short period of time during the Sunrise flight, when the pointing stability was not particularly good. Therefore, the image quality of the analyzed L12-2 data is not quite as good as the V5-6 data analyzed by Riethmüller et al. (2010), which has a better spatial resolution. The LOS velocities were corrected for the wavelength shift over the FOV caused by the IMaX etalon (see Martínez Pillet et al. 2011). In this work, negative LOS velocities correspond to upflows.
We selected the nine data sets acquired at 23:05:08, 23:09:20, 23:20:22, 23:26:09, 23:31:56, 23:36:39, 23:42:26, 23:47:09, and 23:53:28 UT for an in-depth study from the one-hour time series. The selection was done so that the time interval between two consecutive sets was on average five minutes so as to give the BPs some time to evolve between two analyzed data sets. For each data set we checked that the pointing stability of the gondola and hence the image quality was as good as any among the L12-2 data, although it was found to be somewhat lower than of the best V5-6 data.
 |
Fig. 1 Excerpts from an NSO spectral atlas (black lines; Kurucz et al. 1984), spatially averaged synthetic spectra (red lines; see text for details), and instrumental filter profiles (green lines referring to the scale on the right side of the figure) for the part of the OH band around 3118 Å (top panel), the CN band at 3877 Å (middle panel), and the Fe i line at 5250.2 Å (bottom panel). The dotted red line in the bottom panel simulates the Doppler shifted profile of the Fe i line at 5250.2 Å produced by an upflow of 5 km s-1. The red arrows indicate the five scan positions of the IMaX V5-6 mode, while the twelve blue arrows mark them for the L12-2 mode. |
2.2. Simulations
The three-dimensional non-ideal compressible radiation MHD simulations considered here were calculated with the MURaM code which solves a system of equations consisting of the continuity equation, the momentum equation, the energy equation, the induction equation, and the equation of state (Vögler et al. 2005). The radiative energy exchange rate of the energy equation is determined by a non-gray radiative transfer module under the assumption of local thermal equilibrium (LTE). The equation of state takes into account effects of partial ionization because they influence the efficiency of the convective energy transport. Periodic boundary conditions were used in the horizontal directions. A free in- and outflow of matter was allowed at the bottom boundary of the computational box under the constraint of total mass conservation, while the top boundary was closed (i.e., zero vertical velocity). A statistically relaxed purely hydrodynamical simulation was used as an initial condition. From tests with different magnetic fluxes, we estimated the mean unsigned vertical magnetic flux density of our quiet-Sun observations to correspond roughly to a simulation with a starting value of 30 G and hence a unipolar homogeneous vertical magnetic field of Bz = 30 G was introduced into the hydrodynamical simulation (see Sect. 3.1 for a more precise estimate of the mean flux). The simulation was run for an additional 3 h of solar time to reach, and stay for a sufficiently long time, a statistically stationary state. Thirty equidistant snapshots covering 141 min of solar time were then used for this study. The data cubes cover 6 Mm in both horizontal directions with a cell size of 10.42 km (0.′′014). In the vertical direction they extend 1.4 Mm with a 14 km cell size. On average, unit optical depth for the continuum at 5000 Å is reached about 500 km below the upper boundary. To evaluate the dependence of our MHD results on the mean magnetic flux, we also calculated ten snapshots each taken from simulation runs with an initial mean unsigned vertical flux density of 0 G (purely hydrodynamical run), 50 G, and 200 G, while all other parameters were kept identical to the 30 G run.
The output of the MURaM code consisted of data cubes of the density, velocity (x, y, z component), total energy density, magnetic field (x, y, z component), as well as gas pressure and temperature. For a direct comparison with the observations, Stokes profiles had to be derived from these data cubes. This was done by a forward calculation with the SPINOR inversion code (Frutiger 2000; Frutiger et al. 2000; Berdyugina et al. 2003) that uses the STOPRO routines (Solanki 1987) to compute synthetic Stokes spectra for atomic and molecular spectral lines assuming LTE and solving the Unno-Rachkovsky radiative transfer equations (Rachkovsky 1962). All spectral line syntheses in this paper were carried out for the center of the solar disk (μ = 1).
Molecular lines were synthesized using the MOL routine library which is employed in the SPINOR and STOPRO codes and is based on theoretical computations and results presented by Berdyugina & Solanki (2002); Berdyugina et al. (2003, 2005). In particular, they analyzed violet CN and OH lines and suggested that these lines can serve as very sensitive diagnostics of temperature and magnetic field fluctuations in the solar atmosphere and sunspots using both imaging and spectropolarimetry. The CN lines were previously successfully employed for imaging the quiet photosphere (Chapman 1970; Sheeley 1971; Zakharov et al. 2005, 2007; Uitenbroek & Tritschler 2006, 2007) and for measuring weak entangled solar magnetic fields with the Hanle effect (Shapiro et al. 2007, 2011). The violet OH lines have not yet been broadly employed for solar studies because of the impediment by the terrestiral atmosphere. Recently, Prokhorov et al. (2014) have analyzed diagnostic potentials of several molecular bands including the CN and OH violet bands using MHD simulations and 3D radiative transfer.
The SuFI spectral range at 3877 Å includes lines of the CN B2Σ+ − X2Σ+ system and the CH B2Σ− − X2Π system. By comparing synthetic spectra with the quiet-Sun NSO atlas spectrum (Kurucz et al. 1984), we have identified 233 CN lines, 36 CH lines, and 85 atomic lines. A few lines remained unidentified. In fact, the molecular lines completely dominate the chosen spectral range, which includes the CN (0,0) and (1,1) band heads. The maximum absorption in these bands is, however, in the wings of the instrument passband (see green line in the middle panel of Fig. 1), while the maximum transmission was set at a wavelength where both atomic and molecular lines contribute to the absorbtion. We compiled the CN line list using laboratory measured wavelengths and by calculating line oscillator strengths from measured molecular constants and band oscillator strengths (Knowles et al. 1988; Rehfuss et al. 1992; Prasad et al. 1992; Davis et al. 2005; Ram et al. 2006). The CH line list was compiled in the same way using wavelengths, molecular constants, and band oscillator strengths by Krupp (1974); Bembenek et al. (1990). The CN and CH B − X systems are strongly perturbed by relatively weak external magnetic fields: the complete Paschen-Back effect (PBE) starts at 77 G and 305 G for the CN and CH bands, respectively (Berdyugina et al. 2005). This implies that even an order of magnitude weaker magnetic field will cause noticeable effects, such as line asymmetries and alterations of the line strengths. These effects are fully accounted for in our calculations.
Central wavelength λ0, oscillator strength log(gf), energy of the lower level El, and term sysmbol of the lower and upper levels of the 20 synthesized spectral lines around the Fe i line at 5250.2 Å.
The SuFI 3118 Å region includes hydroxyl radical OH lines from the A2Σ+ − X2Π system. We have identified 139 OH lines and 399 atomic lines. Thus, the quiet-Sun spectrum in this spectral region is dominated by atomic lines. However, at lower temperatures, e.g., in a sunspot spectrum, many otherwise weak OH lines become clearly visible. The OH line list was compiled using data by Coxon (1980) and Abrams et al. (1994). The PBE in the OH A − X system starts to be noticeable at field strengths stronger than about 200 G (Berdyugina et al. 2003), which is taken into account.
For the spectral range of IMaX we synthesized 20 spectral lines around the Fe i line at 5250.2 Å, all of which could possibly contribute to the synthesized Stokes signals owing to the width and secondary peaks of the IMaX spectral point spread function (PSF), see green line in the bottom panel of Fig. 1. The atomic parameters of the 20 absorption lines around 5250.2 Å are listed in Table 1. Oscillator strengths, energies of the lower level, and the term sysmbols have been taken from the Kurucz (Kurucz & Bell 1995), the VALD (Piskunov et al. 1995; Kupka et al. 2000), or the NIST (Kramida et al. 2012) database, respectively. Values in brackets are given only for comparison of the various data sources. Central wavelengths and various oscillator strengths are fitted to the NSO spectral atlas.
Molecular number densities were calculated under the assumption of the chemical equilibrium of about 300 molecular species composed of more than 30 atoms, as described in Berdyugina et al. (2003). The solar abundance of iron was taken from Bellot Rubio & Borrero (2002); for all other elements, including carbon, nitrogen, and oxygen, we assumed solar abundances according to Grevesse & Sauval (1998).
For the three considered wavelength ranges, the spatially averaged synthetic spectra (calculated for a snapshot with 30 G average vertical field1) are shown in Fig. 1 (red lines) and compared with the average observed spectra of quiet Sun taken from the NSO atlas (Kurucz et al. 1984). The synthetic spectra were convolved with a Gaussian of FWHM = 1.93 km s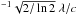 to fit the spectral resolution of the NSO atlas. The spectral PSF of IMaX (green line in the bottom panel) includes the IMaX prefilter and is plotted on a logarithmic scale for a better visibility of the secondary peaks at 5248.32 Å and 5252.10 Å.
to fit the spectral resolution of the NSO atlas. The spectral PSF of IMaX (green line in the bottom panel) includes the IMaX prefilter and is plotted on a logarithmic scale for a better visibility of the secondary peaks at 5248.32 Å and 5252.10 Å.
2.3. Synthetic instrumental effects
One of the most sensitive parts of this work was the introduction of synthetic instrumental effects, i.e., the degradation of the synthetic data to the same spatial and spectral resolution, to the same stray light contamination and noise level as the observed data. The various degradation steps significantly influenced the values of the parameters we compared between simulation and observation. We found that only if all the relevant effects of the Sunrise instrumentation are known to relatively high precision, can the comparison between synthetic and observed data be meaningful. All the used degradation steps are explained in the following. They were applied in the same order as described below.
2.3.1. Spectral resolution and sampling
The synthetic Stokes profiles output from the SPINOR code have perfect spectral resolution and high spectral sampling which had to be reduced to the values of the Sunrise instruments. The transmission profiles of the SuFI filters as well as the spectral PSF of IMaX (including the pre-filter) were measured in the laboratory before the launch of Sunrise. The transmission profiles of the two SuFI filters (3118 Å and 3877 Å) were re-sampled to the wavelength grid points of the synthetic intensity profiles. Then the filter transmission profile were multiplied by the intensity profile point by point and the products were summed up. This scalar product gave the intensity at a spatial pixel of a synthetic SuFI image. In the case of IMaX, the synthetic Stokes profiles were convolved with the spectral PSF of IMaX. Finally, Stokes images at the twelve scan positions of the IMaX L12-2 mode were retrieved.
2.3.2. Spatial resolution and residual pointing jitter
The spatial resolution of the Sunrise data was limited by the 1 m aperture, the considered wavelength, and the stability of the gondola’s pointing. The theoretical diffraction limit was not fully reached during the first science flight of Sunrise owing to the residual pointing jitter. From azimuthally averaged power spectra of the SuFI and IMaX intensity images, a precise determination of the spatial resolution was not possible, but allowed a rough estimate between 0.′′20 and 0.′′24 for the data analyzed here, which are not as highly resolved as data used for earlier publications. In the ideal case of a perfect knowledge of the Sunrise PSF and no pointing jitter, a spatial degradation of the synthesized data would not be needed because we compared with reconstructed Sunrise data. Theoretically, the deconvolution with the PSF reconstructs the original root mean square (rms) contrasts. In the non-ideal case of Sunrise, the residual pointing jitter during the observation was taken into account by convolving all synthetic Stokes images with a two-dimensional Gaussian of FWHM = 0.′′23. This FWHM value led to the best match between the rms contrasts of the observed and synthesized IMaX continuum images as we found after some tests with different FWHM values.
2.3.3. Stray light
In the case of ground-based solar observations, the atmospheric stray light is a significant part of the total amount of stray light. Owing to the flight altitude of approximately 35 km on average, we expect that atmospheric stray light is negligible, so that we have to deal with instrumental stray light alone. By observing the solar limb, intensity profiles of the limb could be recorded for the considered wavelengths. These solar limb profiles were then compared with the intrinsic limb profiles of the Sun taken from the literature (Dunn et al. 1968) which allowed the stray light modulation transfer functions (MTFs) to be calculated. The stray light MTFs were then multiplied with the synthetic Stokes images in Fourier space. Details about the determination of the stray light affecting Sunrise data are given by Feller et al. (in prep.).
 |
Fig. 2 Intensity maps in the wavelength bands 3118 Å and 3877 Å, as well as for the continuum at 5250.4 Å (first three columns), all normalized to the corresponding mean quiet-Sun intensity level, IQS. The LOS velocity (positive velocities correspond to downflows) and the circular polarization degree (see main text for definition) are shown in Cols. 4 and 5, respectively. The color bars at the top refer to the undegraded MHD data shown in the first row, while the lower color bars apply to the degraded MHD data (second row) and to the data obtained from the Sunrise Observatory (third row). |
2.3.4. Noise
The noise level of the IMaX Stokes V images was determined at the continuum wavelength (+192.5 mÅ offset from the core of the line), which is generally free of V signals. The signals found by Borrero et al. (2010) are sufficiently rare not to influence the noise determination significantly. The histograms of the nine PD reconstructed Stokes V continuum images we considered here showed a clear Gaussian shape with a standard deviation of 3.3 × 10-3IQS (IQS is the mean continuum intensity of the quiet Sun).
The retrieval of the Stokes I noise level was more difficult because here the standard deviation is not only determined by the noise, but also by the granulation pattern. For that reason, we determined standard deviations for small regions within granules, assuming the signal to be nearly constant for such small regions. We found similar values as for Stokes V, which confirmed our assumption of small intrinsic variations within the small patches considered. Consequently, we added a Gaussian noise with σ = 3.3 × 10-3IQS to all synthetic Stokes images.
2.3.5. Plate scale
The cell size of the simulation data was 10.42 km and had to be adapted to the pixel size of the IMaX observation of 40.10 km or to that of the SuFI observation of 15.24 km. Various tests showed that the adopted plate scale hardly influenced the parameters we considered and hence did not affect our results (mainly because it is significantly smaller than the width of the spatial PSF). For the sake of simplicity, we therefore skipped this degradation step in the following study.
2.3.6. Retrieval of line parameters
In the last step, we fitted a Gaussian to the twelve points of the Stokes I profile of the 5250.2 Å line for each pixel to determine the two values, LOS velocity and line width (as FWHM value). The Stokes V profiles were used for calculations of the circular polarization degree, defined as 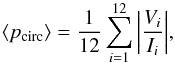 (1)where the averaging was done over the twelve scan positions of the 5250.2 Å line. Additionally, the area (δA) and amplitude (δa) asymmetry of each Stokes V profile was calculated according to Martínez Pillet et al. (1997),
(1)where the averaging was done over the twelve scan positions of the 5250.2 Å line. Additionally, the area (δA) and amplitude (δa) asymmetry of each Stokes V profile was calculated according to Martínez Pillet et al. (1997),  where ab and ar are the unsigned blue and red lobe amplitudes, and sgn(blue) is + 1 for positive blue lobes and −1 for negative ones. The Doppler shifts of the magnetic component are determined from the zero-crossing points of the Stokes V profile. For SuFI data, only the intensity in each filter was available.
where ab and ar are the unsigned blue and red lobe amplitudes, and sgn(blue) is + 1 for positive blue lobes and −1 for negative ones. The Doppler shifts of the magnetic component are determined from the zero-crossing points of the Stokes V profile. For SuFI data, only the intensity in each filter was available.
3. Results
Figure 2 contrasts the MHD data with the observational data. The top two rows of panels depict a snapshot of the original and the degraded MHD data. The bottom panels exhibit an 8.1″ × 8.1″ quiet-Sun region (a subregion of the 13″ × 37″ common FOV of SuFI and IMaX) as observed with Sunrise at 23:05:08 UT. Several bright granules, separated by darker intergranular lanes, can be seen. The undegraded MHD data show many small bright features within the dark lanes. Only the largest of these features can be identified as BPs in the degraded MHD data, the smaller ones are smeared out by the degradation. The BP contrasts exceed the granulation contrasts in the observed OH and CN image, but not for the observed 5250 Å image, in agreement with the results of Riethmüller et al. (2010). The degraded data look fairly similar to the observations, except that some of the observational BP flux concentrations, e.g., the one at position (1.5′′,2.0′′), carry more magnetic flux and are bigger than the largest BPs in the degraded simulations. In particular, the granulation contrasts in the degraded simulated granulation is very similar to that in the observational data at all three wavelengths. This gives us the confidence to proceed with a more detailed analysis with the help of histograms of various quantities, plotted in Figs. 3 to 8.
3.1. Simulations versus observations: all pixels
All pixels of all frames contributed to the histograms plotted in Figs. 3 to 8. In order to ease comparisons between the similarly shaped histograms, the integral over the histograms was always normalized to one.
3.1.1. Intensity at multiple wavelengths
Figure 3 exhibits histograms of the normalized intensities of the OH data at 3118 Å. The upper panel reveals the influence of the various degradation steps on the histogram of the 30 G MHD data. The histogram of the original MHD data is drawn in black. “Original” means that the computed Stokes I spectra are multiplied with the SuFI filter transmission profile, but no other degradation steps have been applied. The blue line represents spectrally and spatially degraded data, while the red line displays the fully degraded data, i.e., after spectral, spatial, stray light, and noise degradation. A comparison of the black and blue lines shows the influence of the spatial degradation. The noise hardly changes the histograms in Figs. 3 to 7 so that the difference between the blue and the red line is mainly due to stray light.
 |
Fig. 3 Intensity histograms over all pixels for the OH band data around 3118 Å. Top panel: the black line corresponds to the original 30 G MHD simulation, the blue line to the spatially degraded data, and the red line to the fully degraded simulation data. The green line displays the Sunrise observations. Bottom panel: influence of the MHD simulations’ mean flux density on the fully degraded OH intensity histogram. The black line shows a purely hydrodynamical simulation, i.e., without any magnetic field. The mean unsigned vertical flux density was 30 G for the histogram colored in red, 50 G for the blue line, and 200 G for the green line. rms contrasts are indicated in the text labels. |
The fully degraded MHD data are then compared with the SuFI observations colored in green. The degradation of the simulated data reduces the rms contrast in the OH band from 32.4% down to 21.1% which is 0.9% higher than the observational contrast of 20.2%. Although all histograms show a certain amount of asymmetry, the histogram of undegraded simulated data is the most extreme and indicates a superposition of two populations: the first one consists of intergranular pixels with low intensities, the second one contains bright pixels from the granules or from bright points. This superposition is still somewhat visible after degradation. The observed histogram does not reveal such a clear superposition of two populations.
The lower panel of Fig. 3 displays OH intensity histograms of fully degraded MHD data for different mean unsigned vertical flux densities. The IQS for the intensity normalization in the considered spectral band is determined from the 30 G data (closest to our observations). The rms contrast is highest in the field-free case, 22.7%, decreasing to 18% in the 200 G simulation (typical mean flux density of a moderate plage region). Without any magnetic field, there are no BPs and hence the fraction of the area covered by dark intergranular lanes is relatively large. With increasing magnetic flux the number density of BPs increases (see discussion of Fig. 13) which reduces the area fraction of the darker regions in the intergranular lanes and the rms contrast is reduced as well, but we think that this effect plays only a minor role. The decreased contrast reflects mainly the fact that the convection is inhibited by a magnetic field (Biermann 1941; Spruit et al. 1990; Vögler 2005; Kobel et al. 2012). We note that the black line in the bottom panel of Fig. 3 not only has more dark pixels than the others, but it also has more bright pixels, in particular when comparing with the 200 G simulation. The bright pixels in the field-free case correspond to the edges of granules, which are in some cases brighter even than the BPs. The presence of a magnetic field lowers the contrast of the surrounding granules. This effect can also be found in the undegraded simulations, where the field-free case leads to a contrast of 33.4%, decreasing to 30.8% in the 200 G simulation. The superposition of two populations is most pronounced in the field-free data, but it is not visible in the 200 G data. The shape and width of the observed histogram, as well as its rms contrast lies between the degraded histograms of synthetic data with Bz = 50 G and 200 G.
The intensity histograms of the CN-band (3877 Å) are displayed in Fig. 4. Compared with the OH histograms, the superposition of two populations is somewhat less pronounced for the simulations. The rms contrast of the simulated 30 G data is reduced from 30.8% to 20.5% after degradation, which is 1.7% higher than the 18.8% contrast of the SuFI data. The main difference between the observations and the degraded MHD data is the stronger asymmetry of the synthetic histogram. The rms contrast reduces from 22.8% to 17.6% if a 200 G magnetic field is present. The histogram also becomes more symmetric.
Intensity histograms of the IMaX continuum wavelength 5250.2 Å + 192.5 mÅ ≈ 5250.4 Å are plotted in Fig. 5. In Figs. 5 to 8, the term “original” MHD data (black lines in the top panels) implies that the Stokes I spectra are convolved with the IMaX spectral PSF, but are not otherwise degraded. The full degradation of the 30 G MHD data leads to a decrease in the rms contrast from 22.1% to 12.1%, which is exactly the observed contrast. A very good match between the degraded MHD data and the observations is not only found for the rms contrast (which is not a big surprise; see Sect. 2.3.2), but also for the shape of the histograms which enhances our trust in the applied degradation method. The superposition of two populations can be seen for the undegraded data, but it is not so clear for the degraded simulations. The fully degraded 200 G MHD data have a 2.7% lower contrast than the corresponding field-free data.
3.1.2. LOS velocity
Figure 6 exhibits histograms of the LOS velocity as determined from the Gaussian fit of the twelve scan positions of the Stokes I profiles of the 5250.2 Å line. Since an absolute wavelength calibration of the Sunrise/IMaX data has not been done, we decided to force the observed LOS velocities to have the same mean value as the degraded 30 G MHD data. The standard deviation of the 30 G simulation is reduced by the degradation from 1050 m s-1 to 580 m s-1, which is close to the standard deviation of the observations of 670 m s-1. The histograms are only weakly asymmetric. Small mean flux densities (0−50 G) led to almost identical velocity histograms. Increasing the average vertical field to 200 G significantly impedes the convection, reducing the standard deviation of the velocities to 460 m s-1.
 |
Fig. 6 Same as Fig. 3, but for the LOS velocity as retrieved from a Gaussian fit to the Stokes I profile of Fe i 5250.2 Å. Mean values and their standard deviations are indicated in the text labels. Negative velocities are upflows. |
3.1.3. Width of the Fe i 5250.2 Å line
Histograms of the 5250.2 Å line width are displayed in Fig. 7. The degradation of the 30 G simulation data (top panel) causes a shift of the position of the histogram’s maximum towards larger line widths, coupled with an increase in the width of the histogram, bringing it closer to the histogram of the observed values. The histograms of the degraded simulations and the observations display a reasonable match for the mean values, but a significant mismatch of their widths, i.e., the mean as well as the most common line widths of the simulated profiles are close to the observed values, but the scatter of the line widths is clearly larger for the observational data. The middle panel of Fig. 7 shows how the MHD line width histogram depends on the mean flux density. A larger magnetic flux increases the mean value of line widths as well as the standard deviation mainly owing to an increased number of larger line width values (partly due to enhanced Zeeman splitting). The number of small line width values is hardly influenced by the mean flux density and hence none of the additionally considered fluxes matches the observational histogram much better than the 30 G case.
In the bottom panel of Fig. 7 we demonstrate the influence of the broad wings and secondary peaks of the IMaX spectral PSF on the degraded 30 G MHD line width histogram. In particular the approximation of the spectral PSF of IMaX by a Gaussian function led to a significantly increased discrepancy between observation and simulation. The best match was reached by doing a full 20-line synthesis and using the measured spectral PSF for the degradation. We note that convolving with a 85 mÅ Gaussian or restricting the line synthesis to just Fe i 5250.2 Å left the histograms of all other quantities considered in this study practically unchanged.
 |
Fig. 7 Top and middle panels: same as Fig. 3, but for the spectral line width (FWHM) as retrieved from a Gaussian fit to the Stokes I profiles of Fe i 5250.2 Å. Bottom panel: influence of different approximations made during the spectral synthesis of the 30 G MHD data on the histogram of the spectral line width. The spectra were fully degraded in all three plotted cases. The black line corresponds to the histogram obtained when the filter transmission profile was approximated by an 85 mÅ Gaussian instead of the measured spectral PSF. The blue line corresponds to a spectral synthesis of only the 5250.2 Å line, i.e., the 19 neighboring lines were not synthesized. For comparison, the red line in the top panel is plotted again and corresponds to the 20-line synthesis and spectral degradation with the measured spectral PSF. |
3.1.4. Circular polarization degree
Histograms of the circular polarization degree ⟨ pcirc ⟩ as defined in Eq. (1) are given in Fig. 8. As in the case of the line widths, we found a strong asymmetry in all histograms. This time the match between the degraded 30 G simulation and the observation was remarkably good. The spatial degradation as well as the stray light contamination made the histogram narrower and left the maximum position nearly unchanged. The influence of the noise was dominant as can be seen by comparing the magenta line (spectral + spatial + stray light degradation) and the red line (spectral + spatial + stray light + noise degradation). The noise broadens the histogram and shifts the maximum position towards higher polarization values. We note that in contrast to ⟨ pcirc ⟩ the histograms of all other parameters considered so far were hardly affected by noise.
 |
Fig. 8 Histograms of the circular polarization degree ⟨ pcirc ⟩ as retrieved from the Stokes I and V profiles of Fe i 5250.2 Å (see Eq. (1) for definition). Top panel: the black line corresponds to the original 30 G MHD simulation, the blue line to the spatially degraded data, the magenta line represents the histogram after stray light contamination has been added. Finally, the red line corresponds to the fully degraded 30 G simulation. The green line displays the Sunrise/IMaX observations. Middle panel: influence of the MHD simulations’ mean flux density on the fully degraded polarization histogram. The black line shows a purely hydrodynamical simulation, i.e., without any magnetic field. The mean unsigned vertical flux density was 30 G for the histogram colored in red, 50 G for the blue line, and 200 G for the green line. The noise level was always 3.30 × 10-3IQS. Bottom panel: influence of the noise level. The flux density was always 30 G. The noise levels in units of the mean quiet-Sun intensity are printed as text labels. |
The middle panel of Fig. 8 displays the dependence of the fully degraded MHD histogram on the mean vertical flux density. The maximum position and the width of the histograms increase with mean flux density. The 0 G simulation has no intrinsic polarization, so that the black line is entirely due to noise that was introduced as part of the degradation. This pure noise histogram differs clearly from the observational histogram, so that from such variations in the mean MHD flux we estimated that the Sunrise data correspond to an average LOS field of around 25 G. (Even the 30 G simulations shown in the top panel of Fig. 8 exhibit a slightly too large mean flux density compared to our observation.) We note, however, that all simulations considered here started with an initially homogeneous, vertical and unipolar field. A comparison with simulations with a different initial condition (or a different Reynolds number) could result in a significantly different estimate of the magnetic field in the observed region (see, e.g., Danilovic et al. 2010; Pietarila Graham et al. 2010). The comparison of the histograms of simulated SuFI intensities for various mean vertical flux densities with the observations actually suggests higher fields of around 50 − 100 G, in better agreement with the above studies. Moreover, the way in which the circular polarization degree is normalized – e.g., division by Ii as in Eq. (1), division by I12 (local continuum), or division by ⟨ I12 ⟩ = IQS, i.e., the mean continuum, see Eq. (4) – can have a slight influence on the average field strength, estimated from a comparison with simulations. Additionally, a possible cross talk from Stokes Q or U into Stokes V, which cannot be corrected because of the lack of Stokes Q and U signals in the IMaX L12 data, could influence our estimate of the mean MHD flux.
The dependence of the degraded 30 G MHD polarization histogram on the level of noise, which was added to all Stokes images, is shown in the bottom panel of Fig. 8. The ⟨ pcirc ⟩ histograms for three noise levels between 3.00 × 10-3IQS and 3.60 × 10-3IQS (see text labels) are plotted in different colors. Again, the position of the maximum and the width of the histograms increase with noise level. Nevertheless, noise level and mean MHD flux density can both be assigned to the observations unambiguously since small variations in the mean flux density mainly change the amplitude and the width of the histogram, while a small variation in the noise level mainly shifts the maximum position. The best-fit noise level was determined to be σfit = 3.30 × 10-3IQS, which is somewhat lower than the standard deviation of the observed Stokes V continuum signals, σall = 3.77 × 10-3IQS, suggesting that the assumption of a signal-free Stokes V continuum is not entirely correct. Such a signal was found by Borrero et al. (2010), but was restricted to 0.005% of all their spatial pixels. Since we do not know how quickly the area covered by these signals increases with decreasing threshold, we use the σfit value as an approximation of the true noise level.
In summary, some parameters show better agreement with simulation snapshots with a higher amount of initial magnetic flux, others (including the circular polarization amplitude) display the best agreement with the 30 G simulations. Therefore, in the following we will concentrate on comparing the observations with this simulation.
3.2. Simulations versus observations: bright points
We now compare BP properties between Sunrise observations and the degraded 30 G simulations. From the flux-tube paradigm one would expect kilogauss fields for the BPs and hence strong polarization signals, but Riethmüller et al. (2010, see their Fig. 2, panel h) find that most of the BPs are only weakly polarized. We use the BP detection method applied by Riethmüller et al. (2010) for a direct comparison with their results.
First of all, we need an additional step in the pre-processing of the observational data because the IMaX and SuFI instruments differed significantly in their plate scales and there was also a slight difference in the plate scales of the various SuFI wavelengths. Therefore, we re-sampled all data to the common plate scale of 0.′′0207 pixel-1 (original plate scale of the SuFI 2995 Å images) via bilinear interpolation. With the help of cross correlation functions the two instruments’ common field of view (FOV) was identified. Finally, the larger IMaX FOV was cropped to the smaller 13″ × 37″ SuFI FOV (see Fig. 1 of Jafarzadeh et al. 2013).
We then manually identified the BPs’ peak intensity in the CN images because of their good visibility in that molecular band (Schüssler et al. 2003). The local intensity maximum in an 11 × 11 pixel patch (i.e., 0.′′22 × 0.′′22) surrounding each BP detected at 3877 Å was determined for each of the other wavelengths. This method takes into account that the various wavelengths are formed in different atmospheric layers so that inclined features may appear at slightly different horizontal positions at different wavelengths (see Jafarzadeh et al. 2013). In addition, the dark background (DB) close to the BPs was retrieved. It was defined as the darkest pixel whose distance to a BP’s local intensity maximum is less than 0.′′3. We extended the simple and manual BP detection method of Riethmüller et al. (2010) by the determination of the BP boundaries with the help of a multilevel tracking (MLT) algorithm (see Bovelet & Wiehr 2001). The MLT algorithm determined the intensity range of the CN images and subdivided this into 25 equidistant levels. Starting with the highest intensity level, all pixels were found whose intensity exceeds this level. This led to several contiguous two-dimensional structures, which were tagged with a unique number. The obtained structures were extended pixel by pixel as long as the intensity was greater than the next lower level. Then the algorithm searched through the whole image again to find all pixels whose intensity was greater than the next lower level, which often led to newly detected contiguous structures. This procedure was repeated until the minimum intensity level was reached. At the end of the iterations, every pixel belonged to exactly one contiguous structure. Finally, contiguous structures which did not contain one of the manually detected BPs were ignored and all pixels of the remaining structures that had an intensity lower than 50% of the local min–max range were rejected, which led to the boundary of the BPs. A more detailed description of MLT, including some illustrative figures, has been given by Riethmüller et al. (2008), who applied the algorithm to the detection of umbral dots. The BP boundary detection via MLT was applied to the SuFI intensity images, to the IMaX continuum intensity images, and also to the maps of the ⟨ pcirc ⟩ (see Sect. 2.3.6). We identified 121 BPs in the nine observational data sets. This number is limited by the relatively few L12 IMaX data sets available. The corresponding BP number density was 0.05 BP per Mm2, which is 1.7 times higher than the value found by Jafarzadeh et al. (2013) in the Ca ii H channel of Sunrise/SuFI. The difference likely stems from the restriction to small BPs by Jafarzadeh et al. (2013).
We applied the same manual detection method to the degraded CN images of the 30 simulation data sets with 30 G field strength. Here we found 277 BPs (0.26 BP per Mm2). We also detected BPs in the 30 undegraded CN images. Owing to the much higher spatial resolution of the undegraded data, we found many more BPs there, in total 898 (0.83 BP per Mm2), although many of them were relatively small. (Histograms for the BP diameter are discussed in Sect. 3.2.1; see also Fig. 9.) In case of the synthetic data, the boundaries of our manually detected BPs were obtained by applying the MLT algorithm to the CN, OH, and 5250.4 Å intensity images as well as to the maps of the circular polarization degree. Furthermore, since we also discuss BP properties which were a direct output of the MHD calculations, such as the magnetic field strength, we additionally applied the MLT algorithm to the field strength maps at constant optical depth log(τ) = 0 and log(τ) = −2. The determination of various boundaries for the same set of BPs takes into account, e.g., that the magnetic features change in size with height and do not always overlap 100% with their brightness enhancements.
3.2.1. Effective diameter and influence of the MHD cell size
Figure 9 compares histograms of the effective BP diameter between the Sunrise observations and various 30 G MHD simulations. The diameters were calculated from the BP boundaries as determined from the CN intensity images. The observed mean BP diameter of 334 km (red line) was fairly similar to the mean diameter of the degraded synthetic BPs, 330 km (black line). The influence of the degradation can be seen by comparing the black with the blue histogram, representing the undegraded MHD simulations. The degradation increased the mean BP diameter from 129 km to 330 km. If the BP boundaries were determined from intensity images at other wavelengths, we found very similar mean diameters for both the observation and the simulation: the observed mean BP diameter is (306 ± 114) km at 3118 Å and (324 ± 96) km at the 5250.4 Å continuum wavelength.
The cell size of the MHD grid may also influence some BP properties. We repeated the 30 G MHD simulation, the full spectral line syntheses, and the BP detections for a cell size of 20.8 km while all other parameters were unmodified. We found 475 BPs in the 30 snapshots of 6 × 6 Mm2 size (number density was 0.44 BP per Mm2) with a mean BP diameter of 163 km (see green line in Fig. 9). This dependence of BP diameter and number density on the grid size of the simulations is interesting in the sense that it indicates that an even smaller grid size could result in smaller BPs. This casts doubts on the claim of Crockett et al. (2010) that they resolved essentially all BPs by comparing observed and simulated BP area distributions, since the simulations they employed had a grid size of 25 km, so that true BP sizes are almost certainly smaller than was claimed.
 |
Fig. 9 Effective BP diameter for the observed BPs (red line), for the undegraded MHD BPs simulated with a cell size of 20.8 km (green line), for the undegraded MHD BPs simulated with a cell size of 10.4 km (blue line), and for the degraded MHD BPs simulated with a cell size of 10.4 km (black line). |
Besides the BP diameter and number density we could not find any significant influence of the MHD cell size on BP properties: We used the original MHD data to average BP properties over all BPs and found for a cell size of 20.8 km [10.4 km] a peak intensity at 3118 Å of (1.60 ± 0.39) IQS [(1.63 ± 0.45) IQS], a peak intensity at 3877 Å of (2.01 ± 0.52) IQS [(2.06 ± 0.61) IQS], a peak continuum intensity at 5250 Å of (1.27 ± 0.19) IQS [(1.29 ± 0.23) IQS], a LOS velocity of (1.28 ± 0.97) km s-1 [(1.25 ± 1.05) km s-1], a circular polarization degree of (6.83 ± 2.03) % [(6.66 ± 1.83) %], and a magnetic field strength at log(τ) = 0 of (1720 ± 380) G [(1760 ± 350) G]. The results in square brackets correspond to MHD simulations with 10.4 km cell size and most of them are discussed in more details in the following text.
We note that we refer to MHD cell sizes of 20.8 km only in Sect. 3.2.1 (with the green line of Fig. 9 as the only plotted result). The rest of the study stems from 10.4 km simulations.
 |
Fig. 10 Bright point (BP) peak intensity in the 3118 Å OH band (red lines), the intensity histograms of the BPs’ dark background (blue lines), and the histograms of all pixels (green lines). Mean values and standard deviations are given in the text labels. The top panel shows the histograms obtained from the observational data recorded by the SuFI instrument; the bottom panel displays the same for the degraded 30 G MHD simulations. The BP histogram of the undegraded MHD data is indicated in the bottom panel by the black line. |
3.2.2. Intensity at multiple wavelengths
Histograms of BP properties are displayed as red lines in Figs. 10 to 13. For comparison, the blue lines represent histograms of the same parameters in the dark background (DB, defined as the darkest pixel within 0.′′3 of each BP’s peak position). Likewise for comparison, we plot in green the corresponding histograms over all pixels in the images (these green histograms have already been plotted in Figs. 3, 5, 6, and 82). The histograms of Figs. 10 to 13 are normalized to their maximum which turned out to be more favorable for comparison between histograms of significantly different shapes than normalization by their integrals. Figures 10 to 13 compare the set of 121 BPs detected from the Sunrise observations (upper panels) with the set of 277 BPs detected from the degraded 30 G MHD simulations (bottom panels). Additionally, the bottom panels in Figs. 10 to 12 show the histogram of the 898 BPs that we detected in the undegraded MHD data (black lines) in order to illustrate the influence of the degradation.
Histograms of the BP peak intensity (intensity of the brightest pixel of a BP) in the OH band at 3118 Å are drawn in Fig. 10. The highest BP intensities coincide with the highest intensities found in these images. The observed BPs exhibit a peak intensity range of (0.86−1.97) IQS (with a mean value of 1.37 IQS), which is considerably higher than the range of (0.73−1.58) IQS with a mean value of 1.05 IQS obtained from the degraded simulations. Hence the observed BPs are brighter. The observed DB histogram is also broader than the simulated one.
Figure 11 shows histograms of the BPs’ peak intensity in the continuum at 5250.4 Å. Again, the range covered by the observational BP histogram, (0.82−1.24) IQS is larger than that covered by the simulational BP histogram, (0.80−1.18) IQS, although the discrepancy is not so marked. In addition, we found an almost perfect agreement between observation and simulation for the histograms of all pixels and a rather good match for the DB histograms. In contrast to the OH band, the highest intensities in the 5250.4 Å continuum images do not belong to BPs but to the brightest parts of granules.
3.2.3. LOS velocity
As mentioned above, the LOS velocity was retrieved from a Gaussian fit to the Stokes I profile of Fe i 5250.2 Å. Hence the BP boundaries determined from the Stokes I continuum images were used for the spatial averaging of velocities. The average over LOS velocities of all pixels belonging to a particular BP was assigned to that BP. The red lines of Fig. 12 exhibit histograms of such spatially averaged BP velocities. The standard deviations of the observational histograms agree with the degraded simulations, but the observed BPs and their DB display on average larger downflows. Clearly, the BPs’ LOS velocitiy lies on the downflow side of the distribution for the whole map. The velocities of the observed BPs range between −980 m s-1 and 1510 m s-1, with an average downflow of 600 m s-1. The downflow of the DB is on average 320 m s-1 stronger. The BPs in the simulations show LOS velocities ranging from −1180 m s-1 to 1620 m s-1 with a mean downflow of 270 m s-1. Here, the downflow of the mean DB is only 160 m s-1 stronger than for the BPs. The degraded simulations lead to a BP velocity distribution which is considerably narrower and shows a smaller mean velocity than in the case of the undegraded simulations (black line). Romano et al. (2012) also reported that a reduced spatial resolution causes a lower mean BP velocity, but a broader BP velocity distribution. Buehler et al. (in prep.) found that downflows are concentrated at the edges of strong-field magnetic features, but not in their cores. At insufficient spatial resolution, however, both may get mixed.
 |
Fig. 12 Same as Fig. 10, but for the LOS velocity as retrieved from a Gaussian fit to the Stokes I profile of Fe i 5250.2 Å. |
 |
Fig. 13 Same as Fig. 10 for the spatial peak value of the circular polarization degree. Additionally, the magenta line shows the histogram of the BP polarization for the degraded 200 G MHD simulations. |
3.2.4. Circular polarization degree
Histograms of the BPs’ circular polarization degree (peak polarization within the magnetic structure, i.e., within the BP boundary as determined from the polarization maps) can be seen in Fig. 13. A comparison of the upper panel of Fig. 13 (IMaX observations with 12 scan positions) with Fig. 2, panel (h) of Riethmüller et al. (2010) (IMaX observations with 5 scan positions) shows that most BPs are only weakly polarized, irrespective of spectral sampling. The strongest BP polarization degree observed in the V5-6 mode reached 9.1%, while it reached only 6.8% in the L12-2 mode. This difference is caused by the fact that we averaged over all twelve scan steps in the L12-2 mode and hence over more wavelengths close to the continuum (i.e., low polarization signals) than in the V5-6 mode. By interpolating L12-2 Stokes V to the wavelength positions of the V5-6 mode, we obtained similar polarization degrees as found in the V5-6 data by Riethmüller et al. (2010). Furthermore, the noise levels of the two data sets were comparable. We also calculated the histogram of the circular polarization degree of the set of V5-6 BPs analyzed by Riethmüller et al. (2010) (not shown) and compared it with their histogram of the total polarization degree, i.e., 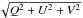 integrated over λ in the line, shown in Fig. 2, panel (h) of Riethmüller et al. (2010). From the similarity of the two histograms we concluded that the Stokes Q and U signals are negligible in BPs, so that the lack of Q and U signals in the L12-2 data should not affect our conclusions.
integrated over λ in the line, shown in Fig. 2, panel (h) of Riethmüller et al. (2010). From the similarity of the two histograms we concluded that the Stokes Q and U signals are negligible in BPs, so that the lack of Q and U signals in the L12-2 data should not affect our conclusions.
A comparison of the observed and degraded 30 G simulation BP ⟨ pcirc ⟩ histograms revealed a good agreement for most of the BPs, but a population of BPs showing strong ⟨ pcirc ⟩ is found only in the observations. We can rule out a possible over-reconstruction of the IMaX data as the cause of these large ⟨ pcirc ⟩ because the rms contrasts matched rather well. Since we also applied the BP boundary detection via MLT to the circular polarization maps, we were able to determine the effective diameter of the polarized features, defined as the diameter of a circle of area equal to that within the ⟨ pcirc ⟩ boundary of the BP. We found that 6 of the 121 observed BPs had ⟨ pcirc ⟩ > 4.8% (strongest BP polarization of the 30 G simulation) and their diameter was on average larger by a factor of 1.5 compared to the mean diameter of the other 115 BPs. Hence, the long tail towards stronger polarization degrees, which we found in the observational BP histogram, is caused by large and strongly polarized BPs which were not present in the 30 G simulations. For comparison, we also plotted the histogram of ⟨ pcirc ⟩ of the 285 BPs that we detected in the ten degraded snapshots of our 200 G simulations (magenta line in the bottom panel of Fig. 13). There the mean polarization degree was 3.32%, with the strongest value being 6.4%, i.e., comparable to the strongest observed signals. The number density was 0.79 BP per Mm2.
3.2.5. Stokes V asymmetry and zero-crossing velocity
In a next step, we azimuthally averaged the Stokes V asymmetries and zero-crossing velocities of all pixels at roughly the same distance to the BP center and plotted these mean values as a function of the distance to the center of the BP. Only Stokes V profiles having a two-lobe shape with a signal-to-noise ratio of at least 3 for each of the two lobes contributed to the averaging. We restricted the distance range to 800 km since the number of pixels fulfilling this condition decreases considerably farther out. Figure 14 displays the Stokes V asymmetries. On average, amplitude and area asymmetry exhibit low values in the core of the BPs and increase quickly up to a radial distance of about 160−180 km (see also Shelyag et al. 2007). For larger distances, the asymmetries of the original MHD data decrease slowly again, while they more or less saturate in the case of the degraded simulations and observations. Even if both kinds of Stokes V asymmetry show slightly larger values for the degraded simulation than for the observation, the qualitative behavior is quite similar. Interestingly, area and amplitude asymmetry show nearly identical values in the undegraded simulations, i.e., the fact that the observations and the degraded simulations lead to area asymmetries that are on average lower than the corresponding amplitude asymmetries is only caused by instrumental effects.
 |
Fig. 14 Stokes V amplitude (green lines) and area (red lines) asymmetries, intensity in the 3877 Å CN band (black lines), and circular polarization degree (blue lines) of the reconstructed IMaX observations (top panel), degraded (middle panel), and original (bottom panel) 30 G MHD simulations as a function of the distance to the BP center. The dashed black lines display the half width half maximum value of the mean intensity profile. |
For comparison, we also plotted the mean BP profile for the normalized intensity of the CN data at 3877 Å and for the circular polarization degree in Fig. 14. (All pixels, and not only those having a clear two-lobe Stokes V profile, contributed to the calculation of the mean BP intensity and ⟨ pcirc ⟩ profiles.) The highest intensities are found in the core of the BP, while the lowest values are associated with the interganular lanes. Farther out the intensity increases again, but only weakly for the observations. As already retrieved from the histograms in Figs. 10 and 11, the BP intensities of the observations are higher than for the degraded simulations. The FWHM values of the mean BP intensity profile, 220 km for the observations, 190 km for the degraded simulations, and 70 km for the original simulations, are a measure of the size of the mean BP brightness structure that is independent of any BP boundary detection. These values are smaller than the averages obtained from Fig. 9. A comparison suggests that the BP boundaries returned by the MLT method correspond roughly to the e-folding width of the intensity.
Additionally, we plotted the mean circular polarization degree and found a monotonic but more gentle decrease with radial distance. The FWHM values of the mean polarization structure, 430 km for the observations, 390 km for the degraded simulations, and 190 km for the original simulations, are roughly twice as big as the mean brightness structure (compare, e.g., the large flux patch at position (1.5′′,2.0′′) in the I3877 and ⟨ pcirc ⟩ maps of the bottom row of Fig. 2). That larger flux concentrations are more diffuse than their brightenings was already reported by Berger & Title (2001) for their spectropolarimetric observations with the 0.5 m SVST telescope on La Palma island and is confirmed by our study for the Sunrise observations as well as for the MHD simulations. Since the mean BP is much larger in polarization than in brightness even in the original MHD data, this is most likely an intrinsic effect and cannot be caused by a pure PSF effect similar to the one pointed out by Title & Berger (1996). We expected that the reason for this is related to the expansion of flux tubes with height. In locations of the magnetic canopy the Stokes V profile is formed higher up, where B ≠ 0, than the Stokes I profile which may get its main contribution from below the canopy. This is particularly true for the broadband 3877 Å SuFI channel. Other possibilities may be that only part of the strong-field magnetic features are bright.
The maximum brightness of a magnetic feature need not be co-spatial with its maximum magnetic field. This could be the case if the brightness is largest near the walls of a flux tube, but its B has its peak in the center of the flux tube. By how much the peak in the CN intensity is offset from the peak in the circular polarization degree can be seen in Fig. 15 for the observed and synthesized set of BPs. Mean values and their standard deviations are given in the text labels. The histograms show a peak at lower offsets and a moderate decrease towards higher offsets. For half of the undegraded synthetic BPs, the offset is smaller than 62 km, which is less than 50% of its effective MLT diameter of 129 km.
 |
Fig. 15 Offset between the BPs’ peak in CN intensity and the peak in the circular polarization degree, O, for the observed BPs (red line), the undegraded MHD BPs (blue line), and for the degraded MHD BPs (black line). |
Finally, the LOS velocity from the Stokes V zero-crossing and the Stokes I Doppler velocities are displayed in Fig. 16 as a function of the radial distance. Owing to the small MHD cell size of 10.4 km, most of the BPs are well resolved in the original MHD data, so that Stokes I and V lead to rather similar velocity values there. The downflows of about 1.4 km s-1 in the BP center decrease continually. Even for the largest shown radial distances, we found remarkable downflows of roughly 500 m s-1 which could possibly be affected by the fact that BPs are often located in regions where several intergranular lanes join up, so that azimuthal averages at these larger distances can be considerably influenced by intergranular lanes.
The spatial smearing as part of the degradation of the MHD data mixes magnetic and non-magnetic components within the resolution element, so that the Stokes I velocities are significantly decreased by the degradation. The Stokes V zero-crossing velocities do not undergo this degradation because they only represent the magnetic component. However, the drop in the MHD Stokes I velocities due to degradation is so strong that the relatively good match between observation and degraded simulation found for the Stokes V velocities cannot be found for the Stokes I velocities. To a minor degree this can be explained by the fact that the observations show more clustering of the magnetic field and the mixture of magnetic and non-magnetic components due to spatial smearing acts mainly at the border of larger flux patches, but is not so significant for their inner parts (see also Buehler et al. in prep.). An analysis in which the degradation of the MHD data was applied step by step revealed that the stray light contamination is the main contributor to the strong Stokes I velocity drop. This becomes understandable considering that the fit of the observed solar limb profiles (which led to the stray light MTF applied in this study; see Feller et al. in prep.) could not disentangle the stray light from the remaining pointing jitter of the gondola. Hence the determined stray light MTF must be seen as an upper limit since it also contains a jitter component. Unfortunately, the jitter varied widely over the Sunrise mission, so that our method of degradation, for all its shortcomings, is the best currently available approach for the Sunrise data.
 |
Fig. 16 LOS velocity as retrieved from a Gaussian fit to the Stokes I profile (green lines) and from the Stokes V zero crossing (red lines) of the reconstructed IMaX observations (top panel), degraded (middle panel), and original (bottom panel) 30 G MHD simulations as a function of the distance to the BP center. The dashed black lines are the same as in Fig. 14. |
 |
Fig. 17 Influence of the various degradation steps on the histogram of the BP circular polarization degree. The degradation was applied to the 30 G MHD simulations. The black line corresponds to the data that were only spectrally degraded. An additional spatial degradation results in the blue histogram. The green line also includes the effect of stray light contamination, while the fully degraded BP signals, i.e., including noise, give the histogram colored in red. |
3.3. Why are most bright points weakly polarized?
According to Fig. 13 most BPs, both synthetic and observed, are only weakly polarized at the resolution of Sunrise/IMaX. The same was noted by Riethmüller et al. (2010). This weak polarization could have a number of causes. Either most BPs are associated with intrinsically weak fields, contrary to standard flux-tube theory (Spruit 1976, see below), or they are very highly inclined, nearly horizontal, also contrary to expectations for strong fields (Schüssler 1986, a highly evacuated flux tube anchored at one end is driven to be nearly vertical by buoyancy). Alternatively, they could be spatially unresolved at the spatial resolution reached by Sunrise, or the weak Stokes V could be caused by thermal weakening of Fe i 5250.2 Å in BPs. Of course, some combination of these effects may also be acting. We searched for the cause by analyzing the simulation data.
Bright points are often modeled by nearly vertical slender flux tubes. In the flux-tube model, only magnetic field strengths in the kilogauss range can explain the brightnesses that are observed in BPs. The field increases the magnetic pressure which leads to an evacuation inside the tube and hence a depressed optical depth unity surface. The lateral inflow of heat through the walls of the flux tube makes it hot and bright.
To determine what polarization signals can be expected for kilogauss fields, we synthesized Stokes profiles for a standard atmosphere, the HSRASP (Chapman 1979), assigned a zero velocity and a height independent field strength of 1 kG. The synthetic profiles were then convolved with the spectral PSF of IMaX and the Stokes V values at the twelve scan positions of the IMaX L12-2 mode were used to calculate ⟨ pcirc ⟩ according to Eq. (1). A value of 10.71% was obtained. This value is significantly higher than the mean value of ⟨ pcirc ⟩ of 1.96% obtained from the fully degraded data.
To analyze the influence of the various degradation steps on the mean BP polarization, we used the set of 898 BPs that we detected in the undegraded CN images for the original3 MHD data and determined their peak ⟨ pcirc ⟩ values (see black line in Fig. 17) for the data that were spectrally and spatially degraded (blue line), for the additionally stray light contaminated images (green line), and the fully degraded data (red line in Fig. 17). The spatial degradation reduced the mean BP polarization from 6.66% down to 2.37%. The stray light led to a further reduction down to 1.45% and the noise increased the mean value to 1.74%. In contrast to the histograms of all pixels (top panel of Fig. 8), here the noise was not the main contributor, but rather the spatial degradation, because the BPs are small (see Fig. 14) and their ⟨ pcirc ⟩ values are much higher than the noise level.
 |
Fig. 18 Demonstration of a weak polarization signal owing to the strong temperature sensitivity of the Fe i line at 5250.2 Å by a comparison of a pixel in a particularly bright BP (red lines) with a pixel located in a much less bright BP (blue lines). a) Vertical temperature stratification as a function of log(τ) at 5000 Å. b) Magnetic field strength stratification. c) and d) Stokes I/IQS and V/IQS signals from the original MHD data at the twelve IMaX L12-2 scan positions in the line. |
We note that the red line in the bottom panel of Fig. 13 and the red line in Fig. 17 are not identical. Both histograms were retrieved from the same fully degraded ⟨ pcirc ⟩ maps, but the lower panel of Fig. 13 was calculated for the 277 BPs that were detected in the degraded CN images, while Fig. 17 displays ⟨ pcirc ⟩ of the 898 BPs detected from the undegraded CN images. These contained many small BPs and hence led to a smaller mean value of 1.74% compared to 1.96% for the 277 BPs detected in the degraded CN images.
Even at the original resolution of the simulations the average ⟨ pcirc ⟩ is only 6.66% and only 2.6% of all BPs reach the 10.71% retrieved from the 1 kG HSRASP atmosphere. This discrepancy can be explained by the high temperature sensitivity of the Fe i line at 5250.2 Å, as illustrated in Fig. 18, where two pixels taken from the simulation data are compared. The pixel colored in blue belongs to a faint BP with a low brightness in the CN band, but one that is still identified as a BP, while the pixel colored in red is part of a BP with a high contrast. Panel a of Fig. 18 shows the vertical temperature stratification, where the atmospheric height is given in logarithmic units of τ (continuum optical depth at 5000 Å). In the middle photosphere (where the spectral line is mainly formed), the red pixel’s temperature is about 800 K higher than the temperature of the blue pixel, but in the lower and upper photosphere both temperatures are almost the same. The vertical stratification of the magnetic field strength is displayed in panel b. In the middle photosphere, e.g., at log(τ) = −2, the blue pixel reveals a field strength of roughly 650 G, while the red pixel has a field strength of 1200 G. As expected for the flux-tube model of BPs, at log(τ) = 0 both pixels show a magnetic field stronger than 1 kG that is nearly vertically oriented (the height averaged field inclinations at the two pixels are 8.9° and 7.6°). The original Stokes I/IQS signals of the twelve scan positions of the 5250.2 Å line are shown in panel c. The continuum intensity near 5250 Å of the red pixel is higher than IQS, while it is lower in the blue pixel. The most striking feature of the figure is the minute line depth of the 5250.2 Å line in the red pixel. This is partly due to the large Zeeman splitting caused by the large field strength in this pixel, but even more to the strong temperature sensitivity. The temperature sensitivity originates not just in the increased ionization of iron as the temperature is raised, but also from the excitation potential of the lower level of this line of only 0.12 eV. The line weakening is also conspicuous in the Stokes V/IQS profiles of panel d. Although the red pixel has a higher magnetic field strength, its circular polarization degree of 1.8% is much smaller than that of the blue pixel, 6.8%. The ratio 1.8/6.8 is larger than the ratio of the line depths due to the contribution of the magnetic field which is stronger for the red pixel (obviously Zeeman saturation, Stenflo 1973, is not complete, so that a residual Zeeman sensitivity of the Stokes V amplitude is present).
 |
Fig. 19 Circular polarization degree versus magnetic field strength at log(τ) = −2 as retrieved for the 898 BPs from the original 30 G MHD data. Pixels with T ≥ 5100 K are colored in red, cooler pixels in blue. The solid lines are linear regressions. |
The temperature effect is statistically relevant for the BPs in general. To show this, in Fig. 19 we plot the circular polarization degree versus the magnetic field strength at log(τ) = −2 (peak values for both quantities) for all 898 BPs in the original 30 G MHD data. At log(τ) = −2 these BPs have a mean temperature of 5100 K, and all BPs hotter than the mean temperature are colored in red, the cooler ones in blue. The solid lines are the linear regressions of these two BP classes. We recognize that for a given field strength, the BPs having a higher temperature show a weaker ⟨ pcirc ⟩ than cooler BPs, although the scatter is large, and there is some overlap. In addition, the hotter features tend to have stronger fields.
Since the Stokes V normalization to Ii chosen by Riethmüller et al. (2010) could enhance the effect of the line weakening of ⟨ pcirc ⟩, we also considered other formulae to analyze the BP polarization or field strength, respectively: 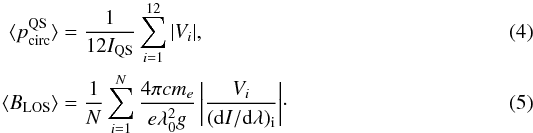 The scatterplot for
The scatterplot for 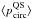 (not shown) exhibits the same qualitative behavior as that for ⟨ pcirc ⟩ (shown in Fig. 19), so that the temperature effect cannot be reduced by this widely used normalization for the circular polarization calculation.
(not shown) exhibits the same qualitative behavior as that for ⟨ pcirc ⟩ (shown in Fig. 19), so that the temperature effect cannot be reduced by this widely used normalization for the circular polarization calculation.
Equation (5) is based on the weak field approximation which holds if the Zeeman splitting is much smaller than the line width (e.g., Landi Degl’Innocenti & Landolfi 2004). The derivative of Stokes I was determined from the Gaussian fit of the Stokes I profile. The values c, me, and e have the usual meaning, λ0 = 5250.2 Å is the reference wavelength, and g = 3 is the Landé factor of the line. To avoid division by zero, the sum in Eq. (5) was only calculated over the N scan positions with |dI/ dλ| > 3σ, where σ is the ratio of the Stokes I noise level and the scanning step size. A scatterplot of ⟨ BLOS ⟩ versus the magnetic field strength at log(τ) = −2 (not shown) revealed that Eq. (5) very significantly reduces the effect of the line weakening. Histograms of the ⟨ BLOS ⟩ values obtained from applying Eq. (5) to observational and degraded synthetic data are plotted in Fig. 20. Similar to ⟨ pcirc ⟩ (Fig. 13), ⟨ BLOS ⟩ shows a long tail of stronger fields which is more pronounced for the observational data. Even under this approximation, only 9.9% of the observed BPs and 3.6% of the synthetic BPs yielded ⟨ BLOS ⟩ values higher than 1 kG.
 |
Fig. 20 Peak value of the BP field strength calculated via the weak field approximation (see main text). The green line shows the observed BPs and the red line displays the BPs from the degraded 30 G MHD data. |
3.4. Properties of simulated bright points
In Sects. 3.2 and 3.3 we showed that the MURaM MHD simulations reproduce the properties of the observed BPs reasonably well. Therefore we can obtain a better understanding of the physical phenomena underlying BPs by analyzing BP properties in undegraded simulations. In the following we used the 898 BPs detected in the undegraded CN images. It is this set of BPs that underlies Figs. 21 to 25.
3.4.1. Magnetic field strength and inclination
Figure 21 shows histograms of the BP peak magnetic field strength taken directly from the 30 G MHD simulations. The peak values were determined as the maximum field strength at a given optical depth within a BP. Owing to lateral force balance, the decreasing gas pressure with height, and the need for magnetic flux conservation, the flux tubes expand, so that the BP field strength drops from an average of 1750 G at log(τ) = 0 to 1070 G at log(τ) = −2. At optical depth unity, only 14 of the considered 898 BPs had a field strength lower than 1000 G, i.e., 98% of the BPs were in the kilogauss range, the strongest BP field was found to be 2825 G, the weakest one was 721 G. On average, the peak field strength in the DB is an order of magnitude lower than in the BPs.
 |
Fig. 21 Magnetic field strength of the BPs in the middle photosphere (green line), and of the BPs (red line) and the DB (blue line) in the lower photosphere as retrieved from the undegraded 30 G MHD data. Mean values and their standard deviations are given in the text labels. |
Figure 22 displays the field inclinations (angle between the field vector and the surface normal) of the 30 G MHD BPs at optical depth unity. The inclinations were averaged over all pixels covered by a BP at optical depth unity. The mean inclination4 at log(τ) = 0 of the BPs is 17°, i.e., the BPs are almost vertical as expected from buoyancy considerations (Schüssler 1986). Four of the 898 BPs showed inclinations greater than 90°, i.e., their magnetic field direction had been reversed from the initial condition of a homogeneous unipolar field. The field in the DB, in contrast, displays all possible inclination values, whereby almost vertical fields of either polarity are slightly preferred. The distribution of the field inclinations of all pixels is quite similar to the distribution of an isotropic field.
 |
Fig. 22 Magnetic field inclination at optical depth unity of BPs, DB, and of all pixels. The color coding is the same as in the top panel of Fig. 10. |
 |
Fig. 23 Temperature for the simulated BPs (red lines), for the BPs’ dark background (blue lines), and for all pixels in all frames (green lines). Mean values and their standard deviations are given in the text labels. The top panel shows the temperature at log(τ) = −2 and the bottom panel at optical depth unity (the T scales are different). |
 |
Fig. 24 Same as Fig. 23 for the LOS velocities (vertical component of the velocity vector taken directly from the MHD output). |
3.4.2. Temperature
In Fig. 23 we compare the BP temperatures between the middle photosphere and the lower photosphere. The temperatures were averaged over all pixels of a BP as determined by the MLT algorithm (applied to the CN maps). The mean BP temperature in the middle photosphere was 440 K higher and the mean DB temperature was 30 K lower than the mean quiet-Sun temperature. In the lower photosphere, the mean BP temperature was 190 K higher than the mean quiet-Sun temperature, while the dark background was 420 K colder than the quiet Sun. The temperature gradient in the BP and in the DB were thus significantly lower than average.
3.4.3. LOS velocity
Histograms of the LOS velocity obtained directly from the MHD calculations are depicted in Fig. 24. Again, the LOS velocities were averaged over all pixels of a BP as determined by MLT applied to 5250.4 Å continuum intensity images (for the same reason as in Sect. 3.2.3). At an optical depth of log(τ) = −2 (top panel) the gas in the BP flows down at roughly 1 km s-1, which is 0.9 km s-1 faster than in the surroundings. At log(τ) = 0 (bottom panel), the BPs showed a strong downflow of 3.2 km s-1. This time the DB downflow was, on average, slightly stronger with 3.4 km s-1. The histogram of all pixels (green line) clearly shows a superposition of two populations. The pixels from the interior of the granules formed the first population with an upflow of around −2 km s-1 as the most numerous velocity. The second population corresponds to intergranular lanes with a 3 km s-1 downflow as the most common velocity.
3.4.4. Correlations between BP properties
Finally, we were interested in correlations between BP properties found by looking at scatterplots and correlation coefficients. The spatial peak values of the field strength at optical depth unity, the CN intensity, as well as the 5250.4 Å continuum intensity were found to be only weakly correlated with the BP diameter (correlation coefficients are 0.17, 0.19, and 0.16). The scatterplots (not shown) exhibited a slight increase in the three quantities for large BP diameters. A decrease in the intensities for very large diameters, expected for micropores and pores, could not be found in our study owing to the BP detection method, which looked for bright features and not for highly magnetized ones. This may also have to do with the rather limited range of BP diameters found in this very quiet region, with less than 4% being broader than 200 km (see the blue line in Fig. 9).
A clear relationship was found between the peak CN intensity and the peak magnetic field strength at optical depth unity with a correlation coefficient of 0.76 (see Fig. 25). The monotonicity over the whole range of field strengths is highlighted by binning points adjacent in B (red crosses in Fig. 25). Again, a decrease in the intensity of very strong fields could not be found owing to the BP detection method which excluded micropores.
 |
Fig. 25 Scatterplot of the BP peak CN intensity versus the magnetic field strength at optical depth unity (black dots). The red line connects binned values and the blue line is the linear regression. Error bars represent standard deviations. |
Of some interest is the relation between the magnetic field inclination at optical depth unity and the peak CN intensity (not shown), which gave a moderate correlation coefficient of −0.32, implying that the more intense BPs are associated not just with a stronger field, but also with one that is on average more vertical. In this case all inclinations were transformed to the interval [0,90 deg] to be independent of the field polarity and they were spatially averaged over the BP to get an estimate of the flux tube’s orientation as a whole. From the darkest BPs (0.68 IQS) to the brightest BPs (4.3 IQS) the binning graph shows a nearly linear decrease in inclination from 23 deg to 5 deg.
4. Discussion
The aim of this study is to learn more about magnetic BPs in the quiet solar atmosphere. To achieve this we combined high-resolution observations with realistic radiation MHD simulations. First we compared a row of parameters deduced from the observations (intensity, LOS velocity, line width, circular polarization degree) with their counterparts obtained from the simulations under conditions matching those of the observations as closely as possible (noise, spatial and spectral resolution, sampling, straylight, etc.). After establishing that the simulations give a reasonable description of the data, both in general and for the BPs in particular, we employed the simulations to deduce more about the BPs than can be gleaned from the observational data alone.
We observed quiet-Sun regions at disk center with the balloon-borne observatory Sunrise. Photometric data at 3118 Å and 3877 Å, as well as spectropolarimetric data at twelve wavelengths in and around the Fe i line at 5250.2 Å were acquired quasi simultaneously. Compared to high-resolution observations with other telescopes, we benefited from the following advantages of Sunrise: a) the Sun was observed not only in the visible but also in the near UV; b) the PSF was measured during the observations, so that the influence of the central obscuration by the secondary mirror, the spiders, and the low-order aberrations like defocus, coma, and astigmatism were known and we did not have to rely on a theoretical PSF; c) a stray light analysis was possible owing to observations of the solar limb; d) the data were practically free of seeing effects. Therefore, it was possible to carefully determine the degradations that were acting during the observations and to apply them to the MHD simulations. In contrast to other studies, which worked with opacity distribution functions (ODFs, e.g., Danilovic et al. 2008; Afram et al. 2011), we applied full spectral line syntheses, for the first time also to the OH band at 3118 Å, in order to compute observables to be compared with the Sunrise data. Our study concentrated on a comparison of the following BP properties at disk center: diameters, intensity in the visible and near UV, LOS velocity, polarization degree, and Stokes V asymmetry; other studies typically only focussed on center to limb variations of intensity histograms (Wedemeyer-Böhm & Rouppe van der Voort 2009; Afram et al. 2011).
A reasonable match between the observations and the degraded simulations was found for the intensity histograms of all pixels for all three considered wavelength ranges, as well as for the LOS velocities and the circular polarizations for an initial field strength of 30 G averaged over the simulated box, although some parameters indicated a better match with simulations containing more magnetic flux. We note that the multitude of considered observables strongly constrains the problem. The tuning of any degradation parameter to reach a better match with a particular observational quantity would significantly increase the mismatch with other observables. The intensity histograms of the undegraded 30 G simulations showed a superposition of two populations which was greatly weakened by the degradation and which was not found in the observations. The two populations were also clearly present in comparable simulations with the Stagger and CO5BOLD code (Wedemeyer-Böhm & Rouppe van der Voort 2009; Beeck et al. 2012). Afram et al. (2010) also used the MURaM code and found the same superposition for their undegraded 0 G and 50 G simulations, but not for their 200 G data. We can confirm this result by our intensity histograms of the degraded MHD data for varying mean flux densities.
The degradation of our MHD data reduced the rms contrast at 3118 Å from 32.4% to 21.1%, at 3877 Å from 30.8% to 20.5% and at 5250.4 Å from 22.1% to 12.1%. With the help of ODFs, Hirzberger et al. (2010) calculated an rms contrast of 28.3% at 3118 Å and of 23.9% at 3877 Å. In both cases, complete spectral line syntheses led to significantly higher contrasts than with the ODF method, although the smaller grid size of our simulation may also have contributed. For the CN band at 3877 Å, Hirzberger et al. (2010) also applied a full spectral line synthesis, but they used an older version of SPINOR with a limited number of wavelength points. They converted from geometrical heights into optical depths with a different opacity package and they also used a different horizontal grid resolution of 20.8 km. They report an rms contrast of 25.3% for the undegraded CN data while we found a value of 30.8% with the improved SPINOR code.
The deviation of the rms contrasts between degraded simulations and observations was 0.9% at 3118 Å, it was negligible at 5250.4 Å, at 3877 Å it was somewhat higher, but at 1.7% the agreement was still remarkably good given the various sources of uncertainty, e.g., slightly varying image quality owing to the remaining pointing jitter of the gondola, inaccuracies of the spectral line synthesis (incomplete spectral line lists, inaccurate atomic or molecular data, differences in the solar abundances found by, e.g., Asplund 2005, and neglected non-LTE effects), and approximations involved in the radiative transfer calculations of the MHD simulation (only four opacity bins, LTE/no scattering, limited angular resolution). Given that the computed CN lines are clearly too strong even for the average quiet Sun (see Fig. 1), we expect the inaccuracies of the spectral line synthesis to play a significant role in producing the discrepancies in the UV. A comparison between several MHD codes by Beeck et al. (2012) led to a variation of up to 1% even in the bolometric intensity contrast. Hirzberger et al. (2010) found rms contrasts of 18.3% and 20.1% for two different Sunrise observations at 3877 Å, while our observation showed 18.8%. Depending on the ratio of the inverse jitter frequency to the exposure time, different image qualities are possible for observations at different wavelengths. The exposure time of the 3877 Å images was by far the shortest one compared to the other wavelengths and thus this wavelength range was expected to have sharpest images.
A comparison of our observed rms intensity contrasts with ground-based observations cannot be done easily owing to the large influence of seeing effects and atmospheric stray light on the image quality. Hence, we compare with data of the space-borne Solar Optical Telescope on board the Hinode satellite. Mathew et al. (2009) determined the PSF of the Broadband Filter Imager with the help of Mercury transit images at different wavelengths and deconvolved quiet-Sun images. For the violet CN band they reported an rms contrast of 21.8% and of 15.8% for the green continuum at 5550 Å (which is a wavelength relatively close to our 5250.4 Å Fe i continuum). These values are somewhat higher than ours, 18.8% and 12.1%, probably because their PSF also removed the stray light while it was still present in our data.
We found that the various degradation steps considerably influenced the shape of the histograms of the parameters. In particular, the stray light influenced histograms of all quantities and often it provided the most important contribution to the degradation. This was also found by Wedemeyer-Böhm & Rouppe van der Voort (2009). Additionally, for the line width histogram a good knowledge of the spectral PSF of the instrument is needed. The circular polarization histograms depended strongly on the noise level of the Stokes V images, while the noise level of the Stokes I images as well as the other degradation steps played only a minor role (due to the high signal-to-noise ratio in Stokes I).
Stray light may also contribute to the last remaining discrepancy between the data and the simulations, the larger scatter of the observed 5250.2 Å line widths than in the simulations. We used the continuum images of the IMaX limb observations, but the IMaX stray light may depend on the wavelength within the spectral line. Because of the sensitivity of the histogram shapes to stray light, we believe that such a wavelength dependence could be a good candidate to explain the larger scatter in the observed line widths. Another possibility is the influence of the evolution of the granulation during the relatively long acquisition time of IMaX of almost 32 s, which may also change the line width histogram. Another possibility, insufficient turbulence in the MHD simulations, would only explain the missing tail of high line widths but not the missing low widths.
The good match between observation and simulation (only a moderate deviation remained for the scatter of line widths) enhanced our trust in the simulations, so that we used them to probe BP properties. We found a BP number density of 0.05 BP per Mm2 in our observations which is at the lower end of the wide spread of values found in the literature: Muller & Roudier (1984) reported 0.04 BP per Mm2, 0.12 BP per Mm2 were found by Bovelet & Wiehr (2008), 0.3 BP per Mm2 by Sánchez Almeida et al. (2004), and even 0.85 BP per Mm2 by Sánchez Almeida et al. (2010). All these were quiet-Sun studies. Active-region data analyzed by Berger et al. (1995) gave 0.37 BP per Mm2. Our BP number density is larger than the 0.03 BP per Mm2 obtained by Jafarzadeh et al. (2013) from Ca ii H observations made by Sunrise, but this is likely because they restricted their study to features narrower than 0.′′3.
The effective BP diameter was, on average, 334 km in our observations using MLT and 220 km from the FWHM of the average BP intensity profile, despite the fact that the MLT boundaries of the BPs are defined by a threshold of 50% of the local min-max intensity range. We note that for an idealized brightness structure of a rotationally symmetric Gaussian shape MLT provides a diameter that is equal to the FWHM value of the mean intensity profile, but already a Gaussian with an elliptical cross-section leads to different results. This demonstrates the sensitivity of the diameter determination on the technique. Most other studies reported BP diameters consistent with our value obtained from the average BP profile; for example, Berger et al. (1995) found a mean FWHM intensity diameter of 250 km by taking the smallest dimension across the BP features (whereas we obtained an effective diameter). Sánchez Almeida et al. (2004) fitted the minor and major axes of the BPs with average values of 135 km and 230 km, respectively. Utz et al. (2009) reported a decrease in the mean BP diameter from 218 km to 166 km by doubling the spatial sampling of data from the Hinode Telescope. Crockett et al. (2010) found a distribution that peaked at an effective BP diameter of 240 km. Combining our observed BP number density with the mean BP diameter results in a 0.5% fraction of the solar surface that is covered by quiet-Sun BPs. This value is only half of the 1% found by Bonet et al. (2012) using reconstructed disk center data from the ground-based 1 m Swedish Solar Telescope.
The observed BP sizes found in the literature are generally larger than the 129 km obtained by MLT directly from the undegraded simulations. We note that this value was reduced by 20% when going from a grid size of 20 km to 10 km, suggesting that the claim of Crockett et al. (2010) that they had resolved all BPs, based on a comparison of observations with MURaM MHD simulations with a grid size of 25 km, was premature. The fact that nearly half of our undegraded synthetic BPs have a diameter smaller than 130 km (see the blue line in Fig. 9) casts doubts on the claim of Wiehr et al. (2004) that there is a true deficit of such small BPs in the observations which does not stem from instrumental artifacts.
A direct comparison of the BP number density and BP diameter from studies made at different telescopes is not straightforward because both quantities depend strongly on the image degradation (i.e., we cannot say much about the underlying true size distribution), on the mean vertical flux density of the observed region, on the method employed to identify the BPs, and possibly on the phase of the solar cycle. For our simulated BPs we found that degrading the data to the Sunrise resolution decreased the BP number density by a factor of 3.2, while the BP diameter was increased by a factor of 2.6. An increase of the mean vertical flux density from 30 G to 200 G led to a 3.1 times higher BP number density. We note that our manual detection method tends to consider larger bright patches (associated with larger concentrations of magnetic flux) as single features whereas other techniques may identify them as chains or clusters of multiple BPs, which might also be a reason that we found a lower BP number density and a higher BP diameter, at least when applying MLT to the individual BPs. Another reason for the relatively low number of BPs could be that Sunrise observed a very quiet region in the deepest part of the last activity minimum. Foukal et al. (1991) and Meunier (2003) found evidence that the number of quiet-Sun BPs is correlated with the solar cycle. However, Muller & Roudier (1984) obtained an anticorrelation from their observations.
Asymmetries of the Stokes V profiles provide insights into the structuring of magnetic fields along the LOS (Solanki & Pahlke 1988; Grossmann-Doerth et al. 1988; Sánchez Almeida et al. 1989; Steiner 2000; López Ariste 2002; Shelyag et al. 2007; Martínez González et al. 2012). The rapidly increasing asymmetries with distance from the mean BP core are indicators of the flux-tube canopy. Flux tubes expand with height owing to pressure balance and magnetic flux conservation. Martínez González et al. (2012) also analyzed IMaX L12 data of a single network element and found evidence for a canopy. By studying a statistical ensemble of BPs, mostly consisting of internetwork elements, we were able to show that the spatial distribution of the asymmetry is consistent with the presence of a canopy, thus further supporting the model of Grossmann-Doerth et al. (1988) and Solanki (1989).
For a deeper understanding of the BP phenomenon, we analyzed properties of the simulated BPs in greater detail. An important finding is that basically all magnetic BPs identified on the basis of their brightness properties in the simulations are associated with kilogauss fields, with the average B at log(τ) = 0 being 1760 G, which drops to 1070 G at log(τ) = −2. This is in contrast to the observations, which gave 540 G (from the weak field approximation). This is comparable with the values obtained from the simulations after all the effects of the instrument have been taken into account. This difference, as well as that between the BP sizes before and after applying instrumental effects, indicates that many BPs are not fully resolved in our data set. We note that because of the higher resolution of Sunrise data taken at other times, more features are expected to be resolved there (e.g., Lagg et al. 2010). We also note that instrument degradations imply that we are missing nearly two thirds of all BPs in the quiet Sun in our data. The fact that the BP contrast increases quickly with B, but does not depend strongly on diameter, suggests that for these slender features the field strength is the main driver of flux-tube brightness.
The histogram of the inclination of the magnetic field vector exhibited a nearly vertical magnetic field for most of the BPs, which is to be expected for kilogauss fields and not too strong horizontal flows (Schüssler 1986). This result is in good agreement with the observational findings of Jafarzadeh et al. (2014a), obtained by comparing the positions of BPs recorded at different heights by Sunrise. Hence this is another point in which Sunrise data and MHD simulations agree.
A significant difference between the middle and lower photosphere was found for the vertical velocities of the simulated BPs. While the BPs showed on average a downflow of 3.2 km s-1 in the lower photosphere, the downflow was reduced to 1.06 km s-1 in the middle photosphere. A decrease of velocity with height was also found by Bellot Rubio et al. (1997) from the inversion of asymmetric Stokes V profiles observed in plage regions. The deeper we look into the atmosphere the stronger are the downflows of the BPs, so that it would be interesting to observe BPs spectropolarimetrically in a spectral line that is formed deep in the photosphere, e.g., the C i line at 5380 Å, which we expect to show BP downflows that are stronger than the ones found with Sunrise. These strong flows in the deep layers of photospheric magnetic elements raise the question of the origin of the mass. Either it diffuses into the magnetic features across field lines, which runs counter to the estimates of Hasan & Schüssler (1985), or the lifetimes of BPs, i.e., kilogauss features are rather short, or the plasma with the strong field is continually mixing with relatively field-free plasma in the immediate surroundings of the magnetic elements. This last process may be related to the vortices found in the simulations around magnetic elements by, e.g., Moll et al. (2011), and observationally by Bonet et al. (2010) and Wedemeyer-Böhm et al. (2012).
5. Conclusions
We have compared high-resolution Sunrise data in three spectral bands with three-dimensional radiative MHD simulations and found that the two agree remarkably well in most areas, as long as all instrumental effects that degrade the data are properly introduced into the simulations as well. This represents a stringent test of the simulations, since we consider many more parameters than just intensities. In addition, we consider both the entire FOV as well as BPs separately.
We showed that although most of the BPs are weakly polarized in the observational data (see also Riethmüller et al. 2010) they correspond to magnetic elements with kilogauss fields. The small signals can be partly explained by a combination of thermal weakening of the temperature sensitive Fe i 5250.2 Å line, spatial smearing due to residual pointing jitter, and instrumental stray light. In the original simulations 98% of the BPs are almost vertically oriented magnetic fields in the kilogauss range, which, together with our findings about the asymmetries in the circular polarization signals, confirms the physical model of magnetic flux concentrations as evacuated and laterally heated structures that expand with height (Spruit 1976; Deinzer et al. 1984). The field strength in the magnetic elements is found to be the quantity with the largest effect on its brightness.
Magnetohydrodynamical simulations with a horizontal cell size of 20 km or larger are widely used in the literature (Afram et al. 2010, 2011; Hirzberger et al. 2010; Orozco Suárez 2008; Röhrbein et al. 2011; Tritschler & Uitenbroek 2006; Wedemeyer-Böhm & Rouppe van der Voort 2009). We found a reduction of the effective BP diameter of 20% and a near doubling of the BP number density by doubling the horizontal grid resolution. We cannot rule out that MHD simulations with a horizontal cell size lower than the 10 km used here will give yet other BP properties.
The observations, in particular when taken together with the simulations, also indicate that phenomena are present in the BPs that are not yet understood. One of these is the average downflow velocity of 0.6 km s-1 in the observed Stokes I profiles and 0.27 km s-1 in the degraded synthesized line profiles. An even higher mean downflow velocity of 1.25 km s-1 is obtained from the original synthesized line profiles, i.e., if we do not consider instrumental degradation effects. Such high universal downflows would lead to an evacuation of the gas by an order of magnitude within the time it takes the gas to flow down two scale heights, i.e., roughly 200 km. At 1.25 km s-1 this will take place within 160 s. Comparing with the mean lifetime of Ca ii H BPs of 673 s in similar Sunrise data sets (Jafarzadeh et al. 2013), this implies that the magnetic elements would be almost completely evacuated within a fraction of their lifetimes unless the gas is continuously replenished. An even stronger need for replenishment is present in the simulations, which show downflows of 3.2 km s-1 at log(τ) = 0 in BPs5. Such flows would evacuate the magnetic element within 63 s.
The plasma can be replenished by gas flowing up along the opposite footpoints of loops that end in the BPs. As shown by Wiegelmann et al. (2010) at the Sunrise resolution in the quiet Sun, strong-field regions, such as BPs, are mainly connected to weak-field regions. Furthermore, most of these loops are rather low-lying, i.e., not reaching above the chromosphere. Along such loops a siphon flow from the footpoint with weaker field to that with the stronger field can take place (Meyer & Schmidt 1968; Montesinos & Thomas 1989). Such a flow would produce a downflow in the BPs, as has been observed along the neutral line of an active region (Rüedi et al. 1992; Degenhardt et al. 1993). However, the simulations also show these downflows and they have a closed upper boundary through which the magnetic field of the BPs passes, but no flow is allowed to go through. Hence the flow must be replenished locally. We note that the observed average downflows of 0.6 km s-1 are larger than the ones obtained from the degraded synthesized line profiles, 0.27 km s-1, and we also note that the observed intensities are higher (see Figs. 10 and 11). The difference may be due to missing siphon flows in the simulations, or just to the lower Reynolds number of the simulations compared with the real Sun. The lower the Reynolds number, the more intense the artificial viscous braking, which leads to lower velocities.
The Sunrise images contain a few large and highly polarized BPs which were possibly part of network elements. Such network elements were not present in our simulations, presumably because the used simulation box is too shallow, which leads to a lack of larger scale flows accumulating magnetic flux. Usually, network elements are observed at the boundaries of supergranules and are possibly formed deeper in the convective zone (Schüssler 2013). In a future study we will analyze MHD simulations with a computational box large and deep enough to contain one or more supergranules.
There are slight differences between the histograms over all pixels plotted in Figs. 3, 5, 6, and 8 on the one hand, and those in Figs. 10−13 on the other hand, because the former are obtained from data of the original plate scale and FOV, while the latter are produced from the re-sampled data of the common FOV of IMaX and SuFI.
Acknowledgments
We thank Robert Cameron for the efficient MURaM lessons. The German contribution to Sunrise is funded by the Bundesministerium für Wirtschaft und Technologie through Deutsches Zentrum für Luft- und Raumfahrt e.V. (DLR), grant No. 50 OU 0401, and by the Innovationsfond of the President of the Max Planck Society (MPG). The Spanish contribution has been funded by the Spanish MICINN under projects ESP2006-13030-C06 and AYA2009-14105-C06 (including European FEDER funds). The HAO contribution was partly funded through NASA grant number NNX08AH38G. This work was partially supported by the BK21 plus program through the National Research Foundation (NRF) funded by the Ministry of Education of Korea.
References
- Abrams, M. C., Davis, S. P., Rao, M. L. P., Engleman, R., & Brault, J. W. 1994, ApJS, 93, 351 [NASA ADS] [CrossRef] [Google Scholar]
- Afram, N., Unruh, Y. C., Solanki, S. K., Schüssler, M., & Mathew, S. K. 2010, Proc. IAU Symp., 264, 63 [NASA ADS] [Google Scholar]
- Afram, N., Unruh, Y. C., Solanki, S. K., et al. 2011, A&A, 526, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Asplund, M. 2005, ARA&A, 43, 481 [NASA ADS] [CrossRef] [Google Scholar]
- Barthol, P., Gandorfer, A., Solanki, S. K., et al. 2011, Sol. Phys., 268, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Beeck, B., Collet, R., Steffen, M., et al. 2012, A&A, 539, A121 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellot Rubio, L. R., & Borrero, J. M. 2002, A&A, 391, 331 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bellot Rubio, L. R., Ruiz Cobo, B., & Collados, M. 1997, ApJ, 478, L45 [NASA ADS] [CrossRef] [Google Scholar]
- Bembenek, Z., KȩPa, R., Para, A., et al. 1990, J. Mol. Spectr., 139, 1 [Google Scholar]
- Berdyugina, S. V., & Solanki, S. K. 2002, A&A, 385, 701 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V., Solanki, S. K., & Frutiger, C. 2003, A&A, 412, 513 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berdyugina, S. V., Braun, P. A., Fluri, D. M., & Solanki, S. K. 2005, A&A, 444, 947 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Berger, T. E., & Title, A. M. 2001, ApJ, 553, 449 [NASA ADS] [CrossRef] [Google Scholar]
- Berger, T. E., Schrijver, C. J., Shine, R. A., et al. 1995, ApJ, 454, 531 [NASA ADS] [CrossRef] [Google Scholar]
- Berkefeld, T., Schmidt, W., Soltau, D., et al. 2011, Sol. Phys., 268, 103 [NASA ADS] [CrossRef] [Google Scholar]
- Biermann, L. 1941, Vierteljahrsschr. Astron. Ges., 76, 194 [Google Scholar]
- Bonet, J. A., Márquez, I., Sánchez Almeida, J., et al. 2010, ApJ, 723, L139 [NASA ADS] [CrossRef] [Google Scholar]
- Bonet, J. A., Cabello, I., & Sánchez Almeida, J. 2012, A&A, 539, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Borrero, J. M., Martínez Pillet, V., Schlichenmaier, R., et al. 2010, ApJ, 723, L144 [NASA ADS] [CrossRef] [Google Scholar]
- Bovelet, B., & Wiehr, E. 2001, Sol. Phys., 201, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Bovelet, B., & Wiehr, E. 2008, A&A, 488, 1101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chapman, G. A. 1970, Sol. Phys., 13, 78 [NASA ADS] [CrossRef] [Google Scholar]
- Chapman, G. A. 1979, ApJ, 232, 923 [NASA ADS] [CrossRef] [Google Scholar]
- Choudhuri, A. R., Auffret, H., & Priest, E. R. 1993, Sol. Phys., 143, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Coxon, J. A. 1980, Can. J. Phys., 58, 933 [Google Scholar]
- Crockett, P. J., Mathioudakis, M., Jess, D. B., et al. 2010, ApJ, 722, L188 [NASA ADS] [CrossRef] [Google Scholar]
- Danilovic, S., Gandorfer, A., Lagg, A., et al. 2008, A&A, 484, L17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Danilovic, S., Schüssler, M., & Solanki, S. K. 2010, A&A, 513, A1 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Davis, S. P., Wallace, L., Brault, J., & Engleman, R. 2005, National Solar Observatory Technical Report No. 05-002 [Google Scholar]
- De Pontieu, B., McIntosh, S. W., Carlsson, M., et al. 2007, Science, 318, 1574 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Degenhardt, D., Solanki, S. K., Montesinos, B., & Thomas, J. H. 1993, A&A, 279, L29 [NASA ADS] [Google Scholar]
- Deinzer, W., Hensler, G., Schüssler, M., & Weisshaar, E. 1984, A&A, 139, 435 [NASA ADS] [Google Scholar]
- Dunn, R. B., Evans, J. W., Jefferies, J. T., et al. 1968, ApJS, 15, 275 [NASA ADS] [CrossRef] [Google Scholar]
- Ermolli, I., Matthes, K., Dudok de Wit, T., et al. 2012, Atmos. Chem. Phys. Discussions, 12, 24557 [Google Scholar]
- Foukal, P., Harvey, K., & Hill, F. 1991, ApJ, 383, L89 [NASA ADS] [CrossRef] [Google Scholar]
- Fröhlich, C. 2013, Space Sci. Rev., 176, 237 [NASA ADS] [CrossRef] [Google Scholar]
- Frutiger, C. 2000, Ph.D. Thesis, Institute of Astronomy, ETH Zürich, Switzerland, No. 13896 [Google Scholar]
- Frutiger, C., Solanki, S. K., Fligge, M., & Bruls, J. H. M. J. 2000, A&A, 358, 1109 [NASA ADS] [Google Scholar]
- Gandorfer, A., Grauf, B., Barthol, P., et al. 2011, Sol. Phys., 268, 35 [NASA ADS] [CrossRef] [Google Scholar]
- Gray, L. J., Beer, J., Geller, M., et al. 2010, Rev. Geophys., 48, RG4001 [Google Scholar]
- Grevesse, N., & Sauval, A. J. 1998, Space Sci. Rev., 85, 161 [NASA ADS] [CrossRef] [Google Scholar]
- Grossmann-Doerth, U., Schüssler, M., & Solanki, S. K. 1988, A&A, 206, L37 [NASA ADS] [Google Scholar]
- Haigh, J. D., Winning, A. R., Toumi, R., & Harder, J. W. 2010, Nature, 467, 696 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Harder, J. W., Fontenla, J. M., Pilewskie, P., Richard, E. C., & Woods, T. N. 2009, Geophys. Res. Lett., 36, 7801 [NASA ADS] [CrossRef] [Google Scholar]
- Hasan, S. S., & Schüssler, M. 1985, A&A, 151, 69 [NASA ADS] [Google Scholar]
- Hirzberger, J., Feller, A., Riethmüller, T. L., et al. 2010, ApJ, 723, L154 [NASA ADS] [CrossRef] [Google Scholar]
- Hirzberger, J., Feller, A., Riethmüller, T. L., Gandorfer, A., & Solanki, S. K. 2011, A&A, 529, A132 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ishikawa, R., Tsuneta, S., Kitakoshi, Y., et al. 2007, A&A, 472, 911 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jafarzadeh, S., Solanki, S. K., Feller, A., et al. 2013, A&A, 549, A116 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jafarzadeh, S., Cameron, R. H., Solanki, S. K., et al. 2014a, A&A, 563, A101 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Jafarzadeh, S., Solanki, S. K., Lagg, A., et al. 2014b, A&A, in press [Google Scholar]
- Knowles, P. J., Werner, H.-J., Hay, P. J., & Cartwright, D. C. 1988, J. Chem. Phys. 89, 7334 [Google Scholar]
- Kobel, P., Solanki, S. K., & Borrero, J. M. 2012, A&A, 542, A96 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Kramida, A., Ralchenko, Yu., Reader, J., & NIST ASD Team 2012, NIST Atomic Spectra Database (version 5.0), available at http://physics.nist.gov/asd [Google Scholar]
- Krivova, N. A., Solanki, S. K., & Floyd, L. 2006, A&A, 452, 631 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Krupp, B. M. 1974, ApJ, 189, 389 [NASA ADS] [CrossRef] [Google Scholar]
- Kupka, F. G., Ryabchikova, T. A., Piskunov, N. E., Stempels, H. C., & Weiss, W. W. 2000, Balt. Astron., 9, 590 [NASA ADS] [Google Scholar]
- Kurucz, R., & Bell, B. 1995, Atomic Line Data. Kurucz CD-ROM No. 23, (Cambridge, MA: Smithsonian Astrophysical Observatory) [Google Scholar]
- Kurucz, R. L., Furenlid, I., Brault, J., & Testerman, L. 1984, Solar Flux Atlas from 296 to 1300 nm (Harvard University Press) [Google Scholar]
- Lagg, A., Solanki, S. K., Riethmüller, T. L., et al. 2010, ApJ, 723, L164 [NASA ADS] [CrossRef] [Google Scholar]
- Landi Degl’Innocenti, E., & Landolfi, M. 2004, Polarization in spectral lines, (Dordrecht: Kluwer Academic Publishers) [Google Scholar]
- Larkin, A., Haigh, J. D., & Djavidnia, S. 2000, Space Sci. Rev., 94, 199 [Google Scholar]
- London, J. 1994, Adv. Space Res., 14, 33 [NASA ADS] [CrossRef] [Google Scholar]
- López Ariste, A. 2002, ApJ, 564, 379 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez González, V., Bellot Rubio, L. R., Solanki, S. K., & Martínez Pillet, V. 2012, ApJ, 758, L40 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez Pillet, V., Lites, B. W., & Skumanich, A. 1997, ApJ, 474, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Martínez Pillet, V., del Toro Iniesta, J. C., Álvarez-Herrero, A., et al. 2011, Sol. Phys., 268, 57 [NASA ADS] [CrossRef] [Google Scholar]
- Mathew, S., Zakharov, V., & Solanki, S. K. 2009, A&A, 501, L19 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meunier, N. 2003, A&A, 405, 1107 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Meyer, F., & Schmidt, H. U. 1968, Z. Angew. Math. Mech., 48, T218 [CrossRef] [Google Scholar]
- Moll, R., Cameron, R. H., & Schüssler, M. 2011, A&A, 533, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Montesinos, B., & Thomas, J. H. 1989, ApJ, 337, 977 [NASA ADS] [CrossRef] [Google Scholar]
- Muller, R., & Roudier, Th. 1984, Sol. Phys., 94, 33 [NASA ADS] [CrossRef] [Google Scholar]
- Orozco Suárez, D. 2008, Ph.D. Thesis, Instituto de Astrofísica de Andalucía, Universidad de Granada, Spain [Google Scholar]
- Parker, E. N. 1988, ApJ, 330, 474 [Google Scholar]
- Pietarila Graham, J., Cameron, R., & Schüssler, M. 2010, ApJ, 714, 1606 [NASA ADS] [CrossRef] [Google Scholar]
- Piskunov, N. E., Kupka, F., Ryabchikova, T. A., Weiss, W. W., & Jeffery, C. S. 1995, A&AS, 112, 525 [NASA ADS] [Google Scholar]
- Prasad, C. V. V., Bernath, P. F., Frum, C., & Engleman, R. 1992, J. Mol. Spectr., 151, 459 [Google Scholar]
- Prokhorov, A., Bruls, J. H. M. J., & Berdyugina, S. V. 2014, A&A submitted [Google Scholar]
- Rachkovsky, D. N. 1962, Izv. Krymskoj Astrofiz. Obs., 28, 259 [NASA ADS] [Google Scholar]
- Ram, R. S., Davis, S. P., Wallace, L., et al. 2006, J. Mol. Spectr., 237, 225 [Google Scholar]
- Rehfuss, B. D., Suh, M.-H., Miller, T. A., & Bondybey, V. E. 1992, J. Mol. Spectr., 151, 437 [Google Scholar]
- Riethmüller, T. L., Solanki, S. K., Zakharov, V., & Gandorfer, A. 2008, A&A, 492, 233 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Riethmüller, T. L., Solanki, S. K., Martínez Pillet, V., et al. 2010, ApJ, 723, L169 [NASA ADS] [CrossRef] [Google Scholar]
- Roberts, B. 1983, Sol. Phys., 87, 77 [NASA ADS] [CrossRef] [Google Scholar]
- Röhrbein, D., Cameron, R., & Schüssler, M. 2011, A&A, 532, A140 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Romano, P., Berrilli, F., Criscuoli, S., et al. 2012, Sol. Phys., 280, 407 [NASA ADS] [CrossRef] [Google Scholar]
- Rüedi, I., Solanki, S. K., & Rabin, D. 1992, A&A, 261, L21 [NASA ADS] [Google Scholar]
- Ruiz Cobo, B., & del Toro Iniesta, J. C. 1992, ApJ, 398, 375 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J., Bonet, J. A., Viticchié, B., & del Moro, D. 2010, ApJ, 715, L26 [NASA ADS] [CrossRef] [Google Scholar]
- Sánchez Almeida, J., Collados, M., & del Toro Iniesta, J. C. 1989, A&A, 222, 311 [NASA ADS] [Google Scholar]
- Sánchez Almeida, J., Márquez, I., Bonet, J. A., Domínguez Cerdeña, I., & Muller, R. 2004, ApJ, 609, L91 [NASA ADS] [CrossRef] [Google Scholar]
- Schüssler, M. 1986, in Proc. Small Scale Magnetic Flux Concentrations in the Solar Photosphere, ed. W. Deinzer, M. Knölker, & H. H. Voigt (Göttingen: Vandenhoeck & Ruprecht), 103 [Google Scholar]
- Schüssler, M. 2013, Solar and Astrophysical Dynamos and Magnetic Activity, eds. A. G. Kosovichev, E. M. de Gouveia Dal Pino, Y. Yan, Proc. IAU Symp., 294, 95 [Google Scholar]
- Schüssler, M., Shelyag, S., Berdyugina, S., Vögler, A., & Solanki, S. K. 2003, ApJ, 597, L173 [NASA ADS] [CrossRef] [Google Scholar]
- Shapiro, A. I., Berdyugina, S. V., Fluri, D. M., & Stenflo, J. O. 2007, A&A, 475, 349 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Shapiro, A. I., Fluri, D. M., Berdyugina, S. V., Bianda, M., & Ramelli, R. 2011, A&A, 529, A139 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Sheeley, N. R., Jr. 1971, Sol. Phys., 20, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Shelyag, S., Schüssler, Solanki, S. K., & Vögler, A. 2007, A&A, 469, 731 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Solanki, S. K. 1987, Ph.D. Thesis, Institute of Astronomy, ETH Zürich, Switzerland, No. 8309 [Google Scholar]
- Solanki, S. K. 1989, A&A, 224, 225 [NASA ADS] [Google Scholar]
- Solanki, S. K. 1993, Space Sci. Rev., 63, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., & Pahlke, K. D. 1988, A&A, 201, 143 [NASA ADS] [Google Scholar]
- Solanki, S. K., Inhester, B., & Schüssler, M. 2006, Rep. Prog. Phys., 69, 563 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., Barthol, P., Danilovic, S., et al. 2010, ApJ, 723, L127 [NASA ADS] [CrossRef] [Google Scholar]
- Solanki, S. K., Krivova, N. A., & Haigh, J. D. 2013, ARA&A, 51, 311 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C. 1976, Sol. Phys., 50, 269 [NASA ADS] [CrossRef] [Google Scholar]
- Spruit, H. C., Nordlund, Å., & Title, A. M. 1990, ARA&A, 28, 263 [NASA ADS] [CrossRef] [Google Scholar]
- Steiner, O. 2000, Sol. Phys., 196, 245 [NASA ADS] [CrossRef] [Google Scholar]
- Stenflo, J. O. 1973, Sol. Phys., 32, 41 [NASA ADS] [CrossRef] [Google Scholar]
- Title, A. M., & Berger, T. E. 1996, ApJ, 463, 797 [NASA ADS] [CrossRef] [Google Scholar]
- Tritschler, A., & Uitenbroek, H. 2006, ApJ, 648, 741 [NASA ADS] [CrossRef] [Google Scholar]
- Uitenbroek, H., & Tritschler, A. 2006, ApJ, 639, 525 [NASA ADS] [CrossRef] [Google Scholar]
- Uitenbroek, H., & Tritschler, A. 2007, A&A, 462, 1157 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Utz, D., Hanslmeier, A., Möstl, C., et al. 2009, A&A, 498, 289 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Vögler, A. 2005, Mem. Soc. Astron. It., 76, 842 [NASA ADS] [Google Scholar]
- Vögler, A., Shelyag, S., Schüssler, M., et al. 2005, A&A, 429, 335 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S., & Rouppe van der Voort, L. 2009, A&A, 503, 225 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wedemeyer-Böhm, S., Scullion, E., Steiner, O., et al. 2012, Nature, 486, 505 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Wiegelmann, T., Solanki, S. K., Borrero, J. M., et al. 2010, ApJ, 723, L185 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wiehr, E., Bovelet, B., & Hirzberger, J. 2004, A&A, 422, L63 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Willson, R. C., & Hudson, H. S. 1988, Nature, 332, 810 [NASA ADS] [CrossRef] [Google Scholar]
- Zakharov, V., Gandorfer, A., Solanki, S. K., & Löfdahl, M. 2005, A&A, 437, L43 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zakharov, V., Gandorfer, A., Solanki, S. K., & Löfdahl, M. 2007, A&A, 461, 695 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
All Tables
Central wavelength λ0, oscillator strength log(gf), energy of the lower level El, and term sysmbol of the lower and upper levels of the 20 synthesized spectral lines around the Fe i line at 5250.2 Å.
All Figures
 |
Fig. 1 Excerpts from an NSO spectral atlas (black lines; Kurucz et al. 1984), spatially averaged synthetic spectra (red lines; see text for details), and instrumental filter profiles (green lines referring to the scale on the right side of the figure) for the part of the OH band around 3118 Å (top panel), the CN band at 3877 Å (middle panel), and the Fe i line at 5250.2 Å (bottom panel). The dotted red line in the bottom panel simulates the Doppler shifted profile of the Fe i line at 5250.2 Å produced by an upflow of 5 km s-1. The red arrows indicate the five scan positions of the IMaX V5-6 mode, while the twelve blue arrows mark them for the L12-2 mode. |
| In the text | |
 |
Fig. 2 Intensity maps in the wavelength bands 3118 Å and 3877 Å, as well as for the continuum at 5250.4 Å (first three columns), all normalized to the corresponding mean quiet-Sun intensity level, IQS. The LOS velocity (positive velocities correspond to downflows) and the circular polarization degree (see main text for definition) are shown in Cols. 4 and 5, respectively. The color bars at the top refer to the undegraded MHD data shown in the first row, while the lower color bars apply to the degraded MHD data (second row) and to the data obtained from the Sunrise Observatory (third row). |
| In the text | |
 |
Fig. 3 Intensity histograms over all pixels for the OH band data around 3118 Å. Top panel: the black line corresponds to the original 30 G MHD simulation, the blue line to the spatially degraded data, and the red line to the fully degraded simulation data. The green line displays the Sunrise observations. Bottom panel: influence of the MHD simulations’ mean flux density on the fully degraded OH intensity histogram. The black line shows a purely hydrodynamical simulation, i.e., without any magnetic field. The mean unsigned vertical flux density was 30 G for the histogram colored in red, 50 G for the blue line, and 200 G for the green line. rms contrasts are indicated in the text labels. |
| In the text | |
 |
Fig. 4 Same as Fig. 3, but for the CN band data around 3877 Å. |
| In the text | |
 |
Fig. 5 Same as Fig. 3, but for the continuum at 5250.4 Å. |
| In the text | |
 |
Fig. 6 Same as Fig. 3, but for the LOS velocity as retrieved from a Gaussian fit to the Stokes I profile of Fe i 5250.2 Å. Mean values and their standard deviations are indicated in the text labels. Negative velocities are upflows. |
| In the text | |
 |
Fig. 7 Top and middle panels: same as Fig. 3, but for the spectral line width (FWHM) as retrieved from a Gaussian fit to the Stokes I profiles of Fe i 5250.2 Å. Bottom panel: influence of different approximations made during the spectral synthesis of the 30 G MHD data on the histogram of the spectral line width. The spectra were fully degraded in all three plotted cases. The black line corresponds to the histogram obtained when the filter transmission profile was approximated by an 85 mÅ Gaussian instead of the measured spectral PSF. The blue line corresponds to a spectral synthesis of only the 5250.2 Å line, i.e., the 19 neighboring lines were not synthesized. For comparison, the red line in the top panel is plotted again and corresponds to the 20-line synthesis and spectral degradation with the measured spectral PSF. |
| In the text | |
 |
Fig. 8 Histograms of the circular polarization degree ⟨ pcirc ⟩ as retrieved from the Stokes I and V profiles of Fe i 5250.2 Å (see Eq. (1) for definition). Top panel: the black line corresponds to the original 30 G MHD simulation, the blue line to the spatially degraded data, the magenta line represents the histogram after stray light contamination has been added. Finally, the red line corresponds to the fully degraded 30 G simulation. The green line displays the Sunrise/IMaX observations. Middle panel: influence of the MHD simulations’ mean flux density on the fully degraded polarization histogram. The black line shows a purely hydrodynamical simulation, i.e., without any magnetic field. The mean unsigned vertical flux density was 30 G for the histogram colored in red, 50 G for the blue line, and 200 G for the green line. The noise level was always 3.30 × 10-3IQS. Bottom panel: influence of the noise level. The flux density was always 30 G. The noise levels in units of the mean quiet-Sun intensity are printed as text labels. |
| In the text | |
 |
Fig. 9 Effective BP diameter for the observed BPs (red line), for the undegraded MHD BPs simulated with a cell size of 20.8 km (green line), for the undegraded MHD BPs simulated with a cell size of 10.4 km (blue line), and for the degraded MHD BPs simulated with a cell size of 10.4 km (black line). |
| In the text | |
 |
Fig. 10 Bright point (BP) peak intensity in the 3118 Å OH band (red lines), the intensity histograms of the BPs’ dark background (blue lines), and the histograms of all pixels (green lines). Mean values and standard deviations are given in the text labels. The top panel shows the histograms obtained from the observational data recorded by the SuFI instrument; the bottom panel displays the same for the degraded 30 G MHD simulations. The BP histogram of the undegraded MHD data is indicated in the bottom panel by the black line. |
| In the text | |
 |
Fig. 11 Same as Fig. 10, but for the peak intensity at the 5250.4 Å continuum. |
| In the text | |
 |
Fig. 12 Same as Fig. 10, but for the LOS velocity as retrieved from a Gaussian fit to the Stokes I profile of Fe i 5250.2 Å. |
| In the text | |
 |
Fig. 13 Same as Fig. 10 for the spatial peak value of the circular polarization degree. Additionally, the magenta line shows the histogram of the BP polarization for the degraded 200 G MHD simulations. |
| In the text | |
 |
Fig. 14 Stokes V amplitude (green lines) and area (red lines) asymmetries, intensity in the 3877 Å CN band (black lines), and circular polarization degree (blue lines) of the reconstructed IMaX observations (top panel), degraded (middle panel), and original (bottom panel) 30 G MHD simulations as a function of the distance to the BP center. The dashed black lines display the half width half maximum value of the mean intensity profile. |
| In the text | |
 |
Fig. 15 Offset between the BPs’ peak in CN intensity and the peak in the circular polarization degree, O, for the observed BPs (red line), the undegraded MHD BPs (blue line), and for the degraded MHD BPs (black line). |
| In the text | |
 |
Fig. 16 LOS velocity as retrieved from a Gaussian fit to the Stokes I profile (green lines) and from the Stokes V zero crossing (red lines) of the reconstructed IMaX observations (top panel), degraded (middle panel), and original (bottom panel) 30 G MHD simulations as a function of the distance to the BP center. The dashed black lines are the same as in Fig. 14. |
| In the text | |
 |
Fig. 17 Influence of the various degradation steps on the histogram of the BP circular polarization degree. The degradation was applied to the 30 G MHD simulations. The black line corresponds to the data that were only spectrally degraded. An additional spatial degradation results in the blue histogram. The green line also includes the effect of stray light contamination, while the fully degraded BP signals, i.e., including noise, give the histogram colored in red. |
| In the text | |
 |
Fig. 18 Demonstration of a weak polarization signal owing to the strong temperature sensitivity of the Fe i line at 5250.2 Å by a comparison of a pixel in a particularly bright BP (red lines) with a pixel located in a much less bright BP (blue lines). a) Vertical temperature stratification as a function of log(τ) at 5000 Å. b) Magnetic field strength stratification. c) and d) Stokes I/IQS and V/IQS signals from the original MHD data at the twelve IMaX L12-2 scan positions in the line. |
| In the text | |
 |
Fig. 19 Circular polarization degree versus magnetic field strength at log(τ) = −2 as retrieved for the 898 BPs from the original 30 G MHD data. Pixels with T ≥ 5100 K are colored in red, cooler pixels in blue. The solid lines are linear regressions. |
| In the text | |
 |
Fig. 20 Peak value of the BP field strength calculated via the weak field approximation (see main text). The green line shows the observed BPs and the red line displays the BPs from the degraded 30 G MHD data. |
| In the text | |
 |
Fig. 21 Magnetic field strength of the BPs in the middle photosphere (green line), and of the BPs (red line) and the DB (blue line) in the lower photosphere as retrieved from the undegraded 30 G MHD data. Mean values and their standard deviations are given in the text labels. |
| In the text | |
 |
Fig. 22 Magnetic field inclination at optical depth unity of BPs, DB, and of all pixels. The color coding is the same as in the top panel of Fig. 10. |
| In the text | |
 |
Fig. 23 Temperature for the simulated BPs (red lines), for the BPs’ dark background (blue lines), and for all pixels in all frames (green lines). Mean values and their standard deviations are given in the text labels. The top panel shows the temperature at log(τ) = −2 and the bottom panel at optical depth unity (the T scales are different). |
| In the text | |
 |
Fig. 24 Same as Fig. 23 for the LOS velocities (vertical component of the velocity vector taken directly from the MHD output). |
| In the text | |
 |
Fig. 25 Scatterplot of the BP peak CN intensity versus the magnetic field strength at optical depth unity (black dots). The red line connects binned values and the blue line is the linear regression. Error bars represent standard deviations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


