| Issue |
A&A
Volume 567, July 2014
|
|
|---|---|---|
| Article Number | A144 | |
| Number of page(s) | 10 | |
| Section | Cosmology (including clusters of galaxies) | |
| DOI | https://doi.org/10.1051/0004-6361/201424047 | |
| Published online | 05 August 2014 | |
Characterising superclusters with the galaxy cluster distribution
1 Max-Planck-Institut für extraterrestrische Physik, 85748 Garching, Germany
e-mail: gchon@mpe.mpg.de
2 Astrophysics Research Institute, Liverpool John Moores University, IC2, Liverpool Science Park, 146 Brownlow Hill, Liverpool L3 5RF, UK
3 Excellence Cluster Universe, Boltzmannstrasse 2, 85748 Garching, Germany
Received: 22 April 2014
Accepted: 17 June 2014
Superclusters are the largest observed matter density structures in the Universe. Recently, we presented the first supercluster catalogue constructed with a well-defined selection function based on the X-ray flux-limited cluster survey, REFLEX II. To construct the sample we proposed a concept to find large objects with a minimum overdensity such that it can be expected that most of their mass will collapse in the future. The main goal is to provide support for our concept here by using simulation that we can, on the basis of our observational sample of X-ray clusters, construct a supercluster sample defined by a certain minimum overdensity. On this sample we also test how superclusters trace the underlying dark matter distribution. Our results confirm that an overdensity in the number of clusters is tightly correlated with an overdensity of the dark matter distribution. This enables us to define superclusters within which most of the mass will collapse in the future. We also obtain first-order mass estimates of superclusters on the basis of the properties of the member clusters. We also show that in this context the ratio of the cluster number density and dark matter mass density is consistent with the theoretically expected cluster bias. Our previous work provided evidence that superclusters are a special environment in which the density structures of the dark matter grow differently from those in the field, as characterised by the X-ray luminosity function. Here we confirm for the first time that this originates from a top-heavy mass function at high statistical significance that is provided by a Kolmogorov-Smirnov test. We also find in close agreement with observations that the superclusters only occupy a small volume of a few per cent, but contain more than half of the clusters in the present-day Universe.
Key words: large-scale structure of Universe / X-rays: galaxies: clusters
© ESO, 2014
1. Introduction
Superclusters are the largest prominent density enhancements in our Universe. They are generally defined as groups of two or more galaxy clusters above a given spatial density enhancement (Bahcall 1988). Their sizes vary between several tens of Mpc to about 150 h-1 Mpc. Because the time a cluster needs to cross a supercluster is longer than the age of the Universe, superclusters cannot be regarded as relaxed systems. Their appearance is irregular, often flattened, elongated, or filamentary, and generally not spherically symmetric. This is a sign that they still reflect, to a large extent, the initial conditions set for the structure formation in the early Universe. They do not necessarily have a central concentration, and are without sharply defined boundaries.
The first evidence of superclusters as agglomerations of rich clusters of galaxies was provided by Abell (1961). The existence of superclusters was confirmed by Bogart & Wagoner (1973), Hauser & Peebles (1973), and Peebles (1974). So far, numerous supercluster catalogues have been published based essentially on optically selected samples of galaxy clusters. Several supercluster catalogues based on samples of Abell/ACO clusters of galaxies followed, for example Rood (1976), Thuan (1980), Bahcall & Soneira (1984), Batuski & Burns (1985), West (1989), Zucca et al. (1993), Kalinkov & Kuneva (1995) and Einasto et al. (1994, 1997, 2001). Einasto et al. (2001) was the first to use X-ray selected clusters in addition to Abell clusters. X-ray selected galaxy clusters are very good tracers of the large-scale structure because their X-ray luminosity correlates well with their mass better than optically selected samples of galaxy clusters, Pratt et al. (2009). Such samples suffer from projection effects among other. However, none of these catalogues is based on cluster catalogues with a well-understood selection criterion. This means that they can neither be used as a representative sample to study the properties of superclusters, nor can they be easily compared with simulations.
Chon et al. (2013) made a fresh approach in this respect by presenting the first statistically well-defined supercluster catalogue based on the extended ROSAT-ESO Flux LimitEd X-ray (REFLEX II) cluster survey (Chon & Böhringer 2012; Böhringer et al. 2013) by using a friends-of-friends algorithm to construct the superclusters. The REFLEX II cluster catalogue comes with a well-understood selection function and it is complete, homogeneous, and of very high purity. This allows a relatively straightforward reconstruction of the survey with simulated data.Chon et al. (2013) hereafter C13 presented the construction of superclusters and studied observed properties of the X-ray superclusters. The strategy of the supercluster sample construction in this previous paper was based on the assumption that by choosing a certain linking length for the cluster association to superclusters we obtain superclusters with a minimum dark matter overdensity. By choosing the correct linking length value in relation to the mean cluster density, we conjectured that we can obtain a supercluster sample that includes the objects that will marginally collapse in the future. This hypothesis relies on two assumptions: (i) a certain linking length corresponds to a certain number overdensity of clusters; and (ii) an overdensity in the number of clusters above a certain mass limit corresponds to a closely correlated value of the overdensity in the dark matter of the supercluster volume.
The main aim of the present paper is to use simulations to test these crucial assumptions, and to examine how superclusters trace the underlying dark matter distribution. By using the dark matter distribution of the Millennium Simulation (Springel et al. 2005), we compare the cluster density with the dark matter density in superclusters that are constructed with a friends-of-friends algorithm so that they are expected to have a minimum spherical overdensity. To determine how superclusters trace the dark matter we consider two quantities. We first study the correlation between the mass fraction of a supercluster represented in its member clusters to the total mass of a supercluster probed by all halos in the Millennium Simulation, and investigate how the cluster number density is correlated with the matter overdensity of a supercluster, analogously to the bias of the power spectrum of clusters, and examine how simulated superclusters trace the underlying matter distribution.
According to Birkhoff’s theorem, structure evolution in a supercluster region can be modelled in a way equivalent to a universe with a higher mean density than that of our Universe. The main difference between these two environments is then a slower growth of structure in the field compared with the denser regions of superclusters in the recent past. Thus, we would expect a more top-heavy X-ray luminosity function in superclusters. Among the properties of the superclusters investigated in C13 two main findings were (1) that the volume occupied by these superclusters is very small, two per cent, while more than half of the REFLEX II clusters are found in the superclusters; and (2) that the cumulative X-ray luminosity function of the volume-limited-sample (VLS) of the REFLEX II superclusters differs from that in the field: this was supported by a Kolmogorov-Smirnov (KS) test. Since the X-ray luminosity of clusters is tightly correlated with their mass, we might expect that there are more massive clusters in superclusters than in the field. In C13 we also discussed an alternative explanation for the top-heavy luminosity function: that the luminosity of clusters is temporarily boosted in a dense region because of an increased rate of merger events. In this case we would not find correspondingly more massive clusters in superclusters. Our study with the Millennium Simulation allows us to distinguish between these hypotheses in this paper. Previous studies investigated various quantities within the supercluster environment, for example, Einasto et al. (2003, 2005, 2012) and Luparello et al. (2013), with the galaxy survey data or N-body simulations, and the future evolution of superclusters were studied by Dünner et al. (2006), Araya-Melo et al. (2009), and Luparello et al. (2011). They found that in the regions of superclusters there are more richer and massive systems, enhanced velocity dispersions, and larger star formation rates, which indicate that the superclusters provide a different environment for structures to grow than does the field. Our approach is different from these previous works because we select the clusters of galaxies as tracer objects to probe superclusters, and because they are selected closely following the flux-limited X-ray observation.
This paper is organised as follows. Section 2 describes the construction of superclusters from the Millennium Simulation and their basic properties. The connection of the linking length to the cluster density ratio is explored in Sect. 3. We investigate how superclusters trace the dark matter distribution by studying the mass fraction of clusters and the bias introduced by the cluster number overdensity in Sect. 4. We probe the supercluster environment by comparing the cluster mass function and volume fraction of superclusters to those of the field in Sect. 5. We conclude in Sect. 6 with some discussions.
2. Construction of superclusters in a simulation
We used the Millennium Simulation to study the properties of superclusters constructed with the dark matter (DM) halos. It contains a total of 21603 particles with a mass of 8.6 × 108 h-1 M⊙ in a box size of 500 h-1 Mpc. It adopts a flat-ΛCDM cosmology with Ωm = 0.25, h = 0.73, σ8 = 0.9.
Our aim with the simulation is to explore whether superclusters can be used to probe the statistics of the large-scale structure in our Universe, and to test the concept of constructing superclusters with a certain minimum overdensity of clusters. To construct the supercluster catalogue with the Millennium Simulation data analogous to typical X-ray cluster observations we defined clusters in the DM simulation as the halos above a given mass limit. We adopted M200 as the halo mass, where M200 is defined as the mass inside the radius where the mean halo density is 200 times the mean density of the universe. We are interested in the mass range above 1013 h-1 M⊙ which encompasses the whole range of clusters and groups of galaxies. To enable a better discussion, two reference catalogues were considered with two lower mass limits of 1014 h-1 M⊙ and 1013 h-1 M⊙. Since the current lower mass limits of cluster surveys are typically about 1014 h-1 M⊙ we defined the halos of mass above 1014 h-1 M⊙ as the clusters, of which our main cluster catalogue consists. The second main catalogue consists of halos with a mass above 1013 h-1 M⊙. These halos correspond to clusters and groups of galaxies that we take as a representative sample for future cluster and group surveys. Throughout we refer to the supercluster catalogue built with halos of mass above 1014 h-1 M⊙ as CS and that above 1013 h-1 M⊙ as GCS for brevity. We restrict our study here to a snapshot at z = 0.
With the definition of clusters given above we constructed a catalogue of superclusters with a friends-of-friends (fof) algorithm in the same way as C13. The key parameter in this algorithm is the linking length within which friends are found, and this parameter determines the types of superclusters that are constructed. We adopted the definition of a linking length in Zucca et al. (1993), which depends on the overdensity, f, meaning that the cluster density enhancement over the mean cluster density, f = n/no. As the local density n ∝ l-3, the linking length is inversely proportional to the density of the sources in the volume, no, and we define it as l = (nof)− 1/3. Hence the choices of f affect the definition of superclusters. We here fixed f to ten for reasons detailed in C13, and we only summarise them here briefly. We calculated this required overdensity value by assuming a spherical top-hat collapse model for the superclusters and by integrating the Friedmann equations, which describe the evolution of the superclusters given ΔCL,m = [(ΔDM,c + 1)/Ωm − 1] bCL. ΔCL,m is the cluster overdensity against the mean density, ΔDM,c the DM overdensity against the critical density in the superclusters, and bCL is the bias in the density fluctuations of clusters with the condition ΔDM,c ≳ 1.4. For superclusters at low redshifts that will collapse in the future we therefore find the condition ΔCL,m ≥ 17 − 35 for a cluster bias of 2−4. As noted in C13, we sample superstructures more comprehensively by taking f = 10, which include those slightly beyond definitely bound structures. Therefore this linking parameter is rather conservative because it includes slightly more material than is gravitationally bound in a ΛCDM Universe. Most of the superclusters are still recovered with f = 50 (C13), and most of the matter in the superclusters will collapse in the future, and in addition, a volume of f = 10 selects superclusters that correspond well to the superclusters described in the literature. Our search for friends of a supercluster starts from the brightest clusters in the halo catalogue, where we call the brightest cluster in a supercluster BSC. We note that the definition of superclusters in our work also includes objects with two cluster members.
2.1. Physical properties
Two main supercluster catalogues were constructed with the recipes described above. The CS contains 3569 clusters, from which 607 superclusters were constructed, while there were 8893 superclusters out of 51 528 clusters in the GCS. In the following we consider two physical properties that result from the choice of the overdensity parameter, f.
We note that Einasto et al. (2007a) compared the properties of superclusters from the 2dF galaxy redshift survey (Einasto et al. 2007b) with those constructed with the Millennium Simulation. Their main conclusion was that most of the properties of the 2dF superclusters agree well with those of the Millennium superclusters, except for the luminosity and multiplicity distributions. Unfortunately, a direct comparison with their results is not possible because our supercluster catalogue is directly constructed from clusters, while their catalogue is based on galaxy overdensities.
2.1.1. Multiplicity function
The multiplicity function is defined as the number of member clusters in a supercluster, equivalent to the richness parameter of an optical cluster of galaxies. We define superclusters as systems with two or more member clusters in our study, and systems with two member clusters are referred to as pair superclusters.
The normalised multiplicity function of the superclusters is shown in Fig. 1 for a range of overdensity parameters, f. Those constructed with the CS are shown as a black solid line, and superclusters constructed with the GCS as a grey dashed line. We note that there are three very rich superclusters with >100 members or more in the f = 2 case in both CS and GCS, which are not shown. For a fixed no a higher value of f corresponds to a smaller linking length, and in this case, there are fewer very rich superclusters, and less rich systems dominate the distribution. Conversely with lower values of f the number of very rich superclusters increases because of a large linking length. In either case, the multiplicity histograms for all f are dominated by pair and less rich superclusters, and the multiplicity spread broadens with a larger linking length. We see these trends in Fig. 1, and the shapes of the multiplicity functions of supercluster samples that are constructed with different mass limits agree well. The KS test for each case of Fig. 1 yields a probability of unity, meaning that it is highly likely that the multiplicity distributions formed by both CS and GCS originate from the same parent distribution.
2.1.2. Extent
Superclusters are the largest objects that are seen in galaxy redshift surveys, for example, and we are interested in determining how large these prominent features of the large-scale structure are. We define the extent of a supercluster by the largest distance between the centre of mass of a supercluster to its farthest member clusters.
 |
Fig. 1 Normalised multiplicity function of the superclusters for a range of overdensity parameters, f, constructed with the halos in the CS (black solid line), and with those in the GCS (grey dashed line). The value of f is indicated in each panel. Richer systems are abundant with decreasing f, which is equivalent to a longer linking length (upper left panel), while less rich systems are more common with higher f values (lower right panel). |
 |
Fig. 2 Distribution of the normalised extent of the superclusters. The superclusters in the CS are shown in black, those in the GCS in grey. Superclusters with three or more member clusters are marked by a dashed line, pair superclusters by a solid line. |
Figure 2 shows the distribution of the supercluster extent for the two nominal mass limits. The extent is normalised by the linking length of the corresponding catalogue, which is 15.2 Mpc h-1 for the CS and 6.2 Mpc h-1 for the GCS. The pair superclusters are denoted by solid lines, and the other richer systems in dashed lines. Fewer than a per cent of superclusters in the GCS are left out in the plot where the normalised extent is larger than three. The two samples of the richer superclusters are strikingly similar. The typical size of the richer superclusters is around 80 per cent of the linking length. Richer systems show a longer tail towards large extents. The distributions in the pair superclusters are very similar as well, which is expected because in both samples the typical size of pairs is half of the linking length. This implies that most of the pairs have almost the largest possible size for systems of similar mass. The similarity between the size distributions of the two samples provides a signature of the self-similarity of the large-scale structure at these mass and length scales.
2.1.3. Percolation
Percolation occurs when structures begin to be linked and permeate through the volume. This means in our context that systems identified as separate systems with a larger overdensity parameter begin to merge and form a single superstructure with decreasing overdensity parameter. These structures will not collapse into a virialised object in the future. Therefore it is important to understand where the percolation occurs in the sample of superclusters, what the level of percolation is, and how one needs to treat the percolated systems in the analysis.
Shandarin et al. (2004) studied the percolation to understand the morphology of the supercluster-void network constructed by smoothed density fields in the N-body simulations. They found that the percolating objects make up a considerable fraction of superclusters, and that they should be studied separately. Liivamägi et al. (2012) also studied the percolation in the supercluster catalogue constructed with galaxy data depending on the density threshold, which is in some way equivalent to our overdensity parameter.
Our strategy here is to build a sample of superclusters that will form collapsed objects in the future. This sample is selected by applying a clear selection function that resembles the X-ray selection. f = 10 was chosen as a physically motivated overdensity parameter based on solving the Friedmann equations, and we explained in Sect. 2 that our nominal catalogues built with f = 10 also include those structures that will also partially collapse. Thus it is interesting to determine the number of percolating superclusters in our sample, and their effect on the subsequent analysis.
Based on the distribution of the multiplicity function, we determined the percolation scale, which isolates very large structures. For instance, the top-left panel of Fig. 1 shows isolated objects beyond a multiplicity of 80, and we identify them as percolating objects. This means that we define the scale of percolation by the largest system in the multiplicity distribution that still belongs to the continuous distribution function before the first gap. This is slightly more conservative than taking the scale at which the isolation starts, but does not modify our conclusion. This categorisation reveals that 11 superclusters in the nominal GCS and 3 in the CS may be the results of percolation, which is very small fraction of the sample. This is reassuring for our choice of the overdensity parameter.
The most evident quantity affected by percolation is the volume fraction of percolating structures to the total volume of superclusters. We show the effect of percolation on the cumulative volume fraction in Fig. 3 as a function of normalised multiplicity. Four cases are considered here with the two overdensity parameters, f = 2 (grey) and f = 10 (black) for the catalogues built with the two mass limits, 1013 h-1 M⊙ (line), and 1014 h-1 M⊙ (filled circles). The percolation scales are marked by asterisks on each curve. For the same mass limit, percolating objects identified in the f = 2 catalogue take up a much larger volume than those in the f = 10 catalogue. In the 1014 h-1 M⊙ catalogues they occupy about 70% of the total volume for f = 2, while the fraction reduces to about 15% in the nominal f = 10 catalogue. Moreover, the percolation starts at smaller normalised multiplicities for a higher mass limit, as shown by the asterisks.
 |
Fig. 3 Cumulative volume fraction of superclusters as a function of normalised multiplicity. The CS is shown as filled circles, GCS as continuous lines. For the same mass limit the catalogues built with f = 2 are shown in grey, and f = 10 in black. Four asterisks mark the estimated starting scale of the percolation. |
With the superclusters built with f = 10 the contribution of potential percolation to the total volume fraction ranges from three to at most 20% for the mass limits between 1013 h-1 M⊙ and 1014 h-1 M⊙. This means that the percolation effect is much less pronounced in our supercluster catalogues than previous findings, for example Shandarin et al. (2004). We attribute this to the fact that clusters of galaxies do not trace long, thin dark matter filaments as closely as galaxies or the smoothed density field. In our nominal catalogues built with f = 10, we find very few percolating structures, therefore their contribution to the quantities that are probed in our paper is very limited. An extreme treatment of these superclusters is to remove them from the analysis, and as we will discuss in the relevant sections, no major differences are found, except for the total volume of superclusters in our analysis.
3. Assessing supercluster density ratio
The nature of a supercluster catalogue critically depends on the choice of the linking length in the fof algorithm since it determines the types of superclusters that are constructed. A too long linking length merges structures that may not be bound gravitationally, but a much lower value might only select the peaks of larger underlying structures. In C13 we showed that the overdensity parameter, f, which is inversely proportional to the linking length, can be formulated such that the corresponding linking length selects the superclusters that will eventually collapse in the future in our standard ΛCDM universe. As we discussed in Sect. 2, we defined a physically motivated linking length, which corresponds to f = 10 as our nominal overdensity parameter to capture systems that are slightly beyond definitely bound structures based on integrating the Friedmann equations. Our aim in this section is to understand how superclusters are represented by their member clusters that are constructed with this overdensity parameter, based on a spherical top-hat collapse model, via a friends-of-friends algorithm. In this approach we approximate superclusters to have a spherical shape, and for consistency with this theoretically motivated characterisation, we keep this geometric approximation throughout this paper.
To answer this question, we checked the distribution of the actual density ratios of superclusters constructed with a given f, in retrospect. We measured the density ratio of the superclusters, defined as the ratio of the cluster number density in a supercluster to the mean number density of clusters in the considered volume. This test also provides a sanity check on our assumption, and a census of the typical departure of these large structures from the mean density of the universe. To calculate the ratio, the volume of a supercluster was assumed to be spherical, and its extent is defined in Sect. 2.
 |
Fig. 4 Measured number density ratio of the clusters in the CS. The cluster number density ratio is defined as the ratio between the cluster density in a supercluster and the mean cluster density in the simulation. |
Figure 4 shows the measured density ratio of the CS as a function of the extent. The apparent line-like structures are due to the discreteness of the multiplicity function, since the density ratio is proportional to the multiplicity and the volume of a supercluster. The dashed line corresponds to the overdensity parameter, f = 10, with which we constructed the superclusters. We note that with a maximum linking length defined by f = 10, a density ratio of ten is the expected lower limit with some scatter, as the cluster distances in a particular supercluster can always be smaller than this maximum. We see this in particular among the pairs in Fig. 5, where we find many systems with linking lengths very much shorter than the largest allowed value. In extreme cases, these are systems that are very close to merging. Therefore it is expected to find systems with the density ratio very much higher than the threshold in Fig. 4. In addition, nine per cent of the superclusters in the CS fall below the dashed line, allowing a scatter of 20 per cent, while 18 per cent of the GCS superclusters fall below for the same scatter.
 |
Fig. 5 Multiplicity of superclusters shown as a function of their extent for the CS as in Fig. 4. The open circles represent the superclusters with a measured density ratio below ten in Fig. 4. |
Superclusters below the overdensity threshold of ten are marked by open circles, while the remainders are marked by crosses in Fig. 5. The former systems are dominantly large in each class of the multiplicity; the smallest system among them is R = 13.5 Mpc h-1 in size. Figure 6 shows an example of such a system in two projections with one of the lowest measured density ratios. Both panels show the member clusters as black filled circles, and all other halos as grey dots in the spherical volume defined by the extent of a supercluster. The upper panel shows a cut through the X–Y plane, the lower panel a cut through the X–Z. In this extreme case, the clusters are located along a long filament in the X-axis, while in the other axes the distribution of clusters is rather compact. In this case, the spherical volume overestimates the volume that is represented by the member clusters.
 |
Fig. 6 Distribution of all halos in the largest supercluster cut through two axes, in X–Y (upper), and in X–Z (lower). The offsets are in units of Mpc h-1. The member clusters are shown as filled circles, and all other halos less massive than the mass limit as grey dots, where the centre of mass is located at the origin. This supercluster, taken as an example from Fig. 4, represents superclusters with a measured density ratio lower than ten. Typically, the member clusters of these superclusters form a thin filament along one axis, which causes an over-estimation of a supercluster volume, leading to an under-estimation of the measured density ratio. The open circles mark the clusters belonging to the neighbouring superclusters whose volumes overlap with the volume of the main supercluster according to the definition of the extent. |
Traditionally, superclusters have been found with a fof algorithm, and this result reflects how well the fof reproduces structures in comparison with a spherical overdensity (SO). This is analogous to compiling dark matter halos in N-body simulations that are found by the fof and characterised by the SO method, except that superclusters are more complex and are not virialised. We find in our analysis that the fof method works similarly well in compiling superclusters as for the study of dark matter halos.
A different concern in this context is that superclusters constructed with a fof algorithm might potentially have an overlapping volume with neighbouring superclusters if their extent is defined as in Sect. 2.1.2 with the assumption of a spherical shape. Therefore we explored whether this occurs in our sample, and show an example in Fig. 6. Clusters in the neighbouring superclusters with an overlapping volume with this supercluster are shown as open circles. For the CS the overlapping volume is 1.5 per cent of the total supercluster volume, and for the GCS it is about six per cent. Since the overlapping volume fraction is so small, we neglect it in the following analysis.
4. Superclusters as dark matter tracers
The fact that the REFLEX II supercluster sample has been constructed by means of a statistically well defined sample of closely mass-selected clusters motivated us to search for a more precise physical characterisation of the simulated superclusters. We are in particular interested in exploring the relation of the cluster density in superclusters to the underlying dark matter distribution. This can be studied with DM simulations by applying criteria equivalent to those used in our X-ray selection. To do this we consider two quantities in this section the mass fraction of the superclusters represented by their member clusters compared with total supercluster mass, and the overdensity of clusters in superclusters as a function of the DM mass overdensity. A better knowledge of these relations would greatly assist interpreting the observations. Since we have almost no direct access to determine the supercluster masses – neither dynamical mass estimates nor gravitational lensing studies have yet been successfully applied to entire superclusters – an indirect mass estimate would be very helpful. Since we have mass estimates of the member clusters through mass-observable scaling relations where the X-ray luminosity is the crucial observable in our case, the total supercluster mass can be estimated if we can calibrate the cluster mass fraction in superclusters. Similarly, we would be able to determine the DM overdensity traced by a supercluster if the mass fraction relation or the overdensity bias could be calibrated. The following analysis constitutes a first exploration of this territory.
In this section we consider a finer grid of mass limits to form a smoother distribution of mass-related quantities between 1013 h-1 M⊙ and 1014 h-1 M⊙ where appropriate. We note that there are approximately 5−10 per cent of superclusters, depending on the mass limit, that will not be included in the samples purely because their extent in one or more dimensions extends farther outside the simulation volume. Since this occurs for the observations near the survey boundaries, we exclude these superclusters. Another technical point is the assumption that we make in terms of the DM particle mass distribution. We assume that the least massive halos in our study are not biased against the DM. This also applies to the particles that do not contribute to the M200 of halos. This is reasonable because of the small mass resolution of particles and because unbound particles are spatially equally distributed throughout the simulation. The assumption that halos less massive than the smallest groups have a bias close to unity is in the first place based on theory, for example Seljak & Warren (2004). We also tested this by comparing the halo distribution for different halo masses with the dark matter density field, and found that it is observed with an accuracy of about 5% on a scale of 5 Mpc h-1 or larger.
4.1. Mass fraction probed by clusters
From the observations and simulations we have a good understanding of the relation between cluster observables and the total mass of a cluster, for instance Böhringer et al. (2012), Sheldon et al. (2009), and Johnston et al. (2007), which means that the visible components of a cluster represent the underlying dark matter component well. If DM had no preferential scale, this argument should apply in a similar way to superclusters, which means that a supercluster mass probed by the total cluster mass is probably also correlated with the true mass of the supercluster. This motivated this subsection, where we investigate whether superclusters can be used to trace the DM distribution by comparing the total cluster and total DM mass of a supercluster in the simulation. This is interesting since it leads to the possibility of mass calibrations for superclusters in just the same way as is done for estimating the total mass of a cluster with its observables. Our aim here is not to provide an exact fitting formulae to calibrate the masses, but to test experimentally how well superclusters are represented in clusters, and to diagnose whether this is a viable way forward with future cluster survey missions. With the definition of the mass fraction as the ratio between the total cluster mass and the true supercluster mass, we study the typical mass fraction of a supercluster that is made up of clusters, and explore whether there is any dependency on the mass limit imposed by an observation. The estimated true mass of a cluster relies on cosmology and a scaling relation in the real observation. However, using simulations where the true mass is known, we can skip these two constraints to directly calculate the mass fraction.
As explained above, the true mass of a supercluster is defined to be the sum of all halos in the volume with the assumption that the simulation mass resolution is sufficiently low. As was mentioned at the beginning of Sect. 3, particles that do not contribute to M200 are excluded in our work. However, we took them into account when calculating the total halo mass of a supercluster as a correction factor, with the reasonable assumption that these particles are spatially distributed in an unbiased way. This correction factor, taken as the ratio between the total halo mass and the total particle mass in the simulation, is 2.02 in our particular case, and is accounted for in the following result. For convenience we denote the total cluster mass in a supercluster as CM, and the total mass traced by halos in the same supercluster as HM so that the mass fraction is defined as CM/HM1.
 |
Fig. 7 Total mass of a supercluster probed by the total mass of member clusters. The sum of the member cluster masses (CM) is plotted as a function of the true supercluster mass, i.e. the total halo masses (HM) with the correction factor applied (see text for details). The superclusters in the CS catalogue are shown in the upper panel, those in the GCS in the lower one. We show a power-law fit as a solid line with 2σ scatter of data points as dashed lines. |
Figure 7 shows the comparison of the total mass estimates CM as a function of the HM for the two nominal mass limits, 1014 h-1 M⊙ in the upper and 1013 h-1 M⊙ in the lower panel. Note that the lack of scatter at the upper limit in both panels arises because in particular for close pairs, the cluster masses make up most of the supercluster mass, and this limit cannot be exceeded. This effect is pronounced because of the applied definition of the cluster volume with an extent of the supercluster which coincides with its outermost cluster member. A more generous volume definition will make this cut-off less sharp. This effect also appears in Fig. 8. A naive expectation is that the mass fraction increases as the mass limit for the constituent clusters decreases. This is only true if we were considering exactly the same superclusters, where we can imagine lowering the mass threshold to include more smaller halos. However, this does not have to hold if the superclusters vary. The mean for this relation for GCS is 0.39 with one sigma scatter of 0.077, and that for CS is 0.34 with 0.092. As expected, the mass fraction decreases with increasing mass limit of the cluster catalogue. We fit a power-law in Fig. 7 just to guide the eye. The power-law model that we used for the fit is defined by Y = B(X/Xo)A, where X is the HM, Y the CM, Xo = 2 × 1015 h-1 M⊙ the pivot point, and A and B are the fitted slope and amplitude. We applied the same weight over the entire mass range for the chi-square fit, and show two sigma scatter of the data points as dashed lines. The fitted slope is lower than unity over the all mass ranges and decreases towards a larger mass limit. We note that removing percolating superclusters does not change this result because they contribute negligibly to the total number of systems. Given the uncertainty in some of the assumptions made above, we refrain here from using the results to determine supercluster masses until we have explored the supercluster properties in even more detail. Our finding is that the total cluster mass is closely correlated with the total halo mass of a supercluster with a power-law relation, and that the mean scatter of the relation is lower than 40 per cent for all cluster mass limits. This result promises success for estimating the masses of superclusters. More details need to be investigated, especially for alternative volume definitions, to truly exploit the potential of this approach in the future work.
4.2. Cluster density bias against dark matter
The rare density enhancements in our Universe are traced by clusters of galaxies. Clusters have an advantage over other probes of large-scale structure, because fluctuations in their density distribution are more biased to the DM, which allows us to trace the DM distribution very sensitively. Biasing means in this case that the amplitude of the density fluctuations in the cluster distribution is higher by a roughly constant factor compared with the amplitude of DM fluctuations. We studied the bias for the REFLEX II clusters in Balaguera-Antolínez et al. (2012) by calculating the theoretically expected bias based on the formulae given by Tinker et al. (2010), and tested the results against N-body simulations with good agreement for the flux-limited and the volume-limited-sample (VLS) of REFLEX II. For this study the volume-limited results are relevant. For the lower luminosity corresponding to a mass limit of 1014 h-1 M⊙ we find a bias factor of 3.3 and for a mass limit of 1013 h-1 M⊙ a bias factor of 2.1.
The power spectrum of clusters of galaxies measures the distribution of clusters as a function of a scale, where the amplitude ratio of this power spectrum in comparison with the power spectrum of the DM is interpreted as a bias that clusters have. Analogous to the power spectrum of clusters of galaxies, we take the number overdensity of clusters in superclusters as a measure of bias against the DM overdensity, for which we take again the halo mass overdensity as a tracer. This approach makes use of the observable, the number overdensity of clusters, so it can be calibrated against a quantity from the simulation, the DM mass overdensity. The cluster number overdensity is defined as 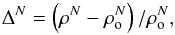 (1)where ρN is the number density of clusters in a supercluster and
(1)where ρN is the number density of clusters in a supercluster and 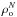 is the mean number density of the clusters in the simulation. Similarly, the halo mass overdensity is defined by
is the mean number density of the clusters in the simulation. Similarly, the halo mass overdensity is defined by 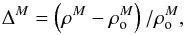 (2)where ρM is the mass density of halos in a supercluster and
(2)where ρM is the mass density of halos in a supercluster and 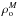 is the mean mass density of the halos in the simulation.
is the mean mass density of the halos in the simulation.
The cluster number overdensity is plotted as a function of the halo mass overdensity in Fig. 8, where the upper plot is for the CS and the lower for the GCS. We indicate the best fit of a power-law model with solid lines, which is given by 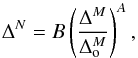 (3)where A and B are the fitted slope and amplitude,
(3)where A and B are the fitted slope and amplitude, 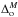 is a pivot point, which is the median of the halo mass overdensity.
is a pivot point, which is the median of the halo mass overdensity.
 |
Fig. 8 Cluster number overdensity, ΔN, as a function of the halo mass overdensity, ΔM, for pair (grey dots) and richer superclusters (black dots). The best-fit model (solid line) is shown for the CS (upper panel) and the GCS (lower panel). The fitted slope and amplitude for different mass limits for the cluster catalogues are shown in Fig. 9. |
The fitted slope (lowest curve) and amplitude (three upper curves) as a function of limiting mass are shown in Fig. 9. The errors were calculated by one thousand bootstrap simulations where we randomly resampled the halo mass overdensity. The mean of the slope remains nearly constant at around 1.1 with a very small scatter for all mass limits. For purely linear bias we would expect a slope of unity. That we find a slope of 1.1 shows that any non-linear effects must be very moderate and the linear bias picture works as a good approximation. Thus we proceed to interpret the scale factor, 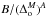 , that relates ΔN and ΔM as a bias. We find that the bias is 1.83 for the 1013 h-1 M⊙ limit, and 3.36 for the 1014 h-1 M⊙. This is in reasonable agreement with the expected bias calculated from the cluster power spectrum for the REFLEX II quoted at the beginning of this section. We note that completely removing the percolating objects identified in Sect. 2.1.3 modifies the best fit by 0.3−0.5% in all mass ranges, hence this result is robust.
, that relates ΔN and ΔM as a bias. We find that the bias is 1.83 for the 1013 h-1 M⊙ limit, and 3.36 for the 1014 h-1 M⊙. This is in reasonable agreement with the expected bias calculated from the cluster power spectrum for the REFLEX II quoted at the beginning of this section. We note that completely removing the percolating objects identified in Sect. 2.1.3 modifies the best fit by 0.3−0.5% in all mass ranges, hence this result is robust.
A closer look at the data shows that pair superclusters have a higher effective bias than richer systems. Because pairs contain a large fraction of extremely compact objects, we also calculated the median bias for the systems richer than pairs. To do this we considered the pairs and richer systems separately by fitting the amplitude for each population while fixing the slope of the relation to that found above. The result of the fit is shown in Fig. 9 . The fair agreement between the cluster biases calculated by the power spectrum and the mass fraction approaches is encouraging because the cluster number overdensity clearly extends into the extreme non-linear regime with overdensities up to 1000, whereas the calculated bias of the power spectrum is mainly based on linear theory. This result motivates the study in Sect. 5 where we will quantitatively test how much this non-linear environment differs from the field.
 |
Fig. 9 Fitted slope and amplitude for the mass bias as a function of the mass limit in the cluster catalogue. The mean of the slope is 1.1, which remains nearly constant over the cluster mass limit range (lower solid line), while the amplitude increases with the increasing mass limit (solid). The errors are calculated with one thousand bootstrappings of the sample. In comparison we show the fitted amplitude of the pair (dotted) and richer (dashed) superclusters separately where the slope is fixed to the fitted slope for the entire sample. |
5. Supercluster environment
To answer the question how rare superclusters are in the Universe, we study in this section the volume fraction that superclusters occupy in the simulation volume. This fraction is equivalent to the probability for a randomly chosen point to lie in superclusters. The rareness and the cluster overdensity in superclusters characterise superclusters as a special environment. Thus we study whether we find different cluster properties in the dense supercluster environment compared with the field in terms of a mass distribution, which are then compared with the X-ray luminosity functions obtained with the REFLEX II superclusters.
5.1. Volume fraction
The first quantity we measured is the volume occupied by superclusters, and calculated the volume fraction, which is defined as a ratio of the total volume of superclusters to the simulation volume.
 |
Fig. 10 Volume fraction of superclusters in the simulation as a function of limiting mass. Richer (solid) and pair (dotted) superclusters are shown. The pair fraction is multiplied by a factor of five for clarity. For comparison we also show the volume fraction of rich superclusters by removing the total volume of possibly percolating superclusters (dashed). The total supercluster volume is completely dominated by the volume of the richer systems, and the pairs occupy an almost constant volume fraction over the mass range. |
Figure 10 shows the volume fraction of rich superclusters. We also explored the contribution from percolated systems to the volume of rich superclusters by removing it completely. For the lowest mass limit the volume fraction of all superclusters is roughly 12.5 per cent, while at the 1014 h-1 M⊙ limit, the fraction decreases to less than 5.4 per cent. In most of the mass range there are typically about five superclusters that may be responsible for the percolation, and the range of volume fraction of those superclusters is 3−20% of the total supercluster volume. This is the largest effect of percolation seen in the properties that we considered in this paper. It is not surprising that most of the total supercluster volume consists of the volume of richer systems. The volume taken up by the pairs is negligible in comparison and remains nearly constant over the entire mass range. This is because the construction of pairs only depends on the linking length, which depends on the number density of the clusters in the volume and the distance between two cluster members. A large fraction of pairs has distances much smaller than the linking length. It is interesting to note that the number fraction of clusters, defined as the number of clusters in superclusters to the total number of clusters in the simulation, is 55 per cent for CS and increases to 64 per cent for GCS. The number of pair superclusters is roughly half the total number of superclusters.
This finding is in line with the observational result reported in C13 for the VLS of REFLEX II. The volume fraction of superclusters in this sample was determined to be two per cent, while slightly more than half of the clusters belong to superclusters. The X-ray luminosity limit of the VLS is 5 × 1043 erg s-1, approximately comparable to a mass limit of 2 ×1014 h-1 M⊙ below redshift z = 0.1 for the scaling relation in Böhringer et al. (2014). Considering this limiting mass of the VLS, we find that the corresponding volume fraction of the simulation is 3.4 per cent. Both the observation and simulation results show how rare these superclusters are, and that they might be interesting study objects probing the non-linear regime of the Universe.
5.2. Mass function
One of the important findings of C13 is that the luminosity function of superclusters in the VLS compared with that of the field is top-heavy, meaning that there are more luminous clusters in superclusters than in the field. This implies that superclusters provide a special environment for the non-linear structures to grow. One possible reason put forward by C13 is that X-ray luminosity is tightly correlated with the mass of a cluster. This top-heavy luminosity function implies the top-heaviness of a mass function of clusters in superclusters. An alternative reason might also be an increased frequency of the cluster merger rate due to enhanced interactions of clusters, where the central region of the cluster is temporarily compressed, giving rise to an increased X-ray luminosity. To numerically quantify the difference in the X-ray luminosity function, C13 subjected the cumulative X-ray luminosity function to a KS test. Here we equivalently form the cumulative mass function with the simulation.
 |
Fig. 11 Cumulative mass fraction of clusters inside (solid) and outside the superclusters (dashed) for the CS (grey) and GCS. |
Figure 11 shows the cumulative mass functions of the two populations of clusters, those in superclusters and those in the field for the CS and GCS. To compare these two unbinned cumulative mass functions we used the KS test as in C13 to calculate the significance of the difference in the two distributions. The KS test shows that the probability that both distributions drawn from the same function is 4.4 × 10-10 for the CS catalogue of Fig. 11, and zero for the GCS. This confirms with very little doubt that the mass function of clusters in superclusters is top-heavy in comparison to that of clusters in the field. This conclusion is in line with what was observed with the REFLEX II clusters in superclusters. The same KS test showed a probability of 0.03 for the REFLEX II superclusters in the VLS. The much lower KS probabilities resulting from the simulation is due to very large number statistics in comparison with the observations. We note that Fig. 11 also spans about a decade larger in the ordinate than Fig. 10 in C13. With this we confirm that both the X-ray luminosity function and the mass function of clusters in superclusters are top-heavy. This is an important evidence that the boost seen in the X-ray luminosity of clusters in an enhanced density region is not just a temporary phenomenon in merging events, but that the mass function of clusters is fundamentally modified so that both mass and luminosity functions in a high-density environment evolve differently from those of the field.
6. Discussion and conclusions
We tested our concept to understand superclusters constructed with a friends-of-friends method on a complete sample of mass-selected or X-ray luminosity selected galaxy clusters by means of dark matter halos from cosmological N-body simulations by applying a set-up equivalent to that used in a typical cluster survey. A friends-of-friends algorithm was applied to DM halos above a mass threshold to construct a supercluster catalogue. One key parameter in this method is the linking length, which is inversely proportional to the overdensity parameter, f. With the simulation we were able to calculate in retrospect the distribution of the number density ratio of clusters in superclusters compared with the mean density in the simulation volume. As a first-order approach motivated by a theoretical spherical collapse model the geometry of a supercluster was assumed to be spherical, and most of superclusters had a higher density ratio than the initial input overdensity with some scatter due to a particular spatial distribution of clusters within a supercluster. This suggests that the fof algorithm provides a reasonable way to construct superclusters, which approximately selects superclusters with pre-defined cluster overdensity.
Our findings are encouraging for future studies that use superclusters as potential tools to probe the properties of the large-scale structure. We considered the fraction of mass that is represented in the cluster content of superclusters in comparison with the total mass. There is a clear power-law correlation between these two quantities, showing that the total member cluster mass in a supercluster is a good first-order estimate of the total mass of a supercluster with a mean scatter of less than 40 per cent. One of our aims in this paper was to learn how the dark matter is traced by superclusters. By comparing the cluster overdensity with the underlying DM overdensity, we verified that the biasing concept as implied in Chon et al. (2013) works. Thus we can indeed select superclusters with prescribed DM overdensity with moderate scatter. In a similar study we examined the cluster number overdensity as a function of the supercluster matter overdensity. The ratio of these two quantities is the bias carried by the clusters in superclusters. We expect that this closely follows the expectation of the bias for the power spectrum of clusters. We find that the relation between the cluster number overdensity and the matter overdensity as a function of the matter overdensity is described well with a power-law model where the slope is within 10% of unity and the amplitude increases as expected from theory with increasing lower mass limit. We interpret the scaling factor between the cluster number density and the halo mass density resulting from the power-law model fit as a bias. For superclusters constructed with the CS the bias is 3.36, while the bias is 1.83 for the GCS supercluster catalogue, which indicates agreement with theory. This implies that the similar bias factors that describe global statistical function such as the power spectrum or the correlation function also applies to local overdensities. Consequently the cluster bias we found reflects once more that superclusters are a special region in our Universe.
This led to the work in Sect. 5 where we tested how the supercluster environment differs from the field by considering the volume occupied by superclusters and the mass function of clusters in superclusters. The volume fraction of superclusters for the VLS-equivalent catalogue is 3.4 per cent, in good agreement with the result of the REFLEX II observations in C13. Superclusters occupy only a very small fraction. A high-density region in our Universe is expected to evolve differently from the background cosmology, and it can be understood as a local universe that evolved from an originally higher mass density. This can be tested by examining the mass function of clusters in superclusters compared with that in the field. We find with a probability close to zero that these two mass functions are drawn from the same parent distribution, confirming that the mass function is top-heavy, analogously to the top-heavy X-ray luminosity function in C13. In both observation and simulation there are more luminous or more massive clusters in superclusters than in the field. Thus we confirm with the volume fraction and the mass function of clusters of galaxies from the simulation, also supported by the REFLEX II observations, that the supercluster environment is distinctly different from the rest of the Universe.
For the first time, this finding is based on the well-understood selection functions of clusters in both simulations and large flux-limited X-ray survey data. It also agrees with previous studies, albeit using different tracer objects to probe superclusters and different methods to construct them, such as Einasto et al. (2003, 2005, 2012). The NORAS II catalogue, complementary to the REFLEX II survey in the Northern sky, is currently being compiled. With this addition the sample will effectively double the current sample size, and will provide an improved ground for further exploration of supercluster properties.
Acknowledgments
We thank the referee for the interesting and constructive comments. We acknowledge support from the DfG Transregio Program TR33 and the DFG cluster of excellence “Origin and Structure of the Universe” (http://www.universe-cluster.de). G.C. acknowledges the support from Deutsches Zentrum für Luft- und Raumfahrt (DLR) with the program 50 OR 1305. The Millennium Simulation databases used in this paper and the web application providing online access to them were constructed as part of the activities of the German Astrophysical Virtual Observatory. We thank Gerard Lemson for his support with the simulation data.
References
- Abell, G. O. 1961, AJ, 66, 607 [NASA ADS] [CrossRef] [Google Scholar]
- Araya-Melo, P. A., Reisenegger, A., Meza, A., et al. 2009, MNRAS, 399, 97 [Google Scholar]
- Bahcall, N. A. 1988, ARA&A, 26, 631 [NASA ADS] [CrossRef] [Google Scholar]
- Bahcall, N. A., & Soneira, R. M. 1984, ApJ, 277, 27 [NASA ADS] [CrossRef] [Google Scholar]
- Balaguera-Antolínez, A., Sánchez, A. G., Böhringer, H., & Collins, C. 2012, MNRAS, 425, 2244 [NASA ADS] [CrossRef] [Google Scholar]
- Batuski, D. J., & Burns, J. O. 1985, AJ, 90, 1413 [NASA ADS] [CrossRef] [Google Scholar]
- Bogart, R. S., & Wagoner, R. V. 1973, ApJ, 181, 609 [NASA ADS] [CrossRef] [Google Scholar]
- Böhringer, H., Dolag, K., & Chon, G. 2012, A&A, 539, A120 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Chon, G., Collins, C. A., et al. 2013, A&A, 555, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Böhringer, H., Chon, G., & Collins, C. A. 2014, A&A, in press, DOI: 10.1051/0004-6361/201323155 [Google Scholar]
- Chon, G., & Böhringer, H. 2012, A&A, 538, A35 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chon, G., Böhringer, H., & Nowak, N. 2013, MNRAS, 429, 3272 [NASA ADS] [CrossRef] [Google Scholar]
- Dünner, R., Araya, P. A., Meza, A., & Reisenegger, A. 2006, MNRAS, 366, 803 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, M., Einasto, J., Tago, E., Dalton, G. B., & Andernach, H. 1994, MNRAS, 269, 301 [NASA ADS] [CrossRef] [Google Scholar]
- Einasto, M., Tago, E., Jaaniste, J., Einasto, J., & Andernach, H. 1997, A&AS, 123, 119 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Einasto, J., Tago, E., Müller, V., & Andernach, H. 2001, AJ, 122, 2222 [CrossRef] [Google Scholar]
- Einasto, M., Jaaniste, J., Einasto, J., et al. 2003, A&A, 405, 821 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Suhhonenko, I., Heinämäki, P., Einasto, J., & Saar, E. 2005, A&A, 436, 17 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, J., Einasto, M., Saar, E., et al. 2007a, A&A, 462, 397 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, J., Einasto, M., Tago, E., et al. 2007b, A&A, 462, 811 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Einasto, M., Liivamägi, L. J., Tempel, E., et al. 2012, A&A, 542, A36 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Hauser, M. G., & Peebles, P. J. E. 1973, ApJ, 185, 757 [NASA ADS] [CrossRef] [MathSciNet] [Google Scholar]
- Johnston, D. E., Sheldon, E. S., Wechsler, R. H., et al. 2007, unpublished [arXiv:0709.1159] [Google Scholar]
- Kalinkov, M., & Kuneva, I. 1995, A&AS, 113, 451 [NASA ADS] [Google Scholar]
- Liivamägi, L. J., Tempel, E., & Saar, E. 2012, A&A, 539, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Luparello, H., Lares, M., Lambas, D. G., & Padilla, N. 2011, MNRAS, 415, 964 [NASA ADS] [CrossRef] [Google Scholar]
- Luparello, H. E., Lares, M., Yaryura, C. Y., et al. 2013, MNRAS, 432, 1367 [NASA ADS] [CrossRef] [Google Scholar]
- Peebles, P. J. E. 1974, Ap&SS, 31, 403 [NASA ADS] [CrossRef] [Google Scholar]
- Pratt, G. W., Croston, J. H., Arnaud, M., & Böhringer, H. 2009, A&A, 498, 361 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rood, H. J. 1976, ApJ, 207, 16 [NASA ADS] [CrossRef] [Google Scholar]
- Seljak, U., & Warren, M. S. 2004, MNRAS, 355, 129 [NASA ADS] [CrossRef] [Google Scholar]
- Shandarin, S. F., Sheth, J. V., & Sahni, V. 2004, MNRAS, 353, 162 [NASA ADS] [CrossRef] [Google Scholar]
- Sheldon, E. S., Johnston, D. E., Masjedi, M., et al. 2009, ApJ, 703, 2232 [NASA ADS] [CrossRef] [Google Scholar]
- Springel, V., White, S. D. M., Jenkins, A., et al. 2005, Nature, 435, 629 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Thuan, T. X. 1980, in Physical Cosmology, Proc. Les Houches Summer School, eds. R. Balian, J. Audouze, & D. N. Schramm, 277 [Google Scholar]
- Tinker, J. L., Robertson, B. E., Kravtsov, A. V., et al. 2010, ApJ, 724, 878 [NASA ADS] [CrossRef] [Google Scholar]
- West, M. J. 1989, ApJ, 347, 610 [NASA ADS] [CrossRef] [Google Scholar]
- Zucca, E., Zamorani, G., Scaramella, R., & Vettolani, G. 1993, ApJ, 407, 470 [NASA ADS] [CrossRef] [Google Scholar]
All Figures
 |
Fig. 1 Normalised multiplicity function of the superclusters for a range of overdensity parameters, f, constructed with the halos in the CS (black solid line), and with those in the GCS (grey dashed line). The value of f is indicated in each panel. Richer systems are abundant with decreasing f, which is equivalent to a longer linking length (upper left panel), while less rich systems are more common with higher f values (lower right panel). |
| In the text | |
 |
Fig. 2 Distribution of the normalised extent of the superclusters. The superclusters in the CS are shown in black, those in the GCS in grey. Superclusters with three or more member clusters are marked by a dashed line, pair superclusters by a solid line. |
| In the text | |
 |
Fig. 3 Cumulative volume fraction of superclusters as a function of normalised multiplicity. The CS is shown as filled circles, GCS as continuous lines. For the same mass limit the catalogues built with f = 2 are shown in grey, and f = 10 in black. Four asterisks mark the estimated starting scale of the percolation. |
| In the text | |
 |
Fig. 4 Measured number density ratio of the clusters in the CS. The cluster number density ratio is defined as the ratio between the cluster density in a supercluster and the mean cluster density in the simulation. |
| In the text | |
 |
Fig. 5 Multiplicity of superclusters shown as a function of their extent for the CS as in Fig. 4. The open circles represent the superclusters with a measured density ratio below ten in Fig. 4. |
| In the text | |
 |
Fig. 6 Distribution of all halos in the largest supercluster cut through two axes, in X–Y (upper), and in X–Z (lower). The offsets are in units of Mpc h-1. The member clusters are shown as filled circles, and all other halos less massive than the mass limit as grey dots, where the centre of mass is located at the origin. This supercluster, taken as an example from Fig. 4, represents superclusters with a measured density ratio lower than ten. Typically, the member clusters of these superclusters form a thin filament along one axis, which causes an over-estimation of a supercluster volume, leading to an under-estimation of the measured density ratio. The open circles mark the clusters belonging to the neighbouring superclusters whose volumes overlap with the volume of the main supercluster according to the definition of the extent. |
| In the text | |
 |
Fig. 7 Total mass of a supercluster probed by the total mass of member clusters. The sum of the member cluster masses (CM) is plotted as a function of the true supercluster mass, i.e. the total halo masses (HM) with the correction factor applied (see text for details). The superclusters in the CS catalogue are shown in the upper panel, those in the GCS in the lower one. We show a power-law fit as a solid line with 2σ scatter of data points as dashed lines. |
| In the text | |
 |
Fig. 8 Cluster number overdensity, ΔN, as a function of the halo mass overdensity, ΔM, for pair (grey dots) and richer superclusters (black dots). The best-fit model (solid line) is shown for the CS (upper panel) and the GCS (lower panel). The fitted slope and amplitude for different mass limits for the cluster catalogues are shown in Fig. 9. |
| In the text | |
 |
Fig. 9 Fitted slope and amplitude for the mass bias as a function of the mass limit in the cluster catalogue. The mean of the slope is 1.1, which remains nearly constant over the cluster mass limit range (lower solid line), while the amplitude increases with the increasing mass limit (solid). The errors are calculated with one thousand bootstrappings of the sample. In comparison we show the fitted amplitude of the pair (dotted) and richer (dashed) superclusters separately where the slope is fixed to the fitted slope for the entire sample. |
| In the text | |
 |
Fig. 10 Volume fraction of superclusters in the simulation as a function of limiting mass. Richer (solid) and pair (dotted) superclusters are shown. The pair fraction is multiplied by a factor of five for clarity. For comparison we also show the volume fraction of rich superclusters by removing the total volume of possibly percolating superclusters (dashed). The total supercluster volume is completely dominated by the volume of the richer systems, and the pairs occupy an almost constant volume fraction over the mass range. |
| In the text | |
 |
Fig. 11 Cumulative mass fraction of clusters inside (solid) and outside the superclusters (dashed) for the CS (grey) and GCS. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


