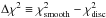| Issue |
A&A
Volume 564, April 2014
|
|
|---|---|---|
| Article Number | A27 | |
| Number of page(s) | 24 | |
| Section | Stellar structure and evolution | |
| DOI | https://doi.org/10.1051/0004-6361/201322779 | |
| Published online | 31 March 2014 | |
Seismic constraints on the radial dependence of the internal rotation profiles of six Kepler subgiants and young red giants⋆
1 Université de Toulouse, UPS-OMP, IRAP, 31028 Toulouse, France
e-mail: sebastien.deheuvels@irap.omp.eu
2 CNRS, IRAP, 14 avenue Edouard Belin, 31400 Toulouse, France
3 High Altitude Observatory, National Center for Atmospheric Research, PO Box 3000, Boulder CO 80307, USA
4 Stellar Astrophysics Centre, Department of Physics and Astronomy, Aarhus University, Ny Munkegade 120, 8000 Aarhus C, Denmark
5 LESIA, UMR8109, Observatoire de Paris, Université Pierre et Marie Curie, Université Denis Diderot, CNRS, 5 place Jules Janssen, 92195 Meudon Cedex, France
6 Institut d’Astrophysique Spatiale, UMR8617, Université Paris XI, Bâtiment 121, 91405 Orsay Cedex, France
7 Sydney Institute for Astronomy (SIfA), School of Physics, University of Sydney, NSW 2006 Sydney, Australia
8 Aarhus Katedralskole, Skolegyde 1, 8000 Aarhus C, Denmark
9 School of Physics and Astronomy, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK
10 Research School of Astronomy and Astrophysics, Mount Stromlo Observatory, The Australian National University, ACT 2611 Mont Stromlo, Australia
11 Laboratoire AIM Paris-Saclay, CEA/DSM-CNRS-Université Paris Diderot, IRFU/SAp, Centre de Saclay, 91191 Gif-sur-Yvette Cedex, France
12 Royal Observatory of Belgium, Ringlaan 3, 1180 Ukkel, Belgium
13 Department of Astronomy, Beijing Normal University, 100875 Beijing, PR China
14 Institut d’Astrophysique et de Géophysique de l’Université de Liège, allée du 6 Août 17, 4000 Liège, Belgium
15 Instituto de Astrofísica de Canarias, 38205 La Laguna, Tenerife, Spain
16 Universidad de La Laguna, Dpto de Astrofísica, 38206 La Laguna, Tenerife, Spain
17 Institut für Astrophysik, Georg-August-Universität Göttingen, 37077 Göttingen, Germany
18 Zentrum für Astronomie der Universität Heidelberg, Landessternwarte, Königstuhl 12, 69117 Heidelberg, Germany
19 Observatoire de Genève, Université de Genève, 51 Ch. des Maillettes, 1290 Sauverny, Suisse
20 Max-Planck-Institut für Sonnensystemforschung, 37191 Katlenburg-Lindau, Germany
21 Instytut Astronomiczny Uniwersytetu Wrocławskiego, ul. Kopernika 11, 51-622 Wrocław, Poland
22 Department of Astronomy, the Ohio State University, Columbus OH 43210, USA
Received: 2 October 2013
Accepted: 24 January 2014
Context. We still do not understand which physical mechanisms are responsible for the transport of angular momentum inside stars. The recent detection of mixed modes that contain the clear signature of rotation in the spectra of Kepler subgiants and red giants gives us the opportunity to make progress on this question.
Aims. Our aim is to probe the radial dependence of the rotation profiles for a sample of Kepler targets. For this purpose, subgiants and early red giants are particularly interesting targets because their rotational splittings are more sensitive to the rotation outside the deeper core than is the case for their more evolved counterparts.
Methods. We first extracted the rotational splittings and frequencies of the modes for six young Kepler red giants. We then performed a seismic modeling of these stars using the evolutionary codes Cesam2k and astec. By using the observed splittings and the rotational kernels of the optimal models, we inverted the internal rotation profiles of the six stars.
Results. We obtain estimates of the core rotation rates for these stars, and upper limits to the rotation in their convective envelope. We show that the rotation contrast between the core and the envelope increases during the subgiant branch. Our results also suggest that the core of subgiants spins up with time, while their envelope spins down. For two of the stars, we show that a discontinuous rotation profile with a deep discontinuity reproduces the observed splittings significantly better than a smooth rotation profile. Interestingly, the depths that are found to be most probable for the discontinuities roughly coincide with the location of the H-burning shell, which separates the layers that contract from those that expand.
Conclusions. We characterized the differential rotation pattern of six young giants with a range of metallicities, and with both radiative and convective cores on the main sequence. This will bring observational constraints to the scenarios of angular momentum transport in stars. Moreover, if the existence of sharp gradients in the rotation profiles of young red giants is confirmed, it is expected to help in distinguishing between the physical processes that could transport angular momentum in the subgiant and red giant branches.
Key words: asteroseismology / stars: rotation / stars: interiors / stars: evolution
Appendices and Tables 3–9 are available in electronic form at http://www.aanda.org
© ESO, 2014
1. Introduction
Rotation is a key element for understanding stellar structure and evolution. However, the way in which angular momentum (AM) is transported inside stars remains uncertain. Hydrodynamic mechanisms and meridional circulation as currently implemented in 1D stellar evolution codes are not efficient enough to account for the solid-body rotation of the solar radiative interior (Zahn 1992; Mathis & Zahn 2004), which has been found through helioseismology (Schou et al. 1998; Chaplin et al. 1999; García et al. 2004; Eff-Darwich & Korzennik 2013). Other processes are probably at work, such as transport through internal gravity waves (e.g. Charbonnel & Talon 2005), through a fossil magnetic field (e.g. Gough & McIntyre 1998), or through magnetic instabilities (e.g. Spruit 1999). However, the importance of the contributions of these processes, as well as the timescales over which they operate, are still unclear.
Asteroseismology can make a significant contribution to this debate by providing observational constraints on the internal rotation profiles of stars. Indeed, rotation is known to lift the degeneracy between non-radial modes of same radial orders and degrees, but different azimuthal orders, and the frequency splitting between these modes (known as rotational splitting) is directly linked to the internal rotation. The space missions CoRoT (Baglin et al. 2006) and Kepler (Borucki et al. 2010) are providing us with unprecedentedly long time series, which have already made it possible to measure rotational splitting for certain stars. For instance, an average of the internal rotation of the main-sequence CoRoT target HD 52265 was successfully estimated by interpreting the observed rotational splitting (Ballot et al. 2011; Gizon et al. 2013). The Kepler satellite, by observing stars over several years, gave the opportunity to measure the rotational splitting of the modes for hundreds of red giants (Mosser et al. 2012b). This result is all the more interesting, since in these stars the non-radial modes have a mixed character: they behave as pressure modes (p modes) in the envelope and as gravity modes (g modes) in the core (Osaki 1975; Aizenman et al. 1977). Mixed modes were first detected from the ground (Kjeldsen et al. 1995) and then from space with CoRoT (Deheuvels & Michel 2010) and Kepler (e.g. Metcalfe et al. 2010; Mathur et al. 2011; Appourchaux et al. 2012). They have already made it possible to probe the core structure of subgiants (Deheuvels & Michel 2011; Benomar et al. 2013) and red giants (Beck et al. 2011; Mosser et al. 2012c), thus allowing us to distinguish RGB stars from clump stars (Bedding et al. 2011; Mosser et al. 2011). The interpretation of the rotational splitting of mixed modes in several red giants showed that there exists a strong radial differential rotation in these stars, with the core rotating at least five times faster than the envelope (Beck et al. 2012; Deheuvels et al. 2012a). Mosser et al. (2012b) found that this is a general feature of red giants, and showed that the core of these stars spins down as they ascend the red giant branch (RGB), in spite of the contraction of the central layers, which should spin it up if AM were conserved. This implies effective AM transport during the ascent of the RGB.
Different classes of theoretical models predict radically different core rotation rates for giants depending on the efficiency of AM transport. The limiting case of an instantaneous exchange of AM (strong core-envelope coupling) for first ascent giant stars would imply that they rotate rigidly, which is clearly inconsistent with the detected level of differential rotation. On the other hand, for higher-mass secondary clump stars, Tayar & Pinsonneault (2013) found that the measured core rotation rates are consistent with strongly coupled models. This is probably linked to the expectedly higher rotation of these stars when they leave the main sequence, compared to their low-mass counterparts. Core rotation for first-ascent giants obtained from asteroseismology is both much faster than predicted from strongly coupled models and slower by several orders of magnitude than expected from models with hydrodynamic AM transport (Eggenberger et al. 2012; Marques et al. 2013; Ceillier et al. 2013), showing the need for a more efficient source of AM transport in these stars. Attempts were recently made to estimate the timescale of AM exchange on the RGB. Eggenberger et al. (2012) found that the ad hoc diffusion coefficients that are required to explain the timescale for core-envelope decoupling in young MS stars (e.g. Denissenkov et al. 2010) can also reproduce the core rotation rates of some giants, suggesting that similar mechanisms might be at play. Assuming a solar-like rotation profile on the MS, Tayar & Pinsonneault (2013) showed that the detected core rotation is consistent with post-MS decoupling during the first dredge-up phase. However, the nature of the physical process responsible for core-envelope coupling remains unknown.
Until now, the interpretation of rotational splittings of red giants brought information exclusively on the rotation of the innermost layers of the star because the rotational kernels of red giants are most sensitive to these regions (Goupil et al. 2013). However, constraining the radial dependence of the rotation profile would undoubtedly provide useful information on the processes of AM transport that are at work. For this purpose, subgiants and young red giants are particularly interesting targets because their rotational splittings are more sensitive to the rotation of the envelope than is the case in more evolved stars. We selected six Kepler subgiants and young red giants that seemed most favorable to probing the internal rotation profile. The selection process is described in Sect. 2. We first extracted the frequencies and rotational splittings of the oscillation modes by analyzing the power spectra of the six targets (Sect. 3). In Sect. 4, we present the atmospheric parameters that were available for these stars prior to this study. Since two of the stars had not been observed spectroscopically before, we observed them from the ground, and the results are presented in Sect. 4. To interpret the observed splittings, we searched for stellar models that reproduce both the surface observables and the observed mode frequencies in Sect. 5. By using these, we performed inversions of the internal rotation profiles of these stars, which are presented in Sect. 6. We obtained precise estimates of the core and the envelope rotation rates of these stars, and we show that for two of them a discontinuous rotation profile with a discontinuity located near the H-burning shell reproduces the observed splittings significantly better than a smooth rotation profile.
Global seismic parameters of the selected targets and estimates of the stars’ masses, radii, and surface gravity inferred from scaling relations.
2. Selection of targets
Among the Kepler targets, we searched for stars for which the internal rotation profile can be probed by following a similar procedure as the one adopted by (Deheuvels et al. 2012a, hereafter D12) for KIC 7341231. For this purpose, the stars had to satisfy the following criteria:
-
The stars need to have been observed over a long enough period so that the frequency resolution is much lower than the rotational splittings. We selected stars that were observed over at least five quarters (~470 days), which corresponds to a frequency resolution below 0.02 μHz.
Their modes should have a linewidth significantly smaller than the rotational splittings, to ensure that the m-components of the rotational multiplets are well separated. It has been shown by Appourchaux et al. (2012) that the mode linewidths increase very rapidly with increasing temperature (
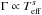 , with s ~ 16). As a result, only the cooler targets have narrow enough modes to make the rotational splittings of the modes clearly visible.
, with s ~ 16). As a result, only the cooler targets have narrow enough modes to make the rotational splittings of the modes clearly visible. We restricted ourselves to stars that are not too evolved. Indeed, the core of subgiants and young red giants is less dense than that of more evolved star, which makes their rotational splittings more sensitive to the rotation in other regions than the innermost layers. In addition, young red giants can be modeled by using existing fitting procedures. For these stars, the combined knowledge of the large separation of acoustic modes Δν and the period spacing ΔΠ1 of l = 1 gravity modes can yield precise estimates of the stellar mass and age for a given set of input physical parameters. This can be used to model these stars (Deheuvels & Michel 2011). For more evolved red giants, the relation between Δν, ΔΠ1, and the stellar mass becomes degenerate (for a given large separation Δν, a large change in mass induces almost no change in ΔΠ1). This degeneracy occurs for stars whose mean large separation is below a threshold limit that varies between 30 and 40 μHz depending on the stellar mass (Mosser et al. 2012c). We therefore retained only stars with ⟨ Δν ⟩ > 30 μHz.
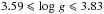 ), and they lie either at the end of the subgiant branch or at the base of the RGB. The absence of younger subgiants is caused by the fact that they are hotter. As a result, their modes have larger linewidths and it is much harder to extract their rotational splittings.
), and they lie either at the end of the subgiant branch or at the base of the RGB. The absence of younger subgiants is caused by the fact that they are hotter. As a result, their modes have larger linewidths and it is much harder to extract their rotational splittings.
 |
Fig. 1 Location of the selected targets in a seismic HR diagram (mean large separation Δν against effective temperature). The blue filled stars indicate the six targets selected in our sample and the gray diamonds correspond to the set of Kepler targets studied by Chaplin et al. (2014). The dashed lines indicate evolutionary tracks of models of different masses and solar metallicity. |
3. Seismic properties
The frequencies of the oscillation modes bear information about the internal structure of a star, and in particular about its internal rotation. Indeed, rotation is known to lift the degeneracy between the non-radial modes of same radial order n and degree l but different azimuthal order m, thus forming rotational multiplets. For slow rotators, the effects of the centrifugal force can be neglected, and if we furthermore assume that the rotation profile is spherically symmetric, the frequency of the (n,l,m) mode can be written as νn,l,m = νn,l,0 + mδνn,l, where δνn,l is known as the rotational splitting and can be expressed as a weighted average of the rotation profile Ω(r)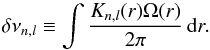 (1)The functions Kn,l(r), known as the rotational kernels, essentially depend on the mode eigenfunctions.
(1)The functions Kn,l(r), known as the rotational kernels, essentially depend on the mode eigenfunctions.
Our goal in the analysis of the oscillation spectra of the stars was twofold:
-
1.
estimating the mode frequencies to use them as observables for the modeling of the stars (see Sect. 5); this requires first to identify the modes in the oscillation spectra;
-
2.
extracting the rotational splittings to invert the internal rotation profiles (see Sect. 6).
3.1. Kepler observations
The targets selected for this study have been observed with Kepler over periods ranging from 470 to 650 days2 with the short-cadence mode (integration time of 58.84876 s). Corrections have been applied to the raw Kepler time series: the light curves were processed using the Kepler pipeline developed by Jenkins et al. (2010), and they were additionally corrected for outliers, occasional jumps, and drifts following García et al. (2011). Long-period instrumental drifts were also corrected for by subtracting a smoothed version of the light curve over a width of 1 day.
The power density spectra of the selected stars were obtained by using the Lomb-Scargle periodogram (Lomb 1976; Scargle 1982). They all clearly show the signature of solar-like oscillations in frequency intervals that range from about [300;550] μHz for the most evolved target (star F) to approximately [550;950] μHz for the least evolved one (star A).
3.2. Identification of the modes
First estimates of the mean large separation of acoustic modes ⟨ Δν ⟩ were obtained by computing an autocorrelation of the power spectra. We built échelle diagrams for the six stars using these estimates of the large separation. In all of them, the neighboring ridges that correspond to l = 0 and l = 2 modes can easily be identified. We then fine-tuned our estimates of ⟨ Δν ⟩ so that the l = 0 ridge is as vertical as possible in the échelle diagram (see Fig. 2). The corresponding values of ⟨ Δν ⟩ are given in Table 1. We note that these estimates might be refined by taking into account the curvature of the l = 0 ridge (Mosser et al. 2013), but in our study the models were constrained using the individual frequencies of the oscillation modes, which contain more precise information on the structure than the mean large separation (see Sects. 3.3.2 and 5). The l = 1 modes all have a mixed behavior, which makes it harder to identify them. The stars we selected have an evolutionary status that is intermediate between the subgiants, for which the g modes that lie in the frequency range of observations have low radial orders (n ~ 1), and typical RGB stars, for which the radial orders of g modes are huge (n ~ 100, Mosser et al. 2012c). Mosser et al. (2012c) proposed a method to identify the degree of the detected mixed modes based on asymptotic relations, which they successfully applied to hundreds of red giants. We used this method to obtain first estimates of the frequencies of l = 1 modes for the six stars.
 |
Fig. 2 Échelle diagrams of the stars from our sample. The mean large separations that were used to build the diagrams are specified in Table 1. For more clarity, the power spectra were binned over a 0.25 μHz boxcar and clipped at a maximum of 20 to 40 times the noise level. |
3.3. Extracting the mode frequencies and rotational splittings
To obtain estimates of the frequencies and rotational splittings of the observed modes, we fitted a model of the power spectral density (PSD) to the power spectra of the six stars. We followed a procedure that is very similar to the one adopted by D12. We here only briefly summarize it, with an emphasis on the few differences.
3.3.1. Model of the PSD
The background was fitted prior to extracting the mode parameters by using a maximum-likelihood estimation (MLE) method in the same way as described in D12. The contribution from granulation to the background was modeled as a Harvey profile (Harvey 1985), and white noise was added, corresponding to photon noise. Karoff et al. (2013) have recently shown that an additional component with a timescale intermediate between that of granulation and the periods of the acoustic modes is needed. This component might be attributed to bright points (Aigrain et al. 2004), a second granulation population (Vázquez Ramió et al. 2005), or more likely faculae based on its timescale (Karoff 2012; Karoff et al. 2013). In this study, we also found that a background including only the contribution from granulation poorly reproduces the observations (see the example of KIC 9574283 in Fig. 3). We thus included an additional Harvey profile, which greatly improved the agreement with the observations (Fig. 3). In the following, the background parameters were held fixed to their fitted values when extracting the mode parameters. We note that to fit the background, the component of the PSD that corresponds to solar-like oscillations was modeled as a Gaussian function. Its central frequency provides an estimate of the frequency of maximum power of the oscillations νmax. The values that were obtained are listed in Table 1.
The stochastically excited oscillation modes were modeled as Lorentzian functions. We assumed that the modes are split by rotation following Eq. (1). We note that in fact, theoretical models predict a fast rotation for the cores of red giants, which could in certain cases invalidate the linear dependence of the splittings on the rotation rate expressed by Eq. (1) (e.g. Marques et al. 2013; Ceillier et al. 2013). In this case, a non-perturbative approach is needed (Ouazzani et al. 2013). However, Kepler observations have shown that the core rotation of red giants is in fact much slower, making the use of Eq. (1) relevant (D12, Mosser et al. 2012b). For the stars of our sample, the l = 1 rotational multiplets show clear symmetry, which justifies the use of linear splittings. The case of l = 2 modes is more complex and is discussed in Sect. 3.3.2.
Within the rotational multiplets, the modes were assumed to have a common width. The ratios between their heights hl,m are given by a visibility factor that depend only on the inclination angle of the star (Gizon & Solanki 2003; Ballot et al. 2006). For global fits, each rotational multiplet thus contributes four free parameters (frequency, height, width, and rotational splittings). One additional free parameter is needed: the inclination angle, which is common to all the modes. For local fits, the inclination angle is left free for all the multiplets, which means that there are five free parameters per multiplet.
Usually, for main-sequence stars, the ratio between the height hl of a multiplet of degree l (defined as the sum of the heights of its components, i.e. hl ≡ ∑ mhl,m) and the height of the closest radial mode h0 is given by a geometric factor obtained by integration over the stellar disk, taking into account the limb-darkening profile. For Kepler stars, typical ratios are h1/h0 = 1.5 and h2/h0 = 0.5 (Ballot et al. 2011). These ratios do not necessarily hold for stars with mixed modes such as the targets of our sample. Indeed, some non-radial modes are mainly trapped in the core and their longer lifetimes prevent us from resolving them, even with 650 days of data. In this case, the mode height depends on the mode inertia (Dupret et al. 2009) and the theoretical visibility ratios are inappropriate. Moreover, recent observations have shown that these visibility ratios vary from one star to another for red giants (Mosser et al. 2012a; Benomar et al. 2013). The mode heights were thus left free in our fits.
 |
Fig. 3 Power spectrum of KIC 9574283 (smoothed over a 10 μHz boxcar) computed with 650 days of Kepler data (gray curve). Two Harvey-type laws (solid black lines) had to be considered to reproduce the shape of the background. The fitted background is represented by the dashed blue line, while the long-dashed red line shows the background that is obtained with only one Harvey profile. The dotted line shows the contribution from the photon noise. |
Characteristics of the fit performed by each fitting group to extract the mode frequencies and rotational splittings from the power spectra.
3.3.2. Results
Two types of fits of the PSD were performed to estimate the mode frequencies and splittings. Six independent teams followed a frequentist approach and used the MLE method, as is commonly done for the analysis of stochastically excited modes. The main difference between these analyses lies in the initial guesses taken for the mode parameters and the type of fitting that was chosen: either a global fit (all the modes are fitted simultaneously) as prescribed by Appourchaux et al. (2008), or a local one (modes are fitted individually), as was done for the Sun (Anderson et al. 1990). Apart from the computational time (which is much shorter for local fits), the only difference between the two approaches is that local fits consider the inclination angle as a free parameter for each mode, whereas the angle is common to all modes in global fits. This enabled us to check the robustness of the optimal angle that is obtained from global fits. One other team fitted the PSD by using a Bayesian approach coupled with a Markov chain Monte Carlo (MCMC) algorithm, following the method described by Benomar et al. (2009). One of the advantages of the latter approach is that it gives access to the probability density function of the fitted parameters. Its computational time is much longer than that of the MLE methods, however. Therefore, we were only able to fit two stars of the sample this way (stars D and F). These two stars were chosen because for them the radial dependence of the rotation profile can be best constrained (see Sect. 6)3. The characteristics of all the fits that were performed are listed in Table 2.
To derive a reliable set of mode frequencies and rotational splittings for the six stars from the results of the different teams, we adopted the following procedure: for each fitted mode, we rejected outliers by applying the Peirce criterion to both the mode frequencies and the rotational splittings in the same way as described by Mathur et al. (2011) (see also Campante et al. 2011; Appourchaux et al. 2012). We then selected only the modes for which at least two fitters agreed within 1σ error bars (maximal mode set, as introduced by Metcalfe et al. 2010). We note that prior to applying the Peirce criterion, a first selection had to be made. Indeed, for a few modes, the splittings found by one team correspond to half or twice the value that is found by the other teams. This can arise when the initial guess for the splittings is too far off, which can lead to a wrong identification of the m components of the multiplet (for instance an m = −1/m = + 1 pair is mistaken for an m = 0/m = + 1 pair). If these wrong splitting estimates were kept, the mean value of the data set would be significantly altered and the first iteration of the Peirce criterion would reject all the data points. We thus found it necessary to discard them first.
Surface parameters.
For the modes that were rejected by the Peirce criterion, we identified several sources of disagreement:
-
At higher frequency, the mode linewidths increase and for several stars, they become larger than the rotational splittings, which prevents us from measuring them. For these modes, the agreement between the teams on the estimated frequencies remained good in most cases, but there are large disagreements on their splittings.
Problems were found to arise when the m-components of an l = 1 mode overlap another mode. If this other mode was a radial mode, then the l = 1 mode was usually recovered correctly. However, if it was an l = 2 mode, the components of the two modes were very hard to disentangle and the results obtained from the different teams varied strongly, and they were rejected by the Peirce criterion.
Large disagreements between the teams were also found for the splittings of l = 2 modes when two neighboring l = 2 mixed modes were observed instead of one p-dominated l = 2 mode. This was already pointed out by D12 for KIC 7341231, and Deheuvels et al. (2012b) showed that for early red giants, the l = 2 rotational multiplets that are undergoing an avoided crossing are not symmetric with respect to their central component. This means that Eq. (1) does not apply to these modes, which are thus not considered in the following.
Even though a few l = 3 modes were detected in several stars of the sample, no reliable frequency or rotational splittings could be estimated for these modes. This is mostly caused by their very low signal-to-noise ratio (S/N).
The question of the inclination angle is interesting. So far, all the studies that extracted mode parameters from solar-like pulsators assumed that the inclination angle is the same for all modes. This is true if the whole star rotates about the same axis. While this assumption seems reasonable, it has been questioned before (e.g. Bai & Sturrock 1993 for the Sun). If the core rotates about a different angle than the envelope, we would expect the height ratios within g-dominated multiplets to correspond to an inclination angle that differs from the p-dominated multiplets (Gough & Kosovichev 1993). In this study, three of the six teams performed local fits, leaving the inclination angle free for each mode. This gave us the opportunity to check the common assumption of a single rotation axis in the stars of our sample. We found that the obtained inclination angles vary very little from one mode to another and agree well with the angle that is found from global fits. An example is given for star E (KIC 7799349) in Fig. 4. This shows that the rotation axis of the core is not significantly inclined from the one of the envelope in these stars.
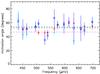 |
Fig. 4 Inclination angles obtained for star E (KIC 7799349). The dashed lines indicate the results of global fits (gray: Campante, green: Davies, blue: Deheuvels, purple: Regulo), and the open symbols correspond to the results of local fits that allow for different angles for each mode (red triangles: Appourchaux, blue squares: Deheuvels, cyan stars: Stahn). |
4. Surface parameters
To characterize the stars of the sample, we derived estimates of their effective temperature and surface metallicity using both spectroscopy and photometry. These estimates will serve as surface observables for our modeling of the stars, which is presented in Sect. 5.
4.1. Spectroscopic observations
Before this study was started, four stars of the sample (stars B, C, D, and E) had already been observed spectroscopically. Since then, star A was also observed by Molenda-Żakowicz et al. (2013), whose results are mentioned below. Star C was observed with the Guo Shou Jing Telescope, also known as the Large sky Area Multi-Object fibre Spectroscopic Telescope, (LAMOST; De Cat et al., in prep.). Stars B, D, and E were among the Kepler targets that were observed by Bruntt et al. (2012) with the ESPaDOnS spectrometer at the 3.6-m Canada-France-Hawaii Telescope (CFHT) in the USA and with the NARVAL spectrometer mounted on the 2 m Bernard Lyot Telescope at the Pic du Midi Observatory in France. The atmospheric parameters obtained by the authors for these stars are given in Table 10.
Specific campaigns of observations were led for the two other stars. Star F was observed with the HERMES instrument of the 1.2-m Mercator Telescope at the Roque de los Muchachos Observatory on La Palma Island (Canary Islands, Spain), which is a high-efficiency bench-mounted échelle spectrograph that observes the complete wavelength range from 420 nm to 900 nm in a single exposure (Raskin et al. 2011). We used the high-resolution fiber mode (R ≃ 80 000) for two concatenated observations of 1800 s. The spectra have a maximum S/N ~ 60 around 600 nm (~35 around 500 nm). The science exposures were co-added to minimize the amount of CCD cosmic-ray hits. The spectra were calibrated using the latest version of the HERMES pipeline (release 4.0) developed at the Royal Observatory of Belgium in collaboration with the HERMES Consortium. Typical calibration steps were performed, including spectral-order tracing and extraction, average flat-fielding, Th-Ar lamp wavelength calibration, and hot-pixel removal using cross-order profiling. The wavelength scale was corrected to the barycentric rest frame, which includes a wavelength-scale rebinning to 0.0015625 nm. The spectrum was analyzed with the semi-automatic software package VWA (Bruntt 2009) and the atmospheric parameters obtained are listed in Table 10.
Star A was observed with the FIber-fed Échelle Spectrograph (FIES) mounted on the 2.56-m Nordic Optical Telescope (NOT) in October 2011. The obtained spectrum has a maximum S/N ~ 80 with a resolving power of 25 000. The reduction of the data and the analysis of the spectrum were performed using the semi-automatic software package VWA by following the same procedure as in Thygesen et al. (2012). The atmospheric parameters that were derived for this star are given in Table 10. We note that since the present study was started, star A was also observed with the HERMES instrument by Molenda-Żakowicz et al. (2013). The authors analyzed its spectrum using two different codes: ROTFIT (Frasca et al. 2003) and a combination of the codes ARES (Sousa et al. 2007) and MOOG (Sneden 1973). They obtained a temperature of Teff = 5134 ± 121 K and a metallicity of [Fe/H] = 0.08 ± 0.22 dex with ROTFIT and Teff = 5281 ± 76 K and [Fe/H] = 0.21 ± 0.06 dex with ARES+MOOG. These values agree well with the results obtained with the FIES data quoted in Table 10.
We note that our data include spectra with very different native resolutions and analysis techniques, and it is difficult to estimate the resulting systematic errors, which are not included here. We have, however, adopted star-by-star uncertainties that reflect the random errors in our measurements.
4.2. Photometric estimates of Teff
The Kepler Input Catalogue (KIC ) provides griz photometry for all the selected targets, except for star D. We followed the recipe prescribed by Pinsonneault et al. (2012) to obtain photometric estimates of the effective temperatures of the stars. The KIC griz photometry was corrected to be consistent with SDSS photometry. The colors were dereddened using the extinctions obtained from the reddening map of Drimmel et al. (2003) and the extinction coefficients given by An et al. (2009). We then used the polynomials given by Pinsonneault et al. (2012) to obtain temperature estimates. Finally, the spectroscopic estimates of metallicity were used to correct our Teff estimates from metallicity effects by interpolating between the tabulated values given by Pinsonneault et al. (2012). The errors on the Teff estimates were computed by varying the metallicity within the spectroscopic error bars and assuming an uncertainty of 0.02 mag for the extinction. The obtained temperatures, referred to as Teff,SDSS are given in Table 10. We note that no KIC photometry is available for star D (KIC 8751420), so the effective temperature of the star could not be estimated by this method.
We also combined the optical griz photometry with the infrared JHKS photometry available from the Two Micron All Sky Survey catalog (2MASS, Skrutskie et al. 2006) and applied the InfraRed Flux Method (IRFM) as prescribed by Casagrande et al. (2010) to obtain an additionnal estimate of the effective temperature. Error bars on these measurements are dominated by the uncertainty on the reddening, which can at present not be estimated to better than 0.01 mag. The values of Teff coming from the IRFM are given in Table 10. For star D, we used BV photometry instead of griz photometry, which is lacking, and applied the polynomials of Casagrande et al. (2010) to obtain an estimate of Teff. We note from Table 10 that the IRFM values of Teff all agree with the griz-color Teff within less than 1.4σ. The largest difference occurs for star F, where the SDSS temperature is higher. However, the IRFM Teff agrees well with the spectroscopic estimate for this star.
For all the stars except one (star F), three distinct measurements of Teff (spectroscopy, SDSS photometry, and IRFM photometry) yielded values that agree within less than 1σ, which shows that these estimates are very reliable. For star F, the IRFM temperature and the spectroscopic one also agree within less than 1σ, but the SDSS temperature is higher than the two other estimates (1.4σ difference with IRFM Teff and 2.8σ difference with spectroscopic Teff). In the following, we adopt the spectroscopic temperatures and examine the consequences of an alternative (larger) Teff for Star F (see Sect. 5).
5. Seismic modeling
To derive information on the internal rotation profile of the stars from the rotational splittings obtained in Sect. 3, we needed to have access to the rotational kernels of the modes. We thus modeled the six stars of the sample. To establish that our conclusions on the rotation profiles of the stars do not critically depend on the choice of a best-fit model, we modeled the stars using two different evolutionary codes: Cesam2k (Morel 1997) and astec (Christensen-Dalsgaard 2008a). In these two codes, the effects of rotation on the structure and evolution was neglected.
5.1. CESAM2K models
5.1.1. Properties of the models
The models that were computed with Cesam2k use the OPAL 2005 equation of state and opacity tables as described in Lebreton et al. (2008). The nuclear reaction rates were computed using the NACRE compilation (Angulo et al. 1999). The atmosphere was described by Eddington’s gray law. We assumed the classical solar mixture of heavy elements of Grevesse & Noels (1993). Convection was treated using the Canuto-Goldman-Mazzitelli (CGM) formalism (Canuto et al. 1996). This description involves a free parameter, the mixing length, which is taken as a fraction αCGM of the pressure scale height Hp. The effects of microscopic diffusion were neglected in this study. We did not include any overshooting at the boundary of convective cores during the main sequence.
The mode frequencies of the models were computed using the oscillation code LOSC (Scuflaire et al. 2008). It is well known that the lack of a satisfactory way of modeling surface convection in stellar models induces shifts in the absolute mode frequencies, which are known as near-surface effects. To correct for these effects, we used the recipe advocated by Kjeldsen et al. (2008), which consists of adding to the mode frequencies a power law whose exponent is calibrated on the Sun. With Cesam2k and the CGM formalism for convection, we found an exponent of 4.25, which was used for the models computed with Cesam2k in this work. Mixed modes are less sensitive to near-surface effects than pure acoustic modes because the contribution to the kinetic energy from the core is larger. To take this into account, the surface correction of non-radial modes were multiplied by a factor 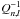 , where Qn,l corresponds to the ratio of the mode inertia to the inertia of the closest radial mode (e.g. Aerts et al. 2010, Chap. 7).
, where Qn,l corresponds to the ratio of the mode inertia to the inertia of the closest radial mode (e.g. Aerts et al. 2010, Chap. 7).
5.1.2. Fitting procedure
To model the stars, we used the method first proposed by Deheuvels & Michel (2011) to model subgiants with mixed modes, which was later adapted to the case of early red giants by D12. This method uses the fact that for these stars, the combined knowledge of the mean large separation ⟨ Δν ⟩ and the mean period spacing of l = 1 modes ⟨ ΔΠ1 ⟩ can yield very precise estimates of the stellar mass and age when other input physical parameters are fixed (see Deheuvels & Michel 2011; and D12 for more details).
To apply this method, we first needed to determine which values of ⟨ Δν ⟩ and ⟨ ΔΠ1 ⟩ should be used. An estimate of ⟨ Δν ⟩ can be obtained observationally from the mean large separation of p modes. However, this value is not directly comparable with the one computed from stellar models because it is affected by near-surface effects. One way of circumventing this problem is to instead require the models to match the observed frequencies of the lowest-order radial modes (which are the least affected by near-surface effects). Two methods have been proposed to estimate ⟨ ΔΠ1 ⟩ from the observations (Benomar et al. 2012; Mosser et al. 2012c). The estimates obtained with the method of Mosser et al. (2012c) for the six stars (denoted 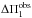 ) are given in Table 11. In principle, these methods can also be applied to the oscillation spectra of stellar models. However, automating them is not straightforward. It would also require computing the frequencies of l = 1 mixed modes very many times for each model during the optimization process, which is time-consuming. We therefore chose to use the period spacing obtained from an asymptotic expansion, which is further denoted
) are given in Table 11. In principle, these methods can also be applied to the oscillation spectra of stellar models. However, automating them is not straightforward. It would also require computing the frequencies of l = 1 mixed modes very many times for each model during the optimization process, which is time-consuming. We therefore chose to use the period spacing obtained from an asymptotic expansion, which is further denoted 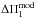 . We note that for red giants,
. We note that for red giants, 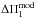 is typically calculated by assuming that the Brunt-Väisälä frequency NBV is much higher than the mode frequency in the whole g-mode cavity, thus yielding the approximate expression
is typically calculated by assuming that the Brunt-Väisälä frequency NBV is much higher than the mode frequency in the whole g-mode cavity, thus yielding the approximate expression 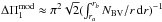 . For subgiants and young red giants this approximation is not justified because the frequencies of the observed mixed modes are higher than those of their more evolved counterparts and the Brunt-Väisälä frequency is lower owing to the less dense core. Making this approximation for the studied targets yields estimates of
. For subgiants and young red giants this approximation is not justified because the frequencies of the observed mixed modes are higher than those of their more evolved counterparts and the Brunt-Väisälä frequency is lower owing to the less dense core. Making this approximation for the studied targets yields estimates of 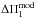 that are overestimated by 3 to 11%. Appendix A explains how the
that are overestimated by 3 to 11%. Appendix A explains how the 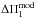 are computed from stellar models.
are computed from stellar models.
Value of ΔΠ1 for each star computed either from the best-fit models (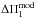 ) or directly from the observations by following the method of Mosser et al. (2012c) (
) or directly from the observations by following the method of Mosser et al. (2012c) (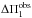 ).
).
We then computed a grid of models by varying the initial helium content (Y0 = 0.24 to 0.30), the mixing length parameter (αCGM = 0.55 to 0.65), and the metallicity in the range (Z/X)obs ± σobs. For each considered set of parameters, an automatic search was performed to determine the stellar mass and age that simultaneously reproduce the frequency of the lowest-order radial mode and the observed value of ΔΠ1. Finally, the mass and age were fine-tuned to reproduce the observations as closely as possible. This last step causes the period spacing of the models to slightly differ from 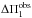 . We computed the value of
. We computed the value of 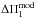 for the best-fit models by following the procedure described in Appendix A. The values obtained for the selected stars are given in Table 11. The values of
for the best-fit models by following the procedure described in Appendix A. The values obtained for the selected stars are given in Table 11. The values of 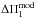 agree with those estimated directly from the observations following the method of Mosser et al. (2012c) (
agree with those estimated directly from the observations following the method of Mosser et al. (2012c) (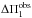 ) within less than 6%. This is similar to the level of agreement reported between the methods of Benomar et al. 2012 and Mosser et al. 2012c to estimate
) within less than 6%. This is similar to the level of agreement reported between the methods of Benomar et al. 2012 and Mosser et al. 2012c to estimate 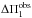 (Benomar et al. 2013).
(Benomar et al. 2013).
 |
Fig. 5 Échelle diagrams of the stars from our sample. The open circles represent the observed frequencies and the colored filled symbols stand for the best model (blue squares: l = 0, red triangles: l = 1, green stars: l = 2). |
Parameters of the best-fit models obtained for the stars of the sample with the codes Cesam2k and astec.
For each point of the grid, we estimated the agreement with the observations by computing a reduced χ2 function defined as 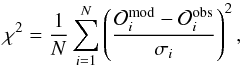 (2)where
(2)where 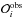 (i = 1,N) are the observables, σi their error bars, and
(i = 1,N) are the observables, σi their error bars, and 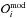 the corresponding values in the computed models. As is commonly done, we separated the contribution of the seismic constraints to the χ2 (
the corresponding values in the computed models. As is commonly done, we separated the contribution of the seismic constraints to the χ2 (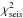 ) from the contribution of the atmospheric constraints (
) from the contribution of the atmospheric constraints (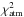 ). Indeed, since there are fewer atmospheric constraints than seismic ones, the total χ2 tends to drown their contribution. The values of
). Indeed, since there are fewer atmospheric constraints than seismic ones, the total χ2 tends to drown their contribution. The values of 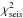 and
and 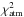 for the best-fit models are listed in Table 12. The evolutionary tracks of these models are shown in Fig. 6. We thus confirm that our stars lie around the base of the RGB. Stars A and B, which have the highest value of log g are obviously still in the subgiant branch, while the four other stars just started their ascent of the RGB.
for the best-fit models are listed in Table 12. The evolutionary tracks of these models are shown in Fig. 6. We thus confirm that our stars lie around the base of the RGB. Stars A and B, which have the highest value of log g are obviously still in the subgiant branch, while the four other stars just started their ascent of the RGB.
Except for star E, the atmospheric constraints are well reproduced, with values of 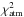 around 1. For star E, the higher value of
around 1. For star E, the higher value of 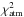 (4.6) is derived because the effective temperature of the model (4898 K) is lower than the spectroscopic one (5115 ± 60 K) by about 3σ. In fact, no model in our grid has a Teff higher than 4900 K for this star. We confirm that each model in our grid is the result of an optimization of the stellar mass and age as described above, which means that this Teff upper limit cannot be increased by simply extending the grid. We note that the photometric estimate of Teff using the IRFM method is lower and would yield
(4.6) is derived because the effective temperature of the model (4898 K) is lower than the spectroscopic one (5115 ± 60 K) by about 3σ. In fact, no model in our grid has a Teff higher than 4900 K for this star. We confirm that each model in our grid is the result of an optimization of the stellar mass and age as described above, which means that this Teff upper limit cannot be increased by simply extending the grid. We note that the photometric estimate of Teff using the IRFM method is lower and would yield 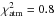 .
.
For star F, we found models that match the spectroscopic estimate of Teff (5120 ± 55 K) and the IRFM temperature (5174 ± 114 K), but no model in our grid was able to reproduce the higher value of Teff obtained from SDSS photometry (5354 ± 61 K). We were able to obtain satisfactory fits with this higher Teff only by decreasing the metallicity to −1 dex, which is more than 7σ lower than the spectroscopic value.
For star D (KIC 8751420), Huber et al. (2012) obtained a precise estimate of the radius of the star from interferometric measurements with the CHARA array (R/R⊙ = 2.703 ± 0.071). The radius of our best-fit model for this star (R = 2.668R⊙) perfectly agrees with the interferometric value.
Even though the agreement between the observed mode frequencies and the frequencies of the models is visually good (see Fig. 5), the values of 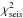 are strikingly high (around 100 for the six stars). We found that the l = 1 modes are by far the largest contributors to the value of
are strikingly high (around 100 for the six stars). We found that the l = 1 modes are by far the largest contributors to the value of 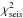 (they represent from 50% to 97% of
(they represent from 50% to 97% of 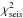 ). These disagreements are at least partly caused by imprecisions in the stellar models. With observation times as long as 650 days, the measurement errors on the mode frequencies reach values as low as 0.01 μHz (see Tables 5 to 3), which certainly gives the possibility to test the physics that is used in current stellar models. Indeed, the frequencies of the l = 1 mixed modes strongly depend on the coupling between the p-mode and the g-mode cavities, and thus on the evanescent zone that separates them (Deheuvels & Michel 2010). However, these high values of
). These disagreements are at least partly caused by imprecisions in the stellar models. With observation times as long as 650 days, the measurement errors on the mode frequencies reach values as low as 0.01 μHz (see Tables 5 to 3), which certainly gives the possibility to test the physics that is used in current stellar models. Indeed, the frequencies of the l = 1 mixed modes strongly depend on the coupling between the p-mode and the g-mode cavities, and thus on the evanescent zone that separates them (Deheuvels & Michel 2010). However, these high values of 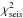 are most probably also caused by the crude way near-surface effects are dealt with in our models, by using the empirical correction prescribed by Kjeldsen et al. (2008). It was already surprising that this correction, which was intended for main-sequence stars, provides good fits to the observed frequencies of mixed modes for post-main-sequence stars – provided it is weighted by the factor
are most probably also caused by the crude way near-surface effects are dealt with in our models, by using the empirical correction prescribed by Kjeldsen et al. (2008). It was already surprising that this correction, which was intended for main-sequence stars, provides good fits to the observed frequencies of mixed modes for post-main-sequence stars – provided it is weighted by the factor 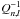 ; (e.g. D12; Doğan et al. 2013). We of course do not expect this correction to reproduce the observed absolute frequencies at a level of precision of 0.01 μHz. To derive information on the core structure of these stars from the frequencies of mixed modes, this matter will need to be thoroughly studied. Such a study is beyond the scope of the present paper, however. Indeed, variations in the mode frequencies on the order of the difference between models and observations induce very little change in the rotational kernels. This will be checked a posteriori in Sect. 6 by showing that our conclusions on the rotation profiles of the stars are not significantly modified when changing the reference model adopted for the inversions.
; (e.g. D12; Doğan et al. 2013). We of course do not expect this correction to reproduce the observed absolute frequencies at a level of precision of 0.01 μHz. To derive information on the core structure of these stars from the frequencies of mixed modes, this matter will need to be thoroughly studied. Such a study is beyond the scope of the present paper, however. Indeed, variations in the mode frequencies on the order of the difference between models and observations induce very little change in the rotational kernels. This will be checked a posteriori in Sect. 6 by showing that our conclusions on the rotation profiles of the stars are not significantly modified when changing the reference model adopted for the inversions.
5.2. ASTEC models
We also computed a grid of models using the Aarhus Stellar Evolution Code (ASTEC). The opacity tables, equation of state and nuclear reaction rates are the same as in the Cesam2k models. Convection was treated using the classical mixing length theory (MLT, Böhm-Vitense 1958) with a fixed value of the mixing length (αMLT = 1.8). Effects of diffusion on the stellar structure and core overshooting were neglected in the models. Models were computed with varying masses (from 1.0 to 1.6 M⊙), initial helium content Y0 (from 0.24 to 0.32), and metallicity with (Z/X) from 0.01 to 0.07. The oscillation frequencies were calculated for the models whose atmospheric properties are within roughly 3σ of the observed values. For frequency calculations, we used the Aarhus adiabatic pulsation package (ADIPLS, Christensen-Dalsgaard 2008b). The near-surface effects were corrected in the same way as described in Sect. 5.1, with an exponent of 4.9 for the power law, as found by Kjeldsen et al. (2008) for the classical MLT. The best models were then selected as those that minimize the function 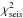 , as defined in Sect. 5.1. We note that here, we did not perform a pre-selection imposing the mean large separation of p modes and the period spacing of g modes as constraints to the models. After selecting the models that reproduced the observations best, their parameters were fine-tuned by decreasing the mesh of the initial grid and/or interpolating between the original time-steps to attempt to reduce the χ2 value. The resulting models are given in Table 12. That the selected astec models have generally higher χ2 values than the Cesam2k models is probably caused by the fact the fitting method adopted here was initially designed for main-sequence stars and early subgiants, for which the density of the grid of models, particularly in terms of stellar age, is less crucial.
, as defined in Sect. 5.1. We note that here, we did not perform a pre-selection imposing the mean large separation of p modes and the period spacing of g modes as constraints to the models. After selecting the models that reproduced the observations best, their parameters were fine-tuned by decreasing the mesh of the initial grid and/or interpolating between the original time-steps to attempt to reduce the χ2 value. The resulting models are given in Table 12. That the selected astec models have generally higher χ2 values than the Cesam2k models is probably caused by the fact the fitting method adopted here was initially designed for main-sequence stars and early subgiants, for which the density of the grid of models, particularly in terms of stellar age, is less crucial.
 |
Fig. 6 Evolutionary tracks of the best-fit models for stars A to F in the HR diagram. The current location of the model in the HR diagram is indicated by a filled circle. |
6. Probing the internal rotation profile
6.1. Rotational splittings vs. trapping of the modes
Having access to stellar models for the stars of the sample, we could relate the observed splittings to the trapping of the corresponding modes. For this purpose, we plot in Fig. 7 the observed splittings against the quantity ζ, which was introduced by Goupil et al. (2013) and is defined as the ratio between the kinetic energy of the mode in the g-mode cavity and the total kinetic energy of the mode, that is, ![\begin{equation} \zeta\equiv\frac{\int_{r\ind{a}}^{r\ind{b}} \rho r^2 \left[\xi_r^2+l(l+1)\xi_h^2\right]\,{\rm d}r}{\int_0^{R_\star} \rho r^2 \left[\xi_r^2+l(l+1)\xi_h^2\right]\,{\rm d}r}, \end{equation}](/articles/aa/full_html/2014/04/aa22779-13/aa22779-13-eq176.png) (3)where l is the degree of the mode, ξr and ξh are the radial and horizontal displacements, and ra and rb are the inner and outer turning points of the g-mode cavity. A value of ζ close to 1 indicates that the mode is mainly trapped in the g-mode cavity (and thus in the core for our stars), and a value of ζ close to 0, that it is trapped in the p-mode cavity. It is clear from Fig. 7 that the splittings of g modes are larger than those of p modes, indicating that the core rotates faster than the envelope in these stars, as was found in previous studies of this type (Beck et al. 2012, D12).
(3)where l is the degree of the mode, ξr and ξh are the radial and horizontal displacements, and ra and rb are the inner and outer turning points of the g-mode cavity. A value of ζ close to 1 indicates that the mode is mainly trapped in the g-mode cavity (and thus in the core for our stars), and a value of ζ close to 0, that it is trapped in the p-mode cavity. It is clear from Fig. 7 that the splittings of g modes are larger than those of p modes, indicating that the core rotates faster than the envelope in these stars, as was found in previous studies of this type (Beck et al. 2012, D12).
There is a roughly linear relation between the rotational splittings of l = 1 modes and the ratio ζ. This phenomenon was theoretically explained before by Goupil et al. (2013). We note that for star E, the splittings obtained for the two highest-frequency l = 1 modes (modes around 670 and 698 μHz, plotted in gray in Fig. 7) lie well outside this linear relation. None of the rotation profiles tested in this study were able to account for the fitted splittings of these modes. In fact, these high-frequency modes have a large linewidth, and a possible explanation might be that they are too wide to reliably determine their rotational splittings. This should appear more clearly when longer time-series are available from Kepler observations. In the following, the splittings of these two modes were excluded from the sets of splittings that were used to perform the inversions.
 |
Fig. 7 Observed splittings (open symbols) for modes of degrees l = 1 (circles) and l = 2 (squares), plotted as a function of the parameter ζ, which indicates the trapping of the modes (a value of ζ closer to 0 indicates a p-dominated mode, whereas a value of ζ closer to 1 indicates a g-dominated mode). The dashed lines indicate linear regressions of the relation between the splittings of l = 1 modes and the parameter ζ. Gray symbols indicate suspicious measurements that were not taken into account (see text). |
Goupil et al. (2013) showed that the coefficients of the linear relation δν(ζ) for l = 1 modes can be used to obtain estimates of the mean rotation rate in the g-mode cavity ⟨ Ωg ⟩ and the mean rotation rate in the p-mode cavity ⟨ Ωp ⟩. By combining their Eqs. (21) and (22), we obtain 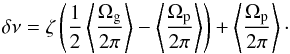 (4)We thus fitted a relation of the type δν = Aζ + B to the observed splittings of l = 1 modes for the six stars (see Fig. 7). From Eq. (4), we derive ⟨ Ωg/(2π) ⟩ = 2(A + B) and ⟨ Ωp/(2π) ⟩ = B. We note that for more evolved red giants, the contribution from the envelope to the rotational splittings becomes negligible and reliable estimates of ⟨ Ωp ⟩ cannot be obtained from the δν(ζ) relation (Goupil et al. 2013). The obtained results are given in Table 13. There are clear trends with the evolutionary status, suggesting that ⟨ Ωg ⟩ increases and ⟨ Ωp ⟩ decreases as stars evolve at the base of the red giant branch, resulting in an increase of the ratio ⟨ Ωg ⟩ / ⟨ Ωp ⟩. These trends are discussed in Sect. 7.
(4)We thus fitted a relation of the type δν = Aζ + B to the observed splittings of l = 1 modes for the six stars (see Fig. 7). From Eq. (4), we derive ⟨ Ωg/(2π) ⟩ = 2(A + B) and ⟨ Ωp/(2π) ⟩ = B. We note that for more evolved red giants, the contribution from the envelope to the rotational splittings becomes negligible and reliable estimates of ⟨ Ωp ⟩ cannot be obtained from the δν(ζ) relation (Goupil et al. 2013). The obtained results are given in Table 13. There are clear trends with the evolutionary status, suggesting that ⟨ Ωg ⟩ increases and ⟨ Ωp ⟩ decreases as stars evolve at the base of the red giant branch, resulting in an increase of the ratio ⟨ Ωg ⟩ / ⟨ Ωp ⟩. These trends are discussed in Sect. 7.
By using the rotational splittings of the modes that were obtained in Sect. 3 and the rotational kernels of the best stellar models from Sect. 5, we applied several inversion techniques to probe the rotational profiles of the six stars of our sample. The results presented below were obtained using the best-fit models of Cesam2k. However, all the inversions were also performed using the best models of astec and yielded results that are quantitatively very similar.
6.2. Core and envelope rotation
We first tried to obtain localized constraints on the rotation profiles of the selected targets. For this purpose, the OLA (optimally localized averages) method is particularly well suited. The OLA method consists of forming combinations of the rotational kernels such that the resulting averaging kernels 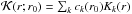 are as localized as possible around a target point r0. Note that for clarity, we now use the subscript k = 1,M for the modes whose splittings we were able to determine, instead of their order n and degree l. If the averaging kernel is sufficiently well localized around r0, then it is straightforward to obtain an estimate of the rotation rate at depth r0 through the relation
are as localized as possible around a target point r0. Note that for clarity, we now use the subscript k = 1,M for the modes whose splittings we were able to determine, instead of their order n and degree l. If the averaging kernel is sufficiently well localized around r0, then it is straightforward to obtain an estimate of the rotation rate at depth r0 through the relation 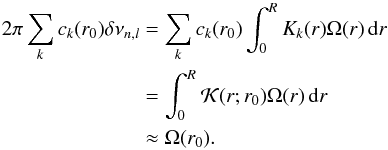 (5)The coefficients ck(r0) were searched so that the averaging kernel
(5)The coefficients ck(r0) were searched so that the averaging kernel 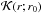 approached the Dirac function δ(r − r0) as closely as possible. For this purpose, Backus & Gilbert (1968) advocated minimizing the function
approached the Dirac function δ(r − r0) as closely as possible. For this purpose, Backus & Gilbert (1968) advocated minimizing the function ![\begin{equation} J=12 \int_0^R \mathcal{K}(r;r_0)^2 (r-r_0)^2\, {\rm d}r + \gamma \sum_{k=1}^M \left[ c_k(r_0)\sigma_{\delta\nu_k} \right]^2 \label{eq_OLA} \end{equation}](/articles/aa/full_html/2014/04/aa22779-13/aa22779-13-eq193.png) (6)for each point r0 considered by requiring that the integral of the averaging kernel be unity. Here, γ is a trade-off parameter between resolution of the averaging kernel and error magnification, and the σδνk are the measurement errors of the rotational splitting estimates. As was pointed out by D12, it is very hard to obtain localized averaging kernels in our case, and we therefore took γ = 0.
(6)for each point r0 considered by requiring that the integral of the averaging kernel be unity. Here, γ is a trade-off parameter between resolution of the averaging kernel and error magnification, and the σδνk are the measurement errors of the rotational splitting estimates. As was pointed out by D12, it is very hard to obtain localized averaging kernels in our case, and we therefore took γ = 0.
Since the modes are mixed, their rotational kernels have a contribution both from the core, due to their g-mode character, and from the envelope where they behave as p modes. The ratio between these contributions depend on where the modes are predominantly trapped. Because of the shape of the mode kernels, it was impossible with the set of modes at our disposal to build averaging kernels that are well localized at intermediate depths inside the star, and we were therefore unable to invert the whole rotation profile throughout the star. But we obtained estimates of the rotation rate in the core and the envelope.
 |
Fig. 8 Core-averaging kernels obtained with the OLA method for stars A (top) and F (bottom). A zoom of the kernels in the core is also shown. Step functions between 0 and 0.025 R (star A) or 0.015 (star F) are overplotted (dashed red lines). |
6.2.1. Core rotation
By minimizing the function J defined by Eq. (6) for values of r0 between 0 and 0.02 R, we obtained averaging kernels that efficiently cancel the contribution from the p-mode cavity. The more evolved the star is, the smaller the envelope contribution to the averaging kernel becomes. We show in Fig. 8 the core-averaging kernels obtained for stars A and F, which are the least and most evolved star of the sample, respectively. It is clear that these averaging kernels are poor approximations to Dirac functions; but if we assume that the rotation profile varies smoothly in the core, they can be well approximated by step functions in the g-mode cavity (i.e. between 0 and 0.015 to 0.025 R), as can be seen in Fig. 8. By applying Eq. (5), we thus obtained estimates of the average rotation rate in the innermost 1.5% to 2.5% for the stars of the sample. The results are summarized in Table 13. The same inversions using the astec models provide core rotation rates that agree with the values quoted in Table 13 within less than 1.3σ. The core rotations obtained with the OLA inversions agree well with the values obtained from the coefficients of the linear regression of the relation δν(ζ) (see Table 13). This validates the prescription of Goupil et al. (2013) for stars at the base of the RGB.
6.2.2. Envelope rotation
The surface-averaging kernels are obtained by choosing r0 = 1 and searching for the coefficients ck(r0) that minimize the function J. We show in Fig. 9 the cumulative integral of the surface kernels 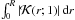 for our stars. First, we note that the contribution of the g-mode cavity to the surface-averaging kernels seems to be efficiently canceled. However, it is clear from Fig. 9 that the surface-averaging kernels provide a weighted average of the rotation rate in the whole p-mode cavity rather than an estimate of the surface rotation itself. Without knowledge of the variations in Ω(r) in the p-mode cavity, no direct information about the rotation profile in the envelope can be inferred. If we assume that the star rotates as a solid-body in the whole p-mode cavity, then the quantity 2π ∑ kck(r0)δνk provides an estimate of the envelope rotation rate. The estimates are listed in Table 13 for the six stars. These estimates can be regarded as upper limits to the rotation rate in the convective envelope. Indeed, Fig. 9 shows that the radiative part of the p-mode cavity, which presumably rotates faster than the convective envelope, also contributes to the surface-averaging kernels. In addition, even though the contribution from the g-mode cavity to the surface-averaging kernel is small, we know that the core rotates much faster than the envelope, which leads us to overestimate the envelope rotation. This leakage from this region can be quantified by separating the contributions from the core and the envelope as follows:
for our stars. First, we note that the contribution of the g-mode cavity to the surface-averaging kernels seems to be efficiently canceled. However, it is clear from Fig. 9 that the surface-averaging kernels provide a weighted average of the rotation rate in the whole p-mode cavity rather than an estimate of the surface rotation itself. Without knowledge of the variations in Ω(r) in the p-mode cavity, no direct information about the rotation profile in the envelope can be inferred. If we assume that the star rotates as a solid-body in the whole p-mode cavity, then the quantity 2π ∑ kck(r0)δνk provides an estimate of the envelope rotation rate. The estimates are listed in Table 13 for the six stars. These estimates can be regarded as upper limits to the rotation rate in the convective envelope. Indeed, Fig. 9 shows that the radiative part of the p-mode cavity, which presumably rotates faster than the convective envelope, also contributes to the surface-averaging kernels. In addition, even though the contribution from the g-mode cavity to the surface-averaging kernel is small, we know that the core rotates much faster than the envelope, which leads us to overestimate the envelope rotation. This leakage from this region can be quantified by separating the contributions from the core and the envelope as follows: 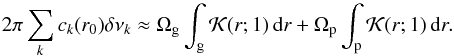 (7)The first term of the right-hand side in Eq. (7) represents the contribution from the g-mode cavity and can be estimated by using the core rotation rates obtained in Sect. 6.2.1. Taking this into account, we found that the estimates of the rotation rates in the p-mode cavity listed in Table 13 are reduced by only 0.6% to 2.6% for stars A through E. In contrast, for star F, which is the most evolved star in our sample, the leakage from the core amounts to 26%. Similar inversions using the astec models yielded an envelope rotation rate that agrees with the values quoted in Table 13 within less than 1σ for all the stars.
(7)The first term of the right-hand side in Eq. (7) represents the contribution from the g-mode cavity and can be estimated by using the core rotation rates obtained in Sect. 6.2.1. Taking this into account, we found that the estimates of the rotation rates in the p-mode cavity listed in Table 13 are reduced by only 0.6% to 2.6% for stars A through E. In contrast, for star F, which is the most evolved star in our sample, the leakage from the core amounts to 26%. Similar inversions using the astec models yielded an envelope rotation rate that agrees with the values quoted in Table 13 within less than 1σ for all the stars.
 |
Fig. 9 Cumulative integral of the surface averaging kernel obtained with the OLA method for the stars of the sample. The vertical lines indicate the base of the convective envelope for each star. |
 |
Fig. 10 Best rotation profiles obtained by applying the RLS method with a smoothness condition on the rotation profile on the entire star (solid blue lines) or only in the radiative interior while the convective envelope is assumed to rotate as a solid body (long-dashed red lines). The dotted lines indicate the 1σ error bars for both types of inversions. |
Estimates of the ratio Ωp/Ωg were obtained by combining our estimates of the envelope rotation rates with the estimates of the core rotation rates obtained in Sect. 6.2.1. The results are given in Table 13. Except for star F, they agree well with the values obtained with the prescription of Goupil et al. (2013). The disagreement for star F probably arises because our estimate of Ωp is too high due to a leakage from the core, as explained above.
6.3. Testing for strong gradients in the rotation profiles
As mentioned above, it is very difficult to obtain localized information about the rotation profile in regions other than the deepest layers, because in these zones the averaging kernels suffer from considerable leakage from the core and the surface. Another approach consists of trying to place constraints on the overall shape of the rotation profiles. One important question is that of the existence of discontinuities or sharp gradients in the rotation profiles. Indeed, if we assume conservation of the specific angular momentum of each layer, the evolution in the post-main sequence leads to a fast-spinning core and a slow-spinning envelope, with a sharp rotation gradient in the intermediate region, where the H-burning shell lies. If we assume, in contrast, an instantaneous AM transport, the whole star rotates as a solid body. We know that the reality probably lies somewhere between these two limiting cases, but the shape of the rotation profile is still very uncertain. We therefore tried to test for strong gradients in the rotation profiles of the stars in our sample. For this purpose, we fitted both smooth and discontinuous rotation profiles to the observed splittings.
6.3.1. Smooth rotation profiles
To ensure that the fitted rotation profiles are smooth, we used the RLS (regularized least-squares) method. It consists of searching the rotation profile that best matches the observed splittings by performing a least-squares fitting. Owing to the few available cases of splittings, which are not sufficient to reconstruct the whole rotation profile in a unique way, the problem must be regularized. The function to be minimized corresponds to the sum of the χ2 residual of the fit and a regularization function that penalizes undesirable features in the solution. Here, since we were searching for smooth rotation profiles, we imposed a smoothness condition by taking the regularization function as the square of the norm of its first derivative. Two options were studied: we either imposed a smoothness condition on the whole rotation profile (hereafter denoted by the index smooth) or to the radiative interior alone, assuming a solid-body rotation in the envelope (denoted by the index SBenv). The balance between minimizing χ2 and having a smooth solution is controlled by a trade-off parameter λ. The value of this trade-off parameter was determined by generating artificial rotation profiles and trying to recover them for different values of λ.
 |
Fig. 11 Contribution of each mode to the χ2 values computed in Sect. 6.3. The symbols correspond to the splittings computed with the best-fit rotation profiles obtained using the RLS method with a smoothness condition on the whole profile (blue crosses), the RLS method with a smoothness condition in the radiative interior only and solid-body rotation in the convective envelope (red circles), or a two-zone model with an optimized depth of discontinuity (see Sect. 6.3.2, green diamonds). |
The best-fitting rotation profiles for the six stars are shown in Fig. 10. When the rotation profile is required to be smooth throughout the star (solid blue lines), the best-fitting profiles vary almost linearly as a function of the radius. For stars C, D, E, and F, the surface is found to be counter-rotating. However, we showed in Sect. 6.2.2 that we can only obtain information about the average rotation in the envelope with our data. Since the shape of the rotation profile cannot be determined in the envelope, it is clear that the smoothness condition dominates and imposes a linear behavior for the recovered profile in this region, thus causing the surface to be counter-rotating. The best-fitting profiles for solid-body rotation in the convective envelope (long-dashed red lines in Fig. 10) produce rotational splittings very similar to those of the previous case, which appears clearly in Fig. 7.
The agreement between the observed splittings and those produced by the best-fitting smooth profiles (noted δνRLS) was estimated by computing the χ2 of the residual of the fits 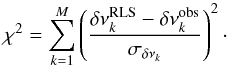 (8)Since our aim is to interpret the obtained values of χ2 in a statistical sense, special care needs to be given to its normalization. It is customary to normalize the χ2 by its expected value, which yields a reduced χ2 of expected value unity. The expected value of χ2 is equal to its number of degrees of freedom. For an ordinary least-squares fit, it corresponds to M − μ, where μ is the number of fitted parameters. For a regularized least-squares fit, it is more delicate and requires computing an effective number of degrees of freedom, which obviously depends on the regularization parameter λ. By following Hastie & Tibshirani (1990), we estimated the effective number of degrees of freedom of the RLS fits for the six studied stars, given the chosen regularization parameter λ. Details of the calculation are presented in Appendix B. We obtained values of around M − 2.2 for all the stars. This is expected because the inverted rotation profiles are almost straight lines (see Fig. 10), and fitting the observed splittings to a straight line would give μ = 2, and thus M − 2 degrees of freedom. We thus defined the reduced χ2 as
(8)Since our aim is to interpret the obtained values of χ2 in a statistical sense, special care needs to be given to its normalization. It is customary to normalize the χ2 by its expected value, which yields a reduced χ2 of expected value unity. The expected value of χ2 is equal to its number of degrees of freedom. For an ordinary least-squares fit, it corresponds to M − μ, where μ is the number of fitted parameters. For a regularized least-squares fit, it is more delicate and requires computing an effective number of degrees of freedom, which obviously depends on the regularization parameter λ. By following Hastie & Tibshirani (1990), we estimated the effective number of degrees of freedom of the RLS fits for the six studied stars, given the chosen regularization parameter λ. Details of the calculation are presented in Appendix B. We obtained values of around M − 2.2 for all the stars. This is expected because the inverted rotation profiles are almost straight lines (see Fig. 10), and fitting the observed splittings to a straight line would give μ = 2, and thus M − 2 degrees of freedom. We thus defined the reduced χ2 as 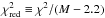 .
.
The obtained 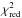 are given in Table 14. First we observe that the case where a smooth profile is assumed throughout, the star produces
are given in Table 14. First we observe that the case where a smooth profile is assumed throughout, the star produces 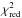 values that are very similar to the case where solid-body rotation is assumed in the envelope. For stars A and E, the observed splittings are very well reproduced by smooth profiles, with reduced χ2 around 1. For stars B and C, the reduced χ2 is around 3, indicating a poorer match with the observations. This might indicate that the rotation profile is not smooth as assumed. However, as can be seen in Fig. 11, the modes that contribute the most to the value of χ2 for these two stars are located at the edges of the frequency range of the oscillations, where the signal-to-noise ratio is the lowest. We can therefore not exclude that this mismatch is caused by wrong splitting estimates. For stars D and F, the reduced χ2 is even higher, reaching values of about 6.0 and 4.4, respectively. For these stars, the splittings of several modes differ from the observed splittings by 3 to 5σ. In addition, Fig. 11 shows that the modes that contribute the most to the χ2 value lie around νmax, so it is very unlikely that this disagreement might be due to an incorrect determination of the splittings.
values that are very similar to the case where solid-body rotation is assumed in the envelope. For stars A and E, the observed splittings are very well reproduced by smooth profiles, with reduced χ2 around 1. For stars B and C, the reduced χ2 is around 3, indicating a poorer match with the observations. This might indicate that the rotation profile is not smooth as assumed. However, as can be seen in Fig. 11, the modes that contribute the most to the value of χ2 for these two stars are located at the edges of the frequency range of the oscillations, where the signal-to-noise ratio is the lowest. We can therefore not exclude that this mismatch is caused by wrong splitting estimates. For stars D and F, the reduced χ2 is even higher, reaching values of about 6.0 and 4.4, respectively. For these stars, the splittings of several modes differ from the observed splittings by 3 to 5σ. In addition, Fig. 11 shows that the modes that contribute the most to the χ2 value lie around νmax, so it is very unlikely that this disagreement might be due to an incorrect determination of the splittings.
 |
Fig. 12 Variations in the reduced χ2 as a function of the radius rc of the assumed discontinuity. The black curves correspond to the inversions performed with the best-fit models of Cesam2k and the gray curves, to the inversions performed with the best-fit models of astec. The circles indicate the lowest value of the χ2 function. The vertical dot-dashed blue line indicates the location of the H-burning shell for the best-fit models. |
6.3.2. Discontinuous profiles
We then tried to fit discontinuous rotation profiles to the data. We here modeled discontinuous profiles in the crudest way, by splitting the star into two zones that are assumed to rotate as solid bodies, that is, profiles of the type 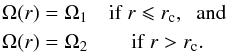 (9)The radius rc that separates these zones was considered a free parameter. We varied the radius rc between 0 and 1, and each time determined the rotation rates Ω1 and Ω2 that fit the observations best. We thus minimized the reduced χ2 defined as
(9)The radius rc that separates these zones was considered a free parameter. We varied the radius rc between 0 and 1, and each time determined the rotation rates Ω1 and Ω2 that fit the observations best. We thus minimized the reduced χ2 defined as ![\begin{equation} \chi^2\ind{red} = \frac{1}{M-2} \sum_{k=1}^M \left[\frac{\delta\nu_k\ex{obs}-\Omega_1A_k(r\ind{c})-\Omega_2 B_k(r\ind{c})}{\sigma_k\ex{obs}}\right]^2, \label{eq_chi2_2zone} \end{equation}](/articles/aa/full_html/2014/04/aa22779-13/aa22779-13-eq221.png) (10)where
(10)where 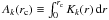 and
and 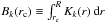 . Here, there are two fitted parameters and the χ2 is thus normalized by M − 2. In the following, the lowest value of the χ2 function is noted
. Here, there are two fitted parameters and the χ2 is thus normalized by M − 2. In the following, the lowest value of the χ2 function is noted 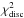 and the corresponding depth of discontinuity, rdisc. The results are presented in Fig. 12. For stars A, B, C, and E, the χ2 function varies little as a function of rc, except at very low values of rc (<0.002 R⋆), where it sharply increases. The minimum χ2 is located very close to the surface for stars A, B, and C (
and the corresponding depth of discontinuity, rdisc. The results are presented in Fig. 12. For stars A, B, C, and E, the χ2 function varies little as a function of rc, except at very low values of rc (<0.002 R⋆), where it sharply increases. The minimum χ2 is located very close to the surface for stars A, B, and C (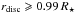 ), and it corresponds to a rotation profile with a thin counter-rotating layer at the surface. D12 have shown that these solutions are in fact most likely spurious, and this is discussed in more detail in Appendix C. For stars D and F, the minimum of the χ2 function is much more pronounced than for the other stars. For these two stars, discontinuities below a depth of about 0.04 R⋆ yield χ2 values that are much lower than discontinuities in other regions of the star. The global minimum of the χ2 function is located at rdisc = 0.005 R⋆ for star D, and rdisc = 0.037 R⋆ for star F, but other depths of discontinuities below 0.04 R⋆ also yield very similar values of χ2. The values of
), and it corresponds to a rotation profile with a thin counter-rotating layer at the surface. D12 have shown that these solutions are in fact most likely spurious, and this is discussed in more detail in Appendix C. For stars D and F, the minimum of the χ2 function is much more pronounced than for the other stars. For these two stars, discontinuities below a depth of about 0.04 R⋆ yield χ2 values that are much lower than discontinuities in other regions of the star. The global minimum of the χ2 function is located at rdisc = 0.005 R⋆ for star D, and rdisc = 0.037 R⋆ for star F, but other depths of discontinuities below 0.04 R⋆ also yield very similar values of χ2. The values of 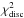 are given in Table 14 for each star. It is striking that for stars D and F, the best-fitting discontinuous rotation profiles yield reduced χ2 of 2.4 and 1.4, respectively, which are much smaller than the reduced χ2 obtained with smooth rotation profiles (
are given in Table 14 for each star. It is striking that for stars D and F, the best-fitting discontinuous rotation profiles yield reduced χ2 of 2.4 and 1.4, respectively, which are much smaller than the reduced χ2 obtained with smooth rotation profiles (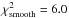 and 4.4 for stars D and F, see Table 14). The question of the significance of this χ2 difference is addressed in 6.4. For this purpose, we introduce the quantity
and 4.4 for stars D and F, see Table 14). The question of the significance of this χ2 difference is addressed in 6.4. For this purpose, we introduce the quantity 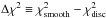 . We thus have Δχ2 = 3.6 for star D and Δχ2 = 3.1 for star F.
. We thus have Δχ2 = 3.6 for star D and Δχ2 = 3.1 for star F.
We observe that regardless of the chosen depth of discontinuity rc, the best-fitting values of Ω1 and Ω2 always agree well with with the mean rotation rate in the g-mode cavity that was obtained with the OLA method in Sect. 6.2.1. We checked this by computing 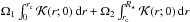 and comparing the result with the values of Ωg listed in Table 13. It is thus understandable that for depths of discontinuity smaller than the outer turning point of the g-mode cavity, the best-fitting value of Ω1 increases and takes values that can become much higher than Ωg. For instance for star D, the best-fitting depth of discontinuity rdisc = 0.005 R⋆ corresponds to Ω1/(2π) = 5254 ± 92 nHz. If the rotation profile is indeed discontinuous in stars D and F, it is therefore possible that the rotation rate in the deeper core is significantly higher than the average rotation rate in the g-mode cavity given in Table 13.
and comparing the result with the values of Ωg listed in Table 13. It is thus understandable that for depths of discontinuity smaller than the outer turning point of the g-mode cavity, the best-fitting value of Ω1 increases and takes values that can become much higher than Ωg. For instance for star D, the best-fitting depth of discontinuity rdisc = 0.005 R⋆ corresponds to Ω1/(2π) = 5254 ± 92 nHz. If the rotation profile is indeed discontinuous in stars D and F, it is therefore possible that the rotation rate in the deeper core is significantly higher than the average rotation rate in the g-mode cavity given in Table 13.
To study the influence of the choice of the best-fit stellar model on the results, we also performed the same inversions as described above using the best model found with the astec code instead of the Cesam2k models. The χ2 are plotted as a function of the rc in Fig. 12 (gray lines). Apart from the absolute values of χ2, which vary a little compared with the case where Cesam2k models were used, the results are very similar. In particular, the radii rdisc where the χ2 functions are minimal are almost unchanged. This justifies the assumption that the results on the internal rotation of the selected stars do not critically depend on the choice of the best-fit stellar model.
6.4. Significance of the results
The results obtained in Sect. 6.3 suggest that there might exist a deep discontinuity in the rotation profiles of stars D and F. To evaluate the significance of these results, we ran a series of simulations with artificial input rotation profiles to determine whether or not we can distinguish between a smooth and a discontinuous profile with a deep discontinuity for the six stars of the sample. These tests are presented in Appendix C, and we here summarize the obtained results.
We found that stars D and F only offer good chances of distinguishing between the two cases for the following reasons:
-
1.
If we assume a discontinuous input profile with a deepdiscontinuity (at 0.04 R⋆), the probability of correctly recovering this depth of discontinuity is high (90% for star D and 97% for star F).
-
2.
If we assume a smooth input profile, the probability of mistaking it with a discontinuous profile with a deep discontinuity is low (4% for star D and 2% for star F).
-
3.
Assuming a smooth or discontinuous input profile yields distributions of Δχ2 that are clearly different from each other (see Fig. C.2).
By comparison, for stars A, B, C, and E, the chances of correctly recovering a deep discontinuity are relatively low (between 28% and 60%), and the distributions of Δχ2 whether we assume a smooth or discontinuous input profile almost overlap (see Fig. C.2). This shows that the available splittings do not allow us to significantly distinguish between a smooth and a discontinuous rotation profile for these stars.
We now use the results of our simulations to interpret the observations. In Sect. 6.3.2, we found that a deep discontinuity yields the smallest reduced χ2 for stars D and F, which has little chance of occurring if the rotation profile is smooth, as we showed in Appendix C. We also obtained Δχ2 = 3.6 for star D and Δχ2 = 3.1 for star F. These values are much better compatible with the case of a discontinuous profile than with the case of a smooth profile (Fig. C.2). We thus conclude that the improvement in the χ2 when considering a discontinuous rotation profile is statistically significant. We note that even with discontinuous profiles, the reduced χ2 that we obtained for stars D and F is higher than 1. This is very likely because the actual rotation profile of the star is more complex than the simple two-zone model we assumed. However, for completeness, we also considered the possibility that it might come from an underestimation of the error bars of the observed splittings. We computed a correcting factor to the errors that would bring the reduced χ2 to 1 and repeated the inversions performed in Sect. 6.3. We found that a discontinuous rotation profile still reproduces the observed splittings significantly better than a smooth profile for both stars.
For stars A, B, C, and E, no evidence for a discontinuous rotation profile was found in the observations. However, this does not mean that the profile is smooth because our simulations showed that it is impossible to distinguish between the two types of profiles. This raises the question of why stars D and F are bette suited for detecting discontinuities in the rotation profiles. Answering this question is beyond the scope of this paper; but several possible explanations can be offered at this point. First of all, stars D and F have the fastest core-rotation (see Table 13). By performing statistical tests similar to those presented in Appendix C for input profiles with increasing core rotations, we indeed found that the probability of detecting a discontinuity increases with the core rotation. Yet, this does not explain why discontinuities cannot be detected for star E, which has a core rotation that is similar to those of stars D and F. This could come from the precision of the splitting estimates. Indeed, we saw from Fig. C.3 that the splittings of several modes are crucial for distinguishing between smooth and discontinuous profiles. The precision with which the splittings of these modes can be determined from the observations is therefore decisive.
7. Discussion and conclusion
We selected a subsample of six subgiants or early red giants observed with Kepler with the objective to obtain constraints on the radial dependence of their rotation profile. For this purpose, spectroscopic estimates of their surface parameters were obtained, either from the literature or by performing ground-based observations. The Kepler light curves of the six stars were analyzed, enabling us to determine the frequencies and rotational splittings of 12 to 18 mixed modes of degree l = 1 or 2 with a very high level of precision (uncertainties on the order of 10 nHz). We then performed a seismic modeling of the six targets and obtained stellar models that reproduce well both the observed atmospheric parameters and the frequencies of the observed modes. By using these models along with our estimates of the rotational splittings, we performed inversions to probe the rotation profiles of the selected targets.
 |
Fig. 13 Core (red symbols) and envelope (blue symbols) rotation rates obtained with the OLA method (see Sects. 6.2.1 and 6.2.2) plotted as a function of the surface gravity. The letter corresponding to each star is specified. The dashed gray lines correspond to the range of surface rotation rates predicted by van Saders & Pinsonneault (2013) for the stars that lie in the range of parameters that they considered. The horizontal and vertical lines indicate 1σ error-bars. |
 |
Fig. 14 Core rotation rate as a function of the stellar radius. The open symbols correspond to the stars studied by Mosser et al. (2012b, circles: RGB stars, squares: clump stars). The filled symbols indicate the stars that were studied in this paper, and the cross corresponds to the young giant KIC 7341231 studied by D12. |
By using the OLA (optimally localized average) method, we were able to obtain estimates of the average rotation in the g-mode cavity (which roughly corresponds to the innermost 2% of the stellar radius) for the six stars of our sample (Sect. 6.2.1). It is interesting that the mean core rotation rate appears to be correlated with the evolutionary status. The two stars that are the least evolved and were identified as subgiants on their way to the RGB (stars A and B) have the slowest cores. To further illustrate this point, we plot in Fig. 13 the estimated core rotation rates as a function of the surface gravities that were obtained from seismic global parameters in Sect. 2. There is a clear trend, which suggests that the core spins up as the star evolves. At first glance, this result seems at odds with the conclusions of Mosser et al. (2012b), who reported that the core of red giant stars spins down as they climb the RGB. However, the authors studied stars that are more evolved than those in our sample. Figure 14 reproduces Fig. 9 of Mosser et al. (2012b), where we added the core rotation rates of the stars that were studied here (filled circles in the plot), as well as the rotation rate of KIC 7341231 obtained by D12 (cross). Our results suggest that the core of subgiant stars spins up until the base of the RGB and subsequently spins down due to an efficient transport of AM from the core to the envelope whose origin is still unknown. This suggests that during the subgiant phase, the AM transport from the core to the envelope is not efficient enough to counterbalance the core contraction, which results in a spin-up of the core in this phase. This result, if confirmed, can be used to place constraints on the mechanisms of AM transport that operate in this phase. The confirmation of this result will require measuring the core rotation for more subgiant stars, which is difficult since Kepler observed fewer of these targets4, and moreover, their modes are wider, which makes it more difficult to estimate the rotational splittings.
We were also able to build averaging kernels that almost erase the contribution from the core, and thus obtained estimates of the rotation rate in the convective envelope for the stars of the sample (see Sect. 6.2.2). We showed that except for star F, these estimates are nearly insensitive to the core rotation. However, if the radiative layers below the envelope spin much faster than the envelope, they could lead us to overestimate the envelope rotation rate. These estimates must therefore be regarded as upper limits of the envelope rotation rate. They are plotted as a function of the surface gravity in Fig. 13. Once again, a clear trend appears. It suggests that the convective envelope is spun down in the subgiant phase. This is expected since the envelope rapidly expends in this phase. However, we know that AM must be redistributed from the core to the envelope to account for the relatively low core rotation rates that are observed (Eggenberger et al. 2012; Marques et al. 2013; Ceillier et al. 2013). Our results show that the AM gained by the envelope is not sufficient to spin it up. Our estimates of the envelope rotation rates can therefore be used to place constraints on the transport of AM in the subgiant phase. van Saders & Pinsonneault (2013) recently built a simplified model to predict the rotation periods of stars across the HR diagram by taking into account the loss of AM through a magnetized wind when relevant. They assumed rigid rotation at all times (i.e. instantaneous internal transport of AM), which is clearly not the case for the stars of our study, but they argued that their results are only weakly sensitive to this hypothesis. Figure 13 shows the ranges of surface rotation rates predicted by van Saders & Pinsonneault (2013) for the stars of our sample that lie in the range of parameters they considered (stars B, D, E, and F). They broadly agree with the estimates found in this study, but are systematically larger, which is consistent with the fact that internal transport of AM is likely less efficient than they assumed. It would be interesting to compare the observed envelope rotation rates with those predicted by models that include an additional viscosity to simulate the unknown physical process of AM transport (Eggenberger et al. 2012).
Finally, we found indications that the rotation profiles of two of our stars (stars D and F) might have a sharp gradient in the core. For these stars, the observed splittings are significantly better reproduced by a discontinuous rotation profile with a deep discontinuity (located at 0.4% of the stellar radius for star D and 3.9% of the radius for star F) than by a rotation profile that decreases smoothly from the core to the surface. The significance of this result was established by performing simulations with our optimal models and by assuming either discontinuous or smooth input rotation profiles. For the four other stars, no observational evidence of a discontinuous rotation profile was found. However, our statistical tests showed that with the current data, it is in fact impossible to distinguish between a smooth and a discontinuous rotation profile for these stars, which means that discontinuities could exist. Interestingly, the depth found to be most probable for the discontinuity in the rotation profiles of stars D and F is close to the location of the H-burning shell, which is located between 1% and 2% of the stellar radius for these stars (see Fig. 12). This suggests that the overall shape of the rotation profile might in fact be similar to that predicted by current theoretical models that include rotationally induced AM transport (e.g. Marques et al. 2013). Of course the problem remains that the core rotation rates predicted by these models are higher by several orders of magnitude than the observed ones.
 |
Fig. 15 Schematic rotation profiles for a star in which a rotation gradient is building up in the g-mode cavity (delimited by the vertical dotted line) between times t1 (black curves) and t2 (blue curves). The dashed lines indicate the mean rotation rate in the g-mode cavity Ωg and the rotation rate in the center is denote Ω0. |
The existence of a sharp gradient within the g-mode cavity of young giants would complicate the interpretation of the average rotation velocity in the g-mode cavity Ωg. Indeed, if it is the case, the layers below this jump could have rotation rates that are much higher than our estimates of Ωg, which are listed in Table 13. As a result, any conclusion on the spin-up or spin-down of the most central layers depends on the evolution of the rotation gradient in the g-mode cavity. Figure 15 illustrates this point schematically. We assumed rotation profiles for an imaginary star in which a rotation gradient would be building up between times t1 and t2. If we only have access to Ωg, we would conclude that the core is spinning down because Ωg(t2) < Ωg(t1). But in fact, Fig. 15 shows that the core spins up (Ω0(t2) > Ω0(t1)) owing to the sharp gradient that is building up in the core.
Moreover, if the existence of sharp gradients in the rotation profiles of early red giants can be confirmed, it would bring very important constraints on the mechanisms that transport AM in these stars. In particular, it seems incompatible with AM transport through a deep fossil magnetic field, as advocated for instance by Gough & McIntyre (1998), because it would very likely erase such sharp features. Indeed, differential rotation is expected to be damped along the poloidal filed lines (Garaud & Garaud 2008; Strugarek et al. 2011). On the other hand, internal gravity waves, which are also able to transport AM and have been reported to be efficient during advanced phases of stellar evolution (Talon & Charbonnel 2008), can give birth to localized weak gradients in the rotation profile caused by the extraction and deposit of AM (e.g. Talon & Charbonnel 2005). Sharp rotation gradients might also potentially trigger magnetohydrodynamic instabilities, such as the magnetorotational instability (MRI), which in turn might transport AM (Balbus & Hawley 1994; Arlt et al. 2003; Menou et al. 2004; Menou & Le Mer 2006).
To conclude, we confirm that the precision with which rotational splittings can be determined from the observations is crucial for studying the shape of the internal rotation profiles of young red giants. This is yet another motivation to try to obtain long time-series for asteroseismic measurements, such as those obtained with Kepler.
Online material
Estimates of the frequencies and rotational splittings of the detected modes for KIC 12508433 (star A), obtained by fitting Lorentzian functions to the mode profiles.
Inclination angles obtained for the stars of the sample from the final fit (see text).
Appendix A: Computation of asymptotic period spacings from stellar models
According to the asymptotic analysis of g modes (e.g. Christensen-Dalsgaard 2003), the frequencies of two g modes of same degree l and consecutive radial order n verify the following equation: ![\appendix \setcounter{section}{1} \begin{equation} L\left[I(\omega_{n+1})-I(\omega_{n})\right] = \pi \label{eq_deltap1} \end{equation}](/articles/aa/full_html/2014/04/aa22779-13/aa22779-13-eq498.png) (A.1)where
(A.1)where 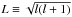 and
and 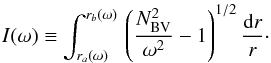 (A.2)The radii ra(ω) and rb(ω) correspond to the turning points of the g-mode cavity for the mode of frequency ω. For red giants, one usually assumes that ω ≪ NBV(r) in the whole g-mode cavity and thus derives
(A.2)The radii ra(ω) and rb(ω) correspond to the turning points of the g-mode cavity for the mode of frequency ω. For red giants, one usually assumes that ω ≪ NBV(r) in the whole g-mode cavity and thus derives 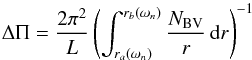 (A.3)from Eq. (A.1). For young giants, this approximation is not legitimate because the core is less dense than in more evolved giants and the integrand of Eq. (A.2) cannot be simplified. In this case, computing the asymptotic period spacing from a model at a frequency ωn requires an iterative method. By definition of the period spacing, we have
(A.3)from Eq. (A.1). For young giants, this approximation is not legitimate because the core is less dense than in more evolved giants and the integrand of Eq. (A.2) cannot be simplified. In this case, computing the asymptotic period spacing from a model at a frequency ωn requires an iterative method. By definition of the period spacing, we have 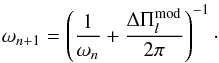 (A.4)This expression of ωn + 1 is then plugged into Eq. (A.1) and we use the Newton method to solve this latter equation for
(A.4)This expression of ωn + 1 is then plugged into Eq. (A.1) and we use the Newton method to solve this latter equation for  . The obtained values are given in Table 11. They differ from those given by Eq. (A.3) by 3% (for the most evolved targets) to 11% (for the least evolved ones). This shows a posteriori that the usual approximation is not valid for the young red giants.
. The obtained values are given in Table 11. They differ from those given by Eq. (A.3) by 3% (for the most evolved targets) to 11% (for the least evolved ones). This shows a posteriori that the usual approximation is not valid for the young red giants.
Appendix B: Effective number of degrees of freedom for an RLS fit
Estimating the number of degrees of freedom for an RLS fit is not straightforward because this number cannot be interpreted as the dimension of a certain vector subspace, as is the case for ordinary least-squares fits. However, the fitted values (the rotational splittings that correspond to the inverted rotation profile δνRLS in our case) remain linear in the observations δνobs. There exists a matrix H, usually referred to as the hat matrix, such that 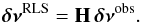 (B.1)We note that both the matrix H and the vector δνRLS depend on the regularization parameter.
(B.1)We note that both the matrix H and the vector δνRLS depend on the regularization parameter.
The number of degrees of freedom of the fit correspond to the expected value of χ2, which is given by Eq. (8). To calculate E(χ2), we assume that the RLS fit is unbiased, that is, we assume that the “true” splittings would be recovered with this method if the observations were noise-free. This assumption is probably not completely justified, but if a bias exists, it will increase the expected value of the χ2. Therefore, by neglecting the bias, we obtain higher values of the reduced χ2 and our assumption is thus conservative. We also consider that the observed splittings are uncorrelated. Under these conditions, we can use the development of Hastie & Tibshirani (1990). The only difference is that in our case the variances of the data points are not all the same. To place ourselves in this particular case, we normalize the rotational splittings by the observed errors by defining 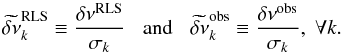 (B.2)We thus have
(B.2)We thus have 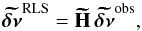 (B.3)where the corresponding hat matrix is such that
(B.3)where the corresponding hat matrix is such that 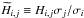 . In this case, Hastie & Tibshirani (1990) have shown that the expected value of χ2 is
. In this case, Hastie & Tibshirani (1990) have shown that the expected value of χ2 is 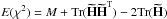 . Finally we obtain
. Finally we obtain 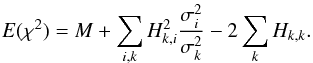 (B.4)
(B.4)
Appendix C: Can we distinguish between a smooth and a discontinuous rotation profile in the stars of the sample?
Appendix C.1: Simulations with a discontinuous rotation profile
To answer this question, we performed simulations by assuming a discontinuous input rotation profile Ωth(r). We took 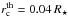 to determine whether or not a discontinuity at this depth can be detected. For each star, the values of Ω1 and Ω2 were fixed to the best-fitting values that were found by assuming rc = 0.04 R⋆ in Sect. 6.3.2. We then used the rotational kernels of the observed modes to compute the theoretical rotational splittings
to determine whether or not a discontinuity at this depth can be detected. For each star, the values of Ω1 and Ω2 were fixed to the best-fitting values that were found by assuming rc = 0.04 R⋆ in Sect. 6.3.2. We then used the rotational kernels of the observed modes to compute the theoretical rotational splittings 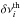 that correspond to Ωth(r). We used the same sets of modes as the observed ones. To simulate the observed splittings, we added to the theoretical splittings
that correspond to Ωth(r). We used the same sets of modes as the observed ones. To simulate the observed splittings, we added to the theoretical splittings 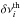 a random noise following a Gaussian distribution with rms
a random noise following a Gaussian distribution with rms 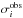 . We then tried to recover the input rotation profile Ωth(r) by performing the same inversion procedures as for the observations. The last two steps were repeated many times (500 iterations per star for each inversion method) to study the statistics.
. We then tried to recover the input rotation profile Ωth(r) by performing the same inversion procedures as for the observations. The last two steps were repeated many times (500 iterations per star for each inversion method) to study the statistics.
We first performed inversions by assuming that the rotation profile is discontinuous. We minimized the χ2 as defined by Eq. (10) for different values of rc. To determine whether or not the input depth of the discontinuity 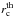 can be recovered, we located the radius rdisc at which the χ2 function is the lowest for each iteration. Correspondingly, the lowest value of the χ2 function is further noted
can be recovered, we located the radius rdisc at which the χ2 function is the lowest for each iteration. Correspondingly, the lowest value of the χ2 function is further noted 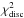 . The distribution of rdisc is shown in Fig. C.1 for all the stars. We remark that for stars D and F, the depth of the discontinuity is correctly recovered in 90% and 97% of the cases, respectively (we arbitrarily considered that the depth of the discontinuity is recovered if
. The distribution of rdisc is shown in Fig. C.1 for all the stars. We remark that for stars D and F, the depth of the discontinuity is correctly recovered in 90% and 97% of the cases, respectively (we arbitrarily considered that the depth of the discontinuity is recovered if 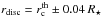 ), which indicates that we should be able to detect a discontinuity in the rotation profile at a depth of
), which indicates that we should be able to detect a discontinuity in the rotation profile at a depth of 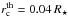 in these stars. For the least evolved stars A and B, the success rate is much lower (28% for both stars). For stars C and E, the correct discontinuity is recovered about 60% of the time.
in these stars. For the least evolved stars A and B, the success rate is much lower (28% for both stars). For stars C and E, the correct discontinuity is recovered about 60% of the time.
 |
Fig. C.1 Distribution of the depth rmin at which a discontinuity in Ω(r) is found to be most probable for simulations considering either a smooth input rotation profile (blue histogram) or discontinuous one at a depth |
 |
Fig. C.2 Distribution of |
We then tried to recover the rotation profile by (incorrectly) assuming that it is smooth for each of the 500 iterations. For this purpose, we used the RLS method with a smoothness condition, as was done for the observations in Sect. 6.3.1. Of course, the resulting profiles contain no discontinuity. For each iteration, the agreement between the simulated splittings and that corresponding to the inverted rotation profile was estimated by computing a χ2, further referred to as 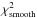 . We compared the values of
. We compared the values of 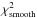 with those of
with those of 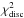 , which were obtained above, assuming that the profile is discontinuous. Figure C.2 shows the distribution of
, which were obtained above, assuming that the profile is discontinuous. Figure C.2 shows the distribution of 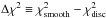 for each star. For stars D and F,
for each star. For stars D and F, 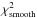 was found larger than
was found larger than 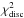 for all the 500 iterations, with Δχ2 = 0.8 ± 0.4 for star D and 1.1 ± 0.6 for star F.
for all the 500 iterations, with Δχ2 = 0.8 ± 0.4 for star D and 1.1 ± 0.6 for star F.
This set of simulations shows that for stars D and F, a discontinuity located at 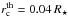 is recovered more than 90% of the time, and the agreement with the input theoretical splittings is better when the rotation profile is assumed to be discontinuous than when it is assumed to be smooth (
is recovered more than 90% of the time, and the agreement with the input theoretical splittings is better when the rotation profile is assumed to be discontinuous than when it is assumed to be smooth (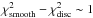 ). To determine whether or not the profile is indeed discontinuous in these stars, we must also show that a smooth profile very probably does not produce the same features.
). To determine whether or not the profile is indeed discontinuous in these stars, we must also show that a smooth profile very probably does not produce the same features.
Appendix C.2: Simulations with a smooth rotation profile
For this purpose, we considered an input rotation profile that is smooth. We took the best-fit profile obtained with the RLS method in Sect. 6.3.1. As before, we computed the theoretical splittings that correspond to this rotation profile, added a random noise to it, and tried to recover the input rotation profile. 500 iterations were performed for each star.
 |
Fig. C.3 Differences between the theoretical splittings that are obtained with a smooth rotation profile and those produced by discontinuous rotation profiles with depths of discontinuity of rc/R⋆ = 0.04 (filled stars), 0.2 (green circles), 0.4 (red circles), 0.6 (blue circles), and 0.8 (purple circles) for star D (KIC 8751420). The differences were normalized by the 1σ errors of the observations to emphasize the contribution of each mode to the χ2. |
We first performed inversions by (incorrectly) assuming that the rotation profile is discontinuous. For each iteration, we determined the radius rdisc at which a discontinuity is most probable and we kept a record of the minimum χ2 (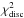 ). The distributions of rdisc that we obtained for all the stars are shown in Fig. C.1 (blue histograms). For stars A, B, C, and E, we observe that rdisc is distributed more or less randomly between 0 and 1. In particular, for stars A and B, the distribution of rdisc is very similar to the one that was obtained when considering a discontinuous input profile, which confirms that it is impossible to detect a discontinuity in the rotation profile for these stars. For stars D and F, some radii are more probable than others (e.g. 0.16, 0.33, 0.50, 0.60, and 0.90 R⋆ for star F). This means that the splittings produced by a smooth rotation profile are quite similar to those produced by discontinuous profiles with specific depths of discontinuity. It would therefore be hopeless to try to detect a discontinuity around these specific radii. However, smooth profiles very seldom produce rotational splittings that are similar to the one corresponding to a discontinuous profile with rc as deep as 0.04 R⋆. Indeed, for stars D and F, a value of rdisc below 0.08 R⋆ was obtained for only 4% and 2% of the iterations, respectively.
). The distributions of rdisc that we obtained for all the stars are shown in Fig. C.1 (blue histograms). For stars A, B, C, and E, we observe that rdisc is distributed more or less randomly between 0 and 1. In particular, for stars A and B, the distribution of rdisc is very similar to the one that was obtained when considering a discontinuous input profile, which confirms that it is impossible to detect a discontinuity in the rotation profile for these stars. For stars D and F, some radii are more probable than others (e.g. 0.16, 0.33, 0.50, 0.60, and 0.90 R⋆ for star F). This means that the splittings produced by a smooth rotation profile are quite similar to those produced by discontinuous profiles with specific depths of discontinuity. It would therefore be hopeless to try to detect a discontinuity around these specific radii. However, smooth profiles very seldom produce rotational splittings that are similar to the one corresponding to a discontinuous profile with rc as deep as 0.04 R⋆. Indeed, for stars D and F, a value of rdisc below 0.08 R⋆ was obtained for only 4% and 2% of the iterations, respectively.
To understand this result, a closer inspection of the theoretical splittings (without noise) is instructive. Figure C.3 shows the difference between the theoretical splittings of the input smooth profile and that of best-fit discontinuous profiles with various values of rc for star D. We observe that for discontinuities between 0.2 and 1, the theoretical splittings does not vary much and is very close to the splitting of the smooth profile. On the other hand, for deeper discontinuities (e.g. around rc = 0.04 R⋆), the splittings of several modes significantly differ from the case of a smooth profile (for example the modes around 454 and 582 μHz for star D, see Fig. C.3), which explains why we can distinguish between these two types of profiles.
For each iteration, we also performed RLS inversions with a smoothness condition and estimated the agreement with the theoretical splittings by computing 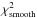 . The distributions of
. The distributions of 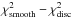 are shown in Fig. C.2 (blue histograms). For all the stars, the values of
are shown in Fig. C.2 (blue histograms). For all the stars, the values of 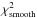 are similar to those of
are similar to those of 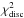 . This was expected since we saw from Fig. C.1 that smooth rotation profiles produce splittings that resemble those of discontinuous profiles with discontinuities at certain depths. However, for stars D and F, if the input profile is smooth,
. This was expected since we saw from Fig. C.1 that smooth rotation profiles produce splittings that resemble those of discontinuous profiles with discontinuities at certain depths. However, for stars D and F, if the input profile is smooth, 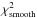 is never larger than
is never larger than 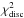 by more than 0.8 and 0.9, respectively, whereas the observed values of Δχ2 are as high as 3.6 and 3.1 for these stars, which is much more consistent with the distribution found for discontinuous input profiles. For all the other stars, the observed Δχ2 are equally consistent with the two types of profiles.
by more than 0.8 and 0.9, respectively, whereas the observed values of Δχ2 are as high as 3.6 and 3.1 for these stars, which is much more consistent with the distribution found for discontinuous input profiles. For all the other stars, the observed Δχ2 are equally consistent with the two types of profiles.
To determine to what extent our results depend on the shape of the smooth rotation profile that is used as an input, we repeated the same simulations considering other smooth profiles (e.g. the best-fit rotation profiles obtained by using the OLA method in Sect. 6.2, or an best-fit linear profile). We obtained results that are quantitatively very similar to those described above.
We note that to apply these scaling relations, estimates of the effective temperatures of the stars are also required. We here used the spectroscopic estimates that are obtained in Sect. 4 of this paper.
Acknowledgments
S.D. thanks W. Ball for his comments on this paper and acknowledges support from the PNPS under the grant “Rotation interne et magnétisme des sous-géantes et géantes Kepler”. Funding for the Stellar Astrophysics Centre is provided by The Danish National Research Foundation (Grant DNRF106). The research is supported by the ASTERISK project (ASTERoseismic Investigations with SONG and Kepler) funded by the European Research Council (Grant agreement No.: 267864). A.O.T acknowledges support from Sonderforschungsbereich SFB 881 “The Milky Way System” (subproject A5) of the German Research Foundation (DFG). J.M.-Ż acknowledges funding by the Polish MNiSW grant N N203 405139. L.G. and J.S. acknowledge research funding by the Deutsche Forschungsgemeinschaft (DFG) under grant SFB 963/1 “Astrophysical flow instabilities and turbulence” (Project A18). T.L.C., G.R.D. and W.J.C. acknowledge financial support from the UK Science and Technology Facilities Council.
References
- Aerts, C., Christensen-Dalsgaard, J., & Kurtz, D. W. 2010, Asteroseismology (Springer Science+Business Media B.V.) [Google Scholar]
- Aigrain, S., Favata, F., & Gilmore, G. 2004, in Stellar Structure and Habitable Planet Finding, eds. F. Favata, S. Aigrain, & A. Wilson, ESA SP, 538, 215 [Google Scholar]
- Aizenman, M., Smeyers, P., & Weigert, A. 1977, A&A, 58, 41 [NASA ADS] [Google Scholar]
- An, D., Pinsonneault, M. H., Masseron, T., et al. 2009, ApJ, 700, 523 [NASA ADS] [CrossRef] [Google Scholar]
- Anderson, E. R., Duvall, Jr., T. L., & Jefferies, S. M. 1990, ApJ, 364, 699 [NASA ADS] [CrossRef] [Google Scholar]
- Angulo, C., Arnould, M., Rayet, M., et al. 1999, Nucl. Phys. A, 656, 3 [NASA ADS] [CrossRef] [Google Scholar]
- Appourchaux, T., Michel, E., Auvergne, M., et al. 2008, A&A, 488, 705 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Appourchaux, T., Benomar, O., Gruberbauer, M., et al. 2012, A&A, 537, A134 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Arlt, R., Hollerbach, R., & Rüdiger, G. 2003, A&A, 401, 1087 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Backus, G., & Gilbert, F. 1968, Geophys. J. Int., 16, 169 [NASA ADS] [CrossRef] [Google Scholar]
- Baglin, A., Auvergne, M., Boisnard, L., et al. 2006, in 36th COSPAR Scientific Assembly, COSPAR, Plenary Meeting, 36, 3749 [Google Scholar]
- Bai, T., & Sturrock, P. A. 1993, ApJ, 409, 476 [NASA ADS] [CrossRef] [Google Scholar]
- Balbus, S. A., & Hawley, J. F. 1994, MNRAS, 266, 769 [NASA ADS] [Google Scholar]
- Ballot, J., García, R. A., & Lambert, P. 2006, MNRAS, 369, 1281 [NASA ADS] [CrossRef] [Google Scholar]
- Ballot, J., Barban, C., & van’t Veer-Menneret, C. 2011, A&A, 531, A124 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Beck, P. G., Bedding, T. R., Mosser, B., et al. 2011, Science, 332, 205 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Beck, P. G., Montalban, J., Kallinger, T., et al. 2012, Nature, 481, 55 [NASA ADS] [CrossRef] [Google Scholar]
- Bedding, T. R., Mosser, B., Huber, D., et al. 2011, Nature, 471, 608 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Belkacem, K., Goupil, M. J., Dupret, M. A., et al. 2011, A&A, 530, A142 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benomar, O., Appourchaux, T., & Baudin, F. 2009, A&A, 506, 15 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Benomar, O., Bedding, T. R., Stello, D., et al. 2012, ApJ, 745, L33 [NASA ADS] [CrossRef] [Google Scholar]
- Benomar, O., Bedding, T. R., Mosser, B., et al. 2013, ApJ, 767, 158 [NASA ADS] [CrossRef] [Google Scholar]
- Böhm-Vitense, E. 1958, ZAp, 46, 108 [NASA ADS] [Google Scholar]
- Borucki, W. J., Koch, D., Basri, G., et al. 2010, Science, 327, 977 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Brown, T. M., Gilliland, R. L., Noyes, R. W., & Ramsey, L. W. 1991, ApJ, 368, 599 [NASA ADS] [CrossRef] [Google Scholar]
- Bruntt, H. 2009, A&A, 506, 235 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Bruntt, H., Basu, S., Smalley, B., et al. 2012, MNRAS, 423, 122 [NASA ADS] [CrossRef] [Google Scholar]
- Campante, T. L., Handberg, R., Mathur, S., et al. 2011, A&A, 534, A6 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Canuto, V. M., Goldman, I., & Mazzitelli, I. 1996, ApJ, 473, 550 [NASA ADS] [CrossRef] [Google Scholar]
- Casagrande, L., Ramírez, I., Meléndez, J., Bessell, M., & Asplund, M. 2010, A&A, 512, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Ceillier, T., Eggenberger, P., García, R. A., & Mathis, S. 2013, A&A, 555, A54 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Chaplin, W. J., Christensen-Dalsgaard, J., Elsworth, Y., et al. 1999, MNRAS, 308, 405 [NASA ADS] [CrossRef] [Google Scholar]
- Chaplin, W. J., Basu, S., Huber, D., et al. 2014, ApJS, 210, 1 [NASA ADS] [CrossRef] [Google Scholar]
- Charbonnel, C., & Talon, S. 2005, Science, 309, 2189 [NASA ADS] [CrossRef] [PubMed] [Google Scholar]
- Christensen-Dalsgaard, J. 2003, Lecture Notes on Stellar Oscillations, 5th edn., available at astro.berkeley.edu/~eliot/Astro202/2009_Dalsgaard.pdf [Google Scholar]
- Christensen-Dalsgaard, J. 2008a, Ap&SS, 316, 13 [NASA ADS] [CrossRef] [Google Scholar]
- Christensen-Dalsgaard, J. 2008b, Ap&SS, 316, 113 [NASA ADS] [CrossRef] [Google Scholar]
- Deheuvels, S., & Michel, E. 2010, Ap&SS, 328, 259 [NASA ADS] [CrossRef] [Google Scholar]
- Deheuvels, S., & Michel, E. 2011, A&A, 535, A91 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Deheuvels, S., García, R. A., Chaplin, W. J., et al. 2012a, ApJ, 756, 19 [NASA ADS] [CrossRef] [Google Scholar]
- Deheuvels, S., Ouazzani, R. M., & Basu, S. 2012b, A&A, submitted [Google Scholar]
- Denissenkov, P. A., Pinsonneault, M., Terndrup, D. M., & Newsham, G. 2010, ApJ, 716, 1269 [NASA ADS] [CrossRef] [Google Scholar]
- Doğan, G., Metcalfe, T. S., Deheuvels, S., et al. 2013, ApJ, 763, 49 [NASA ADS] [CrossRef] [Google Scholar]
- Drimmel, R., Cabrera-Lavers, A., & López-Corredoira, M. 2003, A&A, 409, 205 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Dupret, M.-A., Belkacem, K., Samadi, R., et al. 2009, A&A, 506, 57 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Eff-Darwich, A., & Korzennik, S. G. 2013, Sol. Phys., 287, 43 [NASA ADS] [CrossRef] [Google Scholar]
- Eggenberger, P., Montalbán, J., & Miglio, A. 2012, A&A, 544, L4 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Frasca, A., Alcalá, J. M., Covino, E., et al. 2003, A&A, 405, 149 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Garaud, P., & Garaud, J.-D. 2008, MNRAS, 391, 1239 [NASA ADS] [CrossRef] [Google Scholar]
- García, R. A., Corbard, T., Chaplin, W. J., et al. 2004, Sol. Phys., 220, 269 [NASA ADS] [CrossRef] [Google Scholar]
- García, R. A., Hekker, S., Stello, D., et al. 2011, MNRAS, 414, L6 [NASA ADS] [CrossRef] [Google Scholar]
- Gizon, L., & Solanki, S. K. 2003, ApJ, 589, 1009 [NASA ADS] [CrossRef] [Google Scholar]
- Gizon, L., Ballot, J., Michel, E., et al. 2013, Proc. National Academy of Science, 110, 13267 [NASA ADS] [CrossRef] [Google Scholar]
- Gough, D. O., & Kosovichev, A. G. 1993, in IAU Colloq., 137: Inside the Stars, eds. W. W. Weiss, & A. Baglin, ASP Conf. Ser., 40, 566 [Google Scholar]
- Gough, D. O., & McIntyre, M. E. 1998, Nature, 394, 755 [NASA ADS] [CrossRef] [Google Scholar]
- Goupil, M. J., Mosser, B., Marques, J. P., et al. 2013, A&A, 549, A75 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Grevesse, N., & Noels, A. 1993, in Proc. Symp. Origin and Evolution of the Elements, eds. N. Prantzos, E. Vangioni-Flam, & M. Casse, 15 [Google Scholar]
- Harvey, J. 1985, in ESA SP, 235, 199 [Google Scholar]
- Hastie, T. J., & Tibshirani, R. J. 1990, Generalized Additive Models (CRC Press) [Google Scholar]
- Huber, D., Bedding, T. R., Stello, D., et al. 2011, ApJ, 743, 143 [NASA ADS] [CrossRef] [Google Scholar]
- Huber, D., Ireland, M. J., Bedding, T. R., et al. 2012, ApJ, 760, 32 [NASA ADS] [CrossRef] [Google Scholar]
- Jenkins, J. M., Caldwell, D. A., Chandrasekaran, H., et al. 2010, ApJ, 713, L120 [NASA ADS] [CrossRef] [Google Scholar]
- Karoff, C. 2012, MNRAS, 421, 3170 [NASA ADS] [CrossRef] [Google Scholar]
- Karoff, C., Campante, T. L., Ballot, J., et al. 2013, ApJ, 767, 34 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., Bedding, T. R., Viskum, M., & Frandsen, S. 1995, AJ, 109, 1313 [NASA ADS] [CrossRef] [Google Scholar]
- Kjeldsen, H., Bedding, T. R., & Christensen-Dalsgaard, J. 2008, ApJ, 683, L175 [NASA ADS] [CrossRef] [Google Scholar]
- Lebreton, Y., Monteiro, M. J. P. F. G., Montalbán, J., et al. 2008, Ap&SS, 316, 1 [Google Scholar]
- Lomb, N. R. 1976, Ap&SS, 39, 447 [NASA ADS] [CrossRef] [Google Scholar]
- Marques, J. P., Goupil, M. J., Lebreton, Y., et al. 2013, A&A, 549, A74 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathis, S., & Zahn, J. 2004, A&A, 425, 229 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mathur, S., Handberg, R., Campante, T. L., et al. 2011, ApJ, 733, 95 [NASA ADS] [CrossRef] [Google Scholar]
- Menou, K., & Le Mer, J. 2006, ApJ, 650, 1208 [NASA ADS] [CrossRef] [Google Scholar]
- Menou, K., Balbus, S. A., & Spruit, H. C. 2004, ApJ, 607, 564 [NASA ADS] [CrossRef] [Google Scholar]
- Metcalfe, T. S., Monteiro, M. J. P. F. G., Thompson, M. J., et al. 2010, ApJ, 723, 1583 [NASA ADS] [CrossRef] [Google Scholar]
- Molenda-Żakowicz, J., Sousa, S. G., Frasca, A., et al. 2013, MNRAS, 434, 1422 [NASA ADS] [CrossRef] [Google Scholar]
- Morel, P. 1997, A&AS, 124, 597 [NASA ADS] [CrossRef] [EDP Sciences] [MathSciNet] [PubMed] [Google Scholar]
- Mosser, B., Barban, C., Montalbán, J., et al. 2011, A&A, 532, A86 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Elsworth, Y., Hekker, S., et al. 2012a, A&A, 537, A30 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012b, A&A, 548, A10 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Goupil, M. J., Belkacem, K., et al. 2012c, A&A, 540, A143 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Mosser, B., Michel, E., Belkacem, K., et al. 2013, A&A, 550, A126 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Osaki, J. 1975, PASJ, 27, 237 [NASA ADS] [Google Scholar]
- Ouazzani, R.-M., Goupil, M. J., Dupret, M.-A., & Marques, J. P. 2013, A&A, 554, A80 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Pinsonneault, M. H., An, D., Molenda-Żakowicz, J., et al. 2012, ApJS, 199, 30 [NASA ADS] [CrossRef] [Google Scholar]
- Raskin, G., van Winckel, H., Hensberge, H., et al. 2011, A&A, 526, A69 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Scargle, J. D. 1982, ApJ, 263, 835 [NASA ADS] [CrossRef] [Google Scholar]
- Schou, J., Antia, H. M., Basu, S., et al. 1998, ApJ, 505, 390 [NASA ADS] [CrossRef] [Google Scholar]
- Scuflaire, R., Montalbán, J., Théado, S., et al. 2008, Ap&SS, 316, 149 [NASA ADS] [CrossRef] [Google Scholar]
- Silva Aguirre, V., Casagrande, L., Basu, S., et al. 2012, ApJ, 757, 99 [NASA ADS] [CrossRef] [Google Scholar]
- Skrutskie, M. F., Cutri, R. M., Stiening, R., et al. 2006, AJ, 131, 1163 [NASA ADS] [CrossRef] [Google Scholar]
- Sneden, C. A. 1973, Ph.D. Thesis, the University of Texas at Austin, USA [Google Scholar]
- Sousa, S. G., Santos, N. C., Israelian, G., Mayor, M., & Monteiro, M. J. P. F. G. 2007, A&A, 469, 783 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Spruit, H. C. 1999, A&A, 349, 189 [NASA ADS] [Google Scholar]
- Strugarek, A., Brun, A. S., & Zahn, J.-P. 2011, A&A, 532, A34 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Talon, S., & Charbonnel, C. 2005, A&A, 440, 981 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Talon, S., & Charbonnel, C. 2008, A&A, 482, 597 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Tayar, J., & Pinsonneault, M. H. 2013, ApJ, 775, L1 [NASA ADS] [CrossRef] [Google Scholar]
- Thygesen, A. O., Frandsen, S., Bruntt, H., et al. 2012, A&A, 543, A160 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- van Saders, J. L., & Pinsonneault, M. H. 2013, ApJ, 776, 67 [NASA ADS] [CrossRef] [Google Scholar]
- Vázquez Ramió, H., Régulo, C., & Roca Cortés, T. 2005, A&A, 443, L11 [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Zahn, J.-P. 1992, A&A, 265, 115 [NASA ADS] [Google Scholar]
All Tables
Global seismic parameters of the selected targets and estimates of the stars’ masses, radii, and surface gravity inferred from scaling relations.
Characteristics of the fit performed by each fitting group to extract the mode frequencies and rotational splittings from the power spectra.
Value of ΔΠ1 for each star computed either from the best-fit models (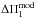 ) or directly from the observations by following the method of Mosser et al. (2012c) (
) or directly from the observations by following the method of Mosser et al. (2012c) (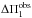 ).
).
Parameters of the best-fit models obtained for the stars of the sample with the codes Cesam2k and astec.
Estimates of the frequencies and rotational splittings of the detected modes for KIC 12508433 (star A), obtained by fitting Lorentzian functions to the mode profiles.
Inclination angles obtained for the stars of the sample from the final fit (see text).
All Figures
 |
Fig. 1 Location of the selected targets in a seismic HR diagram (mean large separation Δν against effective temperature). The blue filled stars indicate the six targets selected in our sample and the gray diamonds correspond to the set of Kepler targets studied by Chaplin et al. (2014). The dashed lines indicate evolutionary tracks of models of different masses and solar metallicity. |
| In the text | |
 |
Fig. 2 Échelle diagrams of the stars from our sample. The mean large separations that were used to build the diagrams are specified in Table 1. For more clarity, the power spectra were binned over a 0.25 μHz boxcar and clipped at a maximum of 20 to 40 times the noise level. |
| In the text | |
 |
Fig. 3 Power spectrum of KIC 9574283 (smoothed over a 10 μHz boxcar) computed with 650 days of Kepler data (gray curve). Two Harvey-type laws (solid black lines) had to be considered to reproduce the shape of the background. The fitted background is represented by the dashed blue line, while the long-dashed red line shows the background that is obtained with only one Harvey profile. The dotted line shows the contribution from the photon noise. |
| In the text | |
 |
Fig. 4 Inclination angles obtained for star E (KIC 7799349). The dashed lines indicate the results of global fits (gray: Campante, green: Davies, blue: Deheuvels, purple: Regulo), and the open symbols correspond to the results of local fits that allow for different angles for each mode (red triangles: Appourchaux, blue squares: Deheuvels, cyan stars: Stahn). |
| In the text | |
 |
Fig. 5 Échelle diagrams of the stars from our sample. The open circles represent the observed frequencies and the colored filled symbols stand for the best model (blue squares: l = 0, red triangles: l = 1, green stars: l = 2). |
| In the text | |
 |
Fig. 6 Evolutionary tracks of the best-fit models for stars A to F in the HR diagram. The current location of the model in the HR diagram is indicated by a filled circle. |
| In the text | |
 |
Fig. 7 Observed splittings (open symbols) for modes of degrees l = 1 (circles) and l = 2 (squares), plotted as a function of the parameter ζ, which indicates the trapping of the modes (a value of ζ closer to 0 indicates a p-dominated mode, whereas a value of ζ closer to 1 indicates a g-dominated mode). The dashed lines indicate linear regressions of the relation between the splittings of l = 1 modes and the parameter ζ. Gray symbols indicate suspicious measurements that were not taken into account (see text). |
| In the text | |
 |
Fig. 8 Core-averaging kernels obtained with the OLA method for stars A (top) and F (bottom). A zoom of the kernels in the core is also shown. Step functions between 0 and 0.025 R (star A) or 0.015 (star F) are overplotted (dashed red lines). |
| In the text | |
 |
Fig. 9 Cumulative integral of the surface averaging kernel obtained with the OLA method for the stars of the sample. The vertical lines indicate the base of the convective envelope for each star. |
| In the text | |
 |
Fig. 10 Best rotation profiles obtained by applying the RLS method with a smoothness condition on the rotation profile on the entire star (solid blue lines) or only in the radiative interior while the convective envelope is assumed to rotate as a solid body (long-dashed red lines). The dotted lines indicate the 1σ error bars for both types of inversions. |
| In the text | |
 |
Fig. 11 Contribution of each mode to the χ2 values computed in Sect. 6.3. The symbols correspond to the splittings computed with the best-fit rotation profiles obtained using the RLS method with a smoothness condition on the whole profile (blue crosses), the RLS method with a smoothness condition in the radiative interior only and solid-body rotation in the convective envelope (red circles), or a two-zone model with an optimized depth of discontinuity (see Sect. 6.3.2, green diamonds). |
| In the text | |
 |
Fig. 12 Variations in the reduced χ2 as a function of the radius rc of the assumed discontinuity. The black curves correspond to the inversions performed with the best-fit models of Cesam2k and the gray curves, to the inversions performed with the best-fit models of astec. The circles indicate the lowest value of the χ2 function. The vertical dot-dashed blue line indicates the location of the H-burning shell for the best-fit models. |
| In the text | |
 |
Fig. 13 Core (red symbols) and envelope (blue symbols) rotation rates obtained with the OLA method (see Sects. 6.2.1 and 6.2.2) plotted as a function of the surface gravity. The letter corresponding to each star is specified. The dashed gray lines correspond to the range of surface rotation rates predicted by van Saders & Pinsonneault (2013) for the stars that lie in the range of parameters that they considered. The horizontal and vertical lines indicate 1σ error-bars. |
| In the text | |
 |
Fig. 14 Core rotation rate as a function of the stellar radius. The open symbols correspond to the stars studied by Mosser et al. (2012b, circles: RGB stars, squares: clump stars). The filled symbols indicate the stars that were studied in this paper, and the cross corresponds to the young giant KIC 7341231 studied by D12. |
| In the text | |
 |
Fig. 15 Schematic rotation profiles for a star in which a rotation gradient is building up in the g-mode cavity (delimited by the vertical dotted line) between times t1 (black curves) and t2 (blue curves). The dashed lines indicate the mean rotation rate in the g-mode cavity Ωg and the rotation rate in the center is denote Ω0. |
| In the text | |
 |
Fig. C.1 Distribution of the depth rmin at which a discontinuity in Ω(r) is found to be most probable for simulations considering either a smooth input rotation profile (blue histogram) or discontinuous one at a depth |
| In the text | |
 |
Fig. C.2 Distribution of |
| In the text | |
 |
Fig. C.3 Differences between the theoretical splittings that are obtained with a smooth rotation profile and those produced by discontinuous rotation profiles with depths of discontinuity of rc/R⋆ = 0.04 (filled stars), 0.2 (green circles), 0.4 (red circles), 0.6 (blue circles), and 0.8 (purple circles) for star D (KIC 8751420). The differences were normalized by the 1σ errors of the observations to emphasize the contribution of each mode to the χ2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.